text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
# Radial Velocity Orbit-fitting with RadVel
## Week 6, Intro-to-Astro 2021
### Written by Ruben Santana & Sarah Blunt, 2018
#### Updated by Joey Murphy, June 2020
#### Updated by Corey Beard, July 2021
## Background information
Radial velocity measurements tell us how the velocity of a star changes along the direction of our line of sight. These measurements are made using Doppler Spectroscopy, which looks at the spectrum of a star and measures shifts in known absorption lines. Here is a nice [GIF](https://polytechexo.files.wordpress.com/2011/12/spectro.gif) showing the movement of a star due to the presence of an orbiting planet, the shift in the stellar spectrum, and the corresponding radial velocity measurements.
This tutorial will cover a lot of new topics and build on ones we just learned. We don't have time to review all of them right now, so you're encouraged to read the following references before coming back to complete the tutorial as one of your weekly assignments.
- [Intro to the Radial Velocity Technique](http://exoplanets.astro.yale.edu/workshop/EPRV/Bibliography_files/Radial_Velocity.pdf) (focus on pgs. 1-6)
- [Intro to Periodograms](https://arxiv.org/pdf/1703.09824.pdf) (focus on pgs. 1-30)
- [Intro to Markov Chain Monte Carlo Methods](https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50) (link also found in the MCMC resources from the Bayesian fitting methods and MCMC tutorial)
## About this tutorial
In this tutorial, you will use the California Planet Search Python package [RadVel](https://github.com/California-Planet-Search/radvel) to characterize the exoplanets orbiting the star K2-24 (EPIC 203771098) using radial velocity measurements. This tutorial is a modification of the "[K2-24 Fitting & MCMC](https://github.com/California-Planet-Search/radvel/blob/master/docs/tutorials/K2-24_Fitting%2BMCMC.ipynb)" tutorial on the RadVel GitHub page.
There are several coding tasks for you to accomplish in this tutorial. Each task is indicated by a `#TODO` comment.
In this tutorial, you will:
- estimate planetary orbital periods using a periodogram
- perform a maximum likelihood orbit fit with RadVel
- create a residuals plot
- perform a Markov Chain Monte Carlo (MCMC) fit to characterize orbital parameter uncertainty
## Outline
1. RadVel Installation
2. Importing Data
3. Finding Periods
4. Defining and Initializing a Model
5. Maximum Likelihood Fitting
6. Residuals
7. MCMC
## 1. Installation
We will begin by making sure we have all the python packages needed for the tutorial. First, [install RadVel](http://radvel.readthedocs.io/en/latest/quickstartcli.html#installation) by typing:
`pip install radvel` at the command line. (Some warning messages may print out, but I (Corey) was able to install RadVel successfully in a new Anaconda environment using python=3.8.3.)
If you want to clone the entire RadVel GitHub repository for easy access to the RadVel source code, type:
`git clone https://github.com/California-Planet-Search/radvel.git`
If everything installed correctly, the following cell should run without errors. If you still see errors try restarting the kernel by using the tab above labeled **kernel >> restart**.
```
# allows us to see plots on the jupyter notebook
%matplotlib inline
# used to interact with operating system
import os
# models used by radvel for calculations, plotting, and model optimization
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import optimize
# for corner plots
import corner
# for radial velocity analysis
import radvel
from radvel.plot import orbit_plots, mcmc_plots
# for periodogram
from astropy.stats import LombScargle
# sets font size for plots
matplotlib.rcParams['font.size'] = 18
```
## 2. Importing and Plotting Data
When you installed RadVel, some .csv files were placed in a directory on your computer called `radvel.DATADIR`. Let's read this data into Python using pandas.
```
# import data
path = os.path.join(radvel.DATADIR,'epic203771098.csv') # path to data file
data = pd.read_csv(path, index_col=0) # read data into pandas DataFrame
print('Path to radvel.DATADIR: {}\n'.format(radvel.DATADIR))
print(data)
# Let's print out the column names of the pandas DataFrame you just created (`data`)
print(data.columns.values)
# TODO: print out the length of `data`
print(len(data))
# Let's plot time (data.t) vs radial velocity (data.vel) using matplotlib.pyplot
plt.plot(data.t, data.vel, 'o')
# Now, on a new figure, let's modify the plotting code so that it adds error
# bars (data.errvel) to each RV measurement
plt.figure()
plt.errorbar(data.t, data.vel, data.errvel, fmt='o')
plt.show()
plt.errorbar(data.t, data.vel, data.errvel, fmt='o',color='maroon')
# Add labels for the x- and y-axes of your plot (time is in days; radial velocity is in m/s)
plt.xlabel('Time [days]')
plt.ylabel('Velocity [m/s]')
plt.show()
# TODO: change the color of the data in your plot
# TODO: What do you notice about the data? Does it look like there is a planet signal?
# What orbital period would you estimate?
# Enter your answer in the triple quotes below.
"""
It definitely doesn't appear to be a pure sinusoid. This means there could be significant eccentricity, additional planets,
stellar activity, or any number of other possible explanations. The periods look like on the order of ~10-20 days,
or so
"""
```
## 3. Finding a Significant Period
Now, we will find probable orbital periods using a Lomb-Scargle periodogram. Periodograms are created using a Fourier transform, which is a mathematical process that takes in continuous time-based data and decomposes it into a combination of functions with various frequencies, as seen in the image below. To build more intuition for how a Fourier transform works, checkout this useful [PhET simulation](https://phet.colorado.edu/en/simulation/fourier).

([wikipedia](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png))
The graph on the left is the continous data which is analagous to our radial velocity data. The three sine waves behind the graphs are the functions that are added to produce a good fit to the original data. Finally, the graph on the right is the periodogram. It shows how much each contributing function's frequency contributes to the data model. The larger the peak in the graph, the more significant that frequency is in the data. We use this frequency to get an idea of periodic behaivor in the data (e.g. the orbital period of an exoplanet). Now, we will calculate a periodogram and use it to give us an estimate of the period of the planet's orbit.
```
def LombScarg(t,v,e,min_per=0.01,max_per=1000):
#Calculate Generalized Lomb-Scargle periodogram and window function
fmin = 1./max_per
fmax = 1./min_per
frequency, power = LombScargle(t, v, e).autopower(minimum_frequency=1/1000,maximum_frequency=1.,method='cython')
per = 1/frequency
#Identify strongest period.
in_window = np.zeros(len(per),dtype=bool)
for s in range(len(per)):
if per[s] > min_per and per[s] < max_per:
in_window[s] += 1
powmax = max(power[in_window])
imax = np.argmax(power[in_window])
fbest = frequency[in_window][imax]
perbest = 1./fbest
return per, power, perbest
minPer = 30 # min period to look for 1st planet (in days)
maxPer = 50 # max period to look for 1st planet (in days)
period, power, period1 = LombScarg(data.t, data.vel,data.errvel,min_per=minPer,max_per=maxPer)
plt.xlim(1,1000)
plt.axvline(period1,color='red',linestyle='--')
plt.semilogx(period,power)
plt.xlabel('Period (days)')
plt.ylabel('GLS Power')
plt.show()
# TODO: change the values of minPer and maxPer. How do the results change? Why? Type your answer
# between the triple quotes below.
"""
`minPer` and `maxPer` control the period range in which the nyquist searcher looks for significant peaks. Changing
them controls which period the searcher returns (it's returning the maximum peak in the allowable range).
"""
```
## 4. Defining and Initializing Model
Let's define a function that we will use to initialize the ``radvel.Parameters`` and ``radvel.RVModel`` objects.
These will be our initial guesses of the planet parameters based on on the radial velocity measurements shown and periodogram shown above.
```
nplanets = 1 # number of planets
def initialize_model():
time_base = 2420.
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
params['per1'] = radvel.Parameter(value=period1) # Insert our guess for period of first planet (from periodogram)
params['tc1'] = radvel.Parameter(value=2080.) # guess for time of transit of 1st planet
params['secosw1'] = radvel.Parameter(value=0.0) # determines eccentricity (assuming circular orbit here)
params['sesinw1'] = radvel.Parameter(value=0.0) # determines eccentriciy (assuming circular orbit here)
params['k1'] = radvel.Parameter(value=3.) # radial velocity semi-amplitude
mod = radvel.RVModel(params, time_base=time_base)
mod.params['dvdt'] = radvel.Parameter(value=-0.02) # possible acceleration of star
mod.params['curv'] = radvel.Parameter(value=0.01) # possible curvature in long-term radial velocity trend
return mod
```
Fit the K2-24 RV data assuming circular orbits.
Set initial guesses for the parameters:
```
mod = initialize_model() # model initiliazed
like = radvel.likelihood.RVLikelihood(mod, data.t, data.vel, data.errvel, '_HIRES') # initialize Likelihood object
# define initial guesses for instrument-related parameters
like.params['gamma_HIRES'] = radvel.Parameter(value=0.1) # zero-point radial velocity offset
like.params['jit_HIRES'] = radvel.Parameter(value=1.0) # white noise
```
Plot the model with our initial parameter guesses:
```
def plot_results(like):
fig = plt.figure(figsize=(12,4))
fig = plt.gcf()
fig.set_tight_layout(True)
plt.errorbar(
like.x, like.model(data.t.values)+like.residuals(),
yerr=like.yerr, fmt='o'
)
ti = np.linspace(data.t.iloc[0] - 5, data.t.iloc[-1] + 5,100) # time array for model
plt.plot(ti, like.model(ti))
plt.xlabel('Time')
plt.ylabel('RV')
plot_results(like)
```
## 5. Maximum Likelihood fit
Well, that solution doesn't look very good! Let's optimize the parameters set to vary by maximizing the likelihood.
Initialize a ``radvel.Posterior`` object.
```
post = radvel.posterior.Posterior(like) # initialize radvel.Posterior object
```
Choose which parameters to change or hold fixed during a fit. By default, all `radvel.Parameter` objects will vary, so you only have to worry about setting the ones you want to hold fixed.
```
post.likelihood.params['secosw1'].vary = False # set as false because we are assuming circular orbit
post.likelihood.params['sesinw1'].vary = False # set as false because we are assuming circular orbit
print(like)
```
Maximize the likelihood and print the updated posterior object
```
res = optimize.minimize(
post.neglogprob_array, # objective function is negative log likelihood
post.get_vary_params(), # initial variable parameters
method='Powell', # Nelder-Mead also works
)
plot_results(like) # plot best fit model
print(post)
```
RadVel comes equipped with some fancy ready-made plotting routines. Check this out!
```
matplotlib.rcParams['font.size'] = 12
RVPlot = orbit_plots.MultipanelPlot(post)
RVPlot.plot_multipanel()
matplotlib.rcParams['font.size'] = 18
```
## 6. Residuals and Repeat
Residuals are the difference of our data and our best-fit model.
Next, we will plot the residuals of our optimized model to see if there is a second planet in our data. When we look at the following residuals, we will see a sinusoidal shape, so another planet may be present! Thus, we will repeat the steps shown earlier (this time using the parameters from the maximum fit for the first planet).
```
residuals1 = post.likelihood.residuals()
# Let's make a plot of data.time versus `residuals1`
plt.figure()
plt.scatter(data.t, residuals1)
plt.xlabel('time [MJD]')
plt.ylabel('RV [m/s]')
plt.show()
# TODO: What do you notice? What would you estimate the period
# of the other exoplanet in this system to be? Write your answer between the triple quotes below.
"""
These residuals appear to go up and down every ~20 days or so. This looks like a more convincing version of the
period we first observed in the original radial velocity data. It's still pretty hard to tell, though! I'm
happy we have algorithms to find orbital periods more effectively than the human eye can.
"""
```
Let's repeat the above analysis with two planets!
```
nyquist = 2 # maximum sampling rate
minPer = 20 # minimum period to look for 2nd planet
maxPer = 30 # max period to look for 2nd planet
# finding 2nd planet period
period, power, period2 = LombScarg(data.t, data.vel, data.errvel, min_per=minPer, max_per=maxPer) # finding possible periords for 2nd planet
period, power, period1 = LombScarg(data.t, data.vel,data.errvel,min_per=minPer,max_per=maxPer)
plt.xlim(1,1000)
plt.axvline(period2,color='red',linestyle='--')
plt.semilogx(period,power)
plt.show()
# TODO: why doesn't the periodogram return the period of the first planet? Write your answer between the triple
# quotes below.
"""
The period of the first planet is not in the allowed period range we specified (`minPer` to `maxPer`).
"""
```
Repeat the RadVel analysis
```
nplanets = 2 # number of planets
def initialize_model():
time_base = 2420
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
# 1st Planet
params['per1'] = post.params['per1'] # period of 1st planet
params['tc1'] = post.params['tc1'] # time transit of 1st planet
params['secosw1'] = post.params['secosw1'] # determines eccentricity (assuming circular orbit here)
params['sesinw1'] = post.params['sesinw1'] # determines eccentricity (assuming circular orbit here)
params['k1'] = post.params['k1'] # velocity semi-amplitude for 1st planet
# 2nd Planet
params['per2'] = radvel.Parameter(value=period2) # Insert our guess for period of second planet (from periodogram)
params['tc2'] = radvel.Parameter(value=2070.)
params['secosw2'] = radvel.Parameter(value=0.0)
params['sesinw2'] = radvel.Parameter(value=0.0)
params['k2'] = radvel.Parameter(value=1.1)
mod = radvel.RVModel(params, time_base=time_base)
mod.params['dvdt'] = radvel.Parameter(value=-0.02) # acceleration of star
mod.params['curv'] = radvel.Parameter(value=0.01) # curvature of radial velocity fit
return mod
mod = initialize_model() # initialize radvel.RVModel object
like = radvel.likelihood.RVLikelihood(mod, data.t, data.vel, data.errvel, '_HIRES')
like.params['gamma_HIRES'] = radvel.Parameter(value=0.1)
like.params['jit_HIRES'] = radvel.Parameter(value=1.0)
like.params['secosw1'].vary = False # set as false because we are assuming circular orbit
like.params['sesinw1'].vary = False
like.params['secosw2'].vary = False # set as false because we are assuming circular orbit
like.params['sesinw2'].vary = False
print(like)
plot_results(like)
post = radvel.posterior.Posterior(like) # initialize radvel.Posterior object
res = optimize.minimize(
post.neglogprob_array, # objective function is negative log likelihood
post.get_vary_params(), # initial variable parameters
method='Powell', # Nelder-Mead also works
)
plot_results(like) # plot best fit model
print(post)
matplotlib.rcParams['font.size'] = 12
RVPlot = orbit_plots.MultipanelPlot(post)
RVPlot.plot_multipanel()
matplotlib.rcParams['font.size'] = 18
residuals2 = post.likelihood.residuals()
# TODO: make a plot of data.time versus `residuals2`. What do you notice?
# TODO: try redoing the above analysis, but this time, allow the eccentricity parameters to vary during the fit.
# How does the fit change?
plt.figure()
plt.scatter(data.t, residuals2)
plt.xlabel('time [MJD]')
plt.ylabel('RV [ms$^{-1}$]')
# Here's the original residuals plot, for comparison purposes:
plt.figure()
plt.scatter(data.t, residuals1, color='red')
plt.xlabel('time [MJD]')
plt.ylabel('RV [ms$^{-1}$]')
"""
The residuals perhaps look a little more randomly distributed than before, but again it's pretty hard to tell
without a periodogram.
"""
"""
The easiest way to do this is to rerun the analysis, except whenever you see a line that says secosw1 = False,
or sesinw1 = False, or secosw2 = False, or sesinw2 = False, you change them to True.
Be careful not to let the model go too crazy with eccentricity, try giving them initial guesses of 0.1.
The planet RV signatures look more angular (less purely sinusoidal) now that they have a non-zero eccentricity.
The data appears to be better-fit by an eccentric orbit model (i.e. the planets probably do have non-negligible
eccentricities).
"""
```
K2-24 only has two known exoplanets so will stop this part of our analysis here. However, when analzying an uncharacterized star system, it's important to continue the analysis until we see no significant reduction in the residuals of the radial velocity.
# 7. Markov Chain Monte Carlo (MCMC)
After reading the intro to MCMC blog post at the beginning of this tutorial, you are an expert on MCMC! Write a 3-sentence introduction to this section yourself.
MCMC is a method of exploring the parameter space of probable orbits using random walks, i.e. randomly changing the parameters of the fit. MCMC is used to find the most probable orbital solution and to determine the uncertainty (error bars) in the fit. MCMC tells you the probability distributions of orbital parameters consistent with the data.
```
# TODO: edit the Markdown cell immediately above this one with a 3 sentence description of the MCMC method.
# What does MCMC do? Why do you think it is important to use MCMC to characterize uncertainties in radial
# velocity fits?
```
Let's use RadVel to perform an MCMC fit:
```
df = radvel.mcmc(post, nwalkers=50, nrun=1000)
# TODO: What type of data structure is `df`, the object returned by RadVel's MCMC method?
"""
It is a pandas dataframe
"""
```
Make a fun plot!
```
Corner = mcmc_plots.CornerPlot(post, df)
Corner.plot()
# TODO: There is a lot going on in this plot. What do you think the off-diagonal boxes are showing?
# What about the on-diagonal boxes? What is the median period of the first planet?
# What is the uncertainty on the period of the first planet? The second planet?
# TODO: Why do you think the uncertainties on the periods of planets b and c are different?
"""
The off-diagonal boxes are 1 dimensional probability distributions over each of the parameters of the fit.
The on-diagonal boxes show 2 dimensional probability distributions (covariances) between pairs of parameters
(the box's row and column show the parameters it corresponds to).
The median period of the first plot (for my eccentric fit) is 52.56 days. The uncertainty is +0.08 days, -0.07 days
(this corresponds to a *68% confidence interval* of [52.49, 52.64] days.)
The median period of the second planet is 20.69 days, with an uncertainty of +/- 0.02 days.
The uncertainties of the two orbital periods are different because the period of the second planet is much better
constrained by the data than the period of the first planet. We see many periods of the second planet repeated
over the ~100 day dataset, but only ~2 periods of the first planet.
"""
```
|
github_jupyter
|
```
import math
import string
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import logit
from IPython.display import display
import tensorflow as tf
from tensorflow.keras.layers import (Input, Dense, Lambda, Flatten, Reshape, BatchNormalization, Layer,
Activation, Dropout, Conv2D, Conv2DTranspose,
Concatenate, add, Add, Multiply)
from tensorflow.keras.losses import sparse_categorical_crossentropy
from tensorflow.keras.optimizers import RMSprop, Adam
from tensorflow.keras.models import Model
from tensorflow.keras import metrics
from tensorflow.keras import backend as K
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.callbacks import TensorBoard
from tensorflow_addons.callbacks import TQDMProgressBar
from realnvp_helpers import Mask, FlowBatchNorm
%matplotlib inline
batch_size = 10
shape = (4, 4, 3)
batch_shape = (batch_size,) + shape
samples = 100
train_data = np.random.normal(0.5, 3, size=(samples,) + (shape))
print(batch_shape)
print(train_data.shape)
train_data[0, :, :, :]
def conv_block(input_shape, kernel_size, filters, stage, block, use_resid=True):
''' Adapted from resnet50 implementation in Keras '''
filters1, filters2, filters3 = filters
if K.image_data_format() == 'channels_last':
bn_axis = 3
else:
bn_axis = 1
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
input_tensor = Input(batch_shape=input_shape)
x = Conv2D(filters1, (1, 1),
kernel_initializer='he_normal',
name=conv_name_base + '2a')(input_tensor)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2a')(x)
x = Activation('relu')(x)
x = Conv2D(filters2, kernel_size,
padding='same',
kernel_initializer='he_normal',
name=conv_name_base + '2b')(x)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2b')(x)
x = Activation('relu')(x)
x = Conv2D(filters3, (1, 1),
kernel_initializer='he_normal',
name=conv_name_base + '2c')(x)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2c')(x)
if use_resid:
x = add([x, input_tensor])
x = Activation('relu')(x)
return Model(input_tensor, x, name='conv_block' + stage + block)
def coupling_layer(input_shape, mask_type, stage):
''' Implements (as per paper):
y = b * x + (1 - b) * [x * exp(s(b * x)) + t(b * x)]
'''
assert mask_type in ['check_even', 'check_odd', 'channel_even', 'channel_odd']
mask_prefix = 'check' if mask_type.startswith('check') else 'channel'
mask_opposite = 'odd' if mask_type.endswith('even') else 'even'
input_tensor = Input(batch_shape=input_shape)
# Raw operations for step
b0 = Mask(mask_type)
b1 = Mask(mask_prefix + '_' + mask_opposite)
s_ = conv_block(input_shape, (3, 3), (32, 32, 3), stage, '_s', use_resid=True)
t_ = conv_block(input_shape, (3, 3), (32, 32, 3), stage, '_t', use_resid=True)
batch = FlowBatchNorm(name='_'.join(['FlowBatchNorm' + mask_type + stage]))
# Forward
masked_input = b1(input_tensor)
s = s_(masked_input)
t = t_(masked_input)
coupling = Lambda(lambda ins: ins[0] * K.exp(ins[1]) + ins[2])([input_tensor, s, t])
coupling_mask = b0(coupling)
out1, out2 = Add()([masked_input, coupling_mask]), b0(s)
out1_norm = batch(out1)
#batch_loss = Lambda(lambda x: - (K.log(gamma) - 0.5 * K.log(x + batch.epsilon)))(var)
#batch_loss = Lambda(lambda x: -K.log(gamma))(var)
#batch_loss = Lambda(lambda x: - ( - 0.5 * K.log(x + batch.epsilon)))(var)
# Reverse
# Return result + masked scale for loss function
return Model(input_tensor, [out1_norm, out2], name='_'.join(['coupling', mask_type, stage]))
def coupling_group(input_tensor, steps, mask_type, stage):
name_mapping = dict(enumerate(string.ascii_lowercase))
# TODO: Only need check/channel, not even/odd right?
assert mask_type in ['check_even', 'check_odd', 'channel_even', 'channel_odd']
mask_prefix = 'check' if mask_type.startswith('check') else 'channel'
x = input_tensor
s_losses = []
batch_losses = []
for i in range(3):
mask_type = mask_prefix + ('_even' if i % 2 == 0 else '_odd')
step = coupling_layer(input_tensor.shape, mask_type, stage=str(stage) + name_mapping[i])
x, s = step(x)
#x, s = step(x)
s_losses.append(s)
return x, s_losses
def realnvp_zloss(target, z):
# log(p_X(x)) = log(p_Z(f(x))) + log(|det(\partial f(x) / \partial X^T)|)
# Prior is standard normal(mu=0, sigma=1)
shape = z.shape
return K.sum(-0.5 * np.log(math.pi) - 0.5 * z**2, axis=list(range(1, len(shape[1:]))))
def const_loss(target, output):
# For debugging
return K.constant(0)
def realnvp_sumloss(target, output):
# Determinant is just sum of "s" or "batch loss" params (already log-space)
shape = output.shape
return K.sum(output, axis=list(range(1, len(shape))))
input_tensor = Input(batch_shape=batch_shape)
#x = conv_block(shape, (3, 3), (32, 32, 3), '0', '_s', use_resid=True)(input_tensor)
step = coupling_layer(batch_shape, 'check_even', stage=str('a') + '0')
x, s = step(input_tensor)
s_losses = [s, s]
#x, s_losses, batch_losses = coupling_group(input_tensor, steps=3, mask_type='check_even', stage=1)
s_losses = Concatenate(name='s_losses')(s_losses)
forward_model = Model(inputs=input_tensor, outputs=[x, s_losses])
optimizer = Adam(lr=0.001)
forward_model.compile(optimizer=optimizer,
loss=[realnvp_zloss, realnvp_sumloss])
#loss=[const_loss, const_loss, realnvp_sumloss])
forward_model.summary()
def get_losses_from_layers(layers):
losses = []
for layer in layers:
if isinstance(layer, Model):
losses.extend(layer._losses)
losses.extend(get_losses_from_layers(layer.layers))
else:
losses.extend(layer.losses)
return losses
get_losses_from_layers(forward_model.layers)
#early_stopping = keras.callbacks.EarlyStopping('val_loss', min_delta=50.0, patience=5)
#reduce_lr = keras.callbacks.ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=2, min_lr=0.0001)
s = [len(train_data)] + [int(x) for x in s_losses.shape[1:]]
#s[0] = int(train_data.shape[0])
#print(train_data.shape, np.zeros(s).shape)
tensorboard = TensorBoard(log_dir='graph',
batch_size=batch_size,
histogram_freq=1,
write_graph=True)
history = forward_model.fit(
train_data, [train_data, np.zeros(s)],
#validation_data=(train_data[:10], [train_data[:10], np.zeros(s)[:10], np.zeros(s)[:10]]),
batch_size=batch_size,
epochs=20,
callbacks=[TQDMProgressBar()], #, tensorboard], #, early_stopping, reduce_lr],
verbose=0
)
df = pd.DataFrame(history.history)
#display(df.describe(percentiles=[0.25 * i for i in range(4)] + [0.95, 0.99]))
col = 'val_loss' if 'val_loss' in df else 'loss'
display(df[-25:])
df[col][-25:].plot(figsize=(8, 6))
```
# 2019-07-28
* Got some framework up to do coupling layers but having trouble passing the scale parameter to the loss function, getting some weird tensorflow error, needs more debugging
* Without the determinant in the loss function, it looks like loss goes down, so maybe on the right track?
* It's actually weird that we're not using the image in the output, but I guess that's what's great about this reversible model!
* TODO:
* Debug scale function in loss
* Add reverse (generator) network to functions above.
# 2019-07-29
* Explanation of how to estimate probability of continuous variables (relevant for computing bits/pixel without an explicit discrete distribution): https://math.stackexchange.com/questions/2818318/probability-that-a-sample-is-generated-from-a-distribution
* Idea for a post, explain likelihood estimation of discrete vs. continuous distributions (like pixels), include:
* Probability of observing a value from continuous distribution = 0
* https://math.stackexchange.com/questions/2818318/probability-that-a-sample-is-generated-from-a-distribution
* Probability of observing a value from a set of discrete hypthesis (models) is non-zero using epsilon trick (see above link):
* https://math.stackexchange.com/questions/920241/can-an-observed-event-in-fact-be-of-zero-probability
* Explain Equation 3 from "A NOTE ON THE EVALUATION OF GENERATIVE MODELS"
* Also include an example using a simpler case, like a bernoulli variable that we're estimating using a continuous distribution
* Bring it back to modelling pixels and how they usually do it
# 2020-03-30
* To make reversible network, build forward and backward network at the same time using `Model()` to have components that I can use in both networks
* Looks like I have some instability here, depending on the run I can get an exact fit (-100s loss) or a poor a fit (+10):
* Turning off residual networks helps
* Adjusting the learning rate, batch size helps but hard to pinpoint a methodology
* Most likely it's the instability of using a scale parameter (RealNVP paper Section 3.7), might need to implement their batch norm for more stable results, especially when adding more layers:
* Reimplement `BatchNorm`: https://github.com/keras-team/keras/blob/master/keras/layers/normalization.py
* Except return regular result AND (variance + eps) term
* Use the (var + eps) term to compute Jacobian for loss function (should just be log-additive)
* Once this is done, add back the other stuff:
* Turn on residual shortcuts
* Change batch size to reasonable number and learning rate=0.01
* If this still doesn't work, might want to implement "Running average over recent minibatches" in Appendix E
# 2020-03-31
* Fixed a bug (I think) in the network where the coupling layer was wrong. However, it still sometimes get stuck at around a loss of 5 but more often than not (on another training run) get to -10 (after 20 iters).
* Trying to get FlowBatchNorm worknig but having some issues passing the determinant batch loss as an output because the `batch_size` is not getting passed (it has dimension (3,) but should have dimension (None, 3)). Need to figure out how to tranlate a tensor to Layer that includes batch.
# 2020-04-05
* Reminder: BatchNormalization on conv layers only need to normalize across [B, W, H, :] layers, not the "C" layer because the filter is identical across a channel (so it uses the same mean/var to normalize). This is nice because it's the same axis (-1) you would normalize across in a Dense layer. See: https://intellipaat.com/community/3872/batch-normalization-in-convolutional-neural-network
* I think I figured out how to return the batchnorm weights back but now I'm hitting a roadblock when I try to merge them together to put as part of the output loss -- maybe I should just forget it and use the tensors directly in the output loss?
* Now that I switched to an explicit batch size, it doesn't run anymore... get this error "Incompatible shapes: [4] vs. [32]", probably some assumption that I had, got to work backwards and fix it I think.
# 2020-04-14
* Okay figured out the weird error I was getting: when a Keras model has multiple outputs you either have to give it a list or dict of loss functions, otherwise it will apply the same loss to each output! Of course, I just assumed that it gives you all outputs in one loss function. So silly!
* I reverted the change to explicitly set batch. Instead in the `BatchNormFlow` layer I just multiply zero by the `inputs` and then add the mean/variance. I think this gives the right shape?
* **TODOs**:
* Check that shape/computation for `BatchNormFlow`/`batch_losses` loss is correct
* Check that loss functions are actually returning a negative log-loss (not just the log)
* Validate the model is fitting what I want (right now I have an elbow effect as I train more) -- should there be backprop through the batch_losses? I guess not? Check the paper and figure out what to do.
* Add back in the bigger model that has multiple coupling layers
# 2020-04-15
* Somehow I suspect that the batch loss is not getting optimized (the var parameter in the batch norm function). When I set the other loss components to zero, I see that hte batch loss is not really getting smaller -- should it?
loss coupling_check_even_1c_loss s_losses_loss batch_losses_loss
0 146.227879 0.0 0.0 146.227879
1 131.294226 0.0 0.0 131.294226
2 135.579913 0.0 0.0 135.579913
3 127.908073 0.0 0.0 127.908073
4 130.301921 0.0 0.0 130.301921
5 139.414369 0.0 0.0 139.414369
6 129.732767 0.0 0.0 129.732767
7 127.321448 0.0 0.0 127.321448
8 130.812973 0.0 0.0 130.812973
9 136.737979 0.0 0.0 136.737979
10 135.001893 0.0 0.0 135.001893
11 140.181680 0.0 0.0 140.181680
12 133.053322 0.0 0.0 133.053322
13 132.912917 0.0 0.0 132.912917
14 122.261415 0.0 0.0 122.261415
15 139.447081 0.0 0.0 139.447081
16 134.216364 0.0 0.0 134.216364
17 133.567210 0.0 0.0 133.567210
18 131.333447 0.0 0.0 131.333447
19 133.022141 0.0 0.0 133.022141
* **IDEA:** I should probably unit test the batch norm flow layer to make sure that it's doing what I think it should be doing... need to think about how to structure this experiment.
* **CHECK**: Should `s` loss be negated also? Seems like I need negative log loss, not just log loss...
# 2020-04-16
* Forgot that BatchNorm has two components: $\mu, \sigma^2$, the mean and variance of the batch, which we scale ($\hat{x} = \frac{x-\mu}{\sqrt{\sigma^2 + \epsilon}}$) AND two learnable parameters: $\gamma, \beta$, which are used to scale the output: $y = \gamma \hat{x} + \beta$. The learnable parameters are the only ones that change!
* Now, how does that work when calculating the determinant? Let's see:
$$\frac{\partial}{\partial y} \hat{y} = \frac{\partial}{\partial y}\big[\gamma * \frac{x-\mu}{\sqrt{\sigma^2 + \epsilon} + \beta}\big]$$
$$ = \frac{\gamma}{\sqrt{\sigma^2 + \epsilon}}$$
Therefore, I need to include gamma in the determinant calculation in the batch norm layer!
Ohhhhh... use `keras.layer.add_loss()` function instead of passing the new things over! Not sure how to deal with batch though... https://www.tensorflow.org/guide/keras/custom_layers_and_models
# 2020-04-17
* Made some progress adding batch norm loss use both `layer.add_loss()` and `layer.add_metric()` so I can view it... BUT I need to upgrade to Tensorflow 2.0.
* After upgrading to 2.0, might as well start using `tf.keras` directly as that's the recommendation from the site.
# 2020-04-20
* Upgraded to Tensorflow 2.1! I hate upgrading things...
* Converted most of my code over too -- still need to add `layer.add_loss()` and `layer.add_metric()` to the `FlowBatchNorm()` layer though. I did convert it over to the TF2 version, inheriting it and assuming that the fancier features are turned off.
```
from scipy.stats import norm
for i in range(-10, 10):
eps = i / 1000
l = norm.cdf(0 - eps)
r = norm.cdf(0 + eps)
print(eps, '\t', l - r)
a = np.array([[[-1, -2], [-3, -4]], [[1,2], [3, 4]], [[5,6], [7, 8]]])
b = np.array([100, 200]).reshape([1, 1, 2])
c = a + b
c[:, :, :]
```
|
github_jupyter
|
```
import pandas as pd
import geopandas
import glob
import matplotlib.pyplot as plt
import numpy as np
import seaborn
import shapefile as shp
from paths import *
from refuelplot import *
setup()
wpNZ = pd.read_csv(data_path + "/NZ/windparks_NZ.csv", delimiter=';')
wpBRA = pd.read_csv(data_path + '/BRA/turbine_data.csv',index_col=0)
wpUSA = pd.read_csv(data_path + '/USA/uswtdb_v2_3_20200109.csv')
# remove Guam
wpUSA = wpUSA[wpUSA.t_state!='GU']
wpZAF = pd.read_csv(data_path + '/ZAF/windparks_ZAF.csv')
shpBRA = geopandas.read_file(data_path + '/country_shapefiles/BRA/BRA_adm1.shp')
shpNZ = geopandas.read_file(data_path + '/country_shapefiles/NZ/CON2017_HD_Clipped.shp')
shpUSA = geopandas.read_file(data_path + '/country_shapefiles/USA/cb_2018_us_state_500k.shp')
shpZAF = geopandas.read_file(data_path + '/country_shapefiles/ZAF/zaf_admbnda_adm1_2016SADB_OCHA.shp')
```
plot windparks: either all with opacity or aggregate to windparks and maybe use size as capacity indicator?
```
fig, ax = plt.subplots(figsize = (9,7))
ax.set_xlim(-180,-65)
ax.set_ylim(20,75)
shpUSA.plot(color=COLORS[4],ax=ax)
plt.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
import xarray as xr
from matplotlib.patches import Rectangle
NZera5 = xr.open_dataset(era_path + '/NZ/era5_wind_NZ_198701.nc')
NZmerra2 = xr.open_dataset(mer_path + '/NZ/merra2_wind_NZ_198701.nc')
def cell_coords(lon,lat):
diflat = NZera5.latitude.values - lat
diflon = NZera5.longitude.values - lon
clat = NZera5.latitude.values[abs(diflat)==min(abs(diflat))][0]
clon = NZera5.longitude.values[abs(diflon)==min(abs(diflon))][0]
return((clon-0.125,clat-0.125))
def cell_coords_mer(lon,lat):
diflat = NZmerra2.lat.values - lat
diflon = NZmerra2.lon.values - lon
clat = NZmerra2.lat.values[abs(diflat)==min(abs(diflat))][0]
clon = NZmerra2.lon.values[abs(diflon)==min(abs(diflon))][0]
return((clon-0.3125,clat-0.25))
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[3]).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
ax = plt.gca()
rect = matplotlib.patches.Rectangle(xy=cell_coords(wpNZ.Longitude[0],wpNZ.Latitude[0]),width= 0.25,height=0.25,alpha=0.7,color=COLORS[1])
ax.add_patch(rect)
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[3],alpha=0.5).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
ax = plt.gca()
for i in range(len(wpNZ)):
rect = matplotlib.patches.Rectangle(xy=cell_coords_mer(wpNZ.Longitude[i],wpNZ.Latitude[i]),width= 0.625,height=0.5,alpha=0.7,color=COLORS[1])
ax.add_patch(rect)
plt.savefig(results_path + '/plots/syssize_NZ.png')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4]).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
shpBRA.plot(color=COLORS[4])
plt.plot(wpBRA.lon,wpBRA.lat,'o',alpha=0.1,markersize=2)
shpZAF.plot(color=COLORS[4])
plt.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=4)
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2,figsize=(10,10),gridspec_kw = {'wspace':0.15, 'hspace':0.15})
shpBRA.plot(color=COLORS[4],ax=ax1)
ax1.set_xlim(-75,-30)
ax1.set_ylim(-35,10)
ax1.plot(wpBRA.groupby('name').mean().lon,
wpBRA.groupby('name').mean().lat,'o',alpha=0.1,markersize=2)
ax1.set_title('Brazil')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4],ax=ax2).set_xlim(165,180)
ax2.set_xlim(165,179)
ax2.set_ylim(-48,-34)
ax2.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=2)
ax2.set_title('New Zealand')
#ax3.set_xlim(-180,-65)
#ax3.set_ylim(-20,95)
ax3.set_xlim(-125,-65)
ax3.set_ylim(5,65)
shpUSA.plot(color=COLORS[4],ax=ax3)
#ax3.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
ax3.plot(wpUSA.groupby('p_name').mean().xlong,
wpUSA.groupby('p_name').mean().ylat,'o',alpha=0.1,markersize=2)
ax3.set_title('USA')
shpZAF.plot(color=COLORS[4],ax=ax4)
ax4.set_xlim(16,33)
ax4.set_ylim(-37,-20)
ax4.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=2)
ax4.set_title('South Africa')
plt.savefig(results_path + '/map_windparks.png')
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2,figsize=(10,10),gridspec_kw = {'wspace':0.1, 'hspace':0.1})
shpBRA.plot(color=COLORS[4],ax=ax1)
#ax1.plot(wpBRA.lon,wpBRA.lat,'o',alpha=0.1,markersize=2)
ax1.plot(wpBRA.groupby('name').mean().lon,
wpBRA.groupby('name').mean().lat,'o',alpha=0.1,markersize=2)
ax1.set_title('Brazil')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4],ax=ax2).set_xlim(165,180)
ax2.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=2)
ax2.set_title('New Zealand')
ax3.set_xlim(-180,-65)
ax3.set_ylim(20,75)
#ax3.set_ylim(0,87)
shpUSA.plot(color=COLORS[4],ax=ax3)
#ax3.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
ax3.plot(wpUSA.groupby('p_name').mean().xlong,
wpUSA.groupby('p_name').mean().ylat,'o',alpha=0.1,markersize=2)
ax3.set_title('USA')
shpZAF.plot(color=COLORS[4],ax=ax4)
ax4.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=2)
ax4.set_title('South Africa')
plt.savefig(results_path + '/map_windparks.png')
```
|
github_jupyter
|
# dwtls: Discrete Wavelet Transform LayerS
This library provides downsampling (DS) layers using discrete wavelet transforms (DWTs), which we call DWT layers.
Conventional DS layers lack either antialiasing filters and the perfect reconstruction property, so downsampled features are aliased and entire information of input features are not preserved.
By contrast, DWT layers have antialiasing filters and the perfect reconstruction property, which enables us to overcome the two problems.
In this library, the DWT layer and its extensions are implemented as below:
- DWT layers with fixed wavelets (Haar, CDF22, CDF26, CDF15, and DD4 wavelets)
- Trainable DWT (TDWT) layers
- Weight-normalized trainable DWT (WN-TDWT) layers
## Install dwtls
```
!pip install dwtls
import torch
import dwtls.dwt_layers
```
## DWT layers with fixed wavelets
The DWT layer (including its extensions) is implemeted as a subclass of `torch.nn.Module` provided by PyTorch, so we can easily use it in PyTorch-based scripts. Also, this layer is differentiable.
```
dwt_layer = dwtls.dwt_layers.DWT(wavelet="haar")
feature = torch.normal(0.0, 1.0, size=(1,1,20)).float()
output_feature = dwt_layer(feature)
print('Input:', feature)
print("Output:", output_feature)
```
## TDWT layer
The TDWT layer has trainable wavelets (precisely, predict and update filters of lifting scheme).
For example, we can define the TDWT layer having a pair of the prediction and update filters initialized with Haar wavelet.
```
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
```
The `tdwt_layer._predict_weight` and `tdwt_layer._update_weight` of this layer are trainable jointly with other DNN components.
We show three structures of the trainable DWT layers used in our music source separation paper [1].
[1] Tomohiko Nakamura, Shihori Kozuka, and Hiroshi Saruwatari, “Time-Domain Audio Source Separation with Neural Networks Based on Multiresolution Analysis,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 29, pp. 1687–1701, Apr. 2021. [pdf](https://doi.org/10.1109/TASLP.2021.3072496), [demo](https://tomohikonakamura.github.io/Tomohiko-Nakamura/demo/MRDLA/)
```
# Type A
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
# Type B
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=1, update_ksize=1,
requires_grad={"predict": False, "update": False},
initial_values={"predict": [1], "update": [0.5]}),
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,0,0], "update": [0,0,0]})
])
# Type C
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]}),
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,0,0], "update": [0,0,0]})
])
```
## WN-TDWT layer
The TDWT layer can be incorporated into many types of DNNs, but such straightforward extension does not guarantee that it has anti-aliasing filters, while it has the perfect reconstruction property owing to the lifting scheme.
The WN-TDWT layer is developed to overcome this problem. It has both properties owing to adequate normalization of the prediction and update filter coefficients.
```
# Type A
tdwt_layer = dwtls.dwt_layers.WeightNormalizedMultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
```
The WN-TDWT layer can be used in the same way as the TDWT layer.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/sprinkler_pgm.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Directed graphical models
We illustrate some basic properties of DGMs.
```
!pip install causalgraphicalmodels
!pip install pgmpy
from causalgraphicalmodels import CausalGraphicalModel
import pgmpy
import numpy as np
import pandas as pd
```
# Make the model
```
sprinkler = CausalGraphicalModel(
nodes=["cloudy", "rain", "sprinkler", "wet", "slippery"],
edges=[
("cloudy", "rain"),
("cloudy", "sprinkler"),
("rain", "wet"),
("sprinkler", "wet"),
("wet", "slippery")
]
)
```
# Draw the model
```
# draw return a graphviz `dot` object, which jupyter can render
out = sprinkler.draw()
type(out)
display(out)
out.render()
```
# Display the factorization
```
print(sprinkler.get_distribution())
```
# D-separation
```
# check for d-seperation of two nodes
sprinkler.is_d_separated("slippery", "cloudy", {"wet"})
```
# Extract CI relationships
```
# get all the conditional independence relationships implied by a CGM
CI = sprinkler.get_all_independence_relationships()
print(CI)
records = []
for ci in CI:
record = (ci[0], ci[1], ', '.join(x for x in ci[2]))
records.append(record)
print(records)
df = pd.DataFrame(records, columns = ('X', 'Y', 'Z'))
display(df)
print(df.to_latex(index=False))
```
# Inference
```
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
# Defining the model structure. We can define the network by just passing a list of edges.
model = BayesianModel([('C', 'S'), ('C', 'R'), ('S', 'W'), ('R', 'W'), ('W', 'L')])
# Defining individual CPDs.
cpd_c = TabularCPD(variable='C', variable_card=2, values=np.reshape([0.5, 0.5],(2,1)))
# In pgmpy the columns are the evidences and rows are the states of the variable.
cpd_s = TabularCPD(variable='S', variable_card=2,
values=[[0.5, 0.9],
[0.5, 0.1]],
evidence=['C'],
evidence_card=[2])
cpd_r = TabularCPD(variable='R', variable_card=2,
values=[[0.8, 0.2],
[0.2, 0.8]],
evidence=['C'],
evidence_card=[2])
cpd_w = TabularCPD(variable='W', variable_card=2,
values=[[1.0, 0.1, 0.1, 0.01],
[0.0, 0.9, 0.9, 0.99]],
evidence=['S', 'R'],
evidence_card=[2, 2])
cpd_l = TabularCPD(variable='L', variable_card=2,
values=[[0.9, 0.1],
[0.1, 0.9]],
evidence=['W'],
evidence_card=[2])
# Associating the CPDs with the network
model.add_cpds(cpd_c, cpd_s, cpd_r, cpd_w, cpd_l)
# check_model checks for the network structure and CPDs and verifies that the CPDs are correctly
# defined and sum to 1.
model.check_model()
from pgmpy.inference import VariableElimination
infer = VariableElimination(model)
# p(R=1)= 0.5*0.2 + 0.5*0.8 = 0.5
probs = infer.query(['R']).values
print('\np(R=1) = ', probs[1])
# P(R=1|W=1) = 0.7079
probs = infer.query(['R'], evidence={'W': 1}).values
print('\np(R=1|W=1) = ', probs[1])
# P(R=1|W=1,S=1) = 0.3204
probs = infer.query(['R'], evidence={'W': 1, 'S': 1}).values
print('\np(R=1|W=1,S=1) = ', probs[1])
```
|
github_jupyter
|
```
import json
from datetime import datetime, timedelta
import matplotlib.pylab as plot
import matplotlib.pyplot as plt
from matplotlib import dates
import pandas as pd
import numpy as np
import matplotlib
matplotlib.style.use('ggplot')
%matplotlib inline
# Read data from http bro logs
with open("http.log",'r') as infile:
file_data = infile.read()
# Split file by newlines
file_data = file_data.split('\n')
# Remove comment lines
http_data = []
for line in file_data:
if line[0] is not None and line[0] != "#":
http_data.append(line)
# Lets analyze user agents
user_agent_analysis = {}
user_agent_overall = {}
for line in http_data:
# Extract the timestamp
timestamp = datetime.fromtimestamp(float(line.split('\t')[0]))
# Strip second and microsecond from timestamp
timestamp = str(timestamp.replace(second=0,microsecond=0))
# Extract the user agent
user_agent = line.split('\t')[11]
# Update status code analysis variable
if user_agent not in user_agent_analysis.keys():
user_agent_analysis[user_agent] = {timestamp: 1}
else:
if timestamp not in user_agent_analysis[user_agent].keys():
user_agent_analysis[user_agent][timestamp] = 1
else:
user_agent_analysis[user_agent][timestamp] += 1
# Update overall user agent count
if user_agent not in user_agent_overall.keys():
user_agent_overall[user_agent] = 1
else:
user_agent_overall[user_agent] += 1
df = pd.DataFrame.from_dict(user_agent_analysis,orient='columns').fillna(0)
df
#df.plot(figsize=(12,9))
ax = df.plot(rot=90,figsize=(12,9))
user_agent_analysis2 = user_agent_analysis
print(user_agent_analysis2.keys())
high_volume_user_agents = [
"Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/46.0.2490.64 Safari/537.36"
]
for ua in high_volume_user_agents:
if ua in user_agent_analysis2.keys():
del user_agent_analysis2[ua]
df2 = pd.DataFrame.from_dict(user_agent_analysis2,orient='columns').fillna(0)
df2
df2.plot(rot=90,figsize=(12,9))
# Lets analyze status codes
status_code_analysis = {}
status_code_overall = {}
earliest_time = None
latest_time = None
for line in http_data:
# Extract the timestamp
timestamp = datetime.fromtimestamp(float(line.split('\t')[0]))
# Strip minute, second and microsecond from timestamp
#timestamp = str(timestamp.replace(minute=0,second=0,microsecond=0))
timestamp = str(timestamp.replace(second=0,microsecond=0))
# Extract the status code
status_code = line.split('\t')[14]
# Update status code analysis variable
if status_code not in status_code_analysis.keys():
status_code_analysis[status_code] = {timestamp: 1}
else:
if timestamp not in status_code_analysis[status_code].keys():
status_code_analysis[status_code][timestamp] = 1
else:
status_code_analysis[status_code][timestamp] += 1
# Update overall status code count
if status_code not in status_code_overall.keys():
status_code_overall[status_code] = 1
else:
status_code_overall[status_code] += 1
# Update our earliest and latest time as needed
if earliest_time is None or timestamp < earliest_time:
earliest_time = timestamp
if latest_time is None or timestamp > latest_time:
latest_time = timestamp
# Format data for the plot function
status_label = []
data = []
for code in sorted(status_code_overall.keys()):
status_label.append(str(code) + " (" + str(status_code_overall[code]) + ")")
data.append(status_code_overall[code])
plot.figure(1,figsize=[8,8])
patches, texts = plot.pie(data, shadow=True, startangle=90)
plot.legend(patches, status_label,loc="best")
plot.title('Status Code Distribution')
plot.axis('equal')
plot.tight_layout()
plot.show()
# Output the status codes in table form
df = pd.DataFrame.from_dict(status_code_analysis,orient='columns').fillna(0)
df
# Plot the status codes
df.plot(rot=90,figsize=(12,9))
# Remove the 200 status code and re-plot the status codes
status_code_analysis2 = status_code_analysis
if '200' in status_code_analysis2.keys():
del status_code_analysis2['200']
print(status_code_analysis2.keys())
df2 = pd.DataFrame.from_dict(status_code_analysis2,orient='columns').fillna(0)
df2.plot(rot=90, figsize=(12,9))
```
|
github_jupyter
|
# Method4 DCT based DOST + Huffman encoding
## Import Libraries
```
import mne
import numpy as np
from scipy.fft import fft,fftshift
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter
from scipy.signal import freqz
from scipy import signal
from scipy.fftpack import fft, dct, idct
from itertools import islice
import pandas as pd
import os
```
## Preprocessing
### Data loading
```
acc = pd.read_csv('ACC.csv')
acc = acc.iloc[1:]
acc.columns = ['column1','column2','column3']
np.savetxt('acc.txt',acc)
acc_c1 = acc["column1"]
acc_c2 = acc["column2"]
acc_c3 = acc["column3"]
acc_array_c1 = acc_c1.to_numpy() #save the data into an ndarray
acc_array_c2 = acc_c2.to_numpy()
acc_array_c3 = acc_c3.to_numpy()
acc_array_c1.shape
acc_array_c1 = acc_array_c1[0:66000] # Remove the signal in first 3minutes and last 5minutes
acc_array_c2 = acc_array_c2[0:66000]
acc_array_c3 = acc_array_c3[0:66000]
sampling_freq = 1/32
N = acc_array_c1.size
xf = np.linspace(-N*sampling_freq/2, N*sampling_freq/2, N)
index = np.linspace(0, round((N-1)*sampling_freq,4), N)
```
### Butterworth Filter to denoising
```
def butter_bandpass(lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(data, lowcut, highcut, fs, order=5):
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
y = lfilter(b, a, data)
return y
from scipy.signal import freqz
from scipy import signal
# Sample rate and desired cutoff frequencies (in Hz).
fs = 1000.0
lowcut = 0.5
highcut = 50.0
# Plot the frequency response for a few different orders.
plt.figure(1)
plt.clf()
for order in [1, 2, 3, 4]:
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
w, h = freqz(b, a, worN=2000)
plt.plot((fs * 0.5 / np.pi) * w, abs(h), label="order = %d" % order)
plt.plot([0, 0.5 * fs], [np.sqrt(0.5), np.sqrt(0.5)],
'--', label='sqrt(0.5)')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Gain')
plt.grid(True)
plt.legend(loc='best')
y1 = butter_bandpass_filter(acc_array_c1, lowcut, highcut, fs, order=2)
y2 = butter_bandpass_filter(acc_array_c2, lowcut, highcut, fs, order=2)
y3 = butter_bandpass_filter(acc_array_c3, lowcut, highcut, fs, order=2)
resampled_signal1 = y1
resampled_signal2 = y2
resampled_signal3 = y3
np.savetxt('processed_acc_col1.txt',resampled_signal1)
np.savetxt('processed_acc_col2.txt',resampled_signal2)
np.savetxt('processed_acc_col3.txt',resampled_signal3)
rounded_signal1 = np.around(resampled_signal1)
rounded_signal2 = np.around(resampled_signal2)
rounded_signal3 = np.around(resampled_signal3)
```
## Transformation --- DCT based DOST
```
from scipy.fftpack import fft, dct
aN1 = dct(rounded_signal1, type = 2, norm = 'ortho')
aN2 = dct(rounded_signal2, type = 2, norm = 'ortho')
aN3 = dct(rounded_signal3, type = 2, norm = 'ortho')
def return_N(target):
if target > 1:
for i in range(1, int(target)):
if (2 ** i >= target):
return i-1
else:
return 1
from itertools import islice
split_list = [1]
for i in range(0,return_N(aN1.size)):
split_list.append(2 ** i)
temp1 = iter(aN1)
res1 = [list(islice(temp1, 0, ele)) for ele in split_list]
temp2 = iter(aN2)
res2 = [list(islice(temp2, 0, ele)) for ele in split_list]
temp3 = iter(aN3)
res3 = [list(islice(temp3, 0, ele)) for ele in split_list]
from scipy.fftpack import fft, dct, idct
cN_idct1 = [list(idct(res1[0], type = 2, norm = 'ortho' )), list(idct(res1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res1)):
cN_idct1.append(list(idct(res1[k], type = 2, norm = 'ortho' )))
cN_idct2 = [list(idct(res2[0], type = 2, norm = 'ortho' )), list(idct(res2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res2)):
cN_idct2.append(list(idct(res2[k], type = 2, norm = 'ortho' )))
cN_idct3 = [list(idct(res3[0], type = 2, norm = 'ortho' )), list(idct(res3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res3)):
cN_idct3.append(list(idct(res3[k], type = 2, norm = 'ortho' )))
all_numbers1 = []
for i in cN_idct1:
for j in i:
all_numbers1.append(j)
all_numbers2 = []
for i in cN_idct2:
for j in i:
all_numbers2.append(j)
all_numbers3 = []
for i in cN_idct3:
for j in i:
all_numbers3.append(j)
all_numbers1 = np.asarray(all_numbers1)
all_numbers2 = np.asarray(all_numbers2)
all_numbers3 = np.asarray(all_numbers3)
int_cN1 = np.round(all_numbers1,3)
int_cN2 = np.round(all_numbers2,3)
int_cN3 = np.round(all_numbers3,3)
np.savetxt('int_cN1.txt',int_cN1, fmt='%.3f')
np.savetxt('int_cN2.txt',int_cN2, fmt='%.3f')
np.savetxt('int_cN3.txt',int_cN3,fmt='%.3f')
```
## Huffman Coding
### INSTRUCTION ON HOW TO COMPRESS THE DATA BY HUFFMAN CODING
(I used the package "tcmpr 0.2" and "pyhuff 1.1". These two packages provided the same compression result. So here, we just use "tcmpr 0.2")
1. Open your termial or git bash, enter "pip install tcmpr" to install the "tcmpr 0.2" package
2. Enter the directory which include the file you want to compress OR copy the path of the file you want to compress
3. Enter "tcmpr filename.txt" / "tcmpr filepath" to compress the file
4. Find the compressed file in the same directory of the original file
```
# Do Huffman encoding based on the instruction above
# or run this trunk if this scratch locates in the same directory with the signal you want to encode
os.system('tcmpr int_cN1.txt')
os.system('tcmpr int_cN2.txt')
os.system('tcmpr int_cN3.txt')
```
## Reconstruction
```
os.system('tcmpr -d int_cN1.txt.huffman')
os.system('tcmpr -d int_cN2.txt.huffman')
os.system('tcmpr -d int_cN3.txt.huffman')
decoded_data1 = np.loadtxt(fname = "int_cN1.txt")
decoded_data2 = np.loadtxt(fname = "int_cN2.txt")
decoded_data3 = np.loadtxt(fname = "int_cN3.txt")
recover_signal1 = decoded_data1
recover_signal2 = decoded_data2
recover_signal3 = decoded_data3
recover_signal1 = list(recover_signal1)
recover_signal2 = list(recover_signal2)
recover_signal3 = list(recover_signal3)
len(recover_signal1)
split_list = [1]
for i in range(0,return_N(len(recover_signal1))+1):
split_list.append(2 ** i)
temp_recovered1 = iter(recover_signal1)
res_recovered1 = [list(islice(temp_recovered1, 0, ele)) for ele in split_list]
temp_recovered2 = iter(recover_signal2)
res_recovered2 = [list(islice(temp_recovered2, 0, ele)) for ele in split_list]
temp_recovered3 = iter(recover_signal3)
res_recovered3 = [list(islice(temp_recovered3, 0, ele)) for ele in split_list]
recover_dct1 = [list(dct(res_recovered1[0], type = 2, norm = 'ortho' )), list(dct(res_recovered1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered1)):
recover_dct1.append(list(dct(res_recovered1[k], type = 2, norm = 'ortho' )))
recover_dct2 = [list(dct(res_recovered2[0], type = 2, norm = 'ortho' )), list(dct(res_recovered2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered2)):
recover_dct2.append(list(dct(res_recovered2[k], type = 2, norm = 'ortho' )))
recover_dct3 = [list(dct(res_recovered3[0], type = 2, norm = 'ortho' )), list(dct(res_recovered3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered3)):
recover_dct3.append(list(dct(res_recovered3[k], type = 2, norm = 'ortho' )))
all_recover1 = []
for i in recover_dct1:
for j in i:
all_recover1.append(j)
all_recover2 = []
for i in recover_dct2:
for j in i:
all_recover2.append(j)
all_recover3 = []
for i in recover_dct3:
for j in i:
all_recover3.append(j)
aN_recover1 = idct(all_recover1, type = 2, norm = 'ortho')
aN_recover2 = idct(all_recover2, type = 2, norm = 'ortho')
aN_recover3 = idct(all_recover3, type = 2, norm = 'ortho')
plt.plot(signal.resample(y1, len(aN_recover1))[31000:31100], label = "origianl")
plt.plot(aN_recover1[31000:31100], label = "recovered")
plt.legend()
plt.title('ACC')
plt.grid()
plt.show()
#resampled_signal_shorter = resampled_signal1[:len(aN_recover1)]
resampled_signal_shorter1 = signal.resample(y1, len(aN_recover1))
from sklearn.metrics import mean_squared_error
from math import sqrt
def PRD_calculation(original_signal, compressed_signal):
PRD = sqrt(sum((original_signal-compressed_signal)**2)/(sum(original_signal**2)))
return PRD
PRD = PRD_calculation(resampled_signal_shorter1, aN_recover1)
print("The PRD is {}%".format(round(PRD*100,3)))
```
|
github_jupyter
|
# Quickstart
In this tutorial, we explain how to quickly use ``LEGWORK`` to calculate the detectability of a collection of sources.
```
%matplotlib inline
```
Let's start by importing the source and visualisation modules of `LEGWORK` and some other common packages.
```
import legwork.source as source
import legwork.visualisation as vis
import numpy as np
import astropy.units as u
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
plt.rc('font', family='serif')
plt.rcParams['text.usetex'] = False
fs = 24
# update various fontsizes to match
params = {'figure.figsize': (12, 8),
'legend.fontsize': fs,
'axes.labelsize': fs,
'xtick.labelsize': 0.7 * fs,
'ytick.labelsize': 0.7 * fs}
plt.rcParams.update(params)
```
Next let's create a random collection of possible LISA sources in order to assess their detectability.
```
# create a random collection of sources
n_values = 1500
m_1 = np.random.uniform(0, 10, n_values) * u.Msun
m_2 = np.random.uniform(0, 10, n_values) * u.Msun
dist = np.random.normal(8, 1.5, n_values) * u.kpc
f_orb = 10**(-5 * np.random.power(3, n_values)) * u.Hz
ecc = 1 - np.random.power(5, n_values)
```
We can instantiate a `Source` class using these random sources in order to analyse the population. There are also a series of optional parameters which we don't cover here but if you are interested in the purpose of these then check out the [Using the Source Class](Source.ipynb) tutorial.
```
sources = source.Source(m_1=m_1, m_2=m_2, ecc=ecc, dist=dist, f_orb=f_orb)
```
This `Source` class has many methods for calculating strains, visualising populations and more. You can learn more about these in the [Using the Source Class](Source.ipynb) tutorial. For now, we shall focus only on the calculation of the signal-to-noise ratio.
Therefore, let's calculate the SNR for these sources. We set `verbose=True` to give an impression of what sort of sources we have created. This function will split the sources based on whether they are stationary/evolving and circular/eccentric and use one of 4 SNR functions for each subpopulation.
```
snr = sources.get_snr(verbose=True)
```
These SNR values are now stored in `sources.snr` and we can mask those that don't meet some detectable threshold.
```
detectable_threshold = 7
detectable_sources = sources.snr > 7
print("{} of the {} sources are detectable".format(len(sources.snr[detectable_sources]), n_values))
```
```
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, xlim=(2e-6, 2e-1), which_sources=sources.snr > 0)
```
The reason for this shape may not be immediately obvious. However, if we also use the visualisation module to overlay the LISA sensitivity curve, it becomes clear that the SNRs increase in step with the decrease in the noise and flatten out as the sensitivity curve does as we would expect. To learn more about the visualisation options that `LEGWORK` offers, check out the [Visualisation](Visualisation.ipynb) tutorial.
```
# create the same plot but set `show=False`
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, show=False, which_sources=sources.snr > 0)
# duplicate the x axis and plot the LISA sensitivity curve
right_ax = ax.twinx()
frequency_range = np.logspace(np.log10(2e-6), np.log10(2e-1), 1000) * u.Hz
vis.plot_sensitivity_curve(frequency_range=frequency_range, fig=fig, ax=right_ax)
plt.show()
```
That's it for this quickstart into using `LEGWORK`. For more details on using `LEGWORK` to calculate strains, evolve binaries and visualise their distributions check out the [other tutorials](../tutorials.rst) and [demos](../demos.rst) in these docs! You can also read more about the scope and limitations of `LEGWORK` [on this page](../limitations.rst).
|
github_jupyter
|
```
from __future__ import division, print_function
import os
import torch
import pandas
import numpy as np
from torch.utils.data import DataLoader,Dataset
from torchvision import utils, transforms
from skimage import io, transform
import matplotlib.pyplot as plt
import warnings
#ignore warnings
warnings.filterwarnings("ignore")
plt.ion() #interactive mode on
```
The dataset being used is the face pose detection dataset, which annotates the data using 68 landmark points. The dataset has a csv file that contains the annotation for the images.
```
# Import CSV file
landmarks_csv = pandas.read_csv("data/faces/face_landmarks.csv")
# Extracting info from the CSV file
n = 65
img_name = landmarks_csv.iloc[n,0]
landmarks = landmarks_csv.iloc[n,1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1,2)
# Print a few of the datasets for having a look at
# the dataset
print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
print('First 4 Landmarks: {}'.format(landmarks[:4]))
```
Now that we have seen the landmark values let's plot a function to display the landmarks on an image
```
def plot_landmarks(image, landmarks):
plt.imshow(image)
plt.scatter(landmarks[:, 0], landmarks[:, 1], s=10, c='r', marker='.')
plt.pause(0.01)
plt.figure()
plot_landmarks(io.imread(os.path.join('data/faces/',img_name)),landmarks)
plt.show()
```
To use customa datasets we need to use the <b>(torch.utils.data.Dataset) Dataset</b> class provided. It is an abstract class and hence the custom class should inherit it and override the
<b>__len__</b> method and the
<b>__getitem__</b> method
The __getitem__ method is used to provide the ith sample from the dataset
```
class FaceLandmarkDataset(Dataset):
# We will read the file here
def __init__(self,csv_file, root_dir, transform=None):
"""
Args:
csv_file : string : path to csv file
root_dir : string : root directory which contains all the images
transform : callable, optional : Optional transform to be applied
to the images
"""
self.landmarks_frame = pandas.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.landmarks_frame)
def __getitem__(self, idx):
"""
Args:
idx (integer): the ith sample
"""
image_name = os.path.join(self.root_dir,self.landmarks_frame.iloc[idx, 0])
image = io.imread(image_name)
landmarks = np.array([self.landmarks_frame.iloc[idx, 1:]])
landmarks = landmarks.astype("float").reshape(-1, 2)
sample = {"image":image,"landmarks":landmarks}
if self.transform:
sample = self.transform(sample)
return sample
face_dataset = FaceLandmarkDataset(csv_file='data/faces/face_landmarks.csv',
root_dir='data/faces/')
fig = plt.figure()
for i in range(len(face_dataset)):
sample = face_dataset[i]
print(i, sample['image'].shape, sample['landmarks'].shape)
ax = plt.subplot(1, 4, i + 1)
plt.tight_layout()
ax.set_title('Sample #{}'.format(i))
ax.axis('off')
plot_landmarks(**sample)
if i == 3:
plt.show()
break
```
Now that we have the dataset , we can move on to preprocessing the data. We use the transforms class for this.
We will be using callable classes of the transformations we need so that the parameters do not need to be passed again and again. For better description refer the <a href="https://pytorch.org/tutorials/beginner/data_loading_tutorial.html">tutorial</a> from PyTorch.
To implement callable classes we just need to implement the __call__ method and if required __init__ method of the class.
Here we will be using autocrop , Reshape and To Tensor transformations.
__** NOTE **__<br>
In PyTorch the default style for image Tensors is <span>n_channels * Height * Width</span> as opposed to the Tensordlow default of <span>Height * Width * n_channels</span>. But all the images in the real world have the tensorflow default format and hence we need to do that change in the ToTensor class that we will implement.
```
# Implementing the Rescale class
class Rescale(object):
"""Rescale the input image to a given size
Args:
output_size (int or tuple):Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same
"""
def __init__(self,output_size):
assert isinstance(output_size,(int,tuple))
self.output_size = output_size
def __call__(self,sample):
image, landmarks = samplep['image'], sample['landmarks']
h, w = image.shape[:2]
if isinstance(self.output_size,int):
if h>w:
new_h, new_w = self.output_size * h/w, self.output_size
else:
new_h, new_w = slef.output_size, self.output_size *w/h
else:
new_h, new_w = self.output_size
image = transform.resize(image, (new_h, new_w))
# h and w are swapped for landmarks because for images,
# x and y axes are axis 1 and 0 respectively
landmarks = landmarks * [new_w / w, new_h / h]
return {"image": image, "landmarks": landmarks}
# Implementing Random Crop
class RandomCrop(object):
"""Crop randomly the image in a sample
Args:
output_size(tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
images, landmarks = sample['image'], sample['landmarks']
h, w = images.shape[:,2]
new_h, new_w = self.output_size
top = np.random.randn(0, h-new_h)
left = np.random.randn(0, w-new_w)
images = images[top:top + new_h, left:left + new_w]
landmarks = landmarks - [left, top]
sample = {"image":images, "landmarks": landmarks}
return sample
# Implementing To Tensor
class ToTensor(object):
"""Convert the PIL image into a tensor"""
def __call__(self,sample):
image, landmarks = sample['image'], sample['landmarks']
# Need to transpose
# Numpy image : H x W x C
# Torch image : C x H x W
image = image.transpose((2, 0, 1))
sample = {"image":torch.from_numpy(image),"landmarks":torch.from_numpy(landmarks)}
```
|
github_jupyter
|
```
%matplotlib inline
import gym
import matplotlib
import numpy as np
import sys
from collections import defaultdict
if "../" not in sys.path:
sys.path.append("../")
from lib.envs.blackjack import BlackjackEnv
from lib import plotting
matplotlib.style.use('ggplot')
env = BlackjackEnv()
def mc_prediction(policy, env, num_episodes, discount_factor=1.0):
"""
Monte Carlo prediction algorithm. Calculates the value function
for a given policy using sampling.
Args:
policy: A function that maps an observation to action probabilities.
env: OpenAI gym environment.
num_episodes: Number of episodes to sample.
discount_factor: Gamma discount factor.
Returns:
A dictionary that maps from state -> value.
The state is a tuple and the value is a float.
"""
# Keeps track of sum and count of returns for each state
# to calculate an average. We could use an array to save all
# returns (like in the book) but that's memory inefficient.
returns_sum = defaultdict(float)
returns_count = defaultdict(float)
# The final value function
V = defaultdict(float)
for i_episode in range(1, num_episodes + 1):
# Print out which episode we're on, useful for debugging.
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# Generate an episode.
# An episode is an array of (state, action, reward) tuples
episode = []
state = env.reset()
for t in range(100):
action = policy(state)
next_state, reward, done, _ = env.step(action)
episode.append((state, action, reward))
if done:
break
state = next_state
# Find all states the we've visited in this episode
# We convert each state to a tuple so that we can use it as a dict key
states_in_episode = set([tuple(x[0]) for x in episode])
for state in states_in_episode:
# Find the first occurance of the state in the episode
first_occurence_idx = next(i for i,x in enumerate(episode) if x[0] == state)
# Sum up all rewards since the first occurance
G = sum([x[2]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
# Calculate average return for this state over all sampled episodes
returns_sum[state] += G
returns_count[state] += 1.0
V[state] = returns_sum[state] / returns_count[state]
return V
def sample_policy(observation):
"""
A policy that sticks if the player score is >= 20 and hits otherwise.
"""
score, dealer_score, usable_ace = observation
return 0 if score >= 20 else 1
V_10k = mc_prediction(sample_policy, env, num_episodes=10000)
plotting.plot_value_function(V_10k, title="10,000 Steps")
V_500k = mc_prediction(sample_policy, env, num_episodes=500000)
plotting.plot_value_function(V_500k, title="500,000 Steps")
```
|
github_jupyter
|
```
#Fill the paths below
PATH_FRC = "" # git repo directory path
PATH_ZENODO = "" # Data and models are available here: https://zenodo.org/record/5831014#.YdnW_VjMLeo
DATA_FLAT = PATH_ZENODO+'/data/goi_1000/flat_1000/*.png'
DATA_NORMAL = PATH_ZENODO+'/data/goi_1000/standard_1000/*.jpg'
GAUSS_L2_MODEL = PATH_ZENODO+'/models/gaussian/noise005_set1000/standard/' # noise 0.05
GAUSS_L2_MODEL_FLAT = PATH_ZENODO+'/models/gaussian/noise005_set1000/flat/' # noise 0.05
import sys
sys.path.append(PATH_FRC)
import glob
import os
import skimage
%matplotlib inline
import matplotlib.pyplot as plt
from skimage.io import imread
import numpy as np
import matplotlib
import tensorflow as tf
from models2 import FRCUnetModel
from skimage.filters import window
from tqdm import tqdm
import pandas as pd
import scipy.stats as stats
from scipy.optimize import fsolve
import pyfftw.interfaces.numpy_fft
np.fft = pyfftw.interfaces.numpy_fft
matplotlib.rcParams.update({'mathtext.default':'regular'})
matplotlib.rcParams.update({'font.size': 8})
matplotlib.rcParams.update({'axes.labelweight': 'bold'})
def normalise_img(image):
image = image - image.min()
image = image/image.max() - 0.5
return image
def plot_power_spectrum(image):
if len(image.shape) == 3:
image = np.sum(image, axis=2)
image = image.astype('float64')
image = image - image.mean()
fourier_image = np.fft.fftn(image) # here the input is grey image
size = image.shape[0]
fourier_amplitudes = np.abs(fourier_image)**2
print("FOURIER AMPLITUDES", np.sum(fourier_amplitudes))
kfreq = np.fft.fftfreq(size) * size # image size
kfreq2D = np.meshgrid(kfreq, kfreq)
knrm = np.sqrt(kfreq2D[0]**2 + kfreq2D[1]**2)
knrm = knrm.flatten()
fourier_amplitudes = fourier_amplitudes.flatten()
kbins = np.arange(0.5, int(size / 2), 1.)
kvals = 0.5 * (kbins[1:] + kbins[:-1])
Abins, _, _ = stats.binned_statistic(
knrm, fourier_amplitudes, statistic="mean", bins=kbins) # mean power
return kvals, Abins
def load_model(model_dir, model_fname):
if model_dir is not None:
return FRCUnetModel(None, model_path=os.path.join(model_dir, model_fname))
files_flat=sorted(glob.glob(DATA_FLAT))
files_flat=files_flat[:50]
files_normal=sorted(glob.glob(DATA_NORMAL))
files_normal=files_normal[:50]
cleans_flat=[]
for file in files_flat:
clean = imread(file)
if len(clean.shape) > 2:
clean = np.mean(clean, axis=2)
minsize = np.array(clean.shape).min()
clean = clean[:minsize,:minsize]
clean = normalise_img(clean)
clean = clean.astype('float32')
#clean = clean*window('hann', clean.shape)
cleans_flat.append(clean)
cleans_flat=np.stack(cleans_flat)
cleans_normal=[]
for file in files_normal:
clean = imread(file)
if len(clean.shape) > 2:
clean = np.mean(clean, axis=2)
minsize = np.array(clean.shape).min()
clean = clean[:minsize,:minsize]
clean = normalise_img(clean)
clean = clean.astype('float32')
#clean = clean*window('hann', clean.shape)
cleans_normal.append(clean)
cleans_normal=np.stack(cleans_normal)
cleans_normal.shape
noise1=np.random.normal(0,0.05,256**2*50).reshape(50,256,256)
noisy_flat=cleans_flat.copy()+noise1
noise2=np.random.normal(0,0.05,256**2*50).reshape(50,256,256)
noisy_normal=cleans_normal.copy()+noise2
l2_model=load_model(GAUSS_L2_MODEL, 'saved-model-epoch-200')
l2_1000_model_flat=load_model(GAUSS_L2_MODEL_FLAT, 'saved-model-epoch-200')
imnr=3
denoised_normal = l2_model.model(np.reshape(noisy_normal[imnr], [1,256, 256,1]))
denoised_normal = np.squeeze(denoised_normal)
denoised_flat = l2_1000_model_flat.model(np.reshape(noisy_flat[imnr], [1,256, 256,1]))
denoised_flat = np.squeeze(denoised_flat)
x=np.array(plot_power_spectrum(noisy_normal[imnr])[0])
x=x*1.0/x.max()
fig = plt.figure()
fig.set_size_inches(7, 7) # 3.5 inch is the width of one column in A4 paper
ax = fig.add_subplot(334)
ax.imshow(cleans_flat[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
#plt.ylabel('Gaussian')
plt.title('Normalised spectrum, GT')
ax = fig.add_subplot(335)
ax.imshow(noisy_flat[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Normalised spectrum, noisy')
ax = fig.add_subplot(336)
ax.imshow(denoised_flat, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Normalised spectrum, denoised')
ax = fig.add_subplot(331)
ax.imshow(cleans_normal[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, GT')
ax = fig.add_subplot(332)
ax.imshow(noisy_normal[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, noisy')
ax = fig.add_subplot(333)
ax.imshow(denoised_normal, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, denoised')
ax = fig.add_subplot(337)
plt.title('Ground truth ')
ax.plot(x,np.array(plot_power_spectrum(cleans_flat[imnr])[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(cleans_normal[imnr])[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
ax.set_ylabel('Power')
plt.yscale('log')
plt.xscale('log')
#ax.locator_params(axis='x', nbins=5)
plt.ylim([10**1.5,10**7.5 ])
plt.legend(loc=1)
ax = fig.add_subplot(338)
plt.title('Noisy')
ax.plot(x,np.array(plot_power_spectrum(noisy_flat[imnr])[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(noisy_normal[imnr])[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
#ax.set_ylabel('Power')
plt.yscale('log')
plt.xscale('log')
plt.ylim([10**1.5,10**7.5 ])
ax = fig.add_subplot(339)
plt.title('Denoised')
ax.plot(x,np.array(plot_power_spectrum(denoised_flat)[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(denoised_normal)[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
plt.yscale('log')
plt.xscale('log')
#ax.locator_params(axis='x', nbins=5)
plt.ylim([10**1.5,10**7.5 ])
plt.tight_layout()
plt.subplots_adjust(wspace=0.23, hspace=0.23)
fig.savefig('figure_s3.png', dpi=300)
```
|
github_jupyter
|
```
import datetime
import os, sys
import numpy as np
import matplotlib.pyplot as plt
import casadi as cas
import pickle
import copy as cp
# from ..</src> import car_plotting
# from .import src.car_plotting
PROJECT_PATH = '/home/nbuckman/Dropbox (MIT)/DRL/2020_01_cooperative_mpc/mpc-multiple-vehicles/'
sys.path.append(PROJECT_PATH)
import src.MPC_Casadi as mpc
import src.TrafficWorld as tw
import src.IterativeBestResponseMPCMultiple as mibr
np.set_printoptions(precision=2)
NEW = True
if NEW:
optional_suffix = "testsave"
subdir_name = datetime.datetime.now().strftime("%Y%m%d-%H%M%S") + optional_suffix
folder = "results/" + subdir_name + "/"
os.makedirs(folder)
os.makedirs(folder+"imgs/")
os.makedirs(folder+"data/")
os.makedirs(folder+"vids/")
else:
subdir_name = "20200224-103456_real_dim_CA"
folder = "results/" + subdir_name + "/"
print(folder)
T = 10 #numbr of time horizons
dt = 0.2
N = int(T/dt) #Number of control intervals
world = tw.TrafficWorld(2, 0, 1000)
# Initial Conditions
all_other_x0 = []
all_other_u = []
n_other = 2
all_other_MPC = []
next_x0 = 0
for i in range(n_other):
x1_MPC = mpc.MPC(dt)
x1_MPC.theta_iamb = np.pi/2.5
x1_MPC.k_final = 1.0
x1_MPC.k_s = -2.0
# x1_MPC.k_s = 0.0
# x1_MPC.k_x = -1.0
x1_MPC.min_y = world.y_min
x1_MPC.max_y = world.y_max
x1_MPC.k_u_v = 0.10
x1_MPC.k_u_delta = 0.10
x1_MPC.k_lat = 1.0
# x1_MPC.k_change_u_v = 1.0
# x1_MPC.k_change_u_delta = 1.0
if i%2 == 0:
lane_number = 0
next_x0 += x1_MPC.L/2.0 + 2*x1_MPC.min_dist
else:
lane_number = 1
initial_speed = 20 * 0.447 # m/s
x1_MPC.fd = x1_MPC.gen_f_desired_lane(world, lane_number, True)
x0 = np.array([next_x0, world.get_lane_centerline_y(lane_number), 0, 0, initial_speed, 0]).T
u1 = np.zeros((2,N))
u1[0,:] = np.clip(np.pi/180 *np.random.normal(size=(1,N)), -2 * np.pi/180, 2 * np.pi/180)
# u1[0,:] = np.ones((1,N)) * np.pi/6
# u1[1,:] = np.clip(np.random.normal(size=(1,N)), -x1_MPC.max_acceleration * x1_MPC.dt, x1_MPC.max_acceleration * x1_MPC.dt)
all_other_MPC += [x1_MPC]
all_other_x0 += [x0]
all_other_u += [u1]
amb_MPC = cp.deepcopy(x1_MPC)
amb_MPC.theta_iamb = 0.0
amb_MPC.k_u_v = 0.10
amb_MPC.k_u_delta = 1.0
amb_MPC.k_change_u_v = 0.01
amb_MPC.k_change_u_delta = 0.0
amb_MPC.k_phi
amb_MPC.k_x = -1/10000.0
amb_MPC.k_s = 0
# amb_MPC.min_v = initial_speed
# amb_MPC.k_u_change = 1.0
# amb_MPC.k_lat = 0
amb_MPC.k_lon = 0.0
# amb_MPC.k_s = -2.0
amb_MPC.max_v = 40 * 0.447 # m/s
# amb_MPC.max_X_dev = 5.0
amb_MPC.fd = amb_MPC.gen_f_desired_lane(world, 0, True)
x0_amb = np.array([0, 0, 0, 0, 1.1*initial_speed , 0]).T
uamb = np.zeros((2,N))
uamb[0,:] = np.clip(np.pi/180 * np.random.normal(size=(1,N)), -2 * np.pi/180, 2 * np.pi/180)
amb_MPC.min_v = 1.1*initial_speed
WARM = True
n_total_round = 60
ibr_sub_it = 1
runtimeerrors = 0
min_slack = 100000.0
for n_round in range(n_total_round):
response_MPC = amb_MPC
response_x0 = x0_amb
nonresponse_MPC_list = all_other_MPC
nonresponse_x0_list = all_other_x0
nonresponse_u_list = all_other_u
bri = mibr.IterativeBestResponseMPCMultiple(response_MPC, None, nonresponse_MPC_list )
bri.k_slack = 999
bri.generate_optimization(N, T, response_x0, None, nonresponse_x0_list, 5, slack=True)
bri.solve(None, nonresponse_u_list)
x1, u1, x1_des, _, _, _, other_x, other_u, other_des = bri.get_solution()
x1 = bri.opti.debug.value(bri.x_opt)
plt.plot(x1[0,:], x1[1,:])
costs = ["self.k_u_delta * self.u_delta_cost",
"self.k_u_v * self.u_v_cost",
"self.k_lat * self.lat_cost",
"self.k_lon * self.lon_cost",
"self.k_phi_error * self.phi_error_cost",
"self.k_phi_dot * self.phidot_cost",
"self.k_s * self.s_cost",
"self.k_v * self.v_cost",
"self.k_change_u_v * self.change_u_v",
"self.k_change_u_delta * self.change_u_delta",
"self.k_final * self.final_costs",
"self.k_x * self.x_cost"]
for i in range(len(bri.car1_costs_list)):
amb_costs = bri.opti.debug.value(bri.car1_costs_list[i])
print('%.03f'%amb_costs, costs[i])
print(bri.opti.debug.value(bri.slack_cost))
```
|
github_jupyter
|
```
import ast
from glob import glob
import sys
import os
from copy import deepcopy
import networkx as nx
from stdlib_list import stdlib_list
STDLIB = set(stdlib_list())
CONVERSIONS = {
'attr': 'attrs',
'PIL': 'Pillow',
'Image': 'Pillow',
'mpl_toolkits': 'matplotlib',
'dateutil': 'python-dateutil'
}
dirtree = nx.DiGraph()
exclude_dirs = {'node_modules', '__pycache__', 'dist'}
exclude_files = {'__init__.py', '_version.py', '_install_requires.py'}
packages_dir = os.path.join(ROOT, 'packages')
for root, dirs, files in os.walk(packages_dir, topdown=True):
dirs[:] = [d for d in dirs if d not in exclude_dirs]
if '__init__.py' in files:
module_init = os.path.join(root, '__init__.py')
files[:] = [f for f in files if f not in exclude_files]
dirtree.add_node(module_init)
parent_init = os.path.join(os.path.dirname(root), '__init__.py')
if os.path.exists(parent_init):
dirtree.add_edge(parent_init, module_init)
for f in files:
if f.endswith('.py'):
filepath = os.path.join(root, f)
dirtree.add_node(filepath)
dirtree.add_edge(module_init, filepath)
package_roots = [n for n, d in dirtree.in_degree() if d == 0]
package_root_map = {
os.path.basename(os.path.dirname(package_root)): package_root
for package_root in package_roots
}
internal_packages = list(package_root_map.keys())
internal_packages
import_types = {
type(ast.parse('import george').body[0]),
type(ast.parse('import george as macdonald').body[0])}
import_from_types = {
type(ast.parse('from george import macdonald').body[0])
}
all_import_types = import_types.union(import_from_types)
all_import_types
def get_imports(filepath):
with open(filepath, 'r') as file:
data = file.read()
parsed = ast.parse(data)
imports = [node for node in ast.walk(parsed) if type(node) in all_import_types]
stdlib_imports = set()
external_imports = set()
internal_imports = set()
near_relative_imports = set()
far_relative_imports = set()
def get_base_converted_module(name):
name = name.split('.')[0]
try:
name = CONVERSIONS[name]
except KeyError:
pass
return name
def add_level_0(name):
if name in STDLIB:
stdlib_imports.add(name)
elif name in internal_packages:
internal_imports.add(name)
else:
external_imports.add(name)
for an_import in imports:
if type(an_import) in import_types:
for alias in an_import.names:
name = get_base_converted_module(alias.name)
add_level_0(name)
elif type(an_import) in import_from_types:
name = get_base_converted_module(an_import.module)
if an_import.level == 0:
add_level_0(name)
elif an_import.level == 1:
near_relative_imports.add(name)
else:
far_relative_imports.add(name)
else:
raise
return {
'stdlib': stdlib_imports,
'external': external_imports,
'internal': internal_imports,
'near_relative': near_relative_imports,
'far_relative': far_relative_imports}
all_imports = {
filepath: get_imports(filepath)
for filepath in dirtree.nodes()
}
def get_descendants_dependencies(filepath):
dependencies = deepcopy(all_imports[filepath])
for descendant in nx.descendants(dirtree, filepath):
for key, item in all_imports[descendant].items():
dependencies[key] |= item
return dependencies
package_dependencies = {
package: get_descendants_dependencies(root)
for package, root in package_root_map.items()
}
package_dependencies
get_descendants_dependencies(package_roots[0])
list(nx.neighbors(dirtree, package_roots[4]))
nx.descendants(dirtree, '/home/simon/git/pymedphys/packages/pymedphys/src/pymedphys/__init__.py')
# nx.neighbors()
imports = [node for node in ast.walk(table) if type(node) in all_import_types]
imports
# external_imports = set()
# near_internal_imports = set()
# far_internal_imports = set()
# for an_import in imports:
# if type(an_import) in import_types:
# for alias in an_import.names:
# external_imports.add(alias.name)
# elif type(an_import) in import_from_types:
# if an_import.level == 0:
# external_imports.add(an_import.module)
# elif an_import.level == 1:
# near_internal_imports.add(an_import.module)
# else:
# far_internal_imports.add(an_import.module)
# else:
# raise
# print(ast.dump(an_import))
external_imports
near_internal_imports
far_internal_imports
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
%matplotlib inline
import joblib
import json
import tqdm
import glob
import numba
import dask
import xgboost
from dask.diagnostics import ProgressBar
import re
ProgressBar().register()
fold1, fold2 = joblib.load("./valid/fold1.pkl.z"), joblib.load("./valid/fold2.pkl.z")
train = pd.read_parquet("./data/train.parquet")
train_melt = pd.read_parquet("./data/22c_train_melt_with_features.parquet")
test_melt = pd.read_parquet("./data/22c_test_melt_with_features.parquet")
test_melt.head()
item_data = pd.read_parquet("./data/item_data.parquet")
item_data.head()
item_title_map = item_data[['item_id', 'title']].drop_duplicates()
item_title_map = item_title_map.set_index("item_id").squeeze().to_dict()
item_price_map = item_data[['item_id', 'price']].drop_duplicates()
item_price_map = item_price_map.set_index("item_id").squeeze().to_dict()
item_domain_map = item_data[['item_id', 'domain_id']].drop_duplicates()
item_domain_map = item_domain_map.set_index("item_id").squeeze().to_dict()
```
# stack gen
```
%%time
log_pos = np.log1p(np.arange(1,11))
best_sellers = [1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574]
best_sellers_domain = [item_domain_map[e] for e in best_sellers]
def pad(lst):
if len(lst) == 0:
return best_sellers
if len(lst) < 10:
lst += best_sellers[:(10 - len(lst))]
return np.array(lst)
def pad_str(lst):
if len(lst) == 0:
return best_sellers_domain
if len(lst) < 10:
lst += best_sellers_domain[:(10 - len(lst))]
return lst
# this is wrong, double counts exact item hits
def ndcg_vec(ytrue, ypred, ytrue_domain, ypred_domain):
relevance = np.zeros((ypred.shape[0], 10))
for i in range(10):
relevance[:, i] = np.equal(ypred_domain[:, i], ytrue_domain) * (np.equal(ypred[:, i], ytrue) * 12 + 1)
dcg = (relevance / log_pos).sum(axis=1)
i_relevance = np.ones(10)
i_relevance[0] = 12.
idcg = np.zeros(ypred.shape[0]) + (i_relevance / log_pos).sum()
return (dcg / idcg).mean()
%%time
tr_list = glob.glob("./stack_2f/*_train.parquet")
ts_list = glob.glob("./stack_2f/*_test.parquet")
train = train_melt[['seq_index','event_info','has_bought', 'item_domain', 'bought_domain', 'bought_id', 'y_rank']].copy()
for f in tr_list:
fname = re.search('/(\d[\d\w]+)_', f).group(1)
fdf = pd.read_parquet(f).rename(columns={"p": fname})
train = pd.merge(train, fdf, on=['seq_index','event_info'])
train = train.sort_values("seq_index")
test = test_melt[['seq_index','event_info']].copy()
for f in ts_list:
fname = re.search('/(\d[\d\w]+)_', f).group(1)
fdf = pd.read_parquet(f).rename(columns={"p": fname})
test = pd.merge(test, fdf, on=['seq_index','event_info'])
test = test.sort_values("seq_index")
train.head()
test.head()
train.columns
from sklearn.model_selection import GroupKFold
from cuml.preprocessing import TargetEncoder
stack_p = list()
for f1, f2 in [(fold1, fold2), (fold2, fold1)]:
Xtr = train[train['seq_index'].isin(f1)]
Xval = train[train['seq_index'].isin(f2)]
features = ['22c', '26']
params = [0.1, 3, 1, 0.5, 1.]
learning_rate, max_depth, min_child_weight, subsample, colsample_bytree = params
Xtrr, ytr = Xtr[features], Xtr['y_rank']
Xvall = Xval[features]
groups = Xtr.groupby('seq_index').size().values
mdl = xgboost.XGBRanker(seed=0, tree_method='gpu_hist', gpu_id=0, n_estimators=100,
learning_rate=learning_rate, max_depth=max_depth, min_child_weight=min_child_weight,
subsample=subsample, colsample_bytree=colsample_bytree, objective='rank:pairwise', num_parallel_tree=5)
mdl.fit(Xtrr, ytr, group=groups)
p = mdl.predict(Xvall)
preds = Xval[['seq_index', 'has_bought', 'item_domain', 'bought_domain', 'event_info', 'bought_id']].copy()
preds['p'] = p
preds = preds.sort_values('p', ascending=False).drop_duplicates(subset=['seq_index', 'event_info'])
ytrue = preds.groupby("seq_index")['bought_id'].apply(lambda x: x.iloc[0]).values
ytrue_domain = preds.groupby("seq_index")['bought_domain'].apply(lambda x: x.iloc[0]).values
ypred = preds.groupby("seq_index")['event_info'].apply(lambda x: pad(x.iloc[:10].tolist()))
ypred = np.array(ypred.tolist())
ypred_domain = preds.groupby("seq_index")['item_domain'].apply(lambda x: pad_str(x.iloc[:10].tolist()))
ypred_domain = np.array(ypred_domain.tolist())
print(ndcg_vec(ytrue, ypred, ytrue_domain, ypred_domain))
```
# test
```
groups = train.groupby('seq_index').size().values
learning_rate, max_depth, min_child_weight, subsample, colsample_bytree = params
mdl = xgboost.XGBRanker(seed=0, tree_method='gpu_hist', gpu_id=0, n_estimators=100,
learning_rate=learning_rate, max_depth=max_depth, min_child_weight=min_child_weight,
subsample=subsample, colsample_bytree=colsample_bytree, objective='rank:pairwise', num_parallel_tree=5)
mdl.fit(train[features], train['y_rank'], group=groups)
test[features].head()
p = mdl.predict(test[features])
preds = test[['seq_index', 'event_info']].copy()
preds['p'] = p
preds = preds.sort_values('p', ascending=False).drop_duplicates(subset=['seq_index', 'event_info'])
def pad(lst):
pad_candidates = [1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574]
if len(lst) == 0:
return pad_candidates
if len(lst) < 10:
lst += [lst[0]] * (10 - len(lst)) # pad_candidates[:(10 - len(lst))]
return np.array(lst)
ypred = preds.groupby("seq_index")['event_info'].apply(lambda x: pad(x.iloc[:10].tolist()))
seq_index = ypred.index
ypred = np.array(ypred.tolist())
ypred_final = np.zeros((177070, 10))
ypred_final[seq_index, :] = ypred
no_views = np.setdiff1d(np.arange(177070), seq_index)
#ypred_final[no_views, :] = np.array([1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574])
ypred_final = ypred_final.astype(int)
#permite produtos repetidos
pd.DataFrame(ypred_final).to_csv("./subs/27.csv", index=False, header=False)
test['seq_index'].max()
!wc -l ./subs/27.csv
!head ./subs/27.csv
```
|
github_jupyter
|
```
from imports import *
import pickle
# device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
device = torch.device("cuda:0")
2048*6*10
def get_encoder(model_name):
if model_name == 'mobile_net':
md = torchvision.models.mobilenet_v2(pretrained=True)
encoder = nn.Sequential(*list(md.children())[:-1])
elif model_name == 'resnet':
md = torchvision.models.resnet50(pretrained=True)
encoder = nn.Sequential(*list(md.children())[:-2])
return encoder
class DecisionGenerator_no_attention(nn.Module):
def __init__(self, encoder, encoder_dims, device, action_num=4, explanation_num=21):
super().__init__()
"""
encoder_dims = (F,H,W)
F:Feature shape (1280 for mobile net, 2048 for resnet)
H,W = image feature height, width
"""
self.encoder = encoder
assert len(encoder_dims) == 3, "encoder_dims has to be a triplet with shape (F,H,W)"
F,H,W = encoder_dims
ind_dim = H*W*F
self.action_branch = nn.Sequential(
nn.Linear(ind_dim,12),
nn.ReLU(),
# nn.Dropout(),
nn.Linear(12,action_num))
self.explanation_branch = nn.Sequential(
nn.Linear(ind_dim,12),
nn.ReLU(),
# nn.Dropout(),
nn.Linear(12, explanation_num))
self.action_loss_fn, self.reason_loss_fn = self.loss_fn(device)
def loss_fn(self,device):
class_weights = [1, 1, 2, 2]
w = torch.FloatTensor(class_weights).to(device)
action_loss = nn.BCEWithLogitsLoss(pos_weight=w).to(device)
explanation_loss = nn.BCEWithLogitsLoss().to(device)
return action_loss,explanation_loss
def forward(self,images,targets=None):
images = torch.stack(images)
if self.training:
assert targets is not None
target_reasons = torch.stack([t['reason'] for t in targets])
target_actions = torch.stack([t['action'] for t in targets])
# print(images.shape)
features = self.encoder(images) #
# print(features.shape)
B,F,H,W = features.shape
# print(features.view(B,F,H*W).transpose(1,2).shape)
# print(transformed_feature.shape)
feature_polled = torch.flatten(features,start_dim=1)
# print(feature_polled.shape)
actions = self.action_branch(feature_polled)
reasons = self.explanation_branch(feature_polled)
if self.training:
action_loss = self.action_loss_fn(actions, target_actions)
reason_loss = self.reason_loss_fn(reasons, target_reasons)
loss_dic = {"action_loss":action_loss, "reason_loss":reason_loss}
return loss_dic
else:
return {"action":torch.sigmoid(actions),"reasons":torch.sigmoid(reasons)}
encoder = get_encoder('resnet')
dg = DecisionGenerator_no_attention(encoder,encoder_dims=(2048,6,10), device='cpu' )
# params = sum([np.prod(p.size()) for p in model_parameters])
# print("len of params: ",params)
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
count_parameters(dg)
class MHSA2(nn.Module):
def __init__(self,
emb_dim,
kqv_dim,
output_dim=10,
num_heads=8):
super(MHSA2, self).__init__()
self.emb_dim = emb_dim
self.kqv_dim = kqv_dim
self.num_heads = num_heads
self.w_k = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_q = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_v = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_out = nn.Linear(kqv_dim * num_heads, output_dim)
def forward(self, x):
b, t, _ = x.shape
e = self.kqv_dim
h = self.num_heads
keys = self.w_k(x).view(b, t, h, e)
values = self.w_v(x).view(b, t, h, e)
queries = self.w_q(x).view(b, t, h, e)
keys = keys.transpose(2, 1)
queries = queries.transpose(2, 1)
values = values.transpose(2, 1)
dot = queries @ keys.transpose(3, 2)
dot = dot / np.sqrt(e)
dot = nn.functional.softmax(dot, dim=3)
out = dot @ values
out = out.transpose(1,2).contiguous().view(b, t, h * e)
out = self.w_out(out)
return out
class DecisionGenerator_whole_attention(nn.Module):
def __init__(self, encoder, encoder_dims, device, num_heads=8, \
attention_out_dim=10, action_num=4, explanation_num=21):
super().__init__()
"""
encoder_dims = (F,H,W)
F:Feature shape (1280 for mobile net, 2048 for resnet)
H,W = image feature height, width
"""
self.encoder = encoder
assert len(encoder_dims) == 3, "encoder_dims has to be a triplet with shape (F,H,W)"
F,H,W = encoder_dims
self.MHSA = MHSA2(emb_dim=F,kqv_dim=10,output_dim=attention_out_dim,num_heads=num_heads)
T = H*W
self.action_branch = nn.Sequential(
nn.Linear(attention_out_dim*T,64),
nn.ReLU(),
# nn.Dropout(),
nn.Linear(64,action_num))
self.explanation_branch = nn.Sequential(
nn.Linear(attention_out_dim*T,64),
nn.ReLU(),
# nn.Dropout(),
nn.Linear(64, explanation_num))
self.action_loss_fn, self.reason_loss_fn = self.loss_fn(device)
def loss_fn(self,device):
class_weights = [1, 1, 2, 2]
w = torch.FloatTensor(class_weights).to(device)
action_loss = nn.BCEWithLogitsLoss(pos_weight=w).to(device)
explanation_loss = nn.BCEWithLogitsLoss().to(device)
return action_loss,explanation_loss
def forward(self,images,targets=None):
images = torch.stack(images)
if self.training:
assert targets is not None
target_reasons = torch.stack([t['reason'] for t in targets])
target_actions = torch.stack([t['action'] for t in targets])
# print(images.shape)
features = self.encoder(images) #
# print(features.shape)
B,F,H,W = features.shape
# print(features.view(B,F,H*W).transpose(1,2).shape)
transformed_feature = self.MHSA(features.view(B,F,H*W).transpose(1,2)) #(B, H, T, 10)
# print(transformed_feature.shape)
feature_polled = torch.flatten(transformed_feature,start_dim=1)
# print(feature_polled.shape)
actions = self.action_branch(feature_polled)
reasons = self.explanation_branch(feature_polled)
if self.training:
action_loss = self.action_loss_fn(actions, target_actions)
reason_loss = self.reason_loss_fn(reasons, target_reasons)
loss_dic = {"action_loss":action_loss, "reason_loss":reason_loss}
return loss_dic
else:
return {"action":torch.sigmoid(actions),"reasons":torch.sigmoid(reasons)}
dga = DecisionGenerator_whole_attention(encoder, encoder_dims=(2048,6,10), device='cpu')
count_parameters(dga)
24078915
classes = {
"bus": 0,
"traffic light": 1,
"traffic sign": 2,
"person": 3,
"bike": 4,
"truck": 5,
"motor": 6,
"car": 7,
"train": 8,
"rider": 9,
}
class_2_name = dict([(value, key) for key, value in classes.items()])
num_classes = len(classes)
```
## 1. Load model
```
def get_model(num_classes):
model = torchvision.models.detection.fasterrcnn_resnet50_fpn(pretrained=True)
in_features = model.roi_heads.box_predictor.cls_score.in_features
#model.roi_heads.box_predictor = FastRCNNPredictor(in_features, num_classes) # replace the pre-trained head with a new one
model.roi_heads.box_predictor = torchvision.models.detection.faster_rcnn.FastRCNNPredictor(in_features,num_classes)
return model.cpu()
model = get_model(num_classes)
checkpoint = torch.load('saved_models/bdd100k_24.pth')
model.load_state_dict(checkpoint['model'])
#optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
#epoch = checkpoint['epoch']
model.eval()
```
## 2. Show sample plot
```
def get_preds(idx,img_datalist,threshold):
im0 = Image.open(img_datalist[idx])
im0_tensor = torchvision.transforms.ToTensor()(im0)
pred = model([im0_tensor])
total_preds = []
for n,confidence in enumerate(pred[0]['scores']):
if confidence>threshold:
pred_update = {}
pred_update['boxes'] = pred[0]['boxes'][n]
pred_update['labels'] = pred[0]['labels'][n]
pred_update['scores'] = pred[0]['scores'][n]
total_preds.append(pred_update)
return im0,total_preds
def plot_from_image_preds(img,total_preds):
fig,ax = plt.subplots(1,figsize=(20,10))
for i in range(len(total_preds)):
xy = total_preds[i]['boxes'][0],total_preds[i]['boxes'][1]
width = total_preds[i]['boxes'][2]-total_preds[i]['boxes'][0]
height = total_preds[i]['boxes'][3]-total_preds[i]['boxes'][1]
rect = patches.Rectangle(xy,width,height,linewidth=1,edgecolor='r',facecolor='none')
ax.text(xy[0],xy[1],class_2_name[total_preds[i]['labels'].item()])
ax.add_patch(rect)
ax.imshow(img)
with open("datalists/bdd100k_val_images_path.txt", "rb") as fp:
val_img_paths = pickle.load(fp)
im, total_preds = get_preds(751,val_img_paths,0.6)
plot_from_image_preds(im,total_preds)
```
## 3. Test
```
im0 = Image.open(val_img_paths[100])
im0_tensor = torchvision.transforms.ToTensor()(im0)
model.backbone.out_channels
images, targets = model.transform([im0_tensor,im0_tensor])
images.tensors.shape
features = model.backbone(images.tensors)
proposals, _ = model.rpn(images, features, targets)
box_features1 = model.roi_heads.box_roi_pool(features,proposals,images.image_sizes)
box_features2 = model.roi_heads.box_head(box_features1)
class_logits, box_regression = model.roi_heads.box_predictor(box_features2)
```
## Test Multihead attention in pytorch
```
box_features2 = box_features2.view(2,1000,1024)
box_features2.shape
class MHSA(nn.Module):
def __init__(self,
emb_dim,
kqv_dim,
num_heads=1):
super(MHSA, self).__init__()
self.emb_dim = emb_dim
self.kqv_dim = kqv_dim
self.num_heads = num_heads
self.w_k = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_q = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_v = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_out = nn.Linear(kqv_dim * num_heads, emb_dim)
def forward(self, x):
b, t, _ = x.shape
e = self.kqv_dim
h = self.num_heads
keys = self.w_k(x).view(b, t, h, e)
values = self.w_v(x).view(b, t, h, e)
queries = self.w_q(x).view(b, t, h, e)
keys = keys.transpose(2, 1)
print("keys",keys.shape)
queries = queries.transpose(2, 1) # b, h, t, e
print("queries",queries.shape)
values = values.transpose(2, 1) # b, h, t, e
print("values",values.shape)
dot = queries @ keys.transpose(3, 2)
dot = dot / np.sqrt(e)
print("dot",dot.shape)
weights = nn.functional.softmax(dot, dim=3)
print(values.shape)
out = weights @ values
print(out.shape)
out = out.transpose(1,2).contiguous().view(b, t, h * e)
out = self.w_out(out)
return out, weights
attention = MHSA(1024,10,num_heads=8)
val, score = attention(box_features2)
score.shape
attention.parameters
model_parameters = filter(lambda p: p.requires_grad, attention.parameters())
params = sum([np.prod(p.size()) for p in model_parameters])
1024*4*80+1024
nn.Linear()
nn.MultiheadAttention()
```
## Test hard attention
```
box_features2.shape
box_features2 = box_features2.view(2,1000,1024)
box_features2.shape
attention = nn.Sequential(nn.Linear(1024,1),nn.Softmax(dim=1))
attention(box_features2)
score = attention(box_features2)
score.shape
box_features2.shape
_,ind = torch.topk(score,k=10,dim=1)
torch.index_select(box_features2,)
ind
torch.gather(box_features2,1,ind.expand(ind.size(0),ind.size(1),box_features2.size(2)))
box_features2[1,399,:]
box_features2[ind,:]
(box_features2*attention(box_features2)).shape
ind.squeeze(-1).shape
proposals[0].shape
boxes, scores, labels = model.roi_heads.postprocess_detections(class_logits, box_regression, proposals, images.image_sizes)
len(boxes)
box_features2_reshaped = box_features2.view(2,1000,1024)
box_features2_reshaped.shape,box_features1.shape
detections, detector_losses = model.roi_heads(features, proposals, images.image_sizes)
detections[0]['boxes'].shape
class MHSA(nn.Module):
def __init__(self,
emb_dim,
kqv_dim,
num_heads=1):
super(MHSA, self).__init__()
self.emb_dim = emb_dim
self.kqv_dim = kqv_dim
self.num_heads = num_heads
self.w_k = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_q = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_v = nn.Linear(emb_dim, kqv_dim * num_heads, bias=False)
self.w_out = nn.Linear(kqv_dim * num_heads, emb_dim)
def forward(self, x):
b, t, _ = x.shape
e = self.kqv_dim
h = self.num_heads
keys = self.w_k(x).view(b, t, h, e)
values = self.w_v(x).view(b, t, h, e)
queries = self.w_q(x).view(b, t, h, e)
keys = keys.transpose(2, 1)
queries = queries.transpose(2, 1)
values = values.transpose(2, 1)
dot = queries @ keys.transpose(3, 2)
dot = dot / np.sqrt(e)
dot = nn.functional.softmax(dot, dim=3)
out = dot @ values
out = out.transpose(1,2).contiguous().view(b, t, h * e)
out = self.w_out(out)
return out
attention = MHSA(1024,10,num_heads=8)
attention_result = attention(box_features2_reshaped)
attention_result.shape
torch.max(attention_result,1)[0]
class DecisionGenerator(nn.Module):
def __init__(self,faster_rcnn_model,batch_size=2,action_num=4,explanation_num=21,freeze_rcnn=True):
super().__init__()
self.rcnn = faster_rcnn_model
self.batch_size = batch_size
if freeze_rcnn:
self.rcnn.params.requires_grad = False
self.object_attention = MHSA(1024, kqv_dim=10, num_heads=8)
self.action_branch = nn.Linear(1024,action_num)
self.explanation_branch = nn.Linear(1024, explanation_num)
def forward(images):
images,_ = rcnn.transform(images)
features = rcnn.backbone(images.tensors)
proposals, _ = rcnn.rpn(images, features)
box_features = rcnn.roi_heads.box_roi_pool(features,proposals,images.image_sizes)
box_features = rcnn.roi_heads.box_head(box_features).view(self.batch_size, -1, 1024) #(B, num_proposal, 1024)
box_features = self.object_attention(box_features) #(B, num_proposal, 1024)
feature_polled,_ = torch.max(box_features,1)
actions = self.action_branch(feature_polled)
explanations = self.explanation_branch(feature_polled)
return actions,explanations
class Self_Attn(nn.Module):
""" Self attention Layer"""
def __init__(self,in_dim,activation):
super(Self_Attn,self).__init__()
self.chanel_in = in_dim
self.activation = activation
self.query_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
self.key_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
self.value_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim , kernel_size= 1)
self.gamma = nn.Parameter(torch.zeros(1))
self.softmax = nn.Softmax(dim=-1) #
def forward(self,x):
"""
inputs :
x : input feature maps( B X C X W X H)
returns :
out : self attention value + input feature
attention: B X N X N (N is Width*Height)
"""
m_batchsize,C,width ,height = x.size()
proj_query = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1) # B X CX(N)
proj_key = self.key_conv(x).view(m_batchsize,-1,width*height) # B X C x (*W*H)
energy = torch.bmm(proj_query,proj_key) # transpose check
attention = self.softmax(energy) # BX (N) X (N)
proj_value = self.value_conv(x).view(m_batchsize,-1,width*height) # B X C X N
out = torch.bmm(proj_value,attention.permute(0,2,1) )
out = out.view(m_batchsize,C,width,height)
out = self.gamma*out + x
return out,attention
```
|
github_jupyter
|
# Write custom inference script and requirements to local folder
```
! mkdir inference_code
%%writefile inference_code/inference.py
# This is the script that will be used in the inference container
import os
import json
import torch
from transformers import AutoModelForSeq2SeqLM, AutoTokenizer
def model_fn(model_dir):
"""
Load the model and tokenizer for inference
"""
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
tokenizer = AutoTokenizer.from_pretrained(model_dir)
model = AutoModelForSeq2SeqLM.from_pretrained(model_dir).to(device)
model_dict = {'model':model, 'tokenizer':tokenizer}
return model_dict
def predict_fn(input_data, model):
"""
Make a prediction with the model
"""
text = input_data.pop('inputs')
parameters = input_data.pop('parameters', None)
tokenizer = model['tokenizer']
model = model['model']
# Parameters may or may not be passed
input_ids = tokenizer(text, truncation=True, padding='longest', return_tensors="pt").input_ids
output = model.generate(input_ids, **parameters) if parameters is not None else model.generate(input_ids)
return tokenizer.batch_decode(output, skip_special_tokens=True)[0]
def input_fn(request_body, request_content_type):
"""
Transform the input request to a dictionary
"""
request = json.loads(request_body)
return request
def output_fn(prediction, response_content_type):
"""
Return model's prediction
"""
return {'generated_text':prediction}
%%writefile inference_code/requirements.txt
transformers
sentencepiece
protobuf
```
# Deploy an endpoint with PyTorchModel
Once you .deploy(), this will upload your model package to S3, create a model in SageMaker, create an endpoint configuration, and deploy an endpoint from that configuration.
```
! pip install -U sagemaker
import sagemaker
session = sagemaker.Session()
session_bucket = session.default_bucket()
role = sagemaker.get_execution_role()
pytorch_version = '1.7.1'
python_version = 'py36'
from sagemaker.huggingface import HuggingFaceModel
model_name = 'summarization-model'
endpoint_name = 'summarization-endpoint'
model_for_deployment = HuggingFaceModel(entry_point='inference.py',
source_dir='inference_code',
model_data=huggingface_estimator.model_data,
# model_data=f'{session_bucket}/{<insert_model_location_key>}/model.tar.gz', in case you don't run this notebook using the initialized huggingface_estimator from 2_finetune.ipynb
role=role,
pytorch_version=pytorch_version,
py_version=python_version,
transformers_version='4.6.1',
name=model_name)
from sagemaker.serializers import JSONSerializer
from sagemaker.deserializers import BytesDeserializer
# Deploy the model
predictor = model_for_deployment.deploy(initial_instance_count=1,
instance_type='ml.m5.xlarge',
endpoint_name=endpoint_name
)
text = ('PG&E stated it scheduled the blackouts in response to forecasts for high winds amid dry conditions.'
' The aim is to reduce the risk of wildfires.'
'Nearly 800 thousand customers were scheduled to be affected by the shutoffs which were expected to last through at least midday tomorrow.'
)
summary_short = predictor.predict({
'inputs':text,
'parameters':{
'length_penalty':0.6
}
})
print(summary_short)
summary_long = predictor.predict({
'inputs':text,
'parameters':{
'length_penalty':1.5
}
})
print(summary_long)
```
# (Optional) If you haven't fine-tuned a model, but want to deploy directly from HuggingFace Hub to experiment
```
# We will pass these as env variables, defining the model and task we want
hub = {
'HF_MODEL_ID':'google/pegasus-xsum',
'HF_TASK':'summarization'
}
hub_model = HuggingFaceModel(env=hub,
role=role,
pytorch_version='1.7',
py_version='py36',
transformers_version='4.6',
name='hub-model')
hub_predictor = hub_model.deploy(initial_instance_count=1,
instance_type='ml.m5.xlarge',
endpoint_name='hub-endpoint')
# You can also pass in a 'parameters' key with valid parameters, just like we did before
summary = hub_predictor.predict({'inputs':text})
print(summary)
```
# Clean up
Use this code to delete the resources created in SageMaker Inference (endpoint configuration, endpoint and model).
```
predictor.delete_endpoint()
predictor.delete_model()
```
|
github_jupyter
|
# Ejercicio: Spectral clustering para documentos
El clustering espectral es una técnica de agrupamiento basada en la topología de gráficas. Es especialmente útil cuando los datos no son convexos o cuando se trabaja, directamente, con estructuras de grafos.
##Preparación d elos documentos
Trabajaremos con documentos textuales. Estos se limpiarán y se convertirán en vectores. Posteriormente, podremos aplicar el método de spectral clustering.
```
#Se importan las librerías necesarias
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
```
La librería de Natural Language Toolkit (nltk) proporciona algunos corpus con los que se puede trabajar. Por ejemplo, el cropus Gutenberg (https://web.eecs.umich.edu/~lahiri/gutenberg_dataset.html) del que usaremos algunos datos. Asimismo, obtendremos de esta librería herramientas de preprocesamiento: stemmer y lista de stopwords.
```
import nltk
#Descarga del corpus
nltk.download('gutenberg')
#Descarga de la lista de stopwords
nltk.download('stopwords')
from nltk.corpus import gutenberg
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
```
Definimos los nombres de los archivos (ids) y la lista de paro
```
#Obtiene ids de los archivos del corpus gutenberg
doc_labels = gutenberg.fileids()
#Lista de stopwords para inglés
lista_paro = stopwords.words('english')
```
Definiremos una función que se encargará de preprocesar los textos. Se eliminan símbolos, se quitan elementos de la lista de stopwords y se pasa todo a minúsculas.
```
def preprocess(document):
#Lista que guarda archivos limpios
text = []
for word in document:
#Minúsculas
word = word.lower()
#Elimina stopwords y símbolos
if word not in lista_paro and word.isalpha() == True:
#Se aplica stemming
text.append(PorterStemmer().stem(word))
return text
```
Por cada documento, obtenemos la lista de sus palabras (stems) aplicando un preprocesado. Cada documento, entonces, es de la forma $d_i = \{w_1, w_2, ..., w_{N_i}\}$, donde $w_k$ son los stems del documento.
```
docs = []
for doc in doc_labels:
#Lista de palabras del documentos
arx = gutenberg.words(doc)
#Aplica la función de preprocesado
arx_prep = preprocess(arx)
docs.append(arx_prep)
#Imprime el nombre del documento, su longitud original y su longitud con preproceso
print(doc,len(arx), len(arx_prep))
```
Posteriormente, convertiremos cada documento en un vector en $\mathbb{R}^d$. Para esto, utilizaremos el algoritmo Doc2Vec.
```
#Dimensión de los vectores
dim = 300
#tamaño de la ventana de contexto
windows_siz = 15
#Indexa los documentos con valores enteros
documents = [TaggedDocument(doc_i, [i]) for i, doc_i in enumerate(docs)]
#Aplica el modelo de Doc2Vec
model = Doc2Vec(documents, vector_size=dim, window=windows_siz, min_count=1)
#Matriz de datos
X = np.zeros((len(doc_labels),dim))
for j in range(0,len(doc_labels)):
#Crea la matriz con los vectores de Doc2Vec
X[j] = model.docvecs[j]
print(X)
```
###Visualización
```
#Función para plotear
def plot_words(Z,ids,color='blue'):
#Reduce a dos dimensiones con PCA
Z = PCA(n_components=2).fit_transform(Z)
r=0
#Plotea las dimensiones
plt.scatter(Z[:,0],Z[:,1], marker='o', c=color)
for label,x,y in zip(ids, Z[:,0], Z[:,1]):
#Agrega las etiquetas
plt.annotate(label, xy=(x,y), xytext=(-1,1), textcoords='offset points', ha='center', va='bottom')
r+=1
plot_words(X, doc_labels)
plt.show()
```
##Aplicación de spectral clustering
Ahora se debe aplicar el algoritmo de spectral clustering a estos datos. Como hemos visto, se debe tomar en cuenta diferentes criterios:
* La función graph kernel se va utilizar
* El método de selección de vecinos (fully connected, k-nn)
* El número de dimensiones que queremos obtener
* El número de clusters en k-means
Pruebe con estos parámetros para obtener un buen agrupamiento de los documentos elegidos.
|
github_jupyter
|
```
# Copyright 2020 IITK EE604A Image Processing. All Rights Reserved.
#
# Licensed under the MIT License. Use and/or modification of this code outside of EE604 must reference:
#
# © IITK EE604A Image Processing
# https://github.com/ee604/ee604_assignments
#
# Author: Shashi Kant Gupta, Chiranjeev Prachand and Prof K. S. Venkatesh, Department of Electrical Engineering, IIT Kanpur
```
# Task 2: Image Enhancement II: Spatial Smoothing
In this task, we will implement average, gaussian, and median spatial filter.
```
%%bash
pip install git+https://github.com/ee604/ee604_plugins
# Importing required libraries
import cv2
import numpy as np
import matplotlib.pyplot as plt
from ee604_plugins import download_dataset, cv2_imshow
download_dataset(assignment_no=2, task_no=2) # download data for this assignment
def avgFilter(img, kernel_size=7):
'''
Write a program to implement average filter. You have to assume square kernels.
Inputs:
+ img - grayscaled image of size N x N
- values between [0, 255] - 'uint8'
+ kernel_size - size of the kernel window which should be used for averaging.
Ouputs:
+ out_img - smoothed grayscaled image of size N x N
- values between [0, 255] - 'uint8'
Allowed modules:
+ Basic numpy operations
+ cv2.filter2D() to perform 2D convolution
Hint:
+ Not needed.
'''
#############################
# Start your code from here #
#############################
# Replace with your code...
#############################
# End your code here ########
#############################
return out_img
def gaussianFilter(img, kernel_size=7, sigma=3):
'''
Write a program to implement gaussian filter. You have to assume square kernels.
Inputs:
+ img - grayscaled image of size N x N
- values between [0, 255] - 'uint8'
+ kernel_size - size of the kernel window which should be used for smoothing.
+ sigma - sigma parameter for gaussian kernel
Ouputs:
+ out_img - smoothed grayscaled image of size N x N
- values between [0, 255] - 'uint8'
Allowed modules:
+ Basic numpy operations
+ cv2.filter2D() to perform 2D convolution
+ cv2.getGaussianKernel(). Note that this will give you 1D gaussian.
Hint:
+ Not needed.
'''
#############################
# Start your code from here #
#############################
# Replace with your code...
#############################
# End your code here ########
#############################
return out_img
def medianFilter(img, kernel_size=7):
'''
Write a program to implement median filter. You have to assume square kernels.
Inputs:
+ img - grayscaled image of size N x N
- values between [0, 255] - 'uint8'
+ kernel_size - size of the kernel window which should be used for smoothing.
Ouputs:
+ out_img - smoothed grayscaled image of size N x N
- values between [0, 255] - 'uint8'
Allowed modules:
+ Basic numpy operations
+ np.median()
Hint:
+ Not needed.
'''
#############################
# Start your code from here #
#############################
# Replace with your code...
#############################
# End your code here ########
#############################
return out_img
```
### Test
---
Your observation should compare the different methods for different images. Must include a sentence on which method + kernel size worked best in each case.
```
# Do not change codes inside this cell
# Add your observations in next to next cell
# Your observation should compare the different methods for different images
lena_orig = cv2.imread('data/lena_gray.jpg', 0)
lena_noisy_1 = cv2.imread('data/lena_noisy_1.jpg', 0)
lena_noisy_2 = cv2.imread('data/lena_noisy_2.jpg', 0)
lena_noisy_3 = cv2.imread('data/lena_noisy_3.jpg', 0)
def plot_frame(gridx, gridy, subplot_id, img, name):
plt.subplot(gridx, gridy, 1 + int(subplot_id))
plt.imshow(np.uint8(img), cmap="gray", vmin=0, vmax=255)
plt.axis("off")
plt.title(name)
# Do not change codes inside this cell
# Add your observations in next cell
img_arr = [lena_noisy_1, lena_noisy_2, lena_noisy_3]
img_caption = ["Noisy 1", "Noisy 2", "Noisy 3"]
for i in range(3):
for kernel_size in [5, 7, 9]:
print("\n-------------------------------------")
print("# Lena", img_caption[i], "| kernel:", kernel_size, "x", kernel_size)
print("-------------------------------------")
plt.figure(figsize=(20, 13))
plot_frame(1, 5, 0, lena_orig, "Original")
plot_frame(1, 5, 1, img_arr[i], "Noisy")
tmp_img = avgFilter(np.copy(img_arr[i]), kernel_size=kernel_size)
plot_frame(1, 5, 2, tmp_img, "Avg.")
tmp_img = gaussianFilter(np.copy(img_arr[i]), kernel_size=kernel_size, sigma=int(kernel_size/5))
plot_frame(1, 5, 3, tmp_img, "Gaussian.")
tmp_img = medianFilter(np.copy(img_arr[i]), kernel_size=kernel_size)
plot_frame(1, 5, 4, tmp_img, "Median.")
plt.show()
your_observation = """
Replace this with your observations.
"""
print(your_observation)
# Submission >>>>>>>>>>>>>>>>>>>>>
# Do not change codes inside this cell.
gen_imgs = []
img_arr = [lena_noisy_1, lena_noisy_2, lena_noisy_3]
for i in range(3):
for kernel_size in [5, 7, 9]:
tmp_img = avgFilter(np.copy(img_arr[i]), kernel_size=kernel_size)
gen_imgs.append(tmp_img)
tmp_img = gaussianFilter(np.copy(img_arr[i]), kernel_size=kernel_size, sigma=int(kernel_size/5))
gen_imgs.append(tmp_img)
tmp_img = medianFilter(np.copy(img_arr[i]), kernel_size=kernel_size)
gen_imgs.append(tmp_img)
task2_submission = np.array(gen_imgs)
```
|
github_jupyter
|
```
# super comms script
import serial
from time import sleep
import math
from tqdm import *
import json
def set_target(motor, location, ser, output=True):
if ser.is_open:
if motor =='A':
ser.write(b'A')
else:
ser.write(b'B')
target_bytes = location.to_bytes(4, byteorder='big')
#print(target_bytes)
ser.write(target_bytes)
sleep(0.02)
while(ser.in_waiting > 0):
b = ser.read()
if output:
print(b.decode('ascii'), end='')
else:
raise Exception("Serial is not open!")
def get_debug(ser):
if ser.is_open:
ser.write(b'D')
sleep(0.02)
while(ser.in_waiting > 0):
b = ser.read()
print(b.decode('ascii'), end='')
print("---")
else:
raise Exception("Serial is not open!")
def gogogo(ser, wait=False, output=True):
if ser.is_open:
ser.write(b'G')
sleep(0.02)
if output:
print("--- Making a move ---")
if wait:
end_found = False
while not end_found:
sleep(0.002)
while(ser.in_waiting > 0):
b = ser.readline().decode('ascii')
if output:
print(b)
if "move-end" in b:
end_found = True
else:
while(ser.in_waiting > 0):
b = ser.read()
print(b.decode('ascii'), end='')
else:
raise Exception("Serial is not open!")
def stop(ser):
if ser.is_open:
ser.write(b'S')
sleep(0.1)
while(ser.in_waiting > 0):
b = ser.read()
print(b.decode('ascii'), end='')
print("---")
else:
raise Exception("Serial is not open!")
def penup(ser):
if ser.is_open:
ser.write(b'C')
sleep(0.1)
while(ser.in_waiting > 0):
b = ser.read()
#print(b.decode('ascii'), end='')
#print("---")
else:
raise Exception("Serial is not open!")
def pendown(ser):
if ser.is_open:
ser.write(b'X')
sleep(0.1)
while(ser.in_waiting > 0):
b = ser.read()
#print(b.decode('ascii'), end='')
#print("---")
else:
raise Exception("Serial is not open!")
def reset(ser, output=True):
if ser.is_open:
ser.write(b'R')
sleep(0.5)
while(ser.in_waiting > 0):
b = ser.read()
if output:
print(b.decode('ascii'), end='')
else:
raise Exception("Serial is not open!")
ser = serial.Serial('/dev/cu.usbserial-141240', baudrate=115200) # open serial port
print(ser.name) # check which port was really used
get_debug(ser)
# Start with thing at home position!
#reset(ser)
target_coord = (300,200)
reset_point = (800,800)
target_lengths = translate_xy_to_ab(target_coord)
travel_lengths = (reset_point[0] - target_lengths[0], reset_point[1] - target_lengths[1])
a_step_mm = 10000/125
b_step_mm = 10000/125
travel_steps = (int(travel_lengths[0] * a_step_mm), int(travel_lengths[1] * b_step_mm))
set_target("A", travel_steps[0], ser, output=True)
set_target("B", travel_steps[1], ser, output=True)
gogogo(ser, wait=True)
set_target("A", 0, ser, output=True)
set_target("B", 0, ser, output=True)
#set_target("A", 132, ser, output=True)
#set_target("B", 9121, ser, output=True)
gogogo(ser, wait=True)
gogogo(ser, wait=True)
abpath = [
(5000,5000),
(10000,10000),
(0, 10000),
(1000, 0)
]
counter = 0
for coord in abpath:
counter += 1
print("Step %s of %s (%s)" % (counter, len(abpath), 100*counter/len(abpath)))
set_target('A', coord[0], ser, output=False)
set_target('B', coord[1], ser, output=False)
gogogo(ser, wait=True, output=False)
ser.close()
reset(ser)
def translate_xy_to_ab(coord):
x = coord[0]
y = coord[1]
a_len = math.sqrt(x**2 + y**2)
b_len = math.sqrt((MAX_WIDTH-x)**2 + y**2)
return [a_len, b_len]
def translate_ab_to_xy(lengths):
a = lengths[0]
b = lengths[1]
# Cosine rule!
#cos(left) = (a**2 + MAX_WIDTH**2 - b**2) / (2 * a * MAX_WIDTH)
try:
left_angle = math.acos((a**2 + MAX_WIDTH**2 - b**2) / (2 * a * MAX_WIDTH))
except Exception as e:
# This specifically happens if the values just arn't a triangle!
# i.e. consider maxwidth = 100, left length = 10, right = 10... one of
# the wires must have broken!
print("Not a triangle!")
print((a**2 + MAX_WIDTH**2 - b**2) / (2 * a * MAX_WIDTH))
raise e
#print(left_angle) # in radians, remember.
# sin(left) = opp / hyp
# cos(right) = adj / hyp
# hyp is 'a'
# Lack of precision here - chop to mm. Rounding 'down'
y = int(math.sin(left_angle) * a)
x = int(math.cos(left_angle) * a)
return [x,y]
# Math time
MAX_WIDTH = 970
a_scale = 10000/130
b_scale = 10000/125
# 0,0 is furthest, then up is less (?)
real_start_mm = (800,800)
orig_length = (real_start_mm[0] * a_scale, real_start_mm[1] * b_scale)
print(orig_length)
xy_path = [
(500, 390),
#(500,500),
#(600,400),
'HOME'
]
ab_path = []
for coord in xy_path:
if coord=='HOME':
movement = (0,0)
else:
short_ab_mm = translate_xy_to_ab(coord)
#print(short_ab_mm)
short_ab_steps = (short_ab_mm[0] * a_scale, short_ab_mm[1] * b_scale)
#print(short_ab_steps)
movement = (int(orig_length[0] - short_ab_steps[0]),int( orig_length[1] - short_ab_steps[1]))
print("Going -> %s" % (movement,))
ab_path.append(movement)
ser = serial.Serial('/dev/cu.usbserial-141210', baudrate=115200) # open serial port
print(ser.name)
reset(ser)
get_debug(ser)
counter = 0
for coord in ab_path:
counter += 1
print("Step %s of %s (%s)" % (counter, len(ab_path), 100*counter/len(ab_path)))
set_target('A', coord[0], ser, output=False)
set_target('B', coord[1], ser, output=False)
gogogo(ser, wait=True, output=False)
ser.close()
with open("spiro.json") as fp:
paths = json.load(fp)
MAX_WIDTH = 970
offset_x = 300
offset_y = 50
scale_x = 1.5
scale_y = 2
path_counter = 0
a_scale = 10000/130
b_scale = 10000/130
paths.append(('HOME',))
# 0,0 is furthest, then up is less (?)
real_start_mm = (800,800)
orig_length = (real_start_mm[0] * a_scale, real_start_mm[1] * b_scale)
reset(ser)
penup(ser)
for xy_path in tqdm(paths):
if len(xy_path) == 0:
continue
print("path %s (%s)" % (path_counter, 100*path_counter/len(paths)))
path_counter += 1
ab_path = []
for coord in tqdm(xy_path):
if coord=='HOME':
movement = (0,0)
else:
coord = (offset_x + coord[0]*scale_x, offset_y + coord[1]*scale_y)
short_ab_mm = translate_xy_to_ab(coord)
#print(short_ab_mm)
short_ab_steps = (short_ab_mm[0] * a_scale, short_ab_mm[1] * b_scale)
#print(short_ab_steps)
movement = (int(orig_length[0] - short_ab_steps[0]),int( orig_length[1] - short_ab_steps[1]))
if movement[0] < 0 or movement[1] < 0:
print("%s -> %s" % (coord, movement))
raise Exception("out of bounds")
#print("Going -> %s" % (movement,))
ab_path.append(movement)
#input("> PENUP !\r\n")
penup(ser)
set_target('A', ab_path[0][0], ser, output=False)
set_target('B', ab_path[0][1], ser, output=False)
gogogo(ser, wait=True, output=False)
pendown(ser)
counter = 0
for coord in tqdm(ab_path[1:]):
counter += 1
#print("Step %s of %s (%s)" % (counter, len(ab_path), 100*counter/len(ab_path)))
set_target('A', coord[0], ser, output=False)
set_target('B', coord[1], ser, output=False)
gogogo(ser, wait=True, output=False)
penup(ser)
#print(len(ab_path))
#print(int(offset_x + xy_path[0][0]*scale_x), int(offset_y + xy_path[0][1]*scale_y))
penup(ser)
set_target('A',1000, ser, output=False)
set_target('B',1000, ser, output=False)
gogogo(ser)
ser.close()
reset(ser)
def go_to_xy(target_coord,ser):
target_lengths = translate_xy_to_ab(target_coord)
travel_lengths = (reset_point[0] - target_lengths[0], reset_point[1] - target_lengths[1])
a_step_mm = 10000/125
b_step_mm = 10000/125
travel_steps = (int(travel_lengths[0] * a_step_mm), int(travel_lengths[1] * b_step_mm))
set_target("A", travel_steps[0], ser, output=True)
set_target("B", travel_steps[1], ser, output=True)
gogogo(ser, wait=True)
reset(ser)
path = [
(650, 400),
(300, 400),
(300, 150),
(650, 150),
(650, 400)
]
for point in path:
go_to_xy(point,ser)
pendown(ser)
```
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
_**Classification of credit card fraudulent transactions on remote compute **_
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Train](#Train)
1. [Results](#Results)
1. [Test](#Test)
1. [Acknowledgements](#Acknowledgements)
## Introduction
In this example we use the associated credit card dataset to showcase how you can use AutoML for a simple classification problem. The goal is to predict if a credit card transaction is considered a fraudulent charge.
This notebook is using remote compute to train the model.
If you are using an Azure Machine Learning Compute Instance, you are all set. Otherwise, go through the [configuration](../../../configuration.ipynb) notebook first if you haven't already to establish your connection to the AzureML Workspace.
In this notebook you will learn how to:
1. Create an experiment using an existing workspace.
2. Configure AutoML using `AutoMLConfig`.
3. Train the model using remote compute.
4. Explore the results.
5. Test the fitted model.
## Setup
As part of the setup you have already created an Azure ML `Workspace` object. For Automated ML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.
```
import logging
from matplotlib import pyplot as plt
import pandas as pd
import os
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.core.dataset import Dataset
from azureml.train.automl import AutoMLConfig
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.22.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
ws = Workspace.from_config()
# choose a name for experiment
experiment_name = 'automl-classification-ccard-remote'
experiment=Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Create or Attach existing AmlCompute
A compute target is required to execute the Automated ML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read [this article](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-manage-quotas) on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
cpu_cluster_name = "cpu-cluster-1"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=cpu_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_DS12_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, cpu_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
# Data
### Load Data
Load the credit card dataset from a csv file containing both training features and labels. The features are inputs to the model, while the training labels represent the expected output of the model. Next, we'll split the data using random_split and extract the training data for the model.
```
data = "https://automlsamplenotebookdata.blob.core.windows.net/automl-sample-notebook-data/creditcard.csv"
dataset = Dataset.Tabular.from_delimited_files(data)
training_data, validation_data = dataset.random_split(percentage=0.8, seed=223)
label_column_name = 'Class'
```
## Train
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|classification or regression|
|**primary_metric**|This is the metric that you want to optimize. Classification supports the following primary metrics: <br><i>accuracy</i><br><i>AUC_weighted</i><br><i>average_precision_score_weighted</i><br><i>norm_macro_recall</i><br><i>precision_score_weighted</i>|
|**enable_early_stopping**|Stop the run if the metric score is not showing improvement.|
|**n_cross_validations**|Number of cross validation splits.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
**_You can find more information about primary metrics_** [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-configure-auto-train#primary-metric)
```
automl_settings = {
"n_cross_validations": 3,
"primary_metric": 'average_precision_score_weighted',
"enable_early_stopping": True,
"max_concurrent_iterations": 2, # This is a limit for testing purpose, please increase it as per cluster size
"experiment_timeout_hours": 0.25, # This is a time limit for testing purposes, remove it for real use cases, this will drastically limit ablity to find the best model possible
"verbosity": logging.INFO,
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
compute_target = compute_target,
training_data = training_data,
label_column_name = label_column_name,
**automl_settings
)
```
Call the `submit` method on the experiment object and pass the run configuration. Depending on the data and the number of iterations this can run for a while. Validation errors and current status will be shown when setting `show_output=True` and the execution will be synchronous.
```
remote_run = experiment.submit(automl_config, show_output = False)
# If you need to retrieve a run that already started, use the following code
#from azureml.train.automl.run import AutoMLRun
#remote_run = AutoMLRun(experiment = experiment, run_id = '<replace with your run id>')
remote_run
```
## Results
#### Widget for Monitoring Runs
The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
**Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details
```
from azureml.widgets import RunDetails
RunDetails(remote_run).show()
remote_run.wait_for_completion(show_output=False)
```
#### Explain model
Automated ML models can be explained and visualized using the SDK Explainability library.
## Analyze results
### Retrieve the Best Model
Below we select the best pipeline from our iterations. The `get_output` method returns the best run and the fitted model. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
```
best_run, fitted_model = remote_run.get_output()
fitted_model
```
#### Print the properties of the model
The fitted_model is a python object and you can read the different properties of the object.
## Test the fitted model
Now that the model is trained, split the data in the same way the data was split for training (The difference here is the data is being split locally) and then run the test data through the trained model to get the predicted values.
```
# convert the test data to dataframe
X_test_df = validation_data.drop_columns(columns=[label_column_name]).to_pandas_dataframe()
y_test_df = validation_data.keep_columns(columns=[label_column_name], validate=True).to_pandas_dataframe()
# call the predict functions on the model
y_pred = fitted_model.predict(X_test_df)
y_pred
```
### Calculate metrics for the prediction
Now visualize the data on a scatter plot to show what our truth (actual) values are compared to the predicted values
from the trained model that was returned.
```
from sklearn.metrics import confusion_matrix
import numpy as np
import itertools
cf =confusion_matrix(y_test_df.values,y_pred)
plt.imshow(cf,cmap=plt.cm.Blues,interpolation='nearest')
plt.colorbar()
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
class_labels = ['False','True']
tick_marks = np.arange(len(class_labels))
plt.xticks(tick_marks,class_labels)
plt.yticks([-0.5,0,1,1.5],['','False','True',''])
# plotting text value inside cells
thresh = cf.max() / 2.
for i,j in itertools.product(range(cf.shape[0]),range(cf.shape[1])):
plt.text(j,i,format(cf[i,j],'d'),horizontalalignment='center',color='white' if cf[i,j] >thresh else 'black')
plt.show()
```
## Acknowledgements
This Credit Card fraud Detection dataset is made available under the Open Database License: http://opendatacommons.org/licenses/odbl/1.0/. Any rights in individual contents of the database are licensed under the Database Contents License: http://opendatacommons.org/licenses/dbcl/1.0/ and is available at: https://www.kaggle.com/mlg-ulb/creditcardfraud
The dataset has been collected and analysed during a research collaboration of Worldline and the Machine Learning Group (http://mlg.ulb.ac.be) of ULB (Université Libre de Bruxelles) on big data mining and fraud detection.
More details on current and past projects on related topics are available on https://www.researchgate.net/project/Fraud-detection-5 and the page of the DefeatFraud project
Please cite the following works:
Andrea Dal Pozzolo, Olivier Caelen, Reid A. Johnson and Gianluca Bontempi. Calibrating Probability with Undersampling for Unbalanced Classification. In Symposium on Computational Intelligence and Data Mining (CIDM), IEEE, 2015
Dal Pozzolo, Andrea; Caelen, Olivier; Le Borgne, Yann-Ael; Waterschoot, Serge; Bontempi, Gianluca. Learned lessons in credit card fraud detection from a practitioner perspective, Expert systems with applications,41,10,4915-4928,2014, Pergamon
Dal Pozzolo, Andrea; Boracchi, Giacomo; Caelen, Olivier; Alippi, Cesare; Bontempi, Gianluca. Credit card fraud detection: a realistic modeling and a novel learning strategy, IEEE transactions on neural networks and learning systems,29,8,3784-3797,2018,IEEE
Dal Pozzolo, Andrea Adaptive Machine learning for credit card fraud detection ULB MLG PhD thesis (supervised by G. Bontempi)
Carcillo, Fabrizio; Dal Pozzolo, Andrea; Le Borgne, Yann-Aël; Caelen, Olivier; Mazzer, Yannis; Bontempi, Gianluca. Scarff: a scalable framework for streaming credit card fraud detection with Spark, Information fusion,41, 182-194,2018,Elsevier
Carcillo, Fabrizio; Le Borgne, Yann-Aël; Caelen, Olivier; Bontempi, Gianluca. Streaming active learning strategies for real-life credit card fraud detection: assessment and visualization, International Journal of Data Science and Analytics, 5,4,285-300,2018,Springer International Publishing
Bertrand Lebichot, Yann-Aël Le Borgne, Liyun He, Frederic Oblé, Gianluca Bontempi Deep-Learning Domain Adaptation Techniques for Credit Cards Fraud Detection, INNSBDDL 2019: Recent Advances in Big Data and Deep Learning, pp 78-88, 2019
Fabrizio Carcillo, Yann-Aël Le Borgne, Olivier Caelen, Frederic Oblé, Gianluca Bontempi Combining Unsupervised and Supervised Learning in Credit Card Fraud Detection Information Sciences, 2019
|
github_jupyter
|
```
import json
import os
from pprint import *
from tqdm import *
from utils.definitions import ROOT_DIR
path_load = "mpd.v1/data/" #json folder
path_save = ROOT_DIR + "/data/original/" #where to save csv
playlist_fields = ['pid','name', 'collaborative', 'modified_at', 'num_albums', 'num_tracks', 'num_followers',
'num_tracks', 'num_edits', 'duration_ms', 'num_artists','description']
### care, the description field is optional
track_fields = ['tid', 'arid' , 'alid', 'track_uri', 'track_name', 'duration_ms']
album_fields = ['alid','album_uri','album_name']
artist_fields = ['arid','artist_uri','artist_name']
interaction_fields = ['pid','tid','pos']
interactions = []
playlists = []
tracks = []
artists = []
albums = []
count_files = 0
count_playlists = 0
count_interactions = 0
count_tracks = 0
count_artists = 0
count_albums = 0
dict_tracks = {}
dict_artists = {}
dict_albums = {}
def process_mpd(path):
global count_playlists
global count_files
filenames = os.listdir(path)
for filename in tqdm(sorted(filenames)):
if filename.startswith("mpd.slice.") and filename.endswith(".json"):
fullpath = os.sep.join((path, filename))
f = open(fullpath)
js = f.read()
f.close()
mpd_slice = json.loads(js)
process_info(mpd_slice['info'])
for playlist in mpd_slice['playlists']:
process_playlist(playlist)
pid = playlist['pid']
for track in playlist['tracks']:
track['pid']=pid
new = add_id_artist(track)
if new: process_artist(track)
new = add_id_album(track)
if new: process_album(track)
new = add_id_track(track)
if new: process_track(track)
process_interaction(track)
count_playlists += 1
count_files +=1
show_summary()
def process_info(value):
#print (json.dumps(value, indent=3, sort_keys=False))
pass
def add_id_track(track):
global count_tracks
if track['track_uri'] not in dict_tracks:
dict_tracks[track['track_uri']] = count_tracks
track['tid'] = count_tracks
count_tracks += 1
return True
else:
track['tid'] = dict_tracks[track['track_uri']]
return False
def add_id_artist(track):
global count_artists
if track['artist_uri'] not in dict_artists:
dict_artists[track['artist_uri']] = count_artists
track['arid'] = count_artists
count_artists += 1
return True
else:
track['arid'] = dict_artists[track['artist_uri']]
return False
def add_id_album(track):
global count_albums
if track['album_uri'] not in dict_albums:
dict_albums[track['album_uri']] = count_albums
track['alid'] = count_albums
count_albums += 1
return True
else:
track['alid'] = dict_albums[track['album_uri']]
return False
def process_track(track):
global track_fields
info = []
for field in track_fields:
info.append(track[field])
tracks.append(info)
def process_album(track):
global album_fields
info = []
for field in album_fields:
info.append(track[field])
albums.append(info)
def process_artist(track):
global artist_fields
info = []
for field in artist_fields:
info.append(track[field])
artists.append(info)
def process_interaction(track):
global interaction_fields
global count_interactions
info = []
for field in interaction_fields:
info.append(track[field])
interactions.append(info)
count_interactions +=1
def process_playlist(playlist):
global playlist_fields
if not 'description' in playlist:
playlist['description'] = None
info = []
for field in playlist_fields:
info.append(playlist[field])
playlists.append(info)
def show_summary():
print (count_files)
print (count_playlists)
print (count_tracks)
print (count_artists)
print (count_albums)
print (count_interactions)
process_mpd(path_load)
import csv
with open(path_save+"artists.csv", "w") as f:
writer = csv.writer(f,delimiter = "\t",)
writer.writerow(artist_fields)
writer.writerows(artists)
print ("artists.csv done")
with open(path_save+"albums.csv", "w") as f:
writer = csv.writer(f,delimiter = "\t",)
writer.writerow(album_fields)
writer.writerows(albums)
print ("albums.csv done")
with open(path_save+"interactions.csv", "w") as f:
writer = csv.writer(f,delimiter = "\t",)
writer.writerow(interaction_fields)
writer.writerows(interactions)
print ("interactions.csv done")
with open(path_save+"tracks.csv", "w") as f:
writer = csv.writer(f,delimiter = "\t",)
writer.writerow(track_fields)
writer.writerows(tracks)
print ("tracks.csv done")
with open(path_save+"playlists.csv", "w") as f:
writer = csv.writer(f,delimiter = "\t",)
writer.writerow(playlist_fields)
writer.writerows(playlists)
print ("playlists.csv done")
```
|
github_jupyter
|
# This Jupyter Notebook contains the full code needed to write the ColumnTransformer blog
## Import Necessary Packages
```
import pandas as pd
import numpy as np
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from pytz import timezone
```
## Import Data and some pre-transformation data prep
```
# read the csvs with waits and weather
df = pd.read_csv('./data/dec2019.csv')
weather_df = pd.read_csv('./data/dec2019weather.csv')
# rename the columns
df.columns = ['date_hour', 'wait_hrs']
# cut the date_hours to the hour (no minutes/seconds) and convert to string for merging
df['date_hour'] = pd.to_datetime(df['date_hour'], utc=True).values.astype('datetime64[h]')
df['date_hour'] = df['date_hour'].astype('str')
# create dataframe of all possible departure hours in the month (as string for merging)
# note that I chose to include non-ferry service hours at this stage
dts = pd.DataFrame(columns=['date_hour'])
dts['date_hour'] = pd.date_range(start='2019-12-01 00:00',
end='2019-12-31 23:30',
freq='H',
).astype('str')
# merge/join the waits to the dataframe of all departures
df_expanded = dts.merge(df, how='left', on='date_hour')
# cast as datetime with timezone UTC
df_expanded['date_hour'] = pd.to_datetime(df_expanded['date_hour'], utc=True)
# adjust time to PST
df_expanded['date_hour'] = [dt.astimezone(timezone('US/Pacific')) for dt in df_expanded['date_hour']]
# remove non-sailing times (1 to 4 am for Edmonds (1-3 for Kingston))
df_expanded = df_expanded.set_index('date_hour')
df_expanded = df_expanded.between_time('5:00', '00:59')
# reset index for modeling
df_expanded = df_expanded.reset_index()
weather_df.columns = ['date', 'max_temp', 'avg_temp', 'min_temp']
weather_df['date'] = pd.to_datetime(weather_df['date'])
df_expanded['date'] = pd.to_datetime(df_expanded['date_hour']).values.astype('datetime64[D]')
df_expanded = df_expanded.merge(weather_df, how='left', on='date')
df_expanded.head()
```
## Simple Column Transformer Example
```
# a little cheating to extract the day of the week
# and hour of the day w/out using a transformer
# (see below for the "real" version)
df_simple = df_expanded.copy()
df_simple['weekday'] = [dt.weekday() for dt in df_simple['date_hour']]
df_simple['hour'] = [dt.hour for dt in df_simple['date_hour']]
df_simple.head()
X = df_simple.drop(columns='wait_hrs')
y = df_simple['wait_hrs'].fillna(value=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=111)
# define column transformer and set n_jobs to have it run on all cores
col_transformer = ColumnTransformer(
transformers=[
('ss', StandardScaler(), ['max_temp', 'avg_temp', 'min_temp']),
('ohe', OneHotEncoder(), ['weekday', 'hour'])],
remainder='drop',
n_jobs=-1
)
X_train_transformed = col_transformer.fit_transform(X_train)
X_train_transformed
lr = LinearRegression()
pipe = Pipeline([
("preprocessing", col_transformer),
("lr", lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
preds_train[0:5]
preds_test[0:5]
col_transformer.get_feature_names
col_transformer.named_transformers_['ohe'].get_feature_names()
for transformer in col_transformer.named_transformers_.values():
try:
transformer.get_feature_names()
except:
print('SS col')
else:
print(transformer.get_feature_names())
```
## More complex column transformer example: imputing THEN standard scale/ohe
```
# define transformers
si_0 = SimpleImputer(strategy='constant', fill_value=0)
ss = StandardScaler()
ohe = OneHotEncoder()
# define column groups with same processing
cat_vars = ['weekday', 'hour']
num_vars = ['max_temp', 'avg_temp', 'min_temp']
# set up pipelines for each column group
categorical_pipe = Pipeline([
('si_0', si_0),
('ohe', ohe)
])
numeric_pipe = Pipeline([
('si_0', si_0),
('ss', ss)
])
# set up columnTransformer
col_transformer = ColumnTransformer(
transformers=[
('nums', numeric_pipe, num_vars),
('cats', categorical_pipe, cat_vars)
],
remainder='drop',
n_jobs=-1
)
pipe = Pipeline([
("preprocessing", col_transformer),
("lr", lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
preds_train[0:10]
preds_test[0:10]
col_transformer.named_transformers_['cats'].named_steps['ohe'].get_feature_names()
```
## Create your own custom transformer
```
from sklearn.base import TransformerMixin, BaseEstimator
class DateTransformer(TransformerMixin, BaseEstimator):
"""Extracts features from datetime column
Returns:
hour: hour
day: Between 1 and the number of days in the given month of the given year.
month: Between 1 and 12 inclusive.
year: four-digit year
weekday:day of the week as an integer, where Monday is 0 and Sunday is 6
"""
def fit(self, x, y=None):
return self
def transform(self, x, y=None):
result = pd.DataFrame(x, columns=['date_hour'])
result['hour'] = [dt.hour for dt in result['date_hour']]
result['day'] = [dt.day for dt in result['date_hour']]
result['month'] = [dt.month for dt in result['date_hour']]
result['year'] = [dt.year for dt in result['date_hour']]
result['weekday'] = [dt.weekday() for dt in result['date_hour']]
return result[['hour', 'day', 'month', 'year', 'weekday']]
def get_feature_names(self):
return ['hour','day', 'month', 'year', 'weekday']
X = df_expanded.drop(columns='wait_hrs')
y = df_simple['wait_hrs'].fillna(value=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=111)
X.head()
time_preprocessing = Pipeline([
('date', DateTransformer()),
('ohe', OneHotEncoder(categories='auto'))
])
ct = ColumnTransformer(
transformers=[
('ss', StandardScaler(), ['max_temp', 'avg_temp', 'min_temp']),
('date_exp', time_preprocessing, ['date_hour'])],
remainder='drop',
)
pipe = Pipeline([('preprocessor', ct),
('lr', lr)])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
lr.coef_
ct.named_transformers_['date_exp'].named_steps['ohe'].get_feature_names()
ct.named_transformers_['date_exp'].named_steps['date'].get_feature_names()
```
## Rare features with ColumnTransformer
```
df = pd.DataFrame()
df['cat1'] = [0, 1, 1, 1, 1, 1, 1, 1, 1, 1]
df['cat2'] = [0, 0, 0, 0, 0, 2, 2, 2, 2, 2]
df['num1'] = [np.nan, 1, 1.1, .9, .8, np.nan, 2, 2.2, 1.5, np.nan]
df['num2'] = [1.1, 1.1, 1.1, 1.1, 1.1, 1.2, 1.2, 1.2, 1.2, 1.2]
target = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
X_train, X_test, y_train, y_test = train_test_split(df, target, random_state=111)
num_pipe = Pipeline([
('si', SimpleImputer(add_indicator=True)),
('ss', StandardScaler())
])
ct = ColumnTransformer(
transformers=[('ohe', OneHotEncoder(categories=[[0,1], [0,2]]), ['cat1', 'cat2']),
('numeric', num_pipe, ['num1', 'num2'])])
pipe = Pipeline([
('preprocessor', ct),
('lr', lr)
])
pipe.fit(X_train, y_train)
preds_train = pipe.predict(X_train)
preds_test = pipe.predict(X_test)
ct.fit_transform(X_train)
ct.fit_transform(X_test)
```
|
github_jupyter
|
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
# Python for Finance
**Analyze Big Financial Data**
O'Reilly (2014)
Yves Hilpisch
<img style="border:0px solid grey;" src="http://hilpisch.com/python_for_finance.png" alt="Python for Finance" width="30%" align="left" border="0">
**Buy the book ** |
<a href='http://shop.oreilly.com/product/0636920032441.do' target='_blank'>O'Reilly</a> |
<a href='http://www.amazon.com/Yves-Hilpisch/e/B00JCYHHJM' target='_blank'>Amazon</a>
**All book codes & IPYNBs** |
<a href="http://oreilly.quant-platform.com">http://oreilly.quant-platform.com</a>
**The Python Quants GmbH** | <a href='http://tpq.io' target='_blank'>http://tpq.io</a>
**Contact us** | <a href='mailto:[email protected]'>[email protected]</a>
# Input-Output Operations
```
from pylab import plt
plt.style.use('ggplot')
import matplotlib as mpl
mpl.rcParams['font.family'] = 'serif'
```
## Basic I/O with Python
### Writing Objects to Disk
```
path = './data/'
import numpy as np
from random import gauss
a = [gauss(1.5, 2) for i in range(1000000)]
# generation of normally distributed randoms
import pickle
pkl_file = open(path + 'data.pkl', 'wb')
# open file for writing
# Note: existing file might be overwritten
%time pickle.dump(a, pkl_file)
pkl_file
pkl_file.close()
ll $path*
pkl_file = open(path + 'data.pkl', 'rb') # open file for reading
%time b = pickle.load(pkl_file)
b[:5]
a[:5]
np.allclose(np.array(a), np.array(b))
np.sum(np.array(a) - np.array(b))
pkl_file = open(path + 'data.pkl', 'wb') # open file for writing
%time pickle.dump(np.array(a), pkl_file)
%time pickle.dump(np.array(a) ** 2, pkl_file)
pkl_file.close()
ll $path*
pkl_file = open(path + 'data.pkl', 'rb') # open file for reading
x = pickle.load(pkl_file)
x
y = pickle.load(pkl_file)
y
pkl_file.close()
pkl_file = open(path + 'data.pkl', 'wb') # open file for writing
pickle.dump({'x' : x, 'y' : y}, pkl_file)
pkl_file.close()
pkl_file = open(path + 'data.pkl', 'rb') # open file for writing
data = pickle.load(pkl_file)
pkl_file.close()
for key in data.keys():
print(key, data[key][:4])
!rm -f $path*
```
### Reading and Writing Text Files
```
rows = 5000
a = np.random.standard_normal((rows, 5)) # dummy data
a.round(4)
import pandas as pd
t = pd.date_range(start='2014/1/1', periods=rows, freq='H')
# set of hourly datetime objects
t
csv_file = open(path + 'data.csv', 'w') # open file for writing
header = 'date,no1,no2,no3,no4,no5\n'
csv_file.write(header)
for t_, (no1, no2, no3, no4, no5) in zip(t, a):
s = '%s,%f,%f,%f,%f,%f\n' % (t_, no1, no2, no3, no4, no5)
csv_file.write(s)
csv_file.close()
ll $path*
csv_file = open(path + 'data.csv', 'r') # open file for reading
for i in range(5):
print(csv_file.readline(), end='')
csv_file = open(path + 'data.csv', 'r')
content = csv_file.readlines()
for line in content[:5]:
print(line, end='')
csv_file.close()
!rm -f $path*
```
### SQL Databases
```
import sqlite3 as sq3
query = 'CREATE TABLE numbs (Date date, No1 real, No2 real)'
con = sq3.connect(path + 'numbs.db')
con.execute(query)
con.commit()
import datetime as dt
con.execute('INSERT INTO numbs VALUES(?, ?, ?)',
(dt.datetime.now(), 0.12, 7.3))
data = np.random.standard_normal((10000, 2)).round(5)
for row in data:
con.execute('INSERT INTO numbs VALUES(?, ?, ?)',
(dt.datetime.now(), row[0], row[1]))
con.commit()
con.execute('SELECT * FROM numbs').fetchmany(10)
pointer = con.execute('SELECT * FROM numbs')
for i in range(3):
print(pointer.fetchone())
con.close()
!rm -f $path*
```
### Writing and Reading Numpy Arrays
```
import numpy as np
dtimes = np.arange('2015-01-01 10:00:00', '2021-12-31 22:00:00',
dtype='datetime64[m]') # minute intervals
len(dtimes)
dty = np.dtype([('Date', 'datetime64[m]'), ('No1', 'f'), ('No2', 'f')])
data = np.zeros(len(dtimes), dtype=dty)
data['Date'] = dtimes
a = np.random.standard_normal((len(dtimes), 2)).round(5)
data['No1'] = a[:, 0]
data['No2'] = a[:, 1]
%time np.save(path + 'array', data) # suffix .npy is added
ll $path*
%time np.load(path + 'array.npy')
data = np.random.standard_normal((10000, 6000))
%time np.save(path + 'array', data)
ll $path*
%time np.load(path + 'array.npy')
data = 0.0
!rm -f $path*
```
## I/O with pandas
```
import numpy as np
import pandas as pd
data = np.random.standard_normal((1000000, 5)).round(5)
# sample data set
filename = path + 'numbs'
```
### SQL Database
```
import sqlite3 as sq3
query = 'CREATE TABLE numbers (No1 real, No2 real,\
No3 real, No4 real, No5 real)'
con = sq3.Connection(filename + '.db')
con.execute(query)
%%time
con.executemany('INSERT INTO numbers VALUES (?, ?, ?, ?, ?)', data)
con.commit()
ll $path*
%%time
temp = con.execute('SELECT * FROM numbers').fetchall()
print(temp[:2])
temp = 0.0
%%time
query = 'SELECT * FROM numbers WHERE No1 > 0 AND No2 < 0'
res = np.array(con.execute(query).fetchall()).round(3)
res = res[::100] # every 100th result
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(res[:, 0], res[:, 1], 'ro')
plt.grid(True); plt.xlim(-0.5, 4.5); plt.ylim(-4.5, 0.5)
# tag: scatter_query
# title: Plot of the query result
# size: 60
```
### From SQL to pandas
```
import pandas.io.sql as pds
%time data = pds.read_sql('SELECT * FROM numbers', con)
data.head()
%time data[(data['No1'] > 0) & (data['No2'] < 0)].head()
%%time
res = data[['No1', 'No2']][((data['No1'] > 0.5) | (data['No1'] < -0.5))
& ((data['No2'] < -1) | (data['No2'] > 1))]
plt.plot(res.No1, res.No2, 'ro')
plt.grid(True); plt.axis('tight')
# tag: data_scatter_1
# title: Scatter plot of complex query results
# size: 55
h5s = pd.HDFStore(filename + '.h5s', 'w')
%time h5s['data'] = data
h5s
h5s.close()
%%time
h5s = pd.HDFStore(filename + '.h5s', 'r')
temp = h5s['data']
h5s.close()
np.allclose(np.array(temp), np.array(data))
temp = 0.0
ll $path*
```
### Data as CSV File
```
%time data.to_csv(filename + '.csv')
ls data/
%%time
pd.read_csv(filename + '.csv')[['No1', 'No2',
'No3', 'No4']].hist(bins=20)
# tag: data_hist_3
# title: Histogram of 4 data sets
# size: 60
```
### Data as Excel File
```
%time data[:100000].to_excel(filename + '.xlsx')
%time pd.read_excel(filename + '.xlsx', 'Sheet1').cumsum().plot()
# tag: data_paths
# title: Paths of random data from Excel file
# size: 60
ll $path*
rm -f $path*
```
## Fast I/O with PyTables
```
import numpy as np
import tables as tb
import datetime as dt
import matplotlib.pyplot as plt
%matplotlib inline
```
### Working with Tables
```
filename = path + 'tab.h5'
h5 = tb.open_file(filename, 'w')
rows = 2000000
row_des = {
'Date': tb.StringCol(26, pos=1),
'No1': tb.IntCol(pos=2),
'No2': tb.IntCol(pos=3),
'No3': tb.Float64Col(pos=4),
'No4': tb.Float64Col(pos=5)
}
filters = tb.Filters(complevel=0) # no compression
tab = h5.create_table('/', 'ints_floats', row_des,
title='Integers and Floats',
expectedrows=rows, filters=filters)
tab
pointer = tab.row
ran_int = np.random.randint(0, 10000, size=(rows, 2))
ran_flo = np.random.standard_normal((rows, 2)).round(5)
%%time
for i in range(rows):
pointer['Date'] = dt.datetime.now()
pointer['No1'] = ran_int[i, 0]
pointer['No2'] = ran_int[i, 1]
pointer['No3'] = ran_flo[i, 0]
pointer['No4'] = ran_flo[i, 1]
pointer.append()
# this appends the data and
# moves the pointer one row forward
tab.flush()
tab
ll $path*
dty = np.dtype([('Date', 'S26'), ('No1', '<i4'), ('No2', '<i4'),
('No3', '<f8'), ('No4', '<f8')])
sarray = np.zeros(len(ran_int), dtype=dty)
sarray
%%time
sarray['Date'] = dt.datetime.now()
sarray['No1'] = ran_int[:, 0]
sarray['No2'] = ran_int[:, 1]
sarray['No3'] = ran_flo[:, 0]
sarray['No4'] = ran_flo[:, 1]
%%time
h5.create_table('/', 'ints_floats_from_array', sarray,
title='Integers and Floats',
expectedrows=rows, filters=filters)
h5
h5.remove_node('/', 'ints_floats_from_array')
tab[:3]
tab[:4]['No4']
%time np.sum(tab[:]['No3'])
%time np.sum(np.sqrt(tab[:]['No1']))
%%time
plt.hist(tab[:]['No3'], bins=30)
plt.grid(True)
print(len(tab[:]['No3']))
# tag: data_hist
# title: Histogram of data
# size: 60
%%time
res = np.array([(row['No3'], row['No4']) for row in
tab.where('((No3 < -0.5) | (No3 > 0.5)) \
& ((No4 < -1) | (No4 > 1))')])[::100]
plt.plot(res.T[0], res.T[1], 'ro')
plt.grid(True)
# tag: scatter_data
# title: Scatter plot of query result
# size: 70
%%time
values = tab.cols.No3[:]
print("Max %18.3f" % values.max())
print("Ave %18.3f" % values.mean())
print("Min %18.3f" % values.min())
print("Std %18.3f" % values.std())
%%time
results = [(row['No1'], row['No2']) for row in
tab.where('((No1 > 9800) | (No1 < 200)) \
& ((No2 > 4500) & (No2 < 5500))')]
for res in results[:4]:
print(res)
%%time
results = [(row['No1'], row['No2']) for row in
tab.where('(No1 == 1234) & (No2 > 9776)')]
for res in results:
print(res)
```
### Working with Compressed Tables
```
filename = path + 'tab.h5c'
h5c = tb.open_file(filename, 'w')
filters = tb.Filters(complevel=4, complib='blosc')
tabc = h5c.create_table('/', 'ints_floats', sarray,
title='Integers and Floats',
expectedrows=rows, filters=filters)
%%time
res = np.array([(row['No3'], row['No4']) for row in
tabc.where('((No3 < -0.5) | (No3 > 0.5)) \
& ((No4 < -1) | (No4 > 1))')])[::100]
%time arr_non = tab.read()
%time arr_com = tabc.read()
ll $path*
h5c.close()
```
### Working with Arrays
```
%%time
arr_int = h5.create_array('/', 'integers', ran_int)
arr_flo = h5.create_array('/', 'floats', ran_flo)
h5
ll $path*
h5.close()
!rm -f $path*
```
### Out-of-Memory Computations
```
filename = path + 'array.h5'
h5 = tb.open_file(filename, 'w')
n = 100
ear = h5.create_earray(h5.root, 'ear',
atom=tb.Float64Atom(),
shape=(0, n))
%%time
rand = np.random.standard_normal((n, n))
for i in range(750):
ear.append(rand)
ear.flush()
ear
ear.size_on_disk
out = h5.create_earray(h5.root, 'out',
atom=tb.Float64Atom(),
shape=(0, n))
expr = tb.Expr('3 * sin(ear) + sqrt(abs(ear))')
# the numerical expression as a string object
expr.set_output(out, append_mode=True)
# target to store results is disk-based array
%time expr.eval()
# evaluation of the numerical expression
# and storage of results in disk-based array
out[0, :10]
%time imarray = ear.read()
# read whole array into memory
import numexpr as ne
expr = '3 * sin(imarray) + sqrt(abs(imarray))'
ne.set_num_threads(16)
%time ne.evaluate(expr)[0, :10]
h5.close()
!rm -f $path*
```
## Conclusions
## Further Reading
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
<a href="http://tpq.io" target="_blank">http://tpq.io</a> | <a href="http://twitter.com/dyjh" target="_blank">@dyjh</a> | <a href="mailto:[email protected]">[email protected]</a>
**Quant Platform** |
<a href="http://quant-platform.com">http://quant-platform.com</a>
**Python for Finance** |
<a href="http://python-for-finance.com" target="_blank">Python for Finance @ O'Reilly</a>
**Derivatives Analytics with Python** |
<a href="http://derivatives-analytics-with-python.com" target="_blank">Derivatives Analytics @ Wiley Finance</a>
**Listed Volatility and Variance Derivatives** |
<a href="http://lvvd.tpq.io" target="_blank">Listed VV Derivatives @ Wiley Finance</a>
**Python Training** |
<a href="http://training.tpq.io" target="_blank">Python for Finance University Certificate</a>
|
github_jupyter
|
# 第6章 スモール言語を作る
```
# !pip install pegtree
import pegtree as pg
from pegtree.colab import peg, pegtree, example
%%peg
Program = { // 開式非終端記号 Expression*
#Program
} EOF
EOF = !. // ファイル終端
Expression =
/ FuncDecl // 関数定義
/ VarDecl // 変数定義
/ IfExpr // if 式
/ Binary // 二項演算
```
import pegtree as pg
peg = pg.grammar('chibi.pegtree') parser = pg.generate(peg)
## 6.2.5 パーザの生成
```
import pegtree as pg
peg = pg.grammar('chibi.pegtree')
parser = pg.generate(peg)
```
## トランスコンパイラ
```
class Visitor(object):
def visit(self, tree):
tag = tree.getTag()
name = f'accept{tag}'
if hasattr(self, name): # accept メソッドがあるか調べる
# メソッド名からメソッドを得る
acceptMethod = getattr(self, name)
return acceptMethod(tree)
print(f'TODO: accept{tag}')
return None
class Compiler(Visitor): # Visitor クラスの継承
def __init__(self):
self.buffers = []
peg = pg.grammar('chibi.pegtree')
self.parser = pg.generate(peg)
def compile(self, source):
tree = self.parser(source) # 構文木に交換
self.buffers = [] # バッファの初期化
self.visit(tree)
return ''.join(self.buffers) # バッファを連結してソースコードにまとめる
def push(self, s): # コード片をバッファに追加
self.buffers.append(s)
c = Compiler()
code = c.compile('1+2*3')
print(code)
```
### 各ノードのコード変換
```
BUILTIN_FUNCTIONS = {
'print': 'console.log'
}
class Compiler(Visitor): # Visitor クラスの継承
def __init__(self):
self.buffers = []
peg = pg.grammar('chibi.pegtree')
self.parser = pg.generate(peg)
def compile(self, source):
tree = self.parser(source) # 構文木に交換
self.buffers = [] # バッファの初期化
self.visit(tree)
return ''.join(self.buffers) # バッファを連結してソースコードにまとめる
def push(self, s): # コード片をバッファに追加
self.buffers.append(s)
def acceptProgram(self, tree):
for child in tree: # 子ノードのリスト
self.visit(child) # 子ノードの変換
self.push('\n') # 改行をバッファに追加
def acceptInt(self, tree):
v = tree.getToken()
self.push(v)
def acceptName(self, tree):
name = tree.getToken()
self.push(name)
def acceptAdd(self, tree):
self.push('(')
self.visit(tree[0])
self.push('+')
self.visit(tree[1])
self.push(')')
def acceptEq(self, tree):
self.push('(')
self.visit(tree[0])
self.push('===')
self.visit(tree[1])
self.push(') ? 1 : 0')
def acceptFuncApp(self, tree):
f = tree.getToken(0)
self.push(BUILTIN_FUNCTIONS.get(f, f))
self.push('(')
self.visit(tree[1])
self.push(')')
def accepterr(self, tree):
print(repr(tree))
c = Compiler()
code = c.compile('''
f(x) = x+1
print(x)
''')
print(code)
```
## インタプリタ
```
class Interpreter(Visitor):
def __init__(self):
self.env = {} # 空の環境を用意する
peg = pg.grammar('chibi.pegtree')
self.parser = pg.generate(peg)
def eval(self, source):
tree = self.parser(source)
return self.visit(tree)
chibi = Interpreter()
source = input('>>> ')
while source != '':
result = chibi.eval(source)
print(result)
source = input('>>> ')
class Interpreter(Visitor):
def __init__(self):
self.env = {} # 空の環境を用意する
peg = pg.grammar('chibi.pegtree')
self.parser = pg.generate(peg)
def eval(self, source):
tree = self.parser(source)
return self.visit(tree)
def acceptProgram(self, tree):
result = None
for child in tree:
result = self.visit(child)
return result
def acceptInt(self, tree):
token = tree.getToken()
return int(token)
def acceptAdd(self, tree):
v0 = self.visit(tree[0])
v1 = self.visit(tree[1])
return v0 + v1
def acceptEq(self, tree):
v0 = self.visit(tree[0])
v1 = self.visit(tree[1])
return 1 if v0 == v1 else 0
def acceptIfExpr(self, tree):
v0 = self.visit(tree[0])
if v0 != 0:
return self.visit(tree[1])
else:
return self.visit(tree[2])
def acceptVarDecl(self, tree):
v = self.visit(tree[1])
x = str(tree[0])
self.env[x] = v
return v
def acceptName(self, t):
x = t.getToken()
if x in self.env:
return self.env[x]
else:
raise NameError(x)
def acceptFuncDecl(self, tree):
f = tree.getToken(0)
x = tree.getToken(1)
e = tree.get(2)
self.env[f] = (x, e)
return self.env[f]
def acceptFuncApp(self, tree):
f = tree.getToken(0) # 関数名を得る
v = self.visit(tree[1]) # 引数を先に評価
x, e = self.env[f] # 関数名から引数名と関数式を取り出す
self.env[x] = v # 環境xをvにする
v = self.visit(e) # 関数式を評価
return v
source = '''
fib(n) = if n < 3 then 1 else fib(n-1)+fib(n-2)
fib(4)
'''
c = Interpreter()
print(c.eval(source))
```
|
github_jupyter
|
## Dataset
https://data.wprdc.org/dataset/allegheny-county-restaurant-food-facility-inspection-violations/resource/112a3821-334d-4f3f-ab40-4de1220b1a0a
This data set is a set of all of the restaurants in Allegheny County with geographic locations including zip code, size, description of use, and a "status" ranging from 0 to 7 to indicate if the restaurant is currently open.
```
import pandas as pd
restaurants_all = pd.read_csv("r.csv")
```
First, I remove the few restaurants that are outside of Pittsburgh and those with a value of 0 or 1 for their status, which indicates that they are closed.
```
query_mask = restaurants_all['status'] > 1
zip_mask_low = restaurants_all['zip'] > 14999.0
zip_mask_high = restaurants_all['zip'] < 16000.0
open_restaurants = restaurants_all[query_mask]
open_restaurants = open_restaurants[zip_mask_low]
open_restaurants = open_restaurants[zip_mask_high]
open_restaurants = open_restaurants[open_restaurants['zip'].notnull()]
open_restaurants.head(5)
```
Then I count up the number of open restaurants within a certain zipcode by keeping track of the data in a dictionary, using the zipcode as a key and incrementing the value associated with it.
```
zipcode_counter = dict()
for row in open_restaurants.index:
zipc = open_restaurants.loc[row, "zip"]
if zipc not in zipcode_counter:
zipcode_counter[zipc] = 1
else:
zipcode_counter[zipc] = zipcode_counter[zipc] + 1
zipcode_counter
zip_sorted = dict(sorted(zipcode_counter.items(), key=lambda item: item[1]))
zip_sorted
import matplotlib.pyplot as plt
names = list(zipcode_counter.keys())
values = list(zipcode_counter.values())
plt.bar(names, values)
plt.xlabel("Zipcodes")
plt.ylabel("Number of Restaurants")
plt.axis([15000, 15300, 0, 1060])
plt.show()
average = sum(zip_sorted.values()) / len(zip_sorted)
print(average)
```
Plotting this data, we find that there is a very wide range from 0 to 1041 and a mean of 124 restaurants per zipcode.
```
#all_values = zipcode_counter.values()
#max_value = max(all_values)
#print(max_value)
max_key = max(zipcode_counter, key=zipcode_counter.get)
print(max_key)
min_key = min(zipcode_counter, key=zipcode_counter.get)
print(min_key)
```
The top ten zipcodes with the most restaurants and their corresponding neighborhoods are:
* 15222.0: 1041 - Strip District
* 15212.0: 694 - North Shore/North Side
* 15213.0: 677 - Oakland
* 15219.0: 639 - Hill District
* 15237.0: 509 - Ross Township
* 15146.0: 482 - Monroeville
* 15205.0: 423 - Crafton
* 15108.0: 408 - Coraoplis
* 15235.0: 396 - Penn Hills
* 15203.0: 392 - South Side
According to our metric, we divide the data into fifths and award points to the total of each of the zipcodes:
```
print(len(zip_sorted))
zipcode_points_restaurants = dict()
i = 1
for key in zip_sorted:
zipcode_points_restaurants[key] = i // 28 + 1
i = i + 1
zipcode_points_restaurants
```
|
github_jupyter
|
# Dimensionality Reduction Example
Using the IMDB data, feature matrix and apply dimensionality reduction to this matrix via PCA and SVD.
```
%matplotlib inline
import json
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import lil_matrix
from sklearn.neighbors import DistanceMetric
from sklearn.metrics import jaccard_score
from sklearn.metrics import pairwise_distances
# Let's restrict ourselves just to US titles
relevant_title_df = pd.read_csv("../data/us_relevant_titles.csv")
# And create a set of just these titles, so we can filter them
relevant_title_set = set(relevant_title_df["title"])
actor_id_to_name_map = {} # Map Actor IDs to actor names
actor_id_to_index_map = {} # Map actor IDs to a unique index of known actors
index_to_actor_ids = [] # Array mapping unique index back to actor ID (invert of actor_id_to_index_map)
index_counter = 0 # Unique actor index; increment for each new actor
known_actors = set()
movie_actor_list = [] # List of all our movies and their actors
test_count = 0
with open("../data/imdb_recent_movies.json", "r") as in_file:
for line in in_file:
this_movie = json.loads(line)
# Restrict to American movies
if this_movie["title_name"] not in relevant_title_set:
continue
# Keep track of all the actors in this movie
for actor_id,actor_name in zip(this_movie['actor_ids'],this_movie['actor_names']):
# Keep names and IDs
actor_id_to_name_map[actor_id] = actor_name
# If we've seen this actor before, skip...
if actor_id in known_actors:
continue
# ... Otherwise, add to known actor set and create new index for them
known_actors.add(actor_id)
actor_id_to_index_map[actor_id] = index_counter
index_to_actor_ids.append(actor_id)
index_counter += 1
# Finished with this film
movie_actor_list.append({
"movie": this_movie["title_name"],
"actors": set(this_movie['actor_ids']),
"genres": this_movie["title_genre"]
})
print("Known Actors:", len(known_actors))
```
## Generate Same DataFrame using Sparse Matrics
The above will break if you have too much data. We can get around that partially with sparse matrices, where we only store the non-zero elements of the feature matrix and their indices.
```
# With sparse matrix, initialize to size of Movies x Actors of 0s
matrix_sparse = lil_matrix((len(movie_actor_list), len(known_actors)), dtype=bool)
# Update the matrix, movie by movie, setting non-zero values for the appropriate actors
for row,movie in enumerate(movie_actor_list):
for actor_id in movie["actors"]:
this_index = actor_id_to_index_map[actor_id]
matrix_sparse[row,this_index] = 1
df = pd.DataFrame.sparse.from_spmatrix(
matrix_sparse,
index=[m["movie"] for m in movie_actor_list],
columns=[index_to_actor_ids[i] for i in range(len(known_actors))]
)
df
top_k_actors = 1000
# Extract the most frequent actors, so we can deal with a reasonable dataset size
actor_df = df.sum(axis=0)
top_actors = set(actor_df.sort_values().tail(top_k_actors).index)
# Restrict the data frame to just the movies containing
#. the top k actors
reduced_df = df[top_actors] # restrict to just these top actors
# throw away movies that don't have any of these actors
reduced_df = reduced_df.loc[reduced_df.sum(axis=1) > 0]
reduced_df
```
## Apply SVD to Feature Matrix
```
# https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.TruncatedSVD.html
from sklearn.decomposition import TruncatedSVD
matrix_dense = reduced_df.to_numpy()
reduced_df
svd = TruncatedSVD(n_components=2)
svd.fit(matrix_dense)
matrix_reduced = svd.transform(matrix_dense)
np.mean(matrix_reduced, axis=0)
plt.scatter(matrix_reduced[:,0], matrix_reduced[:,1])
counter = 0
for index in np.argwhere((matrix_reduced[:,0] > 1.0) & (matrix_reduced[:,1] > 0.8)):
movie_title = reduced_df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
print(this_movie["movie"])
print("\tGenres:", ", ".join(this_movie["genres"]))
print("\tActors:", ", ".join([actor_id_to_name_map[actor] for actor in this_movie["actors"]]))
counter += 1
if counter > 10:
print("...")
break
counter = 0
for index in np.argwhere((matrix_reduced[:,0] < 0.1) & (matrix_reduced[:,1] < 0.1)):
movie_title = reduced_df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
print(this_movie["movie"])
print("\tGenres:", ", ".join(this_movie["genres"]))
print("\tActors:", ", ".join([actor_id_to_name_map[actor] for actor in this_movie["actors"]]))
counter += 1
if counter > 10:
print("...")
break
comp1_genre_map = {}
comp1_actor_map = {}
comp1_counter = 0
for index in np.argwhere((matrix_reduced[:,0] > 1.0) & (matrix_reduced[:,1] < 0.2)):
movie_title = reduced_df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
for g in this_movie["genres"]:
comp1_genre_map[g] = comp1_genre_map.get(g, 0) + 1
for a in [actor_id_to_name_map[actor] for actor in this_movie["actors"]]:
comp1_actor_map[a] = comp1_actor_map.get(a, 0) + 1
comp1_counter += 1
print("Movies in Component 1:", comp1_counter)
print("Genres:")
for g in sorted(comp1_genre_map, key=comp1_genre_map.get, reverse=True)[:10]:
print("\t", g, comp1_genre_map[g])
print("Actors:")
for a in sorted(comp1_actor_map, key=comp1_actor_map.get, reverse=True)[:10]:
print("\t", a, comp1_actor_map[a])
comp2_genre_map = {}
comp2_actor_map = {}
comp2_counter = 0
for index in np.argwhere((matrix_reduced[:,0] < 0.1) & (matrix_reduced[:,1] < 0.1)):
movie_title = reduced_df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
for g in this_movie["genres"]:
comp2_genre_map[g] = comp2_genre_map.get(g, 0) + 1
for a in [actor_id_to_name_map[actor] for actor in this_movie["actors"]]:
comp2_actor_map[a] = comp2_actor_map.get(a, 0) + 1
comp2_counter += 1
print("Movies in Component 2:", comp2_counter)
print("Genres:")
for g in sorted(comp2_genre_map, key=comp2_genre_map.get, reverse=True)[:10]:
print("\t", g, comp2_genre_map[g])
print("Actors:")
for a in sorted(comp2_actor_map, key=comp2_actor_map.get, reverse=True)[:10]:
print("\t", a, comp2_actor_map[a])
```
## Find Similar Movies in Reduced Dimensional Space
```
query_idx = [idx for idx,m in enumerate(reduced_df.index) if m == "The Lord of the Rings: The Fellowship of the Ring"][0]
# query_idx = [idx for idx,m in enumerate(reduced_df.index) if m == "Heavy Metal 2000"][0]
# query_idx = [idx for idx,m in enumerate(reduced_df.index) if m == "Casino Royale"][0]
# query_idx = [idx for idx,m in enumerate(reduced_df.index) if m == "Star Wars: Episode II - Attack of the Clones"][0]
query_idx
query_v = matrix_reduced[query_idx,:]
query_v
# get distances between all films and query film
distances = pairwise_distances(matrix_reduced, [query_v], metric='euclidean')
distances_df = pd.DataFrame(distances, columns=["distance"])
for idx,row in distances_df.sort_values(by="distance", ascending=True).head(20).iterrows():
print(idx, reduced_df.iloc[idx].name, row["distance"])
```
## SVD and Column Feature Space
Above, we focused on the *movies* in the reduced feature/"concept" space. Here, we will use SVD to map the *actors* into the reduced "concept" space.
```
# See that the shape of this matrix is *reduced space* X original features
svd.components_.shape
```
We will use this reduced space to inspect the associations with a given actor and the concept set of concepts (i.e., the reduced space)
```
# query_actor = [idx for idx,name in actor_id_to_name_map.items() if name == "Ewan McGregor"][0]
# query_actor = [idx for idx,name in actor_id_to_name_map.items() if name == "Eric Roberts"][0]
# query_actor = [idx for idx,name in actor_id_to_name_map.items() if name == "Jason Statham"][0]
# query_actor = [idx for idx,name in actor_id_to_name_map.items() if name == "Leonardo DiCaprio"][0]
query_actor = [idx for idx,name in actor_id_to_name_map.items() if name == "George Clooney"][0]
query_actor
query_actor_index = np.argwhere(reduced_df.columns == query_actor)[0,0]
query_actor_index
# Show the actor strengths across these concepts
svd.components_.T[query_actor_index,:]
# And you can use this method to evaluate distances between actors in the concept space
distances = pairwise_distances(svd.components_.T, [svd.components_.T[query_actor_index,:]], metric='euclidean')
distances_df = pd.DataFrame(distances, columns=["distance"])
for idx,row in distances_df.sort_values(by="distance", ascending=True).head(20).iterrows():
print(idx, actor_id_to_name_map[reduced_df.columns[idx]], row["distance"])
```
## SVD is more scalable than PCA
```
from sklearn.decomposition import PCA
matrix_sparse.shape
# This will fail
pca = PCA(n_components=2)
pca.fit(matrix_sparse)
svd = TruncatedSVD(n_components=2)
svd.fit(matrix_sparse)
matrix_reduced = svd.transform(matrix_sparse)
print(np.mean(matrix_reduced, axis=0))
plt.scatter(matrix_reduced[:,0], matrix_reduced[:,1])
comp1_genre_map = {}
comp1_actor_map = {}
comp1_counter = 0
for index in np.argwhere((matrix_reduced[:,0] > 1.0) & (matrix_reduced[:,1] < 0.2)):
movie_title = df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
for g in this_movie["genres"]:
comp1_genre_map[g] = comp1_genre_map.get(g, 0) + 1
for a in [actor_id_to_name_map[actor] for actor in this_movie["actors"]]:
comp1_actor_map[a] = comp1_actor_map.get(a, 0) + 1
comp1_counter += 1
print("Movies in Component 1:", comp1_counter)
print("Genres:")
for g in sorted(comp1_genre_map, key=comp1_genre_map.get, reverse=True)[:10]:
print("\t", g, comp1_genre_map[g])
print("Actors:")
for a in sorted(comp1_actor_map, key=comp1_actor_map.get, reverse=True)[:10]:
print("\t", a, comp1_actor_map[a])
comp2_genre_map = {}
comp2_actor_map = {}
comp2_counter = 0
for index in np.argwhere((matrix_reduced[:,0] < 0.1) & (matrix_reduced[:,1] < 0.1)):
movie_title = df.iloc[index[0]].name
for this_movie in [m for m in movie_actor_list if m['movie'] == movie_title]:
for g in this_movie["genres"]:
comp2_genre_map[g] = comp2_genre_map.get(g, 0) + 1
for a in [actor_id_to_name_map[actor] for actor in this_movie["actors"]]:
comp2_actor_map[a] = comp2_actor_map.get(a, 0) + 1
comp2_counter += 1
print("Movies in Component 2:", comp2_counter)
print("Genres:")
for g in sorted(comp2_genre_map, key=comp2_genre_map.get, reverse=True)[:10]:
print("\t", g, comp2_genre_map[g])
print("Actors:")
for a in sorted(comp2_actor_map, key=comp2_actor_map.get, reverse=True)[:10]:
print("\t", a, comp2_actor_map[a])
```
|
github_jupyter
|
## Image segmentation with CamVid
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
from fastai import *
from fastai.vision import *
from fastai.callbacks.hooks import *
```
The One Hundred Layer Tiramisu paper used a modified version of Camvid, with smaller images and few classes. You can get it from the CamVid directory of this repo:
git clone https://github.com/alexgkendall/SegNet-Tutorial.git
```
path = Path('./data/camvid-tiramisu')
path.ls()
```
## Data
```
fnames = get_image_files(path/'val')
fnames[:3]
lbl_names = get_image_files(path/'valannot')
lbl_names[:3]
img_f = fnames[0]
img = open_image(img_f)
img.show(figsize=(5,5))
def get_y_fn(x): return Path(str(x.parent)+'annot')/x.name
codes = array(['Sky', 'Building', 'Pole', 'Road', 'Sidewalk', 'Tree',
'Sign', 'Fence', 'Car', 'Pedestrian', 'Cyclist', 'Void'])
mask = open_mask(get_y_fn(img_f))
mask.show(figsize=(5,5), alpha=1)
src_size = np.array(mask.shape[1:])
src_size,mask.data
```
## Datasets
```
bs = 8
src = (SegmentationItemList.from_folder(path)
.split_by_folder(valid='val')
.label_from_func(get_y_fn, classes=codes))
data = (src.transform(get_transforms(), tfm_y=True)
.databunch(bs=bs)
.normalize(imagenet_stats))
data.show_batch(2, figsize=(10,7))
```
## Model
```
name2id = {v:k for k,v in enumerate(codes)}
void_code = name2id['Void']
def acc_camvid(input, target):
target = target.squeeze(1)
mask = target != void_code
return (input.argmax(dim=1)[mask]==target[mask]).float().mean()
metrics=acc_camvid
wd=1e-2
learn = unet_learner(data, models.resnet34, metrics=metrics, wd=wd, bottle=True)
lr_find(learn)
learn.recorder.plot()
lr=2e-3
learn.fit_one_cycle(10, slice(lr), pct_start=0.8)
learn.save('stage-1')
learn.load('stage-1');
learn.unfreeze()
lrs = slice(lr/100,lr)
learn.fit_one_cycle(12, lrs, pct_start=0.8)
learn.save('stage-2');
```
## Go big
```
learn=None
gc.collect()
```
You may have to restart your kernel and come back to this stage if you run out of memory, and may also need to decrease `bs`.
```
size = src_size
bs=8
data = (src.transform(get_transforms(), size=size, tfm_y=True)
.databunch(bs=bs)
.normalize(imagenet_stats))
learn = unet_learner(data, models.resnet34, metrics=metrics, wd=wd, bottle=True).load('stage-2');
lr_find(learn)
learn.recorder.plot()
lr=1e-3
learn.fit_one_cycle(10, slice(lr), pct_start=0.8)
learn.save('stage-1-big')
learn.load('stage-1-big');
learn.unfreeze()
lrs = slice(lr/1000,lr/10)
learn.fit_one_cycle(10, lrs)
learn.save('stage-2-big')
learn.load('stage-2-big');
learn.show_results(rows=3, figsize=(9,11))
```
## fin
```
# start: 480x360
print(learn.summary())
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Image Classification using tf.keras
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/examples/blob/master/courses/udacity_intro_to_tensorflow_for_deep_learning/l05c04_exercise_flowers_with_data_augmentation_solution.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/examples/blob/master/courses/udacity_intro_to_tensorflow_for_deep_learning/l05c04_exercise_flowers_with_data_augmentation_solution.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
In this Colab you will classify images of flowers. You will build an image classifier using `tf.keras.Sequential` model and load data using `tf.keras.preprocessing.image.ImageDataGenerator`.
# Importing Packages
Let's start by importing required packages. **os** package is used to read files and directory structure, **numpy** is used to convert python list to numpy array and to perform required matrix operations and **matplotlib.pyplot** is used to plot the graph and display images in our training and validation data.
```
import os
import numpy as np
import glob
import shutil
import matplotlib.pyplot as plt
```
### TODO: Import TensorFlow and Keras Layers
In the cell below, import Tensorflow and the Keras layers and models you will use to build your CNN. Also, import the `ImageDataGenerator` from Keras so that you can perform image augmentation.
```
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Flatten, Dropout, MaxPooling2D
from tensorflow.keras.preprocessing.image import ImageDataGenerator
```
# Data Loading
In order to build our image classifier, we can begin by downloading the flowers dataset. We first need to download the archive version of the dataset and after the download we are storing it to "/tmp/" directory.
After downloading the dataset, we need to extract its contents.
```
_URL = "https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz"
zip_file = tf.keras.utils.get_file(origin=_URL,
fname="flower_photos.tgz",
extract=True)
base_dir = os.path.join(os.path.dirname(zip_file), 'flower_photos')
```
The dataset we downloaded contains images of 5 types of flowers:
1. Rose
2. Daisy
3. Dandelion
4. Sunflowers
5. Tulips
So, let's create the labels for these 5 classes:
```
classes = ['roses', 'daisy', 'dandelion', 'sunflowers', 'tulips']
```
Also, the dataset we have downloaded has following directory structure. n
<pre style="font-size: 10.0pt; font-family: Arial; line-height: 2; letter-spacing: 1.0pt;" >
<b>flower_photos</b>
|__ <b>daisy</b>
|__ <b>dandelion</b>
|__ <b>roses</b>
|__ <b>sunflowers</b>
|__ <b>tulips</b>
</pre>
As you can see there are no folders containing training and validation data. Therefore, we will have to create our own training and validation set. Let's write some code that will do this.
The code below creates a `train` and a `val` folder each containing 5 folders (one for each type of flower). It then moves the images from the original folders to these new folders such that 80% of the images go to the training set and 20% of the images go into the validation set. In the end our directory will have the following structure:
<pre style="font-size: 10.0pt; font-family: Arial; line-height: 2; letter-spacing: 1.0pt;" >
<b>flower_photos</b>
|__ <b>daisy</b>
|__ <b>dandelion</b>
|__ <b>roses</b>
|__ <b>sunflowers</b>
|__ <b>tulips</b>
|__ <b>train</b>
|______ <b>daisy</b>: [1.jpg, 2.jpg, 3.jpg ....]
|______ <b>dandelion</b>: [1.jpg, 2.jpg, 3.jpg ....]
|______ <b>roses</b>: [1.jpg, 2.jpg, 3.jpg ....]
|______ <b>sunflowers</b>: [1.jpg, 2.jpg, 3.jpg ....]
|______ <b>tulips</b>: [1.jpg, 2.jpg, 3.jpg ....]
|__ <b>val</b>
|______ <b>daisy</b>: [507.jpg, 508.jpg, 509.jpg ....]
|______ <b>dandelion</b>: [719.jpg, 720.jpg, 721.jpg ....]
|______ <b>roses</b>: [514.jpg, 515.jpg, 516.jpg ....]
|______ <b>sunflowers</b>: [560.jpg, 561.jpg, 562.jpg .....]
|______ <b>tulips</b>: [640.jpg, 641.jpg, 642.jpg ....]
</pre>
Since we don't delete the original folders, they will still be in our `flower_photos` directory, but they will be empty. The code below also prints the total number of flower images we have for each type of flower.
```
for cl in classes:
img_path = os.path.join(base_dir, cl)
images = glob.glob(img_path + '/*.jpg')
print("{}: {} Images".format(cl, len(images)))
num_train = int(round(len(images)*0.8))
train, val = images[:num_train], images[num_train:]
for t in train:
if not os.path.exists(os.path.join(base_dir, 'train', cl)):
os.makedirs(os.path.join(base_dir, 'train', cl))
shutil.move(t, os.path.join(base_dir, 'train', cl))
for v in val:
if not os.path.exists(os.path.join(base_dir, 'val', cl)):
os.makedirs(os.path.join(base_dir, 'val', cl))
shutil.move(v, os.path.join(base_dir, 'val', cl))
round(len(images)*0.8)
```
For convenience, let us set up the path for the training and validation sets
```
train_dir = os.path.join(base_dir, 'train')
val_dir = os.path.join(base_dir, 'val')
```
# Data Augmentation
Overfitting generally occurs when we have small number of training examples. One way to fix this problem is to augment our dataset so that it has sufficient number of training examples. Data augmentation takes the approach of generating more training data from existing training samples, by augmenting the samples via a number of random transformations that yield believable-looking images. The goal is that at training time, your model will never see the exact same picture twice. This helps expose the model to more aspects of the data and generalize better.
In **tf.keras** we can implement this using the same **ImageDataGenerator** class we used before. We can simply pass different transformations we would want to our dataset as a form of arguments and it will take care of applying it to the dataset during our training process.
## Experiment with Various Image Transformations
In this section you will get some practice doing some basic image transformations. Before we begin making transformations let's define our `batch_size` and our image size. Remember that the input to our CNN are images of the same size. We therefore have to resize the images in our dataset to the same size.
### TODO: Set Batch and Image Size
In the cell below, create a `batch_size` of 100 images and set a value to `IMG_SHAPE` such that our training data consists of images with width of 150 pixels and height of 150 pixels.
```
batch_size = 100
IMG_SHAPE = 150
```
### TODO: Apply Random Horizontal Flip
In the cell below, use ImageDataGenerator to create a transformation that rescales the images by 255 and then applies a random horizontal flip. Then use the `.flow_from_directory` method to apply the above transformation to the images in our training set. Make sure you indicate the batch size, the path to the directory of the training images, the target size for the images, and to shuffle the images.
```
image_gen = ImageDataGenerator(rescale=1./255, horizontal_flip=True)
train_data_gen = image_gen.flow_from_directory(
batch_size=batch_size,
directory=train_dir,
shuffle=True,
target_size=(IMG_SHAPE,IMG_SHAPE)
)
```
Let's take 1 sample image from our training examples and repeat it 5 times so that the augmentation can be applied to the same image 5 times over randomly, to see the augmentation in action.
```
# This function will plot images in the form of a grid with 1 row and 5 columns where images are placed in each column.
def plotImages(images_arr):
fig, axes = plt.subplots(1, 5, figsize=(20,20))
axes = axes.flatten()
for img, ax in zip( images_arr, axes):
ax.imshow(img)
plt.tight_layout()
plt.show()
augmented_images = [train_data_gen[0][0][0] for i in range(5)]
plotImages(augmented_images)
```
### TODO: Apply Random Rotation
In the cell below, use ImageDataGenerator to create a transformation that rescales the images by 255 and then applies a random 45 degree rotation. Then use the `.flow_from_directory` method to apply the above transformation to the images in our training set. Make sure you indicate the batch size, the path to the directory of the training images, the target size for the images, and to shuffle the images.
```
image_gen = ImageDataGenerator(rescale=1./255, rotation_range=45)
train_data_gen = image_gen.flow_from_directory(batch_size=batch_size,
directory=train_dir,
shuffle=True,
target_size=(IMG_SHAPE, IMG_SHAPE))
```
Let's take 1 sample image from our training examples and repeat it 5 times so that the augmentation can be applied to the same image 5 times over randomly, to see the augmentation in action.
```
augmented_images = [train_data_gen[0][0][0] for i in range(5)]
plotImages(augmented_images)
```
### TODO: Apply Random Zoom
In the cell below, use ImageDataGenerator to create a transformation that rescales the images by 255 and then applies a random zoom of up to 50%. Then use the `.flow_from_directory` method to apply the above transformation to the images in our training set. Make sure you indicate the batch size, the path to the directory of the training images, the target size for the images, and to shuffle the images.
```
image_gen = ImageDataGenerator(rescale=1./255, zoom_range=0.5)
train_data_gen = image_gen.flow_from_directory(
batch_size=batch_size,
directory=train_dir,
shuffle=True,
target_size=(IMG_SHAPE, IMG_SHAPE)
)
```
Let's take 1 sample image from our training examples and repeat it 5 times so that the augmentation can be applied to the same image 5 times over randomly, to see the augmentation in action.
```
augmented_images = [train_data_gen[0][0][0] for i in range(5)]
plotImages(augmented_images)
```
### TODO: Put It All Together
In the cell below, use ImageDataGenerator to create a transformation that rescales the images by 255 and that applies:
- random 45 degree rotation
- random zoom of up to 50%
- random horizontal flip
- width shift of 0.15
- height shift of 0.15
Then use the `.flow_from_directory` method to apply the above transformation to the images in our training set. Make sure you indicate the batch size, the path to the directory of the training images, the target size for the images, to shuffle the images, and to set the class mode to `sparse`.
```
image_gen_train = ImageDataGenerator(
rescale=1./255,
rotation_range=45,
width_shift_range=.15,
height_shift_range=.15,
horizontal_flip=True,
zoom_range=0.5
)
train_data_gen = image_gen_train.flow_from_directory(
batch_size=batch_size,
directory=train_dir,
shuffle=True,
target_size=(IMG_SHAPE,IMG_SHAPE),
class_mode='sparse'
)
```
Let's visualize how a single image would look like 5 different times, when we pass these augmentations randomly to our dataset.
```
augmented_images = [train_data_gen[0][0][0] for i in range(5)]
plotImages(augmented_images)
```
### TODO: Create a Data Generator for the Validation Set
Generally, we only apply data augmentation to our training examples. So, in the cell below, use ImageDataGenerator to create a transformation that only rescales the images by 255. Then use the `.flow_from_directory` method to apply the above transformation to the images in our validation set. Make sure you indicate the batch size, the path to the directory of the validation images, the target size for the images, and to set the class mode to `sparse`. Remember that it is not necessary to shuffle the images in the validation set.
```
image_gen_val = ImageDataGenerator(rescale=1./255)
val_data_gen = image_gen_val.flow_from_directory(batch_size=batch_size,
directory=val_dir,
target_size=(IMG_SHAPE, IMG_SHAPE),
class_mode='sparse')
```
# TODO: Create the CNN
In the cell below, create a convolutional neural network that consists of 3 convolution blocks. Each convolutional block contains a `Conv2D` layer followed by a max pool layer. The first convolutional block should have 16 filters, the second one should have 32 filters, and the third one should have 64 filters. All convolutional filters should be 3 x 3. All max pool layers should have a `pool_size` of `(2, 2)`.
After the 3 convolutional blocks you should have a flatten layer followed by a fully connected layer with 512 units. The CNN should output class probabilities based on 5 classes which is done by the **softmax** activation function. All other layers should use a **relu** activation function. You should also add Dropout layers with a probability of 20%, where appropriate.
```
model = Sequential()
model.add(Conv2D(16, 3, padding='same', activation='relu', input_shape=(IMG_SHAPE,IMG_SHAPE, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, 3, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, 3, padding='same', activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(5))
```
# TODO: Compile the Model
In the cell below, compile your model using the ADAM optimizer, the sparse cross entropy function as a loss function. We would also like to look at training and validation accuracy on each epoch as we train our network, so make sure you also pass the metrics argument.
```
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
```
# TODO: Train the Model
In the cell below, train your model using the **fit_generator** function instead of the usual **fit** function. We have to use the `fit_generator` function because we are using the **ImageDataGenerator** class to generate batches of training and validation data for our model. Train the model for 80 epochs and make sure you use the proper parameters in the `fit_generator` function.
```
epochs = 80
history = model.fit_generator(
train_data_gen,
steps_per_epoch=int(np.ceil(train_data_gen.n / float(batch_size))),
epochs=epochs,
validation_data=val_data_gen,
validation_steps=int(np.ceil(val_data_gen.n / float(batch_size)))
)
```
# TODO: Plot Training and Validation Graphs.
In the cell below, plot the training and validation accuracy/loss graphs.
```
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs_range = range(epochs)
plt.figure(figsize=(8, 8))
plt.subplot(1, 2, 1)
plt.plot(epochs_range, acc, label='Training Accuracy')
plt.plot(epochs_range, val_acc, label='Validation Accuracy')
plt.legend(loc='lower right')
plt.title('Training and Validation Accuracy')
plt.subplot(1, 2, 2)
plt.plot(epochs_range, loss, label='Training Loss')
plt.plot(epochs_range, val_loss, label='Validation Loss')
plt.legend(loc='upper right')
plt.title('Training and Validation Loss')
plt.show()
```
|
github_jupyter
|
# Equilibrium analysis Chemical reaction
Number (code) of assignment: 2N4
Description of activity:
Report on behalf of:
name : Pieter van Halem
student number : 4597591
name : Dennis Dane
student number :4592239
Data of student taking the role of contact person:
name :
email address :
```
import numpy as np
import matplotlib.pyplot as plt
```
# Function definitons:
In the following block the function that are used for the numerical analysis are definend. These are functions for calculation the various time steps, functions for plotting tables ands functions for plotting graphs.
```
def f(t,y,a,b,i):
if (t>round(i,2)):
a = 0
du = a-(b+1)*y[0,0]+y[0,0]**2*y[0,1]
dv = b*y[0,0]-y[0,0]**2*y[0,1]
return np.matrix([du,dv])
def FE(t,y,h,a,b,i):
f1 = f(t,y,a,b,i)
pred = y + f1*h
corr = y + (h/2)*(f(t,pred,a,b,i) + f1)
return corr
def Integrate(y0, t0, tend, N,a,b,i):
h = (tend-t0)/N
t_arr = np.zeros(N+1)
t_arr[0] = t0
w_arr = np.zeros((2,N+1))
w_arr[:,0] = y0
t = t0
y = y0
for k in range(1,N+1):
y = FE(t,y,h,a,b,i)
w_arr[:,k] = y
t = round(t + h,4)
t_arr[k] = t
return t_arr, w_arr
def PrintTable(t_arr, w_arr):
print ("%6s %6s: %17s %17s" % ("index", "t", "u(t)", "v(t)"))
for k in range(0,N+1):
print ("{:6d} {:6.2f}: {:17.7e} {:17.7e}".format(k,t_arr[k],
w_arr[0,k],w_arr[1,k]))
def PlotGraphs(t_arr, w_arr):
plt.figure("Initial value problem")
plt.plot(t_arr,w_arr[0,:],'r',t_arr,w_arr[1,:],'--')
plt.legend(("$u(t)$", "$v(t)$"),loc="best", shadow=True)
plt.xlabel("$t$")
plt.ylabel("$u$ and $v$")
plt.title("Graphs of $u(t)$ and $v(t)$")
plt.show()
def PlotGraphs2(t_arr, w_arr):
plt.figure("Initial value problem")
plt.plot(w_arr[0,:],w_arr[1,:],'g')
plt.legend(("$u,v$",""),loc="best", shadow=True)
plt.xlabel("$u(t)$")
plt.ylabel("$v(t)$")
plt.title("$Phase$ $plane$ $(u,v)$")
plt.axis("scaled")
plt.show()
def PlotGraphs3(t_arr, w_arr,t_arr2, w_arr2):
plt.figure("Initial value problem")
plt.plot(t_arr,w_arr[0,:],'r',t_arr,w_arr[1,:],'b--')
plt.plot(t_arr2,w_arr2[0,:],'r',t_arr2,w_arr2[1,:],'b--')
#plt.plot([t_array[80],t_array2[0]],[w_array[0,80],w_array2[0,0]],'r')
plt.legend(("$u(t)$", "$v(t)$"),loc="best", shadow=True)
plt.xlabel("$t$")
plt.ylabel("$u$ and $v$")
plt.title("Graphs of $u(t)$ and $v(t)$")
plt.show()
def PlotGraphs4(t_arr, w_arr,t_arr2, w_arr2):
#plt.figure("Initial value problem")
plt.plot(w_arr[0,:],w_arr[1,:],'g')
plt.plot(w_arr2[0,:],w_arr2[1,:],'g')
#plt.legend(("$u,v$",""),loc="best", shadow=True)
plt.xlabel("$u(t)$")
plt.ylabel("$v(t)$")
plt.title("$Phase$ $plane$ $(u,v)$")
plt.axis("scaled")
plt.show()
```
# Assignment 2.9
Integrate the system with Modified Euler and time step h = 0.15. Make a table of u and v on the time interval 0 ≤ t ≤ 1.5. The table needs to give u and v in an 8-digit floating-point format.
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 1.5
N = 10
t_array, w_array = Integrate(y0, t0, tend, N,2,4.5,11)
print("The integrated system using Modified Euler with time step h = 0.15 is shown in the following table: \n")
PrintTable(t_array, w_array)
```
# Assignmet 2.10
Integrate the system with Modified Euler and time step h = 0.05 for the interval [0,20]. Make plots of u and v as functions of t (put them in one figure). Also make a plot of u and v in the phase plane (u,v-plane). Do your plots correspond to your results of part 2?
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 400
t_array, w_array = Integrate(y0, t0, tend, N,2,4.5, 25)
print("In this assignment the system has to be integrated using Modified Euler with a time step of h = 0.05 on \na interval of [0,20].")
print("The first graph is u(t) and v(t) against time (t).")
PlotGraphs(t_array, w_array)
print("The second graph shows the u-v plane")
PlotGraphs2(t_array, w_array)
print("\n The system is stable and a spiral. Therefor is consistent with the conclusion from assignment 1.3.")
```
# Assignment 2.11
Using the formula derived in question 7, estimate the accuracy of u and v computed with h = 0.05 at t = 8. Hence, integrate once more with time step h = 0.1.
The error can be estimated with Richardsons methode. were we use α = 1/3 found in assignment 7. here the estimated error is: E ≈ α( w(h) - w(2h) ).
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 400
t_array, w_array = Integrate(y0, t0, tend, N, 2, 4.5,25)
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 20
N = 200
t_array2, w_array2 = Integrate(y0, t0, tend, N, 2, 4.5, 25)
print("The value for u and v at t = 8 with h = 0.05 is:",t_array[160], w_array[:,160])
print("The value for u and v at t = 8 with h = 0.10 is:",t_array2[80], w_array2[:,80])
E1 = (w_array[0,160]-w_array2[0,80])*(1/3)
E2 = (w_array[1,160]-w_array2[1,80])*(1/3)
print("The estimated acuracy for u is:", E1)
print("The estimated acuracy for v is:", E2)
```
# Assignment 2.12
Apply Modified Euler with h = 0.05. For 0 ≤ t ≤ t1 it holds that a = 2. At t = t1 the supply of materials A fails, and therefore a = 0 for t > t1. Take t1 = 4.0. Make plot of u and v as a function of t on the intervals [0, 10] in one figure and a plot of u and v in the uv-plane. Evaluate your results by comparing them to your findings form part 8.
```
y0 = np.matrix([0.0,0.0])
t0 = 0.0
tend = 10.0
N = 200
t_array, w_array = Integrate(y0, t0, tend, N, 2, 4.5, 4)
PlotGraphs(t_array, w_array)
```
The first plot shows that u and v indeed converges to a certain value, as predicted in assignment 8. The phase plane shows that uv goes to a point on the u-axis. This was as well predicted in assignment 8.
The first plot shows a corner in the u and v graph (a discontinuity in the first derivative). This does not contradict the theory because the system of differential equations changes the first derivatives does not have to be continuous. The line itself is continuous because it is given in the initial values.
# Assignment 2.13
Take t1 = 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0. Make a table of the value of v-tilda and t-tilda. Evaluate your rsults.
```
for i in np.arange(3.0,6.5,0.50):
t0 = 0.0
tend = 10.0
N = 200
t_array2, w_array2 = Integrate(y0, t0, tend, N, 2.0, 4.5,i)
indices = np.nonzero(w_array2[0,:] >= 0.01)
index = np.max(indices[0])
t_tilde = t_array2[index+1]
v_tilde = w_array2[1,N]
if i == 3:
print("%6s %17s: %17s " % ("t1", "t_tilde", "v_tilde"))
print("{:6.2f} {:17.2f} {:17.7e}".format(i,t_tilde,v_tilde))
```
lkksdndglnsldkgknlsdagn
De waarde moeten zijn: t1 = 6.0 v-tilde = 3.34762, t-tilde = 7.35
|
github_jupyter
|
# Creating a simple PDE model
In the [previous notebook](./1-an-ode-model.ipynb) we show how to create, discretise and solve an ODE model in pybamm. In this notebook we show how to create and solve a PDE problem, which will require meshing of the spatial domain.
As an example, we consider the problem of linear diffusion on a unit sphere,
\begin{equation*}
\frac{\partial c}{\partial t} = \nabla \cdot (\nabla c),
\end{equation*}
with the following boundary and initial conditions:
\begin{equation*}
\left.\frac{\partial c}{\partial r}\right\vert_{r=0} = 0, \quad \left.\frac{\partial c}{\partial r}\right\vert_{r=1} = 2, \quad \left.c\right\vert_{t=0} = 1.
\end{equation*}
As before, we begin by importing the pybamm library into this notebook, along with any other packages we require:
```
%pip install pybamm -q # install PyBaMM if it is not installed
import pybamm
import numpy as np
import matplotlib.pyplot as plt
```
## Setting up the model
As in the previous example, we start with a `pybamm.BaseModel` object and define our model variables. Since we are now solving a PDE we need to tell pybamm the domain each variable belongs to so that it can be discretised in space in the correct way. This is done by passing the keyword argument `domain`, and in this example we choose the domain "negative particle".
```
model = pybamm.BaseModel()
c = pybamm.Variable("Concentration", domain="negative particle")
```
Note that we have given our variable the (useful) name "Concentration", but the symbol representing this variable is simply `c`.
We then state out governing equations. Sometime it is useful to define intermediate quantities in order to express the governing equations more easily. In this example we define the flux, then define the rhs to be minus the divergence of the flux. The equation is then added to the dictionary `model.rhs`
```
N = -pybamm.grad(c) # define the flux
dcdt = -pybamm.div(N) # define the rhs equation
model.rhs = {c: dcdt} # add the equation to rhs dictionary
```
Unlike ODE models, PDE models require both initial and boundary conditions. Similar to initial conditions, boundary conditions can be added using the dictionary `model.boundary_conditions`. Boundary conditions for each variable are provided as a dictionary of the form `{side: (value, type)`, where, in 1D, side can be "left" or "right", value is the value of the boundary conditions, and type is the type of boundary condition (at present, this can be "Dirichlet" or "Neumann").
```
# initial conditions
model.initial_conditions = {c: pybamm.Scalar(1)}
# boundary conditions
lbc = pybamm.Scalar(0)
rbc = pybamm.Scalar(2)
model.boundary_conditions = {c: {"left": (lbc, "Neumann"), "right": (rbc, "Neumann")}}
```
Note that in our example the boundary conditions take constant values, but the value can be any valid pybamm expression.
Finally, we add any variables of interest to the dictionary `model.variables`
```
model.variables = {"Concentration": c, "Flux": N}
```
## Using the model
Now the model is now completely defined all that remains is to discretise and solve. Since this model is a PDE we need to define the geometry on which it will be solved, and choose how to mesh the geometry and discretise in space.
### Defining a geometry and mesh
We can define spatial variables in a similar way to how we defined model variables, providing a domain and a coordinate system. The geometry on which we wish to solve the model is defined using a nested dictionary. The first key is the domain name (here "negative particle") and the entry is a dictionary giving the limits of the domain.
```
# define geometry
r = pybamm.SpatialVariable(
"r", domain=["negative particle"], coord_sys="spherical polar"
)
geometry = {"negative particle": {r: {"min": pybamm.Scalar(0), "max": pybamm.Scalar(1)}}}
```
We then create a mesh using the `pybamm.MeshGenerator` class. As inputs this class takes the type of mesh and any parameters required by the mesh. In this case we choose a uniform one-dimensional mesh which doesn't require any parameters.
```
# mesh and discretise
submesh_types = {"negative particle": pybamm.MeshGenerator(pybamm.Uniform1DSubMesh)}
var_pts = {r: 20}
mesh = pybamm.Mesh(geometry, submesh_types, var_pts)
```
Example of meshes that do require parameters include the `pybamm.Exponential1DSubMesh` which clusters points close to one or both boundaries using an exponential rule. It takes a parameter which sets how closely the points are clustered together, and also lets the users select the side on which more points should be clustered. For example, to create a mesh with more nodes clustered to the right (i.e. the surface in the particle problem), using a stretch factor of 2, we pass an instance of the exponential submesh class and a dictionary of parameters into the `MeshGenerator` class as follows: `pybamm.MeshGenerator(pybamm.Exponential1DSubMesh, submesh_params={"side": "right", "stretch": 2})`
After defining a mesh we choose a spatial method. Here we choose the Finite Volume Method. We then set up a discretisation by passing the mesh and spatial methods to the class `pybamm.Discretisation`. The model is then processed, turning the variables into (slices of) a statevector, spatial variables into vector and spatial operators into matrix-vector multiplications.
```
spatial_methods = {"negative particle": pybamm.FiniteVolume()}
disc = pybamm.Discretisation(mesh, spatial_methods)
disc.process_model(model);
```
Now that the model has been discretised we are ready to solve.
### Solving the model
As before, we choose a solver and times at which we want the solution returned. We then solve, extract the variables we are interested in, and plot the result.
```
# solve
solver = pybamm.ScipySolver()
t = np.linspace(0, 1, 100)
solution = solver.solve(model, t)
# post-process, so that the solution can be called at any time t or space r
# (using interpolation)
c = solution["Concentration"]
# plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13, 4))
ax1.plot(solution.t, c(solution.t, r=1))
ax1.set_xlabel("t")
ax1.set_ylabel("Surface concentration")
r = np.linspace(0, 1, 100)
ax2.plot(r, c(t=0.5, r=r))
ax2.set_xlabel("r")
ax2.set_ylabel("Concentration at t=0.5")
plt.tight_layout()
plt.show()
```
In the [next notebook](./3-negative-particle-problem.ipynb) we build on the example here to to solve the problem of diffusion in the negative electrode particle within the single particle model. In doing so we will also cover how to include parameters in a model.
## References
The relevant papers for this notebook are:
```
pybamm.print_citations()
```
|
github_jupyter
|
# Writing Functions
This lecture discusses the mechanics of writing functions and how to encapsulate scripts as functions.
```
# Example: We're going to use Pandas dataframes to create a gradebook for this course
import pandas as pd
# Student Rosters:
students = ['Hao', 'Jennifer', 'Alex']
# Gradebook columns:
columns = ['raw_grade', 'did_extra_credit', 'final_grade']
# Let's create two dataframes, one for each class section
gradebook = pd.DataFrame(index=students, columns=columns)
print("Gradebook:")
print(gradebook)
# Now let's add some data
# (in real life we might load this from a CSV or other file)
gradebook.loc['Hao']['raw_grade'] = 80
gradebook.loc['Hao']['did_extra_credit'] = True # python supports boolean (True/False) values
gradebook.loc['Jennifer']['raw_grade'] = 98
gradebook.loc['Jennifer']['did_extra_credit'] = False
gradebook.loc['Alex']['raw_grade'] = 85
gradebook.loc['Alex']['did_extra_credit'] = True
print("Gradebook:")
print(gradebook)
```
## Copying and pasting code can introduce bugs:
You might forget to change a variable name.
If you later make a change (like making extra credit worth 10 points instead of 5), you need to remember to change it in multiple places.
If we put the code in a function, we can avoid these problems!
```
# Let's put our extra credit code in a function!
def add_final_grades(student, grade):
print("in add_final_grades")
gradebook.loc[student, 'final_grade'] = grade
add_final_grades('Jennifer', 99)
print(gradebook)
```
## Why write functions?
1. Easily reuse code (without introducing bugs)
2. Easy testing of components
<ul>
<li>Later in the course we will learn about writing unit tests. You will create a set of input values for a function representing potential scenarios, and will test that the function is generating the expected output.
</ul>
3. Better readability
<ul>
<li>Functions encapsulate your code into components with meaningful names. You can get a high-level view of what the code is doing, then dive into the function definitions if you need more detail.
</ul>
## A function should have one task
Functions should usually be pretty short.
It's good to think about functions as trying to do one single thing.
## Mechanics of Writing a Function
- Function definition line - How python knows that this is a function
- Function body - Code that does the computation of the function
- Arguments - the values passed to a function
- Formal parameters - the values accepted by the function
(the arguments become the formal parameters once they are inside the function)
- Return values - value returned to the caller
If you are familiar with other languages like Java, you may have needed to declare the types of the parameters and return value. This is not necessary in Python.
```
def example_addition_function(num_1, num_2):
"""
This function adds two numbers.
example_addition_function is the function name
Parameters:
num_1: This is the first formal parameter
num_2: This is the second formal parameter
Returns:
sum of num_1 and num_2
"""
added_value = num_1 + num_2
return added_value
arg_1 = 5
arg_2 = 10
result_value = example_addition_function(arg_1, arg_2) # arg_1 and arg_2 are the arguments to the function
```
# Variable names and scope
In Python, variables have a scope (a context in which they are valid).
Variables created in a function cannot be referenced outside of a function
```
# Let's put our extra credit code in a function!
section = "Section 1"
def add_final_grades(student, grade):
print("in add_final_grades %s" % section)
gradebook.loc[student, 'final_grade'] = grade
add_final_grades('Jennifer', 99)
print(gradebook)
# Let's put our extra credit code in a function!
section = "Section 1"
def add_final_grades(student, grade):
print("in add_final_grades %s" % section)
gradebook.loc[student, 'final_grade'] = grade
if False:
section = "new"
add_final_grades('Jennifer', 99)
print(gradebook)
def print_message(message):
message_to_print = "Here is your message: " + message
print(message_to_print)
my_message = "Hello, class!"
print_message(my_message)
#print(message_to_print) # this will cause an error. This variable only exists within the function.
```
If you modify an object (like a list or a dataframe) inside of a function, the modifications will affect its value outside of the function
```
def add_name_to_list(name_list, new_name):
name_list.append(new_name)
teachers = ["Bernease", "Dave", "Joe"]
print(teachers)
add_name_to_list(teachers, "Colin")
print(teachers)
```
## Exercise: Write a function to determine if a number is prime
Below is some code that checks if a number is prime. The code has a bug in it!
```
# Determine if num is prime
# This code has a bug. What is it?
# Also, the efficiency of the code can be improved. How?
num = 3
is_prime = True
for integer in range(1, num):
if num % integer == 0:
# The "==" operator checks for equality and returns True or False.
# Note the difference between "==" and "=", which assigns a value to a variable.
#
# The "%" operator calculates the remainder of a division operation
# if the remainder is zero, integer is a divisor of num, so num is not prime
print("Not prime!")
is_prime = False
if is_prime:
print("Is prime!")
```
Once you've identified the bug in the above code, take the code and turn it into a function that takes a number as input and returns True if the number is prime and False if it is not.
See if you can find any ways to make the code more efficient.
|
github_jupyter
|
# 线性回归
:label:`sec_linear_regression`
*回归*(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。
在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系。
在机器学习领域中的大多数任务通常都与*预测*(prediction)有关。
当我们想预测一个数值时,就会涉及到回归问题。
常见的例子包括:预测价格(房屋、股票等)、预测住院时间(针对住院病人等)、
预测需求(零售销量等)。
但不是所有的*预测*都是回归问题。
在后面的章节中,我们将介绍分类问题。分类问题的目标是预测数据属于一组类别中的哪一个。
## 线性回归的基本元素
*线性回归*(linear regression)可以追溯到19世纪初,
它在回归的各种标准工具中最简单而且最流行。
线性回归基于几个简单的假设:
首先,假设自变量$\mathbf{x}$和因变量$y$之间的关系是线性的,
即$y$可以表示为$\mathbf{x}$中元素的加权和,这里通常允许包含观测值的一些噪声;
其次,我们假设任何噪声都比较正常,如噪声遵循正态分布。
为了解释*线性回归*,我们举一个实际的例子:
我们希望根据房屋的面积(平方英尺)和房龄(年)来估算房屋价格(美元)。
为了开发一个能预测房价的模型,我们需要收集一个真实的数据集。
这个数据集包括了房屋的销售价格、面积和房龄。
在机器学习的术语中,该数据集称为*训练数据集*(training data set)
或*训练集*(training set)。
每行数据(比如一次房屋交易相对应的数据)称为*样本*(sample),
也可以称为*数据点*(data point)或*数据样本*(data instance)。
我们把试图预测的目标(比如预测房屋价格)称为*标签*(label)或*目标*(target)。
预测所依据的自变量(面积和房龄)称为*特征*(feature)或*协变量*(covariate)。
通常,我们使用$n$来表示数据集中的样本数。
对索引为$i$的样本,其输入表示为$\mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top$,
其对应的标签是$y^{(i)}$。
### 线性模型
:label:`subsec_linear_model`
线性假设是指目标(房屋价格)可以表示为特征(面积和房龄)的加权和,如下面的式子:
$$\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b.$$
:eqlabel:`eq_price-area`
:eqref:`eq_price-area`中的$w_{\mathrm{area}}$和$w_{\mathrm{age}}$
称为*权重*(weight),权重决定了每个特征对我们预测值的影响。
$b$称为*偏置*(bias)、*偏移量*(offset)或*截距*(intercept)。
偏置是指当所有特征都取值为0时,预测值应该为多少。
即使现实中不会有任何房子的面积是0或房龄正好是0年,我们仍然需要偏置项。
如果没有偏置项,我们模型的表达能力将受到限制。
严格来说, :eqref:`eq_price-area`是输入特征的一个
*仿射变换*(affine transformation)。
仿射变换的特点是通过加权和对特征进行*线性变换*(linear transformation),
并通过偏置项来进行*平移*(translation)。
给定一个数据集,我们的目标是寻找模型的权重$\mathbf{w}$和偏置$b$,
使得根据模型做出的预测大体符合数据里的真实价格。
输出的预测值由输入特征通过*线性模型*的仿射变换决定,仿射变换由所选权重和偏置确定。
而在机器学习领域,我们通常使用的是高维数据集,建模时采用线性代数表示法会比较方便。
当我们的输入包含$d$个特征时,我们将预测结果$\hat{y}$
(通常使用“尖角”符号表示$y$的估计值)表示为:
$$\hat{y} = w_1 x_1 + ... + w_d x_d + b.$$
将所有特征放到向量$\mathbf{x} \in \mathbb{R}^d$中,
并将所有权重放到向量$\mathbf{w} \in \mathbb{R}^d$中,
我们可以用点积形式来简洁地表达模型:
$$\hat{y} = \mathbf{w}^\top \mathbf{x} + b.$$
:eqlabel:`eq_linreg-y`
在 :eqref:`eq_linreg-y`中,
向量$\mathbf{x}$对应于单个数据样本的特征。
用符号表示的矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$
可以很方便地引用我们整个数据集的$n$个样本。
其中,$\mathbf{X}$的每一行是一个样本,每一列是一种特征。
对于特征集合$\mathbf{X}$,预测值$\hat{\mathbf{y}} \in \mathbb{R}^n$
可以通过矩阵-向量乘法表示为:
$${\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b$$
这个过程中的求和将使用广播机制
(广播机制在 :numref:`subsec_broadcasting`中有详细介绍)。
给定训练数据特征$\mathbf{X}$和对应的已知标签$\mathbf{y}$,
线性回归的目标是找到一组权重向量$\mathbf{w}$和偏置$b$:
当给定从$\mathbf{X}$的同分布中取样的新样本特征时,
这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。
虽然我们相信给定$\mathbf{x}$预测$y$的最佳模型会是线性的,
但我们很难找到一个有$n$个样本的真实数据集,其中对于所有的$1 \leq i \leq n$,$y^{(i)}$完全等于$\mathbf{w}^\top \mathbf{x}^{(i)}+b$。
无论我们使用什么手段来观察特征$\mathbf{X}$和标签$\mathbf{y}$,
都可能会出现少量的观测误差。
因此,即使确信特征与标签的潜在关系是线性的,
我们也会加入一个噪声项来考虑观测误差带来的影响。
在开始寻找最好的*模型参数*(model parameters)$\mathbf{w}$和$b$之前,
我们还需要两个东西:
(1)一种模型质量的度量方式;
(2)一种能够更新模型以提高模型预测质量的方法。
### 损失函数
在我们开始考虑如何用模型*拟合*(fit)数据之前,我们需要确定一个拟合程度的度量。
*损失函数*(loss function)能够量化目标的*实际*值与*预测*值之间的差距。
通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。
回归问题中最常用的损失函数是平方误差函数。
当样本$i$的预测值为$\hat{y}^{(i)}$,其相应的真实标签为$y^{(i)}$时,
平方误差可以定义为以下公式:
$$l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.$$
:eqlabel:`eq_mse`
常数$\frac{1}{2}$不会带来本质的差别,但这样在形式上稍微简单一些
(因为当我们对损失函数求导后常数系数为1)。
由于训练数据集并不受我们控制,所以经验误差只是关于模型参数的函数。
为了进一步说明,来看下面的例子。
我们为一维情况下的回归问题绘制图像,如 :numref:`fig_fit_linreg`所示。

:label:`fig_fit_linreg`
由于平方误差函数中的二次方项,
估计值$\hat{y}^{(i)}$和观测值$y^{(i)}$之间较大的差异将导致更大的损失。
为了度量模型在整个数据集上的质量,我们需计算在训练集$n$个样本上的损失均值(也等价于求和)。
$$L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2.$$
在训练模型时,我们希望寻找一组参数($\mathbf{w}^*, b^*$),
这组参数能最小化在所有训练样本上的总损失。如下式:
$$\mathbf{w}^*, b^* = \operatorname*{argmin}_{\mathbf{w}, b}\ L(\mathbf{w}, b).$$
### 解析解
线性回归刚好是一个很简单的优化问题。
与我们将在本书中所讲到的其他大部分模型不同,线性回归的解可以用一个公式简单地表达出来,
这类解叫作解析解(analytical solution)。
首先,我们将偏置$b$合并到参数$\mathbf{w}$中,合并方法是在包含所有参数的矩阵中附加一列。
我们的预测问题是最小化$\|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2$。
这在损失平面上只有一个临界点,这个临界点对应于整个区域的损失极小点。
将损失关于$\mathbf{w}$的导数设为0,得到解析解:
$$\mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.$$
像线性回归这样的简单问题存在解析解,但并不是所有的问题都存在解析解。
解析解可以进行很好的数学分析,但解析解对问题的限制很严格,导致它无法广泛应用在深度学习里。
### 随机梯度下降
即使在我们无法得到解析解的情况下,我们仍然可以有效地训练模型。
在许多任务上,那些难以优化的模型效果要更好。
因此,弄清楚如何训练这些难以优化的模型是非常重要的。
本书中我们用到一种名为*梯度下降*(gradient descent)的方法,
这种方法几乎可以优化所有深度学习模型。
它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)
关于模型参数的导数(在这里也可以称为梯度)。
但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。
因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本,
这种变体叫做*小批量随机梯度下降*(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量$\mathcal{B}$,
它是由固定数量的训练样本组成的。
然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。
最后,我们将梯度乘以一个预先确定的正数$\eta$,并从当前参数的值中减掉。
我们用下面的数学公式来表示这一更新过程($\partial$表示偏导数):
$$(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b).$$
总结一下,算法的步骤如下:
(1)初始化模型参数的值,如随机初始化;
(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
对于平方损失和仿射变换,我们可以明确地写成如下形式:
$$\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\ b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}$$
:eqlabel:`eq_linreg_batch_update`
公式 :eqref:`eq_linreg_batch_update`中的$\mathbf{w}$和$\mathbf{x}$都是向量。
在这里,更优雅的向量表示法比系数表示法(如$w_1, w_2, \ldots, w_d$)更具可读性。
$|\mathcal{B}|$表示每个小批量中的样本数,这也称为*批量大小*(batch size)。
$\eta$表示*学习率*(learning rate)。
批量大小和学习率的值通常是手动预先指定,而不是通过模型训练得到的。
这些可以调整但不在训练过程中更新的参数称为*超参数*(hyperparameter)。
*调参*(hyperparameter tuning)是选择超参数的过程。
超参数通常是我们根据训练迭代结果来调整的,
而训练迭代结果是在独立的*验证数据集*(validation dataset)上评估得到的。
在训练了预先确定的若干迭代次数后(或者直到满足某些其他停止条件后),
我们记录下模型参数的估计值,表示为$\hat{\mathbf{w}}, \hat{b}$。
但是,即使我们的函数确实是线性的且无噪声,这些估计值也不会使损失函数真正地达到最小值。
因为算法会使得损失向最小值缓慢收敛,但却不能在有限的步数内非常精确地达到最小值。
线性回归恰好是一个在整个域中只有一个最小值的学习问题。
但是对于像深度神经网络这样复杂的模型来说,损失平面上通常包含多个最小值。
深度学习实践者很少会去花费大力气寻找这样一组参数,使得在*训练集*上的损失达到最小。
事实上,更难做到的是找到一组参数,这组参数能够在我们从未见过的数据上实现较低的损失,
这一挑战被称为*泛化*(generalization)。
### 用模型进行预测
给定“已学习”的线性回归模型$\hat{\mathbf{w}}^\top \mathbf{x} + \hat{b}$,
现在我们可以通过房屋面积$x_1$和房龄$x_2$来估计一个(未包含在训练数据中的)新房屋价格。
给定特征估计目标的过程通常称为*预测*(prediction)或*推断*(inference)。
本书将尝试坚持使用*预测*这个词。
虽然*推断*这个词已经成为深度学习的标准术语,但其实*推断*这个词有些用词不当。
在统计学中,*推断*更多地表示基于数据集估计参数。
当深度学习从业者与统计学家交谈时,术语的误用经常导致一些误解。
## 矢量化加速
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。
为了实现这一点,需要(**我们对计算进行矢量化,
从而利用线性代数库,而不是在Python中编写开销高昂的for循环**)。
```
%matplotlib inline
import math
import time
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l
```
为了说明矢量化为什么如此重要,我们考虑(**对向量相加的两种方法**)。
我们实例化两个全为1的10000维向量。
在一种方法中,我们将使用Python的for循环遍历向量;
在另一种方法中,我们将依赖对`+`的调用。
```
n = 10000
a = tf.ones(n)
b = tf.ones(n)
```
由于在本书中我们将频繁地进行运行时间的基准测试,所以[**我们定义一个计时器**]:
```
class Timer: #@save
"""记录多次运行时间"""
def __init__(self):
self.times = []
self.start()
def start(self):
"""启动计时器"""
self.tik = time.time()
def stop(self):
"""停止计时器并将时间记录在列表中"""
self.times.append(time.time() - self.tik)
return self.times[-1]
def avg(self):
"""返回平均时间"""
return sum(self.times) / len(self.times)
def sum(self):
"""返回时间总和"""
return sum(self.times)
def cumsum(self):
"""返回累计时间"""
return np.array(self.times).cumsum().tolist()
```
现在我们可以对工作负载进行基准测试。
首先,[**我们使用for循环,每次执行一位的加法**]。
```
c = tf.Variable(tf.zeros(n))
timer = Timer()
for i in range(n):
c[i].assign(a[i] + b[i])
f'{timer.stop():.5f} sec'
```
(**或者,我们使用重载的`+`运算符来计算按元素的和**)。
```
timer.start()
d = a + b
f'{timer.stop():.5f} sec'
```
结果很明显,第二种方法比第一种方法快得多。
矢量化代码通常会带来数量级的加速。
另外,我们将更多的数学运算放到库中,而无须自己编写那么多的计算,从而减少了出错的可能性。
## 正态分布与平方损失
:label:`subsec_normal_distribution_and_squared_loss`
接下来,我们通过对噪声分布的假设来解读平方损失目标函数。
正态分布和线性回归之间的关系很密切。
正态分布(normal distribution),也称为*高斯分布*(Gaussian distribution),
最早由德国数学家高斯(Gauss)应用于天文学研究。
简单的说,若随机变量$x$具有均值$\mu$和方差$\sigma^2$(标准差$\sigma$),其正态分布概率密度函数如下:
$$p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right).$$
下面[**我们定义一个Python函数来计算正态分布**]。
```
def normal(x, mu, sigma):
p = 1 / math.sqrt(2 * math.pi * sigma**2)
return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
```
我们现在(**可视化正态分布**)。
```
# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)
# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])
```
就像我们所看到的,改变均值会产生沿$x$轴的偏移,增加方差将会分散分布、降低其峰值。
均方误差损失函数(简称均方损失)可以用于线性回归的一个原因是:
我们假设了观测中包含噪声,其中噪声服从正态分布。
噪声正态分布如下式:
$$y = \mathbf{w}^\top \mathbf{x} + b + \epsilon,$$
其中,$\epsilon \sim \mathcal{N}(0, \sigma^2)$。
因此,我们现在可以写出通过给定的$\mathbf{x}$观测到特定$y$的*似然*(likelihood):
$$P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right).$$
现在,根据极大似然估计法,参数$\mathbf{w}$和$b$的最优值是使整个数据集的*似然*最大的值:
$$P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}).$$
根据极大似然估计法选择的估计量称为*极大似然估计量*。
虽然使许多指数函数的乘积最大化看起来很困难,
但是我们可以在不改变目标的前提下,通过最大化似然对数来简化。
由于历史原因,优化通常是说最小化而不是最大化。
我们可以改为*最小化负对数似然*$-\log P(\mathbf y \mid \mathbf X)$。
由此可以得到的数学公式是:
$$-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2.$$
现在我们只需要假设$\sigma$是某个固定常数就可以忽略第一项,
因为第一项不依赖于$\mathbf{w}$和$b$。
现在第二项除了常数$\frac{1}{\sigma^2}$外,其余部分和前面介绍的均方误差是一样的。
幸运的是,上面式子的解并不依赖于$\sigma$。
因此,在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。
## 从线性回归到深度网络
到目前为止,我们只谈论了线性模型。
尽管神经网络涵盖了更多更为丰富的模型,我们依然可以用描述神经网络的方式来描述线性模型,
从而把线性模型看作一个神经网络。
首先,我们用“层”符号来重写这个模型。
### 神经网络图
深度学习从业者喜欢绘制图表来可视化模型中正在发生的事情。
在 :numref:`fig_single_neuron`中,我们将线性回归模型描述为一个神经网络。
需要注意的是,该图只显示连接模式,即只显示每个输入如何连接到输出,隐去了权重和偏置的值。

:label:`fig_single_neuron`
在 :numref:`fig_single_neuron`所示的神经网络中,输入为$x_1, \ldots, x_d$,
因此输入层中的*输入数*(或称为*特征维度*,feature dimensionality)为$d$。
网络的输出为$o_1$,因此输出层中的*输出数*是1。
需要注意的是,输入值都是已经给定的,并且只有一个*计算*神经元。
由于模型重点在发生计算的地方,所以通常我们在计算层数时不考虑输入层。
也就是说, :numref:`fig_single_neuron`中神经网络的*层数*为1。
我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络,或称为单层神经网络。
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连,
我们将这种变换( :numref:`fig_single_neuron`中的输出层)
称为*全连接层*(fully-connected layer)或称为*稠密层*(dense layer)。
下一章将详细讨论由这些层组成的网络。
### 生物学
线性回归发明的时间(1795年)早于计算神经科学,所以将线性回归描述为神经网络似乎不合适。
当控制学家、神经生物学家沃伦·麦库洛奇和沃尔特·皮茨开始开发人工神经元模型时,
他们为什么将线性模型作为一个起点呢?
我们来看一张图片 :numref:`fig_Neuron`:
这是一张由*树突*(dendrites,输入终端)、
*细胞核*(nucleu,CPU)组成的生物神经元图片。
*轴突*(axon,输出线)和*轴突端子*(axon terminal,输出端子)
通过*突触*(synapse)与其他神经元连接。

:label:`fig_Neuron`
树突中接收到来自其他神经元(或视网膜等环境传感器)的信息$x_i$。
该信息通过*突触权重*$w_i$来加权,以确定输入的影响(即,通过$x_i w_i$相乘来激活或抑制)。
来自多个源的加权输入以加权和$y = \sum_i x_i w_i + b$的形式汇聚在细胞核中,
然后将这些信息发送到轴突$y$中进一步处理,通常会通过$\sigma(y)$进行一些非线性处理。
之后,它要么到达目的地(例如肌肉),要么通过树突进入另一个神经元。
当然,许多这样的单元可以通过正确连接和正确的学习算法拼凑在一起,
从而产生的行为会比单独一个神经元所产生的行为更有趣、更复杂,
这种想法归功于我们对真实生物神经系统的研究。
当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。
我们援引斯图尔特·罗素和彼得·诺维格谁,在他们的经典人工智能教科书
*Artificial Intelligence:A Modern Approach* :cite:`Russell.Norvig.2016`
中所说:虽然飞机可能受到鸟类的启发,但几个世纪以来,鸟类学并不是航空创新的主要驱动力。
同样地,如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。
## 小结
* 机器学习模型中的关键要素是训练数据、损失函数、优化算法,还有模型本身。
* 矢量化使数学表达上更简洁,同时运行的更快。
* 最小化目标函数和执行极大似然估计等价。
* 线性回归模型也是一个简单的神经网络。
## 练习
1. 假设我们有一些数据$x_1, \ldots, x_n \in \mathbb{R}$。我们的目标是找到一个常数$b$,使得最小化$\sum_i (x_i - b)^2$。
1. 找到最优值$b$的解析解。
1. 这个问题及其解与正态分布有什么关系?
1. 推导出使用平方误差的线性回归优化问题的解析解。为了简化问题,可以忽略偏置$b$(我们可以通过向$\mathbf X$添加所有值为1的一列来做到这一点)。
1. 用矩阵和向量表示法写出优化问题(将所有数据视为单个矩阵,将所有目标值视为单个向量)。
1. 计算损失对$w$的梯度。
1. 通过将梯度设为0、求解矩阵方程来找到解析解。
1. 什么时候可能比使用随机梯度下降更好?这种方法何时会失效?
1. 假定控制附加噪声$\epsilon$的噪声模型是指数分布。也就是说,$p(\epsilon) = \frac{1}{2} \exp(-|\epsilon|)$
1. 写出模型$-\log P(\mathbf y \mid \mathbf X)$下数据的负对数似然。
1. 你能写出解析解吗?
1. 提出一种随机梯度下降算法来解决这个问题。哪里可能出错?(提示:当我们不断更新参数时,在驻点附近会发生什么情况)你能解决这个问题吗?
[Discussions](https://discuss.d2l.ai/t/1776)
|
github_jupyter
|
## Load Model, plain 2D Conv
```
import os
os.chdir("../..")
os.getcwd()
import numpy as np
import torch
import json
from distributed.model_util import choose_model, choose_old_model, load_model, extend_model_config
from distributed.util import q_value_index_to_action
import matplotlib.pyplot as plt
model_name = "conv2d"
model_config_path = "src/config/model_spec/conv_agents_slim.json"
trained_model_path = "threshold_networks/5/72409/conv2d_5_72409.pt"
with open(model_config_path, "r") as jsonfile:
model_config = json.load(jsonfile)[model_name]
code_size, stack_depth = 5, 5
syndrome_size = code_size + 1
model_config = extend_model_config(model_config, syndrome_size, stack_depth)
model_config["network_size"] = "slim"
model_config["rl_type"] = "q"
model = choose_model(model_name, model_config, transfer_learning=0)
model, *_ = load_model(model, trained_model_path, model_device="cpu")
from evaluation.final_evaluation import main_evaluation
all_ground_states = 0
for i in range(10):
is_ground_state, n_syndromes, n_loops = main_evaluation(
model,
model.device,
epsilon=0.0,
code_size=code_size,
stack_depth=stack_depth,
block=False,
verbosity=0,
rl_type=model_config["rl_type"]
)
all_ground_states += is_ground_state
print(all_ground_states)
print(all_ground_states)
```
## Prepare States
```
all_states = []
state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
state[-2:, 1, 2] = 1
all_states.append(state)
state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
state[-1, 1, 2] = 1
state[-1, 2, 3] = 1
all_states.append(state)
state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
state[-1, 2, 3] = 1
all_states.append(state)
state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
state[-2:, 1, 2] = 1
state[-2:, 2, 3] = 1
state[-1:, 2, 3] = 0
all_states.append(state)
state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
state[:, 1, 2] = 1
state[:, 2, 3] = 1
state[-1, 2, 3] = 0
all_states.append(state)
full_error_state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
full_error_state[:, 1, 2] = 1
full_error_state[:, 2, 3] = 1
all_states.append(full_error_state)
torch_all_states = torch.stack(all_states)
# for i in range(0, stack_depth, 2):
# state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
# state[:, 1, 2] = 1
# state[:, 2, 3] = 1
# state[i, 2, 3] = 0
# all_states.append(state)
# for i in range(0, stack_depth, 2):
# state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
# state[i, 2, 3] = 1
# all_states.append(state)
# state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
# state[-1, 1, 2] = 1
# state[-1, 2, 3] = 1
# all_states.append(state)
# state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
# state[-2:, 1, 2] = 1
# state[-2:, 2, 3] = 1
# state[-1:, 2, 3] = 0
# all_states.append(state)
# state = torch.zeros((stack_depth, syndrome_size, syndrome_size), dtype=torch.float32)
# state[-2:, 1, 2] = 1
# all_states.append(state)
# torch_all_states = torch.stack(all_states)
def calculate_state_image(state, stack_depth, syndrome_size):
layer_discount_factor = 0.3
layer_exponents = np.arange(stack_depth - 1, -1, -1)
layer_rewards = np.power(layer_discount_factor, layer_exponents)
layer_rewards = torch.tensor(layer_rewards, dtype=torch.float32)
state_image = torch.zeros((syndrome_size, syndrome_size), dtype=torch.float32)
for j, layer in enumerate(state):
tmp_layer = layer * layer_rewards[j]
state_image += tmp_layer
return state_image
```
## Do the plotting
```
k = 1
# stack_depth = 5
# syndrome_size = 5
from matplotlib import colors
plt.rcParams.update({"font.size": 15})
fig, ax = plt.subplots(1, 3, figsize=(18, 8), gridspec_kw={"width_ratios": [4, 4, 8], "wspace": 0.02, "hspace": 0.0},)
plot_colors = ["#ffffff", "#404E5C", "#F76C5E", "#E9B44C", "#7F95D1", "#CF1259", "#669900"]
markers = ["o", "v", "^", "X", "d", "P"]
cmap = colors.ListedColormap(plot_colors)
boundaries = range(len(torch_all_states))
norm = colors.BoundaryNorm(boundaries, cmap.N, clip=True)
markersize = 70
img_separation = 1
column_width = 8
syndrome_locations = np.array([[1, 2],[2, 3]])
column_filler = np.zeros((stack_depth, 1))
image_filler = np.zeros((stack_depth, img_separation))
img_width = 2 * column_width + img_separation
vline_locations = np.array([
column_width + i * img_width for i in range(len(torch_all_states))
])
image_separators_left = np.array([
(i+1) * 2 * column_width + i * img_separation for i in range(len(torch_all_states))
])
# image_separators_left[1:] += img_separation
image_separators_right = [
i * img_width for i in range(len(torch_all_states))
]
hline_locations = range(0, stack_depth + 1)
complete_image_list = []
for i, state in enumerate(torch_all_states):
ii = i + 1
# TODO: concat the columns multi-pixel wide with an empty space in between
# and empty spaces between each state's column
column1 = np.vstack(state[:, syndrome_locations[0, 0], syndrome_locations[0, 1]])
repeated_column1 = np.repeat(column1, column_width, axis=1)
column2 = np.vstack(state[:, syndrome_locations[1, 0], syndrome_locations[1, 1]])
repeated_column2 = np.repeat(column2, column_width, axis=1)
state_img = np.concatenate((repeated_column1, repeated_column2), axis=1) * ii
complete_image_list.append(state_img)
if i < len(torch_all_states) - 1:
complete_image_list.append(image_filler)
complete_image_array = np.concatenate(complete_image_list, axis=1)
ax2 = ax[2].twinx()
for i, state in enumerate(torch_all_states):
ii = i + 1
q_values = model(state.unsqueeze(0))
q_values = q_values.detach().squeeze().clone().numpy()
ind = np.argpartition(q_values, -k)[-k:]
max_ind = ind
action = q_value_index_to_action(ind[0], code_size)
ind = np.append(ind, [max(ind[0]-1, 0), min(ind[0]+1, len(q_values)-1)])
ind = np.sort(ind)
print(f"{ind=}")
q_hist = np.histogram(q_values)
if i < 3:
ax[0].plot(range(len(q_values)), q_values, label=str(ii), color=plot_colors[ii])
ax[0].scatter(
max_ind, q_values[max_ind], marker=markers[i], c=plot_colors[ii], s=markersize
)
# marker=markers[i], c=plot_colors[ii]
else:
ax[1].plot(range(len(q_values)), q_values, label=str(ii), color=plot_colors[ii]),
ax[1].scatter(
max_ind, q_values[max_ind], marker=markers[i], c=plot_colors[ii], s=markersize
)
ax2.imshow(
complete_image_array, vmin=0, vmax=6, cmap=cmap, aspect='auto', origin='lower'
)
ax2.axvline(x=vline_locations[i] - 0.5, linestyle=':', color='black')
ax2.axhline(y=hline_locations[i] - 0.5, linestyle=':', color='black')
ax2.axvline(x=image_separators_left[i] - 0.5, color='black')
ax2.axvline(x=image_separators_right[i] - 0.5, color='black')
ax2.text(x=image_separators_left[i] - 1.8 * column_width, y=1, s=f"{action}")
ax[0].set(
ylim=(40, 120),
xlabel="Q Value Index",
ylabel="Q Value",
title=f"Q Activation",
)
ax[1].set(
ylim=(40, 120),
xlabel="Q Value Index",
title=f"Q Activation",
)
all_vline_locations = np.concatenate(
[vline_locations - 0.5 * column_width, vline_locations + 0.5 * column_width]
)
x_tick_labels = [f"{tuple(syndrome_locations[0])}"] * len(torch_all_states)
x_tick_labels2 = [f"{tuple(syndrome_locations[1])}"] * len(torch_all_states)
x_tick_labels.extend(x_tick_labels2)
# , f"{tuple(syndrome_locations[1])}"] * len(torch_all_states)
print(f"{x_tick_labels}")
ax2.set(xlabel="", ylabel="h", title="Isolated Syndrome States")
ax[2].set_yticks(all_vline_locations)
ax[2].set_yticks([])
ax[2].set_yticklabels([])
ax2.set_xticklabels(x_tick_labels)
ax2.set_xticks(all_vline_locations)
ax[1].set_yticklabels([])
ax[0].legend()
ax[1].legend()
plt.savefig("plots/q_value_activation.pdf", bbox_inches="tight")
```
## 3D Conv
```
model_name = "conv3d"
model_config_path_3d = "src/config/model_spec/conv_agents_slim.json"
trained_model_path_3d = "threshold_networks/5/69312/conv3d_5_69312.pt"
with open(model_config_path_3d, "r") as jsonfile:
model_config_3d = json.load(jsonfile)[model_name]
code_size, stack_depth = 5, 5
syndrome_size = code_size + 1
model_config_3d = extend_model_config(model_config_3d, syndrome_size, stack_depth)
model_config_3d["network_size"] = "slim"
model_config_3d["rl_type"] = "q"
model3d = choose_old_model(model_name, model_config_3d)
model3d, *_ = load_model(model3d, trained_model_path_3d, model_device="cpu")
from evaluation.final_evaluation import main_evaluation
all_ground_states = 0
for i in range(10):
is_ground_state, n_syndromes, n_loops = main_evaluation(
model3d,
model3d.device,
epsilon=0.0,
code_size=code_size,
stack_depth=stack_depth,
block=False,
verbosity=0,
rl_type=model_config_3d["rl_type"]
)
all_ground_states += is_ground_state
print(all_ground_states)
print(all_ground_states)
k = 1
# stack_depth = 5
# syndrome_size = 5
from matplotlib import colors
plt.rcParams.update({"font.size": 15})
fig, ax = plt.subplots(1, 3, figsize=(18, 8), gridspec_kw={"width_ratios": [4, 4, 8], "wspace": 0.02, "hspace": 0.0},)
plot_colors = ["#ffffff", "#404E5C", "#F76C5E", "#E9B44C", "#7F95D1", "#CF1259", "#669900"]
markers = ["o", "v", "^", "X", "d", "P"]
cmap = colors.ListedColormap(plot_colors)
boundaries = range(len(torch_all_states))
norm = colors.BoundaryNorm(boundaries, cmap.N, clip=True)
markersize = 70
img_separation = 1
column_width = 8
syndrome_locations = np.array([[1, 2],[2, 3]])
column_filler = np.zeros((stack_depth, 1))
image_filler = np.zeros((stack_depth, img_separation))
img_width = 2 * column_width + img_separation
vline_locations = np.array([
column_width + i * img_width for i in range(len(torch_all_states))
])
image_separators_left = np.array([
(i+1) * 2 * column_width + i * img_separation for i in range(len(torch_all_states))
])
# image_separators_left[1:] += img_separation
image_separators_right = [
i * img_width for i in range(len(torch_all_states))
]
hline_locations = range(0, stack_depth + 1)
complete_image_list = []
for i, state in enumerate(torch_all_states):
ii = i + 1
# TODO: concat the columns multi-pixel wide with an empty space in between
# and empty spaces between each state's column
column1 = np.vstack(state[:, syndrome_locations[0, 0], syndrome_locations[0, 1]])
repeated_column1 = np.repeat(column1, column_width, axis=1)
column2 = np.vstack(state[:, syndrome_locations[1, 0], syndrome_locations[1, 1]])
repeated_column2 = np.repeat(column2, column_width, axis=1)
state_img = np.concatenate((repeated_column1, repeated_column2), axis=1) * ii
complete_image_list.append(state_img)
if i < len(torch_all_states) - 1:
complete_image_list.append(image_filler)
complete_image_array = np.concatenate(complete_image_list, axis=1)
ax2 = ax[2].twinx()
for i, state in enumerate(torch_all_states):
ii = i + 1
q_values = model3d(state.unsqueeze(0))
q_values = q_values.detach().squeeze().clone().numpy()
ind = np.argpartition(q_values, -k)[-k:]
max_ind = ind
action = q_value_index_to_action(ind[0], code_size)
ind = np.append(ind, [max(ind[0]-1, 0), min(ind[0]+1, len(q_values)-1)])
ind = np.sort(ind)
print(f"{ind=}")
q_hist = np.histogram(q_values)
if i < 3:
ax[0].plot(range(len(q_values)), q_values, label=str(ii), color=plot_colors[ii])
ax[0].scatter(
max_ind, q_values[max_ind], marker=markers[i], c=plot_colors[ii], s=markersize
)
# marker=markers[i], c=plot_colors[ii]
else:
ax[1].plot(range(len(q_values)), q_values, label=str(ii), color=plot_colors[ii]),
ax[1].scatter(
max_ind, q_values[max_ind], marker=markers[i], c=plot_colors[ii], s=markersize
)
ax2.imshow(
complete_image_array, vmin=0, vmax=6, cmap=cmap, aspect='auto', origin='lower'
)
ax2.axvline(x=vline_locations[i] - 0.5, linestyle=':', color='black')
ax2.axhline(y=hline_locations[i] - 0.5, linestyle=':', color='black')
ax2.axvline(x=image_separators_left[i] - 0.5, color='black')
ax2.axvline(x=image_separators_right[i] - 0.5, color='black')
ax2.text(x=image_separators_left[i] - 1.8 * column_width, y=1, s=f"{action}")
ax[0].set(
ylim=(40, 100),
xlabel="Q Value Index",
ylabel="Q Value",
title=f"Q Activation",
)
ax[1].set(
ylim=(40, 100),
xlabel="Q Value Index",
title=f"Q Activation",
)
all_vline_locations = np.concatenate(
[vline_locations - 0.5 * column_width, vline_locations + 0.5 * column_width]
)
x_tick_labels = [f"{tuple(syndrome_locations[0])}"] * len(torch_all_states)
x_tick_labels2 = [f"{tuple(syndrome_locations[1])}"] * len(torch_all_states)
x_tick_labels.extend(x_tick_labels2)
# , f"{tuple(syndrome_locations[1])}"] * len(torch_all_states)
print(f"{x_tick_labels}")
ax2.set(xlabel="", ylabel="h", title="Isolated Syndrome States")
ax[2].set_yticks(all_vline_locations)
ax[2].set_yticks([])
ax[2].set_yticklabels([])
ax2.set_xticklabels(x_tick_labels)
ax2.set_xticks(all_vline_locations)
ax[1].set_yticklabels([])
ax[0].legend()
ax[1].legend()
plt.savefig("plots/q_value_activation_3d.pdf", bbox_inches="tight")
from distributed.util import select_actions
from surface_rl_decoder.surface_code import SurfaceCode
from surface_rl_decoder.surface_code_util import create_syndrome_output_stack
# q_values = model3d(full_error_state)
action, _ = select_actions(full_error_state.unsqueeze(0), model3d, code_size)
sc = SurfaceCode(code_size=code_size, stack_depth=stack_depth)
sc.qubits[:, 1, 2] = 1
sc.state = create_syndrome_output_stack(
sc.qubits, sc.vertex_mask, sc.plaquette_mask
)
np.argwhere(sc.state)
from copy import deepcopy
torch_state = torch.tensor(deepcopy(sc.state), dtype=torch.float32)
action, _ = select_actions(torch_state.unsqueeze(0), model3d, code_size)
action
new_state, *_ = sc.step(action[0])
torch_state = torch.tensor(deepcopy(sc.state), dtype=torch.float32)
action, _ = select_actions(torch_state.unsqueeze(0), model3d, code_size)
action
new_state, *_ = sc.step(action[0])
new_state
```
|
github_jupyter
|
```
ls ../test-data/
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tables as tb
import h5py
import dask.dataframe as dd
import dask.bag as db
import blaze
fname = '../test-data/EQY_US_ALL_BBO_201402/EQY_US_ALL_BBO_20140206.h5'
max_sym = '/SPY/no_suffix'
fname = '../test-data/small_test_data_public.h5'
max_sym = '/IXQAJE/no_suffix'
# by default, this will be read-only
taq_tb = tb.open_file(fname)
%%time
rec_counts = {curr._v_pathname: len(curr)
for curr in taq_tb.walk_nodes('/', 'Table')}
# What's our biggest table? (in bytes)
max(rec_counts.values()) * 91 / 2 ** 20 # I think it's 91 bytes...
```
Anyway, under a gigabyte. So, nothing to worry about even if we have 24 cores.
```
# But what symbol is that?
max_sym = None
max_rows = 0
for sym, rows in rec_counts.items():
if rows > max_rows:
max_rows = rows
max_sym = sym
max_sym, max_rows
```
Interesting... the S&P 500 ETF
```
# Most symbols also have way less rows - note this is log xvals
plt.hist(list(rec_counts.values()), bins=50, log=True)
plt.show()
```
## Doing some compute
We'll use a "big" table to get some sense of timings
```
spy = taq_tb.get_node(max_sym)
# PyTables is record oriented...
%timeit np.mean(list(x['Bid_Price'] for x in spy.iterrows()))
# But this is faster...
%timeit np.mean(spy[:]['Bid_Price'])
np.mean(spy[:]['Bid_Price'])
```
# Using numexpr?
numexpr is currently not set up to do reductions via HDF5. I've opened an issue here:
https://github.com/PyTables/PyTables/issues/548
```
spy_bp = spy.cols.Bid_Price
# this works...
np.mean(spy_bp)
# But it can't use numexpr
expr = tb.Expr('sum(spy_bp)')
# You can use numexpr to get the values of the column... but that's silly
# (sum doesn't work right, and the axis argument is non-functional)
%timeit result = expr.eval().mean()
tb.Expr('spy_bp').eval().mean()
```
# h5py
```
taq_tb.close()
%%time
spy_h5py = h5py.File(fname)[max_sym]
np.mean(spy_h5py['Bid_Price'])
```
h5py may be a *touch* faster than pytables for this kind of usage. But why does pandas use pytables?
```
%%timeit
np.mean(spy_h5py['Bid_Price'])
```
# Dask
It seems that there should be no need to, e.g., use h5py - but dask's read_hdf doens't seem to be working nicely...
```
taq_tb.close()
```
spy_h5py = h5py.File(fname)[max_sym]
```
store = pd.HDFStore(fname)
store = pd.HDFStore('../test-data/')
# this is a fine way to iterate over our datasets (in addition to what's available in PyTables and h5py)
it = store.items()
key, tab = next(it)
tab
# The columns argument doesn't seem to work...
store.select(max_sym, columns=['Bid_Price']).head()
# columns also doesn't work here...
pd.read_hdf(fname, max_sym, columns=['Bid_Price']).head()
# So we use h5py (actually, pytables appears faster...)
spy_dask = dd.from_array(spy_h5py)
mean_job = spy_dask['Bid_Price'].mean()
mean_job.compute()
# This is appreciably slower than directly computing the mean w/ numpy
%timeit mean_job.compute()
```
## Dask for an actual distributed task (but only on one file for now)
```
class DDFs:
# A (key, table) list
datasets = []
dbag = None
def __init__(self, h5fname):
h5in = h5py.File(h5fname)
h5in.visititems(self.collect_dataset)
def collect_dataset(self, key, table):
if isinstance(table, h5py.Dataset):
self.datasets.append(dd.from_array(table)['Bid_Price'].mean())
def compute_mean(self):
# This is still very slow!
self.results = {key: result for key, result in dd.compute(*self.datasets)}
%%time
ddfs = DDFs(fname)
ddfs.datasets[:5]
len(ddfs.datasets)
dd.compute?
%%time
results = dd.compute(*ddfs.datasets[:20])
import dask.multiprocessing
%%time
# This crashes out throwing lots of KeyErrors
results = dd.compute(*ddfs.datasets[:20], get=dask.multiprocessing.get)
results[0]
```
This ends up being a *little* faster than just using blaze (see below), but about half the time is spent setting thigs up in Dask.
```
from dask import delayed
@delayed
def mean_column(key, data, column='Bid_Price'):
return key, blaze.data(data)[column].mean()
class DDFs:
# A (key, table) list
datasets = []
def __init__(self, h5fname):
h5in = h5py.File(h5fname)
h5in.visititems(self.collect_dataset)
def collect_dataset(self, key, table):
if isinstance(table, h5py.Dataset):
self.datasets.append(mean_column(key, table))
def compute_mean(self, limit=None):
# Note that a limit of None includes all values
self.results = {key: result for key, result in dd.compute(*self.datasets[:limit])}
%%time
ddfs = DDFs(fname)
%%time
ddfs.compute_mean()
next(iter(ddfs.results.items()))
# You can also compute individual results as needed
ddfs.datasets[0].compute()
```
# Blaze?
Holy crap!
```
spy_blaze = blaze.data(spy_h5py)
%time
spy_blaze['Ask_Price'].mean()
taq_tb = tb.open_file(fname)
spy_tb = taq_tb.get_node(max_sym)
spy_blaze = blaze.data(spy_tb)
%time spy_blaze['Bid_Price'].mean()
taq_tb.close()
```
## Read directly with Blaze
Somehow this is not as impressive
```
%%time
blaze_h5_file = blaze.data(fname)
# This is rather nice
blaze_h5_file.SPY.no_suffix.Bid_Price.mean()
blaze_h5_file.ZFKOJB.no_suffix.Bid_Price.mean()
```
# Do some actual compute with Blaze
```
taq_h5py = h5py.File(fname)
class SymStats:
means = {}
def compute_stats(self, key, table):
if isinstance(table, h5py.Dataset):
self.means[key] = blaze.data(table)['Bid_Price'].mean()
ss = SymStats()
%time taq_h5py.visititems(ss.compute_stats)
means = iter(ss.means.items())
next(means)
ss.means['SPY/no_suffix']
```
# Pandas?
### To load with Pandas, you need to close the pytables session
```
taq_tb = tb.open_file(fname)
taq_tb.close()
pd.read_hdf?
pd.read_hdf(fname, max_sym, start=0, stop=1, chunksize=1)
max_sym
fname
%%timeit
node = taq_tb.get_node(max_sym)
pd.DataFrame.from_records(node[0:1])
%%timeit
# I've also tried this with `.get_node()`, same speed
pd.DataFrame.from_records(taq_tb.root.IXQAJE.no_suffix)
%%timeit
pd.read_hdf(fname, max_sym)
# Pandas has optimizations it likes to do with
%timeit spy_df = pd.read_hdf(fname, max_sym)
# Actually do it
spy_df = pd.read_hdf(fname, max_sym)
# This is fast, but loading is slow...
%timeit spy_df.Bid_Price.mean()
```
|
github_jupyter
|
**Copyright 2021 The TensorFlow Authors.**
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/model_optimization/guide/combine/pcqat_example"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/model-optimization/blob/master/tensorflow_model_optimization/g3doc/guide/combine/pcqat_example.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/model-optimization/blob/master/tensorflow_model_optimization/g3doc/guide/combine/pcqat_example.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/model-optimization/tensorflow_model_optimization/g3doc/guide/combine/pcqat_example.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
# Sparsity and cluster preserving quantization aware training (PCQAT) Keras example
## Overview
This is an end to end example showing the usage of the **sparsity and cluster preserving quantization aware training (PCQAT)** API, part of the TensorFlow Model Optimization Toolkit's collaborative optimization pipeline.
### Other pages
For an introduction to the pipeline and other available techniques, see the [collaborative optimization overview page](https://www.tensorflow.org/model_optimization/guide/combine/collaborative_optimization).
### Contents
In the tutorial, you will:
1. Train a `tf.keras` model for the MNIST dataset from scratch.
2. Fine-tune the model with pruning and see the accuracy and observe that the model was successfully pruned.
3. Apply sparsity preserving clustering on the pruned model and observe that the sparsity applied earlier has been preserved.
4. Apply QAT and observe the loss of sparsity and clusters.
5. Apply PCQAT and observe that both sparsity and clustering applied earlier have been preserved.
6. Generate a TFLite model and observe the effects of applying PCQAT on it.
7. Compare the sizes of the different models to observe the compression benefits of applying sparsity followed by the collaborative optimization techniques of sparsity preserving clustering and PCQAT.
8. Compare the accurracy of the fully optimized model with the un-optimized baseline model accuracy.
## Setup
You can run this Jupyter Notebook in your local [virtualenv](https://www.tensorflow.org/install/pip?lang=python3#2.-create-a-virtual-environment-recommended) or [colab](https://colab.sandbox.google.com/). For details of setting up dependencies, please refer to the [installation guide](https://www.tensorflow.org/model_optimization/guide/install).
```
! pip install -q tensorflow-model-optimization
import tensorflow as tf
import numpy as np
import tempfile
import zipfile
import os
```
## Train a tf.keras model for MNIST to be pruned and clustered
```
# Load MNIST dataset
mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Normalize the input image so that each pixel value is between 0 to 1.
train_images = train_images / 255.0
test_images = test_images / 255.0
model = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=(28, 28)),
tf.keras.layers.Reshape(target_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(filters=12, kernel_size=(3, 3),
activation=tf.nn.relu),
tf.keras.layers.MaxPooling2D(pool_size=(2, 2)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10)
])
opt = tf.keras.optimizers.Adam(learning_rate=1e-3)
# Train the digit classification model
model.compile(optimizer=opt,
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.fit(
train_images,
train_labels,
validation_split=0.1,
epochs=10
)
```
### Evaluate the baseline model and save it for later usage
```
_, baseline_model_accuracy = model.evaluate(
test_images, test_labels, verbose=0)
print('Baseline test accuracy:', baseline_model_accuracy)
_, keras_file = tempfile.mkstemp('.h5')
print('Saving model to: ', keras_file)
tf.keras.models.save_model(model, keras_file, include_optimizer=False)
```
## Prune and fine-tune the model to 50% sparsity
Apply the `prune_low_magnitude()` API to achieve the pruned model that is to be clustered in the next step. Refer to the [pruning comprehensive guide](https://www.tensorflow.org/model_optimization/guide/pruning/comprehensive_guide) for more information on the pruning API.
### Define the model and apply the sparsity API
Note that the pre-trained model is used.
```
import tensorflow_model_optimization as tfmot
prune_low_magnitude = tfmot.sparsity.keras.prune_low_magnitude
pruning_params = {
'pruning_schedule': tfmot.sparsity.keras.ConstantSparsity(0.5, begin_step=0, frequency=100)
}
callbacks = [
tfmot.sparsity.keras.UpdatePruningStep()
]
pruned_model = prune_low_magnitude(model, **pruning_params)
# Use smaller learning rate for fine-tuning
opt = tf.keras.optimizers.Adam(learning_rate=1e-5)
pruned_model.compile(
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=opt,
metrics=['accuracy'])
```
### Fine-tune the model, check sparsity, and evaluate the accuracy against baseline
Fine-tune the model with pruning for 3 epochs.
```
# Fine-tune model
pruned_model.fit(
train_images,
train_labels,
epochs=3,
validation_split=0.1,
callbacks=callbacks)
```
Define helper functions to calculate and print the sparsity and clusters of the model.
```
def print_model_weights_sparsity(model):
for layer in model.layers:
if isinstance(layer, tf.keras.layers.Wrapper):
weights = layer.trainable_weights
else:
weights = layer.weights
for weight in weights:
if "kernel" not in weight.name or "centroid" in weight.name:
continue
weight_size = weight.numpy().size
zero_num = np.count_nonzero(weight == 0)
print(
f"{weight.name}: {zero_num/weight_size:.2%} sparsity ",
f"({zero_num}/{weight_size})",
)
def print_model_weight_clusters(model):
for layer in model.layers:
if isinstance(layer, tf.keras.layers.Wrapper):
weights = layer.trainable_weights
else:
weights = layer.weights
for weight in weights:
# ignore auxiliary quantization weights
if "quantize_layer" in weight.name:
continue
if "kernel" in weight.name:
unique_count = len(np.unique(weight))
print(
f"{layer.name}/{weight.name}: {unique_count} clusters "
)
```
Let's strip the pruning wrapper first, then check that the model kernels were correctly pruned.
```
stripped_pruned_model = tfmot.sparsity.keras.strip_pruning(pruned_model)
print_model_weights_sparsity(stripped_pruned_model)
```
## Apply sparsity preserving clustering and check its effect on model sparsity in both cases
Next, apply sparsity preserving clustering on the pruned model and observe the number of clusters and check that the sparsity is preserved.
```
import tensorflow_model_optimization as tfmot
from tensorflow_model_optimization.python.core.clustering.keras.experimental import (
cluster,
)
cluster_weights = tfmot.clustering.keras.cluster_weights
CentroidInitialization = tfmot.clustering.keras.CentroidInitialization
cluster_weights = cluster.cluster_weights
clustering_params = {
'number_of_clusters': 8,
'cluster_centroids_init': CentroidInitialization.KMEANS_PLUS_PLUS,
'preserve_sparsity': True
}
sparsity_clustered_model = cluster_weights(stripped_pruned_model, **clustering_params)
sparsity_clustered_model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
print('Train sparsity preserving clustering model:')
sparsity_clustered_model.fit(train_images, train_labels,epochs=3, validation_split=0.1)
```
Strip the clustering wrapper first, then check that the model is correctly pruned and clustered.
```
stripped_clustered_model = tfmot.clustering.keras.strip_clustering(sparsity_clustered_model)
print("Model sparsity:\n")
print_model_weights_sparsity(stripped_clustered_model)
print("\nModel clusters:\n")
print_model_weight_clusters(stripped_clustered_model)
```
## Apply QAT and PCQAT and check effect on model clusters and sparsity
Next, apply both QAT and PCQAT on the sparse clustered model and observe that PCQAT preserves weight sparsity and clusters in your model. Note that the stripped model is passed to the QAT and PCQAT API.
```
# QAT
qat_model = tfmot.quantization.keras.quantize_model(stripped_clustered_model)
qat_model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
print('Train qat model:')
qat_model.fit(train_images, train_labels, batch_size=128, epochs=1, validation_split=0.1)
# PCQAT
quant_aware_annotate_model = tfmot.quantization.keras.quantize_annotate_model(
stripped_clustered_model)
pcqat_model = tfmot.quantization.keras.quantize_apply(
quant_aware_annotate_model,
tfmot.experimental.combine.Default8BitClusterPreserveQuantizeScheme(preserve_sparsity=True))
pcqat_model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
print('Train pcqat model:')
pcqat_model.fit(train_images, train_labels, batch_size=128, epochs=1, validation_split=0.1)
print("QAT Model clusters:")
print_model_weight_clusters(qat_model)
print("\nQAT Model sparsity:")
print_model_weights_sparsity(qat_model)
print("\nPCQAT Model clusters:")
print_model_weight_clusters(pcqat_model)
print("\nPCQAT Model sparsity:")
print_model_weights_sparsity(pcqat_model)
```
## See compression benefits of PCQAT model
Define helper function to get zipped model file.
```
def get_gzipped_model_size(file):
# It returns the size of the gzipped model in kilobytes.
_, zipped_file = tempfile.mkstemp('.zip')
with zipfile.ZipFile(zipped_file, 'w', compression=zipfile.ZIP_DEFLATED) as f:
f.write(file)
return os.path.getsize(zipped_file)/1000
```
Observe that applying sparsity, clustering and PCQAT to a model yields significant compression benefits.
```
# QAT model
converter = tf.lite.TFLiteConverter.from_keras_model(qat_model)
converter.optimizations = [tf.lite.Optimize.DEFAULT]
qat_tflite_model = converter.convert()
qat_model_file = 'qat_model.tflite'
# Save the model.
with open(qat_model_file, 'wb') as f:
f.write(qat_tflite_model)
# PCQAT model
converter = tf.lite.TFLiteConverter.from_keras_model(pcqat_model)
converter.optimizations = [tf.lite.Optimize.DEFAULT]
pcqat_tflite_model = converter.convert()
pcqat_model_file = 'pcqat_model.tflite'
# Save the model.
with open(pcqat_model_file, 'wb') as f:
f.write(pcqat_tflite_model)
print("QAT model size: ", get_gzipped_model_size(qat_model_file), ' KB')
print("PCQAT model size: ", get_gzipped_model_size(pcqat_model_file), ' KB')
```
## See the persistence of accuracy from TF to TFLite
Define a helper function to evaluate the TFLite model on the test dataset.
```
def eval_model(interpreter):
input_index = interpreter.get_input_details()[0]["index"]
output_index = interpreter.get_output_details()[0]["index"]
# Run predictions on every image in the "test" dataset.
prediction_digits = []
for i, test_image in enumerate(test_images):
if i % 1000 == 0:
print(f"Evaluated on {i} results so far.")
# Pre-processing: add batch dimension and convert to float32 to match with
# the model's input data format.
test_image = np.expand_dims(test_image, axis=0).astype(np.float32)
interpreter.set_tensor(input_index, test_image)
# Run inference.
interpreter.invoke()
# Post-processing: remove batch dimension and find the digit with highest
# probability.
output = interpreter.tensor(output_index)
digit = np.argmax(output()[0])
prediction_digits.append(digit)
print('\n')
# Compare prediction results with ground truth labels to calculate accuracy.
prediction_digits = np.array(prediction_digits)
accuracy = (prediction_digits == test_labels).mean()
return accuracy
```
Evaluate the model, which has been pruned, clustered and quantized, and then see that the accuracy from TensorFlow persists in the TFLite backend.
```
interpreter = tf.lite.Interpreter(pcqat_model_file)
interpreter.allocate_tensors()
pcqat_test_accuracy = eval_model(interpreter)
print('Pruned, clustered and quantized TFLite test_accuracy:', pcqat_test_accuracy)
print('Baseline TF test accuracy:', baseline_model_accuracy)
```
## Conclusion
In this tutorial, you learned how to create a model, prune it using the `prune_low_magnitude()` API, and apply sparsity preserving clustering using the `cluster_weights()` API to preserve sparsity while clustering the weights.
Next, sparsity and cluster preserving quantization aware training (PCQAT) was applied to preserve model sparsity and clusters while using QAT. The final PCQAT model was compared to the QAT one to show that sparsity and clusters are preserved in the former and lost in the latter.
Next, the models were converted to TFLite to show the compression benefits of chaining sparsity, clustering, and PCQAT model optimization techniques and the TFLite model was evaluated to ensure that the accuracy persists in the TFLite backend.
Finally, the PCQAT TFLite model accuracy was compared to the pre-optimization baseline model accuracy to show that collaborative optimization techniques managed to achieve the compression benefits while maintaining a similar accuracy compared to the original model.
|
github_jupyter
|
# Testing cnn for classifying universes
Nov 10, 2020
```
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
from torchsummary import summary
from torch.utils.data import DataLoader, TensorDataset
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
import time
from datetime import datetime
import glob
import pickle
import yaml
import logging
%matplotlib widget
```
## Modules
```
def f_load_config(config_file):
with open(config_file) as f:
config = yaml.load(f, Loader=yaml.SafeLoader)
return config
### Transformation functions for image pixel values
def f_transform(x):
return 2.*x/(x + 4.) - 1.
def f_invtransform(s):
return 4.*(1. + s)/(1. - s)
# custom weights initialization called on netG and netD
def weights_init(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
# Generator Code
class View(nn.Module):
def __init__(self, shape):
super(View, self).__init__()
self.shape = shape
def forward(self, x):
return x.view(*self.shape)
class Discriminator(nn.Module):
def __init__(self, ngpu, nz,nc,ndf,n_classes,kernel_size,stride,d_padding):
super(Discriminator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is (nc) x 64 x 64
# nn.Conv2d(in_channels, out_channels, kernel_size,stride,padding,output_padding,groups,bias, Dilation,padding_mode)
nn.Conv2d(nc, ndf,kernel_size, stride, d_padding, bias=True),
nn.BatchNorm2d(ndf,eps=1e-05, momentum=0.9, affine=True),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf) x 32 x 32
nn.Conv2d(ndf, ndf * 2, kernel_size, stride, d_padding, bias=True),
nn.BatchNorm2d(ndf * 2,eps=1e-05, momentum=0.9, affine=True),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*2) x 16 x 16
nn.Conv2d(ndf * 2, ndf * 4, kernel_size, stride, d_padding, bias=True),
nn.BatchNorm2d(ndf * 4,eps=1e-05, momentum=0.9, affine=True),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*4) x 8 x 8
nn.Conv2d(ndf * 4, ndf * 8, kernel_size, stride, d_padding, bias=True),
nn.BatchNorm2d(ndf * 8,eps=1e-05, momentum=0.9, affine=True),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*8) x 4 x 4
nn.Flatten(),
nn.Linear(nc*ndf*8*8*8, n_classes)
# nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
```
## Main code
```
torch.backends.cudnn.benchmark=True
t0=time.time()
#################################
###### Initialize variables #######
config_file='config_128.yaml'
config_dict=f_load_config(config_file)
print(config_dict)
workers=config_dict['training']['workers']
nc,nz,ngf,ndf=config_dict['training']['nc'],config_dict['training']['nz'],config_dict['training']['ngf'],config_dict['training']['ndf']
lr,beta1=config_dict['training']['lr'],config_dict['training']['beta1']
kernel_size,stride=config_dict['training']['kernel_size'],config_dict['training']['stride']
g_padding,d_padding=config_dict['training']['g_padding'],config_dict['training']['d_padding']
flip_prob=config_dict['training']['flip_prob']
image_size=config_dict['data']['image_size']
checkpoint_size=config_dict['data']['checkpoint_size']
num_imgs=config_dict['data']['num_imgs']
ip_fname=config_dict['data']['ip_fname']
op_loc=config_dict['data']['op_loc']
# Overriding configs in .yaml file (different for jupyter notebook)
ngpu=1
batch_size=128
spec_loss_flag=True
checkpoint_size=50
num_imgs=2000 # Number of images to use
num_epochs=4
lr=0.0002
n_classes=6
### Initialize random seed (different for Jpt notebook)
manualSeed=21245
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
device = torch.device("cuda" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
print('Device:',device)
# #################################
# ####### Read data and precompute ######
# # ip_fname='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_2_smoothing_200k/norm_1_train_val.npy'
# ip_fname='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/data_x.npy'
# labels='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/data_y.npy'
# img=np.load(ip_fname)[:num_imgs].transpose(0,1,2,3)
# t_img=torch.from_numpy(img)
# print(img.shape,t_img.shape)
# dataset=TensorDataset(t_img)
# dataloader=DataLoader(dataset,batch_size=batch_size,shuffle=True,num_workers=1,drop_last=True)
#################################
###### Build Networks ###
print("Building CNN")
# Create Discriminator
netD = Discriminator(ngpu, nz,nc,ndf,n_classes,kernel_size,stride,g_padding).to(device)
netD.apply(weights_init)
print(netD)
summary(netD,(1,128,128))
# Handle multi-gpu if desired
ngpu=torch.cuda.device_count()
print("Number of GPUs used",ngpu)
if (device.type == 'cuda') and (ngpu > 1):
netD = nn.DataParallel(netD, list(range(ngpu)))
# Initialize BCELoss function
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(netD.parameters(), lr=0.001, momentum=0.9)
# fixed_noise = torch.randn(batch_size, 1, 1, nz, device=device) #Latent vectors to view G progress
# Setup Adam optimizers for both G and D
# optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999),eps=1e-7)
#################################
###### Set up directories ####### (different for Jpt notebook)
# run_suffix='_nb_test'
# ### Create prefix for foldername
# now=datetime.now()
# fldr_name=now.strftime('%Y%m%d_%H%M%S') ## time format
# # print(fldr_name)
# save_dir=op_loc+fldr_name+run_suffix
# if not os.path.exists(save_dir):
# os.makedirs(save_dir+'/models')
# os.makedirs(save_dir+'/images')
# Fresh start
# iters = 0; start_epoch=0
# best_chi1,best_chi2=1e10,1e10
# ip_fname='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/data_x.npy'
# labels_file='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/data_y.npy'
# ids_file='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/data_id.npy'
# img=np.load(ip_fname)
# labels=np.load(labels_file)
# ids=np.load(ids_file)
# t_img=torch.from_numpy(img)
# print(img.shape,t_img.shape)
## Read data from dataframe
data_dir='/global/cfs/cdirs/m3363/vayyar/cosmogan_data/raw_data/128_square/dataset_4_four_universes_6k_cnn/'
df_data=pd.read_pickle(data_dir+'/df_data.pkle')
df_data=df_data.sample(frac=1,random_state=20).reset_index(drop=True)
train_size,val_size,test_size=0.7,0.1,0.1
data_size=df_data.shape[0]
df_data[['ID','label']].head()
idx1,idx2,idx3=int(train_size*data_size),int((train_size+val_size)*data_size),int((train_size+val_size+test_size)*data_size)
print(idx1,idx2,idx3)
df_temp=df_data.loc[np.arange(0,idx1)]
dataset=TensorDataset(torch.Tensor(np.stack(df_temp.img.values)),torch.Tensor(df_temp.label.values))
train_loader=DataLoader(dataset,batch_size=batch_size,shuffle=True,num_workers=1,drop_last=True)
df_temp=df_data.loc[np.arange(idx1,idx2)]
dataset=TensorDataset(torch.Tensor(np.stack(df_temp.img.values)),torch.Tensor(df_temp.label.values))
val_loader=DataLoader(dataset,batch_size=16,shuffle=True,num_workers=1,drop_last=True)
df_temp=df_data.loc[np.arange(idx2,idx3)]
dataset=TensorDataset(torch.Tensor(np.stack(df_temp.img.values)),torch.Tensor(df_temp.label.values))
test_loader=DataLoader(dataset,batch_size=8,shuffle=True,num_workers=1,drop_last=True)
## Test model
def f_test(data_loader,netD):
netD.eval()
correct,total=0,0
with torch.no_grad():
for count,data in enumerate(data_loader):
images,labels=data[0].to(device),data[1].to(device)
outputs=netD(images)
_,predictions=torch.max(outputs,1)
total+=labels.size(0)
correct+=(predictions==labels).sum().item()
accuracy=(correct/total)*100
# print("Accuracy %",accuracy)
# print(correct,total)
return accuracy
accuracy=[]
for epoch in range(0,4):
running_loss=0.0
print("Epoch",epoch)
for i, data in enumerate(train_loader):
# print(images.shape,labels.shape)
images,labels=data[0].to(device),data[1].to(device)
optimizer.zero_grad()
# netD.train(); ### Need to add these after inference and before training
netD.zero_grad()
labels=labels.long()
output = netD(images)
loss= criterion(output, labels)
loss.backward()
optimizer.step()
running_loss+=loss.item()
if i%10==0: accuracy.append(f_test(val_loader,netD))
netD.train()
plt.figure()
plt.plot(accuracy)
## Test model
f_test(test_loader,netD)
```
|
github_jupyter
|
#### Abstract Classes: contains abstract methods
Abstract methods are those which are only declared but they've no implementation
**All methods need to be implemented (mandatory)
Module -- abc
|
|
|---> ABC (Class)
|
|---> Abstract method (as a functionality and used as a decorator)
** You cannot create objects of an abstract class (evne there is only one abstract method)
```
from abc import ABC, abstractmethod
class Automobile(ABC):
def __init__(self):
print("Automobile Created")
def start(self):
pass
def start(self):
pass
def start(self):
pass
c = Automobile()
from abc import ABC, abstractmethod
class Automobile(ABC):
def __init__(self):
print("Automobile Created")
@abstractmethod
def start(self):
pass
@abstractmethod
def start(self):
pass
@abstractmethod
def start(self):
pass
c = Automobile()
from abc import ABC, abstractmethod
class Automobile(ABC):
def __init__(self):
print("Automobile Created")
@abstractmethod
def start(self):
pass
@abstractmethod
def start(self):
pass
@abstractmethod
def start(self):
pass
class Car(Automobile):
def __init__(self, name):
print("Car created")
self.name = name
def start(self):
pass
def stop(self):
pass
def drive(self):
pass
class Bus(Automobile):
def __init__(self, name):
print("Bus Created")
self.name = name
def start(self):
pass
def stop(self):
pass
def drive(self):
pass
c = Car("Honda")
d = Bus("Delhi Metro BUs")
```
#### 1) Object of abstract class cannot be created
#### 2) Implement all the abstract methods in the child class
```
# Predict the output:
from abc import ABC,abstractmethod
class A(ABC):
@abstractmethod
def fun1(self):
pass
@abstractmethod
def fun2(self):
pass
o = A()
o.fun1()
# Predict the output:
from abc import ABC,abstractmethod
class A(ABC):
@abstractmethod
def fun1(self):
pass
@abstractmethod
def fun2(self):
pass
class B(A):
def fun1(self):
print("function 1 called")
o = B()
o.fun1()
#Predict the Output:
from abc import ABC,abstractmethod
class A(ABC):
@abstractmethod
def fun1(self):
pass
@abstractmethod
def fun2(self):
pass
class B(A):
def fun1(self):
print("function 1 called")
def fun2(self):
print("function 2 called")
o = B()
o.fun1()
```
** In this 3rd example, it's clearly visible that you've implemented all the abstract funtions of class A, class B inherits class A and created the object for class B. Then finally called the fun1() from the object. So, the output got printed else you can visit the first two examples. It throws an error either if you implement only one class or if you try to create an object for abstract class (Example 1)
|
github_jupyter
|
```
# This mounts your Google Drive to the Colab VM.
from google.colab import drive
drive.mount('/content/drive')
# TODO: Enter the foldername in your Drive where you have saved the unzipped
# assignment folder, e.g. 'cs231n/assignments/assignment1/'
FOLDERNAME = None
assert FOLDERNAME is not None, "[!] Enter the foldername."
# Now that we've mounted your Drive, this ensures that
# the Python interpreter of the Colab VM can load
# python files from within it.
import sys
sys.path.append('/content/drive/My Drive/{}'.format(FOLDERNAME))
# This downloads the CIFAR-10 dataset to your Drive
# if it doesn't already exist.
%cd /content/drive/My\ Drive/$FOLDERNAME/cs231n/datasets/
!bash get_datasets.sh
%cd /content/drive/My\ Drive/$FOLDERNAME
```
# Introduction to PyTorch
You've written a lot of code in this assignment to provide a whole host of neural network functionality. Dropout, Batch Norm, and 2D convolutions are some of the workhorses of deep learning in computer vision. You've also worked hard to make your code efficient and vectorized.
For the last part of this assignment, though, we're going to leave behind your beautiful codebase and instead migrate to one of two popular deep learning frameworks: in this instance, PyTorch (or TensorFlow, if you choose to work with that notebook).
## Why do we use deep learning frameworks?
* Our code will now run on GPUs! This will allow our models to train much faster. When using a framework like PyTorch or TensorFlow you can harness the power of the GPU for your own custom neural network architectures without having to write CUDA code directly (which is beyond the scope of this class).
* In this class, we want you to be ready to use one of these frameworks for your project so you can experiment more efficiently than if you were writing every feature you want to use by hand.
* We want you to stand on the shoulders of giants! TensorFlow and PyTorch are both excellent frameworks that will make your lives a lot easier, and now that you understand their guts, you are free to use them :)
* Finally, we want you to be exposed to the sort of deep learning code you might run into in academia or industry.
## What is PyTorch?
PyTorch is a system for executing dynamic computational graphs over Tensor objects that behave similarly as numpy ndarray. It comes with a powerful automatic differentiation engine that removes the need for manual back-propagation.
## How do I learn PyTorch?
One of our former instructors, Justin Johnson, made an excellent [tutorial](https://github.com/jcjohnson/pytorch-examples) for PyTorch.
You can also find the detailed [API doc](http://pytorch.org/docs/stable/index.html) here. If you have other questions that are not addressed by the API docs, the [PyTorch forum](https://discuss.pytorch.org/) is a much better place to ask than StackOverflow.
# Table of Contents
This assignment has 5 parts. You will learn PyTorch on **three different levels of abstraction**, which will help you understand it better and prepare you for the final project.
1. Part I, Preparation: we will use CIFAR-10 dataset.
2. Part II, Barebones PyTorch: **Abstraction level 1**, we will work directly with the lowest-level PyTorch Tensors.
3. Part III, PyTorch Module API: **Abstraction level 2**, we will use `nn.Module` to define arbitrary neural network architecture.
4. Part IV, PyTorch Sequential API: **Abstraction level 3**, we will use `nn.Sequential` to define a linear feed-forward network very conveniently.
5. Part V, CIFAR-10 open-ended challenge: please implement your own network to get as high accuracy as possible on CIFAR-10. You can experiment with any layer, optimizer, hyperparameters or other advanced features.
Here is a table of comparison:
| API | Flexibility | Convenience |
|---------------|-------------|-------------|
| Barebone | High | Low |
| `nn.Module` | High | Medium |
| `nn.Sequential` | Low | High |
# GPU
You can manually switch to a GPU device on Colab by clicking `Runtime -> Change runtime type` and selecting `GPU` under `Hardware Accelerator`. You should do this before running the following cells to import packages, since the kernel gets restarted upon switching runtimes.
```
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torch.utils.data import sampler
import torchvision.datasets as dset
import torchvision.transforms as T
import numpy as np
USE_GPU = True
dtype = torch.float32 # We will be using float throughout this tutorial.
if USE_GPU and torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')
# Constant to control how frequently we print train loss.
print_every = 100
print('using device:', device)
```
# Part I. Preparation
Now, let's load the CIFAR-10 dataset. This might take a couple minutes the first time you do it, but the files should stay cached after that.
In previous parts of the assignment we had to write our own code to download the CIFAR-10 dataset, preprocess it, and iterate through it in minibatches; PyTorch provides convenient tools to automate this process for us.
```
NUM_TRAIN = 49000
# The torchvision.transforms package provides tools for preprocessing data
# and for performing data augmentation; here we set up a transform to
# preprocess the data by subtracting the mean RGB value and dividing by the
# standard deviation of each RGB value; we've hardcoded the mean and std.
transform = T.Compose([
T.ToTensor(),
T.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))
])
# We set up a Dataset object for each split (train / val / test); Datasets load
# training examples one at a time, so we wrap each Dataset in a DataLoader which
# iterates through the Dataset and forms minibatches. We divide the CIFAR-10
# training set into train and val sets by passing a Sampler object to the
# DataLoader telling how it should sample from the underlying Dataset.
cifar10_train = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=transform)
loader_train = DataLoader(cifar10_train, batch_size=64,
sampler=sampler.SubsetRandomSampler(range(NUM_TRAIN)))
cifar10_val = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=transform)
loader_val = DataLoader(cifar10_val, batch_size=64,
sampler=sampler.SubsetRandomSampler(range(NUM_TRAIN, 50000)))
cifar10_test = dset.CIFAR10('./cs231n/datasets', train=False, download=True,
transform=transform)
loader_test = DataLoader(cifar10_test, batch_size=64)
```
# Part II. Barebones PyTorch
PyTorch ships with high-level APIs to help us define model architectures conveniently, which we will cover in Part II of this tutorial. In this section, we will start with the barebone PyTorch elements to understand the autograd engine better. After this exercise, you will come to appreciate the high-level model API more.
We will start with a simple fully-connected ReLU network with two hidden layers and no biases for CIFAR classification.
This implementation computes the forward pass using operations on PyTorch Tensors, and uses PyTorch autograd to compute gradients. It is important that you understand every line, because you will write a harder version after the example.
When we create a PyTorch Tensor with `requires_grad=True`, then operations involving that Tensor will not just compute values; they will also build up a computational graph in the background, allowing us to easily backpropagate through the graph to compute gradients of some Tensors with respect to a downstream loss. Concretely if x is a Tensor with `x.requires_grad == True` then after backpropagation `x.grad` will be another Tensor holding the gradient of x with respect to the scalar loss at the end.
### PyTorch Tensors: Flatten Function
A PyTorch Tensor is conceptionally similar to a numpy array: it is an n-dimensional grid of numbers, and like numpy PyTorch provides many functions to efficiently operate on Tensors. As a simple example, we provide a `flatten` function below which reshapes image data for use in a fully-connected neural network.
Recall that image data is typically stored in a Tensor of shape N x C x H x W, where:
* N is the number of datapoints
* C is the number of channels
* H is the height of the intermediate feature map in pixels
* W is the height of the intermediate feature map in pixels
This is the right way to represent the data when we are doing something like a 2D convolution, that needs spatial understanding of where the intermediate features are relative to each other. When we use fully connected affine layers to process the image, however, we want each datapoint to be represented by a single vector -- it's no longer useful to segregate the different channels, rows, and columns of the data. So, we use a "flatten" operation to collapse the `C x H x W` values per representation into a single long vector. The flatten function below first reads in the N, C, H, and W values from a given batch of data, and then returns a "view" of that data. "View" is analogous to numpy's "reshape" method: it reshapes x's dimensions to be N x ??, where ?? is allowed to be anything (in this case, it will be C x H x W, but we don't need to specify that explicitly).
```
def flatten(x):
N = x.shape[0] # read in N, C, H, W
return x.view(N, -1) # "flatten" the C * H * W values into a single vector per image
def test_flatten():
x = torch.arange(12).view(2, 1, 3, 2)
print('Before flattening: ', x)
print('After flattening: ', flatten(x))
test_flatten()
```
### Barebones PyTorch: Two-Layer Network
Here we define a function `two_layer_fc` which performs the forward pass of a two-layer fully-connected ReLU network on a batch of image data. After defining the forward pass we check that it doesn't crash and that it produces outputs of the right shape by running zeros through the network.
You don't have to write any code here, but it's important that you read and understand the implementation.
```
import torch.nn.functional as F # useful stateless functions
def two_layer_fc(x, params):
"""
A fully-connected neural networks; the architecture is:
NN is fully connected -> ReLU -> fully connected layer.
Note that this function only defines the forward pass;
PyTorch will take care of the backward pass for us.
The input to the network will be a minibatch of data, of shape
(N, d1, ..., dM) where d1 * ... * dM = D. The hidden layer will have H units,
and the output layer will produce scores for C classes.
Inputs:
- x: A PyTorch Tensor of shape (N, d1, ..., dM) giving a minibatch of
input data.
- params: A list [w1, w2] of PyTorch Tensors giving weights for the network;
w1 has shape (D, H) and w2 has shape (H, C).
Returns:
- scores: A PyTorch Tensor of shape (N, C) giving classification scores for
the input data x.
"""
# first we flatten the image
x = flatten(x) # shape: [batch_size, C x H x W]
w1, w2 = params
# Forward pass: compute predicted y using operations on Tensors. Since w1 and
# w2 have requires_grad=True, operations involving these Tensors will cause
# PyTorch to build a computational graph, allowing automatic computation of
# gradients. Since we are no longer implementing the backward pass by hand we
# don't need to keep references to intermediate values.
# you can also use `.clamp(min=0)`, equivalent to F.relu()
x = F.relu(x.mm(w1))
x = x.mm(w2)
return x
def two_layer_fc_test():
hidden_layer_size = 42
x = torch.zeros((64, 50), dtype=dtype) # minibatch size 64, feature dimension 50
w1 = torch.zeros((50, hidden_layer_size), dtype=dtype)
w2 = torch.zeros((hidden_layer_size, 10), dtype=dtype)
scores = two_layer_fc(x, [w1, w2])
print(scores.size()) # you should see [64, 10]
two_layer_fc_test()
```
### Barebones PyTorch: Three-Layer ConvNet
Here you will complete the implementation of the function `three_layer_convnet`, which will perform the forward pass of a three-layer convolutional network. Like above, we can immediately test our implementation by passing zeros through the network. The network should have the following architecture:
1. A convolutional layer (with bias) with `channel_1` filters, each with shape `KW1 x KH1`, and zero-padding of two
2. ReLU nonlinearity
3. A convolutional layer (with bias) with `channel_2` filters, each with shape `KW2 x KH2`, and zero-padding of one
4. ReLU nonlinearity
5. Fully-connected layer with bias, producing scores for C classes.
Note that we have **no softmax activation** here after our fully-connected layer: this is because PyTorch's cross entropy loss performs a softmax activation for you, and by bundling that step in makes computation more efficient.
**HINT**: For convolutions: http://pytorch.org/docs/stable/nn.html#torch.nn.functional.conv2d; pay attention to the shapes of convolutional filters!
```
def three_layer_convnet(x, params):
"""
Performs the forward pass of a three-layer convolutional network with the
architecture defined above.
Inputs:
- x: A PyTorch Tensor of shape (N, 3, H, W) giving a minibatch of images
- params: A list of PyTorch Tensors giving the weights and biases for the
network; should contain the following:
- conv_w1: PyTorch Tensor of shape (channel_1, 3, KH1, KW1) giving weights
for the first convolutional layer
- conv_b1: PyTorch Tensor of shape (channel_1,) giving biases for the first
convolutional layer
- conv_w2: PyTorch Tensor of shape (channel_2, channel_1, KH2, KW2) giving
weights for the second convolutional layer
- conv_b2: PyTorch Tensor of shape (channel_2,) giving biases for the second
convolutional layer
- fc_w: PyTorch Tensor giving weights for the fully-connected layer. Can you
figure out what the shape should be?
- fc_b: PyTorch Tensor giving biases for the fully-connected layer. Can you
figure out what the shape should be?
Returns:
- scores: PyTorch Tensor of shape (N, C) giving classification scores for x
"""
conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b = params
scores = None
################################################################################
# TODO: Implement the forward pass for the three-layer ConvNet. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x = F.conv2d(x, conv_w1, conv_b1, padding=2)
x = F.relu(x)
x = F.conv2d(x, conv_w2, conv_b2, padding=1)
x = F.relu(x)
scores = flatten(x).mm(fc_w) + fc_b
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
return scores
```
After defining the forward pass of the ConvNet above, run the following cell to test your implementation.
When you run this function, scores should have shape (64, 10).
```
def three_layer_convnet_test():
x = torch.zeros((64, 3, 32, 32), dtype=dtype) # minibatch size 64, image size [3, 32, 32]
conv_w1 = torch.zeros((6, 3, 5, 5), dtype=dtype) # [out_channel, in_channel, kernel_H, kernel_W]
conv_b1 = torch.zeros((6,)) # out_channel
conv_w2 = torch.zeros((9, 6, 3, 3), dtype=dtype) # [out_channel, in_channel, kernel_H, kernel_W]
conv_b2 = torch.zeros((9,)) # out_channel
# you must calculate the shape of the tensor after two conv layers, before the fully-connected layer
fc_w = torch.zeros((9 * 32 * 32, 10))
fc_b = torch.zeros(10)
scores = three_layer_convnet(x, [conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b])
print(scores.size()) # you should see [64, 10]
three_layer_convnet_test()
```
### Barebones PyTorch: Initialization
Let's write a couple utility methods to initialize the weight matrices for our models.
- `random_weight(shape)` initializes a weight tensor with the Kaiming normalization method.
- `zero_weight(shape)` initializes a weight tensor with all zeros. Useful for instantiating bias parameters.
The `random_weight` function uses the Kaiming normal initialization method, described in:
He et al, *Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification*, ICCV 2015, https://arxiv.org/abs/1502.01852
```
def random_weight(shape):
"""
Create random Tensors for weights; setting requires_grad=True means that we
want to compute gradients for these Tensors during the backward pass.
We use Kaiming normalization: sqrt(2 / fan_in)
"""
if len(shape) == 2: # FC weight
fan_in = shape[0]
else:
fan_in = np.prod(shape[1:]) # conv weight [out_channel, in_channel, kH, kW]
# randn is standard normal distribution generator.
w = torch.randn(shape, device=device, dtype=dtype) * np.sqrt(2. / fan_in)
w.requires_grad = True
return w
def zero_weight(shape):
return torch.zeros(shape, device=device, dtype=dtype, requires_grad=True)
# create a weight of shape [3 x 5]
# you should see the type `torch.cuda.FloatTensor` if you use GPU.
# Otherwise it should be `torch.FloatTensor`
random_weight((3, 5))
```
### Barebones PyTorch: Check Accuracy
When training the model we will use the following function to check the accuracy of our model on the training or validation sets.
When checking accuracy we don't need to compute any gradients; as a result we don't need PyTorch to build a computational graph for us when we compute scores. To prevent a graph from being built we scope our computation under a `torch.no_grad()` context manager.
```
def check_accuracy_part2(loader, model_fn, params):
"""
Check the accuracy of a classification model.
Inputs:
- loader: A DataLoader for the data split we want to check
- model_fn: A function that performs the forward pass of the model,
with the signature scores = model_fn(x, params)
- params: List of PyTorch Tensors giving parameters of the model
Returns: Nothing, but prints the accuracy of the model
"""
split = 'val' if loader.dataset.train else 'test'
print('Checking accuracy on the %s set' % split)
num_correct, num_samples = 0, 0
with torch.no_grad():
for x, y in loader:
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.int64)
scores = model_fn(x, params)
_, preds = scores.max(1)
num_correct += (preds == y).sum()
num_samples += preds.size(0)
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f%%)' % (num_correct, num_samples, 100 * acc))
```
### BareBones PyTorch: Training Loop
We can now set up a basic training loop to train our network. We will train the model using stochastic gradient descent without momentum. We will use `torch.functional.cross_entropy` to compute the loss; you can [read about it here](http://pytorch.org/docs/stable/nn.html#cross-entropy).
The training loop takes as input the neural network function, a list of initialized parameters (`[w1, w2]` in our example), and learning rate.
```
def train_part2(model_fn, params, learning_rate):
"""
Train a model on CIFAR-10.
Inputs:
- model_fn: A Python function that performs the forward pass of the model.
It should have the signature scores = model_fn(x, params) where x is a
PyTorch Tensor of image data, params is a list of PyTorch Tensors giving
model weights, and scores is a PyTorch Tensor of shape (N, C) giving
scores for the elements in x.
- params: List of PyTorch Tensors giving weights for the model
- learning_rate: Python scalar giving the learning rate to use for SGD
Returns: Nothing
"""
for t, (x, y) in enumerate(loader_train):
# Move the data to the proper device (GPU or CPU)
x = x.to(device=device, dtype=dtype)
y = y.to(device=device, dtype=torch.long)
# Forward pass: compute scores and loss
scores = model_fn(x, params)
loss = F.cross_entropy(scores, y)
# Backward pass: PyTorch figures out which Tensors in the computational
# graph has requires_grad=True and uses backpropagation to compute the
# gradient of the loss with respect to these Tensors, and stores the
# gradients in the .grad attribute of each Tensor.
loss.backward()
# Update parameters. We don't want to backpropagate through the
# parameter updates, so we scope the updates under a torch.no_grad()
# context manager to prevent a computational graph from being built.
with torch.no_grad():
for w in params:
w -= learning_rate * w.grad
# Manually zero the gradients after running the backward pass
w.grad.zero_()
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss.item()))
check_accuracy_part2(loader_val, model_fn, params)
print()
```
### BareBones PyTorch: Train a Two-Layer Network
Now we are ready to run the training loop. We need to explicitly allocate tensors for the fully connected weights, `w1` and `w2`.
Each minibatch of CIFAR has 64 examples, so the tensor shape is `[64, 3, 32, 32]`.
After flattening, `x` shape should be `[64, 3 * 32 * 32]`. This will be the size of the first dimension of `w1`.
The second dimension of `w1` is the hidden layer size, which will also be the first dimension of `w2`.
Finally, the output of the network is a 10-dimensional vector that represents the probability distribution over 10 classes.
You don't need to tune any hyperparameters but you should see accuracies above 40% after training for one epoch.
```
hidden_layer_size = 4000
learning_rate = 1e-2
w1 = random_weight((3 * 32 * 32, hidden_layer_size))
w2 = random_weight((hidden_layer_size, 10))
train_part2(two_layer_fc, [w1, w2], learning_rate)
```
### BareBones PyTorch: Training a ConvNet
In the below you should use the functions defined above to train a three-layer convolutional network on CIFAR. The network should have the following architecture:
1. Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2
2. ReLU
3. Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1
4. ReLU
5. Fully-connected layer (with bias) to compute scores for 10 classes
You should initialize your weight matrices using the `random_weight` function defined above, and you should initialize your bias vectors using the `zero_weight` function above.
You don't need to tune any hyperparameters, but if everything works correctly you should achieve an accuracy above 42% after one epoch.
```
learning_rate = 3e-3
channel_1 = 32
channel_2 = 16
conv_w1 = None
conv_b1 = None
conv_w2 = None
conv_b2 = None
fc_w = None
fc_b = None
################################################################################
# TODO: Initialize the parameters of a three-layer ConvNet. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
conv_w1 = random_weight((channel_1, 3, 5, 5))
conv_b1 = zero_weight((channel_1, ))
conv_w2 = random_weight((channel_2, channel_1, 3, 3))
conv_b2 = zero_weight((channel_2, ))
fc_w = random_weight((channel_2 * 32 * 32, 10))
fc_b = zero_weight((10, ))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
params = [conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b]
train_part2(three_layer_convnet, params, learning_rate)
```
# Part III. PyTorch Module API
Barebone PyTorch requires that we track all the parameter tensors by hand. This is fine for small networks with a few tensors, but it would be extremely inconvenient and error-prone to track tens or hundreds of tensors in larger networks.
PyTorch provides the `nn.Module` API for you to define arbitrary network architectures, while tracking every learnable parameters for you. In Part II, we implemented SGD ourselves. PyTorch also provides the `torch.optim` package that implements all the common optimizers, such as RMSProp, Adagrad, and Adam. It even supports approximate second-order methods like L-BFGS! You can refer to the [doc](http://pytorch.org/docs/master/optim.html) for the exact specifications of each optimizer.
To use the Module API, follow the steps below:
1. Subclass `nn.Module`. Give your network class an intuitive name like `TwoLayerFC`.
2. In the constructor `__init__()`, define all the layers you need as class attributes. Layer objects like `nn.Linear` and `nn.Conv2d` are themselves `nn.Module` subclasses and contain learnable parameters, so that you don't have to instantiate the raw tensors yourself. `nn.Module` will track these internal parameters for you. Refer to the [doc](http://pytorch.org/docs/master/nn.html) to learn more about the dozens of builtin layers. **Warning**: don't forget to call the `super().__init__()` first!
3. In the `forward()` method, define the *connectivity* of your network. You should use the attributes defined in `__init__` as function calls that take tensor as input and output the "transformed" tensor. Do *not* create any new layers with learnable parameters in `forward()`! All of them must be declared upfront in `__init__`.
After you define your Module subclass, you can instantiate it as an object and call it just like the NN forward function in part II.
### Module API: Two-Layer Network
Here is a concrete example of a 2-layer fully connected network:
```
class TwoLayerFC(nn.Module):
def __init__(self, input_size, hidden_size, num_classes):
super().__init__()
# assign layer objects to class attributes
self.fc1 = nn.Linear(input_size, hidden_size)
# nn.init package contains convenient initialization methods
# http://pytorch.org/docs/master/nn.html#torch-nn-init
nn.init.kaiming_normal_(self.fc1.weight)
self.fc2 = nn.Linear(hidden_size, num_classes)
nn.init.kaiming_normal_(self.fc2.weight)
def forward(self, x):
# forward always defines connectivity
x = flatten(x)
scores = self.fc2(F.relu(self.fc1(x)))
return scores
def test_TwoLayerFC():
input_size = 50
x = torch.zeros((64, input_size), dtype=dtype) # minibatch size 64, feature dimension 50
model = TwoLayerFC(input_size, 42, 10)
scores = model(x)
print(scores.size()) # you should see [64, 10]
test_TwoLayerFC()
```
### Module API: Three-Layer ConvNet
It's your turn to implement a 3-layer ConvNet followed by a fully connected layer. The network architecture should be the same as in Part II:
1. Convolutional layer with `channel_1` 5x5 filters with zero-padding of 2
2. ReLU
3. Convolutional layer with `channel_2` 3x3 filters with zero-padding of 1
4. ReLU
5. Fully-connected layer to `num_classes` classes
You should initialize the weight matrices of the model using the Kaiming normal initialization method.
**HINT**: http://pytorch.org/docs/stable/nn.html#conv2d
After you implement the three-layer ConvNet, the `test_ThreeLayerConvNet` function will run your implementation; it should print `(64, 10)` for the shape of the output scores.
```
class ThreeLayerConvNet(nn.Module):
def __init__(self, in_channel, channel_1, channel_2, num_classes):
super().__init__()
########################################################################
# TODO: Set up the layers you need for a three-layer ConvNet with the #
# architecture defined above. #
########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
self.conv1 = nn.Conv2d(in_channel, channel_1, (5, 5), padding=2)
nn.init.kaiming_normal_(self.conv1.weight)
self.conv2 = nn.Conv2d(channel_1, channel_2, (3, 3), padding=1)
nn.init.kaiming_normal_(self.conv2.weight)
self.fc = nn.Linear(channel_2 * 32 * 32, num_classes)
nn.init.kaiming_normal_(self.fc.weight)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
########################################################################
# END OF YOUR CODE #
########################################################################
def forward(self, x):
scores = None
########################################################################
# TODO: Implement the forward function for a 3-layer ConvNet. you #
# should use the layers you defined in __init__ and specify the #
# connectivity of those layers in forward() #
########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
scores = self.fc(flatten(x))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
########################################################################
# END OF YOUR CODE #
########################################################################
return scores
def test_ThreeLayerConvNet():
x = torch.zeros((64, 3, 32, 32), dtype=dtype) # minibatch size 64, image size [3, 32, 32]
model = ThreeLayerConvNet(in_channel=3, channel_1=12, channel_2=8, num_classes=10)
scores = model(x)
print(scores.size()) # you should see [64, 10]
test_ThreeLayerConvNet()
```
### Module API: Check Accuracy
Given the validation or test set, we can check the classification accuracy of a neural network.
This version is slightly different from the one in part II. You don't manually pass in the parameters anymore.
```
def check_accuracy_part34(loader, model):
if loader.dataset.train:
print('Checking accuracy on validation set')
else:
print('Checking accuracy on test set')
num_correct = 0
num_samples = 0
model.eval() # set model to evaluation mode
with torch.no_grad():
for x, y in loader:
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.long)
scores = model(x)
_, preds = scores.max(1)
num_correct += (preds == y).sum()
num_samples += preds.size(0)
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f)' % (num_correct, num_samples, 100 * acc))
```
### Module API: Training Loop
We also use a slightly different training loop. Rather than updating the values of the weights ourselves, we use an Optimizer object from the `torch.optim` package, which abstract the notion of an optimization algorithm and provides implementations of most of the algorithms commonly used to optimize neural networks.
```
def train_part34(model, optimizer, epochs=1):
"""
Train a model on CIFAR-10 using the PyTorch Module API.
Inputs:
- model: A PyTorch Module giving the model to train.
- optimizer: An Optimizer object we will use to train the model
- epochs: (Optional) A Python integer giving the number of epochs to train for
Returns: Nothing, but prints model accuracies during training.
"""
model = model.to(device=device) # move the model parameters to CPU/GPU
for e in range(epochs):
for t, (x, y) in enumerate(loader_train):
model.train() # put model to training mode
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.long)
scores = model(x)
loss = F.cross_entropy(scores, y)
# Zero out all of the gradients for the variables which the optimizer
# will update.
optimizer.zero_grad()
# This is the backwards pass: compute the gradient of the loss with
# respect to each parameter of the model.
loss.backward()
# Actually update the parameters of the model using the gradients
# computed by the backwards pass.
optimizer.step()
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss.item()))
check_accuracy_part34(loader_val, model)
print()
```
### Module API: Train a Two-Layer Network
Now we are ready to run the training loop. In contrast to part II, we don't explicitly allocate parameter tensors anymore.
Simply pass the input size, hidden layer size, and number of classes (i.e. output size) to the constructor of `TwoLayerFC`.
You also need to define an optimizer that tracks all the learnable parameters inside `TwoLayerFC`.
You don't need to tune any hyperparameters, but you should see model accuracies above 40% after training for one epoch.
```
hidden_layer_size = 4000
learning_rate = 1e-2
model = TwoLayerFC(3 * 32 * 32, hidden_layer_size, 10)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
train_part34(model, optimizer)
```
### Module API: Train a Three-Layer ConvNet
You should now use the Module API to train a three-layer ConvNet on CIFAR. This should look very similar to training the two-layer network! You don't need to tune any hyperparameters, but you should achieve above above 45% after training for one epoch.
You should train the model using stochastic gradient descent without momentum.
```
learning_rate = 3e-3
channel_1 = 32
channel_2 = 16
model = None
optimizer = None
################################################################################
# TODO: Instantiate your ThreeLayerConvNet model and a corresponding optimizer #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
model = ThreeLayerConvNet(3, channel_1, channel_2, 10)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
train_part34(model, optimizer)
```
# Part IV. PyTorch Sequential API
Part III introduced the PyTorch Module API, which allows you to define arbitrary learnable layers and their connectivity.
For simple models like a stack of feed forward layers, you still need to go through 3 steps: subclass `nn.Module`, assign layers to class attributes in `__init__`, and call each layer one by one in `forward()`. Is there a more convenient way?
Fortunately, PyTorch provides a container Module called `nn.Sequential`, which merges the above steps into one. It is not as flexible as `nn.Module`, because you cannot specify more complex topology than a feed-forward stack, but it's good enough for many use cases.
### Sequential API: Two-Layer Network
Let's see how to rewrite our two-layer fully connected network example with `nn.Sequential`, and train it using the training loop defined above.
Again, you don't need to tune any hyperparameters here, but you shoud achieve above 40% accuracy after one epoch of training.
```
# We need to wrap `flatten` function in a module in order to stack it
# in nn.Sequential
class Flatten(nn.Module):
def forward(self, x):
return flatten(x)
hidden_layer_size = 4000
learning_rate = 1e-2
model = nn.Sequential(
Flatten(),
nn.Linear(3 * 32 * 32, hidden_layer_size),
nn.ReLU(),
nn.Linear(hidden_layer_size, 10),
)
# you can use Nesterov momentum in optim.SGD
optimizer = optim.SGD(model.parameters(), lr=learning_rate,
momentum=0.9, nesterov=True)
train_part34(model, optimizer)
```
### Sequential API: Three-Layer ConvNet
Here you should use `nn.Sequential` to define and train a three-layer ConvNet with the same architecture we used in Part III:
1. Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2
2. ReLU
3. Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1
4. ReLU
5. Fully-connected layer (with bias) to compute scores for 10 classes
You can use the default PyTorch weight initialization.
You should optimize your model using stochastic gradient descent with Nesterov momentum 0.9.
Again, you don't need to tune any hyperparameters but you should see accuracy above 55% after one epoch of training.
```
channel_1 = 32
channel_2 = 16
learning_rate = 1e-2
model = None
optimizer = None
################################################################################
# TODO: Rewrite the 2-layer ConvNet with bias from Part III with the #
# Sequential API. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
model = nn.Sequential(
nn.Conv2d(3, channel_1, (5, 5), padding=2),
nn.ReLU(),
nn.Conv2d(channel_1, channel_2, (3, 3), padding=1),
nn.ReLU(),
Flatten(),
nn.Linear(channel_2 * 32 * 32, 10)
)
optimizer = optim.SGD(model.parameters(), lr=learning_rate,
momentum=0.9, nesterov=True)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
train_part34(model, optimizer)
```
# Part V. CIFAR-10 open-ended challenge
In this section, you can experiment with whatever ConvNet architecture you'd like on CIFAR-10.
Now it's your job to experiment with architectures, hyperparameters, loss functions, and optimizers to train a model that achieves **at least 70%** accuracy on the CIFAR-10 **validation** set within 10 epochs. You can use the check_accuracy and train functions from above. You can use either `nn.Module` or `nn.Sequential` API.
Describe what you did at the end of this notebook.
Here are the official API documentation for each component. One note: what we call in the class "spatial batch norm" is called "BatchNorm2D" in PyTorch.
* Layers in torch.nn package: http://pytorch.org/docs/stable/nn.html
* Activations: http://pytorch.org/docs/stable/nn.html#non-linear-activations
* Loss functions: http://pytorch.org/docs/stable/nn.html#loss-functions
* Optimizers: http://pytorch.org/docs/stable/optim.html
### Things you might try:
- **Filter size**: Above we used 5x5; would smaller filters be more efficient?
- **Number of filters**: Above we used 32 filters. Do more or fewer do better?
- **Pooling vs Strided Convolution**: Do you use max pooling or just stride convolutions?
- **Batch normalization**: Try adding spatial batch normalization after convolution layers and vanilla batch normalization after affine layers. Do your networks train faster?
- **Network architecture**: The network above has two layers of trainable parameters. Can you do better with a deep network? Good architectures to try include:
- [conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [conv-relu-conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [batchnorm-relu-conv]xN -> [affine]xM -> [softmax or SVM]
- **Global Average Pooling**: Instead of flattening and then having multiple affine layers, perform convolutions until your image gets small (7x7 or so) and then perform an average pooling operation to get to a 1x1 image picture (1, 1 , Filter#), which is then reshaped into a (Filter#) vector. This is used in [Google's Inception Network](https://arxiv.org/abs/1512.00567) (See Table 1 for their architecture).
- **Regularization**: Add l2 weight regularization, or perhaps use Dropout.
### Tips for training
For each network architecture that you try, you should tune the learning rate and other hyperparameters. When doing this there are a couple important things to keep in mind:
- If the parameters are working well, you should see improvement within a few hundred iterations
- Remember the coarse-to-fine approach for hyperparameter tuning: start by testing a large range of hyperparameters for just a few training iterations to find the combinations of parameters that are working at all.
- Once you have found some sets of parameters that seem to work, search more finely around these parameters. You may need to train for more epochs.
- You should use the validation set for hyperparameter search, and save your test set for evaluating your architecture on the best parameters as selected by the validation set.
### Going above and beyond
If you are feeling adventurous there are many other features you can implement to try and improve your performance. You are **not required** to implement any of these, but don't miss the fun if you have time!
- Alternative optimizers: you can try Adam, Adagrad, RMSprop, etc.
- Alternative activation functions such as leaky ReLU, parametric ReLU, ELU, or MaxOut.
- Model ensembles
- Data augmentation
- New Architectures
- [ResNets](https://arxiv.org/abs/1512.03385) where the input from the previous layer is added to the output.
- [DenseNets](https://arxiv.org/abs/1608.06993) where inputs into previous layers are concatenated together.
- [This blog has an in-depth overview](https://chatbotslife.com/resnets-highwaynets-and-densenets-oh-my-9bb15918ee32)
### Have fun and happy training!
```
################################################################################
# TODO: #
# Experiment with any architectures, optimizers, and hyperparameters. #
# Achieve AT LEAST 70% accuracy on the *validation set* within 10 epochs. #
# #
# Note that you can use the check_accuracy function to evaluate on either #
# the test set or the validation set, by passing either loader_test or #
# loader_val as the second argument to check_accuracy. You should not touch #
# the test set until you have finished your architecture and hyperparameter #
# tuning, and only run the test set once at the end to report a final value. #
################################################################################
model = None
optimizer = None
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
learning_rate = 1e-2
model = nn.Sequential(
nn.Conv2d(3, 32, (3, 3), padding=1),
nn.ReLU(),
nn.Conv2d(32, 32, (3, 3), padding=1),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d((2, 2)),
nn.Conv2d(32, 64, (3, 3), padding=1),
nn.ReLU(),
nn.Conv2d(64, 64, (3, 3), padding=1),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d((2, 2)),
nn.Conv2d(64, 128, (3, 3), padding=1),
nn.ReLU(),
nn.Conv2d(128, 128, (3, 3), padding=1),
nn.ReLU(),
nn.Conv2d(128, 128, (3, 3), padding=1),
nn.BatchNorm2d(128),
nn.ReLU(),
nn.MaxPool2d((2, 2)),
Flatten(),
nn.Linear(128 * 4 * 4, 512),
nn.ReLU(),
nn.Linear(512, 128),
nn.ReLU(),
nn.Linear(128, 10),
)
optimizer = optim.SGD(model.parameters(), lr=learning_rate,
momentum=0.9, nesterov=True)
# train_part34(model, optimizer, epochs=1)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
# You should get at least 70% accuracy
train_part34(model, optimizer, epochs=10)
```
## Describe what you did
In the cell below you should write an explanation of what you did, any additional features that you implemented, and/or any graphs that you made in the process of training and evaluating your network.
**Answer:**
## Test set -- run this only once
Now that we've gotten a result we're happy with, we test our final model on the test set (which you should store in best_model). Think about how this compares to your validation set accuracy.
```
best_model = model
check_accuracy_part34(loader_test, best_model)
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Libraries-and-functions" data-toc-modified-id="Libraries-and-functions-1"><span class="toc-item-num">1 </span>Libraries and functions</a></span><ul class="toc-item"><li><span><a href="#Import-libraries" data-toc-modified-id="Import-libraries-1.1"><span class="toc-item-num">1.1 </span>Import libraries</a></span></li><li><span><a href="#Definition-of--functions-used-locally" data-toc-modified-id="Definition-of--functions-used-locally-1.2"><span class="toc-item-num">1.2 </span>Definition of functions used locally</a></span></li></ul></li><li><span><a href="#Options" data-toc-modified-id="Options-2"><span class="toc-item-num">2 </span>Options</a></span></li><li><span><a href="#Load-data" data-toc-modified-id="Load-data-3"><span class="toc-item-num">3 </span>Load data</a></span></li><li><span><a href="#Create-base-indices" data-toc-modified-id="Create-base-indices-4"><span class="toc-item-num">4 </span>Create base indices</a></span><ul class="toc-item"><li><span><a href="#Market-cap-weighted" data-toc-modified-id="Market-cap-weighted-4.1"><span class="toc-item-num">4.1 </span>Market cap weighted</a></span></li><li><span><a href="#Equal-weights" data-toc-modified-id="Equal-weights-4.2"><span class="toc-item-num">4.2 </span>Equal weights</a></span></li><li><span><a href="#compute-index-returns" data-toc-modified-id="compute-index-returns-4.3"><span class="toc-item-num">4.3 </span>compute index returns</a></span></li></ul></li><li><span><a href="#Index-based-on-model-predictions" data-toc-modified-id="Index-based-on-model-predictions-5"><span class="toc-item-num">5 </span>Index based on model predictions</a></span><ul class="toc-item"><li><span><a href="#Weight-generation" data-toc-modified-id="Weight-generation-5.1"><span class="toc-item-num">5.1 </span>Weight generation</a></span></li><li><span><a href="#Build-your-strategy" data-toc-modified-id="Build-your-strategy-5.2"><span class="toc-item-num">5.2 </span>Build your strategy</a></span></li><li><span><a href="#Build-index" data-toc-modified-id="Build-index-5.3"><span class="toc-item-num">5.3 </span>Build index</a></span><ul class="toc-item"><li><span><a href="#Monthly-index-levels" data-toc-modified-id="Monthly-index-levels-5.3.1"><span class="toc-item-num">5.3.1 </span>Monthly index levels</a></span></li></ul></li></ul></li></ul></div>
# Libraries and functions
## Import libraries
Need to be able to access functions in base_dir/src
```
# libraries
# general
import sys
import os
import itertools
import dateutil.relativedelta as relativedelta
import datetime
import numpy as np
import pandas as pd
# plotting
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
# # statistics and machine learning
from IPython.display import display
pd.options.display.max_columns = None
# # add the base path to python system path
path = os.getcwd()
#dir_up = os.path.abspath(os.path.join(path, os.pardir))
base_path = os.path.abspath(os.path.join(path, os.pardir))
sys.path.append(base_path)
# from mpl_toolkits.axes_grid.anchored_artists import AnchoredText
from matplotlib import gridspec
# # libraries within package
from src.finance_functions import multiple_returns_from_levels_vec, project_to_first
from src.finance_functions import df_restrict_dates
from src.automotive_dictionaries import equity_name2first_date
from src.index_functionality import index_levels_from_returns
from src.financial_metrics import extract_performance
%load_ext autoreload
%autoreload 2
%reload_ext autoreload
```
# Options
# Load data
```
filename = '../data/data_sample_monthly.csv'
infile = filename
df_comb_long = pd.read_csv(infile)
df_comb_long['date'] = pd.to_datetime(df_comb_long['date'])
#df_comb_long.head()
#eq_name = 'Equity Parent'
eq_name = 'company'
df_prices = df_comb_long.pivot(values='stock_price', index='date', columns=eq_name)
# monthly returns
df_returns = multiple_returns_from_levels_vec(df_prices.ffill())
```
# Create base indices
```
df_market_cap = df_comb_long.pivot(values='MarketCap_Mlns', index='date', columns=eq_name)
df_market_cap.index = df_market_cap.index.map(project_to_first)
# deal with the missing values by taking the previously available one
df_market_cap.ffill(inplace=True)
# set to zero when not available, this takes care of the market cap weights
for col in df_market_cap.columns:
first_date = project_to_first(equity_name2first_date[col])
mask = df_market_cap.index < first_date
df_market_cap.loc[mask, col] = 0.0
#print(first_date)
#df_market_cap.head()
```
## Market cap weighted
```
total_market_cap = df_market_cap.sum(axis=1)
# weights determined in the same month as market cap
df_weights = df_market_cap.div(total_market_cap, axis=0)
# the weights for the index should be determined by past information,
# i.e.by previous month market_cap
#df_weights_mc = df_weights.shift(1).bfill()
df_weights_mc = df_weights.shift(1)
```
## Equal weights
```
df_temp = (df_weights_mc > 0.0).astype(int)
df_weights_equal = df_temp.div(df_temp.sum(axis=1), axis=0)
```
## compute index returns
```
df_mc_index_returns = pd.DataFrame((df_returns * df_weights_mc).sum(axis=1),columns=['mc_return'])
df_mc_index_returns.dropna(inplace=True)
df_equal_index_returns = pd.DataFrame((df_returns * df_weights_equal).sum(axis=1),columns=['equal_return'])
df_equal_index_returns.dropna(inplace=True)
```
# Index based on model predictions
Base indices
* market cap weighted
* equal weighted
## Weight generation
```
l_base_weights = ['Market Cap', 'Equal']
l_weighting_schemes = ['0']
# Cartesian product tuples
l_weights = list(itertools.product(*[l_base_weights,l_weighting_schemes]))
# WEIGHT ADJUSTMENTS OPTIONS
d_weights = {}
#execution loop
for base_mod, scheme in l_weights:
print(base_mod, scheme)
if base_mod == 'Market Cap' :
df_base_weights = df_weights_mc.copy()
if base_mod == 'Equal' :
df_base_weights = df_weights_equal.copy()
df_mod_weights = df_base_weights.copy()
name_d = base_mod + ' ' + scheme
d_weights[name_d] = df_mod_weights
```
## Build your strategy
```
# do something better than random
df_rand = pd.DataFrame(np.random.uniform(low=0.0, high=0.01, size=(len(df_weights_mc.index), len(df_weights_mc.columns))),
columns=list(df_weights_mc.columns), index=df_weights_mc.index)
df_w = df_weights_mc + df_rand
df_w = df_w.div(df_w.sum(axis=1), axis=0)
d_weights['Market Cap smart modify'] = df_w
# # SCHEMATIC: CODE DOES NOT EXECUTE LIKE THIS
# # possible loop for training a model
# # and producing df_oos_predictions
# # alternatively use portfolio optimization
# x_names = ['feature1',...]
# y_name = 'returns'
# prediction_dates = df_weights_mc.index[24:]
# for date in prediction_dates:
# #print(date)
# train_ini_date = date + relativedelta.relativedelta(months=-24)
# train_final_date = date + relativedelta.relativedelta(months=-1)
# df1 = df_restrict_dates(df_comb_long, train_ini_date, train_final_date)
# df_x_train = df1[x_names].copy()
# df_y_train = df1[[y_name]].copy()
# X_train_full = df_x_train.values
# y_train_full = df_y_train[y_name].values
# model.fit(X_train_full, y_train_full, sample_weight=sample_weights)
# ##### oos results
# df2 = df_restrict_dates(df_comb_long, date, date)
# df_x = df2[x_names].copy()
# X_oos = df_x.values
# predictions = model.predict(X_oos)
# df_oos_predictions.loc[date] = predictions
# # SCHEMATIC: CODE DOES NOT EXECUTE LIKE THIS
# # possible loop for weight updates (schematic)
# # based on model predictions df_oos_predictions
# df_base_weights = df_weights_mc.copy()
# df_mod_weights = df_base_weights.copy()
# for date in prediction_dates:
# # assume you have made some predictions
# predictions = df_oos_predictions.loc[date].values
# # relate predictions to weight updates
# weights_mod = ....
# # possibly apply capping rules
# df_mod_weights.loc[date] = weights_mod
# name_d = 'xx'
# d_weights[name_d] = df_mod_weights
```
## Build index
### Monthly index levels
```
# build date frame with indices (no rebalancing)
start_date = datetime.datetime(2009,1,1)
end_date = datetime.datetime(2015,12,31)
starting_level = 100
df_r_in = df_restrict_dates(df_returns, start_date, end_date)
frequency = 'monthly'
for k, name in enumerate(sorted(d_weights.keys())):
print(name)
df_w_in = df_restrict_dates(d_weights[name], start_date, end_date)
df_temp = index_levels_from_returns(df_w_in, df_r_in, out_field=name, starting_level=starting_level,
transaction_costs=False, frequency=frequency)
if k == 0:
df_i_comb = df_temp
else:
df_i_comb = df_i_comb.merge(df_temp, left_index=True, right_index=True)
# plot without rebalancing costs
font = {'size' : 24}
mpl.rc('font', **font)
cm = plt.get_cmap('jet')
#cm = plt.get_cmap('viridis')
sns.set(font_scale=2.5)
sns.set_style("whitegrid")
#fields = 'Equal'
#fields = 'Market Cap'
fields = None
headers = df_i_comb.columns
if fields is not None:
headers = list(filter(lambda s: fields in s, df_i_comb.columns))
df_i_comb[headers].plot(figsize=(20,12), colormap=cm)
plt.title(frequency.title() + ' Index performance (no rebalancing costs)')
print()
extract_performance(df_i_comb[headers])
```
|
github_jupyter
|
# Segmentation
Image segmentation is another early as well as an important image processing task. Segmentation is the process of breaking an image into groups, based on similarities of the pixels. Pixels can be similar to each other in multiple ways like brightness, color, or texture. The segmentation algorithms are to find a partition of the image into sets of similar pixels which usually indicating objects or certain scenes in an image.
The segmentations in this chapter can be categorized into two complementary ways: one focussing on detecting the boundaries of these groups, and the other on detecting the groups themselves, typically called regions. We will introduce some principles of some algorithms in this notebook to present the basic ideas in segmentation.
## Probability Boundary Detection
A boundary curve passing through a pixel $(x,y)$ in an image will have an orientation $\theta$, so we can formulize boundary detection problem as a classification problem. Based on features from a local neighborhood, we want to compute the probability $P_b(x,y,\theta)$ that indeed there is a boundary curve at that pixel along that orientation.
One of the sampling ways to calculate $P_b(x,y,\theta)$ is to generate a series sub-divided into two half disks by a diameter oriented at θ. If there is a boundary at (x, y, θ) the two half disks might be expected to differ significantly in their brightness, color, and texture. For detailed proof of this algorithm, please refer to this [article](https://people.eecs.berkeley.edu/~malik/papers/MFM-boundaries.pdf).
### Implementation
We implemented a simple demonstration of probability boundary detector as `probability_contour_detection` in `perception.py`. This method takes three inputs:
- image: an image already transformed into the type of numpy ndarray.
- discs: a list of sub-divided discs.
- threshold: the standard to tell whether the difference between intensities of two discs implying there is a boundary passing the current pixel.
we also provide a helper function `gen_discs` to gen a list of discs. It takes `scales` as the number of sizes of discs will be generated which is default 1. Please note that for each scale size, there will be 8 sub discs generated which are in the horizontal, verticle and two diagnose directions. Another `init_scale` indicates the starting scale size. For instance, if we use `init_scale` of 10 and `scales` of 2, then scales of sizes of 10 and 20 will be generated and thus we will have 16 sub-divided scales.
### Example
Now let's demonstrate the inner mechanism with our navie implementation of the algorithm. First, let's generate some very simple test images. We already generated a grayscale image with only three steps of gray scales in `perceptron.py`:
```
import os, sys
sys.path = [os.path.abspath("../../")] + sys.path
from perception4e import *
from notebook4e import *
import matplotlib.pyplot as plt
```
Let's take a look at it:
```
plt.imshow(gray_scale_image, cmap='gray', vmin=0, vmax=255)
plt.axis('off')
plt.show()
```
You can also generate your own grayscale images by calling `gen_gray_scale_picture` and pass the image size and grayscale levels needed:
```
gray_img = gen_gray_scale_picture(100, 5)
plt.imshow(gray_img, cmap='gray', vmin=0, vmax=255)
plt.axis('off')
plt.show()
```
Now let's generate the discs we are going to use as sampling masks to tell the intensity difference between two half of the care area of an image. We can generate the discs of size 100 pixels and show them:
```
discs = gen_discs(100, 1)
fig=plt.figure(figsize=(10, 10))
for i in range(8):
img = discs[0][i]
fig.add_subplot(1, 8, i+1)
plt.axis('off')
plt.imshow(img, cmap='gray', vmin=0, vmax=255)
plt.show()
```
The white part of disc images is of value 1 while dark places are of value 0. Thus convolving the half-disc image with the corresponding area of an image will yield only half of its content. Of course, discs of size 100 is too large for an image of the same size. We will use discs of size 10 and pass them to the detector.
```
discs = gen_discs(10, 1)
contours = probability_contour_detection(gray_img, discs[0])
show_edges(contours)
```
As we are using discs of size 10 and some boundary conditions are not dealt with in our naive algorithm, the extracted contour has a bold edge with missings near the image border. But the main structures of contours are extracted correctly which shows the ability of this algorithm.
## Group Contour Detection
The alternative approach is based on trying to “cluster” the pixels into regions based on their brightness, color and texture properties. There are multiple grouping algorithms and the simplest and the most popular one is k-means clustering. Basically, the k-means algorithm starts with k randomly selected centroids, which are used as the beginning points for every cluster, and then performs iterative calculations to optimize the positions of the centroids. For a detailed description, please refer to the chapter of unsupervised learning.
### Implementation
Here we will use the module of `cv2` to perform K-means clustering and show the image. To use it you need to have `opencv-python` pre-installed. Using `cv2.kmeans` is quite simple, you only need to specify the input image and the characters of cluster initialization. Here we use modules provide by `cv2` to initialize the clusters. `cv2.KMEANS_RANDOM_CENTERS` can randomly generate centers of clusters and the cluster number is defined by the user.
`kmeans` method will return the centers and labels of clusters, which can be used to classify pixels of an image. Let's try this algorithm again on the small grayscale image we imported:
```
contours = group_contour_detection(gray_scale_image, 3)
```
Now let's show the extracted contours:
```
show_edges(contours)
```
It is not obvious as our generated image already has very clear boundaries. Let's apply the algorithm on the stapler example to see whether it will be more obvious:
```
import numpy as np
import matplotlib.image as mpimg
stapler_img = mpimg.imread('images/stapler.png', format="gray")
contours = group_contour_detection(stapler_img, 5)
plt.axis('off')
plt.imshow(contours, cmap="gray")
```
The segmentation is very rough when using only 5 clusters. Adding to the cluster number will increase the degree of subtle of each group thus the whole picture will be more alike the original one:
```
contours = group_contour_detection(stapler_img, 15)
plt.axis('off')
plt.imshow(contours, cmap="gray")
```
## Minimum Cut Segmentation
Another way to do clustering is by applying the minimum cut algorithm in graph theory. Roughly speaking, the criterion for partitioning the graph is to minimize the sum of weights of connections across the groups and maximize the sum of weights of connections within the groups.
### Implementation
There are several kinds of representations of a graph such as a matrix or an adjacent list. Here we are using a util function `image_to_graph` to convert an image in ndarray type to an adjacent list. It is integrated into the class of `Graph`. `Graph` takes an image as input and offer the following implementations of some graph theory algorithms:
- bfs: performing bread searches from a source vertex to a terminal vertex. Return `True` if there is a path between the two nodes else return `False`.
- min_cut: performing minimum cut on a graph from a source vertex to sink vertex. The method will return the edges to be cut.
Now let's try the minimum cut method on a simple generated grayscale image of size 10:
```
image = gen_gray_scale_picture(size=10, level=2)
show_edges(image)
graph = Graph(image)
graph.min_cut((0,0), (9,9))
```
There are ten edges to be cut. By cutting the ten edges, we can separate the pictures into two parts by the pixel intensities.
|
github_jupyter
|
# Results Analysis
This notebook analyzes results produced by the _anti-entropy reinforcement learning_ experiments. The practical purpose of this notebook is to create graphs that can be used to display anti-entropy topologies, but also to extract information relevant to each experimental run.
```
%matplotlib notebook
import os
import re
import glob
import json
import unicodedata
import numpy as np
import pandas as pd
import seaborn as sns
import networkx as nx
import matplotlib as mpl
import graph_tool.all as gt
import matplotlib.pyplot as plt
from nx2gt import nx2gt
from datetime import timedelta
from collections import defaultdict
```
## Data Loading
The data directory contains directories whose names are the hosts along with configuration files for each run. Each run is stored in its own `metrics.json` file, suffixed by the run number. The data loader yields _all_ rows from _all_ metric files and appends them with the correct configuration data.
```
DATA = "../data"
FIGS = "../figures"
GRAPHS = "../graphs"
HOSTS = "hosts.json"
RESULTS = "metrics-*.json"
CONFIGS = "config-*.json"
NULLDATE = "0001-01-01T00:00:00Z"
DURATION = re.compile("^([\d\.]+)(\w+)$")
def suffix(path):
# Get the run id from the path
name, _ = os.path.splitext(path)
return int(name.split("-")[-1])
def parse_duration(d):
match = DURATION.match(d)
if match is None:
raise TypeError("could not parse duration '{}'".format(d))
amount, units = match.groups()
amount = float(amount)
unitkw = {
"µs": "microseconds",
"ms": "milliseconds",
"s": "seconds",
}[units]
return timedelta(**{unitkw:amount}).total_seconds()
def load_hosts(path=DATA):
with open(os.path.join(path, HOSTS), 'r') as f:
return json.load(f)
def load_configs(path=DATA):
configs = {}
for name in glob.glob(os.path.join(path, CONFIGS)):
with open(name, 'r') as f:
configs[suffix(name)] = json.load(f)
return configs
def slugify(name):
slug = unicodedata.normalize('NFKD', name)
slug = str(slug.encode('ascii', 'ignore')).lower()
slug = re.sub(r'[^a-z0-9]+', '-', slug).strip('-')
slug = re.sub(r'[-]+', '-', slug)
return slug
def load_results(path=DATA):
hosts = load_hosts(path)
configs = load_configs(path)
for host in os.listdir(path):
for name in glob.glob(os.path.join(path, host, "metrics-*.json")):
run = suffix(name)
with open(name, 'r', encoding='utf-8') as f:
for line in f:
row = json.loads(line.strip())
row['name'] = host
row['host'] = hosts[host]["hostname"] + ":3264"
row['runid'] = run
row['config'] = configs[run]
yield row
def merge_results(path, data=DATA):
# Merge all of the results into a single unified file
with open(path, 'w') as f:
for row in load_results(data):
f.write(json.dumps(row))
f.write("\n")
```
## Graph Extraction
This section extracts a NeworkX graph for each of the experimental runs such that each graph defines an anti-entropy topology.
```
def extract_graphs(path=DATA, outdir=None):
graphs = defaultdict(nx.DiGraph)
for row in load_results(path):
# Get the graph for the topology
G = graphs[row["runid"]]
# Update the graph information
name = row["bandit"]["strategy"].title()
epsilon = row["config"]["replicas"].get("epsilon", None)
if epsilon:
name += " ε={}".format(epsilon)
G.graph.update({
"name": name + " (E{})".format(row["runid"]),
"experiment": row["runid"],
"uptime": row["config"]["replicas"]["uptime"],
"bandit": row["config"]["replicas"]["bandit"],
"epsilon": epsilon or "",
"anti_entropy_interval": row["config"]["replicas"]["delay"],
"workload_duration": row["config"]["clients"]["config"]["duration"],
"n_clients": len(row["config"]["clients"]["hosts"]),
# "workload": row["config"]["clients"]["hosts"],
"store": row["store"],
})
# Update the vertex information
vnames = row["name"].split("-")
vertex = {
"duration": row["duration"],
"finished": row["finished"] if row["finished"] != NULLDATE else "",
"started": row["started"] if row["started"] != NULLDATE else "",
"keys_stored": row["nkeys"],
"reads": row["reads"],
"writes": row["writes"],
"throughput": row["throughput"],
"location": " ".join(vnames[1:-1]).title(),
"pid": int(vnames[-1]),
"name": row["name"]
}
source_id = row["host"]
source = G.add_node(source_id, **vertex)
# Get bandit edge information
bandit_counts = dict(zip(row["peers"], row["bandit"]["counts"]))
bandit_values = dict(zip(row["peers"], row["bandit"]["values"]))
# Add the edges from the sync table
for target_id, stats in row["syncs"].items():
edge = {
"count": bandit_counts[target_id],
"reward": bandit_values[target_id],
"misses": stats["Misses"],
"pulls": stats["Pulls"],
"pushes": stats["Pushes"],
"syncs": stats["Syncs"],
"versions": stats["Versions"],
"mean_pull_latency": parse_duration(stats["PullLatency"]["mean"]),
"mean_push_latency": parse_duration(stats["PushLatency"]["mean"]),
}
G.add_edge(source_id, target_id, **edge)
# Write Graphs
if outdir:
for G in graphs.values():
opath = os.path.join(outdir, slugify(G.name)+".graphml.gz")
nx.write_graphml(G, opath)
return graphs
# for G in extract_graphs(outdir=GRAPHS).values():
for G in extract_graphs().values():
print(nx.info(G))
print()
LOCATION_COLORS = {
"Virginia": "#D91E18",
"Ohio": "#E26A6A",
"California": "#8E44AD",
"Sao Paulo": "#6BB9F0",
"London": "#2ECC71",
"Frankfurt": "#6C7A89",
"Seoul": "#F9690E",
"Sydney": "#F7CA18",
}
LOCATION_GROUPS = sorted(list(LOCATION_COLORS.keys()))
LOCATION_CODES = {
"Virginia": "VA",
"Ohio": "OH",
"California": "CA",
"Sao Paulo": "BR",
"London": "GB",
"Frankfurt": "DE",
"Seoul": "KR",
"Sydney": "AU",
}
def filter_edges(h, pulls=0, pushes=0):
# Create a view of the graph with only edges with syncs > 0
efilt = h.new_edge_property('bool')
for edge in h.edges():
efilt[edge] = (h.ep['pulls'][edge] > pulls or h.ep['pushes'][edge] > pushes)
return gt.GraphView(h, efilt=efilt)
def mklabel(name, loc):
code = LOCATION_CODES[loc]
parts = name.split("-")
return "{}{}".format(code, parts[-1])
def visualize_graph(G, layout='sfdp', filter=True, save=True):
print(G.name)
output = None
if save:
output = os.path.join(FIGS, slugify(G.name) + ".pdf")
# Convert the nx Graph to a gt Graph
g = nx2gt(G)
if filter:
g = filter_edges(g)
# Vertex Properties
vgroup = g.new_vertex_property('int32_t')
vcolor = g.new_vertex_property('string')
vlabel = g.new_vertex_property('string')
for vertex in g.vertices():
vcolor[vertex] = LOCATION_COLORS[g.vp['location'][vertex]]
vgroup[vertex] = LOCATION_GROUPS.index(g.vp['location'][vertex])
vlabel[vertex] = mklabel(g.vp['name'][vertex], g.vp['location'][vertex])
vsize = gt.prop_to_size(g.vp['writes'], ma=65, mi=35)
# Edge Properties
esize = gt.prop_to_size(g.ep['versions'], mi=.01, ma=6)
ecolor = gt.prop_to_size(g.ep['mean_pull_latency'], mi=1, ma=5, log=True)
# Compute the layout and draw
if layout == 'fruchterman_reingold':
pos = gt.fruchterman_reingold_layout(g, weight=esize, circular=True, grid=False)
elif layout == 'sfdp':
pos = gt.sfdp_layout(g, eweight=esize, groups=vgroup)
else:
raise ValueError("unknown layout '{}".format(layout))
gt.graph_draw(
g, pos=pos, output_size=(1200,1200), output=output, inline=True,
vertex_size=vsize, vertex_fill_color=vcolor, vertex_text=vlabel,
vertex_halo=False, vertex_pen_width=1.2,
edge_pen_width=esize,
)
visualize_graph(extract_graphs()[5])
```
## Rewards DataFrame
This section extracts a timeseries of rewards on a per-replica basis.
```
def extract_rewards(path=DATA):
for row in load_results(path):
bandit = row["bandit"]
history = bandit["history"]
strategy = bandit["strategy"]
epsilon = row["config"]["replicas"].get("epsilon")
if epsilon:
strategy += " ε={}".format(epsilon)
values = np.array(list(map(float, history["rewards"])))
series = pd.Series(values, name=row["name"] + " " + strategy)
yield series, row['runid']
total_rewards = {}
for series, rowid in extract_rewards():
if rowid not in total_rewards:
total_rewards[rowid] = series
else:
total_rewards[rowid] += series
cumulative_rewards = {
rowid: s.cumsum()
for rowid, s in total_rewards.items()
}
from pandas.plotting import autocorrelation_plot
df = pd.DataFrame({
" ".join(s.name.split(" ")[1:]): s
for s in total_rewards.values()
}).iloc[15:361]
df.reset_index(inplace=True, drop=True)
fig,ax = plt.subplots(figsize=(9,6))
df.rolling(window=15,center=False).mean().plot(ax=ax)
ax.set_ylabel("Rolling Mean of Total System Reward (w=15)")
ax.set_xlabel("Timesteps (Anti-Entropy Sessions)")
ax.grid(True, ls='--')
ax.set_xlim(12, 346)
plt.savefig(os.path.join(FIGS, "rewards.pdf"))
```
|
github_jupyter
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=1
import tensorflow as tf
gpu_devices = tf.config.experimental.list_physical_devices('GPU')
if len(gpu_devices)>0:
tf.config.experimental.set_memory_growth(gpu_devices[0], True)
print(gpu_devices)
tf.keras.backend.clear_session()
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
dataset = 'fmnist'
from tensorflow.keras.datasets import fashion_mnist
# load dataset
(train_images, Y_train), (test_images, Y_test) = fashion_mnist.load_data()
X_train = (train_images/255.).astype('float32')
X_test = (test_images/255.).astype('float32')
X_train = X_train.reshape((len(X_train), np.product(np.shape(X_train)[1:])))
X_test = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
# subset a validation set
n_valid = 10000
X_valid = X_train[-n_valid:]
Y_valid = Y_train[-n_valid:]
X_train = X_train[:-n_valid]
Y_train = Y_train[:-n_valid]
# flatten X
X_train_flat = X_train.reshape((len(X_train), np.product(np.shape(X_train)[1:])))
X_test_flat = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
X_valid_flat= X_valid.reshape((len(X_valid), np.product(np.shape(X_valid)[1:])))
print(len(X_train), len(X_valid), len(X_test))
```
### define networks
```
dims = (28,28,1)
n_components = 64
encoder = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=dims),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation="relu"
),
tf.keras.layers.Conv2D(
filters=128, kernel_size=3, strides=(2, 2), activation="relu"
),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(units=512, activation="relu"),
tf.keras.layers.Dense(units=n_components),
])
decoder = tf.keras.Sequential([
tf.keras.layers.InputLayer(input_shape=(n_components)),
tf.keras.layers.Dense(units=512, activation="relu"),
tf.keras.layers.Dense(units=7 * 7 * 256, activation="relu"),
tf.keras.layers.Reshape(target_shape=(7, 7, 256)),
tf.keras.layers.Conv2DTranspose(
filters=128, kernel_size=3, strides=(2, 2), padding="SAME", activation="relu"
),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=(2, 2), padding="SAME", activation="relu"
),
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding="SAME", activation="sigmoid"
)
])
input_img = tf.keras.Input(dims)
output_img = decoder(encoder(input_img))
autoencoder = tf.keras.Model(input_img, output_img)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
X_train = X_train.reshape([len(X_train)] + list(dims))
history = autoencoder.fit(X_train, X_train,
epochs=50,
batch_size=256,
shuffle=True,
#validation_data=(X_valid, X_valid)
)
z = encoder.predict(X_train)
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)],
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
```
### View loss
```
from tfumap.umap import retrieve_tensors
import seaborn as sns
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
output_dir = MODEL_DIR/'projections'/ dataset / '64' /'ae_only'
ensure_dir(output_dir)
encoder.save(output_dir / 'encoder')
decoder.save(output_dir / 'encoder')
#loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
### compute metrics
```
X_test.shape
z_test = encoder.predict(X_test.reshape((len(X_test), 28,28,1)))
```
#### silhouette
```
from tfumap.silhouette import silhouette_score_block
ss, sil_samp = silhouette_score_block(z, Y_train, n_jobs = -1)
ss
ss_test, sil_samp_test = silhouette_score_block(z_test, Y_test, n_jobs = -1)
ss_test
fig, axs = plt.subplots(ncols = 2, figsize=(10, 5))
axs[0].scatter(z[:, 0], z[:, 1], s=0.1, alpha=0.5, c=sil_samp, cmap=plt.cm.viridis)
axs[1].scatter(z_test[:, 0], z_test[:, 1], s=1, alpha=0.5, c=sil_samp_test, cmap=plt.cm.viridis)
```
#### KNN
```
from sklearn.neighbors import KNeighborsClassifier
neigh5 = KNeighborsClassifier(n_neighbors=5)
neigh5.fit(z, Y_train)
score_5nn = neigh5.score(z_test, Y_test)
score_5nn
neigh1 = KNeighborsClassifier(n_neighbors=1)
neigh1.fit(z, Y_train)
score_1nn = neigh1.score(z_test, Y_test)
score_1nn
```
#### Trustworthiness
```
from sklearn.manifold import trustworthiness
tw = trustworthiness(X_train_flat[:10000], z[:10000])
tw_test = trustworthiness(X_test_flat[:10000], z_test[:10000])
tw, tw_test
```
### Save output metrics
```
from tfumap.paths import ensure_dir, MODEL_DIR, DATA_DIR
```
#### train
```
metrics_df = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"trustworthiness",
"silhouette_score",
"silhouette_samples",
]
)
metrics_df.loc[len(metrics_df)] = [dataset, 'ae_only', n_components, tw, ss, sil_samp]
metrics_df
save_loc = DATA_DIR / 'projection_metrics' / 'ae_only' / 'train' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
metrics_df.to_pickle(save_loc)
```
#### test
```
metrics_df_test = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"trustworthiness",
"silhouette_score",
"silhouette_samples",
]
)
metrics_df_test.loc[len(metrics_df)] = [dataset, 'ae_only', n_components, tw_test, ss_test, sil_samp_test]
metrics_df_test
save_loc = DATA_DIR / 'projection_metrics' / 'ae' / 'test' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
metrics_df.to_pickle(save_loc)
```
#### knn
```
nn_acc_df = pd.DataFrame(columns = ["method_","dimensions","dataset","1NN_acc","5NN_acc"])
nn_acc_df.loc[len(nn_acc_df)] = ['ae_only', n_components, dataset, score_1nn, score_5nn]
nn_acc_df
save_loc = DATA_DIR / 'knn_classifier' / 'ae_only' / 'train' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
nn_acc_df.to_pickle(save_loc)
```
### Reconstruction
```
from sklearn.metrics import mean_squared_error, mean_absolute_error, median_absolute_error, r2_score
X_recon = decoder.predict(encoder.predict(X_test.reshape((len(X_test), 28, 28, 1))))
X_real = X_test.reshape((len(X_test), 28, 28, 1))
x_real = X_test.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
x_recon = X_recon.reshape((len(X_test), np.product(np.shape(X_test)[1:])))
reconstruction_acc_df = pd.DataFrame(
columns=["method_", "dimensions", "dataset", "MSE", "MAE", "MedAE", "R2"]
)
MSE = mean_squared_error(
x_real,
x_recon
)
MAE = mean_absolute_error(
x_real,
x_recon
)
MedAE = median_absolute_error(
x_real,
x_recon
)
R2 = r2_score(
x_real,
x_recon
)
reconstruction_acc_df.loc[len(reconstruction_acc_df)] = ['ae_only', n_components, dataset, MSE, MAE, MedAE, R2]
reconstruction_acc_df
save_loc = DATA_DIR / 'reconstruction_acc' / 'ae_only' / str(n_components) / (dataset + '.pickle')
ensure_dir(save_loc)
reconstruction_acc_df.to_pickle(save_loc)
```
### Compute clustering quality
```
from sklearn.cluster import KMeans
from sklearn.metrics import homogeneity_completeness_v_measure
def get_cluster_metrics(row, n_init=5):
# load cluster information
save_loc = DATA_DIR / 'clustering_metric_df'/ ('_'.join([row.class_, str(row.dim), row.dataset]) + '.pickle')
print(save_loc)
if save_loc.exists() and save_loc.is_file():
cluster_df = pd.read_pickle(save_loc)
return cluster_df
# make cluster metric dataframe
cluster_df = pd.DataFrame(
columns=[
"dataset",
"class_",
"dim",
"silhouette",
"homogeneity",
"completeness",
"v_measure",
"init_",
"n_clusters",
"model",
]
)
y = row.train_label
z = row.train_z
n_labels = len(np.unique(y))
for n_clusters in tqdm(np.arange(n_labels - int(n_labels / 2), n_labels + int(n_labels / 2)), leave=False, desc = 'n_clusters'):
for init_ in tqdm(range(n_init), leave=False, desc='init'):
kmeans = KMeans(n_clusters=n_clusters, random_state=init_).fit(z)
clustered_y = kmeans.labels_
homogeneity, completeness, v_measure = homogeneity_completeness_v_measure(
y, clustered_y
)
ss, _ = silhouette_score_block(z, clustered_y)
cluster_df.loc[len(cluster_df)] = [
row.dataset,
row.class_,
row.dim,
ss,
homogeneity,
completeness,
v_measure,
init_,
n_clusters,
kmeans,
]
# save cluster df in case this fails somewhere
ensure_dir(save_loc)
cluster_df.to_pickle(save_loc)
return cluster_df
projection_df = pd.DataFrame(columns = ['dataset', 'class_', 'train_z', 'train_label', 'dim'])
projection_df.loc[len(projection_df)] = [dataset, 'ae_only', z, Y_train, n_components]
projection_df
get_cluster_metrics(projection_df.iloc[0], n_init=5)
```
|
github_jupyter
|
# **Space X Falcon 9 First Stage Landing Prediction**
## Web scraping Falcon 9 and Falcon Heavy Launches Records from Wikipedia
We will be performing web scraping to collect Falcon 9 historical launch records from a Wikipedia page titled `List of Falcon 9 and Falcon Heavy launches`
[https://en.wikipedia.org/wiki/List_of_Falcon\_9\_and_Falcon_Heavy_launches](https://en.wikipedia.org/wiki/List_of_Falcon\_9\_and_Falcon_Heavy_launches?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01)
More specifically, the launch records are stored in a HTML table.
First let's import required packages for this lab
```
!pip3 install beautifulsoup4
!pip3 install requests
import sys
import requests
from bs4 import BeautifulSoup
import re
import unicodedata
import pandas as pd
```
Some helper functions for processing web scraped HTML table
```
def date_time(table_cells):
"""
This function returns the data and time from the HTML table cell
Input: the element of a table data cell extracts extra row
"""
return [data_time.strip() for data_time in list(table_cells.strings)][0:2]
def booster_version(table_cells):
"""
This function returns the booster version from the HTML table cell
Input: the element of a table data cell extracts extra row
"""
out=''.join([booster_version for i,booster_version in enumerate( table_cells.strings) if i%2==0][0:-1])
return out
def landing_status(table_cells):
"""
This function returns the landing status from the HTML table cell
Input: the element of a table data cell extracts extra row
"""
out=[i for i in table_cells.strings][0]
return out
def get_mass(table_cells):
mass=unicodedata.normalize("NFKD", table_cells.text).strip()
if mass:
mass.find("kg")
new_mass=mass[0:mass.find("kg")+2]
else:
new_mass=0
return new_mass
def extract_column_from_header(row):
"""
This function returns the landing status from the HTML table cell
Input: the element of a table data cell extracts extra row
"""
if (row.br):
row.br.extract()
if row.a:
row.a.extract()
if row.sup:
row.sup.extract()
colunm_name = ' '.join(row.contents)
# Filter the digit and empty names
if not(colunm_name.strip().isdigit()):
colunm_name = colunm_name.strip()
return colunm_name
```
To keep the lab tasks consistent, we will be asked to scrape the data from a snapshot of the `List of Falcon 9 and Falcon Heavy launches` Wikipage updated on
`9th June 2021`
```
static_url = "https://en.wikipedia.org/w/index.php?title=List_of_Falcon_9_and_Falcon_Heavy_launches&oldid=1027686922"
```
Next, request the HTML page from the above URL and get a `response` object
### TASK 1: Request the Falcon9 Launch Wiki page from its URL
First, let's perform an HTTP GET method to request the Falcon9 Launch HTML page, as an HTTP response.
```
# use requests.get() method with the provided static_url
# assign the response to a object
page=requests.get(static_url)
```
Create a `BeautifulSoup` object from the HTML `response`
```
# Use BeautifulSoup() to create a BeautifulSoup object from a response text content
soup = BeautifulSoup(page.text, 'html.parser')
```
Print the page title to verify if the `BeautifulSoup` object was created properly
```
# Use soup.title attribute
soup.title
```
### TASK 2: Extract all column/variable names from the HTML table header
Next, we want to collect all relevant column names from the HTML table header
Let's try to find all tables on the wiki page first.
```
# Use the find_all function in the BeautifulSoup object, with element type `table`
# Assign the result to a list called `html_tables`
html_tables=soup.find_all('table')
```
Starting from the third table is our target table contains the actual launch records.
```
# Let's print the third table and check its content
first_launch_table = html_tables[2]
print(first_launch_table)
```
We can see the columns names embedded in the table header elements `<th>` as follows:
```
<tr>
<th scope="col">Flight No.
</th>
<th scope="col">Date and<br/>time (<a href="/wiki/Coordinated_Universal_Time" title="Coordinated Universal Time">UTC</a>)
</th>
<th scope="col"><a href="/wiki/List_of_Falcon_9_first-stage_boosters" title="List of Falcon 9 first-stage boosters">Version,<br/>Booster</a> <sup class="reference" id="cite_ref-booster_11-0"><a href="#cite_note-booster-11">[b]</a></sup>
</th>
<th scope="col">Launch site
</th>
<th scope="col">Payload<sup class="reference" id="cite_ref-Dragon_12-0"><a href="#cite_note-Dragon-12">[c]</a></sup>
</th>
<th scope="col">Payload mass
</th>
<th scope="col">Orbit
</th>
<th scope="col">Customer
</th>
<th scope="col">Launch<br/>outcome
</th>
<th scope="col"><a href="/wiki/Falcon_9_first-stage_landing_tests" title="Falcon 9 first-stage landing tests">Booster<br/>landing</a>
</th></tr>
```
Next, we just need to iterate through the `<th>` elements and apply the provided `extract_column_from_header()` to extract column name one by one
```
column_names = []
# Apply find_all() function with `th` element on first_launch_table
# Iterate each th element and apply the provided extract_column_from_header() to get a column name
# Append the Non-empty column name (`if name is not None and len(name) > 0`) into a list called column_names
for i in first_launch_table.find_all('th'):
if extract_column_from_header(i)!=None:
if len(extract_column_from_header(i))>0:
column_names.append(extract_column_from_header(i))
```
Check the extracted column names
```
print(column_names)
```
## TASK 3: Create a data frame by parsing the launch HTML tables
We will create an empty dictionary with keys from the extracted column names in the previous task. Later, this dictionary will be converted into a Pandas dataframe
```
launch_dict= dict.fromkeys(column_names)
# Remove an irrelvant column
del launch_dict['Date and time ( )']
# Let's initial the launch_dict with each value to be an empty list
launch_dict['Flight No.'] = []
launch_dict['Launch site'] = []
launch_dict['Payload'] = []
launch_dict['Payload mass'] = []
launch_dict['Orbit'] = []
launch_dict['Customer'] = []
launch_dict['Launch outcome'] = []
# Added some new columns
launch_dict['Version Booster']=[]
launch_dict['Booster landing']=[]
launch_dict['Date']=[]
launch_dict['Time']=[]
```
Next, we just need to fill up the `launch_dict` with launch records extracted from table rows.
Usually, HTML tables in Wiki pages are likely to contain unexpected annotations and other types of noises, such as reference links `B0004.1[8]`, missing values `N/A [e]`, inconsistent formatting, etc.
```
extracted_row = 0
#Extract each table
for table_number,table in enumerate(soup.find_all('table',"wikitable plainrowheaders collapsible")):
# get table row
for rows in table.find_all("tr"):
#check to see if first table heading is as number corresponding to launch a number
if rows.th:
if rows.th.string:
flight_number=rows.th.string.strip()
flag=flight_number.isdigit()
else:
flag=False
#get table element
row=rows.find_all('td')
#if it is number save cells in a dictonary
if flag:
extracted_row += 1
# Flight Number value
# TODO: Append the flight_number into launch_dict with key `Flight No.`
launch_dict['Flight No.'].append(flight_number)
print(flight_number)
datatimelist=date_time(row[0])
# Date value
# TODO: Append the date into launch_dict with key `Date`
date = datatimelist[0].strip(',')
launch_dict['Date'].append(date)
print(date)
# Time value
# TODO: Append the time into launch_dict with key `Time`
time = datatimelist[1]
launch_dict['Time'].append(time)
print(time)
# Booster version
# TODO: Append the bv into launch_dict with key `Version Booster`
bv=booster_version(row[1])
if not(bv):
bv=row[1].a.string
launch_dict['Version Booster'].append(bv)
print(bv)
# Launch Site
# TODO: Append the bv into launch_dict with key `Launch Site`
launch_site = row[2].a.string
launch_dict['Launch site'].append(launch_site)
print(launch_site)
# Payload
# TODO: Append the payload into launch_dict with key `Payload`
payload = row[3].a.string
launch_dict['Payload'].append(payload)
print(payload)
# Payload Mass
# TODO: Append the payload_mass into launch_dict with key `Payload mass`
payload_mass = get_mass(row[4])
launch_dict['Payload mass'].append(payload_mass)
print(payload_mass)
# Orbit
# TODO: Append the orbit into launch_dict with key `Orbit`
orbit = row[5].a.string
launch_dict['Orbit'].append(orbit)
print(orbit)
# Customer
# TODO: Append the customer into launch_dict with key `Customer`
if row[6].a!=None:
customer = row[6].a.string
else:
customer='None'
launch_dict['Customer'].append(customer)
print(customer)
# Launch outcome
# TODO: Append the launch_outcome into launch_dict with key `Launch outcome`
launch_outcome = list(row[7].strings)[0]
launch_dict['Launch outcome'].append(launch_outcome)
print(launch_outcome)
# Booster landing
# TODO: Append the launch_outcome into launch_dict with key `Booster landing`
booster_landing = landing_status(row[8])
launch_dict['Booster landing'].append(booster_landing)
print(booster_landing)
print("******")
```
After we have filled in the parsed launch record values into `launch_dict`, we can create a dataframe from it.
```
df=pd.DataFrame(launch_dict)
df.head()
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import sys
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
from sklearn.feature_selection import RFE
from sklearn.tree import DecisionTreeClassifier
from sklearn import preprocessing
col_names = ["duration","protocol_type","service","flag","src_bytes",
"dst_bytes","land","wrong_fragment","urgent","hot","num_failed_logins",
"logged_in","num_compromised","root_shell","su_attempted","num_root",
"num_file_creations","num_shells","num_access_files","num_outbound_cmds",
"is_host_login","is_guest_login","count","srv_count","serror_rate",
"srv_serror_rate","rerror_rate","srv_rerror_rate","same_srv_rate",
"diff_srv_rate","srv_diff_host_rate","dst_host_count","dst_host_srv_count",
"dst_host_same_srv_rate","dst_host_diff_srv_rate","dst_host_same_src_port_rate",
"dst_host_srv_diff_host_rate","dst_host_serror_rate","dst_host_srv_serror_rate",
"dst_host_rerror_rate","dst_host_srv_rerror_rate","label"]
df = pd.read_csv("KDDTrain+_2.csv", header=None, names = col_names)
df_test = pd.read_csv("KDDTest+_2.csv", header=None, names = col_names)
categorical_columns=['protocol_type', 'service', 'flag']
# insert code to get a list of categorical columns into a variable, categorical_columns
categorical_columns=['protocol_type', 'service', 'flag']
# Get the categorical values into a 2D numpy array
df_categorical_values = df[categorical_columns]
testdf_categorical_values = df_test[categorical_columns]
df_categorical_values.head()
# protocol type
unique_protocol=sorted(df.protocol_type.unique())
string1 = 'Protocol_type_'
unique_protocol2=[string1 + x for x in unique_protocol]
# service
unique_service=sorted(df.service.unique())
string2 = 'service_'
unique_service2=[string2 + x for x in unique_service]
# flag
unique_flag=sorted(df.flag.unique())
string3 = 'flag_'
unique_flag2=[string3 + x for x in unique_flag]
# put together
dumcols=unique_protocol2 + unique_service2 + unique_flag2
print(dumcols)
#do same for test set
unique_service_test=sorted(df_test.service.unique())
unique_service2_test=[string2 + x for x in unique_service_test]
testdumcols=unique_protocol2 + unique_service2_test + unique_flag2
df_categorical_values_enc=df_categorical_values.apply(LabelEncoder().fit_transform)
print(df_categorical_values_enc.head())
# test set
testdf_categorical_values_enc=testdf_categorical_values.apply(LabelEncoder().fit_transform)
enc = OneHotEncoder()
df_categorical_values_encenc = enc.fit_transform(df_categorical_values_enc)
df_cat_data = pd.DataFrame(df_categorical_values_encenc.toarray(),columns=dumcols)
# test set
testdf_categorical_values_encenc = enc.fit_transform(testdf_categorical_values_enc)
testdf_cat_data = pd.DataFrame(testdf_categorical_values_encenc.toarray(),columns=testdumcols)
df_cat_data.head()
trainservice=df['service'].tolist()
testservice= df_test['service'].tolist()
difference=list(set(trainservice) - set(testservice))
string = 'service_'
difference=[string + x for x in difference]
for col in difference:
testdf_cat_data[col] = 0
testdf_cat_data.shape
newdf=df.join(df_cat_data)
newdf.drop('flag', axis=1, inplace=True)
newdf.drop('protocol_type', axis=1, inplace=True)
newdf.drop('service', axis=1, inplace=True)
# test data
newdf_test=df_test.join(testdf_cat_data)
newdf_test.drop('flag', axis=1, inplace=True)
newdf_test.drop('protocol_type', axis=1, inplace=True)
newdf_test.drop('service', axis=1, inplace=True)
print(newdf.shape)
print(newdf_test.shape)
# take label column
labeldf=newdf['label']
labeldf_test=newdf_test['label']
# change the label column
newlabeldf=labeldf.replace({ 'normal' : 0, 'neptune' : 1 ,'back': 1, 'land': 1, 'pod': 1, 'smurf': 1, 'teardrop': 1,'mailbomb': 1, 'apache2': 1, 'processtable': 1, 'udpstorm': 1, 'worm': 1,
'ipsweep' : 2,'nmap' : 2,'portsweep' : 2,'satan' : 2,'mscan' : 2,'saint' : 2
,'ftp_write': 3,'guess_passwd': 3,'imap': 3,'multihop': 3,'phf': 3,'spy': 3,'warezclient': 3,'warezmaster': 3,'sendmail': 3,'named': 3,'snmpgetattack': 3,'snmpguess': 3,'xlock': 3,'xsnoop': 3,'httptunnel': 3,
'buffer_overflow': 4,'loadmodule': 4,'perl': 4,'rootkit': 4,'ps': 4,'sqlattack': 4,'xterm': 4})
newlabeldf_test=labeldf_test.replace({ 'normal' : 0, 'neptune' : 1 ,'back': 1, 'land': 1, 'pod': 1, 'smurf': 1, 'teardrop': 1,'mailbomb': 1, 'apache2': 1, 'processtable': 1, 'udpstorm': 1, 'worm': 1,
'ipsweep' : 2,'nmap' : 2,'portsweep' : 2,'satan' : 2,'mscan' : 2,'saint' : 2
,'ftp_write': 3,'guess_passwd': 3,'imap': 3,'multihop': 3,'phf': 3,'spy': 3,'warezclient': 3,'warezmaster': 3,'sendmail': 3,'named': 3,'snmpgetattack': 3,'snmpguess': 3,'xlock': 3,'xsnoop': 3,'httptunnel': 3,
'buffer_overflow': 4,'loadmodule': 4,'perl': 4,'rootkit': 4,'ps': 4,'sqlattack': 4,'xterm': 4})
# put the new label column back
newdf['label'] = newlabeldf
newdf_test['label'] = newlabeldf_test
print(newdf['label'].head())
to_drop_DoS = [2,3,4]
DoS_df=newdf[~newdf['label'].isin(to_drop_DoS)];
#test
DoS_df_test=newdf_test[~newdf_test['label'].isin(to_drop_DoS)];
print('Train:')
print('Dimensions of DoS:' ,DoS_df.shape)
print('Test:')
print('Dimensions of DoS:' ,DoS_df_test.shape)
X_DoS = DoS_df.drop('label',1)
Y_DoS = DoS_df.label
Y_DoS=Y_DoS.astype('int')
X_DoS_test = DoS_df_test.drop('label',1)
colNames=list(X_DoS)
colNames_test=list(X_DoS_test)
# scaler1 = preprocessing.StandardScaler().fit(X_DoS)
# X_DoS=scaler1.transform(X_DoS)
# scaler5 = preprocessing.StandardScaler().fit(X_DoS_test)
# X_DoS_test=scaler5.transform(X_DoS_test)
from sklearn.feature_selection import SelectPercentile, f_classif
np.seterr(divide='ignore', invalid='ignore');
selector=SelectPercentile(f_classif, percentile=10)
X_newDoS = selector.fit_transform(X_DoS,Y_DoS)
X_newDoS.shape
true=selector.get_support()
newcolindex_DoS=[i for i, x in enumerate(true) if x]
print(newcolindex_DoS)
newcolname_DoS=list( colNames[i] for i in newcolindex_DoS )
newcolname_DoS
# newcolname_DoS_test=list( colNames_test[i] for i in newcolindex_DoS )
# newcolname_DoS_test
from sklearn.feature_selection import RFE
from sklearn.tree import DecisionTreeClassifier
# Create a decision tree classifier. By convention, clf means 'classifier'
clf = DecisionTreeClassifier(random_state=0)
#rank all features, i.e continue the elimination until the last one
# rfe = RFE(clf, n_features_to_select=1)
clf.fit(X_newDoS, Y_DoS)
X_DoS_test=(X_DoS_test[['logged_in',
'count',
'serror_rate',
'srv_serror_rate',
'same_srv_rate',
'dst_host_count',
'dst_host_srv_count',
'dst_host_same_srv_rate',
'dst_host_serror_rate',
'dst_host_srv_serror_rate',
'service_http',
'flag_S0',
'flag_SF']])
clf.predict(X_D)
```
|
github_jupyter
|
Branching GP Regression on hematopoietic data
--
*Alexis Boukouvalas, 2017*
**Note:** this notebook is automatically generated by [Jupytext](https://jupytext.readthedocs.io/en/latest/index.html), see the README for instructions on working with it.
test change
Branching GP regression with Gaussian noise on the hematopoiesis data described in the paper "BGP: Gaussian processes for identifying branching dynamics in single cell data".
This notebook shows how to build a BGP model and plot the posterior model fit and posterior branching times.
```
import time
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import BranchedGP
plt.style.use("ggplot")
%matplotlib inline
```
### Read the hematopoiesis data. This has been simplified to a small subset of 23 genes found to be branching.
We have also performed Monocle2 (version 2.1) - DDRTree on this data. The results loaded include the Monocle estimated pseudotime, branching assignment (state) and the DDRTree latent dimensions.
```
Y = pd.read_csv("singlecelldata/hematoData.csv", index_col=[0])
monocle = pd.read_csv("singlecelldata/hematoMonocle.csv", index_col=[0])
Y.head()
monocle.head()
# Plot Monocle DDRTree space
genelist = ["FLT3", "KLF1", "MPO"]
f, ax = plt.subplots(1, len(genelist), figsize=(10, 5), sharex=True, sharey=True)
for ig, g in enumerate(genelist):
y = Y[g].values
yt = np.log(1 + y / y.max())
yt = yt / yt.max()
h = ax[ig].scatter(
monocle["DDRTreeDim1"],
monocle["DDRTreeDim2"],
c=yt,
s=50,
alpha=1.0,
vmin=0,
vmax=1,
)
ax[ig].set_title(g)
def PlotGene(label, X, Y, s=3, alpha=1.0, ax=None):
fig = None
if ax is None:
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
for li in np.unique(label):
idxN = (label == li).flatten()
ax.scatter(X[idxN], Y[idxN], s=s, alpha=alpha, label=int(np.round(li)))
return fig, ax
```
### Fit BGP model
Notice the cell assignment uncertainty is higher for cells close to the branching point.
```
def FitGene(g, ns=20): # for quick results subsample data
t = time.time()
Bsearch = list(np.linspace(0.05, 0.95, 5)) + [
1.1
] # set of candidate branching points
GPy = (Y[g].iloc[::ns].values - Y[g].iloc[::ns].values.mean())[
:, None
] # remove mean from gene expression data
GPt = monocle["StretchedPseudotime"].values[::ns]
globalBranching = monocle["State"].values[::ns].astype(int)
d = BranchedGP.FitBranchingModel.FitModel(Bsearch, GPt, GPy, globalBranching)
print(g, "BGP inference completed in %.1f seconds." % (time.time() - t))
# plot BGP
fig, ax = BranchedGP.VBHelperFunctions.PlotBGPFit(
GPy, GPt, Bsearch, d, figsize=(10, 10)
)
# overplot data
f, a = PlotGene(
monocle["State"].values,
monocle["StretchedPseudotime"].values,
Y[g].values - Y[g].iloc[::ns].values.mean(),
ax=ax[0],
s=10,
alpha=0.5,
)
# Calculate Bayes factor of branching vs non-branching
bf = BranchedGP.VBHelperFunctions.CalculateBranchingEvidence(d)["logBayesFactor"]
fig.suptitle("%s log Bayes factor of branching %.1f" % (g, bf))
return d, fig, ax
d, fig, ax = FitGene("MPO")
d_c, fig_c, ax_c = FitGene("CTSG")
```
|
github_jupyter
|
```
%matplotlib inline
import itertools
import os
os.environ['CUDA_VISIBLE_DEVICES']=""
import numpy as np
import gpflow
import gpflow.training.monitor as mon
import numbers
import matplotlib.pyplot as plt
import tensorflow as tf
```
# Demo: `gpflow.training.monitor`
In this notebook we'll demo how to use `gpflow.training.monitor` for logging the optimisation of a GPflow model.
## Creating the GPflow model
We first generate some random data and create a GPflow model.
Under the hood, GPflow gives a unique name to each model which is used to name the Variables it creates in the TensorFlow graph containing a random identifier. This is useful in interactive sessions, where people may create a few models, to prevent variables with the same name conflicting. However, when loading the model, we need to make sure that the names of all the variables are exactly the same as in the checkpoint. This is why we pass name="SVGP" to the model constructor, and why we use gpflow.defer_build().
```
np.random.seed(0)
X = np.random.rand(10000, 1) * 10
Y = np.sin(X) + np.random.randn(*X.shape)
Xt = np.random.rand(10000, 1) * 10
Yt = np.sin(Xt) + np.random.randn(*Xt.shape)
with gpflow.defer_build():
m = gpflow.models.SVGP(X, Y, gpflow.kernels.RBF(1), gpflow.likelihoods.Gaussian(),
Z=np.linspace(0, 10, 5)[:, None],
minibatch_size=100, name="SVGP")
m.likelihood.variance = 0.01
m.compile()
```
Let's compute log likelihood before the optimisation
```
print('LML before the optimisation: %f' % m.compute_log_likelihood())
```
We will be using a TensorFlow optimiser. All TensorFlow optimisers have a support for `global_step` variable. Its purpose is to track how many optimisation steps have occurred. It is useful to keep this in a TensorFlow variable as this allows it to be restored together with all the parameters of the model.
The code below creates this variable using a monitor's helper function. It is important to create it before building the monitor in case the monitor includes a checkpoint task. This is because the checkpoint internally uses the TensorFlow Saver which creates a list of variables to save. Therefore all variables expected to be saved by the checkpoint task should exist by the time the task is created.
```
session = m.enquire_session()
global_step = mon.create_global_step(session)
```
## Construct the monitor
Next we need to construct the monitor. `gpflow.training.monitor` provides classes that are building blocks for the monitor. Essengially, a monitor is a function that is provided as a callback to an optimiser. It consists of a number of tasks that may be executed at each step, subject to their running condition.
In this example, we want to:
- log certain scalar parameters in TensorBoard,
- log the full optimisation objective (log marginal likelihood bound) periodically, even though we optimise with minibatches,
- store a backup of the optimisation process periodically,
- log performance for a test set periodically.
We will define these tasks as follows:
```
print_task = mon.PrintTimingsTask().with_name('print')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
sleep_task = mon.SleepTask(0.01).with_name('sleep').with_name('sleep')
saver_task = mon.CheckpointTask('./monitor-saves').with_name('saver')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
file_writer = mon.LogdirWriter('./model-tensorboard')
model_tboard_task = mon.ModelToTensorBoardTask(file_writer, m).with_name('model_tboard')\
.with_condition(mon.PeriodicIterationCondition(10))\
.with_exit_condition(True)
lml_tboard_task = mon.LmlToTensorBoardTask(file_writer, m).with_name('lml_tboard')\
.with_condition(mon.PeriodicIterationCondition(100))\
.with_exit_condition(True)
```
As the above code shows, each task can be assigned a name and running conditions. The name will be shown in the task timing summary.
There are two different types of running conditions: `with_condition` controls execution of the task at each iteration in the optimisation loop. `with_exit_condition` is a simple boolean flag indicating that the task should also run at the end of optimisation.
In this example we want to run our tasks periodically, at every iteration or every 10th or 100th iteration.
Notice that the two TensorBoard tasks will write events into the same file. It is possible to share a file writer between multiple tasks. However it is not possible to share the same event location between multiple file writers. An attempt to open two writers with the same location will result in error.
## Custom tasks
We may also want to perfom certain tasks that do not have pre-defined `Task` classes. For example, we may want to compute the performance on a test set. Here we create such a class by extending `BaseTensorBoardTask` to log the testing benchmarks in addition to all the scalar parameters.
```
class CustomTensorBoardTask(mon.BaseTensorBoardTask):
def __init__(self, file_writer, model, Xt, Yt):
super().__init__(file_writer, model)
self.Xt = Xt
self.Yt = Yt
self._full_test_err = tf.placeholder(gpflow.settings.tf_float, shape=())
self._full_test_nlpp = tf.placeholder(gpflow.settings.tf_float, shape=())
self._summary = tf.summary.merge([tf.summary.scalar("test_rmse", self._full_test_err),
tf.summary.scalar("test_nlpp", self._full_test_nlpp)])
def run(self, context: mon.MonitorContext, *args, **kwargs) -> None:
minibatch_size = 100
preds = np.vstack([self.model.predict_y(Xt[mb * minibatch_size:(mb + 1) * minibatch_size, :])[0]
for mb in range(-(-len(Xt) // minibatch_size))])
test_err = np.mean((Yt - preds) ** 2.0)**0.5
self._eval_summary(context, {self._full_test_err: test_err, self._full_test_nlpp: 0.0})
custom_tboard_task = CustomTensorBoardTask(file_writer, m, Xt, Yt).with_name('custom_tboard')\
.with_condition(mon.PeriodicIterationCondition(100))\
.with_exit_condition(True)
```
Now we can put all these tasks into a monitor.
```
monitor_tasks = [print_task, model_tboard_task, lml_tboard_task, custom_tboard_task, saver_task, sleep_task]
monitor = mon.Monitor(monitor_tasks, session, global_step)
```
## Running the optimisation
We finally get to running the optimisation.
We may want to continue a previously run optimisation by resotring the TensorFlow graph from the latest checkpoint. Otherwise skip this step.
```
if os.path.isdir('./monitor-saves'):
mon.restore_session(session, './monitor-saves')
optimiser = gpflow.train.AdamOptimizer(0.01)
with mon.Monitor(monitor_tasks, session, global_step, print_summary=True) as monitor:
optimiser.minimize(m, step_callback=monitor, maxiter=450, global_step=global_step)
file_writer.close()
```
Now lets compute the log likelihood again. Hopefully we will see an increase in its value
```
print('LML after the optimisation: %f' % m.compute_log_likelihood())
```
|
github_jupyter
|
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# IUCN - Extinct species
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/IUCN/IUCN_Extinct_species.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #iucn #opendata #extinctspecies #analytics #plotly
**Author:** [Martin Delasalle](https://github.com/delasalle-sio-martin)
Source : https://www.iucnredlist.org/statistics
If you want another view of the data : Link : https://ourworldindata.org/extinctions
### History
The initial aim was to compare the number of threatened species per species over time (e.g. number of pandas per year).
After a lot of research, it turns out that this kind of data is not available or it is only data from one year (2015 or 2018).
Therefore, we decided to start another project: Number of threatened species per year, with details by category using data from this site : https://www.iucnredlist.org/resources/summary-statistics#Summary%20Tables
So we took the pdf from this site and turned it into a csv.
But the data was heavy and not easy to use. Moreover, we thought that this would not necessarily be viable and adaptable over time.
So we decided to take another datasource on a similar subject : *Extinct Species*, from this website : https://www.iucnredlist.org/statistics
### Links that we found during the course
- https://donnees.banquemondiale.org/indicator/EN.MAM.THRD.NO (only 2018)
- https://www.eea.europa.eu/data-and-maps/data/european-red-lists-4/european-red-list/european-red-list-csv-files/view (old Dataset, last upload was in 2015)
- https://www.worldwildlife.org/species/directory?page=2 (the years are not available)
- https://www.worldwildlife.org/pages/conservation-science-data-and-tools (apart from the case)
- https://databasin.org/datasets/68635d7c77f1475f9b6c1d1dbe0a4c4c/ (we can't use it)
- https://gisandscience.com/2009/12/01/download-datasets-from-the-world-wildlife-funds-conservation-science-program/ (no datas about threatened species)
- https://data.world/datasets/tiger (only about tigers but there are no datas usefull)
## Input
### Import library
```
import pandas as pd
import plotly.express as px
```
### Setup your variables
👉 Download data in [CSV](https://www.iucnredlist.org/statistics) and drop it on your root folder
```
# Input csv
csv_input = "Table 3 Species by kingdom and class - show all.csv"
```
## Model
### Get data from csv
```
# We load the csv file
data = pd.read_csv(csv_input, ',')
# We set the column Name as index
data.set_index('Name', inplace = True)
# Then we select the columns EX, EW and Name, and all the lines we want in the graph
table = data.loc[["Total",
"GASTROPODA",
"BIVALVIA",
"AVES",
"MAMMALIA",
"ACTINOPTERYGII",
"CEPHALASPIDOMORPHI",
"INSECTA",
"AMPHIBIA",
"REPTILIA",
"ARACHNIDA",
"CLITELLATA",
"DIPLOPODA",
"ENOPLA",
"TURBELLARIA",
"MALACOSTRACA",
"MAXILLOPODA",
"OSTRACODA"]# add species here
,"EX":"EW"]
table
# We add a new column 'CATEGORY' to our Dataframe
table["CATEGORY"] = ["Total",
"Molluscs",
"Molluscs",
"Birds",
"Mammals",
"Fishes",
"Fishes",
"Insects",
"Amphibians",
"Reptiles",
"Others",
"Others",
"Others",
"Others",
"Others",
"Crustaceans",
"Crustaceans",
"Crustaceans"]
table = table.loc[:,["CATEGORY","EX"]] # we drop the column "EW"
table
# ---NOTE : If you want to add new species, you have to also add his category
# We groupby CATEGORIES :
table.reset_index(drop=True, inplace=True)
table = table.groupby(['CATEGORY']).sum().reset_index()
table.rename(columns = {'EX':'Extincted'}, inplace=True)
table
```
## Output
### Plot graph
```
# We use plotly to show datas with an horizontal bar chart
def create_barchart(table):
Graph = table.sort_values('Extincted', ascending=False)
fig = px.bar(Graph,
x="Extincted",
y="CATEGORY",
color="CATEGORY",
orientation="h")
fig.update_layout(title_text="Number of species that have gone extinct since 1500",
title_x=0.5)
fig.add_annotation(x=800,
y=0,
text="Source : IUCN Red List of Threatened Species<br>https://www.iucnredlist.org/statistics",
showarrow=False)
fig.show()
return fig
fig = create_barchart(table)
```
|
github_jupyter
|
# ThaiNER (Bi-LSTM CRF)
using pytorch
By Mr.Wannaphong Phatthiyaphaibun
Bachelor of Science Program in Computer and Information Science, Nong Khai Campus, Khon Kaen University
https://iam.wannaphong.com/
E-mail : [email protected]
Thank you Faculty of Applied Science and Engineering, Nong Khai Campus, Khon Kaen University for server.
```
import torch.nn.functional as F
from torch.autograd import Variable
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim
print(torch.__version__)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
#torch.backends.cudnn.benchmark=torch.cuda.is_available()
#FloatTensor = torch.cuda.FloatTensor if USE_CUDA else torch.FloatTensor
LongTensor = torch.long
#ByteTensor = torch.cuda.ByteTensor if USE_CUDA else torch.ByteTensor
def argmax(vec):
# return the argmax as a python int
_, idx = torch.max(vec, 1)
return idx.item()
def prepare_sequence(seq, to_ix):
idxs = [to_ix[w] if w in to_ix else to_ix["UNK"] for w in seq]
return torch.tensor(idxs, dtype=LongTensor, device=device)
# Compute log sum exp in a numerically stable way for the forward algorithm
def log_sum_exp(vec):
max_score = vec[0, argmax(vec)]
max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])
return max_score + \
torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))
class BiLSTM_CRF(nn.Module):
def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):
super(BiLSTM_CRF, self).__init__()
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.vocab_size = vocab_size
self.tag_to_ix = tag_to_ix
self.tagset_size = len(tag_to_ix)
self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2,
num_layers=1, bidirectional=True)
# Maps the output of the LSTM into tag space.
self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)
# Matrix of transition parameters. Entry i,j is the score of
# transitioning *to* i *from* j.
self.transitions = nn.Parameter(
torch.randn(self.tagset_size, self.tagset_size, device=device))
# These two statements enforce the constraint that we never transfer
# to the start tag and we never transfer from the stop tag
self.transitions.data[tag_to_ix[START_TAG], :] = -10000
self.transitions.data[:, tag_to_ix[STOP_TAG]] = -10000
self.hidden = self.init_hidden()
def init_hidden(self):
return (torch.randn(2, 1, self.hidden_dim // 2,device=device),
torch.randn(2, 1, self.hidden_dim // 2,device=device))
def _forward_alg(self, feats):
# Do the forward algorithm to compute the partition function
init_alphas = torch.full((1, self.tagset_size), -10000., device=device)
# START_TAG has all of the score.
init_alphas[0][self.tag_to_ix[START_TAG]] = 0.
# Wrap in a variable so that we will get automatic backprop
forward_var = init_alphas
# Iterate through the sentence
for feat in feats:
alphas_t = [] # The forward tensors at this timestep
for next_tag in range(self.tagset_size):
# broadcast the emission score: it is the same regardless of
# the previous tag
emit_score = feat[next_tag].view(
1, -1).expand(1, self.tagset_size)
# the ith entry of trans_score is the score of transitioning to
# next_tag from i
trans_score = self.transitions[next_tag].view(1, -1)
# The ith entry of next_tag_var is the value for the
# edge (i -> next_tag) before we do log-sum-exp
next_tag_var = forward_var + trans_score + emit_score
# The forward variable for this tag is log-sum-exp of all the
# scores.
alphas_t.append(log_sum_exp(next_tag_var).view(1))
forward_var = torch.cat(alphas_t).view(1, -1)
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
alpha = log_sum_exp(terminal_var)
return alpha
def _get_lstm_features(self, sentence):
self.hidden = self.init_hidden()
embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)
lstm_out, self.hidden = self.lstm(embeds, self.hidden)
lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
lstm_feats = self.hidden2tag(lstm_out)
return lstm_feats
def _score_sentence(self, feats, tags):
# Gives the score of a provided tag sequence
score = torch.zeros(1,device=device)
tags = torch.cat([torch.tensor([self.tag_to_ix[START_TAG]], dtype=LongTensor, device=device), tags])
for i, feat in enumerate(feats):
score = score + \
self.transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
score = score + self.transitions[self.tag_to_ix[STOP_TAG], tags[-1]]
return score
def _viterbi_decode(self, feats):
backpointers = []
# Initialize the viterbi variables in log space
init_vvars = torch.full((1, self.tagset_size), -10000., device=device)
init_vvars[0][self.tag_to_ix[START_TAG]] = 0
# forward_var at step i holds the viterbi variables for step i-1
forward_var = init_vvars
for feat in feats:
bptrs_t = [] # holds the backpointers for this step
viterbivars_t = [] # holds the viterbi variables for this step
for next_tag in range(self.tagset_size):
# next_tag_var[i] holds the viterbi variable for tag i at the
# previous step, plus the score of transitioning
# from tag i to next_tag.
# We don't include the emission scores here because the max
# does not depend on them (we add them in below)
next_tag_var = forward_var + self.transitions[next_tag]
best_tag_id = argmax(next_tag_var)
bptrs_t.append(best_tag_id)
viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))
# Now add in the emission scores, and assign forward_var to the set
# of viterbi variables we just computed
forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
backpointers.append(bptrs_t)
# Transition to STOP_TAG
terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
best_tag_id = argmax(terminal_var)
path_score = terminal_var[0][best_tag_id]
# Follow the back pointers to decode the best path.
best_path = [best_tag_id]
for bptrs_t in reversed(backpointers):
best_tag_id = bptrs_t[best_tag_id]
best_path.append(best_tag_id)
# Pop off the start tag (we dont want to return that to the caller)
start = best_path.pop()
assert start == self.tag_to_ix[START_TAG] # Sanity check
best_path.reverse()
return path_score, best_path
def neg_log_likelihood(self, sentence, tags):
feats = self._get_lstm_features(sentence)
forward_score = self._forward_alg(feats)
gold_score = self._score_sentence(feats, tags)
return forward_score - gold_score
def forward(self, sentence): # dont confuse this with _forward_alg above.
# Get the emission scores from the BiLSTM
lstm_feats = self._get_lstm_features(sentence)
# Find the best path, given the features.
score, tag_seq = self._viterbi_decode(lstm_feats)
return score, tag_seq
START_TAG = "<START>"
STOP_TAG = "<STOP>"
EMBEDDING_DIM = 64
HIDDEN_DIM = 128
import dill
with open('word_to_ix.pkl', 'rb') as file:
word_to_ix = dill.load(file)
with open('pos_to_ix.pkl', 'rb') as file:
pos_to_ix = dill.load(file)
ix_to_word = dict((v,k) for k,v in word_to_ix.items()) #convert index to word
ix_to_pos = dict((v,k) for k,v in pos_to_ix.items()) #convert index to word
model = BiLSTM_CRF(len(word_to_ix), pos_to_ix, EMBEDDING_DIM, HIDDEN_DIM)
model.load_state_dict(torch.load("thainer.model"), strict=False)
model.to(device)
def predict(input_sent):
y_pred=[]
temp=[]
with torch.no_grad():
precheck_sent = prepare_sequence(input_sent, word_to_ix)
output=model(precheck_sent)[1]
y_pred=[ix_to_pos[i] for i in output]
return y_pred
predict(["ผม","ชื่อ","นาย","บุญ","มาก"," ","ทอง","ดี"])
```
|
github_jupyter
|
# Flight Price Prediction
---
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
pip list
```
## Importing dataset
1. Check whether any null values are there or not. if it is present then following can be done,
1. Imputing data using Imputation method in sklearn
2. Filling NaN values with mean, median and mode using fillna() method
```
train_data = pd.read_excel(r"/home/adarshsrivastava/Github/Flight_Fare_Prediction-/dataset/Data_Train.xlsx")
#pd.set_option('display.max_columns', None)
train_data.head()
train_data.info()
train_data["Duration"].value_counts()
train_data.dropna(inplace = True)
train_data.isnull().sum() #To check if there is any NaN value in any of the column
```
## EDA
From description we can see that Date_of_Journey is a object data type,\
Therefore, we have to convert this datatype into timestamp so as to use this column properly for prediction
For this we require pandas **to_datetime** to convert object data type to datetime dtype.
<span style="color: red;">**.dt.day method will extract only day of that date**</span>\
<span style="color: red;">**.dt.month method will extract only month of that date**</span>
```
train_data["Journey_day"] = pd.to_datetime(train_data.Date_of_Journey, format="%d/%m/%Y").dt.day
train_data["Journey_month"] = pd.to_datetime(train_data["Date_of_Journey"], format = "%d/%m/%Y").dt.month
train_data.head()
# Since we have converted Date_of_Journey column into integers, Now we can drop as it is of no use.
train_data.drop(["Date_of_Journey"], axis = 1, inplace = True)
# Departure time is when a plane leaves the gate.
# Similar to Date_of_Journey we can extract values from Dep_Time
# Extracting Hours
train_data["Dep_hour"] = pd.to_datetime(train_data["Dep_Time"]).dt.hour
# Extracting Minutes
train_data["Dep_min"] = pd.to_datetime(train_data["Dep_Time"]).dt.minute
# Now we can drop Dep_Time as it is of no use
train_data.drop(["Dep_Time"], axis = 1, inplace = True)
train_data.head()
# Arrival time is when the plane pulls up to the gate.
# Similar to Date_of_Journey we can extract values from Arrival_Time
# Extracting Hours
train_data["Arrival_hour"] = pd.to_datetime(train_data.Arrival_Time).dt.hour
# Extracting Minutes
train_data["Arrival_min"] = pd.to_datetime(train_data.Arrival_Time).dt.minute
# Now we can drop Arrival_Time as it is of no use
train_data.drop(["Arrival_Time"], axis = 1, inplace = True)
train_data.head()
# Time taken by plane to reach destination is called Duration
# It is the differnce betwwen Departure Time and Arrival time
# Assigning and converting Duration column into list
duration = list(train_data["Duration"])
for i in range(len(duration)):
if len(duration[i].split()) != 2: # Check if duration contains only hour or mins
if "h" in duration[i]:
duration[i] = duration[i].strip() + " 0m" # Adds 0 minute
else:
duration[i] = "0h " + duration[i] # Adds 0 hour
duration_hours = []
duration_mins = []
for i in range(len(duration)):
duration_hours.append(int(duration[i].split(sep = "h")[0])) # Extract hours from duration
duration_mins.append(int(duration[i].split(sep = "m")[0].split()[-1])) # Extracts only minutes from duration
# Adding duration_hours and duration_mins list to train_data dataframe
train_data["Duration_hours"] = duration_hours
train_data["Duration_mins"] = duration_mins
train_data.drop(["Duration"], axis = 1, inplace = True)
train_data.head()
```
---
## Handling Categorical Data
One can find many ways to handle categorical data. Some of them categorical data are,
1. <span style="color: blue;">**Nominal data**</span> --> data are not in any order --> <span style="color: green;">**OneHotEncoder**</span> is used in this case
2. <span style="color: blue;">**Ordinal data**</span> --> data are in order --> <span style="color: green;">**LabelEncoder**</span> is used in this case
```
train_data["Airline"].value_counts()
# From graph we can see that Jet Airways Business have the highest Price.
# Apart from the first Airline almost all are having similar median
# Airline vs Price
sns.catplot(y = "Price", x = "Airline", data = train_data.sort_values("Price", ascending = False), kind="boxen", height = 12, aspect = 2)
plt.show()
# As Airline is Nominal Categorical data we will perform OneHotEncoding
Airline = train_data[["Airline"]]
Airline = pd.get_dummies(Airline, drop_first= True)
Airline.head()
train_data["Source"].value_counts()
# Source vs Price
sns.catplot(y = "Price", x = "Source", data = train_data.sort_values("Price", ascending = False), kind="boxen", height = 6, aspect = 2)
plt.show()
# As Source is Nominal Categorical data we will perform OneHotEncoding
Source = train_data[["Source"]]
Source = pd.get_dummies(Source, drop_first= True)
Source.head()
train_data["Destination"].value_counts()
# As Destination is Nominal Categorical data we will perform OneHotEncoding
Destination = train_data[["Destination"]]
Destination = pd.get_dummies(Destination, drop_first = True)
Destination.head()
train_data["Route"]
# Additional_Info contains almost 80% no_info
# Route and Total_Stops are related to each other
train_data.drop(["Route", "Additional_Info"], axis = 1, inplace = True)
train_data["Total_Stops"].value_counts()
# As this is case of Ordinal Categorical type we perform LabelEncoder
# Here Values are assigned with corresponding keys
train_data.replace({"non-stop": 0, "1 stop": 1, "2 stops": 2, "3 stops": 3, "4 stops": 4}, inplace = True)
train_data.head()
# Concatenate dataframe --> train_data + Airline + Source + Destination
data_train = pd.concat([train_data, Airline, Source, Destination], axis = 1)
data_train.head()
data_train.drop(["Airline", "Source", "Destination"], axis = 1, inplace = True)
data_train.head()
data_train.shape
```
---
## Test set
```
test_data = pd.read_excel(r"/home/adarshsrivastava/Github/Flight_Fare_Prediction-/dataset/Test_set.xlsx")
test_data.head()
# Preprocessing
print("Test data Info")
print("-"*75)
print(test_data.info())
print()
print()
print("Null values :")
print("-"*75)
test_data.dropna(inplace = True)
print(test_data.isnull().sum())
# EDA
# Date_of_Journey
test_data["Journey_day"] = pd.to_datetime(test_data.Date_of_Journey, format="%d/%m/%Y").dt.day
test_data["Journey_month"] = pd.to_datetime(test_data["Date_of_Journey"], format = "%d/%m/%Y").dt.month
test_data.drop(["Date_of_Journey"], axis = 1, inplace = True)
# Dep_Time
test_data["Dep_hour"] = pd.to_datetime(test_data["Dep_Time"]).dt.hour
test_data["Dep_min"] = pd.to_datetime(test_data["Dep_Time"]).dt.minute
test_data.drop(["Dep_Time"], axis = 1, inplace = True)
# Arrival_Time
test_data["Arrival_hour"] = pd.to_datetime(test_data.Arrival_Time).dt.hour
test_data["Arrival_min"] = pd.to_datetime(test_data.Arrival_Time).dt.minute
test_data.drop(["Arrival_Time"], axis = 1, inplace = True)
# Duration
duration = list(test_data["Duration"])
for i in range(len(duration)):
if len(duration[i].split()) != 2: # Check if duration contains only hour or mins
if "h" in duration[i]:
duration[i] = duration[i].strip() + " 0m" # Adds 0 minute
else:
duration[i] = "0h " + duration[i] # Adds 0 hour
duration_hours = []
duration_mins = []
for i in range(len(duration)):
duration_hours.append(int(duration[i].split(sep = "h")[0])) # Extract hours from duration
duration_mins.append(int(duration[i].split(sep = "m")[0].split()[-1])) # Extracts only minutes from duration
# Adding Duration column to test set
test_data["Duration_hours"] = duration_hours
test_data["Duration_mins"] = duration_mins
test_data.drop(["Duration"], axis = 1, inplace = True)
# Categorical data
print("Airline")
print("-"*75)
print(test_data["Airline"].value_counts())
Airline = pd.get_dummies(test_data["Airline"], drop_first= True)
print()
print("Source")
print("-"*75)
print(test_data["Source"].value_counts())
Source = pd.get_dummies(test_data["Source"], drop_first= True)
print()
print("Destination")
print("-"*75)
print(test_data["Destination"].value_counts())
Destination = pd.get_dummies(test_data["Destination"], drop_first = True)
# Additional_Info contains almost 80% no_info
# Route and Total_Stops are related to each other
test_data.drop(["Route", "Additional_Info"], axis = 1, inplace = True)
# Replacing Total_Stops
test_data.replace({"non-stop": 0, "1 stop": 1, "2 stops": 2, "3 stops": 3, "4 stops": 4}, inplace = True)
# Concatenate dataframe --> test_data + Airline + Source + Destination
data_test = pd.concat([test_data, Airline, Source, Destination], axis = 1)
data_test.drop(["Airline", "Source", "Destination"], axis = 1, inplace = True)
print()
print()
print("Shape of test data : ", data_test.shape)
data_test.head()
```
---
# Feature Selection
Finding out the best feature which will contribute and have good relation with target variable.
Following are some of the feature selection methods,
1. <span style="color: red;">**heatmap**</span>
2. <span style="color: red;">**feature_importance_**</span>
3. <span style="color: red;">**SelectKBest**</span>
```
data_train.shape
data_train.columns
X = data_train.loc[:, ['Total_Stops', 'Journey_day', 'Journey_month', 'Dep_hour',
'Dep_min', 'Arrival_hour', 'Arrival_min', 'Duration_hours',
'Duration_mins', 'Airline_Air India', 'Airline_GoAir', 'Airline_IndiGo',
'Airline_Jet Airways', 'Airline_Jet Airways Business',
'Airline_Multiple carriers',
'Airline_Multiple carriers Premium economy', 'Airline_SpiceJet',
'Airline_Trujet', 'Airline_Vistara', 'Airline_Vistara Premium economy',
'Source_Chennai', 'Source_Delhi', 'Source_Kolkata', 'Source_Mumbai',
'Destination_Cochin', 'Destination_Delhi', 'Destination_Hyderabad',
'Destination_Kolkata', 'Destination_New Delhi']]
X.head()
y = data_train.iloc[:,1]
y.head()
# Finds correlation between Independent and dependent attributes
plt.figure(figsize = (18,18))
sns.heatmap(train_data.corr(), annot = True)
plt.show()
# Important feature using ExtraTreesRegressor
from sklearn.ensemble import ExtraTreesRegressor
selection = ExtraTreesRegressor()
selection.fit(X, y)
print(selection.feature_importances_)
#plot graph of feature importances for better visualization
plt.figure(figsize = (12,8))
feat_importances = pd.Series(selection.feature_importances_, index=X.columns)
feat_importances.nlargest(20).plot(kind='barh')
plt.show()
```
## Fitting model using Random Forest
1. Split dataset into train and test set in order to prediction w.r.t X_test
2. If needed do scaling of data
* Scaling is not done in Random forest
3. Import model
4. Fit the data
5. Predict w.r.t X_test
6. In regression check **RSME** Score
7. Plot graph
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor()
rf.fit(X_train, y_train)
y_pred=rf.predict(X_test)
rf.score(X_train,y_train)
rf.score(X_test,y_test)
sns.distplot(y_test-y_pred)
plt.show()
plt.scatter(y_test,y_pred)
plt.xlabel("y_test")
plt.ylabel("y_pred")
plt.show()
from sklearn import metrics
print("MAE:",metrics.mean_absolute_error(y_test,y_pred))
print("MSE:",metrics.mean_squared_error(y_test,y_pred))
rmse=np.sqrt(metrics.mean_squared_error(y_test,y_pred))
print("RMSE:",rmse)
rmse/(max(y)-min(y))
metrics.r2_score(y_test,y_pred)
import pickle
# open a file, where you ant to store the data
file = open('flight_fare_pred.pkl', 'wb')
# dump information to that file
pickle.dump(rf, file)
model = open('flight_fare_pred.pkl','rb')
forest = pickle.load(model)
y_prediction = forest.predict(X_test)
metrics.r2_score(y_test, y_prediction)
```
|
github_jupyter
|
<h1><center>Solving Linear Equations with Quantum Circuits</center></h1>
<h2><center>Ax = b</center></h2>
<h4><center> Attempt to replicate the following paper </center></h4>

<h3><center>Algorithm for a simpler 2 x 2 example</center></h3>


$\newcommand{\ket}[1]{\left|{#1}\right\rangle}$
$\newcommand{\bra}[1]{\left\langle{#1}\right|}$
The Final state looks like:
$$ \ket{\psi} = \sum_{j=1}^N \beta_j \left( \sqrt{1-\frac{C^2}{\lambda_j^2}} \ket{0} + \frac{C}{\lambda_j} \ket{1} \right) \ket{00} \ket{u_j} $$
```
#Solving a linear system of equation for 2 dimensional equantion of the form Ax = b
### code specific initialization (importing libraries)
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from math import *
import scipy
# importing Qiskit
from qiskit import IBMQ, BasicAer
#from qiskit.providers.ibmq import least_busy
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
# import basic plot tools
from qiskit.tools.visualization import plot_histogram
from qiskit.quantum_info.synthesis import euler_angles_1q
from cmath import exp
### problem specific parameters
# matrix representation of linear equation
A = 0.5*np.array([[3,1],[1,3]])
t0 = 2*pi #time paramter appearing in the unitary
r = 4
q = QuantumRegister(4, 'q')
c = ClassicalRegister(1, 'c')
qpe = QuantumCircuit(q,c)
qpe.h(q[3])
qpe.barrier()
qpe.h(q[1])
qpe.h(q[2])
# 1st unitary corresponding to A
UA = scipy.linalg.expm(complex(0,1)*A*t0/4)
[theta, phi, lmda] = euler_angles_1q(UA)
qpe.cu3(theta, phi, lmda,q[2],q[3])
# 2nd unitary corresponding to A
UA = scipy.linalg.expm(complex(0,1)*A*2*t0/4)
[theta, phi, lmda] = euler_angles_1q(UA)
qpe.cu3(theta, phi, lmda,q[1],q[3])
qpe.barrier()
# quantum fourier transform
qpe.swap(q[1],q[2])
qpe.h(q[2])
qpe.cu1(-pi/2,q[1],q[2])
qpe.h(q[1])
qpe.swap(q[1],q[2])
qpe.barrier()
#controlled rotations gate
qpe.cry(2*pi/(2**r),q[1],q[0])
qpe.cry(pi/(2**r),q[2],q[0])
qpe.barrier()
qpe.draw(output="mpl")
###############################################################
### uncomputation
# reversing fourier transform
qpe.swap(q[1],q[2])
qpe.h(q[1])
qpe.cu1(pi/2,q[1],q[2])
qpe.h(q[2])
qpe.swap(q[1],q[2])
# reversing 2nd unitary corresponding to A
UA = scipy.linalg.expm(complex(0,-1)*A*2*t0/4)
[theta, phi, lmda] = euler_angles_1q(UA)
qpe.cu3(theta, phi, lmda,q[1],q[3])
# reversing 1st unitary corresponding to A
UA = scipy.linalg.expm(complex(0,-1)*A*t0/4)
[theta, phi, lmda] = euler_angles_1q(UA)
qpe.cu3(theta, phi, lmda,q[2],q[3])
qpe.h(q[1])
qpe.h(q[2])
qpe.barrier()
qpe.draw(output="mpl")
qpe.measure(q[0], c[0])
qpe.draw(output="mpl")
circuit = qpe
simulator = BasicAer.get_backend('qasm_simulator')
result = execute(circuit, backend = simulator, shots = 2048).result()
counts = result.get_counts()
from qiskit.tools.visualization import plot_histogram
plot_histogram(counts)
```
|
github_jupyter
|
```
from mocpy import MOC
import numpy as np
from astropy import units as u
from astropy.coordinates import SkyCoord
%matplotlib inline
# Plot the polygon vertices on a matplotlib axis
def plot_graph(vertices):
import matplotlib.pyplot as plt
from matplotlib import path, patches
fig = plt.figure()
ax = fig.add_subplot(111)
p = path.Path(vertices)
patch = patches.PathPatch(p, facecolor='orange', lw=2)
ax.add_patch(patch)
# Methods for defining random polygons
def generate_rand_polygon(num_points):
lon_min, lon_max = (-5, 5)
lat_min, lat_max = (-5, 5)
lon = (np.random.random(num_points) * (lon_max - lon_min) + lon_min) * u.deg
lat = (np.random.random(num_points) * (lat_max - lat_min) + lat_min) * u.deg
vertices = np.vstack((lon.to_value(), lat.to_value())).T
return vertices
def generate_concave_polygon(num_points, lon_offset, lat_offset):
delta_ang = (2 * np.pi) / num_points
radius_max = 10
angles = np.linspace(0, 2 * np.pi, num_points)
radius = np.random.random(angles.shape[0]) * radius_max
lon = (np.cos(angles) * radius + lon_offset) * u.deg
lat = (np.sin(angles) * radius + lat_offset) * u.deg
vertices = np.vstack((lon.to_value(), lat.to_value())).T
return vertices
def generate_convexe_polygon(num_points, lon_offset, lat_offset):
delta_ang = (2 * np.pi) / num_points
radius_max = 10
angles = np.linspace(0, 2 * np.pi, num_points)
radius = np.random.random() * radius_max * np.ones(angles.shape[0])
lon = (np.cos(angles) * radius + lon_offset) * u.deg
lat = (np.sin(angles) * radius + lat_offset) * u.deg
vertices = np.vstack((lon.to_value(), lat.to_value())).T
return vertices
#vertices = generate_convexe_polygon(20, 10, 5)
vertices = generate_concave_polygon(20, 10, 5)
def plot(moc, skycoord):
from matplotlib import path, patches
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10, 10))
from mocpy import World2ScreenMPL
from astropy.coordinates import Angle
with World2ScreenMPL(fig,
fov=20 * u.deg,
center=SkyCoord(10, 5, unit='deg', frame='icrs'),
coordsys="icrs",
rotation=Angle(0, u.degree),
projection="TAN") as wcs:
ax = fig.add_subplot(1, 1, 1, projection=wcs)
moc.fill(ax=ax, wcs=wcs, edgecolor='r', facecolor='r', linewidth=1.0, fill=True, alpha=0.5)
from astropy.wcs.utils import skycoord_to_pixel
x, y = skycoord_to_pixel(skycoord, wcs)
p = path.Path(np.vstack((x, y)).T)
patch = patches.PathPatch(p, facecolor='green', alpha=0.25, lw=2)
ax.add_patch(patch)
plt.xlabel('ra')
plt.ylabel('dec')
plt.grid(color='black', ls='dotted')
plt.title('from polygon')
plt.show()
plt.close()
# Convert the vertices to lon and lat astropy quantities
lon, lat = vertices[:, 0] * u.deg, vertices[:, 1] * u.deg
skycoord = SkyCoord(lon, lat, unit="deg", frame="icrs")
# Define a vertex that is said to belongs to the MOC.
# It is important as there is no way on the sphere to know the area from
# which we want to build the MOC (a set of vertices delimits two finite areas).
%time moc = MOC.from_polygon(lon=lon, lat=lat, max_depth=12)
plot(moc, skycoord)
```
|
github_jupyter
|
# MCMC sampling using the emcee package
## Introduction
The goal of Markov Chain Monte Carlo (MCMC) algorithms is to approximate the posterior distribution of your model parameters by random sampling in a probabilistic space. For most readers this sentence was probably not very helpful so here we'll start straight with and example but you should read the more detailed mathematical approaches of the method [here](https://www.pas.rochester.edu/~sybenzvi/courses/phy403/2015s/p403_17_mcmc.pdf) and [here](https://github.com/jakevdp/BayesianAstronomy/blob/master/03-Bayesian-Modeling-With-MCMC.ipynb).
### How does it work ?
The idea is that we use a number of walkers that will sample the posterior distribution (i.e. sample the Likelihood profile).
The goal is to produce a "chain", i.e. a list of $\theta$ values, where each $\theta$ is a vector of parameters for your model.<br>
If you start far away from the truth value, the chain will take some time to converge until it reaches a stationary state. Once it has reached this stage, each successive elements of the chain are samples of the target posterior distribution.<br>
This means that, once we have obtained the chain of samples, we have everything we need. We can compute the distribution of each parameter by simply approximating it with the histogram of the samples projected into the parameter space. This will provide the errors and correlations between parameters.
Now let's try to put a picture on the ideas described above. With this notebook, we have simulated and carried out a MCMC analysis for a source with the following parameters:<br>
$Index=2.0$, $Norm=5\times10^{-12}$ cm$^{-2}$ s$^{-1}$ TeV$^{-1}$, $Lambda =(1/Ecut) = 0.02$ TeV$^{-1}$ (50 TeV) for 20 hours.
The results that you can get from a MCMC analysis will look like this :
<img src="images/gammapy_mcmc.png" width="800">
On the first two top panels, we show the pseudo-random walk of one walker from an offset starting value to see it evolve to a better solution.
In the bottom right panel, we show the trace of each 16 walkers for 500 runs (the chain described previsouly). For the first 100 runs, the parameter evolve towards a solution (can be viewed as a fitting step). Then they explore the local minimum for 400 runs which will be used to estimate the parameters correlations and errors.
The choice of the Nburn value (when walkers have reached a stationary stage) can be done by eye but you can also look at the autocorrelation time.
### Why should I use it ?
When it comes to evaluate errors and investigate parameter correlation, one typically estimate the Likelihood in a gridded search (2D Likelihood profiles). Each point of the grid implies a new model fitting. If we use 10 steps for each parameters, we will need to carry out 100 fitting procedures.
Now let's say that I have a model with $N$ parameters, we need to carry out that gridded analysis $N*(N-1)$ times.
So for 5 free parameters you need 20 gridded search, resulting in 2000 individual fit.
Clearly this strategy doesn't scale well to high-dimensional models.
Just for fun: if each fit procedure takes 10s, we're talking about 5h of computing time to estimate the correlation plots.
There are many MCMC packages in the python ecosystem but here we will focus on [emcee](https://emcee.readthedocs.io), a lightweight Python package. A description is provided here : [Foreman-Mackey, Hogg, Lang & Goodman (2012)](https://arxiv.org/abs/1202.3665).
```
%matplotlib inline
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import astropy.units as u
from astropy.coordinates import SkyCoord
from gammapy.irf import load_cta_irfs
from gammapy.maps import WcsGeom, MapAxis
from gammapy.modeling.models import (
ExpCutoffPowerLawSpectralModel,
GaussianSpatialModel,
SkyModel,
Models,
FoVBackgroundModel,
)
from gammapy.datasets import MapDataset
from gammapy.makers import MapDatasetMaker
from gammapy.data import Observation
from gammapy.modeling.sampling import (
run_mcmc,
par_to_model,
plot_corner,
plot_trace,
)
from gammapy.modeling import Fit
import logging
logging.basicConfig(level=logging.INFO)
```
## Simulate an observation
Here we will start by simulating an observation using the `simulate_dataset` method.
```
irfs = load_cta_irfs(
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
observation = Observation.create(
pointing=SkyCoord(0 * u.deg, 0 * u.deg, frame="galactic"),
livetime=20 * u.h,
irfs=irfs,
)
# Define map geometry
axis = MapAxis.from_edges(
np.logspace(-1, 2, 15), unit="TeV", name="energy", interp="log"
)
geom = WcsGeom.create(
skydir=(0, 0), binsz=0.05, width=(2, 2), frame="galactic", axes=[axis]
)
empty_dataset = MapDataset.create(geom=geom, name="dataset-mcmc")
maker = MapDatasetMaker(selection=["background", "edisp", "psf", "exposure"])
dataset = maker.run(empty_dataset, observation)
# Define sky model to simulate the data
spatial_model = GaussianSpatialModel(
lon_0="0 deg", lat_0="0 deg", sigma="0.2 deg", frame="galactic"
)
spectral_model = ExpCutoffPowerLawSpectralModel(
index=2,
amplitude="3e-12 cm-2 s-1 TeV-1",
reference="1 TeV",
lambda_="0.05 TeV-1",
)
sky_model_simu = SkyModel(
spatial_model=spatial_model, spectral_model=spectral_model, name="source"
)
bkg_model = FoVBackgroundModel(dataset_name="dataset-mcmc")
models = Models([sky_model_simu, bkg_model])
print(models)
dataset.models = models
dataset.fake()
dataset.counts.sum_over_axes().plot(add_cbar=True);
# If you want to fit the data for comparison with MCMC later
# fit = Fit(dataset)
# result = fit.run(optimize_opts={"print_level": 1})
```
## Estimate parameter correlations with MCMC
Now let's analyse the simulated data.
Here we just fit it again with the same model we had before as a starting point.
The data that would be needed are the following:
- counts cube, psf cube, exposure cube and background model
Luckily all those maps are already in the Dataset object.
We will need to define a Likelihood function and define priors on parameters.<br>
Here we will assume a uniform prior reading the min, max parameters from the sky model.
### Define priors
This steps is a bit manual for the moment until we find a better API to define priors.<br>
Note the you **need** to define priors for each parameter otherwise your walkers can explore uncharted territories (e.g. negative norms).
```
print(dataset)
# Define the free parameters and min, max values
parameters = dataset.models.parameters
parameters["sigma"].frozen = True
parameters["lon_0"].frozen = True
parameters["lat_0"].frozen = True
parameters["amplitude"].frozen = False
parameters["index"].frozen = False
parameters["lambda_"].frozen = False
parameters["norm"].frozen = True
parameters["tilt"].frozen = True
parameters["norm"].min = 0.5
parameters["norm"].max = 2
parameters["index"].min = 1
parameters["index"].max = 5
parameters["lambda_"].min = 1e-3
parameters["lambda_"].max = 1
parameters["amplitude"].min = 0.01 * parameters["amplitude"].value
parameters["amplitude"].max = 100 * parameters["amplitude"].value
parameters["sigma"].min = 0.05
parameters["sigma"].max = 1
# Setting amplitude init values a bit offset to see evolution
# Here starting close to the real value
parameters["index"].value = 2.0
parameters["amplitude"].value = 3.2e-12
parameters["lambda_"].value = 0.05
print(dataset.models)
print("stat =", dataset.stat_sum())
%%time
# Now let's define a function to init parameters and run the MCMC with emcee
# Depending on your number of walkers, Nrun and dimensionality, this can take a while (> minutes)
sampler = run_mcmc(dataset, nwalkers=6, nrun=150) # to speedup the notebook
# sampler=run_mcmc(dataset,nwalkers=12,nrun=1000) # more accurate contours
```
## Plot the results
The MCMC will return a sampler object containing the trace of all walkers.<br>
The most important part is the chain attribute which is an array of shape:<br>
_(nwalkers, nrun, nfreeparam)_
The chain is then used to plot the trace of the walkers and estimate the burnin period (the time for the walkers to reach a stationary stage).
```
plot_trace(sampler, dataset)
plot_corner(sampler, dataset, nburn=50)
```
## Plot the model dispersion
Using the samples from the chain after the burn period, we can plot the different models compared to the truth model. To do this we need to the spectral models for each parameter state in the sample.
```
emin, emax = [0.1, 100] * u.TeV
nburn = 50
fig, ax = plt.subplots(1, 1, figsize=(12, 6))
for nwalk in range(0, 6):
for n in range(nburn, nburn + 100):
pars = sampler.chain[nwalk, n, :]
# set model parameters
par_to_model(dataset, pars)
spectral_model = dataset.models["source"].spectral_model
spectral_model.plot(
energy_range=(emin, emax),
ax=ax,
energy_power=2,
alpha=0.02,
color="grey",
)
sky_model_simu.spectral_model.plot(
energy_range=(emin, emax), energy_power=2, ax=ax, color="red"
);
```
## Fun Zone
Now that you have the sampler chain, you have in your hands the entire history of each walkers in the N-Dimensional parameter space. <br>
You can for example trace the steps of each walker in any parameter space.
```
# Here we plot the trace of one walker in a given parameter space
parx, pary = 0, 1
plt.plot(sampler.chain[0, :, parx], sampler.chain[0, :, pary], "ko", ms=1)
plt.plot(
sampler.chain[0, :, parx],
sampler.chain[0, :, pary],
ls=":",
color="grey",
alpha=0.5,
)
plt.xlabel("Index")
plt.ylabel("Amplitude");
```
## PeVatrons in CTA ?
Now it's your turn to play with this MCMC notebook. For example to test the CTA performance to measure a cutoff at very high energies (100 TeV ?).
After defining your Skymodel it can be as simple as this :
```
# dataset = simulate_dataset(model, geom, pointing, irfs)
# sampler = run_mcmc(dataset)
# plot_trace(sampler, dataset)
# plot_corner(sampler, dataset, nburn=200)
```
|
github_jupyter
|
#Stock Price Predictor
This is a Jupyter notebook that you can use to get prediction of adjusted close stock price per the specified day range after the last day from the training data set. The prediction is made by training the machine learning model with historical trade of the stock data. This is the result of study from the following notebook - https://github.com/pathompong-y/stock_predictor.
To use this notebook, please follow this setup instruction.
##Setup Instructions
1. Download `stock_predictor.ipynb` and `stock_predictor.py` from https://github.com/pathompong-y/stock_predictor.
2. Go to https://colab.research.google.com and go to file and upload new notebook. Upload stock_predictor.ipynb.
3. Upload `stock_predictor.py` to Files panel by drag and drop from your local computer to the root/outmost level folder.
4. Follow how to use to do train the model and do prediction.
##How to use
Provide input into the code cell below per this instruction.
1. At `stock_list`, Provide the list of stock symbol separated by space. Make sure that the symbol is searchable on Yahoo Finance - https://finance.yahoo.com/.
2. At `training_date_start_date` and `training_data_end_date`, specify the start date and end date for historical data of the stock to train the model. The date format is DD/MM/YYYY.
3. Push "Play" button at the cell upper left corner (or alt+enter / cmd+enter). Please wait until you see "Completed" message. For one stock, it could take up to 15 minutes.
```
stock_list = 'ASK.BK GOOGL'
training_data_start_date = '08/05/2000'
training_data_end_date = '13/05/2020'
# ------ DO NOT CHANGE CODE BELOW THIS LINE --------
!pip install yfinance
import yfinance as yf
import os,sys
sys.path.append(os.path.abspath("/content/stock_predictor.py"))
from stock_predictor import *
train_model(stock_list,training_data_start_date,training_data_end_date)
```
##How to use (cont.)
4. You can query for the predicted stock price by adding the list of stock symbol in `query_list`. The symbol must be subset of `stock_list` that you provided in step 1.
5. `prediction_range` is the day range of price prediction after `end_date` in step 2. For example, if `end_date` is 15/05/2020 and `prediction_range` is 5. You will get the prediction for 5 days after 15/05/2020.
6. Push "Play" button at the cell upper left corner (or alt+enter / cmd+enter). You will get the predicted price (Adjusted Close) with mean squared error rate of prediction.
```
query_list = 'ASK.BK GOOGL'
prediction_range = 5
# ------ DO NOT CHANGE CODE BELOW THIS LINE --------
query_price(query_list,prediction_range)
```
|
github_jupyter
|
<a href="https://qworld.net" target="_blank" align="left"><img src="../qworld/images/header.jpg" align="left"></a>
$ \newcommand{\bra}[1]{\langle #1|} $
$ \newcommand{\ket}[1]{|#1\rangle} $
$ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
$ \newcommand{\dot}[2]{ #1 \cdot #2} $
$ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
$ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
$ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
$ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
$ \newcommand{\mypar}[1]{\left( #1 \right)} $
$ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
$ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
$ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
$ \newcommand{\onehalf}{\frac{1}{2}} $
$ \newcommand{\donehalf}{\dfrac{1}{2}} $
$ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
$ \newcommand{\vzero}{\myvector{1\\0}} $
$ \newcommand{\vone}{\myvector{0\\1}} $
$ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
$ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
$ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
$ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
$ \newcommand{\I}{ \mymatrix{rr}{1 & 0 \\ 0 & 1} } $
$ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
$ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
$ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
$ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
$ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
$ \newcommand{\greenbit}[1] {\mathbf{{\color{green}#1}}} $
$ \newcommand{\bluebit}[1] {\mathbf{{\color{blue}#1}}} $
$ \newcommand{\redbit}[1] {\mathbf{{\color{red}#1}}} $
$ \newcommand{\brownbit}[1] {\mathbf{{\color{brown}#1}}} $
$ \newcommand{\blackbit}[1] {\mathbf{{\color{black}#1}}} $
<font style="font-size:28px;" align="left"><b> Basics of Python: Loops </b></font>
<br>
_prepared by Abuzer Yakaryilmaz_
<br><br>
We review using loops in Python here.
Run each cell and check the results.
<h3> For-loop </h3>
```
# let's print all numbers between 0 and 9
for i in range(10): print(i)
# range(n) represents the list of all numbers from 0 to n-1
# i is the variable to take the values in the range(n) iteratively: 0,1,...,9 in our example
# let's write the same code in two lines
for i in range(10): # do not forget to use colon
print(i)
# the second line is indented
# this means that the command in the second line will be executed inside the for-loop
# any other code executed inside the for-loop must be intented in the same way
#my_code_inside_for-loop_2 will come here
#my_code_inside_for-loop_3 will come here
#my_code_inside_for-loop_4 will come here
# now I am out of the scope of for-loop
#my_code_outside_for-loop_1 will come here
#my_code_outside_for-loop_2 will come here
# let's calculate the summation 1+2+...+10 by using a for-loop
# we use variable total for the total summation
total = 0
for i in range(11): # do not forget to use colon
total = total + i # the value of total is increased by i in each iteration
# alternatively, the same assignment can shortly be written as total += i similarly to the languages C, C++, Java, etc.
# now I am out of the scope of for-loop
# let's print the final value of total
print(total)
# let's calculate the summation 10+12+14+...+44
# we create a list having all numbers in the summation
# for this purpose, this time we will use three parameters in range
total = 0
for j in range(10,45,2): # the range is defined between 10 and 44, and the value of j will be increased by 2 after each iteration
total += j # let's use the shortened version of total = total + j this time
print(total)
# let's calculate the summation 1+2+4+8+16+...+256
# remark that 256 = 2*2*...*2 (8 times)
total = 0
current_number = 1 # this value will be multiplied by 2 after each iteration
for k in range(9):
total = total + current_number # current_number is 1 at the beginning, and its value will be doubled after each iteration
current_number = 2 * current_number # let's double the value of the current_number for the next iteration
# short version of the same assignment: current_number *= 2 as in the languages C, C++, Java, etc.
# now I am out of the scope of for-loop
# let's print the latest value of total
print(total)
# instead of range, we may also directly use a list if it is short
for i in [1,10,100,1000,10000]:
print(i)
# instead of [...], we may also use (...)
# but this time it is a tuple, not a list (keep in your mind that the values in a tuple cannot be changed)
for i in (1,10,100,1000,10000):
print(i)
# let's create a range between 10 and 91 that contains the multiples of 7
for j in range(14,92,7):
# 14 is the first multiple of 7 greater than or equal to 10; so we should start with 14
# 91 should be in the range, and so we end the range with 92
print(j)
# let's create a range between 11 and 22
for i in range(11,23):
print(i)
# we can also use variables in range
n = 5
for j in range(n,2*n):
print(j) # we will print all numbers in {n,n+1,n+2,...,2n-1}
# we can use a list of strings
for name in ("Asja","Balvis","Fyodor"):
print("Hello",name,":-)")
# any range indeed returns a list
L1 = list(range(10))
print(L1)
L2 = list(range(55,200,11))
print(L2)
```
<h3> Task 1 </h3>
Calculate the value of summation $ 3+6+9+\cdots+51 $, and then print the result.
Your result should be 459.
```
#
# your solution is here
#
```
<a href="Python12_Basics_Loops_Solutions.ipynb#task1">click for our solution</a>
<h3> Task 2 </h3>
$ 3^k $ means $ 3 \cdot 3 \cdot \cdots \cdot 3 $ ($ k $ times) for $ k \geq 2 $.
Moreover, $ 3^0 $ is 1 and $ 3^1 = 3 $.
Calculate the value of summation $ 3^0 + 3^1 + 3^2 + \cdots + 3^8 $, and then print the result.
Your result should be 9841.
```
#
# your solution is here
#
```
<a href="Python12_Basics_Loops_Solutions.ipynb#task2">click for our solution</a>
<h3> While-loop </h3>
```
# let's calculate the summation 1+2+4+8+...+256 by using a while-loop
total = 0
i = 1
#while condition(s):
# your_code1
# your_code2
# your_code3
while i < 257: # this loop iterates as long as i is less than 257
total = total + i
i = i * 2 # i is doubled in each iteration, and so soon it will be greater than 256
print(total)
# we do the same summation by using for-loop above
L = [0,1,2,3,4,5,11] # this is a list containing 7 integer values
i = 0
while i in L: # this loop will be iterated as long as i is in L
print(i)
i = i + 1 # the value of i iteratively increased, and so soon it will hit a value not in the list L
# the loop is terminated after i is set to 6, because 6 is not in L
# let's use negation in the condition of while-loop
L = [10] # this list has a single element
i = 0
while i not in L: # this loop will be iterated as long as i is not equal to 10
print(i)
i = i+1 # the value of i will hit 10 after ten iterations
# let's rewrite the same loop by using a direct inequality
i = 0
while i != 10: # "!=" is used for operator "not equal to"
print(i)
i=i+1
# let's rewrite the same loop by using negation of equality
i = 0
while not (i == 10): # "==" is used for operator "equal to"
print(i)
i=i+1
# while-loop seems having more fun :-)
# but we should be more careful when writing the condition(s)!
```
Consider the summation $ S(n) = 1+ 2+ 3 + \cdots + n $ for some natural number $ n $.
Let's find the minimum value of $ n $ such that $ S(n) \geq 1000 $.
While-loop works very well for this task.
<ul>
<li>We can iteratively increase $ n $ and update the value of $ S(n) $.</li>
<li>The loop iterates as long as $S(n)$ is less than 1000.</li>
<li>Once it hits 1000 or a greater number, the loop will be terminated.</li>
</ul>
```
# summation and n are zeros at the beginning
S = 0
n = 0
while S < 1000: # this loop will stop after S exceeds 999 (S = 1000 or S > 1000)
n = n +1
S = S + n
# let's print n and S
print("n =",n," S =",S)
```
<h3> Task 3 </h3>
Consider the summation $ T(n) = 1 + \dfrac{1}{2} + \dfrac{1}{4}+ \dfrac{1}{8} + \cdots + \dfrac{1}{2^n} $ for some natural number $ n $.
Remark that $ T(0) = \dfrac{1}{2^0} = \dfrac{1}{1} = 1 $.
This summation can be arbitrarily close to $2$.
Find the minimum value of $ n $ such that $ T(n) $ is close to $2$ by $ 0.01 $, i.e., $ 2 - T(n) < 0.01 $.
In other words, we find the minimum value of $n$ such that $ T(n) > 1.99 $.
The operator for "less than or equal to" in python is "$ < = $".
```
# three examples for the operator "less than or equal to"
#print (4 <= 5)
#print (5 <= 5)
#print (6 <= 5)
# you may comment out the above three lines and see the results by running this cell
#
# your solution is here
#
```
<a href="Python12_Basics_Loops_Solutions.ipynb#task3">click for our solution</a>
<h3> Task 4 </h3>
Randomly pick number(s) between 0 and 9 until hitting 3, and then print the number of attempt(s).
We can use <i>randrange</i> function from <i>random</i> module for randomly picking a number in the given range.
```
# this is the code for including function randrange into our program
from random import randrange
# randrange(n) picks a number from the list [0,1,2,...,n-1] randomly
#r = randrange(100)
#print(r)
#
# your solution is here
#
```
<a href="Python12_Basics_Loops_Solutions.ipynb#task4">click for our solution</a>
<h3> Task 5 </h3>
This task is challenging .
It is designed for the usage of double nested loops: one loop inside of the other loop.
In the fourth task above, the expected number of attempt(s) to hit number 3 is 10.
Do a series of experiments by using your solution for Task 4.
Experiment 1: Execute your solution 20 times, and then calculate the average attempts.
Experiment 2: Execute your solution 200 times, and then calculate the average attempts.
Experiment 3: Execute your solution 2000 times, and then calculate the average attempts.
Experiment 4: Execute your solution 20000 times, and then calculate the average attempts.
Experiment 5: Execute your solution 200000 times, and then calculate the average attempts.
<i>Your experimental average sgould get closer to 10 when the number of executions is increased.</i>
Remark that all five experiments may also be automatically done by using triple loops.
<a href="Python12_Basics_Loops_Solutions.ipynb#task5">click for our solution</a>
```
# here is a schematic example for double nested loops
#for i in range(10):
# your_code1
# your_code2
# while j != 7:
# your_code_3
# your_code_4
#
# your solution is here
#
```
|
github_jupyter
|
```
import os
import struct
import pandas as pd
import numpy as np
import talib as tdx
def readTdxLdayFile(fname="data/sh000001.day"):
dataSet=[]
with open(fname,'rb') as fl:
buffer=fl.read() #读取数据到缓存
size=len(buffer)
rowSize=32 #通信达day数据,每32个字节一组数据
code=os.path.basename(fname).replace('.day','')
for i in range(0,size,rowSize): #步长为32遍历buffer
row=list( struct.unpack('IIIIIfII',buffer[i:i+rowSize]) )
row[1]=row[1]/100
row[2]=row[2]/100
row[3]=row[3]/100
row[4]=row[4]/100
row.pop() #移除最后无意义字段
row.insert(0,code)
dataSet.append(row)
data=pd.DataFrame(data=dataSet,columns=['code','tradeDate','open','high','low','close','amount','vol'])
data=data.set_index(['tradeDate'])
return code, data
def select1(code, data):
# 连续三日缩量
cn = data.close.iloc[-1]
# df=pd.concat([tdx.MA(data.close, x) for x in (5,10,20,30,60,90,120,250,500,750,1000,1500,2000,2500,) ], axis = 1).dropna()[-1:]
df=pd.concat([tdx.MA(data.close, x) for x in (5,10,20,30,60,90,120,250,500,750,1000,1500,2000,2500,) ], axis = 1)[-1:]
df.columns = [u'm5',u'm10',u'm20',u'm30',u'm60',u'm90',u'm120', u'm250', u'm500', u'm750', u'm1000', u'm1500', u'm2000', u'm2500']
df_c2 = df.m5 > df.m10
df_c1 = cn > df.m5
df_c = cn > df.m5
df_h = df.apply(lambda x:cn > x.max() , axis = 1 )
# df_l = df.apply(lambda x:x.min() >= cl, axis = 1 )
df['dfh'] = df_h
df['dfc2'] = df_c2
df['dfc1'] = df_c1
df['code'] =code
# out=df.iloc[-1].apply(lambda x: True if x>cl and x < ch else False)
df=df.reset_index('tradeDate')
df=df.set_index(['code','tradeDate'])
return df
from threading import Thread, current_thread, Lock
import multiprocessing #import Pool, cpu_count, Queue
def asyncCalc(fname, queue):
code, df = readTdxLdayFile(fname)
queue.put(select1(code, df))
def readPath(path):
files = os.listdir(path)
# codes=[]
q = multiprocessing.Queue()
jobs = []
# dataSet=[]multiprocessing
pool_size = multiprocessing.cpu_count()
pool = multiprocessing.Pool(pool_size)
output=pd.DataFrame()
for i in range(0,len(files)):
fname = os.path.join(path,files[i])
if os.path.isdir(fname):
continue
pool.apply_async(asyncCalc, args=(fname))
p = multiprocessing.Process(target=asyncCalc, args=(fname, q))
jobs.append(p)
p.start()
for p in jobs:
p.join()
for j in jobs:
t = q.get()
if t is not None:
output=output.append(t)
return output
output=readPath('/tmp/easyquant/tdx/data') #读取目录下面的所有文件
output
code, data = readTdxLdayFile('/tmp/easyquant/tdx/data/sh000001.day')
select1(code,data)
code
data=df
cn = data.close.iloc[-1]
cn=cn+1000
df=pd.concat([tdx.MA(data.close, x) for x in (5,10,20,30,60,90,120,250,500,750,1000,21500,20000,25000,) ], axis = 1)[-1:]
df
df.columns = [u'm5',u'm10',u'm20',u'm30',u'm60',u'm90',u'm120', u'm250', u'm500', u'm750', u'm1000', u'm1500', u'm2000', u'm2500']
df_c = df.m5 > df.m10
df_c1 = cn > df.m5
df_h = df.apply(lambda x:cn > x.max() , axis = 1 )
df_h
df_h
da=data_df.reset_index('tradeDate')
df_c1
import datetime
pd.to_datetime(da.tradeDate)
# data_df.to_csv('test.csv')
data_df.index[,-1:-1]
def select1(code,data):
# 连续三日缩量
ch= data.close.iloc[-1] * 1.1
cl= data.close.iloc[-1] * 0.9
# ch= data.close * 1.1
# cl = data.close * 0.9
df=pd.concat([tdx.MA(data.close, x) for x in (5,10,20,30,60,90,120,250) ], axis = 1).dropna()[-1:]
df.columns = [u'm5',u'm10',u'm20',u'm30',u'm60',u'm90',u'm120', u'm250']
df_h = df.apply(lambda x:x.max() <= ch, axis = 1 )
df_l = df.apply(lambda x:x.min() >= cl, axis = 1 )
df['dfh'] = df_h
df['dfl'] = df_l
df['code'] =code
# out=df.iloc[-1].apply(lambda x: True if x>cl and x < ch else False)
df=df.reset_index('tradeDate')
df=df.set_index(['code','tradeDate'])
return df
bbb=select1('sh000001',data_df.loc['sh000001',])
bbb
bbb=bbb.set_index(['code','tradeDate'])
data=bbb.set_index(['code','tradeDate'])
output=None
for code in codes:
aaa=data_df.loc[code,]
out=select1(code, aaa)
if output is None:
output = out
else:
# print(code)
output=output.append(out)
output
output.query('dfh==True and dfl==True').to_csv('out1.csv')
bb=select1('000001',aaa)
type(bb)
import talib as tdx
aaa=pd.read_csv('test.csv')
aaa.set_index('vol').sort_index()
df=readTdxLdayFile()
df['mon'] = df.tradeDate.apply(lambda x : str(x)[0:6])
df=df.set_index(['tradeDate'])
dfmax=df.groupby(['mon']).apply(lambda x: x[x.high ==x.high.max()])
dfmax.drop_duplicates(subset=['high','mon'],keep='first',inplace=True)
dfmin=df.groupby(['mon']).apply(lambda x: x[x.low ==x.low.min()])
dfmin.drop_duplicates(subset=['low','mon'],keep='first',inplace=True)
dfmax.to_csv('max.csv')
dfmin.to_csv('min.csv')
dfmax
for x in dfmax.index:
print(df.loc[x[1]])
```
|
github_jupyter
|
```
import argparse
import torch.distributed as dist
import torch.optim as optim
import torch.optim.lr_scheduler as lr_scheduler
import test # import test.py to get mAP after each epoch
from models import *
from utils.datasets import *
from utils.utils import *
from mymodel import *
# Hyperparameters (results68: 59.9 [email protected] yolov3-spp-416) https://github.com/ultralytics/yolov3/issues/310
hyp = {'giou': 3.54, # giou loss gain
'cls': 37.4, # cls loss gain
'cls_pw': 1.0, # cls BCELoss positive_weight
'obj': 64.3, # obj loss gain (*=img_size/320 if img_size != 320)
'obj_pw': 1.0, # obj BCELoss positive_weight
'iou_t': 0.225, # iou training threshold
'lr0': 0.01, # initial learning rate (SGD=5E-3, Adam=5E-4)
'lrf': -4., # final LambdaLR learning rate = lr0 * (10 ** lrf)
'momentum': 0.937, # SGD momentum
'weight_decay': 0.000484, # optimizer weight decay
'fl_gamma': 0.5, # focal loss gamma
'hsv_h': 0.0138, # image HSV-Hue augmentation (fraction)
'hsv_s': 0.678, # image HSV-Saturation augmentation (fraction)
'hsv_v': 0.36, # image HSV-Value augmentation (fraction)
'degrees': 1.98, # image rotation (+/- deg)
'translate': 0.05, # image translation (+/- fraction)
'scale': 0.05, # image scale (+/- gain)
'shear': 0.641} # image shear (+/- deg)
parser = argparse.ArgumentParser()
parser.add_argument('--batch-size', type=int, default=16) # effective bs = batch_size * accumulate = 16 * 4 = 64
parser.add_argument('--accumulate', type=int, default=4, help='batches to accumulate before optimizing')
parser.add_argument('--cfg', type=str, default='cfg/yolov3-tiny-1cls_1.cfg', help='*.cfg path')
parser.add_argument('--data', type=str, default='data/coco2017.data', help='*.data path')
parser.add_argument('--img-size', nargs='+', type=int, default=[320], help='train and test image-sizes')
parser.add_argument('--rect', action='store_true', help='rectangular training')
parser.add_argument('--cache-images', action='store_true', help='cache images for faster training')
parser.add_argument('--weights', type=str, default='/home/denggc/DAC2021/dgc/April/ultra_bypass/weights/test_best.pt', help='initial weights path')
parser.add_argument('--arc', type=str, default='default', help='yolo architecture') # default, uCE, uBCE
parser.add_argument('--name', default='', help='renames results.txt to results_name.txt if supplied')
parser.add_argument('--device', default='1', help='device id (i.e. 0 or 0,1 or cpu)')
parser.add_argument('--single-cls', action='store_true', help='train as single-class dataset')
parser.add_argument('--var', type=float, help='debug variable')
opt = parser.parse_known_args()[0]
print(opt)
print(opt.weights)
device = torch_utils.select_device(opt.device, batch_size=opt.batch_size)
print(device)
img_size, img_size_test = opt.img_size if len(opt.img_size) == 2 else opt.img_size * 2 # train, test sizes
batch_size = opt.batch_size
accumulate = opt.accumulate # effective bs = batch_size * accumulate = 16 * 4 = 64
weights = opt.weights # initial training weights
test_path = '../DAC-SDC2021/dataset/sample'
nc = 1
model = UltraNet_Bypass().to(device)
model.hyp = hyp
model.nc = 1
model.arc = 'default'
if weights.endswith('.pt'): # pytorch format
# possible weights are '*.pt', 'yolov3-spp.pt', 'yolov3-tiny.pt' etc.
print("load weights...")
model.load_state_dict(torch.load(weights, map_location=device)['model'])
batch_size = min(batch_size, 1)
nw = min([os.cpu_count(), batch_size if batch_size > 1 else 0, 8]) # number of workers
dataset = LoadImagesAndLabels(test_path, img_size_test, batch_size * 2,
hyp=hyp,
rect=False,
cache_images=opt.cache_images,
single_cls=opt.single_cls)
testloader = torch.utils.data.DataLoader(dataset,
batch_size=batch_size * 2,
num_workers=nw,
pin_memory=True,
collate_fn=dataset.collate_fn)
results = test.test(opt.cfg,
opt.data,
batch_size=batch_size * 2,
img_size=img_size_test,
model=model,
conf_thres=0.001, # 0.001 if opt.evolve or (final_epoch and is_coco) else 0.01,
iou_thres=0.6,
save_json=False,
single_cls=opt.single_cls,
dataloader=testloader)
print(results)
```
|
github_jupyter
|
```
#hide
%load_ext autoreload
%autoreload 2
# default_exp analysis
```
# Analysis
> The analysis functions help a modeler quickly run a full time series analysis.
An analysis consists of:
1. Initializing a DGLM, using `define_dglm`.
2. Updating the model coefficients at each time step, using `dglm.update`.
3. Forecasting at each time step between `forecast_start` and `forecast_end`, using `dglm.forecast_marginal` or `dglm.forecast_path`.
4. Returning the desired output, specified in the argument `ret`. The default is to return the model and forecast samples.
The analysis starts by defining a new DGLM with `define_dglm`. The default number of observations to use is set at `prior_length=20`. Any arguments that are used to define a model in `define_dglm` can be passed into analysis as keyword arguments. Alternatively, you may define the model beforehand, and pass the pre-initialized DGLM into analysis as the argument `model_prior`.
Once the model has been initialized, the analysis loop begins. If $\text{forecast_start} \leq t \leq \text{forecast_end}$, then the model will forecast ahead. The forecast horizon k must be specified. The default is to simulate `nsamps=500` times from the forecast distribution using `forecast_marginal`, from $1$ to `k` steps into the future. To simulate from the joint forecast distribution over the next `k` steps, set the flag `forecast_path=True`. Note that all forecasts are *out-of-sample*, i.e. they are made before the model has seen the observation. This is to ensure than the forecast accuracy is a more fair representation of future model performance.
After the forecast has been made, the model sees the observation $y_t$, and updates the state vector accordingly.
The analysis ends after seeing the last observation in `Y`. The output is a list specified by the argument `ret`, which may contain:
- `mod`: The final model
- `forecast`: The forecast samples, stored in a 3-dimensional array with axes *nsamps* $\times$ *forecast length* $\times$ *k*
- `model_coef`: A time series of the state vector mean vector and variance matrix
Please note that `analysis` is used on a historic dataset that already exists. This means that a typical sequence of events is to run an analysis on the data you current have, and return the model and forecast samples. The forecast samples are used to evaluate the past forecast performance. Then you can use `dglm.forecast_marginal` and `dglm.forecast_path` to forecast into the future.
```
#hide
#exporti
import numpy as np
import pandas as pd
from pybats.define_models import define_dglm, define_dcmm, define_dbcm, define_dlmm
from pybats.shared import define_holiday_regressors
from collections.abc import Iterable
```
## Analysis for a DGLM
```
#export
def analysis(Y, X=None, k=1, forecast_start=0, forecast_end=0,
nsamps=500, family = 'normal', n = None,
model_prior = None, prior_length=20, ntrend=1,
dates = None, holidays = [],
seasPeriods = [], seasHarmComponents = [],
latent_factor = None, new_latent_factors = None,
ret=['model', 'forecast'],
mean_only = False, forecast_path = False,
**kwargs):
"""
This is a helpful function to run a standard analysis. The function will:
1. Automatically initialize a DGLM
2. Run sequential updating
3. Forecast at each specified time step
"""
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
X = define_holiday_regressors(X, dates, holidays)
# Check if it's a latent factor DGLM
if latent_factor is not None:
is_lf = True
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
if model_prior is None:
mod = define_dglm(Y, X, family=family, n=n, prior_length=prior_length, ntrend=ntrend, nhol=nhol, nlf=nlf,
seasPeriods=seasPeriods, seasHarmComponents=seasHarmComponents,
**kwargs)
else:
mod = model_prior
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Define the run length
T = len(Y) + 1
if ret.__contains__('model_coef'):
m = np.zeros([T-1, mod.a.shape[0]])
C = np.zeros([T-1, mod.a.shape[0], mod.a.shape[0]])
if family == 'normal':
n = np.zeros(T)
s = np.zeros(T)
if new_latent_factors is not None:
if not ret.__contains__('new_latent_factors'):
ret.append('new_latent_factors')
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for lf in new_latent_factors:
tmp.append(lf.copy())
new_latent_factors = tmp
# Create dummy variable if there are no regression covariates
if X is None:
X = np.array([None]*(T+k)).reshape(-1,1)
else:
if len(X.shape) == 1:
X = X.reshape(-1,1)
# Initialize updating + forecasting
horizons = np.arange(1, k + 1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
for t in range(prior_length, T):
if forecast_start <= t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
if ret.__contains__('forecast'):
if is_lf:
if forecast_path:
pm, ps, pp = latent_factor.get_lf_forecast(dates.iloc[t])
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(k=k, X=X[t + horizons - 1, :],
nsamps=nsamps,
phi_mu=pm, phi_sigma=ps, phi_psi=pp)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including path dependency in latent factor
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps:
mod.forecast_marginal_lf_analytic(k=k, X=x, phi_mu=pm, phi_sigma=ps, nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).squeeze().T.reshape(-1, k)#.reshape(-1, 1)
else:
if forecast_path:
forecast[:, t - forecast_start, :] = mod.forecast_path(k=k, X = X[t + horizons - 1, :], nsamps=nsamps)
else:
if family == "binomial":
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, n, x:
mod.forecast_marginal(k=k, n=n, X=x, nsamps=nsamps, mean_only=mean_only),
horizons, n[t + horizons - 1], X[t + horizons - 1, :]))).squeeze().T.reshape(-1, k) # .reshape(-1, 1)
else:
# Get the forecast samples for all the items over the 1:k step ahead marginal forecast distributions
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x:
mod.forecast_marginal(k=k, X=x, nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).squeeze().T.reshape(-1, k)#.reshape(-1, 1)
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates[t], mod=mod, X=X[t + horizons - 1],
k=k, nsamps=nsamps, horizons=horizons)
# Now observe the true y value, and update:
if t < len(Y):
if is_lf:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=X[t],
phi_mu=pm, phi_sigma=ps)
else:
if family == "binomial":
mod.update(y=Y[t], X=X[t], n=n[t])
else:
mod.update(y=Y[t], X=X[t])
if ret.__contains__('model_coef'):
m[t,:] = mod.m.reshape(-1)
C[t,:,:] = mod.C
if family == 'normal':
n[t] = mod.n / mod.delVar
s[t] = mod.s
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates[t], mod=mod, Y=Y[t], X=X[t], k=k, nsamps=nsamps)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'model_coef':
mod_coef = {'m':m, 'C':C}
if family == 'normal':
mod_coef.update({'n':n, 's':s})
out.append(mod_coef)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
This function is core to the PyBATS package, because it allows a modeler to easily run a full time series analysis in one step. Below is a quick example of analysis of quarterly inflation in the US using a normal DLM. We'll start by loading in the data:
```
from pybats.shared import load_us_inflation
from pybats.analysis import analysis
import pandas as pd
from pybats.plot import plot_data_forecast
from pybats.point_forecast import median
import matplotlib.pyplot as plt
from pybats.loss_functions import MAPE
data = load_us_inflation()
pd.concat([data.head(3), data.tail(3)])
```
And then running an analysis. We're going to use the previous (lag-1) value of inflation as a predictor.
```
forecast_start = '1990-Q1'
forecast_end = '2014-Q3'
X = data.Inflation.values[:-1]
mod, samples = analysis(Y = data.Inflation.values[1:], X=X, family="normal",
k = 1, prior_length = 12,
forecast_start = forecast_start, forecast_end = forecast_end,
dates=data.Date,
ntrend = 2, deltrend=.99,
seasPeriods=[4], seasHarmComponents=[[1,2]], delseas=.99,
nsamps = 5000)
```
A couple of things to note here:
- `forecast_start` and `forecast_end` were specified as elements in the `dates` vector. You can also specify forecast_start and forecast_end by row numbers in `Y`, and avoid providing the `dates` argument.
- `ntrend=2` creates a model with an intercept and a local slope term, and `deltrend=.98` discounts the impact of older observations on the trend component by $2\%$ at each time step.
- The seasonal component was set as `seasPeriods=[4]`, because we think the seasonal effect has a cycle of length $4$ in this quarterly inflation data.
Let's examine the output. Here is the mean and standard deviation of the state vector (aka the coefficients) after the model has seen the last observation in `Y`:
```
mod.get_coef()
```
It's clear that the lag-1 regression term is dominant, with a mean of $0.92$. The only other large coefficient is the intercept, with a mean of $0.10$.
The seasonal coefficients turned out to be very small. Most likely this is because the publicly available dataset for US inflation is pre-adjusted for seasonality.
The forecast samples are stored in a 3-dimensional array, with axes *nsamps* $\times$ *forecast length* $\times$ *k*:
- **nsamps** is the number of samples drawn from the forecast distribution
- **forecast length** is the number of time steps between `forecast_start` and `forecast_end`
- **k** is the forecast horizon, or the number of steps that were forecast ahead
We can plot the forecasts using `plot_data_forecast`. We'll plot the 1-quarter ahead forecasts, using the median as our point estimate.
```
forecast = median(samples)
# Plot the 1-quarter ahead forecast
h = 1
start = data[data.Date == forecast_start].index[0] + h
end = data[data.Date == forecast_end].index[0] + h + 1
fig, ax = plt.subplots(figsize=(12, 6))
plot_data_forecast(fig, ax, y = data[start:end].Inflation.values,
f = forecast[:,h-1],
samples = samples[:,:,h-1],
dates = pd.to_datetime(data[start:end].Date.values),
xlabel='Time', ylabel='Quarterly US Inflation', title='1-Quarter Ahead Forecasts');
```
We can see that the forecasts are quite good, and nearly all of the observations fall within the $95\%$ credible interval.
There's also a clear pattern - the forecasts look as if they're shifted forward from the data by 1 step. This is because the lag-1 predictor is very strong, with a coefficient mean of $0.91$. The model is primarily using the previous month's value as its forecast, with some small modifications. Having the previous value as our best forecast is common in many time series.
We can put a number on the quality of the forecast by using a loss function, the Mean Absolute Percent Error (MAPE). We see that on average, our forecasts of quarterly inflation have an error of under $15\%$.
```
MAPE(data[start:end].Inflation.values, forecast[:,0]).round(1)
assert(MAPE(data[start:end].Inflation.values, forecast[:,0]).round(0) <= 15)
```
Finally, we can use the returned model to forecast $1-$step ahead to Q1 2015, which is past the end of the dataset. We need the `X` value to forecast into the future. Luckily, in this model the predictor `X` is simply the previous value of Inflation from Q4 2014.
```
x_future = data.Inflation.iloc[-1]
one_step_forecast_samples = mod.forecast_marginal(k=1,
X=x_future,
nsamps=1000000)
```
From here, we can find the mean and standard deviation of the forecast for next quarter's inflation:
```
print('Mean: ' + str(np.mean(one_step_forecast_samples).round(2)))
print('Std Dev: ' + str(np.std(one_step_forecast_samples).round(2)))
```
We can also plot the full forecast distribution for Q1 2015:
```
fig, ax = plt.subplots(figsize=(10,6))
ax.hist(one_step_forecast_samples.reshape(-1),
bins=200, alpha=0.3, color='b', density=True,
label='Forecast Distribution');
ax.vlines(x=np.mean(one_step_forecast_samples),
ymin=0, ymax=ax.get_ylim()[1],
label='Forecast Mean');
ax.set_title('1-Step Ahead Forecast Distribution for Q1 2015 Inflation');
ax.set_ylabel('Forecast Density')
ax.set_xlabel('Q1 2015 Inflation')
ax.legend();
```
## Analysis for a DCMM
```
#export
def analysis_dcmm(Y, X=None, k=1, forecast_start=0, forecast_end=0,
nsamps=500, rho=.6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays=[],
seasPeriods=[], seasHarmComponents=[],
latent_factor=None, new_latent_factors=None,
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DCMM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X = define_holiday_regressors(X, dates, holidays)
# Initialize the DCMM
if model_prior is None:
mod = define_dcmm(Y, X, prior_length = prior_length, seasPeriods = seasPeriods, seasHarmComponents = seasHarmComponents,
ntrend=ntrend, nlf = nlf, rho = rho, nhol = nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
T = len(Y) + 1 # np.min([len(Y), forecast_end]) + 1
nu = 9
if X is None:
X = np.array([None]*(T+k)).reshape(-1,1)
else:
if len(X.shape) == 1:
X = X.reshape(-1,1)
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including the path dependency of the latent factor
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]),
phi_mu=(pm, pm), phi_sigma=(ps, ps), phi_psi=(pp, pp), nsamps=nsamps, t_dist=True, nu=nu)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x: mod.forecast_marginal(
k=k, X=(x, x), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]), nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DCMM
if t < len(Y):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=(X[t], X[t]),
phi_mu=(pm, pm), phi_sigma=(ps, ps))
else:
mod.update(y = Y[t], X=(X[t], X[t]))
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dcmm` works identically to the standard `analysis`, but is specialized for a DCMM.
The observations must be integer counts, which are modeled as a combination of a Poisson and Bernoulli DGLM. Typically a DCMM is equally good as a Poisson DGLM for modeling series with consistently large integers, while being significantly better at modeling series with many zeros.
Note that by default, all simulated forecasts made with `analysis_dcmm` are *path* forecasts, meaning that they account for the dependence across forecast horizons.
## Analysis for a DBCM
```
#export
def analysis_dbcm(Y_transaction, X_transaction, Y_cascade, X_cascade, excess,
k, forecast_start, forecast_end, nsamps = 500, rho = .6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays = [],
latent_factor = None, new_latent_factors = None,
seasPeriods = [], seasHarmComponents = [],
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DBCM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X_transaction = define_holiday_regressors(X_transaction, dates, holidays)
if model_prior is None:
mod = define_dbcm(Y_transaction, X_transaction, Y_cascade, X_cascade,
excess_values = excess, prior_length = prior_length,
seasPeriods = seasPeriods, seasHarmComponents=seasHarmComponents,
nlf = nlf, rho = rho, nhol=nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
T = len(Y_transaction) + 1 #np.min([len(Y_transaction)- k, forecast_end]) + 1
nu = 9
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
# print(mod.dcmm.pois_mod.param1)
# print(mod.dcmm.pois_mod.param2)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
pp = None # Not including path dependency in latent factor
else:
if latent_factor.forecast_path:
pm, ps, pp = latent_factor.get_lf_forecast(dates.iloc[t])
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x_trans, x_cascade, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X_transaction=x_trans, X_cascade=x_cascade,
phi_mu=pm, phi_sigma=ps, nsamps=nsamps, mean_only=mean_only),
horizons, X_transaction[t + horizons - 1, :], X_cascade[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_lf_copula(
k=k, X_transaction=X_transaction[t + horizons - 1, :], X_cascade=X_cascade[t + horizons - 1, :],
phi_mu=pm, phi_sigma=ps, phi_psi=pp, nsamps=nsamps, t_dist=True, nu=nu)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x_trans, x_cascade: mod.forecast_marginal(
k=k, X_transaction=x_trans, X_cascade=x_cascade, nsamps=nsamps, mean_only=mean_only),
horizons, X_transaction[t + horizons - 1, :], X_cascade[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X_transaction=X_transaction[t + horizons - 1, :], X_cascade=X_cascade[t + horizons - 1, :],
nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X_transaction=X_transaction[t + horizons - 1, :],
X_cascade = X_cascade[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DBCM
if t < len(Y_transaction):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_pois, ps_pois = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_pois)
ps = (ps_bern, ps_pois)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y_transaction=Y_transaction[t], X_transaction=X_transaction[t, :],
y_cascade=Y_cascade[t,:], X_cascade=X_cascade[t, :],
phi_mu=pm, phi_sigma=ps, excess=excess[t])
else:
mod.update(y_transaction=Y_transaction[t], X_transaction=X_transaction[t, :],
y_cascade=Y_cascade[t,:], X_cascade=X_cascade[t, :], excess=excess[t])
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X_transaction=X_transaction[t + horizons - 1, :],
X_cascade = X_cascade[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dbcm` works identically to the standard `analysis`, but is specialized for a DBCM.
Separate data must be specified for the DCMM on transactions, `y_transaction` and `X_transaction`, the binomial cascade,`y_cascade`, `X_cascade`, and any excess counts, `excess`.
Note that by default, all simulated forecasts made with `analysis_dbcm` are *path* forecasts, meaning that they account for the dependence across forecast horizons.
## Analysis for a DLMM
```
#export
def analysis_dlmm(Y, X, k=1, forecast_start=0, forecast_end=0,
nsamps=500, rho=.6,
model_prior=None, prior_length=20, ntrend=1,
dates=None, holidays=[],
seasPeriods=[], seasHarmComponents=[],
latent_factor=None, new_latent_factors=None,
mean_only=False,
ret=['model', 'forecast'],
**kwargs):
"""
This is a helpful function to run a standard analysis using a DLMM.
"""
if latent_factor is not None:
is_lf = True
# Note: This assumes that the bernoulli & poisson components have the same number of latent factor components
if isinstance(latent_factor, (list, tuple)):
nlf = latent_factor[0].p
else:
nlf = latent_factor.p
else:
is_lf = False
nlf = 0
# Convert dates into row numbers
if dates is not None:
dates = pd.Series(dates)
# dates = pd.to_datetime(dates, format='%y/%m/%d')
if type(forecast_start) == type(dates.iloc[0]):
forecast_start = np.where(dates == forecast_start)[0][0]
if type(forecast_end) == type(dates.iloc[0]):
forecast_end = np.where(dates == forecast_end)[0][0]
# Add the holiday indicator variables to the regression matrix
nhol = len(holidays)
if nhol > 0:
X = define_holiday_regressors(X, dates, holidays)
# Initialize the DCMM
if model_prior is None:
mod = define_dlmm(Y, X, prior_length = prior_length, seasPeriods = seasPeriods, seasHarmComponents = seasHarmComponents,
ntrend=ntrend, nlf = nlf, rho = rho, nhol = nhol, **kwargs)
else:
mod = model_prior
if ret.__contains__('new_latent_factors'):
if not isinstance(new_latent_factors, Iterable):
new_latent_factors = [new_latent_factors]
tmp = []
for sig in new_latent_factors:
tmp.append(sig.copy())
new_latent_factors = tmp
if ret.__contains__('model_coef'): ## Return normal dlm params
m = np.zeros([T, mod.dlm_mod.a.shape[0]])
C = np.zeros([T, mod.dlm_mod.a.shape[0], mod.dlm_mod.a.shape[0]])
a = np.zeros([T, mod.dlm_mod.a.shape[0]])
R = np.zeros([T, mod.dlm_mod.a.shape[0], mod.dlm_mod.a.shape[0]])
n = np.zeros(T)
s = np.zeros(T)
# Initialize updating + forecasting
horizons = np.arange(1,k+1)
if mean_only:
forecast = np.zeros([1, forecast_end - forecast_start + 1, k])
else:
forecast = np.zeros([nsamps, forecast_end - forecast_start + 1, k])
T = len(Y) + 1
nu = 9
# Run updating + forecasting
for t in range(prior_length, T):
# if t % 100 == 0:
# print(t)
if ret.__contains__('forecast'):
if t >= forecast_start and t <= forecast_end:
if t == forecast_start:
print('beginning forecasting')
# Get the forecast samples for all the items over the 1:k step ahead path
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf_forecast(dates.iloc[t])
pm_dlm, ps_dlm = latent_factor[1].get_lf_forecast(dates.iloc[t])
pm = (pm_bern, pm_dlm)
ps = (ps_bern, ps_dlm)
else:
pm, ps = latent_factor.get_lf_forecast(dates.iloc[t])
pp = None # Not including the path dependency of the latent factor
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).reshape(1, -1)
else:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x, pm, ps: mod.forecast_marginal_lf_analytic(
k=k, X=(x, x), phi_mu=(pm, pm), phi_sigma=(ps, ps), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :], pm, ps))).squeeze().T.reshape(-1, k)
else:
if mean_only:
forecast[:, t - forecast_start, :] = np.array(list(map(
lambda k, x: mod.forecast_marginal(
k=k, X=(x, x), nsamps=nsamps, mean_only=mean_only),
horizons, X[t + horizons - 1, :]))).reshape(1,-1)
else:
forecast[:, t - forecast_start, :] = mod.forecast_path_copula(
k=k, X=(X[t + horizons - 1, :], X[t + horizons - 1, :]), nsamps=nsamps, t_dist=True, nu=nu)
if ret.__contains__('new_latent_factors'):
if t >= forecast_start and t <= forecast_end:
for lf in new_latent_factors:
lf.generate_lf_forecast(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Update the DLMM
if t < len(Y):
if is_lf:
if isinstance(latent_factor, (list, tuple)):
pm_bern, ps_bern = latent_factor[0].get_lf(dates.iloc[t])
pm_dlm, ps_dlm = latent_factor[1].get_lf(dates.iloc[t])
pm = (pm_bern, pm_dlm)
ps = (ps_bern, ps_dlm)
else:
pm, ps = latent_factor.get_lf(dates.iloc[t])
mod.update_lf_analytic(y=Y[t], X=(X[t], X[t]),
phi_mu=(pm, pm), phi_sigma=(ps, ps))
else:
mod.update(y = Y[t], X=(X[t], X[t]))
if ret.__contains__('new_latent_factors'):
for lf in new_latent_factors:
lf.generate_lf(date=dates.iloc[t], mod=mod, X=X[t + horizons - 1, :],
k=k, nsamps=nsamps, horizons=horizons)
# Store the dlm coefficients
if ret.__contains__('model_coef'):
m[t,:] = mod.dlm.m.reshape(-1)
C[t,:,:] = mod.dlm.C
a[t,:] = mod.dlm.a.reshape(-1)
R[t,:,:] = mod.dlm.R
n[t] = mod.dlm.n / mod.dlm.delVar
s[t] = mod.dlm.s
out = []
for obj in ret:
if obj == 'forecast': out.append(forecast)
if obj == 'model': out.append(mod)
if obj == 'model_coef':
mod_coef = {'m':m, 'C':C, 'a':a, 'R':R, 'n':n, 's':s}
out.append(mod_coef)
if obj == 'new_latent_factors':
#for lf in new_latent_factors:
# lf.append_lf()
# lf.append_lf_forecast()
if len(new_latent_factors) == 1:
out.append(new_latent_factors[0])
else:
out.append(new_latent_factors)
if len(out) == 1:
return out[0]
else:
return out
```
`analysis_dlmm` works identically to the standard `analysis`, but is specialized for a DLMM. `analysis_dlmm` returns the model coefficients for the Normal DLM portion of the model only.
The observations are continuous and are modeled as a combination of a Bernoulli DGLM and a Normal DLM.
Note that by default, all simulated forecasts made with `analysis_dlmm` are *path* forecasts, meaning that they account for the dependence across forecast horizons. The exception is for latent factor DLMMs, which default to marginal forecasting.
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
# Support Vector Machines
Support Vector Machines (SVM) are an extension of the linear methods that attempt to separate classes with hyperplans.
These extensions come in three steps:
1. When classes are linearly separable, maximize the margin between the two classes
2. When classes are not linearly separable, maximize the margin but allow some samples within the margin. That is the soft margin
3. The "Kernel trick" to extend the separation to non linear frontieres
The boost in performance of the Kernel trick has made the SVM the best classification method of the 2000's until the deep neural nets.
### Learning goals
- Understand and implement SVM concepts stated above
- Reminder to the Lagrange multiplier and optimization theory
- Deal with a general purpose solver with constraints
- Apply SVM to a non linear problem (XOR) with a non linear kernel (G-RBF)
### References
- [1] [The Elements of Statistical Learning](https://web.stanford.edu/~hastie/ElemStatLearn/) - Trevor Hastie, Robert Tibshirani, Jerome Friedman, Springer
- [2] Convex Optimization - Stephen Boyd, Lieven Vandenberghe, Cambridge University Press
- [3] [Pattern Recognition and Machine Learning - Ch 7 demo](https://github.com/yiboyang/PRMLPY/blob/master/ch7/svm.py) - Christopher M Bishop, Github
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as pltcolors
from sklearn import linear_model, svm, discriminant_analysis, metrics
from scipy import optimize
import seaborn as sns
```
## Helpers
```
def plotLine(ax, xRange, w, x0, label, color='grey', linestyle='-', alpha=1.):
""" Plot a (separating) line given the normal vector (weights) and point of intercept """
if type(x0) == int or type(x0) == float or type(x0) == np.float64:
x0 = [0, -x0 / w[1]]
yy = -(w[0] / w[1]) * (xRange - x0[0]) + x0[1]
ax.plot(xRange, yy, color=color, label=label, linestyle=linestyle)
def plotSvm(X, y, support=None, w=None, intercept=0., label='Data', separatorLabel='Separator',
ax=None, bound=[[-1., 1.], [-1., 1.]]):
""" Plot the SVM separation, and margin """
if ax is None:
fig, ax = plt.subplots(1)
im = ax.scatter(X[:,0], X[:,1], c=y, cmap=cmap, alpha=0.5, label=label)
if support is not None:
ax.scatter(support[:,0], support[:,1], label='Support', s=80, facecolors='none',
edgecolors='y', color='y')
print("Number of support vectors = %d" % (len(support)))
if w is not None:
xx = np.array(bound[0])
plotLine(ax, xx, w, intercept, separatorLabel)
# Plot margin
if support is not None:
signedDist = np.matmul(support, w)
margin = np.max(signedDist) - np.min(signedDist) * np.sqrt(np.dot(w, w))
supportMaxNeg = support[np.argmin(signedDist)]
plotLine(ax, xx, w, supportMaxNeg, 'Margin -', linestyle='-.', alpha=0.8)
supportMaxPos = support[np.argmax(signedDist)]
plotLine(ax, xx, w, supportMaxPos, 'Margin +', linestyle='--', alpha=0.8)
ax.set_title('Margin = %.3f' % (margin))
ax.legend(loc='upper left')
ax.grid()
ax.set_xlim(bound[0])
ax.set_ylim(bound[1])
cb = plt.colorbar(im, ax=ax)
loc = np.arange(-1,1,1)
cb.set_ticks(loc)
cb.set_ticklabels(['-1','1'])
```
## The data model
Let's use a simple model with two Gaussians that are faraway in order to be separable
```
colors = ['blue','red']
cmap = pltcolors.ListedColormap(colors)
nFeatures = 2
N = 100
def generateBatchBipolar(n, mu=0.5, sigma=0.2):
""" Two gaussian clouds on each side of the origin """
X = np.random.normal(mu, sigma, (n, 2))
yB = np.random.uniform(0, 1, n) > 0.5
# y is in {-1, 1}
y = 2. * yB - 1
X *= y[:, np.newaxis]
X -= X.mean(axis=0)
return X, y
```
# 1. Maximum margin separator
The following explanation is about the binary classification but generalizes to more classes.
Let $X$ be the matrix of $n$ samples of the $p$ features. We want to separate the two classes of $y$ with an hyperplan (a straight line in 2D, that is $p=2$). The separation equation is:
$$ w^T x + b = 0, w \in \mathbb{R}^{p}, x \in \mathbb{R}^{p}, b \in \mathbb{R} $$
Given $x_0$ a point on the hyperplan, the signed distance of any point $x$ to the hyperplan is :
$$ \frac{w}{\Vert w \Vert} (x - x_0) = \frac{1}{\Vert w \Vert} (w^T x + b) $$
If $y$, such that $y \in \{-1, 1\}$, is the corresponding label of $x$, the (unsigned) distance is :
$$ \frac{y}{\Vert w \Vert} (w^T x + b) $$
This is the update quantity used by the Rosenblatt Perceptron.
The __Maximum margin separator__ is aiming at maximizing $M$ such that :
$$ \underset{w, b}{\max} M $$
__Subject to :__
- $y_i(x_i^T w + b) \ge M, i = 1..n$
- $\Vert w \Vert = 1$
$x_i$ and $y_i$ are samples of $x$ and $y$, a row of the matrix $X$ and the vector $y$.
However, we may change the condition on the norm of $w$ such that : $\Vert w \Vert = \frac 1M$
Leading to the equivalent statement of the maximum margin classifier :
$$ \min_{w, b} \frac 12 \Vert w \Vert^2 $$
__Subject to : $y_i(x_i^T w + b) \ge 1, i = 1..n$__
For more details, see [1, chap 4.5]
The corresponding Lagrange primal problem is :
$$\mathcal{L}_p(w, b, \alpha) = \frac 12 \Vert w \Vert^2 - \sum_{i=0}^n \alpha_i (y_i(x_i^T w + b) - 1)$$
__Subject to:__
- $\alpha_i \ge 0, i\in 1..n$
This shall be __minimized__ on $w$ and $b$, using the corresponding partial derivates equal to 0, we get :
$$\begin{align}
\sum_{i=0}^n \alpha_i y_i x_i &= w \\
\sum_{i=0}^n \alpha_i y_i &= 0
\end{align}$$
From $\mathcal{L}_p$, we get the (Wolfe) dual :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \langle \alpha_i y_i x_i, \alpha_k y_k x_k \rangle \\
\end{align}$$
__Subject to :__
- $\alpha_i \ge 0, i\in 1..n$
- $\sum_{i=0}^n \alpha_i y_i = 0$
Which is a concave problem that is __maximized__ using a solver.
Strong duality requires (KKT) [2, chap. 5.5]:
- $\alpha_i (y_i(x_i^T w + b) - 1) = 0, \forall i \in 1..n$
Implying that :
- If $\alpha_i > 0$, then $y_i(x_i^T w + b) = 1$, meaning that $x_i$ is on one of the two hyperplans located at the margin distance from the separating hyperplan. $x_i$ is said to be a support vector
- If $y_i(x_i^T w + b) > 1$, the distance of $x_i$ to the hyperplan is larger than the margin.
### Train data
To demonstrate the maximum margin classifier, a dataset with separable classes is required. Let's use a mixture of two gaussian distributed classes with mean and variance such that the two classes are separated.
```
xTrain0, yTrain0 = generateBatchBipolar(N, sigma=0.2)
plotSvm(xTrain0, yTrain0)
```
## Implementation of the Maximum margin separator
$$\mathcal{L}_d = \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k $$
__Subject to :__
- $\sum_{i=0}^n \alpha_i y_i = \langle \alpha, y \rangle = 0$
- $\alpha_i \ge 0, i\in 1..n$
The classifier is built on the scipy.optimize.minimum solver. The implementation is correct but inefficient as it is not taking into account for the sparsity of the $\alpha$ vector.
```
class MaxMarginClassifier:
def __init__(self):
self.alpha = None
self.w = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# Gram matrix of (X.y)
Xy = X * y[:, np.newaxis]
GramXy = np.matmul(Xy, Xy.T)
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = -np.eye(N)
b = np.zeros(N)
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramXy, a),
constraints=constraints)
self.alpha = optRes.x
self.w = np.sum((self.alpha[:, np.newaxis] * Xy), axis=0)
epsilon = 1e-6
self.supportVectors = X[self.alpha > epsilon]
# Any support vector is at a distance of 1 to the separation plan
# => use support vector #0 to compute the intercept, assume label is in {-1, 1}
supportLabels = y[self.alpha > epsilon]
self.intercept = supportLabels[0] - np.matmul(self.supportVectors[0].T, self.w)
def predict(self, X):
""" Predict y value in {-1, 1} """
assert(self.w is not None)
assert(self.w.shape[0] == X.shape[1])
return 2 * (np.matmul(X, self.w) > 0) - 1
```
Reference:
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize
```
model00 = MaxMarginClassifier()
model00.fit(xTrain0, yTrain0)
model00.w, model00.intercept
fig, ax = plt.subplots(1, figsize=(12, 7))
plotSvm(xTrain0, yTrain0, model00.supportVectors, model00.w, model00.intercept, label='Training', ax=ax)
```
## Maximum margin classifier using Scikit Learn (SVC)
SVC is used in place of LinearSVC as the support vectors are provided. These vectors are displayed in the graph here below.
Set a high $C$ parameter to disable soft margin
```
model01 = svm.SVC(kernel='linear', gamma='auto', C = 1e6)
model01.fit(xTrain0, yTrain0)
model01.coef_[0], model01.intercept_[0]
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain0, yTrain0, model01.support_vectors_, model01.coef_[0], model01.intercept_[0],
label='Training', ax=ax)
```
The two implementations of the linear SVM agree on the ceofficients and margin. Good !
### Comparison of the maximum margin classifier to the Logistic regression and Linear Discriminant Analysis (LDA)
Logistic regression is based on the linear regression that is the computation of the square error of any point $x$ to the separation plan and a projection on the probability space using the sigmoid in order to compute the binary cross entropy, see ([HTML](ClassificationContinuous2Features.html) / [Jupyter](ClassificationContinuous2Features.ipynb)).
LDA is assuming a Gaussian mixture prior (our case) and performs bayesian inference.
```
model02 = linear_model.LogisticRegression(solver='lbfgs')
model02.fit(xTrain0, yTrain0)
model02.coef_[0], model02.intercept_[0]
model03 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model03.fit(xTrain0, yTrain0)
model03.coef_[0], model03.intercept_[0]
```
We observe that the coefficients of the three models are very different in amplitude but globally draw a separator line with slope $-\frac \pi4$ in the 2D plan
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain0, yTrain0, w=model01.coef_[0], intercept=model01.intercept_[0],
separatorLabel='Max Margin SVM', label='Training', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model02.coef_[0], x0=model02.intercept_[0], label='Logistic', color='g')
plotLine(ax, xx, w=model03.coef_[0], x0=model03.intercept_[0], label='LDA', color='c')
ax.legend();
```
# 2. Soft Margin Linear SVM for non separable classes
The example above has little interest as the separation is trivial.
Using the same SVM implementation on a non separable case would not be possible, the solver would fail.
Here comes the soft margin: some $x_i$ are allowed to lie in between the two margin bars.
The __Soft margin linear SVM__ is adding a regularization parameter in maximizing $M$:
$$ \underset{w, b}{\max} M ( 1 - \xi_i) $$
__Subject to $\forall i = 1..n$:__
- $y_i(x_i^T w + b) \ge M$
- $\Vert w \Vert = 1$
- $\xi_i \ge 0$
Equivalently :
$$ \min_{w, b} \frac 12 \Vert w \Vert^2 + C \sum_{i=1}^n \xi_i$$
__Subject to $\forall i = 1..n$:__
- $\xi_i \ge 0$
- $y_i(x_i^T w + b) \ge 1 - \xi_i$
The corresponding Lagrange primal problem is :
$$\mathcal{L}_p(w, b, \alpha, \mu) = \frac 12 \Vert w \Vert^2 - \sum_{i=0}^n \alpha_i (y_i(x_i^T w + b) - (1 - \xi_i) - \sum_{i=0}^n \mu_i \xi_i $$
__Subject to $\forall i\in 1..n$:__
- $\alpha_i \ge 0$
- $\mu_i \ge 0$
- $\xi_i \ge 0$
This shall be minimized on $w$, $b$ and $\xi_i$, using the corresponding partial derivates equal to 0, we get :
$$\begin{align}
\sum_{i=0}^n \alpha_i y_i x_i &= w \\
\sum_{i=0}^n \alpha_i y_i &= 0 \\
\alpha_i &= C - \mu_i
\end{align}$$
From $\mathcal{L}_p$, we get the (Wolfe) dual :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k x_i^T x_k \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \langle \alpha_i y_i x_i, \alpha_k y_k x_k \rangle \\
\end{align}$$
__Subject to $\forall i\in 1..n$:__
- $0 \le \alpha_i \le C$
- $\sum_{i=0}^n \alpha_i y_i = 0$
This problem is very similar to the one of the Maximum margin separator, but with one more constraint on $\alpha$.
It is a concave problem that is maximized using a solver.
Extra conditions to get strong duality are required (KKT), $\forall i \in 1..n$:
- $\alpha_i (y_i(x_i^T w + b) - (1 - \xi_i)) = 0$
- $\mu_i \xi_i = 0$
- $y_i(x_i^T w + b) - (1 - \xi_i) \ge 0$
More detailed explainations are in [1 chap. 12.1, 12.2]
## Data model
Let's reuse the same model made of two gaussians, but with larger variance in order to mix the positive and negative points
```
xTrain1, yTrain1 = generateBatchBipolar(N, mu=0.3, sigma=0.3)
plotSvm(xTrain1, yTrain1, label='Training')
```
## Custom implementation
Changes to the Maximum margin classifier are identified by "# <---"
```
class LinearSvmClassifier:
def __init__(self, C):
self.C = C # <---
self.alpha = None
self.w = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# Gram matrix of (X.y)
Xy = X * y[:, np.newaxis]
GramXy = np.matmul(Xy, Xy.T)
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = np.vstack((-np.eye(N), np.eye(N))) # <---
b = np.hstack((np.zeros(N), self.C * np.ones(N))) # <---
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramXy, a),
constraints=constraints)
self.alpha = optRes.x
self.w = np.sum((self.alpha[:, np.newaxis] * Xy), axis=0)
epsilon = 1e-6
self.supportVectors = X[self.alpha > epsilon]
# Support vectors is at a distance <= 1 to the separation plan
# => use min support vector to compute the intercept, assume label is in {-1, 1}
signedDist = np.matmul(self.supportVectors, self.w)
minDistArg = np.argmin(signedDist)
supportLabels = y[self.alpha > epsilon]
self.intercept = supportLabels[minDistArg] - signedDist[minDistArg]
def predict(self, X):
""" Predict y value in {-1, 1} """
assert(self.w is not None)
assert(self.w.shape[0] == X.shape[1])
return 2 * (np.matmul(X, self.w) > 0) - 1
model10 = LinearSvmClassifier(C=1)
model10.fit(xTrain1, yTrain1)
model10.w, model10.intercept
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, model10.supportVectors, model10.w, model10.intercept, label='Training', ax=ax)
```
### Linear SVM using Scikit Learn
```
model11 = svm.SVC(kernel='linear', gamma='auto', C = 1)
model11.fit(xTrain1, yTrain1)
model11.coef_[0], model11.intercept_[0]
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, model11.support_vectors_, model11.coef_[0], model11.intercept_[0],
label='Training', ax=ax)
```
With the soft margin, the support vectors are all the vectors on the boundary or within the margin slab.
The custom and SKLearn implementations are matching !
### Comparison of the soft margin classifier to the Logistic regression and Linear Discriminant Analysis (LDA)
```
model12 = linear_model.LogisticRegression(solver='lbfgs')
model12.fit(xTrain1, yTrain1)
model12.coef_[0], model12.intercept_[0]
model13 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model13.fit(xTrain1, yTrain1)
model13.coef_[0], model13.intercept_[0]
```
As shown below, the three models separator hyperplans are very similar, negative slope.
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain1, yTrain1, w=model11.coef_[0], intercept=model11.intercept_[0], label='Training',
separatorLabel='Soft Margin SVM', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model12.coef_[0], x0=model12.intercept_[0], label='Logistic reg', color='orange')
plotLine(ax, xx, w=model13.coef_[0], x0=model13.intercept_[0], label='LDA', color='c')
ax.legend();
```
### Validation with test data
```
xTest1, yTest1 = generateBatchBipolar(2*N, mu=0.3, sigma=0.3)
```
#### Helpers for binary classification performance
```
def plotHeatMap(X, classes, title=None, fmt='.2g', ax=None, xlabel=None, ylabel=None):
""" Fix heatmap plot from Seaborn with pyplot 3.1.0, 3.1.1
https://stackoverflow.com/questions/56942670/matplotlib-seaborn-first-and-last-row-cut-in-half-of-heatmap-plot
"""
ax = sns.heatmap(X, xticklabels=classes, yticklabels=classes, annot=True, \
fmt=fmt, cmap=plt.cm.Blues, ax=ax) #notation: "annot" not "annote"
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
if title:
ax.set_title(title)
if xlabel:
ax.set_xlabel(xlabel)
if ylabel:
ax.set_ylabel(ylabel)
def plotConfusionMatrix(yTrue, yEst, classes, title=None, fmt='.2g', ax=None):
plotHeatMap(metrics.confusion_matrix(yTrue, yEst), classes, title, fmt, ax, xlabel='Estimations', \
ylabel='True values');
```
### Confusion matrices
```
fig, axes = plt.subplots(1, 3, figsize=(16, 3))
for model, ax, title in zip([model10, model12, model13], axes, ['Custom linear SVM', 'Logistic reg', 'LDA']):
yEst = model.predict(xTest1)
plotConfusionMatrix(yTest1, yEst, colors, title, ax=ax)
```
There is no clear winner, all models are performing equally well.
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTest1, yTest1, w=model10.w, intercept=model10.intercept, separatorLabel='Cust. linear SVM', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model12.coef_[0], x0=model12.intercept_[0], label='Logistic reg', color='orange')
plotLine(ax, xx, w=model13.coef_[0], x0=model13.intercept_[0], label='LDA', color='c')
ax.legend();
```
# 3. The "kernel trick" for non linearly separable classes
Let's use a very famous dataset showing the main limitation of the Logistic regression and LDA : the XOR.
```
def generateBatchXor(n, mu=0.5, sigma=0.5):
""" Four gaussian clouds in a Xor fashion """
X = np.random.normal(mu, sigma, (n, 2))
yB0 = np.random.uniform(0, 1, n) > 0.5
yB1 = np.random.uniform(0, 1, n) > 0.5
# y is in {-1, 1}
y0 = 2. * yB0 - 1
y1 = 2. * yB1 - 1
X[:,0] *= y0
X[:,1] *= y1
X -= X.mean(axis=0)
return X, y0*y1
xTrain3, yTrain3 = generateBatchXor(2*N, sigma=0.25)
plotSvm(xTrain3, yTrain3)
xTest3, yTest3 = generateBatchXor(2*N, sigma=0.25)
```
## Logistic regression and LDA on XOR problem
```
model32 = linear_model.LogisticRegression(solver='lbfgs')
model32.fit(xTrain3, yTrain3)
model32.coef_[0], model32.intercept_[0]
model33 = discriminant_analysis.LinearDiscriminantAnalysis(solver='svd')
model33.fit(xTrain3, yTrain3)
model33.coef_[0], model33.intercept_[0]
```
The linear separators are sometimes mitigating the issue by isolating a single class within a corner. Or they are simply fully failing (separator is of limit).
```
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, w=model32.coef_[0], intercept=model32.intercept_[0], label='Training',
separatorLabel='Logistic reg', ax=ax)
xx = np.array([-1., 1.])
plotLine(ax, xx, w=model33.coef_[0], x0=model33.intercept_[0], label='LDA', color='c')
ax.legend();
```
## Introducing the Kernel trick
When using linear separators like the regression, the traditional way to deal with non linear functions is to expand the feature space using powers and products of the initial features. This is also necessary in case of multiclass problems as shown in [1 chap. 4.2].
There are limits to this trick. For example, the XOR problem is not handled proprely.
The SVM has used a new method known as the "Kernel trick".
Let's apply a transformation to $x$ using function $h(x)$.
The Lagrange (Wolfe) dual problem becomes :
$$\begin{align}
\mathcal{L}_d (\alpha)
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k y_i y_k h(x_i)^T h(x_k) \\
&= \sum_{i=0}^n \alpha_i - \frac 12 \sum_{i=0}^n \sum_{k=0}^n \alpha_i \alpha_k \langle y_i h(x_i), y_k h(x_k) \rangle \\
\end{align}$$
__Subject to $\forall i\in 1..n$:__
- $0 \le \alpha_i \le C$
- $\sum_{i=0}^n \alpha_i y_i = 0$
Since $ w = \sum_{i=0}^n \alpha_i y_i h(x_i)$, the prediction function is now :
$$ f(x) = sign(w^T h(x) + b) = sign \left(\sum_{i=0}^n \alpha_i y_i \langle h(x_i), h(x) \rangle \right) $$
This prediction needs to be computed for $\alpha_i > 0$, that are support vectors.
Both the fit and prediction are based on the inner product $K(x, x') = \langle h(x), h(x') \rangle$, also known as the kernel function. This function shall be symmetric, semi-definite.
Popular kernel is the Gaussian Radial Basis Function (RBF) : $K(x, x') = exp(- \gamma \Vert x - x' \Vert^2 )$
### Custom implementation of the SVM with G-RBF kernel
Modifications made on the Linear SVM implementation are enclosed in blocks starting with _"# --->"_ and ending with _"# <---"_
```
class KernelSvmClassifier:
def __init__(self, C, kernel):
self.C = C
self.kernel = kernel # <---
self.alpha = None
self.supportVectors = None
def fit(self, X, y):
N = len(y)
# --->
# Gram matrix of h(x) y
hXX = np.apply_along_axis(lambda x1 : np.apply_along_axis(lambda x2: self.kernel(x1, x2), 1, X),
1, X)
yp = y.reshape(-1, 1)
GramHXy = hXX * np.matmul(yp, yp.T)
# <---
# Lagrange dual problem
def Ld0(G, alpha):
return alpha.sum() - 0.5 * alpha.dot(alpha.dot(G))
# Partial derivate of Ld on alpha
def Ld0dAlpha(G, alpha):
return np.ones_like(alpha) - alpha.dot(G)
# Constraints on alpha of the shape :
# - d - C*alpha = 0
# - b - A*alpha >= 0
A = np.vstack((-np.eye(N), np.eye(N))) # <---
b = np.hstack((np.zeros(N), self.C * np.ones(N))) # <---
constraints = ({'type': 'eq', 'fun': lambda a: np.dot(a, y), 'jac': lambda a: y},
{'type': 'ineq', 'fun': lambda a: b - np.dot(A, a), 'jac': lambda a: -A})
# Maximize by minimizing the opposite
optRes = optimize.minimize(fun=lambda a: -Ld0(GramHXy, a),
x0=np.ones(N),
method='SLSQP',
jac=lambda a: -Ld0dAlpha(GramHXy, a),
constraints=constraints)
self.alpha = optRes.x
# --->
epsilon = 1e-8
supportIndices = self.alpha > epsilon
self.supportVectors = X[supportIndices]
self.supportAlphaY = y[supportIndices] * self.alpha[supportIndices]
# <---
def predict(self, X):
""" Predict y values in {-1, 1} """
# --->
def predict1(x):
x1 = np.apply_along_axis(lambda s: self.kernel(s, x), 1, self.supportVectors)
x2 = x1 * self.supportAlphaY
return np.sum(x2)
d = np.apply_along_axis(predict1, 1, X)
return 2 * (d > 0) - 1
# <---
def GRBF(x1, x2):
diff = x1 - x2
return np.exp(-np.dot(diff, diff) * len(x1) / 2)
model30 = KernelSvmClassifier(C=5, kernel=GRBF)
model30.fit(xTrain3, yTrain3)
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, support=model30.supportVectors, label='Training', ax=ax)
# Estimate and plot decision boundary
xx = np.linspace(-1, 1, 50)
X0, X1 = np.meshgrid(xx, xx)
xy = np.vstack([X0.ravel(), X1.ravel()]).T
Y30 = model30.predict(xy).reshape(X0.shape)
ax.contour(X0, X1, Y30, colors='k', levels=[-1, 0], alpha=0.3, linestyles=['-.', '-']);
```
## Scikit Learn SVM with Radial basis kernel
```
model31 = svm.SVC(kernel='rbf', C=10, gamma=1/2, shrinking=False)
model31.fit(xTrain3, yTrain3);
fig, ax = plt.subplots(1, figsize=(11, 7))
plotSvm(xTrain3, yTrain3, support=model31.support_vectors_, label='Training', ax=ax)
# Estimate and plot decision boundary
Y31 = model31.predict(xy).reshape(X0.shape)
ax.contour(X0, X1, Y31, colors='k', levels=[-1, 0], alpha=0.3, linestyles=['-.', '-']);
```
### SVM with RBF performance on XOR
```
fig, axes = plt.subplots(1, 2, figsize=(11, 3))
for model, ax, title in zip([model30, model31], axes, ["Custom SVM with RBF", "SKLearn SVM with RBF"]):
yEst3 = model.predict(xTest3)
plotConfusionMatrix(yTest3, yEst3, colors, title, ax=ax)
```
Both models' predictions are almost matching on the XOR example.
## Conclusion
We have shown the power of SVM classifiers for non linearly separable problems. From the end of the 1990's, SVM was the leading machine learning algorithm family for many problems. This situation has changed a little since 2010 as deep learning has shown better performance for some classes of problems. However, SVM remains stronger in many contexts. For example, the amount of training data for SVM is lower than the one required for deep learning.
### Where to go from here
- Multiclass classifier using Neural Nets in Keras ([HTML](ClassificationMulti2Features-Keras.html) / [Jupyter](ClassificationMulti2Features-Keras.ipynb))
- Multiclass classifier using Decision Trees ([HTML](ClassificationMulti2Features-Tree.html) / [Jupyter](ClassificationMulti2Features-Tree.ipynb))
- Bivariate continuous function approximation with Linear Regression ([HTML](ClassificationContinuous2Features.html) / [Jupyter](ClassificationContinuous2Features.ipynb))
- Bivariate continuous function approximation with k Nearest Neighbors ([HTML](ClassificationContinuous2Features-KNN.html) / [Jupyter](ClassificationContinuous2Features-KNN.ipynb))
|
github_jupyter
|
```
import caffe
import numpy as np
import matplotlib.pyplot as plt
import os
from keras.datasets import mnist
from caffe.proto import caffe_pb2
import google.protobuf.text_format
plt.rcParams['image.cmap'] = 'gray'
%matplotlib inline
```
Loading the model
```
model_def = 'example_caffe_mnist_model.prototxt'
model_weights = 'mnist.caffemodel'
net = caffe.Net(model_def, model_weights, caffe.TEST)
```
A Caffe net offers a layer dict that maps layer names to layer objects. These objects do not provide very much information though, but access to their weights and the type of the layer.
```
net.layer_dict
conv_layer = net.layer_dict['conv2d_1']
conv_layer.type, conv_layer.blobs[0].data.shape
```
### Getting input and output shape.
The net provides a `blobs dict`. These blobs contain `data`, i.e. all the intermediary computation results and `diff`, i.e. the gradients.
```
for name, blob in net.blobs.items():
print('{}: \t {}'.format(name, blob.data.shape))
```
### Getting the weigths.
The net provides access to a `param dict` that contains the weights. The first entry in param corresponds to the weights, the second corresponds to the bias.
```
net.params
for name, param in net.params.items():
print('{}:\t {} \t{}'.format(name, param[0].data.shape, param[1].data.shape))
```
The weights are also accessible through the layer blobs.
```
for layer in net.layers:
try:
print (layer.type + '\t' + str(layer.blobs[0].data.shape), str(layer.blobs[1].data.shape))
except:
continue
weights = net.params['conv2d_1'][0].data
weights.shape
```
For visualizing the weights the axis still have to be moved around.
```
for i in range(32):
plt.imshow(np.moveaxis(weights[i], 0, -1)[..., 0])
plt.show()
```
Layers that have no weights simply keep empty lists as their blob vector.
```
list(net.layer_dict['dropout_1'].blobs)
```
### Getting the activations and the net input.
For getting activations, first data has to be passed through the network. Then the activations can be read out from the blobs. If the activations are defined as in place operations, the net input will not be stored in any blob and can therefore not be recovered. This problem can be circumvented if the network definition is changed so that in place operations are avoided. This can also be done programatically as follows.
```
def remove_inplace(model_def):
protonet = caffe_pb2.NetParameter()
with open(model_def, 'r') as fp:
google.protobuf.text_format.Parse(str(fp.read()), protonet)
replaced_tops = {}
for layer in protonet.layer:
# Check whehter bottoms were renamed.
for i in range(len(layer.bottom)):
if layer.bottom[i] in replaced_tops.keys():
layer.bottom[i] = replaced_tops[layer.bottom[i]]
if layer.bottom == layer.top:
for i in range(len(layer.top)):
# Retain the mapping from the old to the new name.
new_top = layer.top[i] + '_' + layer.name
replaced_tops[layer.top[i]] = new_top
# Redefine layer.top
layer.top[i] = new_top
return protonet
model_def = 'example_caffe_mnist_model_deploy.prototxt'
protonet_no_inplace = remove_inplace(model_def)
protonet_no_inplace
model_def = 'example_caffe_network_no_inplace_deploy.prototxt'
model_weights = 'mnist.caffemodel'
net_no_inplace = caffe.Net(model_def, model_weights, caffe.TEST)
net_no_inplace.layer_dict
net_no_inplace.blobs
# Loading and preprocessing data.
data = mnist.load_data()[1][0]
# Normalize data.
data = data / data.max()
plt.imshow(data[0, :, :])
seven = data[0, :, :]
print(seven.shape)
seven = seven[np.newaxis, ...]
print(seven.shape)
```
Feeding the input and forwarding it.
```
net_no_inplace.blobs['data'].data[...] = seven
output = net_no_inplace.forward()
output['prob'][0].argmax()
activations = net_no_inplace.blobs['relu_1'].data
for i in range(32):
plt.imshow(activations[0, i, :, :])
plt.title('Feature map %d' % i)
plt.show()
net_input = net_no_inplace.blobs['conv2d_1'].data
for i in range(32):
plt.imshow(net_input[0, i, :, :])
plt.title('Feature map %d' % i)
plt.show()
```
### Getting layer properties
From the layer object not more then type information is available. There the original .prototxt has to be parsed to access attributes such as kernel size.
```
model_def = 'example_caffe_mnist_model.prototxt'
f = open(model_def, 'r')
protonet = caffe_pb2.NetParameter()
google.protobuf.text_format.Parse(str(f.read()), protonet)
f.close()
protonet
type(protonet)
```
Parsed messages for the layer can be found in `message.layer` list.
```
for i in range(0, len(protonet.layer)):
if protonet.layer[i].type == 'Convolution':
print('layer %s has kernel_size %d'
% (protonet.layer[i].name,
protonet.layer[i].convolution_param.kernel_size[0]))
lconv_proto = protonet.layer[i]
len(protonet.layer), len(net.layers)
```
|
github_jupyter
|
# Transpose convolution: Upsampling
In section 10.5.3, we discussed how transpose convolutions are can be used to upsample a lower resolution input into a higher resolution output. This notebook contains fully functional PyTorch code for the same.
```
import matplotlib.pyplot as plt
import torch
import math
```
First, let's look at how transpose convolution works on a simple input tensor. Then we will look at a real image. For this purpose, we will consider the example described in Figure 10.17. The input is a 2x2 array as follows:
$$
x = \begin{bmatrix}
5 & 6 \\
7 & 8 \\
\end{bmatrix}
$$
and the transpose convolution kernel is also a 2x2 array as follows
$$
w = \begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
$$
Transpose convolution with stride 1 results in a 3x3 output as shown below.
# Transpose conv 2D with stride 1
```
x = torch.tensor([
[5., 6.],
[7., 8.]
])
w = torch.tensor([
[1., 2.],
[3., 4.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2, stride=1, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
```
# Transpose conv 2D with stride 2
In the above example, we did not get a truly upsampled version of the input because we used a kernel stride of 1. Thei increase in resolution from 2 to 3 comes because of padding. Now, let's see how to truly upsample the image - we will run transpose convolution with stride 2. The step by step demonstration of this is shown in Figure 10.18. As you can see below, we obtained a 4z4 output. This is because we used a kernel a stride 2. Using a larger stride with further increase the output resolution
```
x = torch.tensor([
[5., 6.],
[7., 8.]
])
w = torch.tensor([
[1., 2.],
[3., 4.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
```
Now, let's take a sample image and see how the input compares to the output post transpose convolution with stride 2.
```
import cv2
x = torch.tensor(cv2.imread("./Figures/dog2.jpg", 0), dtype=torch.float32)
w = torch.tensor([
[1., 1.],
[1., 1.]
])
x = x.unsqueeze(0).unsqueeze(0)
w = w.unsqueeze(0).unsqueeze(0)
transpose_conv2d = torch.nn.ConvTranspose2d(1, 1, kernel_size=2,
stride=2, bias=False)
# set weights of the TransposeConv2d object
with torch.no_grad():
transpose_conv2d.weight = torch.nn.Parameter(w)
with torch.no_grad():
y = transpose_conv2d(x)
y
print("Input shape:", x.shape)
print("Output shape:", y.shape)
```
As expected, the output is twice the size of the input. The images below should make this clear
```
def display_image_in_actual_size(im_data, title):
dpi = 80
height, width = im_data.shape
# What size does the figure need to be in inches to fit the image?
figsize = width / float(dpi), height / float(dpi)
# Create a figure of the right size with one axes that takes up the full figure
fig = plt.figure(figsize=figsize)
ax = fig.add_axes([0, 0, 1, 1])
# Hide spines, ticks, etc.
ax.axis('off')
# Display the image.
ax.imshow(im_data, cmap='gray')
ax.set_title(title)
plt.show()
display_image_in_actual_size(x.squeeze().squeeze(), "Input image")
display_image_in_actual_size(y.squeeze().squeeze(), "Output image")
```
|
github_jupyter
|
```
import tensorflow as tf
print(tf.__version__)
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5
# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=42)
plt.figure(figsize=(10, 6))
plot_series(time, series)
plt.show()
```
Now that we have the time series, let's split it so we can start forecasting
```
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
plt.figure(figsize=(10, 6))
plot_series(time_train, x_train)
plt.show()
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plt.show()
```
Naive Forecast
```
naive_forecast = series[split_time - 1:-1]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, naive_forecast)
x = [1,2, 3, 4, 5, 6, 7, 8, 9, 10]
print(x)
split=7
naive=x[split - 1:-1]
print(naive)
x_val = x[split:]
print(x_val)
```
Let's zoom in on the start of the validation period:
```
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid, start=0, end=150)
plot_series(time_valid, naive_forecast, start=1, end=151)
```
You can see that the naive forecast lags 1 step behind the time series.
Now let's compute the mean squared error and the mean absolute error between the forecasts and the predictions in the validation period:
```
print(keras.metrics.mean_squared_error(x_valid, naive_forecast).numpy())
print(keras.metrics.mean_absolute_error(x_valid, naive_forecast).numpy())
```
That's our baseline, now let's try a moving average:
```
def moving_average_forecast(series, window_size):
"""Forecasts the mean of the last few values.
If window_size=1, then this is equivalent to naive forecast"""
forecast = []
for time in range(len(series) - window_size):
forecast.append(series[time:time + window_size].mean())
return np.array(forecast)
moving_avg = moving_average_forecast(series, 30)[split_time - 30:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, moving_avg)
print(keras.metrics.mean_squared_error(x_valid, moving_avg).numpy())
print(keras.metrics.mean_absolute_error(x_valid, moving_avg).numpy())
```
That's worse than naive forecast! The moving average does not anticipate trend or seasonality, so let's try to remove them by using differencing. Since the seasonality period is 365 days, we will subtract the value at time t – 365 from the value at time t.
```
diff_series = (series[365:] - series[:-365])
diff_time = time[365:]
plt.figure(figsize=(10, 6))
plot_series(diff_time, diff_series)
plt.show()
```
Great, the trend and seasonality seem to be gone, so now we can use the moving average:
```
diff_moving_avg = moving_average_forecast(diff_series, 50)[split_time - 365 - 50:]
plt.figure(figsize=(10, 6))
plot_series(time_valid, diff_series[split_time - 365:])
plot_series(time_valid, diff_moving_avg)
plt.show()
```
Now let's bring back the trend and seasonality by adding the past values from t – 365:
```
diff_moving_avg_plus_past = series[split_time - 365:-365] + diff_moving_avg
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, diff_moving_avg_plus_past)
plt.show()
print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_past).numpy())
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_past).numpy())
```
Better than naive forecast, good. However the forecasts look a bit too random, because we're just adding past values, which were noisy. Let's use a moving averaging on past values to remove some of the noise:
```
diff_moving_avg_plus_smooth_past = moving_average_forecast(series[split_time - 370:-360], 10) + diff_moving_avg
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, diff_moving_avg_plus_smooth_past)
plt.show()
print(keras.metrics.mean_squared_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())
print(keras.metrics.mean_absolute_error(x_valid, diff_moving_avg_plus_smooth_past).numpy())
```
|
github_jupyter
|
# Genentech Cervical Cancer - Feature Selection
https://www.kaggle.com/c/cervical-cancer-screening/
```
# imports
import sys # for stderr
import numpy as np
import pandas as pd
import sklearn as skl
from sklearn import metrics
import matplotlib.pyplot as plt
%matplotlib inline
# settings
%logstop
%logstart -o 'cc_feature_selection.log' rotate
plt.style.use('ggplot')
# constants
# plt.rcParams['figure.figsize'] = (10.0, 10.0)
# pd.set_option('display.max_rows', 50)
# pd.set_option('display.max_columns', 50)
# versions
import sys
print(pd.datetime.now())
print('Python: '+sys.version)
print('numpy: '+np.__version__)
print('pandas: '+pd.__version__)
print('sklearn: '+skl.__version__)
from sqlalchemy import create_engine
engine = create_engine('postgresql://paulperry:@localhost:5432/ccancer')
from pyace import ace
```
## Load
```
fdir = './features/'
train_file = './input/patients_train.csv.gz'
train = pd.read_csv(train_file)
train.drop('patient_gender', axis=1, inplace=True)
train.set_index('patient_id', inplace=True)
train[:3]
files =[
'diag_code_0_1000.csv.gz',
'diag_code_1000_2000.csv.gz',
'diag_code_2000_3000.csv.gz',
'diag_code_3000_4000.csv.gz',
'diag_code_4000_5000.csv.gz',
'diag_code_5000_6000.csv.gz',
'diag_code_6000_7000.csv.gz',
'diag_code_7000_8000.csv.gz',
'diag_code_8000_9000.csv.gz',
'diag_code_9000_10000.csv.gz',
'diag_code_10000_11000.csv.gz',
'diag_code_11000_12000.csv.gz',
'diag_code_12000_13000.csv.gz',
'diag_code_13000_14000.csv.gz',
'diag_code_14000_15000.csv.gz',
'diag_code_15000_16000.csv.gz',
]
len(files)
# #
# tab = pd.read_csv(fdir+files[0])
# tab.set_index('patient_id', inplace=True)
# for f in files[1:]:
# tab2 = pd.read_csv(fdir+f)
# tab2.set_index('patient_id', inplace=True)
# tab = tab.merge(tab2, left_index=True, right_index=True, how='left')
# gc.collect()
# print(f)
```
## Run
```
nnn = 4
import datetime
start = datetime.datetime.now()
print(start)
tab = pd.read_csv(fdir+files[nnn])
tab.set_index('patient_id', inplace=True)
tab.shape
dfall = pd.merge(train, tab, left_index=True, right_index=True, how='left')
cat_cols = ['patient_age_group','patient_state','ethinicity','household_income','education_level']
ranks = ace(dfall, 'is_screener', cat_cols=[])
df_ranks = pd.DataFrame(ranks, index=dfall.columns, columns=['ace','mean'])
df_ranks = df_ranks.sort_values(by='ace', ascending=False)
top_ranks = df_ranks[df_ranks.ace > 0]
top_ranks[:20]
top_ranks.to_csv('diagnosis_ranks_'+str(nnn)+'.csv')
import gc
gc.collect()
end = datetime.datetime.now()
print('run time: '+str(end-start)+' at: '+str(end))
break
top_ranks = pd.read_csv('diagnosis_ranks_15.csv')
top_ranks.set_index('Unnamed: 0', inplace=True)
top_ranks[:10]
qlist = list(top_ranks[top_ranks.ace > 0.003891].index)
for c in cat_cols:
qlist.remove(c)
qlist_str = "('"+qlist[0]+"'"
for c in qlist[1:]:
qlist_str=qlist_str+",'"+c+"'"
qlist_str=qlist_str+')'
qlist_str
q = 'select * from diagnosis_code where diagnosis_code in '+qlist_str
diag_codes = pd.read_sql_query(q, engine)
diag_codes
diag_codes.to_csv('diagnosis_top_codes.csv', mode='a', header=False)
qlist
tab[qlist].to_csv('diagnosis_top_'+str(nnn)+'.csv')
```
## Merge feature values
```
diag_top_features = [
'diagnosis_top_0.csv',
'diagnosis_top_3.csv',
'diagnosis_top_4.csv',
'diagnosis_top_6.csv',
'diagnosis_top_10.csv',
'diagnosis_top_12.csv',
'diagnosis_top_15.csv'
]
dff = pd.read_csv(diag_top_features[0])
dff.set_index('patient_id', inplace=True)
print(dff.shape)
for f in diag_top_features[1:]:
df2 = pd.read_csv(f)
df2.set_index('patient_id', inplace=True)
dff = dff.merge(df2, left_index=True, right_index=True, how='outer')
gc.collect()
print(f)
gc.collect()
dff.shape
dff[:5]
dff.columns
big_table = pd.read_csv(fdir+'train_big_table.csv.gz')
big_table.set_index('patient_id', inplace=True)
big_table.shape
big_table[:2]
dff[:2]
dff.columns
big_table.columns
bad_cols = ['CLINIC', 'INPATIENT', 'OTHER', 'OUTPATIENT', 'UNKNOWN',
'0001', '0002', '0003', '0004', '0005', '0006',
'HX01', 'HX02', 'HX03', 'HX04', 'HX05', 'HXPR',
'pract_screen_pct', 'cbsa_pct', 'age_pct', 'state_pct',
'632','650', u'57452', u'57454', u'57455', u'57456',
u'81252', u'90696', u'G0143', u'S4020', u'S4023']
# take only a subset of the features, the rest I think is junk
cols = list(big_table.columns)
cols = [x for x in cols if x not in bad_cols]
test_cols = list(cols)
test_cols.remove('is_screener')
bigt = big_table[cols].merge(dff, left_index=True, right_index=True, how='left')
bigt.columns
bigt.shape
bigt.to_csv(fdir+'train_big_table.csv')
big_table_encoded = pd.read_csv(fdir+'train_big_table_encoded.csv.gz')
big_table_encoded.set_index('patient_id', inplace=True)
big_table_encoded.shape
big_table_encoded[:2]
dffd = dff.copy()
dffd[dffd > 0] = 1
dffd[:10]
bigte = big_table_encoded[cols].merge(dffd,left_index=True, right_index=True, how='left')
bigte.shape
bigte[:10]
bigte.to_csv(fdir+'train_big_table_encoded.csv')
```
## Procedures
```
procs = pd.read_csv(fdir+'procedure/procedure_counts_selected.csv.gz')
procs.shape
procs.set_index('patient_id', inplace=True)
procs[:2]
print(bigt.shape)
bigtp = bigt.merge(procs, left_index=True, right_index=True, how='left')
bigtp.shape
bigtp.to_csv(fdir+'train_big_table.csv')
print(bigte.shape)
bigtep = bigte.merge(procs, left_index=True, right_index=True, how='left')
bigtep.shape
bigtep.to_csv(fdir+'train_big_table_encoded.csv')
```
## test_top
```
test_diagnosis_top = pd.read_csv('test_diagnosis_top.csv')
test_diagnosis_top.shape
#test_diagnosis_top.set_index('patient_id', inplace=True)
test_diagnosis_top[:5]
test_pivot = test_diagnosis_top.pivot(index='patient_id', columns='diagnosis_code', values='diagnosis_code_count')
test_pivot[:5]
test_pivot.shape
test_big_table = pd.read_csv(fdir+'test_big_table.csv.gz')
test_big_table.set_index('patient_id', inplace=True)
test_big_table = test_big_table[test_cols]
test_big_table.shape
test_big_table[:4]
test_big_table.info()
test_bigt = test_big_table.merge(test_pivot, left_index=True, right_index=True, how='left')
test_bigt.shape
test_bigt[:5]
test_bigt.to_csv(fdir+'test_big_table.csv')
test_big_table_encoded = pd.read_csv(fdir+'test_big_table_encoded.csv.gz')
test_big_table_encoded.set_index('patient_id', inplace=True)
test_big_table_encoded = test_big_table_encoded[test_cols]
test_big_table_encoded.shape
test_big_table_encoded.info()
test_big_table_encoded[:2]
test_dffd = test_pivot.copy()
test_dffd[test_dffd > 0] = 1
test_dffd[:10]
test_bigte = test_big_table_encoded.merge(test_dffd,left_index=True, right_index=True, how='left')
test_bigte.shape
test_bigte[:10]
test_bigte.to_csv(fdir+'test_big_table_encoded.csv')
dff.shape
test_pivot.shape
sorted_cols = [u'401.9', u'462', u'496', u'585.3', u'616.0', u'616.10', u'620.2',
u'622.10', u'622.11', u'623.5', u'625.3', u'625.9', u'626.0', u'626.2',
u'626.4', u'626.8', u'646.83', u'648.93', u'650', u'795.00',
u'V22.0', u'V22.1', u'V22.2', u'V24.2', u'V25.2', u'V27.0', u'V28.3',
u'V70.0', u'V74.5']
dff[sorted_cols].to_csv('train_diagnosis_top.csv')
test_pivot.to_csv('test_diagnosis_top.csv')
test_big_table.shape, big_table.shape
test_bigt.columns
len(test_bigt.columns)
len(big_table.columns)
len(bigte.columns)
test_bigt.drop('632_y', axis=1, inplace=True)
test_bigt.rename(columns={'632_x':'632'}, inplace=True)
test_bigte.drop('632_y', axis=1, inplace=True)
test_bigte.rename(columns={'632_x':'632'}, inplace=True)
```
## Check results
```
train_diagnosis_top = fdir+'train_diagnosis_top.csv.gz'
train_diagnosis_top = pd.read_csv(train_diagnosis_top)
train_diagnosis_top.set_index('patient_id', inplace=True)
train_diagnosis_top[:3]
train_diagnosis_top.shape
test_diagnosis_top = fdir+'test_diagnosis_top.csv.gz'
test_diagnosis_top = pd.read_csv(test_diagnosis_top)
test_diagnosis_top.set_index('patient_id', inplace=True)
test_diagnosis_top[:3]
test_diagnosis_top.shape
set(test_diagnosis_top.columns) - set(train_diagnosis_top.columns)
pd.read_csv(fdir+'diagnosis_top_codes.csv')
test_diagnosis_top.columns
train_632 = pd.read_csv(fdir+'train_big_table.csv.gz')
train_632.set_index('patient_id', inplace=True)
train_632['632'][:5]
train_diagnosis_top['632'] = train_632['632']
train_diagnosis_top.sort_index(axis=1, inplace=True)
train_diagnosis_top.columns
train_diagnosis_top.to_csv(fdir+'train_diagnosis_top.csv')
train_632.columns
```
|
github_jupyter
|
```
import nltk
import difflib
import time
import gc
import itertools
import multiprocessing
import pandas as pd
import numpy as np
import xgboost as xgb
import lightgbm as lgb
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.metrics import log_loss
from sklearn.model_selection import train_test_split
from models_utils_fe import *
from models_utils_gbm import *
src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/scripts/features/'
feats_src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/data/features/uncleaned/'
trans_src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/data/features/lemmatized_fullclean/transformations/'
wmd = pd.read_csv(src + 'train_WMD_cleaned_stemmed.csv')
wmd = wmd.astype('float32')
wmd.replace(np.inf, 1000, inplace = True)
skip_thought = pd.read_csv(src + 'train_skipthoughts_Alex_distances.csv')
skip_thought = skip_thought.astype('float32')
compression = pd.read_csv(src + 'train_LZMAcompression_distance.csv')
compression = compression.astype('float32')
edit = pd.read_csv(src + 'train_EDITdistance.csv')
edit = edit.astype('float32')
moments = pd.read_csv(src + 'train_doc2vec_moments.csv')
moments = moments.astype('float32')
networks_NER = pd.read_csv(src + 'train_networkfeats_NER.csv')
networks_NER = networks_NER.astype('float32')
xgb_feats = pd.read_csv(feats_src + '/the_1owl/owl_train.csv')
y_train = xgb_feats[['is_duplicate']]
lsaq1 = pd.DataFrame(np.load(trans_src + 'train_lsa50_CV1gram.npy')[0])
lsaq1.columns = ['{}_lsaCV1_q1'.format(i) for i in range(lsaq1.shape[1])]
lsaq2 = pd.DataFrame(np.load(trans_src + 'train_lsa50_CV1gram.npy')[1])
lsaq2.columns = ['{}_lsaCV1_q2'.format(i) for i in range(lsaq2.shape[1])]
svdq1 = pd.DataFrame(np.load(trans_src + 'train_svd50_CV1gram.npy')[0])
svdq1.columns = ['{}_svdCV1_q1'.format(i) for i in range(svdq1.shape[1])]
svdq2 = pd.DataFrame(np.load(trans_src + 'train_svd50_CV1gram.npy')[1])
svdq2.columns = ['{}_svdCV1_q2'.format(i) for i in range(svdq2.shape[1])]
X_train = pd.read_pickle('Xtrain_500bestCols.pkl')
X_train = pd.concat([X_train, wmd, skip_thought, compression, edit, moments, networks_NER,
lsaq1, lsaq2, svdq1, svdq2], axis = 1)
del xgb_feats, wmd, skip_thought, compression, edit, moments, networks_NER, \
lsaq1, lsaq2, svdq1, svdq2
gc.collect()
best_cols = [
'min_pagerank_sp_network_weighted',
'norm_wmd',
'word_match',
'1wl_tfidf_l2_euclidean',
'm_vstack_svd_q1_q1_euclidean',
'1wl_tfidf_cosine',
'sk_bi_skew_q2vec',
'm_q1_q2_tf_svd0',
'sk_bi_skew_q1vec',
'skew_q2vec',
'trigram_tfidf_cosine',
'sk_uni_skew_q2vec',
'sk_bi_canberra_distance',
'question1_3',
'sk_uni_skew_q1vec',
'sk_uni_kur_q2vec',
'min_eigenvector_centrality_np_network_weighted',
'avg_world_len2',
'z_word_match',
'sk_uni_kur_q1vec',
'skew_doc2vec_pretrained_lemmat']
rescale = False
X_bin = bin_numerical(X_train, best_cols, 0.1)
X_grouped = group_featbyfeat(X_train, best_cols, 'mean')
X_grouped2 = group_featbyfeat(X_train, best_cols, 'sum')
X_combinations = feature_combinations(X_train, best_cols[:5])
X_additional = pd.concat([X_bin, X_grouped, X_grouped2, X_combinations], axis = 1)
X_additional = drop_duplicate_cols(X_additional)
X_additional.replace(np.inf, 999, inplace = True)
X_additional.replace(np.nan, -999, inplace = True)
if rescale:
colnames = X_additional.columns
X_additional = pd.DataFrame(MinMaxScaler().fit_transform(X_additional))
X_additional.columns = colnames
X_train = pd.concat([X_train, X_additional], axis = 1)
X_train = X_train.astype('float32')
print('Final training data shape:', X_train.shape)
del X_bin, X_grouped, X_grouped2, X_combinations, X_additional
gc.collect()
src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/scripts/features/'
feats_src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/data/features/uncleaned/'
trans_src = '/media/w/1c392724-ecf3-4615-8f3c-79368ec36380/DS Projects/Kaggle/Quora/data/features/lemmatized_fullclean/transformations/'
X_train = pd.read_pickle('Xtrain_814colsBest.pkl', compression = 'bz2')
xgb_feats = pd.read_csv(feats_src + '/the_1owl/owl_train.csv')
y_train = xgb_feats[['is_duplicate']]
del xgb_feats
gc.collect()
xgb = True
if xgb:
run_xgb(X_train, y_train)
else:
run_lgb(X_train, y_train)
gbm = xgb.Booster(model_file = 'saved_models/XGB/XGB_500cols_experiments.txt')
dtrain = xgb.DMatrix(X_train, label = y_train)
mapper = {'f{0}'.format(i): v for i, v in enumerate(dtrain.feature_names)}
importance = {mapper[k]: v for k, v in gbm.get_fscore().items()}
importance = sorted(importance.items(), key=lambda x:x[1], reverse=True)[:20]
df_importance = pd.DataFrame(importance, columns=['feature', 'fscore'])
df_importance['fscore'] = df_importance['fscore'] / df_importance['fscore'].sum()
plt.figure()
df_importance.plot()
df_importance.plot(kind='barh', x='feature', y='fscore', legend=False, figsize=(10, 18))
plt.title('XGBoost Feature Importance')
plt.xlabel('relative importance')
retain_cols = df_importance['feature']
X_train2 = X_train.loc[:, retain_cols]
retain_cols.to_pickle('Colnames_best500features.pkl')
```
|
github_jupyter
|
# Homework 1
The maximum score of this homework is 100+10 points. Grading is listed in this table:
| Grade | Score range |
| --- | --- |
| 5 | 85+ |
| 4 | 70-84 |
| 3 | 55-69 |
| 2 | 40-54 |
| 1 | 0-39 |
Most exercises include tests which should pass if your solution is correct.
However successful test do not guarantee that your solution is correct.
The homework is partially autograded using many hidden tests.
Test cells cannot be modified and empty cells cannot be deleted.
Your solution should replace placeholder lines such as:
### YOUR CODE HERE
raise NotImplementedError()
Please do not add new cells, they will be ignored by the autograder.
**VERY IMPORTANT** Before submitting your solution (pushing to the git repo),
run your notebook with `Kernel -> Restart & Run All` and make sure it
runs without exceptions.
## Submission
GitHub Classroom will accept your last pushed version before the deadline.
You do not need to send the homework to the instructor.
## Plagiarism
When preparing their homework, students are reminded to pay special attention to Title 32, Sections 92-93 of Code of Studies (quoted below). Any content from external sources must be stated in the students own words AND accompanied by citations. Copying and pasting from an external source should be avoided and any text copied must be placed between quotation marks. Reports that violate these rules cannot receive a passing grade.
"**Section 92**
(1) The works of another person will be used as follows: a) if a work of another person is used in whole or in part (e.g. by copying, citation, translation from another language or presentation), the source and the name of the author will be indicated if this name is included in the source or – in case of orally presented works – may be clearly identified; b) the work of another person or any part of that will be used – up to a quantity reasonably corresponding to the nature and purpose of the student work – identified as quotations.
(2) Instructors are entitled to review compliance with requirements in this article with computer programmes and databases.
(3) The use of works of another person and the acknowledgement of use will be governed by applicable laws and the relevant rules of the specific discipline.
**Section 93**
(1) If a student fails to meet rules regarding use of works of another person in whole or in part, the student work will be considered as not assessable and the student will not be allowed to obtain the credit of the concerned subject in the specific term.
(2) It will be deemed a disciplinary offence if a student – in breach of the rules regarding use of works of another person – submits or presents a work of another person fully or in a significant part verbatim (word for word) or in terms of its basic concepts or the combined version of several works of another person(s) as their own work.
(3) Based on subsection (1) of Section 52/A. of the Higher Education Act, compliance with the rules regarding the use of works of another person in a master thesis may be reviewed up to five years following the issue of the degree certificate. In case of violation of the above rules, section 52/A of the Higher Education Act will apply."
(BME Code of Studies, p.50)
## 1. Modified Levenshtein distance (20 points)
Standard Levenshtein distance assigns an integer edit distance to any two strings measuring how difficult it would be to turn one string into the other. See [Wikipedia](https://en.wikipedia.org/wiki/Levenshtein_distance).
Create a modify version of Levenshtein distance which discounts letters
that are close to each other on the English keyboard. The keyboard variable below
contains the English keyboard organized into a table.
Two letters are considered close to each other if both their row
and column distance is at most 1. Close keys are at distance 0.5,
others are at distance 1.
This table lists a few examples:
| | | distance |
| ---- | ---- |
| q | w | 0.5 |
| q | e | 1 |
| s | w | 0.5 |
| f | t | 0.5 |
| f | y | 1 |
| f | f | 0 |
Any letter outside the lowercase English alphabet (see the `keyboard` variable below)
is not considered close and you do not need to discount them.
```
keyboard = [
['q', 'w', 'e', 'r', 't', 'y', 'u', 'i', 'o', 'p'],
['a', 's', 'd', 'f', 'g', 'h', 'j', 'k', 'l'],
['z', 'x', 'c', 'v', 'b', 'n', 'm'],
]
keyboard_mapping = {}
for i, row in enumerate(keyboard):
for j, c in enumerate(row):
keyboard_mapping[c] = (i, j)
def keyboard_edit_distance(str1, str2):
# YOUR CODE HERE
raise NotImplementedError()
assert keyboard_edit_distance("abc", "abc") == 0
assert keyboard_edit_distance("abc", "ab") == 1
assert keyboard_edit_distance("a", "s") == 0.5
```
## 2. Replace rare words (10 points)
Write a function that takes a text and a number $N$ as parameters and replaces every word other than the most common $N$ in the text with a common symbol. The symbol by default is `__RARE__` but it can be redefined.
Your code should split on spaces only.
You can derive the function definition from the tests.
```
# YOUR CODE HERE
raise NotImplementedError()
assert replace_rare_words("a b a a a b b b c d d d", 2) == "a b a a a b b b __RARE__ __RARE__ __RARE__ __RARE__"
assert replace_rare_words("a b a b b c", 2, rare_symbol="rare") == "a b a b b rare"
```
## 3. MutableString (30 points)
Python strings are immutable. Create a mutable string class. The internal representation should be mutable too.
Implement the following features (see the tests below).
- initialization from `str`,
- initialization from text file (loads the file's content into the string),
- assignment (i.e. modifying a character),
- if the index is out of range, it should fill the blanks with spaces (see the tests below)
- conversion to built-in `str` and `list`. The latter is a list of the characters.
- addition with other `MutableString` instances and built-in strings,
- multiplication with integers. Multiplying a string with 3 means repeating the string 3 times.
- built-in `len` function,
- comparision with strings,
- substring containment with both built-in strings and other MutableString objects,
- in-place upper and lowercasing,
- shallow copying,
- iteration.
Please read all of the tests before writing your solution.
```
class MutableString(object):
# YOUR CODE HERE
raise NotImplementedError()
```
### Briefly describe what internal representation you chose and why you chose it.
What other possibilities did you think about?
(double-click on the text to edit it)
YOUR ANSWER HERE
### MutableString tests
```
# initialization
m = MutableString()
assert m == "" and len(m) == 0
# initialization from file
import tempfile
import os
with tempfile.NamedTemporaryFile(mode="w+b", delete=False) as tmpfile:
tmpfile.write("abc".encode("utf8"))
m = MutableString.from_file(tmpfile.name)
assert m == "abc"
os.remove(tmpfile.name)
# iteration
m = MutableString("abc")
for c in m:
print(c)
# comparison
m1 = MutableString("abc")
assert m1 == "abc"
m2 = MutableString("abc")
assert id(m1) != id(m2)
assert m1 == m2
# item setting tests
m1 = MutableString("abc")
assert m1[0] == "a" and m1[2] == "c"
m1[1] = "d"
assert(m1[1] == "d")
# slicing
m1 = MutableString("abc")
assert m1[1:] == "bc"
m1[2:4] = "ad"
assert m1 == "abad"
# conversions
m1 = MutableString("abc d")
assert(list(m1) == list("abc d"))
assert(str(m1) == "abc d")
# concatenation
m1 = MutableString("abc")
m2 = MutableString("def")
assert m1 + m2 == "abcdef"
assert m2 + m1 == "defabc"
# multiplication
m1 = MutableString("abc")
m3 = m1 * 3
assert m3 == "abcabcabc"
# operator=
m1 = MutableString("abc")
m2 = m1
m2[0] = "A"
assert m1[1:] == "bc"
# copy
from copy import copy
m1 = MutableString("abc")
m2 = copy(m1)
m2[0] = "A"
assert m2 == "Abc"
# concatenation with strings
m1 = MutableString("abc")
m2 = m1 + "def"
assert m2 == "abcdef"
m3 = "def" + m1
assert m3 == "defabc"
# in place lowercasing and uppercasing
m1 = MutableString("aBc")
m1.to_upper()
assert m1 == "ABC"
m1 = MutableString("aBc")
m1.to_lower()
# containment test
m1 = MutableString("abcdef")
assert "bcd" in m1
m2 = MutableString("bcd")
assert m2 in m1
```
# Text generation
## 3.1 (Same as a laboratory exercise) Write a function that computes N-gram frequencies in a string. (0 point)
```
# YOUR CODE HERE
raise NotImplementedError()
assert(count_ngram_freqs("abcc", 1) == {"a": 1, "b": 1, "c": 2})
assert(count_ngram_freqs("abccab", 2) == {"ab": 2, "bc": 1, "cc": 1, "ca": 1})
```
## 3.2 Define a random text generator function (20 points).
The function takes 4 arguments:
1. starting text (at least $N-1$ long),
2. target length: length of the output string,
3. n-gram frequency dictionary,
4. N, length of the n-grams.
The function generates one character at a time given the last $N-1$ characters.
The probability of `c` being generated after `ab` is defined as:
$$
P(c | a b ) = \frac{\text{freq}(a b c)}{\text{freq}(a b)},
$$
where $\text{freq}(a b c)$ is obtained by counting how many times `abc` occurs in the training corpus (`count_ngram_freqs` function).
If the generated text ends with a $N-1$-gram that does not occur in the training data, generate the next character from the full character or ngram distribution.
```
# YOUR CODE HERE
raise NotImplementedError()
toy_freqs = count_ngram_freqs("abcabcda", 3)
gen = generate_text("abc", 5, toy_freqs, 3)
assert(len(gen) == 5)
assert(set(gen) <= set("abcd"))
```
## 3.3 Test your solution on a small Wikipedia corpus (10 points).
Collect a sample of at least 1 million characters from Wikipedia using the wikipedia module.
```
# YOUR CODE HERE
raise NotImplementedError()
```
## \*3.4 Smoothing (extra exercise, 10 points)
Implement one or more smoothing methods such as Jelinek-Mercer smoothing or Katz's backoff. Train it on your Wikipedia corpus and generate an example.
https://nlp.stanford.edu/~wcmac/papers/20050421-smoothing-tutorial.pdf
```
# YOUR CODE HERE
raise NotImplementedError()
```
## Code cleanness and PEP8 (10 points)
This cell is here for technical reasons, you will receive feedback on your code quality here. You do not need to write anything here.
YOUR ANSWER HERE
|
github_jupyter
|
# Optimiztion with `mystic`
```
%matplotlib notebook
```
`mystic`: approximates that `scipy.optimize` interface
```
"""
Example:
- Minimize Rosenbrock's Function with Nelder-Mead.
- Plot of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using retall
"""
# Nelder-Mead solver
from mystic.solvers import fmin
# Rosenbrock function
from mystic.models import rosen
# tools
import pylab
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
# use Nelder-Mead to minimize the Rosenbrock function
solution = fmin(rosen, x0, disp=0, retall=1)
allvecs = solution[-1]
# plot the parameter trajectories
pylab.plot([i[0] for i in allvecs])
pylab.plot([i[1] for i in allvecs])
pylab.plot([i[2] for i in allvecs])
# draw the plot
pylab.title("Rosenbrock parameter convergence")
pylab.xlabel("Nelder-Mead solver iterations")
pylab.ylabel("parameter value")
pylab.legend(["x", "y", "z"])
pylab.show()
```
Diagnostic tools
* Callbacks
```
"""
Example:
- Minimize Rosenbrock's Function with Nelder-Mead.
- Dynamic plot of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using callback
- solver interactivity
"""
# Nelder-Mead solver
from mystic.solvers import fmin
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.tools import getch
import pylab
pylab.ion()
# draw the plot
def plot_frame():
pylab.title("Rosenbrock parameter convergence")
pylab.xlabel("Nelder-Mead solver iterations")
pylab.ylabel("parameter value")
pylab.draw()
return
iter = 0
step, xval, yval, zval = [], [], [], []
# plot the parameter trajectories
def plot_params(params):
global iter, step, xval, yval, zval
step.append(iter)
xval.append(params[0])
yval.append(params[1])
zval.append(params[2])
pylab.plot(step,xval,'b-')
pylab.plot(step,yval,'g-')
pylab.plot(step,zval,'r-')
pylab.legend(["x", "y", "z"])
pylab.draw()
iter += 1
return
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
# suggest that the user interacts with the solver
print("NOTE: while solver is running, press 'Ctrl-C' in console window")
getch()
plot_frame()
# use Nelder-Mead to minimize the Rosenbrock function
solution = fmin(rosen, x0, disp=1, callback=plot_params, handler=True)
print(solution)
# don't exit until user is ready
getch()
```
**NOTE** IPython does not handle shell prompt interactive programs well, so the above should be run from a command prompt. An IPython-safe version is below.
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
- Dynamic print of parameter convergence to function minimum.
Demonstrates:
- standard models
- minimal solver interface
- parameter trajectories using callback
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
iter = 0
# plot the parameter trajectories
def print_params(params):
global iter
from numpy import asarray
print("Generation %d has best fit parameters: %s" % (iter,asarray(params)))
iter += 1
return
if __name__ == '__main__':
# initial guess
x0 = [0.8,1.2,0.7]
print_params(x0)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, disp=1, callback=print_params, handler=False)
print(solution)
```
* Monitors
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
Demonstrates:
- standard models
- minimal solver interface
- customized monitors
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.monitors import VerboseLoggingMonitor
if __name__ == '__main__':
print("Powell's Method")
print("===============")
# initial guess
x0 = [1.5, 1.5, 0.7]
# configure monitor
stepmon = VerboseLoggingMonitor(1,1)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, itermon=stepmon)
print(solution)
import mystic
mystic.log_reader('log.txt')
```
* Solution trajectory and model plotting
```
import mystic
mystic.model_plotter(mystic.models.rosen, 'log.txt', kwds='-d -x 1 -b "-2:2:.1, -2:2:.1, 1"')
```
Solver "tuning" and extension
* Solver class interface
```
"""
Example:
- Solve 8th-order Chebyshev polynomial coefficients with DE.
- Callable plot of fitting to Chebyshev polynomial.
- Monitor Chi-Squared for Chebyshev polynomial.
Demonstrates:
- standard models
- expanded solver interface
- built-in random initial guess
- customized monitors and termination conditions
- customized DE mutation strategies
- use of monitor to retrieve results information
"""
# Differential Evolution solver
from mystic.solvers import DifferentialEvolutionSolver2
# Chebyshev polynomial and cost function
from mystic.models.poly import chebyshev8, chebyshev8cost
from mystic.models.poly import chebyshev8coeffs
# tools
from mystic.termination import VTR
from mystic.strategy import Best1Exp
from mystic.monitors import VerboseMonitor
from mystic.tools import getch, random_seed
from mystic.math import poly1d
import pylab
pylab.ion()
# draw the plot
def plot_exact():
pylab.title("fitting 8th-order Chebyshev polynomial coefficients")
pylab.xlabel("x")
pylab.ylabel("f(x)")
import numpy
x = numpy.arange(-1.2, 1.2001, 0.01)
exact = chebyshev8(x)
pylab.plot(x,exact,'b-')
pylab.legend(["Exact"])
pylab.axis([-1.4,1.4,-2,8],'k-')
pylab.draw()
return
# plot the polynomial
def plot_solution(params,style='y-'):
import numpy
x = numpy.arange(-1.2, 1.2001, 0.01)
f = poly1d(params)
y = f(x)
pylab.plot(x,y,style)
pylab.legend(["Exact","Fitted"])
pylab.axis([-1.4,1.4,-2,8],'k-')
pylab.draw()
return
if __name__ == '__main__':
print("Differential Evolution")
print("======================")
# set range for random initial guess
ndim = 9
x0 = [(-100,100)]*ndim
random_seed(123)
# draw frame and exact coefficients
plot_exact()
# configure monitor
stepmon = VerboseMonitor(50)
# use DE to solve 8th-order Chebyshev coefficients
npop = 10*ndim
solver = DifferentialEvolutionSolver2(ndim,npop)
solver.SetRandomInitialPoints(min=[-100]*ndim, max=[100]*ndim)
solver.SetGenerationMonitor(stepmon)
solver.enable_signal_handler()
solver.Solve(chebyshev8cost, termination=VTR(0.01), strategy=Best1Exp, \
CrossProbability=1.0, ScalingFactor=0.9, \
sigint_callback=plot_solution)
solution = solver.Solution()
# use monitor to retrieve results information
iterations = len(stepmon)
cost = stepmon.y[-1]
print("Generation %d has best Chi-Squared: %f" % (iterations, cost))
# use pretty print for polynomials
print(poly1d(solution))
# compare solution with actual 8th-order Chebyshev coefficients
print("\nActual Coefficients:\n %s\n" % poly1d(chebyshev8coeffs))
# plot solution versus exact coefficients
plot_solution(solution)
from mystic.solvers import DifferentialEvolutionSolver
print("\n".join([i for i in dir(DifferentialEvolutionSolver) if not i.startswith('_')]))
```
* Algorithm configurability
* Termination conditions
```
from mystic.termination import VTR, ChangeOverGeneration, And, Or
stop = Or(And(VTR(), ChangeOverGeneration()), VTR(1e-8))
from mystic.models import rosen
from mystic.monitors import VerboseMonitor
from mystic.solvers import DifferentialEvolutionSolver
solver = DifferentialEvolutionSolver(3,40)
solver.SetRandomInitialPoints([-10,-10,-10],[10,10,10])
solver.SetGenerationMonitor(VerboseMonitor(10))
solver.SetTermination(stop)
solver.SetObjective(rosen)
solver.SetStrictRanges([-10,-10,-10],[10,10,10])
solver.SetEvaluationLimits(generations=600)
solver.Solve()
print(solver.bestSolution)
```
* Solver population
```
from mystic.solvers import DifferentialEvolutionSolver
from mystic.math import Distribution
import numpy as np
import pylab
# build a mystic distribution instance
dist = Distribution(np.random.normal, 5, 1)
# use the distribution instance as the initial population
solver = DifferentialEvolutionSolver(3,20)
solver.SetSampledInitialPoints(dist)
# visualize the initial population
pylab.hist(np.array(solver.population).ravel())
pylab.show()
```
**EXERCISE:** Use `mystic` to find the minimum for the `peaks` test function, with the bound specified by the `mystic.models.peaks` documentation.
**EXERCISE:** Use `mystic` to do a fit to the noisy data in the `scipy.optimize.curve_fit` example (the least squares fit).
Constraints "operators" (i.e. kernel transformations)
PENALTY: $\psi(x) = f(x) + k*p(x)$
CONSTRAINT: $\psi(x) = f(c(x)) = f(x')$
```
from mystic.constraints import *
from mystic.penalty import quadratic_equality
from mystic.coupler import inner
from mystic.math import almostEqual
from mystic.tools import random_seed
random_seed(213)
def test_penalize():
from mystic.math.measures import mean, spread
def mean_constraint(x, target):
return mean(x) - target
def range_constraint(x, target):
return spread(x) - target
@quadratic_equality(condition=range_constraint, kwds={'target':5.0})
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
def penalty(x):
return 0.0
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
from numpy import array
x = array([1,2,3,4,5])
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_solve():
from mystic.math.measures import mean
def mean_constraint(x, target):
return mean(x) - target
def parameter_constraint(x):
return x[-1] - x[0]
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
@quadratic_equality(condition=parameter_constraint)
def penalty(x):
return 0.0
x = solve(penalty, guess=[2,3,1])
assert round(mean_constraint(x, 5.0)) == 0.0
assert round(parameter_constraint(x)) == 0.0
assert issolution(penalty, x)
def test_solve_constraint():
from mystic.math.measures import mean
@with_mean(1.0)
def constraint(x):
x[-1] = x[0]
return x
x = solve(constraint, guess=[2,3,1])
assert almostEqual(mean(x), 1.0, tol=1e-15)
assert x[-1] == x[0]
assert issolution(constraint, x)
def test_as_constraint():
from mystic.math.measures import mean, spread
def mean_constraint(x, target):
return mean(x) - target
def range_constraint(x, target):
return spread(x) - target
@quadratic_equality(condition=range_constraint, kwds={'target':5.0})
@quadratic_equality(condition=mean_constraint, kwds={'target':5.0})
def penalty(x):
return 0.0
ndim = 3
constraints = as_constraint(penalty, solver='fmin')
#XXX: this is expensive to evaluate, as there are nested optimizations
from numpy import arange
x = arange(ndim)
_x = constraints(x)
assert round(mean(_x)) == 5.0
assert round(spread(_x)) == 5.0
assert round(penalty(_x)) == 0.0
def cost(x):
return abs(sum(x) - 5.0)
npop = ndim*3
from mystic.solvers import diffev
y = diffev(cost, x, npop, constraints=constraints, disp=False, gtol=10)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 5.0*(ndim-1)
def test_as_penalty():
from mystic.math.measures import mean, spread
@with_spread(5.0)
@with_mean(5.0)
def constraint(x):
return x
penalty = as_penalty(constraint)
from numpy import array
x = array([1,2,3,4,5])
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(spread(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_with_penalty():
from mystic.math.measures import mean, spread
@with_penalty(quadratic_equality, kwds={'target':5.0})
def penalty(x, target):
return mean(x) - target
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin
from numpy import array
x = array([1,2,3,4,5])
y = fmin(cost, x, penalty=penalty, disp=False)
assert round(mean(y)) == 5.0
assert round(cost(y)) == 4*(5.0)
def test_with_mean():
from mystic.math.measures import mean, impose_mean
@with_mean(5.0)
def mean_of_squared(x):
return [i**2 for i in x]
from numpy import array
x = array([1,2,3,4,5])
y = impose_mean(5, [i**2 for i in x])
assert mean(y) == 5.0
assert mean_of_squared(x) == y
def test_with_mean_spread():
from mystic.math.measures import mean, spread, impose_mean, impose_spread
@with_spread(50.0)
@with_mean(5.0)
def constrained_squared(x):
return [i**2 for i in x]
from numpy import array
x = array([1,2,3,4,5])
y = impose_spread(50.0, impose_mean(5.0,[i**2 for i in x]))
assert almostEqual(mean(y), 5.0, tol=1e-15)
assert almostEqual(spread(y), 50.0, tol=1e-15)
assert constrained_squared(x) == y
def test_constrained_solve():
from mystic.math.measures import mean, spread
@with_spread(5.0)
@with_mean(5.0)
def constraints(x):
return x
def cost(x):
return abs(sum(x) - 5.0)
from mystic.solvers import fmin_powell
from numpy import array
x = array([1,2,3,4,5])
y = fmin_powell(cost, x, constraints=constraints, disp=False)
assert almostEqual(mean(y), 5.0, tol=1e-15)
assert almostEqual(spread(y), 5.0, tol=1e-15)
assert almostEqual(cost(y), 4*(5.0), tol=1e-6)
if __name__ == '__main__':
test_penalize()
test_solve()
test_solve_constraint()
test_as_constraint()
test_as_penalty()
test_with_penalty()
test_with_mean()
test_with_mean_spread()
test_constrained_solve()
from mystic.coupler import and_, or_, not_
from mystic.constraints import and_ as _and, or_ as _or, not_ as _not
if __name__ == '__main__':
import numpy as np
from mystic.penalty import linear_equality, quadratic_equality
from mystic.constraints import as_constraint
x = x1,x2,x3 = (5., 5., 1.)
f = f1,f2,f3 = (np.sum, np.prod, np.average)
k = 100
solver = 'fmin_powell' #'diffev'
ptype = quadratic_equality
# case #1: couple penalties into a single constraint
p1 = lambda x: abs(x1 - f1(x))
p2 = lambda x: abs(x2 - f2(x))
p3 = lambda x: abs(x3 - f3(x))
p = (p1,p2,p3)
p = [ptype(pi)(lambda x:0.) for pi in p]
penalty = and_(*p, k=k)
constraint = as_constraint(penalty, solver=solver)
x = [1,2,3,4,5]
x_ = constraint(x)
assert round(f1(x_)) == round(x1)
assert round(f2(x_)) == round(x2)
assert round(f3(x_)) == round(x3)
# case #2: couple constraints into a single constraint
from mystic.math.measures import impose_product, impose_sum, impose_mean
from mystic.constraints import as_penalty
from mystic import random_seed
random_seed(123)
t = t1,t2,t3 = (impose_sum, impose_product, impose_mean)
c1 = lambda x: t1(x1, x)
c2 = lambda x: t2(x2, x)
c3 = lambda x: t3(x3, x)
c = (c1,c2,c3)
k=1
solver = 'buckshot' #'diffev'
ptype = linear_equality #quadratic_equality
p = [as_penalty(ci, ptype) for ci in c]
penalty = and_(*p, k=k)
constraint = as_constraint(penalty, solver=solver)
x = [1,2,3,4,5]
x_ = constraint(x)
assert round(f1(x_)) == round(x1)
assert round(f2(x_)) == round(x2)
assert round(f3(x_)) == round(x3)
# etc: more coupling of constraints
from mystic.constraints import with_mean, discrete
@with_mean(5.0)
def meanie(x):
return x
@discrete(list(range(11)))
def integers(x):
return x
c = _and(integers, meanie)
x = c([1,2,3])
assert x == integers(x) == meanie(x)
x = c([9,2,3])
assert x == integers(x) == meanie(x)
x = c([0,-2,3])
assert x == integers(x) == meanie(x)
x = c([9,-200,344])
assert x == integers(x) == meanie(x)
c = _or(meanie, integers)
x = c([1.1234, 4.23412, -9])
assert x == meanie(x) and x != integers(x)
x = c([7.0, 10.0, 0.0])
assert x == integers(x) and x != meanie(x)
x = c([6.0, 9.0, 0.0])
assert x == integers(x) == meanie(x)
x = c([3,4,5])
assert x == integers(x) and x != meanie(x)
x = c([3,4,5.5])
assert x == meanie(x) and x != integers(x)
c = _not(integers)
x = c([1,2,3])
assert x != integers(x) and x != [1,2,3] and x == c(x)
x = c([1.1,2,3])
assert x != integers(x) and x == [1.1,2,3] and x == c(x)
c = _not(meanie)
x = c([1,2,3])
assert x != meanie(x) and x == [1,2,3] and x == c(x)
x = c([4,5,6])
assert x != meanie(x) and x != [4,5,6] and x == c(x)
c = _not(_and(meanie, integers))
x = c([4,5,6])
assert x != meanie(x) and x != integers(x) and x != [4,5,6] and x == c(x)
# etc: more coupling of penalties
from mystic.penalty import quadratic_inequality
p1 = lambda x: sum(x) - 5
p2 = lambda x: min(i**2 for i in x)
p = p1,p2
p = [quadratic_inequality(pi)(lambda x:0.) for pi in p]
p1,p2 = p
penalty = and_(*p)
x = [[1,2],[-2,-1],[5,-5]]
for xi in x:
assert p1(xi) + p2(xi) == penalty(xi)
penalty = or_(*p)
for xi in x:
assert min(p1(xi),p2(xi)) == penalty(xi)
penalty = not_(p1)
for xi in x:
assert bool(p1(xi)) != bool(penalty(xi))
penalty = not_(p2)
for xi in x:
assert bool(p2(xi)) != bool(penalty(xi))
```
In addition to being able to generically apply information as a penalty, `mystic` provides the ability to construct constraints "operators" -- essentially applying kernel transformations that reduce optimizer search space to the space of solutions that satisfy the constraints. This can greatly accelerate convergence to a solution, as the space that the optimizer can explore is restricted.
```
"""
Example:
- Minimize Rosenbrock's Function with Powell's method.
Demonstrates:
- standard models
- minimal solver interface
- parameter constraints solver and constraints factory decorator
- statistical parameter constraints
- customized monitors
"""
# Powell's Directonal solver
from mystic.solvers import fmin_powell
# Rosenbrock function
from mystic.models import rosen
# tools
from mystic.monitors import VerboseMonitor
from mystic.math.measures import mean, impose_mean
if __name__ == '__main__':
print("Powell's Method")
print("===============")
# initial guess
x0 = [0.8,1.2,0.7]
# use the mean constraints factory decorator
from mystic.constraints import with_mean
# define constraints function
@with_mean(1.0)
def constraints(x):
# constrain the last x_i to be the same value as the first x_i
x[-1] = x[0]
return x
# configure monitor
stepmon = VerboseMonitor(1)
# use Powell's method to minimize the Rosenbrock function
solution = fmin_powell(rosen, x0, constraints=constraints, itermon=stepmon)
print(solution)
```
* Range (i.e. 'box') constraints
Use `solver.SetStrictRange`, or the `bounds` keyword on the solver function interface.
* Symbolic constraints interface
```
%%file spring.py
"a Tension-Compression String"
def objective(x):
x0,x1,x2 = x
return x0**2 * x1 * (x2 + 2)
bounds = [(0,100)]*3
# with penalty='penalty' applied, solution is:
xs = [0.05168906, 0.35671773, 11.28896619]
ys = 0.01266523
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
pf = generate_penalty(generate_conditions(equations), k=1e12)
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf, npop=40,
gtol=500, disp=True, full_output=True)
print(result[0])
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
ineql, eql = generate_conditions(equations)
print("CONVERTED SYMBOLIC TO SINGLE CONSTRAINTS FUNCTIONS")
print(ineql)
print(eql)
print("\nTHE INDIVIDUAL INEQUALITIES")
for f in ineql:
print(f.__doc__)
print("\nGENERATED THE PENALTY FUNCTION FOR ALL CONSTRAINTS")
pf = generate_penalty((ineql, eql))
print(pf.__doc__)
x = [-0.1, 0.5, 11.0]
print("\nPENALTY FOR {}: {}".format(x, pf(x)))
```
* Penatly functions
```
equations = """
1.0 - (x1**3 * x2)/(71785*x0**4) <= 0.0
(4*x1**2 - x0*x1)/(12566*x0**3 * (x1 - x0)) + 1./(5108*x0**2) - 1.0 <= 0.0
1.0 - 140.45*x0/(x2 * x1**2) <= 0.0
(x0 + x1)/1.5 - 1.0 <= 0.0
"""
"a Tension-Compression String"
from spring import objective, bounds, xs, ys
from mystic.penalty import quadratic_inequality
def penalty1(x): # <= 0.0
return 1.0 - (x[1]**3 * x[2])/(71785*x[0]**4)
def penalty2(x): # <= 0.0
return (4*x[1]**2 - x[0]*x[1])/(12566*x[0]**3 * (x[1] - x[0])) + 1./(5108*x[0]**2) - 1.0
def penalty3(x): # <= 0.0
return 1.0 - 140.45*x[0]/(x[2] * x[1]**2)
def penalty4(x): # <= 0.0
return (x[0] + x[1])/1.5 - 1.0
@quadratic_inequality(penalty1, k=1e12)
@quadratic_inequality(penalty2, k=1e12)
@quadratic_inequality(penalty3, k=1e12)
@quadratic_inequality(penalty4, k=1e12)
def penalty(x):
return 0.0
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=penalty, npop=40,
gtol=500, disp=True, full_output=True)
print(result[0])
```
* "Operators" that directly constrain search space
```
"""
Crypto problem in Google CP Solver.
Prolog benchmark problem
'''
Name : crypto.pl
Original Source: P. Van Hentenryck's book
Adapted by : Daniel Diaz - INRIA France
Date : September 1992
'''
"""
def objective(x):
return 0.0
nletters = 26
bounds = [(1,nletters)]*nletters
# with penalty='penalty' applied, solution is:
# A B C D E F G H I J K L M N O P Q
xs = [ 5, 13, 9, 16, 20, 4, 24, 21, 25, 17, 23, 2, 8, 12, 10, 19, 7, \
# R S T U V W X Y Z
11, 15, 3, 1, 26, 6, 22, 14, 18]
ys = 0.0
# constraints
equations = """
B + A + L + L + E + T - 45 == 0
C + E + L + L + O - 43 == 0
C + O + N + C + E + R + T - 74 == 0
F + L + U + T + E - 30 == 0
F + U + G + U + E - 50 == 0
G + L + E + E - 66 == 0
J + A + Z + Z - 58 == 0
L + Y + R + E - 47 == 0
O + B + O + E - 53 == 0
O + P + E + R + A - 65 == 0
P + O + L + K + A - 59 == 0
Q + U + A + R + T + E + T - 50 == 0
S + A + X + O + P + H + O + N + E - 134 == 0
S + C + A + L + E - 51 == 0
S + O + L + O - 37 == 0
S + O + N + G - 61 == 0
S + O + P + R + A + N + O - 82 == 0
T + H + E + M + E - 72 == 0
V + I + O + L + I + N - 100 == 0
W + A + L + T + Z - 34 == 0
"""
var = list('ABCDEFGHIJKLMNOPQRSTUVWXYZ')
# Let's say we know the vowels.
bounds[0] = (5,5) # A
bounds[4] = (20,20) # E
bounds[8] = (25,25) # I
bounds[14] = (10,10) # O
bounds[20] = (1,1) # U
from mystic.constraints import unique, near_integers, has_unique
from mystic.symbolic import generate_penalty, generate_conditions
pf = generate_penalty(generate_conditions(equations,var),k=1)
from mystic.penalty import quadratic_equality
@quadratic_equality(near_integers)
@quadratic_equality(has_unique)
def penalty(x):
return pf(x)
from numpy import round, hstack, clip
def constraint(x):
x = round(x).astype(int) # force round and convert type to int
x = clip(x, 1,nletters) #XXX: hack to impose bounds
x = unique(x, range(1,nletters+1))
return x
if __name__ == '__main__':
from mystic.solvers import diffev2
from mystic.monitors import Monitor, VerboseMonitor
mon = VerboseMonitor(50)
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf,
constraints=constraint, npop=52, ftol=1e-8, gtol=1000,
disp=True, full_output=True, cross=0.1, scale=0.9, itermon=mon)
print(result[0])
```
Special cases
* Integer and mixed integer programming
```
"""
Eq 10 in Google CP Solver.
Standard benchmark problem.
"""
def objective(x):
return 0.0
bounds = [(0,10)]*7
# with penalty='penalty' applied, solution is:
xs = [6., 0., 8., 4., 9., 3., 9.]
ys = 0.0
# constraints
equations = """
98527*x0 + 34588*x1 + 5872*x2 + 59422*x4 + 65159*x6 - 1547604 - 30704*x3 - 29649*x5 == 0.0
98957*x1 + 83634*x2 + 69966*x3 + 62038*x4 + 37164*x5 + 85413*x6 - 1823553 - 93989*x0 == 0.0
900032 + 10949*x0 + 77761*x1 + 67052*x4 - 80197*x2 - 61944*x3 - 92964*x5 - 44550*x6 == 0.0
73947*x0 + 84391*x2 + 81310*x4 - 1164380 - 96253*x1 - 44247*x3 - 70582*x5 - 33054*x6 == 0.0
13057*x2 + 42253*x3 + 77527*x4 + 96552*x6 - 1185471 - 60152*x0 - 21103*x1 - 97932*x5 == 0.0
1394152 + 66920*x0 + 55679*x3 - 64234*x1 - 65337*x2 - 45581*x4 - 67707*x5 - 98038*x6 == 0.0
68550*x0 + 27886*x1 + 31716*x2 + 73597*x3 + 38835*x6 - 279091 - 88963*x4 - 76391*x5 == 0.0
76132*x1 + 71860*x2 + 22770*x3 + 68211*x4 + 78587*x5 - 480923 - 48224*x0 - 82817*x6 == 0.0
519878 + 94198*x1 + 87234*x2 + 37498*x3 - 71583*x0 - 25728*x4 - 25495*x5 - 70023*x6 == 0.0
361921 + 78693*x0 + 38592*x4 + 38478*x5 - 94129*x1 - 43188*x2 - 82528*x3 - 69025*x6 == 0.0
"""
from mystic.symbolic import generate_constraint, generate_solvers, solve
cf = generate_constraint(generate_solvers(solve(equations)))
if __name__ == '__main__':
from mystic.solvers import diffev2
result = diffev2(objective, x0=bounds, bounds=bounds, constraints=cf,
npop=4, gtol=1, disp=True, full_output=True)
print(result[0])
```
**EXERCISE:** Solve the `chebyshev8.cost` example exactly, by applying the knowledge that the last term in the chebyshev polynomial will always be be one. Use `numpy.round` or `mystic.constraints.integers` or to constrain solutions to the set of integers. Does using `mystic.suppressed` to supress small numbers accelerate the solution?
**EXERCISE:** Replace the symbolic constraints in the following "Pressure Vessel Design" code with explicit penalty functions (i.e. use a compound penalty built with `mystic.penalty.quadratic_inequality`).
```
"Pressure Vessel Design"
def objective(x):
x0,x1,x2,x3 = x
return 0.6224*x0*x2*x3 + 1.7781*x1*x2**2 + 3.1661*x0**2*x3 + 19.84*x0**2*x2
bounds = [(0,1e6)]*4
# with penalty='penalty' applied, solution is:
xs = [0.72759093, 0.35964857, 37.69901188, 240.0]
ys = 5804.3762083
from mystic.symbolic import generate_constraint, generate_solvers, solve
from mystic.symbolic import generate_penalty, generate_conditions
equations = """
-x0 + 0.0193*x2 <= 0.0
-x1 + 0.00954*x2 <= 0.0
-pi*x2**2*x3 - (4/3.)*pi*x2**3 + 1296000.0 <= 0.0
x3 - 240.0 <= 0.0
"""
pf = generate_penalty(generate_conditions(equations), k=1e12)
if __name__ == '__main__':
from mystic.solvers import diffev2
from mystic.math import almostEqual
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf, npop=40, gtol=500,
disp=True, full_output=True)
print(result[0])
```
* Linear and quadratic constraints
```
"""
Minimize: f = 2*x[0] + 1*x[1]
Subject to: -1*x[0] + 1*x[1] <= 1
1*x[0] + 1*x[1] >= 2
1*x[1] >= 0
1*x[0] - 2*x[1] <= 4
where: -inf <= x[0] <= inf
"""
def objective(x):
x0,x1 = x
return 2*x0 + x1
equations = """
-x0 + x1 - 1.0 <= 0.0
-x0 - x1 + 2.0 <= 0.0
x0 - 2*x1 - 4.0 <= 0.0
"""
bounds = [(None, None),(0.0, None)]
# with penalty='penalty' applied, solution is:
xs = [0.5, 1.5]
ys = 2.5
from mystic.symbolic import generate_conditions, generate_penalty
pf = generate_penalty(generate_conditions(equations), k=1e3)
from mystic.symbolic import generate_constraint, generate_solvers, simplify
cf = generate_constraint(generate_solvers(simplify(equations)))
if __name__ == '__main__':
from mystic.solvers import fmin_powell
from mystic.math import almostEqual
result = fmin_powell(objective, x0=[0.0,0.0], bounds=bounds, constraint=cf,
penalty=pf, disp=True, full_output=True, gtol=3)
print(result[0])
```
**EXERCISE:** Solve the `cvxopt` "qp" example with `mystic`. Use symbolic constaints, penalty functions, or constraints operators. If you get it quickly, do all three methods.
Let's look at how `mystic` gives improved [solver workflow](workflow.ipynb)
|
github_jupyter
|
```
# Load dependencies
import numpy as np
import pandas as pd
from uncertainties import ufloat
from uncertainties import unumpy
```
# Biomass C content estimation
Biomass is presented in the paper on a dry-weight basis. As part of the biomass calculation, we converted biomass in carbon-weight basis to dry-weight basis by multiplying by a conversion factor.
## Conversion factor calculation
The conversion factor was calculated based on C content estimates of the different plant compartments (leaves, stems and roots) of different biomes, from [Tang et al.](https://doi.org/10.1073/pnas.1700295114) (units: (mg/g)).
```
# Upload C content data from Tang et al., units [mg/g]
c_content = pd.read_excel("C_content_Tang.xlsx")
c_content
# Save parameters to unumpy arrays
cleaf = unumpy.uarray(list(c_content['leaf']), list(c_content['leaf std']))
cstem = unumpy.uarray(list(c_content['stem'].fillna(0)), list(c_content['stem std'].fillna(0)))
croot = unumpy.uarray(list(c_content['root']), list(c_content['root std']))
```
For each biome, we calculate the weighted average C content according to the mass fraction of each plant compartment. Information on plants compartmental mass composition was obtained from [Poorter et al.](https://nph.onlinelibrary.wiley.com/doi/full/10.1111/j.1469-8137.2011.03952.x).
```
# Upload compartmental mass composition, from Poorter et al., classified according to Tang et al. biomes
compart_comp = pd.read_excel("compartment_comp_Poorter.xlsx")
compart_comp
# Save parameters to unumpy arrays
fleaf = unumpy.uarray(list(compart_comp['leaf']), list(compart_comp['leaf std']))
fstem = unumpy.uarray(list(compart_comp['stem'].fillna(0)), list(compart_comp['stem std'].fillna(0)))
froot = unumpy.uarray(list(compart_comp['root']), list(compart_comp['root std']))
# Calculate the weighted average for each biome
cbiome = (cleaf*fleaf)+(cstem*fstem)+(croot*froot)
```
Next, we calculate the plants conversion factor, according to the mass fraction of each biome, which was calculated by the corresponding mass of each of the biome categories, derived from [Erb et al.](https://doi.org/10.1038/nature25138).
```
# Upload biomes biomass, from Erb et al., classified according to Tang et al. biomes
mbiome = pd.read_excel('biome_mass_Erb.xlsx')
mbiome
# Save to unumpy array
mbiomes = unumpy.uarray(list(mbiome['biomass [Gt C]']), list(mbiome['biomass std']))
# Calculate the overall conversion factor
cplants_factor = 1000/np.sum((cbiome* (mbiomes/np.sum(mbiomes))))
```
In the overall carbon-weight to dry-weight conversion factor, we also accounted the C content of non-plant biomass, which was based on estimates from [Heldal et al.](https://aem.asm.org/content/50/5/1251.short) and [von Stockar](https://www.sciencedirect.com/science/article/pii/S0005272899000651). We used the current estimate of non-plant biomass fraction - about 10% of the total biomass, according to [Bar-On et al.](https://doi.org/10.1073/pnas.1711842115) and [updates](https://doi.org/10.1038/s41561-018-0221-6).
```
# Upload non plant C content data, units [g/g]
cnon_plant = pd.read_excel('C_content_non_plant.xlsx')
cnon_plant
# Calculate conversion factors
cnon_plant_factor = ufloat(np.average(cnon_plant['C content']) ,np.std(cnon_plant['C content'], ddof = 1))
cfactor = (cplants_factor*0.9) +(0.1*(1/cnon_plant_factor))
cfactor
print 'Our best estimate of the C content conversion factor is: ' + "%.2f" % (cfactor.n) + ', with uncertainty (±1 standard deviation): ' + "%.2f" % (cfactor.s)
```
|
github_jupyter
|
# Introduction
<div class="alert alert-info">
**Code not tidied, but should work OK**
</div>
<img src="../Udacity_DL_Nanodegree/031%20RNN%20Super%20Basics/SimpleRNN01.png" align="left"/>
# Neural Network
```
import numpy as np
import matplotlib.pyplot as plt
import pdb
```
**Sigmoid**
```
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_der(x):
return sigmoid(x) * (1 - sigmoid(x))
```
**Hyperbolic Tangent**
```
def tanh(x):
return np.tanh(x)
def tanh_der(x):
return 1.0 - np.tanh(x)**2
```
**Mean Squared Error**
```
def mse(x, y, Wxh, Whh, Who):
y_hat = forward(x, Wxh, Whh, Who)
return 0.5 * np.mean((y-y_hat)**2)
```
**Forward Pass**
```
def forward(x, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
x_t0 = x[:,0,:]
x_t1 = x[:,1,:]
x_t2 = x[:,2,:]
x_t3 = x[:,3,:]
s_init = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
z_t0 = s_init @ Whh + x_t0 @ Wxh
s_t0 = tanh(z_t0)
z_t1 = s_t0 @ Whh + x_t1 @ Wxh
s_t1 = tanh(z_t1)
z_t2 = s_t1 @ Whh + x_t2 @ Wxh
s_t2 = tanh(z_t2)
z_t3 = s_t2 @ Whh + x_t3 @ Wxh
s_t3 = tanh(z_t3)
z_out = s_t3 @ Who
y_hat = sigmoid( z_out )
return y_hat
def forward(x, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
for t in range(T):
x_t[t] = x[:,t,:]
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = sigmoid( z_out )
return y_hat
```
**Backpropagation**
```
def backward(x, y, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
assert y.ndim==2 and y.shape[1:]==(1,)
assert len(x) == len(y)
# Forward
x_t0 = x[:,0,:]
x_t1 = x[:,1,:]
x_t2 = x[:,2,:]
x_t3 = x[:,3,:]
s_init = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
z_t0 = s_init @ Whh + x_t0 @ Wxh
s_t0 = tanh(z_t0)
z_t1 = s_t0 @ Whh + x_t1 @ Wxh
s_t1 = tanh(z_t1)
z_t2 = s_t1 @ Whh + x_t2 @ Wxh
s_t2 = tanh(z_t2)
z_t3 = s_t2 @ Whh + x_t3 @ Wxh
s_t3 = tanh(z_t3)
z_out = s_t3 @ Who
y_hat = sigmoid( z_out )
# Backward
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
err = -(y-y_hat)/len(x) * sigmoid_der( z_out )
dWho = s_t3.T @ err
ro_t3 = err @ Who.T * tanh_der(z_t3)
dWxh += x_t3.T @ ro_t3
dWhh += s_t2.T @ ro_t3
ro_t2 = ro_t3 @ Whh.T * tanh_der(z_t2)
dWxh += x_t2.T @ ro_t2
dWhh += s_t1.T @ ro_t2
ro_t1 = ro_t2 @ Whh.T * tanh_der(z_t1)
dWxh += x_t1.T @ ro_t1
dWhh += s_t0.T @ ro_t1
ro_t0 = ro_t1 @ Whh.T * tanh_der(z_t0)
dWxh += x_t0.T @ ro_t0
dWhh += s_init.T @ ro_t0
return y_hat, dWxh, dWhh, dWho
def backward(x, y, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
assert y.ndim==2 and y.shape[1:]==(1,)
assert len(x) == len(y)
# Init
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
# Forward
for t in range(T): # t = [0, 1, 2, 3]
x_t[t] = x[:,t,:] # pick time-step input x_[t].shape = (n_batch, n_in)
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = sigmoid( z_out )
# Backward
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
ro = -(y-y_hat)/len(x) * sigmoid_der( z_out ) # Backprop through loss funt.
dWho = s_t[t].T @ ro #
ro = ro @ Who.T * tanh_der(z_t[t]) # Backprop into hidden state
for t in reversed(range(T)): # t = [3, 2, 1, 0]
dWxh += x_t[t].T @ ro
dWhh += s_t[t-1].T @ ro
if t != 0: # don't backprop into t=-1
ro = ro @ Whh.T * tanh_der(z_t[t-1]) # Backprop into previous time step
return y_hat, dWxh, dWhh, dWho
```
**Train Loop**
```
def train_rnn(x, y, nb_epochs, learning_rate, Wxh, Whh, Who):
losses = []
for e in range(nb_epochs):
y_hat, dWxh, dWhh, dWho = backward(x, y, Wxh, Whh, Who)
Wxh += -learning_rate * dWxh
Whh += -learning_rate * dWhh
Who += -learning_rate * dWho
# Log and print
loss_train = mse(x, y, Wxh, Whh, Who)
losses.append(loss_train)
if e % (nb_epochs / 10) == 0:
print('loss ', loss_train.round(4))
return losses
```
# Example: Count Letter 'a'
**Create Dataset**
```
# Encoding: 'a'=[0,0,1] 'b'=[0,1,0] 'c'=[1,0,0]
# < ----- 4x time steps ----- >
x_train = np.array([
[ [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 1, 0] ], # 'bbcb'
[ [1, 0, 0], [0, 1, 0], [1, 0, 0], [0, 1, 0] ], # 'cbcb' ^
[ [0, 1, 0], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'bcbc' ^
[ [1, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0] ], # 'cbbc' ^
[ [1, 0, 0], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'ccbc' ^
[ [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0] ], # 'bacb' | 9x batch size
[ [1, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1] ], # 'ccba' v
[ [0, 0, 1], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'acbc' ^
[ [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0] ], # 'cbac' ^
[ [0, 1, 0], [0, 0, 1], [0, 0, 1], [0, 1, 0] ], # 'baab'
[ [0, 0, 1], [0, 0, 1], [0, 1, 0], [1, 0, 0] ], # 'aabc'
[ [0, 0, 1], [1, 0, 0], [0, 0, 1], [0, 0, 1] ], # 'acaa'
])
y_train = np.array([ [0], # <-> no timesteps
[0], #
[0], #
[0], #
[0], #
[1], # ^
[1], # | 9x batch size
[1], # ^
[1], # | 9x batch size
[0], # v
[0], #
[1] ]) #
x_test = np.array([
[ [0,1,0], [1,0,0], [1,0,0], [0,1,0] ], # 'bccb' -> 0
[ [1,0,0], [1,0,0], [0,1,0], [1,0,0] ], # 'ccbb' -> 0
[ [0,1,0], [1,0,0], [0,0,1], [1,0,0] ], # 'bcac' -> 1
[ [0,1,0], [0,0,1], [1,0,0], [0,1,0] ], # 'bacb' -> 1
])
y_test = np.array([ [0], # <-> no timesteps
[0], #
[1], #
[1], ])
test_gradient()
```
#### Train
```
np.random.seed(0)
W_xh = 0.1 * np.random.randn(3, 2) # Wxh.shape: [n_in, n_hid]
W_hh = 0.1 * np.random.randn(2, 2) # Whh.shape: [n_hid, n_hid]
W_ho = 0.1 * np.random.randn(2, 1) # Who.shape: [n_hid, n_out]
losses = train_rnn(x_train, y_train, 3000, 0.1, W_xh, W_hh, W_ho)
y_hat = forward(x_train, W_xh, W_hh, W_ho).round(0)
y_hat
y_hat == y_train
y_hat = forward(x_test, W_xh, W_hh, W_ho).round(0)
y_hat
y_hat == y_test
plt.plot(losses)
```
# Gradient Check
```
def numerical_gradient(x, y, Wxh, Whh, Who):
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
eps = 1e-4
for r in range(len(Wxh)):
for c in range(Wxh.shape[1]):
Wxh_pls = Wxh.copy()
Wxh_min = Wxh.copy()
Wxh_pls[r, c] += eps
Wxh_min[r, c] -= eps
l_pls = mse(x, y, Wxh_pls, Whh, Who)
l_min = mse(x, y, Wxh_min, Whh, Who)
dWxh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Whh)):
for c in range(Whh.shape[1]):
Whh_pls = Whh.copy()
Whh_min = Whh.copy()
Whh_pls[r, c] += eps
Whh_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh_pls, Who)
l_min = mse(x, y, Wxh, Whh_min, Who)
dWhh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Who)):
for c in range(Who.shape[1]):
Who_pls = Who.copy()
Who_min = Who.copy()
Who_pls[r, c] += eps
Who_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh, Who_pls)
l_min = mse(x, y, Wxh, Whh, Who_min)
dWho[r, c] = (l_pls - l_min) / (2*eps)
return dWxh, dWhh, dWho
def test_gradients():
for i in range(100):
W_xh = 0.1 * np.random.randn(3, 2) # Wxh.shape: [n_in, n_hid]
W_hh = 0.1 * np.random.randn(2, 2) # Whh.shape: [n_hid, n_hid]
W_ho = 0.1 * np.random.randn(2, 1) # Who.shape: [n_hid, n_out]
xx = np.random.randn(100, 4, 3)
yy = np.random.randint(0, 2, size=[100, 1])
_, dW_xh, dW_hh, dW_ho = backward(xx, yy, W_xh, W_hh, W_ho)
ngW_xh, ngW_hh, ngW_ho = numerical_gradient(xx, yy, W_xh, W_hh, W_ho)
assert np.allclose(dW_xh, ngW_xh)
assert np.allclose(dW_hh, ngW_hh)
assert np.allclose(dW_ho, ngW_ho)
test_gradients()
```
|
github_jupyter
|
<a id="title_ID"></a>
# JWST Pipeline Validation Notebook: calwebb_detector1, dark_current unit tests
<span style="color:red"> **Instruments Affected**</span>: NIRCam, NIRISS, NIRSpec, MIRI, FGS
### Table of Contents
<div style="text-align: left">
<br> [Introduction](#intro)
<br> [JWST Unit Tests](#unit)
<br> [Defining Terms](#terms)
<br> [Test Description](#description)
<br> [Data Description](#data_descr)
<br> [Imports](#imports)
<br> [Convenience Functions](#functions)
<br> [Perform Tests](#testing)
<br> [About This Notebook](#about)
<br>
</div>
<a id="intro"></a>
# Introduction
This is the validation notebook that displays the unit tests for the Dark Current step in calwebb_detector1. This notebook runs and displays the unit tests that are performed as a part of the normal software continuous integration process. For more information on the pipeline visit the links below.
* Pipeline description: https://jwst-pipeline.readthedocs.io/en/latest/jwst/dark_current/index.html
* Pipeline code: https://github.com/spacetelescope/jwst/tree/master/jwst/
[Top of Page](#title_ID)
<a id="unit"></a>
# JWST Unit Tests
JWST unit tests are located in the "tests" folder for each pipeline step within the [GitHub repository](https://github.com/spacetelescope/jwst/tree/master/jwst/), e.g., ```jwst/dark_current/tests```.
* Unit test README: https://github.com/spacetelescope/jwst#unit-tests
[Top of Page](#title_ID)
<a id="terms"></a>
# Defining Terms
These are terms or acronymns used in this notebook that may not be known a general audience.
* JWST: James Webb Space Telescope
* NIRCam: Near-Infrared Camera
[Top of Page](#title_ID)
<a id="description"></a>
# Test Description
Unit testing is a software testing method by which individual units of source code are tested to determine whether they are working sufficiently well. Unit tests do not require a separate data file; the test creates the necessary test data and parameters as a part of the test code.
[Top of Page](#title_ID)
<a id="data_descr"></a>
# Data Description
Data used for unit tests is created on the fly within the test itself, and is typically an array in the expected format of JWST data with added metadata needed to run through the pipeline.
[Top of Page](#title_ID)
<a id="imports"></a>
# Imports
* tempfile for creating temporary output products
* pytest for unit test functions
* jwst for the JWST Pipeline
* IPython.display for display pytest reports
[Top of Page](#title_ID)
```
import tempfile
import pytest
import jwst
from IPython.display import IFrame
```
<a id="functions"></a>
# Convenience Functions
Here we define any convenience functions to help with running the unit tests.
[Top of Page](#title_ID)
```
def display_report(fname):
'''Convenience function to display pytest report.'''
return IFrame(src=fname, width=700, height=600)
```
<a id="testing"></a>
# Perform Tests
Below we run the unit tests for the Dark Current step.
[Top of Page](#title_ID)
```
with tempfile.TemporaryDirectory() as tmpdir:
!pytest jwst/dark_current -v --ignore=jwst/associations --ignore=jwst/datamodels --ignore=jwst/stpipe --ignore=jwst/regtest --html=tmpdir/unit_report.html --self-contained-html
report = display_report('tmpdir/unit_report.html')
report
```
<a id="about"></a>
## About This Notebook
**Author:** Alicia Canipe, Staff Scientist, NIRCam
<br>**Updated On:** 01/07/2021
[Top of Page](#title_ID)
<img style="float: right;" src="./stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="stsci_pri_combo_mark_horizonal_white_bkgd" width="200px"/>
|
github_jupyter
|
## Dự án 01: Xây dựng Raspberry PI thành máy tính cho Data Scientist (PIDS)
## Bài 01. Cài đặt TensorFlow và các thư viện cần thiết
##### Người soạn: Dương Trần Hà Phương
##### Website: [Mechasolution Việt Nam](https://mechasolution.vn)
##### Email: [email protected]
---
## 1. Mở đầu
Nếu bạn muốn chạy một Neural network model hoặc một thuật toán dự đoán nào đó trên một hệ thống nhúng thì Raspberry PI là một lựa chọn hoàn hảo cho bạn.
Chỉ cần lựa chọn phiên bản Raspberry phù hợp với dự án của bạn. Sau đó, cài đặt hệ điều hành mới nhất và xong. Bạn đã sẵn sàng để khám phá thế giới Raspberry kì diệu rồi đó.
## 2. Yêu cầu cần thiết
**Hệ điều hành: Raspbian**
* Tải xuống phiên bản mới nhất của hệ điều hành Raspbian tại [ĐÂY](https://downloads.raspberrypi.org/raspbian_latest)
* Sử dụng [Etcher](https://etcher.io/) để copy Raspbian lên thẻ nhớ (MicroSD)
* Tham khảo cách cài đặt và chạy Raspbian tại bài viết [**Thiết lập Raspberry PI**](https://mechasolution.vn/Blog/bai-1-thiet-lap-raspberry-pi)
**Python**
* Ở đây chúng ta sẽ dùng Python làm ngôn ngữ chính để lập trình vì nhiều lý do như: hiện thực thuật toán nhanh, đơn giản, hệ thống thư viện hỗ trợ đa dạng.
* Phiên bản Raspbian mới nhất ([2018–04–18-raspbian-stretch](https://downloads.raspberrypi.org/raspbian_latest)) đã được cài đặt 2 phiên bản Python là Python 3.5.2 và 2.7.13. Ở đây tôi sử dụng phiên bản Python 3.5.x để demo.
## 3. Cài đặt Numpy
Numpy là thư viện toán học cho ngôn ngữ lập trình Python. Numpy hỗ trợ mảng, ma trận có kích thước và số chiều lớn cùng các toán tử đa dạng để tính toán trên mảng, ma trận. Cơ sở của Machine Learning dự trên phần lớn là toán học nên Numpy là một thư viện nền tảng không thể thiếu. Số lượng Commits và Contributors trên Github cũng cực kì ấn tượng: Commits: 15980, Contributors: 522.
Chúng ta cài đặt Numpy với dòng lệnh sau:
> `sudo apt-get install python3-numpy`
## 4. Cài đặt Scipy
Scipy là thư viện dành cho các nhà khoa học và kĩ sư. SciPy bao gồm các modules: linear algebra, optimization, integration, and statistics. Đây cũng là một thư viện nền tảng không thể thiếu cho các dự án Machine Learning. Scipy cũng có số lượng Commits và Contributors trên Github rất lớn: **Commits: 17213, Contributors: 489**
Chúng ta cài đặt Scipy và các thư viện liên quan với các dòng lệnh sau:
> `sudo apt-get install libblas-dev`
> `sudo apt-get install liblapack-dev`
> `sudo apt-get install python3-dev # Có thể đã được cài đặt sẵn`
> `sudo apt-get install libatlas-base-dev # Tuỳ chọn`
> `sudo apt-get install gfortran`
> `sudo apt-get install python3-setuptools # Có thể đã được cài đặt sẵn`
> `sudo apt-get install python3-scipy`
## 5. Cài đặt Scikit-learn
Scikit-learn (Sklearn) là các gói bổ sung của SciPy Stack được thiết kế cho các chức năng cụ thể như xử lý hình ảnh và Machine learning được dễ dàng hơn, nhanh hơn và tiện dụng hơn. Lượt Commits và Contributors trên Github lần lượt là: **Commits: 21793, Contributors: 842**.
> `sudo pip3 install scikit-learn`
> `sudo pip3 install pillow`
> `sudo apt-get install python3-h5py`
## 6. Cài đặt Matplotlib
Matplotlib là một thư viện hỗ trợ trực quan hoá dữ liệu một cách đơn giản nhưng không kém phần mạnh mẽ. Với một chút nỗ lực, bạn có thể trực quan hoá bất kỳ dữ liệu nào: Line plots; Scatter plots; Bar charts and Histograms; Pie charts; Stem plots; Contour plots; Quiver plots; Spectrograms. Số lượng Commits và Contributors trên Github là: **Commits: 21754, Contributors: 588**.
> `sudo apt-get install python3-matplotlib`
## 7. Upgrade pip
Chúng ta hãy cập nhật pip trước khi tiến hành cài đặt thư viện tiếp theo - Jupyter notebook.
> `sudo pip3 install --upgrade pip`
> `reboot`
## 8. Cài đặt Jupyter Notebook
[Jupyter Notebook](http://jupyter.org/) là một ứng dụng web mã nguồn mở cho phép bạn tạo hoặc chia sẻ những văn bản chứa:
* live code
* mô phỏng
* văn bản diễn giải
Sau đó, bạn chạy các lệnh dưới đây trên Terminal:
> `sudo pip3 install jupyter`
Khi cài đặt xong, chạy dòng lệnh dưới đây để khởi động Jupyter Notebook
> `jupyter notebook`
Kết quả, bạn sẽ thấy trình duyệt web được mở lên cùng với giao diện Jupyter Notebook như sau:

Xem bài viết [Sử dụng Jupyter Notebook cho Python](https://mechasolution.vn/Blog/bai-3-su-dung-jupyter-notebook-cho-python) để xem thêm về cách sử dụng Jupyter Notebook
## 9. Cài đặt TensorFlow
[**TensorFlow**](https://www.tensorflow.org/) là một hệ thống chuyên dùng để tính toán trên đồ thị (graph-based computation). Một ví dụ điển hình là sử dụng trong máy học (machine learning).
Ở đây, tôi sử dụng **Python Wheel Package (*.WHL)** được cung cấp bởi [lhelontra](https://github.com/lhelontra) tại [tensorflow-on-arm](https://github.com/lhelontra/tensorflow-on-arm)
### * Với Raspberry PI 2 / 3
###### ♦ Với Python version 3.5.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
###### ♦ Với Python version 2.7.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp27-none-linux_armv7l.wh`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
### * Với Raspberry PI One / Zero
###### ♦ Với Python version 3.5.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp35-none-linux_armv6l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv6l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
###### ♦ Với Python version 2.7.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp27-none-linux_armv6l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp27-none-linux_armv6l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
Sau khi cài đặt xong, bạn có thể kiểm tra xem mình có cài đặt thành công không bằng cách import TensorFlow và in ra phiên bản hiện tại (như hình):

### Tham khảo:
* https://medium.com/@abhizcc/installing-latest-tensor-flow-and-keras-on-raspberry-pi-aac7dbf95f2
* https://medium.com/activewizards-machine-learning-company/top-15-python-libraries-for-data-science-in-in-2017-ab61b4f9b4a7
* http://www.instructables.com/id/Installing-Keras-on-Raspberry-Pi-3/
---
Nếu có thắc mắc hoặc góp ý, các bạn hãy comment bên dưới để bài viết có thể được hoàn thiện hơn.
Xin cảm ơn,
Hà Phương - Mechasolution Việt Nam.
|
github_jupyter
|
# House Price Prediction With TensorFlow
[![open_in_colab][colab_badge]][colab_notebook_link]
[![open_in_binder][binder_badge]][binder_notebook_link]
[colab_badge]: https://colab.research.google.com/assets/colab-badge.svg
[colab_notebook_link]: https://colab.research.google.com/github/UnfoldedInc/examples/blob/master/notebooks/09%20-%20Tensorflow_prediction.ipynb
[binder_badge]: https://mybinder.org/badge_logo.svg
[binder_notebook_link]: https://mybinder.org/v2/gh/UnfoldedInc/examples/master?urlpath=lab/tree/notebooks/09%20-%20Tensorflow_prediction.ipynb
This example demonstrates how the Unfolded Map SDK allows for more engaging exploratory data visualization, helping to simplify the process of building a machine learning model for predicting median house prices in California.
## Dependencies
This notebook uses the following dependencies:
- pandas
- numpy
- scikit-learn
- scipy
- seaborn
- matplotlib
- tensorflow
If running this notebook in Binder, these dependencies should already be installed. If running in Colab, the next cell will install these dependencies. In another environment, you'll need to make sure these dependencies are available by running the following `pip` command in a shell.
```bash
pip install pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
This notebook was originally tested with the following package versions, but likely works with a broad range of versions:
- pandas==1.3.2
- numpy==1.19.5
- scikit-learn==0.24.2
- scipy==1.7.1
- seaborn==0.11.2
- matplotlib==3.4.3
- tensorflow==2.6.0
```
# If in Colab, install this notebook's required dependencies
import sys
if "google.colab" in sys.modules:
!pip install 'unfolded.map_sdk>=0.6.3' pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
## Imports
If you're running this notebook on Binder, you may see a notification like the following when running the next cell.
```
Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
Ignore above cudart dlerror if you do not have a GPU set up on your machine.
```
This is expected behavior because the machines on which Binder is running are not equipped with GPUs. The notebook will still function fine, it will just run slightly slower than on a machine with a GPU available.
```
from uuid import uuid4
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from unfolded.map_sdk import UnfoldedMap
```
## Data Loading
For this example we'll use data from Kaggle's [California Housing Prices](https://www.kaggle.com/camnugent/california-housing-prices) dataset under the CC0 license. This dataset contains information about the housing in each census area in California, as of the 1990 census.
```
dataset_url = "https://raw.githubusercontent.com/UnfoldedInc/examples/master/notebooks/data/housing.csv"
housing = pd.read_csv(dataset_url)
housing.head()
```
## Feature Engineering
First, let's take a look at the input data and try to visualize different aspects of them in a map.
### Population Clustering
In the next cell we'll create a map that clusters rows of the dataset according to population. Note that since the clustering happens within Unfolded Studio, the clusters are re-computed as you zoom in, allowing you to explore your data at various resolutions.
```
population_in_CA = UnfoldedMap()
population_in_CA
# Create a persistent dataset ID that we can reference in both add_dataset and add_layer
dataset_id = uuid4()
population_in_CA.add_dataset(
{"uuid": dataset_id, "label": "Population_in_CA", "data": housing},
auto_create_layers=False,
)
population_in_CA.add_layer(
{
"id": "population_CA",
"type": "cluster",
"config": {
"label": "population in CA",
"data_id": dataset_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "population", "type": "real"},
},
}
)
population_in_CA.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 5}
)
```
### Distances from housing areas to largest cities
Next, we want to explore where the housing areas in our dataset are located in comparison to the largest cities in California. For example purposes, we'll take the five largest cities in California and compare our input data against these locations.
```
# Longitude-latitude pairs for large cities
cities = {
"Los Angeles": (-118.244, 34.052),
"San Diego": (-117.165, 32.716),
"San Jose": (-121.895, 37.339),
"San Francisco": (-122.419, 37.775),
"Fresno": (-119.772, 36.748),
}
```
Next we need to find the closest city for each row in our data sample. First we'll define a couple functions to help compute the distance between cities and the city closest to a specific point. Then we'll apply these functions on our data.
```
def distance(lng1, lat1, lng2, lat2):
"""Vectorized Haversine formula
Computes distances between two sets of points.
From: https://stackoverflow.com/a/51722117
"""
# approximate radius of earth in km
R = 6371.009
lat1 = lat1*np.pi/180.0
lng1 = np.deg2rad(lng1)
lat2 = np.deg2rad(lat2)
lng2 = np.deg2rad(lng2)
d = np.sin((lat2 - lat1)/2)**2 + np.cos(lat1)*np.cos(lat2) * np.sin((lng2 - lng1)/2)**2
return 2 * R * np.arcsin(np.sqrt(d))
def closest_city(lng_array, lat_array, cities):
"""Find the closest_city for each row in lng_array and lat_array input
"""
distances = []
# Compute distance from each row of arrays to each of our city inputs
for city_name, coord in cities.items():
distances.append(distance(lng_array, lat_array, *coord))
# Convert this list of numpy arrays into a 2D numpy array
distances = np.array(distances)
# Find the shortest distance value for each row
shortest_distances = np.amin(distances, axis=0)
# Find the _index_ of the shortest distance for each row. Then use this value to
# lookup the longitude-latitude pair of the closest city
city_index = np.argmin(distances, axis=0)
# Create a 2D numpy array of location coordinates
# Then use the indexes from above to perform a lookup against the order of cities as
# input. (Note: this relies on the fact that in Python 3.6+ dictionaries are
# ordered)
input_coords = np.array(list(cities.values()))
closest_city_coords = input_coords[city_index]
# Return a 2D array with three columns:
# - Distance to closest city
# - Longitude of closest city
# - Latitude of closest city
return np.hstack((shortest_distances[:, np.newaxis], closest_city_coords))
```
Then use the `closest_city` function on our data to create three new columns:
```
housing[['closest_city_dist', 'closest_city_lng', 'closest_city_lat']] = closest_city(
housing['longitude'], housing['latitude'], cities
)
```
The map created in the next cell uses the new columns we computed above in relation to the largest cities in California:
```
distance_to_big_cities = UnfoldedMap()
distance_to_big_cities
dist_data_id = uuid4()
distance_to_big_cities.add_dataset(
{
"uuid": dist_data_id,
"label": "Distance to closest big city",
"data": housing,
},
auto_create_layers=False,
)
distance_to_big_cities.add_layer(
{
"id": "closest_distance",
"type": "arc",
"config": {
"data_id": dist_data_id,
"label": "distance to closest big city",
"columns": {
"lng0": "longitude",
"lat0": "latitude",
"lng1": "closest_city_lng",
"lat1": "closest_city_lat",
},
"visConfig": {"opacity": 0.8, "thickness": 0.3},
"is_visible": True,
},
}
)
distance_to_big_cities.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4.5}
)
```
## Data Preprocessing
In this next section, we want to prepare our dataset to be used for training a TensorFlow model. First, we'll drop rows with null values, since they're quite rare in the dataset.
```
pct_null_rows = housing.isnull().any(axis=1).sum() / len(housing) * 100
print(f'{pct_null_rows:.1f}% of rows have null values')
housing = housing.dropna()
```
In the model we're training, we want to predict the median house value of an area. Thus we split the columns from our dataset `housing` into a dataset `y` with the column `median_house_value` and a dataset `X` with all other columns.
```
predicted_column = ['median_house_value']
other_columns = housing.columns.difference(predicted_column)
X = housing.loc[:, other_columns]
y = housing.loc[:, predicted_column]
```
Most of the columns in `X` are numeric, but one is not. `ocean_proximity` is of type `object`, which here is a string.
```
X.dtypes
```
Looking closer, we see that `ocean_proximity` is a categorical string with only five values.
```
X['ocean_proximity'].value_counts()
```
In order to use this column in our numeric model, we call [`pandas.get_dummies`](https://pandas.pydata.org/docs/reference/api/pandas.get_dummies.html) to create five new boolean columns. Each of these columns contains a `1` if the value of `ocean_proximity` is equal to the value that's now the column name.
```
X = pd.get_dummies(
data=X, columns=["ocean_proximity"], prefix=["ocean_proximity"], drop_first=True
)
```
## Data Splitting
In line with standard machine learning practice, we split our dataset into training, validation and test sets. We first take out 20% of our full dataset to use for testing the model after training. Then of the remaining 80%, we take out 75% to use for training the model and 25% to use for validation.
```
# dividing training data into test, validation and train
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=0.25, random_state=1
)
# We save a copy of our test data to use after model prediction
start_values = X_test.copy(deep=True)
```
## Feature Scaling
We use standard scaling with mean and standard deviation from our training dataset to avoid data leakage.
```
# feature standardization
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)
```
## Price Prediction Model
Next we specify the parameters for the TensorFlow model:
```
# We use a Sequential model from Keras
# https://keras.io/api/models/sequential/
model = Sequential()
# Each column from X is an input feature into our model.
number_of_features = len(X.columns)
# input Layer
model.add(Dense(number_of_features, activation="relu", input_dim=number_of_features))
# hidden Layer
model.add(Dense(512, activation="relu"))
model.add(Dense(512, activation="relu"))
model.add(Dense(256, activation="relu"))
model.add(Dense(128, activation="relu"))
model.add(Dense(64, activation="relu"))
model.add(Dense(32, activation="relu"))
# output Layer
model.add(Dense(1, activation="linear"))
model.compile(loss="mse", optimizer="adam", metrics=["mse", "mae"])
model.summary()
```
### Training
Next we begin model training. Model training can take a long time; the higher the number of epochs, the better the model will be fit, but the longer training will take. Here we default to only 10 epochs because the focus of this notebook is integration with Unfolded Studio, not the machine learning itself.
```
EPOCHS = 10
# Or uncomment the following line if you're happy to wait longer for a better model fit.
# EPOCHS = 70
history = model.fit(
X_train,
y_train.to_numpy(),
batch_size=10,
epochs=EPOCHS,
verbose=1,
validation_data=(X_val, y_val),
)
```
### Evaluation
Next we want to find out how well the model was trained:
```
# summarize history for loss
loss_train = history.history["loss"]
loss_val = history.history["val_loss"]
epochs = range(1, EPOCHS + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss_train, "g", label="Training loss")
plt.plot(epochs, loss_val, "b", label="Validation loss")
plt.title("Training and Validation loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
```
In the above chart we can see that the training loss and validation loss are quite close to each other.
Now we can use our trained model to predict home prices on the _test_ data, which was not used in the training process.
```
y_pred = model.predict(X_test)
```
We can see that loss function value on the test data is similar to the loss value on the training data
```
model.evaluate(X_test, y_test)
```
### Prediction
Let's now visualize our housing price predictions using Unfolded Studio. Here we create a dataframe with predicted values obtained from the model.
```
predict_data = start_values.loc[:, ['longitude', 'latitude']]
predict_data["price"] = y_pred
```
### Visualization
The map we create in the next cell depicts the prices we've predicted for houses in each census area in California.
```
housing_predict_prices = UnfoldedMap()
housing_predict_prices
price_data_id = uuid4()
housing_predict_prices.add_dataset(
{
"uuid": price_data_id,
"label": "Predict housing prices in CA",
"data": predict_data,
},
auto_create_layers=False,
)
housing_predict_prices.add_layer(
{
"id": "housing_prices",
"type": "hexagon",
"config": {
"label": "housing prices",
"data_id": price_data_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "price", "type": "real"},
"vis_config": {
"colorRange": {
"colors": [
"#E6F598",
"#ABDDA4",
"#66C2A5",
"#3288BD",
"#5E4FA2",
"#9E0142",
"#D53E4F",
"#F46D43",
"#FDAE61",
"#FEE08B",
]
}
},
},
}
)
housing_predict_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.6, "zoom": 6}
)
```
## Clustering Model
We'll now cluster the predicted data by price levels using the KMeans algorithm.
```
k = 5
km = KMeans(n_clusters=k, init="k-means++")
X = predict_data.loc[:, ["latitude", "longitude", "price"]]
# Run clustering and add to prediction dataset dataset
predict_data["cluster"] = km.fit_predict(X)
```
### Visualization
Let's show the price clusters in a chart
```
fig, ax = plt.subplots()
sns.scatterplot(
x="latitude",
y="longitude",
data=predict_data,
palette=sns.color_palette("bright", k),
hue="cluster",
size_order=[1, 0],
ax=ax,
).set_title(f"Clustering (k={k})")
```
The next map shows the same clusters in a geographic context. Here we can see that house prices are highest for areas close to the largest cities.
```
unfolded_map_prices = UnfoldedMap()
unfolded_map_prices
prices_dataset_id = uuid4()
unfolded_map_prices.add_dataset(
{"uuid": prices_dataset_id, "label": "Prices", "data": predict_data},
auto_create_layers=False,
)
unfolded_map_prices.add_layer(
{
"id": "prices_CA",
"type": "point",
"config": {
"data_id": prices_dataset_id,
"label": "clustering of prices",
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "cluster", "type": "real"},
"vis_config": {
"colorRange": {
"colors": ["#7FFFD4", "#8A2BE2", "#00008B", "#FF8C00", "#FF1493"]
}
},
},
}
)
unfolded_map_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4}
)
```
|
github_jupyter
|
# Semantic Image Clustering
**Author:** [Khalid Salama](https://www.linkedin.com/in/khalid-salama-24403144/)<br>
**Date created:** 2021/02/28<br>
**Last modified:** 2021/02/28<br>
**Description:** Semantic Clustering by Adopting Nearest neighbors (SCAN) algorithm.
## Introduction
This example demonstrates how to apply the [Semantic Clustering by Adopting Nearest neighbors
(SCAN)](https://arxiv.org/abs/2005.12320) algorithm (Van Gansbeke et al., 2020) on the
[CIFAR-10](https://www.cs.toronto.edu/~kriz/cifar.html) dataset. The algorithm consists of
two phases:
1. Self-supervised visual representation learning of images, in which we use the
[simCLR](https://arxiv.org/abs/2002.05709) technique.
2. Clustering of the learned visual representation vectors to maximize the agreement
between the cluster assignments of neighboring vectors.
The example requires [TensorFlow Addons](https://www.tensorflow.org/addons),
which you can install using the following command:
```python
pip install tensorflow-addons
```
## Setup
```
from collections import defaultdict
import random
import numpy as np
import tensorflow as tf
import tensorflow_addons as tfa
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from tqdm import tqdm
```
## Prepare the data
```
num_classes = 10
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
x_data = np.concatenate([x_train, x_test])
y_data = np.concatenate([y_train, y_test])
print("x_data shape:", x_data.shape, "- y_data shape:", y_data.shape)
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
```
## Define hyperparameters
```
target_size = 32 # Resize the input images.
representation_dim = 512 # The dimensions of the features vector.
projection_units = 128 # The projection head of the representation learner.
num_clusters = 20 # Number of clusters.
k_neighbours = 5 # Number of neighbours to consider during cluster learning.
tune_encoder_during_clustering = False # Freeze the encoder in the cluster learning.
```
## Implement data preprocessing
The data preprocessing step resizes the input images to the desired `target_size` and applies
feature-wise normalization. Note that, when using `keras.applications.ResNet50V2` as the
visual encoder, resizing the images into 255 x 255 inputs would lead to more accurate results
but require a longer time to train.
```
data_preprocessing = keras.Sequential(
[
layers.experimental.preprocessing.Resizing(target_size, target_size),
layers.experimental.preprocessing.Normalization(),
]
)
# Compute the mean and the variance from the data for normalization.
data_preprocessing.layers[-1].adapt(x_data)
```
## Data augmentation
Unlike simCLR, which randomly picks a single data augmentation function to apply to an input
image, we apply a set of data augmentation functions randomly to the input image.
(You can experiment with other image augmentation techniques by following the [data augmentation tutorial](https://www.tensorflow.org/tutorials/images/data_augmentation).)
```
data_augmentation = keras.Sequential(
[
layers.experimental.preprocessing.RandomTranslation(
height_factor=(-0.2, 0.2), width_factor=(-0.2, 0.2), fill_mode="nearest"
),
layers.experimental.preprocessing.RandomFlip(mode="horizontal"),
layers.experimental.preprocessing.RandomRotation(
factor=0.15, fill_mode="nearest"
),
layers.experimental.preprocessing.RandomZoom(
height_factor=(-0.3, 0.1), width_factor=(-0.3, 0.1), fill_mode="nearest"
)
]
)
```
Display a random image
```
image_idx = np.random.choice(range(x_data.shape[0]))
image = x_data[image_idx]
image_class = classes[y_data[image_idx][0]]
plt.figure(figsize=(3, 3))
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(image_class)
_ = plt.axis("off")
```
Display a sample of augmented versions of the image
```
plt.figure(figsize=(10, 10))
for i in range(9):
augmented_images = data_augmentation(np.array([image]))
ax = plt.subplot(3, 3, i + 1)
plt.imshow(augmented_images[0].numpy().astype("uint8"))
plt.axis("off")
```
## Self-supervised representation learning
### Implement the vision encoder
```
def create_encoder(representation_dim):
encoder = keras.Sequential(
[
keras.applications.ResNet50V2(
include_top=False, weights=None, pooling="avg"
),
layers.Dense(representation_dim),
]
)
return encoder
```
### Implement the unsupervised contrastive loss
```
class RepresentationLearner(keras.Model):
def __init__(
self,
encoder,
projection_units,
num_augmentations,
temperature=1.0,
dropout_rate=0.1,
l2_normalize=False,
**kwargs
):
super(RepresentationLearner, self).__init__(**kwargs)
self.encoder = encoder
# Create projection head.
self.projector = keras.Sequential(
[
layers.Dropout(dropout_rate),
layers.Dense(units=projection_units, use_bias=False),
layers.BatchNormalization(),
layers.ReLU(),
]
)
self.num_augmentations = num_augmentations
self.temperature = temperature
self.l2_normalize = l2_normalize
self.loss_tracker = keras.metrics.Mean(name="loss")
@property
def metrics(self):
return [self.loss_tracker]
def compute_contrastive_loss(self, feature_vectors, batch_size):
num_augmentations = tf.shape(feature_vectors)[0] // batch_size
if self.l2_normalize:
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
# The logits shape is [num_augmentations * batch_size, num_augmentations * batch_size].
logits = (
tf.linalg.matmul(feature_vectors, feature_vectors, transpose_b=True)
/ self.temperature
)
# Apply log-max trick for numerical stability.
logits_max = tf.math.reduce_max(logits, axis=1)
logits = logits - logits_max
# The shape of targets is [num_augmentations * batch_size, num_augmentations * batch_size].
# targets is a matrix consits of num_augmentations submatrices of shape [batch_size * batch_size].
# Each [batch_size * batch_size] submatrix is an identity matrix (diagonal entries are ones).
targets = tf.tile(tf.eye(batch_size), [num_augmentations, num_augmentations])
# Compute cross entropy loss
return keras.losses.categorical_crossentropy(
y_true=targets, y_pred=logits, from_logits=True
)
def call(self, inputs):
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Create augmented versions of the images.
augmented = []
for _ in range(self.num_augmentations):
augmented.append(data_augmentation(preprocessed))
augmented = layers.Concatenate(axis=0)(augmented)
# Generate embedding representations of the images.
features = self.encoder(augmented)
# Apply projection head.
return self.projector(features)
def train_step(self, inputs):
batch_size = tf.shape(inputs)[0]
# Run the forward pass and compute the contrastive loss
with tf.GradientTape() as tape:
feature_vectors = self(inputs, training=True)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
# Compute gradients
trainable_vars = self.trainable_variables
gradients = tape.gradient(loss, trainable_vars)
# Update weights
self.optimizer.apply_gradients(zip(gradients, trainable_vars))
# Update loss tracker metric
self.loss_tracker.update_state(loss)
# Return a dict mapping metric names to current value
return {m.name: m.result() for m in self.metrics}
def test_step(self, inputs):
batch_size = tf.shape(inputs)[0]
feature_vectors = self(inputs, training=False)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
self.loss_tracker.update_state(loss)
return {"loss": self.loss_tracker.result()}
```
### Train the model
```
# Create vision encoder.
encoder = create_encoder(representation_dim)
# Create representation learner.
representation_learner = RepresentationLearner(
encoder, projection_units, num_augmentations=2, temperature=0.1
)
# Create a a Cosine decay learning rate scheduler.
lr_scheduler = keras.experimental.CosineDecay(
initial_learning_rate=0.001, decay_steps=500, alpha=0.1
)
# Compile the model.
representation_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=lr_scheduler, weight_decay=0.0001),
)
# Fit the model.
history = representation_learner.fit(
x=x_data,
batch_size=512,
epochs=50, # for better results, increase the number of epochs to 500.
)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Compute the nearest neighbors
### Generate the embeddings for the images
```
batch_size = 500
# Get the feature vector representations of the images.
feature_vectors = encoder.predict(x_data, batch_size=batch_size, verbose=1)
# Normalize the feature vectores.
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
```
### Find the *k* nearest neighbours for each embedding
```
neighbours = []
num_batches = feature_vectors.shape[0] // batch_size
for batch_idx in tqdm(range(num_batches)):
start_idx = batch_idx * batch_size
end_idx = start_idx + batch_size
current_batch = feature_vectors[start_idx:end_idx]
# Compute the dot similarity.
similarities = tf.linalg.matmul(current_batch, feature_vectors, transpose_b=True)
# Get the indices of most similar vectors.
_, indices = tf.math.top_k(similarities, k=k_neighbours + 1, sorted=True)
# Add the indices to the neighbours.
neighbours.append(indices[..., 1:])
neighbours = np.reshape(np.array(neighbours), (-1, k_neighbours))
```
Let's display some neighbors on each row
```
nrows = 4
ncols = k_neighbours + 1
plt.figure(figsize=(12, 12))
position = 1
for _ in range(nrows):
anchor_idx = np.random.choice(range(x_data.shape[0]))
neighbour_indicies = neighbours[anchor_idx]
indices = [anchor_idx] + neighbour_indicies.tolist()
for j in range(ncols):
plt.subplot(nrows, ncols, position)
plt.imshow(x_data[indices[j]].astype("uint8"))
plt.title(classes[y_data[indices[j]][0]])
plt.axis("off")
position += 1
```
You notice that images on each row are visually similar, and belong to similar classes.
## Semantic clustering with nearest neighbours
### Implement clustering consistency loss
This loss tries to make sure that neighbours have the same clustering assignments.
```
class ClustersConsistencyLoss(keras.losses.Loss):
def __init__(self):
super(ClustersConsistencyLoss, self).__init__()
def __call__(self, target, similarity, sample_weight=None):
# Set targets to be ones.
target = tf.ones_like(similarity)
# Compute cross entropy loss.
loss = keras.losses.binary_crossentropy(
y_true=target, y_pred=similarity, from_logits=True
)
return tf.math.reduce_mean(loss)
```
### Implement the clusters entropy loss
This loss tries to make sure that cluster distribution is roughly uniformed, to avoid
assigning most of the instances to one cluster.
```
class ClustersEntropyLoss(keras.losses.Loss):
def __init__(self, entropy_loss_weight=1.0):
super(ClustersEntropyLoss, self).__init__()
self.entropy_loss_weight = entropy_loss_weight
def __call__(self, target, cluster_probabilities, sample_weight=None):
# Ideal entropy = log(num_clusters).
num_clusters = tf.cast(tf.shape(cluster_probabilities)[-1], tf.dtypes.float32)
target = tf.math.log(num_clusters)
# Compute the overall clusters distribution.
cluster_probabilities = tf.math.reduce_mean(cluster_probabilities, axis=0)
# Replacing zero probabilities - if any - with a very small value.
cluster_probabilities = tf.clip_by_value(
cluster_probabilities, clip_value_min=1e-8, clip_value_max=1.0
)
# Compute the entropy over the clusters.
entropy = -tf.math.reduce_sum(
cluster_probabilities * tf.math.log(cluster_probabilities)
)
# Compute the difference between the target and the actual.
loss = target - entropy
return loss
```
### Implement clustering model
This model takes a raw image as an input, generated its feature vector using the trained
encoder, and produces a probability distribution of the clusters given the feature vector
as the cluster assignments.
```
def create_clustering_model(encoder, num_clusters, name=None):
inputs = keras.Input(shape=input_shape)
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Apply data augmentation to the images.
augmented = data_augmentation(preprocessed)
# Generate embedding representations of the images.
features = encoder(augmented)
# Assign the images to clusters.
outputs = layers.Dense(units=num_clusters, activation="softmax")(features)
# Create the model.
model = keras.Model(inputs=inputs, outputs=outputs, name=name)
return model
```
### Implement clustering learner
This model receives the input `anchor` image and its `neighbours`, produces the clusters
assignments for them using the `clustering_model`, and produces two outputs:
1. `similarity`: the similarity between the cluster assignments of the `anchor` image and
its `neighbours`. This output is fed to the `ClustersConsistencyLoss`.
2. `anchor_clustering`: cluster assignments of the `anchor` images. This is fed to the `ClustersEntropyLoss`.
```
def create_clustering_learner(clustering_model):
anchor = keras.Input(shape=input_shape, name="anchors")
neighbours = keras.Input(
shape=tuple([k_neighbours]) + input_shape, name="neighbours"
)
# Changes neighbours shape to [batch_size * k_neighbours, width, height, channels]
neighbours_reshaped = tf.reshape(neighbours, shape=tuple([-1]) + input_shape)
# anchor_clustering shape: [batch_size, num_clusters]
anchor_clustering = clustering_model(anchor)
# neighbours_clustering shape: [batch_size * k_neighbours, num_clusters]
neighbours_clustering = clustering_model(neighbours_reshaped)
# Convert neighbours_clustering shape to [batch_size, k_neighbours, num_clusters]
neighbours_clustering = tf.reshape(
neighbours_clustering,
shape=(-1, k_neighbours, tf.shape(neighbours_clustering)[-1]),
)
# similarity shape: [batch_size, 1, k_neighbours]
similarity = tf.linalg.einsum(
"bij,bkj->bik", tf.expand_dims(anchor_clustering, axis=1), neighbours_clustering
)
# similarity shape: [batch_size, k_neighbours]
similarity = layers.Lambda(lambda x: tf.squeeze(x, axis=1), name="similarity")(
similarity
)
# Create the model.
model = keras.Model(
inputs=[anchor, neighbours],
outputs=[similarity, anchor_clustering],
name="clustering_learner",
)
return model
```
### Train model
```
# If tune_encoder_during_clustering is set to False,
# then freeze the encoder weights.
for layer in encoder.layers:
layer.trainable = tune_encoder_during_clustering
# Create the clustering model and learner.
clustering_model = create_clustering_model(encoder, num_clusters, name="clustering")
clustering_learner = create_clustering_learner(clustering_model)
# Instantiate the model losses.
losses = [ClustersConsistencyLoss(), ClustersEntropyLoss(entropy_loss_weight=5)]
# Create the model inputs and labels.
inputs = {"anchors": x_data, "neighbours": tf.gather(x_data, neighbours)}
labels = tf.ones(shape=(x_data.shape[0]))
# Compile the model.
clustering_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=0.0005, weight_decay=0.0001),
loss=losses,
)
# Begin training the model.
clustering_learner.fit(x=inputs, y=labels, batch_size=512, epochs=50)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Cluster analysis
### Assign images to clusters
```
# Get the cluster probability distribution of the input images.
clustering_probs = clustering_model.predict(x_data, batch_size=batch_size, verbose=1)
# Get the cluster of the highest probability.
cluster_assignments = tf.math.argmax(clustering_probs, axis=-1).numpy()
# Store the clustering confidence.
# Images with the highest clustering confidence are considered the 'prototypes'
# of the clusters.
cluster_confidence = tf.math.reduce_max(clustering_probs, axis=-1).numpy()
```
Let's compute the cluster sizes
```
clusters = defaultdict(list)
for idx, c in enumerate(cluster_assignments):
clusters[c].append((idx, cluster_confidence[idx]))
for c in range(num_clusters):
print("cluster", c, ":", len(clusters[c]))
```
Notice that the clusters have roughly balanced sizes.
### Visualize cluster images
Display the *prototypes*—instances with the highest clustering confidence—of each cluster:
```
num_images = 8
plt.figure(figsize=(15, 15))
position = 1
for c in range(num_clusters):
cluster_instances = sorted(clusters[c], key=lambda kv: kv[1], reverse=True)
for j in range(num_images):
image_idx = cluster_instances[j][0]
plt.subplot(num_clusters, num_images, position)
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(classes[y_data[image_idx][0]])
plt.axis("off")
position += 1
```
### Compute clustering accuracy
First, we assign a label for each cluster based on the majority label of its images.
Then, we compute the accuracy of each cluster by dividing the number of image with the
majority label by the size of the cluster.
```
cluster_label_counts = dict()
for c in range(num_clusters):
cluster_label_counts[c] = [0] * num_classes
instances = clusters[c]
for i, _ in instances:
cluster_label_counts[c][y_data[i][0]] += 1
cluster_label_idx = np.argmax(cluster_label_counts[c])
correct_count = np.max(cluster_label_counts[c])
cluster_size = len(clusters[c])
accuracy = (
np.round((correct_count / cluster_size) * 100, 2) if cluster_size > 0 else 0
)
cluster_label = classes[cluster_label_idx]
print("cluster", c, "label is:", cluster_label, " - accuracy:", accuracy, "%")
```
## Conclusion
To improve the accuracy results, you can: 1) increase the number
of epochs in the representation learning and the clustering phases; 2)
allow the encoder weights to be tuned during the clustering phase; and 3) perform a final
fine-tuning step through self-labeling, as described in the [original SCAN paper](https://arxiv.org/abs/2005.12320).
Note that unsupervised image clustering techniques are not expected to outperform the accuracy
of supervised image classification techniques, rather showing that they can learn the semantics
of the images and group them into clusters that are similar to their original classes.
|
github_jupyter
|
```
import json
import numpy as np
from sklearn.model_selection import train_test_split
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import random
import librosa
import math
# path to json
data_path = "C:\\Users\\Saad\\Desktop\\Project\\MGC\\Data\\data.json"
def load_data(data_path):
with open(data_path, "r") as f:
data = json.load(f)
# convert lists to numpy arrays
X = np.array(data["mfcc"])
y = np.array(data["labels"])
print("No Problems, go ahead!")
return X, y
# load data
X, y = load_data(data_path)
X.shape
```
## ANN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
history = model.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=50)
def plot_history(history):
fig, axs = plt.subplots(2)
axs[0].plot(history.history["accuracy"], label="train accuracy")
axs[0].plot(history.history["val_accuracy"], label="test accuracy")
axs[0].set_ylabel("Accuracy")
axs[0].legend(loc="lower right")
axs[0].set_title("Accuracy eval")
axs[1].plot(history.history["loss"], label="train error")
axs[1].plot(history.history["val_loss"], label="test error")
axs[1].set_ylabel("Error")
axs[1].set_xlabel("Epoch")
axs[1].legend(loc="upper right")
axs[1].set_title("Error eval")
plt.show()
plot_history(history)
model_regularized = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(256, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(64, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_regularized.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model_regularized.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=100)
plot_history(history)
```
## CNN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.2)
X_train = X_train[..., np.newaxis]
X_validation = X_validation[..., np.newaxis]
X_test = X_test[..., np.newaxis]
X_train.shape
input_shape = (X_train.shape[1], X_train.shape[2], 1)
model_cnn = keras.Sequential()
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=input_shape))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (2, 2), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((2, 2), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Flatten())
model_cnn.add(keras.layers.Dense(64, activation='relu'))
model_cnn.add(keras.layers.Dropout(0.3))
model_cnn.add(keras.layers.Dense(10, activation='softmax'))
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_cnn.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model_cnn.summary()
history = model_cnn.fit(X_train, y_train, validation_data=(X_validation, y_validation), batch_size=32, epochs=50)
plot_history(history)
test_loss, test_acc = model_cnn.evaluate(X_test, y_test, verbose=1)
print('\nTest accuracy:', test_acc)
model_cnn.save("Genre_Classifier.h5")
for n in range(10):
i = random.randint(0,len(X_test))
# pick a sample to predict from the test set
X_to_predict = X_test[i]
y_to_predict = y_test[i]
print("\nReal Genre :", y_to_predict)
X_to_predict = X_to_predict[np.newaxis, ...]
prediction = model_cnn.predict(X_to_predict)
# get index with max value
predicted_index = np.argmax(prediction, axis=1)
print("Predicted Genre:", int(predicted_index))
```
|
github_jupyter
|
# Notebook 3 - Advanced Data Structures
So far, we have seen numbers, strings, and lists. In this notebook, we will learn three more data structures, which allow us to organize data. The data structures are `tuple`, `set`, and `dict` (dictionary).
## Tuples
A tuple is like a list, but is immutable, meaning that it cannot be modified.
```
tup = (1,'a',[1,2])
tup
print(tup[1])
print(tup[2][0])
tup[1] = 3
# We can turn a list into a tuple, and visa versa
print(list(tup))
print(tuple(list(tup)))
# We can have a tuple with a single item
single_tup = (1,)
print(single_tup)
```
## Sets
We consider the `set` data structure. The `set` is thought of similarly to how it is defined in mathematics: it is unordered, and has no duplicates. Let's contrast with the data structures we have seen thus far.
* A `list` is an ordered, mutable collection of items
* A `tuple` is an ordered, immutable collection of items
* A `str` is an ordered, immutable collection of characters
* A `set` is an unordered, mutable collection of distinct items
```
some_numbers = [0,2,1,1,2]
my_set = set(some_numbers) # create a set out of the numbers
print(my_set)
```
We observed that, by turning a list into a set, we automatically removed the duplicates. This idea will work on any collection.
```
my_string = 'aabbccda'
my_set = set(my_string)
print(my_set)
'a' in my_set
'a' in my_set and 'e' not in my_set
```
Suppose we wanted to remove `'a'` from `my_set`, but don't know the syntax for it.
Fortunately, there is built-in help features.
* Typing `my_set.<tab>` lists different member functions of `my_set`.
* The function `help(my_set)` also lists different functions, along with explanations.
```
my_set.
help(my_set)
```
## Dictionaries
These are *very* useful!
Given $n$ values, a list `l` store $n$ values, which can be accessed by `l[i]` for each $i = 0,\ldots,n-1$.
A *dictionary* is a data structure that allows us to access values by general types of keys. This is useful in designing efficient algorithms and writing simple code.
```
# Create a dictionary of produce and their prices
product_prices = {}
# Add produce and prices to the dictionary
product_prices['apple'] = 2
product_prices['banana'] = 2
product_prices['carrot'] = 3
# View the dictionary
print(product_prices)
```
Dictionaries behave in ways similar to a list.
```
# Print the price of a banana
print(product_prices['banana'])
# Check if 'banana' is a key in the dictionary.
print('banana' in product_prices)
# Check if `donut` is a key in the dictonary.
print('donut' in product_prices)
```
Dictionaries allow us to access their keys and values directly.
```
# View the keys of the dictionary
produce = product_prices.keys()
print(produce)
# The keys are a list
type(produce)
# Using list comprehensions, we can find all produce that
# have 6 characters in their name.
print([name for name in product_prices if len(name) == 6])
# Python knows that we want to iterate through the keys of product_prices.
# Equivalently, we can use the following syntax.
print([name for name in produce if len(name) == 6])
# We can find all produce that have a price of 2 dollars.
print([name for name in product_prices if product_prices[name] == 2])
# Similarly, we can access the values of the dictionary
print(product_prices.values())
```
Dictionaries don't have to be indexed by strings. It can be indexed by numbers.
```
my_dict = {1: 5, 'abc': '123'}
print(my_dict)
```
Dictionaries can be created in several ways. We have seen two so far.
* Creating an empty dictionary with `{}`, then adding (key,value) pairs, one at a time.
* Creating an dictionary at once as `{key1:val1, key2:val2, ...}`
There are more ways to create dictionaries, that are convenient in different situations. We will see one more way.
* Dictionary comprehension
* Combining lists
```
# Create a dictionary, with a key of i^2 and a value of i for each i in 0,...,1000
squared_numbers = {i**2: i for i in range(10)}
print(81 in squared_numbers)
print(squared_numbers[81])
names = ['alice','bob','cindy']
sports = [['Archery', 'Badmitton'], ['Archery', 'Curling'], ['Badmitton', 'Diving']]
# Create a dictionary mapping names to sports
print({names[i]:sports[i] for i in range(len(names))})
# Alternative approach
print(dict(zip(names,sports)))
```
## Exercise
### Part 1
Obtain the list of common English words from the 'english_words.txt' file.
### Part 2
Create a dictionary called `length_to_words` that maps an integer `i` to the list of common English words that have that have `i` letters.
Example: If the words were `['and','if','the']`, then the dictionary would be `{2: ['if'], 3: ['and','the']}`.
Question: Why is a dictionary the correct choice for this data structure?
### Part 3
Create a dictionary named `length_to_num_words` that maps each length in `length_to_words` to the number of words with that length.
Example: If the words were `['and','if','the']`, then the dictionary would be `{2: 1, 3: 2}`.
|
github_jupyter
|
### Mount Google Drive (Works only on Google Colab)
```
from google.colab import drive
drive.mount('/content/gdrive')
```
# Import Packages
```
import os
import numpy as np
import pandas as pd
from zipfile import ZipFile
from PIL import Image
from tqdm.autonotebook import tqdm
from IPython.display import display
from IPython.display import Image as Dimage
```
# Define Paths
Define paths of all the required directories
```
# Root path of the dataset
ROOT_DATA_DIR = '/content/gdrive/My Drive/modest_museum_dataset.zip'
```
# Data Visualization
Let's visualize some of the foreground and background images
```
def make_grid(images_list, height=140, margin=8, aspect_ratio=False):
"""Combine Images to form a grid.
Args:
images (list): List of PIL images to display in grid.
height (int): Height to which the image will be resized.
margin (int): Amount of padding between the images in grid.
aspect_ratio (bool, optional): Create grid while maintaining
the aspect ratio of the images. (default: False)
Returns:
Image grid.
"""
# Create grid template
widths = []
if aspect_ratio:
for image in images_list:
# Find width according to aspect ratio
h_percent = height / image.size[1]
widths.append(int(image.size[0] * h_percent))
else:
widths = [height] * len(images_list)
start = 0
background = Image.new(
'RGBA', (sum(widths) + (len(images_list) - 1) * margin, height)
)
# Add images to grid
for idx, image in enumerate(images_list):
image = image.resize((widths[idx], height))
offset = (start, 0)
start += (widths[idx] + margin)
background.paste(image, offset)
return background
```
# Data Statistics
Let's calculate mean, standard deviation and total number of images for each type of image category.
## Mean
Mean is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/mean.svg" height="50">
</center>
where, `sum of the terms` represents a pixel value and `number of terms` represents the total number of pixels across all the images.
## Standard Deviation
Standard Deviation is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/population_standard_deviation.svg" height="50">
</center>
where, `x` represents a pixel value, `u` represents the mean calculated above and `N` represents the total number of pixels across all the images.
```
def statistics(filename, channel_num, filetype):
"""Calculates data statistics
Args:
path (str): Path of the directory for which statistics is to be calculated
Returns:
Mean, standard deviation, number of images
"""
counter = 0
mean = []
std = []
images = [] # store PIL instance of the image
pixel_num = 0 # store all pixel number in the dataset
channel_sum = np.zeros(channel_num) # store channel-wise sum
channel_sum_squared = np.zeros(channel_num) # store squared channel-wise sum
with ZipFile(filename) as archive:
img_list = [
x for x in archive.infolist()
if x.filename.split('/')[1] == filetype and x.filename.split('/')[2].endswith('.jpeg')
]
for entry in tqdm(img_list):
with archive.open(entry) as file:
img = Image.open(file)
if len(images) < 5:
images.append(img)
im = np.array(img)
im = im / 255.0
pixel_num += (im.size / channel_num)
channel_sum += np.sum(im, axis=(0, 1))
channel_sum_squared += np.sum(np.square(im), axis=(0, 1))
counter += 1
bgr_mean = channel_sum / pixel_num
bgr_std = np.sqrt(channel_sum_squared / pixel_num - np.square(bgr_mean))
# change the format from bgr to rgb
mean = [round(x, 5) for x in list(bgr_mean)[::-1]]
std = [round(x, 5) for x in list(bgr_std)[::-1]]
return mean, std, counter, im.shape, images
```
# Statistics for Background images
```
# Background
print('Calculating statistics for Backgrounds...')
bg_mean, bg_std, bg_counter, bg_dim, bg_images = statistics(ROOT_DATA_DIR, 3, 'bg')
# Display
print('Background Images:')
make_grid(bg_images, margin=30)
print('Data Statistics for Background images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_mean, bg_std, bg_counter, bg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground images
```
# Background-Foreground
print('Calculating statistics for Background-Foreground Images...')
bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim, bg_fg_image = statistics(ROOT_DATA_DIR, 3, 'bg_fg')
# Display
print('Background-Foreground Images:')
make_grid(bg_fg_image, margin=30)
print('Data Statistics for Background-Foreground images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Masks
```
#Foreground-Background Masks
print('Calculating statistics for Foreground-Background Masks...')
bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim, bg_fg_mask_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_mask')
# Display
print('Background-Foreground Masks:')
make_grid(bg_fg_mask_images, margin=30, aspect_ratio=True)
print('Data Statistics for Background-Foreground Masks images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Depth Maps
```
#Foreground-Background Depth Map
print('Calculating statistics for Foreground-Background Depth Map...')
depth_mean, depth_std, depth_counter, depth_dim, depth_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_depth_map')
# Display
print('Background-Foreground Depth Maps:')
make_grid(depth_images, margin=30)
print('Data Statistics for Background-Foreground Depth Map images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [depth_mean, depth_std, depth_counter, depth_dim]
}
data = pd.DataFrame(stats)
data
```
|
github_jupyter
|
<a id='pd'></a>
<div id="qe-notebook-header" align="right" style="text-align:right;">
<a href="https://quantecon.org/" title="quantecon.org">
<img style="width:250px;display:inline;" width="250px" src="https://assets.quantecon.org/img/qe-menubar-logo.svg" alt="QuantEcon">
</a>
</div>
# Pandas
<a id='index-1'></a>
## Contents
- [Pandas](#Pandas)
- [Overview](#Overview)
- [Series](#Series)
- [DataFrames](#DataFrames)
- [On-Line Data Sources](#On-Line-Data-Sources)
- [Exercises](#Exercises)
- [Solutions](#Solutions)
In addition to what’s in Anaconda, this lecture will need the following libraries:
```
!pip install --upgrade pandas-datareader
```
## Overview
[Pandas](http://pandas.pydata.org/) is a package of fast, efficient data analysis tools for Python.
Its popularity has surged in recent years, coincident with the rise
of fields such as data science and machine learning.
Here’s a popularity comparison over time against STATA, SAS, and [dplyr](https://dplyr.tidyverse.org/) courtesy of Stack Overflow Trends
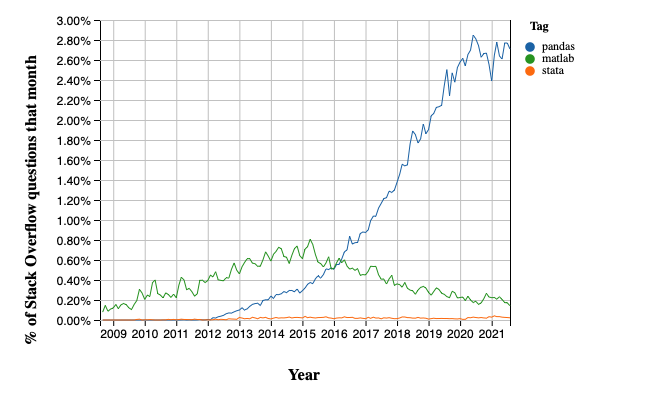
Just as [NumPy](http://www.numpy.org/) provides the basic array data type plus core array operations, pandas
1. defines fundamental structures for working with data and
1. endows them with methods that facilitate operations such as
- reading in data
- adjusting indices
- working with dates and time series
- sorting, grouping, re-ordering and general data munging <sup><a href=#mung id=mung-link>[1]</a></sup>
- dealing with missing values, etc., etc.
More sophisticated statistical functionality is left to other packages, such
as [statsmodels](http://www.statsmodels.org/) and [scikit-learn](http://scikit-learn.org/), which are built on top of pandas.
This lecture will provide a basic introduction to pandas.
Throughout the lecture, we will assume that the following imports have taken
place
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [10,8] # Set default figure size
import requests
```
## Series
<a id='index-2'></a>
Two important data types defined by pandas are `Series` and `DataFrame`.
You can think of a `Series` as a “column” of data, such as a collection of observations on a single variable.
A `DataFrame` is an object for storing related columns of data.
Let’s start with Series
```
s = pd.Series(np.random.randn(4), name='daily returns')
s
```
Here you can imagine the indices `0, 1, 2, 3` as indexing four listed
companies, and the values being daily returns on their shares.
Pandas `Series` are built on top of NumPy arrays and support many similar
operations
```
s * 100
np.abs(s)
```
But `Series` provide more than NumPy arrays.
Not only do they have some additional (statistically oriented) methods
```
s.describe()
```
But their indices are more flexible
```
s.index = ['AMZN', 'AAPL', 'MSFT', 'GOOG']
s
```
Viewed in this way, `Series` are like fast, efficient Python dictionaries
(with the restriction that the items in the dictionary all have the same
type—in this case, floats).
In fact, you can use much of the same syntax as Python dictionaries
```
s['AMZN']
s['AMZN'] = 0
s
'AAPL' in s
```
## DataFrames
<a id='index-3'></a>
While a `Series` is a single column of data, a `DataFrame` is several columns, one for each variable.
In essence, a `DataFrame` in pandas is analogous to a (highly optimized) Excel spreadsheet.
Thus, it is a powerful tool for representing and analyzing data that are naturally organized into rows and columns, often with descriptive indexes for individual rows and individual columns.
Here’s the content of `test_pwt.csv`
```text
"country","country isocode","year","POP","XRAT","tcgdp","cc","cg"
"Argentina","ARG","2000","37335.653","0.9995","295072.21869","75.716805379","5.5788042896"
"Australia","AUS","2000","19053.186","1.72483","541804.6521","67.759025993","6.7200975332"
"India","IND","2000","1006300.297","44.9416","1728144.3748","64.575551328","14.072205773"
"Israel","ISR","2000","6114.57","4.07733","129253.89423","64.436450847","10.266688415"
"Malawi","MWI","2000","11801.505","59.543808333","5026.2217836","74.707624181","11.658954494"
"South Africa","ZAF","2000","45064.098","6.93983","227242.36949","72.718710427","5.7265463933"
"United States","USA","2000","282171.957","1","9898700","72.347054303","6.0324539789"
"Uruguay","URY","2000","3219.793","12.099591667","25255.961693","78.978740282","5.108067988"
```
Supposing you have this data saved as `test_pwt.csv` in the present working directory (type `%pwd` in Jupyter to see what this is), it can be read in as follows:
```
df = pd.read_csv('https://raw.githubusercontent.com/QuantEcon/lecture-python-programming/master/source/_static/lecture_specific/pandas/data/test_pwt.csv')
type(df)
df
```
We can select particular rows using standard Python array slicing notation
```
df[2:5]
```
To select columns, we can pass a list containing the names of the desired columns represented as strings
```
df[['country', 'tcgdp']]
```
To select both rows and columns using integers, the `iloc` attribute should be used with the format `.iloc[rows, columns]`
```
df.iloc[2:5, 0:4]
```
To select rows and columns using a mixture of integers and labels, the `loc` attribute can be used in a similar way
```
df.loc[df.index[2:5], ['country', 'tcgdp']]
```
Let’s imagine that we’re only interested in population (`POP`) and total GDP (`tcgdp`).
One way to strip the data frame `df` down to only these variables is to overwrite the dataframe using the selection method described above
```
df = df[['country', 'POP', 'tcgdp']]
df
```
Here the index `0, 1,..., 7` is redundant because we can use the country names as an index.
To do this, we set the index to be the `country` variable in the dataframe
```
df = df.set_index('country')
df
```
Let’s give the columns slightly better names
```
df.columns = 'population', 'total GDP'
df
```
Population is in thousands, let’s revert to single units
```
df['population'] = df['population'] * 1e3
df
```
Next, we’re going to add a column showing real GDP per capita, multiplying by 1,000,000 as we go because total GDP is in millions
```
df['GDP percap'] = df['total GDP'] * 1e6 / df['population']
df
```
One of the nice things about pandas `DataFrame` and `Series` objects is that they have methods for plotting and visualization that work through Matplotlib.
For example, we can easily generate a bar plot of GDP per capita
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
At the moment the data frame is ordered alphabetically on the countries—let’s change it to GDP per capita
```
df = df.sort_values(by='GDP percap', ascending=False)
df
```
Plotting as before now yields
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
## On-Line Data Sources
<a id='index-4'></a>
Python makes it straightforward to query online databases programmatically.
An important database for economists is [FRED](https://research.stlouisfed.org/fred2/) — a vast collection of time series data maintained by the St. Louis Fed.
For example, suppose that we are interested in the [unemployment rate](https://research.stlouisfed.org/fred2/series/UNRATE).
Via FRED, the entire series for the US civilian unemployment rate can be downloaded directly by entering
this URL into your browser (note that this requires an internet connection)
```text
https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv
```
(Equivalently, click here: [https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv](https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv))
This request returns a CSV file, which will be handled by your default application for this class of files.
Alternatively, we can access the CSV file from within a Python program.
This can be done with a variety of methods.
We start with a relatively low-level method and then return to pandas.
### Accessing Data with requests
<a id='index-6'></a>
One option is to use [requests](https://requests.readthedocs.io/en/master/), a standard Python library for requesting data over the Internet.
To begin, try the following code on your computer
```
r = requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')
```
If there’s no error message, then the call has succeeded.
If you do get an error, then there are two likely causes
1. You are not connected to the Internet — hopefully, this isn’t the case.
1. Your machine is accessing the Internet through a proxy server, and Python isn’t aware of this.
In the second case, you can either
- switch to another machine
- solve your proxy problem by reading [the documentation](https://requests.readthedocs.io/en/master/)
Assuming that all is working, you can now proceed to use the `source` object returned by the call `requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')`
```
url = 'http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv'
source = requests.get(url).content.decode().split("\n")
source[0]
source[1]
source[2]
```
We could now write some additional code to parse this text and store it as an array.
But this is unnecessary — pandas’ `read_csv` function can handle the task for us.
We use `parse_dates=True` so that pandas recognizes our dates column, allowing for simple date filtering
```
data = pd.read_csv(url, index_col=0, parse_dates=True)
```
The data has been read into a pandas DataFrame called `data` that we can now manipulate in the usual way
```
type(data)
data.head() # A useful method to get a quick look at a data frame
pd.set_option('precision', 1)
data.describe() # Your output might differ slightly
```
We can also plot the unemployment rate from 2006 to 2012 as follows
```
ax = data['2006':'2012'].plot(title='US Unemployment Rate', legend=False)
ax.set_xlabel('year', fontsize=12)
ax.set_ylabel('%', fontsize=12)
plt.show()
```
Note that pandas offers many other file type alternatives.
Pandas has [a wide variety](https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html) of top-level methods that we can use to read, excel, json, parquet or plug straight into a database server.
### Using pandas_datareader to Access Data
<a id='index-8'></a>
The maker of pandas has also authored a library called pandas_datareader that gives programmatic access to many data sources straight from the Jupyter notebook.
While some sources require an access key, many of the most important (e.g., FRED, [OECD](https://data.oecd.org/), [EUROSTAT](https://ec.europa.eu/eurostat/data/database) and the World Bank) are free to use.
For now let’s work through one example of downloading and plotting data — this
time from the World Bank.
The World Bank [collects and organizes data](http://data.worldbank.org/indicator) on a huge range of indicators.
For example, [here’s](http://data.worldbank.org/indicator/GC.DOD.TOTL.GD.ZS/countries) some data on government debt as a ratio to GDP.
The next code example fetches the data for you and plots time series for the US and Australia
```
from pandas_datareader import wb
govt_debt = wb.download(indicator='GC.DOD.TOTL.GD.ZS', country=['US', 'AU'], start=2005, end=2016).stack().unstack(0)
ind = govt_debt.index.droplevel(-1)
govt_debt.index = ind
ax = govt_debt.plot(lw=2)
ax.set_xlabel('year', fontsize=12)
plt.title("Government Debt to GDP (%)")
plt.show()
```
The [documentation](https://pandas-datareader.readthedocs.io/en/latest/index.html) provides more details on how to access various data sources.
## Exercises
<a id='pd-ex1'></a>
### Exercise 1
With these imports:
```
import datetime as dt
from pandas_datareader import data
```
Write a program to calculate the percentage price change over 2019 for the following shares:
```
ticker_list = {'INTC': 'Intel',
'MSFT': 'Microsoft',
'IBM': 'IBM',
'BHP': 'BHP',
'TM': 'Toyota',
'AAPL': 'Apple',
'AMZN': 'Amazon',
'BA': 'Boeing',
'QCOM': 'Qualcomm',
'KO': 'Coca-Cola',
'GOOG': 'Google',
'SNE': 'Sony',
'PTR': 'PetroChina'}
```
Here’s the first part of the program
```
def read_data(ticker_list,
start=dt.datetime(2019, 1, 2),
end=dt.datetime(2019, 12, 31)):
"""
This function reads in closing price data from Yahoo
for each tick in the ticker_list.
"""
ticker = pd.DataFrame()
for tick in ticker_list:
prices = data.DataReader(tick, 'yahoo', start, end)
closing_prices = prices['Close']
ticker[tick] = closing_prices
return ticker
ticker = read_data(ticker_list)
```
Complete the program to plot the result as a bar graph like this one:
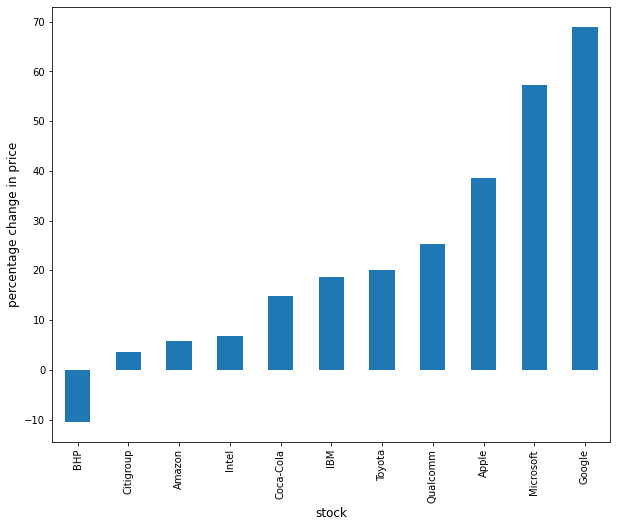
<a id='pd-ex2'></a>
### Exercise 2
Using the method `read_data` introduced in [Exercise 1](#pd-ex1), write a program to obtain year-on-year percentage change for the following indices:
```
indices_list = {'^GSPC': 'S&P 500',
'^IXIC': 'NASDAQ',
'^DJI': 'Dow Jones',
'^N225': 'Nikkei'}
```
Complete the program to show summary statistics and plot the result as a time series graph like this one:
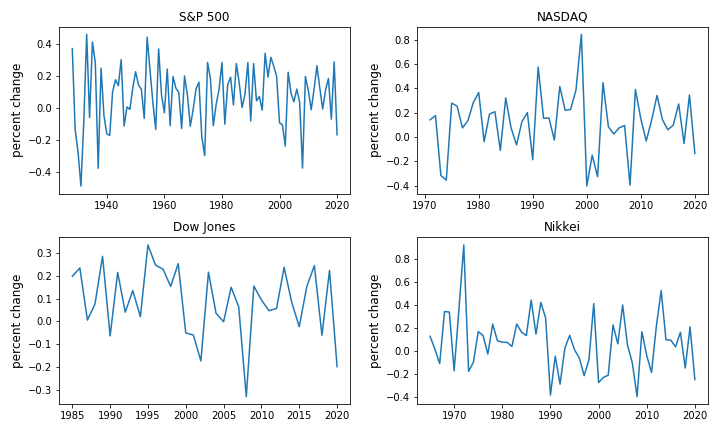
## Solutions
### Exercise 1
There are a few ways to approach this problem using Pandas to calculate
the percentage change.
First, you can extract the data and perform the calculation such as:
```
p1 = ticker.iloc[0] #Get the first set of prices as a Series
p2 = ticker.iloc[-1] #Get the last set of prices as a Series
price_change = (p2 - p1) / p1 * 100
price_change
```
Alternatively you can use an inbuilt method `pct_change` and configure it to
perform the correct calculation using `periods` argument.
```
change = ticker.pct_change(periods=len(ticker)-1, axis='rows')*100
price_change = change.iloc[-1]
price_change
```
Then to plot the chart
```
price_change.sort_values(inplace=True)
price_change = price_change.rename(index=ticker_list)
fig, ax = plt.subplots(figsize=(10,8))
ax.set_xlabel('stock', fontsize=12)
ax.set_ylabel('percentage change in price', fontsize=12)
price_change.plot(kind='bar', ax=ax)
plt.show()
```
### Exercise 2
Following the work you did in [Exercise 1](#pd-ex1), you can query the data using `read_data` by updating the start and end dates accordingly.
```
indices_data = read_data(
indices_list,
start=dt.datetime(1928, 1, 2),
end=dt.datetime(2020, 12, 31)
)
```
Then, extract the first and last set of prices per year as DataFrames and calculate the yearly returns such as:
```
yearly_returns = pd.DataFrame()
for index, name in indices_list.items():
p1 = indices_data.groupby(indices_data.index.year)[index].first() # Get the first set of returns as a DataFrame
p2 = indices_data.groupby(indices_data.index.year)[index].last() # Get the last set of returns as a DataFrame
returns = (p2 - p1) / p1
yearly_returns[name] = returns
yearly_returns
```
Next, you can obtain summary statistics by using the method `describe`.
```
yearly_returns.describe()
```
Then, to plot the chart
```
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
for iter_, ax in enumerate(axes.flatten()): # Flatten 2-D array to 1-D array
index_name = yearly_returns.columns[iter_] # Get index name per iteration
ax.plot(yearly_returns[index_name]) # Plot pct change of yearly returns per index
ax.set_ylabel("percent change", fontsize = 12)
ax.set_title(index_name)
plt.tight_layout()
```
<p><a id=mung href=#mung-link><strong>[1]</strong></a> Wikipedia defines munging as cleaning data from one raw form into a structured, purged one.
|
github_jupyter
|
# In this note book the following steps are taken:
1. Remove highly correlated attributes
2. Find the best hyper parameters for estimator
3. Find the most important features by tunned random forest
4. Find f1 score of the tunned full model
5. Find best hyper parameter of model with selected features
6. Find f1 score of the tuned seleccted model
7. Compare the two f1 scores
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.feature_selection import RFECV,RFE
from sklearn.model_selection import train_test_split, GridSearchCV, KFold,RandomizedSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn import metrics
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score,f1_score
import numpy as np
from sklearn.metrics import make_scorer
f1_score = make_scorer(f1_score)
#import data
Data=pd.read_csv("Halifax-Transfomed-Data-BS-NoBreak - Copy.csv")
X = Data.iloc[:,:-1]
y = Data.iloc[:,-1]
#split test and training set.
np.random.seed(60)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 1000)
#Define estimator and model
classifiers = {}
classifiers.update({"Random Forest": RandomForestClassifier(random_state=1000)})
#Define range of hyperparameters for estimator
np.random.seed(60)
parameters = {}
parameters.update({"Random Forest": { "classifier__n_estimators": [100,105,110,115,120,125,130,135,140,145,150,155,160,170,180,190,200],
# "classifier__n_estimators": [2,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200],
#"classifier__class_weight": [None, "balanced"],
"classifier__max_features": ["auto", "sqrt", "log2"],
"classifier__max_depth" : [4,6,8,10,11,12,13,14,15,16,17,18,19,20,22],
#"classifier__max_depth" : [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20],
"classifier__criterion" :["gini", "entropy"]
}})
# Make correlation matrix
corr_matrix = X_train.corr(method = "spearman").abs()
# Draw the heatmap
sns.set(font_scale = 1.0)
f, ax = plt.subplots(figsize=(11, 9))
sns.heatmap(corr_matrix, cmap= "YlGnBu", square=True, ax = ax)
f.tight_layout()
plt.savefig("correlation_matrix.png", dpi = 1080)
# Select upper triangle of matrix
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k = 1).astype(np.bool))
# Find index of feature columns with correlation greater than 0.8
to_drop = [column for column in upper.columns if any(upper[column] > 0.8)]
# Drop features
X_train = X_train.drop(to_drop, axis = 1)
X_test = X_test.drop(to_drop, axis = 1)
X_train
FEATURE_IMPORTANCE = {"Random Forest"}
selected_classifier = "Random Forest"
classifier = classifiers[selected_classifier]
scaler = StandardScaler()
steps = [("scaler", scaler), ("classifier", classifier)]
pipeline = Pipeline(steps = steps)
#Define parameters that we want to use in gridsearch cv
param_grid = parameters[selected_classifier]
# Initialize GridSearch object for estimator
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
# Fit gscv (Tunes estimator)
print(f"Now tuning {selected_classifier}. Go grab a beer or something.")
gscv.fit(X_train, np.ravel(y_train))
#Getting the best hyperparameters
best_params = gscv.best_params_
best_params
#Getting the best score of model
best_score = gscv.best_score_
best_score
#Check overfitting of the estimator
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
scores_test = cross_val_score(mod, X_test, y_test, scoring='f1', cv=5)
scores_test
tuned_params = {item[12:]: best_params[item] for item in best_params}
classifier.set_params(**tuned_params)
#Find f1 score of the model with all features (Model is tuned for all features)
results={}
model=classifier.set_params(criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
# Select Features using RFECV
class PipelineRFE(Pipeline):
# Source: https://ramhiser.com/post/2018-03-25-feature-selection-with-scikit-learn-pipeline/
def fit(self, X, y=None, **fit_params):
super(PipelineRFE, self).fit(X, y, **fit_params)
self.feature_importances_ = self.steps[-1][-1].feature_importances_
return self
steps = [("scaler", scaler), ("classifier", classifier)]
pipe = PipelineRFE(steps = steps)
np.random.seed(60)
# Initialize RFECV object
feature_selector = RFECV(pipe, cv = 5, step = 1, verbose = 1)
# Fit RFECV
feature_selector.fit(X_train, np.ravel(y_train))
# Get selected features
feature_names = X_train.columns
selected_features = feature_names[feature_selector.support_].tolist()
performance_curve = {"Number of Features": list(range(1, len(feature_names) + 1)),
"F1": feature_selector.grid_scores_}
performance_curve = pd.DataFrame(performance_curve)
# Performance vs Number of Features
# Set graph style
sns.set(font_scale = 1.75)
sns.set_style({"axes.facecolor": "1.0", "axes.edgecolor": "0.85", "grid.color": "0.85",
"grid.linestyle": "-", 'axes.labelcolor': '0.4', "xtick.color": "0.4",
'ytick.color': '0.4'})
colors = sns.color_palette("RdYlGn", 20)
line_color = colors[3]
marker_colors = colors[-1]
# Plot
f, ax = plt.subplots(figsize=(13, 6.5))
sns.lineplot(x = "Number of Features", y = "F1", data = performance_curve,
color = line_color, lw = 4, ax = ax)
sns.regplot(x = performance_curve["Number of Features"], y = performance_curve["F1"],
color = marker_colors, fit_reg = False, scatter_kws = {"s": 200}, ax = ax)
# Axes limits
plt.xlim(0.5, len(feature_names)+0.5)
plt.ylim(0.60, 1)
# Generate a bolded horizontal line at y = 0
ax.axhline(y = 0.625, color = 'black', linewidth = 1.3, alpha = .7)
# Turn frame off
ax.set_frame_on(False)
# Tight layout
plt.tight_layout()
#Define new training and test set based based on selected features by RFECV
X_train_rfecv = X_train[selected_features]
X_test_rfecv= X_test[selected_features]
np.random.seed(60)
classifier.fit(X_train_rfecv, np.ravel(y_train))
#Finding important features
np.random.seed(60)
feature_importance = pd.DataFrame(selected_features, columns = ["Feature Label"])
feature_importance["Feature Importance"] = classifier.feature_importances_
feature_importance = feature_importance.sort_values(by="Feature Importance", ascending=False)
feature_importance
# Initialize GridSearch object for model with selected features
np.random.seed(60)
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
#Tuning random forest classifier with selected features
np.random.seed(60)
gscv.fit(X_train_rfecv,y_train)
#Getting the best parameters of model with selected features
best_params = gscv.best_params_
best_params
#Getting the score of model with selected features
best_score = gscv.best_score_
best_score
#Check overfitting of the tuned model with selected features
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
scores_test
results={}
model=classifier.set_params(criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
model.fit(X_train_rfecv,y_train)
y_pred = model.predict(X_test_rfecv)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
```
|
github_jupyter
|
# Anailís ghramadaí trí [deplacy](https://koichiyasuoka.github.io/deplacy/)
## le [Stanza](https://stanfordnlp.github.io/stanza)
```
!pip install deplacy stanza
import stanza
stanza.download("ga")
nlp=stanza.Pipeline("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [UDPipe 2](http://ufal.mff.cuni.cz/udpipe/2)
```
!pip install deplacy
def nlp(t):
import urllib.request,urllib.parse,json
with urllib.request.urlopen("https://lindat.mff.cuni.cz/services/udpipe/api/process?model=ga&tokenizer&tagger&parser&data="+urllib.parse.quote(t)) as r:
return json.loads(r.read())["result"]
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [COMBO-pytorch](https://gitlab.clarin-pl.eu/syntactic-tools/combo)
```
!pip install --index-url https://pypi.clarin-pl.eu/simple deplacy combo
import combo.predict
nlp=combo.predict.COMBO.from_pretrained("irish-ud27")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Trankit](https://github.com/nlp-uoregon/trankit)
```
!pip install deplacy trankit transformers
import trankit
nlp=trankit.Pipeline("irish")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spacy-udpipe](https://github.com/TakeLab/spacy-udpipe)
```
!pip install deplacy spacy-udpipe
import spacy_udpipe
spacy_udpipe.download("ga")
nlp=spacy_udpipe.load("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-COMBO](https://github.com/KoichiYasuoka/spaCy-COMBO)
```
!pip install deplacy spacy_combo
import spacy_combo
nlp=spacy_combo.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-jPTDP](https://github.com/KoichiYasuoka/spaCy-jPTDP)
```
!pip install deplacy spacy_jptdp
import spacy_jptdp
nlp=spacy_jptdp.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Camphr-Udify](https://camphr.readthedocs.io/en/latest/notes/udify.html)
```
!pip install deplacy camphr en-udify@https://github.com/PKSHATechnology-Research/camphr_models/releases/download/0.7.0/en_udify-0.7.tar.gz
import pkg_resources,imp
imp.reload(pkg_resources)
import spacy
nlp=spacy.load("en_udify")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_python.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# MMClassification Python API tutorial on Colab
In this tutorial, we will introduce the following content:
* How to install MMCls
* Inference a model with Python API
* Fine-tune a model with Python API
## Install MMClassification
Before using MMClassification, we need to prepare the environment with the following steps:
1. Install Python, CUDA, C/C++ compiler and git
2. Install PyTorch (CUDA version)
3. Install mmcv
4. Clone mmcls source code from GitHub and install it
Because this tutorial is on Google Colab, and the basic environment has been completed, we can skip the first two steps.
### Check environment
```
%cd /content
!pwd
# Check nvcc version
!nvcc -V
# Check GCC version
!gcc --version
# Check PyTorch installation
import torch, torchvision
print(torch.__version__)
print(torch.cuda.is_available())
```
### Install MMCV
MMCV is the basic package of all OpenMMLab packages. We have pre-built wheels on Linux, so we can download and install them directly.
Please pay attention to PyTorch and CUDA versions to match the wheel.
In the above steps, we have checked the version of PyTorch and CUDA, and they are 1.9.0 and 11.1 respectively, so we need to choose the corresponding wheel.
In addition, we can also install the full version of mmcv (mmcv-full). It includes full features and various CUDA ops out of the box, but needs a longer time to build.
```
# Install mmcv
!pip install mmcv -f https://download.openmmlab.com/mmcv/dist/cu111/torch1.9.0/index.html
# !pip install mmcv-full -f https://download.openmmlab.com/mmcv/dist/cu110/torch1.9.0/index.html
```
### Clone and install MMClassification
Next, we clone the latest mmcls repository from GitHub and install it.
```
# Clone mmcls repository
!git clone https://github.com/open-mmlab/mmclassification.git
%cd mmclassification/
# Install MMClassification from source
!pip install -e .
# Check MMClassification installation
import mmcls
print(mmcls.__version__)
```
## Inference a model with Python API
MMClassification provides many pre-trained models, and you can check them by the link of [model zoo](https://mmclassification.readthedocs.io/en/latest/model_zoo.html). Almost all models can reproduce the results in original papers or reach higher metrics. And we can use these models directly.
To use the pre-trained model, we need to do the following steps:
- Prepare the model
- Prepare the config file
- Prepare the checkpoint file
- Build the model
- Inference with the model
```
# Get the demo image
!wget https://www.dropbox.com/s/k5fsqi6qha09l1v/banana.png?dl=0 -O demo/banana.png
from PIL import Image
Image.open('demo/banana.png')
```
### Prepare the config file and checkpoint file
We configure a model with a config file and save weights with a checkpoint file.
On GitHub, you can find all these pre-trained models in the config folder of MMClassification. For example, you can find the config files and checkpoints of Mobilenet V2 in [this link](https://github.com/open-mmlab/mmclassification/tree/master/configs/mobilenet_v2).
We have integrated many config files for various models in the MMClassification repository. As for the checkpoint, we can download it in advance, or just pass an URL to API, and MMClassification will download it before load weights.
```
# Confirm the config file exists
!ls configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py
# Specify the path of the config file and checkpoint file.
config_file = 'configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py'
checkpoint_file = 'https://download.openmmlab.com/mmclassification/v0/mobilenet_v2/mobilenet_v2_batch256_imagenet_20200708-3b2dc3af.pth'
```
### Inference the model
MMClassification provides high-level Python API to inference models.
At first, we build the MobilenetV2 model and load the checkpoint.
```
import mmcv
from mmcls.apis import inference_model, init_model, show_result_pyplot
# Specify the device, if you cannot use GPU, you can also use CPU
# by specifying `device='cpu'`.
device = 'cuda:0'
# device = 'cpu'
# Build the model according to the config file and load the checkpoint.
model = init_model(config_file, checkpoint_file, device=device)
# The model's inheritance relationship
model.__class__.__mro__
# The inference result in a single image
img = 'demo/banana.png'
img_array = mmcv.imread(img)
result = inference_model(model, img_array)
result
%matplotlib inline
# Visualize the inference result
show_result_pyplot(model, img, result)
```
## Fine-tune a model with Python API
Fine-tuning is to re-train a model which has been trained on another dataset (like ImageNet) to fit our target dataset. Compared with training from scratch, fine-tuning is much faster can avoid over-fitting problems during training on a small dataset.
The basic steps of fine-tuning are as below:
1. Prepare the target dataset and meet MMClassification's requirements.
2. Modify the training config.
3. Start training and validation.
More details are in [the docs](https://mmclassification.readthedocs.io/en/latest/tutorials/finetune.html).
### Prepare the target dataset
Here we download the cats & dogs dataset directly. You can find more introduction about the dataset in the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb).
```
# Download the cats & dogs dataset
!wget https://www.dropbox.com/s/wml49yrtdo53mie/cats_dogs_dataset_reorg.zip?dl=0 -O cats_dogs_dataset.zip
!mkdir -p data
!unzip -qo cats_dogs_dataset.zip -d ./data/
```
### Read the config file and modify the config
In the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb), we have introduced all parts of the config file, and here we can modify the loaded config by Python code.
```
# Load the base config file
from mmcv import Config
cfg = Config.fromfile('configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py')
# Modify the number of classes in the head.
cfg.model.head.num_classes = 2
cfg.model.head.topk = (1, )
# Load the pre-trained model's checkpoint.
cfg.model.backbone.init_cfg = dict(type='Pretrained', checkpoint=checkpoint_file, prefix='backbone')
# Specify sample size and number of workers.
cfg.data.samples_per_gpu = 32
cfg.data.workers_per_gpu = 2
# Specify the path and meta files of training dataset
cfg.data.train.data_prefix = 'data/cats_dogs_dataset/training_set/training_set'
cfg.data.train.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of validation dataset
cfg.data.val.data_prefix = 'data/cats_dogs_dataset/val_set/val_set'
cfg.data.val.ann_file = 'data/cats_dogs_dataset/val.txt'
cfg.data.val.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of test dataset
cfg.data.test.data_prefix = 'data/cats_dogs_dataset/test_set/test_set'
cfg.data.test.ann_file = 'data/cats_dogs_dataset/test.txt'
cfg.data.test.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the normalization parameters in data pipeline
normalize_cfg = dict(type='Normalize', mean=[124.508, 116.050, 106.438], std=[58.577, 57.310, 57.437], to_rgb=True)
cfg.data.train.pipeline[3] = normalize_cfg
cfg.data.val.pipeline[3] = normalize_cfg
cfg.data.test.pipeline[3] = normalize_cfg
# Modify the evaluation metric
cfg.evaluation['metric_options']={'topk': (1, )}
# Specify the optimizer
cfg.optimizer = dict(type='SGD', lr=0.005, momentum=0.9, weight_decay=0.0001)
cfg.optimizer_config = dict(grad_clip=None)
# Specify the learning rate scheduler
cfg.lr_config = dict(policy='step', step=1, gamma=0.1)
cfg.runner = dict(type='EpochBasedRunner', max_epochs=2)
# Specify the work directory
cfg.work_dir = './work_dirs/cats_dogs_dataset'
# Output logs for every 10 iterations
cfg.log_config.interval = 10
# Set the random seed and enable the deterministic option of cuDNN
# to keep the results' reproducible.
from mmcls.apis import set_random_seed
cfg.seed = 0
set_random_seed(0, deterministic=True)
cfg.gpu_ids = range(1)
```
### Fine-tune the model
Use the API `train_model` to fine-tune our model on the cats & dogs dataset.
```
import time
import mmcv
import os.path as osp
from mmcls.datasets import build_dataset
from mmcls.models import build_classifier
from mmcls.apis import train_model
# Create the work directory
mmcv.mkdir_or_exist(osp.abspath(cfg.work_dir))
# Build the classifier
model = build_classifier(cfg.model)
model.init_weights()
# Build the dataset
datasets = [build_dataset(cfg.data.train)]
# Add `CLASSES` attributes to help visualization
model.CLASSES = datasets[0].CLASSES
# Start fine-tuning
train_model(
model,
datasets,
cfg,
distributed=False,
validate=True,
timestamp=time.strftime('%Y%m%d_%H%M%S', time.localtime()),
meta=dict())
%matplotlib inline
# Validate the fine-tuned model
img = mmcv.imread('data/cats_dogs_dataset/training_set/training_set/cats/cat.1.jpg')
model.cfg = cfg
result = inference_model(model, img)
show_result_pyplot(model, img, result)
```
|
github_jupyter
|
```
```
# **Deep Convolutional Generative Adversarial Network (DC-GAN):**
DC-GAN is a foundational adversarial framework developed in 2015.
It had a major contribution in streamlining the process of designing adversarial frameworks and visualizing intermediate representations, thus, making GANs more accessible to both researchers and practitioners. This was achieved by enhancing the concept of adversarial training (introduced by [Ian Goodfellow](https://arxiv.org/abs/1406.2661) one year prior) with then-state-of-the-art advances in deep learning such as strided and fractional-strided convolutions, batch normalization and LeakyReLU activations.
In this programming exercise, you are tasking with creating a miniature [Deep Convolutional Generative Adversarial Network](https://arxiv.org/pdf/1511.06434.pdf) (DC-GAN) framework for the generation of MNIST digits. The goal is to bridge the gap between the theoretical concept and the practical implementation of GANs.

The desired DC-GAN network should consist of two principal components: the generator $G$ and the discriminator $D$. The generator should receive as input a 100-dimensional random noise vector $z$ and outputs a synthetically generated MNIST digit $G(z)$ of pixel size $28 \times 28 \times 1$. As the adversarial training continues over time, the output digits should increasingly resemble handwritten digits as shown below.

The discriminator network receives both the synthetically generated digits as well as ground-truth MNIST digits $x$ as inputs. $D$ is trained as a binary classifier. In other words, it is trained to assign the correct label (real vs fake) to both sets of input images. On the other hand side, $G$ is motivated to fool the discriminator into making a false decision by implicitly improving the quality of the output synthetic image. This adversarial training procedure, where both networks are trained with opposing goals, is represented by the following min-max optimization task:
>$\underset{G}{\min} \underset{D}{\max} \mathcal{L}_{\textrm{adv}} =\underset{G}{\min} \underset{D}{\max} \; \mathbb{E}_{x} \left[\textrm{log} D(x) \right] + \mathbb{E}_{z} \left[\textrm{log} \left( 1 - D\left(G(z)\right) \right) \right]$
# Implementation
### Import Import TensorFlow and other libraries
```
from __future__ import absolute_import, division, print_function, unicode_literals
!pip install tensorflow-gpu==2.0.0-alpha0
import tensorflow as tf
tf.__version__
# To generate GIFs for illustration
!pip install imageio
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import os
import PIL
from tensorflow.keras import layers
import time
from IPython import display
```
### Load and prepare the dataset
You will use the MNIST dataset to train the generator and the discriminator. The generator will generate handwritten digits resembling the MNIST data.
You can also repeat the exercise for other avaliable variations of the MNIST dataset such as: EMNIST, Fashio-MNIST or KMNIST. For more details, please refer to [tensorflow_datasets](https://www.tensorflow.org/datasets/datasets).
```
(train_images, train_labels), (_, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
train_images = (train_images - 127.5) / 127.5 # Normalize the images to [-1, 1]
BUFFER_SIZE = 60000
BATCH_SIZE = 256
# Batch and shuffle the data
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
```
## Create the models
Both the generator and discriminator are defined using the [Keras Sequential API](https://www.tensorflow.org/guide/keras#sequential_model).
### The Generator
The generator uses `tf.keras.layers.Conv2DTranspose` (fractional-strided convolutional) layers to produce an image from an input noise vector. Start with a fully connected layer that takes this vector as input, then upsample several times until you reach the desired image size of $28\times 28 \times 1$. Utilize the `tf.keras.layers.LeakyReLU` activation and batch normalization for each intermediate layer, except the output layer which should use tanh.
```
def make_generator_model():
model = tf.keras.Sequential()
model.add(layers.Dense(7*7*256, use_bias=False, input_shape=(100,)))
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
model.add(layers.Reshape((7, 7, 256)))
assert model.output_shape == (None, 7, 7, 256) # Note: None is the batch size
# Layer 2: Hint use layers.Conv2DTranspose with 5x5 kernels and appropriate stride
model.add(layers.Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', use_bias=False))
assert model.output_shape == (None, 7, 7, 128)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
# Layer 3
model.add(layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False))
assert model.output_shape == (None, 14, 14, 64)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
#Layer4
model.add(layers.Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', use_bias=False, activation='tanh'))
assert model.output_shape == (None, 28, 28, 1)
return model
```
Use the (as yet untrained) generator to create an image.
```
generator = make_generator_model()
noise = tf.random.normal([1, 100])
generated_image = generator(noise, training=False)
plt.imshow(generated_image[0, :, :, 0], cmap='gray')
```
### The Discriminator
The discriminator is a CNN-based image classifier.
```
def make_discriminator_model():
model = tf.keras.Sequential()
model.add(layers.Conv2D(64, (5, 5), strides=(2, 2), padding='same',
input_shape=[28, 28, 1]))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Conv2D(128, (5, 5), strides=(2, 2), padding='same'))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Flatten())
model.add(layers.Dense(1))
return model
```
Use the (as yet untrained) discriminator to classify the generated images as real or fake. The model will be trained to output positive values for real images, and negative values for fake images.
```
discriminator = make_discriminator_model()
decision = discriminator(generated_image)
print (decision)
```
## Define the loss and optimizers
Define loss functions and optimizers for both models.
```
# This method returns a helper function to compute the binary cross entropy loss
cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)
```
### Discriminator loss
Define the discriminator loss function. [Hint](https://www.tensorflow.org/api_docs/python/tf/keras/losses/BinaryCrossentropy): compare the discriminator's predictions on real images to an array of 1s.
```
def discriminator_loss(real_output, fake_output):
real_loss = cross_entropy(tf.ones_like(real_output), real_output)
fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
total_loss = real_loss + fake_loss
return total_loss
```
### Generator loss
The generator's loss quantifies how well it was able to trick the discriminator. Intuitively, if the generator is performing well, the discriminator will classify the fake images as real (or 1). Again, use the same principle used to define the real_loss to define the generator_loss.
```
def generator_loss(fake_output):
generator_loss = cross_entropy(tf.ones_like(fake_output), fake_output)
return generator_loss
```
The discriminator and the generator optimizers are different since both networks are trained separately. Hint: use Adam optimizers. Experiment with the learning rates.
```
generator_optimizer = tf.keras.optimizers.Adam(1e-4)
discriminator_optimizer = tf.keras.optimizers.Adam(1e-4)
```
### Save checkpoints
This notebook also demonstrates how to save and restore models, which can be helpful in case a long running training task is interrupted (especially for larger datasets).
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
```
## Define the training loop
```
EPOCHS = 100
noise_dim = 100
num_examples_to_generate = 16 # For visualization
# We will reuse this noise_vector overtime (so it's easier)
# to visualize progress in the animated GIF)
noise_vector = tf.random.normal([num_examples_to_generate, noise_dim])
```
The training loop should begin with generator receiving a random vector as input. That vector will be used to produce an image. The discriminator should then be used to classify real images (drawn from the training set) and fakes images (produced by the generator). The loss will be calculated for each of these models, and the gradients used to update the generator and discriminator
```
# Notice the use of `tf.function`
# This annotation causes the function to be "compiled".
@tf.function
def train_step(images):
noise = tf.random.normal([BATCH_SIZE, noise_dim])
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
# Generator output
generated_images = generator(noise, training=True)
# Discriminator output
real_output = discriminator(images, training=True)
fake_output = discriminator(generated_images, training=True)
# Loss functions
gen_loss = generator_loss(fake_output)
disc_loss = discriminator_loss(real_output, fake_output)
# Gradients
gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
# Update both networks
generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for image_batch in dataset:
train_step(image_batch)
# Produce images for the GIF as we go
display.clear_output(wait=True)
generate_and_save_images(generator,
epoch + 1,
noise_vector)
# Save the model every 15 epochs
if (epoch + 1) % 15 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))
# Generate after the final epoch
display.clear_output(wait=True)
generate_and_save_images(generator,
epochs,
noise_vector)
```
**Generate and save images**
```
def generate_and_save_images(model, epoch, test_input):
# Notice `training` is set to False.
# This is so all layers run in inference mode (batchnorm).
predictions = model(test_input, training=False)
fig = plt.figure(figsize=(4,4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')
plt.axis('off')
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
```
## Train the model
Call the `train()` method defined above to train the generator and discriminator simultaneously. Note, training GANs can be tricky. It's important that the generator and discriminator do not overpower each other (e.g., that they train at a similar rate).
At the beginning of the training, the generated images look like random noise. As training progresses, the generated digits will look increasingly real. After about 50 epochs, they resemble MNIST digits. This may take about one minute / epoch with the default settings on Colab.
```
%%time
train(train_dataset, EPOCHS)
```
Restore the latest checkpoint.
```
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Create a GIF
```
# Display a single image using the epoch number
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
display_image(EPOCHS)
```
Use imageio to create an animated gif using the images saved during training.
```
anim_file = 'dcgan.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
last = -1
for i,filename in enumerate(filenames):
frame = 8*(i**0.25)
if round(frame) > round(last):
last = frame
else:
continue
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import IPython
if IPython.version_info > (6,2,0,''):
display.Image(filename=anim_file)
```
If you're working in Colab you can download the animation with the code below:
```
try:
from google.colab import files
except ImportError:
pass
else:
files.download(anim_file)
```
## Next Steps
How does the generated digits compare with the original MNIST? Optimize the network design and training hyperparameters further for better results.
Repeat the above steps for other similar datasets such as Fashion-MNIST or expand the capacities of the network appropriately to suit larger datasets such as the Large-scale Celeb Faces Attributes (CelebA) dataset.
|
github_jupyter
|
```
%matplotlib inline
import matplotlib.pyplot as plt
from functools import reduce
import seaborn as sns; sns.set(rc={'figure.figsize':(15,15)})
import numpy as np
import pandas as pd
from sqlalchemy import create_engine
from sklearn.preprocessing import MinMaxScaler
engine = create_engine('postgresql://postgres:[email protected]:5555/mimic')
common_index = ['hadm_id', 'icustay_id', 'ts']
def get_mortality_label():
label = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', outtime) as ts, hospital_expire_flag, thirtyday_expire_flag
from sepsis3
where excluded=0
""", engine)
label.set_index(common_index, inplace=True)
return label
def get_demo():
demo = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts
, age, is_male, race_white, race_black, race_hispanic, race_other
from sepsis3
where excluded=0
""", engine)
demo.set_index(common_index, inplace=True)
return demo
def get_admit():
admit = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts, icu_los, hosp_los
from sepsis3
where excluded=0
""", engine)
admit.set_index(common_index, inplace=True)
return admit
def get_comorbidity():
com = pd.read_sql('''
select s.icustay_id, date_trunc('day', admittime) as ts, c.*
from comorbidity c
inner join (select icustay_id, hadm_id from sepsis3 where excluded=0) s
on c.hadm_id=s.hadm_id
''', engine)
del com['subject_id']
del com['admittime']
com.set_index(common_index, inplace=True)
return com
def get_gcs():
gcs = pd.read_sql('''
select v.*
from gcsdaily v
inner join (select hadm_id from sepsis3 where excluded=0) s
on v.hadm_id=s.hadm_id
where charttime_by_day is not null
''', engine)
del gcs['subject_id']
gcs.rename(columns = {'charttime_by_day': 'ts'}, inplace=True)
gcs.set_index(common_index, inplace=True)
return gcs
def get_vitalsign():
vital = pd.read_sql('''
select v.*
from vitalsdaily v
inner join (select hadm_id from sepsis3 where excluded=0) s
on v.hadm_id=s.hadm_id
''', engine)
del vital['subject_id']
vital.rename(columns = {'charttime_by_day': 'ts'}, inplace=True)
vital.set_index(common_index, inplace=True)
return vital
def get_drug():
# (48761, 1770) --> (48761, 8)
list_of_abx = ['adoxa','ala-tet','alodox','amikacin','amikin','amoxicillin',
'amoxicillin%claulanate','clavulanate','ampicillin','augmentin',
'avelox','avidoxy','azactam','azithromycin','aztreonam','axetil',
'bactocill','bactrim','bethkis','biaxin','bicillin l-a','cayston',
'cefazolin','cedax','cefoxitin','ceftazidime','cefaclor','cefadroxil',
'cefdinir','cefditoren','cefepime','cefotetan','cefotaxime','cefpodoxime',
'cefprozil','ceftibuten','ceftin','cefuroxime ','cefuroxime','cephalexin',
'chloramphenicol','cipro','ciprofloxacin','claforan','clarithromycin',
'cleocin','clindamycin','cubicin','dicloxacillin','doryx','doxycycline',
'duricef','dynacin','ery-tab','eryped','eryc','erythrocin','erythromycin',
'factive','flagyl','fortaz','furadantin','garamycin','gentamicin',
'kanamycin','keflex','ketek','levaquin','levofloxacin','lincocin',
'macrobid','macrodantin','maxipime','mefoxin','metronidazole',
'minocin','minocycline','monodox','monurol','morgidox','moxatag',
'moxifloxacin','myrac','nafcillin sodium','nicazel doxy 30','nitrofurantoin',
'noroxin','ocudox','ofloxacin','omnicef','oracea','oraxyl','oxacillin',
'pc pen vk','pce dispertab','panixine','pediazole','penicillin',
'periostat','pfizerpen','piperacillin','tazobactam','primsol','proquin',
'raniclor','rifadin','rifampin','rocephin','smz-tmp','septra','septra ds',
'septra','solodyn','spectracef','streptomycin sulfate','sulfadiazine',
'sulfamethoxazole','trimethoprim','sulfatrim','sulfisoxazole','suprax',
'synercid','tazicef','tetracycline','timentin','tobi','tobramycin','trimethoprim',
'unasyn','vancocin','vancomycin','vantin','vibativ','vibra-tabs','vibramycin',
'zinacef','zithromax','zmax','zosyn','zyvox']
drug = pd.read_sql("""
select p.icustay_id, p.hadm_id
, startdate as ts
, 'prescription' as category
, drug
, sum((EXTRACT(EPOCH FROM enddate - startdate))/ 60 / 60 / 24) as duration
from prescriptions p
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on p.hadm_id=s.hadm_id and p.icustay_id=s.icustay_id
group by p.icustay_id, p.hadm_id, ts, drug
""", engine)
drug.duration = drug.duration.replace(0, 1) # avoid null of instant prescription
drug = drug[drug.drug.str.contains('|'.join(list_of_abx), case=False)]
pivot_drug = pd.pivot_table(drug,
index=common_index,
columns=['drug'],
values='duration',
fill_value=0)
return pivot_drug
def get_lab():
lab = pd.read_sql("""
select s.icustay_id, c.hadm_id, date_trunc('day', c.charttime) as ts
, d.label
, valuenum
from labevents c
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on c.hadm_id=s.hadm_id
join d_labitems d using (itemid)
where itemid in (
50912 -- 크레아티닌(creatinine)
,50905, 50906 -- LDL-콜레스테롤(LDL-cholesterol)
,50852 -- 당화혈색소(HbA1c/Hemoglobin A1c)
,50809, 50931 -- 공복혈당(fasting plasma glucose)
,50889 -- C-반응성 단백질(C-reactive protein)
,50811, 51222 -- 헤모글로빈(hemoglobin)
,50907 -- 총콜레스테롤(total cholesterol)
,50945 -- 호모시스테인(Homocysteine)
,51006 -- 혈액 요소 질소(blood urea nitrogen)
,51000 -- 중성지방(triglyceride)
,51105 -- 요산(uric acid)
,50904 -- HDL-콜레스테롤(HDL-cholesterol)
,51265 -- 혈소판(platelet)
,51288 -- 적혈구침강속도(Erythrocyte sedimentation rate)
,51214 -- 피브리노겐(fibrinogen)
,51301 -- 백혈구(white blood cell)
,50963 -- B형 나트륨 이뇨펩타이드(B-type Natriuretic Peptide)
,51002, 51003 -- 트로포닌(Troponin)
,50908 -- 크레아티닌키나제-MB(Creatine Kinase - Muscle Brain)
,50862 -- 알부민(albumin)
,50821 -- 동맥 산소분압(arterial pO2)
,50818 -- 이산화탄소분압(pCO2)
,50820 -- 동맥혈의 산도(arterial PH)
,50910 -- 크레아틴키나제(CK)
,51237 -- 혈액응고검사(PT (INR)/aPTT)
,50885 -- 빌리루빈(bilirubin)
,51144 -- 대상핵세포(band cells)
,50863 -- 알칼리 인산염(alkaline phosphatase)
)
""", engine)
pivot_lab = pd.pivot_table(lab,
index=common_index,
columns=['label'],
values='valuenum',
# aggfunc=['min', 'max', np.mean]
fill_value=0)
return pivot_lab
def get_vaso():
vaso = pd.read_sql("""
select c.icustay_id, s.hadm_id, date_trunc('day', c.starttime) as ts
, duration_hours as vaso_duration_hours
from vasopressordurations c
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on c.icustay_id=s.icustay_id
""", engine)
vaso.set_index(common_index, inplace=True)
return vaso
def get_sepsis():
s = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts
, sofa, qsofa
from sepsis3
where excluded=0
""", engine)
s.set_index(common_index, inplace=True)
return s
def fig_corr_heatmap(labels, df, feature_df):
cols = [labels[0]] + feature_df.columns.tolist()
df_grp = df[cols].groupby(level=0).agg('mean')
corr = df_grp.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cols[0] = labels[1]
df_grp = df[cols].groupby(level=0).agg('mean')
corr_30d = df_grp.corr()
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(15, 5))
sns.heatmap(corr, ax=ax1, mask=mask, vmin=0, vmax=1)
sns.heatmap(corr_30d, ax=ax2, mask=mask, vmin=0, vmax=1)
ax1.set_title('In-hospital Death')
ax2.set_title('30-day Death')
```
- 패혈증 진단받은 환자수, 입원수
```
pd.read_sql(
"""
select count(distinct hadm_id), count(distinct icustay_id) from sepsis3 where excluded=0
""", engine)
```
- ICU, 입원 기간의 최소, 최대
```
pd.read_sql(
"""
select min(icu_los), max(icu_los), min(hosp_los), max(hosp_los) from sepsis3 where excluded=0
""", engine)
```
## 라벨
- 사망: 원내 사망, 30일 이내 사망
```
label = get_mortality_label()
label.head()
```
## 변수 : 인구통계, 입원, 진단
```
demo = get_demo()
demo.head()
admit = get_admit()
admit.head()
com = get_comorbidity()
com.head()
```
## 변수 : 바이탈사인, 투약, 검사, 승압제
```
gcs = get_gcs()
gcs.head()
vital = get_vitalsign()
vital.head()
drug = get_drug()
drug.head()
lab = get_lab()
lab.head()
vaso = get_vaso()
vaso.head()
sepsis = get_sepsis()
sepsis.head()
data_frames = [
label,
demo,
admit,
com,
gcs,
vital,
drug,
lab,
vaso,
sepsis
]
df_merged = reduce(lambda left,right: pd.merge(left, right, how='outer', left_index=True, right_index=True),
data_frames)
df_merged.head()
```
- hdf 포맷으로 저장
```
filename_sepsis = "mimiciii_sepsis_mortality.h5"
df_merged.to_hdf(filename_sepsis, key='all')
```
# 탐색
```
df = pd.read_hdf(filename_sepsis, key='all')
df.head()
```
# Correlation
## mortality and features
```
labels = ['hospital_expire_flag', 'thirtyday_expire_flag']
for f in data_frames[1:]:
fig_corr_heatmap(labels, df, f)
```
# Feature, Label
```
y = df[labels].groupby(level=0).agg('max').fillna(0).values
X = df.drop(columns=labels).groupby(level=0).agg(['mean','max', 'min']).fillna(0)
X.shape, y.shape
y.sum(axis=0) / y.shape[0]
```
# In-hospital Death - Train and Validation
```
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, confusion_matrix, f1_score, accuracy_score
import numpy as np
random_state = 2
X_train, X_test, y_train, y_test = train_test_split(X, y[:, 0], test_size=0.3, random_state=random_state)
clf = LogisticRegression(penalty='l1',
solver='liblinear',
# tol=1e-6,
# max_iter=int(1e6),
# warm_start=True,
random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
params = {'n_estimators': 1000, 'max_leaf_nodes': None, 'max_depth': None, 'random_state': random_state,
'min_samples_split': 4,
'learning_rate': 0.1}
clf = GradientBoostingClassifier(**params)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = RandomForestClassifier(n_estimators=1000, random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
```
# 30day Death - Train and Validation
```
X_train, X_test, y_train, y_test = train_test_split(X, y[:, 1], test_size=0.3, random_state=random_state)
clf = LogisticRegression(penalty='l1',
solver='liblinear',
# tol=1e-6,
# max_iter=int(1e6),
# warm_start=True,
random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = GradientBoostingClassifier(**params)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = RandomForestClassifier(n_estimators=1000, random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
```
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# Any results you write to the current directory are saved as output.
```
This is the post about **Introduction to Data Scinece**, I am going to write about* handling tabular/dataframe* data in python3.
### Importing Data
```
import pandas as pd
df = pd.read_csv('/kaggle/input/california-housing-prices/housing.csv')
display(df.head())
```
During data analysis, we need to use our data to perform some calculations and generate some new data or output from it. Pandas makes it very easy to apply user-defined operations, in Python terminology, on individual data items, rows, and columns of a dataframe.
Pandas has an **apply** function which applies the provided function to the data. One of the reasons for the success of pandas is how fast the apply function performs.
In the Dataset, the field **median_income** has values which are written in tens of thousands of dollars. During analysis, we might want to convert this to Dollars. Let’s see how we can do that with the apply function.
```
def convert(n):
return n * 10000
converted = df['median_income'].apply(convert)
display(converted.head())
# update value
df['median_income'] = converted
display(df.head())
```
### Converting numerical values to categories
----
During analysis, sometimes we want to classify our data into separate classes based on some criteria. For instance, we might want to separate these housing blocks into three distinct categories based on the median income of the households i.e.
* High-incomes
* Moderate-incomes
* Low-incomes
```
def category(n):
value = n / 10000
if value > 10:
return 'high-income'
elif value > 2 and value < 10:
return 'moderate-income'
else:
return 'low-income'
categories = df['median_income'].apply(category)
df['income-category'] = categories
display(df.head())
print(df['income-category'].value_counts())
```
|
github_jupyter
|
```
from pykat import finesse
from pykat.commands import *
import numpy as np
import matplotlib.pyplot as plt
import scipy
from IPython import display
pykat.init_pykat_plotting(dpi=200)
base1 = """
l L0 10 0 n0 #input laser
tem L0 0 0 1 0 #tem modes
tem L0 1 0 1 0
tem L0 2 0 1 0
tem L0 3 0 1 0
tem L0 4 0 1 0
tem L0 5 0 1 0
tem L0 6 0 1 0
tem L0 7 0 1 0
s s1 1 n0 n5
m itmx0 0 1 0 n5 n6 #ITM surface 1
s itmx_l 0.035 1.44963 n6 n7 #thickness of mirror
m2 itmx 0.99 50u 0 n7 n8 #ITM surface 2
s s2 9.1 n8 n9 #cavity length
m2 etmx 0.998 50u 0 n9 n10 #ETM surface 2
s etmx_l 0.035 1.44963 n10 n11 #thickness of mirror
m etmx0 0 1 0 n11 n12 #ETM surface 1
attr etmx Rcx 34 #roc of mirror
attr etmx Rcy 34
xaxis etmx Rcx lin 20 40 6000
func g = 1-(9.1/$x1)
put etmx Rcy $x1
ad order0 0 0 0 n12 #ad detectors
ad order1 1 0 0 n12
ad order2 2 0 0 n12
ad order3 3 0 0 n12
ad order4 4 0 0 n12
ad order5 5 0 0 n12
ad order6 6 0 0 n12
ad order7 7 0 0 n12
cav FP itmx n8 etmx n9
cp FP x finesse
maxtem 7
phase 2
#noplot Rc2
"""
basekat = finesse.kat()
basekat.verbose = 1
basekat.parse(base1)
out = basekat.run()
out.info()
#out.plot(['FP_x_w'])
y=[]
x= out['g']
colors = ['b','g','r','c','m','y','k','teal','violet','pink','olive']
#plt.figure(figsize=(8,4))
#append all output detectors in an array
for i in range(0,7,1):
y.append(out['order'+str(i+1)]/out['order0'])
#plot all outputs
for k in range(0,7,1):
plt.semilogy(x,y[k],antialiased=False,label='order'+str(k),c=colors[k])
#label and other stuff
plt.grid(linewidth=1)
plt.legend(["order1","order2","order3","order4","order5","order6","order7","order8","order9","order10"],loc='center left', bbox_to_anchor=(1, 0.5))
plt.xlabel("g (1-L/R) \n Finesse = "+str(out['FP_x_finesse'][1]))
plt.ylabel("HG modes intensity(rel to fund. mode)",verticalalignment='center')
plt.axvline(x = 0.708, color = 'r', linestyle = 'dashed')
plt.axvline(x = 0.73, color = 'b', linestyle = 'dashed')
display.Image("C:/Users/Parivesh/Desktop/9.1m.jpg",width = 500, height = 300)
base2 = """
l L0 10 0 n0 #input laser
s s1 1 n0 n1 #laser cav
bs bs1 0.5 0.5 0 0 n1 n2 n3 n4 #beam splitter
s sx 1 n2 n5 #BS to ITMx cav
m itmx0 0 1 0 n5 n6 #ITM surface 1
s itmx_l 0.035 1.44963 n6 n7 #thickness of mirror
m2 itmx 0.99 50u 0 n7 n8 #ITM surface 2
s s2 9.1 n8 n9 #arm length
m2 etmx 0.998 50u 0 n9 n10 #ETM surface 2
s etmx_l 0.035 1.44963 n10 n11 #thickness of mirror
m etmx0 0 1 0 n11 dump #ETM surface 1
s sy 1 n3 n13 #BS to ITMy cav
m itmy0 0 1 0 n13 n14
s itmy_l 0.035 1.44963 n14 n15
m2 itmy 0.99 50u 0 n15 n16
s s3 9.1 n16 n17
m2 etmy 0.998 50u 0 n17 n18
s etmy_l 0.035 1.44963 n18 n19
m etmy0 0 1 0 n19 n20
attr etmy Rc 34 #roc of mirror
attr etmx Rc 34
xaxis etmy phi lin -220 220 7000
#maxtem 7
#phase 2
pd pd_out n4
#ad order0 0 0 0 n20 #ad detectors
#ad order1 1 0 0 n20
#ad order2 2 0 0 n20
"""
basekat1 = finesse.kat()
basekat1.verbose = 1
basekat1.parse(base2)
out = basekat1.run()
out.info()
out.plot(['pd_out'])
#out.plot(['order0','order1','order2'])
print("Contrast Ratio : ",(np.max(out['pd_out'])-np.min(out['pd_out']))/(np.max(out['pd_out'])+np.min(out['pd_out'])))
```
|
github_jupyter
|
# Web crawling exercise
```
from selenium import webdriver
```
## Quiz 1
- 아래 URL의 NBA 데이터를 크롤링하여 판다스 데이터 프레임으로 나타내세요.
- http://stats.nba.com/teams/traditional/?sort=GP&dir=-1
### 1.1 webdriver를 실행하고 사이트에 접속하기
```
driver = webdriver.Chrome()
url = "http://stats.nba.com/teams/traditional/?sort=GP&dir=-1"
driver.get(url)
```
링크로 들어가면 GP로 정렬되어 있는 상태임

### 1.2 표 데이터 받아오기
#### (1) column 이름을 받아와서 pandas dataframe 만들기
```
columns = driver.find_elements_by_css_selector("div.nba-stat-table__overflow > table > thead > tr > th")[:28]
len(columns)
ls_column = []
for column in columns:
ls_column.append(column.text)
ls_column
df = pd.DataFrame(columns = ls_column)
df
```
#### (2) 각 row의 팀별 데이터를 받아와서 dataframe에 넣기
```
team_stat = driver.find_elements_by_css_selector("div.nba-stat-table__overflow > table > tbody > tr")
len(team_stat)
for stat in team_stat:
stats = stat.find_elements_by_css_selector("td")
stat = {}
for i in range(len(stats)):
stat[ls_column[i]] = stats[i].text
df.loc[len(df)] = stat
df
driver.quit()
```
## Quiz 2
- Selenium을 이용하여 네이버 IT/과학 기사의 10 페이지 까지의 최신 제목 리스트를 크롤링하세요.
- http://news.naver.com/main/main.nhn?mode=LSD&mid=shm&sid1=105
### 2.1 webdriver를 실행하고 사이트에 접속하기
```
driver = webdriver.Chrome()
def make_url(page=1):
return "http://news.naver.com/main/main.nhn?mode=LSD&mid=shm&sid1=105#&date=%2000:00:00&page="\
+ str(page)
url = make_url()
driver.get(url)
```
### 2.2 기사 제목 리스트 가져오기
#### (1) 1페이지에 대해 기사 제목 가져오기
##### 1페이지의 기사 리스트 가져오기
- 한 페이지에 20개의 기사가 있음
```
articles = driver.find_elements_by_css_selector("#section_body > ul > li")
len(articles)
```
##### 1페이지 안의 기사 제목 가져오기
```
dict_list = []
for article in articles:
dict_list.append({
"title": article.find_element_by_css_selector("dt:nth-child(2)").text
})
df = pd.DataFrame(dict_list)
df.tail()
```
#### (2) 1-10페이지에서 기사 제목 가져오기
- 2페이지와 7페이지에서 에러가 발생해서 try & except 처리함
```
dict_list = []
for i in range(1, 11):
driver.get(make_url(i))
articles = driver.find_elements_by_css_selector("#section_body > ul > li")
print(len(articles))
try:
for article in articles:
dict_list.append({"title": article.find_element_by_css_selector("dl > dt:nth-child(2)").text})
except:
print(str(i)+"페이지 에러 발생")
df = pd.DataFrame(dict_list)
df.tail()
```
총 168개의 기사 제목이 크롤링됨
```
driver.quit()
```
#### 참고자료
- 패스트캠퍼스, ⟪데이터사이언스스쿨 8기⟫ 수업자료
|
github_jupyter
|
# Custom Building Recurrent Neural Network
**Notation**:
- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer.
- Superscript $(i)$ denotes an object associated with the $i^{th}$ example.
- Superscript $\langle t \rangle$ denotes an object at the $t^{th}$ time-step.
- **Sub**script $i$ denotes the $i^{th}$ entry of a vector.
Example:
- $a^{(2)[3]<4>}_5$ denotes the activation of the 2nd training example (2), 3rd layer [3], 4th time step <4>, and 5th entry in the vector.
Let's first import all the packages.
```
import numpy as np
from rnn_utils import *
```
## Forward propagation for the basic Recurrent Neural Network
## RNN cell
```
# GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute next activation state using the formula given above
a_next = a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.dot(Wya, a_next) + by)
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = \n", a_next_tmp.shape)
print("yt_pred[1] =\n", yt_pred_tmp[1])
print("yt_pred.shape = \n", yt_pred_tmp.shape)
```
## 1.2 - RNN forward pass
```
# GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# initialize "a" and "y_pred" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps of the input 'x' (1 line)
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,4)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][1] = \n", a_tmp[4][1])
print("a.shape = \n", a_tmp.shape)
print("y_pred[1][3] =\n", y_pred_tmp[1][3])
print("y_pred.shape = \n", y_pred_tmp.shape)
print("caches[1][1][3] =\n", caches_tmp[1][1][3])
print("len(caches) = \n", len(caches_tmp))
```
## Long Short-Term Memory (LSTM) network
### Overview of gates and states
#### - Forget gate $\mathbf{\Gamma}_{f}$
* Let's assume we are reading words in a piece of text, and plan to use an LSTM to keep track of grammatical structures, such as whether the subject is singular ("puppy") or plural ("puppies").
* If the subject changes its state (from a singular word to a plural word), the memory of the previous state becomes outdated, so we "forget" that outdated state.
* The "forget gate" is a tensor containing values that are between 0 and 1.
* If a unit in the forget gate has a value close to 0, the LSTM will "forget" the stored state in the corresponding unit of the previous cell state.
* If a unit in the forget gate has a value close to 1, the LSTM will mostly remember the corresponding value in the stored state.
##### Equation
$$\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f)\tag{1} $$
##### Explanation of the equation:
* $\mathbf{W_{f}}$ contains weights that govern the forget gate's behavior.
* The previous time step's hidden state $[a^{\langle t-1 \rangle}$ and current time step's input $x^{\langle t \rangle}]$ are concatenated together and multiplied by $\mathbf{W_{f}}$.
* A sigmoid function is used to make each of the gate tensor's values $\mathbf{\Gamma}_f^{\langle t \rangle}$ range from 0 to 1.
* The forget gate $\mathbf{\Gamma}_f^{\langle t \rangle}$ has the same dimensions as the previous cell state $c^{\langle t-1 \rangle}$.
* This means that the two can be multiplied together, element-wise.
* Multiplying the tensors $\mathbf{\Gamma}_f^{\langle t \rangle} * \mathbf{c}^{\langle t-1 \rangle}$ is like applying a mask over the previous cell state.
* If a single value in $\mathbf{\Gamma}_f^{\langle t \rangle}$ is 0 or close to 0, then the product is close to 0.
* This keeps the information stored in the corresponding unit in $\mathbf{c}^{\langle t-1 \rangle}$ from being remembered for the next time step.
* Similarly, if one value is close to 1, the product is close to the original value in the previous cell state.
* The LSTM will keep the information from the corresponding unit of $\mathbf{c}^{\langle t-1 \rangle}$, to be used in the next time step.
##### Variable names in the code
The variable names in the code are similar to the equations, with slight differences.
* `Wf`: forget gate weight $\mathbf{W}_{f}$
* `Wb`: forget gate bias $\mathbf{W}_{b}$
* `ft`: forget gate $\Gamma_f^{\langle t \rangle}$
#### Candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$
* The candidate value is a tensor containing information from the current time step that **may** be stored in the current cell state $\mathbf{c}^{\langle t \rangle}$.
* Which parts of the candidate value get passed on depends on the update gate.
* The candidate value is a tensor containing values that range from -1 to 1.
* The tilde "~" is used to differentiate the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ from the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Equation
$$\mathbf{\tilde{c}}^{\langle t \rangle} = \tanh\left( \mathbf{W}_{c} [\mathbf{a}^{\langle t - 1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{c} \right) \tag{3}$$
##### Explanation of the equation
* The 'tanh' function produces values between -1 and +1.
##### Variable names in the code
* `cct`: candidate value $\mathbf{\tilde{c}}^{\langle t \rangle}$
#### - Update gate $\mathbf{\Gamma}_{i}$
* We use the update gate to decide what aspects of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to add to the cell state $c^{\langle t \rangle}$.
* The update gate decides what parts of a "candidate" tensor $\tilde{\mathbf{c}}^{\langle t \rangle}$ are passed onto the cell state $\mathbf{c}^{\langle t \rangle}$.
* The update gate is a tensor containing values between 0 and 1.
* When a unit in the update gate is close to 1, it allows the value of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to be passed onto the hidden state $\mathbf{c}^{\langle t \rangle}$
* When a unit in the update gate is close to 0, it prevents the corresponding value in the candidate from being passed onto the hidden state.
* Notice that we use the subscript "i" and not "u", to follow the convention used in the literature.
##### Equation
$$\mathbf{\Gamma}_i^{\langle t \rangle} = \sigma(\mathbf{W}_i[a^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_i)\tag{2} $$
##### Explanation of the equation
* Similar to the forget gate, here $\mathbf{\Gamma}_i^{\langle t \rangle}$, the sigmoid produces values between 0 and 1.
* The update gate is multiplied element-wise with the candidate, and this product ($\mathbf{\Gamma}_{i}^{\langle t \rangle} * \tilde{c}^{\langle t \rangle}$) is used in determining the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Variable names in code (Please note that they're different than the equations)
In the code, we'll use the variable names found in the academic literature. These variables don't use "u" to denote "update".
* `Wi` is the update gate weight $\mathbf{W}_i$ (not "Wu")
* `bi` is the update gate bias $\mathbf{b}_i$ (not "bu")
* `it` is the forget gate $\mathbf{\Gamma}_i^{\langle t \rangle}$ (not "ut")
#### - Cell state $\mathbf{c}^{\langle t \rangle}$
* The cell state is the "memory" that gets passed onto future time steps.
* The new cell state $\mathbf{c}^{\langle t \rangle}$ is a combination of the previous cell state and the candidate value.
##### Equation
$$ \mathbf{c}^{\langle t \rangle} = \mathbf{\Gamma}_f^{\langle t \rangle}* \mathbf{c}^{\langle t-1 \rangle} + \mathbf{\Gamma}_{i}^{\langle t \rangle} *\mathbf{\tilde{c}}^{\langle t \rangle} \tag{4} $$
##### Explanation of equation
* The previous cell state $\mathbf{c}^{\langle t-1 \rangle}$ is adjusted (weighted) by the forget gate $\mathbf{\Gamma}_{f}^{\langle t \rangle}$
* and the candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$, adjusted (weighted) by the update gate $\mathbf{\Gamma}_{i}^{\langle t \rangle}$
##### Variable names and shapes in the code
* `c`: cell state, including all time steps, $\mathbf{c}$ shape $(n_{a}, m, T)$
* `c_next`: new (next) cell state, $\mathbf{c}^{\langle t \rangle}$ shape $(n_{a}, m)$
* `c_prev`: previous cell state, $\mathbf{c}^{\langle t-1 \rangle}$, shape $(n_{a}, m)$
#### - Output gate $\mathbf{\Gamma}_{o}$
* The output gate decides what gets sent as the prediction (output) of the time step.
* The output gate is like the other gates. It contains values that range from 0 to 1.
##### Equation
$$ \mathbf{\Gamma}_o^{\langle t \rangle}= \sigma(\mathbf{W}_o[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{o})\tag{5}$$
##### Explanation of the equation
* The output gate is determined by the previous hidden state $\mathbf{a}^{\langle t-1 \rangle}$ and the current input $\mathbf{x}^{\langle t \rangle}$
* The sigmoid makes the gate range from 0 to 1.
##### Variable names in the code
* `Wo`: output gate weight, $\mathbf{W_o}$
* `bo`: output gate bias, $\mathbf{b_o}$
* `ot`: output gate, $\mathbf{\Gamma}_{o}^{\langle t \rangle}$
### LSTM cell
```
# GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
# Retrieve parameters from "parameters"
Wf = parameters["Wf"] # forget gate weight
bf = parameters["bf"]
Wi = parameters["Wi"] # update gate weight (notice the variable name)
bi = parameters["bi"] # (notice the variable name)
Wc = parameters["Wc"] # candidate value weight
bc = parameters["bc"]
Wo = parameters["Wo"] # output gate weight
bo = parameters["bo"]
Wy = parameters["Wy"] # prediction weight
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
# Concatenate a_prev and xt (≈1 line)
concat = np.zeros((n_a + n_x, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft (forget gate), it (update gate),
# cct (candidate value), c_next (cell state),
# ot (output gate), a_next (hidden state) (≈6 lines)
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.dot(Wy, a_next) + by)
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = ", c_next_tmp.shape)
print("c_next[2] = \n", c_next_tmp[2])
print("c_next.shape = ", c_next_tmp.shape)
print("yt[1] =", yt_tmp[1])
print("yt.shape = ", yt_tmp.shape)
print("cache[1][3] =\n", cache_tmp[1][3])
print("len(cache) = ", len(cache_tmp))
```
### Forward pass for LSTM
```
# GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
# Initialize "caches", which will track the list of all the caches
caches = []
# Retrieve dimensions from shapes of x and Wy (≈2 lines)
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros(a_next.shape)
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi']= np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][3][6] = ", a_tmp[4][3][6])
print("a.shape = ", a_tmp.shape)
print("y[1][4][3] =", y_tmp[1][4][3])
print("y.shape = ", y_tmp.shape)
print("caches[1][1][1] =\n", caches_tmp[1][1][1])
print("c[1][2][1]", c_tmp[1][2][1])
print("len(caches) = ", len(caches_tmp))
```
**Expected Output**:
```Python
a[4][3][6] = 0.172117767533
a.shape = (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape = (2, 10, 7)
caches[1][1][1] =
[ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.855544916718
len(caches) = 2
```
## Backpropagation in recurrent neural networks
This section is optional and ungraded. It is more difficult and has fewer details regarding its implementation. This section only implements key elements of the full path.
### Basic RNN backward pass
##### Equations
To compute the rnn_cell_backward you can utilize the following equations. It is a good exercise to derive them by hand. Here, $*$ denotes element-wise multiplication while the absence of a symbol indicates matrix multiplication.
$a^{\langle t \rangle} = \tanh(W_{ax} x^{\langle t \rangle} + W_{aa} a^{\langle t-1 \rangle} + b_{a})\tag{-}$
$\displaystyle \frac{\partial \tanh(x)} {\partial x} = 1 - \tanh^2(x) \tag{-}$
$\displaystyle {dW_{ax}} = da_{next} * ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) x^{\langle t \rangle T}\tag{1}$
$\displaystyle dW_{aa} = da_{next} * (( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) a^{\langle t-1 \rangle T}\tag{2}$
$\displaystyle db_a = da_{next} * \sum_{batch}( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{3}$
$\displaystyle dx^{\langle t \rangle} = da_{next} * { W_{ax}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{4}$
$\displaystyle da_{prev} = da_{next} * { W_{aa}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{5}$
#### Implementing rnn_cell_backward
```
def rnn_cell_backward(da_next, cache):
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute the gradient of the loss with respect to z (optional) (≈1 line)
dtanh = (1 - a_next ** 2) * da_next
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.dot(Wax.T, dtanh)
dWax = np.dot(dtanh, xt.T)
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.dot(Waa.T, dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
dba = np.sum(dtanh, axis = 1,keepdims=1)
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
gradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])
print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
-1.3872130506
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.152399493774
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
0.410772824935
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
1.15034506685
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[ 0.20023491]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
#### Backward pass through the RNN
```
def rnn_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros((n_a, n_x))
dWaa = np.zeros((n_a, n_a))
dba = np.zeros((n_a, 1))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[-2.07101689 -0.59255627 0.02466855 0.01483317]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
-0.314942375127
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
11.2641044965
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
2.30333312658
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[-0.74747722]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
## LSTM backward pass
### One Step backward
### Gate derivatives
Note the location of the gate derivatives ($\gamma$..) between the dense layer and the activation function (see graphic above). This is convenient for computing parameter derivatives in the next step.
$d\gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*\left(1-\Gamma_o^{\langle t \rangle}\right)\tag{7}$
$dp\widetilde{c}^{\langle t \rangle} = \left(dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \Gamma_u^{\langle t \rangle} * da_{next} \right) * \left(1-\left(\widetilde c^{\langle t \rangle}\right)^2\right) \tag{8}$
$d\gamma_u^{\langle t \rangle} = \left(dc_{next}*\widetilde{c}^{\langle t \rangle} + \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \widetilde{c}^{\langle t \rangle} * da_{next}\right)*\Gamma_u^{\langle t \rangle}*\left(1-\Gamma_u^{\langle t \rangle}\right)\tag{9}$
$d\gamma_f^{\langle t \rangle} = \left(dc_{next}* c_{prev} + \Gamma_o^{\langle t \rangle} * (1-\tanh^2(c_{next})) * c_{prev} * da_{next}\right)*\Gamma_f^{\langle t \rangle}*\left(1-\Gamma_f^{\langle t \rangle}\right)\tag{10}$
### Parameter derivatives
$ dW_f = d\gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{11} $
$ dW_u = d\gamma_u^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{12} $
$ dW_c = dp\widetilde c^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{13} $
$ dW_o = d\gamma_o^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{14}$
To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis= 1) axis on $d\gamma_f^{\langle t \rangle}, d\gamma_u^{\langle t \rangle}, dp\widetilde c^{\langle t \rangle}, d\gamma_o^{\langle t \rangle}$ respectively. Note that you should have the `keepdims = True` option.
$\displaystyle db_f = \sum_{batch}d\gamma_f^{\langle t \rangle}\tag{15}$
$\displaystyle db_u = \sum_{batch}d\gamma_u^{\langle t \rangle}\tag{16}$
$\displaystyle db_c = \sum_{batch}d\gamma_c^{\langle t \rangle}\tag{17}$
$\displaystyle db_o = \sum_{batch}d\gamma_o^{\langle t \rangle}\tag{18}$
Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.
$ da_{prev} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle} \tag{19}$
Here, to account for concatenation, the weights for equations 19 are the first n_a, (i.e. $W_f = W_f[:,:n_a]$ etc...)
$ dc_{prev} = dc_{next}*\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh^2(c_{next}))*\Gamma_f^{\langle t \rangle}*da_{next} \tag{20}$
$ dx^{\langle t \rangle} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle}\tag{21} $
where the weights for equation 21 are from n_a to the end, (i.e. $W_f = W_f[:,n_a:]$ etc...)
**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-21$ below.
Note: In the code:
$d\gamma_o^{\langle t \rangle}$ is represented by `dot`,
$dp\widetilde{c}^{\langle t \rangle}$ is represented by `dcct`,
$d\gamma_u^{\langle t \rangle}$ is represented by `dit`,
$d\gamma_f^{\langle t \rangle}$ is represented by `dft`
```
def lstm_cell_backward(da_next, dc_next, cache):
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = xt.shape
n_a, m = a_next.shape
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * it * (1 - cct ** 2)
dit = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * cct * (1 - it) * it
dft = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * c_prev * ft * (1 - ft)
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
dWf = np.dot(dft, np.hstack([a_prev.T, xt.T]))
dWi = np.dot(dit, np.hstack([a_prev.T, xt.T]))
dWc = np.dot(dcct, np.hstack([a_prev.T, xt.T]))
dWo = np.dot(dot, np.hstack([a_prev.T, xt.T]))
dbf = np.sum(dft, axis=1, keepdims=True)
dbi = np.sum(dit, axis=1, keepdims=True)
dbc = np.sum(dcct, axis=1, keepdims=True)
dbo = np.sum(dot, axis=1, keepdims=True)
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = np.dot(Wf[:, :n_a].T, dft) + np.dot(Wc[:, :n_a].T, dcct) + np.dot(Wi[:, :n_a].T, dit) + np.dot(Wo[:, :n_a].T, dot)
dc_prev = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * ft
dxt = np.dot(Wf[:, n_a:].T, dft) + np.dot(Wc[:, n_a:].T, dcct) + np.dot(Wi[:, n_a:].T, dit) + np.dot(Wo[:, n_a:].T, dot)
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
dc_next_tmp = np.random.randn(5,10)
gradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients_tmp["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients_tmp["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
3.23055911511
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.0639621419711
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"][2][3]** =
</td>
<td>
0.797522038797
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.147954838164
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
1.05749805523
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
2.30456216369
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.331311595289
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[ 0.18864637]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.40142491]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[ 0.25587763]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ 0.13893342]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
### LSTM BACKWARD
```
def lstm_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches.
(caches, x) = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈12 lines)
dx = np.zeros((n_x, m, T_x))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
dc_prevt = np.zeros((n_a, m))
dWf = np.zeros((n_a, n_a + n_x))
dWi = np.zeros((n_a, n_a + n_x))
dWc = np.zeros((n_a, n_a + n_x))
dWo = np.zeros((n_a, n_a + n_x))
dbf = np.zeros((n_a, 1))
dbi = np.zeros((n_a, 1))
dbc = np.zeros((n_a, 1))
dbo = np.zeros((n_a, 1))
# loop back over the whole sequence
for t in reversed(range(T_x)):
# Compute all gradients using lstm_cell_backward
gradients = lstm_cell_backward(da[:,:,t] + da_prevt, dc_prevt, caches[t])
# Store or add the gradient to the parameters' previous step's gradient
dx[:,:,t] = gradients["dxt"]
dWf += gradients["dWf"]
dWi += gradients["dWi"]
dWc += gradients["dWc"]
dWo += gradients["dWo"]
dbf += gradients["dbf"]
dbi += gradients["dbi"]
dbc += gradients["dbc"]
dbo += gradients["dbo"]
# Set the first activation's gradient to the backpropagated gradient da_prev.
da0 = gradients["da_prev"]
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.zeros((2,5)) # unused, but needed for lstm_forward
parameters_tmp['by'] = np.zeros((2,1)) # unused, but needed for lstm_forward
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
da_tmp = np.random.randn(5, 10, 4)
gradients_tmp = lstm_backward(da_tmp, caches_tmp)
print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[0.00218254 0.28205375 -0.48292508 -0.43281115]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
0.312770310257
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.0809802310938
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
0.40512433093
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
-0.0793746735512
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.038948775763
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[-0.15745657]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.50848333]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[-0.42510818]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ -0.17958196]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
|
github_jupyter
|
# Data description:
I'm going to solve the International Airline Passengers prediction problem. This is a problem where given a year and a month, the task is to predict the number of international airline passengers in units of 1,000. The data ranges from January 1949 to December 1960 or 12 years, with 144 observations.
# Workflow:
- Load the Time Series (TS) by Pandas Library
- Prepare the data, i.e. convert the problem to a supervised ML problem
- Build and evaluate the RNN model:
- Fit the best RNN model
- Evaluate model by in-sample prediction: Calculate RMSE
- Forecast the future trend: Out-of-sample prediction
Note: For data exploration of this TS, please refer to the notebook of my alternative solution with "Seasonal ARIMA model"
```
import keras
import sklearn
import tensorflow as tf
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics
from sklearn import preprocessing
import random as rn
import math
%matplotlib inline
from keras import backend as K
session_conf = tf.ConfigProto(intra_op_parallelism_threads=5, inter_op_parallelism_threads=5)
sess = tf.Session(graph=tf.get_default_graph(), config=session_conf)
K.set_session(sess)
import warnings
warnings.filterwarnings("ignore")
# Load data using Series.from_csv
from pandas import Series
#TS = Series.from_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/daily-minimum-temperatures.csv', header=0)
# Load data using pandas.read_csv
# in case, specify your own date parsing function and use the date_parser argument
from pandas import read_csv
TS = read_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/AirPassengers.csv', header=0, parse_dates=[0], index_col=0, squeeze=True)
print(TS.head())
#TS=pd.to_numeric(TS, errors='coerce')
TS.dropna(inplace=True)
data=pd.DataFrame(TS.values)
# prepare the data (i.e. convert problem to a supervised ML problem)
def prepare_data(data, lags=1):
"""
Create lagged data from an input time series
"""
X, y = [], []
for row in range(len(data) - lags - 1):
a = data[row:(row + lags), 0]
X.append(a)
y.append(data[row + lags, 0])
return np.array(X), np.array(y)
# normalize the dataset
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(data)
# split into train and test sets
train = dataset[0:120, :]
test = dataset[120:, :]
# LSTM RNN model: _________________________________________________________________
from keras.models import Sequential, Model
from keras.layers import Dense, LSTM, Dropout, average, Input, merge, concatenate
from keras.layers.merge import concatenate
from keras.regularizers import l2, l1
from keras.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.utils.class_weight import compute_sample_weight
from keras.layers.normalization import BatchNormalization
# reshape into X=t and Y=t+1
lags = 3
X_train, y_train = prepare_data(train, lags)
X_test, y_test = prepare_data(test, lags)
# reshape input to be [samples, time steps, features]
X_train = np.reshape(X_train, (X_train.shape[0], lags, 1))
X_test = np.reshape(X_test, (X_test.shape[0], lags, 1))
# create and fit the LSTM network
mdl = Sequential()
#mdl.add(Dense(3, input_shape=(1, lags), activation='relu'))
mdl.add(LSTM(4, activation='relu'))
#mdl.add(Dropout(0.1))
mdl.add(Dense(1))
mdl.compile(loss='mean_squared_error', optimizer='adam')
monitor=EarlyStopping(monitor='loss', min_delta=0.001, patience=100, verbose=1, mode='auto')
history=mdl.fit(X_train, y_train, epochs=1000, batch_size=1, validation_data=(X_test, y_test), callbacks=[monitor], verbose=0)
# To measure RMSE and evaluate the RNN model:
from sklearn.metrics import mean_squared_error
# make predictions
train_predict = mdl.predict(X_train)
test_predict = mdl.predict(X_test)
# invert transformation
train_predict = scaler.inverse_transform(pd.DataFrame(train_predict))
y_train = scaler.inverse_transform(pd.DataFrame(y_train))
test_predict = scaler.inverse_transform(pd.DataFrame(test_predict))
y_test = scaler.inverse_transform(pd.DataFrame(y_test))
# calculate root mean squared error
train_score = math.sqrt(mean_squared_error(y_train, train_predict[:,0]))
print('Train Score: {:.2f} RMSE'.format(train_score))
test_score = math.sqrt(mean_squared_error(y_test, test_predict[:,0]))
print('Test Score: {:.2f} RMSE'.format(test_score))
# list all data in history
#print(history.history.keys())
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
mdl.save('passenger_model.h5')
# shift train predictions for plotting
train_predict_plot =np.full(data.shape, np.nan)
train_predict_plot[lags:len(train_predict)+lags, :] = train_predict
# shift test predictions for plotting
test_predict_plot =np.full(data.shape, np.nan)
test_predict_plot[len(train_predict) + (lags * 2)+1:len(data)-1, :] = test_predict
# plot observation and predictions
plt.figure(figsize=(8,6))
plt.plot(data, label='Observed', color='#006699');
plt.plot(train_predict_plot, label='Prediction for Train Set', color='#006699', alpha=0.5);
plt.plot(test_predict_plot, label='Prediction for Test Set', color='#ff0066');
plt.legend(loc='upper left')
plt.title('LSTM Recurrent Neural Net')
plt.show()
mse = mean_squared_error(y_test, test_predict[:,0])
plt.title('Prediction quality: {:.2f} MSE ({:.2f} RMSE)'.format(mse, math.sqrt(mse)))
plt.plot(y_test.reshape(-1, 1), label='Observed', color='#006699')
plt.plot(test_predict.reshape(-1, 1), label='Prediction', color='#ff0066')
plt.legend(loc='upper left');
plt.show()
```
|
github_jupyter
|
# Comparing soundings from NCEP Reanalysis and various models
We are going to plot the global, annual mean sounding (vertical temperature profile) from observations.
Read in the necessary NCEP reanalysis data from the online server.
The catalog is here: <https://psl.noaa.gov/psd/thredds/catalog/Datasets/ncep.reanalysis.derived/catalog.html>
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
ncep_url = "https://psl.noaa.gov/thredds/dodsC/Datasets/ncep.reanalysis.derived/"
ncep_air = xr.open_dataset( ncep_url + "pressure/air.mon.1981-2010.ltm.nc", decode_times=False)
level = ncep_air.level
lat = ncep_air.lat
```
Take global averages and time averages.
```
Tzon = ncep_air.air.mean(dim=('lon','time'))
weight = np.cos(np.deg2rad(lat)) / np.cos(np.deg2rad(lat)).mean(dim='lat')
Tglobal = (Tzon * weight).mean(dim='lat')
```
Here is code to make a nicely labeled sounding plot.
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000))
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Global, annual mean sounding from NCEP Reanalysis', fontsize = 24)
ax2 = ax.twinx()
ax2.plot( Tglobal + 273.15, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now compute the Radiative Equilibrium solution for the grey-gas column model
```
import climlab
from climlab import constants as const
col = climlab.GreyRadiationModel()
print(col)
col.subprocess['LW'].diagnostics
col.integrate_years(1)
print("Surface temperature is " + str(col.Ts) + " K.")
print("Net energy in to the column is " + str(col.ASR - col.OLR) + " W / m2.")
```
### Plot the radiative equilibrium temperature on the same plot with NCEP reanalysis
```
pcol = col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=20 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue) and radiative equilibrium in grey gas model (red)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now use convective adjustment to compute a Radiative-Convective Equilibrium temperature profile
```
dalr_col = climlab.RadiativeConvectiveModel(adj_lapse_rate='DALR')
print(dalr_col)
dalr_col.integrate_years(2.)
print("After " + str(dalr_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(dalr_col.Ts) + " K.")
print("Net energy in to the column is " + str(dalr_col.ASR - dalr_col.OLR) + " W / m2.")
dalr_col.param
```
Now plot this "Radiative-Convective Equilibrium" on the same graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red) and dry RCE (black)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
The convective adjustment gets rid of the unphysical temperature difference between the surface and the overlying air.
But now the surface is colder! Convection acts to move heat upward, away from the surface.
Also, we note that the observed lapse rate (blue) is always shallower than $\Gamma_d$ (temperatures decrease more slowly with height).
## "Moist" Convective Adjustment
To approximately account for the effects of latent heat release in rising air parcels, we can just adjust to a lapse rate that is a little shallow than $\Gamma_d$.
We will choose 6 K / km, which gets close to the observed mean lapse rate.
We will also re-tune the longwave absorptivity of the column to get a realistic surface temperature of 288 K:
```
rce_col = climlab.RadiativeConvectiveModel(adj_lapse_rate=6, abs_coeff=1.7E-4)
print(rce_col)
rce_col.integrate_years(2.)
print("After " + str(rce_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(rce_col.Ts) + " K.")
print("Net energy in to the column is " + str(rce_col.ASR - rce_col.OLR) + " W / m2.")
```
Now add this new temperature profile to the graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), and moist RCE (magenta)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Adding stratospheric ozone
Our model has no equivalent of the stratosphere, where temperature increases with height. That's because our model has been completely transparent to shortwave radiation up until now.
We can load some climatogical ozone data:
```
# Put in some ozone
import xarray as xr
ozonepath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CLIMLAB/ozone/apeozone_cam3_5_54.nc"
ozone = xr.open_dataset(ozonepath)
ozone
```
Take the global average of the ozone climatology, and plot it as a function of pressure (or height)
```
# Taking annual, zonal, and global averages of the ozone data
O3_zon = ozone.OZONE.mean(dim=("time","lon"))
weight_ozone = np.cos(np.deg2rad(ozone.lat)) / np.cos(np.deg2rad(ozone.lat)).mean(dim='lat')
O3_global = (O3_zon * weight_ozone).mean(dim='lat')
O3_global.shape
ax = plt.figure(figsize=(10,8)).add_subplot(111)
ax.plot( O3_global * 1.E6, np.log(O3_global.lev/const.ps) )
ax.invert_yaxis()
ax.set_xlabel('Ozone (ppm)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
yticks = np.array([1000., 500., 250., 100., 50., 20., 10., 5.])
ax.set_yticks( np.log(yticks/1000.) )
ax.set_yticklabels( yticks )
ax.set_title('Global, annual mean ozone concentration', fontsize = 24);
```
This shows that most of the ozone is indeed in the stratosphere, and peaks near the top of the stratosphere.
Now create a new column model object **on the same pressure levels as the ozone data**. We are also going set an adjusted lapse rate of 6 K / km, and tune the longwave absorption
```
oz_col = climlab.RadiativeConvectiveModel(lev = ozone.lev,
abs_coeff=1.82E-4,
adj_lapse_rate=6,
albedo=0.315)
```
Now we will do something new: let the column absorb some shortwave radiation. We will assume that the shortwave absorptivity is proportional to the ozone concentration we plotted above. We need to weight the absorptivity by the pressure (mass) of each layer.
```
ozonefactor = 75
dp = oz_col.Tatm.domain.axes['lev'].delta
sw_abs = O3_global * dp * ozonefactor
oz_col.subprocess.SW.absorptivity = sw_abs
oz_col.compute()
oz_col.compute()
print(oz_col.SW_absorbed_atm)
```
Now run it out to Radiative-Convective Equilibrium, and plot
```
oz_col.integrate_years(2.)
print("After " + str(oz_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(oz_col.Ts) + " K.")
print("Net energy in to the column is " + str(oz_col.ASR - oz_col.OLR) + " W / m2.")
pozcol = oz_col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), moist RCE (magenta), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we finally have something that looks looks like the tropopause, with temperature increasing above at about the correct rate. Though the tropopause temperature is off by 15 degrees or so.
## Greenhouse warming in the RCE model with ozone
```
oz_col2 = climlab.process_like( oz_col )
oz_col2.subprocess['LW'].absorptivity *= 1.2
oz_col2.integrate_years(2.)
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we find that the troposphere warms, while the stratosphere cools!
### Vertical structure of greenhouse warming in CESM model
```
datapath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CESMA/"
atmstr = ".cam.h0.clim.nc"
cesm_ctrl = xr.open_dataset(datapath + 'som_1850_f19/clim/som_1850_f19' + atmstr)
cesm_2xCO2 = xr.open_dataset(datapath + 'som_1850_2xCO2/clim/som_1850_2xCO2' + atmstr)
cesm_ctrl.T
T_cesm_ctrl_zon = cesm_ctrl.T.mean(dim=('time', 'lon'))
T_cesm_2xCO2_zon = cesm_2xCO2.T.mean(dim=('time', 'lon'))
weight = np.cos(np.deg2rad(cesm_ctrl.lat)) / np.cos(np.deg2rad(cesm_ctrl.lat)).mean(dim='lat')
T_cesm_ctrl_glob = (T_cesm_ctrl_zon*weight).mean(dim='lat')
T_cesm_2xCO2_glob = (T_cesm_2xCO2_zon*weight).mean(dim='lat')
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.plot( T_cesm_ctrl_glob, np.log( cesm_ctrl.lev/const.ps ), 'r-' )
ax.plot( T_cesm_2xCO2_glob, np.log( cesm_ctrl.lev/const.ps ), 'r--' )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan), CESM (red)', fontsize = 18)
ax.grid()
```
And we find that CESM has the same tendency for increased CO2: warmer troposphere, colder stratosphere.
|
github_jupyter
|
# `numpy`
မင်္ဂလာပါ၊ welcome to the week 07 of Data Science Using Python.
We will go into details of `numpy` this week (as well as do some linear algebra stuffs).
## `numpy` အကြောင်း သိပြီးသမျှ
* `numpy` ဟာ array library ဖြစ်တယ်၊
* efficient ဖြစ်တယ်၊
* vector နဲ့ matrix တွေကို လွယ်လွယ်ကူကူ ကိုင်တွယ်နိုင်တယ်၊
* tensor တွေကို ရောပဲ ???
```
# tensor ဆိုတာ 2 ထက်များတဲ့ dimension ရှိတဲ့ array ကြီးတွေကို သင်္ချာဆန်ဆန် ခေါ်တာပါပဲ။
import numpy as np
tensor_3d = np.array(
[
[
[1, 2],
[3, 4]
],
[
[10, 20],
[30, 40]
],
]
)
print (tensor_3d.ndim, tensor_3d.shape, tensor_3d.size)
```
* **array indexing** `numpy` array တွေကို index လုပ်ဖို့ square bracket '[]' ထဲမှာ comma ',' ခံပြီး ရေးရတယ်။ dimension အရေအတွက် ရှိတဲ့အတိုင်း အကုန်ရေးရတယ်။ ချန်ထားရင် ကျန်တဲ့ dimensional တွေအတွက် အကုန်လို့ ယူဆတယ်။
* **slicing/dicing** `numpy` array တွေရဲ့ view တခုကို dimension အတွက် index ဂဏန်း နေရာမှာ start:end:step syntax သုံးပြီး slice လုပ်နိုင်တယ်။
```
from utils import my_data, np_data
print (my_data)
print ('---')
print (np_data)
# so, how to get the id, length, width view and height view ?
```
## `numpy` array creation
`numpy` မှာ array ဖန်တီးဖို့ short-cut function တွေရှိတယ်။
```
import numpy as np
a = np.zeros((2,2)) # Create an array of all zeros
print(a) # Prints "[[ 0. 0.]
# [ 0. 0.]]"
b = np.ones((1,2)) # Create an array of all ones
print(b) # Prints "[[ 1. 1.]]"
c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
e = np.random.random((2,2)) # Create an array filled with random values
print(e) # Might print "[[ 0.91940167 0.08143941]
# [ 0.68744134 0.87236687]]"
r = np.arange(35)
print (r)
```
အသုံးများတာကတော့ ...
* `arange`
* `zeros`
* `ones`
* `full`
* `eye` နဲ့
* `random.random` တို့ ဖြစ်တယ်။
အပြည့်အစုံကို [Numpy official documentation](https://numpy.org/doc/stable/reference/routines.array-creation.html) မှာ ကြည့်နိုင်တယ်။
## `numpy` array manipulation
အသုံးအများဆုံး array manipulation ကတော့ ...
* `copy`
* `reshape`
* `vstack`
* `hstack` နဲ့
* `block` တို့ပဲ ဖြစ်တယ်။
```
v1 = np_data[::2]
v2 = np_data[1::2,0]
print (v1.shape, v2.shape)
print (v1)
print (v2)
v2 =v2.reshape(-1,1) # here, -1 means "ကိုယ့်ဟာကိုယ် ကြည့်ဖြည့်လိုက်"
print (v2.shape)
np.hstack((v1, v2))
A = np.zeros((3,3)) # သတိထားစရာက tuple တွေကို parameter pass တာပဲ
print (A)
print ("---")
B = np.eye(2, 2)
print (B)
print ("---")
A_sub = A[1:3, 1:3]
A_sub += B
print (A)
A = np.zeros((3,3))
print (A)
print ("---")
B = np.eye(2, 2)
print (B)
print ("---")
A_sub = A[1:3, 1:3].copy() # this copy make sure A_sub is a copy (not a view)
A_sub += B
print (A)
A = np.ones(2, 2) # this will give you an error. check it out
B = np.zeros((2, 2))
C = np.block([[A, B, B], [B, A, B]])
print (C)
D = np.hstack((A, B))
E = np.vstack((A, B))
print (D)
print (E)
```
နောက်ထပ် အသုံးများတဲ့ property တခုကတော့ `T` ပဲ။ transpose လုပ်တာ။
```
print (D.T)
print (E.T)
```
## vector/matrix calculations
`dot` function ဟာ matrix/vector တွေကို လွယ်ကူစွာ မြှောက်နိုင်စေတယ်။
```
x = np.array(
[
[1,2],
[3,4]
])
y = np.array(
[
[5,6],
[7,8]
])
v = np.array([9,10])
w = np.array([11, 12])
# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))
# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))
# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
# [43 50]]
print(x.dot(y))
print(np.dot(x, y))
```
## Special Array indexing
`numpy` မှာ array တခုရဲ့ dimension တခုစီအတွက် list တခုနှုန်းနဲ့ (အဲဒီ list ထဲမှာ ကိုယ်လိုချင်တဲ့ element အရေအတွက်အတိုင်း ပါရ) index လုပ်တဲ့ special indexing method လဲ ရှိတယ်။
```
r = np.arange(35).reshape(5, 7)
print (r)
index_x0 = [3, 4, 4]
index_x1 = [6, 2, 3]
print (r[index_x0, index_x1])
```
### `numpy` special boolean ability and boolean indexing
```
r_index = r % 2 == 0
print (r_index)
```
အဲဒီလို boolean array (size တူရမယ်) ကို အသုံးပြုပြီး မူလ array ကနေ data retrieval လုပ်နိုင်တယ်။
```
r_selected = r[r_index]
print (r_selected)
```
|
github_jupyter
|
```
import pandas as pd
import datetime
from finquant.portfolio import build_portfolio
from finquant.moving_average import compute_ma, ema
from finquant.moving_average import plot_bollinger_band
from finquant.efficient_frontier import EfficientFrontier
### DOES OUR OPTIMIZATION ACTUALLY WORK?
# COMPARING AN OPTIMIZED PORTFOLIO WITH OTHER 2: THE FIRST WITH THE SAME AMOUNT OF ALL CURRENCIES AND ONE WITH ETH ONLY
# TIME-FRAME: WINTER 2021 IN WHICH ALL CURRENCIES WERE WERE GOING UP
# NO STABLECOINS
L = ['ETH', 'BTC', 'USDT', 'USDC','ENJ', 'MANA']
names = ['ETH-USD', 'BTC-USD', 'ENJ-USD', 'MANA-USD']
start_date = '2021-01-01'
end_date = '2021-03-01' #datetime.date.today()
pf = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf.data=pf.data.fillna('nan')
for i in range(pf.data.shape[0]):
for k in range(pf.data.shape[1]):
if pf.data.iloc[i,k]=='nan':
pf.data.iloc[i,k]=pf.data.iloc[i-1,k]
pf.data.head()
pf.properties()
ef=EfficientFrontier(pf.comp_mean_returns(freq=30), pf.comp_cov(), risk_free_rate=0.0232)
max_sr=ef.maximum_sharpe_ratio().reset_index().rename({"index":"Crypto"},axis=1)
data = {i : {'Name':max_sr.iloc[i,0], "Allocation":max_sr.iloc[i,1]}for i in range(max_sr.shape[0])}
alloc=[max_sr.iloc[i,1] for i in range(max_sr.shape[0])]
data
pf_allocation = pd.DataFrame.from_dict(data, orient="index")
names=pf_allocation["Name"].values.tolist()
pf_opt = build_portfolio(names=names,pf_allocation=pf_allocation, start_date=start_date ,end_date=end_date,data_api="yfinance")
pf_opt.properties()
# OUR OPTIMIZATION EXPECTS A RETURN OF 578%
start_date = '2021-03-01'
end_date = '2021-04-01'
pf_real = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf_real.data=pf_real.data.fillna('nan')
for i in range(pf_real.data.shape[0]):
for k in range(pf_real.data.shape[1]):
if pf_real.data.iloc[i,k]=='nan':
pf_real.data.iloc[i,k]=pf_real.data.iloc[i-1,k]
ds=pf_real.data
ds
returns = {i : {'Name':ds.columns[i], "Returns":(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i]}for i in range(ds.shape[1])}
r=[(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i] for i in range(ds.shape[1])]
returns,r
DATA = pd.DataFrame(names, columns=['Crypto'])
DATA["p_1"]=alloc
DATA["p_2"]=0.2
DATA["p_3"]=0
DATA.iloc[0,3]=1
DATA["Returns"]=r
DATA
p_1_returns = 0
p_2_returns = 0
p_3_returns = 0
for i in range(DATA.shape[0]):
p_1_returns+=DATA.iloc[i,1]*DATA.iloc[i,4]
p_2_returns+=DATA.iloc[i,2]*DATA.iloc[i,4]
p_3_returns+=DATA.iloc[i,3]*DATA.iloc[i,4]
p_1_returns,p_2_returns,p_3_returns
# AS WE CAN SEE, OUR PORTFOLIO PERFORMED MUCH BETTER, WITH 240% ACTUAL RETURN RATE
# TIME_FRAME: SUMMER 2021, WHEN CRYPTOS WERE GOING DOWN
# WITH STABLECOINS
L = ['ETH', 'BTC', 'USDT', 'USDC','ENJ', 'MANA']
names = ['ETH-USD', 'BTC-USD', 'ENJ-USD', 'MANA-USD', 'USDC-USD','USDT-USD']
start_date = '2021-06-01'
end_date = '2021-09-01' #datetime.date.today()
pf = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf.data=pf.data.fillna('nan')
for i in range(pf.data.shape[0]):
for k in range(pf.data.shape[1]):
if pf.data.iloc[i,k]=='nan':
pf.data.iloc[i,k]=pf.data.iloc[i-1,k]
pf.data.head()
ef=EfficientFrontier(pf.comp_mean_returns(freq=30), pf.comp_cov(), risk_free_rate=0.0232)
max_sr=ef.maximum_sharpe_ratio().reset_index().rename({"index":"Crypto"},axis=1)
data = {i : {'Name':max_sr.iloc[i,0], "Allocation":max_sr.iloc[i,1]}for i in range(max_sr.shape[0])}
alloc=[max_sr.iloc[i,1] for i in range(max_sr.shape[0])]
pf_allocation = pd.DataFrame.from_dict(data, orient="index")
names=pf_allocation["Name"].values.tolist()
pf_opt = build_portfolio(names=names,pf_allocation=pf_allocation, start_date=start_date ,end_date=end_date,data_api="yfinance")
pf_opt.properties()
# OUR OPTIMIZATION EXPECTS A RETURN OF 6.5%
start_date = '2021-09-01'
end_date = '2021-10-01'
pf_real = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf_real.data=pf_real.data.fillna('nan')
for i in range(pf_real.data.shape[0]):
for k in range(pf_real.data.shape[1]):
if pf_real.data.iloc[i,k]=='nan':
pf_real.data.iloc[i,k]=pf_real.data.iloc[i-1,k]
ds=pf_real.data
ds.head()
returns = {i : {'Name':ds.columns[i], "Returns":(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i]}for i in range(ds.shape[1])}
r=[(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i] for i in range(ds.shape[1])]
DATA = pd.DataFrame(names, columns=['Crypto'])
DATA["p_1"]=alloc
DATA["p_2"]=0.2
DATA["p_3"]=0
DATA.iloc[0,3]=1
DATA["Returns"]=r
DATA
p_1_returns = 0
p_2_returns = 0
p_3_returns = 0
for i in range(DATA.shape[0]):
p_1_returns+=DATA.iloc[i,1]*DATA.iloc[i,4]
p_2_returns+=DATA.iloc[i,2]*DATA.iloc[i,4]
p_3_returns+=DATA.iloc[i,3]*DATA.iloc[i,4]
p_1_returns,p_2_returns,p_3_returns
# ACTUAL RETURN RATE IS -0.8%, WAY LOWER THAN THE OTHER PORTFOLIOS
```
|
github_jupyter
|
# Isolation Forest (IF) outlier detector deployment
Wrap a scikit-learn Isolation Forest python model for use as a prediction microservice in seldon-core and deploy on seldon-core running on minikube or a Kubernetes cluster using GCP.
## Dependencies
- [helm](https://github.com/helm/helm)
- [minikube](https://github.com/kubernetes/minikube)
- [s2i](https://github.com/openshift/source-to-image) >= 1.1.13
python packages:
- scikit-learn: pip install scikit-learn --> 0.20.1
## Task
The outlier detector needs to detect computer network intrusions using TCP dump data for a local-area network (LAN) simulating a typical U.S. Air Force LAN. A connection is a sequence of TCP packets starting and ending at some well defined times, between which data flows to and from a source IP address to a target IP address under some well defined protocol. Each connection is labeled as either normal, or as an attack.
There are 4 types of attacks in the dataset:
- DOS: denial-of-service, e.g. syn flood;
- R2L: unauthorized access from a remote machine, e.g. guessing password;
- U2R: unauthorized access to local superuser (root) privileges;
- probing: surveillance and other probing, e.g., port scanning.
The dataset contains about 5 million connection records.
There are 3 types of features:
- basic features of individual connections, e.g. duration of connection
- content features within a connection, e.g. number of failed log in attempts
- traffic features within a 2 second window, e.g. number of connections to the same host as the current connection
The outlier detector is only using 40 out of 41 features.
## Train locally
Train on small dataset where you roughly know the fraction of outliers, defined by the "contamination" parameter.
```
# define columns to keep
cols=['duration','protocol_type','flag','src_bytes','dst_bytes','land',
'wrong_fragment','urgent','hot','num_failed_logins','logged_in',
'num_compromised','root_shell','su_attempted','num_root','num_file_creations',
'num_shells','num_access_files','num_outbound_cmds','is_host_login',
'is_guest_login','count','srv_count','serror_rate','srv_serror_rate',
'rerror_rate','srv_rerror_rate','same_srv_rate','diff_srv_rate',
'srv_diff_host_rate','dst_host_count','dst_host_srv_count','dst_host_same_srv_rate',
'dst_host_diff_srv_rate','dst_host_same_src_port_rate','dst_host_srv_diff_host_rate',
'dst_host_serror_rate','dst_host_srv_serror_rate','dst_host_rerror_rate',
'dst_host_srv_rerror_rate','target']
cols_str = str(cols)
!python train.py \
--dataset 'kddcup99' \
--samples 50000 \
--keep_cols "$cols_str" \
--contamination .1 \
--n_estimators 100 \
--max_samples .8 \
--max_features 1. \
--save_path './models/'
```
## Test using Kubernetes cluster on GCP or Minikube
Run the outlier detector as a model or a transformer. If you want to run the anomaly detector as a transformer, change the SERVICE_TYPE variable from MODEL to TRANSFORMER [here](./.s2i/environment), set MODEL = False and change ```OutlierIsolationForest.py``` to:
```python
from CoreIsolationForest import CoreIsolationForest
class OutlierIsolationForest(CoreIsolationForest):
""" Outlier detection using Isolation Forests.
Parameters
----------
threshold (float) : anomaly score threshold; scores below threshold are outliers
"""
def __init__(self,threshold=0.,load_path='./models/'):
super().__init__(threshold=threshold, load_path=load_path)
```
```
MODEL = True
```
Pick Kubernetes cluster on GCP or Minikube.
```
MINIKUBE = True
if MINIKUBE:
!minikube start --memory 4096
else:
!gcloud container clusters get-credentials standard-cluster-1 --zone europe-west1-b --project seldon-demos
```
Create a cluster-wide cluster-admin role assigned to a service account named “default” in the namespace “kube-system”.
```
!kubectl create clusterrolebinding kube-system-cluster-admin --clusterrole=cluster-admin \
--serviceaccount=kube-system:default
!kubectl create namespace seldon
```
Add current context details to the configuration file in the seldon namespace.
```
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
```
Create tiller service account and give it a cluster-wide cluster-admin role.
```
!kubectl -n kube-system create sa tiller
!kubectl create clusterrolebinding tiller --clusterrole cluster-admin --serviceaccount=kube-system:tiller
!helm init --service-account tiller
```
Check deployment rollout status and deploy seldon/spartakus helm charts.
```
!kubectl rollout status deploy/tiller-deploy -n kube-system
!helm install ../../../helm-charts/seldon-core-operator --name seldon-core --set usage_metrics.enabled=true --namespace seldon-system
```
Check deployment rollout status for seldon core.
```
!kubectl rollout status deploy/seldon-controller-manager -n seldon-system
```
Install Ambassador API gateway
```
!helm install stable/ambassador --name ambassador --set crds.keep=false
!kubectl rollout status deployment.apps/ambassador
```
If Minikube used: create docker image for outlier detector inside Minikube using s2i. Besides the transformer image and the demo specific model image, the general model image for the Isolation Forest outlier detector is also available from Docker Hub as ***seldonio/outlier-if-model:0.1***.
```
if MINIKUBE & MODEL:
!eval $(minikube docker-env) && \
s2i build . seldonio/seldon-core-s2i-python3:0.4 seldonio/outlier-if-model-demo:0.1
elif MINIKUBE:
!eval $(minikube docker-env) && \
s2i build . seldonio/seldon-core-s2i-python3:0.4 seldonio/outlier-if-transformer:0.1
```
Install outlier detector helm charts either as a model or transformer and set *threshold* hyperparameter value.
```
if MODEL:
!helm install ../../../helm-charts/seldon-od-model \
--name outlier-detector \
--namespace=seldon \
--set model.type=isolationforest \
--set model.isolationforest.image.name=seldonio/outlier-if-model-demo:0.1 \
--set model.isolationforest.threshold=0 \
--set oauth.key=oauth-key \
--set oauth.secret=oauth-secret \
--set replicas=1
else:
!helm install ../../../helm-charts/seldon-od-transformer \
--name outlier-detector \
--namespace=seldon \
--set outlierDetection.enabled=true \
--set outlierDetection.name=outlier-if \
--set outlierDetection.type=isolationforest \
--set outlierDetection.isolationforest.image.name=seldonio/outlier-if-transformer:0.1 \
--set outlierDetection.isolationforest.threshold=0 \
--set oauth.key=oauth-key \
--set oauth.secret=oauth-secret \
--set model.image.name=seldonio/mock_classifier:1.0
```
## Port forward Ambassador
Run command in terminal:
```
kubectl port-forward $(kubectl get pods -n seldon -l app.kubernetes.io/name=ambassador -o jsonpath='{.items[0].metadata.name}') -n seldon 8003:8080
```
## Import rest requests, load data and test requests
```
from utils import get_payload, rest_request_ambassador, send_feedback_rest, get_kdd_data, generate_batch
data = get_kdd_data(keep_cols=cols,percent10=True) # load dataset
print(data.shape)
```
Generate a random batch from the data
```
import numpy as np
samples = 1
fraction_outlier = 0.
X, labels = generate_batch(data,samples,fraction_outlier)
print(X.shape)
print(labels.shape)
```
Test the rest requests with the generated data. It is important that the order of requests is respected. First we make predictions, then we get the "true" labels back using the feedback request. If we do not respect the order and eg keep making predictions without getting the feedback for each prediction, there will be a mismatch between the predicted and "true" labels. This will result in errors in the produced metrics.
```
request = get_payload(X)
response = rest_request_ambassador("outlier-detector","seldon",request,endpoint="localhost:8003")
```
If the outlier detector is used as a transformer, the output of the anomaly detection is added as part of the metadata. If it is used as a model, we send model feedback to retrieve custom performance metrics.
```
if MODEL:
send_feedback_rest("outlier-detector","seldon",request,response,0,labels,endpoint="localhost:8003")
```
## Analytics
Install the helm charts for prometheus and the grafana dashboard
```
!helm install ../../../helm-charts/seldon-core-analytics --name seldon-core-analytics \
--set grafana_prom_admin_password=password \
--set persistence.enabled=false \
--namespace seldon
```
## Port forward Grafana dashboard
Run command in terminal:
```
kubectl port-forward $(kubectl get pods -n seldon -l app=grafana-prom-server -o jsonpath='{.items[0].metadata.name}') -n seldon 3000:3000
```
You can then view an analytics dashboard inside the cluster at http://localhost:3000/dashboard/db/prediction-analytics?refresh=5s&orgId=1. Your IP address may be different. get it via minikube ip. Login with:
Username : admin
password : password (as set when starting seldon-core-analytics above)
Import the outlier-detector-if dashboard from ../../../helm-charts/seldon-core-analytics/files/grafana/configs.
## Run simulation
- Sample random network intrusion data with a certain outlier probability.
- Get payload for the observation.
- Make a prediction.
- Send the "true" label with the feedback if the detector is run as a model.
It is important that the prediction-feedback order is maintained. Otherwise there will be a mismatch between the predicted and "true" labels.
View the progress on the grafana "Outlier Detection" dashboard. Most metrics need the outlier detector to be run as a model since they need model feedback.
```
import time
n_requests = 100
samples = 1
for i in range(n_requests):
fraction_outlier = .1
X, labels = generate_batch(data,samples,fraction_outlier)
request = get_payload(X)
response = rest_request_ambassador("outlier-detector","seldon",request,endpoint="localhost:8003")
if MODEL:
send_feedback_rest("outlier-detector","seldon",request,response,0,labels,endpoint="localhost:8003")
time.sleep(1)
if MINIKUBE:
!minikube delete
```
|
github_jupyter
|
```
from IPython.display import Latex
# Latex(r"""\begin{eqnarray} \large
# Z_{n+1} = Z_{n}^(-e^(Z_{n}^p)^(e^(Z_{n}^p)^(-e^(Z_{n}^p)^(e^(Z_{n}^p)^(-e^(Z_{n}^p))))))
# \end{eqnarray}""")
```
# Parameterized machine learning algo:
## tanh(Z) = (a exp(Z) - b exp(-Z)) / (c exp(Z) + d exp(-Z))
### with parameters a,b,c,d s.t. ad - bc = 1
Sequential iteration of difference equation:
Z =
```
import warnings
warnings.filterwarnings('ignore')
import os
import sys
import numpy as np
import time
from IPython.display import display
sys.path.insert(1, '../src');
import z_plane as zp
import graphic_utility as gu;
import itergataters as ig
import numcolorpy as ncp
def rnd_lambda(s=1):
""" random parameters s.t. a*d - b*c = 1 """
b = np.random.random()
c = np.random.random()
ad = b*c + 1
a = np.random.random()
d = ad / a
lamb0 = {'a': a, 'b': b, 'c': c, 'd': d}
lamb0 = np.array([a, b, c, d]) * s
return lamb0
def tanh_lmbd(Z, p, Z0=None, ET=None):
""" Z = starfish_ish(Z, p)
Args:
Z: a real or complex number
p: a real of complex number
Returns:
Z: the result (complex)
"""
Zp = np.exp(Z)
Zm = np.exp(-Z)
return (p[0] * Zp - p[1] * Zm) / (p[2] * Zp + p[3] * Zm)
def plane_gradient(X):
""" DX, DY = plane_gradient(X)
Args:
X: matrix
Returns:
DX: gradient in X direction
DY: gradient in Y direction
"""
n_rows = X.shape[0]
n_cols = X.shape[1]
DX = np.zeros(X.shape)
DY = np.zeros(X.shape)
for r in range(0, n_rows):
xr = X[r, :]
for c in range(0, n_cols - 1):
DX[r,c] = xr[c+1] - xr[c]
for c in range(0, n_cols):
xc = X[:, c]
for r in range(0, n_rows -1):
DY[r, c] = xc[r+1] - xc[r]
return DX, DY
def grad_Im(X):
"""
Args:
X: matrix
Returns:
Gradient_Image: positive matrix representation of the X-Y gradient of X
"""
DX, DY = plane_gradient(X)
return gu.graphic_norm(DX + DY * 1j)
def grad_pct(X):
""" percentage of X s.t gradient > 0 """
I = grad_Im(X)
return (I > 0).sum() / (X.shape[0] * X.shape[1])
def get_half_n_half(X):
""" box counting, fractal dimension submatrix shortcut """
x_rows = X.shape[0]
x_cols = X.shape[1]
x_numel = x_rows * x_cols
y_rows = np.int(np.ceil(x_rows / 2))
y_cols = np.int(np.ceil(x_cols / 2))
y_numel = y_rows * y_cols
Y = np.zeros([y_rows, y_cols])
for r in range(0, y_rows):
for c in range(0, y_cols):
Y[r,c] = X[2*r, 2*c]
return Y, y_numel, x_numel
def get_fractal_dim(X):
""" estimate fractal dimension by box counting """
Y, y_numel, x_numel = get_half_n_half(X)
X_pct = grad_pct(X) + 1
Y_pct = grad_pct(Y) + 1
return X_pct / Y_pct
X = np.random.random([5,5])
X[X < 0.5] = 0
Y, y_numel, x_numel = get_half_n_half(X)
X_pct = grad_pct(X)
Y_pct = grad_pct(Y)
print(X_pct, Y_pct)
print('y_numel', y_numel, '\nx_numel', x_numel)
print(X_pct / Y_pct)
# print(Y)
# print(X)
print(get_fractal_dim(X))
# -- machine with 8 cores --
P0 = [ 1.68458678, 1.72346312, 0.53931956, 2.92623535]
P1 = [ 1.99808082, 0.68298986, 0.80686446, 2.27772581]
P2 = [ 1.97243201, 1.32849475, 0.24972699, 2.19615225]
P3 = [ 1.36537498, 1.02648965, 0.60966423, 3.38794403]
p_scale = 2
P = rnd_lambda(p_scale)
# P = np.array(P3)
N = 200
par_set = {'n_rows': N, 'n_cols': N}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = np.pi / 2
par_set['zoom'] = 1/2
par_set['it_max'] = 16
par_set['max_d'] = 12 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET, Z, Z0 = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(P, '\n', tt, '\t total time')
Zd, Zr, ETn = ncp.etg_norm(Z0, Z, ET)
print('Fractal Dimensionn = ', get_fractal_dim(ETn) - 1)
ZrN = ncp.range_norm(Zr, lo=0.25, hi=1.0)
display(ncp.gray_mat(ZrN))
ZrN = ncp.range_norm(gu.grad_Im(ETn), lo=0.25, hi=1.0)
R = ncp.gray_mat(ZrN)
display(R)
# -- machine with 4 cores --
p_scale = 2
# P = rnd_lambda(p_scale)
P = np.array([1.97243201, 1.32849475, 0.24972699, 2.19615225])
N = 800
par_set = {'n_rows': N, 'n_cols': N}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = np.pi / 2
par_set['zoom'] = 1/2
par_set['it_max'] = 16
par_set['max_d'] = 12 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET, Z, Z0 = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(P, '\n', tt, '\t total time')
t0 = time.time()
Zd, Zr, ETn = ncp.etg_norm(Z0, Z, ET)
print('converstion time =\t', time.time() - t0)
t0 = time.time()
# ZrN = ncp.range_norm(Zr, lo=0.25, hi=1.0)
# R = ncp.gray_mat(ZrN)
ZrN = ncp.range_norm(gu.grad_Im(ETn), lo=0.25, hi=1.0)
R = ncp.gray_mat(ZrN)
print('coloring time =\t',time.time() - t0)
display(R)
# def grad_pct(X):
# """ percentage of X s.t gradient > 0 """
# I = gu.grad_Im(X)
# nz = (I == 0).sum()
# if nz > 0:
# grad_pct = (I > 0).sum() / nz
# else:
# grad_pct = 1
# return grad_pct
I = gu.grad_Im(ETn)
nz = (I == 0).sum()
nb = (I > 0).sum()
print(nz, nb, ETn.shape[0] * ETn.shape[1], nz + nb)
P0 = [ 1.68458678, 1.72346312, 0.53931956, 2.92623535]
P1 = [ 1.99808082, 0.68298986, 0.80686446, 2.27772581]
P2 = [ 1.97243201, 1.32849475, 0.24972699, 2.19615225]
P3 = [ 1.36537498, 1.02648965, 0.60966423, 3.38794403]
H = ncp.range_norm(1 - Zd, lo=0.5, hi=1.0)
S = ncp.range_norm(1 - ETn, lo=0.0, hi=0.15)
V = ncp.range_norm(Zr, lo=0.2, hi=1.0)
t0 = time.time()
Ihsv = ncp.rgb_2_hsv_mat(H, S, V)
print('coloring time:\t',time.time() - t0)
display(Ihsv)
H = ncp.range_norm(Zd, lo=0.05, hi=0.55)
S = ncp.range_norm(1 - ETn, lo=0.0, hi=0.35)
V = ncp.range_norm(Zr, lo=0.0, hi=0.7)
t0 = time.time()
Ihsv = ncp.rgb_2_hsv_mat(H, S, V)
print('coloring time:\t',time.time() - t0)
display(Ihsv)
# smaller for analysis
par_set = {'n_rows': 200, 'n_cols': 200}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = 0.0
par_set['zoom'] = 5/8
par_set['it_max'] = 16
par_set['max_d'] = 10 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
# list_tuple = [(starfish_ish, (-0.040431211565+0.388620268274j))]
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET_sm, Z_sm, Z0_zm = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(tt, '\t total time')
# view smaller - individual escape time starting points
for t in range(1,7):
print('ET =\t',t)
I = np.ones(ET_sm.shape)
I[ET_sm == t] = 0
display(ncp.mat_to_gray(I))
I = np.ones(ET_sm.shape)
I[ET_sm > 7] = 0
display(ncp.mat_to_gray(I))
# view smaller - individual escape time frequency
for k in range(0,int(ET_sm.max())):
print(k, (ET_sm == k).sum())
print('\nHow many never escaped:\n>',(ET_sm > k).sum())
# get the list of unescaped starting points and look for orbit points
Z_overs = Z0_zm[ET_sm == ET_sm.max()]
v1 = Z_overs[0]
d = '%0.2f'%(np.abs(v1))
theta = '%0.1f'%(180*np.arctan2(np.imag(v1), np.real(v1))/np.pi)
print('One Unescaped Vector:\n\tV = ', d, theta, 'degrees\n')
print('%9d'%Z_overs.size, 'total unescaped points\n')
print('%9s'%('points'), 'near V', ' (plane units)')
for denom0 in range(1,12):
neighbor_distance = np.abs(v1) * 1/denom0
v1_list = Z_overs[np.abs(Z_overs-v1) < neighbor_distance]
print('%9d'%len(v1_list), 'within V/%2d (%0.3f)'%(denom0, neighbor_distance))
```
|
github_jupyter
|
# Hashtags
```
from nltk.tokenize import TweetTokenizer
import os
import pandas as pd
import re
import sys
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
from IPython.display import clear_output
def squeal(text=None):
clear_output(wait=True)
if not text is None: print(text)
DATADIR = "../data/text/"
ID_STR = "id_str"
TEXT = "text"
TOPICQUERY = "corona|covid|huisarts|mondkapje|rivm|blijfthuis|flattenthecurve|houvol"
PANDEMICQUERY = "|".join([TOPICQUERY, r'virus|besmet|ziekenhui|\bic\b|intensive.care|^zorg|vaccin|[^ad]arts|uitbraak|uitbrak|pandemie|ggd|'+
r'mondkapje|quarantaine|\bwho\b|avondklok|variant|verple|sympto|e.golf|mutant|^omt$|umc|hcq|'+
r'hydroxychloroquine|virolo|zkh|oversterfte|patiënt|patient|intensivist|🦠|ivermectin'])
DISTANCEQUERY = "1[.,]5[ -]*m|afstand.*hou|hou.*afstand|anderhalve[ -]*meter"
LOCKDOWNQUERY = "lock.down|lockdown"
VACCINQUERY = "vaccin|ingeënt|ingeent|inent|prik|spuit|bijwerking|-->|💉|pfizer|moderna|astrazeneca|astra|zeneca|novavax|biontech"
TESTQUERY = r'\btest|getest|sneltest|pcr'
QUERY = "|".join([PANDEMICQUERY, TESTQUERY, VACCINQUERY, LOCKDOWNQUERY, DISTANCEQUERY])
BASEQUERY = "corona|covid"
HAPPY_QUERY = r'\b(geluk|gelukkig|gelukkige|blij|happy)\b'
LONELY_QUERY = r'eenza|alleen.*voel|voel.*alleen|lonely|loneli'
IK_QUERY = r'\b(ik|mij|mijn|me|mn|m\'n|zelf|mezelf|mijzelf|i)\b'
def get_tweets(file_pattern, query, query2="", spy=False):
tweets = []
file_names = sorted(os.listdir(DATADIR))
for file_name in file_names:
if re.search('^' + file_pattern, file_name):
if spy:
squeal(file_name)
df = pd.read_csv(DATADIR+file_name,index_col=ID_STR)
if query2 == "":
df_query = df[df[TEXT].str.contains(query, flags=re.IGNORECASE)]
else:
df_query = df[df[TEXT].str.contains(query, flags=re.IGNORECASE) & df[TEXT].str.contains(query2, flags=re.IGNORECASE)]
tweets.extend(list(df_query[TEXT]))
return(tweets)
def get_hashtags(tweet):
hashtags = []
for token in TweetTokenizer().tokenize(tweet):
if re.search(r'#', token):
hashtags.append(token)
return(hashtags)
def process_month(month, query=BASEQUERY, query2=""):
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, query, query2=query2, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
pd.DataFrame([{"202105": "measures", "202106": "pandemic", "202107": "measures",
"202108": "pandemic", "202109": "entry pass", "202110": "entry pass"},
{"202105": "pandemic", "202106": "measures", "202107": "pandemic",
"202108": "measures", "202109": "measures", "202110": "measures"},
{"202105": "vaccination", "202106": "vaccination", "202107": "vaccination",
"202108": "vaccination obligation", "202109": "vaccination obligation", "202110": "pandemic"},
{"202105": "entry pass", "202106": "FVD", "202107": "vaccination obligation",
"202108": "vaccination", "202109": "pandemic", "202110": "vaccination obligation"},
{"202105": "Netherlands", "202106": "Netherlands", "202107": "FVD",
"202108": "Netherlands", "202109": "press conference", "202110": "press conference"},
{"202105": "testing", "202106": "facemasks", "202107": "Netherlands",
"202108": "lockdown", "202109": "FVD", "202110": "unvaccinated"},
{"202105": "FVD", "202106": "entry pass", "202107": "lockdown",
"202108": "press conference", "202109": "Hugo de Jonge", "202110": "3 October protest"},
{"202105": "ivermectine", "202106": "app", "202107": "press conference",
"202108": "entry pass", "202109": "hospitality business", "202110": "Netherlands"},
{"202105": "long covid", "202106": "variants", "202107": "long covid",
"202108": "FVD", "202109": "Mark Rutte", "202110": "Hugo de Jonge"},
{"202105": "lockdown", "202106": "lab leak", "202107": "Hugo de Jonge",
"202108": "long covid", "202109": "Mona Keizer", "202110": "FVD"},
])
for month in "202105 202106 202107 202108 202109 202110".split():
process_month(month)
for month in "202105".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, LONELY_QUERY, query2=IK_QUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
for month in "202002 202003 202004 202005 202006 202007 202008 202009 202010 202011 202012 201201".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, BASEQUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
for month in "202101 202102 202103 202104".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, BASEQUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
```
|
github_jupyter
|
# Graph
> in progress
- toc: true
- badges: true
- comments: true
- categories: [self-taught]
- image: images/bone.jpeg
- hide: true
https://towardsdatascience.com/using-graph-convolutional-neural-networks-on-structured-documents-for-information-extraction-c1088dcd2b8f
CNNs effectively capture patterns in data in Euclidean space
data is represented in the form of a Graph and lack a grid-like regularity.
As Graphs can be irregular, they may have a variable size of un-ordered nodes and each node may have a different number of neighbors, resulting in mathematical operations such as convolutions difficult to apply to the Graph domain.
Some examples of such non-Euclidean data include:
- Protein-Protein Interaction Data where interactions between molecules are modeled as graphs
- Citation Networks where scientific papers are nodes and citations are uni- or bi-directional edges
- Social Networks where people on the network are nodes and their relationships are edges
This article particularly discusses the use of Graph Convolutional Neural Networks (GCNs) on structured documents such as Invoices and Bills to automate the extraction of meaningful information by learning positional relationships between text entities.
What is a Graph?
**How to convert Structured Documents to Graphs?**
Such recurring structural information along with text attributes can help a Graph Neural Network learn neighborhood representations and perform node classification as a result
Geometric Algorithm: Connecting objects based on visibility
**Convolution on Document Graphs for Information Extraction**
# References
https://towardsdatascience.com/overview-of-deep-learning-on-graph-embeddings-4305c10ad4a4
Graph embedding
https://towardsdatascience.com/graph-convolutional-networks-for-geometric-deep-learning-1faf17dee008m
Graph Conv
https://arxiv.org/pdf/1611.08097.pdf
https://arxiv.org/pdf/1901.00596.pdf
https://towardsdatascience.com/graph-theory-and-deep-learning-know-hows-6556b0e9891b
**Everything you need to know about Graph Theory for Deep Learning**
Graph Theory — crash course
1. What is a graph?
A graph, in the context of graph theory, is a structured datatype that has nodes (entities that hold information) and edges (connections between nodes that can also hold information). A graph is a way of structuring data, but can be a datapoint itself. Graphs are a type of Non-Euclidean data, which means they exist in 3D, unlike other datatypes like images, text, and audio.
- Graphs can have labels on their edges and/or nodes
- Labels can also be considered weights, but that’s up to the graph’s designer.
- Labels don’t have to be numerical, they can be textual.
- Labels don’t have to be unique;
- Graphs can have features (a.k.a attributes).
Take care not to mix up features and labels.
> Note: a node is a person, a node’s label is a person’s name, and the node’s features are the person’s characteristics.
- Graphs can be directed or undirected
- A node in the graph can even have an edge that points/connects to itself. This is known as a self-loop.
Graphs can be either:
- Heterogeneous — composed of different types of nodes
- Homogeneous — composed of the same type of nodes
and are either:
- Static — nodes and edges do not change, nothing is added or taken away
- Dynamic — nodes and edges change, added, deleted, moved, etc.
graphs can be vaguely described as either
- Dense — composed of many nodes and edges
- Sparse — composed of fewer nodes and edges
Graphs can be made to look neater by turning them into their planar form, which basically means rearranging nodes such that edges don’t intersect
2. Graph Analysis
3. E-graphs — graphs on computers
https://medium.com/@flawnsontong1/what-is-geometric-deep-learning-b2adb662d91d
**What is Geometric Deep Learning?**
The vast majority of deep learning is performed on Euclidean data. This includes datatypes in the 1-dimensional and 2-dimensional domain.
Images, text, audio, and many others are all euclidean data.
`Non-euclidean data` can represent more complex items and concepts with more accuracy than 1D or 2D representation:
When we represent things in a non-euclidean way, we are giving it an inductive bias.
An inductive bias allows a learning algorithm to prioritize one solution (or interpretation) over another, independent of the observed data. Inductive biases can express assumptions about either the data-generating process or the space of solutions.
In the majority of current research pursuits and literature, the inductive bias that is used is relational.
Building on this intuition, `Geometric Deep Learning (GDL)` is the niche field under the umbrella of deep learning that aims to build neural networks that can learn from non-euclidean data.
The prime example of a non-euclidean datatype is a graph. `Graphs` are a type of data structure that consists of `nodes` (entities) that are connected with `edges` (relationships). This abstract data structure can be used to model almost anything.
We want to be able to learn from graphs because:
`
Graphs allow us to represent individual features, while also providing information regarding relationships and structure.
`
`Graph theory` is the study of graphs and what we can learn from them. There are various types of graphs, each with a set of rules, properties, and possible actions.
Examples of Geometric Deep Learning
- Molecular Modeling and learning:
One of the bottlenecks in computational chemistry, biology, and physics is the representation concepts, entities, and interactions. Our current methods of representing these concepts computationally can be considered “lossy”, since we lose a lot of valuable information. By treating atoms as nodes, and bonds as edges, we can save structural information that can be used downstream in prediction or classification.
- 3D Modeling and Learning
5 types of bias
https://twitter.com/math_rachel/status/1113203073051033600
https://arxiv.org/pdf/1806.01261.pdf
https://stackoverflow.com/questions/35655267/what-is-inductive-bias-in-machine-learning
|
github_jupyter
|
# 08 - Common problems & bad data situations
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons Licence" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" title='This work is licensed under a Creative Commons Attribution 4.0 International License.' align="right"/></a>
In this notebook, we will revise common problems that might come up when dealing with real-world data.
Maintainers: [@thempel](https://github.com/thempel), [@cwehmeyer](https://github.com/cwehmeyer), [@marscher](https://github.com/marscher), [@psolsson](https://github.com/psolsson)
**Remember**:
- to run the currently highlighted cell, hold <kbd>⇧ Shift</kbd> and press <kbd>⏎ Enter</kbd>;
- to get help for a specific function, place the cursor within the function's brackets, hold <kbd>⇧ Shift</kbd>, and press <kbd>⇥ Tab</kbd>;
- you can find the full documentation at [PyEMMA.org](http://www.pyemma.org).
---
Most problems in Markov modeling of MD data arise from bad sampling combined with a poor discretization.
For estimating a Markov model, it is required to have a connected data set,
i.e., we must have observed each process we want to describe in both directions.
PyEMMA checks if this requirement is fulfilled but, however, in certain situations this might be less obvious.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import mdshare
import pyemma
```
## Case 1: preprocessed, two-dimensional data (toy model)
### well-sampled double-well potential
Let's again have a look at the double-well potential.
Since we are only interested in the problematic situations here,
we will simplify our data a bit and work with a 1D projection.
```
file = mdshare.fetch('hmm-doublewell-2d-100k.npz', working_directory='data')
with np.load(file) as fh:
data = [fh['trajectory'][:, 1]]
```
Since this particular example is simple enough, we can define a plotting function that combines histograms with trajectory data:
```
def plot_1D_histogram_trajectories(data, cluster=None, max_traj_length=200, ax=None):
if ax is None:
fig, ax = plt.subplots()
for n, _traj in enumerate(data):
ax.hist(_traj, bins=30, alpha=.33, density=True, color='C{}'.format(n));
ylims = ax.get_ylim()
xlims = ax.get_xlim()
for n, _traj in enumerate(data):
ax.plot(
_traj[:min(len(_traj), max_traj_length)],
np.linspace(*ylims, min(len(_traj), max_traj_length)),
alpha=0.6, color='C{}'.format(n), label='traj {}'.format(n))
if cluster is not None:
ax.plot(
cluster.clustercenters[cluster.dtrajs[n][:min(len(_traj), max_traj_length)], 0],
np.linspace(*ylims, min(len(_traj), max_traj_length)),
'.-', alpha=.6, label='dtraj {}'.format(n), linewidth=.3)
ax.annotate(
'', xy=(0.8500001 * xlims[1], 0.7 * ylims[1]), xytext=(0.85 * xlims[1], 0.3 * ylims[1]),
arrowprops=dict(fc='C0', ec='None', alpha=0.6, width=2))
ax.text(0.86 * xlims[1], 0.5 * ylims[1], '$x(time)$', ha='left', va='center', rotation=90)
ax.set_xlabel('TICA coordinate')
ax.set_ylabel('histogram counts & trajectory time')
ax.legend(loc=2)
```
As a reference, we visualize the histogram of this well-sampled trajectory along with the first $200$ steps (left panel) and the MSM implied timescales (right panel):
```
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
cluster = pyemma.coordinates.cluster_regspace(data, dmin=0.05)
plot_1D_histogram_trajectories(data, cluster=cluster, ax=axes[0])
lags = [i + 1 for i in range(10)]
its = pyemma.msm.its(cluster.dtrajs, lags=lags)
pyemma.plots.plot_implied_timescales(its, marker='o', ax=axes[1], nits=4)
fig.tight_layout()
```
We see a nice, reversibly connected trajectory.
That means we have sampled transitions between the basins in both directions that are correctly resolved by the discretization.
As we see from the almost perfect overlay of discrete and continuous trajectory, nearly no discretization error is made.
### irreversibly connected double-well trajectories
In MD simulations, we often face the problem that a process is sampled only in one direction.
For example, consider protein-protein binding.
The unbinding might take on the order of seconds to minutes and is thus difficult to sample.
We will have a look what happens with the MSM in this case.
Our example are two trajectories sampled from a double-well potential, each started in a different basin.
They will be color coded.
```
file = mdshare.fetch('doublewell_oneway.npy', working_directory='data')
data = [trj for trj in np.load(file)]
plot_1D_histogram_trajectories(data, max_traj_length=data[0].shape[0])
```
We note that the orange trajectory does not leave its potential well while the blue trajectory does overcome the barrier exactly once.
⚠️ Even though we have sampled one direction of the process,
we do not sample the way out of one of the potential wells, thus effectively finding a sink state in our data.
Let's have a look at the MSM.
Since in higher dimensions, we often face the problem of poor discretization,
we will simulate this situation by using too few cluster centers.
```
cluster_fine = pyemma.coordinates.cluster_regspace(data, dmin=0.1)
cluster_poor = pyemma.coordinates.cluster_regspace(data, dmin=0.7)
print(cluster_fine.n_clusters, cluster_poor.n_clusters)
fig, axes = plt.subplots(2, 2, figsize=(10, 8), sharey='col')
for cluster, ax in zip([cluster_poor, cluster_fine], axes):
plot_1D_histogram_trajectories(data, cluster=cluster, max_traj_length=data[0].shape[0], ax=ax[0])
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 10, 100, 200, 300, 500, 800, 1000])
pyemma.plots.plot_implied_timescales(its, marker='o', ax=ax[1], nits=4)
axes[0, 0].set_title('poor discretization')
axes[1, 0].set_title('fine discretization')
fig.tight_layout()
```
#### What do we see?
1) We observe implied timescales that even look converged in the fine discretization case.
2) With poor clustering, the process cannot be resolved any more, i.e., the ITS does not convergence before the lag time exceeds the implied time scale.
The obvious question is, what is the process that can be observed in the fine discretization case?
PyEMMA checks for disconnectivity and thus should not find the process between the two wells.
We follow this question by taking a look at the first eigenvector, which corresponds to that process.
```
msm = pyemma.msm.estimate_markov_model(cluster_fine.dtrajs, 200)
fig, ax = plt.subplots()
ax.plot(
cluster_fine.clustercenters[msm.active_set, 0],
msm.eigenvectors_right()[:, 1],
'o:',
label='first eigvec')
tx = ax.twinx()
tx.hist(np.concatenate(data), bins=30, alpha=0.33)
tx.set_yticklabels([])
tx.set_yticks([])
fig.legend()
fig.tight_layout()
```
We observe a process which is entirely taking place in the left potential well.
How come?
PyEMMA estimates MSMs only on the largest connected set because they are only defined on connected sets.
In this particular example, the largest connected set is the microstates in the left potential well.
That means that we find a transition between the right and the left side of this well.
This is not wrong, it might just be non-informative or even irrelevant.
The set of microstates which is used for the MSM estimation is stored in the MSM object `msm` and can be retrieved via `.active_set`.
```
print('Active set: {}'.format(msm.active_set))
print('Active state fraction: {:.2}'.format(msm.active_state_fraction))
```
In this example we clearly see that some states are missing.
### disconnected double-well trajectories with cross-overs
This example covers the worst-case scenario.
We have two trajectories that live in two separated wells and never transition to the other one.
Due to a very bad clustering, we believe that the data is connected.
This can happen if we cluster a large dataset in very high dimensions where it is especially difficult to debug.
```
file = mdshare.fetch('doublewell_disconnected.npy', working_directory='data')
data = [trj for trj in np.load(file)]
plot_1D_histogram_trajectories(data, max_traj_length=data[0].shape[0])
```
We, again, compare a reasonable to a deliberately poor discretization:
```
cluster_fine = pyemma.coordinates.cluster_regspace(data, dmin=0.1)
cluster_poor = pyemma.coordinates.cluster_regspace(data, dmin=0.7)
print(cluster_fine.n_clusters, cluster_poor.n_clusters)
fig, axes = plt.subplots(2, 2, figsize=(10, 8), sharey='col')
for cluster, ax in zip([cluster_poor, cluster_fine], axes):
plot_1D_histogram_trajectories(data, cluster=cluster, max_traj_length=data[0].shape[0], ax=ax[0])
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 10, 100, 200, 300, 500, 800, 1000])
pyemma.plots.plot_implied_timescales(its, marker='o', ax=ax[1], nits=4)
axes[0, 0].set_title('poor discretization')
axes[1, 0].set_title('fine discretization')
fig.tight_layout()
```
#### What do we see?
1) With the fine discretization, we observe some timescales that are converged. These are most probably processes within one of the wells, similar to the ones we saw before.
2) The poor discretization induces a large error and describes artificial short visits to the other basin.
3) The timescales in the poor discretization are much higher but not converged.
The reason for the high timescales in 3) are in fact the artificial cross-over events created by the poor discretization.
This process was not actually sampled and is an artifact of bad clustering.
Let's look at it in more detail and see what happens if we estimate an MSM and even compute metastable states with PCCA++.
```
msm = pyemma.msm.estimate_markov_model(cluster_poor.dtrajs, 200)
nstates = 2
msm.pcca(nstates)
index_order = np.argsort(cluster_poor.clustercenters[:, 0])
fig, axes = plt.subplots(1, 3, figsize=(12, 3))
axes[0].plot(
cluster_poor.clustercenters[index_order, 0],
msm.eigenvectors_right()[index_order, 1],
'o:',
label='1st eigvec')
axes[0].set_title('first eigenvector')
for n, metastable_distribution in enumerate(msm.metastable_distributions):
axes[1].step(
cluster_poor.clustercenters[index_order, 0],
metastable_distribution[index_order],
':',
label='md state {}'.format(n + 1),
where='mid')
axes[1].set_title('metastable distributions (md)')
axes[2].step(
cluster_poor.clustercenters[index_order, 0],
msm.pi[index_order],
'k--',
label='$\pi$',
where='mid')
axes[2].set_title('stationary distribution $\pi$')
for ax in axes:
tx = ax.twinx()
tx.hist(np.concatenate(data), bins=30, alpha=0.33)
tx.set_yticklabels([])
tx.set_yticks([])
fig.legend(loc=7)
fig.tight_layout()
```
We observe that the first eigenvector represents a process that does not exist, i.e., is an artifact.
Nevertheless, the PCCA++ algorithm can separate metastable states in a way we would expect.
It finds the two disconnected states. However, the stationary distribution yields arbitrary results.
#### How to detect disconnectivity?
Generally, hidden Markov models (HMMs) are much more reliable because they come with an additional layer of hidden states.
Cross-over events are thus unlikely to be counted as "real" transitions.
Thus, it is a good idea to estimate an HMM.
What happens if we try to estimate a two state HMM on the same, poorly discretized data?
⚠️ It is important to note that the HMM estimation is initialized from the PCCA++ metastable states that we already analyzed.
```
hmm = pyemma.msm.estimate_hidden_markov_model(cluster_poor.dtrajs, nstates, msm.lag)
```
We are getting an error message which already explains what is going wrong, i.e.,
that the (macro-) states are not connected and thus no unique stationary distribution can be estimated.
This is equivalent to having two eigenvalues of magnitude 1 or an implied timescale of infinity which is what we observe in the implied timescales plot.
```
its = pyemma.msm.timescales_hmsm(cluster_poor.dtrajs, nstates, lags=[1, 3, 4, 10, 100])
pyemma.plots.plot_implied_timescales(its, marker='o', ylog=True);
```
As we see, the requested timescales above $4$ steps could not be computed because the underlying HMM is disconnected,
i.e., the corresponding timescales are infinity.
The implied timescales that could be computed are most likely the same process that we observed from the fine clustering before, i.e., jumps within one basin.
In general, it is a non-trivial problem to show that processes were not sampled reversibly.
In our experience, HMMs are a good choice here, even though situations can occur where they might not detect the problem as easily as in this example.
<a id="poorly_sampled_dw"></a>
### poorly sampled double-well trajectories
Let's now assume that everything worked out fine but our sampling is somewhat poor.
This is a realistic scenario when dealing with large systems that were well-sampled but still contain only few events of interest.
We expect that our trajectories are just long enough to sample a certain process but are too short to capture them with a large lag time.
To rule out discretization issues and to make the example clear, we use the full data set for discretization.
```
file = mdshare.fetch('hmm-doublewell-2d-100k.npz', working_directory='data')
with np.load(file) as fh:
data = [fh['trajectory'][:, 1]]
cluster = pyemma.coordinates.cluster_regspace(data, dmin=0.05)
```
We want to simulate a process that happens on a timescale that is on the order of magnitude of the trajectory length.
To do so, we choose `n_trajs` chunks from the full data set that contain `traj_length` steps by splitting the original trajectory:
```
traj_length = 10
n_trajs = 50
data_short_trajs = list(data[0].reshape((data[0].shape[0] // traj_length, traj_length)))[:n_trajs]
dtrajs_short = list(cluster.dtrajs[0].reshape((data[0].shape[0] // traj_length, traj_length)))[:n_trajs]
```
Now, let's plot the trajectories (left panel) and estimate implied timescales (right panel) as above.
Since we know the true ITS of this process, we visualize it as a dotted line.
```
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
for n, _traj in enumerate(data_short_trajs):
axes[0].plot(_traj, np.linspace(0, 1, _traj.shape[0]) + n)
lags = [i + 1 for i in range(9)]
its = pyemma.msm.its(dtrajs_short, lags=lags)
pyemma.plots.plot_implied_timescales(its, marker='o', ax=axes[1], nits=1)
its_reference = pyemma.msm.its(cluster.dtrajs, lags=lags)
pyemma.plots.plot_implied_timescales(its_reference, linestyle=':', ax=axes[1], nits=1)
fig.tight_layout()
```
We note that the slowest process is clearly contained in the data chunks and is reversibly sampled (left panel, short trajectory pieces color coded and stacked).
Due to very short trajectories, we find that this process can only be captured at a very short MSM lag time (right panel).
Above that interval, the slowest timescale diverges.
Luckily, here we know that it is already converged at $\tau = 1$, so we estimate an MSM:
```
msm_short_trajectories = pyemma.msm.estimate_markov_model(dtrajs_short, 1)
```
Let's now have a look at the CK-test:
```
pyemma.plots.plot_cktest(msm_short_trajectories.cktest(2), marker='.');
```
As already discussed, we cannot expect new estimates above a certain lag time to agree with the model prediction due to too short trajectories.
Indeed, we find that new estimates and model predictions diverge at very high lag times.
This does not necessarily mean that the model at $\tau=1$ is wrong and in this particular case,
we can even explain the divergence and find that it fits to the implied timescales divergence.
This example mirrors another incarnation of the sampling problem: Working with large systems,
we often have comparably short trajectories with few rare events.
Thus, implied timescales convergence can often be achieved only in a certain interval and CK-tests will not converge up to arbitrary multiples of the lag time.
It is the responsibility of the modeler to interpret these results and to ensure that a valid model can be obtained from the data.
Please note that this is only a special case of a failed CK test.
More general information about CK tests and what it means if it fails are explained in
[Notebook 03 ➜ 📓](03-msm-estimation-and-validation.ipynb).
## Case 2: low-dimensional molecular dynamics data (alanine dipeptide)
In this example, we will show how an ill-conducted TICA analysis can yield results that look metastable in the 2D histogram,
but in fact are not describing the slow dynamics.
Please note that this was deliberately broken with a nonsensical TICA-lagtime of almost trajectory length, which is 250 ns.
We start off with adding all atom coordinates.
That is a non-optimal choice because it artificially blows up the dimensionality,
but might still be a reasonable choice depending on the problem.
A well-conducted TICA projection can extract the slow coordinates, as we will see at the end of this example.
```
pdb = mdshare.fetch('alanine-dipeptide-nowater.pdb', working_directory='data')
files = mdshare.fetch('alanine-dipeptide-*-250ns-nowater.xtc', working_directory='data')
feat = pyemma.coordinates.featurizer(pdb)
feat.add_all()
data = pyemma.coordinates.load(files, features=feat)
```
TICA analysis is conducted with an extremely high lag time of almost $249.9$ ns. We map down to two dimensions.
```
tica = pyemma.coordinates.tica(data, lag=data[0].shape[0] - 100, dim=2)
tica_output = tica.get_output()
pyemma.plots.plot_free_energy(*np.concatenate(tica_output).T, legacy=False);
```
In the free energy plot, we recognize two defined basins that are nicely separated by the first TICA component. We thus continue with a discretization of this space and estimate MSM implied timescales.
```
cluster = pyemma.coordinates.cluster_kmeans(tica_output, k=200, max_iter=30, stride=100)
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 5, 10, 20, 30, 50])
pyemma.plots.plot_implied_timescales(its, marker='o', units='ps', nits=3);
```
Indeed, we observe a converged implied timescale.
In this example we already know that it is way lower than expected,
but in the general case we are unaware of the real dynamics of the system.
Thus, we estimate an MSM at lag time $20 $ ps.
Coarse graining and validation will be done with $2$ metastable states since we found $2$ basins in the free energy landscape and have one slow process in the ITS plot.
```
msm = pyemma.msm.estimate_markov_model(cluster.dtrajs, 20)
nstates = 2
msm.pcca(nstates);
stride = 10
metastable_trajs_strided = [msm.metastable_assignments[dtrj[::stride]] for dtrj in cluster.dtrajs]
tica_output_strided = [i[::stride] for i in tica_output]
_, _, misc = pyemma.plots.plot_state_map(*np.concatenate(tica_output_strided).T,
np.concatenate(metastable_trajs_strided));
misc['cbar'].set_ticklabels(range(1, nstates + 1)) # set state numbers 1 ... nstates
```
As we see, the PCCA++ algorithm is perfectly able to separate the two basins.
Let's go on with a Chapman-Kolmogorow validation.
```
pyemma.plots.plot_cktest(msm.cktest(nstates), units='ps');
```
Congratulations, we have estimated a well-validated MSM.
The only question remaining is: What does it actually describe?
For this, we usually extract representative structures as described in [Notebook 00 ➜ 📓](00-pentapeptide-showcase.ipynb).
We will not do this here but look at the metastable trajectories instead.
#### What could be wrong about it?
Let's have a look at the trajectories as assigned to PCCA++ metastable states.
We have already computed them before but not looked at their time dependence.
```
fig, ax = plt.subplots(1, 1, figsize=(15, 6), sharey=True, sharex=True)
ax_yticks_labels = []
for n, pcca_traj in enumerate(metastable_trajs_strided):
ax.plot(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, color='k', linewidth=0.3)
ax.scatter(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, c=pcca_traj, s=0.1)
ax_yticks_labels.append(((msm.n_metastable * (2 * n + 1) - 1) / 2, n + 1))
ax.set_yticks([l[0] for l in ax_yticks_labels])
ax.set_yticklabels([str(l[1]) for l in ax_yticks_labels])
ax.set_ylabel('Trajectory #')
ax.set_xlabel('time / {} ps'.format(stride))
fig.tight_layout()
```
#### What do we see?
The above figure shows the metastable states visited by the trajectory over time.
Each metastable state is color-coded, the trajectory is shown by the black line.
This is clearly not a metastable trajectory as we would have expected.
What did we do wrong?
Let's have a look at the TICA trajectories, not only the histogram!
```
fig, axes = plt.subplots(2, 3, figsize=(12, 6), sharex=True, sharey='row')
for n, trj in enumerate(tica_output):
for dim, traj1d in enumerate(trj.T):
axes[dim, n].plot(traj1d[::stride], linewidth=.5)
for ax in axes[1]:
ax.set_xlabel('time / {} ps'.format(stride))
for dim, ax in enumerate(axes[:, 0]):
ax.set_ylabel('IC {}'.format(dim + 1))
for n, ax in enumerate(axes[0]):
ax.set_title('Trajectory # {}'.format(n + 1))
fig.tight_layout()
```
This is essentially noise, so it is not surprising that the metastable trajectories do not show significant metastability.
The MSM nevertheless found a process in the above TICA components which, however,
does not seem to describe any of the slow dynamics.
Thus, the model is not wrong, it is just not informative.
As we see in this example, it can be instructive to keep the trajectories in mind and not to rely on the histograms alone.
⚠️ Histograms are no proof of metastability,
they can only give us a hint towards defined states in a multi-dimensional state space which can be metastable.
#### How to fix it?
In this particular example, we already know the issue:
the TICA lag time was deliberately chosen way too high.
That's easy to fix.
Let's now have a look at how the metastable trajectories should look for a decent model such as the one estimated in [Notebook 05 ➜ 📓](05-pcca-tpt.ipynb).
We will take the same input data,
do a TICA transform with a realistic lag time of $10$ ps,
and coarse grain into $2$ metastable states in order to compare with the example above.
```
tica = pyemma.coordinates.tica(data, lag=10, dim=2)
tica_output = tica.get_output()
cluster = pyemma.coordinates.cluster_kmeans(tica_output, k=200, max_iter=30, stride=100)
pyemma.plots.plot_free_energy(*np.concatenate(tica_output).T, legacy=False);
```
As wee see, TICA yields a very nice state separation.
We will see that these states are in fact metastable.
```
msm = pyemma.msm.estimate_markov_model(cluster.dtrajs, lag=20)
msm.pcca(nstates);
metastable_trajs_strided = [msm.metastable_assignments[dtrj[::stride]] for dtrj in cluster.dtrajs]
stride = 10
tica_output_strided = [i[::stride] for i in tica_output]
_, _, misc = pyemma.plots.plot_state_map(*np.concatenate(tica_output_strided).T,
np.concatenate(metastable_trajs_strided));
misc['cbar'].set_ticklabels(range(1, nstates + 1)) # set state numbers 1 ... nstates
```
We note that PCCA++ separates the two basins of the free energy plot.
Let's have a look at the metastable trajectories:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 6), sharey=True, sharex=True)
ax_yticks_labels = []
for n, pcca_traj in enumerate(metastable_trajs_strided):
ax.plot(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, color='k', linewidth=0.3)
ax.scatter(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, c=pcca_traj, s=0.1)
ax_yticks_labels.append(((msm.n_metastable * (2 * n + 1) - 1) / 2, n + 1))
ax.set_yticks([l[0] for l in ax_yticks_labels])
ax.set_yticklabels([str(l[1]) for l in ax_yticks_labels])
ax.set_ylabel('Trajectory #')
ax.set_xlabel('time / {} ps'.format(stride))
fig.tight_layout()
```
These trajectories show the expected behavior of a metastable trajectory,
i.e., it does not quickly jump back and forth between the states.
## Wrapping up
In this notebook, we have learned about some problems that can arise when estimating MSMs with "real world" data at simple examples.
In detail, we have seen
- irreversibly connected dynamics and what it means for MSM estimation,
- fully disconnected trajectories and how to identify them,
- connected but poorly sampled trajectories and how convergence looks in this case,
- ill-conducted TICA analysis and what it yields.
The most important lesson from this tutorial is that histograms, which are usually calculated in a projected space, are not a sufficient means of identifying metastability or connectedness.
It is crucial to remember that the underlying trajectories play the role of ground truth for the model.
Ultimately, histograms only help us to understand this ground truth but cannot provide a complete picture.
|
github_jupyter
|
```
import tensorflow as tf
import tensorflow as tf
from tensorflow.python.keras.applications.vgg19 import VGG19
model=VGG19(
include_top=False,
weights='imagenet'
)
model.trainable=False
model.summary()
from tensorflow.python.keras.preprocessing.image import load_img, img_to_array
from tensorflow.python.keras.applications.vgg19 import preprocess_input
from tensorflow.python.keras.models import Model
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def load_and_process_image(image_path):
img=load_img(image_path)
img=img_to_array(img)
img=preprocess_input(img)
img=np.expand_dims(img,axis=0)
return img
def deprocess(x):
x[:,:,0]+=103.939
x[:,:,1]+=116.779
x[:,:,2]+=123.68
x=x[:,:,::-1]
x=np.clip(x,0,255).astype('uint8')
return x
def display_image(image):
if len(image.shape)==4:
img=np.squeeze(image,axis=0)
img=deprocess(img)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img)
return
display_image(load_and_process_image('style.jpg'))
style_layers = [
'block1_conv1',
'block3_conv1',
'block5_conv1'
]
content_layer = 'block5_conv2'
# intermediate models
content_model = Model(
inputs = model.input,
outputs = model.get_layer(content_layer).output
)
style_models = [Model(inputs = model.input,
outputs = model.get_layer(layer).output) for layer in style_layers]
# Content Cost
def content_cost(content, generated):
a_C = content_model(content)
a_G = content_model(generated)
cost = tf.reduce_mean(tf.square(a_C - a_G))
return cost
def gram_matrix(A):
channels = int(A.shape[-1])
a = tf.reshape(A, [-1, channels])
n = tf.shape(a)[0]
gram = tf.matmul(a, a, transpose_a = True)
return gram / tf.cast(n, tf.float32)
lam = 1. / len(style_models)
def style_cost(style, generated):
J_style = 0
for style_model in style_models:
a_S = style_model(style)
a_G = style_model(generated)
GS = gram_matrix(a_S)
GG = gram_matrix(a_G)
current_cost = tf.reduce_mean(tf.square(GS - GG))
J_style += current_cost * lam
return J_style
import time
generated_images = []
def training_loop(content_path, style_path, iterations = 20, a = 10., b = 20.):
# initialise
content = load_and_process_image(content_path)
style = load_and_process_image(style_path)
generated = tf.Variable(content, dtype = tf.float32)
opt = tf.optimizers.Adam(learning_rate = 7.)
best_cost = 1e12+0.1
best_image = None
start_time = time.time()
for i in range(iterations):
with tf.GradientTape() as tape:
J_content = content_cost(content, generated)
J_style = style_cost(style, generated)
J_total = a * J_content + b * J_style
grads = tape.gradient(J_total, generated)
opt.apply_gradients([(grads, generated)])
if J_total < best_cost:
best_cost = J_total
best_image = generated.numpy()
if i % int(iterations/10) == 0:
time_taken = time.time() - start_time
print('Cost at {}: {}. Time elapsed: {}'.format(i, J_total, time_taken))
generated_images.append(generated.numpy())
return best_image
final = training_loop('content.jpg','style.jpg')
plt.figure(figsize = (12, 12))
for i in range(10):
plt.subplot(5, 2, i + 1)
display_image(generated_images[i])
plt.show()
```
|
github_jupyter
|
```
%reload_ext watermark
%matplotlib inline
from os.path import exists
from metapool.metapool import *
from metapool import (validate_plate_metadata, assign_emp_index, make_sample_sheet, KLSampleSheet, parse_prep, validate_and_scrub_sample_sheet, generate_qiita_prep_file)
%watermark -i -v -iv -m -h -p metapool,sample_sheet,openpyxl -u
```
# Knight Lab Amplicon Sample Sheet and Mapping (preparation) File Generator
### What is it?
This Jupyter Notebook allows you to automatically generate sample sheets for amplicon sequencing.
### Here's how it should work.
You'll start out with a **basic plate map** (platemap.tsv) , which just links each sample to it's approprite row and column.
You can use this google sheet template to generate your plate map:
https://docs.google.com/spreadsheets/d/1xPjB6iR3brGeG4bm2un4ISSsTDxFw5yME09bKqz0XNk/edit?usp=sharing
Next you'll automatically assign EMP barcodes in order to produce a **sample sheet** (samplesheet.csv) that can be used in combination with the rest of the sequence processing pipeline.
**Please designate what kind of amplicon sequencing you want to perform:**
```
seq_type = '16S'
#options are ['16S', '18S', 'ITS']
```
## Step 1: read in plate map
**Enter the correct path to the plate map file**. This will serve as the plate map for relating all subsequent information.
```
plate_map_fp = './test_data/amplicon/compressed-map.tsv'
if not exists(plate_map_fp):
print("Error: %s is not a path to a valid file" % plate_map_fp)
```
**Read in the plate map**. It should look something like this:
```
Sample Row Col Blank
GLY_01_012 A 1 False
GLY_14_034 B 1 False
GLY_11_007 C 1 False
GLY_28_018 D 1 False
GLY_25_003 E 1 False
GLY_06_106 F 1 False
GLY_07_011 G 1 False
GLY_18_043 H 1 False
GLY_28_004 I 1 False
```
**Make sure there a no duplicate IDs.** If each sample doesn't have a different name, an error will be thrown and you won't be able to generate a sample sheet.
```
plate_df = read_plate_map_csv(open(plate_map_fp,'r'))
plate_df.head()
```
# Assign barcodes according to primer plate
This portion of the notebook will assign a barcode to each sample according to the primer plate number.
As inputs, it requires:
1. A plate map dataframe (from previous step)
2. Preparation metadata for the plates, importantly we need the Primer Plate # so we know what **EMP barcodes** to assign to each plate.
The workflow then:
1. Joins the preparation metadata with the plate metadata.
2. Assigns indices per sample
## Enter and validate the plating metadata
- In general you will want to update all the fields, but the most important ones are the `Primer Plate #` and the `Plate Position`. `Primer Plate #` determines which EMP barcodes will be used for this plate. `Plate Position` determines the physical location of the plate.
- If you are plating less than four plates, then remove the metadata for that plate by deleting the text between the curly braces.
- For missing fields, write NA between the single quotes for example `'NA'`.
- To enter a plate copy and paste the contents from the plates below.
```
_metadata = [
{
# top left plate
'Plate Position': '1',
'Primer Plate #': '1',
'Sample Plate': 'THDMI_UK_Plate_2',
'Project_Name': 'THDMI UK',
'Plating': 'SF',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF3',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# top right plate
'Plate Position': '2',
'Primer Plate #': '2',
'Sample Plate': 'THDMI_UK_Plate_3',
'Project_Name': 'THDMI UK',
'Plating':'AS',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF4',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# bottom left plate
'Plate Position': '3',
'Primer Plate #': '3',
'Sample Plate': 'THDMI_UK_Plate_4',
'Project_Name': 'THDMI UK',
'Plating':'MB_SF',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF3',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# bottom right plate
'Plate Position': '4',
'Primer Plate #': '4',
'Sample Plate': 'THDMI_US_Plate_6',
'Project_Name': 'THDMI US',
'Plating':'AS',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF4',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
]
plate_metadata = validate_plate_metadata(_metadata)
plate_metadata
```
The `Plate Position` and `Primer Plate #` allow us to figure out which wells are associated with each of the EMP barcodes.
```
if plate_metadata is not None:
plate_df = assign_emp_index(plate_df, plate_metadata, seq_type).reset_index()
plate_df.head()
else:
print('Error: Please fix the errors in the previous cell')
```
As you can see in the table above, the resulting table is now associated with the corresponding EMP barcodes (`Golay Barcode`, `Forward Primer Linker`, etc), and the plating metadata (`Primer Plate #`, `Primer Date`, `Water Lot`, etc).
```
plate_df.head()
```
# Combine plates (optional)
If you would like to combine existing plates with these samples, enter the path to their corresponding sample sheets and mapping (preparation) files below. Otherwise you can skip to the next section.
- sample sheet and mapping (preparation)
```
files = [
# uncomment the line below and point to the correct filepaths to combine with previous plates
# ['test_output/amplicon/2021_08_17_THDMI-4-6_samplesheet.csv', 'test_output/amplicon/2021-08-01-515f806r_prep.tsv'],
]
sheets, preps = [], []
for sheet, prep in files:
sheets.append(KLSampleSheet(sheet))
preps.append(parse_prep(prep))
if len(files):
print('%d pair of files loaded' % len(files))
```
# Make Sample Sheet
This workflow takes the pooled sample information and writes an Illumina sample sheet that can be given directly to the sequencing center or processing pipeline. Note that as of writing `bcl2fastq` does not support error-correction in Golay barcodes so the sample sheet is used to generate a mapping (preparation) file but not to demultiplex sequences. Demultiplexing takes place in [Qiita](https://qiita.ucsd.edu).
As inputs, this notebook requires:
1. A plate map DataFrame (from previous step)
The workflow:
1. formats sample names as bcl2fastq-compatible
2. formats sample data
3. sets values for sample sheet fields and formats sample sheet.
4. writes the sample sheet to a file
## Step 1: Format sample names to be bcl2fastq-compatible
bcl2fastq requires *only* alphanumeric, hyphens, and underscore characters. We'll replace all non-those characters
with underscores and add the bcl2fastq-compatible names to the DataFrame.
```
plate_df['sample sheet Sample_ID'] = plate_df['Sample'].map(bcl_scrub_name)
plate_df.head()
```
## Format the sample sheet data
This step formats the data columns appropriately for the sample sheet, using the values we've calculated previously.
The newly-created `bcl2fastq`-compatible names will be in the `Sample ID` and `Sample Name` columns. The original sample names will be in the Description column.
Modify lanes to indicate which lanes this pool will be sequenced on.
The `Project Name` and `Project Plate` columns will be placed in the `Sample_Project` and `Sample_Name` columns, respectively.
sequencer is important for making sure the i5 index is in the correct orientation for demultiplexing. `HiSeq4000`, `HiSeq3000`, `NextSeq`, and `MiniSeq` all require reverse-complemented i5 index sequences. If you enter one of these exact strings in for sequencer, it will revcomp the i5 sequence for you.
`HiSeq2500`, `MiSeq`, and `NovaSeq` will not revcomp the i5 sequence.
```
sequencer = 'HiSeq4000'
lanes = [1]
metadata = {
'Bioinformatics': [
{
'Sample_Project': 'THDMI_10317',
'QiitaID': '10317',
'BarcodesAreRC': 'False',
'ForwardAdapter': '',
'ReverseAdapter': '',
'HumanFiltering': 'True',
'library_construction_protocol': 'Illumina EMP protocol 515fbc, 806r amplification of 16S rRNA V4',
'experiment_design_description': 'Equipment',
},
],
'Contact': [
{
'Sample_Project': 'THDMI_10317',
# non-admin contacts who want to know when the sequences
# are available in Qiita
'Email': '[email protected],[email protected]'
},
],
'Chemistry': 'Amplicon',
'Assay': 'TruSeq HT',
}
sheet = make_sample_sheet(metadata, plate_df, sequencer, lanes)
sheet.Settings['Adapter'] = 'AGATCGGAAGAGCACACGTCTGAACTCCAGTCA'
sheet.Settings['AdapterRead2'] = 'AGATCGGAAGAGCGTCGTGTAGGGAAAGAGTGT'
```
Check for any possible errors in the sample sheet
```
sheet = validate_and_scrub_sample_sheet(sheet)
```
Add the other sample sheets
```
if len(sheets):
sheet.merge(sheets)
```
## Step 3: Write the sample sheet to file
```
# write sample sheet as .csv
sample_sheet_fp = './test_output/amplicon/2021_08_17_THDMI-4-6_samplesheet16S.csv'
if exists(sample_sheet_fp):
print("Warning! This file exists already.")
with open(sample_sheet_fp,'w') as f:
sheet.write(f)
!head -n 30 {sample_sheet_fp}
!echo ...
!tail -n 15 {sample_sheet_fp}
```
# Create a mapping (preparation) file for Qiita
```
output_filename = 'test_output/amplicon/2021-08-01-515f806r_prep.tsv'
qiita_df = generate_qiita_prep_file(plate_df, seq_type)
qiita_df.head()
qiita_df.set_index('sample_name', verify_integrity=True).to_csv(output_filename, sep='\t')
```
Add the previous sample sheets
```
if len(preps):
prep = prep.append(preps, ignore_index=True)
!head -n 5 {output_filename}
```
|
github_jupyter
|
<img src="../../images/banners/python-basics.png" width="600"/>
# <img src="../../images/logos/python.png" width="23"/> Conda Environments
## <img src="../../images/logos/toc.png" width="20"/> Table of Contents
* [Understanding Conda Environments](#understanding_conda_environments)
* [Understanding Basic Package Management With Conda](#understanding_basic_package_management_with_conda)
* [Searching and Installing Packages](#searching_and_installing_packages)
* [Updating and Removing Packages](#updating_and_removing_packages)
* [Cheat Sheet](#cheat_sheet)
* [<img src="../../images/logos/web.png" width="20"/> Read More](#<img_src="../../images/logos/web.png"_width="20"/>_read_more)
---
<a class="anchor" id="understanding_conda_environments"></a>
## Understanding Conda Environments
When you start developing a project from scratch, it’s recommended that you use the latest versions of the libraries you need. However, when working with someone else’s project, such as when running an example from [Kaggle](https://www.kaggle.com/) or [Github](https://github.com/), you may need to install specific versions of packages or even another version of Python due to compatibility issues.
This problem may also occur when you try to run an application you’ve developed long ago, which uses a particular library version that does not work with your application anymore due to updates.
Virtual environments are a solution to this kind of problem. By using them, it is possible to create multiple environments, each one with different versions of packages. A typical Python set up includes [Virtualenv](https://virtualenv.pypa.io/en/stable/#), a tool to create isolated Python virtual environments, widely used in the Python community.
Conda includes its own environment manager and presents some advantages over Virtualenv, especially concerning numerical applications, such as the ability to manage non-Python dependencies and the ability to manage different versions of Python, which is not possible with Virtualenv. Besides that, Conda environments are entirely compatible with default [Python packages](https://realpython.com/python-modules-packages/) that may be installed using pip.
Miniconda installation provides Conda and a root environment with a version of Python and some basic packages installed. Besides this root environment, it is possible to set up additional environments including different versions of Python and packages.
<a class="anchor" id="conda_environments:"></a>
Using the Anaconda prompt, it is possible to check the available Conda environments by running `conda env list`:
```bash
$ (base) ~ % conda env list
# conda environments:
#
base * /home/ali/anaconda3
```
<a class="anchor" id="package_plan_##"></a>
This base environment is the root environment, created by the Miniconda installer. It is possible to create another environment, named `otherenv`, by running `conda create --name otherenv`:
```bash
$ (base) ~ % conda create --name otherenv
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\otherenv
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate otherenv
#
# To deactivate an active environment, use
#
# $ conda deactivate
```
As notified after the environment creation process is finished, it is possible to activate the otherenv environment by running `conda activate otherenv`. You’ll notice the environment has changed by the indication between parentheses in the beginning of the prompt:
```bash
$ (base) ~ % conda activate otherenv
$ (otherenv) ~ %
```
You can open the Python interpreter within this environment by running `python`:
```bash
$ (otherenv) ~ % python
Python 3.7.0 (default, Jun 28 2018, 08:04:48) [MSC v.1912 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>>>
```
The environment includes Python 3.7.0, the same version included in the root base environment. To exit the Python interpreter, just run `quit()`:
```bash
>>> quit()
(otherenv) ~ %
```
To deactivate the otherenv environment and go back to the root base environment, you should run `deactivate`:
```bash
(otherenv) ~ % conda deactivate
(base) ~ %
```
<a class="anchor" id="package_plan_##"></a>
As mentioned earlier, Conda allows you to easily create environments with different versions of Python, which is not straightforward with Virtualenv. To include a different Python version within an environment, you have to specify it by using `python=<version>` when running conda create. For example, to create an environment named `py2` with `Python 2.7`, you have to run `conda create --name py2 python=2.7`:
```bash
(base) ~ % create --name py2 python=2.7
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\py2
added / updated specs:
- python=2.7
The following NEW packages will be INSTALLED:
certifi: 2018.8.24-py27_1
pip: 10.0.1-py27_0
python: 2.7.15-he216670_0
setuptools: 40.2.0-py27_0
vc: 9-h7299396_1
vs2008_runtime: 9.00.30729.1-hfaea7d5_1
wheel: 0.31.1-py27_0
wincertstore: 0.2-py27hf04cefb_0
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate py2
#
# To deactivate an active environment, use
#
# $ conda deactivate
(base) /mnt/c/Users/username%
```
As shown by the output of `conda create`, this time some new packages were installed, since the new environment uses Python 2. You can check the new environment indeed uses Python 2 by activating it and running the Python interpreter:
```
(base) ~ % conda activate py2
```
<a class="anchor" id="conda_environments:"></a>
Now, if you run `conda env list`, you should see the two environments that were created, besides the root base environment:
```bash
(py2) ~ % conda env list
# conda environments:
#
base C:\Users\IEUser\Miniconda3
otherenv C:\Users\IEUser\Miniconda3\envs\otherenv
py2 * C:\Users\IEUser\Miniconda3\envs\py2
(py2) ~ %
```
<a class="anchor" id="package_plan_##"></a>
In the list, the asterisk indicates the activated environment. It is possible to remove an environment by running `conda remove --name <environment name> --all`. Since it is not possible to remove an activated environment, you should first deactivate the `py2` environment, to remove it:
```bash
(py2) ~ % conda deactivate
(base) ~ % conda remove --name py2 --all
Remove all packages in environment C:\Users\IEUser\Miniconda3\envs\py2:
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\py2
The following packages will be REMOVED:
certifi: 2018.8.24-py27_1
pip: 10.0.1-py27_0
python: 2.7.15-he216670_0
setuptools: 40.2.0-py27_0
vc: 9-h7299396_1
vs2008_runtime: 9.00.30729.1-hfaea7d5_1
wheel: 0.31.1-py27_0
wincertstore: 0.2-py27hf04cefb_0
Proceed ([y]/n)? y
(base) /mnt/c/Users/username%
```
Now that you’ve covered the basics of managing environments with Conda, let’s see how to manage packages within the environments.
<a class="anchor" id="understanding_basic_package_management_with_conda"></a>
## Understanding Basic Package Management With Conda
Within each environment, packages of software can be installed using the Conda package manager. The root base environment created by the Miniconda installer includes some packages by default that are not part of Python standard library.
<a class="anchor" id="packages_in_environment_at_c:\users\ieuser\miniconda3:"></a>
The default installation includes the minimum packages necessary to use Conda. To check the list of installed packages in an environment, you just have to make sure it is activated and run `conda list`. In the root environment, the following packages are installed by default:
```bash
(base) ~ % conda list
# packages in environment at C:\Users\IEUser\Miniconda3:
#
# Name Version Build Channel
asn1crypto 0.24.0 py37_0
ca-certificates 2018.03.07 0
certifi 2018.8.24 py37_1
cffi 1.11.5 py37h74b6da3_1
chardet 3.0.4 py37_1
conda 4.5.11 py37_0
conda-env 2.6.0 1
console_shortcut 0.1.1 3
cryptography 2.3.1 py37h74b6da3_0
idna 2.7 py37_0
menuinst 1.4.14 py37hfa6e2cd_0
openssl 1.0.2p hfa6e2cd_0
pip 10.0.1 py37_0
pycosat 0.6.3 py37hfa6e2cd_0
pycparser 2.18 py37_1
pyopenssl 18.0.0 py37_0
pysocks 1.6.8 py37_0
python 3.7.0 hea74fb7_0
pywin32 223 py37hfa6e2cd_1
requests 2.19.1 py37_0
ruamel_yaml 0.15.46 py37hfa6e2cd_0
setuptools 40.2.0 py37_0
six 1.11.0 py37_1
urllib3 1.23 py37_0
vc 14 h0510ff6_3
vs2015_runtime 14.0.25123 3
wheel 0.31.1 py37_0
win_inet_pton 1.0.1 py37_1
wincertstore 0.2 py37_0
yaml 0.1.7 hc54c509_2
```
To manage the packages, you should also use Conda. Next, let’s see how to search, install, update, and remove packages using Conda.
<a class="anchor" id="searching_and_installing_packages"></a>
### Searching and Installing Packages
Packages are installed from repositories called **channels** by Conda, and some default channels are configured by the installer. To search for a specific package, you can run `conda search <package name>`. For example, this is how you search for the `keras` package (a machine learning library):
```bash
(base) ~ % conda search keras
Loading channels: done
# Name Version Build Channel
keras 2.0.8 py35h15001cb_0 pkgs/main
keras 2.0.8 py36h65e7a35_0 pkgs/main
keras 2.1.2 py35_0 pkgs/main
keras 2.1.2 py36_0 pkgs/main
keras 2.1.3 py35_0 pkgs/main
keras 2.1.3 py36_0 pkgs/main
... (more)
```
According to the previous output, there are different versions of the package and different builds for each version, such as for Python 3.5 and 3.6.
<a class="anchor" id="name_version_build_channel"></a>
The previous search shows only exact matches for packages named `keras`. To perform a broader search, including all packages containing `keras` in their names, you should use the wildcard `*`. For example, when you run conda search `*keras*`, you get the following:
```bash
(base) ~ % conda search "*keras*"
Loading channels: done
# Name Version Build Channel
keras 2.0.8 py35h15001cb_0 pkgs/main
keras 2.0.8 py36h65e7a35_0 pkgs/main
keras 2.1.2 py35_0 pkgs/main
keras 2.1.2 py36_0 pkgs/main
keras 2.1.3 py35_0 pkgs/main
keras 2.1.3 py36_0 pkgs/main
... (more)
keras-applications 1.0.2 py35_0 pkgs/main
keras-applications 1.0.2 py36_0 pkgs/main
keras-applications 1.0.4 py35_0 pkgs/main
... (more)
keras-base 2.2.0 py35_0 pkgs/main
keras-base 2.2.0 py36_0 pkgs/main
... (more)
```
As the previous output shows, there are some other keras related packages in the default channels.
<a class="anchor" id="package_plan_##"></a>
To install a package, you should run `conda install <package name>`. By default, the newest version of the package will be installed in the active environment. So, let’s install the package `keras` in the environment `otherenv` that you’ve already created:
```bash
(base) ~ % conda activate otherenv
(otherenv) ~ % conda install keras
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\otherenv
added / updated specs:
- keras
The following NEW packages will be INSTALLED:
_tflow_1100_select: 0.0.3-mkl
absl-py: 0.4.1-py36_0
astor: 0.7.1-py36_0
blas: 1.0-mkl
certifi: 2018.8.24-py36_1
gast: 0.2.0-py36_0
grpcio: 1.12.1-py36h1a1b453_0
h5py: 2.8.0-py36h3bdd7fb_2
hdf5: 1.10.2-hac2f561_1
icc_rt: 2017.0.4-h97af966_0
intel-openmp: 2018.0.3-0
keras: 2.2.2-0
keras-applications: 1.0.4-py36_1
keras-base: 2.2.2-py36_0
keras-preprocessing: 1.0.2-py36_1
libmklml: 2018.0.3-1
libprotobuf: 3.6.0-h1a1b453_0
markdown: 2.6.11-py36_0
mkl: 2019.0-117
mkl_fft: 1.0.4-py36h1e22a9b_1
mkl_random: 1.0.1-py36h77b88f5_1
numpy: 1.15.1-py36ha559c80_0
numpy-base: 1.15.1-py36h8128ebf_0
pip: 10.0.1-py36_0
protobuf: 3.6.0-py36he025d50_0
python: 3.6.6-hea74fb7_0
pyyaml: 3.13-py36hfa6e2cd_0
scipy: 1.1.0-py36h4f6bf74_1
setuptools: 40.2.0-py36_0
six: 1.11.0-py36_1
tensorboard: 1.10.0-py36he025d50_0
tensorflow: 1.10.0-mkl_py36hb361250_0
tensorflow-base: 1.10.0-mkl_py36h81393da_0
termcolor: 1.1.0-py36_1
vc: 14-h0510ff6_3
vs2013_runtime: 12.0.21005-1
vs2015_runtime: 14.0.25123-3
werkzeug: 0.14.1-py36_0
wheel: 0.31.1-py36_0
wincertstore: 0.2-py36h7fe50ca_0
yaml: 0.1.7-hc54c509_2
zlib: 1.2.11-h8395fce_2
Proceed ([y]/n)?
```
Conda manages the necessary dependencies for a package when it is installed. Since the package keras has a lot of dependencies, when you install it, Conda manages to install this big list of packages.
> **Note:** The paragraph below may not happen when you run it as newer versions of `keras` may be available that use python 3.7.
It’s worth noticing that, since the keras package’s newest build uses Python 3.6 and the otherenv environment was created using Python 3.7, the package python version 3.6.6 was included as a dependency. After confirming the installation, you can check that the Python version for the otherenv environment is downgraded to the 3.6.6 version.
Sometimes, you don’t want packages to be downgraded, and it would be better to just create a new environment with the necessary version of Python. To check the list of new packages, updates, and downgrades necessary for a package without installing it, you should use the parameter `--dry-run`. For example, to check the packages that will be changed by the installation of the package keras, you should run the following:
```
(base) ~ % conda install keras --dry-run
```
<a class="anchor" id="package_plan_##"></a>
However, if necessary, it is possible to change the default Python of a Conda environment by installing a specific version of the package python. To demonstrate that, let’s create a new environment called envpython:
```bash
(otherenv) ~ % conda create --name envpython
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\envpython
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate envpython
#
# To deactivate an active environment, use
#
# $ conda deactivate
```
As you saw before, since the root base environment uses Python 3.7, envpython is created including this same version of Python:
```bash
(base) ~ % conda activate envpython
(envpython) ~ % python
Python 3.7.0 (default, Jun 28 2018, 08:04:48) [MSC v.1912 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> quit()
```
<a class="anchor" id="package_plan_##"></a>
To install a specific version of a package, you can run `conda install <package name>=<version>`. For example, this is how you install Python 3.6 in the envpython environment:
```bash
(envpython) ~ % conda install python=3.6
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\envpython
added / updated specs:
- python=3.6
The following NEW packages will be INSTALLED:
certifi: 2018.8.24-py36_1
pip: 10.0.1-py36_0
python: 3.6.6-hea74fb7_0
setuptools: 40.2.0-py36_0
vc: 14-h0510ff6_3
vs2015_runtime: 14.0.25123-3
wheel: 0.31.1-py36_0
wincertstore: 0.2-py36h7fe50ca_0
Proceed ([y]/n)?
```
<a class="anchor" id="package_plan_##"></a>
In case you need to install more than one package in an environment, it is possible to run conda install only once, passing the names of the packages. To illustrate that, let’s install `numpy`, `scipy`, and `matplotlib`, basic packages for numerical computation:
```bash
(envpython) ~ % conda install numpy scipy matplotlib
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3
added / updated specs:
- matplotlib
- numpy
- scipy
The following packages will be downloaded:
package | build
---------------------------|-----------------
libpng-1.6.34 | h79bbb47_0 1.3 MB
mkl_random-1.0.1 | py37h77b88f5_1 267 KB
intel-openmp-2019.0 | 117 1.7 MB
qt-5.9.6 | vc14h62aca36_0 92.5 MB
matplotlib-2.2.3 | py37hd159220_0 6.5 MB
tornado-5.1 | py37hfa6e2cd_0 668 KB
pyqt-5.9.2 | py37ha878b3d_0 4.6 MB
pytz-2018.5 | py37_0 232 KB
scipy-1.1.0 | py37h4f6bf74_1 13.5 MB
jpeg-9b | hb83a4c4_2 313 KB
python-dateutil-2.7.3 | py37_0 260 KB
numpy-base-1.15.1 | py37h8128ebf_0 3.9 MB
numpy-1.15.1 | py37ha559c80_0 37 KB
mkl_fft-1.0.4 | py37h1e22a9b_1 120 KB
kiwisolver-1.0.1 | py37h6538335_0 61 KB
pyparsing-2.2.0 | py37_1 96 KB
cycler-0.10.0 | py37_0 13 KB
freetype-2.9.1 | ha9979f8_1 470 KB
icu-58.2 | ha66f8fd_1 21.9 MB
sqlite-3.24.0 | h7602738_0 899 KB
sip-4.19.12 | py37h6538335_0 283 KB
------------------------------------------------------------
Total: 149.5 MB
The following NEW packages will be INSTALLED:
blas: 1.0-mkl
cycler: 0.10.0-py37_0
freetype: 2.9.1-ha9979f8_1
icc_rt: 2017.0.4-h97af966_0
icu: 58.2-ha66f8fd_1
intel-openmp: 2019.0-117
jpeg: 9b-hb83a4c4_2
kiwisolver: 1.0.1-py37h6538335_0
libpng: 1.6.34-h79bbb47_0
matplotlib: 2.2.3-py37hd159220_0
mkl: 2019.0-117
mkl_fft: 1.0.4-py37h1e22a9b_1
mkl_random: 1.0.1-py37h77b88f5_1
numpy: 1.15.1-py37ha559c80_0
numpy-base: 1.15.1-py37h8128ebf_0
pyparsing: 2.2.0-py37_1
pyqt: 5.9.2-py37ha878b3d_0
python-dateutil: 2.7.3-py37_0
pytz: 2018.5-py37_0
qt: 5.9.6-vc14h62aca36_0
scipy: 1.1.0-py37h4f6bf74_1
sip: 4.19.12-py37h6538335_0
sqlite: 3.24.0-h7602738_0
tornado: 5.1-py37hfa6e2cd_0
zlib: 1.2.11-h8395fce_2
Proceed ([y]/n)?
```
Now that you’ve covered how to search and install packages, let’s see how to update and remove them using Conda.
<a class="anchor" id="updating_and_removing_packages"></a>
### Updating and Removing Packages
Sometimes, when new packages are released, you need to update them. To do so, you may run `conda update <package name>`. In case you wish to update all the packages within one environment, you should activate the environment and run `conda update --all`.
<a class="anchor" id="package_plan_##"></a>
To remove a package, you can run `conda remove <package name>`. For example, this is how you remove numpy from the root base environment:
```bash
(envpython) ~ % conda remove numpy
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3
removed specs:
- numpy
The following packages will be REMOVED:
matplotlib: 2.2.3-py37hd159220_0
mkl_fft: 1.0.4-py37h1e22a9b_1
mkl_random: 1.0.1-py37h77b88f5_1
numpy: 1.15.1-py37ha559c80_0
scipy: 1.1.0-py37h4f6bf74_1
Proceed ([y]/n)?
```
> **Note:** It’s worth noting that when you remove a package, all packages that depend on it are also removed.
<a class="anchor" id="cheat_sheet"></a>
## Cheat Sheet
[Click here to get access to a Conda cheat sheet](https://static.realpython.com/conda-cheatsheet.pdf) with handy usage examples for managing your Python environment and packages.
<a class="anchor" id="read_more"></a>
## <img src="../../images/logos/web.png" width="20"/> Read More
Also, if you’d like a deeper understanding of Anaconda and Conda, check out the following links:
- [Why you need Python environments and how to manage them with Conda](https://medium.freecodecamp.org/why-you-need-python-environments-and-how-to-manage-them-with-conda-85f155f4353c)
- [Conda: Myths and Misconceptions](http://jakevdp.github.io/blog/2016/08/25/conda-myths-and-misconceptions/)
|
github_jupyter
|
# Configuraciones para el Grupo de Estudio
<img src="./img/f_mail.png" style="width: 700px;"/>
## Contenidos
- ¿Por qué jupyter notebooks?
- Bash
- ¿Que es un *kernel*?
- Instalación
- Deberes
## Python y proyecto Jupyter
<img src="./img/py.jpg" style="width: 500px;"/>
<img src="./img/jp.png" style="width: 100px;"/>
- Necesitamos llevar un registro del avance de cada integrante.
- Lenguaje de programación interpretado de alto nivel.
- Jupyter notebooks: son fáciles de usar
- `Necesitamos que todos tengan una versión de Python con jupyter lab`
## ¿Cómo funciona Jupyter?
- Es un derivado del proyecto `iPython`, que ofrece una interfaz interactiva para programadores.
- Tiene formato `.ipynb`
- Es posible usar otros lenguajes de programación diferentes a Python.
- Permite al usuario configurar cómo se visualiza su código mediante `Markdown`.
- Ahora una demostración
<img src="./img/jupex.png" style="width: 500px;"/>
```
import matplotlib.pyplot as plt
import numpy as np
import math
# constantes
pi = math.pi; h = 6.626e-34; kB = 1.380e-23; c = 3.0e+8;
Temps = [9940.00, 8500.00, 7500.00, 6627.00, 5810.93, 4231.15, 3000.00, 2973.15, 288.15]
labels = ['Sirius', 'White star', 'Yellow-white star', 'Polaris', 'Sol', 'HfC', 'Bombilla', 'TaN', 'Atmósfera ']
colors = ['r','g','#FF9633','c','m','#eeefff','y','b','k']
# arreglo de frecuencias
freq = np.arange(0.25e14,3e15,0.25e14)
# funcion spectral energy density (SED)
def SED(f, T):
energyDensity = ( 8*pi*h*(np.power(f, 3.0))/(c**3) ) / (np.exp((h/kB)*f/T) - 1)
return energyDensity
# Calculo de SED para temperaturas
for i in range(len(Temps)):
r = SED(freq,Temps[i])
plt.plot(freq*1e-12,r,color=colors[i],label=labels[i])
plt.legend(); plt.xlabel('frequency ( THz )'); plt.ylabel('SED_frequency ( J $m^{-3}$ $Hz^{-1}$ )')
plt.xlim(0.25e2,2.5e3); plt.show()
```
### Permite escribir expresiones matemáticas complejas
Es posible escribir código en $\LaTeX$ si es necesario
\begin{align}
\frac{\partial u(\lambda, T)}{\partial \lambda} &= \frac{\partial}{\partial \lambda} \left( \frac{C_{1}}{\lambda^{5}}\left(\frac{1}{e^{C_{2}/T\lambda} -1}\right) \right) \\
0 &= \left(\frac{-5}{e^{C_{2}/T\lambda} -1}\frac{1}{\lambda^{6}}\right) + \left( \frac{C_{2}e^{C_{2}/T\lambda}}{T\lambda^{7}} \right)\left(\frac{1}{e^{C_{2}/T\lambda} -1}\right)^{2} \\
0 &= \frac{-\lambda T5}{C_{2}} + \frac{e^{C_{2}/T\lambda}}{e^{C_{2}/T\lambda} -1} \\
0 &= -5 + \left(\frac{C_{2}}{\lambda T}\right) \left(\frac{e^{C_{2}/T\lambda}}{e^{C_{2}/T\lambda} -1}\right)
\end{align}
## ¿Cómo es que usa un lenguaje diferente a Python?
- Un kernel es una especie de `motor computacional` que ejecuta el código dentro de un archivo `.ipynb`.
- Los kernels hay para varios lengajes de programación, como R, Bash, C++, julia.
<img src="./img/ker.png" style="width: 250px;"/>
## ¿Por qué Bash?
- Bash es un lenguaje de scripting que se comunica con la shell e históricamente ha ayudado a científicos a llevarse mejor con la bioinformática.
## ¿Dónde encontramos las instrucciones para instalar Python?
- Es posible hacerlo de varias maneras: `Anaconda` y el `intérprete oficial` desde https://www.python.org/downloads/
- Usaremos el intérprete de `Anaconda`: es más fácil la instalación si no te acostumbras a usar la línea de comandos.
- Si ustedes ya están familiarizados con Python y no desean instalar el intérprete de `Anaconda` pueden usar `pip` desde https://pypi.org/project/bash_kernel/
<img src="./img/qrgit.png" style="width: 250px;"/>
## Deberes
- Creamos una carpeta en `google Drive` donde harán subirán los archivos `.ipynb` y una conversión a HTML, u otro tipo de archivo dependiendo de la sesión.
- Vamos a tener un quiz cada semana, que les enviaremos por el servidor de Discord del grupo de estudio.
- El deber para la siguiente semana:
1. Instalar Ubuntu si aún no lo poseen usando cualquiera de las alternativas presentadas.
2. Instalar Anaconda, jupyter lab y el kernel de bash.
Se deben enviar un documento word o pdf con capturas de pantalla que compruebe esto.
Si tienen algún problema, usen por favor los foros de `Discord` y nos ayudamos entre todos.
<img src="./img/deberes.png" style="width: 500px;"/>
|
github_jupyter
|
# MHKiT Quality Control Module
The following example runs a simple quality control analysis on wave elevation data using the [MHKiT QC module](https://mhkit-software.github.io/MHKiT/mhkit-python/api.qc.html). The data file used in this example is stored in the [\\\\MHKiT\\\\examples\\\\data](https://github.com/MHKiT-Software/MHKiT-Python/tree/master/examples/data) directory.
Start by importing the necessary Python packages and MHKiT modules.
```
import pandas as pd
from mhkit import qc, utils
```
## Load Data
The wave elevation data used in this example includes several issues, including timestamps that are out of order, corrupt data with values of -999, data outside the expected range, and stagnant data.
The data is loaded into a pandas DataFrame using the pandas method `read_csv`. The first 5 rows of data are shown below, along with a plot.
```
# Load data from the csv file into a DataFrame
data = pd.read_csv('data/qc/wave_elevation_data.csv', index_col='Time')
# Plot the data
data.plot(figsize=(15,5), ylim=(-60,60))
# Print the first 5 rows of data
print(data.head())
```
The data is indexed by time in seconds. To use the quality control functions, the data must be indexed by datetime. The index can be converted to datetime using the following utility function.
```
# Convert the index to datetime
data.index = utils.index_to_datetime(data.index, origin='2019-05-20')
# Print the first 5 rows of data
print(data.head())
```
## Quality control tests
The following quality control tests are used to identify timestamp issues, corrupt data, data outside the expected range, and stagnant data.
Each quality control tests results in the following information:
* Cleaned data, which is a DataFrame that has *NaN* in place of data that did not pass the quality control test
* Boolean mask, which is a DataFrame with True/False that indicates if each data point passed the quality control test
* Summary of the quality control test results, the summary includes the variable name (which is blank for timestamp issues), the start and end time of the test failure, and an error flag for each test failure
### Check timestamp
Quality control analysis generally starts by checking the timestamp index of the data.
The following test checks to see if 1) the data contains duplicate timestamps, 2) timestamps are not monotonically increasing, and 3) timestamps occur at irregular intervals (an interval of 0.002s is expected for this data).
If duplicate timestamps are found, the resulting DataFrames (cleaned data and mask) keep the first occurrence. If timestamps are not monotonic, the timestamps in the resulting DataFrames are reordered.
```
# Define expected frequency of the data, in seconds
frequency = 0.002
# Run the timestamp quality control test
results = qc.check_timestamp(data, frequency)
```
The cleaned data, boolean mask, and test results summary are shown below. The summary is transposed (using .T) so that it is easier to read.
```
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print the first 5 rows of the cleaned data
print(results['cleaned_data'].head())
# Print the first 5 rows of the mask
print(results['mask'].head())
# Print the test results summary
# The summary is transposed (using .T) so that it is easier to read.
print(results['test_results'].T)
```
### Check for corrupt data
In the following quality control tests, the cleaned data from the previous test is used as input to the subsequent test. For each quality control test, a plot of the cleaned data is shown along with the test results summary.
Note, that if you want to run a series of quality control tests before extracting the cumulative cleaned data, boolean mask, and summary, we recommend using Pecos directly with the object-oriented approach, see https://pecos.readthedocs.io/ for more details.
The quality control test below checks for corrupt data, indicated by a value of -999.
```
# Define corrupt values
corrupt_values = [-999]
# Run the corrupt data quality control test
results = qc.check_corrupt(results['cleaned_data'], corrupt_values)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
### Check for data outside the expected range
The next quality control test checks for data that is greater than 50 or less than -50. Note that expected range tests can also be used to compare measured values to a model, or analyze the expected relationships between data columns.
```
# Define expected lower and upper bound ([lower bound, upper bound])
expected_bounds = [-50, 50]
# Run expected range quality control test
results = qc.check_range(results['cleaned_data'], expected_bounds)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
### Check for stagnant data
The final quality control test checks for stagnant data by looking for data that changes by less than 0.001 within a 0.02 second moving window.
```
# Define expected lower bound (no upper bound is specified in this example)
expected_bound = [0.001, None]
# Define the moving window, in seconds
window = 0.02
# Run the delta quality control test
results = qc.check_delta(results['cleaned_data'], expected_bound, window)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
## Cleaned Data
The cleaned data can be used directly in MHKiT analysis, or the missing values can be replaced using various methods before analysis is run.
Data replacement strategies are generally defined on a case by case basis. Pandas includes methods to interpolate, replace, and fill missing values.
```
# Extract final cleaned data for MHKiT analysis
cleaned_data = results['cleaned_data']
```
|
github_jupyter
|
```
import tushare as ts
import sina_data
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
from datetime import datetime, timedelta
from dateutil.parser import parse
import time
import common_util
import os
def get_time(date=False, utc=False, msl=3):
if date:
time_fmt = "%Y-%m-%d %H:%M:%S.%f"
else:
time_fmt = "%H:%M:%S.%f"
if utc:
return datetime.utcnow().strftime(time_fmt)[:(msl-6)]
else:
return datetime.now().strftime(time_fmt)[:(msl-6)]
def print_info(status="I"):
return "\033[0;33;1m[{} {}]\033[0m".format(status, get_time())
def judgement(df, change_rate=0.01, buy1_rate=0.03, buy1_volume=1e5):
float_share = df['float_share'].to_numpy().astype(np.int)
open = df['今日开盘价'].to_numpy().astype(np.float)
pre_close = df['昨日收盘价'].to_numpy().astype(np.float)
limit_up = limit_up_price(pre_close)
price = df['当前价'].to_numpy().astype(np.float)
high = df['今日最高价'].to_numpy().astype(np.float)
low = df['今日最低价'].to_numpy().astype(np.float)
volume = df['成交股票数'].to_numpy().astype(np.int)
buy_1v = df['买一量'].to_numpy().astype(np.int)
judge_list = [
low < limit_up,
price < limit_up,
volume < float_share * change_rate,
buy_1v < float_share * buy1_rate,
buy_1v < buy1_volume
]
return judge_list
# 基于前一交易日收盘价的涨停价计算
def limit_up_price(pre_close):
return np.around(pre_close * 1.1, decimals=2)
# 日K数据判断是否开板
def is_sold(code, start_date):
print(code)
try:
time.sleep(1)
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
start_date = (parse(str(start_date))+timedelta(1)).strftime('%Y%m%d')
end_date = datetime.now().strftime('%Y%m%d')
daily_k = pro.daily(ts_code=code, start_date=start_date, end_date=end_date)
if len(daily_k) > 0:
daily_k['flag'] = daily_k.apply(
lambda x: x['high'] == x['low'] and x['open'] == x['close'] and x['high'] == x['low'],
axis=1
)
flag = daily_k['flag'].sum()
result = True
for each in daily_k['flag'].tolist():
result = result and each
return result
else:
return True
except Exception as e:
print('再次请求ts数据')
time.sleep(1)
a = is_sold(code, start_date)
return a
# 获取流通股本
def get_float_share(code):
print(code)
try:
time.sleep(1)
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
# target_date = datetime.now().strftime('%Y%m%d')
target_data = []
delta = 0
count = 1
while len(target_data) == 0:
target_date = datetime.now() + timedelta(delta)
target_data = pro.daily_basic(
ts_code=code, trade_date=target_date.strftime('%Y%m%d'), fields='free_share'
)
delta = delta - 1
time.sleep(0.5)
count = count + 1
if count > 3:
return 1000000
return target_data.values[0][0] * 10000
except Exception as e:
time.sleep(1)
get_float_share(code)
print('再次请求ts数据.....')
# 新股筛选
# 获取股票列表
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
basic_data = pro.stock_basic()
print('股票筛选')
# basic_data.to_excel(r'C:\Users\duanp\Desktop\test\stock_basic.xlsx')
# basic_data = pd.read_excel(r'C:\Users\duanp\Desktop\test\stock_basic.xlsx')
# 筛选上市日期为近一月的股票
start_date = datetime.now() + timedelta(-30)
end_date = datetime.now() + timedelta(1)
basic_data['list_date'] = basic_data['list_date'].apply(lambda x: parse(str(x)))
basic_data = basic_data[basic_data['list_date'] > start_date]
basic_data = basic_data[basic_data['list_date'] < end_date]
# 剔除科创板股票
basic_data = basic_data[basic_data['market'] != '科创板']
# 筛选未开板的股票
basic_data['target_flag'] = basic_data.apply(lambda x: is_sold(x['ts_code'], x['list_date']), axis=1)
# basic_data = basic_data[basic_data['target_flag']]
print('补充流通股本数据')
# 补充流通股本信息
basic_data['float_share'] = basic_data.apply(lambda x: get_float_share(x['ts_code']), axis=1)
basic_data['float_share'] = basic_data['float_share'].fillna('100000')
print('预警股票如下:')
print(basic_data)
change_rate = 0.01
buy1_rate = 0.03
buy1_volume = 1e5
tick_list = [
'股票代码',
'今日开盘价',
'昨日收盘价',
'当前价',
'今日最高价',
'今日最低价',
'成交股票数',
'买一量'
]
flag_dict = {
"low_flag": "当日曾开板!",
"price_flag": "已经开板!",
"volume_top_flag": "换手率超过 {:.0%}!".format(change_rate),
"buy1_percent_flag": "买一量不足总流通市值的 {:.0%}!".format(buy1_rate),
"buy1_volume_flag": "买一量不足 {} 股!".format(buy1_volume),
}
flag_list = list(flag_dict.keys())
flag_len = len(flag_list)
basic_data['target_code'] = basic_data['ts_code'].apply(lambda x: common_util.get_format_code(x, 'num'))
basic_data['ts_code'].to_list()
tick_data = sina_data.get_tick_data(basic_data['symbol'].to_list())
tick_data['股票代码'] = tick_data['股票代码'].apply(lambda x: common_util.get_format_code(x, 'wind'))
tick_data = tick_data[tick_list]
temp_data = basic_data.merge(tick_data, left_on='ts_code', right_on='股票代码')
judge_list = judgement(temp_data, change_rate, buy1_rate, buy1_volume)
judge_list
alert_dict = dict()
count = 0
for idx in range(flag_len):
temp_data[flag_list[idx]] = judge_list[idx]
alert_dict[flag_list[idx]] = temp_data[temp_data[flag_list[idx]]]["name"].tolist()
if len(alert_dict[flag_list[idx]]) > 0:
print(print_info("W"), end=" ")
print(flag_dict[flag_list[idx]])
print(",".join(alert_dict[flag_list[idx]]))
else:
count += 1
idx=1
temp_data[flag_list[idx]] = judge_list[idx]
alert_dict[flag_list[idx]] = temp_data[temp_data[flag_list[idx]]]
alert_dict
```
|
github_jupyter
|
```
%matplotlib inline
%pylab inline
pylab.rcParams['figure.figsize'] = (10, 6)
import numpy as np
from numpy.lib import stride_tricks
import cv2
from matplotlib.colors import hsv_to_rgb
import matplotlib.pyplot as plt
import numpy as np
np.set_printoptions(precision=3)
class PatchMatch(object):
def __init__(self, a, b, patch_size):
assert a.shape == b.shape, "Dimensions were unequal for patch-matching input"
self.A = a
self.B = b
self.patch_size = patch_size
self.nnf = np.zeros((2, self.A.shape[0], self.A.shape[1])).astype(np.int)
self.nnd = np.zeros((self.A.shape[0], self.A.shape[1]))
self.initialise_nnf()
def initialise_nnf(self):
self.nnf[0] = np.random.randint(self.B.shape[0], size=(self.A.shape[0], self.A.shape[1]))
self.nnf[1] = np.random.randint(self.B.shape[1], size=(self.A.shape[0], self.A.shape[1]))
self.nnf = self.nnf.transpose((1, 2 ,0))
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
pos = self.nnf[i,j]
self.nnd[i,j] = self.cal_dist(i, j, pos[0], pos[1])
def cal_dist(self, ai ,aj, bi, bj):
dx0 = dy0 = self.patch_size//2
dx1 = dy1 = self.patch_size//2 + 1
dx0 = min(ai, bi, dx0)
dx1 = min(self.A.shape[0]-ai, self.B.shape[0]-bi, dx1)
dy0 = min(aj, bj, dy0)
dy1 = min(self.A.shape[1]-aj, self.B.shape[1]-bj, dy1)
return np.sum((self.A[ai-dx0:ai+dx1, aj-dy0:aj+dy1]-self.B[bi-dx0:bi+dx1, bj-dy0:bj+dy1])**2) / (dx1+dx0) / (dy1+dy0)
def reconstruct(self):
ans = np.zeros_like(self.A)
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
pos = self.nnf[i,j]
ans[i,j] = self.B[pos[0], pos[1]]
return ans
def reconstruct_img_voting(self, patch_size=3,arr_v=None):
if patch_size is None:
patch_size = self.patch_size
b_prime = np.zeros_like(self.A,dtype=np.uint8)
for i in range(self.A.shape[0]): #traverse down a
for j in range(self.A.shape[1]): #traverse across a
dx0 = dy0 = patch_size//2
dx1 = dy1 = patch_size//2 + 1
dx0 = min(i,dx0)
dx1 = min(self.A.shape[0]-i, dx1)
dy0 = min(j, dy0)
dy1 = min(self.A.shape[1]-j, dy1)
votes = self.nnf[i-dx0:i+dx1, j-dy0:j+dy1]
b_patch = np.zeros(shape=(votes.shape[0],votes.shape[1],self.A.shape[2]))
for p_i in range(votes.shape[0]):
for p_j in range(votes.shape[1]):
b_patch[p_i, p_j] = self.B[votes[p_i,p_j][0] , votes[p_i,p_j][1]]
averaged_patch = np.average(b_patch,axis=(0,1))
b_prime[i, j] = averaged_patch[:]
plt.imshow(b_prime[:,:,::-1])
plt.show()
def visualize_nnf(self):
nnf = self.nnf
nnd = self.nnd
def angle_between_alt(p1, p2):
ang1 = np.arctan2(*p1[::-1])
ang2 = np.arctan2(*p2[::-1])
return np.rad2deg((ang1 - ang2) % (2 * np.pi))
def norm_dist(arr):
return (arr)/(arr.max())
img = np.zeros((nnf.shape[0], nnf.shape[1], 3),dtype=np.uint8)
for i in range(1, nnf.shape[0]):
for j in range(1, nnf.shape[1]):
angle = angle_between_alt([j, i], [nnf[i, j][0], nnf[i, j][1]])
img[i, j, :] = np.array([angle, nnd[i,j], 250])
img = hsv_to_rgb(norm_dist(img/255))
plt.imshow(img)
plt.show()
def propagate(self):
compare_value = -1
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
x,y = self.nnf[i,j]
bestx, besty, bestd = x, y, self.nnd[i,j]
compare_value *=-1
if (i + compare_value >= 0 and compare_value == -1) or (i + compare_value < self.A.shape[0] and compare_value == 1) :
rx, ry = self.nnf[i+compare_value, j][0] , self.nnf[i+compare_value, j][1]
if rx < self.B.shape[0]:
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
if (j+compare_value >= 0 and compare_value == -1)or (j + compare_value < self.A.shape[1] and compare_value == 1) :
rx, ry = self.nnf[i, j+compare_value][0], self.nnf[i, j+compare_value][1]
if ry < self.B.shape[1]:
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
rand_d = min(self.B.shape[0]//2, self.B.shape[1]//2)
while rand_d > 0:
try:
xmin = max(bestx - rand_d, 0)
xmax = min(bestx + rand_d, self.B.shape[0])
ymin = max(besty - rand_d, 0)
ymax = min(besty + rand_d, self.B.shape[1])
#print(xmin, xmax)
rx = np.random.randint(xmin, xmax)
ry = np.random.randint(ymin, ymax)
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
except:
print(rand_d)
print(xmin, xmax)
print(ymin, ymax)
print(bestx, besty)
print(self.B.shape)
rand_d = rand_d // 2
self.nnf[i, j] = [bestx, besty]
self.nnd[i, j] = bestd
print("Done")
x = cv2.imread("./blue.jpg")
y = cv2.imread("./yellow.jpg")
x = cv2.resize(x,(200,200))
y = cv2.resize(y,(200,200))
pm = PatchMatch(x,y, 3)
pm.visualize_nnf()
def do():
pm.propagate()
pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
do()
pm.visualize_nnf()
do()
plt.figure(1)
plt.subplot(131)
plt.axis('off')
plt.imshow(x[:,:,::-1])
plt.subplot(132)
plt.axis('off')
plt.imshow(y[:,:,::-1])
plt.subplot(133)
plt.axis('off')
plt.imshow(pm.reconstruct()[:,:,::-1])
plt.show()
import os
import sys
# add the 'src' directory as one where we can import modules
src_dir = os.path.join(os.getcwd(), os.pardir)
sys.path.append(src_dir)
os.path.join(os.getcwd(), os.pardir)
from src.PatchMatch import PatchMatchSimple
pm = PatchMatchSimple(x,y,patch_size=3)
for i in range(15):
pm.propagate()
pm.reconstruct_img_voting(patch_size=3)
pm.visualize_nnf()
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.