prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Cell Editing
DataGrid cells can be edited using in-place editors built into DataGrid. Editing can be initiated by double clicking on a cell or by starting typing the new value for the cell.
DataGrids are not editable by default. Editing can be enabled by setting `editable` property to `True`. Selection enablement is required for editing to work and it is set automatically to `cell` mode if it is `none` when editing is enabled.
### Cursor Movement
Editing is initiated for the `cursor` cell. Cursor cell is the same as the selected cell if there is a single cell selected. If there are multiple cells / rectangles selected then cursor cell is the cell where the last selection rectangle was started.
Cursor can be moved in four directions by using the following keyboard keys.
- **Down**: Enter
- **Up**: Shift + Enter
- **Right**: Tab
- **Left**: Shift + Tab
Once done with editing a cell, cursor can be moved to next cell based on the keyboard hit following the rules above.
```
from ipydatagrid import DataGrid
from json import load
import pandas as pd
with open("./cars.json") as fobj:
data = load(fobj)
df = pd.DataFrame(data["data"]).drop("index", axis=1)
datagrid = DataGrid(df, editable=True, layout={"height": "200px"})
datagrid
```
All grid views are updated simultaneously to reflect cell edit changes.
```
datagrid
# keep track of changed cells
changed_cells = {}
def create_cell_key(cell):
return "{row}:{column}".format(row=cell["row"], column=cell["column_index"])
def track_changed_cell(cell):
key = create_cell_key(cell)
changed_cells[key] = cell
```
Changes to cell values can be tracked by subscribing to `on_cell_change` event as below.
```
def on_cell_changed(cell):
track_changed_cell(cell)
print(
"Cell at primary key {row} and column '{column}'({column_index}) changed to {value}".format(
row=cell["row"],
column=cell["column"],
column_index=cell["column_index"],
value=cell["value"],
)
)
datagrid.on_cell_change(on_cell_changed)
```
A cell's value can also be changed programmatically by using the DataGrid methods `set_cell_value` and `set_cell_value_by_index`
```
datagrid.set_cell_value("Cylinders", 2, 12)
```
Whether new cell values are entered using UI or programmatically, both the DataGrid cell rendering and the underlying python data are updated.
```
datagrid.data.iloc[2]["Cylinders"]
datagrid.set_cell_value_by_index("Horsepower", 3, 169)
datagrid.data.iloc[3]["Origin"]
def select_all_changed_cells():
datagrid.clear_selection()
for cell in changed_cells.values():
datagrid.select(cell["row"], cell["column_index"])
return datagrid.selected_cells
```
Show all cells changed using UI or programmatically by selecting them.
```
select_all_changed_cells()
```
| true |
code
| 0.233095 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/AI4Finance-LLC/FinRL/blob/master/FinRL_ensemble_stock_trading_ICAIF_2020.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Deep Reinforcement Learning for Stock Trading from Scratch: Multiple Stock Trading Using Ensemble Strategy
Tutorials to use OpenAI DRL to trade multiple stocks using ensemble strategy in one Jupyter Notebook | Presented at ICAIF 2020
* This notebook is the reimplementation of our paper: Deep Reinforcement Learning for Automated Stock Trading: An Ensemble Strategy, using FinRL.
* Check out medium blog for detailed explanations: https://medium.com/@ai4finance/deep-reinforcement-learning-for-automated-stock-trading-f1dad0126a02
* Please report any issues to our Github: https://github.com/AI4Finance-LLC/FinRL-Library/issues
* **Pytorch Version**
# Content
* [1. Problem Definition](#0)
* [2. Getting Started - Load Python packages](#1)
* [2.1. Install Packages](#1.1)
* [2.2. Check Additional Packages](#1.2)
* [2.3. Import Packages](#1.3)
* [2.4. Create Folders](#1.4)
* [3. Download Data](#2)
* [4. Preprocess Data](#3)
* [4.1. Technical Indicators](#3.1)
* [4.2. Perform Feature Engineering](#3.2)
* [5.Build Environment](#4)
* [5.1. Training & Trade Data Split](#4.1)
* [5.2. User-defined Environment](#4.2)
* [5.3. Initialize Environment](#4.3)
* [6.Implement DRL Algorithms](#5)
* [7.Backtesting Performance](#6)
* [7.1. BackTestStats](#6.1)
* [7.2. BackTestPlot](#6.2)
* [7.3. Baseline Stats](#6.3)
* [7.3. Compare to Stock Market Index](#6.4)
<a id='0'></a>
# Part 1. Problem Definition
This problem is to design an automated trading solution for single stock trading. We model the stock trading process as a Markov Decision Process (MDP). We then formulate our trading goal as a maximization problem.
The algorithm is trained using Deep Reinforcement Learning (DRL) algorithms and the components of the reinforcement learning environment are:
* Action: The action space describes the allowed actions that the agent interacts with the
environment. Normally, a ∈ A includes three actions: a ∈ {−1, 0, 1}, where −1, 0, 1 represent
selling, holding, and buying one stock. Also, an action can be carried upon multiple shares. We use
an action space {−k, ..., −1, 0, 1, ..., k}, where k denotes the number of shares. For example, "Buy
10 shares of AAPL" or "Sell 10 shares of AAPL" are 10 or −10, respectively
* Reward function: r(s, a, s′) is the incentive mechanism for an agent to learn a better action. The change of the portfolio value when action a is taken at state s and arriving at new state s', i.e., r(s, a, s′) = v′ − v, where v′ and v represent the portfolio
values at state s′ and s, respectively
* State: The state space describes the observations that the agent receives from the environment. Just as a human trader needs to analyze various information before executing a trade, so
our trading agent observes many different features to better learn in an interactive environment.
* Environment: Dow 30 consituents
The data of the single stock that we will be using for this case study is obtained from Yahoo Finance API. The data contains Open-High-Low-Close price and volume.
<a id='1'></a>
# Part 2. Getting Started- Load Python Packages
<a id='1.1'></a>
## 2.1. Install all the packages through FinRL library
```
# ## install finrl library
#!pip install git+https://github.com/AI4Finance-LLC/FinRL-Library.git
```
<a id='1.2'></a>
## 2.2. Check if the additional packages needed are present, if not install them.
* Yahoo Finance API
* pandas
* numpy
* matplotlib
* stockstats
* OpenAI gym
* stable-baselines
* tensorflow
* pyfolio
<a id='1.3'></a>
## 2.3. Import Packages
```
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# matplotlib.use('Agg')
from datetime import datetime, timedelta
%matplotlib inline
from finrl.apps import config
from finrl.neo_finrl.preprocessor.yahoodownloader import YahooDownloader
from finrl.neo_finrl.preprocessor.preprocessors import FeatureEngineer, data_split
from finrl.neo_finrl.env_stock_trading.env_stocktrading import StockTradingEnv
from finrl.drl_agents.stablebaselines3.models import DRLAgent,DRLEnsembleAgent
from finrl.plot import backtest_stats, backtest_plot, get_daily_return, get_baseline
from pprint import pprint
import sys
sys.path.append("../FinRL-Library")
import itertools
```
<a id='1.4'></a>
## 2.4. Create Folders
```
import os
if not os.path.exists("./" + config.DATA_SAVE_DIR):
os.makedirs("./" + config.DATA_SAVE_DIR)
if not os.path.exists("./" + config.TRAINED_MODEL_DIR):
os.makedirs("./" + config.TRAINED_MODEL_DIR)
if not os.path.exists("./" + config.TENSORBOARD_LOG_DIR):
os.makedirs("./" + config.TENSORBOARD_LOG_DIR)
if not os.path.exists("./" + config.RESULTS_DIR):
os.makedirs("./" + config.RESULTS_DIR)
import yfinance as yf
data_prefix = [f"{config.DOW_30_TICKER}", f"{config.nas_choosen}", f"{config.sp_choosen}"]
path_mark = ["dow", "nas", "sp"]
choose_number = 0
#注意更改ticker_list
config.START_DATE
config.END_DATE
print(data_prefix[choose_number])
time_current = datetime.now() + timedelta(hours=8)
time_current = time_current.strftime("%Y-%m-%d_%H:%M")
print(f"time_current ====={time_current}")
```
<a id='2'></a>
# Part 3. Download Data
Yahoo Finance is a website that provides stock data, financial news, financial reports, etc. All the data provided by Yahoo Finance is free.
* FinRL uses a class **YahooDownloader** to fetch data from Yahoo Finance API
* Call Limit: Using the Public API (without authentication), you are limited to 2,000 requests per hour per IP (or up to a total of 48,000 requests a day).
-----
class YahooDownloader:
Provides methods for retrieving daily stock data from
Yahoo Finance API
Attributes
----------
start_date : str
start date of the data (modified from config.py)
end_date : str
end date of the data (modified from config.py)
ticker_list : list
a list of stock tickers (modified from config.py)
Methods
-------
fetch_data()
Fetches data from yahoo API
```
#ticker_list = []
#ticker_list = [ticks[i] for i in index]
#getattr(ticker_list, data_prefix[choose_number])
# 缓存数据,如果日期或者股票列表发生变化,需要删除该缓存文件重新下载
SAVE_PATH = f"./datasets/{path_mark[choose_number]}.csv"
if os.path.exists(SAVE_PATH):
df = pd.read_csv(SAVE_PATH)
else:
#注意更改ticker_list
df = YahooDownloader(
config.START_DATE, #'2000-01-01',
config.END_DATE, # 2021-01-01,预计将改日期改为'2021-07-03'(今日日期)
ticker_list=config.DOW_30_TICKER#config.DOW_30_TICKER, config.nas_choosen, config.sp_choosen
).fetch_data()
df.to_csv(SAVE_PATH)
df.head()
df.tail()
df.shape
df.sort_values(['date','tic']).head()
```
# Part 4: Preprocess Data
Data preprocessing is a crucial step for training a high quality machine learning model. We need to check for missing data and do feature engineering in order to convert the data into a model-ready state.
* Add technical indicators. In practical trading, various information needs to be taken into account, for example the historical stock prices, current holding shares, technical indicators, etc. In this article, we demonstrate two trend-following technical indicators: MACD and RSI.
* Add turbulence index. Risk-aversion reflects whether an investor will choose to preserve the capital. It also influences one's trading strategy when facing different market volatility level. To control the risk in a worst-case scenario, such as financial crisis of 2007–2008, FinRL employs the financial turbulence index that measures extreme asset price fluctuation.
```
tech_indicators = ['macd',
'rsi_30',
'cci_30',
'dx_30']
fe = FeatureEngineer(
use_technical_indicator=True,
tech_indicator_list = tech_indicators,
use_turbulence=True,
user_defined_feature = False)
csv_name_func_processed = lambda time: f"./datasets/ensemble_{path_mark[choose_number]}_{time}_processed.csv"
SAVE_PATH = csv_name_func_processed(time_current)
if os.path.exists(SAVE_PATH):
processed = pd.read_csv(SAVE_PATH)
else:
processed = fe.preprocess_data(df)
processed.to_csv(SAVE_PATH)
list_ticker = processed["tic"].unique().tolist()
list_date = list(pd.date_range(processed['date'].min(),processed['date'].max()).astype(str))
combination = list(itertools.product(list_date,list_ticker))
processed_full = pd.DataFrame(combination,columns=["date","tic"]).merge(processed,on=["date","tic"],how="left")
processed_full = processed_full[processed_full['date'].isin(processed['date'])]
processed_full = processed_full.sort_values(['date','tic'])
processed_full = processed_full.fillna(0)
processed_full.sample(5)
```
<a id='4'></a>
# Part 5. Design Environment
Considering the stochastic and interactive nature of the automated stock trading tasks, a financial task is modeled as a **Markov Decision Process (MDP)** problem. The training process involves observing stock price change, taking an action and reward's calculation to have the agent adjusting its strategy accordingly. By interacting with the environment, the trading agent will derive a trading strategy with the maximized rewards as time proceeds.
Our trading environments, based on OpenAI Gym framework, simulate live stock markets with real market data according to the principle of time-driven simulation.
The action space describes the allowed actions that the agent interacts with the environment. Normally, action a includes three actions: {-1, 0, 1}, where -1, 0, 1 represent selling, holding, and buying one share. Also, an action can be carried upon multiple shares. We use an action space {-k,…,-1, 0, 1, …, k}, where k denotes the number of shares to buy and -k denotes the number of shares to sell. For example, "Buy 10 shares of AAPL" or "Sell 10 shares of AAPL" are 10 or -10, respectively. The continuous action space needs to be normalized to [-1, 1], since the policy is defined on a Gaussian distribution, which needs to be normalized and symmetric.
```
#train = data_split(processed_full, '2009-01-01','2019-01-01')
#trade = data_split(processed_full, '2019-01-01','2021-01-01')
#print(len(train))
#print(len(trade))
stock_dimension = len(processed_full.tic.unique())
state_space = 1 + 2*stock_dimension + len(tech_indicators)*stock_dimension
print(f"Stock Dimension: {stock_dimension}, State Space: {state_space}")
env_kwargs = {
"hmax": 100,
"initial_amount": 1000000,
"buy_cost_pct": 0.001,
"sell_cost_pct": 0.001,
"state_space": state_space,
"stock_dim": stock_dimension,
"tech_indicator_list": tech_indicators,
"action_space": stock_dimension,
"reward_scaling": 1e-4,
"print_verbosity":5
}
```
<a id='5'></a>
# Part 6: Implement DRL Algorithms
* The implementation of the DRL algorithms are based on **OpenAI Baselines** and **Stable Baselines**. Stable Baselines is a fork of OpenAI Baselines, with a major structural refactoring, and code cleanups.
* FinRL library includes fine-tuned standard DRL algorithms, such as DQN, DDPG,
Multi-Agent DDPG, PPO, SAC, A2C and TD3. We also allow users to
design their own DRL algorithms by adapting these DRL algorithms.
* In this notebook, we are training and validating 3 agents (A2C, PPO, DDPG) using Rolling-window Ensemble Method ([reference code](https://github.com/AI4Finance-LLC/Deep-Reinforcement-Learning-for-Automated-Stock-Trading-Ensemble-Strategy-ICAIF-2020/blob/80415db8fa7b2179df6bd7e81ce4fe8dbf913806/model/models.py#L92))
```
rebalance_window = 63 # rebalance_window is the number of days to retrain the model
validation_window = 63 # validation_window is the number of days to do validation and trading (e.g. if validation_window=63, then both validation and trading period will be 63 days)
"""
train_start = '2009-01-01'
train_end = "2016-10-03"
val_test_start = "2016-10-03"
val_test_end = "2021-09-18"
"""
train_start = "2009-01-01"
train_end = "2015-12-31"
val_test_start = "2015-12-31"
val_test_end = "2021-05-03"
ensemble_agent = DRLEnsembleAgent(df=processed_full,
train_period=(train_start,train_end),
val_test_period=(val_test_start,val_test_end),
rebalance_window=rebalance_window,
validation_window=validation_window,
**env_kwargs)
A2C_model_kwargs = {
'n_steps': 5,
'ent_coef': 0.01,
'learning_rate': 0.0005
}
PPO_model_kwargs = {
"ent_coef":0.01,
"n_steps": 2048,
"learning_rate": 0.00025,
"batch_size": 128
}
DDPG_model_kwargs = {
"action_noise":"ornstein_uhlenbeck",
"buffer_size": 50_000,
"learning_rate": 0.000005,
"batch_size": 128
}
timesteps_dict = {'a2c' : 1_000,
'ppo' : 1_000,
'ddpg' : 1_000
}
df_summary = ensemble_agent.run_ensemble_strategy(A2C_model_kwargs,
PPO_model_kwargs,
DDPG_model_kwargs,
timesteps_dict)
df_summary
```
<a id='6'></a>
# Part 7: Backtest Our Strategy
Backtesting plays a key role in evaluating the performance of a trading strategy. Automated backtesting tool is preferred because it reduces the human error. We usually use the Quantopian pyfolio package to backtest our trading strategies. It is easy to use and consists of various individual plots that provide a comprehensive image of the performance of a trading strategy.
```
unique_trade_date = processed_full[(processed_full.date > val_test_start)&(processed_full.date <= val_test_end)].date.unique()
import functools
def compare(A, B): # 名字可以随便取,不一定得是“compare"
return -1 if int(A.split("_")[-1][:-4])<int(B.split("_")[-1][:-4]) else 1
from typing import List
with open("paths.txt") as f:
paths: List[str] = f.readlines()
paths = [path.strip().split(" ")[-1] for path in paths]
paths.sort(key=functools.cmp_to_key(compare))
#paths.sort()
#print(paths)
df_account_value=pd.DataFrame()
for i in range(len(df_summary)):
iter = df_summary.iloc[i]["Iter"]
al = df_summary.iloc[i]["Model Used"]
path = f"results/account_value_validation_{al}_{iter}.csv"
#print(path, os.path.exists(path))
df_tmp = pd.read_csv(path)
df_account_value = df_account_value.append(df_tmp,ignore_index=True)
df_account_value
df_account_value.tail()
df_account_value.to_csv("results/account_value_all.csv", index=False)
df_account_value.head()
%matplotlib inline
df_account_value.account_value.plot()
```
<a id='6.1'></a>
## 7.1 BackTestStats
pass in df_account_value, this information is stored in env class
```
print("==============Get Backtest Results===========")
now = datetime.now().strftime('%Y%m%d-%Hh%M')
perf_stats_all = backtest_stats(account_value=df_account_value)
perf_stats_all = pd.DataFrame(perf_stats_all)
#baseline stats
print("==============Get Baseline Stats===========")
baseline_df = get_baseline(
ticker="^GSPC",
start = df_account_value.loc[0,'date'],
end = df_account_value.loc[len(df_account_value)-1,'date'])
stats = backtest_stats(baseline_df, value_col_name = 'close')
```
<a id='6.2'></a>
## 7.2 BackTestPlot
```
print("==============Compare to DJIA===========")
import pandas as pd
%matplotlib inline
# S&P 500: ^GSPC
# Dow Jones Index: ^DJI
# NASDAQ 100: ^NDX
#df_account_value = pd.read_csv("/mnt/wanyao/guiyi/hhf/RL-FIN/datasets/ensemble_2021-09-06_19:36_account_value.csv")
backtest_plot(df_account_value,
baseline_ticker = '^DJI',
baseline_start = df_account_value.loc[0,'date'],
baseline_end = df_account_value.loc[len(df_account_value)-1,'date'])
```
| true |
code
| 0.391464 | null | null | null | null |
|
# Text Classification using LSTM
This Code Template is for Text Classification using Long short-term memory in python
<img src="https://cdn.blobcity.com/assets/gpu_required.png" height="25" style="margin-bottom:-15px" />
### Required Packages
```
!pip install tensorflow
!pip install nltk
import pandas as pd
import tensorflow as tf
from tensorflow.keras.layers import Embedding
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.models import Sequential
from tensorflow.keras.preprocessing.text import one_hot
from tensorflow.keras.layers import LSTM
from tensorflow.keras.layers import Dense
import nltk
import re
from nltk.corpus import stopwords
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
pip install tensorflow==2.1.0
```
### Initialization
Filepath of CSV file
```
df=pd.read_csv('/content/train.csv')
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df.head()
###Drop Nan Values
df=df.dropna()
```
Target variable for prediction.
```
target=''
```
Text column containing all the text data
```
text=""
tf.__version__
### Vocabulary size
voc_size=5000
nltk.download('stopwords')
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
### Dataset Preprocessing
from nltk.stem.porter import PorterStemmer
ps = PorterStemmer()
corpus = []
for i in range(0, len(df)):
review = re.sub('[^a-zA-Z]', ' ', df[text][i])
review = review.lower()
review = review.split()
review = [ps.stem(word) for word in review if not word in stopwords.words('english')]
review = ' '.join(review)
corpus.append(review)
corpus[1:10]
onehot_repr=[one_hot(words,voc_size)for words in corpus]
onehot_repr
```
### Embedding Representation
```
sent_length=20
embedded_docs=pad_sequences(onehot_repr,padding='pre',maxlen=sent_length)
print(embedded_docs)
embedded_docs[0]
```
### Model
#LSTM
The LSTM model will learn a function that maps a sequence of past observations as input to an output observation. As such, the sequence of observations must be transformed into multiple examples from which the LSTM can learn.
Refer [API](https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21) for the parameters
```
## Creating model
embedding_vector_features=40
model=Sequential()
model.add(Embedding(voc_size,embedding_vector_features,input_length=sent_length))
model.add(LSTM(100))
model.add(Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])
print(model.summary())
len(embedded_docs),y.shape
X=np.array(embedded_docs)
Y=df[target]
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.33, random_state=42)
```
### Model Training
```
### Finally Training
model.fit(X_train,y_train,validation_data=(X_test,y_test),epochs=10,batch_size=64)
```
### Performance Metrics And Accuracy
```
y_pred=model.predict_classes(X_test)
confusion_matrix(y_test,y_pred)
```
## Model Accuracy
```
accuracy_score(y_test,y_pred)
```
#### Creator: Ageer Harikrishna , Github: [Profile](https://github.com/ageerHarikrishna)
| true |
code
| 0.686002 | null | null | null | null |
|
# Deep learning models for age prediction on EEG data
This notebook uses deep learning methods to predict the age of infants using EEG data. The EEG data is preprocessed as shown in the notebook 'Deep learning EEG_dataset preprocessing raw'.
```
import sys, os, fnmatch, csv
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
sys.path.insert(0, os.path.dirname(os.getcwd()))
from config import PATH_DATA_PROCESSED_DL_REDUCED, PATH_MODELS
```
## Load preprocessed data (reduced)
The data can be found in 'PATH_DATA_PROCESSED_DL_REDUCED'. This is a single folder with all the data and metadata. The EEG data is in the .zarr files and the metadata is in .csv files. The .zarr files are divided in chunks of 1-second epochs (average of 10 original EEG epochs) from the same subject and the metadata contains the information like the subject's identification code and age. The notebook "Deep learning EEG_DL dataset_reduction.ipynb" takes care of reducing the original processed data set to the reduced size.
Generator loads all the data into memory. The generators generate averaged epochs on the fly. The data is split in train/validation/test and no subject can be found in more than one of these splits.
Originally, we used the original EEG epochs and averaged 30 of them into a new EEG epoch in the generator object. This had two disadvantages: (1) many files had to be openened and closed during the training process, and (2) the data set was too large to fit into memory. Therefore, we decided to randomly create chunks of 10 EEG epochs and average those for each subject/age group. This reduced the data set from ±145GB to ±14.5 GB. We now use these already averaged EEG epochs as "original" epcohs, and average those another 3-5 times to reduce noise. We have also experimented with averaging all EEG epochs of a subject at a specific age into a single EEG epoch, but performance was lower, most likely because this reduced the size of the data set a lot.
```
%%time
# Load all the metadata
from sklearn.model_selection import train_test_split
# Step 1: Get all the files in the output folder
file_names = os.listdir(PATH_DATA_PROCESSED_DL_REDUCED)
# Step 2: Get the full paths of the files (without extensions)
files = [os.path.splitext(os.path.join(PATH_DATA_PROCESSED_DL_REDUCED, file_name))[0] for file_name in fnmatch.filter(file_names, "*.zarr")]
# Step 3: Load all the metadata
frames = []
for idx, feature_file in enumerate(files):
df_metadata = pd.read_csv(feature_file + ".csv")
frames.append(df_metadata)
df_metadata = pd.concat(frames)
# Step 4: Add missing age information based on the age group the subject is in
df_metadata['age_months'].fillna(df_metadata['age_group'], inplace=True)
df_metadata['age_days'].fillna(df_metadata['age_group']*30, inplace=True)
df_metadata['age_years'].fillna(df_metadata['age_group']/12, inplace=True)
# Step 5: List all the unique subject IDs
subject_ids = sorted(list(set(df_metadata["code"].tolist())))
from sklearn.model_selection import train_test_split
IDs_train, IDs_temp = train_test_split(subject_ids, test_size=0.3, random_state=42)
IDs_test, IDs_val = train_test_split(IDs_temp, test_size=0.5, random_state=42)
df_metadata
from dataset_generator_reduced import DataGeneratorReduced
# # Import libraries
# from tensorflow.keras.utils import Sequence
# import numpy as np
# import zarr
# import os
# class DataGeneratorReduced(Sequence):
# """Generates data for loading (preprocessed) EEG timeseries data.
# Create batches for training or prediction from given folders and filenames.
# """
# def __init__(self,
# list_IDs,
# BASE_PATH,
# metadata,
# gaussian_noise=0.0,
# n_average = 3,
# batch_size=10,
# iter_per_epoch = 1,
# n_timepoints = 501,
# n_channels=30,
# shuffle=True,
# warnings=False):
# """Initialization
# Args:
# --------
# list_IDs:
# list of all filename/label ids to use in the generator
# metadata:
# DataFrame containing all the metadata.
# n_average: int
# Number of EEG/time series epochs to average.
# batch_size:
# batch size at each iteration
# iter_per_epoch: int
# Number of iterations over all data points within one epoch.
# n_timepoints: int
# Timepoint dimension of data.
# n_channels:
# number of input channels
# shuffle:
# True to shuffle label indexes after every epoch
# """
# self.list_IDs = list_IDs
# self.BASE_PATH = BASE_PATH
# self.metadata = metadata
# self.metadata_temp = None
# self.gaussian_noise = gaussian_noise
# self.n_average = n_average
# self.batch_size = batch_size
# self.iter_per_epoch = iter_per_epoch
# self.n_timepoints = n_timepoints
# self.n_channels = n_channels
# self.shuffle = shuffle
# self.warnings = warnings
# self.on_epoch_end()
# # Store all data in here
# self.X_data_all = []
# self.y_data_all = []
# self.load_all_data()
# def __len__(self):
# """Denotes the number of batches per epoch
# return: number of batches per epoch
# """
# return int(np.floor(len(self.metadata_temp) / self.batch_size))
# def __getitem__(self, index):
# """Generate one batch of data
# Args:
# --------
# index: int
# index of the batch
# return: X and y when fitting. X only when predicting
# """
# # Generate indexes of the batch
# indexes = self.indexes[index * self.batch_size:((index + 1) * self.batch_size)]
# # Generate data
# X, y = self.generate_data(indexes)
# return X, y
# def load_all_data(self):
# """ Loads all data into memory. """
# for i, metadata_file in self.metadata_temp.iterrows():
# filename = os.path.join(self.BASE_PATH, metadata_file['cnt_file'] + '.zarr')
# X_data = np.zeros((0, self.n_channels, self.n_timepoints))
# data_signal = self.load_signal(filename)
# if (len(data_signal) == 0) and self.warnings:
# print(f"EMPTY SIGNAL, filename: {filename}")
# X_data = np.concatenate((X_data, data_signal), axis=0)
# self.X_data_all.append(X_data)
# self.y_data_all.append(metadata_file['age_months'])
# def on_epoch_end(self):
# """Updates indexes after each epoch."""
# # Create new metadata DataFrame with only the current subject IDs
# if self.metadata_temp is None:
# self.metadata_temp = self.metadata[self.metadata['code'].isin(self.list_IDs)].reset_index(drop=True)
# idx_base = np.arange(len(self.metadata_temp))
# idx_epoch = np.tile(idx_base, self.iter_per_epoch)
# self.indexes = idx_epoch
# if self.shuffle == True:
# np.random.shuffle(self.indexes)
# def generate_data(self, indexes):
# """Generates data containing batch_size averaged time series.
# Args:
# -------
# list_IDs_temp: list
# list of label ids to load
# return: batch of averaged time series
# """
# X_data = np.zeros((0, self.n_channels, self.n_timepoints))
# y_data = []
# for index in indexes:
# X = self.create_averaged_epoch(self.X_data_all[index])
# X_data = np.concatenate((X_data, X), axis=0)
# y_data.append(self.y_data_all[index])
# return np.swapaxes(X_data,1,2), np.array(y_data).reshape((-1,1))
# def create_averaged_epoch(self,
# data_signal):
# """
# Function to create averages of self.n_average epochs.
# Will create one averaged epoch per found unique label from self.n_average random epochs.
# Args:
# --------
# data_signal: numpy array
# Data from one person as numpy array
# """
# # Create new data collection:
# X_data = np.zeros((0, self.n_channels, self.n_timepoints))
# num_epochs = len(data_signal)
# if num_epochs >= self.n_average:
# select = np.random.choice(num_epochs, self.n_average, replace=False)
# signal_averaged = np.mean(data_signal[select,:,:], axis=0)
# else:
# if self.warnings:
# print("Found only", num_epochs, " epochs and will take those!")
# signal_averaged = np.mean(data_signal[:,:,:], axis=0)
# X_data = np.concatenate([X_data, np.expand_dims(signal_averaged, axis=0)], axis=0)
# if self.gaussian_noise != 0.0:
# X_data += np.random.normal(0, self.gaussian_noise, X_data.shape)
# return X_data
# def load_signal(self,
# filename):
# """Load EEG signal from one person.
# Args:
# -------
# filename: str
# filename...
# return: loaded array
# """
# return zarr.open(os.path.join(filename), mode='r')
%%time
# IDs_train = [152, 18, 11, 435, 617]
# IDs_val = [180, 105, 19, 332]
train_generator_noise = DataGeneratorReduced(list_IDs = IDs_train,
BASE_PATH = PATH_DATA_PROCESSED_DL_REDUCED,
metadata = df_metadata,
n_average = 3,
batch_size = 10,
gaussian_noise=0.01,
iter_per_epoch = 3,
n_timepoints = 501,
n_channels=30,
shuffle=True)
val_generator = DataGeneratorReduced(list_IDs = IDs_val,
BASE_PATH = PATH_DATA_PROCESSED_DL_REDUCED,
metadata = df_metadata,
n_average = 3,
batch_size = 10,
n_timepoints = 501,
iter_per_epoch = 3,
n_channels=30,
shuffle=True)
```
# Helper functions
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, Input, Sequential
from tensorflow.keras.layers import Bidirectional, LSTM, Dropout, BatchNormalization, Dense, Conv1D, LeakyReLU, AveragePooling1D, Flatten, Reshape, MaxPooling1D
from tensorflow.keras.optimizers import Adam, Adadelta, SGD
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
from tensorflow.keras.metrics import RootMeanSquaredError, MeanAbsoluteError
import time
n_timesteps = 501
n_features = 30
n_outputs = 1
input_shape = (n_timesteps, n_features)
```
# Testing of different architectures
Below we will test multiple different architectures, most of them as discussed in "Deep learning for time series classification: a review", by Ismail Fawaz et al (2019). Most of them are inspired again on other papers. Refer to the Ismail Fawaz paper for the original papers.
1. Fully-connected NN
2. CNN
3. ResNet
4. Encoder
5. Time-CNN
Other architectures to test:
6. BLSTM-LSTM
7. InceptionTime
# 1. Fully connected NN
```
def fully_connected_model():
""" Returns the fully connected model from Ismail Fawaz et al. (2019). """
input_layer = keras.layers.Input(input_shape)
input_layer_flattened = keras.layers.Flatten()(input_layer)
layer_1 = keras.layers.Dropout(0.1)(input_layer_flattened)
layer_1 = keras.layers.Dense(500, activation='relu')(layer_1)
layer_2 = keras.layers.Dropout(0.2)(layer_1)
layer_2 = keras.layers.Dense(500, activation='relu')(layer_2)
layer_3 = keras.layers.Dropout(0.2)(layer_2)
layer_3 = keras.layers.Dense(500, activation='relu')(layer_3)
output_layer = keras.layers.Dropout(0.3)(layer_3)
output_layer = keras.layers.Dense(1)(output_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = fully_connected_model()
optimizer = Adadelta(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# 01 seems to be incorrect (makes too many predictions, changed model)
# Fully_connected_regressor_01: MSE, Adadelta, N_average=30, 5000 epochs, ES=1000, RLR=200, gaussian=0.01
# Fully_connected_regressor_02: MSE, Adadelta, N_average=30, 5000 epochs, ES=1000, RLR=200, gaussian=0.01
output_filename = 'Fully_connected_regressor_03'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=1000, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=200, min_lr=0.0001, verbose=1)
%%time
epochs = 5000
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer, earlystopper, reduce_lr])
```
# 2. CNN
```
def cnn_model():
""" Returns the CNN (FCN) model from Ismail Fawaz et al. (2019). """
input_layer = keras.layers.Input(input_shape)
conv1 = keras.layers.Conv1D(filters=128, kernel_size=8, padding='same')(input_layer)
conv1 = keras.layers.BatchNormalization()(conv1)
conv1 = keras.layers.Activation(activation='relu')(conv1)
conv2 = keras.layers.Conv1D(filters=256, kernel_size=5, padding='same')(conv1)
conv2 = keras.layers.BatchNormalization()(conv2)
conv2 = keras.layers.Activation('relu')(conv2)
conv3 = keras.layers.Conv1D(128, kernel_size=3, padding='same')(conv2)
conv3 = keras.layers.BatchNormalization()(conv3)
conv3 = keras.layers.Activation('relu')(conv3)
gap_layer = keras.layers.GlobalAveragePooling1D()(conv3)
output_layer = keras.layers.Dense(1)(gap_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = cnn_model()
optimizer = Adam(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# CNN_regressor_01: MSE, Adam, N_average=30, 2000 epochs, ES=250, RLR=50, gaussian=0.01
output_filename = 'CNN_regressor_03'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=250, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=50, min_lr=0.0001, verbose=1)
%%time
epochs = 2000
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer, earlystopper, reduce_lr])
```
# 3. ResNet
```
def resnet_model():
""" Returns the ResNet model from Ismail Fawaz et al. (2019). """
n_feature_maps = 64
input_layer = keras.layers.Input(input_shape)
# BLOCK 1
conv_x = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=8, padding='same')(input_layer)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# expand channels for the sum
shortcut_y = keras.layers.Conv1D(filters=n_feature_maps, kernel_size=1, padding='same')(input_layer)
shortcut_y = keras.layers.BatchNormalization()(shortcut_y)
output_block_1 = keras.layers.add([shortcut_y, conv_z])
output_block_1 = keras.layers.Activation('relu')(output_block_1)
# BLOCK 2
conv_x = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=8, padding='same')(output_block_1)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# expand channels for the sum
shortcut_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=1, padding='same')(output_block_1)
shortcut_y = keras.layers.BatchNormalization()(shortcut_y)
output_block_2 = keras.layers.add([shortcut_y, conv_z])
output_block_2 = keras.layers.Activation('relu')(output_block_2)
# BLOCK 3
conv_x = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=8, padding='same')(output_block_2)
conv_x = keras.layers.BatchNormalization()(conv_x)
conv_x = keras.layers.Activation('relu')(conv_x)
conv_y = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=5, padding='same')(conv_x)
conv_y = keras.layers.BatchNormalization()(conv_y)
conv_y = keras.layers.Activation('relu')(conv_y)
conv_z = keras.layers.Conv1D(filters=n_feature_maps * 2, kernel_size=3, padding='same')(conv_y)
conv_z = keras.layers.BatchNormalization()(conv_z)
# no need to expand channels because they are equal
shortcut_y = keras.layers.BatchNormalization()(output_block_2)
output_block_3 = keras.layers.add([shortcut_y, conv_z])
output_block_3 = keras.layers.Activation('relu')(output_block_3)
# FINAL
gap_layer = keras.layers.GlobalAveragePooling1D()(output_block_3)
output_layer = keras.layers.Dense(1)(gap_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = resnet_model()
optimizer = Adam(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# ResNet_regressor_01: MSE, Adam, N_average=30, 1500 epochs, ES=250, RLR=50, gaussian=0.01
output_filename = 'ResNet_regressor_02'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=250, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=50, min_lr=0.0001, verbose=1)
%%time
epochs = 1500
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer, earlystopper, reduce_lr])
```
# 4. Encoder
```
import tensorflow_addons as tfa
def encoder_model():
""" Returns the Encoder model from Ismail Fawaz et al. (2019). """
input_layer = keras.layers.Input(input_shape)
# conv block -1
conv1 = keras.layers.Conv1D(filters=128,kernel_size=5,strides=1,padding='same')(input_layer)
conv1 = tfa.layers.InstanceNormalization()(conv1)
conv1 = keras.layers.PReLU(shared_axes=[1])(conv1)
conv1 = keras.layers.Dropout(rate=0.2)(conv1)
conv1 = keras.layers.MaxPooling1D(pool_size=2)(conv1)
# conv block -2
conv2 = keras.layers.Conv1D(filters=256,kernel_size=11,strides=1,padding='same')(conv1)
conv2 = tfa.layers.InstanceNormalization()(conv2)
conv2 = keras.layers.PReLU(shared_axes=[1])(conv2)
conv2 = keras.layers.Dropout(rate=0.2)(conv2)
conv2 = keras.layers.MaxPooling1D(pool_size=2)(conv2)
# conv block -3
conv3 = keras.layers.Conv1D(filters=512,kernel_size=21,strides=1,padding='same')(conv2)
conv3 = tfa.layers.InstanceNormalization()(conv3)
conv3 = keras.layers.PReLU(shared_axes=[1])(conv3)
conv3 = keras.layers.Dropout(rate=0.2)(conv3)
# split for attention
attention_data = keras.layers.Lambda(lambda x: x[:,:,:256])(conv3)
attention_softmax = keras.layers.Lambda(lambda x: x[:,:,256:])(conv3)
# attention mechanism
attention_softmax = keras.layers.Softmax()(attention_softmax)
multiply_layer = keras.layers.Multiply()([attention_softmax,attention_data])
# last layer
dense_layer = keras.layers.Dense(units=256,activation='sigmoid')(multiply_layer)
dense_layer = tfa.layers.InstanceNormalization()(dense_layer)
# output layer
flatten_layer = keras.layers.Flatten()(dense_layer)
output_layer = keras.layers.Dense(1)(flatten_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = encoder_model()
optimizer = Adam(learning_rate=0.00001)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# Encoder_regressor_01: MSE, Adam, N_average=30, 1500 epochs, ES=250, RLR=50, gaussian=0.01 (LR = 0.0001, no reduction)
output_filename = 'Encoder_regressor_02'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
%%time
epochs = 100
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer])
```
# 5. Time-CNN
```
# https://github.com/hfawaz/dl-4-tsc/blob/master/classifiers/cnn.py
def timecnn_model():
""" Returns the Time-CNN model from Ismail Fawaz et al. (2019). """
padding = 'valid'
input_layer = keras.layers.Input(input_shape)
conv1 = keras.layers.Conv1D(filters=6,kernel_size=7,padding=padding,activation='sigmoid')(input_layer)
conv1 = keras.layers.AveragePooling1D(pool_size=3)(conv1)
conv2 = keras.layers.Conv1D(filters=12,kernel_size=7,padding=padding,activation='sigmoid')(conv1)
conv2 = keras.layers.AveragePooling1D(pool_size=3)(conv2)
flatten_layer = keras.layers.Flatten()(conv2)
output_layer = keras.layers.Dense(units=1)(flatten_layer)
model = keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = cnn_model()
optimizer = Adam(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# TimeCNN_regressor_01: MSE, Adam, N_average=30, 2000 epochs, ES=250, RLR=50, gaussian=0.01
output_filename = 'TimeCNN_regressor_02'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=250, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=50, min_lr=0.0001, verbose=1)
%%time
epochs = 2000
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer, earlystopper, reduce_lr])
```
# 6. BLSTM-LSTM
```
def blstm_lstm_model():
""" Returns the BLSTM-LSTM model from Kaushik et al. (2019). """
# MARK: This model compresses too much in the last phase, check if possible to improve.
model = keras.Sequential()
# BLSTM layer
model.add(Bidirectional(LSTM(256, return_sequences=True), input_shape=input_shape))
model.add(Dropout(.2))
model.add(BatchNormalization())
# LSTM layer
model.add(LSTM(128, return_sequences=True))
model.add(BatchNormalization())
# LSTM layer
model.add(LSTM(64, return_sequences=False))
model.add(BatchNormalization())
# Fully connected layer
model.add(Dense(32))
model.add(Dense(n_outputs))
return model
model = blstm_lstm_model()
optimizer = Adam(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# BLSTM_regressor_01: MSE, Adam, N_average=30, 1500 epochs, ES=250, RLR=50, gaussian=0.01
output_filename = 'BLSTM_regressor_01'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=250, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=50, min_lr=0.0001, verbose=1)
model.summary()
%%time
epochs = 1500
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks=[checkpointer, earlystopper, reduce_lr])
```
# 7. InceptionTime
```
class Regressor_Inception:
def __init__(self, output_directory, input_shape, verbose=False, build=True, batch_size=64,
nb_filters=32, use_residual=True, use_bottleneck=True, depth=6, kernel_size=41, nb_epochs=1500):
self.output_directory = output_directory
self.nb_filters = nb_filters
self.use_residual = use_residual
self.use_bottleneck = use_bottleneck
self.depth = depth
self.kernel_size = kernel_size - 1
self.callbacks = None
self.batch_size = batch_size
self.bottleneck_size = 32
self.nb_epochs = nb_epochs
if build == True:
self.model = self.build_model(input_shape)
if (verbose == True):
self.model.summary()
self.verbose = verbose
self.model.save_weights(self.output_directory + 'inception_model_init.hdf5')
def _inception_module(self, input_tensor, stride=1, activation='linear'):
if self.use_bottleneck and int(input_tensor.shape[-1]) > 1:
input_inception = tf.keras.layers.Conv1D(filters=self.bottleneck_size, kernel_size=1,
padding='same', activation=activation, use_bias=False)(input_tensor)
else:
input_inception = input_tensor
# kernel_size_s = [3, 5, 8, 11, 17]
kernel_size_s = [self.kernel_size // (2 ** i) for i in range(3)]
conv_list = []
for i in range(len(kernel_size_s)):
conv_list.append(tf.keras.layers.Conv1D(filters=self.nb_filters, kernel_size=kernel_size_s[i],
strides=stride, padding='same', activation=activation, use_bias=False)(
input_inception))
max_pool_1 = tf.keras.layers.MaxPool1D(pool_size=3, strides=stride, padding='same')(input_tensor)
conv_6 = tf.keras.layers.Conv1D(filters=self.nb_filters, kernel_size=1,
padding='same', activation=activation, use_bias=False)(max_pool_1)
conv_list.append(conv_6)
x = tf.keras.layers.Concatenate(axis=2)(conv_list)
x = tf.keras.layers.BatchNormalization()(x)
x = tf.keras.layers.Activation(activation='relu')(x)
return x
def _shortcut_layer(self, input_tensor, out_tensor):
shortcut_y = tf.keras.layers.Conv1D(filters=int(out_tensor.shape[-1]), kernel_size=1,
padding='same', use_bias=False)(input_tensor)
shortcut_y = tf.keras.layers.BatchNormalization()(shortcut_y)
x = tf.keras.layers.Add()([shortcut_y, out_tensor])
x = tf.keras.layers.Activation('relu')(x)
return x
def build_model(self, input_shape):
input_layer = tf.keras.layers.Input(input_shape)
x = input_layer
input_res = input_layer
for d in range(self.depth):
x = self._inception_module(x)
if self.use_residual and d % 3 == 2:
x = self._shortcut_layer(input_res, x)
input_res = x
pooling_layer = tf.keras.layers.AveragePooling1D(pool_size=50)(x)
flat_layer = tf.keras.layers.Flatten()(pooling_layer)
dense_layer = tf.keras.layers.Dense(128, activation='relu')(flat_layer)
output_layer = tf.keras.layers.Dense(1)(dense_layer)
model = tf.keras.models.Model(inputs=input_layer, outputs=output_layer)
return model
model = Regressor_Inception(PATH_MODELS, input_shape, verbose=True).model
optimizer = Adam(learning_rate=0.01)
model.compile(loss='mean_squared_error',
optimizer=optimizer,
metrics=[RootMeanSquaredError(), MeanAbsoluteError()])
# 'Inception_regressor_01' (n_average = 40, gaussian_noise = 0.01, MAE)
# 'Inception_regressor_02' (n_average = 1, gaussian_noise = 0.01, MAE)
# 'Inception_regressor_03' (n_average = 40, gaussian_noise = 0.01, MSE)
# 'Inception_regressor_04' (n_average = 1, gaussian_noise = 0.01, MSE)
# 'Inception_regressor_05' (n_average = 100, gaussian_noise = 0.01, MAE)
output_filename = 'Inception_regressor_05'
output_file = os.path.join(PATH_MODELS, output_filename)
checkpointer = ModelCheckpoint(filepath = output_file + ".hdf5", monitor='val_loss', verbose=1, save_best_only=True)
earlystopper = EarlyStopping(monitor='val_loss', patience=100, verbose=1)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=20, min_lr=0.0001, verbose=1)
%%time
epochs = 1500
# fit network
history = model.fit(x=train_generator_noise,
validation_data=val_generator,
epochs=epochs,
callbacks = [checkpointer, earlystopper, reduce_lr])
```
# Compare models
### Helper functions for comparison
```
# 'Inception_regressor_01' (n_average = 40, gaussian_noise = 0.01, MAE)
model_path = os.path.join(PATH_MODELS, 'Inception_regressor_01.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# 'Inception_regressor_02' (n_average = 1, gaussian_noise = 0.01, MAE)
model_path = os.path.join(PATH_MODELS, 'Inception_regressor_02.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# 'Inception_regressor_03' (n_average = 40, gaussian_noise = 0.01, MSE)
model_path = os.path.join(PATH_MODELS, 'Inception_regressor_03.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# 'Inception_regressor_04' (n_average = 1, gaussian_noise = 0.01, MSE)
model_path = os.path.join(PATH_MODELS, 'Inception_regressor_04.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# 'Inception_regressor_05' (n_average = 100, gaussian_noise = 0.01, MAE)
model_path = os.path.join(PATH_MODELS, 'Inception_regressor_05.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# Fully_connected_regressor_02: MSE, Adadelta, N_average=30, 5000 epochs, ES=1000, RLR=200, gaussian=0.01
model_path = os.path.join(PATH_MODELS, 'Fully_connected_regressor_02.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# CNN_regressor_01: MSE, Adam, N_average=30, 2000 epochs, ES=250, RLR=50, gaussian=0.01
model_path = os.path.join(PATH_MODELS, 'CNN_regressor_01.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# ResNet_regressor_01: MSE, Adam, N_average=30, 1500 epochs, ES=250, RLR=50, gaussian=0.01
model_path = os.path.join(PATH_MODELS, 'ResNet_regressor_01.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# Encoder_regressor_01: MSE, Adam, N_average=30, 1500 epochs, ES=250, RLR=50, gaussian=0.01 (LR = 0.0001, no reduction)
model_path = os.path.join(PATH_MODELS, 'Encoder_regressor_01.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
# TimeCNN_regressor_01: MSE, Adam, N_average=30, 2000 epochs, ES=250, RLR=50, gaussian=0.01
model_path = os.path.join(PATH_MODELS, 'TimeCNN_regressor_01.hdf5')
loaded_model = tf.keras.models.load_model(model_path)
evaluate_model(loaded_model)
```
| true |
code
| 0.587292 | null | null | null | null |
|
# Descriptive statistics
```
import numpy as np
import seaborn as sns
import scipy.stats as st
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import pandas as pd
import statsmodels.api as sm
import statistics
import os
from scipy.stats import norm
```
## Probability data, binomial distribution
We already got to know data that follow a binomial distribution, but we actually had not looked at the distribution. We will do this now. 10% of the 100 cells we count have deformed nuclei. To illustrate the distribution we will count repeatedly....
```
n = 100 # number of trials
p = 0.1 # probability of each trial
s = np.random.binomial(n, p, 1000) #simulation repeating the experiment 1000 times
print(s)
```
As you can see, the result of the distribution is in absolute counts, not proportions - they can easyly be converted by deviding with n, but they dont have to...
```
props = s/n
print(props)
```
Now we plot the distribution. The easiest first look is a histogram.
```
plt.hist(props, bins = 5)
plt.xlabel("proportion")
plt.ylabel("frequency")
plt.show()
```
The resolution is a bit inappropriate, given that we deal with integers. To increase the bin number would be a good idea. Maybe we should also plot a confidence interval.
```
CI= sm.stats.proportion_confint(n*p, n, alpha=0.05)
print(CI)
plt.axvspan(CI[0],CI[1], alpha=0.2, color='yellow')
plt.hist(props, bins = 50)
plt.xlabel("proportion")
plt.ylabel("frequency")
plt.axvline(p, color="black")
```
In a binomial distribution, the distribution is given by the proportion and the sample size. Therefore we could calculate a confidence interval from one measurement.
#### How can we now describe the distribution?
Summary statistics:
```
print("the minimum is:", min(props))
print("the maximum is:", max(props))
print(statistics.mean(props))
```
Is the mean a good way to look at our distribution?
```
n = 50 # number of trials
p = 0.02 # probability of each trial
s = np.random.binomial(n, p, 1000) #simulation repeating the experiment 1000 times
props = s/n
CI= sm.stats.proportion_confint(n*p, n, alpha=0.05)
print(CI)
plt.axvspan(CI[0],CI[1], alpha=0.2, color='yellow')
plt.hist(props, bins = 20)
plt.xlabel("proportion")
plt.ylabel("frequency")
plt.axvline(p, color="black")
plt.axvline(statistics.mean(props), color="red")
print(statistics.mean(props))
```
## Count data/ the Poisson distribution
The Poisson distribution is built on count data, e.g. the numbers of raisins in a Dresdner Christstollen, the number of geese at any given day between Blaues Wunder and Waldschlösschenbrücke, or radioactive decay. So lets use a Geiger counter and count the numbers of decay per min.
```
freq =1.6
s = np.random.poisson(freq, 1000)
plt.hist(s, bins = 20)
plt.xlabel("counts per minute")
plt.ylabel("frequency")
plt.axvline(freq, color="black")
```
### Confidence intervals for a Poisson distribution
Similar to the binomial distribution, the distribution is defined by sample size and the mean.
Also for Poisson, one can calculate an also asymmetrical confidence interval:
```
freq =1.6
s = np.random.poisson(freq, 1000)
CI = st.poisson.interval(0.95,freq)
plt.axvspan(CI[0],CI[1], alpha=0.2, color='yellow')
plt.hist(s, bins = 20)
plt.xlabel("counts per minute")
plt.ylabel("frequency")
plt.axvline(freq, color="black")
```
For a poisson distribution, poisson error can be reduced, when increasing the counting population, in our case lets count for 10 min instead of 1 min, and see what happens.
```
CI = np.true_divide(st.poisson.interval(0.95,freq*10),10)
print(CI)
s = np.true_divide(np.random.poisson(freq*10, 1000),10)
plt.axvspan(CI[0],CI[1], alpha=0.2, color='yellow')
plt.hist(s, bins = 70)
plt.xlabel("counts per minute")
plt.ylabel("frequency")
plt.axvline(freq, color="black")
```
What is the difference between Poisson and Binomial? Aren't they both kind of looking at count data?
Yes, BUT:
Binomial counts events versus another event, e.g. for the cells there are two options, normal versus deformed. A binomial distribution is about comparing the two options.
Poisson counts with an open end, e.g. number of mutations.
## Continuous data
Let's import the count data you have generated with Robert. When you download it from Google sheets (https://docs.google.com/spreadsheets/d/1Ek-23Soro5XZ3y1kJHpvaTaa1f4n2C7G3WX0qddD-78/edit#gid=0), it comes with spaces. Try to avoid spaces and special characters in file names, they tend to make trouble.
I renamed it to 'BBBC001.csv'.
```
dat = pd.read_csv(os.path.join('data','BBBC001.csv'), header=1, sep=';')
print(dat)
```
For now we will focus on the manual counts, visualise it and perform summary statistics.
```
man_count = dat.iloc[:,1].values
plt.hist(man_count,bins=100)
```
There are different alternatives of displaying such data, some of which independent of distribution. You will find documentation in the graph galery: https://www.python-graph-gallery.com/
```
sns.kdeplot(man_count)
```
A density plot is sometimes helpful to see the distribution, but be aware of the smoothing and that you loose the information on sample size.
```
sns.stripplot(y=man_count)
sns.swarmplot(y=man_count)
sns.violinplot(y=man_count)
```
this plot is useful, but the density function can sometimes be misleading and lead to artefacts dependent on the sample size. Unless explicitely stated, sample sizes are usually normalised and therefore hidden!
```
sns.boxplot(y=man_count)
```
Be aware that boxplots hide the underlying distribution and the sample size.
So the "safest" plot, when in doubt, is to combine boxplot and jitter:
```
ax = sns.swarmplot(y=man_count, color="black")
ax = sns.boxplot(y=man_count,color="lightgrey")
```
The boxplot is very useful, because it directly provides non-parametric summary statistics:
Min, Max, Median, Quartiles and therefore the inter-quartile range (IQR). The whiskers are usually the highest point that is within 1.5x the quartile plus the IQR. Everything beyond that is considered an outlier. Whiskers are however not always used in this way!
The mean and standard diviation are not visible in a boxplot, because it is only meaningful in distributions that center around the mean. It is however a part of summary statistics:
```
dat["BBBC001 manual count"].describe()
```
## Normal distribution
We assume that our distribution is "normal".
First we fit a normal distribution to our data.
```
(mu, sigma) = norm.fit(man_count)
n, bins, patches = plt.hist(man_count, 100,density=1)
# add a 'best fit' line
y = norm.pdf(bins, mu, sigma)
l = plt.plot(bins, y, 'r--', linewidth=2)
#plot
plt.xlabel('manual counts counts')
plt.ylabel('binned counts')
plt.title(r'$\mathrm{Histogram\ of\ manual\ counts:}\ \mu=%.3f,\ \sigma=%.3f$' %(mu, sigma))
plt.show()
```
Is it really normally distributed? What we see here is already one of the most problematic properties of a normal distribution: The susceptibility to outliers.
In normal distributions the confidence interval is determined by the standard diviation. A confidence level of 95% equals 1.96 x sigma.
```
#plot
(mu, sigma) = norm.fit(man_count)
n, bins, patches = plt.hist(man_count, 100,density=1)
# add a 'best fit' line
y = norm.pdf(bins, mu, sigma)
l = plt.plot(bins, y, 'r--', linewidth=2)
plt.xlabel('manual counts counts')
plt.ylabel('binned counts')
plt.title(r'$\mathrm{Histogram\ of\ manual\ counts:}\ \mu=%.3f,\ \sigma=%.3f$' %(mu, sigma))
plt.axvspan((mu-1.96*sigma),(mu+1.96*sigma), alpha=0.2, color='yellow')
plt.axvline(mu, color="black")
plt.show()
```
This shows even nicer that our outlier messes up the distribution :-)
How can we solve this in practise?
1. Ignore the problem and continue with the knowledge that we are overestimating the width of the distribution and underestimating the mean.
2. Censor the outlier.
3. Decide that we cannot assume normality and move to either a different distribution or non-parametric statistics.
## Other distributions
Of course there are many more distributions, e.g.
Lognormal is a distribution that becomes normal, when log transformed. It is important for the "geometric mean".
Bimodal distributions may arise from imaging data with background signal, or DNA methylation data.
Negative binomial distributions are very important in genomics, especially RNA-Seq analysis.
## Exercise
1. We had imported the total table with also the automated counts. Visualise the distribution of the data next to each other
2. Generate the summary statistics and compare the different distributions
3. Two weeks ago you learned how to analyze a folder of images and measured the average size of beads:
https://nbviewer.jupyter.org/github/BiAPoL/Bio-image_Analysis_with_Python/blob/main/image_processing/12_process_folders.ipynb
Go back to the bead-analysis two weeks ago and measure the intensity of the individual beads (do not average over the image). Plot the beads' intensities as different plots. Which one do you find most approproiate for these data?
| true |
code
| 0.6329 | null | null | null | null |
|
# Qiskit: Open-Source Quantum Development, an introduction
---
### Workshop contents
1. Intro IBM Quantum Lab and Qiskit modules
2. Circuits, backends, visualization
3. Quantum info, circuit lib, algorithms
4. Circuit compilation, pulse, opflow
## 1. Intro IBM Quantum Lab and Qiskit modules
### https://quantum-computing.ibm.com/lab
### https://qiskit.org/documentation/
### https://github.com/qiskit
## 2. Circuits, backends and visualization
```
from qiskit import IBMQ
# Loading your IBM Quantum account(s)
#provider = IBMQ.load_account()
#provider = IBMQ.enable_account(<token>)
IBMQ.providers()
```
### Your first quantum circuit
Let's begin exploring the different tools in Qiskit Terra. For that, we will now create a Quantum Circuit.
```
from qiskit import QuantumCircuit
# Create circuit
# <INSERT CODE>
# print circuit
# <INSERT CODE>
```
Now let's run the circuit in the Aer simulator and plot the results in a histogram.
```
from qiskit import Aer
# run circuit on Aer simulator
# <INSERT CODE>
from qiskit.visualization import plot_histogram
# and display it on a histogram
# <INSERT CODE>
```
### Qiskit Visualization tools
```
from qiskit.visualization import plot_state_city
from qiskit.visualization import plot_state_paulivec, plot_state_hinton
circuit = QuantumCircuit(2, 2)
circuit.h(0)
circuit.cx(0, 1)
backend = Aer.get_backend('statevector_simulator') # the device to run on
result = backend.run(circuit).result()
psi = result.get_statevector(circuit)
# plot state city
# <INSERT CODE>
# plot state hinton
# <INSERT CODE>
# plot state paulivec
# <INSERT CODE>
```
#### Circuit Visualization
```
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
# Build a quantum circuit
circuit = QuantumCircuit(3, 3)
circuit.x(1)
circuit.h(range(3))
circuit.cx(0, 1)
circuit.measure(range(3), range(3));
# print circuit
# <INSERT CODE>
# print circuit using draw method
# <INSERT CODE>
```
There are different drawing formats. The parameter output (str) selects the output method to use for drawing the circuit. Valid choices are ``text, mpl, latex, latex_source``. See [qiskit.circuit.QuantumCircuit.draw](https://qiskit.org/documentation/stubs/qiskit.circuit.QuantumCircuit.draw.html?highlight=draw)
```
# print circuit using different drawer (mlp for example)
# <INSERT CODE>
```
##### Disable Plot Barriers and Reversing Bit Order
```
# Draw a new circuit with barriers and more registers
q_a = QuantumRegister(3, name='qa')
q_b = QuantumRegister(5, name='qb')
c_a = ClassicalRegister(3)
c_b = ClassicalRegister(5)
circuit = QuantumCircuit(q_a, q_b, c_a, c_b)
circuit.x(q_a[1])
circuit.x(q_b[1])
circuit.x(q_b[2])
circuit.x(q_b[4])
circuit.barrier()
circuit.h(q_a)
circuit.barrier(q_a)
circuit.h(q_b)
circuit.cswap(q_b[0], q_b[1], q_b[2])
circuit.cswap(q_b[2], q_b[3], q_b[4])
circuit.cswap(q_b[3], q_b[4], q_b[0])
circuit.barrier(q_b)
circuit.measure(q_a, c_a)
circuit.measure(q_b, c_b);
# Draw the circuit
# <INSERT CODE>
# Draw the circuit with reversed bit order
# <INSERT CODE>
# Draw the circuit without barriers
# <INSERT CODE>
```
##### MPL specific costumizations
```
# Change the background color in mpl
# <INSERT CODE>
# Scale the mpl output to 1/2 the normal size
# <INSERT CODE>
```
### Simulators
```
import numpy as np
# Import Qiskit
from qiskit import QuantumCircuit
from qiskit import Aer, transpile
from qiskit.tools.visualization import plot_histogram, plot_state_city
import qiskit.quantum_info as qi
Aer.backends()
simulator = Aer.get_backend('aer_simulator')
# Create circuit
circ = QuantumCircuit(2)
circ.h(0)
circ.cx(0, 1)
circ.measure_all()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get counts
result = simulator.run(circ).result()
counts = result.get_counts(circ)
plot_histogram(counts, title='Bell-State counts')
# Run and get memory (measurement outcomes for each individual shot)
result = simulator.run(circ, shots=10, memory=True).result()
memory = result.get_memory(circ)
print(memory)
```
##### Simulation methods
```
# Increase shots to reduce sampling variance
shots = 10000
# Stabilizer simulation method
sim_stabilizer = Aer.get_backend('aer_simulator_stabilizer')
job_stabilizer = sim_stabilizer.run(circ, shots=shots)
counts_stabilizer = job_stabilizer.result().get_counts(0)
# Statevector simulation method
sim_statevector = Aer.get_backend('aer_simulator_statevector')
job_statevector = sim_statevector.run(circ, shots=shots)
counts_statevector = job_statevector.result().get_counts(0)
# Density Matrix simulation method
sim_density = Aer.get_backend('aer_simulator_density_matrix')
job_density = sim_density.run(circ, shots=shots)
counts_density = job_density.result().get_counts(0)
# Matrix Product State simulation method
sim_mps = Aer.get_backend('aer_simulator_matrix_product_state')
job_mps = sim_mps.run(circ, shots=shots)
counts_mps = job_mps.result().get_counts(0)
plot_histogram([counts_stabilizer, counts_statevector, counts_density, counts_mps],
title='Counts for different simulation methods',
legend=['stabilizer', 'statevector',
'density_matrix', 'matrix_product_state'])
```
##### Simulation precision
```
# Configure a single-precision statevector simulator backend
simulator = Aer.get_backend('aer_simulator_statevector')
simulator.set_options(precision='single')
# Run and get counts
result = simulator.run(circ).result()
counts = result.get_counts(circ)
print(counts)
```
##### Device backend noise model simulations
```
from qiskit import IBMQ, transpile
from qiskit import QuantumCircuit
from qiskit.providers.aer import AerSimulator
from qiskit.tools.visualization import plot_histogram
from qiskit.test.mock import FakeVigo
device_backend = FakeVigo()
# Construct quantum circuit
circ = QuantumCircuit(3, 3)
circ.h(0)
circ.cx(0, 1)
circ.cx(1, 2)
circ.measure([0, 1, 2], [0, 1, 2])
# Create ideal simulator and run
# <INSERT CODE>
# Create simulator from backend
# <INSERT CODE>
# Transpile the circuit for the noisy basis gates and get results
# <INSERT CODE>
```
#### Usefull operations with circuits
```
qc = QuantumCircuit(12)
for idx in range(5):
qc.h(idx)
qc.cx(idx, idx+5)
qc.cx(1, 7)
qc.x(8)
qc.cx(1, 9)
qc.x(7)
qc.cx(1, 11)
qc.swap(6, 11)
qc.swap(6, 9)
qc.swap(6, 10)
qc.x(6)
qc.draw()
# width of circuit
# <INSERT CODE>
# number of qubits
# <INSERT CODE>
# count of operations
# <INSERT CODE>
# size of circuit
# <INSERT CODE>
# depth of circuit
# <INSERT CODE>
```
#### Final statevector
```
# Saving the final statevector
# Construct quantum circuit without measure
from qiskit.visualization import array_to_latex
circuit = QuantumCircuit(2)
circuit.h(0)
circuit.cx(0, 1)
# save statevector, run circuit and get results
# <INSERT CODE>
# Saving the circuit unitary
# Construct quantum circuit without measure
circuit = QuantumCircuit(2)
circuit.h(0)
circuit.cx(0, 1)
# save unitary, run circuit and get results
# <INSERT CODE>
```
Saving multiple statevectors
```
# Saving multiple states
# Construct quantum circuit without measure
steps = 5
circ = QuantumCircuit(1)
for i in range(steps):
circ.save_statevector(label=f'psi_{i}')
circ.rx(i * np.pi / steps, 0)
circ.save_statevector(label=f'psi_{steps}')
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
data = result.data(0)
data
```
Saving custom statevector
```
# Generate a random statevector
num_qubits = 2
psi = qi.random_statevector(2 ** num_qubits, seed=100)
# Set initial state to generated statevector
circ = QuantumCircuit(num_qubits)
circ.set_statevector(psi)
circ.save_state()
# Transpile for simulator
simulator = Aer.get_backend('aer_simulator')
circ = transpile(circ, simulator)
# Run and get saved data
result = simulator.run(circ).result()
result.data(0)
```
### Parametric circuits
```
# Parameterized Quantum Circuits
from qiskit.circuit import Parameter
# create parameter and use it in circuit
# <INSERT CODE>
res = sim.run(circuit, parameter_binds=[{theta: [np.pi/2, np.pi, 0]}]).result() # Different bindings
res.get_counts()
from qiskit.circuit import Parameter
theta = Parameter('θ')
n = 5
qc = QuantumCircuit(5, 1)
qc.h(0)
for i in range(n-1):
qc.cx(i, i+1)
qc.barrier()
qc.rz(theta, range(5))
qc.barrier()
for i in reversed(range(n-1)):
qc.cx(i, i+1)
qc.h(0)
qc.measure(0, 0)
qc.draw('mpl')
#We can inspect the circuit’s parameters
# <INSERT CODE>
import numpy as np
theta_range = np.linspace(0, 2 * np.pi, 128)
circuits = [qc.bind_parameters({theta: theta_val})
for theta_val in theta_range]
circuits[-1].draw()
backend = Aer.get_backend('aer_simulator')
job = backend.run(transpile(circuits, backend))
counts = job.result().get_counts()
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
ax.plot(theta_range, list(map(lambda c: c.get('0', 0), counts)), '.-', label='0')
ax.plot(theta_range, list(map(lambda c: c.get('1', 0), counts)), '.-', label='1')
ax.set_xticks([i * np.pi / 2 for i in range(5)])
ax.set_xticklabels(['0', r'$\frac{\pi}{2}$', r'$\pi$', r'$\frac{3\pi}{2}$', r'$2\pi$'], fontsize=14)
ax.set_xlabel('θ', fontsize=14)
ax.set_ylabel('Counts', fontsize=14)
ax.legend(fontsize=14)
# Random Circuit
from qiskit.circuit.random import random_circuit
# create random circuit
# <INSERT CODE>
# add unitary matrix to circuit
matrix = [[0, 0, 0, 1],
[0, 0, 1, 0],
[1, 0, 0, 0],
[0, 1, 0, 0]]
# <INSERT CODE>
# Classical logic
from qiskit.circuit import classical_function, Int1
@classical_function
def oracle(x: Int1, y: Int1, z: Int1) -> Int1:
return not x and (y or z)
circuit = QuantumCircuit(4)
circuit.append(oracle, [0, 1, 2, 3])
circuit.draw()
# circuit.decompose().draw() #synthesis
# Classical logic
from qiskit.circuit import classical_function, Int1
@classical_function
def oracle(x: Int1) -> Int1:
return not x
circuit = QuantumCircuit(2)
circuit.append(oracle, [0, 1])
circuit.draw()
circuit.decompose().draw()
```
https://qiskit.org/documentation/tutorials/circuits_advanced/02_operators_overview.html
## 3. Quantum info, circuit lib and algorithms
### Circuit lib
```
from qiskit.circuit.library import InnerProduct, QuantumVolume, clifford_6_2, C3XGate
# inner product circuit
# <INSERT CODE>
# clifford
# <INSERT CODE>
```
### Quantum info
```
from qiskit.quantum_info.operators import Operator
# Create an operator
# <INSERT CODE>
# add operator to circuit
# <INSERT CODE>
# Pauli
from qiskit.quantum_info.operators import Pauli
# use Pauli operator
# <INSERT CODE>
# Pauli with phase
from qiskit.quantum_info.operators import Pauli
circuit = QuantumCircuit(4)
iIXYZ = Pauli('iIXYZ') # ['', '-i', '-', 'i']
circuit.append(iIXYZ, [0, 1, 2, 3])
circuit.draw()
# create clifford
from qiskit.quantum_info import random_clifford
# random clifford
# <INSERT CODE>
# stabilizer and destabilizer
# <INSERT CODE>
```
### Algorithms
#### VQE
```
from qiskit.algorithms import VQE
from qiskit.algorithms.optimizers import SLSQP
from qiskit.circuit.library import TwoLocal
num_qubits = 2
ansatz = TwoLocal(num_qubits, 'ry', 'cz')
opt = SLSQP(maxiter=1000)
vqe = VQE(ansatz, optimizer=opt)
from qiskit.opflow import X, Z, I
H2_op = (-1.052373245772859 * I ^ I) + \
(0.39793742484318045 * I ^ Z) + \
(-0.39793742484318045 * Z ^ I) + \
(-0.01128010425623538 * Z ^ Z) + \
(0.18093119978423156 * X ^ X)
from qiskit.utils import algorithm_globals
seed = 50
algorithm_globals.random_seed = seed
qi = QuantumInstance(Aer.get_backend('statevector_simulator'), seed_transpiler=seed, seed_simulator=seed)
ansatz = TwoLocal(rotation_blocks='ry', entanglement_blocks='cz')
slsqp = SLSQP(maxiter=1000)
vqe = VQE(ansatz, optimizer=slsqp, quantum_instance=qi)
result = vqe.compute_minimum_eigenvalue(H2_op)
print(result)
```
#### Grover's algorithm
```
from qiskit.algorithms import Grover
from qiskit.algorithms import AmplificationProblem
# the state we desire to find is '11'
good_state = ['11']
# specify the oracle that marks the state '11' as a good solution
oracle = QuantumCircuit(2)
oracle.cz(0, 1)
# define Grover's algorithm
problem = AmplificationProblem(oracle, is_good_state=good_state)
# now we can have a look at the Grover operator that is used in running the algorithm
problem.grover_operator.draw(output='mpl')
from qiskit import Aer
from qiskit.utils import QuantumInstance
from qiskit.algorithms import Grover
aer_simulator = Aer.get_backend('aer_simulator')
grover = Grover(quantum_instance=aer_simulator)
result = grover.amplify(problem)
print('Result type:', type(result))
print('Success!' if result.oracle_evaluation else 'Failure!')
print('Top measurement:', result.top_measurement)
```
## 4. Transpiling, pulse and opflow
### Compiling circuits
```
[(b.name(), b.configuration().n_qubits) for b in provider.backends()]
from qiskit.tools.jupyter import *
%qiskit_backend_overview
from qiskit.providers.ibmq import least_busy
# get least busy backend
# <INSERT CODE>
# bell state
circuit = QuantumCircuit(2)
circuit.h(0)
circuit.cx(0, 1)
circuit.measure_all()
circuit.draw()
# run it in simulator
sim = Aer.get_backend('aer_simulator')
result = sim.run(circuit).result()
counts = result.get_counts()
plot_histogram(counts)
# run on least busy backend
# <INSERT CODE>
# get results
# <INSERT CODE>
circuit.draw('mpl')
from qiskit import transpile
# transpile with specified backend
# <INSERT CODE>
# rerun job
# <INSERT CODE>
# job status
# <INSERT CODE>
# get results
# <INSERT CODE>
from qiskit.visualization import plot_circuit_layout, plot_gate_map
display(transpiled_circuit.draw(idle_wires=False))
display(plot_gate_map(backend))
plot_circuit_layout(transpiled_circuit, backend)
# a slightly more interesting example:
circuit = QuantumCircuit(3)
circuit.h([0,1,2])
circuit.ccx(0, 1, 2)
circuit.h([0,1,2])
circuit.ccx(2, 0, 1)
circuit.h([0,1,2])
circuit.measure_all()
circuit.draw()
transpiled = transpile(circuit, backend)
transpiled.draw(idle_wires=False, fold=-1)
# Initial layout
# transpiling with initial layout
# <INSERT CODE>
transpiled.draw(idle_wires=False, fold=-1)
level0 = transpile(circuit, backend, optimization_level=0)
level1 = transpile(circuit, backend, optimization_level=1)
level2 = transpile(circuit, backend, optimization_level=2)
level3 = transpile(circuit, backend, optimization_level=3)
for level in [level0, level1, level2, level3]:
print(level.count_ops()['cx'], level.depth())
# transpiling is a stochastic process
transpiled = transpile(circuit, backend, optimization_level=2, seed_transpiler=42)
transpiled.depth()
transpiled = transpile(circuit, backend, optimization_level=2, seed_transpiler=1)
transpiled.depth()
# Playing with other transpiler options (without a backend)
transpiled = transpile(circuit)
transpiled.draw(fold=-1)
# Set a basis gates
backend.configuration().basis_gates
# specify basis gates
# <INSERT CODE>
# Set a coupling map
backend.configuration().coupling_map
from qiskit.transpiler import CouplingMap
# specify coupling map
# <INSERT CODE>
# Set an initial layout in a coupling map
transpiled = transpile(circuit,
coupling_map=CouplingMap([(0,1),(1,2)]),
initial_layout=[1, 0, 2])
transpiled.draw(fold=-1)
# Set an initial_layout in the coupling map with basis gates
transpiled = transpile(circuit,
coupling_map=CouplingMap([(0,1),(1,2)]),
initial_layout=[1, 0, 2],
basis_gates=['x', 'cx', 'h', 'p']
)
transpiled.draw(fold=-1)
transpiled.count_ops()['cx']
# Plus optimization level
transpiled = transpile(circuit,
coupling_map=CouplingMap([(0,1),(1,2)]),
initial_layout=[1, 0, 2],
basis_gates=['x', 'cx', 'h', 'p'],
optimization_level=3
)
transpiled.draw(fold=-1)
transpiled.count_ops()['cx']
# Last parameter, approximation degree
transpiled = transpile(circuit,
coupling_map=CouplingMap([(0,1),(1,2)]),
initial_layout=[1, 0, 2],
basis_gates=['x', 'cx', 'h', 'p'],
approximation_degree=0.99,
optimization_level=3
)
transpiled.draw(fold=-1)
transpiled.depth()
transpiled = transpile(circuit,
coupling_map=CouplingMap([(0,1),(1,2)]),
initial_layout=[1, 0, 2],
basis_gates=['x', 'cx', 'h', 'p'],
approximation_degree=0.01,
optimization_level=3
)
transpiled.draw(fold=-1)
transpiled.depth()
```
#### Qiskit is hardware agnostic!
```
# !pip install qiskit-ionq
# from qiskit_ionq import IonQProvider
# provider = IonQProvider(<your token>)
# circuit = QuantumCircuit(2)
# circuit.h(0)
# circuit.cx(0, 1)
# circuit.measure_all()
# circuit.draw()
# backend = provider.get_backend("ionq_qpu")
# job = backend.run(circuit)
# plot_histogram(job.get_counts())
```
### Pulse
```
from qiskit import pulse
# create dummy pusle program
# <INSERT CODE>
from qiskit.pulse import DriveChannel
channel = DriveChannel(0)
from qiskit.test.mock import FakeValencia
# build backend aware pulse schedule
# <INSERT CODE>
```
#### Delay instruction
```
# delay instruction
# <INSERT CODE>
```
#### Play instruction
#### Parametric pulses
```
from qiskit.pulse import library
# build parametric pulse
# <INSERT CODE>
# play parametric pulse
# <INSERT CODE>
# set frequency
# <INSERT CODE>
# shift phase
# <INSERT CODE>
from qiskit.pulse import Acquire, AcquireChannel, MemorySlot
# aqure instruction
# <INSERT CODE>
# example with left align schedule
# <INSERT CODE>
from qiskit import pulse
dc = pulse.DriveChannel
d0, d1, d2, d3, d4 = dc(0), dc(1), dc(2), dc(3), dc(4)
with pulse.build(name='pulse_programming_in') as pulse_prog:
pulse.play([1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1], d0)
pulse.play([1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0], d1)
pulse.play([1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0], d2)
pulse.play([1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0], d3)
pulse.play([1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0], d4)
pulse_prog.draw()
```
### Opflow
```
from qiskit.opflow import I, X, Y, Z
print(I, X, Y, Z)
# These operators may also carry a coefficient.
# <INSERT CODE>
# These coefficients allow the operators to be used as terms in a sum.
# <INSERT CODE>
# Tensor products are denoted with a caret, like this.
# <INSERT CODE>
# Composition is denoted by the @ symbol.
# <INSERT CODE>
```
### State functions and measurements
```
from qiskit.opflow import (StateFn, Zero, One, Plus, Minus, H,
DictStateFn, VectorStateFn, CircuitStateFn, OperatorStateFn)
# zero, one
# <INSERT CODE>
# plus, minus
# <INSERT CODE>
# evaulation
# <INSERT CODE>
# adjoint
# <INSERT CODE>
# other way of writing adjoint
# <INSERT CODE>
```
#### Algebraic operations
```
import math
v_zero_one = (Zero + One) / math.sqrt(2)
print(v_zero_one)
print(StateFn({'0':1}))
print(StateFn({'0':1}) == Zero)
print(StateFn([0,1,1,0]))
from qiskit.circuit.library import RealAmplitudes
print(StateFn(RealAmplitudes(2)))
from qiskit.opflow import Zero, One, H, CX, I
# bell state
# <INSERT CODE>
# implement arbitrary circuits
# <INSERT CODE>
```
| true |
code
| 0.6585 | null | null | null | null |
|
# Pivotal method vs Percentile Method
In this notebook we will explore the difference between the **pivotal** and **percentile** bootstrapping methods.
tldr -
* The **percentile method** generates a bunch of re-samples and esimates confidence intervals based on the percentile values of those re-samples.
* The **pivotal method** is similar to percentile but does a correction for the fact that your input sample may not be a good representation of your population. Bootstrapped uses this as the default.
We will show that the pviotal method has generally better power. This does come at a cost - the pivotal method can warp the confidence interval to give non-sencical interval values.
See [Link1](https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading24.pdf), [Link2](http://www.stat.cmu.edu/~cshalizi/402/lectures/08-bootstrap/lecture-08.pdf) for explanations of both methods.
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import numpy.random as npr
import bootstrapped.bootstrap as bs
import bootstrapped.stats_functions as bs_stats
import bootstrapped.power as bs_power
```
### Setup
The bootstrap is based on a sample of your larger population. A sample is only as good as how representitave it is. If you happen to be unlucky in your sample then you are going to make some very bad inferences!
We pick the exponential distribution because it should differentiate the difference between the two methods somewhat. We will also look at an extreme case.
```
population = np.random.exponential(scale=1000, size=500000)
# Plot the population
count, bins, ignored = plt.hist(population, 30, normed=True)
plt.title('Distribution of the population')
plt.show()
population = pd.Series(population)
# Do a bunch of simpulations and track the percent of the time the error bars overlap the true mean
def bootstrap_vs_pop_mean(population, num_samples, is_pivotal, num_loops=3000):
population_mean = population.mean()
pop_results = []
for _ in range(num_loops):
samples = population.sample(num_samples)
result = bs.bootstrap(samples.values, stat_func=bs_stats.mean, is_pivotal=is_pivotal)
# we want to 0 center this for our power plotting below
# we want our error bars to overlap zero
result = result - population_mean
pop_results.append(result)
return pop_results
def bounds_squared_distance(results):
'''The squared distance from zero for both the lower and the upper bound
This is a rough measure of how 'good' the confidence intervals are in terms of near misses vs extreme misses.
It is minimized when (1) the confidence interval is symmetric over zero and (2) when it is narrow.
'''
return np.sum([r.upper_bound**2 for r in results]) + np.sum([r.lower_bound**2 for r in results])
def squared_dist_ratio(x, y):
'Compare bounds_squared_distance for two sets of bootstrap results'
return bounds_squared_distance(x) / bounds_squared_distance(y)
```
### Pivotal vs Percentile for very small input sample size - 10 elements
```
pivotal_tiny_sample_count = bootstrap_vs_pop_mean(population, num_samples=10, is_pivotal=True)
percentile_tiny_sample_count = bootstrap_vs_pop_mean(population, num_samples=10, is_pivotal=False)
squared_dist_ratio(pivotal_tiny_sample_count, percentile_tiny_sample_count)
# more insignificant results is better
print(bs_power.power_stats(pivotal_tiny_sample_count))
bs_power.plot_power(pivotal_tiny_sample_count[::20])
# more insignificant results is better
print(bs_power.power_stats(percentile_tiny_sample_count))
bs_power.plot_power(percentile_tiny_sample_count[::20])
```
### Pivotal vs Percentile for small input sample size - 100 elements
```
pivotal_small_sample_count = bootstrap_vs_pop_mean(population, num_samples=100, is_pivotal=True)
percentile_small_sample_count = bootstrap_vs_pop_mean(population, num_samples=100, is_pivotal=False)
squared_dist_ratio(pivotal_small_sample_count, percentile_small_sample_count)
print(bs_power.power_stats(pivotal_small_sample_count))
bs_power.plot_power(pivotal_small_sample_count[::20])
print(bs_power.power_stats(percentile_small_sample_count))
bs_power.plot_power(percentile_small_sample_count[::20])
```
### Pivotal vs Percentile for medium input sample size - 1000 elements
```
pivotal_med_sample_count = bootstrap_vs_pop_mean(population, num_samples=1000, is_pivotal=True)
percentile_med_sample_count = bootstrap_vs_pop_mean(population, num_samples=1000, is_pivotal=False)
squared_dist_ratio(pivotal_med_sample_count, percentile_med_sample_count)
print(bs_power.power_stats(pivotal_med_sample_count))
bs_power.plot_power(pivotal_med_sample_count[::20])
print(bs_power.power_stats(percentile_med_sample_count))
bs_power.plot_power(percentile_med_sample_count[::20])
```
### Pivotal vs Percentile for somewhat large input sample size - 10k elements
### Bad Populaiton
```
bad_population = pd.Series([1]*10000 + [100000])
# Plot the population
count, bins, ignored = plt.hist(bad_population, 30, normed=True)
plt.title('Distribution of the population')
plt.show()
samples = bad_population.sample(10000)
print('Mean:\t\t{}'.format(bad_population.mean()))
print('Pivotal CI:\t{}'.format(bs.bootstrap(samples.values, stat_func=bs_stats.mean, is_pivotal=True)))
print('Percentile CI:\t{}'.format(bs.bootstrap(samples.values, stat_func=bs_stats.mean, is_pivotal=False)))
```
**Analysis:** The correction from the pivotal method causes a negative lower bound for the estimate in this instance. Generalization: the pivotal correction may not always produce realisitc intervals. In this situation we know that the mean cant be less than one. Still, we have seen from above that the piovtal method seems to be more reliable - this is why it is the default.
| true |
code
| 0.610599 | null | null | null | null |
|
# Image Classification Neo Compilation Example - Local Mode
This notebook shows an intermediate step in the process of developing an Edge image classification algorithm.
## Notebook Setup
```
%matplotlib inline
import time
import os
#os.environ["CUDA_VISIBLE_DEVICES"]="0"
import tensorflow as tf
import numpy as np
import cv2
from tensorflow.python.client import device_lib
tf.__version__
```
## Helper Functions and scripts
```
def get_img(img_path):
img = cv2.imread(img_path)
img = cv2.resize(img.astype(float), (224, 224)) #resize
imgMean = np.array([104, 117, 124], np.float)
img -= imgMean #subtract image mean
return img
def get_label_encode(class_id):
enc = np.zeros((257),dtype=int)
enc[class_id] = 1
return enc
def freeze_graph(model_dir, output_node_names):
"""Extract the sub graph defined by the output nodes and convert
all its variables into constant
Args:
model_dir: the root folder containing the checkpoint state file
output_node_names: a string, containing all the output node's names,
comma separated
"""
if not tf.gfile.Exists(model_dir):
raise AssertionError(
"Export directory doesn't exists. Please specify an export "
"directory: %s" % model_dir)
if not output_node_names:
print("You need to supply the name of a node to --output_node_names.")
return -1
# We retrieve our checkpoint fullpath
checkpoint = tf.train.get_checkpoint_state(model_dir)
input_checkpoint = checkpoint.model_checkpoint_path
# We precise the file fullname of our freezed graph
absolute_model_dir = "/".join(input_checkpoint.split('/')[:-1])
output_graph = absolute_model_dir + "/frozen_model.pb"
# We clear devices to allow TensorFlow to control on which device it will load operations
clear_devices = True
# We start a session using a temporary fresh Graph
with tf.Session(graph=tf.Graph()) as sess:
# We import the meta graph in the current default Graph
saver = tf.train.import_meta_graph(input_checkpoint + '.meta', clear_devices=clear_devices)
# We restore the weights
saver.restore(sess, input_checkpoint)
# We use a built-in TF helper to export variables to constants
output_graph_def = tf.graph_util.convert_variables_to_constants(
sess, # The session is used to retrieve the weights
tf.get_default_graph().as_graph_def(), # The graph_def is used to retrieve the nodes
output_node_names.split(",") # The output node names are used to select the usefull nodes
)
# Finally we serialize and dump the output graph to the filesystem
with tf.gfile.GFile(output_graph, "wb") as f:
f.write(output_graph_def.SerializeToString())
print("%d ops in the final graph." % len(output_graph_def.node))
return output_graph_def
class VGG(object):
"""alexNet model"""
def __init__(self, n_classes, batch_size=None):
self.NUM_CLASSES = n_classes
self.BATCH_SIZE = batch_size
self.x = tf.placeholder(tf.float32, [None, 224, 224, 3])
self.y = tf.placeholder(tf.float32, [None, self.NUM_CLASSES])
self.buildCNN()
def buildCNN(self):
"""build model"""
input_layer = self.x
conv1_1 = tf.layers.conv2d(
input_layer, filters=64, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv1_1'
)
conv1_2 = tf.layers.conv2d(
conv1_1, filters=64, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv1_2'
)
pool1 = tf.layers.max_pooling2d(conv1_2, pool_size=(2, 2), strides=(2, 2), padding='SAME', name='pool1')
# conv2
conv2_1 = tf.layers.conv2d(
pool1, filters=128, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv2_1'
)
conv2_2 = tf.layers.conv2d(
conv2_1, filters=128, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv2_2'
)
pool2 = tf.layers.max_pooling2d(conv2_2, pool_size=(2, 2), strides=(2, 2), padding='SAME', name='pool2')
# conv3
conv3_1 = tf.layers.conv2d(
pool2, filters=256, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv3_1'
)
conv3_2 = tf.layers.conv2d(
conv3_1, filters=256, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv3_2'
)
conv3_3 = tf.layers.conv2d(
conv3_2, filters=256, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv3_3'
)
pool3 = tf.layers.max_pooling2d(conv3_3, pool_size=(2, 2), strides=(2, 2), padding='SAME', name='pool3')
# conv4
conv4_1 = tf.layers.conv2d(
pool3, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv4_1'
)
conv4_2 = tf.layers.conv2d(
conv4_1, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv4_2'
)
conv4_3 = tf.layers.conv2d(
conv4_2, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv4_3'
)
pool4 = tf.layers.max_pooling2d(conv4_3, pool_size=(2, 2), strides=(2, 2), padding='SAME', name='pool4')
# conv5
conv5_1 = tf.layers.conv2d(
pool4, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv5_1'
)
conv5_2 = tf.layers.conv2d(
conv5_1, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv5_2'
)
conv5_3 = tf.layers.conv2d(
conv5_2, filters=512, kernel_size=(3, 3), strides=(1, 1), activation=tf.nn.relu, padding='SAME', name='conv5_3'
)
pool5 = tf.layers.max_pooling2d(conv5_3, pool_size=(2, 2), strides=(2, 2), padding='SAME', name='pool5')
#print('POOL5', pool5.shape)
#CULPADO flatten = tf.layers.flatten(pool5, name='flatten')
flatten = tf.reshape(pool5, [-1, 7*7*512])
fc1_relu = tf.layers.dense(flatten, units=4096, activation=tf.nn.relu, name='fc1_relu')
fc2_relu = tf.layers.dense(fc1_relu, units=4096, activation=tf.nn.relu, name='fc2_relu')
self.logits = tf.layers.dense(fc2_relu, units=self.NUM_CLASSES, name='fc3_relu')
#fc3 = tf.nn.softmax(logits)
print(self.logits.shape)
# Return the complete AlexNet model
return self.logits
net = VGG(257)
net.x, net.y, net.logits
```
## Dataset
The example is no longer on this URL. Now it has to be downloaded from Google Drive: https://drive.google.com/uc?id=1r6o0pSROcV1_VwT4oSjA2FBUSCWGuxLK
```
!conda install -c conda-forge -y gdown
!mkdir -p ../data/Caltech256
import gdown
url = "https://drive.google.com/uc?id=1r6o0pSROcV1_VwT4oSjA2FBUSCWGuxLK"
destination = "../data/Caltech256/256_ObjectCategories.tar"
gdown.download(url, destination, quiet=False)
#!curl http://www.vision.caltech.edu/Image_Datasets/Caltech256/256_ObjectCategories.tar -o ../data/Caltech256/256_ObjectCategories.tar
%%sh
pushd ../data/Caltech256/
tar -xvf 256_ObjectCategories.tar
popd
import glob
import random
from sklearn.model_selection import train_test_split
counter = 0
classes = {}
all_image_paths = list(glob.glob('../data/Caltech256/256_ObjectCategories/*/*.jpg'))
x = []
y = []
for i in all_image_paths:
_,cat,fname = i.split('/')[3:]
if classes.get(cat) is None:
classes[cat] = counter
counter += 1
x.append(i)
y.append(classes.get(cat))
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=42)
```
## Training
```
# (6) Define model's cost and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=net.logits, labels=net.y))
optimizer = tf.train.AdamOptimizer().minimize(cost)
# (7) Defining evaluation metrics
correct_prediction = tf.equal(tf.argmax(net.logits, 1), tf.argmax(net.y, 1))
accuracy_pct = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) * 100
# (8) initialize
initializer_op = tf.global_variables_initializer()
epochs = 1
batch_size = 128
test_batch_size = 256
# (9) Run
with tf.Session() as session:
session.run(initializer_op)
print("Training for", epochs, "epochs.")
# looping over epochs:
for epoch in range(epochs):
# To monitor performance during training
avg_cost = 0.0
avg_acc_pct = 0.0
# loop over all batches of the epoch- 1088 records
# batch_size = 128 is already defined
n_batches = int(len(x_train) / batch_size)
counter = 1
for i in range(n_batches):
# Get the random int for batch
#random_indices = np.random.randint(len(x_train), size=batch_size) # 1088 is the no of training set records
pivot = i * batch_size
feed = {
net.x: [get_img(i) for i in x_train[pivot:pivot+batch_size]],
net.y: [get_label_encode(i) for i in y_train[pivot:pivot+batch_size]]
}
# feed batch data to run optimization and fetching cost and accuracy:
_, batch_cost, batch_acc = session.run([optimizer, cost, accuracy_pct],
feed_dict=feed)
# Print batch cost to see the code is working (optional)
# print('Batch no. {}: batch_cost: {}, batch_acc: {}'.format(counter, batch_cost, batch_acc))
# Get the average cost and accuracy for all batches:
avg_cost += batch_cost / n_batches
avg_acc_pct += batch_acc / n_batches
counter += 1
if counter % 50 == 0:
print("Batch {}/{}: batch_cost={:.3f}, batch_acc={:.3f},avg_cost={:.3f},avg_acc={:.3f}".format(
i,n_batches, batch_cost, batch_acc, avg_cost, avg_acc_pct
))
# Get cost and accuracy after one iteration
test_cost = cost.eval({net.x: [get_img(i) for i in x_test[:test_batch_size]], net.y: [get_label_encode(i) for i in y_test[:test_batch_size]]})
test_acc_pct = accuracy_pct.eval({net.x: [get_img(i) for i in x_test[:test_batch_size]], net.y: [get_label_encode(i) for i in y_test[:test_batch_size]]})
# output logs at end of each epoch of training:
print("Epoch {}: Training Cost = {:.3f}, Training Acc = {:.2f} -- Test Cost = {:.3f}, Test Acc = {:.2f}"\
.format(epoch + 1, avg_cost, avg_acc_pct, test_cost, test_acc_pct))
# Getting Final Test Evaluation
print('\n')
print("Training Completed. Final Evaluation on Test Data Set.\n")
test_cost = cost.eval({net.x: [get_img(i) for i in x_test[:test_batch_size]], net.y: [get_label_encode(i) for i in y_test[:test_batch_size]]})
test_accy_pct = accuracy_pct.eval({net.x: [get_img(i) for i in x_test[:test_batch_size]], net.y: [get_label_encode(i) for i in y_test[:test_batch_size]]})
print("Test Cost:", '{:.3f}'.format(test_cost))
print("Test Accuracy: ", '{:.2f}'.format(test_accy_pct), "%", sep='')
print('\n')
# Getting accuracy on Validation set
val_cost = cost.eval({net.x: [get_img(i) for i in x_test[test_batch_size:test_batch_size*2]], net.y: [get_label_encode(i) for i in y_test[test_batch_size:test_batch_size*2]]})
val_acc_pct = accuracy_pct.eval({net.x: [get_img(i) for i in x_test[test_batch_size:test_batch_size*2]], net.y: [get_label_encode(i) for i in y_test[test_batch_size:test_batch_size*2]]})
print("Evaluation on Validation Data Set.\n")
print("Evaluation Cost:", '{:.3f}'.format(val_cost))
print("Evaluation Accuracy: ", '{:.2f}'.format(val_acc_pct), "%", sep='')
```
## Saving/exporting the model
```
!rm -rf vgg16/
exporter = tf.saved_model.builder.SavedModelBuilder('vgg16/model')
saver = tf.train.Saver()
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
img = get_img('TestImage.jpg')
batch = np.array([img for i in range(batch_size)]).reshape((batch_size,224,224,3))
print(batch.shape)
x = net.x
y = net.logits
start_time = time.time()
out = sess.run(y, feed_dict = {x: batch})
print("Elapsed time: {}".format(time.time() - start_time))
exporter.add_meta_graph_and_variables(
sess,
tags=[tf.saved_model.tag_constants.SERVING],
signature_def_map={
tf.saved_model.signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY:
tf.saved_model.signature_def_utils.predict_signature_def(
inputs={"inputs": net.x},
outputs={"outputs": net.logits }
)
},
strip_default_attrs=True)
#exporter.save()
saver.save(sess, 'vgg16/model/model')
_ = freeze_graph('vgg16/model', 'fc3_relu/BiasAdd')
!cd vgg16 && rm -f model.tar.gz && cd model && tar -czvf ../model.tar.gz frozen_model.pb
import time
import sagemaker
import os
import json
import boto3
# Retrieve the default bucket
sagemaker_session = sagemaker.Session()
default_bucket = sagemaker_session.default_bucket()
type(sagemaker_session)
role=sagemaker.session.get_execution_role()
job_prefix='VGG16'
path='neo/%s' % job_prefix
sm = boto3.client('sagemaker')
!aws s3 cp vgg16/model.tar.gz s3://$default_bucket/$path/model.tar.gz
target_device='ml_m5'
# 'lambda'|'ml_m4'|'ml_m5'|'ml_c4'|'ml_c5'|'ml_p2'|'ml_p3'|'ml_g4dn'|'ml_inf1'|'jetson_tx1'|'jetson_tx2'|'jetson_nano'|'jetson_xavier'|
# 'rasp3b'|'imx8qm'|'deeplens'|'rk3399'|'rk3288'|'aisage'|'sbe_c'|'qcs605'|'qcs603'|'sitara_am57x'|'amba_cv22'|'x86_win32'|'x86_win64'
job_name="%s-%d" % (job_prefix, int(time.time()))
sm.create_compilation_job(
CompilationJobName=job_name,
RoleArn=role,
InputConfig={
'S3Uri': "s3://%s/%s/model.tar.gz" % (default_bucket, path),
'DataInputConfig': '{"data":[1,224,224,3]}',
'Framework': 'TENSORFLOW'
},
OutputConfig={
'S3OutputLocation': "s3://%s/%s/" % (default_bucket, path),
'TargetDevice': target_device
},
StoppingCondition={
'MaxRuntimeInSeconds': 300
}
)
print(job_name)
default_bucket
```
## NEO
```
!echo s3://$default_bucket/neo/VGG16/model-$target_device\.tar.gz
!aws s3 cp s3://$default_bucket/neo/VGG16/model-$target_device\.tar.gz .
!tar -tzvf model-$target_device\.tar.gz
!rm -rf neo_test && mkdir neo_test
!tar -xzvf model-$target_device\.tar.gz -C neo_test
!ldd neo_test/compiled.so
%%time
import os
import numpy as np
import cv2
import time
from dlr import DLRModel
model_path='neo_test'
imgMean = np.array([104, 117, 124], np.float)
img = cv2.imread("TestImage.jpg")
img = cv2.resize(img.astype(float), (224, 224)) # resize
img -= imgMean #subtract image mean
img = img.reshape((1, 224, 224, 3))
device = 'cpu' # Go, Raspberry Pi, go!
model = DLRModel(model_path, dev_type=device)
print(model.get_input_names())
def predict(img):
start = time.time()
input_data = {'Placeholder': img}
out = model.run(input_data)
return (out, time.time()-start)
startTime = time.time()
out = [predict(img)[1] for i in (range(1))]
print("Elapsed time: {}".format((time.time() - start_time)))
#top1 = np.argmax(out[0])
#prob = np.max(out)
#print("Class: %d, probability: %f" % (top1, prob))
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(20,10))
ax = plt.axes()
ax.plot(out)
```
| true |
code
| 0.731173 | null | null | null | null |
|
# Basic Distributions
### A. Taylan Cemgil
### Boğaziçi University, Dept. of Computer Engineering
### Notebook Summary
* We review the notation and parametrization of densities of some basic distributions that are often encountered
* We show how random numbers are generated using python libraries
* We show some basic visualization methods such as displaying histograms
# Sampling From Basic Distributions
Sampling from basic distribution is easy using the numpy library.
Formally we will write
$x \sim p(X|\theta)$
where $\theta$ is the _parameter vector_, $p(X| \theta)$ denotes the _density_ of the random variable $X$ and $x$ is a _realization_, a particular draw from the density $p$.
The following distributions are building blocks from which more complicated processes may be constructed. It is important to have a basic understanding of these distributions.
### Continuous Univariate
* Uniform $\mathcal{U}$
* Univariate Gaussian $\mathcal{N}$
* Gamma $\mathcal{G}$
* Inverse Gamma $\mathcal{IG}$
* Beta $\mathcal{B}$
### Discrete
* Poisson $\mathcal{P}$
* Bernoulli $\mathcal{BE}$
* Binomial $\mathcal{BI}$
* Categorical $\mathcal{M}$
* Multinomial $\mathcal{M}$
### Continuous Multivariate (todo)
* Multivariate Gaussian $\mathcal{N}$
* Dirichlet $\mathcal{D}$
### Continuous Matrix-variate (todo)
* Wishart $\mathcal{W}$
* Inverse Wishart $\mathcal{IW}$
* Matrix Gaussian $\mathcal{N}$
## Sampling from the standard uniform $\mathcal{U}(0,1)$
For generating a single random number in the interval $[0, 1)$ we use the notation
$$
x_1 \sim \mathcal{U}(x; 0,1)
$$
In python, this is implemented as
```
import numpy as np
x_1 = np.random.rand()
print(x_1)
```
We can also generate an array of realizations $x_i$ for $i=1 \dots N$,
$$
x_i \sim \mathcal{U}(x; 0,1)
$$
```
import numpy as np
N = 5
x = np.random.rand(N)
print(x)
```
For large $N$, it is more informative to display an histogram of generated data:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# Number of realizations
N = 50000
x = np.random.rand(N)
plt.hist(x, bins=20)
plt.xlabel('x')
plt.ylabel('Count')
plt.show()
```
$\newcommand{\indi}[1]{\left[{#1}\right]}$
$\newcommand{\E}[1]{\left\langle{#1}\right\rangle}$
We know that the density of the uniform distribution $\mathcal{U}(0,1)$ is
$$
\mathcal{U}(x; 0,1) = \left\{ \begin{array}{cc} 1 & 0 \leq x < 1 \\ 0 & \text{otherwise} \end{array} \right.
$$
or using the indicator notation
$$
\mathcal{U}(x; 0,1) = \left[ x \in [0,1) \right]
$$
#### Indicator function
To write and manipulate discrete probability distributions in algebraic expression, the *indicator* function is useful:
$$ \left[x\right] = \left\{ \begin{array}{cc}
1 & x\;\;\text{is true} \\
0 & x\;\;\text{is false}
\end{array}
\right.$$
This notation is also known as the Iverson's convention.
#### Aside: How to plot the density and the histogram onto the same plot?
In one dimension, the histogram is simply the count of the data points that fall to a given interval. Mathematically, we have
$j = 1\dots J$ intervals where $B_j = [b_{j-1}, b_j]$ and $b_j$ are bin boundries such that $b_0 < b_1 < \dots < b_J$.
$$
h(x) = \sum_{j=1}^J \sum_{i=1}^N \indi{x \in B_j} \indi{x_i \in B_j}
$$
This expression, at the first sight looks somewhat more complicated than it really is. The indicator product just encodes the logical condition $x \in B_j$ __and__ $x_i \in B_j$. The sum over $j$ is just a convenient way of writing the result instead of specifying the histogram as a case by case basis for each bin. It is important to get used to such nested sums.
When the density $p(x)$ is given, the probability that a single realization is in bin $B_j$ is given by
$$
\Pr\left\{x \in B_j\right\} = \int_{B_j} dx p(x) = \int_{-\infty}^{\infty} dx \indi{x\in B_j} p(x) = \E{\indi{x\in B_j}}
$$
In other words, the probability is just the expectation of the indicator.
The histogram can be written as follows
$$
h(x) = \sum_{j=1}^J \indi{x \in B_j} \sum_{i=1}^N \indi{x_i \in B_j}
$$
We define the counts at each bin as
$$
c_j \equiv \sum_{i=1}^N \indi{x_i \in B_j}
$$
If all bins have the same width, i.e., $b_j - b_{j-1} = \Delta$ for $\forall j$, and if $\Delta$ is sufficiently small we have
$$
\E{\indi{x\in B_j}} \approx p(b_{j-1}+\Delta/2) \Delta
$$
i.e., the probability is roughly the interval width times the density evaluated at the middle point of the bin. The expected value of the counts is
$$
\E{c_j} = \sum_{i=1}^N \E{\indi{x_i \in B_j}} \approx N \Delta p(b_{j-1}+\Delta/2)
$$
Hence, the density should be roughly
$$
p(b_{j-1}+\Delta/2) \approx \frac{\E{c_j} }{N \Delta}
$$
The $N$ term is intuitive but the $\Delta$ term is easily forgotten. When plotting the histograms on top of the corresponding densities, we should scale the normalized histogram ${ c_j }/{N}$ by dividing by $\Delta$.
```
N = 1000
# Bin width
Delta = 0.02
# Bin edges
b = np.arange(0 ,1+Delta, Delta)
# Evaluate the density
g = np.ones(b.size)
# Draw the samples
u = np.random.rand(N)
counts,edges = np.histogram(u, bins=b)
plt.bar(b[:-1], counts/N/Delta, width=Delta)
#plt.hold(True)
plt.plot(b, g, linewidth=3, color='y')
#plt.hold(False)
plt.show()
```
The __plt.hist__ function (calling __np.histogram__) can do this calculation automatically if the option normed=True. However, when the grid is not uniform, it is better to write your own code to be sure what is going on.
```
N = 1000
Delta = 0.05
b = np.arange(0 ,1+Delta, Delta)
g = np.ones(b.size)
u = np.random.rand(N)
#plt.hold(True)
plt.plot(b, g, linewidth=3, color='y')
plt.hist(u, bins=b, normed=True)
#plt.hold(False)
plt.show()
```
# Continuous Univariate Distributions
* Uniform $\mathcal{U}$
* Univariate Gaussian $\mathcal{N}$
$${\cal N}(x;\mu, v) = \frac{1}{\sqrt{2\pi v}} \exp\left(-\frac12 \frac{(x - \mu)^2}{v}\right) $$
* Gamma $\mathcal{G}$
$${\cal G}(\lambda; a, b) = \frac{b^a \lambda^{a-1}}{\Gamma(a)} \exp( - b \lambda)$$
* Inverse Gamma $\mathcal{IG}$
$${\cal IG}(v; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha) v^{\alpha+1}} \exp(- \frac{\beta}{v}) $$
* Beta $\mathcal{B}$
$${\cal B}(r; \alpha, \beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta) } r^{\alpha-1} (1-r)^{\beta-1}$$
In derivations, the distributions are often needed as building blocks. The following code segment prints the latex strings to be copied and pasted.
$\DeclareMathOperator{\trace}{Tr}$
```
from IPython.display import display, Math, Latex, HTML
import notes_utilities as nut
print('Gaussian')
L = nut.pdf2latex_gauss(x=r'Z_{i,j}', m=r'\mu_{i,j}',v=r'l_{i,j}')
display(HTML(nut.eqs2html_table(L)))
print('Gamma')
L = nut.pdf2latex_gamma(x=r'u', a=r'a',b=r'b')
display(HTML(nut.eqs2html_table(L)))
print('Inverse Gamma')
L = nut.pdf2latex_invgamma(x=r'z', a=r'a',b=r'b')
display(HTML(nut.eqs2html_table(L)))
print('Beta')
L = nut.pdf2latex_beta(x=r'\pi', a=r'\alpha',b=r'\beta')
display(HTML(nut.eqs2html_table(L)))
```
We will illustrate two alternative ways for sampling from continuous distributions.
- The first method has minimal dependence on the numpy and scipy libraries. This is initially the preferred method. Only random variable generators and the $\log \Gamma(x)$ (__gammaln__) function is used and nothing more.
- The second method uses scipy. This is a lot more practical but requires knowing more about the internals of the library.
### Aside: The Gamma function $\Gamma(x)$
The gamma function $\Gamma(x)$ is the (generalized) factorial.
- Defined by
$$\Gamma(x) = \int_0^{\infty} t^{x-1} e^{-t}\, dt$$
- For integer $x$, $\Gamma(x) = (x-1)!$. Remember that for positive integers $x$, the factorial function can be defined recursively $x! = (x-1)! x $ for $x\geq 1$.
- For real $x>1$, the gamma function satisfies
$$
\Gamma(x+1) = \Gamma(x) x
$$
- Interestingly, we have
$$\Gamma(1/2) = \sqrt{\pi}$$
- Hence
$$\Gamma(3/2) = \Gamma(1/2 + 1) = \Gamma(1/2) (1/2) = \sqrt{\pi}/2$$
- It is available in many numerical computation packages, in python it is available as __scipy.special.gamma__.
- To compute $\log \Gamma(x)$, you should always use the implementation as __scipy.special.gammaln__. The gamma function blows up super-exponentially so numerically you should never evaluate $\log \Gamma(x)$ as
```python
import numpy as np
import scipy.special as sps
np.log(sps.gamma(x)) # Don't
sps.gammaln(x) # Do
```
- A related function is the Beta function
$$B(x,y) = \int_0^{1} t^{x-1} (1-t)^{y-1}\, dt$$
- We have
$$B(x,y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$
- Both $\Gamma(x)$ and $B(x)$ pop up as normalizing constant of the gamma and beta distributions.
#### Derivatives of $\Gamma(x)$
- <span style="color:red"> </span> The derivatives of $\log \Gamma(x)$ pop up quite often when fitting densities. The first derivative has a specific name, often called the digamma function or the psi function.
$$
\Psi(x) \equiv \frac{d}{d x} \log \Gamma(x)
$$
- It is available as __scipy.special.digamma__ or __scipy.special.psi__
- Higher order derivatives of the $\log \Gamma(x)$ function (including digamma itself) are available as __scipy.special.polygamma__
```
import numpy as np
import scipy.special as sps
import matplotlib.pyplot as plt
x = np.arange(0.1,5,0.01)
f = sps.gammaln(x)
df = sps.psi(x)
# First derivative of the digamma function
ddf = sps.polygamma(1,x)
# sps.psi(x) == sps.polygamma(0,x)
plt.figure(figsize=(8,10))
plt.subplot(3,1,1)
plt.plot(x, f, 'r')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('log Gamma(x)')
plt.subplot(3,1,2)
plt.grid(True)
plt.plot(x, df, 'b')
plt.xlabel('x')
plt.ylabel('Psi(x)')
plt.subplot(3,1,3)
plt.plot(x, ddf, 'k')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('Psi\'(x)')
plt.show()
```
#### Stirling's approximation
An important approximation to the factorial is the famous Stirling's approximation
\begin{align}
n! \sim \sqrt{2 \pi n}\left(\frac{n}{e}\right)^n
\end{align}
\begin{align}
\log \Gamma(x+1) \approx \frac{1}{2}\log(2 \pi) + x \log(x) - \frac{1}{2} \log(x)
\end{align}
```
import matplotlib.pylab as plt
import numpy as np
from scipy.special import polygamma
from scipy.special import gammaln as loggamma
from scipy.special import psi
x = np.arange(0.001,6,0.001)
ylim = [-1,8]
xlim = [-1,6]
plt.plot(x, loggamma(x), 'b')
stir = x*np.log(x)-x +0.5*np.log(2*np.pi*x)
plt.plot(x+1, stir,'r')
plt.hlines(0,0,8)
plt.vlines([0,1,2],ylim[0],ylim[1],linestyles=':')
plt.hlines(range(ylim[0],ylim[1]),xlim[0],xlim[1],linestyles=':',colors='g')
plt.ylim(ylim)
plt.xlim(xlim)
plt.legend([r'\log\Gamma(x)',r'\log(x-1)'],loc=1)
plt.xlabel('x')
plt.show()
```
# Sampling from Continuous Univariate Distributions
## Sampling using numpy.random
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import gammaln
def plot_histogram_and_density(N, c, edges, dx, g, title='Put a title'):
'''
N : Number of Datapoints
c : Counts, as obtained from np.histogram function
edges : bin edges, as obtained from np.histogram
dx : The bin width
g : Density evaluated at the points given in edges
title : for the plot
'''
plt.bar(edges[:-1], c/N/dx, width=dx)
# plt.hold(True)
plt.plot(edges, g, linewidth=3, color='y')
# plt.hold(False)
plt.title(title)
def log_gaussian_pdf(x, mu, V):
return -0.5*np.log(2*np.pi*V) -0.5*(x-mu)**2/V
def log_gamma_pdf(x, a, b):
return (a-1)*np.log(x) - b*x - gammaln(a) + a*np.log(b)
def log_invgamma_pdf(x, a, b):
return -(a+1)*np.log(x) - b/x - gammaln(a) + a*np.log(b)
def log_beta_pdf(x, a, b):
return - gammaln(a) - gammaln(b) + gammaln(a+b) + np.log(x)*(a-1) + np.log(1-x)*(b-1)
N = 1000
# Univariate Gaussian
mu = 2 # mean
V = 1.2 # Variance
x_normal = np.random.normal(mu, np.sqrt(V), N)
dx = 10*np.sqrt(V)/50
x = np.arange(mu-5*np.sqrt(V) ,mu+5*np.sqrt(V),dx)
g = np.exp(log_gaussian_pdf(x, mu, V))
#g = scs.norm.pdf(x, loc=mu, scale=np.sqrt(V))
c,edges = np.histogram(x_normal, bins=x)
plt.figure(num=None, figsize=(16, 5), dpi=80, facecolor='w', edgecolor='k')
plt.subplot(2,2,1)
plot_histogram_and_density(N, c, x, dx, g, 'Gaussian')
## Gamma
# Shape
a = 1.2
# inverse scale
b = 30
# Generate unit scale first than scale with inverse scale parameter b
x_gamma = np.random.gamma(a, 1, N)/b
dx = np.max(x_gamma)/500
x = np.arange(dx, 250*dx, dx)
g = np.exp(log_gamma_pdf(x, a, b))
c,edges = np.histogram(x_gamma, bins=x)
plt.subplot(2,2,2)
plot_histogram_and_density(N, c, x, dx, g, 'Gamma')
## Inverse Gamma
a = 3.5
b = 0.2
x_invgamma = b/np.random.gamma(a, 1, N)
dx = np.max(x_invgamma)/500
x = np.arange(dx, 150*dx, dx)
g = np.exp(log_invgamma_pdf(x,a,b))
c,edges = np.histogram(x_invgamma, bins=x)
plt.subplot(2,2,3)
plot_histogram_and_density(N, c, x, dx, g, 'Inverse Gamma')
## Beta
a = 0.5
b = 1
x_beta = np.random.beta(a, b, N)
dx = 0.01
x = np.arange(dx, 1, dx)
g = np.exp(log_beta_pdf(x, a, b))
c,edges = np.histogram(x_beta, bins=x)
plt.subplot(2,2,4)
plot_histogram_and_density(N, c, x, dx, g, 'Beta')
plt.show()
```
## Sampling using scipy.stats
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as scs
N = 2000
# Univariate Gaussian
mu = 2 # mean
V = 1.2 # Variance
rv_normal = scs.norm(loc=mu, scale=np.sqrt(V))
x_normal = rv_normal.rvs(size=N)
dx = 10*np.sqrt(V)/50
x = np.arange(mu-5*np.sqrt(V) ,mu+5*np.sqrt(V),dx)
g = rv_normal.pdf(x)
c,edges = np.histogram(x_normal, bins=x)
plt.figure(num=None, figsize=(16, 5), dpi=80, facecolor='w', edgecolor='k')
plt.subplot(2,2,1)
plot_histogram_and_density(N, c, x, dx, g, 'Gaussian')
## Gamma
a = 3.2
b = 30
# The following is equivalent to our parametrization of gamma, note the 1/b term
rv_gamma = scs.gamma(a, scale=1/b)
x_gamma = rv_gamma.rvs(N)
dx = np.max(x_gamma)/500
x = np.arange(0, 250*dx, dx)
g = rv_gamma.pdf(x)
c,edges = np.histogram(x_gamma, bins=x)
plt.subplot(2,2,2)
plot_histogram_and_density(N, c, x, dx, g, 'Gamma')
## Inverse Gamma
a = 3.5
b = 0.2
# Note the b term
rv_invgamma = scs.invgamma(a, scale=b)
x_invgamma = rv_invgamma.rvs(N)
dx = np.max(x_invgamma)/500
x = np.arange(dx, 150*dx, dx)
g = rv_invgamma.pdf(x)
c,edges = np.histogram(x_invgamma, bins=x)
plt.subplot(2,2,3)
plot_histogram_and_density(N, c, x, dx, g, 'Inverse Gamma')
## Beta
a = 0.7
b = 0.8
rv_beta = scs.beta(a, b)
x_beta = rv_beta.rvs(N)
dx = 0.02
x = np.arange(0, 1+dx, dx)
g = rv_beta.pdf(x)
c,edges = np.histogram(x_beta, bins=x)
plt.subplot(2,2,4)
plot_histogram_and_density(N, c, x, dx, g, 'Beta')
plt.show()
```
# Sampling from Discrete Densities
* Bernoulli $\mathcal{BE}$
$$
{\cal BE}(r; w) = w^r (1-w)^{1-r} \;\; \text{if} \; r \in \{0, 1\}
$$
* Binomial $\mathcal{BI}$
$${\cal BI}(r; L, w) = \binom{L}{r, (L-r)} w^r (1-w)^{L-r} \;\; \text{if} \; r \in \{0, 1, \dots, L\} $$
Here, the binomial coefficient is defined as
$$
\binom{L}{r, (L-r)} = \frac{N!}{r!(L-r)!}
$$
Note that
$$
{\cal BE}(r; w) = {\cal BI}(r; L=1, w)
$$
* Poisson $\mathcal{PO}$, with intensity $\lambda$
$${\cal PO}(x;\lambda) = \frac{e^{-\lambda} \lambda^x}{x!} = \exp(x \log \lambda - \lambda - \log\Gamma(x+1)) $$
Given samples on nonnegative integers, we can obtain histograms easily using __np.bincount__.
```python
c = np.bincount(samples)
```
The functionality is equivalent to the following sniplet, while implementation is possibly different and more efficient.
```python
upper_bound = np.max()
c = np.zeros(upper_bound+1)
for i in samples:
c[i] += 1
```
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def plot_histogram_and_pmf(N, c, domain, dx, g, title='Put a title'):
'''
N : Number of Datapoints
c : Counts, as obtained from np.bincount function
domain : integers for each c, same size as c
dx : The bin width
g : Density evaluated at the points given in edges
title : for the plot
'''
plt.bar(domain-dx/2, c/N, width=dx)
# plt.hold(True)
plt.plot(domain, g, 'ro:', linewidth=3, color='y')
# plt.hold(False)
plt.title(title)
def log_poisson_pdf(x, lam):
return -lam + x*np.log(lam) - gammaln(x+1)
def log_bernoulli_pdf(r, pr):
return r*np.log(pr) + (1-r)*np.log(1 - pr)
def log_binomial_pdf(r, pr, L):
return gammaln(L+1) - gammaln(r+1) - gammaln(L-r+1) + r*np.log(pr) + (L-r)*np.log(1 - pr)
N = 100
pr = 0.8
# For plots
bin_width = 0.3
# Bernoulli
L = 1
x_bern = np.random.binomial(n=L, p=pr, size=N)
c = np.bincount(x_bern, minlength=L+1)
g = np.exp(log_bernoulli_pdf(np.arange(L+1), pr))
plt.figure(figsize=(20,4))
plt.subplot(1,3,1)
plot_histogram_and_pmf(N, c, np.arange(L+1), bin_width, g, 'Bernoulli')
plt.xticks([0,1])
# Binomial
L = 10
pr = 0.7
x_binom = np.random.binomial(n=L, p=pr, size=N)
c = np.bincount(x_binom, minlength=L+1)
g = np.exp(log_binomial_pdf(np.arange(L+1), pr, L))
plt.subplot(1,3,2)
plot_histogram_and_pmf(N, c, np.arange(L+1), bin_width, g, 'Binomial')
plt.xticks(np.arange(L+1))
# Poisson
intensity = 10.5
x_poiss = np.random.poisson(intensity, size =N )
c = np.bincount(x_poiss)
x = np.arange(len(c))
g = np.exp(log_poisson_pdf(x, intensity))
plt.subplot(1,3,3)
plot_histogram_and_pmf(N, c, x, bin_width, g, 'Poisson')
```
## Bernoulli, Binomial, Categorical and Multinomial Distributions
The Bernoulli and Binomial distributions are quite simple and well known distributions on small integers, so it may come as a surprise that they have another, less obvious but arguably more useful representation as discrete multivariate densities. This representation makes the link to categorical distributions where there are more than two possible outcomes. Finally, all Bernoulli, Binomial or Categorical distributions are special cases of Multinomial distribution.
### Bernoulli
Recall the Bernoulli distribution $r \in \{0, 1\}$
$$
{\cal BE}(r; w) = w^r (1-w)^{1-r}
$$
We will define $\pi_0 = 1-w$ and $\pi_1 = w$, such that $\pi_0 + \pi_1 = 1$. The parameter vector is $\pi = (\pi_0, \pi_1)$
We will also introduce a positional encoding such that
\begin{eqnarray}
r = 0 & \Rightarrow & s = (1, 0) \\
r = 1 & \Rightarrow & s = (0, 1)
\end{eqnarray}
In other words $s = (s_0, s_1)$ is a 2-dimensional vector where
$$s_0, s_1 \in \{0,1\}\;\text{and}\; s_0 + s_1 = 1$$
We can now write the Bernoulli density
$$
p(s | \pi) = \pi_0^{s_0} \pi_1^{s_1}
$$
### Binomial
Similarly, recall the Binomial density where $r \in \{0, 1, \dots, L\}$
$${\cal BI}(r; L, w) = \binom{L}{r, (L-r)} w^r (1-w)^{L-r} $$
We will again define $\pi_0 = 1-w$ and $\pi_1 = w$, such that $\pi_0 + \pi_1 = 1$. The parameter vector is $\pi = (\pi_0, \pi_1)$
\begin{eqnarray}
r = 0 & \Rightarrow & s = (L, 0) \\
r = 1 & \Rightarrow & s = (L-1, 1)\\
r = 2 & \Rightarrow & s = (L-2, 2)\\
\dots \\
r = L & \Rightarrow & s = (0, L)
\end{eqnarray}
where $s = (s_0, s_1)$ is a 2-dimensional vector where $$s_0, s_1 \in \{0,\dots,L\} \;\text{and}\; s_0 + s_1 = L$$
We can now write the Binomial density as
$$
p(s | \pi) = \binom{L}{s_0, s_1} \pi_0^{s_0} \pi_1^{s_1}
$$
### Categorical (Multinouilli)
One of the advantages of this new notation is that we can write the density even if the outcomes are not numerical. For example, the result of a single coin flip experiment when $r \in \{$ 'Tail', 'Head' $\}$ where the probability of 'Tail' is $w$ can be written as
$$
p(r | w) = w^{\indi{r=\text{'Tail'}}} (1-w)^{\indi{r=\text{'Head'}}}
$$
We define $s_0 = \indi{r=\text{'Head'}}$ and $s_1 = \indi{r=\text{'Tail'}}$, then the density can be written in the same form as
$$
p(s | \pi) = \pi_0^{s_0} \pi_1^{s_1}
$$
where $\pi_0 = 1-w$ and $\pi_1 = w$.
More generally, when $r$ is from a set with $K$ elements, i.e., $r \in R = \{ v_0, v_1, \dots, v_{K-1} \}$ with probability of the event $r = v_k$ given as $\pi_k$, we define $s = (s_0, s_1, \dots, s_{K-1})$ for $k=0,\dots, K-1$
$$
s_k = \indi{r=v_k}
$$
Note that by construction, we have $\sum_k s_k = 1$.
The resulting density, known as the Categorical density, can be writen as
$$
p(s|\pi) = \pi_0^{s_0} \pi_1^{s_1} \dots \pi_{K-1}^{s_{K-1}}
$$
### Multinomial
When drawing from a categorical distribution, one chooses a single category from $K$ options with given probabilities. A standard model for this is placing a single ball into $K$ different bins. The vector $s = (s_0, s_1, \dots,s_k, \dots, s_{K-1})$ represents how many balls eack bin $k$ contains.
Now, place $L$ balls instead of one into $K$ bins with placing each ball idependently into bin $k$ where $k \in\{0,\dots,K-1\}$ with the probability $\pi_k$. The multinomial is the joint distribution of $s$ where $s_k$ is the number of balls placed into bin $k$.
The density will be denoted as
$${\cal M}(s; L, \pi) = \binom{L}{s_0, s_1, \dots, s_{K-1}}\prod_{k=0}^{K-1} \pi_k^{s_k} $$
Here $\pi \equiv [\pi_0, \pi_2, \dots, \pi_{K-1} ]$ is the probability vector and $L$ is referred as the _index parameter_.
Clearly, we have the normalization constraint $ \sum_k \pi_k = 1$ and realization of the counts $s$ satisfy
$ \sum_k s_k = L $.
Here, the _multinomial_ coefficient is defined as
$$\binom{L}{s_0, s_1, \dots, s_{K-1}} = \frac{L!}{s_0! s_1! \dots s_{K-1}!}$$
Binomial, Bernoulli and Categorical distributions are all special cases of the Multinomial distribution, with a suitable representation.
The picture is as follows:
~~~
|Balls/Bins | $2$ Bins | $K$ Bins |
|-------- | -------- | ---------|
| $1$ Ball | Bernoulli ${\cal BE}$ | Categorical ${\cal C}$ |
|-------- | -------- | ---------|
| $L$ Balls | Binomial ${\cal BI}$ | Multinomial ${\cal M}$ |
~~~
Murphy calls the categorical distribution ($1$ Ball, $K$ Bins) as the Multinoulli. This is non-standard but logical (and somewhat cute).
It is common to consider Bernoulli and Binomial as scalar random variables. However, when we think of them as special case of a Multinomial it is better to think of them as bivariate, albeit degenerate, random variables, as
illustrated in the following cell along with an alternative visualization.
```
# The probability parameter
pr = 0.3
fig = plt.figure(figsize=(16,50), edgecolor=None)
maxL = 12
plt.subplot(maxL-1,2,1)
plt.grid(False)
# Set up the scalar binomial density as a bivariate density
for L in range(1,maxL):
r = np.arange(L+1)
p = np.exp(log_binomial_pdf(r, pr=pr, L=L))
A = np.zeros(shape=(13,13))
for s in range(L):
s0 = s
s1 = L-s
A[s0, s1] = p[s]
#plt.subplot(maxL-1,2,2*L-1)
# plt.bar(r-0.25, p, width=0.5)
# ax.set_xlim(-1,maxL)
# ax.set_xticks(range(0,maxL))
if True:
plt.subplot(maxL-1,2,2*L-1)
plt.barh(bottom=r-0.25, width=p, height=0.5)
ax2 = fig.gca()
pos = ax2.get_position()
pos2 = [pos.x0, pos.y0, 0.04, pos.height]
ax2.set_position(pos2)
ax2.set_ylim(-1,maxL)
ax2.set_yticks(range(0,maxL))
ax2.set_xlim([0,1])
ax2.set_xticks([0,1])
plt.ylabel('s1')
ax2.invert_xaxis()
plt.subplot(maxL-1,2,2*L)
plt.imshow(A, interpolation='nearest', origin='lower',cmap='gray_r',vmin=0,vmax=0.7)
plt.xlabel('s0')
ax1 = fig.gca()
pos = ax1.get_position()
pos2 = [pos.x0-0.45, pos.y0, pos.width, pos.height]
ax1.set_position(pos2)
ax1.set_ylim(-1,maxL)
ax1.set_yticks(range(0,maxL))
ax1.set_xlim(-1,maxL)
ax1.set_xticks(range(0,maxL))
plt.show()
```
The following cell illustrates sampling from the Multinomial density.
```
# Number of samples
sz = 3
# Multinomial
p = np.array([0.3, 0.1, 0.1, 0.5])
K = len(p) # number of Bins
L = 20 # number of Balls
print('Multinomial with number of bins K = {K} and Number of balls L = {L}'.format(K=K,L=L))
print(np.random.multinomial(L, p, size=sz))
# Categorical
L = 1 # number of Balls
print('Categorical with number of bins K = {K} and a single ball L=1'.format(K=K))
print(np.random.multinomial(L, p, size=sz))
# Binomial
p = np.array([0.3, 0.7])
K = len(p) # number of Bins = 2
L = 20 # number of Balls
print('Binomial with two bins K=2 and L={L} balls'.format(L=L))
print(np.random.multinomial(L, p, size=sz))
# Bernoulli
L = 1 # number of Balls
p = np.array([0.3, 0.7])
K = len(p) # number of Bins = 2
print('Bernoulli, two bins and a single ball')
print(np.random.multinomial(L, p, size=sz))
```
| true |
code
| 0.63077 | null | null | null | null |
|
# Ex 12
```
import tensorflow as tf
from tensorflow import keras
import os
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras import models
from tensorflow.keras import layers
from tensorflow.keras.utils import to_categorical
from matplotlib.pyplot import figure
from time import time
seed=0
np.random.seed(seed) # fix random seed
start_time = time()
OTTIMIZZATORE = 'rmsprop'
LOSS = 'categorical_crossentropy'
BATCH = 120
EPOCHS = 10
BATCH_CONV = 120
EPOCHS_CONV = 10
```
### Exercise 12.1
By keeping fixed all the other parameters, try to use at least two other optimizers, different from SGD. <span style="color:red">Watch to accuracy and loss for training and validation data and comment on the performances</span>.
```
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
pixel_rows = train_images.shape[1]
pixel_col = train_images.shape[2]
def prepare_data(array):
array = array.reshape(array.shape[0], array.shape[1]*array.shape[2])
return array.astype('float32')/255.
x_train = prepare_data(train_images)
x_test = prepare_data(test_images)
y_train = to_categorical(train_labels)
y_test = to_categorical(test_labels)
def dense_model():
model = models.Sequential()
model.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(10, activation='softmax'))
return model
network = dense_model()
network.compile(optimizer=OTTIMIZZATORE,
loss=LOSS,
metrics=['accuracy'])
history = network.fit(x_train, y_train,
batch_size = BATCH,
epochs = EPOCHS,
validation_split = 0.1,
verbose=True,
shuffle=True)
figure(figsize=((10,5)), dpi=200)
plt.subplot(1,2,1)
plt.plot(history.history['loss'], label='Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title("Model Loss")
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend(loc='best')
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], label='Accuracy')
plt.plot(history.history['val_accuracy'], label='Validation Accuracy')
plt.title("Model Accuracy")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend(loc='best')
plt.show()
network.evaluate(x_test, y_test)
```
### Exercise 12.2
Change the architecture of your DNN using convolutional layers. Use `Conv2D`, `MaxPooling2D`, `Dropout`, but also do not forget `Flatten`, a standard `Dense` layer and `soft-max` in the end. I have merged step 2 and 3 in the following definition of `create_CNN()` that **<span style="color:red">you should complete</span>**:
```
def prepare_data_conv(array):
if keras.backend.image_data_format() == 'channels_first':
array = array.reshape(array.shape[0], 1, array.shape[1], array.shape[2])
shape = (1, array.shape[1], array.shape[2])
else:
array = array.reshape(array.shape[0], array.shape[1], array.shape[2], 1)
shape = (array.shape[1], array.shape[2], 1)
return array.astype('float32')/255., shape
x_train, INPUT_SHAPE = prepare_data_conv(train_images)
x_test, test_shape = prepare_data_conv(test_images)
def conv_model():
model = models.Sequential()
model.add(layers.Conv2D(32,
(3,3),
activation='relu',
input_shape=INPUT_SHAPE))
model.add(layers.MaxPooling2D((2,2)))
model.add(layers.Conv2D(64, (3,3), activation='relu',))
model.add(layers.MaxPooling2D((2,2)))
model.add(layers.Conv2D(64, (3,3), activation='relu',))
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
return model
network_conv = conv_model()
network_conv.compile(optimizer=OTTIMIZZATORE, loss=LOSS, metrics=['accuracy'])
history = network_conv.fit(x_train,
y_train,
validation_split=0.1,
verbose=True,
batch_size=BATCH,
epochs=5,
shuffle=True)
figure(figsize=((10,5)), dpi=200)
plt.subplot(1,2,1)
plt.plot(history.history['loss'], label='Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title("Model Loss")
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid(True)
plt.legend(loc='best')
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], label='Accuracy')
plt.plot(history.history['val_accuracy'], label='Validation Accuracy')
plt.title("Model Accuracy")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend(loc='best')
plt.grid(True)
plt.show()
network_conv.evaluate(x_test, y_test)
```
### Exercise 12.3
Use the `gimp` application to create 10 pictures of your "handwritten" digits, import them in your jupyter-notebook and try to see if your CNN is able to recognize your handwritten digits.
For example, you can use the following code to import a picture of an handwritten digit:
```
from PIL import Image
import os
plt.figure(figsize=(20,40), dpi=50)
full_data = np.zeros((10,28,28))
for k in range(0,10):
digit_filename = str(k)+".png"
digit_in = Image.open(digit_filename).convert('L')
pix=digit_in.load();
data = np.zeros((28, 28))
for j in range(28):
for i in range(28):
data[i,j]=pix[j,i]
plt.subplot(1,10,k+1)
plt.imshow(data, cmap='gray')
full_data[k,:,:] = data[:,:]
#data /= 255
plt.show()
print(data.shape)
```
Test di accuratezza con i numeri scritti a mano da me.
```
plt.figure(figsize=(20,40), dpi=50)
for k in range(0,10):
data = full_data[k,:,:]
data_conv = np.zeros((1,data.shape[0], data.shape[1]))
data_conv[0,:,:] = data[:,:]
data_conv, aa = prepare_data_conv(data_conv)
data = data.reshape(1, 28*28)
pred_0 = network.predict(data)
pred_1 = network_conv.predict(data_conv)
data = data.reshape(28,28)
plt.subplot(1,10,k+1)
plt.imshow(data, cmap='gray')
plt.title("Dense {}".format(np.argmax(pred_0))+"\n \nConv {}".format(np.argmax(pred_1)))
plt.axis('off')
plt.show()
```
Test di accuratezza con alcune cifre sempre dal ```MNIST```.
```
#X_test = X_test.reshape(X_test.shape[0], img_rows*img_cols)
predictions = network_conv.predict(x_test)
x_test = x_test.reshape(x_test.shape[0], 28, 28,1)
plt.figure(figsize=(15, 15))
for i in range(10):
ax = plt.subplot(2, 10, i + 1)
plt.imshow(x_test[i, :, :, 0], cmap='gray')
plt.title("Digit: {}\nPredicted: {}".format(np.argmax(y_test[i]), np.argmax(predictions[i])))
plt.axis('off')
plt.show()
end_time = time()
minutes = int((end_time - start_time)/60.)
seconds = int((end_time - start_time) - minutes*60)
print("Computation time: ", minutes, "min ", seconds, "sec.")
```
| true |
code
| 0.654453 | null | null | null | null |
|
```
# code for loading the format for the notebook
import os
# path : store the current path to convert back to it later
path = os.getcwd()
os.chdir( os.path.join('..', 'notebook_format') )
from formats import load_style
load_style()
os.chdir(path)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1. magic for inline plot
# 2. magic to print version
# 3. magic so that the notebook will reload external python modules
%matplotlib inline
%load_ext watermark
%load_ext autoreload
%autoreload 2
from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
%watermark -a 'Ethen' -d -t -v -p numpy,pandas,matplotlib,sklearn
```
# Softmax Regression
**Softmax Regression** is a generalization of logistic regression that we can use for multi-class classification. If we want to assign probabilities to an object being one of several different things, softmax is the thing to do. Even later on, when we start training neural network models, the final step will be a layer of softmax.
A softmax regression has two steps: first we add up the evidence of our input being in certain classes, and then we convert that evidence into probabilities.
In **Softmax Regression**, we replace the sigmoid logistic function by the so-called *softmax* function $\phi(\cdot)$.
$$P(y=j \mid z^{(i)}) = \phi(z^{(i)}) = \frac{e^{z^{(i)}}}{\sum_{j=1}^{k} e^{z_{j}^{(i)}}}$$
where we define the net input *z* as
$$z = w_1x_1 + ... + w_mx_m + b= \sum_{l=1}^{m} w_l x_l + b= \mathbf{w}^T\mathbf{x} + b$$
(**w** is the weight vector, $\mathbf{x}$ is the feature vector of 1 training sample. Each $w$ corresponds to a feature $x$ and there're $m$ of them in total. $b$ is the bias unit. $k$ denotes the total number of classes.)
Now, this softmax function computes the probability that the $i_{th}$ training sample $\mathbf{x}^{(i)}$ belongs to class $l$ given the weight and net input $z^{(i)}$. So given the obtained weight $w$, we're basically compute the probability, $p(y = j \mid \mathbf{x^{(i)}; w}_j)$, the probability of the training sample belonging to class $j$ for each class label in $j = 1, \ldots, k$. Note the normalization term in the denominator which causes these class probabilities to sum up to one.
We can picture our softmax regression as looking something like the following, although with a lot more $x_s$. For each output, we compute a weighted sum of the $x_s$, add a bias, and then apply softmax.
<img src='images/softmax1.png' width="60%">
If we write that out as equations, we get:
<img src='images/softmax2.png' width="60%">
We can "vectorize" this procedure, turning it into a matrix multiplication and vector addition. This is helpful for computational efficiency. (It's also a useful way to think.)
<img src='images/softmax3.png' width="60%">
To illustrate the concept of softmax, let us walk through a concrete example. Suppose we have a training set consisting of 4 samples from 3 different classes (0, 1, and 2)
- $x_0 \rightarrow \text{class }0$
- $x_1 \rightarrow \text{class }1$
- $x_2 \rightarrow \text{class }2$
- $x_3 \rightarrow \text{class }2$
First, we apply one-hot encoding to encode the class labels into a format that we can more easily work with.
```
y = np.array([0, 1, 2, 2])
def one_hot_encode(y):
n_class = np.unique(y).shape[0]
y_encode = np.zeros((y.shape[0], n_class))
for idx, val in enumerate(y):
y_encode[idx, val] = 1.0
return y_encode
y_encode = one_hot_encode(y)
y_encode
```
A sample that belongs to class 0 (the first row) has a 1 in the first cell, a sample that belongs to class 1 has a 1 in the second cell of its row, and so forth.
Next, let us define the feature matrix of our 4 training samples. Here, we assume that our dataset consists of 2 features; thus, we create a 4x2 dimensional matrix of our samples and features.
Similarly, we create a 2x3 dimensional weight matrix (one row per feature and one column for each class).
```
X = np.array([[0.1, 0.5],
[1.1, 2.3],
[-1.1, -2.3],
[-1.5, -2.5]])
W = np.array([[0.1, 0.2, 0.3],
[0.1, 0.2, 0.3]])
bias = np.array([0.01, 0.1, 0.1])
print('Inputs X:\n', X)
print('\nWeights W:\n', W)
print('\nbias:\n', bias)
```
To compute the net input, we multiply the 4x2 matrix feature matrix `X` with the 2x3 (n_features x n_classes) weight matrix `W`, which yields a 4x3 output matrix (n_samples x n_classes) to which we then add the bias unit:
$$\mathbf{Z} = \mathbf{X}\mathbf{W} + \mathbf{b}$$
```
def net_input(X, W, b):
return X.dot(W) + b
net_in = net_input(X, W, bias)
print('net input:\n', net_in)
```
Now, it's time to compute the softmax activation that we discussed earlier:
$$P(y=j \mid z^{(i)}) = \phi_{softmax}(z^{(i)}) = \frac{e^{z^{(i)}}}{\sum_{j=1}^{k} e^{z_{j}^{(i)}}}$$
```
def softmax(z):
return np.exp(z) / np.sum(np.exp(z), axis = 1, keepdims = True)
smax = softmax(net_in)
print('softmax:\n', smax)
```
As we can see, the values for each sample (row) nicely sum up to 1 now. E.g., we can say that the first sample `[ 0.29450637 0.34216758 0.36332605]` has a 29.45% probability to belong to class 0. Now, in order to turn these probabilities back into class labels, we could simply take the argmax-index position of each row:
[[ 0.29450637 0.34216758 **0.36332605**] -> 2
[ 0.21290077 0.32728332 **0.45981591**] -> 2
[ **0.42860913** 0.33380113 0.23758974] -> 0
[ **0.44941979** 0.32962558 0.22095463]] -> 0
```
def to_classlabel(z):
return z.argmax(axis = 1)
print('predicted class labels: ', to_classlabel(smax))
```
As we can see, our predictions are terribly wrong, since the correct class labels are `[0, 1, 2, 2]`. Now, in order to train our model we need to measuring how inefficient our predictions are for describing the truth and then optimize on it. To do so we first need to define a loss/cost function $J(\cdot)$ that we want to minimize. One very common function is "cross-entropy":
$$J(\mathbf{W}; \mathbf{b}) = \frac{1}{n} \sum_{i=1}^{n} H( T^{(i)}, O^{(i)} )$$
which is the average of all cross-entropies $H$ over our $n$ training samples. The cross-entropy function is defined as:
$$H( T^{(i)}, O^{(i)} ) = -\sum_k T^{(i)} \cdot log(O^{(i)})$$
Where:
- $T$ stands for "target" (i.e., the *true* class labels)
- $O$ stands for output -- the computed *probability* via softmax; **not** the predicted class label.
- $\sum_k$ denotes adding up the difference between the target and the output for all classes.
```
def cross_entropy_cost(y_target, output):
return np.mean(-np.sum(y_target * np.log(output), axis = 1))
cost = cross_entropy_cost(y_target = y_encode, output = smax)
print('Cross Entropy Cost:', cost)
```
## Gradient Descent
Our objective in training a neural network is to find a set of weights that gives us the lowest error when we run it against our training data. There're many ways to find these weights and simplest one is so called **gradient descent**. It does this by giving us directions (using derivatives) on how to "shift" our weights to an optimum. It tells us whether we should increase or decrease the value of a specific weight in order to lower the error function.
Let's imagine we have a function $f(x) = x^4 - 3x^3 + 2$ and we want to find the minimum of this function using gradient descent. Here's a graph of that function:
```
from sympy.plotting import plot
from sympy import symbols, init_printing
# change default figure and font size
plt.rcParams['figure.figsize'] = 6, 4
plt.rcParams['font.size'] = 12
# plotting f(x) = x^4 - 3x^3 + 2, showing -2 < x <4
init_printing()
x = symbols('x')
fx = x ** 4 - 3 * x ** 3 + 2
p1 = plot(fx, (x, -2, 4), ylim = (-10, 50))
```
As you can see, there appears to be a minimum around ~2.3 or so. Gradient descent answers this question: If we were to start with a random value of x, which direction should we go if we want to get to the lowest point on this function? Let's imagine we pick a random x value, say <b>x = 4</b>, which would be somewhere way up on the right side of the graph. We obviously need to start going to the left if we want to get to the bottom. This is obvious when the function is an easily visualizable 2d plot, but when dealing with functions of multiple variables, we need to rely on the raw mathematics.
Calculus tells us that the derivative of a function at a particular point is the rate of change/slope of the tangent to that part of the function. So let's use derivatives to help us get to the bottom of this function. The derivative of $f(x) = x^4 - 3x^3 + 2$ is $f'(x) = 4x^3 - 9x^2$. So if we plug in our random point from above (x=4) into the first derivative of $f(x)$ we get $f'(4) = 4(4)^3 - 9(4)^2 = 112$. So how does 112 tell us where to go? Well, first of all, it's positive. If we were to compute $f'(-1)$ we get a negative number (-13). So it looks like we can say that whenever the $f'(x)$ for a particular $x$ is positive, we should move to the left (decrease x) and whenever it's negative, we should move to the right (increase x).
We'll now formalize this: When we start with a random x and compute it's deriative $f'(x)$, our <b>new x</b> should then be proportional to $x - f'(x)$. The word proportional is there because we wish to control <em>to what degree</em> we move at each step, for example when we compute $f'(4)=112$, do we really want our new $x$ to be $x - 112 = -108$? No, if we jump all the way to -108, we're even farther from the minimum than we were before. Instead, we want to take relatively <em>small</em> steps toward the minimum.
Let's say that for any random $x$, we want to take a step (change $x$ a little bit) such that our <b>new $x$</b> $ = x - \alpha*f'(x)$. We'll call $\alpha$ (alpha) our <em>learning rate or step size</em> because it determines how big of a step we take. $\alpha$ is something we will just have to play around with to find a good value. Some functions might require bigger steps, others smaller steps.
Suppose we've set our $\alpha$ to be 0.001. This means, if we randomly started at $f'(4)=112$ then our new $x$ will be $ = 4 - (0.001 * 112) = 3.888$. So we moved to the left a little bit, toward the optimum. Let's do it again. $x_{new} = x - \alpha*f'(3.888) = 3.888 - (0.001 * 99.0436) = 3.79$. Nice, we're indeed moving to the left, closer to the minimum of $f(x)$, little by little. And we'll keep on doing this until we've reached convergence. By convergence, we mean that if the absolute value of the difference between the updated $x$ and the old $x$ is smaller than some randomly small number that we set, denoted as $\epsilon$ (epsilon).
```
x_old = 0
x_new = 4 # The algorithm starts at x = 4
alpha = 0.01 # step size
epsilon = 0.00001
def f_derivative(x):
return 4 * x ** 3 - 9 * x ** 2
while abs(x_new - x_old) > epsilon:
x_old = x_new
x_new = x_old - alpha * f_derivative(x_old)
print("Local minimum occurs at", x_new)
```
The script above says that if the absolute difference of $x$ between the two iterations is not changing by more than 0.00001, then we're probably at the bottom of the "bowl" because our slope is approaching 0, and therefore we should stop and call it a day. Now, if you remember some calculus and algebra, you could have solved for this minimum analytically, and you should get 2.25. Very close to what our gradient descent algorithm above found.
## More Gradient Descent...
As you might imagine, when we use gradient descent for a neural network, things get a lot more complicated. Not because gradient descent gets more complicated, it still ends up just being a matter of taking small steps downhill, it's that we need that pesky derivative in order to use gradient descent, and the derivative of a neural network cost function (with respect to its weights) is pretty intense. It's not a matter of just analytically solving $f(x)=x^2, f'(x)=2x$ , because the output of a neural net has many nested or "inner" functions.
Also unlike our toy math problem above, a neural network may have many weights. We need to find the optimal value for each individual weight to lower the cost for our entire neural net output. This requires taking the partial derivative of the cost/error function with respect to a single weight, and then running gradient descent for each individual weight. Thus, for any individual weight $W_j$, we'll compute the following:
$$ W_j^{(t + 1)} = W_j^{(t)} - \alpha * \frac{\partial L}{\partial W_j}$$
Where:
- $L$ denotes the loss function that we've defined.
- $W_j^{(t)}$ denotes the weight of the $j_{th}$ feature at iteration $t$.
And as before, we do this iteratively for each weight, many times, until the whole network's cost function is minimized.
In order to learn the weight for our softmax model via gradient descent, we then need to compute the gradient of our cost function for each class $j \in \{0, 1, ..., k\}$.
$$\nabla \mathbf{w}_j \, J(\mathbf{W}; \mathbf{b})$$
We won't be going through the tedious details here, but this cost's gradient turns out to be simply:
$$\nabla \mathbf{w}_j \, J(\mathbf{W}; \mathbf{b}) = \frac{1}{n} \sum^{n}_{i=0} \big[\mathbf{x}^{(i)}_j\ \big( O^{(i)} - T^{(i)} \big) \big]$$
We can then use the cost derivate to update the weights in opposite direction of the cost gradient with learning rate $\eta$:
$$\mathbf{w}_j := \mathbf{w}_j - \eta \nabla \mathbf{w}_j \, J(\mathbf{W}; \mathbf{b})$$
(note that $\mathbf{w}_j$ is the weight vector for the class $y=j$), and we update the bias units using:
$$
\mathbf{b}_j := \mathbf{b}_j - \eta \bigg[ \frac{1}{n} \sum^{n}_{i=0} \big( O^{(i)} - T^{(i)} \big) \bigg]
$$
As a penalty against complexity, an approach to reduce the variance of our model and decrease the degree of overfitting by adding additional bias, we can further add a regularization term such as the L2 term with the regularization parameter $\lambda$:
$$\frac{\lambda}{2} ||\mathbf{w}||_{2}^{2}$$
where $||\mathbf{w}||_{2}^{2}$ simply means adding up the squared weights across all the features and classes.
$$||\mathbf{w}||_{2}^{2} = \sum^{m}_{l=0} \sum^{k}_{j=0} w_{l, j}^2$$
so that our cost function becomes
$$
J(\mathbf{W}; \mathbf{b}) = \frac{1}{n} \sum_{i=1}^{n} H( T^{(i)}, O^{(i)} ) + \frac{\lambda}{2} ||\mathbf{w}||_{2}^{2}
$$
and we define the "regularized" weight update as
$$
\mathbf{w}_j := \mathbf{w}_j - \eta \big[\nabla \mathbf{w}_j \, J(\mathbf{W}) + \lambda \mathbf{w}_j \big]
$$
Note that we don't regularize the bias term, thus the update function for it stays the same.
## Softmax Regression Code
Bringing the concepts together, we could come up with an implementation as follows: Note that for the weight and bias parameter, we'll have initialize a value for it. Here we'll simply draw the weights from a normal distribution and set the bias as zero. The code can be obtained [here](https://github.com/ethen8181/machine-learning/blob/master/deep_learning/softmax.py).
```
# import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
# standardize the input features
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
from softmax import SoftmaxRegression
# train the softmax using batch gradient descent,
# eta: learning rate, epochs : number of iterations, minibatches, number of
# training data to use for training at each iteration
softmax_reg = SoftmaxRegression(eta = 0.1, epochs = 10, minibatches = y.shape[0])
softmax_reg.fit(X_std, y)
# print the training accuracy
y_pred = softmax_reg.predict(X_std)
accuracy = np.sum(y_pred == y) / y.shape[0]
print('accuracy: ', accuracy)
# use a library to ensure comparable results
log_reg = LogisticRegression()
log_reg.fit(X_std, y)
y_pred = log_reg.predict(X_std)
print('accuracy library: ', accuracy_score(y_true = y, y_pred = y_pred))
```
# Reference
- [Blog: Softmax Regression](http://nbviewer.jupyter.org/github/rasbt/python-machine-learning-book/blob/master/code/bonus/softmax-regression.ipynb)
- [Blog: Gradient Descent with Backpropagation](http://outlace.com/Beginner-Tutorial-Backpropagation/)
- [TensorFlow Documentation: MNIST For ML Beginners](https://www.tensorflow.org/get_started/mnist/beginners)
| true |
code
| 0.624637 | null | null | null | null |
|
## Imports
```
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Lasso, Ridge
```
## Generate Data
```
samples = 500
np.random.seed(10) ## seed for reproducibility
f1 = np.random.uniform(low=0, high=10, size=samples) ## garbage feature
f2 = np.random.rand(samples)
f3 = np.random.binomial(n=1, p=0.5, size=samples)
f4 = None
f5 = np.random.normal(1, 2.5, samples)
d = {'f1':f1, 'f2':f2, 'f3':f3, 'f4':f4, 'f5':f5}
df = pd.DataFrame(d)
df['target'] = None
df.head()
# Set target values w/noise
for i, _ in df.iterrows():
df.loc[i, 'target'] = df.loc[i, 'f2'] * df.loc[i, 'f3'] + df.loc[i, 'f5'] * df.loc[i, 'f3'] + np.random.rand() * 3
df.loc[i, 'f4'] = df.loc[i, 'f2'] ** 2.8 + np.random.normal(loc=0, scale=1.25, size=1)
df['f4'] = df.f4.astype('float')
df['target'] = df.target.astype('float')
df.head()
df.describe()
df.corr()
sns.pairplot(df);
```
## Train/Test Split
```
X_train, X_test, y_train, y_test = train_test_split(df[['f1', 'f2', 'f3', 'f4', 'f5']],
df['target'],
test_size=0.2,
random_state=42)
```
## StandardScale
```
ss = StandardScaler()
ss.fit(X_train)
X_train_std = ss.transform(X_train)
X_test_std = ss.transform(X_test)
```
## Modeling
```
lr = LinearRegression()
lasso = Lasso(alpha=0.01, random_state=42)
ridge = Ridge(alpha=0.01, random_state=42)
lr.fit(X_train_std, y_train)
lasso.fit(X_train_std, y_train)
ridge.fit(X_train_std, y_train)
```
## Results
```
def pretty_print_coef(obj):
print('intercept: {0:.4}'.format(obj.intercept_))
print('coef: {0:.3} {1:.4} {2:.4} {3:.3} {4:.3}'.format(obj.coef_[0],
obj.coef_[1],
obj.coef_[2],
obj.coef_[3],
obj.coef_[4]))
models = (lr, lasso, ridge)
for model in models:
print(str(model))
pretty_print_coef(model)
print('R^2:', model.score(X_train_std, y_train))
print('MSE:', mean_squared_error(y_test, model.predict(X_test_std)))
print()
np.mean(cross_val_score(lr, X_train_std, y_train, scoring='neg_mean_squared_error', cv=5, n_jobs=-1) * -1)
np.mean(cross_val_score(lasso, X_train_std, y_train, scoring='neg_mean_squared_error', cv=5, n_jobs=-1) * -1)
np.mean(cross_val_score(ridge, X_train_std, y_train, scoring='neg_mean_squared_error', cv=5, n_jobs=-1) * -1)
```
## Residuals
```
fig, axes = plt.subplots(1, 3, sharex=False, sharey=False)
fig.suptitle('[Residual Plots]')
fig.set_size_inches(18,5)
axes[0].plot(lr.predict(X_test_std), y_test-lr.predict(X_test_std), 'bo')
axes[0].axhline(y=0, color='k')
axes[0].grid()
axes[0].set_title('Linear')
axes[0].set_xlabel('predicted values')
axes[0].set_ylabel('residuals')
axes[1].plot(lasso.predict(X_test_std), y_test-lasso.predict(X_test_std), 'go')
axes[1].axhline(y=0, color='k')
axes[1].grid()
axes[1].set_title('Lasso')
axes[1].set_xlabel('predicted values')
axes[1].set_ylabel('residuals')
axes[2].plot(ridge.predict(X_test_std), y_test-ridge.predict(X_test_std), 'ro')
axes[2].axhline(y=0, color='k')
axes[2].grid()
axes[2].set_title('Ridge')
axes[2].set_xlabel('predicted values')
axes[2].set_ylabel('residuals');
```
## Notes
We can tell from the residuals that there's signal that we're not catching with our current model. The reason is obvious in this case, because we know how the data was generated. The **target** is built on interaction terms.
## Random Forest (for fun)
```
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(n_estimators=10, max_depth=5, n_jobs=-1, random_state=42)
rf.fit(X_train, y_train)
mean_squared_error(y_test, rf.predict(X_test))
rf.feature_importances_
fig, axes = plt.subplots(1, 4, sharex=False, sharey=False)
fig.suptitle('[Residual Plots]')
fig.set_size_inches(18,5)
axes[0].plot(lr.predict(X_test_std), y_test-lr.predict(X_test_std), 'bo')
axes[0].axhline(y=0, color='k')
axes[0].grid()
axes[0].set_title('Linear')
axes[0].set_xlabel('predicted values')
axes[0].set_ylabel('residuals')
axes[1].plot(lasso.predict(X_test_std), y_test-lasso.predict(X_test_std), 'go')
axes[1].axhline(y=0, color='k')
axes[1].grid()
axes[1].set_title('Lasso')
axes[1].set_xlabel('predicted values')
axes[1].set_ylabel('residuals')
axes[2].plot(ridge.predict(X_test_std), y_test-ridge.predict(X_test_std), 'ro')
axes[2].axhline(y=0, color='k')
axes[2].grid()
axes[2].set_title('Ridge')
axes[2].set_xlabel('predicted values')
axes[2].set_ylabel('residuals');
axes[3].plot(rf.predict(X_test), y_test-rf.predict(X_test), 'ko')
axes[3].axhline(y=0, color='k')
axes[3].grid()
axes[3].set_title('RF')
axes[3].set_xlabel('predicted values')
axes[3].set_ylabel('residuals');
```
While random forest does a better job catching the interaction between variables, we still see some pattern in the residuals meaning we haven't captured all the signal. Nonetheless, random forest is signficantly better than linear regression, lasso, and ridge on the raw features. We can combat this with feature engineering, however.
| true |
code
| 0.642376 | null | null | null | null |
|
<h1> Time series prediction using RNNs, with TensorFlow and Cloud ML Engine </h1>
This notebook illustrates:
<ol>
<li> Creating a Recurrent Neural Network in TensorFlow
<li> Creating a Custom Estimator in tf.contrib.learn
<li> Training on Cloud ML Engine
</ol>
<p>
<h3> Simulate some time-series data </h3>
Essentially a set of sinusoids with random amplitudes and frequencies.
```
!pip install --upgrade tensorflow
import tensorflow as tf
print tf.__version__
import numpy as np
import tensorflow as tf
import seaborn as sns
import pandas as pd
SEQ_LEN = 10
def create_time_series():
freq = (np.random.random()*0.5) + 0.1 # 0.1 to 0.6
ampl = np.random.random() + 0.5 # 0.5 to 1.5
x = np.sin(np.arange(0,SEQ_LEN) * freq) * ampl
return x
for i in xrange(0, 5):
sns.tsplot( create_time_series() ); # 5 series
def to_csv(filename, N):
with open(filename, 'w') as ofp:
for lineno in xrange(0, N):
seq = create_time_series()
line = ",".join(map(str, seq))
ofp.write(line + '\n')
to_csv('train.csv', 1000) # 1000 sequences
to_csv('valid.csv', 50)
!head -5 train.csv valid.csv
```
<h2> RNN </h2>
For more info, see:
<ol>
<li> http://colah.github.io/posts/2015-08-Understanding-LSTMs/ for the theory
<li> https://www.tensorflow.org/tutorials/recurrent for explanations
<li> https://github.com/tensorflow/models/tree/master/tutorials/rnn/ptb for sample code
</ol>
Here, we are trying to predict from 8 values of a timeseries, the next two values.
<p>
<h3> Imports </h3>
Several tensorflow packages and shutil
```
import tensorflow as tf
import shutil
import tensorflow.contrib.learn as tflearn
import tensorflow.contrib.layers as tflayers
from tensorflow.contrib.learn.python.learn import learn_runner
import tensorflow.contrib.metrics as metrics
import tensorflow.contrib.rnn as rnn
```
<h3> Input Fn to read CSV </h3>
Our CSV file structure is quite simple -- a bunch of floating point numbers (note the type of DEFAULTS). We ask for the data to be read BATCH_SIZE sequences at a time. The Estimator API in tf.contrib.learn wants the features returned as a dict. We'll just call this timeseries column 'rawdata'.
<p>
Our CSV file sequences consist of 10 numbers. We'll assume that 8 of them are inputs and we need to predict the next two.
```
DEFAULTS = [[0.0] for x in xrange(0, SEQ_LEN)]
BATCH_SIZE = 20
TIMESERIES_COL = 'rawdata'
N_OUTPUTS = 2 # in each sequence, 1-8 are features, and 9-10 is label
N_INPUTS = SEQ_LEN - N_OUTPUTS
```
Reading data using the Estimator API in tf.learn requires an input_fn. This input_fn needs to return a dict of features and the corresponding labels.
<p>
So, we read the CSV file. The Tensor format here will be batchsize x 1 -- entire line. We then decode the CSV. At this point, all_data will contain a list of Tensors. Each tensor has a shape batchsize x 1. There will be 10 of these tensors, since SEQ_LEN is 10.
<p>
We split these 10 into 8 and 2 (N_OUTPUTS is 2). Put the 8 into a dict, call it features. The other 2 are the ground truth, so labels.
```
# read data and convert to needed format
def read_dataset(filename, mode=tf.contrib.learn.ModeKeys.TRAIN):
def _input_fn():
num_epochs = 100 if mode == tf.contrib.learn.ModeKeys.TRAIN else 1
# could be a path to one file or a file pattern.
input_file_names = tf.train.match_filenames_once(filename)
filename_queue = tf.train.string_input_producer(
input_file_names, num_epochs=num_epochs, shuffle=True)
reader = tf.TextLineReader()
_, value = reader.read_up_to(filename_queue, num_records=BATCH_SIZE)
value_column = tf.expand_dims(value, -1)
print 'readcsv={}'.format(value_column)
# all_data is a list of tensors
all_data = tf.decode_csv(value_column, record_defaults=DEFAULTS)
inputs = all_data[:len(all_data)-N_OUTPUTS] # first few values
label = all_data[len(all_data)-N_OUTPUTS : ] # last few values
# from list of tensors to tensor with one more dimension
inputs = tf.concat(inputs, axis=1)
label = tf.concat(label, axis=1)
print 'inputs={}'.format(inputs)
return {TIMESERIES_COL: inputs}, label # dict of features, label
return _input_fn
```
<h3> Define RNN </h3>
A recursive neural network consists of possibly stacked LSTM cells.
<p>
The RNN has one output per input, so it will have 8 output cells. We use only the last output cell, but rather use it directly, we do a matrix multiplication of that cell by a set of weights to get the actual predictions. This allows for a degree of scaling between inputs and predictions if necessary (we don't really need it in this problem).
<p>
Finally, to supply a model function to the Estimator API, you need to return a ModelFnOps. The rest of the function creates the necessary objects.
```
LSTM_SIZE = 3 # number of hidden layers in each of the LSTM cells
# create the inference model
def simple_rnn(features, targets, mode):
# 0. Reformat input shape to become a sequence
x = tf.split(features[TIMESERIES_COL], N_INPUTS, 1)
#print 'x={}'.format(x)
# 1. configure the RNN
lstm_cell = rnn.BasicLSTMCell(LSTM_SIZE, forget_bias=1.0)
outputs, _ = rnn.static_rnn(lstm_cell, x, dtype=tf.float32)
# slice to keep only the last cell of the RNN
outputs = outputs[-1]
#print 'last outputs={}'.format(outputs)
# output is result of linear activation of last layer of RNN
weight = tf.Variable(tf.random_normal([LSTM_SIZE, N_OUTPUTS]))
bias = tf.Variable(tf.random_normal([N_OUTPUTS]))
predictions = tf.matmul(outputs, weight) + bias
# 2. loss function, training/eval ops
if mode == tf.contrib.learn.ModeKeys.TRAIN or mode == tf.contrib.learn.ModeKeys.EVAL:
loss = tf.losses.mean_squared_error(targets, predictions)
train_op = tf.contrib.layers.optimize_loss(
loss=loss,
global_step=tf.contrib.framework.get_global_step(),
learning_rate=0.01,
optimizer="SGD")
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(targets, predictions)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. return ModelFnOps
return tflearn.ModelFnOps(
mode=mode,
predictions=predictions_dict,
loss=loss,
train_op=train_op,
eval_metric_ops=eval_metric_ops)
```
<h3> Experiment </h3>
Distributed training is launched off using an Experiment. The key line here is that we use tflearn.Estimator rather than, say tflearn.DNNRegressor. This allows us to provide a model_fn, which will be our RNN defined above. Note also that we specify a serving_input_fn -- this is how we parse the input data provided to us at prediction time.
```
def get_train():
return read_dataset('train.csv', mode=tf.contrib.learn.ModeKeys.TRAIN)
def get_valid():
return read_dataset('valid.csv', mode=tf.contrib.learn.ModeKeys.EVAL)
def serving_input_fn():
feature_placeholders = {
TIMESERIES_COL: tf.placeholder(tf.float32, [None, N_INPUTS])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
features[TIMESERIES_COL] = tf.squeeze(features[TIMESERIES_COL], axis=[2])
print 'serving: features={}'.format(features[TIMESERIES_COL])
return tflearn.utils.input_fn_utils.InputFnOps(
features,
None,
feature_placeholders
)
from tensorflow.contrib.learn.python.learn.utils import saved_model_export_utils
def experiment_fn(output_dir):
# run experiment
return tflearn.Experiment(
tflearn.Estimator(model_fn=simple_rnn, model_dir=output_dir),
train_input_fn=get_train(),
eval_input_fn=get_valid(),
eval_metrics={
'rmse': tflearn.MetricSpec(
metric_fn=metrics.streaming_root_mean_squared_error
)
},
export_strategies=[saved_model_export_utils.make_export_strategy(
serving_input_fn,
default_output_alternative_key=None,
exports_to_keep=1
)]
)
shutil.rmtree('outputdir', ignore_errors=True) # start fresh each time
learn_runner.run(experiment_fn, 'outputdir')
```
<h3> Standalone Python module </h3>
To train this on Cloud ML Engine, we take the code in this notebook, make an standalone Python module.
```
%bash
# run module as-is
REPO=$(pwd)
echo $REPO
rm -rf outputdir
export PYTHONPATH=${PYTHONPATH}:${REPO}/simplernn
python -m trainer.task \
--train_data_paths="${REPO}/train.csv*" \
--eval_data_paths="${REPO}/valid.csv*" \
--output_dir=${REPO}/outputdir \
--job-dir=./tmp
```
Try out online prediction. This is how the REST API will work after you train on Cloud ML Engine
```
%writefile test.json
{"rawdata": [0.0,0.0527,0.10498,0.1561,0.2056,0.253,0.2978,0.3395]}
%bash
MODEL_DIR=$(ls ./outputdir/export/Servo/)
gcloud ml-engine local predict --model-dir=./outputdir/export/Servo/$MODEL_DIR --json-instances=test.json
```
<h3> Cloud ML Engine </h3>
Now to train on Cloud ML Engine.
```
%bash
# run module on Cloud ML Engine
REPO=$(pwd)
BUCKET=cloud-training-demos-ml # CHANGE AS NEEDED
OUTDIR=gs://${BUCKET}/simplernn/model_trained
JOBNAME=simplernn_$(date -u +%y%m%d_%H%M%S)
REGION=us-central1
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=trainer.task \
--package-path=${REPO}/simplernn/trainer \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC \
--runtime-version=1.2 \
-- \
--train_data_paths="gs://${BUCKET}/train.csv*" \
--eval_data_paths="gs://${BUCKET}/valid.csv*" \
--output_dir=$OUTDIR \
--num_epochs=100
```
<h2> Variant: long sequence </h2>
To create short sequences from a very long sequence.
```
import tensorflow as tf
import numpy as np
def breakup(sess, x, lookback_len):
N = sess.run(tf.size(x))
windows = [tf.slice(x, [b], [lookback_len]) for b in xrange(0, N-lookback_len)]
windows = tf.stack(windows)
return windows
x = tf.constant(np.arange(1,11, dtype=np.float32))
with tf.Session() as sess:
print 'input=', x.eval()
seqx = breakup(sess, x, 5)
print 'output=', seqx.eval()
```
Copyright 2017 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| true |
code
| 0.579579 | null | null | null | null |
|
# *CoNNear*: A convolutional neural-network model of human cochlear mechanics and filter tuning for real-time applications
Python notebook for reproducing the evaluation results of the proposed CoNNear model.
## Prerequisites
- First, let us compile the cochlea_utils.c file that is used for solving the transmission line (TL) model of the cochlea. This requires some C++ compiler which should be installed beforehand. Then go the connear folder from the terminal and run:
```
gcc -shared -fpic -O3 -ffast-math -o tridiag.so cochlea_utils.c
```
- Install numpy, scipy, keras and tensorflow
## Import required python packages and functions
Import required python packages and load the connear model.
```
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import keras
from keras.models import model_from_json
from keras.utils import CustomObjectScope
from keras.initializers import glorot_uniform
from tlmodel.get_tl_vbm_and_oae import tl_vbm_and_oae
json_file = open("connear/Gmodel.json", "r")
loaded_model_json = json_file.read()
json_file.close()
connear = model_from_json(loaded_model_json)
connear.load_weights("connear/Gmodel.h5")
connear.summary()
```
Define some functions here
```
def rms (x):
# compute rms of a matrix
sq = np.mean(np.square(x), axis = 0)
return np.sqrt(sq)
# Define model specific variables
down_rate = 2
fs = 20e3
fs_tl = 100e3
p0 = 2e-5
factor_fs = int(fs_tl / fs)
right_context = 256
left_context = 256
# load CFs
CF = np.loadtxt('tlmodel/cf.txt')
```
## Click response
Compare the responses of the models to a click stimulus.
**Notice that for all the simulations, TL model operates at 100kHz and the CoNNear model operates at 20kHz.**
```
#Define the click stimulus
dur = 128.0e-3 # for 2560 samples #CONTEXT
click_duration = 2 # 100 us click
stim = np.zeros((1, int(dur * fs)))
L = 70.0
samples = dur * fs
click_duration = 2 # 100 us click
click_duration_tl = factor_fs * click_duration
silence = 60 #samples in silence
samples = int(samples - right_context - left_context)
'''
# GET TL model response
stim = np.zeros((1, (samples + right_context + left_context)*factor_fs))
stim[0, (factor_fs * (right_context+silence)) : (factor_fs * (right_context+silence)) + click_duration_tl] = 2 * np.sqrt(2) * p0 * 10**(L/20)
output = tl_vbm_and_oae(stim , L)
CF = output[0]['cf'][::down_rate]
# basilar membrane motion for click response
# the context samples (first and last 256 samples)
# are removed. Also downsample it to 20kHz
bmm_click_out_full = np.array(output[0]['v'])
stimrange = range(right_context*factor_fs, (right_context*factor_fs) + (factor_fs*samples))
bmm_click_tl = sp_sig.resample_poly(output[0]['v'][stimrange,::down_rate], fs, fs_tl)
bmm_click_tl = bmm_click_tl.T
'''
# Prepare the same for CoNNear model
stim = np.zeros((1, int(dur * fs)))
stim[0, right_context + silence : right_context + silence + click_duration] = 2 * np.sqrt(2) * p0 * 10**(L/20)
# Get the CoNNear response
stim = np.expand_dims(stim, axis=2)
connear_pred_click = connear.predict(stim.T, verbose=1)
bmm_click_connear = connear_pred_click[0,:,:].T * 1e-6
```
Plotting the results.
```
plt.plot(stim[0,256:-256]), plt.xlim(0,2000)
plt.show()
'''
plt.imshow(bmm_click_tl, aspect='auto', cmap='jet')
plt.xlim(0,2000), plt.clim(-4e-7,5e-7)
plt.colorbar()
plt.show()
'''
plt.imshow(bmm_click_connear, aspect='auto', cmap='jet')
plt.xlim(0,2000), plt.clim(-4e-7,5e-7)
plt.colorbar()
plt.show()
```
## Cochlear Excitation Patterns
Here, we plot the simulated RMS levels of basilar memberane (BM) displacement across CF for tone stimuli presented at SPLs between 0 and 90 dB SPL.
```
f_tone = 1e3 # You can change this tone frequency to see how the excitation pattern changes
# with stimulus frequency
fs = 20e3
p0 = 2e-5
dur = 102.4e-3 # for 2048 samples
window_len = int(fs * dur)
L = np.arange(0., 91.0, 10.) # SPLs from 0 to 90dB
#CoNNear
t = np.arange(0., dur, 1./fs)
hanlength = int(10e-3 * fs) # 10ms length hanning window
stim_sin = np.sin(2 * np.pi * f_tone * t)
han = signal.windows.hann(hanlength)
stim_sin[:int(hanlength/2)] = stim_sin[:int(hanlength/2)] * han[:int(hanlength/2)]
stim_sin[-int(hanlength/2):] = stim_sin[-int(hanlength/2):] * han[int(hanlength/2):]
stim = np.zeros((len(L), int(len(stim_sin))))
#total_length = 2560 #CONTEXT
total_length = window_len + right_context + left_context # CONTEXT
stim = np.zeros((len(L), total_length)) #CONTEXT
for j in range(len(L)):
stim[j,right_context:window_len+right_context] = p0 * np.sqrt(2) * 10**(L[j]/20) * stim_sin
# prepare for feeding to the DNN
stim = np.expand_dims(stim, axis=2)
connear_pred_tone = connear.predict(stim, verbose=1)
bmm_tone_connear = connear_pred_tone# * 1e-6
bmm_tone_connear.shape
# Compute rms for each level
cochlear_pred_tone_rms = np.vstack([rms(bmm_tone_connear[i]) for i in range(len(L))])
# Plot the RMS
cftile=np.tile(CF, (len(L),1))
plt.semilogx(cftile.T, 20.*np.log10(cochlear_pred_tone_rms.T))
plt.xlim(0.25,8.), plt.grid(which='both'),
plt.xticks(ticks=(0.25, 0.5, 1., 2., 4., 8.) , labels=(0.25, 0.5, 1., 2., 4., 8.))
plt.ylim(-80, 20)
plt.xlabel('CF (kHz)')
plt.ylabel('RMS of y_bm (dB)')
plt.title('CoNNear Predicted')
plt.show()
```
| true |
code
| 0.613584 | null | null | null | null |
|
# cadCAD Tutorials: The Robot and the Marbles, part 2
In [Part 1](../robot-marbles-part-1/robot-marbles-part-1.ipynb) we introduced the 'language' in which a system must be described in order for it to be interpretable by cadCAD and some of the basic concepts of the library:
* State Variables
* Timestep
* State Update Functions
* Partial State Update Blocks
* Simulation Configuration Parameters
This article will introduce the concept of __Policies__. But first let's copy the base configuration from Part 1. As a reminder, here's the description of the simple system we are using for illustration purposes.
__The robot and the marbles__
* Picture a box (`box_A`) with ten marbles in it; an empty box (`box_B`) next to the first one; and a robot arm capable of taking a marble from any one of the boxes and dropping it into the other one.
* The robot is programmed to take one marble at a time from the box containing the largest number of marbles and drop it in the other box. It repeats that process until the boxes contain an equal number of marbles.
```
%%capture
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# List of all the state variables in the system and their initial values
genesis_states = {
'box_A': 10, # as per the description of the example, box_A starts out with 10 marbles in it
'box_B': 0 # as per the description of the example, box_B starts out empty
}
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
def update_A(params, step, sH, s, _input):
y = 'box_A'
add_to_A = 0
if (s['box_A'] > s['box_B']):
add_to_A = -1
elif (s['box_A'] < s['box_B']):
add_to_A = 1
x = s['box_A'] + add_to_A
return (y, x)
def update_B(params, step, sH, s, _input):
y = 'box_B'
add_to_B = 0
if (s['box_B'] > s['box_A']):
add_to_B = -1
elif (s['box_B'] < s['box_A']):
add_to_B = 1
x = s['box_B'] + add_to_B
return (y, x)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# In the Partial State Update Blocks, the user specifies if state update functions will be run in series or in parallel
partial_state_update_blocks = [
{
'policies': { # We'll ignore policies for now
},
'variables': { # The following state variables will be updated simultaneously
'box_A': update_A,
'box_B': update_B
}
}
]
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# Settings of general simulation parameters, unrelated to the system itself
# `T` is a range with the number of discrete units of time the simulation will run for;
# `N` is the number of times the simulation will be run (Monte Carlo runs)
# In this example, we'll run the simulation once (N=1) and its duration will be of 10 timesteps
# We'll cover the `M` key in a future article. For now, let's omit it
sim_config_dict = {
'T': range(10),
'N': 1,
#'M': {}
}
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
#imported some addition utilities to help with configuration set-up
from cadCAD.configuration.utils import config_sim
from cadCAD.configuration import Experiment
exp = Experiment()
c = config_sim(sim_config_dict)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# The configurations above are then packaged into a `Configuration` object
exp.append_configs(initial_state=genesis_states, #dict containing variable names and initial values
partial_state_update_blocks=partial_state_update_blocks, #dict containing state update functions
sim_configs=c #preprocessed dictionaries containing simulation parameters
)
from cadCAD.engine import ExecutionMode, ExecutionContext
exec_mode = ExecutionMode()
local_mode_ctx = ExecutionContext(exec_mode.local_mode)
from cadCAD.engine import Executor
from cadCAD import configs
simulation = Executor(exec_context=local_mode_ctx, configs=configs) # Pass the configuration object inside an array
raw_system_events, tensor_field, sessions = simulation.execute() # The `execute()` method returns a tuple; its first elements contains the raw results
%matplotlib inline
import pandas as pd
simulation_result = pd.DataFrame(raw_result)
simulation_result.plot('timestep', ['box_A', 'box_B'], grid=True,
colormap = 'RdYlGn',
xticks=list(simulation_result['timestep'].drop_duplicates()),
yticks=list(range(1+(simulation_result['box_A']+simulation_result['box_B']).max())));
```
# Policies
In part 1, we ignored the `_input` argument of state update functions. That argument is a signal passed to the state update function by another set of functions: Policy Functions.
Policy Functions are most commonly used as representations of the behavior of agents that interact with the components of the system we're simulating in cadCAD. But more generally, they describe the logic of some component or mechanism of the system. It is possible to encode the functionality of a policy function in the state update functions themselves (as we did in part 1, where we had the robot's algorithm reside in the `update_A` and `update_B` functions), but as systems grow more complex this approach makes the code harder to read and maintain, and in some cases more inefficient because of unnecessary repetition of computational steps.
The general structure of a policy function is:
```python
def policy_function(params, step, sL, s):
...
return {'value1': value1, 'value2': value2, ...}
```
Just like State Update Functions, policies can read the current state of the system from argument `s`, a Python `dict` where the `dict_keys` are the __names of the variables__ and the `dict_values` are their __current values__. The Policy Function must return a dictionary, which will be passed as an argument (`_input`) to the state update functions.

Let's update our simulation so that the robot arm's logic is encoded in a Policy instead of in the State Update Functions.
```
%%capture
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# We specify the robot arm's logic in a Policy Function
def robot_arm(params, step, sH, s):
add_to_A = 0
if (s['box_A'] > s['box_B']):
add_to_A = -1
elif (s['box_A'] < s['box_B']):
add_to_A = 1
return({'add_to_A': add_to_A, 'add_to_B': -add_to_A})
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# We make the state update functions less "intelligent",
# ie. they simply add the number of marbles specified in _input
# (which, per the policy function definition, may be negative)
def increment_A(params, step, sH, s, _input):
y = 'box_A'
x = s['box_A'] + _input['add_to_A']
return (y, x)
def increment_B(params, step, sH, s, _input):
y = 'box_B'
x = s['box_B'] + _input['add_to_B']
return (y, x)
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# In the Partial State Update Blocks,
# the user specifies if state update functions will be run in series or in parallel
# and the policy functions that will be evaluated in that block
partial_state_update_blocks = [
{
'policies': { # The following policy functions will be evaluated and their returns will be passed to the state update functions
'robot_arm': robot_arm
},
'states': { # The following state variables will be updated simultaneously
'box_A': increment_A,
'box_B': increment_B
}
}
]
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
del configs[:] # Clear any prior configs
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# The configurations above are then packaged into a `Configuration` object
exp.append_configs(initial_state=genesis_states, #dict containing variable names and initial values
partial_state_update_blocks=partial_state_update_blocks, #dict containing state update functions
sim_configs=c #preprocessed dictionaries containing simulation parameters
)
executor = Executor(local_mode_ctx, configs) # Pass the configuration object inside an array
raw_result, tensor, sessions = executor.execute() # The `execute()` method returns a tuple; its first elements contains the raw results
%matplotlib inline
simulation_result = pd.DataFrame(raw_result)
simulation_result.plot('timestep', ['box_A', 'box_B'], grid=True,
xticks=list(simulation_result['timestep'].drop_duplicates()),
colormap = 'RdYlGn',
yticks=list(range(1+(simulation_result['box_A']+simulation_result['box_B']).max())));
```
As expected, the results are the same as when the robot arm logic was encoded within the state update functions.
Several policies may be evaluated within a Partial State Update Block. When that's the case, cadCAD's engine aggregates the outputs of the policies and passes them as a single signal to the state update functions.

Aggregation of policies is defined in cadCAD as __key-wise sum (+) of the elements of the outputted `dict`s__.
```python
>policy_1_output = {'int': 1, 'str': 'abc', 'list': [1, 2], '1-only': 'Specific to policy 1'}
>policy_2_output = {'int': 2, 'str': 'def', 'list': [3, 4], '2-only': 'Specific to policy 2'}
>print(aggregate([policy_1_output, policy_2_output]))
```
```
{'int': 3, 'str': 'abcdef', 'list': [1, 2, 3, 4], '1-only': 'Specific to policy 1', '2-only': 'Specific to policy 2'}
```
To illustrate, let's add to another system another robot arm identical to the first one, that acts in tandem with it. All it takes is to add a policy to the `dict` that describes the partial state update block.
```
%%capture
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# In the Partial State Update Blocks,
# the user specifies if state update functions will be run in series or in parallel
# and the policy functions that will be evaluated in that block
partial_state_update_blocks = [
{
'policies': { # The following policy functions will be evaluated and their returns will be passed to the state update functions
'robot_arm_1': robot_arm,
'robot_arm_2': robot_arm
},
'variables': { # The following state variables will be updated simultaneously
'box_A': increment_A,
'box_B': increment_B
}
}
]
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
del configs[:] # Clear any prior configs
# # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # # #
# The configurations above are then packaged into a `Configuration` object
exp.append_configs(initial_state=genesis_states, #dict containing variable names and initial values
partial_state_update_blocks=partial_state_update_blocks, #dict containing state update functions
sim_configs=c #preprocessed dictionaries containing simulation parameters
)
executor = Executor(local_mode_ctx, configs) # Pass the configuration object inside an array
raw_result, tensor, sessions = executor.execute() # The `execute()` method returns a tuple; its first elements contains the raw results
%matplotlib inline
simulation_result = pd.DataFrame(raw_result)
simulation_result.plot('timestep', ['box_A', 'box_B'], grid=True,
xticks=list(simulation_result['timestep'].drop_duplicates()),
colormap = 'RdYlGn',
yticks=list(range(1+(simulation_result['box_A']+simulation_result['box_B']).max())));
```
Because we have made it so that both robots read and update the state of the system at the same time, the equilibrium we had before (with 5 marbles in each box) is never reached. Instead, the system oscillates around that point.
---
_About BlockScience_
[BlockScience](http://bit.ly/github_articles_M_02) is a research and engineering firm specialized in complex adaptive systems and applying practical methodologies from engineering design, development and testing to projects in emerging technologies such as blockchain. Follow us on [Medium](http://bit.ly/bsci-medium) or [Twitter](http://bit.ly/bsci-twitter) to stay in touch.
| true |
code
| 0.45181 | null | null | null | null |
|
# Example Gawain notebook
In this notebook I show how to set up, run, and plot a simple simulation using the gawain plasma physics module.
```
import numpy as np
from gawain.main import run_gawain
from gawain.io import Reader
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
```
# Set up run
Here we define the simulation parameters and initial and boundary conditions.
For this simple example, I use the Sod shock tube problem. This is a 1D hydrodynamics problem, and so mhd routines are turned off.
First define the run_name and output directory, this will create a directory containing the output from the simulation.
```
run_name = "sod_shock_tube"
output_dir = "."
```
Here I choose whether to run an MHD or Hydro simulation, and whether to turn on thermal conductivity and resistivty. As the Sod shock tube is a hydrodynamic problem, MHD and resistivity are turned off. I also do not turn on thermal conductivity.
```
with_mhd = False
with_thermal_conductivity = False
with_resistivity = False
```
These cells define the cfl number, the total simulation time, and which time integrator and flux calculation methods are to be used.
Currently the supported time integration methods are
- euler forward step
- 2nd order Runge-Kutta
- Leapfrog
- Predictor-Corrector
The currently supported flux calculation methods are
- Lax-Wendroff (two-step Richtmeyer form)
- Lax-Friedrichs
- HLLE with MUSCL reconstruction
For all but the simplest simulations it is strongly advised to use HLL, as Lax-Wendroff is susceptible to oscillations about sharp discontinuities and Lax-Friedrichs is very diffusive.
```
cfl = 0.5
t_max = 0.25
# "euler", "rk2", "leapfrog", "predictor-corrector"
integrator = "euler"
# "lax-wendroff", "lax-friedrichs", "hll"
fluxer = "hll"
```
## Define mesh
This cell defines the mesh shape (number of cells in each direction), dimensions (length of each dimension) and the number of output dumps to use.
```
nx, ny, nz = 200, 1, 1
mesh_shape = (nx, ny, nz)
n_outputs = 100
lx, ly, lz = 1.0, 0.001, 0.001
mesh_size = (lx, ly, lz)
x = np.linspace(0.0, lx,num=nx)
y = np.linspace(0.0, ly,num=ny)
z = np.linspace(0.0, lz,num=nz)
X,Y,Z =np.meshgrid(x,y,z, indexing='ij')
```
## Define initial condition
The mesh information is used to create an initial condition. If this were an mhd simulation, the magnetic field initial condition would also need to be included.
```
adiabatic_idx = 7.0/5.0
rho = np.piecewise(X, [X < 0.5, X >= 0.5], [1.0, 0.125])
pressure = np.piecewise(X, [X < 0.5, X >= 0.5], [1.0, 0.1])
mx = np.zeros(X.shape)
my = np.zeros(X.shape)
mz = np.zeros(X.shape)
e = pressure/(adiabatic_idx-1) + 0.5*mx*mx/rho
initial_condition = np.array([rho, mx, my, mz, e])
source = 0.0*np.ones(initial_condition.shape)
```
adiabatic_idx = 7.0/5.0
rho = np.ones(mesh_shape)
pressure = np.ones(mesh_shape)
mx = np.zeros(mesh_shape)
my = np.zeros(mesh_shape)
mz = np.zeros(mesh_shape)
e = pressure/(adiabatic_idx-1) + 0.5*mx*mx/rho
initial_condition = np.array([rho, mx, my, mz, e])
rho_s= np.zeros(mesh_shape)
mx_s= np.zeros(mesh_shape)
my_s= np.zeros(mesh_shape)
mz_s= np.zeros(mesh_shape)
e_s=np.zeros(mesh_shape)
e_s[80:120, :, :]=1.0
source = np.array([rho_s, mx_s, my_s, mz_s, e_s])
## Define boundary conditions
The available boundary conditions are
- periodic
- fixed (to the value specified in the initial condition)
- reflective
```
boundary_conditions = ['fixed', 'periodic', 'periodic']
config = {
"run_name": run_name,
"cfl": cfl,
"mesh_shape": mesh_shape,
"mesh_size": mesh_size,
"t_max": t_max,
"n_dumps": n_outputs,
"initial_condition": initial_condition,
"boundary_type": boundary_conditions,
"adi_idx": adiabatic_idx,
"integrator": integrator,
"fluxer": fluxer,
"output_dir": output_dir,
"with_mhd": with_mhd,
"source":source,
}
```
# Run Simulation
Combine all the above simulation parameters into a parameter dictionary. This dictionary is then fed to the run_gawain function which begins the simulation. Ensure the all keys for this dictionary are defined, and ensure the names are spelt correctly.
```
run_gawain(config)
```
# Plot Results
One can create simple plots to visualise the results using the Reader object
```
data = Reader(run_name)
data.variables
data.plot('density', timesteps=[0,10,20,50,90])
```
One can also create animations from the raw data using the method below
```
raw_data = data.get_data('energy')
raw_data.shape
fig, ax = plt.subplots()
ax.set_xlim(( 0, 200))
ax.set_ylim((0, 1))
line, = ax.plot([], [], lw=2)
# initialization function: plot the background of each frame
def init():
line.set_data([], [])
return (line,)
# animation function. This is called sequentially
def animate(i):
x = np.linspace(0, 200, 200)
y = raw_data[i].reshape(200,)
line.set_data(x, y)
return (line,)
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=100, interval=20,
blit=True)
HTML(anim.to_jshtml())
```
| true |
code
| 0.633779 | null | null | null | null |
|
```
test_index = 0
```
#### testing
```
from load_data import *
# load_data()
```
## Loading the data
```
from load_data import *
X_train,X_test,y_train,y_test = load_data()
len(X_train),len(y_train)
len(X_test),len(y_test)
```
## Test Modelling
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
class Test_Model(nn.Module):
def __init__(self) -> None:
super().__init__()
self.c1 = nn.Conv2d(1,64,5)
self.c2 = nn.Conv2d(64,128,5)
self.c3 = nn.Conv2d(128,256,5)
self.fc4 = nn.Linear(256*10*10,256)
self.fc6 = nn.Linear(256,128)
self.fc5 = nn.Linear(128,4)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.c1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.c2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.c3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,256*10*10)
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc6(preds))
preds = self.fc5(preds)
return preds
device = torch.device('cuda')
BATCH_SIZE = 32
IMG_SIZE = 112
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
EPOCHS = 12
from tqdm import tqdm
PROJECT_NAME = 'Weather-Clf'
import wandb
# test_index += 1
# wandb.init(project=PROJECT_NAME,name=f'test-{test_index}')
# for _ in tqdm(range(EPOCHS)):
# for i in range(0,len(X_train),BATCH_SIZE):
# X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
# y_batch = y_train[i:i+BATCH_SIZE].to(device)
# model.to(device)
# preds = model(X_batch.float())
# preds.to(device)
# loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
# optimizer.zero_grad()
# loss.backward()
# optimizer.step()
# wandb.log({'loss':loss.item()})
# wandb.finish()
# for index in range(10):
# print(torch.argmax(preds[index]))
# print(y_batch[index])
# print('\n')
class Test_Model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1,64,5)
self.conv2 = nn.Conv2d(64,128,5)
self.conv3 = nn.Conv2d(128,256,5)
self.fc1 = nn.Linear(256*10*10,64)
self.fc2 = nn.Linear(64,128)
self.fc3 = nn.Linear(128,256)
self.fc4 = nn.Linear(256,128)
self.fc5 = nn.Linear(128,6)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.conv1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.conv2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.conv3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,256*10*10)
preds = F.relu(self.fc1(preds))
preds = F.relu(self.fc2(preds))
preds = F.relu(self.fc3(preds))
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc5(preds))
return preds
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
test_index += 1
wandb.init(project=PROJECT_NAME,name=f'test-{test_index}')
for _ in tqdm(range(EPOCHS)):
for i in range(0,len(X_train),BATCH_SIZE):
X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
y_batch = y_train[i:i+BATCH_SIZE].to(device)
model.to(device)
preds = model(X_batch.float())
preds.to(device)
loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
optimizer.zero_grad()
loss.backward()
optimizer.step()
wandb.log({'loss':loss.item()})
wandb.finish()
for index in range(10):
print(torch.argmax(preds[index]))
print(y_batch[index])
print('\n')
```
| true |
code
| 0.771381 | null | null | null | null |
|
# Quantum Machine Learning with Amazon Braket: Binary Classifiers
This post details an approach taken by Aioi to build an exploratory
quantum machine learning application using Amazon Braket. Quantum
machine learning has been defined as "a research area that explores the
interplay of ideas from quantum computing and machine learning." Specifically, we explore how to use quantum computers to build a proof-of-principle classifier for risk assessment in a hypothetical car insurance use case. We use a hybrid quantum-classical approach and train a so-called quantum neural network to perform binary classification.
## Background
This demonstration is a result of collaboration with Aioi USA -
subsidiary of Aioi Nissay Dowa Insurance which is a member of MS&AD
Insurance Group Holdings - a major worldwide insurance organization
with close ties to the Toyota group, offering Toyota Insurance in 37
countries. Aioi USA is a full-service "insurtech" insurance agency
that develops data science-based products and services for the
transportation industry. Aioi was one of the first insurance companies
to work with Amazon Braket.
Aioi analyzes telematics data from self-driving vehicles to predict
driving risks. The vehicles are equipped with a multitude of sensors and
the goal is to use the sensor data to assign each vehicle a binary score
(safe or fail) that indicates the health of the vehicle. The problem can
be formalized computationally as a binary classification task in which
the driving risk score is a binary label to vehicle's sensor data.
To learn label assignments for each data point, classical machine learning
techniques such as e.g., linear regression (LR) or deep learning (DL)
can be applied. LR is a popular approach when the data-label mapping
is described by a linear function. For large and complex data structures, DL offers a way to capture
nonlinear behavior in data-label mapping.
So, we have powerful classical methods to perform classification tasks; how can quantum computers help here? The short answer is, we don't quite know yet. There are results ([arXiv:1204.5242](https://arxiv.org/abs/1204.5242), [arXiv:1601.07823](https://arxiv.org/abs/1601.07823) ) indicating that quantum LR algorithms applied to quantum data under specific assumptions can be exponentially faster than their classical counterparts operating on classical data. The flip side is that these quantum algorithms output a solution in the form of a quantum state which may not be immediately useful for further processing on a classical computer. On the DL front, quantum neural networks (QNNs) emerged as a potential replacement for classical neural nets ([arXiv:quant-ph/0201144](https://arxiv.org/abs/quant-ph/0201144)) . QNN designs to perform binary classification tasks were proposed recently (see e.g., [arXiv:1802.06002](https://arxiv.org/abs/1802.06002)) as well. An advantage of QNNs is that they can directly output a classical label value, though one still has to input data in the form of a quantum state. Whether or not QNNs have practical computational advantage over classical neural nets in DL task is very much an area of active research and the jury is not out yet on QNNs. This motivated us to explore how QNNs can be utilized for the driving risk
assignment in the case of binary sensor data with an eye towards near-term hardware implementation that constraints QNN's circuit depth due to decoherence.
In this post we build quantum machine learning applications using [Amazon Braket](https://aws.amazon.com/braket/). To run the example applications developed here, you need access to the [Amazon Braket SDK](https://github.com/aws/amazon-braket-sdk-python). You can either install the Braket SDK locally from the [Amazon Braket GitHub repo](https://github.com/aws/amazon-braket-sdk-python) or, alternatively, create a managed notebook in the [Amazon Braket console](https://aws.amazon.com/console/). (Please note that you need an AWS account, if you would like to run this demo on one of the quantum hardware backends offered by Amazon Braket.)
## Problem Setting
Binary classification is an example of supervised machine learning. It
requires a training data set to build a model that can be used to predict
labels (driving risk scores). We assume that we are given a training set
$T$ that consists of $M$ data-label pairs ${\bf x}, {\bf y}$
$(T=\{{\bf x}_i, {\bf y}_i\}$,$i=1,M)$. Here, ${\bf x}_i$ represents vehicle sensor data as a $N$-bit string
${\bf x}_i=\{x_{i0},\cdots,x_{iN-1}\}$ ($x_{ij}=\{0,1\}$). A label
${\bf y}_i=\{0,1\}$ represents the driving risk score associated with ${\bf x}_i$.
Before we proceed with a quantum solution, it is instructive to recall
the main steps of constructing a classical neural net (NN) based
solution. A classical NN takes data ${\bf x}$ and a set of
parameters $\vec{\theta}$ (so-called weights) as an input and transforms it into an output
label ${\bf z}$ such that $\hat{{\bf y} }= f({\bf x},\vec{\theta})$ where
$f$ is determined by NN. The goal is then
to use a training set to train the NN, i.e. to determine the values of
$\vec{\theta}$ for which the discrepancy between the output labels and
the training set labels is minimized. You achieve this by minimizing a
suitably chosen loss function $L(\hat{{\bf y}},{\bf y})$ over the NN
parameters $\vec{\theta}$ using e.g., a gradient-based optimizer.
To construct a quantum binary classifier we follow a similar procedure
with a couple of modifications
- We map our classical $N$-bit data $\{{\bf x}_i\}$ onto $N$-qubit quantum states $\{|\psi_i\rangle \}$. For example, a classical bit string $\{{\bf x}_i\}=0010$ maps onto $|\psi_i\rangle = |0010\rangle$
- Instead of a classical NN we construct a QNN - a $N+1$-qubit circuit $\mathcal{C}(\{\vec{\theta}\})$ (a sequence of elementary single- and two-qubit gates) that transforms the input states $\{|\psi_i\rangle|0\rangle \}$ into output states $\{|\phi_i \rangle \}$ $|\phi_i\rangle = \mathcal{C}|\psi_i\rangle $. The QNN circuit $\mathcal{C}(\{\vec{\theta}\})$ depends on classical parameters $\{\vec{\theta}\}$ that can be adjusted to change the output $\{|\phi_i\rangle \}$
- We use the $N+1$-th qubit to read out labels after the QNN acted on the input state. Every time we run the QNN with the same input state and parameters $\{\vec{\theta}\}$, we measure in what quantum state the $N+1$-th qubit ends up ($|0\rangle$ or $|1\rangle$). We denote the frequency of observing the state $|0\rangle$ ($|1\rangle$ ) as $p_0$ ($p_1$). We define the observed label $\hat{{\bf y}}$ as $\hat{{\bf y}} = \frac{1 - (p_0-p_1)}{2}$. (Note: in the language of quantum computing the difference $p_0-p_1$ equals the expected value of the Pauli $\hat{Z}$ operator measured on the $N+1$-th qubit.) By definition, $p_0-p_1$ is a function of the QNN parameters $\{\vec{\theta}\}$ in the range $ [-1,1] $ and, thus, $\hat{{\bf y}}$ has the range $ [0,1] $ .
In the training of the QNN circuit $\mathcal{C}$ our goal is to find a set of parameters $\{\vec{\theta}_o\}$ such that for each data point in the training set $T$ the label value ${\bf y}_i$ is close
to $\hat{{\bf y}}_i$.
To achieve this, we minimize the log loss function $L(\{\vec{\theta}\})$ defined as,
$L(\{\vec{\theta}\})=-(\sum\limits_{i=1}^{M}{\bf y}_i\log(\hat{{\bf y}}_i)+(1-{\bf y}_i)\log(1-\hat{{\bf y}}_i))$.
We use the Amazon Braket local simulator to evaluate $L(\{\vec{\theta}\})$ and a classical optimizer from $\verb+scipy.optimize+$ to minimize it.
## Mapping classical data onto quantum states.
The first step in the implementation of a quantum binary classifier is to specify a quantum circuit that maps classical data onto quantum states. We map classical bit values "0" and "1" onto quantum states
$|0\rangle$ and $|1\rangle$, respectively. By convention, the
initial state of a qubit is always assumed to be $|0\rangle$. If the
input quantum state is $|1\rangle$ then we obtain it from
$|0\rangle$ by applying a qubit flip gate $X$ i.e.
$|1\rangle = X|0\rangle$. Similarly, a quantum circuit to prepare an
input state, corresponding to classical data, consists of $X$
gates acting on qubits that are in state $|1\rangle$. For example, a
quantum circuit to prepare $|\psi_i\rangle =|101\rangle$ will consist
of two $X$ gate acting on qubits 0 and 2. Below we provide code that
generates a quantum circuit for preparing an arbitrary computational basis state
$|\psi_i\rangle$ using Amazon Braket.
```
# Import Braket libraries
from braket.circuits import Circuit
from braket.aws import AwsDevice
# A function that converts a bit string bitStr into a quantum circuit
def bit_string_to_circuit(bitStr):
circuit = Circuit()
for ind in range(len(bitStr)):
if bitStr[ind]=='1':
circuit.x(ind)
return circuit
# provide a feature string to test the function above
feature = '00101010'
# print quantum circuit that prepares corresponding quantum state
print(bit_string_to_circuit(feature))
```
## Designing Quantum Neural Networks and Training
Now that we know how to prepare input quantum states that correspond to classical data, the next step is to define and constuct a QNN circuit $\mathcal{C}(\{\vec{\theta}\})$ that we will train to
perform binary classification. We use the QNN design layout depicted in
the figure below. It is has $2N+1$ classical parameters defining:
$N$ two-qubit gates
$XX(\theta_k) = e^{-i\frac{\theta_k}{2} \hat{X}_j\hat{X}_{N+1}}$, $N$
single-qubit gates $R_{y}(\theta_m) = e^{-i\frac{\theta_m}{2}\hat{Y}_j}$, and one single-qubit gate $R_{x}(\theta) = e^{-i\frac{\theta}{2}\hat{X}_N}$ acting on the $N+1$-th qubit..

The code below implements this QNN, applies it to an arbitrary input state defined by a classical bit string, and measures the values of the label qubit using Amazon Braket.
```
# import standard numpy libraries and optimizers
import numpy as np
from scipy.optimize import minimize
# Braket imports
from braket.circuits import Circuit, Gate, Instruction, circuit, Observable
from braket.aws import AwsDevice, AwsQuantumTask
from braket.devices import LocalSimulator
# set Braket backend to local simulator (can be changed to other backends)
device = LocalSimulator()
# Quantum Neural Net from the QNN figure implemented in Braket
# Inputs: bitStr - data bit string (e.g. '01010101')
# pars - array of parameters theta (see the QNN figure for more details)
def QNN(bitStr,pars):
## size of the quantum neural net circuit
nQbts = len(bitStr) + 1 # extra qubit is allocated for the label
## initialize the circuit
qnn = Circuit()
## add single-qubit X rotation to the label qubit,
## initialize the input state to the one specified by bitStr
## add single-qubit Y rotations to data qubits,
## add XX gate between qubit i and the label qubit,
qnn.rx(nQbts-1, pars[0])
for ind in range(nQbts-1):
angles = pars[2*ind + 1:2*ind+1+2]
if bitStr[ind] == '1': # by default Braket sets input states to '0',
# qnn.x(ind) flips qubit number ind to state |1\
qnn.x(ind)
qnn.ry(ind, angles[0]).xx(ind, nQbts-1, angles[1])
## add Z observable to the label qubit
observZ = Observable.Z()
qnn.expectation(observZ, target=[nQbts-1])
return qnn
```
With the QNN defined, we need to code up the loss function $L(\{\vec{\theta}\})$ that we minimize in order to train
the QNN to perform binary classification. Below is the code that computes $L(\{\vec{\theta}\})$ using the local simulator in Amazon Braket.
```
## Function that computes the label of a given feature bit sting bitStr
def parity(bitStr):
return bitStr.count('1') % 2
## Log loss function L(theta,phi) for a given training set trainSet
## inputs: trainSet - array of feature bit strings e.g. ['0101','1110','0000']
## pars - quantum neural net parameters theta (See the QNN figure)
## device - Braket backend that will compute the log loss
def loss(trainSet, pars, device):
loss = 0.0
for ind in range(np.size(trainSet)):
## run QNN on Braket device
task = device.run(QNN(trainSet[ind], pars), shots=0)
## retrieve the run results <Z>
result = task.result()
if parity(trainSet[ind])==0:
loss += -np.log2(1.0-0.5*(1.0-result.values[0]))
else:
loss += -np.log2(0.5*(1.0-result.values[0]))
print ("Current value of the loss function: ", loss)
return loss
```
Putting it all together we are now ready to train our QNN circuit to reproduce binary classification of a training set $T$. For the example below, we assume that labels ${\bf y}_i$ are generated by a Boolean function $\hat{f}({\bf x}_i) = (\sum\limits_{j=0}^{N-1}x_{ij})\ {\rm mod}\ 2$. To emulate data in the training set $T$, we generated $11$ random $10$-bit strings (data) and assign them labels according to $\hat{f}$.
```
## Training the QNN using gradient-based optimizer
nBits = 10 # number of bits per feature
## Random training set consisting of 11 10-bit features
## Please explore other training sets
trainSet = ['1101011010',
'1000110011',
'0101001001',
'0010000110',
'0101111010',
'0000100010',
'1001010000',
'1100110001',
'1000010001',
'0000111101',
'0000000001']
## Initial assignment of QNN parameters theta and phi (random angles in [-pi,pi])
pars0 = 2 * np.pi * np.random.rand(2*nBits+1) - np.pi
## Run minimization
res = minimize(lambda pars: loss(trainSet, pars, device), pars0, method='BFGS', options={'disp':True})
```
Run the code and wait for the optimizer to converge. It outputs a message that looks like this when the optimizer finishes.
```
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 55
Function evaluations: 1430
Gradient evaluations: 65
```
We note that our QNN circuit is designed to compute the parity of input data exactly for an appropriate choice of the parameters $\{\vec{\theta}\}$. Thus, the global minimum of the loss function using this QNN is zero. This is generally not the case in DL applications, however. Note also that $L(\{\vec{\theta}\})$ is not convex
with respect to the parameters $\{\vec{\theta}\}$. This means that if the final value of the loss function value is not zero, the optimizer got stuck in a local minimum. Do not panic. Try running the optimizer with a
different set of initial parameters \verb+pars0+. You can also explore various minimization algorithms by
specifying $\verb+method=' '+$ in the minimize function.
Calling $\verb+res.x+$ outputs the optimal values of the parameters $\{\vec{\theta}\}$
and you can use them to run the "optimal" QNN and perform binary classification on the data that is not a part of the training set. Try that and compute the mean square error of the classifier.
For our 10-bit data example there are $2^{10}=1024$ possible
10-bit strings, we chose a training set that has only 11 data points. Yet it is
sufficiently large to train the QNN to act as a perfect
binary classifier for all 1024 possible features. Can you demonstrate
that?
```
## Print the predicted label values for all N-bit data points using the optimal QNN parameters res.x
for ind in range(2**nBits):
data = format(ind, '0'+str(nBits)+'b')
task = device.run(QNN(data, res.x), shots=100)
result = task.result()
if (data in trainSet):
inSet = 'in the training set'
else:
inSet = 'NOT in the training set'
print('Feature:', data, '| QNN predicted parity: ', 0.5*(1-result.values[0]), ' | ', inSet)
print('---------------------------------------------------')
```
As an exercise, use the optimal QNN parameters in $\verb+res.x+$ and apply the
resulting QNN to all 10-bit strings that are not in the training set.
Record the mean square error between the predicted and computed label
values.
### Conclusion
This post explored the use case of binary classification to analyze
binary (telematic) data by combining QNNs with Amazon Braket. The QNN binary classifier designed in this post
requires the number of two-qubit gates that scales linearly with the
feature size. This is advantageous for Noisy Intermediate Scale Quantum
(NISQ) devices that are limited in the circuit depth due to noise. A
future area of investigation for the team is to apply more complex
feature sets, and constructing QNNs to classify them. You can download and play with the code from this post here.
| true |
code
| 0.57081 | null | null | null | null |
|
# M² Experimental Design
**Scott Prahl**
**Mar 2021**
The basic idea for measuring M² is simple. Use a CCD imager to capture changing beam profile at different points along the direction of propagation. Doing this accurately is a challenge because the beam must always fit within camera sensor and the measurement locations should include both points near the focus and far from the focus. Moreover, in most situations, the focus is not accessible. In this case a lens is used to create an artificial focus that can be measured.
One of the nice properties of M² is that it is not affected by refocusing: the artificially focused beam will have different beam waist and Rayleigh distances but the M² value will be the same as the original beam.
This notebook describes a set of constraints for selection of an imaging lens and then gives an example of a successful measurement and an unsuccessful measurement.
---
*If* `` laserbeamsize `` *is not installed, uncomment the following cell (i.e., delete the initial #) and execute it with* `` shift-enter ``. *Afterwards, you may need to restart the kernel/runtime before the module will import successfully.*
```
#!pip install --user laserbeamsize
import numpy as np
import matplotlib.pyplot as plt
try:
import laserbeamsize as lbs
except ModuleNotFoundError:
print('laserbeamsize is not installed. To install, uncomment and run the cell above.')
print('Once installation is successful, rerun this cell again.')
pixel_size = 3.75e-6 # pixel size in m
pixel_size_mm = pixel_size * 1e3
pixel_size_µm = pixel_size * 1e6
```
## Designing an M² measurement
We first need to to figure out the focal length of the lens that will be used. The design example that we will use is for a low divergence beam. (High divergence lasers (e.g. diodes) are more suited to other techniques.)
Obviously, we do not want to introduce experimental artifacts into the measurement and therefore we want to minimize introducing wavefront aberrations with the lens. In general, to avoid spherical aberrations the f-number (the focal length divided by the beam diameter) of the lens should be over 20. For a low divergence beam the beam diameter will be about 1mm at the lens and, as we will see below, the allowed f-numbers will all be much greater than 20 and we don't need to worry about it further (as long as a plano-convex lens or doublet is used in the right orientation).
### Creating an artificial focus
An example of beam propagation is shown below. The beam waist is at -500mm and a lens is located at 0mm. The beam cross section is exaggerated because the aspect ratio on the axes is 1000:1.
```
lambda0 = 632.8e-9 # wavelength of light [m]
w0 = 450e-6 # radius at beam waist [m]
f = 300e-3 # focal length of lens [m]
lbs.M2_focus_plot(w0, lambda0, f, z0=-500e-3, M2=2)
plt.show()
```
### Axial measurement positions
The ISO 11146-1 document, [Lasers and laser-related equipment - Test methods for laser beam widths, divergence angles and beam propagation, Part 1: Stigmatic and simple astigmatic beams](https://www.iso.org/obp/ui/#iso:std:iso:11146:-1:ed-1:v1:en) gives specific instructions for how to measure the M² value.
> If the beam waist is accessible for direct measurement, the beam waist location, beam widths, divergence angles and beam propagation ratios shall be determined by a hyperbolic fit to different measurements of the beam width along the propagation axis $z$. Hence, measurements at at least 10 different $z$ positions shall be taken. Approximately half of the measurements shall be distributed within one Rayleigh length on either side of the beam waist, and approximately half of them shall be distributed beyond two Rayleigh lengths from the beam waist. For simple astigmatic beams this procedure shall be applied separately for both principal directions.
In the picture above, the artificial beam waist is at 362mm and the Rayleigh distance for the artificial beam is 155mm. Therefore, to comply with the requirements above, five measurements should be made between 207 and 517mm of the lens and then five more at distances greater than 672mm. One possibility might be the ten measurements shown below.
```
lambda0 = 632.8e-9 # wavelength of light [m]
w0 = 450e-6 # radius at beam waist [m]
f = 300e-3 # focal length of lens [m]
z = np.array([250, 300, 350, 400, 450, 675, 725, 775, 825, 875])*1e-3
lbs.M2_focus_plot(w0, lambda0, f, z0=-500e-3, M2=2)
r = lbs.beam_radius(250e-6, lambda0, z, z0=362e-3, M2=2)
plt.plot(z*1e3,r*1e6,'or')
plt.show()
```
### Camera sensor size constraints
If the beam is centered on the camera sensor then should be larger than 20 pixels and it should less than 1/4 of the narrower sensor dimension. The first constraint is critical for weakly divergent beams (e.g., HeNe) and the second is critical for strongly divergent beams (e.g., diode laser).
For a HeNe, this ensures that the focal length of the lens should be greater than 100mm. If we want 40 pixel diameters then the requirement is that the focal length must be more than 190mm.
(Use M²=1 so that the beam size is smallest possible.)
```
w0 = (1e-3)/2
lambda0 = 632.8e-9
f = np.linspace(10,250)*1e-3
s = -400e-3
max_size = 960 * 0.25 * pixel_size_µm
min_size = 20 * pixel_size_µm
w0_artificial = w0 * lbs.magnification(w0,lambda0,s,f,M2=1)
plt.plot(f*1e3, w0_artificial*1e6)
plt.axhspan(min_size, 0, color='blue', alpha=0.1)
plt.text(70, 20, "Image too small")
plt.xlabel("Focal Length (mm)")
plt.ylabel("Beam Radius (µm)")
plt.axvline(190,color='black')
plt.show()
```
### Working size constraints (i.e., the optical table is only so big)
The measurements must be made on an optical table. Now, while mirrors could be used to bounce the light around the table, this makes exact measurements of the lens to the camera sensor difficult. Thus we would like the distance from the lens to the focus + 4 Rayleigh distances to be less than a meter.
Longer focal length lenses reduce the relative error in the positioning of the camera sensor relative to the lens. If one is doing these measurements by hand then ±1mm might be a typical positioning error. A motorized stage could minimize such errors, but who has the money for a stage that moves half of a meter!
This means the focal distance needs to be less than 320mm. However, at this distance, the beam becomes too large and the largest focal length lens is now about 275mm.
```
w0 = 1e-3 / 2
lambda0 = 632.8e-9
f = np.linspace(50,500)*1e-3
s = -400e-3
M2 = 2
w0_artificial = w0 * lbs.magnification(w0,lambda0,s,f,M2=M2)
z0_artificial = lbs.image_distance(w0,lambda0,s,f,M2=M2)
zR_artificial = lbs.z_rayleigh(w0_artificial, lambda0, M2=M2)
lens_to_4zr_distance = z0_artificial + 4 * zR_artificial
plt.plot(f*1e3, lens_to_4zr_distance*1e3)
plt.axhspan(1000, lens_to_4zr_distance[-1]*1e3, color='blue', alpha=0.1)
plt.text(350, 1050, "Axial distance too far")
plt.xlabel("Focal Length (mm)")
plt.ylabel("$z_0+4z_R$ (mm)")
plt.axvline(320,color='black')
plt.show()
radius_at_4zr = lbs.beam_radius(w0_artificial, lambda0, lens_to_4zr_distance, z0=z0_artificial, M2=M2)
max_size = 960 * 0.25 * pixel_size_µm
plt.plot(f*1e3, radius_at_4zr*1e6)
plt.axhspan(1600, max_size, color='blue', alpha=0.1)
plt.text(350, 1000, "Beam too big")
plt.axvline(275,color='black')
plt.xlabel("Focal Length (mm)")
plt.ylabel("Beam Radius (mm)")
plt.show()
```
### Putting it all together
The focal length of the lens to measure a multimode HeNe beam should then be between 190 and 275 mm. Here is what a reasonable set of measurements should be for a f=250mm lens.
```
lambda0 = 632.8e-9 # wavelength of light [m]
w0 = 500e-6 # radius at beam waist [m]
f = 250e-3 # focal length of lens [m]
s = -400e-3 # beam waist in laser to lens distance [m]
M2 = 2
lbs.M2_focus_plot(w0, lambda0, f, z0=s, M2=M2)
z0_after = lbs.image_distance(w0,lambda0,s,f,M2=M2)
w0_after = w0 * lbs.magnification(w0,lambda0,s,f,M2=M2)
zR_after = lbs.z_rayleigh(w0_after,lambda0,M2=M2)
zn = np.linspace(z0_after-zR_after,z0_after+zR_after,5)
zf = np.linspace(z0_after+2*zR_after,z0_after+4*zR_after,5)
rn = lbs.beam_radius(w0_after, lambda0, zn, z0=z0_after, M2=2)
rf = lbs.beam_radius(w0_after, lambda0, zf, z0=z0_after, M2=2)
plt.plot(zn*1e3,rn*1e6,'or')
plt.plot(zf*1e3,rf*1e6,'ob')
plt.show()
```
## Good spacing of beam size measurements
```
# datapoints digitized by hand from the graph at https://www.rp-photonics.com/beam_quality.html
lambda1=308e-9
z1_all=np.array([-200,-180,-160,-140,-120,-100,-80,-60,-40,-20,0,20,40,60,80,99,120,140,160,180,200])*1e-3
d1_all=2*np.array([416,384,366,311,279,245,216,176,151,120,101,93,102,120,147,177,217,256,291,316,348])*1e-6
lbs.M2_radius_plot(z1_all, d1_all, lambda1, strict=True)
```
## Poor spacing of beam size measurements
A nice fit of the beam is achieved, however the fitted value for M²<1. This is impossible. Basically the problem boils down to the fact that the measurements in the beam waist are terrible for determining the actual divergence of the beam. The fit then severely underestimates the divergence of the beam and claims that the beam diverges more slowly than a simple Gaussian beam!!
```
## Some Examples
f=500e-3 # m
lambda2 = 632.8e-9 # m
z2_all = np.array([168, 210, 280, 348, 414, 480, 495, 510, 520, 580, 666, 770]) * 1e-3 # [m]
d2_all = 2*np.array([597, 572, 547, 554, 479, 404, 415, 399, 377, 391, 326, 397]) * 1e-6 # [m]
lbs.M2_radius_plot(z2_all, d2_all, lambda2, strict=True)
plt.show()
```
| true |
code
| 0.67174 | null | null | null | null |
|
# Scene Classification
## 3. Build Model-InceptionV3 BatchTrain Top2Layer
- Import pkg
- Load sample data, only first 1000 objects
-
Reference:
- https://challenger.ai/competitions
- https://github.com/jupyter/notebook/issues/2287
**Tensorboard**
1. Input at command: **tensorboard --logdir=./log**
2. Input at browser: **http://127.0.0.1:6006**
### Import pkg
```
import numpy as np
import pandas as pd
# import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import seaborn as sns
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from keras.utils.np_utils import to_categorical # convert to one-hot-encoding
from keras.models import Sequential, load_model
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D, BatchNormalization
from keras.optimizers import Adam, SGD
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import LearningRateScheduler, TensorBoard
# import zipfile
import os
import zipfile
import math
import time
from IPython.display import display
import pdb
import json
from PIL import Image
import glob
import pickle
```
### Load sample data, only first 1000 objects
```
input_path = './input'
datasetName = 'train'
date = '20170904'
zip_path = input_path + '/ai_challenger_scene_{0}_{1}.zip'.format(datasetName, date)
extract_path = input_path + '/ai_challenger_scene_{0}_{1}'.format(datasetName, date)
image_path = extract_path + '/scene_{0}_images_{1}'.format(datasetName, date)
scene_classes_path = extract_path + '/scene_classes.csv'
scene_annotations_path = extract_path + '/scene_{0}_annotations_{1}.json'.format(datasetName, date)
print(input_path)
print(zip_path)
print(extract_path)
print(image_path)
print(scene_classes_path)
print(scene_annotations_path)
scene_classes = pd.read_csv(scene_classes_path, header=None)
display(scene_classes.head())
def get_scene_name(lable_number, scene_classes_path):
scene_classes = pd.read_csv(scene_classes_path, header=None)
return scene_classes.loc[lable_number, 2]
print(get_scene_name(0, scene_classes_path))
def load_pickle_data(dataset, index):
pickleFolder = './input/pickle_{0}'.format(dataset)
print(pickleFolder)
x_path = pickleFolder + '/x_data{0}.p'.format(index)
y_path = pickleFolder + '/y_data{0}.p'.format(index)
print(x_path)
print(y_path)
if not os.path.exists(x_path):
print(x_path + ' do not exist!')
return
if not os.path.exists(y_path):
print(y_path + ' do not exist!')
return
x_data = pickle.load(open(x_path, mode='rb'))
y_data = pickle.load(open(y_path, mode='rb'))
# y_data = to_categorical(y_train)
print(x_data.shape)
print(y_data.shape)
return (x_data, y_data)
x_train, y_train = load_pickle_data("train", 0)
print(x_train.shape)
print(y_train.shape)
del x_train
del y_train
%%time
x_train, y_train = load_pickle_data("train", 0)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(x_train[0])
ax[0].set_title(get_scene_name(y_train[0], scene_classes_path))
ax[1].imshow(x_train[1])
ax[1].set_title(get_scene_name(y_train[1], scene_classes_path))
del x_train
del y_train
%%time
x_val, y_val = load_pickle_data("validation", 0)
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(x_val[0])
ax[0].set_title(get_scene_name(y_val[0], scene_classes_path))
ax[1].imshow(x_val[1])
ax[1].set_title(get_scene_name(y_val[1], scene_classes_path))
del x_val
del y_val
```
### Load model
```
from keras.preprocessing import image
from keras.models import Model
from keras.layers import Dense, GlobalAveragePooling2D
from keras import backend as K
from keras.applications.inception_v3 import InceptionV3
base_model = InceptionV3(weights='imagenet', include_top=False)
# add a global spatial average pooling layer
x = base_model.output
x = GlobalAveragePooling2D()(x)
# let's add a fully-connected layer
x = Dense(1024, activation='relu')(x)
# and a logistic layer -- let's say we have 200 classes
predictions = Dense(80, activation='softmax')(x)
# this is the model we will train
model = Model(inputs=base_model.input, outputs=predictions)
# first: train only the top layers (which were randomly initialized)
# i.e. freeze all convolutional InceptionV3 layers
for layer in base_model.layers:
layer.trainable = False
model.compile(loss='categorical_crossentropy', optimizer = Adam(lr=1e-4), metrics=["accuracy"])
for i, layer in enumerate(model.layers):
print(i, layer.name)
def saveModel(model, middleName):
modelPath = './model'
if not os.path.isdir(modelPath):
os.mkdir(modelPath)
fileName = middleName + time.strftime("%Y-%m-%d_%H-%M-%S", time.localtime())
jsonFileName = modelPath + '/' + fileName + '.json'
yamlFileName = modelPath + '/' + fileName + '.yaml'
json_string = model.to_json()
with open(jsonFileName, 'w') as file:
file.write(json_string)
yaml_string = model.to_yaml()
with open(yamlFileName, 'w') as file:
file.write(yaml_string)
weigthsFile = modelPath + '/' + fileName + '.h5'
model.save(weigthsFile)
# saveModel(model, 'ModelSaveTest')
```
**Train top 2 inception**
```
train_datagen = ImageDataGenerator(rescale=1./255,
rotation_range = 20,
zoom_range = 0.1,
width_shift_range = 0.1,
height_shift_range = 0.1,
horizontal_flip = True,
vertical_flip = True)
train_generator = train_datagen.flow_from_directory('./input/data_train',
target_size=(224, 224),
batch_size=64,
class_mode = "categorical")
print(train_generator.classes[0:1000])
# annealer = LearningRateScheduler(lambda x: 1e-3 * 0.9 ** x)
tensorBoard = TensorBoard(log_dir='./log_Top2Inc_171001')
x_val, y_val = load_pickle_data("validation", 0)
y_val = to_categorical(y_val)
# model.compile(loss='categorical_crossentropy', optimizer = Adam(lr=1e-4), metrics=["accuracy"])
hist = model.fit_generator(train_generator,
steps_per_epoch=128,
epochs=32, #Increase this when not on Kaggle kernel
verbose=2, #1 for ETA, 0 for silent
validation_data=(x_val, y_val),
callbacks=[tensorBoard])
saveModel(model, 'TrainImageFolder')
final_loss, final_acc = model.evaluate(x_val, y_val, verbose=0)
print("Final loss: {0:.4f}, final accuracy: {1:.4f}".format(final_loss, final_acc))
plt.plot(hist.history['loss'], color='b')
plt.plot(hist.history['val_loss'], color='r')
plt.show()
plt.plot(hist.history['acc'], color='b')
plt.plot(hist.history['val_acc'], color='r')
plt.show()
print('Done!')
```
| true |
code
| 0.522811 | null | null | null | null |
|
# NESTS algorithm **Kopuru Vespa Velutina Competition**
Purpose: Bring together weather data, geographic data, food availability data, and identified nests in each municipality of Biscay in order to have a dataset suitable for analysis and potential predictions in a Machine Learning model.
Outputs: QUEENtrain and QUEENpredict datasets *(WBds03_QUEENtrain.csv & WBds03_QUEENpredict.csv)*
@authors:
* [email protected]
* [email protected]
* [email protected]
* [email protected]
## Libraries
```
import pandas as pd
import numpy as np
import math
from plotnine import *
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn import preprocessing
```
## Functions
```
def silueta(iterations_int, features_df):
silhouettes = []
for i in range(2,iterations_int,1):
model = KMeans(n_clusters=i)
aux = features_df
model.fit(aux)
labels = model.labels_
sol = silhouette_score(aux, labels)
silhouettes.append(sol)
silhouette = pd.DataFrame()
silhouette['Labels'] = silhouettes
silhouette['NumberOfClusters'] = range(2,iterations_int,1)
return silhouette
def codos(numClusters_int, features_df):
inertias = []
for i in range(1,numClusters_int,1):
model = KMeans(n_clusters=i)
aux = features_df
model.fit(aux)
inertias.append(model.inertia_)
elbow = pd.DataFrame()
elbow['Inertia'] = inertias
elbow['NumberOfClusters'] = range(1,numClusters_int,1)
return elbow
def kmedias(numClusters_int, features_df):
model = KMeans(n_clusters = numClusters_int)
aux = features_df
model.fit(aux)
modelLabels = model.labels_
modelCenters = model.cluster_centers_
return pd.Series(modelLabels, index=features_df.index)
```
## Get the data
```
df01 = pd.read_csv('../../../Input_open_data/ds01_PLANTILLA-RETO-AVISPAS-KOPURU.csv', sep=";")
df02 = pd.read_csv('../../../Input_open_data/ds02_datos-nidos-avispa-asiatica.csv', sep=",")
df03 = pd.read_csv('../../../Input_open_data/ds03_APICULTURA_COLMENAS_KOPURU.csv', sep=";")
df04 = pd.read_csv('../../../Input_open_data/ds04_FRUTALES-DECLARADOS-KOPURU.csv', sep=";")
WBdf01 = pd.read_csv('./WBds01_GEO.csv', sep=',')
WBdf02 = pd.read_csv('./WBds02_METEO.csv', sep=',')
df_population = pd.read_csv('../../../Other_open_data/population.csv', sep=',')
```
## Data cleanup
### Getting the names right
```
# Dropping and Renaming columns in accordance to the DataMap
# DataMap's URL: https://docs.google.com/spreadsheets/d/1Ad7s4IOmj9Tn2WcEOz4ArwedTzDs9Y0_EaUSm6uRHMQ/edit#gid=0
df01.columns = ['municip_code', 'municip_name', 'nests_2020']
df01.drop(columns=['nests_2020'], inplace=True) # just note that this is the final variable to predict in the competition
df02.drop(columns=['JARDUERA_ZENBAKIA/NUM_ACTUACION', 'ERABILTZAILEA_EU/USUARIO_EU', 'ERABILTZAILEA_CAS/USUARIO_CAS', 'HELBIDEA/DIRECCION', 'EGOERA_EU/ESTADO_EU', 'ITXIERA_DATA/FECHA CIERRE', 'ITXIERAKO AGENTEA_EU/AGENTE CIERRE_EU', 'ITXIERAKO AGENTEA_CAS/AGENTE CIERRE_CAS'], inplace=True)
df02.columns = ['waspbust_id', 'year', 'nest_foundDate', 'municip_name', 'species', 'nest_locType', 'nest_hight', 'nest_diameter', 'nest_longitude', 'nest_latitude', 'nest_status']
df03.drop(columns=['CP'], inplace=True)
df03.columns = ['municip_name','municip_code','colonies_amount']
df04.columns = ['agriculture_type','municip_code','municip_name']
# We don't have the "months" specified for any of the records in 2017 ('nest_foundDate' is incorrect for this year), so we'll drop those records
df02 = df02.drop(df02[df02['year'] == 2017].index, inplace = False)
# Cleaning municipality names in ds02 with names from ds01
df02_wrong_mun = ['ABADIÑO' ,'ABANTO Y CIERVANA' ,'ABANTO Y CIERVANA-ABANTO ZIERBENA' ,'AJANGIZ' ,'ALONSOTEGI' ,'AMOREBIETA-ETXANO' ,'AMOROTO' ,'ARAKALDO' ,'ARANTZAZU' ,'AREATZA' ,'ARRANKUDIAGA' ,'ARRATZU' ,'ARRIETA' ,'ARRIGORRIAGA' ,'ARTEA' ,'ARTZENTALES' ,'ATXONDO' ,'AULESTI' ,'BAKIO' ,'BALMASEDA' ,'BARAKALDO' ,'BARRIKA' ,'BASAURI' ,'BEDIA' ,'BERANGO' ,'BERMEO' ,'BERRIATUA' ,'BERRIZ' ,'BUSTURIA' ,'DERIO' ,'DIMA' ,'DURANGO' ,'EA' ,'ELANTXOBE' ,'ELORRIO' ,'ERANDIO' ,'EREÑO' ,'ERMUA' ,'ERRIGOITI' ,'ETXEBARRI' ,'ETXEBARRIA', 'ETXEBARRIa','FORUA' ,'FRUIZ' ,'GALDAKAO' ,'GALDAMES' ,'GAMIZ-FIKA' ,'GARAI' ,'GATIKA' ,'GAUTEGIZ ARTEAGA' ,'GERNIKA-LUMO' ,'GETXO' ,'GETXO ' ,'GIZABURUAGA' ,'GORDEXOLA' ,'GORLIZ' ,'GUEÑES' ,'IBARRANGELU' ,'IGORRE' ,'ISPASTER' ,'IURRETA' ,'IZURTZA' ,'KARRANTZA HARANA/VALLE DE CARRANZA' ,'KARRANTZA HARANA-VALLE DE CARRANZA' ,'KORTEZUBI' ,'LANESTOSA' ,'LARRABETZU' ,'LAUKIZ' ,'LEIOA' ,'LEKEITIO' ,'LEMOA' ,'LEMOIZ' ,'LEZAMA' ,'LOIU' ,'MALLABIA' ,'MAÑARIA' ,'MARKINA-XEMEIN' ,'MARURI-JATABE' ,'MEÑAKA' ,'MENDATA' ,'MENDEXA' ,'MORGA' ,'MUNDAKA' ,'MUNGIA' ,'MUNITIBAR-ARBATZEGI' ,'MUNITIBAR-ARBATZEGI GERRIKAITZ' ,'MURUETA' ,'MUSKIZ' ,'MUXIKA' ,'NABARNIZ' ,'ONDARROA' ,'OROZKO' ,'ORTUELLA' ,'OTXANDIO' ,'PLENTZIA' ,'PORTUGALETE' ,'SANTURTZI' ,'SESTAO' ,'SONDIKA' ,'SOPELA' ,'SOPUERTA' ,'SUKARRIETA' ,'TRUCIOS-TURTZIOZ' ,'UBIDE' ,'UGAO-MIRABALLES' ,'URDULIZ' ,'URDUÑA/ORDUÑA' ,'URDUÑA-ORDUÑA' ,'VALLE DE TRAPAGA' ,'VALLE DE TRAPAGA-TRAPAGARAN' ,'ZALDIBAR' ,'ZALLA' ,'ZAMUDIO' ,'ZARATAMO' ,'ZEANURI' ,'ZEBERIO' ,'ZIERBENA' ,'ZIORTZA-BOLIBAR' ]
df02_correct_mun = ['Abadiño' ,'Abanto y Ciérvana-Abanto Zierbena' ,'Abanto y Ciérvana-Abanto Zierbena' ,'Ajangiz' ,'Alonsotegi' ,'Amorebieta-Etxano' ,'Amoroto' ,'Arakaldo' ,'Arantzazu' ,'Areatza' ,'Arrankudiaga' ,'Arratzu' ,'Arrieta' ,'Arrigorriaga' ,'Artea' ,'Artzentales' ,'Atxondo' ,'Aulesti' ,'Bakio' ,'Balmaseda' ,'Barakaldo' ,'Barrika' ,'Basauri' ,'Bedia' ,'Berango' ,'Bermeo' ,'Berriatua' ,'Berriz' ,'Busturia' ,'Derio' ,'Dima' ,'Durango' ,'Ea' ,'Elantxobe' ,'Elorrio' ,'Erandio' ,'Ereño' ,'Ermua' ,'Errigoiti' ,'Etxebarri' , 'Etxebarria', 'Etxebarria','Forua' ,'Fruiz' ,'Galdakao' ,'Galdames' ,'Gamiz-Fika' ,'Garai' ,'Gatika' ,'Gautegiz Arteaga' ,'Gernika-Lumo' ,'Getxo' ,'Getxo' ,'Gizaburuaga' ,'Gordexola' ,'Gorliz' ,'Güeñes' ,'Ibarrangelu' ,'Igorre' ,'Ispaster' ,'Iurreta' ,'Izurtza' ,'Karrantza Harana/Valle de Carranza' ,'Karrantza Harana/Valle de Carranza' ,'Kortezubi' ,'Lanestosa' ,'Larrabetzu' ,'Laukiz' ,'Leioa' ,'Lekeitio' ,'Lemoa' ,'Lemoiz' ,'Lezama' ,'Loiu' ,'Mallabia' ,'Mañaria' ,'Markina-Xemein' ,'Maruri-Jatabe' ,'Meñaka' ,'Mendata' ,'Mendexa' ,'Morga' ,'Mundaka' ,'Mungia' ,'Munitibar-Arbatzegi Gerrikaitz' ,'Munitibar-Arbatzegi Gerrikaitz' ,'Murueta' ,'Muskiz' ,'Muxika' ,'Nabarniz' ,'Ondarroa' ,'Orozko' ,'Ortuella' ,'Otxandio' ,'Plentzia' ,'Portugalete' ,'Santurtzi' ,'Sestao' ,'Sondika' ,'Sopela' ,'Sopuerta' ,'Sukarrieta' ,'Trucios-Turtzioz' ,'Ubide' ,'Ugao-Miraballes' ,'Urduliz' ,'Urduña/Orduña' ,'Urduña/Orduña' ,'Valle de Trápaga-Trapagaran' ,'Valle de Trápaga-Trapagaran' ,'Zaldibar' ,'Zalla' ,'Zamudio' ,'Zaratamo' ,'Zeanuri' ,'Zeberio' ,'Zierbena' ,'Ziortza-Bolibar',]
df02.municip_name.replace(to_replace = df02_wrong_mun, value = df02_correct_mun, inplace = True)
df02.shape
# Translate the `species` variable contents to English
df02.species.replace(to_replace=['AVISPA ASIÁTICA', 'AVISPA COMÚN', 'ABEJA'], value=['Vespa Velutina', 'Common Wasp', 'Wild Bee'], inplace=True)
# Translate the contents of the `nest_locType` and `nest_status` variables to English
# But note that this data makes is of no use from a "forecastoing" standpoint eventually, since we will predict with a one-year offset (and thus, use thigs like weather mostly)
df02.nest_locType.replace(to_replace=['CONSTRUCCIÓN', 'ARBOLADO'], value=['Urban Environment', 'Natural Environment'], inplace=True)
df02.nest_status.replace(to_replace=['CERRADA - ELIMINADO', 'CERRADA - NO ELIMINABLE', 'PENDIENTE DE GRUPO'], value=['Nest Terminated', 'Cannot Terminate', 'Pending classification'], inplace=True)
```
### Getting the dates right
Including the addition of a `year_offset` variable to comply with the competition's rules
```
# Changing 'nest_foundDate' the to "datetime" format
df02['nest_foundDate'] = pd.to_datetime(df02['nest_foundDate'])
# Create a "month" variable in the main dataframe
df02['month'] = pd.DatetimeIndex(df02['nest_foundDate']).month
# Create a "year_offset" variable in the main dataframe
# IMPORTANT: THIS REFLECTS OUR ASSUMPTION THAT `YEAR-1` DATA CAN BE USE TO PREDICT `YEAR` DATA, AS MANDATED BY THE COMPETITION'S BASE REQUIREMENTS
df02['year_offset'] = pd.DatetimeIndex(df02['nest_foundDate']).year - 1
df02.columns
```
### Creating distinct dataFrames for each `species`
```
df02.species.value_counts()
df02_vespas = df02.loc[df02.species == 'Vespa Velutina', :]
df02_wasps = df02.loc[df02.species == 'Common Wasp', :]
df02_bees = df02.loc[df02.species == 'Wild Bee', :]
df02_vespas.shape
```
## Create a TEMPLATE dataframe with the missing municipalities and months
```
template = pd.read_csv('../../../Input_open_data/ds01_PLANTILLA-RETO-AVISPAS-KOPURU.csv', sep=";")
template.drop(columns='NIDOS 2020', inplace=True)
template.columns = ['municip_code', 'municip_name']
template['year2019'] = 2019
template['year2018'] = 2018
template['year2017'] = 2017
template = pd.melt(template, id_vars=['municip_code', 'municip_name'], value_vars=['year2019', 'year2018', 'year2017'], value_name = 'year_offset')
template.drop(columns='variable', inplace=True)
for i in range(1,13,1):
template[i] = i
template = pd.melt(template, id_vars=['municip_code', 'municip_name', 'year_offset'],\
value_vars=[1,2,3,4,5,6,7,8,9,10,11,12], value_name = 'month')
template.drop(columns='variable', inplace=True)
template.shape
112*12*3 == template.shape[0]
template.columns
```
## Merge the datasets
### Match each `municip_name` to its `municip_code` as per the competition's official template (i.e. `df01`)
```
# Merge dataFrames df01 and df02 by 'municip_name', in order to identify every wasp nest with its 'municip_code'
# The intention is that 'all_the_queens-wasps' will be the final dataFrame to use in the ML model eventually
all_the_queens_wasps = pd.merge(df02_vespas, df01, how = 'left', on = 'municip_name')
# check if there are any municipalities missing from the df02 dataframe, and add them if necessary
df01.municip_code[~df01.municip_code.isin(all_the_queens_wasps.municip_code.unique())]
```
### Input municipalities and months missing from the dataset
```
all_the_queens_wasps = pd.merge(all_the_queens_wasps, template,\
how = 'outer', left_on = ['municip_code', 'municip_name', 'year_offset', 'month'],\
right_on = ['municip_code', 'municip_name', 'year_offset', 'month'])
all_the_queens_wasps.isnull().sum()
all_the_queens_wasps.year.fillna(value='no registers', inplace=True)
all_the_queens_wasps.shape
```
### Discarding some variables
Namely: **species** (since by now they are all Vespa Velutina only), **nest_foundDate**,**nest_longitude**, and **nest_latitude**.
```
all_the_queens_wasps.drop(columns=['nest_foundDate', 'nest_longitude', 'nest_latitude', 'species'], inplace=True)
```
### Creating a new categorical variable for Nest Size
[Formula for nest volume](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6723431/)
[Example calculation in cubic meters](https://www.easycalculation.com/shapes/volume-of-prolate-spheroid.php)
```
#ggplot(aes(x='nest_hight', y='nest_diameter'), all_the_queens_wasps) + geom_point(stat='identity')
#all_the_queens_wasps['nest_volume_l'] = 4/3 * math.pi * (all_the_queens_wasps['nest_hight']/100/2)**2 * (all_the_queens_wasps['nest_diameter']/100/2) * 1000
#all_the_queens_wasps['nest_volume_l'].fillna(0, inplace=True)
all_the_queens_wasps['nest_size'] = all_the_queens_wasps['nest_hight'] * all_the_queens_wasps['nest_diameter']
all_the_queens_wasps['nest_size'].fillna(0, inplace=True)
all_the_queens_wasps['nest_size'].describe()
vespaVoluminous = all_the_queens_wasps.loc[:, ['municip_code', 'nest_size']].groupby(by='municip_code', as_index=False).mean()
ggplot(aes(x='nest_size'), vespaVoluminous) + geom_histogram()
#vespaVoluminous['nest_size_equals'] = pd.qcut(vespaVoluminous['nest_size'], 3, labels=['small', 'mid', 'large'])
#vespaVoluminous['nest_size_equals'].value_counts()
vespaVoluminous['nest_size'] = pd.cut(vespaVoluminous['nest_size'], bins=3, labels=['small', 'mid', 'large'])
vespaVoluminous['nest_size'].value_counts()
all_the_queens_wasps = pd.merge(all_the_queens_wasps, vespaVoluminous, how = 'left', on= 'municip_code')
#all_the_queens_wasps
```
### Converting categoricals to dummy variables
... and dropping some variables. Namely: **nest_locType**, **nest_hight**, **nest_diameter**, **nest_size_x**, **nest_size_y**, and **nest_latitude**.
```
queen_big = pd.get_dummies(all_the_queens_wasps.nest_size_y)
all_the_queens_wasps = pd.concat([all_the_queens_wasps, queen_big], axis=1)
queen_cosmo = pd.get_dummies(all_the_queens_wasps.nest_locType)
all_the_queens_wasps = pd.concat([all_the_queens_wasps, queen_cosmo], axis=1)
queen_hastalavista = pd.get_dummies(all_the_queens_wasps.nest_status)
all_the_queens_wasps = pd.concat([all_the_queens_wasps, queen_hastalavista], axis=1)
all_the_queens_wasps.drop(columns=['nest_locType', 'nest_hight', 'nest_diameter', 'nest_size_y', 'nest_size_x', 'nest_status'], inplace=True)
all_the_queens_wasps.rename(columns = {"small":"fv_size_small", "mid":"fv_size_mid", "large":"fv_size_large",\
"Natural Environment":"fv_type_natural", "Urban Environment":"fv_type_urban",\
"Cannot Terminate":"fv_status_cantkill", "Nest Terminated":"fv_status_dead", "Pending classification":"fv_status_pending"}, inplace = True)
#all_the_queens_wasps
#all_the_queens_wasps.isnull().sum()
```
### Counting the amount of wasp nests in each municipality, for each year, ~not for the months~
```
all_the_queens_wasps = all_the_queens_wasps.loc[:, ['waspbust_id', 'fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural', 'fv_type_urban',\
'fv_status_cantkill', 'fv_status_dead', 'fv_status_pending',\
'year', 'municip_name', 'municip_code', 'year_offset']]\
.groupby(by =['year', 'municip_name', 'municip_code', 'year_offset'], as_index=False)\
.agg({'waspbust_id':'count', 'fv_size_small':'sum', 'fv_size_mid':'sum', 'fv_size_large':'sum', 'fv_type_natural':'sum', 'fv_type_urban':'sum',\
'fv_status_cantkill':'sum', 'fv_status_dead':'sum', 'fv_status_pending':'sum'})
# let's rename the id to NESTS, now that it has been counted
all_the_queens_wasps.rename(columns = {"waspbust_id":"NESTS"}, inplace = True)
all_the_queens_wasps.columns
# for all those "outer merge" rows with no associated year, set their NESTS to zero
all_the_queens_wasps.loc[all_the_queens_wasps.year == 'no registers', ['NESTS']] = 0
all_the_queens_wasps.NESTS.sum() == df02_vespas.shape[0]
# grouping by 'year_offset' and making the former 'year' variable dissappear
all_the_queens_wasps = all_the_queens_wasps.loc[:, ['municip_name', 'municip_code', 'year_offset', 'NESTS', 'fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural', 'fv_type_urban', 'fv_status_cantkill', 'fv_status_dead', 'fv_status_pending']]\
.groupby(by =['municip_name', 'municip_code', 'year_offset'], as_index = False).sum()
# verifying that the DataFrame has the right number of rows
all_the_queens_wasps.shape[0] == 112*3
#all_the_queens_wasps.isnull().sum()
```
### Food sources
```
# Group df03 by 'municip_code' because there are multiple rows for each municipality (and we need a 1:1 relationship)
df03 = df03.groupby(by = 'municip_code', as_index= False).colonies_amount.sum()
# Now merge df03 to add number of bee hives (which is a food source for the wasp) in each municipality
# Note that NaNs (unknown amount of hives) are replaced with zeroes for the 'colonies_amount' variable
all_the_queens_wasps = pd.merge(all_the_queens_wasps, df03, how = 'left', on = 'municip_code')
all_the_queens_wasps.colonies_amount.fillna(value=0, inplace=True)
all_the_queens_wasps.shape
#all_the_queens_wasps.isnull().sum()
# Group df04 (agricultural food sources) by municipality code, after appending variables with the amount of each type of agricultural product
aux = df04.copy(deep=True)
aux.drop(columns=['municip_name'], inplace=True)
aux['food_fruit'] = np.where(aux['agriculture_type'] == 'FRUTALES', '1', '0')
aux['food_fruit'] = aux['food_fruit'].astype('int')
aux['food_apple'] = np.where(aux['agriculture_type'] == 'MANZANO', '1', '0')
aux['food_apple'] = aux['food_apple'].astype('int')
txakoli_string = df04.agriculture_type[45]
aux['food_txakoli'] = np.where(aux['agriculture_type'] == txakoli_string, '1', '0')
aux['food_txakoli'] = aux['food_txakoli'].astype('int')
aux['food_kiwi'] = np.where(aux['agriculture_type'] == 'AKTINIDIA (KIWI)', '1', '0')
aux['food_kiwi'] = aux['food_kiwi'].astype('int')
aux['food_pear'] = np.where(aux['agriculture_type'] == 'PERAL', '1', '0')
aux['food_pear'] = aux['food_pear'].astype('int')
aux['food_blueberry'] = np.where(aux['agriculture_type'] == 'ARANDANOS', '1', '0')
aux['food_blueberry'] = aux['food_blueberry'].astype('int')
aux['food_raspberry'] = np.where(aux['agriculture_type'] == 'FRAMBUESAS', '1', '0')
aux['food_raspberry'] = aux['food_raspberry'].astype('int')
aux = aux.groupby(by='municip_code', as_index=False).sum()
df04 = aux.copy(deep=True)
# Now merge df04 to add number of each type of food source ('agriculture_type') present in each municipality
# Any municipality not present in df04 will get assigned 'zero' food sources for any given type of fruit
all_the_queens_wasps = pd.merge(all_the_queens_wasps, df04, how = 'left', on= 'municip_code')
all_the_queens_wasps.food_fruit.fillna(value=0, inplace=True)
all_the_queens_wasps.food_apple.fillna(value=0, inplace=True)
all_the_queens_wasps.food_txakoli.fillna(value=0, inplace=True)
all_the_queens_wasps.food_kiwi.fillna(value=0, inplace=True)
all_the_queens_wasps.food_pear.fillna(value=0, inplace=True)
all_the_queens_wasps.food_blueberry.fillna(value=0, inplace=True)
all_the_queens_wasps.food_raspberry.fillna(value=0, inplace=True)
all_the_queens_wasps.shape
#all_the_queens_wasps.isnull().sum()
```
### Geographic
Here, a very important assumption regarding which station corresponds to each municipality is being brought from the HONEYCOMB script
```
# Adding weather station code to each municipality in all_the_queens_wasps. "No municipality left behind!"
all_the_queens_wasps = pd.merge(all_the_queens_wasps, WBdf01, how = 'left', on= 'municip_code')
all_the_queens_wasps.shape
#all_the_queens_wasps.isnull().sum()
all_the_queens_wasps.year_offset.value_counts()
```
### Weather
MANDATORY ASSUMPTION: As per the competition's rules. 2020 weather data cannot be used to predict 2020's number of wasp nests.
Therefore, **this merge links 2018's wasp nests to 2017's weather data** (all of which falls under the $2017$ value for `year_offset`).
Likewise, **2019's wasp nests are linked to 2018's weather data** (all of which falls under the $2018$ value for `year_offset`).
Finally, the $2019$ value for `year_offset` contains zero NESTS and the year 2019's weather which we will use to predict 2020's number of NESTS (the target variable of the competition)
```
# Now, merge the Main 'all_the_queens_wasps' dataFrame with the weather data 'WBdf02' dataFrame
all_the_queens_wasps = pd.merge(all_the_queens_wasps, WBdf02, how = 'left',\
left_on = ['station_code', 'year_offset'],\
right_on = ['codigo', 'year'])
all_the_queens_wasps.columns
all_the_queens_wasps_TRAIN = all_the_queens_wasps.loc[all_the_queens_wasps.year_offset.isin([2017, 2018]),:]
all_the_queens_wasps_PREDICT = all_the_queens_wasps.loc[all_the_queens_wasps.year_offset.isin([2019]),:]
```
### Adding `Population`, a publicly available dataset
```
# Adding population by municipality
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, df_population, how = 'left',\
left_on= ['municip_code', 'year_offset'],\
right_on = ['municip_code', 'year'])
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, df_population, how = 'left',\
left_on= ['municip_code', 'year_offset'],\
right_on = ['municip_code', 'year'])
all_the_queens_wasps_TRAIN.shape
all_the_queens_wasps_PREDICT.shape
```
## Further cleanup
```
#dropping unnecessary/duplicate columns
all_the_queens_wasps_TRAIN.drop(columns=['year_x', 'year_y', 'codigo'], inplace=True)
all_the_queens_wasps_TRAIN.columns
# this step shouldn't be necessary
all_the_queens_wasps_TRAIN.columns = ['municip_name', 'municip_code', 'year_offset', 'NESTS',\
'fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural',\
'fv_type_urban', 'fv_status_cantkill', 'fv_status_dead',\
'fv_status_pending', 'colonies_amount', 'food_fruit', 'food_apple',\
'food_txakoli', 'food_kiwi', 'food_pear', 'food_blueberry',\
'food_raspberry', 'station_code', 'weath_days_frost',\
'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel',\
'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall',\
'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar',\
'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp',\
'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind',\
'population']
all_the_queens_wasps_TRAIN.columns
all_the_queens_wasps_PREDICT.drop(columns=['year_x', 'year_y', 'codigo'], inplace=True)
all_the_queens_wasps_PREDICT.columns
# this step shouldn't be necessary
all_the_queens_wasps_PREDICT.columns = ['municip_name', 'municip_code', 'year_offset', 'NESTS',\
'fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural',\
'fv_type_urban', 'fv_status_cantkill', 'fv_status_dead',\
'fv_status_pending', 'colonies_amount', 'food_fruit', 'food_apple',\
'food_txakoli', 'food_kiwi', 'food_pear', 'food_blueberry',\
'food_raspberry', 'station_code', 'weath_days_frost',\
'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel',\
'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall',\
'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar',\
'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp',\
'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind',\
'population']
all_the_queens_wasps_TRAIN.NESTS.sum() == df02_vespas.shape[0]
all_the_queens_wasps_PREDICT.NESTS.sum() == 0
```
## Clustering municipalities
### by the size of its Vespa Velutina nests (`fv_...`)
```
sizeMatters = all_the_queens_wasps_TRAIN.loc[:, ['municip_code', 'fv_size_small', 'fv_size_mid', 'fv_size_large']].groupby(by='municip_code', as_index=True).mean()
sizeSilhouette = silueta(15, sizeMatters)
ggplot(aes(x='NumberOfClusters', y='Labels'), sizeSilhouette) + geom_line() + geom_point()
clustersby_size = 5
sizeClusters = pd.DataFrame()
sizeClusters['cluster_size'] = kmedias(clustersby_size, sizeMatters)
sizeClusters['cluster_size'].reset_index()
sizeClusters['cluster_size'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, sizeClusters['cluster_size'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, sizeClusters['cluster_size'], how = 'left', on= 'municip_code')
```
### by the usual environment of its wasp nests (`fv_...`)
```
cosmopolitan = all_the_queens_wasps_TRAIN.loc[:, ['municip_code', 'fv_type_natural', 'fv_type_urban']].groupby(by='municip_code', as_index=True).mean()
cosmoSilhouette = silueta(10, cosmopolitan)
ggplot(aes(x='NumberOfClusters', y='Labels'), cosmoSilhouette) + geom_line() + geom_point()
clustersby_cosmo = 2
cosmoClusters = pd.DataFrame()
cosmoClusters['cluster_cosmo'] = kmedias(clustersby_cosmo, cosmopolitan)
cosmoClusters['cluster_cosmo'].reset_index()
cosmoClusters['cluster_cosmo'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, cosmoClusters['cluster_cosmo'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, cosmoClusters['cluster_cosmo'], how = 'left', on= 'municip_code')
```
### by the usual status its wasp nests are left in (`fv_...`)
```
survivalists = all_the_queens_wasps_TRAIN.loc[:, ['municip_code', 'fv_status_cantkill', 'fv_status_dead', 'fv_status_pending']].groupby(by='municip_code', as_index=True).mean()
surviveSilhouette = silueta(10, survivalists)
ggplot(aes(x='NumberOfClusters', y='Labels'), surviveSilhouette) + geom_line() + geom_point()
clustersby_survive = 2
surviveClusters = pd.DataFrame()
surviveClusters['cluster_survive'] = kmedias(clustersby_cosmo, survivalists)
surviveClusters['cluster_survive'].reset_index()
surviveClusters['cluster_survive'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, surviveClusters['cluster_survive'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, surviveClusters['cluster_survive'], how = 'left', on= 'municip_code')
```
### Dropping all that future information (aka, future variables (`fv_...`)) from the dataset
```
all_the_queens_wasps_TRAIN.drop(columns=['fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural', 'fv_type_urban', 'fv_status_cantkill', 'fv_status_dead', 'fv_status_pending'], inplace=True)
all_the_queens_wasps_PREDICT.drop(columns=['fv_size_small', 'fv_size_mid', 'fv_size_large', 'fv_type_natural', 'fv_type_urban', 'fv_status_cantkill', 'fv_status_dead', 'fv_status_pending'], inplace=True)
```
### by the availability of food sources (`food_`)
```
foodies = all_the_queens_wasps_TRAIN.loc[:, ['municip_code', 'colonies_amount', 'food_fruit', 'food_apple', 'food_txakoli', 'food_kiwi', 'food_pear', 'food_blueberry', 'food_raspberry']].groupby(by='municip_code', as_index=True).mean()
slimSilhouette = silueta(10, foodies)
ggplot(aes(x='NumberOfClusters', y='Labels'), slimSilhouette) + geom_line() + geom_point()
clustersby_foodie = 2
foodieClusters = pd.DataFrame()
foodieClusters['cluster_food'] = kmedias(clustersby_foodie, foodies)
foodieClusters['cluster_food'].reset_index()
foodieClusters['cluster_food'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, foodieClusters['cluster_food'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, foodieClusters['cluster_food'], how = 'left', on= 'municip_code')
```
### Exploring clustering of weather variables (`weath_...`)
#### Humidity-related variables
```
# scale the dataset using MinMaxScaler, the most common approach
#scalators = ['weath_days_frost', 'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel', 'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall', 'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar', 'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp', 'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind']
scalators_wet = ['municip_code', 'weath_days_frost', 'weath_humidity', 'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall', 'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar']
weathercock_water = all_the_queens_wasps_TRAIN[scalators_wet].copy()
weathercock_water.iloc[:,1:] = preprocessing.minmax_scale(weathercock_water.iloc[:,1:])
weathercock_water = weathercock_water.groupby(by='municip_code', as_index=True).mean()
wetSilhouette = silueta(15, weathercock_water)
ggplot(aes(x='NumberOfClusters', y='Labels'), wetSilhouette) + geom_line() + geom_point()
clustersby_weather_humid = 2
weatherWetClusters = pd.DataFrame()
weatherWetClusters['cluster_weather_wet'] = kmedias(clustersby_weather_humid, weathercock_water)
weatherWetClusters['cluster_weather_wet'].reset_index()
weatherWetClusters['cluster_weather_wet'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, weatherWetClusters['cluster_weather_wet'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, weatherWetClusters['cluster_weather_wet'], how = 'left', on= 'municip_code')
```
#### Temperature-related variables
```
# scale the dataset using MinMaxScaler, the most common approach
#scalators = ['weath_days_frost', 'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel', 'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall', 'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar', 'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp', 'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind']
scalators_temp = ['municip_code', 'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp']
weathercock_temp = all_the_queens_wasps_TRAIN[scalators_temp].copy()
weathercock_temp.iloc[:,1:] = preprocessing.minmax_scale(weathercock_temp.iloc[:,1:])
weathercock_temp = weathercock_temp.groupby(by='municip_code', as_index=True).mean()
tempSilhouette = silueta(10, weathercock_temp)
ggplot(aes(x='NumberOfClusters', y='Labels'), tempSilhouette) + geom_line() + geom_point()
clustersby_weather_temp = 2
weatherTempClusters = pd.DataFrame()
weatherTempClusters['cluster_weather_temp'] = kmedias(clustersby_weather_temp, weathercock_temp)
weatherTempClusters['cluster_weather_temp'].reset_index()
weatherTempClusters['cluster_weather_temp'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, weatherTempClusters['cluster_weather_temp'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, weatherTempClusters['cluster_weather_temp'], how = 'left', on= 'municip_code')
```
#### Wind-related variables
```
# scale the dataset using MinMaxScaler, the most common approach
#scalators = ['weath_days_frost', 'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel', 'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall', 'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar', 'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp', 'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind']
scalators_wind = ['municip_code', 'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind']
weathercock_wind = all_the_queens_wasps_TRAIN[scalators_wind].copy()
weathercock_wind.iloc[:,1:] = preprocessing.minmax_scale(weathercock_wind.iloc[:,1:])
weathercock_wind = weathercock_wind.groupby(by='municip_code', as_index=True).mean()
windSilhouette = silueta(15, weathercock_wind)
ggplot(aes(x='NumberOfClusters', y='Labels'), windSilhouette) + geom_line() + geom_point()
clustersby_weather_wind = 2
weatherWindClusters = pd.DataFrame()
weatherWindClusters['cluster_weather_wind'] = kmedias(clustersby_weather_wind, weathercock_wind)
weatherWindClusters['cluster_weather_wind'].reset_index()
weatherWindClusters['cluster_weather_wind'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, weatherWindClusters['cluster_weather_wind'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, weatherWindClusters['cluster_weather_wind'], how = 'left', on= 'municip_code')
```
#### Other weather variables
```
# scale the dataset using MinMaxScaler, the most common approach
#scalators = ['weath_days_frost', 'weath_humidity', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel', 'weath_days_rain', 'weath_days_rain1mm', 'weath_accuRainfall', 'weath_10minRainfall', 'weath_1dayRainfall', 'weath_solar', 'weath_meanTemp', 'weath_maxTemp', 'weath_maxMeanTemp', 'weath_minTemp', 'weath_meanWindM', 'weath_maxWindM', 'weath_meanDayMaxWind']
scalators_level = ['municip_code', 'weath_maxLevel', 'weath_midLevel', 'weath_minLevel']
weathercock_level = all_the_queens_wasps_TRAIN[scalators_level].copy()
weathercock_level.iloc[:,1:] = preprocessing.minmax_scale(weathercock_level.iloc[:,1:])
weathercock_level = weathercock_level.groupby(by='municip_code', as_index=True).mean()
levelSilhouette = silueta(10, weathercock_level)
ggplot(aes(x='NumberOfClusters', y='Labels'), slimSilhouette) + geom_line() + geom_point()
clustersby_weather_level = 2
weatherLevelClusters = pd.DataFrame()
weatherLevelClusters['cluster_weather_level'] = kmedias(clustersby_weather_level, weathercock_level)
weatherLevelClusters['cluster_weather_level'].reset_index()
weatherLevelClusters['cluster_weather_level'].value_counts()
all_the_queens_wasps_TRAIN = pd.merge(all_the_queens_wasps_TRAIN, weatherLevelClusters['cluster_weather_level'], how = 'left', on= 'municip_code')
all_the_queens_wasps_PREDICT = pd.merge(all_the_queens_wasps_PREDICT, weatherLevelClusters['cluster_weather_level'], how = 'left', on= 'municip_code')
```
### Cluster table
## Final check
```
all_the_queens_wasps_TRAIN.isnull().sum()
# check how many rows (municipalities) are there in the dataframe for each year/month combination
pd.crosstab(all_the_queens_wasps.municip_code, all_the_queens_wasps.year_offset)
all_the_queens_wasps_TRAIN.NESTS.sum() == df02_vespas.shape[0]
all_the_queens_wasps_PREDICT.NESTS.sum() == 0
```
## Export the TRAINING dataset for the model
A dataset which relates the weather from a previous year (12 months ago) to an amount of NESTS in any given year (and month).
```
#all_the_queens_wasps.to_csv('WBds03_QUEEN.csv', index=False)
all_the_queens_wasps_TRAIN.to_csv('WBds03_QUEENtrainYEARS.csv', index=False)
```
## Export the PREDICTION dataset for the model
```
all_the_queens_wasps_PREDICT.to_csv('WBds03_QUEENpredictYEARS.csv', index=False)
```
| true |
code
| 0.375936 | null | null | null | null |
|
# Training Models
We will practice training machine learning models for both regression and for classification problems.
# 1) Regression Models
We will start by fitting regression models. We will download the time series of the GPS station deployed on Montague Island.
<img src="AC29_map.png" alt="AC29 GPS stations on Montague Island" width="600"/>
```
import requests, zipfile, io, gzip, glob, os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
%matplotlib inline
# Download data
sta="AC29"
file_url="http://geodesy.unr.edu/gps_timeseries/tenv/IGS14/"+ sta + ".tenv"
r = requests.get(file_url).text.splitlines() # download, read text, split lines into a list
ue=[];un=[];uv=[];se=[];sn=[];sv=[];date=[];date_year=[];df=[]
for iday in r: # this loops through the days of data
crap=iday.split()
if len(crap)<10:
continue
date.append((crap[1]))
date_year.append(float(crap[2]))
ue.append(float(crap[6])*1000)
un.append(float(crap[7])*1000)
uv.append(float(crap[8])*1000)
# # errors
se.append(float(crap[10])*1000)
sn.append(float(crap[11])*1000)
sv.append(float(crap[12])*1000)
# make dataframe
crap={'station':sta,'date':date,'date_year':date_year,'east':ue,'north':un,'up':uv}
if len(df)==0:
df = pd.DataFrame(crap, columns = ['station', 'date','date_year','east','north','up'])
else:
df=pd.concat([df,pd.DataFrame(crap, columns = ['station', 'date','date_year','east','north','up'])])
df.head()
# select the first 2 years of data from the east component
y = ue[0:365*5]
plt.plot(df['date_year'],df['east']);plt.grid(True)
```
### 1.1 Linear regression
Let $y$ be the data, and $\hat{y}$ be the predicted value of the data. A general linear regression can be formulated as
$\hat{y} = w_0 + w_1 x_1 + ... + w_n x_n = h_w (\mathbf{x})$.
$\mathbf{\hat{y}} = \mathbf{G} \mathbf{w}$.
$y$ is a data vector of length $m$, $\mathbf{x}$ is a feature vector of length $n$. $\mathbf{w}$ is a vector of model parameter, $h_w$ is refered to as the *hypothesis function* or the *model* using the model parameter $w$. In the most simple case of a linear regression with time, the formulation becomes:
$\hat{y} = w_0 + w_1 t$,
where $x_1 = t$ the time feature.
To evaluate how well the model performs, we will compute a *loss score*, or a *residual*. It is the result of applying a *loss* or *cost* or *objective* function to the prediction and the data. The most basic *cost function* is the **Mean Square Error (MSE)**:
$MSE(\mathbf{x},h_w) = \frac{1}{m} \sum_{i=1}^{m} \left( h_w(\mathbf{x})_i - y_i \right)^2 = \frac{1}{m} \sum_{i=1}^{m} \left( \hat{y}_i - y_i \right)^2 $, in the case of a linear regression.
The *Normal Equation* is the solution to the linear regression that minimize the MSE.
$\mathbf{w} = \left( \mathbf{x}^T\mathbf{x} \right)^{-1} \mathbf{x}^T \mathbf{y}$
This compares with the classic inverse problem framed by $\mathbf{d} = \mathbf{G} \mathbf{m}$.
$\mathbf{m} = \left( \mathbf{G}^T\mathbf{G} \right)^{-1} \mathbf{G}^T \mathbf{d} $
It can be solved using Numpy linear algebra module. If $\left( \mathbf{x}^T\mathbf{x} \right) $ is singular and cannot be inverted, a lower rank matrix called the *pseudoinverse* can be calculated using singular value decomposition. We also used in a previous class that the Scikit-learn function for ``sklearn.linear_model.LinearRegression``, which is the implementation of the *pseudoinverse* We practice below how to use these standard inversions:
```
x = np.asarray(date_year[0:2*365])
x = x-np.min(x)
y = np.asarray(ue[0:2*365])
G = np.c_[np.ones((2*365,1)),x]
m = len(y)
print(G)
#normal equation
w1 = np.linalg.inv(G.T.dot(G)).dot(G.T).dot(y)
# Pseudoinverse
w2 = np.linalg.pinv(G).dot(y)
# scikitlearn LinearRegression
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x.reshape(1,-1),y.reshape(1,-1))
print(lin_reg)
w3 = [lin_reg.intercept_, lin_reg.coef_]
y_predict1=G.dot(w1)
y_predict2=G.dot(w2)
y_predict3=lin_reg.predict(x.reshape(1,-1))
plt.plot(x,y);plt.grid(True)
plt.plot(x,y_predict1,'r',linewidth=3);
plt.plot(x,y_predict2,'g--');
plt.plot(x.reshape(1,-1),y_predict3,'k');
plt.xlabel("Time (years)")
plt.ylabel('East displacement (mm) at AC29')
print("modeled parameters. Normal equation")
print(w1)
print("modeled parameters. pseudoinverse")
print(w2)
```
## 1.2 Loss functions for regressions
Loss functions are used to measure the difference between the data and the predictions. Loss functions $\mathcal{L}(\mathbf{w}) $ are differentiable with respect to models.
In the previous example, we used the MSE as a loss function:
$ MSE(\mathbf{x},h_w) = \frac{1}{m} \sum_{i=1}^m \left( \hat{y}_i - y_i \right) ^2 $
The regression aims to find $h_w$ that minimizes the loss function $\mathcal{L}(\mathbf{w}) $. Other examples of loss functions are:
$MAE(\mathbf{x},h_w) = \frac{1}{m} \sum_{i=1}^m |\hat{y}_i - y_i|$
You can find interesting comparisons of Loss functions for regression problems here: https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0
# 2) Gradient Descent
Gradient Descent is used to *train* machine learning models.
Gradient Descent marches down the misfit function through the parameter space: it evaluates the loss function and attempting to find its global minimum. The model $\mathbf{w}$ is updated iteratively in the direction that reduces the loss/misfit:
$w_j^{(k + 1)} = w_j^{(k)} - \alpha \frac{\partial \mathcal{L}}{\partial w_j}$ for $j = 1 , \cdots , n ,$
where $\alpha$ is the **learning rate**.
<table><tr>
<td> <img src="GD_cartoon.jpeg" alt="Gradient Descent" style="width: 400px;"/> </td>
<td> <img src="GD_non_global.png" alt="Gradient Descent non convex" style="width: 400px;"/> </td>
</tr>
<tr>
<td>Gradient descent for a convex, well behaved loss function. </td>
<td> Gradient descent in a poorly behaved loss function with local minima. <td>
</tr>
</table>
## 2.1 Batch Gradient Descent
Batch GD is performing the GD over the entire data and taking the steps to go down the gradient by finding the appropriate learning rate $\alpha$.
<table><tr>
<td> <img src="GD_AlphaTooSmall.png" alt="Learning rate too small" style="width: 400px;"/> </td>
<td> <img src="GD_AlphaTooLarge.png" alt="Learning rate too large" style="width: 400px;"/> </td>
</tr>
<tr>
<td>Learning rate $\alpha$ is too small. It will take longer to converge. </td>
<td> Learning rate $\alpha$ is too large. Converge to global minimum. <td>
</tr>
</table>
The iteration in GD can be stopped by imposing a convergence rate (tolerance) that is a thershold under which the error will not longer be calculated. Gradient Descent require re-scaling the data.
```
# normalize the data. Without normalization this will fail!
x = np.asarray(date_year[0:3*365]).reshape(-1,1)
y = np.asarray(ue[0:3*365]).reshape(-1,1)
x = x-np.min(x)
G = np.c_[np.ones((len(x),1)),x]
scale = (np.max(y)-np.min(y)) # minmax scaling
newy = y / scale
plt.plot(x,newy*scale);plt.grid(True)
alpha = 0.1
n_iterations =1000
for k in range(100): # perform 100 times the random initialization
w = np.random.rand(2,1) # initialize the model parameters.
for iteration in range(n_iterations):
gradients = 2/m *G.T.dot(G.dot(w)-newy.reshape(-1,1))
w = w - alpha * gradients
plt.plot(x,G.dot(w)*scale,'r')
# Now let's vary the learning rate
n_iterations =1000
for alpha in [0.001,0.01,0.1]:
fig,ax=plt.subplots(1,1)
ax.plot(x,newy*scale);ax.grid(True)
for k in range(100): # perform 100 times the random initialization
w = np.random.rand(2,1) # initialize the model parameters.
for iteration in range(n_iterations):
gradients = 2/m *G.T.dot(G.dot(w)-newy.reshape(-1,1))
w = w - alpha * gradients
ax.plot(x,G.dot(w)*scale,'r')
ax.set_title("alpha = "+str(alpha))
```
## 2.2 Stochastic Gradient Descent
SGD takes the gradient for each single instance. By default, SGD in Scikit-learn will minimize the MSE cost function. The advantages of GD are:
* Efficiency.
* Ease of implementation (lots of opportunities for code tuning).
The disadvantages of Stochastic Gradient Descent include:
* SGD requires a number of hyperparameters such as the regularization parameter and the number of iterations.
* SGD is sensitive to feature scaling.
```
from sklearn.linear_model import SGDRegressor
alpha = 0.01 # learning rate
sgd_reg = SGDRegressor(max_iter=1000,tol=1e-2,penalty=None,eta0=alpha)
sgd_reg.fit(x,y)
w=[sgd_reg.intercept_[0],sgd_reg.coef_[0]]
print(w)
fig,ax=plt.subplots(1,1)
ax.plot(x,y);ax.grid(True)
ax.plot(x,G.dot(w),'r')
```
## 2.3 Mini Batch Gradient Descent
It is a combination of Batch GD and SGD. Minibatch computes the gradient over a subset of instances (as against a single one in SGD or the full one in Batched GD). At each step, using one minibatch randomly drawn from our dataset, we will estimate the gradient of the loss with respect to our parameters. Next, we will update our parameters in the direction that may reduce the loss.
# 2) Under-fitting and Overfitting
**Bias**
This part of the generalization error is due to wrong assumptions, such as assuming that the data is linear when it is actually quadratic. A high-bias model is most likely to underfit the training data. Biased is reduced by adjusting, optimizing the model to get the best performance possible on the training data.
**Variance**
This part is due to the model’s excessive sensitivity to small variations in the training data. A model with many degrees of freedom (such as a high-degree polynomial model) is likely to have high variance, and thus to overfit the training data. Variance is reduced
**Irreducible error**
This part is due to the noisiness of the data itself. The only way to reduce this part of the error is to clean up the data (e.g., fix the data sources, such as broken sensors, or detect and remove outliers).
**Underfitting**: the model is too simple, the bias is high but the model variance is low. This occurs in most cases at the beginning of training, where the model has not yet learned to fit the data. With iterative training, the algorithm starts by underfitting the data (high loss for both validation and training data) and progressively "learn" and improve the fit. It remains a problem with the loss in both training and validation have high values.
The solution is to increase the complexity of the model, or to design better feature from the data (feature engineering), and to reduce the constrains on the model (such as the parameterization of model regularization). Underfitting is identified by having a high bias and low variance of the residuals. It is usually obvious and rarely a problem because the training and validation errors are high.
**Overfitting**: the model is too complex, the bias is low but the model variance is high. Data may contain noise that should not be fit by the algorithm. It happens when the model is too complex relative to the amount and the noisiness of the training data. Overfitting is a common problem in geoscience machine learning problems. Overfitting can be detected when the model performs perfectly on the training data, but poorly on the validation and test data. It can also be detected using **cross-validation metrics** and **learning curves**.
Some solutions are to reduce the model size, reduce the number of attributes in the training data, gather more training data, to reduce the noise in the training data (fix data errors and remove outliers). Another way to keep the model complexity but constrain its variance is called **regularization**.
***You do not know if you overfit, until you do***. The model may not be complex enough until your reached overfitting. Once reached, back up a little bit to find the best tradeoff in optimization and generalization.
**Assessing Overfitting**
To evaluate the model's ability to generalize to other data sets, and have the appropriate level of variance, we plot **learning curves**. These plots the model performance on the training and validation set as a function of the training set size.
```
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y,c1="b+",c2="b"):
# Setting the random_state variable in the train_test_split is necessary to reproduce the results.
# When tuning parameters such as test_size, you need to set the random state otherwise too many parameters change.
X_train, X_val, y_train, y_val = train_test_split(x, y, test_size=0.2,random_state=42)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), c1, linewidth=2, label="train")
plt.plot(np.sqrt(val_errors),c2, linewidth=3, label="val")
plt.legend(['training','validation'])
plt.grid(True)
plt.title("Learning curve")
plt.ylabel("RMSE")
plt.xlabel('Training size')
x = np.asarray(date_year[0:2*365]).reshape(-1,1)
y = np.asarray(ue[0:2*365]).reshape(-1,1)
x = x-np.min(x)
# G = np.c_[np.ones((len(x),1)),x]
scale = (np.max(y)-np.min(y)) # minmax scaling
newy = y / scale
alpha = 0.01 # learning rate
sgd_reg = SGDRegressor(max_iter=1000,tol=1e-2,penalty=None,eta0=alpha)
sgd_reg.fit(x,newy)
y_predict=sgd_reg.predict(x)
plt.plot(x,y);plt.grid(True)
plt.plot(x,y_predict*scale,"m",linewidth=3)
plt.ylabel('East displacement (mm) at AC29')
plot_learning_curves(sgd_reg, x.ravel(), y.ravel())
plt.ylim([1,2])
```
Let's read and interpret these curves.
You will notice that when you re-run the cell with ``plot_learning_curves`` that you will get different answers: this is because the initialization of the SGD will give different answers. This is a first reason why one should run these multiple times and then average over the curves.
* **The good signs**:
Loss curves plateau at low value for both training and validation. Training loss should be smaller, but not by much, than the validation loss. Low loss values are signs of good fit and good generalization.
* **The bad signs: underfitting**:
RMSE are high for both training and validation.
* **The bad signs: overfitting**:
RMSE is low for training but high for validation.
# 3) Regularization
Constraining a model of a given complexity to make it simpler is called **regularization**.
## 3.1 Ridge Regression
To regularize the model, we can reduce model parameter variance by imposing that the norm of the model parameters is small. Assuming that the model parameters follow a normal (Gaussian) distribution, we want to minimize the L2 norm (equivalent to the mean square of the model parameters:
$\mathcal{L}(\mathbf{w}) = MSE(\mathbf{w}) + \lambda \frac{1}{2} || \mathbf{w} ||_2^2$,
where $|| \mathbf{w} ||_2 = \sum_{i=1}^n w_i^2$ is the L2 norm of the model parameters, $\lambda$ is a hyperparameter to tune to balance the contribution of model norm as against the residual norms. L2 norm is sensitive to outliers in the distributions.
Ridge Regression is sensitive to data scale, so do not forget to scale input data.
## 3.2 Lasso Regression
Lasso Regression is just like the Ridge Regression a way to minimize model variance. Instead of mimizing the L2 norm, we mimize the L1 norn:
$\mathcal{L}(\mathbf{w}) = MSE(\mathbf{w}) + \lambda || \mathbf{w} ||_1$,
The L1 norm $|| \mathbf{w} ||_1 = \sum_{i=1}^n | w_i |$ is appropriate for exponential (Laplace) distribution, and allow to not be penalized by outliers. It tends to eliminate the weights of the least important features. It effectively performs a *feature reduction* and output a *sparse model*. It can be called in SGD by using the argument ``penalty="l1"``.
## 3.3 Elastic Net
Combine Ridge and Lasso, weigh the contribution of each norm (L1 and L2) using the hyperparameter $r$, and the contribution of the regularization in the loss function with $\lambda$.
$\mathcal{L}(\mathbf{w}) = MSE(\mathbf{w}) + r \lambda|| \mathbf{w} ||_1 + \frac{1-r}{2} \lambda|| \mathbf{w} ||_2^2$,
```
from sklearn.linear_model import SGDRegressor, ElasticNet, Lasso, Ridge
sgd_reg = SGDRegressor()
ridge_reg = Ridge(alpha=0.1)
lasso_reg = Lasso(alpha=0.1)
ela_reg = ElasticNet(alpha=0.1,l1_ratio=0.5)
# prep the data again
x = np.asarray(date_year[0:4*365]).reshape(-1,1)
y = np.asarray(ue[0:4*365]).reshape(-1,1)
x = x-np.min(x)
G = np.c_[np.ones((len(x),1)),x]
scale = (np.max(y)-np.min(y)) # minmax scaling
# Fit
sgd_reg.fit(x,y)
ridge_reg.fit(x,y)
lasso_reg.fit(x,y)
ela_reg.fit(x,y)
# make prediction
y_sgd=sgd_reg.predict(x)
y_sridge=ridge_reg.predict(x)
y_lasso=lasso_reg.predict(x)
y_ela=ela_reg.predict(x)
w_sgd=[sgd_reg.intercept_[0],sgd_reg.coef_[0]]
w_ridge=[ridge_reg.intercept_[0],ridge_reg.coef_[0]]
w_lasso=[lasso_reg.intercept_[0],lasso_reg.coef_[0]]
w_ela=[ela_reg.intercept_[0],ela_reg.coef_[0]]
print(w_sgd,w_ridge,w_lasso,w_ela)
fig,ax=plt.subplots(1,1)
ax.plot(x,y);ax.grid(True)
ax.plot(x,G.dot(w_sgd))
ax.plot(x,G.dot(w_ridge))
ax.plot(x,G.dot(w_lasso))
ax.plot(x,G.dot(w_ela))
ax.legend(['data','SGD','Ridge','Lasso','Elastic'])
# perform the regressions
plot_learning_curves(sgd_reg, x.ravel(), y.ravel(),"r-+","r")
plot_learning_curves(ridge_reg, x.ravel(), y.ravel(),"g-+","g")
plot_learning_curves(lasso_reg, x.ravel(), y.ravel(),"m-+","m")
plot_learning_curves(ela_reg, x.ravel(), y.ravel(),"y-+","y")
plt.ylim([0,6])
plt.xlim([0,30])
```
We see that there needs to be at least 10 samples in the training set for the models to generalize reasonably well. We also see that all of the regularization mechanisms yield seemingly similar behavior at the training. After a sufficient number of samples, validation loss goes below training loss.
**model complexity**
Now we will try and fit the step in the data.
```
x = np.asarray(date_year[3*365:4*365]).reshape(-1,1)
y = np.asarray(ue[3*365:4*365]).reshape(-1,1)
x = x-np.min(x)
# G = np.c_[np.ones((len(x),1)),x]
scale = (np.max(y)-np.min(y)) # minmax scaling
newy = y / scale
plt.plot(x,newy*scale);plt.grid(True)
```
The data looks complex, with the superposition of a linear trend and oscillatory signals. Let's fit a general polynomial form. We will start with a simple model.
```
from sklearn.preprocessing import PolynomialFeatures
#Let's start with a simple
poly_features = PolynomialFeatures(degree=2)
G = poly_features.fit_transform(x) # G now contains the original feature of X plus the power of the features.
ridge_reg = Ridge(alpha=0.1)
ridge_reg.fit(G,y)
y_ridge=ridge_reg.predict(G)
print(G.shape)
plt.plot(x,y);plt.grid(True)
plt.plot(x,y_ridge)
plot_learning_curves(ridge_reg, G.ravel(), y.ravel(),"b-+","b");plt.xlim([0,100])
# Let's make it complex
poly_features = PolynomialFeatures(degree=400)
G2 = poly_features.fit_transform(x) # G now contains the original feature of X plus the power of the features.
ridge_reg2 = Ridge(alpha=0.001)
ridge_reg2.fit(G2,y)
y_ridge2=ridge_reg2.predict(G2)
fix,ax=plt.subplots(1,2,figsize=(20,8))
ax[0].plot(x,y);ax[0].grid(True)
ax[0].plot(x,y_ridge,"m",linewidth=3)
ax[0].plot(x,y_ridge2,"y",linewidth=3)
# ax[0].set_ylim([-10,20])
ax[0].set_ylabel('Vertical displacement (mm)at AC29')
plot_learning_curves(ridge_reg, G.ravel(), y.ravel(),"m-+","m");#plt.xlim([0,200])
plot_learning_curves(ridge_reg2, G2.ravel(), y.ravel(),"y-+","y");#plt.xlim([0,200])
plt.ylim([2,4])
```
# 4) Early stopping
In gradient descent, learning of the algorithm means that we are "training" the algorithm iteratively. As we keep training the model.
Another strategy to regularize the learning is to stop training as soon as the validation error reaches a minimum. Now instead of looking at the errors as a function of training size, we look at them as a function of epoch.
```
from sklearn.base import clone
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
x = np.asarray(date_year[:]).reshape(-1,1)
x=x-np.min(x)
y = np.asarray(uv[:]).reshape(-1,1)
X_train, X_val, y_train, y_val = train_test_split(x, y, test_size=0.3,random_state=42)
# use the Pipeline function from sklearn to get prepare your data.
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=50)),
("std_scaler", StandardScaler()) ])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_poly = poly_scaler.fit_transform(x)
X_val_poly_scaled = poly_scaler.transform(X_val)
# set the gradient with a single iteration since we will iterate over epochs.
# warm_start=True says that you should keep the previous state of the model to retrain.
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
val_error=np.zeros(1000)
train_error=np.zeros(1000)
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train.ravel()) # continues where it left off
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
val_error[epoch] = mean_squared_error(y_val, y_val_predict)
train_error[epoch] = mean_squared_error(y_train, y_train_predict)
if val_error[epoch] < minimum_val_error: # you will stop and save the best model
minimum_val_error = val_error[epoch]
best_epoch = epoch
best_model = clone(sgd_reg)
best_y = sgd_reg.predict(X_poly)
fig,ax=plt.subplots(1,2,figsize=(16,6))
ax[0].plot(x,y);
ax[0].plot(x,best_y)
ax[1].plot(np.arange(1000),val_error)
ax[1].plot(np.arange(1000),train_error)
plt.legend(["validation error","training error"])
plt.xlim([0,100]);plt.ylim([0,30])
```
You may also consider the parameter ``early_stopping=True`` in SGD to automatically implement early stopping and deal with overfitting.
# 5) Training Classification algorithms
Last week, we explored the ***logistic regression***, a classification method to estimate the probability that an instance belongs to a particular class. Here we take example of a binary classificaiton. The Logistic regression estimates the probability that an instance belongs to the positive class. If the probably is ablove a threshold, then the instance is classified in the positive class. The probability is estimted using a **logistic sigmoid function**:
$\sigma(x) = \frac{1}{1+ \exp(-x)}$
Training a logistic regression is to tune the model such that the output score is low for a negative instance and high for a positive instance. The loss function associated with logistic regression is the $\log$ function due to its property that it is really high at low values of $x$ and really low at high values of $x$. The cost function over a batch of $m$ instances it the sum of the individual instance cost functions, which is called the ***Log Loss**:
$ \mathcal{L}(\mathbf{w}) = - \frac{1}{m} \sum_{i=1}^m \left[ y_i \log(\hat{p}_i(\mathbf{w})) + (1 - y_i) \log(1-\hat{p}_i(\mathbf{w}))\right] $,
where $m$ is the number of instances, $\hat{p}_i = \sigma(\mathbf{w}(x)) $ is the probability output by the model of the instence $x$, and $y_i$ is the class of the instance. The log loss is differentiable with respect to the model parameters, and one can use Gradient Descent to optimize the model parameters.
In Scikit-learn, ``LogisticRegression`` is equivalent to training an logistic regression using a log loss ``SGDClassifier(loss='log')``.
The K-class version of logistical regression is the ***softmax or multinomial regression***. The softmax regression model first computes scores $s_k$ for each class, which are computing using a simple linear regression prediction. The probabilities are calculated using the softmax function:
$\hat{p}_k = \sigma(s_k) = \frac{\exp(s_k)}{ \sum_{i=1}^K \exp(s_i)}$
An appropriate loss function to use is called ***Cross Entropy*** cost function:
$ \mathcal{L}(\mathbf{w}) = - \frac{1}{m} \sum_{i=1}^m \sum_{i=1}^K y_i \log(\hat{p}_i(\mathbf{w})) $.
The rest of the training requires similar tricks than the regression model training. The performance metrics are precision, recall, F1 scores etc etc as seen in previous notes.
# Checklist for training an ML model
1. Set the test set aside.
2. Initialize model parameters for optimizer (e.g. SGD)
3. Identify and define machine learning methods
4. Define the Loss Function
There are loss functions for classification (most of them use logs) and for regressions (they may use exponentials). Follow the documentation of your ML API: https://keras.io/api/losses/, https://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics, https://pytorch.org/docs/stable/nn.html#loss-functions
5. Define the optimization algorithm
The most popular optimizer algorithms compute the first derivative (gradient) of the loss functions. They include Gradient Descent, Momentum, Adagrad, RMSProp, Adam.
6. Model training
Prepare the folds for K-fold cross validation. Scale the data.
Define the model parameters in a dictionary. Define the number of epochs, learning rate, batch size.
For each fold:
Initialize the model parameters.
for each epoch (iteration), train the algorithm on a minibatch of training examples. Training consists in 1) passing the training data through our model to obtain a set of predictions, 2) calculating the loss, 3) computing the gradient (either known, or using backward passes in neural networks), and 4) updating the model parameters using an optimization algorithm (e.g. Stochastic Gradient Descent).
7. Fine tune the training
Compute learning rate as a function of training size to get a sense for the batch size desired to properly train.
Compute the validation and training error as a function of epochs. Find the minimum of the validation error and stop the training there.
| true |
code
| 0.534127 | null | null | null | null |
|
# Support Vector Machine
```
!pip install six
!pip install pandas
!pip install numpy
!pip install sklearn
!pip install matplotlib
!pip install imbalanced-learn
import pandas as pd
import numpy as np
import sklearn
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from imblearn.under_sampling import RandomUnderSampler
train_set = pd.read_csv('train_set_with_features.csv')
```
## Data Prep
```
# Random undersampler to reduce the number of majority class instances to match number of minority class instance.
undersample = RandomUnderSampler(sampling_strategy='majority')
# Extract only engineered features into x and y
x = train_set.drop(['id', 'qid1', 'qid2', 'question1', 'question2', 'is_duplicate', 'Unnamed: 0'], axis=1)
y = train_set[['is_duplicate']]
# Because gridSearch parameter tuning is slow, only use 50% of model data for training the gridSearch model while searching for best parameters for final SVM model.
x_grid_train, x_grid_test, y_grid_train, y_grid_test = train_test_split(x, y, test_size = 0.5, random_state = 42)
# Split 80% of data for the final model training and 20% for testing.
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state = 42)
# Normalize then undersample data used by final model
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_test = scaler.transform(x_test)
x_train, y_train = undersample.fit_resample(x_train, y_train)
# Normalize then undersample data used by gridSearch model
x_grid_train = scaler.fit_transform(x_grid_train)
x_grid_test = scaler.transform(x_grid_test)
x_grid_train, y_grid_train = undersample.fit_resample(x_grid_train, y_grid_train)
# gridSearch requires labels to be of a particular shape.
y_grid_train = y_grid_train.to_numpy().reshape(-1)
y_grid_test = y_grid_test.to_numpy().reshape(-1)
```
## Parameter tuning
```
# Execute gridSearch to try these parameters for SVM.
param_grid = {'C': [0.1,1, 10, 100], 'gamma': [1,0.1,0.01,0.001],'kernel': ['rbf', 'sigmoid']}
grid = GridSearchCV(SVC(),param_grid,refit=True,verbose=2, n_jobs=3)
grid.fit(x_grid_train ,y_grid_train)
# Best parameters for SVM, but best kernel is not shown
print(grid.best_estimator_)
# Print out the performance of the SVM model trained by gridSearch using the best parameters.
grid_predictions = grid.predict(x_test)
print(confusion_matrix(y_test,grid_predictions))
print(classification_report(y_test,grid_predictions))
```
## Fitting model based on tuned parameters
```
# Use the parameters found by gridSearch to train the final SVM model with more data (80% instead of 50%).
# After trying multiple kernel types since gridSearch did not reveal the best kernel type, 'rbf' is the best.
# Kernel = 'rbf'
SVM = SVC(C=10, kernel='rbf', degree=3, gamma=0.01)
clf = SVM.fit(x_train,y_train)
predictions_SVM = SVM.predict(x_test)
# Print out the performance of SVM that is trained using the best parameters and
print(classification_report(y_test,predictions_SVM))
```
### Process:
1. Normalize feature engineered training data
2. Parameter tuning using GridSearchCV which fits the SVM model using several values of each parameter and evaluating it with a 5-fold cross validation. (10000 rows)
3. Resulting parameters are C = 100, gamma = 0.01.
4. Upon testing, best kernel for those parameters is rbf.
Results suggest that the model is better used to predict that a question is NOT a duplicate.
### Advantages:
1. By using a kernel, there can be separation of the classes even if the data provided is not linearly separable. (https://core.ac.uk/reader/6302770)
2. SVM provides good out of sample generalization as it makes use of regularization which helps to prevent overfitting on the dataset.
3. SVM can classify data points faster than some other models because it only relies on the support vectors to decide the decision boundary and not all of the data points used to train the model (like kNN).
### Disadvantages:
1. Does not perform too well with skewed dataset, as in our case. There would be high variance of the decision boundary as the under represented class can skew the decision boundary by a lot.
https://www.quora.com/Why-does-SVM-not-perform-well-for-imbalanced-data
2. Takes a long time to train the model if the data set is large. "As you mention, storing the kernel matrix requires memory that scales quadratically with the number of data points. Training time for traditional SVM algorithms also scales superlinearly with the number of data points. So, these algorithms aren't feasible for large data sets."
https://stats.stackexchange.com/questions/314329/can-support-vector-machine-be-used-in-large-data
| true |
code
| 0.642517 | null | null | null | null |
|
# Problem Statement:
Given profiles representing fictional customers from an e-commerce company. The profiles contain information about the customer, their orders, their transactions ,what payment methods they used and whether the customer is fraudulent or not. We need to predict the given customer is fraudulent or not based on the above factors
##The data given below represents fictional customers from an e-commerce website
The data contain information about the customerEmail,orders,transaction they have made,what payment method they have used,through which card the payment has been done and whether the customer is fraudulent or not
1)The first thing is loading the dataset
```
import pandas as pd
import numpy as np
data1 = pd.read_csv('Customer_DF (1).csv')
data2 = pd.read_csv('cust_transaction_details (1).csv')
#this code is just to make the copy of the dataset
data_copy_1 = pd.read_csv('Customer_DF (1).csv')
data_copy_2 = pd.read_csv('cust_transaction_details (1).csv')
data1.head()
data2.head()
```
Checking whether if they are some null values
```
data1.isnull().sum()
data2.isnull().sum()
```
Printing the columns of both the table
```
data1.columns
data2.columns
```
Shape of the datasets
```
data1.shape
data2.shape
print('total customers records',data1.shape[0], 'and total unique customers',len(data1.customerEmail.unique()))
```
Duplicates customersEmail ID's are....
```
data1[data1['customerEmail'].duplicated()]
```
We see that all the records that are duplicated are fraudulent
So now our job is to remove all the duplicate entries from the dataset
```
data2=data2.drop(["transactionId","transactionId","paymentMethodId","orderId","Unnamed: 0"],axis=1)
#filtering the email if their is "." present in them
data2["customerEmail"]=data2.apply(lambda x:x.customerEmail if("." in x.customerEmail) else "f",axis=1)
#setting customerEmail as the index of the dataframe
data2 = data2.set_index("customerEmail")
#dropping the email which does not have '.' in them
data2=data2.drop("f",axis=0)
#taking out the mean of the customerEmail to avoid duplicates
n1=data2.groupby("customerEmail")["paymentMethodRegistrationFailure"].mean().astype(int)
n2=data2.groupby("customerEmail")["transactionAmount"].mean().astype(int)
n3=data2.groupby("customerEmail")["transactionFailed"].mean().astype(int)
data2=data2.drop(["transactionFailed","transactionAmount","paymentMethodRegistrationFailure"],axis=1)
data2=data2.drop(["paymentMethodProvider"],axis=1)
#creating dummy variables for the dataset
data2= pd.get_dummies(data2)
data2
m1=data2.groupby("customerEmail")["orderState_failed"].mean().astype(int)
m2=data2.groupby("customerEmail")["orderState_fulfilled"].mean().astype(int)
m3=data2.groupby("customerEmail")["orderState_pending"].mean().astype(int)
l1=data2.groupby("customerEmail")["paymentMethodType_card"].mean().astype(int)
l2=data2.groupby("customerEmail")["paymentMethodType_paypal"].mean().astype(int)
l3=data2.groupby("customerEmail")["paymentMethodType_apple pay"].mean().astype(int)
l4=data2.groupby("customerEmail")["paymentMethodType_bitcoin"].mean().astype(int)
#concatenating the variables after removing duplicates
nresult = pd.concat([m1,m2,m3,l1,l2,l3,l4,n1,n2,n3], axis=1, join='inner')
data1=data1.drop(["customerPhone","customerDevice","customerIPAddress","customerBillingAddress","Unnamed: 0"],axis=1)
#converting the target variable from bool to int for the creation of dummy variable
data1['Fraud'] = data1['Fraud'].astype(int)
#merging both the datasets into single object called result
result = pd.merge(data1,nresult, on='customerEmail')
result.isnull().sum()
#unique email id's in result dataset
len(result["customerEmail"].unique())
#dropping the email id as it is of no use now
result=result.drop(["customerEmail"],axis=1)
result.columns
#creating the dummies for the merged dataset
result2= pd.get_dummies(result)
result2
```
Now exploring the data and analysing it
```
#maximum number of transaction done by the customer
data1[data1['No_Transactions']==data1['No_Transactions'].max()]
#maximum number of orders done by the customer
data1[data1['No_Orders']==data1['No_Orders'].max()]
#maximum number of payments done by the customer
data1[data1['No_Payments']==data1['No_Payments'].max()]
data_copy_2['paymentMethodRegistrationFailure'].value_counts()
import seaborn as sns
import matplotlib.pyplot as plt
sns.countplot(x='paymentMethodRegistrationFailure',data=data_copy_2,palette='hls')
plt.show()
```
Count of Payment method Registration Failure occ
INFERENCE --> There is a very less probability of payment to fail
```
data_copy_2['paymentMethodType'].value_counts()
sns.countplot(x='paymentMethodType',data=data_copy_2,palette='hls')
plt.show()
```
PREFERRED PAYMENT METHOD
INFERENCE --> People prefer Card over other payment methods types
```
data_copy_2['paymentMethodProvider'].value_counts()
sns.countplot(y="paymentMethodProvider",data=data_copy_2)
```
Payment Method Provider
INFERENCE --> JCB 16 DIGIT is widely used followed by VISA 16 DIGIT and rest
```
data_copy_2['transactionFailed'].value_counts()
sns.countplot(x='transactionFailed',data=data_copy_2,orient='vertical',palette='hls')
plt.show()
```
transaction failed
INFERENCE --> after the payment is completed , the probability of transaction to fail is low
```
data_copy_2['orderState'].value_counts()
sns.countplot(x='orderState',data=data_copy_2,orient='vertical',palette='hls')
plt.show()
```
Order State
INFERENCE --> it is found out that the most of the orders were fullfilled
```
result['Fraud'].value_counts()
sns.countplot(x='Fraud',data=data1,orient='vertical',palette='hls')
plt.show()
```
FRAUD
INFERENCE --> it is seen that the cases aof fraud is neaarly half of those that are not fraud
```
result
#number of transaction that went fraud and not fraud
plt.scatter(result['No_Transactions'],result['Fraud'],color='#2ca02c')
#number of orders that went fraud and not fraud
plt.scatter(result['No_Orders'],result['Fraud'],color='#2ca02c')
#number of payments that went fraud and not fraud
plt.scatter(result['No_Payments'],result['Fraud'],color='#2ca02c')
sns.catplot(x="No_Payments",y="No_Transactions",data=result,kind="box")
```
INFERENCE --> although there is no particular trend , but it seems that as the no.of payments increase the no,of transactions tend to decrease
```
sns.barplot(y="No_Payments",x="No_Orders",data=result)
```
INFERENCE --> as the no,of orders increase the no.of payments tend to increase
```
data1[data1['No_Payments']==0]
#No. number of fullfilled orders
len(result[result['orderState_fulfilled'] == 1])
#No. number of pending orders
len(result[result['orderState_pending'] == 1])
#No. number of failed orders
len(result[result['orderState_failed'] == 1])
%matplotlib inline
pd.crosstab(result['paymentMethodType_card'],result['Fraud']).plot(kind='bar')
plt.title('paymentMethodProvider for card vs fraud')
plt.xlabel('paymentMethodProvider')
plt.ylabel('Fraud')
```
INFERENCE --> when the payment method is not card then it is seen that the not fraud and fraud cases are nearly same and when card is used the non fraud case is higher than the fraud case
```
%matplotlib inline
pd.crosstab(result['paymentMethodType_paypal'],result['Fraud']).plot(kind='bar')
plt.title('paymentMethodProvider for paypal vs fraud')
plt.xlabel('paymentMethodProvider')
plt.ylabel('Fraud')
```
INFERENCE --> when the payment method is not paypal then the cases of not fraud is higher than cases of fraud and when paypal is used there is no case of fraud at all
```
%matplotlib inline
pd.crosstab(result['paymentMethodType_bitcoin'],result['Fraud']).plot(kind='bar')
plt.title('paymentMethodProvider for bitcoin vs fraud')
plt.xlabel('paymentMethodProvider')
plt.ylabel('Fraud')
```
INFERENCE --> when the payment type is not bitcoin it is found that the cases of non fraud is higher than the cases of fraud and when bitcoin is used it is found that fraud and non fraud cases is almost same
Till Now we have done some EDA for our datasets
Now we have to construct our model to predict if the customer if fraudulent or not
```
result.describe(include='all')
#creating dependent and independent variables
features = result2.drop('Fraud',axis=1) #->independent variables
labels = result2['Fraud'] #->dependent variable
#splitting the data into training and testing
#and performing Logistic Regression and fitting the training dataset in the Logistic model
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(features,labels,test_size=0.20,random_state=0)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train,y_train)
#predicating the output from the test data
ypred = lr.predict(X_test)
ypred
from sklearn.metrics import confusion_matrix
#creating a confusion matrix to check if the variable is predicated correctly or not
confusion_matrix(y_test,ypred)
#normalizing the data and plotting the confusion matrix
from sklearn.metrics import confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Oranges):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.figure(figsize = (10, 10))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title, size = 24)
plt.colorbar(aspect=4)
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45, size = 14)
plt.yticks(tick_marks, classes, size = 14)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
# Labeling the plot
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt), fontsize = 20,
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.grid(None)
plt.tight_layout()
plt.ylabel('True label', size = 18)
plt.xlabel('Predicted label', size = 18)
cm = confusion_matrix(y_test, ypred)
plot_confusion_matrix(cm, classes = ['fraud', 'not fraud'],
title = 'FRAUD DETECTION CONFUSION MATRIX')
#finding out the accuracy_score for the model
#the below accuracy for the model is 68%,hyperparameters are yet to be applied
from sklearn.metrics import accuracy_score
print("Logistic regression")
accuracy_score(y_test,ypred) * 100
from sklearn.metrics import classification_report
print(classification_report(y_test,ypred))
#basically in the below code we are performing pipelining in the model itself will Normalize the data and perform PCA
from sklearn import linear_model, decomposition, datasets
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV, cross_val_score
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
pca = decomposition.PCA(n_components=2)
logistic = linear_model.LogisticRegression()
pipe = Pipeline(steps=[('sc', sc),
('pca', pca),
('logistic', logistic)])
n_components = list(range(1,features.shape[1]+1,1))
# Create a list of values of the regularization parameter
C = np.logspace(-4, 4, 15)
# Create a list of options for the regularization penalty
penalty = ['l1', 'l2']
# Create a dictionary of all the parameter options
# accessing the parameters of steps of a pipeline by using '__’
parameters = dict(pca__n_components=n_components,
logistic__C=C,
logistic__penalty=penalty)
clf = GridSearchCV(pipe, parameters,verbose = True,n_jobs=-1,scoring='accuracy')
# Fit the grid search
clf.fit(features, labels)
print('Best Penalty:', clf.best_estimator_.get_params()['logistic__penalty'])
print('Best C:', clf.best_estimator_.get_params()['logistic__C'])
print('Best Number Of Components:', clf.best_estimator_.get_params()['pca__n_components'])
#this will return the best parameters that are required for our model
clf.best_params_
#this will return the mean accuracy of the model
clf.best_score_
clf.best_estimator_
clf.best_estimator_.get_params()['logistic']
#here cross_val_score will split the whole data into training and testing and perforn cross validations
cross_val = cross_val_score(clf,features,labels,cv=3,scoring='accuracy',n_jobs=-1)
#this will return the accuracy of each dataset that was splitted on the basics of 'cv' value which is 3
cross_val * 100
print('the mean accuracy of our model is',(cross_val * 100).mean())
print('the maximum accuracy of our model is',max(cross_val * 100))
ypred_new = clf.predict(X_test)
ypred_new
accuracy_score(y_test,ypred_new) * 100
```
# INFERENCES
* There is a very less probability of payment to fail
* People prefer Card over other payment methods types
* JCB 16 DIGIT is widely used followed by VISA 16 DIGIT and rest
* After the payment is completed , the probability of transaction to fail is low
* It is found out that the most of the orders were fullfilled
* It is seen that the cases of fraud is nearly half of those that are not fraud
* It seems that as the no.of payments increase the no,of transactions tend to decrease
* As the no.of orders increase the no.of payments tend to increase
* When the payment method is not card then it is seen that the not fraud and fraud cases are nearly same and when card is used the non fraud case is higher than the fraud case
* When the payment method is not paypal then the cases of not fraud is higher than cases of fraud and when paypal is used there is no case of fraud at all
* When the payment type is not bitcoin it is found that the cases of non fraud is higher than the cases of fraud and when bitcoin is used it is found that fraud and non fraud cases is almost same
# Model_Selection
* Initially , we decided to use Logistic Regression as it seems to appear as a binary problem and achieved an accuracy of 75%
*
* Implemented a pipeline such that it will Normalize the data and perform PCA
*
* Applied CrossValidation and fitting the model via GridSearch
*
* The mean accuracy of our model is 77.13536848596978 %
The highest accuracy of our model is 82.97872340425532 %
The testing accuracy of our model is 78.57142857142857 %
```
#applying ANN here
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.fit_transform(X_test)
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import GridSearchCV
from keras.models import Sequential
from keras.layers import Dense, Activation, Embedding, Flatten, LeakyReLU, BatchNormalization, Dropout
from keras.activations import relu, sigmoid
def create_model(layers,activation):
model = Sequential()
for i,node in enumerate(layers):
if i == 0:
model.add(Dense(node,input_dim=X_train.shape[1]))
model.add(Activation(activation))
model.add(Dropout(0.3))
else:
model.add(Dense(node))
model.add(Activation(activation))
model.add(Dropout(0.3))
model.add(Dense(units=1,activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy',metrics=['accuracy'])
return model
model = KerasClassifier(build_fn=create_model,verbose=0)
layers = [[20,15],[40,20,15],[45,25,20,15]]
activation = ['sigmoid','relu']
param_grid = dict(layers=layers, activation=activation, batch_size = [64,128,150,175], epochs=[35])
grid = GridSearchCV(estimator=model, param_grid=param_grid,cv=3)
grid_result = grid.fit(X_train, y_train)
ypred_new = grid.predict(X_test)
ypred_new
accuracy_score(ypred_new,y_test)
grid_result.best_params_
grid_result.best_score_
```
| true |
code
| 0.46794 | null | null | null | null |
|
$\newcommand{\mb}[1]{\mathbf{ #1 }}$
$\newcommand{\bb}[1]{\mathbb{ #1 }}$
$\newcommand{\bs}[1]{\boldsymbol{ #1 }}$
$\newcommand{\norm}[1]{\left\Vert #1 \right\Vert}$
$\newcommand{\der}[2]{\frac{ \mathrm{d} #1 }{ \mathrm{d} #2 }}$
$\newcommand{\derp}[2]{\frac{ \partial #1 }{ \partial #2 }}$
$\newcommand{\R}{\bb{R}}$
# Learning Dynamics
```
from matplotlib.pyplot import show, subplots
```
## Robotic Systems
Let $\mathcal{Q} \subseteq \R^n$ be a configuration space. Consider a robotic system governed by:
\begin{equation}
\mb{D}(\mb{q})\ddot{\mb{q}} + \mb{C}(\mb{q}, \dot{\mb{q}})\dot{\mb{q}} + \mb{G}(\mb{q}) = \mb{B}\mb{u},
\end{equation}
for generalized coordinates $\mb{q} \in \mathcal{Q}$, coordinate rates $\dot{\mb{q}} \in \R^n$, actions $\mb{u} \in \R^m$, inertia matrix function $\mb{D}: \mathcal{Q} \to \bb{S}^n_{++}$ (the space of $n \times n$ positive definite matrices), Coriolis terms $\mb{C}: \mathcal{Q} \times \R^n \to \R^{n \times n}$, potential terms $\mb{G}: \mathcal{Q} \to \R^n$, and static actuation matrix $\mb{B} \in \R^{n \times m}$. Assume $m \leq n$ and $\mb{B}$ is full rank.
### Inverted Pendulum
```
from numpy import array, identity, linspace
from core.controllers import FBLinController, LQRController
from core.systems import InvertedPendulum
ip = InvertedPendulum(m=0.25, l=0.5)
Q_ip = identity(2)
R_ip = identity(1)
lqr_ip = LQRController.build(ip, Q_ip, R_ip)
fb_lin_ip = FBLinController(ip, lqr_ip)
x_0_ip = array([1, 0])
ts_ip = linspace(0, 10, 1000 + 1)
xs_ip, _ = ip.simulate(x_0_ip, fb_lin_ip, ts_ip)
fig_ip, ax_ip = subplots(figsize=(6, 4))
ax_ip.plot(ts_ip, xs_ip[:, 0], linewidth=3, label='Oracle')
ax_ip.grid()
ax_ip.legend(fontsize=16)
ax_ip.set_title('Inverted Pendulum', fontsize=16)
ax_ip.set_xlabel('$t$ (sec)', fontsize=16)
ax_ip.set_ylabel('$\\theta$ (rad)', fontsize=16)
show()
```
### Double Inverted Pendulum
```
from core.systems import DoubleInvertedPendulum
dip = DoubleInvertedPendulum(m_1=0.25, m_2=0.25, l_1=0.5, l_2=0.5)
Q_dip = identity(4)
R_dip = identity(2)
lqr_dip = LQRController.build(dip, Q_dip, R_dip)
fb_lin_dip = FBLinController(dip, lqr_dip)
x_0_dip = array([1, 0, 0, 0])
ts_dip = linspace(0, 10, 1000 + 1)
xs_dip, _ = dip.simulate(x_0_dip, fb_lin_dip, ts_dip)
fig_dip, (ax_dip_1, ax_dip_2) = subplots(2, figsize=(6, 8))
ax_dip_1.set_title('Double Inverted Pendulum', fontsize=16)
ax_dip_1.plot(ts_dip, xs_dip[:, 0], linewidth=3, label='Oracle')
ax_dip_1.grid()
ax_dip_1.legend(fontsize=16)
ax_dip_1.set_xlabel('$t$ (sec)', fontsize=16)
ax_dip_1.set_ylabel('$\\theta_1$ (rad)', fontsize=16)
ax_dip_2.plot(ts_dip, xs_dip[:, 1], linewidth=3, label='Oracle')
ax_dip_2.grid()
ax_dip_2.legend(fontsize=16)
ax_dip_2.set_xlabel('$t$ (sec)', fontsize=16)
ax_dip_2.set_ylabel('$\\theta_2$ (rad)', fontsize=16)
show()
```
## Uncertain Robotic Systems
Suppose $\mb{D}$, $\mb{C}$, $\mb{G}$, and $\mb{B}$ are unknown, and instead we have access to corresponding estimates $\hat{\mb{D}}$, $\hat{\mb{C}}$, $\hat{\mb{G}}$, and $\hat{\mb{B}}$ satisfying:
\begin{equation}
\hat{\mb{D}}(\mb{q})\ddot{\mb{q}} + \hat{\mb{C}}(\mb{q}, \dot{\mb{q}})\dot{\mb{q}} + \hat{\mb{G}}(\mb{q}) = \hat{\mb{B}}\mb{u}.
\end{equation}
Assume that $\hat{\mb{B}}$ is also full rank.
The system dynamics can be in terms of the estimated terms as:
\begin{equation}
\der{}{t} \begin{bmatrix} \mb{q} \\ \dot{\mb{q}} \end{bmatrix} = \begin{bmatrix} \dot{\mb{q}} \\ -\hat{\mb{D}}(\mb{q})^{-1}(\hat{\mb{C}}(\mb{q}, \dot{\mb{q}})\dot{\mb{q}} + \hat{\mb{G}}(\mb{q})) \end{bmatrix} + \begin{bmatrix} \mb{0}_{n \times m} \\ \hat{\mb{D}}(\mb{q})^{-1}\hat{\mb{B}} \end{bmatrix} \mb{u} + \begin{bmatrix} \mb{0}_n \\ \hat{\mb{D}}(\mb{q})^{-1}(\hat{\mb{C}}(\mb{q}, \dot{\mb{q}})\dot{\mb{q}} + \hat{\mb{G}}(\mb{q}))-\mb{D}(\mb{q})^{-1}(\mb{C}(\mb{q}, \dot{\mb{q}})\dot{\mb{q}} + \mb{G}(\mb{q})) \end{bmatrix} + \begin{bmatrix} \mb{0}_{n \times m} \\ \mb{D}(\mb{q})^{-1}\mb{B} - \hat{\mb{D}}(\mb{q})^{-1}\hat{\mb{B}} \end{bmatrix} \mb{u}
\end{equation}
### Inverted Pendulum
```
ip_est = InvertedPendulum(m=0.24, l=0.48)
lqr_ip_est = LQRController.build(ip_est, Q_ip, R_ip)
fb_lin_ip_est = FBLinController(ip_est, lqr_ip_est)
xs_ip, us_ip = ip.simulate(x_0_ip, fb_lin_ip_est, ts_ip)
ax_ip.plot(ts_ip, xs_ip[:, 0], linewidth=3, label='Estimated')
ax_ip.legend(fontsize=16)
fig_ip
```
### Double Inverted Pendulum
```
dip_est = DoubleInvertedPendulum(m_1=0.24, m_2=0.24, l_1=0.48, l_2=0.48)
lqr_dip_est = LQRController.build(dip_est, Q_dip, R_dip)
fb_lin_dip_est = FBLinController(dip_est, lqr_dip_est)
xs_dip, us_dip = dip.simulate(x_0_dip, fb_lin_dip_est, ts_dip)
ax_dip_1.plot(ts_dip, xs_dip[:, 0], linewidth=3, label='Esimated')
ax_dip_1.legend(fontsize=16)
ax_dip_2.plot(ts_dip, xs_dip[:, 1], linewidth=3, label='Esimated')
ax_dip_2.legend(fontsize=16)
fig_dip
```
## Learning Dynamics
```
from tensorflow.logging import ERROR, set_verbosity
set_verbosity(ERROR)
```
### Inverted Pendulum
```
from core.dynamics import LearnedFBLinDynamics
from core.learning.keras import KerasResidualAffineModel
d_drift_in_ip = 3
d_act_in_ip = 3
d_hidden_ip = 20
d_out_ip = 1
res_model_ip = KerasResidualAffineModel(d_drift_in_ip, d_act_in_ip, d_hidden_ip, 1, d_out_ip)
ip_learned = LearnedFBLinDynamics(ip_est, res_model_ip)
data = ip_learned.process_episode(xs_ip, us_ip, ts_ip)
ip_learned.fit(data, num_epochs=10, validation_split=0.1)
x_dots = array([ip.eval_dot(x, u, t) for x, u, t in zip(xs_ip, us_ip, ts_ip)])
_, (ax_ip_1, ax_ip_2) = subplots(2, figsize=(6, 8))
ax_ip_1.set_title('Inverted Pendulum', fontsize=16)
ax_ip_1.plot(ts_ip[:-1], x_dots[:, 0], linewidth=3, label='True')
ax_ip_1.grid()
ax_ip_1.set_xlabel('$t$ (sec)', fontsize=16)
ax_ip_1.set_ylabel('$\\dot{\\theta}$ (rad / sec)', fontsize=16)
ax_ip_2.plot(ts_ip[:-1], x_dots[:, 1], linewidth=3, label='True')
ax_ip_2.grid()
ax_ip_2.set_xlabel('$t$ (sec)', fontsize=16)
ax_ip_2.set_ylabel('$\\ddot{\\theta}$ (rad / sec$^2$)', fontsize=16)
x_dots = array([ip_learned.eval_dot(x, u, t) for x, u, t in zip(xs_ip, us_ip, ts_ip)])
ax_ip_1.plot(ts_ip[:-1], x_dots[:, 0], linewidth=3, label='Learned')
ax_ip_1.legend(fontsize=16)
ax_ip_2.plot(ts_ip[:-1], x_dots[:, 1], linewidth=3, label='Learned')
ax_ip_2.legend(fontsize=16)
show()
```
### Double Inverted Pendulum
```
d_drift_in_dip = 5
d_act_in_dip = 5
d_hidden_dip = 40
d_out_dip = 2
res_model_dip = KerasResidualAffineModel(d_drift_in_dip, d_act_in_dip, d_hidden_dip, 2, d_out_dip)
dip_learned = LearnedFBLinDynamics(dip_est, res_model_dip)
data = dip_learned.process_episode(xs_dip, us_dip, ts_dip)
dip_learned.fit(data, num_epochs=10, validation_split=0.1)
x_dots = array([dip.eval_dot(x, u, t) for x, u, t in zip(xs_dip, us_dip, ts_dip)])
_, axs_dip = subplots(4, figsize=(6, 16))
axs_dip[0].set_title('Double Inverted Pendulum', fontsize=16)
ylabels = ['$\\dot{\\theta}_1$ (rad / sec)', '$\\dot{\\theta}_2$ (rad / sec)', '$\\ddot{\\theta}_1$ (rad / sec$^2$)', '$\\ddot{\\theta}_2$ (rad / sec$^2$)']
for ax, data, ylabel in zip(axs_dip, x_dots.T, ylabels):
ax.plot(ts_dip[:-1], data, linewidth=3, label='True')
ax.grid()
ax.set_xlabel('$t$ (sec)', fontsize=16)
ax.set_ylabel(ylabel, fontsize=16)
x_dots = array([dip_learned.eval_dot(x, u, t) for x, u, t in zip(xs_dip, us_dip, ts_dip)])
for ax, data in zip(axs_dip, x_dots.T):
ax.plot(ts_dip[:-1], data, linewidth=3, label='Learned')
ax.legend(fontsize=16)
show()
```
## Overfitting
### Inverted Pendulum
```
lqr_learned_ip = LQRController.build(ip_learned, Q_ip, R_ip)
fb_lin_learned_ip = FBLinController(ip_learned, lqr_learned_ip)
xs, _ = ip.simulate(x_0_ip, fb_lin_learned_ip, ts_ip)
_, ax = subplots(figsize=(6, 4))
ax.plot(ts_ip, xs[:, 0], linewidth=3)
ax.grid()
ax.set_title('Inverted Pendulum', fontsize=16)
ax.set_xlabel('$t$ (sec)', fontsize=16)
ax.set_ylabel('$\\theta$ (rad)', fontsize=16)
show()
```
### Double Inverted Pendulum
```
lqr_learned_dip = LQRController.build(dip_learned, Q_dip, R_dip)
fb_lin_learned_dip = FBLinController(dip_learned, lqr_learned_dip)
xs, _ = dip.simulate(x_0_dip, fb_lin_learned_dip, ts_dip)
_, (ax_1, ax_2) = subplots(2, figsize=(6, 8))
ax_1.set_title('Double Inverted Pendulum', fontsize=16)
ax_1.plot(ts_dip, xs[:, 0], linewidth=3)
ax_1.grid()
ax_1.set_xlabel('$t$ (sec)', fontsize=16)
ax_1.set_ylabel('$\\theta_1$ (rad)', fontsize=16)
ax_2.plot(ts_dip, xs[:, 1], linewidth=3)
ax_2.grid()
ax_2.set_xlabel('$t$ (sec)', fontsize=16)
ax_2.set_ylabel('$\\theta_2$ (rad)', fontsize=16)
show()
```
| true |
code
| 0.642629 | null | null | null | null |
|
# 量子神经网络在自然语言处理中的应用
[](https://mindspore.cn/mindquantum/api/zh-CN/master/index.html) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/zh_cn/mindspore_qnn_for_nlp.ipynb) [](https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/notebook/master/mindquantum/zh_cn/mindspore_qnn_for_nlp.py) [](https://gitee.com/mindspore/docs/blob/master/docs/mindquantum/docs/source_zh_cn/qnn_for_nlp.ipynb)
## 概述
在自然语言处理过程中,词嵌入(Word embedding)是其中的重要步骤,它是一个将高维度空间的词向量嵌入到一个维数更低的连续向量空间的过程。当给予神经网络的语料信息不断增加时,网络的训练过程将越来越困难。利用量子力学的态叠加和纠缠等特性,我们可以利用量子神经网络来处理这些经典语料信息,加入其训练过程,并提高收敛精度。下面,我们将简单地搭建一个量子经典混合神经网络来完成一个词嵌入任务。
## 环境准备
导入本教程所依赖模块
```
import numpy as np
import time
from mindquantum.core import QubitOperator
import mindspore.ops as ops
import mindspore.dataset as ds
from mindspore import nn
from mindspore.train.callback import LossMonitor
from mindspore import Model
from mindquantum.framework import MQLayer
from mindquantum import Hamiltonian, Circuit, RX, RY, X, H, UN
```
本教程实现的是一个[CBOW模型](https://blog.csdn.net/u010665216/article/details/78724856),即利用某个词所处的环境来预测该词。例如对于“I love natural language processing”这句话,我们可以将其切分为5个词,\["I", "love", "natural", "language", "processing”\],在所选窗口为2时,我们要处理的问题是利用\["I", "love", "language", "processing"\]来预测出目标词汇"natural"。这里我们以窗口为2为例,搭建如下的量子神经网络,来完成词嵌入任务。

这里,编码线路会将"I"、"love"、"language"和"processing"的编码信息编码到量子线路中,待训练的量子线路由四个Ansatz线路构成,最后我们在量子线路末端对量子比特做$\text{Z}$基矢上的测量,具体所需测量的比特的个数由所需嵌入空间的维数确定。
## 数据预处理
我们对所需要处理的语句进行处理,生成关于该句子的词典,并根据窗口大小来生成样本点。
```
def GenerateWordDictAndSample(corpus, window=2):
all_words = corpus.split()
word_set = list(set(all_words))
word_set.sort()
word_dict = {w: i for i, w in enumerate(word_set)}
sampling = []
for index, _ in enumerate(all_words[window:-window]):
around = []
for i in range(index, index + 2*window + 1):
if i != index + window:
around.append(all_words[i])
sampling.append([around, all_words[index + window]])
return word_dict, sampling
word_dict, sample = GenerateWordDictAndSample("I love natural language processing")
print(word_dict)
print('word dict size: ', len(word_dict))
print('samples: ', sample)
print('number of samples: ', len(sample))
```
根据如上信息,我们得到该句子的词典大小为5,能够产生一个样本点。
## 编码线路
为了简单起见,我们使用的编码线路由$\text{RX}$旋转门构成,结构如下。

我们对每个量子门都作用一个$\text{RX}$旋转门。
```
def GenerateEncoderCircuit(n_qubits, prefix=''):
if prefix and prefix[-1] != '_':
prefix += '_'
circ = Circuit()
for i in range(n_qubits):
circ += RX(prefix + str(i)).on(i)
return circ
GenerateEncoderCircuit(3, prefix='e')
```
我们通常用$\left|0\right>$和$\left|1\right>$来标记二能级量子比特的两个状态,由态叠加原理,量子比特还可以处于这两个状态的叠加态:
$$\left|\psi\right>=\alpha\left|0\right>+\beta\left|1\right>$$
对于$n$比特的量子态,其将处于$2^n$维的希尔伯特空间中。对于上面由5个词构成的词典,我们只需要$\lceil \log_2 5 \rceil=3$个量子比特即可完成编码,这也体现出量子计算的优越性。
例如对于上面词典中的"love",其对应的标签为2,2的二进制表示为`010`,我们只需将编码线路中的`e_0`、`e_1`和`e_2`分别设为$0$、$\pi$和$0$即可。下面来验证一下。
```
from mindquantum.simulator import Simulator
from mindspore import context
from mindspore import Tensor
n_qubits = 3 # number of qubits of this quantum circuit
label = 2 # label need to encode
label_bin = bin(label)[-1: 1: -1].ljust(n_qubits, '0') # binary form of label
label_array = np.array([int(i)*np.pi for i in label_bin]).astype(np.float32) # parameter value of encoder
encoder = GenerateEncoderCircuit(n_qubits, prefix='e') # encoder circuit
encoder_params_names = encoder.params_name # parameter names of encoder
print("Label is: ", label)
print("Binary label is: ", label_bin)
print("Parameters of encoder is: \n", np.round(label_array, 5))
print("Encoder circuit is: \n", encoder)
print("Encoder parameter names are: \n", encoder_params_names)
# quantum state evolution operator
state = encoder.get_qs(pr=dict(zip(encoder_params_names, label_array)))
amp = np.round(np.abs(state)**2, 3)
print("Amplitude of quantum state is: \n", amp)
print("Label in quantum state is: ", np.argmax(amp))
```
通过上面的验证,我们发现,对于标签为2的数据,最后得到量子态的振幅最大的位置也是2,因此得到的量子态正是对输入标签的编码。我们将对数据编码生成参数数值的过程总结成如下函数。
```
def GenerateTrainData(sample, word_dict):
n_qubits = np.int(np.ceil(np.log2(1 + max(word_dict.values()))))
data_x = []
data_y = []
for around, center in sample:
data_x.append([])
for word in around:
label = word_dict[word]
label_bin = bin(label)[-1: 1: -1].ljust(n_qubits, '0')
label_array = [int(i)*np.pi for i in label_bin]
data_x[-1].extend(label_array)
data_y.append(word_dict[center])
return np.array(data_x).astype(np.float32), np.array(data_y).astype(np.int32)
GenerateTrainData(sample, word_dict)
```
根据上面的结果,我们将4个输入的词编码的信息合并为一个更长向量,便于后续神经网络调用。
## Ansatz线路
Ansatz线路的选择多种多样,我们选择如下的量子线路作为Ansatz线路,它的一个单元由一层$\text{RY}$门和一层$\text{CNOT}$门构成,对此单元重复$p$次构成整个Ansatz线路。

定义如下函数生成Ansatz线路。
```
def GenerateAnsatzCircuit(n_qubits, layers, prefix=''):
if prefix and prefix[-1] != '_':
prefix += '_'
circ = Circuit()
for l in range(layers):
for i in range(n_qubits):
circ += RY(prefix + str(l) + '_' + str(i)).on(i)
for i in range(l % 2, n_qubits, 2):
if i < n_qubits and i + 1 < n_qubits:
circ += X.on(i + 1, i)
return circ
GenerateAnsatzCircuit(5, 2, 'a')
```
## 测量
我们把对不同比特位上的测量结果作为降维后的数据。具体过程与比特编码类似,例如当我们想将词向量降维为5维向量时,对于第3维的数据可以如下产生:
- 3对应的二进制为`00011`。
- 测量量子线路末态对$Z_0Z_1$哈密顿量的期望值。
下面函数将给出产生各个维度上数据所需的哈密顿量(hams),其中`n_qubits`表示线路的比特数,`dims`表示词嵌入的维度:
```
def GenerateEmbeddingHamiltonian(dims, n_qubits):
hams = []
for i in range(dims):
s = ''
for j, k in enumerate(bin(i + 1)[-1:1:-1]):
if k == '1':
s = s + 'Z' + str(j) + ' '
hams.append(Hamiltonian(QubitOperator(s)))
return hams
GenerateEmbeddingHamiltonian(5, 5)
```
## 量子版词向量嵌入层
量子版词向量嵌入层结合前面的编码量子线路和待训练量子线路,以及测量哈密顿量,将`num_embedding`个词嵌入为`embedding_dim`维的词向量。这里我们还在量子线路的最开始加上了Hadamard门,将初态制备为均匀叠加态,用以提高量子神经网络的表达能力。
下面,我们定义量子嵌入层,它将返回一个量子线路模拟算子。
```
def QEmbedding(num_embedding, embedding_dim, window, layers, n_threads):
n_qubits = int(np.ceil(np.log2(num_embedding)))
hams = GenerateEmbeddingHamiltonian(embedding_dim, n_qubits)
circ = Circuit()
circ = UN(H, n_qubits)
encoder_param_name = []
ansatz_param_name = []
for w in range(2 * window):
encoder = GenerateEncoderCircuit(n_qubits, 'Encoder_' + str(w))
ansatz = GenerateAnsatzCircuit(n_qubits, layers, 'Ansatz_' + str(w))
encoder.no_grad()
circ += encoder
circ += ansatz
encoder_param_name.extend(encoder.params_name)
ansatz_param_name.extend(ansatz.params_name)
grad_ops = Simulator('projectq', circ.n_qubits).get_expectation_with_grad(hams,
circ,
None,
None,
encoder_param_name,
ansatz_param_name,
n_threads)
return MQLayer(grad_ops)
```
整个训练模型跟经典网络类似,由一个嵌入层和两个全连通层构成,然而此处的嵌入层是由量子神经网络构成。下面定义量子神经网络CBOW。
```
class CBOW(nn.Cell):
def __init__(self, num_embedding, embedding_dim, window, layers, n_threads,
hidden_dim):
super(CBOW, self).__init__()
self.embedding = QEmbedding(num_embedding, embedding_dim, window,
layers, n_threads)
self.dense1 = nn.Dense(embedding_dim, hidden_dim)
self.dense2 = nn.Dense(hidden_dim, num_embedding)
self.relu = ops.ReLU()
def construct(self, x):
embed = self.embedding(x)
out = self.dense1(embed)
out = self.relu(out)
out = self.dense2(out)
return out
```
下面我们对一个稍长的句子来进行训练。首先定义`LossMonitorWithCollection`用于监督收敛过程,并搜集收敛过程的损失。
```
class LossMonitorWithCollection(LossMonitor):
def __init__(self, per_print_times=1):
super(LossMonitorWithCollection, self).__init__(per_print_times)
self.loss = []
def begin(self, run_context):
self.begin_time = time.time()
def end(self, run_context):
self.end_time = time.time()
print('Total time used: {}'.format(self.end_time - self.begin_time))
def epoch_begin(self, run_context):
self.epoch_begin_time = time.time()
def epoch_end(self, run_context):
cb_params = run_context.original_args()
self.epoch_end_time = time.time()
if self._per_print_times != 0 and cb_params.cur_step_num % self._per_print_times == 0:
print('')
def step_end(self, run_context):
cb_params = run_context.original_args()
loss = cb_params.net_outputs
if isinstance(loss, (tuple, list)):
if isinstance(loss[0], Tensor) and isinstance(loss[0].asnumpy(), np.ndarray):
loss = loss[0]
if isinstance(loss, Tensor) and isinstance(loss.asnumpy(), np.ndarray):
loss = np.mean(loss.asnumpy())
cur_step_in_epoch = (cb_params.cur_step_num - 1) % cb_params.batch_num + 1
if isinstance(loss, float) and (np.isnan(loss) or np.isinf(loss)):
raise ValueError("epoch: {} step: {}. Invalid loss, terminating training.".format(
cb_params.cur_epoch_num, cur_step_in_epoch))
self.loss.append(loss)
if self._per_print_times != 0 and cb_params.cur_step_num % self._per_print_times == 0:
print("\repoch: %+3s step: %+3s time: %5.5s, loss is %5.5s" % (cb_params.cur_epoch_num, cur_step_in_epoch, time.time() - self.epoch_begin_time, loss), flush=True, end='')
```
接下来,利用量子版本的`CBOW`来对一个长句进行词嵌入。运行之前请在终端运行`export OMP_NUM_THREADS=4`,将量子模拟器的线程数设置为4个,当所需模拟的量子系统比特数较多时,可设置更多的线程数来提高模拟效率。
```
import mindspore as ms
from mindspore import context
from mindspore import Tensor
context.set_context(mode=context.PYNATIVE_MODE, device_target="CPU")
corpus = """We are about to study the idea of a computational process.
Computational processes are abstract beings that inhabit computers.
As they evolve, processes manipulate other abstract things called data.
The evolution of a process is directed by a pattern of rules
called a program. People create programs to direct processes. In effect,
we conjure the spirits of the computer with our spells."""
ms.set_seed(42)
window_size = 2
embedding_dim = 10
hidden_dim = 128
word_dict, sample = GenerateWordDictAndSample(corpus, window=window_size)
train_x, train_y = GenerateTrainData(sample, word_dict)
train_loader = ds.NumpySlicesDataset({
"around": train_x,
"center": train_y
}, shuffle=False).batch(3)
net = CBOW(len(word_dict), embedding_dim, window_size, 3, 4, hidden_dim)
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
net_opt = nn.Momentum(net.trainable_params(), 0.01, 0.9)
loss_monitor = LossMonitorWithCollection(500)
model = Model(net, net_loss, net_opt)
model.train(350, train_loader, callbacks=[loss_monitor], dataset_sink_mode=False)
```
打印收敛过程中的损失函数值:
```
import matplotlib.pyplot as plt
plt.plot(loss_monitor.loss, '.')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.show()
```
通过如下方法打印量子嵌入层的量子线路中的参数:
```
net.embedding.weight.asnumpy()
```
## 经典版词向量嵌入层
这里我们利用经典的词向量嵌入层来搭建一个经典的CBOW神经网络,并与量子版本进行对比。
首先,搭建经典的CBOW神经网络,其中的参数跟量子版本的类似。
```
class CBOWClassical(nn.Cell):
def __init__(self, num_embedding, embedding_dim, window, hidden_dim):
super(CBOWClassical, self).__init__()
self.dim = 2 * window * embedding_dim
self.embedding = nn.Embedding(num_embedding, embedding_dim, True)
self.dense1 = nn.Dense(self.dim, hidden_dim)
self.dense2 = nn.Dense(hidden_dim, num_embedding)
self.relu = ops.ReLU()
self.reshape = ops.Reshape()
def construct(self, x):
embed = self.embedding(x)
embed = self.reshape(embed, (-1, self.dim))
out = self.dense1(embed)
out = self.relu(out)
out = self.dense2(out)
return out
```
生成适用于经典CBOW神经网络的数据集。
```
train_x = []
train_y = []
for i in sample:
around, center = i
train_y.append(word_dict[center])
train_x.append([])
for j in around:
train_x[-1].append(word_dict[j])
train_x = np.array(train_x).astype(np.int32)
train_y = np.array(train_y).astype(np.int32)
print("train_x shape: ", train_x.shape)
print("train_y shape: ", train_y.shape)
```
我们对经典CBOW网络进行训练。
```
context.set_context(mode=context.GRAPH_MODE, device_target="CPU")
train_loader = ds.NumpySlicesDataset({
"around": train_x,
"center": train_y
}, shuffle=False).batch(3)
net = CBOWClassical(len(word_dict), embedding_dim, window_size, hidden_dim)
net_loss = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
net_opt = nn.Momentum(net.trainable_params(), 0.01, 0.9)
loss_monitor = LossMonitorWithCollection(500)
model = Model(net, net_loss, net_opt)
model.train(350, train_loader, callbacks=[loss_monitor], dataset_sink_mode=False)
```
打印收敛过程中的损失函数值:
```
import matplotlib.pyplot as plt
plt.plot(loss_monitor.loss, '.')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.show()
```
由上可知,通过量子模拟得到的量子版词嵌入模型也能很好的完成嵌入任务。当数据集大到经典计算机算力难以承受时,量子计算机将能够轻松处理这类问题。
## 参考文献
[1] Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean. [Efficient Estimation of Word Representations in
Vector Space](https://arxiv.org/pdf/1301.3781.pdf)
| true |
code
| 0.545044 | null | null | null | null |
|
```
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Author(s): Kevin P. Murphy ([email protected]) and Mahmoud Soliman ([email protected])
```
<a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/figures//chapter20_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Figure 20.1:<a name='20.1'></a> <a name='pcaDemo2d'></a>
An illustration of PCA where we project from 2d to 1d. Circles are the original data points, crosses are the reconstructions. The red star is the data mean.
Figure(s) generated by [pcaDemo2d.py](https://github.com/probml/pyprobml/blob/master/scripts/pcaDemo2d.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/pcaDemo2d.py")
```
## Figure 20.2:<a name='20.2'></a> <a name='pcaDigits'></a>
An illustration of PCA applied to MNIST digits from class 9. Grid points are at the 5, 25, 50, 75, 95 \% quantiles of the data distribution along each dimension. The circled points are the closest projected images to the vertices of the grid. Adapted from Figure 14.23 of <a href='#HastieBook'>[HTF09]</a> .
Figure(s) generated by [pca_digits.py](https://github.com/probml/pyprobml/blob/master/scripts/pca_digits.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/pca_digits.py")
```
## Figure 20.3:<a name='20.3'></a> <a name='eigenFace'></a>
a) Some randomly chosen $64 \times 64$ pixel images from the Olivetti face database. (b) The mean and the first three PCA components represented as images.
Figure(s) generated by [pcaImageDemo.m](https://github.com/probml/pmtk3/blob/master/demos/pcaImageDemo.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaImages-faces-images.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaImages-faces-basis.png")
```
## Figure 20.4:<a name='20.4'></a> <a name='pcaProjVar'></a>
Illustration of the variance of the points projected onto different 1d vectors. $v_1$ is the first principal component, which maximizes the variance of the projection. $v_2$ is the second principal component which is direction orthogonal to $v_1$. Finally $v'$ is some other vector in between $v_1$ and $v_2$. Adapted from Figure 8.7 of <a href='#Geron2019'>[Aur19]</a> .
Figure(s) generated by [pca_projected_variance.py](https://github.com/probml/pyprobml/blob/master/scripts/pca_projected_variance.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/pca_projected_variance.py")
```
## Figure 20.5:<a name='20.5'></a> <a name='heightWeightPCA'></a>
Effect of standardization on PCA applied to the height/weight dataset. (Red=female, blue=male.) Left: PCA of raw data. Right: PCA of standardized data.
Figure(s) generated by [pcaStandardization.py](https://github.com/probml/pyprobml/blob/master/scripts/pcaStandardization.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/pcaStandardization.py")
```
## Figure 20.6:<a name='20.6'></a> <a name='pcaErr'></a>
Reconstruction error on MNIST vs number of latent dimensions used by PCA. (a) Training set. (b) Test set.
Figure(s) generated by [pcaOverfitDemo.m](https://github.com/probml/pmtk3/blob/master/demos/pcaOverfitDemo.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaOverfitReconTrain.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaOverfitReconTest.png")
```
## Figure 20.7:<a name='20.7'></a> <a name='pcaFrac'></a>
(a) Scree plot for training set, corresponding to \cref fig:pcaErr (a). (b) Fraction of variance explained.
Figure(s) generated by [pcaOverfitDemo.m](https://github.com/probml/pmtk3/blob/master/demos/pcaOverfitDemo.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaOverfitScree.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaOverfitVar.png")
```
## Figure 20.8:<a name='20.8'></a> <a name='pcaProfile'></a>
Profile likelihood corresponding to PCA model in \cref fig:pcaErr (a).
Figure(s) generated by [pcaOverfitDemo.m](https://github.com/probml/pmtk3/blob/master/demos/pcaOverfitDemo.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaOverfitProfile.png")
```
## Figure 20.9:<a name='20.9'></a> <a name='sprayCan'></a>
Illustration of the FA generative process, where we have $L=1$ latent dimension generating $D=2$ observed dimensions; we assume $\boldsymbol \Psi =\sigma ^2 \mathbf I $. The latent factor has value $z \in \mathbb R $, sampled from $p(z)$; this gets mapped to a 2d offset $\boldsymbol \delta = z \mathbf w $, where $\mathbf w \in \mathbb R ^2$, which gets added to $\boldsymbol \mu $ to define a Gaussian $p(\mathbf x |z) = \mathcal N (\mathbf x |\boldsymbol \mu + \boldsymbol \delta ,\sigma ^2 \mathbf I )$. By integrating over $z$, we ``slide'' this circular Gaussian ``spray can'' along the principal component axis $\mathbf w $, which induces elliptical Gaussian contours in $\mathbf x $ space centered on $\boldsymbol \mu $. Adapted from Figure 12.9 of <a href='#BishopBook'>[Bis06]</a> .
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/PPCAsprayCan.png")
```
## Figure 20.10:<a name='20.10'></a> <a name='pcaSpring'></a>
Illustration of EM for PCA when $D=2$ and $L=1$. Green stars are the original data points, black circles are their reconstructions. The weight vector $\mathbf w $ is represented by blue line. (a) We start with a random initial guess of $\mathbf w $. The E step is represented by the orthogonal projections. (b) We update the rod $\mathbf w $ in the M step, keeping the projections onto the rod (black circles) fixed. (c) Another E step. The black circles can 'slide' along the rod, but the rod stays fixed. (d) Another M step. Adapted from Figure 12.12 of <a href='#BishopBook'>[Bis06]</a> .
Figure(s) generated by [pcaEmStepByStep.m](https://github.com/probml/pmtk3/blob/master/demos/pcaEmStepByStep.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaEmStepByStepEstep1.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaEmStepByStepMstep1.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaEmStepByStepEstep2.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/pcaEmStepByStepMstep2.png")
```
## Figure 20.11:<a name='20.11'></a> <a name='mixFAdgm'></a>
Mixture of factor analyzers as a PGM.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/mixFAdgmC.png")
```
## Figure 20.12:<a name='20.12'></a> <a name='ppcaMixNetlab'></a>
Mixture of PPCA models fit to a 2d dataset, using $L=1$ latent dimensions and $K=1$ and $K=10$ mixture components.
Figure(s) generated by [mixPpcaDemoNetlab.m](https://github.com/probml/pmtk3/blob/master/demos/mixPpcaDemoNetlab.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/mixPpcaAnnulus1.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/mixPpcaAnnulus10.png")
```
## Figure 20.13:<a name='20.13'></a> <a name='MFAGANsamples'></a>
Random samples from the MixFA model fit to CelebA. From Figure 4 of <a href='#Richardson2018'>[EY18]</a> . Used with kind permission of Yair Weiss
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/MFAGAN-samples.png")
```
## Figure 20.14:<a name='20.14'></a> <a name='binaryPCA'></a>
(a) 150 synthetic 16 dimensional bit vectors. (b) The 2d embedding learned by binary PCA, fit using variational EM. We have color coded points by the identity of the true ``prototype'' that generated them. (c) Predicted probability of being on. (d) Thresholded predictions.
Figure(s) generated by [binaryFaDemoTipping.m](https://github.com/probml/pmtk3/blob/master/demos/binaryFaDemoTipping.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/binaryPCAinput.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/binaryPCAembedding.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/binaryPCApostpred.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/binaryPCArecon.png")
```
## Figure 20.15:<a name='20.15'></a> <a name='PLS'></a>
Gaussian latent factor models for paired data. (a) Supervised PCA. (b) Partial least squares.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/eSPCAxy.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ePLSxy.png")
```
## Figure 20.16:<a name='20.16'></a> <a name='CCA'></a>
Canonical correlation analysis as a PGM.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/eCCAxy.png")
```
## Figure 20.17:<a name='20.17'></a> <a name='autoencoder'></a>
An autoencoder with one hidden layer.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/autoencoder.png")
```
## Figure 20.18:<a name='20.18'></a> <a name='aeFashion'></a>
Results of applying an autoencoder to the Fashion MNIST data. Top row are first 5 images from validation set. Bottom row are reconstructions. (a) MLP model (trained for 20 epochs). The encoder is an MLP with architecture 784-100-30. The decoder is the mirror image of this. (b) CNN model (trained for 5 epochs). The encoder is a CNN model with architecture Conv2D(16, 3x3, same, selu), MaxPool2D(2x2), Conv2D(32, 3x3, same, selu), MaxPool2D(2x2), Conv2D(64, 3x3, same, selu), MaxPool2D(2x2). The decoder is the mirror image of this, using transposed convolution and without the max pooling layers. Adapted from Figure 17.4 of <a href='#Geron2019'>[Aur19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/ae_mnist_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/ae_fashion_mlp_recon.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae_fashion_cnn_recon.png")
```
## Figure 20.19:<a name='20.19'></a> <a name='aeFashionTSNE'></a>
tSNE plot of the first 2 latent dimensions of the Fashion MNIST validation set computed using an MLP-based autoencoder. Adapted from Figure 17.5 of <a href='#Geron2019'>[Aur19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/ae_mnist_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-mlp-fashion-tsne.png")
```
## Figure 20.20:<a name='20.20'></a> <a name='DAEfashion'></a>
Denoising autoencoder (MLP architecture) applied to some noisy Fashion MNIST images from the validation set. (a) Gaussian noise. (b) Bernoulli dropout noise. Top row: input. Bottom row: output Adapted from Figure 17.9 of <a href='#Geron2019'>[Aur19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/ae_mnist_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-denoising-gaussian.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-denoising-dropout.png")
```
## Figure 20.21:<a name='20.21'></a> <a name='DAEfield'></a>
The residual error from a DAE, $\mathbf e (\mathbf x )=r( \cc@accent "707E \mathbf x )-\mathbf x $, can learn a vector field corresponding to the score function. Arrows point towards higher probability regions. The length of the arrow is proportional to $||\mathbf e (\mathbf x )||$, so points near the 1d data manifold (represented by the curved line) have smaller arrows. From Figure 5 of <a href='#Alain2014'>[GY14]</a> . Used with kind permission of Guillaume Alain.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/DAE.png")
```
## Figure 20.22:<a name='20.22'></a> <a name='sparseAE'></a>
Neuron activity (in the bottleneck layer) for an autoencoder applied to Fashion MNIST. We show results for three models, with different kinds of sparsity penalty: no penalty (left column), $\ell _1$ penalty (middle column), KL penalty (right column). Top row: Heatmap of 300 neuron activations (columns) across 100 examples (rows). Middle row: Histogram of activation levels derived from this heatmap. Bottom row: Histogram of the mean activation per neuron, averaged over all examples in the validation set. Adapted from Figure 17.11 of <a href='#Geron2019'>[Aur19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/ae_mnist_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-noreg-heatmap.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-L1reg-heatmap.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-KLreg-heatmap.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-noreg-act.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-L1reg-act.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-KLreg-act.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-noreg-neurons.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-L1reg-neurons.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-sparse-KLreg-neurons.png")
```
## Figure 20.23:<a name='20.23'></a> <a name='vaeSchematic'></a>
Schematic illustration of a VAE. From a figure from http://krasserm.github.io/2018/07/27/dfc-vae/ . Used with kind permission of Martin Krasser.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/vae-krasser.png")
```
## Figure 20.24:<a name='20.24'></a> <a name='VAEcelebaRecon'></a>
Comparison of reconstruction abilities of an autoencoder and VAE. Top row: Original images. Middle row: Reconstructions from a VAE. Bottom row: Reconstructions from an AE. We see that the VAE reconstructions (middle) are blurrier. Both models have the same shallow convolutional architecture (3 hidden layers, 200 latents), and are trained on identical data (20k images of size $64 \times 64$ extracted from CelebA) for the same number of epochs (20).
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/vae_celeba_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-celeba-orig.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/vae-celeba-recon.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-celeba-recon.png")
```
## Figure 20.25:<a name='20.25'></a> <a name='VAEcelebaSamples'></a>
Unconditional samples from a VAE (top row) or AE (bottom row) trained on CelebA. Both models have the same structure and both are trained for 20 epochs.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/vae_celeba_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/vae-celeba-samples.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/ae-celeba-samples.png")
```
## Figure 20.26:<a name='20.26'></a> <a name='VAEcelebaInterpGender'></a>
Interpolation between two real images (first and last columns) in the latent space of a VAE. Adapted from Figure 3.22 of <a href='#Foster2019'>[Dav19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/vae_celeba_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/vae-celeba-interp-gender.png")
```
## Figure 20.27:<a name='20.27'></a> <a name='VAEcelebaAddGlasses'></a>
Adding or removing the ``sunglasses'' vector to an image using a VAE. The first column is an input image, with embedding $\mathbf z $. Subsequent columns show the decoding of $\mathbf z + s \boldsymbol \Delta $, where $s \in \ -4,-3,-2,-1,0,1,2,3,4\ $ and $\boldsymbol \Delta = \overline \mathbf z ^+ - \overline \mathbf z ^-$ is the difference in the average embeddings of images of people with or without sunglasses. Adapted from Figure 3.21 of <a href='#Foster2019'>[Dav19]</a> .
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/dimred/vae_celeba_tf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/vae-celeba-glasses-scale.png")
```
## Figure 20.28:<a name='20.28'></a> <a name='tangentSpace'></a>
Illustration of the tangent space and tangent vectors at two different points on a 2d curved manifold. From Figure 1 of <a href='#Bronstein2017'>[MM+17]</a> . Used with kind permission of Michael Bronstein
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/tangentSpace.png")
```
## Figure 20.29:<a name='20.29'></a> <a name='manifold-6-rotated'></a>
Illustration of the image manifold. (a) An image of the digit 6 from the USPS dataset, of size $64 \times 57 = 3,648$. (b) A random sample from the space $\ 0,1\ ^ 3648 $ reshaped as an image. (c) A dataset created by rotating the original image by one degree 360 times. We project this data onto its first two principal components, to reveal the underlying 2d circular manifold. From Figure 1 of <a href='#Lawrence2012'>[Nei12]</a> . Used with kind permission of Neil Lawrence
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/manifold-6-original.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/manifold-6-rnd.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/manifold-6-rotated.png")
```
## Figure 20.30:<a name='20.30'></a> <a name='manifoldData'></a>
Illustration of some data generated from low-dimensional manifolds. (a) The 2d Swiss-roll manifold embedded into 3d.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.31:<a name='20.31'></a> <a name='metricMDS'></a>
Metric MDS applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.32:<a name='20.32'></a> <a name='KNNgraph'></a>
(a) If we measure distances along the manifold, we find $d(1,6) > d(1,4)$, whereas if we measure in ambient space, we find $d(1,6) < d(1,4)$. The plot at the bottom shows the underlying 1d manifold. (b) The $K$-nearest neighbors graph for some datapoints; the red path is the shortest distance between A and B on this graph. From <a href='#HintonEmbedding'>[Hin13]</a> . Used with kind permission of Geoff Hinton.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/hinton-isomap1.png")
pmlt.show_image("/pyprobml/notebooks/figures/images/hinton-isomap2.png")
```
## Figure 20.33:<a name='20.33'></a> <a name='isomap'></a>
Isomap applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.34:<a name='20.34'></a> <a name='isomapNoisy'></a>
(a) Noisy version of Swiss roll data. We perturb each point by adding $\mathcal N (0, 0.5^2)$ noise. (b) Results of Isomap applied to this data.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
```
## Figure 20.35:<a name='20.35'></a> <a name='kpcaScholkopf'></a>
Visualization of the first 8 kernel principal component basis functions derived from some 2d data. We use an RBF kernel with $\sigma ^2=0.1$.
Figure(s) generated by [kpcaScholkopf.m](https://github.com/probml/pmtk3/blob/master/demos/kpcaScholkopf.m)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/kpcaScholkopfNoShade.png")
```
## Figure 20.36:<a name='20.36'></a> <a name='kPCA'></a>
Kernel PCA applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.37:<a name='20.37'></a> <a name='LLE'></a>
LLE applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.38:<a name='20.38'></a> <a name='eigenmaps'></a>
Laplacian eigenmaps applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.39:<a name='20.39'></a> <a name='graphLaplacian'></a>
Illustration of the Laplacian matrix derived from an undirected graph. From https://en.wikipedia.org/wiki/Laplacian_matrix . Used with kind permission of Wikipedia author AzaToth.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/graphLaplacian.png")
```
## Figure 20.40:<a name='20.40'></a> <a name='graphFun'></a>
Illustration of a (positive) function defined on a graph. From Figure 1 of <a href='#Shuman2013'>[DI+13]</a> . Used with kind permission of Pascal Frossard.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/graphFun.png")
```
## Figure 20.41:<a name='20.41'></a> <a name='tSNE'></a>
tSNE applied to (a) Swiss roll.
Figure(s) generated by [manifold_swiss_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_swiss_sklearn.py) [manifold_digits_sklearn.py](https://github.com/probml/pyprobml/blob/master/scripts/manifold_digits_sklearn.py)
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_and_run("/pyprobml/scripts/manifold_swiss_sklearn.py")
pmlt.show_and_run("/pyprobml/scripts/manifold_digits_sklearn.py")
```
## Figure 20.42:<a name='20.42'></a> <a name='tsneWattenberg'></a>
Illustration of the effect of changing the perplexity parameter when t-SNE is applied to some 2d data. From <a href='#Wattenberg2016how'>[MFI16]</a> . See http://distill.pub/2016/misread-tsne for an animated version of these figures. Used with kind permission of Martin Wattenberg.
```
#@title Setup { display-mode: "form" }
%%time
# If you run this for the first time it would take ~25/30 seconds
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null && git clone https://github.com/Sekhen/colab_powertoys.git &> /dev/null
!pip3 install nbimporter -qqq
%cd -q /content/colab_powertoys
from colab_powertoys.probml_toys import probml_toys as pmlt
%cd -q /content/
pmlt.show_image("/pyprobml/notebooks/figures/images/tSNE-wattenberg0.png.png")
```
## References:
<a name='Geron2019'>[Aur19]</a> G. Aur'elien "Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques for BuildingIntelligent Systems (2nd edition)". (2019).
<a name='BishopBook'>[Bis06]</a> C. Bishop "Pattern recognition and machine learning". (2006).
<a name='Shuman2013'>[DI+13]</a> S. DI, N. SK, F. P, O. A and V. P. "The emerging field of signal processing on graphs: Extendinghigh-dimensional data analysis to networks and other irregulardomains". In: IEEE Signal Process. Mag. (2013).
<a name='Foster2019'>[Dav19]</a> F. David "Generative Deep Learning: Teaching Machines to Paint, WriteCompose, and Play". (2019).
<a name='Richardson2018'>[EY18]</a> R. Eitan and W. Yair. "On GANs and GMMs". (2018).
<a name='Alain2014'>[GY14]</a> A. Guillaume and B. Yoshua. "What Regularized Auto-Encoders Learn from the Data-GeneratingDistribution". In: jmlr (2014).
<a name='HastieBook'>[HTF09]</a> T. Hastie, R. Tibshirani and J. Friedman. "The Elements of Statistical Learning". (2009).
<a name='HintonEmbedding'>[Hin13]</a> G. Hinton "CSC 2535 Lecture 11: Non-linear dimensionality reduction". (2013).
<a name='Wattenberg2016how'>[MFI16]</a> W. Martin, V. Fernanda and J. Ian. "How to Use t-SNE Effectively". In: Distill (2016).
<a name='Bronstein2017'>[MM+17]</a> B. MM, B. J, L. Y, S. A and V. P. "Geometric Deep Learning: Going beyond Euclidean data". In: IEEE Signal Process. Mag. (2017).
<a name='Lawrence2012'>[Nei12]</a> L. NeilD "A Unifying Probabilistic Perspective for Spectral DimensionalityReduction: Insights and New Models". In: jmlr (2012).
| true |
code
| 0.611498 | null | null | null | null |
|
```
!cp drive/My\ Drive/time-series-analysis/london_bike_sharing_dataset.csv .
```
### Importing libraries
```
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import pandas as pd
import tensorflow as tf
from tensorflow import keras
import seaborn as sns
from matplotlib import rc
from pylab import rcParams
rcParams['figure.figsize'] = 22, 6
```
### Load data
```
df = pd.read_csv('london_bike_sharing_dataset.csv',parse_dates=['timestamp'],index_col='timestamp')
df.head()
```
#### Get a copy of the data
```
df_copy = df.copy()
```
## Exploratory data analysis
### Extracting extra features from timestamps
```
df['hour'] = df.index.hour
df['day_of_week'] = df.index.dayofweek
df['day_of_month'] = df.index.day
df['month'] = df.index.month
df.head()
```
### total numbers of bike shared during the period
```
sns.lineplot(x=df.index, y=df.cnt);
```
### total numbers of bike shared during each month
```
df_by_month = df.resample('M').sum()
sns.lineplot(x=df_by_month.index, y='cnt', data=df_by_month, color='b');
```
### total numbers of bike shared in each hour in comparison with holidays
```
sns.pointplot(x='hour',y='cnt', data=df, hue='is_holiday');
```
### total numbers of bike shared during each day of the week
```
sns.pointplot(x='day_of_week',y='cnt', data=df, color='b');
```
## Splitting train & test
```
train_size = int(len(df_)*0.9)
test_size = len(df) - train_size
train , test = df.iloc[:train_size], df.iloc[train_size:]
print(train.shape, test.shape)
```
## Feature scaling
```
from sklearn.preprocessing import RobustScaler
pd.options.mode.chained_assignment = None
f_columns = ['t1', 't2', 'hum', 'wind_speed']
f_transformer = RobustScaler()
cnt_transformer = RobustScaler()
f_transformer = f_transformer.fit(train[f_columns].to_numpy())
cnt_transformer = cnt_transformer.fit(train[['cnt']])
train.loc[:, f_columns] = f_transformer.transform(train[f_columns].to_numpy())
train['cnt'] = cnt_transformer.transform(train[['cnt']])
test.loc[:, f_columns] = f_transformer.transform(test[f_columns].to_numpy())
test['cnt'] = cnt_transformer.transform(test[['cnt']])
```
### Converting the data to a time series format
```
def to_sequence(X, y, time_steps=1):
Xs, ys = [], []
for i in range(len(X) - time_steps):
v = X.iloc[i: (i + time_steps)].to_numpy()
Xs.append(v)
ys.append(y.iloc[i + time_steps])
return np.asarray(Xs), np.asarray(ys)
TIMESTEPS = 24
x_train, y_train = to_sequence(train, train['cnt'], TIMESTEPS)
x_test, y_test = to_sequence(test, test['cnt'], TIMESTEPS)
print(f"X_train shape is {x_train.shape}, and y_train shape is {y_train.shape}")
```
## Defining a model
```
from keras.models import Sequential
from keras.layers import LSTM, Dropout, Bidirectional, Dense
model = Sequential()
model.add(Bidirectional(LSTM(units=128),input_shape=(x_train.shape[1], x_train.shape[2])))
model.add(Dropout(rate=0.3))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse', metrics=['acc'])
model.summary()
```
### Fitting the model on data
```
history = model.fit(x_train, y_train, batch_size=16, validation_split=0.1, epochs=100, shuffle=False)
```
### Model loss visualization
```
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='validation')
plt.legend();
```
### Model prediction
```
y_pred = model.predict(x_test)
y_test_inv = cnt_transformer.inverse_transform(y_test.reshape(1,-1))
y_train_inv = cnt_transformer.inverse_transform(y_train.reshape(1,-1))
y_pred_inv = cnt_transformer.inverse_transform(y_pred)
```
### Model prediction visualization
```
plt.plot(y_test_inv.flatten(), marker='.', label='True')
plt.plot(y_pred_inv, marker='.', label='Prediction')
plt.legend();
```
| true |
code
| 0.57821 | null | null | null | null |
|
.. meta::
:description: A guide which introduces the most important steps to get started with pymoo, an open-source multi-objective optimization framework in Python.
.. meta::
:keywords: Multi-objective Optimization, Python, Evolutionary Computation, Optimization Test Problem, Hypervolume
# Getting Started
In the following, we like to introduce *pymoo* by presenting an example optimization scenario. This guide goes through the essential steps to get started with our framework. This guide is structured as follows:
1. Introduction to Multi-objective Optimization and an exemplarily Test Problem
2. Implementation of a Problem (vectorized, element-wise or functional)
3. Initialization of an Algorithm (in our case NSGA2)
4. Definition of a Termination Criterion
5. Optimize (functional through `minimize` or object-oriented by calling `next()`)
6. Visualization of Results and Convergence
7. Summary
8. Source code (in one piece)
We try to cover the essential steps you have to follow to get started optimizing your own optimization problem and have also included some posteriori analysis which is known to be particularly important in multi-objective optimization.
## 1. Introduction
### Multi-Objective Optimization
In general, multi-objective optimization has several objective functions with subject to inequality and equality constraints to optimize <cite data-cite="multi_objective_book"></cite>. The goal is to find a set of solutions that do not have any constraint violation and are as good as possible regarding all its objectives values. The problem definition in its general form is given by:
\begin{align}
\begin{split}
\min \quad& f_{m}(x) \quad \quad \quad \quad m = 1,..,M \\[4pt]
\text{s.t.} \quad& g_{j}(x) \leq 0 \quad \; \; \, \quad j = 1,..,J \\[2pt]
\quad& h_{k}(x) = 0 \quad \; \; \quad k = 1,..,K \\[4pt]
\quad& x_{i}^{L} \leq x_{i} \leq x_{i}^{U} \quad i = 1,..,N \\[2pt]
\end{split}
\end{align}
The formulation above defines a multi-objective optimization problem with $N$ variables, $M$ objectives, $J$ inequality and $K$ equality constraints. Moreover, for each variable $x_i$ lower and upper variable boundaries ($x_i^L$ and $x_i^U$) are defined.
### Test Problem
In the following, we investigate exemplarily a bi-objective optimization with two constraints.
We tried to select a suitable optimization problem with enough complexity for demonstration purposes, but not too difficult to lose track of the overall idea. Its definition is given by:
\begin{align}
\begin{split}
\min \;\; & f_1(x) = (x_1^2 + x_2^2) \\
\max \;\; & f_2(x) = -(x_1-1)^2 - x_2^2 \\[1mm]
\text{s.t.} \;\; & g_1(x) = 2 \, (x_1 - 0.1) \, (x_1 - 0.9) \leq 0\\
& g_2(x) = 20 \, (x_1 - 0.4) \, (x_1 - 0.6) \geq 0\\[1mm]
& -2 \leq x_1 \leq 2 \\
& -2 \leq x_2 \leq 2
\end{split}
\end{align}
It consists of two objectives ($M=2$) where $f_1(x)$ is minimized and $f_2(x)$ maximized. The optimization is with subject to two inequality constraints ($J=2$) where $g_1(x)$ is formulated as a less than and $g_2(x)$ as a greater than constraint. The problem is defined with respect to two variables ($N=2$), $x_1$ and $x_2$, which both are in the range $[-2,2]$. The problem does not contain any equality constraints ($K=0$).
```
import numpy as np
X1, X2 = np.meshgrid(np.linspace(-2, 2, 500), np.linspace(-2, 2, 500))
F1 = X1**2 + X2**2
F2 = (X1-1)**2 + X2**2
G = X1**2 - X1 + 3/16
G1 = 2 * (X1[0] - 0.1) * (X1[0] - 0.9)
G2 = 20 * (X1[0] - 0.4) * (X1[0] - 0.6)
import matplotlib.pyplot as plt
plt.rc('font', family='serif')
levels = [0.02, 0.1, 0.25, 0.5, 0.8]
plt.figure(figsize=(7, 5))
CS = plt.contour(X1, X2, F1, levels, colors='black', alpha=0.5)
CS.collections[0].set_label("$f_1(x)$")
CS = plt.contour(X1, X2, F2, levels, linestyles="dashed", colors='black', alpha=0.5)
CS.collections[0].set_label("$f_2(x)$")
plt.plot(X1[0], G1, linewidth=2.0, color="green", linestyle='dotted')
plt.plot(X1[0][G1<0], G1[G1<0], label="$g_1(x)$", linewidth=2.0, color="green")
plt.plot(X1[0], G2, linewidth=2.0, color="blue", linestyle='dotted')
plt.plot(X1[0][X1[0]>0.6], G2[X1[0]>0.6], label="$g_2(x)$",linewidth=2.0, color="blue")
plt.plot(X1[0][X1[0]<0.4], G2[X1[0]<0.4], linewidth=2.0, color="blue")
plt.plot(np.linspace(0.1,0.4,100), np.zeros(100),linewidth=3.0, color="orange")
plt.plot(np.linspace(0.6,0.9,100), np.zeros(100),linewidth=3.0, color="orange")
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.12),
ncol=4, fancybox=True, shadow=False)
plt.tight_layout()
plt.show()
```
The figure above shows the contours of the problem. The contour lines of the objective function $f_1(x)$ is represented by a solid and $f_2(x)$ by a dashed line. The constraints $g_1(x)$ and $g_2(x)$ are parabolas which intersect the $x_1$-axis at $(0.1, 0.9)$ and $(0.4, 0.6)$. A thick orange line illustrates the pareto-optimal set. Through the combination of both constraints, the pareto-set is split into two parts.
Analytically, the pareto-optimal set is given by $PS = \{(x_1, x_2) \,|\, (0.1 \leq x_1 \leq 0.4) \lor (0.6 \leq x_1 \leq 0.9) \, \land \, x_2 = 0\}$ and the Pareto-front by $f_2 = (\sqrt{f_1} - 1)^2$ where $f_1$ is defined in $[0.01,0.16]$ and $[0.36,0.81]$.
## 2. Implementation of a Problem
In *pymoo*, we consider **minimization** problems for optimization in all our modules. However, without loss of generality, an objective that is supposed to be maximized can be multiplied by $-1$ and be minimized. Therefore, we minimize $-f_2(x)$ instead of maximizing $f_2(x)$ in our optimization problem. Furthermore, all constraint functions need to be formulated as a $\leq 0$ constraint.
The feasibility of a solution can, therefore, be expressed by:
$$ \begin{cases}
\text{feasible,} \quad \quad \sum_i^n \langle g_i(x)\rangle = 0\\
\text{infeasbile,} \quad \quad \quad \text{otherwise}\\
\end{cases}
$$
$$
\text{where} \quad \langle g_i(x)\rangle =
\begin{cases}
0, \quad \quad \; \text{if} \; g_i(x) \leq 0\\
g_i(x), \quad \text{otherwise}\\
\end{cases}
$$
For this reason, $g_2(x)$ needs to be multiplied by $-1$ in order to flip the $\geq$ to a $\leq$ relation. We recommend the normalization of constraints to give equal importance to each of them.
For $g_1(x)$, the coefficient results in $2 \cdot (-0.1) \cdot (-0.9) = 0.18$ and for $g_2(x)$ in $20 \cdot (-0.4) \cdot (-0.6) = 4.8$, respectively. We achieve normalization of constraints by dividing $g_1(x)$ and $g_2(x)$ by its corresponding coefficient.
Finally, the optimization problem to be optimized using *pymoo* is defined by:
\begin{align}
\label{eq:getting_started_pymoo}
\begin{split}
\min \;\; & f_1(x) = (x_1^2 + x_2^2) \\
\min \;\; & f_2(x) = (x_1-1)^2 + x_2^2 \\[1mm]
\text{s.t.} \;\; & g_1(x) = 2 \, (x_1 - 0.1) \, (x_1 - 0.9) \, / \, 0.18 \leq 0\\
& g_2(x) = - 20 \, (x_1 - 0.4) \, (x_1 - 0.6) \, / \, 4.8 \leq 0\\[1mm]
& -2 \leq x_1 \leq 2 \\
& -2 \leq x_2 \leq 2
\end{split}
\end{align}
This getting started guide demonstrates **3** different ways of defining a problem:
- **By Class**
- **Vectorized evaluation:** A set of solutions is evaluated directly.
- **Elementwise evaluation:** Only one solution is evaluated at a time.
- **By Functions**: Functional interface as commonly defined in other optimization libraries.
**Optional**: Define a Pareto set and front for the optimization problem to track convergence to the analytically derived optimum/optima.
Please choose the most convenient implementation for your purpose.
### By Class
Defining a problem through a class allows defining the problem very naturally, assuming the metadata, such as the number of variables and objectives, are known.
The problem inherits from the [Problem](problems/index.ipynb) class. By calling the `super()` function in the constructor `__init__` the problem properties such as the number of variables `n_var`, objectives `n_obj` and constraints `n_constr` are supposed to be initialized. Furthermore, lower `xl` and upper variables boundaries `xu` are supplied as a NumPy array. Please note that most algorithms in our framework require the lower and upper boundaries to be provided and not equal to negative or positive infinity. Finally, the evaluation function `_evaluate` needs to be overwritten to calculated the objective and constraint values.
#### Vectorized Evaluation
The `_evaluate` method takes a **two-dimensional** NumPy array `X` with *n* rows and *m* columns as an input. Each row represents an individual, and each column an optimization variable. After doing the necessary calculations, the objective values must be added to the dictionary out with the key `F` and the constraints with key `G`.
**Note**: This method is only called once per iteration for most algorithms. This gives you all the freedom to implement your own parallelization.
```
import numpy as np
from pymoo.model.problem import Problem
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2,
n_obj=2,
n_constr=2,
xl=np.array([-2,-2]),
xu=np.array([2,2]))
def _evaluate(self, X, out, *args, **kwargs):
f1 = X[:,0]**2 + X[:,1]**2
f2 = (X[:,0]-1)**2 + X[:,1]**2
g1 = 2*(X[:, 0]-0.1) * (X[:, 0]-0.9) / 0.18
g2 = - 20*(X[:, 0]-0.4) * (X[:, 0]-0.6) / 4.8
out["F"] = np.column_stack([f1, f2])
out["G"] = np.column_stack([g1, g2])
vectorized_problem = MyProblem()
```
#### Elementwise Evaluation
The `_evaluate` method takes a **one-dimensional** NumPy array `x` number of entries equal to `n_var`. This behavior is enabled by setting `elementwise_evaluation=True` while calling the `super()` method.
**Note**: This method is called in each iteration for **each** solution exactly once.
```
import numpy as np
from pymoo.util.misc import stack
from pymoo.model.problem import Problem
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2,
n_obj=2,
n_constr=2,
xl=np.array([-2,-2]),
xu=np.array([2,2]),
elementwise_evaluation=True)
def _evaluate(self, x, out, *args, **kwargs):
f1 = x[0]**2 + x[1]**2
f2 = (x[0]-1)**2 + x[1]**2
g1 = 2*(x[0]-0.1) * (x[0]-0.9) / 0.18
g2 = - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8
out["F"] = [f1, f2]
out["G"] = [g1, g2]
elementwise_problem = MyProblem()
```
### By Functions
The definition by functions is a common way in Python and available and many other optimization frameworks. It reduces the problem's definitions without any overhead, and the number of objectives and constraints is simply derived from the list of functions.
After having defined the functions, the problem object is created by initializing `FunctionalProblem`. Please note that the number of variables `n_var` must be passed as an argument.
**Note**: This definition is recommended to be used to define a problem through simple functions. It is worth noting that the evaluation can require many functions calls. For instance, for 100 individuals with 2 objectives and 2 constraints 400 function calls are necessary for evaluation. Whereas, a vectorized definition through the `Problem` class requires only a single function call. Moreover, if metrics are shared between objectives or constraints, they need to be calculated twice.
```
import numpy as np
from pymoo.model.problem import FunctionalProblem
objs = [
lambda x: x[0]**2 + x[1]**2,
lambda x: (x[0]-1)**2 + x[1]**2
]
constr_ieq = [
lambda x: 2*(x[0]-0.1) * (x[0]-0.9) / 0.18,
lambda x: - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8
]
functional_problem = FunctionalProblem(2,
objs,
constr_ieq=constr_ieq,
xl=np.array([-2,-2]),
xu=np.array([2,2]))
```
### (Optional) Pareto front (pf) and Pareto set (ps)
In this case, we have a test problem where the optimum is **known**. For illustration, we like to measure the convergence of the algorithm to the known true optimum. Thus, we implement override the `_calc_pareto_front` and `_calc_pareto_set` for this purpose. Please note that both have to be mathematically derived.
**Note: This is not necessary if your goal is solely optimizing a function**. For test problems, this is usually done to measure and visualize the performance of an algorithm.
The implementation of `func_pf` and `func_ps` looks as follows:
```
from pymoo.util.misc import stack
def func_pf(flatten=True, **kwargs):
f1_a = np.linspace(0.1**2, 0.4**2, 100)
f2_a = (np.sqrt(f1_a) - 1)**2
f1_b = np.linspace(0.6**2, 0.9**2, 100)
f2_b = (np.sqrt(f1_b) - 1)**2
a, b = np.column_stack([f1_a, f2_a]), np.column_stack([f1_b, f2_b])
return stack(a, b, flatten=flatten)
def func_ps(flatten=True, **kwargs):
x1_a = np.linspace(0.1, 0.4, 50)
x1_b = np.linspace(0.6, 0.9, 50)
x2 = np.zeros(50)
a, b = np.column_stack([x1_a, x2]), np.column_stack([x1_b, x2])
return stack(a,b, flatten=flatten)
```
This information can be passed to the definition via class or functions as follows:
#### Add to Class
```
import numpy as np
from pymoo.util.misc import stack
from pymoo.model.problem import Problem
class MyTestProblem(MyProblem):
def _calc_pareto_front(self, *args, **kwargs):
return func_pf(**kwargs)
def _calc_pareto_set(self, *args, **kwargs):
return func_ps(**kwargs)
test_problem = MyTestProblem()
```
#### Add to Function
```
from pymoo.model.problem import FunctionalProblem
functional_test_problem = FunctionalProblem(2,
objs,
constr_ieq=constr_ieq,
xl=-2,
xu=2,
func_pf=func_pf,
func_ps=func_ps
)
```
### Initialize the object
Choose the way you have defined your problem and initialize it:
```
problem = test_problem
```
Moreover, we would like to mention that in many test optimization problems, implementation already exists. For example, the test problem *ZDT1* can be initiated by:
```
from pymoo.factory import get_problem
zdt1 = get_problem("zdt1")
```
Our framework has various single- and many-objective optimization test problems already implemented. Furthermore, a more advanced guide for custom problem definitions is available. In case problem functions are computationally expensive, more sophisticated parallelization of the evaluation functions might be worth looking at.
[Optimization Test Problems](problems/index.ipynb) |
[Define a Custom Problem](problems/custom.ipynb) |
[Parallelization](problems/parallelization.ipynb) |
[Callback](interface/callback.ipynb) |
[Constraint Handling](misc/constraint_handling.ipynb)
## 3. Initialization of an Algorithm
Moreover, we need to initialize a method to optimize the problem.
In *pymoo*, factory methods create an `algorithm` object to be used for optimization. For each of those methods, an API documentation is available, and through supplying different parameters, algorithms can be customized in a plug-and-play manner.
Depending on the optimization problem, different algorithms can be used to optimize the problem. Our framework offers various [Algorithms](algorithms/index.ipynb), which can be used to solve problems with different characteristics.
In general, the choice of a suitable algorithm for optimization problems is a challenge itself. Whenever problem characteristics are known beforehand, we recommended using those through customized operators.
However, in our case, the optimization problem is rather simple, but the aspect of having two objectives and two constraints should be considered. We decided to use [NSGA-II](algorithms/nsga2.ipynb) with its default configuration with minor modifications. We chose a population size of 40 (`pop_size=40`) and decided instead of generating the same number of offsprings to create only 10 (`n_offsprings=40`). Such an implementation is a greedier variant and improves the convergence of rather simple optimization problems without difficulties regarding optimization, such as the existence of local Pareto fronts.
Moreover, we enable a duplicate check (`eliminate_duplicates=True`), making sure that the mating produces offsprings that are different from themselves and the existing population regarding their design space values. To illustrate the customization aspect, we listed the other unmodified default operators in the code snippet below.
```
from pymoo.algorithms.nsga2 import NSGA2
from pymoo.factory import get_sampling, get_crossover, get_mutation
algorithm = NSGA2(
pop_size=40,
n_offsprings=10,
sampling=get_sampling("real_random"),
crossover=get_crossover("real_sbx", prob=0.9, eta=15),
mutation=get_mutation("real_pm", eta=20),
eliminate_duplicates=True
)
```
The `algorithm` object contains the implementation of NSGA-II with the custom settings supplied to the factory method.
## 4. Definition of a Termination Criterion
Furthermore, a termination criterion needs to be defined to start the optimization procedure finally. Different kind of [Termination Criteria](interface/termination.ipynb) are available. Here, since the problem is rather simple, we run the algorithm for some number of generations.
```
from pymoo.factory import get_termination
termination = get_termination("n_gen", 40)
```
Instead of the number of generations (or iterations), other criteria such as the number of function evaluations or the improvement in design or objective space between generations can be used.
## 5. Optimize
Finally, we are solving the problem with the algorithm and termination criterion we have defined.
In *pymoo*, we provide two interfaces for solving an optimization problem:
- **Functional:** Commonly in Python, a function is used as a global interface. In pymoo, the `minimize` method is the most crucial method which is responsible for using an algorithm to solve a problem using
other attributes such as `seed`, `termination`, and others.
- **Object Oriented:** The object-oriented interface directly uses the algorithm object to perform an iteration.
This allows the flexibility of executing custom code very quickly between iterations. However, features already
implemented in the functional approach, such as displaying metrics, saving the history, or pre-defined callbacks, need to be incorporated manually.
Both ways have their benefits and drawbacks depending on the different use cases.
### Functional Interface
The functional interface is provided by the `minimize` method. By default, the method performs deep-copies of the algorithm and the termination object. Which means the objects are not altered during the function call. This ensures repetitive function calls end up with the same results. The `minimize` function returns the [Result](interface/result.ipynb) object, which provides attributes such as the optimum.
```
from pymoo.optimize import minimize
res = minimize(problem,
algorithm,
termination,
seed=1,
save_history=True,
verbose=True)
```
The [Result](interface/result.ipynb) object provides the corresponding X and F values and some more information.
### Object-Oriented Interface
On the contrary, the object-oriented approach directly modifies the algorithm object by calling the `next` method. Thus, it makes sense to create a deepcopy of the algorithm object beforehand, as shown in the code below.
In the while loop, the algorithm object can be accessed to be modified or for other purposes.
**NOTE**: In this guide, we have used the functional interface because the history is used during analysis.
```
import copy
# perform a copy of the algorithm to ensure reproducibility
obj = copy.deepcopy(algorithm)
# let the algorithm know what problem we are intending to solve and provide other attributes
obj.setup(problem, termination=termination, seed=1)
# until the termination criterion has not been met
while obj.has_next():
# perform an iteration of the algorithm
obj.next()
# access the algorithm to print some intermediate outputs
print(f"gen: {obj.n_gen} n_nds: {len(obj.opt)} constr: {obj.opt.get('CV').min()} ideal: {obj.opt.get('F').min(axis=0)}")
# finally obtain the result object
result = obj.result()
```
## 6. Visualization of Results and Convergence
### Results
The optimization results are illustrated below (design and objective space). The solid lines represent the analytically derived Pareto set, and front in the corresponding space, and the circles represent solutions found by the algorithm. It can be observed that the algorithm was able to converge, and a set of nearly-optimal solutions was obtained.
```
from pymoo.visualization.scatter import Scatter
# get the pareto-set and pareto-front for plotting
ps = problem.pareto_set(use_cache=False, flatten=False)
pf = problem.pareto_front(use_cache=False, flatten=False)
# Design Space
plot = Scatter(title = "Design Space", axis_labels="x")
plot.add(res.X, s=30, facecolors='none', edgecolors='r')
if ps is not None:
plot.add(ps, plot_type="line", color="black", alpha=0.7)
plot.do()
plot.apply(lambda ax: ax.set_xlim(-0.5, 1.5))
plot.apply(lambda ax: ax.set_ylim(-2, 2))
plot.show()
# Objective Space
plot = Scatter(title = "Objective Space")
plot.add(res.F)
if pf is not None:
plot.add(pf, plot_type="line", color="black", alpha=0.7)
plot.show()
```
Visualization is a vital post-processing step in multi-objective optimization. Although it seems to be pretty easy for our example optimization problem, it becomes much more difficult in higher dimensions where trade-offs between solutions are not readily observable. For visualizations in higher dimensions, various more advanced [Visualizations](visualization/index.ipynb) are implemented in our framework.
### Convergence
A not negligible step is the post-processing after having obtained the results. We strongly recommend not only analyzing the final result but also the algorithm's behavior. This gives more insights into the convergence of the algorithm.
For such an analysis, intermediant steps of the algorithm need to be considered. This can either be achieved by:
- A `Callback` class storing the necessary information in each iteration of the algorithm.
- Enabling the `save_history` flag when calling the minimize method to store a deepcopy of the algorithm's objective each iteration.
We provide some more details about each variant in our [convergence](misc/convergence.ipynb) tutorial.
As you might have already seen, we have set `save_history=True` when calling the `minmize` method in this getting started guide and, thus, will you the `history` for our analysis. Moreover, we need to decide what metric should be used to measure the performance of our algorithm. In this tutorial, we are going to use `Hypervolume` and `IGD`. Feel free to look at our [performance indicators](misc/performance_indicator.ipynb) to find more information about metrics to measure the performance of multi-objective algorithms.
As a first step we have to extract the population in each generation of the algorithm. We extract the constraint violation (`cv`), the objective space values (`F`) and the number of function evaluations (`n_evals`) of the corresponding generation.
```
n_evals = [] # corresponding number of function evaluations\
F = [] # the objective space values in each generation
cv = [] # constraint violation in each generation
# iterate over the deepcopies of algorithms
for algorithm in res.history:
# store the number of function evaluations
n_evals.append(algorithm.evaluator.n_eval)
# retrieve the optimum from the algorithm
opt = algorithm.opt
# store the least contraint violation in this generation
cv.append(opt.get("CV").min())
# filter out only the feasible and append
feas = np.where(opt.get("feasible"))[0]
_F = opt.get("F")[feas]
F.append(_F)
```
**NOTE:** If your problem has different scales on the objectives (e.g. first objective in range of [0.1, 0.2] and the second objective [100, 10000] you **HAVE** to normalize to measure the performance in a meaningful way! This example assumes no normalization is necessary to keep things a bit simple.
### Constraint Violation (CV)
Here, in the first generation, a feasible solution was already found.
Since the constraints of the problem are rather simple, the constraints are already satisfied in the initial population.
```
import matplotlib.pyplot as plt
k = min([i for i in range(len(cv)) if cv[i] <= 0])
first_feas_evals = n_evals[k]
print(f"First feasible solution found after {first_feas_evals} evaluations")
plt.plot(n_evals, cv, '--', label="CV")
plt.scatter(first_feas_evals, cv[k], color="red", label="First Feasible")
plt.xlabel("Function Evaluations")
plt.ylabel("Constraint Violation (CV)")
plt.legend()
plt.show()
```
### Hypvervolume (HV)
Hypervolume is a very well-known performance indicator for multi-objective problems. It is known to be pareto-compliant and is based on the volume between a predefined reference point and the solution provided. Hypervolume requires to define a reference point `ref_point` which shall be larger than the maximum value of the Pareto front.
**Note:** Hypervolume becomes computationally expensive with increasing dimensionality. The exact hypervolume can be calculated efficiently for 2 and 3 objectives. For higher dimensions, some researchers use a hypervolume approximation, which is not available yet in pymoo.
```
import matplotlib.pyplot as plt
from pymoo.performance_indicator.hv import Hypervolume
# MODIFY - this is problem dependend
ref_point = np.array([1.0, 1.0])
# create the performance indicator object with reference point
metric = Hypervolume(ref_point=ref_point, normalize=False)
# calculate for each generation the HV metric
hv = [metric.calc(f) for f in F]
# visualze the convergence curve
plt.plot(n_evals, hv, '-o', markersize=4, linewidth=2)
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("Hypervolume")
plt.show()
```
### IGD
For IGD the Pareto front needs to be known or to be approximated.
In our framework the Pareto front of **test problems** can be obtained by:
```
pf = problem.pareto_front(flatten=True, use_cache=False)
```
For real-world problems, you have to use an **approximation**. An approximation can be obtained by running an algorithm a couple of times and extracting the non-dominated solutions out of all solution sets. If you have only a single run, an alternative is to use the obtain a non-dominated set of solutions as an approximation. However, the result does then only indicate how much the algorithm's progress in converging to the final set.
```
import matplotlib.pyplot as plt
from pymoo.performance_indicator.igd import IGD
if pf is not None:
# for this test problem no normalization for post prcessing is needed since similar scales
normalize = False
metric = IGD(pf=pf, normalize=normalize)
# calculate for each generation the HV metric
igd = [metric.calc(f) for f in F]
# visualze the convergence curve
plt.plot(n_evals, igd, '-o', markersize=4, linewidth=2, color="green")
plt.yscale("log") # enable log scale if desired
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("IGD")
plt.show()
```
### Running Metric
Another way of analyzing a run when the true Pareto front is **not** known is using are recently proposed [running metric](https://www.egr.msu.edu/~kdeb/papers/c2020003.pdf). The running metric shows the difference in the objective space from one generation to another and uses the algorithm's survival to visualize the improvement.
This metric is also being used in pymoo to determine the termination of a multi-objective optimization algorithm if no default termination criteria have been defined.
For instance, this analysis reveals that the algorithm was able to improve from the 4th to the 5th generation significantly.
```
from pymoo.util.running_metric import RunningMetric
running = RunningMetric(delta_gen=5,
n_plots=3,
only_if_n_plots=True,
key_press=False,
do_show=True)
for algorithm in res.history[:15]:
running.notify(algorithm)
```
Plotting until the final population shows the the algorithm seems to have more a less converged and only a small improvement has been made.
```
from pymoo.util.running_metric import RunningMetric
running = RunningMetric(delta_gen=10,
n_plots=4,
only_if_n_plots=True,
key_press=False,
do_show=True)
for algorithm in res.history:
running.notify(algorithm)
```
## 7. Summary
We hope you have enjoyed the getting started guide. For more topics we refer to each section covered by on the [landing page](https://pymoo.org). If you have any question or concern do not hesitate to [contact us](contact.rst).
### Citation
If you have used **pymoo** for research purposes please refer to our framework in your reports or publication by:
## 8. Source Code
In this guide, we have provided a couple of options on defining your problem and how to run the optimization.
You might have already copied the code into your IDE. However, if not, the following code snippets cover the problem definition, algorithm initializing, solving the optimization problem, and visualization of the non-dominated set of solutions altogether.
```
import numpy as np
from pymoo.algorithms.nsga2 import NSGA2
from pymoo.model.problem import Problem
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter
class MyProblem(Problem):
def __init__(self):
super().__init__(n_var=2,
n_obj=2,
n_constr=2,
xl=np.array([-2, -2]),
xu=np.array([2, 2]),
elementwise_evaluation=True)
def _evaluate(self, x, out, *args, **kwargs):
f1 = x[0] ** 2 + x[1] ** 2
f2 = (x[0] - 1) ** 2 + x[1] ** 2
g1 = 2 * (x[0] - 0.1) * (x[0] - 0.9) / 0.18
g2 = - 20 * (x[0] - 0.4) * (x[0] - 0.6) / 4.8
out["F"] = [f1, f2]
out["G"] = [g1, g2]
problem = MyProblem()
algorithm = NSGA2(pop_size=100)
res = minimize(problem,
algorithm,
("n_gen", 100),
verbose=True,
seed=1)
plot = Scatter()
plot.add(res.F, color="red")
plot.show()
```
| true |
code
| 0.57332 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
from prml.utils.datasets import load_mnist,load_iris
from prml.kernel_method import BaseKernelMachine
```
# PCA
```
class PCA():
"""PCA
Attributes:
X_mean (1-D array): mean of data
weight (2-D array): proj matrix
importance (1-D array): contirbution of ratio
"""
def __init__(self):
pass
def fit(self,X):
"""fit
Args:
X (2-D array): shape = (N_samples,N_dim), data
"""
N = X.shape[0]
X_mean = X.mean(axis = 0)
S = (X - X_mean).T@(X - X_mean)/N
eig_val,eig_vec = np.linalg.eigh(S)
eig_val,eig_vec = np.real(eig_val),np.real(eig_vec.real)
idx = np.argsort(eig_val)[::-1]
eig_val,eig_vec = eig_val[idx],eig_vec[:,idx]
self.X_mean = X_mean
self.importance = eig_val/eig_val.sum()
self.weight = eig_vec
def transform(self,X,M,return_importance=False,whitening=False):
"""transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, if M > N_dim, M = N_dim
return_importance (bool): return importance or not
whitening (bool): if whitening or not
Retunrs:
X_proj (2-D array): shape = (N_samples,M), projected data
impotance_rate (float): how important X_proj is
"""
if whitening:
return (X-self.X_mean)@self.weight[:,:M]/np.sqrt(self.importance[:M])
elif return_importance:
return [email protected][:,:M],self.importance[:M].sum()
else:
return [email protected][:,:M]
def fit_transform(self,X,M,return_importance=False,whitening=False):
"""fit_transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, if M > N_dim, M = N_dim
return_importance (bool): return importance or not
whitening (bool): if whitening or not
Retunrs:
X_proj (2-D array): shape = (N_samples,M), projected data
impotance_rate (float): how important X_proj is
"""
self.fit(X)
return self.transform(X,M,return_importance,whitening)
X,y = load_iris()
pca = PCA()
X_proj = pca.fit_transform(X,2,whitening=True)
fig,axes = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
axes.scatter(x=X_proj[y == label,0],
y=X_proj[y == label,1],
alpha=0.8,
label=label)
axes.set_title("iris PCA (4dim -> 2dim)")
plt.legend()
plt.show()
```
### mnist image compression
```
X,y = load_mnist([3])
X = X[:600].reshape(-1,28*28)
X_mean = X.mean(axis=0)
pca = PCA()
pca.fit(X)
img = X[0]
fig = plt.figure(figsize=(10,7))
ax = fig.add_subplot(231)
ax.imshow(img.reshape(28,28))
ax.set_title("original image")
ax.axis("off")
img = img.ravel()
weight = pca.weight
approximate = np.dot(weight.T,img - X_mean)*weight
for n,M in enumerate([1,10,50,100,250]):
ax = fig.add_subplot(int(f"23{n+2}"))
img_proj = X_mean + np.sum(approximate[:,:M],axis = 1)
i,j = (n+1)//2,(n+1)%3
ax.imshow(img_proj.reshape(28,28))
ax.set_title(f"M = {M}")
ax.axis("off")
plt.show()
```
# ProbabilisticPCA
```
class ProbabilisticPCA():
"""ProbabilisticPCA
find parameter by maximum likelihood method, O(D^3)
Attributes:
D (int): original dim of data
mu (1-D array): mean of data
W (2-D array): param of density of data
sigma (float): param of density of data
U (2-D array): eigen vectors of covariance matrix of data
lamda (1-D array): eigen values of covariance matrix of data
"""
def __init__(self) -> None:
pass
def fit(self,X):
"""
Args:
X (2-D array): shape = (N_samples,N_dim), data
"""
N = X.shape[0]
X_mean = X.mean(axis = 0)
S = (X - X_mean).T@(X - X_mean)/N
eig_val,eig_vec = np.linalg.eigh(S)
eig_val,eig_vec = np.real(eig_val),np.real(eig_vec.real)
idx = np.argsort(eig_val)[::-1]
eig_val,eig_vec = eig_val[idx],eig_vec[:,idx]
self.D = X.shape[1]
self.mu = X_mean
self.U = eig_vec
self.lamda = eig_val
def transform(self,X,M):
"""transform
after this method is called, attribute W,sigma can be used
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, M is less than X.shape[1]
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
if self.D == M:
raise ValueError("M is less than X.shape[1]")
sigma = np.mean(self.lamda[M:])
W = self.U[:,:M]@(np.diag((self.lamda[:M] - sigma)**0.5))
Mat = W.T@W + sigma*np.eye(M)
proj_weight = [email protected](Mat) # x -> z
return (X - self.mu)@proj_weight
def fit_transform(self,X,M):
"""fit_transform
after this method is called, attribute W,sigma can be used
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, M is less than X.shape[1]
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
self.fit(X)
return self.transform(X,M)
X,y = load_iris()
ppca = ProbabilisticPCA()
X_proj = ppca.fit_transform(X,2)
fig,axes = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
axes.scatter(x=X_proj[y == label,0],
y=X_proj[y == label,1],
alpha=0.8,
label=label)
axes.set_title("iris PCA (4dim -> 2dim)")
plt.legend()
plt.show()
```
# Probablistic PCA
```
class ProbabilisticPCAbyEM():
"""ProbabilisticPCAbyEM
Attributes:
M (int): dimension of latent variables
mu (1-D array): mean of data
W (2-D array): param of density of data
sigma (float): param of density of data
"""
def __init__(self,max_iter=100,threshold=1e-5) -> None:
"""
Args:
max_iter (int): maximum iteration
threshold (float): threshold
"""
self.max_iter = max_iter
self.threshold = threshold
def fit(self,X,M,find_M=False,alpha_limit=10):
"""
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): dimension of latent variables
find_M (bool): if appropriate M will be found or not, if this is True, appropriate_M <= M
alpha_limit (float): if alpha is more than this, this component is removed
"""
N = X.shape[0]
D = X.shape[1]
# init param
self.mu = X.mean(axis = 0)
W = np.random.randn(D,M)
sigma = np.random.rand() + 1e-1
if find_M:
alpha = np.random.rand(M) + 1e-1
Y = X - self.mu
Ysum = np.sum(Y**2)
for _ in range(self.max_iter):
# E step
Mat = W.T@W + sigma*np.eye(M)
Minv = np.linalg.inv(Mat)
E_z = Y@W@Minv
E_zz = sigma*Minv + E_z.reshape(-1,M,1)@E_z.reshape(-1,1,M)
# M step
if find_M:
W_new = Y.T@[email protected](E_zz.sum(axis = 0) + sigma*np.diag(alpha))
else:
W_new = Y.T@[email protected](E_zz.sum(axis = 0))
sigma_new = (Ysum - 2*np.diag(E_z@[email protected]).sum() + np.diag(np.sum(E_zz@W_new.T@W_new,axis=0)).sum())/(N*D)
diff = ((sigma_new - sigma)**2 + np.mean((W_new - W)**2)) ** 0.5
if diff < self.threshold:
W = W_new
sigma = sigma_new
break
W = W_new
sigma = sigma_new
if find_M:
alpha = D/np.diag(W.T@W)
idx = alpha < alpha_limit
alpha = alpha[idx]
W = W[:,idx]
M = idx.astype("int").sum()
self.M = M
self.W = W
self.sigma = sigma
def transform(self,X):
"""transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
Note:
unlike other method you should choose M when you call `fit()`
"""
Mat = [email protected] + self.sigma*np.eye(self.M)
proj_weight = [email protected](Mat) # x -> z
return (X - self.mu)@proj_weight
def fit_transform(self,X,M,find_M=False,alpha_limit=10):
"""fit_transform
after this method is called, attribute W,sigma can be used
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, M is less than X.shape[1]
find_M (bool): if appropriate M will be found or not, if this is True, appropriate_M <= M
alpha_limit (float): if alpha is more than this, this component is removed
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
self.fit(X,M,find_M,alpha_limit)
return self.transform(X)
```
you can find appropriate `M` by EM algorhithm
```
X,y = load_iris()
em = ProbabilisticPCAbyEM(max_iter=1000)
X_proj = em.fit_transform(X,4,find_M=True)
M = X_proj.shape[1]
if M == 1:
fig,ax = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
ax.hist(x=X_proj[y == label,0],
alpha=0.8,
label=label)
ax.set_title("iris PCA by EM (4dim -> 1dim)")
plt.legend()
plt.show()
elif M == 2:
fig,axes = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
axes.scatter(x=X_proj[y == label,0],
y=X_proj[y == label,1],
alpha=0.8,
label=label)
axes.set_title("mnist PCA by EM (10dim -> 2dim)")
plt.legend()
plt.show()
else:
print(f"M = {M} >= 3 ...")
```
# Factor Analysis
```
class FactorAnalysis():
"""FactorAnalysis
"""
def __init__(self,max_iter=100,threshold=1e-5) -> None:
"""
Args:
max_iter (int): maximum iteration
threshold (float): threshold
"""
self.max_iter = max_iter
self.threshold = threshold
def fit(self,X,M):
"""fit
"""
N = X.shape[0]
D = X.shape[1]
self.mu = X.mean(axis = 0)
W = np.random.randn(D,M)
Sigma = np.random.rand(D) + 1e-1
Y = X - self.mu
S = Y.T@Y/N
for _ in range(self.max_iter):
# E step
G = np.linalg.inv(np.eye(M) + (W.T/Sigma)@W)
E_z = Y/Sigma@[email protected]
E_zz = G + E_z.reshape(-1,M,1)@E_z.reshape(-1,1,M)
# M step
W_new = Y.T@[email protected](E_zz.sum(axis = 0))
Sigma_new = np.diag(S - W_new@E_z.T@Y/N)
diff = (np.mean((Sigma_new - Sigma)**2) + np.mean((W_new - W)**2))**0.5
if diff < self.threshold:
W = W_new
Sigma = Sigma_new
break
W = W_new
Sigma = Sigma_new
self.W = W
self.Sigma = Sigma
self.G = G = np.linalg.inv(np.eye(M) + (W.T/Sigma)@W)
def transform(self,X):
"""transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
return (X - self.mu)/[email protected]@self.G.T
def fit_transform(self,X,M):
"""fit_transform
after this method is called, attribute W,sigma can be used
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, M is less than X.shape[1]
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
self.fit(X,M)
return self.transform(X)
X,y = load_iris()
fa = FactorAnalysis()
X_proj = fa.fit_transform(X,M=2)
fig,axes = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
axes.scatter(x=X_proj[y == label,0],
y=X_proj[y == label,1],
alpha=0.8,
label=label)
axes.set_title("iris Factor Analysis (4dim -> 2dim)")
plt.legend()
plt.show()
```
# Kernel PCA
```
class KernelPCA(BaseKernelMachine):
"""KernelPCA
Attributes:
a (2-D array): projection weight of pca
kernel_func (function) : kernel function k(x,y)
gram_func (function) : function which make gram matrix
"""
def __init__(self,kernel="Linear",sigma=0.1,a=1.0,b=0.0,h=None,theta=1.0):
"""
Args:
kernel (string) : kernel type (default "Linear"). you can choose "Linear","Gaussian","Sigmoid","RBF","Exponential"
sigma (float) : for "Gaussian" kernel
a,b (float) : for "Sigmoid" kernel
h (function) : for "RBF" kernel
theta (float) : for "Exponential" kernel
"""
super(KernelPCA,self).__init__(kernel=kernel,sigma=sigma,a=a,b=b,h=h,theta=theta)
def fit(self,X):
"""
Args:
X (2-D array): shape = (N_samples,N_dim), data
"""
# make gram mat
N = X.shape[0]
gram_mat = self.gram_func(X)
divN = np.ones((N,N))/N
K = gram_mat - divN@gram_mat - gram_mat@divN + divN@gram_mat@divN
# eig
eig_val,eig_vec = np.linalg.eigh(K)
eig_val,eig_vec = np.real(eig_val),np.real(eig_vec.real)
idx = np.argsort(eig_val)[::-1]
eig_val,eig_vec = eig_val[idx],eig_vec[:,idx]
plus = eig_val > 0
eig_val,eig_vec = eig_val[plus],eig_vec[:,plus] # if dimension of kernel space is lower than N, K can have eigen values of 0
eig_vec /= eig_val**0.5
self.a = eig_vec
self.X = X
def transform(self,X,M):
"""transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
gram_mat = np.zeros((self.X.shape[0],X.shape[0]))
for i in range(self.X.shape[0]):
gram_mat[i] = np.array([self.kernel_func(self.X[i],X[j]) for j in range(X.shape[0])])
return [email protected][:,:M]
def fit_transform(self,X,M):
"""fit_transform
Args:
X (2-D array): shape = (N_samples,N_dim), data
M (int): number of principal component, M is less than X.shape[1]
Returns:
X_proj (2-D array): shape = (N_samples,M), projected data
"""
self.fit(X)
return self.transform(X,M)
X,y = load_iris()
kpca = KernelPCA(kernel="Gaussian",sigma=3.0)
X_proj = kpca.fit_transform(X,2)
fig,axes = plt.subplots(1,1,figsize=(10,7))
for idx,label in enumerate(np.unique(y)):
axes.scatter(x=X_proj[y == label,0],
y=X_proj[y == label,1],
alpha=0.8,
label=label)
axes.set_title("iris KPCA (4im -> 2dim)")
plt.legend()
plt.show()
```
| true |
code
| 0.777743 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/PacktPublishing/Hands-On-Computer-Vision-with-PyTorch/blob/master/Chapter11/Generating_deep_fakes.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import os
if not os.path.exists('Faceswap-Deepfake-Pytorch'):
!wget -q https://www.dropbox.com/s/5ji7jl7httso9ny/person_images.zip
!wget -q https://raw.githubusercontent.com/sizhky/deep-fake-util/main/random_warp.py
!unzip -q person_images.zip
!pip install -q torch_snippets torch_summary
from torch_snippets import *
from random_warp import get_training_data
face_cascade = cv2.CascadeClassifier(cv2.data.haarcascades + 'haarcascade_frontalface_default.xml')
def crop_face(img):
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
faces = face_cascade.detectMultiScale(gray, 1.3, 5)
if(len(faces)>0):
for (x,y,w,h) in faces:
img2 = img[y:(y+h),x:(x+w),:]
img2 = cv2.resize(img2,(256,256))
return img2, True
else:
return img, False
!mkdir cropped_faces_personA
!mkdir cropped_faces_personB
def crop_images(folder):
images = Glob(folder+'/*.jpg')
for i in range(len(images)):
img = read(images[i],1)
img2, face_detected = crop_face(img)
if(face_detected==False):
continue
else:
cv2.imwrite('cropped_faces_'+folder+'/'+str(i)+'.jpg',cv2.cvtColor(img2, cv2.COLOR_RGB2BGR))
crop_images('personA')
crop_images('personB')
class ImageDataset(Dataset):
def __init__(self, items_A, items_B):
self.items_A = np.concatenate([read(f,1)[None] for f in items_A])/255.
self.items_B = np.concatenate([read(f,1)[None] for f in items_B])/255.
self.items_A += self.items_B.mean(axis=(0, 1, 2)) - self.items_A.mean(axis=(0, 1, 2))
def __len__(self):
return min(len(self.items_A), len(self.items_B))
def __getitem__(self, ix):
a, b = choose(self.items_A), choose(self.items_B)
return a, b
def collate_fn(self, batch):
imsA, imsB = list(zip(*batch))
imsA, targetA = get_training_data(imsA, len(imsA))
imsB, targetB = get_training_data(imsB, len(imsB))
imsA, imsB, targetA, targetB = [torch.Tensor(i).permute(0,3,1,2).to(device) for i in [imsA, imsB, targetA, targetB]]
return imsA, imsB, targetA, targetB
a = ImageDataset(Glob('cropped_faces_personA'), Glob('cropped_faces_personB'))
x = DataLoader(a, batch_size=32, collate_fn=a.collate_fn)
inspect(*next(iter(x)))
for i in next(iter(x)):
subplots(i[:8], nc=4, sz=(4,2))
def _ConvLayer(input_features, output_features):
return nn.Sequential(
nn.Conv2d(input_features, output_features, kernel_size=5, stride=2, padding=2),
nn.LeakyReLU(0.1, inplace=True)
)
def _UpScale(input_features, output_features):
return nn.Sequential(
nn.ConvTranspose2d(input_features, output_features, kernel_size=2, stride=2, padding=0),
nn.LeakyReLU(0.1, inplace=True)
)
class Reshape(nn.Module):
def forward(self, input):
output = input.view(-1, 1024, 4, 4) # channel * 4 * 4
return output
class Autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
self.encoder = nn.Sequential(
_ConvLayer(3, 128),
_ConvLayer(128, 256),
_ConvLayer(256, 512),
_ConvLayer(512, 1024),
nn.Flatten(),
nn.Linear(1024 * 4 * 4, 1024),
nn.Linear(1024, 1024 * 4 * 4),
Reshape(),
_UpScale(1024, 512),
)
self.decoder_A = nn.Sequential(
_UpScale(512, 256),
_UpScale(256, 128),
_UpScale(128, 64),
nn.Conv2d(64, 3, kernel_size=3, padding=1),
nn.Sigmoid(),
)
self.decoder_B = nn.Sequential(
_UpScale(512, 256),
_UpScale(256, 128),
_UpScale(128, 64),
nn.Conv2d(64, 3, kernel_size=3, padding=1),
nn.Sigmoid(),
)
def forward(self, x, select='A'):
if select == 'A':
out = self.encoder(x)
out = self.decoder_A(out)
else:
out = self.encoder(x)
out = self.decoder_B(out)
return out
from torchsummary import summary
model = Autoencoder()
summary(model, torch.zeros(32,3,64,64), 'A');
def train_batch(model, data, criterion, optimizes):
optA, optB = optimizers
optA.zero_grad()
optB.zero_grad()
imgA, imgB, targetA, targetB = data
_imgA, _imgB = model(imgA, 'A'), model(imgB, 'B')
lossA = criterion(_imgA, targetA)
lossB = criterion(_imgB, targetB)
lossA.backward()
lossB.backward()
optA.step()
optB.step()
return lossA.item(), lossB.item()
model = Autoencoder().to(device)
dataset = ImageDataset(Glob('cropped_faces_personA'), Glob('cropped_faces_personB'))
dataloader = DataLoader(dataset, 32, collate_fn=dataset.collate_fn)
optimizers = optim.Adam([{'params': model.encoder.parameters()},
{'params': model.decoder_A.parameters()}],
lr=5e-5, betas=(0.5, 0.999)), \
optim.Adam([{'params': model.encoder.parameters()},
{'params': model.decoder_B.parameters()}],
lr=5e-5, betas=(0.5, 0.999))
criterion = nn.L1Loss()
n_epochs = 10000
log = Report(n_epochs)
!mkdir checkpoint
for ex in range(n_epochs):
N = len(dataloader)
for bx,data in enumerate(dataloader):
lossA, lossB = train_batch(model, data, criterion, optimizers)
log.record(ex+(1+bx)/N, lossA=lossA, lossB=lossB, end='\r')
log.report_avgs(ex+1)
if (ex+1)%100 == 0:
state = {
'state': model.state_dict(),
'epoch': ex
}
torch.save(state, './checkpoint/autoencoder.pth')
if (ex+1)%100 == 0:
bs = 5
a,b,A,B = data
line('A to B')
_a = model(a[:bs], 'A')
_b = model(a[:bs], 'B')
x = torch.cat([A[:bs],_a,_b])
subplots(x, nc=bs, figsize=(bs*2, 5))
line('B to A')
_a = model(b[:bs], 'A')
_b = model(b[:bs], 'B')
x = torch.cat([B[:bs],_a,_b])
subplots(x, nc=bs, figsize=(bs*2, 5))
log.plot_epochs()
```
| true |
code
| 0.757744 | null | null | null | null |
|
# Overfitting Figure Generation
We're going to generate `n_points` points distributed along a line, remembering that the formula for a line is $y = mx+b$. Modified (slightly) from [here](https://stackoverflow.com/a/35730618/8068638).
```
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
n_points = 12
m = 1
b = 0
training_delta = 1.0
test_points_offset = 0.5
test_points_jitter = 0.1
test_delta = 1.0
np.random.seed(3)
```
Now, we need to generate the testing and training "data"
```
points_x = np.arange(n_points)
training_delta = np.random.uniform(-training_delta, training_delta, size=(n_points))
training_points_y = m*points_x + b + training_delta
testing_points_x = points_x + np.random.uniform(-test_points_jitter, test_points_jitter, size=(n_points)) + test_points_offset
testing_delta = np.random.uniform(-test_delta, test_delta, size=(n_points))
testing_points_y = m*testing_points_x + b + testing_delta
```
We'll overfit by generating a $n$-dimensional polynomial
```
overfitted = np.poly1d(np.polyfit(points_x, training_points_y, n_points - 1))
x_space = np.linspace(-(n_points/5), 2*n_points+(n_points/5), n_points*100)
overfitted_x_space = np.linspace(-(n_points/5), 2*n_points+(n_points/5), n_points*100)
y_overfitted = overfitted(x_space)
```
## Plot it
Colors chosen from [Wong, B. (2011). Points of view: Color blindness. *Nature Methods, 8*(6), 441–441. doi:10.1038/nmeth.1618](doi.org/10.1038/nmeth.1618). I had to do some magic to make the arrays colors play nicely with matplotlib
```
def rgb_to_np_rgb(r, g, b):
return (r / 255, g / 255, b / 255)
orange = rgb_to_np_rgb(230, 159, 0)
blueish_green = rgb_to_np_rgb(0, 158, 115)
vermillion = rgb_to_np_rgb(213, 94, 0)
blue = rgb_to_np_rgb(0, 114, 178)
# configure the plot
plt.rcParams["figure.figsize"] = (12.8 * 0.75, 9.6 * 0.75)
plt.rcParams['svg.fonttype'] = 'path'
plt.rcParams['axes.spines.left'] = True
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False
plt.rcParams['axes.spines.bottom'] = True
plt.rcParams["xtick.labelbottom"] = False
plt.rcParams["xtick.bottom"] = False
plt.rcParams["ytick.left"] = False
plt.rcParams["ytick.labelleft"] = False
plt.xkcd() # for fun (see https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1003858#s12)
# plot the data
plt.scatter(points_x, training_points_y, zorder=3,label="Training data", s=100, c=[blue])
plt.scatter(testing_points_x, testing_points_y, zorder=3,label="Test data", s=100, c=[vermillion])
plt.plot(x_space, m*x_space + b, zorder=2, label="Properly fit model", c=blueish_green)
plt.plot(x_space, y_overfitted, zorder=1, label="Overfit model", c=orange)
plt.xlim(-(n_points/5) - 1, max(testing_points_x) + 1)
plt.ylim(-(n_points/5) - 1, max(testing_points_y)+(n_points/5) + 1)
# plt.rcParams["figure.figsize"] = [6.4*2, 4.8*2]
plt.legend(loc=2)
plt.savefig('overfitting.svg', bbox_inches='tight')
plt.savefig('overfitting.png', dpi=150, bbox_inches='tight')
```
| true |
code
| 0.648411 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#EDA-and-pre-processing" data-toc-modified-id="EDA-and-pre-processing-1"><span class="toc-item-num">1 </span>EDA and pre-processing</a></span><ul class="toc-item"><li><span><a href="#Descriptive-statistics-(data-shape,-balance,-etc)" data-toc-modified-id="Descriptive-statistics-(data-shape,-balance,-etc)-1.1"><span class="toc-item-num">1.1 </span>Descriptive statistics (data shape, balance, etc)</a></span></li><li><span><a href="#Data-pre-processing" data-toc-modified-id="Data-pre-processing-1.2"><span class="toc-item-num">1.2 </span>Data pre-processing</a></span></li></ul></li><li><span><a href="#ML-template-starts---training-session" data-toc-modified-id="ML-template-starts---training-session-2"><span class="toc-item-num">2 </span>ML template starts - training session</a></span><ul class="toc-item"><li><span><a href="#Training-model-(LGBM)-with-stratisfied-CV" data-toc-modified-id="Training-model-(LGBM)-with-stratisfied-CV-2.1"><span class="toc-item-num">2.1 </span>Training model (LGBM) with stratisfied CV</a></span></li></ul></li><li><span><a href="#Model-evaluation" data-toc-modified-id="Model-evaluation-3"><span class="toc-item-num">3 </span>Model evaluation</a></span><ul class="toc-item"><li><span><a href="#Plot-of-the-CV-folds---F1-macro-and-F1-for-the-positive-class" data-toc-modified-id="Plot-of-the-CV-folds---F1-macro-and-F1-for-the-positive-class-3.1"><span class="toc-item-num">3.1 </span>Plot of the CV folds - F1 macro and F1 for the positive class</a></span></li><li><span><a href="#Scikit-learn---Classification-report" data-toc-modified-id="Scikit-learn---Classification-report-3.2"><span class="toc-item-num">3.2 </span>Scikit learn - Classification report</a></span></li><li><span><a href="#ROC-curve-with-AUC" data-toc-modified-id="ROC-curve-with-AUC-3.3"><span class="toc-item-num">3.3 </span>ROC curve with AUC</a></span></li><li><span><a href="#Confusion-Matrix-plot-(normalized-and-with-absolute-values)" data-toc-modified-id="Confusion-Matrix-plot-(normalized-and-with-absolute-values)-3.4"><span class="toc-item-num">3.4 </span>Confusion Matrix plot (normalized and with absolute values)</a></span></li><li><span><a href="#Feature-Importance-plot" data-toc-modified-id="Feature-Importance-plot-3.5"><span class="toc-item-num">3.5 </span>Feature Importance plot</a></span></li><li><span><a href="#Correlations-analysis-(on-top-features)" data-toc-modified-id="Correlations-analysis-(on-top-features)-3.6"><span class="toc-item-num">3.6 </span>Correlations analysis (on top features)</a></span></li><li><span><a href="#Anomaly-detection-on-the-training-set-(on-top-features-alone)" data-toc-modified-id="Anomaly-detection-on-the-training-set-(on-top-features-alone)-3.7"><span class="toc-item-num">3.7 </span>Anomaly detection on the training set (on top features alone)</a></span></li><li><span><a href="#Data-leakage-test" data-toc-modified-id="Data-leakage-test-3.8"><span class="toc-item-num">3.8 </span>Data leakage test</a></span></li>
<li><span><a href="##-Analysis-of-FPs/FNs" data-toc-modified-id="##-Analysis-of-FPs/FNs"><span class="toc-item-num">3.9 </span>Analysis of FPs/FNs</a></span></li></ul></li></ul></div>
```
import warnings
import pandas as pd
import numpy as np
from pandas_summary import DataFrameSummary
import octopus_ml as oc
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import seaborn as sns
import re
import optuna
pd.set_option('display.max_columns', None) # or 1000
pd.set_option('display.max_rows', None) # or 1000
pd.set_option('display.max_colwidth', -1) # or 199
%matplotlib inline
warnings.simplefilter("ignore")
```
### Read the Kaggle Titanic competition dataset
https://www.kaggle.com/c/titanic
```
pwd
XY_df=pd.read_csv('../../datasets/Kaggle_titanic_train.csv')
test_df=pd.read_csv('../../datasets/Kaggle_titanic_test.csv')
```
# EDA and pre-processing
## Descriptive statistics (data shape, balance, etc)
```
XY_df.shape
XY_df.head(5)
```
### Target distribution
```
XY_df['Survived'].value_counts()
oc.target_pie(XY_df,'Survived')
XY_df.shape
def convert_to_categorical(df):
categorical_features = []
for c in df.columns:
col_type = df[c].dtype
if col_type == "object" or col_type.name == "category":
# an option in case the data(pandas dataframe) isn't passed with the categorical column type
df[c] = df[c].astype('category')
categorical_features.append(c)
return df, categorical_features
def lgbm_fast(X_train, y_train, num, params=None):
# Training function for LGBM with basic categorical features treatment and close to default params
X_train, categorical_features=convert_to_categorical(X_train)
lgb_train = lgb.Dataset(X_train, y_train, categorical_feature=categorical_features)
if params == None:
params = {
"objective": "binary",
"boosting": "gbdt",
"scale_pos_weight": 0.02,
"learning_rate": 0.005,
"seed": 100,
"verbose":-1
# 'categorical_feature': 'auto',
# 'metric': 'auc',
# 'scale_pos_weight':0.1,
# 'learning_rate': 0.02,
# 'num_boost_round':2000,
# "min_sum_hessian_in_leaf":1,
# 'max_depth' : 100,
# "num_leaves":31,
# "bagging_fraction" : 0.4,
# "feature_fraction" : 0.05,
}
clf = lgb.train(
params, lgb_train, num_boost_round=num
)
return clf
```
## Dataset comparisons
```
features=XY_df.columns.to_list()
print ('number of features ', len(features))
features_remove=['PassengerId','Survived']
for f in features_remove:
features.remove(f)
def dataset_comparison(df1,df2, top=3):
print ('Datasets shapes:\n df1: '+str(df1.shape)+'\n df2: '+str(df2.shape))
df1['label']=0
df2['label']=1
df=pd.concat([df1,df2])
print (df.shape)
clf=lgbm_fast(df,df['label'], 100, params=None)
oc.plot_imp( clf, df, title="Datasets differences", model="lgbm", num=12, importaince_type="split", save_path=None)
return df
df=dataset_comparison(XY_df[features],test_df)
import lightgbm as lgb
def dataset_comparison(df1,df2, top=3):
print ('Datasets shapes:\n df1: '+str(df1.shape)+'\n df2: '+str(df2.shape))
df1['label']=0
df2['label']=1
df=pd.concat([df1,df2])
print (df.shape)
clf=lgbm_fast(df,df['label'], 100, params=None)
feature_imp_list=oc.plot_imp( clf, df, title="Datasets differences", model="lgbm", num=10, importaince_type="gain", save_path=None)
oc.target_corr(df,df['label'],feature_imp_list)
return df
df=dataset_comparison(XY_df[features],test_df)
df[1700:1800]
```
### Selected features vs target historgrams
```
oc.hist_target(XY_df, 'Sex', 'Survived')
oc.hist_target(XY_df, 'Fare', 'Survived')
```
### Data summary - and missing values analysis
```
import missingno as msno
from pandas_summary import DataFrameSummary
dfs = DataFrameSummary(XY_df)
dfs.summary()
# Top 5 sparse features, mainly labs results
pd.Series(1 - XY_df.count() / len(XY_df)).sort_values(ascending=False).head(5)
```
## Data pre-processing
```
XY_df['Cabin'] = XY_df['Cabin'].astype('str').fillna("U0")
deck = {"A": 1, "B": 2, "C": 3, "D": 4, "E": 5, "F": 6, "G": 7, "U": 8}
XY_df['Deck'] = XY_df['Cabin'].map(lambda x: re.compile("([a-zA-Z]+)").search(x).group())
XY_df['Deck'] = XY_df['Deck'].map(deck)
XY_df['Deck'] = XY_df['Deck'].fillna(0)
XY_df['Deck'] = XY_df['Deck'].astype('category')
XY_df['relatives'] = XY_df['SibSp'] + XY_df['Parch']
XY_df.loc[XY_df['relatives'] > 0, 'not_alone'] = 0
XY_df.loc[XY_df['relatives'] == 0, 'not_alone'] = 1
XY_df['not_alone'] = XY_df['not_alone'].astype(int)
def encodeAgeFare(train):
train.loc[train['Age'] <= 16, 'Age_fare'] = 0
train.loc[(train['Age'] > 16) & (train['Age'] <= 32), 'Age_fare'] = 1
train.loc[(train['Age'] > 32) & (train['Age'] <= 48), 'Age_fare'] = 2
train.loc[(train['Age'] > 48) & (train['Age'] <= 64), 'Age_fare'] = 3
train.loc[ (train['Age'] > 48) & (train['Age'] <= 80), 'Age_fare'] = 4
train.loc[train['Fare'] <= 7.91, 'Fare'] = 0
train.loc[(train['Fare'] > 7.91) & (train['Fare'] <= 14.454), 'Fare_adj'] = 1
train.loc[(train['Fare'] > 14.454) & (train['Fare'] <= 31.0), 'Fare_adj'] = 2
train.loc[(train['Fare'] > 31.0) & (train['Fare'] <= 512.329), 'Fare_adj'] = 3
encodeAgeFare(XY_df)
# Categorical features pre-proccesing
cat_list ,XY_df=oc.cat_features_proccessing(XY_df)
print (cat_list)
features=XY_df.columns.to_list()
print ('number of features ', len(features))
features_remove=['PassengerId','Survived']
for f in features_remove:
features.remove(f)
X=XY_df[features]
y=XY_df['Survived']
from IPython.display import Image
Image("../images/octopus_know_your_data.PNG", width=600, height=600)
XY_sampled=oc.sampling(XY_df,'Survived',200)
```
# ML template starts - training session
## Training model (LGBM) with stratisfied CV
```
def create(hyperparams):
"""Create LGBM Classifier for a given set of hyper-parameters."""
model = LGBMClassifier(**hyperparams)
return model
def kfold_evaluation(X, y, k, hyperparams, esr=50):
scores = []
kf = KFold(k)
for i, (train_idx, test_idx) in enumerate(kf.split(X)):
X_train = X.iloc[train_idx]
y_train = y.iloc[train_idx]
X_val = X.iloc[test_idx]
y_val = y.iloc[test_idx]
model = create(hyperparams)
model = fit_with_stop(model, X_train, y_train, X_val, y_val, esr)
train_score = evaluate(model, X_train, y_train)
val_score = evaluate(model, X_val, y_val)
scores.append((train_score, val_score))
scores = pd.DataFrame(scores, columns=['train score', 'validation score'])
return scores
# Constant
K = 5
# Objective function
def objective(trial):
# Search spaces
hyperparams = {
'reg_alpha': trial.suggest_float('reg_alpha', 0.001, 10.0),
'reg_lambda': trial.suggest_float('reg_lambda', 0.001, 10.0),
'num_leaves': trial.suggest_int('num_leaves', 5, 1000),
'min_child_samples': trial.suggest_int('min_child_samples', 5, 100),
'max_depth': trial.suggest_int('max_depth', 5, 64),
'colsample_bytree': trial.suggest_float('colsample_bytree', 0.1, 0.5),
'cat_smooth' : trial.suggest_int('cat_smooth', 10, 100),
'cat_l2': trial.suggest_int('cat_l2', 1, 20),
'min_data_per_group': trial.suggest_int('min_data_per_group', 50, 200)
}
hyperparams.update(best_params)
scores = kfold_evaluation(X, y, K, hyperparams, 10)
return scores['validation score'].mean()
def create(hyperparams):
model = LGBMClassifier(**hyperparams)
return model
def fit(model, X, y):
model.fit(X, y,verbose=-1)
return model
def fit_with_stop(model, X, y, X_val, y_val, esr):
#model.fit(X, y,
# eval_set=(X_val, y_val),
# early_stopping_rounds=esr,
# verbose=-1)
model.fit(X, y,
eval_set=(X_val, y_val),
verbose=-1)
return model
def evaluate(model, X, y):
yp = model.predict_proba(X)[:, 1]
auc_score = roc_auc_score(y, yp)
return auc_score
```
## Hyper Parameter Optimization
```
best_params = {
'n_estimators': 1000,
'learning_rate': 0.05,
'metric': 'auc',
'verbose': -1
}
from lightgbm import LGBMClassifier
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
study = optuna.create_study(direction='maximize')
study.optimize(objective, n_trials=50)
study.best_value
best_params.update(study.best_params)
best_params
#plot_param_importances(study)
#plot_optimization_history(study)
params = {
'boosting_type': 'gbdt',
'objective': 'binary',
'metric': 'auc',
'learning_rate': 0.1,
'n_estimators': 500,
'verbose': -1,
'max_depth': -1,
'seed':100,
'min_split_gain': 0.01,
'num_leaves': 18,
'reg_alpha': 0.01,
'reg_lambda': 1.50,
'feature_fraction':0.2,
'bagging_fraction':0.84
}
metrics= oc.cv_adv(X,y,0.5,1000,shuffle=True,params=best_params)
```
# Model evaluation
### Plot of the CV folds - F1 macro and F1 for the positive class
(in this case it's an unbalanced dataset)
```
oc.cv_plot(metrics['f1_weighted'],metrics['f1_macro'],metrics['f1_positive'],'Titanic Kaggle competition')
```
## Scikit learn - Classification report
```
print(classification_report(metrics['y'], metrics['predictions_folds']))
```
## ROC curve with AUC
```
oc.roc_curve_plot(metrics['y'], metrics['predictions_proba'])
```
## Confusion Matrix plot (normalized and with absolute values)
```
oc.confusion_matrix_plot(metrics['y'], metrics['predictions_folds'])
```
## Feature Importance plot
```
feature_imp_list=oc.plot_imp(metrics['final_clf'],X,'LightGBM Mortality Kaggle',num=15)
top_features=feature_imp_list.sort_values(by='Value', ascending=False).head(20)
top_features
```
## Correlations analysis (on top features)
```
list_for_correlations=top_features['Feature'].to_list()
list_for_correlations.append('Survived')
oc.correlations(XY_df,list_for_correlations)
```
## Data leakage test
```
oc.data_leakage(X,top_features['Feature'].to_list())
```
## Analysis of FPs/FNs
```
fps=oc.recieve_fps(XY_df, metrics['index'] ,metrics['y'], metrics['predictions_proba'],top=10)
fns=oc.recieve_fns(XY_df, metrics['index'] ,metrics['y'], metrics['predictions_proba'],top=10)
fps
fns
filter_fps = XY_df[XY_df.index.isin(fps['index'])]
filter_fns = XY_df[XY_df.index.isin(fns['index'])]
filter_fps_with_prediction=pd.merge(filter_fps,fps[['index','preds_proba']], left_on=[pd.Series(filter_fps.index.values)], right_on=fps['index'])
filter_fns_with_prediction=pd.merge(filter_fns,fns[['index','preds_proba']], left_on=[pd.Series(filter_fns.index.values)], right_on=fns['index'])
```
### Top FPs with full features
```
filter_fps_with_prediction
```
### Top FNs with full features
```
filter_fns_with_prediction
```
| true |
code
| 0.40392 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/pabair/rl-course-ss21/blob/main/solutions/S6_LunarLander_PolicyBased.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Install Dependencies
```
# source: https://medium.com/coinmonks/landing-a-rocket-with-simple-reinforcement-learning-3a0265f8b58c
!pip3 install box2d-py
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Categorical
import matplotlib.pyplot as plt
from collections import deque
torch.manual_seed(1)
np.random.seed(1)
```
# Neural Network
```
class Net(nn.Module):
def __init__(self, obs_size, hidden_size, n_actions):
super(Net, self).__init__()
self.fc1 = nn.Linear(obs_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, n_actions)
def forward(self, x):
x = F.relu(self.fc1(x))
return self.fc2(x)
```
# Generate Episodes
```
def generate_batch(env, batch_size, t_max=5000):
activation = nn.Softmax(dim=1)
batch_actions,batch_states, batch_rewards = [],[],[]
for b in range(batch_size):
states,actions = [],[]
total_reward = 0
s = env.reset()
for t in range(t_max):
s_v = torch.FloatTensor([s])
act_probs_v = activation(net(s_v))
act_probs = act_probs_v.data.numpy()[0]
a = np.random.choice(len(act_probs), p=act_probs)
new_s, r, done, info = env.step(a)
#record sessions like you did before
states.append(s)
actions.append(a)
total_reward += r
s = new_s
if done:
batch_actions.append(actions)
batch_states.append(states)
batch_rewards.append(total_reward)
break
return batch_states, batch_actions, batch_rewards
```
# Training
```
def filter_batch(states_batch, actions_batch, rewards_batch, percentile):
reward_threshold = np.percentile(rewards_batch, percentile)
elite_states = []
elite_actions = []
for i in range(len(rewards_batch)):
if rewards_batch[i] > reward_threshold:
for j in range(len(states_batch[i])):
elite_states.append(states_batch[i][j])
elite_actions.append(actions_batch[i][j])
return elite_states, elite_actions
batch_size = 100
session_size = 500
percentile = 80
hidden_size = 200
completion_score = 100
learning_rate = 0.01
env = gym.make("LunarLander-v2")
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
#neural network
net = Net(n_states, hidden_size, n_actions)
#loss function
objective = nn.CrossEntropyLoss()
#optimisation function
optimizer = optim.Adam(params=net.parameters(), lr=learning_rate)
for i in range(session_size):
#generate new sessions
batch_states, batch_actions, batch_rewards = generate_batch(env, batch_size, t_max=500)
elite_states, elite_actions = filter_batch(batch_states, batch_actions, batch_rewards, percentile)
optimizer.zero_grad()
tensor_states = torch.FloatTensor(elite_states)
tensor_actions = torch.LongTensor(elite_actions)
action_scores_v = net(tensor_states)
loss_v = objective(action_scores_v, tensor_actions)
loss_v.backward()
optimizer.step()
#show results
mean_reward, threshold = np.mean(batch_rewards), np.percentile(batch_rewards, percentile)
print("%d: loss=%.3f, reward_mean=%.1f, reward_threshold=%.1f" % (
i, loss_v.item(), mean_reward, threshold))
#check if
if np.mean(batch_rewards)> completion_score:
print("Environment has been successfullly completed!")
break
```
# Evaluation
```
import time
FPS = 25
record_folder="video"
env = gym.make('LunarLander-v2')
env = gym.wrappers.Monitor(env, record_folder, force=True)
state = env.reset()
total_reward = 0.0
activation = nn.Softmax(dim=1)
while True:
start_ts = time.time()
env.render()
s_v = torch.FloatTensor([state])
act_probs_v = activation(net(s_v))
act_probs = act_probs_v.data.numpy()[0]
a = np.random.choice(len(act_probs), p=act_probs)
state, reward, done, _ = env.step(a)
total_reward += reward
if done:
break
delta = 1/FPS - (time.time() - start_ts)
if delta > 0:
time.sleep(delta)
print("Total reward: %.2f" % total_reward)
env.close()
```
| true |
code
| 0.787482 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/graviraja/100-Days-of-NLP/blob/applications%2Fclassification/applications/classification/grammatically_correct_sentence/CoLA%20with%20DistilBERT.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Installations
```
!pip install transformers
!pip install wget
```
### CoLA (Corpus of Linguistic Acceptability) Dataset
```
import os
import wget
print('Downloading dataset')
# The URL for the dataset zip file.
url = 'https://nyu-mll.github.io/CoLA/cola_public_1.1.zip'
# Download the file (if we haven't already)
if not os.path.exists('./cola_public_1.1.zip'):
wget.download(url, './cola_public_1.1.zip')
if not os.path.exists('./cola_public'):
!unzip cola_public_1.1.zip
!ls
```
### Imports
```
import time
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import transformers
from transformers import AdamW, get_linear_schedule_with_warmup
from sklearn import model_selection
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
torch.backends.cudnn.deterministic = True
train_file = "cola_public/raw/in_domain_train.tsv"
test_file = "cola_public/raw/in_domain_dev.tsv"
df_train = pd.read_csv(train_file, sep='\t', header=None, names=['sentence_source', 'label', 'label_notes', 'sentence'])
df_valid = pd.read_csv(test_file, sep='\t', header=None, names=['sentence_source', 'label', 'label_notes', 'sentence'])
```
### Data Analysis
```
df_train.head()
df_train = df_train.drop(columns=['sentence_source', 'label_notes'])
df_train.head()
df_valid = df_valid.drop(columns=['sentence_source', 'label_notes'])
df_train.shape, df_valid.shape
df_train = df_train.sample(frac=1).reset_index(drop=True)
df_train.head()
sns.countplot(df_train['label'].values)
plt.xlabel("Training Data Distribution")
sns.countplot(df_valid['label'].values)
plt.xlabel("Testing Data Distribution")
```
#### Choosing maximum sequence length
```
token_lens = []
for txt in df_train.sentence:
tokens = txt.split()
token_lens.append(len(tokens))
sns.distplot(token_lens)
plt.xlim([0, 512]);
plt.xlabel('Token lengths');
```
### Configurations
```
OUTPUT_DIM = 1
MAX_LEN = 100
TRAIN_BATCH_SIZE = 8
VALID_BATCH_SIZE = 8
EPOCHS = 3
TEACHER_MODEL_NAME = "bert-base-uncased"
STUDENT_MODEL_NAME = "distilbert-base-uncased"
TEACHER_MODEL_PATH = "teacher_model.bin"
STUDENTSA_MODEL_PATH = "studentsa_model.bin"
STUDENT_MODEL_PATH = "student_model.bin"
TOKENIZER = transformers.BertTokenizer.from_pretrained(TEACHER_MODEL_NAME)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
```
### CoLA Dataset
```
class CoLADataset:
def __init__(self, sentences, labels):
self.sentences = sentences
self.labels = labels
self.tokenizer = TOKENIZER
self.max_len = MAX_LEN
def __len__(self):
return len(self.labels)
def __getitem__(self, item):
sentence = self.sentences[item]
label = self.labels[item]
encoding = self.tokenizer.encode_plus(
sentence,
add_special_tokens=True,
max_length=self.max_len,
return_token_type_ids=False,
pad_to_max_length=True,
return_attention_mask=True,
truncation=True,
return_tensors='pt',
)
return {
"ids": encoding["input_ids"].flatten(),
"mask": encoding["attention_mask"].flatten(),
"targets": torch.tensor(label, dtype=torch.float)
}
train_dataset = CoLADataset(
sentences=df_train.sentence.values,
labels=df_train.label.values
)
valid_dataset = CoLADataset(
sentences=df_valid.sentence.values,
labels=df_valid.label.values
)
```
### DataLoaders
```
train_data_loader = torch.utils.data.DataLoader(
train_dataset,
TRAIN_BATCH_SIZE,
shuffle=True
)
valid_data_loader = torch.utils.data.DataLoader(
valid_dataset,
VALID_BATCH_SIZE
)
sample = next(iter(train_data_loader))
sample["ids"].shape, sample["mask"].shape, sample["targets"].shape
```
## BERT Model (Teacher)
```
class BERTModel(nn.Module):
def __init__(self):
super().__init__()
self.bert = transformers.BertModel.from_pretrained(TEACHER_MODEL_NAME)
self.bert_drop = nn.Dropout(0.3)
self.out = nn.Linear(768, OUTPUT_DIM)
def forward(self, ids, mask):
_, o2 = self.bert(ids, attention_mask=mask)
bo = self.bert_drop(o2)
output = self.out(bo)
return output
teacher_model = BERTModel()
teacher_model.to(device)
```
### Optimizer
```
# create parameters we want to optimize
# we generally dont use any decay for bias and weight layers
param_optimizer = list(teacher_model.named_parameters())
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
optimizer_parameters = [
{
"params": [
p for n, p in param_optimizer if not any(nd in n for nd in no_decay)
],
"weight_decay": 0.001,
},
{
"params": [
p for n, p in param_optimizer if any(nd in n for nd in no_decay)
],
"weight_decay": 0.0
}
]
num_train_steps = int(len(df_train) / TRAIN_BATCH_SIZE * EPOCHS)
num_train_steps
optimizer = AdamW(optimizer_parameters, lr=3e-5)
```
### Scheduler
```
scheduler = get_linear_schedule_with_warmup(
optimizer,
num_warmup_steps=0,
num_training_steps=num_train_steps
)
```
### Loss Criterion
```
criterion = nn.BCEWithLogitsLoss().to(device)
```
### Training Method
```
def train_fn(data_loader, model, optimizer, criterion, device, scheduler):
model.train()
epoch_loss = 0
for batch in data_loader:
ids = batch['ids'].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
optimizer.zero_grad()
outputs = model(
ids=ids,
mask=mask
)
loss = criterion(outputs, targets.view(-1, 1))
epoch_loss += loss.item()
loss.backward()
optimizer.step()
scheduler.step()
return epoch_loss / len(data_loader)
```
### Evaluation Method
```
def eval_fn(data_loader, model, criterion, device):
model.eval()
fin_outputs = []
fin_targets = []
epoch_loss = 0
with torch.no_grad():
for batch in data_loader:
ids = batch["ids"].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
outputs = model(
ids=ids,
mask=mask
)
loss = criterion(outputs, targets.view(-1, 1))
epoch_loss += loss.item()
targets = targets.cpu().detach()
fin_targets.extend(targets.numpy().tolist())
outputs = torch.sigmoid(outputs).cpu().detach()
fin_outputs.extend(outputs.numpy().tolist())
outputs = np.array(fin_outputs) >= 0.5
accuracy = metrics.accuracy_score(fin_targets, outputs)
mat_cor = metrics.matthews_corrcoef(fin_targets, outputs)
return epoch_loss / len(data_loader), accuracy, mat_cor
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
```
### Training
```
best_valid_loss = float('inf')
for epoch in range(EPOCHS):
start_time = time.time()
train_loss = train_fn(train_data_loader, teacher_model, optimizer, criterion, device, scheduler)
val_loss, val_acc, val_mat_cor = eval_fn(valid_data_loader, teacher_model, criterion, device)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if val_loss < best_valid_loss:
best_valid_loss = val_loss
torch.save(teacher_model.state_dict(), TEACHER_MODEL_PATH)
print(f"Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s")
print(f"\t Train Loss: {train_loss:.3f}")
print(f"\t Valid Loss: {val_loss:.3f} | Valid Acc: {val_acc * 100:.2f} | Matthews Cor: {val_mat_cor:.3f}")
teacher_model.load_state_dict(torch.load(TEACHER_MODEL_PATH))
```
### Inference
```
def inference(sentence, model, device):
encoded = TOKENIZER.encode_plus(
sentence,
max_length=MAX_LEN,
add_special_tokens=True,
return_token_type_ids=False,
pad_to_max_length=True,
return_attention_mask=True,
truncation=True,
return_tensors='pt',
)
input_ids = encoded['input_ids'].to(device)
attention_mask = encoded['attention_mask'].to(device)
output = model(input_ids, attention_mask)
prediction = torch.round(torch.sigmoid(output))
print(f'Sentence: {sentence}')
print(f'Grammatically Correct: {prediction.item()}')
sentence = "I like coding"
inference(sentence, teacher_model, device)
sentence = "I myself talking to"
inference(sentence, teacher_model, device)
sentence = "I am talking to myself"
inference(sentence, teacher_model, device)
torch.cuda.empty_cache()
```
## DistilBERT Model (Standalone)
Without any teacher forcing from BERT Model
```
class DistilBERTModelSA(nn.Module):
def __init__(self):
super().__init__()
self.bert = transformers.DistilBertModel.from_pretrained(STUDENT_MODEL_NAME)
self.bert_drop = nn.Dropout(0.3)
self.out = nn.Linear(768, OUTPUT_DIM)
def forward(self, ids, mask):
output = self.bert(ids, attention_mask=mask)
hidden = output[0]
bo = self.bert_drop(hidden[:, 0])
output = self.out(bo)
return output
student_model_sa = DistilBERTModelSA()
student_model_sa.to(device)
param_optimizer = list(student_model_sa.named_parameters())
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
optimizer_parameters = [
{
"params": [
p for n, p in param_optimizer if not any(nd in n for nd in no_decay)
],
"weight_decay": 0.001,
},
{
"params": [
p for n, p in param_optimizer if any(nd in n for nd in no_decay)
],
"weight_decay": 0.0
}
]
num_train_steps = int(len(df_train) / TRAIN_BATCH_SIZE * EPOCHS)
num_train_steps
optimizer = AdamW(optimizer_parameters, lr=3e-5)
scheduler = get_linear_schedule_with_warmup(
optimizer,
num_warmup_steps=0,
num_training_steps=num_train_steps
)
criterion = nn.BCEWithLogitsLoss().to(device)
def train_fn(data_loader, model, optimizer, criterion, device, scheduler):
model.train()
epoch_loss = 0
for batch in data_loader:
ids = batch['ids'].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
optimizer.zero_grad()
outputs = model(
ids=ids,
mask=mask
)
loss = criterion(outputs, targets.view(-1, 1))
epoch_loss += loss.item()
loss.backward()
optimizer.step()
scheduler.step()
return epoch_loss / len(data_loader)
def eval_fn(data_loader, model, criterion, device):
model.eval()
fin_outputs = []
fin_targets = []
epoch_loss = 0
with torch.no_grad():
for batch in data_loader:
ids = batch["ids"].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
outputs = model(
ids=ids,
mask=mask
)
loss = criterion(outputs, targets.view(-1, 1))
epoch_loss += loss.item()
targets = targets.cpu().detach()
fin_targets.extend(targets.numpy().tolist())
outputs = torch.sigmoid(outputs).cpu().detach()
fin_outputs.extend(outputs.numpy().tolist())
outputs = np.array(fin_outputs) >= 0.5
accuracy = metrics.accuracy_score(fin_targets, outputs)
mat_cor = metrics.matthews_corrcoef(fin_targets, outputs)
return epoch_loss / len(data_loader), accuracy, mat_cor
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
best_valid_loss = float('inf')
for epoch in range(EPOCHS):
start_time = time.time()
train_loss = train_fn(train_data_loader, student_model_sa, optimizer, criterion, device, scheduler)
val_loss, val_acc, val_mat_cor = eval_fn(valid_data_loader, student_model_sa, criterion, device)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if val_loss < best_valid_loss:
best_valid_loss = val_loss
torch.save(student_model_sa.state_dict(), STUDENTSA_MODEL_PATH)
print(f"Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s")
print(f"\t Train Loss: {train_loss:.3f}")
print(f"\t Valid Loss: {val_loss:.3f} | Valid Acc: {val_acc * 100:.2f} | Matthews Cor: {val_mat_cor:.3f}")
student_model_sa.load_state_dict(torch.load(STUDENTSA_MODEL_PATH))
def inference(sentence, model, device):
encoded = TOKENIZER.encode_plus(
sentence,
max_length=MAX_LEN,
add_special_tokens=True,
return_token_type_ids=False,
pad_to_max_length=True,
return_attention_mask=True,
truncation=True,
return_tensors='pt',
)
input_ids = encoded['input_ids'].to(device)
attention_mask = encoded['attention_mask'].to(device)
output = model(input_ids, attention_mask)
prediction = torch.round(torch.sigmoid(output))
print(f'Sentence: {sentence}')
print(f'Grammatically Correct: {prediction.item()}')
sentence = "I like coding"
inference(sentence, student_model_sa, device)
torch.cuda.empty_cache()
```
## DistilBERT Model (With Teacher Forcing)
```
class DistilBERTModel(nn.Module):
def __init__(self):
super().__init__()
self.bert = transformers.DistilBertModel.from_pretrained(STUDENT_MODEL_NAME)
self.bert_drop = nn.Dropout(0.3)
self.out = nn.Linear(768, OUTPUT_DIM)
def forward(self, ids, mask):
output = self.bert(ids, attention_mask=mask)
hidden = output[0]
bo = self.bert_drop(hidden[:, 0])
output = self.out(bo)
return output
student_model = DistilBERTModel()
student_model.to(device)
param_optimizer = list(student_model.named_parameters())
no_decay = ["bias", "LayerNorm.bias", "LayerNorm.weight"]
optimizer_parameters = [
{
"params": [
p for n, p in param_optimizer if not any(nd in n for nd in no_decay)
],
"weight_decay": 0.001,
},
{
"params": [
p for n, p in param_optimizer if any(nd in n for nd in no_decay)
],
"weight_decay": 0.0
}
]
num_train_steps = int(len(df_train) / TRAIN_BATCH_SIZE * EPOCHS)
num_train_steps
optimizer = AdamW(optimizer_parameters, lr=3e-5)
scheduler = get_linear_schedule_with_warmup(
optimizer,
num_warmup_steps=0,
num_training_steps=num_train_steps
)
criterion = nn.BCEWithLogitsLoss().to(device)
MSE_loss = nn.MSELoss(reduction='mean')
KLD_loss = nn.KLDivLoss(reduction="batchmean")
def train_fn(data_loader, model, teacher_model, optimizer, criterion, device, scheduler, alpha_clf=1.0, alpha_teacher=1.0, temperature=2.0):
model.train()
epoch_clf_loss = 0
epoch_total_loss = 0
for batch in data_loader:
ids = batch['ids'].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
optimizer.zero_grad()
student_logits = model(
ids=ids,
mask=mask
)
with torch.no_grad():
teacher_logits = teacher_model(
ids=ids,
mask=mask
)
mse_loss = MSE_loss(student_logits, teacher_logits)
kld_loss = KLD_loss(
(student_logits / temperature),
(teacher_logits / temperature),
)
clf_loss = criterion(student_logits, targets.view(-1, 1))
teacher_loss = mse_loss + kld_loss
loss = alpha_clf * clf_loss + alpha_teacher * teacher_loss
epoch_clf_loss += clf_loss.item()
epoch_total_loss += loss.item()
loss.backward()
optimizer.step()
scheduler.step()
return epoch_clf_loss / len(data_loader), epoch_total_loss / len(data_loader)
def eval_fn(data_loader, model, teacher_model, criterion, device, alpha_clf=1.0, alpha_teacher=1.0, temperature=2.0):
model.eval()
fin_outputs = []
fin_targets = []
epoch_clf_loss = 0
epoch_total_loss = 0
with torch.no_grad():
for batch in data_loader:
ids = batch["ids"].to(device)
mask = batch["mask"].to(device)
targets = batch["targets"].to(device)
student_logits = model(
ids=ids,
mask=mask
)
with torch.no_grad():
teacher_logits = teacher_model(
ids=ids,
mask=mask
)
mse_loss = MSE_loss(student_logits, teacher_logits)
kld_loss = KLD_loss(
(student_logits / temperature),
(teacher_logits / temperature),
)
clf_loss = criterion(student_logits, targets.view(-1, 1))
teacher_loss = mse_loss + kld_loss
loss = alpha_clf * clf_loss + alpha_teacher * teacher_loss
epoch_clf_loss += clf_loss.item()
epoch_total_loss += loss.item()
targets = targets.cpu().detach()
fin_targets.extend(targets.numpy().tolist())
outputs = torch.sigmoid(student_logits).cpu().detach()
fin_outputs.extend(outputs.numpy().tolist())
outputs = np.array(fin_outputs) >= 0.5
accuracy = metrics.accuracy_score(fin_targets, outputs)
mat_cor = metrics.matthews_corrcoef(fin_targets, outputs)
return epoch_clf_loss / len(data_loader), epoch_total_loss / len(data_loader), accuracy, mat_cor
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
teacher_model.load_state_dict(torch.load(TEACHER_MODEL_PATH))
best_valid_loss = float('inf')
for epoch in range(EPOCHS):
start_time = time.time()
train_clf_loss, train_total_loss = train_fn(train_data_loader, student_model, teacher_model, optimizer, criterion, device, scheduler)
val_clf_loss, val_total_loss, val_acc, val_mat_cor = eval_fn(valid_data_loader, student_model, teacher_model, criterion, device)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if val_loss < best_valid_loss:
best_valid_loss = val_loss
torch.save(student_model.state_dict(), STUDENT_MODEL_PATH)
print(f"Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s")
print(f"\t Train CLF Loss: {train_clf_loss:.3f} | Train total Loss: {train_total_loss:.3f}")
print(f"\t Valid CLF Loss: {val_clf_loss:.3f} | Valid total Loss: {val_total_loss:.3f}")
print(f"\t Valid Acc: {val_acc * 100:.2f} | Matthews Cor: {val_mat_cor:.3f}")
student_model.load_state_dict(torch.load(STUDENT_MODEL_PATH))
def inference(sentence, model, device):
encoded = TOKENIZER.encode_plus(
sentence,
max_length=MAX_LEN,
add_special_tokens=True,
return_token_type_ids=False,
pad_to_max_length=True,
return_attention_mask=True,
truncation=True,
return_tensors='pt',
)
input_ids = encoded['input_ids'].to(device)
attention_mask = encoded['attention_mask'].to(device)
output = model(input_ids, attention_mask)
prediction = torch.round(torch.sigmoid(output))
print(f'Sentence: {sentence}')
print(f'Grammatically Correct: {prediction.item()}')
sentence = "I like coding"
inference(sentence, student_model, device)
```
| true |
code
| 0.81322 | null | null | null | null |
|
Classical probability distributions can be written as a stochastic vector, which can be transformed to another stochastic vector by applying a stochastic matrix. In other words, the evolution of stochastic vectors can be described by a stochastic matrix.
Quantum states also evolve and their evolution is described by unitary matrices. This leads to some interesting properties in quantum computing. Unitary evolution is true for a closed system, that is, a quantum system perfectly isolated from the environment. This is not the case in the quantum computers we have today: these are open quantum systems that evolve differently due to to uncontrolled interactions with the environment. In this notebook, we take a glimpse at both types of evolution.
# Unitary evolution
A unitary matrix has the property that its conjugate transpose is its inverse. Formally, it means that a matrix $U$ is unitary if $UU^\dagger=U^\dagger U=\mathbb{1}$, where $^\dagger$ stands for conjugate transpose, and $\mathbb{1}$ is the identity matrix. A quantum computer is a machine that implements unitary operations.
As an example, we have seen the NOT operation before, which is performed by the X gate in a quantum computer. While the generic discussion on gates will only occur in a subsequent notebook, we can study the properties of the X gate. Its matrix representation is $X = \begin{bmatrix} 0 & 1\\ 1 & 0\end{bmatrix}$. Let's check if it is indeed unitary:
```
import numpy as np
X = np.array([[0, 1], [1, 0]])
print("XX^dagger")
print(X.dot(X.T.conj()))
print("X^daggerX")
print(X.T.conj().dot(X))
```
It looks like a legitimate unitary operation. The unitary nature ensures that the $l_2$ norm is preserved, that is, quantum states are mapped to quantum states.
```
print("The norm of the state |0> before applying X")
zero_ket = np.array([[1], [0]])
print(np.linalg.norm(zero_ket))
print("The norm of the state after applying X")
print(np.linalg.norm(X.dot(zero_ket)))
```
Furthermore, since the unitary operation is a matrix, it is linear. Measurements are also represented by matrices. These two observations imply that everything a quantum computer implements is actually linear. If we want to see some form of nonlinearity, that must involve some classical intervention.
Another consequence of the unitary operations is reversibility. Any unitary operation can be reversed. Quantum computing libraries often provide a function to reverse entire circuits. Reversing the X gate is simple: we just apply it again (its conjugate transpose is itself, therefore $X^2=\mathbb{1}$).
```
import numpy as np
from pyquil import Program, get_qc
from pyquil.gates import *
from forest_tools import *
%matplotlib inline
qvm_server, quilc_server, fc = init_qvm_and_quilc('/home/local/bin/qvm', '/home/local/bin/quilc')
qc = get_qc('1q-qvm', connection=fc)
circuit = Program()
circuit += X(0)
circuit += X(0)
results = qc.run_and_measure(circuit, trials=100)
plot_histogram(results)
```
which is exactly $|0\rangle$ as we would expect.
In the next notebook, you will learn about classical and quantum many-body systems and the Hamiltonian. In the notebook on adiabatic quantum computing, you will learn that a unitary operation is in fact the Schrödinger equation solved for a Hamiltonian for some duration of time. This connects the computer science way of thinking about gates and unitary operations to actual physics, but there is some learning to be done before we can make that connection. Before that, let us take another look at the interaction with the environment.
# Interaction with the environment: open systems
Actual quantum systems are seldom closed: they constantly interact with their environment in a largely uncontrolled fashion, which causes them to lose coherence. This is true for current and near-term quantum computers too.
<img src="figures/open_system.svg" alt="A quantum processor as an open quantum system" style="width: 400px;"/>
This also means that their actual time evolution is not described by a unitary matrix as we would want it, but some other operator (the technical name for it is a completely positive trace-preserving map).
Quantum computing libraries often offer a variety of noise models that mimic different types of interaction, and increasing the strength of the interaction with the environment leads to faster decoherence. The timescale for decoherence is often called $T_2$ time. Among a couple of other parameters, $T_2$ time is critically important for the number of gates or the duration of the quantum computation we can perform.
A very cheap way of studying the effects of decoherence is mixing a pure state with the maximally mixed state $\mathbb{1}/2^d$, where $d$ is the number of qubits, with some visibility parameter in $[0,1]$. This way we do not have to specify noise models or any other map modelling decoherence. For instance, we can mix the $|\phi^+\rangle$ state with the maximally mixed state:
```
def mixed_state(pure_state, visibility):
density_matrix = pure_state.dot(pure_state.T.conj())
maximally_mixed_state = np.eye(4)/2**2
return visibility*density_matrix + (1-visibility)*maximally_mixed_state
ϕ = np.array([[1],[0],[0],[1]])/np.sqrt(2)
print("Maximum visibility is a pure state:")
print(mixed_state(ϕ, 1.0))
print("The state is still entangled with visibility 0.8:")
print(mixed_state(ϕ, 0.8))
print("Entanglement is lost by 0.6:")
print(mixed_state(ϕ, 0.6))
print("Barely any coherence remains by 0.2:")
print(mixed_state(ϕ, 0.2))
```
Another way to look at what happens to a quantum state in an open system is through equilibrium processes. Think of a cup of coffee: left alone, it will equilibrate with the environment, eventually reaching the temperature of the environment. This includes energy exchange. A quantum state does the same thing and the environment has a defined temperature, just the environment of a cup of coffee.
The equilibrium state is called the thermal state. It has a very specific structure and we will revisit it, but for now, suffice to say that the energy of the samples pulled out of a thermal state follows a Boltzmann distribution. The Boltzmann -- also called Gibbs -- distribution is described as $P(E_i) = \frac {e^{-E_{i}/T}}{\sum _{j=1}^{M}{e^{-E_{j}/T}}}$, where $E_i$ is an energy, and $M$ is the total number of possible energy levels. Temperature enters the definition: the higher the temperature, the closer we are to the uniform distribution. In the infinite temperature limit, it recovers the uniform distribution. At high temperatures, all energy levels have an equal probability. In contrast, at zero temperature, the entire probability mass is concentrated on the lowest energy level, the ground state energy. To get a sense of this, let's plot the Boltzmann distribution with vastly different temperatures:
```
import matplotlib.pyplot as plt
temperatures = [.5, 5, 2000]
energies = np.linspace(0, 20, 100)
fig, ax = plt.subplots()
for i, T in enumerate(temperatures):
probabilities = np.exp(-energies/T)
Z = probabilities.sum()
probabilities /= Z
ax.plot(energies, probabilities, linewidth=3, label = "$T_" + str(i+1)+"$")
ax.set_xlim(0, 20)
ax.set_ylim(0, 1.2*probabilities.max())
ax.set_xticks([])
ax.set_yticks([])
ax.set_xlabel('Energy')
ax.set_ylabel('Probability')
ax.legend()
```
Here $T_1<T_2<T_3$. Notice that $T_1$ is a low temperature, and therefore it is highly peaked at low energy levels. In contrast, $T_3$ is a very high temperature and the probability distribution is almost completely flat.
```
qvm_server.terminate()
quilc_server.terminate()
```
| true |
code
| 0.484807 | null | null | null | null |
|
## Learning Objectives
- How we can exctract keywords from corpus (collections of texts) using TF-IDF
- Explain what is TF-IDF
- Applications of keywords exctraction algorithm and Word2Vec
## Review: What are the pre-processings to apply a machine learning algorithm on text data?
1. The text must be parsed to words, called tokenization
2. Then the words need to be encoded as integers or floating point values
3. scikit-learn library offers easy-to-use tools to perform both tokenization and feature extraction of text data
## What is TF-IDF Vectorizer?
- Word counts are a good starting point, but are very basic
An alternative is to calculate word frequencies, and by far the most popular method is called TF-IDF.
**Term Frequency**: This summarizes how often a given word appears within a document
**Inverse Document Frequency**: This downscales words that appear a lot across documents
## Intuitive idea behind TF-IDF:
- If a word appears frequently in a document, it's important. Give the word a high score
- But if a word appears in many documents, it's not a unique identifier. Give the word a low score
<img src="Images/tfidf_slide.png" width="700" height="700">
## Activity: Obtain the keywords from TF-IDF
1- First obtain the TF-IDF matrix for given corpus
2- Do column-wise addition
3- Sort the score from highest to lowest
4- Return the associated words based on step 3
```
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
import numpy as np
def keyword_sklearn(docs, k):
vectorizer = TfidfVectorizer(stop_words='english')
tfidf_matrix = vectorizer.fit_transform(docs)
print(tfidf_matrix.toarray())
print(vectorizer.get_feature_names())
tfidf_scores = np.sum(tfidf_matrix, axis=0)
tfidf_scores = np.ravel(tfidf_scores)
return sorted(dict(zip(vectorizer.get_feature_names(), tfidf_scores)).items(), key=lambda x: x[1], reverse=True)[:k]
documnets = ['The sky is bule', 'The sun is bright', 'The sun in the sky is bright', 'we can see the shining sun, the bright sun']
print(keyword_sklearn(documnets, 3))
```
## Word2Vec
- Data Scientists have assigned a vector to each english word
- This process of assignning vectors to each word is called Word2Vec
- In DS 2.4, we will learn how they accomplished Word2Vec task
- Download this huge Word2Vec file: https://nlp.stanford.edu/projects/glove/
- Do not open the extracted file
## What is the property of vectors associated to each word in Word2Vec?
- Words with similar meanings would be closer to each other in Euclidean Space
- For example if $V_{pizza}$, $V_{food}$ and $V_{sport}$ represent the vector associated to pizza, food and sport then:
${\| V_{pizza} - V_{food}}\|$ < ${\| V_{pizza} - V_{sport}}\|$
## Acitivity: Obtain the vector associated to pizza in Glove
```
import codecs
with codecs.open('/Users/miladtoutounchian/Downloads/glove.840B.300d.txt', 'r') as f:
for c, r in enumerate(f):
sr = r.split()
if sr[0] == 'pizza':
print(sr[0])
print([float(i) for i in sr[1:]])
print(len([float(i) for i in sr[1:]]))
break
```
## Activity: Obtain the vectors associated to pizza, food and sport in Glove
```
import codecs
with codecs.open('/Users/miladtoutounchian/Downloads/glove.840B.300d.txt', 'r') as f:
ls = {}
for c, r in enumerate(f):
sr = r.split()
if sr[0] in ['pizza', 'food', 'sport']:
ls[sr[0]] =[float(i) for i in sr[1:]]
if len(ls) == 3:
break
print(ls)
```
## Acitivty: Show that the vector of pizza is closer to vector of food than vector of sport
```
import numpy as np
np.linalg.norm(np.array(ls['pizza']) - np.array(ls['food']))
np.linalg.norm(np.array(ls['pizza']) - np.array(ls['sport']))
np.linalg.norm(np.array(ls['food']) - np.array(ls['sport']))
```
| true |
code
| 0.346928 | null | null | null | null |
|
# Multi-Fidelity
<div class="btn btn-notebook" role="button">
<img src="../_static/images/colab_logo_32px.png"> [Run in Google Colab](https://colab.research.google.com/drive/1Cc9TVY_Tl_boVzZDNisQnqe6Qx78svqe?usp=sharing)
</div>
<div class="btn btn-notebook" role="button">
<img src="../_static/images/github_logo_32px.png"> [View on GitHub](https://github.com/adapt-python/notebooks/blob/d0364973c642ea4880756cef4e9f2ee8bb5e8495/Multi_fidelity.ipynb)
</div>
The following example is a 1D regression multi-fidelity issue. Blue points are low fidelity observations and orange points are high fidelity observations. The goal is to use both datasets to learn the task on the [0, 1] interval.
To tackle this challenge, we use here the parameter-based method: [RegularTransferNN](#RegularTransferNN)
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from sklearn.metrics import mean_absolute_error, mean_squared_error
import tensorflow as tf
from tensorflow.keras import Model, Sequential
from tensorflow.keras.optimizers import Adam, SGD, RMSprop, Adagrad
from tensorflow.keras.layers import Dense, Input, Dropout, Conv2D, MaxPooling2D, Flatten, Reshape, GaussianNoise, BatchNormalization
from tensorflow.keras.constraints import MinMaxNorm
from tensorflow.keras.regularizers import l2
from tensorflow.keras.callbacks import Callback
from tensorflow.keras.models import clone_model
from adapt.parameter_based import RegularTransferNN
```
## Setup
```
np.random.seed(0)
Xs = np.linspace(0, 1, 200)
ys = (1 - Xs**2) * np.sin(2 * 2 * np.pi * Xs) - Xs + 0.1 * np.random.randn(len(Xs))
Xt = Xs[:100]
yt = (1 - Xt**2) * np.sin(2 * 2 * np.pi * Xt) - Xt - 1.5
gt = (1 - Xs**2) * np.sin(2 * 2 * np.pi * Xs) - Xs - 1.5
plt.figure(figsize=(10,6))
plt.plot(Xs, ys, '.', label="low fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xt, yt, '.', label="high fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xs, gt, c="black", alpha=0.7, ls="--", label="Ground truth")
plt.legend(fontsize=14)
plt.xlabel("X", fontsize=16)
plt.ylabel("y = f(X)", fontsize=16)
plt.show()
```
## Network
```
np.random.seed(0)
tf.random.set_seed(0)
model = Sequential()
model.add(Dense(100, activation='relu', input_shape=(1,)))
model.add(Dense(100, activation='relu'))
model.add(Dense(1))
model.compile(optimizer=Adam(0.001), loss='mean_squared_error')
```
## Low fidelity only
```
np.random.seed(0)
tf.random.set_seed(0)
model_low = clone_model(model)
model_low.compile(optimizer=Adam(0.001), loss='mean_squared_error')
model_low.fit(Xs, ys, epochs=800, batch_size=34, verbose=0);
yp = model_low.predict(Xs.reshape(-1,1))
score = mean_absolute_error(gt.ravel(), yp.ravel())
plt.figure(figsize=(10,6))
plt.plot(Xs, ys, '.', label="low fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xt, yt, '.', label="high fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xs, gt, c="black", alpha=0.7, ls="--", label="Ground truth")
plt.plot(Xs, yp, c="red", alpha=0.9, lw=3, label="Predictions")
plt.legend(fontsize=14)
plt.xlabel("X", fontsize=16)
plt.ylabel("y = f(X)", fontsize=16)
plt.title("Low Fidelity Only -- MAE = %.3f"%score, fontsize=18)
plt.show()
```
## High fidelity only
```
np.random.seed(0)
tf.random.set_seed(0)
model_high = clone_model(model)
model_high.compile(optimizer=Adam(0.001), loss='mean_squared_error')
model_high.fit(Xt, yt, epochs=800, batch_size=34, verbose=0);
yp = model_high.predict(Xs.reshape(-1,1))
score = mean_absolute_error(gt.ravel(), yp.ravel())
plt.figure(figsize=(10,6))
plt.plot(Xs, ys, '.', label="low fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xt, yt, '.', label="high fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xs, gt, c="black", alpha=0.7, ls="--", label="Ground truth")
plt.plot(Xs, yp, c="red", alpha=0.9, lw=3, label="Predictions")
plt.legend(fontsize=14)
plt.xlabel("X", fontsize=16)
plt.ylabel("y = f(X)", fontsize=16)
plt.title("Low Fidelity Only -- MAE = %.3f"%score, fontsize=18)
plt.show()
```
## [RegularTransferNN](https://adapt-python.github.io/adapt/generated/adapt.parameter_based.RegularTransferNN.html)
```
model_reg = RegularTransferNN(model_low, lambdas=1000., random_state=1, optimizer=Adam(0.0001))
model_reg.fit(Xt.reshape(-1,1), yt, epochs=1200, batch_size=34, verbose=0);
yp = model_reg.predict(Xs.reshape(-1,1))
score = mean_absolute_error(gt.ravel(), yp.ravel())
plt.figure(figsize=(10,6))
plt.plot(Xs, ys, '.', label="low fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xt, yt, '.', label="high fidelity", ms=15, alpha=0.9, markeredgecolor="black")
plt.plot(Xs, gt, c="black", alpha=0.7, ls="--", label="Ground truth")
plt.plot(Xs, yp, c="red", alpha=0.9, lw=3, label="Predictions")
plt.legend(fontsize=14)
plt.xlabel("X", fontsize=16)
plt.ylabel("y = f(X)", fontsize=16)
plt.title("Low Fidelity Only -- MAE = %.3f"%score, fontsize=18)
plt.show()
```
| true |
code
| 0.802846 | null | null | null | null |
|
## **Semana de Data Science**
- Minerando Dados
## Aula 01
### Conhecendo a base de dados
Monta o drive
```
from google.colab import drive
drive.mount('/content/drive')
```
Importando as bibliotecas básicas
```
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Carregando a Base de Dados
```
# carrega o dataset de london
from sklearn.datasets import load_boston
boston = load_boston()
# descrição do dataset
print (boston.DESCR)
# cria um dataframe pandas
data = pd.DataFrame(boston.data, columns=boston.feature_names)
# imprime as 5 primeiras linhas do dataset
data.head()
```
Conhecendo as colunas da base de dados
**`CRIM`**: Taxa de criminalidade per capita por cidade.
**`ZN`**: Proporção de terrenos residenciais divididos por lotes com mais de 25.000 pés quadrados.
**`INDUS`**: Essa é a proporção de hectares de negócios não comerciais por cidade.
**`CHAS`**: variável fictícia Charles River (= 1 se o trecho limita o rio; 0 caso contrário)
**`NOX`**: concentração de óxido nítrico (partes por 10 milhões)
**`RM`**: Número médio de quartos entre as casas do bairro
**`IDADE`**: proporção de unidades ocupadas pelos proprietários construídas antes de 1940
**`DIS`**: distâncias ponderadas para cinco centros de emprego em Boston
**`RAD`**: Índice de acessibilidade às rodovias radiais
**`IMPOSTO`**: taxa do imposto sobre a propriedade de valor total por US $ 10.000
**`B`**: 1000 (Bk - 0,63) ², onde Bk é a proporção de pessoas de descendência afro-americana por cidade
**`PTRATIO`**: Bairros com maior proporção de alunos para professores (maior valor de 'PTRATIO')
**`LSTAT`**: porcentagem de status mais baixo da população
**`MEDV`**: valor médio de casas ocupadas pelos proprietários em US $ 1000
Adicionando a coluna que será nossa variável alvo
```
# adiciona a variável MEDV
data['MEDV'] = boston.target
# imprime as 5 primeiras linhas do dataframe
data.head()
data.describe()
```
### Análise e Exploração dos Dados
Nesta etapa nosso objetivo é conhecer os dados que estamos trabalhando.
Podemos a ferramenta **Pandas Profiling** para essa etapa:
```
# Instalando o pandas profiling
pip install https://github.com/pandas-profiling/pandas-profiling/archive/master.zip
# import o ProfileReport
from pandas_profiling import ProfileReport
# executando o profile
profile = ProfileReport(data, title='Relatório - Pandas Profiling', html={'style':{'full_width':True}})
profile
# salvando o relatório no disco
profile.to_file(output_file="Relatorio01.html")
```
**Observações**
* *O coeficiente de correlação varia de `-1` a `1`.
Se valor é próximo de 1, isto significa que existe uma forte correlação positiva entre as variáveis. Quando esse número é próximo de -1, as variáveis tem uma forte correlação negativa.*
* *A relatório que executamos acima nos mostra que a nossa variável alvo (**MEDV**) é fortemente correlacionada com as variáveis `LSTAT` e `RM`*
* *`RAD` e `TAX` são fortemente correlacionadas, podemos remove-las do nosso modelo para evitar a multi-colinearidade.*
* *O mesmo acontece com as colunas `DIS` and `AGE` a qual tem a correlação de -0.75*
* *A coluna `ZN` possui 73% de valores zero.*
## Aula 02
Obtendo informações da base de dados manualmente
```
# Check missing values
data.isnull().sum()
# um pouco de estatística descritiva
data.describe()
```
Analisando a Correlação das colunas da base de dados
```
# Calcule a correlaçao
correlacoes = data.corr()
# Usando o método heatmap do seaborn
%matplotlib inline
plt.figure(figsize=(16, 6))
sns.heatmap(data=correlacoes, annot=True)
```
Visualizando a relação entre algumas features e variável alvo
```
# Importando o Plot.ly
import plotly.express as px
# RM vs MEDV (Número de quartos e valor médio do imóvel)
fig = px.scatter(data, x=data.RM, y=data.MEDV)
fig.show()
# LSTAT vs MEDV (índice de status mais baixo da população e preço do imóvel)
fig = px.scatter(data, x=data.LSTAT, y=data.MEDV)
fig.show()
# PTRATIO vs MEDV (percentual de proporção de alunos para professores e o valor médio de imóveis)
fig = px.scatter(data, x=data.PTRATIO, y=data.MEDV)
fig.show()
```
#### Analisando Outliers
```
# estatística descritiva da variável RM
data.RM.describe()
# visualizando a distribuição da variável RM
import plotly.figure_factory as ff
labels = ['Distribuição da variável RM (número de quartos)']
fig = ff.create_distplot([data.RM], labels, bin_size=.2)
fig.show()
# Visualizando outliers na variável RM
import plotly.express as px
fig = px.box(data, y='RM')
fig.update_layout(width=800,height=800)
fig.show()
```
Visualizando a distribuição da variável MEDV
```
# estatística descritiva da variável MEDV
data.MEDV.describe()
# visualizando a distribuição da variável MEDV
import plotly.figure_factory as ff
labels = ['Distribuição da variável MEDV (preço médio do imóvel)']
fig = ff.create_distplot([data.MEDV], labels, bin_size=.2)
fig.show()
```
Analisando a simetria do dado
```
# carrega o método stats da scipy
from scipy import stats
# imprime o coeficiente de pearson
stats.skew(data.MEDV)
```
Coeficiente de Pearson
* Valor entre -1 e 1 - distribuição simétrica.
* Valor maior que 1 - distribuição assimétrica positiva.
* Valor maior que -1 - distribuição assimétrica negativa.
```
# Histogram da variável MEDV (variável alvo)
fig = px.histogram(data, x="MEDV", nbins=50, opacity=0.50)
fig.show()
# Visualizando outliers na variável MEDV
import plotly.express as px
fig = px.box(data, y='MEDV')
fig.update_layout( width=800,height=800)
fig.show()
# imprimindo os 16 maiores valores de MEDV
data[['RM','LSTAT','PTRATIO','MEDV']].nlargest(16, 'MEDV')
# filtra os top 16 maiores registro da coluna MEDV
top16 = data.nlargest(16, 'MEDV').index
# remove os valores listados em top16
data.drop(top16, inplace=True)
# visualizando a distribuição da variável MEDV
import plotly.figure_factory as ff
labels = ['Distribuição da variável MEDV (número de quartos)']
fig = ff.create_distplot([data.MEDV], labels, bin_size=.2)
fig.show()
# Histogram da variável MEDV (variável alvo)
fig = px.histogram(data, x="MEDV", nbins=50, opacity=0.50)
fig.show()
# imprime o coeficiente de pearson
# o valor de inclinação..
stats.skew(data.MEDV)
```
**Definindo um Baseline**
- `Uma baseline é importante para ter marcos no projeto`.
- `Permite uma explicação fácil para todos os envolvidos`.
- `É algo que sempre tentaremos ganhar na medida do possível`.
```
# converte os dados
data.RM = data.RM.astype(int)
data.info()
# definindo a regra para categorizar os dados
categorias = []
# Se número de quartos for menor igual a 4 este será pequeno, senão se for menor que 7 será médio, senão será grande.
# alimenta a lista categorias
for i in data.RM.iteritems():
valor = (i[1])
if valor <= 4:
categorias.append('Pequeno')
elif valor < 7:
categorias.append('Medio')
else:
categorias.append('Grande')
# imprimindo categorias
categorias
# cria a coluna categorias no dataframe data
data['categorias'] = categorias
# imprime 5 linhas do dataframe
data.head()
# imprime a contagem de categorias
data.categorias.value_counts()
# agrupa as categorias e calcula as médias
medias_categorias = data.groupby(by='categorias')['MEDV'].mean()
# imprime a variável medias_categorias
medias_categorias
# criando o dicionario com chaves medio, grande e pequeno e seus valores
dic_baseline = {'Grande': medias_categorias[0], 'Medio': medias_categorias[1], 'Pequeno': medias_categorias[2]}
# imprime dicionario
dic_baseline
# cria a função retorna baseline
def retorna_baseline(num_quartos):
if num_quartos <= 4:
return dic_baseline.get('Pequeno')
elif num_quartos < 7:
return dic_baseline.get('Medio')
else:
return dic_baseline.get('Grande')
# chama a função retorna baseline
retorna_baseline(10)
# itera sobre os imoveis e imprime o valor médio pelo número de quartos.
for i in data.RM.iteritems():
n_quartos = i[1]
print('Número de quartos é: {} , Valor médio: {}'.format(n_quartos,retorna_baseline(n_quartos)))
# imprime as 5 primeiras linhas do dataframe
data.head()
```
| true |
code
| 0.557484 | null | null | null | null |
|
# Deep Neural Networks (DNN) Model Development
## Preparing Packages
```
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
from sklearn import metrics
from numpy import genfromtxt
from scipy import stats
from sklearn import preprocessing
from keras.callbacks import ModelCheckpoint
from keras.callbacks import Callback
from keras.models import load_model
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score, f1_score, precision_score, recall_score
import keras
from keras.layers import Dense, Flatten, Reshape,Dropout
from keras.layers import Conv2D, MaxPooling2D, LSTM
from keras.models import Sequential
from sklearn.model_selection import train_test_split
import timeit #package for recording the model running time
import time
from keras.callbacks import EarlyStopping
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential, load_model
from keras.layers import Activation, Dropout, Flatten, Dense, Conv2D, Conv3D, MaxPooling3D, Reshape, BatchNormalization, MaxPooling2D
from keras.applications.inception_resnet_v2 import InceptionResNetV2
from keras.callbacks import ModelCheckpoint
from keras import metrics
from keras.optimizers import Adam
from keras import backend as K
from sklearn.metrics import fbeta_score
from sklearn.model_selection import KFold,StratifiedKFold,ShuffleSplit,StratifiedShuffleSplit
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report,f1_score,accuracy_score
```
## Preparing Functions
```
def win_seg(data,windowsize,overlap):#function for overlap segmentation
length=int((data.shape[0]*data.shape[1]-windowsize)/(windowsize*overlap)+1)
newdata=np.empty((length,windowsize, data.shape[2],1))
data_dim=data.shape[2]
layers=data.shape[3]
data=data.reshape(-1,data_dim,layers)
for i in range(0,length) :
start=int(i*windowsize*overlap)
end=int(start+windowsize)
newdata[i]=data[start:end]
return newdata
def lab_vote(data,windowsize):
y_data=data.reshape(-1,windowsize,1,1)
y_data=win_seg(y_data,windowsize,0.5)
y_data=y_data.reshape(y_data.shape[0],y_data.shape[1],y_data.shape[2])
y_data=stats.mode(y_data,axis=1)
y_data=y_data.mode
y_data=y_data.reshape(-1,1)
y_data=np.float64(keras.utils.to_categorical(y_data))
return y_data
def lab_vote_cat(data,windowsize): # non one-hot coding
y_data=data.reshape(-1,windowsize,1,1)
y_data=win_seg(y_data,windowsize,0.5)
y_data=y_data.reshape(y_data.shape[0],y_data.shape[1],y_data.shape[2])
y_data=stats.mode(y_data,axis=1)
y_data=y_data.mode
y_data=y_data.reshape(-1,1)
return y_data
def write_csv(data):
a = np.asarray(data)
a.tofile('check.csv',sep=',',format='%10.5f')
def average(lst):
a = np.array(lst)
return np.mean(a)
class TimeHistory(keras.callbacks.Callback):
def on_train_begin(self, logs={}):
self.times = []
def on_epoch_begin(self, batch, logs={}):
self.epoch_time_start = time.time()
def on_epoch_end(self, batch, logs={}):
self.times.append(time.time() - self.epoch_time_start)
def f1(y_true, y_pred):
y_pred = K.round(y_pred)
tp = K.sum(K.cast(y_true*y_pred, 'float'), axis=0)
# tn = K.sum(K.cast((1-y_true)*(1-y_pred), 'float'), axis=0)
fp = K.sum(K.cast((1-y_true)*y_pred, 'float'), axis=0)
fn = K.sum(K.cast(y_true*(1-y_pred), 'float'), axis=0)
p = tp / (tp + fp + K.epsilon())
r = tp / (tp + fn + K.epsilon())
f1 = 2*p*r / (p+r+K.epsilon())
f1 = tf.where(tf.is_nan(f1), tf.zeros_like(f1), f1)
return K.mean(f1)
```
## Convolutional LSTM Model Development
```
#loading the training and testing data
os.chdir("...") #changing working directory
buffer = np.float64(preprocessing.scale(genfromtxt('S3_X.csv', delimiter=','))) # using S3 as an example
x_data=buffer.reshape(-1,40,30,1)
x_data=win_seg(x_data,40,0.5) # data segmentation with 0.5 overlap
#majority vote on training label
buffer = np.float64(genfromtxt('S3_Y.csv', delimiter=','))-1 #0 based index
y_data=lab_vote(buffer,40)
y_data2=lab_vote_cat(buffer,40) # for stratification purposes
#five round Stratified Random Shuffle
SRS=StratifiedShuffleSplit(n_splits=5, test_size=0.1, random_state=42) #split the train and test by 9:1
#model evaluation metrics
acc_score=list()
f_score=list()
eopch_time_record=list()
oper_time_record=list()
i=0
for train_index, test_index in SRS.split(x_data,y_data):
X_train, X_test = x_data[train_index], x_data[test_index]
y_train, y_test = y_data[train_index], y_data[test_index]
#split the train data into training (training the model) and validation (tuning hypeparameters) by 8:2
X_training, X_validation, y_training, y_validation = train_test_split(X_train, y_train, test_size=0.20)
#setup model parameters
data_dim = X_train.shape[2] #y of 2D Motion Image
timesteps = X_train.shape[1] #x of 2D Motion Image
num_classes = y_train.shape[1]
batchsize=300
epcoh=300
#build model
model = Sequential()
#five convolutional layers as an exmaple, adjust the convolutional layer depth if needed
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh',input_shape=(timesteps, data_dim,1)))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
#turn the multilayer tensor into single layer tensor
model.add(Reshape((40, -1),input_shape=(40,30,64)))
model.add(Dropout(0.5)) #add dropout layers for controlling overfitting
model.add(LSTM(128, return_sequences=True, input_shape=(40, 1920))) # returns a sequence of vectors
model.add(Dropout(0.5)) #add dropout layers for controlling overfitting
model.add(LSTM(128)) # return a single vector
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),metrics=['accuracy',f1])
checkpointer = ModelCheckpoint(filepath="2D_CNN5_LSTM_checkpoint(F1)_sss_%s.h5" % i, monitor='val_f1',verbose=1, mode='max', save_best_only=True)
time_callback = TimeHistory() #record the model training time for each epoch
callbacks_list = [checkpointer,time_callback]
train_history=model.fit(X_training, y_training,
batch_size=batchsize, epochs=epcoh,callbacks=callbacks_list,
validation_data=(X_validation, y_validation))
eopch_time=time_callback.times
eopch_time_record.append(eopch_time) #record the traing time of each epoch
CNN_LSTM_model=load_model("2D_CNN5_LSTM_checkpoint(F1)_sss_%s.h5" % i, custom_objects={'f1': f1})
#model operation and timing
start=timeit.default_timer()
y_pred=CNN_LSTM_model.predict(X_test)
stop=timeit.default_timer()
oper_time=stop-start
oper_time_record.append(oper_time)
#check the model test result
y_pred=CNN_LSTM_model.predict(X_test)
y_pred = np.argmax(y_pred, axis=1)
Y_test=np.argmax(y_test, axis=1)
acc_score.append(accuracy_score(Y_test, y_pred)) # Evaluation of accuracy
f_score.append(f1_score(Y_test, y_pred,average='macro')) # Evaluation of F1 score
print("This is the", i+1, "out of ",5, "Shuffle")
i+=1
del model #delete the model for retrain the neural network from scrach, instead of starting from trained model
# record performance
performance=pd.DataFrame(columns=['Acc_score','Macro_Fscore','Average_Epoch','Average_Run'])
performance['Acc_score']=acc_score
performance['Macro_Fscore']=f_score
performance['Average_Epoch']=average(eopch_time_record)
performance['Average_Run']=average(oper_time_record)
performance.to_csv("2DConv5LSTM_Performance_sss_test.csv")
```
## Baseline LSTM Model Development
```
acc_score=list()
f_score=list()
eopch_time_record=list()
oper_time_record=list()
#loading data
buffer = np.float64(preprocessing.scale(genfromtxt('S3_X.csv', delimiter=',')))
x_data=buffer.reshape(-1,40,30,1)
x_data=win_seg(x_data,40,0.5) # data segmentation with 0.5 overlap
x_data=x_data.reshape(x_data.shape[0],x_data.shape[1],x_data.shape[2]) #reshape the dataset as LSTM input shape
#majority vote on training label
buffer = np.float64(genfromtxt('S3_Y.csv', delimiter=','))-1 #0 based index
y_data=lab_vote(buffer,40)
i=0
for train_index, test_index in SRS.split(x_data,y_data):
X_train, X_test = x_data[train_index], x_data[test_index]
y_train, y_test = y_data[train_index], y_data[test_index]
#split the train data into training (training the model) and validation (tuning hypeparameters) by 8:2
X_training, X_validation, y_training, y_validation = train_test_split(X_train, y_train, test_size=0.20)
#setup model parameters
data_dim = X_train.shape[2] #y of figure
timesteps = X_train.shape[1] #x of figure
num_classes = y_train.shape[1]
batchsize=300
epcoh=300
#Build Model
model = Sequential()
model.add(LSTM(128, return_sequences=True, input_shape=(timesteps, data_dim))) # returns a sequence of vectors of dimension 64
model.add(Dropout(0.5)) #add dropout layers for controlling overfitting
model.add(LSTM(128)) # return a single vector of dimension 64
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),metrics=['accuracy',f1])
checkpointer = ModelCheckpoint(filepath='LSTM_checkpoint(F1)_sss_%s.h5' % i, monitor='val_f1',verbose=1,mode='max', save_best_only=True)
time_callback = TimeHistory() #record the model training time for each epoch
callbacks_list = [checkpointer,time_callback]
model.fit(X_training, y_training,
batch_size=batchsize, epochs=epcoh,callbacks=callbacks_list,
validation_data=(X_validation, y_validation))
eopch_time=time_callback.times
eopch_time_record.append(eopch_time) #record the traing time of each epoch
LSTM_model=load_model('LSTM_checkpoint(F1)_sss_%s.h5' % i,custom_objects={'f1': f1})
#model operation and timing
start=timeit.default_timer()
y_pred=LSTM_model.predict(X_test)
stop=timeit.default_timer()
oper_time=stop-start
oper_time_record.append(oper_time)
#check the model test result
y_pred = np.argmax(y_pred, axis=1)
Y_test=np.argmax(y_test, axis=1)
acc_score.append(accuracy_score(Y_test, y_pred))
f_score.append(f1_score(Y_test, y_pred,average='macro'))
print("This is the", i+1, "out of ",5, "Shuffle")
del model #delete the model for retrain the neural network from scrach, instead of starting from trained model
i+=1
# record performance
performance=pd.DataFrame(columns=['Acc_score','Macro_Fscore','Average_Epoch','Average_Run'])
performance['Acc_score']=acc_score
performance['Macro_Fscore']=f_score
performance['Average_Epoch']=average(eopch_time_record)
performance['Average_Run']=average(oper_time_record)
performance.to_csv("LSTM_Performance_sss_test.csv")
```
## Baseline CNN Model
```
acc_score=list()
f_score=list()
eopch_time_record=list()
oper_time_record=list()
i=0
for train_index, test_index in SRS.split(x_data,y_data):
X_train, X_test = x_data[train_index], x_data[test_index]
y_train, y_test = y_data[train_index], y_data[test_index]
#split the train data into training (training the model) and validation (tuning hypeparameters) by 8:2
X_training, X_validation, y_training, y_validation = train_test_split(X_train, y_train, test_size=0.20)
#setup model parameters
data_dim = X_train.shape[2] #y of figure
timesteps = X_train.shape[1] #x of figure
num_classes = y_train.shape[1]
batchsize=300
epcoh=300
#Build Model
model = Sequential()
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh',input_shape=(timesteps, data_dim,1)))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Conv2D(64, kernel_size=(5, 30), strides=(1, 1),padding='same',
activation='tanh'))
model.add(Flatten())
model.add(Dropout(0.5)) #add dropout layers for controlling overfitting
model.add(Dense(128, activation='tanh'))
model.add(Dropout(0.5)) #add dropout layers for controlling overfitting
model.add(Dense(128, activation='tanh'))
model.add(Dense(num_classes, activation='softmax'))#second flat fully connected layer for softmatrix (classification)
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adam(),metrics=['accuracy',f1])
checkpointer = ModelCheckpoint(filepath='2D_CNN_checkpoint(F1)_sss_%s.h5' % i, monitor='val_f1',mode='max',verbose=1, save_best_only=True)
time_callback = TimeHistory() #record the model training time for each epoch
callbacks_list = [checkpointer,time_callback]
model.fit(X_training, y_training,
batch_size=batchsize, epochs=epcoh,callbacks=callbacks_list,
validation_data=(X_validation, y_validation))
eopch_time=time_callback.times
eopch_time_record.append(eopch_time) #record the traingtime of each epoch
CNN_model=load_model('2D_CNN_checkpoint(F1)_sss_%s.h5' % i, custom_objects={'f1': f1})
#model operation and timing
start=timeit.default_timer()
y_pred=CNN_model.predict(X_test)
stop=timeit.default_timer()
oper_time=stop-start
oper_time_record.append(oper_time)
#check the model test result
y_pred = np.argmax(y_pred, axis=1)
Y_test=np.argmax(y_test, axis=1)
acc_score.append(accuracy_score(Y_test, y_pred))
f_score.append(f1_score(Y_test, y_pred,average='macro'))
print("This is the", i+1, "out of ",5, "Shuffle")
del model #delete the model for retrain the neural network from scrach, instead of starting from trained model
i+=1
# record performance
import pandas as pd
performance=pd.DataFrame(columns=['Acc_score','Macro_Fscore','Average_Epoch','Average_Run'])
performance['Acc_score']=acc_score
performance['Macro_Fscore']=f_score
performance['Average_Epoch']=average(eopch_time_record)
performance['Average_Run']=average(oper_time_record)
performance.to_csv("2DConv_Performance_sss_test.csv")
```
# Benchmark Machine Learing-based Model Development
## Packages Preparation
```
import os
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report,f1_score,accuracy_score
import timeit
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score, f1_score, precision_score, recall_score
import matplotlib.pyplot as plt
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_selection import RFECV
from sklearn.datasets import make_classification
```
## Functions Preparation
```
def win_seg(data,windowsize,overlap):#function for overlap segmentation
length=int((data.shape[0]*data.shape[1]-windowsize)/(windowsize*overlap)+1)
newdata=np.empty((length,windowsize, data.shape[2],1))
data_dim=data.shape[2]
layers=data.shape[3]
data=data.reshape(-1,data_dim,layers)
for i in range(0,length) :
start=int(i*windowsize*overlap)
end=int(start+windowsize)
newdata[i]=data[start:end]
return newdata
def lab_vote(data,windowsize):
y_data=data.reshape(-1,windowsize,1,1)
y_data=win_seg(y_data,windowsize,0.5)
y_data=y_data.reshape(y_data.shape[0],y_data.shape[1],y_data.shape[2])
y_data=stats.mode(y_data,axis=1)
y_data=y_data.mode
y_data=y_data.reshape(-1,1)
y_data=np.float64(keras.utils.to_categorical(y_data))
return y_data
def lab_vote_cat(data,windowsize): # non one-hot coding
y_data=data.reshape(-1,windowsize,1,1)
y_data=win_seg(y_data,windowsize,0.5)
y_data=y_data.reshape(y_data.shape[0],y_data.shape[1],y_data.shape[2])
y_data=stats.mode(y_data,axis=1)
y_data=y_data.mode
y_data=y_data.reshape(-1,1)
return y_data
def preparation(dataset):
x_data=preprocessing.scale(pd.read_csv(dataset).iloc[:,1:]) #Column-wise normalization
y_data=pd.read_csv(dataset).iloc[:,0]
X_train, X_test, y_train, y_test = train_test_split(x_data, y_data, test_size=0.20, random_state=42)#split the data into train and test by 8:2
return X_train, X_test, x_data,y_train, y_test, y_data
def TrainModels(X_train, X_test, y_train, y_test):
# Time cost
train_time=[]
run_time=[]
#SVM
svm=SVC(gamma='auto',random_state=42)
start = timeit.default_timer()
svm.fit(X_train,y_train)
stop = timeit.default_timer()
train_time.append(stop - start)
start = timeit.default_timer()
svm_pre=pd.DataFrame(data=svm.predict(X_test))
stop = timeit.default_timer()
run_time.append(stop - start)
#Naive Bayes
nb=GaussianNB()
start = timeit.default_timer()
nb.fit(X_train,y_train)
stop = timeit.default_timer()
train_time.append(stop - start)
start = timeit.default_timer()
nb_pre=pd.DataFrame(data=nb.predict(X_test))
stop = timeit.default_timer()
run_time.append(stop - start)
#KNN
knn=KNeighborsClassifier(n_neighbors=7) # based on a simple grid search
start = timeit.default_timer()
knn.fit(X_train,y_train)
stop = timeit.default_timer()
train_time.append(stop - start)
start = timeit.default_timer()
knn_pre=pd.DataFrame(data=knn.predict(X_test))
stop = timeit.default_timer()
run_time.append(stop - start)
#Decision Tree
dt=DecisionTreeClassifier(random_state=42)
start = timeit.default_timer()
dt.fit(X_train,y_train)
stop = timeit.default_timer()
train_time.append(stop - start)
start = timeit.default_timer()
dt_pre= pd.DataFrame(data=dt.predict(X_test))
stop = timeit.default_timer()
run_time.append(stop - start)
#Random Forest
rf=RandomForestClassifier(n_estimators=100)
start = timeit.default_timer()
rf.fit(X_train,y_train)
stop = timeit.default_timer()
train_time.append(stop - start)
start = timeit.default_timer()
rf_pre=pd.DataFrame(data=rf.predict(X_test))
stop = timeit.default_timer()
run_time.append(stop - start)
report = pd.DataFrame(columns=['Models','Accuracy','Macro F1','Micro F1','Train Time','Run Time'])
report['Models']=modelnames
for i in range(len(result.columns)):
report.iloc[i,1]=accuracy_score(y_test, result.iloc[:,i])
report.iloc[i,2]=f1_score(y_test, result.iloc[:,i],average='macro')
report.iloc[i,3]=f1_score(y_test, result.iloc[:,i],average='micro')
if i<len(train_time):
report.iloc[i,4]=train_time[i]
report.iloc[i,5]=run_time[i]
return report
```
## Sliding Window Segmentation
```
#loading the training and testing data
os.chdir("...") #changing working directory
buffer = np.float64(genfromtxt('S3_X.csv', delimiter=','))
x_data=buffer.reshape(-1,40,30,1)
x_data=win_seg(x_data,40,0.5) # data segmentation with 0.5 overlap
x_data=x_data.reshape(-1,40,30)
x_data_pd=x_data.reshape(-1,30)
x_data_pd = pd.DataFrame(data=x_data_pd)
adj_win=[i//40+1 for i in range(len(x_data_pd.iloc[:,0]))]
x_data_pd["adjwin"]=adj_win
x_data_pd.to_csv("S3_X_ML.csv")
#majority vote on training label
buffer = np.float64(genfromtxt('S3_Y.csv', delimiter=',')) #0 based index
y_data=lab_vote(buffer,40)
y_data2=lab_vote_cat(buffer,40) # for stratification purposes
y_data_pd = pd.DataFrame(data=y_data2)
y_data_pd.to_csv("S3_Y_ML.csv")
```
## Feature Selection Using Recursive Feature Elimination
```
X, y = X_train, y_train
svc = SVC(kernel="linear")
rfecv = RFECV(estimator=svc, step=1, cv=StratifiedKFold(10),scoring='f1_macro')
rfecv.fit(X, y)
print("Optimal number of features : %d" % rfecv.n_features_)
#plot number of features VS. cross-validation scores
plt.figure()
plt.xlabel("Number of features selected")
plt.ylabel("Cross validation score (nb of correct classifications)")
plt.plot(range(1, len(rfecv.grid_scores_) + 1), rfecv.grid_scores_)
plt.show()
# Export the best features
sel_features=pd.DataFrame()
sel_features["label"]=y_test
fullfeatures=pd.read_csv("fullfeatures.csv")
names=list(fullfeatures.columns.values)[1:]
for index, val in enumerate(list(rfecv.support_)):
if val:
sel_features=pd.concat([sel_features,fullfeatures.iloc[:,index+1]],axis=1)
sel_features.to_csv("S3_Dataset_ML_SelectetedFeatures.csv")
```
## Test on Selected Features
```
X_train, X_test, X_data,y_train, y_test, y_data=preparation("S3_Dataset_ML_SelectetedFeatures.csv")
sf = ShuffleSplit(n_splits=5, test_size=0.1, random_state=42) # Random Shuffle
SRS = StratifiedShuffleSplit(n_splits=5, test_size=0.1, random_state=42) # Stratified Shuffle
finalreport = pd.DataFrame(columns=['Models','Accuracy','Macro F1','Micro F1','Train Time','Run Time'])
for train_index, test_index in SRS.split(X_data, y_data):
X_train, X_test = X_data[train_index], X_data[test_index]
y_train, y_test = y_data[train_index], y_data[test_index]
finalreport=finalreport.append(TrainModels(X_train, X_test, y_train, y_test))
finalreport.to_csv("S3_Dataset_ML_SelectetedFeatures_Evalucation.csv")
```
| true |
code
| 0.672842 | null | null | null | null |
|
## Classification - Before and After MMLSpark
### 1. Introduction
<p><img src="https://images-na.ssl-images-amazon.com/images/G/01/img16/books/bookstore/landing-page/1000638_books_landing-page_bookstore-photo-01.jpg" style="width: 500px;" title="Image from https://images-na.ssl-images-amazon.com/images/G/01/img16/books/bookstore/landing-page/1000638_books_landing-page_bookstore-photo-01.jpg" /><br /></p>
In this tutorial, we perform the same classification task in two
different ways: once using plain **`pyspark`** and once using the
**`mmlspark`** library. The two methods yield the same performance,
but one of the two libraries is drastically simpler to use and iterate
on (can you guess which one?).
The task is simple: Predict whether a user's review of a book sold on
Amazon is good (rating > 3) or bad based on the text of the review. We
accomplish this by training LogisticRegression learners with different
hyperparameters and choosing the best model.
### 2. Read the data
We download and read in the data. We show a sample below:
```
rawData = spark.read.parquet("wasbs://[email protected]/BookReviewsFromAmazon10K.parquet")
rawData.show(5)
```
### 3. Extract more features and process data
Real data however is more complex than the above dataset. It is common
for a dataset to have features of multiple types: text, numeric,
categorical. To illustrate how difficult it is to work with these
datasets, we add two numerical features to the dataset: the **word
count** of the review and the **mean word length**.
```
from pyspark.sql.functions import udf
from pyspark.sql.types import *
def wordCount(s):
return len(s.split())
def wordLength(s):
import numpy as np
ss = [len(w) for w in s.split()]
return round(float(np.mean(ss)), 2)
wordLengthUDF = udf(wordLength, DoubleType())
wordCountUDF = udf(wordCount, IntegerType())
from mmlspark.stages import UDFTransformer
wordLength = "wordLength"
wordCount = "wordCount"
wordLengthTransformer = UDFTransformer(inputCol="text", outputCol=wordLength, udf=wordLengthUDF)
wordCountTransformer = UDFTransformer(inputCol="text", outputCol=wordCount, udf=wordCountUDF)
from pyspark.ml import Pipeline
data = Pipeline(stages=[wordLengthTransformer, wordCountTransformer]) \
.fit(rawData).transform(rawData) \
.withColumn("label", rawData["rating"] > 3).drop("rating")
data.show(5)
```
### 4a. Classify using pyspark
To choose the best LogisticRegression classifier using the `pyspark`
library, need to *explictly* perform the following steps:
1. Process the features:
* Tokenize the text column
* Hash the tokenized column into a vector using hashing
* Merge the numeric features with the vector in the step above
2. Process the label column: cast it into the proper type.
3. Train multiple LogisticRegression algorithms on the `train` dataset
with different hyperparameters
4. Compute the area under the ROC curve for each of the trained models
and select the model with the highest metric as computed on the
`test` dataset
5. Evaluate the best model on the `validation` set
As you can see below, there is a lot of work involved and a lot of
steps where something can go wrong!
```
from pyspark.ml.feature import Tokenizer, HashingTF
from pyspark.ml.feature import VectorAssembler
# Featurize text column
tokenizer = Tokenizer(inputCol="text", outputCol="tokenizedText")
numFeatures = 10000
hashingScheme = HashingTF(inputCol="tokenizedText",
outputCol="TextFeatures",
numFeatures=numFeatures)
tokenizedData = tokenizer.transform(data)
featurizedData = hashingScheme.transform(tokenizedData)
# Merge text and numeric features in one feature column
featureColumnsArray = ["TextFeatures", "wordCount", "wordLength"]
assembler = VectorAssembler(
inputCols = featureColumnsArray,
outputCol="features")
assembledData = assembler.transform(featurizedData)
# Select only columns of interest
# Convert rating column from boolean to int
processedData = assembledData \
.select("label", "features") \
.withColumn("label", assembledData.label.cast(IntegerType()))
from pyspark.ml.evaluation import BinaryClassificationEvaluator
from pyspark.ml.classification import LogisticRegression
# Prepare data for learning
train, test, validation = processedData.randomSplit([0.60, 0.20, 0.20], seed=123)
# Train the models on the 'train' data
lrHyperParams = [0.05, 0.1, 0.2, 0.4]
logisticRegressions = [LogisticRegression(regParam = hyperParam)
for hyperParam in lrHyperParams]
evaluator = BinaryClassificationEvaluator(rawPredictionCol="rawPrediction",
metricName="areaUnderROC")
metrics = []
models = []
# Select the best model
for learner in logisticRegressions:
model = learner.fit(train)
models.append(model)
scoredData = model.transform(test)
metrics.append(evaluator.evaluate(scoredData))
bestMetric = max(metrics)
bestModel = models[metrics.index(bestMetric)]
# Get AUC on the validation dataset
scoredVal = bestModel.transform(validation)
print(evaluator.evaluate(scoredVal))
```
### 4b. Classify using mmlspark
Life is a lot simpler when using `mmlspark`!
1. The **`TrainClassifier`** Estimator featurizes the data internally,
as long as the columns selected in the `train`, `test`, `validation`
dataset represent the features
2. The **`FindBestModel`** Estimator find the best model from a pool of
trained models by find the model which performs best on the `test`
dataset given the specified metric
3. The **`CompueModelStatistics`** Transformer computes the different
metrics on a scored dataset (in our case, the `validation` dataset)
at the same time
```
from mmlspark.train import TrainClassifier, ComputeModelStatistics
from mmlspark.automl import FindBestModel
# Prepare data for learning
train, test, validation = data.randomSplit([0.60, 0.20, 0.20], seed=123)
# Train the models on the 'train' data
lrHyperParams = [0.05, 0.1, 0.2, 0.4]
logisticRegressions = [LogisticRegression(regParam = hyperParam)
for hyperParam in lrHyperParams]
lrmodels = [TrainClassifier(model=lrm, labelCol="label", numFeatures=10000).fit(train)
for lrm in logisticRegressions]
# Select the best model
bestModel = FindBestModel(evaluationMetric="AUC", models=lrmodels).fit(test)
# Get AUC on the validation dataset
predictions = bestModel.transform(validation)
metrics = ComputeModelStatistics().transform(predictions)
print("Best model's AUC on validation set = "
+ "{0:.2f}%".format(metrics.first()["AUC"] * 100))
```
| true |
code
| 0.620564 | null | null | null | null |
|
# DRF of CNS-data
```
%load_ext autoreload
%autoreload 2
%matplotlib notebook
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import networkx as nx
from matplotlib.colors import LogNorm
from sklearn.utils import shuffle
from itertools import groupby
from matplotlib.figure import figaspect
# package developed for the analysis
from world_viewer.cns_world import CNSWorld
from world_viewer.glasses import Glasses
# DTU Data Wrapper
from sensible_raw.loaders import loader
```
## 1) Load and Prepare Data
```
# load data for analysis
cns = CNSWorld()
cns.load_world(opinions = ['fitness'], read_cached = False, stop=False, write_pickle = False, continous_op=False)
# load analysis tools
cns_glasses = Glasses(cns)
# remove not needed data in order to save mermory
cns.d_ij = None
# set analysis parameters
analysis = 'expo_frac'
opinion_type = "op_fitness"
binning = True
n_bins = 10
save_plots = True
show_plot = True
4.1_CopenhagenDataRelativeExposure.ipynb# load previously calculated exposure instead of recalculate it
exposure = pd.read_pickle("tmp/fitness_exposure_tx7.pkl")
# alternative: recalculate exposure value
# exposure = cns_glasses.calc_exposure("expo_frac", "op_fitness", exposure_time = 7)
# filter by degre
degree = exposure.groupby("node_id").n_nbs.mean().to_frame("avg").reset_index()
exposure = exposure.loc[degree.loc[degree.avg >= 4,"node_id"]]
exposure = exposure.loc[exposure.n_nbs_mean > 1/7]
# cut time series in time slices: spring + summer
exposure.reset_index(inplace=True)
start_spring = "2014-02-01"
end_spring = "2014-04-30"
exposure_spring = exposure.loc[(exposure.time >= pd.to_datetime(start_spring)) & (exposure.time <= pd.to_datetime(end_spring))].copy()
start_summer = "2014-07-01"
end_summer = "2014-09-30"
exposure_summer = exposure.loc[(exposure.time >= pd.to_datetime(start_summer)) & (exposure.time <= pd.to_datetime(end_summer))].copy()
exposure_spring.set_index(['node_id','time'],inplace=True)
exposure_summer.set_index(['node_id','time'],inplace=True)
exposure.set_index(['node_id','time'],inplace=True)
# column "exposure" equals relative exposure
# column "n_influencer_summed" equals absolute exposure
# use absolute exposure for further calculations
exposure.rename(columns={"exposure":"exposure_old", "n_influencer_summed":"exposure"},inplace=True)
exposure_spring.rename(columns={"exposure":"exposure_old", "n_influencer_summed":"exposure"},inplace=True)
exposure_summer.rename(columns={"exposure":"exposure_old", "n_influencer_summed":"exposure"},inplace=True)
# calculate if nodes changed trait after experiencing a certain exposure
# save value as column "op_change" (bool)
data_spring, expo_agg_spring = cns_glasses.opinion_change_per_exposure(exposure_spring, opinion_type, opinion_change_time = 1)
data_summer, expo_agg_summer = cns_glasses.opinion_change_per_exposure(exposure_summer, opinion_type, opinion_change_time = 1)
data_full, expo_agg_full = cns_glasses.opinion_change_per_exposure(exposure, opinion_type, opinion_change_time = 1)
# save calculated values on hard drive
expo_agg_spring.to_pickle("tmp/final/exposure_filtered_spring.pkl")
```
## 2) Plot Dose Response Functions (FIG.: 4.9)
```
# plot drf for full timeseries
fig, ax = plt.subplots(1,2,subplot_kw = {"adjustable":'box', "aspect":200/0.25})
cns_glasses.output_folder = "final/"
suffix = "_full"
data = data_full[data_full.exposure <= 200]
bin_width=1
q_binning=True
bin_width=5
n_bins=15
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == True], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=False, show_plot=show_plot, y_lower_lim=0, y_upper_lim = 0.2, fig=fig, ax=ax[0], label="become active", q_binning = q_binning, \
loglog=False, step_plot=True, color="forestgreen", suffix=suffix,x_lim=200)
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == False], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=True, show_plot=show_plot, y_lower_lim=0, y_upper_lim = 0.2, fig=fig, ax=ax[1], label="become passive", loglog=False, \
q_binning=q_binning, step_plot=True, color="darkorange", suffix=suffix,x_lim=200)
# plot drf for summer timeseries
fig, ax = plt.subplots(1,2,subplot_kw = {"adjustable":'box', "aspect":200/0.25})
cns_glasses.output_folder = "final/"
suffix = "_summer"
data = data_summer[data_summer.exposure <= 200]
q_binning=False
bin_width=15
n_bins=20
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == True].dropna(), "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=False, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.25, fig=fig, ax=ax[0], label="become active", q_binning = q_binning, loglog=False, step_plot=True, color="forestgreen", suffix=suffix,x_lim=200)
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == False].dropna(), "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=True, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.25, fig=fig, ax=ax[1], label="become passive", loglog=False, q_binning=q_binning, step_plot=True, color="darkorange", suffix=suffix,x_lim=200)
# plot drf for spring timeseries
x_max = 330
w, h = figaspect(0.5)
fig, ax = plt.subplots(1,2,figsize=(w,h))
cns_glasses.output_folder = "final/"
suffix = "_spring"
data = data_spring[data_spring.exposure <= x_max]
q_binning=False
bin_width=15
n_bins=15
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == True], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=False, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax[0], label="become active", \
q_binning = q_binning, loglog=False, step_plot=True, color="forestgreen", suffix=suffix, x_lim=x_max)
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == False], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=True, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax[1], label="become passive", loglog=False, \
q_binning=q_binning, step_plot=True, color="darkorange", suffix=suffix, x_lim=x_max)
fig.savefig("tmp/final/empirical_drfs.pdf" , bbox_inches='tight')
x_max = 330
fig, ax = plt.subplots()
cns_glasses.output_folder = "final/"
suffix = "_spring"
data = data_spring[data_spring.exposure <= x_max]
q_binning=False
bin_width=15
n_bins=15
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == True], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=False, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax, label="become active", \
q_binning = q_binning, loglog=False, step_plot=True, color="forestgreen", suffix=suffix, x_lim=x_max,marker="^", markersize=5)
fig.savefig("tmp/final/empirical_drf_1.pdf" , bbox_inches='tight')
cns_glasses.plot_opinion_change_per_exposure_number(data[data.op_fitness == False], "expo_nmb", binning, n_bins=n_bins, bin_width=bin_width, \
save_plots=True, show_plot=show_plot, y_lower_lim=-0.01, y_upper_lim = 0.2, fig=fig, ax=ax, label="become passive", loglog=False, \
q_binning=q_binning, step_plot=True, color="darkorange", suffix=suffix, x_lim=x_max, marker=".")
fig.savefig("tmp/final/empirical_drf_2.pdf" , bbox_inches='tight')
```
## 3) Plot Distribution of the Absolute Exposure (FIG.: 4.10)
```
expo = expo_agg_spring[expo_agg_spring.op_fitness==True].reset_index()
#expo = expo.loc[(expo.time > "2013-09-01") & (expo.time < "2014-09-01")]
#expo.time = expo.time.dt.dayofyear
expo.time = expo.time.astype("int")
mean_expo = expo.groupby("time").exposure.mean().to_frame("mean exposure").reset_index()
mean_expo.set_index("time",inplace=True)
fig,ax = plt.subplots()
expo.dropna(inplace=True)
#expo = expo[expo.exposure < 250]
plot = ax.hist2d(expo.time,expo.exposure,norm=LogNorm(), bins = [len(expo.time.unique())
,120])#, vmin=1, vmax=100)
expo.groupby("time").exposure.mean().plot(label=r"mean exposure $<K>$",color="red",linestyle="--")
ax.legend(loc="upper left")
ax.set_xlabel("time")
ax.set_ylabel(r"absolute exposure $K$")
ax.set_xticklabels(pd.to_datetime(ax.get_xticks()).strftime('%d. %B %Y'), rotation=40, ha="right")
cbar = fig.colorbar(plot[3])
cbar.set_label('# number of occurrences')
fig.savefig("tmp/final/abs_expo_distrib_spring.pdf",bbox_inches='tight')
```
| true |
code
| 0.634345 | null | null | null | null |
|
# Policy Evaluation in Contextual Bandits
** *
This IPython notebook illustrates the usage of the [contextualbandits](https://www.github.com/david-cortes/contextualbandits) package's `evaluation` module through a simulation with public datasets.
** Small note: if the TOC here is not clickable or the math symbols don't show properly, try visualizing this same notebook from nbviewer following [this link](http://nbviewer.jupyter.org/github/david-cortes/contextualbandits/blob/master/example/policy_evaluation.ipynb). **
** *
### Sections
[1. Problem description](#p1)
[2. Methods](#p2)
[3. Experiments](#p3)
[4. References](#p4)
** *
<a id="p1"></a>
## 1. Problem description
For a general description of the contextual bandits problem, see the first part of the package's guide [Online Contextual Bandits](http://nbviewer.jupyter.org/github/david-cortes/contextualbandits/blob/master/example/online_contextual_bandits.ipynb).
The previous two guides [Online Contextual Bandits](http://nbviewer.jupyter.org/github/david-cortes/contextualbandits/blob/master/example/online_contextual_bandits.ipynb) and [Off-policy Learning in Contextual Bandits](http://nbviewer.jupyter.org/github/david-cortes/contextualbandits/blob/master/example/offpolicy_learning.ipynb) evaluated the performance of different policies by looking at the actions they would have chosen in a fully-labeled dataset for multi-label classification.
However, in contextual bandits settings one doesn't have access to fully-labeled data, and the data that one has is usually very biased, as it is collected through some policy that aims to maximize rewards. In this situation, it is a lot more difficult to evaluate the performance of a new policy. This module deals with such problem.
** *
<a id="p2"></a>
## 2. Methods
This module implements two policy evaluation methods:
* `evaluateRejectionSampling` (see _"A contextual-bandit approach to personalized news article recommendation"_), for both online and offline policies.
* `evaluateDoublyRobust` (see _"Doubly Robust Policy Evaluation and Learning"_).
Both of these are based on a train-test split - that is, the policy is trained with some data and evaluated on different data.
The best way to obtain a good estimate of the performance of a policy is to collect some data on which actions are chosen at random. When such data is available, one can iterate through it, let the policy choose an action for each observation, and if it matches with what was chosen, take it along with its rewards for evaluation purposes, skip it if not. This simple rejection sampling method is unbiased and let's you evaluate both online and offline algorithms. **It must be stressed that evaluating data like this only works when the actions of this test sample are chosen at random, otherwise the estimates will be biased (and likely very wrong)**.
When such data is not available and there is reasonable variety of actions chosen, another option is doubly-robust estimates. These are meant for the case of continuous rewards, and don't work as well with discrete rewards though, especially when there are many labels, but they can still be tried.
The doubly-robust estimate requires, as it names suggests, two estimates: one of the reward that each arm will give, and another of the probability or score that the policy that collected the data gave to each arm it chose for each observation.
In a scenario such as online advertising, we don't need the second estimate if we record the scores that the models output along with the covariates-action-reward history. When using the functions from this package's `online` module, you can get such estimates for some of the policies by using their `predict_proba_separate` function.
For the first estimate, there are different options to obtain it. One option is to fit a (non-online) model to both the train and test sets to make reward estimates on the test set, or fit it only on the test set (while the policy to be evaluated is fitted to the training set); or perhaps even use the score estimates from the old policy (which chose the actions on the training and test data) or from the new policy. The function `evaluateDoublyRobust` provides an API that can accomodate all these methods.
** *
<a id="p3"></a>
## 3. Experiments
Just like in the previous guide [Off-policy Learning in Contextual Bandits](http://nbviewer.jupyter.org/github/david-cortes/contextualbandits/blob/master/example/offpolicy_learning.ipynb), I will simualate data generated from a policy by fitting a logistic regression model with a sample of the **fully-labeled** data, then let it choose actions for some more data, and take those actions and rewards as input for a new policy, along with the estimated reward probabilities for the actions that were chosen.
The new policy will then be evaluated on a test sample with actions already pre-selected, and the estimates from the methods here will be compared with the real rewards, which we can know because the data is fully labeled.
The data are again the Bibtext and Mediamill datasets.
** *
Loading the Bibtex dataset again:
```
import pandas as pd, numpy as np, re
from sklearn.preprocessing import MultiLabelBinarizer
def parse_data(file_name):
features = list()
labels = list()
with open(file_name, 'rt') as f:
f.readline()
for l in f:
if bool(re.search("^[0-9]", l)):
g = re.search("^(([0-9]{1,2},?)+)\s(.*)$", l)
labels.append([int(i) for i in g.group(1).split(",")])
features.append(eval("{" + re.sub("\s", ",", g.group(3)) + "}"))
else:
l = l.strip()
labels.append([])
features.append(eval("{" + re.sub("\s", ",", l) + "}"))
features = pd.DataFrame.from_dict(features).fillna(0).as_matrix()
mlb = MultiLabelBinarizer()
y = mlb.fit_transform(labels)
return features, y
features, y = parse_data("Bibtex_data.txt")
print(features.shape)
print(y.shape)
```
Simulating a stationary exploration policy and a test set:
```
from sklearn.linear_model import LogisticRegression
# the 'explorer' polcy will be fit with this small sample of the rows
st_seed = 0
end_seed = 2000
# then it will choose actions for this larger sample, which will be the input for the new policy
st_exploration = 0
end_exploration = 3000
# the new policy will be evaluated with a separate test set
st_test = 3000
end_test = 7395
# separating the covariates data for each case
Xseed = features[st_seed:end_seed, :]
Xexplore_sample = features[st_exploration:end_exploration, :]
Xtest = features[st_test:end_test, :]
nchoices = y.shape[1]
# now constructing an exploration policy as explained above, with fully-labeled data
explorer = LogisticRegression()
np.random.seed(100)
explorer.fit(Xseed, np.argmax(y[st_seed:end_seed], axis=1))
# letting the exploration policy choose actions for the new policy input
np.random.seed(100)
actions_explore_sample=explorer.predict(Xexplore_sample)
rewards_explore_sample=y[st_exploration:end_exploration, :]\
[np.arange(end_exploration - st_exploration), actions_explore_sample]
# extracting the probabilities it estimated
ix_internal_actions = {j:i for i,j in enumerate(explorer.classes_)}
ix_internal_actions = [ix_internal_actions[i] for i in actions_explore_sample]
ix_internal_actions = np.array(ix_internal_actions)
prob_actions_explore = explorer.predict_proba(Xexplore_sample)[np.arange(Xexplore_sample.shape[0]),
ix_internal_actions]
# generating a test set with random actions
actions_test = np.random.randint(nchoices, size=end_test - st_test)
rewards_test = y[st_test:end_test, :][np.arange(end_test - st_test), actions_test]
```
Rejection sampling estimate:
```
from contextualbandits.online import SeparateClassifiers
from contextualbandits.evaluation import evaluateRejectionSampling
new_policy = SeparateClassifiers(LogisticRegression(C=0.1), y.shape[1])
np.random.seed(100)
new_policy.fit(Xexplore_sample, actions_explore_sample, rewards_explore_sample)
np.random.seed(100)
est_r, ncases = evaluateRejectionSampling(new_policy, X=Xtest, a=actions_test, r=rewards_test, online=False)
np.random.seed(100)
real_r = np.mean(y[st_test:end_test,:][np.arange(end_test - st_test), new_policy.predict(Xtest)])
print('Test set Rejection Sampling mean reward estimate (new policy)')
print('Estimated mean reward: ',est_r)
print('Sample size: ', ncases)
print('----------------')
print('Real mean reward: ', real_r)
```
We can also evaluate the exploration policy with the same method:
```
np.random.seed(100)
est_r, ncases = evaluateRejectionSampling(explorer, X=Xtest, a=actions_test, r=rewards_test, online=False)
real_r = np.mean(y[st_test:end_test, :][np.arange(end_test - st_test), explorer.predict(Xtest)])
print('Test set Rejection Sampling mean reward estimate (old policy)')
print('Estimated mean reward: ', est_r)
print('Sample size: ', ncases)
print('----------------')
print('Real mean reward: ', real_r)
```
_(Remember that the exploration policy was fit with a smaller set of fully-labeled data, thus it's no surprise it performs a lot better)_
The estimates are not exact, but they are somewhat close to the real values as expected. They get better the more cases are successfully sampled, and their estimate should follow the central limit theorem.
** *
To be stressed again, such an evaluation method only works when the data was collected by choosing actions at random. **If we evaluate it with the actions chosen by the exploration policy, the results will be totally biased as demonstrated here:**
```
actions_test_biased = explorer.predict(Xtest)
rewards_test_biased = y[st_test:end_test, :][np.arange(end_test - st_test), actions_test_biased]
est_r, ncases = evaluateRejectionSampling(new_policy, X=Xtest, a=actions_test_biased,\
r=rewards_test_biased, online=False)
real_r = np.mean(y[st_test:end_test, :][np.arange(end_test - st_test), new_policy.predict(Xtest)])
print('Biased Test set Rejection Sampling mean reward estimate (new policy)')
print('Estimated mean reward: ', est_r)
print('Sample size: ', ncases)
print('----------------')
print('Real mean reward: ', real_r)
print("(Don't try rejection sampling on a biased test set)")
```
We can also try Doubly-Robust estimates, but these work poorly for a dataset like this:
```
from contextualbandits.evaluation import evaluateDoublyRobust
# getting estimated probabilities for the biased test sample chosen by the old policy
ix_internal_actions = {j:i for i,j in enumerate(explorer.classes_)}
ix_internal_actions = [ix_internal_actions[i] for i in actions_test_biased]
ix_internal_actions = np.array(ix_internal_actions)
prob_actions_test_biased = explorer.predict_proba(Xtest)[np.arange(Xtest.shape[0]), ix_internal_actions]
# actions that the new policy will choose
np.random.seed(1)
pred = new_policy.predict(Xtest)
# method 1: estimating rewards by fitting another model to the whole data (train + test)
model_fit_on_all_data = SeparateClassifiers(LogisticRegression(), y.shape[1])
np.random.seed(1)
model_fit_on_all_data.fit(np.r_[Xexplore_sample, Xtest],
np.r_[actions_explore_sample, actions_test_biased],
np.r_[rewards_explore_sample, rewards_test_biased])
np.random.seed(1)
est_r_dr_whole = evaluateDoublyRobust(pred, X=Xtest, a=actions_test_biased, r=rewards_test_biased,\
p=prob_actions_test_biased, reward_estimator = model_fit_on_all_data)
# method 2: estimating rewards by fitting another model to the test data only
np.random.seed(1)
est_r_dr_test_only = evaluateDoublyRobust(pred, X=Xtest, a=actions_test_biased, r=rewards_test_biased,\
p=prob_actions_test_biased, reward_estimator = LogisticRegression(), nchoices=y.shape[1])
print('Biased Test set mean reward estimates (new policy)')
print('DR estimate (reward estimator fit on train+test): ', est_r_dr_whole)
print('DR estimate (reward estimator fit on test only): ', est_r_dr_test_only)
print('----------------')
print('Real mean reward: ', real_r)
```
Both estimates are very wrong, but they are still less wrong than the wrongly-conducted rejection sampling from before.
** *
Finally, rejection sampling can also be used to evaluate online policies - in this case though, be aware that the estimate will only be considered up to a certain number of rounds (as many as it accepts, but it will end up rejecting the majority), but online policies keep improving with time.
Here I will use the Mediamill dataset instead, as it has a lot more data:
```
from contextualbandits.online import BootstrappedUCB
features, y = parse_data("Mediamill_data.txt")
nchoices = y.shape[1]
Xall=features
actions_random = np.random.randint(nchoices, size = Xall.shape[0])
rewards_actions = y[np.arange(y.shape[0]), actions_random]
online_policy = BootstrappedUCB(LogisticRegression(), y.shape[1])
evaluateRejectionSampling(online_policy,
X = Xall,
a = actions_random,
r = rewards_actions,
online = True,
start_point_online = 'random',
batch_size = 5)
```
** *
<a id="p4"></a>
## 4. References
* Li, L., Chu, W., Langford, J., & Schapire, R. E. (2010, April). A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th international conference on World wide web (pp. 661-670). ACM.
* Dudík, M., Langford, J., & Li, L. (2011). Doubly robust policy evaluation and learning. arXiv preprint arXiv:1103.4601.
| true |
code
| 0.481027 | null | null | null | null |
|
# Import libraries needed to plot data
```
import math
import numpy as np
import pandas as pd
import scipy.special
from bokeh.layouts import gridplot
from bokeh.io import show, output_notebook, save, output_file
from bokeh.plotting import figure
from bokeh.models import BoxAnnotation, HoverTool, ColumnDataSource, NumeralTickFormatter
from scipy.stats import lognorm, norm
```
Set plots to ouput in notebook instead of as a new tab in the browser, comment out or delete if you want the output as a new browser tab
```
# Bokeh output to notebook setting
output_notebook()
```
# Create main functions used to plot the different outputs, CHANGE AT YOUR OWN RISK
```
# Find P10, P50, and P90
def find_nearest(array, value):
array = np.asarray(array)
idx = (np.abs(array - value)).argmin()
return (array[idx], idx)
def make_plot_cdf(title, hist, edges, x, pdf, cdf, x_label):
p = figure(title=title, background_fill_color="#fafafa", x_axis_type='log')
p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],
fill_color="navy", line_color="white", alpha=0.5)
p.line(x, cdf, line_color="orange", line_width=2, alpha=0.7, legend="CDF")
p.x_range.start = 1
p.y_range.start = 0
p.legend.location = "center_right"
p.legend.background_fill_color = "#fefefe"
p.xaxis.axis_label = x_label
p.yaxis.axis_label = 'Pr(x)'
p.grid.grid_line_color = "white"
p.left[0].formatter.use_scientific = False
p.xaxis[0].formatter = NumeralTickFormatter(format="0,0")
return p
def make_plot_probit(title, input_data, x_label):
'''Creates Probit plot for EUR and data that has a log-normal distribution.
'''
# Calculate log-normal distribtion for input data
sigma, floc, scale = lognorm.fit(input_data, floc=0)
mu = math.log(scale)
x = np.linspace(0.001, np.max(input_data) + np.mean(input_data), 1000)
pdf = 1/(x * sigma * np.sqrt(2*np.pi)) * \
np.exp(-(np.log(x)-mu)**2 / (2*sigma**2))
cdf = (1+scipy.special.erf((np.log(x)-mu)/(np.sqrt(2)*sigma)))/2
p = figure(title=title, background_fill_color="#fafafa", x_axis_type='log')
# Prepare input data for plot
input_data_log = np.log(input_data)
# Get percentile of each point by getting rank/len(data)
input_data_log_sorted = np.argsort(input_data_log)
ranks = np.empty_like(input_data_log_sorted)
ranks[input_data_log_sorted] = np.arange(len(input_data_log))
# Add 1 to length of data because norm._ppf(1) is infinite, which will occur for highest ranked value
input_data_log_perc = [(x + 1)/(len(input_data_log_sorted) + 1)
for x in ranks]
input_data_y_values = norm._ppf(input_data_log_perc)
# Prepare fitted line for plot
x_y_values = norm._ppf(cdf)
# Values to display on y axis instead of z values from ppf
y_axis = [1 - x for x in cdf]
# Plot input data values
p.scatter(input_data, input_data_y_values, size=15,
line_color="navy", legend="Input Data", marker='circle_cross')
p.line(x, x_y_values, line_width=3, line_color="red", legend="Best Fit")
# calculate P90, P50, P10
p10_param = find_nearest(cdf, 0.9)
p10 = round(x[p10_param[1]])
p50_param = find_nearest(cdf, 0.5)
p50 = round(x[p50_param[1]])
p90_param = find_nearest(cdf, 0.1)
p90 = round(x[p90_param[1]])
# Add P90, P50, P10 markers
p.scatter(p90, norm._ppf(0.10), size=15, line_color="black",
fill_color='darkred', legend=f"P90 = {int(p90)}", marker='square_x')
p.scatter(p50, norm._ppf(0.50), size=15, line_color="black",
fill_color='blue', legend=f"P50 = {int(p50)}", marker='square_x')
p.scatter(p10, norm._ppf(0.90), size=15, line_color="black",
fill_color='red', legend=f"P10 = {int(p10)}", marker='square_x')
# Add P90, P50, P10 segments
# p.segment(1, norm._ppf(0.10), np.max(x), norm._ppf(0.10), line_dash='dashed', line_width=2, line_color='black', legend="P90")
# p.segment(1, norm._ppf(0.50), np.max(x), norm._ppf(0.50), line_dash='dashed', line_width=2, line_color='black', legend="P50")
# p.segment(1, norm._ppf(0.90), np.max(x), norm._ppf(0.90), line_dash='dashed', line_width=2, line_color='black', legend="P10")
p.segment(p90, -4, p90, np.max(x_y_values), line_dash='dashed',
line_width=2, line_color='darkred', legend=f"P90 = {int(p90)}")
p.segment(p50, -4, p50, np.max(x_y_values), line_dash='dashed',
line_width=2, line_color='blue', legend=f"P50 = {int(p50)}")
p.segment(p10, -4, p10, np.max(x_y_values), line_dash='dashed',
line_width=2, line_color='red', legend=f"P10 = {int(p10)}")
# Find min for x axis
x_min = int(np.log10(np.min(input_data)))
power_of_10 = 10**(x_min)
# Plot Styling
p.x_range.start = power_of_10
p.y_range.start = -3
p.legend.location = "top_left"
p.legend.background_fill_color = "#fefefe"
p.xaxis.axis_label = x_label
p.yaxis.axis_label = 'Z'
p.left[0].formatter.use_scientific = False
p.xaxis[0].formatter = NumeralTickFormatter(format="0,0")
p.yaxis.visible = False
p.title.text = title
p.title.align = 'center'
p.legend.click_policy = "hide"
return p
def make_plot_pdf(title, hist, edges, x, pdf, x_label):
source = ColumnDataSource(data = {
'x' : x,
'pdf': pdf,
})
p = figure(background_fill_color="#fafafa", )
p.quad(top=hist, bottom=0, left=edges[:-1], right=edges[1:],
fill_color="navy", line_color="white", alpha=0.5)
p.line('x', 'pdf', line_color="black", line_width=4, alpha=0.8, legend="PDF",
hover_alpha=0.4, hover_line_color="black", source=source)
# calculate P90, P50, P10
p10_param = find_nearest(cdf, 0.9)
p10 = round(x[p10_param[1]])
p50_param = find_nearest(cdf, 0.5)
p50 = round(x[p50_param[1]])
p90_param = find_nearest(cdf, 0.1)
p90 = round(x[p90_param[1]])
p.line((p90, p90), [0, np.max(pdf)],
line_color='darkred', line_width=3, legend=f"P90 = {int(p90)}")
p.line((p50, p50), [0, np.max(pdf)],
line_color='blue', line_width=3, legend=f"P50 = {int(p50)}")
p.line((p10, p10), [0, np.max(pdf)],
line_color='red', line_width=3, legend=f"P10 = {int(p10)}")
lower = BoxAnnotation(left=p90, right=p50,
fill_alpha=0.1, fill_color='darkred')
middle = BoxAnnotation(left=p50, right=p10,
fill_alpha=0.1, fill_color='blue')
upper = BoxAnnotation(
left=p10, right=x[-1], fill_alpha=0.1, fill_color='darkred')
# Hover Tool
p.add_tools(HoverTool(
tooltips=[
( x_label, '@x{f}' ),
( 'Probability', '@pdf{%0.6Ff}' ), # use @{ } for field names with spaces
]))
# Plot Styling
p.add_layout(lower)
p.add_layout(middle)
p.add_layout(upper)
p.y_range.start = 0
p.x_range.start = 0
p.legend.location = "center_right"
p.legend.background_fill_color = "#fefefe"
p.xaxis.axis_label = x_label
p.yaxis.axis_label = 'Pr(x)'
p.grid.grid_line_color = "white"
p.left[0].formatter.use_scientific = False
p.xaxis[0].formatter = NumeralTickFormatter(format="0,0")
p.title.text = title
p.title.align = 'center'
return p
```
## The data you want to analyze needs to be set equal to the **input_data** variable below. This example uses the dataset supplied in the /Test_Data tab. The input data can be a list, numpy array, pandas series, or DataFrame Column.
```
data = pd.read_csv(
"https://raw.githubusercontent.com/mwentzWW/petrolpy/master/petrolpy/Test_Data/EUR_Data.csv")
data
input_data = data["CUM_MBO"]
```
The **input_data** is fit to a log normal model
```
# lognorm.fit returns (shape, floc, scale)
# shape is sigma or the standard deviation, scale = exp(median)
sigma, floc, scale = lognorm.fit(input_data, floc=0)
mu = math.log(scale)
```
The model parameters are used to construct the histogram, probability density function (pdf) and cumulative density function (cdf)
```
hist, edges = np.histogram(input_data, density=True, bins='auto')
x = np.linspace(0.001, np.max(input_data) + np.mean(input_data), 1000)
pdf = 1/(x * sigma * np.sqrt(2*np.pi)) * \
np.exp(-(np.log(x)-mu)**2 / (2*sigma**2))
cdf = (1+scipy.special.erf((np.log(x)-mu)/(np.sqrt(2)*sigma)))/2
mean = np.exp(mu + 0.5*(sigma**2))
```
Now we create one of each plot, for basic use the only thing you will want to change is the label argument. Replace 'Cum MBO' with whatever label you want for your data.
```
plot_cdf = make_plot_cdf("Log Normal Distribution (n = {}, mean = {}, σ = {})".format(round(len(
input_data), 2), int(mean), round(sigma, 2)), hist, edges, x, pdf, cdf, 'Cum MBO')
plot_pdf = make_plot_pdf("Log Normal Distribution (n = {}, mean = {}, σ = {})".format(round(
len(input_data), 2), int(mean), round(sigma, 2)), hist, edges, x, pdf, 'Cum MBO')
plot_dist = make_plot_probit("Log Normal Distribution (n = {}, mean = {}, σ = {})".format(
round(len(input_data), 2), int(mean), round(sigma, 2)), input_data, 'Cum MBO')
show(plot_cdf)
```
# The show function will return the plot generated. If you want to save the output as an html file, remove the # from the lines below.
```
#output_file("plot_pdf.html")
#save(plot_pdf)
show(plot_pdf)
#output_file("plot_dist.html")
#save(plot_dist)
show(plot_dist)
```
Below are examples of how to calculate the value of each percentile in the cdf. The P50, P10, and P90 are calculated below.
```
# P50 value
p50_param = find_nearest(cdf, 0.5)
p50_value = round(x[p50_param[1]])
p50_value
# P10 value, only 10% of values will have this value or more
p10_param = find_nearest(cdf, 0.9)
p10_value = round(x[p10_param[1]])
p10_value
# P90 value, 90% of values will have this value or more
p90_param = find_nearest(cdf, 0.1)
p90_value = round(x[p90_param[1]])
p90_value
```
| true |
code
| 0.655557 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/hbayes_binom_rats_pymc3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
We fit a hierarchical beta-binomial model to some count data derived from rat survival. (In the book, we motivate this in terms of covid incidence rates.)
Based on https://docs.pymc.io/notebooks/GLM-hierarchical-binominal-model.html
```
import sklearn
import scipy.stats as stats
import scipy.optimize
import matplotlib.pyplot as plt
import seaborn as sns
import time
import numpy as np
import os
import pandas as pd
#!pip install pymc3 # colab uses 3.7 by default (as of April 2021)
# arviz needs 3.8+
#!pip install pymc3>=3.8 # fails to update
!pip install pymc3==3.11
import pymc3 as pm
print(pm.__version__)
import arviz as az
print(az.__version__)
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np
import pandas as pd
#import seaborn as sns
import pymc3 as pm
import arviz as az
import theano.tensor as tt
np.random.seed(123)
# rat data (BDA3, p. 102)
y = np.array([
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 5, 2,
5, 3, 2, 7, 7, 3, 3, 2, 9, 10, 4, 4, 4, 4, 4, 4, 4,
10, 4, 4, 4, 5, 11, 12, 5, 5, 6, 5, 6, 6, 6, 6, 16, 15,
15, 9, 4
])
n = np.array([
20, 20, 20, 20, 20, 20, 20, 19, 19, 19, 19, 18, 18, 17, 20, 20, 20,
20, 19, 19, 18, 18, 25, 24, 23, 20, 20, 20, 20, 20, 20, 10, 49, 19,
46, 27, 17, 49, 47, 20, 20, 13, 48, 50, 20, 20, 20, 20, 20, 20, 20,
48, 19, 19, 19, 22, 46, 49, 20, 20, 23, 19, 22, 20, 20, 20, 52, 46,
47, 24, 14
])
N = len(n)
def logp_ab(value):
''' prior density'''
return tt.log(tt.pow(tt.sum(value), -5/2))
with pm.Model() as model:
# Uninformative prior for alpha and beta
ab = pm.HalfFlat('ab',
shape=2,
testval=np.asarray([1., 1.]))
pm.Potential('p(a, b)', logp_ab(ab))
alpha = pm.Deterministic('alpha', ab[0])
beta = pm.Deterministic('beta', ab[1])
X = pm.Deterministic('X', tt.log(ab[0]/ab[1]))
Z = pm.Deterministic('Z', tt.log(tt.sum(ab)))
theta = pm.Beta('theta', alpha=ab[0], beta=ab[1], shape=N)
p = pm.Binomial('y', p=theta, observed=y, n=n)
#trace = pm.sample(1000, tune=2000, target_accept=0.95)
trace = pm.sample(1000, tune=500)
#az.plot_trace(trace)
#plt.savefig('../figures/hbayes_binom_rats_trace.png', dpi=300)
print(az.summary(trace))
J = len(n)
post_mean = np.zeros(J)
samples = trace[theta]
post_mean = np.mean(samples, axis=0)
print('post mean')
print(post_mean)
alphas = trace['alpha']
betas = trace['beta']
alpha_mean = np.mean(alphas)
beta_mean = np.mean(betas)
hyper_mean = alpha_mean/(alpha_mean + beta_mean)
print('hyper mean')
print(hyper_mean)
mle = y / n
pooled_mle = np.sum(y) / np.sum(n)
print('pooled mle')
print(pooled_mle)
#axes = az.plot_forest(
# trace, var_names='theta', credible_interval=0.95, combined=True, colors='cycle')
axes = az.plot_forest(
trace, var_names='theta', hdi_prob=0.95, combined=True, colors='cycle')
y_lims = axes[0].get_ylim()
axes[0].vlines(hyper_mean, *y_lims)
#plt.savefig('../figures/hbayes_binom_rats_forest95.pdf', dpi=300)
J = len(n)
fig, axs = plt.subplots(4,1, figsize=(10,10))
plt.subplots_adjust(hspace=0.3)
axs = np.reshape(axs, 4)
xs = np.arange(J)
ax = axs[0]
ax.bar(xs, y)
ax.set_title('number of postives')
ax = axs[1]
ax.bar(xs, n)
ax.set_title('popn size')
ax = axs[2]
ax.bar(xs, mle)
ax.set_ylim(0, 0.5)
ax.hlines(pooled_mle, 0, J, 'r', lw=3)
ax.set_title('MLE (red line = pooled)')
ax = axs[3]
ax.bar(xs, post_mean)
ax.hlines(hyper_mean, 0, J, 'r', lw=3)
ax.set_ylim(0, 0.5)
ax.set_title('posterior mean (red line = hparam)')
#plt.savefig('../figures/hbayes_binom_rats_barplot.pdf', dpi=300)
J = len(n)
xs = np.arange(J)
fig, ax = plt.subplots(1,1)
ax.bar(xs, y)
ax.set_title('number of postives')
#plt.savefig('../figures/hbayes_binom_rats_outcomes.pdf', dpi=300)
fig, ax = plt.subplots(1,1)
ax.bar(xs, n)
ax.set_title('popn size')
#plt.savefig('../figures/hbayes_binom_rats_popsize.pdf', dpi=300)
fig, ax = plt.subplots(1,1)
ax.bar(xs, mle)
ax.set_ylim(0, 0.5)
ax.hlines(pooled_mle, 0, J, 'r', lw=3)
ax.set_title('MLE (red line = pooled)')
#plt.savefig('../figures/hbayes_binom_rats_MLE.pdf', dpi=300)
fig, ax = plt.subplots(1,1)
ax.bar(xs, post_mean)
ax.hlines(hyper_mean, 0, J, 'r', lw=3)
ax.set_ylim(0, 0.5)
ax.set_title('posterior mean (red line = hparam)')
#plt.savefig('../figures/hbayes_binom_rats_postmean.pdf', dpi=300)
```
| true |
code
| 0.509093 | null | null | null | null |
|
# Think Bayes
This notebook presents example code and exercise solutions for Think Bayes.
Copyright 2018 Allen B. Downey
MIT License: https://opensource.org/licenses/MIT
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import classes from thinkbayes2
from thinkbayes2 import Hist, Pmf, Suite, Beta
import thinkplot
import numpy as np
```
## The dinner party
Suppose you are having a dinner party with 10 guests and 4 of them are allergic to cats. Because you have cats, you expect 50% of the allergic guests to sneeze during dinner. At the same time, you expect 10% of the non-allergic guests to sneeze. What is the distribution of the total number of guests who sneeze?
```
# Solution
n_allergic = 4
n_non = 6
p_allergic = 0.5
p_non = 0.1
pmf = MakeBinomialPmf(n_allergic, p_allergic) + MakeBinomialPmf(n_non, p_non)
thinkplot.Hist(pmf)
# Solution
pmf.Mean()
```
## The Gluten Problem
[This study from 2015](http://onlinelibrary.wiley.com/doi/10.1111/apt.13372/full) showed that many subjects diagnosed with non-celiac gluten sensitivity (NCGS) were not able to distinguish gluten flour from non-gluten flour in a blind challenge.
Here is a description of the study:
>"We studied 35 non-CD subjects (31 females) that were on a gluten-free diet (GFD), in a double-blind challenge study. Participants were randomised to receive either gluten-containing flour or gluten-free flour for 10 days, followed by a 2-week washout period and were then crossed over. The main outcome measure was their ability to identify which flour contained gluten.
>"The gluten-containing flour was correctly identified by 12 participants (34%)..."
Since 12 out of 35 participants were able to identify the gluten flour, the authors conclude "Double-blind gluten challenge induces symptom recurrence in just one-third of patients fulfilling the clinical diagnostic criteria for non-coeliac gluten sensitivity."
This conclusion seems odd to me, because if none of the patients were sensitive to gluten, we would expect some of them to identify the gluten flour by chance. So the results are consistent with the hypothesis that none of the subjects are actually gluten sensitive.
We can use a Bayesian approach to interpret the results more precisely. But first we have to make some modeling decisions.
1. Of the 35 subjects, 12 identified the gluten flour based on resumption of symptoms while they were eating it. Another 17 subjects wrongly identified the gluten-free flour based on their symptoms, and 6 subjects were unable to distinguish. So each subject gave one of three responses. To keep things simple I follow the authors of the study and lump together the second two groups; that is, I consider two groups: those who identified the gluten flour and those who did not.
2. I assume (1) people who are actually gluten sensitive have a 95% chance of correctly identifying gluten flour under the challenge conditions, and (2) subjects who are not gluten sensitive have only a 40% chance of identifying the gluten flour by chance (and a 60% chance of either choosing the other flour or failing to distinguish).
Using this model, estimate the number of study participants who are sensitive to gluten. What is the most likely number? What is the 95% credible interval?
```
# Solution
# Here's a class that models the study
class Gluten(Suite):
def Likelihood(self, data, hypo):
"""Computes the probability of the data under the hypothesis.
data: tuple of (number who identified, number who did not)
hypothesis: number of participants who are gluten sensitive
"""
# compute the number who are gluten sensitive, `gs`, and
# the number who are not, `ngs`
gs = hypo
yes, no = data
n = yes + no
ngs = n - gs
pmf1 = MakeBinomialPmf(gs, 0.95)
pmf2 = MakeBinomialPmf(ngs, 0.4)
pmf = pmf1 + pmf2
return pmf[yes]
# Solution
prior = Gluten(range(0, 35+1))
thinkplot.Pdf(prior)
# Solution
posterior = prior.Copy()
data = 12, 23
posterior.Update(data)
# Solution
thinkplot.Pdf(posterior)
thinkplot.Config(xlabel='# who are gluten sensitive',
ylabel='PMF', legend=False)
# Solution
posterior.CredibleInterval(95)
```
| true |
code
| 0.707796 | null | null | null | null |
|
<img src='./img/logoline_12000.png' align='right' width='100%'></img>
# Tutorial on creating a climate index for wind chill
In this tutorial we will plot a map of wind chill over Europe using regional climate reanalysis data (UERRA) of wind speed and temperature. From the WEkEO Jupyterhub we will download this data from the Climate Data Store (CDS) of the Copernicus Climate Change Service (C3S). The tutorial comprises the following steps:
1. [Search and download](#search_download) regional climate reanalysis data (UERRA) of 10m wind speed and 2m temperature.
2. [Read data](#read_data): Once downloaded, we will read and understand the data, including its variables and coordinates.
3. [Calculate wind chill index](#wind_chill): We will calculate the wind chill index from the two parameters of wind speed and temperature, and view a map of average wind chill over Europe.
4. [Calculate wind chill with ERA5](#era5): In order to assess the reliability of the results, repeat the process with ERA5 reanalysis data and compare the results with those derived with UERRA.
<img src='./img/climate_indices.png' align='center' width='100%'></img>
## <a id='search_download'></a>1. Search and download data
Before we begin we must prepare our environment. This includes installing the Application Programming Interface (API) of the CDS, and importing the various python libraries that we will need.
#### Install CDS API
To install the CDS API, run the following command. We use an exclamation mark to pass the command to the shell (not to the Python interpreter).
```
!pip install cdsapi
```
#### Import libraries
We will be working with data in NetCDF format. To best handle this data we need a number of libraries for working with multidimensional arrays, in particular Xarray. We will also need libraries for plotting and viewing data, in particular Matplotlib and Cartopy.
```
# CDS API
import cdsapi
# Libraries for working with multidimensional arrays
import numpy as np
import xarray as xr
# Libraries for plotting and visualising data
import matplotlib.path as mpath
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature
```
#### Enter your CDS API key
Please follow the steps at this link to obtain a User ID and a CDS API key:
https://cds.climate.copernicus.eu/api-how-to
Once you have these, please enter them in the fields below by replacing "UID" with your User ID, and "API_KEY" with your API key.
```
CDS_URL = "https://cds.climate.copernicus.eu/api/v2"
# enter your CDS authentication key:
CDS_KEY = "UID:API_KEY"
```
#### Search for climate data to calculate wind chill index
The wind chill index we will calculate takes two parameters as input, these are 2m near-surface air temperature, and 10m wind speed. Data for these parameters are available as part of the UERRA regional reanalysis dataset for Europe for the period 1961 to 2019. We will search for this data on the CDS website: http://cds.climate.copernicus.eu. The specific dataset we will use is the UERRA regional reanalysis for Europe on single levels from 1961 to 2019.
<img src='./img/CDS.jpg' align='left' width='45%'></img> <img src='./img/CDS_UERRA.png' align='right' width='45%'></img>
Having selected the dataset, we now need to specify what product type, variables, temporal and geographic coverage we are interested in. These can all be selected in the **"Download data"** tab. In this tab a form appears in which we will select the following parameters to download:
- Origin: `UERRA-HARMONIE`
- Variable: `10m wind speed` and `2m temperature` (these will need to be selected one at a time)
- Year: `1998 to 2019`
- Month: `December`
- Day: `15`
- Time: `12:00`
- Format: `NetCDF`
<img src='./img/CDS_UERRA_download.png' align='center' width='45%'></img>
At the end of the download form, select **"Show API request"**. This will reveal a block of code, which you can simply copy and paste into a cell of your Jupyter Notebook (see cells below). You will do this twice: once for 10m wind speed and again for 2m temperature.
#### Download data
Having copied the API requests into the cells below, run these to retrieve and download the data you requested into your local directory.
```
c = cdsapi.Client(url=CDS_URL, key=CDS_KEY)
c.retrieve(
'reanalysis-uerra-europe-single-levels',
{
'origin': 'uerra_harmonie',
'variable': '10m_wind_speed',
'year': [
'1998', '1999', '2000',
'2001', '2002', '2003',
'2004', '2005', '2006',
'2007', '2008', '2009',
'2010', '2011', '2012',
'2013', '2014', '2015',
'2016', '2017', '2018',
],
'month': '12',
'day': '15',
'time': '12:00',
'format': 'netcdf',
},
'UERRA_ws10m.nc')
c = cdsapi.Client(url=CDS_URL, key=CDS_KEY)
c.retrieve(
'reanalysis-uerra-europe-single-levels',
{
'origin': 'uerra_harmonie',
'variable': '2m_temperature',
'year': [
'1998', '1999', '2000',
'2001', '2002', '2003',
'2004', '2005', '2006',
'2007', '2008', '2009',
'2010', '2011', '2012',
'2013', '2014', '2015',
'2016', '2017', '2018',
],
'month': '12',
'day': '15',
'time': '12:00',
'format': 'netcdf',
},
'UERRA_t2m.nc')
```
## <a id='read_data'></a>2. Read Data
Now that we have downloaded the data, we can start to play ...
We have requested the data in NetCDF format. This is a commonly used format for array-oriented scientific data.
To read and process this data we will make use of the Xarray library. Xarray is an open source project and Python package that makes working with labelled multi-dimensional arrays simple, efficient, and fun! We will read the data from our NetCDF file into an Xarray **"dataset"**
```
fw = 'UERRA_ws10m.nc'
ft = 'UERRA_t2m.nc'
# Create Xarray Dataset
dw = xr.open_dataset(fw)
dt = xr.open_dataset(ft)
```
Now we can query our newly created Xarray datasets ...
```
dw
dt
```
We see that dw (dataset for wind speed) has one variable called **"si10"**. If you view the documentation for this dataset on the CDS you will see that this is the wind speed valid for a grid cell at the height of 10m above the surface. It is computed from both the zonal (u) and the meridional (v) wind components by $\sqrt{(u^{2} + v^{2})}$. The units are m/s.
The other dataset, dt (2m temperature), has a variable called **"t2m"**. According to the documentation on the CDS this is air temperature valid for a grid cell at the height of 2m above the surface, in units of Kelvin.
While an Xarray **dataset** may contain multiple variables, an Xarray **data array** holds a single multi-dimensional variable and its coordinates. To make the processing of the **si10** and **t2m** data easier, we will convert them into Xarray data arrays.
```
# Create Xarray Data Arrays
aw = dw['si10']
at = dt['t2m']
```
## <a id='wind_chill'></a>3. Calculate wind chill index
There are several indices to calculate wind chill based on air temperature and wind speed. Until recently, a commonly applied index was the following:
$\textit{WCI} = (10 \sqrt{\upsilon}-\upsilon + 10.5) \cdot (33 - \textit{T}_{a})$
where:
- WCI = wind chill index, $kg*cal/m^{2}/h$
- $\upsilon$ = wind velocity, m/s
- $\textit{T}_{a}$ = air temperature, °C
We will use the more recently adopted North American and United Kingdom wind chill index, which is calculated as follows:
$\textit{T}_{WC} = 13.12 + 0.6215\textit{T}_{a} - 11.37\upsilon^{0.16} + 0.3965\textit{T}_{a}\upsilon^{0.16}$
where:
- $\textit{T}_{WC}$ = wind chill index
- $\textit{T}_{a}$ = air temperature in degrees Celsius
- $\upsilon$ = wind speed at 10 m standard anemometer height, in kilometres per hour
To calculate $\textit{T}_{WC}$ we first have to ensure our data is in the right units. For the wind speed we need to convert from m/s to km/h, and for air temperature we need to convert from Kelvin to degrees Celsius:
```
# wind speed, convert from m/s to km/h: si10 * 1000 / (60*60)
w = aw * 3600 / 1000
# air temperature, convert from Kelvin to Celsius: t2m - 273.15
t = at - 273.15
```
Now we can calculate the North American and United Kingdom wind chill index:
$\textit{T}_{WC} = 13.12 + 0.6215\textit{T}_{a} - 11.37\upsilon^{0.16} + 0.3965\textit{T}_{a}\upsilon^{0.16}$
```
twc = 13.12 + (0.6215*t) - (11.37*(w**0.16)) + (0.3965*t*(w**0.16))
```
Let's calculate the average wind chill for 12:00 on 15 December for the 20 year period from 1998 to 2019:
```
twc_mean = twc.mean(dim='time')
```
Now let's plot the average wind chill for this time over Europe:
```
# create the figure panel
fig = plt.figure(figsize=(10,10))
# create the map using the cartopy Orthographic projection
ax = plt.subplot(1,1,1, projection=ccrs.Orthographic(central_longitude=8., central_latitude=42.))
# add coastlines
ax.coastlines()
ax.gridlines(draw_labels=False, linewidth=1, color='gray', alpha=0.5, linestyle='--')
# provide a title
ax.set_title('Wind Chill Index 12:00, 15 Dec, 1998 to 2019')
# plot twc
im = plt.pcolormesh(twc_mean.longitude, twc_mean.latitude,
twc_mean, cmap='viridis', transform=ccrs.PlateCarree())
# add colourbar
cbar = plt.colorbar(im)
cbar.set_label('Wind Chill Index')
```
Can you identify areas where frostbite may occur (see chart below)?
<img src='./img/Windchill_effect_en.svg' align='left' width='60%'></img>
RicHard-59, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons
## <a id='era5'></a>4. Exercise: Repeat process with ERA5 data and compare results
So far you have plotted wind chill using the UERRA regional reanalysis dataset, but how accurate is this plot? One way to assess a dataset is to compare it with an alternative independent one to see what differences there may be. An alternative to UERRA is the ERA5 reanalysis data that you used in the previous tutorials. Repeat the steps above with ERA5 and compare your results with those obtained using UERRA.
<hr>
| true |
code
| 0.606673 | null | null | null | null |
|
# Automatic music generation system (AMGS) - Pop genre
An affective rule-based generative music system that generates retro pop music.
```
import numpy as np
import pandas as pd
import mido
import scipy.io
import time
import statistics
from numpy.random import choice
from IPython.display import clear_output
import math
import json
# set up midi ports
print(mido.get_output_names())
percussion = mido.open_output('IAC Driver Bus 1')
piano = mido.open_output('IAC Driver Bus 2')
# read in composed progressions
with open('composed_progressions.txt') as json_file:
data = json.load(json_file)
```
# Scales, progressions and patterns
This section determines the scales, chord progressions, melodic patterns and rhythmic patterns used by the system.
```
import playerContainer
import progressionsContainer as progs
# initialize helper functions
player = playerContainer.PlayerContainer()
# set relative positions of notes in major and parallel minor scales
# MIDI note numbers for C major: 60 (C4), 62 (D), 64 (E), 65 (F), 67 (G), 69 (A), 71 (B)
tonic = 60
majorScale = [tonic, tonic+2, tonic+4, tonic+5, tonic+7, tonic+9, tonic+11]
minorScale = [tonic, tonic+2, tonic+3, tonic+5, tonic+7, tonic+8, tonic+10]
# test sound -> should hear note being played through audio workstation
ichannel = 1
ivelocity = 64
msg = mido.Message('note_on',channel=ichannel,note=tonic,velocity=ivelocity)
piano.send(msg)
time.sleep(0.50)
msg = mido.Message('note_off',channel=ichannel,note=tonic,velocity=ivelocity)
piano.send(msg)
# draft: percussion
# Ableton's drum pads are mapped by default to MIDI notes 36-51
ichannel = 10
ivelocity = 64
inote = 51
msg = mido.Message('note_on',channel=ichannel,note=inote,velocity=ivelocity)
percussion.send(msg)
```
# Player (Main)
This section puts together all the functions and generates music based on the current arousal and valence values.
**Arousal-based params**
1. roughness. Lower roughness -> higher note density.
3. loudness
4. tempo. Minimum = 60bpm, maximum = 160bpm
**Valence-based params**
1. voicing
2. chord progression
```
# artificially determine arousal-valence trajectory
#np.array([0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2])
input_arousal = np.array([0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
input_arousal = np.repeat(input_arousal, 8)
input_valence = np.array([0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
input_valence = np.repeat(input_valence, 8)
# or randomly generate a trajectory
rng = np.random.default_rng()
# low arousal, low valence, 40-bar progression
input_arousal = rng.integers(50, size=40)/100
input_valence = rng.integers(50, size=40)/100
# high arousal, low valence, 40-bar progression
input_arousal = rng.integers(50, high=100, size=40)/100
input_valence = rng.integers(50, size=40)/100
# low arousal, high valence, 40-bar progression
input_arousal = rng.integers(50, size=40)/100
input_valence = rng.integers(50, high=100, size=40)/100
# high arousal, high valence, 40-bar progression
input_arousal = rng.integers(50, high=100, size=40)/100
input_valence = rng.integers(50, high=100, size=40)/100
input_arousal
input_arousal = np.array([0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
input_arousal = np.repeat(input_arousal, 4)
input_valence = np.array([0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
input_valence = np.repeat(input_valence, 4)
print(input_valence)
print(input_arousal)
```
* melody generator, harmony generator, bass generator
* implement voice leading logic
**POSSIBLE CHANGES**
* maybe we can do moving average tempo instead -> but is that sacrificing accuracy of emotion feedback?
```
# initialize params: next_chord, minimal loudness, velocity, current_motive
next_chord = []
current_motive=0
# initialize memory of previous harmony and melody notes (partially determines current harmony/melody notes)
prev_noteset, melody_note = [], []
# keep track of current bar
for bar in range(len(input_arousal)):
# set arousal and valence, keep track of current bar in 8-bar progressions
arousal = input_arousal[bar]
valence = input_valence[bar]
bar = bar%8
print("arousal: ", arousal, "---valence: ", valence, "---bar: ", bar)
# set simple params: roughness, voicing, loudness, tempo
roughness = 1-arousal
low_loudness = 40 + (arousal*40)
loudness = (round(arousal*10))/10*40+60
bpm = 60 + arousal * 100
volume = int(50 + (arousal*30))
# allocate note densities
n_subdivisions = 8
if arousal >= 0.75:
arousal_cat='high'
elif arousal >= 0.40:
arousal_cat='moderate'
else:
arousal_cat='low'
activate1 = [x for x in data['rhythmic_motives'] if x['bar']==bar if x['arousal']==arousal_cat][0]['motive']
activate2 = player.setRoughness(n_subdivisions, roughness+0.3)
# change volume of instruments
# instruments[0]: piano, instruments[1]: clarinet, instruments[2]: strings
msg = mido.Message('control_change',channel=ichannel,control=7,value=volume)
instruments[0].send(msg), instruments[1].send(msg), instruments[1].send(msg)
# select chord to be sounded
if next_chord==[]:
# if next chord has not already been determined, then select randomly as usual
chord, next_chord = progs.selectChord(data['progressions'], valence, bar)
else:
chord = next_chord.pop(0)
# generate set of all valid notes within range (based on current valence)
noteset = progs.createChord(chord, majorScale)
n_notes = len(noteset)
midi_low = [x for x in data['range'] if x['valence']==math.floor(valence * 10)/10][0]['midi_low']
midi_high = [x for x in data['range'] if x['valence']==math.floor(valence * 10)/10][0]['midi_high']
range_noteset = player.setRange(midi_low, midi_high, noteset)
print("chord: ", chord[3], "---notes in noteset: ", noteset, "----notes in full range: ", range_noteset)
# initialize memory of previous chord
if prev_noteset==[]:
prev_noteset=noteset
# allocate probabilities of register for each note in chord.
bright = player.setPitch(n_notes, valence)
# determine if scale patterns should be drawn from major or minor scale
if valence<0.4:
scale = player.setRange(midi_low, midi_high, minorScale)
else:
scale = player.setRange(midi_low, midi_high, majorScale)
scale.sort()
# do we want to add in a percussion instrument?
# play bass (root note) -> want to try bassoon? instruments = [piano, clarinet, strings]
current_velocity = np.random.randint(low_loudness,loudness)
note = mido.Message('note_on', channel=1, note=min(noteset) - 12, velocity=current_velocity)
instruments[2].send(note)
# play "accompaniment"/harmony chords
chord_voicing = progs.harmonyVL(prev_noteset, noteset, range_noteset)
print("chord voicing: ", chord_voicing)
for i in range(len(chord_voicing)):
note = mido.Message('note_on',
channel=1,
note=int(chord_voicing[i]+bright[i]*12),
velocity=current_velocity)
instruments[0].send(note)
# update value of prev_noteset
prev_noteset=chord_voicing
# plays "foreground" melody
for beat in range(0,n_subdivisions):
# determine which extensions to sound and create tone
if (activate1[beat] == 1):
note1 = int(noteset[0]+bright[0]*12)
msg = mido.Message('note_on',
channel=1,
note=note1,
velocity=current_velocity)
instruments[0].send(msg)
if (activate2[beat] == 1):
# use melodic motives for voice leading logic
current_motive = player.selectMotive(data['melodic_motives'], current_motive, arousal)
melody_note = player.melodyVL_motives(current_motive, melody_note, noteset, scale)
print('melody note is: ',melody_note)
msg = mido.Message('note_on',
channel=1,
note=melody_note,
velocity=current_velocity+10)
instruments[0].send(msg)
# length of pause determined by tempo.
time.sleep((60/bpm)/(n_subdivisions/4))
# shut all down
instruments[0].reset()
instruments[1].reset()
instruments[2].reset()
instruments[0].reset()
instruments[1].reset()
instruments[2].reset()
#clear_output()
```
Three voices: bass, harmony and melody
* Bass - String ensemble, Harmony and melody - Piano
* Bass - String ensemble, Harmony and melody - Piano, melody - Clarinet (doubling)
* Bass - Clarinet, Harmony and melody - Piano
```
[x for x in zip(chord_voicing, bright*12)]
melody_note
```
# Archive
```
if np.random.rand(1)[0] < arousal:
violin.send(msg)
# write control change (cc) message. Controller number 7 maps to volume.
volume = 80
msg = mido.Message('control_change',channel=ichannel,control=7,value=volume)
piano.send(msg)
# initial idea for melody voice leading - pick closest note
# note how this doesn't depend on arousal or valence at all, basically only controls musicality
def melodyVL_closestNote(melody_note, noteset, range_noteset):
"""
Controls voice leading of melodic line by picking the closest available next note based on previous note
the melody tends to stay around the same register with this implementation
"""
rand_idx = np.random.randint(2,n_notes)
# randomly initialize melody
if melody_note==[]:
melody_note = int(noteset[rand_idx]+bright[rand_idx]*12)
else:
melody_note = min(range_noteset, key=lambda x:abs(x-melody_note))
return melody_note
# initialize params: next_chord, minimal loudness, stadard velocity, current_motive
next_chord = []
low_loudness = 50
default_velocity = 80
current_motive=0
# initialize memory of previous harmony and melody notes (partially determines current harmony/melody notes)
prev_chord, melody_note = [], []
# keep track of current bar
for bar in range(len(input_arousal)):
# set arousal and valence, keep track of current bar in 8-bar progressions
arousal = input_arousal[bar]
valence = input_valence[bar]
bar = bar%8
print("arousal: ", arousal, "---valence: ", valence, "---bar: ", bar)
# set simple params: roughness, voicing, loudness, tempo
roughness = 1-arousal
voicing = valence
loudness = (round(arousal*10))/10*40+60
bpm = 60 + arousal * 100
# first vector (activate1) determines density of background chords
# second vector (activate2) determines density of melody played by piano
# TBC: n_subdivisions should eventually be determined by rhythmic pattern
n_subdivisions = 4
activate1 = player.setRoughness(n_subdivisions, roughness+0.4)
activate2 = player.setRoughness(n_subdivisions, roughness+0.2)
# select chord to be sounded
if next_chord==[]:
# if next chord has not already been determined, then select randomly as usual
chord, next_chord = progs.selectChord(data['progressions'], valence, bar)
else:
chord = next_chord.pop(0)
# generate set of all valid notes within range (based on current valence)
noteset = progs.createChord(chord, majorScale)
n_notes = len(noteset)
midi_low = [x for x in data['range'] if x['valence']==valence][0]['midi_low']
midi_high = [x for x in data['range'] if x['valence']==valence][0]['midi_high']
range_noteset = player.setRange(midi_low, midi_high, noteset)
print("chord: ", chord[3], "---notes in noteset: ", noteset, "----notes in full range: ", range_noteset)
# allocate probabilities of register for each note in chord.
bright = player.setPitch(n_notes, voicing)
# determine if scale patterns should be drawn from major or minor scale
if valence<0.4:
scale = player.setRange(midi_low, midi_high, minorScale)
else:
scale = player.setRange(midi_low, midi_high, majorScale)
scale.sort()
# play "accompaniment"/harmony chords
# TO CHANGE: if all notes in noteset above C4 octave, tranpose whole noteset down an octave.
# Create tone for each note in chord. Serves as the harmony of the generated music
for n in noteset:
note = mido.Message('note_on',
channel=1,
#note=int(noteset[i]+bright[i]*12),
note=n,
velocity=np.random.randint(low_loudness,loudness))
piano.send(note)
# NEW: added in bass (taking lowest value in noteset and transpose down 1-2 octaves)
# this should probably be played by cello, not piano
note = mido.Message('note_on', channel=1, note=min(noteset) - 24, velocity=default_velocity)
piano.send(note)
# plays "foreground" melody [0, 0, 0, 0] [0, 1, 1, 0]
for beat in range(0,n_subdivisions):
# determine which extensions to sound and create tone
#activate1 = player.setRoughness(n_subdivisions, roughness) -> moving this here lets us change subdivision every beat
# alternatively: determine downbeat probability separately.
if (activate1[beat] == 1):
note1 = int(noteset[0]+bright[0]*12)
msg = mido.Message('note_on',
channel=1,
note=note1,
velocity=np.random.randint(low_loudness,loudness))
piano.send(msg)
# add note_off message
if (activate2[beat] == 1):
# use "closest note" voice leading logic
#melody_note = melodyVL_closestNote(melody_note)
# use melodic motives for voice leading logic
current_motive = selectMotive(data['melodic_motives'], current_motive, arousal)
melody_note = melodyVL_motives(current_motive, melody_note, noteset, scale)
print('melody note is: ',melody_note)
msg = mido.Message('note_on',
channel=1,
note=melody_note,
velocity=np.random.randint(low_loudness,loudness))
piano.send(msg)
# length of pause determined by tempo. This formula works when smallest subdivision = eighth notes
time.sleep(0.50/(bpm/60))
#piano.send(mido.Message('note_off', channel=1, note=note1, velocity=64))
#piano.send(mido.Message('note_off', channel=1, note=note2, velocity=64))
# shut all down
# see if you can change the release param
piano.reset()
# generate scale for maximum range of player (C1-C6, MIDI note numbers 24-84)
range_majorScale = player.setRange(24, 84, majorScale)
range_majorScale.sort()
range_minorScale = player.setRange(24, 84, minorScale)
range_minorScale.sort()
range_majorScale.index(60)
temp = [1, 2, 3, 4]
temp[-1]
[x for x in data['melodic_motives'] if x['arousal']=='low' if x['current_motive']=='CT'][0]['motive_weights']
motives = [1, -1, 0, 'CT']
motive_weights=[0.15, 0.15, 0.3, 0.4]
choice(len(motives), 1, p=motive_weights)[0]
def inversion(noteset, inversion):
"""
increases the chord (noteset)'s inversion
"""
noteset.sort()
for i in range(inversion):
while noteset[i] < noteset[-1]:
noteset[i]+=12
return noteset
def decrease_inversion(noteset, inversion):
"""
decreases the chord (noteset)'s inversion
"""
noteset.sort()
for i in range(inversion):
while noteset[-1-i] > noteset[0]:
noteset[-1-i]-=12
return noteset
# implement voice leading logic for bass
temp = 61
print(range_noteset)
# this chooses the closest available note
min(range_noteset, key=lambda x:abs(x-temp))
# I think another possibility is to min. total distance moved for the hamony chords (which is more human)
print(noteset)
setRange(data['range'], 0.1, noteset)
```
| true |
code
| 0.239572 | null | null | null | null |
|
<img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# Remotive - Post daily jobs on slack
<a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Remotive/Remotive_Post_daily_jobs_on_slack.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
**Tags:** #remotive #jobs #slack #gsheet #naas_drivers #automation #opendata #text
**Author:** [Sanjeet Attili](https://www.linkedin.com/in/sanjeet-attili-760bab190/)
## Input
### Import libraries
```
import pandas as pd
from bs4 import BeautifulSoup
import requests
from datetime import datetime
import time
from naas_drivers import gsheet, slack
import naas
```
### Setup slack channel configuration
```
SLACK_TOKEN = "xoxb-1481042297777-3085654341191-xxxxxxxxxxxxxxxxxxxxxxxxx"
SLACK_CHANNEL = "05_work"
```
### Setup sheet log data
```
spreadsheet_id = "1EBefhkbmqaXMZLRCiafabf6xxxxxxxxxxxxxxxxxxx"
sheet_name = "SLACK_CHANNEL_POSTS"
```
### Setup Remotive
#### Get categories from Remotive
```
def get_remotejob_categories():
req_url = f"https://remotive.io/api/remote-jobs/categories"
res = requests.get(req_url)
try:
res.raise_for_status()
except requests.HTTPError as e:
return e
res_json = res.json()
# Get categories
jobs = res_json.get('jobs')
return pd.DataFrame(jobs)
df_categories = get_remotejob_categories()
df_categories
```
#### Enter your parameters
```
categories = ['data'] # Pick the list of categories in columns "slug"
date_from = - 10 # Choose date difference in days from now => must be negative
```
### Set the Scheduler
```
naas.scheduler.add(recurrence="0 9 * * *")
# # naas.scheduler.delete() # Uncomment this line to delete your scheduler if needed
```
## Model
### Get the sheet log of jobs
```
df_jobs_log = gsheet.connect(spreadsheet_id).get(sheet_name=sheet_name)
df_jobs_log
```
### Get all jobs posted after timestamp_date
All jobs posted after the date from will be fetched.<br>
In summary, we can set the value, in seconds, of 'search_data_from' to fetch all jobs posted since this duration
```
REMOTIVE_DATETIME = "%Y-%m-%dT%H:%M:%S"
NAAS_DATETIME = "%Y-%m-%d %H:%M:%S"
def get_remotive_jobs_since(jobs, date):
ret = []
for job in jobs:
publication_date = datetime.strptime(job['publication_date'], REMOTIVE_DATETIME).timestamp()
if publication_date > date:
ret.append({
'URL': job['url'],
'TITLE': job['title'],
'COMPANY': job['company_name'],
'PUBLICATION_DATE': datetime.fromtimestamp(publication_date).strftime(NAAS_DATETIME)
})
return ret
def get_category_jobs_since(category, date, limit):
url = f"https://remotive.io/api/remote-jobs?category={category}&limit={limit}"
res = requests.get(url)
if res.json()['jobs']:
publication_date = datetime.strptime(res.json()['jobs'][-1]['publication_date'], REMOTIVE_DATETIME).timestamp()
if len(res.json()['jobs']) < limit or date > publication_date:
print(f"Jobs from catgory {category} fetched ✅")
return get_remotive_jobs_since(res.json()['jobs'], date)
else:
return get_category_jobs_since(category, date, limit + 5)
return []
def get_jobs_since(categories: list,
date_from: int):
if date_from >= 0:
return("'date_from' must be negative. Please update your parameter.")
# Transform datefrom int to
search_jobs_from = date_from * 24 * 60 * 60 # days in seconds
timestamp_date = time.time() + search_jobs_from
jobs = []
for category in categories:
jobs += get_category_jobs_since(category, timestamp_date, 5)
print(f'- All job since {datetime.fromtimestamp(timestamp_date)} have been fetched -')
return pd.DataFrame(jobs)
df_jobs = get_jobs_since(categories, date_from=date_from)
df_jobs
```
### Remove duplicate jobs
```
def remove_duplicates(df1, df2):
# Get jobs log
jobs_log = df1.URL.unique()
# Exclude jobs already log from jobs
df2 = df2[~df2.URL.isin(jobs_log)]
return df2.sort_values(by="PUBLICATION_DATE")
df_new_jobs = remove_duplicates(df_jobs_log, df_jobs)
df_new_jobs
```
## Output
### Add new jobs on the sheet log
```
gsheet.connect(spreadsheet_id).send(sheet_name=sheet_name,
data=df_new_jobs,
append=True)
```
### Send all jobs link to the slack channel
```
if len(df_new_jobs) > 0:
for _, row in df_new_jobs.iterrows():
url = row.URL
slack.connect(SLACK_TOKEN).send(SLACK_CHANNEL, f"<{url}>")
else:
print("Nothing to published in Slack !")
```
| true |
code
| 0.339359 | null | null | null | null |
|
AMUSE tutorial on multiple code in a single bridge
====================
A cascade of bridged codes to address the problem of running multiple planetary systems in, for example, a star cluster. This is just an example of how to initialize such a cascaded bridge without any stellar evolution, background potentials. The forces for one planetary system on the planets in the other systems are ignored to save computer time. This gives rise to some energy errors, and inconsistencies (for example when one star tries to capture planets from another system. The latter will not happen here.
This can be addressed by intorducing some logic in checking what stars are nearby which planets.
```
import numpy
from amuse.units import (units, constants)
from amuse.lab import Particles
from amuse.units import nbody_system
from matplotlib import pyplot
## source https://en.wikipedia.org/wiki/TRAPPIST-1
trappist= {"b": {"m": 1.374 | units.MEarth,
"a": 0.01154 | units.au,
"e": 0.00622,
"i": 89.56},
"c": {"m": 1.308 | units.MEarth,
"a": 0.01580 | units.au,
"e": 0.00654,
"i": 89.70},
"d": {"m": 0.388 | units.MEarth,
"a": 0.02227 | units.au,
"e": 0.00837,
"i": 89.89},
"e": {"m": 0.692 | units.MEarth,
"a": 0.02925 | units.au,
"e": 0.00510,
"i": 89.736},
"f": {"m": 1.039 | units.MEarth,
"a": 0.03849 | units.au,
"e": 0.01007,
"i": 89.719},
"g": {"m": 1.321 | units.MEarth,
"a": 0.04683 | units.au,
"e": 0.00208,
"i": 89.721},
"h": {"m": 0.326 | units.MEarth,
"a": 0.06189 | units.au,
"e": 0.00567,
"i": 89.796}
}
def trappist_system():
from amuse.ext.orbital_elements import new_binary_from_orbital_elements
from numpy.random import uniform
star = Particles(1)
setattr(star, "name", "")
setattr(star, "type", "")
star[0].mass = 0.898 | units.MSun
star[0].position = (0,0,0) | units.au
star[0].velocity = (0,0,0) | units.kms
star[0].name = "trappist"
star[0].type = "star"
bodies = Particles(len(trappist))
setattr(bodies, "name", "")
setattr(bodies, "type", "")
for bi, planet in zip(bodies, trappist):
true_anomaly = uniform(0, 360)
b = new_binary_from_orbital_elements(star.mass,
trappist[planet]['m'],
trappist[planet]["a"],
trappist[planet]["e"],
true_anomaly = true_anomaly,
inclination = trappist[planet]["i"],
G = constants.G)
bi.name = planet
bi.type = "planet"
bi.mass = b[1].mass
bi.position = b[1].position - b[0].position
bi.velocity = b[1].velocity - b[0].velocity
return star | bodies
from amuse.community.ph4.interface import ph4
from amuse.community.hermite.interface import Hermite
from amuse.ic.plummer import new_plummer_model
import numpy.random
numpy.random.seed(1624973942)
converter=nbody_system.nbody_to_si(1 | units.MSun, 0.1|units.parsec)
t1 = trappist_system()
t2 = trappist_system()
t3 = trappist_system()
p = new_plummer_model(3, convert_nbody=converter)
t1.position += p[0].position
t1.velocity += p[0].velocity
t2.position += p[1].position
t2.velocity += p[1].velocity
t3.position += p[2].position
t3.velocity += p[2].velocity
converter=nbody_system.nbody_to_si(t1.mass.sum(), 0.1|units.au)
bodies = Particles(0)
gravity1 = ph4(converter)
t = gravity1.particles.add_particles(t1)
bodies.add_particles(t1)
gravity2 = ph4(converter)
t = gravity2.particles.add_particles(t2)
bodies.add_particles(t2)
gravity3 = Hermite(converter)
t = gravity3.particles.add_particles(t3)
bodies.add_particles(t3)
channel_from_g1 = gravity1.particles.new_channel_to(bodies)
channel_from_g2 = gravity2.particles.new_channel_to(bodies)
channel_from_g3 = gravity3.particles.new_channel_to(bodies)
from amuse.plot import scatter
from matplotlib import pyplot
scatter(bodies.x-bodies[0].x, bodies.z-bodies[0].z)
#pyplot.xlim(-0.1, 0.1)
#pyplot.ylim(-0.1, 0.1)
pyplot.show()
def plot(bodies):
from amuse.plot import scatter
from matplotlib import pyplot
stars = bodies[bodies.type=='star']
planets = bodies-stars
pyplot.scatter((stars.x-bodies[0].x).value_in(units.au),
(stars.z-bodies[0].z).value_in(units.au), c='r', s=100)
pyplot.scatter((planets.x-bodies[0].x).value_in(units.au),
(planets.z-bodies[0].z).value_in(units.au), c='b', s=10)
pyplot.xlim(-0.1, 0.1)
pyplot.ylim(-0.1, 0.1)
pyplot.show()
plot(bodies)
from amuse.couple import bridge
gravity = bridge.Bridge()
gravity.add_system(gravity1, (gravity2,gravity3))
gravity.add_system(gravity2, (gravity1,gravity3))
gravity.add_system(gravity3, (gravity1,gravity2))
from amuse.lab import zero
Etot_init = gravity.kinetic_energy + gravity.potential_energy
Etot_prev = Etot_init
gravity.timestep = 100.0| units.yr
time = zero
dt = 200.0|units.yr
t_end = 1000.0| units.yr
while time < t_end:
time += dt
gravity.evolve_model(time)
Etot_prev_se = gravity.kinetic_energy + gravity.potential_energy
channel_from_g1.copy()
channel_from_g2.copy()
channel_from_g3.copy()
plot(bodies)
print(bodies[1].position.in_(units.au))
Ekin = gravity.kinetic_energy
Epot = gravity.potential_energy
Etot = Ekin + Epot
print("T=", time.in_(units.yr), end=' ')
print("E= ", Etot/Etot_init, "Q= ", Ekin/Epot, end=' ')
print("dE=", (Etot_init-Etot)/Etot, "ddE=", (Etot_prev-Etot)/Etot)
Etot_prev = Etot
gravity.stop()
```
| true |
code
| 0.490236 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/moh2236945/Natural-language-processing/blob/master/Multichannel_CNN_Model_for_Text_Classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
```
model can be expanded by using multiple parallel convolutional neural networks that read the source document using different kernel sizes. This, in effect, creates a multichannel convolutional neural network for text that reads text with different n-gram sizes (groups of words).
Movie Review Dataset
Data Preparation
In this section, we will look at 3 things:
Separation of data into training and test sets.
Loading and cleaning the data to remove punctuation and numbers.
Prepare all reviews and save to file.
```
from string import punctuation
from os import listdir
from nltk.corpus import stopwords
from pickle import dump
# load doc into memory
def load_doc(filename):
# open the file as read only
file = open(filename, 'r')
# read all text
text = file.read()
# close the file
file.close()
return text
# turn a doc into clean tokens
def clean_doc(doc):
# split into tokens by white space
tokens = doc.split()
# remove punctuation from each token
table = str.maketrans('', '', punctuation)
tokens = [w.translate(table) for w in tokens]
# remove remaining tokens that are not alphabetic
tokens = [word for word in tokens if word.isalpha()]
# filter out stop words
stop_words = set(stopwords.words('english'))
tokens = [w for w in tokens if not w in stop_words]
# filter out short tokens
tokens = [word for word in tokens if len(word) > 1]
tokens = ' '.join(tokens)
return tokens
# load all docs in a directory
def process_docs(directory, is_trian):
documents = list()
# walk through all files in the folder
for filename in listdir(directory):
# skip any reviews in the test set
if is_trian and filename.startswith('cv9'):
continue
if not is_trian and not filename.startswith('cv9'):
continue
# create the full path of the file to open
path = directory + '/' + filename
# load the doc
doc = load_doc(path)
# clean doc
tokens = clean_doc(doc)
# add to list
documents.append(tokens)
return documents
# save a dataset to file
def save_dataset(dataset, filename):
dump(dataset, open(filename, 'wb'))
print('Saved: %s' % filename)
# load all training reviews
negative_docs = process_docs('txt_sentoken/neg', True)
positive_docs = process_docs('txt_sentoken/pos', True)
trainX = negative_docs + positive_docs
trainy = [0 for _ in range(900)] + [1 for _ in range(900)]
save_dataset([trainX,trainy], 'train.pkl')
# load all test reviews
negative_docs = process_docs('txt_sentoken/neg', False)
positive_docs = process_docs('txt_sentoken/pos', False)
testX = negative_docs + positive_docs
testY = [0 for _ in range(100)] + [1 for _ in range(100)]
save_dataset([testX,testY], 'test.pkl')
from nltk.corpus import stopwords
import string
# load doc into memory
def load_doc(filename):
# open the file as read only
file = open(filename, 'r')
# read all text
text = file.read()
# close the file
file.close()
return text
# turn a doc into clean tokens
def clean_doc(doc):
# split into tokens by white space
tokens = doc.split()
# remove punctuation from each token
table = str.maketrans('', '', string.punctuation)
tokens = [w.translate(table) for w in tokens]
# remove remaining tokens that are not alphabetic
tokens = [word for word in tokens if word.isalpha()]
# filter out stop words
stop_words = set(stopwords.words('english'))
tokens = [w for w in tokens if not w in stop_words]
# filter out short tokens
tokens = [word for word in tokens if len(word) > 1]
return tokens
# load the document
filename = 'txt_sentoken/pos/cv000_29590.txt'
text = load_doc(filename)
tokens = clean_doc(text)
print(tokens)
# load all docs in a directory
def process_docs(directory, is_trian):
documents = list()
# walk through all files in the folder
for filename in listdir(directory):
# skip any reviews in the test set
if is_trian and filename.startswith('cv9'):
continue
if not is_trian and not filename.startswith('cv9'):
continue
# create the full path of the file to open
path = directory + '/' + filename
# load the doc
doc = load_doc(path)
# clean doc
tokens = clean_doc(doc)
# add to list
documents.append(tokens)
return documents
negative_docs = process_docs('txt_sentoken/neg', True)
trainy = [0 for _ in range(900)] + [1 for _ in range(900)]
testY = [0 for _ in range(100)] + [1 for _ in range(100)]
def save_dataset(dataset, filename):
dump(dataset, open(filename, 'wb'))
print('Saved: %s' % filename)
# load all test reviews
negative_docs = process_docs('txt_sentoken/neg', False)
positive_docs = process_docs('txt_sentoken/pos', False)
testX = negative_docs + positive_docs
testY = [0 for _ in range(100)] + [1 for _ in range(100)]
save_dataset([testX,testY], 'test.pkl')
```
develop a multichannel convolutional neural network for the sentiment analysis prediction problem.
This section is divided into 3 part
```
# load a clean dataset
def load_dataset(filename):
return load(open(filename, 'rb'))
trainLines, trainLabels = load_dataset('train.pkl')
# fit a tokenizer
def create_tokenizer(lines):
tokenizer = Tokenizer()
tokenizer.fit_on_texts(lines)
return tokenizer
# calculate the maximum document length
def max_length(lines):
return max([len(s.split()) for s in lines])
# calculate vocabulary size
vocab_size = len(tokenizer.word_index) + 1
# calculate vocabulary size
vocab_size = len(tokenizer.word_index) + 1
# encode a list of lines
def encode_text(tokenizer, lines, length):
# integer encode
encoded = tokenizer.texts_to_sequences(lines)
# pad encoded sequences
padded = pad_sequences(encoded, maxlen=length, padding='post')
return padded
# encode a list of lines
def encode_text(tokenizer, lines, length):
# integer encode
encoded = tokenizer.texts_to_sequences(lines)
# pad encoded sequences
padded = pad_sequences(encoded, maxlen=length, padding='post')
return padded
# define the model
def define_model(length, vocab_size):
# channel 1
inputs1 = Input(shape=(length,))
embedding1 = Embedding(vocab_size, 100)(inputs1)
conv1 = Conv1D(filters=32, kernel_size=4, activation='relu')(embedding1)
drop1 = Dropout(0.5)(conv1)
pool1 = MaxPooling1D(pool_size=2)(drop1)
flat1 = Flatten()(pool1)
# channel 2
inputs2 = Input(shape=(length,))
embedding2 = Embedding(vocab_size, 100)(inputs2)
conv2 = Conv1D(filters=32, kernel_size=6, activation='relu')(embedding2)
drop2 = Dropout(0.5)(conv2)
pool2 = MaxPooling1D(pool_size=2)(drop2)
flat2 = Flatten()(pool2)
# channel 3
inputs3 = Input(shape=(length,))
embedding3 = Embedding(vocab_size, 100)(inputs3)
conv3 = Conv1D(filters=32, kernel_size=8, activation='relu')(embedding3)
drop3 = Dropout(0.5)(conv3)
pool3 = MaxPooling1D(pool_size=2)(drop3)
flat3 = Flatten()(pool3)
# merge
merged = concatenate([flat1, flat2, flat3])
# interpretation
dense1 = Dense(10, activation='relu')(merged)
outputs = Dense(1, activation='sigmoid')(dense1)
model = Model(inputs=[inputs1, inputs2, inputs3], outputs=outputs)
# compile
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# summarize
print(model.summary())
plot_model(model, show_shapes=True, to_file='multichannel.png')
return model
# load training dataset
trainLines, trainLabels = load_dataset('train.pkl')
# create tokenizer
tokenizer = create_tokenizer(trainLines)
# calculate max document length
length = max_length(trainLines)
# calculate vocabulary size
vocab_size = len(tokenizer.word_index) + 1
print('Max document length: %d' % length)
print('Vocabulary size: %d' % vocab_size)
# encode data
trainX = encode_text(tokenizer, trainLines, length)
print(trainX.shape)
# define model
model = define_model(length, vocab_size)
# fit model
model.fit([trainX,trainX,trainX], array(trainLabels), epochs=10, batch_size=16)
# save the model
model.save('model.h5')
#Evaluation
# load datasets
trainLines, trainLabels = load_dataset('train.pkl')
testLines, testLabels = load_dataset('test.pkl')
# create tokenizer
tokenizer = create_tokenizer(trainLines)
# calculate max document length
length = max_length(trainLines)
# calculate vocabulary size
vocab_size = len(tokenizer.word_index) + 1
print('Max document length: %d' % length)
print('Vocabulary size: %d' % vocab_size)
# encode data
trainX = encode_text(tokenizer, trainLines, length)
testX = encode_text(tokenizer, testLines, length)
print(trainX.shape, testX.shape)
```
| true |
code
| 0.754542 | null | null | null | null |
|
# Federated Learning Training Plan: Host Plan & Model
Here we load Plan and Model params created earlier in "Create Plan" notebook, host them to PyGrid,
and run sample syft.js app that executes them.
```
%load_ext autoreload
%autoreload 2
import websockets
import json
import base64
import requests
import torch
import syft as sy
from syft.grid.grid_client import GridClient
from syft.serde import protobuf
from syft_proto.execution.v1.plan_pb2 import Plan as PlanPB
from syft_proto.execution.v1.state_pb2 import State as StatePB
sy.make_hook(globals())
# force protobuf serialization for tensors
hook.local_worker.framework = None
async def sendWsMessage(data):
async with websockets.connect('ws://' + gatewayWsUrl) as websocket:
await websocket.send(json.dumps(data))
message = await websocket.recv()
return json.loads(message)
def deserializeFromBin(worker, filename, pb):
with open(filename, "rb") as f:
bin = f.read()
pb.ParseFromString(bin)
return protobuf.serde._unbufferize(worker, pb)
```
## Step 4a: Host in PyGrid
Here we load "ops list" Plan.
PyGrid should translate it to other types (e.g. torchscript) automatically.
```
# Load files with protobuf created in "Create Plan" notebook.
training_plan = deserializeFromBin(hook.local_worker, "tp_full.pb", PlanPB())
model_params_state = deserializeFromBin(hook.local_worker, "model_params.pb", StatePB())
```
Follow PyGrid README.md to build `openmined/grid-gateway` image from the latest `dev` branch
and spin up PyGrid using `docker-compose up --build`.
```
# Default gateway address when running locally
gatewayWsUrl = "127.0.0.1:5000"
grid = GridClient(id="test", address=gatewayWsUrl, secure=False)
grid.connect()
```
Define name, version, configs.
```
# These name/version you use in worker
name = "mnist"
version = "1.0.0"
client_config = {
"name": name,
"version": version,
"batch_size": 64,
"lr": 0.01,
"max_updates": 100 # custom syft.js option that limits number of training loops per worker
}
server_config = {
"min_workers": 3, # temporarily this plays role "min # of worker's diffs" for triggering cycle end event
"max_workers": 3,
"pool_selection": "random",
"num_cycles": 5,
"do_not_reuse_workers_until_cycle": 4,
"cycle_length": 28800,
"minimum_upload_speed": 0,
"minimum_download_speed": 0
}
```
Shoot!
If everything's good, success is returned.
If the name/version already exists in PyGrid, change them above or cleanup PyGrid db by re-creating docker containers (e.g. `docker-compose up --force-recreate`).
```
response = grid.host_federated_training(
model=model_params_state,
client_plans={'training_plan': training_plan},
client_protocols={},
server_averaging_plan=None,
client_config=client_config,
server_config=server_config
)
print("Host response:", response)
```
Let's double-check that data is loaded by requesting a cycle.
(Request is made directly, will be methods on grid client in the future)
```
auth_request = {
"type": "federated/authenticate",
"data": {}
}
auth_response = await sendWsMessage(auth_request)
print('Auth response: ', json.dumps(auth_response, indent=2))
cycle_request = {
"type": "federated/cycle-request",
"data": {
"worker_id": auth_response['data']['worker_id'],
"model": name,
"version": version,
"ping": 1,
"download": 10000,
"upload": 10000,
}
}
cycle_response = await sendWsMessage(cycle_request)
print('Cycle response:', json.dumps(cycle_response, indent=2))
worker_id = auth_response['data']['worker_id']
request_key = cycle_response['data']['request_key']
model_id = cycle_response['data']['model_id']
training_plan_id = cycle_response['data']['plans']['training_plan']
```
Let's download model and plan (both versions) and check they are actually workable.
```
# Model
req = requests.get(f"http://{gatewayWsUrl}/federated/get-model?worker_id={worker_id}&request_key={request_key}&model_id={model_id}")
model_data = req.content
pb = StatePB()
pb.ParseFromString(req.content)
model_params_downloaded = protobuf.serde._unbufferize(hook.local_worker, pb)
print(model_params_downloaded)
# Plan "list of ops"
req = requests.get(f"http://{gatewayWsUrl}/federated/get-plan?worker_id={worker_id}&request_key={request_key}&plan_id={training_plan_id}&receive_operations_as=list")
pb = PlanPB()
pb.ParseFromString(req.content)
plan_ops = protobuf.serde._unbufferize(hook.local_worker, pb)
print(plan_ops.role.actions)
print(plan_ops.torchscript)
# Plan "torchscript"
req = requests.get(f"http://{gatewayWsUrl}/federated/get-plan?worker_id={worker_id}&request_key={request_key}&plan_id={training_plan_id}&receive_operations_as=torchscript")
pb = PlanPB()
pb.ParseFromString(req.content)
plan_ts = protobuf.serde._unbufferize(hook.local_worker, pb)
print(plan_ts.role.actions)
print(plan_ts.torchscript.code)
```
## Step 5a: Train
Start and open "with-grid" example in syft.js project (http://localhost:8080 by default),
enter model name and version and start FL training.
## Step 6a: Submit diff
This emulates submitting worker's diff (created earlier in Execute Plan notebook) to PyGrid.
After several diffs submitted, PyGrid will end the cycle and create new model checkpoint and cycle.
(Request is made directly, will be methods on grid client in the future)
```
with open("diff.pb", "rb") as f:
diff = f.read()
report_request = {
"type": "federated/report",
"data": {
"worker_id": auth_response['data']['worker_id'],
"request_key": cycle_response['data']['request_key'],
"diff": base64.b64encode(diff).decode("utf-8")
}
}
report_response = await sendWsMessage(report_request)
print('Report response:', json.dumps(report_response, indent=2))
```
| true |
code
| 0.386271 | null | null | null | null |
|
```
"""
A randomly connected network learning a sequence
This example contains a reservoir network of 500 neurons.
400 neurons are excitatory and 100 neurons are inhibitory.
The weights are initialized randomly, based on a log-normal distribution.
The network activity is stimulated with three different inputs (A, B, C).
The inputs are given in i a row (A -> B -> C -> A -> ...)
The experiment is defined in 'pelenet/experiments/sequence.py' file.
A log file, parameters, and plot figures are stored in the 'log' folder for every run of the simulation.
NOTE: The main README file contains some more information about the structure of pelenet
"""
# Load pelenet modules
from pelenet.utils import Utils
from pelenet.experiments.sequence import SequenceExperiment
# Official modules
import numpy as np
import matplotlib.pyplot as plt
# Overwrite default parameters (pelenet/parameters/ and pelenet/experiments/sequence.py)
parameters = {
# Experiment
'seed': 1, # Random seed
'trials': 10, # Number of trials
'stepsPerTrial': 60, # Number of simulation steps for every trial
# Neurons
'refractoryDelay': 2, # Refactory period
'voltageTau': 100, # Voltage time constant
'currentTau': 5, # Current time constant
'thresholdMant': 1200, # Spiking threshold for membrane potential
# Network
'reservoirExSize': 400, # Number of excitatory neurons
'reservoirConnPerNeuron': 35, # Number of connections per neuron
'isLearningRule': True, # Apply a learning rule
'learningRule': '2^-2*x1*y0 - 2^-2*y1*x0 + 2^-4*x1*y1*y0 - 2^-3*y0*w*w', # Defines the learning rule
# Input
'inputIsSequence': True, # Activates sequence input
'inputSequenceSize': 3, # Number of input clusters in sequence
'inputSteps': 20, # Number of steps the trace input should drive the network
'inputGenSpikeProb': 0.8, # Probability of spike for the generator
'inputNumTargetNeurons': 40, # Number of neurons activated by the input
# Probes
'isExSpikeProbe': True, # Probe excitatory spikes
'isInSpikeProbe': True, # Probe inhibitory spikes
'isWeightProbe': True # Probe weight matrix at the end of the simulation
}
# Initilizes the experiment, also initializes the log
# Creating a new object results in a new log entry in the 'log' folder
# The name is optional, it is extended to the folder in the log directory
exp = SequenceExperiment(name='random-network-sequence-learning', parameters=parameters)
# Instantiate the utils singleton
utils = Utils.instance()
# Build the network, in this function the weight matrix, inputs, probes, etc. are defined and created
exp.build()
# Run the network simulation, afterwards the probes are postprocessed to nice arrays
exp.run()
# Weight matrix before learning (randomly initialized)
exp.net.plot.initialExWeightMatrix()
# Plot distribution of weights
exp.net.plot.initialExWeightDistribution(figsize=(12,3))
# Plot spike trains of the excitatory (red) and inhibitory (blue) neurons
exp.net.plot.reservoirSpikeTrain(figsize=(12,6), to=600)
# Weight matrix after learning
exp.net.plot.trainedExWeightMatrix()
# Sorted weight matrix after learning
supportMask = utils.getSupportWeightsMask(exp.net.trainedWeightsExex)
exp.net.plot.weightsSortedBySupport(supportMask)
```
| true |
code
| 0.879432 | null | null | null | null |
|
# Computingthe mean of a bunch of images:
```
# computing statistics:
import torch
from torchvision import transforms, datasets
import numpy as np
import time
unlab_ddset = datasets.ImageFolder('./surrogate_dataset/unlab_dataset_055/train_set/',
transform = transforms.Compose([transforms.ToTensor()]))
unlab_loader = torch.utils.data.DataLoader(unlab_ddset,
batch_size = 20,
shuffle = True,
) # iterating over the DataLoader gives the tuple (input, target)
def compute_mean(loader):
mean = [0, 0, 0]
std = [0, 0, 0]
for i, (images, targets) in enumerate(unlab_loader):
mean0, mean1, mean2 = (0.0, 0.0, 0.0)
std0, std1, std2 = (0.0, 0.0, 0.0)
for num, t in enumerate(images):
mean0 += t[0].mean()
mean1 += t[1].mean()
mean2 += t[2].mean()
std0 += t[0].std()
std1 += t[1].std()
std2 += t[2].std()
mean[0] += mean0/num
mean[1] += mean1/num
mean[2] += mean2/num
std[0] += std0/num
std[1] += std1/num
std[2] += std2/num
return ([x / i for x in mean], [x / i for x in std])
st = time.time()
mean, std = compute_mean(unlab_loader)
end = time.time()
print 'Time to compute the statistics: ' + str(end-st)
print "Mean of xxx random images transformed 100 each:"
print mean
print std
# computing statistics:
import torch
from torchvision import transforms, datasets
import numpy as np
import time
unlab_ddset = datasets.ImageFolder('./surrogate_dataset/unlab_dataset007/data/',
transform = transforms.Compose([transforms.ToTensor()]))
unlab_loader = torch.utils.data.DataLoader(unlab_ddset,
batch_size = 20,
shuffle = True,
) # iterating over the DataLoader gives the tuple (input, target)
def compute_mean(loader):
mean = [0, 0, 0]
for i, (images, targets) in enumerate(unlab_loader):
mean0, mean1, mean2 = (0, 0, 0)
for num, t in enumerate(images):
mean0 += t[0].mean()
mean1 += t[1].mean()
mean2 += t[2].mean()
mean[0] += mean0/num
mean[1] += mean1/num
mean[2] += mean2/num
return [x / i for x in mean]
st = time.time()
mean = compute_mean(unlab_loader)
end = time.time()
print 'Time to compute the statistics: ' + str(end-st)
print "Mean of xxx random images transformed 100 each:"
print mean
```
# Checking how the normalization affects the images:
```
import torch
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as datasets
from matplotlib import pyplot as plt
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import os
import time
import numpy as np
from PIL import Image
experiment = '002_6'
path = '../saving_model/alexNet' + str(experiment) + '.pth.tar'
#print path
normalize = transforms.Normalize(mean = [0.6128879173491645, 0.6060359745417173, 0.5640660479324938],
std=[1, 1, 1])
batch_size = 100
unlab_ddset = datasets.ImageFolder('./surrogate_dataset/unlab_train/',
transform = transforms.Compose([transforms.ToTensor()]))
unlab_loader = torch.utils.data.DataLoader(unlab_ddset,
batch_size = batch_size,
shuffle = True,
)
for i, data in enumerate(unlab_loader):
break
# data loaded with the pytorch loader and no normalization
type(data[0]), type(data[1]), data[1][5], data[0][5].max(), data[0][5].min(), data[0][5].mean()
experiment = '002_6'
path = '../saving_model/alexNet' + str(experiment) + '.pth.tar'
#print path
normalize = transforms.Normalize(mean = [0.6128879173491645, 0.6060359745417173, 0.5640660479324938],
std=[1, 1, 1])
batch_size = 100
unlab_ddset = datasets.ImageFolder('./surrogate_dataset/unlab_train/',
transform = transforms.Compose([transforms.ToTensor(), normalize]))
unlab_loader = torch.utils.data.DataLoader(unlab_ddset,
batch_size = batch_size,
shuffle = True,
)
for i, data in enumerate(unlab_loader):
break
# data loaded with the pytorch loader and normalization like follows:
# (mean = [0.6128879173491645, 0.6060359745417173, 0.5640660479324938], std=[1, 1, 1])
type(data[0]), type(data[1]), data[1][5], data[0][5].max(), data[0][5].min(), data[0][5].mean()
```
| true |
code
| 0.551453 | null | null | null | null |
|
[Reinforcement Learning TF-Agents](https://colab.research.google.com/drive/1FXh1BQgMI5xE1yIV1CQ25TyRVcxvqlbH?usp=sharing)
```
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
# nice plot figures
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
import matplotlib.animation as animation
# smooth animations
mpl.rc('animation', html='jshtml')
import PIL
import os
import gym
import tf_agents
from tf_agents.environments import suite_atari, suite_gym
from tf_agents.environments.atari_preprocessing import AtariPreprocessing
from tf_agents.environments.atari_wrappers import FrameStack4
from tf_agents.environments.tf_py_environment import TFPyEnvironment
from tf_agents.networks.q_network import QNetwork
from tf_agents.agents.dqn.dqn_agent import DqnAgent
from tf_agents.replay_buffers.tf_uniform_replay_buffer import TFUniformReplayBuffer
from tf_agents.metrics import tf_metrics
from tf_agents.drivers.dynamic_step_driver import DynamicStepDriver
from tf_agents.policies.random_tf_policy import RandomTFPolicy
from tf_agents.utils.common import function
# functions to plot animations on a per frame basis
def update_scene(num, frames, patch):
patch.set_data(frames[num])
return patch,
def plot_animation(frames, repeat=False, interval=40):
fig = plt.figure()
patch = plt.imshow(frames[0])
plt.axis('off')
anim = animation.FuncAnimation(
fig, update_scene, fargs=(frames, patch),
frames=len(frames), repeat=repeat, interval=interval)
plt.close()
return anim
# save an agent's demo (after training)
saved_frames = []
def save_frames(trajectory):
global saved_frames
saved_frames.append(tf_env.pyenv.envs[0].render(mode="rgb_array"))
def play_game_demo(tf_env, the_agent, obs_list, n_steps):
watch_driver = DynamicStepDriver(
tf_env,
the_agent.policy,
observers=[save_frames] + obs_list,
num_steps=n_steps)
final_time_step, final_policy_state = watch_driver.run()
def save_animated_gif(frames): # saved_frames is passed in
image_path = os.path.join("images", "rl", "breakout.gif")
frame_images = [PIL.Image.fromarray(frame) for frame in frames[:150]]
frame_images[0].save(image_path, format='GIF',
append_images=frame_images[1:],
save_all=True,
duration=30,
loop=0)
# %%html
# <img src="images/rl/breakout.gif" /> runs the gif in a jupyter/colab environment
# 8
# install this dependency for LunarLander
# pip install gym[box2d]
test_env = gym.make("LunarLander-v2")
test_env # seems like there is a time limit
test_env.reset() # 8 values from each observation
```
From the source code, we can see that these each 8D observation (x, y, h, v, a, w, l, r) correspond to:
+ x,y: the coordinates of the spaceship. It starts at a random location near (0, 1.4) and must land near the target at (0, 0).
+ h,v: the horizontal and vertical speed of the spaceship. It starts with a small random speed.
+ a,w: the spaceship's angle and angular velocity.
+ l,r: whether the left or right leg touches the ground (1.0) or not (0.0).
```
print(test_env.observation_space) #
print(test_env.action_space, test_env.action_space.n) # 4 possible values
```
Looking at the https://gym.openai.com/envs/LunarLander-v2/, these actions are:
+ do nothing
+ fire left orientation engine
+ fire main engine
+ fire right orientation engine
```
# PG REINFORCE algorithm
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
n_inputs = test_env.observation_space.shape[0]
n_outputs = test_env.action_space.n
model = keras.models.Sequential([
keras.layers.Dense(32, activation="relu", input_shape=[n_inputs]),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(32, activation='relu'),
keras.layers.Dense(n_outputs, activation="softmax")
])
# play multiple episodes, exploring the environment randomly and recording
# gradients and rewards
def play_one_step(env, obs, model, loss_fn):
with tf.GradientTape() as tape:
probas = model(obs[np.newaxis])
logits = tf.math.log(probas + keras.backend.epsilon())
action = tf.random.categorical(logits, num_samples=1)
loss = tf.reduce_mean(loss_fn(action, probas))
grads = tape.gradient(loss, model.trainable_variables)
return obs, reward, done, grads
def play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
all_grads, all_rewards = [], []
for episode in range(n_episodes):
current_grads, current_rewards = [], []
obs = env.reset()
for step in range(n_max_steps):
obs, reward, done, grads = play_one_step(env, obs, model, loss_fn)
current_rewards.append(reward)
current_grads.append(grads)
if done:
break
all_grads.append(current_grads)
all_rewards.append(current_rewards)
return all_rewards, all_grads
# compute sum of future discounted rewards and standardize to differentiate
# good and bad decisions
def discount_rewards(discounted, discount_rate):
discounted = np.array(discounted)
for step in range(len(discounted) - 2, -1, -1):
discounted[step] += discounted[step + 1] * discount_rate
return discount
def discount_and_normalize_rewards(all_rewards, discount_rate):
discounted_rewards = [discount_rewards(reward, discount_rate) for reward in all_rewards]
flattened_rewards = np.concatenate(discounted_rewards)
rewards_mean = flattened_rewards.mean()
rewards_stddev = flattened_rewards.std()
return [(reward - rewards_mean) / rewards_stddev for reward in discounted_rewards]
n_iterations = 200
n_episodes_per_update = 16
n_max_steps = 1000
discount_rate = 0.99
env = gym.make("LunarLander-v2")
optimizer = keras.optimizers.Nadam(lr=0.005)
loss_fn = keras.losses.sparse_categorical_crossentropy
# the model outputs probabilities for each class so we use categorical_crossentropy
# and the action is just 1 value (not a 1 hot vector so we use sparse_categorical_crossentropy)
env.seed(42)
# this will take very long, so I'm not calling it for the sake of my computer's mental health
def train(n_iterations, env, n_episodes_per_update, n_max_steps, model, loss_fn, discount_rate):
for iteration in range(n_iterations):
all_rewards, all_grads = play_multiple_episodes(env, n_episodes_per_update, n_max_steps, model, loss_fn)
# for plotting the learning curve with undiscounted rewards
# alternatively, just use a reduce_sum from tf and extract the numpy scalar value using .numpy()
mean_reward = sum(map(sum, all_rewards)) / n_episodes_per_update
print("\rIteration: {}/{}, mean reward: {:.1f} ".format( # \r means that it will not return a new line, it will just replace the current line
iteration + 1, n_iterations, mean_reward), end="")
mean_rewards.append(mean_reward)
all_discounted_rewards = discount_and_normalize_rewards(all_rewards, discount_rate)
all_mean_grads = []
for var_index in range(len(model.trainable_variables)):
mean_grads = tf.reduce_mean(
[final_reward * all_grads[episode_index][step][var_index]
for episode_index, final_rewards in enumerate(all_discounted_rewards)
for step, final_reward in enumerate(final_rewards)], axis=0)
all_mean_grads.append(mean_grads)
optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))
# 9 TF-Agents SpaceInvaders-v4
environment_name = "SpaceInvaders-v4"
env = suite_atari.load(
environment_name,
max_episode_steps=27000,
gym_env_wrappers=[AtariPreprocessing, FrameStack4]
)
env
```
+ environment ✓
+ driver ✓
+ observer(s) ✓
+ replay buffer ✓
+ dataset ✓
+ agent with collect policy ✓
+ DQN ✓
+ training loop ✓
```
# environment officially built
tf_env = TFPyEnvironment(env)
dropout_params = [0.4]
fc_params = [512]
conv_params = [(32, (8, 8), 5),
(64, (4, 4), 4),
(64, (3, 3), 1),]
preprocessing_layer = keras.layers.Lambda(lambda obs: tf.cast(obs, np.float32) / 255.) # uint8 beforehand
dqn = QNetwork(
tf_env.observation_spec(),
tf_env.action_spec(),
preprocessing_layers=preprocessing_layer,
conv_layer_params=conv_params,
fc_layer_params=fc_params,
dropout_layer_params=dropout_params,
activation_fn=keras.activations.relu,
)
# dqn agent with collect policy officially built
update_period = 4
train_step = tf.Variable(0)
epsilon_greedy_policy = keras.optimizers.schedules.PolynomialDecay(
initial_learning_rate=1.0,
decay_steps=250000 // update_period,
end_learning_rate=0.01,
)
dqn_agent = DqnAgent(
tf_env.time_step_spec(),
tf_env.action_spec(),
q_network=dqn,
optimizer=keras.optimizers.RMSprop(learning_rate=0.001, rho=0.9, momentum=0.0, epsilon=1e-07, centered=False),
train_step_counter=train_step,
gamma=0.99,
td_errors_loss_fn=keras.losses.Huber(reduction="none"),
target_update_period=2000,
epsilon_greedy=lambda: epsilon_greedy_policy(train_step)
)
dqn_agent.initialize()
# uniform replay buffer officially built
replay_buffer = TFUniformReplayBuffer(
dqn_agent.collect_data_spec,
batch_size = tf_env.batch_size,
max_length=100000,
)
replay_buffer_observer = replay_buffer.add_batch
# observers + metrics officially built
training_metrics = [
tf_metrics.AverageEpisodeLengthMetric(),
tf_metrics.AverageReturnMetric(),
tf_metrics.NumberOfEpisodes(),
tf_metrics.EnvironmentSteps(),
]
class ShowProgress:
def __init__(self, total):
self.counter = 0
self.total = total
def __call__(self, trajectory):
if not trajectory.is_boundary():
self.counter += 1
if self.counter % 100 == 0:
print("\r{}/{}".format(self.counter, self.total), end="")
# driver officially created
driver = DynamicStepDriver(
tf_env,
dqn_agent.collect_policy,
observers = training_metrics + [ShowProgress(2000)],
num_steps=update_period
)
random_policy = RandomTFPolicy(
tf_env.time_step_spec(),
tf_env.action_spec()
)
initial_driver = DynamicStepDriver(
tf_env,
random_policy,
observers = [replay_buffer.add_batch] + [ShowProgress(2000)],
num_steps=update_period
)
final_time_step, final_policy_state = initial_driver.run()
# dataset officially built
dataset = replay_buffer.as_dataset(
sample_batch_size=64,
num_steps=2,
num_parallel_calls=3,
).prefetch(3)
driver.run = function(driver.run)
dqn_agent.train = function(dqn_agent.train)
# I would train it, but my computer suffers from dementia
# training loop officially built
def training(n_iterations, agent, driver, tf_env, dataset):
time_step = None
initial_policy_state = agent.collect_policy.get_initial_state(tf_env.batch_size)
iterator = iter(dataset) # forgot to do this!
for iteration in range(n_iterations):
time_step, policy_state = driver.run(time_step, policy_state)
trajectories, buffer_info = next(iterator)
train_loss = agent.train(trajectories)
```
| true |
code
| 0.658472 | null | null | null | null |
|
# A quick introduction to Blackjax
BlackJAX is an MCMC sampling library based on [JAX](https://github.com/google/jax). BlackJAX provides well-tested and ready to use sampling algorithms. It is also explicitly designed to be modular: it is easy for advanced users to mix-and-match different metrics, integrators, trajectory integrations, etc.
In this notebook we provide a simple example based on basic Hamiltonian Monte Carlo and the NUTS algorithm to showcase the architecture and interfaces in the library
```
import jax
import jax.numpy as jnp
import jax.scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as np
import blackjax
%load_ext watermark
%watermark -d -m -v -p jax,jaxlib,blackjax
jax.devices()
```
## The problem
We'll generate observations from a normal distribution of known `loc` and `scale` to see if we can recover the parameters in sampling. Let's take a decent-size dataset with 1,000 points:
```
loc, scale = 10, 20
observed = np.random.normal(loc, scale, size=1_000)
def logprob_fn(loc, scale, observed=observed):
"""Univariate Normal"""
logpdf = stats.norm.logpdf(observed, loc, scale)
return jnp.sum(logpdf)
logprob = lambda x: logprob_fn(**x)
```
## HMC
### Sampler parameters
```
inv_mass_matrix = np.array([0.5, 0.5])
num_integration_steps = 60
step_size = 1e-3
hmc = blackjax.hmc(logprob, step_size, inv_mass_matrix, num_integration_steps)
```
### Set the initial state
The initial state of the HMC algorithm requires not only an initial position, but also the potential energy and gradient of the potential energy at this position. BlackJAX provides a `new_state` function to initialize the state from an initial position.
```
initial_position = {"loc": 1.0, "scale": 2.0}
initial_state = hmc.init(initial_position)
initial_state
```
### Build the kernel and inference loop
The HMC kernel is easy to obtain:
```
%%time
hmc_kernel = jax.jit(hmc.step)
```
BlackJAX does not provide a default inference loop, but it easy to implement with JAX's `lax.scan`:
```
def inference_loop(rng_key, kernel, initial_state, num_samples):
@jax.jit
def one_step(state, rng_key):
state, _ = kernel(rng_key, state)
return state, state
keys = jax.random.split(rng_key, num_samples)
_, states = jax.lax.scan(one_step, initial_state, keys)
return states
```
### Inference
```
%%time
rng_key = jax.random.PRNGKey(0)
states = inference_loop(rng_key, hmc_kernel, initial_state, 10_000)
loc_samples = states.position["loc"].block_until_ready()
scale_samples = states.position["scale"]
fig, (ax, ax1) = plt.subplots(ncols=2, figsize=(15, 6))
ax.plot(loc_samples)
ax.set_xlabel("Samples")
ax.set_ylabel("loc")
ax1.plot(scale_samples)
ax1.set_xlabel("Samples")
ax.set_ylabel("scale")
```
## NUTS
NUTS is a *dynamic* algorithm: the number of integration steps is determined at runtime. We still need to specify a step size and a mass matrix:
```
inv_mass_matrix = np.array([0.5, 0.5])
step_size = 1e-3
nuts = blackjax.nuts(logprob, step_size, inv_mass_matrix)
initial_position = {"loc": 1.0, "scale": 2.0}
initial_state = nuts.init(initial_position)
initial_state
%%time
rng_key = jax.random.PRNGKey(0)
states = inference_loop(rng_key, nuts.step, initial_state, 4_000)
loc_samples = states.position["loc"].block_until_ready()
scale_samples = states.position["scale"]
fig, (ax, ax1) = plt.subplots(ncols=2, figsize=(15, 6))
ax.plot(loc_samples)
ax.set_xlabel("Samples")
ax.set_ylabel("loc")
ax1.plot(scale_samples)
ax1.set_xlabel("Samples")
ax1.set_ylabel("scale")
```
### Use Stan's window adaptation
Specifying the step size and inverse mass matrix is cumbersome. We can use Stan's window adaptation to get reasonable values for them so we have, in practice, no parameter to specify.
The adaptation algorithm takes a function that returns a transition kernel given a step size and an inverse mass matrix:
```
%%time
warmup = blackjax.window_adaptation(
blackjax.nuts,
logprob,
1000,
)
state, kernel, _ = warmup.run(
rng_key,
initial_position,
)
```
We can use the obtained parameters to define a new kernel. Note that we do not have to use the same kernel that was used for the adaptation:
```
%%time
states = inference_loop(rng_key, nuts.step, initial_state, 1_000)
loc_samples = states.position["loc"].block_until_ready()
scale_samples = states.position["scale"]
fig, (ax, ax1) = plt.subplots(ncols=2, figsize=(15, 6))
ax.plot(loc_samples)
ax.set_xlabel("Samples")
ax.set_ylabel("loc")
ax1.plot(scale_samples)
ax1.set_xlabel("Samples")
ax1.set_ylabel("scale")
```
## Sample multiple chains
We can easily sample multiple chains using JAX's `vmap` construct. See the [documentation](https://jax.readthedocs.io/en/latest/jax.html?highlight=vmap#jax.vmap) to understand how the mapping works.
```
num_chains = 4
initial_positions = {"loc": np.ones(num_chains), "scale": 2.0 * np.ones(num_chains)}
initial_states = jax.vmap(nuts.init, in_axes=(0))(initial_positions)
def inference_loop_multiple_chains(
rng_key, kernel, initial_state, num_samples, num_chains
):
def one_step(states, rng_key):
keys = jax.random.split(rng_key, num_chains)
states, _ = jax.vmap(kernel)(keys, states)
return states, states
keys = jax.random.split(rng_key, num_samples)
_, states = jax.lax.scan(one_step, initial_state, keys)
return states
%%time
states = inference_loop_multiple_chains(
rng_key, nuts.step, initial_states, 2_000, num_chains
)
states.position["loc"].block_until_ready()
```
This scales very well to hundreds of chains on CPU, tens of thousand on GPU:
```
%%time
num_chains = 40
initial_positions = {"loc": np.ones(num_chains), "scale": 2.0 * np.ones(num_chains)}
initial_states = jax.vmap(nuts.init, in_axes=(0,))(initial_positions)
states = inference_loop_multiple_chains(
rng_key, nuts.step, initial_states, 1_000, num_chains
)
states.position["loc"].block_until_ready()
```
In this example the result is a dictionnary and each entry has shape `(num_samples, num_chains)`. Here's how to access the samples of the second chains for `loc`:
| true |
code
| 0.699216 | null | null | null | null |
|
# NLP model creation and training
```
from fastai.gen_doc.nbdoc import *
from fastai.text import *
```
The main thing here is [`RNNLearner`](/text.learner.html#RNNLearner). There are also some utility functions to help create and update text models.
## Quickly get a learner
```
show_doc(language_model_learner)
```
`bptt` (for backprop trough time) is the number of words we will store the gradient for, and use for the optimization step.
The model used is an [AWD-LSTM](https://arxiv.org/abs/1708.02182) that is built with embeddings of size `emb_sz`, a hidden size of `nh`, and `nl` layers (the `vocab_size` is inferred from the [`data`](/text.data.html#text.data)). All the dropouts are put to values that we found worked pretty well and you can control their strength by adjusting `drop_mult`. If <code>qrnn</code> is True, the model uses [QRNN cells](https://arxiv.org/abs/1611.01576) instead of LSTMs. The flag `tied_weights` control if we should use the same weights for the encoder and the decoder, the flag `bias` controls if the last linear layer (the decoder) has bias or not.
You can specify `pretrained_model` if you want to use the weights of a pretrained model. If you have your own set of weights and the corrsesponding dictionary, you can pass them in `pretrained_fnames`. This should be a list of the name of the weight file and the name of the corresponding dictionary. The dictionary is needed because the function will internally convert the embeddings of the pretrained models to match the dictionary of the [`data`](/text.data.html#text.data) passed (a word may have a different id for the pretrained model). Those two files should be in the models directory of `data.path`.
```
path = untar_data(URLs.IMDB_SAMPLE)
data = TextLMDataBunch.from_csv(path, 'texts.csv')
learn = language_model_learner(data, pretrained_model=URLs.WT103, drop_mult=0.5)
show_doc(text_classifier_learner)
```
`bptt` (for backprop trough time) is the number of words we will store the gradient for, and use for the optimization step.
The model used is the encoder of an [AWD-LSTM](https://arxiv.org/abs/1708.02182) that is built with embeddings of size `emb_sz`, a hidden size of `nh`, and `nl` layers (the `vocab_size` is inferred from the [`data`](/text.data.html#text.data)). All the dropouts are put to values that we found worked pretty well and you can control their strength by adjusting `drop_mult`. If <code>qrnn</code> is True, the model uses [QRNN cells](https://arxiv.org/abs/1611.01576) instead of LSTMs.
The input texts are fed into that model by bunch of `bptt` and only the last `max_len` activations are considerated. This gives us the backbone of our model. The head then consists of:
- a layer that concatenates the final outputs of the RNN with the maximum and average of all the intermediate outputs (on the sequence length dimension),
- blocks of ([`nn.BatchNorm1d`](https://pytorch.org/docs/stable/nn.html#torch.nn.BatchNorm1d), [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout), [`nn.Linear`](https://pytorch.org/docs/stable/nn.html#torch.nn.Linear), [`nn.ReLU`](https://pytorch.org/docs/stable/nn.html#torch.nn.ReLU)) layers.
The blocks are defined by the `lin_ftrs` and `drops` arguments. Specifically, the first block will have a number of inputs inferred from the backbone arch and the last one will have a number of outputs equal to data.c (which contains the number of classes of the data) and the intermediate blocks have a number of inputs/outputs determined by `lin_ftrs` (of course a block has a number of inputs equal to the number of outputs of the previous block). The dropouts all have a the same value ps if you pass a float, or the corresponding values if you pass a list. Default is to have an intermediate hidden size of 50 (which makes two blocks model_activation -> 50 -> n_classes) with a dropout of 0.1.
```
jekyll_note("Using QRNN require to have cuda installed (same version as pytorhc is using).")
path = untar_data(URLs.IMDB_SAMPLE)
data = TextClasDataBunch.from_csv(path, 'texts.csv')
learn = text_classifier_learner(data, drop_mult=0.5)
show_doc(RNNLearner)
```
Handles the whole creation from <code>data</code> and a `model` with a text data using a certain `bptt`. The `split_func` is used to properly split the model in different groups for gradual unfreezing and differential learning rates. Gradient clipping of `clip` is optionally applied. `adjust`, `alpha` and `beta` are all passed to create an instance of [`RNNTrainer`](/callbacks.rnn.html#RNNTrainer). Can be used for a language model or an RNN classifier. It also handles the conversion of weights from a pretrained model as well as saving or loading the encoder.
```
show_doc(RNNLearner.get_preds)
```
If `ordered=True`, returns the predictions in the order of the dataset, otherwise they will be ordered by the sampler (from the longest text to the shortest). The other arguments are passed [`Learner.get_preds`](/basic_train.html#Learner.get_preds).
### Loading and saving
```
show_doc(RNNLearner.load_encoder)
show_doc(RNNLearner.save_encoder)
show_doc(RNNLearner.load_pretrained)
```
Opens the weights in the `wgts_fname` of `self.model_dir` and the dictionary in `itos_fname` then adapts the pretrained weights to the vocabulary of the <code>data</code>. The two files should be in the models directory of the `learner.path`.
## Utility functions
```
show_doc(lm_split)
show_doc(rnn_classifier_split)
show_doc(convert_weights)
```
Uses the dictionary `stoi_wgts` (mapping of word to id) of the weights to map them to a new dictionary `itos_new` (mapping id to word).
## Get predictions
```
show_doc(LanguageLearner, title_level=3)
show_doc(LanguageLearner.predict)
```
If `no_unk=True` the unknown token is never picked. Words are taken randomly with the distribution of probabilities returned by the model. If `min_p` is not `None`, that value is the minimum probability to be considered in the pool of words. Lowering `temperature` will make the texts less randomized.
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(RNNLearner.get_preds)
show_doc(LanguageLearner.show_results)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.707739 | null | null | null | null |
|
# HyperParameter Tuning
### `keras.wrappers.scikit_learn`
Example adapted from: [https://github.com/fchollet/keras/blob/master/examples/mnist_sklearn_wrapper.py]()
## Problem:
Builds simple CNN models on MNIST and uses sklearn's GridSearchCV to find best model
```
import numpy as np
np.random.seed(1337) # for reproducibility
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.utils import np_utils
from keras.wrappers.scikit_learn import KerasClassifier
from keras import backend as K
from sklearn.model_selection import GridSearchCV
```
# Data Preparation
```
nb_classes = 10
# input image dimensions
img_rows, img_cols = 28, 28
# load training data and do basic data normalization
(X_train, y_train), (X_test, y_test) = mnist.load_data()
if K.image_dim_ordering() == 'th':
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X_train = X_train.reshape(X_train.shape[0], img_rows, img_cols, 1)
X_test = X_test.reshape(X_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
# convert class vectors to binary class matrices
y_train = np_utils.to_categorical(y_train, nb_classes)
y_test = np_utils.to_categorical(y_test, nb_classes)
```
## Build Model
```
def make_model(dense_layer_sizes, filters, kernel_size, pool_size):
'''Creates model comprised of 2 convolutional layers followed by dense layers
dense_layer_sizes: List of layer sizes. This list has one number for each layer
nb_filters: Number of convolutional filters in each convolutional layer
nb_conv: Convolutional kernel size
nb_pool: Size of pooling area for max pooling
'''
model = Sequential()
model.add(Conv2D(filters, (kernel_size, kernel_size),
padding='valid', input_shape=input_shape))
model.add(Activation('relu'))
model.add(Conv2D(filters, (kernel_size, kernel_size)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(pool_size, pool_size)))
model.add(Dropout(0.25))
model.add(Flatten())
for layer_size in dense_layer_sizes:
model.add(Dense(layer_size))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(nb_classes))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy',
optimizer='adadelta',
metrics=['accuracy'])
return model
dense_size_candidates = [[32], [64], [32, 32], [64, 64]]
my_classifier = KerasClassifier(make_model, batch_size=32)
```
## GridSearch HyperParameters
```
validator = GridSearchCV(my_classifier,
param_grid={'dense_layer_sizes': dense_size_candidates,
# nb_epoch is avail for tuning even when not
# an argument to model building function
'epochs': [3, 6],
'filters': [8],
'kernel_size': [3],
'pool_size': [2]},
scoring='neg_log_loss',
n_jobs=1)
validator.fit(X_train, y_train)
print('The parameters of the best model are: ')
print(validator.best_params_)
# validator.best_estimator_ returns sklearn-wrapped version of best model.
# validator.best_estimator_.model returns the (unwrapped) keras model
best_model = validator.best_estimator_.model
metric_names = best_model.metrics_names
metric_values = best_model.evaluate(X_test, y_test)
for metric, value in zip(metric_names, metric_values):
print(metric, ': ', value)
```
---
# There's more:
The `GridSearchCV` model in scikit-learn performs a complete search, considering **all** the possible combinations of Hyper-parameters we want to optimise.
If we want to apply for an optmised and bounded search in the hyper-parameter space, I strongly suggest to take a look at:
* `Keras + hyperopt == hyperas`: [http://maxpumperla.github.io/hyperas/](http://maxpumperla.github.io/hyperas/)
| true |
code
| 0.704541 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
**Module 14: Other Neural Network Techniques**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 14 Video Material
* Part 14.1: What is AutoML [[Video]](https://www.youtube.com/watch?v=TFUysIR5AB0&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_14_01_automl.ipynb)
* Part 14.2: Using Denoising AutoEncoders in Keras [[Video]](https://www.youtube.com/watch?v=4bTSu6_fucc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_14_02_auto_encode.ipynb)
* Part 14.3: Training an Intrusion Detection System with KDD99 [[Video]](https://www.youtube.com/watch?v=1ySn6h2A68I&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_14_03_anomaly.ipynb)
* **Part 14.4: Anomaly Detection in Keras** [[Video]](https://www.youtube.com/watch?v=VgyKQ5MTDFc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_14_04_ids_kdd99.ipynb)
* Part 14.5: The Deep Learning Technologies I am Excited About [[Video]]() [[Notebook]](t81_558_class_14_05_new_tech.ipynb)
# Part 14.4: Training an Intrusion Detection System with KDD99
The [KDD-99 dataset](http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html) is very famous in the security field and almost a "hello world" of intrusion detection systems in machine learning.
# Read in Raw KDD-99 Dataset
```
import pandas as pd
from tensorflow.keras.utils import get_file
try:
path = get_file('kddcup.data_10_percent.gz', origin='http://kdd.ics.uci.edu/databases/kddcup99/kddcup.data_10_percent.gz')
except:
print('Error downloading')
raise
print(path)
# This file is a CSV, just no CSV extension or headers
# Download from: http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html
df = pd.read_csv(path, header=None)
print("Read {} rows.".format(len(df)))
# df = df.sample(frac=0.1, replace=False) # Uncomment this line to sample only 10% of the dataset
df.dropna(inplace=True,axis=1) # For now, just drop NA's (rows with missing values)
# The CSV file has no column heads, so add them
df.columns = [
'duration',
'protocol_type',
'service',
'flag',
'src_bytes',
'dst_bytes',
'land',
'wrong_fragment',
'urgent',
'hot',
'num_failed_logins',
'logged_in',
'num_compromised',
'root_shell',
'su_attempted',
'num_root',
'num_file_creations',
'num_shells',
'num_access_files',
'num_outbound_cmds',
'is_host_login',
'is_guest_login',
'count',
'srv_count',
'serror_rate',
'srv_serror_rate',
'rerror_rate',
'srv_rerror_rate',
'same_srv_rate',
'diff_srv_rate',
'srv_diff_host_rate',
'dst_host_count',
'dst_host_srv_count',
'dst_host_same_srv_rate',
'dst_host_diff_srv_rate',
'dst_host_same_src_port_rate',
'dst_host_srv_diff_host_rate',
'dst_host_serror_rate',
'dst_host_srv_serror_rate',
'dst_host_rerror_rate',
'dst_host_srv_rerror_rate',
'outcome'
]
# display 5 rows
df[0:5]
```
# Analyzing a Dataset
The following script can be used to give a high-level overview of how a dataset appears.
```
ENCODING = 'utf-8'
def expand_categories(values):
result = []
s = values.value_counts()
t = float(len(values))
for v in s.index:
result.append("{}:{}%".format(v,round(100*(s[v]/t),2)))
return "[{}]".format(",".join(result))
def analyze(df):
print()
cols = df.columns.values
total = float(len(df))
print("{} rows".format(int(total)))
for col in cols:
uniques = df[col].unique()
unique_count = len(uniques)
if unique_count>100:
print("** {}:{} ({}%)".format(col,unique_count,int(((unique_count)/total)*100)))
else:
print("** {}:{}".format(col,expand_categories(df[col])))
expand_categories(df[col])
# Analyze KDD-99
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
analyze(df)
```
# Encode the feature vector
Encode every row in the database. This is not instant!
```
# Encode a numeric column as zscores
def encode_numeric_zscore(df, name, mean=None, sd=None):
if mean is None:
mean = df[name].mean()
if sd is None:
sd = df[name].std()
df[name] = (df[name] - mean) / sd
# Encode text values to dummy variables(i.e. [1,0,0],[0,1,0],[0,0,1] for red,green,blue)
def encode_text_dummy(df, name):
dummies = pd.get_dummies(df[name])
for x in dummies.columns:
dummy_name = f"{name}-{x}"
df[dummy_name] = dummies[x]
df.drop(name, axis=1, inplace=True)
# Now encode the feature vector
encode_numeric_zscore(df, 'duration')
encode_text_dummy(df, 'protocol_type')
encode_text_dummy(df, 'service')
encode_text_dummy(df, 'flag')
encode_numeric_zscore(df, 'src_bytes')
encode_numeric_zscore(df, 'dst_bytes')
encode_text_dummy(df, 'land')
encode_numeric_zscore(df, 'wrong_fragment')
encode_numeric_zscore(df, 'urgent')
encode_numeric_zscore(df, 'hot')
encode_numeric_zscore(df, 'num_failed_logins')
encode_text_dummy(df, 'logged_in')
encode_numeric_zscore(df, 'num_compromised')
encode_numeric_zscore(df, 'root_shell')
encode_numeric_zscore(df, 'su_attempted')
encode_numeric_zscore(df, 'num_root')
encode_numeric_zscore(df, 'num_file_creations')
encode_numeric_zscore(df, 'num_shells')
encode_numeric_zscore(df, 'num_access_files')
encode_numeric_zscore(df, 'num_outbound_cmds')
encode_text_dummy(df, 'is_host_login')
encode_text_dummy(df, 'is_guest_login')
encode_numeric_zscore(df, 'count')
encode_numeric_zscore(df, 'srv_count')
encode_numeric_zscore(df, 'serror_rate')
encode_numeric_zscore(df, 'srv_serror_rate')
encode_numeric_zscore(df, 'rerror_rate')
encode_numeric_zscore(df, 'srv_rerror_rate')
encode_numeric_zscore(df, 'same_srv_rate')
encode_numeric_zscore(df, 'diff_srv_rate')
encode_numeric_zscore(df, 'srv_diff_host_rate')
encode_numeric_zscore(df, 'dst_host_count')
encode_numeric_zscore(df, 'dst_host_srv_count')
encode_numeric_zscore(df, 'dst_host_same_srv_rate')
encode_numeric_zscore(df, 'dst_host_diff_srv_rate')
encode_numeric_zscore(df, 'dst_host_same_src_port_rate')
encode_numeric_zscore(df, 'dst_host_srv_diff_host_rate')
encode_numeric_zscore(df, 'dst_host_serror_rate')
encode_numeric_zscore(df, 'dst_host_srv_serror_rate')
encode_numeric_zscore(df, 'dst_host_rerror_rate')
encode_numeric_zscore(df, 'dst_host_srv_rerror_rate')
# display 5 rows
df.dropna(inplace=True,axis=1)
df[0:5]
# This is the numeric feature vector, as it goes to the neural net
# Convert to numpy - Classification
x_columns = df.columns.drop('outcome')
x = df[x_columns].values
dummies = pd.get_dummies(df['outcome']) # Classification
outcomes = dummies.columns
num_classes = len(outcomes)
y = dummies.values
df.groupby('outcome')['outcome'].count()
```
# Train the Neural Network
```
import pandas as pd
import io
import requests
import numpy as np
import os
from sklearn.model_selection import train_test_split
from sklearn import metrics
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.callbacks import EarlyStopping
# Create a test/train split. 25% test
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.25, random_state=42)
# Create neural net
model = Sequential()
model.add(Dense(10, input_dim=x.shape[1], activation='relu'))
model.add(Dense(50, input_dim=x.shape[1], activation='relu'))
model.add(Dense(10, input_dim=x.shape[1], activation='relu'))
model.add(Dense(1, kernel_initializer='normal'))
model.add(Dense(y.shape[1],activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam')
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3,
patience=5, verbose=1, mode='auto')
model.fit(x_train,y_train,validation_data=(x_test,y_test),
callbacks=[monitor],verbose=2,epochs=1000)
# Measure accuracy
pred = model.predict(x_test)
pred = np.argmax(pred,axis=1)
y_eval = np.argmax(y_test,axis=1)
score = metrics.accuracy_score(y_eval, pred)
print("Validation score: {}".format(score))
```
| true |
code
| 0.253584 | null | null | null | null |
|
# An Introduction to FEAST v2.0
FEAST v2.0 is a Python implementation of the Fugitive Emmissions Abatement Simulation Toolkit (FEAST) published by the Environmental Assessment and Optimization group at Stanford University. FEAST v2.0 generates similar results to FEAST v1.0 and includes some updates to the code structure to make the model more accessible. Extended documentation of FEAST is available [here](https://github.com/EAOgroup/FEAST/blob/master/Archive/FEAST_v1.0/FEASTDocumentation.pdf).
This tutorial gives an example of how to generate a realization of the default scenario in FEAST v2.0, analyze results, and change settings to generate a custom realization. The tutorial is interactive, so feel free to experiment with the code cells and discover how your changes affect the results.
## Running the default scenario
The default scenario simulates four leak detection and repair (LDAR) programs over a 10 year period. Leak distribution data sets, LDAR parameters and gas field properties are all assumed in order to generate the results.
Producing a single realization of the default scenario requires two lines of code: one to load the function *field_simulation* to the active python kernel, and the second to call the function. The code cell below illustrates the commands. The optional argument *dir_out* specifies the directory in which to save results from the simulation. It will take about one minute to complete the simulation.
```
from field_simulation import field_simulation
field_simulation(dir_out='../Results')
```
Each new realization is saved under the name "realization0," and the final integer is incremented by one with each new realization generated. The results can be viewed by using the built in plotting functions. There are three plotting functions available. The first produces a time series of the leakage in single realization file. It is shown in the code cell below.
```
# First the necessary functions are loaded to the active kernel
from GeneralClassesFunctions import plotting_functions
# Then the time series plotting function is called with a path to a
# specific results file
plotting_functions.time_series('../Results/realization0.p')
```
The other two plotting functions accumulate the data from all realizations in a directory. In order to illustrate their utility, multiple realizations should be used. For illustration purposes, four more realizations are generated below. To suppress the time step updates from *field_simulation()*, the optional command *display_status=False* was added.
```
for ind in range(0,4):
print("Currently evaluating iteration number " + str(ind))
field_simulation(display_status=False, dir_out='../Results')
```
Now there are five realizations of the default scenario in the "Results" folder. The *summary_plotter* function compiles results from all five to show the mean net present value, the estimated uncertainty in the sample mean from the mean of infinite realizations of the same scenario, and the types of costs and benefits that contributed to to the net present value. *summary_plotter* was already loaded to the kernel as part of the *plotting_functions* module, so it is called directly in the cell below.
```
# summary_plotter requires a path to a results directory as an input
plotting_functions.summary_plotter('../Results')
```
*hist_plotter* allows the leak repair performance of each LDAR program to be evaluated without regard to financial value. The function generates a histogram of the sizes of leaks found by each program. Like *summary_plotter*, *hist_plotter* combines results from all realizations in a directory. Unlike *summary_plotter*, *hist_plotter* generates the plots in separate windows from the notebook by default. An optional *inline=True* command was added to ensure that the plots pop up in this notebook.
```
plotting_functions.hist_plotter('../Results', inline=True)
```
FEAST has the capability to rapidly calculate the value of improving detection technology or changing operating procedures. Users can define any parameters they choose in existing LDAR program simulations, and more ambitious users can create their own LDAR program modules. The cell below illustrates how unique technology instances can be generated and simulated simultaneously for easy comparison. The call to *field_simulation* uses the option argument *dir_out* to define a directory to place the results in.
```
# This cell compares the performance of three AIR LDAR programs
# with varying camera sensitivities.
# First, the modules neaded to create the AIR objects must be
# imported to the kernel
from DetectionModules import ir
from GeneralClassesFunctions import simulation_classes
# The loop is used to generate 5 independent realizations of the
# desired simulation
for ind in range(0,5):
print("Currently evaluating iteration number " + str(ind))
# Before creating the LDAR objects, a few properties of the
# simulation need to be set.
# The default GasField settings are used
gas_field = simulation_classes.GasField()
# A time step of 10 days is specified (instead of the default
# timestep of 1 day) to speed up the simulation
time = simulation_classes.Time(delta_t = 10)
# Each camera is defined below by its noise equivalent
# temperature difference (netd).
# In the default scenario, the netd is 0.015 K
Default_AIR = ir.AIR(time=time, gas_field=gas_field)
Better_AIR = ir.AIR(time=time, gas_field=gas_field, netd=0.005)
Best_AIR = ir.AIR(time=time, gas_field=gas_field, netd=0.001)
# All of the tetchnologies are combined into a dict to be passed
# to field_simulation()
tech_dict = {'Default_AIR': Default_AIR, 'Better_AIR': Better_AIR,
'Best_AIR': Best_AIR}
# field_simulation is called with the predefined objects,
# and an output directory is specified
field_simulation(time=time, gas_field=gas_field, tech_dict=tech_dict,
dir_out='../Results/AIR_Sample', display_status=False)
```
The function *hist_plotter* shows how the improved sensitivity affects the size of leaks detected:
```
plotting_functions.hist_plotter('../Results/AIR_Sample',inline=True)
```
*summary_plotter* is used to illustrate the financial value of improving camera sensitivity.
```
plotting_functions.summary_plotter('../Results/AIR_Sample')
```
The above AIR example gives a glimpse into the possible analyses using FEAST v2.0. Any of the default parameters in FEAST v2.0 can be modified from the command line, stored in an object and used in a gas field simulation. The model is open source and freely available so that code can be customized and new technology modules can be added by private users.
The default parameters in FEAST v2.0 are intended to provide a realistic starting point but should be customized to accurately portray any particular gas field or LDAR program. In this tutorial, a sample size of five realizations was used to demonstrate the plotting functions, but a larger sample size should be used in any rigorous analysis in order to understand the stochastic error in the model.
Please contact [email protected] with any questions or suggestions regarding the code contained in FEAST.
| true |
code
| 0.641535 | null | null | null | null |
|
# AIMSim Demo
This notebook demonstrates the key uses of _AIMSim_ as a graphical user interface, command line tool, and scripting utility. For detailed explanations and to view the source code for _AIMSim_, visit our [documentation page](https://vlachosgroup.github.io/AIMSim/).
## Installing _AIMSim_
For users with Python already in use on their devices, it is _highly_ recommended to first create a virtual environment before installing _AIMSim_. This package has a large number of dependencies with only a handful of versions supported, so conflicts are likely unless a virtual environment is used.
For new Python users, the authors recommended installing anaconda navigator to manage dependencies for _AIMSim_ and make installation easier overall. Once anaconda navigator is ready, create a new environment with Python 3.7, open a terminal or command prompt in this environment, and follow the instructions below.
We reccomend installing _AIMSim_ using the commands shown below (omit exclamation points and the %%capture, unless you are running in a Jupyter notebook):
```
%%capture
!pip install aimsim
```
Now, start the _AIMSim_ GUI by typing `python -m aimsim` or simply `aimsim` into the command line.
## Graphical User Interface Walkthrough
For most users, the Graphical User Interface (GUI) will provide access to all the key functionalities in _AIMSim_. The GUI works by serving the user with drop downs and text fields which represent settings that would otherwise need to be configured in a file by hand. This file is written to the disk by the GUI as part of execution so that the file can be used as a 'starting point' for more advanced use cases.
**Important Note**: Jupyter Notebook _cannot_ run _AIMSim_ from Binder. In order to actually run the _AIMSim_ GUI alongside this tutorial, you will need to download this notebook and run it from a local installation of Jupyter, or follow the installation instructions above and start _AIMSim_ from there. You can install Jupyter [here](https://jupyter.org/install).
<div>
<img src="attachment:image-6.png" width="250"/>
</div>
### A. Database File
This field accepts a file or directory path containing an input set of molecules in one of the accepted formats: SMILES strings, Protein Data Bank files, and excel files containing these data types.
Example:
`/Users/chemist/Desktop/SMILES_database.smi`
#### A1. Similarity Plots
Checking this box will generate a similarity distribution with _AIMSim's_ default color scheme and labels. To customize this plot further, edit the configuration file produced by _AIMSim_ by clicking `Open Config`, then re-submit the file through the command line interface.
Example:
<div>
<img src="attachment:image-4.png" width="200"/>
</div>
In addition to the similarity distribution, this will create a heatmap showing pairwise comparisons between the two species. As above, edit the configuration file to control the appearance of this plot.
Example:
<div>
<img src="attachment:image-5.png" width="200"/>
</div>
#### A2. Property Similarity Checkboxes
Like in the previous two examples, checking this box will create a plot showing how a provided molecular property varies according to the chosen molecular fingerprint. For this to work, data must be provided in a comma-separated value format (which can be generated using Excel with Save As... -> CSV) where the rightmost column is a numerical value (the property of interest).
Example:
| SMILES | Boiling Point |
|--------|---------------|
| C | -161.6 |
| CC | -89 |
| CCC | -42 |
### B. Target Molecule
Provide a SMILES string representing a single molecule for comparison to the provided database of molecules. In the screenshot above, the provided molecule is "CO", methanol. Any valid SMILES strings are accepted, and any errors in the SMILES string will not affect the execution of other tasks.
#### B1. Similarity Heatmap
Like the similarity heatmap shown above, this checkbox will generate a similarity distribution for the single target molecule specified above to the entire molecular database. This is particularly useful when considering a new addition to a dataset, where _AIMSim_ can help in determining if the provided molecule's structural motif's are already well represented in the data.
### C. Similarity Measure
This dropdown includes all of the similarity metrics currently implemented in _AIMSim_. The default selected metric is likely a great starting point for most users, and the additional metrics are provided for advanced users or more specific use cases.
Available Similarity Measures are automatically updated according to the fingerprint currently selected. Not all metrics are compatible with all fingerprints, and _AIMSim_ recognizes will only allow the user to select valid combinations.
Below is a complete list of all similarity measures currently implemented in _AIMSim_.
| # | Name | Input Aliases |
| -- | ---------------------- | ---------------------------------------------------------------------------------------------------------------------------------------------- |
| 1 | l0\_similarity | \- |
| 2 | l1\_similarity | manhattan\_similarity, taxicab\_similarity, city\_block\_similarity, snake\_similarity |
| 3 | l2\_similarity | euclidean\_similarity |
| 4 | cosine | driver-kroeber, ochiai |
| 5 | dice | sorenson, gleason |
| 6 | dice\_2 | \- |
| 7 | dice\_3 | \- |
| 8 | tanimoto | jaccard-tanimoto |
| 9 | simple\_matching | sokal-michener, rand |
| 10 | rogers-tanimoto | \- |
| 11 | russel-rao | \- |
| 12 | forbes | \- |
| 13 | simpson | \- |
| 14 | braun-blanquet | \- |
| 15 | baroni-urbani-buser | \- |
| 16 | kulczynski | \- |
| 17 | sokal-sneath | sokal-sneath\_1 |
| 18 | sokal-sneath\_2 | sokal-sneath-2, symmetric\_sokal\_sneath, symmetric-sokal-sneath, |
| 19 | sokal-sneath\_3 | sokal-sneath-3 |
| 20 | sokal-sneath\_4 | sokal-sneath-4 |
| 21 | jaccard | \- |
| 22 | faith | \- |
| 23 | michael | \- |
| 24 | mountford | \- |
| 25 | rogot-goldberg | \- |
| 26 | hawkins-dotson | \- |
| 27 | maxwell-pilliner | \- |
| 28 | harris-lahey | \- |
| 29 | consonni−todeschini\_1 | consonni−todeschini-1 |
| 30 | consonni−todeschini\_2 | consonni−todeschini-2 |
| 31 | consonni−todeschini\_3 | consonni−todeschini-3 |
| 32 | consonni−todeschini\_4 | consonni−todeschini-4 |
| 33 | consonni−todeschini\_5 | consonni−todeschini-5 |
| 34 | austin-colwell | \- |
| 35 | yule\_1 | yule-1 |
| 36 | yule\_2 | yule-2 |
| 37 | holiday-fossum | fossum, holiday\_fossum |
| 38 | holiday-dennis | dennis, holiday\_dennis |
| 39 | cole\_1 | cole-1 |
| 40 | cole\_2 | cole-2 |
| 41 | dispersion | choi |
| 42 | goodman-kruskal | goodman\_kruskal |
| 43 | pearson-heron | pearson\_heron |
| 44 | sorgenfrei | \- |
| 45 | cohen | \- |
| 46 | peirce\_1 | peirce-1 |
| 47 | peirce\_2 | peirce-2 |
### D. Molecular Descriptor
This dropdown includes all of the molecular descriptors, mainly fingerprints, currently implemented in _AIMSim_:
|#|Fingerprint|
|---|---|
|1|morgan|
|2|topological|
|3|daylight|
Each of these fingerprints should be generally applicable for chemical problems, though they are all provided to serve as an easy way to compare the results according to fingerprinting approach.
Additional descriptors are included with _AIMSim_ which are not mathematically compatible with some of the similarity measures. When such a descriptor is selected, the corresponding similarity measure will be removed from the dropdown.
#### D1. Show Experimental Descriptors
This checkbox adds additional molecular descriptors into the `Molecular Descriptor` dropdown. These are marked as _experimental_ because they are generated using third-party libraries over which we have very little or no control. The descriptors generated by these libraries should be used only when the user has a very specific need for a descriptor as implemented in one of the packages below:
- [ccbmlib](https://doi.org/10.12688/f1000research.22292.2): All molecular fingerprints included in the `ccbmlib` library have been reproduced in _AIMSim_. Read about these fingerprints [in the `ccbmlib` repository](https://github.com/vogt-m/ccbmlib).
- [mordred](https://doi.org/10.1186/s13321-018-0258-y): All 1000+ descriptors included in `mordred` are available in _AIMSim_, though as of Januray 2022 it seems that `mordred` is no longer being maintained and has a significant amount of bugs. Use at your own risk.
- [PaDELPy](https://doi.org/10.1002/jcc.21707): [This package](https://github.com/ecrl/padelpy) provides access to all of the molecular descriptors included as part of the PaDEL-Descriptor standalone Java program.
### E. Run
Pressing this button will call a number of input checkers to verify that the information entered into the fields above is valid, and then the tasks will be passed into _AIMSim_ for execution. Additional input to _AIMSim_ needed for some tasks may be requested from the command line.
For large collections of molecules with substantial run times, your operating system may report that _AIMSim_ has stopped responding and should be closed. This is likely not the case, and _AIMSim_ is simply executing your requested tasks. If unsure, try checking the `Verbose` checkbox discussed below, which will provide near-constant output while _AIMSim_ is running.
### F. Open Config
Using your system's default text editor, this button will open the configuration file generated by _AIMSim_ after pressing the run button. This is useful for fine-tuning your plots or re-running the exact same tasks in the future. This configuration file can also access additional functionality present in _AIMSim_ which is not included in the GUI, such as the sampling ratio for the data (covered in greater depth in the __Command Line and Configuration Files__ section below). To use this configuration file, include the name of the file after your call to _AIMSim_ on the command line, i.e.:
`aimsim aimsim-ui-config.yaml` or `python -m aimsim aimsim-ui-config.yaml`
Because of the way Python install libraries like _AIMSim_, this file will likely be saved somewhere difficult to find among many other internal Python files. It is highly recommended to make a copy of this file in a more readily accessible location, or copy the contents of this file into another one. The name of the file can also be changed to something more meaningful (i.e., JWB-Solvent-Screen-123.yaml) as long as the file extension (.yaml) is still included.
### G. Verbose
Selecting this checkbox will cause _AIMSim_ to emit near-constant updates to the command line on its status during execution. This is useful to confirm that _AIMSim_ is executing and has not crashed, and also to provide additional information about errors in the input data.
For large datasets, this may generate a _significant_ amount of command line output. A pairwise comparison of 10,000 molecules would require 100,000,000 (10,000 \* 10,000) operations, generating at least that many lines of text in the console.
Example __Verbose__ output:
```
Reading SMILES strings from C:\path\to\file\small.smi
Processing O=S(C1=CC=CC=C1)(N2CCOCC2)=O (1/5)
Processing O=S(C1=CC=C(C(C)(C)C)C=C1)(N2CCOCC2)=O (2/5)
Processing O=S(C1=CC=C(C2=CC=CC=C2)C=C1)(N3CCOCC3)=O (3/5)
Processing O=S(C1=CC=C(OC)C=C1)(N2CCOCC2)=O (4/5)
Processing O=S(C1=CC=C(SC)C=C1)(N2CCOCC2)=O (5/5)
Computing similarity of molecule num 1 against 1
Computing similarity of molecule num 2 against 1
Computing similarity of molecule num 3 against 1
Computing similarity of molecule num 4 against 1
Computing similarity of molecule num 5 against 1
Computing similarity of molecule num 1 against 2
```
### H. Outlier Check
Checking this will have _AIMSim_ create an Isolation Forest (read more about this in [Sklearn's documentation](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html)) to identify possible outliers in the input database of molecules. The results from this approach are _non-deterministic_ because of the underlying algorithm driving the Isolation Forest, so this feature is intended to be a "sanity check" rather than a quantitative measure of 'outlier-ness'. To truly determine how different a single example molecule is to a set of molecules, use the `Compare Target Molecule` functionality discussed above.
### I. Enable Multiple Workers
This checkbox will enable multiprocessing, speeding up execution time on the data. By default, _AIMSim_ will use __all__ physical cores available on your machine, which may impact performance of other programs.
The user should only enable this option with datasets off a few hundred or more molecules. This is because there is additional processing time associated with creating and destroying multiple processes, so for small data sets it is faster to simply execute the comparisons serially.
## Command Line and Configuration Files
For users who prefer to use _AIMSim_ without a user interface, a command line interface is provided. This requires the user to manually write configuration files, but allows access to more granular control and some additional features which are not included in the GUI. This can be invoked by typing `aimsim config.yaml` into your terminal or command window, where `config.yaml` is a configuration file you have provided or copied from the _AIMSim_ repository.
Below is a 'maximum specification' file to be used with _AIMSim_, showing all possible settings and tasks which _AIMSim_ can ingest. Any overall settings which are left out will be inferred by _AIMSim_, and any tasks which are not included will simply not be executed. Each field used in the file is explained afterward.
### Maximum Specification File
```
is_verbose (bool):
molecule_database (str): # path to excel / csv/ text file
molecule_database_source_type (str): # Type of source file. 'excel', 'csv', 'text'
similarity_measure (str): #Set to determine if auto identification required
fingerprint_type (str): # Set to determine if auto identification required
measure_id_subsample (float): # [0, 1] Subsample used for measure search
sampling_ratio (float): # [0, 1] Subsample used for all tasks
n_workers (int / str): # [int, 'auto'] number of processes, or let AIMSim decide
global_random_seed (int / str): # int or 'random'
tasks:
compare_target_molecule:
target_molecule_smiles (str):
draw_molecule (bool): # If true, strucures of target, most and least similar molecules are displayed
similarity_plot_settings:
plot_color (str): # Set a color recognized by matplotlib
shade (bool): # If true, the similarity density is shaded
plot_title (str):
log_file_path (str):
visualize_dataset:
heatmap_plot_settings:
cmap (str): # matplotlib recognized cmap (color map) used for heatmap.
plot_title (str):
annotate (bool): # If true, heatmap is annotated
similarity_plot_settings:
plot_color (str):
shade (bool): # If true, the similarity density is shaded
embedding_plot_settings:
plot_title (str):
embedding:
method (str): # algorithm used for embedding molecule set in 2 dimensions.
params: # method specific parameters
random_state (int): #used for seeding stochastic algorithms
see_property_variation_w_similarity:
log_file_path (str):
property_plot_settings:
plot_color (str): # Set a color recognized by matplotlib
identify_outliers:
random_state (int):
output (str): # filepath or "terminal" to control where results are shown
plot_outliers (bool):
pair_similarity_plot_settings: # Only meaningful if plot_outliers is True
plot_color (str): # Set a color recognized by matplotlib
cluster:
n_clusters (int):
clustering_method (str):
log_file_path (str):
cluster_file_path (str):
cluster_plot_settings:
cluster_colors (list): # Ensure len(list) >= n_cluster
embedding_plot_settings:
plot_title (str):
embedding:
method (str): # algorithm used for embedding molecule set in 2 dimensions.
params: # method specific parameters
random_state (int): #used for seeding stochastic algorithms
```
#### Overall _AIMSim_ Settings
These settings impact how all tasks run by _AIMSim_ will be executed.
- `is_verbose`: Must be either `True` or `False`. When `True`, _AIMSim_ will emit text updates of during execution to the command line, useful for debugging.
- `molecule_database`: A file path to an Excel workbook, text file containing SMILES strings, or PDB file surrounded by single quotes, i.e. `'/User/my_user/smiles_database.smi'`. Can also point to a directory containing a group of PDB files, but the file path must end with a '/' (or '\' for Windows).
- `molecule_database_source_type`: The type of data to be input to _AIMSim_, being either `text`, `excel`, or `pdb`.
- `similarity_measure`: The similarity measure to be used during all tasks, chosen from the list of supported similarity measures. Automatic similarity measure determination is also supported, and can be performed by specifying `determine`.
- `fingerprint_type`: The fingerprint type or molecular descriptor to be used during all tasks, chosen from the list of supported descriptors. Automatic determination is also supported, and can be performed by specifying `determine`.
- `measure_id_subsample`: A decimal number between 0 and 1 specifying what fraction of the dataset to use for automatic determination of similarity measure and fingerprint. For a dataset of 10,000 molecules, setting this to `0.1` would run only 1000 randomly selected molecules, dramatically reducing runtime. This field is only needed if `determine` is used in either of the prior fields.
- `sampling_ratio`: A decimal number between 0 and 1 specifying what fraction of the dataset to use for tasks. For a dataset of 10,000 molecules, setting this to `0.1` would run only 1000 randomly selected molecules, dramatically reducing runtime.
- `n_workers`: Either an integer or the string 'auto'. With an integer, _AIMSim_ will create that many processes for its operation. This number should be less than or equal to the number of _physical_ CPU cores in your computer. Set this option to 'auto' to let _AIMSim_ configure multiprocessing for you.
- `global_random_seed`: Integer to be passed to all non-deterministic functions in _AIMSim_. By default, this value is 42 to ensure consistent results between subsequent executions of _AIMSim_. This seed will override the random seeds provided to any other _AIMSim_ tasks. Alternatively, specify 'random' to allow _AIMSim_ to randomly generate a seed.
#### Task-Specific Settings
The settings fields below dictate the behavior of _AIMSim_ when performing its various tasks.
##### Compare Target Molecule
Generates a similarity distribution for the dataset compared to an individual molecule.
- `target_molecule_smiles`: SMILES string for the molecule used in comparison to the dataset.
- `draw_molecule`: If this is set to True, then _AIMSim_ draws the structure of the target molecule, and of the molecule most and least similar to it.
- `similarity_plot_settings`: Controls the appearance of the distribution.
- `plot_color`: Can be any color recognized by the _matplotlib_ library.
- `shade`: `True` or `False`, whether or not to shade in the area under the curve.
- `plot_title`: String containing text to be written above the plot.
- `log_file_path`: String specifying a file to write output to for the execution of this task. Useful for debugging.
##### Visualize Dataset
Generates a pairwise comparison matrix for all molecules in the dataset.
- `heatmap_plot_settings`: Control the appearance of the plot.
- `cmap`: _matplotlib_ recognized cmap (color map) used for heatmap.
- `plot_title`: String containing text to be written above the plot.
- `annotate`: `True` or `False`, controls whether or not _AIMSim_ will write annotations over the heatmap.
- `similarity_plot_settings`: Controls the appearance of the distribution.
- `plot_color`: Can be any color recognized by the _matplotlib_ library.
- `shade`: `True` or `False`, whether or not to shade in the area under the curve.
- `embedding_plot_settings`: Constrols the lower dimensional embedding of the dataset.
- `plot_title`: String containing text to be written above the plot.
- `embedding`: Set the algorithmic aspects of the embedding
- `method`: Label specifying the algorithm embedding the molecule set in 2 dimensions.
- `params`: Specific hyperparameters which are passed through to the underlying implementation
- `random_state`: Number used for seeding stochastic algorithms
##### Property Variation Visualization
Creates a plot of how a given property in the input molecule set varies according to the structural fingerprint chosen.
- `log_file_path`: String specifying a file to write output to for the execution of this task. Useful for debugging or retrospection.
- `property_plot_settings`: Control the appearance of the plot.
- `plot_color`: Any color recognized by the _matplotlib_ library.
##### Identify Outliers
Trains an [IsolationForest](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.IsolationForest.html) on the input data to check for potential outliers.
- `random_state`: An integer to pass through to random_state in sklearn. _AIMSim_ sets this to 42 by default.
- `output`: A string which specifies where the output of the outlier search should go. This can be either a filepath or "terminal" to write the output directly to the terminal.
- `plot_outliers`: Set this to `True` to generate a 2D plot of which molecules are potential outliers.
- `pair_similarity_plot_settings`: Only meaningful if plot_outliers is True, allows access to plot settings.
- `plot_color`: Any color recognized by the _matplotlib_ library.
##### Cluster
Use a clustering algorithm to make groups from the database of molecules.
- `n_clusters`: The number of clusters to group the molecules into.
- `clustering_method`: Optional string specifying a clustering method implemented in `sklearn`, one of `kmedoids`, `ward`, or `complete_linkage`. `complete_linkage` will be chosen by default if no alternative is provided.
- `log_file_path`: String specifying a file to write output to for the execution of this task. Useful for debugging.
- `cluster_file_path`: String specifying a file path where _AIMSim_ will output the result of clustering. Useful for comparing multiple clustering approaches or saving the results of large data sets.
- `cluster_plot_settings`: Control the appearance of the clustering plot.
- `cluster_colors`: A list of strings, each of which is a color recognized by _matplotlib_ to use for the clusters. Must specify at least as many colors as there are clusters. Additional colors will be ignored.
- `embedding_plot_settings`: Constrols the lower dimensional embedding of the dataset.
- `plot_title`: String containing text to be written above the plot.
- `embedding`: Set the algorithmic aspects of the embedding
- `method`: Label specifying the algorithm embedding the clustered molecule set in 2 dimensions.
- `params`: Specific hyperparameters which are passed through to the underlying implementation
- `random_state`: Number used for seeding stochastic algorithms
## Writing Scripts with _AIMSim_
Advanced users may wish to use _AIMSim_ to create their own descriptors, use the descriptor's provided in _AIMSim_ for something else entirely, or utilize the various similarity scores. Brief explanations for how to access the core functionalities of _AIMSim_ from a Python script are shown below.
### Making Custom Descriptors
Any arbitrary numpy array can be provided as a molecular descriptor, though correct function with the similarity metrics provided with _AIMSim_ is not guaranteed.
```
from aimsim.ops.descriptor import Descriptor
desc = Descriptor()
```
With the `Descriptor` class instantiated, one can then call the methods to set the value(s) of the descriptor.
```
import numpy as np
custom_desc = np.array([1, 2, 3])
desc.set_manually(custom_desc)
desc.numpy_
```
This same function can be achieved by passing in a numpy array for the keyword argument `value` in the constructor for `Descriptor`, as shown below:
```
desc = Descriptor(custom_desc)
desc.numpy_
```
The above code is useful for individually changing a descriptor for one molecule in a `MoleculeSet` but is obviously not practical for bulk custom descriptors. To assign descriptors for an entire set of molecules at once, instantiate the `MoleculeSet` class and call the `_set_descriptor` method passing in a 2-dimensional numpy array of descriptors.
```
from AIMSim.chemical_datastructures.molecule_set import MoleculeSet
molset = MoleculeSet(
'/path/to/databse/smiles.txt',
'text',
False,
'tanimoto'
)
molset._set_descriptor([[1, 2, 3], [4, 5, 6]])
```
### Generating Descriptors with _AIMSim_
Because _AIMSim_ is able to generate such a wise variety of molecular fingerprints and descriptors from only the SMILES strings, you may want to avoid re-inventing the wheel and use the descriptors that it generates. There are two general approaches to doing this, and the approach used depends on what other code you already have in place:
1. If you have only SMILES strings to turn into fingerprints/descriptors, the `Molecule` class should be used to handle generating the molecule object and generating the descriptors.
2. If you have already created a molecule using `RDKit`, you must provide the existing molecule in your call to the constructor in `Molecule`.
These approaches are covered in this order below.
```
# with a SMILES string
smiles = "CO"
from aimsim.chemical_datastructures.molecule import Molecule
mol = Molecule(mol_smiles=smiles)
mol.set_descriptor(fingerprint_type="atom-pair_fingerprint")
mol.get_descriptor_val()
# with an RDKit molecule
from rdkit import Chem
mol_graph = Chem.MolFromSmiles(smiles)
mol = Molecule(mol_graph=mol_graph)
mol.set_descriptor(fingerprint_type="mordred:nAtom")
mol.get_descriptor_val()
```
### Acessing _AIMSim_ Similarity Metrics
As of January 2022, _AIMSim_ implements 47 unique similarity metrics for use in comparing two numbers and/or two sets of numbers. These metrics were pulled from a variety of sources, including some original implementations, so it may be of interest to use this code in your own work.
All of the similarity metrics can be accessed through the `SimilarityMeasure` class, as shown below.
```
from aimsim.ops.similarity_measures import SimilarityMeasure
from rdkit.Chem import MolFromSmiles
sim_mes = SimilarityMeasure("driver-kroeber")
desc_1 = Descriptor()
desc_1.make_fingerprint(
MolFromSmiles("COC"),
"morgan_fingerprint",
)
desc_2 = Descriptor()
desc_2.make_fingerprint(
MolFromSmiles("CCCC"),
"morgan_fingerprint",
)
out = sim_mes(
desc_1,
desc_2,
)
out
```
A complete list of supported similarity measures and the names by which _AIMSim_ recognizes them is listed in the GUI walkthrough section.
## Using AIMSim Tasks inside custom Python pipelines
In this section we will take a look at using some of the Tasks provided by AIMSim inside custom Python scripts.
### Visualizing a Dataset
First we create the dataset which consists of 100 samples, each containing 3 features. We will first create an Excel file and load that file via _AIMSim_ to visualize it. <b>Note that </b> columns corresponding to sample names or features in the Excel have to be prefixed by <i>'feature_'</i>
```
%%capture
!pip install openpyxl # for using the excel writer
import pandas as pd
from numpy.random import random
n_samples = 100
dataset = {'feature_f1': random(size=n_samples),
'feature_f2': random(size=n_samples),
'feature_f3': random(size=n_samples)}
df = pd.DataFrame(dataset)
dataset_file = 'dataset.xlsx'
df.to_excel(dataset_file)
```
First we load the data into a MoleculeSet object. We use the arbitrary features defined above and L2- similarity to define the similarity in this feature space.
```
from aimsim.chemical_datastructures import MoleculeSet
# load a MoleculeSet from the file
molecule_set = MoleculeSet(molecule_database_src=dataset_file,
molecule_database_src_type='excel',
similarity_measure='l2_similarity',
is_verbose=False)
```
Now we visualize it using the VisualizeDataset Task.
Note that the arguments to the VisualizeDataset constructor are used to edit the plot settings (such as colors and axis labels) as well as the type and parameters of the 2D embedding (here we use PCA to embed the dataset in 2 dimensions). A complete list of the keywords accepted and their default values can be found in the docstring of the constructor in our [documentation page](https://vlachosgroup.github.io/AIMSim/).
```
from aimsim.tasks import VisualizeDataset
# instantiate the task
viz = VisualizeDataset(embedding_plot_settings={"embedding": {"method": "pca"}})
viz(molecule_set)
```
### Clustering
The dataset can also be clustered using the ClusterData Task in _AIMSim_. The following code snippets clusters the dataset using the K-Medoids algorithm. Note that we reuse the MoleculeSet object, therefore we are still using the L2 similarity for clustering. The data is clustered into 5 clusters and the 2D embedding is again generated using PCA. A complete list of the keywords accepted by the ClusterData constructor and their default values can be found in the docstring of the constructor in our [documentation page](https://vlachosgroup.github.io/AIMSim/).
```
from aimsim.tasks import ClusterData
clustering = ClusterData(n_clusters=5, # data is clustered into 5 clusters
clustering_method='kmedoids',
embedding_plot_settings={"embedding": {"method": "pca"}}
)
clustering(molecule_set)
```
| true |
code
| 0.617801 | null | null | null | null |
|
# Amazon SageMaker Processing と AWS Step Functions Data Science SDK で機械学習ワークフローを構築する
Amazon SageMaker Processing を使うと、データの前/後処理やモデル評価のワークロードを Amazon SageMaker platform 上で簡単に実行することができます。Processingジョブは Amazon Simple Storage Service (Amazon S3) から入力データをダウンロードし、処理結果を Amazon S3 にアップロードします。
Step Functions SDK は AWS Step Function と Amazon SageMaker を使って、データサイエンティストが機械学習ワークフローを簡単に作成して実行するためのものです。詳しい情報は以下のドキュメントをご参照ください。
* [AWS Step Functions](https://aws.amazon.com/step-functions/)
* [AWS Step Functions Developer Guide](https://docs.aws.amazon.com/step-functions/latest/dg/welcome.html)
* [AWS Step Functions Data Science SDK](https://aws-step-functions-data-science-sdk.readthedocs.io)
AWS Step Functions Data Science SDK の SageMaker Processing Step [ProcessingStep](https://aws-step-functions-data-science-sdk.readthedocs.io/en/stable/sagemaker.html#stepfunctions.steps.sagemaker.ProcessingStep) によって、AWS Step Functions ワークフローで実装された Sageaker Processing を機械学習エンジニアが直接システムに統合することができます。
このノートブックは、SageMaker Processing Job を使ってデータの前処理、モデルの学習、モデルの精度評価の機械学習ワークフローを AWS Step Functions Data Science SDK を使って作成する方法をご紹介します。大まかな流れは以下の通りです。
1. AWS Step Functions Data Science SDK の `ProcessingStep` を使ってデータの前処理、特徴量エンジニアリング、学習用とテスト用への分割を行う scikit-learn スクリプトを実行する SageMaker Processing Job を実行
1. AWS Step Functions Data Science SDK の `TrainingStep` を使って前処理された学習データを使ったモデルの学習を実行
1. AWS Step Functions Data Science SDK の `ProcessingStep` を使って前処理したテスト用データを使った学習済モデルの評価を実行
このノートブックで使用するデータは [Census-Income KDD Dataset](https://archive.ics.uci.edu/ml/datasets/Census-Income+%28KDD%29) です。このデータセットから特徴量を選択し、データクレンジングを実施し、二値分類モデルの利用できる形にデータを変換し、最後にデータを学習用とテスト用に分割します。このノートブックではロジスティック回帰モデルを使って、国勢調査の回答者の収入が 5万ドル以上か 5万ドル未満かを予測します。このデータセットはクラスごとの不均衡が大きく、ほとんどのデータに 5万ドル以下というラベルが付加されています。
## Setup
このノートブックを実行するのに必要なライブラリをインストールします。
```
# Import the latest sagemaker, stepfunctions and boto3 SDKs
import sys
!{sys.executable} -m pip install --upgrade pip
!{sys.executable} -m pip install -qU awscli boto3 "sagemaker>=2.0.0"
!{sys.executable} -m pip install -qU "stepfunctions>=2.0.0"
!{sys.executable} -m pip show sagemaker stepfunctions
```
### 必要なモジュールのインポート
```
import io
import logging
import os
import random
import time
import uuid
import boto3
import stepfunctions
from stepfunctions import steps
from stepfunctions.inputs import ExecutionInput
from stepfunctions.steps import (
Chain,
ChoiceRule,
ModelStep,
ProcessingStep,
TrainingStep,
TransformStep,
)
from stepfunctions.template import TrainingPipeline
from stepfunctions.template.utils import replace_parameters_with_jsonpath
from stepfunctions.workflow import Workflow
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import image_uris
from sagemaker.processing import ProcessingInput, ProcessingOutput
from sagemaker.s3 import S3Uploader
from sagemaker.sklearn.processing import SKLearnProcessor
# SageMaker Session
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_region_name
# SageMaker Execution Role
# You can use sagemaker.get_execution_role() if running inside sagemaker's notebook instance
role = get_execution_role()
```
次に、ノートブックから Step Functions を実行するための IAM ロール設定を行います。
## ノートブックインスタンスの IAM ロールに権限を追加
以下の手順を実行して、ノートブックインスタンスに紐づけられた IAM ロールに、AWS Step Functions のワークフローを作成して実行するための権限を追加してください。
1. [Amazon SageMaker console](https://console.aws.amazon.com/sagemaker/) を開く
2. **ノートブックインスタンス** を開いて現在使用しているノートブックインスタンスを選択する
3. **アクセス許可と暗号化** の部分に表示されている IAM ロールへのリンクをクリックする
4. IAM ロールの ARN は後で使用するのでメモ帳などにコピーしておく
5. **ポリシーをアタッチします** をクリックして `AWSStepFunctionsFullAccess` を検索する
6. `AWSStepFunctionsFullAccess` の横のチェックボックスをオンにして **ポリシーのアタッチ** をクリックする
もしこのノートブックを SageMaker のノートブックインスタンス以外で実行している場合、その環境で AWS CLI 設定を行ってください。詳細は [Configuring the AWS CLI](https://docs.aws.amazon.com/cli/latest/userguide/cli-chap-configure.html) をご参照ください。
次に Step Functions で使用する実行ロールを作成します。
## Step Functions の実行ロールの作成
作成した Step Functions ワークフローは、AWS の他のサービスと連携するための IAM ロールを必要とします。
1. [IAM console](https://console.aws.amazon.com/iam/) にアクセス
2. 左側のメニューの **ロール** を選択し **ロールの作成** をクリック
3. **ユースケースの選択** で **Step Functions** をクリック
4. **次のステップ:アクセス権限** **次のステップ:タグ** **次のステップ:確認**をクリック
5. **ロール名** に `AmazonSageMaker-StepFunctionsWorkflowExecutionRole` と入力して **ロールの作成** をクリック
Next, attach a AWS Managed IAM policy to the role you created as per below steps.
次に、作成したロールに AWS マネージド IAM ポリシーをアタッチします。
1. [IAM console](https://console.aws.amazon.com/iam/) にアクセス
2. 左側のメニューの **ロール** を選択
3. 先ほど作成した `AmazonSageMaker-StepFunctionsWorkflowExecutionRole`を検索
4. **ポリシーをアタッチします** をクリックして `CloudWatchEventsFullAccess` を検索
5. `CloudWatchEventsFullAccess` の横のチェックボックスをオンにして **ポリシーのアタッチ** をクリック
次に、別の新しいポリシーをロールにアタッチします。ベストプラクティスとして、以下のステップで特定のリソースのみのアクセス権限とこのサンプルを実行するのに必要なアクションのみを有効にします。
1. 左側のメニューの **ロール** を選択
1. 先ほど作成した `AmazonSageMaker-StepFunctionsWorkflowExecutionRole`を検索
1. **ポリシーをアタッチします** をクリックして **ポリシーの作成** をクリック
1. **JSON** タブをクリックして以下の内容をペースト<br>
NOTEBOOK_ROLE_ARN の部分をノートブックインスタンスで使用している IAM ロールの ARN に置き換えてください。
```json
{
"Version": "2012-10-17",
"Statement": [
{
"Sid": "VisualEditor0",
"Effect": "Allow",
"Action": [
"events:PutTargets",
"events:DescribeRule",
"events:PutRule"
],
"Resource": [
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTrainingJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTransformJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForSageMakerTuningJobsRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForECSTaskRule",
"arn:aws:events:*:*:rule/StepFunctionsGetEventsForBatchJobsRule"
]
},
{
"Sid": "VisualEditor1",
"Effect": "Allow",
"Action": "iam:PassRole",
"Resource": "NOTEBOOK_ROLE_ARN",
"Condition": {
"StringEquals": {
"iam:PassedToService": "sagemaker.amazonaws.com"
}
}
},
{
"Sid": "VisualEditor2",
"Effect": "Allow",
"Action": [
"batch:DescribeJobs",
"batch:SubmitJob",
"batch:TerminateJob",
"dynamodb:DeleteItem",
"dynamodb:GetItem",
"dynamodb:PutItem",
"dynamodb:UpdateItem",
"ecs:DescribeTasks",
"ecs:RunTask",
"ecs:StopTask",
"glue:BatchStopJobRun",
"glue:GetJobRun",
"glue:GetJobRuns",
"glue:StartJobRun",
"lambda:InvokeFunction",
"sagemaker:CreateEndpoint",
"sagemaker:CreateEndpointConfig",
"sagemaker:CreateHyperParameterTuningJob",
"sagemaker:CreateModel",
"sagemaker:CreateProcessingJob",
"sagemaker:CreateTrainingJob",
"sagemaker:CreateTransformJob",
"sagemaker:DeleteEndpoint",
"sagemaker:DeleteEndpointConfig",
"sagemaker:DescribeHyperParameterTuningJob",
"sagemaker:DescribeProcessingJob",
"sagemaker:DescribeTrainingJob",
"sagemaker:DescribeTransformJob",
"sagemaker:ListProcessingJobs",
"sagemaker:ListTags",
"sagemaker:StopHyperParameterTuningJob",
"sagemaker:StopProcessingJob",
"sagemaker:StopTrainingJob",
"sagemaker:StopTransformJob",
"sagemaker:UpdateEndpoint",
"sns:Publish",
"sqs:SendMessage"
],
"Resource": "*"
}
]
}
```
5. **次のステップ:タグ** **次のステップ:確認**をクリック
6. **名前** に `AmazonSageMaker-StepFunctionsWorkflowExecutionPolicy` と入力して **ポリシーの作成** をクリック
7. 左側のメニューで **ロール** を選択して `AmazonSageMaker-StepFunctionsWorkflowExecutionRole` を検索
8. **ポリシーをアタッチします** をクリック
9. 前の手順で作成した `AmazonSageMaker-StepFunctionsWorkflowExecutionPolicy` ポリシーを検索してチェックボックスをオンにして **ポリシーのアタッチ** をクリック
11. AmazonSageMaker-StepFunctionsWorkflowExecutionRole の *Role ARN** をコピーして以下のセルにペースト
```
# paste the AmazonSageMaker-StepFunctionsWorkflowExecutionRole ARN from above
workflow_execution_role = "arn:aws:iam::420964472730:role/StepFunctionsWorkflowExecutionRole"
```
### Step Functions ワークフロー実行時の入力スキーマ作成
Step Functions ワークフローを実行する際に、パラメタなどを引数として渡すことができます。ここではそれらの引数のスキーマを作成します。
```
# Generate unique names for Pre-Processing Job, Training Job, and Model Evaluation Job for the Step Functions Workflow
training_job_name = "scikit-learn-training-{}".format(
uuid.uuid1().hex
) # Each Training Job requires a unique name
preprocessing_job_name = "scikit-learn-sm-preprocessing-{}".format(
uuid.uuid1().hex
) # Each Preprocessing job requires a unique name,
evaluation_job_name = "scikit-learn-sm-evaluation-{}".format(
uuid.uuid1().hex
) # Each Evaluation Job requires a unique name
# SageMaker expects unique names for each job, model and endpoint.
# If these names are not unique the execution will fail. Pass these
# dynamically for each execution using placeholders.
execution_input = ExecutionInput(
schema={
"PreprocessingJobName": str,
"TrainingJobName": str,
"EvaluationProcessingJobName": str,
}
)
```
## データの前処理と特徴量エンジニアリング
データクレンジング 、前処理、特徴量エンジニアリングのスクリプトの前に、データセットの初めの 20行をのぞいてみましょう。ターゲット変数は `income` 列です。選択する特徴量は `age`, `education`, `major industry code`, `class of worker`, `num persons worked for employer`, `capital gains`, `capital losses`, `dividends from stocks` です。
```
import pandas as pd
input_data = "s3://sagemaker-sample-data-{}/processing/census/census-income.csv".format(region)
df = pd.read_csv(input_data, nrows=10)
df.head(n=10)
```
scikit-learn の前処理スクリプトを実行するために `SKLearnProcessor`を作成します。これは、SageMaker が用意している scikit-learn のコンテナイメージを使って Processing ジョブを実行するためのものです。
```
sklearn_processor = SKLearnProcessor(
framework_version="0.20.0",
role=role,
instance_type="ml.m5.xlarge",
instance_count=1,
max_runtime_in_seconds=1200,
)
```
以下のセルを実行すると `preprocessing.py` が作成されます。これは前処理のためのスクリプトです。以下のセルを書き換えて実行すれば、`preprocessing.py` が上書き保存されます。このスクリプトでは、以下の処理が実行されます。
n the next cell. In this script, you
* 重複データやコンフリクトしているデータの削除
* ターゲット変数 `income` 列をカテゴリ変数から 2つのラベルを持つ列に変換
* `age` と `num persons worked for employer` をビニングして数値からカテゴリ変数に変換
* 連続値である`capital gains`, `capital losses`, `dividends from stocks` を学習しやすいようスケーリング
* `education`, `major industry code`, `class of worker`を学習しやすいようエンコード
* データを学習用とテスト用に分割し特徴量とラベルの値をそれぞれ保存
学習スクリプトでは、前処理済みの学習用データとラベル情報を使用してモデルを学習します。また、モデル評価スクリプトでは学習済みモデルと前処理済みのテスト用データトラベル情報を使用してモデルを評価します。
```
%%writefile preprocessing.py
import argparse
import os
import warnings
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder, LabelBinarizer, KBinsDiscretizer
from sklearn.preprocessing import PolynomialFeatures
from sklearn.compose import make_column_transformer
from sklearn.exceptions import DataConversionWarning
warnings.filterwarnings(action="ignore", category=DataConversionWarning)
columns = [
"age",
"education",
"major industry code",
"class of worker",
"num persons worked for employer",
"capital gains",
"capital losses",
"dividends from stocks",
"income",
]
class_labels = [" - 50000.", " 50000+."]
def print_shape(df):
negative_examples, positive_examples = np.bincount(df["income"])
print(
"Data shape: {}, {} positive examples, {} negative examples".format(
df.shape, positive_examples, negative_examples
)
)
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("--train-test-split-ratio", type=float, default=0.3)
args, _ = parser.parse_known_args()
print("Received arguments {}".format(args))
input_data_path = os.path.join("/opt/ml/processing/input", "census-income.csv")
print("Reading input data from {}".format(input_data_path))
df = pd.read_csv(input_data_path)
df = pd.DataFrame(data=df, columns=columns)
df.dropna(inplace=True)
df.drop_duplicates(inplace=True)
df.replace(class_labels, [0, 1], inplace=True)
negative_examples, positive_examples = np.bincount(df["income"])
print(
"Data after cleaning: {}, {} positive examples, {} negative examples".format(
df.shape, positive_examples, negative_examples
)
)
split_ratio = args.train_test_split_ratio
print("Splitting data into train and test sets with ratio {}".format(split_ratio))
X_train, X_test, y_train, y_test = train_test_split(
df.drop("income", axis=1), df["income"], test_size=split_ratio, random_state=0
)
preprocess = make_column_transformer(
(
["age", "num persons worked for employer"],
KBinsDiscretizer(encode="onehot-dense", n_bins=10),
),
(
["capital gains", "capital losses", "dividends from stocks"],
StandardScaler(),
),
(
["education", "major industry code", "class of worker"],
OneHotEncoder(sparse=False),
),
)
print("Running preprocessing and feature engineering transformations")
train_features = preprocess.fit_transform(X_train)
test_features = preprocess.transform(X_test)
print("Train data shape after preprocessing: {}".format(train_features.shape))
print("Test data shape after preprocessing: {}".format(test_features.shape))
train_features_output_path = os.path.join("/opt/ml/processing/train", "train_features.csv")
train_labels_output_path = os.path.join("/opt/ml/processing/train", "train_labels.csv")
test_features_output_path = os.path.join("/opt/ml/processing/test", "test_features.csv")
test_labels_output_path = os.path.join("/opt/ml/processing/test", "test_labels.csv")
print("Saving training features to {}".format(train_features_output_path))
pd.DataFrame(train_features).to_csv(train_features_output_path, header=False, index=False)
print("Saving test features to {}".format(test_features_output_path))
pd.DataFrame(test_features).to_csv(test_features_output_path, header=False, index=False)
print("Saving training labels to {}".format(train_labels_output_path))
y_train.to_csv(train_labels_output_path, header=False, index=False)
print("Saving test labels to {}".format(test_labels_output_path))
y_test.to_csv(test_labels_output_path, header=False, index=False)
```
前処理用スクリプトを S3 にアップロードします。
```
PREPROCESSING_SCRIPT_LOCATION = "preprocessing.py"
input_code = sagemaker_session.upload_data(
PREPROCESSING_SCRIPT_LOCATION,
bucket=sagemaker_session.default_bucket(),
key_prefix="data/sklearn_processing/code",
)
```
Processing ジョブの出力を保存する S3 パスを作成します。
```
s3_bucket_base_uri = "{}{}".format("s3://", sagemaker_session.default_bucket())
output_data = "{}/{}".format(s3_bucket_base_uri, "data/sklearn_processing/output")
preprocessed_training_data = "{}/{}".format(output_data, "train_data")
```
### `ProcessingStep` の作成
それでは、SageMaker Processing ジョブを起動するための [ProcessingStep](https://aws-step-functions-data-science-sdk.readthedocs.io/en/stable/sagemaker.html#stepfunctions.steps.sagemaker.ProcessingStep) を作成しましょう。
このステップは、前の手順で定義した SKLearnProcessor に入力と出力の情報を追加して使用します。
#### [ProcessingInputs](https://sagemaker.readthedocs.io/en/stable/api/training/processing.html#sagemaker.processing.ProcessingInput) と [ProcessingOutputs](https://sagemaker.readthedocs.io/en/stable/api/training/processing.html#sagemaker.processing.ProcessingOutput) オブジェクトを作成して SageMaker Processing ジョブに入力と出力の情報を追加
```
inputs = [
ProcessingInput(
source=input_data, destination="/opt/ml/processing/input", input_name="input-1"
),
ProcessingInput(
source=input_code,
destination="/opt/ml/processing/input/code",
input_name="code",
),
]
outputs = [
ProcessingOutput(
source="/opt/ml/processing/train",
destination="{}/{}".format(output_data, "train_data"),
output_name="train_data",
),
ProcessingOutput(
source="/opt/ml/processing/test",
destination="{}/{}".format(output_data, "test_data"),
output_name="test_data",
),
]
```
#### `ProcessingStep` の作成
```
# preprocessing_job_name = generate_job_name()
processing_step = ProcessingStep(
"SageMaker pre-processing step",
processor=sklearn_processor,
job_name=execution_input["PreprocessingJobName"],
inputs=inputs,
outputs=outputs,
container_arguments=["--train-test-split-ratio", "0.2"],
container_entrypoint=["python3", "/opt/ml/processing/input/code/preprocessing.py"],
)
```
## 前処理済みデータを使ったモデルの学習
学習スクリプト `train.py` を使って学習ジョブを実行するための `SKLearn` インスタンスを作成します。これはあとで `TrainingStep` を作成する際に使用します。
```
from sagemaker.sklearn.estimator import SKLearn
sklearn = SKLearn(
entry_point="train.py",
train_instance_type="ml.m5.xlarge",
role=role,
framework_version="0.20.0",
py_version="py3",
)
```
学習スクリプト `train.py` は、ロジスティック回帰モデルを学習し、学習済みモデルを `/opt/ml/model` に保存します。Amazon SageMaker は、学習ジョブの最後にそこに保存されているモデルを `model.tar.gz` に圧縮して S3 にアップロードします。
```
%%writefile train.py
import os
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.externals import joblib
if __name__ == "__main__":
training_data_directory = "/opt/ml/input/data/train"
train_features_data = os.path.join(training_data_directory, "train_features.csv")
train_labels_data = os.path.join(training_data_directory, "train_labels.csv")
print("Reading input data")
X_train = pd.read_csv(train_features_data, header=None)
y_train = pd.read_csv(train_labels_data, header=None)
model = LogisticRegression(class_weight="balanced", solver="lbfgs")
print("Training LR model")
model.fit(X_train, y_train)
model_output_directory = os.path.join("/opt/ml/model", "model.joblib")
print("Saving model to {}".format(model_output_directory))
joblib.dump(model, model_output_directory)
```
### `TrainingStep` の作成
```
training_step = steps.TrainingStep(
"SageMaker Training Step",
estimator=sklearn,
data={"train": sagemaker.TrainingInput(preprocessed_training_data, content_type="text/csv")},
job_name=execution_input["TrainingJobName"],
wait_for_completion=True,
)
```
## モデルの評価
`evaluation.py` はモデル評価用のスクリプトです。このスクリプトは scikit-learn を用いるため、以前の手順で使用した`SKLearnProcessor` を使用します。このスクリプトは学習済みモデルとテスト用データセットを入力として受け取り、各分類クラスの分類評価メトリクス、precision、リコール、F1スコア、accuracy と ROC AUC が記載された JSON ファイルを出力します。
```
%%writefile evaluation.py
import json
import os
import tarfile
import pandas as pd
from sklearn.externals import joblib
from sklearn.metrics import classification_report, roc_auc_score, accuracy_score
if __name__ == "__main__":
model_path = os.path.join("/opt/ml/processing/model", "model.tar.gz")
print("Extracting model from path: {}".format(model_path))
with tarfile.open(model_path) as tar:
tar.extractall(path=".")
print("Loading model")
model = joblib.load("model.joblib")
print("Loading test input data")
test_features_data = os.path.join("/opt/ml/processing/test", "test_features.csv")
test_labels_data = os.path.join("/opt/ml/processing/test", "test_labels.csv")
X_test = pd.read_csv(test_features_data, header=None)
y_test = pd.read_csv(test_labels_data, header=None)
predictions = model.predict(X_test)
print("Creating classification evaluation report")
report_dict = classification_report(y_test, predictions, output_dict=True)
report_dict["accuracy"] = accuracy_score(y_test, predictions)
report_dict["roc_auc"] = roc_auc_score(y_test, predictions)
print("Classification report:\n{}".format(report_dict))
evaluation_output_path = os.path.join("/opt/ml/processing/evaluation", "evaluation.json")
print("Saving classification report to {}".format(evaluation_output_path))
with open(evaluation_output_path, "w") as f:
f.write(json.dumps(report_dict))
MODELEVALUATION_SCRIPT_LOCATION = "evaluation.py"
input_evaluation_code = sagemaker_session.upload_data(
MODELEVALUATION_SCRIPT_LOCATION,
bucket=sagemaker_session.default_bucket(),
key_prefix="data/sklearn_processing/code",
)
```
モデル評価用の ProcessingStep の入力と出力オブジェクトを作成します。
```
preprocessed_testing_data = "{}/{}".format(output_data, "test_data")
model_data_s3_uri = "{}/{}/{}".format(s3_bucket_base_uri, training_job_name, "output/model.tar.gz")
output_model_evaluation_s3_uri = "{}/{}/{}".format(
s3_bucket_base_uri, training_job_name, "evaluation"
)
inputs_evaluation = [
ProcessingInput(
source=preprocessed_testing_data,
destination="/opt/ml/processing/test",
input_name="input-1",
),
ProcessingInput(
source=model_data_s3_uri,
destination="/opt/ml/processing/model",
input_name="input-2",
),
ProcessingInput(
source=input_evaluation_code,
destination="/opt/ml/processing/input/code",
input_name="code",
),
]
outputs_evaluation = [
ProcessingOutput(
source="/opt/ml/processing/evaluation",
destination=output_model_evaluation_s3_uri,
output_name="evaluation",
),
]
model_evaluation_processor = SKLearnProcessor(
framework_version="0.20.0",
role=role,
instance_type="ml.m5.xlarge",
instance_count=1,
max_runtime_in_seconds=1200,
)
processing_evaluation_step = ProcessingStep(
"SageMaker Processing Model Evaluation step",
processor=model_evaluation_processor,
job_name=execution_input["EvaluationProcessingJobName"],
inputs=inputs_evaluation,
outputs=outputs_evaluation,
container_entrypoint=["python3", "/opt/ml/processing/input/code/evaluation.py"],
)
```
いずれかのステップが失敗したときにワークフローが失敗だとわかるように `Fail` 状態を作成します。
```
failed_state_sagemaker_processing_failure = stepfunctions.steps.states.Fail(
"ML Workflow failed", cause="SageMakerProcessingJobFailed"
)
```
#### ワークフローの中のエラーハンドリングを追加
エラーハンドリングのために [Catch Block](https://aws-step-functions-data-science-sdk.readthedocs.io/en/stable/states.html#stepfunctions.steps.states.Catch) を使用します。もし Processing ジョブステップか学習ステップが失敗したら、`Fail` 状態に遷移します。
```
catch_state_processing = stepfunctions.steps.states.Catch(
error_equals=["States.TaskFailed"],
next_step=failed_state_sagemaker_processing_failure,
)
processing_step.add_catch(catch_state_processing)
processing_evaluation_step.add_catch(catch_state_processing)
training_step.add_catch(catch_state_processing)
```
## `Workflow` の作成と実行
```
workflow_graph = Chain([processing_step, training_step, processing_evaluation_step])
branching_workflow = Workflow(
name="SageMakerProcessingWorkflow",
definition=workflow_graph,
role=workflow_execution_role,
)
branching_workflow.create()
# branching_workflow.update(workflow_graph)
# Execute workflow
execution = branching_workflow.execute(
inputs={
"PreprocessingJobName": preprocessing_job_name, # Each pre processing job (SageMaker processing job) requires a unique name,
"TrainingJobName": training_job_name, # Each Sagemaker Training job requires a unique name,
"EvaluationProcessingJobName": evaluation_job_name, # Each SageMaker processing job requires a unique name,
}
)
execution_output = execution.get_output(wait=True)
execution.render_progress()
```
### ワークフローの出力を確認
Amazon S3 から `evaluation.json` を取得して確認します。ここにはモデルの評価レポートが書かれています。なお、以下のセルは Step Functions でワークフローの実行が完了してから(`evaluation.json` が出力されてから)実行してください。
```
workflow_execution_output_json = execution.get_output(wait=True)
from sagemaker.s3 import S3Downloader
import json
evaluation_output_config = workflow_execution_output_json["ProcessingOutputConfig"]
for output in evaluation_output_config["Outputs"]:
if output["OutputName"] == "evaluation":
evaluation_s3_uri = "{}/{}".format(output["S3Output"]["S3Uri"], "evaluation.json")
break
evaluation_output = S3Downloader.read_file(evaluation_s3_uri)
evaluation_output_dict = json.loads(evaluation_output)
print(json.dumps(evaluation_output_dict, sort_keys=True, indent=4))
```
## リソースの削除
このノートブックの実行が終わったら、不要なリソースを削除することを忘れないでください。以下のコードのコメントアウトを外してから実行すると、このノートブックで作成した Step Functions のワークフローを削除することができます。ノートブックインスタンス、各種データを保存した S3 バケットも不要であれば削除してください。
```
# branching_workflow.delete()
```
| true |
code
| 0.513973 | null | null | null | null |
|
This notebook is designed to run in a IBM Watson Studio default runtime (NOT the Watson Studio Apache Spark Runtime as the default runtime with 1 vCPU is free of charge). Therefore, we install Apache Spark in local mode for test purposes only. Please don't use it in production.
In case you are facing issues, please read the following two documents first:
https://github.com/IBM/skillsnetwork/wiki/Environment-Setup
https://github.com/IBM/skillsnetwork/wiki/FAQ
Then, please feel free to ask:
https://coursera.org/learn/machine-learning-big-data-apache-spark/discussions/all
Please make sure to follow the guidelines before asking a question:
https://github.com/IBM/skillsnetwork/wiki/FAQ#im-feeling-lost-and-confused-please-help-me
If running outside Watson Studio, this should work as well. In case you are running in an Apache Spark context outside Watson Studio, please remove the Apache Spark setup in the first notebook cells.
```
from IPython.display import Markdown, display
def printmd(string):
display(Markdown('# <span style="color:red">'+string+'</span>'))
if ('sc' in locals() or 'sc' in globals()):
printmd('<<<<<!!!!! It seems that you are running in a IBM Watson Studio Apache Spark Notebook. Please run it in an IBM Watson Studio Default Runtime (without Apache Spark) !!!!!>>>>>')
!pip install pyspark==2.4.5
try:
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
except ImportError as e:
printmd('<<<<<!!!!! Please restart your kernel after installing Apache Spark !!!!!>>>>>')
sc = SparkContext.getOrCreate(SparkConf().setMaster("local[*]"))
spark = SparkSession \
.builder \
.getOrCreate()
```
In case you want to learn how ETL is done, please run the following notebook first and update the file name below accordingly
https://github.com/IBM/coursera/blob/master/coursera_ml/a2_w1_s3_ETL.ipynb
```
# delete files from previous runs
!rm -f hmp.parquet*
# download the file containing the data in PARQUET format
!wget https://github.com/IBM/coursera/raw/master/hmp.parquet
# create a dataframe out of it
df = spark.read.parquet('hmp.parquet')
# register a corresponding query table
df.createOrReplaceTempView('df')
df_energy = spark.sql("""
select sqrt(sum(x*x)+sum(y*y)+sum(z*z)) as label, class from df group by class
""")
df_energy.createOrReplaceTempView('df_energy')
df_join = spark.sql('select * from df inner join df_energy on df.class=df_energy.class')
splits = df_join.randomSplit([0.8, 0.2])
df_train = splits[0]
df_test = splits[1]
df_train.count()
df_test.count()
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.feature import MinMaxScaler
vectorAssembler = VectorAssembler(inputCols=["x","y","z"],
outputCol="features")
normalizer = MinMaxScaler(inputCol="features", outputCol="features_norm")
from pyspark.ml.regression import LinearRegression
lr = LinearRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)
from pyspark.ml import Pipeline
pipeline = Pipeline(stages=[vectorAssembler, normalizer,lr])
model = pipeline.fit(df_train)
model.stages[2].summary.r2
model = pipeline.fit(df_test)
model.stages[2].summary.r2
```
| true |
code
| 0.506958 | null | null | null | null |
|

# NYC Taxi Data Regression Model
This is an [Azure Machine Learning Pipelines](https://aka.ms/aml-pipelines) version of two-part tutorial ([Part 1](https://docs.microsoft.com/en-us/azure/machine-learning/service/tutorial-data-prep), [Part 2](https://docs.microsoft.com/en-us/azure/machine-learning/service/tutorial-auto-train-models)) available for Azure Machine Learning.
You can combine the two part tutorial into one using AzureML Pipelines as Pipelines provide a way to stitch together various steps involved (like data preparation and training in this case) in a machine learning workflow.
In this notebook, you learn how to prepare data for regression modeling by using open source library [pandas](https://pandas.pydata.org/). You run various transformations to filter and combine two different NYC taxi datasets. Once you prepare the NYC taxi data for regression modeling, then you will use [AutoMLStep](https://docs.microsoft.com/python/api/azureml-train-automl-runtime/azureml.train.automl.runtime.automl_step.automlstep?view=azure-ml-py) available with [Azure Machine Learning Pipelines](https://aka.ms/aml-pipelines) to define your machine learning goals and constraints as well as to launch the automated machine learning process. The automated machine learning technique iterates over many combinations of algorithms and hyperparameters until it finds the best model based on your criterion.
After you complete building the model, you can predict the cost of a taxi trip by training a model on data features. These features include the pickup day and time, the number of passengers, and the pickup location.
## Prerequisite
If you are using an Azure Machine Learning Notebook VM, you are all set. Otherwise, make sure you go through the configuration Notebook located at https://github.com/Azure/MachineLearningNotebooks first if you haven't. This sets you up with a working config file that has information on your workspace, subscription id, etc.
## Prepare data for regression modeling
First, we will prepare data for regression modeling. We will leverage the convenience of Azure Open Datasets along with the power of Azure Machine Learning service to create a regression model to predict NYC taxi fare prices. Perform `pip install azureml-opendatasets` to get the open dataset package. The Open Datasets package contains a class representing each data source (NycTlcGreen and NycTlcYellow) to easily filter date parameters before downloading.
### Load data
Begin by creating a dataframe to hold the taxi data. When working in a non-Spark environment, Open Datasets only allows downloading one month of data at a time with certain classes to avoid MemoryError with large datasets. To download a year of taxi data, iteratively fetch one month at a time, and before appending it to green_df_raw, randomly sample 500 records from each month to avoid bloating the dataframe. Then preview the data. To keep this process short, we are sampling data of only 1 month.
Note: Open Datasets has mirroring classes for working in Spark environments where data size and memory aren't a concern.
```
import azureml.core
# Check core SDK version number
print("SDK version:", azureml.core.VERSION)
from azureml.opendatasets import NycTlcGreen, NycTlcYellow
import pandas as pd
from datetime import datetime
from dateutil.relativedelta import relativedelta
green_df_raw = pd.DataFrame([])
start = datetime.strptime("1/1/2016","%m/%d/%Y")
end = datetime.strptime("1/31/2016","%m/%d/%Y")
number_of_months = 1
sample_size = 5000
for sample_month in range(number_of_months):
temp_df_green = NycTlcGreen(start + relativedelta(months=sample_month), end + relativedelta(months=sample_month)) \
.to_pandas_dataframe()
green_df_raw = green_df_raw.append(temp_df_green.sample(sample_size))
yellow_df_raw = pd.DataFrame([])
start = datetime.strptime("1/1/2016","%m/%d/%Y")
end = datetime.strptime("1/31/2016","%m/%d/%Y")
sample_size = 500
for sample_month in range(number_of_months):
temp_df_yellow = NycTlcYellow(start + relativedelta(months=sample_month), end + relativedelta(months=sample_month)) \
.to_pandas_dataframe()
yellow_df_raw = yellow_df_raw.append(temp_df_yellow.sample(sample_size))
```
### See the data
```
from IPython.display import display
display(green_df_raw.head(5))
display(yellow_df_raw.head(5))
```
### Download data locally and then upload to Azure Blob
This is a one-time process to save the dave in the default datastore.
```
import os
dataDir = "data"
if not os.path.exists(dataDir):
os.mkdir(dataDir)
greenDir = dataDir + "/green"
yelloDir = dataDir + "/yellow"
if not os.path.exists(greenDir):
os.mkdir(greenDir)
if not os.path.exists(yelloDir):
os.mkdir(yelloDir)
greenTaxiData = greenDir + "/unprepared.parquet"
yellowTaxiData = yelloDir + "/unprepared.parquet"
green_df_raw.to_csv(greenTaxiData, index=False)
yellow_df_raw.to_csv(yellowTaxiData, index=False)
print("Data written to local folder.")
from azureml.core import Workspace
ws = Workspace.from_config()
print("Workspace: " + ws.name, "Region: " + ws.location, sep = '\n')
# Default datastore
default_store = ws.get_default_datastore()
default_store.upload_files([greenTaxiData],
target_path = 'green',
overwrite = True,
show_progress = True)
default_store.upload_files([yellowTaxiData],
target_path = 'yellow',
overwrite = True,
show_progress = True)
print("Upload calls completed.")
```
### Create and register datasets
By creating a dataset, you create a reference to the data source location. If you applied any subsetting transformations to the dataset, they will be stored in the dataset as well. You can learn more about the what subsetting capabilities are supported by referring to [our documentation](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabular_dataset.tabulardataset?view=azure-ml-py#remarks). The data remains in its existing location, so no extra storage cost is incurred.
```
from azureml.core import Dataset
green_taxi_data = Dataset.Tabular.from_delimited_files(default_store.path('green/unprepared.parquet'))
yellow_taxi_data = Dataset.Tabular.from_delimited_files(default_store.path('yellow/unprepared.parquet'))
```
Register the taxi datasets with the workspace so that you can reuse them in other experiments or share with your colleagues who have access to your workspace.
```
green_taxi_data = green_taxi_data.register(ws, 'green_taxi_data')
yellow_taxi_data = yellow_taxi_data.register(ws, 'yellow_taxi_data')
```
### Setup Compute
#### Create new or use an existing compute
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
amlcompute_cluster_name = "cpu-cluster"
# Verify that cluster does not exist already
try:
aml_compute = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=4)
aml_compute = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
aml_compute.wait_for_completion(show_output=True)
```
#### Define RunConfig for the compute
We will also use `pandas`, `scikit-learn` and `automl`, `pyarrow` for the pipeline steps. Defining the `runconfig` for that.
```
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
# Create a new runconfig object
aml_run_config = RunConfiguration()
# Use the aml_compute you created above.
aml_run_config.target = aml_compute
# Enable Docker
aml_run_config.environment.docker.enabled = True
# Set Docker base image to the default CPU-based image
aml_run_config.environment.docker.base_image = "mcr.microsoft.com/azureml/base:0.2.1"
# Use conda_dependencies.yml to create a conda environment in the Docker image for execution
aml_run_config.environment.python.user_managed_dependencies = False
# Specify CondaDependencies obj, add necessary packages
aml_run_config.environment.python.conda_dependencies = CondaDependencies.create(
conda_packages=['pandas','scikit-learn'],
pip_packages=['azureml-sdk[automl,explain]', 'pyarrow'])
print ("Run configuration created.")
```
### Prepare data
Now we will prepare for regression modeling by using `pandas`. We run various transformations to filter and combine two different NYC taxi datasets.
We achieve this by creating a separate step for each transformation as this allows us to reuse the steps and saves us from running all over again in case of any change. We will keep data preparation scripts in one subfolder and training scripts in another.
> The best practice is to use separate folders for scripts and its dependent files for each step and specify that folder as the `source_directory` for the step. This helps reduce the size of the snapshot created for the step (only the specific folder is snapshotted). Since changes in any files in the `source_directory` would trigger a re-upload of the snapshot, this helps keep the reuse of the step when there are no changes in the `source_directory` of the step.
#### Define Useful Columns
Here we are defining a set of "useful" columns for both Green and Yellow taxi data.
```
display(green_df_raw.columns)
display(yellow_df_raw.columns)
# useful columns needed for the Azure Machine Learning NYC Taxi tutorial
useful_columns = str(["cost", "distance", "dropoff_datetime", "dropoff_latitude",
"dropoff_longitude", "passengers", "pickup_datetime",
"pickup_latitude", "pickup_longitude", "store_forward", "vendor"]).replace(",", ";")
print("Useful columns defined.")
```
#### Cleanse Green taxi data
```
from azureml.pipeline.core import PipelineData
from azureml.pipeline.steps import PythonScriptStep
# python scripts folder
prepare_data_folder = './scripts/prepdata'
# rename columns as per Azure Machine Learning NYC Taxi tutorial
green_columns = str({
"vendorID": "vendor",
"lpepPickupDatetime": "pickup_datetime",
"lpepDropoffDatetime": "dropoff_datetime",
"storeAndFwdFlag": "store_forward",
"pickupLongitude": "pickup_longitude",
"pickupLatitude": "pickup_latitude",
"dropoffLongitude": "dropoff_longitude",
"dropoffLatitude": "dropoff_latitude",
"passengerCount": "passengers",
"fareAmount": "cost",
"tripDistance": "distance"
}).replace(",", ";")
# Define output after cleansing step
cleansed_green_data = PipelineData("cleansed_green_data", datastore=default_store).as_dataset()
print('Cleanse script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# cleansing step creation
# See the cleanse.py for details about input and output
cleansingStepGreen = PythonScriptStep(
name="Cleanse Green Taxi Data",
script_name="cleanse.py",
arguments=["--useful_columns", useful_columns,
"--columns", green_columns,
"--output_cleanse", cleansed_green_data],
inputs=[green_taxi_data.as_named_input('raw_data')],
outputs=[cleansed_green_data],
compute_target=aml_compute,
runconfig=aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("cleansingStepGreen created.")
```
#### Cleanse Yellow taxi data
```
yellow_columns = str({
"vendorID": "vendor",
"tpepPickupDateTime": "pickup_datetime",
"tpepDropoffDateTime": "dropoff_datetime",
"storeAndFwdFlag": "store_forward",
"startLon": "pickup_longitude",
"startLat": "pickup_latitude",
"endLon": "dropoff_longitude",
"endLat": "dropoff_latitude",
"passengerCount": "passengers",
"fareAmount": "cost",
"tripDistance": "distance"
}).replace(",", ";")
# Define output after cleansing step
cleansed_yellow_data = PipelineData("cleansed_yellow_data", datastore=default_store).as_dataset()
print('Cleanse script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# cleansing step creation
# See the cleanse.py for details about input and output
cleansingStepYellow = PythonScriptStep(
name="Cleanse Yellow Taxi Data",
script_name="cleanse.py",
arguments=["--useful_columns", useful_columns,
"--columns", yellow_columns,
"--output_cleanse", cleansed_yellow_data],
inputs=[yellow_taxi_data.as_named_input('raw_data')],
outputs=[cleansed_yellow_data],
compute_target=aml_compute,
runconfig=aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("cleansingStepYellow created.")
```
#### Merge cleansed Green and Yellow datasets
We are creating a single data source by merging the cleansed versions of Green and Yellow taxi data.
```
# Define output after merging step
merged_data = PipelineData("merged_data", datastore=default_store).as_dataset()
print('Merge script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# merging step creation
# See the merge.py for details about input and output
mergingStep = PythonScriptStep(
name="Merge Taxi Data",
script_name="merge.py",
arguments=["--output_merge", merged_data],
inputs=[cleansed_green_data.parse_parquet_files(file_extension=None),
cleansed_yellow_data.parse_parquet_files(file_extension=None)],
outputs=[merged_data],
compute_target=aml_compute,
runconfig=aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("mergingStep created.")
```
#### Filter data
This step filters out coordinates for locations that are outside the city border. We use a TypeConverter object to change the latitude and longitude fields to decimal type.
```
# Define output after merging step
filtered_data = PipelineData("filtered_data", datastore=default_store).as_dataset()
print('Filter script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# filter step creation
# See the filter.py for details about input and output
filterStep = PythonScriptStep(
name="Filter Taxi Data",
script_name="filter.py",
arguments=["--output_filter", filtered_data],
inputs=[merged_data.parse_parquet_files(file_extension=None)],
outputs=[filtered_data],
compute_target=aml_compute,
runconfig = aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("FilterStep created.")
```
#### Normalize data
In this step, we split the pickup and dropoff datetime values into the respective date and time columns and then we rename the columns to use meaningful names.
```
# Define output after normalize step
normalized_data = PipelineData("normalized_data", datastore=default_store).as_dataset()
print('Normalize script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# normalize step creation
# See the normalize.py for details about input and output
normalizeStep = PythonScriptStep(
name="Normalize Taxi Data",
script_name="normalize.py",
arguments=["--output_normalize", normalized_data],
inputs=[filtered_data.parse_parquet_files(file_extension=None)],
outputs=[normalized_data],
compute_target=aml_compute,
runconfig = aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("normalizeStep created.")
```
#### Transform data
Transform the normalized taxi data to final required format. This steps does the following:
- Split the pickup and dropoff date further into the day of the week, day of the month, and month values.
- To get the day of the week value, uses the derive_column_by_example() function. The function takes an array parameter of example objects that define the input data, and the preferred output. The function automatically determines the preferred transformation. For the pickup and dropoff time columns, split the time into the hour, minute, and second by using the split_column_by_example() function with no example parameter.
- After new features are generated, use the drop_columns() function to delete the original fields as the newly generated features are preferred.
- Rename the rest of the fields to use meaningful descriptions.
```
# Define output after transform step
transformed_data = PipelineData("transformed_data", datastore=default_store).as_dataset()
print('Transform script is in {}.'.format(os.path.realpath(prepare_data_folder)))
# transform step creation
# See the transform.py for details about input and output
transformStep = PythonScriptStep(
name="Transform Taxi Data",
script_name="transform.py",
arguments=["--output_transform", transformed_data],
inputs=[normalized_data.parse_parquet_files(file_extension=None)],
outputs=[transformed_data],
compute_target=aml_compute,
runconfig = aml_run_config,
source_directory=prepare_data_folder,
allow_reuse=True
)
print("transformStep created.")
```
### Split the data into train and test sets
This function segregates the data into dataset for model training and dataset for testing.
```
train_model_folder = './scripts/trainmodel'
# train and test splits output
output_split_train = PipelineData("output_split_train", datastore=default_store).as_dataset()
output_split_test = PipelineData("output_split_test", datastore=default_store).as_dataset()
print('Data spilt script is in {}.'.format(os.path.realpath(train_model_folder)))
# test train split step creation
# See the train_test_split.py for details about input and output
testTrainSplitStep = PythonScriptStep(
name="Train Test Data Split",
script_name="train_test_split.py",
arguments=["--output_split_train", output_split_train,
"--output_split_test", output_split_test],
inputs=[transformed_data.parse_parquet_files(file_extension=None)],
outputs=[output_split_train, output_split_test],
compute_target=aml_compute,
runconfig = aml_run_config,
source_directory=train_model_folder,
allow_reuse=True
)
print("testTrainSplitStep created.")
```
## Use automated machine learning to build regression model
Now we will use **automated machine learning** to build the regression model. We will use [AutoMLStep](https://docs.microsoft.com/python/api/azureml-train-automl-runtime/azureml.train.automl.runtime.automl_step.automlstep?view=azure-ml-py) in AML Pipelines for this part. Perform `pip install azureml-sdk[automl]`to get the automated machine learning package. These functions use various features from the data set and allow an automated model to build relationships between the features and the price of a taxi trip.
### Automatically train a model
#### Create experiment
```
from azureml.core import Experiment
experiment = Experiment(ws, 'NYCTaxi_Tutorial_Pipelines')
print("Experiment created")
```
#### Define settings for autogeneration and tuning
Here we define the experiment parameter and model settings for autogeneration and tuning. We can specify automl_settings as **kwargs as well.
Use your defined training settings as a parameter to an `AutoMLConfig` object. Additionally, specify your training data and the type of model, which is `regression` in this case.
Note: When using AmlCompute, we can't pass Numpy arrays directly to the fit method.
```
import logging
from azureml.train.automl import AutoMLConfig
# Change iterations to a reasonable number (50) to get better accuracy
automl_settings = {
"iteration_timeout_minutes" : 10,
"iterations" : 2,
"primary_metric" : 'spearman_correlation',
"n_cross_validations": 5
}
training_dataset = output_split_train.parse_parquet_files(file_extension=None).keep_columns(['pickup_weekday','pickup_hour', 'distance','passengers', 'vendor', 'cost'])
automl_config = AutoMLConfig(task = 'regression',
debug_log = 'automated_ml_errors.log',
path = train_model_folder,
compute_target = aml_compute,
featurization = 'auto',
training_data = training_dataset,
label_column_name = 'cost',
**automl_settings)
print("AutoML config created.")
```
#### Define AutoMLStep
```
from azureml.pipeline.steps import AutoMLStep
trainWithAutomlStep = AutoMLStep(name='AutoML_Regression',
automl_config=automl_config,
allow_reuse=True)
print("trainWithAutomlStep created.")
```
#### Build and run the pipeline
```
from azureml.pipeline.core import Pipeline
from azureml.widgets import RunDetails
pipeline_steps = [trainWithAutomlStep]
pipeline = Pipeline(workspace = ws, steps=pipeline_steps)
print("Pipeline is built.")
pipeline_run = experiment.submit(pipeline, regenerate_outputs=False)
print("Pipeline submitted for execution.")
RunDetails(pipeline_run).show()
```
### Explore the results
```
# Before we proceed we need to wait for the run to complete.
pipeline_run.wait_for_completion()
# functions to download output to local and fetch as dataframe
def get_download_path(download_path, output_name):
output_folder = os.listdir(download_path + '/azureml')[0]
path = download_path + '/azureml/' + output_folder + '/' + output_name
return path
def fetch_df(step, output_name):
output_data = step.get_output_data(output_name)
download_path = './outputs/' + output_name
output_data.download(download_path, overwrite=True)
df_path = get_download_path(download_path, output_name) + '/processed.parquet'
return pd.read_parquet(df_path)
```
#### View cleansed taxi data
```
green_cleanse_step = pipeline_run.find_step_run(cleansingStepGreen.name)[0]
yellow_cleanse_step = pipeline_run.find_step_run(cleansingStepYellow.name)[0]
cleansed_green_df = fetch_df(green_cleanse_step, cleansed_green_data.name)
cleansed_yellow_df = fetch_df(yellow_cleanse_step, cleansed_yellow_data.name)
display(cleansed_green_df.head(5))
display(cleansed_yellow_df.head(5))
```
#### View the combined taxi data profile
```
merge_step = pipeline_run.find_step_run(mergingStep.name)[0]
combined_df = fetch_df(merge_step, merged_data.name)
display(combined_df.describe())
```
#### View the filtered taxi data profile
```
filter_step = pipeline_run.find_step_run(filterStep.name)[0]
filtered_df = fetch_df(filter_step, filtered_data.name)
display(filtered_df.describe())
```
#### View normalized taxi data
```
normalize_step = pipeline_run.find_step_run(normalizeStep.name)[0]
normalized_df = fetch_df(normalize_step, normalized_data.name)
display(normalized_df.head(5))
```
#### View transformed taxi data
```
transform_step = pipeline_run.find_step_run(transformStep.name)[0]
transformed_df = fetch_df(transform_step, transformed_data.name)
display(transformed_df.describe())
display(transformed_df.head(5))
```
#### View training data used by AutoML
```
split_step = pipeline_run.find_step_run(testTrainSplitStep.name)[0]
train_split = fetch_df(split_step, output_split_train.name)
display(train_split.describe())
display(train_split.head(5))
```
#### View the details of the AutoML run
```
from azureml.train.automl.run import AutoMLRun
#from azureml.widgets import RunDetails
# workaround to get the automl run as its the last step in the pipeline
# and get_steps() returns the steps from latest to first
for step in pipeline_run.get_steps():
automl_step_run_id = step.id
print(step.name)
print(automl_step_run_id)
break
automl_run = AutoMLRun(experiment = experiment, run_id=automl_step_run_id)
#RunDetails(automl_run).show()
```
#### Retrieve all Child runs
We use SDK methods to fetch all the child runs and see individual metrics that we log.
```
children = list(automl_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata
```
### Retreive the best model
Uncomment the below cell to retrieve the best model
```
# best_run, fitted_model = automl_run.get_output()
# print(best_run)
# print(fitted_model)
```
### Test the model
#### Get test data
Uncomment the below cell to get test data
```
# split_step = pipeline_run.find_step_run(testTrainSplitStep.name)[0]
# x_test = fetch_df(split_step, output_split_test.name)[['distance','passengers', 'vendor','pickup_weekday','pickup_hour']]
# y_test = fetch_df(split_step, output_split_test.name)[['cost']]
# display(x_test.head(5))
# display(y_test.head(5))
```
#### Test the best fitted model
Uncomment the below cell to test the best fitted model
```
# y_predict = fitted_model.predict(x_test)
# y_actual = y_test.values.tolist()
# display(pd.DataFrame({'Actual':y_actual, 'Predicted':y_predict}).head(5))
# import matplotlib.pyplot as plt
# fig = plt.figure(figsize=(14, 10))
# ax1 = fig.add_subplot(111)
# distance_vals = [x[0] for x in x_test.values]
# ax1.scatter(distance_vals[:100], y_predict[:100], s=18, c='b', marker="s", label='Predicted')
# ax1.scatter(distance_vals[:100], y_actual[:100], s=18, c='r', marker="o", label='Actual')
# ax1.set_xlabel('distance (mi)')
# ax1.set_title('Predicted and Actual Cost/Distance')
# ax1.set_ylabel('Cost ($)')
# plt.legend(loc='upper left', prop={'size': 12})
# plt.rcParams.update({'font.size': 14})
# plt.show()
```
| true |
code
| 0.312819 | null | null | null | null |
|
**Chapter 3 – Classification**
_This notebook contains all the sample code and solutions to the exercices in chapter 3._
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import numpy.random as rnd
import os
# to make this notebook's output stable across runs
rnd.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# MNIST
```
from shutil import copyfileobj
from six.moves import urllib
from sklearn.datasets.base import get_data_home
import os
def fetch_mnist(data_home=None):
mnist_alternative_url = "https://github.com/amplab/datascience-sp14/raw/master/lab7/mldata/mnist-original.mat"
data_home = get_data_home(data_home=data_home)
data_home = os.path.join(data_home, 'mldata')
if not os.path.exists(data_home):
os.makedirs(data_home)
mnist_save_path = os.path.join(data_home, "mnist-original.mat")
if not os.path.exists(mnist_save_path):
mnist_url = urllib.request.urlopen(mnist_alternative_url)
with open(mnist_save_path, "wb") as matlab_file:
copyfileobj(mnist_url, matlab_file)
fetch_mnist()
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata("MNIST original")
# from six.moves import urllib
# from sklearn.datasets import fetch_mldata
# try:
# mnist = fetch_mldata('MNIST original')
# except urllib.error.HTTPError as ex:
# print("Could not download MNIST data from mldata.org, trying alternative...")
# # Alternative method to load MNIST, if mldata.org is down
# from scipy.io import loadmat
# mnist_alternative_url = "https://github.com/amplab/datascience-sp14/raw/master/lab7/mldata/mnist-original.mat"
# mnist_path = "./mnist-original.mat"
# response = urllib.request.urlopen(mnist_alternative_url)
# with open(mnist_path, "wb") as f:
# content = response.read()
# f.write(content)
# mnist_raw = loadmat(mnist_path)
# mnist = {
# "data": mnist_raw["data"].T,
# "target": mnist_raw["label"][0],
# "COL_NAMES": ["label", "data"],
# "DESCR": "mldata.org dataset: mnist-original",
# }
# print("Success!")
mnist
X, y = mnist["data"], mnist["target"]
X.shape
y.shape
28*28
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = matplotlib.cm.binary,
interpolation="nearest")
plt.axis("off")
some_digit_index = 36000
some_digit = X[some_digit_index]
plot_digit(some_digit)
save_fig("some_digit_plot")
plt.show()
# EXTRA
def plot_digits(instances, images_per_row=10, **options):
size = 28
images_per_row = min(len(instances), images_per_row)
images = [instance.reshape(size,size) for instance in instances]
n_rows = (len(instances) - 1) // images_per_row + 1
row_images = []
n_empty = n_rows * images_per_row - len(instances)
images.append(np.zeros((size, size * n_empty)))
for row in range(n_rows):
rimages = images[row * images_per_row : (row + 1) * images_per_row]
row_images.append(np.concatenate(rimages, axis=1))
image = np.concatenate(row_images, axis=0)
plt.imshow(image, cmap = matplotlib.cm.binary, **options)
plt.axis("off")
plt.figure(figsize=(9,9))
example_images = np.r_[X[:12000:600], X[13000:30600:600], X[30600:60000:590]]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()
y[some_digit_index]
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
shuffle_index = rnd.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
```
# Binary classifier
```
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([some_digit])
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf)
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
4344 / (4344 + 1307)
recall_score(y_train_5, y_train_pred)
4344 / (4344 + 1077)
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)
4344 / (4344 + (1077 + 1307)/2)
y_scores = sgd_clf.decision_function([some_digit])
y_scores
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
threshold = 200000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
plt.xlabel("Threshold", fontsize=16)
plt.legend(loc="center left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
save_fig("precision_recall_vs_threshold_plot")
plt.show()
(y_train_pred == (y_scores > 0)).all()
y_train_pred_90 = (y_scores > 70000)
precision_score(y_train_5, y_train_pred_90)
recall_score(y_train_5, y_train_pred_90)
def plot_precision_vs_recall(precisions, recalls):
plt.plot(recalls, precisions, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
save_fig("precision_vs_recall_plot")
plt.show()
```
# ROC curves
```
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, **options):
plt.plot(fpr, tpr, linewidth=2, **options)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('False Positive Rate', fontsize=16)
plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
save_fig("roc_curve_plot")
plt.show()
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, label="Random Forest")
plt.legend(loc="lower right", fontsize=16)
save_fig("roc_curve_comparison_plot")
plt.show()
roc_auc_score(y_train_5, y_scores_forest)
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)
recall_score(y_train_5, y_train_pred_forest)
```
# Multiclass classification
```
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
some_digit_scores = sgd_clf.decision_function([some_digit])
some_digit_scores
np.argmax(some_digit_scores)
sgd_clf.classes_
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict([some_digit])
len(ovo_clf.estimators_)
forest_clf.fit(X_train, y_train)
forest_clf.predict([some_digit])
forest_clf.predict_proba([some_digit])
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx
def plot_confusion_matrix(matrix):
"""If you prefer color and a colorbar"""
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
cax = ax.matshow(conf_mx)
fig.colorbar(cax)
plt.matshow(conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221)
plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222)
plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223)
plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224)
plot_digits(X_bb[:25], images_per_row=5)
save_fig("error_analysis_digits_plot")
plt.show()
```
# Multilabel classification
```
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
knn_clf.predict([some_digit])
y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_train, cv=3)
f1_score(y_train, y_train_knn_pred, average="macro")
```
# Multioutput classification
```
noise = rnd.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = rnd.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
some_index = 5500
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
save_fig("noisy_digit_example_plot")
plt.show()
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
save_fig("cleaned_digit_example_plot")
plt.show()
```
# Extra material
## Dummy (ie. random) classifier
```
from sklearn.dummy import DummyClassifier
dmy_clf = DummyClassifier()
y_probas_dmy = cross_val_predict(dmy_clf, X_train, y_train_5, cv=3, method="predict_proba")
y_scores_dmy = y_probas_dmy[:, 1]
fprr, tprr, thresholdsr = roc_curve(y_train_5, y_scores_dmy)
plot_roc_curve(fprr, tprr)
```
## KNN classifier
```
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_jobs=-1, weights='distance', n_neighbors=4)
knn_clf.fit(X_train, y_train)
y_knn_pred = knn_clf.predict(X_test)
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_knn_pred)
from scipy.ndimage.interpolation import shift
def shift_digit(digit_array, dx, dy, new=0):
return shift(digit_array.reshape(28, 28), [dy, dx], cval=new).reshape(784)
plot_digit(shift_digit(some_digit, 5, 1, new=100))
X_train_expanded = [X_train]
y_train_expanded = [y_train]
for dx, dy in ((1, 0), (-1, 0), (0, 1), (0, -1)):
shifted_images = np.apply_along_axis(shift_digit, axis=1, arr=X_train, dx=dx, dy=dy)
X_train_expanded.append(shifted_images)
y_train_expanded.append(y_train)
X_train_expanded = np.concatenate(X_train_expanded)
y_train_expanded = np.concatenate(y_train_expanded)
X_train_expanded.shape, y_train_expanded.shape
knn_clf.fit(X_train_expanded, y_train_expanded)
y_knn_expanded_pred = knn_clf.predict(X_test)
accuracy_score(y_test, y_knn_expanded_pred)
ambiguous_digit = X_test[2589]
knn_clf.predict_proba([ambiguous_digit])
plot_digit(ambiguous_digit)
```
# Exercise solutions
**Coming soon**
| true |
code
| 0.610686 | null | null | null | null |
|
# Tutorial 7: Graph Neural Networks

**Filled notebook:**
[](https://github.com/phlippe/uvadlc_notebooks/blob/master/docs/tutorial_notebooks/tutorial7/GNN_overview.ipynb)
[](https://colab.research.google.com/github/phlippe/uvadlc_notebooks/blob/master/docs/tutorial_notebooks/tutorial7/GNN_overview.ipynb)
**Pre-trained models:**
[](https://github.com/phlippe/saved_models/tree/main/tutorial7)
[](https://drive.google.com/drive/folders/1DOTV_oYt5boa-MElbc2izat4VMSc1gob?usp=sharing)
**Recordings:**
[](https://youtu.be/fK7d56Ly9q8)
[](https://youtu.be/ZCNSUWe4a_Q)
In this tutorial, we will discuss the application of neural networks on graphs. Graph Neural Networks (GNNs) have recently gained increasing popularity in both applications and research, including domains such as social networks, knowledge graphs, recommender systems, and bioinformatics. While the theory and math behind GNNs might first seem complicated, the implementation of those models is quite simple and helps in understanding the methodology. Therefore, we will discuss the implementation of basic network layers of a GNN, namely graph convolutions, and attention layers. Finally, we will apply a GNN on a node-level, edge-level, and graph-level tasks.
Below, we will start by importing our standard libraries. We will use PyTorch Lightning as already done in Tutorial 5 and 6.
```
## Standard libraries
import os
import json
import math
import numpy as np
import time
## Imports for plotting
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf') # For export
from matplotlib.colors import to_rgb
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2.0
import seaborn as sns
sns.reset_orig()
sns.set()
## Progress bar
from tqdm.notebook import tqdm
## PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import torch.optim as optim
# Torchvision
import torchvision
from torchvision.datasets import CIFAR10
from torchvision import transforms
# PyTorch Lightning
try:
import pytorch_lightning as pl
except ModuleNotFoundError: # Google Colab does not have PyTorch Lightning installed by default. Hence, we do it here if necessary
!pip install --quiet pytorch-lightning>=1.4
import pytorch_lightning as pl
from pytorch_lightning.callbacks import LearningRateMonitor, ModelCheckpoint
# Path to the folder where the datasets are/should be downloaded (e.g. CIFAR10)
DATASET_PATH = "../data"
# Path to the folder where the pretrained models are saved
CHECKPOINT_PATH = "../saved_models/tutorial7"
# Setting the seed
pl.seed_everything(42)
# Ensure that all operations are deterministic on GPU (if used) for reproducibility
torch.backends.cudnn.determinstic = True
torch.backends.cudnn.benchmark = False
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
print(device)
```
We also have a few pre-trained models we download below.
```
import urllib.request
from urllib.error import HTTPError
# Github URL where saved models are stored for this tutorial
base_url = "https://raw.githubusercontent.com/phlippe/saved_models/main/tutorial7/"
# Files to download
pretrained_files = ["NodeLevelMLP.ckpt", "NodeLevelGNN.ckpt", "GraphLevelGraphConv.ckpt"]
# Create checkpoint path if it doesn't exist yet
os.makedirs(CHECKPOINT_PATH, exist_ok=True)
# For each file, check whether it already exists. If not, try downloading it.
for file_name in pretrained_files:
file_path = os.path.join(CHECKPOINT_PATH, file_name)
if "/" in file_name:
os.makedirs(file_path.rsplit("/",1)[0], exist_ok=True)
if not os.path.isfile(file_path):
file_url = base_url + file_name
print(f"Downloading {file_url}...")
try:
urllib.request.urlretrieve(file_url, file_path)
except HTTPError as e:
print("Something went wrong. Please try to download the file from the GDrive folder, or contact the author with the full output including the following error:\n", e)
```
## Graph Neural Networks
### Graph representation
Before starting the discussion of specific neural network operations on graphs, we should consider how to represent a graph. Mathematically, a graph $\mathcal{G}$ is defined as a tuple of a set of nodes/vertices $V$, and a set of edges/links $E$: $\mathcal{G}=(V,E)$. Each edge is a pair of two vertices, and represents a connection between them. For instance, let's look at the following graph:
<center width="100%" style="padding:10px"><img src="example_graph.svg" width="250px"></center>
The vertices are $V=\{1,2,3,4\}$, and edges $E=\{(1,2), (2,3), (2,4), (3,4)\}$. Note that for simplicity, we assume the graph to be undirected and hence don't add mirrored pairs like $(2,1)$. In application, vertices and edge can often have specific attributes, and edges can even be directed. The question is how we could represent this diversity in an efficient way for matrix operations. Usually, for the edges, we decide between two variants: an adjacency matrix, or a list of paired vertex indices.
The **adjacency matrix** $A$ is a square matrix whose elements indicate whether pairs of vertices are adjacent, i.e. connected, or not. In the simplest case, $A_{ij}$ is 1 if there is a connection from node $i$ to $j$, and otherwise 0. If we have edge attributes or different categories of edges in a graph, this information can be added to the matrix as well. For an undirected graph, keep in mind that $A$ is a symmetric matrix ($A_{ij}=A_{ji}$). For the example graph above, we have the following adjacency matrix:
$$
A = \begin{bmatrix}
0 & 1 & 0 & 0\\
1 & 0 & 1 & 1\\
0 & 1 & 0 & 1\\
0 & 1 & 1 & 0
\end{bmatrix}
$$
While expressing a graph as a list of edges is more efficient in terms of memory and (possibly) computation, using an adjacency matrix is more intuitive and simpler to implement. In our implementations below, we will rely on the adjacency matrix to keep the code simple. However, common libraries use edge lists, which we will discuss later more.
Alternatively, we could also use the list of edges to define a sparse adjacency matrix with which we can work as if it was a dense matrix, but allows more memory-efficient operations. PyTorch supports this with the sub-package `torch.sparse` ([documentation](https://pytorch.org/docs/stable/sparse.html)) which is however still in a beta-stage (API might change in future).
### Graph Convolutions
Graph Convolutional Networks have been introduced by [Kipf et al.](https://openreview.net/pdf?id=SJU4ayYgl) in 2016 at the University of Amsterdam. He also wrote a great [blog post](https://tkipf.github.io/graph-convolutional-networks/) about this topic, which is recommended if you want to read about GCNs from a different perspective. GCNs are similar to convolutions in images in the sense that the "filter" parameters are typically shared over all locations in the graph. At the same time, GCNs rely on message passing methods, which means that vertices exchange information with the neighbors, and send "messages" to each other. Before looking at the math, we can try to visually understand how GCNs work. The first step is that each node creates a feature vector that represents the message it wants to send to all its neighbors. In the second step, the messages are sent to the neighbors, so that a node receives one message per adjacent node. Below we have visualized the two steps for our example graph.
<center width="100%" style="padding:10px"><img src="graph_message_passing.svg" width="700px"></center>
If we want to formulate that in more mathematical terms, we need to first decide how to combine all the messages a node receives. As the number of messages vary across nodes, we need an operation that works for any number. Hence, the usual way to go is to sum or take the mean. Given the previous features of nodes $H^{(l)}$, the GCN layer is defined as follows:
$$H^{(l+1)} = \sigma\left(\hat{D}^{-1/2}\hat{A}\hat{D}^{-1/2}H^{(l)}W^{(l)}\right)$$
$W^{(l)}$ is the weight parameters with which we transform the input features into messages ($H^{(l)}W^{(l)}$). To the adjacency matrix $A$ we add the identity matrix so that each node sends its own message also to itself: $\hat{A}=A+I$. Finally, to take the average instead of summing, we calculate the matrix $\hat{D}$ which is a diagonal matrix with $D_{ii}$ denoting the number of neighbors node $i$ has. $\sigma$ represents an arbitrary activation function, and not necessarily the sigmoid (usually a ReLU-based activation function is used in GNNs).
When implementing the GCN layer in PyTorch, we can take advantage of the flexible operations on tensors. Instead of defining a matrix $\hat{D}$, we can simply divide the summed messages by the number of neighbors afterward. Additionally, we replace the weight matrix with a linear layer, which additionally allows us to add a bias. Written as a PyTorch module, the GCN layer is defined as follows:
```
class GCNLayer(nn.Module):
def __init__(self, c_in, c_out):
super().__init__()
self.projection = nn.Linear(c_in, c_out)
def forward(self, node_feats, adj_matrix):
"""
Inputs:
node_feats - Tensor with node features of shape [batch_size, num_nodes, c_in]
adj_matrix - Batch of adjacency matrices of the graph. If there is an edge from i to j, adj_matrix[b,i,j]=1 else 0.
Supports directed edges by non-symmetric matrices. Assumes to already have added the identity connections.
Shape: [batch_size, num_nodes, num_nodes]
"""
# Num neighbours = number of incoming edges
num_neighbours = adj_matrix.sum(dim=-1, keepdims=True)
node_feats = self.projection(node_feats)
node_feats = torch.bmm(adj_matrix, node_feats)
node_feats = node_feats / num_neighbours
return node_feats
```
To further understand the GCN layer, we can apply it to our example graph above. First, let's specify some node features and the adjacency matrix with added self-connections:
```
node_feats = torch.arange(8, dtype=torch.float32).view(1, 4, 2)
adj_matrix = torch.Tensor([[[1, 1, 0, 0],
[1, 1, 1, 1],
[0, 1, 1, 1],
[0, 1, 1, 1]]])
print("Node features:\n", node_feats)
print("\nAdjacency matrix:\n", adj_matrix)
```
Next, let's apply a GCN layer to it. For simplicity, we initialize the linear weight matrix as an identity matrix so that the input features are equal to the messages. This makes it easier for us to verify the message passing operation.
```
layer = GCNLayer(c_in=2, c_out=2)
layer.projection.weight.data = torch.Tensor([[1., 0.], [0., 1.]])
layer.projection.bias.data = torch.Tensor([0., 0.])
with torch.no_grad():
out_feats = layer(node_feats, adj_matrix)
print("Adjacency matrix", adj_matrix)
print("Input features", node_feats)
print("Output features", out_feats)
```
As we can see, the first node's output values are the average of itself and the second node. Similarly, we can verify all other nodes. However, in a GNN, we would also want to allow feature exchange between nodes beyond its neighbors. This can be achieved by applying multiple GCN layers, which gives us the final layout of a GNN. The GNN can be build up by a sequence of GCN layers and non-linearities such as ReLU. For a visualization, see below (figure credit - [Thomas Kipf, 2016](https://tkipf.github.io/graph-convolutional-networks/)).
<center width="100%" style="padding: 10px"><img src="gcn_network.png" width="600px"></center>
However, one issue we can see from looking at the example above is that the output features for nodes 3 and 4 are the same because they have the same adjacent nodes (including itself). Therefore, GCN layers can make the network forget node-specific information if we just take a mean over all messages. Multiple possible improvements have been proposed. While the simplest option might be using residual connections, the more common approach is to either weigh the self-connections higher or define a separate weight matrix for the self-connections. Alternatively, we can re-visit a concept from the last tutorial: attention.
### Graph Attention
If you remember from the last tutorial, attention describes a weighted average of multiple elements with the weights dynamically computed based on an input query and elements' keys (if you haven't read Tutorial 6 yet, it is recommended to at least go through the very first section called [What is Attention?](https://uvadlc-notebooks.readthedocs.io/en/latest/tutorial_notebooks/tutorial6/Transformers_and_MHAttention.html#What-is-Attention?)). This concept can be similarly applied to graphs, one of such is the Graph Attention Network (called GAT, proposed by [Velickovic et al., 2017](https://arxiv.org/abs/1710.10903)). Similarly to the GCN, the graph attention layer creates a message for each node using a linear layer/weight matrix. For the attention part, it uses the message from the node itself as a query, and the messages to average as both keys and values (note that this also includes the message to itself). The score function $f_{attn}$ is implemented as a one-layer MLP which maps the query and key to a single value. The MLP looks as follows (figure credit - [Velickovic et al.](https://arxiv.org/abs/1710.10903)):
<center width="100%" style="padding:10px"><img src="graph_attention_MLP.svg" width="250px"></center>
$h_i$ and $h_j$ are the original features from node $i$ and $j$ respectively, and represent the messages of the layer with $\mathbf{W}$ as weight matrix. $\mathbf{a}$ is the weight matrix of the MLP, which has the shape $[1,2\times d_{\text{message}}]$, and $\alpha_{ij}$ the final attention weight from node $i$ to $j$. The calculation can be described as follows:
$$\alpha_{ij} = \frac{\exp\left(\text{LeakyReLU}\left(\mathbf{a}\left[\mathbf{W}h_i||\mathbf{W}h_j\right]\right)\right)}{\sum_{k\in\mathcal{N}_i} \exp\left(\text{LeakyReLU}\left(\mathbf{a}\left[\mathbf{W}h_i||\mathbf{W}h_k\right]\right)\right)}$$
The operator $||$ represents the concatenation, and $\mathcal{N}_i$ the indices of the neighbors of node $i$. Note that in contrast to usual practice, we apply a non-linearity (here LeakyReLU) before the softmax over elements. Although it seems like a minor change at first, it is crucial for the attention to depend on the original input. Specifically, let's remove the non-linearity for a second, and try to simplify the expression:
$$
\begin{split}
\alpha_{ij} & = \frac{\exp\left(\mathbf{a}\left[\mathbf{W}h_i||\mathbf{W}h_j\right]\right)}{\sum_{k\in\mathcal{N}_i} \exp\left(\mathbf{a}\left[\mathbf{W}h_i||\mathbf{W}h_k\right]\right)}\\[5pt]
& = \frac{\exp\left(\mathbf{a}_{:,:d/2}\mathbf{W}h_i+\mathbf{a}_{:,d/2:}\mathbf{W}h_j\right)}{\sum_{k\in\mathcal{N}_i} \exp\left(\mathbf{a}_{:,:d/2}\mathbf{W}h_i+\mathbf{a}_{:,d/2:}\mathbf{W}h_k\right)}\\[5pt]
& = \frac{\exp\left(\mathbf{a}_{:,:d/2}\mathbf{W}h_i\right)\cdot\exp\left(\mathbf{a}_{:,d/2:}\mathbf{W}h_j\right)}{\sum_{k\in\mathcal{N}_i} \exp\left(\mathbf{a}_{:,:d/2}\mathbf{W}h_i\right)\cdot\exp\left(\mathbf{a}_{:,d/2:}\mathbf{W}h_k\right)}\\[5pt]
& = \frac{\exp\left(\mathbf{a}_{:,d/2:}\mathbf{W}h_j\right)}{\sum_{k\in\mathcal{N}_i} \exp\left(\mathbf{a}_{:,d/2:}\mathbf{W}h_k\right)}\\
\end{split}
$$
We can see that without the non-linearity, the attention term with $h_i$ actually cancels itself out, resulting in the attention being independent of the node itself. Hence, we would have the same issue as the GCN of creating the same output features for nodes with the same neighbors. This is why the LeakyReLU is crucial and adds some dependency on $h_i$ to the attention.
Once we obtain all attention factors, we can calculate the output features for each node by performing the weighted average:
$$h_i'=\sigma\left(\sum_{j\in\mathcal{N}_i}\alpha_{ij}\mathbf{W}h_j\right)$$
$\sigma$ is yet another non-linearity, as in the GCN layer. Visually, we can represent the full message passing in an attention layer as follows (figure credit - [Velickovic et al.](https://arxiv.org/abs/1710.10903)):
<center width="100%"><img src="graph_attention.jpeg" width="400px"></center>
To increase the expressiveness of the graph attention network, [Velickovic et al.](https://arxiv.org/abs/1710.10903) proposed to extend it to multiple heads similar to the Multi-Head Attention block in Transformers. This results in $N$ attention layers being applied in parallel. In the image above, it is visualized as three different colors of arrows (green, blue, and purple) that are afterward concatenated. The average is only applied for the very final prediction layer in a network.
After having discussed the graph attention layer in detail, we can implement it below:
```
class GATLayer(nn.Module):
def __init__(self, c_in, c_out, num_heads=1, concat_heads=True, alpha=0.2):
"""
Inputs:
c_in - Dimensionality of input features
c_out - Dimensionality of output features
num_heads - Number of heads, i.e. attention mechanisms to apply in parallel. The
output features are equally split up over the heads if concat_heads=True.
concat_heads - If True, the output of the different heads is concatenated instead of averaged.
alpha - Negative slope of the LeakyReLU activation.
"""
super().__init__()
self.num_heads = num_heads
self.concat_heads = concat_heads
if self.concat_heads:
assert c_out % num_heads == 0, "Number of output features must be a multiple of the count of heads."
c_out = c_out // num_heads
# Sub-modules and parameters needed in the layer
self.projection = nn.Linear(c_in, c_out * num_heads)
self.a = nn.Parameter(torch.Tensor(num_heads, 2 * c_out)) # One per head
self.leakyrelu = nn.LeakyReLU(alpha)
# Initialization from the original implementation
nn.init.xavier_uniform_(self.projection.weight.data, gain=1.414)
nn.init.xavier_uniform_(self.a.data, gain=1.414)
def forward(self, node_feats, adj_matrix, print_attn_probs=False):
"""
Inputs:
node_feats - Input features of the node. Shape: [batch_size, c_in]
adj_matrix - Adjacency matrix including self-connections. Shape: [batch_size, num_nodes, num_nodes]
print_attn_probs - If True, the attention weights are printed during the forward pass (for debugging purposes)
"""
batch_size, num_nodes = node_feats.size(0), node_feats.size(1)
# Apply linear layer and sort nodes by head
node_feats = self.projection(node_feats)
node_feats = node_feats.view(batch_size, num_nodes, self.num_heads, -1)
# We need to calculate the attention logits for every edge in the adjacency matrix
# Doing this on all possible combinations of nodes is very expensive
# => Create a tensor of [W*h_i||W*h_j] with i and j being the indices of all edges
edges = adj_matrix.nonzero(as_tuple=False) # Returns indices where the adjacency matrix is not 0 => edges
node_feats_flat = node_feats.view(batch_size * num_nodes, self.num_heads, -1)
edge_indices_row = edges[:,0] * num_nodes + edges[:,1]
edge_indices_col = edges[:,0] * num_nodes + edges[:,2]
a_input = torch.cat([
torch.index_select(input=node_feats_flat, index=edge_indices_row, dim=0),
torch.index_select(input=node_feats_flat, index=edge_indices_col, dim=0)
], dim=-1) # Index select returns a tensor with node_feats_flat being indexed at the desired positions along dim=0
# Calculate attention MLP output (independent for each head)
attn_logits = torch.einsum('bhc,hc->bh', a_input, self.a)
attn_logits = self.leakyrelu(attn_logits)
# Map list of attention values back into a matrix
attn_matrix = attn_logits.new_zeros(adj_matrix.shape+(self.num_heads,)).fill_(-9e15)
attn_matrix[adj_matrix[...,None].repeat(1,1,1,self.num_heads) == 1] = attn_logits.reshape(-1)
# Weighted average of attention
attn_probs = F.softmax(attn_matrix, dim=2)
if print_attn_probs:
print("Attention probs\n", attn_probs.permute(0, 3, 1, 2))
node_feats = torch.einsum('bijh,bjhc->bihc', attn_probs, node_feats)
# If heads should be concatenated, we can do this by reshaping. Otherwise, take mean
if self.concat_heads:
node_feats = node_feats.reshape(batch_size, num_nodes, -1)
else:
node_feats = node_feats.mean(dim=2)
return node_feats
```
Again, we can apply the graph attention layer on our example graph above to understand the dynamics better. As before, the input layer is initialized as an identity matrix, but we set $\mathbf{a}$ to be a vector of arbitrary numbers to obtain different attention values. We use two heads to show the parallel, independent attention mechanisms working in the layer.
```
layer = GATLayer(2, 2, num_heads=2)
layer.projection.weight.data = torch.Tensor([[1., 0.], [0., 1.]])
layer.projection.bias.data = torch.Tensor([0., 0.])
layer.a.data = torch.Tensor([[-0.2, 0.3], [0.1, -0.1]])
with torch.no_grad():
out_feats = layer(node_feats, adj_matrix, print_attn_probs=True)
print("Adjacency matrix", adj_matrix)
print("Input features", node_feats)
print("Output features", out_feats)
```
We recommend that you try to calculate the attention matrix at least for one head and one node for yourself. The entries are 0 where there does not exist an edge between $i$ and $j$. For the others, we see a diverse set of attention probabilities. Moreover, the output features of node 3 and 4 are now different although they have the same neighbors.
## PyTorch Geometric
We had mentioned before that implementing graph networks with adjacency matrix is simple and straight-forward but can be computationally expensive for large graphs. Many real-world graphs can reach over 200k nodes, for which adjacency matrix-based implementations fail. There are a lot of optimizations possible when implementing GNNs, and luckily, there exist packages that provide such layers. The most popular packages for PyTorch are [PyTorch Geometric](https://pytorch-geometric.readthedocs.io/en/latest/) and the [Deep Graph Library](https://www.dgl.ai/) (the latter being actually framework agnostic). Which one to use depends on the project you are planning to do and personal taste. In this tutorial, we will look at PyTorch Geometric as part of the PyTorch family. Similar to PyTorch Lightning, PyTorch Geometric is not installed by default on GoogleColab (and actually also not in our `dl2020` environment due to many dependencies that would be unnecessary for the practicals). Hence, let's import and/or install it below:
```
# torch geometric
try:
import torch_geometric
except ModuleNotFoundError:
# Installing torch geometric packages with specific CUDA+PyTorch version.
# See https://pytorch-geometric.readthedocs.io/en/latest/notes/installation.html for details
TORCH = torch.__version__.split('+')[0]
CUDA = 'cu' + torch.version.cuda.replace('.','')
!pip install torch-scatter -f https://pytorch-geometric.com/whl/torch-{TORCH}+{CUDA}.html
!pip install torch-sparse -f https://pytorch-geometric.com/whl/torch-{TORCH}+{CUDA}.html
!pip install torch-cluster -f https://pytorch-geometric.com/whl/torch-{TORCH}+{CUDA}.html
!pip install torch-spline-conv -f https://pytorch-geometric.com/whl/torch-{TORCH}+{CUDA}.html
!pip install torch-geometric
import torch_geometric
import torch_geometric.nn as geom_nn
import torch_geometric.data as geom_data
```
PyTorch Geometric provides us a set of common graph layers, including the GCN and GAT layer we implemented above. Additionally, similar to PyTorch's torchvision, it provides the common graph datasets and transformations on those to simplify training. Compared to our implementation above, PyTorch Geometric uses a list of index pairs to represent the edges. The details of this library will be explored further in our experiments.
In our tasks below, we want to allow us to pick from a multitude of graph layers. Thus, we define again below a dictionary to access those using a string:
```
gnn_layer_by_name = {
"GCN": geom_nn.GCNConv,
"GAT": geom_nn.GATConv,
"GraphConv": geom_nn.GraphConv
}
```
Additionally to GCN and GAT, we added the layer `geom_nn.GraphConv` ([documentation](https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html#torch_geometric.nn.conv.GraphConv)). GraphConv is a GCN with a separate weight matrix for the self-connections. Mathematically, this would be:
$$
\mathbf{x}_i^{(l+1)} = \mathbf{W}^{(l + 1)}_1 \mathbf{x}_i^{(l)} + \mathbf{W}^{(\ell + 1)}_2 \sum_{j \in \mathcal{N}_i} \mathbf{x}_j^{(l)}
$$
In this formula, the neighbor's messages are added instead of averaged. However, PyTorch Geometric provides the argument `aggr` to switch between summing, averaging, and max pooling.
## Experiments on graph structures
Tasks on graph-structured data can be grouped into three groups: node-level, edge-level and graph-level. The different levels describe on which level we want to perform classification/regression. We will discuss all three types in more detail below.
### Node-level tasks: Semi-supervised node classification
Node-level tasks have the goal to classify nodes in a graph. Usually, we have given a single, large graph with >1000 nodes of which a certain amount of nodes are labeled. We learn to classify those labeled examples during training and try to generalize to the unlabeled nodes.
A popular example that we will use in this tutorial is the Cora dataset, a citation network among papers. The Cora consists of 2708 scientific publications with links between each other representing the citation of one paper by another. The task is to classify each publication into one of seven classes. Each publication is represented by a bag-of-words vector. This means that we have a vector of 1433 elements for each publication, where a 1 at feature $i$ indicates that the $i$-th word of a pre-defined dictionary is in the article. Binary bag-of-words representations are commonly used when we need very simple encodings, and already have an intuition of what words to expect in a network. There exist much better approaches, but we will leave this to the NLP courses to discuss.
We will load the dataset below:
```
cora_dataset = torch_geometric.datasets.Planetoid(root=DATASET_PATH, name="Cora")
```
Let's look at how PyTorch Geometric represents the graph data. Note that although we have a single graph, PyTorch Geometric returns a dataset for compatibility to other datasets.
```
cora_dataset[0]
```
The graph is represented by a `Data` object ([documentation](https://pytorch-geometric.readthedocs.io/en/latest/modules/data.html#torch_geometric.data.Data)) which we can access as a standard Python namespace. The edge index tensor is the list of edges in the graph and contains the mirrored version of each edge for undirected graphs. The `train_mask`, `val_mask`, and `test_mask` are boolean masks that indicate which nodes we should use for training, validation, and testing. The `x` tensor is the feature tensor of our 2708 publications, and `y` the labels for all nodes.
After having seen the data, we can implement a simple graph neural network. The GNN applies a sequence of graph layers (GCN, GAT, or GraphConv), ReLU as activation function, and dropout for regularization. See below for the specific implementation.
```
class GNNModel(nn.Module):
def __init__(self, c_in, c_hidden, c_out, num_layers=2, layer_name="GCN", dp_rate=0.1, **kwargs):
"""
Inputs:
c_in - Dimension of input features
c_hidden - Dimension of hidden features
c_out - Dimension of the output features. Usually number of classes in classification
num_layers - Number of "hidden" graph layers
layer_name - String of the graph layer to use
dp_rate - Dropout rate to apply throughout the network
kwargs - Additional arguments for the graph layer (e.g. number of heads for GAT)
"""
super().__init__()
gnn_layer = gnn_layer_by_name[layer_name]
layers = []
in_channels, out_channels = c_in, c_hidden
for l_idx in range(num_layers-1):
layers += [
gnn_layer(in_channels=in_channels,
out_channels=out_channels,
**kwargs),
nn.ReLU(inplace=True),
nn.Dropout(dp_rate)
]
in_channels = c_hidden
layers += [gnn_layer(in_channels=in_channels,
out_channels=c_out,
**kwargs)]
self.layers = nn.ModuleList(layers)
def forward(self, x, edge_index):
"""
Inputs:
x - Input features per node
edge_index - List of vertex index pairs representing the edges in the graph (PyTorch geometric notation)
"""
for l in self.layers:
# For graph layers, we need to add the "edge_index" tensor as additional input
# All PyTorch Geometric graph layer inherit the class "MessagePassing", hence
# we can simply check the class type.
if isinstance(l, geom_nn.MessagePassing):
x = l(x, edge_index)
else:
x = l(x)
return x
```
Good practice in node-level tasks is to create an MLP baseline that is applied to each node independently. This way we can verify whether adding the graph information to the model indeed improves the prediction, or not. It might also be that the features per node are already expressive enough to clearly point towards a specific class. To check this, we implement a simple MLP below.
```
class MLPModel(nn.Module):
def __init__(self, c_in, c_hidden, c_out, num_layers=2, dp_rate=0.1):
"""
Inputs:
c_in - Dimension of input features
c_hidden - Dimension of hidden features
c_out - Dimension of the output features. Usually number of classes in classification
num_layers - Number of hidden layers
dp_rate - Dropout rate to apply throughout the network
"""
super().__init__()
layers = []
in_channels, out_channels = c_in, c_hidden
for l_idx in range(num_layers-1):
layers += [
nn.Linear(in_channels, out_channels),
nn.ReLU(inplace=True),
nn.Dropout(dp_rate)
]
in_channels = c_hidden
layers += [nn.Linear(in_channels, c_out)]
self.layers = nn.Sequential(*layers)
def forward(self, x, *args, **kwargs):
"""
Inputs:
x - Input features per node
"""
return self.layers(x)
```
Finally, we can merge the models into a PyTorch Lightning module which handles the training, validation, and testing for us.
```
class NodeLevelGNN(pl.LightningModule):
def __init__(self, model_name, **model_kwargs):
super().__init__()
# Saving hyperparameters
self.save_hyperparameters()
if model_name == "MLP":
self.model = MLPModel(**model_kwargs)
else:
self.model = GNNModel(**model_kwargs)
self.loss_module = nn.CrossEntropyLoss()
def forward(self, data, mode="train"):
x, edge_index = data.x, data.edge_index
x = self.model(x, edge_index)
# Only calculate the loss on the nodes corresponding to the mask
if mode == "train":
mask = data.train_mask
elif mode == "val":
mask = data.val_mask
elif mode == "test":
mask = data.test_mask
else:
assert False, f"Unknown forward mode: {mode}"
loss = self.loss_module(x[mask], data.y[mask])
acc = (x[mask].argmax(dim=-1) == data.y[mask]).sum().float() / mask.sum()
return loss, acc
def configure_optimizers(self):
# We use SGD here, but Adam works as well
optimizer = optim.SGD(self.parameters(), lr=0.1, momentum=0.9, weight_decay=2e-3)
return optimizer
def training_step(self, batch, batch_idx):
loss, acc = self.forward(batch, mode="train")
self.log('train_loss', loss)
self.log('train_acc', acc)
return loss
def validation_step(self, batch, batch_idx):
_, acc = self.forward(batch, mode="val")
self.log('val_acc', acc)
def test_step(self, batch, batch_idx):
_, acc = self.forward(batch, mode="test")
self.log('test_acc', acc)
```
Additionally to the Lightning module, we define a training function below. As we have a single graph, we use a batch size of 1 for the data loader and share the same data loader for the train, validation, and test set (the mask is picked inside the Lightning module). Besides, we set the argument `progress_bar_refresh_rate` to zero as it usually shows the progress per epoch, but an epoch only consists of a single step. The rest of the code is very similar to what we have seen in Tutorial 5 and 6 already.
```
def train_node_classifier(model_name, dataset, **model_kwargs):
pl.seed_everything(42)
node_data_loader = geom_data.DataLoader(dataset, batch_size=1)
# Create a PyTorch Lightning trainer with the generation callback
root_dir = os.path.join(CHECKPOINT_PATH, "NodeLevel" + model_name)
os.makedirs(root_dir, exist_ok=True)
trainer = pl.Trainer(default_root_dir=root_dir,
callbacks=[ModelCheckpoint(save_weights_only=True, mode="max", monitor="val_acc")],
gpus=1 if str(device).startswith("cuda") else 0,
max_epochs=200,
progress_bar_refresh_rate=0) # 0 because epoch size is 1
trainer.logger._default_hp_metric = None # Optional logging argument that we don't need
# Check whether pretrained model exists. If yes, load it and skip training
pretrained_filename = os.path.join(CHECKPOINT_PATH, f"NodeLevel{model_name}.ckpt")
if os.path.isfile(pretrained_filename):
print("Found pretrained model, loading...")
model = NodeLevelGNN.load_from_checkpoint(pretrained_filename)
else:
pl.seed_everything()
model = NodeLevelGNN(model_name=model_name, c_in=dataset.num_node_features, c_out=dataset.num_classes, **model_kwargs)
trainer.fit(model, node_data_loader, node_data_loader)
model = NodeLevelGNN.load_from_checkpoint(trainer.checkpoint_callback.best_model_path)
# Test best model on the test set
test_result = trainer.test(model, test_dataloaders=node_data_loader, verbose=False)
batch = next(iter(node_data_loader))
batch = batch.to(model.device)
_, train_acc = model.forward(batch, mode="train")
_, val_acc = model.forward(batch, mode="val")
result = {"train": train_acc,
"val": val_acc,
"test": test_result[0]['test_acc']}
return model, result
```
Finally, we can train our models. First, let's train the simple MLP:
```
# Small function for printing the test scores
def print_results(result_dict):
if "train" in result_dict:
print(f"Train accuracy: {(100.0*result_dict['train']):4.2f}%")
if "val" in result_dict:
print(f"Val accuracy: {(100.0*result_dict['val']):4.2f}%")
print(f"Test accuracy: {(100.0*result_dict['test']):4.2f}%")
node_mlp_model, node_mlp_result = train_node_classifier(model_name="MLP",
dataset=cora_dataset,
c_hidden=16,
num_layers=2,
dp_rate=0.1)
print_results(node_mlp_result)
```
Although the MLP can overfit on the training dataset because of the high-dimensional input features, it does not perform too well on the test set. Let's see if we can beat this score with our graph networks:
```
node_gnn_model, node_gnn_result = train_node_classifier(model_name="GNN",
layer_name="GCN",
dataset=cora_dataset,
c_hidden=16,
num_layers=2,
dp_rate=0.1)
print_results(node_gnn_result)
```
As we would have hoped for, the GNN model outperforms the MLP by quite a margin. This shows that using the graph information indeed improves our predictions and lets us generalizes better.
The hyperparameters in the model have been chosen to create a relatively small network. This is because the first layer with an input dimension of 1433 can be relatively expensive to perform for large graphs. In general, GNNs can become relatively expensive for very big graphs. This is why such GNNs either have a small hidden size or use a special batching strategy where we sample a connected subgraph of the big, original graph.
### Edge-level tasks: Link prediction
In some applications, we might have to predict on an edge-level instead of node-level. The most common edge-level task in GNN is link prediction. Link prediction means that given a graph, we want to predict whether there will be/should be an edge between two nodes or not. For example, in a social network, this is used by Facebook and co to propose new friends to you. Again, graph level information can be crucial to perform this task. The output prediction is usually done by performing a similarity metric on the pair of node features, which should be 1 if there should be a link, and otherwise close to 0. To keep the tutorial short, we will not implement this task ourselves. Nevertheless, there are many good resources out there if you are interested in looking closer at this task.
Tutorials and papers for this topic include:
* [PyTorch Geometric example](https://github.com/rusty1s/pytorch_geometric/blob/master/examples/link_pred.py)
* [Graph Neural Networks: A Review of Methods and Applications](https://arxiv.org/pdf/1812.08434.pdf), Zhou et al. 2019
* [Link Prediction Based on Graph Neural Networks](https://papers.nips.cc/paper/2018/file/53f0d7c537d99b3824f0f99d62ea2428-Paper.pdf), Zhang and Chen, 2018.
### Graph-level tasks: Graph classification
Finally, in this part of the tutorial, we will have a closer look at how to apply GNNs to the task of graph classification. The goal is to classify an entire graph instead of single nodes or edges. Therefore, we are also given a dataset of multiple graphs that we need to classify based on some structural graph properties. The most common task for graph classification is molecular property prediction, in which molecules are represented as graphs. Each atom is linked to a node, and edges in the graph are the bonds between atoms. For example, look at the figure below.
<center width="100%"><img src="molecule_graph.svg" width="600px"></center>
On the left, we have an arbitrary, small molecule with different atoms, whereas the right part of the image shows the graph representation. The atom types are abstracted as node features (e.g. a one-hot vector), and the different bond types are used as edge features. For simplicity, we will neglect the edge attributes in this tutorial, but you can include by using methods like the [Relational Graph Convolution](https://arxiv.org/abs/1703.06103) that uses a different weight matrix for each edge type.
The dataset we will use below is called the MUTAG dataset. It is a common small benchmark for graph classification algorithms, and contain 188 graphs with 18 nodes and 20 edges on average for each graph. The graph nodes have 7 different labels/atom types, and the binary graph labels represent "their mutagenic effect on a specific gram negative bacterium" (the specific meaning of the labels are not too important here). The dataset is part of a large collection of different graph classification datasets, known as the [TUDatasets](https://chrsmrrs.github.io/datasets/), which is directly accessible via `torch_geometric.datasets.TUDataset` ([documentation](https://pytorch-geometric.readthedocs.io/en/latest/modules/datasets.html#torch_geometric.datasets.TUDataset)) in PyTorch Geometric. We can load the dataset below.
```
tu_dataset = torch_geometric.datasets.TUDataset(root=DATASET_PATH, name="MUTAG")
```
Let's look at some statistics for the dataset:
```
print("Data object:", tu_dataset.data)
print("Length:", len(tu_dataset))
print(f"Average label: {tu_dataset.data.y.float().mean().item():4.2f}")
```
The first line shows how the dataset stores different graphs. The nodes, edges, and labels of each graph are concatenated to one tensor, and the dataset stores the indices where to split the tensors correspondingly. The length of the dataset is the number of graphs we have, and the "average label" denotes the percentage of the graph with label 1. As long as the percentage is in the range of 0.5, we have a relatively balanced dataset. It happens quite often that graph datasets are very imbalanced, hence checking the class balance is always a good thing to do.
Next, we will split our dataset into a training and test part. Note that we do not use a validation set this time because of the small size of the dataset. Therefore, our model might overfit slightly on the validation set due to the noise of the evaluation, but we still get an estimate of the performance on untrained data.
```
torch.manual_seed(42)
tu_dataset.shuffle()
train_dataset = tu_dataset[:150]
test_dataset = tu_dataset[150:]
```
When using a data loader, we encounter a problem with batching $N$ graphs. Each graph in the batch can have a different number of nodes and edges, and hence we would require a lot of padding to obtain a single tensor. Torch geometric uses a different, more efficient approach: we can view the $N$ graphs in a batch as a single large graph with concatenated node and edge list. As there is no edge between the $N$ graphs, running GNN layers on the large graph gives us the same output as running the GNN on each graph separately. Visually, this batching strategy is visualized below (figure credit - PyTorch Geometric team, [tutorial here](https://colab.research.google.com/drive/1I8a0DfQ3fI7Njc62__mVXUlcAleUclnb?usp=sharing#scrollTo=2owRWKcuoALo)).
<center width="100%"><img src="torch_geometric_stacking_graphs.png" width="600px"></center>
The adjacency matrix is zero for any nodes that come from two different graphs, and otherwise according to the adjacency matrix of the individual graph. Luckily, this strategy is already implemented in torch geometric, and hence we can use the corresponding data loader:
```
graph_train_loader = geom_data.DataLoader(train_dataset, batch_size=64, shuffle=True)
graph_val_loader = geom_data.DataLoader(test_dataset, batch_size=64) # Additional loader if you want to change to a larger dataset
graph_test_loader = geom_data.DataLoader(test_dataset, batch_size=64)
```
Let's load a batch below to see the batching in action:
```
batch = next(iter(graph_test_loader))
print("Batch:", batch)
print("Labels:", batch.y[:10])
print("Batch indices:", batch.batch[:40])
```
We have 38 graphs stacked together for the test dataset. The batch indices, stored in `batch`, show that the first 12 nodes belong to the first graph, the next 22 to the second graph, and so on. These indices are important for performing the final prediction. To perform a prediction over a whole graph, we usually perform a pooling operation over all nodes after running the GNN model. In this case, we will use the average pooling. Hence, we need to know which nodes should be included in which average pool. Using this pooling, we can already create our graph network below. Specifically, we re-use our class `GNNModel` from before, and simply add an average pool and single linear layer for the graph prediction task.
```
class GraphGNNModel(nn.Module):
def __init__(self, c_in, c_hidden, c_out, dp_rate_linear=0.5, **kwargs):
"""
Inputs:
c_in - Dimension of input features
c_hidden - Dimension of hidden features
c_out - Dimension of output features (usually number of classes)
dp_rate_linear - Dropout rate before the linear layer (usually much higher than inside the GNN)
kwargs - Additional arguments for the GNNModel object
"""
super().__init__()
self.GNN = GNNModel(c_in=c_in,
c_hidden=c_hidden,
c_out=c_hidden, # Not our prediction output yet!
**kwargs)
self.head = nn.Sequential(
nn.Dropout(dp_rate_linear),
nn.Linear(c_hidden, c_out)
)
def forward(self, x, edge_index, batch_idx):
"""
Inputs:
x - Input features per node
edge_index - List of vertex index pairs representing the edges in the graph (PyTorch geometric notation)
batch_idx - Index of batch element for each node
"""
x = self.GNN(x, edge_index)
x = geom_nn.global_mean_pool(x, batch_idx) # Average pooling
x = self.head(x)
return x
```
Finally, we can create a PyTorch Lightning module to handle the training. It is similar to the modules we have seen before and does nothing surprising in terms of training. As we have a binary classification task, we use the Binary Cross Entropy loss.
```
class GraphLevelGNN(pl.LightningModule):
def __init__(self, **model_kwargs):
super().__init__()
# Saving hyperparameters
self.save_hyperparameters()
self.model = GraphGNNModel(**model_kwargs)
self.loss_module = nn.BCEWithLogitsLoss() if self.hparams.c_out == 1 else nn.CrossEntropyLoss()
def forward(self, data, mode="train"):
x, edge_index, batch_idx = data.x, data.edge_index, data.batch
x = self.model(x, edge_index, batch_idx)
x = x.squeeze(dim=-1)
if self.hparams.c_out == 1:
preds = (x > 0).float()
data.y = data.y.float()
else:
preds = x.argmax(dim=-1)
loss = self.loss_module(x, data.y)
acc = (preds == data.y).sum().float() / preds.shape[0]
return loss, acc
def configure_optimizers(self):
optimizer = optim.AdamW(self.parameters(), lr=1e-2, weight_decay=0.0) # High lr because of small dataset and small model
return optimizer
def training_step(self, batch, batch_idx):
loss, acc = self.forward(batch, mode="train")
self.log('train_loss', loss)
self.log('train_acc', acc)
return loss
def validation_step(self, batch, batch_idx):
_, acc = self.forward(batch, mode="val")
self.log('val_acc', acc)
def test_step(self, batch, batch_idx):
_, acc = self.forward(batch, mode="test")
self.log('test_acc', acc)
```
Below we train the model on our dataset. It resembles the typical training functions we have seen so far.
```
def train_graph_classifier(model_name, **model_kwargs):
pl.seed_everything(42)
# Create a PyTorch Lightning trainer with the generation callback
root_dir = os.path.join(CHECKPOINT_PATH, "GraphLevel" + model_name)
os.makedirs(root_dir, exist_ok=True)
trainer = pl.Trainer(default_root_dir=root_dir,
callbacks=[ModelCheckpoint(save_weights_only=True, mode="max", monitor="val_acc")],
gpus=1 if str(device).startswith("cuda") else 0,
max_epochs=500,
progress_bar_refresh_rate=0)
trainer.logger._default_hp_metric = None # Optional logging argument that we don't need
# Check whether pretrained model exists. If yes, load it and skip training
pretrained_filename = os.path.join(CHECKPOINT_PATH, f"GraphLevel{model_name}.ckpt")
if os.path.isfile(pretrained_filename):
print("Found pretrained model, loading...")
model = GraphLevelGNN.load_from_checkpoint(pretrained_filename)
else:
pl.seed_everything(42)
model = GraphLevelGNN(c_in=tu_dataset.num_node_features,
c_out=1 if tu_dataset.num_classes==2 else tu_dataset.num_classes,
**model_kwargs)
trainer.fit(model, graph_train_loader, graph_val_loader)
model = GraphLevelGNN.load_from_checkpoint(trainer.checkpoint_callback.best_model_path)
# Test best model on validation and test set
train_result = trainer.test(model, test_dataloaders=graph_train_loader, verbose=False)
test_result = trainer.test(model, test_dataloaders=graph_test_loader, verbose=False)
result = {"test": test_result[0]['test_acc'], "train": train_result[0]['test_acc']}
return model, result
```
Finally, let's perform the training and testing. Feel free to experiment with different GNN layers, hyperparameters, etc.
```
model, result = train_graph_classifier(model_name="GraphConv",
c_hidden=256,
layer_name="GraphConv",
num_layers=3,
dp_rate_linear=0.5,
dp_rate=0.0)
print(f"Train performance: {100.0*result['train']:4.2f}%")
print(f"Test performance: {100.0*result['test']:4.2f}%")
```
The test performance shows that we obtain quite good scores on an unseen part of the dataset. It should be noted that as we have been using the test set for validation as well, we might have overfitted slightly to this set. Nevertheless, the experiment shows us that GNNs can be indeed powerful to predict the properties of graphs and/or molecules.
## Conclusion
In this tutorial, we have seen the application of neural networks to graph structures. We looked at how a graph can be represented (adjacency matrix or edge list), and discussed the implementation of common graph layers: GCN and GAT. The implementations showed the practical side of the layers, which is often easier than the theory. Finally, we experimented with different tasks, on node-, edge- and graph-level. Overall, we have seen that including graph information in the predictions can be crucial for achieving high performance. There are a lot of applications that benefit from GNNs, and the importance of these networks will likely increase over the next years.
| true |
code
| 0.896795 | null | null | null | null |
|
# Numerical Differentiation
Teng-Jui Lin
Content adapted from UW AMATH 301, Beginning Scientific Computing, in Spring 2020.
- Numerical differentiation
- First order methods
- Forward difference
- Backward difference
- Second order methods
- Central difference
- Other second order methods
- Errors
- `numpy` implementation
- Data differentiation by [`numpy.gradient()`](https://numpy.org/doc/stable/reference/generated/numpy.gradient.html)
## Numerical differentiation of known function
From the definition of derivative, the forward difference approximation is given by
$$
f'(x) = \dfrac{f(x+\Delta x) - f(x)}{\Delta x}
$$
The backward difference approximation is given by
$$
f'(x) = \dfrac{f(x) - f(x-\Delta x)}{\Delta x}
$$
The central difference approximation is given by
$$
f'(x) = \dfrac{f(x + \Delta x) - f(x-\Delta x)}{2\Delta x}
$$
which is the average of forward and backward difference.
Forward and backward difference are $\mathcal{O}(\Delta x)$, or first order method. Central difference is $\mathcal{O}(\Delta x^2)$, being a second order method. Note that we also have second order method at the left and right end points:
$$
f'(x) = \dfrac{-3f(x) + 4f(x+\Delta x) - 4f(x+2\Delta x)}{2\Delta x}
$$
$$
f'(x) = \dfrac{3f(x) - 4f(x-\Delta x) + 4f(x-2\Delta x)}{2\Delta x}
$$
### Implementation
**Problem Statement.** Find the derivative of the function
$$
f(x) = \sin x
$$
using analytic expression, forward difference, backward difference, and central difference. compare their accuracy using a plot.
```
import numpy as np
import matplotlib.pyplot as plt
# target function
f = lambda x : np.sin(x)
df = lambda x : np.cos(x) # analytic for comparison
x = np.arange(0, 2*np.pi, 0.1)
def forward_diff(f, x, dx):
return (f(x + dx) - f(x))/dx
def backward_diff(f, x, dx):
return (f(x) - f(x - dx))/dx
def central_diff(f, x, dx):
return (f(x + dx) - f(x - dx))/(2*dx)
dx = 0.1
forward_df = forward_diff(f, x, dx)
backward_df = backward_diff(f, x, dx)
central_df = central_diff(f, x, dx)
# plot settings
%config InlineBackend.figure_format = 'retina'
%matplotlib inline
plt.rcParams.update({
'font.family': 'Arial', # Times New Roman, Calibri
'font.weight': 'normal',
'mathtext.fontset': 'cm',
'font.size': 18,
'lines.linewidth': 2,
'axes.linewidth': 2,
'axes.spines.top': False,
'axes.spines.right': False,
'axes.titleweight': 'bold',
'axes.titlesize': 18,
'axes.labelweight': 'bold',
'xtick.major.size': 8,
'xtick.major.width': 2,
'ytick.major.size': 8,
'ytick.major.width': 2,
'figure.dpi': 80,
'legend.framealpha': 1,
'legend.edgecolor': 'black',
'legend.fancybox': False,
'legend.fontsize': 14
})
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x, df(x), label='Analytic', color='black')
ax.plot(x, forward_df, '--', label='Forward')
ax.plot(x, backward_df, '--', label='Backward')
ax.plot(x, central_df, '--', label='Central')
ax.set_xlabel('$x$')
ax.set_ylabel('$f\'(x)$')
ax.set_title('Numerical differentiation methods')
ax.set_xlim(0, 2*np.pi)
ax.set_ylim(-1, 1)
ax.legend()
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x, df(x), label='Analytic', color='black')
ax.plot(x, forward_df, '--', label='Forward')
ax.plot(x, backward_df, '--', label='Backward')
ax.plot(x, central_df, '--', label='Central')
ax.set_xlabel('$x$')
ax.set_ylabel('$f\'(x)$')
ax.set_title('Numerical differentiation methods')
ax.set_xlim(1.5, 2.5)
ax.set_ylim(-0.9, 0.5)
ax.legend()
```
### Error and method order
**Problem Statement.** Compare the error of forward difference, backward difference, and central difference with analytic derivative of the function
$$
f(x) = \sin x
$$
Compare the error of the methods using a plot.
```
# target function
f = lambda x : np.sin(x)
df = lambda x : np.cos(x) # analytic for comparison
x = np.arange(0, 2*np.pi, 0.1)
dx = np.array([0.1 / 2**i for i in range(5)])
forward_errors = np.zeros(len(dx))
backward_errors = np.zeros(len(dx))
central_errors = np.zeros(len(dx))
for i in range(len(dx)):
forward_df = forward_diff(f, x, dx[i])
backward_df = backward_diff(f, x, dx[i])
central_df = central_diff(f, x, dx[i])
forward_errors[i] = np.linalg.norm(df(x) - forward_df)
backward_errors[i] = np.linalg.norm(df(x) - backward_df)
central_errors[i] = np.linalg.norm(df(x) - central_df)
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(dx, forward_errors, '.-', label='Forward')
ax.plot(dx, backward_errors, 'o-.', label='Backward', alpha=0.5)
ax.plot(dx, central_errors, 'o--', label='Central', alpha=0.8)
ax.set_xlabel('$dx$')
ax.set_ylabel('Error')
ax.set_title('Error of numerical methods')
# ax.set_xlim(1.5, 2.5)
# ax.set_ylim(-0.9, 0.5)
ax.legend()
```
## Numerical differentiation of data
### Implementation
**Problem Statement.** The Gaussian function has the form
$$
f(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right)
$$
(a) Generate an equidistant Gaussian dataset of such form in the domain $[0, 5]$ with $\sigma = 1, \mu = 2.5$.
(b) Find the numerical derivative of the data points using second order methods and [`numpy.gradient()`](https://numpy.org/doc/stable/reference/generated/numpy.gradient.html). Plot the data and the derivative.
```
# generate data
gaussian = lambda x, sigma, mu : 1/np.sqrt(2*np.pi*sigma**2) * np.exp(-(x - mu)**2 / (2*sigma**2))
gaussian_data_x = np.linspace(0, 5, 50)
gaussian_data_y = np.array([gaussian(i, 1, 2.5) for i in gaussian_data_x])
def numerical_diff(data_x, data_y):
'''
Numerically differentiate given equidistant data points.
Central difference is used in middle.
Second order forward and backward difference used at end points.
:param data_x: x-coordinates of data points
:param data_y: y-coordinates of data points
:returns: numerical derivative of data points
'''
df = np.zeros_like(data_x)
dx = data_x[1] - data_x[0] # assume equidistant points
df[0] = (-3*data_y[0] + 4*data_y[1] - data_y[2])/(2*dx)
df[-1] = (3*data_y[-1] - 4*data_y[-2] + data_y[-3])/(2*dx)
df[1:-1] = (data_y[2:] - data_y[0:-2])/(2*dx)
return df
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(gaussian_data_x, gaussian_data_y, 'o', label='Data points')
ax.plot(gaussian_data_x, numerical_diff(gaussian_data_x, gaussian_data_y), '.', label='Derivative')
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x), f\'(x)$')
ax.set_title('Numerical differentiation of data')
# ax.set_xlim(1.5, 2.5)
# ax.set_ylim(-0.9, 0.5)
ax.legend()
```
### Numerical differentiation of data with `numpy`
[`numpy.gradient()`](https://numpy.org/doc/stable/reference/generated/numpy.gradient.html) has similar implementation as above. It uses central difference in the middle, and forward and backward differences at the end points.
```
dx = gaussian_data_x[1] - gaussian_data_x[0]
gaussian_df = np.gradient(gaussian_data_y, dx)
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(gaussian_data_x, gaussian_data_y, 'o', label='Data points')
ax.plot(gaussian_data_x, gaussian_df, '.', label='Derivative')
ax.set_xlabel('$x$')
ax.set_ylabel('$f(x), f\'(x)$')
ax.set_title('Numerical differentiation of data')
# ax.set_xlim(1.5, 2.5)
# ax.set_ylim(-0.9, 0.5)
ax.legend()
```
| true |
code
| 0.65437 | null | null | null | null |
|
#### Xl Juleoriansyah Nksrsb / 13317005
#### Muhamad Asa Nurrizqita Adhiem / 13317018
#### Oktoni Nur Pambudi / 13317022
#### Bernardus Rendy / 13317041
# Definisi Masalah
#### Dalam tangki dengan luas permukaan A, luas luaran a, dalam percepatan gravitasi g [Parameter A,a,g]
#### Diisi dengan flow fluida Vin (asumsi fluida incompressible) sehingga terdapat ketinggian h [Variabel Input Vin dan output h]
#### Akan memiliki luaran $V_{out}$ dengan
$V_{out} = a \sqrt{2gh} $
#### Sehingga akan didapat hubungan persamaan diferensial non-linear
$ \frac {dh}{dt} = \frac {V_{in}}{A} - \frac {a}{A}\sqrt{2gh}$
<img src="./dinsis_nonlinear.png" style="width:50%;">
#### Sumber Gambar: Slide Kuliah Dinamika Sistem dan Simulasi (Eko M. Budi & Estiyanti Ekawati) System Modeling: Fluidic Systems
```
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def dhdt_non(h,t,Vin,A,a,g):
return (Vin/A)-(a/A)*np.sqrt(2*g*h)
# initial condition
h0 = 0
# Parameter
A = 1
g = 9.8
Vin =100
a = 1
# time points
t = np.linspace(0,100)
# solve ODEs
hnon = odeint(dhdt_non,h0,t,args=(Vin,A,a,g))
# plot results
plt.plot(t,hnon,'r-',linewidth=2,label='h_non_linear')
plt.xlabel('time')
plt.ylabel('h(t)')
plt.legend()
plt.show()
```
# Alternatif Penyelesaian: Linearisasi
#### Dalam sebuah persamaan diferensial non-linear, sulit ditentukan fungsi transfer (karena h dalam akar sehingga tidak dapat dikeluarkan dengan mudah) dan penyelesaian analitik tanpa menggunakan numerik sehingga dibentuk suatu metode bernama linearisasi. Linearisasi juga mengimplikasi operasi matematika yang jauh lebih mudah
#### Linearisasi menggunakan ekspansi taylor orde 1 untuk mengubah persamaan diferensial $ \frac {dh(t)}{dt} = \frac {q_i(t)}{A} - \frac {a}{A}\sqrt{2gh(t)}$ menjadi linear
<img src="./dinsis_linear1.png" style="width:50%">
#### Sumber Gambar: Slide Kuliah Dinamika Sistem dan Simulasi (Eko M. Budi & Estiyanti Ekawati) System Modeling: Fluidic Systems
#### Menghasilkan (dengan catatan qi adalah Vin)
# $ \frac {dh}{dt} - \frac {d\bar h}{dt} = \frac {V_{in}- \bar {V_{in}}}{A} - (\frac {a \sqrt {2g}}{2A \sqrt {\bar h}})(h - \bar h) $
#### Setelah linearisasi, dihasilkan persamaan diferensial linear yang dapat beroperasi dekat $ \bar h $
#### Secara sederhana, ditulis
# $ \frac {d\hat h}{dt} = \frac {\hat {V_{in}}}{A} - \frac{\hat h}{R} $
#### Dimana
### $ \hat h = h-\bar h $
### $ \hat {V_{in}} = V_{in} - \bar {V_{in}} $
### $ R=\frac {A \sqrt {2 \bar {h}}}{a \sqrt{g}} $
#### Sehingga harus dipilih kondisi dimana $ \bar h $ sesuai untuk daerah operasi persamaan
#### Terlihat bahwa persamaan digunakan pada 0 hingga steady state, saat steady state
# $ \frac {dh}{dt} = 0 $
#### Berdasarkan persamaan
# $ \frac {dh}{dt} = \frac {V_{in}}{A} - \frac {a}{A}\sqrt{2gh}$
# $ 0 = V_{in} - a \sqrt{2g\bar {h}} $
# $ \bar {h} = \frac {V_{in}^2}{2ga^2} $
#### Juga harus dipilih kondisi dimana $ \bar V_{in} $ sesuai untuk daerah operasi persamaan
#### Terlihat bahwa jika input merupakan fungsi step,
# $ \bar V_{in} = V_{in} $
#### Karena $ V_{in} $ konstan, maka pada kondisi akhir dimana $ \bar V_{in} $ beroperasi, juga tetap sama dengan $ V_{in} $
#### Menggunakan persamaan yang sebelumnya telah diturunkan
# $ \frac {d\hat h}{dt} = \frac {\hat {V_{in}}}{A} - \frac{\hat h}{R} $
#### Dimana
### $ \hat h = h-\bar h $
### $ \hat {V_{in}} = V_{in} - \bar {V_{in}} $
### $ R=\frac {A \sqrt {2 \bar {h}}}{a \sqrt{g}} $
```
def dhhatdt_lin(hhat,t,Vinhat,A,a,g,R):
return (Vinhat/A)-(hhat/R)
# Initial condition
h0 = 0
# Input
Vin=100
# Parameter
A = 1
g = 9.8
a = 1
hbar = Vin**2/(2*g*a**2)
R=(A*np.sqrt(2*hbar))/(a*np.sqrt(g))
hhat0 = h0-hbar
Vinbar= Vin
Vinhat= Vin-Vinbar
# time points
t = np.linspace(0,100)
# solve ODEs, karena hasil ODE yang didapat adalah untuk hhat, maka harus dilakukan penambahan hbar karena h = hhat+hbar
hlin = odeint(dhhatdt_lin,hhat0,t,args=(Vinhat,A,a,g,R))
hlin = hlin+hbar
# plot results
plt.plot(t,hlin,'b-',linewidth=2,label='h_linear')
plt.xlabel('time')
plt.ylabel('h(t)')
plt.legend()
plt.show()
```
# Perbandingan Non-linear dan Linearisasi
```
plt.plot(t,hnon,'r-',linewidth=2,label='h_non_linear')
plt.plot(t,hlin,'b-',linewidth=2,label='h_linear')
plt.xlabel('time')
plt.ylabel('h(t)')
plt.legend()
plt.show()
```
#### Terlihat perbedaan respon sistem ketika dilakukan aproksimasi linearisasi terhadap dhdt
#### Walaupun terjadi perbedaan, perbedaan tersebut kurang signifikan pada sistem ini dengan Sum Squared Error sebesar:
```
err=hnon-hlin
err=err*err
sum(err)
```
# Interface Parameter
```
from ipywidgets import interact,fixed,widgets
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from ipywidgets import interact,fixed,widgets,Button,Layout
def dhhatdt_lin(hhat,t,Vinhat,A,a,g,R):
return (Vinhat/A)-(hhat/R)
def dhdt_non(h,t,Vin,A,a,g):
return (Vin/A)-(a/A)*np.sqrt(2*g*h)
g = 9.8
range_A = widgets.FloatSlider(
value=2.,
min=1.,
max=10.0,
step=0.1,
description='Luas Alas Tangki ($dm^2$):',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
range_a = widgets.FloatSlider(
value=2.,
min=0.1, max=+3., step=0.1,
description='Luas Pipa ($dm^2$) :',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
range_Vin = widgets.FloatSlider(
value= 2.,
min=0.1,
max=100.0,
step=0.1,
description='Debit Fluida Masuk ($dm^2 / s$)',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
range_h0 = widgets.FloatSlider(
value= 2.,
min=0.,
max=500.0,
step=0.1,
description='Ketinggian Mula-Mula ($dm$):',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
range_amplitude = widgets.FloatSlider(
value= 2.,
min=0.,
max=100.0,
step=0.1,
description='Amplituda Gangguan Sinusoidal:',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
time_slider = widgets.IntSlider(
min=100, max=1000, step=1, value=100,
description='Waktu Maksimum ($s$):',
layout=Layout(width='80%', height='50px'),
style={'description_width': '200px'},
readout_format='.1f',
)
max_err_button = widgets.Button(
description='Error Maksimum',
)
max_err_sin_button = widgets.Button(
description='Error Maksimum Sinusoidal',
)
min_err_button = widgets.Button(
description='Error Minimum',
)
tab1 = widgets.VBox(children=[range_A,range_a,range_Vin,range_h0,time_slider,max_err_button,min_err_button])
tab2 = widgets.VBox(children=[range_A,range_a,range_Vin,range_h0,range_amplitude,time_slider,max_err_sin_button,min_err_button])
tab = widgets.Tab(children=[tab1, tab2])
tab.set_title(0, 'Step')
tab.set_title(1, 'GangguanSinusoidal')
A = range_A.value
a = range_a.value
Vin = range_Vin.value
h0 = range_h0.value
tmax = time_slider.value
amp = range_amplitude.value
#Max error untuk step
def max_err_set(b=None):
range_A.value=10.0
range_a.value=0.1
range_Vin.value=100
range_h0.value=0
time_slider.value=1000
@max_err_button.on_click
def maximum_err_set(b):
max_err_set()
#Max error untuk sinusoidal
def max_err_sin_set(b=None):
range_A.value=10.0
range_a.value=2.9
range_Vin.value=100
range_h0.value=0
time_slider.value=150
range_amplitude.value=100
@max_err_sin_button.on_click
def maximum_err_sin_set(b):
max_err_sin_set()
#Min error untuk step dan sinusoidal
def min_err_set(b=None):
range_A.value=1.0
range_a.value=2.9
range_Vin.value=100
range_h0.value=50
time_slider.value=100
range_amplitude.value=0
@min_err_button.on_click
def minimum_err_set(b):
min_err_set()
def plot3(A,a,Vin,h0,amp,tmax):
t = np.linspace(50,tmax,1000)
f, ax = plt.subplots(1, 1, figsize=(8, 6))
if tab.selected_index == 1 :
def dhdt_non_sin(h,t,Vin,A,a,g,amp):
return ((Vin+abs(amp*np.sin(np.pi*t)))/A)-(a/A)*np.sqrt(2*g*h)
def dhhatdt_lin_sin(hhat,t,Vin,A,a,g,amp):
V=Vin+abs(amp*np.sin(np.pi*t))
R=(A*np.sqrt(2*hbar))/(a*np.sqrt(g))
Vinbar=Vin
Vinhat=V-Vinbar
return ((Vinhat/A)-(hhat/R))
hbar = Vin**2/(2*g*a**2)
hhat0 = h0-hbar
hlin = odeint(dhhatdt_lin_sin,hhat0,t,args=(Vin,A,a,g,amp))
hlin = hlin+hbar
hnon = odeint(dhdt_non_sin,h0,t,args=(Vin,A,a,g,amp))
ax.plot(t, hlin , color = 'blue', label ='linier')
ax.plot(t, hnon , color = 'red', label ='non-linier')
ax.title.set_text('Input Step dengan Gangguan Sinusoidal')
ax.legend()
if tab.selected_index == 0 :
hbar = Vin**2/(2*g*a**2)
R=(A*np.sqrt(2*hbar))/(a*np.sqrt(g))
hhat0 = h0-hbar
Vinbar= Vin
Vinhat= Vin-Vinbar
hlin = odeint(dhhatdt_lin,hhat0,t,args=(Vinhat,A,a,g,R))
hlin = hlin+hbar
hnon = odeint(dhdt_non,h0,t,args=(Vin,A,a,g))
ax.plot(t, hlin , color = 'blue' , label ='linier')
ax.plot(t, hnon , color = 'red', label='non-linier')
ax.title.set_text('Input Step')
ax.legend()
ui = tab
out = widgets.interactive_output(plot3,{'A':range_A,'a':range_a,'Vin':range_Vin,'h0':range_h0,'amp':range_amplitude,'tmax':time_slider})
display(ui,out)
```
# Pembahasan
Dari grafik di atas: kurva biru (linear) dan merah (non linear), dapat dilihat bahwa kurva merah dan biru tersebut terkadang sama atau hampir berhimpit yang berarti error antara linear dan non-linear kecil, namun terkadang juga tidak berhimpit dan error antara linear dan non-linear menjadi besar. Dapat digunakan interaksi untuk meninjau efek perubahan parameter terhadap model respon sistem yang dibentuk dengan persamaan non-linear dan linear. Untuk dapat melihat perbedaan respon persamaan linar dan persamaan nonlinear serta menentukan keterbatasan persamaan hasil linearisasi, kita akan membuat error tersebut agar menjadi besar. Untuk error maksimum atau minimum dapat digunakan tombol "error maksimum" dan "error minimum". Adapun cara yang dilakukan adalah:
#### 1) Memperkecil ketinggian awal (h0) dari fluida di tabung, sehingga rentang h0 dan hfinal semakin besar
Hal ini akan menyebabkan h dan hbar memiliki perbedaan nilai yang besar saat proses transien. Ketika rentang h0 dan hfinal membesar, pada saat respon belum steady, h dan hbar akan semakin menjauh karena nilai hbar yang diambil adalah saat keadaan steady.
#### 2) Meningkatkan luas alas tabung (A)
Untuk nilai A, semakin besar A, maka akan semakin lama keadaan steady tercapai. Maka semakin lama proses h menuju hbar pada steady state, sehingga error semakin besar.
#### 3) Mengecilkan luas pipa luaran (a) [saat respon sisem sedang meningkat]
#### 4) Memperbesar luas pipa luaran (a) [saat respon sistem sedang menurun]
Kemudian untuk a, yang merupakan variabel penentu banyaknya fluida yang keluar dari tangki menentukan apakah respon tersebut menurun atau meningkat. Di faktor 2, 3, dan 4 ini kita juga mengetahui bahwa error akan terjadi saat keadaan transien akibat hbar diasumsikan saat keadaan steady. Saat respon sistem meningkat, jika a semakin kecil, perubahan
## $ \frac{dh}{dt} - \frac{\bar{dh}}{dt} $
semakin besar sehingga error semakin besar pada saat transien. Berlaku sebaliknya saat respon sistem sedang menurun.
#### 5) Vin meningkat (saat respon sedang meningkat)
#### 6) Vin menurun (saat respon sedang menurun)
Dari faktor 5 dan 6 dapat dilihat bahwa saat kita meningkatkan nilai Vin, kurva biru (linear) akan semakin memperlambat keadaan steady (kurva semakin ke kanan) yang berarti error dari linearisasi semakin besar. Hal ini berhubungan dengan asumsi hbar diambil saat keadaan steady.
#### 7) Amplitudo sinusoidal yang meningkat
Faktor 7 menjelaskan hubungan Vinbar dan Vin harus berbeda nilai sekecil mungkin dan harus sesuai dengan rentang kerja sistem.
| true |
code
| 0.523786 | null | null | null | null |
|
# Simple ray tracing
```
# setup path to ray_tracing package
import sys
sys.path.append('~/Documents/python/ray_tracing/')
import ray_tracing as rt
from matplotlib import rcParams
rcParams['figure.figsize'] = [8, 4]
import matplotlib.pyplot as plt
plt.ion()
```
## Principle
The package 'ray_tracing.py' provides you with the means to quickly plot an optical system. Currently included are Lenses (L) with and without an aperture and simple apertures (A), such as irises, that are separated by distances (D). All ray tracing is done according to the paraxial approximation: $\sin \alpha \approx \tan \alpha \approx \alpha$, the larger $\alpha$ the larger the error!
### Example 1: one lens
Lets look at one lens of focal length 100 mm, an object shall be placed 150 mm apart from it and we look at two rays, __[the marginal and the principle ray](https://en.wikipedia.org/wiki/Ray_(optics))__. A ray is given as a vector $(h, \varphi)$, where $h$ is the height of the starting point and $\varphi$ is the angle measured against the optical axis in rad.
```
osys = rt.OpticalSystem(' d150 | L100 | d500 ')
height_1 = 0.0; phi_1 = 0.005;
ray_1 = (height_1, phi_1)
height_2 = 1.0; phi_2 = -1/150;
ray_2 = (height_2, phi_2)
ax = osys.plot_statics()
osys.plot_ray(ray_1, label="marginal ray")
osys.plot_ray(ray_2, label="chief ray")
ax.legend()
```
You can see that the marginal ray (blue) crosses the optical axis again at 450 mm. This is where the image is formed. The height of the chief (orange) ray at that position is 2.0 mm. Lets check that:
```
rt.get_image_pos(object_distance=150, focal_length=100)
rt.get_image_size(object_size=1.0, object_distance=150, focal_length=100)
```
The image is formed 300 mm after the lens, hence at 450 mm and it's magnified twice.
### Example 2: two lens system
```
osys = rt.OpticalSystem(' d150 | L100 | d400 | L50 | d150 ')
height_1 = 0.0; phi_1 = 0.005;
ray_1 = (height_1, phi_1)
height_2 = 1.0; phi_2 = -1/150;
ray_2 = (height_2, phi_2)
ax = osys.plot_statics()
osys.plot_ray(ray_1, label="marginal ray")
osys.plot_ray(ray_2, label="meridional ray")
ax.legend();
```
### Example 3: two lens system with apertures
Let's now consider an optical sytem with lenses of finite size. Apertures of lenses can be added by '/' following a number. Apertures of lenses are plotted as thick black lines.
```
osys = rt.OpticalSystem(' d150 | L100/1 | d400 | L50/2 | d150 ')
height_1 = 0.0; phi_1 = 0.005;
ray_1 = (height_1, phi_1)
height_2 = 1.0; phi_2 = -1/150;
ray_2 = (height_2, phi_2)
height_2 = 1.0; phi_2 = -1/150;
ray_2 = (height_2, phi_2)
height_3 = 0.5; phi_3 = -0.5/150;
ray_3 = (height_3, phi_3)
ax = osys.plot_statics()
osys.plot_ray(ray_1, label="marginal ray")
osys.plot_ray(ray_2, label="chief ray")
osys.plot_ray(ray_3, label="meridional ray")
ax.legend();
```
Rays not passing an aperture
```
"""
ray traycing: led | d0 | l1 | d1 | l2 | d2 | d3 | l3 | d4 | l4 | d5 | d6 | obj | d7
"""
trace = 'd15 | L15/5.5 | d10 | L40/12.5 | d40 | d80 | L80/15 | d60 | L300/16 | d300 | d3.33 | L3.33/4.4 | d3.33'
sequence = rt.trace_parser(trace)
from numpy import arange
plt.ion()
plt.close('all')
fig = plt.figure()
ax = fig.add_subplot(111)
for idx, h in enumerate(arange(-0.5, 0.6, 0.125)):
rt.plot_ray(h, sequence, axis=ax )
fig.subplots_adjust(right=0.8)
ax.legend(loc='center right', bbox_to_anchor=(1.3, 0.5));
```
| true |
code
| 0.624723 | null | null | null | null |
|
```
#default_exp utils
```
# Utility Functions
> Utility functions to help with downstream tasks
```
#hide
from nbdev.showdoc import *
from self_supervised.byol import *
from self_supervised.simclr import *
from self_supervised.swav import *
#export
from fastai.vision.all import *
```
## Loading Weights for Downstream Tasks
```
#export
def transfer_weights(learn:Learner, weights_path:Path, device:torch.device=None):
"Load and freeze pretrained weights inplace from `weights_path` using `device`"
if device is None: device = learn.dls.device
new_state_dict = torch.load(weights_path, map_location=device)
if 'model' in new_state_dict.keys(): new_state_dict = new_state_dict['model']
#allow for simply exporting the raw PyTorch model
learn_state_dict = learn.model.state_dict()
matched_layers = 0
for name, param in learn_state_dict.items():
name = 'encoder.'+name[2:]
if name in new_state_dict:
matched_layers += 1
input_param = new_state_dict[name]
if input_param.shape == param.shape:
param.copy_(input_param)
else:
raise ValueError(f'Shape mismatch at {name}, please ensure you have the same backbone')
else: pass # these are weights that weren't in the original model, such as a new head
if matched_layers == 0: raise Exception("No shared weight names were found between the models")
learn.model.load_state_dict(learn_state_dict)
learn.freeze()
print("Weights successfully transferred!")
```
When training models with this library, the `state_dict` will change, so loading it back into `fastai` as an encoder won't be a perfect match. This helper function aims to make that simple.
Example usage:
First prepare the downstream-task dataset (`ImageWoof` is shown here):
```
def get_dls(bs:int=32):
"Prepare `IMAGEWOOF` `DataLoaders` with `bs`"
path = untar_data(URLs.IMAGEWOOF)
tfms = [[PILImage.create], [parent_label, Categorize()]]
item_tfms = [ToTensor(), Resize(224)]
batch_tfms = [FlipItem(), RandomResizedCrop(224, min_scale=0.35),
IntToFloatTensor(), Normalize.from_stats(*imagenet_stats)]
items = get_image_files(path)
splits = GrandparentSplitter(valid_name='val')(items)
dsets = Datasets(items, tfms, splits=splits)
dls = dsets.dataloaders(after_item=item_tfms, after_batch=batch_tfms,
bs=32)
return dls
dls = get_dls(bs=32)
```
For the sake of example we will make and save a SWaV model trained for one epoch (in reality you'd want to train for many more):
```
net = create_swav_model(arch=xresnet34, pretrained=False)
learn = Learner(dls, net, SWAVLoss(), cbs=[SWAV()])
learn.save('../../../swav_test');
```
Followed by a `Learner` designed for classification with a simple custom head for our `xresnet`:
```
learn = cnn_learner(dls, xresnet34, pretrained=False)
```
Before loading in all the weights:
```
transfer_weights(learn, '../../swav_test.pth')
```
Now we can do downstream tasks with our pretrained models!
| true |
code
| 0.676393 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
from scipy import stats
from statsmodels.stats.proportion import proportion_confint
from statsmodels.stats.weightstats import CompareMeans, DescrStatsW, ztest
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from statsmodels.stats.weightstats import *
from statsmodels.stats.proportion import proportion_confint
import warnings
warnings.filterwarnings('ignore')
```
Прежде всего, скопируем нужные функции из учебного ноутбука. Они понадобятся.
```
def proportions_diff_confint_ind(sample1, sample2, alpha = 0.05):
z = scipy.stats.norm.ppf(1 - alpha / 2.)
p1 = float(sum(sample1)) / len(sample1)
p2 = float(sum(sample2)) / len(sample2)
left_boundary = (p1 - p2) - z * np.sqrt(p1 * (1 - p1)/ len(sample1) + p2 * (1 - p2)/ len(sample2))
right_boundary = (p1 - p2) + z * np.sqrt(p1 * (1 - p1)/ len(sample1) + p2 * (1 - p2)/ len(sample2))
return (left_boundary, right_boundary)
def proportions_diff_z_stat_ind(sample1, sample2):
n1 = len(sample1)
n2 = len(sample2)
p1 = float(sum(sample1)) / n1
p2 = float(sum(sample2)) / n2
P = float(p1*n1 + p2*n2) / (n1 + n2)
return (p1 - p2) / np.sqrt(P * (1 - P) * (1. / n1 + 1. / n2))
def proportions_diff_z_test(z_stat, alternative = 'two-sided'):
if alternative not in ('two-sided', 'less', 'greater'):
raise ValueError("alternative not recognized\n"
"should be 'two-sided', 'less' or 'greater'")
if alternative == 'two-sided':
return 2 * (1 - scipy.stats.norm.cdf(np.abs(z_stat)))
if alternative == 'less':
return scipy.stats.norm.cdf(z_stat)
if alternative == 'greater':
return 1 - scipy.stats.norm.cdf(z_stat)
def proportions_diff_confint_rel(sample1, sample2, alpha = 0.05):
z = scipy.stats.norm.ppf(1 - alpha / 2.)
sample = list(zip(sample1, sample2))
n = len(sample)
f = sum([1 if (x[0] == 1 and x[1] == 0) else 0 for x in sample])
g = sum([1 if (x[0] == 0 and x[1] == 1) else 0 for x in sample])
left_boundary = float(f - g) / n - z * np.sqrt(float((f + g)) / n**2 - float((f - g)**2) / n**3)
right_boundary = float(f - g) / n + z * np.sqrt(float((f + g)) / n**2 - float((f - g)**2) / n**3)
return (left_boundary, right_boundary)
def proportions_diff_z_stat_rel(sample1, sample2):
sample = list(zip(sample1, sample2))
n = len(sample)
f = sum([1 if (x[0] == 1 and x[1] == 0) else 0 for x in sample])
g = sum([1 if (x[0] == 0 and x[1] == 1) else 0 for x in sample])
return float(f - g) / np.sqrt(f + g - float((f - g)**2) / n )
```
В одном из выпусков программы "Разрушители легенд" проверялось, действительно ли заразительна зевота. В эксперименте участвовало 50 испытуемых, проходивших собеседование на программу. Каждый из них разговаривал с рекрутером; в конце 34 из 50 бесед рекрутер зевал. Затем испытуемых просили подождать решения рекрутера в соседней пустой комнате.
Во время ожидания 10 из 34 испытуемых экспериментальной группы и 4 из 16 испытуемых контрольной начали зевать. Таким образом, разница в доле зевающих людей в этих двух группах составила примерно 4.4%. Ведущие заключили, что миф о заразительности зевоты подтверждён.
Можно ли утверждать, что доли зевающих в контрольной и экспериментальной группах отличаются статистически значимо? Посчитайте достигаемый уровень значимости при альтернативе заразительности зевоты, округлите до четырёх знаков после десятичной точки.
Имеются данные измерений двухсот швейцарских тысячефранковых банкнот, бывших в обращении в первой половине XX века. Сто из банкнот были настоящими, и сто — поддельными.
Отделите 50 случайных наблюдений в тестовую выборку с помощью функции $\textbf{sklearn.cross_validation.train_test_split}$ (зафиксируйте $\textbf{random state = 1)}$. На оставшихся $150$ настройте два классификатора поддельности банкнот:
1. логистическая регрессия по признакам $X_1,X_2,X_3$
2. логистическая регрессия по признакам $X_4,X_5,X_6$
Каждым из классификаторов сделайте предсказания меток классов на тестовой выборке. Одинаковы ли доли ошибочных предсказаний двух классификаторов? Проверьте гипотезу, вычислите достигаемый уровень значимости. Введите номер первой значащей цифры (например, если вы получили $5.5\times10^{-8}$, нужно ввести 8).
```
df = pd.read_table('banknotes.txt')
y = df['real']
X = df.drop(['real'], axis=1)
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state = 1, test_size = 50)
X1_train = X_train[['X1', 'X2','X3']]
X2_train = X_train[['X4','X5','X6']]
X1_test = X_test[['X1', 'X2','X3']]
X2_test = X_test[['X4','X5','X6']]
logreg = LogisticRegression()
logreg.fit(X1_train, y_train)
pred1 = logreg.predict(X1_test)
logreg.fit(X2_train, y_train)
pred2 = logreg.predict(X2_test)
pred1_acc = np.array([1 if pred1[i] == np.array(y_test)[i] else 0 for i in range(len(pred1))])
pred2_acc = np.array([1 if pred2[i] == np.array(y_test)[i] else 0 for i in range(len(pred2))])
print('First prediction accuracy:', sum(pred1_acc)/len(pred1_acc),
'\n','Second prediction accuracy:', sum(pred2_acc)/len(pred2_acc))
```
Вывод - доли ошибок не одинаковы
В предыдущей задаче посчитайте $95\%$ доверительный интервал для разности долей ошибок двух классификаторов. Чему равна его ближайшая к нулю граница? Округлите до четырёх знаков после десятичной точки.
Построим $95\%$ доверительный интервал для разницы предсказаний
```
print('95%% доверительный интервал для разницы предсказаний: [%.4f, %.4f]' %
proportions_diff_confint_rel(pred1_acc, pred2_acc))
print ("p-value: %f" % proportions_diff_z_test(proportions_diff_z_stat_rel(pred1_acc, pred2_acc)))
```
Ежегодно более 200000 людей по всему миру сдают стандартизированный экзамен GMAT при поступлении на программы MBA. Средний результат составляет 525 баллов, стандартное отклонение — 100 баллов.
Сто студентов закончили специальные подготовительные курсы и сдали экзамен. Средний полученный ими балл — 541.4. Проверьте гипотезу о неэффективности программы против односторонней альтернативы о том, что программа работает. Отвергается ли на уровне значимости 0.05 нулевая гипотеза? Введите достигаемый уровень значимости, округлённый до 4 знаков после десятичной точки.
```
n = 100
mean_result = 525
stand_dev = 100
mean_spec = 541.4
alpha = 0.05
```
Реализуем формулу: $Z(X^n) = \frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}$
```
def z_conf(mu, sigma, n, x_mean):
return (x_mean - mu)/(sigma / np.sqrt(n))
print((z_conf(mu = mean_result, x_mean=mean_spec, n=n, sigma=stand_dev)))
print(round(1-stats.norm.cdf(z_conf(mu = mean_result, x_mean=mean_spec, n=n, sigma=stand_dev)),4))
```
Оцените теперь эффективность подготовительных курсов, средний балл 100 выпускников которых равен 541.5. Отвергается ли на уровне значимости 0.05 та же самая нулевая гипотеза против той же самой альтернативы? Введите достигаемый уровень значимости, округлённый до 4 знаков после десятичной точки.
```
print((z_conf(mu = mean_result, x_mean=541.5, n=n, sigma=stand_dev)))
print(round(1-stats.norm.cdf(z_conf(mu = mean_result, x_mean=541.5, n=n, sigma=stand_dev)),4))
```
| true |
code
| 0.453262 | null | null | null | null |
|
```
import sys # for automation and parallelisation
manual, scenario = (True, 'base') if 'ipykernel' in sys.argv[0] else (False, sys.argv[1])
if manual:
%matplotlib inline
import numpy as np
import pandas as pd
from quetzal.model import stepmodel
```
# Modelling steps 1 and 2.
## Saves transport demand between zones
## Needs zones
```
input_path = '../input/transport_demand/'
output_path = '../output/'
model_path = '../model/'
sm = stepmodel.read_json(model_path + 'de_zones')
```
### Emission and attraction with quetzal
Steps: Generation and distribution --> Transport demand in volumes<br>
Transport volumes can be generated by using the function<br>
step_distribution(impedance_matrix=None, **od_volume_from_zones_kwargs)<br>
:param impedance_matrix: an OD unstaked friction dataframe<br>
used to compute the distribution.<br>
:param od_volume_from_zones_kwargs: if the friction matrix is not<br>
provided, it will be automatically computed using a gravity<br>
distribution which uses the following parameters:<br>
param power: (int) the gravity exponent<br>
param intrazonal: (bool) set the intrazonal distance to 0 if False,<br>
compute a characteristic distance otherwise.<br>
Or create the volumes from input data<br>
### Load transport demand data from VP2030
The German federal government's transport study "[Bundesverkehrswegeplan 2030](https://www.bmvi.de/SharedDocs/DE/Artikel/G/BVWP/bundesverkehrswegeplan-2030-inhalte-herunterladen.html)" uses origin destination matrices on NUTS3-level resolution and makes them accessible under copyright restrictions for the base year and the year of prognosis. These matrices cannot be published in their original form.
```
vp2010 = pd.read_excel(input_path + 'PVMatrix_BVWP15_A2010.xlsx')
vp2030 = pd.read_excel(input_path + 'PVMatrix_BVWP15_P2030.xlsx')
#print(vp2010.shape)
vp2010[vp2010.isna().any(axis=1)]
for df in [vp2010, vp2030]:
df.rename(columns={'# Quelle': 'origin', 'Ziel': 'destination'}, inplace=True)
def get_vp2017(vp2010_i, vp2030_i):
return vp2010_i + (vp2030_i - vp2010_i) * (7/20)
# Calculate a OD table for the year 2017
vp2017 = get_vp2017(vp2010.set_index(['origin', 'destination']),
vp2030.set_index(['origin', 'destination']))
vp2017.dropna(how='all', inplace=True)
#print(vp2010.shape)
vp2017[vp2017.isna().any(axis=1)]
vp2017 = vp2017[list(vp2017.columns)].astype(int)
#vp2017.head()
```
### Create the volumes table
```
# Sum up trips by purpose
for suffix in ['Fz1', 'Fz2', 'Fz3', 'Fz4', 'Fz5', 'Fz6']:
vp2017[suffix] = vp2017[[col for col in list(vp2017.columns) if col[-3:] == suffix]].sum(axis=1)
# Merge purpose 5 and 6 due to calibration data limitations
vp2017['Fz6'] = vp2017['Fz5'] + vp2017['Fz6']
# Replace LAU IDs with NUTS IDs in origin and destination
nuts_lau_dict = sm.zones.set_index('lau_id')['NUTS_ID'].to_dict()
vp2017.reset_index(level=['origin', 'destination'], inplace=True)
# Zones that appear in the VP (within Germany) but not in the model
sorted([i for i in set(list(vp2017['origin'])+list(vp2017['destination'])) -
set([int(k) for k in nuts_lau_dict.keys()]) if i<=16077])
# Most of the above numbers are airports in the VP, however
# NUTS3-level zones changed after the VP2030
# Thus the VP table needs to be updated manually
update_dict = {3156: 3159, 3152: 3159, # Göttingen
13001: 13075, 13002: 13071, 13005: 13073, 13006: 13074,
13051: 13072, 13052: 13071, 13053: 13072, 13054: 13076, 13055: 13071, 13056: 13071,
13057: 13073, 13058: 13074, 13059: 13075, 13060: 13076, 13061: 13073, 13062: 13075}
# What is the sum of all trips? For Validation
cols = [c for c in vp2017.columns if c not in ['origin', 'destination']]
orig_sum = vp2017[cols].sum().sum()
orig_sum
# Update LAU codes
vp2017['origin'] = vp2017['origin'].replace(update_dict)
vp2017['destination'] = vp2017['destination'].replace(update_dict)
sorted([i for i in set(list(vp2017['origin'])+list(vp2017['destination'])) -
set([int(k) for k in nuts_lau_dict.keys()]) if i<=16077])
# Replace LAU with NUTS
vp2017['origin'] = vp2017['origin'].astype(str).map(nuts_lau_dict)
vp2017['destination'] = vp2017['destination'].astype(str).map(nuts_lau_dict)
# Restrict to cells in the model
vp2017 = vp2017[~vp2017.isna().any(axis=1)]
vp2017.shape
# What is the sum of all trips after ditching outer-German trips?
vp_sum = vp2017[cols].sum().sum()
vp_sum / orig_sum
# Aggregate OD pairs
vp2017 = vp2017.groupby(['origin', 'destination']).sum().reset_index()
vp2017[cols].sum().sum() / orig_sum
```
### Add car ownership segments
```
sm.volumes = vp2017[['origin', 'destination', 'Fz1', 'Fz2', 'Fz3', 'Fz4', 'Fz6']
].copy().set_index(['origin', 'destination'], drop=True)
# Car availabilities from MiD2017 data
av = dict(zip(list(sm.volumes.columns),
[0.970375, 0.965208, 0.968122, 0.965517, 0.95646]))
# Split purpose cells into car ownership classes
for col in sm.volumes.columns for car in [0,1]:
sm.volumes[(col, car)] = sm.volumes[col] * abs(((1-car)*1 - av[col]))
sm.volumes.drop(col, inplace=True)
sm.volumes.reset_index(inplace=True)
```
## Save model
```
sm.volumes.shape
sm.volumes.columns
# Empty rows?
assert len(sm.volumes.loc[sm.volumes.sum(axis=1)==0])==0
# Saving volumes
sm.to_json(model_path + 'de_volumes', only_attributes=['volumes'], encoding='utf-8')
```
## Create validation table
Generate a normalised matrix for the year 2017 in order to validate model results against each other. It is needed for the calibration step.
```
# Merge purpose 5 and 6
for prefix in ['Bahn', 'MIV', 'Luft', 'OESPV', 'Rad', 'Fuß']:
vp2017[prefix + '_Fz6'] = vp2017[prefix + '_Fz5'] + vp2017[prefix + '_Fz6']
vp2017 = vp2017[[col for col in list(vp2017.columns) if col[-1]!='5']]
# Merge bicycle and foot
for p in [1,2,3,4,6]:
vp2017['non_motor_Fz' + str(p)] = vp2017['Rad_Fz' + str(p)] + vp2017['Fuß_Fz' + str(p)]
vp2017 = vp2017[[col for col in list(vp2017.columns) if not col[:3] in ['Rad', 'Fuß']]]
# Prepare columns
vp2017.set_index(['origin', 'destination'], drop=True, inplace=True)
vp2017 = vp2017[[col for col in vp2017.columns if col[:2]!='Fz']]
vp2017.columns
# Normalise
vp2017_norm = (vp2017-vp2017.min())/(vp2017.max()-vp2017.min()).max()
vp2017_norm.sample(5)
# Save normalised table
vp2017_norm.to_csv(input_path + 'vp2017_validation_normalised.csv')
vp2017_norm.columns = pd.MultiIndex.from_tuples(
[(col.split('_')[0], col.split('_')[-1]) for col in vp2017_norm.columns],
names=['mode', 'segment'])
if manual:
vp2017_norm.T.sum(axis=1).unstack('segment').plot.pie(
subplots=True, figsize=(16, 4), legend=False)
# Restrict to inter-cell traffic and cells of the model
vp2017_norm.reset_index(level=['origin', 'destination'], inplace=True)
vp2017_norm = vp2017_norm.loc[(vp2017_norm['origin']!=vp2017_norm['destination']) &
(vp2017_norm['origin'].notna()) &
(vp2017_norm['destination'].notna())]
vp2017_norm.set_index(['origin', 'destination'], drop=True, inplace=True)
if manual:
vp2017_norm.T.sum(axis=1).unstack('segment').plot.pie(
subplots=True, figsize=(16, 4), legend=False)
# Clear the RAM if notebook stays open
vp2010 = None
vp2030 = None
```
| true |
code
| 0.220175 | null | null | null | null |
|
# Customize a TabNet Model
## This tutorial gives examples on how to easily customize a TabNet Model
### 1 - Customizing your learning rate scheduler
Almost all classical pytroch schedulers are now easy to integrate with pytorch-tabnet
### 2 - Use your own loss function
It's really easy to use any pytorch loss function with TabNet, we'll walk you through that
### 3 - Customizing your evaluation metric and evaluations sets
Like XGBoost, you can easily monitor different metrics on different evaluation sets with pytorch-tabnet
```
from pytorch_tabnet.tab_model import TabNetClassifier
import torch
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import roc_auc_score
import pandas as pd
import numpy as np
np.random.seed(0)
import os
import wget
from pathlib import Path
from matplotlib import pyplot as plt
%matplotlib inline
```
### Download census-income dataset
```
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data"
dataset_name = 'census-income'
out = Path(os.getcwd()+'/data/'+dataset_name+'.csv')
out.parent.mkdir(parents=True, exist_ok=True)
if out.exists():
print("File already exists.")
else:
print("Downloading file...")
wget.download(url, out.as_posix())
```
### Load data and split
```
train = pd.read_csv(out)
target = ' <=50K'
if "Set" not in train.columns:
train["Set"] = np.random.choice(["train", "valid", "test"], p =[.8, .1, .1], size=(train.shape[0],))
train_indices = train[train.Set=="train"].index
valid_indices = train[train.Set=="valid"].index
test_indices = train[train.Set=="test"].index
```
### Simple preprocessing
Label encode categorical features and fill empty cells.
```
nunique = train.nunique()
types = train.dtypes
categorical_columns = []
categorical_dims = {}
for col in train.columns:
if types[col] == 'object' or nunique[col] < 200:
print(col, train[col].nunique())
l_enc = LabelEncoder()
train[col] = train[col].fillna("VV_likely")
train[col] = l_enc.fit_transform(train[col].values)
categorical_columns.append(col)
categorical_dims[col] = len(l_enc.classes_)
else:
train.fillna(train.loc[train_indices, col].mean(), inplace=True)
```
### Define categorical features for categorical embeddings
```
unused_feat = ['Set']
features = [ col for col in train.columns if col not in unused_feat+[target]]
cat_idxs = [ i for i, f in enumerate(features) if f in categorical_columns]
cat_dims = [ categorical_dims[f] for i, f in enumerate(features) if f in categorical_columns]
```
# 1 - Customizing your learning rate scheduler
TabNetClassifier, TabNetRegressor and TabNetMultiTaskClassifier all takes two arguments:
- scheduler_fn : Any torch.optim.lr_scheduler should work
- scheduler_params : A dictionnary that contains the parameters of your scheduler (without the optimizer)
----
NB1 : Some schedulers like torch.optim.lr_scheduler.ReduceLROnPlateau depend on the evolution of a metric, pytorch-tabnet will use the early stopping metric you asked (the last eval_metric, see 2-) to perform the schedulers updates
EX1 :
```
scheduler_fn=torch.optim.lr_scheduler.ReduceLROnPlateau
scheduler_params={"mode":'max', # max because default eval metric for binary is AUC
"factor":0.1,
"patience":1}
```
-----
NB2 : Some schedulers require updates at batch level, they can be used very easily the only thing to do is to add `is_batch_level` to True in your `scheduler_params`
EX2:
```
scheduler_fn=torch.optim.lr_scheduler.CyclicLR
scheduler_params={"is_batch_level":True,
"base_lr":1e-3,
"max_lr":1e-2,
"step_size_up":100
}
```
-----
NB3: Note that you can also customize your optimizer function, any torch optimizer should work
```
# Network parameters
max_epochs = 20 if not os.getenv("CI", False) else 2
batch_size = 1024
clf = TabNetClassifier(cat_idxs=cat_idxs,
cat_dims=cat_dims,
cat_emb_dim=1,
optimizer_fn=torch.optim.Adam, # Any optimizer works here
optimizer_params=dict(lr=2e-2),
scheduler_fn=torch.optim.lr_scheduler.OneCycleLR,
scheduler_params={"is_batch_level":True,
"max_lr":5e-2,
"steps_per_epoch":int(train.shape[0] / batch_size)+1,
"epochs":max_epochs
},
mask_type='entmax', # "sparsemax",
)
```
### Training
```
X_train = train[features].values[train_indices]
y_train = train[target].values[train_indices]
X_valid = train[features].values[valid_indices]
y_valid = train[target].values[valid_indices]
X_test = train[features].values[test_indices]
y_test = train[target].values[test_indices]
```
# 2 - Use your own loss function
The default loss for classification is torch.nn.functional.cross_entropy
The default loss for regression is torch.nn.functional.mse_loss
Any derivable loss function of the type lambda y_pred, y_true : loss(y_pred, y_true) should work if it uses torch computation (to allow gradients computations).
In particular, any pytorch loss function should work.
Once your loss is defined simply pass it loss_fn argument when defining your model.
/!\ : One important thing to keep in mind is that when computing the loss for TabNetClassifier and TabNetMultiTaskClassifier you'll need to apply first torch.nn.Softmax() to y_pred as the final model prediction is softmaxed automatically.
NB : Tabnet also has an internal loss (the sparsity loss) which is summed to the loss_fn, the importance of the sparsity loss can be mitigated using `lambda_sparse` parameter
```
def my_loss_fn(y_pred, y_true):
"""
Dummy example similar to using default torch.nn.functional.cross_entropy
"""
softmax_pred = torch.nn.Softmax(dim=-1)(y_pred)
logloss = (1-y_true)*torch.log(softmax_pred[:,0])
logloss += y_true*torch.log(softmax_pred[:,1])
return -torch.mean(logloss)
```
# 3 - Customizing your evaluation metric and evaluations sets
When calling the `fit` method you can speficy:
- eval_set : a list of tuples like (X_valid, y_valid)
Note that the last value of this list will be used for early stopping
- eval_name : a list to name each eval set
default will be val_0, val_1 ...
- eval_metric : a list of default metrics or custom metrics
Default : "auc", "accuracy", "logloss", "balanced_accuracy", "mse", "rmse"
NB : If no eval_set is given no early stopping will occure (patience is then ignored) and the weights used will be the last epoch's weights
NB2 : If `patience<=0` this will disable early stopping
NB3 : Setting `patience` to `max_epochs` ensures that training won't be early stopped, but best weights from the best epochs will be used (instead of the last weight if early stopping is disabled)
```
from pytorch_tabnet.metrics import Metric
class my_metric(Metric):
"""
2xAUC.
"""
def __init__(self):
self._name = "custom" # write an understandable name here
self._maximize = True
def __call__(self, y_true, y_score):
"""
Compute AUC of predictions.
Parameters
----------
y_true: np.ndarray
Target matrix or vector
y_score: np.ndarray
Score matrix or vector
Returns
-------
float
AUC of predictions vs targets.
"""
return 2*roc_auc_score(y_true, y_score[:, 1])
clf.fit(
X_train=X_train, y_train=y_train,
eval_set=[(X_train, y_train), (X_valid, y_valid)],
eval_name=['train', 'val'],
eval_metric=["auc", my_metric],
max_epochs=max_epochs , patience=0,
batch_size=batch_size,
virtual_batch_size=128,
num_workers=0,
weights=1,
drop_last=False,
loss_fn=my_loss_fn
)
# plot losses
plt.plot(clf.history['loss'])
# plot auc
plt.plot(clf.history['train_auc'])
plt.plot(clf.history['val_auc'])
# plot learning rates
plt.plot(clf.history['lr'])
```
## Predictions
```
preds = clf.predict_proba(X_test)
test_auc = roc_auc_score(y_score=preds[:,1], y_true=y_test)
preds_valid = clf.predict_proba(X_valid)
valid_auc = roc_auc_score(y_score=preds_valid[:,1], y_true=y_valid)
print(f"FINAL VALID SCORE FOR {dataset_name} : {clf.history['val_auc'][-1]}")
print(f"FINAL TEST SCORE FOR {dataset_name} : {test_auc}")
# check that last epoch's weight are used
assert np.isclose(valid_auc, clf.history['val_auc'][-1], atol=1e-6)
```
# Save and load Model
```
# save tabnet model
saving_path_name = "./tabnet_model_test_1"
saved_filepath = clf.save_model(saving_path_name)
# define new model with basic parameters and load state dict weights
loaded_clf = TabNetClassifier()
loaded_clf.load_model(saved_filepath)
loaded_preds = loaded_clf.predict_proba(X_test)
loaded_test_auc = roc_auc_score(y_score=loaded_preds[:,1], y_true=y_test)
print(f"FINAL TEST SCORE FOR {dataset_name} : {loaded_test_auc}")
assert(test_auc == loaded_test_auc)
```
# Global explainability : feat importance summing to 1
```
clf.feature_importances_
```
# Local explainability and masks
```
explain_matrix, masks = clf.explain(X_test)
fig, axs = plt.subplots(1, 3, figsize=(20,20))
for i in range(3):
axs[i].imshow(masks[i][:50])
axs[i].set_title(f"mask {i}")
```
# XGB
```
from xgboost import XGBClassifier
clf_xgb = XGBClassifier(max_depth=8,
learning_rate=0.1,
n_estimators=1000,
verbosity=0,
silent=None,
objective='binary:logistic',
booster='gbtree',
n_jobs=-1,
nthread=None,
gamma=0,
min_child_weight=1,
max_delta_step=0,
subsample=0.7,
colsample_bytree=1,
colsample_bylevel=1,
colsample_bynode=1,
reg_alpha=0,
reg_lambda=1,
scale_pos_weight=1,
base_score=0.5,
random_state=0,
seed=None,)
clf_xgb.fit(X_train, y_train,
eval_set=[(X_valid, y_valid)],
early_stopping_rounds=40,
verbose=10)
preds = np.array(clf_xgb.predict_proba(X_valid))
valid_auc = roc_auc_score(y_score=preds[:,1], y_true=y_valid)
print(valid_auc)
preds = np.array(clf_xgb.predict_proba(X_test))
test_auc = roc_auc_score(y_score=preds[:,1], y_true=y_test)
print(test_auc)
```
| true |
code
| 0.65861 | null | null | null | null |
|
# `pymdptoolbox` demo
```
import warnings
from mdptoolbox import mdp
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
```
## The problem
* You have a 20-sided die, and you get to roll repeatedly until the sum of your rolls either gets as close as possible to 21 or you bust.
* Your score is the numerical value of the sum of your rolls; if you bust, you get zero.
* What is the optimal strategy?

## The solution
Let's look at what we have to deal with:
* State space is 23-dimensional (sum of rolls can be 0-21 inclusive, plus the terminal state)
* Action space is 2-dimensional (roll/stay)
* State transitions are stochastic; requires transition matrix $T(s^\prime;s,a)$
* $T$ is mildly sparse (some transitions like 9->5 or 0->21 are impossible)
* Rewards depend on both state and action taken from that state, but are not stochastic (only ever get positive reward when choosing "stay")
We're going to use the [*value iteration*](https://pymdptoolbox.readthedocs.io/en/latest/api/mdp.html#mdptoolbox.mdp.ValueIteration) algorithm. Looking at the documentation, we can see that it requires as input a transition matrx, a reward matrix, and a discount factor (we will use $\gamma = 1$).
Let's first specify the transition "matrix". It's going to be a 3-dimensional tensor of shape $(|\mathcal{A}|,|\mathcal{S}|,|\mathcal{S}|) = (2, 23, 23)$. Most entries are probably zero, so let's start with a zero matrix and fill in the blanks. I'm going reserve the very last state (the 23rd entry) for the terminal state.
```
def make_transition_matrix(n_sides=20, max_score=21):
"""Constructs the transition matrix for the MDP
Arguments:
n_sides: number of sides on the die being rolled
max_score: the maximum score of the game before going bust
Returns:
np.ndarray: array of shape (A,S,S), where A=2, and S=max_score+2
representing the transition matrix for the MDP
"""
A = 2
S = max_score + 2
T = np.zeros(shape=(A, S, S))
p = 1/n_sides
# All the "roll" action transitions
# First, the transition from state s to any non terminal state s' has probability
# 1/n_sides unless s' <= s or s' > s + n_sides
for s in range(0, S-1):
for sprime in range(s+1, S-1):
if sprime <= s + n_sides:
T[0,s,sprime] = p
# The rows of T[0] must all sum to one, so all the remaining probability goes to
# the terminal state
for s in range(0, S-1):
T[0,s,S-1] = 1 - T[0,s].sum()
# It is impossible to transition out of the terminal state; it is "absorbing"
T[0,S-1,S-1] = 1
# All the "stay" action transitions
# This one is simple - all "stay" transitions dump you in the terminal state,
# regardless of starting state
T[1,:,S-1] = 1
T[T<0] = 0 # There may be some very small negative probabilities due to rounding
# errors - this fixes errythang
return T
# Take a peek at a smaller version
T = make_transition_matrix(n_sides=4, max_score=5)
print("roll transitions:")
print(T[0])
print("\nstay transitions:")
print(T[1])
```
Now let's build the reward matrix. This is going to be a tensor of shape $(|\mathcal{S}|,|\mathcal{A}|) = (23,2)$. This one is even simpler than the transition matrix because only "stay" actions generate nonzero rewards, which are equal to the index of the state itself.
```
def make_reward_matrix(max_score=21):
"""Create the reward matrix for the MDP.
Arguments:
max_score: the maximum score of the game before going bust
Returns:
np.ndarray: array of shape (S,A), where A=2, and S=max_score+2
representing the reward matrix for the MDP
"""
A = 2
S = max_score + 2
R = np.zeros(shape=(S, A))
# Only need to create rewards for the "stay" action
# Rewards are equal to the state index, except for the terminal state, which
# always returns zero
for s in range(0, S-1):
R[s,1] = s
return R
# Take a peek at a smaller version
R = make_reward_matrix(max_score=5)
print("roll rewards:")
print(R[:,0])
print("\nstay rewards:")
print(R[:,1])
```
## The algorithm
Alright, now that we have the transition and reward matrices, our MDP is completely defined, and we can use the `pymdptoolbox` to help us figure out the optimal policy/strategy.
```
n_sides = 20
max_score = 21
T = make_transition_matrix(n_sides, max_score)
R = make_reward_matrix(max_score)
model = mdp.ValueIteration(
transitions=T,
reward=R,
discount=1,
epsilon=0.001,
max_iter=1000,
)
model.setVerbose()
model.run()
print(f"Algorithm finished running in {model.time:.2e} seconds")
```
That ran pretty fast, didn't it? Unfortunately most realistic MDP problems have millions or billions of possible states (or more!), so this doesn't really scale very well. But it works for our small problem very well.
## The results
Now let's analyze the results. The `ValueIteration` object gives us easy access to the optimal value function and policy.
```
plt.plot(model.V, marker='o')
x = np.linspace(0, max_score, 10)
plt.plot(x, x, linestyle="--", color='black')
ticks = list(range(0, max_score+1, 5)) + [max_score+1]
labels = [str(x) for x in ticks[:-1]] + ["\u2205"]
plt.xticks(ticks, labels)
plt.xlim(-1, max_score+2)
plt.xlabel("State sum of rolls $s$")
plt.ylabel("State value $V$")
plt.title("MDP optimal value function $V^*(s)$")
plt.show()
plt.plot(model.policy, marker='o')
ticks = list(range(0, max_score+1, 5)) + [max_score+1]
labels = [str(x) for x in ticks[:-1]] + ["\u2205"]
plt.xticks(ticks, labels)
plt.xlim(-1, max_score+2)
ticks = [0, 1]
labels = ["roll", "stay"]
plt.yticks(ticks, labels)
plt.ylim(-0.25, 1.25)
plt.xlabel("State sum of rolls $s$")
plt.ylabel("Policy $\pi$")
plt.title("MDP optimal policy $\pi^*(s)$")
plt.show()
```
Looks like the optimal policy is to keep rolling until the sum gets to 10. This is why $V(s) = s$ for $s>=10$ (black dashed line); because that's the score you end up with when following this policy. For $s<10$, it's actually a bit higher than $s$ because you get an opportunity to roll again to get a higher score, and the sum is low enough that your chances of busting are relatively low. We can see the slope is positive for $s \le 21 - 20 = 1$ because it's impossible to bust below that point, but the slope becomes negative between $1 \le s \le 10$ because you're more likely to bust the higher you get.
We can also calculate the state distribution $\rho_\pi(s_0 \rightarrow s,t)$, which tells us the probability to be in any one of the states $s$ after a time $t$ when starting from state $s_0$:
$$
\rho_\pi(s_0 \rightarrow s,t) = \sum_{s^\prime} T(s;s^\prime,\pi(s^\prime)) \rho_\pi(s_0 \rightarrow s^\prime, t-1) \\
\text{where }\rho_\pi(s_0 \rightarrow s, 0) = \delta_{s, s_0}
$$
```
def calculate_state_distribution(policy, T, t_max=10):
S = len(policy)
# Reduce transition matrix to T(s';s) since policy is fixed
T_ = np.zeros(shape=(S, S))
for s in range(S):
for sprime in range(S):
T_[s,sprime] = T[policy[s],s,sprime]
T = T_
# Initialize rho
rho = np.zeros(shape=(S, S, t_max+1))
for s in range(0, S):
rho[s,s,0] = 1
# Use the iterative update equation
for t in range(1, t_max+1):
rho[:,:,t] = np.einsum("ji,kj->ki", T, rho[:,:,t-1])
return rho
rho = calculate_state_distribution(model.policy, T, 5)
with warnings.catch_warnings():
warnings.simplefilter('ignore') # Ignore the divide by zero error from taking log(0)
plt.imshow(np.log10(rho[0].T), cmap='viridis')
cbar = plt.colorbar(shrink=0.35, aspect=9)
cbar.ax.set_title(r"$\log_{10}(\rho)$")
ticks = list(range(0, max_score+1, 5)) + [max_score+1]
labels = [str(x) for x in ticks[:-1]] + ["\u2205"]
plt.xticks(ticks, labels)
plt.xlabel("State sum of rolls $s$")
plt.ylabel("Number of rolls/turns $t$")
plt.title(r"Optimal state distribution $\rho_{\pi^*}(s_0\rightarrow s;t)$")
plt.subplots_adjust(right=2, top=2)
plt.show()
```
| true |
code
| 0.737288 | null | null | null | null |
|
# Building deep retrieval models
**Learning Objectives**
1. Converting raw input examples into feature embeddings.
2. Splitting the data into a training set and a testing set.
3. Configuring the deeper model with losses and metrics.
## Introduction
In [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) we incorporated multiple features into our models, but the models consist of only an embedding layer. We can add more dense layers to our models to increase their expressive power.
In general, deeper models are capable of learning more complex patterns than shallower models. For example, our [user model](fhttps://www.tensorflow.org/recommenders/examples/featurization#user_model) incorporates user ids and timestamps to model user preferences at a point in time. A shallow model (say, a single embedding layer) may only be able to learn the simplest relationships between those features and movies: a given movie is most popular around the time of its release, and a given user generally prefers horror movies to comedies. To capture more complex relationships, such as user preferences evolving over time, we may need a deeper model with multiple stacked dense layers.
Of course, complex models also have their disadvantages. The first is computational cost, as larger models require both more memory and more computation to fit and serve. The second is the requirement for more data: in general, more training data is needed to take advantage of deeper models. With more parameters, deep models might overfit or even simply memorize the training examples instead of learning a function that can generalize. Finally, training deeper models may be harder, and more care needs to be taken in choosing settings like regularization and learning rate.
Finding a good architecture for a real-world recommender system is a complex art, requiring good intuition and careful [hyperparameter tuning](https://en.wikipedia.org/wiki/Hyperparameter_optimization). For example, factors such as the depth and width of the model, activation function, learning rate, and optimizer can radically change the performance of the model. Modelling choices are further complicated by the fact that good offline evaluation metrics may not correspond to good online performance, and that the choice of what to optimize for is often more critical than the choice of model itself.
Each learning objective will correspond to a _#TODO_ in this student lab notebook -- try to complete this notebook first and then review the [solution notebook](../solutions/deep_recommenders.ipynb)
## Preliminaries
We first import the necessary packages.
```
!pip install -q tensorflow-recommenders
!pip install -q --upgrade tensorflow-datasets
```
**NOTE: Please ignore any incompatibility warnings and errors and re-run the above cell before proceeding.**
```
!pip install tensorflow==2.5.0
```
**NOTE: Please ignore any incompatibility warnings and errors.**
**NOTE: Restart your kernel to use updated packages.**
```
import os
import tempfile
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
plt.style.use('seaborn-whitegrid')
```
This notebook uses TF2.x.
Please check your tensorflow version using the cell below.
```
# Show the currently installed version of TensorFlow
print("TensorFlow version: ",tf.version.VERSION)
```
In this tutorial we will use the models from [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) to generate embeddings. Hence we will only be using the user id, timestamp, and movie title features.
```
ratings = tfds.load("movielens/100k-ratings", split="train")
movies = tfds.load("movielens/100k-movies", split="train")
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"],
"timestamp": x["timestamp"],
})
movies = movies.map(lambda x: x["movie_title"])
```
We also do some housekeeping to prepare feature vocabularies.
```
timestamps = np.concatenate(list(ratings.map(lambda x: x["timestamp"]).batch(100)))
max_timestamp = timestamps.max()
min_timestamp = timestamps.min()
timestamp_buckets = np.linspace(
min_timestamp, max_timestamp, num=1000,
)
unique_movie_titles = np.unique(np.concatenate(list(movies.batch(1000))))
unique_user_ids = np.unique(np.concatenate(list(ratings.batch(1_000).map(
lambda x: x["user_id"]))))
```
## Model definition
### Query model
We start with the user model defined in [the featurization tutorial](https://www.tensorflow.org/recommenders/examples/featurization) as the first layer of our model, tasked with converting raw input examples into feature embeddings.
```
class UserModel(tf.keras.Model):
def __init__(self):
super().__init__()
self.user_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_user_ids, mask_token=None),
tf.keras.layers.Embedding(len(unique_user_ids) + 1, 32),
])
self.timestamp_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.Discretization(timestamp_buckets.tolist()),
tf.keras.layers.Embedding(len(timestamp_buckets) + 1, 32),
])
self.normalized_timestamp = tf.keras.layers.experimental.preprocessing.Normalization()
self.normalized_timestamp.adapt(timestamps)
def call(self, inputs):
# Take the input dictionary, pass it through each input layer,
# and concatenate the result.
return tf.concat([
self.user_embedding(inputs["user_id"]),
self.timestamp_embedding(inputs["timestamp"]),
self.normalized_timestamp(inputs["timestamp"]),
], axis=1)
```
Defining deeper models will require us to stack mode layers on top of this first input. A progressively narrower stack of layers, separated by an activation function, is a common pattern:
```
+----------------------+
| 128 x 64 |
+----------------------+
| relu
+--------------------------+
| 256 x 128 |
+--------------------------+
| relu
+------------------------------+
| ... x 256 |
+------------------------------+
```
Since the expressive power of deep linear models is no greater than that of shallow linear models, we use ReLU activations for all but the last hidden layer. The final hidden layer does not use any activation function: using an activation function would limit the output space of the final embeddings and might negatively impact the performance of the model. For instance, if ReLUs are used in the projection layer, all components in the output embedding would be non-negative.
We're going to try something similar here. To make experimentation with different depths easy, let's define a model whose depth (and width) is defined by a set of constructor parameters.
```
class QueryModel(tf.keras.Model):
"""Model for encoding user queries."""
def __init__(self, layer_sizes):
"""Model for encoding user queries.
Args:
layer_sizes:
A list of integers where the i-th entry represents the number of units
the i-th layer contains.
"""
super().__init__()
# We first use the user model for generating embeddings.
# TODO 1a -- your code goes here
# Then construct the layers.
# TODO 1b -- your code goes here
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
for layer_size in layer_sizes[-1:]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size))
def call(self, inputs):
feature_embedding = self.embedding_model(inputs)
return self.dense_layers(feature_embedding)
```
The `layer_sizes` parameter gives us the depth and width of the model. We can vary it to experiment with shallower or deeper models.
### Candidate model
We can adopt the same approach for the movie model. Again, we start with the `MovieModel` from the [featurization](https://www.tensorflow.org/recommenders/examples/featurization) tutorial:
```
class MovieModel(tf.keras.Model):
def __init__(self):
super().__init__()
max_tokens = 10_000
self.title_embedding = tf.keras.Sequential([
tf.keras.layers.experimental.preprocessing.StringLookup(
vocabulary=unique_movie_titles,mask_token=None),
tf.keras.layers.Embedding(len(unique_movie_titles) + 1, 32)
])
self.title_vectorizer = tf.keras.layers.experimental.preprocessing.TextVectorization(
max_tokens=max_tokens)
self.title_text_embedding = tf.keras.Sequential([
self.title_vectorizer,
tf.keras.layers.Embedding(max_tokens, 32, mask_zero=True),
tf.keras.layers.GlobalAveragePooling1D(),
])
self.title_vectorizer.adapt(movies)
def call(self, titles):
return tf.concat([
self.title_embedding(titles),
self.title_text_embedding(titles),
], axis=1)
```
And expand it with hidden layers:
```
class CandidateModel(tf.keras.Model):
"""Model for encoding movies."""
def __init__(self, layer_sizes):
"""Model for encoding movies.
Args:
layer_sizes:
A list of integers where the i-th entry represents the number of units
the i-th layer contains.
"""
super().__init__()
self.embedding_model = MovieModel()
# Then construct the layers.
self.dense_layers = tf.keras.Sequential()
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
for layer_size in layer_sizes[-1:]:
self.dense_layers.add(tf.keras.layers.Dense(layer_size))
def call(self, inputs):
feature_embedding = self.embedding_model(inputs)
return self.dense_layers(feature_embedding)
```
### Combined model
With both `QueryModel` and `CandidateModel` defined, we can put together a combined model and implement our loss and metrics logic. To make things simple, we'll enforce that the model structure is the same across the query and candidate models.
```
class MovielensModel(tfrs.models.Model):
def __init__(self, layer_sizes):
super().__init__()
self.query_model = QueryModel(layer_sizes)
self.candidate_model = CandidateModel(layer_sizes)
self.task = tfrs.tasks.Retrieval(
metrics=tfrs.metrics.FactorizedTopK(
candidates=movies.batch(128).map(self.candidate_model),
),
)
def compute_loss(self, features, training=False):
# We only pass the user id and timestamp features into the query model. This
# is to ensure that the training inputs would have the same keys as the
# query inputs. Otherwise the discrepancy in input structure would cause an
# error when loading the query model after saving it.
query_embeddings = self.query_model({
"user_id": features["user_id"],
"timestamp": features["timestamp"],
})
movie_embeddings = self.candidate_model(features["movie_title"])
return self.task(
query_embeddings, movie_embeddings, compute_metrics=not training)
```
## Training the model
### Prepare the data
We first split the data into a training set and a testing set.
```
tf.random.set_seed(42)
shuffled = ratings.shuffle(100_000, seed=42, reshuffle_each_iteration=False)
# Split the data into a training set and a testing set
# TODO 2a -- your code goes here
```
### Shallow model
We're ready to try out our first, shallow, model!
**NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
```
num_epochs = 300
model = MovielensModel([32])
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.1))
one_layer_history = model.fit(
cached_train,
validation_data=cached_test,
validation_freq=5,
epochs=num_epochs,
verbose=0)
accuracy = one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"][-1]
print(f"Top-100 accuracy: {accuracy:.2f}.")
```
This gives us a top-100 accuracy of around 0.27. We can use this as a reference point for evaluating deeper models.
### Deeper model
What about a deeper model with two layers?
**NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
```
model = MovielensModel([64, 32])
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.1))
two_layer_history = model.fit(
cached_train,
validation_data=cached_test,
validation_freq=5,
epochs=num_epochs,
verbose=0)
accuracy = two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"][-1]
print(f"Top-100 accuracy: {accuracy:.2f}.")
```
The accuracy here is 0.29, quite a bit better than the shallow model.
We can plot the validation accuracy curves to illustrate this:
```
num_validation_runs = len(one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"])
epochs = [(x + 1)* 5 for x in range(num_validation_runs)]
plt.plot(epochs, one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="1 layer")
plt.plot(epochs, two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="2 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy");
plt.legend()
```
Even early on in the training, the larger model has a clear and stable lead over the shallow model, suggesting that adding depth helps the model capture more nuanced relationships in the data.
However, even deeper models are not necessarily better. The following model extends the depth to three layers:
**NOTE: The below cell will take approximately 15~20 minutes to get executed completely.**
```
# Model extends the depth to three layers
# TODO 3a -- your code goes here
```
In fact, we don't see improvement over the shallow model:
```
plt.plot(epochs, one_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="1 layer")
plt.plot(epochs, two_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="2 layers")
plt.plot(epochs, three_layer_history.history["val_factorized_top_k/top_100_categorical_accuracy"], label="3 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy");
plt.legend()
```
This is a good illustration of the fact that deeper and larger models, while capable of superior performance, often require very careful tuning. For example, throughout this tutorial we used a single, fixed learning rate. Alternative choices may give very different results and are worth exploring.
With appropriate tuning and sufficient data, the effort put into building larger and deeper models is in many cases well worth it: larger models can lead to substantial improvements in prediction accuracy.
## Next Steps
In this tutorial we expanded our retrieval model with dense layers and activation functions. To see how to create a model that can perform not only retrieval tasks but also rating tasks, take a look at [the multitask tutorial](https://www.tensorflow.org/recommenders/examples/multitask).
| true |
code
| 0.797911 | null | null | null | null |
|
# KNeighborsClassifier with MaxAbsScaler
This Code template is for the Classification task using a simple KNeighborsClassifier based on the K-Nearest Neighbors algorithm using MaxAbsScaler technique.
### Required Packages
```
!pip install imblearn
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from imblearn.over_sampling import RandomOverSampler
from sklearn.preprocessing import LabelEncoder,MaxAbsScaler
from sklearn.metrics import classification_report,plot_confusion_matrix
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
file_path= ""
```
List of features which are required for model training .
```
features = []
```
Target feature for prediction.
```
target = ''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
def EncodeY(df):
if len(df.unique())<=2:
return df
else:
un_EncodedT=np.sort(pd.unique(df), kind='mergesort')
df=LabelEncoder().fit_transform(df)
EncodedT=[xi for xi in range(len(un_EncodedT))]
print("Encoded Target: {} to {}".format(un_EncodedT,EncodedT))
return df
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=EncodeY(NullClearner(Y))
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
#### Distribution Of Target Variable
```
plt.figure(figsize = (10,6))
se.countplot(Y)
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
#### Handling Target Imbalance
The challenge of working with imbalanced datasets is that most machine learning techniques will ignore, and in turn have poor performance on the minority class, although typically it is performing on the minority class that is most important.
One approach to address imbalanced datasets is to oversample the minority class. The simplest approach involves duplicating examples in the minority class.We will perform overspampling using imblearn library.
```
x_train,y_train = RandomOverSampler(random_state=123).fit_resample(x_train, y_train)
```
### Model
KNN is one of the easiest Machine Learning algorithms based on Supervised Machine Learning technique. The algorithm stores all the available data and classifies a new data point based on the similarity. It assumes the similarity between the new data and data and put the new case into the category that is most similar to the available categories.KNN algorithm at the training phase just stores the dataset and when it gets new data, then it classifies that data into a category that is much similar to the available data.
#### Model Tuning Parameters
> - **n_neighbors** -> Number of neighbors to use by default for kneighbors queries.
> - **weights** -> weight function used in prediction. {**uniform,distance**}
> - **algorithm**-> Algorithm used to compute the nearest neighbors. {**‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’**}
> - **p** -> Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan_distance (l1), and euclidean_distance (l2) for p = 2. For arbitrary p, minkowski_distance (l_p) is used.
> - **leaf_size** -> Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
## Data Rescaling
MaxAbsScaler scales each feature by its maximum absolute value.
This estimator scales and translates each feature individually such that the maximal absolute value of each feature in the training set will be 1.0. It does not shift/center the data, and thus does not destroy any sparsity.
[For More Reference](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MaxAbsScaler.html)
```
model=make_pipeline(MaxAbsScaler(),KNeighborsClassifier(n_jobs=-1))
model.fit(x_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
#### Confusion Matrix
A confusion matrix is utilized to understand the performance of the classification model or algorithm in machine learning for a given test set where results are known.
```
plot_confusion_matrix(model,x_test,y_test,cmap=plt.cm.Blues)
```
#### Classification Report
A Classification report is used to measure the quality of predictions from a classification algorithm. How many predictions are True, how many are False.
* where:
- Precision:- Accuracy of positive predictions.
- Recall:- Fraction of positives that were correctly identified.
- f1-score:- percent of positive predictions were correct
- support:- Support is the number of actual occurrences of the class in the specified dataset.
```
print(classification_report(y_test,model.predict(x_test)))
```
#### Creator: Vikas Mishra, Github: [Profile](https://github.com/Vikaas08)
| true |
code
| 0.272847 | null | null | null | null |
|
# Connect 4 sur un SenseHat
---
## Introduction
### Règles du Jeu
Le Connect 4, Four in a Row, ou Puissance 4 en français est un jeu se déroulant sur une grille de 6 rangées et 7 colonnes. En insérant tour à tour un jeton coloré dans la dernière rangée, qui tombe ensuite dans le plus bas emplacement disponible, les joueurs tentent d'avoir quatre jetons de leur couleur alignés horizontalement, verticalement, ou diagonalement.
Si toutes les cases sont remplies sans gagnant, la partie est déclarée nulle.
### Mise en place sur SenseHat
L'écran du SenseHat étant fait de 8\*8 pixels, il a été décidé d'utiliser cette surface de la manière suivante :
- Une **zone de jeu**, de 6*7 pixels bleus
- Un espace de sélection, avec un **curseur** de la couleur du joueur en train de jouer

## Installation
### 1. Importer SenseHat & autres modules
La première étape de la programmation de ce jeu est l'importation du module Sense_Hat afin de pouvoir communiquer avec le SenseHat.
```
from sense_hat import SenseHat
#from sense_emu import SenseHat
from time import sleep, time
from gamelib import *
sense = SenseHat()
```
```from sense_hat import SenseHat``` permet l'intéraction avec le module SenseHat. <br/>
```#from sense_emu import SenseHat``` permet d'utiliser l'émulateur SenseHat si la ligne est décommentée <br/>
```from time import sleep, time``` permet d'utiliser la fonction sleep(time) afin de pouvoir ralentir le programme <br/>
```from gamelib import *``` importe les couleurs de ```gamelib``` <br/>
<br/>
```sense = SenseHat()``` permet d'appeler les fonctions liées au SenseHat.
### 2. Définir et initialiser les variables générales
Ces variables seront cruciales au bon fonctionnement du jeu.
```
repeat = 1 # Repeats the program if launched as standalone
playerScore = [0, 0] # Score of the players
turns = 0 # Amount of turns passed
gameOver = 0 # Is the game over?
stopGame = 0 # =1 makes main() stop the game
# Creates two lists of 4 pixels to make winning streaks detection easier
fourYellow = [[248, 252, 0]] * 4
fourRed = [[248, 0, 0]] * 4
# Puts BLUE, RED and YELLOW from gamelib into a list
colors = (BLUE, RED, YELLOW)
```
### 3. Fonction ```main()```
La fonction ```main()``` est la fonction principale du jeu, qui le fait démarrer, continuer, où l'arrête.
```
def main():
"""
Main function, initialises the game, starts it, and stops it when needed.
"""
global gameOver
global playerScore
global stopGame
global turns
turns = 0 # Resets the turns passed
# Stops the game if a player has 2 points or if stop_game() set
# stopGame to 1 and the game is supposed to stop now
if (
repeat == 0 and
(playerScore[0] == 2 or playerScore[1] == 2 or stopGame == 1)
):
stopGame = 0 # Resets stopGame
gameOver = 0 # Resets gameOver
return
# If the game should continue, resets gameOver and playerScore to 0
else:
gameOver = 0 # Resets gameOver
if playerScore[0] == 2 or playerScore[1] == 2 or stopGame == 1:
stopGame = 0 # Resets stopGame
playerScore = [0, 0] # Resets the playerScore
show() # Resets the display for a new game
turn() # Starts a new turn
```
Le morceau de code <br/>
```
if (
repeat == 0 and
(playerScore[0] == 2 or playerScore[1] == 2 or stopGame == 1)
):
```
est indenté spécialement pour suivre le standard PEP8 tout en ne faisant pas plus de 79 caractères de long.
La fonction ```main()``` appèle les fonctions ```show()``` et ```turn()```, décrites ci-dessous en sections 4. et 5.
### 4. Fonction ```show()```
La fonction ```show()``` réinitialise l'affichage, puis y créé la zone de jeu en bleu de 6\*7 pixels.
```
def show():
"""
Sets up the playing field : 6*7 blue pixels
"""
sense.clear() # Resets the pixels
# Creates the 6*7 blue playing field
for y in range(6):
for x in range(7):
sense.set_pixel(x, 7-y, colors[0])
```
### 5. Fonction ```turn()```
La fonction ```turn()``` gère les tours, appèle la fonction ```select_column(p)``` pour que le joueur `p` sélectionne où placer son jeton, et cause un match nul si toutes les cases sont pleines (42 tours écoulés).
```
def turn():
"""
Decides whose turn it is, then calls select_column(p) to allow the player p
to make their selection
"""
global turns
if gameOver == 0: # Checks that the game isn't over
if turns % 2 == 0 and turns != 42: # If the turn is even it's p1's
turns += 1 # Increments turns
select_column(1) # Asks p1 to select a column for their token
elif turns % 2 == 1 and turns != 42: # If the turn is odd, it's p2's
turns += 1 # Increments turns
select_column(2) # Asks p2 to select a column for their token
elif turns == 42: # If 42 turns have passed..
player_scored(0) # ..then it's a draw
```
### 6. Fonction ```player_score(p)```
La fonction ```player_score(p)``` est appelée lorsqu'un joueur ```p``` marque un point, ou lorsqu'il y a match nul (p vaut alors 0). <br/>
Lorsqu'un joueur marque son premier point, son score s'affiche dans sa couleur sur l'écran, avant que le jeu ne soit relancé. <br/>
Lorsqu'un joueur marque son deuxième point, son score s'affiche dans sa couleur, puis l'écran entier, avant que le jeu et les scores ne soient réinitialisés. Si le jeu est appelé comme module, il renvoie à la sélection de jeu, sinon le jeu recommence.
```
def player_scored(p):
"""
Manages the scoring system.
p in player_scored(p) is the player who just scored.
p == 0 -> draw
p == 1 -> p1 scored
p == 2 -> p2 scored
If one of the players won the round, show their score in their color and
prepare the field for the next round. If one of the players has two points,
they win the game, the screen turns to their color and the game is reset.
If it's a draw, no points are given and the field gets prepared for the
next round.
"""
global gameOver
gameOver = 1 # The game has ended
global playerScore
if p != 0: # Checks if it's a draw
playerScore[p - 1] += 1 # Increments the winner's score
sense.show_letter(str(playerScore[p - 1]), colors[p]) # Shows score
# Ends the game if the player already had a point
if playerScore[0] == 2 or playerScore[1] == 2 or stopGame == 1:
sleep(1.5) # Pauses long enough to see the score
sense.clear(colors[p]) # Turns the screen into the winner's color
sleep(1.5) # Pauses long enough to see the winner's screen
sense.clear() # Clears the display
main() # Calls the main game function
```
### 7. Fonction ```select_column(p)```
La fonction ```select_column(p)``` permet au joueur ```p``` de sélectionner dans quelle colonne il veut poser son jeton en déplaçant le joystick à droite ou à gauche. La sélection commence au centre pour l'aspect pratique. <br/>
<br/>
```x = (x + 1) % 7``` permet de s'assurer que `x` reste dans la zone de jeu faisant 7 pixels.<br/>
Lorsque le choix est fait, et que le joueur a appuyé sur le joystick vers le bas, la fonction ```put_down(x, p)``` est appelée, avec ```x``` comme colonne choisie. Cette fonction va vérifier que l'espace est libre, et si ce n'est pas le cas, rappeler ```select_column(p)``` afin que le joueur ne gaspille pas son tour.
```
def select_column(p):
"""
Asks the player to select a column with the joystick, then calls for the
function to drop the token if it is clear.
p is the player whose turn it is.
If the joystick is moved upwards, the game is ended.
The function calls put_down(x,p) in order to drop the token down.
If it turns out the column is full,
put_down(x,p) will call select_column(p) back.
show_selection(x,p) is used to show the current selection.
Returns the selected column with x.
"""
x = 3 # Starts the selection in the middle of the playing field
selection = True # Is the player selecting?
while selection:
for event in sense.stick.get_events(): # Listens for joystick events
if event.action == 'pressed': # When the joystick is moved..
if event.direction == 'right': # ..to the right..
x = (x + 1) % 7 # ..then move the cursor to the right
elif event.direction == 'left': # ..to the left..
x = (x - 1) % 7 # ..then move the cursor to the left
elif event.direction == 'down': # Pressing down confirms
selection = False # Ends selection
put_down(x, p) # Calls the function that drops the token
elif event.direction == 'up': # Pressing up..
global stopGame
stopGame = 1 # ..will make main() end the game..
player_scored(0) # ..and causes a draw
show_selection(x, p) # Calls the function that shows the selection
return x # Returns which column was selected
```
Si le joueur appuie vers le haut, `stopGame` devient `True`, ce qui va faire que le jeu s'arrête à la prochaine invocation de `main()`, qui arrive après que `player_scored(0)` soit appelé. <br/>
<br/>
La fonction renvoie `x`, c'est à dire la coordonée de la colonne choisie, et appèle ```show_selection(x, p)``` afin que le curseur du joueur soit affiché correctement pendant la sélection.
### 8. Fonction ```show_selection(x, p)```
La fonction ```show_selection(x, p)``` affiche l'emplacement du curseur du joueur `p` avec la couleur appropriée, et rend aux pixels leur couleur originelle après le passage du curseur.
```
def show_selection(x, p):
"""
Shows the cursor for the column selection.
x is the currently selected column
p is the player playing
Ensures that the replacement to black stops when the game is over in order
to prevent conflict with the score display.
"""
for i in range(7):
if i == x and gameOver == 0: # Checks that i is in the playing field
# Colors the selection with the player p's color
sense.set_pixel(i, 0, colors[p])
elif gameOver == 0:
# Resets the pixels once the cursor has moved
sense.set_pixel(i, 0, (0, 0, 0))
```
Lorsque le jeu n'est pas en cours (```gameOver =! 0```), la fonction ne fait plus rien, afin d'éviter qu'elle n'interfère avec par exemple l'affichage des résultats.
### 9. Fonction ```put_down(x, p)```
La fonction ```put_down(x, p)``` vérifie que la colonne `x` choisie par le joueur est bien libre, puis trouve le plus bas emplacement libre, appèle la fonction ```animate_down(x, y, p)``` afin d'animer la chute puis y affiche le jeton du joueur.<br/>
Si la colonne n'est pas libre, ```put_down(x, p)``` rappèle ```select_column(p)``` afin d'éviter que le joueur ne gaspille son tour.<br/>
Une fois le jeton placé, la fonction appèle ```check_connectfour(x, y)``` afin de regarder si le jeton posé créé une suite de quatre. S'il n'y a pas de connection, c'est au tour de l'autre joueur avec ```turn()```.
```
def put_down(x, p):
"""
Puts the token down in the selected column.
x is the selected column
p is the player playing
If the selected column is full, select_column(p) is called back to ensure
the player doesn't waste their turn.
The token is animated down with animate_down(x,y,p) before being set.
If the token is not a winning one, calls for the next turn with turn().
"""
# Checks that the column is free (BLUE)
if sense.get_pixel(x, 2) == [0, 0, 248]:
for y in range(7): # Finds the lowest available spot
if sense.get_pixel(x, 7-y) == [0, 0, 248]: # If it's free then..
animate_down(x, y, p) # ..calls for the animation down and..
sense.set_pixel(x, 7 - y, colors[p]) # ..puts the token there
# Checks if it's a winning move
if check_connectfour(x, 7 - y) is False:
turn() # If not, starts the next turn
return
return
else:
select_column(p) # If there is no free spot, restarts selection
return
```
La fonction ```sense.get_pixel(x, y)``` ne renvoie pas la valeur qui a été assignée au pixel directement, mais la fait passer à travers une autre opération, ce qui explique l'utilisation d'une valeur de bleu (```[0,0,248]```) qui n'est pas ```BLUE```.
### 10. Fonction ```animate_down(x, y, p)```
La fonction ```animate_down(x, y, p)``` fait apparaître puis disparaître un pixel de la couleur du joueur `p` dans chaque case de la colonne `x` jusqu'au point `y`, avant de redonner aux pixels leur couleur d'origine (Noire `[0,0,0]` ou `BLUE`)
```
def animate_down(x, y, p):
"""
Creates an animation that makes a pixel move down the selected column to
the lowest available spot.
x is the selected column
y is the lowest available spot
p is the player playing
Ensures that the first two rows stay black, and that the others turn BLUE
again after the animation.
"""
# For each available spot from the top of the column
for z in range(7 - y):
sense.set_pixel(x, z, colors[p]) # Set the pixel to the player's color
sleep(0.03) # Wait long enough for it to be noticeable
if z != 1 and z != 0: # If it's not the first two rows
sense.set_pixel(x, z, colors[0]) # Set the pixel back to BLUE
else: # Otherwise
sense.set_pixel(x, 1, [0, 0, 0]) # Set it to black
```
### 11. Fonction ```check_connectfour(x, y)```
La fonction ```check_connectfour(x, y)``` va faire une série de tests afin de regarder si le jeton posé à l'emplacement `x, y` cause une suite de 4 pixels horizontalement, verticalement et en diagonale.
```
def check_connectfour(x, y):
"""
Checks if there is four same-colored token next to each other.
x is the last played token's column
y is the last played token's row
Returns False if there is no winning move this turn. Return True and thus
makes the game end if it was a winning move.
"""
# First asks if there is a win horizontally and vertically
if check_horizontal(x, y) is False and check_vertical(x, y) is False:
# Then diagonally from the bottom left to the upper right
if check_diagonal_downleft_upright(x, y) is False:
# And then diagonally the other way
if check_diagonal_downright_upleft(x, y) is False:
# If not, then continue playing by returning False
return(False)
```
La fonction appèle d'abord 1) ```check_horizontal(x, y)``` et 2) ```check_vertical(x, y)```, puis regarde pour les deux diagonales 3) ```check_diagonal_downleft_upright(x, y)``` et 4) ```check_diagonal_downright_upleft(x, y)```. <br/>
<br/>
Si le pixel ne fait aucune suite, alors toutes les conditions seront `False`, ce que la fonction retournera, et ce sera le tour de l'autre joueur.

#### 11.1 ```check_horizontal(x, y)```
La fonction ```check_horizontal(x, y)``` va faire une liste `horizontal` de tous les pixels de la rangée `y` où le jeton a été placé, puis va la comparer à `fourYellow` et `fourRed` par groupe de quatre pixels, quatre fois de suite afin de couvrir l'entièreté de la rangée.<br/>
Si l'une des conditions est remplie, le joueur `p` qui a posé le jeton recevra un point à travers la fonction `player_scored(p)`, et la fonction retournera `True`. Sinon, la fonction retournera `False`.
```
def check_horizontal(x, y):
"""
Checks if there is four same-colored tokens in the same row.
x is the last played token's column
y is the last played token's row
Returns False if there isn't four same-colored tokens on the same row.
Returns True if there are, and calls player_scored(p) for the appropriate
player based on color (RED == p1, YELLOW == p2)
"""
# Makes a list out of the row
horizontal = sense.get_pixels()[8 * y:8 * y + 7]
for z in range(4): # Checks the row by four groups of four tokens
if horizontal[z:z + 4] == fourYellow: # Is there four yellow tokens?
player_scored(2) # If yes, p2 scored
return True # Returns that there was a winning move
if horizontal[z:z + 4] == fourRed: # Is there four red tokens?
player_scored(1) # If yes, p1 scored
return True # Returns that there was a winning move.
return False # Returns that there were no winning move.
```
#### 11.2 ```check_vertical(x, y)```
La fonction ```check_vertical(x, y)``` va faire une liste `vertical` de tous les pixels de la colonne `x` où le jeton a été placé, puis va la comparer à `fourYellow` et `fourRed` par groupe de quatre pixels, trois fois de suite afin de couvrir l'entièreté de la colonne.<br/>
Si l'une des conditions est remplie, le joueur `p` qui a posé le jeton recevra un point à travers la fonction `player_scored(p)`, et la fonction retournera `True`. Sinon, la fonction retournera `False`.
```
def check_vertical(x, y):
"""
Checks if there is four same-colored tokens in the same column.
x is the last played token's column
y is the last played token's row
Returns False if there isn't four same-colored tokens in the column.
Returns True if there are, and calls player_scored(p) for the appropriate
player based on color (RED == p1, YELLOW == p2)
"""
# Makes a list out of the column
vertical = [sense.get_pixel(x, 2), sense.get_pixel(x, 3),
sense.get_pixel(x, 4), sense.get_pixel(x, 5),
sense.get_pixel(x, 6), sense.get_pixel(x, 7)]
for z in range(3): # Checks the column by three groups of four tokens
if vertical[z:z + 4] == fourYellow: # Is there four yellow tokens?
player_scored(2) # If yes, p2 scored
return True # Returns that there was a winning move
if vertical[z:z + 4] == fourRed: # Is there four red tokens?
player_scored(1) # If yes, p1 scored
return True # Returns that there was a winning move
return False # Returns that there were no winning move
```
#### 11.3 ```check_diagonal_downleft_upright(x, y)```
La fonction ```check_diagonal_downleft_upright(x, y)``` va faire une liste `diagonal` de tous les pixels de la diagonale allant d'en bas à gauche à en haut à droite en passant par le point `x, y` où le jeton a été placé grâce à la fonction ```create_diagonal_downleft_upright(diagonal, x, y)```, puis va la comparer à `fourYellow` et `fourRed` par groupe de quatre pixels, quatre fois de suite afin de couvrir l'entièreté de la rangée.<br/>
Si l'une des conditions est remplie, le joueur `p` qui a posé le jeton recevra un point à travers la fonction `player_scored(p)`, et la fonction retournera `True`. Sinon, la fonction retournera `False`.
```
def check_diagonal_downleft_upright(x, y):
"""
Checks if there is four same-colored token in the bottom-left to
upper-right diagonal.
x is the last played token's column
y is the last played token's row
Calls create_diagonal_downleft_upright to create a list from the diagonal.
Returns False if there isn't four same-colored tokens in the diagonal.
Returns True if there are, and calls player_scored(p) for the appropriate
player based on color (RED == p1, YELLOW == p2)
"""
diagonal = [] # Resets the list
# Calls a function to create a list from the pixels in a bottom-left to
# upper-right diagonal
create_diagonal_downleft_upright(diagonal, x, y)
for z in range(4): # Checks the diagonal by four groups of four tokens
if diagonal[z:z + 4] == fourYellow: # Is there four yellow tokens?
player_scored(2) # If yes, p2 scored
return True # Returns that there was a winning move
if diagonal[z:z + 4] == fourRed: # Is there four red tokens?
player_scored(1) # If yes, p1 scored
return True # Returns that there was a winning move
return False # Returns that there were no winning move
```
##### 11.3.1 ```create_diagonal_downleft_upright(diagonal, x, y)```
En utilisant `try` et `except`, la fonction ```create_diagonal_downleft_upright(diagonal, x, y)``` tente de créer une liste de 7 pixels passant en diagonale du point `x, y` d'en bas à gauche à en haut à droite.<br/>
L'utilisation de `try` et `except` permet d'éviter que le programme crashe lorsque la fonction tente d'ajouter un pixel hors limites à la liste. <br/><br/>
La fonction retourne la liste `diagonale` aussi grande que ce qu'elle a pu obtenir.
```
def create_diagonal_downleft_upright(diagonal, x, y):
"""
Creates a list of seven pixels in a bottom left to upper right diagonal
centered around the last placed token.
diagonal is the list
x is the last played token's column
y is the last played token's row
As the function might try to take into account pixels that are out of
bounds, there is a try except ValueError in order to prevent out of bounds
errors. The list might be shorter than seven pixels, but the function works
anyway.
Returns the list of diagonal pixels.
"""
for z in range(7): # To have a 7 pixel list
# Tries to get values that might be out of bounds, three pixels down
# left and three pixels up right in a diagonal from the token
try:
diagonal.append(sense.get_pixel(x - z + 3, y + z - 3))
except: # Catches out of bounds errors
ValueError
return(diagonal) # Returns the list of pixels
```
#### 11.4 ```check_diagonal_downright_upleft(x, y)```
La fonction ```check_diagonal_downright_upleft(x, y)``` va faire une liste `diagonal` de tous les pixels de la diagonale allant d'en bas à droite à en haut à gauche en passant par le point `x, y` où le jeton a été placé grâce à la fonction ```create_diagonal_downright_upleft(diagonal, x, y)```, puis va la comparer à `fourYellow` et `fourRed` par groupe de quatre pixels, quatre fois de suite afin de couvrir l'entièreté de la rangée.<br/>
Si l'une des conditions est remplie, le joueur `p` qui a posé le jeton recevra un point à travers la fonction `player_scored(p)`, et la fonction retournera `True`. Sinon, la fonction retournera `False`.
```
def check_diagonal_downright_upleft(x, y):
"""
Checks if there is four same-colored token in the bottom-right to
upper-left diagonal.
x is the last played token's column
y is the last played token's row
Calls create_diagonal_downright_upleft to create a list from the diagonal.
Returns False if there isn't four same-colored tokens in the diagonal.
Returns True if there are, and calls player_scored(p) for the appropriate
player based on color (RED == p1, YELLOW == p2)
"""
diagonal = [] # Resets the list
# Calls a function to create a list from the pixels in a bottom-right to
# upper-left diagonal
create_diagonal_downright_upleft(diagonal, x, y)
for z in range(4): # Checks the diagonal by four groups of four tokens
if diagonal[z:z + 4] == fourYellow: # Is there four yellow tokens?
player_scored(2) # If yes, p2 scored
return True # Returns that there was a winning move
if diagonal[z:z + 4] == fourRed: # Is there four red tokens?
player_scored(1) # If yes, p1 scored
return True # Returns that there was a winning move
return False # Returns that there were no winning move
```
##### 11.4.1 ```create_diagonal_downright_upleft(diagonal, x, y)```
En utilisant `try` et `except`, la fonction ```create_diagonal_downright_upleft(diagonal, x, y)``` tente de créer une liste de 7 pixels passant en diagonale du point `x, y` d'en bas à droite à en haut à gauche.<br/>
L'utilisation de `try` et `except` permet d'éviter que le programme crashe lorsque la fonction tente d'ajouter un pixel hors limites à la liste.<br/>
<br/>
La fonction retourne la liste `diagonale` aussi grande que ce qu'elle a pu obtenir.
```
def create_diagonal_downright_upleft(diagonal, x, y):
"""
Creates a list of seven pixels in a bottom right to upper left diagonal
centered around the last placed token.
diagonal is the list
x is the last played token's column
y is the last played token's row
As the function might try to take into account pixels that are out of
bounds, there is a try except ValueError in order to prevent out of bounds
errors. The list might be shorter than seven pixels, but the function works
anyway.
Returns the list of diagonal pixels.
"""
for z in range(7): # To have a 7 pixel list
# Tries to get values that might be out of bounds, three pixels down
# right and three pixels up left in a diagonal from the token
try:
diagonal.append(sense.get_pixel(x - z + 3, y - z + 3))
except: # Catches out of bounds errors
ValueError
return(diagonal) # Returns the list of pixels
```
### 12. Module ou Standalone?
Ce morceau de code fait en sorte que le jeu se répète s'il est standalone `repeat = 1` mais pas s'il est importé comme module `repeat = 0` afin de permettre de retourner à la sélection de jeux.
```
# Execute the main() function when the file is executed,
# but do not execute when the module is imported as a module.
print('module name =', __name__)
if __name__ == '__main__':
main()
global repeat
repeat = 1 # If the game is played as standalone, make it repeat
else:
global repeat
repeat = 0 # If the game is played as a module, make it quit when over
```
| true |
code
| 0.613642 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/technologyhamed/Neuralnetwork/blob/Single/ArticleSummarization/ArticleSummarization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
*قسمت 1: پیدا کردن امتیاز TF IDF هر کلمه
ابتدا فایل خوانده می شود و تمام رشته ها در قالب Pandas DataFrame ذخیره می شوند
```
#Import libraries
%matplotlib inline
import pandas as pd
import numpy as np
import os
import glob
import requests as requests
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.datasets import load_files
import nltk
nltk.download('stopwords')
# Just making the plots look better
mpl.style.use('ggplot')
mpl.rcParams['figure.figsize'] = (8,6)
mpl.rcParams['font.size'] = 12
url='https://raw.githubusercontent.com/technologyhamed/Neuralnetwork/Single/Datasets/Article_Summarization_project/Article.txt'
filename='../content/sample_data/Article.txt'
df = pd.read_csv(url)
df.to_csv(filename)
str_article = list()
article_files = glob.glob(filename)
d = list()
for article in article_files:
with open(article, encoding='utf-8') as f:
filename = os.path.basename(article.split('.')[0])
lines = (line.rstrip() for line in f) # All lines including the blank ones
lines = list(line for line in lines if line) # Non-blank lines
#str_article.rstrip()
d.append(pd.DataFrame({'article': "اخبار", 'paragraph': lines}))
doc = pd.concat(d)
doc
#doc['article'].value_counts().plot.bar();
```
Importing NLTK corpus to remove stop words from the vector.
```
from nltk.corpus import stopwords
```
Split the lines into sentences/words.
```
doc['sentences'] = doc.paragraph.str.rstrip('.').str.split('[\.]\s+')
doc['words'] = doc.paragraph.str.strip().str.split('[\W_]+')
#This line is used to remove the English stop words
stop = stopwords.words('english')
doc['words'] = doc['words'].apply(lambda x: [item for item in x if item not in stop])
#doc.head()
doc
```
```
# This is formatted as code
```
Split the paragraph into sentences.
```
rows = list()
for row in doc[['paragraph', 'sentences']].iterrows():
r = row[1]
for sentence in r.sentences:
rows.append((r.paragraph, sentence))
sentences = pd.DataFrame(rows, columns=['paragraph', 'sentences'])
#sentences = sentences[sentences.sentences.str.len() > 0]
sentences.head()
```
Split the paragraph into words.
```
rows = list()
for row in doc[['paragraph', 'words']].iterrows():
r = row[1]
for word in r.words:
rows.append((r.paragraph, word))
words = pd.DataFrame(rows, columns=['paragraph', 'words'])
#remove empty spaces and change words to lower case
words = words[words.words.str.len() > 0]
words['words'] = words.words.str.lower()
#words.head()
#words
```
Calculate word counts in the article.
```
rows = list()
for row in doc[['article', 'words']].iterrows():
r = row[1]
for word in r.words:
rows.append((r.article, word))
wordcount = pd.DataFrame(rows, columns=['article', 'words'])
wordcount['words'] = wordcount.words.str.lower()
wordcount.words = wordcount.words.str.replace('\d+', '')
wordcount.words = wordcount.words.str.replace(r'^the', '')
wordcount = wordcount[wordcount.words.str.len() > 2]
counts = wordcount.groupby('article')\
.words.value_counts()\
.to_frame()\
.rename(columns={'words':'n_w'})
#counts.head()
counts
#wordcount
#wordcount.words.tolist()
#counts.columns
```
Plot number frequency graph.
```
def pretty_plot_top_n(series, top_n=20, index_level=0):
r = series\
.groupby(level=index_level)\
.nlargest(top_n)\
.reset_index(level=index_level, drop=True)
r.plot.bar()
return r.to_frame()
pretty_plot_top_n(counts['n_w'])
word_sum = counts.groupby(level=0)\
.sum()\
.rename(columns={'n_w': 'n_d'})
word_sum
tf = counts.join(word_sum)
tf['tf'] = tf.n_w/tf.n_d
tf.head()
#tf
```
Plot top 20 words based on TF
```
pretty_plot_top_n(tf['tf'])
c_d = wordcount.article.nunique()
c_d
idf = wordcount.groupby('words')\
.article\
.nunique()\
.to_frame()\
.rename(columns={'article':'i_d'})\
.sort_values('i_d')
idf.head()
idf['idf'] = np.log(c_d/idf.i_d.values)
idf.head()
#idf
```
IDF values are all zeros because in this example, only 1 article is considered & all unique words appeared in the same article. IDF values are 0 if it appears in all the documents.
```
tf_idf = tf.join(idf)
tf_idf.head()
#tf_idf
tf_idf['tf_idf'] = tf_idf.tf * tf_idf.idf
tf_idf.head()
#tf_idf
```
-------------------------------------------------
**Part 2: Using Hopfield Network to find the most important words**
In this part, the TF scores are treated as the Frequency Vector i.e. the input to Hopfield Network.
Frequency Matrix is constructed to be treated as Hopfield Network weights.
```
freq_matrix = pd.DataFrame(np.outer(tf_idf["tf"], tf_idf["tf"]), tf_idf["tf"].index, tf_idf["tf"].index)
#freq_matrix.head()
freq_matrix
```
Finding the maximum of the frequency vector and matrix
```
vector_max = tf_idf['tf'].max()
print(vector_max)
matrix_max = freq_matrix.max().max()
print(matrix_max)
```
Normalizing the frequency vector
```
tf_idf['norm_freq'] = tf_idf.tf / vector_max
temp_df = tf_idf[['tf', 'norm_freq']]
#temp_df
temp_df.head(20)
#tf_idf.head()
#tf_idf
```
Normalizing the frequency matrix
```
freq_matrix_norm = freq_matrix.div(matrix_max)
freq_matrix_norm
np.fill_diagonal(freq_matrix_norm.values, 0)
freq_matrix_norm
```
.
```
#define sigmoid function
#currently just a placeholder because tanh activation function is selected instead
def sigmoid(x):
beta = 1
return 1 / (1 + np.exp(-x * beta))
tf_idf["hopfield_value"] = np.tanh(freq_matrix_norm @ tf_idf["norm_freq"])
temp = np.tanh(freq_matrix_norm @ tf_idf["hopfield_value"])
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
temp = np.tanh(freq_matrix_norm @ temp)
#temp
#temp
#temp.head()
temp.head(20)
```
# **الگوریتم هابفیلد**
```
#safe limit
itr = 0
zero_itr = 0
max_itr = 5 #maximum iteration where Delta Energy is 0
char_list = []
delta_energy = 0
threshold = 0
energy = 0
init_energy = 0
tf_idf["hopfield_value"] = np.tanh(freq_matrix_norm @ tf_idf["norm_freq"])
while (delta_energy < 0.0001):
itr = itr + 1
#Calculation of output vector from Hopfield Network
#y = activation_function(sum(W * x))
tf_idf["hopfield_value"] = np.tanh(freq_matrix_norm @ tf_idf["hopfield_value"])
#Calculation of Hopfield Energy Function and its Delta
#E = [-1/2 * sum(Wij * xi * xj)] + [sum(threshold*xi)]
energy = (-0.5 * tf_idf["hopfield_value"] @ freq_matrix_norm @ tf_idf["hopfield_value"]) \
+ (np.sum(threshold * tf_idf["hopfield_value"]))
#Append to list for characterization
char_list.append(energy)
#Find Delta for Energy
delta_energy = energy - init_energy
#print ('Energy = {}'.format(energy))
#print ('Init_Energy = {}'.format(init_energy))
#print ('Delta_Energy = {}'.format(delta_energy))
#print ()
init_energy = energy #Setting the current energy to be previous energy in next iteration
#break the loop if Delta Energy reached zero after a certain iteration
if (delta_energy == 0):
zero_itr = zero_itr + 1
if (zero_itr == max_itr):
print("Hopfield Loop exited at Iteration {}".format(itr))
break
big_grid = np.arange(0,itr)
plt.plot(big_grid,char_list, color ='blue')
plt.suptitle('Hopfield Energy Value After Each Iteration')
# Customize the major grid
plt.grid(which='major', linestyle='-', linewidth='0.5', color='red')
# Customize the minor grid
plt.grid(which='minor', linestyle=':', linewidth='0.5', color='black')
plt.minorticks_on()
plt.rcParams['figure.figsize'] = [13, 6]
plt.show()
#tf_idf.head()
#tf_idf
#final_hopfield_output = tf_idf["hopfield_value"]
final_output_vector = tf_idf["hopfield_value"]
final_output_vector.head(10)
#final_output_vector.head()
#final_output_vector
#tf_idf
```
Once again, it is shown that the words <font color=green>***kipchoge***</font> and <font color=green>***marathon***</font> are the the most important word. It is highly likely that it is accurate because the article was about the performance of Eliud Kipchoge running a marathon.
-------------------------------------------------
**Part 3: خلاصه مقاله**
```
txt_smr_sentences = pd.DataFrame({'sentences': sentences.sentences})
txt_smr_sentences['words'] = txt_smr_sentences.sentences.str.strip().str.split('[\W_]+')
rows = list()
for row in txt_smr_sentences[['sentences', 'words']].iterrows():
r = row[1]
for word in r.words:
rows.append((r.sentences, word))
txt_smr_sentences = pd.DataFrame(rows, columns=['sentences', 'words'])
#remove empty spaces and change words to lower case
txt_smr_sentences['words'].replace('', np.nan, inplace=True)
txt_smr_sentences.dropna(subset=['words'], inplace=True)
txt_smr_sentences.reset_index(drop=True, inplace=True)
txt_smr_sentences['words'] = txt_smr_sentences.words.str.lower()
##Initialize 3 new columns
# w_ind = New word index
# s_strt = Starting index of a sentence
# s_stp = Stopping index of a sentence
# w_scr = Hopfield Value for words
txt_smr_sentences['w_ind'] = txt_smr_sentences.index + 1
txt_smr_sentences['s_strt'] = 0
txt_smr_sentences['s_stp'] = 0
txt_smr_sentences['w_scr'] = 0
#Iterate through the rows to check if the current sentence is equal to
#previous sentence. If not equal, determine the "start" & "stop"
start = 0
stop = 0
prvs_string = ""
for i in txt_smr_sentences.index:
#print (i)
if (i == 0):
start = 1
txt_smr_sentences.iloc[i,3] = 1
prvs_string = txt_smr_sentences.iloc[i,0]
else:
if (txt_smr_sentences.iloc[i,0] != prvs_string):
stop = txt_smr_sentences.iloc[i-1,2]
txt_smr_sentences.iloc[i-(stop-start)-1:i,4] = stop
start = txt_smr_sentences.iloc[i,2]
txt_smr_sentences.iloc[i,3] = start
prvs_string = txt_smr_sentences.iloc[i,0]
else:
txt_smr_sentences.iloc[i,3] = start
if (i == len(txt_smr_sentences.index)-1):
last_ind = txt_smr_sentences.w_ind.max()
txt_smr_sentences.iloc[i-(last_ind-start):i+1,4] = last_ind
#New Column for length of sentence
txt_smr_sentences['length'] = txt_smr_sentences['s_stp'] - txt_smr_sentences['s_strt'] + 1
#Rearrange the Columns
txt_smr_sentences = txt_smr_sentences[['sentences', 's_strt', 's_stp', 'length', 'words', 'w_ind', 'w_scr']]
txt_smr_sentences.head(100)
#txt_smr_sentences
```
Check if word has Hopfield Score value, and update *txt_smr_sentences*
```
for index, value in final_output_vector.items():
for i in txt_smr_sentences.index:
if(index[1] == txt_smr_sentences.iloc[i,4]):
txt_smr_sentences.iloc[i,6] = value
#New Column for placeholder of sentences score
txt_smr_sentences['s_scr'] = txt_smr_sentences.w_scr
txt_smr_sentences.head(100)
# three_sigma = 3 * math.sqrt((tf_idf.loc[:,"hopfield_value"].var()))
# three_sigma
# tf_idf["hopfield_value"]
aggregation_functions = {'s_strt': 'first', \
's_stp': 'first', \
'length': 'first', \
's_scr': 'sum'}
tss_new = txt_smr_sentences.groupby(txt_smr_sentences['sentences']).aggregate(aggregation_functions)\
.sort_values(by='s_scr', ascending=False).reset_index()
tss_new
import math
max_word = math.floor(0.1 * tss_new['s_stp'].max())
print("Max word amount for summary: {}\n".format(max_word))
summary = tss_new.loc[tss_new['s_strt'] == 1, 'sentences'].iloc[0] + ". " ##Consider the Title of the Article
length_printed = 0
for i in tss_new.index:
if (length_printed <= max_word):
summary += tss_new.iloc[i,0] + ". "
length_printed += tss_new.iloc[i,3] ##Consider the sentence where max_word appear in the middle
else:
break
class style:
BOLD = '\033[1m'
END = '\033[0m'
print('\n','--------------------------------------------------------')
s = pd.Series([style.BOLD+summary+style.END])
print(s.str.split(' '))
print('\n')
#!jupyter nbconvert --to html ./ArticleSummarization.ipynb
```
| true |
code
| 0.424352 | null | null | null | null |
|
```
import numpy as np
from scipy.stats import norm
from stochoptim.scengen.scenario_tree import ScenarioTree
from stochoptim.scengen.scenario_process import ScenarioProcess
from stochoptim.scengen.variability_process import VariabilityProcess
from stochoptim.scengen.figure_of_demerit import FigureOfDemerit
```
We illustrate on a Geometric Brownian Motion (GBM) the two ways (forward vs. backward) to build a scenario tree with **optimized scenarios**.
# Define a `ScenarioProcess` instance for the GBM
```
S_0 = 2 # initial value (at stage 0)
delta_t = 1 # time lag between 2 stages
mu = 0 # drift
sigma = 1 # volatility
```
The `gbm_recurrence` function below implements the dynamic relation of a GBM:
* $S_{t} = S_{t-1} \exp[(\mu - \sigma^2/2) \Delta t + \sigma \epsilon_t\sqrt{\Delta t}], \quad t=1,2,\dots$
where $\epsilon_t$ is a standard normal random variable $N(0,1)$.
The discretization of $\epsilon_t$ is done by quasi-Monte Carlo (QMC) and is implemented by the `epsilon_sample_qmc` method.
```
def gbm_recurrence(stage, epsilon, scenario_path):
if stage == 0:
return {'S': np.array([S_0])}
else:
return {'S': scenario_path[stage-1]['S'] \
* np.exp((mu - sigma**2 / 2) * delta_t + sigma * np.sqrt(delta_t) * epsilon)}
def epsilon_sample_qmc(n_samples, stage, u=0.5):
return norm.ppf(np.linspace(0, 1-1/n_samples, n_samples) + u / n_samples).reshape(-1, 1)
scenario_process = ScenarioProcess(gbm_recurrence, epsilon_sample_qmc)
```
# Define a `VariabilityProcess` instance
A `VariabilityProcess` provides the *variability* of a stochastic problem along the stages and the scenarios. What we call 'variability' is a positive number that indicates how variable the future is given the present scenario.
Mathematically, a `VariabilityProcess` must implement one of the following two methods:
* the `lookback_fct` method which corresponds to the function $\mathcal{V}_{t}(S_{1}, ..., S_{t})$ that provides the variability at stage $t+1$ given the whole past scenario,
* the `looknow_fct` method which corresponds to the function $\mathcal{\tilde{V}}_{t}(\epsilon_t)$ that provides the variability at stage $t+1$ given the present random perturbation $\epsilon_t$.
If the `lookback_fct` method is provided, the scenarios can be optimized using the key world argument `optimized='forward'`.
If the `looknow_fct` method is provided, the scenarios can be optimized using the key world argument `optimized='backward'`.
```
def lookback_fct(stage, scenario_path):
return scenario_path[stage]['S'][0]
def looknow_fct(stage, epsilon):
return np.exp(epsilon[0])
my_variability = VariabilityProcess(lookback_fct, looknow_fct)
```
# Define a `FigureOfDemerit` instance
```
def demerit_fct(stage, epsilons, weights):
return 1 / len(epsilons)
my_demerit = FigureOfDemerit(demerit_fct, my_variability)
```
# Optimized Assignment of Scenarios to Nodes
### `optimized='forward'`
```
scen_tree = ScenarioTree.from_recurrence(last_stage=3, init=3, recurrence={1: (2,), 2: (1,2), 3: (1,2,3)})
scen_tree.fill(scenario_process,
optimized='forward',
variability_process=my_variability,
demerit=my_demerit)
scen_tree.plot('S')
scen_tree.plot_scenarios('S')
```
### `optimized='backward'`
```
scen_tree = ScenarioTree.from_recurrence(last_stage=3, init=3, recurrence={1: (2,), 2: (1,2), 3: (1,2,3)})
scen_tree.fill(scenario_process,
optimized='backward',
variability_process=my_variability,
demerit=my_demerit)
scen_tree.plot('S')
scen_tree.plot_scenarios('S')
```
| true |
code
| 0.58053 | null | null | null | null |
|
### 3. Tackle the Titanic dataset
```
# To support both python 2 and python 3
# 让这份笔记同步支持 python 2 和 python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
# 让笔记全程输入稳定
np.random.seed(42)
# To plot pretty figures
# 导入绘图工具
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# Where to save the figures
# 设定图片保存路径,这里写了一个函数,后面直接调用即可
PROJECT_ROOT_DIR = "F:\ML\Machine learning\Hands-on machine learning with scikit-learn and tensorflow"
CHAPTER_ID = "Classification_MNIST_03"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Ignore useless warnings (see SciPy issue #5998)
# 忽略无用警告
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
```
**目标**是根据年龄,性别,乘客等级,他们的出发地等属性来预测乘客是否幸存下来。
* 首先,登录Kaggle并前往泰坦尼克号挑战下载train.csv和test.csv。 将它们保存到datasets / titanic目录中。
* 接下来,让我们加载数据:
```
import os
TITANIC_PATH = os.path.join("datasets", "titanic")
import pandas as pd
def load_titanic_data(filename, titanic_path=TITANIC_PATH):
csv_path = os.path.join(titanic_path, filename)
return pd.read_csv(csv_path)
train_data = load_titanic_data("train.csv")
test_data = load_titanic_data("test.csv")
```
数据已经分为训练集和测试集。 但是,测试数据不包含标签:
* 你的目标是使用培训数据培训最佳模型,
* 然后对测试数据进行预测并将其上传到Kaggle以查看最终得分。
让我们来看看训练集的前几行:
```
train_data.head()
```
* **Survived**: 这是目标,0表示乘客没有生存,1表示他/她幸存。
* **Pclass**: 乘客客舱级别
* **Name, Sex, Age**: 这个不需要解释
* **SibSp**:乘坐泰坦尼克号的乘客中有多少兄弟姐妹和配偶。
* **Parch**: 乘坐泰坦尼克号的乘客中有多少孩子和父母。
* **Ticket**: 船票 id
* **Fare**: 支付的价格(英镑)
* **Cabin**: 乘客的客舱号码
* **Embarked**: 乘客登上泰坦尼克号的地点
```
train_data.info()
```
Okay, the **Age, Cabin** and **Embarked** attributes are sometimes null (less than 891 non-null), especially the **Cabin** (77% are null). We will **ignore the Cabin for now and focus on the rest**. The **Age** attribute has about 19% null values, so we will need to decide what to do with them.
* Replacing null values with the median age seems reasonable.
The **Name** and **Ticket** attributes may have some value, but they will be a bit tricky to convert into useful numbers that a model can consume. So for now, we will **ignore them**.
Let's take a look at the **numerical attributes**:
**Age,Cabin和Embarked**属性有时为null(小于891非null),尤其是**Cabin**(77%为null)。 我们现在将忽略Cabin并专注于其余部分。 Age属性有大约19%的空值,因此我们需要决定如何处理它们。
* 用年龄中位数替换空值似乎是合理的。
**Name和Ticket**属性可能有一些值,但转换为模型可以使用的有用数字会有点棘手。 所以现在,我们将忽略它们。
我们来看看数值属性:
```
train_data.describe()
# only in a Jupyter notebook
# 另一种快速了解数据的方法是绘制直方图
%matplotlib inline
import matplotlib.pyplot as plt
train_data.hist(bins=50, figsize=(20,15))
plt.show()
```
* 只有38%幸存。 :(这足够接近40%,因此准确度将是评估我们模型的合理指标。
* 平均票价是32.20英镑,这看起来并不那么昂贵(但当时可能还有很多钱)。
* 平均年龄不到30岁。
让我们检查目标是否确实为0或1:
```
train_data["Survived"].value_counts()
```
现在让我们快速浏览所有分类属性:
```
train_data["Pclass"].value_counts()
train_data["Sex"].value_counts()
train_data["Embarked"].value_counts()
```
“ Embarked ”属性告诉我们乘客的出发地点:C = Cherbourg 瑟堡,Q = Queenstown 皇后镇,S = Southampton 南安普敦。
现在让我们构建我们的预处理流水线。 我们将重用我们在前一章中构建的DataframeSelector来从DataFrame中选择特定属性:
```
from sklearn.base import BaseEstimator, TransformerMixin
# A class to select numerical or categorical columns
# since Scikit-Learn doesn't handle DataFrames yet
class DataFrameSelector(BaseEstimator, TransformerMixin):
def __init__(self, attribute_names):
self.attribute_names = attribute_names
def fit(self, X, y=None):
return self
def transform(self, X):
return X[self.attribute_names]
```
让我们为数值属性构建管道:
```
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
num_pipeline = Pipeline([
("select_numeric", DataFrameSelector(["Age", "SibSp", "Parch", "Fare"])),
("imputer", Imputer(strategy="median")),
])
num_pipeline.fit_transform(train_data)
```
我们还需要一个用于字符串分类列的imputer(常规Imputer不适用于那些):
```
# Inspired from stackoverflow.com/questions/25239958
class MostFrequentImputer(BaseEstimator, TransformerMixin):
def fit(self, X, y=None):
self.most_frequent_ = pd.Series([X[c].value_counts().index[0] for c in X],
index=X.columns)
return self
def transform(self, X, y=None):
return X.fillna(self.most_frequent_)
```
我们可以使用**OneHotEncoder**将每个分类值转换为**单热矢量**。
现在这个类只能处理整数分类输入,但在Scikit-Learn 0.20中它也会处理字符串分类输入(参见PR#10521)。 所以现在我们从future_encoders.py导入它,但是当Scikit-Learn 0.20发布时,你可以从sklearn.preprocessing导入它:
```
from sklearn.preprocessing import OneHotEncoder
```
现在我们可以为分类属性构建管道:
```
cat_pipeline = Pipeline([
("select_cat", DataFrameSelector(["Pclass", "Sex", "Embarked"])),
("imputer", MostFrequentImputer()),
("cat_encoder", OneHotEncoder(sparse=False)),
])
cat_pipeline.fit_transform(train_data)
```
最后,合并数值和分类管道:
```
from sklearn.pipeline import FeatureUnion
preprocess_pipeline = FeatureUnion(transformer_list=[
("num_pipeline", num_pipeline),
("cat_pipeline", cat_pipeline),
])
```
现在我们有一个很好的预处理管道,它可以获取原始数据并输出数字输入特征,我们可以将这些特征提供给我们想要的任何机器学习模型。
```
X_train = preprocess_pipeline.fit_transform(train_data)
X_train
```
让我们不要忘记获得标签:
```
y_train = train_data["Survived"]
```
我们现在准备训练分类器。 让我们从SVC开始吧
```
from sklearn.svm import SVC
svm_clf = SVC()
svm_clf.fit(X_train, y_train)
```
模型经过训练,让我们用它来测试测试集:
```
X_test = preprocess_pipeline.transform(test_data)
y_pred = svm_clf.predict(X_test)
```
现在我们可以:
* 用这些预测构建一个CSV文件(尊重Kaggle除外的格式)
* 然后上传它并希望能有好成绩。
可是等等! 我们可以比希望做得更好。 为什么我们不使用交叉验证来了解我们的模型有多好?
```
from sklearn.model_selection import cross_val_score
svm_scores = cross_val_score(svm_clf, X_train, y_train, cv=10)
svm_scores.mean()
```
好吧,超过73%的准确率,明显优于随机机会,但它并不是一个好成绩。 看看Kaggle泰坦尼克号比赛的排行榜,你可以看到你需要达到80%以上的准确率才能进入前10%的Kagglers。 有些人达到了100%,但由于你可以很容易地找到泰坦尼克号的受害者名单,似乎很少有机器学习涉及他们的表现! ;-)所以让我们尝试建立一个达到80%准确度的模型。
我们来试试**RandomForestClassifier**:
```
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
forest_scores = cross_val_score(forest_clf, X_train, y_train, cv=10)
forest_scores.mean()
```
这次好多了!
* 让我们为每个模型绘制所有10个分数,而不只是查看10个交叉验证折叠的平均准确度
* 以及突出显示下四分位数和上四分位数的方框图,以及显示分数范围的“whiskers(胡须)”(感谢Nevin Yilmaz建议这种可视化)。
请注意,**boxplot()函数**检测异常值(称为“fliers”)并且不包括它们在whiskers中。 特别:
* 如果下四分位数是$ Q_1 $而上四分位数是$ Q_3 $
* 然后四分位数范围$ IQR = Q_3 - Q_1 $(这是盒子的高度)
* 且任何低于$ Q_1 - 1.5 \ IQR $ 的分数都是一个**异常值**,任何分数都高于$ Q3 + 1.5 \ IQR $也是一个异常值。
```
plt.figure(figsize=(8, 4))
plt.plot([1]*10, svm_scores, ".")
plt.plot([2]*10, forest_scores, ".")
plt.boxplot([svm_scores, forest_scores],
labels=("SVM","Random Forest"))
plt.ylabel("Accuracy", fontsize=14)
plt.show()
```
为了进一步改善这一结果,你可以:比较更多模型并使用交叉验证和网格搜索调整超参数,做更多的特征工程,例如:
* 用他们的总和取代SibSp和Parch,
* 尝试识别与Survived属性相关的名称部分(例如,如果名称包含“Countess”,那么生存似乎更有可能),
* 尝试将数字属性转换为分类属性:例如,
* 不同年龄组的存活率差异很大(见下文),因此可能有助于创建一个年龄段类别并使用它代替年龄。
* 同样,为独自旅行的人设置一个特殊类别可能是有用的,因为只有30%的人幸存下来(见下文)。
```
train_data["AgeBucket"] = train_data["Age"] // 15 * 15
train_data[["AgeBucket", "Survived"]].groupby(['AgeBucket']).mean()
train_data["RelativesOnboard"] = train_data["SibSp"] + train_data["Parch"]
train_data[["RelativesOnboard", "Survived"]].groupby(['RelativesOnboard']).mean()
```
### 4. Spam classifier
Apache SpamAssassin的公共数据集下载spam and ham的示例
* 解压缩数据集并熟悉数据格式。
* 将数据集拆分为训练集和测试集。
* 编写数据preparation pipeline,将每封电子邮件转换为特征向量。您的preparation pipeline应将电子邮件转换为(稀疏)向量,指示每个可能单词的存在或不存在。例如,如果全部电子邮件只包含四个单词:
“Hello,” “how,” “are,” “you,”
then the email“Hello you Hello Hello you” would be converted into a vector [1, 0, 0, 1]
意思是:[“Hello” is present, “how” is absent, “are” is absent, “you” is present]),
或者[3, 0, 0, 2],如果你更喜欢计算每个单词的出现次数。
* 您可能希望在preparation pipeline中添加超参数以对是否剥离电子邮件标题进行控制,将每封电子邮件转换为小写,删除标点符号,将所有网址替换为“URL”用“NUMBER”替换所有数字,甚至执行*stemming*(即,修剪单词结尾;有可用的Python库)。
* 然后尝试几个分类器,看看你是否可以建立一个伟大的垃圾邮件分类器,具有高召回率和高精度。
First, let's fetch the data:
```
import os
import tarfile
from six.moves import urllib
DOWNLOAD_ROOT = "http://spamassassin.apache.org/old/publiccorpus/"
HAM_URL = DOWNLOAD_ROOT + "20030228_easy_ham.tar.bz2"
SPAM_URL = DOWNLOAD_ROOT + "20030228_spam.tar.bz2"
SPAM_PATH = os.path.join("datasets", "spam")
def fetch_spam_data(spam_url=SPAM_URL, spam_path=SPAM_PATH):
if not os.path.isdir(spam_path):
os.makedirs(spam_path)
for filename, url in (("ham.tar.bz2", HAM_URL), ("spam.tar.bz2", SPAM_URL)):
path = os.path.join(spam_path, filename)
if not os.path.isfile(path):
urllib.request.urlretrieve(url, path)
tar_bz2_file = tarfile.open(path)
tar_bz2_file.extractall(path=SPAM_PATH)
tar_bz2_file.close()
fetch_spam_data()
```
Next, let's load all the emails:
```
HAM_DIR = os.path.join(SPAM_PATH, "easy_ham")
SPAM_DIR = os.path.join(SPAM_PATH, "spam")
ham_filenames = [name for name in sorted(os.listdir(HAM_DIR)) if len(name) > 20]
spam_filenames = [name for name in sorted(os.listdir(SPAM_DIR)) if len(name) > 20]
len(ham_filenames)
len(spam_filenames)
```
We can use Python's email module to parse these emails (this handles headers, encoding, and so on):
```
import email
import email.policy
def load_email(is_spam, filename, spam_path=SPAM_PATH):
directory = "spam" if is_spam else "easy_ham"
with open(os.path.join(spam_path, directory, filename), "rb") as f:
return email.parser.BytesParser(policy=email.policy.default).parse(f)
ham_emails = [load_email(is_spam=False, filename=name) for name in ham_filenames]
spam_emails = [load_email(is_spam=True, filename=name) for name in spam_filenames]
```
Let's look at one example of ham and one example of spam, to get a feel of what the data looks like:
```
print(ham_emails[1].get_content().strip())
```
Your use of Yahoo! Groups is subject to http://docs.yahoo.com/info/terms/
```
print(spam_emails[6].get_content().strip())
```
Some emails are actually multipart, with images and attachments (which can have their own attachments). Let's look at the various types of structures we have:
```
def get_email_structure(email):
if isinstance(email, str):
return email
payload = email.get_payload()
if isinstance(payload, list):
return "multipart({})".format(", ".join([
get_email_structure(sub_email)
for sub_email in payload
]))
else:
return email.get_content_type()
fromfrom collectionscollectio import Counter
def structures_counter(emails):
structures = Counter()
for email in emails:
structure = get_email_structure(email)
structures[structure] += 1
return structures
structures_counter(ham_emails).most_common()
structures_counter(spam_emails).most_common()
```
It seems that the ham emails are more often plain text, while spam has quite a lot of HTML. Moreover, quite a few ham emails are signed using PGP, while no spam is. In short, it seems that the email structure is useful information to have.
Now let's take a look at the email headers:
```
for header, value in spam_emails[0].items():
print(header,":",value)
```
There's probably a lot of useful information in there, such as the sender's email address ([email protected] looks fishy), but we will just focus on the Subject header:
```
spam_emails[0]["Subject"]
```
Okay, before we learn too much about the data, let's not forget to split it into a training set and a test set:
```
import numpy as np
from sklearn.model_selection import train_test_split
X = np.array(ham_emails + spam_emails)
y = np.array([0] * len(ham_emails) + [1] * len(spam_emails))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
```
Okay, let's start writing the preprocessing functions. First, we will need a function to convert HTML to plain text. Arguably the best way to do this would be to use the great BeautifulSoup library, but I would like to avoid adding another dependency to this project, so let's hack a quick & dirty solution using regular expressions (at the risk of un̨ho͞ly radiańcé destro҉ying all enli̍̈́̂̈́ghtenment). The following function first drops the <head> section, then converts all <a> tags to the word HYPERLINK, then it gets rid of all HTML tags, leaving only the plain text. For readability, it also replaces multiple newlines with single newlines, and finally it unescapes html entities (such as > or ):
```
import re
from html import unescape
def html_to_plain_text(html):
text = re.sub('<head.*?>.*?</head>', '', html, flags=re.M | re.S | re.I)
text = re.sub('<a\s.*?>', ' HYPERLINK ', text, flags=re.M | re.S | re.I)
text = re.sub('<.*?>', '', text, flags=re.M | re.S)
text = re.sub(r'(\s*\n)+', '\n', text, flags=re.M | re.S)
return unescape(text)
```
Let's see if it works. This is HTML spam:
```
html_spam_emails = [email for email in X_train[y_train==1]
if get_email_structure(email) == "text/html"]
sample_html_spam = html_spam_emails[7]
print(sample_html_spam.get_content().strip()[:1000], "...")
```
And this is the resulting plain text:
```
print(html_to_plain_text(sample_html_spam.get_content())[:1000], "...")
```
Great! Now let's write a function that takes an email as input and returns its content as plain text, whatever its format is:
```
def email_to_text(email):
html = None
for part in email.walk():
ctype = part.get_content_type()
if not ctype in ("text/plain", "text/html"):
continue
try:
content = part.get_content()
except: # in case of encoding issues
content = str(part.get_payload())
if ctype == "text/plain":
return content
else:
html = content
if html:
return html_to_plain_text(html)
print(email_to_text(sample_html_spam)[:100], "...")
```
Let's throw in some stemming! For this to work, you need to install the Natural Language Toolkit (NLTK). It's as simple as running the following command (don't forget to activate your virtualenv first; if you don't have one, you will likely need administrator rights, or use the --user option):
$ pip3 install nltk
```
try:
import nltk
stemmer = nltk.PorterStemmer()
for word in ("Computations", "Computation", "Computing", "Computed", "Compute", "Compulsive"):
print(word, "=>", stemmer.stem(word))
except ImportError:
print("Error: stemming requires the NLTK module.")
stemmer = None
```
We will also need a way to replace URLs with the word "URL". For this, we could use hard core regular expressions but we will just use the urlextract library. You can install it with the following command (don't forget to activate your virtualenv first; if you don't have one, you will likely need administrator rights, or use the --user option):
$ pip3 install urlextract
```
try:
import urlextract # may require an Internet connection to download root domain names
url_extractor = urlextract.URLExtract()
print(url_extractor.find_urls("Will it detect github.com and https://youtu.be/7Pq-S557XQU?t=3m32s"))
except ImportError:
print("Error: replacing URLs requires the urlextract module.")
url_extractor = None
```
We are ready to put all this together into a transformer that we will use to convert emails to word counters. Note that we split sentences into words using Python's split() method, which uses whitespaces for word boundaries. This works for many written languages, but not all. For example, Chinese and Japanese scripts generally don't use spaces between words, and Vietnamese often uses spaces even between syllables. It's okay in this exercise, because the dataset is (mostly) in English.
```
from sklearn.base import BaseEstimator, TransformerMixin
class EmailToWordCounterTransformer(BaseEstimator, TransformerMixin):
def __init__(self, strip_headers=True, lower_case=True, remove_punctuation=True,
replace_urls=True, replace_numbers=True, stemming=True):
self.strip_headers = strip_headers
self.lower_case = lower_case
self.remove_punctuation = remove_punctuation
self.replace_urls = replace_urls
self.replace_numbers = replace_numbers
self.stemming = stemming
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
X_transformed = []
for email in X:
text = email_to_text(email) or ""
if self.lower_case:
text = text.lower()
if self.replace_urls and url_extractor is not None:
urls = list(set(url_extractor.find_urls(text)))
urls.sort(key=lambda url: len(url), reverse=True)
for url in urls:
text = text.replace(url, " URL ")
if self.replace_numbers:
text = re.sub(r'\d+(?:\.\d*(?:[eE]\d+))?', 'NUMBER', text)
if self.remove_punctuation:
text = re.sub(r'\W+', ' ', text, flags=re.M)
word_counts = Counter(text.split())
if self.stemming and stemmer is not None:
stemmed_word_counts = Counter()
for word, count in word_counts.items():
stemmed_word = stemmer.stem(word)
stemmed_word_counts[stemmed_word] += count
word_counts = stemmed_word_counts
X_transformed.append(word_counts)
return np.array(X_transformed)
```
Let's try this transformer on a few emails:
```
X_few = X_train[:3]
X_few_wordcounts = EmailToWordCounterTransformer().fit_transform(X_few)
X_few_wordcounts
```
This looks about right!
Now we have the word counts, and we need to convert them to vectors. For this, we will build another transformer whose fit() method will build the vocabulary (an ordered list of the most common words) and whose transform() method will use the vocabulary to convert word counts to vectors. The output is a sparse matrix.
```
from scipy.sparse import csr_matrix
class WordCounterToVectorTransformer(BaseEstimator, TransformerMixin):
def __init__(self, vocabulary_size=1000):
self.vocabulary_size = vocabulary_size
def fit(self, X, y=None):
total_count = Counter()
for word_count in X:
for word, count in word_count.items():
total_count[word] += min(count, 10)
most_common = total_count.most_common()[:self.vocabulary_size]
self.most_common_ = most_common
self.vocabulary_ = {word: index + 1 for index, (word, count) in enumerate(most_common)}
return self
def transform(self, X, y=None):
rows = []
cols = []
data = []
for row, word_count in enumerate(X):
for word, count in word_count.items():
rows.append(row)
cols.append(self.vocabulary_.get(word, 0))
data.append(count)
return csr_matrix((data, (rows, cols)), shape=(len(X), self.vocabulary_size + 1))
vocab_transformer = WordCounterToVectorTransformer(vocabulary_size=10)
X_few_vectors = vocab_transformer.fit_transform(X_few_wordcounts)
X_few_vectors
X_few_vectors.toarray()
```
What does this matrix mean? Well, the 64 in the third row, first column, means that the third email contains 64 words that are not part of the vocabulary. The 1 next to it means that the first word in the vocabulary is present once in this email. The 2 next to it means that the second word is present twice, and so on. You can look at the vocabulary to know which words we are talking about. The first word is "of", the second word is "and", etc.
```
vocab_transformer.vocabulary_
```
We are now ready to train our first spam classifier! Let's transform the whole dataset:
```
from sklearn.pipeline import Pipeline
preprocess_pipeline = Pipeline([
("email_to_wordcount", EmailToWordCounterTransformer()),
("wordcount_to_vector", WordCounterToVectorTransformer()),
])
X_train_transformed = preprocess_pipeline.fit_transform(X_train)
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
log_clf = LogisticRegression(random_state=42)
score = cross_val_score(log_clf, X_train_transformed, y_train, cv=3, verbose=3)
score.mean()
```
Over 98.7%, not bad for a first try! :) However, remember that we are using the "easy" dataset. You can try with the harder datasets, the results won't be so amazing. You would have to try multiple models, select the best ones and fine-tune them using cross-validation, and so on.
But you get the picture, so let's stop now, and just print out the precision/recall we get on the test set:
```
from sklearn.metrics import precision_score, recall_score
X_test_transformed = preprocess_pipeline.transform(X_test)
log_clf = LogisticRegression(random_state=42)
log_clf.fit(X_train_transformed, y_train)
y_pred = log_clf.predict(X_test_transformed)
print("Precision: {:.2f}%".format(100 * precision_score(y_test, y_pred)))
print("Recall: {:.2f}%".format(100 * recall_score(y_test, y_pred)))
```
| true |
code
| 0.504333 | null | null | null | null |
|
[Binary Tree Tilt](https://leetcode.com/problems/binary-tree-tilt/)。定义倾斜程度,节点的倾斜程度等于左子树节点和与右子树节点和的绝对差,而整棵树的倾斜程度等于所有节点倾斜度的和。求一棵树的倾斜程度。
思路:因为求倾斜程度牵涉到节点的累计和,所以在设计递归函数时返回一个累加和。
```
def findTilt(root: TreeNode) -> int:
res = 0
def rec(root): # 返回累加和的递归函数
if not root:
return 0
nonlocal res
left_sum = rec(root.left)
right_sum = rec(root.right)
res += abs(left_sum-right_sum)
return left_sum+right_sum+root.val
rec(root)
return res
```
京东2019实习笔试题:
体育场突然着火了,现场需要紧急疏散,但是过道真的是太窄了,同时只能容许一个人通过。现在知道了体育场的所有座位分布,座位分布图是一棵树,已知每个座位上都坐了一个人,安全出口在树的根部,也就是1号结点的位置上。其他节点上的人每秒都能向树根部前进一个结点,但是除了安全出口以外,没有任何一个结点可以同时容纳两个及以上的人,这就需要一种策略,来使得人群尽快疏散,问在采取最优策略的情况下,体育场最快可以在多长时间内疏散完成。
示例数据:
6
2 1
3 2
4 3
5 2
6 1
思路:在第二层以下的所有节点,每次均只能移动一个节点,所以散场的时间由第二层以下的节点数决定。找到所有分支中节点数最大的那一支,返回其节点数即可
```
n = int(input())
branches = list()
for _ in range(n-1):
a, b = map(int, input().split())
if b == 1: # 新分支
branches.append(set([a]))
for branch in branches:
if b in branch:
branch.add(a)
print(branches)
print(max(map(len, branches)))
```
[Leaf-Similar Trees](https://leetcode.com/problems/leaf-similar-trees/)。一颗二叉树,从左往右扫描经过的所有叶节点构成的序列为叶节点序列。给两颗二叉树,判断两棵树的叶节点序列是否相同。
思路:易得叶节点序列可以通过中序遍历得到。
```
def leafSimilar(root1: TreeNode, root2: TreeNode) -> bool:
def get_leaf_seq(root):
res=list()
if not root:
return res
s=list()
while root or s:
while root:
s.append(root)
root=root.left
vis_node=s.pop()
if not vis_node.left and not vis_node.right:
res.append(vis_node.val)
if vis_node.right:
root=vis_node.right
return res
seq_1,seq_2=get_leaf_seq(root1),get_leaf_seq(root2)
if len(seq_1)!=len(seq_2):
return False
for val_1,val_2 in zip(seq_1,seq_2):
if val_1!=val_2:
return False
return True
```
[Increasing Order Search Tree](https://leetcode.com/problems/increasing-order-search-tree/)。给一颗BST,将其转化成只有右分支的单边树。
思路:只有右分支的BST,那么根节点是最小节点,一直往右一直增。BST的递增序列是通过中序遍历得到,新建一棵树即可。
```
def increasingBST(root: TreeNode) -> TreeNode:
res = None
s = list()
while s or root:
while root:
s.append(root)
root = root.left
vis_node = s.pop()
if res is None: # 第一个节点特殊处理
res = TreeNode(vis_node.val)
ptr = res
else:
ptr.right = TreeNode(vis_node.val)
ptr = ptr.right
if vis_node.right:
root = vis_node.right
return res
```
| true |
code
| 0.394493 | null | null | null | null |
|
# Modeling and Simulation in Python
Chapter 10
Copyright 2017 Allen Downey
License: [Creative Commons Attribution 4.0 International](https://creativecommons.org/licenses/by/4.0)
```
# Configure Jupyter so figures appear in the notebook
%matplotlib inline
# Configure Jupyter to display the assigned value after an assignment
%config InteractiveShell.ast_node_interactivity='last_expr_or_assign'
# import functions from the modsim.py module
from modsim import *
from pandas import read_html
```
### Under the hood
To get a `DataFrame` and a `Series`, I'll read the world population data and select a column.
`DataFrame` and `Series` contain a variable called `shape` that indicates the number of rows and columns.
```
filename = 'data/World_population_estimates.html'
tables = read_html(filename, header=0, index_col=0, decimal='M')
table2 = tables[2]
table2.columns = ['census', 'prb', 'un', 'maddison',
'hyde', 'tanton', 'biraben', 'mj',
'thomlinson', 'durand', 'clark']
table2.shape
census = table2.census / 1e9
census.shape
un = table2.un / 1e9
un.shape
```
A `DataFrame` contains `index`, which labels the rows. It is an `Int64Index`, which is similar to a NumPy array.
```
table2.index
```
And `columns`, which labels the columns.
```
table2.columns
```
And `values`, which is an array of values.
```
table2.values
```
A `Series` does not have `columns`, but it does have `name`.
```
census.name
```
It contains `values`, which is an array.
```
census.values
```
And it contains `index`:
```
census.index
```
If you ever wonder what kind of object a variable refers to, you can use the `type` function. The result indicates what type the object is, and the module where that type is defined.
`DataFrame`, `Int64Index`, `Index`, and `Series` are defined by Pandas.
`ndarray` is defined by NumPy.
```
type(table2)
type(table2.index)
type(table2.columns)
type(table2.values)
type(census)
type(census.index)
type(census.values)
```
## Optional exercise
The following exercise provides a chance to practice what you have learned so far, and maybe develop a different growth model. If you feel comfortable with what we have done so far, you might want to give it a try.
**Optional Exercise:** On the Wikipedia page about world population estimates, the first table contains estimates for prehistoric populations. The following cells process this table and plot some of the results.
Select `tables[1]`, which is the second table on the page.
```
table1 = tables[1]
table1.head()
```
Not all agencies and researchers provided estimates for the same dates. Again `NaN` is the special value that indicates missing data.
```
table1.tail()
```
Some of the estimates are in a form we can't read as numbers. We could clean them up by hand, but for simplicity I'll replace any value that has an `M` in it with `NaN`.
```
table1.replace('M', np.nan, regex=True, inplace=True)
```
Again, we'll replace the long column names with more convenient abbreviations.
```
table1.columns = ['prb', 'un', 'maddison', 'hyde', 'tanton',
'biraben', 'mj', 'thomlinson', 'durand', 'clark']
```
This function plots selected estimates.
```
def plot_prehistory(table):
"""Plots population estimates.
table: DataFrame
"""
plot(table.prb, 'ro', label='PRB')
plot(table.un, 'co', label='UN')
plot(table.hyde, 'yo', label='HYDE')
plot(table.tanton, 'go', label='Tanton')
plot(table.biraben, 'bo', label='Biraben')
plot(table.mj, 'mo', label='McEvedy & Jones')
```
Here are the results. Notice that we are working in millions now, not billions.
```
plot_prehistory(table1)
decorate(xlabel='Year',
ylabel='World population (millions)',
title='Prehistoric population estimates')
```
We can use `xlim` to zoom in on everything after Year 0.
```
plot_prehistory(table1)
decorate(xlim=[0, 2000], xlabel='Year',
ylabel='World population (millions)',
title='Prehistoric population estimates')
```
See if you can find a model that fits these data well from Year -1000 to 1940, or from Year 1 to 1940.
How well does your best model predict actual population growth from 1950 to the present?
```
# Solution
def update_func_prop(pop, t, system):
"""Compute the population next year with proportional growth.
pop: current population
t: current year
system: system object containing parameters of the model
returns: population next year
"""
net_growth = system.alpha * pop
return pop + net_growth
# Solution
t_0 = 1
p_0 = table1.biraben[t_0]
prehistory = System(t_0=t_0,
t_end=2016,
p_0=p_0,
alpha=0.0011)
# Solution
def run_simulation(system, update_func):
"""Simulate the system using any update function.
system: System object
update_func: function that computes the population next year
returns: TimeSeries
"""
results = TimeSeries()
results[system.t_0] = system.p_0
for t in linrange(system.t_0, system.t_end):
results[t+1] = update_func(results[t], t, system)
return results
# Solution
results = run_simulation(prehistory, update_func_prop)
plot_prehistory(table1)
plot(results, color='gray', label='model')
decorate(xlim=[0, 2000], xlabel='Year',
ylabel='World population (millions)',
title='Prehistoric population estimates')
# Solution
plot(census, ':', label='US Census')
plot(un, '--', label='UN DESA')
plot(results / 1000, color='gray', label='model')
decorate(xlim=[1950, 2016], xlabel='Year',
ylabel='World population (billions)',
title='Prehistoric population estimates')
```
| true |
code
| 0.714858 | null | null | null | null |
|
```
import os
import sys
import torch
import gpytorch
from tqdm.auto import tqdm
import timeit
if os.path.abspath('..') not in sys.path:
sys.path.insert(0, os.path.abspath('..'))
from gpytorch_lattice_kernel import RBFLattice as BilateralKernel
# device = "cuda" if torch.cuda.is_available() else "cpu"
device = "cpu"
N_vals = torch.linspace(100, 10000000, 10).int().tolist()
D_vals = torch.linspace(1, 100, 10).int().tolist()
```
# Matmul
```
N_vary = []
for N in tqdm(N_vals):
D = 1
x = torch.randn(N, D).to(device)
K = BilateralKernel().to(device)(x)
v = torch.randn(N, 1).to(device)
def matmul():
return K @ v
time = timeit.timeit(matmul , number=10)
N_vary.append([N, D, time])
del x
del K
del v
del matmul
D_vary = []
for D in tqdm(D_vals):
N = 1000
x = torch.randn(N, D).to(device)
K = BilateralKernel().to(device)(x)
v = torch.randn(N, 1).to(device)
def matmul():
return K @ v
time = timeit.timeit(matmul , number=10)
D_vary.append([N, D, time])
del x
del K
del v
del matmul
import pandas as pd
N_vary = pd.DataFrame(N_vary, columns=["N", "D", "Time"])
D_vary = pd.DataFrame(D_vary, columns=["N", "D", "Time"])
import seaborn as sns
ax = sns.lineplot(data=N_vary, x="N", y="Time")
ax.set(title="Matmul (D=1)")
from sklearn.linear_model import LinearRegression
import numpy as np
regr = LinearRegression()
regr.fit(np.log(D_vary["D"].to_numpy()[:, None]), np.log(D_vary["Time"]))
print('Coefficients: \n', regr.coef_)
pred_time = regr.predict(np.log(D_vary["D"].to_numpy()[:, None]))
ax = sns.lineplot(data=D_vary, x="D", y="Time")
ax.set(title="Matmul (N=1000)", xscale="log", yscale="log")
ax.plot(D_vary["D"].to_numpy(), np.exp(pred_time))
```
# Gradient
```
N_vary = []
for N in tqdm(N_vals):
D = 1
x = torch.randn(N, D, requires_grad=True).to(device)
K = BilateralKernel().to(device)(x)
v = torch.randn(N, 1, requires_grad=True).to(device)
sum = (K @ v).sum()
def gradient():
torch.autograd.grad(sum, [x, v], retain_graph=True)
x.grad = None
v.grad = None
return
time = timeit.timeit(gradient, number=10)
N_vary.append([N, D, time])
del x
del K
del v
del gradient
D_vary = []
for D in tqdm(D_vals):
N = 1000
x = torch.randn(N, D, requires_grad=True).to(device)
K = BilateralKernel().to(device)(x)
v = torch.randn(N, 1, requires_grad=True).to(device)
sum = (K @ v).sum()
def gradient():
torch.autograd.grad(sum, [x, v], retain_graph=True)
x.grad = None
v.grad = None
return
time = timeit.timeit(gradient, number=10)
D_vary.append([N, D, time])
del x
del K
del v
del gradient
import pandas as pd
N_vary = pd.DataFrame(N_vary, columns=["N", "D", "Time"])
D_vary = pd.DataFrame(D_vary, columns=["N", "D", "Time"])
import seaborn as sns
ax = sns.lineplot(data=N_vary, x="N", y="Time")
ax.set(title="Gradient computation of (K@v).sum() (D=1)")
from sklearn.linear_model import LinearRegression
import numpy as np
regr = LinearRegression()
regr.fit(np.log(D_vary["D"].to_numpy()[:, None]), np.log(D_vary["Time"]))
print('Coefficients: \n', regr.coef_)
pred_time = regr.predict(np.log(D_vary["D"].to_numpy()[:, None]))
ax = sns.lineplot(data=D_vary, x="D", y="Time")
ax.set(title="Gradient computation of (K@v).sum() (N=100)", xscale="log", yscale="log")
ax.plot(D_vary["D"].to_numpy(), np.exp(pred_time))
```
| true |
code
| 0.501404 | null | null | null | null |
|
### Linear SCM simulations with variance shift noise interventions in Section 5.2.2
variance shift instead of mean shift
| Sim Num | name | better estimator | baseline |
| :-----------: | :--------------------------------|:----------------:| :-------:|
| (viii) | Single source anti-causal DA without Y interv + variance shift | DIP-std+ | DIP |
| (ix) | Multiple source anti-causal DA with Y interv + variance shift | CIRMweigh-std+ | OLSPool |
```
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
plt.rcParams['axes.facecolor'] = 'lightgray'
np.set_printoptions(precision=3)
sns.set(style="darkgrid")
```
#### Helper functions
```
def boxplot_all_methods(plt_handle, res_all, title='', names=[], colors=[], ylim_option=0):
res_all_df = pd.DataFrame(res_all.T)
res_all_df.columns = names
res_all_df_melt = res_all_df.melt(var_name='methods', value_name='MSE')
res_all_mean = np.mean(res_all, axis=1)
plt_handle.set_title(title, fontsize=20)
plt_handle.axhline(res_all_mean[1], ls='--', color='b')
plt_handle.axhline(res_all_mean[0], ls='--', color='r')
ax = sns.boxplot(x="methods", y="MSE", data=res_all_df_melt,
palette=colors,
ax=plt_handle)
ax.set_xticklabels(ax.get_xticklabels(), rotation=-70, ha='left', fontsize=20)
ax.tick_params(labelsize=20)
# ax.yaxis.set_major_formatter(matplotlib.ticker.FormatStrFormatter('%.2f'))
ax.yaxis.grid(False) # Hide the horizontal gridlines
ax.xaxis.grid(True) # Show the vertical gridlines
# ax.xaxis.set_visible(False)
ax.set_xlabel("")
ax.set_ylabel("MSE", fontsize=20)
if ylim_option == 1:
lower_ylim = res_all_mean[0] - (res_all_mean[1] - res_all_mean[0]) *0.3
# upper_ylim = max(res_all_mean[1] + (res_all_mean[1] - res_all_mean[0]) *0.3, res_all_mean[0]*1.2)
upper_ylim = res_all_mean[1] + (res_all_mean[1] - res_all_mean[0]) *0.3
# get the boxes that are outside of the plot
outside_index = np.where(res_all_mean > upper_ylim)[0]
for oindex in outside_index:
ax.annotate("box\nbeyond\ny limit", xy=(oindex - 0.3, upper_ylim - (upper_ylim-lower_ylim)*0.15 ), fontsize=15)
plt_handle.set_ylim(lower_ylim, upper_ylim)
def scatterplot_two_methods(plt_handle, res_all, index1, index2, names, colors=[], title="", ylimmax = -1):
plt_handle.scatter(res_all[index1], res_all[index2], alpha=1.0, marker='+', c = np.array(colors[index2]).reshape(1, -1), s=100)
plt_handle.set_xlabel(names[index1], fontsize=20)
plt_handle.set_ylabel(names[index2], fontsize=20)
plt_handle.tick_params(labelsize=20)
#
if ylimmax <= 0:
# set ylim automatically
# ylimmax = np.max((np.max(res_all[index1]), np.max(res_all[index2])))
ylimmax = np.percentile(np.concatenate((res_all[index1], res_all[index2])), 90)
print(ylimmax)
plt_handle.plot([0, ylimmax],[0, ylimmax], 'k--', alpha=0.5)
# plt.axis('equal')
plt_handle.set_xlim(0.0, ylimmax)
plt_handle.set_ylim(0.0, ylimmax)
plt_handle.set_title(title, fontsize=20)
```
#### 8. Single source anti-causal DA without Y interv + variance shift - boxplots
boxplots showwing thatDIP-std+ and DIP-MMD works
```
names_short = ["OLSTar", "OLSSrc[1]", "DIP[1]-mean", "DIP[1]-std+", "DIP[1]-MMD"]
COLOR_PALETTE1 = sns.color_palette("Set1", 9, desat=1.)
COLOR_PALETTE2 = sns.color_palette("Set1", 9, desat=.7)
COLOR_PALETTE3 = sns.color_palette("Set1", 9, desat=.5)
COLOR_PALETTE4 = sns.color_palette("Set1", 9, desat=.3)
# this corresponds to the methods in names_short
COLOR_PALETTE = [COLOR_PALETTE2[0], COLOR_PALETTE2[1], COLOR_PALETTE2[3], COLOR_PALETTE2[3], COLOR_PALETTE3[3], COLOR_PALETTE4[3]]
sns.palplot(COLOR_PALETTE)
interv_type = 'sv1'
M = 2
lamL2 = 0.
lamL1 = 0.
epochs = 20000
lr = 1e-4
n = 5000
prefix_template_exp8_box = "simu_results/sim_exp8_box_r0%sd31020_%s_lamMatch%s_n%d_epochs%d_repeats%d"
save_dir = 'paper_figures'
nb_ba = 4
results_src_ba = np.zeros((3, M-1, nb_ba, 2, 10))
results_tar_ba = np.zeros((3, 1, nb_ba, 2, 10))
savefilename_prefix = prefix_template_exp8_box %(interv_type, 'baseline', 1.,
n, epochs, 10)
res_all_ba = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
for i in range(3):
for j in range(1):
results_src_ba[i, :], results_tar_ba[i, :] = res_all_ba.item()[i, j]
lamMatches = [10.**(k) for k in (np.arange(10)-5)]
print(lamMatches)
nb_damean = 2 # DIP, DIPOracle
results_src_damean = np.zeros((3, len(lamMatches), M-1, nb_damean, 2, 10))
results_tar_damean = np.zeros((3, len(lamMatches), 1, nb_damean, 2, 10))
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_box %(interv_type, 'DAmean', lam,
n, epochs, 10)
res_all_damean = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
for i in range(3):
for j in range(1):
results_src_damean[i, k, :], results_tar_damean[i, k, 0, :] = res_all_damean.item()[i, j]
nb_dastd = 2 # DIP-std, DIP-std+
results_src_dastd = np.zeros((3, len(lamMatches), M-1, nb_dastd, 2, 10))
results_tar_dastd = np.zeros((3, len(lamMatches), 1, nb_dastd, 2, 10))
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_box %(interv_type, 'DAstd', lam,
n, epochs, 10)
res_all_dastd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
for i in range(3):
for j in range(1):
# run methods on data generated from sem
results_src_dastd[i, k, :], results_tar_dastd[i, k, 0, :] = res_all_dastd.item()[i, j]
nb_dammd = 1 # DIP-MMD
results_src_dammd = np.zeros((3, len(lamMatches), M-1, nb_dammd, 2, 10))
results_tar_dammd = np.zeros((3, len(lamMatches), 1, nb_dammd, 2, 10))
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_box %(interv_type, 'DAMMD', lam,
n, 2000, 10)
res_all_dammd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
for i in range(3):
for j in range(1):
# run methods on data generated from sem
results_src_dammd[i, k, :], results_tar_dammd[i, k, 0, :] = res_all_dammd.item()[i, j]
# now add the methods
results_tar_plot = {}
lamMatchIndex = 6
print("Fix lambda choice: lmabda = ", lamMatches[lamMatchIndex])
for i in range(3):
results_tar_plot[i] = np.concatenate((results_tar_ba[i, 0, :2, 0, :],
results_tar_damean[i, lamMatchIndex, 0, 0, 0, :].reshape(1, -1),
results_tar_dastd[i, lamMatchIndex, 0, 1, 0, :].reshape(1, -1),
results_tar_dammd[i, lamMatchIndex, 0, 0, 0, :].reshape(1, -1)), axis=0)
ds = [3, 10, 20]
fig, axs = plt.subplots(1, 3, figsize=(20,5))
for i in range(3):
boxplot_all_methods(axs[i], results_tar_plot[i],
title="linear SCM: d=%d" %(ds[i]), names=names_short, colors=COLOR_PALETTE[:len(names_short)])
plt.subplots_adjust(top=0.9, bottom=0.1, left=0.1, right=0.9, hspace=0.6,
wspace=0.2)
plt.savefig("%s/sim_6_2_exp_%s.pdf" %(save_dir, interv_type), bbox_inches="tight")
plt.show()
fig, axs = plt.subplots(1, 1, figsize=(5,5))
boxplot_all_methods(axs, results_tar_plot[1],
title="linear SCM: d=%d" %(10), names=names_short, colors=COLOR_PALETTE[:len(names_short)])
plt.subplots_adjust(top=0.9, bottom=0.1, left=0.1, right=0.9, hspace=0.6,
wspace=0.2)
plt.savefig("%s/sim_6_2_exp_%s_single10.pdf" %(save_dir, interv_type), bbox_inches="tight")
plt.show()
```
#### 8 Single source anti-causal DA without Y interv + variance shift - scatterplots
Scatterplots showing that DIP-std+ and DIP-MMD works
```
interv_type = 'sv1'
M = 2
lamL2 = 0.
lamL1 = 0.
epochs = 20000
lr = 1e-4
n = 5000
prefix_template_exp8_scat = "simu_results/sim_exp8_scat_r0%sd10_%s_lamMatch%s_n%d_epochs%d_seed%d"
nb_ba = 4
repeats = 100
results_scat_src_ba = np.zeros((M-1, nb_ba, 2, repeats))
results_scat_tar_ba = np.zeros((1, nb_ba, 2, repeats))
for myseed in range(100):
savefilename_prefix = prefix_template_exp8_scat %(interv_type, 'baseline', 1.,
n, epochs, myseed)
res_all_ba = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results_scat_src_ba[0, :, :, myseed] = res_all_ba.item()['src'][:, :, 0]
results_scat_tar_ba[0, :, :, myseed] = res_all_ba.item()['tar'][:, :, 0]
lamMatches = [10.**(k) for k in (np.arange(10)-5)]
nb_damean = 2 # DIP, DIPOracle
results_scat_src_damean = np.zeros((len(lamMatches), M-1, nb_damean, 2, 100))
results_scat_tar_damean = np.zeros((len(lamMatches), 1, nb_damean, 2, 100))
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_scat %(interv_type, 'DAmean', lam,
n, epochs, myseed)
res_all_damean = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results_scat_src_damean[k, 0, :, :, myseed] = res_all_damean.item()['src'][:, :, 0]
results_scat_tar_damean[k, 0, :, :, myseed] = res_all_damean.item()['tar'][:, :, 0]
nb_dastd = 2 # DIP-std, DIP-std+
results_scat_src_dastd = np.zeros((len(lamMatches), M-1, nb_dastd, 2, 100))
results_scat_tar_dastd = np.zeros((len(lamMatches), 1, nb_dastd, 2, 100))
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_scat %(interv_type, 'DAstd', lam,
n, epochs, myseed)
res_all_dastd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results_scat_src_dastd[k, 0, :, :, myseed] = res_all_dastd.item()['src'][:, :, 0]
results_scat_tar_dastd[k, 0, :, :, myseed] = res_all_dastd.item()['tar'][:, :, 0]
nb_dammd = 1 # DIP-MMD
results_scat_src_dammd = np.zeros((len(lamMatches), M-1, nb_dammd, 2, 100))
results_scat_tar_dammd = np.zeros((len(lamMatches), 1, nb_dammd, 2, 100))
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp8_scat %(interv_type, 'DAMMD', lam,
n, 2000, myseed)
res_all_dammd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results_scat_src_dammd[k, 0, :, :, myseed] = res_all_dammd.item()['src'][:, :, 0]
results_scat_tar_dammd[k, 0, :, :, myseed] = res_all_dammd.item()['tar'][:, :, 0]
# now add the methods
results_tar_plot = {}
lamMatchIndex = 6
print("Fix lambda choice: lmabda = ", lamMatches[lamMatchIndex])
results_scat_tar_plot = np.concatenate((results_scat_tar_ba[0, :2, 0, :],
results_scat_tar_damean[lamMatchIndex, 0, 0, 0, :].reshape(1, -1),
results_scat_tar_dastd[lamMatchIndex, 0, 0, 0, :].reshape(1, -1),
results_scat_tar_dammd[lamMatchIndex, 0, 0, 0, :].reshape(1, -1)), axis=0)
for index1, name1 in enumerate(names_short):
for index2, name2 in enumerate(names_short):
if index2 > index1:
fig, axs = plt.subplots(1, 1, figsize=(5,5))
nb_below_diag = np.sum(results_scat_tar_plot[index1, :] >= results_scat_tar_plot[index2, :])
scatterplot_two_methods(axs, results_scat_tar_plot, index1, index2, names_short, COLOR_PALETTE[:len(names_short)],
title="%d%% of pts below the diagonal" % (nb_below_diag),
ylimmax = -1)
plt.savefig("%s/sim_6_2_exp_%s_single_repeat_%s_vs_%s.pdf" %(save_dir, interv_type, name1, name2), bbox_inches="tight")
plt.show()
```
#### 9 Multiple source anti-causal DA with Y interv + variance shift - scatterplots
Scatterplots showing that CIRM-std+ and CIRM-MMD works
```
interv_type = 'smv1'
M = 15
lamL2 = 0.
lamL1 = 0.
epochs = 20000
lr = 1e-4
n = 5000
prefix_template_exp9 = "simu_results/sim_exp9_scat_r0%sd20x4_%s_lamMatch%s_lamCIP%s_n%d_epochs%d_seed%d"
nb_ba = 4 # OLSTar, SrcPool, OLSTar, SrcPool
results9_src_ba = np.zeros((M-1, nb_ba, 2, 100))
results9_tar_ba = np.zeros((1, nb_ba, 2, 100))
for myseed in range(100):
savefilename_prefix = prefix_template_exp9 %(interv_type, 'baseline',
1., 0.1, n, epochs, myseed)
res_all_ba = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results9_src_ba[0, :, :, myseed] = res_all_ba.item()['src'][0, :, 0]
results9_tar_ba[0, :, :, myseed] = res_all_ba.item()['tar'][:, :, 0]
lamMatches = [10.**(k) for k in (np.arange(10)-5)]
nb_damean = 5 # DIP, DIPOracle, DIPweigh, CIP, CIRMweigh
results9_src_damean = np.zeros((len(lamMatches), M-1, nb_damean, 2, 100))-1
results9_tar_damean = np.zeros((len(lamMatches), 1, nb_damean, 2, 100))-1
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp9 %(interv_type, 'DAmean',
lam, 0.1, 5000, epochs, myseed)
res_all_damean = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results9_src_damean[k, :, :, :, myseed] = res_all_damean.item()['src'][:, :, :, 0]
results9_tar_damean[k, 0, :, :, myseed] = res_all_damean.item()['tar'][:, :, 0]
nb_dastd = 4 # DIP-std+, DIPweigh-std+, CIP-std+, CIRMweigh-std+
results9_src_dastd = np.zeros((len(lamMatches), M-1, nb_dastd, 2, 100))-1
results9_tar_dastd = np.zeros((len(lamMatches), 1, nb_dastd, 2, 100))-1
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp9 %(interv_type, 'DAstd',
lam, 0.1, 5000, epochs, myseed)
res_all_dastd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results9_src_dastd[k, :, :, :, myseed] = res_all_dastd.item()['src'][:, :, :, 0]
results9_tar_dastd[k, 0, :, :, myseed] = res_all_dastd.item()['tar'][:, :, 0]
nb_dammd = 4 # DIP-MMD, DIPweigh-MMD, CIP-MMD, CIRMweigh-MMMD
results9_src_dammd = np.zeros((len(lamMatches), M-1, nb_dammd, 2, 100))-1
results9_tar_dammd = np.zeros((len(lamMatches), 1, nb_dammd, 2, 100))-1
for myseed in range(100):
for k, lam in enumerate(lamMatches):
savefilename_prefix = prefix_template_exp9 %(interv_type, 'DAMMD',
lam, 0.1, 5000, 2000, myseed)
res_all_dammd = np.load("%s.npy" %savefilename_prefix, allow_pickle=True)
results9_src_dammd[k, :, :, :, myseed] = res_all_dammd.item()['src'][:, :, :, 0]
results9_tar_dammd[k, 0, :, :, myseed] = res_all_dammd.item()['tar'][:, :, 0]
# now add the methods
names_short = ["Tar", "SrcPool", "CIRMweigh-mean", "CIRMweigh-std+", "DIPweigh-MMD", "CIRMweigh-MMD"]
COLOR_PALETTE1 = sns.color_palette("Set1", 9, desat=1.)
COLOR_PALETTE = [COLOR_PALETTE1[k] for k in [0, 1, 2, 3, 4, 7, 6]]
COLOR_PALETTE = [COLOR_PALETTE[k] for k in [0, 1, 6, 6, 4, 6]]
sns.palplot(COLOR_PALETTE)
lamMatchIndex = 6
print("Fix lambda choice: lmabda = ", lamMatches[lamMatchIndex])
results9_tar_plot = np.concatenate((results9_tar_ba[0, :2, 0, :],
results9_tar_damean[lamMatchIndex, 0, 4, 0, :].reshape(1, -1),
results9_tar_dastd[lamMatchIndex, 0, 3, 0, :].reshape(1, -1),
results9_tar_dammd[lamMatchIndex, 0, 1, 0, :].reshape(1, -1),
results9_tar_dammd[lamMatchIndex, 0, 3, 0, :].reshape(1, -1)), axis=0)
for index1, name1 in enumerate(names_short):
for index2, name2 in enumerate(names_short):
if index2 > index1:
fig, axs = plt.subplots(1, 1, figsize=(5,5))
nb_below_diag = np.sum(results9_tar_plot[index1, :] >= results9_tar_plot[index2, :])
scatterplot_two_methods(axs, results9_tar_plot, index1, index2, names_short, COLOR_PALETTE[:len(names_short)],
title="%d%% of pts below the diagonal" % (nb_below_diag),
ylimmax = -1)
plt.savefig("%s/sim_6_2_exp_%s_y_shift_single_repeat_%s_vs_%s.pdf" %(save_dir, interv_type, name1, name2), bbox_inches="tight")
plt.show()
```
| true |
code
| 0.436562 | null | null | null | null |
|
# Linear algebra
Linear algebra is the branch of mathematics that deals with **vector spaces**.
```
import re, math, random # regexes, math functions, random numbers
import matplotlib.pyplot as plt # pyplot
from collections import defaultdict, Counter
from functools import partial, reduce
```
# Vectors
Vectors are points in some finite-dimensional space.
```
v = [1, 2]
w = [2, 1]
vectors = [v, w]
def vector_add(v, w):
"""adds two vectors componentwise"""
return [v_i + w_i for v_i, w_i in zip(v,w)]
vector_add(v, w)
def vector_subtract(v, w):
"""subtracts two vectors componentwise"""
return [v_i - w_i for v_i, w_i in zip(v,w)]
vector_subtract(v, w)
def vector_sum(vectors):
return reduce(vector_add, vectors)
vector_sum(vectors)
def scalar_multiply(c, v):
# c is a number, v is a vector
return [c * v_i for v_i in v]
scalar_multiply(2.5, v)
def vector_mean(vectors):
"""compute the vector whose i-th element is the mean of the
i-th elements of the input vectors"""
n = len(vectors)
return scalar_multiply(1/n, vector_sum(vectors))
vector_mean(vectors)
def dot(v, w):
"""v_1 * w_1 + ... + v_n * w_n"""
return sum(v_i * w_i for v_i, w_i in zip(v, w))
dot(v, w)
```
The dot product measures how far the vector v extends in the w direction.
- For example, if w = [1, 0] then dot(v, w) is just the first component of v.
The dot product measures the length of the vector you’d get if you projected v onto w.
```
def sum_of_squares(v):
"""v_1 * v_1 + ... + v_n * v_n"""
return dot(v, v)
sum_of_squares(v)
def magnitude(v):
return math.sqrt(sum_of_squares(v))
magnitude(v)
def squared_distance(v, w):
return sum_of_squares(vector_subtract(v, w))
squared_distance(v, w)
def distance(v, w):
return math.sqrt(squared_distance(v, w))
distance(v, w)
```
Using lists as vectors
- is great for exposition
- but terrible for performance.
- to use the NumPy library.
# Matrices
A matrix is a two-dimensional collection of numbers.
- We will represent matrices as lists of lists
- If A is a matrix, then A[i][j] is the element in the ith row and the jth column.
```
A = [[1, 2, 3],
[4, 5, 6]]
B = [[1, 2],
[3, 4],
[5, 6]]
def shape(A):
num_rows = len(A)
num_cols = len(A[0]) if A else 0
return num_rows, num_cols
shape(A)
def get_row(A, i):
return A[i]
get_row(A, 1)
def get_column(A, j):
return [A_i[j] for A_i in A]
get_column(A, 2)
def make_matrix(num_rows, num_cols, entry_fn):
"""returns a num_rows x num_cols matrix
whose (i,j)-th entry is entry_fn(i, j),
entry_fn is a function for generating matrix elements."""
return [[entry_fn(i, j)
for j in range(num_cols)]
for i in range(num_rows)]
def entry_add(i, j):
"""a function for generating matrix elements. """
return i+j
make_matrix(5, 5, entry_add)
def is_diagonal(i, j):
"""1's on the 'diagonal',
0's everywhere else"""
return 1 if i == j else 0
identity_matrix = make_matrix(5, 5, is_diagonal)
identity_matrix
```
### Matrices will be important.
- using a matrix to represent a dataset
- using an n × k matrix to represent a linear function that maps k-dimensional vectors to n-dimensional vectors.
- using matrix to represent binary relationships.
```
friendships = [(0, 1),
(0, 2),
(1, 2),
(1, 3),
(2, 3),
(3, 4),
(4, 5),
(5, 6),
(5, 7),
(6, 8),
(7, 8),
(8, 9)]
friendships = [[0, 1, 1, 0, 0, 0, 0, 0, 0, 0], # user 0
[1, 0, 1, 1, 0, 0, 0, 0, 0, 0], # user 1
[1, 1, 0, 1, 0, 0, 0, 0, 0, 0], # user 2
[0, 1, 1, 0, 1, 0, 0, 0, 0, 0], # user 3
[0, 0, 0, 1, 0, 1, 0, 0, 0, 0], # user 4
[0, 0, 0, 0, 1, 0, 1, 1, 0, 0], # user 5
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 6
[0, 0, 0, 0, 0, 1, 0, 0, 1, 0], # user 7
[0, 0, 0, 0, 0, 0, 1, 1, 0, 1], # user 8
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0]] # user 9
friendships[0][2] == 1 # True, 0 and 2 are friends
def matrix_add(A, B):
if shape(A) != shape(B):
raise ArithmeticError("cannot add matrices with different shapes")
num_rows, num_cols = shape(A)
def entry_fn(i, j): return A[i][j] + B[i][j]
return make_matrix(num_rows, num_cols, entry_fn)
A = make_matrix(5, 5, is_diagonal)
B = make_matrix(5, 5, entry_add)
matrix_add(A, B)
v = [2, 1]
w = [math.sqrt(.25), math.sqrt(.75)]
c = dot(v, w)
vonw = scalar_multiply(c, w)
o = [0,0]
plt.figure(figsize=(4, 5), dpi = 100)
plt.arrow(0, 0, v[0], v[1],
width=0.002, head_width=.1, length_includes_head=True)
plt.annotate("v", v, xytext=[v[0] + 0.01, v[1]])
plt.arrow(0 ,0, w[0], w[1],
width=0.002, head_width=.1, length_includes_head=True)
plt.annotate("w", w, xytext=[w[0] - 0.1, w[1]])
plt.arrow(0, 0, vonw[0], vonw[1], length_includes_head=True)
plt.annotate(u"(v•w)w", vonw, xytext=[vonw[0] - 0.1, vonw[1] + 0.02])
plt.arrow(v[0], v[1], vonw[0] - v[0], vonw[1] - v[1],
linestyle='dotted', length_includes_head=True)
plt.scatter(*zip(v,w,o),marker='.')
plt.axis('equal')
plt.show()
```
| true |
code
| 0.769221 | null | null | null | null |
|
```
from scipy.cluster.hierarchy import linkage, fcluster
import matplotlib.pyplot as plt
import seaborn as sns, pandas as pd
x_coords = [80.1, 93.1, 86.6, 98.5, 86.4, 9.5, 15.2, 3.4, 10.4, 20.3, 44.2, 56.8, 49.2, 62.5]
y_coords = [87.2, 96.1, 95.6, 92.4, 92.4, 57.7, 49.4, 47.3, 59.1, 55.5, 25.6, 2.1, 10.9, 24.1]
df = pd.DataFrame({"x_coord" : x_coords, "y_coord": y_coords})
df.head()
Z = linkage(df, "ward")
df["cluster_labels"] = fcluster(Z, 3, criterion="maxclust")
df.head(3)
sns.scatterplot(x="x_coord", y="y_coord", hue="cluster_labels", data=df)
plt.show()
```
### K-means clustering in SciPy
#### two steps of k-means clustering:
* Define cluster centers through kmeans() function.
* It has two required arguments: observations and number of clusters.
* Assign cluster labels through the vq() function.
* It has two required arguments: observations and cluster centers.
```
from scipy.cluster.vq import kmeans, vq
import random
# Generate cluster centers
cluster_centers, distortion = kmeans(comic_con[["x_scaled","y_scaled"]], 2)
# Assign cluster labels
comic_con['cluster_labels'], distortion_list = vq(comic_con[["x_scaled","y_scaled"]], cluster_centers)
# Plot clusters
sns.scatterplot(x='x_scaled', y='y_scaled',
hue='cluster_labels', data = comic_con)
plt.show()
random.seed((1000,2000))
centroids, _ = kmeans(df, 3)
df["cluster_labels_kmeans"], _ = vq(df, centroids)
sns.scatterplot(x="x_coord", y="y_coord", hue="cluster_labels_kmeans", data=df)
plt.show()
```
### Normalization of Data
```
# Process of rescaling data to a standard deviation of 1
# x_new = x / std(x)
from scipy.cluster.vq import whiten
data = [5, 1, 3, 3, 2, 3, 3, 8, 1, 2, 2, 3, 5]
scaled_data = whiten(data)
scaled_data
plt.figure(figsize=(12,4))
plt.subplot(131)
plt.plot(data, label="original")
plt.legend()
plt.subplot(132)
plt.plot(scaled_data, label="scaled")
plt.legend()
plt.subplot(133)
plt.plot(data, label="original")
plt.plot(scaled_data, label="scaled")
plt.legend()
plt.show()
```
### Normalization of small numbers
```
# Prepare data
rate_cuts = [0.0025, 0.001, -0.0005, -0.001, -0.0005, 0.0025, -0.001, -0.0015, -0.001, 0.0005]
# Use the whiten() function to standardize the data
scaled_rate_cuts = whiten(rate_cuts)
plt.figure(figsize=(12,4))
plt.subplot(131)
plt.plot(rate_cuts, label="original")
plt.legend()
plt.subplot(132)
plt.plot(scaled_rate_cuts, label="scaled")
plt.legend()
plt.subplot(133)
plt.plot(rate_cuts, label='original')
plt.plot(scaled_rate_cuts, label='scaled')
plt.legend()
plt.show()
```
#### Hierarchical clustering: ward method
```
# Import the fcluster and linkage functions
from scipy.cluster.hierarchy import fcluster, linkage
# Use the linkage() function
distance_matrix = linkage(comic_con[['x_scaled', 'y_scaled']], method = "ward", metric = 'euclidean')
# Assign cluster labels
comic_con['cluster_labels'] = fcluster(distance_matrix, 2, criterion='maxclust')
# Plot clusters
sns.scatterplot(x='x_scaled', y='y_scaled',
hue='cluster_labels', data = comic_con)
plt.show()
```
#### Hierarchical clustering: single method
```
# Use the linkage() function
distance_matrix = linkage(comic_con[["x_scaled", "y_scaled"]], method = "single", metric = "euclidean")
# Assign cluster labels
comic_con['cluster_labels'] = fcluster(distance_matrix, 2, criterion="maxclust")
# Plot clusters
sns.scatterplot(x='x_scaled', y='y_scaled',
hue='cluster_labels', data = comic_con)
plt.show()
```
#### Hierarchical clustering: complete method
```
# Import the fcluster and linkage functions
from scipy.cluster.hierarchy import linkage, fcluster
# Use the linkage() function
distance_matrix = linkage(comic_con[["x_scaled", "y_scaled"]], method = "complete", metric = "euclidean")
# Assign cluster labels
comic_con['cluster_labels'] = fcluster(distance_matrix, 2, criterion="maxclust")
# Plot clusters
sns.scatterplot(x='x_scaled', y='y_scaled',
hue='cluster_labels', data = comic_con)
plt.show()
```
### Visualizing Data
```
# Import the pyplot class
import matplotlib.pyplot as plt
# Define a colors dictionary for clusters
colors = {1:'red', 2:'blue'}
# Plot a scatter plot
comic_con.plot.scatter(x="x_scaled",
y="y_scaled",
c=comic_con['cluster_labels'].apply(lambda x: colors[x]))
plt.show()
# Import the seaborn module
import seaborn as sns
# Plot a scatter plot using seaborn
sns.scatterplot(x="x_scaled",
y="y_scaled",
hue="cluster_labels",
data = comic_con)
plt.show()
```
### Dendogram
```
from scipy.cluster.hierarchy import dendrogram
Z = linkage(df[['x_whiten', 'y_whiten']], method='ward', metric='euclidean')
dn = dendrogram(Z)
plt.show()
### timing using %timeit
%timeit sum([1,3,5])
```
### Finding optimum "k" Elbow Method
```
distortions = []
num_clusters = range(1, 7)
# Create a list of distortions from the kmeans function
for i in num_clusters:
cluster_centers, distortion = kmeans(comic_con[["x_scaled","y_scaled"]], i)
distortions.append(distortion)
# Create a data frame with two lists - num_clusters, distortions
elbow_plot_data = pd.DataFrame({'num_clusters': num_clusters, 'distortions': distortions})
# Creat a line plot of num_clusters and distortions
sns.lineplot(x="num_clusters", y="distortions", data = elbow_plot_data)
plt.xticks(num_clusters)
plt.show()
```
### Elbow method on uniform data
```
# Let us now see how the elbow plot looks on a data set with uniformly distributed points.
distortions = []
num_clusters = range(2, 7)
# Create a list of distortions from the kmeans function
for i in num_clusters:
cluster_centers, distortion = kmeans(uniform_data[["x_scaled","y_scaled"]], i)
distortions.append(distortion)
# Create a data frame with two lists - number of clusters and distortions
elbow_plot = pd.DataFrame({'num_clusters': num_clusters, 'distortions': distortions})
# Creat a line plot of num_clusters and distortions
sns.lineplot(x="num_clusters", y="distortions", data=elbow_plot)
plt.xticks(num_clusters)
plt.show()
```
### Impact of seeds on distinct clusters
Notice that kmeans is unable to capture the three visible clusters clearly, and the two clusters towards the top have taken in some points along the boundary. This happens due to the underlying assumption in kmeans algorithm to minimize distortions which leads to clusters that are similar in terms of area.
### Dominant Colors in Images
#### Extracting RGB values from image
There are broadly three steps to find the dominant colors in an image:
* Extract RGB values into three lists.
* Perform k-means clustering on scaled RGB values.
* Display the colors of cluster centers.
To extract RGB values, we use the imread() function of the image class of matplotlib.
```
# Import image class of matplotlib
import matplotlib.image as img
from matplotlib.pyplot import imshow
# Read batman image and print dimensions
sea_horizon = img.imread("../00_DataSets/img/sea_horizon.jpg")
print(sea_horizon.shape)
imshow(sea_horizon)
# Store RGB values of all pixels in lists r, g and b
r, g, b = [], [], []
for row in sea_horizon:
for temp_r, temp_g, temp_b in row:
r.append(temp_r)
g.append(temp_g)
b.append(temp_b)
sea_horizon_df = pd.DataFrame({'red': r, 'blue': b, 'green': g})
sea_horizon_df.head()
distortions = []
num_clusters = range(1, 7)
# Create a list of distortions from the kmeans function
for i in num_clusters:
cluster_centers, distortion = kmeans(sea_horizon_df[["red", "blue", "green"]], i)
distortions.append(distortion)
# Create a data frame with two lists, num_clusters and distortions
elbow_plot_data = pd.DataFrame({"num_clusters":num_clusters, "distortions":distortions})
# Create a line plot of num_clusters and distortions
sns.lineplot(x="num_clusters", y="distortions", data = elbow_plot_data)
plt.xticks(num_clusters)
plt.show()
# scaling the data
sea_horizon_df["scaled_red"] = whiten(sea_horizon_df["red"])
sea_horizon_df["scaled_blue"] = whiten(sea_horizon_df["blue"])
sea_horizon_df["scaled_green"] = whiten(sea_horizon_df["green"])
distortions = []
num_clusters = range(1, 7)
# Create a list of distortions from the kmeans function
for i in num_clusters:
cluster_centers, distortion = kmeans(sea_horizon_df[["scaled_red", "scaled_blue", "scaled_green"]], i)
distortions.append(distortion)
# Create a data frame with two lists, num_clusters and distortions
elbow_plot_data = pd.DataFrame({"num_clusters":num_clusters, "distortions":distortions})
# Create a line plot of num_clusters and distortions
sns.lineplot(x="num_clusters", y="distortions", data = elbow_plot_data)
plt.xticks(num_clusters)
plt.show()
```
#### Show Dominant colors
To display the dominant colors, convert the colors of the cluster centers to their raw values and then converted them to the range of 0-1, using the following formula: converted_pixel = standardized_pixel * pixel_std / 255
```
# Get standard deviations of each color
r_std, g_std, b_std = sea_horizon_df[['red', 'green', 'blue']].std()
colors = []
for cluster_center in cluster_centers:
scaled_red, scaled_green, scaled_blue = cluster_center
# Convert each standardized value to scaled value
colors.append((
scaled_red * r_std / 255,
scaled_green * g_std / 255,
scaled_blue * b_std / 255
))
# Display colors of cluster centers
plt.imshow([colors])
plt.show()
```
### Document clustering
```
# TF-IDF of movie plots
from sklearn.feature_extraction.text import TfidfVectorizer
# Import TfidfVectorizer class from sklearn
from sklearn.feature_extraction.text import TfidfVectorizer
# Initialize TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer(max_df=0.75, min_df=0.1, max_features=50, tokenizer=remove_noise)
# Use the .fit_transform() method on the list plots
tfidf_matrix = tfidf_vectorizer.fit_transform(plots)
num_clusters = 2
# Generate cluster centers through the kmeans function
cluster_centers, distortion = kmeans(tfidf_matrix.todense(), num_clusters)
# Generate terms from the tfidf_vectorizer object
terms = tfidf_vectorizer.get_feature_names()
for i in range(num_clusters):
# Sort the terms and print top 3 terms
center_terms = dict(zip(terms, list(cluster_centers[i])))
sorted_terms = sorted(center_terms, key=center_terms.get, reverse=True)
print(sorted_terms[:3])
```
| true |
code
| 0.741702 | null | null | null | null |
|
## Demo 4: HKR multiclass and fooling
[](https://colab.research.google.com/github/deel-ai/deel-lip/blob/master/doc/notebooks/demo4.ipynb)
This notebook will show how to train a lispchitz network in a multiclass setup.
The HKR is extended to multiclass using a one-vs all setup. It will go through
the process of designing and training the network. It will also show how to create robustness certificates from the output of the network. Finally these
certificates will be checked by attacking the network.
### installation
First, we install the required libraries. `Foolbox` will allow to perform adversarial attacks on the trained network.
```
# pip install deel-lip foolbox -qqq
from deel.lip.layers import (
SpectralDense,
SpectralConv2D,
ScaledL2NormPooling2D,
ScaledAveragePooling2D,
FrobeniusDense,
)
from deel.lip.model import Sequential
from deel.lip.activations import GroupSort, FullSort
from deel.lip.losses import MulticlassHKR, MulticlassKR
from deel.lip.callbacks import CondenseCallback
from tensorflow.keras.layers import Input, Flatten
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.datasets import mnist, fashion_mnist, cifar10
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import numpy as np
```
For this example, the dataset `fashion_mnist` will be used. In order to keep things simple, no data augmentation will be performed.
```
# load data
(x_train, y_train_ord), (x_test, y_test_ord) = fashion_mnist.load_data()
# standardize and reshape the data
x_train = np.expand_dims(x_train, -1) / 255
x_test = np.expand_dims(x_test, -1) / 255
# one hot encode the labels
y_train = to_categorical(y_train_ord)
y_test = to_categorical(y_test_ord)
```
Let's build the network.
### the architecture
The original one vs all setup would require 10 different networks ( 1 per class ), however, in practice we use a network with
a common body and 10 1-lipschitz heads. Experiments have shown that this setup don't affect the network performance. In order to ease the creation of such network, `FrobeniusDense` layer has a parameter for this: whenr `disjoint_neurons=True` it act as the stacking of 10 single neurons head. Note that, altough each head is a 1-lipschitz function the overall network is not 1-lipschitz (Concatenation is not 1-lipschitz). We will see later how this affects the certficate creation.
### the loss
The multiclass loss can be found in `HKR_multiclass_loss`. The loss has two params: `alpha` and `min_margin`. Decreasing `alpha` and increasing `min_margin` improve robustness (at the cost of accuracy). note also in the case of lipschitz networks, more robustness require more parameters. For more information see [our paper](https://arxiv.org/abs/2006.06520).
In this setup choosing `alpha=100`, `min_margin=.25` provide a good robustness without hurting the accuracy too much.
Finally the `KR_multiclass_loss()` indicate the robustness of the network ( proxy of the average certificate )
```
# Sequential (resp Model) from deel.model has the same properties as any lipschitz model.
# It act only as a container, with features specific to lipschitz
# functions (condensation, vanilla_exportation...)
model = Sequential(
[
Input(shape=x_train.shape[1:]),
# Lipschitz layers preserve the API of their superclass ( here Conv2D )
# an optional param is available: k_coef_lip which control the lipschitz
# constant of the layer
SpectralConv2D(
filters=16,
kernel_size=(3, 3),
activation=GroupSort(2),
use_bias=True,
kernel_initializer="orthogonal",
),
# usual pooling layer are implemented (avg, max...), but new layers are also available
ScaledL2NormPooling2D(pool_size=(2, 2), data_format="channels_last"),
SpectralConv2D(
filters=32,
kernel_size=(3, 3),
activation=GroupSort(2),
use_bias=True,
kernel_initializer="orthogonal",
),
ScaledL2NormPooling2D(pool_size=(2, 2), data_format="channels_last"),
# our layers are fully interoperable with existing keras layers
Flatten(),
SpectralDense(
64,
activation=GroupSort(2),
use_bias=True,
kernel_initializer="orthogonal",
),
FrobeniusDense(
y_train.shape[-1], activation=None, use_bias=False, kernel_initializer="orthogonal"
),
],
# similary model has a parameter to set the lipschitz constant
# to set automatically the constant of each layer
k_coef_lip=1.0,
name="hkr_model",
)
# HKR (Hinge-Krantorovich-Rubinstein) optimize robustness along with accuracy
model.compile(
# decreasing alpha and increasing min_margin improve robustness (at the cost of accuracy)
# note also in the case of lipschitz networks, more robustness require more parameters.
loss=MulticlassHKR(alpha=100, min_margin=.25),
optimizer=Adam(1e-4),
metrics=["accuracy", MulticlassKR()],
)
model.summary()
```
### notes about constraint enforcement
There are currently 3 way to enforce a constraint in a network:
1. regularization
2. weight reparametrization
3. weight projection
The first one don't provide the required garanties, this is why `deel-lip` focuses on the later two. Weight reparametrization is done directly in the layers (parameter `niter_bjorck`) this trick allow to perform arbitrary gradient updates without breaking the constraint. However this is done in the graph, increasing ressources consumption. The last method project the weights between each batch, ensuring the constraint at an more affordable computational cost. It can be done in `deel-lip` using the `CondenseCallback`. The main problem with this method is a reduced efficiency of each update.
As a rule of thumb, when reparametrization is used alone, setting `niter_bjorck` to at least 15 is advised. However when combined with weight projection, this setting can be lowered greatly.
```
# fit the model
model.fit(
x_train,
y_train,
batch_size=4096,
epochs=100,
validation_data=(x_test, y_test),
shuffle=True,
verbose=1,
)
```
### model exportation
Once training is finished, the model can be optimized for inference by using the `vanilla_export()` method.
```
# once training is finished you can convert
# SpectralDense layers into Dense layers and SpectralConv2D into Conv2D
# which optimize performance for inference
vanilla_model = model.vanilla_export()
```
### certificates generation and adversarial attacks
```
import foolbox as fb
from tensorflow import convert_to_tensor
import matplotlib.pyplot as plt
import tensorflow as tf
# we will test it on 10 samples one of each class
nb_adv = 10
hkr_fmodel = fb.TensorFlowModel(vanilla_model, bounds=(0., 1.), device="/GPU:0")
```
In order to test the robustness of the model, the first correctly classified element of each class are selected.
```
# strategy: first
# we select a sample from each class.
images_list = []
labels_list = []
# select only a few element from the test set
selected=np.random.choice(len(y_test_ord), 500)
sub_y_test_ord = y_test_ord[:300]
sub_x_test = x_test[:300]
# drop misclassified elements
misclassified_mask = tf.equal(tf.argmax(vanilla_model.predict(sub_x_test), axis=-1), sub_y_test_ord)
sub_x_test = sub_x_test[misclassified_mask]
sub_y_test_ord = sub_y_test_ord[misclassified_mask]
# now we will build a list with input image for each element of the matrix
for i in range(10):
# select the first element of the ith label
label_mask = [sub_y_test_ord==i]
x = sub_x_test[label_mask][0]
y = sub_y_test_ord[label_mask][0]
# convert it to tensor for use with foolbox
images = convert_to_tensor(x.astype("float32"), dtype="float32")
labels = convert_to_tensor(y, dtype="int64")
# repeat the input 10 times, one per misclassification target
images_list.append(images)
labels_list.append(labels)
images = convert_to_tensor(images_list)
labels = convert_to_tensor(labels_list)
```
In order to build a certficate, we take for each sample the top 2 output and apply this formula:
$$ \epsilon \geq \frac{\text{top}_1 - \text{top}_2}{2} $$
Where epsilon is the robustness radius for the considered sample.
```
values, classes = tf.math.top_k(hkr_fmodel(images), k=2)
certificates = (values[:, 0] - values[:, 1]) / 2
certificates
```
now we will attack the model to check if the certificates are respected. In this setup `L2CarliniWagnerAttack` is used but in practice as these kind of networks are gradient norm preserving, other attacks gives very similar results.
```
attack = fb.attacks.L2CarliniWagnerAttack(binary_search_steps=6, steps=8000)
imgs, advs, success = attack(hkr_fmodel, images, labels, epsilons=None)
dist_to_adv = np.sqrt(np.sum(np.square(images - advs), axis=(1,2,3)))
dist_to_adv
```
As we can see the certificate are respected.
```
tf.assert_less(certificates, dist_to_adv)
```
Finally we can take a visual look at the obtained examples.
We first start with utility functions for display.
```
class_mapping = {
0: "T-shirt/top",
1: "Trouser",
2: "Pullover",
3: "Dress",
4: "Coat",
5: "Sandal",
6: "Shirt",
7: "Sneaker",
8: "Bag",
9: "Ankle boot",
}
def adversarial_viz(model, images, advs, class_mapping):
"""
This functions shows for each sample:
- the original image
- the adversarial image
- the difference map
- the certificate and the observed distance to adversarial
"""
scale = 1.5
kwargs={}
nb_imgs = images.shape[0]
# compute certificates
values, classes = tf.math.top_k(model(images), k=2)
certificates = (values[:, 0] - values[:, 1]) / 2
# compute difference distance to adversarial
dist_to_adv = np.sqrt(np.sum(np.square(images - advs), axis=(1,2,3)))
# find classes labels for imgs and advs
orig_classes = [class_mapping[i] for i in tf.argmax(model(images), axis=-1).numpy()]
advs_classes = [class_mapping[i] for i in tf.argmax(model(advs), axis=-1).numpy()]
# compute differences maps
if images.shape[-1] != 3:
diff_pos = np.clip(advs - images, 0, 1.)
diff_neg = np.clip(images - advs, 0, 1.)
diff_map = np.concatenate([diff_neg, diff_pos, np.zeros_like(diff_neg)], axis=-1)
else:
diff_map = np.abs(advs - images)
# expands image to be displayed
if images.shape[-1] != 3:
images = np.repeat(images, 3, -1)
if advs.shape[-1] != 3:
advs = np.repeat(advs, 3, -1)
# create plot
figsize = (3 * scale, nb_imgs * scale)
fig, axes = plt.subplots(
ncols=3,
nrows=nb_imgs,
figsize=figsize,
squeeze=False,
constrained_layout=True,
**kwargs,
)
for i in range(nb_imgs):
ax = axes[i][0]
ax.set_title(orig_classes[i])
ax.set_xticks([])
ax.set_yticks([])
ax.axis("off")
ax.imshow(images[i])
ax = axes[i][1]
ax.set_title(advs_classes[i])
ax.set_xticks([])
ax.set_yticks([])
ax.axis("off")
ax.imshow(advs[i])
ax = axes[i][2]
ax.set_title(f"certif: {certificates[i]:.2f}, obs: {dist_to_adv[i]:.2f}")
ax.set_xticks([])
ax.set_yticks([])
ax.axis("off")
ax.imshow(diff_map[i]/diff_map[i].max())
```
When looking at the adversarial examples we can see that the network has interresting properties:
#### predictability
by looking at the certificates, we can predict if the adversarial example will be close of not
#### disparity among classes
As we can see, the attacks are very efficent on similar classes (eg. T-shirt/top, and Shirt ). This denote that all classes are not made equal regarding robustness.
#### explainability
The network is more explainable: attacks can be used as counterfactuals.
We can tell that removing the inscription on a T-shirt turns it into a shirt makes sense. Non robust examples reveals that the network rely on textures rather on shapes to make it's decision.
```
adversarial_viz(hkr_fmodel, images, advs, class_mapping)
```
| true |
code
| 0.710239 | null | null | null | null |
|
# Representing Qubit States
You now know something about bits, and about how our familiar digital computers work. All the complex variables, objects and data structures used in modern software are basically all just big piles of bits. Those of us who work on quantum computing call these *classical variables.* The computers that use them, like the one you are using to read this article, we call *classical computers*.
In quantum computers, our basic variable is the _qubit:_ a quantum variant of the bit. These have exactly the same restrictions as normal bits do: they can store only a single binary piece of information, and can only ever give us an output of `0` or `1`. However, they can also be manipulated in ways that can only be described by quantum mechanics. This gives us new gates to play with, allowing us to find new ways to design algorithms.
To fully understand these new gates, we first need to understand how to write down qubit states. For this we will use the mathematics of vectors, matrices and complex numbers. Though we will introduce these concepts as we go, it would be best if you are comfortable with them already. If you need a more in-depth explanation or refresher, you can find a guide [here](../ch-prerequisites/linear_algebra.html).
## Contents
1. [Classical vs Quantum Bits](#cvsq)
1.1 [Statevectors](#statevectors)
1.2 [Qubit Notation](#notation)
1.3 [Exploring Qubits with Qiskit](#exploring-qubits)
2. [The Rules of Measurement](#rules-measurement)
2.1 [A Very Important Rule](#important-rule)
2.2 [The Implications of this Rule](#implications)
3. [The Bloch Sphere](#bloch-sphere)
3.1 [Describing the Restricted Qubit State](#bloch-sphere-1)
3.2 [Visually Representing a Qubit State](#bloch-sphere-2)
## 1. Classical vs Quantum Bits <a id="cvsq"></a>
### 1.1 Statevectors<a id="statevectors"></a>
In quantum physics we use _statevectors_ to describe the state of our system. Say we wanted to describe the position of a car along a track, this is a classical system so we could use a number $x$:

$$ x=4 $$
Alternatively, we could instead use a collection of numbers in a vector called a _statevector._ Each element in the statevector contains the probability of finding the car in a certain place:

$$
|x\rangle = \begin{bmatrix} 0\\ \vdots \\ 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}
\begin{matrix} \\ \\ \\ \leftarrow \\ \\ \\ \\ \end{matrix}
\begin{matrix} \\ \\ \text{Probability of} \\ \text{car being at} \\ \text{position 4} \\ \\ \\ \end{matrix}
$$
This isn’t limited to position, we could also keep a statevector of all the possible speeds the car could have, and all the possible colours the car could be. With classical systems (like the car example above), this is a silly thing to do as it requires keeping huge vectors when we only really need one number. But as we will see in this chapter, statevectors happen to be a very good way of keeping track of quantum systems, including quantum computers.
### 1.2 Qubit Notation <a id="notation"></a>
Classical bits always have a completely well-defined state: they are either `0` or `1` at every point during a computation. There is no more detail we can add to the state of a bit than this. So to write down the state of a classical bit (`c`), we can just use these two binary values. For example:
c = 0
This restriction is lifted for quantum bits. Whether we get a `0` or a `1` from a qubit only needs to be well-defined when a measurement is made to extract an output. At that point, it must commit to one of these two options. At all other times, its state will be something more complex than can be captured by a simple binary value.
To see how to describe these, we can first focus on the two simplest cases. As we saw in the last section, it is possible to prepare a qubit in a state for which it definitely gives the outcome `0` when measured.
We need a name for this state. Let's be unimaginative and call it $0$ . Similarly, there exists a qubit state that is certain to output a `1`. We'll call this $1$. These two states are completely mutually exclusive. Either the qubit definitely outputs a ```0```, or it definitely outputs a ```1```. There is no overlap. One way to represent this with mathematics is to use two orthogonal vectors.
$$
|0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \, \, \, \, |1\rangle =\begin{bmatrix} 0 \\ 1 \end{bmatrix}.
$$
This is a lot of notation to take in all at once. First, let's unpack the weird $|$ and $\rangle$. Their job is essentially just to remind us that we are talking about the vectors that represent qubit states labelled $0$ and $1$. This helps us distinguish them from things like the bit values ```0``` and ```1``` or the numbers 0 and 1. It is part of the bra-ket notation, introduced by Dirac.
If you are not familiar with vectors, you can essentially just think of them as lists of numbers which we manipulate using certain rules. If you are familiar with vectors from your high school physics classes, you'll know that these rules make vectors well-suited for describing quantities with a magnitude and a direction. For example, the velocity of an object is described perfectly with a vector. However, the way we use vectors for quantum states is slightly different from this, so don't hold on too hard to your previous intuition. It's time to do something new!
With vectors we can describe more complex states than just $|0\rangle$ and $|1\rangle$. For example, consider the vector
$$
|q_0\rangle = \begin{bmatrix} \tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix} .
$$
To understand what this state means, we'll need to use the mathematical rules for manipulating vectors. Specifically, we'll need to understand how to add vectors together and how to multiply them by scalars.
<p>
<details>
<summary>Reminder: Matrix Addition and Multiplication by Scalars (Click here to expand)</summary>
<p>To add two vectors, we add their elements together:
$$|a\rangle = \begin{bmatrix}a_0 \\ a_1 \\ \vdots \\ a_n \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$|a\rangle + |b\rangle = \begin{bmatrix}a_0 + b_0 \\ a_1 + b_1 \\ \vdots \\ a_n + b_n \end{bmatrix} $$
</p>
<p>And to multiply a vector by a scalar, we multiply each element by the scalar:
$$x|a\rangle = \begin{bmatrix}x \times a_0 \\ x \times a_1 \\ \vdots \\ x \times a_n \end{bmatrix}$$
</p>
<p>These two rules are used to rewrite the vector $|q_0\rangle$ (as shown above):
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
& = \tfrac{1}{\sqrt{2}}\begin{bmatrix}1\\0\end{bmatrix} + \tfrac{i}{\sqrt{2}}\begin{bmatrix}0\\1\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}}\\0\end{bmatrix} + \begin{bmatrix}0\\\tfrac{i}{\sqrt{2}}\end{bmatrix}\\
& = \begin{bmatrix}\tfrac{1}{\sqrt{2}} \\ \tfrac{i}{\sqrt{2}} \end{bmatrix}\\
\end{aligned}
$$
</details>
</p>
<p>
<details>
<summary>Reminder: Orthonormal Bases (Click here to expand)</summary>
<p>
It was stated before that the two vectors $|0\rangle$ and $|1\rangle$ are orthonormal, this means they are both <i>orthogonal</i> and <i>normalised</i>. Orthogonal means the vectors are at right angles:
</p><p><img src="images/basis.svg"></p>
<p>And normalised means their magnitudes (length of the arrow) is equal to 1. The two vectors $|0\rangle$ and $|1\rangle$ are <i>linearly independent</i>, which means we cannot describe $|0\rangle$ in terms of $|1\rangle$, and vice versa. However, using both the vectors $|0\rangle$ and $|1\rangle$, and our rules of addition and multiplication by scalars, we can describe all possible vectors in 2D space:
</p><p><img src="images/basis2.svg"></p>
<p>Because the vectors $|0\rangle$ and $|1\rangle$ are linearly independent, and can be used to describe any vector in 2D space using vector addition and scalar multiplication, we say the vectors $|0\rangle$ and $|1\rangle$ form a <i>basis</i>. In this case, since they are both orthogonal and normalised, we call it an <i>orthonormal basis</i>.
</details>
</p>
Since the states $|0\rangle$ and $|1\rangle$ form an orthonormal basis, we can represent any 2D vector with a combination of these two states. This allows us to write the state of our qubit in the alternative form:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
This vector, $|q_0\rangle$ is called the qubit's _statevector,_ it tells us everything we could possibly know about this qubit. For now, we are only able to draw a few simple conclusions about this particular example of a statevector: it is not entirely $|0\rangle$ and not entirely $|1\rangle$. Instead, it is described by a linear combination of the two. In quantum mechanics, we typically describe linear combinations such as this using the word 'superposition'.
Though our example state $|q_0\rangle$ can be expressed as a superposition of $|0\rangle$ and $|1\rangle$, it is no less a definite and well-defined qubit state than they are. To see this, we can begin to explore how a qubit can be manipulated.
### 1.3 Exploring Qubits with Qiskit <a id="exploring-qubits"></a>
First, we need to import all the tools we will need:
```
from qiskit import QuantumCircuit, execute, Aer
from qiskit.visualization import plot_histogram, plot_bloch_vector
from math import sqrt, pi
```
In Qiskit, we use the `QuantumCircuit` object to store our circuits, this is essentially a list of the quantum gates in our circuit and the qubits they are applied to.
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
```
In our quantum circuits, our qubits always start out in the state $|0\rangle$. We can use the `initialize()` method to transform this into any state. We give `initialize()` the vector we want in the form of a list, and tell it which qubit(s) we want to initialise in this state:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
qc.draw('text') # Let's view our circuit (text drawing is required for the 'Initialize' gate due to a known bug in qiskit)
```
We can then use one of Qiskit’s simulators to view the resulting state of our qubit. To begin with we will use the statevector simulator, but we will explain the different simulators and their uses later.
```
backend = Aer.get_backend('statevector_simulator') # Tell Qiskit how to simulate our circuit
```
To get the results from our circuit, we use `execute` to run our circuit, giving the circuit and the backend as arguments. We then use `.result()` to get the result of this:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
result = execute(qc,backend).result() # Do the simulation, returning the result
```
from `result`, we can then get the final statevector using `.get_statevector()`:
```
qc = QuantumCircuit(1) # Create a quantum circuit with one qubit
initial_state = [0,1] # Define initial_state as |1>
qc.initialize(initial_state, 0) # Apply initialisation operation to the 0th qubit
result = execute(qc,backend).result() # Do the simulation, returning the result
out_state = result.get_statevector()
print(out_state) # Display the output state vector
```
**Note:** Python uses `j` to represent $i$ in complex numbers. We see a vector with two complex elements: `0.+0.j` = 0, and `1.+0.j` = 1.
Let’s now measure our qubit as we would in a real quantum computer and see the result:
```
qc.measure_all()
qc.draw('text')
```
This time, instead of the statevector we will get the counts for the `0` and `1` results using `.get_counts()`:
```
result = execute(qc,backend).result()
counts = result.get_counts()
plot_histogram(counts)
```
We can see that we (unsurprisingly) have a 100% chance of measuring $|1\rangle$. This time, let’s instead put our qubit into a superposition and see what happens. We will use the state $|q_0\rangle$ from earlier in this section:
$$ |q_0\rangle = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle $$
We need to add these amplitudes to a python list. To add a complex amplitude we use `complex`, giving the real and imaginary parts as arguments:
```
initial_state = [1/sqrt(2), 1j/sqrt(2)] # Define state |q>
```
And we then repeat the steps for initialising the qubit as before:
```
qc = QuantumCircuit(1) # Must redefine qc
qc.initialize(initial_state, 0) # Initialise the 0th qubit in the state `initial_state`
state = execute(qc,backend).result().get_statevector() # Execute the circuit
print(state) # Print the result
results = execute(qc,backend).result().get_counts()
plot_histogram(results)
```
We can see we have an equal probability of measuring either $|0\rangle$ or $|1\rangle$. To explain this, we need to talk about measurement.
## 2. The Rules of Measurement <a id="rules-measurement"></a>
### 2.1 A Very Important Rule <a id="important-rule"></a>
There is a simple rule for measurement. To find the probability of measuring a state $|\psi \rangle$ in the state $|x\rangle$ we do:
$$p(|x\rangle) = | \langle x| \psi \rangle|^2$$
The symbols $\langle$ and $|$ tell us $\langle x |$ is a row vector. In quantum mechanics we call the column vectors _kets_ and the row vectors _bras._ Together they make up _bra-ket_ notation. Any ket $|a\rangle$ has a corresponding bra $\langle a|$, and we convert between them using the conjugate transpose.
<details>
<summary>Reminder: The Inner Product (Click here to expand)</summary>
<p>There are different ways to multiply vectors, here we use the <i>inner product</i>. The inner product is a generalisation of the <i>dot product</i> which you may already be familiar with. In this guide, we use the inner product between a bra (row vector) and a ket (column vector), and it follows this rule:
$$\langle a| = \begin{bmatrix}a_0^*, & a_1^*, & \dots & a_n^* \end{bmatrix}, \quad
|b\rangle = \begin{bmatrix}b_0 \\ b_1 \\ \vdots \\ b_n \end{bmatrix}$$
$$\langle a|b\rangle = a_0^* b_0 + a_1^* b_1 \dots a_n^* b_n$$
</p>
<p>We can see that the inner product of two vectors always gives us a scalar. A useful thing to remember is that the inner product of two orthogonal vectors is 0, for example if we have the orthogonal vectors $|0\rangle$ and $|1\rangle$:
$$\langle1|0\rangle = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 0$$
</p>
<p>Additionally, remember that the vectors $|0\rangle$ and $|1\rangle$ are also normalised (magnitudes are equal to 1):
$$
\begin{aligned}
\langle0|0\rangle & = \begin{bmatrix} 1 , & 0\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} = 1 \\
\langle1|1\rangle & = \begin{bmatrix} 0 , & 1\end{bmatrix}\begin{bmatrix}0 \\ 1\end{bmatrix} = 1
\end{aligned}
$$
</p>
</details>
In the equation above, $|x\rangle$ can be any qubit state. To find the probability of measuring $|x\rangle$, we take the inner product of $|x\rangle$ and the state we are measuring (in this case $|\psi\rangle$), then square the magnitude. This may seem a little convoluted, but it will soon become second nature.
If we look at the state $|q_0\rangle$ from before, we can see the probability of measuring $|0\rangle$ is indeed $0.5$:
$$
\begin{aligned}
|q_0\rangle & = \tfrac{1}{\sqrt{2}}|0\rangle + \tfrac{i}{\sqrt{2}}|1\rangle \\
\langle 0| q_0 \rangle & = \tfrac{1}{\sqrt{2}}\langle 0|0\rangle - \tfrac{i}{\sqrt{2}}\langle 0|1\rangle \\
& = \tfrac{1}{\sqrt{2}}\cdot 1 - \tfrac{i}{\sqrt{2}} \cdot 0\\
& = \tfrac{1}{\sqrt{2}}\\
|\langle 0| q_0 \rangle|^2 & = \tfrac{1}{2}
\end{aligned}
$$
You should verify the probability of measuring $|1\rangle$ as an exercise.
This rule governs how we get information out of quantum states. It is therefore very important for everything we do in quantum computation. It also immediately implies several important facts.
### 2.2 The Implications of this Rule <a id="implications"></a>
### #1 Normalisation
The rule shows us that amplitudes are related to probabilities. If we want the probabilities to add up to 1 (which they should!), we need to ensure that the statevector is properly normalized. Specifically, we need the magnitude of the state vector to be 1.
$$ \langle\psi|\psi\rangle = 1 \\ $$
Thus if:
$$ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle $$
Then:
$$ \sqrt{|\alpha|^2 + |\beta|^2} = 1 $$
This explains the factors of $\sqrt{2}$ you have seen throughout this chapter. In fact, if we try to give `initialize()` a vector that isn’t normalised, it will give us an error:
```
vector = [1,1]
qc.initialize(vector, 0)
```
#### Quick Exercise
1. Create a state vector that will give a $1/3$ probability of measuring $|0\rangle$.
2. Create a different state vector that will give the same measurement probabilities.
3. Verify that the probability of measuring $|1\rangle$ for these two states is $2/3$.
You can check your answer in the widget below (you can use 'pi' and 'sqrt' in the vector):
```
# Run the code in this cell to interact with the widget
from qiskit_textbook.widgets import state_vector_exercise
state_vector_exercise(target=1/3)
```
### #2 Alternative measurement
The measurement rule gives us the probability $p(|x\rangle)$ that a state $|\psi\rangle$ is measured as $|x\rangle$. Nowhere does it tell us that $|x\rangle$ can only be either $|0\rangle$ or $|1\rangle$.
The measurements we have considered so far are in fact only one of an infinite number of possible ways to measure a qubit. For any orthogonal pair of states, we can define a measurement that would cause a qubit to choose between the two.
This possibility will be explored more in the next section. For now, just bear in mind that $|x\rangle$ is not limited to being simply $|0\rangle$ or $|1\rangle$.
### #3 Global Phase
We know that measuring the state $|1\rangle$ will give us the output `1` with certainty. But we are also able to write down states such as
$$\begin{bmatrix}0 \\ i\end{bmatrix} = i|1\rangle.$$
To see how this behaves, we apply the measurement rule.
$$ |\langle x| (i|1\rangle) |^2 = | i \langle x|1\rangle|^2 = |\langle x|1\rangle|^2 $$
Here we find that the factor of $i$ disappears once we take the magnitude of the complex number. This effect is completely independent of the measured state $|x\rangle$. It does not matter what measurement we are considering, the probabilities for the state $i|1\rangle$ are identical to those for $|1\rangle$. Since measurements are the only way we can extract any information from a qubit, this implies that these two states are equivalent in all ways that are physically relevant.
More generally, we refer to any overall factor $\gamma$ on a state for which $|\gamma|=1$ as a 'global phase'. States that differ only by a global phase are physically indistinguishable.
$$ |\langle x| ( \gamma |a\rangle) |^2 = | \gamma \langle x|a\rangle|^2 = |\langle x|a\rangle|^2 $$
Note that this is distinct from the phase difference _between_ terms in a superposition, which is known as the 'relative phase'. This becomes relevant once we consider different types of measurements and multiple qubits.
### #4 The Observer Effect
We know that the amplitudes contain information about the probability of us finding the qubit in a specific state, but once we have measured the qubit, we know with certainty what the state of the qubit is. For example, if we measure a qubit in the state:
$$ |q\rangle = \alpha|0\rangle + \beta|1\rangle$$
And find it in the state $|0\rangle$, if we measure again, there is a 100% chance of finding the qubit in the state $|0\rangle$. This means the act of measuring _changes_ the state of our qubits.
$$ |q\rangle = \begin{bmatrix} \alpha \\ \beta \end{bmatrix} \xrightarrow{\text{Measure }|0\rangle} |q\rangle = |0\rangle = \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$
We sometimes refer to this as _collapsing_ the state of the qubit. It is a potent effect, and so one that must be used wisely. For example, were we to constantly measure each of our qubits to keep track of their value at each point in a computation, they would always simply be in a well-defined state of either $|0\rangle$ or $|1\rangle$. As such, they would be no different from classical bits and our computation could be easily replaced by a classical computation. To achieve truly quantum computation we must allow the qubits to explore more complex states. Measurements are therefore only used when we need to extract an output. This means that we often place the all measurements at the end of our quantum circuit.
We can demonstrate this using Qiskit’s statevector simulator. Let's initialise a qubit in superposition:
```
qc = QuantumCircuit(1) # Redefine qc
initial_state = [0.+1.j/sqrt(2),1/sqrt(2)+0.j]
qc.initialize(initial_state, 0)
qc.draw('text')
```
This should initialise our qubit in the state:
$$ |q\rangle = \tfrac{i}{\sqrt{2}}|0\rangle + \tfrac{1}{\sqrt{2}}|1\rangle $$
We can verify this using the simulator:
```
state = execute(qc, backend).result().get_statevector()
print("Qubit State = " + str(state))
```
We can see here the qubit is initialised in the state `[0.+0.70710678j 0.70710678+0.j]`, which is the state we expected.
Let’s now measure this qubit:
```
qc.measure_all()
qc.draw('text')
```
When we simulate this entire circuit, we can see that one of the amplitudes is _always_ 0:
```
state = execute(qc, backend).result().get_statevector()
print("State of Measured Qubit = " + str(state))
```
You can re-run this cell a few times to reinitialise the qubit and measure it again. You will notice that either outcome is equally probable, but that the state of the qubit is never a superposition of $|0\rangle$ and $|1\rangle$. Somewhat interestingly, the global phase on the state $|0\rangle$ survives, but since this is global phase, we can never measure it on a real quantum computer.
### A Note about Quantum Simulators
We can see that writing down a qubit’s state requires keeping track of two complex numbers, but when using a real quantum computer we will only ever receive a yes-or-no (`0` or `1`) answer for each qubit. The output of a 10-qubit quantum computer will look like this:
`0110111110`
Just 10 bits, no superposition or complex amplitudes. When using a real quantum computer, we cannot see the states of our qubits mid-computation, as this would destroy them! This behaviour is not ideal for learning, so Qiskit provides different quantum simulators: The `qasm_simulator` behaves as if you are interacting with a real quantum computer, and will not allow you to use `.get_statevector()`. Alternatively, `statevector_simulator`, (which we have been using in this chapter) does allow peeking at the quantum states before measurement, as we have seen.
## 3. The Bloch Sphere <a id="bloch-sphere"></a>
### 3.1 Describing the Restricted Qubit State <a id="bloch-sphere-1"></a>
We saw earlier in this chapter that the general state of a qubit ($|q\rangle$) is:
$$
|q\rangle = \alpha|0\rangle + \beta|1\rangle
$$
$$
\alpha, \beta \in \mathbb{C}
$$
(The second line tells us $\alpha$ and $\beta$ are complex numbers). The first two implications in section 2 tell us that we cannot differentiate between some of these states. This means we can be more specific in our description of the qubit.
Firstly, since we cannot measure global phase, we can only measure the difference in phase between the states $|0\rangle$ and $|1\rangle$. Instead of having $\alpha$ and $\beta$ be complex, we can confine them to the real numbers and add a term to tell us the relative phase between them:
$$
|q\rangle = \alpha|0\rangle + e^{i\phi}\beta|1\rangle
$$
$$
\alpha, \beta, \phi \in \mathbb{R}
$$
Finally, since the qubit state must be normalised, i.e.
$$
\sqrt{\alpha^2 + \beta^2} = 1
$$
we can use the trigonometric identity:
$$
\sqrt{\sin^2{x} + \cos^2{x}} = 1
$$
to describe the real $\alpha$ and $\beta$ in terms of one variable, $\theta$:
$$
\alpha = \cos{\tfrac{\theta}{2}}, \quad \beta=\sin{\tfrac{\theta}{2}}
$$
From this we can describe the state of any qubit using the two variables $\phi$ and $\theta$:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
$$
\theta, \phi \in \mathbb{R}
$$
### 3.2 Visually Representing a Qubit State <a id="bloch-sphere-2"></a>
We want to plot our general qubit state:
$$
|q\rangle = \cos{\tfrac{\theta}{2}}|0\rangle + e^{i\phi}\sin{\tfrac{\theta}{2}}|1\rangle
$$
If we interpret $\theta$ and $\phi$ as spherical co-ordinates ($r = 1$, since the magnitude of the qubit state is $1$), we can plot any qubit state on the surface of a sphere, known as the _Bloch sphere._
Below we have plotted a qubit in the state $|{+}\rangle$. In this case, $\theta = \pi/2$ and $\phi = 0$.
(Qiskit has a function to plot a bloch sphere, `plot_bloch_vector()`, but at the time of writing it only takes cartesian coordinates. We have included a function that does the conversion automatically).
```
from qiskit_textbook.widgets import plot_bloch_vector_spherical
coords = [pi/2,0,1] # [Theta, Phi, Radius]
plot_bloch_vector_spherical(coords) # Bloch Vector with spherical coordinates
```
#### Warning!
When first learning about qubit states, it's easy to confuse the qubits _statevector_ with its _Bloch vector_. Remember the statevector is the vector discussed in [1.1](#notation), that holds the amplitudes for the two states our qubit can be in. The Bloch vector is a visualisation tool that maps the 2D, complex statevector onto real, 3D space.
#### Quick Exercise
Use `plot_bloch_vector()` or `plot_bloch_sphere_spherical()` to plot a qubit in the states:
1. $|0\rangle$
2. $|1\rangle$
3. $\tfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$
4. $\tfrac{1}{\sqrt{2}}(|0\rangle - i|1\rangle)$
5. $\tfrac{1}{\sqrt{2}}\begin{bmatrix}i\\1\end{bmatrix}$
We have also included below a widget that converts from spherical co-ordinates to cartesian, for use with `plot_bloch_vector()`:
```
from qiskit_textbook.widgets import bloch_calc
bloch_calc()
import qiskit
qiskit.__qiskit_version__
```
| true |
code
| 0.836621 | null | null | null | null |
|
# Loading Medicare and Medicaid Claims data into i2b2
[CMS RIF][] docs
This notebook is on demographics.
[CMS RIF]: https://www.resdac.org/cms-data/file-availability#research-identifiable-files
## Python Data Science Tools
especially [pandas](http://pandas.pydata.org/pandas-docs/)
```
import pandas as pd
import numpy as np
import sqlalchemy as sqla
dict(pandas=pd.__version__, numpy=np.__version__, sqlalchemy=sqla.__version__)
```
## DB Access: Luigi Config, Logging
[luigi docs](https://luigi.readthedocs.io/en/stable/)
```
# Passwords are expected to be in the environment.
# Prompt if it's not already there.
def _fix_password():
from os import environ
import getpass
keyname = getpass.getuser().upper() + '_SGROUSE'
if keyname not in environ:
environ[keyname] = getpass.getpass()
_fix_password()
import luigi
def _reset_config(path):
'''Reach into luigi guts and reset the config.
Don't ask.'''
cls = luigi.configuration.LuigiConfigParser
cls._instance = None # KLUDGE
cls._config_paths = [path]
return cls.instance()
_reset_config('luigi-sgrouse.cfg')
luigi.configuration.LuigiConfigParser.instance()._config_paths
import cx_ora_fix
help(cx_ora_fix)
cx_ora_fix.patch_version()
import cx_Oracle as cx
dict(cx_Oracle=cx.__version__, version_for_sqlalchemy=cx.version)
import logging
concise = logging.Formatter(fmt='%(asctime)s %(levelname)s %(message)s',
datefmt='%02H:%02M:%02S')
def log_to_notebook(log,
formatter=concise):
log.setLevel(logging.DEBUG)
to_notebook = logging.StreamHandler()
to_notebook.setFormatter(formatter)
log.addHandler(to_notebook)
return log
from cms_etl import CMSExtract
try:
log.info('Already logging to notebook.')
except NameError:
cms_rif_task = CMSExtract()
log = log_to_notebook(logging.getLogger())
log.info('We try to log non-trivial DB access.')
with cms_rif_task.connection() as lc:
lc.log.info('first bene_id')
first_bene_id = pd.read_sql('select min(bene_id) bene_id_first from %s.%s' % (
cms_rif_task.cms_rif, cms_rif_task.table_eg), lc._conn)
first_bene_id
```
## Demographics: MBSF_AB_SUMMARY, MAXDATA_PS
### Breaking work into groups by beneficiary
```
from cms_etl import BeneIdSurvey
from cms_pd import MBSFUpload
survey_d = BeneIdSurvey(source_table=MBSFUpload.table_name)
chunk_m0 = survey_d.results()[0]
chunk_m0 = pd.Series(chunk_m0, index=chunk_m0.keys())
chunk_m0
dem = MBSFUpload(bene_id_first=chunk_m0.bene_id_first,
bene_id_last=chunk_m0.bene_id_last,
chunk_rows=chunk_m0.chunk_rows)
dem
```
## Column Info: Value Type, Level of Measurement
```
with dem.connection() as lc:
col_data_d = dem.column_data(lc)
col_data_d.head(3)
colprops_d = dem.column_properties(col_data_d)
colprops_d.sort_values(['valtype_cd', 'column_name'])
with dem.connection() as lc:
for x, pct_in in dem.obs_data(lc, upload_id=100):
break
pct_in
x.sort_values(['instance_num', 'valtype_cd']).head(50)
```
### MAXDATA_PS: skip custom for now
```
from cms_pd import MAXPSUpload
survey_d = BeneIdSurvey(source_table=MAXPSUpload.table_name)
chunk_ps0 = survey_d.results()[0]
chunk_ps0 = pd.Series(chunk_ps0, index=chunk_ps0.keys())
chunk_ps0
dem2 = MAXPSUpload(bene_id_first=chunk_ps0.bene_id_first,
bene_id_last=chunk_ps0.bene_id_last,
chunk_rows=chunk_ps0.chunk_rows)
dem2
with dem2.connection() as lc:
col_data_d2 = dem2.column_data(lc)
col_data_d2.head(3)
```
`maxdata_ps` has many groups of columns with names ending in `_1`, `_2`, `_3`, and so on:
```
col_groups = col_data_d2[col_data_d2.column_name.str.match('.*_\d+$')]
col_groups.tail()
pd.DataFrame([dict(all_cols=len(col_data_d2),
cols_in_groups=len(col_groups),
plain_cols=len(col_data_d2) - len(col_groups))])
from cms_pd import col_valtype
def _cprop(cls, valtype_override, info: pd.DataFrame) -> pd.DataFrame:
info['valtype_cd'] = [col_valtype(c).value for c in info.column.values]
for cd, pat in valtype_override:
info.valtype_cd = info.valtype_cd.where(~ info.column_name.str.match(pat), cd)
info.loc[info.column_name.isin(cls.i2b2_map.values()), 'valtype_cd'] = np.nan
return info.drop('column', 1)
_vo = [
('@', r'.*race_code_\d$'),
('@custom_postpone', r'.*_\d+$')
]
#dem2.column_properties(col_data_d2)
colprops_d2 = _cprop(dem2.__class__, _vo, col_data_d2)
colprops_d2.query('valtype_cd != "@custom_postpone"').sort_values(['valtype_cd', 'column_name'])
colprops_d2.dtypes
```
## Patient, Encounter Mapping
```
obs_facts = obs_dx.append(obs_cd).append(obs_num).append(obs_txt).append(obs_dt)
with cc.connection('patient map') as lc:
pmap = cc.patient_mapping(lc, (obs_facts.bene_id.min(), obs_facts.bene_id.max()))
from etl_tasks import I2B2ProjectCreate
obs_patnum = obs_facts.merge(pmap, on='bene_id')
obs_patnum.sort_values('start_date').head()[[
col.name for col in I2B2ProjectCreate.observation_fact_columns
if col.name in obs_patnum.columns.values]]
with cc.connection() as lc:
emap = cc.encounter_mapping(lc, (obs_dx.bene_id.min(), obs_dx.bene_id.max()))
emap.head()
'medpar_id' in obs_patnum.columns.values
obs_pmap_emap = cc.pat_day_rollup(obs_patnum, emap)
x = obs_pmap_emap
(x[(x.encounter_num > 0) | (x.encounter_num % 8 == 0) ][::5]
.reset_index().set_index(['patient_num', 'start_date', 'encounter_num']).sort_index()
.head(15)[['medpar_id', 'start_day', 'admsn_dt', 'dschrg_dt', 'concept_cd']])
```
### Provider etc. done?
```
obs_mapped = cc.with_mapping(obs_dx, pmap, emap)
obs_mapped.columns
[col.name for col in I2B2ProjectCreate.observation_fact_columns
if not col.nullable and col.name not in obs_mapped.columns.values]
test_run = False
if test_run:
cc.run()
```
## Drugs: PDE
```
from cms_pd import DrugEventUpload
du = DrugEventUpload(bene_id_first=bene_chunks.iloc[0].bene_id_first,
bene_id_last=bene_chunks.iloc[0].bene_id_last,
chunk_rows=bene_chunks.iloc[0].chunk_rows,
chunk_size=1000)
with du.connection() as lc:
du_cols = du.column_data(lc)
du.column_properties(du_cols).sort_values('valtype_cd')
with du.connection() as lc:
for x, pct_in in du.obs_data(lc, upload_id=100):
break
x.sort_values(['instance_num', 'valtype_cd']).head(50)
```
## Performance Results
```
bulk_migrate = '''
insert /*+ parallel(24) append */ into dconnolly.observation_fact
select * from dconnolly.observation_fact_2440
'''
with cc.connection() as lc:
lc.execute('truncate table my_plan_table')
print(lc._conn.engine.url.query)
print(pd.read_sql('select count(*) from my_plan_table', lc._conn))
lc._conn.execute('explain plan into my_plan_table for ' + bulk_migrate)
plan = pd.read_sql('select * from my_plan_table', lc._conn)
plan
with cc.connection() as lc:
lc.execute('truncate table my_plan_table')
print(pd.read_sql('select * from my_plan_table', lc._conn))
db = lc._conn.engine
cx = db.dialect.dbapi
dsn = cx.makedsn(db.url.host, db.url.port, db.url.database)
conn = cx.connect(db.url.username, db.url.password, dsn,
threaded=True, twophase=True)
cur = conn.cursor()
cur.execute('explain plan into my_plan_table for ' + bulk_migrate)
cur.close()
conn.commit()
conn.close()
plan = pd.read_sql('select * from my_plan_table', lc._conn)
plan
select /*+ parallel(24) */ max(bene_enrollmt_ref_yr)
from cms_deid.mbsf_ab_summary;
select * from upload_status
where upload_id >= 2799 -- and message is not null -- 2733
order by upload_id desc;
-- order by end_date desc;
select load_status, count(*), min(upload_id), max(upload_id), min(load_date), max(end_date)
, to_char(sum(loaded_record), '999,999,999') loaded_record
, round(sum(loaded_record) / 1000 / ((max(end_date) - min(load_date)) * 24 * 60)) krows_min
from (
select upload_id, loaded_record, load_status, load_date, end_date, end_date - load_date elapsed
from upload_status
where upload_label like 'MBSFUp%'
)
group by load_status
;
```
## Reimport code into running notebook
```
import importlib
import cms_pd
import cms_etl
import etl_tasks
import eventlog
import script_lib
importlib.reload(script_lib)
importlib.reload(eventlog)
importlib.reload(cms_pd)
importlib.reload(cms_etl)
importlib.reload(etl_tasks);
```
| true |
code
| 0.241154 | null | null | null | null |
|
# Pixelwise Segmentation
Use the `elf.segmentation` module for feature based instance segmentation from pixels.
Note that this example is educational and there are easier and better performing method for the image used here. These segmentation methods are very suitable for pixel embeddings learned with neural networks, e.g. with methods like [Semantic Instance Segmentation with a Discriminateive Loss Function](https://arxiv.org/abs/1708.02551).
## Image and Features
Load the relevant libraries. Then load an image from the skimage examples and compute per pixel features.
```
%gui qt5
import time
import numpy as np
# import napari for data visualisation
import napari
# import vigra to compute per pixel features
import vigra
# elf segmentation functionality we need for the problem setup
import elf.segmentation.features as feats
from elf.segmentation.utils import normalize_input
# we use the coins example image
from skimage.data import coins
image = coins()
# We use blurring and texture filters from vigra.filters computed for different scales to obain pixel features.
# Note that it's certainly possible to compute better features for the segmentation problem at hand.
# But for our purposes, these features are good enough.
im_normalized = normalize_input(image)
scales = [4., 8., 12.]
image_features = [im_normalized[None]] # use the normal image as
for scale in scales:
image_features.append(normalize_input(vigra.filters.gaussianSmoothing(im_normalized, scale))[None])
feats1 = vigra.filters.hessianOfGaussianEigenvalues(im_normalized, scale)
image_features.append(normalize_input(feats1[..., 0])[None])
image_features.append(normalize_input(feats1[..., 1])[None])
feats2 = vigra.filters.structureTensorEigenvalues(im_normalized, scale, 1.5 * scale)
image_features.append(normalize_input(feats2[..., 0])[None])
image_features.append(normalize_input(feats2[..., 1])[None])
image_features = np.concatenate(image_features, axis=0)
print("Feature shape:")
print(image_features.shape)
# visualize the image and the features with napari
viewer = napari.Viewer()
viewer.add_image(im_normalized)
viewer.add_image(image_features)
```
## Segmentation Problem
Set up a graph segmentation problem based on the image and features with elf functionality.
To this end, we construct a grid graph and compute edge features for the inter pixel edges in this graph.
```
# compute a grid graph for the image
shape = image.shape
grid_graph = feats.compute_grid_graph(shape)
# compute the edge features
# elf supports three different distance metrics to compute edge features
# from the image features:
# - 'l1': the l1 distance
# - 'l2': the l2 distance
# - 'cosine': the cosine distance (= 1. - cosine similarity)
# here, we use the l2 distance
distance_type = 'l2'
# 'compute_grid-graph-image_features' returns both the edges (=list of node ids connected by the edge)
# and the edge weights. Here, the edges are the same as grid_graph.uvIds()
edges, edge_weights = feats.compute_grid_graph_image_features(grid_graph, image_features, distance_type)
# we normalize the edge weigths to the range [0, 1]
edge_weights = normalize_input(edge_weights)
# simple post-processing to ensure the background label is '0',
# filter small segments with a size of below 100 pixels
# and ensure that the segmentation ids are consecutive
def postprocess_segmentation(seg, shape, min_size=100):
if seg.ndim == 1:
seg = seg.reshape(shape)
ids, sizes = np.unique(seg, return_counts=True)
bg_label = ids[np.argmax(sizes)]
if bg_label != 0:
if 0 in seg:
seg[seg == 0] = seg.max() + 1
seg[seg == bg_label] = 0
filter_ids = ids[sizes < min_size]
seg[np.isin(seg, filter_ids)] = 0
vigra.analysis.relabelConsecutive(seg, out=seg, start_label=1, keep_zeros=True)
return seg
```
## Multicut
As the first segmentation method, we use Multicut segmentation, based on the grid graph and the edge weights we have just computed.
```
# the elf multicut funtionality
import elf.segmentation.multicut as mc
# In order to apply multicut segmentation, we need to map the edge weights from their initial value range [0, 1]
# to [-inf, inf]; where positive values represent attractive edges and negative values represent repulsive edges.
# When computing these "costs" for the multicut, we can set the threshold for when an edge is counted
# as repulsive with the so called boundary bias, or beta, parameter.
# For values smaller than 0.5 the multicut segmentation will under-segment more,
# for values larger than 0.4 it will over-segment more.
beta = .75
costs = mc.compute_edge_costs(edge_weights, beta=beta)
print("Mapped edge weights in range", edge_weights.min(), edge_weights.max(), "to multicut costs in range", costs.min(), costs.max())
# compute the multicut segmentation
t = time.time()
mc_seg = mc.multicut_kernighan_lin(grid_graph, costs)
print("Computing the segmentation with multicut took", time.time() - t, "s")
mc_seg = postprocess_segmentation(mc_seg, shape)
# visualize the multicut segmentation
viewer = napari.Viewer()
viewer.add_image(image)
viewer.add_labels(mc_seg)
```
## Long-range Segmentation Problem
For now, we have only taken "local" information into account for the segmentation problem.
More specifically, we have only solved the Multicut with edges derived from nearest neighbor pixel transitions.
Next, we will use two algorithms, Mutex Watershed and Lifted Multicut, that can take long range edges into account. This has the advantage that feature differences are often more pronounced along larger distances, thus yielding much better information with respect to label transition.
Here, we extract this information by defining a "pixel offset pattern" and comparing the pixel features for these offsets. For details about this segmentation approach check out [The Mutex Watershed: Efficient, Parameter-Free Image Partitioning](https://openaccess.thecvf.com/content_ECCV_2018/html/Steffen_Wolf_The_Mutex_Watershed_ECCV_2018_paper.html).
```
# here, we define the following offset pattern:
# straight and diagonal transitions at a radius of 3, 9 and 27 pixels
# note that the offsets [-1, 0] and [0, -1] would correspond to the edges of the grid graph
offsets = [
[-3, 0], [0, -3], [-3, 3], [3, 3],
[-9, 0], [0, -9], [-9, 9], [9, 9],
[-27, 0], [0, -27], [-27, 27], [27, 27]
]
# we have significantly more long range than normal edges.
# hence, we subsample the offsets, for which actual long range edges will be computed by setting a stride factor
strides = [2, 2]
distance_type = 'l2' # we again use l2 distance
lr_edges, lr_edge_weights = feats.compute_grid_graph_image_features(grid_graph, image_features, distance_type,
offsets=offsets, strides=strides,
randomize_strides=False)
lr_edge_weights = normalize_input(lr_edge_weights)
print("Have computed", len(lr_edges), "long range edges, compared to", len(edges), "normal edges")
```
## Mutex Watershed
We use the Mutex Watershed to segment the image. This algorithm functions similar to (Lifted) Multicut, but is greedy and hence much faster. Despite its greedy nature, for many problems the solutions are of similar quality than Multicut segmentation.
```
# elf mutex watershed functionality
import elf.segmentation.mutex_watershed as mws
t = time.time()
mws_seg = mws.mutex_watershed_clustering(edges, lr_edges, edge_weights, lr_edge_weights)
print("Computing the segmentation with mutex watershed took", time.time() - t, "s")
mws_seg = postprocess_segmentation(mws_seg, shape)
viewer = napari.Viewer()
viewer.add_image(image)
viewer.add_labels(mws_seg)
```
## Lifted Multicut
Finally, we use Lifted Multicut segmentation. The Lifted Multicut is an extension to the Multicut, which can incorporate long range edges.
```
# elf lifted multicut functionality
import elf.segmentation.lifted_multicut as lmc
# For the lifted multicut, we again need to transform the edge weights in [0, 1] to costs in [-inf, inf]
beta = .75 # we again use a boundary bias of 0.75
lifted_costs = mc.compute_edge_costs(lr_edge_weights, beta=beta)
t = time.time()
lmc_seg = lmc.lifted_multicut_kernighan_lin(grid_graph, costs, lr_edges, lifted_costs)
print("Computing the segmentation with lifted multicut took", time.time() - t, "s")
lmc_seg = postprocess_segmentation(lmc_seg, shape)
viewer = napari.Viewer()
viewer.add_image(image)
viewer.add_labels(lmc_seg)
```
## Comparing the segmentations
We can now compare the three different segmentation. Note that the comparison is not quite fair here, because we have used the beta parameter to bias the segmentation to more over-segmentation for Multicut and Lifted Multicut while applying the Mutex Watershed to unbiased edge weights.
```
viewer = napari.Viewer()
viewer.add_image(image)
viewer.add_labels(mc_seg)
viewer.add_labels(mws_seg)
viewer.add_labels(lmc_seg)
```
| true |
code
| 0.566378 | null | null | null | null |
|
## test.ipynb: Test the training result and Evaluate model
```
# Import the necessary libraries
from sklearn.decomposition import PCA
import os
import scipy.io as sio
import numpy as np
from keras.models import load_model
from keras.utils import np_utils
from sklearn.metrics import classification_report, confusion_matrix
import itertools
import spectral
# Define the neccesary functions for later use
# load the Indian pines dataset which is the .mat format
def loadIndianPinesData():
data_path = os.path.join(os.getcwd(),'data')
data = sio.loadmat(os.path.join(data_path, 'Indian_pines.mat'))['indian_pines']
labels = sio.loadmat(os.path.join(data_path, 'Indian_pines_gt.mat'))['indian_pines_gt']
return data, labels
# load the Indian pines dataset which is HSI format
# refered from http://www.spectralpython.net/fileio.html
def loadHSIData():
data_path = os.path.join(os.getcwd(), 'HSI_data')
data = spectral.open_image(os.path.join(data_path, '92AV3C.lan')).load()
data = np.array(data).astype(np.int32)
labels = spectral.open_image(os.path.join(data_path, '92AV3GT.GIS')).load()
labels = np.array(labels).astype(np.uint8)
labels.shape = (145, 145)
return data, labels
# Get the model evaluation report,
# include classification report, confusion matrix, Test_Loss, Test_accuracy
target_names = ['Alfalfa', 'Corn-notill', 'Corn-mintill', 'Corn'
,'Grass-pasture', 'Grass-trees', 'Grass-pasture-mowed',
'Hay-windrowed', 'Oats', 'Soybean-notill', 'Soybean-mintill',
'Soybean-clean', 'Wheat', 'Woods', 'Buildings-Grass-Trees-Drives',
'Stone-Steel-Towers']
def reports(X_test,y_test):
Y_pred = model.predict(X_test)
y_pred = np.argmax(Y_pred, axis=1)
classification = classification_report(np.argmax(y_test, axis=1), y_pred, target_names=target_names)
confusion = confusion_matrix(np.argmax(y_test, axis=1), y_pred)
score = model.evaluate(X_test, y_test, batch_size=32)
Test_Loss = score[0]*100
Test_accuracy = score[1]*100
return classification, confusion, Test_Loss, Test_accuracy
# apply PCA preprocessing for data sets
def applyPCA(X, numComponents=75):
newX = np.reshape(X, (-1, X.shape[2]))
pca = PCA(n_components=numComponents, whiten=True)
newX = pca.fit_transform(newX)
newX = np.reshape(newX, (X.shape[0],X.shape[1], numComponents))
return newX, pca
def Patch(data,height_index,width_index):
#transpose_array = data.transpose((2,0,1))
#print transpose_array.shape
height_slice = slice(height_index, height_index+PATCH_SIZE)
width_slice = slice(width_index, width_index+PATCH_SIZE)
patch = data[height_slice, width_slice, :]
return patch
# Global Variables
windowSize = 5
numPCAcomponents = 30
testRatio = 0.50
# show current path
PATH = os.getcwd()
print (PATH)
# Read PreprocessedData from file
X_test = np.load("./predata/XtestWindowSize"
+ str(windowSize) + "PCA" + str(numPCAcomponents) + "testRatio" + str(testRatio) + ".npy")
y_test = np.load("./predata/ytestWindowSize"
+ str(windowSize) + "PCA" + str(numPCAcomponents) + "testRatio" + str(testRatio) + ".npy")
# X_test = np.load("./predata/XAllWindowSize"
# + str(windowSize) + "PCA" + str(numPCAcomponents) + "testRatio" + str(testRatio) + ".npy")
# y_test = np.load("./predata/yAllWindowSize"
# + str(windowSize) + "PCA" + str(numPCAcomponents) + "testRatio" + str(testRatio) + ".npy")
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[3], X_test.shape[1], X_test.shape[2]))
y_test = np_utils.to_categorical(y_test)
# load the model architecture and weights
model = load_model('./model/HSI_model_epochs100.h5')
# calculate result, loss, accuray and confusion matrix
classification, confusion, Test_loss, Test_accuracy = reports(X_test,y_test)
classification = str(classification)
confusion_str = str(confusion)
# show result and save to file
print('Test loss {} (%)'.format(Test_loss))
print('Test accuracy {} (%)'.format(Test_accuracy))
print("classification result: ")
print('{}'.format(classification))
print("confusion matrix: ")
print('{}'.format(confusion_str))
file_name = './result/report' + "WindowSize" + str(windowSize) + "PCA" + str(numPCAcomponents) + "testRatio" + str(testRatio) +".txt"
with open(file_name, 'w') as x_file:
x_file.write('Test loss {} (%)'.format(Test_loss))
x_file.write('\n')
x_file.write('Test accuracy {} (%)'.format(Test_accuracy))
x_file.write('\n')
x_file.write('\n')
x_file.write(" classification result: \n")
x_file.write('{}'.format(classification))
x_file.write('\n')
x_file.write(" confusion matrix: \n")
x_file.write('{}'.format(confusion_str))
import matplotlib.pyplot as plt
%matplotlib inline
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.get_cmap("Blues")):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
Normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
if normalize:
cm = Normalized
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(Normalized, interpolation='nearest', cmap=cmap)
plt.colorbar()
plt.title(title)
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=90)
plt.yticks(tick_marks, classes)
fmt = '.4f' if normalize else 'd'
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
thresh = cm[i].max() / 2.
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.figure(figsize=(10,10))
plot_confusion_matrix(confusion, classes=target_names, normalize=False,
title='Confusion matrix, without normalization')
plt.savefig("./result/confusion_matrix_without_normalization.svg")
plt.show()
plt.figure(figsize=(15,15))
plot_confusion_matrix(confusion, classes=target_names, normalize=True,
title='Normalized confusion matrix')
plt.savefig("./result/confusion_matrix_with_normalization.svg")
plt.show()
# load the original image
# X, y = loadIndianPinesData()
X, y = loadHSIData()
X, pca = applyPCA(X, numComponents=numPCAcomponents)
height = y.shape[0]
width = y.shape[1]
PATCH_SIZE = 5
numComponents = 30
# calculate the predicted image
outputs = np.zeros((height,width))
for i in range(height-PATCH_SIZE+1):
for j in range(width-PATCH_SIZE+1):
p = int(PATCH_SIZE/2)
# print(y[i+p][j+p])
# target = int(y[i+PATCH_SIZE/2, j+PATCH_SIZE/2])
target = y[i+p][j+p]
if target == 0 :
continue
else :
image_patch=Patch(X,i,j)
# print (image_patch.shape)
X_test_image = image_patch.reshape(1,image_patch.shape[2],image_patch.shape[0],image_patch.shape[1]).astype('float32')
prediction = (model.predict_classes(X_test_image))
outputs[i+p][j+p] = prediction+1
ground_truth = spectral.imshow(classes=y, figsize=(10, 10))
predict_image = spectral.imshow(classes=outputs.astype(int), figsize=(10, 10))
```
| true |
code
| 0.673178 | null | null | null | null |
|
# __Conceptos de estadística e introducción al análisis estadístico de datos usando Python__
```
#Importa las paqueterías necesarias
import numpy as np
import matplotlib.pyplot as pit
import pandas as pd
import seaborn as sns
import pandas_profiling as pp
from joblib import load, dump
import statsmodels.api as sm
```
Para este ejemplo ocuparemos bases de datos abiertas de crimen, registrados en Estados Unidos, específicamente una submuestra de la base de datos de crimen en Nueva York.
```
#Usar pandas para leer los datos y guardarlos como data frame
df_NY = load( "./datos_NY_crimen_limpios.pkl")
#Revisar si los datos fueron leidos correctamente
df_NY.head()
```
Diccionario de variables de la base de datos de crimenes en NY.
1. Ciudad: lugar en el que ocurrio el incidente
2. Fecha: año, mes y día en el que ocurrio el incidente
3. Hora: hora en la que ocurrio el incidente
4. Estatus: indicador de si el incidente fue completado o no
5. Gravedad: nivel del incidente; violación, delito mayor, delito menor
6. Lugar: lugar de ocurrencia del incidente; dentro, detras de, enfrente a y opuesto a...
7. Lugar especifico: lugar específico dónde ocurrio el incidente; tienda, casa habitación...
8. Crimen_tipo: descripción del tipo de delito
9. Edad_sospechoso: grupo de edad del sospechoso
10. Raza_sospechoso: raza del sospechoso
11. Sexo_sospechoso: sexo del sospechoso; M hombre, F mujer, U desconocido
12. Edad_victima: grupo de edad de la victima
13. Raza_victima: raza a la que pertenece la víctima
14. Sexo_victima: sexo de la victima; M hombre, F mujer, U desconocido
## 1.0 __Estadística descriptiva__
## 1.1 Conceptos de estadística descriptiva:
**Población**: conjunto de todos los elementos de interés (N).
**Parámetros**: métricas que obtenemos al trabajar con una población.
**Muestra**: subgrupo de la población (n).
**Estadísticos**: métricas que obtenemos al trabajar con poblaciones.

## 1.2 Una muestra debe ser:
**Representativa**: una muestra representativa es un subgrupo de la poblaciòn que refleja exactamente a los miembros de toda la población.
**Tomada al azar**: una muestra azarosa es recolectada cuando cada miembro de la muestra es elegida de la población estrictamente por casualidad
*¿Cómo sabemos que una muestra es representativa?¿Cómo calculamos el tamaño de muestra?*
Depende de los siguientes factores:
1. **Nivel de confianza**: ¿qué necesitamos para estar seguros de que nuestros resultados no ocurrieron solo por azar? Tipicamente se utiliza un nivel de confianza del _95% al 99%_
2. **Porcentaje de diferencia que deseemos detectar**: entre más pequeña sea la diferencia que quieres detectar, más grande debe ser la muestra
3. **Valor absoluto de las probabilidades en las que desea detectar diferencias**: depende de la prueba con la que estamos trabajando. Por ejemplo, detectar una diferencia entre 50% y 51% requiere un tamaño de muestra diferente que detectar una diferencia entre 80% y 81%. Es decir que, el tamaño de muestra requerido es una función de N1.
4. **La distribución de los datos (principalmente del resultado)**
## 1.3 ¿Qué es una variable?
**Variable**: es una característica, número o cantidad que puede ser descrita, medida o cuantíficada.
__Tipos de variables__:
1. Cualitativas o catégoricas: ordinales y nominales
2. Cuantitativas o numericas: discretas y continuas
```
#ORDINALES
#
#NOMINALES
#
#DISCRETAS
#
#CONTINUA
#
```
Variables de nuestra base de datos
```
df_NY.columns
```
## 1.4 ¿Cómo representar correctamente los diferentes tipos de variables?
__Datos categóricos:__ gráfica de barras, pastel, diagrama de pareto (tienen ambas barras y porcentajes)
__Datos numéricos:__ histograma y scatterplot
## 1.5 Atributos de las variables: medidas de tendencia central
Medidas de tendencia central: __media, mediana y moda__
1. **Media**: es la más común y la podemos obtener sumando todos los elementos de una variable y dividiéndola por el número de ellos. Es afectada por valores extremos
2. **Mediana**: número de la posición central de las observaciones (en orden ascendente). No es afectada por valores extremos.
3. **Moda**: el dato más común (puede existir más de una moda).

## 1.6 Atributos de las variables: medidas de asimetría (sesgo) o dispersión
__Sesgo__: indica si los datos se concentran en un lado de la curva
Por ejemplo:
1) cuando la medias es > que la mediana los datos se concentran del lado izquierdo de la curva, es decir que los outlier se encuentra del lado derecho de la distribución.
2) cuando la mediana < que la media, la mayor parte de los datos se concentran del lado derecho de la distribución y los outliers se encuentran en el lado izquierdo de la distribución.
En ambos casos la moda es la medida con mayor representación.
__Sin sesgo__: cuando la mediana, la moda y la media son iguales, la distribución es simétrica.
__El sesgo nos habla de donde se encuentran nuestros datos!__
## 1.7 Varianza
La __varianza__ es una medida de dispersión de un grupo de datos alrededor de la media.
Una forma más fácil de “visualizar” la varianza es por medio de la __desviación estandar__, en la mayoría de los casos esta es más significativa.
El __coeficiente de variación__ es igual a la desviación estándar dividida por el promedio
La desviación estandar es la medida más común de variabilidad para una base de datos única. Una de las principales ventajas de usar desviación estandar es que las unidades no estan elevadas al cuadrado y son más facil de interpretar
## 1.8 Relación entre variables
__Covarianza y Coeficiente de correlación lineal__
La covarianza puede ser >0, =0 o <0:
1. >0 las dos variables se mueven juntas
2. <0 las dos variables se mueven en direcciones opuestas
3. =0 las dos variables son independientes
El coeficiente de correlación va de -1 a 1
__Para explorar los atributos de cada una de las variables dentro de nuestra base de datos podemos hacer un profile report (podemos resolver toda la estadística descrptiva con un solo comando!!). Este reporte es el resultado de un análisis de cada una de las variables que integran la base de datos. Por medio de este, podemos verificar a que tipo de dato pertenece cada variable y obtener las medidas de tendencia central y asímetria. Con el fin de tener una idea general del comportamiento de nuestras variables.
Además, el profile report arroja un análisis de correlación entre variables (ver más adelante), que nos indica que tan relacionadas están entre si dos pares de variables__.
```
#pp.ProfileReport(df_NY[['Ciudad', 'Fecha', 'Hora', 'Estatus', 'Gravedad', 'Lugar','Crimen_tipo', 'Lugar_especifico', 'Edad_sospechoso', 'Raza_sospechoso','Sexo_sospechoso', 'Edad_victima', 'Raza_victima', 'Sexo_victima']])
```
## __2.0 Estadística inferencial__
## 2.1 Distribuciónes de probabilidad
Una __distribución__ es una función que muestra los valores posibles de una variable y que tan frecuentemente ocurren.
Es decir la __frecuencia__ en la que los posibles valores de una variable ocurren en un intervalo.
Las distribución más famosa en estadística(no precisamente la más común)es la __distribución normal__, donde la media moda y mediana son =. Es decir no hay sesgo
Frecuentemente, cuando los valores de una variable no tienen una distribución normal se recurre a transformaciones o estandarizaciones.
## 2.2 Regresión lineal
Una __regresión lineal__ es un modelo matemático para aproximar la relación de dependencia entre dos variables, una variable independiente y otra dependiente.
*Los valores de las variables dependientes dependen de los valores de las variables independientes*
## 2.3 Análisis de varianza
__Analisis de Varianza (ANOVA)__ se utiliza para comparar los promedios de dos o más grupos. Una prueba de ANOVA puede indicarte si hay diferencia en el promedio entre los grupos. Sin embargo,no nos da información sobre dónde se encuentra la diferencia (entre cuál y cuál grupo). Para resolver esto, podemos realizar una prueba post-hoc.
## __Análisis de base de datos abierta de delitos en NY__
### 1.0 Evaluar frecuencia de delitos
Podemos empezar por análizar los tipos de crimenes registrados, así como frecuencia de cada tipo de crimen.
```
#Usar value_counts en Pandas para cuantificar y organizar el tipo de crimenes
df_NY.Crimen_tipo.value_counts().iloc[:10]
df_NY.Crimen_tipo.value_counts().iloc[:10]
```
Ahora vamos a crear una grafica de los resultados para tener una mejor visualización de los datos.
```
df_NY.Crimen_tipo.value_counts().iloc[:10].plot(kind= "barh")
```
Podemos observar que los crimenes con mayor ocurrencia son "Petit larceny" y "Harraament 2"
### 1.1 Evaluar frecuencia de un delito específico: por ejemplo "Harrassment"
```
df_NY.dropna(inplace=True)
acoso = df_NY[df_NY["Crimen_tipo"].str.contains("HARRASSMENT 2")]
acoso.head(5)
```
## 2.0 Relaciones entre dos variables dependiente e independiente (de manera visual).
### 2.1 Análisis de la ocurrencia del __delito__ por __sitio__
¿Existen diferencias en la frecuencia de acoso en las diferentes localidades en NY? Es decir, qué lugares son más peligrosos.
En este ejemplo, la variable dependiente sería la ocurrecia del delito y la indenpendiente el sitio.
Para ello, usaremos la función __"groupby"__ de Pandas para agrupar por el tipo de localidades, y la función __size__ para revisar el número registrado en cada localidad.
```
acoso.columns
acoso.head()
acoso.groupby("Ciudad").size().sort_values(ascending=False)
acoso.Ciudad.value_counts().iloc[:10].plot(kind= "barh")
```
Al observar los resultados podemos distinguir en cuál de las localidades de NY hay mayores reportes de acoso. Brooklyn presenta más reportes de acoso.
```
acoso.Lugar_especifico.value_counts().iloc[:10].plot(kind= "barh")
```
El acoso ocurrió con mayor frecuencia dentro de casas y lugares de residencia.
### 2.2. Análisis de la ocurrencia del delito en el tiempo
Si queremos saber la frecuencia de ocurrencia del delito en diferentes años (2004-2018) y meses del año.
Aquí la variable dependiente es nuevamente la ocurrencia del delito y la independiente el tiempo.
```
acoso.groupby("anio").size().plot(kind="bar")
```
Podemos observar la mayoria de los resportes de acoso ocurrieron del 2016 al 2018. El 2011 fue el año con menor número de reportes de la ocurrencia de acoso
### 2.3. Analisis de ocurrencia del delito por sexo de la víctima y del agresor
En este ejemplo, la variable dependiente es el sexo de la víctima y la independiente el sexo del agresor
#### VICTIMAS
```
acoso.groupby("Sexo_victima").size().sort_values(ascending=False)
acoso.Sexo_victima.value_counts().iloc[:10].plot(kind= "pie")
acoso.groupby("Edad_victima").size().sort_values(ascending=False)
acoso.Edad_victima.value_counts().iloc[:10].plot(kind= "pie")
```
#### SOSPECHOSOS
```
acoso.groupby("Sexo_sospechoso").size().sort_values(ascending=False)
acoso.Sexo_sospechoso.value_counts().iloc[:10].plot(kind= "pie")
acoso.groupby("Edad_sospechoso").size().sort_values(ascending=False)
acoso.Edad_sospechoso.value_counts().iloc[:10].plot(kind= "pie")
```
### 2.4. Analisis de ocurrencia del delito por raza de la víctima y del agresor
En este ultimo ejemplo de relación entre variables, la variable dependiente es la raza de la víctima y la independiente es la raza del agresor.
#### VICTIMAS
```
acoso.groupby("Raza_victima").size().sort_values(ascending=False)
acoso.Raza_victima.value_counts().iloc[:10].plot(kind= "pie")
```
#### SOSPECHOSOS
```
acoso.groupby("Raza_sospechoso").size().sort_values(ascending=False)
acoso.Raza_sospechoso.value_counts().iloc[:10].plot(kind= "pie")
```
## 3.0 Regresión lineal
Pongamos a prueba la relación entre un par de variables. Por ejemplo, pero de la victima y peso del agresor. La relación puede ser negativa o positiva.
```
import pandas as pd
import statsmodels.api as sm
from sklearn import datasets, linear_model
df_w = pd.read_csv('Weight.csv')
df_w.head()
model = sm.OLS(y,X).fit()
predictions = model.predict(X)
print_model = model.summary()
print(print_model)
from scipy.stats import shapiro
stat, p = shapiro (y)
print('statistics=%.3f, p=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('its Gaussian')
else:
print('not Gaussian')
import statsmodels.api as sm
import pylab
sm.qqplot(y, loc = 4, scale = 3, line = 's')
pylab.show()
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(color_codes = True)
sns.regplot(x = "AGRE_Weight ", y = "VIC_Weight", data = tamano);
```
## 4.0 ANOVA
Para realizar un análisis de variaza utilizando nuestros datos inicialmente debemos plantearnos una hipótesis. Por ejemplo: Existe diferencias en la edad de las víctimas entre los sitios donde ocurre ocoso.
Podemos probar nuetra hipótesis de manera estadística.
En este caso generaremos una columna extra de datos numericos continuos aproximados de "Edad_calculada_victima" y "Edad_calculada_agresor" para hacer el análisis
```
import pandas as pd
import scipy.stats as stats
import statsmodels. api as sm
from statsmodels.formula.api import ols
acoso["Edad_sospechoso"].unique()
from random import randint
def rango_a_random(s):
if type(s)==str:
s = s.split('-')
s = [int(i) for i in s]
s = randint(s[0],s[1]+1)
return s
acoso["Edad_calculada_victima"] = acoso["Edad_victima"]
acoso["Edad_calculada_victima"] = acoso["Edad_calculada_victima"].replace("65+","65-90").replace("<18","15-18").replace("UNKNOWN",np.nan)
acoso["Edad_calculada_victima"] = acoso["Edad_calculada_victima"].apply(rango_a_random)
acoso["Edad_calculada_sospechoso"] = acoso["Edad_sospechoso"]
acoso["Edad_calculada_sospechoso"] = acoso["Edad_calculada_sospechoso"].replace("65+","65-90").replace("<18","15-18").replace("UNKNOWN",np.nan)
acoso["Edad_calculada_sospechoso"] = acoso["Edad_calculada_sospechoso"].apply(rango_a_random)
acoso.head(5)
acoso.dropna ()
results = ols('Edad_calculada_victima ~ C(Ciudad)', data = acoso).fit()
results.summary()
```
En un análisis de varianza los dos "datos" de mayor importancia son el valor de F (F-statistic) y el valor de P (Prof F-statistic). Debemos obtener un avalor de P <0.05 para poder aceptar nuestra hipótesis.
En el ejemplo nuestro valor de F=4.129 y el de P=0.002. Es decir que podemos aceptar nuestra hipótesis.
| true |
code
| 0.484136 | null | null | null | null |
|
# Default of credit card clients Data Set
### Data Set Information:
This research aimed at the case of customers’ default payments in Taiwan and compares the predictive accuracy of probability of default among six data mining methods. From the perspective of risk management, the result of predictive accuracy of the estimated probability of default will be more valuable than the binary result of classification - credible or not credible clients. Because the real probability of default is unknown, this study presented the novel “Sorting Smoothing Method†to estimate the real probability of default. With the real probability of default as the response variable (Y), and the predictive probability of default as the independent variable (X), the simple linear regression result (Y = A + BX) shows that the forecasting model produced by artificial neural network has the highest coefficient of determination; its regression intercept (A) is close to zero, and regression coefficient (B) to one. Therefore, among the six data mining techniques, artificial neural network is the only one that can accurately estimate the real probability of default.
### Attribute Information:
This research employed a binary variable, default payment (Yes = 1, No = 0), as the response variable. This study reviewed the literature and used the following 23 variables as explanatory variables:
X1: Amount of the given credit (NT dollar): it includes both the individual consumer credit and his/her family (supplementary) credit.
X2: Gender (1 = male; 2 = female).
X3: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others).
X4: Marital status (1 = married; 2 = single; 3 = others).
X5: Age (year).
X6 - X11: History of past payment. We tracked the past monthly payment records (from April to September, 2005) as follows:
X6 = the repayment status in September, 2005;
X7 = the repayment status in August, 2005;
. . .;
X11 = the repayment status in April, 2005. The measurement scale for the repayment status is: -1 = pay duly; 1 = payment delay for one month; 2 = payment delay for two months; . . .; 8 = payment delay for eight months; 9 = payment delay for nine months and above.
X12-X17: Amount of bill statement (NT dollar).
X12 = amount of bill statement in September, 2005;
X13 = amount of bill statement in August, 2005;
. . .;
X17 = amount of bill statement in April, 2005.
X18-X23: Amount of previous payment (NT dollar).
X18 = amount paid in September, 2005;
X19 = amount paid in August, 2005;
. . .;
X23 = amount paid in April, 2005.
```
%matplotlib inline
import os
import json
import time
import pickle
import requests
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
URL = "http://archive.ics.uci.edu/ml/machine-learning-databases/00350/default%20of%20credit%20card%20clients.xls"
def fetch_data(fname='default_of_credit_card_clients.xls'):
"""
Helper method to retreive the ML Repository dataset.
"""
response = requests.get(URL)
outpath = os.path.abspath(fname)
with open(outpath, 'w') as f:
f.write(response.content)
return outpath
# Fetch the data if required
# DATA = fetch_data()
# IMPORTANT - Issue saving xls file needed to be fix in fetch_data. Using a valid manually downloaded files instead for this example.
DATA = "./default_of_credit_card_clients2.xls"
FEATURES = [
"ID",
"LIMIT_BAL",
"SEX",
"EDUCATION",
"MARRIAGE",
"AGE",
"PAY_0",
"PAY_2",
"PAY_3",
"PAY_4",
"PAY_5",
"PAY_6",
"BILL_AMT1",
"BILL_AMT2",
"BILL_AMT3",
"BILL_AMT4",
"BILL_AMT5",
"BILL_AMT6",
"PAY_AMT1",
"PAY_AMT2",
"PAY_AMT3",
"PAY_AMT4",
"PAY_AMT5",
"PAY_AMT6",
"label"
]
LABEL_MAP = {
1: "Yes",
0: "No",
}
# Read the data into a DataFrame
df = pd.read_excel(DATA,header=None, skiprows=2, names=FEATURES)
# Convert class labels into text
for k,v in LABEL_MAP.items():
df.ix[df.label == k, 'label'] = v
# Describe the dataset
print df.describe()
df.head(5)
# Determine the shape of the data
print "{} instances with {} features\n".format(*df.shape)
# Determine the frequency of each class
print df.groupby('label')['label'].count()
from pandas.tools.plotting import scatter_matrix
scatter_matrix(df, alpha=0.2, figsize=(12, 12), diagonal='kde')
plt.show()
from pandas.tools.plotting import parallel_coordinates
plt.figure(figsize=(12,12))
parallel_coordinates(df, 'label')
plt.show()
from pandas.tools.plotting import radviz
plt.figure(figsize=(12,12))
radviz(df, 'label')
plt.show()
```
## Data Extraction
One way that we can structure our data for easy management is to save files on disk. The Scikit-Learn datasets are already structured this way, and when loaded into a `Bunch` (a class imported from the `datasets` module of Scikit-Learn) we can expose a data API that is very familiar to how we've trained on our toy datasets in the past. A `Bunch` object exposes some important properties:
- **data**: array of shape `n_samples` * `n_features`
- **target**: array of length `n_samples`
- **feature_names**: names of the features
- **target_names**: names of the targets
- **filenames**: names of the files that were loaded
- **DESCR**: contents of the readme
**Note**: This does not preclude database storage of the data, in fact - a database can be easily extended to load the same `Bunch` API. Simply store the README and features in a dataset description table and load it from there. The filenames property will be redundant, but you could store a SQL statement that shows the data load.
In order to manage our data set _on disk_, we'll structure our data as follows:
```
with open('./../data/cc_default/meta.json', 'w') as f:
meta = {'feature_names': FEATURES, 'target_names': LABEL_MAP}
json.dump(meta, f, indent=4)
from sklearn.datasets.base import Bunch
DATA_DIR = os.path.abspath(os.path.join(".", "..", "data", "cc_default"))
# Show the contents of the data directory
for name in os.listdir(DATA_DIR):
if name.startswith("."): continue
print "- {}".format(name)
def load_data(root=DATA_DIR):
# Construct the `Bunch` for the wheat dataset
filenames = {
'meta': os.path.join(root, 'meta.json'),
'rdme': os.path.join(root, 'README.md'),
'data_xls': os.path.join(root, 'default_of_credit_card_clients.xls'),
'data': os.path.join(root, 'default_of_credit_card_clients.csv'),
}
# Load the meta data from the meta json
with open(filenames['meta'], 'r') as f:
meta = json.load(f)
target_names = meta['target_names']
feature_names = meta['feature_names']
# Load the description from the README.
with open(filenames['rdme'], 'r') as f:
DESCR = f.read()
# Load the dataset from the EXCEL file.
df = pd.read_excel(filenames['data_xls'],header=None, skiprows=2, names=FEATURES)
df.to_csv(filenames['data'],header=False)
dataset = np.loadtxt(filenames['data'],delimiter=",")
# Extract the target from the data
data = dataset[:, 0:-1]
target = dataset[:, -1]
# Create the bunch object
return Bunch(
data=data,
target=target,
filenames=filenames,
target_names=target_names,
feature_names=feature_names,
DESCR=DESCR
)
# Save the dataset as a variable we can use.
dataset = load_data()
print dataset.data.shape
print dataset.target.shape
```
## Classification
Now that we have a dataset `Bunch` loaded and ready, we can begin the classification process. Let's attempt to build a classifier with kNN, SVM, and Random Forest classifiers.
```
from sklearn import metrics
from sklearn import cross_validation
from sklearn.cross_validation import KFold
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
def fit_and_evaluate(dataset, model, label, **kwargs):
"""
Because of the Scikit-Learn API, we can create a function to
do all of the fit and evaluate work on our behalf!
"""
start = time.time() # Start the clock!
scores = {'precision':[], 'recall':[], 'accuracy':[], 'f1':[]}
for train, test in KFold(dataset.data.shape[0], n_folds=12, shuffle=True):
X_train, X_test = dataset.data[train], dataset.data[test]
y_train, y_test = dataset.target[train], dataset.target[test]
estimator = model(**kwargs)
estimator.fit(X_train, y_train)
expected = y_test
predicted = estimator.predict(X_test)
# Append our scores to the tracker
scores['precision'].append(metrics.precision_score(expected, predicted, average="weighted"))
scores['recall'].append(metrics.recall_score(expected, predicted, average="weighted"))
scores['accuracy'].append(metrics.accuracy_score(expected, predicted))
scores['f1'].append(metrics.f1_score(expected, predicted, average="weighted"))
# Report
print "Build and Validation of {} took {:0.3f} seconds".format(label, time.time()-start)
print "Validation scores are as follows:\n"
print pd.DataFrame(scores).mean()
# Write official estimator to disk
estimator = model(**kwargs)
estimator.fit(dataset.data, dataset.target)
outpath = label.lower().replace(" ", "-") + ".pickle"
with open(outpath, 'w') as f:
pickle.dump(estimator, f)
print "\nFitted model written to:\n{}".format(os.path.abspath(outpath))
# Perform SVC Classification
#fit_and_evaluate(dataset, SVC, "CC Defaut - SVM Classifier")
# Perform kNN Classification
fit_and_evaluate(dataset, KNeighborsClassifier, "CC Defaut - kNN Classifier", n_neighbors=12)
# Perform Random Forest Classification
fit_and_evaluate(dataset, RandomForestClassifier, "CC Defaut - Random Forest Classifier")
```
| true |
code
| 0.599661 | null | null | null | null |
|
MNIST classification (drawn from sklearn example)
=====================================================
MWEM is not particularly well suited for image data (where there are tons of features with relatively large ranges) but it is still able to capture some important information about the underlying distributions if tuned correctly.
We use a feature included with MWEM that allows a column to be specified for a custom bin count, if we are capping every other bin count at a small value. In this case, we specify that the numerical column (784) has 10 possible values. We do this with the dict {'784': 10}.
Here we borrow from a scikit-learn example, and insert MWEM synthetic data into their training example/visualization, to understand the tradeoffs.
https://scikit-learn.org/stable/auto_examples/linear_model/plot_sparse_logistic_regression_mnist.html#sphx-glr-download-auto-examples-linear-model-plot-sparse-logistic-regression-mnist-py
```
import time
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.utils import check_random_state
# pip install scikit-image
from skimage import data, color
from skimage.transform import rescale
# Author: Arthur Mensch <[email protected]>
# License: BSD 3 clause
# Turn down for faster convergence
t0 = time.time()
train_samples = 5000
# Load data from https://www.openml.org/d/554
data = fetch_openml('mnist_784', version=1, return_X_y=False)
data_np = np.hstack((data.data,np.reshape(data.target.astype(int), (-1, 1))))
from opendp.smartnoise.synthesizers.mwem import MWEMSynthesizer
# Here we set max bin count to be 10, so that we retain the numeric labels
synth = MWEMSynthesizer(10.0, 40, 15, 10, split_factor=1, max_bin_count = 128, custom_bin_count={'784':10})
synth.fit(data_np)
sample_size = 2000
synthetic = synth.sample(sample_size)
from sklearn.linear_model import RidgeClassifier
import utils
real = pd.DataFrame(data_np[:sample_size])
model_real, model_fake = utils.test_real_vs_synthetic_data(real, synthetic, RidgeClassifier, tsne=True)
# Classification
coef = model_real.coef_.copy()
plt.figure(figsize=(10, 5))
scale = np.abs(coef).max()
for i in range(10):
l1_plot = plt.subplot(2, 5, i + 1)
l1_plot.imshow(coef[i].reshape(28, 28), interpolation='nearest',
cmap=plt.cm.RdBu, vmin=-scale, vmax=scale)
l1_plot.set_xticks(())
l1_plot.set_yticks(())
l1_plot.set_xlabel('Class %i' % i)
plt.suptitle('Classification vector for...')
run_time = time.time() - t0
print('Example run in %.3f s' % run_time)
plt.show()
coef = model_fake.coef_.copy()
plt.figure(figsize=(10, 5))
scale = np.abs(coef).max()
for i in range(10):
l1_plot = plt.subplot(2, 5, i + 1)
l1_plot.imshow(coef[i].reshape(28, 28), interpolation='nearest',
cmap=plt.cm.RdBu, vmin=-scale, vmax=scale)
l1_plot.set_xticks(())
l1_plot.set_yticks(())
l1_plot.set_xlabel('Class %i' % i)
plt.suptitle('Classification vector for...')
run_time = time.time() - t0
print('Example run in %.3f s' % run_time)
plt.show()
```
| true |
code
| 0.699921 | null | null | null | null |
|
# k-NN movie reccomendation
| User\Film | Movie A | Movie B | Movie C | ... | Movie # |
|---------------------------------------------------------|
| **User A**| 3 | 4 | 0 | ... | 5 |
| **User B**| 0 | 3 | 2 | ... | 0 |
| **User C**| 4 | 1 | 3 | ... | 4 |
| **User D**| 5 | 3 | 2 | ... | 3 |
| ... | ... | ... | ... | ... | ... |
| **User #**| 2 | 1 | 1 | ... | 4 |
Task: For a new user find k similar users based on movie rating and recommend few new, previously unseen, movies to the new user. Use mean rating of k users to find which one to recommend. Use cosine similarity as distance function. User didnt't see a movie if he didn't rate the movie.
```
# Import necessary libraries
import tensorflow as tf
import numpy as np
# Define paramaters
set_size = 1000 # Number of users in dataset
n_features = 300 # Number of movies in dataset
K = 3 # Number of similary users
n_movies = 6 # Number of movies to reccomend
# Generate dummy data
data = np.array(np.random.randint(0, 6, size=(set_size, n_features)), dtype=np.float32)
new_user = np.array(np.random.randint(0, 6, size=(1, n_features)), dtype=np.float32)
# Find the number of movies that user did not rate
not_rated = np.count_nonzero(new_user == 0)
# Case in which the new user rated all movies in our dataset
if not_rated == 0:
print('Regenerate new user')
# Case in which we try to recommend more movies than user didn't see
if not_rated < n_movies:
print('Regenerate new user')
# Print few examples
# print(data[:3])
# print(new_user)
# Input train vector
X1 = tf.placeholder(dtype=tf.float32, shape=[None, n_features], name="X1")
# Input test vector
X2 = tf.placeholder(dtype=tf.float32, shape=[1, n_features], name="X2")
# Cosine similarity
norm_X1 = tf.nn.l2_normalize(X1, axis=1)
norm_X2 = tf.nn.l2_normalize(X2, axis=1)
cos_similarity = tf.reduce_sum(tf.matmul(norm_X1, tf.transpose(norm_X2)), axis=1)
with tf.Session() as sess:
# Find all distances
distances = sess.run(cos_similarity, feed_dict={X1: data, X2: new_user})
# print(distances)
# Find indices of k user with highest similarity
_, user_indices = sess.run(tf.nn.top_k(distances, K))
# print(user_indices)
# Get users rating
# print(data[user_indices])
# New user ratings
# print(new_user[0])
# NOTICE:
# There is a possibility that we can incorporate
# user for e.g. movie A which he didn't see.
movie_ratings = sess.run(tf.reduce_mean(data[user_indices], axis=0))
# print(movie_ratings)
# Positions where the new user doesn't have rating
# NOTICE:
# In random generating there is a possibility that
# the new user rated all movies in data set, if that
# happens regenerate the new user.
movie_indices = sess.run(tf.where(tf.equal(new_user[0], 0)))
# print(movie_indices)
# Pick only the avarege rating of movies that have been rated by
# other users and haven't been rated by the new user and among
# those movies pick n_movies for recommend to the new user
_, top_rated_indices = sess.run(tf.nn.top_k(movie_ratings[movie_indices].reshape(-1), n_movies))
# print(top_rated_indices)
# Indices of the movies with the highest mean rating, which new user did not
# see, from the k most similary users based on movie ratings
print('Movie indices to reccomend: ', movie_indices[top_rated_indices].T)
```
# Locally weighted regression (LOWESS)
```
# Import necessary libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
tf.reset_default_graph()
# Load data as numpy array
x, y = np.loadtxt('../../data/02_LinearRegression/polynomial.csv', delimiter=',', unpack=True)
m = x.shape[0]
x = (x - np.mean(x, axis=0)) / np.std(x, axis=0)
y = (y - np.mean(y)) / np.std(y)
# Graphical preview
%matplotlib inline
fig, ax = plt.subplots()
ax.set_xlabel('X Labe')
ax.set_ylabel('Y Label')
ax.scatter(x, y, edgecolors='k', label='Data')
ax.grid(True, color='gray', linestyle='dashed')
X = tf.placeholder(tf.float32, name='X')
Y = tf.placeholder(tf.float32, name='Y')
w = tf.Variable(0.0, name='weights')
b = tf.Variable(0.0, name='bias')
point_x = -0.5
tau = 0.15 # 0.22
t_w = tf.exp(tf.div(-tf.pow(tf.subtract(X, point_x), 2), tf.multiply(tf.pow(tau, 2), 2)))
Y_predicted = tf.add(tf.multiply(X, w), b)
cost = tf.reduce_mean(tf.multiply(tf.square(Y - Y_predicted), t_w), name='cost')
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)
with tf.Session() as sess:
# Initialize the necessary variables, in this case, w and b
sess.run(tf.global_variables_initializer())
# Train the model in 50 epochs
for i in range(500):
total_cost = 0
# Session runs train_op and fetch values of loss
for sample in range(m):
# Session looks at all trainable variables that loss depends on and update them
_, l = sess.run([optimizer, cost], feed_dict={X: x[sample], Y:y[sample]})
total_cost += l
# Print epoch and loss
if i % 50 == 0:
print('Epoch {0}: {1}'.format(i, total_cost / m))
# Output the values of w and b
w1, b1 = sess.run([w, b])
print(sess.run(t_w, feed_dict={X: 1.4}))
print('W: %f, b: %f' % (w1, b1))
print('Cost: %f' % sess.run(cost, feed_dict={X: x, Y: y}))
# Append hypothesis that we found on the plot
x1 = np.linspace(-1.0, 0.0, 50)
ax.plot(x1, x1 * w1 + b1, color='r', label='Predicted')
ax.plot(x1, np.exp(-(x1 - point_x) ** 2 / (2 * 0.15 ** 2)), color='g', label='Weight function')
ax.legend()
fig
```
| true |
code
| 0.712182 | null | null | null | null |
|
# Django2.2
**Python Web Framework**:<https://wiki.python.org/moin/WebFrameworks>
先说句大实话,Web端我一直都是`Net技术站`的`MVC and WebAPI`,Python我一直都是用些数据相关的知识(爬虫、简单的数据分析等)Web这块只是会Flask,其他框架也都没怎么接触过,都说`Python`的`Django`是`建站神器`,有`自动生成后端管理页面`的功能,于是乎就接触了下`Django2.2`(目前最新版本)
> 逆天点评:Net的MVC最擅长的就是(通过Model+View)`快速生成前端页面和对应的验证`,而Python的`Django`最擅长的就是(通过注册Model)`快速生成后台管理页面`。**这两个语言都是快速建站的常用编程语言**(项目 V1~V2 阶段)
网上基本上都是Django1.x的教程,很多东西在2下都有点不适用,所以简单记录下我的学习笔记以及一些心得:
> PS:ASP.Net MVC相关文章可以参考我16年写的文章:<https://www.cnblogs.com/dunitian/tag/MVC/>
官方文档:<https://docs.djangoproject.com/zh-hans/2.2/releases/2.2/>
## 1.环境
### 1.虚拟环境
这个之前的确没太大概念,我一直都是用Conda来管理不同版本的包,现在借助Python生态圈里的工具`virtualenv`和`virtualenvwapper`
---
### 2.Django命令
1.**创建一个空项目:`django-admin startproject 项目名称`**
> PS:项目名不要以数字开头哦~
```shell
# 创建一个base_demo的项目
django-admin startproject base_demo
# 目录结构
|-base_demo (文件夹)
|---__init__.py(说明这个文件夹是一个Python包)
|---settings.py(项目配置文件:创建应用|模块后进行配置)
|---urls.py(URL路由配置)
|---wsgi.py(遵循wsgi协议:web服务器和Django的交互入口)
|-manage.py(项目管理文件,用来生成应用|模块)
```
2.**创建一个应用:`python manage.py startapp 应用名称`**
> 项目中一个模块就是一个应用,eg:商品模块、订单模块等
```shell
# 创建一个用户模块
python manage.py startapp users
├─base_demo
│ __init__.py
│ settings.py
│ urls.py
│ wsgi.py
├─manage.py(项目管理文件,用来生成应用|模块)
│
└─users(新建的模块|应用)
│ │ __init__.py
│ │ admin.py(后台管理相关)
│ │ models.py(数据库相关模型)
│ │ views.py(相当于MVC中的C,用来定义处理|视图函数)
│ │ tests.py(写测试代码)
│ │ apps.py:配置应用的元数据(可选)
│ │
│ └─migrations:数据迁移模块(根据Model内容生成的)
│ __init__.py
```
**PS:记得在项目(`base_demo`)的settings.py注册一下应用模块哦~**
```py
INSTALLED_APPS = [
......
'users', # 注册自己创建的模块|应用
]
```
3.**运行项目:`python manage.py runserver`**
> PS:指定端口:`python manage.py runserver 8080`
## 2.MVT入门
**大家都知道MVC(模型-视图-控制器),而Django的MVC叫做MVT(模型-视图-模版)**
> PS:Django出来很早,名字是自己定义的,用法和理念是一样的
### 2.1.M(模型)
#### 2.1.1.类的定义
- 1.**生成迁移文件:`python manage.py makemigrations`**
- PS:根据编写好的Model文件生成(模型里面可以不用定义ID属性)
- 2.**执行迁移生成表:`python mange.py migrate`**
- PS:执行生成的迁移文件
PS:类似于EF的`CodeFirst`,Django默认使用的是`sqlite`,更改数据库后面会说的
先看个演示案例:
**1.定义类文件**(会根据Code来生成DB)
```py
# users > models.py
from django.db import models
# 用户信息表
class UserInfo(models.Model):
# 字符串类型,最大长度为20
name = models.CharField(max_length=20)
# 创建时间:日期类型
create_time = models.DateTimeField()
# 更新时间
update_time = models.DateTimeField()
```
**2. 生成数据库**
```shell
# 生成迁移文件
> python manage.py makemigrations
Migrations for 'userinfo':
userinfo\migrations\0001_initial.py
- Create model UserInfo
# 执行迁移生成表
> python manage.py migrate
Operations to perform:
Apply all migrations: admin, auth, contenttypes, sessions, userinfo
Running migrations:
Applying contenttypes.0001_initial... OK
Applying auth.0001_initial... OK
Applying admin.0001_initial... OK
Applying admin.0002_logentry_remove_auto_add... OK
Applying admin.0003_logentry_add_action_flag_choices... OK
Applying contenttypes.0002_remove_content_type_name... OK
Applying auth.0002_alter_permission_name_max_length... OK
Applying auth.0003_alter_user_email_max_length... OK
Applying auth.0004_alter_user_username_opts... OK
Applying auth.0005_alter_user_last_login_null... OK
Applying auth.0006_require_contenttypes_0002... OK
Applying auth.0007_alter_validators_add_error_messages... OK
Applying auth.0008_alter_user_username_max_length... OK
Applying auth.0009_alter_user_last_name_max_length... OK
Applying sessions.0001_initial... OK
Applying userinfo.0001_initial... OK
```
然后就自动生成对应的表了 ==> **`users_userinfo`**(应用名_模块中的类名)
知识拓展:默认时间相关文章:<https://www.cnblogs.com/huchong/p/7895263.html>
#### 2.1.2.生成后台
##### 1.配置本地化(设置后台管理页面是中文)
主要就是修改`settings.py`文件的`语言`和`时区`(后台管理的语言和时间)
```py
# 使用中文(zh-hans可以这么记==>zh-汉'字')
LANGUAGE_CODE = 'zh-hans'
# 设置中国时间
TIME_ZONE = 'Asia/Shanghai'
```
##### 2.创建管理员
**创建系统管理员:`python manage.py createsuperuser`**
```shell
python manage.py createsuperuser
用户名 (leave blank to use 'win10'): dnt # 如果不填,默认是计算机用户名
电子邮件地址: # 可以不设置
Password:
Password (again):
Superuser created successfully.
```
**经验:如果忘记密码可以创建一个新管理员账号,然后把旧的删掉就行了**
> PS:根据新password字段,修改下旧账号的password也可以
课后拓展:<a href="https://blog.csdn.net/dsjakezhou/article/details/84319228">修改django后台管理员密码</a>
##### 3.后台管理页面
主要就是**在admin中注册模型类**
比如给之前创建的UserInfo类创建对应的管理页面:
```py
# base_demo > users > admin.py
from users.models import UserInfo
# from .models import UserInfo
# 注册模型类(自动生成后台管理页面)
admin.site.register(UserInfo) # .site别忘记
```
然后运行Django(`python manage.py runserver`),访问"127.0.0.1:8080/admin",登录后就就可以管理了
> PS:如果不想交admin,而是想在root下。那么可以修改项目的`urls.py`(后面会说)
##### 4.制定化显示
注册模型类就ok了,但是显示稍微有点不人性化,eg:
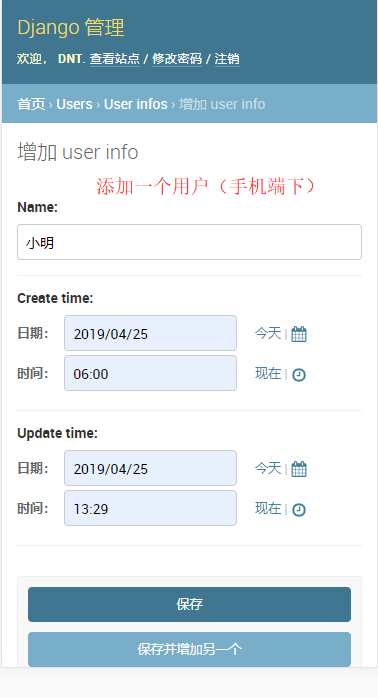
列表页显示出来的标题是UserInfo对象,而我们平时一般显示用户名等信息
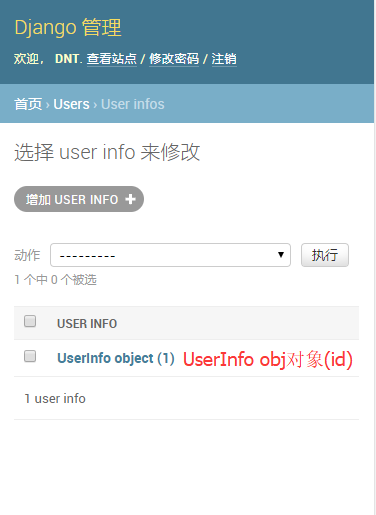
so ==> 可以自己改写下
回顾下之前讲的:(程序是显示的`str(对象)`,那么我们重写魔方方法`__str__`即可改写显示了)
```py
# base_demo > users > models.py
# 用户信息表
class UserInfo(models.Model):
# 字符串类型,最大长度为20
name = models.CharField(max_length=20)
# 创建时间:日期类型
create_time = models.DateTimeField()
# 更新时间
update_time = models.DateTimeField()
def __str__(self):
"""为了后台管理页面的美化"""
return self.name
```
这时候再访问就美化了:(**不用重启Django**)
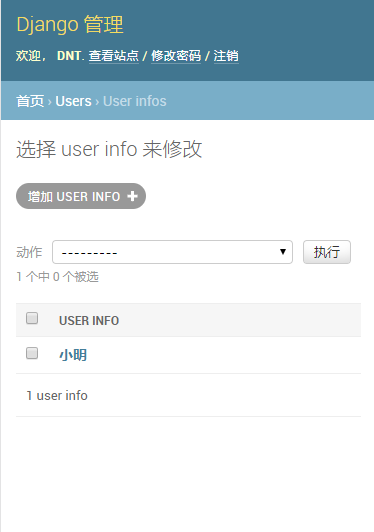
Django就没有提供对应的方法?NoNoNo,我们继续看:
```py
# base_demo > users > admin.py
from .models import UserInfo
# 自定义模型管理页面
class UserInfoAdmin(admin.ModelAdmin):
# 自定义管理页面的列表显示字段(和类属性相对应)
list_display = ["id", "name", "create_time", "update_time", "datastatus"]
# 注册模型类和模型管理类(自动生成后台管理页面)
admin.site.register(UserInfo, UserInfoAdmin)
```
其他什么都不用修改,后端管理列表的布局就更新了:
> PS:设置Model的`verbose_name`就可以在后台显示中文,eg:`name = models.CharField(max_length=25, verbose_name="姓名")`
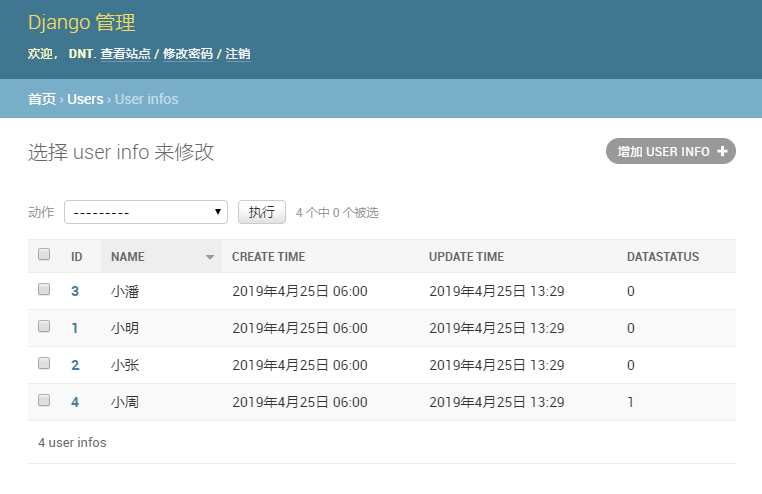
还有更多个性化的内容后面会继续说的~
### 2.3.V(视图)
这个类比于MVC的C(控制器)
> PS:这块比Net的MVC和Python的Flask要麻烦点,url地址要简单配置下映射关系(小意思,不花太多时间)
这块刚接触稍微有点绕,所以我们借助图来看:
**比如我们想访问users应用下的首页(`/users/index`)**
#### 2.3.1.设置视图函数
这个和定义控制器里面的方法没区别:
> PS:函数必须含`request`(类比下类方法必须含的self)
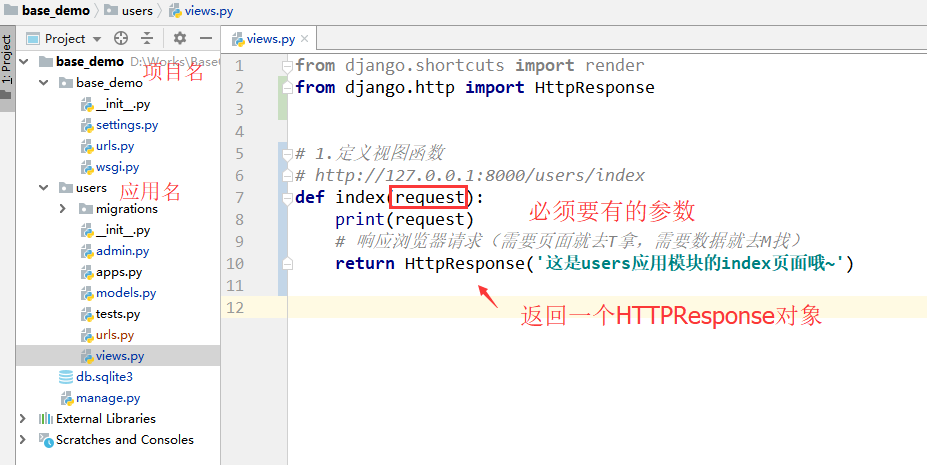
```py
from django.http import HttpResponse
# 1.定义视图函数
# http://127.0.0.1:8000/users/index
def index(request):
print(request)
# 响应浏览器请求(需要页面就去T拿,需要数据就去M找)
return HttpResponse('这是users应用模块的index页面哦~')
```
#### 2.3.2.配置路由
因为我想要的地址是:`/users/index`,那么我在项目urls中也需要配置下访问`/users`的路由规则:
> PS:我是防止以后模块多了管理麻烦,所以分开写,要是你只想在一个urls中配置也无妨
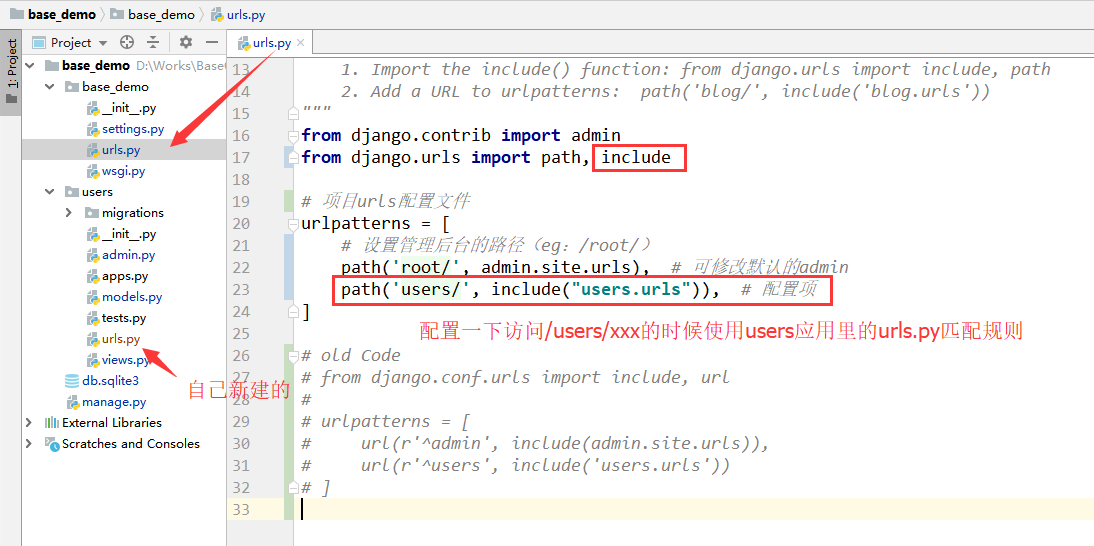
```py
# base_demo > urls.py
from django.contrib import admin
from django.urls import path, include
# 项目urls配置文件
urlpatterns = [
path('users/', include("users.urls")), # 配置项
]
```
最后再贴一下users应用模块的匹配:
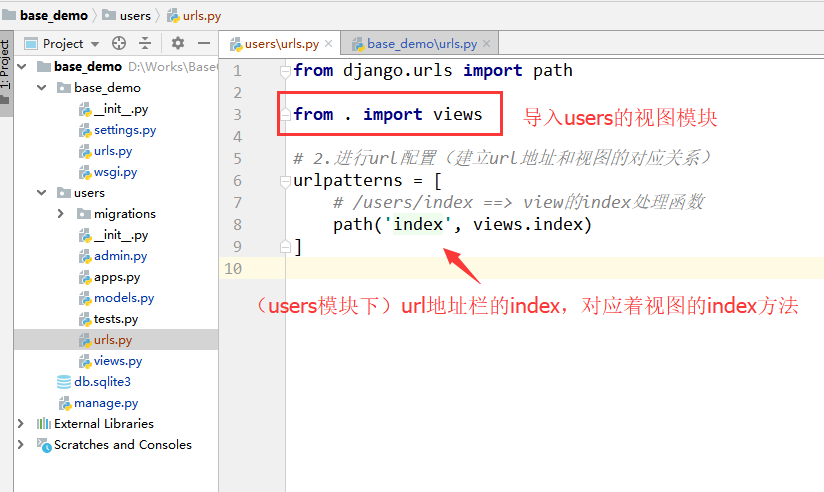
```py
# users > urls.py
from django.urls import path
from . import views
# 2.进行url配置(建立url地址和视图的对应关系)
urlpatterns = [
# /users/index ==> view的index处理函数
path('index', views.index),
]
```
#### 2.3.3.url访问
这时候你访问`127.0.0.1:8000/users/index`就可以了:
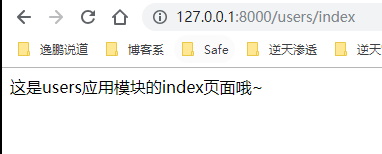
简单说下这个过程:
1. 先去项目的urls.py中进行匹配
- `path('users/', include("users.urls")), # 配置项`
2. 发现只要是以`/users/`开头的都使用了`users`模块自己的`urls.py`来匹配
- `path('index', views.index),`
3. 发现访问`/users/index`最后进入的视图函数是`index`
4. 然后执行`def index(request):pass`里面的内容并返回
### 2.4.T(模版)
这个类比于MVC的V,我们来看个简单案例:
#### 2.4.1.创建模版
Django1.x版本需要配置下模版路径之类的,现在只要在对应模块下创建`templates`文件夹就可以直接访问了
我们来定义一个list的模版:
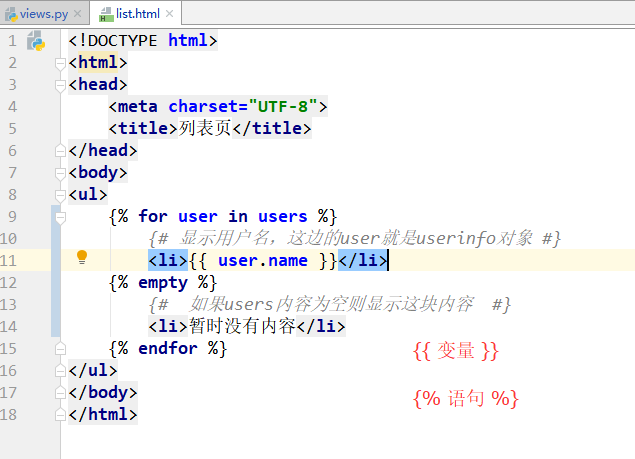
定义视图函数(类比定义控制器方法)
配置对应的路由:
然后就出效果了:
如果把之前添加的数据删除掉,也会显示默认效果:
#### 2.4.2.指定模版
也可以指定模版位置:(看个人习惯)
打开项目`settings.py`文件,设置`TEMPLATES`的`DIRS`值,来指定默认模版路径:
```py
# Base_dir:当前项目的绝对路径
# BASE_DIR = os.path.dirname(os.path.dirname(os.path.abspath(__file__)))
# https://docs.djangoproject.com/zh-hans/2.2/ref/settings/#templates
TEMPLATES = [
{
...
'DIRS': [os.path.join(BASE_DIR, 'templates')], # 模版文件的绝对路径
...
},
]
```
### 扩展:使用MySQL数据库
这篇详细流程可以查看之前写的文章:<a href="" title="https://www.cnblogs.com/dotnetcrazy/p/10782441.html" target="_blank">稍微记录下Django2.2使用MariaDB和MySQL遇到的坑</a>
这边简单过下即可:
#### 1.创建数据库
Django不会帮你创建数据库,需要自己创建,eg:`create database django charset=utf8;`
#### 2.配置数据库
我把对应的文档url也贴了:
```py
# https://docs.djangoproject.com/en/2.2/ref/settings/#databases
DATABASES = {
'default': {
'ENGINE': 'django.db.backends.mysql',
'NAME': 'django', # 使用哪个数据库
'USER': 'root', # mysql的用户名
'PASSWORD': 'dntdnt', # 用户名对应的密码
'HOST': '127.0.0.1', # 数据库服务的ip地址
'PORT': 3306, # 对应的端口
# https://docs.djangoproject.com/en/2.2/ref/settings/#std:setting-OPTIONS
'OPTIONS': {
# https://docs.djangoproject.com/zh-hans/2.2/ref/databases/#setting-sql-mode
# SQLMode可以看我之前写的文章:https://www.cnblogs.com/dotnetcrazy/p/10374091.html
'init_command': "SET sql_mode='STRICT_TRANS_TABLES'", # 设置SQL_Model
},
}
}
```
最小配置:

项目init.py文件中配置:
```py
import pymysql
# Django使用的MySQLdb对Python3支持力度不够,我们用PyMySQL来代替
pymysql.install_as_MySQLdb()
```
图示:
#### 3.解决干扰
如果你的Django是最新的2.2,PyMySQL也是最新的0.93的话,你会发现Django会报错:
> django.core.exceptions.ImproperlyConfigured: mysqlclient 1.3.13 or newer is required; you have 0.9.3.
这个是Django对MySQLdb版本的限制,我们使用的是PyMySQL,所以不用管它
再继续运行发现又冒了个错误:`AttributeError: 'str' object has no attribute 'decode'`
这个就不能乱改了,所以先调试输出下:
发现是对字符串进行了decode解码操作:(一般对字符串进行编码,二进制进行解码)
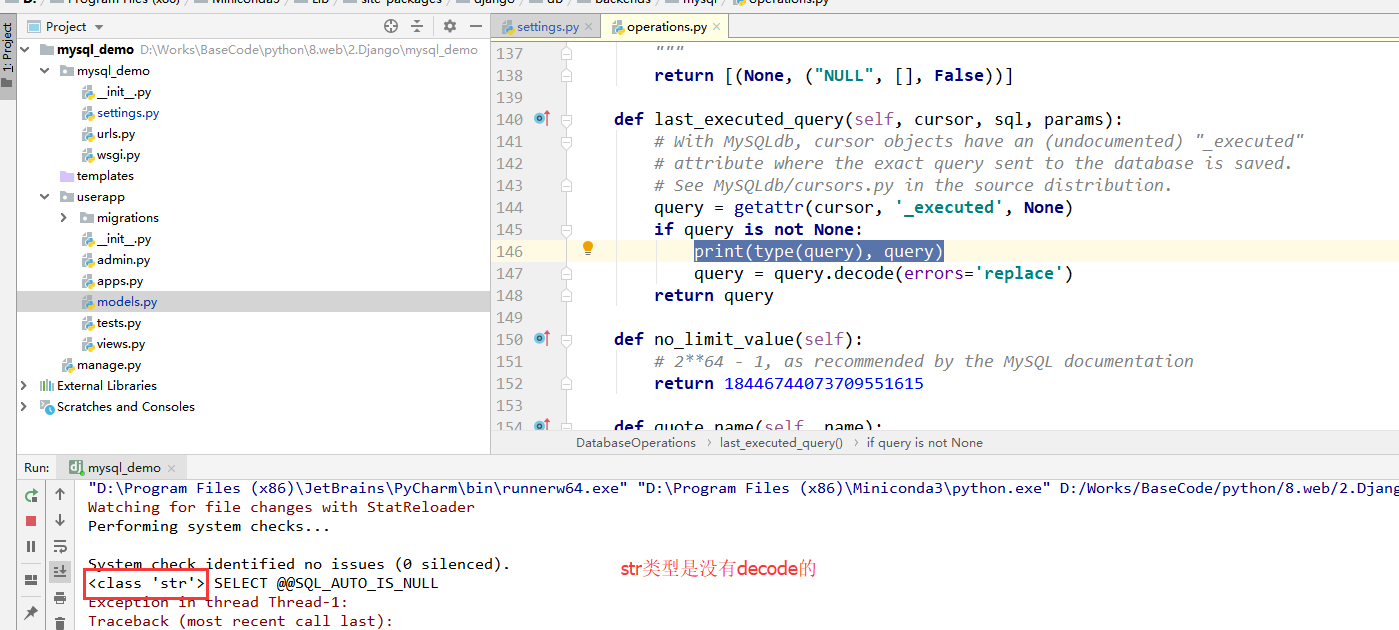
解决也很简单,改成encode即可
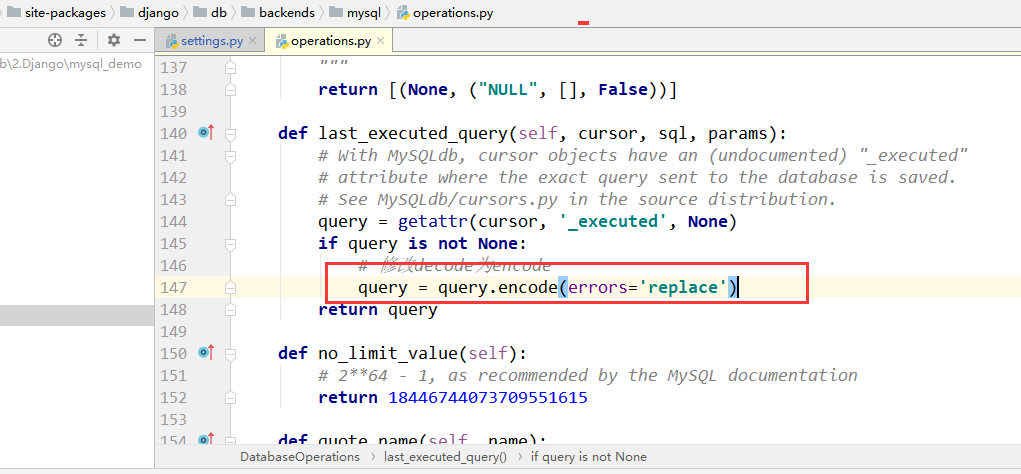
然后就没问题了,之后创建新项目也不会有问题了
### 扩展:避免命令忘记
## 3.MVT基础
### 3.1.M基础
#### 3.1.字段类型
模型类的命名规则基本上和变量命名一致,然后添加一条:**不能含`__`**(双下划线)
> PS:这个后面讲查询的时候你就秒懂了(`__`来间隔关键词)
这边简单罗列下**常用字段类型**:**模型类数据库字段的定义:`属性名=models.字段类型(选项)`**
| 字段类型 | 备注 |
| ----------------------------------------------------------------------- | ---------------------------------------------------------------------------- |
| `AutoField` | **自增长的int类型**(Django默认会自动创建属性名为id的自动增长属性) |
| `BigAutoField` | **自增长的bigint类型**(Django默认会自动创建属性名为id的自动增长属性) |
| **`BooleanField`** | **布尔类型**,值为True或False |
| `NullBooleanField` | **可空布尔类型**,支持Null、True、False三种值 |
| **`CharField(max_length=最大长度)`** | `varchar`**字符串**。参数max_length表示最大字符个数 |
| **`TextField`** | **大文本类型**,一般超过4000个字符时使用。 |
| **`IntegerField`** | **整型** |
| `BigIntegerField` | **长整型** |
| **`DecimalField(max_digits=None, decimal_places=None)`** | **十进制浮点数**,`max_digits`:总位数。`decimal_places`:小数占几位 |
| `FloatField(max_digits=None, decimal_places=None)` | **浮点数**,`max_digits`:总位数。`decimal_places`:小数占几位 |
| `DateField([auto_now=True] | [auto_now_add=True])` | **日期类型**,`auto_now_add`:自动设置创建时间,`auto_now`:自动设置修改时间 |
| `TimeField([auto_now=True] | [auto_now_add=True])` | **时间类型**,参数同`DateField` |
| **`DateTimeField([auto_now=True] | [auto_now_add=True])`** | **日期时间类型**,参数同`DateField` |
| **`UUIDField([primary_key=True,] default=uuid.uuid4, editable=False)`** | **UUID字段** |
后端常用字段:
| 字段类型 | 备注 |
| ---------------- | ----------------------------------------------------------- |
| `EmailField` | `CharField`子类,专门用于**Email**的字段 |
| **`FileField`** | **文件字段** |
| **`ImageField`** | **图片字段**,FileField子类,对内容进行校验以保证是有效图片 |
#### 3.2.字段选项
通过选项可以约束数据库字段,简单罗列几个常用的:
| 字段选项 | 描述 |
| -------------- | -------------------------------------------------------- |
| **`default`** | `default=函数名|默认值`设置字段的**默认值** |
| `primary_key` | `primary_key=True`设置**主键**(一般在`AutoField`中使用) |
| `unique` | `unique=True`设置**唯一键** |
| **`db_index`** | `db_index=True`设置**索引** |
| `db_column` | `db_column='xx'`设置数据库的字段名(默认就是属性名) |
| `null` | 字段是否可以为`null`(现在基本上都是不为`null`) |
和Django自动生成的后台管理相关的选项:(后台管理页面表单验证)
| 管理页的表单选项 | 描述 |
| ------------------ | ---------------------------------------------------------------------- |
| **`blank`** | `blank=True`设置表单验证中字段**是否可以为空** |
| **`verbose_name`** | `verbose_name='xxx'`设置字段对应的**中文显示**(下划线会转换为空格) |
| **`help_text`** | `help_text='xxx'`设置字段对应的**文档提示**(可以包含HTML) |
| `editable` | `editable=False`设置字段**是否可编辑**(不可编辑就不显示在后台管理页) |
| `validators` | `validators=xxx`设置字段**验证**(<http://mrw.so/4LzsEq>) |
补充说明:
1. 除非要覆盖默认的主键行为,否则不需要设置任何字段的`primary_key=True`(Django默认会创建`AutoField`来保存主键)
2. ***`auto_now_add`和`auto_now`是互斥的,一个字段中只能设置一个,不能同时设置**
3. 修改模型类时:如果添加的选项不影响表的结构,就不需要重新迁移
- 字段选项中`default`和`管理表单选项`(`blank`、`verbose_name`、`help_text`等)不影响表结构
### ORM基础
官方文档:<https://docs.djangoproject.com/zh-hans/2.2/ref/models/querysets/>
`O`(objects):类和对象,`R`(Relation):关系型数据库,`M`(Mapping):映射
> PS:表 --> 类、每行数据 --> 对象、字段 --> 对象的属性
进入命令模式:python manager.py shell
增(有连接关系的情况)
删(逻辑删除、删)
改(内连接关联修改)
查(总数、条件查询据、分页查询)
表与表之间的关系(relation),主要有这三种:
1. 一对一(one-to-one):一种对象与另一种对象是一一对应关系
- eg:一个学生只能在一个班级。
2. 一对多(one-to-many): 一种对象可以属于另一种对象的多个实例
- eg:一张唱片包含多首歌。
3. 多对多(many-to-many):两种对象彼此都是"一对多"关系
- eg:比如一张唱片包含多首歌,同时一首歌可以属于多张唱片。
#### 执行SQL语句
官方文档:<https://docs.djangoproject.com/zh-hans/2.2/topics/db/sql/>
#### 扩展:查看生成SQL
课后拓展:<https://www.jianshu.com/p/b69a7321a115>
#### 3.3.模型管理器类
1. 改变查询的结果集
- eg:程序里面都是假删除,而默认的`all()`把那些假删除的数据也查询出来了
2. 添加额外的方法
- eg:
---
### 3.2.V基础
返回Json格式(配合Ajax)
JsonResponse
#### 3.2.1.
#### URL路由
#### 模版配置
#### 重定向
跳转到视图函数
知识拓展:<https://www.cnblogs.com/attila/p/10420702.html>
#### 动态生成URL
模版中动态生成URL地址,类似于Net里面的`@Url.Action("Edit","Home",new {id=13})`
> <https://docs.djangoproject.com/zh-hans/2.2/intro/tutorial03/#removing-hardcoded-urls-in-templates>
#### 404和500页面
调试信息关闭
### 扩展:HTTPRequest
**HTTPRequest的常用属性**:
1. **`path`**:请求页面的完整路径(字符串)
- 不含域名和参数
2. **`method`**:请求使用的HTTP方式(字符串)
- eg:`GET`、`POST`
3. `encoding`:提交数据的编码方式(字符串)
- 如果为`None`:使用浏览器默认设置(PS:一般都是UTF-8)
4. **`GET`**:包含get请求方式的所有参数(QueryDict类型,类似于Dict)
5. **`POST`**:包含post请求方式的所有参数(类型同上)
6. **`FILES`**:包含所有上传的文件(MultiValueDict类型,类似于Dict)
7. **`COOKIES`**:以key-value形式包含所有cookie(Dict类型)
8. **`session`**:状态保持使用(类似于Dict)
#### 获取URL参数
复选框:勾选on,不勾选None
reques.POST.get("xxx")
#### Cookies
基于域名来存储的,如果不指定过期时间则关闭浏览器就过期
```py
# set cookie
response = Htpresponse对象(eg:JsonResponse,Response)
# max_age:多少秒后过期
# response.set_cookie(key,value,max_age=7*24*3600) # 1周过期
# expires:过期时间,timedelta:时间间隔
response.set_cookie(key,value,expires=datatime.datatime.now()+datatime.timedelta(days=7))
return response;
# get cookie
value = request.COOKIES.get(key)
```
**PS:Cookie不管保存什么类型,取出来都是str字符串**
知识拓展:<https://blog.csdn.net/cuishizun/article/details/81537316>
#### Session
Django的Session信息存储在`django_session`里面,可以根据sessionid(`session_key`)获取对应的`session_data`值
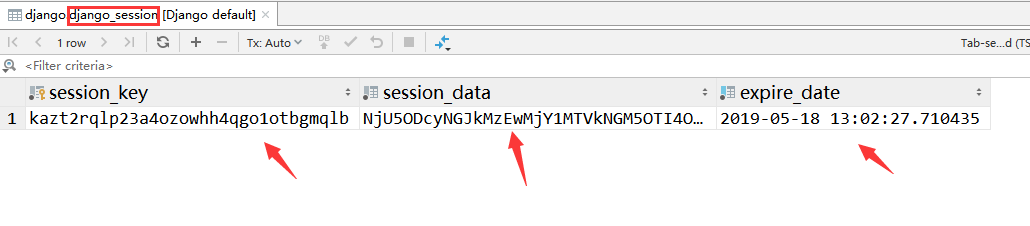
**PS:Session之所以依赖于Cookie,是因为Sessionid(唯一标识)存储在客户端,没有sessionid你怎么获取?**
```py
# 设置
request.session["key"] = value
# 获取
request.session.get("key",默认值)
# 删除指定session
del request.session["key"] # get(key) ?
# 删除所有session的value
# sessiondata里面只剩下了sessionid,而对于的value变成了{}
request.session.clear()
# 删除所有session(数据库内容全删了)
request.session.flush()
# 设置过期时间(默认过期时间是2周)
request.session.set_expiry(不活动多少秒后失效)
# PS:都是request里面的方法
```
**PS:Session保存什么类型,取出来就是什么类型**(Cookie取出来都是str)
---
#### 文件上传
---
### 3.3.T基础
自定义404页面
## 4.Admin后台
上面演示了一些简单的制定化知识点:<a href="#2.1.2.生成后台">上节回顾</a>,现在简单归纳下`Django2.2`admin相关设置:
### 4.1.修改后台管理页面的标题
大致效果如下:
在`admin.py`中设置`admin.site.site_header`和`admin.site.site_title`:
### 4.2.修改app在Admin后台显示的名称
大致效果如下:

先设置应用模块的中文名:**`verbose_name = 'xxx'`**
让配置生效:**`default_app_config = '应用名.apps.应用名Config'`**
### 4.3.汉化显示应用子项
大致效果如下:
在每个模型类中设置**`Meta`**类,并设置`verbose_name`和`verbose_name_plural`
### 4.4.汉化表单字段和提示
大致效果如下:
汉化表单的字段:**`verbose_name`**,显示字段提示:**`help_text`**
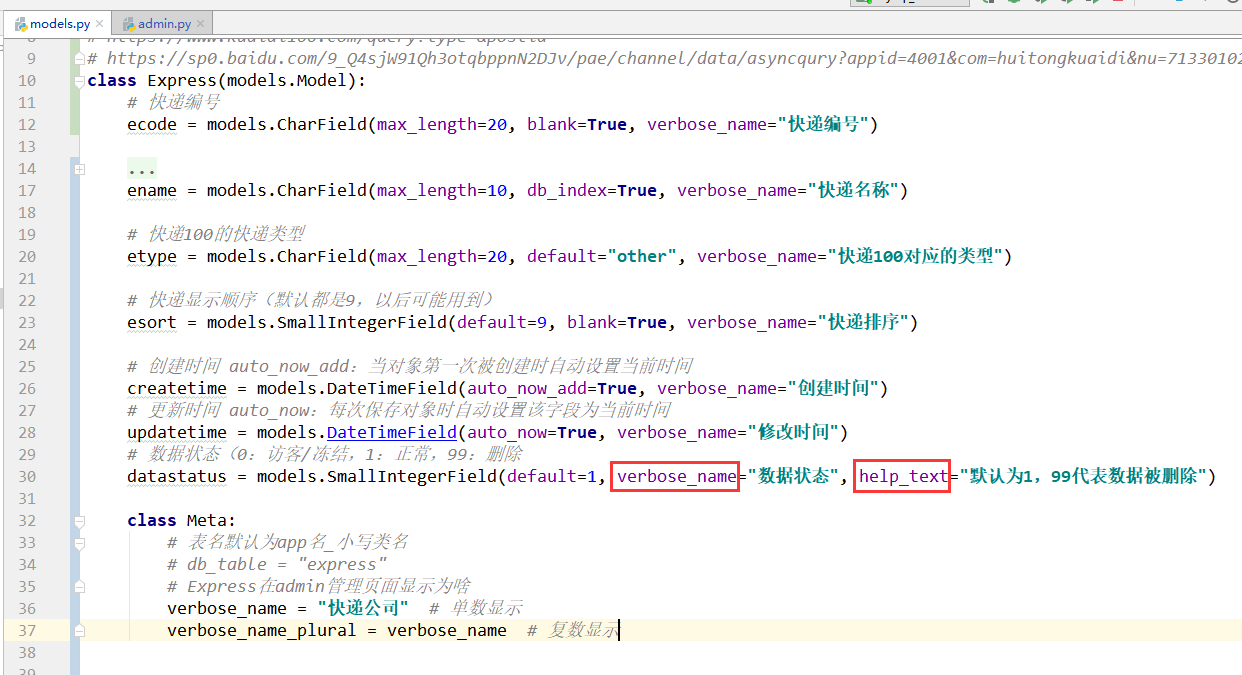
### 4.5.
列表显示
状态显示+字体颜色
文件上传
文本验证
Tag过滤
apt install sqliteman
| true |
code
| 0.317833 | null | null | null | null |
|
# 1A.data - Décorrélation de variables aléatoires
On construit des variables corrélées gaussiennes et on cherche à construire des variables décorrélées en utilisant le calcul matriciel.
```
from jyquickhelper import add_notebook_menu
add_notebook_menu()
```
Ce TD appliquera le calcul matriciel aux vecteurs de variables normales [corrélées](http://fr.wikipedia.org/wiki/Covariance) ou aussi [décomposition en valeurs singulières](https://fr.wikipedia.org/wiki/D%C3%A9composition_en_valeurs_singuli%C3%A8res).
## Création d'un jeu de données
### Q1
La première étape consiste à construire des variables aléatoires normales corrélées dans une matrice $N \times 3$. On cherche à construire cette matrice au format [numpy](http://www.numpy.org/). Le programme suivant est un moyen de construire un tel ensemble à l'aide de combinaisons linéaires. Complétez les lignes contenant des ``....``.
```
import random
import numpy as np
def combinaison () :
x = random.gauss(0,1) # génère un nombre aléatoire
y = random.gauss(0,1) # selon une loi normale
z = random.gauss(0,1) # de moyenne null et de variance 1
x2 = x
y2 = 3*x + y
z2 = -2*x + y + 0.2*z
return [x2, y2, z2]
# mat = [ ............. ]
# npm = np.matrix ( mat )
```
### Q2
A partir de la matrice ``npm``, on veut construire la matrice des corrélations.
```
npm = ... # voir question précédente
t = npm.transpose ()
a = t * npm
a /= npm.shape[0]
```
A quoi correspond la matrice ``a`` ?
### Corrélation de matrices
### Q3
Construire la matrice des corrélations à partir de la matrice ``a``. Si besoin, on pourra utiliser le module [copy](https://docs.python.org/3/library/copy.html).
```
import copy
b = copy.copy (a) # remplacer cette ligne par b = a
b[0,0] = 44444444
print(b) # et comparer le résultat ici
```
### Q4
Construire une fonction qui prend comme argument la matrice ``npm`` et qui retourne la matrice de corrélation. Cette fonction servira plus pour vérifier que nous avons bien réussi à décorréler.
```
def correlation(npm):
# ..........
return "....."
```
## Un peu de mathématiques
Pour la suite, un peu de mathématique. On note $M$ la matrice ``npm``. $V=\frac{1}{n}M'M$ correspond à la matrice des *covariances* et elle est nécessairement symétrique. C'est une matrice diagonale si et seulement si les variables normales sont indépendantes. Comme toute matrice symétrique, elle est diagonalisable. On peut écrire :
$$\frac{1}{n}M'M = P \Lambda P'$$
$P$ vérifie $P'P= PP' = I$. La matrice $\Lambda$ est diagonale et on peut montrer que toutes les valeurs propres sont positives ($\Lambda = \frac{1}{n}P'M'MP = \frac{1}{n}(MP)'(MP)$).
On définit alors la racine carrée de la matrice $\Lambda$ par :
$$\begin{array}{rcl} \Lambda &=& diag(\lambda_1,\lambda_2,\lambda_3) \\ \Lambda^{\frac{1}{2}} &=& diag\left(\sqrt{\lambda_1},\sqrt{\lambda_2},\sqrt{\lambda_3}\right)\end{array}$$
On définit ensuite la racine carrée de la matrice $V$ :
$$V^{\frac{1}{2}} = P \Lambda^{\frac{1}{2}} P'$$
On vérifie que $\left(V^{\frac{1}{2}}\right)^2 = P \Lambda^{\frac{1}{2}} P' P \Lambda^{\frac{1}{2}} P' = P \Lambda^{\frac{1}{2}}\Lambda^{\frac{1}{2}} P' = V = P \Lambda P' = V$.
## Calcul de la racine carrée
### Q6
Le module [numpy](http://www.numpy.org/) propose une fonction qui retourne la matrice $P$ et le vecteur des valeurs propres $L$ :
```
L,P = np.linalg.eig(a)
```
Vérifier que $P'P=I$. Est-ce rigoureusement égal à la matrice identité ?
### Q7
Que fait l'instruction suivante : ``np.diag(L)`` ?
### Q8
Ecrire une fonction qui calcule la racine carrée de la matrice $\frac{1}{n}M'M$ (on rappelle que $M$ est la matrice ``npm``). Voir aussi [Racine carrée d'une matrice](https://fr.wikipedia.org/wiki/Racine_carr%C3%A9e_d%27une_matrice).
## Décorrélation
``np.linalg.inv(a)`` permet d'obtenir l'inverse de la matrice ``a``.
### Q9
Chaque ligne de la matrice $M$ représente un vecteur de trois variables corrélées. La matrice de covariance est $V=\frac{1}{n}M'M$. Calculer la matrice de covariance de la matrice $N=M V^{-\frac{1}{2}}$ (mathématiquement).
### Q10
Vérifier numériquement.
## Simulation de variables corrélées
### Q11
A partir du résultat précédent, proposer une méthode pour simuler un vecteur de variables corrélées selon une matrice de covariance $V$ à partir d'un vecteur de lois normales indépendantes.
### Q12
Proposer une fonction qui crée cet échantillon :
```
def simultation (N, cov) :
# simule un échantillon de variables corrélées
# N : nombre de variables
# cov : matrice de covariance
# ...
return M
```
### Q13
Vérifier que votre échantillon a une matrice de corrélations proche de celle choisie pour simuler l'échantillon.
| true |
code
| 0.278772 | null | null | null | null |
|
# CME Session
### Goals
1. Search and download some coronagraph images
2. Load into Maps
3. Basic CME front enhancement
4. Extract CME front positions
6. Convert positions to height
5. Fit some simple models to height-time data
```
%matplotlib notebook
import warnings
warnings.filterwarnings("ignore")
import astropy.units as u
import numpy as np
from astropy.time import Time
from astropy.coordinates import SkyCoord
from astropy.visualization import time_support, quantity_support
from matplotlib import pyplot as plt
from matplotlib.colors import LogNorm, SymLogNorm
from scipy import ndimage
from scipy.optimize import curve_fit
from sunpy.net import Fido, attrs as a
from sunpy.map import Map
from sunpy.coordinates.frames import Heliocentric, Helioprojective
```
# LASCO C2
## Data Search and Download
```
c2_query = Fido.search(a.Time('2017-09-10T15:10', '2017-09-10T18:00'),
a.Instrument.lasco, a.Detector.c2)
c2_query
c2_results = Fido.fetch(c2_query);
c2_results
c2_results
```
## Load into maps and plot
```
# results = ['/Users/shane/sunpy/data/22650296.fts', '/Users/shane/sunpy/data/22650294.fts', '/Users/shane/sunpy/data/22650292.fts', '/Users/shane/sunpy/data/22650297.fts', '/Users/shane/sunpy/data/22650295.fts', '/Users/shane/sunpy/data/22650290.fts', '/Users/shane/sunpy/data/22650293.fts', '/Users/shane/sunpy/data/22650291.fts', '/Users/shane/sunpy/data/22650298.fts', '/Users/shane/sunpy/data/22650289.fts']
c2_maps = Map(c2_results, sequence=True);
c2_maps.plot();
```
Check the polarisation and filter to make sure they don't change
```
[(m.exposure_time, m.meta.get('polar'), m.meta.get('filter')) for m in c2_maps]
```
Rotate the map so standard orintation and pixel are aligned with wcs axes
```
c2_maps = [m.rotate() for m in c2_maps];
```
# Running and Base Difference
The corona above $\sim 2 R_{Sun}$ is dominated by the F-corona (Fraunhofer corona) which is composed of photospheric radiation Rayleigh scattered off dust particles It forms a continuous spectrum with the Fraunhofer absorption lines superimposed. The radiation has a very low degree of polarisation.
There are a number of approaches to remove this the most straight forward are
* Running Difference $I(x,y)=I_i(x,y) - I_{i-1}(x,y)$
* Base Difference $I(x,y)=I_i(x,y) - I_{B}(x,y)$
* Background Subtraction $I(x,y)=I_i(x,y) - I_{BG}(x,y)$$
Can create new map using data and meta from other maps
```
c2_bdiff_maps = Map([(c2_maps[i+1].data/c2_maps[i+1].exposure_time
- c2_maps[0].data/c2_maps[0].exposure_time, c2_maps[i+1].meta)
for i in range(len(c2_maps)-1)], sequence=True)
```
In jupyter notebook sunpy has very nice preview functionality
```
c2_bdiff_maps
```
## CME front
One technique to help extract CME front is to create a space-time plot or j-plot we can define a region of interest and then sum ovber the region to increase signal to noise.
```
fig, ax = plt.subplots(subplot_kw={'projection': c2_bdiff_maps[3]})
c2_bdiff_maps[3].plot(clip_interval=[1,99]*u.percent, axes=ax)
bottom_left = SkyCoord(0*u.arcsec, -200*u.arcsec, frame=c2_bdiff_maps[3].coordinate_frame)
top_right = SkyCoord(6500*u.arcsec, 200*u.arcsec, frame=c2_bdiff_maps[3].coordinate_frame)
c2_bdiff_maps[9].draw_quadrangle(bottom_left, top_right=top_right, axes=ax)
```
Going to extract the data in the region above and then sum over the y-direction to a 1-d plot of intensity vs pixel coordinate.
```
c2_submaps = []
for m in c2_bdiff_maps:
# define the coordinates of the bottom left and top right for each map should really define once and then transform
bottom_left = SkyCoord(0*u.arcsec, -200*u.arcsec, frame=m.coordinate_frame)
top_right = SkyCoord(6500*u.arcsec, 200*u.arcsec, frame=m.coordinate_frame)
c2_submaps.append(m.submap(bottom_left, top_right=top_right))
c2_submaps[0].data.shape
```
No we can create a space-time diagram by stack these slices one after another,
```
c2_front_pix = []
def onclick(event):
global coords
ax.plot(event.xdata, event.ydata, 'o', color='r')
c2_front_pix.append((event.ydata, event.xdata))
fig, ax = plt.subplots()
ax.imshow(np.stack([m.data.mean(axis=0)/m.data.mean(axis=0).max() for m in c2_submaps]).T,
aspect='auto', origin='lower', interpolation='none', norm=SymLogNorm(0.1,vmax=2))
cid = fig.canvas.mpl_connect('button_press_event', onclick)
if not c2_front_pix:
c2_front_pix = [(209.40188156061873, 3.0291329045449533),
(391.58261749135465, 3.9464716142223724)]
pix, index = c2_front_pix[0]
index = round(index)
fig, ax = plt.subplots(subplot_kw={'projection': c2_bdiff_maps[index]})
c2_bdiff_maps[index].plot(clip_interval=[1,99]*u.percent, axes=ax)
pp = c2_submaps[index].pixel_to_world(*[pix,34/4]*u.pix)
ax.plot_coord(pp, marker='x', ms=20, color='k');
```
Extract the times an coordinates for later
```
c2_times = [m.date for m in c2_submaps[3:5] ]
c2_coords = [c2_submaps[i].pixel_to_world(*[c2_front_pix[i][0],34/4]*u.pix) for i, m in enumerate(c2_submaps[3:5])]
c2_times, c2_coords
```
# Lasco C3
## Data seach and download
```
c3_query = Fido.search(a.Time('2017-09-10T15:10', '2017-09-10T19:00'),
a.Instrument.lasco, a.Detector.c3)
c3_query
```
Download
```
c3_results = Fido.fetch(c3_query);
```
Load into maps
```
c3_maps = Map(c3_results, sequence=True);
c3_maps
```
Rotate
```
c3_maps = [m.rotate() for m in c3_maps]
```
## Create Base Differnce maps
```
c3_bdiff_maps = Map([(c3_maps[i+1].data/c3_maps[i+1].exposure_time.to_value('s')
- c3_maps[0].data/c3_maps[0].exposure_time.to_value('s'),
c3_maps[i+1].meta)
for i in range(0, len(c3_maps)-1)], sequence=True)
c3_bdiff_maps
```
Can use a median filter to reduce some of the noise and make front easier to identify
```
c3_bdiff_maps = Map([(ndimage.median_filter(c3_maps[i+1].data/c3_maps[i+1].exposure_time.to_value('s')
- c3_maps[0].data/c3_maps[0].exposure_time.to_value('s'), size=5),
c3_maps[i+1].meta)
for i in range(0, len(c3_maps)-1)], sequence=True)
```
## CME front
```
fig, ax = plt.subplots(subplot_kw={'projection': c3_bdiff_maps[9]})
c3_bdiff_maps[9].plot(clip_interval=[1,99]*u.percent, axes=ax)
bottom_left = SkyCoord(0*u.arcsec, -2000*u.arcsec, frame=c3_bdiff_maps[9].coordinate_frame)
top_right = SkyCoord(29500*u.arcsec, 2000*u.arcsec, frame=c3_bdiff_maps[9].coordinate_frame)
c3_bdiff_maps[9].draw_quadrangle(bottom_left, top_right=top_right,
axes=ax)
```
Extract region of data
```
c3_submaps = []
for m in c3_bdiff_maps:
bottom_left = SkyCoord(0*u.arcsec, -2000*u.arcsec, frame=m.coordinate_frame)
top_right = SkyCoord(29500*u.arcsec, 2000*u.arcsec, frame=m.coordinate_frame)
c3_submaps.append(m.submap(bottom_left, top_right=top_right))
c3_front_pix = []
def onclick(event):
global coords
ax.plot(event.xdata, event.ydata, 'o', color='r')
c3_front_pix.append((event.ydata, event.xdata))
fig, ax = plt.subplots()
ax.imshow(np.stack([m.data.mean(axis=0)/m.data.mean(axis=0).max() for m in c3_submaps]).T,
aspect='auto', origin='lower', interpolation='none', norm=SymLogNorm(0.1,vmax=2))
cid = fig.canvas.mpl_connect('button_press_event', onclick)
if not c3_front_pix:
c3_front_pix = [(75.84577056752656, 3.007459455920803),
(124.04923377098979, 3.9872981655982223),
(173.6704458922019, 5.039717520436931),
(216.20291342466945, 5.874394939791771),
(248.81113853289455, 6.854233649469189),
(287.0903593121153, 7.797782036565963),
(328.20507792683395, 8.995362681727254),
(369.3197965415526, 9.866330423662738),
(401.92802164977775, 10.991330423662738)]
pix, index = c3_front_pix[5]
index = round(index)
fig, ax = plt.subplots(subplot_kw={'projection': c3_bdiff_maps[index]})
c3_bdiff_maps[index].plot(clip_interval=[1,99]*u.percent, axes=ax)
pp = c3_submaps[index].pixel_to_world(*[pix,37/4]*u.pix)
ax.plot_coord(pp, marker='x', ms=20, color='r');
```
Extract times and coordinates for later
```
c3_times = [m.date for m in c3_submaps[3:12] ]
c3_coords = [c3_submaps[i].pixel_to_world(*[c3_front_pix[i][0],37/4]*u.pix) for i, m in enumerate(c3_submaps[3:12])]
```
# Coordintes to Heights
```
times = Time(np.concatenate([c2_times, c3_times]))
coords = c2_coords + c3_coords
heights_pos = np.hstack([(c.observer.radius * np.tan(c.Tx)) for c in coords])
heights_pos
heights_pos_error = np.hstack([(c.observer.radius * np.tan(c.Tx + 56*u.arcsecond*5)) for c in coords])
height_err = heights_pos_error - heights_pos
heights_pos, height_err
times.shape, height_err.shape
with Helioprojective.assume_spherical_screen(center=coords[0].observer):
heights_sph = np.hstack([np.sqrt(c.transform_to('heliocentric').x**2
+ c.transform_to('heliocentric').y**2
+ c.transform_to('heliocentric').z**2) for c in coords])
heights_sph
fig, axs = plt.subplots()
axs.errorbar(times.datetime, heights_pos.to_value(u.Rsun), yerr=height_err.to_value(u.Rsun), fmt='.')
axs.plot(times.datetime, heights_sph.to(u.Rsun), '+')
```
C2 data points look off not uncommon as different telescope different sensetivity we'll just drop these for the moment
```
times = Time(np.hstack([c2_times, c3_times]))
heights_pos = heights_pos
height_err = height_err
```
# Model Fitting
### Models
Constant velocity model
\begin{align}
a = \frac{dv}{dt} = 0 \\
h(t) = h_0 + v_0 t \\
\end{align}
Constant acceleration model
\begin{align}
a = a_{0} \\
v(t) = v_0 + a_0 t \\
h(t) = h_0 + v_0 t + \frac{1}{2}a_0 t^{2}
\end{align}
```
def const_vel(t0, h0, v0):
return h0 + v0*t0
def const_accel(t0, h0, v0, a0):
return h0 + v0*t0 + 0.5 * a0*t0**2
t0 = (times-times[0]).to(u.s)
const_vel_fit = curve_fit(const_vel, t0, heights_pos, sigma=height_err,
p0=[heights_pos[0].to_value(u.m), 350000])
h0, v0 = const_vel_fit[0]
delta_h0, delta_v0 = np.sqrt(const_vel_fit[1].diagonal())
h0 = h0*u.m
v0 = v0*u.m/u.s
delta_h0 = delta_h0*u.m
delta_v0 = delta_v0*(u.m/u.s)
print(f'h0: {h0.to(u.Rsun).round(2)} +/- {delta_h0.to(u.Rsun).round(2)}')
print(f'v0: {v0.to(u.km/u.s).round(2)} +/- {delta_v0.to(u.km/u.s).round(2)}')
const_accel_fit = curve_fit(const_accel, t0, heights_pos, p0=[heights_pos[0].to_value(u.m), 600000, -5])
h0, v0, a0 = const_accel_fit[0]
delta_h0, delta_v0, delta_a0 = np.sqrt(const_accel_fit[1].diagonal())
h0 = h0*u.m
v0 = v0*u.m/u.s
a0 = a0*u.m/u.s**2
delta_h0 = delta_h0*u.m
delta_v0 = delta_v0*(u.m/u.s)
delta_a0 = delta_a0*(u.m/u.s**2)
print(f'h0: {h0.to(u.Rsun).round(2)} +/- {delta_h0.to(u.Rsun).round(2)}')
print(f'v0: {v0.to(u.km/u.s).round(2)} +/- {delta_v0.to(u.km/u.s).round(2)}')
print(f'a0: {a0.to(u.m/u.s**2).round(2)} +/- {delta_a0.to(u.m/u.s**2).round(2)}')
```
# Check against CDAW CME list
* https://cdaw.gsfc.nasa.gov/CME_list/UNIVERSAL/2017_09/univ2017_09.html
```
with quantity_support():
fig, axes = plt.subplots()
axes.errorbar(times.datetime, heights_pos.to(u.Rsun), fmt='.', yerr=height_err)
axes.plot(times.datetime, const_vel(t0.value, *const_vel_fit[0])*u.m, 'r-')
axes.plot(times.datetime, const_accel(t0.value, *const_accel_fit[0])*u.m, 'r-')
fig.autofmt_xdate()
with quantity_support() and time_support(format='isot'):
fig, axes = plt.subplots()
axes.plot(times, heights_pos.to(u.Rsun), 'x')
axes.plot(times, const_vel(t0.value, *const_vel_fit[0])*u.m, 'r-')
axes.plot(times, const_accel(t0.value, *const_accel_fit[0])*u.m, 'r-')
fig.autofmt_xdate()
```
Estimate the arrival time at Earth like distance for constant velocity model
```
(((1*u.AU) - const_vel_fit[0][0] * u.m) / (const_vel_fit[0][1] * u.m/u.s)).decompose().to(u.hour)
roots = np.roots([((1*u.AU) - const_accel_fit[0][0] * u.m).to_value(u.m),
const_accel_fit[0][1], 0.5*const_accel_fit[0][2]][::-1])
(roots*u.s).to(u.hour)
```
| true |
code
| 0.55097 | null | null | null | null |
|
# Predictable t-SNE
[t-SNE](https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html) is not a transformer which can produce outputs for other inputs than the one used to train the transform. The proposed solution is train a predictor afterwards to try to use the results on some other inputs the model never saw.
```
from jyquickhelper import add_notebook_menu
add_notebook_menu()
%matplotlib inline
```
## t-SNE on MNIST
Let's reuse some part of the example of [Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html#sphx-glr-auto-examples-manifold-plot-lle-digits-py).
```
import numpy
from sklearn import datasets
digits = datasets.load_digits(n_class=6)
Xd = digits.data
yd = digits.target
imgs = digits.images
n_samples, n_features = Xd.shape
n_samples, n_features
```
Let's split into train and test.
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test, imgs_train, imgs_test = train_test_split(Xd, yd, imgs)
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, init='pca', random_state=0)
X_train_tsne = tsne.fit_transform(X_train, y_train)
X_train_tsne.shape
import matplotlib.pyplot as plt
from matplotlib import offsetbox
def plot_embedding(Xp, y, imgs, title=None, figsize=(12, 4)):
x_min, x_max = numpy.min(Xp, 0), numpy.max(Xp, 0)
X = (Xp - x_min) / (x_max - x_min)
fig, ax = plt.subplots(1, 2, figsize=figsize)
for i in range(X.shape[0]):
ax[0].text(X[i, 0], X[i, 1], str(y[i]),
color=plt.cm.Set1(y[i] / 10.),
fontdict={'weight': 'bold', 'size': 9})
if hasattr(offsetbox, 'AnnotationBbox'):
# only print thumbnails with matplotlib > 1.0
shown_images = numpy.array([[1., 1.]]) # just something big
for i in range(X.shape[0]):
dist = numpy.sum((X[i] - shown_images) ** 2, 1)
if numpy.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = numpy.r_[shown_images, [X[i]]]
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(imgs[i], cmap=plt.cm.gray_r),
X[i])
ax[0].add_artist(imagebox)
ax[0].set_xticks([]), ax[0].set_yticks([])
ax[1].plot(Xp[:, 0], Xp[:, 1], '.')
if title is not None:
ax[0].set_title(title)
return ax
plot_embedding(X_train_tsne, y_train, imgs_train, "t-SNE embedding of the digits");
```
## Repeatable t-SNE
We use class *PredictableTSNE* but it works for other trainable transform too.
```
from mlinsights.mlmodel import PredictableTSNE
ptsne = PredictableTSNE()
ptsne.fit(X_train, y_train)
X_train_tsne2 = ptsne.transform(X_train)
plot_embedding(X_train_tsne2, y_train, imgs_train, "Predictable t-SNE of the digits");
```
The difference now is that it can be applied on new data.
```
X_test_tsne2 = ptsne.transform(X_test)
plot_embedding(X_test_tsne2, y_test, imgs_test, "Predictable t-SNE on new digits on test database");
```
By default, the output data is normalized to get comparable results over multiple tries such as the *loss* computed between the normalized output of *t-SNE* and their approximation.
```
ptsne.loss_
```
## Repeatable t-SNE with another predictor
The predictor is a [MLPRegressor](https://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html).
```
ptsne.estimator_
```
Let's replace it with a [KNeighborsRegressor](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html) and a normalizer [StandardScaler](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html).
```
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import StandardScaler
ptsne_knn = PredictableTSNE(normalizer=StandardScaler(),
estimator=KNeighborsRegressor())
ptsne_knn.fit(X_train, y_train)
X_train_tsne2 = ptsne_knn.transform(X_train)
plot_embedding(X_train_tsne2, y_train, imgs_train,
"Predictable t-SNE of the digits\nStandardScaler+KNeighborsRegressor");
X_test_tsne2 = ptsne_knn.transform(X_test)
plot_embedding(X_test_tsne2, y_test, imgs_test,
"Predictable t-SNE on new digits\nStandardScaler+KNeighborsRegressor");
```
The model seems to work better as the loss is better but as it is evaluated on the training dataset, it is just a way to check it is not too big.
```
ptsne_knn.loss_
```
| true |
code
| 0.766139 | null | null | null | null |
|
# Wiener Filter + UNet
https://github.com/vpronina/DeepWienerRestoration
```
# Import some libraries
import numpy as np
from skimage import color, data, restoration
import matplotlib.pyplot as plt
import torch
import utils
import torch.nn as nn
from networks import UNet
import math
import os
from skimage import io
import skimage
import warnings
warnings.filterwarnings('ignore')
def show_images(im1, im1_title, im2, im2_title, im3, im3_title, font):
fig, (image1, image2, image3) = plt.subplots(1, 3, figsize=(15, 50))
image1.imshow(im1, cmap='gray')
image1.set_title(im1_title, fontsize=font)
image1.set_axis_off()
image2.imshow(im2, cmap='gray')
image2.set_title(im2_title, fontsize=font)
image2.set_axis_off()
image3.imshow(im3, cmap='gray')
image3.set_title(im3_title, fontsize=font)
image3.set_axis_off()
fig.subplots_adjust(wspace=0.02, hspace=0.2,
top=0.9, bottom=0.05, left=0, right=1)
fig.show()
```
# Load the data
```
#Load the target image
image = io.imread('./image.tif')
#Load the blurred and distorted images
blurred = io.imread('./blurred.tif')
distorted = io.imread('./distorted.tif')
#Load the kernel
psf = io.imread('./PSF.tif')
show_images(image, 'Original image', blurred, 'Blurred image',\
distorted, 'Blurred and noisy image', font=18)
```
We know, that the solution is described as follows:
$\hat{\mathbf{x}} = \arg\min_\mathbf{x}\underbrace{\frac{1}{2}\|\mathbf{y}-\mathbf{K} \mathbf{x}\|_{2}^{2}+\lambda r(\mathbf{x})}_{\mathbf{J}(\mathbf{x})}$,
where $\mathbf{J}$ is the objective function.
According to the gradient descent iterative scheme,
$\hat{\mathbf{x}}_{k+1}=\hat{\mathbf{x}}_{k}-\beta \nabla \mathbf{J}(\mathbf{x})$.
Solution is described with the iterative gradient descent equation:
$\hat{\mathbf{x}}_{k+1} = \hat{\mathbf{x}}_{k} - \beta\left[\mathbf{K}^\top(\mathbf{K}\hat{\mathbf{x}}_{k} - \mathbf{y}) + e^\alpha f^{CNN}(\hat{\mathbf{x}}_{k})\right]$, and here $\lambda = e^\alpha$ and $r(\mathbf{x}) = f^{CNN}(\hat{\mathbf{x}})$.
```
# Anscombe transform to transform Poissonian data into Gaussian
#https://en.wikipedia.org/wiki/Anscombe_transform
def anscombe(x):
'''
Compute the anscombe variance stabilizing transform.
the input x is noisy Poisson-distributed data
the output fx has variance approximately equal to 1.
Reference: Anscombe, F. J. (1948), "The transformation of Poisson,
binomial and negative-binomial data", Biometrika 35 (3-4): 246-254
'''
return 2.0*torch.sqrt(x + 3.0/8.0)
# Exact unbiased Anscombe transform to transform Gaussian data back into Poissonian
def exact_unbiased(z):
return (1.0 / 4.0 * z.pow(2) +
(1.0/4.0) * math.sqrt(3.0/2.0) * z.pow(-1) -
(11.0/8.0) * z.pow(-2) +
(5.0/8.0) * math.sqrt(3.0/2.0) * z.pow(-3) - (1.0 / 8.0))
class WienerUNet(torch.nn.Module):
def __init__(self):
'''
Deconvolution function for a batch of images. Although the regularization
term does not have a shape of Tikhonov regularizer, with a slight abuse of notations
the function is called WienerUNet.
The function is built upon the iterative gradient descent scheme:
x_k+1 = x_k - lamb[K^T(Kx_k - y) + exp(alpha)*reg(x_k)]
Initial parameters are:
regularizer: a neural network to parametrize the prior on each iteration x_k.
alpha: power of the trade-off coefficient.
lamb: step of the gradient descent algorithm.
'''
super(WienerUNet, self).__init__()
self.regularizer = UNet(mode='instance')
self.alpha = nn.Parameter(torch.FloatTensor([0.0]))
self.lamb = nn.Parameter(torch.FloatTensor([0.3]))
def forward(self, x, y, ker):
'''
Function that performs one iteration of the gradient descent scheme of the deconvolution algorithm.
:param x: (torch.(cuda.)Tensor) Image, restored with the previous iteration of the gradient descent scheme, B x C x H x W
:param y: (torch.(cuda.)Tensor) Input blurred and noisy image, B x C x H x W
:param ker: (torch.(cuda.)Tensor) Blurring kernel, B x C x H_k x W_k
:return: (torch.(cuda.)Tensor) Restored image, B x C x H x W
'''
#Calculate Kx_k
x_filtered = utils.imfilter2D_SpatialDomain(x, ker, padType='symmetric', mode="conv")
Kx_y = x_filtered - y
#Calculate K^T(Kx_k - y)
y_filtered = utils.imfilter_transpose2D_SpatialDomain(Kx_y, ker,
padType='symmetric', mode="conv")
#Calculate exp(alpha)*reg(x_k)
regul = torch.exp(self.alpha) * self.regularizer(x)
brackets = y_filtered + regul
out = x - self.lamb * brackets
return out
class WienerFilter_UNet(nn.Module):
'''
Module that uses UNet to predict individual gradient of a regularizer for each input image and then
applies gradient descent scheme with predicted gradient of a regularizers per-image.
'''
def __init__(self):
super(WienerFilter_UNet, self).__init__()
self.function = WienerUNet()
#Perform gradient descent iterations
def forward(self, y, ker, n_iter):
output = y.clone()
for i in range(n_iter):
output = self.function(output, y, ker)
return output
#Let's transform our numpy data into pytorch data
x = torch.Tensor(distorted[None, None])
ker = torch.Tensor(psf[None, None])
#Define the model
model = WienerFilter_UNet()
#Load the pretrained weights
state_dict = torch.load(os.path.join('./', 'WF_UNet_poisson'))
state_dict = state_dict['model_state_dict']
from collections import OrderedDict
new_state_dict = OrderedDict()
for k, v in state_dict.items():
name = k[7:] # remove `module.`
new_state_dict[name] = v
# load params
model.load_state_dict(new_state_dict)
model.eval()
#Perform Anscombe transform
x = anscombe(x)
#Calculate output
out = model(x, ker, 10)
#Perform inverse Anscombe transform
out = exact_unbiased(out)
#Some post-processing of data
out = out/image.max()
image = image/image.max()
show_images(image, 'Original image', distorted, 'Blurred image',\
out[0][0].detach().cpu().numpy().clip(0,1), 'Restored with WF-UNet', font=18)
```
| true |
code
| 0.835282 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.