prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Session #5: Automate ML workflows and focus on innovation (300)
In this session, you will learn how to use [SageMaker Pipelines](https://docs.aws.amazon.com/sagemaker/latest/dg/pipelines-sdk.html) to train a [Hugging Face](https://docs.aws.amazon.com/sagemaker/latest/dg/hugging-face.html) Transformer model and deploy it. The SageMaker integration with Hugging Face makes it easy to train and deploy advanced NLP models. A Lambda step in SageMaker Pipelines enables you to easily do lightweight model deployments and other serverless operations.
You will learn how to:
1. Setup Environment and Permissions
2. define pipeline with preprocessing, training & deployment steps
3. Run Pipeline
4. Test Inference
Let's get started! 🚀
---
*If you are going to use Sagemaker in a local environment (not SageMaker Studio or Notebook Instances). You need access to an IAM Role with the required permissions for Sagemaker. You can find [here](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html) more about it.*
**Prerequisites**:
- Make sure your notebook environment has IAM managed policy `AmazonSageMakerPipelinesIntegrations` as well as `AmazonSageMakerFullAccess`
**Blog Post**
* [Use a SageMaker Pipeline Lambda step for lightweight model deployments](https://aws.amazon.com/de/blogs/machine-learning/use-a-sagemaker-pipeline-lambda-step-for-lightweight-model-deployments/)
# Development Environment and Permissions
## Installation & Imports
We'll start by updating the SageMaker SDK, and importing some necessary packages.
```
!pip install "sagemaker>=2.48.0" --upgrade
import boto3
import os
import numpy as np
import pandas as pd
import sagemaker
import sys
import time
from sagemaker.workflow.parameters import ParameterInteger, ParameterFloat, ParameterString
from sagemaker.lambda_helper import Lambda
from sagemaker.sklearn.processing import SKLearnProcessor
from sagemaker.processing import ProcessingInput, ProcessingOutput
from sagemaker.workflow.steps import CacheConfig, ProcessingStep
from sagemaker.huggingface import HuggingFace, HuggingFaceModel
import sagemaker.huggingface
from sagemaker.inputs import TrainingInput
from sagemaker.workflow.steps import TrainingStep
from sagemaker.processing import ScriptProcessor
from sagemaker.workflow.properties import PropertyFile
from sagemaker.workflow.step_collections import CreateModelStep, RegisterModel
from sagemaker.workflow.conditions import ConditionLessThanOrEqualTo,ConditionGreaterThanOrEqualTo
from sagemaker.workflow.condition_step import ConditionStep, JsonGet
from sagemaker.workflow.pipeline import Pipeline, PipelineExperimentConfig
from sagemaker.workflow.execution_variables import ExecutionVariables
```
## Permissions
_If you are going to use Sagemaker in a local environment. You need access to an IAM Role with the required permissions for Sagemaker. You can find [here](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-roles.html) more about it._
```
import sagemaker
sess = sagemaker.Session()
region = sess.boto_region_name
# sagemaker session bucket -> used for uploading data, models and logs
# sagemaker will automatically create this bucket if it not exists
sagemaker_session_bucket=None
if sagemaker_session_bucket is None and sess is not None:
# set to default bucket if a bucket name is not given
sagemaker_session_bucket = sess.default_bucket()
role = sagemaker.get_execution_role()
sagemaker_session = sagemaker.Session(default_bucket=sagemaker_session_bucket)
print(f"sagemaker role arn: {role}")
print(f"sagemaker bucket: {sagemaker_session.default_bucket()}")
print(f"sagemaker session region: {sagemaker_session.boto_region_name}")
```
# Pipeline Overview

# Defining the Pipeline
## 0. Pipeline parameters
Before defining the pipeline, it is important to parameterize it. SageMaker Pipeline can directly be parameterized, including instance types and counts.
Read more about Parameters in the [documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/build-and-manage-parameters.html)
```
# S3 prefix where every assets will be stored
s3_prefix = "hugging-face-pipeline-demo"
# s3 bucket used for storing assets and artifacts
bucket = sagemaker_session.default_bucket()
# aws region used
region = sagemaker_session.boto_region_name
# base name prefix for sagemaker jobs (training, processing, inference)
base_job_prefix = s3_prefix
# Cache configuration for workflow
cache_config = CacheConfig(enable_caching=False, expire_after="30d")
# package versions
transformers_version = "4.11.0"
pytorch_version = "1.9.0"
py_version = "py38"
model_id_="distilbert-base-uncased"
dataset_name_="imdb"
model_id = ParameterString(name="ModelId", default_value="distilbert-base-uncased")
dataset_name = ParameterString(name="DatasetName", default_value="imdb")
```
## 1. Processing Step
A SKLearn Processing step is used to invoke a SageMaker Processing job with a custom python script - `preprocessing.py`.
### Processing Parameter
```
processing_instance_type = ParameterString(name="ProcessingInstanceType", default_value="ml.c5.2xlarge")
processing_instance_count = ParameterInteger(name="ProcessingInstanceCount", default_value=1)
processing_script = ParameterString(name="ProcessingScript", default_value="./scripts/preprocessing.py")
```
### Processor
```
processing_output_destination = f"s3://{bucket}/{s3_prefix}/data"
sklearn_processor = SKLearnProcessor(
framework_version="0.23-1",
instance_type=processing_instance_type,
instance_count=processing_instance_count,
base_job_name=base_job_prefix + "/preprocessing",
sagemaker_session=sagemaker_session,
role=role,
)
step_process = ProcessingStep(
name="ProcessDataForTraining",
cache_config=cache_config,
processor=sklearn_processor,
job_arguments=["--transformers_version",transformers_version,
"--pytorch_version",pytorch_version,
"--model_id",model_id_,
"--dataset_name",dataset_name_],
outputs=[
ProcessingOutput(
output_name="train",
destination=f"{processing_output_destination}/train",
source="/opt/ml/processing/train",
),
ProcessingOutput(
output_name="test",
destination=f"{processing_output_destination}/test",
source="/opt/ml/processing/test",
),
ProcessingOutput(
output_name="validation",
destination=f"{processing_output_destination}/test",
source="/opt/ml/processing/validation",
),
],
code=processing_script,
)
```
## 2. Model Training Step
We use SageMaker's [Hugging Face](https://sagemaker.readthedocs.io/en/stable/frameworks/huggingface/sagemaker.huggingface.html) Estimator class to create a model training step for the Hugging Face [DistilBERT](https://huggingface.co/distilbert-base-uncased) model. Transformer-based models such as the original BERT can be very large and slow to train. DistilBERT, however, is a small, fast, cheap and light Transformer model trained by distilling BERT base. It reduces the size of a BERT model by 40%, while retaining 97% of its language understanding capabilities and being 60% faster.
The Hugging Face estimator also takes hyperparameters as a dictionary. The training instance type and size are pipeline parameters that can be easily varied in future pipeline runs without changing any code.
### Training Parameter
```
# training step parameters
training_entry_point = ParameterString(name="TrainingEntryPoint", default_value="train.py")
training_source_dir = ParameterString(name="TrainingSourceDir", default_value="./scripts")
training_instance_type = ParameterString(name="TrainingInstanceType", default_value="ml.p3.2xlarge")
training_instance_count = ParameterInteger(name="TrainingInstanceCount", default_value=1)
# hyperparameters, which are passed into the training job
epochs=ParameterString(name="Epochs", default_value="1")
eval_batch_size=ParameterString(name="EvalBatchSize", default_value="32")
train_batch_size=ParameterString(name="TrainBatchSize", default_value="16")
learning_rate=ParameterString(name="LearningRate", default_value="3e-5")
fp16=ParameterString(name="Fp16", default_value="True")
```
### Hugging Face Estimator
```
huggingface_estimator = HuggingFace(
entry_point=training_entry_point,
source_dir=training_source_dir,
base_job_name=base_job_prefix + "/training",
instance_type=training_instance_type,
instance_count=training_instance_count,
role=role,
transformers_version=transformers_version,
pytorch_version=pytorch_version,
py_version=py_version,
hyperparameters={
'epochs':epochs,
'eval_batch_size': eval_batch_size,
'train_batch_size': train_batch_size,
'learning_rate': learning_rate,
'model_id': model_id,
'fp16': fp16
},
sagemaker_session=sagemaker_session,
)
step_train = TrainingStep(
name="TrainHuggingFaceModel",
estimator=huggingface_estimator,
inputs={
"train": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"train"
].S3Output.S3Uri
),
"test": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"test"
].S3Output.S3Uri
),
},
cache_config=cache_config,
)
```
## 3. Model evaluation Step
A ProcessingStep is used to evaluate the performance of the trained model. Based on the results of the evaluation, either the model is created, registered, and deployed, or the pipeline stops.
In the training job, the model was evaluated against the test dataset, and the result of the evaluation was stored in the `model.tar.gz` file saved by the training job. The results of that evaluation are copied into a `PropertyFile` in this ProcessingStep so that it can be used in the ConditionStep.
### Evaluation Parameter
```
evaluation_script = ParameterString(name="EvaluationScript", default_value="./scripts/evaluate.py")
```
### Evaluator
```
script_eval = SKLearnProcessor(
framework_version="0.23-1",
instance_type=processing_instance_type,
instance_count=processing_instance_count,
base_job_name=base_job_prefix + "/evaluation",
sagemaker_session=sagemaker_session,
role=role,
)
evaluation_report = PropertyFile(
name="HuggingFaceEvaluationReport",
output_name="evaluation",
path="evaluation.json",
)
step_eval = ProcessingStep(
name="HuggingfaceEvalLoss",
processor=script_eval,
inputs=[
ProcessingInput(
source=step_train.properties.ModelArtifacts.S3ModelArtifacts,
destination="/opt/ml/processing/model",
)
],
outputs=[
ProcessingOutput(
output_name="evaluation",
source="/opt/ml/processing/evaluation",
destination=f"s3://{bucket}/{s3_prefix}/evaluation_report",
),
],
code=evaluation_script,
property_files=[evaluation_report],
cache_config=cache_config,
)
```
## 4. Register the model
The trained model is registered in the Model Registry under a Model Package Group. Each time a new model is registered, it is given a new version number by default. The model is registered in the "Approved" state so that it can be deployed. Registration will only happen if the output of the [6. Condition for deployment](#6.-Condition-for-deployment) is true, i.e, the metrics being checked are within the threshold defined.
```
model = HuggingFaceModel(
model_data=step_train.properties.ModelArtifacts.S3ModelArtifacts,
role=role,
transformers_version=transformers_version,
pytorch_version=pytorch_version,
py_version=py_version,
sagemaker_session=sagemaker_session,
)
model_package_group_name = "HuggingFaceModelPackageGroup"
step_register = RegisterModel(
name="HuggingFaceRegisterModel",
model=model,
content_types=["application/json"],
response_types=["application/json"],
inference_instances=["ml.g4dn.xlarge", "ml.m5.xlarge"],
transform_instances=["ml.g4dn.xlarge", "ml.m5.xlarge"],
model_package_group_name=model_package_group_name,
approval_status="Approved",
)
```
## 5. Model Deployment
We create a custom step `ModelDeployment` derived from the provided `LambdaStep`. This Step will create a Lambda function and invocate to deploy our model as SageMaker Endpoint.
```
# custom Helper Step for ModelDeployment
from utils.deploy_step import ModelDeployment
# we will use the iam role from the notebook session for the created endpoint
# this role will be attached to our endpoint and need permissions, e.g. to download assets from s3
sagemaker_endpoint_role=sagemaker.get_execution_role()
step_deployment = ModelDeployment(
model_name=f"{model_id_}-{dataset_name_}",
registered_model=step_register.steps[0],
endpoint_instance_type="ml.g4dn.xlarge",
sagemaker_endpoint_role=sagemaker_endpoint_role,
autoscaling_policy=None,
)
```
## 6. Condition for deployment
For the condition to be `True` and the steps after evaluation to run, the evaluated accuracy of the Hugging Face model must be greater than our `TresholdAccuracy` parameter.
### Condition Parameter
```
threshold_accuracy = ParameterFloat(name="ThresholdAccuracy", default_value=0.8)
```
### Condition
```
cond_gte = ConditionGreaterThanOrEqualTo(
left=JsonGet(
step=step_eval,
property_file=evaluation_report,
json_path="eval_accuracy",
),
right=threshold_accuracy,
)
step_cond = ConditionStep(
name="CheckHuggingfaceEvalAccuracy",
conditions=[cond_gte],
if_steps=[step_register, step_deployment],
else_steps=[],
)
```
# Pipeline definition and execution
SageMaker Pipelines constructs the pipeline graph from the implicit definition created by the way pipeline steps inputs and outputs are specified. There's no need to specify that a step is a "parallel" or "serial" step. Steps such as model registration after the condition step are not listed in the pipeline definition because they do not run unless the condition is true. If so, they are run in order based on their specified inputs and outputs.
Each Parameter we defined holds a default value, which can be overwritten before starting the pipeline. [Parameter Documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/build-and-manage-parameters.html)
### Overwriting Parameters
```
# define parameter which should be overwritten
pipeline_parameters=dict(
ModelId="distilbert-base-uncased",
ThresholdAccuracy=0.7,
Epochs="3",
TrainBatchSize="32",
EvalBatchSize="64",
)
```
### Create Pipeline
```
pipeline = Pipeline(
name=f"HuggingFaceDemoPipeline",
parameters=[
model_id,
dataset_name,
processing_instance_type,
processing_instance_count,
processing_script,
training_entry_point,
training_source_dir,
training_instance_type,
training_instance_count,
evaluation_script,
threshold_accuracy,
epochs,
eval_batch_size,
train_batch_size,
learning_rate,
fp16
],
steps=[step_process, step_train, step_eval, step_cond],
sagemaker_session=sagemaker_session,
)
```
We can examine the pipeline definition in JSON format. You also can inspect the pipeline graph in SageMaker Studio by going to the page for your pipeline.
```
import json
json.loads(pipeline.definition())
```

`upsert` creates or updates the pipeline.
```
pipeline.upsert(role_arn=role)
```
### Run the pipeline
```
execution = pipeline.start(parameters=pipeline_parameters)
execution.wait()
```
## Getting predictions from the endpoint
After the previous cell completes, you can check whether the endpoint has finished deploying.
We can use the `endpoint_name` to create up a `HuggingFacePredictor` object that will be used to get predictions.
```
from sagemaker.huggingface import HuggingFacePredictor
endpoint_name = f"{model_id}-{dataset_name}"
# check if endpoint is up and running
print(f"https://console.aws.amazon.com/sagemaker/home?region={region}#/endpoints/{endpoint_name}")
hf_predictor = HuggingFacePredictor(endpoint_name,sagemaker_session=sagemaker_session)
```
### Test data
Here are a couple of sample reviews we would like to classify as positive (`pos`) or negative (`neg`). Demonstrating the power of advanced Transformer-based models such as this Hugging Face model, the model should do quite well even though the reviews are mixed.
```
sentiment_input1 = {"inputs":"Although the movie had some plot weaknesses, it was engaging. Special effects were mind boggling. Can't wait to see what this creative team does next."}
hf_predictor.predict(sentiment_input1)
sentiment_input2 = {"inputs":"There was some good acting, but the story was ridiculous. The other sequels in this franchise were better. It's time to take a break from this IP, but if they switch it up for the next one, I'll check it out."}
hf_predictor.predict(sentiment_input2)
```
## Cleanup Resources
The following cell will delete the resources created by the Lambda function and the Lambda itself.
Deleting other resources such as the S3 bucket and the IAM role for the Lambda function are the responsibility of the notebook user.
```
sm_client = boto3.client("sagemaker")
# Delete the Lambda function
step_deployment.func.delete()
# Delete the endpoint
hf_predictor.delete_endpoint()
```
| true |
code
| 0.662933 | null | null | null | null |
|
# Assignment 2
For this assignment you'll be looking at 2017 data on immunizations from the CDC. Your datafile for this assignment is in [assets/NISPUF17.csv](assets/NISPUF17.csv). A data users guide for this, which you'll need to map the variables in the data to the questions being asked, is available at [assets/NIS-PUF17-DUG.pdf](assets/NIS-PUF17-DUG.pdf). **Note: you may have to go to your Jupyter tree (click on the Coursera image) and navigate to the assignment 2 assets folder to see this PDF file).**
## Question 1
Write a function called `proportion_of_education` which returns the proportion of children in the dataset who had a mother with the education levels equal to less than high school (<12), high school (12), more than high school but not a college graduate (>12) and college degree.
*This function should return a dictionary in the form of (use the correct numbers, do not round numbers):*
```
{"less than high school":0.2,
"high school":0.4,
"more than high school but not college":0.2,
"college":0.2}
```
```
import pandas as pd
def proportion_of_education():
df = pd.read_csv("assets/NISPUF17.csv", index_col="SEQNUMC")
del df['Unnamed: 0']
df.sort_index(inplace=True)
df = df["EDUC1"].to_frame()
count = len(df.index)
lhs = df.loc[df["EDUC1"] == 1].count()["EDUC1"] / count
hs = df.loc[df["EDUC1"] == 2].count()["EDUC1"] / count
mhs = df.loc[df["EDUC1"] == 3].count()["EDUC1"] / count
college = df.loc[df["EDUC1"] == 4].count()["EDUC1"] / count
return {"less than high school": lhs,
"high school": hs,
"more than high school but not college": mhs,
"college": college
}
assert type(proportion_of_education())==type({}), "You must return a dictionary."
assert len(proportion_of_education()) == 4, "You have not returned a dictionary with four items in it."
assert "less than high school" in proportion_of_education().keys(), "You have not returned a dictionary with the correct keys."
assert "high school" in proportion_of_education().keys(), "You have not returned a dictionary with the correct keys."
assert "more than high school but not college" in proportion_of_education().keys(), "You have not returned a dictionary with the correct keys."
assert "college" in proportion_of_education().keys(), "You have not returned a dictionary with the correct keys."
```
## Question 2
Let's explore the relationship between being fed breastmilk as a child and getting a seasonal influenza vaccine from a healthcare provider. Return a tuple of the average number of influenza vaccines for those children we know received breastmilk as a child and those who know did not.
*This function should return a tuple in the form (use the correct numbers:*
```
(2.5, 0.1)
```
```
def average_influenza_doses():
df = pd.read_csv("assets/NISPUF17.csv", index_col="SEQNUMC")
del df['Unnamed: 0']
df.sort_index(inplace=True)
df = df[["CBF_01", "P_NUMFLU"]]
df = df.dropna()
df = df.groupby(["CBF_01"]).mean()
return (df.loc[1]["P_NUMFLU"], df.loc[2]["P_NUMFLU"])
assert len(average_influenza_doses())==2, "Return two values in a tuple, the first for yes and the second for no."
```
## Question 3
It would be interesting to see if there is any evidence of a link between vaccine effectiveness and sex of the child. Calculate the ratio of the number of children who contracted chickenpox but were vaccinated against it (at least one varicella dose) versus those who were vaccinated but did not contract chicken pox. Return results by sex.
*This function should return a dictionary in the form of (use the correct numbers):*
```
{"male":0.2,
"female":0.4}
```
Note: To aid in verification, the `chickenpox_by_sex()['female']` value the autograder is looking for starts with the digits `0.0077`.
```
def chickenpox_by_sex():
df = pd.read_csv("assets/NISPUF17.csv", index_col="SEQNUMC")
del df['Unnamed: 0']
df.sort_index(inplace=True)
df = df[["SEX", "HAD_CPOX", "P_NUMVRC"]]
df["SEX"] = df["SEX"].replace({1: "Male", 2: "Female"})
df = df.fillna(0)
df = df[(df["P_NUMVRC"]>0) & (df["HAD_CPOX"].isin((1,2)))]
# number of males vaccinated that contracted
nmvc = df[(df["SEX"] == "Male") & (df["HAD_CPOX"] == 1)].count()["SEX"]
# number of males vaccinated that did not contracted
nmvnc = df[(df["SEX"] == "Male") & (df["HAD_CPOX"] == 2)].count()["SEX"]
# number of females vaccinated that contracted
nfvc = df[(df["SEX"] == "Female") & (df["HAD_CPOX"] == 1)].count()["SEX"]
# number of females vaccinated that did not contracted
nfvnc = df[(df["SEX"] == "Female") & (df["HAD_CPOX"] == 2)].count()["SEX"]
return {"male":nmvc/nmvnc,"female":nfvc/nfvnc}
chickenpox_by_sex()
assert len(chickenpox_by_sex())==2, "Return a dictionary with two items, the first for males and the second for females."
```
## Question 4
A correlation is a statistical relationship between two variables. If we wanted to know if vaccines work, we might look at the correlation between the use of the vaccine and whether it results in prevention of the infection or disease [1]. In this question, you are to see if there is a correlation between having had the chicken pox and the number of chickenpox vaccine doses given (varicella).
Some notes on interpreting the answer. The `had_chickenpox_column` is either `1` (for yes) or `2` (for no), and the `num_chickenpox_vaccine_column` is the number of doses a child has been given of the varicella vaccine. A positive correlation (e.g., `corr > 0`) means that an increase in `had_chickenpox_column` (which means more no’s) would also increase the values of `num_chickenpox_vaccine_column` (which means more doses of vaccine). If there is a negative correlation (e.g., `corr < 0`), it indicates that having had chickenpox is related to an increase in the number of vaccine doses.
Also, `pval` is the probability that we observe a correlation between `had_chickenpox_column` and `num_chickenpox_vaccine_column` which is greater than or equal to a particular value occurred by chance. A small `pval` means that the observed correlation is highly unlikely to occur by chance. In this case, `pval` should be very small (will end in `e-18` indicating a very small number).
[1] This isn’t really the full picture, since we are not looking at when the dose was given. It’s possible that children had chickenpox and then their parents went to get them the vaccine. Does this dataset have the data we would need to investigate the timing of the dose?
```
def corr_chickenpox():
import scipy.stats as stats
import numpy as np
import pandas as pd
# this is just an example dataframe
df=pd.DataFrame({"had_chickenpox_column":np.random.randint(1,3,size=(100)),
"num_chickenpox_vaccine_column":np.random.randint(0,6,size=(100))})
# here is some stub code to actually run the correlation
corr, pval=stats.pearsonr(df["had_chickenpox_column"],df["num_chickenpox_vaccine_column"])
# just return the correlation
# return corr
df = pd.read_csv("assets/NISPUF17.csv")
df.sort_index(inplace=True)
df = df[["HAD_CPOX", "P_NUMVRC"]]
df = df.dropna()
df = df[df["HAD_CPOX"]<=3]
corr, pval = stats.pearsonr(df["HAD_CPOX"],df["P_NUMVRC"])
return corr
assert -1<=corr_chickenpox()<=1, "You must return a float number between -1.0 and 1.0."
corr_chickenpox()
```
| true |
code
| 0.433262 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/BRIJNANDA1979/CNN-Sentinel/blob/master/Understand_band_data_info_using_histogram_and_classifying_pixel_values.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#https://www.earthdatascience.org/courses/use-data-open-source-python/multispectral-remote-sensing/vegetation-indices-in-python/calculate-NDVI-python/
#Sentinel 2 Use Handbook. https://sentinels.copernicus.eu/documents/247904/685211/Sentinel-2_User_Handbook
!pip install rioxarray
!pip install geopandas
import os
import matplotlib.pyplot as plt
import numpy as np
import rioxarray as rxr
import geopandas as gpd
path = '/content/drive/MyDrive/Big/S2A_MSIL2A_20170613T101031_0_55/S2A_MSIL2A_20170613T101031_0_55_B01.tif'
#os.chdir(path)
#data_path = os.path.join("/content/drive/MyDrive/Big/S2A_MSIL2A_20170613T101031_0_55/S2A_MSIL2A_20170613T101031_0_55_B01.tif")
data = rxr.open_rasterio(path)
data.shape
!pip install earthpy
import earthpy as et
import earthpy.spatial as es
import earthpy.plot as ep
ep.plot_bands(data,
title="Bigearthnet Band 1 Raster")
plt.show()
#https://earthpy.readthedocs.io/en/latest/gallery_vignettes/plot_bands_functionality.html
#Stack all bands of BigEarthNet Data sample one band tiff images
import glob
files = glob.glob(os.path.join('/content/drive/MyDrive/Big/S2A_MSIL2A_20170613T101031_0_55/S2A_MSIL2A_20170613T101031_0_55_B*.tif'))
files.sort()
print("Number of Bands",len(files))
print(files)
print(files[0]) # Band1
print(files[1]) # Band2
print(files[10]) # Band12
#array_stack, meta_data = es.stack(path, nodata=-9999)
```
# New Section
```
print(files[0])
band1= rxr.open_rasterio(files[0])
ep.plot_bands(band1,
title="Bigearthnet Band 1 Raster")
plt.show()
print("The CRS of this data is:", band1.rio.crs)
#Converting EPSG to Proj4 in Python
# Convert to project string using earthpy
proj4 = et.epsg['32634']
print(proj4)
#Spatial Extent
#You can access the spatial extent using the .bounds() attribute in rasterio.
print(band1.rio.bounds())
#Raster Resolution: area covered by 1 pixel on ground e.g 60m * 60m
# What is the x and y resolution for your raster data?
print(band1.rio.resolution())
print("The nodatavalue of your data is:", band1.rio.nodata)
# How many bands / layers does the object have?
print("Number of bands", band1.rio.count)
print("The shape of your data is:", band1.shape)
print('min value:', np.nanmin(band1))
print('max value:', np.nanmax(band1))
import matplotlib.pyplot as plt
f, ax = plt.subplots()
band1.plot.hist(color="purple")
ax.set(title="Distribution of Raster Cell Values Band 1 Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
print(files[1])
band2= rxr.open_rasterio(files[1])
ep.plot_bands(band2,
title="Bigearthnet Band 2 Raster")
plt.show()
print("The CRS of this data is:", band2.rio.crs)
#Converting EPSG to Proj4 in Python
# Convert to project string using earthpy
proj4 = et.epsg['32634']
print(proj4)
#Spatial Extent
#You can access the spatial extent using the .bounds() attribute in rasterio.
print(band2.rio.bounds())
#Raster Resolution: area covered by 1 pixel on ground e.g 60m * 60m
# What is the x and y resolution for your raster data?
print(band2.rio.resolution())
print("The nodatavalue of your data is:", band2.rio.nodata)
# How many bands / layers does the object have?
print("Number of bands", band2.rio.count)
print("The shape of your data is:", band2.shape)
print('min value:', np.nanmin(band2))
print('max value:', np.nanmax(band2))
import matplotlib.pyplot as plt
f, ax = plt.subplots()
band1.plot.hist(color="purple")
ax.set(title="Distribution of Raster Cell Values Band 2 Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
#https://rasterio.readthedocs.io/en/latest/api/rasterio.plot.html
#rasterio.plot.reshape_as_image(arr)
#Returns the source array reshaped into the order expected by image processing and visualization software (matplotlib, scikit-image, etc) by swapping the axes order from (bands, rows, columns) to (rows, columns, bands)
print('min value:', np.nanmin(data))
print('max value:', np.nanmax(data))
#https://www.earthdatascience.org/courses/use-data-open-source-python/intro-raster-data-python/raster-data-processing/classify-plot-raster-data-in-python/
import matplotlib.pyplot as plt
f, ax = plt.subplots()
data.plot.hist(color="purple")
ax.set(title="Distribution of Raster Cell Values Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
bins=[0, 100, 200, 250, 275, 300,350]
f, ax = plt.subplots()
data.plot.hist(color="purple",bins=[0, 100, 200, 250, 275, 300,350])
ax.set(title="Distribution of Raster Cell Values Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
class_bins = [-np.inf,250,275,300,350,+np.inf]
import xarray as xr
data_class = xr.apply_ufunc(np.digitize,
data,
class_bins)
print(data_class.shape)
#data_class = np.array(data_class[0])
import matplotlib.pyplot as plt
f, ax = plt.subplots()
data_class.plot.hist(color="purple")
ax.set(title="Distribution of Raster Cell Values Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
#https://www.spatialreference.org/ref/epsg/32634/
#/*EPSG:32634
#WGS 84 / UTM zone 34N (Google it)
#WGS84 Bounds: 18.0000, 0.0000, 24.0000, 84.0000
#Projected Bounds: 166021.4431, 0.0000, 833978.5569, 9329005.1825
#Scope: Large and medium scale topographic mapping and engineering survey.
#Last Revised: June 2, 1995
#Area: World - N hemisphere - 18°E to 24°E - by country*/
#Proj4js.defs["EPSG:32634"] = "+proj=utm +zone=34 +ellps=WGS84 +datum=WGS84 +units=m +no_defs";
print(files[10])
band12= rxr.open_rasterio(files[10])
ep.plot_bands(band12,
title="Bigearthnet Band 12 Raster")
plt.show()
print("The CRS of this data is:", band12.rio.crs)
#Converting EPSG to Proj4 in Python
# Convert to project string using earthpy
proj4 = et.epsg['32634']
print(proj4)
#Spatial Extent
#You can access the spatial extent using the .bounds() attribute in rasterio.
print(band12.rio.bounds())
#Raster Resolution: area covered by 1 pixel on ground e.g 60m * 60m
# What is the x and y resolution for your raster data?
print(band12.rio.resolution())
print("The nodatavalue of your data is:", band12.rio.nodata)
# How many bands / layers does the object have?
print("Number of bands", band12.rio.count)
print("The shape of your data is:", band12.shape)
print('min value:', np.nanmin(band12))
print('max value:', np.nanmax(band12))
import matplotlib.pyplot as plt
f, ax = plt.subplots()
band1.plot.hist(color="purple")
ax.set(title="Distribution of Raster Cell Values Band 12 Data",
xlabel="",
ylabel="Number of Pixels")
plt.show()
```
## New Section : Making Dataframe for min/max values of each bands of 1,2 and 12
```
import pandas as pd
df = pd.DataFrame(columns= ['filename','min','max'])
df.head()
import glob
import os
files_batch=[] #batch of same bands
min=[]
max=[]
mean_min =[]
mean_max =[]
path = '/content/drive/MyDrive/Big'
os.chdir(path)
dirs = os.listdir()
dirs.sort()
print(dirs)
print(len(dirs))
#remove last element of list
del dirs[0]
print(dirs)
print(len(dirs))
step_size = len(dirs)
# Add batch of band1 tif files to files list
path = '/content/drive/MyDrive/Big'
for i in dirs:
s = ""
s = s + path + '/' + str(i) + '/' +'*01.tif'
print(s)
temp = (glob.glob(os.path.join(s)))
files_batch.append(temp[0])
# Fetch Filenames of band 1
print(files_batch,files_batch[0],len(files_batch)) #Batch of Band 1 files
# Add min/max values of band 1 to min/max list
for i in range(0,step_size):
band1= rxr.open_rasterio(files_batch[i])
min.append(np.nanmin(band1))
max.append(np.nanmax(band1))
print(min)
print(max)
mean_min.append(np.mean(min))
mean_max.append(np.mean(max))
#df['B1_min'] = min
#df['B1_max'] = max
#print(df)
# Add batch of band2 tif files to files list
path = '/content/drive/MyDrive/Big'
for i in dirs:
s = ""
s = s + path + '/' + str(i) + '/' +'*02.tif'
print(s)
temp = (glob.glob(os.path.join(s)))
files_batch.append(temp[0])
print(files_batch)
print(files_batch[len(files_batch)-1], len(files_batch))
# Add min/max values of band 2 to min/max list
for i in range(step_size,2*step_size):
band2= rxr.open_rasterio(files_batch[i])
min.append(np.nanmin(band2))
max.append(np.nanmax(band2))
print(min)
print(max)
mean_min.append(np.mean(min))
mean_max.append(np.mean(max))
# Add batch of band 12 tif files to files list
path = '/content/drive/MyDrive/Big'
for i in dirs:
s = ""
s = s + path + '/' + str(i) + '/' +'*12.tif'
print(s)
temp = (glob.glob(os.path.join(s)))
files_batch.append(temp[0])
print(files_batch)
print(files_batch[len(files_batch)-1], len(files_batch))
# Add min/max values of band 12 to min/max list
for i in range(2*step_size,3*step_size):
band2= rxr.open_rasterio(files_batch[i])
min.append(np.nanmin(band2))
max.append(np.nanmax(band2))
print(min)
print(max)
mean_min.append(np.mean(min))
mean_max.append(np.mean(max))
```
# Add files and min/max lists to dataframe
```
print(files_batch)
df['filename'] = files_batch
df['min'] = min
df['max'] = max
df.head()
#print means of min and max values for each band 1 2 and 12
print(mean_min)
print(mean_max)
# Plot histogram
import matplotlib.pyplot as plt
x=np.array(min)
y=np.array(max)
plt.bar(x,y,align='center') # A bar chart
plt.xlabel('Min')
plt.ylabel('Max')
plt.show()
# Plot histogram for mean min and mean max
import matplotlib.pyplot as plt
x=np.array(mean_min)
y=np.array(mean_max)
plt.bar(x,y,align='center') # A bar chart
plt.xlabel('Mean_Min')
plt.ylabel('Mean_Max')
plt.show()
```
### **USE RASTERIO module to open Raster images and read it to Array**
```
band1 = np.array(band1)
band1.shape
print(files)
band2= rxr.open_rasterio(files[1])
band2 = np.array(band2)
band2.shape
band12 = np.array(band12)
band12.shape
print(df['filename'])
files_bands = []
files_bands = df['filename']
print(files_bands[0:6])
# Reading raster geotif files
#https://automating-gis-processes.github.io/CSC18/lessons/L6/reading-raster.html
import rasterio
band1_batch = files_bands[0:6]
print(band1_batch[0])
band1_raster = rasterio.open(band1_batch[0])
print(type(band1_raster))
#Projection
print(band1_raster.crs)
#Affine transform (how raster is scaled, rotated, skewed, and/or translated
band1_raster.transform
band1_raster.meta
#reading raster to array
band1_array = band1_raster.read()
print(band1_array)
stats = []
for band in band1_array:
stats.append({
'mean' : band.mean(),
'min' : band.min(),
'max' : band.max(),
'median': np.median(band)
})
print(stats)
```
# Read all Band1 files and find mean of all 6 Forest class Band1 data
```
print(df['filename'])
files_bands = []
files_bands = df['filename']
print(files_bands[0:6])
# Reading raster geotif files using Rasterio
#https://automating-gis-processes.github.io/CSC18/lessons/L6/reading-raster.html
import rasterio
band1_batch = files_bands[0:6]
print(band1_batch[0])
band1_array=[]
for i in band1_batch:
band1_raster = rasterio.open(i)
band1_array.append(band1_raster.read())
band1_mean=[]
band1_min = []
band1_max = []
print(len(band1_array))
for i in band1_array:
for band in i:
band1_mean.append(band.mean())
band1_min.append(band.min())
band1_max.append(band.max())
print("Band 1 stat for 6 images is :------>")
print(band1_mean)
print(band1_min)
print(band1_max)
# Stat for band 2 images
band2_batch = files_bands[6:12]
print(band2_batch)
band2_array=[]
for i in band2_batch:
band2_raster = rasterio.open(i)
band2_array.append(band2_raster.read())
band2_mean=[]
band2_min = []
band2_max = []
print(len(band2_array))
for i in band2_array:
for band in i:
band2_mean.append(band.mean())
band2_min.append(band.min())
band2_max.append(band.max())
print("Band 2 stat for 6 images is :------>")
print(band2_mean)
print(band2_min)
print(band2_max)
# Stat for band 12 images
band12_batch = files_bands[12:18]
print(band12_batch)
band12_array=[]
for i in band12_batch:
band12_raster = rasterio.open(i)
band12_array.append(band12_raster.read())
band12_mean=[]
band12_min = []
band12_max = []
print(len(band12_array))
for i in band12_array:
for band in i:
band12_mean.append(band.mean())
band12_min.append(band.min())
band12_max.append(band.max())
print("Band 12 stat for 6 images is :------>")
print(band12_mean)
print(band12_min)
print(band12_max)
y=np.array(band1_mean)
x=(1,2,3,4,5,6)
plt.bar(x,y,align='center')
plt.axis([0, 6, 100, 600])
plt.xlabel('Bands')
plt.ylabel('Commulative Mean')
plt.show()
y=np.array(band2_mean)
x=(1,2,3,4,5,6)
plt.bar(x,y,align='center')
plt.axis([0, 6, 100, 600])
plt.xlabel('Bands')
plt.ylabel('Commulative Mean')
plt.show()
y=np.array(band12_mean)
x=(1,2,3,4,5,6)
plt.bar(x,y,align='center')
plt.axis([0, 6, 100, 600])
plt.xlabel('Bands')
plt.ylabel('Commulative Mean')
plt.show()
df = pd.DataFrame(columns = ['mean_band1','mean_band2','mean_band12'])
df['mean_band1'] = np.array(band1_mean)
df['mean_band2'] = np.array(band2_mean)
df['mean_band12'] = np.array(band12_mean)
df
df.plot()
```
| true |
code
| 0.661923 | null | null | null | null |
|
# Rank Classification using BERT on Amazon Review dataset
## Introduction
In this tutorial, you learn how to train a rank classification model using [Transfer Learning](https://en.wikipedia.org/wiki/Transfer_learning). We will use a pretrained DistilBert model to train on the Amazon review dataset.
## About the dataset and model
[Amazon Customer Review dataset](https://s3.amazonaws.com/amazon-reviews-pds/readme.html) consists of all different valid reviews from amazon.com. We will use the "Digital_software" category that consists of 102k valid reviews. As for the pre-trained model, use the DistilBERT[[1]](https://arxiv.org/abs/1910.01108) model. It's a light-weight BERT model already trained on [Wikipedia text corpora](https://en.wikipedia.org/wiki/List_of_text_corpora), a much larger dataset consisting of over millions text. The DistilBERT served as a base layer and we will add some more classification layers to output as rankings (1 - 5).
<img src="https://djl-ai.s3.amazonaws.com/resources/images/amazon_review.png" width="500">
<center>Amazon Review example</center>
We will use review body as our data input and ranking as label.
## Pre-requisites
This tutorial assumes you have the following knowledge. Follow the READMEs and tutorials if you are not familiar with:
1. How to setup and run [Java Kernel in Jupyter Notebook](https://github.com/awslabs/djl/blob/master/jupyter/README.md)
2. Basic components of Deep Java Library, and how to [train your first model](https://github.com/awslabs/djl/blob/master/jupyter/tutorial/02_train_your_first_model.ipynb).
## Getting started
Load the Deep Java Libarary and its dependencies from Maven:
```
%mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.9.0-SNAPSHOT
%maven ai.djl:basicdataset:0.9.0-SNAPSHOT
%maven ai.djl.mxnet:mxnet-model-zoo:0.9.0-SNAPSHOT
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven net.java.dev.jna:jna:5.3.0
// See https://github.com/awslabs/djl/blob/master/mxnet/mxnet-engine/README.md
// for more MXNet library selection options
%maven ai.djl.mxnet:mxnet-native-auto:1.7.0-backport
```
Now let's import the necessary modules:
```
import ai.djl.Application;
import ai.djl.Device;
import ai.djl.MalformedModelException;
import ai.djl.Model;
import ai.djl.basicdataset.CsvDataset;
import ai.djl.basicdataset.utils.DynamicBuffer;
import ai.djl.inference.Predictor;
import ai.djl.metric.Metrics;
import ai.djl.modality.Classifications;
import ai.djl.modality.nlp.SimpleVocabulary;
import ai.djl.modality.nlp.bert.BertFullTokenizer;
import ai.djl.ndarray.NDArray;
import ai.djl.ndarray.NDList;
import ai.djl.ndarray.types.Shape;
import ai.djl.nn.Activation;
import ai.djl.nn.Block;
import ai.djl.nn.SequentialBlock;
import ai.djl.nn.core.Linear;
import ai.djl.nn.norm.Dropout;
import ai.djl.repository.zoo.*;
import ai.djl.training.*;
import ai.djl.training.dataset.Batch;
import ai.djl.training.dataset.RandomAccessDataset;
import ai.djl.training.evaluator.Accuracy;
import ai.djl.training.listener.CheckpointsTrainingListener;
import ai.djl.training.listener.TrainingListener;
import ai.djl.training.loss.Loss;
import ai.djl.training.util.ProgressBar;
import ai.djl.translate.*;
import java.io.IOException;
import java.nio.file.Paths;
import java.util.List;
import org.apache.commons.csv.CSVFormat;
```
## Prepare Dataset
First step is to prepare the dataset for training. Since the original data was in TSV format, we can use CSVDataset to be the dataset container. We will also need to specify how do we want to preprocess the raw data. For BERT model, the input data are required to be tokenized and mapped into indices based on the inputs. In DJL, we defined an interface called Fearurizer, it is designed to allow user customize operation on each selected row/column of a dataset. In our case, we would like to clean and tokenize our sentencies. So let's try to implement it to deal with customer review sentencies.
```
final class BertFeaturizer implements CsvDataset.Featurizer {
private final BertFullTokenizer tokenizer;
private final int maxLength; // the cut-off length
public BertFeaturizer(BertFullTokenizer tokenizer, int maxLength) {
this.tokenizer = tokenizer;
this.maxLength = maxLength;
}
/** {@inheritDoc} */
@Override
public void featurize(DynamicBuffer buf, String input) {
SimpleVocabulary vocab = tokenizer.getVocabulary();
// convert sentence to tokens
List<String> tokens = tokenizer.tokenize(input);
// trim the tokens to maxLength
tokens = tokens.size() > maxLength ? tokens.subList(0, maxLength) : tokens;
// BERT embedding convention "[CLS] Your Sentence [SEP]"
buf.put(vocab.getIndex("[CLS]"));
tokens.forEach(token -> buf.put(vocab.getIndex(token)));
buf.put(vocab.getIndex("[SEP]"));
}
}
```
Once we got this part done, we can apply the `BertFeaturizer` into our Dataset. We take `review_body` column and apply the Featurizer. We also pick `star_rating` as our label set. Since we go for batch input, we need to tell the dataset to pad our data if it is less than the `maxLength` we defined. `PaddingStackBatchifier` will do the work for you.
```
CsvDataset getDataset(int batchSize, BertFullTokenizer tokenizer, int maxLength) {
String amazonReview =
"https://s3.amazonaws.com/amazon-reviews-pds/tsv/amazon_reviews_us_Digital_Software_v1_00.tsv.gz";
float paddingToken = tokenizer.getVocabulary().getIndex("[PAD]");
return CsvDataset.builder()
.optCsvUrl(amazonReview) // load from Url
.setCsvFormat(CSVFormat.TDF.withQuote(null).withHeader()) // Setting TSV loading format
.setSampling(batchSize, true) // make sample size and random access
.addFeature(
new CsvDataset.Feature(
"review_body", new BertFeaturizer(tokenizer, maxLength)))
.addNumericLabel("star_rating") // set label
.optDataBatchifier(
PaddingStackBatchifier.builder()
.optIncludeValidLengths(false)
.addPad(0, 0, (m) -> m.ones(new Shape(1)).mul(paddingToken))
.build()) // define how to pad dataset to a fix length
.build();
}
```
## Construct your model
We will load our pretrained model and prepare the classification. First construct the `criteria` to specify where to load the embedding (DistiledBERT), then call `loadModel` to download that embedding with pre-trained weights. Since this model is built without classification layer, we need to add a classification layer to the end of the model and train it. After you are done modifying the block, set it back to model using `setBlock`.
### Load the word embedding
We will download our word embedding and load it to memory (this may take a while)
```
Criteria<NDList, NDList> criteria = Criteria.builder()
.optApplication(Application.NLP.WORD_EMBEDDING)
.setTypes(NDList.class, NDList.class)
.optModelUrls("https://resources.djl.ai/test-models/distilbert.zip")
.optProgress(new ProgressBar())
.build();
ZooModel<NDList, NDList> embedding = ModelZoo.loadModel(criteria);
```
### Create classification layers
Then let's build a simple MLP layer to classify the ranks. We set the output of last FullyConnected (Linear) layer to 5 to get the predictions for star 1 to 5. Then all we need to do is to load the block into the model. Before applying the classification layer, we also need to add text embedding to the front. In our case, we just create a Lambda function that do the followings:
1. batch_data (batch size, token indices) -> batch_data + max_length (size of the token indices)
2. generate embedding
```
Predictor<NDList, NDList> embedder = embedding.newPredictor();
Block classifier = new SequentialBlock()
// text embedding layer
.add(
ndList -> {
NDArray data = ndList.singletonOrThrow();
long batchSize = data.getShape().get(0);
float maxLength = data.getShape().get(1);
try {
return embedder.predict(
new NDList(data, data.getManager()
.full(new Shape(batchSize), maxLength)));
} catch (TranslateException e) {
throw new IllegalArgumentException("embedding error", e);
}
})
// classification layer
.add(Linear.builder().setUnits(768).build()) // pre classifier
.add(Activation::relu)
.add(Dropout.builder().optRate(0.2f).build())
.add(Linear.builder().setUnits(5).build()) // 5 star rating
.addSingleton(nd -> nd.get(":,0")); // Take [CLS] as the head
Model model = Model.newInstance("AmazonReviewRatingClassification");
model.setBlock(classifier);
```
## Start Training
Finally, we can start building our training pipeline to train the model.
### Creating Training and Testing dataset
Firstly, we need to create a voabulary that is used to map token to index such as "hello" to 1121 (1121 is the index of "hello" in dictionary). Then we simply feed the vocabulary to the tokenizer that used to tokenize the sentence. Finally, we just need to split the dataset based on the ratio.
Note: we set the cut-off length to 64 which means only the first 64 tokens from the review will be used. You can increase this value to achieve better accuracy.
```
// Prepare the vocabulary
SimpleVocabulary vocabulary = SimpleVocabulary.builder()
.optMinFrequency(1)
.addFromTextFile(embedding.getArtifact("vocab.txt").getPath())
.optUnknownToken("[UNK]")
.build();
// Prepare dataset
int maxTokenLength = 64; // cutoff tokens length
int batchSize = 8;
BertFullTokenizer tokenizer = new BertFullTokenizer(vocabulary, true);
CsvDataset amazonReviewDataset = getDataset(batchSize, tokenizer, maxTokenLength);
// split data with 7:3 train:valid ratio
RandomAccessDataset[] datasets = amazonReviewDataset.randomSplit(7, 3);
RandomAccessDataset trainingSet = datasets[0];
RandomAccessDataset validationSet = datasets[1];
```
### Setup Trainer and training config
Then, we need to setup our trainer. We set up the accuracy and loss function. The model training logs will be saved to `build/modlel`.
```
CheckpointsTrainingListener listener = new CheckpointsTrainingListener("build/model");
listener.setSaveModelCallback(
trainer -> {
TrainingResult result = trainer.getTrainingResult();
Model model = trainer.getModel();
// track for accuracy and loss
float accuracy = result.getValidateEvaluation("Accuracy");
model.setProperty("Accuracy", String.format("%.5f", accuracy));
model.setProperty("Loss", String.format("%.5f", result.getValidateLoss()));
});
DefaultTrainingConfig config = new DefaultTrainingConfig(Loss.softmaxCrossEntropyLoss()) // loss type
.addEvaluator(new Accuracy())
.optDevices(Device.getDevices(1)) // train using single GPU
.addTrainingListeners(TrainingListener.Defaults.logging("build/model"))
.addTrainingListeners(listener);
```
### Start training
We will start our training process. Training on GPU will takes approximately 10 mins. For CPU, it will take more than 2 hours to finish.
```
int epoch = 2;
Trainer trainer = model.newTrainer(config);
trainer.setMetrics(new Metrics());
Shape encoderInputShape = new Shape(batchSize, maxTokenLength);
// initialize trainer with proper input shape
trainer.initialize(encoderInputShape);
EasyTrain.fit(trainer, epoch, trainingSet, validationSet);
System.out.println(trainer.getTrainingResult());
```
### Save the model
```
model.save(Paths.get("build/model"), "amazon-review.param");
```
## Verify the model
We can create a predictor from the model to run inference on our customized dataset. Firstly, we can create a `Translator` for the model to do preprocessing and post processing. Similar to what we have done before, we need to tokenize the input sentence and get the output ranking.
```
class MyTranslator implements Translator<String, Classifications> {
private BertFullTokenizer tokenizer;
private SimpleVocabulary vocab;
private List<String> ranks;
public MyTranslator(BertFullTokenizer tokenizer) {
this.tokenizer = tokenizer;
vocab = tokenizer.getVocabulary();
ranks = Arrays.asList("1", "2", "3", "4", "5");
}
@Override
public Batchifier getBatchifier() { return new StackBatchifier(); }
@Override
public NDList processInput(TranslatorContext ctx, String input) {
List<String> tokens = tokenizer.tokenize(input);
float[] indices = new float[tokens.size() + 2];
indices[0] = vocab.getIndex("[CLS]");
for (int i = 0; i < tokens.size(); i++) {
indices[i+1] = vocab.getIndex(tokens.get(i));
}
indices[indices.length - 1] = vocab.getIndex("[SEP]");
return new NDList(ctx.getNDManager().create(indices));
}
@Override
public Classifications processOutput(TranslatorContext ctx, NDList list) {
return new Classifications(ranks, list.singletonOrThrow().softmax(0));
}
}
```
Finally, we can create a `Predictor` to run the inference. Let's try with a random customer review:
```
String review = "It works great, but it takes too long to update itself and slows the system";
Predictor<String, Classifications> predictor = model.newPredictor(new MyTranslator(tokenizer));
System.out.println(predictor.predict(review));
```
| true |
code
| 0.841858 | null | null | null | null |
|
# Graph Neural Network (GCN)-based Synthetic Binding Logic Classification with Graph-SafeML
The eisting example of GCN-based Synthetic Binding Logic Classification from google research team is used to test the idea of SafeML for Graph-based classifiers. You can find the source code [here](https://github.com/google-research/graph-attribution) and the related paper for the code is available [here](https://papers.nips.cc/paper/2020/file/417fbbf2e9d5a28a855a11894b2e795a-Paper.pdf) [[1]](https://papers.nips.cc/paper/2020/file/417fbbf2e9d5a28a855a11894b2e795a-Paper.pdf).
Regarding the Graph-based distance measure, the theory of "Graph distance for complex networks" provided by of Yutaka Shimada et al. is used [[2]](https://www.nature.com/articles/srep34944). The code related to this paper is avaialble [here](https://github.com/msarrias/graph-distance-for-complex-networks).
You can read more about the idea of SafeML in [[3]](https://github.com/ISorokos/SafeML). To read more about "Synthetic Binding Logic Classification" and the related dataset that is used in this notebook, please check [[4]](https://www.pnas.org/content/pnas/116/24/11624.full.pdf).

The SafeML project takes place at the University of Hull in collaboration with Fraunhofer IESE and Nuremberg Institute of Technology
## Table of Content
* [Initialization and Installations](#init)
* [Importing Required Libraries](#lib)
* [Graph Attribution Specific Imports](#glib)
* [Load Experiment Data, Task and Attribution Techniques](#load)
* [Creating a GNN Model](#model)
* [Graph Vizualization](#gviz)
* [Graph Distance Measures and SafeML Idea](#SafeML)
* [Discussion](#dis)
### References:
[[1]. Wiltschko, A. B., Sanchez-Lengeling, B., Lee, B., Reif, E., Wei, J., McCloskey, K. J., & Wang, Y. (2020). Evaluating Attribution for Graph Neural Networks.](https://papers.nips.cc/paper/2020/file/417fbbf2e9d5a28a855a11894b2e795a-Paper.pdf)
[[2]. Shimada, Y., Hirata, Y., Ikeguchi, T., & Aihara, K. (2016). Graph distance for complex networks. Scientific reports, 6(1), 1-6.](https://www.nature.com/articles/srep34944)
[[3]. Aslansefat, K., Sorokos, I., Whiting, D., Kolagari, R. T., & Papadopoulos, Y. (2020, September). SafeML: Safety Monitoring of Machine Learning Classifiers Through Statistical Difference Measures. In International Symposium on Model-Based Safety and Assessment (pp. 197-211). Springer, Cham.](https://arxiv.org/pdf/2005.13166.pdf)
[[4]. McCloskey, K., Taly, A., Monti, F., Brenner, M. P., & Colwell, L. J. (2019). Using attribution to decode binding mechanism in neural network models for chemistry. Proceedings of the National Academy of Sciences, 116(24), 11624-11629.](https://www.pnas.org/content/pnas/116/24/11624.full.pdf)
<a id = "init"></a>
## Initialization and Installations
```
import warnings
warnings.filterwarnings('ignore')
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('..')
import sys
IN_COLAB = 'google.colab' in sys.modules
REPO_DIR = '..' if IN_COLAB else '..'
!git clone https://github.com/google-research/graph-attribution.git --quiet
import sys
sys.path.insert(1, '/kaggle/working/graph-attribution')
!pip install tensorflow tensorflow-probability -q
!pip install dm-sonnet -q
!pip install graph_nets "tensorflow>=2.1.0-rc1" "dm-sonnet>=2.0.0b0" tensorflow_probability
!pip install git+https://github.com/google-research/graph-attribution -quiet
!pip install git+https://github.com/google-research/graph-attribution
```
<a id = "lib"></a>
## Importing Required Libraries
```
import os
import itertools
import collections
import tqdm.auto as tqdm
from IPython.display import display
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
import sonnet as snt
import graph_nets
from graph_nets.graphs import GraphsTuple
import graph_attribution as gatt
from tqdm import tqdm
import time
import networkx as nx
# Ignore tf/graph_nets UserWarning:
# Converting sparse IndexedSlices to a dense Tensor of unknown shape
import warnings
warnings.simplefilter("ignore", UserWarning)
for mod in [tf, snt, gatt]:
print(f'{mod.__name__:20s} = {mod.__version__}')
```
<a id = "glib"></a>
## Graph Attribution specific imports
```
from graph_attribution import tasks
from graph_attribution import graphnet_models as gnn_models
from graph_attribution import graphnet_techniques as techniques
from graph_attribution import datasets
from graph_attribution import experiments
from graph_attribution import templates
from graph_attribution import graphs as graph_utils
#datasets.DATA_DIR = os.path.join(REPO_DIR, 'data')
#print(f'Reading data from: {datasets.DATA_DIR}')
datasets.DATA_DIR = './graph-attribution/data'
```
<a id = "load"></a>
# Load Experiment Data, Task and Attribution Techniques
```
print(f'Available tasks: {[t.name for t in tasks.Task]}')
print(f'Available model types: {[m.name for m in gnn_models.BlockType]}')
print(f'Available ATT techniques: {list(techniques.get_techniques_dict(None,None).keys())}')
task_type = 'logic7'
block_type = 'gcn'
#task_dir = datasets.get_task_dir(task_type)
task_dir = './graph-attribution/data/logic7'
exp, task, methods = experiments.get_experiment_setup(task_type, block_type)
task_act, task_loss = task.get_nn_activation_fn(), task.get_nn_loss_fn()
graph_utils.print_graphs_tuple(exp.x_train)
print(f'Experiment data fields:{list(exp.__dict__.keys())}')
```
<a id = "model"></a>
## Creating a GNN Model
### Defining Hyperparams of the Experiment
```
hp = gatt.hparams.get_hparams({'block_type':block_type, 'task_type':task_type})
hp
```
### Instantiate model
```
model = experiments.GNN(node_size = hp.node_size,
edge_size = hp.edge_size,
global_size = hp.global_size,
y_output_size = task.n_outputs,
block_type = gnn_models.BlockType(hp.block_type),
activation = task_act,
target_type = task.target_type,
n_layers = hp.n_layers)
model(exp.x_train)
gnn_models.print_model(model)
```
<a id ="train"></a>
## Training the GNN Model
```
optimizer = snt.optimizers.Adam(hp.learning_rate)
opt_one_epoch = gatt.training.make_tf_opt_epoch_fn(exp.x_train, exp.y_train, hp.batch_size, model,
optimizer, task_loss)
pbar = tqdm(range(hp.epochs))
losses = collections.defaultdict(list)
start_time = time.time()
for _ in pbar:
train_loss = opt_one_epoch(exp.x_train, exp.y_train).numpy()
losses['train'].append(train_loss)
losses['test'].append(task_loss(exp.y_test, model(exp.x_test)).numpy())
#pbar.set_postfix({key: values[-1] for key, values in losses.items()})
losses = {key: np.array(values) for key, values in losses.items()}
# Plot losses
for key, values in losses.items():
plt.plot(values, label=key)
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend()
plt.show()
y_pred = model(exp.x_test).numpy()
y_pred[y_pred > 0.5] = 1
y_pred[y_pred <= 0.5] = 0
#y_pred
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
print(accuracy_score(exp.y_test, y_pred))
print(confusion_matrix(exp.y_test, y_pred))
print(classification_report(exp.y_test, y_pred))
# Evaluate predictions and attributions
results = []
for method in tqdm(methods.values(), total=len(methods)):
results.append(experiments.generate_result(model, method, task, exp.x_test, exp.y_test, exp.att_test))
pd.DataFrame(results)
```
<a id = "gviz"></a>
## Graph Vizualization
```
# Source: https://notebook.community/deepmind/graph_nets/graph_nets/demos/graph_nets_basics
graphs_nx = graph_nets.utils_np.graphs_tuple_to_networkxs(exp.x_test)
def nx_g_plotter(graphs_nx, ColNum=8, node_clr='#ff8080'):
_, axs = plt.subplots(ncols=ColNum, nrows = 1, figsize=(30, 5))
for iax, (graph_nx2, ax) in enumerate(zip(graphs_nx, axs)):
nx.draw(graph_nx2, ax=ax, node_color=node_clr)
ax.set_title("Graph {}".format(iax))
graphs_nx_1 = []
graphs_nx_0 = []
for ii, g_net_ii in enumerate(graphs_nx):
if exp.y_test[ii] == 1:
graphs_nx_1.append(g_net_ii)
else:
graphs_nx_0.append(g_net_ii)
nx_g_plotter(graphs_nx_1, ColNum=8, node_clr='#ff8080')
nx_g_plotter(graphs_nx_0, ColNum=8, node_clr='#00bfff')
y_wrong1[1] - y_wrong1[0]
graphs_nx_wrong0 = []
graphs_nx_wrong1 = []
graphs_nx_correct0 = []
graphs_nx_correct1 = []
y_pred2 = model(exp.x_test).numpy()
y_wrong0 = []
y_wrong1 = []
y_correct0 = []
y_correct1 = []
for ii, g_net_ii in enumerate(graphs_nx):
if exp.y_test[ii] != y_pred[ii] and exp.y_test[ii] == 0:
graphs_nx_wrong0.append(g_net_ii)
y_wrong0.append(y_pred2[ii])
elif exp.y_test[ii] != y_pred[ii] and exp.y_test[ii] == 1:
graphs_nx_wrong1.append(g_net_ii)
y_wrong1.append(y_pred2[ii])
elif exp.y_test[ii] == y_pred[ii] and exp.y_test[ii] == 0:
graphs_nx_correct0.append(g_net_ii)
y_correct0.append(y_pred2[ii])
elif exp.y_test[ii] == y_pred[ii] and exp.y_test[ii] == 1:
graphs_nx_correct1.append(g_net_ii)
y_correct1.append(y_pred2[ii])
print(len(graphs_nx_wrong0), len(graphs_nx_wrong1), len(graphs_nx_correct0), len(graphs_nx_correct1))
nx_g_plotter(graphs_nx_wrong0, ColNum=8, node_clr='#ff8080')
nx_g_plotter(graphs_nx_wrong1, ColNum=8, node_clr='#00bfff')
nx_g_plotter(graphs_nx_correct0, ColNum=8, node_clr='#00e600')
nx_g_plotter(graphs_nx_correct1, ColNum=8, node_clr='#e600ac')
y_yes = exp.y_test[exp.y_test == 1]
y_no = exp.y_test[exp.y_test != 1]
y_yes.shape, y_no.shape
recovered_data_dict_list = graph_nets.utils_np.graphs_tuple_to_data_dicts(exp.x_test)
graphs_tuple_1 = graph_nets.utils_np.data_dicts_to_graphs_tuple(recovered_data_dict_list)
```
<a id = "SafeML"></a>
## Graph Distance Measures and SafeML Idea
```
!git clone https://github.com/msarrias/graph-distance-for-complex-networks --quiet
import sys
sys.path.insert(1, '/kaggle/working/graph-distance-for-complex-networks')
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.ticker import MultipleLocator
import scipy.linalg as la
import networkx as nx
import random, time, math
from collections import Counter
import fun as f
from Graph import Graph
from Watts_Strogatz import watts_strogatz_graph
from Erdos_Renyi import erdos_renyi_graph
def Wasserstein_Dist(cdfX, cdfY):
Res = 0
power = 1
n = len(cdfX)
for ii in range(0, n-2):
height = abs(cdfX[ii]-cdfY[ii])
width = cdfX[ii+1] - cdfX[ii]
Res = Res + (height ** power) * width
return Res
def r_eigenv(G_i, G_j):
#Eigen-decomposition of G_j
A_Gi = (nx.adjacency_matrix(G_i)).todense()
D_i = np.diag(np.asarray(sum(A_Gi))[0])
eigenvalues_Gi, eigenvectors_Gi = la.eig(D_i - A_Gi)
r_eigenv_Gi = sorted(zip(eigenvalues_Gi.real, eigenvectors_Gi.T), key=lambda x: x[0])
#Eigen-decomposition of G_j
A_Gj = (nx.adjacency_matrix(G_j)).todense()
D_j = np.diag(np.asarray(sum(A_Gj))[0])
eigenvalues_Gj, eigenvectors_Gj = la.eig(D_j - A_Gj)
r_eigenv_Gj = sorted(zip(eigenvalues_Gj.real, eigenvectors_Gj.T), key=lambda x: x[0])
r = 4
signs =[-1,1]
temp = []
for sign_s in signs:
for sign_l in signs:
vri = sorted(f.normalize_eigenv(sign_s * r_eigenv_Gi[r][1]))
vrj = sorted(f.normalize_eigenv(sign_l * r_eigenv_Gj[r][1]))
cdf_dist = f.cdf_dist(vri, vrj)
temp.append(cdf_dist)
#Compute empirical CDF
step = 0.005
x=np.arange(0, 1, step)
cdf_grid_Gip = f.cdf(len(r_eigenv_Gi[r][1]),x,
f.normalize_eigenv(sorted(r_eigenv_Gi[r][1], key=lambda x: x)))
cdf_grid_Gin = f.cdf(len(r_eigenv_Gi[r][1]),x,
f.normalize_eigenv(sorted(-r_eigenv_Gi[r][1], key=lambda x: x)))
cdf_grid_Gjp = f.cdf(len(r_eigenv_Gj[r][1]),x,
f.normalize_eigenv(sorted(r_eigenv_Gj[r][1], key=lambda x: x)))
cdf_grid_Gjn = f.cdf(len(r_eigenv_Gj[r][1]),x,
f.normalize_eigenv(sorted(-r_eigenv_Gj[r][1], key=lambda x: x)))
WD1 = Wasserstein_Dist(cdf_grid_Gip, cdf_grid_Gjp)
WD2 = Wasserstein_Dist(cdf_grid_Gip, cdf_grid_Gjn)
WD3 = Wasserstein_Dist(cdf_grid_Gin, cdf_grid_Gjp)
WD4 = Wasserstein_Dist(cdf_grid_Gin, cdf_grid_Gjn)
WD = [WD1, WD2, WD3, WD4]
return max(temp), max(WD)
distt_wrong1_correct1 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_correct1)))
WDist_wrong1_correct1 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_correct1)))
Conf_W1_C1 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_correct1)))
for ii, g_net_ii in enumerate(graphs_nx_wrong1):
for jj, g_net_jj in enumerate(graphs_nx_correct1):
distt_wrong1_correct1[ii,jj], WDist_wrong1_correct1[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
Conf_W1_C1[ii,jj] = y_correct1[jj] - y_wrong1[ii]
import seaborn as sns; sns.set_theme()
#ax = sns.heatmap(distt)
#ax = sns.displot(distt_wrong1_correct1.flatten())
df = pd.DataFrame()
df['WDist_W1_C1'] = WDist_wrong1_correct1.flatten()
df['Conf_W1_C1'] = Conf_W1_C1.flatten()
sns.scatterplot(data=df, x="Conf_W1_C1", y="WDist_W1_C1")
graphs_nx_train = graph_nets.utils_np.graphs_tuple_to_networkxs(exp.x_train)
graphs_nx_train_1 = []
graphs_nx_train_0 = []
for ii, g_net_ii in enumerate(graphs_nx_train):
if exp.y_train[ii] == 1:
graphs_nx_train_1.append(g_net_ii)
else:
graphs_nx_train_0.append(g_net_ii)
distt_wrong1_train1 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_train_1)))
WDist_wrong1_train1 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_train_1)))
for ii, g_net_ii in enumerate(graphs_nx_wrong1):
for jj, g_net_jj in enumerate(graphs_nx_train_1):
distt_wrong1_train1[ii,jj], WDist_wrong1_train1[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
distt_wrong1_train0 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_train_0)))
WDist_wrong1_train0 = np.zeros((len(graphs_nx_wrong1),len(graphs_nx_train_0)))
for ii, g_net_ii in enumerate(graphs_nx_wrong1):
for jj, g_net_jj in enumerate(graphs_nx_train_0):
distt_wrong1_train0[ii,jj], WDist_wrong1_train0[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
#ax = sns.displot(distt_wrong1_train1.flatten())
ax2 = sns.displot(WDist_wrong1_correct1.flatten(), kind = 'kde')
ax2 = sns.displot(WDist_wrong1_train1.flatten(), kind = 'kde')
ax2 = sns.displot(WDist_wrong1_train0.flatten(), kind = 'kde')
distt_wrong0_correct0 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_correct0)))
WDist_wrong0_correct0 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_correct0)))
for ii, g_net_ii in enumerate(graphs_nx_wrong0):
for jj, g_net_jj in enumerate(graphs_nx_correct0):
distt_wrong0_correct0[ii,jj], WDist_wrong0_correct0[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
distt_wrong0_train0 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_train_0)))
WDist_wrong0_train0 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_train_0)))
for ii, g_net_ii in enumerate(graphs_nx_wrong0):
for jj, g_net_jj in enumerate(graphs_nx_train_0):
distt_wrong0_train0[ii,jj], WDist_wrong0_train0[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
distt_wrong0_train1 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_train_1)))
WDist_wrong0_train1 = np.zeros((len(graphs_nx_wrong0),len(graphs_nx_train_1)))
for ii, g_net_ii in enumerate(graphs_nx_wrong0):
for jj, g_net_jj in enumerate(graphs_nx_train_1):
distt_wrong0_train1[ii,jj], WDist_wrong0_train1[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
ax2 = sns.displot(WDist_wrong0_correct0.flatten(), kind = 'kde')
ax2 = sns.displot(WDist_wrong0_train0.flatten(), kind = 'kde')
ax2 = sns.displot(WDist_wrong0_train1.flatten(), kind = 'kde')
distt_correct0_train0 = np.zeros((len(graphs_nx_correct0),len(graphs_nx_train_0)))
WDist_correct0_train0 = np.zeros((len(graphs_nx_correct0),len(graphs_nx_train_0)))
for ii, g_net_ii in enumerate(graphs_nx_correct0):
for jj, g_net_jj in enumerate(graphs_nx_train_0):
distt_correct0_train0[ii,jj], WDist_correct0_train0[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
distt_correct0_train1 = np.zeros((len(graphs_nx_correct0),len(graphs_nx_train_1)))
WDist_correct0_train1 = np.zeros((len(graphs_nx_correct0),len(graphs_nx_train_1)))
for ii, g_net_ii in enumerate(graphs_nx_correct0):
for jj, g_net_jj in enumerate(graphs_nx_train_1):
distt_correct0_train1[ii,jj], WDist_correct0_train1[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
if 0:
distt_correct1_train0 = np.zeros((len(graphs_nx_correct1),len(graphs_nx_train_0)))
WDist_correct1_train0 = np.zeros((len(graphs_nx_correct1),len(graphs_nx_train_0)))
for ii, g_net_ii in enumerate(graphs_nx_correct1):
for jj, g_net_jj in enumerate(graphs_nx_train_0):
distt_correct1_train0[ii,jj], WDist_correct1_train0[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
distt_correct1_train1 = np.zeros((len(graphs_nx_correct1),len(graphs_nx_train_1)))
WDist_correct1_train1 = np.zeros((len(graphs_nx_correct1),len(graphs_nx_train_1)))
for ii, g_net_ii in enumerate(graphs_nx_correct1):
for jj, g_net_jj in enumerate(graphs_nx_train_1):
distt_correct1_train1[ii,jj], WDist_correct1_train1[ii,jj] = r_eigenv(g_net_ii, g_net_jj)
def Wasserstein_Dist(XX, YY):
import numpy as np
nx = len(XX)
ny = len(YY)
n = nx + ny
XY = np.concatenate([XX,YY])
X2 = np.concatenate([np.repeat(1/nx, nx), np.repeat(0, ny)])
Y2 = np.concatenate([np.repeat(0, nx), np.repeat(1/ny, ny)])
S_Ind = np.argsort(XY)
XY_Sorted = XY[S_Ind]
X2_Sorted = X2[S_Ind]
Y2_Sorted = Y2[S_Ind]
Res = 0
E_CDF = 0
F_CDF = 0
power = 1
for ii in range(0, n-2):
E_CDF = E_CDF + X2_Sorted[ii]
F_CDF = F_CDF + Y2_Sorted[ii]
height = abs(F_CDF-E_CDF)
width = XY_Sorted[ii+1] - XY_Sorted[ii]
Res = Res + (height ** power) * width;
return Res
def Wasserstein_Dist_PVal(XX, YY):
# Information about Bootstrap: https://towardsdatascience.com/an-introduction-to-the-bootstrap-method-58bcb51b4d60
import random
nboots = 1000
WD = Wasserstein_Dist(XX,YY)
na = len(XX)
nb = len(YY)
n = na + nb
comb = np.concatenate([XX,YY])
reps = 0
bigger = 0
for ii in range(1, nboots):
e = random.sample(range(n), na)
f = random.sample(range(n), nb)
boost_WD = Wasserstein_Dist(comb[e],comb[f]);
if (boost_WD > WD):
bigger = 1 + bigger
pVal = bigger/nboots;
return pVal, WD
pVal, WD = Wasserstein_Dist_PVal(WDist_wrong0_train0.flatten(), WDist_wrong0_train1.flatten())
print(pVal, WD)
#pVal, WD = Wasserstein_Dist_PVal(WDist_correct0_train0.flatten(), WDist_correct0_train1.flatten())
#print(pVal, WD)
pVal, WD = Wasserstein_Dist_PVal(WDist_wrong1_train1.flatten(), WDist_wrong1_train0.flatten())
print(pVal, WD)
```
<a id = "dis"></a>
## Discussion
It seems that the current idea is not successful and we should do more investigation. We can also consider about model-specific SafeML.
| true |
code
| 0.481881 | null | null | null | null |
|
[@LorenaABarba](https://twitter.com/LorenaABarba)
12 steps to Navier–Stokes
=====
***
For a moment, recall the Navier–Stokes equations for an incompressible fluid, where $\vec{v}$ represents the velocity field:
$$
\begin{eqnarray*}
\nabla \cdot\vec{v} &=& 0 \\
\frac{\partial \vec{v}}{\partial t}+(\vec{v}\cdot\nabla)\vec{v} &=& -\frac{1}{\rho}\nabla p + \nu \nabla^2\vec{v}
\end{eqnarray*}
$$
The first equation represents mass conservation at constant density. The second equation is the conservation of momentum. But a problem appears: the continuity equation for incompressble flow does not have a dominant variable and there is no obvious way to couple the velocity and the pressure. In the case of compressible flow, in contrast, mass continuity would provide an evolution equation for the density $\rho$, which is coupled with an equation of state relating $\rho$ and $p$.
In incompressible flow, the continuity equation $\nabla \cdot\vec{v}=0$ provides a *kinematic constraint* that requires the pressure field to evolve so that the rate of expansion $\nabla \cdot\vec{v}$ should vanish everywhere. A way out of this difficulty is to *construct* a pressure field that guarantees continuity is satisfied; such a relation can be obtained by taking the divergence of the momentum equation. In that process, a Poisson equation for the pressure shows up!
Step 10: 2D Poisson Equation
----
***
Poisson's equation is obtained from adding a source term to the right-hand-side of Laplace's equation:
$$\frac{\partial ^2 p}{\partial x^2} + \frac{\partial ^2 p}{\partial y^2} = b$$
So, unlinke the Laplace equation, there is some finite value inside the field that affects the solution. Poisson's equation acts to "relax" the initial sources in the field.
In discretized form, this looks almost the same as [Step 9](./12_Step_9.ipynb), except for the source term:
$$\frac{p_{i+1,j}^{n}-2p_{i,j}^{n}+p_{i-1,j}^{n}}{\Delta x^2}+\frac{p_{i,j+1}^{n}-2 p_{i,j}^{n}+p_{i,j-1}^{n}}{\Delta y^2}=b_{i,j}^{n}$$
As before, we rearrange this so that we obtain an equation for $p$ at point $i,j$. Thus, we obtain:
$$p_{i,j}^{n}=\frac{(p_{i+1,j}^{n}+p_{i-1,j}^{n})\Delta y^2+(p_{i,j+1}^{n}+p_{i,j-1}^{n})\Delta x^2-b_{i,j}^{n}\Delta x^2\Delta y^2}{2(\Delta x^2+\Delta y^2)}$$
We will solve this equation by assuming an initial state of $p=0$ everywhere, and applying boundary conditions as follows:
$p=0$ at $x=0, \ 2$ and $y=0, \ 1$
and the source term consists of two initial spikes inside the domain, as follows:
$b_{i,j}=100$ at $i=\frac{1}{4}nx, j=\frac{1}{4}ny$
$b_{i,j}=-100$ at $i=\frac{3}{4}nx, j=\frac{3}{4}ny$
$b_{i,j}=0$ everywhere else.
The iterations will advance in pseudo-time to relax the initial spikes. The relaxation under Poisson's equation gets slower and slower as they progress. *Why?*
Let's look at one possible way to write the code for Poisson's equation. As always, we load our favorite Python libraries. We also want to make some lovely plots in 3D. Let's get our parameters defined and the initialization out of the way. What do you notice of the approach below?
```
import numpy
from matplotlib import pyplot, cm
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
# Parameters
nx = 50
ny = 50
nt = 100
xmin = 0
xmax = 2
ymin = 0
ymax = 1
dx = (xmax - xmin) / (nx - 1)
dy = (ymax - ymin) / (ny - 1)
# Initialization
p = numpy.zeros((ny, nx))
pd = numpy.zeros((ny, nx))
b = numpy.zeros((ny, nx))
x = numpy.linspace(xmin, xmax, nx)
y = numpy.linspace(xmin, xmax, ny)
# Source
b[int(ny / 4), int(nx / 4)] = 100
b[int(3 * ny / 4), int(3 * nx / 4)] = -100
```
With that, we are ready to advance the initial guess in pseudo-time. How is the code below different from the function used in [Step 9](./12_Step_9.ipynb) to solve Laplace's equation?
```
for it in range(nt):
pd = p.copy()
p[1:-1,1:-1] = (((pd[1:-1, 2:] + pd[1:-1, :-2]) * dy**2 +
(pd[2:, 1:-1] + pd[:-2, 1:-1]) * dx**2 -
b[1:-1, 1:-1] * dx**2 * dy**2) /
(2 * (dx**2 + dy**2)))
p[0, :] = 0
p[ny-1, :] = 0
p[:, 0] = 0
p[:, nx-1] = 0
```
Maybe we could reuse our plotting function from [Step 9](./12_Step_9.ipynb), don't you think?
```
def plot2D(x, y, p):
fig = pyplot.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
X, Y = numpy.meshgrid(x, y)
surf = ax.plot_surface(X, Y, p[:], rstride=1, cstride=1, cmap=cm.viridis,
linewidth=0, antialiased=False)
ax.view_init(30, 225)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plot2D(x, y, p)
```
Ah! The wonders of code reuse! Now, you probably think: "Well, if I've written this neat little function that does something so useful, I want to use it over and over again. How can I do this without copying and pasting it each time? —If you are very curious about this, you'll have to learn about *packaging*. But this goes beyond the scope of our CFD lessons. You'll just have to Google it if you really want to know.
***
## Learn More
To learn more about the role of the Poisson equation in CFD, watch **Video Lesson 11** on You Tube:
```
from IPython.display import YouTubeVideo
YouTubeVideo('ZjfxA3qq2Lg')
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
> (The cell above executes the style for this notebook.)
| true |
code
| 0.381824 | null | null | null | null |
|
# Fibonacci Series Classifier
*Author: Brianna Gopaul*
The fibonacci series is a sequence of numbers that increases as it sums up it's two subsequent values. For example, 1, 1, 2, 3 are numbers within the fibonacci series because 1 + 1 = 2 + 1 = 3.
Below we create a supervised model that classifies fibonacci sequences from non-fibonacci sequences in Strawberry Fields using The [Quantum Machine Learning Toolbox](https://github.com/XanaduAI/qmlt).

## Supervised Model Tutorial
```
import tensorflow as tf
import strawberryfields as sf
from strawberryfields.ops import *
from qmlt.tf.helpers import make_param
from qmlt.tf import CircuitLearner
```
Here we define the number of iterations we want our model to run through.
```
steps = 100
```
Now we create a circuit that contains trainable parameters. The line proceeding it takes the shape of the input and runs the circuit. The tensorflow backend 'tf' is used and arguments eval, cutoff_dim and batch_size are defined. Different arguments will be required depending on the backend used. The fock backend can alternatively be used.
The output of the circuit is measure using photon counting. If we measure zero photons in the first mode and two photons in the second mode, this output is defined as p0
```
def circuit(X):
kappa = make_param('kappa', constant=0.9)
theta = make_param('theta', constant=2.25)
eng, q = sf.Engine(2)
with eng:
Dgate(X[:, 0], X[:, 1]) | q[0]
BSgate(theta=theta) | (q[0], q[1])
Sgate(X[:, 0], X[:, 1]) | q[0]
Sgate(X[:, 0], X[:, 1]) | q[1]
BSgate(theta=theta) | (q[0], q[1])
Dgate(X[:, 0], X[:, 1]) | q[0]
Kgate(kappa=kappa) | q[0]
Kgate(kappa=kappa) | q[1]
num_inputs = X.get_shape().as_list()[0]
state = eng.run('tf', cutoff_dim=10, eval=False, batch_size=num_inputs)
p0 = state.fock_prob([0, 2])
p1 = state.fock_prob([2, 0])
normalisation = p0 + p1 + 1e-10
circuit_output = p1/normalisation
return circuit_output
```
In machine learning, the loss function tells us how much error there is between the correct value and the output value.
Mean Squared Error (MSE) minimizes the summation of all errors squared.
```
def myloss(circuit_output, targets):
return tf.losses.mean_squared_error(labels=circuit_output, predictions=targets)
def outputs_to_predictions(circuit_output):
return tf.round(circuit_output)
#training and testing data
X_train = [[0.1, 0.1, 0.2, 0.3],[0.3, 0.4, 0.5, 0.8], [0.3,0.6,0.9,0.13], [0.5, 0.8, 0.14, 0.21],[0.3, 0.5, 0.8, 0.13],[0.08, 0.13, 0.21, 0.34],[0.21, 0.36, 0.59, 0.99], [1, 1, 2, 3], [0.3, 0.5, 0.8, 0.13],[0.13, 0.21, 0.34, 0.55], [0.10, 0.777, 0.13434334, 0.88809], [0.1, 0.9, 0.13, 0.17],[0.43, 0.675, 0.2, 0.9], [0.98, 0.32, 0.1, 0.3], [0.15, 0.21, 0.34, 0.56], [0.1, 0.1, 0.2, 0.3], [0.1, 0.15, 0.3, 0.5],[0.1, 0.2, 0.4, 0.5],[0.3, 0.4, 0.5, 0.8],[0.3,0.6,0.9,0.13],[0.15, 0.15, 0.25, 0.35],[0.15, 0.25, 0.35, 0.45],[0.46, 0.29, 0.7, 0.57],[0.55,0.89,1.44,2.33],[0.233, 0.377, 0.61, 0.987], [0.987, 1.597, 2.584, 4.181],[0.6, 0.7, 0.13, 0.20],[0.233, 0.377, 0.61, 0.987],[0.0008, 0.013, 0.0021, 0.0034], [0.5, 0.6, 0.11, 0.17], [0.4, 0.5, 0.9, 0.13], [0.3, 0.5, 0.8, 0.18],[0.1, 0.1, 0.2, 0.6], [0.4, 0.5, 0.10, 0.15], [0.2, 0.3, 0.5, 0.10], [0.2, 0.3, 0.6, 0.43], [0.1, 0.3, 0.4, 0.2], [0.3, 0.5, 0.8, 0.787687], [0.5, 0.8, 1.3, 1], [0.08, 0.13, 0.21, 0.4]]
Y_train = [1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
X_test = [[0.5, 0.8, 0.13, 0.21], [0.21, 0.34, 0.55, 0.89], [0.7, 0.1, 0.879, 0.444], [0.20, 0.56, 0.909, 0.11], [0.2, 0.4, 0.6, 0.99],[0.53, 0.66, 0.06, 0.31], [0.24, 0.79, 0.25, 0.69], [0.008, 0.013, 0.021, 0.034], [0.144, 0.233, 0.377, 0.61], [0.61, 0.987, 1.597, 2.584], [0.34, 0.55, 0.89, 1.44], [0.034, 0.055, 0.089, 0.144],[0.2, 0.3, 0.5, 0.8], [0.5, 0.8, 1.3, 2.1], [0.413, 0.875, 0.066, 0.63], [0.3, 0.5, 0.7, 0.9], [0.2, 0.5, 0.14, 0.12], [0.5, 0.6, 0.7, 0.8],[0.5, 0.6, 0.9, 0.7],[0.5, 0.2, 0.9, 0.7],[0.4, 0.6, 0.4, 0.3],[0.9, 0.6, 0.4, 0.9],[0.9, 0.1, 0.6, 0.9],[0.8, 0.8, 0.6, 0.5]]
Y_test = [1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
X_pred = [[0.233, 0.377, 0.61, 0.987], [0.55, 0.89, 1.44, 2.33], [0.0013, 0.0021, 0.0034, 0.0055], [0.5, 0.8, 1.3, 2.1], [0.89, 1.44, 2.33, 3.77], [0.03, 0.05, 0.3, 0.13], [0.40, 0.34, 0.55, 0.89], [0.2, 0.45, 0.5, 0.8], [0.08, 0.13, 0.30, 0.34], [0.13, 0.21, 0.34, 0.80]]
```
Hyperparameters that define the task, optimizer and various other parameters listed in the QMLT docs are defined below.
A learner is then fed the hyperparameters and data.
```
hyperparams= {'circuit': circuit,
'task': 'supervised',
'loss': myloss,
'optimizer': 'SGD',
'init_learning_rate': 0.1,
'print_log': True}
learner = CircuitLearner(hyperparams=hyperparams)
learner.train_circuit(X=X_train, Y=Y_train, steps=steps)
test_score = learner.score_circuit(X=X_test, Y=Y_test,outputs_to_predictions=outputs_to_predictions)
print("Accuracy on test set: ", test_score['accuracy'])
outcomes = learner.run_circuit(X=X_pred, outputs_to_predictions=outputs_to_predictions)
print("Predictions for new inputs: {}".format(outcomes['predictions']))
```
## Observations
### Small Dataset vs Large Dataset
Here we fix the value of x_pred in each test and feed the model two different datasets in order to see the success rate of using each model. The difficulty of x_pred will vary depending on the model's success rate.
```
X_pred_level1 = [[0.08, 0.13, 0.21, 0.34], [0.2, 0.3, 0.5, 0.8],[0.01, 0.01, 0.02, 0.03],[0.008, 0.013, 0.021, 0.034], [0.3, 0.5, 0.8, 0.13], [0.55, 0.64, 0.77, 0.21], [0.62, 0.93, 0.38, 0.23],[0.9, 0.8, 0.7, 0.6], [0.4, 0.6, 0.78, 0.77],[0.44, 0.96, 0.28, 0.33]]
X_pred_level2 = [[0.34, 0.55, 0.89, 1.44], [0.003, 0.005, 0.008, 0.013], [0.3, 0.5, 0.8, 1.3], [0.08, 0.13, 0.21, 0.34], [0.5, 0.8, 1.3, 2.1], [0.413, 0.875, 0.066, 0.63], [0.3, 0.5, 0.7, 0.4], [0.3, 0.8, 0.12, 0.2], [0.4, 0.5, 0.7, 0.7], [0.7, 0.0, 0.6, 0.5]]
X_pred_level3 = [[0.233, 0.377, 0.61, 0.987], [0.55, 0.89, 1.44, 2.33], [0.0013, 0.0021, 0.0034, 0.0055], [0.5, 0.8, 1.3, 2.1], [0.89, 1.44, 2.33, 3.77], [0.03, 0.05, 0.3, 0.13], [0.40, 0.34, 0.55, 0.89], [0.2, 0.45, 0.5, 0.8], [0.08, 0.13, 0.30, 0.34], [0.13, 0.21, 0.34, 0.80]]
```
### Sparse Dataset
```
X_train = [[0.1, 0.1, 0.2, 0.3],[0.5, 0.8, 0.14, 0.21],[0.3, 0.4, 0.5, 0.8], [0.3, 0.6, 0.9, 0.13]]
Y_train = [1, 1, 0, 0]
X_test = [[0.5, 0.8, 0.13, 0.21], [0.21, 0.34, 0.55, 0.89], [0.7, 0.1, 0.879, 0.444], [0.20, 0.56, 0.909, 0.11]]
Y_test = [1, 1, 0, 0]
```
### Large Dataset
```
X_train = [[0.1, 0.1, 0.2, 0.3],[0.3, 0.4, 0.5, 0.8], [0.3,0.6,0.9,0.13], [0.5, 0.8, 0.14, 0.21],[0.3, 0.5, 0.8, 0.13],[0.08, 0.13, 0.21, 0.34],[0.21, 0.36, 0.59, 0.99], [1, 1, 2, 3], [0.3, 0.5, 0.8, 0.13],[0.13, 0.21, 0.34, 0.55], [0.10, 0.777, 0.13434334, 0.88809], [0.1, 0.9, 0.13, 0.17],[0.43, 0.675, 0.2, 0.9], [0.98, 0.32, 0.1, 0.3], [0.15, 0.21, 0.34, 0.56], [0.1, 0.1, 0.2, 0.3], [0.1, 0.15, 0.3, 0.5],[0.1, 0.2, 0.4, 0.5],[0.3, 0.4, 0.5, 0.8],[0.3,0.6,0.9,0.13],[0.15, 0.15, 0.25, 0.35],[0.15, 0.25, 0.35, 0.45],[0.46, 0.29, 0.7, 0.57],[0.55,0.89,1.44,2.33],[0.233, 0.377, 0.61, 0.987], [0.987, 1.597, 2.584, 4.181],[0.6, 0.7, 0.13, 0.20],[0.233, 0.377, 0.61, 0.987],[0.0008, 0.013, 0.0021, 0.0034], [0.5, 0.6, 0.11, 0.17], [0.4, 0.5, 0.9, 0.13], [0.3, 0.5, 0.8, 0.18],[0.1, 0.1, 0.2, 0.6], [0.4, 0.5, 0.10, 0.15], [0.2, 0.3, 0.5, 0.10], [0.2, 0.3, 0.6, 0.43], [0.1, 0.3, 0.4, 0.2], [0.3, 0.5, 0.8, 0.787687], [0.5, 0.8, 1.3, 1], [0.08, 0.13, 0.21, 0.4]]
Y_train = [1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
X_test = [[0.5, 0.8, 0.13, 0.21], [0.21, 0.34, 0.55, 0.89], [0.7, 0.1, 0.879, 0.444], [0.20, 0.56, 0.909, 0.11], [0.2, 0.4, 0.6, 0.99],[0.53, 0.66, 0.06, 0.31], [0.24, 0.79, 0.25, 0.69], [0.008, 0.013, 0.021, 0.034], [0.144, 0.233, 0.377, 0.61], [0.61, 0.987, 1.597, 2.584], [0.34, 0.55, 0.89, 1.44], [0.034, 0.055, 0.089, 0.144],[0.2, 0.3, 0.5, 0.8], [0.5, 0.8, 1.3, 2.1], [0.413, 0.875, 0.066, 0.63], [0.3, 0.5, 0.7, 0.9], [0.2, 0.5, 0.14, 0.12], [0.5, 0.6, 0.7, 0.8],[0.5, 0.6, 0.9, 0.7],[0.5, 0.2, 0.9, 0.7],[0.4, 0.6, 0.4, 0.3],[0.9, 0.6, 0.4, 0.9],[0.9, 0.1, 0.6, 0.9],[0.8, 0.8, 0.6, 0.5]]
Y_test = [1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
```
### Data Generation
```
import random
import numpy as np
x=np.random.random(4)
np.set_printoptions(precision=2)
print(x)
a = [1,1]
idx = 0
for i in range(30):
a.append(a[idx] + a[idx+1])
idx +=1
print(a[-1]/100)
```
## Results
### Level 1
```
X_pred_level1 = [[0.08, 0.13, 0.21, 0.34], [0.2, 0.3, 0.5, 0.8],[0.01, 0.01, 0.02, 0.03],[0.008, 0.013, 0.021, 0.034], [0.3, 0.5, 0.8, 0.13], [0.55, 0.64, 0.77, 0.21], [0.62, 0.93, 0.38, 0.23],[0.9, 0.8, 0.7, 0.6], [0.4, 0.6, 0.78, 0.77],[0.44, 0.96, 0.28, 0.33]]
```
Level 1 is the easiest classification task. To challenge the model, the non-fibonacci sequences are close in value to each other.
__Tasks Classified Correctly:__
* Large Dataset: 20%
* Small Dataset: 80%
### Level 2
```
X_pred_level2 = [[0.34, 0.55, 0.89, 1.44], [0.003, 0.005, 0.008, 0.013], [0.3, 0.5, 0.8, 1.3], [0.08, 0.13, 0.21, 0.34], [0.5, 0.8, 1.3, 2.1], [0.413, 0.875, 0.066, 0.63], [0.3, 0.5, 0.7, 0.4], [0.3, 0.8, 0.12, 0.2], [0.4, 0.5, 0.7, 0.7], [0.7, 0.0, 0.6, 0.5]]
```
Level 2 challenges the model by testing it against unfamiliar fibonacci sequences. The non-fibonacci numbers also become closer in value.
__Tasks Classified Correctly:__
* Large Dataset: 40%
* Small Dataset: 70%
### Level 3
```
X_pred_level3 = [[0.233, 0.377, 0.61, 0.987], [0.55, 0.89, 1.44, 2.33], [0.0013, 0.0021, 0.0034, 0.0055], [0.5, 0.8, 1.3, 2.1], [0.89, 1.44, 2.33, 3.77], [0.03, 0.05, 0.3, 0.13], [0.40, 0.34, 0.55, 0.89], [0.2, 0.45, 0.5, 0.8], [0.08, 0.13, 0.30, 0.34], [0.13, 0.21, 0.34, 0.80]]
```
Level 3 is the most difficult test set.
<br>
It contains number sequences that appear to follow the fibonacci pattern but are off by a small value. e.g. 0.13, 0.21, 0.34, 0.80
**Tasks Classified Correctly:**
* Large Dataset: 70%
* Small Dataset: 30%
The graph below illustrates the performance of the small dataset model and the large dataset model on each test set.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
N = 3
B = (20, 40, 70)
A = (80, 70, 30)
BB = (1, 1, 1)
AA = (1, 1, 1)
ind = np.arange(N) # the x locations for the groups
width = 0.35 # the width of the bars: can also be len(x) sequence
p1 = plt.bar(ind, B, width, yerr=BB)
p2 = plt.bar(ind, A, width,
bottom=B, yerr=AA)
plt.ylabel('Correct Classifications(%)')
plt.title('Large Dataset vs Small Dataset Performance')
plt.xticks(ind, ('L1', 'L2', 'L3'))
plt.yticks(np.arange(0, 81, 10))
plt.legend((p1[0], p2[0]), ('Large Dataset', 'Small Dataset'))
plt.show()
```
| true |
code
| 0.513181 | null | null | null | null |
|
# Predicting Concrete Compressive Strength - Comparison with Linear Models
In this code notebook, we will analyze the statistics pertaining the various models presented in this project. In the Exploratory Data Analysis notebook, we explored the various relationships that each consituent of concrete has on the cured compressive strength. The materials that held the strongest relationships, regardless of curing time, were cement, cementitious ratio, superplasticizer ratio, and fly ash ratio. We will examine each of the linear ratios independent of age, as well as at the industry-standard 28 day cure time mark.
## Dataset Citation
This dataset was retrieved from the UC Irvine Machine Learning Repository from the following URL: <https://archive.ics.uci.edu/ml/datasets/Concrete+Compressive+Strength>.
The dataset was donated to the UCI Repository by Prof. I-Cheng Yeh of Chung-Huah University, who retains copyright for the following published paper: I-Cheng Yeh, "Modeling of strength of high performance concrete using artificial neural networks," Cement and Concrete Research, Vol. 28, No. 12, pp. 1797-1808 (1998). Additional papers citing this dataset are listed at the reference link above.
## Import the Relevant Libraries
```
# Data Manipulation
import numpy as np
import pandas as pd
# Data Visualization
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set()
# Data Preprocessing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# Linear Regresssion Model
from sklearn.linear_model import LinearRegression
# Model Evaluation
from sklearn.metrics import mean_squared_error,mean_absolute_error,explained_variance_score
```
## Import & Check the Data
```
df1 = pd.read_csv('2020_1124_Modeling_Data.csv')
df2 = pd.read_csv('2020_1123_Concrete_Data_Loaded_Transformed.csv')
original_data = df1.copy()
transformed_data = df2.copy()
# The original data contains kg/m^3 values
original_data.head()
# Original data
original_data.describe()
# The transformed data contains ratios to total mass of the concrete mix
transformed_data.head()
# Transformed data
transformed_data.describe()
```
## Cement Modeling - Including All Cure Times
We understand that the ratio of cement to compressive strength is linear. We will model this relationship in Python and evaluate its performance compared to our ANN model.
### Visualization
```
# We will visualize the linear relationship between quantity of cement and compressive strength
cement = original_data['Cement']
strength = original_data['Compressive_Strength']
plt.scatter(cement,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(cement).reshape(1030,1)
y = np.array(strength).reshape(1030,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_cement = mean_absolute_error(y_test, y_pred)
MSE_cement = mean_squared_error(y_test, y_pred)
RMSE_cement = np.sqrt(mean_squared_error(y_test, y_pred))
cement_stats = [MAE_cement,MSE_cement,RMSE_cement] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR CEMENT VS. COMPRESSIVE STRENGTH")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_cement}\nMean Squared Error:\t\t\t{MSE_cement}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_cement}")
print('-----------------------------\n\n')
```
## Cement Modeling - 28 Day Cure Time
We will model the cement vs compressive strength relationship for a constant cure time (28 days).
### Visualization
```
# We will visualize the linear relationship between quantity of cement and compressive strength at 28 days
cement = original_data[original_data['Age']==28]['Cement']
strength = original_data[original_data['Age']==28]['Compressive_Strength']
plt.scatter(cement,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(cement).reshape(425,1)
y = np.array(strength).reshape(425,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_cement_28 = mean_absolute_error(y_test, y_pred)
MSE_cement_28 = mean_squared_error(y_test, y_pred)
RMSE_cement_28 = np.sqrt(mean_squared_error(y_test, y_pred))
cement_28_stats = [MAE_cement_28,MSE_cement_28,RMSE_cement_28] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR CEMENT VS. COMPRESSIVE STRENGTH")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_cement_28}\nMean Squared Error:\t\t\t{MSE_cement_28}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_cement_28}")
print('-----------------------------\n\n')
```
## Cementitious Ratio Modeling - Including All Cure Times
We know that the ratio of cementitious materials to the total mass is (cement + fly ash)/(total mass) to compressive strength is linear. We will model this relationship in Python and evaluate its performance.
### Visualization
```
# We will visualize the linear relationship between quantity of cementitious materials and compressive strength
cementitious = transformed_data['Cementitious_Ratio']
strength = transformed_data['Compressive_Strength']
plt.scatter(cementitious,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(cementitious).reshape(1030,1)
y = np.array(strength).reshape(1030,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_cementitious = mean_absolute_error(y_test, y_pred)
MSE_cementitious = mean_squared_error(y_test, y_pred)
RMSE_cementitious = np.sqrt(mean_squared_error(y_test, y_pred))
cementitious_stats = [MAE_cementitious,MSE_cementitious,RMSE_cementitious] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR CEMENTITIOUS RATIO VS. COMPRESSIVE STRENGTH")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_cementitious}\nMean Squared Error:\t\t\t{MSE_cementitious}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_cementitious}")
print('-----------------------------\n\n')
```
## Cementitious Ratio Modeling - 28 Day Cure Time
### Visualization
```
# We will visualize the linear relationship between quantity of cementitious materials and compressive strength at 28 days
cementitious = transformed_data[original_data['Age']==28]['Cementitious_Ratio']
strength = transformed_data[original_data['Age']==28]['Compressive_Strength']
plt.scatter(cementitious,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(cementitious).reshape(425,1)
y = np.array(strength).reshape(425,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_cementitious_28 = mean_absolute_error(y_test, y_pred)
MSE_cementitious_28 = mean_squared_error(y_test, y_pred)
RMSE_cementitious_28 = np.sqrt(mean_squared_error(y_test, y_pred))
cementitious_28_stats = [MAE_cementitious_28,MSE_cementitious_28,RMSE_cementitious_28] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR CEMENTITIOUS RATIO VS. COMPRESSIVE STRENGTH AT 28 DAYS")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_cementitious_28}\nMean Squared Error:\t\t\t{MSE_cementitious_28}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_cementitious_28}")
print('-----------------------------\n\n')
```
## Fly Ash Ratio Modeling - Including All Cure Times
The fly ash ratio is interpreted as the percentage of fly ash within the cementitious materials mix, that is, Fly_Ash_Ratio = (fly ash + cement)/(total mass).
### Visualization
```
# We will visualize the linear relationship between fly ash ratio and compressive strength
fly = transformed_data['Fly_Ash_Ratio']
strength = transformed_data['Compressive_Strength']
plt.scatter(fly,strength)
```
### Data Preprocessing
We see from the graph above that there are many instances where there is no fly ash in the mix design. Let us use only nonzero entries for our analysis.
```
fly = transformed_data[transformed_data['Fly_Ash_Ratio']!=0]['Fly_Ash_Ratio']
strength = transformed_data[transformed_data['Fly_Ash_Ratio']!=0]['Compressive_Strength']
plt.scatter(fly,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(fly).reshape(464,1)
y = np.array(strength).reshape(464,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_fly = mean_absolute_error(y_test, y_pred)
MSE_fly = mean_squared_error(y_test, y_pred)
RMSE_fly = np.sqrt(mean_squared_error(y_test, y_pred))
fly_stats = [MAE_fly,MSE_fly,RMSE_fly] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR FLY ASH RATIO VS. COMPRESSIVE STRENGTH")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_fly}\nMean Squared Error:\t\t\t{MSE_fly}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_fly}")
print('-----------------------------\n\n')
```
## Fly Ash Ratio Modeling - 28 Day Cure Time
The fly ash ratio is interpreted as the percentage of fly ash within the cementitious materials mix, that is, Fly_Ash_Ratio = (fly ash + cement)/(total mass).
```
fly = transformed_data[((transformed_data['Fly_Ash_Ratio']!=0)&(transformed_data['Age']==28))]['Fly_Ash_Ratio']
strength = transformed_data[((transformed_data['Fly_Ash_Ratio']!=0)&(transformed_data['Age']==28))]['Compressive_Strength']
plt.scatter(fly,strength)
```
### Train the Linear Model
```
# Reshape the data so it complies with the linear model requirements
X = np.array(fly).reshape(217,1)
y = np.array(strength).reshape(217,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_fly_28 = mean_absolute_error(y_test, y_pred)
MSE_fly_28 = mean_squared_error(y_test, y_pred)
RMSE_fly_28 = np.sqrt(mean_squared_error(y_test, y_pred))
fly_28_stats = [MAE_fly_28,MSE_fly_28,RMSE_fly_28] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR FLY ASH RATIO VS. COMPRESSIVE STRENGTH AT 28 DAYS")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_fly_28}\nMean Squared Error:\t\t\t{MSE_fly_28}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_fly_28}")
print('-----------------------------\n\n')
```
## Superplasticizer Ratio Modeling - Including All Cure Times
The superplasticizer ratio is the ratio of superplasticizer contained within the total mix design, by weight.
### Visualization
```
# We will visualize the linear relationship between superplasticizer ratio and compressive strength
superplasticizer = transformed_data['Superplasticizer_Ratio']
strength = transformed_data['Compressive_Strength']
plt.scatter(superplasticizer,strength)
```
### Data Preprocessing
Once agaain, we see from the graph above that there are many instances where there is no superplasticizer in the mix design. Let us use only nonzero entries for our analysis.
```
superplasticizer = transformed_data[transformed_data['Superplasticizer_Ratio']!=0]['Superplasticizer_Ratio']
strength = transformed_data[transformed_data['Superplasticizer_Ratio']!=0]['Compressive_Strength']
plt.scatter(superplasticizer,strength)
```
This is better, but we see a large spread in the data. Let's remove any outliers first, before training our model.
```
superplasticizer.describe()
mean = 0.004146
three_sigma = 3*0.001875
upper = mean + three_sigma
lower = mean - three_sigma
print(f"The lower bound is:\t{lower}\nThe upper bound is:\t{upper}")
```
Since there are no negative ratios, we only need to remove data points where the superplasticizer ratio is greater than 0.009771.
```
superplasticizer = transformed_data[transformed_data['Superplasticizer_Ratio']!=0][transformed_data['Superplasticizer_Ratio'] < upper]['Superplasticizer_Ratio']
strength = transformed_data[transformed_data['Superplasticizer_Ratio']!=0][transformed_data['Superplasticizer_Ratio'] < upper]['Compressive_Strength']
plt.scatter(superplasticizer,strength)
```
### Train the Linear Model
```
# We will train and test our model only on the data above, that does not contain outliers
# Reshape the data so it complies with the linear model requirements
X = np.array(superplasticizer).reshape(641,1)
y = np.array(strength).reshape(641,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_super = mean_absolute_error(y_test, y_pred)
MSE_super = mean_squared_error(y_test, y_pred)
RMSE_super = np.sqrt(mean_squared_error(y_test, y_pred))
super_stats = [MAE_super,MSE_super,RMSE_super] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR SUPERPLASTICIZER RATIO VS. COMPRESSIVE STRENGTH")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_super}\nMean Squared Error:\t\t\t{MSE_super}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_super}")
print('-----------------------------\n\n')
```
## Superplasticizer Ratio Modeling - 28 Day Cure Time
The superplasticizer ratio is the ratio of superplasticizer contained within the total mix design, by weight.
### Visualization
```
superplasticizer = transformed_data[((transformed_data['Superplasticizer_Ratio']!=0)&(transformed_data['Age']==28))]['Superplasticizer_Ratio']
strength = transformed_data[((transformed_data['Superplasticizer_Ratio']!=0)&(transformed_data['Age']==28))]['Compressive_Strength']
plt.scatter(superplasticizer,strength)
```
This is better, but we see a large spread in the data. Let's remove any outliers first, before training our model.
```
superplasticizer.describe()
mean = 0.004146
three_sigma = 3*0.001875
upper = mean + three_sigma
lower = mean - three_sigma
print(f"The lower bound is:\t{lower}\nThe upper bound is:\t{upper}")
```
Since there are no negative ratios, we only need to remove data points where the superplasticizer ratio is greater than 0.009771.
```
superplasticizer = transformed_data[((transformed_data['Superplasticizer_Ratio']!=0)&(transformed_data['Age']==28)&(transformed_data['Superplasticizer_Ratio']<upper))]['Superplasticizer_Ratio']
strength = transformed_data[((transformed_data['Superplasticizer_Ratio']!=0)&(transformed_data['Age']==28)&(transformed_data['Superplasticizer_Ratio']<upper))]['Compressive_Strength']
plt.scatter(superplasticizer,strength)
```
### Train the Linear Model
```
# We will train and test our model only on the data above, that does not contain outliers
# Reshape the data so it complies with the linear model requirements
X = np.array(superplasticizer).reshape(315,1)
y = np.array(strength).reshape(315,1)
# Perform a train-test split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)
# Train the linear model
lm = LinearRegression()
lm.fit(X_train,y_train)
```
### Test the Linear Model
```
y_pred = lm.predict(X_test)
```
### Linear Equation
```
# print the intercept
print(lm.intercept_)
coeff = pd.DataFrame(lm.coef_,columns=['Coefficient'])
coeff
```
### Model Evaluation
```
# Plot the linear model preditions as a line superimposed on a scatter plot of the testing data
plt.scatter(X_test,y_test)
plt.plot(X_test,y_pred,'r')
# Evaluation Metrics
MAE_super_28 = mean_absolute_error(y_test, y_pred)
MSE_super_28 = mean_squared_error(y_test, y_pred)
RMSE_super_28 = np.sqrt(mean_squared_error(y_test, y_pred))
super_stats_28 = [MAE_super_28,MSE_super_28,RMSE_super_28] # storing for model comparison at the end of this notebook
# Print the metrics
print(f"EVALUATION METRICS, LINEAR MODEL FOR SUPERPLASTICIZER RATIO VS. COMPRESSIVE STRENGTH AT 28 DAYS")
print('-----------------------------')
print(f"Mean Absolute Error (MAE):\t\t{MAE_super_28}\nMean Squared Error:\t\t\t{MSE_super_28}\nRoot Mean Squared Error (RMSE):\t\t{RMSE_super_28}")
print('-----------------------------\n\n')
```
## Model Comparisons Analysis
Neither superplasticizer linear model appeared to represent the data well from a visual perspective. The cement, cementitious ratio, and fly ash ratio linear models, however, did. We can display all of the evaluation metrics below and compare them to the artificial neural network's (ANN) performance.
```
ANN_metrics = [5.083552,6.466492**2,6.466492]
metrics = [cement_stats, cementitious_stats, fly_stats, super_stats, ANN_metrics]
metrics_28 = [cement_28_stats, cementitious_28_stats, fly_28_stats, super_stats_28, ANN_metrics]
metrics_df = pd.DataFrame(data=metrics, index=['Cement (Ignoring Cure Time)','Cementitious_Ratio (Ignoring Cure Time)','Fly_Ash_Ratio (Ignoring Cure Time)','Superplasticizer_Ratio (Ignoring Cure Time)','ANN (Function of Time)'], columns=['MAE','MSE','RMSE'])
metrics_28_df = pd.DataFrame(data=metrics_28, index=['Cement (Cure Time = 28 Days)','Cementitious_Ratio (Cure Time = 28 Days)','Fly_Ash_Ratio (Cure Time = 28 Days)','Superplasticizer_Ratio (Cure Time = 28 Days)','ANN (Function of Time)'], columns=['MAE','MSE','RMSE'])
metrics_df
metrics_28_df
```
## Conclusions & Recommendations
By comparing the evaluation metrics for all models, we conclude that the ANN model performed significantly better than all of the linear models. It outperformed the best linear model's RMSE (for Fly_Ash_Ratio at 28 Days) by over 30%! An important note is that the linear models were not scaled, and the ANN model was. We kept the linear models biased in order to maintain coefficient interpretabililty, whereas that was not relevant to the ANN model.
What is surprising is that the ANN model still outperformed the linear models, even when controlling for cure time at 28 days. Perhaps the most startling insight is that the fly ash ratio was even more accurate at predicting concrete compressive strength than the cement quantity, to the point that it had the lowest errors of all of the linear models. We therefore recommend that engineers give very conservative fly ash ratio specifications when allowing substitutions for Portland cement.
| true |
code
| 0.601184 | null | null | null | null |
|
# `logictools` WaveDrom Tutorial
[WaveDrom](http://wavedrom.com) is a tool for rendering digital timing waveforms. The waveforms are defined in a simple textual format.
This notebook will show how to render digital waveforms using the pynq library.
The __`logictools`__ overlay uses the same format as WaveDrom to specify and generate real signals on the board.
A full tutorial of WaveDrom can be found [here](http://wavedrom.com/tutorial.html)
### Step 1: Import the `draw_wavedrom()` method from the pynq library
```
from pynq.lib.logictools.waveform import draw_wavedrom
```
A simple function to add wavedrom diagrams into a jupyter notebook. It utilizes the wavedrom java script library.
<font color="DodgerBlue">**Example usage:**</font>
```python
from pynq.lib.logictools.waveform import draw_wavedrom
clock = {'signal': [{'name': 'clk', 'wave': 'h....l...'}]}
draw_wavedrom(clock)
```
<font color="DodgerBlue">**Method:**</font>
```python
def draw_wavedrom(data, width=None):
# Note the optional argument width forces the width in pixels
```
### Step 2: Specify and render a waveform
```
from pynq.lib.logictools.waveform import draw_wavedrom
clock = {'signal': [{'name': 'clock_0', 'wave': 'hlhlhlhlhlhlhlhl'}],
'foot': {'tock': 1},
'head': {'text': 'Clock Signal'}}
draw_wavedrom(clock)
```
### Step 3: Adding more signals to the waveform
```
from pynq.lib.logictools.waveform import draw_wavedrom
pattern = {'signal': [{'name': 'clk', 'wave': 'hl' * 8},
{'name': 'clkn', 'wave': 'lh' * 8},
{'name': 'data0', 'wave': 'l.......h.......'},
{'name': 'data1', 'wave': 'h.l...h...l.....'}],
'foot': {'tock': 1},
'head': {'text': 'Pattern'}}
draw_wavedrom(pattern)
```
__Adding multiple wave groups and spaces__
```
from pynq.lib.logictools.waveform import draw_wavedrom
pattern_group = {'signal': [['Group1',
{'name': 'clk', 'wave': 'hl' * 8},
{'name': 'clkn', 'wave': 'lh' * 8},
{'name': 'data0', 'wave': 'l.......h.......'},
{'name': 'data1', 'wave': 'h.l...h...l.....'}],
{},
['Group2',
{'name': 'data2', 'wave': 'l...h..l.h......'},
{'name': 'data3', 'wave': 'l.h.' * 4}]],
'foot': {'tock': 1},
'head': {'text': 'Pattern'}}
draw_wavedrom(pattern_group)
```
# WaveDrom for real-time pattern generation and trace analysis
### The __`logictools`__ overlay uses WaveJSON format to specify and generate real signals on the board.

* As shown in the figure above, the Pattern Generator is an output-only block that specifies a sequence of logic values (patterns) which appear on the output pins of the ARDUINO interface. The logictools API for Pattern Generator accepts **WaveDrom** specification syntax with some enhancements.
* The Trace Analyzer is an input-only block that captures and records all the IO signals. These signals may be outputs driven by the generators or inputs to the PL that are driven by external circuits. The Trace Analyzer allows us to verify that the output signals we have specified from the generators are being applied correctly. It also allows us to debug and analyze the operation of the external interface.
* The signals generated or captured by both the blocks can be displayed in the notebook by populating the WaveJSON dictionary that we have seen in this notebook. Users can access this dictionary through the provided API to extend or modify the waveform with special annotations.
* we use a subset of the wave tokens that are allowed by WaveDrom to specify the waveforms for the Pattern Generator. However, users can call the `draw_waveform()` method on the dictionary populated by the Trace Analyzer to extend and modify the dictionary with annotations.
__In the example below, we are going to generate 3 signals on the Arduino interface pins D0, D1 and D2 using the Pattern Generator. Since all IOs are accessible to the Trace analyzer, we will capture the data on the pins as well. This operation will serve as an internal loopback. __
### Step 1: Download the `logictools` overlay and specify the pattern
The pattern to be generated is specified in the WaveJSON format. The Waveform class is used to display the specified waveform.
```
from pynq.lib.logictools import Waveform
from pynq.overlays.logictools import LogicToolsOverlay
from pynq.lib.logictools import PatternGenerator
logictools_olay = LogicToolsOverlay('logictools.bit')
loopback_test = {'signal': [
['stimulus',
{'name': 'output0', 'pin': 'D0', 'wave': 'lh' * 8},
{'name': 'output1', 'pin': 'D1', 'wave': 'l.h.' * 4},
{'name': 'output2', 'pin': 'D2', 'wave': 'l...h...' * 2}],
{},
['analysis',
{'name': 'input0', 'pin': 'D0'},
{'name': 'input1', 'pin': 'D1'},
{'name': 'input2', 'pin': 'D2'}]],
'foot': {'tock': 1},
'head': {'text': 'loopback_test'}}
waveform = Waveform(loopback_test)
waveform.display()
```
**Note:** Since there are no captured samples at this moment, the analysis group will be empty.
### Step 2: Run the pattern generator and trace the loopback signals.
This step populates the WaveJSON dict with the captured trace analyzer samples. The dict can now serve as an output that we can further modify. It is shown in the next step.
```
pattern_generator = logictools_olay.pattern_generator
pattern_generator.trace(num_analyzer_samples=16)
pattern_generator.setup(loopback_test,
stimulus_group_name='stimulus',
analysis_group_name='analysis')
pattern_generator.run()
pattern_generator.show_waveform()
```
### Step 3: View the output waveJSON dict.
```
import pprint
output_wavejson = pattern_generator.waveform.waveform_dict
pprint.pprint(output_wavejson)
```

### Step 4: Extending the output waveJSON dict with state annotation
```
state_list = ['S0', 'S1', 'S2', 'S3', 'S4', 'S5', 'S6', 'S7',
'S0', 'S1', 'S2', 'S3', 'S4', 'S5', 'S6', 'S7']
color_dict = {'white': '2', 'yellow': '3', 'orange': '4', 'blue': '5'}
output_wavejson['signal'].extend([{}, ['Annotation',
{'name': 'state',
'wave': color_dict['yellow'] * 8 +
color_dict['blue'] * 8,
'data': state_list}]])
```
__Note: __ The color_dict is a color code map as defined by WaveDrom
```
draw_wavedrom(output_wavejson)
```
| true |
code
| 0.477128 | null | null | null | null |
|
# Confidence Interval:
In this notebook you will find:
- Get confidence intervals for predicted survival curves using XGBSE estimators;
- How to use XGBSEBootstrapEstimator, a meta estimator for bagging;
- A nice function to help us plot survival curves.
```
import matplotlib.pyplot as plt
plt.style.use('bmh')
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
# to easily plot confidence intervals
def plot_ci(mean, upper_ci, lower_ci, i=42, title='Probability of survival $P(T \geq t)$'):
# plotting mean and confidence intervals
plt.figure(figsize=(12, 4), dpi=120)
plt.plot(mean.columns,mean.iloc[i])
plt.fill_between(mean.columns, lower_ci.iloc[i], upper_ci.iloc[i], alpha=0.2)
plt.title(title)
plt.xlabel('Time [days]')
plt.ylabel('Probability')
plt.tight_layout()
```
## Metrabic
We will be using the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) dataset from [pycox](https://github.com/havakv/pycox#datasets) as base for this example.
```
from xgbse.converters import convert_to_structured
from pycox.datasets import metabric
import numpy as np
# getting data
df = metabric.read_df()
df.head()
```
## Split and Time Bins
Split the data in train and test, using sklearn API. We also setup the TIME_BINS array, which will be used to fit the survival curve.
```
from xgbse.converters import convert_to_structured
from sklearn.model_selection import train_test_split
# splitting to X, T, E format
X = df.drop(['duration', 'event'], axis=1)
T = df['duration']
E = df['event']
y = convert_to_structured(T, E)
# splitting between train, and validation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=1/3, random_state = 0)
TIME_BINS = np.arange(15, 315, 15)
TIME_BINS
```
## Calculating confidence intervals
We will be using the XGBSEKaplanTree estimator to fit the model and predict a survival curve for each point in our test data, and via <i>return_ci</i> parameter we will get upper and lower bounds for the confidence interval.
```
from xgbse import XGBSEKaplanTree, XGBSEBootstrapEstimator
from xgbse.metrics import concordance_index, approx_brier_score
# xgboost parameters to fit our model
PARAMS_TREE = {
'objective': 'survival:cox',
'eval_metric': 'cox-nloglik',
'tree_method': 'hist',
'max_depth': 10,
'booster':'dart',
'subsample': 1.0,
'min_child_weight': 50,
'colsample_bynode': 1.0
}
```
### Numerical Form
The KaplanTree and KaplanNeighbors models support estimation of confidence intervals via the Exponential Greenwood formula.
```
%%time
# fitting xgbse model
xgbse_model = XGBSEKaplanTree(PARAMS_TREE)
xgbse_model.fit(X_train, y_train, time_bins=TIME_BINS)
# predicting
mean, upper_ci, lower_ci = xgbse_model.predict(X_test, return_ci=True)
# print metrics
print(f"C-index: {concordance_index(y_test, mean)}")
print(f"Avg. Brier Score: {approx_brier_score(y_test, mean)}")
# plotting CIs
plot_ci(mean, upper_ci, lower_ci)
```
### Non-parametric Form
We can also use the XGBSEBootstrapEstimator to wrap any XGBSE model and get confidence intervals via bagging, which also slighty increase our performance at the cost of computation time.
```
%%time
# base model as XGBSEKaplanTree
base_model = XGBSEKaplanTree(PARAMS_TREE)
# bootstrap meta estimator
bootstrap_estimator = XGBSEBootstrapEstimator(base_model, n_estimators=100)
# fitting the meta estimator
bootstrap_estimator.fit(X_train, y_train, time_bins=TIME_BINS)
# predicting
mean, upper_ci, lower_ci = bootstrap_estimator.predict(X_test, return_ci=True)
# print metrics
print(f"C-index: {concordance_index(y_test, mean)}")
print(f"Avg. Brier Score: {approx_brier_score(y_test, mean)}")
# plotting CIs
plot_ci(mean, upper_ci, lower_ci)
```
| true |
code
| 0.695752 | null | null | null | null |
|
## Precision-Recall Curves in Multiclass
For multiclass classification, we have 2 options:
- determine a PR curve for each class.
- determine the overall PR curve as the micro-average of all classes
Let's see how to do both.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.multiclass import OneVsRestClassifier
# to convert the 1-D target vector in to a matrix
from sklearn.preprocessing import label_binarize
from sklearn.metrics import precision_recall_curve
from yellowbrick.classifier import PrecisionRecallCurve
```
## Load data (multiclass)
```
# load data
data = load_wine()
data = pd.concat([
pd.DataFrame(data.data, columns=data.feature_names),
pd.DataFrame(data.target, columns=['target']),
], axis=1)
data.head()
# target distribution:
# multiclass and (fairly) balanced
data.target.value_counts(normalize=True)
# separate dataset into train and test
X_train, X_test, y_train, y_test = train_test_split(
data.drop(labels=['target'], axis=1), # drop the target
data['target'], # just the target
test_size=0.3,
random_state=0)
X_train.shape, X_test.shape
# the target is a vector with the 3 classes
y_test[0:10]
```
## Train ML models
The dataset we are using is very, extremely simple, so I am creating dumb models intentionally, that is few trees and very shallow for the random forests and few iterations for the logit. This is, so that we can get the most out of the PR curves by inspecting them visually.
### Random Forests
The Random Forests in sklearn are not trained as a 1 vs Rest. So in order to produce a 1 vs rest probability vector for each class, we need to wrap this estimator with another one from sklearn:
- [OneVsRestClassifier](https://scikit-learn.org/stable/modules/generated/sklearn.multiclass.OneVsRestClassifier.html)
```
# set up the model, wrapped by the OneVsRestClassifier
rf = OneVsRestClassifier(
RandomForestClassifier(
n_estimators=10, random_state=39, max_depth=1, n_jobs=4,
)
)
# train the model
rf.fit(X_train, y_train)
# produce the predictions (as probabilities)
y_train_rf = rf.predict_proba(X_train)
y_test_rf = rf.predict_proba(X_test)
# note that the predictions are an array of 3 columns
# first column: the probability of an observation of being of class 0
# second column: the probability of an observation of being of class 1
# third column: the probability of an observation of being of class 2
y_test_rf[0:10, :]
pd.DataFrame(y_test_rf).sum(axis=1)[0:10]
# The final prediction is that of the biggest probabiity
rf.predict(X_test)[0:10]
```
### Logistic Regression
The Logistic regression supports 1 vs rest automatically though its multi_class parameter:
```
# set up the model
logit = LogisticRegression(
random_state=0, multi_class='ovr', max_iter=10,
)
# train
logit.fit(X_train, y_train)
# obtain the probabilities
y_train_logit = logit.predict_proba(X_train)
y_test_logit = logit.predict_proba(X_test)
# note that the predictions are an array of 3 columns
# first column: the probability of an observation of being of class 0
# second column: the probability of an observation of being of class 1
# third column: the probability of an observation of being of class 2
y_test_logit[0:10, :]
# The final prediction is that of the biggest probabiity
logit.predict(X_test)[0:10]
```
## Precision-Recall Curve
### Per class with Sklearn
```
# with label_binarize we transform the target vector
# into a multi-label matrix, so that it matches the
# outputs of the models
# then we have 1 class per column
y_test = label_binarize(y_test, classes=[0, 1, 2])
y_test[0:10, :]
# now we determine the precision and recall at different thresholds
# considering only the probability vector for class 2 and the true
# target for class 2
# so we treat the problem as class 2 vs rest
p, r, thresholds = precision_recall_curve(y_test[:, 2], y_test_rf[:, 2])
# precision values
p
# recall values
r
# threhsolds examined
thresholds
```
Go ahead and examine the precision and recall for the other classes see how these values change.
```
# now let's do these for all classes and capture the results in
# dictionaries, so we can plot the values afterwards
# determine the Precision and recall
# at various thresholds of probability
# in a 1 vs all fashion, for each class
precision_rf = dict()
recall_rf = dict()
# for each class
for i in range(3):
# determine precision and recall at various thresholds
# in a 1 vs all fashion
precision_rf[i], recall_rf[i], _ = precision_recall_curve(
y_test[:, i], y_test_rf[:, i])
precision_rf
# plot the curves for each class
for i in range(3):
plt.plot(recall_rf[i], precision_rf[i], label='class {}'.format(i))
plt.xlabel("recall")
plt.ylabel("precision")
plt.legend(loc="best")
plt.title("precision vs. recall curve")
plt.show()
# and now for the logistic regression
precision_lg = dict()
recall_lg = dict()
# for each class
for i in range(3):
# determine precision and recall at various thresholds
# in a 1 vs all fashion
precision_lg[i], recall_lg[i], _ = precision_recall_curve(
y_test[:, i], y_test_logit[:, i])
plt.plot(recall_lg[i], precision_lg[i], label='class {}'.format(i))
plt.xlabel("recall")
plt.ylabel("precision")
plt.legend(loc="best")
plt.title("precision vs. recall curve")
plt.show()
# and now, just because it is a bit difficult to compare
# between models, we plot the PR curves class by class,
# but the 2 models in the same plot
# for each class
for i in range(3):
plt.plot(recall_lg[i], precision_lg[i], label='logit class {}'.format(i))
plt.plot(recall_rf[i], precision_rf[i], label='rf class {}'.format(i))
plt.xlabel("recall")
plt.ylabel("precision")
plt.legend(loc="best")
plt.title("precision vs. recall curve for class{}".format(i))
plt.show()
```
We see that the Random Forest does a better job for all classes.
### Micro-average with sklearn
In order to do this, we concatenate all the probability vectors 1 after the other, and so we do with the real values.
```
# probability vectors for all classes in 1-d vector
y_test_rf.ravel()
# see that the unravelled prediction vector has 3 times the size
# of the origina target
len(y_test), len(y_test_rf.ravel())
# A "micro-average": quantifying score on all classes jointly
# for random forests
precision_rf["micro"], recall_rf["micro"], _ = precision_recall_curve(
y_test.ravel(), y_test_rf.ravel(),
)
# for logistic regression
precision_lg["micro"], recall_lg["micro"], _ = precision_recall_curve(
y_test.ravel(), y_test_logit.ravel(),
)
# now we plot them next to each other
i = "micro"
plt.plot(recall_lg[i], precision_lg[i], label='logit micro {}')
plt.plot(recall_rf[i], precision_rf[i], label='rf micro {}')
plt.xlabel("recall")
plt.ylabel("precision")
plt.legend(loc="best")
plt.title("precision vs. recall curve for class{}".format(i))
plt.show()
```
## Yellowbrick
### Per class with Yellobrick
https://www.scikit-yb.org/en/latest/api/classifier/prcurve.html
**Note:**
In the cells below, we are passing to Yellobrick classes a model that is already fit. When we fit() the Yellobrick class, it will check if the model is fit, in which case it will do nothing.
If we pass a model that is not fit, and a multiclass target, Yellowbrick will wrap the model automatically with a 1 vs Rest classifier.
Check Yellobrick's documentation for more details.
```
visualizer = PrecisionRecallCurve(
rf, per_class=True, cmap="cool", micro=False,
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and show the figure
visualizer = PrecisionRecallCurve(
logit, per_class=True, cmap="cool", micro=False, cv=0.05,
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and show the figure
```
### Micro yellowbrick
```
visualizer = PrecisionRecallCurve(
rf, cmap="cool", micro=True,
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and show the figure
visualizer = PrecisionRecallCurve(
logit, cmap="cool", micro=True, cv=0.05,
)
visualizer.fit(X_train, y_train) # Fit the training data to the visualizer
visualizer.score(X_test, y_test) # Evaluate the model on the test data
visualizer.show() # Finalize and show the figure
```
That's all for PR curves
| true |
code
| 0.740723 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/EmilSkaaning/DeepStruc/blob/main/DeepStruc.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# DeepStruc
**Github:** https://github.com/EmilSkaaning/DeepStruc
**Paper:** DeepStruc: Towards structure solution from pair distribution function data using deep generative models
**Questions:** [email protected] or [email protected]
Welcome to DeepStruc that is a Deep Generative Model (DGM) which learns the relation between PDF and atomic structure and thereby solve a structure based on a PDF!
This script guides you through a simple example of how to use DeepStruc to predict a structure on a given PDF.
Aftwerwards, you can upload a PDF and use DeepStruc to predict the structure.
# First install requirements for DeepStruc (this step takes 5 - 10 minutes)
```
%%capture
!git clone https://github.com/EmilSkaaning/DeepStruc
!pip3 install torch==1.10.1+cpu torchvision==0.11.2+cpu torchaudio==0.10.1+cpu -f https://download.pytorch.org/whl/cpu/torch_stable.html
!pip install pytorch_lightning torch-geometric==1.7.2 torch-scatter
!pip3 install torch-sparse -f https://data.pyg.org/whl/torch-1.10.1+cpu.html
!pip install matplotlib==3.4.3 ase nglview ipywidgets
from google.colab import output, files
from ase.io import read
from ase.visualize import view
from IPython.display import Image
import shutil
import os
os.chdir("DeepStruc")
```
# Example of how to use DeepStruc on a simulated dataset
We here provide an example of how to use DeepStruc on simulated data. The script can both take a single PDF or a directory of PDFs as input.
Be aware that the PDF(s) will be made to have an r-range between 2 - 30 Å in steps of 0.01 Å (2800 points PDF). Any data outside this range will not be used. Check the dataformat of our datasets (often made with PDFGui) if in doubt.
```
PDFFile = "/data/PDFs_simulated/FCC_h_3_k_6_l_7.gr" # Path to PDF(s).
Nstructures = 10 # Number of samples/structures generated for each unique PDF
structure = 0 # Which of the Nstructures to visualize. (Goes from 0 to Nstructures - 1)
sigma = 3 # Sample to '-s' sigma in the normal distribution
plot = True # Plots sampled structures on top of DeepStruc training data.
```
**Outcomment the following line to use DeepStruc on experimental PDF(s) from your local computer.** <br>
Some browsers do not support this upload option. Use Google Chrome or simply upload the file manually in the left menu in the DeepStruc-main' folder.
```
#PDFFile = list(files.upload())[0] # Upload PDF(s) from local computer
```
## Predict with DeepStruc
```
# Use DeepStruc on the uploaded PDF(s)
!python predict.py -d $PDFFile -n $Nstructures -s $sigma -p $plot -i $structure
# Get the latest results
all_subdirs = [d for d in os.listdir('.') if os.path.isdir(d)]
latest_subdir = max(all_subdirs, key=os.path.getmtime)
# Plot the latent space
Image(latest_subdir + '/PDFs.png', width = 480, height = 360)
```
**The raw input PDF and the normalised PDF.** The raw input PDF is normalised to have the highest peak at G(r) = 1 and to be in between r = 2 Å and 30 Å.
## Visualization of the two-dimensional latent space (compressed feature space of the structures)
```
# Plot the latent space
Image(latest_subdir + '/ls.png', width = 900, height = 360)
```
**The two-dimensional latent space with location of the input.** The size of the points relates to the size of the embedded structure. Each point is coloured after its structure type, FCC (light blue), octahedral (dark grey), decahedral (orange), BCC (green), icosahedral (dark blue), HCP (pink) and SC (red). Each point in the latent space corresponds to a structure based on its simulated PDF. Test data point are plotted on top of the training and validation data, which is made semi-transparent. The latent space locations of the reconstructed structures from the input are shown with black markers and the specific reconstructed structure that is shown in the next box is shown with a black and white marker.
## Visualization of a reconstructed structure
```
# Get folder of structures
subfolder = [f.path for f in os.scandir(latest_subdir) if f.is_dir()]
# Define which structure to plot and plot it
output.enable_custom_widget_manager()
view(read(subfolder[0] + "/" + os.listdir(subfolder[0])[structure]) , viewer='ngl')
```
**The reconstructed structure from the input.** The reconstructed structure is indicated at the latent space above using a black and white marker.
**Be aware** that DeepStruc are only created to predict mono-metallic nanoparticles (MMNP) of up to 200 atoms. If the PDF file is not a MMNP, it is highly likely that DeepStruc will not output an meaningful structure.
## Download the latest results
```
# Download the latest results
shutil.make_archive(latest_subdir, 'zip', latest_subdir)
files.download(latest_subdir + ".zip")
```
# Cite
If you use DeepStruc, please consider citing our paper. Thanks in advance!
```
@article{kjær2022DeepStruc,
title={DeepStruc: Towards structure solution from pair distribution function data using deep generative models},
author={Emil T. S. Kjær, Andy S. Anker, Marcus N. Weng, Simon J. L. Billinge, Raghavendra Selvan, Kirsten M. Ø. Jensen},
year={2022}}
```
# LICENSE
This project is licensed under the Apache License Version 2.0, January 2004 - see the LICENSE file at https://github.com/EmilSkaaning/DeepStruc/blob/main/LICENSE.md for details.
| true |
code
| 0.615435 | null | null | null | null |
|
# DC Resistivity: 1D parametric inversion
_Inverting for Resistivities and Layers_
Here we use the module *SimPEG.electromangetics.static.resistivity* to invert
DC resistivity sounding data and recover the resistivities and layer thicknesses
for a 1D layered Earth. In this tutorial, we focus on the following:
- How to define sources and receivers from a survey file
- How to define the survey
- Defining a model that consists of resistivities and layer thicknesses
For this tutorial, we will invert sounding data collected over a layered Earth using
a Wenner array. The end product is layered Earth model which explains the data.
## Import modules
```
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from discretize import TensorMesh
from SimPEG import (
maps, data, data_misfit, regularization,
optimization, inverse_problem, inversion, directives
)
from SimPEG.electromagnetics.static import resistivity as dc
from SimPEG.electromagnetics.static.utils.StaticUtils import plot_layer
mpl.rcParams.update({'font.size': 14})
```
## Define Parameters for the Inversion
```
# Define the file path to the data file. Also define the AB/2, MN/2 and apparent resistivity columns.
# Recall that python counts starting at 0
data_filename = './sounding_data/Aung_San_Location_1_raw.csv'
half_AB_column = 'AB/2 (m)'
half_MN_column = 'MN/2 (m)'
apparent_resistivity_column = 'App. Res. (Ohm m)'
# Define the floor and percent uncertainty you would like to apply to apparent resistivity data
uncertainty_floor = 5
uncertainty_percent = 10.
# Define layer thicknesses and resistivities for the starting model. The thickness
# of the bottom layer is not used, as we assume it extends downward to infinity.
layer_thicknesses = np.r_[10, 10]
halfspace_resistivity = 300.
```
## Load Data, Define Survey and Plot
Here we load the observed data, define the DC survey geometry and plot the
data values.
```
# Load data
df = pd.read_csv(data_filename)
# Extract source and receiver electrode locations and the observed data
half_AB_separations = df[half_AB_column]
half_MN_separations = df[half_MN_column]
dobs = df[apparent_resistivity_column].values
resistivities = halfspace_resistivity*np.ones(layer_thicknesses.size+1)
# Define survey
unique_tx, k = np.unique(half_AB_separations, return_index=True)
n_sources = len(k)
k = np.sort(k)
k = np.r_[k, len(dobs)+1]
source_list = []
for ii in range(0, n_sources):
# MN electrode locations for receivers. Each is an (N, 3) numpy array
M_locations = -half_MN_separations[k[ii]:k[ii+1]]
M_locations = np.c_[M_locations, np.zeros((np.shape(M_locations)[0], 2))]
N_locations = half_MN_separations[k[ii]:k[ii+1]]
N_locations = np.c_[N_locations, np.zeros((np.shape(N_locations)[0], 2))]
receiver_list = [dc.receivers.Dipole(M_locations, N_locations)]
# AB electrode locations for source. Each is a (1, 3) numpy array
A_location = np.r_[-half_AB_separations[k[ii]], 0., 0.]
B_location = np.r_[half_AB_separations[k[ii]], 0., 0.]
source_list.append(dc.sources.Dipole(receiver_list, A_location, B_location))
# Define survey
survey = dc.Survey(source_list)
# Compute the A, B, M and N electrode locations.
survey.getABMN_locations()
# Plot apparent resistivities on sounding curve as a function of Wenner separation
# parameter.
electrode_separations = np.sqrt(
np.sum((survey.m_locations - survey.n_locations)**2, axis=1)
)
fig, ax = plt.subplots(1, 1, figsize=(11, 5))
ax.loglog(half_AB_separations, dobs, 'b', lw=2)
ax.grid(True, which='both', ls="--", c='gray')
ax.set_xlabel("AB/2 (m)")
ax.set_ylabel("Apparent Resistivity ($\Omega m$)")
```
## Assign Uncertainties
Inversion with SimPEG requires that we define uncertainties on our data. The
uncertainty represents our estimate of the standard deviation of the noise on
our data.
```
uncertainties = uncertainty_floor + 0.01*uncertainty_percent*np.abs(dobs)
```
## Define Data
Here is where we define the data that are inverted. The data are defined by
the survey, the observation values and the uncertainties.
```
data_object = data.Data(survey, dobs=dobs, standard_deviation=uncertainties)
```
## Defining the Starting Model and Mapping
```
# Define the layers as a mesh
mesh = TensorMesh([layer_thicknesses], '0')
print(mesh)
# Define model. We are inverting for the layer resistivities and layer thicknesses.
# Since the bottom layer extends to infinity, it is not a model parameter for
# which we need to invert. For a 3 layer model, there is a total of 5 parameters.
# For stability, our model is the log-resistivity and log-thickness.
starting_model = np.r_[np.log(resistivities), np.log(layer_thicknesses)]
# Since the model contains two different properties for each layer, we use
# wire maps to distinguish the properties.
wire_map = maps.Wires(('rho', mesh.nC+1), ('t', mesh.nC))
resistivity_map = maps.ExpMap(nP=mesh.nC+1) * wire_map.rho
layer_map = maps.ExpMap(nP=mesh.nC) * wire_map.t
```
## Define the Physics
Here we define the physics of the problem using the DCSimulation_1D class.
```
simulation = dc.simulation_1d.Simulation1DLayers(
survey=survey, rhoMap=resistivity_map, thicknessesMap=layer_map,
data_type="apparent_resistivity"
)
```
## Define Inverse Problem
The inverse problem is defined by 3 things:
1) Data Misfit: a measure of how well our recovered model explains the field data
2) Regularization: constraints placed on the recovered model and a priori information
3) Optimization: the numerical approach used to solve the inverse problem
```
# Define the data misfit. Here the data misfit is the L2 norm of the weighted
# residual between the observed data and the data predicted for a given model.
# The weighting is defined by the reciprocal of the uncertainties.
dmis = data_misfit.L2DataMisfit(simulation=simulation, data=data_object)
# Define the regularization on the parameters related to resistivity
mesh_rho = TensorMesh([mesh.hx.size+1])
reg_rho = regularization.Simple(
mesh_rho, alpha_s=1., alpha_x=1,
mapping=wire_map.rho
)
# Define the regularization on the parameters related to layer thickness
mesh_t = TensorMesh([mesh.hx.size])
reg_t = regularization.Simple(
mesh_t, alpha_s=1., alpha_x=1,
mapping=wire_map.t
)
# Combine to make regularization for the inversion problem
reg = reg_rho + reg_t
# Define how the optimization problem is solved. Here we will use an inexact
# Gauss-Newton approach that employs the conjugate gradient solver.
opt = optimization.InexactGaussNewton(
maxIter=20, maxIterCG=30, print_type='ubc'
)
# Define the inverse problem
inv_prob = inverse_problem.BaseInvProblem(dmis, reg, opt)
```
## Define Inversion Directives
Here we define any directives that are carried out during the inversion. This
includes the cooling schedule for the trade-off parameter (beta), stopping
criteria for the inversion and saving inversion results at each iteration.
```
# Defining a starting value for the trade-off parameter (beta) between the data
# misfit and the regularization.
starting_beta = directives.BetaEstimate_ByEig(beta0_ratio=1.)
# Set the rate of reduction in trade-off parameter (beta) each time the
# the inverse problem is solved. And set the number of Gauss-Newton iterations
# for each trade-off paramter value.
beta_schedule = directives.BetaSchedule(coolingFactor=2., coolingRate=1.)
# Apply and update sensitivity weighting as the model updates
update_sensitivity_weights = directives.UpdateSensitivityWeights()
# Options for outputting recovered models and predicted data for each beta.
save_iteration = directives.SaveOutputEveryIteration(save_txt=False)
# Setting a stopping criteria for the inversion.
target_misfit = directives.TargetMisfit(chifact=1)
# The directives are defined in a list
directives_list = [
starting_beta, beta_schedule, target_misfit
]
```
## Running the Inversion
To define the inversion object, we need to define the inversion problem and
the set of directives. We can then run the inversion.
```
# Here we combine the inverse problem and the set of directives
inv = inversion.BaseInversion(inv_prob, directives_list)
# Run the inversion
recovered_model = inv.run(starting_model)
# Inversion result from Mon DRD Mawlamyine location 3
res_tmp = np.array([348.4, 722.9, 282, 100.8, 51.4, 170.8, 31.1, 184.3])
thick_tmp = np.array([1.4, 1.6, 1.4, 12.1, 11.4, 25.1, 54.2])
plotting_mesh_tmp = TensorMesh([np.r_[thick_tmp, layer_thicknesses[-1]]], '0')
```
## Examining the Results
```
# Plot true model and recovered model
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
plotting_mesh = TensorMesh([np.r_[layer_map*recovered_model, layer_thicknesses[-1]]], '0')
x_min = np.min(resistivity_map*recovered_model)
x_max = np.max(resistivity_map*recovered_model)
plot_layer(resistivity_map*recovered_model, plotting_mesh, ax=ax, depth_axis=False, color='k')
#plot_layer(res_tmp, plotting_mesh_tmp, ax=ax, depth_axis=False, color='r')
#ax.set_xlim(10, 5000)
#ax.set_ylim(-300, 0)
#ax.legend(("SimPEG", "Mon State DRD"))
ax.grid(True, which='both', ls="--", c='gray')
# Plot the true and apparent resistivities on a sounding curve
fig, ax = plt.subplots(1, 1, figsize=(7, 5))
ax.loglog(half_AB_separations, dobs, 'kx', lw=2, ms=10, mew=2)
ax.loglog(half_AB_separations, inv_prob.dpred, 'k', lw=2)
ax.set_xlabel("AB/2 (m)")
ax.set_ylabel("Apparent Resistivity ($\Omega m$)")
ax.legend(['Observed data','Predicted data'])
#ax.set_ylim(50, 1000)
ax.grid(True, which='both')
```
| true |
code
| 0.694432 | null | null | null | null |
|
# **DIVE INTO CODE COURSE**
## **Graduation Assignment**
**Student Name**: Doan Anh Tien<br>
**Student ID**: 1852789<br>
**Email**: [email protected]
## Introduction
The graduation assignment was based on one of the challenges from the Vietnamese competition **Zalo AI Challenge**. The description of the challenge is described as follows:
> During the Covid-19 outbreak, the Vietnamese government pushed the "5K" public health safety message. In the message, masking and keeping a safe distance are two key rules that have been shown to be extremely successful in preventing people from contracting or spreading the virus. Enforcing these principles on a large scale is where technology may help. In this challenge, you will create algorithm to detect whether or not a person or group of individuals in a picture adhere to the "mask" and "distance" standards.
**Basic rules**
We are given the dataset contains images of people either wearing mask or not and they are standing either close of far from each other. Our mission is to predict whether the formation of these people adhere the 5k standard.
The 5k standard is also based on the two conditions, mask (0 == not wearing, 1 == wearing) and distancing (0 == too close, 1 == far enough). People that adhere the 5k standard will not likely to expose the virus to each other in case they did caught it before, and it is to prevent the spread of the COVID-19 pandamic through people interactions.
---
```
import tensorflow as tf
tf.data.experimental.enable_debug_mode()
print("Num GPUs Available: ", len(tf.config.list_physical_devices('GPU')))
#@title
!pip install cloud_tpu_client
from cloud_tpu_client import Client
c = Client(tpu='') # For TPU runtime
print(c.runtime_version())
#@title
c.configure_tpu_version(tf.__version__, restart_type='ifNeeded')
#@title
print(c.runtime_version())
!nvidia-smi # For GPU runtime
# For when the TPU is used
tpu = tf.distribute.cluster_resolver.TPUClusterResolver()
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.TPUStrategy(tpu)
!pip install wandb
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/MyDrive/Colab Notebooks/DIVE INTO CODE/Graduation
!ls
```
## **1. Resources preparation**
### Libraries
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import wandb
from wandb.keras import WandbCallback
from tensorflow.data import AUTOTUNE
from tensorflow import keras
from tensorflow.keras import layers
from PIL import Image
# Some libraries will be imported later throughout the notebook
print('Tensorflow version:', tf.__version__)
print('Keras version:', keras.__version__)
```
### W&B login and init project
```
!wandb login 88c91a7dc6dd5574f423e38f852c6fe640a7fcd0
wandb.init(project="diveintocode-grad-1st-approach", entity="atien228")
```
### Hyperparamaters
```
standard = 'mask' #@param ['mask', 'distancing']
SEED = 42 #@param {type:'integer'}
wandb.config = {
"learning_rate": 0.001,
"epochs": 15,
"batch_size": 16,
"momentum": 0.85,
"smoothing": 0.1
}
```
### Preprocessing data-set
```
data_path = '/content/drive/MyDrive/Colab Notebooks/DIVE INTO CODE/Graduation/data'
img_dir = os.path.join(data_path, 'images')
os.listdir(img_dir)[:10]
meta = pd.read_csv(os.path.join(data_path, 'train_meta.csv'))
meta
img1 = meta.iloc[0]
print(r'Image ID: {}, Mask: {}, Distancing: {}'.format(img1['image_id'], img1['mask'], img1['distancing']))
img = Image.open(os.path.join(img_dir, img1['fname']))
img
dataset = []
label = []
for idx, row in meta.iterrows():
if pd.notna(row[standard]):
dataset.append(os.path.join(img_dir, row['fname'])) # Mask or distancing
label.append(row[standard])
for i in range(5):
print(f'img: {dataset[i]} label: {label[i]}')
len(label_val)
```
Create a small portion of test set since the competition won't let me submit a new entry to check my score
```
df_test = df_train[1200:1500]
label_test = label_train[1200:1500]
df_train = df_train[:1200]
df_val = df_val[:300]
label_train = label_train[:1200]
label_val = label_val[:300]
df_train[0]
label_train[0]
meta.iloc[3713]
```
Create tuple of train and validation set for further process
```
df_train = tuple(zip(df_train, label_train))
df_val = tuple(zip(df_val, label_val))
df_train = tuple(zip(*df_train))
df_val = tuple(zip(*df_val))
```
### Tensorflow Hub for a variety of CNN models
EfficientNet models and ckpts (and other image classifer models too)
```
import tensorflow_hub as hub
print("Hub version:", hub.__version__)
print("GPU is", "available" if tf.config.list_physical_devices('GPU') else "NOT AVAILABLE")
def get_hub_url_and_isize(model_name):
model_handle_map = {
"efficientnetv2-s": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_s/feature_vector/2",
"efficientnetv2-m": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_m/feature_vector/2",
"efficientnetv2-l": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_l/feature_vector/2",
"efficientnetv2-s-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_s/feature_vector/2",
"efficientnetv2-m-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_m/feature_vector/2",
"efficientnetv2-l-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_l/feature_vector/2",
"efficientnetv2-xl-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_xl/feature_vector/2",
"efficientnetv2-b0-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_b0/feature_vector/2",
"efficientnetv2-b1-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_b1/feature_vector/2",
"efficientnetv2-b2-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_b2/feature_vector/2",
"efficientnetv2-b3-21k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_b3/feature_vector/2",
"efficientnetv2-s-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_s/feature_vector/2",
"efficientnetv2-m-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_m/feature_vector/2",
"efficientnetv2-l-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_l/feature_vector/2",
"efficientnetv2-xl-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_xl/feature_vector/2",
"efficientnetv2-b0-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_b0/feature_vector/2",
"efficientnetv2-b1-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_b1/feature_vector/2",
"efficientnetv2-b2-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_b2/feature_vector/2",
"efficientnetv2-b3-21k-ft1k": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet21k_ft1k_b3/feature_vector/2",
"efficientnetv2-b0": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_b0/feature_vector/2",
"efficientnetv2-b1": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_b1/feature_vector/2",
"efficientnetv2-b2": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_b2/feature_vector/2",
"efficientnetv2-b3": "https://tfhub.dev/google/imagenet/efficientnet_v2_imagenet1k_b3/feature_vector/2",
"efficientnet_b0": "https://tfhub.dev/tensorflow/efficientnet/b0/feature-vector/1",
"efficientnet_b1": "https://tfhub.dev/tensorflow/efficientnet/b1/feature-vector/1",
"efficientnet_b2": "https://tfhub.dev/tensorflow/efficientnet/b2/feature-vector/1",
"efficientnet_b3": "https://tfhub.dev/tensorflow/efficientnet/b3/feature-vector/1",
"efficientnet_b4": "https://tfhub.dev/tensorflow/efficientnet/b4/feature-vector/1",
"efficientnet_b5": "https://tfhub.dev/tensorflow/efficientnet/b5/feature-vector/1",
"efficientnet_b6": "https://tfhub.dev/tensorflow/efficientnet/b6/feature-vector/1",
"efficientnet_b7": "https://tfhub.dev/tensorflow/efficientnet/b7/feature-vector/1",
"bit_s-r50x1": "https://tfhub.dev/google/bit/s-r50x1/1",
"inception_v3": "https://tfhub.dev/google/imagenet/inception_v3/feature-vector/4",
"inception_resnet_v2": "https://tfhub.dev/google/imagenet/inception_resnet_v2/feature-vector/4",
"resnet_v1_50": "https://tfhub.dev/google/imagenet/resnet_v1_50/feature-vector/4",
"resnet_v1_101": "https://tfhub.dev/google/imagenet/resnet_v1_101/feature-vector/4",
"resnet_v1_152": "https://tfhub.dev/google/imagenet/resnet_v1_152/feature-vector/4",
"resnet_v2_50": "https://tfhub.dev/google/imagenet/resnet_v2_50/feature-vector/4",
"resnet_v2_101": "https://tfhub.dev/google/imagenet/resnet_v2_101/feature-vector/4",
"resnet_v2_152": "https://tfhub.dev/google/imagenet/resnet_v2_152/feature-vector/4",
"nasnet_large": "https://tfhub.dev/google/imagenet/nasnet_large/feature_vector/4",
"nasnet_mobile": "https://tfhub.dev/google/imagenet/nasnet_mobile/feature_vector/4",
"pnasnet_large": "https://tfhub.dev/google/imagenet/pnasnet_large/feature_vector/4",
"mobilenet_v2_100_224": "https://tfhub.dev/google/imagenet/mobilenet_v2_100_224/feature_vector/4",
"mobilenet_v2_130_224": "https://tfhub.dev/google/imagenet/mobilenet_v2_130_224/feature_vector/4",
"mobilenet_v2_140_224": "https://tfhub.dev/google/imagenet/mobilenet_v2_140_224/feature_vector/4",
"mobilenet_v3_small_100_224": "https://tfhub.dev/google/imagenet/mobilenet_v3_small_100_224/feature_vector/5",
"mobilenet_v3_small_075_224": "https://tfhub.dev/google/imagenet/mobilenet_v3_small_075_224/feature_vector/5",
"mobilenet_v3_large_100_224": "https://tfhub.dev/google/imagenet/mobilenet_v3_large_100_224/feature_vector/5",
"mobilenet_v3_large_075_224": "https://tfhub.dev/google/imagenet/mobilenet_v3_large_075_224/feature_vector/5",
}
model_image_size_map = {
"efficientnetv2-s": 384,
"efficientnetv2-m": 480,
"efficientnetv2-l": 480,
"efficientnetv2-b0": 224,
"efficientnetv2-b1": 240,
"efficientnetv2-b2": 260,
"efficientnetv2-b3": 300,
"efficientnetv2-s-21k": 384,
"efficientnetv2-m-21k": 480,
"efficientnetv2-l-21k": 480,
"efficientnetv2-xl-21k": 512,
"efficientnetv2-b0-21k": 224,
"efficientnetv2-b1-21k": 240,
"efficientnetv2-b2-21k": 260,
"efficientnetv2-b3-21k": 300,
"efficientnetv2-s-21k-ft1k": 384,
"efficientnetv2-m-21k-ft1k": 480,
"efficientnetv2-l-21k-ft1k": 480,
"efficientnetv2-xl-21k-ft1k": 512,
"efficientnetv2-b0-21k-ft1k": 224,
"efficientnetv2-b1-21k-ft1k": 240,
"efficientnetv2-b2-21k-ft1k": 260,
"efficientnetv2-b3-21k-ft1k": 300,
"efficientnet_b0": 224,
"efficientnet_b1": 240,
"efficientnet_b2": 260,
"efficientnet_b3": 300,
"efficientnet_b4": 380,
"efficientnet_b5": 456,
"efficientnet_b6": 528,
"efficientnet_b7": 600,
"inception_v3": 299,
"inception_resnet_v2": 299,
"nasnet_large": 331,
"pnasnet_large": 331,
}
model_type = model_handle_map.get(model_name)
pixels = model_image_size_map.get(model_name)
print(f"Selected model: {model_name} : {model_type}")
IMAGE_SIZE = (pixels, pixels)
print(f"Input size {IMAGE_SIZE}")
return model_type, IMAGE_SIZE, pixels
model_name = "efficientnetv2-b3-21k-ft1k" # @param ['efficientnetv2-s', 'efficientnetv2-m', 'efficientnetv2-l', 'efficientnetv2-s-21k', 'efficientnetv2-m-21k', 'efficientnetv2-l-21k', 'efficientnetv2-xl-21k', 'efficientnetv2-b0-21k', 'efficientnetv2-b1-21k', 'efficientnetv2-b2-21k', 'efficientnetv2-b3-21k', 'efficientnetv2-s-21k-ft1k', 'efficientnetv2-m-21k-ft1k', 'efficientnetv2-l-21k-ft1k', 'efficientnetv2-xl-21k-ft1k', 'efficientnetv2-b0-21k-ft1k', 'efficientnetv2-b1-21k-ft1k', 'efficientnetv2-b2-21k-ft1k', 'efficientnetv2-b3-21k-ft1k', 'efficientnetv2-b0', 'efficientnetv2-b1', 'efficientnetv2-b2', 'efficientnetv2-b3', 'efficientnet_b0', 'efficientnet_b1', 'efficientnet_b2', 'efficientnet_b3', 'efficientnet_b4', 'efficientnet_b5', 'efficientnet_b6', 'efficientnet_b7', 'bit_s-r50x1', 'inception_v3', 'inception_resnet_v2', 'resnet_v1_50', 'resnet_v1_101', 'resnet_v1_152', 'resnet_v2_50', 'resnet_v2_101', 'resnet_v2_152', 'nasnet_large', 'nasnet_mobile', 'pnasnet_large', 'mobilenet_v2_100_224', 'mobilenet_v2_130_224', 'mobilenet_v2_140_224', 'mobilenet_v3_small_100_224', 'mobilenet_v3_small_075_224', 'mobilenet_v3_large_100_224', 'mobilenet_v3_large_075_224']
# num_epochs = 5 #@param {type: "integer"}
trainable = True #@param {type: "boolean"}
model_url, img_size, pixels = get_hub_url_and_isize(model_name)
IMG_HEIGHT = IMG_WIDTH = pixels
```
### Data-set interpretion
#### Load Image function for W&B
```
def load_img(path, label):
img = tf.io.read_file(path) # <= For non-TPU
# with open(path, "rb") as local_file: # <= For TPU
# img = local_file.read()
img = tf.image.decode_jpeg(img, channels=3)
img = tf.image.resize(img, (IMG_HEIGHT, IMG_WIDTH))
onehot_label = tf.argmax(label == [0.0, 1.0])
# img = np.load(img.numpy(), allow_pickle=True)
# onehot_label = np.load(onehot_label.numpy(), allow_pickle=True)
return img, onehot_label # ,img.shape(), onehot_label.shape()
```
#### Tensorflow Data-set
```
ds_train = tf.data.Dataset.from_tensor_slices((list(df_train[0]), list(df_train[1])))
# Configure with W&B settings
ds_train = (ds_train
.shuffle(buffer_size=1024)
.map(load_img, num_parallel_calls=AUTOTUNE)
.batch(wandb.config['batch_size'])
.cache()
.prefetch(AUTOTUNE))
ds_val = tf.data.Dataset.from_tensor_slices((list(df_val[0]), list(df_val[1])))
# Configure with W&B settings
ds_val = (ds_val
.shuffle(buffer_size=1024)
.map(load_img, num_parallel_calls=AUTOTUNE)
.batch(wandb.config['batch_size'])
.cache()
.prefetch(AUTOTUNE))
ds_train
```
## **2. Modeling**
### Define model structure and metrics
```
from sklearn.metrics import f1_score
tf.config.run_functions_eagerly(True)
@tf.autograph.experimental.do_not_convert
def f1(y_true, y_pred):
return f1_score(y_true,
tf.math.argmax(y_pred, 1))
# Data augmentation layer for image
tf.keras.backend.clear_session()
# =============== TPU ==================
# with strategy.scope():
# data_augmentation = tf.keras.Sequential([
# keras.layers.InputLayer(input_shape=img_size + (3,)),
# layers.RandomFlip("horizontal_and_vertical", seed=SEED),
# layers.RandomRotation(0.2, seed=SEED),
# layers.RandomZoom(0.1, seed=SEED)
# ])
# model = tf.keras.Sequential([
# data_augmentation,
# hub.KerasLayer(model_url, trainable=trainable), # Trainable: Fine tuning
# layers.Dropout(rate=0.2, seed=SEED),
# layers.Dense(units=2, # Binary classifcation
# activation='softmax')
# ])
# model.build((None,) + img_size + (3,)) # (IMG_SIZE, IMG_SIZE, 3)
# model.summary()
# # Update formula rule
# # velocity = momentum * velocity - learning_rate * g
# # w = w + momentum * velocity - learning_rate * g
# model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=wandb.config['learning_rate'], momentum=wandb.config['momentum'], nesterov=True),
# #loss=tf.keras.losses.CategoricalCrossentropy(from_logits=True, label_smoothing=wandb.config['label_smoothing'])
# loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
# metrics=['accuracy', f1])
# =============== GPU ==================
data_augmentation = tf.keras.Sequential([
keras.layers.InputLayer(input_shape=[IMG_HEIGHT, IMG_WIDTH, 3]),
layers.RandomFlip("horizontal_and_vertical", seed=SEED),
# layers.RandomRotation(0.2, seed=SEED),
layers.RandomZoom(0.1, seed=SEED),
layers.experimental.preprocessing.RandomWidth(0.1, seed=SEED),
])
model = tf.keras.Sequential([
data_augmentation,
hub.KerasLayer(model_url, trainable=trainable), # Trainable: Fine tuning
layers.Dropout(rate=0.2, seed=SEED),
layers.Dense(units=2, # Binary classifcation
activation='softmax',
kernel_regularizer=tf.keras.regularizers.l2(0.0001))
])
model.build((None,) + img_size + (3,)) # (IMG_SIZE, IMG_SIZE, 3)
model.summary()
# Update formula rule (when nesterov=True)
# velocity = momentum * velocity - learning_rate * g
# w = w + momentum * velocity - learning_rate * g
model.compile(optimizer=tf.keras.optimizers.SGD(learning_rate=wandb.config['learning_rate'], momentum=wandb.config['momentum'], nesterov=False),
#loss=tf.keras.losses.CategoricalCrossentropy(from_logits=True, label_smoothing=wandb.config['label_smoothing'])
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['accuracy', f1])
```
### Train model with W&B monitoring
```
hist = model.fit(ds_train, validation_data=ds_val,
epochs=wandb.config['epochs'],
callbacks=[WandbCallback()],
verbose=1).history
```
### Save model and weights
```
model.save(data_path + f'/{standard}.keras')
model.save_weights(
data_path + f'/{standard}_weight.h5', overwrite=True, save_format=None, options=None
)
```
## **3. Evaluation**
### Self-made test dataset
We will evaluate the model performance with the small proportion of the test data-set that we have created
#### Mask detection
Predict trial for one image
```
x_test = df_test[0] # Path to 655.jpg
y_test = label_test[0] # Mask label of 655.jpg
image = tf.io.read_file(x_test)
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, (IMG_HEIGHT, IMG_WIDTH))
true_label = 'No mask' if (np.argmax(y_test) == 0) else 'Mask'
plt.imshow(image/255.0)
plt.axis('off')
plt.show()
prediction_scores = model.predict(np.expand_dims(image, axis=0))
predicted_label = 'No mask' if (np.argmax(prediction_scores) == 0) else 'Mask'
print("True label: " + true_label)
print("Predicted label: " + predicted_label)
```
Evaluate the test dataset
```
from sklearn.metrics import accuracy_score
prediction_list = []
for i in range(len(df_test)):
image = tf.io.read_file(df_test[i])
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, (IMG_HEIGHT, IMG_WIDTH))
prediction_scores = model.predict(np.expand_dims(image, axis=0))
prediction_list.append(np.argmax(prediction_scores))
if (i % 10 == 0):
print(f"Predicted {i} images.")
acc = accuracy_score(label_test, prediction_list)
print(f"Test accuracy: {acc}")
```
The test dataset was originally cut down from the train dataset and have not even interfere the training process of the model. So this accuracy is quite reasonable. Currently we have trained the model for detecting mask on people and predict whether they have adhered the 5K standards.
From here, we can change the `standard` variable from `'mask'` to `'distancing'` to train the second model that specifically serves for the distance detection purpose. After finished all requirements, we can use the results from both models to conclude the `5k attribute` and export the final submission.
The 5k attribute can be evaluated as the pseudo code below:
```
5k = 1 if (mask == 1 and distancing == 1) else 0
```
#### Distancing detection
Predict trial for one image
```
x_test = df_test[10] # Path to 1995.jpg
y_test = label_test[10] # Mask label of 1995.jpg
image = tf.io.read_file(x_test)
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, (IMG_HEIGHT, IMG_WIDTH))
true_label = 'Too close' if (np.argmax(y_test) == 0) else 'Good distance'
plt.imshow(image/255.0)
plt.axis('off')
plt.show()
prediction_scores = model.predict(np.expand_dims(image, axis=0))
predicted_label = 'Too close' if (np.argmax(prediction_scores) == 0) else 'Good distance'
print("True label: " + true_label)
print("Predicted label: " + predicted_label)
```
Because there are many images missing either mask, distancing or 5k labels (even all of them), the model cannot determine so well and hence the accuracy is reduced.
Evaluate the test dataset
```
from sklearn.metrics import accuracy_score
prediction_list = []
for i in range(len(df_test)):
image = tf.io.read_file(df_test[i])
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, (IMG_HEIGHT, IMG_WIDTH))
prediction_scores = model.predict(np.expand_dims(image, axis=0))
prediction_list.append(np.argmax(prediction_scores))
if (i % 10 == 0):
print(f"Predicted {i} images.")
acc = accuracy_score(label_test, prediction_list)
print(f"Test accuracy: {acc}")
```
Apparently, the **dataset** is missing a lot of distancing attribute compared to the **mask**. As said, the accuracy for detecting the distance is quite lower than the model of mask detection.
### Public Test set
```
meta_test = pd.read_csv(data_path + '/test/public_test_meta.csv')
df_public_test = meta_test['fname']
test_img_path = data_path + '/test/images/'
```
#### Mask prediction
Load Model
```
dependencies = {
'f1': f1,
'KerasLayer': hub.KerasLayer(model_url, trainable=trainable)
}
model_mask = keras.models.load_model(data_path + f'/{standard}.keras', custom_objects=dependencies)
```
Predict
```
def predict_public_test(model, img_path):
prediction_list = []
for i, row in enumerate(df_public_test):
image = tf.io.read_file(img_path + row)
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, (IMG_HEIGHT, IMG_WIDTH))
prediction_scores = model.predict(np.expand_dims(image, axis=0))
prediction_list.append(np.argmax(prediction_scores))
if (i % 10 == 0):
print(f"Predicted {i} images.")
return prediction_list
# Mask prediction
prediction_mask_list = predict_public_test(model_mask, test_img_path)
```
#### Distancing prediction
```
# Switch standards
standard = 'distancing' #@param ['mask', 'distancing']
```
Load model
```
dependencies = {
'f1': f1,
'KerasLayer': hub.KerasLayer(model_url, trainable=trainable)
}
model_distancing = keras.models.load_model(data_path + f'/{standard}.keras', custom_objects=dependencies)
```
Predict
```
# Distancing prediction
prediction_distancing_list = predict_public_test(model_distancing, test_img_path)
meta_test_results = meta_test.copy()
meta_test['5k'] = [1 if prediction_mask_list[i] == 1 and prediction_distancing_list[i] == 1 else 0 for i in range(len(meta_test))]
meta_test_results[:10]
import os
os.makedirs(data_path + '/submission', exist_ok=True)
meta_test_results.to_csv(data_path + '/submission/5k-compliance-submission.csv')
```
## **4. Recreate the pipeline**
Since making the process of detecting mask and distancing to be seperated procedures, evaluate new models or changing hyperparameters would be exhausted. In this section, I manage to create the pipeline that can be run once to train, predict and monitor the metrics.
But before heading to that part, we can re-examine our problem to find a better way for a better results. One problem still remains is that the dataset contain so many missing values, and it is in fact can affect our model predictions, hence getting less accuracy.
Missing values
```
#@title
plt.figure(figsize=(10,6))
sns.heatmap(meta.isnull(), cbar=False)
#@title
print('Num. missing mask',\
len(meta[meta['mask'].isna()]))
print('Num. missing distancing',\
len(meta[meta['distancing'].isna()]))
print('Num. missing 5k',\
len(meta[meta['5k'].isna()]))
print('Num. missing mask and distancing:',\
len(meta[(meta['mask'].isna()) & (meta['distancing'].isna())]))
print('Num. missing mask and 5k:',\
len(meta[(meta['mask'].isna()) & (meta['5k'].isna())]))
print('Num. missing distancing and 5k:',\
len(meta[(meta['distancing'].isna()) & (meta['5k'].isna())]))
print('Num. missing all three attributes:',\
len(meta[(meta['mask'].isna()) & (meta['distancing'].isna()) & (meta['5k'].isna())]))
```
Apparently, the missing values are occurs as either missing one of three attribute, or a pair of attributes respectively (except for mask and distancing). None of row missing all three attributes.
To get the 5k value, we should have know the mask and distancing value first. Luckily, none of row miss these two variables. Therefore, we can fill the missing values with our own logics (not all the cases).
The original rule for 5k evaluation can be described as follow:
```
5k = 1 if (mask == 1 and distancing == 1) else 0
```
Base on this, we can design a pipeline that can fill out the missing values and produce better results:
> 1. Model mask detection -> Use to predict the missing mask values -> From there continue to fill the missing distancing values
```
if (mask == 1) and (5k == 1):
distancing = 1
elif (mask == 1) and (5k == 0):
distancing = 0
elif (mask == 0) and (5k == 0)
distancing = 0
```
In case the mask is 0, we can skip it since `mask == 0 and 5k == 0` is the only case we can intepret with and in that case, I have run the code:
`meta[(meta['mask'] == 0) & (meta['5k'] == 0) & (meta['distancing'].isna())]` and it return nothing. So it is safe to assume this part does not miss any values and is skippable.
> 2. Model distancing -> Use to predict the missing 5k values
```
if (distancing == 1) and (mask == 1)
5k == 1
elif (distancing == 0) or (mask == 0)
5k == 0
```
> 3. Model 5k -> Use to predict the final output 5k
In conclusion, the difference between the previous section and this section is that we will make three models instead of two. This is doable as we are going to fill the missing 5k values, thus we can use this attribute for our final prediction. For the new approach, please switch to `new_approach_kaggle.ipynb`
**Note 1**: After having a bad experience with Google Colab, I have switched the later approach to Kaggle with a longer session period and stronger GPU. But since Kaggle does not adapt the data storage/data retrieval well as Google Drive, I did had some trouble during using it. Thus some of the output files will need to download onto my PC in order to save the progress.
**Note 2**: The approach and procedures applied in this notebook is the initial one that I come up with first. In summary, I trained two models of mask detection and distancing detection. And after having the model trained, they will predict the `mask` and `distancing` labels. Based on the mask and distancing label, I use conditions to get the final label 5k. This approach is heavily unreliable since I skip all the missing values here.
For the new approach, I trained the mask model to predict the original train data-set again and fill all missing mask values. Then I used the updated data-set to continue to train the distance model and predict again to fill all missing distance values. After this step, I use the conditions again to fill the missing 5k values. In final step, I train the 5k model in order to predict the 5k label, which is differ from the initial approach where I did not use the 5k label for the train and evaluation process but instead generate it immediately based on the mask and distancing labels.
Comparing these two approaches, I personally think that the later one is better since it rely on all of the data. For example, having the results based on the mask and distancing only is not a good way since errors can occur in either predictions. Therefore, if we want to have 5k results for submission, we should train the model based on 5k values as well. And to make it happen, we should have investigate and interpret the missing values too.
| true |
code
| 0.421195 | null | null | null | null |
|
# Непараметрические криетрии
Критерий | Одновыборочный | Двухвыборочный | Двухвыборочный (связанные выборки)
------------- | -------------|
**Знаков** | $\times$ | | $\times$
**Ранговый** | $\times$ | $\times$ | $\times$
**Перестановочный** | $\times$ | $\times$ | $\times$
## Недвижимость в Сиэттле
Имеются данные о продажной стоимости недвижимости в Сиэтле для 50 сделок в 2001 году и 50 в 2002. Изменились ли в среднем цены?
```
import numpy as np
import pandas as pd
import itertools
from scipy import stats
from statsmodels.stats.descriptivestats import sign_test
from statsmodels.stats.weightstats import zconfint
from statsmodels.stats.weightstats import *
%pylab inline
```
### Загрузка данных
```
seattle_data = pd.read_csv('seattle.txt', sep = '\t', header = 0)
seattle_data.shape
seattle_data.head()
price2001 = seattle_data[seattle_data['Year'] == 2001].Price
price2002 = seattle_data[seattle_data['Year'] == 2002].Price
pylab.figure(figsize=(12,4))
pylab.subplot(1,2,1)
pylab.grid()
pylab.hist(price2001, color = 'r')
pylab.xlabel('2001')
pylab.subplot(1,2,2)
pylab.grid()
pylab.hist(price2002, color = 'b')
pylab.xlabel('2002')
pylab.show()
```
## Двухвыборочные критерии для независимых выборок
```
print('95%% confidence interval for the mean: [%f, %f]' % zconfint(price2001))
print('95%% confidence interval for the mean: [%f, %f]' % zconfint(price2002))
```
### Ранговый критерий Манна-Уитни
$H_0\colon F_{X_1}(x) = F_{X_2}(x)$
$H_1\colon F_{X_1}(x) = F_{X_2}(x + \Delta), \Delta\neq 0$
```
stats.mannwhitneyu(price2001, price2002)
```
### Перестановочный критерий
$H_0\colon F_{X_1}(x) = F_{X_2}(x)$
$H_1\colon F_{X_1}(x) = F_{X_2}(x + \Delta), \Delta\neq 0$
```
def permutation_t_stat_ind(sample1, sample2):
return np.mean(sample1) - np.mean(sample2)
def get_random_combinations(n1, n2, max_combinations):
index = list(range(n1 + n2))
indices = set([tuple(index)])
for i in range(max_combinations - 1):
np.random.shuffle(index)
indices.add(tuple(index))
return [(index[:n1], index[n1:]) for index in indices]
def permutation_zero_dist_ind(sample1, sample2, max_combinations = None):
joined_sample = np.hstack((sample1, sample2))
n1 = len(sample1)
n = len(joined_sample)
if max_combinations:
indices = get_random_combinations(n1, len(sample2), max_combinations)
else:
indices = [(list(index), filter(lambda i: i not in index, range(n))) \
for index in itertools.combinations(range(n), n1)]
distr = [joined_sample[list(i[0])].mean() - joined_sample[list(i[1])].mean() \
for i in indices]
return distr
pylab.hist(permutation_zero_dist_ind(price2001, price2002, max_combinations = 1000))
pylab.show()
def permutation_test(sample, mean, max_permutations = None, alternative = 'two-sided'):
if alternative not in ('two-sided', 'less', 'greater'):
raise ValueError("alternative not recognized\n"
"should be 'two-sided', 'less' or 'greater'")
t_stat = permutation_t_stat_ind(sample, mean)
zero_distr = permutation_zero_dist_ind(sample, mean, max_permutations)
if alternative == 'two-sided':
return sum([1. if abs(x) >= abs(t_stat) else 0. for x in zero_distr]) / len(zero_distr)
if alternative == 'less':
return sum([1. if x <= t_stat else 0. for x in zero_distr]) / len(zero_distr)
if alternative == 'greater':
return sum([1. if x >= t_stat else 0. for x in zero_distr]) / len(zero_distr)
print("p-value: %f" % permutation_test(price2001, price2002, max_permutations = 10000))
print("p-value: %f" % permutation_test(price2001, price2002, max_permutations = 50000))
```
| true |
code
| 0.449272 | null | null | null | null |
|
### Specify a text string to examine with NEMO
```
# specify query string
payload = 'The World Health Organization on Sunday reported the largest single-day increase in coronavirus cases by its count, at more than 183,000 new cases in the latest 24 hours. The UN health agency said Brazil led the way with 54,771 cases tallied and the U.S. next at 36,617. Over 15,400 came in in India.'
payload = 'is strongly affected by large ground-water withdrawals at or near Tupelo, Aberdeen, and West Point.'
# payload = 'Overall design: Teliospores of pathogenic races T-1, T-5 and T-16 of T. caries provided by a collection in Aberdeen, ID, USA'
payload = 'The results provide evidence of substantial population structure in C. posadasii and demonstrate presence of distinct geographic clades in Central and Southern Arizona as well as dispersed populations in Texas, Mexico and South and Central America'
payload = 'Most frequent numerical abnormalities in B-NHL were gains of chromosomes 3 and 18, although gains of chromosome 3 were less prominent in FL.'
```
### Load functions
```
# import credentials file
import yaml
with open("config.yml", 'r') as ymlfile:
cfg = yaml.safe_load(ymlfile)
# general way to extract values for a given key. Returns an array. Used to parse Nemo response and extract wikipedia id
# from https://hackersandslackers.com/extract-data-from-complex-json-python/
def extract_values(obj, key):
"""Pull all values of specified key from nested JSON."""
arr = []
def extract(obj, arr, key):
"""Recursively search for values of key in JSON tree."""
if isinstance(obj, dict):
for k, v in obj.items():
if isinstance(v, (dict, list)):
extract(v, arr, key)
elif k == key:
arr.append(v)
elif isinstance(obj, list):
for item in obj:
extract(item, arr, key)
return arr
results = extract(obj, arr, key)
return results
# getting wikipedia ID
# see he API at https://www.mediawiki.org/wiki/API:Query#Example_5:_Batchcomplete
# also, https://stackoverflow.com/questions/37024807/how-to-get-wikidata-id-for-an-wikipedia-article-by-api
def get_WPID (name):
import json
url = 'https://en.wikipedia.org/w/api.php?action=query&prop=pageprops&ppprop=wikibase_item&redirects=1&format=json&titles=' +name
r=requests.get(url).json()
return extract_values(r,'wikibase_item')
```
### Send a request to NEMO, and get a response
```
# make a service request
import requests
# payloadutf = payload.encode('utf-8')
url = "https://nemoservice.azurewebsites.net/nemo?appid=" + cfg['api_creds']['nmo1']
newHeaders = {'Content-type': 'application/json', 'Accept': 'text/plain'}
response = requests.post(url,
data='"{' + payload + '}"',
headers=newHeaders)
# display the results as string (remove json braces)
a = response.content.decode()
resp_full = a[a.find('{')+1 : a.find('}')]
resp_full
```
### Parse the response and load all found elements into a dataframe
```
# create a dataframe with entities, remove duplicates, then add wikipedia/wikidata concept IDs
import pandas as pd
import re
import xml.etree.ElementTree as ET
df = pd.DataFrame(columns=["Type","Ref","EntityType","Name","Form","WP","Value","Alt","WP_ID"])
# note that the last column is to be populated later, via Wikipedia API
# all previous columns are from Nemo: based on "e" (entity) and "d" (data) elements. "c" (concept) to be explored
# get starting and ending positions of xml fragments in the Nemo output
pattern_start = "<(e|d|c)\s"
iter = re.finditer(pattern_start,resp_full)
indices1 = [m.start(0) for m in iter]
pattern_end = "</(e|d|c)>"
iter = re.finditer(pattern_end,resp_full)
indices2 = [m.start(0) for m in iter]
# iterate over xml fragments returned by Nemo, extracting attributes from each and adding to dataframe
for i, entity in enumerate(indices1):
a = resp_full[indices1[i] : indices2[i]+4]
root = ET.fromstring(a)
tag = root.tag
attributes = root.attrib
df = df.append({"Type":root.tag,
"Ref":attributes.get('ref'),
"EntityType":attributes.get('type'),
"Name":attributes.get('name'),
"Form":attributes.get('form'),
"WP":attributes.get('wp'),
"Value":attributes.get('value'),
"Alt":attributes.get('alt')},
ignore_index=True)
```
E stands for entity;
the attribute ref gives you the title of the corresponding Wikipedia page when the attribute wp has the value “y”;
the attribute type gives you the type of entity for known entities; the types of interest for you are G, which is geo-political entity, L – geographic form/location (such as a mountain), and F, which is facility (such as an airport).
D stands for datafield, which comprises dates, NUMEX, email addresses and URLs, tracking numbers, and so on.
C stands for concept; these appear in Wikipedia and are deemed as relevant for the input text, but they do not get disambiguated
```
# remove duplicate records from the df
df = df.drop_duplicates(keep='first')
# for each found entity, add wikidata unique identifiers to the dataframe
for index, row in df.iterrows():
if (row['WP']=='y'):
row['WP_ID'] = get_WPID(row['Name'])[0]
df
```
| true |
code
| 0.542803 | null | null | null | null |
|
# Logistic regression model
## Setup
```
!git clone --depth 1 https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
!pip install -q optax
!pip install -q blackjax
!pip install -q sgmcmcjax
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import itertools
import warnings
from functools import partial
import jax
import jax.numpy as jnp
from jax.random import uniform, normal, bernoulli, split
from jax import jit, grad, value_and_grad, vmap
from jax.experimental import optimizers
from jax.scipy.special import logsumexp
from blackjax import nuts, stan_warmup
import optax
import sgmcmc_subspace_lib as sub
from sgmcmc_utils import build_optax_optimizer, build_nuts_sampler
from sgmcmcjax.samplers import *
```
## Generate Data
This part is based on https://github.com/jeremiecoullon/SGMCMCJax/blob/master/docs/nbs/models/logistic_regression.py
```
#ignore by GPU/TPU message (generated by jax module)
warnings.filterwarnings("ignore", message='No GPU/TPU found, falling back to CPU.')
# Sample initial beta values from random normal
def init_params(rng_key, d):
return normal(rng_key, (d,))
def gen_cov_mat(key, d, rho):
Sigma0 = np.diag(np.ones(d))
for i in range(1,d):
for j in range(0, i):
Sigma0[i,j] = (uniform(key)*2*rho - rho)**(i-j)
Sigma0[j,i] = Sigma0[i,j]
return jnp.array(Sigma0)
def logistic(theta, x):
return 1/(1+jnp.exp(-jnp.dot(theta, x)))
def gen_data(key, dim, N):
"""
Generate data with dimension `dim` and `N` data points
Parameters
----------
key: uint32
random key
dim: int
dimension of data
N: int
Size of dataset
Returns
-------
theta_true: ndarray
Theta array used to generate data
X: ndarray
Input data, shape=(N,dim)
y: ndarray
Output data: 0 or 1s. shape=(N,)
"""
key, theta_key, cov_key, x_key = split(key, 4)
rho = 0.4
print(f"Generating data, with N={N} and dim={dim}")
theta_true = normal(theta_key, shape=(dim, ))*jnp.sqrt(10)
covX = gen_cov_mat(cov_key, dim, rho)
X = jnp.dot(normal(x_key, shape=(N,dim)), jnp.linalg.cholesky(covX))
p_array = batch_logistic(theta_true, X)
keys = split(key, N)
y = batch_benoulli(keys, p_array).astype(jnp.int32)
return theta_true, X, y
@jit
def predict(params, inputs):
return batch_logistic(params, inputs) > 0.5
@jit
def accuracy(params, batch):
inputs, targets = batch
predicted_class = predict(params, inputs)
return jnp.mean(predicted_class == targets)
@jit
def loglikelihood(theta, x_val, y_val):
return -logsumexp(jnp.array([0., (1.-2.*y_val)*jnp.dot(theta, x_val)]))
@jit
def logprior(theta):
return -(0.5/10)*jnp.dot(theta,theta)
batch_logistic = jit(vmap(logistic, in_axes=(None, 0)))
batch_benoulli = vmap(bernoulli, in_axes=(0, 0))
batch_loglikelihood = vmap(loglikelihood, in_axes=(None, 0, 0))
dim = 10 # Choose a dimension for the parameters (10, 50,100 in the paper)
subspace_dim = 2 # Choose a dimension for the subspace parameters
ndata = 10000 # Number of data points
nwarmup = 1000 # Number of iterations during warmup phase
nsamples = 10000 # Number of SGMCMC iterations
nsamplesCV = nsamples // 2
key = jax.random.PRNGKey(42)
theta_true, X, y = gen_data(key, dim, ndata)
batch_size = int(0.01*X.shape[0])
data = (X, y)
init_key, key = split(key)
theta_init = init_params(init_key, dim)
```
## SGD
```
niters = 5000
learning_rate = 6e-5
opt = optax.sgd(learning_rate=learning_rate)
optimizer = build_optax_optimizer(opt, loglikelihood, logprior,
data, batch_size, pbar=False)
opt_key, key = split(key)
sgd_params, logpost_array = optimizer(opt_key, niters, theta_init)
train_accuracy = accuracy(sgd_params, data)
print("Training set accuracy {}".format(train_accuracy))
plt.plot(-logpost_array, color='tab:orange')
plt.show()
```
### Subspace Model
```
sub_opt_key, key = split(key)
sgd_sub_params, _, opt_log_post_trace, _ = sub.subspace_optimizer(
sub_opt_key, loglikelihood, logprior, theta_init, data, batch_size,
subspace_dim, nwarmup, nsamples, opt, pbar=False)
train_accuracy = accuracy(sgd_sub_params, data)
print("Training set accuracy {}".format(train_accuracy))
plt.plot(-opt_log_post_trace, color='tab:pink')
plt.show()
```
## NUTS
```
nuts_sampler = build_nuts_sampler(nwarmup, loglikelihood, logprior,
data, batch_size=ndata, pbar=False)
nuts_key, key = split(key)
nuts_params = nuts_sampler(nuts_key, nsamples//10, theta_init)
train_accuracy = accuracy(jnp.mean(nuts_params, axis=0), data)
print("Training set accuracy {}".format(train_accuracy))
```
### Subspace Model
```
build_nuts_sampler_partial = partial(build_nuts_sampler, nwarmup=nwarmup)
nuts_key, key = split(key)
nuts_sub_params = sub.subspace_sampler(nuts_key, loglikelihood, logprior,
theta_init, build_nuts_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=0, nsteps_sub=0, use_cv=False, opt=None, pbar=False)
```
## SGLD
```
dt = 1e-5
# Run sampler
sgld_sampler = build_sgld_sampler(dt, loglikelihood, logprior, data, batch_size)
sgld_key, key = split(key)
sgld_output = sgld_sampler(sgld_key, nsamples, theta_init)
```
### Subspace Sampler
```
build_sgld_sampler_partial = partial(build_sgld_sampler, dt=dt)
sgld_key, key = split(key)
sgld_sub_output = sub.subspace_sampler(sgld_key, loglikelihood, logprior,
theta_init, build_sgld_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=0, nsteps_sub=0, use_cv=False,
opt=None, pbar=False)
```
## SGLDCV
```
dt = 1e-5
sgldCV_sampler = build_sgldCV_sampler(dt, loglikelihood, logprior,
data, batch_size, sgd_params)
sgldCV_key, key = split(key)
sgldCV_output = sgldCV_sampler(sgldCV_key, nsamplesCV, sgd_params)
```
### Subspace Sampler
```
build_sgldCV_sampler_partial = partial(build_sgldCV_sampler, dt=dt)
sgldCV_key, key = split(key)
sgldCV_sub_output = sub.subspace_sampler(sgldCV_key, loglikelihood, logprior,
theta_init, build_sgldCV_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=niters//2, nsteps_sub=niters//2,
use_cv=True, opt=opt, pbar=False)
```
## SGHMC
```
L = 5
dt = 1e-6
sghmc_sampler = build_sghmc_sampler(dt, L, loglikelihood,
logprior, data, batch_size)
sghmc_key, key = split(key)
sghmc_output = sghmc_sampler(sghmc_key, nsamples, theta_init)
```
### Subspace Sampler
```
build_sghmc_sampler_partial = partial(build_sghmc_sampler, dt=dt, L=L)
sghmc_key, key = split(key)
sghmc_sub_output = sub.subspace_sampler(sghmc_key, loglikelihood, logprior,
theta_init, build_sghmc_sampler_partial,
data, batch_size, subspace_dim,
nsamples, nsteps_full=0, nsteps_sub=0,
use_cv=False, opt=None, pbar=False)
```
## SGHMCCV
```
dt = 1e-7 # step size parameter
L = 5
sghmcCV_sampler = build_sghmcCV_sampler(dt, L, loglikelihood, logprior, data, batch_size, sgd_params)
sghmcCV_key, key = split(key)
sghmcCV_output = sghmcCV_sampler(sghmcCV_key, nsamplesCV, sgd_params)
```
### Subspace Sampler
```
build_sghmcCV_sampler_partial = partial(build_sghmcCV_sampler, dt=dt, L=L)
sghmcCV_key, key = split(key)
sghmcCV_sub_output = sub.subspace_sampler(sghmcCV_key, loglikelihood, logprior,
theta_init, build_sghmcCV_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=niters//2, nsteps_sub=niters//2,
use_cv=True, opt=opt, pbar=False)
```
## SGNHT
```
dt = 1e-6 # step size parameter
a = 0.02
sgnht_sampler = build_sgnht_sampler(dt, loglikelihood, logprior,
data, batch_size, a=a)
sgnht_key, key = split(key)
sgnht_output = sgnht_sampler(sgnht_key, nsamples, theta_init)
```
### Subspace Sampler
```
build_sgnht_sampler_partial = partial(build_sgnht_sampler, dt=dt, a=a)
sgnht_key, key = split(key)
sgnht_sub_output = sub.subspace_sampler(sgnht_key, loglikelihood, logprior,
theta_init, build_sgnht_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=0, nsteps_sub=0, use_cv=False,
opt=opt, pbar=False)
```
## SGHNTCV
```
dt = 1e-6 # step size parameter
a = 0.02
sgnhtCV_sampler = build_sgnhtCV_sampler(dt, loglikelihood, logprior,
data, batch_size, sgd_params, a=a)
sgnhtCV_key, key = split(key)
sgnhtCV_output = sgnhtCV_sampler(sgnhtCV_key, nsamplesCV, sgd_params)
```
### Subspace Sampler
```
build_sgnhtCV_sampler_partial = partial(build_sgnhtCV_sampler, dt=dt, a=a)
sgnhtCV_key, key = split(key)
sgnhtCV_sub_output = sub.subspace_sampler(sgnhtCV_key, loglikelihood, logprior,
theta_init, build_sgnhtCV_sampler_partial,
data, batch_size, subspace_dim, nsamples,
nsteps_full=niters//2, nsteps_sub=niters//2,
use_cv=True, opt=opt, pbar=False)
```
## ULA - SGLD with the full dataset
```
dt = 4e-5 # step size parameter
ula_sampler = build_sgld_sampler(dt, loglikelihood, logprior,
data, batch_size=ndata)
ula_key, key = split(key)
ula_output = ula_sampler(ula_key, nsamples, theta_init)
```
### Subspace Sampler
```
build_sgld_sampler_partial = partial(build_sgld_sampler, dt=dt)
ula_key, key = split(key)
ula_sub_output = sub.subspace_sampler(ula_key, loglikelihood, logprior,
theta_init, build_sgld_sampler_partial,
data, ndata, subspace_dim, nsamples,
nsteps_full=0, nsteps_sub=0, use_cv=False,
opt=None, pbar=False)
```
## Trace plots
```
def trace_plot(outs):
nrows, ncols = 2, 4
fig, axes = plt.subplots(nrows=nrows, ncols=ncols, figsize=(16, 12))
for ax, (title, out) in zip(axes.flatten(), outs.items()):
ax.plot(out)
ax.set_title(title)
ax.set_xlabel("Iteration")
ax.grid(color='white', linestyle='-', linewidth=2)
ax.set_axisbelow(True)
ax.set_facecolor("#EAEBF0")
plt.tight_layout()
plt.savefig("traceplot.pdf", dpi=300)
plt.show()
outs = {"STAN": nuts_params, "SGLD": sgld_output, "SGLDCV": sgldCV_output, "ULA": ula_output, "SGHMC": sghmc_output, "SGHMCCV":sghmcCV_output, "SGNHT": sgnht_output, "SGNHTCV": sgnhtCV_output}
trace_plot(outs)
subspace_outs = {"STAN": nuts_sub_params, "SGLD": sgld_sub_output, "SGLDCV": sgldCV_sub_output, "ULA": ula_sub_output, "SGHMC": sghmc_sub_output, "SGHMCCV":sghmcCV_sub_output, "SGNHT": sgnht_sub_output, "SGNHTCV": sgnhtCV_sub_output}
trace_plot(subspace_outs)
```
| true |
code
| 0.85558 | null | null | null | null |
|
# Finding locations to establish temporary emergency facilities
Run this notebook to create a Decision Optimization model with Decision Optimization for Watson Studio and deploy the model using Watson Machine Learning.
The deployed model can later be accessed using the [Watson Machine Learning client library](https://wml-api-pyclient-dev-v4.mybluemix.net/) to find optimal location based on given constraints.
The model created here is a basic Decision Optimization model. The main purpose is to demonstrate creating a model and deploying using Watson Machine Learning. This model can and should be improved upon to include better constraints that can provide a more optimal solution.
## Steps
**Build and deploy model**
1. [Provision a Watson Machine Learning service](#provision-a-watson-machine-learning-service)
1. [Set up the Watson Machine Learning client library](#set-up-the-watson-machine-learning-client-library)
1. [Build the Decision Optimization model](#build-the-decision-optimization-model)
1. [Deploy the Decision Optimization model](#deploy-the-decision-optimization-model)
**Test the deployed model**
1. [Generate an API Key from the HERE Developer Portal](#generate-an-api-key-from-the-here-developer-portal)
1. [Query HERE API for Places](#query-here-api-for-places)
1. [Create and monitor a job to test the deployed model](#create-and-monitor-a-job-to-test-the-deployed-model)
1. [Extract and display solution](#extract-and-display-solution)
<br>
### Provision a Watson Machine Learning service
- If you do not have an IBM Cloud account, [register for a free trial account](https://cloud.ibm.com/registration).
- Log into [IBM Cloud](https://cloud.ibm.com/login)
- Create a [create a Watson Machine Learning instance](https://cloud.ibm.com/catalog/services/machine-learning)
<br>
### Set up the Watson Machine Learning client library
Install the [Watson Machine Learning client library](https://wml-api-pyclient-dev-v4.mybluemix.net/). This notebook uses the preview Python client based on v4 of Watson Machine Learning APIs.
> **Important** Do not load both (V3 and V4) WML API client libraries into a notebook.
```
# Uninstall the Watson Machine Learning client Python client based on v3 APIs
!pip uninstall watson-machine-learning-client -y
# Install the WML client API v4
!pip install watson-machine-learning-client-V4
```
<br>
#### Create a client instance
Use your [Watson Machine Learning service credentials](https://dataplatform.cloud.ibm.com/docs/content/wsj/analyze-data/ml-get-wml-credentials.html) and update the next cell.
```
# @hidden_cell
WML_API_KEY = '...'
WML_INSTANCE_ID = '...'
WML_URL = 'https://us-south.ml.cloud.ibm.com'
from watson_machine_learning_client import WatsonMachineLearningAPIClient
# Instantiate a client using credentials
wml_credentials = {
'apikey': WML_API_KEY,
'instance_id': WML_INSTANCE_ID,
'url': WML_URL
}
client = WatsonMachineLearningAPIClient(wml_credentials)
client.version
```
<br>
### Build the Decision Optimization model
- The Decision Optimization model will be saved to a `model.py` file in a subdirectory (i.e., `model/`) of the current working directory.
- The model will be placed in a tar archive and uploaded to Watson Machine Learning.
Set up variables for model and deployment
```
import os
model_dir = 'model'
model_file = 'model.py'
model_path = '{}/{}'.format(model_dir, model_file)
model_tar = 'model.tar.gz'
model_tar_path = '{}/{}'.format(os.getcwd(), model_tar)
model_name = 'DO_HERE_DEMO'
model_desc = 'Finding locations for short-term emergency facilities'
deployment_name = 'DO_HERE_DEMO Deployment'
deployment_desc = 'Deployment of DO_HERE_DEMO model'
print(model_path)
print(model_tar_path)
```
<br>
#### Create the model.py in a model subdirectory
Use the `mkdir` and `write_file` commands to create the subdirectory and write the model code to a file.
```
%mkdir $model_dir
%%writefile $model_path
from docplex.util.environment import get_environment
from os.path import splitext
import pandas
from six import iteritems
import json
def get_all_inputs():
'''Utility method to read a list of files and return a tuple with all
read data frames.
Returns:
a map { datasetname: data frame }
'''
result = {}
env = get_environment()
for iname in [f for f in os.listdir('.') if splitext(f)[1] == '.csv']:
with env.get_input_stream(iname) as in_stream:
df = pandas.read_csv(in_stream)
datasetname, _ = splitext(iname)
result[datasetname] = df
return result
def write_all_outputs(outputs):
'''Write all dataframes in ``outputs`` as .csv.
Args:
outputs: The map of outputs 'outputname' -> 'output df'
'''
for (name, df) in iteritems(outputs):
if isinstance(df, pandas.DataFrame):
csv_file = '%s.csv' % name
print(csv_file)
with get_environment().get_output_stream(csv_file) as fp:
if sys.version_info[0] < 3:
fp.write(df.to_csv(index=False, encoding='utf8'))
else:
fp.write(df.to_csv(index=False).encode(encoding='utf8'))
elif isinstance(df, str):
txt_file = '%s.txt' % name
with get_environment().get_output_stream(txt_file) as fp:
fp.write(df.encode(encoding='utf8'))
if len(outputs) == 0:
print('Warning: no outputs written')
%%writefile -a $model_path
from docplex.mp.model import Model
from statistics import mean
def get_distance(routes_df, start, destination):
s = getattr(start, 'geocode', start)
d = getattr(destination, 'geocode', destination)
row = routes_df.loc[
(routes_df['start'] == s) &
(routes_df['destination'] == d)
]
return row['distance'].values[0]
def build_and_solve(places_df, routes_df, number_sites=3):
print('Building and solving model')
mean_dist = mean(routes_df['distance'].unique())
p_only = places_df.loc[places_df['is_medical'] == False]
h_only = places_df.loc[places_df['is_medical'] == True]
places = list(p_only.itertuples(name='Place', index=False))
postal_codes = p_only['postal_code'].unique()
hospital_geocodes = h_only['geocode'].unique()
mdl = Model(name='temporary emergency sites')
## decision variables
places_vars = mdl.binary_var_dict(places, name='is_place')
postal_link_vars = mdl.binary_var_matrix(postal_codes, places, 'link')
hosp_link_vars = mdl.binary_var_matrix(hospital_geocodes, places, 'link')
## objective function
# minimize hospital distances
h_total_distance = mdl.sum(hosp_link_vars[h, p] * abs(mean_dist - get_distance(routes_df, h, p)) for h in hospital_geocodes for p in places)
mdl.minimize(h_total_distance)
## constraints
# match places with their correct postal_code
for p in places:
for c in postal_codes:
if p.postal_code != c:
mdl.add_constraint(postal_link_vars[c, p] == 0, 'ct_forbid_{0!s}_{1!s}'.format(c, p))
# # each postal_code should have one only place
# mdl.add_constraints(
# mdl.sum(postal_link_vars[c, p] for p in places) == 1 for c in postal_codes
# )
# # each postal_code must be associated with a place
# mdl.add_constraints(
# postal_link_vars[c, p] <= places_vars[p] for p in places for c in postal_codes
# )
# solve for 'number_sites' places
mdl.add_constraint(mdl.sum(places_vars[p] for p in places) == number_sites)
## model info
mdl.print_information()
stats = mdl.get_statistics()
## model solve
mdl.solve(log_output=True)
details = mdl.solve_details
status = '''
Model stats
number of variables: {}
number of constraints: {}
Model solve
time (s): {}
status: {}
'''.format(
stats.number_of_variables,
stats.number_of_constraints,
details.time,
details.status
)
possible_sites = [p for p in places if places_vars[p].solution_value == 1]
return possible_sites, status
%%writefile -a $model_path
import pandas
def run():
# Load CSV files into inputs dictionary
inputs = get_all_inputs()
places_df = inputs['places']
routes_df = inputs['routes']
site_suggestions, status = build_and_solve(places_df, routes_df)
solution_df = pandas.DataFrame(site_suggestions)
outputs = {
'solution': solution_df,
'status': status
}
# Generate output files
write_all_outputs(outputs)
run()
```
<br>
#### Create the model tar archive
Use the `tar` command to create a tar archive with the model file.
```
import tarfile
def reset(tarinfo):
tarinfo.uid = tarinfo.gid = 0
tarinfo.uname = tarinfo.gname = 'root'
return tarinfo
tar = tarfile.open(model_tar, 'w:gz')
tar.add(model_path, arcname=model_file, filter=reset)
tar.close()
```
<br>
### Deploy the Decision Optimization model
Store model in Watson Machine Learning with:
- the tar archive previously created,
- metadata including the model type and runtime
```
# All available meta data properties
client.repository.ModelMetaNames.show()
# All available runtimes
client.runtimes.list(pre_defined=True)
```
<br>
#### Upload the model to Watson Machine Learning
Configure the model metadata and set the model type (i.e., `do-docplex_12.9`) and runtime (i.e., `do_12.9`)
```
import os
model_metadata = {
client.repository.ModelMetaNames.NAME: model_name,
client.repository.ModelMetaNames.DESCRIPTION: model_desc,
client.repository.ModelMetaNames.TYPE: 'do-docplex_12.9',
client.repository.ModelMetaNames.RUNTIME_UID: 'do_12.9'
}
model_details = client.repository.store_model(model=model_tar_path, meta_props=model_metadata)
model_uid = client.repository.get_model_uid(model_details)
print('Model GUID: {}'.format(model_uid))
```
<br>
#### Create a deployment
Create a batch deployment for the model, providing deployment metadata and model UID.
```
deployment_metadata = {
client.deployments.ConfigurationMetaNames.NAME: deployment_name,
client.deployments.ConfigurationMetaNames.DESCRIPTION: deployment_desc,
client.deployments.ConfigurationMetaNames.BATCH: {},
client.deployments.ConfigurationMetaNames.COMPUTE: {'name': 'S', 'nodes': 1}
}
deployment_details = client.deployments.create(model_uid, meta_props=deployment_metadata)
deployment_uid = client.deployments.get_uid(deployment_details)
print('Deployment GUID: {}'.format(deployment_uid))
```
<br>
**Congratulations!** The model has been succesfully deployed. Please make a note of the deployment UID.
<br>
## Test the deployed model
### Generate an API Key from the HERE Developer Portal
To test your deployed model using actual data from HERE Location services, you'll need an API key.
Follow the instructions outlined in the [HERE Developer Portal](https://developer.here.com/sign-up) to [generate an API key](https://developer.here.com/documentation/authentication/dev_guide/topics/api-key-credentials.html).
Use your [HERE.com API key](https://developer.here.com/sign-up) and update the next cell.
```
# @hidden_cell
HERE_APIKEY = '...'
```
<br>
Set up helper functions to query HERE APIs
```
import re
import requests
geocode_endpoint = 'https://geocode.search.hereapi.com/v1/geocode?q={address}&apiKey={api_key}'
browse_endpoint = 'https://browse.search.hereapi.com/v1/browse?categories=%s&at=%s&apiKey=%s'
matrix_routing_endpoint = 'https://matrix.route.ls.hereapi.com/routing/7.2/calculatematrix.json?mode=%s&summaryAttributes=%s&apiKey=%s'
coordinates_regex = '^[-+]?([1-8]?\d(\.\d+)?|90(\.0+)?),\s*[-+]?(180(\.0+)?|((1[0-7]\d)|([1-9]?\d))(\.\d+)?)$'
def is_geocode (location):
geocode = None
if isinstance(location, str):
l = location.split(',')
if len(l) == 2:
geocode = '{},{}'.format(l[0].strip(), l[1].strip())
elif isinstance(location, list) and len(location) == 2:
geocode = ','.join(str(l) for l in location)
if geocode is not None and re.match(coordinates_regex, geocode):
return [float(l) for l in geocode.split(',')]
else:
return False
def get_geocode (address):
g = is_geocode(address)
if not g:
url = geocode_endpoint.format(address=address, api_key=HERE_APIKEY)
response = requests.get(url)
if response.ok:
jsonResponse = response.json()
position = jsonResponse['items'][0]['position']
g = [position['lat'], position['lng']]
else:
print(response.text)
return g
def get_browse_url (location, categories, limit=25):
categories = ','.join(c for c in categories)
geocode = get_geocode(location)
coordinates = ','.join(str(g) for g in geocode)
browse_url = browse_endpoint % (
categories,
coordinates,
HERE_APIKEY
)
if limit > 0:
browse_url = '{}&limit={}'.format(browse_url, limit)
return browse_url
def browse_places (location, categories=[], results_limit=100):
places_list = []
browse_url = get_browse_url(location, categories, limit=results_limit)
response = requests.get(browse_url)
if response.ok:
json_response = response.json()
places_list = json_response['items']
else:
print(response.text)
return places_list
def get_places_nearby (location, categories=[], results_limit=100, max_distance_km=50):
places_list = browse_places(location, categories=categories, results_limit=results_limit)
filtered_places = []
for p in places_list:
if p['distance'] <= max_distance_km * 1000:
filtered_places.append(Place(p))
return filtered_places
def get_hospitals_nearby (location, results_limit=100, max_distance_km=50):
h_cat = ['800-8000-0159']
hospitals_list = browse_places(location, categories=h_cat, results_limit=results_limit)
filtered_hospitals = []
for h in hospitals_list:
if h['distance'] <= max_distance_km * 1000:
filtered_hospitals.append(Place(h, is_medical=True))
return filtered_hospitals
def get_matrix_routing_url ():
route_mode = 'shortest;car;traffic:disabled;'
summary_attributes = 'routeId,distance'
matrix_routing_url = matrix_routing_endpoint % (
route_mode,
summary_attributes,
HERE_APIKEY
)
return matrix_routing_url
def get_route_summaries (current_geocode, places, hospitals):
# Request should not contain more than 15 start positions
num_starts = 15
postal_codes_set = set()
postal_codes_geocodes = []
places_waypoints = {}
for i, p in enumerate(places):
if p.postal_code:
postal_codes_set.add('{}:{}'.format(p.postal_code, p.country))
places_waypoints['destination{}'.format(i)] = p.geocode
for p in postal_codes_set:
geocode = get_geocode(p)
postal_codes_geocodes.append({
'postal_code': p.split(':')[0],
'geocode': ','.join(str(g) for g in geocode)
})
current = {
'geocode': ','.join(str(g) for g in current_geocode)
}
start_geocodes = [current] + postal_codes_geocodes + [h.to_dict() for h in hospitals]
start_coords = [
start_geocodes[i:i+num_starts]
for i in range(0, len(start_geocodes), num_starts)
]
route_summaries = []
matrix_routing_url = get_matrix_routing_url()
for sc in start_coords:
start_waypoints = {}
for i, s in enumerate(sc):
start_waypoints['start{}'.format(i)] = s['geocode']
coords = {**start_waypoints, **places_waypoints}
response = requests.post(matrix_routing_url, data = coords)
if not response.ok:
print(response.text)
else:
json_response = response.json()
for entry in json_response['response']['matrixEntry']:
start_geocode = start_waypoints['start{}'.format(entry['startIndex'])]
dest_geocode = places_waypoints[
'destination{}'.format(entry['destinationIndex'])
]
for s in sc:
if 'address' not in s and 'postal_code' in s and s['geocode'] == start_geocode:
route_summaries.append({
'start': s['postal_code'],
'destination': dest_geocode,
'distance': entry['summary']['distance'],
'route_id': entry['summary']['routeId']
})
break
route_summaries.append({
'start': start_geocode,
'destination': dest_geocode,
'distance': entry['summary']['distance'],
'route_id': entry['summary']['routeId']
})
return route_summaries
```
<br>
Define a Place class
```
class Place(object):
def __init__(self, p, is_medical=False):
self.id = p['id']
self.title = p['title']
self.address = p['address']['label'] if 'label' in p['address'] else p['address']
self.postal_code = p['address']['postalCode'] if 'postalCode' in p['address'] else p['postal_code']
self.distance = p['distance']
self.primary_category = p['categories'][0]['id'] if 'categories' in p else p['primary_category']
self.geocode = '{},{}'.format(p['position']['lat'], p['position']['lng']) if 'position' in p else p['geocode']
self.country = p['address']['countryCode'] if 'countryCode' in p['address'] else p['country']
self.is_medical = p['is_medical'] if 'is_medical' in p else is_medical
if isinstance(self.is_medical, str):
self.is_medical = self.is_medical.lower() in ['true', '1']
def to_dict(self):
location = self.geocode.split(',')
return({
'id': self.id,
'title': self.title,
'address': self.address,
'postal_code': self.postal_code,
'distance': self.distance,
'primary_category': self.primary_category,
'geocode': self.geocode,
'country': self.country,
'is_medical': self.is_medical
})
def __str__(self):
return self.address
```
<br>
### Query HERE API for Places
Use the HERE API to get a list of Places in the vicinity of an address
Example of `Place` entity returned by HERE API:
```json
{
'title': 'Duane Street Hotel',
'id': 'here:pds:place:840dr5re-fba2a2b91f944ee4a699eea7556896bd',
'resultType': 'place',
'address': {
'label': 'Duane Street Hotel, 130 Duane St, New York, NY 10013, United States',
'countryCode': 'USA',
'countryName': 'United States',
'state': 'New York',
'county': 'New York',
'city': 'New York',
'district': 'Tribeca',
'street': 'Duane St',
'postalCode': '10013',
'houseNumber': '130'
},
'position': { 'lat': 40.71599, 'lng': -74.00735 },
'access': [ { 'lat': 40.71608, 'lng': -74.00728 } ],
'distance': 161,
'categories': [
{ 'id': '100-1000-0000' },
{ 'id': '200-2000-0000' },
{ 'id': '500-5000-0000' },
{ 'id': '500-5000-0053' },
{ 'id': '500-5100-0000' },
{ 'id': '700-7400-0145' }
],
'foodTypes': [ { 'id': '101-000' } ],
'contacts': [ ],
'openingHours': [
{
'text': [ 'Mon-Sun: 00:00 - 24:00' ],
'isOpen': true,
'structured': [
{
'start': 'T000000',
'duration': 'PT24H00M',
'recurrence': 'FREQ:DAILY;BYDAY:MO,TU,WE,TH,FR,SA,SU'
}
]
}
]
}
```
```
address = 'New York, NY'
max_results = 20
# HERE Place Category System
# https://developer.here.com/documentation/geocoding-search-api/dev_guide/topics-places/places-category-system-full.html
places_categories = ['500-5000'] # Hotel-Motel
current_geocode = get_geocode(address)
places = get_places_nearby(
current_geocode,
categories=places_categories,
results_limit=max_results
)
hospitals = get_hospitals_nearby(
current_geocode,
results_limit=3
)
print('Places:')
for p in places:
print(p)
print('\nHospitals:')
for h in hospitals:
print(h)
```
<br>
### Create and monitor a job to test the deployed model
Create a payload containing places data received from HERE
```
import pandas as pd
places_df = pd.DataFrame.from_records([p.to_dict() for p in (places + hospitals)])
places_df.head()
route_summaries = get_route_summaries(current_geocode, places, hospitals)
routes_df = pd.DataFrame.from_records(route_summaries)
routes_df.drop_duplicates(keep='last', inplace=True)
routes_df.head()
solve_payload = {
client.deployments.DecisionOptimizationMetaNames.INPUT_DATA: [
{ 'id': 'places.csv', 'values' : places_df },
{ 'id': 'routes.csv', 'values' : routes_df }
],
client.deployments.DecisionOptimizationMetaNames.OUTPUT_DATA: [
{ 'id': '.*\.csv' },
{ 'id': '.*\.txt' }
]
}
```
<br>
Submit a new job with the payload and deployment.
Set the UID of the deployed model.
```
# deployment_uid = '...'
job_details = client.deployments.create_job(deployment_uid, solve_payload)
job_uid = client.deployments.get_job_uid(job_details)
print('Job UID: {}'.format(job_uid))
```
Display job status until it is completed.
The first job of a new deployment might take some time as a compute node must be started.
```
from time import sleep
while job_details['entity']['decision_optimization']['status']['state'] not in ['completed', 'failed', 'canceled']:
print(job_details['entity']['decision_optimization']['status']['state'] + '...')
sleep(3)
job_details=client.deployments.get_job_details(job_uid)
print(job_details['entity']['decision_optimization']['status']['state'])
# job_details
job_details['entity']['decision_optimization']['status']
```
<br>
### Extract and display solution
Display the output solution.
```
import base64
output_data = job_details['entity']['decision_optimization']['output_data']
solution = None
stats = None
for i, d in enumerate(output_data):
if d['id'] == 'solution.csv':
solution = pd.DataFrame(output_data[i]['values'],
columns = job_details['entity']['decision_optimization']['output_data'][0]['fields'])
else:
stats = base64.b64decode(output_data[i]['values'][0][0]).decode('utf-8')
print(stats)
solution.head()
```
<br>
Check out the online documentation at <a href="https://dataplatform.cloud.ibm.com/docs" target="_blank" rel="noopener noreferrer">https://dataplatform.cloud.ibm.com/docs</a> for more samples, tutorials and documentation.
<br>
## Helper functions
See `watson-machine-learning-client(V4)` Python library documentation for more info on the API:
https://wml-api-pyclient-dev-v4.mybluemix.net/
```
## List models
def list_models(wml_client):
wml_client.repository.list_models()
## List deployments
def list_deployments(wml_client):
wml_client.deployments.list()
## Delete a model
def delete_model(wml_client, model_uid):
wml_client.repository.delete(model_uid)
## Delete a deployment
def delete_deployment(wml_client, deployment_uid):
wml_client.deployments.delete(deployment_uid)
## Get details of all models
def details_all_models(wml_client):
return wml_client.repository.get_model_details()['resources']
## Get details of all deployments
def details_all_deployments(wml_client):
return wml_client.deployments.get_details()['resources']
# Find model using model name
def get_models_by_name(wml_client, model_name):
all_models = wml_client.repository.get_model_details()['resources']
models = [m for m in all_models if m['entity']['name'] == model_name]
return models
# Find deployment using deployment name
def get_deployments_by_name(wml_client, deployment_name):
all_deployments = wml_client.deployments.get_details()['resources']
deployments = [d for d in all_deployments if d['entity']['name'] == deployment_name][0]
return deployments
delete_deployment(client, deployment_uid)
delete_model(client, model_uid)
list_deployments(client)
list_models(client)
```
| true |
code
| 0.630201 | null | null | null | null |
|
# Data Analysis
This is the main notebook performing all feature engineering, model selection, training, evaluation etc.
The different steps are:
- Step1 - import dependencies
- Step2 - load payloads into memory
- Step3A - Feature engineering custom features
- Step3B - Feature engineering bag-of-words
- Step3C - Feature space visualization
- Step4 - Model selection
- (Step4B - Load pre-trained classifiers)
- Step5 - Visualization
- Step6 - Website integration extract
# Step1
import dependencies
```
%matplotlib inline
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
import seaborn
import string
from IPython.display import display
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import learning_curve
from sklearn.decomposition import TruncatedSVD
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import AdaBoostClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.neighbors import NearestNeighbors
from sklearn.neighbors.nearest_centroid import NearestCentroid
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.tree import DecisionTreeClassifier
import sklearn.gaussian_process.kernels as kernels
from sklearn.cross_validation import ShuffleSplit
from sklearn.cross_validation import KFold
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
from scipy.stats import expon
```
# Step2
load the payloads into memory
```
payloads = pd.read_csv("data/payloads.csv",index_col='index')
display(payloads.head(30))
```
# Step3A - feature engineering custom features
We will create our own feature space with features that might be important for this task, this includes:
- length of payload
- number of non-printable characters in payload
- number of punctuation characters in payload
- the minimum byte value of payload
- the maximum byte value of payload
- the mean byte value of payload
- the standard deviation of payload byte values
- number of distinct bytes in payload
- number of SQL keywords in payload
- number of javascript keywords in payload
```
def plot_feature_distribution(features):
print('Properties of feature: ' + features.name)
print(features.describe())
f, ax = plt.subplots(1, figsize=(10, 6))
ax.hist(features, bins=features.max()-features.min()+1, normed=1)
ax.set_xlabel('value')
ax.set_ylabel('fraction')
plt.show()
def create_feature_length(payloads):
'''
Feature describing the lengh of the input
'''
payloads['length'] = [len(str(row)) for row in payloads['payload']]
return payloads
payloads = create_feature_length(payloads)
display(payloads.head())
plot_feature_distribution(payloads['length'])
def create_feature_non_printable_characters(payloads):
'''
Feature
Number of non printable characthers within payload
'''
payloads['non-printable'] = [ len([1 for letter in str(row) if letter not in string.printable]) for row in payloads['payload']]
return payloads
create_feature_non_printable_characters(payloads)
display(payloads.head())
plot_feature_distribution(payloads['non-printable'])
def create_feature_punctuation_characters(payloads):
'''
Feature
Number of punctuation characthers within payload
'''
payloads['punctuation'] = [ len([1 for letter in str(row) if letter in string.punctuation]) for row in payloads['payload']]
return payloads
create_feature_punctuation_characters(payloads)
display(payloads.head())
plot_feature_distribution(payloads['punctuation'])
def create_feature_min_byte_value(payloads):
'''
Feature
Minimum byte value in payload
'''
payloads['min-byte'] = [ min(bytearray(str(row), 'utf8')) for row in payloads['payload']]
return payloads
create_feature_min_byte_value(payloads)
display(payloads.head())
plot_feature_distribution(payloads['min-byte'])
def create_feature_max_byte_value(payloads):
'''
Feature
Maximum byte value in payload
'''
payloads['max-byte'] = [ max(bytearray(str(row), 'utf8')) for row in payloads['payload']]
return payloads
create_feature_max_byte_value(payloads)
display(payloads.head())
plot_feature_distribution(payloads['max-byte'])
def create_feature_mean_byte_value(payloads):
'''
Feature
Maximum byte value in payload
'''
payloads['mean-byte'] = [ np.mean(bytearray(str(row), 'utf8')) for row in payloads['payload']]
return payloads
create_feature_mean_byte_value(payloads)
display(payloads.head())
plot_feature_distribution(payloads['mean-byte'].astype(int))
def create_feature_std_byte_value(payloads):
'''
Feature
Standard deviation byte value in payload
'''
payloads['std-byte'] = [ np.std(bytearray(str(row), 'utf8')) for row in payloads['payload']]
return payloads
create_feature_std_byte_value(payloads)
display(payloads.head())
plot_feature_distribution(payloads['std-byte'].astype(int))
def create_feature_distinct_bytes(payloads):
'''
Feature
Number of distinct bytes in payload
'''
payloads['distinct-bytes'] = [ len(list(set(bytearray(str(row), 'utf8')))) for row in payloads['payload']]
return payloads
create_feature_distinct_bytes(payloads)
display(payloads.head())
plot_feature_distribution(payloads['distinct-bytes'])
sql_keywords = pd.read_csv('data/SQLKeywords.txt', index_col=False)
def create_feature_sql_keywords(payloads):
'''
Feature
Number of SQL keywords within payload
'''
payloads['sql-keywords'] = [ len([1 for keyword in sql_keywords['Keyword'] if str(keyword).lower() in str(row).lower()]) for row in payloads['payload']]
return payloads
create_feature_sql_keywords(payloads)
display(type(sql_keywords))
display(payloads.head())
plot_feature_distribution(payloads['sql-keywords'])
js_keywords = pd.read_csv('data/JavascriptKeywords.txt', index_col=False)
def create_feature_javascript_keywords(payloads):
'''
Feature
Number of Javascript keywords within payload
'''
payloads['js-keywords'] = [len([1 for keyword in js_keywords['Keyword'] if str(keyword).lower() in str(row).lower()]) for row in payloads['payload']]
return payloads
create_feature_javascript_keywords(payloads)
display(payloads.head())
plot_feature_distribution(payloads['js-keywords'])
```
define a function that makes a feature vector from the payload using the custom features
```
def create_features(payloads):
features = create_feature_length(payloads)
features = create_feature_non_printable_characters(features)
features = create_feature_punctuation_characters(features)
features = create_feature_max_byte_value(features)
features = create_feature_min_byte_value(features)
features = create_feature_mean_byte_value(features)
features = create_feature_std_byte_value(features)
features = create_feature_distinct_bytes(features)
features = create_feature_sql_keywords(features)
features = create_feature_javascript_keywords(features)
del features['payload']
return features
```
### Scoring custom features
Score the custom features using the SelectKBest function, then visualize the scores in a graph
to see which features are less significant
```
Y = payloads['is_malicious']
X = create_features(pd.DataFrame(payloads['payload'].copy()))
test = SelectKBest(score_func=chi2, k='all')
fit = test.fit(X, Y)
# summarize scores
print(fit.scores_)
features = fit.transform(X)
# summarize selected features
# summarize scores
np.set_printoptions(precision=2)
print(fit.scores_)
# Get the indices sorted by most important to least important
indices = np.argsort(fit.scores_)
# To get your top 10 feature names
featuress = []
for i in range(10):
featuress.append(X.columns[indices[i]])
display(featuress)
display([featuress[i] + ' ' + str(fit.scores_[i]) for i in indices[range(10)]])
plt.rcdefaults()
fig, ax = plt.subplots()
y_pos = np.arange(len(featuress))
performance = 3 + 10 * np.random.rand(len(featuress))
error = np.random.rand(len(featuress))
ax.barh(y_pos, fit.scores_[indices[range(10)]], align='center',
color='green', ecolor='black')
ax.set_yticks(y_pos)
ax.set_yticklabels(featuress)
ax.set_xscale('log')
#ax.invert_yaxis() # labels read top-to-bottom
ax.set_xlabel('Points')
ax.set_title('SelectKBest()')
plt.show()
```
# Step3B - Feature engineering using bag of words techniques.
Additional to our custom feature space, we will create 6 more feature spaces using bag-of-words techniques
The following vectorizers below is another way of creating features for text input.
We will test the performance of these techniques independently from our custom features in Step 3A.
We will create vectorizers of these combinations:
- 1-grams CountVectorizer
- 2-grams CountVectorizer
- 3-grams CountVectorizer
- 1-grams TfidfVectorizer
- 2-grams TfidfVectorizer
- 3-grams TfidfVectorizer
The type of N-gram function determines how the actual "words" should be created from the payload string
Each vectorizer is used later in Step4 in Pipeline objects before training
See report for further explanation
### 1-Grams features
create a Countvectorizer and TF-IDFvectorizer that uses 1-grams.
1-grams equals one feature for each letter/symbol recorded
```
def get1Grams(payload_obj):
'''Divides a string into 1-grams
Example: input - payload: "<script>"
output- ["<","s","c","r","i","p","t",">"]
'''
payload = str(payload_obj)
ngrams = []
for i in range(0,len(payload)-1):
ngrams.append(payload[i:i+1])
return ngrams
tfidf_vectorizer_1grams = TfidfVectorizer(tokenizer=get1Grams)
count_vectorizer_1grams = CountVectorizer(min_df=1, tokenizer=get1Grams)
```
### 2-Grams features
create a Countvectorizer and TF-IDFvectorizer that uses 2-grams.
```
def get2Grams(payload_obj):
'''Divides a string into 2-grams
Example: input - payload: "<script>"
output- ["<s","sc","cr","ri","ip","pt","t>"]
'''
payload = str(payload_obj)
ngrams = []
for i in range(0,len(payload)-2):
ngrams.append(payload[i:i+2])
return ngrams
tfidf_vectorizer_2grams = TfidfVectorizer(tokenizer=get2Grams)
count_vectorizer_2grams = CountVectorizer(min_df=1, tokenizer=get2Grams)
```
### 3-Grams features
Create a Countvectorizer and TF-IDFvectorizer that uses 3-grams
```
def get3Grams(payload_obj):
'''Divides a string into 3-grams
Example: input - payload: "<script>"
output- ["<sc","scr","cri","rip","ipt","pt>"]
'''
payload = str(payload_obj)
ngrams = []
for i in range(0,len(payload)-3):
ngrams.append(payload[i:i+3])
return ngrams
tfidf_vectorizer_3grams = TfidfVectorizer(tokenizer=get3Grams)
count_vectorizer_3grams = CountVectorizer(min_df=1, tokenizer=get3Grams)
```
## Step3C - Feature space visualization
After creating our different feature spaces to later train each classifier on,
we first examine them visually by projecting the feature spaces into two dimensions using Principle Component Analysis
Graphs are shown below displaying the data in 3 out of 7 of our feature spaces
```
def visualize_feature_space_by_projection(X,Y,title='PCA'):
'''Plot a two-dimensional projection of the dataset in the specified feature space
input: X - data
Y - labels
title - title of plot
'''
pca = TruncatedSVD(n_components=2)
X_r = pca.fit(X).transform(X)
# Percentage of variance explained for each components
print('explained variance ratio (first two components): %s'
% str(pca.explained_variance_ratio_))
plt.figure()
colors = ['blue', 'darkorange']
lw = 2
#Plot malicious and non-malicious separately with different colors
for color, i, y in zip(colors, [0, 1], Y):
plt.scatter(X_r[Y == i, 0], X_r[Y == i, 1], color=color, alpha=.3, lw=lw,
label=i)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title(title)
plt.show()
```
### 1-Grams CountVectorizer feature space visualization
```
X = count_vectorizer_1grams.fit_transform(payloads['payload'])
Y = payloads['is_malicious']
visualize_feature_space_by_projection(X,Y,title='PCA visualization of 1-grams CountVectorizer feature space')
```
### 3-Grams TFIDFVectorizer feature space visualization
```
X = tfidf_vectorizer_3grams.fit_transform(payloads['payload'])
Y = payloads['is_malicious']
visualize_feature_space_by_projection(X,Y,title='PCA visualization of 3-grams TFIDFVectorizer feature space')
```
### Custom feature space visualization
```
X = create_features(pd.DataFrame(payloads['payload'].copy()))
Y = payloads['is_malicious']
visualize_feature_space_by_projection(X,Y,title='PCA visualization of custom feature space')
```
# Step4 - Model selection and evaluation
First, we will automate hyperparameter tuning and out of sample testing using train_model below
```
def train_model(clf, param_grid, X, Y):
'''Trains and evaluates the model clf from input
The function selects the best model of clf by optimizing for the validation data,
then evaluates its performance using the out of sample test data.
input - clf: the model to train
param_grid: a dict of hyperparameters to use for optimization
X: features
Y: labels
output - the best estimator (trained model)
the confusion matrix from classifying the test data
'''
#First, partition into train and test data
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
n_iter = 5
#If number of possible iterations are less than prefered number of iterations,
#set it to the number of possible iterations
#number of possible iterations are not less than prefered number of iterations if any argument is expon()
#because expon() is continous (writing 100 instead, could be any large number)
n_iter = min(n_iter,np.prod([
100 if type(xs) == type(expon())
else len(xs)
for xs in param_grid.values()
]))
#perform a grid search for the best parameters on the training data.
#Cross validation is made to select the parameters, so the training data is actually split into
#a new train data set and a validation data set, K number of times
cv = ShuffleSplit(n=len(X_train), n_iter=5, test_size=0.2, random_state=0) #DEBUG: n_iter=10
#cv = KFold(n=len(X), n_folds=10)
random_grid_search = RandomizedSearchCV(
clf,
param_distributions=param_grid,
cv=cv,
scoring='f1',
n_iter=n_iter, #DEBUG 1
random_state=5,
refit=True,
verbose=10
)
'''Randomized search used instead. We have limited computing power
grid_search = GridSearchCV(
clf,
param_grid=param_grid,
cv=cv,
scoring='f1', #accuracy/f1/f1_weighted all give same result?
verbose=10,
n_jobs=-1
)
grid_search.fit(X_train, Y_train)
'''
random_grid_search.fit(X_train, Y_train)
#Evaluate the best model on the test data
Y_test_predicted = random_grid_search.best_estimator_.predict(X_test)
Y_test_predicted_prob = random_grid_search.best_estimator_.predict_proba(X_test)[:, 1]
confusion = confusion_matrix(Y_test, Y_test_predicted)
TP = confusion[1, 1]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
#Calculate recall (sensitivity) from confusion matrix
sensitivity = TP / float(TP + FN)
#Calculate specificity from confusion matrix
specificity = TN / float(TN + FP)
#Calculate accuracy
accuracy = (confusion[0][0] + confusion[1][1]) / (confusion.sum().sum())
#Calculate axes of ROC curve
fpr, tpr, thresholds = roc_curve(Y_test, Y_test_predicted_prob)
#Area under the ROC curve
auc = roc_auc_score(Y_test, Y_test_predicted_prob)
return {
'conf_matrix':confusion,
'accuracy':accuracy,
'sensitivity':sensitivity,
'specificity':specificity,
'auc':auc,
'params':random_grid_search.best_params_,
'model':random_grid_search.best_estimator_,
'roc':{'fpr':fpr,'tpr':tpr,'thresholds':thresholds}
}
```
Then, we will use the train_model function to train, optimize and retrieve out of sample testing results from a range of classifiers.
Classifiers tested using our custom feature space:
- AdaBoost
- SGD classifier
- MultiLayerPerceptron classifier
- Logistic Regression
- Support Vector Machine
- Random forest
- Decision Tree
- Multinomial Naive Bayes
Classifiers tested using bag-of-words feature spaces:
- MultiLayerPerceptron classifier
- Logistic Regression
- Support Vector Machine
- Random forest
- Multinomial Naive Bayes
Some classifiers were unable to train using a bag-of-words feature space because they couldn't handle sparse graphs
All their best parameters with their performance is stored in a dataframe called classifier_results
Make dictionary of models with parameters to optimize using bag-of-words feature spaces
```
def create_classifier_inputs_using_vectorizers(vectorizer, subscript):
'''make pipelines of the specified vectorizer with the classifiers to train
input - vectorizer: the vectorizer to add to the pipelines
subscript: subscript name for the dictionary key
output - A dict of inputs to use for train_model(); a pipeline and a dict of params to optimize
'''
classifier_inputs = {}
classifier_inputs[subscript + ' MLPClassifier'] = {
'pipeline':Pipeline([('vect', vectorizer),('clf',MLPClassifier(
activation='relu',
solver='adam',
early_stopping=False,
verbose=True
))]),
'dict_params': {
'vect__min_df':[1,2,5,10,20,40],
'clf__hidden_layer_sizes':[(500,250,125,62)],
'clf__alpha':[0.0005,0.001,0.01,0.1,1],
'clf__learning_rate':['constant','invscaling'],
'clf__learning_rate_init':[0.001,0.01,0.1,1],
'clf__momentum':[0,0.9],
}
}
'''
classifier_inputs[subscript + ' MultinomialNB'] = {
'pipeline':Pipeline([('vect', vectorizer),('clf',MultinomialNB())]),
'dict_params': {
'vect__min_df':[1,2,5,10,20,40]
}
}
classifier_inputs[subscript + ' RandomForest'] = {
'pipeline':Pipeline([('vect', vectorizer),('clf',RandomForestClassifier(
max_depth=None,min_samples_split=2, random_state=0))]),
'dict_params': {
'vect__min_df':[1,2,5,10,20,40],
'clf__n_estimators':[10,20,40,60]
}
}
classifier_inputs[subscript + ' Logistic'] = {
'pipeline':Pipeline([('vect', vectorizer), ('clf',LogisticRegression())]),
'dict_params': {
'vect__min_df':[1,2,5,10,20,40],
'clf__C':[0.001, 0.01, 0.1, 1, 10, 100, 1000]
}
}
classifier_inputs[subscript + ' SVM'] = {
'pipeline':Pipeline([('vect', vectorizer), ('clf',SVC(probability=True))]),
'dict_params': {
'vect__min_df':[1,2,5,10,20,40],
'clf__C':[0.001, 0.01, 0.1, 1, 10, 100, 1000],
'clf__gamma':[0.001, 0.0001,'auto'],
'clf__kernel':['rbf']
}
}
'''
return classifier_inputs
```
Make dictionary of models with parameters to optimize using custom feature spaces
```
def create_classifier_inputs(subscript):
classifier_inputs = {}
'''classifier_inputs[subscript + ' GPC'] = {
'pipeline':GaussianProcessClassifier(),
'dict_params': {
'kernel':[
1.0*kernels.RBF(1.0),
1.0*kernels.Matern(),
1.0*kernels.RationalQuadratic(),
1.0*kernels.DotProduct()
]
}
}'''
classifier_inputs[subscript + ' AdaBoostClassifier'] = {
'pipeline':AdaBoostClassifier(n_estimators=100),
'dict_params': {
'n_estimators':[10,20,50, 100],
'learning_rate':[0.1, 0.5, 1.0, 2.0]
}
}
classifier_inputs[subscript + ' SGD'] = {
'pipeline':SGDClassifier(loss="log", penalty="l2"),
'dict_params': {
'learning_rate': ['optimal']
}
}
classifier_inputs[subscript + ' RandomForest'] = {
'pipeline':RandomForestClassifier(
max_depth=None,min_samples_split=2, random_state=0),
'dict_params': {
'n_estimators':[10,20,40,60]
}
}
classifier_inputs[subscript + ' DecisionTree'] = {
'pipeline': DecisionTreeClassifier(max_depth=5),
'dict_params': {
'min_samples_split': [2]
}
}
'''classifier_inputs[subscript + ' MLPClassifier'] = {
'pipeline':MLPClassifier(
activation='relu',
solver='adam',
early_stopping=False,
verbose=True
),
'dict_params': {
'hidden_layer_sizes':[(300, 200, 150, 150), (30, 30, 30), (150, 30, 30, 150),
(400, 250, 100, 100) , (150, 200, 300)],
'alpha':[0.0005,0.001,0.01,0.1,1],
'learning_rate':['constant','invscaling'],
'learning_rate_init':[0.0005,0.001,0.01,0.1,1],
'momentum':[0,0.9],
}
}'''
classifier_inputs[subscript + ' Logistic'] = {
'pipeline':LogisticRegression(),
'dict_params': {
'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]
}
}
classifier_inputs[subscript + ' MultinomialNB'] = {
'pipeline':MultinomialNB(),
'dict_params': {
'alpha': [1.0]
}
}
'''classifier_inputs[subscript + ' SVM'] = {
'pipeline':SVC(probability=True),
'dict_params': {
'C':[0.001, 0.01, 0.1, 1, 10, 100, 1000],
'gamma':[0.001, 0.0001,'auto'],
'kernel':['rbf']
}
}'''
return classifier_inputs
```
Create a new result table
```
classifier_results = pd.DataFrame(columns=['accuracy','sensitivity','specificity','auc','conf_matrix','params','model','roc'])#,index=classifier_inputs.keys())
```
Use the 6 different feature spaces generated from the vectorizers previously above,
and train every classifier in classifier_inputs in every feature space
### P.S! Don't try to run this, it will take several days to complete
### Instead skip to Step4B
```
classifier_inputs = {}
classifier_inputs.update(create_classifier_inputs_using_vectorizers(count_vectorizer_1grams,'count 1grams'))
classifier_inputs.update(create_classifier_inputs_using_vectorizers(count_vectorizer_2grams,'count 2grams'))
classifier_inputs.update(create_classifier_inputs_using_vectorizers(count_vectorizer_3grams,'count 3grams'))
classifier_inputs.update(create_classifier_inputs_using_vectorizers(tfidf_vectorizer_1grams,'tfidf 1grams'))
classifier_inputs.update(create_classifier_inputs_using_vectorizers(tfidf_vectorizer_2grams,'tfidf 2grams'))
classifier_inputs.update(create_classifier_inputs_using_vectorizers(tfidf_vectorizer_3grams,'tfidf 3grams'))
X = payloads['payload']
Y = payloads['is_malicious']
for classifier_name, inputs in classifier_inputs.items():
display(inputs['dict_params'])
if classifier_name in classifier_results.index.values.tolist():
print('Skipping ' + classifier_name + ', already trained')
else:
result_dict = train_model(inputs['pipeline'],inputs['dict_params'],X,Y)
classifier_results.loc[classifier_name] = result_dict
display(classifier_results)
display(pd.DataFrame(payloads['payload'].copy()))
```
Use our custom feature space,
and train every classifier in classifier_inputs_custom with
### P.S! Don't try to run this, it will take many hours to complete
### Instead skip to Step4B
```
classifier_inputs_custom = {}
#Get classifiers and parameters to optimize
classifier_inputs_custom.update(create_classifier_inputs('custom'))
#Extract payloads and labels
Y = payloads['is_malicious']
X = create_features(pd.DataFrame(payloads['payload'].copy()))
#Select the best features
X_new = SelectKBest(score_func=chi2, k=4).fit_transform(X,Y)
#Call train_model for every classifier and save results to classifier_results
for classifier_name, inputs in classifier_inputs_custom.items():
if classifier_name in classifier_results.index.values.tolist():
print('Skipping ' + classifier_name + ', already trained')
else:
result_dict = train_model(inputs['pipeline'],inputs['dict_params'],X,Y)
classifier_results.loc[classifier_name] = result_dict
display(classifier_results)
#pickle.dump( classifier_results, open( "data/trained_classifiers_custom_all_features.p", "wb" ) )
#Save classifiers in a pickle file to be able to re-use them without re-training
pickle.dump( classifier_results, open( "data/trained_classifiers.p", "wb" ) )
```
### Classifier results
```
#Display the results for the classifiers that were trained using our custom feature space
custom_features_classifiers = pickle.load( open("data/trained_classifier_custom_all_features.p", "rb"))
display(custom_features_classifiers)
#Display the results for the classifiers that were using bag of words feature spaces
classifier_results = pickle.load( open( "data/trained_classifiers.p", "rb" ) )
display(classifier_results)
#Combine the two tables into one table
classifier_results = classifier_results.append(custom_features_classifiers)
classifier_results = classifier_results.sort_values(['sensitivity','accuracy'], ascending=[False,False])
display(classifier_results)
```
### F1-score
Calculate F1-score of each classifier and add to classifiers table
(We didn't implement this in the train_model function as with the other performance metrics because we've already done a 82 hour training session before this and didn't want to re-run the entire training just to add F1-score from inside train_model)
```
def f1_score(conf_matrix):
precision = conf_matrix[0][0] / (conf_matrix[0][0] + conf_matrix[0][1] )
recall = conf_matrix[0][0] / (conf_matrix[0][0] + conf_matrix[1][0] )
return (2 * precision * recall) / (precision + recall)
#load classifier table if not yet loaded
classifier_results = pickle.load( open( "data/trained_classifiers.p", "rb" ) )
#Calculate F1-scores
classifier_results['F1-score'] = [ f1_score(conf_matrix) for conf_matrix in classifier_results['conf_matrix']]
#Re-arrange columns
classifier_results = classifier_results[['F1-score','accuracy','sensitivity','specificity','auc','conf_matrix','params','model','roc']]
#re-sort on F1-score
classifier_results = classifier_results.sort_values(['F1-score','accuracy'], ascending=[False,False])
display(classifier_results)
```
Final formating
Convert numeric columns to float
Round numeric columns to 4 decimals
```
classifier_results[['F1-score','accuracy','sensitivity','specificity','auc']] = classifier_results[['F1-score','accuracy','sensitivity','specificity','auc']].apply(pd.to_numeric)
classifier_results = classifier_results.round({'F1-score':4,'accuracy':4,'sensitivity':4,'specificity':4,'auc':4})
#classifier_results[['F1-score','accuracy','sensitivity','specificity','auc','conf_matrix','params']].to_csv('data/classifiers_result_table.csv')
display(classifier_results.dtypes)
```
### Export classifiers
First, export full list of trained classifiers for later use
Second, pick one classifier to save in a separate pickle, used later to implement in a dummy server
```
#save complete list of classifiers to 'trained_classifiers'
pickle.dump( classifier_results, open( "data/trained_classifiers.p", "wb" ) )
#In this case, we are going to implement tfidf 2grams RandomForest in our dummy server
classifier = (custom_features_classifiers['model'].iloc[0])
print(classifier)
#Save classifiers in a pickle file to be able to re-use them without re-training
pickle.dump( classifier, open( "data/tfidf_2grams_randomforest.p", "wb" ) )
```
## Step4B - load pre-trained classifiers
Instead of re-training all classifiers, load the classifiers from disk that we have already trained
```
classifier_results = pickle.load( open( "data/trained_classifiers.p", "rb" ) )
```
## Step5 - Visualization
In this section we will visualize:
- Histogram of classifier performances
- Learning curves
- ROC curves
### Performance histogram
First, make a histogram of classifier performance measured by F1-score.
Same classifier using different feature spaces are clustered together in the graph
Also, print the table of F1-scores and computes the averages along the x-axis and y-axis,
e.g. the average F1-score for each classifier, and the average F1-score for each feature space
```
def get_classifier_name(index):
'''
Returns the name of the classifier at the given index name
'''
return index.split()[len(index.split())-1]
#Group rows together using same classifier
grouped = classifier_results.groupby(get_classifier_name)
hist_df = pd.DataFrame(columns=['custom','count 1grams','count 2grams','count 3grams','tfidf 1grams','tfidf 2grams','tfidf 3grams'])
for classifier, indices in grouped.groups.items():
#Make a list of feature spaces
feature_spaces = indices.tolist()
feature_spaces = [feature_space.replace(classifier,'') for feature_space in feature_spaces]
feature_spaces = [feature_space.strip() for feature_space in feature_spaces]
#If no result exists, it will stay as 0
hist_df.loc[classifier] = {
'custom':0,
'count 1grams':0,
'count 2grams':0,
'count 3grams':0,
'tfidf 1grams':0,
'tfidf 2grams':0,
'tfidf 3grams':0
}
#Extract F1-score from classifier_results to corrensponding entry in hist_df
for fs in feature_spaces:
hist_df[fs].loc[classifier] = classifier_results['F1-score'].loc[fs + ' ' + classifier]
#Plot the bar plot
f, ax = plt.subplots()
ax.set_ylim([0.989,1])
hist_df.plot(kind='bar', figsize=(12,7), title='F1-score of all models grouped by classifiers', ax=ax, width=0.8)
#Make Avgerage F1-score row and cols for the table and print the table
hist_df_nonzero = hist_df.copy()
hist_df_nonzero[hist_df > 0] = True
hist_df['Avg Feature'] = (hist_df.sum(axis=1) / np.array(hist_df_nonzero.sum(axis=1)))
hist_df_nonzero = hist_df.copy()
hist_df_nonzero[hist_df > 0] = True
hist_df.loc['Avg Classifier'] = (hist_df.sum(axis=0) / np.array(hist_df_nonzero.sum(axis=0)))
hist_df = hist_df.round(4)
display(hist_df)
```
### Learning curves
Create learning curves for a sample of classifiers. This is to visualize how the dataset size impacts the performance
```
def plot_learning_curve(df_row,X,Y):
'''Plots the learning curve of a classifier with its parameters
input - df_row: row of classifier_result
X: payload data
Y: labels
'''
#The classifier to plot learning curve for
estimator = df_row['model']
title = 'Learning curves for classifier ' + df_row.name
train_sizes = np.linspace(0.1,1.0,5)
cv = ShuffleSplit(n=len(X), n_iter=3, test_size=0.2, random_state=0)
#plot settings
plt.figure()
plt.title(title)
plt.xlabel("Training examples")
plt.ylabel("Score")
print('learning curve in process...')
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, Y, cv=cv, n_jobs=-1, train_sizes=train_sizes, verbose=0) #Change verbose=10 to print progress
print('Learning curve done!')
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
plt.show()
```
Three examples of learning curves from the trained classifiers.
All learning curves have upsloping cross-validation score at the end,
which means that adding more data would potentially increase the accuracy
```
#plot learning curve for tfidf 1grams RandomForest
X = payloads['payload']
Y = payloads['is_malicious']
plot_learning_curve(classifier_results.iloc[0],X,Y)
#plot learning curve for count 3grams MultinomialNB
X = payloads['payload']
Y = payloads['is_malicious']
plot_learning_curve(classifier_results.iloc[6],X,Y)
#plot learning curve for custom svm
X = create_features(pd.DataFrame(payloads['payload'].copy()))
Y = payloads['is_malicious']
plot_learning_curve(classifier_results.iloc[5],X,Y)
```
### ROC curves
Plot ROC curves for a range of classifiers to visualize the sensitivity/specificity trade-off and the AUC
```
def visualize_result(classifier_list):
'''Plot the ROC curve for a list of classifiers in the same graph
input - classifier_list: a subset of classifier_results
'''
f, (ax1, ax2) = plt.subplots(1,2)
f.set_figheight(6)
f.set_figwidth(15)
#Subplot 1, ROC curve
for classifier in classifier_list:
ax1.plot(classifier['roc']['fpr'], classifier['roc']['tpr'])
ax1.scatter(1-classifier['specificity'],classifier['sensitivity'], edgecolor='k')
ax1.set_xlim([0, 1])
ax1.set_ylim([0, 1.0])
ax1.set_title('ROC curve for top3 and bottom3 classifiers')
ax1.set_xlabel('False Positive Rate (1 - Specificity)')
ax1.set_ylabel('True Positive Rate (Sensitivity)')
ax1.grid(True)
#subplot 2, ROC curve zoomed
for classifier in classifier_list:
ax2.plot(classifier['roc']['fpr'], classifier['roc']['tpr'])
ax2.scatter(1-classifier['specificity'],classifier['sensitivity'], edgecolor='k')
ax2.set_xlim([0, 0.3])
ax2.set_ylim([0.85, 1.0])
ax2.set_title('ROC curve for top3 and bottom3 classifiers (Zoomed)')
ax2.set_xlabel('False Positive Rate (1 - Specificity)')
ax2.set_ylabel('True Positive Rate (Sensitivity)')
ax2.grid(True)
#Add further zoom
left, bottom, width, height = [0.7, 0.27, 0.15, 0.15]
ax3 = f.add_axes([left, bottom, width, height])
for classifier in classifier_list:
ax3.plot(classifier['roc']['fpr'], classifier['roc']['tpr'])
ax3.scatter(1-classifier['specificity'],classifier['sensitivity'], edgecolor='k')
ax3.set_xlim([0, 0.002])
ax3.set_ylim([0.983, 1.0])
ax3.set_title('Zoomed even further')
ax3.grid(True)
plt.show()
```
Plot ROC curves for the top3 classifiers and the bottom 3 classifiers, sorted by F1-score
Left: standard scale ROC curve
Right: zoomed in version of same graph, to easier see in the upper right corner
```
indices = [0,1,2, len(classifier_results)-1,len(classifier_results)-2,len(classifier_results)-3]
visualize_result([classifier_results.iloc[index] for index in indices])
```
## Step6 - Website integration extract
This is the code needed when implementing the saved classifier in tfidf_2grams_randomforest.p on a server
```
import pickle
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.ensemble import RandomForestClassifier
def get2Grams(payload_obj):
'''Divides a string into 2-grams
Example: input - payload: "<script>"
output- ["<s","sc","cr","ri","ip","pt","t>"]
'''
payload = str(payload_obj)
ngrams = []
for i in range(0,len(payload)-2):
ngrams.append(payload[i:i+2])
return ngrams
classifier = pickle.load( open("data/tfidf_2grams_randomforest.p", "rb"))
def injection_test(inputs):
variables = inputs.split('&')
values = [ variable.split('=')[1] for variable in variables]
print(values)
return 'MALICIOUS' if classifier.predict(values).sum() > 0 else 'NOT_MALICIOUS'
#test injection_test
display(injection_test("val1=%3Cscript%3Ekiddie"))
```
# (Step7)
we can display which types of queries the classifiers failed to classify. These are interesting to examine for further work on how to improve the classifiers and the quality of the data set
```
pipe = Pipeline([('vect', vectorizer), ('clf',LogisticRegression(C=10))])
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
cv = ShuffleSplit(n=len(X_train), n_iter=1, test_size=0.2, random_state=0) #DEBUG: n_iter=10
random_grid_search = RandomizedSearchCV(
pipe,
param_distributions={
'clf__C':[10]
},
cv=cv,
scoring='roc_auc',
n_iter=1,
random_state=5,
refit=True
)
random_grid_search.fit(X_train, Y_train)
#Evaluate the best model on the test data
Y_test_predicted = random_grid_search.best_estimator_.predict(X_test)
#Payloads classified incorrectly
pd.options.display.max_colwidth = 200
print('False positives')
print(X_test[(Y_test == 0) & (Y_test_predicted == 1)])
print('False negatives')
print(X_test[(Y_test == 1) & (Y_test_predicted == 0)])
```
| true |
code
| 0.53437 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Dynamic-Schedule" data-toc-modified-id="Dynamic-Schedule-1"><span class="toc-item-num">1 </span>Dynamic Schedule</a></span><ul class="toc-item"><li><span><a href="#Homogeneous-Exponential-Case" data-toc-modified-id="Homogeneous-Exponential-Case-1.1"><span class="toc-item-num">1.1 </span>Homogeneous Exponential Case</a></span></li><li><span><a href="#Heterogeneous-Exponential-Case" data-toc-modified-id="Heterogeneous-Exponential-Case-1.2"><span class="toc-item-num">1.2 </span>Heterogeneous Exponential Case</a></span></li><li><span><a href="#Phase-Type-Case" data-toc-modified-id="Phase-Type-Case-1.3"><span class="toc-item-num">1.3 </span>Phase-Type Case</a></span><ul class="toc-item"><li><span><a href="#Phase-Type-Fit" data-toc-modified-id="Phase-Type-Fit-1.3.1"><span class="toc-item-num">1.3.1 </span>Phase-Type Fit</a></span></li><li><span><a href="#Weighted-Erlang-Distribution" data-toc-modified-id="Weighted-Erlang-Distribution-1.3.2"><span class="toc-item-num">1.3.2 </span>Weighted Erlang Distribution</a></span></li><li><span><a href="#Hyperexponential-Distribution" data-toc-modified-id="Hyperexponential-Distribution-1.3.3"><span class="toc-item-num">1.3.3 </span>Hyperexponential Distribution</a></span></li></ul></li></ul></li></ul></div>
# Dynamic Schedule
_Roshan Mahes, Michel Mandjes, Marko Boon_
In this notebook we determine dynamic schedules that minimize the following cost function:
\begin{align*}
\omega \sum_{i=1}^{n}\mathbb{E}I_i + (1 - \omega)\sum_{i=1}^{n}\mathbb{E}W_i,\quad \omega\in(0,1),
\end{align*}
where $I_i$ and $W_i$ are the expected idle and waiting time associated to client $i$, respectively. We assume that the service tasks $B_1,\dots,B_n$ are independent and solve the problem assuming different types of distributions.
The following packages are required:
```
# math
import numpy as np
import scipy
import math
from scipy.stats import binom, erlang, poisson
from scipy.optimize import minimize
# web scraping
from urllib.request import urlopen
from bs4 import BeautifulSoup as soup
import pandas as pd
# plotting
import plotly.graph_objects as go
import plotly.express as px
from itertools import cycle
# caching
from functools import cache
```
## Homogeneous Exponential Case
In the first case, we assume $B_1,\dots,B_n \stackrel{i.i.d.}{\sim} B \stackrel{d}{=} \text{Exp}(\mu)$ for some $\mu > 0$. In our thesis, we have determined a recursive procedure. We state the result.
<div class="alert alert-warning">
<b>Corollary 2.5.</b>
For arrival time $t$ we have, with $X_t \sim \text{Pois}(\mu t)$ and $\ell = 2,\dots,k+1$,
\begin{align*}
p_{k1}(t) = \mathbb{P}(X_t\geq k),\quad
p_{k\ell}(t) = \mathbb{P}(X_t = k-\ell+1).
\end{align*}
</div>
<div class="alert alert-warning">
<b>Proposition 2.7.</b>
Let $X_t \sim \text{Pois}(\mu t)$. Then
\begin{align*}
f_k(t) &= t\mathbb{P}(X_t\geq k) - \frac{k}{\mu}\mathbb{P}(X_t\geq k+1), \\
g_k(t) &= \frac{k(k-1)}{2\mu}\mathbb{P}(X_t\geq k+1) + (k-1)t\mathbb{P}(X_t\leq k-1) - \frac{\mu t^2}{2}\mathbb{P}(X_t\leq k-2).
\end{align*}
</div>
<div class="alert alert-warning">
<b>Theorem 3.5.</b>
Let $p_{k\ell}(t)$, $f_k(t)$ and $g_k(t)$ be given by Corollary 2.5 and Proposition 2.7. The following recursion holds: for $i=1,\dots,n-1$ and $k=1,\dots,i$,
\[
C_i^{\star}(k) = \inf_{t\geq 0}\left(\omega f_k(t) + (1 - \omega)g_k(t) + \sum_{\ell=1}^{k+1}p_{k\ell}(t)C_{i+1}^{\star}(\ell)\right),
\]
whereas, for $k=1,\dots,n$,
\[
C_n^{\star}(k) = (1-\omega)g_{k}(\infty) = (1-\omega)\frac{k(k-1)}{2\mu}.
\]
</div>
We have implemented the formulas as follows.
```
def cost(t,i,k,mu,omega,n,C_matrix,use_h=True):
"""
Computes the cost of the (remaining) schedule
when t is the next interarrival time.
"""
Fk = [poisson.cdf(k,mu*t), poisson.cdf(k-2,mu*t), poisson.cdf(k-1,mu*t)]
f = (1 - Fk[-1]) * t - (1 - Fk[0]) * k / mu
if use_h:
g = (k - 1) / mu
else:
g = Fk[-1] * (k - 1) * t - Fk[-2] * mu * t**2 / 2 + (1 - Fk[0]) * k * (k - 1) / (2 * mu)
cost = omega * f + (1 - omega) * g
cost += (1 - Fk[-1]) * Cstar_homexp(i+1,1,mu,omega,n,C_matrix,use_h)
for l in range(2,k+2):
cost += poisson.pmf(k-l+1,mu*t) * Cstar_homexp(i+1,l,mu,omega,n,C_matrix,use_h)
return cost
def Cstar_homexp(i,k,mu=1,omega=1/2,n=15,C_matrix=None,use_h=True):
"""
Computes C*_i(k) in the homogeneous exponential case.
"""
if C_matrix[i-1][k-1] != None: # retrieve stored value
pass
elif i == n: # initial condition
if use_h:
C_matrix[i-1][k-1] = (1 - omega) * (k - 1) / mu
else:
C_matrix[i-1][k-1] = (1 - omega) * k * (k - 1) / (2 * mu)
else:
optimization = minimize(cost,0,args=(i,k,mu,omega,n,C_matrix,use_h),method='Nelder-Mead')
C_matrix[i-1][k-1] = optimization.fun
minima[i-1][k-1] = optimization.x[0]
return C_matrix[i-1][k-1]
```
Now we plot our dynamic schedule for $n = 15$ and $\omega = 0.5$:
```
omega = 0.5
n = 15
# compute schedule
C_matrix = [[None for k in range(n+1)] for i in range(n)]
minima = [[None for k in range(n+1)] for i in range(n)]
for i in range(1,n+1):
for k in range(1,i+1):
Cstar_homexp(i,k,mu=1,omega=omega,n=n,C_matrix=C_matrix,use_h=True)
# plot schedule
palette = cycle(px.colors.cyclical.mrybm[2:])
fig = go.Figure()
for k in range(1,n):
fig.add_trace(go.Scatter(x=np.arange(1,n+2), y=[minima[i][k-1] for i in range(n)],
name=k, marker_color=next(palette)))
fig.update_layout(
template='plotly_white',
title='$\\text{Dynamic Schedule}\ (n=' + f'{n},\ \omega={omega})$',
legend_title='$\\text{Clients in System}\ (k)$',
xaxis = {'title': '$\\text{Client Position}\ (i)$', 'range': [0.7, n - 0.7], 'dtick': 1},
yaxis = {'title': '$\\text{Interarrival Time}\ (\\tau_{i}(k))$', 'dtick': 1}
)
fig.show()
print(f'Cost: {C_matrix[0][0]}')
minima
```
## Heterogeneous Exponential Case
Now we consider the case that the service tasks $B_i$ are independent and _heterogeneous exponentially_ distributed, i.e. $B_i \sim \text{Exp}(\mu_i)$, $i=1,\dots,n$. For ease we assume that all $\mu_i$ are distinct, i.e., $\mu_i \neq \mu_j$ for $i,j = 1,\dots,n$, $i\neq j$, but the case that some of the $\mu_i$ coincide can be considered analogously. We obtain the following result.
<div class="alert alert-warning">
<b>Lemma 2.12.</b>
For $k=1,\dots,n$ and $\ell=0,\dots,n-k$, we can write the density $\varphi_{k\ell}$ as
\[
\varphi_{k\ell}(s) := \mathbb{P}\left(\sum_{j=k}^{k+\ell}B_j \in\mathrm{d}s\right)
= \sum_{j=k}^{k+\ell}c_{k\ell j}e^{-\mu_j s},\quad s \geq 0.
\]
The coefficients $c_{k\ell j}$ are given recursively through $c_{k0k} = \mu_k$ and
\[
c_{k,\ell+1,j} = c_{k\ell j}\frac{\mu_{k+\ell+1}}{\mu_{k+\ell+1} - \mu_j}\quad \text{for}\ j = k,\dots,k+\ell,\quad c_{k,\ell+1,k+\ell+1} = \sum_{j=k}^{k+\ell}c_{k\ell j}\frac{\mu_{k+\ell+1}}{\mu_j - \mu_{k+\ell+1}}.
\]
</div>
<div class="alert alert-warning">
<b>Proposition 2.16.</b>
For $i=1,\dots,n-1$, $k=1,\dots,i$, $\ell = 2,\dots,k+1$ and $t\geq 0$,
\[
p_{k1,i}(t) = 1 - \sum_{\ell=2}^{k+1}p_{k\ell,i}(t),\quad
p_{k\ell,i}(t) = \frac{\varphi_{i-k+1,k-\ell+1}(t)}{\mu_{i-\ell+2}}.
\]
</div>
<div class="alert alert-warning">
<b>Proposition 2.17.</b>
For $i=1,\dots,n-1$ and $k=1,\dots,i$,
\begin{align*}
f_{k,i}(t) = t - \sum_{j=i-k+1}^{i}\frac{c_{i-k+1,k-1,j}}{\mu_j}\psi_{j}(t),
\quad
g_{k,i}(t) = \sum_{\ell=0}^{k-1}(k-\ell-1)\sum_{j=i-k+1}^{i-k+\ell+1}\frac{c_{i-k+1,\ell,j}}{\mu_{i-k+\ell+1}}\psi_{j}(t),
\end{align*}
with $\psi_{j}(t) = (1 - e^{-\mu_j t})/\mu_j$.
</div>
<div class="alert alert-warning">
<b>Theorem 3.9.</b>
We can determine the $C^{\star}_i(k)$ recursively: for $i=1,\dots,n-1$ and $k=1,\dots,i$,
\[
C^{\star}_i(k) = \inf_{t\ge 0}\left(\omega f_{k,i}(t) + (1-\omega)g_{k,i}(t) + \sum_{\ell=1}^{k+1}p_{k\ell,i}(t)C^{\star}_{i+1}(\ell)\right),
\]
whereas, for $k=1,\dots,n$,
\[
C^{\star}_n(k) = (1 - \omega)g_{k,n}(\infty) = (1 - \omega)\sum_{\ell=0}^{k-1}(k-\ell-1)\frac{1}{\mu_{n-k+\ell+1}}.
\]
</div>
These formulas lead to the following implementation.
```
# helper functions
def c(k,l,j,mu):
"""Computes the weights c of phi recursively (Lemma 2.23)."""
# storage indices
k_, l_, j_ = k - 1, l, j - 1
if c_stored[k_][l_][j_] != None:
pass
elif k == j and not l:
c_stored[k_][l_][j_] = mu[k_]
elif l:
if j >= k and j < k + l:
c_stored[k_][l_][j_] = c(k,l-1,j,mu) * mu[k_+l_] / (mu[k_+l_] - mu[j-1])
elif k + l == j:
c_stored[k_][l_][j_] = sum([c(k,l-1,m,mu) * mu[j-1] / (mu[m-1] - mu[j-1])
for m in range(k,k+l)])
return c_stored[k_][l_][j_]
def phi(k,l,s,mu):
return sum([c(k,l,j,mu) * math.exp(-mu[j-1] * s) for j in range(k,k+l+1)])
def psi(j,t,mu):
return (1 - math.exp(-mu[j-1] * t)) / mu[j-1]
# transition probabilities
def trans_prob_het(t,i,k,mu):
"""Computes the transition probabilities (Prop. 2.25)."""
p = [phi(i-k+1,k-l+1,t,mu) / mu[i-l+1] for l in range(2,k+2)]
return [1 - sum(p)] + p
# cost function
def cost_het(t,i,k,mu,omega,n,C_matrix,use_h=True):
"""Computes the cost of the (remaining) schedule
when t is the next interarrival time."""
f = t - sum([c(i-k+1,k-1,j,mu) * psi(j,t,mu) / mu[j-1] for j in range(i-k+1,i+1)])
if use_h:
g = sum(1 / mu[i-k:i-1])
else:
g = 0
for l in range(k-1):
g += (k - l - 1) * sum([c(i-k+1,l,j,mu) * psi(j,t,mu) / mu[i-k+l] for j in range(i-k+1,i-k+l+2)])
p = trans_prob_het(t,i,k,mu)
cost = omega * f + (1 - omega) * g
cost += sum([Cstar_het(i+1,l,mu,omega,n,C_matrix,use_h) * p[l-1] for l in range(1,k+2)])
return cost
def Cstar_het(i,k,mu,omega,n,C_matrix,use_h=True):
"""Computes C*_i(k) in the heterogeneous exponential case."""
if C_matrix[i-1][k-1] != None: # retrieve stored value
pass
elif i == n: # initial condition
if use_h:
C_matrix[i-1][k-1] = (1 - omega) * sum(1 / mu[i-k:i-1])
else:
C_matrix[i-1][k-1] = (1 - omega) * sum([(k - l - 1) / mu[n-k+l] for l in range(k)])
else:
optimization = minimize(cost_het,0,args=(i,k,mu,omega,n,C_matrix,use_h))#,bounds=((0,500),))
C_matrix[i-1][k-1] = optimization.fun
minima[i-1][k-1] = optimization.x[0]
return C_matrix[i-1][k-1]
```
Again we can plot our dynamic schedule:
```
omega = 0.5
n = 11
mus = np.linspace(0.5,1.5,n)
# plot schedule
palette = cycle(px.colors.cyclical.mrybm[2:])
fig = go.Figure()
print(f'omega = {omega}\nmu = {mus}\n')
C_matrix = [[None for k in range(n)] for i in range(n)]
minima = [[None for k in range(n)] for i in range(n)]
c_stored = [[[None for j in range(n)] for l in range(n)] for k in range(n)]
# compute values
for i in range(1,n+1):
for k in range(1,i+1):
Cstar_het(i,k,mus,omega=omega,n=n,C_matrix=C_matrix,use_h=True)
# cost
print(f'Cost: {C_matrix[0][0]}')
for k in range(1,n):
fig.add_trace(go.Scatter(x=np.arange(1,n+2), y=[minima[i][k-1] for i in range(n)],
name=k, marker_color=next(palette)))
fig.update_layout(
template='plotly_white',
title='$\\text{Dynamic Schedule}\ (n=' + f'{n},\ \omega={omega})$',
legend_title='$\\text{Clients in System}\ (k)$',
xaxis = {'title': '$\\text{Client Position}\ (i)$', 'range': [0.7, n - 0.7], 'dtick': 1},
yaxis = {'title': '$\\text{Interarrival Time}\ (\\tau_{i}(k))$', 'dtick': 1},
width=800,
height=600
)
fig.show()
```
## Phase-Type Case
Our most general case consists of service time distributions constructed by convolutions and mixtures of exponential distributions, the so-called _phase-type distributions_.
### Phase-Type Fit
There are two special cases of phase-type distributions that are of particular interest: the weighted Erlang distribution and the hyperexponential distribution. The idea is to fit the first two moments of the real service-time distribution. The former distribution can be used to approximate any non-negative distribution with coefficient of variation below 1, whereas the latter can be used if this coefficient of variation is larger than 1. The parameters of the weighted Erlang and hyperexponential distribution are obtained with the following function.
```
def SCV_to_params(SCV, mean=1):
# weighted Erlang case
if SCV <= 1:
K = math.floor(1/SCV)
p = ((K + 1) * SCV - math.sqrt((K + 1) * (1 - K * SCV))) / (SCV + 1)
mu = (K + 1 - p) / mean
return K, p, mu
# hyperexponential case
else:
p = 0.5 * (1 + np.sqrt((SCV - 1) / (SCV + 1)))
mu = 1 / mean
mu1 = 2 * p * mu
mu2 = 2 * (1 - p) * mu
return p, mu1, mu2
```
In the following subsections we develop procedures for finding the optimal static schedule in the weighted Erlang case and the hyperexponential case, respectively.
### Weighted Erlang Distribution
In this case, we assume that the service time $B$ equals w.p. $p\in[0,1]$ an Erlang-distributed random variable with $K$ exponentially distributed phases, each of them having mean $\mu^{-1}$, and with probability $1-p$ an Erlang-distributed random variable with $K+1$ exponentially distributed phases, again with mean $\mu^{-1}$:
\begin{align*}
B \stackrel{\text{d}}{=} \sum_{i=1}^{K}X_i + X_{K+1}\mathbb{1}_{\{U > p\}},
\end{align*}
where $X_i \stackrel{iid}{\sim} \text{Exp}(\mu)$ and $U\sim\text{Unif}[0,1]$. The following recursion can be found in the thesis.
<div class="alert alert-warning">
<b>Theorem 3.16 (discrete version).</b>
For $i=1,\dots,n-1$, $k=1,\dots,i$, and $m\in\mathbb{N}_0$,
\[
\xi_i(k,m) = \inf_{t\in \mathbb{N}_0}\Bigg(\omega \bar{f}^{\circ}_{k,m\Delta}(t\Delta)
+ (1 - \omega)\bar{h}^{\circ}_{k,m\Delta} + \sum_{\ell=2}^{k}\sum_{j=0}^{t}\bar{q}_{k\ell,mj}(t)\xi_{i+1}(\ell,j)
+ P^{\downarrow}_{k,m\Delta}(t\Delta)\xi_{i+1}(1,0) + P^{\uparrow}_{k,m\Delta}(t\Delta)\xi_{i+1}(k+1,m+t) \Bigg),
\]
whereas, for $k=1,\dots,n$ and $m \in \mathbb{N}_0$,
\[
\xi_n(k,m) = (1 - \omega)\bar{h}^{\circ}_{k,m\Delta}.
\]
</div>
Below is our implementation.
```
### helper functions
@cache
def gamma(z, u):
gamma_circ = poisson.pmf(z-1, mu*u)
if z == K + 1:
gamma_circ *= (1 - p)
return gamma_circ / B_sf(u)
@cache
def B_sf(t):
"""The survival function P(B > t)."""
return poisson.cdf(K-1, mu*t) + (1 - p) * poisson.pmf(K, mu*t)
@cache
def P_k0(k, z, t):
"""Computes P(N_t- = 0 | N_0 = k, Z_0 = z)."""
if z <= K:
return sum([binom.pmf(m, k, 1-p) * erlang.cdf(t, k*K-z+1+m, scale=1/mu) for m in range(k+1)])
elif z == K + 1:
return sum([binom.pmf(m, k-1, 1-p) * erlang.cdf(t, (k-1)*K+1+m, scale=1/mu) for m in range(k)])
@cache
def psi(v, t, k, l):
"""
Computes P(t-v < Erl(k,mu) < t, Erl(k,mu) + Erl(l-k,mu) > t),
where Erl(k,mu) and Erl(l-k,mu) are independent.
"""
return sum([poisson.pmf(j, mu*t) * binom.sf(j-k, j, v/t) for j in range(k, l)])
@cache
def f(k, t):
return poisson.sf(k-1, mu*t) * t - poisson.sf(k, mu*t) * k / mu
@cache
def f_bar(k, z, t):
"""Computes the mean idle time given (N_0, Z_0) = (k,z)."""
if z <= K:
return sum([binom.pmf(m, k, 1 - p) * f(k*K+1-z+m, t) for m in range(k+1)])
elif z == K + 1:
return sum([binom.pmf(m, k-1, 1 - p) * f((k-1)*K+1+m, t) for m in range(k)])
@cache
def f_circ(k, u, t):
"""Computes the mean idle time given (N_0, B_0) = (k,u)."""
return sum([gamma(z, u) * f_bar(k, z, t) for z in range(1, K+2)])
@cache
def h_bar(k, z):
"""Computes the mean waiting time given (N_0, Z_0) = (k,z)."""
if k == 1:
return 0
elif z <= K:
return ((k - 1) * (K + 1 - p) + 1 - z) / mu
elif z == K + 1:
return ((k - 2) * (K + 1 - p) + 1) / mu
@cache
def h_circ(k, u):
"""Computes the mean waiting time given (N_0, B_0) = (k,u)."""
return sum([gamma(z, u) * h_bar(k, z) for z in range(1, K+2)])
### transition probabilities
# 1. No client has been served before time t.
@cache
def P_up(k, u, t):
"""Computes P(N_t- = k | N_0 = k, B_0 = u)."""
return B_sf(u+t) / B_sf(u)
# 2. All clients have been served before time t.
@cache
def P_down(k, u, t):
"""Computes P(N_t- = 0 | N_0 = k, B_0 = u)."""
return sum([gamma(z, u) * P_k0(k, z, t) for z in range(1, K+2)])
# 3. Some (but not all) clients have been served before time t.
@cache
def q(diff, z, v, t):
"""
Computes P(N_t = l, B_t < v | N_0 = k, Z_0 = z).
Note: diff = k-l.
"""
q = 0
if z <= K:
for m in range(diff+2):
I_klmz = (diff + 1) * K - z + m + 1
E = p * psi(v, t, I_klmz, I_klmz+K) + (1 - p) * psi(v, t, I_klmz, I_klmz+K+1)
q += binom.pmf(m, diff+1, 1-p) * E
elif z == K + 1:
for m in range(diff+1):
I_klm = diff * K + m + 1
E = p * psi(v, t, I_klm, I_klm+K) + (1 - p) * psi(v, t, I_klm, I_klm+K+1)
q += binom.pmf(m, diff, 1-p) * E
return q
@cache
def q_bar(diff, m, j, t):
"""
Approximates P(N_{t*Delta} = l, B_{t*Delta} in d(j*Delta) | N_0 = k, B_0 = m * Delta).
Note: diff = k-l.
"""
lower = min(max(0, (j - 0.5) * Delta), t*Delta)
upper = min(max(0, (j + 0.5) * Delta), t*Delta)
q_bar = sum([gamma(z, m*Delta) * (q(diff, z, upper, t*Delta) - q(diff, z, lower, t*Delta)) for z in range(1, K+2)])
return q_bar
### cost function
@cache
def cost_we(t, i, k, m):
"""Computes (approximately) the cost when
t/Delta is the next interarrival time."""
cost = omega * f_circ(k, m*Delta, t*Delta) + (1 - omega) * h_circ(k, m*Delta)
cost += P_down(k, m*Delta, t*Delta) * xi_we(i+1, 1, 0) + P_up(k, m*Delta, t*Delta) * xi_we(i+1, k+1, m+t) ####
# print('f_circ(k, m*Delta, t*Delta)', f_circ(k, m*Delta, t*Delta))
# print('h_circ(k, m*Delta)', h_circ(k, m*Delta))
# print('P_down(k, m*Delta, t*Delta)', P_down(k, m*Delta, t*Delta))
# print('xi_we(i+1, 1, 0)', xi_we(i+1, 1, 0))
# print('P_up(k, m*Delta, t*Delta', P_up(k, m*Delta, t*Delta))
# print('xi_we(i+1, k+1, m+t)', xi_we(i+1, k+1, m+t))
for l in range(2, k+1):
for j in range(t+1):
cost += q_bar(k-l, m, j, t) * xi_we(i+1, l, j)
return cost
k, u = 3, 4
h_circ(k, u)
i = 2
k = 1
m = 1
t = 9
# cost_we(t, i, k, m)
# for t in range(1,21):
# print(t, cost_we(t, i, k, m) - cost_we(t-1, i, k, m))
(1 - 0.5) * h_circ(2, 1)
xi_we(3,2,10) #### 0.4362059564857282
i = 3
k = 2
m = 1
t = 9
(1 - omega) * h_circ(k, (m+t)*Delta)
# def xi_we(i, k, m):
# """Implements the Weighted Erlang Case."""
# # truncate time in service m
# if m >= t_MAX:
# m_new = t_MAX-1
# else:
# m_new = m
# if xi_matrix[i-1][k-1][m]: # retrieve stored value
# pass
# elif i == n: # initial condition
# xi_matrix[i-1][k-1][m] = (1 - omega) * h_circ(k, m*Delta)
# else:
# # initial guess
# if m > 0 and minima[i-1][k-1][m-1]:
# t_guess = minima[i-1][k-1][m-1]
# else:
# t_guess = eval(old_minima[i-1][k-1])[m]
# cost_guess = cost_we(t_guess, i, k, m)
# t_new = t_guess
# # walk to the left
# while True:
# t_new -= 1
# cost_new = cost_we(t_new, i, k, m)
# if cost_new < cost_guess:
# t_guess = t_new
# cost_guess = cost_new
# elif cost_new > cost_guess:
# break
# # walk to the right
# while True:
# t_new += 1
# cost_new = cost_we(t_new, i, k, m)
# if cost_new < cost_guess:
# t_guess = t_new
# cost_guess = cost_new
# elif cost_new > cost_guess:
# break
# xi_matrix[i-1][k-1][m] = cost_guess
# minima[i-1][k-1][m] = t_guess
# print("end",i,k,m,t_guess,cost_guess)
# return xi_matrix[i-1][k-1][m]
def xi_we(i, k, m):
"""Implements the Weighted Erlang Case."""
if m <= t_MAX and xi_matrix[i-1][k-1][m]: # retrieve stored value
pass
elif i == n: # initial condition
if m <= t_MAX:
xi_matrix[i-1][k-1][m] = (1 - omega) * h_circ(k, m*Delta)
else:
return (1 - omega) * h_circ(k, m*Delta)
else:
if m <= t_MAX:
# initial guess
if m > 0 and minima[i-1][k-1][m-1]:
t_guess = minima[i-1][k-1][m-1]
else:
t_guess = eval(old_minima[i-1][k-1])[m]
else:
if minima[i-1][k-1][t_MAX]:
t_guess = minima[i-1][k-1][t_MAX]
else:
t_guess = old_minima[i-1][k-1][t_MAX]
cost_guess = cost_we(t_guess, i, k, m)
t_new = t_guess
# walk to the left
while True:
t_new -= 1
cost_new = cost_we(t_new, i, k, m)
if cost_new < cost_guess:
t_guess = t_new
cost_guess = cost_new
elif cost_new > cost_guess:
break
# walk to the right
while True:
t_new += 1
cost_new = cost_we(t_new, i, k, m)
if cost_new < cost_guess:
t_guess = t_new
cost_guess = cost_new
elif cost_new > cost_guess:
break
if m <= t_MAX:
xi_matrix[i-1][k-1][m] = cost_guess
minima[i-1][k-1][m] = t_guess
else:
return cost_guess
if m <= 2:
print("end",i,k,m,t_guess,cost_guess)
return xi_matrix[i-1][k-1][m]
SCV = 0.6
K, p, mu = SCV_to_params(SCV)
Delta = 0.01
# epsilon = 0.005
t_MAX = int(5/Delta) # int(5/Delta)
n = 5
omega = 0.5
import csv
C_matrix = [[None for k in range(n)] for i in range(n)]
minima = [[None for k in range(n-1)] for i in range(n-1)]
# compute values
for i in range(1,n+1):
for k in range(1,i+1):
Cstar_homexp(i,k,mu=1,omega=omega,n=n,C_matrix=C_matrix)
# # cost
print("\nCost:", C_matrix[0][0])
new_minima = [[[None for m in range(t_MAX+1)] for k in range(n-1)] for i in range(n-1)]
for i in range(n-1):
for k in range(i+1):
new_minima[i][k] = [int(round(minima[i][k],2) / Delta)] * t_MAX * 2
with open(f'SCV_1.00_omega_{omega}_minima.csv','w', newline='') as myfile:
out = csv.writer(myfile)
out.writerows(new_minima)
with open(f'SCV_1.00_omega_{omega:.1f}_minima.csv','r') as csvfile:
reader = csv.reader(csvfile)
old_minima = list(reader)
xi_matrix = [[[None for m in range(t_MAX+1)] for k in range(i+1)] for i in range(n)]
minima = [[[None for m in range(t_MAX+1)] for k in range(i+1)] for i in range(n)]
for i in np.arange(n,0,-1):
for k in range(1,i+1):
print("i =",i,"k =",k)
for m in range(t_MAX+1):
xi_we(i,k,m)
i, k, m = 5, 4, 2
print(xi_we(i,k,m))
print(minima[i-1][k-1][m])
```
We proceed by analyzing the second case, i.e., the hyperexponential case.
### Hyperexponential Distribution
In this case the service times $B_i$ are independent and distributed as $B$, where $B$ equals with probability $p\in [0,1]$ an exponentially distributed random variable with mean $\mu_1^{-1}$, and with probability $1-p$ an exponentially distributed random variable with mean $\mu_{2}^{-1}$. The following recursion can be derived from the thesis.
<div class="alert alert-warning">
<b>Theorem 3.19 (discrete version).</b>
For $i=1,\dots,n-1$, $k=1,\dots,i$, and $m\in\mathbb{N}_0$,
\[
\xi_i(k,m) = \inf_{t\in \mathbb{N}_0}\Bigg(\omega \bar{f}^{\circ}_{k,m\Delta}(t\Delta)
+ (1 - \omega)\bar{h}^{\circ}_{k,m\Delta} + \sum_{\ell=2}^{k}\sum_{j=0}^{t}\bar{q}_{k\ell,mj}(t)\xi_{i+1}(\ell,j)
+ P^{\downarrow}_{k,m\Delta}(t\Delta)\xi_{i+1}(1,0) + P^{\uparrow}_{k,m\Delta}(t\Delta)\xi_{i+1}(k+1,m+t) \Bigg),
\]
whereas, for $k=1,\dots,n$ and $m \in \mathbb{N}_0$,
\[
\xi_n(k,m) = (1 - \omega)\bar{h}^{\circ}_{k,m\Delta}.
\]
</div>
Below is our implementation.
```
### helper functions
# @cache
def gamma(z, u):
if z == 1:
return p * np.exp(-mu1 * u) / B_sf(u)
elif z == 2:
return (1 - p) * np.exp(-mu2 * u) / B_sf(u)
# @cache
def B_sf(t):
return p * np.exp(-mu1 * t) + (1 - p) * np.exp(-mu2 * t) ### gamma_circ
# @cache
def zeta(alpha, t, k):
if not k:
return (np.exp(alpha * t) - 1) / alpha
else:
return ((t ** k) * np.exp(alpha * t) - k * zeta(alpha, t, k-1)) / alpha
# @cache
def rho(t,m,k):
if not k:
return np.exp(-mu2 * t) * (mu1 ** m) / ((mu1 - mu2) ** (m + 1)) * erlang.cdf(t, m+1, scale=1/(mu1 - mu2))
elif not m:
return np.exp(-mu1 * t) * (mu2 ** k) / math.factorial(k) * zeta(mu1-mu2, t, k)
else:
return (mu1 * rho(t, m-1, k) - mu2 * rho(t, m, k-1)) / (mu1 - mu2)
# @cache
def Psi(t,m,k):
if not m:
return erlang.cdf(t, k, scale=1/mu2)
else:
return erlang.cdf(t, m, scale=1/mu1) - mu1 * sum([rho(t, m-1, i) for i in range(k)])
# @cache
def chi(v, t, z, k, l):
"""
Computes P(t-v < Erl(k,mu1) + Erl(l,mu2) < t, Erl(k,mu1) + Erl(l,mu2) + E(1,mu_z) > t),
where Erl(k,mu1) and Erl(l,mu2) are independent.
"""
if z == 1:
if not k and l:
return np.exp(-mu1 * t) * ((mu2) ** l) \
* (zeta(mu1-mu2, t, l-1) - zeta(mu1-mu2, t-v, l-1)) / math.factorial(l-1)
elif k and not l:
return poisson.pmf(k, mu1*t) * binom.sf(0, k, v/t)
else:
return mu2 * (rho(t, k, l-1) - np.exp(-mu1 * v) * rho(t-v, k, l-1))
elif z == 2:
if not k and l:
return poisson.pmf(l, mu2*t) * binom.sf(0, l, v/t)
elif k and not l:
return np.exp(-mu2 * t) * (erlang.cdf(t, k, scale=1/(mu1-mu2)) - erlang.cdf(t-v, k, scale=1/(mu1-mu2))) \
* (mu1 / (mu1 - mu2)) ** k
else:
return mu1 * (rho(t, k-1, l) - np.exp(-mu2 * v) * rho(t-v, k-1, l))
# @cache
def sigma(t, m, k):
if not k:
return t * erlang.cdf(t, m, scale=1/mu1) - (m / mu1) * erlang.cdf(t, m+1, scale=1/mu1)
elif not m:
return t * erlang.cdf(t, k, scale=1/mu2) - (k / mu2) * erlang.cdf(t, k+1, scale=1/mu2)
else:
return (t - k / mu2) * erlang.cdf(t, m, scale=1/mu1) - (m / mu1) * erlang.cdf(t, m+1, scale=1/mu1) \
+ (mu1 / mu2) * sum([(k - i) * rho(t, m-1, i) for i in range(k)])
# @cache
def f_bar(k, z, t):
"""Computes the mean idle time given (N_0, Z_0) = (k,z)."""
if z == 1:
return sum([binom.pmf(m, k-1, p) * sigma(t, m+1, k-1-m) for m in range(k)])
elif z == 2:
return sum([binom.pmf(m, k-1, p) * sigma(t, m, k-m) for m in range(k)])
# @cache
def h_bar(k, z):
"""Computes the mean waiting time given (N_0, Z_0) = (k,z)."""
if k == 1:
return 0
else:
if z == 1:
return (k-2) + (1/mu1)
elif z == 2:
return (k-2) + (1/mu2)
# @cache
def f_circ(k, u, t):
"""Computes the mean idle time given (N_0, B_0) = (k,u)."""
return gamma(1, u) * f_bar(k, 1, t) + gamma(2, u) * f_bar(k, 2, t)
# @cache
def h_circ(k, u):
"""Computes the mean waiting time given (N_0, B_0) = (k,u)."""
return gamma(1, u) * h_bar(k, 1) + gamma(2, u) * h_bar(k, 2)
### transition probabilities
# 1. No client has been served before time t.
# @cache
def P_up(k, u, t):
"""Computes P(N_t- = k | N_0 = k, B_0 = u)."""
return B_sf(u + t) / B_sf(u)
# 2. All clients have been served before time t.
# @cache
def P_down(k, u, t):
"""Computes P(N_t- = 0 | N_0 = k, B_0 = u)."""
return sum([binom.pmf(m, k-1, p) * (Psi(t, m+1, k-1-m) * gamma(1, u) \
+ Psi(t, m, k-m) * gamma(2, u)) for m in range(k)])
# 3. Some (but not all) clients have been served before time t.
# @cache
def q(diff, z, v, t):
"""
Computes P(N_t = l, B_t < v | N_0 = k, Z_0 = z).
Note: diff = k-l.
"""
if z == 1:
return sum([binom.pmf(m, diff, p) * (p * chi(v, t, 1, m+1, diff-m) \
+ (1 - p) * chi(v, t, 2, m+1, diff-m)) for m in range(diff+1)])
elif z == 2:
return sum([binom.pmf(m, diff, p) * (p * chi(v, t, 1, m, diff-m+1) \
+ (1 - p) * chi(v, t, 2, m, diff-m+1)) for m in range(diff+1)])
# @cache
def q_bar(diff, m, j, t):
"""
Approximates P(N_{t*Delta} = l, B_{t*Delta} in d(j*Delta) | N_0 = k, B_0 = m * Delta).
Note: diff = k-l.
"""
lower = min(max(0, (j - 0.5) * Delta), t*Delta)
upper = min(max(0, (j + 0.5) * Delta), t*Delta)
q1_low = q(diff, 1, lower, t*Delta)
q1_upp = q(diff, 1, upper, t*Delta)
q2_low = q(diff, 2, lower, t*Delta)
q2_upp = q(diff, 2, upper, t*Delta)
return gamma(1, m*Delta) * (q1_upp - q1_low) + gamma(2, m*Delta) * (q2_upp - q2_low)
### cost function
# @cache
def cost_he(t, i, k, m):
"""
Computes (approximately) the cost when
t/Delta is the next interarrival time.
"""
cost = omega * f_circ(k, m*Delta, t*Delta) + (1 - omega) * h_circ(k, m*Delta)
cost += P_down(k, m*Delta, t*Delta) * xi_he(i+1, 1, 0) + P_up(k, m*Delta, t*Delta) * xi_he(i+1, k+1, m+t)
for l in range(2, k+1):
for j in range(t+1):
cost_diff = q_bar(k-l, m, j, t) * xi_he(i+1, l, j)
# if cost_diff > 1e-10:
cost += cost_diff
return cost
# k = 2
# np.exp(-mu1 * t) * (mu2 ** k) / math.factorial(k) * zeta(mu1-mu2, t, k)
# (np.exp(-mu1 * t) * (mu2 ** k) / (mu2 - mu1) ** (k+1)) * \
# (1 - sum([np.exp((mu1 - mu2) * t) * ((((mu2 - mu1) * t) ** i) / math.factorial(i)) for i in range(k+1)]))
l = 2
# chi_1[0,l]
np.exp(-mu1 * t) * ((mu2) ** l) \
* (zeta(mu1-mu2, t, l-1) - zeta(mu1-mu2, t-v, l-1)) / math.factorial(l-1)
(np.exp(-mu1 * t) * ((mu2 / (mu2 - mu1)) ** l)) * \
(sum([np.exp(-(mu2-mu1)*(t-v)) * (((mu2 - mu1) * (t - v)) ** i) / math.factorial(i) for i in range(l)]) - \
sum([np.exp(-(mu2-mu1)*t) * (((mu2 - mu1) * t) ** i) / math.factorial(i) for i in range(l)]))
f_circ(k, m*Delta, t*Delta)
h_circ(k, m*Delta)
P_down(k, m*Delta, t*Delta)
xi_he(i+1, 1, 0)
P_up(k, m*Delta, t*Delta)
xi_he(i+1, k+1, m+t)
t = 2
i = 4
k = 2 ### k > 1
m = 0
cost_he(t,i,k,m)
v = 1.3
t = 2.8
z = 2
k = 4
l = 0
q(k-l,z,v,t) ### q hangt alleen af van k-l
q_bar(k-l, v, v, t)
np.exp(-mu2 * t) * ((mu1 ** k) / math.factorial(k-1)) * (zeta(mu2 - mu1, t, k-1) - zeta(mu2 - mu1, t-v, k-1))
SCV = 2
p, mu1, mu2 = SCV_to_params(SCV)
n = 5
v = 0.05
t = 0.10
print(chi(v,t,1,1,0)) ## 0.00776 (klopt)
print(chi(v,t,1,0,1)) ## 0.02081 (FOUT) bij mij 0????
print(chi(v,t,2,0,1)) ## 0.0021 (klopt)
print(chi(v,t,2,1,0)) ## 0.0077 (klopt)
mu2-mu1
l = 1
np.exp(-mu1 * t) * ((mu2 / (mu1 - mu2)) ** l) * \
(
sum([np.exp(-(mu1-mu2)*(t-v)) * (((mu2 - mu1) * (t - v)) ** i) / math.factorial(i) for i in range(l)])) - \
sum([np.exp(-(mu1-mu2)*t) * (((mu2 - mu1) * t) ** i) / math.factorial(i) for i in range(l)]
)
l = 1
np.exp(-mu1 * t) * ((mu2 / (mu2 - mu1)) ** l) * \
(1 - sum([np.exp(-(mu2-mu1)*t) * (((mu2 - mu1) * t) ** i) / math.factorial(i) for i in range(l)])) \
- np.exp(-mu1*(t-v)) * ((mu2 / (mu2 - mu1)) ** l) * \
(1 - sum([np.exp(-(mu2-mu1)*(t-v)) * (((mu2 - mu1) * (t - v)) ** i) / math.factorial(i) for i in range(l)]))
def xi_he(i, k, m):
"""Implements the Hyperexponential Case."""
# truncate time in service m
if m >= t_MAX:
m = t_MAX-1
if xi_matrix[i-1][k-1][m]: # retrieve stored value
pass
elif i == n: # initial condition
xi_matrix[i-1][k-1][m] = (1 - omega) * h_circ(k, m*Delta)
else:
# if m >= 2 and xi_matrix[i-1][k-1][m-1] and xi_matrix[i-1][k-1][m-2]:
# # fill all coming values with current cost & minimum
# if abs(xi_matrix[i-1][k-1][m-1] - xi_matrix[i-1][k-1][m-2]) < epsilon:
# xi_matrix[i-1][k-1][m:] = [xi_matrix[i-1][k-1][m-1]] * (t_MAX - (m - 1))
# minima[i-1][k-1][m:] = [minima[i-1][k-1][m-1]] * (t_MAX - (m - 1))
# print(i,k,m,"break")
# return xi_matrix[i-1][k-1][m]
# initial guess
if m > 0 and minima[i-1][k-1][m-1]:
t_guess = minima[i-1][k-1][m-1]
else:
t_guess = eval(old_minima[i-1][k-1])[m]
cost_guess = cost_he(t_guess, i, k, m)
t_new = t_guess
# walk to the left
while True:
t_new -= 1
cost_new = cost_he(t_new, i, k, m)
if cost_new < cost_guess:
t_guess = t_new
cost_guess = cost_new
elif cost_new > cost_guess:
break
# walk to the right
while True:
t_new += 1
cost_new = cost_he(t_new, i, k, m)
if cost_new < cost_guess:
t_guess = t_new
cost_guess = cost_new
elif cost_new > cost_guess:
break
xi_matrix[i-1][k-1][m] = cost_guess
minima[i-1][k-1][m] = t_guess
if m <= 20:
print("end",i,k,m,t_guess,cost_guess)
return xi_matrix[i-1][k-1][m]
```
With this program, we can obtain dynamic schedules in the hyperexponential case:
```
SCV = 2.5
p, mu1, mu2 = SCV_to_params(SCV)
Delta = 0.01
epsilon = 0.005
t_MAX = int(5/Delta)
n = 5
omega = 0.5
import csv
C_matrix = [[None for k in range(n)] for i in range(n)]
minima = [[None for k in range(n-1)] for i in range(n-1)]
# compute values
for i in range(1,n+1):
for k in range(1,i+1):
Cstar_homexp(i,k,mu=1,omega=omega,n=n,C_matrix=C_matrix)
# # cost
print("\nCost:", C_matrix[0][0])
new_minima = [[[None for m in range(t_MAX)] for k in range(n-1)] for i in range(n-1)]
for i in range(n-1):
for k in range(i+1):
new_minima[i][k] = [int(round(minima[i][k],2) / Delta)] * t_MAX * 2
with open(f'SCV_1.00_omega_{omega}_minima.csv','w', newline='') as myfile:
out = csv.writer(myfile)
out.writerows(new_minima)
with open(f'SCV_1.00_omega_{omega:.1f}_minima.csv','r') as csvfile:
reader = csv.reader(csvfile)
old_minima = list(reader)
xi_matrix = [[[None for m in range(t_MAX)] for k in range(i+1)] for i in range(n)]
minima = [[[None for m in range(t_MAX)] for k in range(i+1)] for i in range(n)]
# i = 3
# k = 1
# # m = 0
# # for k in np.arange(1,5):
# for m in np.arange(3):
# print(i,k,m,xi_he(i,k,m))
xi_matrix = [[[None for m in range(t_MAX)] for k in range(i+1)] for i in range(n)]
minima = [[[None for m in range(t_MAX)] for k in range(i+1)] for i in range(n)]
for i in np.arange(n,0,-1):
for k in range(1,i+1):
print("i =",i,"k =",k)
for m in range(101):
xi_he(i,k,m)
xi_he(1,1,0)
print('Function Summary')
functions = ['gamma', 'B_sf', 'zeta', 'rho', 'Psi', 'chi', 'sigma', 'f_bar', 'h_bar',
'f_circ', 'h_circ', 'P_up', 'P_down', 'q', 'q_bar', 'cost_he']
for function in functions:
info = eval(function).cache_info()
print(f'{str(function):8s}: {info.hits:8d} hits\
{info.misses:8d} misses\
{info.hits/(info.hits + info.misses):.2%} gain')
```
| true |
code
| 0.695183 | null | null | null | null |
|
# Create a circuit to generate any two-qubit quantum state in Qiskit
Build a general 2-qubit circuit that could output all Hilbert space of states by tuning its parameters.
```
from qiskit import *
import numpy as np
def state_maker(theta, ang0, ang1):
circ = QuantumCircuit(2,2)
circ.u3(theta, 0, 0, 0)
circ.cx(0, 1)
circ.u3(*ang1, 1)
circ.u3(*ang0, 0)
return circ
def get_ensemble(theta0, theta1, theta2, N=1024):
circuit = state_maker(theta0, [theta1,0,0], [theta2,0,0])
circuit.measure(0,0)
circuit.measure(1,1)
simulator = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend = simulator, shots = N).result()
counts = result.get_counts()
return counts
from qiskit.tools.visualization import plot_histogram
#angi = [theta, phi, lam]
ang0 = [0,0,0]
ang1 = [0,0,0]
theta = 0
circ = state_maker(theta, ang0, ang1)
%matplotlib inline
#circ.draw(output='mpl')
circ.measure(0,0)
circ.measure(1,1)
circ.draw(output='mpl')
```
Example of the count result for some parameters $\theta_0$, $\theta_1$ and $\theta_2$.
```
from ttq.optimizer import optimize
pi = np.pi
_EXPECTED_VALUES = {
'00' : 0.5,
'01' : 0.2,
'10' : 0.2,
'11' : 0.1
}
_MAX_ERROR = 0.05
_N = 1024
_STEP = 0.1
_PARAMS = 3
theta0, theta1, theta2 = optimize(conf = {
'bound': [0, 2 * pi],
'expected_values': _EXPECTED_VALUES,
'max_error': _MAX_ERROR,
'max_iter': None,
'n_states': _N,
'step': _STEP,
'x0': [0] * _PARAMS
})
counts = get_ensemble(theta0, theta1, theta2)
print(counts)
plot_histogram(counts)
```
Example of the generated state result for some parameters $\theta_0$, $\theta_1$ and $\theta_2$.
```
circ = state_maker(theta0, [theta1, 0, 0], [theta2, 0, 0])
simulator = Aer.get_backend('statevector_simulator')
result = execute(circ, backend = simulator).result()
statevector = result.get_statevector()
print(statevector)
```
# For some $\theta$'s
Plot the probability of measuring each state for a given set of parameters.
```
ntheta = 100
N = 1024
theta = np.linspace(0, 2*np.pi, ntheta)
prob00, prob01, prob10, prob11 = [], [], [], []
for t in theta: # to check it we only change one parameter
counts = get_ensemble(t, t, t, N)
prob00.append(counts['00']/N if '00' in counts.keys() else 0)
prob01.append(counts['01']/N if '01' in counts.keys() else 0)
prob10.append(counts['10']/N if '10' in counts.keys() else 0)
prob11.append(counts['11']/N if '11' in counts.keys() else 0)
import matplotlib.pyplot as plt
plt.plot(theta, prob00, label='| 00 >')
plt.plot(theta, prob01, label='| 01 >')
plt.plot(theta, prob10, label='| 10 >')
plt.plot(theta, prob11, label='| 11 >')
plt.legend(loc = 'upper right')
plt.show()
```
# Measuring the 'entanglement'
We measure the realtion between the amplidudes of states $| 00 >$ and $| 01 >$ for different $\theta_0$'s.
```
import matplotlib.pyplot as plt
ang0 = [0,0,0]
ang1 = [0,0,0]
entang = []
e00 = []
e11 = []
thetas = np.linspace(0, 2*np.pi, 10)
thetas = thetas[2:-2]
for theta in thetas:
circ = state_maker(theta, ang0, ang1)
simulator = Aer.get_backend('statevector_simulator')
result = execute(circ, backend = simulator).result()
statevector = result.get_statevector()
print('theta = {:2.2f}pi '.format(theta/np.pi) )
print('state = ', statevector)
print()
entang.append(abs(statevector[0])/(abs(statevector[3])+.0001))
plt.plot(thetas, entang)
```
| true |
code
| 0.554229 | null | null | null | null |
|
# First fitting from amalgams
In this phase, we are not considering sequences, leave alone syntax trees, in prediction. Instead we are using the frequency of (shallow) occurence of names in types to predict the (shallow) occurence in definitions.
Here we consider the first two models. The second has some depth and shows overfitting.
## Structure of the models
Both the models have a similar structure.
* there is a common representation of the input data.
* a prediction is made from this of a component the output name distribution (we call this the _low rank prediction_).
* the other component is the input scaled, i.e., it is assumed that elements in the statement are in the proofs.
- this should be rectified, currently the scaling is uniform, depending on the amalgams. It should depend on the specific elements.
* the scaling is also determined from the representation (not too good as mentioned)
* the components are put together.
```
import amalgam_predict as pred
import keras
from matplotlib import pyplot as plt
```
We fit the first model.
* The fit is reasonable.
* More importantly, the validation data fits almost as well as the training data.
```
hist1 = pred.fit(1024, pred.model1)
plt.rcParams['figure.figsize'] = [20, 15]
plt.plot(hist1.history['kullback_leibler_divergence'])
plt.plot(hist1.history['val_kullback_leibler_divergence'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
```
As we see, the final KL-divergence is `2.7425` for the training data, and `2.8078` for the validation data.
We now fit the second model. As mentioned, this fits much better, but that is clearly a case of overfitting.
```
hist2 = pred.fit(1024, pred.model2)
plt.plot(hist2.history['kullback_leibler_divergence'])
plt.plot(hist2.history['val_kullback_leibler_divergence'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
```
We see the fit keeps improving (this was before the early stop), reaching `1.2060`, but the validation error flattens, ending at `2.4163`
To do:
* use better model for persistence
After adding the dropout layer, we get a similar validation fit without the overfitting.
```
hist3 = pred.fit(1024, pred.model3)
plt.plot(hist3.history['kullback_leibler_divergence'])
plt.plot(hist3.history['val_kullback_leibler_divergence'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
```
The above shows really no overfitting. So one can try to improve the model.
### Better persistence model (TODO)
* Have a variable which is a row by which to scale each term by pointwise multiplication.
* Initialize from data.
* Multiply and then apply sigmoid to get a probability distribution on terms.
* Use this instead of the input when mixing in.
```
pred.data.keys()
pred.data['types']
import numpy as np
def count_matrix(pairs, dim):
vec = np.zeros((dim, ), np.float32)
for d in pairs:
name = d['name']
count = d['count']
vec[pred.indices[name]] = count
return vec
term_count = count_matrix(pred.data['terms'], pred.dim)
term_count
np.sum(term_count)
```
| true |
code
| 0.598488 | null | null | null | null |
|

# Magnetometer Calibration
Kevin Walchko, Phd
30 May 2020
---
To calibrate a magnetometer, you need to get readings from all directions in 3D space. Ideally, when you plot the readings out, you should get a perfect sphere centered at (0,0,0). However, due to misalignments, offset, etc ... you end up with ellipsoids centered at some biased location.
Here we are going to try and get enough readings to estimate these errors and properly calibrate the sensor. We will load in a pre-recorded data set, where the sensor was tumbled around and calibrate it.
## Errors

- **Soft iron errors:** caused by distortion of the Earth's magnetic field due to materials in the environment. Think of it like electricity - the magnetic field is looking for the easiest path to get to where it is going. Since magnetic fields can flow more easily through ferromagnetic materials than air, more of the field will flow through the ferromagnetic material than you would expect if it were just air. This distortion effect causes the magnetic field lines to be bent sometimes quite a bit. Note that unlike hard iron interference which is the result of materials which actually have a magnetic field of their own, soft iron interference is caused by non-magnetic materials distorting the Earth's magnetic field. This type of interference has a squishing effect on the magnetic data circle turning it into more of an ellipsoid shape. The distortion in this case depends on the direction that the compass is facing. Because of this, the distortion cannot be calibrated out with a simple offset
- **Hard iron errors:** caused by static magnetic fields associated with the enviornment. For example, this could include any minor (or major) magnetism in the metal chassis or frame of a vehicle, any actual magnets such as speakers, etc... This interference pattern is unique to the environment but is constant. If you have your compass in an enclosure that is held together with metal screws, these relatively small amounts of ferromagnetic material can cause issues. If we consider the magnetic data circle, hard iron interference has the effect of shifting the entire circle away from the origin by some amount. The amount is dependent on any number of different factors and can be very large.
## References
- Ozyagcilar, T. ["Calibrating an eCompass in the Presence of Hard and Soft-iron Interference."](AN4246.pdf) Freescale Semiconductor Ltd. 1992, pp. 1-17.
- Teslabs: [Magnetometer Calibration](https://teslabs.com/articles/magnetometer-calibration/)
- ThePoorEngineer: [Calibrating the Magnetometer](https://www.thepoorengineer.com/en/calibrating-the-magnetometer/)
- Mathworks: [magcal](https://www.mathworks.com/help/fusion/ref/magcal.html#mw_34252c54-1f78-46b9-8c30-1a2b7351b0ce)
```
import numpy as np
np.set_printoptions(precision=3)
np.set_printoptions(suppress=True)
from scipy import linalg
import sys
from squaternion import Quaternion
import pandas as pd
%matplotlib inline
from matplotlib import pyplot as plt
# from math import sqrt, atan2, asin, pi
from math import radians as deg2rad
from math import degrees as rad2deg
from slurm import storage
from datetime import datetime
import os
import pickle
def loadPickle(filename):
with open(filename, 'rb') as fd:
d = pickle.load(fd)
return d
# let's load in some data and have a look at what we have
def bag_info(bag):
print('Bag keys:')
print('-'*50)
for k in bag.keys():
print(f' {k:>10}: {len(bag[k]):<7}')
# fname = "../../software/python/data.pickle"
fname = "../../software/python/dddd.pickle"
data = loadPickle(fname)
accel = []
gyro = []
mag = []
pres = []
temp = []
stamp = []
# bnoq = []
# bnoe = []
bno = {
"euler": {
"roll": [],
"pitch": [],
"yaw": [],
"time": []
},
"q": {
"w": [],
"x": [],
"y": [],
"z": [],
"time": []
}
}
tstart = data[0][-1]
for d in data:
a,g,m,p,t,q,e,dt = d
accel.append(a)
gyro.append(g)
mag.append(m)
pres.append(p)
temp.append(t)
bno["q"]["w"].append(q[0])
bno["q"]["x"].append(q[1])
bno["q"]["y"].append(q[2])
bno["q"]["z"].append(q[3])
bno["q"]["time"].append(dt - tstart)
bno["euler"]["roll"].append(e[0])
bno["euler"]["pitch"].append(e[1])
bno["euler"]["yaw"].append(e[2])
bno["euler"]["time"].append(dt - tstart)
stamp.append(dt)
accel = np.array(accel)
gyro = np.array(gyro)
uT = 50.8862
Bpp = np.array(mag)
print(f">> Mag data size: {Bpp.shape}")
def plotMagnetometer(data):
x = [v[0] for v in data]
rx = (max(x)-min(x))/2
cx = min(x)+rx
y = [v[1] for v in data]
ry = (max(y)-min(y))/2
cy = min(y)+ry
z = [v[2] for v in data]
rz = (max(z)-min(z))/2
cz = min(z)+rz
alpha = 0.1
u = np.linspace(0, 2 * np.pi, 100)
plt.plot(rx*np.cos(u)+cx, ry*np.sin(u)+cy,'-r',label='xy')
plt.plot(x,y,'.r',alpha=alpha)
plt.plot(rx*np.cos(u)+cx, rz*np.sin(u)+cz,'-g',label='xz')
plt.plot(x,z,'.g',alpha=alpha)
plt.plot(rz*np.cos(u)+cz, ry*np.sin(u)+cy,'-b',label='zy')
plt.plot(z,y, '.b',alpha=alpha)
plt.title(f"CM:({cx:.1f}, {cy:.1f}, {cz:.1f}) uT R:({rx:.1f}, {ry:.1f}, {rz:.1f}) uT")
plt.xlabel('$\mu$T')
plt.ylabel('$\mu$T')
plt.grid(True);
plt.axis('equal')
plt.legend();
def magcal(Bp, uT=None):
"""
Modelled after the matlab function: magcal(D) -> A, b, expmfs
inputs:
Bp: data points
uT: expected field strength for longitude/altitude. If None
is given, then automatically calculated and used
returns:
A: soft-iron 3x3 matrix of scaling
b: hard-iron offsets
expmfs: expected field strength"""
Y = np.array([v[0]**2+v[1]**2+v[2]**2 for v in Bp])
X = np.hstack((Bp,np.ones((Bp.shape[0],1))))
beta = np.linalg.inv(X.T.dot(X)).dot(X.T.dot(Y))
b=0.5*beta[:3]
# expected mag field strength
expmfs=np.sqrt(beta[3]+b[0]**2+b[1]**2+b[2]**2)
if uT is None:
uT = expmfs
x = [v[0] for v in Bp]
rx = (max(x)-min(x))/2
y = [v[1] for v in Bp]
ry = (max(y)-min(y))/2
z = [v[2] for v in Bp]
rz = (max(z)-min(z))/2
A = np.diag([uT/rx,uT/ry,uT/rz])
return A,b,expmfs
# Raw uncalibrated values - you can see the hard-iron offsets
# and the soft-iron ellipses
plotMagnetometer(Bpp)
# calibrated w/o expected field strength
A,vv,bb = magcal(Bpp)
print(f">> soft-iron correction:\n{A}")
print(f">> hard-iron offset: {vv}uT expmfs: {bb:.1f}uT")
plotMagnetometer((Bpp-vv).dot(A))
# calibrated with expected field strength - it only changes
# the radius of the circles
A,vv,bb = magcal(Bpp,uT)
print(f">> soft-iron correction:\n{A}")
print(f">> hard-iron offset: {vv}uT expmfs: {bb:.1f}uT")
plotMagnetometer((Bpp-vv).dot(A))
```
```
>> soft-iron correction:
[[0.983 0. 0. ]
[0. 0.947 0. ]
[0. 0. 0.941]]
>> hard-iron offset: [-20.438 34.429 -2.368]uT expmfs: 52.6uT
```
```
>> soft-iron correction:
[[0.951 0. 0. ]
[0. 0.916 0. ]
[0. 0. 0.91 ]]
>> hard-iron offset: [-20.438 34.429 -2.368]uT expmfs: 52.6uT
```
# Save Parameters
```
M = np.vstack((A,vv))
print(M)
params = {}
params["imu"] = "adafruit NXP"
params["timestamp"] = datetime.now()
params["mag"] = M.tolist()
params["shape"] = M.shape
storage.write("magnetometer-alt.yaml", params)
np.hstack((A,vv.reshape((3,1))))
rr = ["# hello",
{
"A": A.tolist(),
"b": vv.tolist()
}]
storage.write("temp.yaml", rr)
```
| true |
code
| 0.385808 | null | null | null | null |
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Imports
This tutorial imports [Plotly](https://plot.ly/python/getting-started/), [Numpy](http://www.numpy.org/), and [Pandas](https://plot.ly/pandas/intro-to-pandas-tutorial/).
```
import plotly.plotly as py
from plotly.tools import FigureFactory as FF
import numpy as np
import pandas as pd
```
#### Import Data
For this histogram example, we will import some real data.
```
import plotly.plotly as py
from plotly.tools import FigureFactory as FF
data = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/wind_speed_laurel_nebraska.csv')
df = data[0:10]
table = FF.create_table(df)
py.iplot(table, filename='wind-data-sample')
```
#### Histogram
Using `np.histogram()` we can compute histogram data from a data array. This function returns the values of the histogram (i.e. the number for each bin) and the bin endpoints as well, which denote the intervals for which the histogram values correspond to.
```
import plotly.plotly as py
import plotly.graph_objs as go
data_array = np.array((data['10 Min Std Dev']))
hist_data = np.histogram(data_array)
binsize = hist_data[1][1] - hist_data[1][0]
trace1 = go.Histogram(
x=data_array,
histnorm='count',
name='Histogram of Wind Speed',
autobinx=False,
xbins=dict(
start=hist_data[1][0],
end=hist_data[1][-1],
size=binsize
)
)
trace_data = [trace1]
layout = go.Layout(
bargroupgap=0.3
)
fig = go.Figure(data=trace_data, layout=layout)
py.iplot(fig)
hist_data
help(np.histogram)
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'Histogram.ipynb', 'numpy/histogram/', 'Histogram | plotly',
'A histogram is a chart which divides data into bins with a numeric range, and each bin gets a bar corresponding to the number of data points in that bin.',
title = 'Numpy Histogram | plotly',
name = 'Histogram',
has_thumbnail='true', thumbnail='thumbnail/histogram.jpg',
language='numpy', page_type='example_index',
display_as='numpy-statistics', order=2)
```
| true |
code
| 0.686028 | null | null | null | null |
|
## Exercise 3 - Quantum error correction
### Importing Packages
```
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, Aer, transpile
from qc_grader import grade_ex3
import qiskit.tools.jupyter
from qiskit.test.mock import FakeTokyo
```
#### --------------------------------------------------------------------------------------------------------------------
### 1. Circuit
In this example we'll use 5 qubits that we'll call code qubits. To keep track of them, we'll define a special quantum register.
```
code = QuantumRegister(5,'code')
```
We'll also have an additional four qubits we'll call syndrome qubits.
```
syn = QuantumRegister(4,'syn')
```
Similarly we define a register for the four output bits, used when measuring the syndrome qubits.
```
out = ClassicalRegister(4,'output')
```
We consider the qubits to be laid out as follows, with the code qubits forming the corners of four triangles, and the syndrome qubits living inside each triangle.
```
c0----------c1
| \ s0 / |
| \ / |
| s1 c2 s2 |
| / \ |
| / s3 \ |
c3----------c4
```
For each triangle we associate a stabilizer operation on its three qubits. For the qubits on the sides, the stabilizers are $ZZZ$. For the top and bottom ones, they are $XXX$.
The syndrome measurement circuit corresponds to a measurement of these observables. This is done in a similar way to surface code stabilizers (in fact, this code is a small version of a surface code).
```
qc_syn = QuantumCircuit(code,syn,out)
# Left ZZZ
qc_syn.cx(code[0],syn[1])
qc_syn.cx(code[2],syn[1])
qc_syn.cx(code[3],syn[1])
#qc_syn.barrier()
# Right ZZZ
qc_syn.swap(code[1],code[2])
qc_syn.cx(code[2],syn[2])
qc_syn.swap(code[1],code[2])
qc_syn.cx(code[2],syn[2])
qc_syn.cx(code[4],syn[2])
#qc_syn.barrier()
# Top XXX
qc_syn.h(syn[0])
qc_syn.cx(syn[0],code[0])
qc_syn.cx(syn[0],code[1])
qc_syn.cx(syn[0],code[2])
qc_syn.h(syn[0])
#qc_syn.barrier()
# Bottom XXX
qc_syn.h(syn[3])
qc_syn.cx(syn[3],code[2])
qc_syn.cx(syn[3],code[3])
qc_syn.cx(syn[3],code[4])
qc_syn.h(syn[3])
#qc_syn.barrier()
# Measure the auxilliary qubits
qc_syn.measure(syn,out)
qc_syn.draw('mpl')
qc_init = QuantumCircuit(code,syn,out)
qc_init.h(syn[0])
qc_init.cx(syn[0],code[0])
qc_init.cx(syn[0],code[1])
qc_init.cx(syn[0],code[2])
qc_init.cx(code[2],syn[0])
qc_init.h(syn[3])
qc_init.cx(syn[3],code[2])
qc_init.cx(syn[3],code[3])
qc_init.cx(syn[3],code[4])
qc_init.cx(code[4],syn[3])
#qc_init.barrier()
qc_init.draw('mpl')
```
The initialization circuit prepares an eigenstate of these observables, such that the output of the syndrome measurement will be `0000` with certainty.
```
qc = qc_init.compose(qc_syn)
display(qc.draw('mpl'))
job = Aer.get_backend('qasm_simulator').run(qc)
job.result().get_counts()
```
#### --------------------------------------------------------------------------------------------------------------------
### 2. Error Qubits
```
error_qubits = [0,4]
```
Here 0 and 4 refer to the positions of the qubits in the following list, and hence are qubits `code[0]` and `code[4]`.
```
qc.qubits
```
To check that the code does as we require, we can use the following function to create circuits for inserting artificial errors. Here the errors we want to add are listed in `errors` as a simple text string, such as `x0` for an `x` on `error_qubits[0]`.
```
def insert(errors,error_qubits,code,syn,out):
qc_insert = QuantumCircuit(code,syn,out)
if 'x0' in errors:
qc_insert.x(error_qubits[0])
if 'x1' in errors:
qc_insert.x(error_qubits[1])
if 'z0' in errors:
qc_insert.z(error_qubits[0])
if 'z1' in errors:
qc_insert.z(error_qubits[1])
return qc_insert
```
Rather than all 16 possibilities, let's just look at the four cases where a single error is inserted.
```
for error in ['x0','x1','z0','z1']:
qc = qc_init.compose(insert([error],error_qubits,code,syn,out)).compose(qc_syn)
job = Aer.get_backend('qasm_simulator').run(qc)
print('\nFor error '+error+':')
counts = job.result().get_counts()
for output in counts:
print('Output was',output,'for',counts[output],'shots.')
```
### 2. Backend
```
backend = FakeTokyo()
backend
```
As a simple idea of how our original circuit is laid out, let's see how many two-qubit gates it contains.
```
qc = qc_init.compose(qc_syn)
qc = transpile(qc, basis_gates=['u','cx'])
qc.num_nonlocal_gates()
qc1 = transpile(qc,backend,basis_gates=['u','cx'], optimization_level=3)
qc1.num_nonlocal_gates()
```
#### --------------------------------------------------------------------------------------------------------------------
### 3. Initial Layout
```
initial_layout = [0,2,6,10,12,1,5,7,11]
qc2 = transpile(qc,backend,initial_layout=initial_layout, basis_gates=['u','cx'], optimization_level=3)
qc2.num_nonlocal_gates()
```
#### --------------------------------------------------------------------------------------------------------------------
### 4. Grading
```
grade_ex3(qc_init,qc_syn,error_qubits,initial_layout)
```
#### --------------------------------------------------------------------------------------------------------------------
| true |
code
| 0.389169 | null | null | null | null |
|
```
%pylab inline
from __future__ import division
from __future__ import print_function
import pandas as pd
import seaborn as sb
from collections import Counter
```
## Malware Classification Through Dynamically Mined Traces
### 1. The Dataset
The dataset used in this notebook can be freely downloaded from the [csmining website](http://www.csmining.org/index.php/malicious-software-datasets-.html), where there's also an easy explanation on the nature of the dataset and its strenghts/weaknesses.
For a quick recap: the dataset is a made of traces of API calls from 387 windows programs, some of which are malware.
The malware programs are labelled as 1, whereas the 'goodware' programs have a 0 label. Here's a line:
1,LoadLibraryW HeapAlloc HeapAlloc HeapFree HeapAlloc HeapFree HeapFree NtOpenKey LoadLibraryW GetProcAddress GetProcAddress [...]
Let's start exploring the dataset.
```
dataset = pd.read_csv('CSDMC_API_Train.csv')
dataset.columns = ['target','trace']
print(dataset.keys())
print(dataset.columns)
```
Each trace is simply a string, representing a list of API calls separated with a space and residing all in the first column.
So the first thing to do is to split it into an actual python list, creating a list of traces that will each be represented by a tuple containing the trace itself and its classification into 'malware' or 'goodware'.
```
traces = []
for i in dataset.index:
traces.append((dataset.iloc[i]['trace'].strip().split(' '), dataset.iloc[i]['target']))
print ('A trace: ' , type(traces[0][0]))
print ('A label: ', type(traces[8][1]))
```
To gain some additional knowledge on the dataset we could check its bias, or how well are the samples distributed between malware and goodware.
Let's count how many ones and zeroes there are in the target column.
```
c_target = Counter([x[1] for x in traces])
print(c_target)
```
It seems like the dataset is pretty biased towards malware, as there are few samples of benign applications being run.
It's almost the polar opposite of what would happen in a randomly sampled dataset from real world applications, as malware is usually a one digit percentage of the set of every application being released.
But let's not despair, this will actually make learning easier. It might hurt in the generalization tho.
Here's a graph showing the obvious bias:
```
plt.figure(figsize=(6,8))
plt.xticks(np.arange(2) + 1.4, ['Goodware', 'Malware'])
plt.title('Dataset Bias')
plt.ylabel('Number of Program Traces')
plt.xlabel('Classification')
plt.bar([1,2], c_target.values())
```
### 2. Initial Feature Mining
Now it's time to mine for features, as the dataset itself doesn't really lend itself to an easy classification with a Machine Learning algorithm.
Not out of the box at least.
The raw traces present some peculiar challenges for a smooth classification:
1. They are composed of strings
2. They have various length (makes it hard to fit them in a matrix with fixed width)
3. They present a lot of repeated data points
We need numerical features, and possibly a way to organize everything.
The first idea is to count how many times a given API call is contained in each trace, this should yield positive results during learning if there's any correlation at all with the quantity of calls made to a specific API during a program run and a malicious behaviour.
```
counted_traces = []
for trace, target in traces:
counted_traces.append((Counter(trace), target))
```
Just to get an immediate feedback let's print a list of the first 20 traces, and look at the 3 most used API calls in each trace.
The diagnosis is printed at the end to give some perspective.
```
diagnosis = ''
for i in range(20):
if counted_traces[i][1] == 0:
diagnosis = 'OK'
else:
diagnosis = 'MALWARE'
trace_sample = counted_traces[i][0].most_common(3)
print(i, ')', trace_sample, diagnosis)
```
We can obtain some good information and maybe some ideas from this alone:
1. The only two good samples have the shortest program run and the longest one, this might not be relevant in general but it's worth investigating
2. The most popular API calls are roughly the same for each program run, so maybe they won't be incredibly useful for classification
Also, this might be the shortest program run ever (my guess is it crashed soon after loading):
```
counted_traces[11][0]
```
Maybe then it's possible we'll need the length of each trace and the number of times an API has been called during a program run, and that's all information we can freely gather from the data we have assembled so far.
But the *absolute* number of API calls in a program trace isn't a very useful feature, as it mostly depends on the length of each trace, so we'll normalize it by searching for the **frequency** of each API call in a program run.
And since we will have the frequencies associated to each API call, maybe we can see if the frequency of the most used API call is useful for classification.
Since it's now time to gather more than one feature and it's better to keep everything tidy, let's generate a list of dictionaries that will contain the following fields:
**'ID'** : index of the trace, given by the enumerate() method
**'Counter'** : Counter containing the API calls and how many times they have been called
**'Freq'** : frequency at which a certain API call has been used in a program trace
**'Length'** : Length of the trace
**'MostFreqCall'** : The most common API call and its frequency
**'Target'** : 1 or 0, depending on the maliciousness of the sample
To be honest I'm just glad I could use the name 'dict_traces'.
```
dict_traces = [] #a list of dicts
for i, t in enumerate(counted_traces):
trace, target = t
max_freq = 0
most_common = ()
length = len(traces[i][0])
freq_dict = {}
for key in trace:
freq = trace[key] / length
freq_dict[key] = freq
if freq > max_freq:
max_freq = freq
most_common = (key, freq)
d = {'ID' : i,
'Counter' : trace,
'Freq' : freq_dict,
'Length' : length,
'MostFreqCall' : most_common,
'Target' : target}
dict_traces.append(d)
print(dict_traces[0].keys())
print(dict_traces[0]['MostFreqCall'])
```
What is the most frequent "most frequent call"?
Since the most popular API calls will inevitably be used by every program run, be it malicious or not, maybe we can avoid them.
```
most_freq_call_list = []
for d_t in dict_traces:
call, freq = d_t['MostFreqCall']
most_freq_call_list.append(call)
c = Counter(most_freq_call_list)
print('Maybe we can avoid these: ', c.most_common(3))
```
Here's a graph showing the N most frequent "most frequent call".
As we can see the first 4 are pretty noticeable, then they drop fast:
```
N = 12
plt.figure(figsize=(12,8))
plt.title('Most frequent "most frequent call"')
plt.ylabel('Frequency')
y = [x[1]/len(dict_traces) for x in c.most_common(N)]
plt.bar(np.arange(N) + 0.2, y)
plt.xticks(np.arange(N) + 0.6, [x[0] for x in c.most_common(N)], rotation=60)
plt.ylim((0, 0.5))
```
A further trasformation in our data is needed before we start learning, let's separate the target from the data points.
This will be useful to render the code more readable, and to have another quick glimpse into how biased the dataset is.
```
target = []
for d in dict_traces:
target.append(d['Target'])
print(target)
```
As we can see from the density of the ones, our algorithm would do pretty well if it just guessed 'malware' all the time:
```
p_malware = c_target[1] / len(target)
print('Accuracy if I always guess "malware" = ', p_malware)
print('False positives: ', 1 - p_malware)
```
Of course false negatives will be exactly 0% in this particular instance so, generally speaking, this wouldn't be a bad result.
But that wouldn't be a very realistic scenario in a learned classifier, and even then that would mean that it actually learnt something from the dataset (the target's distribution), although it shoudln't be useful at all for generalizing.
Let's see how a really dumb classifier would fare, by just guessing 'malware' and 'goodware' with 50% chance (this time accounting for both false positives and false negatives):
```
p_chance_mal = (p_malware * 0.5)
p_chance_good = (c_target[0] / len(target)) * 0.5
print ('''Probability of getting it right by guessing with 50%%:
- False Positive Ratio: %f
- False Negative Ratio: %f
''' % (1 - p_chance_mal, 1 - p_chance_good))
```
Now these are horrible ratios, let's hope we can do better than this.
## 3. Learning
It's time to finally try and learn something.
Throughout the rest of the notebook we'll use various classifiers and functions from the [scikit-learn](http://scikit-learn.org/) library.
First off we'll need a classifier, and since I'm a fan of ensemble learning we'll start with a Random Forest classifier initialized with 20 estimators and a random state set to 42.
The random state is very important, as it will help with the reproducibility of this study.
```
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=20, random_state=42)
```
Now we can't start learning right away, as our dataset should be first divided into a 'train' set and a 'test' set, to ensure a bit of generalization.
We could do this manually, by randomly selecting a chunk of the dataset (usually 75%) for the training part and leaving the rest for testing, but we could still generate a lucky division and receive optimistic results that won't generalize well in the real world.
Thankfully scikit-learn has provided a neat implementation of the KFold algorithm that will allow us to generate how many folds we need.
```
from sklearn.cross_validation import KFold
kf = KFold(len(target), n_folds=3, random_state=42)
```
Another little adjustment is needed before using scikit-learn's algorithms, as they expect the data to be indexed vertically, but thankfully again, numpy has the solution.
We're going to create a numpy array with each trace length and reshape it accordingly.
Let'stry and learn only from the length of the traces:
```
scores = []
for train, test in kf:
train_data = np.array([dict_traces[i]['Length'] for i in train]).reshape(len(train), 1)
test_data = np.array([dict_traces[i]['Length'] for i in test]).reshape(len(test), 1)
model.fit(train_data, [target[i] for i in train])
scores.append(model.score(test_data, [target[i] for i in test]))
print(scores)
print(np.array(scores).mean())
```
We have chosen to learn from 3 folds and already our classifier seems to produce good results even with one feature.
This might be because it's a pretty small dataset and it's kinda biased.
Since we're going to try and learn from different features and maybe different classifiers, it's best to keep track of the scores in a global way, just to visualize the improvements over time (or lack thereof).
```
global_scores = {}
global_scores['Length'] = scores
```
Another feature we mined is the most frequent API call, let's see how well it does by itself.
Since classifiers work mainly in dimensional data, we need a way to encode the API call into an integer, maybe by using a dictionary.
This is a very rudementary but effective way:
```
most_freq_list = [x['MostFreqCall'][0] for x in dict_traces]
most_freq_counter = Counter(most_freq_list)
most_freq_dict = {}
index = 0
for call in most_freq_counter.keys():
most_freq_dict[call] = index
index += 1
print(most_freq_dict)
```
The learning process is basically the same as before, so maybe it's time to encode it in a function.
```
model = RandomForestClassifier(n_estimators=20, random_state=42)
scores = []
for train, test in kf:
train_data = np.array([most_freq_dict[dict_traces[i]['MostFreqCall'][0]] for i in train]).reshape(len(train), 1)
test_data = np.array([most_freq_dict[dict_traces[i]['MostFreqCall'][0]] for i in test]).reshape(len(test), 1)
model.fit(train_data, [target[i] for i in train])
scores.append(model.score(test_data, [target[i] for i in test]))
global_scores['MostFreqCall'] = scores
print(scores)
print(np.array(scores).mean())
```
Wait.
```
print(p_malware)
print(np.array(scores).mean())
```
This is probably just a coincidence, but the accuracy of our classifier is exactly the same as the hypothetical classifier that always guesses 'malware'.
And it's a weirdly good result, since the most frequent api call might be correlated with the classification but this is too much. Again, it's probably due to the size of the dataset or its skewness.
I think we can safely assume this is the lowest score we can get with any classifier.
To improve on this, lets try to learn from the 2 features we just mined.
```
model = RandomForestClassifier(n_estimators=20, random_state=42)
scores = []
for train, test in kf:
most_freq_train_data = np.array([most_freq_dict[dict_traces[i]['MostFreqCall'][0]] for i in train]).reshape(len(train), 1)
length_train_data = np.array([dict_traces[i]['Length'] for i in train]).reshape(len(train), 1)
train_data = np.append(most_freq_train_data, length_train_data,1)
most_freq_test_data = np.array([most_freq_dict[dict_traces[i]['MostFreqCall'][0]] for i in test]).reshape(len(test), 1)
length_test_data = np.array([dict_traces[i]['Length'] for i in test]).reshape(len(test), 1)
test_data = np.append(most_freq_test_data, length_test_data,1)
model.fit(train_data, [target[i] for i in train])
scores.append(model.score(test_data, [target[i] for i in test]))
global_scores['Length + MostFreqCall'] = scores
print(scores)
print(np.array(scores).mean())
```
This is a good improvement, even a 5% increase at this stage can be beneficial, we'll see if this is the right direction.
## 4. Reorganizing Features
One of the best aspects of the scikit-learn library is their readily-available datasets, which are either already present in the library's path, or provide a simple function that will download them.
Since we're mining features from our dataset, we could use the same structure as shown below:
```
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.keys())
print(iris['feature_names'])
```
This is good practice, in case we later want to release this to the public or even in case someone wants to expand on this.
Starting with the easy things, a description and the target:
```
m_descr = """
Malware Traces Dataset
Notes:
---------
Dataset characteristics:
:Number of Instances: 387 (319 malware and 68 goodware)
:Number of Attributes: 2
:Attribute Information:
- trace length
- most frequent API call (encoded with an integer)
- class:
- Malware
- Goodware
"""
malware_dataset = {
'target_names' : ['Goodware', 'Malware'],
'DESCR' : m_descr,
'target' : np.array(target)
}
```
Now for the hard part: data and feature_names.
We'll need to unify the 2 features we have used until now:
```
m_most_freq_data = np.array([most_freq_dict[dict_traces[i]['MostFreqCall'][0]] for i in range(len(dict_traces))]).reshape(len(dict_traces), 1)
m_length_data = np.array([dict_traces[i]['Length'] for i in range(len(dict_traces))]).reshape(len(dict_traces), 1)
m_data = np.append(m_most_freq_data, m_length_data,1)
malware_dataset['data'] = m_data
malware_dataset['feature_names'] = ['trace length', 'most frequent call']
```
## 5. Reorganizing Learning
Since now our dataset is clean and organized, we can streamline the learning process aswell.
The function learn() will take in input a classifier, the features and the target points, while returning the scores as we have used until now (raw scores and their mean).
I also added an option to plot the confusion matrix for the learn classifier and the possibility to save the scores into the global_scores variable we have initialized a while ago.
```
from sklearn.metrics import confusion_matrix
def learn(model, data, target, descr=None, n_folds=3, plot=False):
'''
"descr" is an optional parameter that will save the results in global_scores for later visualization
"n_folds" is there just in case I want to change it
'''
kf = KFold(data.shape[0], n_folds=n_folds, random_state=42)
scores = []
best_score = 0
best_split = ()
for train, test in kf:
#this is easier to read
model.fit(data[train], target[train])
m_score = model.score(data[test], target[test])
scores.append(m_score)
if plot and m_score > best_score:
best_score = m_score
best_split = (train, test)
#this plots a simple confusion matrix
if plot:
train, test = best_split
model.fit(data[train], target[train])
cm = confusion_matrix(target[test], model.predict(data[test]))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.xticks(np.arange(len(malware_dataset['target_names'])), malware_dataset['target_names'])
plt.yticks(np.arange(len(malware_dataset['target_names'])), malware_dataset['target_names'], rotation=90)
plt.ylabel('Actual Label')
plt.xlabel('Predicted Label')
plt.tight_layout()
if descr != None:
global_scores[descr] = scores
return (scores, np.array(scores).mean())
```
Let's try it out:
```
model = RandomForestClassifier(n_estimators=20, random_state = 42)
data = malware_dataset['data']
target = malware_dataset['target']
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target, plot=True))
```
This is exactly the same result as before but this was expected, as that's why we initialized the same random state.
Now it's time to mine for more features, since the most frequent call kinda improved our classification when paired with the length of the trace, maybe the 2nd and 3rd most frequent calls will add to it?
```
print(dict_traces[0].keys())
print(dict_traces[0]['Counter'].most_common(4)[0])
m_second_most_freq = []
for trace in dict_traces:
m_second_most_freq.append(trace['Counter'].most_common(2)[1])
m_s_counter = Counter([x[0] for x in m_second_most_freq])
```
This is the same process we used to encode numerically the API calls in the first 'most frequent' feature, it's very rough but it gets the job done.
It could also be methodologically wrong, as we're using different encodings for some of the same API calls.
```
m_s_dict = {}
index = 0
for item in m_s_counter.keys():
m_s_dict[item] = index
index += 1
print(m_s_dict)
m_s_list = [m_s_dict[x[0]] for x in m_second_most_freq]
m_s_data = np.array(m_s_list).reshape(len(m_s_list), 1)
```
Let's add it to the existing feature set.
```
malware_dataset['data'] = np.append(malware_dataset['data'], m_s_data, 1)
malware_dataset['feature_names'].append('second most frequent call')
print(malware_dataset['feature_names'])
```
Has it already impacted the classification?
```
model = RandomForestClassifier(n_estimators=20, random_state=42)
data = malware_dataset['data']
target = malware_dataset['target']
descr = 'Length + MostFreqCall + SecondMostFreqCall'
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target, descr, plot=True))
```
The overall improvement is negligible, but looking at the folds it seems like two of them were more susceptible to the new feature and the middle one didn't really take notice.
So it could be a step in the right direction.
Maybe it would help to visualize our improvements over time:
```
def plot_improvement():
plt.figure(figsize=(13,5))
t_counter = Counter(target)
#assuming an algorithm that always guesses "Malware" as the baseline
best_guess = t_counter[1] / len(target)
plt.plot(np.arange(len(global_scores.keys()) + 1), [best_guess] + [np.array(x).mean() for x in global_scores.values()])
plt.xticks(np.arange(len(global_scores.keys())) + 1, global_scores.keys(), rotation=60)
plt.xlim((0, len(global_scores.keys()) + 0.2))
plt.ylabel('Accuracy')
print('If we just guess "malware" we get an accuracy of: ', best_guess)
print('Our best classificator has an accuracy of: ', np.array([np.array(x).mean() for x in global_scores.values()]).max())
plot_improvement()
```
The improvement on the second most frequent call is clearly negligible, so we'll stop investigating in that direction.
But it seems apparent that the frequency of the api calls has to be correlated in some way with the malicious behaviors of the samples so we might aswell try this new approach.
The idea is simple, there are 10 most frequent apis throughout the dataset, and each trace presents them with a certain frequency:
```
m_10_most_common = []
for trace in dict_traces:
freq_list = []
for t, f in most_freq_counter.most_common(10):
freq_list.append(trace['Counter'][t] / trace['Length'])
m_10_most_common.append(freq_list)
print(m_10_most_common[2])
m_data_10 = np.array(m_10_most_common)
```
Let's update our feature set and the feature names:
```
malware_dataset['data'] = np.append(malware_dataset['data'], m_data_10, 1)
print(malware_dataset['data'].shape)
for i in range(10):
malware_dataset['feature_names'].append(str(i + 1) + ' API call')
```
Now we can try to learn from all the features just mined at once:
```
model = RandomForestClassifier(n_estimators=20, random_state=42)
data = malware_dataset['data']
target = malware_dataset['target']
descr = '10 MostFreqPerc'
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target, descr, plot=True))
plot_improvement()
```
Now, this is a very good improvement, and it seems like every fold is responding in the same way so it's not dependent on the random selection of the training set.
But it's interesting to wonder if the newly mined features are just improving on the old ones or if they can be used on their own without any detraction from the classificiation.
So, what is the accuracy of our classifier if we only learn from the 10 new features?
```
model = RandomForestClassifier(n_estimators=20, random_state=42)
data = malware_dataset['data'][:, 2:]
target = malware_dataset['target']
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
Not bad, as expected.
As a side note, I stopped plotting the confusion matrix as only false negatives were present.
## 6. Trying Different Classifiers
We could go on and mine for features for a while, but an algorithm wich can discern between malware and goodware with ~95% accuracy is already a pretty good result for such a short study.
Also, there's another direction where we could improve, and that's by trying out new models.
- ***AdaBoost***
Until now we used Random Forest, which is just an ensemble classifier that uses Decision Trees as base classifier, but the scikit-learn library also provides us with an implementation of AdaBoost, an ensemble classifier that seems to do just the same thing (its default base classifier is a Decision Tree).
So it might be interesting to see if we can get the same results.
*Note: on the surface Ada Boost and Random Forest seem to be fairly similar, as they both combine the results of many underlying 'weaker' classifiers and construct a stronger learner, but they differ a lot in their core.
Random Forest is a bagging algorithm and Ada Boost is a boosting algorithm.*
```
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
base_class = DecisionTreeClassifier(random_state=42)
model = AdaBoostClassifier(n_estimators=120,learning_rate=1.2, random_state=42)
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
The result is pretty similar, we can play a bit with the estimators and the learning rate but we won't get much better results than this.
Also, if we put back the first 2 features it actually becomes worse.
As a quick side note, we started with ensemble classifiers, but what about linear classifiers?
Well, there's a reason to ignore them:
```
from sklearn.linear_model import Perceptron
model = Perceptron(random_state=42)
data = malware_dataset['data'][:, 2:] #if we try to learn from the first 2 features, the perceptron will take a dive
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
It would be pretty weird if the feature set we just constructed had any linear way to separate it into classes.
So any linear model is out of the question, but there are weaker models than Ada Boost to try against our feature set:
- ***Decision Tree Classifier***
This is the base classifier for both the Random Forest algorithm and for Ada Boost (at least in scikit-learn's implementation).
It's basically an algorithm that tries to learn a Decision Tree to classify the problem at hand, using several heuristics. The learned Decision Tree isn't guaranteed to be the optimal one, as that would entail solving an NP-complete problem and breaking everything.
```
model = DecisionTreeClassifier(random_state=42)
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
- ***Naive Bayes***
Since ours is a simple classification job with only 2 classes, we might aswell try the most used classifier out there, Naive Bayes.
Now, this might not be a really good idea, since Naive Bayes assumes each feature to be independent from the others (and it's not really our case), but it's worth a try since it usually works anyway.
We'll try 3 different implementation of Naive Bayes, with different assumed probability distributions.
```
from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB
models = [MultinomialNB(), GaussianNB(), BernoulliNB()]
#try different first and last_index (0, 2)
first_index = 0
last_index = 4
data = malware_dataset['data'][:, first_index : last_index]
for model in models:
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
- ***Support Vector Machines***
SVMs technically are non-probabilistic binary linear classifiers, but with the kernel trick they can easily perform non-linear classifications.
There are lots of parameters for SVMs (gamma, tolerance, penalty [...]) and of course the various kernels, so we'll see a handy way to automate the choice of these parameters with Grid Search.
```
from sklearn.svm import SVC
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
model = SVC(kernel='rbf')
print('''Our algorithm has:
- scores: %s
- mean: %f
''' % learn(model, data, target))
```
Instead of manually trying out new models and parameters, we can automate everything using the handy GridSearch:
```
from sklearn.grid_search import GridSearchCV
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10],
'gamma': [0.001, 0.01, 0.1, 1],
'kernel' : ['rbf', 'sigmoid'], #poly and linear hang up the whole notebook, beware
'degree' : [3, 4, 5]}
KF = KFold(len(target), n_folds=2, random_state=42)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=kf)#, verbose=3) #uncomment to see lots of prints
first_index = 0
last_index = 10
data = malware_dataset['data'][:, first_index : last_index]
grid.fit(data, target)
print(grid.best_score_)
print(grid.best_params_)
```
## 8. Future Improvements
This notebook might be updated or divided into more notebooks (it is pretty long), anyway there's lots of directions to take from here.
a. Ulterior Feature Mining
I doubt that we've found the best features for this classification job.
b. Dimensionality Reduction
Once we've mined for more features we can try to reduce the dimensionality of the problem using:
- Isomap
- TSNE (this works very well apparently)
c. Biclustering
| true |
code
| 0.348368 | null | null | null | null |
|
# TensorFlow Visual Recognition Sample Application Part 1
## Define the model metadata
```
import tensorflow as tf
import requests
models = {
"mobilenet": {
"base_url":"https://github.com/DTAIEB/Thoughtful-Data-Science/raw/master/chapter%206/Visual%20Recognition/mobilenet_v1_0.50_224",
"model_file_url": "frozen_graph.pb",
"label_file": "labels.txt",
"output_layer": "MobilenetV1/Predictions/Softmax"
}
}
# helper method for reading attributes from the model metadata
def get_model_attribute(model, key, default_value = None):
if key not in model:
if default_value is None:
raise Exception("Require model attribute {} not found".format(key))
return default_value
return model[key]
```
## Helper methods for loading the graph and labels for a given model
```
# Helper method for resolving url relative to the selected model
def get_url(model, path):
return model["base_url"] + "/" + path
# Download the serialized model and create a TensorFlow graph
def load_graph(model):
graph = tf.Graph()
graph_def = tf.GraphDef()
graph_def.ParseFromString(
requests.get( get_url( model, model["model_file_url"] ) ).content
)
with graph.as_default():
tf.import_graph_def(graph_def)
return graph
# Load the labels
def load_labels(model, as_json = False):
labels = [line.rstrip() \
for line in requests.get( get_url( model, model["label_file"] ) ).text.split("\n") \
if line != ""]
if as_json:
return [{"index": item.split(":")[0], "label" : item.split(":")[1]} for item in labels]
return labels
```
## Use BeautifulSoup to scrape the images from a given url
```
from bs4 import BeautifulSoup as BS
import re
# return an array of all the images scraped from an html page
def get_image_urls(url):
# Instantiate a BeautifulSoup parser
soup = BS(requests.get(url).text, "html.parser")
# Local helper method for extracting url
def extract_url(val):
m = re.match(r"url\((.*)\)", val)
val = m.group(1) if m is not None else val
return "http:" + val if val.startswith("//") else val
# List comprehension that look for <img> elements and backgroud-image styles
return [extract_url(imgtag['src']) for imgtag in soup.find_all('img')] + [ \
extract_url(val.strip()) for key,val in \
[tuple(selector.split(":")) for elt in soup.select("[style]") \
for selector in elt["style"].strip(" ;").split(";")] \
if key.strip().lower()=='background-image' \
]
```
## Helper method for downloading an image into a temp file
```
import tempfile
def download_image(url):
response = requests.get(url, stream=True)
if response.status_code == 200:
with tempfile.NamedTemporaryFile(delete=False) as f:
for chunk in response.iter_content(2048):
f.write(chunk)
return f.name
else:
raise Exception("Unable to download image: {}".format(response.status_code))
```
## Decode an image into a tensor
```
# decode a given image into a tensor
def read_tensor_from_image_file(model, file_name):
file_reader = tf.read_file(file_name, "file_reader")
if file_name.endswith(".png"):
image_reader = tf.image.decode_png(file_reader, channels = 3,name='png_reader')
elif file_name.endswith(".gif"):
image_reader = tf.squeeze(tf.image.decode_gif(file_reader,name='gif_reader'))
elif file_name.endswith(".bmp"):
image_reader = tf.image.decode_bmp(file_reader, name='bmp_reader')
else:
image_reader = tf.image.decode_jpeg(file_reader, channels = 3, name='jpeg_reader')
float_caster = tf.cast(image_reader, tf.float32)
dims_expander = tf.expand_dims(float_caster, 0);
# Read some info from the model metadata, providing default values
input_height = get_model_attribute(model, "input_height", 224)
input_width = get_model_attribute(model, "input_width", 224)
input_mean = get_model_attribute(model, "input_mean", 0)
input_std = get_model_attribute(model, "input_std", 255)
resized = tf.image.resize_bilinear(dims_expander, [input_height, input_width])
normalized = tf.divide(tf.subtract(resized, [input_mean]), [input_std])
sess = tf.Session()
result = sess.run(normalized)
return result
```
## Score_image method that run the model and return the top 5 candidate answers
```
import numpy as np
# classify an image given its url
def score_image(graph, model, url):
# Get the input and output layer from the model
input_layer = get_model_attribute(model, "input_layer", "input")
output_layer = get_model_attribute(model, "output_layer")
# Download the image and build a tensor from its data
t = read_tensor_from_image_file(model, download_image(url))
# Retrieve the tensors corresponding to the input and output layers
input_tensor = graph.get_tensor_by_name("import/" + input_layer + ":0");
output_tensor = graph.get_tensor_by_name("import/" + output_layer + ":0");
with tf.Session(graph=graph) as sess:
# Execute the output, overriding the input tensor with the one corresponding
# to the image in the feed_dict argument
results = sess.run(output_tensor, {input_tensor: t})
results = np.squeeze(results)
# select the top 5 candidate and match them to the labels
top_k = results.argsort()[-5:][::-1]
labels = load_labels(model)
return [(labels[i].split(":")[1], results[i]) for i in top_k]
```
## Test the model using a Flickr page
```
model = models['mobilenet']
graph = load_graph(model)
image_urls = get_image_urls("https://www.flickr.com/search/?text=cats")
for url in image_urls:
results = score_image(graph, model, url)
print("Results for {}: \n\t{}".format(url, results))
```
| true |
code
| 0.513242 | null | null | null | null |
|
## Quantum Fourier Transform
```
import numpy as np
from numpy import pi
from qiskit import QuantumCircuit, transpile, assemble, Aer, IBMQ
from qiskit.providers.ibmq import least_busy
from qiskit.tools.monitor import job_monitor
from qiskit.visualization import plot_histogram, plot_bloch_multivector
# doing it for a 3 qubit case
qc = QuantumCircuit(3)
qc.h(2)
qc.draw('mpl')
# we want to turn this to extra quarter if qubit 1 is in |1>
# apply the CROT from qubit 1 to to qubit 2
qc.cp(pi/2,1,2)
qc.draw('mpl')
# we want an another eighsths turn if the least significant bit
# 0 has the value |1>
# apply CROT from qubit 2 to qubit 1
qc.cp(pi/4,0,2)
qc.draw('mpl')
# doing the same for the rest two qubits
qc.h(1)
qc.cp(pi/2,0,1)
qc.h(0)
qc.draw('mpl')
# and then swap the 0 and 2 qubit to complete the QFT
qc.swap(0,2)
qc.draw('mpl')
```
This is one way to create the QFT circuit, but we can also make a function to make that.
```
def qft_rotations(circuit,n):
if n == 0:
return circuit
n -= 1
circuit.h(0)
for qubit in range(n):
circuit.cp(pi/2**(n-qubit), qubit,n)
# so
qc = QuantumCircuit(4)
qft_rotations(qc,4)
qc.draw('mpl')
# how scaling works
from qiskit_textbook.widgets import scalable_circuit
scalable_circuit(qft_rotations)
# we can modify the prev function
def qft_rotations(circuit,n):
if n == 0:
return circuit
n -= 1
circuit.h(n)
for qubit in range(n):
circuit.cp(pi/2**(n-qubit), qubit,n)
qft_rotations(circuit,n)
qc = QuantumCircuit(4)
qft_rotations(qc,4)
qc.draw('mpl')
scalable_circuit(qft_rotations)
# now adding the swap gates
def swap_registeres(circuit, n):
for qubit in range(n//2):
circuit.swap(qubit, n-qubit-1)
return circuit
def qft(circuit,n):
qft_rotations(circuit,n)
swap_registeres(circuit,n)
return circuit
qc = QuantumCircuit(8)
qft(qc,8)
qc.draw('mpl')
scalable_circuit(qft)
```
## How the Circuit Works?
```
bin(7)
# encode this
qc = QuantumCircuit(3)
for i in range(3):
qc.x(i)
qc.draw('mpl')
# display in the aer simulator
sim = Aer.get_backend("aer_simulator")
qc_init = qc.copy()
qc_init.save_statevector()
statevector = sim.run(qc_init).result().get_statevector()
plot_bloch_multivector(statevector)
# now call the qft function
qft(qc,3)
qc.draw('mpl')
qc.save_statevector()
statevector = sim.run(qc).result().get_statevector()
plot_bloch_multivector(statevector)
```
### Running it on Real Quantum Device
```
def inverse_qft(circuit,n):
qft_circ = qft(QuantumCircuit(n), n)
invqft_circuit = qft_circ.inverse()
# add it to first n qubits
circuit.append(invqft_circuit, circuit.qubits[:n])
return circuit.decompose()
# now do it fo the 7
nqubits = 3
number = 7
qc = QuantumCircuit(nqubits)
for qubit in range(nqubits):
qc.h(qubit)
qc.p(number*pi/4,0)
qc.p(number*pi/2,1)
qc.p(number*pi,2)
qc.draw('mpl')
qc_init = qc.copy()
qc_init.save_statevector()
sim = Aer.get_backend("aer_simulator")
statevector = sim.run(qc_init).result().get_statevector()
plot_bloch_multivector(statevector)
# now the inverse QFT
qc = inverse_qft(qc, nqubits)
qc.measure_all()
qc.draw('mpl')
# Load our saved IBMQ accounts and get the least busy backend device with less than or equal to nqubits
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= nqubits
and not x.configuration().simulator
and x.status().operational==True))
print("least busy backend: ", backend)
shots = 2048
transpiled_qc = transpile(qc, backend, optimization_level=3)
job = backend.run(transpiled_qc, shots=shots)
job_monitor(job)
counts = job.result().get_counts()
plot_histogram(counts)
```
| true |
code
| 0.640439 | null | null | null | null |
|
#### 1 - 3 summarized below:
#### Lineraly Seperable Experiment
- **Training data:** X training points were randomly generated (values bounded between -100 and 100). Y training labels were generated by applying a randomly generated target function to the X training points.
- **Test data:** X test points were randomly generated (values bounded between -100 and 100). Y test labels were generated by applying the same target function to the X test points.
#### Non-lineraly Separable Experiment
- **Training data:** X training points were randomly generated (values bounded between -100 and 100). Y training labels randomly generated (-1 and 1). Then, the randomly generated target function was applied with a probaility of .75 to create 'somewhat' lineraly separable data.
- **Test data:** X test points were randomly generated (values bounded between -100 and 100). Y test labels randomly generated (-1 and 1). Then, the randomly generated target function was applied with a probaility of .75 to create 'somewhat' lineraly separable data.
**4.** The initial choice of the weights is random.
#### Answers to questions 5 - 8 can be seen in the statistics (and graphs) on pages 3-4.
#### Variation Results
1. The weights that give the lowest in-sample error rate is best.
2. The step size correlates with the amount the vector changes. i.e., A larger step size makes the vector adjustment larger.
3. It is best to consider training points that reduce the error rate the most first.
```
%matplotlib inline
import numpy as np
import random
from perceptron_learning import Perceptron
from perceptron_learning import two_d_vector as tdv
def main():
bound = 100 # the value that the x and y values are bounded by
num_pts = 80
num_train_pts = 50
perceptron = Perceptron(alpha=0.005)
target_fn = np.random.uniform(-10, 10, 3)
x = get_random_x(num_pts, bound)
x_train, x_test = x[:num_train_pts, :], x[num_train_pts:, :]
y_test = np.sign(np.dot(x_test, target_fn))
print('---------- Linearly Separable Data ----------')
perceptron.fit(x_train, target_fn=target_fn)
predictions = perceptron.predict(x_test)
print('{:28s}: y = {:.2f}x + {:.2f}'.format('Target Function',
tdv.get_slope(target_fn),
tdv.get_y_intercept(target_fn)))
print_error(predictions, y_test)
print()
y = get_y(x[:, 1:], target_fn)
y_train, y_test = y[:num_train_pts], y[num_train_pts:]
print('-------- Non-Linearly Separable Data --------')
perceptron.fit(x_train, y_train=y_train)
predictions = perceptron.predict(x_test)
print_error(predictions, y_test)
perceptron.visualize_training()
def print_error(predictions, y_test):
error = np.sum(np.not_equal(predictions, y_test)) / y_test.shape[0]
print('{0:28s}: {1:.2f}%'.format('Out of Sample (Test) Error', error * 100))
def get_y(training_pts, w_target):
# Have y be somewhat linearly separable
y = np.random.choice([-1, 1], training_pts.shape[0])
for i, pt in enumerate(training_pts):
pct_chance = .75
pt_above_line = tdv.pt_above_line(pt, w_target)
if pt_above_line and random.random() < pct_chance:
y[i] = 1
if not pt_above_line and random.random() < pct_chance:
y[i] = -1
return y
def get_random_x(num_points, bound):
pts = get_random_pts(num_points, bound)
x = np.insert(pts, 0, 1, axis=1) # Let x0 equal 1
return x
def get_random_pts(num_points, bound):
return np.random.randint(-bound, bound, size=(num_points, 2))
if __name__ == '__main__':
main()
"""
two_d_vector.py
Functions that operate on 2d vectors.
w0 (or x0) is a bias "dummy" weight,
so even though the vector is 3 dimensional,
we call it a 2 dimensional vector.
"""
import numpy as np
from random import uniform
def get_perpendicular_vector(w):
# Two lines are perpendicular if: m1 * m2 = -1.
# The two slopes must be negative reciprocals of each other.
m1 = get_slope(w)
m2 = -1 / m1
# m2 = - w[1] / w[2]
random_num = uniform(0, 10)
return np.array([uniform(0, 10), -1 * m2 * random_num, random_num])
def get_line(w, x_bound):
x_range = np.array(range(-x_bound, x_bound))
# Formula for line is: w1x1 + w2x2 + w0 = 0
# we let x2 = y, and x1 = x, then solve for y = mx + b
slope = get_slope(w)
y_intercept = get_y_intercept(w)
y_line = (slope * x_range) + y_intercept
return x_range, y_line
def pt_above_line(pt, w):
return pt[1] > get_slope(w) * pt[0] + get_y_intercept(w)
def get_y_intercept(w):
return - w[0] / w[2]
def get_slope(w):
return - w[1] / w[2]
"""
DataVisualizer.py
"""
import numpy as np
import matplotlib.pyplot as plt
from . import two_d_vector as tdv
class DataVisualizer:
def __init__(self, title, subtitle, x_bound, y_bound):
plt.style.use('seaborn-whitegrid')
self.fig, self.ax = plt.subplots()
self.title = title
self.subtitle = subtitle
self.x_bound = x_bound
self.y_bound = y_bound
def setup_axes(self):
self.ax.cla()
self.fig.canvas.set_window_title(self.subtitle)
self.fig.suptitle(self.title, fontsize=18)
self.ax.set_title(self.subtitle, fontsize=14)
self.ax.set_xlim(-self.x_bound, self.x_bound)
self.ax.set_ylim(-self.y_bound, self.y_bound)
@staticmethod
def red_pts_above_line(pts, w_target, true_classes):
pt_above_line = tdv.pt_above_line(pts[0, :], w_target)
pt_is_positive_class = true_classes[0] > 0
if pt_above_line and pt_is_positive_class:
# positive pt above line
return True
if not pt_above_line and not pt_is_positive_class:
# negative pt below line
return True
return False
def plot_hypothesis(self, pts, true_classes, w_hypothesis, w_target=None):
self.setup_axes()
self.ax.scatter(x=pts[:, 0], y=pts[:, 1], marker='x',
color=['r' if sign >= 0 else 'b' for sign in true_classes])
if w_target is not None:
x, y = tdv.get_line(w_target, self.x_bound)
self.ax.plot(x, y, label='target', color='m')
x, y = tdv.get_line(w_hypothesis, self.x_bound)
self.ax.plot(x, y, label='hypothesis', color='g')
if w_target is not None:
if self.red_pts_above_line(pts, w_target, true_classes):
self.ax.fill_between(x, y, np.full((1,), self.y_bound), color=(1, 0, 0, 0.15))
self.ax.fill_between(x, y, np.full((1,), -self.y_bound), color=(0, 0, 1, 0.15))
else:
self.ax.fill_between(x, y, np.full((1,), self.y_bound), color=(0, 0, 1, 0.15))
self.ax.fill_between(x, y, np.full((1,), -self.y_bound), color=(1, 0, 0, 0.15))
self.ax.legend(facecolor='w', fancybox=True, frameon=True, edgecolor='black', borderpad=1)
# plt.pause(0.01)
@staticmethod
def visualize():
plt.show()
"""
Logger.py
"""
class Logger:
def __init__(self):
self.num_iterations = 0
self.num_vector_updates = 0
def print_statistics(self):
print('{:28s}: {:}'.format('Number of iterations', self.num_iterations))
print('{:28s}: {:}'.format('Number of vector updates', self.num_vector_updates))
"""
Perceptron.py
"""
import numpy as np
from . import two_d_vector as tdv
from . import DataVisualizer, Logger
class Perceptron:
"""Uses 'pocket' algorithm to keep best hypothesis in it's 'pocket'"""
def __init__(self, alpha):
self.alpha = alpha
self.best_hypothesis = np.random.uniform(-10, 10, 3)
self.lowest_error = float('inf')
self.logger = Logger()
self.dv = None
def fit(self, x_train, y_train=None, target_fn=None):
"""Fits the model to the training data (class labels) or target function.
:param x_train: the training data
:param y_train: will be passed in in the non-linearly separable case
:param target_fn: will be passed in in the linearly separable case
:return: None
"""
self.best_hypothesis = np.random.uniform(-10, 10, 3)
self.lowest_error = float('inf')
self.logger = Logger()
self.dv = get_data_visualizer(target_fn, x_train)
if target_fn is not None:
y_train = np.sign(np.dot(x_train, target_fn))
self.best_hypothesis = tdv.get_perpendicular_vector(target_fn)
pts = x_train[:, 1:]
hypothesis = self.best_hypothesis
misclassified_pts = predict_and_evaluate(hypothesis, x_train, y_train)
while self.logger.num_vector_updates < 100000 and np.sum(misclassified_pts) > 0:
for i, misclassified_pt in enumerate(np.nditer(misclassified_pts)):
if misclassified_pt:
# update rule: w(t + 1) = w(t) + y(t) * x(t) * alpha
hypothesis += y_train[i] * x_train[i] * self.alpha
these_misclassified_pts = predict_and_evaluate(hypothesis, x_train, y_train)
this_error = calculate_error(np.sum(these_misclassified_pts), x_train.shape[0])
if this_error < self.lowest_error:
self.best_hypothesis = hypothesis
self.lowest_error = this_error
self.logger.num_vector_updates += 1
misclassified_pts = predict_and_evaluate(hypothesis, x_train, y_train)
self.logger.num_iterations += 1
self.dv.plot_hypothesis(pts, y_train, self.best_hypothesis, target_fn)
self.print_fit_statistics()
def print_fit_statistics(self):
self.logger.print_statistics()
print('{:28s}: y = {:.2f}x + {:.2f}'.format('Hypothesis',
tdv.get_slope(self.best_hypothesis),
tdv.get_y_intercept(self.best_hypothesis)))
print('{0:28s}: {1:.2f}%'.format('In Sample (Training) Error', self.lowest_error * 100))
def visualize_training(self):
self.dv.visualize()
def predict(self, x):
return predict(x, self.best_hypothesis)
def predict_and_evaluate(hypothesis, x_train, y_train):
pred_classes = predict(hypothesis, x_train)
misclassified_pts = np.not_equal(pred_classes, y_train)
return misclassified_pts
def predict(x, hypothesis):
return np.sign(np.dot(x, hypothesis.T))
def calculate_error(num_misclassified_pts, num_pts):
return num_misclassified_pts / float(num_pts)
def get_data_visualizer(target_fn, x_train):
plot_title = 'Perceptron Learning'
if target_fn is not None:
plot_subtitle = 'Linearly Separable Training Data'
else:
plot_subtitle = 'Non-linearly Separable Training Data'
x_bound = np.max(np.absolute(x_train[:, 1]))
y_bound = np.max(np.absolute(x_train[:, 2]))
return DataVisualizer(plot_title, plot_subtitle, x_bound, y_bound)
```
| true |
code
| 0.680401 | null | null | null | null |
|
# Authorise Notebook server to access Earth Engine
This notebook is a reproduction of the workflow originally developed by **Datalab**, which describes how to setup a Google Datalab container in your local machine using Docker.
You can check out the full tutorial by going to this link: https://developers.google.com/earth-engine/python_install-datalab-local
```
# Code to check the IPython Widgets library.
try:
import ipywidgets
except ImportError:
print('The IPython Widgets library is not available on this server.\n'
'Please see https://github.com/jupyter-widgets/ipywidgets '
'for information on installing the library.')
raise
print('The IPython Widgets library (version {0}) is available on this server.'.format(
ipywidgets.__version__
))
```
Next, check if the Earth Engine API is available on the server.
```
# Code to check the Earth Engine API library.
try:
import ee
except ImportError:
print('The Earth Engine Python API library is not available on this server.\n'
'Please see https://developers.google.com/earth-engine/python_install '
'for information on installing the library.')
raise
print('The Earth Engine Python API (version {0}) is available on this server.'.format(
ee.__version__
))
```
Finally, check if the notebook server is authorized to access the Earth Engine backend servers.
```
# Code to check if authorized to access Earth Engine.
import io
import os
import urllib
from IPython import display
# Define layouts used by the form.
row_wide_layout = ipywidgets.Layout(flex_flow="row nowrap", align_items="center", width="100%")
column_wide_layout = ipywidgets.Layout(flex_flow="column nowrap", align_items="center", width="100%")
column_auto_layout = ipywidgets.Layout(flex_flow="column nowrap", align_items="center", width="auto")
form_definition = {'form': None}
response_box = ipywidgets.HTML('')
def isAuthorized():
try:
ee.Initialize()
test = ee.Image(0).getInfo()
except:
return False
return True
def ShowForm(auth_status_button, instructions):
"""Show a form to the user."""
form_definition['form'] = ipywidgets.VBox([
auth_status_button,
instructions,
ipywidgets.VBox([response_box], layout=row_wide_layout)
], layout=column_wide_layout)
display.display(form_definition.get('form'))
def ShowAuthorizedForm():
"""Show a form for a server that is currently authorized to access Earth Engine."""
def revoke_credentials(sender):
credentials = ee.oauth.get_credentials_path()
if os.path.exists(credentials):
os.remove(credentials)
response_box.value = ''
Init()
auth_status_button = ipywidgets.Button(
layout=column_wide_layout,
disabled=True,
description='The server is authorized to access Earth Engine',
button_style='success',
icon='check'
)
instructions = ipywidgets.Button(
layout = row_wide_layout,
description = 'Click here to revoke authorization',
disabled = False,
)
instructions.on_click(revoke_credentials)
ShowForm(auth_status_button, instructions)
def ShowUnauthorizedForm():
"""Show a form for a server that is not currently authorized to access Earth Engine."""
auth_status_button = ipywidgets.Button(
layout=column_wide_layout,
button_style='danger',
description='The server is not authorized to access Earth Engine',
disabled=True
)
auth_link = ipywidgets.HTML(
'<a href="{url}" target="auth">Open Authentication Tab</a><br/>'
.format(url=ee.oauth.get_authorization_url()
)
)
instructions = ipywidgets.VBox(
[
ipywidgets.HTML(
'Click on the link below to start the authentication and authorization process. '
'Once you have received an authorization code, use it to replace the '
'REPLACE_WITH_AUTH_CODE in the code cell below and run the cell.'
),
auth_link,
],
layout=column_auto_layout
)
ShowForm(auth_status_button, instructions)
def Init():
# If a form is currently displayed, close it.
if form_definition.get('form'):
form_definition['form'].close()
# Display the appropriate form according to whether the server is authorized.
if isAuthorized():
ShowAuthorizedForm()
else:
ShowUnauthorizedForm()
Init()
```
If the server **is authorized**, you do not need to run the next code cell.
If the server **is not authorized**:
1. Copy the authentication code generated in the previous step.
2. Replace the REPLACE_WITH_AUTH_CODE string in the cell below with the authentication code.
3. Run the code cell to save authentication credentials.
```
auth_code = 'REPLACE_WITH_AUTH_CODE'
response_box = ipywidgets.HTML('')
try:
token = ee.oauth.request_token(auth_code.strip())
ee.oauth.write_token(token)
if isAuthorized():
Init()
else:
response_box.value = '<font color="red">{0}</font>'.format(
'The account was authenticated, but does not have permission to access Earth Engine.'
)
except Exception as e:
response_box.value = '<font color="red">{0}</font>'.format(e)
response_box
# Code to display an Earth Engine generated image.
from IPython.display import Image
url = ee.Image("CGIAR/SRTM90_V4").getThumbUrl({'min':0, 'max':3000})
Image(url=url)
```
| true |
code
| 0.453625 | null | null | null | null |
|
# Fairness and Explainability with SageMaker Clarify
1. [Overview](#Overview)
1. [Prerequisites and Data](#Prerequisites-and-Data)
1. [Initialize SageMaker](#Initialize-SageMaker)
1. [Download data](#Download-data)
1. [Loading the data: Adult Dataset](#Loading-the-data:-Adult-Dataset)
1. [Data inspection](#Data-inspection)
1. [Data encoding and upload to S3](#Encode-and-Upload-the-Data)
1. [Train and Deploy XGBoost Model](#Train-XGBoost-Model)
1. [Train Model](#Train-Model)
1. [Deploy Model to Endpoint](#Deploy-Model)
1. [Amazon SageMaker Clarify](#Amazon-SageMaker-Clarify)
1. [Detecting Bias](#Detecting-Bias)
1. [Writing BiasConfig](#Writing-BiasConfig)
1. [Pre-training Bias](#Pre-training-Bias)
1. [Post-training Bias](#Post-training-Bias)
1. [Viewing the Bias Report](#Viewing-the-Bias-Report)
1. [Explaining Predictions](#Explaining-Predictions)
1. [Viewing the Explainability Report](#Viewing-the-Explainability-Report)
1. [Clean Up](#Clean-Up)
## Overview
Amazon SageMaker Clarify helps improve your machine learning models by detecting potential bias and helping explain how these models make predictions. The fairness and explainability functionality provided by SageMaker Clarify takes a step towards enabling AWS customers to build trustworthy and understandable machine learning models. The product comes with the tools to help you with the following tasks.
* Measure biases that can occur during each stage of the ML lifecycle (data collection, model training and tuning, and monitoring of ML models deployed for inference).
* Generate model governance reports targeting risk and compliance teams and external regulators.
* Provide explanations of the data, models, and monitoring used to assess predictions.
This sample notebook walks you through:
1. Key terms and concepts needed to understand SageMaker Clarify
1. Measuring the pre-training bias of a dataset and post-training bias of a model
1. Explaining the importance of the various input features on the model's decision
1. Accessing the reports through SageMaker Studio if you have an instance set up.
In doing so, the notebook will first train a [SageMaker XGBoost](https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost.html) model using training dataset, then use SageMaker Clarify to analyze a testing dataset in CSV format. SageMaker Clarify also supports analyzing dataset in [SageMaker JSONLines dense format](https://docs.aws.amazon.com/sagemaker/latest/dg/cdf-inference.html#common-in-formats), which is illustrated in [another notebook](https://github.com/aws/amazon-sagemaker-examples/blob/master/sagemaker_processing/fairness_and_explainability/fairness_and_explainability_jsonlines_format.ipynb).
## Prerequisites and Data
### Initialize SageMaker
```
from sagemaker import Session
session = Session()
bucket = session.default_bucket()
prefix = "sagemaker/DEMO-sagemaker-clarify"
region = session.boto_region_name
# Define IAM role
from sagemaker import get_execution_role
import pandas as pd
import numpy as np
import os
import boto3
role = get_execution_role()
s3_client = boto3.client("s3")
```
### Download data
Data Source: [https://archive.ics.uci.edu/ml/machine-learning-databases/adult/](https://archive.ics.uci.edu/ml/machine-learning-databases/adult/)
Let's __download__ the data and save it in the local folder with the name adult.data and adult.test from UCI repository$^{[2]}$.
$^{[2]}$Dua Dheeru, and Efi Karra Taniskidou. "[UCI Machine Learning Repository](http://archive.ics.uci.edu/ml)". Irvine, CA: University of California, School of Information and Computer Science (2017).
```
adult_columns = [
"Age",
"Workclass",
"fnlwgt",
"Education",
"Education-Num",
"Marital Status",
"Occupation",
"Relationship",
"Ethnic group",
"Sex",
"Capital Gain",
"Capital Loss",
"Hours per week",
"Country",
"Target",
]
if not os.path.isfile("adult.data"):
s3_client.download_file(
"sagemaker-sample-files", "datasets/tabular/uci_adult/adult.data", "adult.data"
)
print("adult.data saved!")
else:
print("adult.data already on disk.")
if not os.path.isfile("adult.test"):
s3_client.download_file(
"sagemaker-sample-files", "datasets/tabular/uci_adult/adult.test", "adult.test"
)
print("adult.test saved!")
else:
print("adult.test already on disk.")
```
### Loading the data: Adult Dataset
From the UCI repository of machine learning datasets, this database contains 14 features concerning demographic characteristics of 45,222 rows (32,561 for training and 12,661 for testing). The task is to predict whether a person has a yearly income that is more or less than $50,000.
Here are the features and their possible values:
1. **Age**: continuous.
1. **Workclass**: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
1. **Fnlwgt**: continuous (the number of people the census takers believe that observation represents).
1. **Education**: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
1. **Education-num**: continuous.
1. **Marital-status**: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
1. **Occupation**: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
1. **Relationship**: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.
1. **Ethnic group**: White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black.
1. **Sex**: Female, Male.
* **Note**: this data is extracted from the 1994 Census and enforces a binary option on Sex
1. **Capital-gain**: continuous.
1. **Capital-loss**: continuous.
1. **Hours-per-week**: continuous.
1. **Native-country**: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.
Next, we specify our binary prediction task:
15. **Target**: <=50,000, >$50,000.
```
training_data = pd.read_csv(
"adult.data", names=adult_columns, sep=r"\s*,\s*", engine="python", na_values="?"
).dropna()
testing_data = pd.read_csv(
"adult.test", names=adult_columns, sep=r"\s*,\s*", engine="python", na_values="?", skiprows=1
).dropna()
training_data.head()
```
### Data inspection
Plotting histograms for the distribution of the different features is a good way to visualize the data. Let's plot a few of the features that can be considered _sensitive_.
Let's take a look specifically at the Sex feature of a census respondent. In the first plot we see that there are fewer Female respondents as a whole but especially in the positive outcomes, where they form ~$\frac{1}{7}$th of respondents.
```
training_data["Sex"].value_counts().sort_values().plot(kind="bar", title="Counts of Sex", rot=0)
training_data["Sex"].where(training_data["Target"] == ">50K").value_counts().sort_values().plot(
kind="bar", title="Counts of Sex earning >$50K", rot=0
)
```
### Encode and Upload the Dataset
Here we encode the training and test data. Encoding input data is not necessary for SageMaker Clarify, but is necessary for the model.
```
from sklearn import preprocessing
def number_encode_features(df):
result = df.copy()
encoders = {}
for column in result.columns:
if result.dtypes[column] == np.object:
encoders[column] = preprocessing.LabelEncoder()
# print('Column:', column, result[column])
result[column] = encoders[column].fit_transform(result[column].fillna("None"))
return result, encoders
training_data = pd.concat([training_data["Target"], training_data.drop(["Target"], axis=1)], axis=1)
training_data, _ = number_encode_features(training_data)
training_data.to_csv("train_data.csv", index=False, header=False)
testing_data, _ = number_encode_features(testing_data)
test_features = testing_data.drop(["Target"], axis=1)
test_target = testing_data["Target"]
test_features.to_csv("test_features.csv", index=False, header=False)
```
A quick note about our encoding: the "Female" Sex value has been encoded as 0 and "Male" as 1.
```
training_data.head()
```
Lastly, let's upload the data to S3
```
from sagemaker.s3 import S3Uploader
from sagemaker.inputs import TrainingInput
train_uri = S3Uploader.upload("train_data.csv", "s3://{}/{}".format(bucket, prefix))
train_input = TrainingInput(train_uri, content_type="csv")
test_uri = S3Uploader.upload("test_features.csv", "s3://{}/{}".format(bucket, prefix))
```
### Train XGBoost Model
#### Train Model
Since our focus is on understanding how to use SageMaker Clarify, we keep it simple by using a standard XGBoost model.
```
from sagemaker.image_uris import retrieve
from sagemaker.estimator import Estimator
container = retrieve("xgboost", region, version="1.2-1")
xgb = Estimator(
container,
role,
instance_count=1,
instance_type="ml.m5.xlarge",
disable_profiler=True,
sagemaker_session=session,
)
xgb.set_hyperparameters(
max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
objective="binary:logistic",
num_round=800,
)
xgb.fit({"train": train_input}, logs=False)
```
#### Deploy Model
Here we create the SageMaker model.
```
model_name = "DEMO-clarify-model"
model = xgb.create_model(name=model_name)
container_def = model.prepare_container_def()
session.create_model(model_name, role, container_def)
```
## Amazon SageMaker Clarify
Now that you have your model set up. Let's say hello to SageMaker Clarify!
```
from sagemaker import clarify
clarify_processor = clarify.SageMakerClarifyProcessor(
role=role, instance_count=1, instance_type="ml.m5.xlarge", sagemaker_session=session
)
```
### Detecting Bias
SageMaker Clarify helps you detect possible pre- and post-training biases using a variety of metrics.
#### Writing DataConfig and ModelConfig
A `DataConfig` object communicates some basic information about data I/O to SageMaker Clarify. We specify where to find the input dataset, where to store the output, the target column (`label`), the header names, and the dataset type.
```
bias_report_output_path = "s3://{}/{}/clarify-bias".format(bucket, prefix)
bias_data_config = clarify.DataConfig(
s3_data_input_path=train_uri,
s3_output_path=bias_report_output_path,
label="Target",
headers=training_data.columns.to_list(),
dataset_type="text/csv",
)
```
A `ModelConfig` object communicates information about your trained model. To avoid additional traffic to your production models, SageMaker Clarify sets up and tears down a dedicated endpoint when processing.
* `instance_type` and `instance_count` specify your preferred instance type and instance count used to run your model on during SageMaker Clarify's processing. The testing dataset is small so a single standard instance is good enough to run this example. If your have a large complex dataset, you may want to use a better instance type to speed up, or add more instances to enable Spark parallelization.
* `accept_type` denotes the endpoint response payload format, and `content_type` denotes the payload format of request to the endpoint.
```
model_config = clarify.ModelConfig(
model_name=model_name,
instance_type="ml.m5.xlarge",
instance_count=1,
accept_type="text/csv",
content_type="text/csv",
)
```
A `ModelPredictedLabelConfig` provides information on the format of your predictions. XGBoost model outputs probabilities of samples, so SageMaker Clarify invokes the endpoint then uses `probability_threshold` to convert the probability to binary labels for bias analysis. Prediction above the threshold is interpreted as label value `1` and below or equal as label value `0`.
```
predictions_config = clarify.ModelPredictedLabelConfig(probability_threshold=0.8)
```
#### Writing BiasConfig
SageMaker Clarify also needs information on what the sensitive columns (`facets`) are, what the sensitive features (`facet_values_or_threshold`) may be, and what the desirable outcomes are (`label_values_or_threshold`).
SageMaker Clarify can handle both categorical and continuous data for `facet_values_or_threshold` and for `label_values_or_threshold`. In this case we are using categorical data.
We specify this information in the `BiasConfig` API. Here that the positive outcome is earning >$50,000, Sex is a sensitive category, and Female respondents are the sensitive group. `group_name` is used to form subgroups for the measurement of Conditional Demographic Disparity in Labels (CDDL) and Conditional Demographic Disparity in Predicted Labels (CDDPL) with regards to Simpson’s paradox.
```
bias_config = clarify.BiasConfig(
label_values_or_threshold=[1], facet_name="Sex", facet_values_or_threshold=[0], group_name="Age"
)
```
#### Pre-training Bias
Bias can be present in your data before any model training occurs. Inspecting your data for bias before training begins can help detect any data collection gaps, inform your feature engineering, and help you understand what societal biases the data may reflect.
Computing pre-training bias metrics does not require a trained model.
#### Post-training Bias
Computing post-training bias metrics does require a trained model.
Unbiased training data (as determined by concepts of fairness measured by bias metric) may still result in biased model predictions after training. Whether this occurs depends on several factors including hyperparameter choices.
You can run these options separately with `run_pre_training_bias()` and `run_post_training_bias()` or at the same time with `run_bias()` as shown below.
```
clarify_processor.run_bias(
data_config=bias_data_config,
bias_config=bias_config,
model_config=model_config,
model_predicted_label_config=predictions_config,
pre_training_methods="all",
post_training_methods="all",
)
```
#### Viewing the Bias Report
In Studio, you can view the results under the experiments tab.
<img src="./recordings/bias_report.gif">
Each bias metric has detailed explanations with examples that you can explore.
<img src="./recordings/bias_detail.gif">
You could also summarize the results in a handy table!
<img src="./recordings/bias_report_chart.gif">
If you're not a Studio user yet, you can access the bias report in pdf, html and ipynb formats in the following S3 bucket:
```
bias_report_output_path
```
### Explaining Predictions
There are expanding business needs and legislative regulations that require explanations of _why_ a model made the decision it did. SageMaker Clarify uses SHAP to explain the contribution that each input feature makes to the final decision.
Kernel SHAP algorithm requires a baseline (also known as background dataset). Baseline dataset type shall be the same as `dataset_type` of `DataConfig`, and baseline samples shall only include features. By definition, `baseline` should either be a S3 URI to the baseline dataset file, or an in-place list of samples. In this case we chose the latter, and put the first sample of the test dataset to the list.
```
shap_config = clarify.SHAPConfig(
baseline=[test_features.iloc[0].values.tolist()],
num_samples=15,
agg_method="mean_abs",
save_local_shap_values=True,
)
explainability_output_path = "s3://{}/{}/clarify-explainability".format(bucket, prefix)
explainability_data_config = clarify.DataConfig(
s3_data_input_path=train_uri,
s3_output_path=explainability_output_path,
label="Target",
headers=training_data.columns.to_list(),
dataset_type="text/csv",
)
clarify_processor.run_explainability(
data_config=explainability_data_config,
model_config=model_config,
explainability_config=shap_config,
)
```
#### Viewing the Explainability Report
As with the bias report, you can view the explainability report in Studio under the experiments tab
<img src="./recordings/explainability_detail.gif">
The Model Insights tab contains direct links to the report and model insights.
If you're not a Studio user yet, as with the Bias Report, you can access this report at the following S3 bucket.
```
explainability_output_path
```
#### Analysis of local explanations
It is possible to visualize the the local explanations for single examples in your dataset. You can use the obtained results from running Kernel SHAP algorithm for global explanations.
You can simply load the local explanations stored in your output path, and visualize the explanation (i.e., the impact that the single features have on the prediction of your model) for any single example.
```
local_explanations_out = pd.read_csv(explainability_output_path + "/explanations_shap/out.csv")
feature_names = [str.replace(c, "_label0", "") for c in local_explanations_out.columns.to_series()]
local_explanations_out.columns = feature_names
selected_example = 111
print(
"Example number:",
selected_example,
"\nwith model prediction:",
sum(local_explanations_out.iloc[selected_example]) > 0,
)
print("\nFeature values -- Label", training_data.iloc[selected_example])
local_explanations_out.iloc[selected_example].plot(
kind="bar", title="Local explanation for the example number " + str(selected_example), rot=90
)
```
### Clean Up
Finally, don't forget to clean up the resources we set up and used for this demo!
```
session.delete_model(model_name)
```
| true |
code
| 0.420064 | null | null | null | null |
|
This notebook was prepared by [Donne Martin](http://donnemartin.com). Source and license info is on [GitHub](https://github.com/donnemartin/data-science-ipython-notebooks).
# Kaggle Machine Learning Competition: Predicting Titanic Survivors
* Competition Site
* Description
* Evaluation
* Data Set
* Setup Imports and Variables
* Explore the Data
* Feature: Passenger Classes
* Feature: Sex
* Feature: Embarked
* Feature: Age
* Feature: Family Size
* Final Data Preparation for Machine Learning
* Data Wrangling Summary
* Random Forest: Training
* Random Forest: Predicting
* Random Forest: Prepare for Kaggle Submission
* Support Vector Machine: Training
* Support Vector Machine: Predicting
## Competition Site
Description, Evaluation, and Data Set taken from the [competition site](https://www.kaggle.com/c/titanic-gettingStarted).
## Description

The sinking of the RMS Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.
One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.
In this challenge, we ask you to complete the analysis of what sorts of people were likely to survive. In particular, we ask you to apply the tools of machine learning to predict which passengers survived the tragedy.
## Evaluation
The historical data has been split into two groups, a 'training set' and a 'test set'. For the training set, we provide the outcome ( 'ground truth' ) for each passenger. You will use this set to build your model to generate predictions for the test set.
For each passenger in the test set, you must predict whether or not they survived the sinking ( 0 for deceased, 1 for survived ). Your score is the percentage of passengers you correctly predict.
The Kaggle leaderboard has a public and private component. 50% of your predictions for the test set have been randomly assigned to the public leaderboard ( the same 50% for all users ). Your score on this public portion is what will appear on the leaderboard. At the end of the contest, we will reveal your score on the private 50% of the data, which will determine the final winner. This method prevents users from 'overfitting' to the leaderboard.
## Data Set
| File Name | Available Formats |
|------------------|-------------------|
| train | .csv (59.76 kb) |
| gendermodel | .csv (3.18 kb) |
| genderclassmodel | .csv (3.18 kb) |
| test | .csv (27.96 kb) |
| gendermodel | .py (3.58 kb) |
| genderclassmodel | .py (5.63 kb) |
| myfirstforest | .py (3.99 kb) |
<pre>
VARIABLE DESCRIPTIONS:
survival Survival
(0 = No; 1 = Yes)
pclass Passenger Class
(1 = 1st; 2 = 2nd; 3 = 3rd)
name Name
sex Sex
age Age
sibsp Number of Siblings/Spouses Aboard
parch Number of Parents/Children Aboard
ticket Ticket Number
fare Passenger Fare
cabin Cabin
embarked Port of Embarkation
(C = Cherbourg; Q = Queenstown; S = Southampton)
SPECIAL NOTES:
Pclass is a proxy for socio-economic status (SES)
1st ~ Upper; 2nd ~ Middle; 3rd ~ Lower
Age is in Years; Fractional if Age less than One (1)
If the Age is Estimated, it is in the form xx.5
With respect to the family relation variables (i.e. sibsp and parch)
some relations were ignored. The following are the definitions used
for sibsp and parch.
Sibling: Brother, Sister, Stepbrother, or Stepsister of Passenger Aboard Titanic
Spouse: Husband or Wife of Passenger Aboard Titanic (Mistresses and Fiances Ignored)
Parent: Mother or Father of Passenger Aboard Titanic
Child: Son, Daughter, Stepson, or Stepdaughter of Passenger Aboard Titanic
Other family relatives excluded from this study include cousins,
nephews/nieces, aunts/uncles, and in-laws. Some children travelled
only with a nanny, therefore parch=0 for them. As well, some
travelled with very close friends or neighbors in a village, however,
the definitions do not support such relations.
</pre>
## Setup Imports and Variables
```
import pandas as pd
import numpy as np
import pylab as plt
# Set the global default size of matplotlib figures
plt.rc('figure', figsize=(10, 5))
# Size of matplotlib figures that contain subplots
fizsize_with_subplots = (10, 10)
# Size of matplotlib histogram bins
bin_size = 10
```
## Explore the Data
Read the data:
```
df_train = pd.read_csv('../data/titanic/train.csv')
df_train.head()
df_train.tail()
```
View the data types of each column:
```
df_train.dtypes
```
Type 'object' is a string for pandas, which poses problems with machine learning algorithms. If we want to use these as features, we'll need to convert these to number representations.
Get some basic information on the DataFrame:
```
df_train.info()
```
Age, Cabin, and Embarked are missing values. Cabin has too many missing values, whereas we might be able to infer values for Age and Embarked.
Generate various descriptive statistics on the DataFrame:
```
df_train.describe()
```
Now that we have a general idea of the data set contents, we can dive deeper into each column. We'll be doing exploratory data analysis and cleaning data to setup 'features' we'll be using in our machine learning algorithms.
Plot a few features to get a better idea of each:
```
# Set up a grid of plots
fig = plt.figure(figsize=fizsize_with_subplots)
fig_dims = (3, 2)
# Plot death and survival counts
plt.subplot2grid(fig_dims, (0, 0))
df_train['Survived'].value_counts().plot(kind='bar',
title='Death and Survival Counts')
# Plot Pclass counts
plt.subplot2grid(fig_dims, (0, 1))
df_train['Pclass'].value_counts().plot(kind='bar',
title='Passenger Class Counts')
# Plot Sex counts
plt.subplot2grid(fig_dims, (1, 0))
df_train['Sex'].value_counts().plot(kind='bar',
title='Gender Counts')
plt.xticks(rotation=0)
# Plot Embarked counts
plt.subplot2grid(fig_dims, (1, 1))
df_train['Embarked'].value_counts().plot(kind='bar',
title='Ports of Embarkation Counts')
# Plot the Age histogram
plt.subplot2grid(fig_dims, (2, 0))
df_train['Age'].hist()
plt.title('Age Histogram')
```
Next we'll explore various features to view their impact on survival rates.
## Feature: Passenger Classes
From our exploratory data analysis in the previous section, we see there are three passenger classes: First, Second, and Third class. We'll determine which proportion of passengers survived based on their passenger class.
Generate a cross tab of Pclass and Survived:
```
pclass_xt = pd.crosstab(df_train['Pclass'], df_train['Survived'])
pclass_xt
```
Plot the cross tab:
```
# Normalize the cross tab to sum to 1:
pclass_xt_pct = pclass_xt.div(pclass_xt.sum(1).astype(float), axis=0)
pclass_xt_pct.plot(kind='bar',
stacked=True,
title='Survival Rate by Passenger Classes')
plt.xlabel('Passenger Class')
plt.ylabel('Survival Rate')
```
We can see that passenger class seems to have a significant impact on whether a passenger survived. Those in First Class the highest chance for survival.
## Feature: Sex
Gender might have also played a role in determining a passenger's survival rate. We'll need to map Sex from a string to a number to prepare it for machine learning algorithms.
Generate a mapping of Sex from a string to a number representation:
```
sexes = sorted(df_train['Sex'].unique())
genders_mapping = dict(zip(sexes, range(0, len(sexes) + 1)))
genders_mapping
```
Transform Sex from a string to a number representation:
```
df_train['Sex_Val'] = df_train['Sex'].map(genders_mapping).astype(int)
df_train.head()
```
Plot a normalized cross tab for Sex_Val and Survived:
```
sex_val_xt = pd.crosstab(df_train['Sex_Val'], df_train['Survived'])
sex_val_xt_pct = sex_val_xt.div(sex_val_xt.sum(1).astype(float), axis=0)
sex_val_xt_pct.plot(kind='bar', stacked=True, title='Survival Rate by Gender')
```
The majority of females survived, whereas the majority of males did not.
Next we'll determine whether we can gain any insights on survival rate by looking at both Sex and Pclass.
Count males and females in each Pclass:
```
# Get the unique values of Pclass:
passenger_classes = sorted(df_train['Pclass'].unique())
for p_class in passenger_classes:
print 'M: ', p_class, len(df_train[(df_train['Sex'] == 'male') &
(df_train['Pclass'] == p_class)])
print 'F: ', p_class, len(df_train[(df_train['Sex'] == 'female') &
(df_train['Pclass'] == p_class)])
```
Plot survival rate by Sex and Pclass:
```
# Plot survival rate by Sex
females_df = df_train[df_train['Sex'] == 'female']
females_xt = pd.crosstab(females_df['Pclass'], df_train['Survived'])
females_xt_pct = females_xt.div(females_xt.sum(1).astype(float), axis=0)
females_xt_pct.plot(kind='bar',
stacked=True,
title='Female Survival Rate by Passenger Class')
plt.xlabel('Passenger Class')
plt.ylabel('Survival Rate')
# Plot survival rate by Pclass
males_df = df_train[df_train['Sex'] == 'male']
males_xt = pd.crosstab(males_df['Pclass'], df_train['Survived'])
males_xt_pct = males_xt.div(males_xt.sum(1).astype(float), axis=0)
males_xt_pct.plot(kind='bar',
stacked=True,
title='Male Survival Rate by Passenger Class')
plt.xlabel('Passenger Class')
plt.ylabel('Survival Rate')
```
The vast majority of females in First and Second class survived. Males in First class had the highest chance for survival.
## Feature: Embarked
The Embarked column might be an important feature but it is missing a couple data points which might pose a problem for machine learning algorithms:
```
df_train[df_train['Embarked'].isnull()]
```
Prepare to map Embarked from a string to a number representation:
```
# Get the unique values of Embarked
embarked_locs = sorted(df_train['Embarked'].unique())
embarked_locs_mapping = dict(zip(embarked_locs,
range(0, len(embarked_locs) + 1)))
embarked_locs_mapping
```
Transform Embarked from a string to a number representation to prepare it for machine learning algorithms:
```
df_train['Embarked_Val'] = df_train['Embarked'] \
.map(embarked_locs_mapping) \
.astype(int)
df_train.head()
```
Plot the histogram for Embarked_Val:
```
df_train['Embarked_Val'].hist(bins=len(embarked_locs), range=(0, 3))
plt.title('Port of Embarkation Histogram')
plt.xlabel('Port of Embarkation')
plt.ylabel('Count')
plt.show()
```
Since the vast majority of passengers embarked in 'S': 3, we assign the missing values in Embarked to 'S':
```
if len(df_train[df_train['Embarked'].isnull()] > 0):
df_train.replace({'Embarked_Val' :
{ embarked_locs_mapping[nan] : embarked_locs_mapping['S']
}
},
inplace=True)
```
Verify we do not have any more NaNs for Embarked_Val:
```
embarked_locs = sorted(df_train['Embarked_Val'].unique())
embarked_locs
```
Plot a normalized cross tab for Embarked_Val and Survived:
```
embarked_val_xt = pd.crosstab(df_train['Embarked_Val'], df_train['Survived'])
embarked_val_xt_pct = \
embarked_val_xt.div(embarked_val_xt.sum(1).astype(float), axis=0)
embarked_val_xt_pct.plot(kind='bar', stacked=True)
plt.title('Survival Rate by Port of Embarkation')
plt.xlabel('Port of Embarkation')
plt.ylabel('Survival Rate')
```
It appears those that embarked in location 'C': 1 had the highest rate of survival. We'll dig in some more to see why this might be the case. Below we plot a graphs to determine gender and passenger class makeup for each port:
```
# Set up a grid of plots
fig = plt.figure(figsize=fizsize_with_subplots)
rows = 2
cols = 3
col_names = ('Sex_Val', 'Pclass')
for portIdx in embarked_locs:
for colIdx in range(0, len(col_names)):
plt.subplot2grid((rows, cols), (colIdx, portIdx - 1))
df_train[df_train['Embarked_Val'] == portIdx][col_names[colIdx]] \
.value_counts().plot(kind='bar')
```
Leaving Embarked as integers implies ordering in the values, which does not exist. Another way to represent Embarked without ordering is to create dummy variables:
```
df_train = pd.concat([df_train, pd.get_dummies(df_train['Embarked_Val'], prefix='Embarked_Val')], axis=1)
```
## Feature: Age
The Age column seems like an important feature--unfortunately it is missing many values. We'll need to fill in the missing values like we did with Embarked.
Filter to view missing Age values:
```
df_train[df_train['Age'].isnull()][['Sex', 'Pclass', 'Age']].head()
```
Determine the Age typical for each passenger class by Sex_Val. We'll use the median instead of the mean because the Age histogram seems to be right skewed.
```
# To keep Age in tact, make a copy of it called AgeFill
# that we will use to fill in the missing ages:
df_train['AgeFill'] = df_train['Age']
# Populate AgeFill
df_train['AgeFill'] = df_train['AgeFill'] \
.groupby([df_train['Sex_Val'], df_train['Pclass']]) \
.apply(lambda x: x.fillna(x.median()))
```
Ensure AgeFill does not contain any missing values:
```
len(df_train[df_train['AgeFill'].isnull()])
```
Plot a normalized cross tab for AgeFill and Survived:
```
# Set up a grid of plots
fig, axes = plt.subplots(2, 1, figsize=fizsize_with_subplots)
# Histogram of AgeFill segmented by Survived
df1 = df_train[df_train['Survived'] == 0]['Age']
df2 = df_train[df_train['Survived'] == 1]['Age']
max_age = max(df_train['AgeFill'])
axes[0].hist([df1, df2],
bins=max_age / bin_size,
range=(1, max_age),
stacked=True)
axes[0].legend(('Died', 'Survived'), loc='best')
axes[0].set_title('Survivors by Age Groups Histogram')
axes[0].set_xlabel('Age')
axes[0].set_ylabel('Count')
# Scatter plot Survived and AgeFill
axes[1].scatter(df_train['Survived'], df_train['AgeFill'])
axes[1].set_title('Survivors by Age Plot')
axes[1].set_xlabel('Survived')
axes[1].set_ylabel('Age')
```
Unfortunately, the graphs above do not seem to clearly show any insights. We'll keep digging further.
Plot AgeFill density by Pclass:
```
for pclass in passenger_classes:
df_train.AgeFill[df_train.Pclass == pclass].plot(kind='kde')
plt.title('Age Density Plot by Passenger Class')
plt.xlabel('Age')
plt.legend(('1st Class', '2nd Class', '3rd Class'), loc='best')
```
When looking at AgeFill density by Pclass, we see the first class passengers were generally older then second class passengers, which in turn were older than third class passengers. We've determined that first class passengers had a higher survival rate than second class passengers, which in turn had a higher survival rate than third class passengers.
```
# Set up a grid of plots
fig = plt.figure(figsize=fizsize_with_subplots)
fig_dims = (3, 1)
# Plot the AgeFill histogram for Survivors
plt.subplot2grid(fig_dims, (0, 0))
survived_df = df_train[df_train['Survived'] == 1]
survived_df['AgeFill'].hist(bins=max_age / bin_size, range=(1, max_age))
# Plot the AgeFill histogram for Females
plt.subplot2grid(fig_dims, (1, 0))
females_df = df_train[(df_train['Sex_Val'] == 0) & (df_train['Survived'] == 1)]
females_df['AgeFill'].hist(bins=max_age / bin_size, range=(1, max_age))
# Plot the AgeFill histogram for first class passengers
plt.subplot2grid(fig_dims, (2, 0))
class1_df = df_train[(df_train['Pclass'] == 1) & (df_train['Survived'] == 1)]
class1_df['AgeFill'].hist(bins=max_age / bin_size, range=(1, max_age))
```
In the first graph, we see that most survivors come from the 20's to 30's age ranges and might be explained by the following two graphs. The second graph shows most females are within their 20's. The third graph shows most first class passengers are within their 30's.
## Feature: Family Size
Feature enginering involves creating new features or modifying existing features which might be advantageous to a machine learning algorithm.
Define a new feature FamilySize that is the sum of Parch (number of parents or children on board) and SibSp (number of siblings or spouses):
```
df_train['FamilySize'] = df_train['SibSp'] + df_train['Parch']
df_train.head()
```
Plot a histogram of FamilySize:
```
df_train['FamilySize'].hist()
plt.title('Family Size Histogram')
```
Plot a histogram of AgeFill segmented by Survived:
```
# Get the unique values of Embarked and its maximum
family_sizes = sorted(df_train['FamilySize'].unique())
family_size_max = max(family_sizes)
df1 = df_train[df_train['Survived'] == 0]['FamilySize']
df2 = df_train[df_train['Survived'] == 1]['FamilySize']
plt.hist([df1, df2],
bins=family_size_max + 1,
range=(0, family_size_max),
stacked=True)
plt.legend(('Died', 'Survived'), loc='best')
plt.title('Survivors by Family Size')
```
Based on the histograms, it is not immediately obvious what impact FamilySize has on survival. The machine learning algorithms might benefit from this feature.
Additional features we might want to engineer might be related to the Name column, for example honorrary or pedestrian titles might give clues and better predictive power for a male's survival.
## Final Data Preparation for Machine Learning
Many machine learning algorithms do not work on strings and they usually require the data to be in an array, not a DataFrame.
Show only the columns of type 'object' (strings):
```
df_train.dtypes[df_train.dtypes.map(lambda x: x == 'object')]
```
Drop the columns we won't use:
```
df_train = df_train.drop(['Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'],
axis=1)
```
Drop the following columns:
* The Age column since we will be using the AgeFill column instead.
* The SibSp and Parch columns since we will be using FamilySize instead.
* The PassengerId column since it won't be used as a feature.
* The Embarked_Val as we decided to use dummy variables instead.
```
df_train = df_train.drop(['Age', 'SibSp', 'Parch', 'PassengerId', 'Embarked_Val'], axis=1)
df_train.dtypes
```
Convert the DataFrame to a numpy array:
```
train_data = df_train.values
train_data
```
## Data Wrangling Summary
Below is a summary of the data wrangling we performed on our training data set. We encapsulate this in a function since we'll need to do the same operations to our test set later.
```
def clean_data(df, drop_passenger_id):
# Get the unique values of Sex
sexes = sorted(df['Sex'].unique())
# Generate a mapping of Sex from a string to a number representation
genders_mapping = dict(zip(sexes, range(0, len(sexes) + 1)))
# Transform Sex from a string to a number representation
df['Sex_Val'] = df['Sex'].map(genders_mapping).astype(int)
# Get the unique values of Embarked
embarked_locs = sorted(df['Embarked'].unique())
# Generate a mapping of Embarked from a string to a number representation
embarked_locs_mapping = dict(zip(embarked_locs,
range(0, len(embarked_locs) + 1)))
# Transform Embarked from a string to dummy variables
df = pd.concat([df, pd.get_dummies(df['Embarked'], prefix='Embarked_Val')], axis=1)
# Fill in missing values of Embarked
# Since the vast majority of passengers embarked in 'S': 3,
# we assign the missing values in Embarked to 'S':
if len(df[df['Embarked'].isnull()] > 0):
df.replace({'Embarked_Val' :
{ embarked_locs_mapping[nan] : embarked_locs_mapping['S']
}
},
inplace=True)
# Fill in missing values of Fare with the average Fare
if len(df[df['Fare'].isnull()] > 0):
avg_fare = df['Fare'].mean()
df.replace({ None: avg_fare }, inplace=True)
# To keep Age in tact, make a copy of it called AgeFill
# that we will use to fill in the missing ages:
df['AgeFill'] = df['Age']
# Determine the Age typical for each passenger class by Sex_Val.
# We'll use the median instead of the mean because the Age
# histogram seems to be right skewed.
df['AgeFill'] = df['AgeFill'] \
.groupby([df['Sex_Val'], df['Pclass']]) \
.apply(lambda x: x.fillna(x.median()))
# Define a new feature FamilySize that is the sum of
# Parch (number of parents or children on board) and
# SibSp (number of siblings or spouses):
df['FamilySize'] = df['SibSp'] + df['Parch']
# Drop the columns we won't use:
df = df.drop(['Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1)
# Drop the Age column since we will be using the AgeFill column instead.
# Drop the SibSp and Parch columns since we will be using FamilySize.
# Drop the PassengerId column since it won't be used as a feature.
df = df.drop(['Age', 'SibSp', 'Parch'], axis=1)
if drop_passenger_id:
df = df.drop(['PassengerId'], axis=1)
return df
```
## Random Forest: Training
Create the random forest object:
```
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100)
```
Fit the training data and create the decision trees:
```
# Training data features, skip the first column 'Survived'
train_features = train_data[:, 1:]
# 'Survived' column values
train_target = train_data[:, 0]
# Fit the model to our training data
clf = clf.fit(train_features, train_target)
score = clf.score(train_features, train_target)
"Mean accuracy of Random Forest: {0}".format(score)
```
## Random Forest: Predicting
Read the test data:
```
df_test = pd.read_csv('../data/titanic/test.csv')
df_test.head()
```
Note the test data does not contain the column 'Survived', we'll use our trained model to predict these values.
```
# Data wrangle the test set and convert it to a numpy array
df_test = clean_data(df_test, drop_passenger_id=False)
test_data = df_test.values
```
Take the decision trees and run it on the test data:
```
# Get the test data features, skipping the first column 'PassengerId'
test_x = test_data[:, 1:]
# Predict the Survival values for the test data
test_y = clf.predict(test_x)
```
## Random Forest: Prepare for Kaggle Submission
Create a DataFrame by combining the index from the test data with the output of predictions, then write the results to the output:
```
df_test['Survived'] = test_y
df_test[['PassengerId', 'Survived']] \
.to_csv('../data/titanic/results-rf.csv', index=False)
```
## Evaluate Model Accuracy
Submitting to Kaggle will give you an accuracy score. It would be helpful to get an idea of accuracy without submitting to Kaggle.
We'll split our training data, 80% will go to "train" and 20% will go to "test":
```
from sklearn import metrics
from sklearn.cross_validation import train_test_split
# Split 80-20 train vs test data
train_x, test_x, train_y, test_y = train_test_split(train_features,
train_target,
test_size=0.20,
random_state=0)
print (train_features.shape, train_target.shape)
print (train_x.shape, train_y.shape)
print (test_x.shape, test_y.shape)
```
Use the new training data to fit the model, predict, and get the accuracy score:
```
clf = clf.fit(train_x, train_y)
predict_y = clf.predict(test_x)
from sklearn.metrics import accuracy_score
print ("Accuracy = %.2f" % (accuracy_score(test_y, predict_y)))
```
View the Confusion Matrix:
| | condition True | condition false|
|------|----------------|---------------|
|prediction true|True Positive|False positive|
|Prediction False|False Negative|True Negative|
```
from IPython.core.display import Image
Image(filename='../data/confusion_matrix.png', width=800)
```
Get the model score and confusion matrix:
```
model_score = clf.score(test_x, test_y)
print ("Model Score %.2f \n" % (model_score))
confusion_matrix = metrics.confusion_matrix(test_y, predict_y)
print ("Confusion Matrix ", confusion_matrix)
print (" Predicted")
print (" | 0 | 1 |")
print (" |-----|-----|")
print (" 0 | %3d | %3d |" % (confusion_matrix[0, 0],
confusion_matrix[0, 1]))
print ("Actual |-----|-----|")
print (" 1 | %3d | %3d |" % (confusion_matrix[1, 0],
confusion_matrix[1, 1]))
print (" |-----|-----|")
```
Display the classification report:
$$Precision = \frac{TP}{TP + FP}$$
$$Recall = \frac{TP}{TP + FN}$$
$$F1 = \frac{2TP}{2TP + FP + FN}$$
```
from sklearn.metrics import classification_report
print(classification_report(test_y,
predict_y,
target_names=['Not Survived', 'Survived']))
```
| true |
code
| 0.508422 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/kpe/bert-for-tf2/blob/master/examples/movie_reviews_with_bert_for_tf2_on_gpu.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
This is a modification of https://github/google-research/bert/blob/master/predicting_movie_reviews_with_bert_on_tf_hub.ipynb using the Tensorflow 2.0 Keras implementation of BERT from [kpe/bert-for-tf2](https://github.com/kpe/bert-for-tf2) with the original [google-research/bert](https://github.com/google-research/bert) weights.
```
# Copyright 2019 Google Inc.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Predicting Movie Review Sentiment with [kpe/bert-for-tf2](https://github.com/kpe/bert-for-tf2)
First install some prerequisites:
```
!pip install tqdm >> /dev/null
import os
import math
import datetime
from tqdm import tqdm
import pandas as pd
import numpy as np
import tensorflow as tf
tf.__version__
if tf.__version__.startswith("1."):
tf.enable_eager_execution()
```
In addition to the standard libraries we imported above, we'll need to install the [bert-for-tf2](https://github.com/kpe/bert-for-tf2) python package, and do the imports required for loading the pre-trained weights and tokenizing the input text.
```
!pip install bert-for-tf2 >> /dev/null
import bert
from bert import BertModelLayer
from bert.loader import StockBertConfig, map_stock_config_to_params, load_stock_weights
from bert.tokenization.bert_tokenization import FullTokenizer
```
#Data
First, let's download the dataset, hosted by Stanford. The code below, which downloads, extracts, and imports the IMDB Large Movie Review Dataset, is borrowed from [this Tensorflow tutorial](https://www.tensorflow.org/hub/tutorials/text_classification_with_tf_hub).
```
from tensorflow import keras
import os
import re
# Load all files from a directory in a DataFrame.
def load_directory_data(directory):
data = {}
data["sentence"] = []
data["sentiment"] = []
for file_path in tqdm(os.listdir(directory), desc=os.path.basename(directory)):
with tf.io.gfile.GFile(os.path.join(directory, file_path), "r") as f:
data["sentence"].append(f.read())
data["sentiment"].append(re.match("\d+_(\d+)\.txt", file_path).group(1))
return pd.DataFrame.from_dict(data)
# Merge positive and negative examples, add a polarity column and shuffle.
def load_dataset(directory):
pos_df = load_directory_data(os.path.join(directory, "pos"))
neg_df = load_directory_data(os.path.join(directory, "neg"))
pos_df["polarity"] = 1
neg_df["polarity"] = 0
return pd.concat([pos_df, neg_df]).sample(frac=1).reset_index(drop=True)
# Download and process the dataset files.
def download_and_load_datasets(force_download=False):
dataset = tf.keras.utils.get_file(
fname="aclImdb.tar.gz",
origin="http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz",
extract=True)
train_df = load_dataset(os.path.join(os.path.dirname(dataset),
"aclImdb", "train"))
test_df = load_dataset(os.path.join(os.path.dirname(dataset),
"aclImdb", "test"))
return train_df, test_df
```
Let's use the `MovieReviewData` class below, to prepare/encode
the data for feeding into our BERT model, by:
- tokenizing the text
- trim or pad it to a `max_seq_len` length
- append the special tokens `[CLS]` and `[SEP]`
- convert the string tokens to numerical `ID`s using the original model's token encoding from `vocab.txt`
```
import bert
from bert import BertModelLayer
from bert.loader import StockBertConfig, map_stock_config_to_params, load_stock_weights
from bert.tokenization import FullTokenizer
class MovieReviewData:
DATA_COLUMN = "sentence"
LABEL_COLUMN = "polarity"
def __init__(self, tokenizer: FullTokenizer, sample_size=None, max_seq_len=1024):
self.tokenizer = tokenizer
self.sample_size = sample_size
self.max_seq_len = 0
train, test = download_and_load_datasets()
train, test = map(lambda df: df.reindex(df[MovieReviewData.DATA_COLUMN].str.len().sort_values().index),
[train, test])
if sample_size is not None:
assert sample_size % 128 == 0
train, test = train.head(sample_size), test.head(sample_size)
# train, test = map(lambda df: df.sample(sample_size), [train, test])
((self.train_x, self.train_y),
(self.test_x, self.test_y)) = map(self._prepare, [train, test])
print("max seq_len", self.max_seq_len)
self.max_seq_len = min(self.max_seq_len, max_seq_len)
((self.train_x, self.train_x_token_types),
(self.test_x, self.test_x_token_types)) = map(self._pad,
[self.train_x, self.test_x])
def _prepare(self, df):
x, y = [], []
with tqdm(total=df.shape[0], unit_scale=True) as pbar:
for ndx, row in df.iterrows():
text, label = row[MovieReviewData.DATA_COLUMN], row[MovieReviewData.LABEL_COLUMN]
tokens = self.tokenizer.tokenize(text)
tokens = ["[CLS]"] + tokens + ["[SEP]"]
token_ids = self.tokenizer.convert_tokens_to_ids(tokens)
self.max_seq_len = max(self.max_seq_len, len(token_ids))
x.append(token_ids)
y.append(int(label))
pbar.update()
return np.array(x), np.array(y)
def _pad(self, ids):
x, t = [], []
token_type_ids = [0] * self.max_seq_len
for input_ids in ids:
input_ids = input_ids[:min(len(input_ids), self.max_seq_len - 2)]
input_ids = input_ids + [0] * (self.max_seq_len - len(input_ids))
x.append(np.array(input_ids))
t.append(token_type_ids)
return np.array(x), np.array(t)
```
## A tweak
Because of a `tf.train.load_checkpoint` limitation requiring list permissions on the google storage bucket, we need to copy the pre-trained BERT weights locally.
```
bert_ckpt_dir="gs://bert_models/2018_10_18/uncased_L-12_H-768_A-12/"
bert_ckpt_file = bert_ckpt_dir + "bert_model.ckpt"
bert_config_file = bert_ckpt_dir + "bert_config.json"
%%time
bert_model_dir="2018_10_18"
bert_model_name="uncased_L-12_H-768_A-12"
!mkdir -p .model .model/$bert_model_name
for fname in ["bert_config.json", "vocab.txt", "bert_model.ckpt.meta", "bert_model.ckpt.index", "bert_model.ckpt.data-00000-of-00001"]:
cmd = f"gsutil cp gs://bert_models/{bert_model_dir}/{bert_model_name}/{fname} .model/{bert_model_name}"
!$cmd
!ls -la .model .model/$bert_model_name
bert_ckpt_dir = os.path.join(".model/",bert_model_name)
bert_ckpt_file = os.path.join(bert_ckpt_dir, "bert_model.ckpt")
bert_config_file = os.path.join(bert_ckpt_dir, "bert_config.json")
```
# Preparing the Data
Now let's fetch and prepare the data by taking the first `max_seq_len` tokenens after tokenizing with the BERT tokenizer, und use `sample_size` examples for both training and testing.
To keep training fast, we'll take a sample of about 2500 train and test examples, respectively, and use the first 128 tokens only (transformers memory and computation requirements scale quadraticly with the sequence length - so with a TPU you might use `max_seq_len=512`, but on a GPU this would be too slow, and you will have to use a very small `batch_size`s to fit the model into the GPU memory).
```
%%time
tokenizer = FullTokenizer(vocab_file=os.path.join(bert_ckpt_dir, "vocab.txt"))
data = MovieReviewData(tokenizer,
sample_size=10*128*2,#5000,
max_seq_len=128)
print(" train_x", data.train_x.shape)
print("train_x_token_types", data.train_x_token_types.shape)
print(" train_y", data.train_y.shape)
print(" test_x", data.test_x.shape)
print(" max_seq_len", data.max_seq_len)
```
## Adapter BERT
If we decide to use [adapter-BERT](https://arxiv.org/abs/1902.00751) we need some helpers for freezing the original BERT layers.
```
def flatten_layers(root_layer):
if isinstance(root_layer, keras.layers.Layer):
yield root_layer
for layer in root_layer._layers:
for sub_layer in flatten_layers(layer):
yield sub_layer
def freeze_bert_layers(l_bert):
"""
Freezes all but LayerNorm and adapter layers - see arXiv:1902.00751.
"""
for layer in flatten_layers(l_bert):
if layer.name in ["LayerNorm", "adapter-down", "adapter-up"]:
layer.trainable = True
elif len(layer._layers) == 0:
layer.trainable = False
l_bert.embeddings_layer.trainable = False
def create_learning_rate_scheduler(max_learn_rate=5e-5,
end_learn_rate=1e-7,
warmup_epoch_count=10,
total_epoch_count=90):
def lr_scheduler(epoch):
if epoch < warmup_epoch_count:
res = (max_learn_rate/warmup_epoch_count) * (epoch + 1)
else:
res = max_learn_rate*math.exp(math.log(end_learn_rate/max_learn_rate)*(epoch-warmup_epoch_count+1)/(total_epoch_count-warmup_epoch_count+1))
return float(res)
learning_rate_scheduler = tf.keras.callbacks.LearningRateScheduler(lr_scheduler, verbose=1)
return learning_rate_scheduler
```
#Creating a model
Now let's create a classification model using [adapter-BERT](https//arxiv.org/abs/1902.00751), which is clever way of reducing the trainable parameter count, by freezing the original BERT weights, and adapting them with two FFN bottlenecks (i.e. `adapter_size` bellow) in every BERT layer.
**N.B.** The commented out code below show how to feed a `token_type_ids`/`segment_ids` sequence (which is not needed in our case).
```
def create_model(max_seq_len, adapter_size=64):
"""Creates a classification model."""
#adapter_size = 64 # see - arXiv:1902.00751
# create the bert layer
with tf.io.gfile.GFile(bert_config_file, "r") as reader:
bc = StockBertConfig.from_json_string(reader.read())
bert_params = map_stock_config_to_params(bc)
bert_params.adapter_size = adapter_size
bert = BertModelLayer.from_params(bert_params, name="bert")
input_ids = keras.layers.Input(shape=(max_seq_len,), dtype='int32', name="input_ids")
# token_type_ids = keras.layers.Input(shape=(max_seq_len,), dtype='int32', name="token_type_ids")
# output = bert([input_ids, token_type_ids])
output = bert(input_ids)
print("bert shape", output.shape)
cls_out = keras.layers.Lambda(lambda seq: seq[:, 0, :])(output)
cls_out = keras.layers.Dropout(0.5)(cls_out)
logits = keras.layers.Dense(units=768, activation="tanh")(cls_out)
logits = keras.layers.Dropout(0.5)(logits)
logits = keras.layers.Dense(units=2, activation="softmax")(logits)
# model = keras.Model(inputs=[input_ids, token_type_ids], outputs=logits)
# model.build(input_shape=[(None, max_seq_len), (None, max_seq_len)])
model = keras.Model(inputs=input_ids, outputs=logits)
model.build(input_shape=(None, max_seq_len))
# load the pre-trained model weights
load_stock_weights(bert, bert_ckpt_file)
# freeze weights if adapter-BERT is used
if adapter_size is not None:
freeze_bert_layers(bert)
model.compile(optimizer=keras.optimizers.Adam(),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=[keras.metrics.SparseCategoricalAccuracy(name="acc")])
model.summary()
return model
adapter_size = None # use None to fine-tune all of BERT
model = create_model(data.max_seq_len, adapter_size=adapter_size)
%%time
log_dir = ".log/movie_reviews/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%s")
tensorboard_callback = keras.callbacks.TensorBoard(log_dir=log_dir)
total_epoch_count = 50
# model.fit(x=(data.train_x, data.train_x_token_types), y=data.train_y,
model.fit(x=data.train_x, y=data.train_y,
validation_split=0.1,
batch_size=48,
shuffle=True,
epochs=total_epoch_count,
callbacks=[create_learning_rate_scheduler(max_learn_rate=1e-5,
end_learn_rate=1e-7,
warmup_epoch_count=20,
total_epoch_count=total_epoch_count),
keras.callbacks.EarlyStopping(patience=20, restore_best_weights=True),
tensorboard_callback])
model.save_weights('./movie_reviews.h5', overwrite=True)
%%time
_, train_acc = model.evaluate(data.train_x, data.train_y)
_, test_acc = model.evaluate(data.test_x, data.test_y)
print("train acc", train_acc)
print(" test acc", test_acc)
```
# Evaluation
To evaluate the trained model, let's load the saved weights in a new model instance, and evaluate.
```
%%time
model = create_model(data.max_seq_len, adapter_size=None)
model.load_weights("movie_reviews.h5")
_, train_acc = model.evaluate(data.train_x, data.train_y)
_, test_acc = model.evaluate(data.test_x, data.test_y)
print("train acc", train_acc)
print(" test acc", test_acc)
```
# Prediction
For prediction, we need to prepare the input text the same way as we did for training - tokenize, adding the special `[CLS]` and `[SEP]` token at begin and end of the token sequence, and pad to match the model input shape.
```
pred_sentences = [
"That movie was absolutely awful",
"The acting was a bit lacking",
"The film was creative and surprising",
"Absolutely fantastic!"
]
tokenizer = FullTokenizer(vocab_file=os.path.join(bert_ckpt_dir, "vocab.txt"))
pred_tokens = map(tokenizer.tokenize, pred_sentences)
pred_tokens = map(lambda tok: ["[CLS]"] + tok + ["[SEP]"], pred_tokens)
pred_token_ids = list(map(tokenizer.convert_tokens_to_ids, pred_tokens))
pred_token_ids = map(lambda tids: tids +[0]*(data.max_seq_len-len(tids)),pred_token_ids)
pred_token_ids = np.array(list(pred_token_ids))
print('pred_token_ids', pred_token_ids.shape)
res = model.predict(pred_token_ids).argmax(axis=-1)
for text, sentiment in zip(pred_sentences, res):
print(" text:", text)
print(" res:", ["negative","positive"][sentiment])
```
| true |
code
| 0.651549 | null | null | null | null |
|
# The soil production function
This lesson produced by Simon M Mudd and Fiona J Clubb. Last update (13/09/2021)
Back in the late 1800s, people (including G.K. Gilbert) were speculating about the rates at which soil was formed. This might depend on things like the number of burrowing animals, the rock type, the number of plants, and other factors.
The soil is "produced" from somewhere, and usually it is produced from some combination of conversion of rock to sediments, addition of organic matter, and deposition of dust. But we are going to focus on the conversion of rock material to sediment that can move.
Gilbert suggested that the rate soil was produced (from underlying rocks) depended on the thickness of the soil. We can make a prediction about the relationship between soil thickness and the rate soil is produced, and we call this the *soil production function*.
This function has proposed to have a few different forms, which we will explore below.
## Exponential Soil Production
In lectures we identified that the rate of weathering on a hillslope could be described as an exponential function that depends on soil depth, with weathering rates declining as soil gets deeper (Heimsath et al., 1997):
$p = W_0 e^{-\frac{h}{\gamma}}$
where $W_0$ is the soil production rate with no soil, and $\gamma$ is a length scale that determines how quickly soil production falls off with depth.
Typical values for $W_0$ are in the range 0.01-1 mm/yr [(Perron, 2017)](http://www.annualreviews.org/doi/abs/10.1146/annurev-earth-060614-105405). Note that when you're doing numerical calculations you have to be consistent with units. We will always do calculations in length units of ***metres*** (m), time units of ***years*** (y) and mass units of ***kilograms*** (kg). However we might convert to other units for the purposes of plotting sensible numbers (e.g. Weathering rates in mm/y = m/y $\times$ 1000).
Let's take a look at what this function looks like by plotting it with python:
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
h_locs = np.arange(0,2,0.1)
```
We define the soil production function:
```
def soil_prod_function(h_locs, W_0 = 0.0001, gamma = 0.4):
P = np.multiply(W_0, np.exp( - np.divide(h_locs,gamma) ) )
return P
```
Now lets plot the function and see what it looks like.
In the code below there are two soil production functions that you can compare. For example if you make `W_0` twice as much as `W_02` that means the second soil production function produces soil twice as fast as the first when there is no soil.
```
plt.rcParams['figure.figsize'] = [10, 4]
plt.clf()
# TRY CHANGING THE FOUR PARAMETER BELOW
# These two are for the first soil production function
W_0 = 0.0001
gamma = 0.4
# These two are for the second soil production function
W_02 = 0.0002
gamma2 = 0.4
# This bit calculates the functions
P = soil_prod_function(h_locs, W_0 = W_0, gamma = gamma)
P2 = soil_prod_function(h_locs, W_0 = W_02, gamma = gamma2)
# The rest of this stuff makes the figure
f, ax = plt.subplots(1, 1)
ax.plot(h_locs, P*1000,label="P1")
ax.plot(h_locs, P2*1000,label="P2")
ax.set_xlabel("Soil thickness ($m$)")
ax.set_ylabel("Soil production (mm/yr)")
plt.title("Two soil production function. Try playing with the parameters!")
ax.legend()
plt.tight_layout()
```
## The peaked soil production function
We also discussed in the lecture an alternative way in which soil may be produced: where there are very slow rates of soil production where there is bare bedrock, then soil peaks at some intermediate thickness before decreasing exponentially with increasing soil thickness. This model dates back to Gilbert (1877), and makes intuitive sense: water is needed for weathering processes as we discussed today. If there is bare bedrock, water is quickly transported through overland flow and little weathering can take place. If there is too much soil, then it's unlikely to be fully saturated down to the bedrock--soil interface.
In this section, we will make some plots of a hypothetical peaked (or humped) soil production function.
We will use the theoretical formulation from [Cox (1980)](https://onlinelibrary.wiley.com/doi/abs/10.1002/esp.3760050305) to calculate the weathering rate for a range of soil depths. This is a bit more complicated than the exponential function and has a bigger range of parameters:
\begin{equation}
W = W_0 (\alpha e^{-kh}) + (1 - \alpha)f \\
f = \Bigg(1 + c\frac{h}{h_c} - \frac{h^2}{{h_c}^2}\Bigg)
\end{equation}
You should recognise some of these parameters from the exponential equation. The first part of the equation is the exponential function multiplied by a coefficient, $\alpha$. $W$ is still the weathering rate, $W_0$ is the inital rate of soil production where there is no soil, and $h$ is soil depth. There are two new parameters: $h_c$ is a critical soil depth (m), and $c$ is an empirical constant. Anhert (1977) suggests that $c$ might vary between 1.7 - 2.3, $h_c$ might vary between 0.6 - 1.5, and $\alpha$ between 0 - 1. If $\alpha = 1$, then the relationship is simply the exponential function.
```
# first, let's clear the original figure
plt.clf()
# make a new figure
fig, ax = plt.subplots()
k = 1
# define the critical depth for soil production
h_c = 0.5 #metres
# define the initial rate of soil production
W_0 = 0.0005 #m/year
# define the constant c
c = 2 #dimensionless
# define alpha
alpha = 0.2
# calculate the weathering rate for the range of soil depths, h
f = (1 + c*(h_locs/h_c) - h_locs**2/h_c**2)
W = W_0 * (alpha * np.exp(-k*h_locs) + (1 - alpha)*f)
# plot the new result with a blue dashed line
ax.plot(h_locs,W*1000.,'--', color='blue', label = 'Peaked function')
# add a legend
plt.legend(loc = 'upper right')
# set the y limit of the humped function to 0 (so we don't get negative weathering rates), and set the axis labels
ax.set_ylim(0,)
plt.xlabel("Soil Depth (m)")
plt.ylabel("Weathering Rate (mm/y)")
plt.title("The peaked soil production function")
plt.tight_layout()
```
Optional Exercise 1
---
1. Have a play around and try to change some of the parameters in the peaked function (simply modify in the code block above). How does this affect the curve?
2. Try to make a plot with the exponential and peaked functions on the same set of axes, so you can compare them (HINT - copy the line that creates the exponential soil production function into the code block above, and then give it a different colour).
---
---
## Optional Exercise 2
<p>Create a figure from the practical today that shows the difference between the peaked and exponential soil production functions for different initial soil production rates. You should write a figure caption that annotates what your soil production plot is showing. The caption should be a paragraph of text that describes each line, and the parameters that have been used to create them, and offers a brief explanation of how the parameters used influence rates of soil production. For an indication of the level of detail required, you could look at examples of captions to figures in journal articles, such as Figure 3 in
[Heimsath et al. (2012)](https://www.nature.com/ngeo/journal/v5/n3/pdf/ngeo1380.pdf). You can use any program you like, such as Microsoft Word, to create your figure.
**Note**: the exercises from the practicals in this module will not be marked, but they are all teaching you important skills that will be used in the summative assessment. I would therefore really encourage you to engage with them. I will go over the answers and discuss the exercises at the start of the next session.
For your independent project, you will be expected to present 5 figures with captions, so this is a good chance to practice how to write a good figure caption!
| true |
code
| 0.690376 | null | null | null | null |
|
# Homework 4 - Reinforcement Learning in a Smart Factory
Optimization of the robots route for pick-up and storage of items in a warehouse:
1. Implement a reinforcement-learning based algorithm
2. The robot is the agent and decides where to place the next part
3. Use the markov decision process toolbox for your solution
4. Choose the best performing MDP
```
#!pip install pymdptoolbox
## Imports
import mdptoolbox
import pandas as pd
import itertools as it
import numpy as np
import pickle
import time
from scipy import sparse
```
## Import data
```
file_path = 'Exercise 4 - Reinforcement Learning Data - warehousetraining.txt'
file_path_test= 'Exercise 4 - Reinforcement Learning Data - warehouseorder.txt'
# Name the data colums corectly
data = pd.read_csv(file_path, sep='\t', names=["action", "color_state"])
test_data = pd.read_csv(file_path_test, sep='\t', names=["action", "color_state"])
#print(data.info()) print(data.dtypes)
data.head()
data.groupby(["action", "color_state"]).count()
actions = list(np.unique(data.action)) #['restore', 'store']
item_colors = list(np.unique(data.color_state)) #['blue' 'red' 'white']
train_data = np.array( [[actions.index(v[0]), item_colors.index(v[1])] for v in data.values] , dtype=int)
```
## Reinforcement-learning based algorithm: Markov Descision Process (MDP)
A MDP is a discrete time stochastic control process where the markov property is satisfied
1. Create Transitions Matrix represeting the probabilities to lead from state *s0* another state *s1* within the action *a*
2. Generate Reward Matrix defined reward after action *a* in state *s0* to reach state *s1*
Optimize the route with following constraints:
- Size of warehouse is {1..3} x {1..3}
- Separate start/stop position outside the 3x3 storage space where the robot have to go at the end of storage and pick-up
- The first position the robot can move into is always (1,1)
- Robot can move to adjacent fields
- Robot cannot move diagonally
- There are three types of items: (white, blue, red)
```
# Set Markov Descision Process (MDP) Constrains
warehouse_size = [2,2] #2x2 grid
grid_size = np.prod(warehouse_size)
grids_cells = [(i+1,j+1) for j in range(warehouse_size[1]) for i in range(warehouse_size[0]) ]
# The actions is equal to grid size
actions_moves = grid_size.copy()
items = len(item_colors) + 1 # Consider also no item
moves = len(actions)*len(item_colors)
#Total posibilities of item in any satate on the field
items_grid = items ** grid_size
total_states = items_grid * moves
print("The total number of states is: ", total_states)
item_states_ID = dict((k,v) for v,k in enumerate( ["noitem"] + item_colors ))# dict.fromkeys(item_colors + ["noitem"], 0)
item_states_ID
# Create all the posible states indexing
def compute_grid_index(grid_size, item_states_ID):
grids = [s for s in it.product(item_states_ID.values(), repeat=grid_size)]
return np.array(grids)
grids = compute_grid_index(grid_size, item_states_ID)
print("Number of posible states: ", len(grids))
grid_states= pd.DataFrame(data=grids, columns=grids_cells)
grid_states[20:30]
def generate_warehosue_states(grid_states, item_states_ID,):
warehouse_states = pd.DataFrame()
for k,v in item_states_ID.items():
warehouse_states[k] = np.sum(grid_states ==v, axis =1)
return warehouse_states
warehouse_states = generate_warehosue_states(grid_states, item_states_ID)
warehouse_states[20:30]
```
### Transition Probability Matrix (action, state, next state)
```
def create_TPM(data, grids):
# Initialize TMP with shape (action, posible states, posible states)
P = np.zeros(( actions_moves, total_states, total_states),dtype=np.float16)
# Compute Each action probability as the count of each action on the data
move_action_probability = np.array([a*c for a in data["action"].value_counts() / len(data) for c in data["color_state"].value_counts() / len(data) ])
for action in range(actions_moves):
idx = 0
for mov in range(moves):
for s in grids:
for m in range(moves):
if m >= (moves//2): # restore actions
i = ((idx % items_grid) - (items**(actions_moves - action - 1) * (mov+1))) + (items_grid * m)
else:
i = ((idx % items_grid) - (items**(actions_moves - action - 1) * (mov+1))) + (items_grid * m)
P[action][idx][i] = move_action_probability[m]
idx += 1
return P
TMP = create_TPM(data, grids)
def create_rewards(moves, total_states, grid_states):
distances = [sum(np.array(c) - np.array(grids_cells[0])) for c in grids_cells]
rewards = dict(keys=grids_cells, values =distances )
R = np.zeros((actions_moves, total_states, ))
for action in range(actions_moves):
for idx, s in grid_states.iterrows():
next_state = idx//(len(grid_states)//moves)
try:
if(next_state < (moves//len(actions)) and s[action] == 0):
reward = rewards[str(s)]
elif (next_state > (moves//len(actions) ) and (s[action] == (next_state - len(actions)))):
reward = 10000*rewards[str(s)] #+=100
# Invalid movements
else:
reward = -10000
R[action][idx] = reward
except:
pass
return np.asarray(R).T
R = create_rewards(moves, total_states, grid_states)
assert TMP.shape[:-1] == R.shape[::-1], "The actions and states should match"
discount = 0.9
max_iter = 750
policy = mdptoolbox.mdp.PolicyIteration(TMP, R, 0.9, max_iter=max_iter)
value = mdptoolbox.mdp.ValueIteration(TMP, R, 0.9, max_iter=max_iter)
value.run()
policy.run()
p = policy.policy
iterations = policy.iter
print("Policy iterations:", iterations)
print("Value iterations:", value.iter)
```
| true |
code
| 0.424054 | null | null | null | null |
|
# Practice for understanding image classification with neural network
- Single layer neural network with gradient descent
## 1) Import Packages
```
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
import random
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import math
import sklearn.metrics as metrics
```
## 2) Make Dataset
```
x_orig = []
y_orig = np.zeros((1,100))
for i in range(1,501):
if i <= 100 :
folder = 0
elif i <=200 :
folder = 1
elif i <=300 :
folder = 2
elif i <=400 :
folder = 3
else :
folder = 4
img = np.array(Image.open('dataset/{0}/{1}.jpg'.format(folder,i)))
img = Image.fromarray(img).convert('L') # gray
data = img.resize((64,64))
data = np.array(data)
x_orig.append(data)
for i in range(1,5):
y_orig = np.append(y_orig, np.full((1, 100),i), axis = 1)
x_orig = np.array(x_orig)
print(x_orig.shape)
print(y_orig.shape)
# Random shuffle
s = np.arange(x_orig.shape[0])
np.random.shuffle(s)
x_shuffle = x_orig[s,:]
y_shuffle = y_orig[:,s]
print(x_shuffle.shape)
print(y_shuffle.shape)
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(x_shuffle[i,:])
plt.xlabel(y_shuffle[:,i])
plt.show()
# Split train and test datasets
x_train_orig, x_test_orig, y_train_orig, y_test_orig = train_test_split(x_shuffle,y_shuffle.T,
test_size=0.2, shuffle=True, random_state=1004)
print(x_train_orig.shape)
print (y_train_orig.shape)
# Flatten the training and test images
x_train_flatten = x_train_orig.reshape(x_train_orig.shape[0], -1).T
x_test_flatten = x_test_orig.reshape(x_test_orig.shape[0], -1).T
# Normalize image vectors
x_train = x_train_flatten/255.
x_test = x_test_flatten/255.
# Convert training and test labels to one hot matrices
enc = OneHotEncoder()
y1 = y_train_orig.reshape(-1,1)
enc.fit(y1)
y_train = enc.transform(y1).toarray()
y_train = y_train.T
y2 = y_test_orig.reshape(-1,1)
enc.fit(y2)
y_test = enc.transform(y2).toarray()
y_test = y_test.T
# Explore dataset
print ("number of training examples = " + str(x_train.shape[1]))
print ("number of test examples = " + str(x_test.shape[1]))
print ("x_train shape: " + str(x_train.shape))
print ("y_train shape: " + str(y_train.shape))
print ("x_test shape: " + str(x_test.shape))
print ("y_test shape: " + str(y_test.shape))
```
## 3) Definie required functions
```
def initialize_parameters(nx, ny):
"""
Argument:
nx -- size of the input layer (4096)
ny -- size of the output layer (3)
Returns:
W -- weight matrix of shape (ny, nx)
b -- bias vector of shape (ny, 1)
"""
np.random.seed(1)
W = np.random.randn(ny,nx)*0.01
b = np.zeros((ny,1))
assert(W.shape == (ny, nx))
assert(b.shape == (ny, 1))
return W, b
def softmax(Z):
# compute the softmax activation
S = np.exp(Z + np.max(Z)) / np.sum(np.exp(Z + np.max(Z)), axis = 0)
return S
def classlabel(Z):
# probabilities back into class labels
y_hat = Z.argmax(axis=0)
return y_hat
def propagate(W, b, X, Y):
m = X.shape[1]
# Forward Propagation
Z = np.dot(W, X)+ b
A = softmax(Z) # compute activation
cost = (-1/m) * np.sum(Y * np.log(A)) # compute cost (Cross_entropy)
# Backward propagation
dW = (1/m) * (np.dot(X,(A-Y).T)).T
db = (1/m) * (np.sum(A-Y))
grads = {"dW": dW,
"db": db}
return grads, cost
```
## 4) Single-Layer Neural Network with Gradient Descent
```
def optimize(X, Y, num_iterations, learning_rate, print_cost = False):
costs = []
W, b = initialize_parameters(4096,5)
for i in range(num_iterations):
grads, cost = propagate(W,b,X,Y)
dW = grads["dW"]
db = grads["db"]
W = W - (learning_rate) * dW
b = b - (learning_rate) * db
# Record the costs for plotting
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training iterations
if print_cost and i % 200 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per 200)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# Lets save the trainded parameters in a variable
params = {"W": W,
"b": b}
grads = {"dW": dW,
"db": db}
return params, grads, costs
params, grads, costs = optimize(x_train, y_train, num_iterations= 1000, learning_rate = 0.01, print_cost = True)
print ("W = " + str(params["W"]))
print ("b = " + str(params["b"]))
```
## 5) Accuracy Analysis
```
def predict(W, b, X) :
m = X.shape[1]
# Compute "A" predicting the probabilities
Z = np.dot(W, X)+ b
A = softmax(Z)
# Convert probabilities A to actual predictions
y_prediction = A.argmax(axis=0)
return y_prediction
# Predict test/train set
W1 = params['W']
b1 = params['b']
y_prediction_train = predict(W1, b1, x_train)
y_prediction_test = predict(W1, b1, x_test)
print(y_prediction_train)
print(y_prediction_test)
# Print train/test accuracy
print("train accuracy : ", metrics.accuracy_score(y_prediction_train, y_train_orig))
print("test accuracy : ", metrics.accuracy_score(y_prediction_test, y_test_orig))
```
| true |
code
| 0.545407 | null | null | null | null |
|
# Iterables
Some steps in a neuroimaging analysis are repetitive. Running the same preprocessing on multiple subjects or doing statistical inference on multiple files. To prevent the creation of multiple individual scripts, Nipype has as execution plugin for ``Workflow``, called **``iterables``**.
<img src="../static/images/iterables.png" width="240">
If you are interested in more advanced procedures, such as synchronizing multiple iterables or using conditional iterables, check out the `synchronize `and `intersource` section in the [`JoinNode`](basic_joinnodes.ipynb) notebook.
## Realistic example
Let's assume we have a workflow with two nodes, node (A) does simple skull stripping, and is followed by a node (B) that does isometric smoothing. Now, let's say, that we are curious about the effect of different smoothing kernels. Therefore, we want to run the smoothing node with FWHM set to 2mm, 8mm, and 16mm.
```
from nipype import Node, Workflow
from nipype.interfaces.fsl import BET, IsotropicSmooth
# Initiate a skull stripping Node with BET
skullstrip = Node(BET(mask=True,
in_file='/data/ds000114/sub-01/ses-test/anat/sub-01_ses-test_T1w.nii.gz'),
name="skullstrip")
```
Create a smoothing Node with IsotropicSmooth
```
isosmooth = Node(IsotropicSmooth(), name='iso_smooth')
```
Now, to use ``iterables`` and therefore smooth with different ``fwhm`` is as simple as that:
```
isosmooth.iterables = ("fwhm", [4, 8, 16])
```
And to wrap it up. We need to create a workflow, connect the nodes and finally, can run the workflow in parallel.
```
# Create the workflow
wf = Workflow(name="smoothflow")
wf.base_dir = "/output"
wf.connect(skullstrip, 'out_file', isosmooth, 'in_file')
# Run it in parallel (one core for each smoothing kernel)
wf.run('MultiProc', plugin_args={'n_procs': 3})
```
**Note**, that ``iterables`` is set on a specific node (``isosmooth`` in this case), but ``Workflow`` is needed to expend the graph to three subgraphs with three different versions of the ``isosmooth`` node.
If we visualize the graph with ``exec``, we can see where the parallelization actually takes place.
```
# Visualize the detailed graph
from IPython.display import Image
wf.write_graph(graph2use='exec', format='png', simple_form=True)
Image(filename='/output/smoothflow/graph_detailed.png')
```
If you look at the structure in the workflow directory, you can also see, that for each smoothing, a specific folder was created, i.e. ``_fwhm_16``.
```
!tree /output/smoothflow -I '*txt|*pklz|report*|*.json|*js|*.dot|*.html'
```
Now, let's visualize the results!
```
from nilearn import plotting
%matplotlib inline
plotting.plot_anat(
'/data/ds000114/sub-01/ses-test/anat/sub-01_ses-test_T1w.nii.gz', title='original',
display_mode='z', dim=-1, cut_coords=(-50, -35, -20, -5), annotate=False);
plotting.plot_anat(
'/output/smoothflow/skullstrip/sub-01_ses-test_T1w_brain.nii.gz', title='skullstripped',
display_mode='z', dim=-1, cut_coords=(-50, -35, -20, -5), annotate=False);
plotting.plot_anat(
'/output/smoothflow/_fwhm_4/iso_smooth/sub-01_ses-test_T1w_brain_smooth.nii.gz', title='FWHM=4',
display_mode='z', dim=-0.5, cut_coords=(-50, -35, -20, -5), annotate=False);
plotting.plot_anat(
'/output/smoothflow/_fwhm_8/iso_smooth/sub-01_ses-test_T1w_brain_smooth.nii.gz', title='FWHM=8',
display_mode='z', dim=-0.5, cut_coords=(-50, -35, -20, -5), annotate=False);
plotting.plot_anat(
'/output/smoothflow/_fwhm_16/iso_smooth/sub-01_ses-test_T1w_brain_smooth.nii.gz', title='FWHM=16',
display_mode='z', dim=-0.5, cut_coords=(-50, -35, -20, -5), annotate=False);
```
# ``IdentityInterface`` (special use case of ``iterables``)
We often want to start our worflow from creating subgraphs, e.g. for running preprocessing for all subjects. We can easily do it with setting ``iterables`` on the ``IdentityInterface``. The ``IdentityInterface`` interface allows you to create ``Nodes`` that does simple identity mapping, i.e. ``Nodes`` that only work on parameters/strings.
For example, you want to start your workflow by collecting anatomical files for 5 subjects.
```
# First, let's specify the list of subjects
subject_list = ['01', '02', '03', '07']
```
Now, we can create the IdentityInterface Node
```
from nipype import IdentityInterface
infosource = Node(IdentityInterface(fields=['subject_id']),
name="infosource")
infosource.iterables = [('subject_id', subject_list)]
```
That's it. Now, we can connect the output fields of this ``infosource`` node to ``SelectFiles`` and ``DataSink`` nodes.
```
from os.path import join as opj
from nipype.interfaces.io import SelectFiles, DataSink
anat_file = opj('sub-{subject_id}', 'ses-test', 'anat', 'sub-{subject_id}_ses-test_T1w.nii.gz')
templates = {'anat': anat_file}
selectfiles = Node(SelectFiles(templates,
base_directory='/data/ds000114'),
name="selectfiles")
# Datasink - creates output folder for important outputs
datasink = Node(DataSink(base_directory="/output",
container="datasink"),
name="datasink")
wf_sub = Workflow(name="choosing_subjects")
wf_sub.connect(infosource, "subject_id", selectfiles, "subject_id")
wf_sub.connect(selectfiles, "anat", datasink, "anat_files")
wf_sub.run()
```
Now we can check that five anatomicl images are in ``anat_files`` directory:
```
! ls -lh /output/datasink/anat_files/
```
This was just a simple example of using ``IdentityInterface``, but a complete example of preprocessing workflow you can find in [Preprocessing Example](example_preprocessing.ipynb)).
## Exercise 1
Create a workflow to calculate various powers of ``2`` using two nodes, one for ``IdentityInterface`` with ``iterables``, and one for ``Function`` interface to calculate the power of ``2``.
```
# write your solution here
# lets start from the Identity node
from nipype import Function, Node, Workflow
from nipype.interfaces.utility import IdentityInterface
iden = Node(IdentityInterface(fields=['number']), name="identity")
iden.iterables = [("number", range(8))]
# the second node should use the Function interface
def power_of_two(n):
return 2**n
# Create Node
power = Node(Function(input_names=["n"],
output_names=["pow"],
function=power_of_two),
name='power')
#and now the workflow
wf_ex1 = Workflow(name="exercise1")
wf_ex1.connect(iden, "number", power, "n")
res_ex1 = wf_ex1.run()
# we can print the results
for i in range(8):
print(list(res_ex1.nodes())[i].result.outputs)
```
| true |
code
| 0.614625 | null | null | null | null |
|
# 2つのガウス分布を含む混合ガウス分布のためのEMアルゴリズム
(細かいコメントはもうちょっと待ってくださーい)
千葉工業大学 上田 隆一
(c) 2017 Ryuichi Ueda
This software is released under the MIT License, see LICENSE.
## はじめに
このコードは、2つの2次元ガウス分布を含む混合ガウス分布から生成されたデータについて、EMアルゴリズムでパラメータを求めるためのEMアルゴリズムの実装例です。処理の流れは、次のようなものです。
* (準備)2つのガウス分布からサンプリング
* 推定対象は、この2つのガウス分布のパラメータと、どちらからどれだけサンプリングされたかの比
* 適当なパラメータで2つガウス分布を準備し、収束するまで以下の繰り返し
* Eステップ: 各サンプルがどちらの分布から生成されたらしいかを、2つのガウス分布の確率密度関数から得られる値の比で計算
* Mステップ: Eステップで得た比を利用して、推定対象の値を計算
* 収束したら、推定値を出力
## アルゴリズムを適用される対象になるデータの生成
クラスタリングの対象となるデータを作ります。二つの2次元ガウス分布から、2:1の割合で標本抽出します。(GitHubだと行列が崩れて表示されますが、$\mathcal{N}$の二番目の引数は2x2行列です。)
* 2つの分布
* 分布A(200個抽出): $\mathcal{N}\left( \begin{bmatrix}170 \\ 70 \end{bmatrix}, \begin{bmatrix}6^2 & -30 \\ -30 & 8^2\end{bmatrix} \right)$
* 分布B(100個抽出): $\mathcal{N}\left( \begin{bmatrix}165 \\ 50 \end{bmatrix}, \begin{bmatrix}5^2 & 20 \\ 20 & 6^2\end{bmatrix} \right)$
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import math
def make_samples():
# グループAのガウス分布
muA_ans = [170,70] # 横軸、縦軸をx,y軸とすると、x=170, y=70が中心
covA_ans = [[6**2,-30],[-30,8**2]] # x軸の標準偏差6、y軸の標準偏差-30、共分散-30
samplesA = np.random.multivariate_normal(muA_ans,covA_ans,200).T #200個の点をサンプリング
# グループBのガウス分布
muB_ans = [165,50] # x=165, y=50が中心
covB_ans = [[5.**2,20],[20,6**2]] # x軸の標準偏差5、y軸の標準偏差6、共分散20
samplesB = np.random.multivariate_normal(muB_ans,covB_ans,100).T #100個の点をサンプリング
# 2つのグループのリストをくっつけて返す
return np.column_stack((samplesA,samplesB))
# データを作る
samples = make_samples()
#描画してみましょう
plt.scatter(samples[0],samples[1],color='g',marker='+') # sample[0]がx値のずらっと入ったリスト、sample[1]がy値
# このデータに関する既知のパラメータ
K = 2 # クラスタの数
N = len(samples[0]) # サンプルの数
```
以後、サンプルは$\boldsymbol{x}_n = (x_n,y_n) \quad (n=0,1,2,\dots,N)$と表現します。
## パラメータの初期設定
2つの分布のパラメータを格納する変数を準備して、このパラメータを上記の分布の式に近づけていきます。また、混合係数の変数も準備します。混合係数というのは、どっちからどれだけサンプルが生成されたかの割合のことです。上の例だと分布1で$2/3$、分布2で$1/3$となります。
* パラメータ
* 各分布(リストdistributions): $\mathcal{N}(\boldsymbol{x} | \boldsymbol{\mu}_k, \Sigma_k)\quad (k=0,1)$
* 混合係数(リストmixing_coefs): $\pi_k \quad (k=0,1; \pi_0 + \pi_1 = 1)$
```
from scipy.stats import multivariate_normal # これを使うと多次元ガウス分布のオブジェクトが生成できます
# 2つのガウス分布のオブジェクトを作る
distributions = []
distributions.append(multivariate_normal(mean=[160,80],cov= [[100,0],[0,100]]) ) # 分布1を適当な分布の中心、共分散行列で初期化
distributions.append(multivariate_normal(mean=[170,100],cov= [[100,0],[0,100]]) ) # 分布2を同様に初期化。分布1と少し値を変える必要アリ
# 混合係数のリスト
mixing_coefs = [1.0/K for k in range(K)] # 回りくどい書き方をしていますが、両方0.5で初期化されます。
```
描画の関係でサンプルの分布に重なるようにガウス分布を初期化していますが、辺鄙な値でも大丈夫です。
## 描画用の関数
```
def draw(ds,X):
# 分布を等高線で描画
x, y = np.mgrid[(min(X[0])):(max(X[0])):1, (min(X[1])):(max(X[1])):1] # 描画範囲の指定
for d in ds:
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x; pos[:, :, 1] = y
plt.contour(x, y, d.pdf(pos),alpha=0.2)
# サンプルの描画
plt.scatter(X[0],X[1],color='g',marker='+')
draw(distributions,samples)
```
以後、描かれた2つの楕円がサンプルの上に重なるように計算していきます。
## Eステップの実装
分布を固定し、各サンプルがどっちの分布に属すかを表した確率である負担率$\gamma(z_{nk})$のリストを各サンプル、各分布に対して計算して返します。
$\gamma(z_{nk}) = \dfrac{\pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \Sigma_k)
}{\sum_j^K\pi_j \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_j, \Sigma_j)}$
```
def expectation_step(ds,X,pis): # 負担率の計算
ans = [] # 負担率のリスト
for n in range(N): # サンプルの数だけ繰り返し
# サンプルの地点における各分布の値(密度)を計算
ws = [ pis[k] * ds[k].pdf([X[0][n],X[1][n]]) for k in range(K) ] # 各クラスタに対して負担率の分子を計算
ans.append([ws[k]/sum(ws) for k in range(K)]) # 各クラスタの負担率の合計が1になるように正規化しているだけ
return ans # K * N 個のリスト
```
## Mステップの実装
各分布のパラメータと混合係数を更新します。次のコードの2行目の$N_k = \sum_{n=0}^{N-1} \gamma(z_{nk}) $は、各分布に関する全サンプルの負担率を合計して、各分布に「いくつ」サンプルが所属するかを求めたものです。負担率はゼロイチではないので、$N_k$は小数になります。
* 分布の中心の更新: $\boldsymbol{\mu}_k \longleftarrow \dfrac{1}{N_k} \sum_{n=0}^{N-1} \gamma(z_{nk})\boldsymbol{x}_n$
* 分布の共分散行列の更新: $\Sigma_k \longleftarrow \dfrac{1}{N_k} \sum_{n=0}^{N-1} \gamma(z_{nk}) (\boldsymbol{x}_n - \boldsymbol{\mu}_k)(\boldsymbol{x}_n - \boldsymbol{\mu}_k)^T$(更新後の$\boldsymbol{\mu}_k$を使用します。)
* 混合係数の更新: $\pi_k \longleftarrow \dfrac{N_k}{N}$
```
def maximization_step(k,X,gammas): # 引数は分布の番号、全サンプル、全サンプルと分布の負担率
N_k = sum ( [ gammas[n][k] for n in range(N) ])
# 分布の中心の更新
tmp_x = sum ( [ gammas[n][k] * X[0][n] for n in range(N) ]) / N_k # 全サンプルのx軸の値の平均値を、その分布に対する負担率で重み付き平均で計算
tmp_y = sum ( [ gammas[n][k] * X[1][n] for n in range(N) ]) / N_k # 同様にy軸の重み付き平均を計算
mu = [tmp_x,tmp_y] # 更新値
# 共分散行列の更新
ds= [ np.array([[X[0][n],X[1][n]]]) - np.array([mu]) for n in range(N) ] # 分布の中心に対するサンプルの位置のリスト
sigma = sum( [ gammas[n][k]* ds[n].T.dot(ds[n]) for n in range(N)] ) / N_k # 上のリストをかけて2x2行列を作り、負担率で重み付き平均をとる
return multivariate_normal(mean=mu,cov=sigma), N_k/N
```
### とりあえず1回ずつEステップとMステップを実行
Eステップで負担率のリストを作り、Mステップでパラメータを更新します。
```
def log_likelihood(ds,X,pis): # 収束の判断のために対数尤度を返す関数
ans = 0.0
for n in range(N):
ws = [ pis[k] * ds[k].pdf([X[0][n],X[1][n]]) for k in range(K) ]
ans += math.log1p(sum(ws) )
return ans
def one_step():
# Eステップ
gammas = expectation_step(distributions,samples,mixing_coefs)
# Mステップ
for k in range(K):
distributions[k], mixing_coefs[k] = maximization_step(k,samples,gammas)
return log_likelihood(distributions,samples,mixing_coefs)
one_step()
draw(distributions,samples)
```
少し二つの分布の位置がサンプルのある場所に近づいているのが分かります。
## 対数尤度が収束するまで繰り返し
対数尤度は次の式で与えられます。
$\ln p(\boldsymbol{x}_{0:N-1} | \boldsymbol{\mu}_{0:1}, \Sigma_{0:1}, \pi_{0:1}) = \sum_{n=0}^{N-1} \ln \left\{ \sum_{k=0}^{K-1} \pi_k \mathcal{N}(\boldsymbol{x}_n | \boldsymbol{\mu}_k, \Sigma_k) \right\}$
```
prev_log_likelihood = 0.0
for i in range(99):
after_log_likelihood = one_step()
if prev_log_likelihood/after_log_likelihood > 0.999: # 0.1%以上対数尤度が改善しなければ抜ける
break
else:
prev_log_likelihood = after_log_likelihood
if i % 3 == 0:
plt.figure()
draw(distributions,samples)
plt.figure()
draw(distributions,samples)
print("---------------------------------------------")
print("repeat: ", i+1)
for k in range(K):
print("Gauss",k,": ")
print(" share: ", mixing_coefs[k])
print(" mean: ", distributions[k].mean)
print(" cov: ", distributions[k].cov)
```
| true |
code
| 0.375735 | null | null | null | null |
|
# Delicious Asian and Indian Cuisines
Install Imblearn which will enable SMOTE. This is a Scikit-learn package that helps handle imbalanced data when performing classification. (https://imbalanced-learn.org/stable/)
```
pip install imblearn
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from imblearn.over_sampling import SMOTE
df = pd.read_csv('../../data/cuisines.csv')
```
This dataset includes 385 columns indicating all kinds of ingredients in various cuisines from a given set of cuisines.
```
df.head()
df.info()
df.cuisine.value_counts()
```
Show the cuisines in a bar graph
```
df.cuisine.value_counts().plot.barh()
thai_df = df[(df.cuisine == "thai")]
japanese_df = df[(df.cuisine == "japanese")]
chinese_df = df[(df.cuisine == "chinese")]
indian_df = df[(df.cuisine == "indian")]
korean_df = df[(df.cuisine == "korean")]
print(f'thai df: {thai_df.shape}')
print(f'japanese df: {japanese_df.shape}')
print(f'chinese df: {chinese_df.shape}')
print(f'indian df: {indian_df.shape}')
print(f'korean df: {korean_df.shape}')
```
## What are the top ingredients by class
```
def create_ingredient_df(df):
# transpose df, drop cuisine and unnamed rows, sum the row to get total for ingredient and add value header to new df
ingredient_df = df.T.drop(['cuisine','Unnamed: 0']).sum(axis=1).to_frame('value')
# drop ingredients that have a 0 sum
ingredient_df = ingredient_df[(ingredient_df.T != 0).any()]
# sort df
ingredient_df = ingredient_df.sort_values(by='value', ascending=False, inplace=False)
return ingredient_df
thai_ingredient_df = create_ingredient_df(thai_df)
thai_ingredient_df.head(10).plot.barh()
japanese_ingredient_df = create_ingredient_df(japanese_df)
japanese_ingredient_df.head(10).plot.barh()
chinese_ingredient_df = create_ingredient_df(chinese_df)
chinese_ingredient_df.head(10).plot.barh()
indian_ingredient_df = create_ingredient_df(indian_df)
indian_ingredient_df.head(10).plot.barh()
korean_ingredient_df = create_ingredient_df(korean_df)
korean_ingredient_df.head(10).plot.barh()
```
Drop very common ingredients (common to all cuisines)
```
feature_df= df.drop(['cuisine','Unnamed: 0','rice','garlic','ginger'], axis=1)
labels_df = df.cuisine #.unique()
feature_df.head()
```
Balance data with SMOTE oversampling to the highest class. Read more here: https://imbalanced-learn.org/dev/references/generated/imblearn.over_sampling.SMOTE.html
```
oversample = SMOTE()
transformed_feature_df, transformed_label_df = oversample.fit_resample(feature_df, labels_df)
print(f'new label count: {transformed_label_df.value_counts()}')
print(f'old label count: {df.cuisine.value_counts()}')
transformed_feature_df.head()
# export transformed data to new df for classification
transformed_df = pd.concat([transformed_label_df,transformed_feature_df],axis=1, join='outer')
transformed_df
transformed_df.info()
```
Save the file for future use
```
transformed_df.to_csv("../../data/cleaned_cuisine.csv")
```
| true |
code
| 0.333415 | null | null | null | null |
|
## Manual publication DB insertion from raw text using syntax features
### Publications and conferences of Prof. Darabant Sergiu Adrian
#### http://www.cs.ubbcluj.ro/~dadi/
```
text = """
A Versatile 3D Face Reconstruction from Multiple Images for Face Shape Classification
Conference Paper
Sep 2019
Alexandru Ion Marinescu
Tudor Ileni
Adrian Sergiu Darabant
View
Fast In-the-Wild Hair Segmentation and Color Classification
Conference Paper
Jan 2019
Tudor Ileni
Diana Borza
Adrian Sergiu Darabant
In this paper we address the problem of hair segmentation and hair color classification in facial images using a machine learning approach based on both convolutional neural networks and classical neural networks. Hair with its color shades, shape and length represents an important feature of the human face and is used in domains like biometrics, v...
View
A Deep Learning Approach to Hair Segmentation and Color Extraction from Facial Images: 19th International Conference, ACIVS 2018, Poitiers, France, September 24–27, 2018, Proceedings
Chapter
Sep 2018
Diana Borza
Tudor Ileni
Adrian Sergiu Darabant
In this paper we tackle the problem of hair analysis in unconstrained images. We propose a fully convolutional, multi-task neural network to segment the image pixels into hair, face and background classes. The network also decides if the person is bald or not. The detected hair pixels are analyzed by a color recognition module which uses color feat...
View
Micro-Expressions Detection Based on Micro-Motions Dense Optical Flows
Conference Paper
Sep 2018
Sergiu Cosmin Nistor
Adrian Sergiu Darabant
Diana Borza
View
Automatic Skin Tone Extraction for Visagism Applications
Conference Paper
Jan 2018
Diana Borza
Adrian Sergiu Darabant
Radu Danescu
View
Figure 1. High-speed video acquisition and analysis process.
Figure 1. High-speed video acquisition and analysis process.
High-Speed Video System for Micro-Expression Detection and Recognition
Article
Full-text available
Dec 2017
Diana Borza
Radu Danescu
Razvan Itu
Adrian Sergiu Darabant
Micro-expressions play an essential part in understanding non-verbal communication and deceit detection. They are involuntary, brief facial movements that are shown when a person is trying to conceal something. Automatic analysis of micro-expression is challenging due to their low amplitude and to their short duration (they occur as fast as 1/15 to...
View
Supplementary Material
Data
Dec 2017
Diana Borza
Radu Danescu
Razvan Itu
Adrian Sergiu Darabant
View
Towards Automatic Skin Tone Classification in Facial Images
Conference Paper
Oct 2017
Diana Borza
Sergiu Cosmin Nistor
Adrian Sergiu Darabant
In this paper, we address the problem of skin tone classification in facial images, which has applications in various domains: visagisme, soft biometry and surveillance systems. We propose four skin tone classification algorithms and analyze their performance using different color spaces. The first two methods rely directly on pixel values, while t...
View
A linear approach to distributed database optimization using data reallocation
Conference Paper
Sep 2017
Adrian Sergiu Darabant
Viorica Varga
Leon Tambulea
View
Fig. 1. Flowchart of the proposed solution for gender classification
Fig. 4. Loss function of Inception-v4 trained with image distortions
Automatic gender recognition for “in the wild” facial images using convolutional neural networks
Conference Paper
Full-text available
Sep 2017
Sergiu Cosmin Nistor
Alexandra-Cristina Marina
Adrian Sergiu Darabant
Diana Borza
View
Fig. 1: The evaluation tree and the values associated to an example query.
Fig. 2: Fragment used by a binary operator-one operand is always a leaf...
Table 2 : Costs and exec times for MFRN=1 and MFRN=5, cases (a) and (b)
Fig. 4: Cost Improvements Percents for MFRN=1 and MFRN=5
Access Patterns Optimization in Distributed Databases Using Data Reallocation
Conference Paper
Full-text available
Aug 2017
Adrian Sergiu Darabant
Leon Tambulea
Viorica Varga
Large distributed databases are split into fragments stored on far distant nodes that communicate through a communication network. Query execution requires data transfers between the processing sites of the system. In this paper we propose a solution for minimizing raw data transfers by re-arranging and replicating existing data within the constrai...
View
Fast Eye Tracking and Feature Measurement using a Multi-stage Particle Filter
Conference Paper
Jan 2017
Radu Danescu
Adrian Sergiu Darabant
Diana Borza
View
Table 1 . Iris center localization accuracies compared to the...
Table 2 . Iris center localization results on the University of...
Table 3 . Iris radius computation results on the University of Michigan...
Table 4 . Performance of the eye shape segmentation algorithm the UMFD...
+3Table 5 . Mean error normalized by the inter-pupillary distance.
Real-Time Detection and Measurement of Eye Features from Color Images
Article
Full-text available
Jul 2016
Diana Borza
Adrian Sergiu Darabant
Radu Danescu
The accurate extraction and measurement of eye features is crucial to a variety of domains, including human-computer interaction, biometry, and medical research. This paper presents a fast and accurate method for extracting multiple features around the eyes: the center of the pupil, the iris radius, and the external shape of the eye. These features...
View
Magnetic Stimulation of the Spinal Cord: Evaluating the Characteristics of an Appropriate Stimulator
Article
Oct 2015
Mihaela Cretu
Adrian Sergiu Darabant
Radu V. Ciupa
This article aims to determine the necessary characteristics of a magnetic stimulator, capable of stimulating neural tracts of the spinal cord in a healthy subject. Our previous preliminary tests had shown that the commercial clinical magnetic stimulator Magstim Rapid2 was unable to reach excitable structures within the spinal cord, and only adjace...
View
Eyeglasses contour extraction using genetic algorithms
Conference Paper
Sep 2015
Diana Borza
Radu Danescu
Adrian Sergiu Darabant
This paper presents an eyeglasses contour extraction method that uses genetic algorithms to find the exact shape of the lenses. An efficient shape description, based on Fourier coefficients, is used to represent the shape of the eyeglasses, allowing a wide range of shapes to be represented with a small number of parameters. The proposed method does...
View
Figure 1. Eyeglasses detection algorithm outline.
Figure 2. Reconstruction of the rim contour using Fourier descriptors....
Table 2 . Detection rates.
Table 3 . Comparison of the proposed method with related works.
+4Figure 7. Eyeglasses region of interest (ROI). The detected position of...
Eyeglasses Lens Contour Extraction from Facial Images Using an Efficient Shape Description
Article
Full-text available
Oct 2013
Diana Borza
Adrian Sergiu Darabant
Radu Danescu
This paper presents a system that automatically extracts the position of the eyeglasses and the accurate shape and size of the frame lenses in facial images. The novelty brought by this paper consists in three key contributions. The first one is an original model for representing the shape of the eyeglasses lens, using Fourier descriptors. The seco...
View
Magnetic Stimulation of the Spinal Cord: Experimental Results and Simulations
Article
May 2013
Laura Darabant
Mihaela Cretu
Adrian Sergiu Darabant
This paper aims in interpreting the leg muscles responses recorded by electromyography during magnetic stimulation of the spinal cord by computing the electric field induced in the spinal cord and the nearby areas during this procedure. A simplified model of the spine was created and a Finite Difference Method algorithm was implemented in Matlab.
View
Fig. 4. Comparative FPE clustering results.
Fig. 5. Comparative results for small, medium and large datasets.
Clustering methods in data fragmentation
Article
Full-text available
Jan 2011
Adrian Sergiu Darabant
L. Darabant
This paper proposes an enhanced version for three clustering algorithms: hierarchical, k-means and fuzzy c-means applied in horizontal object oriented data fragmentation. The main application is focusing in distributed object oriented database (OODB) fragmentation, but the method applicability is not limited to this research area. The proposed algo...
View
Figure 1. Illuminated center of pupils
Figure 2. Auxiliary object with markers
Figure 3. Multiple reflections issue
Figure 4. Final preprocessing step: Canny Edge Detection and Closing
+2Figure 6. Center detection on binarized image of circle
Computer Vision Aided Measurement of Morphological Features in Medical Optics
Article
Full-text available
Sep 2010
Bologa Bogdana
Adrian Sergiu Darabant
This paper presents a computer vision aided method for non invasive interupupillary (IPD) distance measurement. IPD is a morphological feature requirement in any oftalmological frame prescription. A good frame prescription is highly dependent nowadays on accurate IPD estimation in order for the lenses to be eye strain free. The idea is to replace t...
View
Figure 1. Original video frame from the input video.
Figure 2. Foreground objects after subtraction.
Figure 3. Binary image(a), Eroded image(b).
Figure 4. Dilated image-blobs are well separated and compact.
+3Figure 5. Normal blobs(a), Blobs with holes(b), Fragmented blobs(c).
A Computer Vision Approach to Object Tracking and Counting
Article
Full-text available
Sep 2010
Mezei Sergiu
Adrian Sergiu Darabant
This paper, introduces a new method for counting people or more generally objects that enter or exit a certain area/building or perimeter. We propose an algorithm (method) that analyzes a video sequence, detects moving objects and their moving direction and filters them according to some criteria (ex only humans). As result one obtains in and out c...
View
Energy Efficient Coils for Magnetic Stimulation of Peripheral Nerves
Article
Apr 2009
Laura Darabant
M. Plesa
Dan Micu[...]
Adrian Sergiu Darabant
The preoccupation for improving the quality of life, for persons with different handicaps, led to extended research in the area of functional stimulation. Due to its advantages compared to electrical stimulation, magnetic stimulation of the human nervous system is now a common technique in modern medicine. A difficulty of this technique is the need...
View
Hierarchical clustering in large object datasets – a study on complexity, quality and scalability
Article
Jan 2009
Adrian Sergiu Darabant
Anca Andreica
Object database fragmentation (horizontal fragmentation) deals with splitting the extension of classes into subsets according to some criteria. The resulting fragments are then used either in distributed database processing or in parallel data processing in order to spread the computation power over multiple nodes or to increase data locality featu...
View
A medical application of electromagnetic fields: The magnetic stimulation of nerve fibers inside a cylindrical tissue
Conference Paper
Jun 2008
M. Plesa
L. Darabant
R. Ciupa
Adrian Sergiu Darabant
A model is presented that predicts the electric field induced in the arm during magnetic stimulation of a peripheral nerve. The arm is represented as a homogeneous, cylindrical volume conductor. The electric field arises from two sources: the time - varying magnetic field and the accumulation of charge on the tissue - air surface. In magnetic stimu...
View
Fig. 2-The MobMed System Architecture and Integration with the Hospital...
Fig 3-Merge Replication Architecture .
Fig. 6 MobMed's login window
Fig. 7 MobMed's main and patient form
Mobile Devices and Data Synchronization Assisting Medical Diagnosis
Article
Full-text available
Jun 2008
Adrian Sergiu Darabant
Horea Todoran
In order to be able to establish the most accurate diagnostics as quick as possible, medical doctors need fast access not only to the current patient state and test results but also to its historical medical data. With the diversity of the malady symptoms today a correct diagnostic often requires a valuable time that is not always available due to...
View
Web services for e-learning and e-recruitment
Article
Jan 2007
George Chis
Horea Grebla
D. Matis[...]
Adrian Sergiu Darabant
Mobile phone communication can no longer be conceived as a communication mean only, but also as a way to integrate voice services together with data services which are oriented towards large consumer groups. Together with voice services, mobile Internet represents the second most important component of the service packages offered in Romania. The a...
View
Fig. 3 Comparative PE costs for variant M1 on all classes.
Fig. 5-PE values for M1 on complex class fragmentation and primary...
The similarity measures and their impact on OODB fragmentation using hierarchical clustering algorithms
Article
Full-text available
Sep 2006
Adrian Sergiu Darabant
Horea Todoran
Octavian Creţ
George Chis
Class fragmentation is an essential phase in the design of Distributed Object Oriented Databases (DOODB). Due to their semantic similarity with the purpose of database fragmentation (obtaining sets of similar objects with respect to the user applications running in the system), clustering algorithms have recently begun to be investigated in the pro...
View
Building an efficient architecture for data synchronization on mobile wireless agents
Article
Aug 2006
Adrian Sergiu Darabant
H. Todoran
Nowadays, negotiation between a representative of a commercial enterprise and its clients is a pre-requisite for selling most of the industrial goods in large quantities. In many cases, it is the task of a mobile salesman to conduct the negotiation on behalf of the supplier. But this is not an easy task to accomplish, since the mobile agent must br...
View
Fig.1 Business information flow
Fig. 2 – The MobSel System Architecture and Integration with the...
Fig 5 Controlling the synchronized data.
Implementing data synchronization on mobile wireless agents
Conference Paper
Full-text available
Jul 2006
Adrian Sergiu Darabant
Horea Todoran
Mobile salesmen out in the wild and the entire commercial store with them? A while ago this would have seemed atypical. Nowadays, it has become a must have asset for any salesmen-based commercial enterprise. In the past, the Web brought the virtual store to the client's premises. While this is still enough for certain types of commerce, negotiation...
View
Table 1 . Results of the software (C++) implementation
Table 2 . Results of the software implementation
Fig. 3. The hardware architecture in the 1D case
Solving the Maximum Subsequence Problem with a Hardware Agents-based System
Article
Full-text available
Jul 2006
Octavian Creţ
Zsolt Mathe
Cristina Grama[...]
Adrian Sergiu Darabant
The maximum subsequence problem is widely encountered in various digital processing systems. Given a stream of both positive and negative integers, it consists of determining the subsequence of maximal sum inside the input stream. In its two-dimensional version, the input is an array of both positive and negative integers, and the problem consists...
View
Figure 1: The fragmentation costs for the CBAk(incremental) and...
Table 1 : Comparative results for the CBAk and k-means algorithms
Incremental Horizontal Fragmentation: A new Approach in the Design of Distributed Object Oriented Databases
Article
Full-text available
Jan 2006
Adrian Sergiu Darabant
Alina Campan
Horea Todoran
Distributed relational or more recently object-oriented databases usually employ data fragmenta-tion techniques during the design phase in order to split and allocate the database entities across the nodes of the system. Most of the design algorithms are usually static and do not take into account the system evolution: data updates and addition of...
View
A Hardware Implementation of the Kadane’s Algorithm for the Maximum Subsequence Problem
Conference Paper
Jan 2006
Octavian Creţ
Zsolt Mathe
Lucia Văcariu[...]
Levente-Karoly Gorog
View
"The School in Your Pocket": Useful PoeketPC applications for students
Article
Jan 2006
Horea Todoran
Adrian Sergiu Darabant
Much smaller than laptops and still suitable for almost all kinds of applications, hand-held devices have the potential to rapidly become interesting tools for various daily activities. They can be successfully used in education by all participants (students, educators, administrative staff), if helpful applications are carefully designed and imple...
View
Figure 2. Macroflows composed of connections originating from different...
Fine-Grained Macroflow Granularity in Congestion Control Management
Article
Full-text available
Jun 2005
Darius Bufnea
Alina Campan
Adrian Sergiu Darabant
A recent approach in Internet congestion control suggests collaboration between sets of streams that should share network resources and learn from each other about the state of the network. Currently such a set of collaborating streams – a macroflow – is organized on host pair basis. We propose in this paper a new method for grouping streams into m...
View
Figure 3 Fuzzy fragmentation vs k-means primary and k-means...
Using Fuzzy Clustering for Advanced OODB Horizontal Fragmentation with Fine-Grained Replication.
Conference Paper
Full-text available
Jan 2005
Adrian Sergiu Darabant
Alina Campan
Octavian Creţ
In this paper we present a new approach for horizontal object oriented database fragmentation combined with fine-grained object level replication in one step. We build our fragmentation/replication method using AI probabilis- tic clustering (fuzzy clustering). Fragmentation quality evaluation is provided using an evaluator function.
View
Figure 1: The database class hierarchy
Figure 2: Experimental results
CLUSTERING TECHNIQUES FOR ADAPTIVE HORIZONTAL FRAGMENTATION IN OBJECT ORIENTED DATABASES
Article
Full-text available
Jan 2005
Alina Campan
Adrian Sergiu Darabant
Gabriela Serban
Optimal application performance in a Distributed Object Ori- ented System requires class fragmentation and the development of allocation schemes to place fragments at distributed sites so data transfer is minimal. A horizontal fragmentation approach that uses data mining clustering methods for partitioning object instances into fragments has alread...
View
Figure 1: The database class hierarchy
Figure 2: The database aggregation/association graph
Figure 3: Comparative PE values for our fragmentation method,...
Figure 4: Comparative class PE values for each similarity measure
Figure 5: Comparative PE values for primary only fragmentation and our...
A NEW APPROACH IN FRAGMENTATION OF DISTRIBUTED OBJECT ORIENTED DATABASES USING CLUSTERING TECHNIQUES
Article
Full-text available
Jan 2005
Adrian Sergiu Darabant
Horizontal fragmentation plays an important role in the design phase of Distributed Databases. Complex class relationships: associations, aggregations and complex methods, require fragmentation algorithms to take into account the new problem dimensions induced by these features of the object oriented models. We propose in this paper a new method fo...
View
Table 1 .
Table 2 .
Figure 3. Parameter transmission in the SW array
Figure 4. The interface of a PE and the connections between adjacent...
FPGA-based Scalable Implementation of the General Smith-Waterman Algorithm
Conference Paper
Full-text available
Nov 2004
Octavian Creţ
Stefan Mathe
Balint Szente[...]
Adrian Sergiu Darabant
The Smith-Waterman algorithm is fundamental in Bioinformatics. This paper presents an FPGA-based systolic implementation of the Smith-Waterman algorithm that addresses a general case of it. A solution that improves the scalability of the design is proposed. The architecture is optimized for both speed and space, by reusing the hardware resources fo...
View
TABLE 2 . Allocation of Fragments to Distributed Sites
Fig. 3. Comparative quality measures for each class.
Fig. 4. Comparative PE for k-means, full replication and centralized case.
Fig. 5. Comparative PE values for our fragmentation methods.
Semi-supervised learning techniques: k-means clustering in OODB Fragmentation
Conference Paper
Full-text available
Feb 2004
Adrian Sergiu Darabant
Alina Campan
Vertical and horizontal fragmentations are central issues in the design process of distributed object based systems. A good fragmentation scheme followed by an optimal allocation could greatly enhance performance in such systems, as data transfer between distributed sites is minimized. In this paper we present a horizontal fragmentation approach th...
View
Figure 1: The database inheritance hierarchy
Figure 2: The database aggregation hierarchy
Figure 3: Partial RelGraph-CAN values and weights
Figure 4: Comparative PE values for each class
Figure 5: Comparative PE values for different fragmentation orders
A new approach for optimal fragmentation order in distributed object oriented databases
Article
Full-text available
Feb 2004
Adrian Sergiu Darabant
Alina Campan
Class fragmentation is an important task in the design of Distributed OODBs and there are many algorithms handling it. Almost none of them deals however with the class fragmentation order details. We claim that class fragmentation order can induce severe performance penalties if not considered in the frag- mentation phase. We propose here two varia...
View
Figure 1. The database inheritance hierarchy
Figure 2. The database aggregation hierarchy
OPTIMAL CLASS FRAGMENTATION ORDERING IN OBJECT ORIENTED DATABASES
Article
Full-text available
Jan 2004
Adrian Sergiu Darabant
Alina Campan
Distributed Object Oriented Databases require class fragmenta- tion, performed either horizontally or vertically. Complex class relationships like aggregation and/or association are often represented as two-way refer- ences or object-links between classes. In order to obtain a good quality horizontal fragmentation, an optimal class processing order...
View
TABLE 1.
Figure 3 Comparative PE values for our fragmentation method,...
Figure 4 Comparative class PE values for each similarity measure.
AI CLUSTERING TECHNIQUES: A NEW APPROACH IN HORIZONTAL FRAGMENTATION OF CLASSES WITH COMPLEX ATTRIBUTES AND METHODS IN OBJECT ORIENTED DATABASES
Article
Full-text available
Jan 2004
Adrian Sergiu Darabant
Alina Campan
Grigor Moldovan
Horea Grebla
Horizontal fragmentation plays an important role in the design phase of Distributed Databases. Complex class relationships: associations, aggregations and complex methods, require fragmentation algorithms to take into account the new problem dimensions induced by these features of the object oriented models. We propose in this paper a new method fo...
View
DATA ALLOCATION IN DISTRIBUTED DATABASE SYSTEMS PERFORMED BY MOBILE INTELLIGENT AGENTS
Article
Full-text available
Jan 2004
Horea Grebla
Grigor Moldovan
Adrian Sergiu Darabant
Alina Campan
As the European Union extends its boundaries the major companies have extended their presence on different markets resulting sales expansion and marketing specialization. Moreover, globalization brings a bigger impact on vital business's data because of the applications that have been developed on platforms having specific aspects by means of datab...
View
Figure 2. Comparative PE for k-means, full replication and centralized...
Figure 3. Comparison quality measures for each of our fragmentation...
Advanced Object Database Design Techniques
Article
Full-text available
Jan 2004
Adrian Sergiu Darabant
Alina Ampan
Class fragmentation is an important task in the design of Distributed Object Oriented Databases (DOOD). However, fragmentation in DOOD is still at its beginnings and mostly adapted from the relational approaches. In this paper we propose an alternative approach for horizontal fragmentation of DOOD. Our method uses two different AI clustering techni...
View
Fig. 2 . CREC development system
A hardware/software codesign method for general purpose reconfigurable computing
Conference Paper
Full-text available
Jul 2003
Octavian Creţ
Kalman Pusztai
Cristian Cosmin Vancea[...]
Adrian Sergiu Darabant
CREC is an original, low-cost general-purpose Reconfigurable Computer whose architecture is generated through a Hardware / Software CoDesign process. The main idea of the CREC computer is to generate the best-suited hardware architecture for the execution of each software application. The CREC Parallel Compiler parses the source code and generates...
View
Current Technologies in Automatic Test Suites Generation and Verification of Complex Systems
Article
Full-text available
Jan 1999
Adrian Sergiu Darabant
View
Multi-tiered client-server techniques for distributed database systems
Article
Jan 1998
Adrian Sergiu Darabant
Information explosion across all areas has determined an increase in hardware requirements for application that provide data to the users. As hardware evelopment is quite susceptible to be bound after a top barrier is reached, new technologies must be developed in the software area in order to keep up with the requirements. We present here such a t...
View
Fig. 2. The database class hierarchy
Fig. 3. The database aggregation/association graph
Hierarchical clustering in object oriented data models with complex class relationships
Article
Full-text available
Adrian Sergiu Darabant
Alina Campan
Octavian Creţ
Class fragmentation is an essential phase in the design of Distributed Object Oriented Databases (DOODB). Horizontal and vertical fragmentation are the two commonly used fragmentation techniques. We propose here two new methods for horizontal fragmentation of objects with complex attributes. They rely on AI clustering techniques for grouping object...
View
Energy Efficient Coils for Transcranial Magnetic Stimulation (TMS)
Article
Laura DARABANT
M. Plesa
Radu CIUPA[...]
Adrian Sergiu Darabant
The preoccupation for improving the quality of life, for persons with different handicaps, led to extended research in the area of functional stimulation. Due to its advantages compared to electrical stimulation, magnetic stimulation of the human nervous system is now a common technique in modern medicine. A difficulty of this technique is the need...
View
Fig.2: Web Services for E-Learning
E-Learning Services as a Recruitment Tool
Article
Full-text available
George Chis
Horea Grebla
DUMITRU MATIS[...]
Adrian Sergiu Darabant
Networks expansion and Internet provide a good platform for e-learning in the idea of connecting learners with educational resources. The various systems that are already implemented consider the learning process as a remote task to gather knowledge in order to pass some exams. In the learning process evaluation represents a final step for a course...
View
A Comparative Study of Horizontal Object Clustering-based Fragmentation Techniques
Article
Adrian Sergiu Darabant
Alina Campan
Design of modern Distributed Object Oriented Databases (DOODs) requires class fragmentation techniques. Although research has been conducted in this area, most of the developed methods are inspired from the relational fragmentation algorithms. In this paper we develop a comparative approach of two new methods for horizontal class fragmentation in a...
View
TABLE 2 . OCM -exceptional case
TABLE 3 . CVM -for OCM
Fig. 4. Comparative quality measures for fragmentation variants,...
TABLE 4 . OCM -with phantom object
TABLE 5 . CVM -with phantom object
AI Clustering Techniques: a New Approach to Object Oriented Database Fragmentation
Article
Full-text available
Adrian Sergiu Darabant
Alina Campan
Cluj Napoca
M Kogalniceanu
Optimal application performance on a Distributed Object Based System requires class fragmentation and the development of allocation schemes to place fragments at distributed sites so data transfer is minimal. In this paper we present a horizontal fragmentation approach that uses the k-means centroid based clustering method for partitioning object i...
View
A Comparative Study on the Influence of Similarity Measures in Hierarchical Clustering in Complex Distributed Object-Oriented Databases
Article
Full-text available
Adrian Sergiu Darabant
Horea Todoran
Octavian Creţ
George Chis
Class fragmentation is an essential phase in the design of Distributed Object Oriented Databases (DOODB). Due to their semantic similarity with the purpose of database fragmentation (obtaining sets of similar objects with respect to the user applications running in the system), clustering algorithms have recently begun to be investigated in the pro...
View
Figure 1. Medical information flow
Figure 2. The MobMed Architecture and Integration with the Hospital...
Figure 3. Merge Replication Architecture
EFFICIENT DATA SYNCHRONIZATION FOR MOBILE WIRELESS MEDICAL USERS
Article
Full-text available
Adrian Sergiu Darabant
Darabant And
Horea Todoran
In order to take the appropriate decisions as quick as possible, medical doctors need fast access to various pieces of information on their pa-tients. The required information should be accurate, up-to-date, and avail-able on the spot. Even more, after finishing his/her investigation, the medical doctor should be able to immediately forward the rel...
View
Implementing Efficient Data Synchronization for Mobile Wireless Medical Users
Article
Full-text available
Adrian Sergiu Darabant
In order to take the appropriate decisions as quick as possible, medical doctors need fast access to various pieces of information on their patients. The required information should be accurate, up-to-date, and available on the spot. Even more, after finishing his/her investigation, the medical doctor should be able to immediately forward the relev...
View
"""
import re
class HelperMethods:
@staticmethod
def IsDate(text):
# print("text")
# print(text)
val = re.match("(Jan|Feb|Mar|Apr|May|Jun|Jul|Aug|Sep|Oct|Nov|Dec) (1|2)(0|9)[0-9]{2}", text)
if not val:
return False
return True
mylines = []
ctr = 0
title = ""
authors = ""
affiliations = ""
date = ""
papers = []
titles = []
dates = []
for line in text.split('View')[1:-1]:
fields = []
current_date = None
print(line.split('\n'))
for field in line.split('\n'):
val = re.match("(\+[0-9])?(Figure|Fig[\.]?|Table|TABLE)( )?[0-9]+", field)
if val:
continue
if field == "":
continue
print("field: ", field)
fields.append(field)
if HelperMethods.IsDate(field):
current_date = field
title = fields[0]
papers.append((title, current_date))
print(len(papers))
print(papers)
for i, paper in enumerate(papers):
print(i, paper)
#mylines[i][0] = mylines[i][1]
```
# DB Storage (TODO)
Time to store the entries in the `papers` DB table.

```
import mariadb
import json
with open('../credentials.json', 'r') as crd_json_fd:
json_text = crd_json_fd.read()
json_obj = json.loads(json_text)
credentials = json_obj["Credentials"]
username = credentials["username"]
password = credentials["password"]
table_name = "publications_cache"
db_name = "ubbcluj"
mariadb_connection = mariadb.connect(user=username, password=password, database=db_name)
mariadb_cursor = mariadb_connection.cursor()
import datetime
from datetime import datetime
for paper in papers:
title = ""
authors = ""
pub_date = ""
affiliations = ""
try:
title = paper[0].lstrip()
except:
pass
try:
# print(paper[1])
pub_date = datetime.strptime(paper[1], "%b %Y").strftime("%Y-%m-%d")
except:
pass
insert_string = "INSERT INTO {0} SET ".format(table_name)
insert_string += "Title=\'{0}\', ".format(title)
insert_string += "ProfessorId=\'{0}\', ".format(12)
if pub_date != "":
insert_string += "PublicationDate=\'{0}\', ".format(str(pub_date))
insert_string += "Authors=\'{0}\', ".format(authors)
insert_string += "Affiliations=\'{0}\' ".format(affiliations)
print(insert_string)
# print(paper)
# continue
try:
mariadb_cursor.execute(insert_string)
except mariadb.ProgrammingError as pe:
print("Error")
raise pe
except mariadb.IntegrityError:
continue
mariadb_connection.close()
```
# Conclusion
### In the end, the DB only required ~1 manual modifications with this code.
This was first stored in a DB cache table which is a duplicate of the main, reviewed, then inserted in the main table.
| true |
code
| 0.724103 | null | null | null | null |
|
```
from IPython.core.display import HTML
def css_styling():
styles = open("./styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
# Approximate solutions to the Riemann Problem
## Solutions in practice
Solutions to the Riemann problem are mainly used in two contexts:
1. As reference solutions against which a numerical method is benchmarked, or
2. As part of a numerical method, such as a high resolution shock capturing method, where the flux between two numerical cells is required.
In the first case, accuracy is paramount and the complete solution (all wave speeds, and all intermediate states) is required. In the second case only one thing is required: the flux ${\bf f}^*$ between the cells, which is the flux on the characteristic line $\xi = x / t = 0$.
In this second case, the numerical method will have to repeatedly solve the Riemann problem. In a general problem, the solution may be needed tens of times *per cell, per timestep*, leading to millions (or more!) solutions in a simulation. The speed of the solution is then extremely important, and approximate solutions are often used.
## Roe-type solutions
The most obvious simplification is to reduce the nonlinear problem
\begin{equation}
\partial_t {\bf q} + \partial_x {\bf f}({\bf q}) = {\bf 0}
\end{equation}
to the *linear* problem
\begin{equation}
\partial_t {\bf q} + A \partial_x {\bf q} = {\bf 0},
\end{equation}
where $A$ is a *constant* matrix that approximates the Jacobian $\partial {\bf f} / \partial {\bf q}$. We can then solve the linear problem exactly (e.g. by diagonalising the matrix and solving the resulting uncoupled advection equations), to find
\begin{align}
{\bf q}(x, t) & = {\bf q}_l + \sum_{p: \lambda^{(p)} < \tfrac{x}{t}} \left\{ {\bf l}^{(p)} \cdot \left( {\bf q}_r - {\bf q}_l \right) \right\} {\bf r}^{(p)}, \\
& = {\bf q}_r - \sum_{p: \lambda^{(p)} > \tfrac{x}{t}} \left\{ {\bf l}^{(p)} \cdot \left( {\bf q}_r - {\bf q}_l \right) \right\} {\bf r}^{(p)}, \\
& = \frac{1}{2} \left( {\bf q}_l + {\bf q}_r \right) + \sum_{p: \lambda^{(p)} < \tfrac{x}{t}} \left\{ {\bf l}^{(p)} \cdot \left( {\bf q}_r - {\bf q}_l \right) \right\} {\bf r}^{(p)} - \sum_{p: \lambda^{(p)} > \tfrac{x}{t}} \left\{ {\bf l}^{(p)} \cdot \left( {\bf q}_r - {\bf q}_l \right) \right\} {\bf r}^{(p)}.
\end{align}
where $\lambda^{(p)}, {\bf r}^{(p)},$ and ${\bf l}^{(p)}$ are the eigenvalues and the (right and left respectively) eigenvectors of $A$, ordered such that $\lambda^{(1)} \le \dots \le \lambda^{(N)}$ as usual. All three solutions are equivalent; the last is typically used.
Given this complete solution, it is easily evaluated along $x = 0$, and the flux calculated from the result.
An even greater shortcut can be found by noting that we are approximating ${\bf f} = A {\bf q}$. Therefore the standard form is to write
\begin{equation}
{\bf f}^* = \frac{1}{2} \left( {\bf f}_l + {\bf f}_r \right) + \sum_{p} \left| \lambda^{(p)} \right| \left\{ {\bf l}^{(p)} \cdot \left( {\bf q}_r - {\bf q}_l \right) \right\} {\bf r}^{(p)},
\end{equation}
where now we are summing over all eigenvalues and eigenvectors. It should be noted that ${\bf f}^* \ne {\bf f}({\bf q}^*)$ in general, as the calculation of ${\bf f}^*$ relied on an approximation to the flux.
In order to complete this specification of the solver, we only need to say how $A$ is defined. Roe gave the suggestion that
\begin{equation}
A = A({\bf q}_{\textrm{Roe}}) = \left. \frac{\partial {\bf f}}{\partial {\bf q}} \right|_{{\bf q}_{\textrm{Roe}}},
\end{equation}
where the *Roe average* ${\bf q}_{\textrm{Roe}}$ satisfies
1. $A({\bf q}_{\textrm{Roe}}) \left( {\bf q}_r - {\bf q}_l \right) = {\bf f}_r - {\bf f}_l$,
2. $A({\bf q}_{\textrm{Roe}})$ is diagonalizable with real eigenvalues, and
3. $A({\bf q}_{\textrm{Roe}}) \to \partial {\bf f} / \partial {\bf q}$ smoothly as ${\bf q}_{\textrm{Roe}} \to {\bf q}$.
It is *possible* to construct the Roe average for many systems (such as the Euler equations, and the relativistic Euler equations). However, a simple arithmetic average is often nearly as good - in the sense that the algorithm will fail only slightly more often than the algorithm with the full Roe average!
The problem with Roe type solvers is that it approximates all waves as discontinuities. This leads to inaccuracies near rarefactions, and these can be catastrophically bad when the rarefaction fan crosses $\xi = 0$ (a *sonic rarefaction*). It is possible to detect when these problems will occur (e.g. by looking at when $\lambda^{(p)}$ changes sign between the left and right states) and change the approximation at this point, often known as an *entropy fix*. More systematic and complex methods that extend the Roe approach whilst avoiding this problem include the *Marquina* solver.
## HLL-type solutions
An alternative type of method simplifies the wave structure even more, by simplifying the number of waves. HLL (for Harten, Lax and van Leer) type solutions assume that
1. there are two waves, both discontinuities, separating a constant central state in the solution, and
2. the waves propagate at the (known) speeds $\xi_{(\pm)}$.
From these assumptions, and the Rankine-Hugoniot conditions, we have the two equations
\begin{align}
\xi_{(-)} \left[ {\bf q}_m - {\bf q}_l \right] & = {\bf f}_m - {\bf f}_l, \\
\xi_{(+)} \left[ {\bf q}_r - {\bf q}_m \right] & = {\bf f}_r - {\bf f}_m.
\end{align}
These are immediately solved to give
\begin{align}
{\bf q}_m & = \frac{\xi_{(+)} {\bf q}_r - \xi_{(-)} {\bf q}_l - {\bf f}_r + {\bf f}_l}{\xi_{(+)} - \xi_{(-)}}, \\
{\bf f}_m & = \frac{\hat{\xi}_{(+)} {\bf f}_l - \hat{\xi}_{(-)} {\bf f}_r + \hat{\xi}_{(+)} \hat{\xi}_{(-)} \left( {\bf q}_r - {\bf q}_r \right)}{\hat{\xi}_{(+)} - \hat{\xi}_{(-)}},
\end{align}
where
\begin{equation}
\hat{\xi}_{(-)} = \min(0, \xi_{(-)}), \qquad \hat{\xi}_{(+)} = \max(0, \xi_{(+)}).
\end{equation}
Again it should be noted that, in general, ${\bf f}_m \ne {\bf f}({\bf q}_m)$.
We still need some way to compute the wave speeds $\xi_{(\pm)}$. The simplest method is to make them as large as possible, compatible with stability. This means (via the CFL condition) setting
\begin{equation}
-\xi_{(-)} = \xi_{(+)} = \frac{\Delta x}{\Delta t}
\end{equation}
which implies that (as the central state is now guaranteed to include the origin, as the waves have different signs)
\begin{equation}
{\bf f}^* = \frac{1}{2} \left( {\bf f}_l + {\bf f}_r + \frac{\Delta x}{\Delta t} \left[ {\bf q}_l - {\bf q}_r \right] \right).
\end{equation}
This is the *Lax-Friedrichs* flux, as [used in HyperPython](https://github.com/ketch/HyperPython). We can also easily see how the *local* Lax-Friedrichs method, [used in lesson 3 of HyperPython](http://nbviewer.ipython.org/github/ketch/HyperPython/blob/master/Lesson_03_High-resolution_methods.ipynb), comes about: simply choose
\begin{equation}
-\xi_{(-)} = \xi_{(+)} = \alpha = \min \left( \left| \lambda \left( {\bf q}_l \right) \right|, \left| \lambda \left( {\bf q}_r \right) \right| \right)
\end{equation}
to get
\begin{equation}
{\bf f}^* = \frac{1}{2} \left( {\bf f}_l + {\bf f}_r + \alpha \left[ {\bf q}_l - {\bf q}_r \right] \right).
\end{equation}
HLL type methods are straightforward to use but typically do not capture linear waves, such as the contact wave in the Euler equations, well. Extending the HLL method by including more waves is possible (see the *HLLC* method in Toro's book as an example), but rapidly increases the complexity of the solver.
| true |
code
| 0.22657 | null | null | null | null |
|
```
import numpy as np
import tensorflow as tf
import matplotlib.pylab as plt
from modules.spectral_pool import max_pool, l2_loss_images
from modules.frequency_dropout import test_frequency_dropout
from modules.create_images import open_image, downscale_image
from modules.utils import load_cifar10
np.set_printoptions(precision=3, linewidth=200)
% matplotlib inline
% load_ext autoreload
% autoreload 2
images, _ = load_cifar10(1, get_test_data=False)
images.shape
```
### In the cell below, we choose two random images and show how the quality progressively degradees as frequency dropout is applied.
```
batch_size=2
random_selection_indices = np.random.choice(len(images), size=batch_size)
for cutoff in range(16,1,-2):
minibatch_cutoff = tf.cast(tf.constant(cutoff), dtype=tf.float32)
random_selection = images[random_selection_indices]
downsampled_images = np.moveaxis(
test_frequency_dropout(
np.moveaxis(random_selection, 3, 1),
minibatch_cutoff
), 1, 3
)
print('Cutoff = {0}'.format(cutoff))
for i in range(batch_size):
plt.imshow(np.clip(downsampled_images[i],0,1), cmap='gray')
plt.show()
```
### The next cell demonstrates how the random cutoff is applied to all images in a minibatch, but changes from batch to batch.
```
batch_size = 2
minibatch_cutoff = tf.random_uniform([], 2, 12)
for iter_idx in range(3):
random_selection_indices = np.random.choice(len(images), size=batch_size)
random_selection = images[random_selection_indices]
downsampled_images = np.moveaxis(
test_frequency_dropout(
np.moveaxis(random_selection, 3, 1),
minibatch_cutoff
), 1, 3
)
print('Minibatch {0}'.format(iter_idx+1))
for i in range(batch_size):
plt.imshow(random_selection[i], cmap='gray')
plt.show()
plt.imshow(np.clip(downsampled_images[i],0,1), cmap='gray')
plt.show()
```
### max pool test
```
images_pool = max_pool(images, 2)
images_pool.shape
plt.imshow(images_pool[1], cmap='gray')
```
### spectral pool test
```
cutoff_freq = int(32 / (2 * 2))
tf_cutoff_freq = tf.cast(tf.constant(cutoff_freq), tf.float32)
images_spectral_pool = np.clip(np.moveaxis(
test_frequency_dropout(
np.moveaxis(images, 3, 1),
tf_cutoff_freq
), 1, 3
), 0, 1)
images_spectral_pool.shape
plt.imshow(images_spectral_pool[1], cmap='gray')
```
## Iterate and plot
```
images_sample = images[np.random.choice(len(images), size=256)]
# calculate losses for max_pool:
pool_size_mp = [2, 4, 8, 16, 32]
max_pool_errors = []
for s in pool_size_mp:
images_pool = max_pool(images_sample, s)
loss = l2_loss_images(images_sample, images_pool)
max_pool_errors.append(loss)
# calculate losses for spectral_pool:
filter_size_sp = np.arange(16)
spec_pool_errors = []
for s in filter_size_sp:
tf_cutoff_freq = tf.cast(tf.constant(s), tf.float32)
images_sp = np.moveaxis(
test_frequency_dropout(
np.moveaxis(images_sample, 3, 1),
tf_cutoff_freq
), 1, 3
)
loss = l2_loss_images(images_sample, images_sp)
spec_pool_errors.append(loss)
pool_frac_kept = [1/x**2 for x in pool_size_mp]
sp_frac_kept = [(x/16)**2 for x in filter_size_sp]
fig, ax = plt.subplots(1, 1)
ax.semilogy(pool_frac_kept, max_pool_errors, basey=2,
marker='o', linestyle='--', color='r', label='Max Pooling')
ax.semilogy(sp_frac_kept, spec_pool_errors, basey=2,
marker='o', linestyle='--', color='b', label='Spectral Pooling')
ax.legend()
ax.grid(linestyle='--', alpha=0.5)
ax.set_xlabel('Fraction of Parameters Kept')
ax.set_ylabel('Relative Loss')
fig.savefig('../Images/Figure4_Approximation_Loss.png')
```
| true |
code
| 0.739594 | null | null | null | null |
|
# How to use OpenNMT-py as a Library
The example notebook (available [here](https://github.com/OpenNMT/OpenNMT-py/blob/master/docs/source/examples/Library.ipynb)) should be able to run as a standalone execution, provided `onmt` is in the path (installed via `pip` for instance).
Some parts may not be 100% 'library-friendly' but it's mostly workable.
### Import a few modules and functions that will be necessary
```
import yaml
import torch
import torch.nn as nn
from argparse import Namespace
from collections import defaultdict, Counter
import onmt
from onmt.inputters.inputter import _load_vocab, _build_fields_vocab, get_fields, IterOnDevice
from onmt.inputters.corpus import ParallelCorpus
from onmt.inputters.dynamic_iterator import DynamicDatasetIter
from onmt.translate import GNMTGlobalScorer, Translator, TranslationBuilder
from onmt.utils.misc import set_random_seed
```
### Enable logging
```
# enable logging
from onmt.utils.logging import init_logger, logger
init_logger()
```
### Set random seed
```
is_cuda = torch.cuda.is_available()
set_random_seed(1111, is_cuda)
```
### Retrieve data
To make a proper example, we will need some data, as well as some vocabulary(ies).
Let's take the same data as in the [quickstart](https://opennmt.net/OpenNMT-py/quickstart.html):
```
!wget https://s3.amazonaws.com/opennmt-trainingdata/toy-ende.tar.gz
!tar xf toy-ende.tar.gz
ls toy-ende
```
### Prepare data and vocab
As for any use case of OpenNMT-py 2.0, we can start by creating a simple YAML configuration with our datasets. This is the easiest way to build the proper `opts` `Namespace` that will be used to create the vocabulary(ies).
```
yaml_config = """
## Where the vocab(s) will be written
save_data: toy-ende/run/example
# Corpus opts:
data:
corpus:
path_src: toy-ende/src-train.txt
path_tgt: toy-ende/tgt-train.txt
transforms: []
weight: 1
valid:
path_src: toy-ende/src-val.txt
path_tgt: toy-ende/tgt-val.txt
transforms: []
"""
config = yaml.safe_load(yaml_config)
with open("toy-ende/config.yaml", "w") as f:
f.write(yaml_config)
from onmt.utils.parse import ArgumentParser
parser = ArgumentParser(description='build_vocab.py')
from onmt.opts import dynamic_prepare_opts
dynamic_prepare_opts(parser, build_vocab_only=True)
base_args = (["-config", "toy-ende/config.yaml", "-n_sample", "10000"])
opts, unknown = parser.parse_known_args(base_args)
opts
from onmt.bin.build_vocab import build_vocab_main
build_vocab_main(opts)
ls toy-ende/run
```
We just created our source and target vocabularies, respectively `toy-ende/run/example.vocab.src` and `toy-ende/run/example.vocab.tgt`.
### Build fields
We can build the fields from the text files that were just created.
```
src_vocab_path = "toy-ende/run/example.vocab.src"
tgt_vocab_path = "toy-ende/run/example.vocab.tgt"
# initialize the frequency counter
counters = defaultdict(Counter)
# load source vocab
_src_vocab, _src_vocab_size = _load_vocab(
src_vocab_path,
'src',
counters)
# load target vocab
_tgt_vocab, _tgt_vocab_size = _load_vocab(
tgt_vocab_path,
'tgt',
counters)
# initialize fields
src_nfeats, tgt_nfeats = 0, 0 # do not support word features for now
fields = get_fields(
'text', src_nfeats, tgt_nfeats)
fields
# build fields vocab
share_vocab = False
vocab_size_multiple = 1
src_vocab_size = 30000
tgt_vocab_size = 30000
src_words_min_frequency = 1
tgt_words_min_frequency = 1
vocab_fields = _build_fields_vocab(
fields, counters, 'text', share_vocab,
vocab_size_multiple,
src_vocab_size, src_words_min_frequency,
tgt_vocab_size, tgt_words_min_frequency)
```
An alternative way of creating these fields is to run `onmt_train` without actually training, to just output the necessary files.
### Prepare for training: model and optimizer creation
Let's get a few fields/vocab related variables to simplify the model creation a bit:
```
src_text_field = vocab_fields["src"].base_field
src_vocab = src_text_field.vocab
src_padding = src_vocab.stoi[src_text_field.pad_token]
tgt_text_field = vocab_fields['tgt'].base_field
tgt_vocab = tgt_text_field.vocab
tgt_padding = tgt_vocab.stoi[tgt_text_field.pad_token]
```
Next we specify the core model itself. Here we will build a small model with an encoder and an attention based input feeding decoder. Both models will be RNNs and the encoder will be bidirectional
```
emb_size = 100
rnn_size = 500
# Specify the core model.
encoder_embeddings = onmt.modules.Embeddings(emb_size, len(src_vocab),
word_padding_idx=src_padding)
encoder = onmt.encoders.RNNEncoder(hidden_size=rnn_size, num_layers=1,
rnn_type="LSTM", bidirectional=True,
embeddings=encoder_embeddings)
decoder_embeddings = onmt.modules.Embeddings(emb_size, len(tgt_vocab),
word_padding_idx=tgt_padding)
decoder = onmt.decoders.decoder.InputFeedRNNDecoder(
hidden_size=rnn_size, num_layers=1, bidirectional_encoder=True,
rnn_type="LSTM", embeddings=decoder_embeddings)
device = "cuda" if torch.cuda.is_available() else "cpu"
model = onmt.models.model.NMTModel(encoder, decoder)
model.to(device)
# Specify the tgt word generator and loss computation module
model.generator = nn.Sequential(
nn.Linear(rnn_size, len(tgt_vocab)),
nn.LogSoftmax(dim=-1)).to(device)
loss = onmt.utils.loss.NMTLossCompute(
criterion=nn.NLLLoss(ignore_index=tgt_padding, reduction="sum"),
generator=model.generator)
```
Now we set up the optimizer. This could be a core torch optim class, or our wrapper which handles learning rate updates and gradient normalization automatically.
```
lr = 1
torch_optimizer = torch.optim.SGD(model.parameters(), lr=lr)
optim = onmt.utils.optimizers.Optimizer(
torch_optimizer, learning_rate=lr, max_grad_norm=2)
```
### Create the training and validation data iterators
Now we need to create the dynamic dataset iterator.
This is not very 'library-friendly' for now because of the way the `DynamicDatasetIter` constructor is defined. It may evolve in the future.
```
src_train = "toy-ende/src-train.txt"
tgt_train = "toy-ende/tgt-train.txt"
src_val = "toy-ende/src-val.txt"
tgt_val = "toy-ende/tgt-val.txt"
# build the ParallelCorpus
corpus = ParallelCorpus("corpus", src_train, tgt_train)
valid = ParallelCorpus("valid", src_val, tgt_val)
# build the training iterator
train_iter = DynamicDatasetIter(
corpora={"corpus": corpus},
corpora_info={"corpus": {"weight": 1}},
transforms={},
fields=vocab_fields,
is_train=True,
batch_type="tokens",
batch_size=4096,
batch_size_multiple=1,
data_type="text")
# make sure the iteration happens on GPU 0 (-1 for CPU, N for GPU N)
train_iter = iter(IterOnDevice(train_iter, 0))
# build the validation iterator
valid_iter = DynamicDatasetIter(
corpora={"valid": valid},
corpora_info={"valid": {"weight": 1}},
transforms={},
fields=vocab_fields,
is_train=False,
batch_type="sents",
batch_size=8,
batch_size_multiple=1,
data_type="text")
valid_iter = IterOnDevice(valid_iter, 0)
```
### Training
Finally we train.
```
report_manager = onmt.utils.ReportMgr(
report_every=50, start_time=None, tensorboard_writer=None)
trainer = onmt.Trainer(model=model,
train_loss=loss,
valid_loss=loss,
optim=optim,
report_manager=report_manager,
dropout=[0.1])
trainer.train(train_iter=train_iter,
train_steps=1000,
valid_iter=valid_iter,
valid_steps=500)
```
### Translate
For translation, we can build a "traditional" (as opposed to dynamic) dataset for now.
```
src_data = {"reader": onmt.inputters.str2reader["text"](), "data": src_val}
tgt_data = {"reader": onmt.inputters.str2reader["text"](), "data": tgt_val}
_readers, _data = onmt.inputters.Dataset.config(
[('src', src_data), ('tgt', tgt_data)])
dataset = onmt.inputters.Dataset(
vocab_fields, readers=_readers, data=_data,
sort_key=onmt.inputters.str2sortkey["text"])
data_iter = onmt.inputters.OrderedIterator(
dataset=dataset,
device="cuda",
batch_size=10,
train=False,
sort=False,
sort_within_batch=True,
shuffle=False
)
src_reader = onmt.inputters.str2reader["text"]
tgt_reader = onmt.inputters.str2reader["text"]
scorer = GNMTGlobalScorer(alpha=0.7,
beta=0.,
length_penalty="avg",
coverage_penalty="none")
gpu = 0 if torch.cuda.is_available() else -1
translator = Translator(model=model,
fields=vocab_fields,
src_reader=src_reader,
tgt_reader=tgt_reader,
global_scorer=scorer,
gpu=gpu)
builder = onmt.translate.TranslationBuilder(data=dataset,
fields=vocab_fields)
```
**Note**: translations will be very poor, because of the very low quantity of data, the absence of proper tokenization, and the brevity of the training.
```
for batch in data_iter:
trans_batch = translator.translate_batch(
batch=batch, src_vocabs=[src_vocab],
attn_debug=False)
translations = builder.from_batch(trans_batch)
for trans in translations:
print(trans.log(0))
break
```
| true |
code
| 0.762945 | null | null | null | null |
|
# Pessimistic Neighbourhood Aggregation for States in Reinforcement Learning
*Author: Maleakhi Agung Wijaya
Supervisors: Marcus Hutter, Sultan Javed Majeed
Date Created: 21/12/2017*
```
import random
import math
import sys
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import display, clear_output
# Set grid color for seaborn
sns.set(style="whitegrid")
```
## Mountain Car Environment
**Mountain Car** is a standard testing domain in Reinforcement Learning, in which an under-powered car must drive up a steep hill. Since gravity is stronger than the car's engine, even at full throttle, the car cannot simply accelerate up the steep slope. The car is situated in a valley and must learn to leverage potential energy by driving up the opposite hill before the car is able to make it to the goal at the top of the rightmost hill.
**Technical Details**
- *State:* feature vectors consisting of velocity and position represented by an array [velocity, position]
- *Reward:* -1 for every step taken, 0 for achieving the goal
- *Action:* (left, neutral, right) represented by (-1, 0, 1)
- *Initial state:* velocity = 0.0, position = -0.5 represented by [0.0, -0.5]
- *Terminal state:* position >= 0.6
- *Boundaries:* velocity = (-0.07, 0.07), position = (-1.2, 0.6)
- *Update function:* velocity = velocity + (Action) \* 0.001 + cos(3\*Position) * (-0.0025), position = position + velocity
```
class MountainCarEnvironment:
"""
Description: Environment for Mountain Car problem, adapted from Sutton and Barto's Introduction to Reinforcement Learning.
Author: Maleakhi Agung Wijaya
"""
VELOCITY_BOUNDARIES = (-0.07, 0.07)
POSITION_BOUNDARIES = (-1.2, 0.6)
INITIAL_VELOCITY = 0.0
INITIAL_POSITION = -0.5
REWARD_STEP = -1
REWARD_TERMINAL = 0
# Constructor for MountainCarEnvironment
# Input: agent for the MountainCarEnvironment
# Output: MountainCarEnvironment object
def __init__(self, car):
self.car = car
self.reset()
# Compute next state (feature)
# Output: [new velocity, new position]
def nextState(self, action):
# Get current state (velocity, position) and the action chosen by the agent
velocity = self.car.state[0]
position = self.car.state[1]
# Calculate the new velocity and new position
velocity += action * 0.001 + math.cos(3*position) * (-0.0025)
# Consider boundary for velocity
if (velocity < MountainCarEnvironment.VELOCITY_BOUNDARIES[0]):
velocity = MountainCarEnvironment.VELOCITY_BOUNDARIES[0]
elif (velocity > MountainCarEnvironment.VELOCITY_BOUNDARIES[1]):
velocity = MountainCarEnvironment.VELOCITY_BOUNDARIES[1]
position += velocity
# Consider boundary for position
if (position < MountainCarEnvironment.POSITION_BOUNDARIES[0]):
position = MountainCarEnvironment.POSITION_BOUNDARIES[0]
velocity = 0
elif (position > MountainCarEnvironment.POSITION_BOUNDARIES[1]):
position = MountainCarEnvironment.POSITION_BOUNDARIES[1]
new_state = [velocity, position]
return(new_state)
# Reset to the initial state
def reset(self):
self.car.state[0] = MountainCarEnvironment.INITIAL_VELOCITY
self.car.state[1] = MountainCarEnvironment.INITIAL_POSITION
# Give reward for each of the chosen action, depending on what the next state that the agent end up in
# Output: terminal state = 0, non-terminal state = -1
def calculateReward(self):
# Get current position of the agent
position = self.car.state[1]
# Determine the reward given
if (position >= MountainCarEnvironment.POSITION_BOUNDARIES[1]):
return(MountainCarEnvironment.REWARD_TERMINAL)
else:
return(MountainCarEnvironment.REWARD_STEP)
```
## KNN-TD Agent
**kNN-TD** combines the concept of *K-Nearest Neighbours* and *TD-Learning* to learn and evaluate Q values in both continuous and discrete state space RL problems. This method is especially useful in continuous states RL problems as the number of (state, action) pairs is very large and thus impossible to store and learn this information. By choosing a particular k-values and decided some initial points over continuous states, one can estimate Q values based on calculated the weighted average of Q values of the k-nearest neighbours for the state that the agent are currently in and use that values to decide the next move using some decision methods (i.e. UCB or epsilon-greedy). As for the learning process, one can update all of the k-nearest neighbours that contribute for the Q calculation.
**Algorithm:**
1. Cover the whole state space by some initial Q(s,a) pairs, possibly scatter it uniformly across the whole state space and give an initial value of 0/ -1
2. When an agent in a particular state, get the feature vectors representing the state and possible actions from the state
3. For each possible action from the state, calculate Q(s,a) pairs by taking the expected value from previous Q values based on k-nearest neighbours of a particular action.
*Steps for k-nearest neighbours:*
- Standardise every feature in the feature vectors to (-1, 1) or other ranges to make sure that one feature scale not dominate the distance calculation (i.e. if position ranges between (-50, 50) and velocity (-0.7, 0.7) position will dominate distance calculation).
- Calculate the distance between current state and all of other points with the same action using distance formula (i.e. Euclidean distance) and store the k-nearest neighbours to knn vector, and it's distance (for weight) in weight vector
- Determine the probability p(x) for the expected value by using weight calculation (i.e. weight = 1/distance). To calculate weight, one can use other formula as long as that formula gives more weight to closer point. To calculate p(x) just divide individual weight with sum of all weights to get probability
- Estimate the Q(s,a) pairs using expectation formula from kNN previous Q values
4. Using epsilon greedy/ UCB/ other decision methods to choose the next move
5. Observe the reward and update the Q values for all of the neighbours on knn vector using SARSA or Q Learning. (on the code below, I use Q Learning)
6. Repeat step 2-5
```
class KNNAgent:
"""
Description: Mountain Car problem agent based on kNN-TD(0) algorithm
Author: Maleakhi Agung Wijaya
"""
INITIAL_VELOCITY = 0.0
INITIAL_POSITION = -0.5
INITIAL_VALUE = -1
ACTIONS = [-1, 0, 1]
GAMMA = 0.995
EPSILON = 0.05
INDEX_DISTANCE = 0
INDEX_ORIGINAL = 1
INDEX_WEIGHT = 2
REWARD_STEP = -1
REWARD_TERMINAL = 0
# Constructor
# Input: size of the storage for previous Q values, parameters for how many neighbours which the agent will choose
def __init__(self, size, k):
self.state = [KNNAgent.INITIAL_VELOCITY, KNNAgent.INITIAL_POSITION]
self.q_storage = []
self.k = k # fixed number of nearest neighbours that we will used
self.alpha = 1 # will be decaying and change later
# Storage of the k nearest neighbour (data) and weight (inverse of distance) for a particular step
self.knn = []
self.weight = []
# Initialise the storage with random point
for i in range(size):
initial_action = random.randint(-1, 1)
initial_state = [random.uniform(-0.07, 0.07), random.uniform(-1.2, 0.6)]
# Each data on the array will consist of state, action pair + value
data = {"state": initial_state, "value": KNNAgent.INITIAL_VALUE, "action": initial_action}
self.q_storage.append(data)
# Find all index for a given value
# Input: value, list to search
# Output: list of all index where you find that value on the list
def findAllIndex(self, value, list_value):
indices = []
for i in range(len(list_value)):
if (value == list_value[i]):
indices.append(i)
return indices
# Standardise feature vector given
# Input: feature vector to be standardised
# Output: standardised feature vector
def standardiseState(self, state):
standardised_state = []
# The number is taken from VELOCITY_BOUNDARIES and POSITION_BOUNDARIES using normal standardisation formula
standardised_velocity = 2 * ((state[0]+0.07) / (0.07+0.07)) - 1
standardised_position = 2 * ((state[1]+1.2) / (0.6+1.2)) - 1
standardised_state.append(standardised_velocity)
standardised_state.append(standardised_position)
return(standardised_state)
# Calculate Euclidean distance between 2 vectors
# Input: 2 feature vectors
# Output: distance between them
def calculateDistance(self, vector1, vector2):
return(math.sqrt((vector1[0]-vector2[0])**2 + (vector1[1]-vector2[1])**2))
# Calculate total weight
# Input: list of weights
# Output: total weight
def calculateTotalWeight(self, weight_list):
total_weight = 0
for i in range(len(weight_list)):
total_weight += weight_list[i][KNNAgent.INDEX_WEIGHT]
return(total_weight)
# Apply the kNN algorithm for feature vector and store the data point on the neighbours array
# Input: feature vector of current state, actions array consisting of all possible actions, list that will store knn data and weights data
# Output: vector containing the value of taking each action (left, neutral, right)
def kNNTD(self, state, actions, knn_list, weight_list):
approximate_action = []
# Get the standardised version of state
standardised_state = self.standardiseState(state)
# Loop through every element in the storage array and only calculate for particular action
for action in actions:
temp = [] # array consisting of tuple (distance, original index, weight) for each point in the q_storage
for i in range(len(self.q_storage)):
data = self.q_storage[i]
# Only want to calculate the nearest neighbour state which has the same action
if (data["action"] == action):
vector_2 = data["state"]
standardised_vector_2 = self.standardiseState(vector_2)
distance = self.calculateDistance(standardised_state, standardised_vector_2)
index = i
weight = 1 / (1+distance**2) # weight formula
# Create the tuple and append that to temp
temp.append(tuple((distance, index, weight)))
else:
continue
# After we finish looping through all of the point and calculating the standardise distance,
# Sort the tuple based on the distance and only take k of it and append that to the neighbours array
# We also need to calculate the total weight to make it into valid probability that we can compute it's expectation
sorted_temp = sorted(temp, key=lambda x: x[0])
for i in range(self.k):
try:
weight_list.append(sorted_temp[i])
knn_list.append(self.q_storage[sorted_temp[i][KNNAgent.INDEX_ORIGINAL]])
except IndexError:
sys.exit(0)
# Calculate the expected value of the action and append it to the approximate_action array
expected_value = 0
total_weight = self.calculateTotalWeight(weight_list[(action+1)*self.k:(action+1)*self.k + self.k])
for i in range((action+1)*self.k, (action+1)*self.k + self.k):
weight = weight_list[i][KNNAgent.INDEX_WEIGHT]
probability = weight / total_weight
expected_value += probability * knn_list[i]["value"]
approximate_action.append(expected_value)
return(approximate_action)
# Select which action to choose, whether left, neutral, or right (using epsilon greedy)
# Output: -1 (left), 0 (neutral), 1 (right)
def selectAction(self):
# First call the knn-td algorithm to determine the value of each Q(s,a) pairs
action_value = self.kNNTD(self.state, KNNAgent.ACTIONS, self.knn, self.weight)
# Use the epsilon-greedy method to choose value
random_number = random.uniform(0.0, 1.0)
if (random_number <= KNNAgent.EPSILON):
action_chosen = random.randint(-1, 1)
else:
# Return the action with highest Q(s,a)
possible_index = self.findAllIndex(max(action_value), action_value)
action_chosen = possible_index[random.randrange(len(possible_index))] - 1
# Only store chosen data in the knn and weight list
# Clearance step
chosen_knn = []
chosen_weight = []
for i in range(self.k*(action_chosen+1), self.k*(action_chosen+1) + self.k):
chosen_knn.append(self.knn[i])
chosen_weight.append(self.weight[i])
self.knn = chosen_knn
self.weight = chosen_weight
return action_chosen
# Calculate TD target based on Q Learning/ SARSAMAX
# Input: Immediate reward based on what the environment gave
# Output: TD target based on off policy Q learning
def calculateTDTarget(self, immediate_reward):
# Consider condition on the final state, return 0 immediately
if (immediate_reward == KNNAgent.REWARD_TERMINAL):
return(immediate_reward)
knn_prime = []
weight_prime = []
action_value = self.kNNTD(self.state, KNNAgent.ACTIONS, knn_prime, weight_prime)
return(immediate_reward + KNNAgent.GAMMA*max(action_value))
# Q learning TD updates on every neighbours on the kNN based on the contribution that are calculated using probability weight
# Input: Immediate reward based on what the environment gave
def TDUpdate(self, immediate_reward, alpha):
self.alpha = alpha
# First, calculate the TD target
td_target = self.calculateTDTarget(immediate_reward)
# Iterate every kNN and update using Q learning method based on the weighting
total_weight = self.calculateTotalWeight(self.weight)
for i in range(len(self.weight)):
index = self.weight[i][KNNAgent.INDEX_ORIGINAL]
probability = self.weight[i][KNNAgent.INDEX_WEIGHT] / total_weight
# Begin updating
td_error = td_target - self.q_storage[index]["value"]
self.q_storage[index]["value"] = self.q_storage[index]["value"] + self.alpha*td_error*probability
self.cleanList() # clean list to prepare for another step
# Clear the knn list and also the weight list
def cleanList(self):
self.knn = []
self.weight = []
```
## KNN Main Function
**KNN Main function** is responsible for initiating the KNN agent, environment and handling agent-environment interaction. It consists of a non-terminate inner loop that direct agent decision while also giving reward and next state from the environment. This inner loop will only break after the agent successfully get out of the environment, which in this case the mountain. The outer loop can also be created to control the number of episodes which the agent will perform before the main function ends.
Apart from handling agent-environment interaction, main function also responsible to display three kinds of visualisation which will be explain below the appropriate graph.
```
# Generate decaying alphas
# Input: minimum alpha, number of episodes
# Output: list containing alpha
def generateAlphas(minimum_alpha, n_episodes):
return(np.linspace(1.0, MIN_ALPHA, N_EPISODES))
N_EPISODES = 1000
MIN_ALPHA = 0.02
alphas = generateAlphas(MIN_ALPHA, N_EPISODES)
# Initialise the environment and the agent
size = 1000 # size of the q_storage
k = 6 # knn parameter (this is the best k so far that we have)
agent = KNNAgent(size, k)
mountain_car_environment = MountainCarEnvironment(agent)
# Used for graphing purposes
count_step = [] # counter for how many step in each episodes
# Iterate the process, train the agent (training_iteration episodes)
training_iteration = N_EPISODES
for i in range(training_iteration):
step = 0
alpha = alphas[i]
mountain_car_environment.reset()
while (True):
action = agent.selectAction()
next_state = mountain_car_environment.nextState(action)
# Change agent current state and getting reward
agent.state = next_state
immediate_reward = mountain_car_environment.calculateReward()
# Used for graphing
step += 1
# Test for successful learning
if (immediate_reward == MountainCarEnvironment.REWARD_TERMINAL):
agent.TDUpdate(immediate_reward, alpha)
count_step.append(step)
clear_output(wait=True) # clear previous output
# Create table
d = {"Steps": count_step}
episode_table = pd.DataFrame(data=d, index=np.arange(1, len(count_step)+1))
episode_table.index.names = ['Episodes']
display(episode_table)
break
# Update using Q Learning and kNN
agent.TDUpdate(immediate_reward, alpha)
```
The table above displays total step data taken from 1000 episodes simulation. The first column represents episode and the second column represents total steps taken in a particular episode. It can be seen from the table that during the first few episodes, the agent hasn't learned the environment and hence it chose action unoptimally represented by huge number of steps taken to get to goal. Despite that, after experiencing hundred of episodes the agent have learnt the environment and Q values which enable it to reach the goal in just 200-400 steps.
```
# Create graph for step vs episodes
y = count_step
x = np.arange(1, len(y) + 1)
plt.plot(x, y)
plt.title("Steps vs Episodes (Log Scale)", fontsize=16)
plt.xlabel("Episodes")
plt.ylabel("Steps")
plt.xscale('log')
plt.yscale('log')
plt.show()
```
The line plot visualise the table that are explained above. On the y axis, the plot displays steps taken on each episode, while on the x axis the number of episodes (1000 in the simulation). The line plot is displayed in log-log scale to make it easy to visualise small fluctuation within episode and making sure that large steps in first few episodes don't dominate the graph. From the plot we can see that the overall trend is going downward. This result implies that over many episodes the Q values is getting better and better which eventually will converge to true Q values. Consequently, the agent perform better and better and the step taken to get out of the mountain will decrease with respect to number of episodes.
```
# Create heatmap for Q values
data = pd.DataFrame()
data_left = []
data_neutral = []
data_right = []
position_left = []
position_neutral = []
position_right = []
velocity_left = []
velocity_neutral = []
velocity_right = []
# Sort q_storage based on position and velocity
q_storage_sorted = sorted(agent.q_storage, key=lambda k: k['state'][0])
# Separate action left, neutral, and right
for elem in q_storage_sorted:
if (elem["action"] == -1):
data_left.append(elem["value"])
position_left.append(elem["state"][1])
velocity_left.append(elem["state"][0])
elif (elem["action"] == 0):
data_neutral.append(elem["value"])
position_neutral.append(elem["state"][1])
velocity_neutral.append(elem["state"][0])
else:
data_right.append(elem["value"])
position_right.append(elem["state"][1])
velocity_right.append(elem["state"][0])
# Make scatter plot for 3 actions (left, neutral, right)
# Left
plt.scatter(x=velocity_left, y=position_left, c=data_left, cmap="YlGnBu")
plt.title("Q Values (Action Left)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
# Neutral
plt.scatter(x=velocity_neutral, y=position_neutral, c=data_neutral, cmap="YlGnBu")
plt.title("Q Values (Action Neutral)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
# Right
plt.scatter(x=velocity_right, y=position_right, c=data_right, cmap="YlGnBu")
plt.title("Q Values (Action Right)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
```
Three scatter plots above display Q values for every action on the last episode (1000). Y axis represents position and x axis represents velocity of the 1000 points that we scattered random uniformly initially. To represent Q values for every point, these scatter plots use color indicating value that can be seen from the color bar. When the point is darker, the Q value is around -20. On the other hand, if the point is lighter the Q value is around -100. These Q values are later used for comparison with PNA Algorithm
## PNA Agent
**PNA** may be viewed as a refinement for kNN, with k adapting to the situation. On the one hand, it is beneficial to use large k since that means large data can be learn from. On the other hand, it is beneficial to learn only from the most similar past experiences (small k), as the data they provide should be the most relevant.
PNA suggests that when predicting the value of an action a in a state s, k should be chosen dynamically to minimise:

where c = 1 and Var(Nsa) is the variance of observed rewards in the neighbourhood Nsa. This is a negative version of the term endorsing exploration in the UCB algorithm. Here it promotes choosing neighbourhoods that contain as much data as possible but with small variation between rewards. For example, in the ideal choice of k, all k nearest neighbours of (s, a) behave similarly, but actions farther away behave very differently.
Action are chosen optimistically according to the UCB:

with c > 0 a small constant. The upper confidence bound is composed of two terms: The first terms is the estimated value, and the second term is an exploration bonus for action whose value is uncertain. Actions can have uncertain value either because they have rarely been selected or have a high variance among previous returns. Meanwhile, the neighbourhoods are chosen "pessimistically" for each action to minimise the exploration bonus.
**Algorithm:**
1. Cover the whole state space by some initial Q(s,a) pairs, possibly scatter it uniformly across the whole state space and give an initial value of 0/ -1
2. When an agent in a particular state, get the feature vectors representing the state and possible actions from the state
3. For each possible action from the state, calculate Q(s,a) pairs by taking the expected value from previous Q values based on k-nearest neighbours of a particular action. With PNA, we also need to dynamically consider the k values
*Steps for PNA:*
- Standardise every feature in the feature vectors to (-1, 1) or other ranges to make sure that one feature scale not dominate the distance calculation (i.e. if position ranges between (-50, 50) and velocity (-0.7, 0.7) position will dominate distance calculation).
- Calculate the distance between current state and all of other points with the same action using distance formula (i.e. Euclidean distance) and sort based on the closest distance
- Determine k by minimising the variance function described above
- Store the k-nearest neighbours to knn vector, and it's distance (for weight) in weight vector
- Determine the probability p(x) for the expected value by using weight calculation (i.e. weight = 1/distance). To calculate weight, one can use other formula as long as that formula gives more weight to closer point. To calculate p(x) just divide individual weight with sum of all weights to get probability
- Estimate the Q(s,a) pairs using expectation formula from kNN previous Q values
4. Using epsilon greedy/ UCB/ other decision methods to choose the next move
5. Observe the reward and update the Q values for only the closest neighbour (1 point or chosen by hyperparametric) from KNN array using SARSA or Q Learning. (on the code below, I use Q Learning)
6. Repeat step 2-5
```
class PNAAgent:
"""
Description: Mountain Car problem agent based on PNA algorithm adapted from Marcus Hutter's literatures
Author: Maleakhi Agung Wijaya
"""
INITIAL_VELOCITY = 0.0
INITIAL_POSITION = -0.5
INITIAL_VALUE = -1
ACTIONS = [-1, 0, 1]
GAMMA = 0.995
C = 0.01 # UCB constant
EPSILON = 0.05
RADIUS = 1
INDEX_DISTANCE = 0
INDEX_ORIGINAL = 1
INDEX_WEIGHT = 2
REWARD_STEP = -1
REWARD_TERMINAL = 0
# Constructor
# Input: size of the storage for previous Q values
def __init__(self, size):
self.state = [PNAAgent.INITIAL_VELOCITY, PNAAgent.INITIAL_POSITION]
self.q_storage = []
self.alpha = 1 # choose fixed alpha, but we will vary alpha later
# Storage of the k nearest neighbour (data) and weight (inverse of distance) for a particular step
self.knn = []
self.weight = []
self.k_history = [] # used to store history of k chosen for each action
# For plotting expected PNA function graph
self.var_function_left = []
self.var_function_neutral = []
self.var_function_right = []
self.converge_function_left = []
self.converge_function_neutral = []
self.converge_function_right = []
self.episode = 0 # keep count of how many episodes for plotting purposes as well
# Initialise the storage with random point
for i in range(size):
initial_value = PNAAgent.INITIAL_VALUE
initial_action = random.randint(-1, 1)
initial_state = [random.uniform(-0.07, 0.07), random.uniform(-1.2, 0.6)]
# Fill the graph with all possible k
if (initial_action == -1):
self.var_function_left.append(0)
self.converge_function_left.append(0)
elif (initial_action == 0):
self.var_function_neutral.append(0)
self.converge_function_neutral.append(0)
else:
self.var_function_right.append(0)
self.converge_function_right.append(0)
# Each data on the array will consist of state, action pair + value
data = {"state": initial_state, "value": initial_value, "action": initial_action}
self.q_storage.append(data)
# Since the k start at 2 that we want to calculate, just pop 1
self.var_function_left.pop()
self.var_function_neutral.pop()
self.var_function_right.pop()
self.converge_function_left.pop()
self.converge_function_neutral.pop()
self.converge_function_right.pop()
# Standardise feature vector given
# Input: feature vector to be standardised
# Output: standardised feature vector
def standardiseState(self, state):
standardised_state = []
standardised_velocity = 2 * ((state[0]+0.07) / (0.07+0.07)) - 1
standardised_position = 2 * ((state[1]+1.2) / (0.6+1.2)) - 1
standardised_state.append(standardised_velocity)
standardised_state.append(standardised_position)
return(standardised_state)
# Find all index for a given value
# Input: value, list to search
# Output: list of all index where you find that value on the list
def findAllIndex(self, value, list_value):
indices = []
for i in range(len(list_value)):
if (value == list_value[i]):
indices.append(i)
return indices
# Calculate Euclidean distance between 2 vectors
# Input: 2 feature vectors
# Output: distance between them
def calculateDistance(self, vector1, vector2):
return(math.sqrt((vector1[0]-vector2[0])**2 + (vector1[1]-vector2[1])**2))
# Calculate total weight
# Input: list of weights
# Output: total weight
def calculateTotalWeight(self, weight_list):
total_weight = 0
for i in range(len(weight_list)):
total_weight += weight_list[i][PNAAgent.INDEX_WEIGHT]
return(total_weight)
# Clear the knn list, k_history, and also the weight list
def cleanList(self):
self.knn = []
self.weight = []
self.k_history = []
# Choose the appropriate k by minimising variance and maximising the number of data to learn
# Input: sorted neighbourhood list based on distance (distance, index, weight)
# Output: k (numbers of nearest neighbour) that minimise neighbourhood variance function
def chooseK(self, neighbourhood_list):
data_list = []
# Extract the data (Q value from the neighbourhood_list) and append it to the data_list
for data in neighbourhood_list:
data_list.append(self.q_storage[data[PNAAgent.INDEX_ORIGINAL]]["value"])
action = self.q_storage[data[PNAAgent.INDEX_ORIGINAL]]["action"]
# Initialise minimum variance
minimum_k = 2 # Variable that will be return that minimise the variance of the neighbourhood
minimum_function = self.neighbourhoodVariance(1, data_list[:2])
# For plotting variance function graph
list_var = []
if (action == -1):
list_var = self.var_function_left
elif (action == 0):
list_var = self.var_function_neutral
else:
list_var = self.var_function_right
list_var[0] += minimum_function
if (self.episode > 900):
list_var_converge = []
if (action == -1):
list_var_converge = self.converge_function_left
elif (action == 0):
list_var_converge = self.converge_function_neutral
else:
list_var_converge = self.converge_function_right
list_var_converge[0] += minimum_function
previous_sum_variance = np.var(data_list[:2]) * 2
previous_mean = np.mean(data_list[:2])
k = 2
# Iterate to find optimal k that will minimise the neighbourhood variance function
for i in range(2, len(neighbourhood_list)):
target_x = data_list[i]
mean = (previous_mean * k + target_x) / (k + 1)
current_sum_variance = previous_sum_variance + (target_x - previous_mean) * (target_x - mean)
# Update for next iteration
k = k + 1
previous_sum_variance = current_sum_variance
previous_mean = mean
function = self.neighbourhoodVariance(1, [], previous_sum_variance / k, k)
list_var[k-2] += function
if (self.episode > 900):
list_var_converge[k-2] += function
# Update the k value and minimum var value if find parameter which better minimise than the previous value
if (function <= minimum_function):
minimum_k = k
minimum_function = function
return(minimum_k)
# PNA variance function that needed to be minimise
# Input: constant c, list containing data points
# Output: calculation result from the neighbourhood variance function
def neighbourhoodVariance(self, c, data_list, var = None, k = None):
if (var == None):
return(math.sqrt(c * np.var(data_list) / len(data_list)))
else:
return(math.sqrt(c * var / k))
# Get starting index for the weight list
# Input: action, k_history
# Output: starting index for the weight list
def getStartingIndex(self, action, k_history):
count_action = action + 1
if (count_action == 0):
return(0)
else:
index = 0
for i in range(count_action):
index += k_history[i]
return(index)
# Apply the PNA algorithm for feature vector and store the data point on the neighbours array
# Input: feature vector of current state, actions array consisting of all possible actions, list that will store knn data and weights data, k_history
# Output: vector containing the value of taking each action (left, neutral, right)
def PNA(self, state, actions, knn_list, weight_list, k_history):
approximate_action = []
# Get the standardised version of state
standardised_state = self.standardiseState(state)
# Loop through every element in the storage array and only calculate for particular action
for action in actions:
temp = [] # array consisting of tuple (distance, original index, weight) for each point in the q_storage
for i in range(len(self.q_storage)):
data = self.q_storage[i]
# Only want to calculate the nearest neighbour state which has the same action
if (data["action"] == action):
vector_2 = data["state"]
standardised_vector_2 = self.standardiseState(vector_2)
distance = self.calculateDistance(standardised_state, standardised_vector_2)
index = i
weight = 1 / (1+distance**2)
# Create the tuple and append that to temp
temp.append(tuple((distance, index, weight)))
else:
continue
# After we finish looping through all of the point and calculating the standardise distance,
# Sort the tuple based on the distance and only take k of it and append that to the neighbours array
sorted_temp = sorted(temp, key=lambda x: x[0])
# Get the value of the k dynamically
k = self.chooseK(sorted_temp)
k_history.append(k)
for i in range(k):
try:
weight_list.append(sorted_temp[i])
knn_list.append(self.q_storage[sorted_temp[i][PNAAgent.INDEX_ORIGINAL]])
except IndexError:
sys.exit(0)
# Calculate the expected value of the action and append it to the approximate_action array
expected_value = 0
# We also need to calculate the total weight to make it into valid probability that we can compute it's expectation
total_weight = self.calculateTotalWeight(weight_list[self.getStartingIndex(action, k_history):self.getStartingIndex(action, k_history)+k])
for i in range(self.getStartingIndex(action, k_history), self.getStartingIndex(action, k_history) + k):
try:
weight = weight_list[i][PNAAgent.INDEX_WEIGHT]
probability = weight / total_weight
expected_value += probability * knn_list[i]["value"]
except IndexError:
sys.exit(0)
approximate_action.append(expected_value)
return(approximate_action)
# Calculate TD target based on Q Learning/ SARSAMAX
# Input: Immediate reward based on what the environment gave
# Output: TD target based on off policy Q learning
def calculateTDTarget(self, immediate_reward):
# Condition if final state
if (immediate_reward == PNAAgent.REWARD_TERMINAL):
return(immediate_reward)
k_history = []
knn_prime = []
weight_prime = []
action_value = self.PNA(self.state, PNAAgent.ACTIONS, knn_prime, weight_prime, k_history)
return(immediate_reward + PNAAgent.GAMMA * max(action_value))
# Q learning TD updates on every neighbours on the kNN based on the contribution that are calculated using probability weight
# Input: Immediate reward based on what the environment gave
def TDUpdate(self, immediate_reward, alpha):
self.alpha = alpha
# First, calculate the TD target
td_target = self.calculateTDTarget(immediate_reward)
try:
# Update only the #radius closest point
total_weight = self.calculateTotalWeight(self.weight[0:PNAAgent.RADIUS])
for i in range(PNAAgent.RADIUS):
index = self.weight[i][PNAAgent.INDEX_ORIGINAL]
probability = self.weight[i][PNAAgent.INDEX_WEIGHT] / total_weight
td_error = td_target - self.q_storage[index]["value"]
self.q_storage[index]["value"] += self.alpha * td_error * probability
except IndexError:
total_weight = self.calculateTotalWeight(self.weight)
for i in range(len(self.weight)):
index = self.weight[i][PNAAgent.INDEX_ORIGINAL]
probability = self.weight[i][PNAAgent.INDEX_WEIGHT] / total_weight
# Begin updating
td_error = td_target - self.q_storage[index]["value"]
self.q_storage[index]["value"] += self.alpha * td_error * probability
self.cleanList() # clean list to prepare for another step
# Choosing based on Epsilon Greedy method
# Input: action_value array consisting the Q value of every action
# Output: action chosen (-1, 0, 1)
def epsilonGreedy(self, action_value):
# Use the epsilon-greedy method to choose value
random_number = random.uniform(0.0, 1.0)
if (random_number <= PNAAgent.EPSILON):
action_chosen = random.randint(-1, 1)
else:
# Return the action with highest Q(s,a)
possible_index = self.findAllIndex(max(action_value), action_value)
action_chosen = possible_index[random.randrange(len(possible_index))] - 1
return action_chosen
# Getting the maximum of the ucb method
# Input: action_value list, bonus_variance list
# Output: action which maximise
def maximumUCB(self, action_value, bonus_variance):
max_index = 0
max_value = action_value[0] + bonus_variance[0]
# Check 1, 2 (all possible action)
for i in range(1, 3):
value = action_value[i] + bonus_variance[i]
if (value >= max_value):
max_value = value
max_index = i
return(max_index - 1) # return the action which maximise
# Select which action to choose, whether left, neutral, or right (using UCB)
# Output: -1 (left), 0 (neutral), 1 (right)
def selectAction(self):
action_value = self.PNA(self.state, PNAAgent.ACTIONS, self.knn, self.weight, self.k_history)
# Second term of ucb, calculate the bonus variance
start_index = [] # used to calculate start index for each action
finish_index = [] # used to calculate end index for each action
for action in PNAAgent.ACTIONS:
# Prevent index out of bound
if (action != 1):
# Data extraction
start_index.append(self.getStartingIndex(action, self.k_history))
finish_index.append(self.getStartingIndex(action+1, self.k_history))
else:
# Data extraction
start_index.append(self.getStartingIndex(action, self.k_history))
finish_index.append(len(self.weight))
# Choose the action based on ucb method
action_chosen = self.epsilonGreedy(action_value)
# Only store chosen data in the knn and weight list
# Clearance step
chosen_knn = []
chosen_weight = []
for i in range(start_index[action_chosen+1], finish_index[action_chosen+1]):
chosen_knn.append(self.knn[i])
chosen_weight.append(self.weight[i])
self.knn = chosen_knn
self.weight = chosen_weight
return action_chosen
```
## PNA Main Function
**PNA Main function** is responsible for initiating the PNA agent, environment and handling agent-environment interaction. It consists of a non-terminate inner loop that direct agent decision while also giving reward and next state from the environment. This inner loop will only break after the agent successfully get out of the environment, which in this case the mountain or if it is taking too long to converge. The outer loop can also be created to control the number of episodes which the agent will perform before the main function ends.
Apart from handling agent-environment interaction, main function also responsible to display five kinds of visualisation. First, table/ DataFrame displaying episodes and step that are required by the agent to get out of the mountain on each episode. Second, scatter plot displaying steps on the y axis and episodes on the x axis to learn about algorithm convergence property. Third, expected standard error function for every actions. Fourth, heatmap of the Q value for the last episode. Lastly, as the k is dynamically changing each steps, I have created a heatmap indicating k chosen each steps for first episode and last episode.
```
# Generate decaying alphas
# Input: minimum alpha, number of episodes
# Output: list containing alpha
def generateAlphas(minimum_alpha, n_episodes):
return(np.linspace(1.0, MIN_ALPHA, N_EPISODES))
N_EPISODES = 1000
MIN_ALPHA = 0.02
alphas = generateAlphas(MIN_ALPHA, N_EPISODES)
# Initialise the environment and the agent
size = 1000 # size of the q_storage
agent = PNAAgent(size)
mountain_car_environment = MountainCarEnvironment(agent)
convergence = 100 # used to extract data when agent has converges
# Used for graphing purposes
count_step = [] # counter for how many step in each episodes
k_first_left = []
k_first_neutral = []
k_first_right = []
k_last_left = []
k_last_neutral = []
k_last_right = []
k_convergence_left = agent.var_function_left[:]
k_convergence_neutral = agent.var_function_neutral[:]
k_convergence_right = agent.var_function_right[:]
# Iterate the process, train the agent (training_iteration episodes)
total_step = 0
training_iteration = N_EPISODES
for i in range(training_iteration):
step = 0
alpha = alphas[i]
mountain_car_environment.reset()
agent.episode = i + 1
while (True):
action = agent.selectAction()
next_state = mountain_car_environment.nextState(action)
# Change agent current state and getting reward
agent.state = next_state
immediate_reward = mountain_car_environment.calculateReward()
# Used for graphing
step += 1
total_step += 1
# Only append first and last episode (for the k)
if (i == 1):
k_first_left.append(agent.k_history[0])
k_first_neutral.append(agent.k_history[1])
k_first_right.append(agent.k_history[2])
if (i == (training_iteration - 1)):
k_last_left.append(agent.k_history[0])
k_last_neutral.append(agent.k_history[1])
k_last_right.append(agent.k_history[2])
# Count how many k chosen after converge
if (agent.episode > 900):
# Increment count when a particular k is chosen, 2 is just scaling factor since the k starts from 2 in the array
k_convergence_left[agent.k_history[0]-2] += 1
k_convergence_neutral[agent.k_history[1]-2] += 1
k_convergence_right[agent.k_history[2]-2] += 1
# Test for successful learning
if (immediate_reward == MountainCarEnvironment.REWARD_TERMINAL):
agent.TDUpdate(immediate_reward, alpha)
count_step.append(step)
clear_output(wait=True) # clear previous output
# Create table
d = {"Steps": count_step}
episode_table = pd.DataFrame(data=d, index=np.arange(1, len(count_step)+1))
episode_table.index.names = ['Episodes']
display(episode_table)
break
# Update using Q Learning and kNN
agent.TDUpdate(immediate_reward, alpha)
```
The table above displays total step data taken from 1000 episodes simulation. The first column represents episode and the second column represents total steps taken in a particular episode. It can be seen from the table that during the first few episodes, the agent hasn't learned the environment and hence it chose action unoptimally represented by huge number of steps taken to get to goal. Despite that, after experiencing hundred of episodes the agent have learnt the environment and Q values which enable it to reach the goal in around 300-600 steps.
```
# Create graph for step vs episodes
y = count_step
x = np.arange(1, len(y) + 1)
plt.plot(x, y)
plt.title("Steps vs Episodes (Log Scale)", fontsize=16)
plt.xlabel("Episodes (Log)")
plt.ylabel("Steps (Log)")
plt.xscale('log')
plt.yscale('log')
plt.show()
```
The line plot visualise the table that are explained above. On the y axis, the plot displays steps taken on each episode, while on the x axis the number of episodes (1000 in the simulation). The line plot is displayed in log-log scale to make it easy to visualise small fluctuation within episode and making sure that large steps in first few episodes don't dominate the graph. From the plot we can see that the overall trend is going downward. The result implies that over many episodes the Q values is getting better and better which eventually will converge to true Q values. Consequently, the agent perform better and better and the step taken to get out of the mountain will decrease with respect to number of episodes.
```
# Create plot for the average standard error function
average_var_left = []
average_var_neutral = []
average_var_right = []
for elem in agent.var_function_left:
average_var_left.append(elem / total_step)
for elem in agent.var_function_neutral:
average_var_neutral.append(elem / total_step)
for elem in agent.var_function_right:
average_var_right.append(elem / total_step)
# Make a scatter plot
# Left
y = average_var_left
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#55A868")
plt.title("Average Standard Error Function vs K (Action Left)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
# Make a scatter plot
# Neutral
y = average_var_neutral
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#55A868")
plt.title("Average Standard Error Function vs K (Action Neutral)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
# Make a scatter plot
# Right
y = average_var_right
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#55A868")
plt.title(" Average Standard Error Function vs K (Action Right)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
# Now plot the standard error function after convergence
reverse_count_step = count_step[::-1]
total_last_step = 0
for i in range(convergence):
total_last_step += reverse_count_step[i]
average_converge_left = []
average_converge_neutral = []
average_converge_right = []
for elem in agent.converge_function_left:
average_converge_left.append(elem / total_last_step)
for elem in agent.converge_function_neutral:
average_converge_neutral.append(elem / total_last_step)
for elem in agent.converge_function_right:
average_converge_right.append(elem / total_last_step)
# Make a scatter plot
# Left
y = average_converge_left
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#B14C4D")
plt.title("Average Standard Error Function vs K After Convergence (Action Left)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
# Make a scatter plot
# Neutral
y = average_converge_neutral
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#B14C4D")
plt.title("Average Standard Error Function vs K After Convergence (Action Neutral)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
# Make a scatter plot
# Right
y = average_converge_right
x = np.arange(2, len(y)+2)
plt.plot(x, y, color="#B14C4D")
plt.title(" Average Standard Error Function vs K After Convergence (Action Right)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Average f(K)")
plt.xticks(np.arange(2, len(y) + 2, 50))
plt.show()
```
The first 3 graphs display average standard error function calculated for every steps from episode 1 - episode 1000. X axis display the possible k for every actions, while y axis display the average standard error function for each k. From both the plot above and bar plot below, it can be seen that k = 2 is chosen most of the time since it's mostly minimise the standard error function compare to other k. Even though 2 is the most frequent k chosen, if we dissect the plot for every episodes, it is not always the case. On some steps/ episodes, the graph are dominated by the number of neighbourhood which makes the graph looks like 1/sqrt(n) resulted in large amount of k (200-300) chosen.
The last 3 graphs display average standard error function calculated for the last 100 episodes out of 1000 episodes (converges). These graphs have similar value with the first 3 graphs and hence the explanation is similar.
```
# Create heatmap for Q values
data = pd.DataFrame()
data_left = []
data_neutral = []
data_right = []
position_left = []
position_neutral = []
position_right = []
velocity_left = []
velocity_neutral = []
velocity_right = []
# Sort q_storage based on position and velocity
q_storage_sorted = sorted(agent.q_storage, key=lambda k: k['state'][0])
# Separate action left, neutral, and right
for elem in q_storage_sorted:
if (elem["action"] == -1):
data_left.append(elem["value"])
position_left.append(elem["state"][1])
velocity_left.append(elem["state"][0])
elif (elem["action"] == 0):
data_neutral.append(elem["value"])
position_neutral.append(elem["state"][1])
velocity_neutral.append(elem["state"][0])
else:
data_right.append(elem["value"])
position_right.append(elem["state"][1])
velocity_right.append(elem["state"][0])
# Make scatter plot for 3 actions (left, neutral, right)
# Left
plt.scatter(x=velocity_left, y=position_left, c=data_left, cmap="YlGnBu")
plt.title("Q Values (Action Left)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
# Neutral
plt.scatter(x=velocity_neutral, y=position_neutral, c=data_neutral, cmap="YlGnBu")
plt.title("Q Values (Action Neutral)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
# Right
plt.scatter(x=velocity_right, y=position_right, c=data_right, cmap="YlGnBu")
plt.title("Q Values (Action Right)", fontsize=16)
plt.xlabel("Velocity")
plt.ylabel("Position")
plt.colorbar()
plt.show()
```
Three scatter plots above display Q values for every action on the last episode (1000). Y axis represents position and x axis represents velocity of the 1000 points that we scattered random uniformly initially. To represent Q values for every point, these scatter plots use color indicating the value that can be seen from the color bar. When the point is darker, the Q value is around -20. On the other hand, if the point is lighter the Q value is around -100.
If we observe the Q values for both KNN-TD and PNA, it can be seen that the Q values are roughly similar. This result implies that both of the algorithm converges for the Mountain Car problem and eventually after numerous episodes, the agent Q values will converge to the true Q values.
```
# Create heatmap showing the k (first episode)
data = pd.DataFrame()
data["Action Left"] = k_first_left
data["Action Neutral"] = k_first_neutral
data["Action Right"] = k_first_right
data["Steps"] = np.arange(1, len(k_first_left) + 1)
data.set_index("Steps", inplace=True)
grid_kws = {"height_ratios": (.9, .05), "hspace": .3}
f, (ax, cbar_ax) = plt.subplots(2, gridspec_kw=grid_kws)
ax = sns.heatmap(data, ax=ax, cbar_ax=cbar_ax, cbar_kws={"orientation": "horizontal"}, yticklabels=False)
ax.set_title("Number of K Chosen Each Step (First Episode)", fontsize=16)
plt.show()
# Create heatmap showing the k (last episode)
data = pd.DataFrame()
data["Action Left"] = k_last_left
data["Action Neutral"] = k_last_neutral
data["Action Right"] = k_last_right
data["Steps"] = np.arange(1, len(k_last_left) + 1)
data.set_index("Steps", inplace=True)
grid_kws = {"height_ratios": (.9, .05), "hspace": .3}
f, (ax, cbar_ax) = plt.subplots(2, gridspec_kw=grid_kws)
ax = sns.heatmap(data, ax=ax, cbar_ax=cbar_ax, cbar_kws={"orientation": "horizontal"}, yticklabels=False)
ax.set_title("Number of K Chosen Each Step (Last Episode)", fontsize=16)
plt.show()
```
The heatmap displayed above represents k chosen each step for every actions. Each strip on the heatmap represents the k chosen on a step. The first heatmap displayed data from the first episode. Based on the heatmap, it can be seen that the k chosen each step during the first episode is large (around 120-180). This occurs because all points are initialise to have a uniform value of -1. As the Q values is uniformly/ roughly -1 across the whole space, this will make the variance approximately 0 and hence resulted in the standard error function depends largely on the number of k chosen/ neighbourhoods. As the algorithm prefer to minimise the standard error function, it will chooses as many point as possible.
The second heatmap displayed data from the last episode. Based on the heatmap, it can be seen that the k chosen each step is relatively small (around 2-60). This occurs since the agent has gain large amount of experience and Q values greatly differ in different region. As a result, if the agent choose a really large k to learn, it will make the variance very high and hence really large standard error. Consequently, the agent will minimise standard error function by repeatedly choose k around 2-60.
```
# Plot bar chart displaying number of k chosen after convergence
y_bar = k_convergence_left
x_bar = np.arange(2, len(y_bar) + 2)
plt.bar(x_bar, y_bar, color="#FFD700")
plt.yscale('log')
plt.title("Number of K Chosen vs K After Convergence (Action Left)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Number of K Chosen")
plt.xticks(np.arange(2, len(y_bar) + 2, 50))
plt.show()
y_bar = k_convergence_neutral
x_bar = np.arange(2, len(y_bar) + 2)
plt.bar(x_bar, y_bar, color="#FFD700")
plt.yscale('log')
plt.title("Number of K Chosen vs K After Convergence (Action Neutral)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Number of K Chosen")
plt.xticks(np.arange(2, len(y_bar) + 2, 50))
plt.show()
y_bar = k_convergence_right
x_bar = np.arange(2, len(y_bar) + 2)
plt.bar(x_bar, y_bar, color="#FFD700")
plt.yscale('log')
plt.title("Number of K Chosen vs K After Convergence (Action Right)", fontsize=16)
plt.xlabel("K")
plt.ylabel("Number of K Chosen")
plt.xticks(np.arange(2, len(y_bar) + 2, 50))
plt.show()
```
These bar plots represent the number of k chosen for each k after convergence for every actions. X axis represents possible k for each action, while y axis represents how many times the k chosen for a particular k after convergence. The convergence defined in the code is the last 100 episodes out of 1000 episodes.
In all of bar plots, we can see that after convergence the agent mostly choose k equals 2 and relatively small k such as from 2 - 150. This condition occurs because the agent has lots of experience which thus make the Q values highly differ between region. Based on the result, we can see that mostly variance dominates the standard error function which force the agent to choose small k to minimise the standard error function.
| true |
code
| 0.579043 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
```
# **COVID-19 Twitter Sentiments**
# A. **Problem**: Do Twitter-tweet sentiments have any correlations with COVID19 death counts? That is, do states with higher death counts have a particular sentiment correlated to its tweets?
# **B. Datasets used**
## Tweet Source:
I constructed the twextual dataset by using a guide on twitter webscraping. I used the Twint library to construct a twitter webscraper that did not need to use Twitter's API.
https://pypi.org/project/twint/
Twint allowed me to filter by tweet date, querey (keyword being COIVD19), number of tweets that are to be scraped, location of the tweet (state), and finally an output file in `.csv` of the scarped data.
The code can be found on my github. The code may be ran in an UNIX-Based OS via terminal. If that's not possible, one could make an args data class and delete the argparse part from the code.
Code: https://github.com/kwxk/twitter-textual-scraper with comments for each line.
Here is the general format for the crawler within the argparse of the code:
`python tweet_crawler -q [write here query] -d [write here since date] -c [write here how many tweets you want from each state] -s [provide here a list of states each state between quotation marks] -o [write here output file name]`
So for example: `python tweet_crawler -q covid19 -d 2020-01-01 -c 100 -s "New Jersey" "Florida" -o output.csv`
Tweets were collected from a year to date (Decemeber 01, 2021).
**I treated this as if it were an ETL pipeline.**
## **Tweet Dataset**
The main dataset must be split between states and english (en) tweets must be preserved in each dataset.
### **Main tweet data frame**
```
df = pd.read_csv('covid19.csv')
df.head()
```
## **Split Tweet Dataframe (split by states)**
```
flp = df[df['near'].str.contains('Florida',na=False)]
fl = flp[flp['language'].str.contains('en',na=False)]
fl
txp = df[df['near'].str.contains('Texas',na=False)]
tx = txp[txp['language'].str.contains('en',na=False)]
tx
njp = df[df['near'].str.contains('New Jersey',na=False)]
njp = njp[njp['language'].str.contains('en',na=False)]
nj
nyp = df[df['near'].str.contains('New York',na=False)]
ny = nyp[nyp['language'].str.contains('en',na=False)]
ny
```
## **Stopwords**
```
### Stopwords List
stop= open("stopwords.txt").read().replace("\n",' ').split(" ")[:-1]
stat = pd.read_csv('us-states.csv')
stat
ny_stat = stat[stat['state'].str.contains('New York',na=False)]
nystat2 = ny_stat.drop(['fips','cases','state'], axis = 1)
nj_stat = stat[stat['state'].str.contains('New Jersey',na=False)]
njstat2 = nj_stat.drop(['fips','cases','state'], axis = 1)
tx_stat = stat[stat['state'].str.contains('Texas',na=False)]
txstat2 = tx_stat.drop(['fips','cases','state'], axis = 1)
fl_stat = stat[stat['state'].str.contains('Florida',na=False)]
flstat2 = fl_stat.drop(['fips','cases','state'], axis = 1)
fl_stat = stat[stat['state'].str.contains('Florida',na=False)]
fl_stat
```
## **Sentiment Analysis**
```
from nltk.stem.wordnet import WordNetLemmatizer
from gensim import corpora, models
from nltk.tokenize import word_tokenize
import gensim
#import pyLDAvis.gensim_models as gensimvis
from gensim import corpora
from matplotlib.patches import Rectangle
import pandas as pd
import numpy as np
import nltk
nltk.downloader.download('vader_lexicon')
nltk.downloader.download('stopwords')
from nltk.corpus import stopwords
from nltk.tokenize import RegexpTokenizer
from wordcloud import WordCloud, STOPWORDS
import matplotlib.colors as mcolors
import string
import matplotlib.pyplot as plt
import seaborn as sns
from wordcloud import WordCloud
import itertools
import collections
import re
import nltk
from nltk.corpus import stopwords
import re
import networkx
from textblob import TextBlob
df1= df.copy()
df1.drop(["Unnamed: 0","username","link","language"],axis=1, inplace=True)
df1
def cleaner(text):
text = re.sub("@[A-Za-z0-9]+","",text)
text = re.sub("#[A-Za-z0-9]+","",text)#Remove @ sign
text = re.sub(r"(?:\@|http?\://|https?\://|www)\S+", "", text) #Remove http links
text = text.replace("\n", "")
text=text.lower()
return text
df1['tweet'] = df1['tweet'].map(lambda x: cleaner(x))
punct = "\n\r"+string.punctuation
df1['tweet'] = df1['tweet'].str.translate(str.maketrans('','',punct))
def clean_sentence(val):
"remove chars that are not letters or number or down case then remove"
regex=re.compile('([^\sa-zA-Z0-9]|_)+')
sentence=regex.sub('',val).lower()
sentence = sentence.replace('\n'," ")
sentence = sentence.replace(','," ")
sentence = sentence.replace('\\~'," ")
sentence = sentence.replace('QAQ\\~\\~'," ")
sentence=sentence.split(" ")
for word in list(sentence):
if word in stop:
sentence.remove(word)
sentence=" ".join(sentence)
return sentence
def clean_dataframe(data):
"drop nans,thenb apply clean sentence function to description"
# data=data.dropna(how="any")
for col in ['tweet']:
df1[col]=df1[col].apply(clean_sentence)
return df1
cleaned_text = clean_dataframe(df1)
# Create textblob objects of the tweets
sentiment_objects = [TextBlob(text) for text in df1['tweet']]
sentiment_objects[2].polarity, sentiment_objects[0]
sentiment_values = [[text.sentiment.polarity, str(text)] for text in sentiment_objects]
sentiment_df = pd.DataFrame(sentiment_values, columns=["polarity", "tweet"])
a=sentiment_df['polarity'].round(2)
b=list(a)
sentiment_df['Polar']=b
new_list=[]
for i in range(len(sentiment_df['Polar'])):
a = sentiment_df['Polar'][i]
if a == 0:
new_list.append("Neutral")
continue
if a >0:
new_list.append("Positive")
continue
if a <0:
new_list.append("Negative")
continue
sentiment_df['Sentiments']=new_list
sentiment_df
df1['Sentiments']=sentiment_df['Sentiments']
df1['Polar']=sentiment_df['Polar']
df1
```
## **Florida Sentiments Analysis**
```
df_fl= df1[df1['near']=="Florida"].reset_index(drop=True)
df_fl
```
## **New York Sentiments Analysis**
```
df_ny= df1[df1['near']=="New York"].reset_index(drop=True)
df_ny
```
## **New Jersy Sentiments Analysis**
```
df_nj= df1[df1['near']=="New Jersey"].reset_index(drop=True)
df_nj
```
## **Texas Sentiments Analysis**
```
df_tx= df1[df1['near']=="Texas"].reset_index(drop=True)
df_tx
```
# **C. Findings:**
## **Overall Sentiments among all states**
```
## Visualizing the Text sentiments
pos=df1[df1['Sentiments']=='Positive']
neg=df1[df1['Sentiments']=='Negative']
neu=df1[df1['Sentiments']=='Neutral']
import plotly.express as px
#Frist_Day = Frist_Day
fig = px.pie(df1, names='Sentiments')
fig.show()
plt.title('Total number of tweets and sentiments')
plt.xlabel('Emotions')
plt.ylabel('Number of Tweets')
sns.countplot(x='Sentiments', data=df1)
```
**Finding: Neutral Sentiments are the most prevalent of sentiments from the combine dataframe of NJ, NY, FL, TX tweets. There are slightly more positive sentiments than negative sentiments.**
```
df1['near'].unique()
```
## **Barplot for the Sentiments (New Jersey)**
```
b=df_nj['Sentiments'].value_counts().reset_index()
plt.title('NJ number of tweets and sentiments')
plt.xlabel('Emotions')
plt.ylabel('Number of Tweets')
plt.bar(x=b['index'], height=b['Sentiments'])
```
**Findings: New Jersey has a majority neutral sentiment tweets from the dataframe. It has slightly more positive sentiment tweets than there are negative sentiment tweets.**
## **Barplot for the Sentiments (New York)**
```
b=df_ny['Sentiments'].value_counts().reset_index()
plt.title('NY number of tweets and sentiments')
plt.xlabel('Emotions')
plt.ylabel('Number of Tweets')
plt.bar(x=b['index'], height=b['Sentiments'])
```
**Findings: New York has a majority neutral sentiment tweets from the dataframe. It has more positive sentiment tweets than there are negative sentiment tweets.**
```
stat
df1
import datetime
lst=[]
#df1['date'] = datetime.datetime.strptime(df1['date'], '%Y-%m-%d' )
for i in range(len(df1)):
dat= datetime.datetime.strptime(df1['date'][i], '%Y-%m-%d %H:%M:%S')
df1['date'][i]= dat.date()
df1.sort_values(by='date').reset_index(drop=True)
a= ['New Jersey', 'Florida', 'Texas', 'New York']
lst=[]
for i in range(len(stat)):
if stat['state'][i] in a:
lst.append(i)
df_stat= stat.iloc[lst].reset_index(drop=True)
df_stat
```
## **Barplot for the Sentiments (Texas)**
```
b=df_tx['Sentiments'].value_counts().reset_index()
plt.title('TX number of tweets and sentiments')
plt.xlabel('Emotions')
plt.ylabel('Number of Tweets')
plt.bar(x=b['index'], height=b['Sentiments'])
```
**Findings: Texas has a majority neutral sentiment tweets from the dataframe. It has slightly more negative sentiment tweets than there are positive sentiment tweets.**
## **Barplot for the Sentiments (Florida)**
```
b=df_fl['Sentiments'].value_counts().reset_index()
plt.title('FL number of tweets and sentiments')
plt.xlabel('Emotions')
plt.ylabel('Number of Tweets')
plt.bar(x=b['index'], height=b['Sentiments'])
```
**Findings: Florida has a majority neutral sentiment tweets from the dataframe. It has slightly more positive sentiment tweets than there are negative sentiment tweets.**
# **Total Covid Deaths Year to Date (Decemeber 4th)**
---
Source: https://github.com/nytimes/covid-19-data
```
import plotly.express as px
fig = px.line(df_stat, x='date', y='deaths', color='state')
fig.show()
```
The above graph shows the total covid deaths from 02/13/2020 until 12/04/2021 for the states of Texas, Florida, New York, and New Jersey. Texas and Florida have the two most deaths with Texas leading. New York and New Jersey have the least deaths with New York leading New Jersey with the most deaths out of the two.
## **Initial Questions ▶**
1. **Would it stand to reason that the states with more positive-neutral sentiments toward COVID-19 had lower total deaths?**
There are no correlations between tweet sentiments and total deaths according to the curated dataset. Looking at the CSV dataset from the New York Times' Github on the total COVID-19 deaths for the states of Texas, Florida, New York, and New Jersey, it shows that Texas and Florida are top out of the states in terms of the total death count. Texas and Florida had different Positive to Negative sentiments as is apparent from the graph.
2. **Which state had a higher infection death count?**
Texas has the higher death count out of all of the states. New Jersey has the least.
3. **Which states had more negative than positive twitter sentiment to 'COVID-19' in their dataset?**
Texas was the only state that had more negative twitter sentiments in its dataset than positive.
4. **What was the most common sentiment in all datasets?**
Neutral sentiment tweet was the most popular category having much of the tweets in the total dataset: 45.7% of textual data was neutral. 28% of the total textual dataset was positive in sentiment and 26.3% was negative.
5. **Are the sentiment results correlated or related to total death count?**
No. There are no correlations/realtions between sentiment and total death counts. In the Texas dataset, its graph observed more negative sentiments than positive. In the Florida dataset, its graph observed more positive sentiments than negative.
If we look at New Jersey and New York, both datasets have more positive than negative sentiment tweets. New York has considerably more positive tweets than negative tweets. NJ has slightly more positive tweets than negative tweets.
If we wanted to make a statement that states that have more positive tweets to negative tweets have higher total death counts, Texas would have to have that same trend. Texas breaks this trend such that there are more negative tweets than positive tweets in its dataset despite it having the highest total death count out of all of the states.
```
## Visualizing the Text sentiments
pos=df1[df1['Sentiments']=='Positive']
neg=df1[df1['Sentiments']=='Negative']
neu=df1[df1['Sentiments']=='Neutral']
import plotly.express as px
#Frist_Day = Frist_Day
fig = px.pie(df1, names='Sentiments')
fig.show()
```
# **D. Implications**
**For the hiring firm:**
According to the dataset, twitter sentiments alone cannot give any meaningful indication as to whether or not tweets and their emotions have any bearing on COVID-19's death total death count. Better methodologies must be made: perhaps tweets of a certain popularity (perhaps a ratio between likes, retweets, sharing, etc) should be curated into a dataset. Simply looking at tweets at random is a good measure against bias however there is too much statistical noise within the dataset to make any meaningful correlations.
**For Social Science:**
Better methodologies in general should be developed when looking at social media posts. Considerable weight should be given to popular/viral content when curating a dataset as that is a category of data that inherently has the most interaction and 'social proof' due to its popularity on the website.
# **E. Learning Outcomes**
The more I developed my analytical skills, the more I realized that my project had a lot of statsitcal noise. First, I should have developed a better methodolgy for curating tweets. I simply used TWINT to currated 1300+ tweets randomly according to a fixed criteria. I did not add factors such as popularity of a tweet or its general social-media interaction score (primarily because I do not know how to do that yet).
If I were to do this project again, I would start off by curating textual data that had a certain virality to it. I would alone curate tweets with specific likes, shares, and comments.
This would be a difficult task, as I don't know if twitter has an ELO score for tweets: If twitter had a virality ratio for a tweet I would likely curate on that factor as it would come from a class of textual data that has genderated a certain amount of influence.
However, this would add additional questions that would have to be considered as well: How much of the virality score would be coming from a particular state?
For instance, if a score of 10 is VERY viral and that tweet comes from New York, are New York twitter users responsible for that tweet being a score of 10 or could it be users from another geographic location? This is a fair question because I would want to know how much influence the tweet has in its geographic location. It may be possible to develope a webscraper capable of achieving this goal, but It may involve many calculations that still would not gaurantee the results being adequately parsed.
| true |
code
| 0.246193 | null | null | null | null |
|

# **Amazon SageMaker in Practice - Workshop**
## **Click-Through Rate Prediction**
This lab covers the steps for creating a click-through rate (CTR) prediction pipeline. The source code of the workshop prepared by [Pattern Match](https://pattern-match.com) is available on the [company's Github account](https://github.com/patternmatch/amazon-sagemaker-in-practice).
You can reach authors us via the following emails:
- [Sebastian Feduniak](mailto:[email protected])
- [Wojciech Gawroński](mailto:[email protected])
- [Paweł Pikuła](mailto:[email protected])
Today we use the [Criteo Labs](http://labs.criteo.com/) dataset, used for the old [Kaggle competition](https://www.kaggle.com/c/criteo-display-ad-challenge) for the same purpose.
**WARNING**: First you need to update `pandas` to 0.23.4 for the `conda_python3` kernel.
# Background
In advertising, the most critical aspect when it comes to revenue is the final click on the ad. It is one of the ways to compensate for ad delivery for the provider. In the industry, an individual view of the specific ad is called an *impression*.
To compare different algorithms and heuristics of ad serving, "clickability" of the ad is measured and presented in the form of [*click-through rate* metric (CTR)](https://en.wikipedia.org/wiki/Click-through_rate):

If you present randomly sufficient amount of ads to your user base, you get a baseline level of clicks. It is the easiest and simple solution. However, random ads have multiple problems - starting with a lack of relevance, causing distrust and annoyance.
**Ad targeting** is a crucial technique for increasing the relevance of the ad presented to the user. Because resources and a customer's attention is limited, the goal is to provide an ad to most interested users. Predicting those potential clicks based on readily available information like device metadata, demographics, past interactions, and environmental factors is a universal machine learning problem.
# Steps
This notebook presents an example problem to predict if a customer clicks on a given advertisement. The steps include:
- Prepare your *Amazon SageMaker* notebook.
- Download data from the internet into *Amazon SageMaker*.
- Investigate and transforming the data for usage inside *Amazon SageMaker* algorithms.
- Estimate a model using the *Gradient Boosting* algorithm (`xgboost`).
- Leverage hyperparameter optimization for training multiple models with varying hyperparameters in parallel.
- Evaluate and compare the effectiveness of the models.
- Host the model up to make on-going predictions.
# What is *Amazon SageMaker*?
*Amazon SageMaker* is a fully managed machine learning service. It enables discovery and exploration with use of *Jupyter* notebooks and then allows for very easy industrialization on a production-grade, distributed environment - that can handle and scale to extensive datasets.
It provides solutions and algorithms for existing problems, but you can bring your algorithms into service without any problem. Everything mentioned above happens inside your *AWS infrastructure*. That includes secure and isolated *VPC* (*Virtual Private Cloud*), supported by the full power of the platform.
[Typical workflow](https://docs.aws.amazon.com/sagemaker/latest/dg/how-it-works-mlconcepts.html) for creating machine learning models:
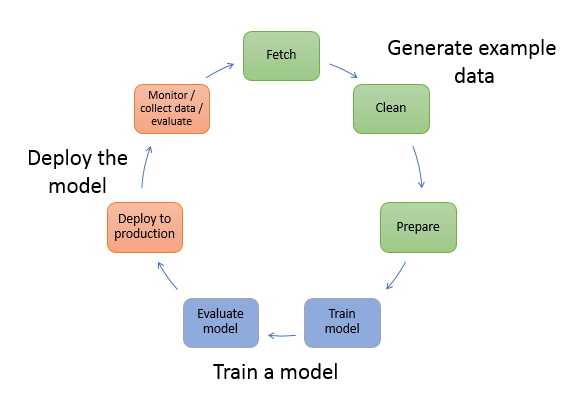
## Note about *Amazon* vs. *AWS* prefix
Why *Amazon* and not *AWS*?
Some services available in *Amazon Web Services* portfolio are branded by *AWS* itself, and some by Amazon.
Everything depends on the origin and team that maintains it - in that case, it originated from the core of the Amazon, and they maintain this service inside the core division.
## Working with *Amazon SageMaker* locally
It is possible to fetch *Amazon SageMaker SDK* library via `pip` and use containers provided by *Amazon* locally, and you are free to do it. The reason why and when you should use *Notebook Instance* is when your datasets are far more significant than you want to store locally and they are residing on *S3* - for such cases it is very convenient to have the *Amazon SageMaker* notebooks available.
# Preparation
The primary way for interacting with *Amazon SageMaker* is to use *S3* as storage for input data and output results.
For our workshops, we have prepared two buckets. One is a dedicated bucket for each user (see the credentials card you have received at the beginning of the workshop) - you should put the name of that bucket into `output_bucket` variable. That bucket is used for storing output models and transformed and split input datasets.
We have also prepared a shared bucket called `amazon-sagemaker-in-practice-workshop` which contains the input dataset inside a path presented below.
```
data_bucket = 'amazon-sagemaker-in-practice-workshop'
user_number = 'CHANGE_TO_YOUR_NUMBER'
user_name = 'user-{}'.format(user_number)
output_bucket = 'amazon-sagemaker-in-practice-bucket-{}'.format(user_name)
path = 'criteo-display-ad-challenge'
key = 'sample.csv'
data_location = 's3://{}/{}/{}'.format(data_bucket, path, key)
```
*Amazon SageMaker* as a service runs is a specific security context applied via *IAM role*. You have created that role when creating *notebook instance* before we have uploaded this content.
Each *notebook* instance provides a *Jupyter* environment with preinstalled libraries and *AWS SDKs*. One of such *SDKs* is *Amazon SageMaker SDK* available from the *Python* environment. With the use of that *SDK* we can check which security context we can use:
```
import boto3
from sagemaker import get_execution_role
role = get_execution_role()
print(role)
```
As a next, we need to import some stuff. It includes *IPython*, *Pandas*, *numpy*, commonly used libraries from *Python's* Standard Library and *Amazon SageMaker* utilities:
```
import numpy as np # For matrix operations and numerical processing
import pandas as pd # For munging tabular data
import matplotlib.pyplot as plt # For charts and visualizations
from IPython.display import Image # For displaying images in the notebook
from IPython.display import display # For displaying outputs in the notebook
from time import gmtime, strftime # For labeling SageMaker models, endpoints, etc.
import sys # For writing outputs to notebook
import math # For ceiling function
import json # For parsing hosting outputs
import os # For manipulating filepath names
import sagemaker # Amazon SageMaker's Python SDK provides helper functions
from sagemaker.predictor import csv_serializer # Converts strings for HTTP POST requests on inference
from sagemaker.tuner import IntegerParameter # Importing HPO elements.
from sagemaker.tuner import CategoricalParameter
from sagemaker.tuner import ContinuousParameter
from sagemaker.tuner import HyperparameterTuner
```
Now we are ready to investigate the dataset.
# Data
The training dataset consists of a portion of Criteo's traffic over a period of 7 days. Each row corresponds to a display ad served by Criteo and the first column indicates whether this ad was clicked or not. The positive (clicked) and negative (non-clicked) examples have both been subsampled (but at different rates) to reduce the dataset size.
There are 13 features taking integer values (mostly count features) and 26 categorical features. Authors hashed values of the categorical features onto 32 bits for anonymization purposes. The semantics of these features is undisclosed. Some features may have missing values (represented as a `-1` for integer values and empty string for categorical ones). Order of the rows is chronological.
You may ask, why in the first place we are investigating such *obfuscated* dataset. In *ad tech* it is not unusual to deal with anonymized, or pseudonymized data, which are not semantical - mostly due to privacy and security reasons.
The test set is similar to the training set but, it corresponds to events on the day following the training period. For that dataset author removed *label* (the first column).
Unfortunately, because of that, it is hard to guess for sure which feature means what, but we can infer that based on the distribution - as we can see below.
## Format
The columns are tab separeted with the following schema:
```
<label> <integer feature 1> ... <integer feature 13> <categorical feature 1> ... <categorical feature 26>
```
When a value is missing, the field is just empty. There is no label field in the test set.
Sample dataset (`sample.csv`) contains *100 000* random rows which are taken from a training dataset to ease the exploration.
## How to load the dataset?
Easy, if it is less than 5 GB - as the disk available on our Notebook instance is equal to 5 GB.
However, there is no way to increase that. :(
It is because of that EBS volume size is fixed at 5GB. As a workaround, you can use the `/tmp` directory for storing large files temporarily. The `/tmp` directory is on the root drive that has around 20GB of free space. However, data stored there cannot be persisted across stopping and restarting of the notebook instance.
What if we need more? We need to preprocess the data in another way (e.g., using *AWS Glue*) and store it on *S3* available for *Amazon SageMaker* training machines.
To read a *CSV* correctly we use *Pandas*. We need to be aware that dataset uses tabs as separators and we do not have the header:
```
data = pd.read_csv(data_location, header = None, sep = '\t')
pd.set_option('display.max_columns', 500) # Make sure we can see all of the columns.
pd.set_option('display.max_rows', 20) # Keep the output on one page.
```
## Exploration
Now we would like to explore our data, especially that we do not know anything about the semantics. How can we do that?
We can do that by reviewing the histograms, frequency tables, correlation matrix, and scatter matrix. Based on that we can try to infer and *"sniff"* the meaning and semantics of the particular features.
### Integer features
First 13 features from the dataset are represented as an integer features, let's review them:
```
# Histograms for each numeric features:
display(data.describe())
%matplotlib inline
hist = data.hist(bins = 30, sharey = True, figsize = (10, 10))
display(data.corr())
pd.plotting.scatter_matrix(data, figsize = (12, 12))
plt.show()
```
### Categorical features
Next 26 features from the dataset are represented as an categorical features. Now it's time to review those:
```
# Frequency tables for each categorical feature:
for column in data.select_dtypes(include = ['object']).columns:
display(pd.crosstab(index = data[column], columns = '% observations', normalize = 'columns'))
categorical_feature = data[14]
unique_values = data[14].unique()
print("Number of unique values in 14th feature: {}\n".format(len(unique_values)))
print(data[14])
```
As for *integer features*, we can push them as-is to the *Amazon SageMaker* algorithms. We cannot do the same thing for *categorical* one.
As you can see above, we have many unique values inside the categorical column. They hashed that into a *32-bit number* represented in a hexadecimal format - as a *string*.
We need to convert that into a number, and we can leverage *one-hot encoding* for that.
#### One-Hot Encoding
It is a way of converting categorical data (e.g., type of animal - *dog*, *cat*, *bear*, and so on) into a numerical one, one-hot encoding means that for a row we create `N` additional columns and we put a `1` if that category is applicable for such row.
#### Sparse Vectors
It is the more efficient way to store data points which are not dense and do not contain all features. It is possible to efficiently compute various operations between those two forms - dense and sparse.
### Problem with *one-hot encoding* in this dataset
Unfortunately, we cannot use *OHE* as-is for this dataset. Why?
```
for column in data.select_dtypes(include=['object']).columns:
size = data.groupby([column]).size()
print("Column '{}' - number of categories: {}".format(column, len(size)))
for column in data.select_dtypes(include=['number']).columns:
size = data.groupby([column]).size()
print("Column '{}' - number of categories: {}".format(column, len(size)))
```
We have too many distinct categories per feature! In the worst case, for an individual feature, we create couple hundred thousands of new columns. Even with the sparse representation it significantly affects memory usage and execution time.
What kind of features are represented by that? Examples of such features are *Device ID*, *User Agent* strings and similar.
How to workaround that? We can use *indexing*.
```
for column in data.select_dtypes(include = ['object']).columns:
print("Converting '{}' column to indexed values...".format(column))
indexed_column = "{}_index".format(column)
data[indexed_column] = pd.Categorical(data[column])
data[indexed_column] = data[indexed_column].cat.codes
categorical_feature = data['14_index']
unique_values = data['14_index'].unique()
print("Number of unique values in 14th feature: {}\n".format(len(unique_values)))
print(data['14_index'])
for column in data.select_dtypes(include=['object']).columns:
data.drop([ column ], axis = 1, inplace = True)
display(data)
```
It is another way of representing a categorical feature in *encoded* form. It is not friendly for *Linear Learner* and classical logistic regression, but we use `xgboost` library - which can leverage such a column without any problems.
## Finishing Touches
Last, but not least - we need to unify the values that are pointing out a missing value `NaN` and `-1`. We use `NaN` everywhere:
```
# Replace all -1 to NaN:
for column in data.columns:
data[column] = data[column].replace(-1, np.nan)
testing = data[2]
testing_unique_values = data[2].unique()
print("Number of unique values in 2nd feature: {}\n".format(len(testing_unique_values)))
print(testing)
```
## Splitting the dataset
We need to split the dataset. We decided to randomize the dataset, and split into 70% for training, 20% for validation and 10% for the test.
```
# Randomly sort the data then split out first 70%, second 20%, and last 10%:
data_len = len(data)
sampled_data = data.sample(frac = 1)
train_data, validation_data, test_data = np.split(sampled_data, [ int(0.7 * data_len), int(0.9 * data_len) ])
```
After splitting, we need to save new training and validation dataset as *CSV* files. After saving, we upload them to the `output_bucket`.
```
train_data.to_csv('train.sample.csv', index = False, header = False)
validation_data.to_csv('validation.sample.csv', index = False, header = False)
s3client = boto3.Session().resource('s3')
train_csv_file = os.path.join(path, 'train/train.csv')
validation_csv_file = os.path.join(path, 'validation/validation.csv')
s3client.Bucket(output_bucket).Object(train_csv_file).upload_file('train.sample.csv')
s3client.Bucket(output_bucket).Object(validation_csv_file).upload_file('validation.sample.csv')
```
Now we are ready to leverage *Amazon SageMaker* for training.
# Training
## Preparation
As a first step, we need to point which libraries we want to use. We do that by fetching the container name based on the name of the library we want to use. In our case, it is `xgboost`.
```
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(boto3.Session().region_name, 'xgboost')
```
Then, we need to point out where to look for input data. In our case, we use *CSV* files uploaded in the previous section to `output_bucket`.
```
train_csv_key = 's3://{}/{}/train/train.csv'.format(output_bucket, path)
validation_csv_key = 's3://{}/{}/validation/validation.csv'.format(output_bucket, path)
s3_input_train = sagemaker.s3_input(s3_data = train_csv_key, content_type = 'csv')
s3_input_validation = sagemaker.s3_input(s3_data = validation_csv_key, content_type = 'csv')
```
## Differences from usual workflow and frameworks usage
Even that *Amazon SageMaker* supports *CSV* files, most of the algorithms work best when you use the optimized `protobuf` `recordIO` format for the training data.
Using this format allows you to take advantage of *pipe mode* when training the algorithms that support it. File mode loads all of your data from *Amazon S3* to the training instance volumes. In *pipe mode*, your training job streams data directly from *Amazon S3*. Streaming can provide faster start times for training jobs and better throughput.
With this mode, you also reduce the size of the *Amazon EBS* volumes for your training instances. *Pipe mode* needs only enough disk space to store your final model artifacts. File mode needs disk space to store both your final model artifacts and your full training dataset.
For our use case - we leverage *CSV* files.
## Single training job
```
sess = sagemaker.Session()
xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count = 1,
train_instance_type = 'ml.m4.xlarge',
base_job_name = user_name,
output_path = 's3://{}/{}/output'.format(output_bucket, path),
sagemaker_session = sess)
xgb.set_hyperparameters(eval_metric = 'logloss',
objective = 'binary:logistic',
eta = 0.2,
max_depth = 10,
colsample_bytree = 0.7,
colsample_bylevel = 0.8,
min_child_weight = 4,
rate_drop = 0.3,
num_round = 75,
gamma = 0.8)
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
Now, we are ready to create *Amazon SageMaker session* and `xgboost` framework objects.
For a single training job, we need to create *Estimator*, where we point the container and *security context*. In this step, we are specifying the instance type and amount of those used for learning. Last, but not least - we need to specify `output_path` and pass the session object.
For the created *Estimator* instance we need to specify the `objective`, `eval_metric` and other hyperparameters used for that training session.
As the last step, we need to start the training process passing the training and validation datasets. Whole training job takes approximately 1-2 minutes at most for the following setup.
## FAQ
**Q**: I see a strange error: `ClientError: Hidden file found in the data path! Remove that before training`. What is that?
**A**: There is something wrong with your input files, probably you messed up the *S3* path passed into training job.
## Hyperparameter Tuning (HPO)
The single job is just one way. We can automate the whole process with use of *hyperparameter tuning*.
As in the case of a single training job, we need to create *Estimator* with the specification for an individual job and set up initial and fixed values for *hyperparameters*. However, outside those - we are setting up the ranges in which algorithm automatically tune in, inside the process of the *HPO*.
Inside the *HyperparameterTuner* specification we are specifying how many jobs we want to run and how many of them we want to run in parallel.
```
hpo_sess = sagemaker.Session()
hpo_xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count = 1,
train_instance_type = 'ml.m4.xlarge',
output_path = 's3://{}/{}/output_hpo'.format(output_bucket, path),
sagemaker_session = hpo_sess)
hpo_xgb.set_hyperparameters(eval_metric = 'logloss',
objective = 'binary:logistic',
colsample_bytree = 0.7,
colsample_bylevel = 0.8,
num_round = 75,
rate_drop = 0.3,
gamma = 0.8)
hyperparameter_ranges = {
'eta': ContinuousParameter(0, 1),
'min_child_weight': ContinuousParameter(1, 10),
'alpha': ContinuousParameter(0, 2),
'max_depth': IntegerParameter(1, 10),
}
objective_metric_name = 'validation:logloss'
objective_type = 'Minimize'
tuner = HyperparameterTuner(hpo_xgb,
objective_metric_name,
hyperparameter_ranges,
base_tuning_job_name = user_name,
max_jobs = 20,
max_parallel_jobs = 5,
objective_type = objective_type)
tuner.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
Another thing that is different is how we see the progress of that particular type of the job. In the previous case, logs were shipped automatically into a *notebook*. For *HPO*, we need to fetch job status via *Amazon SageMaker SDK*. Unfortunately, it allows fetching the only status - logs are available in *Amazon CloudWatch*.
**Beware**, that with current setup whole *HPO* job may take 20-30 minutes.
```
smclient = boto3.client('sagemaker')
job_name = tuner.latest_tuning_job.job_name
hpo_job = smclient.describe_hyper_parameter_tuning_job(HyperParameterTuningJobName = job_name)
hpo_job['HyperParameterTuningJobStatus']
```
# Hosting the single model
After finishing the training, *Amazon SageMaker* by default saves the model inside *S3* bucket we have specified. Moreover, based on that model we can either download the archive and use inside our source code and services when deploying, or we can leverage the hosting mechanism available in the *Amazon SageMaker* service.
## How it works?
After you deploy a model into production using *Amazon SageMaker* hosting services, it creates the endpoint with its configuration.
Your client applications use `InvokeEndpoint` API to get inferences from the model hosted at the specified endpoint. *Amazon SageMaker* strips all `POST` headers except those supported by the *API*. Service may add additional headers.
Does it mean that everyone can call our model? No, calls to `InvokeEndpoint` are authenticated by using *AWS Signature Version 4*.
A customer's model containers must respond to requests within 60 seconds. The model itself can have a maximum processing time of 60 seconds before responding to the /invocations. If your model is going to take 50-60 seconds of processing time, the SDK socket timeout should be set to be 70 seconds.
```
xgb_predictor = xgb.deploy(initial_instance_count = 1, instance_type = 'ml.m4.xlarge')
```
**Beware**, the '!' in the output after hosting model means that it deployed with success.
# Hosting the best model from HPO
Hosting *HPO* model is no different from a single job. *Amazon SageMaker SDK* in very convenient way selects the best model automatically and uses that as a back-end for the endpoint.
```
xgb_predictor_hpo = tuner.deploy(initial_instance_count = 1, instance_type = 'ml.m4.xlarge')
```
# Evaluation
After training and hosting the best possible model, we would like to evaluate its performance with `test_data` subset prepared when splitting data.
As a first step, we need to prepare our hosted predictors to expect `text/csv` payload, which deserializes via *Amazon SageMaker SDK* entity `csv_serializer`.
```
xgb_predictor.content_type = 'text/csv'
xgb_predictor.serializer = csv_serializer
xgb_predictor_hpo.content_type = 'text/csv'
xgb_predictor_hpo.serializer = csv_serializer
```
As a next step, we need to prepare a helper function that split `test_data` into smaller chunks and serialize them before passing it to predictors.
```
def predict(predictor, data, rows = 500):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = ''
for array in split_array:
predictions = ','.join([predictions, predictor.predict(array).decode('utf-8')])
return np.fromstring(predictions[1:], sep =',')
predictions = predict(xgb_predictor, test_data.drop([0], axis=1).values)
hpo_predictions = predict(xgb_predictor_hpo, test_data.drop([0], axis=1).values)
```
As a final step, we would like to compare how many clicks available in `test_data` subset were predicted correctly for job trained individually and with *HPO* jobs.
```
rows = ['actuals']
cols = ['predictions']
clicks = np.round(predictions)
result = pd.crosstab(index = test_data[0], columns = clicks, rownames = rows, colnames = cols)
display("Single job results:")
display(result)
display(result.apply(lambda r: r/r.sum(), axis = 1))
hpo_clicks = np.round(hpo_predictions)
result_hpo = pd.crosstab(index = test_data[0], columns = hpo_clicks, rownames = rows, colnames = cols)
display("HPO job results:")
display(result_hpo)
display(result_hpo.apply(lambda r: r/r.sum(), axis = 1))
```
As you may expect, the model trained with the use of *HPO* works better.
What is interesting - without any tuning and significant improvements, we were able to be classified in the first 25-30 results of the leaderboard from the old [Kaggle competition](https://www.kaggle.com/c/criteo-display-ad-challenge/leaderboard). Impressive!
# Clean-up
To avoid incurring unnecessary charges, use the *AWS Management Console* to delete the resources that you created for this exercise.
Open the *Amazon SageMaker* console at and delete the following resources:
1. The endpoint - that also deletes the ML compute instance or instances.
2. The endpoint configuration.
3. The model.
4. The notebook instance. You need to stop the instance before deleting it.
Keep in mind that *you can not* delete the history of trained individual and hyperparameter optimization jobs, but that do not incur any charges.
Open the Amazon S3 console at and delete the bucket that you created for storing model artifacts and the training dataset. Remember, that before deleting you need to empty it, by removing all objects.
Open the *IAM* console at and delete the *IAM* role. If you created permission policies, you could delete them, too.
Open the *Amazon CloudWatch* console at and delete all of the log groups that have names starting with `/aws/sagemaker`.
When it comes to *endpoints* you can leverage the *Amazon SageMaker SDK* for that operation:
```
sagemaker.Session().delete_endpoint(xgb_predictor.endpoint)
sagemaker.Session().delete_endpoint(xgb_predictor_hpo.endpoint)
```
| true |
code
| 0.466906 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/patprem/IMDb-SentimentAnalysis/blob/main/SentimentAnalysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**Sentiment Analysis of IMDb Movie Reviews**
Importing the basic and required libraries used in this project
```
import torch
from torchtext.legacy import data
from torchtext.legacy import datasets
import torchvision
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import torch.nn as nn
import torch.nn.functional as F
import random
```
Mounting personal Google Drive to load the dataset. **IMPORTANT: Change the directory and root path variable accordingly to yours.**
```
from google.colab import drive
import sys
#Mount your Google drive to the VM
drive.mount('/content/gdrive')
sys.path.append("/content/gdrive/My Drive/ECE4179 S1 2021 Prathik")
#set a root path variable to use
ROOT = "/content/gdrive/My Drive/ECE4179 S1 2021 Prathik/Final Project"
#Follow link and give permission, copy code and paste in text box
#You only have to do this once per session
```
Reading the data from the loaded dataset
**IMPORTANT:**
1. Download the dataset provided under Datasets section on README.md or download from this links: [IMDB Dataset (csv)](https://www.kaggle.com/lakshmi25npathi/sentiment-analysis-of-imdb-movie-reviews/data) and [Large Movie Review Dataset](https://ai.stanford.edu/~amaas/data/sentiment/).
2. Import the downloaded datasets onto your local Google Drive and **change the path variable** accordingly.
```
#from google.colab import files
#uploaded = files.upload()
#import io
#dataset = pd.read_csv(io.BytesIO(uploaded['IMDB Dataset.csv']))
# Dataset is now stored in a Pandas Dataframe
# Reading the data from the dataset.
dataset = pd.read_csv('gdrive/My Drive/ECE4179 S1 2021 Prathik/Final Project/IMDB Dataset.csv')
```
### If you have successfully executed all cells upto this point, then just simply click *Run all* under Runtime tab or press *Ctrl+F9* to execute the remanining cells or follow through the comments besides each cell below to get an understanding of the methodology of this project.
Exploring the loaded dataset
```
pd.set_option('display.max_colwidth',2000) # set the column width to 2000 so that we can read the complete review.
pd.set_option('max_rows', 200)
dataset.head(10) # setting .head(10) to read just the first 10 reviews from the dataset.
dataset.info() # information about the dataset; two columns: review and sentiment,
# where sentiment is the target column or the column that we need to predict.
# number of positive and negative reviews in the dataset.
# dataset is completely balanced and has equal number of positive and negative
# sentiments.
dataset['sentiment'].value_counts()
# reading second review from the dataset and checking how the contents of the review is
# and why we need to use NLP (Natural Language Processing) tasks on this dataset.
review = dataset['review'].loc[10]
review
```
From the above review (output), we can see that there HTML contents, punctuations, special characters, stopwords and others which do not offer much insight into the prediction of our model. The following NLP tasks (text cleaning technqiues) are implemented.
1. Eliminating HTML tags/contents like 'br"
2. Removing punctuations and special characters like |, /, apostrophes, commas and other punctuation marks and etc.
3. Remove stopwords that do not affect the prediction of our outcome and does not offer much insight such as 'are', 'is', 'the' and etc.
4. Use Lemmatization to bring back multiple forms of the same word to their common/base root. For example, words like 'ran', 'running', 'runs' to 'run'.
5. Using Text Tokenization and Vectorization to encode numerical values to our data after the above text cleaning techniques.
6. Lastly, fit these data to a deep learning model like Convolutional Neural Network (CNN) and LinearSVC model and compare the discrepancies between them
```
# Removing HTML contents like "<br>"
# BeautifulSoup is a Python library for extracting data out of HTML and XML files,
# by omitting HTML contents such as "<br>"
from bs4 import BeautifulSoup
soup = BeautifulSoup(review, "html.parser")
review = soup.get_text()
review
# notice that the HTML tags are eliminated.
# Removal of other special characters or punctuations except upper or lower case
# letters using Regular Expressions (Regex)
import re # importing Regex
review = re.sub('\[[^]]*\]', ' ', review) # removing punctuations
review = re.sub('[^a-zA-Z]', ' ', review) # regex; removing strings that contains a non-letter
# i.e., remove except a-z to A-Z
review
# set all characters to lower case for simplicity
review = review.lower()
review
```
Tokenization of reviews in the dataset
```
# Tokenization of reviews
# Stopwords removal: Split the text into tokens since stopwords removal
# works on every word in the text.
review = review.split()
review
```
Removal of Stopwords
```
# importing nltk library to remove stopwords
# Stopwords are words (English language words) that does not add much
# meaning to a sentence. Could be safely ignored without sacrificing the
# meaning of the sentence or review in this case. Words like 'he', 'have',
# 'the' does not provide any insights.
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
review = [word for word in review if not word in set(stopwords.words('english'))]
review
```
**Stemming technique**
Stemming is a process to extract the base form of the words by removing affixes from the words.
Both Stemming and Lemmatization technqiues are implemented on a sample review here to observe the discrepancies between them and why Lemmatization is a better algorithm.
```
# importing PorterStemmer library to perform stemming
from nltk.stem.porter import PorterStemmer
p_stem = PorterStemmer()
review_p_stem = [p_stem.stem(word) for word in review]
review_p_stem
```
**Lemmatization technique**
Lemmatization has the same objective as Stemming, however, it takes into consideration the morphological analysis of the words, i.e., it ensures that the root word is a valid English word alphabetically and meaningfully.
```
from nltk.stem import WordNetLemmatizer
nltk.download('wordnet')
lemma = WordNetLemmatizer()
review = [lemma.lemmatize(word) for word in review]
review
```
From the above results, we can notice that there is a huge difference between the techniques used. For example, 'little' has become 'littl' after Stemming, whereas it remained as 'little' after Lemmatization. Stemming tries to achieve a reduction in words to their root form but the stem itself is not a valid English word. Hence, Lemmatization is used in this project.
```
# merging the words to form a cleaned up version of the text.
review = ' '.join(review)
review
```
We can now see that the text is all cleaned up with no HTML tags, punctuations, special characters and stopwords, and it is ready for vectorization and training the model.
**Vectorization of reviews in the dataset**
```
# create a corpus to convert the text to mathematical forms or numeric values
corpus = [] # empty vector
corpus.append(review)
```
Two Vectorization techniques are applied to check the discrepancy between them and the technique with the highest accuracy will be choosen.
1. CountVectorizer (Bag of Words (BoW) Model)
2. Tfidf Vectorizer (Bag of Words (BoW) Model)
CountVectorizer (Bag of Words (BoW) Model)
```
# importing CountVectorizer to perform vectorization
# Data becomes numeric with 1,2,3s based on the number of times
# they appear in the text
from sklearn.feature_extraction.text import CountVectorizer
count_vect = CountVectorizer()
review_count_vect = count_vect.fit_transform(corpus) # fitting this technique
# onto the corpus
review_count_vect.toarray()
```
Tfidf Vectorizer (Bag of Words (BoW) Model)
1. Text Frequency (TF): how many times a word appears in a review
2. Inverse Document Frequency (IDF): log(total number of reviews/# reviews with that particular word)
TF-IDF score = TF*IDF
```
# importing TfidfVectorizer to perform vectorization
from sklearn.feature_extraction.text import TfidfVectorizer
# IDF acts as a diminishing factor and diminishes the weights of terms that
# occurs frequently in the text and increases the weights of the terms
# that occurs rarely.
tfidf_vect = TfidfVectorizer()
review_tfidf_vect = tfidf_vect.fit_transform(corpus)
review_tfidf_vect.toarray()
```
So far, the techniques mentioned above have been implemented on only one sample review. Now, the above techniques will be applied on all the reviews in the dataset. As there is no test dataset, the dataset is split into 25% of the data as test dataset to test the performance of the model.
```
# splitting the dataset into training and test data
# 25% of the data as test dataset and pseudo random generator
# to randomly distribute the reviews to each dataset
from sklearn.model_selection import train_test_split
train_dataset, test_dataset, traindata_label, testdata_label = train_test_split(dataset['review'], dataset['sentiment'], test_size=0.25, random_state=42)
# Convert the sentiments (target column) to numeric forms (1s and 0s) for simplicity
traindata_label = (traindata_label.replace({'positive': 1, 'negative': 0})).values
testdata_label = (testdata_label.replace({'positive': 1, 'negative': 0})).values
```
Implementation of text cleaning techniques discussed above on the whole dataset and build the train and test corpus.
```
# test and training corpus
train_corpus = []
test_corpus = []
# text cleaning techniques for training dataset
for i in range(train_dataset.shape[0]):
soup = BeautifulSoup(train_dataset.iloc[i], "html.parser")
review = soup.get_text()
review = re.sub('\[[^]]*\]', ' ', review)
review = re.sub('[^a-zA-Z]', ' ', review)
review = review.lower()
review = review.split()
review = [word for word in review if not word in set(stopwords.words('english'))]
lemma = WordNetLemmatizer()
review = [lemma.lemmatize(word) for word in review]
review = ' '.join(review)
train_corpus.append(review)
# text cleaning techniques for test dataset
for j in range(test_dataset.shape[0]):
soup = BeautifulSoup(test_dataset.iloc[j], "html.parser")
review = soup.get_text()
review = re.sub('\[[^]]*\]', ' ', review)
review = re.sub('[^a-zA-Z]', ' ', review)
review = review.lower()
review = review.split()
review = [word for word in review if not word in set(stopwords.words('english'))]
lemma = WordNetLemmatizer()
review = [lemma.lemmatize(word) for word in review]
review = ' '.join(review)
test_corpus.append(review)
```
Validate one sample entry
```
# training corpus
train_corpus[1]
# test corpus
test_corpus[1]
```
Vectorize the training and test corpus using TFIDF technique
```
# lower and upper boundary of the range of n-values for different word n-grams to be extracted.
# (1,3) means unigrams and trigrams.
tfidf_vect = TfidfVectorizer(ngram_range=(1, 3))
# fitting training corpus and test corpus onto TFIDF Vectorizer
tfidf_vect_train = tfidf_vect.fit_transform(train_corpus)
tfidf_vect_test = tfidf_vect.transform(test_corpus)
```
**First model: LinearSVC**
```
# importing LinearSVC library and fitting the data onto the model
from sklearn.svm import LinearSVC
# C: float; regularization parameter, must be positive.
# random_state: controls pseudo random number generation for
# shuffling data for dual coordinate descent.
linear_SVC = LinearSVC(C = 0.5, random_state = 42)
linear_SVC.fit(tfidf_vect_train, traindata_label)
predict = linear_SVC.predict(tfidf_vect_test)
```
LinearSVC with TFIDF Vectorization
```
# Check the performance of the model
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
print("Classification Report of LinearSVC model with TFIDF: \n", classification_report(testdata_label, predict,target_names=['Negative','Positive']))
print("Confusion Matrix of LinearSVC with TFIDF: \n", confusion_matrix(testdata_label, predict))
print("Accuracy of LinearSVC with TFIDF: \n", accuracy_score(testdata_label, predict))
import seaborn as sns
con_matrix = confusion_matrix(testdata_label, predict)
plt.figure(figsize = (10,10))
sns.heatmap(con_matrix, cmap= "Blues", linecolor = 'black', linewidth = 1, annot = True, fmt= '', xticklabels = ['Negative Reviews','Positive Reviews'], yticklabels = ['Negative Reviews','Positive Reviews'])
plt.xlabel("Predicted Sentiment")
plt.ylabel("Actual Sentiment")
```
LinearSVC with CountVectorizer (binary=False) Vectorization
```
# fitting the data onto the model using CountVectorizer technique
# binary = False -> If you set binary=True then CountVectorizer no longer uses the counts of terms/tokens.
# If a token is present in a document, it is 1, if absent it is 0 regardless of its frequency of occurrence.
# So you will be dealing with just binary values. By default, binary=False.
# If True, all non zero counts are set to 1. This is useful for discrete probabilistic models that model binary events rather than integer counts.
count_vect = CountVectorizer(ngram_range=(1, 3), binary = False) # lower and upper boundary
# of the range of n-values for different word n-grams to be extracted.
# (1,3) means unigrams and trigrams.
count_vect_train = count_vect.fit_transform(train_corpus)
count_vect_test = count_vect.transform(test_corpus)
linear_SVC_count = LinearSVC(C = 0.5, random_state = 42, max_iter = 5000)
linear_SVC_count.fit(count_vect_train, traindata_label)
predict_count = linear_SVC_count.predict(count_vect_test)
# Check the performance of the model
print("Classification Report of LinearSVC with CountVectorizer: \n", classification_report(testdata_label, predict_count,target_names=['Negative','Positive']))
print("Confusion Matrix of LinearSVC with CountVectorizer: \n", confusion_matrix(testdata_label, predict_count))
print("Accuracy of LinearSVC with CountVectorizer: \n", accuracy_score(testdata_label, predict_count))
con_matrix = confusion_matrix(testdata_label, predict_count)
plt.figure(figsize = (10,10))
sns.heatmap(con_matrix,cmap= "Blues", linecolor = 'black' , linewidth = 1 , annot = True, fmt='' , xticklabels = ['Negative Reviews','Positive Reviews'] , yticklabels = ['Negative Reviews','Positive Reviews'])
plt.xlabel("Predicted Sentiment")
plt.ylabel("Actual Sentiment")
```
From the above results, we can observe that **LinearSVC with TFIDF vectorization** gives the maximum accuracy and the outcome on our test dataset can be observed.
```
# prediction of data using the above model
predict_dataset = test_dataset.copy()
predict_dataset = pd.DataFrame(predict_dataset)
# setting columns of the predicted outcomes on the dataset
predict_dataset.columns = ['Review']
predict_dataset = predict_dataset.reset_index()
predict_dataset = predict_dataset.drop(['index'], axis=1)
# set the maximum column width to 100000 or more to view the complete review
pd.set_option('display.max_colwidth',100000)
pd.set_option('max_rows', 200)
predict_dataset.head(10)
# comparing the actual/original label with the predicted label
testactual_label = testdata_label.copy()
testactual_label = pd.DataFrame(testactual_label)
testactual_label.columns = ['Sentiment']
# replacing back the numeric forms of the sentiments to positive and negative respectively
testactual_label['Sentiment'] = testactual_label['Sentiment'].replace({1: 'positive', 0: 'negative'})
# predicted sentiments
testpredicted_label = predict.copy()
testpredicted_label = pd.DataFrame(testpredicted_label)
testpredicted_label.columns = ['Predicted Sentiment']
testpredicted_label['Predicted Sentiment'] = testpredicted_label['Predicted Sentiment'].replace({1: 'positive', 0: 'negative'})
# concatenate the original and predicted labels along with its corresponding review
test_result = pd.concat([predict_dataset, testactual_label, testpredicted_label], axis=1)
pd.set_option('display.max_colwidth',100000)
pd.set_option('max_rows', 200)
test_result.head(10)
```
**Second model: Convolutional Neural Network (CNN)**
Using CNN to conduct sentiment analysis
Preparing the data using a different dataset
```
n = 1234
random.seed(n)
np.random.seed(n)
torch.manual_seed(n)
torch.backends.cudnn.deterministic = True
# for convolutional layers
# batch dimension is first
# 'batch_first = true' argument used to tell torchtext to return the permuted data
# in CNN, batch dimension is first, so no need to permute data as 'batch_first' is set to true in TEXT field
TEXT = data.Field(tokenize = 'spacy', tokenizer_language = 'en_core_web_sm', batch_first = True)
LABEL = data.LabelField(dtype = torch.float)
# splitting the dataset into training and test data
train_dataset, test_dataset = datasets.IMDB.splits(TEXT, LABEL)
train_dataset, valid_dataset = train_dataset.split(random_state = random.seed(n))
# building the vocabulary and loading the pre-trained word embeddings
MAX_VOCAB_SIZE = 25_000
TEXT.build_vocab(train_dataset, max_size = MAX_VOCAB_SIZE, vectors = "glove.6B.100d", unk_init = torch.Tensor.normal_)
LABEL.build_vocab(train_dataset)
# creating the iterators
# batch size of 64 is used
BATCH_SIZE = 64
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits((train_dataset, valid_dataset, test_dataset), batch_size = BATCH_SIZE, device = device)
# checking the number of reviews in training, test and validation datasets
print(f'Training reviews: {len(train_dataset)}')
print(f'Validation reviews: {len(valid_dataset)}')
print(f'Testing reviews : {len(test_dataset)}')
```
Building a CNN for the dataset (Text is 1 dimensional)
1. Convert words into word embeddings to visualize words in 2 dimensions, each word along one axis and other axis for the elements of vectors.
2. Use a filter size of [n*width]. 'n' is the number of sequential words (n-grams, number of tokens in the review) and width is the dimensions of the word or dimensional embeddings (depth of filter).
3. Bi-grams are filters that covers two words at a time, tri-grams covers three words and so on. And each element of the filter has a weight associated with it.
4. The output of this filter is the weighted sum of all elements covered by the filter (single real number). Similarly, the filter moves to cover the next bi-gram and another output is calculated and so on.
5. This is an example of one such filter. CNNs has a plethora of these filters. The main idea is that each filter will learn a different feature to extract. For example, each of the [2*width] filters looks for the occurence of different bi-grams that are relevant for analysing sentiment of movie reviews. And the same goes for different sizes of filters (n-grams) with heights of 3,4,5 etc.
6. Then, use max pooling on the output of the convolutional layers, which takes the maximum value over a dimension.
7. The maximum value is the most important feature for determining the sentiment of the review, which corresponds to the most essential n-gram within the review. Through backpropagation, the weights of the filters are updated so that whenever certain n-grams that are highly indicative of the sentiment are seen, the output of the filter is a high or the highest value amongst all. This high value is then passed through the max pooling layer if it is the maximum value in the output.
8. This model has 100 filters of 3 different sizes (n-grams), i.e., 300 different n-grams. Later, these are concatenated into a single vector and passed through a linear layer to predict the sentiment.
9. Most importantly, input review has to be atleast as long as the largest filter height used.
```
import torch.nn as nn
import torch.nn.functional as F
# implementing the convolutional layers (nn.Conv2d)
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim, dropout, pad_idx):
# in_channels: number of channels in text/image fed into convolutional layer
# in text, only one single channel
# in_channels: number of filters
# kernel_size: size of filters (n*emb_dim); n is the size of n-grams
# and emb_dim is the dimensional embedding or width of the text
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.conv_0 = nn.Conv2d(in_channels = 1, out_channels = n_filters, kernel_size = (filter_sizes[0], embedding_dim))
self.conv_1 = nn.Conv2d(in_channels = 1, out_channels = n_filters, kernel_size = (filter_sizes[1], embedding_dim))
self.conv_2 = nn.Conv2d(in_channels = 1, out_channels = n_filters, kernel_size = (filter_sizes[2], embedding_dim))
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text):
# pass review to an embedding layer to get embeddings
# second dimension of the input to nn.Conv2d is the channel dimension
embed_done = self.embedding(text)
# text has no channel dimension, so unsqueeze to make one
# and matches with in_channels (=1) dimension
embed_done = embed_done.unsqueeze(1)
# pass tensors through convolutional and pooling layers using ReLU
# (non-linearity) activation function after the conv layers
conv_layer0 = F.relu(self.conv_0(embed_done).squeeze(3))
conv_layer1 = F.relu(self.conv_1(embed_done).squeeze(3))
conv_layer2 = F.relu(self.conv_2(embed_done).squeeze(3))
# pooling layers handles reviews of different lengths
# with max pooling, input to linear layer is the total no. of filters
max_pool0 = F.max_pool1d(conv_layer0, conv_layer0.shape[2]).squeeze(2)
max_pool1 = F.max_pool1d(conv_layer1, conv_layer1.shape[2]).squeeze(2)
max_pool2 = F.max_pool1d(conv_layer2, conv_layer2.shape[2]).squeeze(2)
# output size of conv layers depends on the input size
# different batches contains reviews of different lengths
# lastly, apply dropout on the concatenated filter outputs
concatenation = self.dropout(torch.cat((max_pool0, max_pool1, max_pool2), dim = 1))
# pass through a linear layer (fully-connected layer) to make predictions
return self.fc(concatenation)
```
The above CNN uses only 3 different sized filters. The below code is a generic CNN that takes in any number of filters.
```
# place all conv layers in a nn.ModuleList - function in PyTorch to hold a list
# of PyTorch nn.Module
# pass arbitrary sized list of filter sizes (generic model)
# creates a conv layer for each
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim, dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.convs = nn.ModuleList([nn.Conv2d(in_channels = 1, out_channels = n_filters, kernel_size = (fs, embedding_dim)) for fs in filter_sizes])
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
# iterate through the list applying each conv layer to get a list of
# conv outputs which is fed into max pooling layer in a list
# comprehension before concatenation and passing through dropout
# and linear layers
def forward(self, text):
embed_done = self.embedding(text)
embed_done = embed_done.unsqueeze(1)
conv_layer_relu = [F.relu(conv(embed_done)).squeeze(3) for conv in self.convs]
max_pool_drop = [F.max_pool1d(conv, conv.shape[2]).squeeze(2) for conv in conv_layer_relu]
concatenation = self.dropout(torch.cat(max_pool_drop, dim = 1))
return self.fc(concatenation)
```
Creating an instance of our CNN model
```
dimension_input = len(TEXT.vocab)
# dimensional embeddings
dimn_embedding = 100
# number of filters
number_filters = 100
# size of the filters
size_filter = [3,4,5]
# output size
dimension_output = 1
# dropout (value of 'p')
p = 0.5
# padding
padding = TEXT.vocab.stoi[TEXT.pad_token]
# applying all these to the CNN
model = CNN(dimension_input, dimn_embedding, number_filters, size_filter, dimension_output, p, padding)
# check number of parameters in CNN model
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f'The model has {count_parameters(model):,} trainable parameters')
```
Loading the pre-trained embeddings
```
embed_pretrain = TEXT.vocab.vectors
# weights
model.embedding.weight.data.copy_(embed_pretrain)
# zero the initial weights of the unknown and padding tokens
token = TEXT.vocab.stoi[TEXT.unk_token]
model.embedding.weight.data[token] = torch.zeros(dimn_embedding)
model.embedding.weight.data[padding] = torch.zeros(dimn_embedding)
```
Next, now it is ready to train our model. The optimizer and loss function (criterion) are initialized. Here, I have used the ADAM optimizer and Binary Cross Entropy with Logits Loss function.
```
# importing ADAM optimizer
import torch.optim as optim
# set ADAM optimizer
optimizer = optim.Adam(model.parameters())
# set the loss function
criterion = nn.BCEWithLogitsLoss()
# set model and criterion on GPU
model = model.to(device)
criterion = criterion.to(device)
```
Implementing a function to calculate accuracy in order to check the performance of the model
```
# returns accuracy per batch, will return, for example, 0.8 instead of 8.
def binary_accuracy(preds, y):
# rounds predictions to the closest integer
predictions_rounded = torch.round(torch.sigmoid(preds))
true_prediction = (predictions_rounded == y).float() # float better for division purposes
accuracy = true_prediction.sum() / len(true_prediction)
return accuracy
# function for training the model
def train(model, iterator, optimizer, criterion):
# initialise the epoch loss and accuracy
epoch_accuracy = 0
epoch_loss = 0
model.train() # to ensure dropout is turned ON while training
for batch in iterator:
optimizer.zero_grad()
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
accuracy = binary_accuracy(predictions, batch.label)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_accuracy += accuracy .item()
return epoch_loss / len(iterator), epoch_accuracy / len(iterator)
# function for testing the model
def evaluate(model, iterator, criterion):
# initialise the epoch loss and accuracy
epoch_loss = 0
epoch_accuracy = 0
model.eval() # to ensure dropout is turned OFF while evaluating/testing
with torch.no_grad():
for batch in iterator:
predictions = model(batch.text).squeeze(1)
loss = criterion(predictions, batch.label)
accuracy = binary_accuracy(predictions, batch.label)
epoch_loss += loss.item()
epoch_accuracy += accuracy.item()
return epoch_loss / len(iterator), epoch_accuracy / len(iterator)
# importing time library to define function to tell the time taken of our
# epochs
import time
def epoch_time(start_time, end_time):
time_taken = end_time - start_time
time_taken_mins = int(time_taken / 60)
time_taken_secs = int(time_taken - (time_taken_mins * 60))
return time_taken_mins, time_taken_secs
```
**Training the CNN model**
```
# 5 epochs are enough to view the values of loss and accuracy
number_epochs = 5
good_validationloss = float('inf') # set to float
for epoch in range(number_epochs):
start_time = time.time()
# calculating the training loss and accuracy and the validation loss
# and accuracy
train_loss, train_accuracy = train(model, train_iterator, optimizer, criterion)
valid_loss, valid_accuracy = evaluate(model, valid_iterator, criterion)
end_time = time.time()
epoch_minutes, epoch_secs = epoch_time(start_time, end_time)
if valid_loss < good_validationloss:
good_validationloss = valid_loss
torch.save(model.state_dict(), 'tut4-model.pt')
# print the training loss and accuracy and validation loss and accuracy
print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_minutes}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_accuracy*100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_accuracy*100:.2f}%')
```
This function will prompt the user to input their reviews. Based on the review, the model will the predict whether the sentiment of the review is positive or negative along with how accurate the model predicts the sentiment.
```
import spacy
prompt = spacy.load('en_core_web_sm')
# minimum_length is set to 10000 so that utmost 10000 tokens are accepted for computing
# the outcome, i.e., 10000 words in a review which is more than enough
def classify_predict_sentiment(model, sentence, minimum_length = 10000):
model.eval()
tokenization_done = [tok.text for tok in prompt.tokenizer(sentence)]
# classify_predict_sentiment function accepts minimum length argument also by changing
# minimum_length
# If tokenization_done input sentence is less than minimum_length tokens, then we append
# padding tokens ('<pad>') to make it minimum_length tokens
if len(tokenization_done) < minimum_length:
tokenization_done += ['<pad>'] * (minimum_length - len(tokenization_done))
indexing = [TEXT.vocab.stoi[t] for t in tokenization_done]
box = torch.LongTensor(indexing).to(device)
box = box.unsqueeze(0)
prediction = torch.sigmoid(model(box))
# if the accuracy of the review is less than 0.5, it shall be considered
# a negative review and anything above 0.5 shall be considered a positive
# review
if prediction.item() < 0.5:
print(f'Negative Review')
else:
print(f'Positive Review')
return print(f'Accuracy of this review: {prediction.item():.8f}')
```
The following positive and negative reviews are fed into the model and the outcome is displayed along with the accuracy from the model, i.e., how accurate the model predicts whether it is a positive or negative review.
```
classify_predict_sentiment(model, "I thought this was a wonderful way to spend time on a too hot summer weekend, sitting in the air conditioned theater and watching a light-hearted comedy. The plot is simplistic, but the dialogue is witty and the characters are likable (even the well bread suspected serial killer). While some may be disappointed when they realize this is not Match Point 2: Risk Addiction, I thought it was proof that Woody Allen is still fully in control of the style many of us have grown to love.<br /><br />This was the most I'd laughed at one of Woody's comedies in years (dare I say a decade?). While I've never been impressed with Scarlet Johanson, in this she managed to tone down her sexy image and jumped right into a average, but spirited young woman.<br /><br />This may not be the crown jewel of his career, but it was wittier than Devil Wears Prada and more interesting than Superman a great comedy to go see with friends.")
classify_predict_sentiment(model, "This show was an amazing, fresh & innovative idea in the 70's when it first aired. The first 7 or 8 years were brilliant, but things dropped off after that. By 1990, the show was not really funny anymore, and it's continued its decline further to the complete waste of time it is today.<br /><br />It's truly disgraceful how far this show has fallen. The writing is painfully bad, the performances are almost as bad - if not for the mildly entertaining respite of the guest-hosts, this show probably wouldn't still be on the air. I find it so hard to believe that the same creator that hand-selected the original cast also chose the band of hacks that followed. How can one recognize such brilliance and then see fit to replace it with such mediocrity? I felt I must give 2 stars out of respect for the original cast that made this show such a huge success. As it is now, the show is just awful. I can't believe it's still on the air.")
classify_predict_sentiment(model, "This a fantastic movie of three prisoners who become famous. One of the actors is george clooney and I'm not a fan but this roll is not bad. Another good thing about the movie is the soundtrack (The man of constant sorrow). I recommand this movie to everybody. Greetings Bart")
classify_predict_sentiment(model,"I saw this movie when I was about 12 when it came out. I recall the scariest scene was the big bird eating men dangling helplessly from parachutes right out of the air. The horror. The horror.<br /><br />As a young kid going to these cheesy B films on Saturday afternoons, I still was tired of the formula for these monster type movies that usually included the hero, a beautiful woman who might be the daughter of a professor and a happy resolution when the monster died in the end. I didn't care much for the romantic angle as a 12 year old and the predictable plots. I love them now for the unintentional humor.<br /><br />But, about a year or so later, I saw Psycho when it came out and I loved that the star, Janet Leigh, was bumped off early in the film. I sat up and took notice at that point. Since screenwriters are making up the story, make it up to be as scary as possible and not from a well-worn formula. There are no rules.")
classify_predict_sentiment(model,"The Karen Carpenter Story shows a little more about singer Karen Carpenter's complex life. Though it fails in giving accurate facts, and details.<br /><br />Cynthia Gibb (portrays Karen) was not a fine election. She is a good actress , but plays a very naive and sort of dumb Karen Carpenter. I think that the role needed a stronger character. Someone with a stronger personality.<br /><br />Louise Fletcher role as Agnes Carpenter is terrific, she does a great job as Karen's mother.<br /><br />It has great songs, which could have been included in a soundtrack album. Unfortunately they weren't, though this movie was on the top of the ratings in USA and other several countries.")
classify_predict_sentiment(model,"I watched this film not really expecting much, I got it in a pack of 5 films, all of which were pretty terrible in their own way for under a fiver so what could I expect? and you know what I was right, they were all terrible, this movie has a few (and a few is stretching it) interesting points, the occasional camcorder view is a nice touch, the drummer is very like a drummer, i.e damned annoying and, well thats about it actually, the problem is that its just so boring, in what I can only assume was an attempt to build tension, a whole lot of nothing happens and when it does its utterly tedious (I had my thumb on the fast forward button, ready to press for most of the movie, but gave it a go) and seriously is the lead singer of the band that great looking, coz they don't half mention how beautiful he is a hell of a lot, I thought he looked a bit like a meercat, all this and I haven't even mentioned the killer, I'm not even gonna go into it, its just not worth explaining. Anyway as far as I'm concerned Star and London are just about the only reason to watch this and with the exception of London (who was actually quite funny) it wasn't because of their acting talent, I've certainly seen a lot worse, but I've also seen a lot better. Best avoid unless your bored of watching paint dry.")
```
| true |
code
| 0.543045 | null | null | null | null |
|
### Linear Problem
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.utils.data import DataLoader, Dataset
import seaborn as sns
from torch import nn
from torch.nn import functional as F
```
### Data Preparation
```
data = pd.read_csv('data/test.csv')
data.head()
sns.scatterplot(data=data, x='x', y='y',hue='color')
class Data(Dataset):
def __init__(self, path, transform=None, shuffle=True):
self.dataFrame = pd.read_csv(path)
self.xy = pd.read_csv(path).values
if shuffle:
np.random.shuffle(self.xy)
self.len = self.xy.shape[0]
self.x = self.xy[:, :-1]
self.y = self.xy[:, -1]
self.transform = transform
print(self.x.shape)
def __getitem__(self, index):
sample = self.x[index], self.y[index]
if self.transform:
sample = self.transform(sample)
return sample
def __len__(self):
return self.len
def plot(self):
sns.scatterplot(data=self.dataFrame, x='x', y='y',hue='color')
plt.show()
```
### Transformers on our data
```
class ToTensor:
def __call__(self, samples):
x, y = samples
return torch.from_numpy(x.astype('float32')) ,torch.from_numpy(np.array(y, dtype='float32'))
train = Data(path='data/train.csv', transform=ToTensor(), shuffle=True)
test = Data(path='data/test.csv', transform=ToTensor(),shuffle=True )
train.plot()
test.plot()
train_set = DataLoader(dataset=train,
batch_size =5,
shuffle=True)
test_set = DataLoader(dataset=test,
batch_size =5,
shuffle=False)
```
### Predicting the Color
```
class Net(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(2,32)
self.fc2 = nn.Linear(32,64)
self.fc3 = nn.Linear(64, 1)
def forward(self,x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = torch.sigmoid(self.fc3(x))
return x
net = Net()
net
criterion = torch.nn.BCELoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
EPOCHS = 5
for epoch in range(EPOCHS):
print(f'Epochs: {epoch+1}/{EPOCHS}')
for data in train_set:
X, y = data
optimizer.zero_grad()
# forward pass
output = net(X.view(-1, 2))
#calculate loss
loss = criterion(output, y.unsqueeze(1))
## backward pass
loss.backward()
# update the weights
optimizer.step()
print("loss: ", loss.item())
total, correct = 0, 0
with torch.no_grad():
for data in test_set:
X, y = data
outputs = net(X.view(-1, 2))
for i in range(len(torch.round(outputs))):
if y[i] == torch.round(outputs[i]):
correct +=1
total +=1
print(correct/total)
total, correct = 0, 0
with torch.no_grad():
for data in train_set:
X, y = data
outputs = net(X.view(-1, 2))
for i in range(len(torch.round(outputs))):
if y[i] == torch.round(outputs[i]):
correct +=1
total +=1
print(correct/total)
```
### Making Predictions
```
test.plot()
test[0]
torch.Tensor([1., 0.])
torch.round(net(torch.Tensor([1., 2.]))).item()
```
> Done
| true |
code
| 0.723981 | null | null | null | null |
|
# NBAiLab - Finetuning and Evaluating a BERT model for NER and POS
<img src="https://raw.githubusercontent.com/NBAiLab/notram/master/images/nblogo_2.png">
In this notebook we will finetune the [NB-BERTbase Model](https://github.com/NBAiLab/notram) released by the National Library of Norway. This is a model trained on a large corpus (110GB) of Norwegian texts.
We will finetune this model on the [NorNE dataset](https://github.com/ltgoslo/norne). for Named Entity Recognition (NER) and Part of Speech (POS) tags using the [Transformers Library by Huggingface](https://huggingface.co/transformers/). After training the model should be able to accept any text string input (up to 512 tokens) and return POS or NER-tags for this text. This is useful for a number of NLP tasks, for instance for extracting/removing names/places from a document. After training, we will save the model, evaluate it and use it for predictions.
The Notebook is intended for experimentation with the pre-release NoTram models from the National Library of Norway, and is made for educational purposes. If you just want to use the model, you can instead initiate one of our finetuned models.
## Before proceeding
Create a copy of this notebook by going to "File - Save a Copy in Drive"
# Install Dependencies and Define Helper Functions
You need to run the code below to install some libraries and initiate some helper functions. Click "Show Code" if you later want to examine this part as well.
```
#@title
#The notebook is using some functions for reporting that are only available in Transformers 4.2.0. Until that is released, we are installing from the source.
!pip -q install https://github.com/huggingface/transformers/archive/0ecbb698064b94560f24c24fbfbd6843786f088b.zip
!pip install -qU scikit-learn datasets seqeval conllu pyarrow
import logging
import os
import sys
from dataclasses import dataclass
from dataclasses import field
from typing import Optional
import numpy as np
import pandas as pd
import tensorflow as tf
import tensorflow_datasets as tfds
import transformers
from datasets import load_dataset
from seqeval.metrics import accuracy_score
from seqeval.metrics import f1_score
from seqeval.metrics import precision_score
from seqeval.metrics import recall_score
from seqeval.metrics import classification_report
from transformers.training_args import TrainingArguments
from tqdm import tqdm
from transformers import (
AutoConfig,
AutoModelForTokenClassification,
AutoTokenizer,
DataCollatorForTokenClassification,
PreTrainedTokenizerFast,
Trainer,
TrainingArguments,
pipeline,
set_seed
)
from google.colab import output
from IPython.display import Markdown
from IPython.display import display
# Helper Funtions - Allows us to format output by Markdown
def printm(string):
display(Markdown(string))
## Preprocessing the dataset
# Tokenize texts and align the labels with them.
def tokenize_and_align_labels(examples):
tokenized_inputs = tokenizer(
examples[text_column_name],
max_length=max_length,
padding=padding,
truncation=True,
# We use this argument because the texts in our dataset are lists of words (with a label for each word).
is_split_into_words=True,
)
labels = []
for i, label in enumerate(examples[label_column_name]):
word_ids = tokenized_inputs.word_ids(batch_index=i)
previous_word_idx = None
label_ids = []
for word_idx in word_ids:
# Special tokens have a word id that is None. We set the label to -100 so they are automatically
# ignored in the loss function.
if word_idx is None:
label_ids.append(-100)
# We set the label for the first token of each word.
elif word_idx != previous_word_idx:
label_ids.append(label_to_id[label[word_idx]])
# For the other tokens in a word, we set the label to either the current label or -100, depending on
# the label_all_tokens flag.
else:
label_ids.append(label_to_id[label[word_idx]] if label_all_tokens else -100)
previous_word_idx = word_idx
labels.append(label_ids)
tokenized_inputs["labels"] = labels
return tokenized_inputs
# Metrics
def compute_metrics(pairs):
predictions, labels = pairs
predictions = np.argmax(predictions, axis=2)
# Remove ignored index (special tokens)
true_predictions = [
[label_list[p] for (p, l) in zip(prediction, label) if l != -100]
for prediction, label in zip(predictions, labels)
]
true_labels = [
[label_list[l] for (p, l) in zip(prediction, label) if l != -100]
for prediction, label in zip(predictions, labels)
]
return {
"accuracy_score": accuracy_score(true_labels, true_predictions),
"precision": precision_score(true_labels, true_predictions),
"recall": recall_score(true_labels, true_predictions),
"f1": f1_score(true_labels, true_predictions),
"report": classification_report(true_labels, true_predictions, digits=4)
}
```
# Settings
Try running this with the default settings first. The default setting should give you a pretty good result. If you want training to go even faster, reduce the number of epochs. The first variables you should consider changing are the one in the dropdown menus. Later you can also experiment with the other settings to get even better results.
```
#Model, Dataset, and Task
#@markdown Set the main model that the training should start from
model_name = 'NbAiLab/nb-bert-base' #@param ["NbAiLab/nb-bert-base", "bert-base-multilingual-cased"]
#@markdown ---
#@markdown Set the dataset for the task we are training on
dataset_name = "NbAiLab/norne" #@param ["NbAiLab/norne", "norwegian_ner"]
dataset_config = "bokmaal" #@param ["bokmaal", "nynorsk"]
task_name = "ner" #@param ["ner", "pos"]
#General
overwrite_cache = False #@#param {type:"boolean"}
cache_dir = ".cache" #param {type:"string"}
output_dir = "./output" #param {type:"string"}
overwrite_output_dir = False #param {type:"boolean"}
seed = 42 #param {type:"number"}
set_seed(seed)
#Tokenizer
padding = False #param ["False", "'max_length'"] {type: 'raw'}
max_length = 512 #param {type: "number"}
label_all_tokens = False #param {type:"boolean"}
# Training
#@markdown ---
#@markdown Set training parameters
per_device_train_batch_size = 8 #param {type: "integer"}
per_device_eval_batch_size = 8 #param {type: "integer"}
learning_rate = 3e-05 #@param {type: "number"}
weight_decay = 0.0 #param {type: "number"}
adam_beta1 = 0.9 #param {type: "number"}
adam_beta2 = 0.999 #param {type: "number"}
adam_epsilon = 1e-08 #param {type: "number"}
max_grad_norm = 1.0 #param {type: "number"}
num_train_epochs = 4.0 #@param {type: "number"}
num_warmup_steps = 750 #@param {type: "number"}
save_total_limit = 1 #param {type: "integer"}
load_best_model_at_end = True #@param {type: "boolean"}
```
# Load the Dataset used for Finetuning
The default setting is to use the NorNE dataset. This is currently the largest (and best) dataset with annotated POS/NER tags that are available today. All sentences is tagged both for POS and NER. The dataset is available as a Huggingface dataset, so loading it is very easy.
```
#Load the dataset
dataset = load_dataset(dataset_name, dataset_config)
#Getting some variables from the dataset
column_names = dataset["train"].column_names
features = dataset["train"].features
text_column_name = "tokens" if "tokens" in column_names else column_names[0]
label_column_name = (
f"{task_name}_tags" if f"{task_name}_tags" in column_names else column_names[1]
)
label_list = features[label_column_name].feature.names
label_to_id = {i: i for i in range(len(label_list))}
num_labels = len(label_list)
#Look at the dataset
printm(f"###Quick Look at the NorNE Dataset")
print(dataset["train"].data.to_pandas()[[text_column_name, label_column_name]])
printm(f"###All labels ({num_labels})")
print(label_list)
if task_name == "ner":
mlabel_list = {label.split("-")[-1] for label in label_list}
printm(f"###Main labels ({len(mlabel_list)})")
print(mlabels)
```
# Initialize Training
We are here using the native Trainer interface provided by Huggingface. Huggingface also has an interface for Tensorflow and PyTorch. To see an example of how to use the Tensorflow interface, please take a look at our notebook about classification.
```
config = AutoConfig.from_pretrained(
model_name,
num_labels=num_labels,
finetuning_task=task_name,
cache_dir=cache_dir,
)
tokenizer = AutoTokenizer.from_pretrained(
model_name,
cache_dir=cache_dir,
use_fast=True,
)
model = AutoModelForTokenClassification.from_pretrained(
model_name,
from_tf=bool(".ckpt" in model_name),
config=config,
cache_dir=cache_dir,
)
data_collator = DataCollatorForTokenClassification(tokenizer)
tokenized_datasets = dataset.map(
tokenize_and_align_labels,
batched=True,
load_from_cache_file=not overwrite_cache,
num_proc=os.cpu_count(),
)
training_args = TrainingArguments(
output_dir=output_dir,
overwrite_output_dir=overwrite_output_dir,
do_train=True,
do_eval=True,
do_predict=True,
per_device_train_batch_size=per_device_train_batch_size,
per_device_eval_batch_size=per_device_eval_batch_size,
learning_rate=learning_rate,
weight_decay=weight_decay,
adam_beta1=adam_beta1,
adam_beta2=adam_beta2,
adam_epsilon=adam_epsilon,
max_grad_norm=max_grad_norm,
num_train_epochs=num_train_epochs,
warmup_steps=num_warmup_steps,
load_best_model_at_end=load_best_model_at_end,
seed=seed,
save_total_limit=save_total_limit,
)
# Initialize our Trainer
trainer = Trainer(
model=model,
args=training_args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["validation"],
tokenizer=tokenizer,
data_collator=data_collator,
compute_metrics=compute_metrics,
)
```
# Start Training
Training for the default 4 epochs should take around 10-15 minutes if you have access to GPU.
```
%%time
train_result = trainer.train()
trainer.save_model() # Saves the tokenizer too for easy upload
# Need to save the state, since Trainer.save_model saves only the tokenizer with the model
trainer.state.save_to_json(os.path.join(training_args.output_dir, "trainer_state.json"))
#Print Results
output_train_file = os.path.join(output_dir, "train_results.txt")
with open(output_train_file, "w") as writer:
printm("**Train results**")
for key, value in sorted(train_result.metrics.items()):
printm(f"{key} = {value}")
writer.write(f"{key} = {value}\n")
```
# Evaluate the Model
The model is now saved on your Colab disk. This is a temporary disk that will disappear when the Colab is closed. You should copy it to another place if you want to keep the result. Now we can evaluate the model and play with it. Expect some UserWarnings since there might be errors in the training file.
```
printm("**Evaluate**")
results = trainer.evaluate()
output_eval_file = os.path.join(output_dir, "eval_results.txt")
with open(output_eval_file, "w") as writer:
printm("**Eval results**")
for key, value in results.items():
printm(f"{key} = {value}")
writer.write(f"{key} = {value}\n")
```
# Run Preditions on the Test Dataset
You should be able to end up with a result not far from what we have reported for the NB-BERT-model:
<table align="left">
<tr><td></td><td>Bokmål</td><td>Nynorsk</td></tr>
<tr><td>POS</td><td>98.86</td><td>98.77</td></tr>
<tr><td>NER</td><td>93.66</td><td>92.02</td></tr>
</table>
```
printm("**Predict**")
test_dataset = tokenized_datasets["test"]
predictions, labels, metrics = trainer.predict(test_dataset)
predictions = np.argmax(predictions, axis=2)
output_test_results_file = os.path.join(output_dir, "test_results.txt")
with open(output_test_results_file, "w") as writer:
printm("**Predict results**")
for key, value in sorted(metrics.items()):
printm(f"{key} = {value}")
writer.write(f"{key} = {value}\n")
# Remove ignored index (special tokens)
true_predictions = [
[label_list[p] for (p, l) in zip(prediction, label) if l != -100]
for prediction, label in zip(predictions, labels)
]
# Save predictions
output_test_predictions_file = os.path.join(output_dir, "test_predictions.txt")
with open(output_test_predictions_file, "w") as writer:
for prediction in true_predictions:
writer.write(" ".join(prediction) + "\n")
```
# Use the model
This model will assign labels to the different word/tokens. B-TAG marks the beginning of the entity, while I-TAG is a continuation of the entity. In the example below the model should be able to pick out the individual names as well as understand how many places and organisations that are mentioned.
```
text = "Svein Arne Brygfjeld, Freddy Wetjen, Javier de la Rosa og Per E Kummervold jobber alle ved AILABen til Nasjonalbiblioteket. Nasjonalbiblioteket har lokaler b\xE5de i Mo i Rana og i Oslo. " #@param {type:"string"}
group_entities = True #param {type:"boolean"}
#Load the saved model in the pipeline, and run some predicions
model = AutoModelForTokenClassification.from_pretrained(output_dir)
try:
tokenizer = AutoTokenizer.from_pretrained(output_dir)
except TypeError:
tokenizer = AutoTokenizer.from_pretrained(model_name)
ner_model = pipeline(
"ner", model=model, tokenizer=tokenizer, grouped_entities=group_entities
)
result = ner_model(text)
output = []
for token in result:
entity = int(token['entity_group'].replace("LABEL_", ""))
output.append({
"word": token['word'],
"entity": label_list[entity],
"score": token['score'],
})
pd.DataFrame(output).style.hide_index()
```
---
##### Copyright 2020 © National Library of Norway
| true |
code
| 0.654646 | null | null | null | null |
|
# Table of Contents
<p><div class="lev1"><a href="#Introduction-to-Pandas"><span class="toc-item-num">1 </span>Introduction to Pandas</a></div><div class="lev2"><a href="#Pandas-Data-Structures"><span class="toc-item-num">1.1 </span>Pandas Data Structures</a></div><div class="lev3"><a href="#Series"><span class="toc-item-num">1.1.1 </span>Series</a></div><div class="lev3"><a href="#DataFrame"><span class="toc-item-num">1.1.2 </span>DataFrame</a></div><div class="lev3"><a href="#Exercise-1"><span class="toc-item-num">1.1.3 </span>Exercise 1</a></div><div class="lev3"><a href="#Exercise-2"><span class="toc-item-num">1.1.4 </span>Exercise 2</a></div><div class="lev2"><a href="#Importing-data"><span class="toc-item-num">1.2 </span>Importing data</a></div><div class="lev3"><a href="#Microsoft-Excel"><span class="toc-item-num">1.2.1 </span>Microsoft Excel</a></div><div class="lev2"><a href="#Pandas-Fundamentals"><span class="toc-item-num">1.3 </span>Pandas Fundamentals</a></div><div class="lev3"><a href="#Manipulating-indices"><span class="toc-item-num">1.3.1 </span>Manipulating indices</a></div><div class="lev2"><a href="#Indexing-and-Selection"><span class="toc-item-num">1.4 </span>Indexing and Selection</a></div><div class="lev3"><a href="#Exercise-3"><span class="toc-item-num">1.4.1 </span>Exercise 3</a></div><div class="lev2"><a href="#Operations"><span class="toc-item-num">1.5 </span>Operations</a></div><div class="lev2"><a href="#Sorting-and-Ranking"><span class="toc-item-num">1.6 </span>Sorting and Ranking</a></div><div class="lev3"><a href="#Exercise-4"><span class="toc-item-num">1.6.1 </span>Exercise 4</a></div><div class="lev2"><a href="#Hierarchical-indexing"><span class="toc-item-num">1.7 </span>Hierarchical indexing</a></div><div class="lev2"><a href="#Missing-data"><span class="toc-item-num">1.8 </span>Missing data</a></div><div class="lev3"><a href="#Exercise-5"><span class="toc-item-num">1.8.1 </span>Exercise 5</a></div><div class="lev2"><a href="#Data-summarization"><span class="toc-item-num">1.9 </span>Data summarization</a></div><div class="lev2"><a href="#Writing-Data-to-Files"><span class="toc-item-num">1.10 </span>Writing Data to Files</a></div><div class="lev3"><a href="#Advanced-Exercise:-Compiling-Ebola-Data"><span class="toc-item-num">1.10.1 </span>Advanced Exercise: Compiling Ebola Data</a></div><div class="lev2"><a href="#References"><span class="toc-item-num">1.11 </span>References</a></div>
# Introduction to Pandas
**pandas** is a Python package providing fast, flexible, and expressive data structures designed to work with *relational* or *labeled* data both. It is a fundamental high-level building block for doing practical, real world data analysis in Python.
pandas is well suited for:
- Tabular data with heterogeneously-typed columns, as in an SQL table or Excel spreadsheet
- Ordered and unordered (not necessarily fixed-frequency) time series data.
- Arbitrary matrix data (homogeneously typed or heterogeneous) with row and column labels
- Any other form of observational / statistical data sets. The data actually need not be labeled at all to be placed into a pandas data structure
Key features:
- Easy handling of **missing data**
- **Size mutability**: columns can be inserted and deleted from DataFrame and higher dimensional objects
- Automatic and explicit **data alignment**: objects can be explicitly aligned to a set of labels, or the data can be aligned automatically
- Powerful, flexible **group by functionality** to perform split-apply-combine operations on data sets
- Intelligent label-based **slicing, fancy indexing, and subsetting** of large data sets
- Intuitive **merging and joining** data sets
- Flexible **reshaping and pivoting** of data sets
- **Hierarchical labeling** of axes
- Robust **IO tools** for loading data from flat files, Excel files, databases, and HDF5
- **Time series functionality**: date range generation and frequency conversion, moving window statistics, moving window linear regressions, date shifting and lagging, etc.
```
import pandas as pd
import numpy as np
pd.options.mode.chained_assignment = None # default='warn'
```
## Pandas Data Structures
### Series
A **Series** is a single vector of data (like a NumPy array) with an *index* that labels each element in the vector.
```
counts = pd.Series([632, 1638, 569, 115])
counts
```
If an index is not specified, a default sequence of integers is assigned as the index. A NumPy array comprises the values of the `Series`, while the index is a pandas `Index` object.
```
counts.values
counts.index
```
We can assign meaningful labels to the index, if they are available:
```
bacteria = pd.Series([632, 1638, 569, 115],
index=['Firmicutes', 'Proteobacteria', 'Actinobacteria', 'Bacteroidetes'])
bacteria
```
These labels can be used to refer to the values in the `Series`.
```
bacteria['Actinobacteria']
bacteria[[name.endswith('bacteria') for name in bacteria.index]]
[name.endswith('bacteria') for name in bacteria.index]
```
Notice that the indexing operation preserved the association between the values and the corresponding indices.
We can still use positional indexing if we wish.
```
bacteria[0]
```
We can give both the array of values and the index meaningful labels themselves:
```
bacteria.name = 'counts'
bacteria.index.name = 'phylum'
bacteria
```
NumPy's math functions and other operations can be applied to Series without losing the data structure.
```
# natural logarithm
np.log(bacteria)
# log base 10
np.log10(bacteria)
```
We can also filter according to the values in the `Series`:
```
bacteria[bacteria>1000]
```
A `Series` can be thought of as an ordered key-value store. In fact, we can create one from a `dict`:
```
bacteria_dict = {'Firmicutes': 632, 'Proteobacteria': 1638, 'Actinobacteria': 569,
'Bacteroidetes': 115}
pd.Series(bacteria_dict)
```
Notice that the `Series` is created in key-sorted order.
If we pass a custom index to `Series`, it will select the corresponding values from the dict, and treat indices without corrsponding values as missing. Pandas uses the `NaN` (not a number) type for missing values.
```
bacteria2 = pd.Series(bacteria_dict,
index=['Cyanobacteria','Firmicutes',
'Proteobacteria','Actinobacteria'])
bacteria2
bacteria2.isnull()
```
Critically, the labels are used to **align data** when used in operations with other Series objects:
```
bacteria + bacteria2
```
Contrast this with NumPy arrays, where arrays of the same length will combine values element-wise; adding Series combined values with the same label in the resulting series. Notice also that the missing values were propogated by addition.
### DataFrame
Inevitably, we want to be able to store, view and manipulate data that is *multivariate*, where for every index there are multiple fields or columns of data, often of varying data type.
A `DataFrame` is a tabular data structure, encapsulating multiple series like columns in a spreadsheet. Data are stored internally as a 2-dimensional object, but the `DataFrame` allows us to represent and manipulate higher-dimensional data.
```
data = pd.DataFrame({'value':[632, 1638, 569, 115, 433, 1130, 754, 555],
'patient':[1, 1, 1, 1, 2, 2, 2, 2],
'phylum':['Firmicutes', 'Proteobacteria', 'Actinobacteria',
'Bacteroidetes', 'Firmicutes', 'Proteobacteria', 'Actinobacteria', 'Bacteroidetes']})
data
```
Notice the `DataFrame` is sorted by column name. We can change the order by indexing them in the order we desire:
```
data[['phylum','value','patient']]
```
A `DataFrame` has a second index, representing the columns:
```
data.columns
```
The `dtypes` attribute reveals the data type for each column in our DataFrame.
- `int64` is numeric integer values
- `object` strings (letters and numbers)
- `float64` floating-point values
```
data.dtypes
```
If we wish to access columns, we can do so either by dict-like indexing or by attribute:
```
data['patient']
data.patient
type(data.value)
data[['value']]
```
Notice this is different than with `Series`, where dict-like indexing retrieved a particular element (row).
If we want access to a row in a `DataFrame`, we index its `loc` attribute.
```
data.loc[3]
```
### Exercise 1
Try out these commands to see what they return:
- `data.head()`
- `data.tail(3)`
- `data.shape`
```
data.head() # returns the first (5 by default) rows of data.
data.tail(3) # returns the 3 last rows of data
data.shape # returns the dimension of data (nbr rows, nbr cols)
```
An alternative way of initializing a `DataFrame` is with a list of dicts:
```
data = pd.DataFrame([{'patient': 1, 'phylum': 'Firmicutes', 'value': 632},
{'patient': 1, 'phylum': 'Proteobacteria', 'value': 1638},
{'patient': 1, 'phylum': 'Actinobacteria', 'value': 569},
{'patient': 1, 'phylum': 'Bacteroidetes', 'value': 115},
{'patient': 2, 'phylum': 'Firmicutes', 'value': 433},
{'patient': 2, 'phylum': 'Proteobacteria', 'value': 1130},
{'patient': 2, 'phylum': 'Actinobacteria', 'value': 754},
{'patient': 2, 'phylum': 'Bacteroidetes', 'value': 555}])
data
```
Its important to note that the Series returned when a DataFrame is indexted is merely a **view** on the DataFrame, and not a copy of the data itself. So you must be cautious when manipulating this data:
```
vals = data.value
vals
vals[5] = 0
vals
```
If we plan on modifying an extracted Series, its a good idea to make a copy.
```
vals = data.value.copy()
vals[5] = 1000
vals
```
We can create or modify columns by assignment:
```
data.value[[3,4,6]] = [14, 21, 5]
data
data['year'] = 2013
data
```
But note, we cannot use the attribute indexing method to add a new column:
```
data.treatment = 1
data
data.treatment
```
### Exercise 2
From the `data` table above, create an index to return all rows for which the phylum name ends in "bacteria" and the value is greater than 1000.
----------------------------
Find the values of 'phylum' ending in 'bacteria'
```
colwitbacteria = [col for col in data['phylum'] if col.endswith('bacteria')]
colwitbacteria
```
then filter the rows having one of the 'bacteria' values
```
rowswithbacteria = data[data['phylum'].isin(colwitbacteria)]
```
then take the values bigger than 1000
```
rowswithbacteria[rowswithbacteria.value > 1000]
```
Note that it is probably faster to first filter the values bigger than 1000 as it filters more values out.
Specifying a `Series` as a new columns cause its values to be added according to the `DataFrame`'s index:
```
treatment = pd.Series([0]*4 + [1]*2)
treatment
data['treatment'] = treatment
data
```
Other Python data structures (ones without an index) need to be the same length as the `DataFrame`:
```
month = ['Jan', 'Feb', 'Mar', 'Apr']
# data['month'] = month # throws error (done on puropse)
data['month'] = ['Jan']*len(data)
data
```
We can use the `drop` method to remove rows or columns, which by default drops rows. We can be explicit by using the `axis` argument:
```
data_nomonth = data.drop('month', axis=1)
data_nomonth
```
We can extract the underlying data as a simple `ndarray` by accessing the `values` attribute:
```
data.values
```
Notice that because of the mix of string and integer (and `NaN`) values, the dtype of the array is `object`. The dtype will automatically be chosen to be as general as needed to accomodate all the columns.
```
df = pd.DataFrame({'foo': [1,2,3], 'bar':[0.4, -1.0, 4.5]})
df.values
```
Pandas uses a custom data structure to represent the indices of Series and DataFrames.
```
data.index
```
Index objects are immutable:
```
# data.index[0] = 15 # throws error
```
This is so that Index objects can be shared between data structures without fear that they will be changed.
```
bacteria2.index = bacteria.index
bacteria2
```
## Importing data
A key, but often under-appreciated, step in data analysis is importing the data that we wish to analyze. Though it is easy to load basic data structures into Python using built-in tools or those provided by packages like NumPy, it is non-trivial to import structured data well, and to easily convert this input into a robust data structure:
genes = np.loadtxt("genes.csv", delimiter=",", dtype=[('gene', '|S10'), ('value', '<f4')])
Pandas provides a convenient set of functions for importing tabular data in a number of formats directly into a `DataFrame` object. These functions include a slew of options to perform type inference, indexing, parsing, iterating and cleaning automatically as data are imported.
Let's start with some more bacteria data, stored in csv format.
```
!cat Data/microbiome.csv
```
This table can be read into a DataFrame using `read_csv`:
```
mb = pd.read_csv("Data/microbiome.csv")
mb
```
Notice that `read_csv` automatically considered the first row in the file to be a header row.
We can override default behavior by customizing some the arguments, like `header`, `names` or `index_col`.
```
pd.read_csv("Data/microbiome.csv", header=None).head()
```
`read_csv` is just a convenience function for `read_table`, since csv is such a common format:
```
mb = pd.read_table("Data/microbiome.csv", sep=',')
```
The `sep` argument can be customized as needed to accomodate arbitrary separators. For example, we can use a regular expression to define a variable amount of whitespace, which is unfortunately very common in some data formats:
sep='\s+'
For a more useful index, we can specify the first two columns, which together provide a unique index to the data.
```
mb = pd.read_csv("Data/microbiome.csv", index_col=['Patient','Taxon'])
mb.head()
```
This is called a *hierarchical* index, which we will revisit later in the section.
If we have sections of data that we do not wish to import (for example, known bad data), we can populate the `skiprows` argument:
```
pd.read_csv("Data/microbiome.csv", skiprows=[3,4,6]).head()
```
If we only want to import a small number of rows from, say, a very large data file we can use `nrows`:
```
pd.read_csv("Data/microbiome.csv", nrows=4)
```
Alternately, if we want to process our data in reasonable chunks, the `chunksize` argument will return an iterable object that can be employed in a data processing loop. For example, our microbiome data are organized by bacterial phylum, with 14 patients represented in each:
```
pd.read_csv("Data/microbiome.csv", chunksize=14)
data_chunks = pd.read_csv("Data/microbiome.csv", chunksize=14)
mean_tissue = pd.Series({chunk.Taxon[0]: chunk.Tissue.mean() for chunk in data_chunks})
mean_tissue
```
Most real-world data is incomplete, with values missing due to incomplete observation, data entry or transcription error, or other reasons. Pandas will automatically recognize and parse common missing data indicators, including `NA` and `NULL`.
```
!cat Data/microbiome_missing.csv
pd.read_csv("Data/microbiome_missing.csv").head(20)
```
Above, Pandas recognized `NA` and an empty field as missing data.
```
pd.isnull(pd.read_csv("Data/microbiome_missing.csv")).head(20)
```
Unfortunately, there will sometimes be inconsistency with the conventions for missing data. In this example, there is a question mark "?" and a large negative number where there should have been a positive integer. We can specify additional symbols with the `na_values` argument:
```
pd.read_csv("Data/microbiome_missing.csv", na_values=['?', -99999]).head(20)
```
These can be specified on a column-wise basis using an appropriate dict as the argument for `na_values`.
### Microsoft Excel
Since so much financial and scientific data ends up in Excel spreadsheets (regrettably), Pandas' ability to directly import Excel spreadsheets is valuable. This support is contingent on having one or two dependencies (depending on what version of Excel file is being imported) installed: `xlrd` and `openpyxl` (these may be installed with either `pip` or `easy_install`).
The read_excel convenience function in pandas imports a specific sheet from an Excel file
```
mb = pd.read_excel('Data/microbiome/MID2.xls', sheetname='Sheet 1', header=None)
mb.head()
```
There are several other data formats that can be imported into Python and converted into DataFrames, with the help of buitl-in or third-party libraries. These include JSON, XML, HDF5, relational and non-relational databases, and various web APIs. These are beyond the scope of this tutorial, but are covered in [Python for Data Analysis](http://shop.oreilly.com/product/0636920023784.do).
## Pandas Fundamentals
This section introduces the new user to the key functionality of Pandas that is required to use the software effectively.
For some variety, we will leave our digestive tract bacteria behind and employ some baseball data.
```
baseball = pd.read_csv("Data/baseball.csv", index_col='id')
baseball.head()
```
Notice that we specified the `id` column as the index, since it appears to be a unique identifier. We could try to create a unique index ourselves by combining `player` and `year`:
```
player_id = baseball.player + baseball.year.astype(str)
baseball_newind = baseball.copy()
baseball_newind.index = player_id
baseball_newind.head()
```
This looks okay, but let's check:
```
baseball_newind.index.is_unique
```
So, indices need not be unique. Our choice is not unique because some players change teams within years.
```
pd.Series(baseball_newind.index).value_counts()
```
The most important consequence of a non-unique index is that indexing by label will return multiple values for some labels:
```
baseball_newind.loc['wickmbo012007']
```
We will learn more about indexing below.
We can create a truly unique index by combining `player`, `team` and `year`:
```
player_unique = baseball.player + baseball.team + baseball.year.astype(str)
baseball_newind = baseball.copy()
baseball_newind.index = player_unique
baseball_newind.head()
baseball_newind.index.is_unique
```
We can create meaningful indices more easily using a hierarchical index; for now, we will stick with the numeric `id` field as our index.
### Manipulating indices
**Reindexing** allows users to manipulate the data labels in a DataFrame. It forces a DataFrame to conform to the new index, and optionally, fill in missing data if requested.
A simple use of `reindex` is to alter the order of the rows:
```
baseball.reindex(baseball.index[::-1]).head()
```
Notice that the `id` index is not sequential. Say we wanted to populate the table with every `id` value. We could specify and index that is a sequence from the first to the last `id` numbers in the database, and Pandas would fill in the missing data with `NaN` values:
```
id_range = range(baseball.index.values.min(), baseball.index.values.max())
baseball.reindex(id_range).head()
```
Missing values can be filled as desired, either with selected values, or by rule:
```
baseball.reindex(id_range, method='ffill', columns=['player','year']).head()
baseball.reindex(id_range, fill_value='charliebrown', columns=['player']).head()
```
Keep in mind that `reindex` does not work if we pass a non-unique index series.
We can remove rows or columns via the `drop` method:
```
baseball.shape
baseball.drop([89525, 89526])
baseball.drop(['ibb','hbp'], axis=1)
```
## Indexing and Selection
Indexing works analogously to indexing in NumPy arrays, except we can use the labels in the `Index` object to extract values in addition to arrays of integers.
```
# Sample Series object
hits = baseball_newind.h
hits
# Numpy-style indexing
hits[:3]
# Indexing by label
hits[['womacto01CHN2006','schilcu01BOS2006']]
```
We can also slice with data labels, since they have an intrinsic order within the Index:
```
hits['womacto01CHN2006':'gonzalu01ARI2006']
hits['womacto01CHN2006':'gonzalu01ARI2006'] = 5
hits
```
In a `DataFrame` we can slice along either or both axes:
```
baseball_newind[['h','ab']]
baseball_newind[baseball_newind.ab>500]
```
For a more concise (and readable) syntax, we can use the new `query` method to perform selection on a `DataFrame`. Instead of having to type the fully-specified column, we can simply pass a string that describes what to select. The query above is then simply:
```
baseball_newind.query('ab > 500')
```
The `DataFrame.index` and `DataFrame.columns` are placed in the query namespace by default. If you want to refer to a variable in the current namespace, you can prefix the variable with `@`:
```
min_ab = 450
baseball_newind.query('ab > @min_ab')
```
The indexing field `loc` allows us to select subsets of rows and columns in an intuitive way:
```
baseball_newind.loc['gonzalu01ARI2006', ['h','X2b', 'X3b', 'hr']]
baseball_newind.loc[:'myersmi01NYA2006', 'hr']
```
In addition to using `loc` to select rows and columns by **label**, pandas also allows indexing by **position** using the `iloc` attribute.
So, we can query rows and columns by absolute position, rather than by name:
```
baseball_newind.iloc[:5, 5:8]
```
### Exercise 3
You can use the `isin` method query a DataFrame based upon a list of values as follows:
data['phylum'].isin(['Firmacutes', 'Bacteroidetes'])
Use `isin` to find all players that played for the Los Angeles Dodgers (LAN) or the San Francisco Giants (SFN). How many records contain these values?
```
baseball[baseball['team'].isin(['LAN', 'SFN'])]
```
15 records contains those values
## Operations
`DataFrame` and `Series` objects allow for several operations to take place either on a single object, or between two or more objects.
For example, we can perform arithmetic on the elements of two objects, such as combining baseball statistics across years. First, let's (artificially) construct two Series, consisting of home runs hit in years 2006 and 2007, respectively:
```
hr2006 = baseball.loc[baseball.year==2006, 'hr']
hr2006.index = baseball.player[baseball.year==2006]
hr2007 = baseball.loc[baseball.year==2007, 'hr']
hr2007.index = baseball.player[baseball.year==2007]
hr2007
```
Now, let's add them together, in hopes of getting 2-year home run totals:
```
hr_total = hr2006 + hr2007
hr_total
```
Pandas' data alignment places `NaN` values for labels that do not overlap in the two Series. In fact, there are only 6 players that occur in both years.
```
hr_total[hr_total.notnull()]
```
While we do want the operation to honor the data labels in this way, we probably do not want the missing values to be filled with `NaN`. We can use the `add` method to calculate player home run totals by using the `fill_value` argument to insert a zero for home runs where labels do not overlap:
```
hr2007.add(hr2006, fill_value=0)
```
Operations can also be **broadcast** between rows or columns.
For example, if we subtract the maximum number of home runs hit from the `hr` column, we get how many fewer than the maximum were hit by each player:
```
baseball.hr - baseball.hr.max()
```
Or, looking at things row-wise, we can see how a particular player compares with the rest of the group with respect to important statistics
```
baseball.loc[89521, "player"]
stats = baseball[['h','X2b', 'X3b', 'hr']]
diff = stats - stats.loc[88641]
diff[:10]
```
We can also apply functions to each column or row of a `DataFrame`
```
stats.apply(np.median)
def range_calc(x):
return x.max() - x.min()
stat_range = lambda x: x.max() - x.min()
stats.apply(stat_range)
```
Lets use apply to calculate a meaningful baseball statistics, [slugging percentage](https://en.wikipedia.org/wiki/Slugging_percentage):
$$SLG = \frac{1B + (2 \times 2B) + (3 \times 3B) + (4 \times HR)}{AB}$$
And just for fun, we will format the resulting estimate.
```
def slugging(x):
bases = x['h']-x['X2b']-x['X3b']-x['hr'] + 2*x['X2b'] + 3*x['X3b'] + 4*x['hr']
ab = x['ab']+1e-6
return bases/ab
baseball.apply(slugging, axis=1).round(3)
```
## Sorting and Ranking
Pandas objects include methods for re-ordering data.
```
baseball_newind.sort_index().head()
baseball_newind.sort_index(ascending=False).head()
```
Try sorting the **columns** instead of the rows, in ascending order:
```
baseball_newind.sort_index(axis=1).head()
```
We can also use `sort_values` to sort a `Series` by value, rather than by label.
```
baseball.hr.sort_values(ascending=False)
```
For a `DataFrame`, we can sort according to the values of one or more columns using the `by` argument of `sort_values`:
```
baseball[['player','sb','cs']].sort_values(ascending=[False,True],
by=['sb', 'cs']).head(10)
```
**Ranking** does not re-arrange data, but instead returns an index that ranks each value relative to others in the Series.
```
baseball.hr.rank()
```
Ties are assigned the mean value of the tied ranks, which may result in decimal values.
```
pd.Series([100,100]).rank()
```
Alternatively, you can break ties via one of several methods, such as by the order in which they occur in the dataset:
```
baseball.hr.rank(method='first')
```
Calling the `DataFrame`'s `rank` method results in the ranks of all columns:
```
baseball.rank(ascending=False).head()
baseball[['r','h','hr']].rank(ascending=False).head()
```
### Exercise 4
Calculate **on base percentage** for each player, and return the ordered series of estimates.
$$OBP = \frac{H + BB + HBP}{AB + BB + HBP + SF}$$
define the function and appy it.
```
def on_base_perc(pl):
nominator = pl['h'] + pl['bb'] + pl['hbp'] #H+BB+HBP
denom = pl['ab'] + pl['bb'] +pl['hbp'] +pl['sf']
if(denom == 0) : # If the denom == 0 we can not compute nominator/denom, hence we retrun NaN
return np.NaN
return nominator / denom
baseball.apply(on_base_perc, axis=1).round(3)
```
and again but ordered
```
baseball.apply(on_base_perc, axis=1).round(3).sort_values(ascending=False)
```
## Hierarchical indexing
In the baseball example, I was forced to combine 3 fields to obtain a unique index that was not simply an integer value. A more elegant way to have done this would be to create a hierarchical index from the three fields.
```
baseball_h = baseball.set_index(['year', 'team', 'player'])
baseball_h.head(10)
```
This index is a `MultiIndex` object that consists of a sequence of tuples, the elements of which is some combination of the three columns used to create the index. Where there are multiple repeated values, Pandas does not print the repeats, making it easy to identify groups of values.
```
baseball_h.index[:10]
baseball_h.index.is_unique
```
Try using this hierarchical index to retrieve Julio Franco (`francju01`), who played for the Atlanta Braves (`ATL`) in 2007:
```
baseball_h.loc[(2007, 'ATL', 'francju01')]
```
Recall earlier we imported some microbiome data using two index columns. This created a 2-level hierarchical index:
```
mb = pd.read_csv("Data/microbiome.csv", index_col=['Taxon','Patient'])
mb.head(10)
```
With a hierachical index, we can select subsets of the data based on a *partial* index:
```
mb.loc['Proteobacteria']
```
Hierarchical indices can be created on either or both axes. Here is a trivial example:
```
frame = pd.DataFrame(np.arange(12).reshape(( 4, 3)),
index =[['a', 'a', 'b', 'b'], [1, 2, 1, 2]],
columns =[['Ohio', 'Ohio', 'Colorado'], ['Green', 'Red', 'Green']])
frame
```
If you want to get fancy, both the row and column indices themselves can be given names:
```
frame.index.names = ['key1', 'key2']
frame.columns.names = ['state', 'color']
frame
```
With this, we can do all sorts of custom indexing:
```
frame.loc['a', 'Ohio']
```
Try retrieving the value corresponding to `b2` in `Colorado`:
---------------------------
fetch b2 and then Colorado
```
frame.loc['b', 2]['Colorado']
```
Additionally, the order of the set of indices in a hierarchical `MultiIndex` can be changed by swapping them pairwise:
```
mb.swaplevel('Patient', 'Taxon').head()
```
Data can also be sorted by any index level, using `sortlevel`:
```
mb.sortlevel('Patient', ascending=False).head()
```
## Missing data
The occurence of missing data is so prevalent that it pays to use tools like Pandas, which seamlessly integrates missing data handling so that it can be dealt with easily, and in the manner required by the analysis at hand.
Missing data are represented in `Series` and `DataFrame` objects by the `NaN` floating point value. However, `None` is also treated as missing, since it is commonly used as such in other contexts (*e.g.* NumPy).
```
foo = pd.Series([np.nan, -3, None, 'foobar'])
foo
foo.isnull()
```
Missing values may be dropped or indexed out:
```
bacteria2
bacteria2.dropna()
bacteria2.isnull()
bacteria2[bacteria2.notnull()]
```
By default, `dropna` drops entire rows in which one or more values are missing.
```
data.dropna()
```
This can be overridden by passing the `how='all'` argument, which only drops a row when every field is a missing value.
```
data.dropna(how='all')
```
This can be customized further by specifying how many values need to be present before a row is dropped via the `thresh` argument.
```
data.loc[7, 'year'] = np.nan
data
data.dropna(thresh=5)
```
This is typically used in time series applications, where there are repeated measurements that are incomplete for some subjects.
### Exercise 5
Try using the `axis` argument to drop columns with missing values:
```
data.dropna(axis=1)
```
Rather than omitting missing data from an analysis, in some cases it may be suitable to fill the missing value in, either with a default value (such as zero) or a value that is either imputed or carried forward/backward from similar data points. We can do this programmatically in Pandas with the `fillna` argument.
```
bacteria2.fillna(0)
data.fillna({'year': 2013, 'treatment':2})
```
Notice that `fillna` by default returns a new object with the desired filling behavior, rather than changing the `Series` or `DataFrame` in place (**in general, we like to do this, by the way!**).
We can alter values in-place using `inplace=True`.
```
data.year.fillna(2013, inplace=True)
data
```
Missing values can also be interpolated, using any one of a variety of methods:
```
bacteria2.fillna(method='bfill')
```
## Data summarization
We often wish to summarize data in `Series` or `DataFrame` objects, so that they can more easily be understood or compared with similar data. The NumPy package contains several functions that are useful here, but several summarization or reduction methods are built into Pandas data structures.
```
baseball.sum()
```
Clearly, `sum` is more meaningful for some columns than others. For methods like `mean` for which application to string variables is not just meaningless, but impossible, these columns are automatically exculded:
```
baseball.mean()
```
The important difference between NumPy's functions and Pandas' methods is that the latter have built-in support for handling missing data.
```
bacteria2
bacteria2.mean()
```
Sometimes we may not want to ignore missing values, and allow the `nan` to propagate.
```
bacteria2.mean(skipna=False)
```
Passing `axis=1` will summarize over rows instead of columns, which only makes sense in certain situations.
```
extra_bases = baseball[['X2b','X3b','hr']].sum(axis=1)
extra_bases.sort_values(ascending=False)
```
A useful summarization that gives a quick snapshot of multiple statistics for a `Series` or `DataFrame` is `describe`:
```
baseball.describe()
```
`describe` can detect non-numeric data and sometimes yield useful information about it.
```
baseball.player.describe()
```
We can also calculate summary statistics *across* multiple columns, for example, correlation and covariance.
$$cov(x,y) = \sum_i (x_i - \bar{x})(y_i - \bar{y})$$
```
baseball.hr.cov(baseball.X2b)
```
$$corr(x,y) = \frac{cov(x,y)}{(n-1)s_x s_y} = \frac{\sum_i (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_i (x_i - \bar{x})^2 \sum_i (y_i - \bar{y})^2}}$$
```
baseball.hr.corr(baseball.X2b)
baseball.ab.corr(baseball.h)
```
Try running `corr` on the entire `baseball` DataFrame to see what is returned:
----------------------------
```
baseball.corr()
```
it returns the correlation matrix for all features
----------------------------
If we have a `DataFrame` with a hierarchical index (or indices), summary statistics can be applied with respect to any of the index levels:
```
mb.head()
mb.sum(level='Taxon')
```
## Writing Data to Files
As well as being able to read several data input formats, Pandas can also export data to a variety of storage formats. We will bring your attention to just a couple of these.
```
mb.to_csv("mb.csv")
```
The `to_csv` method writes a `DataFrame` to a comma-separated values (csv) file. You can specify custom delimiters (via `sep` argument), how missing values are written (via `na_rep` argument), whether the index is writen (via `index` argument), whether the header is included (via `header` argument), among other options.
An efficient way of storing data to disk is in binary format. Pandas supports this using Python’s built-in pickle serialization.
```
baseball.to_pickle("baseball_pickle")
```
The complement to `to_pickle` is the `read_pickle` function, which restores the pickle to a `DataFrame` or `Series`:
```
pd.read_pickle("baseball_pickle")
```
As Wes warns in his book, it is recommended that binary storage of data via pickle only be used as a temporary storage format, in situations where speed is relevant. This is because there is no guarantee that the pickle format will not change with future versions of Python.
### Advanced Exercise: Compiling Ebola Data
The `Data/ebola` folder contains summarized reports of Ebola cases from three countries during the recent outbreak of the disease in West Africa. For each country, there are daily reports that contain various information about the outbreak in several cities in each country.
From these data files, use pandas to import them and create a single data frame that includes the daily totals of new cases and deaths for each country.
### Our solution is in a seperate notebook
| true |
code
| 0.267145 | null | null | null | null |
|
# Image Compression and Decompression
## Downloading the data and preprocessing it
```
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
print(x_train.shape,x_test.shape)
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
x_train.shape,x_test.shape
```
## Visualising training data image
```
from matplotlib import pyplot as plt
import numpy as np
first_image = x_train[0]
first_image = np.array(first_image, dtype='float')
pixels = first_image.reshape((28, 28))
plt.imshow(pixels, cmap='gray')
plt.show()
```
## Creating the Autoencoder
```
import keras
from keras import layers
input_img = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2, 2), padding='same')(x)
# at this point the representation is (4, 4, 8) i.e. 128-dimensional
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(16, (3, 3), activation='relu')(x)
x = layers.UpSampling2D((2, 2))(x)
decoded = layers.Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.summary()
from keras.utils import plot_model
plot_model(autoencoder, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
```
## Training the autoencoder
```
history = autoencoder.fit(x_train, x_train,
epochs=5,
batch_size=128,
shuffle=True,
validation_data=(x_test, x_test))
autoencoder.save("autoencoder.h5")
from keras.models import load_model
autoencoder=load_model("autoencoder.h5")
```
## Testing the trained model and comparing it with the original data
```
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(1, n + 1):
# Display original
ax = plt.subplot(2, n, i)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# Display reconstruction
ax = plt.subplot(2, n, i + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
```
## Visualising the states of a image through the autoencoder
```
from tensorflow.keras import Sequential
import tensorflow as tf
#encoder model
model=tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16,(3,3),activation ='relu', input_shape=(28,28,1)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(8,(3,3),activation ='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(8,(3,3),activation ='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
])
def visualize(img,encoder):
code = encoder.predict(img[None])[0]
# Display original
plt.title("Original Image")
plt.imshow(x_test[0].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
#Display compressed
plt.subplot(1,3,2)
plt.title("Compressed Image")
plt.imshow(code.reshape([code.shape[-1]//2,-1]))
plt.show()
# Display reconstruction
plt.title("Decompressed Image")
plt.imshow(decoded_imgs[0].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
visualize(x_test[0],model)
```
## Analysing the loss wrt epoch
```
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
# Denoising model for the Decompressed Image
## Adding noise to the train and test data
```
# Adding random noise to the images
noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
```
## Visualising the training data
```
n = 10
plt.figure(figsize=(20, 2))
for i in range(1, n + 1):
ax = plt.subplot(1, n, i)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
print("Training Data:")
plt.show()
```
## Creating the encoder model
```
input_img = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2, 2), padding='same')(x)
# At this point the representation is (7, 7, 32)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2, 2))(x)
decoded = layers.Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
```
## Training the model
```
history2 = autoencoder.fit(x_train_noisy, x_train,
epochs=50,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test))
from keras import models
autoencoder = models.load_model('denoising_model.h5')
```
## Visualising the results of denoising the decompressed data
```
denoised_imgs = autoencoder.predict(decoded_imgs)
n = 10
plt.figure(figsize=(20, 4))
for i in range(1, n + 1):
# Display original
ax = plt.subplot(2, n, i)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# Display reconstruction
ax = plt.subplot(2, n, i + n)
plt.imshow(denoised_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
```
## Analysing the loss wrt epoch
```
plt.plot(history2.history['loss'])
plt.plot(history2.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
```
## Quality Metrics - PSNR
```
from math import log10, sqrt
import cv2
import numpy as np
def PSNR(original, compressed):
mse = np.mean((original - decompressed) ** 2)
if(mse == 0): # MSE is zero means no noise is present in the signal .
# Therefore PSNR have no importance.
return 100
max_pixel = 255.0
psnr = 20 * log10(max_pixel / sqrt(mse))
return psnr
psnr=0
for i in range(0,50):
original = x_test[i].reshape(28, 28)
decompressed =denoised_imgs[i].reshape(28,28)
value = PSNR(original, decompressed)
psnr+=value
psnr=psnr/50
print(f"PSNR value is {psnr} dB")
```
| true |
code
| 0.867036 | null | null | null | null |
|
This application demonstrates how to build a simple neural network using the Graph mark.
Interactions can be enabled by adding event handlers (click, hover etc) on the nodes of the network.
See the [Mark Interactions notebook](../Interactions/Mark Interactions.ipynb) and the [Scatter Notebook](../Marks/Scatter.ipynb) for details.
```
from itertools import chain, product
import numpy as np
from bqplot import *
class NeuralNet(Figure):
def __init__(self, **kwargs):
self.height = kwargs.get('height', 600)
self.width = kwargs.get('width', 960)
self.directed_links = kwargs.get('directed_links', False)
self.num_inputs = kwargs['num_inputs']
self.num_hidden_layers = kwargs['num_hidden_layers']
self.nodes_output_layer = kwargs['num_outputs']
self.layer_colors = kwargs.get('layer_colors',
['Orange'] * (len(self.num_hidden_layers) + 2))
self.build_net()
super(NeuralNet, self).__init__(**kwargs)
def build_net(self):
# create nodes
self.layer_nodes = []
self.layer_nodes.append(['x' + str(i+1) for i in range(self.num_inputs)])
for i, h in enumerate(self.num_hidden_layers):
self.layer_nodes.append(['h' + str(i+1) + ',' + str(j+1) for j in range(h)])
self.layer_nodes.append(['y' + str(i+1) for i in range(self.nodes_output_layer)])
self.flattened_layer_nodes = list(chain(*self.layer_nodes))
# build link matrix
i = 0
node_indices = {}
for layer in self.layer_nodes:
for node in layer:
node_indices[node] = i
i += 1
n = len(self.flattened_layer_nodes)
self.link_matrix = np.empty((n,n))
self.link_matrix[:] = np.nan
for i in range(len(self.layer_nodes) - 1):
curr_layer_nodes_indices = [node_indices[d] for d in self.layer_nodes[i]]
next_layer_nodes = [node_indices[d] for d in self.layer_nodes[i+1]]
for s, t in product(curr_layer_nodes_indices, next_layer_nodes):
self.link_matrix[s, t] = 1
# set node x locations
self.nodes_x = np.repeat(np.linspace(0, 100,
len(self.layer_nodes) + 1,
endpoint=False)[1:],
[len(n) for n in self.layer_nodes])
# set node y locations
self.nodes_y = np.array([])
for layer in self.layer_nodes:
n = len(layer)
ys = np.linspace(0, 100, n+1, endpoint=False)[1:]
self.nodes_y = np.append(self.nodes_y, ys[::-1])
# set node colors
n_layers = len(self.layer_nodes)
self.node_colors = np.repeat(np.array(self.layer_colors[:n_layers]),
[len(layer) for layer in self.layer_nodes]).tolist()
xs = LinearScale(min=0, max=100)
ys = LinearScale(min=0, max=100)
self.graph = Graph(node_data=[{'label': d,
'label_display': 'none'} for d in self.flattened_layer_nodes],
link_matrix=self.link_matrix,
link_type='line',
colors=self.node_colors,
directed=self.directed_links,
scales={'x': xs, 'y': ys},
x=self.nodes_x,
y=self.nodes_y,
# color=2 * np.random.rand(len(self.flattened_layer_nodes)) - 1
)
self.graph.hovered_style = {'stroke': '1.5'}
self.graph.unhovered_style = {'opacity': '0.4'}
self.graph.selected_style = {'opacity': '1',
'stroke': 'red',
'stroke-width': '2.5'}
self.marks = [self.graph]
self.title = 'Neural Network'
self.layout.width = str(self.width) + 'px'
self.layout.height = str(self.height) + 'px'
NeuralNet(num_inputs=3, num_hidden_layers=[10, 10, 8, 5], num_outputs=1)
```
| true |
code
| 0.573021 | null | null | null | null |
|
# TF-Slim Walkthrough
This notebook will walk you through the basics of using TF-Slim to define, train and evaluate neural networks on various tasks. It assumes a basic knowledge of neural networks.
## Table of contents
<a href="#Install">Installation and setup</a><br>
<a href='#MLP'>Creating your first neural network with TF-Slim</a><br>
<a href='#ReadingTFSlimDatasets'>Reading Data with TF-Slim</a><br>
<a href='#CNN'>Training a convolutional neural network (CNN)</a><br>
<a href='#Pretained'>Using pre-trained models</a><br>
## Installation and setup
<a id='Install'></a>
Since the stable release of TF 1.0, the latest version of slim has been available as `tf.contrib.slim`.
To test that your installation is working, execute the following command; it should run without raising any errors.
```
python -c "import tensorflow.contrib.slim as slim; eval = slim.evaluation.evaluate_once"
```
Although, to use TF-Slim for image classification (as we do in this notebook), you also have to install the TF-Slim image models library from [here](https://github.com/tensorflow/models/tree/master/research/slim). Let's suppose you install this into a directory called TF_MODELS. Then you should change directory to TF_MODELS/research/slim **before** running this notebook, so that these files are in your python path.
To check you've got these two steps to work, just execute the cell below. If it complains about unknown modules, restart the notebook after moving to the TF-Slim models directory.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import matplotlib
%matplotlib inline
import matplotlib.pyplot as plt
import math
import numpy as np
import tensorflow.compat.v1 as tf
import time
from datasets import dataset_utils
# Main slim library
import tf_slim as slim
```
## Creating your first neural network with TF-Slim
<a id='MLP'></a>
Below we give some code to create a simple multilayer perceptron (MLP) which can be used
for regression problems. The model has 2 hidden layers.
The output is a single node.
When this function is called, it will create various nodes, and silently add them to whichever global TF graph is currently in scope. When a node which corresponds to a layer with adjustable parameters (eg., a fully connected layer) is created, additional parameter variable nodes are silently created, and added to the graph. (We will discuss how to train the parameters later.)
We use variable scope to put all the nodes under a common name,
so that the graph has some hierarchical structure.
This is useful when we want to visualize the TF graph in tensorboard, or if we want to query related
variables.
The fully connected layers all use the same L2 weight decay and ReLu activations, as specified by **arg_scope**. (However, the final layer overrides these defaults, and uses an identity activation function.)
We also illustrate how to add a dropout layer after the first fully connected layer (FC1). Note that at test time,
we do not drop out nodes, but instead use the average activations; hence we need to know whether the model is being
constructed for training or testing, since the computational graph will be different in the two cases
(although the variables, storing the model parameters, will be shared, since they have the same name/scope).
```
def regression_model(inputs, is_training=True, scope="deep_regression"):
"""Creates the regression model.
Args:
inputs: A node that yields a `Tensor` of size [batch_size, dimensions].
is_training: Whether or not we're currently training the model.
scope: An optional variable_op scope for the model.
Returns:
predictions: 1-D `Tensor` of shape [batch_size] of responses.
end_points: A dict of end points representing the hidden layers.
"""
with tf.variable_scope(scope, 'deep_regression', [inputs]):
end_points = {}
# Set the default weight _regularizer and acvitation for each fully_connected layer.
with slim.arg_scope([slim.fully_connected],
activation_fn=tf.nn.relu,
weights_regularizer=slim.l2_regularizer(0.01)):
# Creates a fully connected layer from the inputs with 32 hidden units.
net = slim.fully_connected(inputs, 32, scope='fc1')
end_points['fc1'] = net
# Adds a dropout layer to prevent over-fitting.
net = slim.dropout(net, 0.8, is_training=is_training)
# Adds another fully connected layer with 16 hidden units.
net = slim.fully_connected(net, 16, scope='fc2')
end_points['fc2'] = net
# Creates a fully-connected layer with a single hidden unit. Note that the
# layer is made linear by setting activation_fn=None.
predictions = slim.fully_connected(net, 1, activation_fn=None, scope='prediction')
end_points['out'] = predictions
return predictions, end_points
```
### Let's create the model and examine its structure.
We create a TF graph and call regression_model(), which adds nodes (tensors) to the graph. We then examine their shape, and print the names of all the model variables which have been implicitly created inside of each layer. We see that the names of the variables follow the scopes that we specified.
```
with tf.Graph().as_default():
# Dummy placeholders for arbitrary number of 1d inputs and outputs
inputs = tf.placeholder(tf.float32, shape=(None, 1))
outputs = tf.placeholder(tf.float32, shape=(None, 1))
# Build model
predictions, end_points = regression_model(inputs)
# Print name and shape of each tensor.
print("Layers")
for k, v in end_points.items():
print('name = {}, shape = {}'.format(v.name, v.get_shape()))
# Print name and shape of parameter nodes (values not yet initialized)
print("\n")
print("Parameters")
for v in slim.get_model_variables():
print('name = {}, shape = {}'.format(v.name, v.get_shape()))
```
### Let's create some 1d regression data .
We will train and test the model on some noisy observations of a nonlinear function.
```
def produce_batch(batch_size, noise=0.3):
xs = np.random.random(size=[batch_size, 1]) * 10
ys = np.sin(xs) + 5 + np.random.normal(size=[batch_size, 1], scale=noise)
return [xs.astype(np.float32), ys.astype(np.float32)]
x_train, y_train = produce_batch(200)
x_test, y_test = produce_batch(200)
plt.scatter(x_train, y_train)
```
### Let's fit the model to the data
The user has to specify the loss function and the optimizer, and slim does the rest.
In particular, the slim.learning.train function does the following:
- For each iteration, evaluate the train_op, which updates the parameters using the optimizer applied to the current minibatch. Also, update the global_step.
- Occasionally store the model checkpoint in the specified directory. This is useful in case your machine crashes - then you can simply restart from the specified checkpoint.
```
def convert_data_to_tensors(x, y):
inputs = tf.constant(x)
inputs.set_shape([None, 1])
outputs = tf.constant(y)
outputs.set_shape([None, 1])
return inputs, outputs
# The following snippet trains the regression model using a mean_squared_error loss.
ckpt_dir = '/tmp/regression_model/'
with tf.Graph().as_default():
tf.logging.set_verbosity(tf.logging.INFO)
inputs, targets = convert_data_to_tensors(x_train, y_train)
# Make the model.
predictions, nodes = regression_model(inputs, is_training=True)
# Add the loss function to the graph.
loss = tf.losses.mean_squared_error(labels=targets, predictions=predictions)
# The total loss is the user's loss plus any regularization losses.
total_loss = slim.losses.get_total_loss()
# Specify the optimizer and create the train op:
optimizer = tf.train.AdamOptimizer(learning_rate=0.005)
train_op = slim.learning.create_train_op(total_loss, optimizer)
# Run the training inside a session.
final_loss = slim.learning.train(
train_op,
logdir=ckpt_dir,
number_of_steps=5000,
save_summaries_secs=5,
log_every_n_steps=500)
print("Finished training. Last batch loss:", final_loss)
print("Checkpoint saved in %s" % ckpt_dir)
```
### Training with multiple loss functions.
Sometimes we have multiple objectives we want to simultaneously optimize.
In slim, it is easy to add more losses, as we show below. (We do not optimize the total loss in this example,
but we show how to compute it.)
```
with tf.Graph().as_default():
inputs, targets = convert_data_to_tensors(x_train, y_train)
predictions, end_points = regression_model(inputs, is_training=True)
# Add multiple loss nodes.
mean_squared_error_loss = tf.losses.mean_squared_error(labels=targets, predictions=predictions)
absolute_difference_loss = slim.losses.absolute_difference(predictions, targets)
# The following two ways to compute the total loss are equivalent
regularization_loss = tf.add_n(slim.losses.get_regularization_losses())
total_loss1 = mean_squared_error_loss + absolute_difference_loss + regularization_loss
# Regularization Loss is included in the total loss by default.
# This is good for training, but not for testing.
total_loss2 = slim.losses.get_total_loss(add_regularization_losses=True)
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init_op) # Will initialize the parameters with random weights.
total_loss1, total_loss2 = sess.run([total_loss1, total_loss2])
print('Total Loss1: %f' % total_loss1)
print('Total Loss2: %f' % total_loss2)
print('Regularization Losses:')
for loss in slim.losses.get_regularization_losses():
print(loss)
print('Loss Functions:')
for loss in slim.losses.get_losses():
print(loss)
```
### Let's load the saved model and use it for prediction.
```
with tf.Graph().as_default():
inputs, targets = convert_data_to_tensors(x_test, y_test)
# Create the model structure. (Parameters will be loaded below.)
predictions, end_points = regression_model(inputs, is_training=False)
# Make a session which restores the old parameters from a checkpoint.
sv = tf.train.Supervisor(logdir=ckpt_dir)
with sv.managed_session() as sess:
inputs, predictions, targets = sess.run([inputs, predictions, targets])
plt.scatter(inputs, targets, c='r');
plt.scatter(inputs, predictions, c='b');
plt.title('red=true, blue=predicted')
```
### Let's compute various evaluation metrics on the test set.
In TF-Slim termiology, losses are optimized, but metrics (which may not be differentiable, e.g., precision and recall) are just measured. As an illustration, the code below computes mean squared error and mean absolute error metrics on the test set.
Each metric declaration creates several local variables (which must be initialized via tf.initialize_local_variables()) and returns both a value_op and an update_op. When evaluated, the value_op returns the current value of the metric. The update_op loads a new batch of data, runs the model, obtains the predictions and accumulates the metric statistics appropriately before returning the current value of the metric. We store these value nodes and update nodes in 2 dictionaries.
After creating the metric nodes, we can pass them to slim.evaluation.evaluation, which repeatedly evaluates these nodes the specified number of times. (This allows us to compute the evaluation in a streaming fashion across minibatches, which is usefulf for large datasets.) Finally, we print the final value of each metric.
```
with tf.Graph().as_default():
inputs, targets = convert_data_to_tensors(x_test, y_test)
predictions, end_points = regression_model(inputs, is_training=False)
# Specify metrics to evaluate:
names_to_value_nodes, names_to_update_nodes = slim.metrics.aggregate_metric_map({
'Mean Squared Error': slim.metrics.streaming_mean_squared_error(predictions, targets),
'Mean Absolute Error': slim.metrics.streaming_mean_absolute_error(predictions, targets)
})
# Make a session which restores the old graph parameters, and then run eval.
sv = tf.train.Supervisor(logdir=ckpt_dir)
with sv.managed_session() as sess:
metric_values = slim.evaluation.evaluation(
sess,
num_evals=1, # Single pass over data
eval_op=names_to_update_nodes.values(),
final_op=names_to_value_nodes.values())
names_to_values = dict(zip(names_to_value_nodes.keys(), metric_values))
for key, value in names_to_values.items():
print('%s: %f' % (key, value))
```
# Reading Data with TF-Slim
<a id='ReadingTFSlimDatasets'></a>
Reading data with TF-Slim has two main components: A
[Dataset](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/slim/python/slim/data/dataset.py) and a
[DatasetDataProvider](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/slim/python/slim/data/dataset_data_provider.py). The former is a descriptor of a dataset, while the latter performs the actions necessary for actually reading the data. Lets look at each one in detail:
## Dataset
A TF-Slim
[Dataset](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/slim/python/slim/data/dataset.py)
contains descriptive information about a dataset necessary for reading it, such as the list of data files and how to decode them. It also contains metadata including class labels, the size of the train/test splits and descriptions of the tensors that the dataset provides. For example, some datasets contain images with labels. Others augment this data with bounding box annotations, etc. The Dataset object allows us to write generic code using the same API, regardless of the data content and encoding type.
TF-Slim's Dataset works especially well when the data is stored as a (possibly sharded)
[TFRecords file](https://www.tensorflow.org/versions/r0.10/how_tos/reading_data/index.html#file-formats), where each record contains a [tf.train.Example protocol buffer](https://github.com/tensorflow/tensorflow/blob/r0.10/tensorflow/core/example/example.proto).
TF-Slim uses a consistent convention for naming the keys and values inside each Example record.
## DatasetDataProvider
A
[DatasetDataProvider](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/slim/python/slim/data/dataset_data_provider.py) is a class which actually reads the data from a dataset. It is highly configurable to read the data in various ways that may make a big impact on the efficiency of your training process. For example, it can be single or multi-threaded. If your data is sharded across many files, it can read each files serially, or from every file simultaneously.
## Demo: The Flowers Dataset
For convenience, we've include scripts to convert several common image datasets into TFRecord format and have provided
the Dataset descriptor files necessary for reading them. We demonstrate how easy it is to use these dataset via the Flowers dataset below.
### Download the Flowers Dataset
<a id='DownloadFlowers'></a>
We've made available a tarball of the Flowers dataset which has already been converted to TFRecord format.
```
import tensorflow.compat.v1 as tf
from datasets import dataset_utils
url = "http://download.tensorflow.org/data/flowers.tar.gz"
flowers_data_dir = '/tmp/flowers'
if not tf.gfile.Exists(flowers_data_dir):
tf.gfile.MakeDirs(flowers_data_dir)
dataset_utils.download_and_uncompress_tarball(url, flowers_data_dir)
```
### Display some of the data.
```
from datasets import flowers
import tensorflow.compat.v1 as tf
from tensorflow.contrib import slim
with tf.Graph().as_default():
dataset = flowers.get_split('train', flowers_data_dir)
data_provider = slim.dataset_data_provider.DatasetDataProvider(
dataset, common_queue_capacity=32, common_queue_min=1)
image, label = data_provider.get(['image', 'label'])
with tf.Session() as sess:
with slim.queues.QueueRunners(sess):
for i in range(4):
np_image, np_label = sess.run([image, label])
height, width, _ = np_image.shape
class_name = name = dataset.labels_to_names[np_label]
plt.figure()
plt.imshow(np_image)
plt.title('%s, %d x %d' % (name, height, width))
plt.axis('off')
plt.show()
```
# Convolutional neural nets (CNNs).
<a id='CNN'></a>
In this section, we show how to train an image classifier using a simple CNN.
### Define the model.
Below we define a simple CNN. Note that the output layer is linear function - we will apply softmax transformation externally to the model, either in the loss function (for training), or in the prediction function (during testing).
```
def my_cnn(images, num_classes, is_training): # is_training is not used...
with slim.arg_scope([slim.max_pool2d], kernel_size=[3, 3], stride=2):
net = slim.conv2d(images, 64, [5, 5])
net = slim.max_pool2d(net)
net = slim.conv2d(net, 64, [5, 5])
net = slim.max_pool2d(net)
net = slim.flatten(net)
net = slim.fully_connected(net, 192)
net = slim.fully_connected(net, num_classes, activation_fn=None)
return net
```
### Apply the model to some randomly generated images.
```
import tensorflow as tf
with tf.Graph().as_default():
# The model can handle any input size because the first layer is convolutional.
# The size of the model is determined when image_node is first passed into the my_cnn function.
# Once the variables are initialized, the size of all the weight matrices is fixed.
# Because of the fully connected layers, this means that all subsequent images must have the same
# input size as the first image.
batch_size, height, width, channels = 3, 28, 28, 3
images = tf.random_uniform([batch_size, height, width, channels], maxval=1)
# Create the model.
num_classes = 10
logits = my_cnn(images, num_classes, is_training=True)
probabilities = tf.nn.softmax(logits)
# Initialize all the variables (including parameters) randomly.
init_op = tf.global_variables_initializer()
with tf.Session() as sess:
# Run the init_op, evaluate the model outputs and print the results:
sess.run(init_op)
probabilities = sess.run(probabilities)
print('Probabilities Shape:')
print(probabilities.shape) # batch_size x num_classes
print('\nProbabilities:')
print(probabilities)
print('\nSumming across all classes (Should equal 1):')
print(np.sum(probabilities, 1)) # Each row sums to 1
```
### Train the model on the Flowers dataset.
Before starting, make sure you've run the code to <a href="#DownloadFlowers">Download the Flowers</a> dataset. Now, we'll get a sense of what it looks like to use TF-Slim's training functions found in
[learning.py](https://github.com/tensorflow/tensorflow/blob/master/tensorflow/contrib/slim/python/slim/learning.py). First, we'll create a function, `load_batch`, that loads batches of dataset from a dataset. Next, we'll train a model for a single step (just to demonstrate the API), and evaluate the results.
```
from preprocessing import inception_preprocessing
import tensorflow as tf
from tensorflow.contrib import slim
def load_batch(dataset, batch_size=32, height=299, width=299, is_training=False):
"""Loads a single batch of data.
Args:
dataset: The dataset to load.
batch_size: The number of images in the batch.
height: The size of each image after preprocessing.
width: The size of each image after preprocessing.
is_training: Whether or not we're currently training or evaluating.
Returns:
images: A Tensor of size [batch_size, height, width, 3], image samples that have been preprocessed.
images_raw: A Tensor of size [batch_size, height, width, 3], image samples that can be used for visualization.
labels: A Tensor of size [batch_size], whose values range between 0 and dataset.num_classes.
"""
data_provider = slim.dataset_data_provider.DatasetDataProvider(
dataset, common_queue_capacity=32,
common_queue_min=8)
image_raw, label = data_provider.get(['image', 'label'])
# Preprocess image for usage by Inception.
image = inception_preprocessing.preprocess_image(image_raw, height, width, is_training=is_training)
# Preprocess the image for display purposes.
image_raw = tf.expand_dims(image_raw, 0)
image_raw = tf.image.resize_images(image_raw, [height, width])
image_raw = tf.squeeze(image_raw)
# Batch it up.
images, images_raw, labels = tf.train.batch(
[image, image_raw, label],
batch_size=batch_size,
num_threads=1,
capacity=2 * batch_size)
return images, images_raw, labels
from datasets import flowers
# This might take a few minutes.
train_dir = '/tmp/tfslim_model/'
print('Will save model to %s' % train_dir)
with tf.Graph().as_default():
tf.logging.set_verbosity(tf.logging.INFO)
dataset = flowers.get_split('train', flowers_data_dir)
images, _, labels = load_batch(dataset)
# Create the model:
logits = my_cnn(images, num_classes=dataset.num_classes, is_training=True)
# Specify the loss function:
one_hot_labels = slim.one_hot_encoding(labels, dataset.num_classes)
slim.losses.softmax_cross_entropy(logits, one_hot_labels)
total_loss = slim.losses.get_total_loss()
# Create some summaries to visualize the training process:
tf.summary.scalar('losses/Total Loss', total_loss)
# Specify the optimizer and create the train op:
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train_op = slim.learning.create_train_op(total_loss, optimizer)
# Run the training:
final_loss = slim.learning.train(
train_op,
logdir=train_dir,
number_of_steps=1, # For speed, we just do 1 epoch
save_summaries_secs=1)
print('Finished training. Final batch loss %d' % final_loss)
```
### Evaluate some metrics.
As we discussed above, we can compute various metrics besides the loss.
Below we show how to compute prediction accuracy of the trained model, as well as top-5 classification accuracy. (The difference between evaluation and evaluation_loop is that the latter writes the results to a log directory, so they can be viewed in tensorboard.)
```
from datasets import flowers
# This might take a few minutes.
with tf.Graph().as_default():
tf.logging.set_verbosity(tf.logging.DEBUG)
dataset = flowers.get_split('train', flowers_data_dir)
images, _, labels = load_batch(dataset)
logits = my_cnn(images, num_classes=dataset.num_classes, is_training=False)
predictions = tf.argmax(logits, 1)
# Define the metrics:
names_to_values, names_to_updates = slim.metrics.aggregate_metric_map({
'eval/Accuracy': slim.metrics.streaming_accuracy(predictions, labels),
'eval/Recall@5': slim.metrics.streaming_recall_at_k(logits, labels, 5),
})
print('Running evaluation Loop...')
checkpoint_path = tf.train.latest_checkpoint(train_dir)
metric_values = slim.evaluation.evaluate_once(
master='',
checkpoint_path=checkpoint_path,
logdir=train_dir,
eval_op=names_to_updates.values(),
final_op=names_to_values.values())
names_to_values = dict(zip(names_to_values.keys(), metric_values))
for name in names_to_values:
print('%s: %f' % (name, names_to_values[name]))
```
# Using pre-trained models
<a id='Pretrained'></a>
Neural nets work best when they have many parameters, making them very flexible function approximators.
However, this means they must be trained on big datasets. Since this process is slow, we provide various pre-trained models - see the list [here](https://github.com/tensorflow/models/tree/master/research/slim#pre-trained-models).
You can either use these models as-is, or you can perform "surgery" on them, to modify them for some other task. For example, it is common to "chop off" the final pre-softmax layer, and replace it with a new set of weights corresponding to some new set of labels. You can then quickly fine tune the new model on a small new dataset. We illustrate this below, using inception-v1 as the base model. While models like Inception V3 are more powerful, Inception V1 is used for speed purposes.
Take into account that VGG and ResNet final layers have only 1000 outputs rather than 1001. The ImageNet dataset provied has an empty background class which can be used to fine-tune the model to other tasks. VGG and ResNet models provided here don't use that class. We provide two examples of using pretrained models: Inception V1 and VGG-19 models to highlight this difference.
### Download the Inception V1 checkpoint
```
from datasets import dataset_utils
url = "http://download.tensorflow.org/models/inception_v1_2016_08_28.tar.gz"
checkpoints_dir = '/tmp/checkpoints'
if not tf.gfile.Exists(checkpoints_dir):
tf.gfile.MakeDirs(checkpoints_dir)
dataset_utils.download_and_uncompress_tarball(url, checkpoints_dir)
```
### Apply Pre-trained Inception V1 model to Images.
We have to convert each image to the size expected by the model checkpoint.
There is no easy way to determine this size from the checkpoint itself.
So we use a preprocessor to enforce this.
```
import numpy as np
import os
import tensorflow as tf
try:
import urllib2 as urllib
except ImportError:
import urllib.request as urllib
from datasets import imagenet
from nets import inception
from preprocessing import inception_preprocessing
from tensorflow.contrib import slim
image_size = inception.inception_v1.default_image_size
with tf.Graph().as_default():
url = 'https://upload.wikimedia.org/wikipedia/commons/7/70/EnglishCockerSpaniel_simon.jpg'
image_string = urllib.urlopen(url).read()
image = tf.image.decode_jpeg(image_string, channels=3)
processed_image = inception_preprocessing.preprocess_image(image, image_size, image_size, is_training=False)
processed_images = tf.expand_dims(processed_image, 0)
# Create the model, use the default arg scope to configure the batch norm parameters.
with slim.arg_scope(inception.inception_v1_arg_scope()):
logits, _ = inception.inception_v1(processed_images, num_classes=1001, is_training=False)
probabilities = tf.nn.softmax(logits)
init_fn = slim.assign_from_checkpoint_fn(
os.path.join(checkpoints_dir, 'inception_v1.ckpt'),
slim.get_model_variables('InceptionV1'))
with tf.Session() as sess:
init_fn(sess)
np_image, probabilities = sess.run([image, probabilities])
probabilities = probabilities[0, 0:]
sorted_inds = [i[0] for i in sorted(enumerate(-probabilities), key=lambda x:x[1])]
plt.figure()
plt.imshow(np_image.astype(np.uint8))
plt.axis('off')
plt.show()
names = imagenet.create_readable_names_for_imagenet_labels()
for i in range(5):
index = sorted_inds[i]
print('Probability %0.2f%% => [%s]' % (probabilities[index] * 100, names[index]))
```
### Download the VGG-16 checkpoint
```
from datasets import dataset_utils
import tensorflow as tf
url = "http://download.tensorflow.org/models/vgg_16_2016_08_28.tar.gz"
checkpoints_dir = '/tmp/checkpoints'
if not tf.gfile.Exists(checkpoints_dir):
tf.gfile.MakeDirs(checkpoints_dir)
dataset_utils.download_and_uncompress_tarball(url, checkpoints_dir)
```
### Apply Pre-trained VGG-16 model to Images.
We have to convert each image to the size expected by the model checkpoint.
There is no easy way to determine this size from the checkpoint itself.
So we use a preprocessor to enforce this. Pay attention to the difference caused by 1000 classes instead of 1001.
```
import numpy as np
import os
import tensorflow as tf
try:
import urllib2
except ImportError:
import urllib.request as urllib
from datasets import imagenet
from nets import vgg
from preprocessing import vgg_preprocessing
from tensorflow.contrib import slim
image_size = vgg.vgg_16.default_image_size
with tf.Graph().as_default():
url = 'https://upload.wikimedia.org/wikipedia/commons/d/d9/First_Student_IC_school_bus_202076.jpg'
image_string = urllib.urlopen(url).read()
image = tf.image.decode_jpeg(image_string, channels=3)
processed_image = vgg_preprocessing.preprocess_image(image, image_size, image_size, is_training=False)
processed_images = tf.expand_dims(processed_image, 0)
# Create the model, use the default arg scope to configure the batch norm parameters.
with slim.arg_scope(vgg.vgg_arg_scope()):
# 1000 classes instead of 1001.
logits, _ = vgg.vgg_16(processed_images, num_classes=1000, is_training=False)
probabilities = tf.nn.softmax(logits)
init_fn = slim.assign_from_checkpoint_fn(
os.path.join(checkpoints_dir, 'vgg_16.ckpt'),
slim.get_model_variables('vgg_16'))
with tf.Session() as sess:
init_fn(sess)
np_image, probabilities = sess.run([image, probabilities])
probabilities = probabilities[0, 0:]
sorted_inds = [i[0] for i in sorted(enumerate(-probabilities), key=lambda x:x[1])]
plt.figure()
plt.imshow(np_image.astype(np.uint8))
plt.axis('off')
plt.show()
names = imagenet.create_readable_names_for_imagenet_labels()
for i in range(5):
index = sorted_inds[i]
# Shift the index of a class name by one.
print('Probability %0.2f%% => [%s]' % (probabilities[index] * 100, names[index+1]))
```
### Fine-tune the model on a different set of labels.
We will fine tune the inception model on the Flowers dataset.
```
# Note that this may take several minutes.
import os
from datasets import flowers
from nets import inception
from preprocessing import inception_preprocessing
from tensorflow.contrib import slim
image_size = inception.inception_v1.default_image_size
def get_init_fn():
"""Returns a function run by the chief worker to warm-start the training."""
checkpoint_exclude_scopes=["InceptionV1/Logits", "InceptionV1/AuxLogits"]
exclusions = [scope.strip() for scope in checkpoint_exclude_scopes]
variables_to_restore = []
for var in slim.get_model_variables():
for exclusion in exclusions:
if var.op.name.startswith(exclusion):
break
else:
variables_to_restore.append(var)
return slim.assign_from_checkpoint_fn(
os.path.join(checkpoints_dir, 'inception_v1.ckpt'),
variables_to_restore)
train_dir = '/tmp/inception_finetuned/'
with tf.Graph().as_default():
tf.logging.set_verbosity(tf.logging.INFO)
dataset = flowers.get_split('train', flowers_data_dir)
images, _, labels = load_batch(dataset, height=image_size, width=image_size)
# Create the model, use the default arg scope to configure the batch norm parameters.
with slim.arg_scope(inception.inception_v1_arg_scope()):
logits, _ = inception.inception_v1(images, num_classes=dataset.num_classes, is_training=True)
# Specify the loss function:
one_hot_labels = slim.one_hot_encoding(labels, dataset.num_classes)
slim.losses.softmax_cross_entropy(logits, one_hot_labels)
total_loss = slim.losses.get_total_loss()
# Create some summaries to visualize the training process:
tf.summary.scalar('losses/Total Loss', total_loss)
# Specify the optimizer and create the train op:
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train_op = slim.learning.create_train_op(total_loss, optimizer)
# Run the training:
final_loss = slim.learning.train(
train_op,
logdir=train_dir,
init_fn=get_init_fn(),
number_of_steps=2)
print('Finished training. Last batch loss %f' % final_loss)
```
### Apply fine tuned model to some images.
```
import numpy as np
import tensorflow as tf
from datasets import flowers
from nets import inception
from tensorflow.contrib import slim
image_size = inception.inception_v1.default_image_size
batch_size = 3
with tf.Graph().as_default():
tf.logging.set_verbosity(tf.logging.INFO)
dataset = flowers.get_split('train', flowers_data_dir)
images, images_raw, labels = load_batch(dataset, height=image_size, width=image_size)
# Create the model, use the default arg scope to configure the batch norm parameters.
with slim.arg_scope(inception.inception_v1_arg_scope()):
logits, _ = inception.inception_v1(images, num_classes=dataset.num_classes, is_training=True)
probabilities = tf.nn.softmax(logits)
checkpoint_path = tf.train.latest_checkpoint(train_dir)
init_fn = slim.assign_from_checkpoint_fn(
checkpoint_path,
slim.get_variables_to_restore())
with tf.Session() as sess:
with slim.queues.QueueRunners(sess):
sess.run(tf.initialize_local_variables())
init_fn(sess)
np_probabilities, np_images_raw, np_labels = sess.run([probabilities, images_raw, labels])
for i in range(batch_size):
image = np_images_raw[i, :, :, :]
true_label = np_labels[i]
predicted_label = np.argmax(np_probabilities[i, :])
predicted_name = dataset.labels_to_names[predicted_label]
true_name = dataset.labels_to_names[true_label]
plt.figure()
plt.imshow(image.astype(np.uint8))
plt.title('Ground Truth: [%s], Prediction [%s]' % (true_name, predicted_name))
plt.axis('off')
plt.show()
```
| true |
code
| 0.887619 | null | null | null | null |
|
Evaluation of the frame-based matching algorithm
================================================
This notebook aims at evaluating the performance of the Markov Random Field (MRF) algorithm implemented in `stereovis/framed/algorithms/mrf.py` on the three datasets presented above. For each, the following experiments have been done:
* running MRF on each dataset without any SNN-based prior
* running MRF with prior initialisation from best-performing SNN configuration
* running MRF with prior initialisation and adjustment from motion
* comparing difference between the above scenarios and visually assessing their quality for no ground truth is recorded or computed.
A slightly altered and abbreviated version of this notebook can also be found under `notebooks/evaluation.ipynb`.
```
%matplotlib inline
import numpy as np
import sys
import skimage.io as skio
import os
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from matplotlib.colors import Normalize
from skimage import transform, filters, feature, morphology
sys.path.append("../")
from stereovis.framed.algorithms.mrf import StereoMRF
from stereovis.spiking.algorithms.vvf import VelocityVectorField
from stereovis.utils.frames_io import load_frames, load_ground_truth, generate_frames_from_spikes, split_frames_by_time
from stereovis.utils.spikes_io import load_spikes
from stereovis.utils.config import load_config
```
In the next we define some usefull functions to load, compute and plot data. They should be used for each dataset independetly and although they export some experiment-specific parametes to the user, other configuration options are "hard-coded" into configuration files -- at least one for each dataset. They define the data paths, camera resolution, frame rate and similar parameters and can be found under `experiments/config/hybrid/experiment_name.yaml`, where `experiment_name` shoud be substituded with the respective name of the experiment.
```
def load_mrf_frames(config):
"""
Load the images used for the frame-based matching.
Args:
config: dict, configuration object. Should be loaded beforehand.
Returns:
A tuple of numpy arrays with the left-camera frames, right-camera frames and the timestamps
provided by the left-camera.
"""
frames_left, times = load_frames(input_path=os.path.join('..', config['input']['frames_path'], 'left'),
resolution=config['input']['resolution'],
crop_region=config['input']['crop'],
scale_down_factor=config['input']['scale_down_factor'],
simulation_time=config['simulation']['duration'],
timestamp_unit=config['input']['timestamp_unit'],
adjust_contrast=True)
frames_right, _ = load_frames(input_path=os.path.join('..', config['input']['frames_path'], 'right'),
resolution=config['input']['resolution'],
crop_region=config['input']['crop'],
scale_down_factor=config['input']['scale_down_factor'],
simulation_time=config['simulation']['duration'],
timestamp_unit=config['input']['timestamp_unit'],
adjust_contrast=True)
return frames_left, frames_right, times
def load_retina_spikes(config, build_frames=True, pivots=None, buffer_length=10):
"""
Load the events used for visualisation purposes.
Args:
config: dict, configuration object.
build_frames: bool, whether to load the events in buffered frame-wise manner or as a continuous stream.
pivots: list, timestamps which serve as ticks to buffer the events in frames at precise locations.
Otherwise, equdistant buffering will be performed, according to the buffer length.
buffer_length: int, buffer span time in ms.
Returns:
Buffered left and right retina events, or non-buffered numpy array.
Notes:
The SNN's output is assumed fixed for this evaluation
and only the MRF tests are performed. To experiment with the SNN, please see the framework.
"""
retina_spikes = load_spikes(input_file=os.path.join('..', config['input']['spikes_path']),
resolution=config['input']['resolution'],
crop_region=config['input']['crop'],
simulation_time=config['simulation']['duration'],
timestep_unit=config['input']['timestamp_unit'],
dt_thresh=1,
scale_down_factor=config['input']['scale_down_factor'],
as_spike_source_array=False)
if not build_frames:
return retina_spikes
effective_frame_resolution = (np.asarray(config['input']['resolution'])
/ config['input']['scale_down_factor']).astype(np.int32)
retina_frames_l, times_l = \
generate_frames_from_spikes(resolution=effective_frame_resolution,
xs=retina_spikes['left'][:, 1],
ys=retina_spikes['left'][:, 2],
ts=retina_spikes['left'][:, 0],
zs=retina_spikes['left'][:, 3],
time_interval=buffer_length,
pivots=pivots,
non_pixel_value=-1)
retina_frames_r, times_r = \
generate_frames_from_spikes(resolution=effective_frame_resolution,
xs=retina_spikes['right'][:, 1],
ys=retina_spikes['right'][:, 2],
ts=retina_spikes['right'][:, 0],
zs=retina_spikes['right'][:, 3],
time_interval=buffer_length,
pivots=pivots,
non_pixel_value=-1)
assert retina_frames_l.shape == retina_frames_r.shape
return retina_spikes, retina_frames_l, retina_frames_r
def load_snn_spikes(spikes_file, build_frames=True, pivots=None,
buffer_length=10, non_pixel_value=-1):
"""
Load the SNN output events used as a prior for the frame-based matching.
Args:
spikes_file: str, filepath for the SNN output events.
build_frames: bool, whether to buffer the events as frames.
pivots: list, timestamps for the frames.
buffer_length: int, buffered frame time span in ms
non_pixel_value: numerical value for the frame pixels for which there is no event
Returns:
Buffered frames, timestamps and indices of the events that hass been buffered in each frame accordingly.
"""
prior_disparities = load_spikes(spikes_file)
if not build_frames:
return prior_disparities
effective_frame_resolution = prior_disparities['meta']['resolution']
prior_frames, timestamps, prior_frame_indices = \
generate_frames_from_spikes(resolution=effective_frame_resolution,
xs=prior_disparities['xs'],
ys=prior_disparities['ys'],
ts=prior_disparities['ts'],
zs=prior_disparities['disps'],
time_interval=buffer_length,
pivots=pivots,
non_pixel_value=non_pixel_value,
return_time_indices=True)
return prior_frames, timestamps, prior_frame_indices
def eval_mrf(left_img, right_img, max_disp, prior=None,
prior_mode='adaptive', prior_const=1.0, n_iter=10,
show_outline=False, show_plots=True):
"""
Run the MRF frame-based matching from given frames and algorithm parameters.
Args:
left_img: 2d array with the pre-processed left image
right_img: 2d array with the pre-processed right image
max_dist: int, largest detectable disparity value
prior: optionally a 2d array with the prior frame oriented to the left image
prior_mode: str, mode of incorporating the prior frame. Can be 'adaptive' for mixing proportionally to the
data cost, or 'const' for normal mixing.
prior_const: float, if the prior mode is 'const', this is the mixing coefficient.
n_iter: int, number of BP iterations
show_outline: bool, whether to plot the outline of the objects (using Canny filter)
show_plots: bool, whether to plot the results
Returns:
A 2d numpy array with the resulted disparity map.
"""
img_res = left_img.shape
mrf = StereoMRF(img_res, n_levels=max_disp)
disp_map = mrf.lbp(left_img, right_img, prior=prior,
prior_influence_mode=prior_mode,
prior_trust_factor=prior_const,
n_iter=n_iter).astype(np.float32)
disp_map[:, :max_disp] = np.nan
if not show_plots:
return disp_map
fig, axs = plt.subplots(2, 2)
fig.set_size_inches(10, 8)
axs[0, 0].imshow(left_img, interpolation='none', cmap='gray')
axs[0, 0].set_title("Left frame")
axs[0, 1].imshow(right_img, interpolation='none', cmap='gray')
axs[0, 1].set_title("Right frame")
print("Image resolution is: {}".format(img_res))
if show_outline:
val = filters.threshold_otsu(left_img)
ref_shape = (left_img > val).reshape(img_res).astype(np.float32)
ref_outline = feature.canny(ref_shape, sigma=1.0) > 0
disp_map[ref_outline] = np.nan
cmap = plt.cm.jet
cmap.set_bad((1, 1, 1, 1))
depth_map_im = axs[1, 0].imshow(disp_map, interpolation='none')
axs[1, 0].set_title("Depth frame")
depth_map_pos = axs[1, 0].get_position()
cbaxes = plt.axes([depth_map_pos.x0*1.05 + depth_map_pos.width * 1.05,
depth_map_pos.y0, 0.01, depth_map_pos.height])
fig.colorbar(depth_map_im, cax=cbaxes)
axs[1, 1].set_visible(False)
return disp_map
def eval_snn(experiment_name, disparity_max, frame_id, buffer_len=20):
"""
Visualise the pre-computed SNN output along with the retina input.
Args:
experiment_name: str, the name of the experiment which also match an existing config file.
disparity_max: int, maximum computable disparity
frame_id: int, the index of the frame (pair of frames) which are used to produce a depth map.
buffer_len: int, time in ms for the buffer length of retina events
Returns:
The bufferen SNN output at the timestamps of the frames.
"""
print("Sample images from experiment: {}".format(experiment_name))
config = load_config(os.path.join("..", "experiments", "configs", "hybrid", experiment_name + ".yaml"))
left_frames, right_frames, timestamps = load_mrf_frames(config)
left_img = left_frames[frame_id]
right_img = right_frames[frame_id]
# remove the _downsampled suffix in the experiment name for the pivots
pivots = np.load(os.path.join("..", "data", "input", "frames", experiment_name[:-12],
"left", "timestamps.npy")) / 1000.
retina_spikes, left_retina, right_retina = \
load_retina_spikes(config, build_frames=True,
pivots=pivots,
buffer_length=buffer_len)
snn_spikes_file = os.path.join("..", "data", "output", "experiments",
"best_snn_spikes", experiment_name + '.pickle')
prior_frames, _, prior_frame_indices = \
load_snn_spikes(snn_spikes_file, build_frames=True,
pivots=pivots, buffer_length=buffer_len)
fig, axs = plt.subplots(3, 2)
fig.set_size_inches(11, 11)
# fig.tight_layout()
axs[0, 0].imshow(left_img, interpolation='none', cmap='gray')
axs[0, 0].set_title("Left frame")
axs[0, 1].imshow(right_img, interpolation='none', cmap='gray')
axs[0, 1].set_title("Right frame")
axs[1, 0].imshow(left_retina[frame_id], interpolation='none')
axs[1, 0].set_title("Left retina frame")
axs[1, 1].imshow(right_retina[frame_id], interpolation='none')
axs[1, 1].set_title("Right retina frame")
depth_map_snn = axs[2, 0].imshow(prior_frames[frame_id], interpolation='none', vmin=0, vmax=disparity_max)
depth_map_pos = axs[2, 0].get_position()
cbaxes = plt.axes([depth_map_pos.x0*1.05 + depth_map_pos.width * 1.05,
depth_map_pos.y0, 0.01, depth_map_pos.height])
fig.colorbar(depth_map_snn, cax=cbaxes)
axs[2, 0].set_title("Network depth map")
axs[2, 1].set_visible(False)
return prior_frames
def compute_optical_flow(experiment_name, background=None):
pivots = np.load(os.path.join("..", "data", "input", "frames", experiment_name[:-12],
"left", "timestamps.npy")) / 1000.
config = load_config(os.path.join("..", "experiments", "configs", "hybrid", experiment_name + ".yaml"))
vvf = VelocityVectorField(time_interval=20,
neighbourhood_size=(3, 3),
rejection_threshold=0.005,
convergence_threshold=1e-5,
max_iter_steps=5,
min_num_events_in_timespace_interval=30)
events = load_spikes(input_file=os.path.join('..', config['input']['spikes_path']),
resolution=config['input']['resolution'],
crop_region=config['input']['crop'],
simulation_time=config['simulation']['duration'],
timestep_unit=config['input']['timestamp_unit'],
dt_thresh=1,
scale_down_factor=config['input']['scale_down_factor'],
as_spike_source_array=False)
time_ind, _ = split_frames_by_time(ts=events['left'][:, 0],
time_interval=50,
pivots=pivots)
velocities = vvf.fit_velocity_field(events['left'][time_ind[frame_id_head], :], assume_sorted=False,
concatenate_polarity_groups=True)
xs, ys, us, vs = events['left'][time_ind[frame_id_head], 1], \
events['left'][time_ind[frame_id_head], 2], \
velocities[:, 0], velocities[:, 1]
fig, axs = plt.subplots(1, 1)
# fig.set_size_inches(5, 5)
if background is not None:
plt.imshow(background)
colors = np.arctan2(us, vs)
norm = Normalize()
if colors.size > 0:
norm.autoscale(colors)
colormap = cm.inferno
axs.invert_yaxis()
plt.quiver(xs, ys, us, vs, angles='xy', scale_units='xy', scale=1, color=colormap(norm(colors)))
return xs, ys, us, vs
def adjust_events_from_motion(prior_frame, velocities):
"""
Modify the position of the events according to the detected motion. As the algorithm for optical flow
operates on the 3d non-buffered retina events, some additional parameters such as frame resolution etc. will
be required (unfortunately they cannot be inferred).
Args:
prior_frame: ndarray, the buffered SNN output used as a prior.
velocities: tuple, xs, ys, us, vs -- start and end positions of the velocity vectors.
Returns:
One adjusted prior frame.
"""
xs, ys, us, vs = velocities
# store the velocities onto a 2D image plane which will be queried for a shift
velocity_lut = np.zeros(prior_frame.shape + (2,))
for x, y, u, v in zip(xs, ys, us, vs):
velocity_lut[int(y), int(x), :] = np.array([u, v])
# compute shift based on 8 directional compass
shifts = np.asarray([(1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1), (1, -1)], dtype=np.int32)
compute_shift = lambda x, y: shifts[int(np.floor(np.round(8 * np.arctan2(y, x) / (2 * np.pi)))) % 8] \
if np.linalg.norm([x, y]) > 1. else np.array([0, 0])
adjusted_frame = np.ones_like(prior_frame) * -1
# compute the corresponding shift for all detected disparity event_frames
for row, col in np.argwhere(prior_frame >= 0):
x, y = velocity_lut[row, col]
dcol, drow = compute_shift(y, x)
# going up in the image is equivalent to decrementing the row number, hence the minus in row - drow
if 0 <= col + dcol < prior_frame.shape[1] and 0 <= row - drow < prior_frame.shape[0]:
adjusted_frame[row - drow, col + dcol] = prior_frame[row, col]
return adjusted_frame
def run_mrf_without_prior(experiment_name, disparity_max, frame_id=0, n_iter=5):
"""
Perform the MRF depth map computation on a pair of images without any prior knowledge. The experiment parameters
are loaded from the corresponding configuration yaml file.
Args:
experiment_name: str, the name of the experiment which also match an existing config file.
disparity_max: int, maximum computable disparity.
frame_id: int, the index of the frame (pair of frames) which are used to produce a depth map.
n_iter: int, number of MRF BP iterations.
Returns:
The resolved depth map.
"""
print("Sample images from experiment: {}".format(experiment_name))
config = load_config(os.path.join("..", "experiments", "configs", "hybrid", experiment_name + ".yaml"))
left_frames, right_frames, timestamps = load_mrf_frames(config)
left_img = left_frames[frame_id]
right_img = right_frames[frame_id]
depth_map_raw = eval_mrf(left_img, right_img, disparity_max, n_iter=n_iter)
return depth_map_raw
def run_mrf_with_prior(experiment_name, disparity_max, prior_frames,
frame_id=0, n_iter=5, prior_mode='const', prior_const=1):
"""
Run the MRF computation on an image pair using a SNN prior frame in the initialisation phase. Again, load the
experiment parameters from a configuration file.
Args:
experiment_name: str, the name of the experiment which also match an existing config file.
disparity_max: int, maximum computable disparity
prior_frames: ndarray, list of all buffered frames from the SNN output.
frame_id: int, the index of the frame (pair of frames) which are used to produce a depth map.
n_iter: int, number of MRF BP iterations.
prior_mode: str, the way of incorporating the prior. Can be `adaptive` or `const`.
prior_const: float, if the chosen mode is `const` than this is the influence of the prior.
Returns:
The depth map of the MRF using the prior frame.
"""
config = load_config(os.path.join("..", "experiments", "configs", "hybrid", experiment_name + ".yaml"))
left_frames, right_frames, timestamps = load_mrf_frames(config)
left_img = left_frames[frame_id]
right_img = right_frames[frame_id]
depth_map_prior = eval_mrf(left_img, right_img, disparity_max,
prior=prior_frames[frame_id],
prior_mode=prior_mode,
prior_const=prior_const,
n_iter=n_iter, show_plots=False)
return depth_map_prior
def plot_difference_prior_raw(depth_map_raw, depth_map_prior, disparity_max):
"""
Visualise the outcome from the MRF with the prior and without and show the absolute value difference.
Args:
depth_map_raw: ndarray, depth map result of the MRF applied on the frames only.
depth_map_prior: ndarray, depth map of the MRF applied on the image and prior frames.
disparity_max: int, maximum detectable disparity, used to normalise the plot colors.
"""
fig, axs = plt.subplots(1, 3)
fig.set_size_inches(12, 20)
axs[0].imshow(depth_map_prior, interpolation='none', vmax=disparity_max)
axs[0].set_title("With prior")
axs[1].imshow(depth_map_raw, interpolation='none', vmax=disparity_max)
axs[1].set_title("Without prior")
axs[2].imshow(np.abs(depth_map_raw - depth_map_prior), interpolation='none', vmax=disparity_max)
axs[2].set_title("Absolute value difference")
def plot_adjusted_prior(experiment_name, frame_id=0):
"""
Visualise the prior before and after the adjustment.
Args:
experiment_name: str, name of the experiment to load
frame_id: int, the index of the frame to plot as background
"""
config = load_config(os.path.join("..", "experiments", "configs", "hybrid", experiment_name + ".yaml"))
left_frames, _, _ = load_mrf_frames(config)
left_img = left_frames[frame_id]
fig, axs = plt.subplots(1, 2)
fig.set_size_inches(10, 16)
axs[0].imshow(left_img, interpolation='none', cmap='gray')
axs[0].imshow(prior_frames_head[frame_id_head], interpolation='none', alpha=0.7)
axs[0].set_title("Reference frame with prior overlayed")
axs[1].imshow(left_img, interpolation='none', cmap='gray')
axs[1].imshow(adjusted_events, interpolation='none', alpha=0.7)
axs[1].set_title("Reference frame with adjusted prior overlayed")
```
## MRF on frames without prior information
The following experiment provides a baseline for the stereo-matching performance of the MRF algorothm.
For an algorithm test on a standard stereo benchmark dataset see the notebook `MRF_StereoMatching.ipynb`. These results also provide a baseline for the next experiment in which prior information is included. For the sake of completeness, a [third-party algorithm](http://www.ivs.auckland.ac.nz/quick_stereo/index.php) was applied on a subset of the data to compare against our MRF implementation. The results are included in the submitted data (see `data/output/demo/online_algorithm`).
### Head experiment
```
experiment_name = 'head_downsampled'
disparity_max_head = 30 # note that these should be scaled if the scale factor in the config file is changed.
frame_id_head = 40
depth_map_raw_head = run_mrf_without_prior(experiment_name, disparity_max_head, frame_id=frame_id_head, n_iter=5)
```
**Result Analysis:**
The head is mostly correctly matched, with some errors in the middle. However, if one increases the number of iterations, then in some cases (different `frame_id`s) these spots tend to disappear.
Another interesting effect is the misclassified backgorund area on the left side of the head and the correctly classified right side. This can be explained as follows: when comparing the left and right images for the zero disparity case, the background of the two images overlap and due to the homogeneity of the color, the energy values for the right-side background pixels are quite small and the algorithm correctly assigns the small disparity. On the left side however, the background, albeit not really shifted, is occluded from the object in the right image and the nearest matching point to the left of the object (the direction of search) is some 26-27 pixels apart from the reference location. This inevitably produces the wrong depth values on the left side of the reference object.
Altough the situation below the head statue is different, the algorithm produces unsatisfying results due to the absence of corresponding pixels (as the shadow is not the same in the left and the right image, and the signal from neighbours from above gets propagated to the lower rows of the depth image).
### Checkerboard experiment
```
experiment_name = 'checkerboard_downsampled'
disparity_max_checkerboard = 22 # note that these should be scaled if the scale factor in the config file is changed.
frame_id_checkerboard = 40
depth_map_raw_checkerboard = run_mrf_without_prior(experiment_name, disparity_max_checkerboard,
frame_id=frame_id_checkerboard, n_iter=5)
```
**Result Analysis:**
The outcome of this experiment shows that the MRF is producing good results for the regions which can be matched unambigously, such as object edges. The detected disparities for the regions with homogeneuos colors, e.g. the floor or the wall are mostly incorrect. Nevertheless, the pixel correspondece there is not trivially computable and without any additional knowledge, such as "the floor spans perpendicularly to the image plane" no known to us matching algorithm will be able to generate an adequate depth map. In the experiment with the checkerboard, special difficulty is posed by the repetitive patterns, which in some frames (e.g. No. 40) is fully visible and has therefore a globally optimal matching configuration. There is, however, no guarantee that this configuraiton will be found by the algorithm and in practice we see that only a small portion is correctly matched.
### Boxes and cones experiment
```
experiment_name = 'boxes_and_cones_downsampled'
disparity_max_boxes = 20 # note that these should be scaled if the scale factor in the config file is changed.
frame_id_boxes = 20
depth_map_raw_boxes = run_mrf_without_prior(experiment_name, disparity_max_boxes,
frame_id=frame_id_boxes, n_iter=5)
```
**Result Analysis:**
Some depth maps from frames in this dataset are particularly badly computed as they are overexposed and wash out the object edges. Although the first several frames of the video present a table with sharply outlined edges, some parts which are present in the reference image are missing from the target one, which makes their matching impossible and hinders the correspondence assignment of the visible sections. It is worth putting more effort into pre-processing, such the contrast it normalised locally and overexposed areas do not affect the global contrast normalisation.
## MRF on frames with prior information from SNN output
This experiment will take the pre-computed depth events from the spiking network and will run the MRF on the same data. This time however the initial state of the random field will be computed as a convex combination between the data (i.e. image differences) and the prior. The reader is encouraged to play with the parameters. The arguably well-performing parameters are set as the default in the cell below.
### Head experiment
```
experiment_name = 'head_downsampled'
prior_frames_head = eval_snn(experiment_name, disparity_max_head, frame_id=frame_id_head, buffer_len=20)
```
The prior frame, obtained from the buffered SNN output in the time interval `buffer_len` ms before the actual frames, is mixed with the data-term computed in the image difference operation. The mixing coefficient can be proportional to the difference term, which has the following interpretation: _the lower the matching confidence from the data, the higher the prior influence should be_.
```
depth_map_prior_head = run_mrf_with_prior(experiment_name, disparity_max_head, prior_frames_head,
frame_id=frame_id_head, n_iter=5, prior_mode='const',
prior_const=1)
plot_difference_prior_raw(depth_map_raw=depth_map_raw_head,
depth_map_prior=depth_map_prior_head,
disparity_max=disparity_max_head)
```
Part of this experiment is to evaluate the contribution of the prior with varying prior constants. Below we plot the results from several independent evaluations with the `prior_const` ranging in [0, 0.1, 0.5, 1, 2, 10, 100] and finaly the result from the adaptive mode.
```
prior_consts = [0, 0.5, 1, 10, 100]
depth_maps = []
fig, axs = plt.subplots(1, len(prior_consts)+1)
fig.set_size_inches(40, 40)
for i, p_c in enumerate(prior_consts):
depth_map = run_mrf_with_prior(experiment_name, disparity_max_head, prior_frames_head,
frame_id=frame_id_head, n_iter=5, prior_mode='const',
prior_const=p_c)
axs[i].imshow(depth_map, interpolation='none', vmax=disparity_max_head)
axs[i].set_title("Prior const: {}".format(p_c))
depth_map = run_mrf_with_prior(experiment_name, disparity_max_head, prior_frames_head,
frame_id=frame_id_head, n_iter=5, prior_mode='adaptive')
axs[i+1].imshow(depth_map, interpolation='none', vmax=disparity_max_head)
axs[i+1].set_title("Adaptive Prior const")
```
**Result Analysis:**
In some examples the prior has visually deteriorated the results (especially if taken with great influence, i.e, >> 1) and in the rest of the cases it hasn't change much of the quality of the depth map. The former is due to the noisy output that the SNN produces on these datasets and the latter - due to its sparsity. In any case, these results do not support the claim that using SNN as prior initialisation for the MRF will improve the quality of the depth map.
### Checkerboard experiment
```
experiment_name = 'checkerboard_downsampled'
prior_frames = eval_snn(experiment_name, disparity_max_checkerboard, frame_id=frame_id_checkerboard, buffer_len=20)
depth_map_prior_checkerboard = run_mrf_with_prior(experiment_name, disparity_max_checkerboard, prior_frames,
frame_id=frame_id_checkerboard, n_iter=5, prior_mode='const',
prior_const=1)
plot_difference_prior_raw(depth_map_raw=depth_map_raw_checkerboard,
depth_map_prior=depth_map_prior_checkerboard,
disparity_max=disparity_max_checkerboard)
```
**Result Analysis:**
The same observations as in the _head experiment_: prior doesn't change much, and if it does, then the depth map has not become better in quality.
### Boxes and cones experiment
```
experiment_name = 'boxes_and_cones_downsampled'
prior_frames = eval_snn(experiment_name, disparity_max_boxes, frame_id=frame_id_boxes, buffer_len=20)
depth_map_prior_boxes = run_mrf_with_prior(experiment_name, disparity_max_boxes, prior_frames,
frame_id=frame_id_boxes, n_iter=5, prior_mode='const',
prior_const=1)
plot_difference_prior_raw(depth_map_raw=depth_map_raw_boxes,
depth_map_prior=depth_map_prior_boxes,
disparity_max=disparity_max_boxes)
```
**Result Analysis:**
Same as above.
## Inspecting the spatial precision of the prior
Since the prior is an accumulated information from the past, and motion is present, it can happend that the SNN output will have spikes on locations which are slightly off form the gray-scale image. If this is the case (which, by the way, is not easily detectable in an automatic fashion) then one can try to compute the motion of the object and adapt the SNN output accordingly. An optical flow algorithm on the SNN events is applied to estimate the future posiiton of the object and the shift is added to the prior.
We will perform this experiment on the _head_ dataset only, as this is rather unnecessary evaluation and serves only to show that this approach has been considered. Feel free to try on different frames and/or datasets. The optical flow algorithm is implemented according to _Benosman, Ryad, et al., "Event-based visual flow."_ [10], which in short is based on fitting a plane in 3D space-time (2D image space and 1D time dimensions), where the inverse of the slopes of the plane in the orthogonal _x_, _y_ directions (partial derivatives) are used to compute the velocities.
```
experiment_name = 'head_downsampled'
xs, ys, us, vs = compute_optical_flow(experiment_name)
pivots = np.load(os.path.join("..", "data", "input", "frames", experiment_name[:-12],
"left", "timestamps.npy")) / 1000.
adjusted_events = adjust_events_from_motion(prior_frames_head[frame_id_head], (xs, ys, us, vs))
plot_adjusted_prior(experiment_name, frame_id=frame_id_head)
```
**Result Analysis:**
Since the prior adjustment did not turn out to be beneficial, we decided to stop any furhter analysis of the performance. In a different application or under different circumstances (e.g. when immediate depth SNN spikes cannot be computed and older result should be extrapolated in the future) this technique might prove helpful.
| true |
code
| 0.764176 | null | null | null | null |
|
# Similarity Functions
This notebook describes about the similarity functions that can be used to measure the similarity between two sets.
Firstly we import the shingling functions and other helpful functions.
```
from src.shingle import *
from math import ceil, floor
import numpy as np
```
We will then count how frequent a shingle is in the document. For this I have calculated the frequencies in the document called `data/portuguese/two_ends.txt`. Here we are using portuguese corpus.
Then we create a dictionary called `frequencies` which goes like from the word to its frequency.
```
# Initialize counts
frequencies = {}
text = open("data/portuguese/two_ends.txt", "r+")
for line in text:
word = line.strip().split(' ')
frequencies[word[0]] = float(word[1])
```
## TF - IDF
TF-IDF (Term-frequency and Inverse Document Frequency) measures similarity using this:
<img src="utils/tfidf.png" alt="tfidf" width="400px"/>
Firstly, we define `tf` using this, which is just the frequency counts in the intersection.
```
def tf(intersection, query):
'''Counts term frequency'''
tf = [query.count(word) for word in intersection]
return np.array(tf)
```
Afterwards, we compute `idf`, which is inverse document frequency. Here we will make use of the dictionary that we created earlier in order to compute document frequencies.
```
def idf(intersection, document, N):
'''Counts inverse document frequency'''
idf = np.array([frequencies[word] for word in intersection])
idf = np.log10(np.divide(N + 1, idf + 0.5))
return idf
```
Finally we simulate the function `tf_idf` which takes the dot product of `tf` and `idf` arrays.
```
def tf_idf(query, document, N):
intersection = [word for word in document if word in query] # intersection
score = np.dot(tf(intersection, query), idf(intersection, document, N))
return score
```
We can then run the similarity function in the following manner:
```
query = two_ends("pizza", 2)
document = two_ends("pizza", 2)
tf_idf(query, document, 50000) # number of documents are around 50000
```
## BM25
The formula of BM25 is given like this:
<img src="utils/bm25.png" alt="tfidf" width="800px"/>
Here we define the `bm25_tf` in the following manner:
```
def bm25_tf(intersection, query, document, k1, b, avgdl, N):
tf_ = tf(intersection, document)
numerator = tf_ * (k1 + 1.0)
denominator = tf_ + k1 * (1.0 - b + b * (len(query) / avgdl))
bm25_tf = np.divide(numerator, denominator)
return bm25_tf
```
Finally we will take the dot product of `bm25_tf` and `idf` to get this:
```
def bm25(query, document, k1 = 1.2, b = 0.75, avgdl = 8.3, N = 50000):
intersection = [word for word in document if word in query] # intersection
score = np.dot(bm25_tf(intersection, query, document, k1, b, avgdl, N), idf(intersection, document, N))
return score
```
We can run the function in the following manner:
```
query = two_ends("pizza", 2)
document = two_ends("pizza", 2)
bm25(query, document)
```
## Dirichlet
The formula of Dirichlet is given like this:
<img src="utils/dir.png" alt="tfidf" width="800px"/>
Firstly, we will compute the sum dependent function here in the form of `smooth`.
```
shingles = 470751
def smooth(intersection, document, mu):
smooth = []
for word in intersection:
prob = 1.0 + np.divide(document.count(word), mu * frequencies[word] / shingles)
smooth.append(np.log10(prob))
smooth = np.array(smooth)
return smooth
```
We will add the sum independent function to `smooth` and take the dot product to `tf`.
```
def dirichlet(query, document, mu = 100.0):
intersection = [word for word in document if word in query] # intersection
add = len(query) * np.log10(np.divide(mu, mu + len(document)))
score = np.dot(tf(intersection, query), smooth(intersection , document, mu)) + add
return score
```
We can this function in following manner:
```
query = two_ends("pizzzza", 2)
document = two_ends("pizzza", 2)
print(dirichlet(query, document))
```
| true |
code
| 0.504455 | null | null | null | null |
|
# Numerical solution to the 1-dimensional Time Independent Schroedinger Equation
Based on the paper "Matrix Numerov method for solving Schroedinger's equation" by Mohandas Pillai, Joshua Goglio, and Thad G. Walker, _American Journal of Physics_ **80** (11), 1017 (2012). [doi:10.1119/1.4748813](http://dx.doi.org/10.1119/1.4748813)
```
# import some needed libraries
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
%matplotlib inline
autoscale = False # set this equal to true to use Pillai's recommended step sizes
# values of constants
hbar = 1.0
mass = 1.0 # changing the mass will also change the energy scale
omega = 1.0
L = 1.0 # width of SW
# bounds (These are overwritten if autoscale=True)
xmin = -L # lower bound of position
xmax = 5.0 # upper bound of position
n = 100 # number of steps (may be overwritten if autoscale == True)
dx = (xmax-xmin)/(n-1)
# the function V is the potential energy function
def V(x):
# make sure there is no division by zero
# this also needs to be a "vectorizable" function
# uncomment one of the examples below, or write your own.
return 0.5*mass*omega**2*x*x*(0.5*(x+np.abs(x))) # half harmonic oscillator
if (autoscale):
#Emax is the maximum energy for which to check for eigenvalues
Emax = 20.0
#The next lines make some reasonable choices for the position grid size and spacing
xt = opt.brentq(lambda x: V(x)-Emax ,0,5*Emax) #classical turning point
dx = 1.0/np.sqrt(2*Emax) #step size
# bounds and number of steps
n = np.int(0.5+2*(xt/dx + 4.0*np.pi)) #number of steps
xmin = -dx*(n+1)/2
xmax = dx*(n+1)/2
xmin, xmax, n #show the limits and number of steps
#define the x coordinates
x = np.linspace(xmin,xmax,n)
#define the numerov matrices
B = np.matrix((np.eye(n,k=-1)+10.0*np.eye(n,k=0)+np.eye(n,k=1))/12.0)
A = np.matrix((np.eye(n,k=-1)-2.0*np.eye(n,k=0)+np.eye(n,k=1))/(dx**2))
#calculate kinetic energy operator using Numerov's approximation
KE = -0.5*hbar**2/mass*B.I*A
#calculate hamiltonian operator approximation
H = KE + np.diag(V(x))
#Calculate eigenvalues and eigenvectors of H
energies, wavefunctions = np.linalg.eigh(H) # "wavefunctions" is a matrix with one eigenvector in each column.
energies[0:5] #display the lowest four energies
# extract color settings to help plotting
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
plt.figure(figsize=(6,8))
number = [0,1,2,3,4,5] #which wavefunctions to plot, starting counting from zero
zoom = -3.0 # zoom factor for wavefunctions to make them more visible
plt.plot(x,V(x),'-k',label="V(x)") # plot the potential
plt.vlines(-1,0,15,color="black")
plt.vlines(0,0,15,color="black",lw=0.5)
for num in number:
plt.plot(x,zoom*wavefunctions[:,num]+energies[num],label="n={}".format(num)) #plot the num-th wavefunction
plt.hlines(energies[num],-1,5,lw=0.5, color=colors[num])
plt.ylim(-1,15); # set limits of vertical axis for plot
plt.legend();
plt.xlabel("x");
plt.ylabel("Energy or ϕ(x)");
```
| true |
code
| 0.655143 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/rs-delve/tti-explorer/blob/master/notebooks/tti-experiment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# TTI Explorer
#### `tti_explorer` is a library for simulating infection spread. This library is built to explore the impact of various test-trace-isolate strategies and social distancing measures on the spread of COVID-19 in the UK.
This notebook is an introduction to the functionality offered by `tti-explorer`.
```
%pwd
%cd ~/Desktop/College\ Work/Fourth\ Year/L48/L48Project/tti-explorer
%pip install -q .
import os
import numpy as np
import pandas as pd
from tqdm.notebook import trange
from tqdm import tqdm
from tti_explorer import config, utils
from tti_explorer.case import simulate_case, CaseFactors
from tti_explorer.contacts import EmpiricalContactsSimulator
from tti_explorer.strategies import TTIFlowModel, RETURN_KEYS
def print_doc(func):
print(func.__doc__)
```
Before we do anything, let's make a random state
```
rng = np.random.RandomState(0)
```
We will first do a short tour of the functionality, then show how this is put together to generate simulation results.
## Generate a case
The function we use for this is `simulate_case` in `case.py`
```
print_doc(simulate_case)
```
We store our config values in `config.py`. You can retrieve them as follows
```
case_config = config.get_case_config("delve")
case_config
```
We use these parameters to simulate a case
```
primary_case = simulate_case(rng, **case_config)
print_doc(primary_case)
```
Returned is a `case.Case` with stochastically generated attributes.
### Deeper: Case attributes
Let's go through the simulated attributes of a `case.Case`. The attributes `.under18`, `.covid` and `.symptomatic` are `bool` types indicating whether the generated `case.Case` is under 18, COVID positive and symptomatic respectively. All possible values of these attributes are possible apart from the combination `.covid = False` and `.symptomatic = False` (a configuration irrelevant for the purpose of simulating infection spread). The primary case we just simulated has the following attributes:
```
print(f'Under 18: {primary_case.under18}.')
print(f'COVID positive: {primary_case.covid}.')
print(f'Symptomatic: {primary_case.symptomatic}.')
```
Each `case.Case` also has an attribute `.day_noticed_symptoms` of type `int`, indicating the number of days from start of infectiousness until the `case.Case` noticed the symptoms. If a `case.Case` is asymptomatic, the attribute `.day_noticed_symptoms` is set to `-1`.
```
print(f'primary_case noticed symptoms {primary_case.day_noticed_symptoms} days after start of infectiousness.')
```
Finally, the attribute `.inf_profile` is a `list` describing the relative infectiousness of the case for each day of the infectious period. If `.covid = False` for a `case.Case`, this is `0` throughout.
```
print(f'inf_profile is: {primary_case.inf_profile}')
```
As mentioned above, the configuration for simulating these attributes are stored in `config.py`. This includes the distributions used for sampling attributes. For instance, the attribute `.under18` is sampled from a Bernoulli distribution with probability `0.21`:
```
print(f'Probability of case being under 18: {case_config["p_under18"]}')
```
As another example, if `case.Case` is symptomatic, the attribute `.days_noticed_symptoms` is sampled from a categorical distribution over the set {0, 1, ..., 9} (since we model an infection period of ten days in this configuration) with probabilities:
```
print(f'Probability distribution of .day_noticed_symptoms: {case_config["p_day_noticed_symptoms"]}')
```
## Generate contacts
Social contacts are represented by `Contacts` and defined in `contacts.py`.
To simulate social contacts, we use the BBC Pandemic Dataset. This is stratified as over/under 18 to give different patterns of social contact depending on the age of the case.
```
def load_csv(pth):
return np.loadtxt(pth, dtype=int, skiprows=1, delimiter=",")
path_to_bbc_data = os.path.join("..", "data", "bbc-pandemic")
over18 = load_csv(os.path.join(path_to_bbc_data, "contact_distributions_o18.csv"))
under18 = load_csv(os.path.join(path_to_bbc_data, "contact_distributions_u18.csv"))
```
Now that we have the data loaded, we use `EmpiricalContactsSimulator` to sample these tables for contacts of the primary case, then simulate their infection under a no measures scenario (i.e. no government intervention)
```
print_doc(EmpiricalContactsSimulator.__init__)
simulate_contacts = EmpiricalContactsSimulator(over18, under18, rng)
```
We can now use the callable `simulate_contacts` to simulate social contacts of the primary case
```
print_doc(simulate_contacts.__call__)
```
To do this we need some more parameters, which we also load from `config.py`. The user can, of course, specify this themselves if they would like.
```
contacts_config = config.get_contacts_config("delve")
contacts_config.keys()
```
We now do the same as we did with when simulating a primary case.
```
social_contacts = simulate_contacts(primary_case, **contacts_config)
print_doc(social_contacts)
```
### Deeper: Contacts attributes
Let's examine the attributes of `social_contacts`, which is an instance of `contacts.Contacts`. Note that `social_contacts` is simulated above by calling `simulate_contacts` which takes `primary_case` as in argument, so contact generation of course depends on the case simulated first.
The first attribute to note is `.n_daily`, which is a `dict` containing the average number of daily contacts (split into three categories) of the case. This is simulated by sampling one row of the tables `over18` or `under18` depending on the value of `primary_case.under18`. In the case of `primary_case`, we can look at `social_contacts.n_daily`:
```
print(f'Average number of daily contacts for primary_case:')
print(f'Home: {social_contacts.n_daily["home"]}')
print(f'Work: {social_contacts.n_daily["work"]}')
print(f'Other: {social_contacts.n_daily["other"]}')
```
The three remaining attributes `.home`, `.work` and `.other` are arrays containing information about each contact made by the case, with one row per contact. More specifically, for each contact, the row contains the first day (always measured relative to the start of infectiousness) of encounter between the case and contact and, if transmission occurred, then the day of transmission.
Also, recall that home contacts are assumed to repeat every day of the infectious period, whereas work/other contacts are new for each day. This means the lengths of the arrays `.work` and `.other` are `10 * .n_daily['work']` and `10 * .n_daily['other']` respectively (recalling the infection period is assumed to last ten days, a parameter set in `contacts_config['period']`). Whereas, the length of the `.home` array is just `.n_daily['home']`.
```
print(f'Lengths of .home, .work and .other attributes:')
print(f'Home: {len(social_contacts.home)}')
print(f'Work: {len(social_contacts.work)}')
print(f'Other: {len(social_contacts.other)}')
```
Digging further into the array, each row contains two integers. The first integer indicates the day of transmission, which is set to `-1` if no transmission occurred. The second integer contains the day of first encounter. So for instance, looking at one of the home contacts, we see transmission didn't occur and the day of first encounter is `0`, i.e. the first day of the infection period:
```
print(social_contacts.home[0])
```
Looking at the first six work contacts, we see none of them were infected either. This is consistent with the fact that `primary_case.covid = False` so no transmission can occur in this case.
```
print(social_contacts.work[:6])
```
In simulations where `case.Case` is COVID positive, each contact may get infected and the probability of getting infected depends on parameters such as the secondary attack rates (SARs), all of which are set in `contacts_config`. For details on the precise simulation procedure used to generate `contacts.Contacts`, see either Appendix A of the report or the `__call__` method of `EmpiricalContactsSimulator`.
## TTI Strategies
All of the information about the primary case's infection and how they infect their social contacts (under no government intervention) is now contained in `primary_case` and `social_contacts`.
Now we run a simulation, which works as follows. We start by generating a large number of cases, each with associated contacts. Given a particular strategy (e.g. test-based TTI with NPI of stringency level S3), each case is passed through the strategy, which computes various metrics for the case. For example, it computes the number of secondary cases due to primary case (reproduction number) and the number of tests required. We then collect the results for each case and average them, returning the final evaluation of the strategy.
## Running a Simulation
```
from tti_explorer.strategies import TTIFlowModel
```
We will analyse the `S3_test_based_TTI` strategy from our report. For clarity, we will show the whole process.
First get the configurations:
```
name = 'S3_test_based_TTI'
case_config = config.get_case_config("delve")
print(case_config)
contacts_config = config.get_contacts_config("delve")
policy_config = config.get_strategy_configs("delve", name)[name]
factor_config = utils.get_sub_dictionary(policy_config, config.DELVE_CASE_FACTOR_KEYS)
strategy_config = utils.get_sub_dictionary(policy_config, config.DELVE_STRATEGY_FACTOR_KEYS)
```
Set a random state:
```
rng = np.random.RandomState(42)
```
Make contact simulator:
```
simulate_contacts = EmpiricalContactsSimulator(over18, under18, rng)
```
Make the TTI Model:
```
tti_model = TTIFlowModel(rng, **strategy_config)
```
Generate cases, contacts and run simulation:
```
n_cases = 10000
outputs = list()
for i in tqdm(range(n_cases)):
case = simulate_case(rng, **case_config)
case_factors = CaseFactors.simulate_from(rng, case, **factor_config)
contacts = simulate_contacts(case, **contacts_config)
res = tti_model(case, contacts, case_factors)
outputs.append(res)
```
Collate and average results across the cases simulated:
```
# This cell is mosltly just formatting results...
to_show = [
RETURN_KEYS.base_r,
RETURN_KEYS.reduced_r,
RETURN_KEYS.man_trace,
RETURN_KEYS.app_trace,
RETURN_KEYS.tests
]
# scale factor to turn simulation numbers into UK population numbers
nppl = case_config['infection_proportions']['nppl']
scales = [1, 1, nppl, nppl, nppl]
results = pd.DataFrame(
outputs
).mean(
0
).loc[
to_show
].mul(
scales
).to_frame(
name=f"Simulation results: {name.replace('_', ' ')}"
).rename(
index=lambda x: x + " (k per day)" if x.startswith("#") else x
)
results.round(1)
```
| true |
code
| 0.398641 | null | null | null | null |
|
<a href="https://colab.research.google.com/drive/1F22gG4PqDIuM0R4zbzEKu1DlGbnHeNxM?usp=sharing" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
By [Ibrahim Sobh](https://www.linkedin.com/in/ibrahim-sobh-phd-8681757/)
## In this code, we are going to implement a basic image classifier:
- Load the dataset (MNIST hand written digits)
- Design a deep learning model and inspect its learnable parameters
- Train the model on the training data and inspect learning curves
- Evaluate the trained model on the never seen testing data
- Save the model for later use
- Load and use the model
```
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.utils import plot_model
from PIL import Image
from keras import backend as K
import matplotlib.pyplot as plt
batch_size = 128
num_classes = 10
epochs = 10 #50
# input image dimensions
img_rows, img_cols = 28, 28
```
## Load the data

```
# load data, split into train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
# small data
data_size = 10000
x_train = x_train[:data_size]
y_train = y_train[:data_size]
x_test = x_test[:data_size]
y_test = y_test[:data_size]
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
```
## Build the DNN model
```
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
model.summary()
plot_model(model, to_file="mnistcnn.png", show_shapes=True)
img = Image.open('./mnistcnn.png')
img
```
## Train the model
```
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
```
## Evalaute the model
```
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
plt.figure(figsize=(10, 7))
plt.plot(history.history['loss'], label='Train')
plt.plot(history.history['val_loss'], label='Test')
plt.title('Learning curve')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend()
```
## Save and load the trained model
```
from keras.models import load_model
# save the model
model.save('my_model.h5') # creates a HDF5 file 'my_model.h5'
del model # deletes the existing model
!ls -l
# load the saved model
myloadednewmodel = load_model('my_model.h5')
myloadednewmodel.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
| true |
code
| 0.781153 | null | null | null | null |
|
# Announcements
- __Please familiarize yourself with the term projects, and sign up for your (preliminary) choice__ using [this form](https://forms.gle/ByLLpsthrpjCcxG89). _You may revise your choice, but I'd recommend settling on a choice well before Thanksgiving._
- Recommended reading on ODEs: [Lecture notes by Prof. Hjorth-Jensen (University of Oslo)](https://www.asc.ohio-state.edu/physics/ntg/6810/readings/hjorth-jensen_notes2013_08.pdf)
- Problem Set 5 will be posted on D2L on Oct 12, due Oct 20.
- __Outlook__: algorithms for solving high-dimensional linear and non-linear equations; then Boundary Value Problems and Partial Differential Equations.
- Conference for Undergraduate Women in Physics: online event in 2021, [applications accepted until 10/25](https://www.aps.org/programs/women/cuwip/)
This notebook presents as selection of topics from the book "Numerical Linear Algebra" by Trefethen and Bau (SIAM, 1997), and uses notebooks by Kyle Mandli.
# Numerical Linear Algebra
Numerical methods for linear algebra problems lies at the heart of many numerical approaches and is something we will spend some time on. Roughly we can break down problems that we would like to solve into two general problems, solving a system of equations
$$A \vec{x} = \vec{b}$$
and solving the eigenvalue problem
$$A \vec{v} = \lambda \vec{v}.$$
We examine each of these problems separately and will evaluate some of the fundamental properties and methods for solving these problems. We will be careful in deciding how to evaluate the results of our calculations and try to gain some understanding of when and how they fail.
## General Problem Specification
The number and power of the different tools made available from the study of linear algebra makes it an invaluable field of study. Before we dive in to numerical approximations we first consider some of the pivotal problems that numerical methods for linear algebra are used to address.
For this discussion we will be using the common notation $m \times n$ to denote the dimensions of a matrix $A$. The $m$ refers to the number of rows and $n$ the number of columns. If a matrix is square, i.e. $m = n$, then we will use the notation that $A$ is $m \times m$.
### Systems of Equations
The first type of problem is to find the solution to a linear system of equations. If we have $m$ equations for $m$ unknowns it can be written in matrix/vector form,
$$A \vec{x} = \vec{b}.$$
For this example $A$ is an $m \times m$ matrix, denoted as being in $\mathbb{R}^{m\times m}$, and $\vec{x}$ and $\vec{b}$ are column vectors with $m$ entries, denoted as $\mathbb{R}^m$.
#### Example: Vandermonde Matrix
We have data $(x_i, y_i), ~~ i = 1, 2, \ldots, m$ that we want to fit a polynomial of order $m-1$. Solving the linear system $A p = y$ does this for us where
$$A = \begin{bmatrix}
1 & x_1 & x_1^2 & \cdots & x_1^{m-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{m-1} \\
\vdots & \vdots & \vdots & & \vdots \\
1 & x_m & x_m^2 & \cdots & x_m^{m-1}
\end{bmatrix} \quad \quad y = \begin{bmatrix}
y_1 \\ y_2 \\ \vdots \\ y_m
\end{bmatrix}$$
and $p$ are the coefficients of the interpolating polynomial $\mathcal{P}_N(x) = p_0 + p_1 x + p_2 x^2 + \cdots + p_m x^{m-1}$. The solution to this system satisfies $\mathcal{P}_N(x_i)=y_i$ for $i=1, 2, \ldots, m$.
#### Example: Linear least squares 1
In a similar case as above, say we want to fit a particular function (could be a polynomial) to a given number of data points except in this case we have more data points than free parameters. In the case of polynomials this could be the same as saying we have $m$ data points but only want to fit a $n - 1$ order polynomial through the data where $n - 1 \leq m$. One of the common approaches to this problem is to minimize the "least-squares" error between the data and the resulting function:
$$
E = \left( \sum^m_{i=1} |y_i - f(x_i)|^2 \right )^{1/2}.
$$
But how do we do this if our matrix $A$ is now $m \times n$ and looks like
$$
A = \begin{bmatrix}
1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\
1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & & \vdots \\
1 & x_m & x_m^2 & \cdots & x_m^{n-1}
\end{bmatrix}?
$$
Turns out if we solve the system
$$A^T A x = A^T b$$
we can gaurantee that the error is minimized in the least-squares sense[<sup>1</sup>](#footnoteRegression).
#### Practical Example: Linear least squares implementation
Fitting a line through data that has random noise added to it.
```
%matplotlib inline
%precision 3
import numpy
import matplotlib.pyplot as plt
# Linear Least Squares Problem
# First define the independent and dependent variables.
N = 20
x = numpy.linspace(-1.0, 1.0, N)
y = x + numpy.random.random((N))
# Define the Vandermonde matrix based on our x-values
A = numpy.ones((x.shape[0], 2))
A[:, 1] = x
# Determine the coefficients of the polynomial that will
# result in the smallest sum of the squares of the residual.
p = numpy.linalg.solve(numpy.dot(A.transpose(), A), numpy.dot(A.transpose(), y))
print("Error in slope = %s, y-intercept = %s" % (numpy.abs(p[1] - 1.0), numpy.abs(p[0] - 0.5)))
# Plot it out, cuz pictures are fun!
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'ko')
axes.plot(x, p[0] + p[1] * x, 'r')
axes.set_title("Least Squares Fit to Data")
axes.set_xlabel("$x$")
axes.set_ylabel("$f(x)$ and $y_i$")
plt.show()
```
### Eigenproblems
Eigenproblems come up in a variety of contexts and often are integral to many problem of scientific and engineering interest. It is such a powerful idea that it is not uncommon for us to take a problem and convert it into an eigenproblem. We will covered detailed algorithms for eigenproblems in the next lectures, but for now let's remind ourselves of the problem and analytic solution:
If $A \in \mathbb{C}^{m\times m}$ (a square matrix with complex values), a non-zero vector $\vec{v}\in\mathbb{C}^m$ is an **eigenvector** of $A$ with a corresponding **eigenvalue** $\lambda \in \mathbb{C}$ if
$$A \vec{v} = \lambda \vec{v}.$$
One way to interpret the eigenproblem is that we are attempting to ascertain the "action" of the matrix $A$ on some subspace of $\mathbb{C}^m$ where this action acts like scalar multiplication. This subspace is called an **eigenspace**.
#### Example
Compute the eigenspace of the matrix
$$
A = \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix}
$$
Recall that we can find the eigenvalues of a matrix by computing $\det(A - \lambda I) = 0$.
In this case we have
$$\begin{aligned}
A - \lambda I &= \begin{bmatrix}
1 & 2 \\
2 & 1
\end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \lambda\\
&= \begin{bmatrix}
1 - \lambda & 2 \\
2 & 1 - \lambda
\end{bmatrix}.
\end{aligned}$$
The determinant of the matrix is
$$\begin{aligned}
\begin{vmatrix}
1 - \lambda & 2 \\
2 & 1 - \lambda
\end{vmatrix} &= (1 - \lambda) (1 - \lambda) - 2 \cdot 2 \\
&= 1 - 2 \lambda + \lambda^2 - 4 \\
&= \lambda^2 - 2 \lambda - 3.
\end{aligned}$$
This result is sometimes referred to as the characteristic equation of the matrix, $A$.
Setting the determinant equal to zero we can find the eigenvalues as
$$\begin{aligned}
& \\
\lambda &= \frac{2 \pm \sqrt{4 - 4 \cdot 1 \cdot (-3)}}{2} \\
&= 1 \pm 2 \\
&= -1 \mathrm{~and~} 3
\end{aligned}$$
The eigenvalues are used to determine the eigenvectors. The eigenvectors are found by going back to the equation $(A - \lambda I) \vec{v}_i = 0$ and solving for each vector. A trick that works some of the time is to normalize each vector such that the first entry is 1 ($\vec{v}_1 = 1$):
$$
\begin{bmatrix}
1 - \lambda & 2 \\
2 & 1 - \lambda
\end{bmatrix} \begin{bmatrix} 1 \\ v_2 \end{bmatrix} = 0
$$
$$\begin{aligned}
1 - \lambda + 2 v_2 &= 0 \\
v_2 &= \frac{\lambda - 1}{2}
\end{aligned}$$
We can check this by
$$\begin{aligned}
2 + \left(1- \lambda \frac{\lambda - 1}{2}\right) & = 0\\
(\lambda - 1)^2 - 4 &=0
\end{aligned}$$
which by design is satisfied by our eigenvalues. Another sometimes easier approach is to plug-in the eigenvalues to find each corresponding eigenvector. The eigenvectors are therefore
$$\vec{v} = \begin{bmatrix}1 \\ -1 \end{bmatrix}, \begin{bmatrix}1 \\ 1 \end{bmatrix}.$$
Note that these are linearly independent.
## Fundamentals
### Matrix-Vector Multiplication
One of the most basic operations we can perform with matrices is to multiply them be a vector. This matrix-vector product $A \vec{x} = \vec{b}$ is defined as
$$
b_i = \sum^n_{j=1} a_{ij} x_j \quad \text{where}\quad i = 1, \ldots, m
$$
Writing the matrix-vector product this way we see that one interpretation of this product is that each column of $A$ is weighted by the value $x_j$, or in other words $\vec{b}$ is a linear combination of the columns of $A$ where each column's weighting is $x_j$.
$$
\begin{align}
\vec{b} &= A \vec{x}, \\
\vec{b} &=
\begin{bmatrix} & & & \\ & & & \\ \vec{a}_1 & \vec{a}_2 & \cdots & \vec{a}_n \\ & & & \\ & & & \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}, \\
\vec{b} &= x_1 \vec{a}_1 + x_2 \vec{a}_2 + \cdots + x_n \vec{a}_n.
\end{align}
$$
This view will be useful later when we are trying to interpret various types of matrices.
One important property of the matrix-vector product is that is a **linear** operation, also known as a **linear operator**. This means that the for any $\vec{x}, \vec{y} \in \mathbb{C}^n$ and any $c \in \mathbb{C}$ we know that
1. $A (\vec{x} + \vec{y}) = A\vec{x} + A\vec{y}$
1. $A\cdot (c\vec{x}) = c A \vec{x}$
#### Example: Vandermonde Matrix
In the case where we have $m$ data points and want $m - 1$ order polynomial interpolant the matrix $A$ is a square, $m \times m$, matrix as before. Using the above interpretation the polynomial coefficients $p$ are the weights for each of the monomials that give exactly the $y$ values of the data.
#### Example: Numerical matrix-vector multiply
Write a matrix-vector multiply function and check it with the appropriate `numpy` routine. Also verify the linearity of the matrix-vector multiply.
```
#A x = b
#(m x n) (n x 1) = (m x 1)
def matrix_vector_product(A, x):
m, n = A.shape
b = numpy.zeros(m)
for i in range(m):
for j in range(n):
b[i] += A[i, j] * x[j]
return b
m = 4
n = 3
A = numpy.random.uniform(size=(m,n))
x = numpy.random.uniform(size=(n))
y = numpy.random.uniform(size=(n))
c = numpy.random.uniform()
b = matrix_vector_product(A, x)
print(numpy.allclose(b, numpy.dot(A, x)))
print(numpy.allclose(matrix_vector_product(A, (x + y)), matrix_vector_product(A, x) + matrix_vector_product(A, y)))
print(numpy.allclose(matrix_vector_product(A, c * x), c*matrix_vector_product(A, x)))
```
### Matrix-Matrix Multiplication
The matrix product with another matrix $A C = B$ is defined as
$$
b_{ij} = \sum^m_{k=1} a_{ik} c_{kj}.
$$
Again, a useful interpretation of this operation is that the product result $B$ is the a linear combination of the columns of $A$.
_What are the dimensions of $A$ and $C$ so that the multiplication works?_
#### Example: Outer Product
The product of two vectors $\vec{u} \in \mathbb{C}^m$ and $\vec{v} \in \mathbb{C}^n$ is a $m \times n$ matrix where the columns are the vector $u$ multiplied by the corresponding value of $v$:
$$
\begin{align}
\vec{u} \vec{v}^T &=
\begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix}
\begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix}, \\
& = \begin{bmatrix} v_1u_1 & \cdots & v_n u_1 \\ \vdots & & \vdots \\ v_1 u_m & \cdots & v_n u_m \end{bmatrix}.
\end{align}
$$
It is useful to think of these as operations on the column vectors, and an equivalent way to express this relationship is
$$
\begin{align}
\vec{u} \vec{v}^T &=
\begin{bmatrix} \\ \vec{u} \\ \\ \end{bmatrix}
\begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix}, \\
&=
\begin{bmatrix} & & & \\ & & & \\ \vec{u}v_1 & \vec{u} v_2 & \cdots & \vec{u} v_n \\ & & & \\ & & & \end{bmatrix}, \\
& = \begin{bmatrix} v_1u_1 & \cdots & v_n u_1 \\ \vdots & & \vdots \\ v_1 u_m & \cdots & v_n u_m \end{bmatrix}.
\end{align}
$$
#### Example: Upper Triangular Multiplication
Consider the multiplication of a matrix $A \in \mathbb{C}^{m\times n}$ and the **upper-triangular** matrix $R$ defined as the $n \times n$ matrix with entries $r_{ij} = 1$ for $i \leq j$ and $r_{ij} = 0$ for $i > j$. The product can be written as
$$
\begin{bmatrix} \\ \\ \vec{b}_1 & \cdots & \vec{b}_n \\ \\ \\ \end{bmatrix} = \begin{bmatrix} \\ \\ \vec{a}_1 & \cdots & \vec{a}_n \\ \\ \\ \end{bmatrix} \begin{bmatrix} 1 & \cdots & 1 \\ & \ddots & \vdots \\ & & 1 \end{bmatrix}.
$$
The columns of $B$ are then
$$
\vec{b}_j = A \vec{r}_j = \sum^j_{k=1} \vec{a}_k
$$
so that $\vec{b}_j$ is the sum of the first $j$ columns of $A$.
#### Example: Write Matrix-Matrix Multiplication
Write a function that computes matrix-matrix multiplication and demonstrate the following properties:
1. $A (B + C) = AB + AC$ (for square matrices))
1. $A (cB) = c AB$ where $c \in \mathbb{C}$
1. $AB \neq BA$ in general
```
def matrix_matrix_product(A, B):
C = numpy.zeros((A.shape[0], B.shape[1]))
for i in range(A.shape[0]):
for j in range(B.shape[1]):
for k in range(A.shape[1]):
C[i, j] += A[i, k] * B[k, j]
return C
m = 4
n = 4
p = 4
A = numpy.random.uniform(size=(m, n))
B = numpy.random.uniform(size=(n, p))
C = numpy.random.uniform(size=(m, p))
c = numpy.random.uniform()
print(numpy.allclose(matrix_matrix_product(A, B), numpy.dot(A, B)))
print(numpy.allclose(matrix_matrix_product(A, (B + C)), matrix_matrix_product(A, B) + matrix_matrix_product(A, C)))
print(numpy.allclose(matrix_matrix_product(A, c * B), c*matrix_matrix_product(A, B)))
print(numpy.allclose(matrix_matrix_product(A, B), matrix_matrix_product(B, A)))
```
### Matrices in NumPy
NumPy and SciPy contain routines that ware optimized to perform matrix-vector and matrix-matrix multiplication. Given two `ndarray`s you can take their product by using the `dot` function.
```
n = 10
m = 5
# Matrix vector with identity
A = numpy.identity(n)
x = numpy.random.random(n)
print(numpy.allclose(x, numpy.dot(A, x)))
# Matrix vector product
A = numpy.random.random((m, n))
print(numpy.dot(A, x))
# Matrix matrix product
B = numpy.random.random((n, m))
print(numpy.dot(A, B))
```
### Range and Null-Space
#### Range
- The **range** of a matrix $A \in \mathbb R^{m \times n}$ (similar to any function), denoted as $\text{range}(A)$, is the set of vectors that can be expressed as $A x$ for $x \in \mathbb R^n$.
- We can also then say that that $\text{range}(A)$ is the space **spanned** by the columns of $A$. In other words the columns of $A$ provide a basis for $\text{range}(A)$, also called the **column space** of the matrix $A$.
#### Null-Space
- Similarly the **null-space** of a matrix $A$, denoted $\text{null}(A)$ is the set of vectors $x$ that satisfy $A x = 0$.
- A similar concept is the **rank** of the matrix $A$, denoted as $\text{rank}(A)$, is the dimension of the column space. A matrix $A$ is said to have **full-rank** if $\text{rank}(A) = \min(m, n)$. This property also implies that the matrix mapping is **one-to-one**.
### Inverse
A **non-singular** or **invertible** matrix is characterized as a matrix with full-rank. This is related to why we know that the matrix is one-to-one, we can use it to transform a vector $x$ and using the inverse, denoted $A^{-1}$, we can map it back to the original matrix. The familiar definition of this is
\begin{align*}
A \vec{x} &= \vec{b}, \\
A^{-1} A \vec{x} & = A^{-1} \vec{b}, \\
x &=A^{-1} \vec{b}.
\end{align*}
Since $A$ has full rank, its columns form a basis for $\mathbb{R}^m$ and the vector $\vec{b}$ must be in the column space of $A$.
There are a number of important properties of a non-singular matrix A. Here we list them as the following equivalent statements
1. $A$ has an inverse $A^{-1}$
1. $\text{rank}(A) = m$
1. $\text{range}(A) = \mathbb{C}^m$
1. $\text{null}(A) = {0}$
1. 0 is not an eigenvalue of $A$
1. $\text{det}(A) \neq 0$
#### Example: Properties of invertible matrices
Show that given an invertible matrix that the rest of the properties hold. Make sure to search the `numpy` packages for relevant functions.
```
m = 3
for n in range(100):
A = numpy.random.uniform(size=(m, m))
if numpy.linalg.det(A) != 0:
break
print(numpy.dot(numpy.linalg.inv(A), A))
print(numpy.linalg.matrix_rank(A))
print("range")
print(numpy.linalg.solve(A, numpy.zeros(m)))
print(numpy.linalg.eigvals(A))
```
### Orthogonal Vectors and Matrices
Orthogonality is a very important concept in linear algebra that forms the basis of many of the modern methods used in numerical computations.
Two vectors are said to be orthogonal if their **inner-product** or **dot-product** defined as
$$
< \vec{x}, \vec{y} > \equiv (\vec{x}, \vec{y}) \equiv \vec{x}^T\vec{y} \equiv \vec{x} \cdot \vec{y} = \sum^m_{i=1} x_i y_i
$$
Here we have shown the various notations you may run into (the inner-product is in-fact a general term for a similar operation for mathematical objects such as functions).
If $\langle \vec{x},\vec{y} \rangle = 0$ then we say $\vec{x}$ and $\vec{y}$ are orthogonal. The reason we use this terminology is that the inner-product of two vectors can also be written in terms of the angle between them where
$$
\cos \theta = \frac{\langle \vec{x}, \vec{y} \rangle}{||\vec{x}||_2~||\vec{y}||_2}
$$
and $||\vec{x}||_2$ is the Euclidean ($\ell^2$) norm of the vector $\vec{x}$.
We can write this in terms of the inner-product as well as
$$
||\vec{x}||_2^2 = \langle \vec{x}, \vec{x} \rangle = \vec{x}^T\vec{x} = \sum^m_{i=1} |x_i|^2.
$$
The generalization of the inner-product to complex spaces is defined as
$$
\langle x, y \rangle = \sum^m_{i=1} x_i^* y_i
$$
where $x_i^*$ is the complex-conjugate of the value $x_i$.
#### Orthonormality
Taking this idea one step further we can say a set of vectors $\vec{x} \in X$ are orthogonal to $\vec{y} \in Y$ if $\forall \vec{x},\vec{y}$ $< \vec{x}, \vec{y} > = 0$. If $\forall \vec{x},\vec{y}$ $||\vec{x}|| = 1$ and $||\vec{y}|| = 1$ then they are also called orthonormal. Note that we dropped the 2 as a subscript to the notation for the norm of a vector. Later we will explore other ways to define a norm of a vector other than the Euclidean norm defined above.
Another concept that is related to orthogonality is linear-independence. A set of vectors $\vec{x} \in X$ are **linearly independent** if $\forall \vec{x} \in X$ that each $\vec{x}$ cannot be written as a linear combination of the other vectors in the set $X$.
An equivalent statement is that there does not exist a set of scalars $c_i$ such that
$$
\vec{x}_k = \sum^n_{i=1, i \neq k} c_i \vec{x}_i.
$$
Another way to write this is that $\vec{x}_k \in X$ is orthogonal to all the rest of the vectors in the set $X$.
This can be related directly through the idea of projection. If we have a set of vectors $\vec{x} \in X$ we can project another vector $\vec{v}$ onto the vectors in $X$ by using the inner-product. This is especially powerful if we have a set of linearly-independent vectors $X$, which are said to **span** a space (or provide a **basis** for a space), s.t. any vector in the space spanned by $X$ can be expressed as a linear combination of the basis vectors $X$
$$
\vec{v} = \sum^n_{i=1} \, \langle \vec{v}, \vec{x}_i \rangle \, \vec{x}_i.
$$
Note if $\vec{v} \in X$ that
$$
\langle \vec{v}, \vec{x}_i \rangle = 0 \quad \forall \vec{x}_i \in X \setminus \vec{v}.
$$
Looping back to matrices, the column space of a matrix is spanned by its linearly independent columns. Any vector $v$ in the column space can therefore be expressed via the equation above. A special class of matrices are called **unitary** matrices when complex-valued and **orthogonal** when purely real-valued if the columns of the matrix are orthonormal to each other. Importantly this implies that for a unitary matrix $Q$ we know the following
1. $Q^* = Q^{-1}$
1. $Q^*Q = I$
where $Q^*$ is called the **adjoint** of $Q$. The adjoint is defined as the transpose of the original matrix with the entries being the complex conjugate of each entry as the notation implies.
### Vector Norms
Norms (and also measures) provide a means for measure the "size" or distance in a space. In general a norm is a function, denoted by $||\cdot||$, that maps $\mathbb{C}^m \rightarrow \mathbb{R}$. In other words we stick in a multi-valued object and get a single, real-valued number out the other end. All norms satisfy the properties:
1. $||\vec{x}|| \geq 0$, and $||\vec{x}|| = 0$ only if $\vec{x} = \vec{0}$
1. $||\vec{x} + \vec{y}|| \leq ||\vec{x}|| + ||\vec{y}||$ (triangle inequality)
1. $||c \vec{x}|| = |c| ~ ||\vec{x}||$ where $c \in \mathbb{C}$
There are a number of relevant norms that we can define beyond the Euclidean norm, also know as the 2-norm or $\ell_2$ norm:
1. $\ell_1$ norm:
$$
||\vec{x}||_1 = \sum^m_{i=1} |x_i|,
$$
1. $\ell_2$ norm:
$$
||\vec{x}||_2 = \left( \sum^m_{i=1} |x_i|^2 \right)^{1/2},
$$
1. $\ell_p$ norm:
$$
||\vec{x}||_p = \left( \sum^m_{i=1} |x_i|^p \right)^{1/p}, \quad \quad 1 \leq p < \infty,
$$
1. $\ell_\infty$ norm:
$$
||\vec{x}||_\infty = \max_{1\leq i \leq m} |x_i|,
$$
1. weighted $\ell_p$ norm:
$$
||\vec{x}||_{W_p} = \left( \sum^m_{i=1} |w_i x_i|^p \right)^{1/p}, \quad \quad 1 \leq p < \infty,
$$
These are also related to other norms denoted by capital letters ($L_2$ for instance). In this case we use the lower-case notation to denote finite or discrete versions of the infinite dimensional counterparts.
#### Example: Comparisons Between Norms
Compute the norms given some vector $\vec{x}$ and compare their values. Verify the properties of the norm for one of the norms.
```
m = 10
p = 4
x = numpy.random.uniform(size=m)
ell_1 = 0.0
for i in range(m):
ell_1 += numpy.abs(x[i])
ell_2 = 0.0
for i in range(m):
ell_2 += numpy.abs(x[i])**2
ell_2 = numpy.sqrt(ell_2)
ell_p = 0.0
for i in range(m):
ell_p += numpy.abs(x[i])**p
ell_p = (ell_2)**(1.0 / p)
ell_infty = numpy.max(numpy.abs(x))
print("L_1 = %s, L_2 = %s, L_%s = %s, L_infty = %s" % (ell_1, ell_2, p, ell_p, ell_infty))
y = numpy.random.uniform(size=m)
print()
print("Properties of norms:")
print(numpy.max(numpy.abs(x + y)), numpy.max(numpy.abs(x)) + numpy.max(numpy.abs(y)))
print(numpy.max(numpy.abs(0.1 * x)), 0.1 * numpy.max(numpy.abs(x)))
```
### Matrix Norms
The most direct way to consider a matrix norm is those induced by a vector-norm. Given a vector norm, we can define a matrix norm as the smallest number $C$ that satisfies the inequality
$$
||A \vec{x}||_{m} \leq C ||\vec{x}||_{n}.
$$
or as the supremum of the ratios so that
$$
C = \sup_{\vec{x}\in\mathbb{C}^n ~ \vec{x}\neq\vec{0}} \frac{||A \vec{x}||_{m}}{||\vec{x}||_n}.
$$
Noting that $||A \vec{x}||$ lives in the column space and $||\vec{x}||$ on the domain we can think of the matrix norm as the "size" of the matrix that maps the domain to the range. Also noting that if $||\vec{x}||_n = 1$ we also satisfy the condition we can write the induced matrix norm as
$$
||A||_{(m,n)} = \sup_{\vec{x} \in \mathbb{C}^n ~ ||\vec{x}||_{n} = 1} ||A \vec{x}||_{m}.
$$
#### Example: Induced Matrix Norms
Consider the matrix
$$
A = \begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix}.
$$
Compute the induced-matrix norm of $A$ for the vector norms $\ell_2$ and $\ell_\infty$.
$\ell^2$: For both of the requested norms the unit-length vectors $[1, 0]$ and $[0, 1]$ can be used to give an idea of what the norm might be and provide a lower bound.
$$
||A||_2 = \sup_{x \in \mathbb{R}^n} \left( ||A \cdot [1, 0]^T||_2, ||A \cdot [0, 1]^T||_2 \right )
$$
computing each of the norms we have
$$\begin{aligned}
\begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} &= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\
\begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix} &= \begin{bmatrix} 2 \\ 2 \end{bmatrix}
\end{aligned}$$
which translates into the norms $||A \cdot [1, 0]^T||_2 = 1$ and $||A \cdot [0, 1]^T||_2 = 2 \sqrt{2}$. This implies that the $\ell_2$ induced matrix norm of $A$ is at least $||A||_{2} = 2 \sqrt{2} \approx 2.828427125$.
The exact value of $||A||_2$ can be computed using the spectral radius defined as
$$
\rho(A) = \max_{i} |\lambda_i|,
$$
where $\lambda_i$ are the eigenvalues of $A$. With this we can compute the $\ell_2$ norm of $A$ as
$$
||A||_2 = \sqrt{\rho(A^\ast A)}
$$
Computing the norm again here we find
$$
A^\ast A = \begin{bmatrix} 1 & 0 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & 2 \end{bmatrix} = \begin{bmatrix} 1 & 2 \\ 2 & 8 \end{bmatrix}
$$
which has eigenvalues
$$
\lambda = \frac{1}{2}\left(9 \pm \sqrt{65}\right )
$$
so $||A||_2 \approx 2.9208096$.
$\ell^\infty$: We can again bound $||A||_\infty$ by looking at the unit vectors which give us the matrix lower bound of 2. To compute it turns out $||A||_{\infty} = \max_{1 \leq i \leq m} ||a^\ast_i||_1$ where $a^\ast_i$ is the $i$th row of $A$. This represents then the maximum of the row sums of $A$. Therefore $||A||_\infty = 3$.
```
A = numpy.array([[1, 2], [0, 2]])
print(numpy.linalg.norm(A, ord=2))
print(numpy.linalg.norm(A, ord=numpy.infty))
```
#### Example: General Norms of a Matrix
Compute a bound on the induced norm of the $m \times n$ dimensional matrix $A$ using $\ell_1$ and $\ell_2$
One of the most useful ways to think about matrix norms is as a transformation of a unit-ball to an ellipse. Depending on the norm in question, the norm will be some combination of the resulting ellipse. For the above cases we have some nice relations based on these ideas.
1. $||A \vec{x}||_1 = || \sum^n_{j=1} x_j \vec{a}_j ||_1 \leq \sum^n_{j=1} |x_j| ||\vec{a}_j||_1 \leq \max_{1\leq j\leq n} ||\vec{a}_j||_1$
1. $||A \vec{x}||_\infty = || \sum^n_{j=1} x_j \vec{a_j} ||_\infty \leq \sum^n_{j=1} |x_j| ||\vec{a}_j||_\infty \leq \max_{1 \leq i \leq m} ||a^*_i||_1$
```
# Note: that this code is a bit fragile to angles that go beyond pi
# due to the use of arccos.
import matplotlib.patches as patches
A = numpy.array([[1, 2], [0, 2]])
def draw_unit_vectors(axes, A, head_width=0.1):
head_length = 1.5 * head_width
image_e = numpy.empty(A.shape)
angle = numpy.empty(A.shape[0])
image_e[:, 0] = numpy.dot(A, numpy.array((1.0, 0.0)))
image_e[:, 1] = numpy.dot(A, numpy.array((0.0, 1.0)))
for i in range(A.shape[0]):
angle[i] = numpy.arccos(image_e[0, i] / numpy.linalg.norm(image_e[:, i], ord=2))
axes.arrow(0.0, 0.0, image_e[0, i] - head_length * numpy.cos(angle[i]),
image_e[1, i] - head_length * numpy.sin(angle[i]),
head_width=head_width, color='b', alpha=0.5)
head_width = 0.2
head_length = 1.5 * head_width
# ============
# 1-norm
# Unit-ball
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 2)
fig.suptitle("1-Norm")
axes = fig.add_subplot(1, 2, 1, aspect='equal')
axes.plot((1.0, 0.0, -1.0, 0.0, 1.0), (0.0, 1.0, 0.0, -1.0, 0.0), 'r')
draw_unit_vectors(axes, numpy.eye(2))
axes.set_title("Unit Ball")
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
axes.grid(True)
# Image
axes = fig.add_subplot(1, 2, 2, aspect='equal')
axes.plot((1.0, 2.0, -1.0, -2.0, 1.0), (0.0, 2.0, 0.0, -2.0, 0.0), 'r')
draw_unit_vectors(axes, A, head_width=0.2)
axes.set_title("Images Under A")
axes.grid(True)
plt.show()
# ============
# 2-norm
# Unit-ball
fig = plt.figure()
fig.suptitle("2-Norm")
fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 2, 1, aspect='equal')
axes.add_artist(plt.Circle((0.0, 0.0), 1.0, edgecolor='r', facecolor='none'))
draw_unit_vectors(axes, numpy.eye(2))
axes.set_title("Unit Ball")
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
axes.grid(True)
# Image
# Compute some geometry
u, s, v = numpy.linalg.svd(A)
theta = numpy.empty(A.shape[0])
ellipse_axes = numpy.empty(A.shape)
theta[0] = numpy.arccos(u[0][0]) / numpy.linalg.norm(u[0], ord=2)
theta[1] = theta[0] - numpy.pi / 2.0
for i in range(theta.shape[0]):
ellipse_axes[0, i] = s[i] * numpy.cos(theta[i])
ellipse_axes[1, i] = s[i] * numpy.sin(theta[i])
axes = fig.add_subplot(1, 2, 2, aspect='equal')
axes.add_artist(patches.Ellipse((0.0, 0.0), 2 * s[0], 2 * s[1], theta[0] * 180.0 / numpy.pi,
edgecolor='r', facecolor='none'))
for i in range(A.shape[0]):
axes.arrow(0.0, 0.0, ellipse_axes[0, i] - head_length * numpy.cos(theta[i]),
ellipse_axes[1, i] - head_length * numpy.sin(theta[i]),
head_width=head_width, color='k')
draw_unit_vectors(axes, A, head_width=0.2)
axes.set_title("Images Under A")
axes.set_xlim((-s[0] + 0.1, s[0] + 0.1))
axes.set_ylim((-s[0] + 0.1, s[0] + 0.1))
axes.grid(True)
plt.show()
# ============
# infty-norm
# Unit-ball
fig = plt.figure()
fig.suptitle("$\infty$-Norm")
fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 2, 1, aspect='equal')
axes.plot((1.0, -1.0, -1.0, 1.0, 1.0), (1.0, 1.0, -1.0, -1.0, 1.0), 'r')
draw_unit_vectors(axes, numpy.eye(2))
axes.set_title("Unit Ball")
axes.set_xlim((-1.1, 1.1))
axes.set_ylim((-1.1, 1.1))
axes.grid(True)
# Image
# Geometry - Corners are A * ((1, 1), (1, -1), (-1, 1), (-1, -1))
# Symmetry implies we only need two. Here we just plot two
u = numpy.empty(A.shape)
u[:, 0] = numpy.dot(A, numpy.array((1.0, 1.0)))
u[:, 1] = numpy.dot(A, numpy.array((-1.0, 1.0)))
theta[0] = numpy.arccos(u[0, 0] / numpy.linalg.norm(u[:, 0], ord=2))
theta[1] = numpy.arccos(u[0, 1] / numpy.linalg.norm(u[:, 1], ord=2))
axes = fig.add_subplot(1, 2, 2, aspect='equal')
axes.plot((3, 1, -3, -1, 3), (2, 2, -2, -2, 2), 'r')
for i in range(A.shape[0]):
axes.arrow(0.0, 0.0, u[0, i] - head_length * numpy.cos(theta[i]),
u[1, i] - head_length * numpy.sin(theta[i]),
head_width=head_width, color='k')
draw_unit_vectors(axes, A, head_width=0.2)
axes.set_title("Images Under A")
axes.set_xlim((-4.1, 4.1))
axes.set_ylim((-3.1, 3.1))
axes.grid(True)
plt.show()
```
#### General Matrix Norms (induced and non-induced)
In general matrix-norms have the following properties whether they are induced from a vector-norm or not:
1. $||A|| \geq 0$ and $||A|| = 0$ only if $A = 0$
1. $||A + B|| \leq ||A|| + ||B||$ (Triangle Inequality)
1. $||c A|| = |c| ||A||$
The most widely used matrix norm not induced by a vector norm is the **Frobenius norm** defined by
$$
||A||_F = \left( \sum^m_{i=1} \sum^n_{j=1} |A_{ij}|^2 \right)^{1/2}.
$$
#### Invariance under unitary multiplication
One important property of the matrix 2-norm (and Forbenius norm) is that multiplication by a unitary matrix does not change the product (kind of like multiplication by 1). In general for any $A \in \mathbb{C}^{m\times n}$ and unitary matrix $Q \in \mathbb{C}^{m \times m}$ we have
\begin{align*}
||Q A||_2 &= ||A||_2 \\ ||Q A||_F &= ||A||_F.
\end{align*}
## Singular Value Decomposition
Definition: Let $A \in \mathbb R^{m \times n}$, then $A$ can be factored as
$$
A = U\Sigma V^{T}
$$
where,
* $U \in \mathbb R^{m \times m}$ and is the orthogonal matrix whose columns are the eigenvectors of $AA^{T}$
* $V \in \mathbb R^{n \times n}$ and is the orthogonal matrix whose columns are the eigenvectors of $A^{T}A$
* $\Sigma \in \mathbb R^{m \times n}$ and is a diagonal matrix with elements $\sigma_{1}, \sigma_{2}, \sigma_{3}, ... \sigma_{r}$ where $r = rank(A)$ corresponding to the square roots of the eigenvalues of $A^{T}A$. They are called the singular values of $A$ and are non negative arranged in descending order. ($\sigma_{1} \geq \sigma_{2} \geq \sigma_{3} \geq ... \sigma_{r} \geq 0$).
The SVD has a number of applications mostly related to reducing the dimensionality of a matrix.
### Full SVD example
Consider the matrix
$$
A = \begin{bmatrix}
2 & 0 & 3 \\
5 & 7 & 1 \\
0 & 6 & 2
\end{bmatrix}.
$$
The example below demonstrates the use of the `numpy.linalg.svd` function and shows the numerical result.
```
A = numpy.array([
[2.0, 0.0, 3.0],
[5.0, 7.0, 1.0],
[0.0, 6.0, 2.0]
])
U, sigma, V_T = numpy.linalg.svd(A, full_matrices=True)
print(numpy.dot(U, numpy.dot(numpy.diag(sigma), V_T)))
```
### Eigenvalue Decomposition vs. SVD Decomposition
Let the matrix $X$ contain the eigenvectors of $A$ which are linearly independent, then we can write a decomposition of the matrix $A$ as
$$
A = X \Lambda X^{-1}.
$$
How does this differ from the SVD?
- The basis of the SVD representation differs from the eigenvalue decomposition
- The basis vectors are not in general orthogonal for the eigenvalue decomposition where it is for the SVD
- The SVD effectively contains two basis sets.
- All matrices have an SVD decomposition whereas not all have eigenvalue decompositions.
### Existence and Uniqueness
Every matrix $A \in \mathbb{C}^{m \times n}$ has a singular value decomposition. Furthermore, the singular values $\{\sigma_{j}\}$ are uniquely determined, and if $A$ is square and the $\sigma_{j}$ are distinct, the left and right singular vectors $\{u_{j}\}$ and $\{v_{j}\}$ are uniquely determined up to complex signs (i.e., complex scalar factors of absolute value 1).
### Matrix Properties via the SVD
- The $\text{rank}(A) = r$ where $r$ is the number of non-zero singular values.
- The $\text{range}(A) = [u_1, ... , u_r]$ and $\text{null}(a) = [v_{r+1}, ... , v_n]$.
- The $|| A ||_2 = \sigma_1$ and $||A||_F = \sqrt{\sigma_{1}^{2}+\sigma_{2}^{2}+...+\sigma_{r}^{2}}$.
- The nonzero singular values of A are the square roots of the nonzero eigenvalues of $A^{T}A$ or $AA^{T}$.
- If $A = A^{T}$, then the singular values of $A$ are the absolute values of the eigenvalues of $A$.
- For $A \in \mathbb{C}^{m \times n}$ then $|det(A)| = \Pi_{i=1}^{m} \sigma_{i}$
### Low-Rank Approximations
- $A$ is the sum of the $r$ rank-one matrices:
$$
A = U \Sigma V^T = \sum_{j=1}^{r} \sigma_{j}u_{j}v_{j}^{T}
$$
- For any $k$ with $0 \leq k \leq r$, define
$$
A = \sum_{j=1}^{k} \sigma_{j}u_{j}v_{j}^{T}
$$
Let $k = min(m,n)$, then
$$
||A - A_{v}||_{2} = \text{inf}_{B \in \mathbb{C}^{m \times n}} \text{rank}(B)\leq k|| A-B||_{2} = \sigma_{k+1}
$$
- For any $k$ with $0 \leq k \leq r$, the matrix $A_{k}$ also satisfies
$$
||A - A_{v}||_{F} = \text{inf}_{B \in \mathbb{C}^{m \times n}} \text{rank}(B)\leq v ||A-B||_{F} = \sqrt{\sigma_{v+1}^{2} + ... + \sigma_{r}^{2}}
$$
#### Example: Putting the above equations into code
How does this work in practice?
```
data = numpy.zeros((15,40))
#H
data[2:10,2:4] = 1
data[5:7,4:6] = 1
data[2:10,6:8] = 1
#E
data[3:11,10:12] = 1
data[3:5,12:16] = 1
data[6:8, 12:16] = 1
data[9:11, 12:16] = 1
#L
data[4:12,18:20] = 1
data[10:12,20:24] = 1
#L
data[5:13,26:28] = 1
data[11:13,28:32] = 1
#0
data[6:14,34:36] = 1
data[6:8, 36:38] = 1
data[12:14, 36:38] = 1
data[6:14,38:40] = 1
plt.imshow(data)
plt.show()
u, diag, vt = numpy.linalg.svd(data, full_matrices=True)
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 3)
fig.set_figheight(fig.get_figheight() * 4)
for i in range(1, 16):
diag_matrix = numpy.concatenate((numpy.zeros((len(diag[:i]) -1),), diag[i-1: i], numpy.zeros((40-i),)))
reconstruct = numpy.dot(numpy.dot(u, numpy.diag(diag_matrix)[:15,]), vt)
axes = fig.add_subplot(5, 3, i)
mappable = axes.imshow(reconstruct, vmin=0.0, vmax=1.0)
axes.set_title('Component = %s' % i)
plt.show()
u, diag, vt = numpy.linalg.svd(data, full_matrices=True)
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 3)
fig.set_figheight(fig.get_figheight() * 4)
for i in range(1, 16):
diag_matrix = numpy.concatenate((diag[:i], numpy.zeros((40-i),)))
reconstruct = numpy.dot(numpy.dot(u, numpy.diag(diag_matrix)[:15,]), vt)
axes = fig.add_subplot(5, 3, i)
mappable = axes.imshow(reconstruct, vmin=0.0, vmax=1.0)
axes.set_title('Component = %s' % i)
plt.show()
```
<sup>1</sup><span id="footnoteRegression"> http://www.utstat.toronto.edu/~brunner/books/LinearModelsInStatistics.pdf</span>
| true |
code
| 0.511473 | null | null | null | null |
|
# 4. Categorical Model
Author: _Carlos Sevilla Salcedo (Updated: 18/07/2019)_
This notebook presents the categorical approach of the algorithm. for our model we understand that the view we are analysing is composed of one among several categories (The data given to the model must be an integer). To do so, we have to use the graphic model shown in the next image modifying the relation between the variables $X$ and $t$.
<img src="Images/Graphic_Model_Categorical.png" style="max-width:100%; width: 70%">
where, in this case, variable $t$ is now a vector instead of a matrix.
In order to have this relationship we have stablished a multinomial probit function as the connection between them, as proposed by _Girolami (2016)_.
## Synthetic data generation
We can now generate data in a similar manner to the regression model to compare the performance of both apporaches. In this case we are going to change the regression data to a categorical approach, to work with classes.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import math
np.random.seed(0)
N = 1000 # number of samples
D0 = 55 # input features
D1 = 3 # output features
myKc = 20
K = 2 # common latent variables
K0 = 3 # first view's latent variables
K1 = 3 # second view's latent variables
Kc=K+K0+K1 # latent variables
# Generation of matrix W
A0 = np.random.normal(0.0, 1, D0 * K).reshape(D0, K)
A1 = np.random.normal(0.0, 1, D1 * K).reshape(D1, K)
B0 = np.random.normal(0.0, 1, D0 * K0).reshape(D0, K0)
B1 = np.random.normal(0.0, 1, D1 * K1).reshape(D1, K1)
W0 = np.hstack((np.hstack((A0,B0)),np.zeros((D0,K1))))
W1 = np.hstack((np.hstack((A1,np.zeros((D1,K0)))),B1))
W_tot = np.vstack((W0,W1))
# Generation of matrix Z
Z = np.random.normal(0.0, 1, Kc * N).reshape(N, Kc)
# Generation of matrix X
X0 = np.dot(Z,W0.T) + np.random.normal(0.0, 0.1, D0 * N).reshape(N, D0)
X1 = np.dot(Z,W1.T) + np.random.normal(0.0, 0.1, D1 * N).reshape(N, D1)
# Generation of matrix t
t1 = np.argmax(X1,axis=1)
```
Once the data is generated we divide it into train and test in order to be able to test the performance of the model. After that, we can normalize the data.
```
from sklearn.model_selection import train_test_split
X_tr, X_tst, Y_tr, Y_tst = train_test_split(X0, t1, test_size=0.3, random_state = 31)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_tr = scaler.fit_transform(X_tr)
X_tst = scaler.transform(X_tst)
```
## Training the model
Once the data is prepared we just have to feed it to the model. As the model has so many possibilities we have decided to pass the data to the model following a particular structure so that we can now, for each view, if the data corresponds to real, multilabel or categorical as well as knowing if we want to calculate the model with sparsity in the features.
```
import os
os.sys.path.append('lib')
import sshiba
myKc = 20 # number of latent features
max_it = int(5*1e4) # maximum number of iterations
tol = 1e-6 # tolerance of the stopping condition (abs(1 - L[-2]/L[-1]) < tol)
prune = 1 # whether to prune the irrelevant latent features
myModel = sshiba.SSHIBA(myKc, prune)
X0_tr = myModel.struct_data(X_tr, 0, 0)
X1_tr = myModel.struct_data(Y_tr, 1, 0)
X0_tst = myModel.struct_data(X_tst, 0, 0)
X1_tst = myModel.struct_data(Y_tst, 1, 0)
myModel.fit(X0_tr, X1_tr, max_iter = max_it, tol = tol, Y_tst = X1_tst, X_tst = X0_tst, AUC = 1)
print('Final AUC %.3f' %(myModel.AUC[-1]))
```
## Visualization of the results
### Lower Bound and MSE
Now the model is trained we can plot the evolution of the lower bound through out the iterations. This lower bound is calculated using the values of the variables the model is calculating and is the value we are maximizing. As we want to maximize this value it has to be always increasing with each iteration.
At the same time, we are plotting now the evolution of the Minimum Square Error (MSE) with each update of the model. As we are not minimizing this curve, this doesn't necessarily have to be always decreasing and might need more iterations to reach a minimum.
```
def plot_AUC(AUC):
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(AUC, linewidth=2, marker='s',markersize=5, label='SSHIBA', markerfacecolor='red')
ax.grid()
ax.set_xlabel('Iteration')
ax.set_ylabel('Multiclass AUC')
plt.legend()
def plot_L(L):
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(L, linewidth=2, marker='s',markersize=5, markerfacecolor='red')
ax.grid()
ax.set_xlabel('Iteration')
ax.set_ylabel('L(Q)')
plot_L(myModel.L)
plt.title('Lower Bound')
plot_AUC(myModel.AUC)
plt.title('AUC test')
plt.show()
```
## LFW Dataset
In order to improve the analysis of the results, we are showing in this section the results obtained using the _LFW_ database. This database is composed by different images of famous people and the goal is to identify what person each of them is. For the purpose of this example we have included the images of the people with more images, having that our data is now composed of 7 people or categories.
First of all, we can prepare the data we want to work with.
```
import pickle
resize = 0.4
my_dict = pickle.load( open('Databases/data_lfwa_'+str(resize)+'_7classes.pkl', "rb" ), encoding='latin1' )
X = my_dict['X'].astype(float)
Y = (my_dict['Y_cat']).astype(int)
h = my_dict['h']
w = my_dict['w']
target_names = my_dict['target']
from sklearn.model_selection import train_test_split
X_tr, X_tst, Y_tr, Y_tst = train_test_split(X, Y.astype(int), test_size=0.3, random_state = 31)
n_samples = X.shape[0]
n_features = X.shape[1]
n_classes = target_names.shape[0]
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
```
Here we can see what the images we have downloaded look like.
```
n_col, n_row = 6,3
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(X_tst[i,:].reshape((h, w)), cmap=plt.cm.gray)
plt.xticks(())
plt.yticks(())
```
At this point, the model can be trained with the train and test splits.
```
myKc = 50 # number of latent features
max_it = int(5*1e4) # maximum number of iterations
tol = 1e-7 # tolerance of the stopping condition (abs(1 - L[-2]/L[-1]) < tol)
prune = 1 # whether to prune the irrelevant latent features
myModel = sshiba.SSHIBA(myKc, prune)
X0_tr = myModel.struct_data(X_tr, 0, 0)
X1_tr = myModel.struct_data(Y_tr, 1, 0)
X0_tst = myModel.struct_data(X_tst, 0, 0)
X1_tst = myModel.struct_data(Y_tst, 1, 0)
myModel.fit(X0_tr, X1_tr, max_iter = max_it, tol = tol, Y_tst = X1_tst, X_tst = X0_tst, AUC = 1)
print('Final AUC %.3f' %(myModel.AUC[-1]))
```
Now the model is trained, we can visualize the results, seeing how the image look like as well as both the true and predicted label for each one of them.
```
def plot_gallery(images, titles, h, w, n_row=3, n_col=6):
"""Helper function to plot a gallery of portraits"""
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(titles[i], size=12)
plt.xticks(())
plt.yticks(())
# plot the result of the prediction on a portion of the test set
def title(y_pred, y_test, target_names, i):
pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
return 'predicted: %s\ntrue: %s' % (pred_name, true_name)
def plot_W(W):
plt.figure()
plt.imshow((np.abs(W)), aspect=W.shape[1]/W.shape[0])
plt.colorbar()
plt.title('W')
plt.ylabel('features')
plt.xlabel('K')
y_pred = myModel.predict([0],1,0, X0_tst)
prediction_titles = [title(y_pred, Y_tst, target_names, i)
for i in range(y_pred.shape[0])]
plot_gallery(X_tst, prediction_titles, h, w)
```
## LFW Dataset with Sparsity
Finally, we can use the sparse version of the method to make the model learn not only which latent features are relevant but also which features are the more relevant as well in order to learn the labels given.
To do so, we just need to train the model as we did before, specifying which views are to be learned with the before mentioned sparsity.
```
myKc = 50 # number of latent features
max_it = int(5*1e4) # maximum number of iterations
tol = 1e-7 # tolerance of the stopping condition (abs(1 - L[-2]/L[-1]) < tol)
prune = 1 # whether to prune the irrelevant latent features
myModel = sshiba.SSHIBA(myKc, prune)
X0_tr = myModel.struct_data(X_tr, 0, 1)
X1_tr = myModel.struct_data(Y_tr, 1, 0)
X0_tst = myModel.struct_data(X_tst, 0, 1)
X1_tst = myModel.struct_data(Y_tst, 1, 0)
myModel.fit(X0_tr, X1_tr, max_iter = max_it, tol = tol, Y_tst = X1_tst, X_tst = X0_tst, AUC = 1)
print('Final AUC %.3f' %(myModel.AUC[-1]))
import pickle
my_dict = {}
my_dict['models'] = myModel
filename = 'Models_categorical_sparse'
with open(filename+'.pkl', 'wb') as output:
pickle.dump(my_dict, output, pickle.HIGHEST_PROTOCOL)
import pickle
filename = 'Models_categorical_sparse'
my_dict = pickle.load( open( filename+'.pkl', "rb" ))
myModel = my_dict['models']
y_pred = myModel.predict([0],1,0, X0_tst)
prediction_titles = [title(y_pred, Y_tst, target_names, i)
for i in range(y_pred.shape[0])]
plot_gallery(X_tst, prediction_titles, h, w)
```
## Visualization of the results
### Vector $\gamma$
Once the model is trained, we can visualize the variable $\gamma$ to see which parts of the image are considered as relevant and which ones irrelevant.
```
q = myModel.q_dist
gamma = q.gamma_mean(0)
ax1 = plt.subplot(2, 1, 1)
plt.title('Feature selection analysis')
plt.hist(gamma,100)
ax2 = plt.subplot(2, 1, 2)
plt.plot(gamma,'.')
plt.ylabel('gamma')
plt.xlabel('feature')
plt.show()
```
### Matrix $W$
Now we can see as we did in the _sparse notebook_ how the model is learning matrix $W$ to trasnform $X$ to the latent space, $Z$.
```
pos_ord_var=np.argsort(gamma)[::-1]
plot_W(q.W[0]['mean'][pos_ord_var,:])
```
### Vector $\gamma$ mask visualization
Finally, as the data we are working with are images, we could visualize the values the variable $\gamma$ takes as an image to see the relevance each pixel has.
In our case, we can see that the method is capable of finding the most relevant features to describe the different attributes we have as labels.
```
q = myModel.q_dist
gamma = q.gamma_mean(0)
plt.figure(figsize=(3, 5))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
plt.imshow(gamma.reshape((h, w)), cmap=plt.cm.gray)
plt.xticks(())
plt.yticks(())
plt.title('Gamma mask')
plt.show()
```
### Matrix $W$ masks visualization
Conversely, we can plot the projection matrix W to see the how the latent features are learning the different parts of face learning.
```
alpha = q.alpha_mean(0)
pos_ord_var = np.argsort(alpha)
W_0 = q.W[0]['mean'][:,pos_ord_var]
Wface_titles = ["Latent feature %d" % i for i in range(W_0.shape[0])]
n_col, n_row = 6,8
plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
for i in range(n_row * n_col):
plt.subplot(n_row, n_col, i + 1)
plt.imshow(W_0[:,i].reshape((h, w)), cmap=plt.cm.gray)
plt.title(Wface_titles[i], size=12)
plt.xticks(())
plt.yticks(())
plt.show()
```
| true |
code
| 0.634543 | null | null | null | null |
|
# Single NFW profile
Here we demonstrate most of the NFW functionality using a single NFW profile.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from profiley.nfw import NFW
mass = 1e14
concentration = 4
redshift = 0.5
nfw = NFW(mass, concentration, redshift)
print(nfw)
```
Note that the profile attributes are always arrays, even if scalars are passed to it.
The first thing to look at is the 3-dimensional density profile. For all profiles we need to pass the distances at which these will be computed, as a 1d array, so let's define that first.
These distances must be in Mpc.
```
R = np.logspace(-2, 1, 100)
```
With that, getting the density profile is as simple as
```
rho = nfw.profile(R)
```
That's it!
```
plt.loglog(R, rho)
plt.xlabel('$r$ (Mpc)', fontsize=16)
plt.ylabel(r'$\rho(r)$ (M$_\odot$/Mpc$^3$)', fontsize=16);
```
Similarly, we can obtain the projected surface density or the excess surface density (the weak lensing observable):
```
sigma = nfw.surface_density(R)
esd = nfw.excess_surface_density(R)
fig, axes = plt.subplots(figsize=(14,5), ncols=2)
axes[0].plot(R, sigma)
axes[0].set_ylabel(r'$\Sigma(R)$ (M$_\odot$/Mpc$^2$)', fontsize=16)
axes[1].plot(R, esd)
axes[1].set_ylabel(r'$\Delta\Sigma(R)$ (M$_\odot$/Mpc$^2$)', fontsize=16)
for ax in axes:
ax.set_xlabel('$R$ (Mpc)', fontsize=16)
ax.set_xscale('log')
ax.set_yscale('log')
```
The ESD can also be calculated "manually":
```
barsigma = nfw.enclosed_surface_density(R)
esd_manual = barsigma - sigma
np.allclose(esd, esd_manual)
```
We can also calculate the convergence profile for a given source redshift:
```
z_source = 1.0
kappa = nfw.convergence(R, z_source)
plt.loglog(R, kappa)
plt.xlabel('$R$ (Mpc)', fontsize=16)
plt.ylabel(f'$\kappa(R)$ ($z_s={z_source}$)', fontsize=16);
```
Finally, we can also obtain offset profiles like so:
```
Roff = np.linspace(0.2, 1, 5)
sigma_off = nfw.offset_surface_density(R, Roff)
sigma_off.shape
for Ri, sigma_i in zip(Roff, sigma_off):
plt.loglog(R, sigma_i[0], label=rf'$R_\mathrm{{off}}={Ri:.1f}$ Mpc')
plt.plot(R, sigma, 'k-')
plt.legend()
plt.xlabel('$R$ (Mpc)', fontsize=16)
plt.ylabel(r'$\Sigma(R)$ (M$_\odot$/Mpc$^2$)', fontsize=16);
```
There is a similar `offset_excess_surface_density` method, as well as `offset_density` and `ofset_enclosed_density`, though these would not be used so often. The offset convergence has a different signature:
```
kappa_off = nfw.convergence(R, z_source, Roff=Roff)
for Ri, kappa_i in zip(Roff, kappa_off):
plt.loglog(R, kappa_i[0], label=rf'$R_\mathrm{{off}}={Ri:.1f}$ Mpc')
plt.plot(R, kappa, 'k-')
plt.legend()
plt.xlabel('$R$ (Mpc)', fontsize=16)
plt.ylabel(r'$\kappa(R)$', fontsize=16);
```
| true |
code
| 0.695752 | null | null | null | null |
|
# GraviPy - tutorial
## _Coordinates_ and _MetricTensor_
To start working with the gravipy package you must load the package and initialize a pretty-printing mode in Jupyter environment
```
from gravipy.tensorial import * # import GraviPy package
from sympy import init_printing
import inspect
init_printing()
```
The next step is to choose coordinates and define a metric tensor of a particular space. Let's take, for example, the Schwarzschild metric - vacuum solution to the Einstein's field equations which describes the gravitational field of a spherical mass distribution.
```
# define some symbolic variables
t, r, theta, phi, M = symbols('t, r, \\theta, \phi, M')
# create a coordinate four-vector object instantiating
# the Coordinates class
x = Coordinates('\chi', [t, r, theta, phi])
# define a matrix of a metric tensor components
Metric = diag(-(1-2*M/r), 1/(1-2*M/r), r**2, r**2*sin(theta)**2)
# create a metric tensor object instantiating the MetricTensor class
g = MetricTensor('g', x, Metric)
```
Each component of any tensor object, can be computed by calling the appropriate instance of the _GeneralTensor_ subclass with indices as arguments. The covariant indices take positive integer values (1, 2, ..., dim). The contravariant indices take negative values (-dim, ..., -2, -1).
```
x(-1)
g(1, 1)
x(1)
```
Matrix representation of a tensor can be obtained in the following way
```
x(-All)
g(All, All)
g(All, 4)
```
## Predefined _Tensor_ Classes
The GraviPy package contains a number of the _Tensor_ subclasses that can be used to calculate a tensor components. The _Tensor_ subclasses available in the current version of GraviPy package are
```
print([cls.__name__ for cls in vars()['Tensor'].__subclasses__()])
```
### The _Christoffel_ symbols
The first one is the _Christoffel_ class that represents Christoffel symbols of the first and second kind. (Note that the Christoffel symbols are not tensors) Components of the _Christoffel_ objects are computed from the below formula
$$ \Gamma_{\rho \mu \nu} = g_{\rho \sigma}\Gamma^{\sigma}_{\ \mu \nu} = \frac{1}{2}(g_{\rho \mu, \nu} + g_{\rho \nu, \mu} - g_{\mu \nu, \rho})$$
Let's create an instance of the _Christoffel_ class for the Schwarzschild metric g and compute some components of the object
```
Ga = Christoffel('Ga', g)
Ga(1, 2, 1)
```
Each component of the _Tensor_ object is computed only once due to memoization procedure implemented in the _Tensor_ class. Computed value of a tensor component is stored in _components_ dictionary (attribute of a _Tensor_ instance) and returned by the next call to the instance.
```
Ga.components
```
The above dictionary consists of two elements because the symmetry of the Christoffel symbols is implemented in the _Christoffel_ class.
If necessary, you can clear the _components_ dictionary
```
Ga.components = {}
Ga.components
```
The _Matrix_ representation of the Christoffel symbols is the following
```
Ga(All, All, All)
```
You can get help on any of classes mentioned before by running the command
```
help(Christoffel)
```
Try also "_Christoffel?_" and "_Christoffel??_"
### The _Ricci_ tensor
$$ R_{\mu \nu} = \frac{\partial \Gamma^{\sigma}_{\ \mu \nu}}{\partial x^{\sigma}} - \frac{\partial \Gamma^{\sigma}_{\ \mu \sigma}}{\partial x^{\nu}} + \Gamma^{\sigma}_{\ \mu \nu}\Gamma^{\rho}_{\ \sigma \rho} - \Gamma^{\rho}_{\ \mu \sigma}\Gamma^{\sigma}_{\ \nu \rho} $$
```
Ri = Ricci('Ri', g)
Ri(All, All)
```
Contraction of the _Ricci_ tensor $R = R_{\mu}^{\ \mu} = g^{\mu \nu}R_{\mu \nu}$
```
Ri.scalar()
```
### The _Riemann_ tensor
$$ R_{\mu \nu \rho \sigma} = \frac{\partial \Gamma_{\mu \nu \sigma}}{\partial x^{\rho}} - \frac{\partial \Gamma_{\mu \nu \rho}}{\partial x^{\sigma}} + \Gamma^{\alpha}_{\ \nu \sigma}\Gamma_{\mu \rho \alpha} - \Gamma^{\alpha}_{\ \nu \rho}\Gamma_{\mu \sigma \alpha} - \frac{\partial g_{\mu \alpha}}{\partial x^{\rho}}\Gamma^{\alpha}_{\ \nu \sigma} + \frac{\partial g_{\mu \alpha}}{\partial x^{\sigma}}\Gamma^{\alpha}_{\ \nu \rho} $$
```
Rm = Riemann('Rm', g)
```
Some nonzero components of the _Riemann_ tensor are
```
from IPython.display import display, Math
from sympy import latex
for i, j, k, l in list(variations(range(1, 5), 4, True)):
if Rm(i, j, k, l) != 0 and k<l and i<j:
display(Math('R_{'+str(i)+str(j)+str(k)+str(l)+'} = '+ latex(Rm(i, j, k, l))))
```
You can also display the matrix representation of the tensor
```
# Rm(All, All, All, All)
```
Contraction of the _Riemann_ tensor $R_{\mu \nu} = R^{\rho}_{\ \mu \rho \nu} $
```
ricci = sum([Rm(i, All, k, All)*g(-i, -k)
for i, k in list(variations(range(1, 5), 2, True))],
zeros(4))
ricci.simplify()
ricci
```
### The _Einstein_ tensor
$$ G_{\mu \nu} = R_{\mu \nu} - \frac{1}{2}g_{\mu \nu}R $$
```
G = Einstein('G', Ri)
G(All, All)
```
### _Geodesics_
$$ w_{\mu} = \frac{Du_{\mu}}{d\tau} = \frac{d^2x_{\mu}}{d\tau^2} - \frac{1}{2}g_{\rho \sigma, \mu} \frac{dx^{\rho}}{d\tau}\frac{dx^{\sigma}}{d\tau} $$
```
tau = Symbol('\\tau')
w = Geodesic('w', g, tau)
w(All).transpose()
```
Please note that instantiation of a _Geodesic_ class for the metric $g$ automatically turns on a _Parametrization_ mode for the metric $g$. Then all coordinates are functions of a world line parameter $\tau$
```
Parametrization.info()
x(-All)
g(All, All)
```
_Parametrization_ mode can be deactivated by typing
```
Parametrization.deactivate(x)
Parametrization.info()
x(-All)
g(All, All)
```
## Derivatives
### Partial derivative
All instances of a _GeneralTensor_ subclasses inherits _partialD_ method which works exactly the same way as SymPy _diff_ method.
```
T = Tensor('T', 2, g)
T(1, 2)
T.partialD(1, 2, 1, 3) # The first two indices belongs to second rank tensor T
T(1, 2).diff(x(-1), x(-3))
```
The only difference is that computed value of _partialD_ is saved in "_partial_derivative_components_" dictionary an then returned by the next call to the _partialD_ method.
```
T.partial_derivative_components
```
### Covariant derivative
Covariant derivative components of the tensor ___T___ can be computed by the covariantD method from the formula
$$ \nabla_{\sigma} T_{\mu}^{\ \nu} = T_{\mu \ ;\sigma}^{\ \nu} = \frac{\partial T_{\mu}^{\ \nu}}{\partial x^{\sigma}} - \Gamma^{\rho}_{\ \mu \sigma}T_{\rho}^{\ \nu} + \Gamma^{\nu}_{\ \rho \sigma}T_{\mu}^{\ \rho}$$
Let's compute some covariant derivatives of a scalar field C
```
C = Tensor('C', 0, g)
C()
C.covariantD(1)
C.covariantD(2, 3)
```
All _covariantD_ components of every _Tensor_ object are also memoized
```
for k in C.covariant_derivative_components:
display(Math(str(k) + ': '
+ latex(C.covariant_derivative_components[k])))
C.covariantD(1, 2, 3)
```
Proof that the covariant derivative of the metric tensor $g$ is zero
```
not any([g.covariantD(i, j, k).simplify()
for i, j, k in list(variations(range(1, 5), 3, True))])
```
Bianchi identity in the Schwarzschild spacetime
$$ R_{\mu \nu \sigma \rho ;\gamma} + R_{\mu \nu \gamma \sigma ;\rho} + R_{\mu \nu \rho \gamma ;\sigma} = 0$$
```
not any([(Rm.covariantD(i, j, k, l, m) + Rm.covariantD(i, j, m, k, l)
+ Rm.covariantD(i, j, l, m, k)).simplify()
for i, j, k, l, m in list(variations(range(1, 5), 5, True))])
```
## User-defined tensors
To define a new scalar/vector/tensor field in some space you should __extend__ the _Tensor_ class or __create an instance__ of the _Tensor_ class.
### _Tensor_ class instantiation
Let's create a third-rank tensor field living in the Schwarzshild spacetime as an instance of the _Tensor_ class
```
S = Tensor('S', 3, g)
```
Until you define (override) the _\_compute\_covariant\_component_ method of the __S__ object, all of $4^3$ components are arbitrary functions of coordinates
```
S(1, 2, 3)
inspect.getsourcelines(T._compute_covariant_component)
```
Let's assume that tensor __S__ is the commutator of the covariant derivatives of some arbitrary vector field __V__ and create a new _\_compute\_covariant\_component_ method for the object __S__
```
V = Tensor('V', 1, g)
V(All)
def S_new_method(idxs): # definition
component = (V.covariantD(idxs[0], idxs[1], idxs[2])
- V.covariantD(idxs[0], idxs[2], idxs[1])).simplify()
S.components.update({idxs: component}) # memoization
return component
S._compute_covariant_component = S_new_method
# _compute_covariant_component method was overriden
S(1, 1, 3)
```
One can check that the well known formula is correct
$$ V_{\mu ;\nu \rho} - V_{\mu ;\rho \nu} = R^{\sigma}_{\ \mu \nu \rho}V_{\sigma} $$
```
zeros = reduce(Matrix.add, [Rm(-i, All, All, All)*V(i)
for i in range(1, 5)]) - S(All, All, All)
zeros.simplify()
zeros
```
Another way of tensor creation is to make an instance of the _Tensor_ class with components option. Tensor components stored in _Matrix_ object are writen to the _components_ dictionary of the instance by this method.
```
Z = Tensor('Z', 3, g, components=zeros, components_type=(1, 1, 1))
not any(Z.components.values())
```
### _Tensor_ class extension
As an example of the _Tensor_ class extension you can get the source code of any of the predefined _Tensor_ subclasses
```
print([cls.__name__ for cls in vars()['Tensor'].__subclasses__()])
inspect.getsourcelines(Christoffel)
```
| true |
code
| 0.460107 | null | null | null | null |
|
**Connect With Me in Linkedin :-** https://www.linkedin.com/in/dheerajkumar1997/
## One Hot Encoding - variables with many categories
We observed in the previous lecture that if a categorical variable contains multiple labels, then by re-encoding them using one hot encoding we will expand the feature space dramatically.
See below:
```
import pandas as pd
import numpy as np
# let's load the mercedes benz dataset for demonstration, only the categorical variables
data = pd.read_csv('mercedesbenz.csv', usecols=['X1', 'X2', 'X3', 'X4', 'X5', 'X6'])
data.head()
# let's have a look at how many labels each variable has
for col in data.columns:
print(col, ': ', len(data[col].unique()), ' labels')
# let's examine how many columns we will obtain after one hot encoding these variables
pd.get_dummies(data, drop_first=True).shape
```
We can see that from just 6 initial categorical variables, we end up with 117 new variables.
These numbers are still not huge, and in practice we could work with them relatively easily. However, in business datasets and also other Kaggle or KDD datasets, it is not unusual to find several categorical variables with multiple labels. And if we use one hot encoding on them, we will end up with datasets with thousands of columns.
What can we do instead?
In the winning solution of the KDD 2009 cup: "Winning the KDD Cup Orange Challenge with Ensemble Selection" (http://www.mtome.com/Publications/CiML/CiML-v3-book.pdf), the authors limit one hot encoding to the 10 most frequent labels of the variable. This means that they would make one binary variable for each of the 10 most frequent labels only. This is equivalent to grouping all the other labels under a new category, that in this case will be dropped. Thus, the 10 new dummy variables indicate if one of the 10 most frequent labels is present (1) or not (0) for a particular observation.
How can we do that in python?
```
# let's find the top 10 most frequent categories for the variable X2
data.X2.value_counts().sort_values(ascending=False).head(10)
# let's make a list with the most frequent categories of the variable
top_10 = [x for x in data.X2.value_counts().sort_values(ascending=False).head(10).index]
top_10
# and now we make the 10 binary variables
for label in top_10:
data[label] = np.where(data['X2']==label, 1, 0)
data[['X2']+top_10].head(10)
# get whole set of dummy variables, for all the categorical variables
def one_hot_top_x(df, variable, top_x_labels):
# function to create the dummy variables for the most frequent labels
# we can vary the number of most frequent labels that we encode
for label in top_x_labels:
df[variable+'_'+label] = np.where(data[variable]==label, 1, 0)
# read the data again
data = pd.read_csv('mercedesbenz.csv', usecols=['X1', 'X2', 'X3', 'X4', 'X5', 'X6'])
# encode X2 into the 10 most frequent categories
one_hot_top_x(data, 'X2', top_10)
data.head()
# find the 10 most frequent categories for X1
top_10 = [x for x in data.X1.value_counts().sort_values(ascending=False).head(10).index]
# now create the 10 most frequent dummy variables for X1
one_hot_top_x(data, 'X1', top_10)
data.head()
```
### One Hot encoding of top variables
### Advantages
- Straightforward to implement
- Does not require hrs of variable exploration
- Does not expand massively the feature space (number of columns in the dataset)
### Disadvantages
- Does not add any information that may make the variable more predictive
- Does not keep the information of the ignored labels
Because it is not unusual that categorical variables have a few dominating categories and the remaining labels add mostly noise, this is a quite simple and straightforward approach that may be useful on many occasions.
It is worth noting that the top 10 variables is a totally arbitrary number. You could also choose the top 5, or top 20.
This modelling was more than enough for the team to win the KDD 2009 cup. They did do some other powerful feature engineering as we will see in following lectures, that improved the performance of the variables dramatically.
**Connect With Me in Linkedin :-** https://www.linkedin.com/in/dheerajkumar1997/
| true |
code
| 0.393764 | null | null | null | null |
|
# GSEA analysis on leukemia dataset
```
%load_ext autoreload
%autoreload 2
from gsea import *
import numpy as np
%pylab
%matplotlib inline
```
## Load data
```
genes, D, C = read_expression_file("data/leukemia.txt")
gene_sets, gene_set_names = read_genesets_file("data/pathways.txt", genes)
gene_set_hash = {}
for i in range(len(gene_sets)):
gene_set_hash[gene_set_names[i][0]] = {'indexes':gene_sets[i],'desc':gene_set_names[i][1]}
# verify that the dimensions make sense
len(genes),D.shape,len(C)
```
## Enrichment score calculations
We graphically present the calculation of ES.
```
L,r = rank_genes(D,C)
```
See if the first genes in *L* are indeed correlated with *C*
```
scatter(D[L[1],:],C)
scatter(D[L[-1],:],C)
scatter(D[L[1000],:],C)
```
## Graphical ilustration of ES calculations
```
p_exp = 1
def plot_es_calculations(name, L, r):
S = gene_set_hash[name]['indexes']
N = len(L)
S_mask = np.zeros(N)
S_mask[S] = 1
# reorder gene set mask
S_mask = S_mask[L]
N_R = sum(abs(r*S_mask)**p_exp)
P_hit = np.cumsum(abs(r*S_mask)**p_exp)/N_R if N_R!=0 else np.zeros_like(S_mask)
N_H = len(S)
P_mis = np.cumsum((1-S_mask))/(N-N_H) if N!=N_H else np.zeros_like(S_mask)
idx = np.argmax(abs(P_hit - P_mis))
print("ES =", P_hit[idx]-P_mis[idx])
f, axarr = plt.subplots(3, sharex=True)
axarr[0].plot(S_mask)
axarr[0].set_title('gene set %s' % name)
axarr[1].plot(r)
axarr[1].set_title('correlation with phenotype')
axarr[2].plot(P_hit-P_mis)
axarr[2].set_title('random walk')
L,r = rank_genes(D,C)
plot_es_calculations('CBF_LEUKEMIA_DOWNING_AML', L, r)
```
## Random phenotype labels
Now let's assign phenotype labels randomly. Is the ES much different?
```
N, k = D.shape
pi = np.array([np.random.randint(0,2) for i in range(k)])
L, r = rank_genes(D,pi)
print(pi)
plot_es_calculations('CBF_LEUKEMIA_DOWNING_AML', L, r)
```
## GSEA analysis
```
# use `n_jobs=-1` to use all cores
%time order, NES, p_values = gsea(D, C, gene_sets, n_jobs=-1)
from IPython.display import display, Markdown
s = "| geneset | NES | p-value | number of genes in geneset |\n |-------|---|---|---|\n "
for i in range(len(order)):
s = s + "| **%s** | %.3f | %.7f | %d |\n" % (gene_set_names[order[i]][0], NES[i], p_values[i], len(gene_sets[order[i]]))
display(Markdown(s))
```
## Multiple Hypotesis testing
We present two example gene sets. One with a high *NES* and low *p-value* and one with a low *NES* and a high *p-value*. We plot the histograms of null distribution for ES.
```
name = 'DNA_DAMAGE_SIGNALLING'
L,r = rank_genes(D,C)
plot_es_calculations(name, L, r)
n = 1000
S = gene_set_hash[name]['indexes']
L, r = rank_genes(D,C)
ES = enrichment_score(L,r,S)
ES_pi = np.zeros(n)
for i in range(n):
pi = np.array([np.random.randint(0,2) for i in range(k)])
L, r = rank_genes(D,pi)
ES_pi[i] = enrichment_score(L,r,S)
hist(ES_pi,bins=100)
plot([ES,ES],[0,20],'r-',label="ES(S)")
title("Histogram of ES vlues for random phenotype labels.\nRed line is ES for the selected gene set.")
name = 'tcrPathway'
L,r = rank_genes(D,C)
plot_es_calculations(name, L, r)
n = 1000
S = gene_set_hash[name]['indexes']
L, r = rank_genes(D,C)
ES = enrichment_score(L,r,S)
ES_pi = np.zeros(n)
for i in range(n):
pi = np.array([np.random.randint(0,2) for i in range(k)])
L, r = rank_genes(D,pi)
ES_pi[i] = enrichment_score(L,r,S)
hist(ES_pi,bins=100)
plot([ES,ES],[0,20],'r-',label="ES(S)")
title("Histogram of ES vlues for random phenotype labels.\nRed line is ES for the selected gene set.")
```
## Performance optimizations
```
%timeit L,R = rank_genes(D,C)
%timeit ES = enrichment_score(L,r,S)
%prun order, NES, p_values = gsea(D, C, gene_sets)
```
| true |
code
| 0.364919 | null | null | null | null |
|
# 15-minutes Realized Variance Notebook
This notebook analyzes the best subfrequency for computing the 15-minutes Realized Variance by creating a variance signature plot.
```
# Required libraries
# Required libraries
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:80% !important; }</style>"))
from pathlib import Path
import sys
import os
import pandas as pd
import numpy as np
from itertools import chain
import matplotlib.pyplot as plt
import datetime
import zipfile
from timeit import default_timer as timer
import sqlalchemy as db
import matplotlib.pylab as pylab
# Paths
sys.path.append(os.path.join(Path(os.getcwd()).parent))
data_path = os.path.join(os.path.join(Path(os.getcwd()).parent), 'data')
data_per_day_path = os.path.join(os.path.join(Path(os.getcwd()).parent), 'data','data_per_day')
results_path = os.path.join(os.path.join(Path(os.getcwd()).parent), 'results')
# create connection to sqlite database
db_path = os.path.join(data_path, 'database.db')
db_engine = db.create_engine('sqlite:///' + db_path)
params = {
'axes.labelsize': 'x-large',
'axes.titlesize':'x-large',
'xtick.labelsize':'x-large',
'ytick.labelsize':'x-large'}
pylab.rcParams.update(params)
# get the data folders file now
data_folders = [f for f in os.listdir(data_per_day_path) if not os.path.isfile(os.path.join(data_per_day_path, f))]
data_folders = [file for file in data_folders if '.' not in file]
data_folders = [os.path.join(data_per_day_path, x) for x in data_folders]
# get the csv file now
data_folder = data_folders[1]
table_name = data_folder[-3:]
csv_files = [f for f in os.listdir(data_folder) if os.path.isfile(os.path.join(data_folder, f))]
csv_files = [file for file in csv_files if '.csv' in file and '201912' in file]
csv_files = np.sort([os.path.join(data_folder, x) for x in csv_files])
def compute_second_data(csv_file):
data_df = pd.read_csv(csv_file)
data_df.DT = pd.to_datetime(data_df.DT)
data_df.sort_values(by=['DT'], inplace=True)
data_df.index = data_df.DT
data_df.drop(columns=['DT'],inplace=True)
data_df = data_df.between_time('9:30', '16:00')
data_df.reset_index(drop=False, inplace=True)
# non zero quotes
data_df = data_df.loc[(data_df.BID>0) & (data_df.BIDSIZ>0) & (data_df.ASK>0) & (data_df.ASKSIZ>0)]
# autoselect exchange
data_df['total_size'] = data_df.BIDSIZ + data_df.ASKSIZ
#data_df = data_df.loc[data_df.EX == data_df.groupby(['EX']).sum().total_size.idxmax()]
# delete negative spreads
data_df = data_df.loc[data_df.ASK > data_df.BID]
# mergeQuotesSameTimestamp
ex = data_df.EX.values[0]
sym_root = data_df.SYM_ROOT.values[0]
data_df.drop(columns=['SYM_SUFFIX', 'total_size'], inplace=True)
data_df = data_df.groupby(['DT']).median()
data_df['EX'] = ex
data_df['SYM_ROOT'] = sym_root
data_df.reset_index(drop=False, inplace=True)
# remove entries with spread > 50 * daily median spread
data_df['SPREAD'] = data_df.ASK - data_df.BID
data_df = data_df.loc[data_df['SPREAD'] < 50 * data_df['SPREAD'].median()]
# remove outliers using the centered rolling window approach
def compute_diff(x):
return x.values[window] - np.median(np.delete(x.values,window))
window = 25
data_df.sort_values(by=['DT'], inplace=True)
data_df['SPREAD_DIFF'] = data_df.SPREAD.rolling(2*window+1, min_periods=2*window+1, center=True).apply(compute_diff)
data_df = data_df.loc[(data_df['SPREAD_DIFF'] < 10 * data_df['SPREAD_DIFF'].mean()) | (data_df['SPREAD_DIFF'].isna())]
data_df = data_df.reset_index(drop=True)
# resample data to 15 seconds level
data_df.set_index(['DT'], inplace=True)
data_df["MID"] = data_df.apply(lambda x: (x.ASK * x.ASKSIZ + x.BID * x.BIDSIZ) / (x.ASKSIZ + x.BIDSIZ), axis=1)
data_df = data_df[['MID', 'SYM_ROOT']]
df_resampled = data_df.resample('1s').ffill()
df_resampled = df_resampled.append(pd.DataFrame(data_df[-1:].values,
index=[df_resampled.index[-1] + datetime.timedelta(seconds=1)],columns=data_df.columns)) # get last observation that is not added by ffill
# set new index and forward fill the price data
first_date = datetime.datetime(year=2019,month=12,day=int(csv_file[-6:-4]),hour=9,minute=45,second=0)
df_resampled = df_resampled.iloc[1:,:] # observation at 9:30 is going to be NA
new_index = pd.date_range(start=first_date, periods=22501, freq='1s') # index from 9:45 until 16:00
df_resampled = df_resampled.reindex(new_index, method='ffill')
df_resampled.reset_index(drop=False, inplace=True)
df_resampled.rename(columns={'index': 'DT'}, inplace = True)
return df_resampled
%%time
from joblib import Parallel, delayed
df_data_all_days_SPY = Parallel(n_jobs=14)(delayed(compute_second_data)(i) for i in csv_files)
%%time
from joblib import Parallel, delayed
df_data_all_days_EEM = Parallel(n_jobs=14)(delayed(compute_second_data)(i) for i in csv_files)
%%time
from joblib import Parallel, delayed
df_data_all_days_EZU = Parallel(n_jobs=14)(delayed(compute_second_data)(i) for i in csv_files)
```
# Analysis best sampling for 15min realized variance
The result indicates that 1min is more than enough
```
def compute_rv(df, sampling):
df.index = df.DT
df_resampled = df.resample(sampling).ffill()
df_resampled['RET'] = df_resampled.MID.pct_change().apply(np.vectorize(lambda x: np.log(1+x)))
df_resampled = df_resampled.iloc[1:,:] # first return is NA
df_resampled.reset_index(drop=True, inplace=True)
df_resampled['RET2'] = df_resampled['RET'].apply(lambda x: x ** 2)
df_resampled.iloc[-1,0] = df_resampled.iloc[-1,0] - datetime.timedelta(seconds=1)
df_resampled.index = df_resampled.DT
df_resampled = df_resampled.resample('15min').sum()
df_resampled.reset_index(drop=False, inplace=True)
df_resampled.DT = df_resampled.DT + datetime.timedelta(minutes=15)
return list(df_resampled['RET2'].values)
samplings = ['1s', '2s', '5s', '10s', '20s', '30s', '40s', '50s', '1min','3min', '5min']
rv_plot = []
for sampling in samplings:
rv_sample = []
for df in df_data_all_days_SPY:
rv_sample +=compute_rv(df, sampling)
rv_plot.append(np.mean(rv_sample))
fig,ax = plt.subplots(1,1,figsize=(20,15))
plt.plot(samplings, rv_plot)
plt.savefig(os.path.join(results_path, 'rv_15_signature_plot.png'), dpi=400, facecolor='aliceblue',edgecolor='k',bbox_inches='tight')
plt.show()
df_test = pd.DataFrame(columns=['varEEM', 'varSPY', 'varEZU', 'cov(EEM,SPY)', 'cov(EEM, EZU)', 'cov(SPY, EZU)'])
for day in range(len(df_data_all_days_SPY)):
df_SPY = df_data_all_days_SPY[day]
df_SPY.index = df_SPY.DT
df_SPY = df_SPY.resample('1min').ffill()
df_SPY['RET'] = df_SPY.MID.pct_change().apply(np.vectorize(lambda x: np.log(1+x)))
df_SPY = df_SPY[1:]
df_EEM = df_data_all_days_EEM[day]
df_EEM.index = df_EEM.DT
df_EEM = df_EEM.resample('1min').ffill()
df_EEM['RET'] = df_EEM.MID.pct_change().apply(np.vectorize(lambda x: np.log(1+x)))
df_EEM = df_EEM[1:]
df_EZU = df_data_all_days_EZU[day]
df_EZU.index = df_EZU.DT
df_EZU = df_EZU.resample('1min').ffill()
df_EZU['RET'] = df_EZU.MID.pct_change().apply(np.vectorize(lambda x: np.log(1+x)))
df_EZU = df_EZU[1:]
master_df = pd.DataFrame(index = df_SPY.index, columns=['varEEM', 'varSPY', 'varEZU', 'cov(EEM,SPY)', 'cov(EEM, EZU)', 'cov(SPY, EZU)'])
master_df['varEEM'] = df_EEM.RET.apply(lambda x: x**2)
master_df['varSPY'] = df_SPY.RET.apply(lambda x: x**2)
master_df['varEZU'] = df_EZU.RET.apply(lambda x: x**2)
master_df['cov(EEM,SPY)'] = np.multiply(df_EEM.RET.values, df_SPY.RET.values)
master_df['cov(EEM, EZU)'] = np.multiply(df_EEM.RET.values, df_EZU.RET.values)
master_df['cov(SPY, EZU)'] = np.multiply(df_SPY.RET.values, df_EZU.RET.values)
master_df.reset_index(drop=False, inplace=True)
master_df.iloc[-1,0] = master_df.iloc[-1,0] - datetime.timedelta(seconds=1)
master_df.index = master_df.DT
master_df = master_df.resample('15min').sum()
master_df.reset_index(drop=False, inplace=True)
master_df.DT = master_df.DT + datetime.timedelta(minutes=15)
df_test = pd.concat([df_test, master_df])
df_test.to_excel(os.path.join(data_path, 'RV15min.xlsx'))
```
| true |
code
| 0.398055 | null | null | null | null |
|
# Custom Distributions
You might want to model input uncertanty with a distribution not currenlty available in Golem. In this case you can create your own class implementing such distribution.
Here, we will reimplement a uniform distribution as a toy example.
```
from golem import *
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import matplotlib
%matplotlib inline
import seaborn as sns
sns.set(context='talk', style='ticks')
```
To create your own distribution class to be used in Golem, you need to create a class that:
(1) Inherits from the ``BaseDist`` class;
(2) Implements a ``cdf`` method that returns the cumulative density for the distribution of interest. The ``cdf`` method needs to to take in two arguments, ``x`` and ``loc``. ``loc`` is the location of the distribution, e.g. the mean for a Gaussian, and ``x`` is where the CDF needs to be evaluated at.
In addition, even though this is not required for the code to run, the ``__init__`` method should allow to define the scale of the distribution. In the example below, we allow the user to define the range of the uniform. For a Gaussian distribution this would be the standard deviation, and so on.
```
# Here is a custom, user-implemented, uniform distribution class
class MyDistribution(BaseDist):
def __init__(self, urange):
self.urange = urange
def cdf(self, x, loc):
"""Cumulative density function.
Parameters
----------
x : float
The point where to evaluate the cdf.
loc : float
The location of the Uniform distribution.
Returns
-------
cdf : float
Cumulative density evaluated at ``x``.
"""
a = loc - 0.5 * self.urange
b = loc + 0.5 * self.urange
# calc cdf
if x < a:
return 0.
elif x > b:
return 1.
else:
return (x - a) / (b - a)
```
To demonstrate how this can be used, we use a simple objective function and we will compute its robust counterpart using the ``Uniform`` class available in Golem as well as the above, user-defined equivalent ``MyDistribution``.
```
# a sample 1d objective function
def objective(x):
def sigmoid(x, l, k, x0):
return l / (1 + np.exp(-k*(x-x0)))
sigs = [sigmoid(x, 1, 100, 0.1),
sigmoid(x, -1, 100, 0.2),
sigmoid(x, 0.7, 80, 0.5),
sigmoid(x, -0.7, 80, 0.9)
]
return np.sum(sigs, axis=0)
```
First, using the ``Golem.Uniform`` class...
```
# take 1000 samples in x
x = np.linspace(0, 1, 1000)
# compute objective
y = objective(x)
# compute robust objective with Golem
golem = Golem(goal='max', random_state=42, nproc=1)
golem.fit(X=x.reshape(-1,1), y=y)
# use the Golem.Uniform class here
dists = [Uniform(0.2)]
y_robust = golem.predict(X=x.reshape(-1,1), distributions=dists)
# plot results
plt.plot(x, y, linewidth=5, label='Objective')
plt.plot(x, y_robust, linewidth=5, label='Robust Objective')
_ = plt.legend(loc='lower center', ncol=2, bbox_to_anchor=(0.5 ,1.), frameon=False)
_ = plt.xlabel('$x$')
_ = plt.ylabel('$f(x)$')
```
...then with our new custom ``MyDistribution`` class:
```
# use MyDistribution for the prediction/convolution
dists = [MyDistribution(0.2)]
y_robust = golem.predict(X=x.reshape(-1,1), distributions=dists)
# plot the results
plt.plot(x, y, linewidth=5, label='Objective')
plt.plot(x, y_robust, linewidth=5, label='Robust Objective')
_ = plt.legend(loc='lower center', ncol=2, bbox_to_anchor=(0.5 ,1.), frameon=False)
_ = plt.xlabel('$x$')
_ = plt.ylabel('$f(x)$')
```
As you can see, the result above (orange line) obtained with the user-defined uniform is the same to that obtained with ``Golem.Uniform`` as expected.
However, note that while with ``Golem.Uniform`` the 1000 samples were processed in less than 10 ms, with ``MyDistribution`` it took almost 300 ms (~30 times slower). This is because the method ``cdf`` is called many times (about 1 million times in this example) and ``Golem.Uniform`` is implemented in Cython rather than Python. Therefore, if the execution time of the ``predict`` method in Golem with your custom distribution is too slow, you shuold consider a Cython implementation.
| true |
code
| 0.77 | null | null | null | null |
|
# In this notebook a Q learner with dyna will be trained and evaluated. The Q learner recommends when to buy or sell shares of one particular stock, and in which quantity (in fact it determines the desired fraction of shares in the total portfolio value).
```
# Basic imports
import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import datetime as dt
import scipy.optimize as spo
import sys
from time import time
from sklearn.metrics import r2_score, median_absolute_error
from multiprocessing import Pool
%matplotlib inline
%pylab inline
pylab.rcParams['figure.figsize'] = (20.0, 10.0)
%load_ext autoreload
%autoreload 2
sys.path.append('../../')
import recommender.simulator as sim
from utils.analysis import value_eval
from recommender.agent import Agent
from functools import partial
NUM_THREADS = 1
LOOKBACK = 252*2 + 28
STARTING_DAYS_AHEAD = 20
POSSIBLE_FRACTIONS = [0.0, 1.0]
DYNA = 20
# Get the data
SYMBOL = 'SPY'
total_data_train_df = pd.read_pickle('../../data/data_train_val_df.pkl').stack(level='feature')
data_train_df = total_data_train_df[SYMBOL].unstack()
total_data_test_df = pd.read_pickle('../../data/data_test_df.pkl').stack(level='feature')
data_test_df = total_data_test_df[SYMBOL].unstack()
if LOOKBACK == -1:
total_data_in_df = total_data_train_df
data_in_df = data_train_df
else:
data_in_df = data_train_df.iloc[-LOOKBACK:]
total_data_in_df = total_data_train_df.loc[data_in_df.index[0]:]
# Create many agents
index = np.arange(NUM_THREADS).tolist()
env, num_states, num_actions = sim.initialize_env(total_data_in_df,
SYMBOL,
starting_days_ahead=STARTING_DAYS_AHEAD,
possible_fractions=POSSIBLE_FRACTIONS)
agents = [Agent(num_states=num_states,
num_actions=num_actions,
random_actions_rate=0.98,
random_actions_decrease=0.999,
dyna_iterations=DYNA,
name='Agent_{}'.format(i)) for i in index]
def show_results(results_list, data_in_df, graph=False):
for values in results_list:
total_value = values.sum(axis=1)
print('Sharpe ratio: {}\nCum. Ret.: {}\nAVG_DRET: {}\nSTD_DRET: {}\nFinal value: {}'.format(*value_eval(pd.DataFrame(total_value))))
print('-'*100)
initial_date = total_value.index[0]
compare_results = data_in_df.loc[initial_date:, 'Close'].copy()
compare_results.name = SYMBOL
compare_results_df = pd.DataFrame(compare_results)
compare_results_df['portfolio'] = total_value
std_comp_df = compare_results_df / compare_results_df.iloc[0]
if graph:
plt.figure()
std_comp_df.plot()
```
## Let's show the symbols data, to see how good the recommender has to be.
```
print('Sharpe ratio: {}\nCum. Ret.: {}\nAVG_DRET: {}\nSTD_DRET: {}\nFinal value: {}'.format(*value_eval(pd.DataFrame(data_in_df['Close'].iloc[STARTING_DAYS_AHEAD:]))))
# Simulate (with new envs, each time)
n_epochs = 4
for i in range(n_epochs):
tic = time()
env.reset(STARTING_DAYS_AHEAD)
results_list = sim.simulate_period(total_data_in_df,
SYMBOL,
agents[0],
starting_days_ahead=STARTING_DAYS_AHEAD,
possible_fractions=POSSIBLE_FRACTIONS,
verbose=False,
other_env=env)
toc = time()
print('Epoch: {}'.format(i))
print('Elapsed time: {} seconds.'.format((toc-tic)))
print('Random Actions Rate: {}'.format(agents[0].random_actions_rate))
show_results([results_list], data_in_df)
env.reset(STARTING_DAYS_AHEAD)
results_list = sim.simulate_period(total_data_in_df,
SYMBOL, agents[0],
learn=False,
starting_days_ahead=STARTING_DAYS_AHEAD,
possible_fractions=POSSIBLE_FRACTIONS,
other_env=env)
show_results([results_list], data_in_df, graph=True)
```
## Let's run the trained agent, with the test set
### First a non-learning test: this scenario would be worse than what is possible (in fact, the q-learner can learn from past samples in the test set without compromising the causality).
```
TEST_DAYS_AHEAD = 20
env.set_test_data(total_data_test_df, TEST_DAYS_AHEAD)
tic = time()
results_list = sim.simulate_period(total_data_test_df,
SYMBOL,
agents[0],
learn=False,
starting_days_ahead=TEST_DAYS_AHEAD,
possible_fractions=POSSIBLE_FRACTIONS,
verbose=False,
other_env=env)
toc = time()
print('Epoch: {}'.format(i))
print('Elapsed time: {} seconds.'.format((toc-tic)))
print('Random Actions Rate: {}'.format(agents[0].random_actions_rate))
show_results([results_list], data_test_df, graph=True)
```
### And now a "realistic" test, in which the learner continues to learn from past samples in the test set (it even makes some random moves, though very few).
```
env.set_test_data(total_data_test_df, TEST_DAYS_AHEAD)
tic = time()
results_list = sim.simulate_period(total_data_test_df,
SYMBOL,
agents[0],
learn=True,
starting_days_ahead=TEST_DAYS_AHEAD,
possible_fractions=POSSIBLE_FRACTIONS,
verbose=False,
other_env=env)
toc = time()
print('Epoch: {}'.format(i))
print('Elapsed time: {} seconds.'.format((toc-tic)))
print('Random Actions Rate: {}'.format(agents[0].random_actions_rate))
show_results([results_list], data_test_df, graph=True)
```
## What are the metrics for "holding the position"?
```
print('Sharpe ratio: {}\nCum. Ret.: {}\nAVG_DRET: {}\nSTD_DRET: {}\nFinal value: {}'.format(*value_eval(pd.DataFrame(data_test_df['Close'].iloc[TEST_DAYS_AHEAD:]))))
```
## Conclusion:
```
import pickle
with open('../../data/simple_q_learner_fast_learner_full_training.pkl', 'wb') as best_agent:
pickle.dump(agents[0], best_agent)
```
| true |
code
| 0.247373 | null | null | null | null |
|
*Sebastian Raschka*
last modified: 04/03/2014
<hr>
I am really looking forward to your comments and suggestions to improve and extend this tutorial! Just send me a quick note
via Twitter: [@rasbt](https://twitter.com/rasbt)
or Email: [[email protected]](mailto:[email protected])
<hr>
### Problem Category
- Statistical Pattern Recognition
- Supervised Learning
- Parametric Learning
- Bayes Decision Theory
- Multivariate data (2-dimensional)
- 2-class problem
- equal variances
- equal prior probabilities
- Gaussian model (2 parameters)
- no conditional Risk (1-0 loss functions)
<hr>
<p><a name="sections"></a>
<br></p>
# Sections
<p>• <a href="#given">Given information</a><br>
• <a href="#deriving_db">Deriving the decision boundary</a><br>
• <a href="#classify_rand">Classifying some random example data</a><br>
• <a href="#chern_err">Calculating the Chernoff theoretical bounds for P(error)</a><br>
• <a href="#emp_err">Calculating the empirical error rate</a><br>
<hr>
<p><a name="given"></a>
<br></p>
## Given information:
[<a href="#sections">back to top</a>] <br>
<br>
####model: continuous univariate normal (Gaussian) model for the class-conditional densities
$p(\vec{x} | \omega_j) \sim N(\vec{\mu}|\Sigma)$
$p(\vec{x} | \omega_j) \sim \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} \exp{ \bigg[-\frac{1}{2} (\vec{x}-\vec{\mu})^t \Sigma^{-1}(\vec{x}-\vec{\mu}) \bigg] }$
####Prior probabilities:
$P(\omega_1) = P(\omega_2) = 0.5$
The samples are of 2-dimensional feature vectors:
$\vec{x} = \bigg[
\begin{array}{c}
x_1 \\
x_2 \\
\end{array} \bigg]$
#### Means of the sample distributions for 2-dimensional features:
$\vec{\mu}_{\,1} = \bigg[
\begin{array}{c}
0 \\
0 \\
\end{array} \bigg]$,
$\; \vec{\mu}_{\,2} = \bigg[
\begin{array}{c}
1 \\
1 \\
\end{array} \bigg]$
#### Covariance matrices for the statistically independend and identically distributed ('i.i.d') features:
$\Sigma_i = \bigg[
\begin{array}{cc}
\sigma_{11}^2 & \sigma_{12}^2\\
\sigma_{21}^2 & \sigma_{22}^2 \\
\end{array} \bigg], \;
\Sigma_1 = \Sigma_2 = I = \bigg[
\begin{array}{cc}
1 & 0\\
0 & 1 \\
\end{array} \bigg], \;$
####Class conditional probabilities:
$p(\vec{x}\;|\;\omega_1) \sim N \bigg( \vec{\mu_1} = \; \bigg[
\begin{array}{c}
0 \\
0 \\
\end{array} \bigg], \Sigma = I \bigg)$
$p(\vec{x}\;|\;\omega_2) \sim N \bigg( \vec{\mu_2} = \; \bigg[
\begin{array}{c}
1 \\
1 \\
\end{array} \bigg], \Sigma = I \bigg)$
<p><a name="deriving_db"></a>
<br></p>
## Deriving the decision boundary
[<a href="#sections">back to top</a>] <br>
### Bayes' Rule:
$P(\omega_j|x) = \frac{p(x|\omega_j) * P(\omega_j)}{p(x)}$
### Discriminant Functions:
The goal is to maximize the discriminant function, which we define as the posterior probability here to perform a **minimum-error classification** (Bayes classifier).
$g_1(\vec{x}) = P(\omega_1 | \; \vec{x}), \quad g_2(\vec{x}) = P(\omega_2 | \; \vec{x})$
$\Rightarrow g_1(\vec{x}) = P(\vec{x}|\;\omega_1) \;\cdot\; P(\omega_1) \quad | \; ln \\
\quad g_2(\vec{x}) = P(\vec{x}|\;\omega_2) \;\cdot\; P(\omega_2) \quad | \; ln$
<br>
We can drop the prior probabilities (since we have equal priors in this case):
$\Rightarrow g_1(\vec{x}) = ln(P(\vec{x}|\;\omega_1))\\
\quad g_2(\vec{x}) = ln(P(\vec{x}|\;\omega_2))$
$\Rightarrow g_1(\vec{x}) = \frac{1}{2\sigma^2} \bigg[\; \vec{x}^{\,t} - 2 \vec{\mu_1}^{\,t} \vec{x} + \vec{\mu_1}^{\,t} \bigg] \mu_1 \\
= - \frac{1}{2} \bigg[ \vec{x}^{\,t} \vec{x} -2 \; [0 \;\; 0] \;\; \vec{x} + [0 \;\; 0] \;\; \bigg[
\begin{array}{c}
0 \\
0 \\
\end{array} \bigg] \bigg] \\
= -\frac{1}{2} \vec{x}^{\,t} \vec{x}$
$\Rightarrow g_2(\vec{x}) = \frac{1}{2\sigma^2} \bigg[\; \vec{x}^{\,t} - 2 \vec{\mu_2}^{\,t} \vec{x} + \vec{\mu_2}^{\,t} \bigg] \mu_2 \\
= - \frac{1}{2} \bigg[ \vec{x}^{\,t} \vec{x} -2 \; 2\; [1 \;\; 1] \;\; \vec{x} + [1 \;\; 1] \;\; \bigg[
\begin{array}{c}
1 \\
1 \\
\end{array} \bigg] \bigg] \\
= -\frac{1}{2} \; \bigg[ \; \vec{x}^{\,t} \vec{x} - 2\; [1 \;\; 1] \;\; \vec{x} + 2\; \bigg] \;$
### Decision Boundary
$g_1(\vec{x}) = g_2(\vec{x})$
$\Rightarrow -\frac{1}{2} \vec{x}^{\,t} \vec{x} = -\frac{1}{2} \; \bigg[ \; \vec{x}^{\,t} \vec{x} - 2\; [1 \;\; 1] \;\; \vec{x} + 2\; \bigg] \;$
$\Rightarrow -2[1\;\; 1] \vec{x} + 2 = 0$
$\Rightarrow [-2\;\; -2] \;\;\vec{x} + 2 = 0$
$\Rightarrow -2x_1 - 2x_2 + 2 = 0$
$\Rightarrow -x_1 - x_2 + 1 = 0$
<p><a name="classify_rand"></a>
<br></p>
## Classifying some random example data
[<a href="#sections">back to top</a>] <br>
```
%pylab inline
import numpy as np
from matplotlib import pyplot as plt
def decision_boundary(x_1):
""" Calculates the x_2 value for plotting the decision boundary."""
return -x_1 + 1
# Generate 100 random patterns for class1
mu_vec1 = np.array([0,0])
cov_mat1 = np.array([[1,0],[0,1]])
x1_samples = np.random.multivariate_normal(mu_vec1, cov_mat1, 100)
mu_vec1 = mu_vec1.reshape(1,2).T # to 1-col vector
# Generate 100 random patterns for class2
mu_vec2 = np.array([1,1])
cov_mat2 = np.array([[1,0],[0,1]])
x2_samples = np.random.multivariate_normal(mu_vec2, cov_mat2, 100)
mu_vec2 = mu_vec2.reshape(1,2).T # to 1-col vector
# Scatter plot
f, ax = plt.subplots(figsize=(7, 7))
ax.scatter(x1_samples[:,0], x1_samples[:,1], marker='o', color='green', s=40, alpha=0.5)
ax.scatter(x2_samples[:,0], x2_samples[:,1], marker='^', color='blue', s=40, alpha=0.5)
plt.legend(['Class1 (w1)', 'Class2 (w2)'], loc='upper right')
plt.title('Densities of 2 classes with 100 bivariate random patterns each')
plt.ylabel('x2')
plt.xlabel('x1')
ftext = 'p(x|w1) ~ N(mu1=(0,0)^t, cov1=I)\np(x|w2) ~ N(mu2=(1,1)^t, cov2=I)'
plt.figtext(.15,.8, ftext, fontsize=11, ha='left')
plt.ylim([-3,4])
plt.xlim([-3,4])
# Plot decision boundary
x_1 = np.arange(-5, 5, 0.1)
bound = decision_boundary(x_1)
plt.annotate('R1', xy=(-2, 2), xytext=(-2, 2), size=20)
plt.annotate('R2', xy=(2.5, 2.5), xytext=(2.5, 2.5), size=20)
plt.plot(x_1, bound, color='r', alpha=0.8, linestyle=':', linewidth=3)
x_vec = np.linspace(*ax.get_xlim())
x_1 = np.arange(0, 100, 0.05)
plt.show()
```
<p><a name="chern_err"></a>
<br></p>
## Calculating the Chernoff theoretical bounds for P(error)
[<a href="#sections">back to top</a>] <br>
$P(error) \le p^{\beta}(\omega_1) \; p^{1-\beta}(\omega_2) \; e^{-(\beta(1-\beta))}$
$\Rightarrow 0.5^\beta \cdot 0.5^{(1-\beta)} \; e^{-(\beta(1-\beta))}$
$\Rightarrow 0.5 \cdot e^{-\beta(1-\beta)}$
$min[P(\omega_1), \; P(\omega_2)] \le 0.5 \; e^{-(\beta(1-\beta))} \quad for \; P(\omega_1), \; P(\omega_2) \ge \; 0 \; and \; 0 \; \le \; \beta \; \le 1$
### Plotting the Chernoff Bound for $0 \le \beta \le 1$
```
def chernoff_bound(beta):
return 0.5 * np.exp(-beta * (1-beta))
betas = np.arange(0, 1, 0.01)
c_bound = chernoff_bound(betas)
plt.plot(betas, c_bound)
plt.title('Chernoff Bound')
plt.ylabel('P(error)')
plt.xlabel('parameter beta')
plt.show()
```
#### Finding the global minimum:
```
from scipy.optimize import minimize
x0 = [0.39] # initial guess (here: guessed based on the plot)
res = minimize(chernoff_bound, x0, method='Nelder-Mead')
print(res)
```
<p><a name="emp_err"></a>
<br></p>
## Calculating the empirical error rate
[<a href="#sections">back to top</a>] <br>
```
def decision_rule(x_vec):
""" Returns value for the decision rule of 2-d row vectors """
x_1 = x_vec[0]
x_2 = x_vec[1]
return -x_1 - x_2 + 1
w1_as_w2, w2_as_w1 = 0, 0
for x in x1_samples:
if decision_rule(x) < 0:
w1_as_w2 += 1
for x in x2_samples:
if decision_rule(x) > 0:
w2_as_w1 += 1
emp_err = (w1_as_w2 + w2_as_w1) / float(len(x1_samples) + len(x2_samples))
print('Empirical Error: {}%'.format(emp_err * 100))
test complete; Gopal
```
| true |
code
| 0.679923 | null | null | null | null |
|
# 04: Matrix - An Exercise in Parallelism
An early use for Spark has been Machine Learning. Spark's `MLlib` of algorithms contains classes for vectors and matrices, which are important for many ML algorithms. This exercise uses a simpler representation of matrices to explore another topic; explicit parallelism.
The sample data is generated internally; there is no input that is read. The output is written to the file system as before.
See the corresponding Spark job [Matrix4.scala](https://github.com/deanwampler/spark-scala-tutorial/blob/master/src/main/scala/sparktutorial/Matrix4.scala).
Let's start with a class to represent a Matrix.
```
/**
* A special-purpose matrix case class. Each cell is given the value
* i*N + j for indices (i,j), counting from 0.
* Note: Must be serializable, which is automatic for case classes.
*/
case class Matrix(m: Int, n: Int) {
assert(m > 0 && n > 0, "m and n must be > 0")
private def makeRow(start: Long): Array[Long] =
Array.iterate(start, n)(i => i+1)
private val repr: Array[Array[Long]] =
Array.iterate(makeRow(0), m)(rowi => makeRow(rowi(0) + n))
/** Return row i, <em>indexed from 0</em>. */
def apply(i: Int): Array[Long] = repr(i)
/** Return the (i,j) element, <em>indexed from 0</em>. */
def apply(i: Int, j: Int): Long = repr(i)(j)
private val cellFormat = {
val maxEntryLength = (m*n - 1).toString.length
s"%${maxEntryLength}d"
}
private def rowString(rowI: Array[Long]) =
rowI map (cell => cellFormat.format(cell)) mkString ", "
override def toString = repr map rowString mkString "\n"
}
```
Some variables:
```
val nRows = 5
val nCols = 10
val out = "output/matrix4"
```
Let's create a matrix.
```
val matrix = Matrix(nRows, nCols)
```
With a Scala data structure like this, we can use `SparkContext.parallelize` to convert it into an `RDD`. In this case, we'll actually create an `RDD` with a count of indices for the number of rows, `1 to nRows`. Then we'll map over that `RDD` and use it compute the average of each row's columns. Finally, we'll "collect" the results back to an `Array` in the driver.
```
val sums_avgs = sc.parallelize(1 to nRows).map { i =>
// Matrix indices count from 0.
val sum = matrix(i-1) reduce (_ + _) // Recall that "_ + _" is the same as "(i1, i2) => i1 + i2".
(sum, sum/nCols) // We'll return RDD[(sum, average)]
}.collect // ... then convert to an array
```
## Recap
`RDD.parallelize` is a convenient way to convert a data structure into an RDD.
## Exercises
### Exercise 1: Try different values of nRows and nCols
### Exercise 2: Try other statistics, like standard deviation
The code for the standard deviation that you would add is the following:
```scala
val row = matrix(i-1)
...
val sumsquares = row.map(x => x*x).reduce(_+_)
val stddev = math.sqrt(1.0*sumsquares) // 1.0* => so we get a Double for the sqrt!
```
Given the synthesized data in the matrix, are the average and standard deviation actually very meaningful here, if this were representative of real data?
| true |
code
| 0.687696 | null | null | null | null |
|
# Text Analysis - Dictionary of the Spanish language
- **Created by: Andrés Segura-Tinoco**
- **Created on: Aug 20, 2020**
- **Created on: Aug 02, 2021**
- **Data: Dictionary of the Spanish language**
### Text Analysis
1. Approximate number of words in the DSL
2. Number of words with acute accent in Spanish language
3. Frequency of words per size
4. Top 15 bigger words
5. Frequency of letters in DSL words
6. Vowel and consonant ratio
7. Frequency of words per letter of the alphabet
8. Most frequent n-grams
```
# Load Python libraries
import re
import codecs
import pandas as pd
from collections import Counter
# Import plot libraries
import matplotlib.pyplot as plt
```
### Util functions
```
# Util function - Read a plain text file
def read_file_lines(file_path):
lines = []
with codecs.open(file_path, encoding='utf-8') as f:
for line in f:
lines.append(line)
return lines
# Util function - Apply data quality to words
def apply_dq_word(word):
new_word = word.replace('\n', '')
# Get first token
if ',' in new_word:
new_word = new_word.split(',')[0]
# Remove extra whitespaces
new_word = new_word.strip()
# Remove digits
while re.search("\d", new_word):
new_word = new_word[0:len(new_word)-1]
return new_word
# Util function - Plot column chart
def plot_col_chart(df, figsize, x_var, y_var, title, color='#1f77b4', legend=None, x_label=None):
fig, ax = plt.subplots()
df.plot.bar(ax=ax, x=x_var, y=y_var, color=color, figsize=figsize)
if legend:
ax.legend(legend)
else:
ax.get_legend().remove()
if x_label:
x = np.arange(len(x_label))
plt.xticks(x, x_label, rotation=0)
else:
plt.xticks(rotation=0)
plt.title(title, fontsize=16)
plt.xlabel(x_var.capitalize())
plt.ylabel(y_var.capitalize())
plt.show()
# Util function - Plot bar chart
def plot_bar_chart(df, figsize, x_var, y_var, title, color='#1f77b4', legend=None):
fig, ax = plt.subplots()
df.plot.barh(ax=ax, x=x_var, y=y_var, figsize=figsize)
if legend:
ax.legend(legend)
else:
ax.get_legend().remove()
plt.title(title, fontsize=16)
plt.xlabel(y_var.capitalize())
plt.ylabel(x_var.capitalize())
plt.show()
```
## 1. Approximate number of words in the DSL
```
# Range of files by first letter of word
letter_list = list(map(chr, range(97, 123)))
letter_list.append('ñ')
len(letter_list)
# Read words by letter [a-z]
word_dict = Counter()
file_path = '../data/dics/'
# Read data only first time
for letter in letter_list:
filename = file_path + letter + '.txt'
word_list = read_file_lines(filename)
for word in word_list:
word = apply_dq_word(word)
word_dict[word] += 1
# Show results
n_words = len(word_dict)
print('Total of different words: %d' % n_words)
```
## 2. Number of words with acute accent in Spanish language
```
# Counting words with acute accent
aa_freq = Counter()
regexp = re.compile('[áéíóúÁÉÍÓÚ]')
for word in word_dict.keys():
match = regexp.search(word.lower())
if match:
l = match.group(0)
aa_freq[l] += 1
# Show results
count = sum(aa_freq.values())
perc_words = 100.0 * count / n_words
print('Total words with acute accent: %d (%0.2f %s)' % (count, perc_words, '%'))
# Cooking dataframe
df = pd.DataFrame.from_records(aa_freq.most_common(), columns = ['vowel', 'frequency']).sort_values(by=['vowel'])
df['perc'] = round(100.0 * df['frequency'] / count, 2)
df
# Plotting data
figsize = (12, 6)
x_var = 'vowel'
y_var = 'perc'
title = 'Frequency of accented vowels'
plot_col_chart(df, figsize, x_var, y_var, title)
```
## 3. Frequency of words per size
```
# Processing
word_size = Counter()
for word in word_dict.keys():
size = len(word)
word_size[size] += 1
# Cooking dataframe
df = pd.DataFrame.from_records(word_size.most_common(), columns = ['size', 'frequency']).sort_values(by=['size'])
df['perc'] = 100.0 * df['frequency'] / n_words
df
# Plotting data
figsize = (12, 6)
x_var = 'size'
y_var = 'frequency'
title = 'Frequency of words per size'
plot_col_chart(df, figsize, x_var, y_var, title)
```
## 4. Top 15 bigger words
```
# Processing
top_size = Counter()
threshold = 21
for word in word_dict.keys():
size = len(word)
if size >= threshold:
top_size[word] = size
# Top 15 bigger words
top_size.most_common()
```
## 5. Frequency of letters in DSL words
```
# Processing
letter_freq = Counter()
for word in word_dict.keys():
word = word.lower()
for l in word:
letter_freq[l] += 1
n_total = sum(letter_freq.values())
n_total
# Cooking dataframe
df = pd.DataFrame.from_records(letter_freq.most_common(), columns = ['letter', 'frequency']).sort_values(by=['letter'])
df['perc'] = 100.0 * df['frequency'] / n_total
df
# Plotting data
figsize = (12, 6)
x_var = 'letter'
y_var = 'frequency'
title = 'Letter frequency in DSL words'
plot_col_chart(df, figsize, x_var, y_var, title)
# Plotting sorted data
figsize = (12, 6)
x_var = 'letter'
y_var = 'perc'
title = 'Letter frequency in DSL words (Sorted)'
color = '#2ca02c'
plot_col_chart(df.sort_values(by='perc', ascending=False), figsize, x_var, y_var, title, color)
```
## 6. Vowel and consonant ratio
```
vowel_list = 'aeiouáéíóúèîü'
vowel_total = 0
consonant_total = 0
for ix, row in df.iterrows():
letter = str(row['letter'])
freq = int(row['frequency'])
if letter in vowel_list:
vowel_total += freq
elif letter.isalpha():
consonant_total += freq
letter_total = vowel_total + consonant_total
# Initialize list of lists
data = [['vowels', vowel_total, (100.0 * vowel_total / letter_total)],
['consonant', consonant_total, (100.0 * consonant_total / letter_total)]]
# Create the pandas DataFrame
df = pd.DataFrame(data, columns = ['type', 'frequency', 'perc'])
df
# Plotting data
figsize = (6, 6)
x_var = 'type'
y_var = 'perc'
title = 'Vowel and consonant ratio'
plot_col_chart(df, figsize, x_var, y_var, title)
```
## 7. Frequency of words per letter of the alphabet
```
norm_dict = {'á':'a', 'é':'e', 'í':'i', 'ó':'o', 'ú':'u'}
# Processing
first_letter_freq = Counter()
for word in word_dict.keys():
first_letter = word[0].lower()
if first_letter.isalpha():
if first_letter in norm_dict.keys():
first_letter = norm_dict[first_letter]
first_letter_freq[first_letter] += 1
# Cooking dataframe
df = pd.DataFrame.from_records(first_letter_freq.most_common(), columns = ['letter', 'frequency']).sort_values(by=['letter'])
df['perc'] = 100.0 * df['frequency'] / n_words
df
# Plotting data
figsize = (12, 6)
x_var = 'letter'
y_var = 'frequency'
title = 'Frequency of words per letter of the alphabet'
plot_col_chart(df, figsize, x_var, y_var, title)
# Plotting sorted data
figsize = (12, 6)
x_var = 'letter'
y_var = 'perc'
title = 'Frequency of words per letter of the alphabet (Sorted)'
color = '#2ca02c'
plot_col_chart(df.sort_values(by='perc', ascending=False), figsize, x_var, y_var, title, color)
```
## 8. Most frequent n-grams
```
# Processing
top_ngrams = 25
bi_grams = Counter()
tri_grams = Counter()
for word in word_dict.keys():
word = word.lower()
n = len(word)
size = 2
for i in range(size, n+1):
n_grams = word[i-size:i]
bi_grams[n_grams] += 1
size = 3
for i in range(size, n+1):
n_grams = word[i-size:i]
tri_grams[n_grams] += 1
# Cooking dataframe
df_bi = pd.DataFrame.from_records(bi_grams.most_common(top_ngrams), columns=['bi-grams', 'frequency'])
df_tri = pd.DataFrame.from_records(tri_grams.most_common(top_ngrams), columns=['tri-grams', 'frequency'])
# Plotting sorted data
figsize = (8, 10)
x_var = 'bi-grams'
y_var = 'frequency'
title = str(top_ngrams) + ' bi-grams most frequent in Spanish'
plot_bar_chart(df_bi.sort_values(by=['frequency']), figsize, x_var, y_var, title)
# Plotting sorted data
figsize = (8, 10)
x_var = 'tri-grams'
y_var = 'frequency'
title = str(top_ngrams) + ' tri-grams most frequent in Spanish'
plot_bar_chart(df_tri.sort_values(by=['frequency']), figsize, x_var, y_var, title)
```
---
<a href="https://ansegura7.github.io/DSL_Analysis/">« Home</a>
| true |
code
| 0.464051 | null | null | null | null |
|
```
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '1'
import pickle
import numpy as np
import pandas as pd
import skimage.io as io
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
from keras.applications.resnet50 import preprocess_input
from keras.models import Model
```
### In this part, we conduct the following procedure to make our data be analytic-ready.
**Step 1.** For every species, we select out the **representative images**.
**Step 2.** For every species representative image, we calculate its **HSV values with regard of different parts** (body, forewing, hindwing, whole)
**Step 3.** For every species representative image, we extract its **2048-dimensional features** from the well-trained neural network model
**Step 4.** We cluster species based on either the 2-dimensional t-SNE map or 2048D features into **k assemblages through k-Means Clustering**
**Step 5.** We use **t-SNE to compress its 2048-dimensional features** into one dimension as the trait value
**Step 6.** We quantify the **assemblage-level color diversity** by calculating the average cosine distance among every pair of species in the same assemblage
### output files:
1. **all_complete_table.csv**: main result for further analysis where a row implies a **species**
2. **trait_analysis.csv**: trait value for T-statistics analysis (T stands for trait), where a row implies an **image**
3. **cluster_center.csv**: information about assemblage centers where a row implies an assemblage center
4. **in-cluser_pairwise_diversity.csv**: result of pair-wise color distance where a row implies a pair of species
```
model_dirname = '/home/put_data/moth/code/cmchang/regression/fullcrop_dp0_newaug-rmhue+old_species_keras_resnet_fold_20181121_4'
# read testing dataset and set the path to obtain every part's mask
Xtest = pd.read_csv(os.path.join(model_dirname, 'test.csv'))
Xtest['img_rmbg_path'] = Xtest.Number.apply(lambda x: '/home/put_data/moth/data/whole_crop/'+str(x)+'.png')
Xtest['img_keep_body_path'] = Xtest.img_rmbg_path.apply(lambda x: x.replace('whole_crop','KEEP_BODY'))
Xtest['img_keep_down_path'] = Xtest.img_rmbg_path.apply(lambda x: x.replace('whole_crop','KEEP_DOWN'))
Xtest['img_keep_up_path'] = Xtest.img_rmbg_path.apply(lambda x: x.replace('whole_crop','KEEP_UP'))
Xtest = Xtest.reset_index()
Xtest.drop(columns='index', inplace=True)
# get the dictionary to look up the average elevation of a species
with open(os.path.join('/home/put_data/moth/metadata/1121_Y_mean_dict.pickle'), 'rb') as handle:
Y_dict = pickle.load(handle)
Ytest = np.vstack(Xtest['Species'].apply(lambda x: Y_dict[x]))
# aggregate the testing data by Species
df_species_group = Xtest.groupby('Species').apply(
lambda g: pd.Series({
'indices': g.index.tolist(),
}))
df_species_group = df_species_group.sample(frac=1).reset_index()
display(df_species_group.head())
```
### Step 1.
```
# select out the representative image which is the closest to its average elevation
sel = list()
for k in range(df_species_group.shape[0]):
row = df_species_group.iloc[k]
i = np.argmin(np.abs(np.array(Xtest.Alt[row['indices']]) - Y_dict[row['Species']]))
sel.append(row['indices'][i])
# Xout: DataFrame only contains representative images
Xout = Xtest.iloc[sel]
Yout = Ytest[sel]
Xout = Xout.reset_index()
Xout.drop(columns='index', inplace=True)
Xout.head()
```
### Step 2.
```
# extract the HSV features for species representatives
import skimage.color as color
def img_metrics(img):
hsv = color.rgb2hsv(img)
mask = 1.0 - (np.mean(img, axis=2)==255.0) + 0.0
x,y = np.where(mask)
mean_hsv = np.mean(hsv[x,y], axis=0)
std_hsv = np.std(hsv[x,y], axis=0)
return mean_hsv, std_hsv
df_reg_list = list()
species_list = list()
filename_list = list()
for k in range(Xout.shape[0]):
print(k, end='\r')
species = Xout.iloc[k]['Species']
species_list.append(species)
body_img = io.imread(Xout.iloc[k]['img_keep_body_path'])
mask = 1.0 - (np.mean(body_img, axis=2)==255.0) + 0.0
body_img[:,:,0] = body_img[:,:,0]*mask
body_img[:,:,1] = body_img[:,:,1]*mask
body_img[:,:,2] = body_img[:,:,2]*mask
img = io.imread(Xout.iloc[k]['img_keep_up_path'])
img += body_img
alt = Y_dict[Xout.iloc[k]['Species']]
mean_hsv, std_hsv = img_metrics(img)
whole_img = io.imread(Xout.iloc[k]['img_rmbg_path'])
whole_mean_hsv, whole_std_hsv = img_metrics(whole_img)
res = np.append(whole_mean_hsv[:3], mean_hsv[:3])
res = np.append(res, [alt])
df_reg_list.append(res)
df_reg_output = pd.DataFrame(data=df_reg_list,
columns=['h.whole', 's.whole', 'v.whole',
'h.body_fore','s.body_fore', 'v.body_fore','alt'])
```
### Step 3.
```
# extract 2048-dimensional features
from keras.models import load_model
model = load_model(os.path.join(model_dirname,'model.h5'))
features = model.get_layer('global_average_pooling2d_1')
extractor = Model(inputs=model.input, outputs=features.output)
TestImg = list()
for i in range(Xout.shape[0]):
img = io.imread(list(Xout['img_rmbg_path'])[i])
TestImg.append(img)
TestImg = np.stack(TestImg)
TestInput = preprocess_input(TestImg.astype(float))
Fout = extractor.predict(x=TestInput)
Yout = np.array([Y_dict[sp] for sp in Xout.Species])
np.save(file='Species_Representative_1047x2048.npy', arr=Fout)
Fout.shape
```
### Step 4.
```
# compress 2048-D features to 2-D map for visualization and clustering
from sklearn.manifold import TSNE
F_embedded = TSNE(n_components=2, perplexity=120).fit_transform(Fout)
from sklearn.cluster import KMeans
from sklearn import metrics
from time import time
def bench_k_means(estimator, name, data):
t0 = time()
estimator.fit(data)
print('%-9s\t%.2fs\t%.3f\t%.3f'
% (name, (time() - t0), estimator.inertia_,
metrics.silhouette_score(data, estimator.labels_,
metric='cosine',
sample_size=500)))
return estimator
for k in [30]:
km = KMeans(init='k-means++', n_clusters=k, n_init=20)
km = bench_k_means(km, name="k-means++", data=Fout)
from collections import Counter
Counter(km.labels_)
Xout['tsne.0'] = F_embedded[:,0]
Xout['tsne.1'] = F_embedded[:,1]
Xout['km_label'] = km.labels_
# representative image information
resout = pd.concat([Xout, df_reg_output], axis=1)
resout.to_csv(os.path.join(model_dirname, 'all_complete_table.csv'), index=False)
```
#### - If clustering based on t-SNE maps
```
# # cluster information
# stat = Xout[['km_label','Alt']].groupby('km_label').apply(np.mean)
# stat = stat.sort_values('Alt')
# stat.columns = ['km_label', 'class_alt']
# # center information
# centers = km.cluster_centers_
# myk = km.cluster_centers_.shape[0]
# centx, centy = list(), list()
# for i in range(stat.shape[0]):
# centx.append(centers[int(stat.iloc[i]['km_label']),0])
# centy.append(centers[int(stat.iloc[i]['km_label']),1])
# # add center information into clustere information
# stat['center_x'] = centx
# stat['center_y'] = centy
# stat['order'] = np.arange(myk)
# # output cluster information
# stat.to_csv(os.path.join(model_dirname,'cluster_center.csv'), index=False)
```
#### - If clustering based on 2048D features
```
from sklearn.metrics.pairwise import pairwise_distances
# cluster information
stat = Xout[['km_label','Alt']].groupby('km_label').apply(np.mean)
stat = stat.sort_values('km_label')
stat.columns = ['km_label', 'class_alt']
# center information
centers = km.cluster_centers_
myk = km.cluster_centers_.shape[0]
centx, centy = list(), list()
for i in range(myk):
center = centers[i:(i+1),:]
sel = np.where(km.labels_==i)[0]
nearest_species = np.argmin(pairwise_distances(X=center, Y=Fout2[sel], metric='cosine'))
i_nearest_species = sel[nearest_species]
centx.append(F_embedded[i_nearest_species, 0])
centy.append(F_embedded[i_nearest_species, 1])
# add center information into clustere information
stat['center_x'] = centx
stat['center_y'] = centy
stat = stat.sort_values('class_alt')
# stat.columns = ['km_label', 'class_alt']
stat['order'] = np.arange(myk)
# output cluster information
stat.to_csv(os.path.join(model_dirname,'cluster_center.csv'), index=False)
```
### Step 5.
```
# compress 2048-D features to 1-D trait for functional trait analysis
TestImg = list()
for i in range(Xtest.shape[0]):
img = io.imread(list(Xtest['img_rmbg_path'])[i])
TestImg.append(img)
TestImg = np.stack(TestImg)
TestInput = preprocess_input(TestImg.astype(float))
Ftest = extractor.predict(x=TestInput)
from sklearn.manifold import TSNE
F_trait = TSNE(n_components=1, perplexity=100).fit_transform(Ftest)
F_trait = F_trait - np.min(F_trait)
Xtest['trait'] = F_trait[:,0]
np.save(file='Species_TestingInstance_4249x2048.npy', arr=Ftest)
# image trait information table
dtrait = pd.merge(Xtest[['Species', 'trait']], resout[['Species','km_label','alt']], how='left', on='Species')
dtrait.to_csv(os.path.join(model_dirname, 'trait_analysis.csv'), index=False)
```
### Step 6.
```
# calculate in-cluster pairwise distance
from sklearn.metrics.pairwise import pairwise_distances
# just convert the cluster labels to be ordered for better visualization in the next analysis
km_label_to_order = dict()
order_to_km_label = dict()
for i in range(myk):
km_label_to_order[int(stat.iloc[i]['km_label'])] = i
order_to_km_label[i] = int(stat.iloc[i]['km_label'])
pair_diversity = np.array([])
order = np.array([])
for k in range(myk):
this_km_label = order_to_km_label[k]
sel = np.where(resout.km_label == this_km_label)[0]
if len(sel) == 1:
t = np.array([[0]])
dist_list = np.array([0])
else:
t = pairwise_distances(Fout[sel, :], metric='cosine')
dist_list = np.array([])
for i in range(t.shape[0]):
dist_list = np.append(dist_list,t[i,(i+1):])
pair_diversity = np.append(pair_diversity, dist_list)
order = np.append(order, np.repeat(k, len(dist_list)))
di = pd.DataFrame({'diversity': pair_diversity,
'order': order})
di.to_csv(os.path.join(model_dirname, 'in-cluser_pairwise_diversity.csv'), index=False)
```
| true |
code
| 0.376537 | null | null | null | null |
|
# Benchmark ML Computation Speed
In this notebook, we test the computational performance of [digifellow](https://digifellow.swfcloud.de/hub/spawn) jupyterhub performance against free access like *Colab* and *Kaggle*. The baseline of this comparison is an average PC *(Core i5 2.5GHz - 8GB RAM - No GPU)*
The task of this test is classifying the MNIST dataset with different algorithms *(LR, ANN, CNN)* involving different libraries *(SKLearn, Tensorflow)* and comparing the performance with and without GPU acceleration.
## Dependencies
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.datasets import mnist
from tensorflow.keras import layers
from sklearn.linear_model import LogisticRegression
readings = []
```
## Preprocessing
```
(train_images, train_labels), (_i, _l) = mnist.load_data()
train_images = train_images.reshape(-1,28*28)
train_images = train_images / 255.0
```
## SieKitLearn - Logistic Regression
```
LG = LogisticRegression(penalty='l1', solver='saga', tol=0.1)
```
### sklearn timer
```
%%timeit -n 1 -r 10 -o
LG.fit(train_images, train_labels)
readings.append(_.all_runs)
```
## Tensorflow - ANN
```
annModel = keras.Sequential()
annModel.add(tf.keras.Input(shape=(28*28,)))
annModel.add(layers.Dense(128, activation='relu'))
annModel.add(layers.Dense(10, activation='softmax'))
annModel.compile('sgd','sparse_categorical_crossentropy',['accuracy'])
```
### ANN timer (CPU)
```
%%timeit -n 1 -r 10 -o
with tf.device('/CPU:0'):
annModel.fit(train_images, train_labels, epochs=5, verbose=0)
readings.append(_.all_runs)
```
### ANN timer (GPU)
```
%%timeit -n 1 -r 10 -o
with tf.device('/GPU:0'):
annModel.fit(train_images, train_labels, epochs=5, verbose=0)
readings.append(_.all_runs)
```
## Tensorflow - CNN
```
cnnModel = keras.Sequential()
cnnModel.add(tf.keras.Input(shape=(28, 28, 1)))
cnnModel.add(layers.Conv2D(filters=16,kernel_size=(3, 3),activation='relu'))
cnnModel.add(layers.BatchNormalization())
cnnModel.add(layers.MaxPooling2D())
cnnModel.add(layers.Flatten())
cnnModel.add(layers.Dense(128, activation='relu'))
cnnModel.add(layers.Dropout(0.2))
cnnModel.add(layers.Dense(10, activation='softmax'))
cnnModel.compile('sgd','sparse_categorical_crossentropy',['accuracy'])
```
### CNN timer (CPU)
```
%%timeit -n 1 -r 10 -o
with tf.device('/CPU:0'):
cnnModel.fit(train_images.reshape(-1, 28, 28, 1), train_labels, epochs=5, verbose=0)
readings.append(_.all_runs)
```
### CNN timer (GPU)
```
%%timeit -n 1 -r 10 -o_.all_runs
with tf.device('/GPU:0'):
cnnModel.fit(train_images.reshape(-1, 28, 28, 1), train_labels, epochs=5, verbose=0)
readings.append(_.all_runs)
```
## Storing readings
```
import csv
with open('readings', 'w') as f:
wr = csv.writer(f)
wr.writerow(readings)
```
Done :)
| true |
code
| 0.68541 | null | null | null | null |
|
# Motivación: Redes Neuronales Convolucionales
La información que extraemos de las entradas sensoriales a menudo está determinada por su contexto. Con las imágenes, podemos suponer que los píxeles cercanos están estrechamente relacionados y su información colectiva es más relevante cuando se toma como una unidad. Por el contrario, podemos suponer que los píxeles individuales no transmiten información relacionada entre sí. Por ejemplo, para reconocer letras o dígitos, necesitamos analizar la dependencia de píxeles cercanos, porque determinan la forma del elemento. De esta manera, podríamos calcular la diferencia entre, por ejemplo, un 0 o un 1. Los píxeles de una imagen están organizados en una cuadrícula bidimensional, y si la imagen no es en escala de grises, tendremos una tercera dimensión para Los mapas de colores. Alternativamente, una imagen de resonancia magnética (MRI) también usa espacio tridimensional. Puede recordar que, hasta ahora, si queríamos alimentar una imagen a una red neuronal, teníamos que cambiarla de una matriz bidimensional a una matriz unidimensional. Las CNN están diseñadas para abordar este problema: cómo hacer que la información perteneciente a las neuronas que están más cerca sea más relevante que la información proveniente de las neuronas que están más separadas. En problemas visuales, esto se traduce en hacer que las neuronas procesen información proveniente de píxeles que están cerca uno del otro. Con CNNs, podremos alimentar entradas de una, dos o tres dimensiones y la red producirá una salida de la misma dimensionalidad. Como veremos más adelante, esto nos dará varias ventajas
Cuando tratamos de clasificar las imágenes CIFAR-10 usando una red de capas completamente conectadas con poco éxito. Una de las razones es que se sobreajustan. Si miramos la primera capa oculta de esa red, que tiene 1.024 neuronas. El tamaño de entrada de la imagen es 32x32x3 = 3,072. Por lo tanto, la primera capa oculta tenía un total de 2072 * 1024 = 314, 5728 pesos. ¡Ese no es un número pequeño! No solo es fácil sobreajustar una red tan grande, sino que también es ineficiente en la memoria. Además, cada neurona de entrada (o píxel) está conectada a cada neurona en la capa oculta. Debido a esto, la red no puede aprovechar la proximidad espacial de los píxeles, ya que no tiene una manera de saber qué píxeles están cerca uno del otro. Por el contrario, las CNN tienen propiedades que proporcionan una solución efectiva a estos problemas:
- Conectan neuronas, que solo corresponden a píxeles vecinos de la imagen. De esta manera, las neuronas están "forzadas" a recibir información de otras neuronas que están espacialmente cercanas. Esto también reduce el número de pesos, ya que no todas las neuronas están interconectadas.
- Una CNN utiliza el uso compartido de parámetros. En otras palabras, se comparte un número limitado de pesos entre todas las neuronas de una capa. Esto reduce aún más la cantidad de pesas y ayuda a combatir el sobreajuste. Puede sonar confuso, pero quedará claro en la siguiente sección.
La capa convolucional es el bloque de construcción más importante de una CNN. Consiste en un conjunto de filtros (también conocidos como núcleos o detectores de características), donde cada filtro se aplica en todas las áreas de los datos de entrada. Un filtro se define por un conjunto de pesos aprendibles. Como un guiño al tema en cuestión, la siguiente imagen ilustra esto muy bien:

Se muestra una capa de entrada bidimensional de una red neuronal. Por el bien de la simplicidad, asumiremos que esta es la capa de entrada, pero puede ser cualquier capa de la red. Como hemos visto en los capítulos anteriores, cada neurona de entrada representa la intensidad de color de un píxel (asumiremos que es una imagen en escala de grises por simplicidad). Primero, aplicaremos un filtro 3x3 en la parte superior derecha esquina de la imagen. Cada neurona de entrada está asociada con un solo peso del filtro. Tiene nueve pesos, debido a las nueve neuronas de entrada, pero, en general, el tamaño es arbitrario (2x2, 4x4, 5x5, etc.). La salida del filtro es una suma ponderada de sus entradas (el activaciones de las neuronas de entrada). Su propósito es resaltar una característica específica en la entrada, por ejemplo, una arista o una línea. El grupo de neuronas cercanas, que participan en la entrada. se llaman el campo receptivo. En el contexto de la red, la salida del filtro representa el valor de activación de una neurona en la siguiente capa. La neurona estará activa, si la función es presente en esta ubicación espacial.
Para cada nueva neurona, deslizaremos el filtro por la imagen de entrada y calcularemos su salida (la suma ponderada) con cada nuevo conjunto de neuronas de entrada. En el siguiente diagrama, puede ver cómo calcular las activaciones de las siguientes dos posiciones (un píxel para derecho):

- Al decir "arrastrar", queremos decir que los pesos del filtro no cambian en la imagen. En efecto, utilizaremos los mismos nueve pesos de filtro para calcular las activaciones de todas las neuronas de salida, cada vez con un conjunto diferente de neuronas de entrada. Llamamos a este parámetro compartir, y lo hacemos por dos razones:
- Al reducir el número de pesos, reducimos la huella de la memoria y evitamos el sobreajuste. El filtro resalta características específicas. Podemos suponer que esta característica es útil, independientemente de su posición en la imagen. Al compartir pesos, garantizamos que el filtro podrá ubicar la función en toda la imagen.
Hasta ahora, hemos descrito la relación de corte uno a uno, donde la salida es un solo corte, que toma la entrada de otro segmento (o una imagen). Esto funciona bien en escala de grises, pero cómo ¿Lo adaptamos para imágenes en color (relación n a 1)? ¡Una vez más, es simple! Primero, dividiremos el imagen en canales de color. En el caso de RGB, serían tres. Podemos pensar en cada color canal como un segmento de profundidad, donde los valores son las intensidades de píxeles para el color dado (R, G, o B), como se muestra en el siguiente ejemplo:
La combinación de sectores se denomina volumen de entrada con una profundidad de 3. Un filtro único de 3x3 es
aplicado a cada rebanada. La activación de una neurona de salida es solo la suma ponderada de filtros aplicados en todos los sectores. En otras palabras, combinaremos los tres filtros en un gran 3 x 3 x 3 + 1 filtro con 28 pesos (agregamos profundidad y un solo sesgo). Entonces, calcularemos el suma ponderada aplicando los pesos relevantes a cada segmento.
- Los mapas de características de entrada y salida tienen diferentes dimensiones. Digamos que tenemos una capa de entrada con tamaño (ancho, alto) y un filtro con dimensiones (filter_w, filter_h). Después de aplicar la convolución, las dimensiones de la capa de salida son (ancho - filtro_w + 1, altura - filtro_h + 1).
Como mencionamos, un filtro resalta una característica específica, como bordes o líneas. Pero, en general, muchas características son importantes y nos interesarán todas. ¿Cómo los destacamos a todos? Como de costumbre, es simple. Aplicaremos varios filtros en el conjunto de sectores de entrada. Cada filtro generará un segmento de salida único, que resalta la característica, detectada por el filtro (relación de n a m). Un sector de salida puede recibir información de:
- Todos los sectores de entrada, que es el estándar para capas convolucionales. En este escenario, un segmento de salida único es un caso de la relación n-a-1, que describimos anteriormente. Con múltiples segmentos de salida, la relación se convierte en n-m. En otras palabras, cada segmento de entrada contribuye a la salida de cada segmento de salida.
- Una sola porción de entrada. Esta operación se conoce como convolución profunda. Es un
tipo de reversión del caso anterior. En su forma más simple, aplicamos un filtro sobre un único segmento de entrada para producir un único segmento de salida. Este es un caso de la relación uno a uno, que describimos en la sección anterior. Pero también podemos especificar un multiplicador de canal (un entero m), donde aplicamos filtros m sobre un solo sector de salida para producir m sectores de salida. Este es un caso de relación de 1 a m. El número total de segmentos de salida es n * m.
Denotemos el ancho y la altura del filtro con Fw y Fh, la profundidad del volumen de entrada con D y la profundidad del volumen de salida con M. Luego, podemos calcular el número total de pesos W en una capa convolucional con el siguiente ecuación:
\begin{equation}
W=(D*F_w *F_h+1)*M
\end{equation}
Digamos que tenemos tres sectores y queremos aplicarles cuatro filtros de 5x5. Entonces la la capa convolucional tendrá un total de (3x5x5 + 1) * 4 = 304 pesos, y cuatro cortes de salida (volumen de salida con una profundidad de 4), un sesgo por corte. El filtro para cada segmento de salida tendrá tres parches de filtro de 5x5 para cada uno de los tres segmentos de entrada y un sesgo para un total de 3x5x5 + 1 = 76 pesos. La combinación de los mapas de salida se denomina volumen de salida con una profundidad de cuatro.
```
import numpy as np
def conv(image, im_filter):
"""
:param image: grayscale image as a 2-dimensional numpy array
:param im_filter: 2-dimensional numpy array
"""
# input dimensions
height = image.shape[0]
width = image.shape[1]
# output image with reduced dimensions
im_c = np.zeros((height - len(im_filter) + 1,width - len(im_filter) + 1))
# iterate over all rows and columns
for row in range(len(im_c)):
for col in range(len(im_c[0])):
# apply the filter
for i in range(len(im_filter)):
for j in range(len(im_filter[0])):
im_c[row, col] += image[row + i, col + j] *im_filter[i][j]
# fix out-of-bounds values
im_c[im_c > 255] = 255
im_c[im_c < 0] = 0
# plot images for comparison
import matplotlib.pyplot as plt
import matplotlib.cm as cm
plt.figure()
plt.imshow(image, cmap=cm.Greys_r)
plt.show()
plt.imshow(im_c, cmap=cm.Greys_r)
plt.show()
import requests
from PIL import Image
from io import BytesIO
# Cargar la imagen
url ="https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/Commander_Eileen_Collins_-_GPN-2000-001177.jpg/382px-Commander_Eileen_Collins_-_GPN-2000-001177.jpg?download"
resp = requests.get(url)
image_rgb =np.asarray(Image.open(BytesIO(resp.content)).convert("RGB"))
# Convertirla a escala de grises
image_grayscale = np.mean(image_rgb, axis=2, dtype=np.uint)
# Aplicar filtro de blur
blur = np.full([10, 10], 1. / 100)
conv(image_grayscale, blur)
sobel_x = [[-1, -2, -1],[0, 0, 0],
[1, 2, 1]]
conv(image_grayscale, sobel_x)
sobel_y = [[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]]
conv(image_grayscale, sobel_y)
```
# Stride y relleno en capas convolucionales
Hasta ahora, asumimos que el deslizamiento del filtro ocurre un píxel a la vez, pero ese no es siempre el caso. Podemos deslizar el filtro en múltiples posiciones. Este parámetro de las capas convolucionales se llama zancada. Por lo general, el paso es el mismo en todas las dimensiones de la entrada. En el siguiente diagrama, podemos ver una capa convolucional con un paso de 2:

Al usar una zancada mayor que 1, reducimos el tamaño del segmento de salida. En la sección anterior, presentamos una fórmula simple para el tamaño de salida, que incluía los tamaños de la entrada y el núcleo. Ahora, lo ampliaremos para incluir también el paso: ((ancho - filtro_w) / stride_w + 1, ((altura - filtro_h) / stride_h + 1).
Por ejemplo, el tamaño de salida de un corte cuadrado generado por una imagen de entrada de 28x28, convolucionado con un filtro 3x3 con zancada 1, sería 28-3 + 1 = 26. Pero con zancada 2, obtenemos (28-3) / 2 + 1 = 13. El efecto principal del paso más grande es un aumento en el campo receptivo de las neuronas de salida. Vamos a explicar esto con un ejemplo. Si usamos Stride 2, el tamaño del segmento de salida será aproximadamente cuatro veces menor que el de entrada. En otras palabras, una neurona de salida "cubrirá" el área, que es cuatro veces más grande, en comparación con las neuronas de entrada. Las neuronas en el
Las siguientes capas capturarán gradualmente la entrada de regiones más grandes de la imagen de entrada. Esto es importante, porque les permitiría detectar características más grandes y más complejas de la entrada.
Las operaciones de convolución que hemos discutido hasta ahora han producido una salida menor que la entrada. Pero, en la práctica, a menudo es deseable controlar el tamaño de la salida. Podemos resolver esto rellenando los bordes del segmento de entrada con filas y columnas de ceros antes de la operación de convolución. La forma más común de usar relleno es producir resultados con las mismas dimensiones que la entrada. En el siguiente diagrama, podemos ver una capa convolucional con relleno de 1:

Las neuronas blancas representan el relleno. Los segmentos de entrada y salida tienen las mismas dimensiones (neuronas oscuras). Esta es la forma más común de usar relleno. Los ceros recién rellenados participarán en la operación de convolución con el corte, pero no afectarán el resultado. La razón es que, aunque las áreas rellenadas estén conectadas con pesos a la siguiente capa, siempre multiplicaremos esos pesos por el valor rellenado, que es 0. Ahora agregaremos relleno a la fórmula del tamaño de salida. Deje que el tamaño del segmento de entrada sea I = (Iw, Ih), el tamaño del filtro F = (Fw, Fh), la zancada S = (Sw, Sh) y el relleno P = (Pw, Ph). Entonces el tamaño O = (Ow, Oh) del segmento de salida viene dado por las siguientes ecuaciones:
\begin{equation}
O_w=\frac{I_w+2P_w-F_w}{S_w}+1
\end{equation}
\begin{equation}
O_h=\frac{I_h+2P_h-F_h}{S_h}+1
\end{equation}
# Capas de pooling
En la sección anterior, explicamos cómo aumentar el campo receptivo de las neuronas usando un paso más grande que 1. Pero también podemos hacer esto con la ayuda de la agrupación de capas. Una capa de agrupación divide la porción de entrada en una cuadrícula, donde cada celda de la cuadrícula representa un campo receptivo de varias neuronas (tal como lo hace una capa convolucional). Luego, se aplica una operación de agrupación sobre cada celda de la cuadrícula. Existen diferentes tipos de capas de agrupación. Las capas de agrupación no cambian la profundidad del volumen, porque la operación de agrupación se realiza de forma independiente en cada segmento.
- Max pooling: es la forma más popular de pooling. La operación de agrupación máxima lleva a la neurona con el valor de activación más alto en cada campo receptivo local (celda de cuadrícula) y propaga solo ese valor hacia adelante. En la siguiente figura, podemos ver un ejemplo de agrupación máxima con un campo receptivo de 2x2:

- Average Pooling: es otro tipo de agrupación, donde la salida de cada campo receptivo es el valor medio de todas las activaciones dentro del campo. El siguiente es un ejemplo de agrupación promedio

Las capas de agrupación se definen por dos parámetros:
- Stride, que es lo mismo que con las capas convolucionales
- Tamaño del campo receptivo, que es el equivalente del tamaño del filtro en capas convolucionales.
# Estructura de una red neuronal convolucional

Normalmente, alternaríamos una o más capas convolucionales con una capa de agrupación. De esta forma, las capas convolucionales pueden detectar características en cada nivel del tamaño del campo receptivo. El tamaño del campo receptivo agregado de las capas más profundas es mayor que las del comienzo de la red. Esto les permite capturar características más complejas de regiones de entrada más grandes. Vamos a ilustrar esto con un ejemplo. Imagine que la red utiliza convoluciones de 3x3 con zancada 1 y agrupación de 2x2 con zancada 2:
- las neuronas de la primera capa convolucional recibirán información de 3x3 píxeles de la imagen.
- Un grupo de neuronas de salida 2x2 de la primera capa tendrá un tamaño de campo receptivo combinado de 4x4 (debido a la zancada).
- Después de la primera operación de agrupación, este grupo se combinará en una sola neurona de la capa de agrupación.
- La segunda operación de convolución toma información de las neuronas de agrupación 3x3. Por lo tanto, recibirá la entrada de un cuadrado con lados 3x4 = 12 (o un total de 12x12 = 144) píxeles de la imagen de entrada.
Utilizamos las capas convolucionales para extraer características de la entrada. Las características detectadas por las capas más profundas son muy abstractas, pero tampoco son legibles por los humanos. Para resolver este problema, generalmente agregamos una o más capas completamente conectadas después de la última capa convolucional / agrupación. En este ejemplo, la última capa (salida) completamente conectada utilizará softmax para estimar las probabilidades de clase de la entrada. Puede pensar en las capas totalmente conectadas como traductores entre el idioma de la red (que no entendemos) y el nuestro. Las capas convolucionales más profundas generalmente tienen más filtros (por lo tanto, mayor profundidad de volumen), en comparación con los iniciales. Un detector de características al comienzo de la red funciona en un pequeño campo receptivo. Solo puede detectar un número limitado de características, como bordes o líneas, compartidas entre todas las clases. Por otro lado, una capa más profunda detectaría características más complejas y numerosas. Por ejemplo, si tenemos varias clases, como automóviles, árboles o personas, cada una tendrá su propio conjunto de características, como neumáticos, puertas, hojas y caras, etc. Esto requeriría más detectores de características.
```
#Importen tensorflow, keras, de keras, importen Sequential, Dense, Activation,
#Convolution2D, MaxPooling, Flatten y np_utils
#Primero: Carguen datos de mnist
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.layers import Convolution2D, MaxPooling2D
from keras.layers import Flatten
from keras.utils import np_utils
(X_train, Y_train), (X_test, Y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 28, 28, 1)
X_test = X_test.reshape(10000, 28, 28, 1)
Y_train = np_utils.to_categorical(Y_train, 10)
Y_test = np_utils.to_categorical(Y_test, 10)
#Segundo: creen una red neuronal convolucional
model = Sequential([Convolution2D(filters=64,kernel_size=(3, 3),input_shape=(28, 28, 1)),Activation('sigmoid'),Convolution2D(filters=32,kernel_size=(3, 3)), Activation('sigmoid'),MaxPooling2D(pool_size=(4, 4)), Flatten(), Dense(64), Activation('relu'), Dense(10), Activation('softmax')])
model.compile(loss='categorical_crossentropy',metrics=['accuracy'], optimizer='adadelta')
model.fit(X_train, Y_train, batch_size=100, epochs=5,validation_split=0.1, verbose=1)
score = model.evaluate(X_test, Y_test, verbose=1)
print('Test accuracy:', score[1])
import warnings
warnings.filterwarnings("ignore")
```
# Preprocesamiento de datos
Hasta ahora, hemos alimentado la red con entradas no modificadas. En el caso de las imágenes, estas son intensidades de píxeles en el rango [0: 255]. Pero eso no es óptimo. Imagine que tenemos una imagen RGB, donde las intensidades en uno de los canales de color son muy altas en comparación con los otros dos. Cuando alimentamos la imagen a la red, los valores de este canal serán dominantes, disminuyendo los demás. Esto podría sesgar los resultados, porque en realidad cada canal tiene la misma importancia. Para resolver esto, necesitamos preparar (o normalizar) los datos, antes de alimentarlos a la red. En la práctica, usaremos dos tipos de normalización:
- Feature Scaling: Esta operación escala todas las entradas en el rango [0,1]. Por ejemplo, un píxel con intensidad 125 tendría un valor escalado de. El escalado de características es rápido y fácil de implementar.
- Standard Score: Aquí μ y σ son la media y la desviación estándar de todos los datos de entrenamiento. Por lo general, se calculan por separado para cada dimensión de entrada. Por ejemplo, en una imagen RGB, calcularíamos la media μ y σ para cada canal. Debemos tener en cuenta que μ y σ deben calcularse solo en los datos de entrenamiento y luego aplicarse a los datos de la prueba.
# Dropout
Dropout es una técnica de regularización, que se puede aplicar a la salida de algunas de las capas de red. El dropout aleatorio y periódico elimina algunas de las neuronas (junto con sus conexiones de entrada y salida) de la red. Durante un mini lote de entrenamiento, cada neurona tiene una probabilidad p de ser descartada estocásticamente. Esto es para asegurar que ninguna neurona termine confiando demasiado en otras neuronas y "aprenda" algo útil para la red. El abandono se puede aplicar después de capas convolucionales, de agrupación o completamente conectadas. En la siguiente ilustración, podemos ver un abandono de capas completamente conectadas:

# Aumento de datos
Una de las técnicas de regularización más eficientes es el aumento de datos. Si los datos de entrenamiento son demasiado pequeños, la red podría comenzar a sobreajustarse. El aumento de datos ayuda a contrarrestar esto al aumentar artificialmente el tamaño del conjunto de entrenamiento. Usemos un ejemplo. En los ejemplos de MNIST y CIFAR-10, hemos entrenado la red en varias épocas. La red "verá" cada muestra del conjunto de datos una vez por época. Para evitar esto, podemos aplicar aumentos aleatorios a las imágenes, antes de usarlas para el entrenamiento. Las etiquetas permanecerán igual. Algunos de los aumentos de imagen más populares son:

```
import keras
from keras.datasets import cifar10
from keras.layers import Conv2D, MaxPooling2D
from keras.layers import Dense, Dropout, Activation, Flatten,BatchNormalization
from keras.models import Sequential
from keras.preprocessing.image import ImageDataGenerator
batch_size = 50
(X_train, Y_train), (X_test, Y_test) = cifar10.load_data()
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = keras.utils.to_categorical(Y_train, 10)
Y_test = keras.utils.to_categorical(Y_test, 10)
data_generator = ImageDataGenerator(rotation_range=90, width_shift_range=0.1,height_shift_range=0.1, featurewise_center=True, featurewise_std_normalization=True, horizontal_flip=True)
data_generator.fit(X_train)
# standardize the test set
for i in range(len(X_test)):
X_test[i] = data_generator.standardize(X_test[i])
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',input_shape=X_train.shape[1:]))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(Conv2D(32, (3, 3), padding='same'))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.2))
model.add(Conv2D(128, (3, 3)))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(Conv2D(128, (3, 3)))
model.add(BatchNormalization())
model.add(Activation('elu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam',
metrics=['accuracy'])
model.fit_generator( generator=data_generator.flow(x=X_train, y=Y_train, batch_size=batch_size),steps_per_epoch=len(X_train),epochs=100, validation_data=(X_test, Y_test),workers=4)
```
| true |
code
| 0.742693 | null | null | null | null |
|
# Import necessary depencencies
```
import pandas as pd
import numpy as np
import text_normalizer as tn
import model_evaluation_utils as meu
np.set_printoptions(precision=2, linewidth=80)
```
# Load and normalize data
```
dataset = pd.read_csv(r'movie_reviews.csv')
# take a peek at the data
print(dataset.head())
reviews = np.array(dataset['review'])
sentiments = np.array(dataset['sentiment'])
# build train and test datasets
train_reviews = reviews[:35000]
train_sentiments = sentiments[:35000]
test_reviews = reviews[35000:]
test_sentiments = sentiments[35000:]
# normalize datasets
norm_train_reviews = tn.normalize_corpus(train_reviews)
norm_test_reviews = tn.normalize_corpus(test_reviews)
```
# Traditional Supervised Machine Learning Models
## Feature Engineering
```
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
# build BOW features on train reviews
cv = CountVectorizer(binary=False, min_df=0.0, max_df=1.0, ngram_range=(1,2))
cv_train_features = cv.fit_transform(norm_train_reviews)
# build TFIDF features on train reviews
tv = TfidfVectorizer(use_idf=True, min_df=0.0, max_df=1.0, ngram_range=(1,2),
sublinear_tf=True)
tv_train_features = tv.fit_transform(norm_train_reviews)
# transform test reviews into features
cv_test_features = cv.transform(norm_test_reviews)
tv_test_features = tv.transform(norm_test_reviews)
print('BOW model:> Train features shape:', cv_train_features.shape, ' Test features shape:', cv_test_features.shape)
print('TFIDF model:> Train features shape:', tv_train_features.shape, ' Test features shape:', tv_test_features.shape)
```
## Model Training, Prediction and Performance Evaluation
```
from sklearn.linear_model import SGDClassifier, LogisticRegression
lr = LogisticRegression(penalty='l2', max_iter=100, C=1)
svm = SGDClassifier(loss='hinge', n_iter=100)
# Logistic Regression model on BOW features
lr_bow_predictions = meu.train_predict_model(classifier=lr,
train_features=cv_train_features, train_labels=train_sentiments,
test_features=cv_test_features, test_labels=test_sentiments)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=lr_bow_predictions,
classes=['positive', 'negative'])
# Logistic Regression model on TF-IDF features
lr_tfidf_predictions = meu.train_predict_model(classifier=lr,
train_features=tv_train_features, train_labels=train_sentiments,
test_features=tv_test_features, test_labels=test_sentiments)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=lr_tfidf_predictions,
classes=['positive', 'negative'])
svm_bow_predictions = meu.train_predict_model(classifier=svm,
train_features=cv_train_features, train_labels=train_sentiments,
test_features=cv_test_features, test_labels=test_sentiments)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=svm_bow_predictions,
classes=['positive', 'negative'])
svm_tfidf_predictions = meu.train_predict_model(classifier=svm,
train_features=tv_train_features, train_labels=train_sentiments,
test_features=tv_test_features, test_labels=test_sentiments)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=svm_tfidf_predictions,
classes=['positive', 'negative'])
```
# Newer Supervised Deep Learning Models
```
import gensim
import keras
from keras.models import Sequential
from keras.layers import Dropout, Activation, Dense
from sklearn.preprocessing import LabelEncoder
```
## Prediction class label encoding
```
le = LabelEncoder()
num_classes=2
# tokenize train reviews & encode train labels
tokenized_train = [tn.tokenizer.tokenize(text)
for text in norm_train_reviews]
y_tr = le.fit_transform(train_sentiments)
y_train = keras.utils.to_categorical(y_tr, num_classes)
# tokenize test reviews & encode test labels
tokenized_test = [tn.tokenizer.tokenize(text)
for text in norm_test_reviews]
y_ts = le.fit_transform(test_sentiments)
y_test = keras.utils.to_categorical(y_ts, num_classes)
# print class label encoding map and encoded labels
print('Sentiment class label map:', dict(zip(le.classes_, le.transform(le.classes_))))
print('Sample test label transformation:\n'+'-'*35,
'\nActual Labels:', test_sentiments[:3], '\nEncoded Labels:', y_ts[:3],
'\nOne hot encoded Labels:\n', y_test[:3])
```
## Feature Engineering with word embeddings
```
# build word2vec model
w2v_num_features = 500
w2v_model = gensim.models.Word2Vec(tokenized_train, size=w2v_num_features, window=150,
min_count=10, sample=1e-3)
def averaged_word2vec_vectorizer(corpus, model, num_features):
vocabulary = set(model.wv.index2word)
def average_word_vectors(words, model, vocabulary, num_features):
feature_vector = np.zeros((num_features,), dtype="float64")
nwords = 0.
for word in words:
if word in vocabulary:
nwords = nwords + 1.
feature_vector = np.add(feature_vector, model[word])
if nwords:
feature_vector = np.divide(feature_vector, nwords)
return feature_vector
features = [average_word_vectors(tokenized_sentence, model, vocabulary, num_features)
for tokenized_sentence in corpus]
return np.array(features)
# generate averaged word vector features from word2vec model
avg_wv_train_features = averaged_word2vec_vectorizer(corpus=tokenized_train, model=w2v_model,
num_features=500)
avg_wv_test_features = averaged_word2vec_vectorizer(corpus=tokenized_test, model=w2v_model,
num_features=500)
# feature engineering with GloVe model
train_nlp = [tn.nlp(item) for item in norm_train_reviews]
train_glove_features = np.array([item.vector for item in train_nlp])
test_nlp = [tn.nlp(item) for item in norm_test_reviews]
test_glove_features = np.array([item.vector for item in test_nlp])
print('Word2Vec model:> Train features shape:', avg_wv_train_features.shape, ' Test features shape:', avg_wv_test_features.shape)
print('GloVe model:> Train features shape:', train_glove_features.shape, ' Test features shape:', test_glove_features.shape)
```
## Modeling with deep neural networks
### Building Deep neural network architecture
```
def construct_deepnn_architecture(num_input_features):
dnn_model = Sequential()
dnn_model.add(Dense(512, activation='relu', input_shape=(num_input_features,)))
dnn_model.add(Dropout(0.2))
dnn_model.add(Dense(512, activation='relu'))
dnn_model.add(Dropout(0.2))
dnn_model.add(Dense(512, activation='relu'))
dnn_model.add(Dropout(0.2))
dnn_model.add(Dense(2))
dnn_model.add(Activation('softmax'))
dnn_model.compile(loss='categorical_crossentropy', optimizer='adam',
metrics=['accuracy'])
return dnn_model
w2v_dnn = construct_deepnn_architecture(num_input_features=500)
```
### Visualize sample deep architecture
```
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
SVG(model_to_dot(w2v_dnn, show_shapes=True, show_layer_names=False,
rankdir='TB').create(prog='dot', format='svg'))
```
### Model Training, Prediction and Performance Evaluation
```
batch_size = 100
w2v_dnn.fit(avg_wv_train_features, y_train, epochs=5, batch_size=batch_size,
shuffle=True, validation_split=0.1, verbose=1)
y_pred = w2v_dnn.predict_classes(avg_wv_test_features)
predictions = le.inverse_transform(y_pred)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predictions,
classes=['positive', 'negative'])
glove_dnn = construct_deepnn_architecture(num_input_features=300)
batch_size = 100
glove_dnn.fit(train_glove_features, y_train, epochs=5, batch_size=batch_size,
shuffle=True, validation_split=0.1, verbose=1)
y_pred = glove_dnn.predict_classes(test_glove_features)
predictions = le.inverse_transform(y_pred)
meu.display_model_performance_metrics(true_labels=test_sentiments, predicted_labels=predictions,
classes=['positive', 'negative'])
```
| true |
code
| 0.59302 | null | null | null | null |
|
[Sascha Spors](https://orcid.org/0000-0001-7225-9992),
Professorship Signal Theory and Digital Signal Processing,
[Institute of Communications Engineering (INT)](https://www.int.uni-rostock.de/),
Faculty of Computer Science and Electrical Engineering (IEF),
[University of Rostock, Germany](https://www.uni-rostock.de/en/)
# Tutorial Signals and Systems (Signal- und Systemtheorie)
Summer Semester 2021 (Bachelor Course #24015)
- lecture: https://github.com/spatialaudio/signals-and-systems-lecture
- tutorial: https://github.com/spatialaudio/signals-and-systems-exercises
WIP...
The project is currently under heavy development while adding new material for the summer semester 2021
Feel free to contact lecturer [[email protected]](https://orcid.org/0000-0002-3010-0294)
# Exercise 8: Discrete-Time Convolution
```
import matplotlib.pyplot as plt
import numpy as np
#from matplotlib.ticker import MaxNLocator
#from scipy import signal
# we create a undersampled and windowed impulse response of a RC-circuit lowpass
TRC = 1/6 # time constant in s
wRC = 1/TRC # cutoff angular frequency in rad/s
ws = 200/3*wRC # sampling angular frequency in rad/s, this yields aliasing!!
fs = ws/(2*np.pi) # sampling frequency in Hz
Ts = 1/fs # sampling intervall s
w = np.linspace(-10*ws, ws*10, 2**11) # angular frequency in rad/s
s = 1j*w # laplace variable along im-axis in rad/s
H = 1 / (s/wRC + 1) # frequency response
k = np.arange(np.int32(np.ceil(0.5/Ts)+1)) # sample index
h = (1/TRC * np.exp(-k*Ts/TRC)) # sampled impulse response, windowed!!
# normalize to achieve h[k=0] = 1, cf. convolution_ct_example2_AF3B15E0D3.ipynb
h *= TRC
Nh = h.size
kh = 0 # start of impulse response
plt.figure(figsize=(6, 6))
plt.subplot(2, 1, 1)
for nu in np.arange(-4, 5, 1):
plt.plot(w+nu*ws, 20*np.log10(np.abs(H)), 'C1')
plt.plot(w, 20*np.log10(np.abs(H)))
plt.plot([ws/2, ws/2], [-40, 0], 'C7')
plt.xticks(ws*np.arange(-4, 5, 1))
plt.xlim(-4*ws, +4*ws)
plt.ylim(-40, 0)
plt.xlabel(r'$\omega$ / (rad/s)')
plt.ylabel(r'$20 \log_{10} |H(\omega)|$')
plt.grid(True)
plt.subplot(2, 1, 2)
plt.stem(k*Ts, h, use_line_collection=True,
linefmt='C0:', markerfmt='C0o', basefmt='C0:',
label=r'$h_d[k] = h[k T_s] \cdot T_{RC} = \mathrm{e}^{-k\cdot\frac{T_s}{T_{RC}}}$')
plt.xlabel(r'$k \cdot T_s$')
plt.legend()
plt.grid(True)
print(Ts, ws)
# signal
x = 2*np.ones(np.int32(np.ceil(2 / Ts))) # non-zero elements
Nx = x.size
kx = np.int32(np.ceil(1/Ts)) # start index for first non-zero entry
# discrete-time convolution
Ny = Nx+Nh-1
ky = kx+kh
y = np.convolve(x, h)
plt.figure(figsize=(12, 4))
k = np.arange(kx, kx+Nx)
ax = plt.subplot(1, 3, 1)
plt.stem(k*Ts, x, use_line_collection=True,
linefmt='C0:', markerfmt='C0.', basefmt='C0:',
label=r'$x[k]$')
plt.xlim(1, 3)
plt.xlabel(r'$k \cdot T_s$ / s')
plt.legend(loc='upper right')
k = np.arange(kh, kh+Nh)
ax = plt.subplot(1, 3, 2)
plt.stem(k*Ts, h, use_line_collection=True,
linefmt='C1:', markerfmt='C1.', basefmt='C1:',
label=r'$h[k]$')
plt.xlim(0, 0.5)
plt.ylim(0, 1)
plt.yticks(np.arange(0, 1.25, 0.25))
plt.xlabel(r'$k \cdot T_s$ / s')
plt.legend(loc='upper right')
plt.grid(True)
k = np.arange(ky, ky+Ny)
ax = plt.subplot(1, 3, 3)
plt.stem(k*Ts, y*Ts, use_line_collection=True,
linefmt='C2:', markerfmt='C2.', basefmt='C2:',
label=r'$y[k]\,/\,T_s = x[k]\ast h[k]$')
tmp = (1-np.exp(-3))/3
plt.plot([1, 3.5], [tmp, tmp], 'C3')
plt.xlim(1, 3.5)
plt.ylim(0, 0.4)
plt.yticks(np.arange(0, 0.5, 0.1))
plt.xlabel(r'$k \cdot T_s$ / s')
plt.legend(loc='upper right')
plt.grid(True)
plt.savefig('convolution_discrete_pt1_xhy.pdf')
plt.figure(figsize=(8, 4))
k = np.arange(ky, ky+Ny)
ax = plt.subplot(1, 2, 1)
plt.stem(k*Ts, y*Ts, use_line_collection=True,
linefmt='C2:', markerfmt='C2o', basefmt='C2:',
label=r'$y[k]\,/\,T_s = x[k]\ast h[k]$')
tmp = (1-np.exp(-3))/3
plt.plot([1, 3.5], [tmp, tmp], 'C3')
plt.xlim(1, 1.5)
plt.ylim(0, 0.4)
plt.yticks(np.arange(0, 0.5, 0.1))
plt.xlabel(r'$k \cdot T_s$ / s')
plt.legend(loc='upper right')
plt.grid(True)
ax = plt.subplot(1, 2, 2)
plt.stem(k, y*Ts, use_line_collection=True,
linefmt='C2:', markerfmt='C2o', basefmt='C2:',
label=r'$y[k]\,/\,T_s = x[k]\ast h[k]$')
tmp = (1-np.exp(-3))/3
plt.plot([1/Ts, 3.5/Ts], [tmp, tmp], 'C3')
plt.xlim(1/Ts, 1.5/Ts)
plt.ylim(0, 0.4)
plt.yticks(np.arange(0, 0.5, 0.1))
plt.xlabel(r'$k$')
plt.legend(loc='upper right')
plt.grid(True)
plt.savefig('convolution_discrete_pt1_y_over_kt_zoom.pdf')
```
## Copyright
This tutorial is provided as Open Educational Resource (OER), to be found at
https://github.com/spatialaudio/signals-and-systems-exercises
accompanying the OER lecture
https://github.com/spatialaudio/signals-and-systems-lecture.
Both are licensed under a) the Creative Commons Attribution 4.0 International
License for text and graphics and b) the MIT License for source code.
Please attribute material from the tutorial as *Frank Schultz,
Continuous- and Discrete-Time Signals and Systems - A Tutorial Featuring
Computational Examples, University of Rostock* with
``main file, github URL, commit number and/or version tag, year``.
| true |
code
| 0.667541 | null | null | null | null |
|
# PixdosepiX-OpenKBP---2020-AAPM-Grand-Challenge-
## Introduction
The aim of the OpenKBP Challenge is to advance fair and consistent comparisons of dose prediction methods for knowledge-based planning (KBP). Participants of the challenge will use a large dataset to train, test, and compare their prediction methods, using a set of standardized metrics, with those of other participants.
## Get and prepare data
```
!wget "###REPLACE WITH LINK TO DATASET IN CODALAB###"
from google.colab import drive
drive.mount('/content/drive')
!mv /content/e25ae3d9-03e1-4d2c-8af2-f9991193f54b train.zip
!unzip train.zip
!rm "/content/train-pats/.DS_Store"
!rm "/content/validation-pats-no-dose/.DS_Store"
```
## Import libraries
```
%tensorflow_version 2.x
import shutil
import json
import pandas as pd
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import tensorflow as tf
from tensorflow.keras import *
from tensorflow.keras.layers import *
from IPython.display import clear_output
```
## Data loader and general functions
```
def create_hist(img):
h = np.squeeze(img).flatten()*100
return h
def create_out_file(in_url,out_url):
dir_main = os.listdir(in_url)
for patient in dir_main:
os.mkdir(out_url + "/" + patient)
def unravel_ct_dose(data_img):
array = np.zeros((128,128,128))
indices = tuple(map(tuple,np.unravel_index(tuple(data_img.index),(128,128,128),order="C")))
array[indices] = data_img.data.values
return array
def unravel_masks(data_img):
array = np.zeros((128,128,128))
indices = tuple(map(tuple,np.unravel_index(tuple(data_img.index),(128,128,128),order="C")))
array[indices] = 1
return array
def decode_to_CT_Dose(url_element):
array = pd.read_csv(url_element,index_col=0)
array = np.expand_dims(np.expand_dims(unravel_ct_dose(array),axis = 0),axis = 4)
return array
def decode_unique_mask(url_element):
array = pd.read_csv(url_element,index_col=0)
array = np.expand_dims(np.expand_dims(unravel_masks(array),axis = 0),axis = 4)
return array
def decode_voxel_dimensions(url_element):
array = np.loadtxt(url_element)
return array
def decode_fusion_maks(link,list_name_masks,dict_num_mask):
masks = np.zeros([1,128,128,128,10])
organs_patien = os.listdir(link)
for name in list_name_masks:
if name + ".csv" in organs_patien:
dir_mask = link + "/" + name + ".csv"
array = pd.read_csv(dir_mask,index_col=0)
array = unravel_masks(array)
masks[0,:,:,:,dict_num_mask[name]] = array
return masks
def get_patient_list(url_main):
return os.listdir(url_main)
def load_patient_train(dir_patient):
dict_images = {"ct":None,"dose":None,"masks":None}
ct = decode_to_CT_Dose(dir_patient + "/" + "ct.csv")
dose = decode_to_CT_Dose(dir_patient + "/" + "dose.csv")
list_masks = ['Brainstem',
'SpinalCord',
'RightParotid',
'LeftParotid',
'Esophagus',
'Larynx',
'Mandible',
'PTV56',
'PTV63',
'PTV70']
dict_num_mask = {"Brainstem":0,
"SpinalCord":1,
"RightParotid":2,
"LeftParotid":3,
"Esophagus":4,
"Larynx":5,
"Mandible":6,
"PTV56":7,
"PTV63":8,
"PTV70":9}
masks = decode_fusion_maks(dir_patient,list_masks,dict_num_mask)
dict_images["ct"] = ct
dict_images["dose"] = dose
dict_images["masks"] = masks
return dict_images
def load_patient(dir_patient):
dict_images = {"ct":None,"dose":None,"possible_dose_mask":None,"voxel_dimensions":None,"masks":None}
ct = decode_to_CT_Dose(dir_patient + "/" + "ct.csv")
dose = decode_to_CT_Dose(dir_patient + "/" + "dose.csv")
possible_dose_mask = decode_unique_mask(dir_patient + "/" + "possible_dose_mask.csv")
voxel_dimensions = decode_voxel_dimensions(dir_patient + "/" + "voxel_dimensions.csv")
list_masks = ['Brainstem',
'SpinalCord',
'RightParotid',
'LeftParotid',
'Esophagus',
'Larynx',
'Mandible',
'PTV56',
'PTV63',
'PTV70']
dict_num_mask = {"Brainstem":0,
"SpinalCord":1,
"RightParotid":2,
"LeftParotid":3,
"Esophagus":4,
"Larynx":5,
"Mandible":6,
"PTV56":7,
"PTV63":8,
"PTV70":9}
masks = decode_fusion_maks(dir_patient,list_masks,dict_num_mask)
dict_images["ct"] = ct
dict_images["dose"] = dose
dict_images["possible_dose_mask"] = possible_dose_mask
dict_images["voxel_dimensions"] = voxel_dimensions
dict_images["masks"] = masks
return dict_images
def load_patient_test(dir_patient):
dict_images = {"ct":None,"possible_dose_mask":None,"voxel_dimensions":None,"masks":None}
ct = decode_to_CT_Dose(dir_patient + "/" + "ct.csv")
possible_dose_mask = decode_unique_mask(dir_patient + "/" + "possible_dose_mask.csv")
voxel_dimensions = decode_voxel_dimensions(dir_patient + "/" + "voxel_dimensions.csv")
list_masks = ['Brainstem',
'SpinalCord',
'RightParotid',
'LeftParotid',
'Esophagus',
'Larynx',
'Mandible',
'PTV56',
'PTV63',
'PTV70']
dict_num_mask = {"Brainstem":0,
"SpinalCord":1,
"RightParotid":2,
"LeftParotid":3,
"Esophagus":4,
"Larynx":5,
"Mandible":6,
"PTV56":7,
"PTV63":8,
"PTV70":9}
masks = decode_fusion_maks(dir_patient,list_masks,dict_num_mask)
dict_images["ct"] = ct
dict_images["possible_dose_mask"] = possible_dose_mask
dict_images["voxel_dimensions"] = voxel_dimensions
dict_images["masks"] = masks
return dict_images
url_train = "/content/train-pats"
patients = get_patient_list(url_train)
for i,patient in enumerate(patients):
patients[i] = os.path.join(url_train,patient)
def load_images_to_net(patient_url):
images = load_patient_train(patient_url)
ct = tf.cast(np.where(images["ct"] <= 4500,images["ct"],0),dtype=tf.float32)
ct = (2*ct/4500) - 1
masks = tf.cast(images["masks"],dtype=tf.float32)
dose = tf.cast(np.where(images["dose"] <= 100,images["dose"],0),dtype=tf.float32)
dose = (2*dose/100) - 1
return ct,masks,dose
def load_images_to_net_test(patient_url):
images = load_patient_test(patient_url)
ct = ct = tf.cast(np.where(images["ct"] <= 4500,images["ct"],0),dtype=tf.float32)
ct = (2*ct/4500) - 1
masks = tf.cast(images["masks"],dtype=tf.float32)
possible_dose_mask = tf.cast(images["possible_dose_mask"],dtype=tf.float32)
voxel_dimensions = tf.cast(images["voxel_dimensions"],dtype=tf.float32)
return ct,masks,possible_dose_mask,voxel_dimensions
```
## Architecture

https://blog.paperspace.com/unpaired-image-to-image-translation-with-cyclegan/
### Create downsample and upsample functions
```
def downsample(filters, apply_batchnorm=True):
result = Sequential()
initializer = tf.random_normal_initializer(0,0.02)
#capa convolucional
result.add(Conv3D(filters,
kernel_size = 4,
strides = 2,
padding = "same",
kernel_initializer = initializer,
use_bias = not apply_batchnorm))
# Capa de batch normalization
if apply_batchnorm:
result.add(BatchNormalization())
#Capa de activacion (leak relu)
result.add(ReLU())
return result
def upsample(filters, apply_dropout=False):
result = Sequential()
initializer = tf.random_normal_initializer(0,0.02)
#capa convolucional
result.add(Conv3DTranspose(filters,
kernel_size = 4,
strides = 2,
padding = "same",
kernel_initializer = initializer,
use_bias = False))
# Capa de batch normalization
result.add(BatchNormalization())
if apply_dropout:
result.add(Dropout(0.5))
#Capa de activacion (leak relu)
result.add(ReLU())
return result
```
### Create generator-net
```
def Generator():
ct_image = Input(shape=[128,128,128,1])
roi_masks = Input(shape=[128,128,128,10])
inputs = concatenate([ct_image, roi_masks])
down_stack = [
downsample(64, apply_batchnorm=False), # (64x64x64x64)
downsample(128), #32 (32x32x32x128)
downsample(256), #16 (16x16x16x16x256)
downsample(512), #8 (8x8x8x512)
downsample(512), #4 (4x4x4x512)
downsample(512), #2 (2x2x2x512)
downsample(512), #1 (1x1x1x512)
]
up_stack = [
upsample(512,apply_dropout=True), #2 (2x2x2x512)
upsample(512,apply_dropout=True), #4 (4x4x4x512)
upsample(512), #8 (8x8x8x512)
upsample(256), #16 (16x16x16x256)
upsample(128), #32 (32x32x32x128)
upsample(64), #64 (64x64x64x64)
]
initializer = tf.random_normal_initializer(0,0.02)
last = Conv3DTranspose(filters=1,
kernel_size = 4,
strides = 2,
padding = "same",
kernel_initializer = initializer,
activation = "tanh") #(128x128x128x3)
x = inputs
s = []
concat = Concatenate()
for down in down_stack:
x = down(x)
s.append(x)
s = reversed(s[:-1])
for up,sk in zip(up_stack,s):
x = up(x)
x = concat([x,sk])
last = last(x)
return Model(inputs = [ct_image,roi_masks], outputs = last)
generator = Generator()
```
### Run generator-net
```
ct,masks,dose = load_images_to_net("/content/train-pats/pt_150")
gen_output = generator([ct,masks],training=True)
c = (ct[0,:,:,88,0]+1)/2
d = (dose[0,:,:,88,0]+1)/2
p = (gen_output[0,:,:,88,0]+1)/2
fig=plt.figure(figsize=(16, 16))
fig.add_subplot(3,3,1)
plt.title("ct")
plt.imshow(c)
fig.add_subplot(3,3,2)
plt.title("dose")
plt.imshow(d)
fig.add_subplot(3,3,3)
plt.title("predict")
plt.imshow(p)
fig.add_subplot(3,3,4)
plt.hist(create_hist(c), normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
fig.add_subplot(3,3,5)
plt.hist(create_hist(d), normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
fig.add_subplot(3,3,6)
plt.hist(create_hist(p), normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
fig.add_subplot(3,3,7)
plt.hist(create_hist((ct+1)/2),normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
fig.add_subplot(3,3,8)
plt.hist(create_hist((dose+1)/2), normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
fig.add_subplot(3,3,9)
plt.hist(create_hist((gen_output+1)/2), normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
plt.show()
```
### Create discriminator-net
```
def Discriminator():
ct_dis = Input(shape=[128,128,128,1], name = "ct_dis")
ct_masks = Input(shape=[128,128,128,10], name = "ct_masks")
dose_gen = Input(shape=[128,128,128,1], name = "dose_gen")
con = concatenate([ct_dis,ct_masks,dose_gen])
initializer = tf.random_normal_initializer(0,0.02)
down1 = downsample(64, apply_batchnorm = False)(con)
down2 = downsample(128)(down1)
down3 = downsample(256)(down2)
last = tf.keras.layers.Conv3D(filters = 1,
kernel_size = 4,
strides = 1,
kernel_initializer = initializer,
padding = "same")(down3)
return tf.keras.Model(inputs = [ct_dis,ct_masks,dose_gen],outputs = last)
discriminator = Discriminator()
```
### Run discriminator-net
```
disc_out = discriminator([ct,masks,gen_output],training = True)
w=16
h=16
fig=plt.figure(figsize=(8, 8))
columns = 4
rows = 4
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i +1)
plt.imshow(disc_out[0,:,:,i,0],vmin=-1,vmax=1,cmap = "RdBu_r")
plt.colorbar()
plt.show()
fig=plt.figure(figsize=(8, 8))
columns = 4
rows = 4
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i +1)
plt.imshow(disc_out[0,:,i,:,0],vmin=-1,vmax=1,cmap = "RdBu_r")
plt.colorbar()
plt.show()
fig=plt.figure(figsize=(8, 8))
columns = 4
rows = 4
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i +1)
plt.imshow(disc_out[0,i,:,:,0],vmin=-1,vmax=1,cmap = "RdBu_r")
plt.colorbar()
plt.show()
```
### Loss functions
```
# Funciones de coste adversarias
loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=True)
def discriminator_loss(disc_real_output,disc_generated_output):
#Diferencia entre los true por ser real y el detectado por el discriminador
real_loss = loss_object(tf.ones_like(disc_real_output),disc_real_output)
#Diferencia entre los false por ser generado y el detectado por el discriminador
generated_loss = loss_object(tf.zeros_like(disc_generated_output),disc_generated_output)
total_dics_loss = real_loss + generated_loss
return total_dics_loss
LAMBDA = 100
def generator_loss(disc_generated_output,gen_output,target):
gen_loss = loss_object(tf.ones_like(disc_generated_output),disc_generated_output)
#mean absolute error
l1_loss = tf.reduce_mean(tf.abs(target-gen_output))
total_gen_loss = gen_loss + (LAMBDA*l1_loss)
return total_gen_loss
```
### Configure checkpoint
```
import os
generator_optimizer = tf.keras.optimizers.Adam(2e-4,beta_1=0.5)
discriminator_optimizer = tf.keras.optimizers.Adam(2e-4,beta_1=0.5)
cpath = "/content/drive/My Drive/PAE_PYTHONQUANTIC/IA/OpenKBP/Auxiliary/checkpoint" #dir to checkpoints
checkpoint = tf.train.Checkpoint(generator_optimizer = generator_optimizer,
discriminator_optimizer = discriminator_optimizer,
generator = generator,
discriminator = discriminator)
```
## Train
### Train step
```
@tf.function
def train_step(ct,masks,dose):
with tf.GradientTape() as gen_tape, tf.GradientTape() as discr_tape:
output_image = generator([ct,masks], training=True)
output_gen_discr = discriminator([ct,masks,gen_output],training = True)
output_trg_discr = discriminator([ct,masks,dose], training = True)
discr_loss = discriminator_loss(output_trg_discr,output_gen_discr)
gen_loss = generator_loss(output_gen_discr,output_image,dose)
generator_grads = gen_tape.gradient(gen_loss, generator.trainable_variables)
discriminator_grads = discr_tape.gradient(discr_loss,discriminator.trainable_variables)
generator_optimizer.apply_gradients(zip(generator_grads,generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(discriminator_grads,discriminator.trainable_variables))
```
### Restore metrics
```
def update_metrics():
with open(cpath + 'metrics_GAN.json') as f:
metrics_GAN = json.load(f)
return metrics_GAN
metrics_GAN = {"gen_loss":[],"discr_loss":[]}
check = os.listdir(cpath)
if "metrics_GAN.json" in check:
print("upadte metrics")
metrics_GAN = update_metrics()
```
### Define train-loop
```
def train(epochs):
check = os.listdir(cpath)
if len(cpath) > 0:
if "state.txt" in check:
start = int(np.loadtxt(cpath + "/state.txt"))
print("upload checkpoint model")
checkpoint.restore(tf.train.latest_checkpoint(cpath+"/"+str(start)))
else:
start = 0
metrics_GAN["gen_loss"].append("epoch" + str(start))
metrics_GAN["discr_loss"].append("epoch" + str(start))
print("Start training in epoch",start)
for epoch in range(start,epochs):
np.random.shuffle(patients)
imgi = 0
for patient in patients:
ct,masks,dose = load_images_to_net(patient)
print("epoch " + str(epoch) + " - train: " + str(imgi) + "/" + str(len(patients)))
train_step(ct,masks,dose)
if imgi % 10 == 0:
output_image = generator([ct,masks], training=True)
output_gen_discr = discriminator([ct,masks,gen_output],training = True)
output_trg_discr = discriminator([ct,masks,dose], training = True)
discr_loss = discriminator_loss(output_trg_discr,output_gen_discr)
gen_loss = generator_loss(output_gen_discr,output_image,dose)
metrics_GAN["gen_loss"].append(str(np.mean(gen_loss)))
metrics_GAN["discr_loss"].append(str(np.mean(discr_loss)))
imgi += 1
clear_output(wait=True)
imgi = 0
metrics_GAN["gen_loss"].append("epoch" + str(epoch))
metrics_GAN["discr_loss"].append("epoch" + str(epoch))
# saving (checkpoint) the model every 20 epochs
if (epoch + 1) % 20 == 0:
with open(cpath + '/metrics_GAN.json', 'w') as fp:
json.dump(metrics_GAN, fp)
state = np.array([epoch+1])
np.savetxt(cpath + "/state.txt",state)
os.mkdir(cpath+"/"+str(epoch+1))
checkpoint_prefix = os.path.join(cpath+"/"+str(epoch+1),"ckpt")
checkpoint.save(file_prefix = checkpoint_prefix)
```
### Initialize train for epochs
```
train(230)
```
## Evaluate
### Restore model
```
def upload_model():
check = os.listdir(cpath)
if len(cpath) > 0:
if "state.txt" in check:
start = int(np.loadtxt(cpath + "/state.txt"))
print("upload checkpoint model")
checkpoint.restore(tf.train.latest_checkpoint(cpath+"/"+str(start)))
upload_model()
```
### Loader patient to evaluate
```
ct,masks,possible_dose_mask,voxel_dimensions = load_images_to_net_test("/content/validation-pats-no-dose/pt_201")
gen_output = generator([ct,masks],training=True)
gen_mask = ((gen_output+1)/2)*possible_dose_mask
plt.imshow(gen_mask[0,:,:,75,0])
plt.imshow((ct[0,:,:,75,0]+1)/2)
plt.imshow((gen_output[0,:,:,75,0]+1)/2)
w = np.squeeze(gen_mask ).flatten()*100
plt.hist(w, normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
x = (gen_output[0,:,:,:,0]+1)/2
y = masks[0,:,:,:,8]
z = x * y
w = np.squeeze(z).flatten()*100
plt.hist(w, normed=True, bins=100,range=[1,100])
plt.ylabel('Probability')
```
## Export doses predictions
```
@tf.function
def predict_step(ct,masks):
output_image = generator([ct,masks], training=True)
return output_image
url_main_results = "/content/drive/My Drive/PAE_PYTHONQUANTIC/IA/OpenKBP/Auxiliary/results_v1"
url_main_validation = "/content/validation-pats-no-dose"
def export_csv(predict_dose,patient):
dictionary = {"data":np.ravel(predict_dose,order="C")}
array = pd.DataFrame(dictionary)
array = array[array["data"] != 0]
array.to_csv(url_main_results + "/" + patient + ".csv")
def validation():
patients = get_patient_list(url_main_validation)
os.mkdir(url_main_results)
inimg = 0
for patient in patients:
ct,masks,possible_dose_mask,voxel_dimensions = load_images_to_net_test(url_main_validation + "/" + patient)
output_image = predict_step(ct,masks)
#output_image = generator([ct,masks], training=True)
predict_dose = np.squeeze((((output_image+1)/2)*possible_dose_mask)*100)
export_csv(predict_dose,patient)
print(" - predict: " + str(inimg) + "/" + str(len(patients)))
inimg = inimg + 1
validation()
shutil.make_archive('/content/drive/My Drive/PAE_PYTHONQUANTIC/IA/OpenKBP/Auxiliary/submisions_v1/baseline', 'zip','/content/drive/My Drive/PAE_PYTHONQUANTIC/IA/OpenKBP/Auxiliary/results_v1')
```
| true |
code
| 0.368619 | null | null | null | null |
|
# Convolutional Networks
So far we have worked with deep fully-connected networks, using them to explore different optimization strategies and network architectures. Fully-connected networks are a good testbed for experimentation because they are very computationally efficient, but in practice all state-of-the-art results use convolutional networks instead.
First you will implement several layer types that are used in convolutional networks. You will then use these layers to train a convolutional network on the CIFAR-10 dataset.
```
import os
os.chdir(os.getcwd() + '/..')
# Run some setup code for this notebook
import random
import numpy as np
import matplotlib.pyplot as plt
from utils.data_utils import get_CIFAR10_data
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
# Load the (preprocessed) CIFAR10 data.
data = get_CIFAR10_data('datasets/cifar-10-batches-py', subtract_mean=True)
for k, v in data.iteritems():
print('%s: ' % k, v.shape)
from utils.metrics_utils import rel_error
```
# Convolution: Naive forward pass
The core of a convolutional network is the convolution operation. In the file `layers/layers.py`, implement the forward pass for the convolution layer in the function `conv_forward_naive`.
You don't have to worry too much about efficiency at this point; just write the code in whatever way you find most clear.
You can test your implementation by running the following:
```
from layers.layers import conv_forward_naive
x_shape = (2, 3, 4, 4)
w_shape = (3, 3, 4, 4)
x = np.linspace(-0.1, 0.5, num=np.prod(x_shape)).reshape(x_shape)
w = np.linspace(-0.2, 0.3, num=np.prod(w_shape)).reshape(w_shape)
b = np.linspace(-0.1, 0.2, num=3)
conv_param = {'stride': 2, 'pad': 1}
out, _ = conv_forward_naive(x, w, b, conv_param)
correct_out = np.array([[[[-0.08759809, -0.10987781],
[-0.18387192, -0.2109216 ]],
[[ 0.21027089, 0.21661097],
[ 0.22847626, 0.23004637]],
[[ 0.50813986, 0.54309974],
[ 0.64082444, 0.67101435]]],
[[[-0.98053589, -1.03143541],
[-1.19128892, -1.24695841]],
[[ 0.69108355, 0.66880383],
[ 0.59480972, 0.56776003]],
[[ 2.36270298, 2.36904306],
[ 2.38090835, 2.38247847]]]])
# Compare your output to ours; difference should be around 2e-8
print('Testing conv_forward_naive')
print('difference: ', rel_error(out, correct_out))
```
# Aside: Image processing via convolutions
As fun way to both check your implementation and gain a better understanding of the type of operation that convolutional layers can perform, we will set up an input containing two images and manually set up filters that perform common image processing operations (grayscale conversion and edge detection). The convolution forward pass will apply these operations to each of the input images. We can then visualize the results as a sanity check.
```
from scipy.misc import imread, imresize
kitten, puppy = imread('test/kitten.jpg'), imread('test/puppy.jpg')
# kitten is wide, and puppy is already square
print kitten.shape, puppy.shape
d = kitten.shape[1] - kitten.shape[0]
kitten_cropped = kitten[:, d//2:-d//2, :]
print kitten_cropped.shape, puppy.shape
img_size = 200 # Make this smaller if it runs too slow
x = np.zeros((2, 3, img_size, img_size))
x[0, :, :, :] = imresize(puppy, (img_size, img_size)).transpose((2, 0, 1))
x[1, :, :, :] = imresize(kitten_cropped, (img_size, img_size)).transpose((2, 0, 1))
# Set up a convolutional weights holding 2 filters, each 3x3
w = np.zeros((2, 3, 3, 3))
# The first filter converts the image to grayscale.
# Set up the red, green, and blue channels of the filter.
w[0, 0, :, :] = [[0, 0, 0], [0, 0.3, 0], [0, 0, 0]]
w[0, 1, :, :] = [[0, 0, 0], [0, 0.6, 0], [0, 0, 0]]
w[0, 2, :, :] = [[0, 0, 0], [0, 0.1, 0], [0, 0, 0]]
# Second filter detects horizontal edges in the blue channel.
w[1, 2, :, :] = [[1, 2, 1], [0, 0, 0], [-1, -2, -1]]
# Vector of biases. We don't need any bias for the grayscale
# filter, but for the edge detection filter we want to add 128
# to each output so that nothing is negative.
b = np.array([0, 128])
# Compute the result of convolving each input in x with each filter in w,
# offsetting by b, and storing the results in out.
out, _ = conv_forward_naive(x, w, b, {'stride': 1, 'pad': 1})
def imshow_noax(img, normalize=True):
""" Tiny helper to show images as uint8 and remove axis labels """
if normalize:
img_max, img_min = np.max(img), np.min(img)
img = 255.0 * (img - img_min) / (img_max - img_min)
plt.imshow(img.astype('uint8'))
plt.gca().axis('off')
# Show the original images and the results of the conv operation
plt.subplot(2, 3, 1)
imshow_noax(puppy, normalize=False)
plt.title('Original image')
plt.subplot(2, 3, 2)
imshow_noax(out[0, 0])
plt.title('Grayscale')
plt.subplot(2, 3, 3)
imshow_noax(out[0, 1])
plt.title('Edges')
plt.subplot(2, 3, 4)
imshow_noax(kitten_cropped, normalize=False)
plt.subplot(2, 3, 5)
imshow_noax(out[1, 0])
plt.subplot(2, 3, 6)
imshow_noax(out[1, 1])
plt.show()
```
# Convolution: Naive backward pass
Implement the backward pass for the convolution operation in the function `conv_backward_naive` in the file `layers/layers.py`. Again, you don't need to worry too much about computational efficiency.
When you are done, run the following to check your backward pass with a numeric gradient check.
```
from layers.layers import conv_backward_naive
from utils.gradient_check import eval_numerical_gradient_array
np.random.seed(231)
x = np.random.randn(4, 3, 5, 5)
w = np.random.randn(2, 3, 3, 3)
b = np.random.randn(2,)
dout = np.random.randn(4, 2, 5, 5)
conv_param = {'stride': 1, 'pad': 1}
dx_num = eval_numerical_gradient_array(lambda x: conv_forward_naive(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_forward_naive(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_forward_naive(x, w, b, conv_param)[0], b, dout)
out, cache = conv_forward_naive(x, w, b, conv_param)
dx, dw, db = conv_backward_naive(dout, cache)
# Your errors should be around 1e-8'
print('Testing conv_backward_naive function')
print('dx error: ', rel_error(dx, dx_num))
print('dw error: ', rel_error(dw, dw_num))
print('db error: ', rel_error(db, db_num))
```
# Max pooling: Naive forward
Implement the forward pass for the max-pooling operation in the function `max_pool_forward_naive` in the file `layers/layers.py`. Again, don't worry too much about computational efficiency.
Check your implementation by running the following:
```
from layers.layers import max_pool_forward_naive
x_shape = (2, 3, 4, 4)
x = np.linspace(-0.3, 0.4, num=np.prod(x_shape)).reshape(x_shape)
pool_param = {'pool_width': 2, 'pool_height': 2, 'stride': 2}
out, _ = max_pool_forward_naive(x, pool_param)
correct_out = np.array([[[[-0.26315789, -0.24842105],
[-0.20421053, -0.18947368]],
[[-0.14526316, -0.13052632],
[-0.08631579, -0.07157895]],
[[-0.02736842, -0.01263158],
[ 0.03157895, 0.04631579]]],
[[[ 0.09052632, 0.10526316],
[ 0.14947368, 0.16421053]],
[[ 0.20842105, 0.22315789],
[ 0.26736842, 0.28210526]],
[[ 0.32631579, 0.34105263],
[ 0.38526316, 0.4 ]]]])
# Compare your output with ours. Difference should be around 1e-8.
print('Testing max_pool_forward_naive function:')
print('difference: ', rel_error(out, correct_out))
```
# Max pooling: Naive backward
Implement the backward pass for the max-pooling operation in the function `max_pool_backward_naive` in the file `layers/layers.py`. You don't need to worry about computational efficiency.
from aCheck your implementation with numeric gradient checking by running the following:
```
from layers.layers import max_pool_backward_naive
np.random.seed(231)
x = np.random.randn(3, 2, 8, 8)
dout = np.random.randn(3, 2, 4, 4)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
dx_num = eval_numerical_gradient_array(lambda x: max_pool_forward_naive(x, pool_param)[0], x, dout)
out, cache = max_pool_forward_naive(x, pool_param)
dx = max_pool_backward_naive(dout, cache)
# Your error should be around 1e-12
print('Testing max_pool_backward_naive function:')
print('dx error: ', rel_error(dx, dx_num))
```
# Fast layers
Making convolution and pooling layers fast can be challenging. To spare you the pain, we've provided fast implementations of the forward and backward passes for convolution and pooling layers in the file `layers/fast_conv_layers.py`.
The fast convolution implementation depends on a Cython extension; to compile it you need to run the following from the `layers` directory:
```bash
python setup.py build_ext --inplace
```
The API for the fast versions of the convolution and pooling layers is exactly the same as the naive versions that you implemented above: the forward pass receives data, weights, and parameters and produces outputs and a cache object; the backward pass recieves upstream derivatives and the cache object and produces gradients with respect to the data and weights.
**NOTE:** The fast implementation for pooling will only perform optimally if the pooling regions are non-overlapping and tile the input. If these conditions are not met then the fast pooling implementation will not be much faster than the naive implementation.
You can compare the performance of the naive and fast versions of these layers by running the following:
```
from layers.fast_conv_layers import conv_forward_fast, conv_backward_fast
from time import time
np.random.seed(231)
x = np.random.randn(100, 3, 31, 31)
w = np.random.randn(25, 3, 3, 3)
b = np.random.randn(25,)
dout = np.random.randn(100, 25, 16, 16)
conv_param = {'stride': 2, 'pad': 1}
t0 = time()
out_naive, cache_naive = conv_forward_naive(x, w, b, conv_param)
t1 = time()
out_fast, cache_fast = conv_forward_fast(x, w, b, conv_param)
t2 = time()
print('Testing conv_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('Difference: ', rel_error(out_naive, out_fast))
print
t0 = time()
dx_naive, dw_naive, db_naive = conv_backward_naive(dout, cache_naive)
t1 = time()
dx_fast, dw_fast, db_fast = conv_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting conv_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('dx difference: ', rel_error(dx_naive, dx_fast))
print('dw difference: ', rel_error(dw_naive, dw_fast))
print('db difference: ', rel_error(db_naive, db_fast))
from layers.fast_conv_layers import max_pool_forward_fast, max_pool_backward_fast
np.random.seed(231)
x = np.random.randn(100, 3, 32, 32)
dout = np.random.randn(100, 3, 16, 16)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
t0 = time()
out_naive, cache_naive = max_pool_forward_naive(x, pool_param)
t1 = time()
out_fast, cache_fast = max_pool_forward_fast(x, pool_param)
t2 = time()
print('Testing pool_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('fast: %fs' % (t2 - t1))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('difference: ', rel_error(out_naive, out_fast))
t0 = time()
dx_naive = max_pool_backward_naive(dout, cache_naive)
t1 = time()
dx_fast = max_pool_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting pool_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('dx difference: ', rel_error(dx_naive, dx_fast))
```
# Convolutional "sandwich" layers
Previously we introduced the concept of "sandwich" layers that combine multiple operations into commonly used patterns. In the file `layers/layer_utils.py`, you will find sandwich layers that implement a few commonly used patterns for convolutional networks.
```
from layers.layer_utils import conv_relu_pool_forward, conv_relu_pool_backward
np.random.seed(231)
x = np.random.randn(2, 3, 16, 16)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
out, cache = conv_relu_pool_forward(x, w, b, conv_param, pool_param)
dx, dw, db = conv_relu_pool_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], b, dout)
print('Testing conv_relu_pool')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
from layers.layer_utils import conv_relu_forward, conv_relu_backward
np.random.seed(231)
x = np.random.randn(2, 3, 8, 8)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
out, cache = conv_relu_forward(x, w, b, conv_param)
dx, dw, db = conv_relu_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_forward(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_forward(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_forward(x, w, b, conv_param)[0], b, dout)
print('Testing conv_relu:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
```
# Three-layer ConvNet
Now that you have implemented all the necessary layers, we can put them together into a simple convolutional network.
Open the file `classifiers/cnn.py` and complete the implementation of the `ThreeLayerConvNet` class. Run the following cells to help you debug:
## Sanity check loss
After you build a new network, one of the first things you should do is sanity check the loss. When we use the softmax loss, we expect the loss for random weights (and no regularization) to be about `log(C)` for `C` classes. When we add regularization this should go up.
```
from classifiers.cnn import ThreeLayerConvNet
model = ThreeLayerConvNet()
N = 50
X = np.random.randn(N, 3, 32, 32)
y = np.random.randint(10, size=N)
loss, grads = model.loss(X, y)
print('Initial loss (no regularization): ', loss)
model.reg = 0.5
loss, grads = model.loss(X, y)
print('Initial loss (with regularization): ', loss)
print(np.log(10))
```
## Gradient check
After the loss looks reasonable, use numeric gradient checking to make sure that your backward pass is correct. When you use numeric gradient checking you should use a small amount of artifical data and a small number of neurons at each layer. Note: correct implementations may still have relative errors up to 1e-2.
```
from utils.gradient_check import eval_numerical_gradient
num_inputs = 2
input_dim = (3, 16, 16)
reg = 0.0
num_classes = 10
np.random.seed(231)
X = np.random.randn(num_inputs, *input_dim)
y = np.random.randint(num_classes, size=num_inputs)
model = ThreeLayerConvNet(num_filters=3, filter_size=3,
input_dim=input_dim, hidden_dim=7,
dtype=np.float64)
loss, grads = model.loss(X, y)
for param_name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
param_grad_num = eval_numerical_gradient(f, model.params[param_name], verbose=False, h=1e-6)
e = rel_error(param_grad_num, grads[param_name])
print('%s max relative error: %e' % (param_name, rel_error(param_grad_num, grads[param_name])))
```
## Overfit small data
A nice trick is to train your model with just a few training samples. You should be able to overfit small datasets, which will result in very high training accuracy and comparatively low validation accuracy.
```
from base.solver import Solver
np.random.seed(231)
num_train = 100
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
model = ThreeLayerConvNet(weight_scale=1e-2)
solver = Solver(model, small_data,
num_epochs=15, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=1)
solver.train()
```
Plotting the loss, training accuracy, and validation accuracy should show clear overfitting:
```
plt.subplot(2, 1, 1)
plt.plot(solver.loss_history, 'o')
plt.xlabel('iteration')
plt.ylabel('loss')
plt.subplot(2, 1, 2)
plt.plot(solver.train_acc_history, '-o')
plt.plot(solver.val_acc_history, '-o')
plt.legend(['train', 'val'], loc='upper left')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
```
## Train the net
By training the three-layer convolutional network for one epoch, you should achieve greater than 40% accuracy on the training set:
```
model = ThreeLayerConvNet(weight_scale=0.001, hidden_dim=500, reg=0.001)
solver = Solver(model, data,
num_epochs=1, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=20)
solver.train()
```
## Visualize Filters
You can visualize the first-layer convolutional filters from the trained network by running the following:
```
from utils.vis_utils import visualize_grid
grid = visualize_grid(model.params['W1'].transpose(0, 2, 3, 1))
plt.imshow(grid.astype('uint8'))
plt.axis('off')
plt.gcf().set_size_inches(5, 5)
plt.show()
```
# Spatial Batch Normalization
We already saw that batch normalization is a very useful technique for training deep fully-connected networks. Batch normalization can also be used for convolutional networks, but we need to tweak it a bit; the modification will be called "spatial batch normalization."
Normally batch-normalization accepts inputs of shape `(N, D)` and produces outputs of shape `(N, D)`, where we normalize across the minibatch dimension `N`. For data coming from convolutional layers, batch normalization needs to accept inputs of shape `(N, C, H, W)` and produce outputs of shape `(N, C, H, W)` where the `N` dimension gives the minibatch size and the `(H, W)` dimensions give the spatial size of the feature map.
If the feature map was produced using convolutions, then we expect the statistics of each feature channel to be relatively consistent both between different imagesand different locations within the same image. Therefore spatial batch normalization computes a mean and variance for each of the `C` feature channels by computing statistics over both the minibatch dimension `N` and the spatial dimensions `H` and `W`.
## Spatial batch normalization: forward
In the file `layers/layers.py`, implement the forward pass for spatial batch normalization in the function `spatial_batchnorm_forward`. Check your implementation by running the following:
```
from layers.layers import spatial_batchnorm_forward, spatial_batchnorm_backward
np.random.seed(231)
# Check the training-time forward pass by checking means and variances
# of features both before and after spatial batch normalization
N, C, H, W = 2, 3, 4, 5
x = 4 * np.random.randn(N, C, H, W) + 10
print('Before spatial batch normalization:')
print(' Shape: ', x.shape)
print(' Means: ', x.mean(axis=(0, 2, 3)))
print(' Stds: ', x.std(axis=(0, 2, 3)))
# Means should be close to zero and stds close to one
gamma, beta = np.ones(C), np.zeros(C)
bn_param = {'mode': 'train'}
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization:')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
# Means should be close to beta and stds close to gamma
gamma, beta = np.asarray([3, 4, 5]), np.asarray([6, 7, 8])
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization (nontrivial gamma, beta):')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
np.random.seed(231)
# Check the test-time forward pass by running the training-time
# forward pass many times to warm up the running averages, and then
# checking the means and variances of activations after a test-time
# forward pass.
N, C, H, W = 10, 4, 11, 12
bn_param = {'mode': 'train'}
gamma = np.ones(C)
beta = np.zeros(C)
for t in range(50):
x = 2.3 * np.random.randn(N, C, H, W) + 13
spatial_batchnorm_forward(x, gamma, beta, bn_param)
bn_param['mode'] = 'test'
x = 2.3 * np.random.randn(N, C, H, W) + 13
a_norm, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
# Means should be close to zero and stds close to one, but will be
# noisier than training-time forward passes.
print('After spatial batch normalization (test-time):')
print(' means: ', a_norm.mean(axis=(0, 2, 3)))
print(' stds: ', a_norm.std(axis=(0, 2, 3)))
```
## Spatial batch normalization: backward
In the file `layers/layers.py`, implement the backward pass for spatial batch normalization in the function `spatial_batchnorm_backward`. Run the following to check your implementation using a numeric gradient check:
```
np.random.seed(231)
N, C, H, W = 2, 3, 4, 5
x = 5 * np.random.randn(N, C, H, W) + 12
gamma = np.random.randn(C)
beta = np.random.randn(C)
dout = np.random.randn(N, C, H, W)
bn_param = {'mode': 'train'}
fx = lambda x: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fg = lambda a: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fb = lambda b: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
_, cache = spatial_batchnorm_forward(x, gamma, beta, bn_param)
dx, dgamma, dbeta = spatial_batchnorm_backward(dout, cache)
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))
```
| true |
code
| 0.507995 | null | null | null | null |
|
Wayne Nixalo - 2017-Jun-12 17:27
Code-Along of Lesson 5 JNB.
Lesson 5 NB: https://github.com/fastai/courses/blob/master/deeplearning1/nbs/lesson5.ipynb
[Lecture](https://www.youtube.com/watch?v=qvRL74L81lg)
```
import theano
%matplotlib inline
import sys, os
sys.path.insert(1, os.path.join('utils'))
import utils; reload(utils)
from utils import *
from __future__ import division, print_function
model_path = 'data/imdb/models/'
%mkdir -p $model_path # -p : make intermediate directories as needed
```
## Setup data
We're going to look at the IMDB dataset, which contains movie reviews from IMDB, along with their sentiment. Keras comes with some helpers for this dataset.
```
from keras.datasets import imdb
idx = imdb.get_word_index()
```
This is the word list:
```
idx_arr = sorted(idx, key=idx.get)
idx_arr[:10]
```
...and this is the mapping from id to word:
```
idx2word = {v: k for k, v in idx.iteritems()}
```
We download the reviews using code copied from keras.datasets:
```
# getting the dataset directly bc keras's versn makes some changes
path = get_file('imdb_full.pkl',
origin='https://s3.amazonaws.com/text-datasets/imdb_full.pkl',
md5_hash='d091312047c43cf9e4e38fef92437263')
f = open(path, 'rb')
(x_train, labels_train), (x_test, labels_test) = pickle.load(f)
# apparently cpickle can be x1000 faster than pickle? hmm
len(x_train)
```
Here's the 1st review. As you see, the words have been replaced by ids. The ids can be looked up in idx2word.
```
', '.join(map(str, x_train[0]))
```
The first word of the first review is 23022. Let's see what that is.
```
idx2word[23022]
x_train[0]
```
Here's the whole review, mapped from ids to words.
```
' '.join([idx2word[o] for o in x_train[0]])
```
The labels are 1 for positive, 0 for negative
```
labels_train[:10]
```
Reduce vocabulary size by setting rare words to max index.
```
vocab_size = 5000
trn = [np.array([i if i < vocab_size-1 else vocab_size-1 for i in s]) for s in x_train]
test = [np.array([i if i < vocab_size-1 else vocab_size-1 for i in s]) for s in x_test]
```
Look at distribution of lengths of sentences
```
lens = np.array(map(len, trn))
(lens.max(), lens.min(), lens.mean())
```
Pad (with zero) or truncate each sentence to make consistent length.
```
seq_len = 500
# keras.preprocessing.sequence
trn = sequence.pad_sequences(trn, maxlen=seq_len, value=0)
test = sequence.pad_sequences(test, maxlen=seq_len, value=0)
```
This results in nice rectangular matrices that can be passed to ML algorithms. Reviews shorter than 500 words are prepadded with zeros, those greater are truncated.
```
trn.shape
trn[0]
```
## Create simple models
### Single hidden layer NN
This simplest model that tends to give reasonable results is a single hidden layer net. So let's try that. Note that we can't expect to get any useful results by feeding word ids directly into a neural net - so instead we use an embedding to replace them with a vector of 32 (initially random) floats for each word in the vocab.
```
model = Sequential([
Embedding(vocab_size, 32, input_length=seq_len),
Flatten(),
Dense(100, activation='relu'),
Dropout(0.7),
Dense(1, activation='sigmoid')])
model.compile(loss='binary_crossentropy', optimizer=Adam(), metrics=['accuracy'])
model.summary()
# model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# redoing on Linux
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
```
The [Stanford paper](http://ai.stanford.edu/~amaas/papers/wvSent_acl2011.pdf) that this dataset is from cites a state of the art accuacy (without unlabelled data) of 0.883. So we're short of that, but on the right track.
### Single Conv layer with Max Pooling
A CNN is likely to work better, since it's designed to take advantage of ordered data. We'll need to use a 1D CNN, since a sequence of words is 1D.
```
# the embedding layer is always the first step in every NLP model
# --> after that layer, you don't have words anymore: vectors
conv1 = Sequential([
Embedding(vocab_size, 32, input_length=seq_len, dropout=0.2),
Dropout(0.2),
Convolution1D(64, 5, border_mode='same', activation='relu'),
Dropout(0.2),
MaxPooling1D(),
Flatten(),
Dense(100, activation='relu'),
Dropout(0.7),
Dense(1, activation='sigmoid')])
conv1.summary()
conv1.compile(loss='binary_crossentropy', optimizer=Adam(), metrics=['accuracy'])
# conv1.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=4, batch_size=64)
# redoing on Linux w/ GPU
conv1.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=4, batch_size=64)
```
That's well past the Stanford paper's accuracy - another win for CNNs!
*Heh, the above take a lot longer than 4s on my Mac*
```
conv1.save_weights(model_path + 'conv1.h5')
# conv1.load_weights(model_path + 'conv1.h5')
```
## Pre-trained Vectors
You may want to look at wordvectors.ipynb before moving on.
In this section, we replicate the previous CNN, but using pre-trained embeddings.
```
def get_glove_dataset(dataset):
"""Download the requested glove dataset from files.fast.ai
and return a location that can be passed to load_vectors.
"""
# see wordvectors.ipynb for info on how these files were
# generated from the original glove data.
md5sums = {'6B.50d' : '8e1557d1228decbda7db6dfd81cd9909',
'6B.100d': 'c92dbbeacde2b0384a43014885a60b2c',
'6B.200d': 'af271b46c04b0b2e41a84d8cd806178d',
'6B.300d': '30290210376887dcc6d0a5a6374d8255'}
glove_path = os.path.abspath('data/glove.6B/results')
%mkdir -p $glove_path
return get_file(dataset,
'https://files.fast.ai/models/glove/' + dataset + '.tgz',
cache_subdir=glove_path,
md5_hash=md5sums.get(dataset, None),
untar=True)
# not able to download from above, so using code from wordvectors_CodeAlong.ipynb to load
def get_glove(name):
with open(path+ 'glove.' + name + '.txt', 'r') as f: lines = [line.split() for line in f]
words = [d[0] for d in lines]
vecs = np.stack(np.array(d[1:], dtype=np.float32) for d in lines)
wordidx = {o:i for i,o in enumerate(words)}
save_array(res_path+name+'.dat', vecs)
pickle.dump(words, open(res_path+name+'_words.pkl','wb'))
pickle.dump(wordidx, open(res_path+name+'_idx.pkl','wb'))
# # adding return filename
# return res_path + name + '.dat'
def load_glove(loc):
return (load_array(loc + '.dat'),
pickle.load(open(loc + '_words.pkl', 'rb')),
pickle.load(open(loc + '_idx.pkl', 'rb')))
def load_vectors(loc):
return (load_array(loc + '.dat'),
pickle.load(open(loc + '_words.pkl', 'rb')),
pickle.load(open(loc + '_idx.pkl', 'rb')))
# apparently pickle is a `bit-serializer` or smth like that?
# this isn't working, so instead..
vecs, words, wordidx = load_vectors(get_glove_dataset('6B.50d'))
# trying to load the glove data I downloaded directly, before:
vecs, words, wordix = load_vectors('data/glove.6B/' + 'glove.' + '6B.50d' + '.txt')
# vecs, words, wordix = load_vectors('data/glove.6B/' + 'glove.' + '6B.50d' + '.tgz')
# not successful. get_file(..) returns filepath as '.tar' ? as .tgz doesn't work.
# ??get_file # keras.utils.data_utils.get_file(..)
# that doesn't work either, but method from wordvectors JNB worked so:
path = 'data/glove.6B/'
# res_path = path + 'results/'
res_path = 'data/imdb/results/'
%mkdir -p $res_path
# this way not working; so will pull vecs,words,wordidx manually:
# vecs, words, wordidx = load_vectors(get_glove('6B.50d'))
get_glove('6B.50d')
vecs, words, wordidx = load_glove(res_path + '6B.50d')
# NOTE: yay it worked..!..
def create_emb():
n_fact = vecs.shape[1]
emb = np.zeros((vocab_size, n_fact))
for i in xrange(1, len(emb)):
word = idx2word[i]
if word and re.match(r"^[a-zA-Z0-9\-]*$", word):
src_idx = wordidx[word]
emb[i] = vecs[src_idx]
else:
# If we can't find the word in glove, randomly initialize
emb[i] = normal(scale=0.6, size=(n_fact,))
# This is our "rare word" id - we want to randomly initialize
emb[-1] = normal(scale=0.6, size=(n_fact,))
emb /= 3
return emb
emb = create_emb()
# this embedding matrix is now the glove word vectors, indexed according to
# the imdb dataset.
```
We pass out embedding matrix to the Embedding constructor, and set it to non-trainable.
```
model = Sequential([
Embedding(vocab_size, 50, input_length=seq_len, dropout=0.2,
weights=[emb], trainable=False),
Dropout(0.25),
Convolution1D(64, 5, border_mode='same', activation='relu'),
Dropout(0.25),
MaxPooling1D(),
Flatten(),
Dense(100, activation='relu'),
Dropout(0.7),
Dense(1, activation='sigmoid')])
# this is copy-pasted of the previous code, with the addition of the
# weights being the pre-trained embeddings.
# We figure the weights are pretty good, so we'll initially set
# trainable to False. Will finetune due to some words missing or etc..
model.compile(loss='binary_crossentropy', optimizer=Adam(), metrics=['accuracy'])
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# running on GPU
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
```
We've already beated our previous model! But let's fine-tune the embedding weights - especially since the words we couldn't find in glove just have random embeddings.
```
model.layers[0].trainable=True
model.optimizer.lr=1e-4
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# running on GPU
model.optimizer.lr=1e-4
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# the above was supposed to be 3 total epochs but I did 4 by mistake
model.save_weights(model_path+'glove50.h5')
```
## Multi-size CNN
This is an implementation of a multi-size CNN as show in Ben Bowles' [blog post.](https://quid.com/feed/how-quid-uses-deep-learning-with-small-data)
```
from keras.layers import Merge
```
We use the functional API to create multiple ocnv layers of different sizes, and then concatenate them.
```
graph_in = Input((vocab_size, 50))
convs = [ ]
for fsz in xrange(3, 6):
x = Convolution1D(64, fsz, border_mode='same', activation='relu')(graph_in)
x = MaxPooling1D()(x)
x = Flatten()(x)
convs.append(x)
out = Merge(mode='concat')(convs)
graph = Model(graph_in, out)
emb = create_emb()
```
We then replace the conv/max-pool layer in our original CNN with the concatenated conv layers.
```
model = Sequential ([
Embedding(vocab_size, 50, input_length=seq_len, dropout=0.2, weights=[emb]),
Dropout(0.2),
graph,
Dropout(0.5),
Dense(100, activation='relu'),
Dropout(0.7),
Dense(1, activation='sigmoid')
])
model.compile(loss='binary_crossentropy', optimizer=Adam(), metrics=['accuracy'])
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# on GPU
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
```
Interestingly, I found that in this case I got best results when I started the embedding layer as being trainable, and then set it to non-trainable after a couple of epochs. I have no idea why! *hmmm*
```
model.layers[0].trainable=False
model.optimizer.lr=1e-5
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
# on gpu
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=2, batch_size=64)
conv1.save_weights(model_path + 'conv1_1.h5')
# conv1.load_weights(model_path + 'conv1.h5')
```
This more complex architecture has given us another boost in accuracy.
## LSTM
We haven't covered this bit yet!
```
model = Sequential([
Embedding(vocab_size, 32, input_length=seq_len, mask_zero=True,
W_regularizer=l2(1e-6), dropout=0.2),
LSTM(100, consume_less='gpu'),
Dense(1, activation='sigmoid')])
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.summary()
model.fit(trn, labels_train, validation_data=(test, labels_test), nb_epoch=5, batch_size=64)
# NOTE: if this took 100s/epoch using TitanX's or Tesla K80s ... use the Linux machine for this
conv1.save_weights(model_path + 'LSTM_1.h5')
```
| true |
code
| 0.607197 | null | null | null | null |
|
# Barycenters of persistence diagrams
Theo Lacombe
https://tlacombe.github.io/
## A statistical descriptor in the persistence diagram space
This tutorial presents the concept of barycenter, or __Fréchet mean__, of a family of persistence diagrams. Fréchet means, in the context of persistence diagrams, were initially introduced in the seminal papers:
- Probability measures on the space of persistence diagrams, by Mileyko, Mukherjee, and Harer. https://math.hawaii.edu/~yury/papers/probpers.pdf ,
- Fréchet means for distributions of persistence diagrams, by Turner, Mileyko, Mukherjee and Harer, https://arxiv.org/pdf/1206.2790.pdf
and later studied in https://arxiv.org/pdf/1901.03048.pdf (theoretical viewpoint) and https://arxiv.org/pdf/1805.08331.pdf (computational viewpoint).
## Motivation and mathematical formulation
Recall that given an object $X$, say a point cloud embedded in the Euclidean space $\mathbb{R}^d$, one can compute its persistence diagram $\mathrm{Dgm}(X)$ which is a point cloud supported on a half-plane $\Omega \subset \mathbb{R}^2$ (see this tutorial https://github.com/GUDHI/TDA-tutorial/blob/master/Tuto-GUDHI-persistence-diagrams.ipynb for an introduction to persistence diagrams).
Now, consider that instead of building one diagram $\mathrm{Dgm}(X)$ from one object $X$, you observe a collection of objects $X_1 \dots X_n$ and compute their respective diagrams, let's call them $\mu_1 \dots \mu_n$. How can you build a statistical summary of this information?
Fréchet means is one way to do so. It mimics the notion of arithmetic mean in metric spaces. First, recall that the space of persistence diagrams, equipped with either the bottleneck (https://gudhi.inria.fr/python/latest/bottleneck_distance_user.html) or the Wasserstein (https://gudhi.inria.fr/python/latest/wasserstein_distance_user.html) metrics is **not** a linear space. Therefore, the notion of arithmetic mean cannot be faithfully transposed to the context of persistence diagrams.
To overcome this limitation, one relies on _Fréchet means_. In Euclidean spaces, one of the characterization of the arithmetic mean
$$ \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i $$
of a sample $x_1 \dots x_n \in \mathbb{R}^d$ is that it minimizes the _variance_ of the sample, that is the map
$$\mathcal{E} : x \mapsto \sum_{i=1}^n \|x - x_i \|_2^2 $$
has a unique minimizer, that turns out to be $\overline{x}$.
Although the former formula does not make sense in general metric spaces, the map $\mathcal{E}$ can still be defined, in particular in the context of persistence diagrams. Therefore, a _Fréchet mean_ of $\mu_1 \dots \mu_n$ is any minimizer, should it exist, of the map
$$ \mathcal{E} : \mu \mapsto \sum_{i=1}^n d_2(\mu, \mu_i)^2, $$
where $d_2$ denotes the so-called Wasserstein-2 distance between persistence diagrams.
It has been proved that Fréchet means of persistence diagrams always exist in the context of averaging finitely many diagrams. Their computation remains however challenging.
## A Lagrangian algorithm
We showcase here one of the algorithm used to _estimate_ barycenters of a (finite) family of persistence diagrams (note that their exact computation is intractable in general). This algorithm was introduced by Turner et al. (https://arxiv.org/pdf/1206.2790.pdf) and adopts a _lagrangian_ perspective. Roughly speaking (see details in their paper), this algorithm consists in iterating the following:
- Let $\mu$ be a current estimation of the barycenter of $\mu_1 \dots \mu_n$.
- (1) Compute $\sigma_i$ ($1 \leq i \leq n$) the optimal (partial) matching between $\mu$ and $\mu_i$.
- (2) For each point $x$ of the diagram $\mu$, apply $x \mapsto \mathrm{mean}((\sigma_i(x))_i)$, where $\mathrm{mean}$ is the arithemtic mean in $\mathbb{R}^2$.
- (3) If $\mu$ didn't change, return $\mu$. Otherwise, go back to (1).
This algorithm is proved to converge ($\mathcal{E}$ decreases at each iteration) to a _local_ minimum of the map $\mathcal{E}$. Indeed, the map $\mathcal{E}$ is **not convex**, which can unfortunately lead to arbritrary bad local minima. Furthermore, its combinatorial aspect (one must compute $n$ optimal partial matching at each iteration step), makes it too computationally expensive when dealing with a large number of large diagrams. It is however a fairly decent attempt when dealing with few diagrams with few points.
The solution $\mu^*$ returned by the algorithm is a persistence diagram with the following property:
each point $x \in \mu^*$ is the mean of one point (or the diagonal) $\sigma_i(x)$ in each of the $\mu_i$s. These are called _groupings_.
**Note:** This algorithm is said to be based on a _Lagrangian_ approach by opposition to _Eulerian_ , from fluid dynamics formalism (https://en.wikipedia.org/wiki/Lagrangian_and_Eulerian_specification_of_the_flow_field). Roughly speaking, Lagrangian models track the position of each particule individually (here, the points in the barycenter estimate), while Eulerian models instead measure the quantity of mass that is present in each location of the space. We will present in a next version of this tutorial an Eulerian approach to solve (approximately) this problem.
## Illustration
### Imports and preliminary tests
```
import gudhi
print("Current gudhi version:", gudhi.__version__)
print("Version >= 3.2.0 is required for this tutorial")
# Note: %matplotlib notebook allows for iteractive 3D plot.
#%matplotlib notebook
%matplotlib inline
from gudhi.wasserstein.barycenter import lagrangian_barycenter as bary
from gudhi.persistence_graphical_tools import plot_persistence_diagram
import numpy as np
import matplotlib.pyplot as plt
```
### Exemple
Let us consider three persistence diagrams.
```
diag1 = np.array([[0., 1.], [0, 2], [1, 2], [1.32, 1.87], [0.7, 1.2]])
diag2 = np.array([[0, 1.5], [0.5, 2], [1.2, 2], [1.3, 1.8], [0.4, 0.8]])
diag3 = np.array([[0.2, 1.1], [0.1, 2.2], [1.3, 2.1], [0.5, 0.9], [0.6, 1.1]])
diags = [diag1, diag2, diag3]
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111)
colors=['r', 'b', 'g']
for diag, c in zip(diags, colors):
plot_persistence_diagram(diag, axes=ax, colormap=c)
ax.set_title("Set of 3 persistence diagrams", fontsize=22)
```
Now, let us compute (more precisely, estimate) a barycenter of `diags`.
Using the verbose option, we can get access to a `log` (dictionary) that contains complementary informations.
```
b, log = bary(diags,
init=0,
verbose=True) # we initialize our estimation on the first diagram (the red one.)
print("Energy reached by this estimation of the barycenter: E=%.2f." %log['energy'])
print("Convergenced made after %s steps." %log['nb_iter'])
```
Using the `groupings` provided in logs, we can have a better visibility on what is happening.
```
G = log["groupings"]
def proj_on_diag(x):
return ((x[1] + x[0]) / 2, (x[1] + x[0]) / 2)
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111)
colors = ['r', 'b', 'g']
for diag, c in zip(diags, colors):
plot_persistence_diagram(diag, axes=ax, colormap=c)
def plot_bary(b, diags, groupings, axes):
# n_y = len(Y.points)
for i in range(len(diags)):
indices = G[i]
n_i = len(diags[i])
for (y_j, x_i_j) in indices:
y = b[y_j]
if y[0] != y[1]:
if x_i_j >= 0: # not mapped with the diag
x = diags[i][x_i_j]
else: # y_j is matched to the diagonal
x = proj_on_diag(y)
ax.plot([y[0], x[0]], [y[1], x[1]], c='black',
linestyle="dashed")
ax.scatter(b[:,0], b[:,1], color='purple', marker='d', label="barycenter (estim)")
ax.legend()
ax.set_title("Set of diagrams and their barycenter", fontsize=22)
plot_bary(b, diags, G, axes=ax)
```
Note that, as the problem is not convex, the output (and its quality, i.e. energy) might depend on optimization.
Energy: lower is better.
```
fig, axs = plt.subplots(1, 3, figsize=(15, 5))
colors = ['r', 'b', 'g']
for i, ax in enumerate(axs):
for diag, c in zip(diags, colors):
plot_persistence_diagram(diag, axes=ax, colormap=c)
b, log = bary(diags, init=i, verbose=True)
e = log["energy"]
G = log["groupings"]
# print(G)
plot_bary(b, diags, groupings=G, axes=ax)
ax.set_title("Barycenter estim with init=%s. Energy: %.2f" %(i, e), fontsize=14)
```
| true |
code
| 0.576721 | null | null | null | null |
|
# 基于 BipartiteGraphSage 的二部图无监督学习
二部图是电子商务推荐场景中很常见的一种图,GraphScope提供了针对二部图处理学习任务的模型。本次教程,我们将会展示GraphScope如何使用BipartiteGraphSage算法在二部图上训练一个无监督学习模型。
本次教程的学习任务是链接预测,通过计算在图中用户顶点和商品顶点之间存在边的概率来预测链接。
在这一任务中,我们使用GraphScope内置的BipartiteGraphSage算法在 [U2I](http://graph-learn-dataset.oss-cn-zhangjiakou.aliyuncs.com/u2i.zip) 数据集上训练一个模型,这一训练模型可以用来预测用户顶点和商品顶点之间的链接。这一任务可以被看作在一个异构链接网络上的无监督训练任务。
在这一任务中,BipartiteGraphSage算法会将图中的结构信息和属性信息压缩为每个节点上的低维嵌入向量,这些嵌入和表征可以进一步用来预测节点间的链接。
这一教程将会分为以下几个步骤:
- 启动GraphScope的学习引擎,并将图关联到引擎上
- 使用内置的GCN模型定义训练过程,并定义相关的超参
- 开始训练
```
# Install graphscope package if you are NOT in the Playground
!pip3 install graphscope
!pip3 uninstall -y importlib_metadata # Address an module conflict issue on colab.google. Remove this line if you are not on colab.
# Import the graphscope module.
import graphscope
graphscope.set_option(show_log=False) # enable logging
# Load u2i dataset
from graphscope.dataset import load_u2i
graph = load_u2i()
```
## Launch learning engine
然后,我们需要定义一个特征列表用于图的训练。训练特征集合必须从点的属性集合中选取。在这个例子中,我们选择了 "feature" 属性作为训练特征集,这一特征集也是 U2I 数据中用户顶点和商品顶点的特征集。
借助定义的特征列表,接下来,我们使用 [graphlearn](https://graphscope.io/docs/reference/session.html#graphscope.Session.graphlearn) 方法来开启一个学习引擎。
在这个例子中,我们在 "graphlearn" 方法中,指定在数据中 "u" 类型的顶点和 "i" 类型顶点和 "u-i" 类型边上进行模型训练。
```
# launch a learning engine.
lg = graphscope.graphlearn(
graph,
nodes=[("u", ["feature"]), ("i", ["feature"])],
edges=[(("u", "u-i", "i"), ["weight"]), (("i", "u-i_reverse", "u"), ["weight"])],
)
```
这里我们使用内置的`BipartiteGraphSage`模型定义训练过程。你可以在 [Graph Learning Model](https://graphscope.io/docs/learning_engine.html#data-model) 获取更多内置学习模型的信息。
在本次示例中,我们使用 tensorflow 作为神经网络后端训练器。
```
import numpy as np
import tensorflow as tf
import graphscope.learning
from graphscope.learning.examples import BipartiteGraphSage
from graphscope.learning.graphlearn.python.model.tf.optimizer import get_tf_optimizer
from graphscope.learning.graphlearn.python.model.tf.trainer import LocalTFTrainer
# Unsupervised GraphSage.
def train(config, graph):
def model_fn():
return BipartiteGraphSage(
graph,
config["batch_size"],
config["hidden_dim"],
config["output_dim"],
config["hops_num"],
config["u_neighs_num"],
config["i_neighs_num"],
u_features_num=config["u_features_num"],
u_categorical_attrs_desc=config["u_categorical_attrs_desc"],
i_features_num=config["i_features_num"],
i_categorical_attrs_desc=config["i_categorical_attrs_desc"],
neg_num=config["neg_num"],
use_input_bn=config["use_input_bn"],
act=config["act"],
agg_type=config["agg_type"],
need_dense=config["need_dense"],
in_drop_rate=config["drop_out"],
ps_hosts=config["ps_hosts"],
)
graphscope.learning.reset_default_tf_graph()
trainer = LocalTFTrainer(
model_fn,
epoch=config["epoch"],
optimizer=get_tf_optimizer(
config["learning_algo"], config["learning_rate"], config["weight_decay"]
),
)
trainer.train()
u_embs = trainer.get_node_embedding("u")
np.save("u_emb", u_embs)
i_embs = trainer.get_node_embedding("i")
np.save("i_emb", i_embs)
# Define hyperparameters
config = {
"batch_size": 128,
"hidden_dim": 128,
"output_dim": 128,
"u_features_num": 1,
"u_categorical_attrs_desc": {"0": ["u_id", 10000, 64]},
"i_features_num": 1,
"i_categorical_attrs_desc": {"0": ["i_id", 10000, 64]},
"hops_num": 1,
"u_neighs_num": [10],
"i_neighs_num": [10],
"neg_num": 10,
"learning_algo": "adam",
"learning_rate": 0.001,
"weight_decay": 0.0005,
"epoch": 5,
"use_input_bn": True,
"act": tf.nn.leaky_relu,
"agg_type": "gcn",
"need_dense": True,
"drop_out": 0.0,
"ps_hosts": None,
}
```
## 执行训练过程
在定义完训练过程和超参后,现在我们可以使用学习引擎和定义的超参开始训练过程。
```
train(config, lg)
```
| true |
code
| 0.694549 | null | null | null | null |
|
# Object Detection @Edge with SageMaker Neo + Pytorch Yolov5
**SageMaker Studio Kernel**: Data Science
In this exercise you'll:
- Get a pre-trained model: Yolov5
- Prepare the model to compile it with Neo
- Compile the model for the target: **X86_64**
- Get the optimized model and run a simple local test
### install dependencies
```
!apt update -y && apt install -y libgl1
!pip install torch==1.7.0 torchvision==0.8.0 opencv-python dlr==1.8.0
```
## 1) Get a pre-trained model and export it to torchscript
-> SagMaker Neo expectes the model in the traced format
```
import os
import urllib.request
if not os.path.isdir('yolov5'):
!git clone https://github.com/ultralytics/yolov5 && \
cd yolov5 && git checkout v5.0 && \
git apply ../../models/01_YoloV5/01_Pytorch/yolov5_inplace.patch
if not os.path.exists('yolov5s.pt'):
urllib.request.urlretrieve('https://github.com/ultralytics/yolov5/releases/download/v5.0/yolov5s.pt', 'yolov5s.pt')
import torch.nn as nn
import torch
import sys
sys.path.insert(0, 'yolov5')
model = torch.load('yolov5s.pt')['model'].float().cpu()
## We need to replace these two activation functions to make it work with TVM.
# SiLU https://arxiv.org/pdf/1606.08415.pdf ----------------------------------------------------------------------------
class SiLU(nn.Module): # export-friendly version of nn.SiLU()
@staticmethod
def forward(x):
return x * torch.sigmoid(x)
class Hardswish(nn.Module): # export-friendly version of nn.Hardswish()
@staticmethod
def forward(x):
# return x * F.hardsigmoid(x) # for torchscript and CoreML
return x * F.hardtanh(x + 3, 0., 6.) / 6. # for torchscript, CoreML and ONNX
for k,m in model.named_modules():
t = type(m)
layer_name = f"{t.__module__}.{t.__name__}"
if layer_name == 'models.common.Conv': # assign export-friendly activations
if isinstance(m.act, nn.Hardswish):
m.act = Hardswish()
elif isinstance(m.act, nn.SiLU):
m.act = SiLU()
img_size=640
inp = torch.rand(1,3,img_size,img_size).float().cpu()
model.eval()
p = model(inp)
model_trace = torch.jit.trace(model, inp, strict=False)
model_trace.save('model.pth')
```
## 2) Create a package with the model and upload to S3
```
import tarfile
import sagemaker
sagemaker_session = sagemaker.Session()
model_name='yolov5'
with tarfile.open("model.tar.gz", "w:gz") as f:
f.add("model.pth")
f.list()
s3_uri = sagemaker_session.upload_data('model.tar.gz', key_prefix=f'{model_name}/model')
print(s3_uri)
```
## 3) Compile the model with SageMaker Neo (X86_64)
```
import time
import boto3
import sagemaker
role = sagemaker.get_execution_role()
sm_client = boto3.client('sagemaker')
compilation_job_name = f'{model_name}-pytorch-{int(time.time()*1000)}'
sm_client.create_compilation_job(
CompilationJobName=compilation_job_name,
RoleArn=role,
InputConfig={
'S3Uri': s3_uri,
'DataInputConfig': f'{{"input": [1,3,{img_size},{img_size}]}}',
'Framework': 'PYTORCH'
},
OutputConfig={
'S3OutputLocation': f's3://{sagemaker_session.default_bucket()}/{model_name}-pytorch/optimized/',
'TargetPlatform': {
'Os': 'LINUX',
'Arch': 'X86_64'
}
},
StoppingCondition={ 'MaxRuntimeInSeconds': 900 }
)
while True:
resp = sm_client.describe_compilation_job(CompilationJobName=compilation_job_name)
if resp['CompilationJobStatus'] in ['STARTING', 'INPROGRESS']:
print('Running...')
else:
print(resp['CompilationJobStatus'], compilation_job_name)
break
time.sleep(5)
```
## 4) Download the compiled model
```
output_model_path = f's3://{sagemaker_session.default_bucket()}/{model_name}-pytorch/optimized/model-LINUX_X86_64.tar.gz'
!aws s3 cp $output_model_path /tmp/model.tar.gz
!rm -rf model_object_detection && mkdir model_object_detection
!tar -xzvf /tmp/model.tar.gz -C model_object_detection
```
## 5) Run the model locally
```
import urllib.request
urllib.request.urlretrieve('https://i2.wp.com/petcaramelo.com/wp-content/uploads/2020/05/doberman-cores.jpg', 'dogs.jpg')
%matplotlib inline
import numpy as np
import cv2
import matplotlib.pyplot as plt
import os
# Classes
labels= ['person', 'bicycle', 'car', 'motorcycle', 'airplane', 'bus', 'train', 'truck', 'boat', 'traffic light',
'fire hydrant', 'stop sign', 'parking meter', 'bench', 'bird', 'cat', 'dog', 'horse', 'sheep', 'cow',
'elephant', 'bear', 'zebra', 'giraffe', 'backpack', 'umbrella', 'handbag', 'tie', 'suitcase', 'frisbee',
'skis', 'snowboard', 'sports ball', 'kite', 'baseball bat', 'baseball glove', 'skateboard', 'surfboard',
'tennis racket', 'bottle', 'wine glass', 'cup', 'fork', 'knife', 'spoon', 'bowl', 'banana', 'apple',
'sandwich', 'orange', 'broccoli', 'carrot', 'hot dog', 'pizza', 'donut', 'cake', 'chair', 'couch',
'potted plant', 'bed', 'dining table', 'toilet', 'tv', 'laptop', 'mouse', 'remote', 'keyboard', 'cell phone',
'microwave', 'oven', 'toaster', 'sink', 'refrigerator', 'book', 'clock', 'vase', 'scissors', 'teddy bear',
'hair drier', 'toothbrush'] # class names
```
### load the model using the runtime DLR
```
import dlr
# load the model (CPU x86_64)
model = dlr.DLRModel('model_object_detection', 'cpu')
import sys
sys.path.insert(0,'../models/01_YoloV5/01_Pytorch')
from processing import Processor
proc = Processor(labels, threshold=0.25, iou_threshold=0.45)
img = cv2.imread('dogs.jpg')
x = proc.pre_process(img)
y = model.run(x)[0]
(bboxes, scores, cids), image = proc.post_process(y, img.shape, img.copy())
plt.figure(figsize=(10,10))
plt.imshow(image)
```
# Done! :)
| true |
code
| 0.718011 | null | null | null | null |
|
# Imports
```
import sys
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler
from sklearn.externals import joblib
import torch
import torchvision
import torchvision.transforms as transforms
import pickle
import pandas as pd
import os
sys.path.append('../../Utils')
from SVC_Utils import *
```
# Load CIFAR100
```
def unpickle(file):
with open(file, 'rb') as fo:
res = pickle.load(fo, encoding='bytes')
return res
transform = transforms.Compose(
[transforms.ToTensor()])
#training data;
trainset = torchvision.datasets.CIFAR100(root='./data', train=True, download=True, transform=transforms.ToTensor())
trainloader = torch.utils.data.DataLoader(trainset, batch_size=int((trainset.__len__())/2), shuffle=True, num_workers=2)
trainloader_final=torch.utils.data.DataLoader(trainset, batch_size=trainset.__len__(), shuffle=True, num_workers=2)
#test data
testset = torchvision.datasets.CIFAR100(root='./data', train=False, download=True, transform=transforms.ToTensor())
testloader = torch.utils.data.DataLoader(testset, batch_size=testset.__len__(),shuffle=False, num_workers=2)
classes=None
traininputs, traintargets=load(trainloader)
testinputs, testtargets=load(testloader)
ftraininputs, ftraintargets=load(trainloader_final)
```
# Model Training
```
n_components=180
C_range=np.logspace(0,1,2)
gamma_range=np.logspace(-2,-1,2)
clfs=hp_grid(n_components=n_components, C_range=C_range, gamma_range=gamma_range)
#fitted_clfs=train_grid(clfs, traininputs, traintargets)
fitted_clfs=joblib.load('fclfs')
```
# Model Testing/Evaluation
```
#Stores training and testing accuracies in matrices (Rows: C_range, Cols: gamma_range)
train_accs=np.random.randn(len(C_range),len(gamma_range))
test_accs=np.random.randn(len(C_range),len(gamma_range))
test_preds=[]
k=0;
for i in range(len(C_range)):
for j in range(len(gamma_range)):
train_accs[i,j]=predict_eval(fitted_clfs[k], traininputs, traintargets, training=True)[1]
preds, test_accs[i,j]=predict_eval(fitted_clfs[k], testinputs, testtargets)
test_preds.append(preds)
k+=1
idx=['C = 1','C = 10']
cols=['gamma = .01','gamma = .1']
trainacc_df=pd.DataFrame(data=train_accs, index=idx, columns=cols)
testacc_df=pd.DataFrame(data=test_accs, index=idx, columns=cols)
#training accuracy for C/gamma grid
trainacc_df.style.background_gradient(cmap='GnBu')
#test accuracy for C/gamma grid
testacc_df.style.background_gradient(cmap='GnBu')
```
# Save Model
```
maxacc, gen=maxacc_gen(test_accs, train_accs, clfs)
fn_max_acc = 'SVMCIFAR100_maxacc_proba.pkl'
fn_gen = 'SVMCIFAR100_gen_proba.pkl'
print(maxacc)
save_proba(fn_max_acc, maxacc, traininputs, traintargets)
save_proba(fn_gen, gen, traininputs, traintargets)
```
| true |
code
| 0.47792 | null | null | null | null |
|
# Table of Contents
<p><div class="lev1 toc-item"><a href="#Initialize-Environment" data-toc-modified-id="Initialize-Environment-1"><span class="toc-item-num">1 </span>Initialize Environment</a></div><div class="lev1 toc-item"><a href="#Load-Toy-Data" data-toc-modified-id="Load-Toy-Data-2"><span class="toc-item-num">2 </span>Load Toy Data</a></div><div class="lev1 toc-item"><a href="#Measure-Functional-Connectivity" data-toc-modified-id="Measure-Functional-Connectivity-3"><span class="toc-item-num">3 </span>Measure Functional Connectivity</a></div><div class="lev1 toc-item"><a href="#Optimize-Dynamic-Subgraphs-Parameters" data-toc-modified-id="Optimize-Dynamic-Subgraphs-Parameters-4"><span class="toc-item-num">4 </span>Optimize Dynamic Subgraphs Parameters</a></div><div class="lev2 toc-item"><a href="#Generate-Cross-Validation-Parameter-Sets" data-toc-modified-id="Generate-Cross-Validation-Parameter-Sets-41"><span class="toc-item-num">4.1 </span>Generate Cross-Validation Parameter Sets</a></div><div class="lev2 toc-item"><a href="#Run-NMF-Cross-Validation-Parameter-Sets" data-toc-modified-id="Run-NMF-Cross-Validation-Parameter-Sets-42"><span class="toc-item-num">4.2 </span>Run NMF Cross-Validation Parameter Sets</a></div><div class="lev2 toc-item"><a href="#Visualize-Quality-Measures-of-Search-Space" data-toc-modified-id="Visualize-Quality-Measures-of-Search-Space-43"><span class="toc-item-num">4.3 </span>Visualize Quality Measures of Search Space</a></div><div class="lev1 toc-item"><a href="#Detect-Dynamic-Subgraphs" data-toc-modified-id="Detect-Dynamic-Subgraphs-5"><span class="toc-item-num">5 </span>Detect Dynamic Subgraphs</a></div><div class="lev2 toc-item"><a href="#Stochastic-Factorization-with-Consensus" data-toc-modified-id="Stochastic-Factorization-with-Consensus-51"><span class="toc-item-num">5.1 </span>Stochastic Factorization with Consensus</a></div><div class="lev2 toc-item"><a href="#Plot--Subgraphs-and-Spectrotemporal-Dynamics" data-toc-modified-id="Plot--Subgraphs-and-Spectrotemporal-Dynamics-52"><span class="toc-item-num">5.2 </span>Plot Subgraphs and Spectrotemporal Dynamics</a></div>
# Initialize Environment
```
from __future__ import division
import os
os.environ['MKL_NUM_THREADS'] = '1'
os.environ['NUMEXPR_NUM_THREADS'] = '1'
os.environ['OMP_NUM_THREADS'] = '1'
import sys
# Data manipulation
import numpy as np
import scipy.io as io
import NMF
# Echobase
sys.path.append('../Echobase/')
import Echobase
# Plotting
import matplotlib.pyplot as plt
import seaborn as sns
```
# Load Toy Data
```
# df contains the following keys:
# -- evData contains ECoG with dims: n_sample x n_channels
# -- Fs contains sampling frequency: 1 x 1
# -- channel_lbl contains strings of channel labels with dims: n_channels
# -- channel_ix_soz contains indices of seizure-onset channels: n_soz
df = io.loadmat('./ToyData/Seizure_ECoG.mat')
evData = df['evData']
fs = int(df['Fs'][0,0])
n_sample, n_chan = evData.shape
```
# Measure Functional Connectivity
```
def compute_dynamic_windows(n_sample, fs, win_dur=1.0, win_shift=1.0):
"""
Divide samples into bins based on window duration and shift.
Parameters
----------
n_sample: int
Number of samples
fs: int
Sampling frequency
win_dur: float
Duration of the dynamic window
win_shift: float
Shift of the dynamic window
Returns
-------
win_ix: ndarray with dims: (n_win, n_ix)
"""
n_samp_per_win = int(fs * win_dur)
n_samp_per_shift = int(fs * win_shift)
curr_ix = 0
win_ix = []
while (curr_ix+n_samp_per_win) <= n_sample:
win_ix.append(np.arange(curr_ix, curr_ix+n_samp_per_win))
curr_ix += n_samp_per_shift
win_ix = np.array(win_ix)
return win_ix
# Transform to a configuration matrix (n_window x n_connection)
triu_ix, triu_iy = np.triu_indices(n_chan, k=1)
n_conn = len(triu_ix)
# Measure dynamic functional connectivity using Echobase
#win_bin = compute_dynamic_windows(n_sample, fs)
win_bin = compute_dynamic_windows(fs*100, fs)
n_win = win_bin.shape[0]
n_fft = win_bin.shape[1] // 2
# Notch filter the line-noise
fft_freq = np.linspace(0, fs // 2, n_fft)
notch_60hz = ((fft_freq > 55.0) & (fft_freq < 65.0))
notch_120hz = ((fft_freq > 115.0) & (fft_freq < 125.0))
notch_180hz = ((fft_freq > 175.0) & (fft_freq < 185.0))
fft_freq_ix = np.setdiff1d(np.arange(n_fft),
np.flatnonzero(notch_60hz | notch_120hz | notch_180hz))
fft_freq = fft_freq[fft_freq_ix]
n_freq = len(fft_freq_ix)
# Compute dFC
A_tensor = np.zeros((n_win, n_freq, n_conn))
for w_ii, w_ix in enumerate(win_bin):
evData_hat = evData[w_ix, :]
evData_hat = Echobase.Sigproc.reref.common_avg_ref(evData_hat)
for tr_ii, (tr_ix, tr_iy) in enumerate(zip(triu_ix, triu_iy)):
out = Echobase.Pipelines.ecog_network.coherence.mt_coherence(
df=1.0/fs, xi=evData_hat[:, tr_ix], xj=evData_hat[:, tr_iy],
tbp=5.0, kspec=9, nf=n_fft,
p=0.95, iadapt=1,
cohe=True, freq=True)
A_tensor[w_ii, :, tr_ii] = out['cohe'][fft_freq_ix]
A_hat = A_tensor.reshape(-1, n_conn)
```
# Optimize Dynamic Subgraphs Parameters
## Generate Cross-Validation Parameter Sets
```
def generate_folds(n_win, n_fold):
"""
Generate folds for cross-validation by randomly dividing the windows
into different groups for train/test-set.
Parameters
----------
n_win: int
Number of windows (observations) in the configuration matrix
n_fold: int
Number of folds desired
Returns
-------
fold_list: list[list]
List of index lists that can be further divided into train
and test sets
"""
# discard incomplete folds
n_win_per_fold = int(np.floor(n_win / n_fold))
win_list = np.arange(n_win)
win_list = np.random.permutation(win_list)
win_list = win_list[:(n_win_per_fold*n_fold)]
win_list = win_list.reshape(n_fold, -1)
fold_list = [list(ff) for ff in win_list]
return fold_list
fold_list = generate_folds(n_win, n_fold=5)
# Set the bounds of the search space
# Random sampling scheme
param_search_space = {'rank_range': (2, 20),
'alpha_range': (0.01, 1.0),
'beta_range': (0.01, 1.0),
'n_param': 20}
# Get parameter search space
# Each sampled parameter set will be evaluated n_fold times
param_list = NMF.optimize.gen_random_sampling_paramset(
fold_list=fold_list,
**param_search_space)
```
## Run NMF Cross-Validation Parameter Sets
```
# **This cell block should be parallelized. Takes time to run**
# Produces a list of quality measures for each parameter set in param_list
qmeas_list = [NMF.optimize.run_xval_paramset(A_hat, pdict)
for pdict in param_list]
```
## Visualize Quality Measures of Search Space
```
all_param, opt_params = NMF.optimize.find_optimum_xval_paramset(param_list, qmeas_list, search_pct=5)
# Generate quality measure plots
for qmeas in ['error', 'pct_sparse_subgraph', 'pct_sparse_coef']:
for param in ['rank', 'alpha', 'beta']:
param_unq = np.unique(all_param[param])
qmeas_mean = [np.mean(all_param[qmeas][all_param[param]==pp]) for pp in param_unq]
ax_jp = sns.jointplot(all_param[param], all_param[qmeas], kind='kde',
space=0, n_levels=60, shade_lowest=False)
ax = ax_jp.ax_joint
ax.plot([opt_params[param], opt_params[param]],
[ax.get_ylim()[0], ax.get_ylim()[1]],
lw=1.0, alpha=0.75, linestyle='--')
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.set_xlabel(param)
ax.set_ylabel(qmeas)
plt.show()
plt.close()
```
# Detect Dynamic Subgraphs
## Stochastic Factorization with Consensus
```
def refactor_connection_vector(conn_vec):
n_node = int(np.ceil(np.sqrt(2*len(conn_vec))))
triu_ix, triu_iy = np.triu_indices(n_node, k=1)
adj = np.zeros((n_node, n_node))
adj[triu_ix, triu_iy] = conn_vec[...]
adj += adj.T
return adj
fac_subgraph, fac_coef, err = NMF.optimize.consensus_nmf(A_hat, n_seed=2, n_proc=1,
opt_alpha=opt_params['alpha'],
opt_beta=opt_params['beta'],
opt_rank=opt_params['rank'])
fac_subgraph = np.array([refactor_connection_vector(subg)
for subg in fac_subgraph])
fac_coef = fac_coef.reshape(-1, n_win, n_freq)
```
## Plot Subgraphs and Spectrotemporal Dynamics
```
n_row = fac_subgraph.shape[0]
n_col = 2
plt.figure(figsize=(12,36))
for fac_ii in xrange(fac_subgraph.shape[0]):
ax = plt.subplot(n_row, n_col, 2*fac_ii+1)
ax.matshow(fac_subgraph[fac_ii, ...] / fac_subgraph.max(), cmap='viridis')
ax.set_axis_off()
ax = plt.subplot(n_row, n_col, 2*fac_ii+2)
ax.matshow(fac_coef[fac_ii, ...].T / fac_coef.max(), aspect=n_win/n_freq, cmap='inferno')
plt.show()
```
| true |
code
| 0.849722 | null | null | null | null |
|
# Energy Meter Examples
## Monsoon Power Monitor
*NOTE*: the **monsoon.py** tool is required to collect data from the power monitor.
Instructions on how to install it can be found here:
https://github.com/ARM-software/lisa/wiki/Energy-Meters-Requirements#monsoon-power-monitor.
```
import logging
from conf import LisaLogging
LisaLogging.setup()
```
#### Import required modules
```
# Generate plots inline
%matplotlib inline
import os
# Support to access the remote target
import devlib
from env import TestEnv
# RTApp configurator for generation of PERIODIC tasks
from wlgen import RTA, Ramp
```
## Target Configuration
The target configuration is used to describe and configure your test environment.
You can find more details in **examples/utils/testenv_example.ipynb**.
```
# Let's assume the monsoon binary is installed in the following path
MONSOON_BIN = os.path.join(os.getenv('LISA_HOME'), 'tools', 'scripts', 'monsoon.py')
# Setup target configuration
my_conf = {
# Target platform and board
"platform" : 'android',
"board" : 'wahoo',
# Android tools
"ANDROID_HOME" : "/home/derkling/Code/lisa/tools/android-sdk-linux",
# Folder where all the results will be collected
"results_dir" : "EnergyMeter_Monsoon",
# Define devlib modules to load
"exclude_modules" : [ 'hwmon' ],
# Energy Meters Configuration for ARM Energy Probe
"emeter" : {
"instrument" : "monsoon",
"conf" : {
'monsoon_bin' : MONSOON_BIN,
},
},
# Tools required by the experiments
"tools" : [ 'trace-cmd', 'rt-app' ],
# Comment this line to calibrate RTApp in your own platform
"rtapp-calib" : {"0": 360, "1": 142, "2": 138, "3": 352, "4": 352, "5": 353},
}
# Once powered the Monsoon Power Monitor does not enable the output voltage.
# Since the devlib's API expects that the device is powered and available for
# an ADB connection, let's manually power on the device before initializing the TestEnv
# Power on the device
!$MONSOON_BIN --device /dev/ttyACM1 --voltage 4.2
# Enable USB passthrough to be able to connect the device
!$MONSOON_BIN --usbpassthrough on
# Initialize a test environment using:
te = TestEnv(my_conf, wipe=False, force_new=True)
target = te.target
# If your device support charge via USB, let's disable it in order
# to read the overall power consumption from the main output channel
# For example, this is the API for a Pixel phone:
te.target.write_value('/sys/class/power_supply/battery/charging_enabled', 0)
```
## Workload Execution and Power Consumptions Samping
Detailed information on RTApp can be found in **examples/wlgen/rtapp_example.ipynb**.
Each **EnergyMeter** derived class has two main methods: **reset** and **report**.
- The **reset** method will reset the energy meter and start sampling from channels specified in the target configuration. <br>
- The **report** method will stop capture and will retrieve the energy consumption data. This returns an EnergyReport composed of the measured channels energy and the report file. Each of the samples can also be obtained, as you can see below.
```
# Create and RTApp RAMP task
rtapp = RTA(te.target, 'ramp', calibration=te.calibration())
rtapp.conf(kind='profile',
params={
'ramp' : Ramp(
start_pct = 60,
end_pct = 20,
delta_pct = 5,
time_s = 0.5).get()
})
# EnergyMeter Start
te.emeter.reset()
rtapp.run(out_dir=te.res_dir)
# EnergyMeter Stop and samples collection
nrg_report = te.emeter.report(te.res_dir)
logging.info("Collected data:")
!tree $te.res_dir
```
## Power Measurements Data
```
logging.info("Measured channels energy:")
logging.info("%s", nrg_report.channels)
logging.info("Generated energy file:")
logging.info(" %s", nrg_report.report_file)
!cat $nrg_report.report_file
logging.info("Samples collected for the Output and Battery channels (only first 10)")
samples_file = os.path.join(te.res_dir, 'samples.csv')
!head $samples_file
logging.info("DataFrame of collected samples (only first 5)")
nrg_report.data_frame.head()
logging.info("Plot of collected power samples")
axes = nrg_report.data_frame[('output', 'power')].plot(
figsize=(16,8), drawstyle='steps-post');
axes.set_title('Power samples');
axes.set_xlabel('Time [s]');
axes.set_ylabel('Output power [W]');
logging.info("Plot of collected power samples")
nrg_report.data_frame.describe(percentiles=[0.90, 0.95, 0.99]).T
logging.info("Power distribution")
axes = nrg_report.data_frame[('output', 'power')].plot(
kind='hist', bins=32,
figsize=(16,8));
axes.set_title('Power Histogram');
axes.set_xlabel('Output power [W] buckets');
axes.set_ylabel('Samples per bucket');
```
| true |
code
| 0.605099 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/conquerv0/Pynaissance/blob/master/1.%20Basic%20Framework/Data_Visualization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Data Visualization Guide
This notebook features data visualization techniques in areas such as static 2D, 3D plotting and interactive 2D plotting using packages `matplotlib, ploly`.
__I. Static 2D Plotting__
```
# Import necessary packages and configuration.
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
# Optional for displaying inline
%matplotlib inline
# Sample data source for plotting
np.random.seed(1000)
y = np.random.standard_normal(20)
x = np.arange(len(y))
# Plotting
plt.plot(x, y)
plt.plot(y.cumsum())
# Some modification to plotting: Turning off the grid and create equal scalling for the two axes.
plt.plot(y.cumsum())
plt.grid(False)
plt.axis('equal')
```
Some options for `plt.axis()`
Parameter | Description
------------ | -------------
Empty | Returns current axis limit
off | Turns axis lines and labels off
equal | Leads to equal scalling
scaled | Produces equal scaling via dimension changes
tight | Makes all data visible(tighten limits)
image | Makes all data visible(with data limits)
[xmin, xmax, ymin, ymax] | Sets limits to given list of values
```
plt.plot(y.cumsum())
plt.xlim(-1, 20)
plt.ylim(np.min(y.cumsum())-1,
np.max(y.cumsum()) + 1)
# Add labelling in the plot for Readability
plt.xlabel('Index')
plt.ylabel('Value')
plt.title('Simple Plot')
plt.legend(loc=0)
```
Creating mutilple plots on one line
```
y = np.random.standard_normal((20, 2)).cumsum(axis=0)
plt.figure(figsize=(10, 6))
plt.subplot(121)
plt.plot(y[:, 0], lw=1.5, label='1st')
plt.plot(y[:, 0], 'r')
plt.xlabel('index')
plt.ylabel('value')
plt.title('1st Data Set')
# Second plot
plt.subplot(122)
plt.bar(np.arange(len(y)), y[:,1], width=0.5, color='b', label='2nd')
plt.legend(loc=0)
plt.xlabel('index')
plt.title('2nd Data Set')
```
__Other Plotting Style__
```
# Regular Scatter plot
y = np.random.standard_normal((1000, 2))
plt.figure(figsize=(10, 6))
plt.scatter(y[:, 0], y[:, 1], marker='o')
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot')
# Integrate Color map to Scatter plot
c = np.random.randint(0, 10, len(y))
plt.figure(figsize=(10, 6))
plt.scatter(y[:, 0], y[:, 1], c=c, cmap='coolwarm', marker='o') # Define the dot to be marked as a bigger dot
plt.colorbar()
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot with Color Map')
# Histogram
plt.figure(figsize=(10, 6))
plt.hist(y, label=['1st', '2nd'], bins=30)
plt.legend(loc=0)
plt.xlabel('value')
plt.ylabel('frequency')
plt.title('Histogram')
# Boxplot
fig, ax = plt.subplots(figsize=(10, 6))
plt.boxplot(y)
plt.setp(ax, xticklabels=['1st', '2nd'])
plt.xlabel('data set')
plt.ylabel('value')
plt.title('Boxplot')
# Plotting of mathematical function
def func(x):
return 0.5*np.exp(x)+1
a, b = 0.5, 1.5
x = np.linspace(0, 2)
y = func(x)
Ix = np.linspace(a, b) # Integral limits of x value
Iy = func(Ix) # Integral limits of y value
verts = [(a, 0)] + list(zip(Ix, Iy)) + [(b, 0)]
#
from matplotlib.patches import Polygon
fig, ax = plt.subplots(figsize = (10, 6))
plt.plot(x, y, 'b', linewidth=2)
plt.ylim(bottom=0)
poly = Polygon(verts, facecolor='0.7', edgecolor='0.5')
ax.add_patch(poly)
plt.text(0.5 * (a+b), 1, r'$\int_a^b f(x)\mathrm{d}x$',
horizontalalignment='center', fontsize=20) # Labelling for plot
plt.figtext(0.9, 0.075, '$x$')
plt.figtext(0.075, 0.9, '$f(x)$')
ax.set_xticks((a, b))
ax.set_xticklabels(('$a$', '$b$'))
ax.set_yticks([func(a), func(b)])
ax.set_yticklabels(('$f(a)$', '$f(b)$'))
```
__II. Static 3D Plotting__
Using `np.meshgrid()` function to generate a two-dimensional coordinates system out of two one-dimensional ndarray.
```
# Set a call option data values with
# Strike values = [50, 150]
# Time-to-Maturity = [0.5, 2.5]
strike = np.linspace(50, 150, 24)
ttm = np.linspace(0.5, 2.5, 24)
strike, ttm = np.meshgrid(strike, ttm)
strike[:2].round(2)
# Calculate implied volatility
iv = (strike - 100) ** 2 / (100 * strike) / ttm
iv[:5, :3]
```
Plotting a 3D figure using the generated Call options data with `Axes3D`
```
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 6))
ax = fig.gca(projection = '3d')
surf = ax.plot_surface(strike, ttm, iv, rstride=2, cstride=2,
cmap = plt.cm.coolwarm, linewidth = 0.5, antialiased=True)
ax.set_xlabel('Strike Price')
ax.set_ylabel('Time-to-Maturity')
ax.set_zlabel('Implied Volatility')
fig.colorbar(surf, shrink = 0.5, aspect =5)
```
| true |
code
| 0.742603 | null | null | null | null |
|
# Doc2Vec to wikipedia articles
We conduct the replication to **Document Embedding with Paragraph Vectors** (http://arxiv.org/abs/1507.07998).
In this paper, they showed only DBOW results to Wikipedia data. So we replicate this experiments using not only DBOW but also DM.
## Basic Setup
Let's import Doc2Vec module.
```
from gensim.corpora.wikicorpus import WikiCorpus
from gensim.models.doc2vec import Doc2Vec, TaggedDocument
from pprint import pprint
import multiprocessing
```
## Preparing the corpus
First, download the dump of all Wikipedia articles from [here](http://download.wikimedia.org/enwiki/) (you want the file enwiki-latest-pages-articles.xml.bz2, or enwiki-YYYYMMDD-pages-articles.xml.bz2 for date-specific dumps).
Second, convert the articles to WikiCorpus. WikiCorpus construct a corpus from a Wikipedia (or other MediaWiki-based) database dump.
For more details on WikiCorpus, you should access [Corpus from a Wikipedia dump](https://radimrehurek.com/gensim/corpora/wikicorpus.html).
```
wiki = WikiCorpus("enwiki-latest-pages-articles.xml.bz2")
#wiki = WikiCorpus("enwiki-YYYYMMDD-pages-articles.xml.bz2")
```
Define **TaggedWikiDocument** class to convert WikiCorpus into suitable form for Doc2Vec.
```
class TaggedWikiDocument(object):
def __init__(self, wiki):
self.wiki = wiki
self.wiki.metadata = True
def __iter__(self):
for content, (page_id, title) in self.wiki.get_texts():
yield TaggedDocument([c.decode("utf-8") for c in content], [title])
documents = TaggedWikiDocument(wiki)
```
## Preprocessing
To set the same vocabulary size with original papar. We first calculate the optimal **min_count** parameter.
```
pre = Doc2Vec(min_count=0)
pre.scan_vocab(documents)
for num in range(0, 20):
print('min_count: {}, size of vocab: '.format(num), pre.scale_vocab(min_count=num, dry_run=True)['memory']['vocab']/700)
```
In the original paper, they set the vocabulary size 915,715. It seems similar size of vocabulary if we set min_count = 19. (size of vocab = 898,725)
## Training the Doc2Vec Model
To train Doc2Vec model by several method, DBOW and DM, we define the list of models.
```
cores = multiprocessing.cpu_count()
models = [
# PV-DBOW
Doc2Vec(dm=0, dbow_words=1, size=200, window=8, min_count=19, iter=10, workers=cores),
# PV-DM w/average
Doc2Vec(dm=1, dm_mean=1, size=200, window=8, min_count=19, iter =10, workers=cores),
]
models[0].build_vocab(documents)
print(str(models[0]))
models[1].reset_from(models[0])
print(str(models[1]))
```
Now we’re ready to train Doc2Vec of the English Wikipedia.
```
for model in models:
%%time model.train(documents)
```
## Similarity interface
After that, let's test both models! DBOW model show the simillar results with the original paper. First, calculating cosine simillarity of "Machine learning" using Paragraph Vector. Word Vector and Document Vector are separately stored. We have to add .docvecs after model name to extract Document Vector from Doc2Vec Model.
```
for model in models:
print(str(model))
pprint(model.docvecs.most_similar(positive=["Machine learning"], topn=20))
```
DBOW model interpret the word 'Machine Learning' as a part of Computer Science field, and DM model as Data Science related field.
Second, calculating cosine simillarity of "Lady Gaga" using Paragraph Vector.
```
for model in models:
print(str(model))
pprint(model.docvecs.most_similar(positive=["Lady Gaga"], topn=10))
```
DBOW model reveal the similar singer in the U.S., and DM model understand that many of Lady Gaga's songs are similar with the word "Lady Gaga".
Third, calculating cosine simillarity of "Lady Gaga" - "American" + "Japanese" using Document vector and Word Vectors. "American" and "Japanese" are Word Vectors, not Paragraph Vectors. Word Vectors are already converted to lowercases by WikiCorpus.
```
for model in models:
print(str(model))
vec = [model.docvecs["Lady Gaga"] - model["american"] + model["japanese"]]
pprint([m for m in model.docvecs.most_similar(vec, topn=11) if m[0] != "Lady Gaga"])
```
As a result, DBOW model demonstrate the similar artists with Lady Gaga in Japan such as 'Perfume', which is the Most famous Idol in Japan. On the other hand, DM model results don't include the Japanese aritsts in top 10 simillar documents. It's almost same with no vector calculated results.
This results demonstrate that DBOW employed in the original paper is outstanding for calculating the similarity between Document Vector and Word Vector.
| true |
code
| 0.341104 | null | null | null | null |
|
# NLP (Natural Language Processing) with Python
This is the notebook that goes along with the NLP video lecture!
In this lecture we will discuss a higher level overview of the basics of Natural Language Processing, which basically consists of combining machine learning techniques with text, and using math and statistics to get that text in a format that the machine learning algorithms can understand!
Once you've completed this lecture you'll have a project using some Yelp Text Data!
**Requirements: You will need to have NLTK installed, along with downloading the corpus for stopwords. To download everything with a conda installation, run the cell below. Or reference the full video lecture**
```
import nltk
nltk.download_shell()
```
## Part 1: Get the Data
We'll be using a dataset from the [UCI datasets](https://archive.ics.uci.edu/ml/datasets/SMS+Spam+Collection)! This dataset is already located in the folder for this section.
The file we are using contains a collection of more than 5 thousand SMS phone messages. You can check out the **readme** file for more info.
*Recall that __rstrip()__ is used to return a copy of the string with the trailing characters removed.*
<br>
<br>
Let's go ahead and use __rstrip()__ plus a list comprehension to get a list of all the lines of text messages:
```
messages = [line.rstrip() for line in open('smsspamcollection/SMSSpamCollection')]
print(len(messages))
messages[10]
```
<font color=#2948ff>A collection of texts is also sometimes called __"corpus"__. Let's print the first ten messages and number them using **enumerate**:</font>
```
for message_number, message in enumerate(messages[:11]):
print(message_number, message)
print('\n')
```
Due to the spacing we can tell that this is a **[TSV](http://en.wikipedia.org/wiki/Tab-separated_values) ("tab separated values") file**, where the first column is a label saying whether the given message is a normal message (commonly known as <font color=#a80077>"ham"</font>) or <font color=#a80077>"spam"</font>. The second column is the message itself. (Note our numbers aren't part of the file, they are just from the **enumerate** call).
Using these labeled ham and spam examples, we'll **train a machine learning model to learn to discriminate between ham/spam automatically**. Then, with a trained model, we'll be able to **classify arbitrary unlabeled messages** as ham or spam.
From the official SciKit Learn documentation, we can visualize our process:
Instead of parsing TSV manually using Python, we can just take advantage of pandas! Let's go ahead and import it!
```
import pandas as pd
```
We'll use **read_csv** and make note of the **sep** argument, we can also specify the desired column names by passing in a list of *names*.
```
messages = pd.read_csv('smsspamcollection/SMSSpamCollection', sep='\t', names=['label', 'message'])
messages.head()
```
## Part 2: Exploratory Data Analysis
Let's check out some of the stats with some plots and the built-in methods in pandas!
```
messages.describe()
```
<font color=#a80077>Let's use **groupby** to use describe by label, this way we can begin to think about the features that separate ham and spam!</font>
```
messages.groupby('label').describe()
```
As we continue our analysis we want to start thinking about the features we are going to be using. This goes along with the general idea of [feature engineering](https://en.wikipedia.org/wiki/Feature_engineering). The better your domain knowledge on the data, the better your ability to engineer more features from it. Feature engineering is a very large part of spam detection in general. I encourage you to read up on the topic!
Let's make a new column to detect how long the text messages are:
```
messages['length'] = messages['message'].apply(len)
messages.head()
```
### Data Visualization
Let's visualize this! Let's do the imports:
```
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style('whitegrid')
plt.figure(figsize=(12,6))
messages['length'].plot(kind='hist', bins=150, colormap='magma')
```
Play around with the bin size! Looks like text length may be a good feature to think about! Let's try to explain why the x-axis goes all the way to 1000ish, this must mean that there is some really long message!
```
messages['length'].describe()
# messages.length.describe() can also be used here
```
Woah! 910 characters, let's use masking to find this message:
```
messages[messages['length'] == 910]
messages[messages['length'] == 910]['message'].iloc[0]
```
Looks like we have some sort of Romeo sending texts! But let's focus back on the idea of trying to see if message length is a distinguishing feature between ham and spam:
```
messages.hist(column='length', by='label', bins=60, figsize=(12,6))
```
Very interesting! Through just basic EDA we've been able to discover a trend that spam messages tend to have more characters. (Sorry Romeo!)
Now let's begin to process the data so we can eventually use it with SciKit Learn!
## Part 3: Text Pre-processing
Our main issue with our data is that it is all in text format (strings). The classification algorithms that we've learned about so far will need some sort of numerical feature vector in order to perform the classification task. __<font color=#a80077>There are actually many methods to convert a corpus to a vector format. The simplest is the the [bag-of-words](http://en.wikipedia.org/wiki/Bag-of-words_model) approach, where each unique word in a text will be represented by one number.</font>__
In this section we'll convert the raw messages (sequence of characters) into vectors (sequences of numbers).
1. __As a first step, let's write a function that will split a message into its individual words and return a list.__
<br>
2. __We'll also remove very common words, ('the', 'a', etc..).__ To do this we will take advantage of the NLTK library. It's pretty much the standard library in Python for processing text and has a lot of useful features. We'll only use some of the basic ones here.
Let's create a function that will process the string in the message column, then we can just use **apply()** in pandas do process all the text in the DataFrame.
First removing punctuation. We can just take advantage of Python's built-in **string** library to get a quick list of all the possible punctuation:
```
import string
example = 'Sample message! Notice: it has punctuation.'
# Check characters to see if they are in punctuation
nopunc = [char for char in example if char not in string.punctuation]
# Join the characters again to form the string.
nopunc = ''.join(nopunc)
nopunc = ''.join(nopunc)
nopunc
```
Now let's see how to remove stopwords. We can import a list of english stopwords from NLTK (check the documentation for more languages and info).
```
from nltk.corpus import stopwords
# Some English stop words
stopwords.words('english')[:10]
# back to the example, we are going to remove the stopwords in nopunc
nopunc.split()
# remove stopwords
nopunc_clean = [word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
nopunc_clean
```
Now let's put both of these together in a function to apply it to our DataFrame later on:
```
def text_process(mess):
"""
Takes in a string of text, then performs the following:
1. Remove all punctuation
2. Remove all stopwords
3. Returns a list of the cleaned text
"""
# check characters to see if they contain punctuation
nopunc = [char for char in mess if char not in string.punctuation]
# join the characters again to form the string.
nopunc = ''.join(nopunc)
# remove any stopwords
return[word for word in nopunc.split() if word.lower() not in stopwords.words('english')]
```
Here is the original DataFrame again:
```
messages.head()
```
Now let's "tokenize" these messages. <font color=#a80077>__Tokenization__ is just the term used to describe the process of converting the normal text strings in to a list of tokens (words that we actually want).</font>
Let's see an example output on on column:
**Note:**
We may get some warnings or errors for symbols we didn't account for or that weren't in Unicode (like a British pound symbol)
```
# Check to make sure its working
messages['message'].head().apply(text_process)
# Original dataframe
messages.head()
```
### Continuing Normalization
__There are a lot of ways to continue normalizing this text. Such as [Stemming](https://en.wikipedia.org/wiki/Stemming) or distinguishing by [part of speech](http://www.nltk.org/book/ch05.html).__
NLTK has lots of built-in tools and great documentation on a lot of these methods. __*Sometimes they don't work well for text-messages due to the way a lot of people tend to use abbreviations or shorthand*__, For example:
'Nah dawg, IDK! Wut time u headin to da club?'
versus
'No dog, I don't know! What time are you heading to the club?'
Some text normalization methods will have trouble with this type of shorthand and so I'll leave you to explore those more advanced methods through the __[NLTK book online](http://www.nltk.org/book/).__
For now we will just focus on using what we have to convert our list of words to an actual vector that SciKit-Learn can use.
## Part 4: Vectorization
Currently, we have the messages as lists of tokens (also known as [lemmas](http://nlp.stanford.edu/IR-book/html/htmledition/stemming-and-lemmatization-1.html)) and now we need to convert each of those messages into a vector the SciKit Learn's algorithm models can work with.
Now we'll convert each message, represented as a list of tokens (lemmas) above, into a vector that machine learning models can understand.
__We'll do that in three steps using the bag-of-words model:__
1. __Count how many times a word occurs in each message <font color=#a80077>(Term frequency)</font>__
2. __Weigh the counts, so that frequent tokens get lower weight <font color=#a80077>(Inverse document frequency)</font>__
3. __Normalize the vectors to unit length, to abstract from the original text length <font color=#a80077>(L2 norm)</font>__
Let's begin the first step:
Each vector will have as many dimensions as there are unique words in the SMS corpus. We will first use SciKit Learn's **CountVectorizer**. This model will convert a collection of text documents to a matrix of token counts.
We can imagine this as a 2-Dimensional matrix. Where the 1-dimension is the entire vocabulary (1 row per word) and the other dimension are the actual documents, in this case a column per text message.
For example:
<table border = “1“>
<tr>
<th></th> <th>Message 1</th> <th>Message 2</th> <th>...</th> <th>Message N</th>
</tr>
<tr>
<td><b>Word 1 Count</b></td><td>0</td><td>1</td><td>...</td><td>0</td>
</tr>
<tr>
<td><b>Word 2 Count</b></td><td>0</td><td>0</td><td>...</td><td>0</td>
</tr>
<tr>
<td><b>...</b></td> <td>1</td><td>2</td><td>...</td><td>0</td>
</tr>
<tr>
<td><b>Word N Count</b></td> <td>0</td><td>1</td><td>...</td><td>1</td>
</tr>
</table>
Since there are so many messages, we can expect a lot of zero counts for the presence of that word in that document. Because of this, SciKit Learn will output a [Sparse Matrix](https://en.wikipedia.org/wiki/Sparse_matrix).
__<font color=#a80077>Shape Matrix or sparse array is a matrix where most of the elements are zero. If most of the elements are nonzero, then the matrix is considered dense</font>__
```
from sklearn.feature_extraction.text import CountVectorizer
```
There are a lot of arguments and parameters that can be passed to the CountVectorizer. In this case we will just specify the **analyzer** to be our own previously defined function:
```
bow_transformer = CountVectorizer(analyzer=text_process).fit(messages['message'])
# print total number of vocab words
print(len(bow_transformer.vocabulary_))
```
Let's take one text message and get its bag-of-words counts as a vector, putting to use our new `bow_transformer`:
```
message4 = messages['message'][3]
print(message4)
```
Now let's see its vector representation:
```
bow4 = bow_transformer.transform([message4])
print(bow4)
print('\n')
print(bow4.shape)
```
__This means that there are seven unique words in message number 4 (after removing common stop words). Two of them appear twice, the rest only once.__ Let's go ahead and check and confirm which ones appear twice:
```
print(bow_transformer.get_feature_names()[4068])
print(bow_transformer.get_feature_names()[9554])
```
Now we can use **.transform** on our Bag-of-Words (bow) transformed object and transform the entire DataFrame of messages. Let's go ahead and check out how the bag-of-words counts for the entire SMS corpus is a large, sparse matrix:
```
messages_bow = bow_transformer.transform(messages['message'])
print('Shape of Sparse Matrix: ', messages_bow.shape)
# Shape Matrix or sparse array is a matrix where most of the elements are zero.
print('Amount of Non-Zero occurences: ', messages_bow.nnz)
# .nnz == non zero occurences
sparsity = (100.0 * messages_bow.nnz / (messages_bow.shape[0] * messages_bow.shape[1]))
# print('sparsity: {}'.format(sparsity))
print('sparsity: {}'.format(round(sparsity)))
```
After the counting, the term weighting and normalization can be done with [TF-IDF](http://en.wikipedia.org/wiki/Tf%E2%80%93idf), using scikit-learn's `TfidfTransformer`.
____
### So what is TF-IDF?
__<font color=#a80077>TF-IDF stands for *term frequency-inverse document frequency.* The tf-idf weight is a weight often used in information retrieval and text mining. This weight is a statistical measure used to evaluate how important a word is to a document in a collection or corpus. The importance increases proportionally to the number of times a word appears in the document but is *offset* by the frequency of the word in the corpus. Variations of the tf-idf weighting scheme are often used by search engines as a central tool in scoring and ranking a document's relevance given a user query.</font>__
__One of the simplest ranking functions is computed by summing the tf-idf for each query term;__ many more sophisticated ranking functions are variants of this simple model.
__Typically, the tf-idf weight is composed by two terms:__
__<font color=#a80077>The first computes the normalized Term Frequency (TF),</font> aka the number of times a word appears in a document, divided by the total number of words in that document;__
__<font color=#a80077>The second term is the Inverse Document Frequency (IDF),</font> computed as the logarithm of the number of the documents in the corpus divided by the number of documents where the specific term appears.__
<font color=#a80077>**TF: Term Frequency**</font>, which measures how frequently a term occurs in a document. Since every document is different in length, it is possible that a term would appear much more times in long documents than shorter ones. Thus, the term frequency is often divided by the document length (aka the total number of terms in the document) as a way of normalization:
<font color=#2C7744>*TF(t) = (Number of times term t appears in a document) / (Total number of terms in the document)*</font>
<font color=#a80077>**IDF: Inverse Document Frequency**</font>, which measures how important a term is. While computing TF, all terms are considered equally important. However it is known that certain terms, such as "is", "of", and "that", may appear a lot of times but have little importance. Thus we need to weigh down the frequent terms while scale up the rare ones, by computing the following:
<font color=#2C7744>*IDF(t) = log_e(Total number of documents / Number of documents with term t in it)*</font>
See below for a simple example.
**Example:**
Consider a document containing 100 words wherein the word cat appears 3 times.
The term frequency (i.e., tf) for cat is then (3 / 100) = 0.03. Now, assume we have 10 million documents and the word cat appears in one thousand of these. Then, the inverse document frequency (i.e., idf) is calculated as log(10,000,000 / 1,000) = 4. Thus, the Tf-idf weight is the product of these quantities: 0.03 * 4 = 0.12.
____
Let's go ahead and see how we can do this in SciKit Learn:
```
from sklearn.feature_extraction.text import TfidfTransformer
tfidf_transformer = TfidfTransformer().fit(messages_bow)
tfidf4 = tfidf_transformer.transform(bow4)
print(tfidf4)
```
We'll go ahead and check what is the IDF (inverse document frequency) of the word `"u"` and of word `"university"`?
```
print(tfidf_transformer.idf_[bow_transformer.vocabulary_['u']])
print(tfidf_transformer.idf_[bow_transformer.vocabulary_['university']])
```
To transform the entire bag-of-words corpus into TF-IDF corpus at once:
```
messages_tfidf = tfidf_transformer.transform(messages_bow)
print(messages_tfidf.shape)
```
__There are many ways the data can be preprocessed and vectorized. These steps involve feature engineering and building a "pipeline".__ I encourage you to check out SciKit Learn's documentation on dealing with text data as well as the expansive collection of available papers and books on the general topic of NLP.
## Part 5: Training a model
With messages represented as vectors, we can finally train our spam/ham classifier. Now we can actually use almost any sort of classification algorithms. For a [variety of reasons](http://www.inf.ed.ac.uk/teaching/courses/inf2b/learnnotes/inf2b-learn-note07-2up.pdf), the __Naive Bayes classifier algorithm__ is a good choice.
We'll be using scikit-learn here, choosing the [Naive Bayes](http://en.wikipedia.org/wiki/Naive_Bayes_classifier) classifier to start with:
```
from sklearn.naive_bayes import MultinomialNB
spam_detect_model = MultinomialNB().fit(messages_tfidf, messages['label'])
```
Let's try classifying our single random message and checking how we do:
```
print('predicted: ', spam_detect_model.predict(tfidf4)[0])
print('expected: ', messages.label[3])
```
Fantastic! We've developed a model that can attempt to predict spam vs ham classification!
## Part 6: Model Evaluation
Now we want to determine how well our model will do overall on the entire dataset. Let's begin by getting all the predictions:
```
all_predictions = spam_detect_model.predict(messages_tfidf)
print(all_predictions)
```
__We can use SciKit Learn's built-in classification report, which returns [precision, recall,](https://en.wikipedia.org/wiki/Precision_and_recall) [f1-score](https://en.wikipedia.org/wiki/F1_score), and a column for support (meaning how many cases supported that classification).__ Check out the links for more detailed info on each of these metrics and the figure below:
<img src='https://upload.wikimedia.org/wikipedia/commons/thumb/2/26/Precisionrecall.svg/700px-Precisionrecall.svg.png' width=400 />
```
from sklearn.metrics import classification_report
print(classification_report(messages['label'], all_predictions))
```
There are quite a few possible metrics for evaluating model performance. Which one is the most important depends on the task and the business effects of decisions based off of the model. For example, the cost of mis-predicting "spam" as "ham" is probably much lower than mis-predicting "ham" as "spam".
In the above "evaluation", we evaluated accuracy on the same data we used for training. <font color=#DC281E>**You should never actually evaluate on the same dataset you train on!**</font>
Such evaluation tells us nothing about the true predictive power of our model. If we simply remembered each example during training, the accuracy on training data would trivially be 100%, even though we wouldn't be able to classify any new messages.
A proper way is to split the data into a training/test set, where the model only ever sees the **training data** during its model fitting and parameter tuning. The **test data** is never used in any way. This is then our final evaluation on test data is representative of true predictive performance.
## Train Test Split
```
from sklearn.model_selection import train_test_split
msg_train, msg_test, label_train, label_test = train_test_split(messages['message'], messages['label'], test_size=0.3)
print(len(msg_train), len(msg_test), len(msg_train) + len(msg_test))
```
The test size is 30% of the entire dataset (1672 messages out of total 5572), and the training is the rest (3900 out of 5572). Note: this is the default split(30/70).
## Creating a Data Pipeline
Let's run our model again and then predict off the test set. __We will use SciKit Learn's [pipeline](http://scikit-learn.org/stable/modules/pipeline.html) capabilities to store a pipeline of workflow.__ This will allow us to set up all the transformations that we will do to the data for future use. Let's see an example of how it works:
```
from sklearn.pipeline import Pipeline
pipeline = Pipeline([
# strings to token integer counts
('bow', CountVectorizer(analyzer=text_process)),
# integer counts to weighted TF-IDF scores
('tfidf', TfidfTransformer()),
# train on TF-IDF vectors w/ Naive Bayes classifier
('classifier', MultinomialNB()),
])
```
Now we can directly pass message text data and the pipeline will do our pre-processing for us! We can treat it as a model/estimator API:
```
pipeline.fit(msg_train, label_train)
predictions = pipeline.predict(msg_test)
print(classification_report(label_test, predictions))
```
Now we have a classification report for our model on a true testing set! You can try out different classification models. There is a lot more to Natural Language Processing than what we've covered here, and its vast expanse of topic could fill up several college courses! I encourage you to check out the resources below for more information on NLP!
## More Resources
Check out the links below for more info on Natural Language Processing:
[NLTK Book Online](http://www.nltk.org/book/)
[Kaggle Walkthrough](https://www.kaggle.com/c/word2vec-nlp-tutorial/details/part-1-for-beginners-bag-of-words)
[SciKit Learn's Tutorial](http://scikit-learn.org/stable/tutorial/text_analytics/working_with_text_data.html)
# Good Job!
| true |
code
| 0.462473 | null | null | null | null |
|
In this note book, I
* replicate some of the simulations in the paers, and
* add some variations of my own.
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/facebookresearch/mc/blob/master/notebooks/simulations_py.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
```
# install the mc package
!pip install -q git+https://github.com/facebookresearch/mc
#@title imports {form-width: "20%"}
import pandas as pd
import numpy as np
import mc
#@title function mc {form-width: "20%"}
def one_run(
N=400, # sample size for main data
n=100, # sample size for calibration data
pi=[0.2, 0.8], # true membership proportions
p=[[[0.9, 0.2], [0.1, 0.8]], [[0.9, 0.2], [0.1, 0.8]]], # miscalssification matrix
mu=[0.8, 0.4], # true mean of y
seed=123, # seed for random data generation
verbose=False, # if true, print details
):
# N = 400; n = 100; pi = [0.2, 0.8];
# p =[[[0.9, 0.2], [0.1, 0.8]], [[0.9, 0.2], [0.1, 0.8]]]
# mu = [0.8, 0.4]; seed=123
np.random.seed(seed)
pi = np.array(pi)
p = np.array(p)
mu = np.array(mu)
i = np.random.binomial(n=1, p=pi[1], size=N + n) # true group
y = np.random.binomial(n=1, p=mu[i]) # y_value depends on true group info i
j = np.random.binomial(n=1, p=p[y, 1, i]) # observed group
df = pd.DataFrame({
"sample": ["P"] * N + ["V"] * n,
"i": i, "j": j, "y": y, "y_squared": y ** 2,
})
# start calculation
df_P = df.query("sample == 'P'")
df_V = df.query("sample == 'V'")
n_jd_P = df_P.groupby("j").size().to_numpy()
y_sum_jd_P = df_P.groupby("j")["y"].sum().to_numpy()
n_ji_V = pd.crosstab(df_V["j"], df_V["i"]).to_numpy()
y_sum_ji_V = df_V.pivot_table(
index="j", columns="i", values="y", aggfunc=np.sum, fill_value=0).to_numpy()
y2_sum_ji_V = df_V.pivot_table(
index="j", columns="i", values="y_squared",
aggfunc=np.sum, fill_value=0).to_numpy()
# get estimates
mom = mc.mc_mom(n_jd_P, y_sum_jd_P, n_ji_V, y_sum_ji_V)
rmle = mc.mc_rmle(n_jd_P, y_sum_jd_P, n_ji_V, y_sum_ji_V, y2_sum_ji_V)
out = pd.concat(
(pd.DataFrame({"mu": mu}), mom, rmle),
axis=1
)
for col in out.columns:
if col not in ("mu", "mak_li_var"):
if any(~out[col].between(0., 1.)):
out[col] = np.nan
return out
#@title function simulation {form-width: "20%"}
def simulation(n_reps=1000, verbose=True, *args, **kwargs):
# n_reps=100; verbose=True; args=[]; kwargs={}
res = pd.concat([
one_run(seed=seed + 8101352, *args, **kwargs) for seed in range(n_reps)
])
pct_bad = res.isna().mean()
est_cols = [col for col in res.columns if col not in ("mu", "mak_li_var")]
err = res[est_cols].sub(res["mu"], axis=0)
bias = err.groupby(level=0).mean()
mse = err.groupby(level=0).apply(lambda df: (df ** 2).mean())
estimated_var = res.groupby(level=0)['mak_li_var'].mean().to_numpy()
empirical_var = res.groupby(level=0)["mak_li"].var().to_numpy()
right_direction = (
res[est_cols]
.diff().loc[1].apply(lambda x: (x[~np.isnan(x)] < 0).mean())
)
if verbose:
print(res.head(2))
print(f"\nbias: \n {bias}")
print(f"MSE: \n {mse}")
print(f"\n\n % with bad estimates:\n {pct_bad}")
print(f"\n\nestimated mak_li_var: {estimated_var}")
print(f"\n\nempirical mak_li_var: {empirical_var}")
print(f"\n\nright_direction:\n {right_direction}")
return {
"res":res, "err": err, "bias": bias, "mse": mse,
"pct_bad": pct_bad, "empirical_var": empirical_var,
"right_direction": right_direction
}
# simulation()
```
## simulations in paper
```
#@title p's that define simulation setup {form-width: "20%"}
p_a = [[[0.9, 0.2], [0.1, 0.8]], [[0.9, 0.2], [0.1, 0.8]]]
p_b = [[[0.8, 0.3], [0.2, 0.7]], [[0.8, 0.3], [0.2, 0.7]]]
p_c = [[[0.93, 0.23], [0.07, 0.77]], [[0.87, 0.17], [0.13, 0.83]]]
p_d = [[[0.95, 0.25], [0.05, 0.75]], [[0.85, 0.15], [0.15, 0.85]]]
#@title a {form-width: "20%"}
a = simulation(p=p_a)
#@title b {form-width: "20%"}
b = simulation(p=p_b)
#@title c {form-width: "20%"}
c = simulation(p=p_c)
#@title d {form-width: "20%"}
d = simulation(p=p_d)
```
## simulations with larger primary data
```
#@title a2 {form-width: "20%"}
big_N = 40_000
a2 = simulation(
N=big_N,
p=p_a
)
#@title b2 {form-width: "20%"}
b2 = simulation(
N=big_N,
p=p_a
)
#@title c2 {form-width: "20%"}
c2 = simulation(
N=big_N,
p=p_c
)
#@title d2 {form-width: "20%"}
d2 = simulation(
N=big_N,
p=p_d
)
```
## Collected results
```
#@title 1000 X bias and mse {form-width: "20%"}
setups = np.repeat(("a", "b", "c", "d", "a2", "b2", "c2", "d2"), 2)
setups = np.tile(setups, 2)
multipler = 1000
metrics = np.repeat((f"bia X {multipler}", f"mse X {multipler}"), len(setups)/2)
biases = pd.concat([
r["bias"] * multipler
for r in (a,b,c,d,a2,b2,c2,d2)
])
mses = pd.concat([
r["mse"] * multipler
for r in (a,b,c,d,a2,b2,c2,d2)
])
all = pd.concat([biases, mses])
all["setup"] = setups
all["metric"] = metrics
all["parameter"] = all.index.map({0: "mu1", 1: "mu2"})
all = (
all.sort_values(["parameter", "metric", "setup",])
[["parameter", "metric", "setup", "naive", "validation", "no_y_V", "with_y_V", "mak_li"]]
.round(2)
)
all
```
## smaller effect size
```
s1 = simulation(mu=[0.5, 0.4])
s2 = simulation(mu=[0.5, 0.45])
s3 = simulation(mu=[0.5, 0.48])
```
| true |
code
| 0.438124 | null | null | null | null |
|
Blankenbach Benchmark Case 2a
======
Temperature dependent convection
----
This is a benchmark case of two-dimensional, incompressible, bottom heated, temperature dependent convection. This example is based on case 2a in Blankenbach *et al.* 1989 for a single Rayleigh number ($Ra = 10^7$).
Here a temperature field that is already in equilibrium is loaded and a single Stokes solve is used to get the velocity and pressure fields. A few advection time steps are carried out as a demonstration of the new viscosity function.
**This lesson introduces the concepts of:**
1. material rheologies with functional dependencies
**Keywords:** Stokes system, advective diffusive systems, analysis tools, tools for post analysis, rheologies
**References**
1. B. Blankenbach, F. Busse, U. Christensen, L. Cserepes, D. Gunkel, U. Hansen, H. Harder, G. Jarvis, M. Koch, G. Marquart, D. Moore, P. Olson, H. Schmeling and T. Schnaubelt. A benchmark comparison for mantle convection codes. Geophysical Journal International, 98, 1, 23–38, 1989
http://onlinelibrary.wiley.com/doi/10.1111/j.1365-246X.1989.tb05511.x/abstract
```
import numpy as np
import underworld as uw
import math
from underworld import function as fn
import glucifer
```
Setup parameters
-----
Set simulation parameters for test.
```
Temp_Min = 0.0
Temp_Max = 1.0
res = 128
```
**Set physical values in SI units**
```
alpha = 2.5e-5
rho = 4e3
g = 10
dT = 1e3
h = 1e6
kappa = 1e-6
eta = 2.5e19
```
**Set viscosity function constants as per Case 2a**
```
Ra = 1e7
eta0 = 1.0e3
```
**Input file path**
Set input directory path
```
inputPath = 'input/1_04_BlankenbachBenchmark_Case2a/'
outputPath = 'output/'
# Make output directory if necessary.
if uw.rank()==0:
import os
if not os.path.exists(outputPath):
os.makedirs(outputPath)
```
Create mesh and finite element variables
------
```
mesh = uw.mesh.FeMesh_Cartesian( elementType = ("Q1/dQ0"),
elementRes = (res, res),
minCoord = (0., 0.),
maxCoord = (1., 1.))
velocityField = mesh.add_variable( nodeDofCount=2 )
pressureField = mesh.subMesh.add_variable( nodeDofCount=1 )
temperatureField = mesh.add_variable( nodeDofCount=1 )
temperatureDotField = mesh.add_variable( nodeDofCount=1 )
```
Initial conditions
-------
Load an equilibrium case with 128$\times$128 resolution and $Ra = 10^7$. This can be changed as per **1_03_BlankenbachBenchmark** if required.
```
meshOld = uw.mesh.FeMesh_Cartesian( elementType = ("Q1/dQ0"),
elementRes = (128, 128),
minCoord = (0., 0.),
maxCoord = (1., 1.),
partitioned = False )
temperatureFieldOld = meshOld.add_variable( nodeDofCount=1 )
temperatureFieldOld.load( inputPath + 'tempfield_case2_128_Ra1e7_10000.h5' )
temperatureField.data[:] = temperatureFieldOld.evaluate( mesh )
temperatureDotField.data[:] = 0.
velocityField.data[:] = [0.,0.]
pressureField.data[:] = 0.
```
**Plot initial temperature**
```
figtemp = glucifer.Figure()
figtemp.append( glucifer.objects.Surface(mesh, temperatureField) )
figtemp.show()
```
**Boundary conditions**
```
for index in mesh.specialSets["MinJ_VertexSet"]:
temperatureField.data[index] = Temp_Max
for index in mesh.specialSets["MaxJ_VertexSet"]:
temperatureField.data[index] = Temp_Min
iWalls = mesh.specialSets["MinI_VertexSet"] + mesh.specialSets["MaxI_VertexSet"]
jWalls = mesh.specialSets["MinJ_VertexSet"] + mesh.specialSets["MaxJ_VertexSet"]
freeslipBC = uw.conditions.DirichletCondition( variable = velocityField,
indexSetsPerDof = ( iWalls, jWalls) )
tempBC = uw.conditions.DirichletCondition( variable = temperatureField,
indexSetsPerDof = ( jWalls, ) )
```
Set up material parameters and functions
-----
Setup the viscosity to be a function of the temperature. Recall that these functions and values are preserved for the entire simulation time.
```
b = math.log(eta0)
T = temperatureField
fn_viscosity = eta0 * fn.math.exp( -1.0 * b * T )
densityFn = Ra*temperatureField
gravity = ( 0.0, 1.0 )
buoyancyFn = gravity*densityFn
```
**Plot the initial viscosity**
Plot the viscosity, which is a function of temperature, using the initial temperature conditions set above.
```
figEta = glucifer.Figure()
figEta.append( glucifer.objects.Surface(mesh, fn_viscosity) )
figEta.show()
```
System setup
-----
Since we are using a previously constructed temperature field, we will use a single Stokes solve to get consistent velocity and pressure fields.
**Setup a Stokes system**
```
stokes = uw.systems.Stokes( velocityField = velocityField,
pressureField = pressureField,
conditions = [freeslipBC,],
fn_viscosity = fn_viscosity,
fn_bodyforce = buoyancyFn )
```
**Set up and solve the Stokes system**
```
solver = uw.systems.Solver(stokes)
solver.solve()
```
**Create an advective diffusive system**
```
advDiff = uw.systems.AdvectionDiffusion( temperatureField, temperatureDotField, velocityField, fn_diffusivity = 1.,
conditions = [tempBC,], )
```
Analysis tools
-----
**Nusselt number**
```
nuTop = uw.utils.Integral( fn=temperatureField.fn_gradient[1], mesh=mesh, integrationType='Surface',
surfaceIndexSet=mesh.specialSets["MaxJ_VertexSet"])
Nu = -nuTop.evaluate()[0]
if(uw.rank()==0):
print('Initial Nusselt number = {0:.3f}'.format(Nu))
```
**RMS velocity**
```
v2sum_integral = uw.utils.Integral( mesh=mesh, fn=fn.math.dot( velocityField, velocityField ) )
volume_integral = uw.utils.Integral( mesh=mesh, fn=1. )
Vrms = math.sqrt( v2sum_integral.evaluate()[0] )/volume_integral.evaluate()[0]
if(uw.rank()==0):
print('Initial Vrms = {0:.3f}'.format(Vrms))
```
**Temperature gradients at corners**
Uses global evaluate function which can evaluate across multiple processors, but may slow the model down for very large runs.
```
def calcQs():
q1 = temperatureField.fn_gradient[1].evaluate_global( (0., 1.) )
q2 = temperatureField.fn_gradient[1].evaluate_global( (1., 1.) )
q3 = temperatureField.fn_gradient[1].evaluate_global( (1., 0.) )
q4 = temperatureField.fn_gradient[1].evaluate_global( (0., 0.) )
return q1, q2, q3, q4
q1, q2, q3, q4 = calcQs()
if(uw.rank()==0):
print('Initial T gradients = {0:.3f}, {1:.3f}, {2:.3f}, {3:.3f}'.format(q1[0][0], q2[0][0], q3[0][0], q4[0][0]))
```
Main simulation loop
-----
Run a few advection and Stokes solver steps to make sure we are in, or close to, equilibrium.
```
time = 0.
step = 0
step_end = 4
# define an update function
def update():
# Determining the maximum timestep for advancing the a-d system.
dt = advDiff.get_max_dt()
# Advect using this timestep size.
advDiff.integrate(dt)
return time+dt, step+1
while step < step_end:
# solve Stokes and advection systems
solver.solve()
# Calculate the RMS velocity and Nusselt number.
Vrms = math.sqrt( v2sum_integral.evaluate()[0] )/volume_integral.evaluate()[0]
Nu = -nuTop.evaluate()[0]
q1, q2, q3, q4 = calcQs()
if(uw.rank()==0):
print('Step {0:2d}: Vrms = {1:.3f}; Nu = {2:.3f}; q1 = {3:.3f}; q2 = {4:.3f}; q3 = {5:.3f}; q4 = {6:.3f}'
.format(step, Vrms, Nu, q1[0][0], q2[0][0], q3[0][0], q4[0][0]))
# update
time, step = update()
```
Comparison of benchmark values
-----
Compare values from Underworld against those from Blankenbach *et al.* 1989 for case 2a in the table below.
```
if(uw.rank()==0):
print('Nu = {0:.3f}'.format(Nu))
print('Vrms = {0:.3f}'.format(Vrms))
print('q1 = {0:.3f}'.format(q1[0][0]))
print('q2 = {0:.3f}'.format(q2[0][0]))
print('q3 = {0:.3f}'.format(q3[0][0]))
print('q4 = {0:.3f}'.format(q4[0][0]))
np.savetxt(outputPath+'summary.txt', [Nu, Vrms, q1, q2, q3, q4])
```
| $Ra$ | $Nu$ | $v_{rms}$| $q_1$ | $q_2$ | $q_3$ | $q_4$ |
|:------:|:--------:|:-------:|:--------:|:-------:|:-------:|:--------:|
| 10$^7$ | 10.0660 | 480.4 | 17.53136 | 1.00851 | 26.8085 | 0.497380 |
| true |
code
| 0.501282 | null | null | null | null |
|
#Demo: Interpolator
*This script provides a few examples on using the Interpolator class.
Last updated: April 14, 2015.
Copyright (C) 2014 Randall Romero-Aguilar
Licensed under the MIT license, see LICENSE.txt*
*Interpolator* is a subclass of *Basis*.
* A *Basis* object contains data to compute the interpolation matrix $\Phi(x)$ at arbitrary values of $x$ (within the interpolation box).
* An *Interpolator* is used to interpolate a given function $f(x)$, when the value of $f$ is known at the basis nodes. It adds methods to the *Basis* class to compute interpolation coefficients $c$ and to interpolate $f$ at arbitrary $x$.
Evaluation of this objects is straighforward:
* If B is a Basis, then B(x, k) computes the interpolating matrix $D^{(k)}\Phi(x)$, the k-derivative of $\Phi$
* If V is an Interpolator, then V(x, k) interpolates $D^{(k)}f(x)$, the k-derivative of $f$.
```
%matplotlib notebook
import numpy as np
from compecon import Basis, Interpolator
import matplotlib.pyplot as plt
import seaborn as sns
import time
np.set_printoptions(precision=3, suppress=True)
#sns.set(style='whitegrid')
```
##EXAMPLE 1:
Using BasisChebyshev to interpolate a 1-D function with a Chebyshev basis
**PROBLEM:** Interpolate the function $y = f(x) = 1 + sin(2x)^2$ on the domain $[0,\pi]$, using 5 Gaussian nodes.
There are two ways to create an *Interpolator* object.
* Defining the basis first, then the interpolator with known function values at nodes
```
f = lambda x: (1 + np.sin(2*x)**2)
B = Basis(5,0,np.pi)
V = Interpolator(B, y=f(B.nodes))
```
We are goint to make the same plot several times, so define it with a function
```
xx = np.linspace(0,np.pi,120)
def plot(P):
plt.figure()
plt.plot(xx,f(xx))
plt.plot(xx,P(xx))
plt.scatter(P.nodes,P(),color='red') #add nodes
```
Plot the interpolation at a refined grid. Notice how the interpolation is exact at the nodes.
```
plot(V)
```
* The second option is to create the *Interpolator* just as a regular *Basis*, adding the known function values at the next step. The difference is that we end up with only one object.
```
S = Interpolator(5,0,np.pi)
S.y = f(S.nodes)
plot(S)
```
* When we have a callable object (like the lambda f) we can pass it directly to the constructor, which will evaluate it at the nodes:
```
U = Interpolator(5,0,np.pi, y = f)
plot(U)
```
### Let's time it
Interpolate the first derivative of $S$ at the $xx$ values, repeat $10^4$ times.
```
t0 = time.time()
for k in range(10000):
S(xx, 1)
time.time() - t0
```
In MATLAB, it takes around 6 seconds!!
| true |
code
| 0.406626 | null | null | null | null |
|
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
MAX_EVALUE = 1e-2
```
# Data Overview
This notebook provides an overview of source datasets - training, testing and 3k bacteria.
# Training data
## ClusterFinder BGCs (positives)
** Used for: Model training **
CSV file with protein domains in genomic order. Contigs (samples) are defined by the `contig_id` column.
```
domains = pd.read_csv('../data/training/positive/CF_bgcs.csv')
domains = domains[domains['evalue'] <= MAX_EVALUE]
domains.head()
num_contigs = len(domains['contig_id'].unique())
num_contigs
contig_proteins = domains.groupby("contig_id")['protein_id'].nunique()
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
ax = contig_proteins.hist(bins=40, ax=axes[0])
ax.set_xlabel('# proteins in BGC sample')
ax.set_ylabel('Frequency')
ax = contig_proteins.hist(bins=100, ax=axes[1], cumulative=True)
ax.set_xlabel('# proteins in BGC sample')
ax.set_ylabel('Cumulative frequency')
plt.tight_layout()
contig_domains = domains.groupby("contig_id")['pfam_id'].size()
ax = contig_domains.hist(bins=20)
ax.set_xlabel('# domains in BGC sample')
ax.set_ylabel('Frequency')
```
## MIBiG BGCs (positives)
** Used for: LCO validation, 10-fold Cross-validation **
CSV file with protein domains in genomic order. Contigs (samples) are defined by the `contig_id` column.
```
domains = pd.read_csv('../data/training/positive/mibig_bgcs_all.csv')
domains = domains[domains['evalue'] <= MAX_EVALUE]
domains.head()
num_contigs = len(domains['contig_id'].unique())
num_contigs
contig_proteins = domains.groupby("contig_id")['protein_id'].nunique()
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
ax = contig_proteins.hist(bins=40, ax=axes[0])
ax.set_xlabel('# proteins in BGC sample')
ax.set_ylabel('Frequency')
ax = contig_proteins.hist(bins=100, ax=axes[1], cumulative=True)
ax.set_xlabel('# proteins in BGC sample')
ax.set_ylabel('Cumulative frequency')
plt.tight_layout()
contig_domains = domains.groupby("contig_id")['pfam_id'].size()
ax = contig_domains.hist(bins=20)
ax.set_xlabel('# domains in BGC sample')
ax.set_ylabel('Frequency')
contig_domains.describe(percentiles=np.arange(0, 1, 0.05))
properties = pd.read_csv('../data/mibig/mibig_properties.csv')
properties.head()
properties['classes'].value_counts().plot.barh(figsize=(5, 10))
classes_split = properties['classes'].apply(lambda c: c.split(';'))
class_counts = pd.Series([c for classes in classes_split for c in classes]).value_counts()
class_counts.plot.barh()
print(class_counts)
```
# GeneSwap negatives
** Used for: Model training, LCO validation **
```
domains = pd.read_csv('../data/training/negative/geneswap_negatives.csv')
domains = domains[domains['evalue'] <= MAX_EVALUE]
domains.head()
num_contigs = len(domains['contig_id'].unique())
num_contigs
contig_proteins = domains.groupby("contig_id")['protein_id'].nunique()
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
ax = contig_proteins.hist(bins=40, ax=axes[0])
ax.set_xlabel('# proteins in negative sample')
ax.set_ylabel('Frequency')
ax = contig_proteins.hist(bins=100, ax=axes[1], cumulative=True)
ax.set_xlabel('# proteins in negative sample')
ax.set_ylabel('Cumulative frequency')
plt.tight_layout()
contig_domains = domains.groupby("contig_id")['pfam_id'].size()
ax = contig_domains.hist(bins=20)
ax.set_xlabel('# domains in negative sample')
ax.set_ylabel('Frequency')
```
# Validation and testing data
## ClusterFinder labelled contigs
** Used for: Model validation - ROC curves **
10 labelled genomes (13 contigs) with non-BGC and BGC regions (stored in `in_cluster` column for each domain)
```
contigs = pd.read_csv('../data/clusterfinder/labelled/CF_labelled_contig_summary.csv', sep=';')
contigs
domains = pd.read_csv('../data/clusterfinder/labelled/CF_labelled_contigs_domains.csv')
domains = domains[domains['evalue'] <= MAX_EVALUE]
domains.head()
def count_y_clusters(y):
prev = 0
clusters = 0
for val in y:
if val == 1 and prev == 0:
clusters += 1
prev = val
return clusters
```
### non-BGC and BGC regions
```
for contig_id, contig_domains in domains.groupby('contig_id'):
in_cluster = contig_domains.reset_index()['in_cluster']
num_bgcs = count_y_clusters(in_cluster)
title = '{} ({} BGCs)'.format(contig_id, num_bgcs)
ax = in_cluster.plot(figsize=(15, 1), title=title, color='grey', lw=1)
in_cluster.plot(kind='area', ax=ax, color='grey', alpha=0.2)
plt.show()
```
## ClusterFinder 75 BGCs in genomic context
** Used for: Model validation - TPR evaluation **
6 labelled genomes with annotated BGC regions. Remaining regions are not known.
75 BGCs are annotated (10 are duplicates found twice, so only 65 are unique)
```
bgc75_locations = pd.read_csv('../data/clusterfinder/74validation/74validation_locations.csv')
bgc75_locations.head()
fig, axes = plt.subplots(len(bgc75_locations['Accession'].unique()), figsize=(8, 8))
i = 0
for contig_id, contig_bgcs in bgc75_locations.groupby('Accession'):
num_bgcs = len(contig_bgcs)
title = '{} ({} BGCs)'.format(contig_id, num_bgcs)
axes[i].set_title(title)
axes[i].set_ylim([0, 1.2])
for b, bgc in contig_bgcs.iterrows():
axes[i].plot([bgc['BGC_start'], bgc['BGC_stop']], [1, 1], color='grey')
axes[i].fill_between([bgc['BGC_start'], bgc['BGC_stop']], [1, 1], color='grey', alpha=0.3)
i += 1
plt.tight_layout()
bgc75_domains = pd.read_csv('../data/clusterfinder/74validation/74validation_domains.csv')
bgc75_domains = bgc75_domains[bgc75_domains['evalue'] <= MAX_EVALUE]
bgc75_domains.head()
```
# 3k reference genomes
3376 bacterial genomes, preprocessed using Prodigal & Pfam Hmmscan.
## Reference genomes species
```
bac_species = pd.read_csv('../data/bacteria/species.tsv', sep='\t').set_index('contig_id')
bac_species['family'] = bac_species['species'].apply(lambda species: species.split('_')[0])
bac_species['subspecies'] = bac_species['species'].apply(lambda species: ' '.join(species.split('_')[:2]))
bac_species.head()
bac_families_top = bac_species['family'].value_counts()[:20]
print('Unique families:', len(bac_species['family'].unique()))
bac_families_top
bac_species_top = bac_species['subspecies'].value_counts()[:20]
print('Unique species:', len(bac_species['subspecies'].unique()))
bac_species_top
```
## Reference genomes domains
** Used for: Pfam2vec corpus generation, Novel BGC candidate prediction **
Domain CSV files, one for each bacteria.
```
bac_domains = pd.read_csv('../data/bacteria/domains/AE000511.1.domains.csv', nrows=10)
bac_domains.head()
```
## Reference genomes pfam corpus
** Used for: Pfam2vec training **
Corpus of 23,425,967 pfams domains (words) used to train the pfam2vec embedding using the word2vec algorithm.
Corpus contains pfam domains from one bacteria per line, separated by space.
```
corpus = pd.read_csv('../data/bacteria/corpus/corpus-1e-02.txt', nrows=10, header=None)
corpus.head()
corpus_counts = pd.read_csv('../data/bacteria/corpus/corpus-1e-02.counts.csv').set_index('pfam_id')
corpus_counts[:10][::-1].plot.barh()
```
The pfam counts have a very long-tail distribution with a median of only 101 occurences.
```
corpus_counts.plot.hist(bins=100)
print(corpus_counts.describe())
```
| true |
code
| 0.453685 | null | null | null | null |
|
## Classes for callback implementors
```
from fastai.gen_doc.nbdoc import *
from fastai.callback import *
from fastai.basics import *
```
fastai provides a powerful *callback* system, which is documented on the [`callbacks`](/callbacks.html#callbacks) page; look on that page if you're just looking for how to use existing callbacks. If you want to create your own, you'll need to use the classes discussed below.
A key motivation for the callback system is that additional functionality can be entirely implemented in a single callback, so that it's easily read. By using this trick, we will have different methods categorized in different callbacks where we will find clearly stated all the interventions the method makes in training. For instance in the [`LRFinder`](/callbacks.lr_finder.html#LRFinder) callback, on top of running the fit function with exponentially growing LRs, it needs to handle some preparation and clean-up, and all this code can be in the same callback so we know exactly what it is doing and where to look if we need to change something.
In addition, it allows our [`fit`](/basic_train.html#fit) function to be very clean and simple, yet still easily extended. So far in implementing a number of recent papers, we haven't yet come across any situation where we had to modify our training loop source code - we've been able to use callbacks every time.
```
show_doc(Callback)
```
To create a new type of callback, you'll need to inherit from this class, and implement one or more methods as required for your purposes. Perhaps the easiest way to get started is to look at the source code for some of the pre-defined fastai callbacks. You might be surprised at how simple they are! For instance, here is the **entire** source code for [`GradientClipping`](/train.html#GradientClipping):
```python
@dataclass
class GradientClipping(LearnerCallback):
clip:float
def on_backward_end(self, **kwargs):
if self.clip:
nn.utils.clip_grad_norm_(self.learn.model.parameters(), self.clip)
```
You generally want your custom callback constructor to take a [`Learner`](/basic_train.html#Learner) parameter, e.g.:
```python
@dataclass
class MyCallback(Callback):
learn:Learner
```
Note that this allows the callback user to just pass your callback name to `callback_fns` when constructing their [`Learner`](/basic_train.html#Learner), since that always passes `self` when constructing callbacks from `callback_fns`. In addition, by passing the learner, this callback will have access to everything: e.g all the inputs/outputs as they are calculated, the losses, and also the data loaders, the optimizer, etc. At any time:
- Changing self.learn.data.train_dl or self.data.valid_dl will change them inside the fit function (we just need to pass the [`DataBunch`](/basic_data.html#DataBunch) object to the fit function and not data.train_dl/data.valid_dl)
- Changing self.learn.opt.opt (We have an [`OptimWrapper`](/callback.html#OptimWrapper) on top of the actual optimizer) will change it inside the fit function.
- Changing self.learn.data or self.learn.opt directly WILL NOT change the data or the optimizer inside the fit function.
In any of the callbacks you can unpack in the kwargs:
- `n_epochs`, contains the number of epochs the training will take in total
- `epoch`, contains the number of the current
- `iteration`, contains the number of iterations done since the beginning of training
- `num_batch`, contains the number of the batch we're at in the dataloader
- `last_input`, contains the last input that got through the model (eventually updated by a callback)
- `last_target`, contains the last target that got through the model (eventually updated by a callback)
- `last_output`, contains the last output spitted by the model (eventually updated by a callback)
- `last_loss`, contains the last loss computed (eventually updated by a callback)
- `smooth_loss`, contains the smoothed version of the loss
- `last_metrics`, contains the last validation loss and metrics computed
- `pbar`, the progress bar
- [`train`](/train.html#train), flag to know if we're in training mode or not
- `stop_training`, that will stop the training at the end of the current epoch if True
- `stop_epoch`, that will break the current epoch loop
- `skip_step`, that will skip the next optimizer step
- `skip_zero`, that will skip the next zero grad
When returning a dictionary with those key names, the state of the [`CallbackHandler`](/callback.html#CallbackHandler) will be updated with any of those changes, so in any [`Callback`](/callback.html#Callback), you can change those values.
### Methods your subclass can implement
All of these methods are optional; your subclass can handle as many or as few as you require.
```
show_doc(Callback.on_train_begin)
```
Here we can initiliaze anything we need.
The optimizer has now been initialized. We can change any hyper-parameters by typing, for instance:
```
self.opt.lr = new_lr
self.opt.mom = new_mom
self.opt.wd = new_wd
self.opt.beta = new_beta
```
```
show_doc(Callback.on_epoch_begin)
```
This is not technically required since we have `on_train_begin` for epoch 0 and `on_epoch_end` for all the other epochs,
yet it makes writing code that needs to be done at the beginning of every epoch easy and more readable.
```
show_doc(Callback.on_batch_begin)
```
Here is the perfect place to prepare everything before the model is called.
Example: change the values of the hyperparameters (if we don't do it on_batch_end instead)
At the end of that event `xb`,`yb` will be set to `last_input`, `last_target` of the state of the [`CallbackHandler`](/callback.html#CallbackHandler).
```
show_doc(Callback.on_loss_begin)
```
Here is the place to run some code that needs to be executed after the output has been computed but before the
loss computation.
Example: putting the output back in FP32 when training in mixed precision.
At the end of that event the output will be set to `last_output` of the state of the [`CallbackHandler`](/callback.html#CallbackHandler).
```
show_doc(Callback.on_backward_begin)
```
Here is the place to run some code that needs to be executed after the loss has been computed but before the gradient computation.
Example: `reg_fn` in RNNs.
At the end of that event the output will be set to `last_loss` of the state of the [`CallbackHandler`](/callback.html#CallbackHandler).
```
show_doc(Callback.on_backward_end)
```
Here is the place to run some code that needs to be executed after the gradients have been computed but
before the optimizer is called.
If `skip_step` is `True` at the end of this event, the optimizer step is skipped.
```
show_doc(Callback.on_step_end)
```
Here is the place to run some code that needs to be executed after the optimizer step but before the gradients
are zeroed.
If `skip_zero` is `True` at the end of this event, the gradients are not zeroed.
```
show_doc(Callback.on_batch_end)
```
Here is the place to run some code that needs to be executed after a batch is fully done.
Example: change the values of the hyperparameters (if we don't do it on_batch_begin instead)
If `end_epoch` is `True` at the end of this event, the current epoch is interrupted (example: lr_finder stops the training when the loss explodes).
```
show_doc(Callback.on_epoch_end)
```
Here is the place to run some code that needs to be executed at the end of an epoch.
Example: Save the model if we have a new best validation loss/metric.
If `end_training` is `True` at the end of this event, the training stops (example: early stopping).
```
show_doc(Callback.on_train_end)
```
Here is the place to tidy everything. It's always executed even if there was an error during the training loop,
and has an extra kwarg named exception to check if there was an exception or not.
Examples: save log_files, load best model found during training
```
show_doc(Callback.get_state)
```
This is used internally when trying to export a [`Learner`](/basic_train.html#Learner). You won't need to subclass this function but you can add attribute names to the lists `exclude` or `not_min`of the [`Callback`](/callback.html#Callback) you are designing. Attributes in `exclude` are never saved, attributes in `not_min` only if `minimal=False`.
## Annealing functions
The following functions provide different annealing schedules. You probably won't need to call them directly, but would instead use them as part of a callback. Here's what each one looks like:
```
annealings = "NO LINEAR COS EXP POLY".split()
fns = [annealing_no, annealing_linear, annealing_cos, annealing_exp, annealing_poly(0.8)]
for fn, t in zip(fns, annealings):
plt.plot(np.arange(0, 100), [fn(2, 1e-2, o)
for o in np.linspace(0.01,1,100)], label=t)
plt.legend();
show_doc(annealing_cos)
show_doc(annealing_exp)
show_doc(annealing_linear)
show_doc(annealing_no)
show_doc(annealing_poly)
show_doc(CallbackHandler)
```
You probably won't need to use this class yourself. It's used by fastai to combine all the callbacks together and call any relevant callback functions for each training stage. The methods below simply call the equivalent method in each callback function in [`self.callbacks`](/callbacks.html#callbacks).
```
show_doc(CallbackHandler.on_backward_begin)
show_doc(CallbackHandler.on_backward_end)
show_doc(CallbackHandler.on_batch_begin)
show_doc(CallbackHandler.on_batch_end)
show_doc(CallbackHandler.on_epoch_begin)
show_doc(CallbackHandler.on_epoch_end)
show_doc(CallbackHandler.on_loss_begin)
show_doc(CallbackHandler.on_step_end)
show_doc(CallbackHandler.on_train_begin)
show_doc(CallbackHandler.on_train_end)
show_doc(CallbackHandler.set_dl)
show_doc(OptimWrapper)
```
This is a convenience class that provides a consistent API for getting and setting optimizer hyperparameters. For instance, for [`optim.Adam`](https://pytorch.org/docs/stable/optim.html#torch.optim.Adam) the momentum parameter is actually `betas[0]`, whereas for [`optim.SGD`](https://pytorch.org/docs/stable/optim.html#torch.optim.SGD) it's simply `momentum`. As another example, the details of handling weight decay depend on whether you are using `true_wd` or the traditional L2 regularization approach.
This class also handles setting different WD and LR for each layer group, for discriminative layer training.
```
show_doc(OptimWrapper.clear)
show_doc(OptimWrapper.create)
show_doc(OptimWrapper.new)
show_doc(OptimWrapper.read_defaults)
show_doc(OptimWrapper.read_val)
show_doc(OptimWrapper.set_val)
show_doc(OptimWrapper.step)
show_doc(OptimWrapper.zero_grad)
show_doc(SmoothenValue)
```
Used for smoothing loss in [`Recorder`](/basic_train.html#Recorder).
```
show_doc(SmoothenValue.add_value)
show_doc(Scheduler)
```
Used for creating annealing schedules, mainly for [`OneCycleScheduler`](/callbacks.one_cycle.html#OneCycleScheduler).
```
show_doc(Scheduler.step)
show_doc(AverageMetric)
```
See the documentation on [`metrics`](/metrics.html#metrics) for more information.
### Callback methods
You don't call these yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
```
show_doc(AverageMetric.on_epoch_begin)
show_doc(AverageMetric.on_batch_end)
show_doc(AverageMetric.on_epoch_end)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.914482 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/moh2236945/Natural-language-processing/blob/master/Apply%20features%20extrating%20and%20text%20normalization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import re
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import string
import nltk
import numpy as np
%matplotlib inline
train=pd.read_csv('/content/train_E6oV3lV.csv')
test=pd.read_csv('/content/test_tweets_anuFYb8.csv')
train.head()
```
data has 3 columns id, label, and tweet. ***label*** is the binary target variable and ***tweet*** contains the tweets that we will clean and preprocess.
```
#Removing @ to do this we sure to combine train and test together fires
combi=train.append(test,ignore_index=True)
combi.shape
def remove_pattern(input_text,pattern):
r=re.findall(pattern,input_text)
for i in r:
input_text=re.sub(i,'',input_text)
return input_text
```
create a new column tidy_tweet,
it contain the cleaned and processed tweets. **Note** that we have passed “@[\w]*” as the pattern to the remove_pattern function. It is actually a regular expression which will pick any word starting with ‘@’.
```
combi['tidy_tweet']=np.vectorize(remove_pattern)(combi['tweet'],"@[\w]*")
combi.head()
#removing Punction,Number&Special chars
combi['tidy_tweet']=combi['tidy_tweet'].str.replace('[^a-zA-Z#]', "")
combi.head()
```
Removing Short Words
```
combi['tidy_tweet'] = combi['tidy_tweet'].apply(lambda x: ' '.join([w for w in x.split() if len(w)>3]))
```
Text Normalization
Steps:
Tokenization > Normalization
```
tokenized_tweet = combi['tidy_tweet'].apply(lambda x: x.split()) # tokenizing
tokenized_tweet.head()
from nltk.stem.porter import *
stemmer = PorterStemmer()
tokenized_tweet = tokenized_tweet.apply(lambda x: [stemmer.stem(i) for i in x]) # stemming
#stitch these tokens back together.
for i in range(len(tokenized_tweet)):
tokenized_tweet[i] = ' '.join(tokenized_tweet[i])
combi['tidy_tweet'] = tokenized_tweet
#Understanding the common words used in the tweets: WordCloud
#A wordcloud is a visualization wherein the most frequent words appear in large size and the less frequent words appear in smaller sizes.
all_words = ' '.join([text for text in combi['tidy_tweet']])
from wordcloud import WordCloud
wordcloud = WordCloud(width=800, height=500, random_state=21, max_font_size=110).generate(all_words)
plt.figure(figsize=(10, 7))
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis('off')
plt.show()
#Words in non racist/sexist tweets
normal_words =' '.join([text for text in combi['tidy_tweet'][combi['label'] == 0]])
wordcloud = WordCloud(width=800, height=500, random_state=21, max_font_size=110).generate(normal_words)
plt.figure(figsize=(10, 7))
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis('off')
plt.show()
# Understanding the impact of Hashtags on tweets sentiment
# function to collect hashtags
def hashtag_extract(x):
hashtags = []
# Loop over the words in the tweet
for i in x:
ht = re.findall(r"#(\w+)", i)
hashtags.append(ht)
return hashtags
# extracting hashtags from non racist/sexist tweets
HT_regular = hashtag_extract(combi['tidy_tweet'][combi['label'] == 0])
# extracting hashtags from racist/sexist tweets
HT_negative = hashtag_extract(combi['tidy_tweet'][combi['label'] == 1])
# unnesting list
HT_regular = sum(HT_regular,[])
HT_negative = sum(HT_negative,[])
#Non-Racist/Sexist Tweets
a = nltk.FreqDist(HT_regular)
d = pd.DataFrame({'Hashtag': list(a.keys()),
'Count': list(a.values())})
# selecting top 20 most frequent hashtags
d = d.nlargest(columns="Count", n = 20)
plt.figure(figsize=(16,5))
ax = sns.barplot(data=d, x= "Hashtag", y = "Count")
ax.set(ylabel = 'Count')
plt.show()
#extract Features from Cleaned tweets
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
import gensim
#Bag-of-Words Features
bow_vectorizer = CountVectorizer(max_df=0.90, min_df=2, max_features=1000, stop_words='english')
bow = bow_vectorizer.fit_transform(combi['tidy_tweet'])
bow.shape
#TF-IDF Features
tfidf_vectorizer = TfidfVectorizer(max_df=0.90, min_df=2, max_features=1000, stop_words='english')
tfidf = tfidf_vectorizer.fit_transform(combi['tidy_tweet'])
tfidf.shape
#Word Embedding
tokenized_tweet = combi['tidy_tweet'].apply(lambda x: x.split()) # tokenizing
model_w2v = gensim.models.Word2Vec(
tokenized_tweet,
size=200, # desired no. of features/independent variables
window=5, # context window size
min_count=2,
sg = 1, # 1 for skip-gram model
hs = 0,
negative = 10, # for negative sampling
workers= 2, # no.of cores
seed = 34)
model_w2v.train(tokenized_tweet, total_examples= len(combi['tidy_tweet']), epochs=20)
#Preparing Vectors for Tweets
def word_vector(tokens, size):
vec = np.zeros(size).reshape((1, size))
count = 0.
for word in tokens:
try:
vec += model_w2v[word].reshape((1, size))
count += 1.
except KeyError: # handling the case where the token is not in vocabulary
continue
if count != 0:
vec /= count
return vec
wordvec_arrays = np.zeros((len(tokenized_tweet), 200))
for i in range(len(tokenized_tweet)):
wordvec_arrays[i,:] = word_vector(tokenized_tweet[i], 200)
wordvec_df = pd.DataFrame(wordvec_arrays)
wordvec_df.shape
from tqdm import tqdm
tqdm.pandas(desc="progress-bar")
from gensim.models.doc2vec import LabeledSentence
def add_label(twt):
output = []
for i, s in zip(twt.index, twt):
output.append(LabeledSentence(s, ["tweet_" + str(i)]))
return output
labeled_tweets = add_label(tokenized_tweet) # label all the tweets
labeled_tweets[:6]
```
| true |
code
| 0.369329 | null | null | null | null |
|
# A sample example to tuning the hyperparameters of Prophet classifier is shown as usecase.
```
from mango.tuner import Tuner
from mango.domain.distribution import loguniform
param_dict = {"changepoint_prior_scale": loguniform(-3, 4),
'seasonality_prior_scale' : loguniform(1, 2)
}
```
# userObjective
```
from classifiers.prophet import Prophet
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_val_score
import numpy as np
model = Prophet()
import os
data_path = os.path.abspath('.')+'/classifiers/data/'
X_train, y_train =model.load_train_dataset(data_path+"PJME/train_data")
X_test, y_test = model.load_train_dataset(data_path+"PJME/test_data")
X_validate, y_validate = model.load_train_dataset(data_path+"PJME/validate_data")
count_called = 1
def objective_Prophet(args_list):
global X_train, y_train,X_validate,y_validate, count_called
print('count_called:',count_called)
count_called = count_called + 1
hyper_evaluated = []
results = []
for hyper_par in args_list:
clf = Prophet(**hyper_par)
clf.fit(X_train, y_train.ravel())
y_pred = clf.predict(X_validate)
mse = mean_squared_error(y_validate, y_pred)
mse = mse/10e5
result = (-1.0) * mse
results.append(result)
hyper_evaluated.append(hyper_par)
return hyper_evaluated, results
conf_Dict = dict()
conf_Dict['batch_size'] = 2
conf_Dict['num_iteration'] = 10
conf_Dict['initial_random'] = 5
#conf_Dict['domain_size'] = 10000
```
# Defining Tuner
```
tuner_user = Tuner(param_dict, objective_Prophet,conf_Dict)
tuner_user.getConf()
import time
start_time = time.clock()
results = tuner_user.maximize()
end_time = time.clock()
print(end_time - start_time)
```
# Inspect the results
```
print('best hyper parameters:',results['best_params'])
print('best objective:',results['best_objective'])
print('Sample hyper parameters tried:',len(results['params_tried']))
print(results['params_tried'][:2])
print('Sample objective values',len(results['objective_values']))
print(results['objective_values'][:5])
```
# Plotting the actual variation in objective values of the tried results
```
Size = 201
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,5))
plt.title('Variation of Objective',fontsize=20)
plt.plot(results['objective_values'][:Size],lw=4,label='BL')
plt.xlabel('Iterations', fontsize=25)
plt.ylabel('objective_values',fontsize=25)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(prop={'size': 30})
plt.show()
```
# Plotting the variation of Max objective values of the tried results
```
Size = 201
import numpy as np
results_obj = np.array(results['objective_values'])
y_max=[]
for i in range(results_obj.shape[0]):
y_max.append(np.max(results_obj[:i+1]))
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,5))
plt.title('Max variation of Objective',fontsize=20)
plt.plot(y_max[:Size],lw=4,label='BL')
plt.xlabel('Iterations', fontsize=25)
plt.ylabel('objective_values',fontsize=25)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend(prop={'size': 30})
plt.show()
```
# See the Result
```
import pprint
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(results)
```
# See the learned classifier result on the test data
```
model = Prophet(**results['best_params'])
model.fit(X_train, y_train.ravel())
y_pred = model.predict(X_test)
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,10))
plt.rcParams.update({'font.size': 18})
plt.plot(X_test,y_test,label='Test')
plt.plot(X_test,y_pred,label='Prediction')
plt.title('Testing Data')
plt.legend()
plt.show()
```
# All the Data
```
from classifiers.prophet import Prophet
model = Prophet()
import os
data_path = os.path.abspath('.')+'/classifiers/data/'
X_train, y_train =model.load_train_dataset(data_path+"PJME/train_data")
X_test, y_test = model.load_train_dataset(data_path+"PJME/test_data")
X_validate, y_validate = model.load_train_dataset(data_path+"PJME/validate_data")
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(30,10))
plt.rcParams.update({'font.size': 18})
plt.plot(X_train,y_train,label='Train')
plt.plot(X_validate,y_validate,label='validate')
plt.plot(X_test,y_test,label='Test')
plt.title('All Data')
plt.legend()
plt.show()
```
| true |
code
| 0.533337 | null | null | null | null |
|
# Vector Norm
```
import numpy as np
from scipy import signal
from scipy.spatial import distance
A = np.array([1+1j, 2+2j, 3+3j, 4+4j, 5+5j])
B = np.array([6-6j, 7-7j, 8-8j, 9-9j, 10-10j])
C = np.array([2,3,5,7,11])
Z = np.array([0,0,0,0,0])
D = np.array([A,B])
```
For every complex inner product space V(-,-), we can define a norm or length which is a function defined as
\begin{align}
| |: V -> E
\end{align}
defined as
\begin{align}
|V| = |\sqrt{V . V}|
\end{align}
```
[
np.linalg.norm(A) == np.abs(np.sqrt(np.dot(A,A))),
np.linalg.norm(B) == np.abs(np.sqrt(np.dot(B,B))),
np.linalg.norm(C) == np.abs(np.sqrt(np.dot(C,C)))
]
[
np.linalg.norm(A),
np.linalg.norm(B),
np.linalg.norm(C),
]
```
# Vector Distance
For every complex inner product space V(-,-), we can define a distance function
\begin{align}
d(,) : V x V -> E
\end{align}
where
\begin{align}
d(V1,V2) : |V1 - V2| = \sqrt{V1-V2, V1-V2}
\end{align}
```
distance.euclidean(A, B)
np.linalg.norm(A-B) == distance.euclidean(A, B)
np.round( distance.euclidean(A, B), 10) == \
np.round( np.abs(np.sqrt(np.dot(A,A)-np.dot(B,B))), 10)
```
Distance is symmetric: d(V, W) = d(W, V)
```
distance.euclidean(A, B) == distance.euclidean(B, A)
```
Distance satisfies the triangle inequality: d(U, V) ≤ d(U, W) + d(W, V)
```
distance.euclidean(A, C), distance.euclidean(A, B) + distance.euclidean(B, C)
distance.euclidean(A, C) <= distance.euclidean(A, B) + distance.euclidean(B, C)
```
Distance is nondegenerate: d(V, W) > 0 if V ≠ W and d(V, V) = 0.
```
distance.euclidean(Z,Z)
distance.euclidean(A,Z), distance.euclidean(A,Z) > 0
```
## Orthogonal Vectors
The dot product of orthogonal vectors is zero
```
X = np.array([1,0])
Y = np.array([0,1])
np.dot(X,Y)
```
## Kronecker Delta
δj,k is called the Kronecker delta function.
δj,k =
1 (if i == j);
0 (if i != j);
```
M = np.matrix([[1,2,3],[4,5,6],[7,8,9]]); X
{ "shape": M.shape, "size": M.size }
def kronecker_delta(matrix):
output = np.copy(matrix)
for i in range(0, matrix.shape[0]):
for j in range(0, matrix.shape[1]):
output[i,j] = output[i,j] if i == j else 0
return output
kronecker_delta(M)
```
It is equlivant to element wise multiplication by the identity matrx
```
np.multiply(M, np.identity(3))
kronecker_delta(M) == np.multiply(M, np.identity(M.shape[0]))
```
NOTE: np.kron is the Kronecker (tensor) product function, and not the Kronecker DELTA
```
np.kron(M,M)
```
| true |
code
| 0.492493 | null | null | null | null |
|
```
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
"""
# If you're using Google Colab and not running locally, run this cell
# install NeMo
BRANCH = 'main'
!python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[nlp]
# If you're not using Colab, you might need to upgrade jupyter notebook to avoid the following error:
# 'ImportError: IProgress not found. Please update jupyter and ipywidgets.'
! pip install ipywidgets
! jupyter nbextension enable --py widgetsnbextension
# Please restart the kernel after running this cell
from nemo.collections import nlp as nemo_nlp
from nemo.utils.exp_manager import exp_manager
import os
import wget
import torch
import pytorch_lightning as pl
from omegaconf import OmegaConf
```
In this tutorial, we are going to describe how to finetune BioMegatron - a [BERT](https://arxiv.org/abs/1810.04805)-like [Megatron-LM](https://arxiv.org/pdf/1909.08053.pdf) model pre-trained on large biomedical text corpus ([PubMed](https://pubmed.ncbi.nlm.nih.gov/) abstracts and full-text commercial use collection) - on [RE: Text mining chemical-protein interactions (CHEMPROT)](https://biocreative.bioinformatics.udel.edu/tasks/biocreative-vi/track-5/).
The model size of Megatron-LM can be larger than BERT, up to multi-billion parameters, compared to 345 million parameters of BERT-large.
There are some alternatives of BioMegatron, most notably [BioBERT](https://arxiv.org/abs/1901.08746). Compared to BioBERT BioMegatron is larger by model size and pre-trained on larger text corpus.
A more general tutorial of using BERT-based models, including Megatron-LM, for downstream natural language processing tasks can be found [here](https://github.com/NVIDIA/NeMo/blob/stable/tutorials/nlp/01_Pretrained_Language_Models_for_Downstream_Tasks.ipynb).
# Task Description
**Relation Extraction (RE)** can be regarded as a type of sentence classification.
The task is to classify the relation of a [GENE] and [CHEMICAL] in a sentence, for example like the following:
```html
14967461.T1.T22 <@CHEMICAL$> inhibitors currently under investigation include the small molecules <@GENE$> (Iressa, ZD1839) and erlotinib (Tarceva, OSI-774), as well as monoclonal antibodies such as cetuximab (IMC-225, Erbitux). <CPR:4>
14967461.T2.T22 <@CHEMICAL$> inhibitors currently under investigation include the small molecules gefitinib (<@GENE$>, ZD1839) and erlotinib (Tarceva, OSI-774), as well as monoclonal antibodies such as cetuximab (IMC-225, Erbitux). <CPR:4>
```
to one of the following class:
| Relation Class | Relations |
| ----------- | ----------- |
| CPR:3 | Upregulator and activator |
| CPR:4 | Downregulator and inhibitor |
| CPR:5 | Agonist |
| CPR:6 | Antagonist |
| CPR:9 | Substrate and product of |
# Datasets
Details of ChemProt Relation Extraction task and the original data can be found on the [BioCreative VI website](https://biocreative.bioinformatics.udel.edu/tasks/biocreative-vi/track-5/)
ChemProt dataset pre-processed for easier consumption can be downloaded from [here](https://github.com/arwhirang/recursive_chemprot/blob/master/Demo/tree_LSTM/data/chemprot-data_treeLSTM.zip) or [here](https://github.com/ncbi-nlp/BLUE_Benchmark/releases/download/0.1/bert_data.zip)
```
TASK = 'ChemProt'
DATA_DIR = os.path.join(os.getcwd(), 'DATA_DIR')
RE_DATA_DIR = os.path.join(DATA_DIR, 'RE')
WORK_DIR = os.path.join(os.getcwd(), 'WORK_DIR')
MODEL_CONFIG = 'text_classification_config.yaml'
os.makedirs(DATA_DIR, exist_ok=True)
os.makedirs(os.path.join(DATA_DIR, 'RE'), exist_ok=True)
os.makedirs(WORK_DIR, exist_ok=True)
# download the dataset
wget.download('https://github.com/arwhirang/recursive_chemprot/blob/master/Demo/tree_LSTM/data/chemprot-data_treeLSTM.zip?raw=true',
os.path.join(DATA_DIR, 'data_re.zip'))
!unzip -o {DATA_DIR}/data_re.zip -d {RE_DATA_DIR}
! ls -l $RE_DATA_DIR
```
## Pre-process dataset
Let's convert the dataset into the format that is compatible for [NeMo text-classification module](https://github.com/NVIDIA/NeMo/blob/stable/examples/nlp/text_classification/text_classification_with_bert.py).
```
wget.download(f'https://raw.githubusercontent.com/NVIDIA/NeMo/{BRANCH}/examples/nlp/text_classification/data/import_datasets.py')
! python import_datasets.py --dataset_name=chemprot --source_data_dir={RE_DATA_DIR} --target_data_dir={RE_DATA_DIR}
# let's take a look at the training data
! head -n 5 {RE_DATA_DIR}/train.tsv
# let's check the label mapping
! cat {RE_DATA_DIR}/label_mapping.tsv
```
It is not necessary to have the mapping exactly like this - it can be different.
We use the same [mapping used by BioBERT](https://github.com/dmis-lab/biobert/blob/master/run_re.py#L438) so that comparison can be more straightforward.
# Model configuration
Now, let's take a closer look at the model's configuration and learn to train the model.
The model is defined in a config file which declares multiple important sections. They are:
- **model**: All arguments that are related to the Model - language model, a classifier, optimizer and schedulers, datasets and any other related information
- **trainer**: Any argument to be passed to PyTorch Lightning
```
# download the model's configuration file
config_dir = WORK_DIR + '/configs/'
os.makedirs(config_dir, exist_ok=True)
if not os.path.exists(config_dir + MODEL_CONFIG):
print('Downloading config file...')
wget.download(f'https://raw.githubusercontent.com/NVIDIA/NeMo/{BRANCH}/examples/nlp/text_classification/conf/' + MODEL_CONFIG, config_dir)
else:
print ('config file is already exists')
# this line will print the entire config of the model
config_path = f'{WORK_DIR}/configs/{MODEL_CONFIG}'
print(config_path)
config = OmegaConf.load(config_path)
config.model.train_ds.file_path = os.path.join(RE_DATA_DIR, 'train.tsv')
config.model.validation_ds.file_path = os.path.join(RE_DATA_DIR, 'dev.tsv')
config.model.task_name = 'chemprot'
# Note: these are small batch-sizes - increase as appropriate to available GPU capacity
config.model.train_ds.batch_size=8
config.model.validation_ds.batch_size=8
config.model.dataset.num_classes=6
print(OmegaConf.to_yaml(config))
```
# Model Training
## Setting up Data within the config
Among other things, the config file contains dictionaries called **dataset**, **train_ds** and **validation_ds**. These are configurations used to setup the Dataset and DataLoaders of the corresponding config.
We assume that both training and evaluation files are located in the same directory, and use the default names mentioned during the data download step.
So, to start model training, we simply need to specify `model.dataset.data_dir`, like we are going to do below.
Also notice that some config lines, including `model.dataset.data_dir`, have `???` in place of paths, this means that values for these fields are required to be specified by the user.
Let's now add the data directory path, task name and output directory for saving predictions to the config.
```
config.model.task_name = TASK
config.model.output_dir = WORK_DIR
config.model.dataset.data_dir = RE_DATA_DIR
```
## Building the PyTorch Lightning Trainer
NeMo models are primarily PyTorch Lightning modules - and therefore are entirely compatible with the PyTorch Lightning ecosystem.
Let's first instantiate a Trainer object
```
print("Trainer config - \n")
print(OmegaConf.to_yaml(config.trainer))
# lets modify some trainer configs
# checks if we have GPU available and uses it
cuda = 1 if torch.cuda.is_available() else 0
config.trainer.gpus = cuda
# for PyTorch Native AMP set precision=16
config.trainer.precision = 16 if torch.cuda.is_available() else 32
# remove distributed training flags
config.trainer.accelerator = None
trainer = pl.Trainer(**config.trainer)
```
## Setting up a NeMo Experiment
NeMo has an experiment manager that handles logging and checkpointing for us, so let's use it:
```
config.exp_manager.exp_dir = WORK_DIR
exp_dir = exp_manager(trainer, config.get("exp_manager", None))
# the exp_dir provides a path to the current experiment for easy access
exp_dir = str(exp_dir)
exp_dir
```
Before initializing the model, we might want to modify some of the model configs. Here we are modifying it to use BioMegatron, [Megatron-LM BERT](https://arxiv.org/abs/1909.08053) pre-trained on [PubMed](https://pubmed.ncbi.nlm.nih.gov/) biomedical text corpus.
```
# complete list of supported BERT-like models
print(nemo_nlp.modules.get_pretrained_lm_models_list())
# specify BERT-like model, you want to use, for example, "megatron-bert-345m-uncased" or 'bert-base-uncased'
PRETRAINED_BERT_MODEL = "biomegatron-bert-345m-uncased"
# add the specified above model parameters to the config
config.model.language_model.pretrained_model_name = PRETRAINED_BERT_MODEL
```
Now, we are ready to initialize our model. During the model initialization call, the dataset and data loaders we'll be prepared for training and evaluation.
Also, the pretrained BERT model will be downloaded, note it can take up to a few minutes depending on the size of the chosen BERT model.
```
model = nemo_nlp.models.TextClassificationModel(cfg=config.model, trainer=trainer)
```
## Monitoring training progress
Optionally, you can create a Tensorboard visualization to monitor training progress.
If you're not using Colab, refer to [https://www.tensorflow.org/tensorboard/tensorboard_in_notebooks](https://www.tensorflow.org/tensorboard/tensorboard_in_notebooks) if you're facing issues with running the cell below.
```
try:
from google import colab
COLAB_ENV = True
except (ImportError, ModuleNotFoundError):
COLAB_ENV = False
# Load the TensorBoard notebook extension
if COLAB_ENV:
%load_ext tensorboard
%tensorboard --logdir {exp_dir}
else:
print("To use tensorboard, please use this notebook in a Google Colab environment.")
# start model training
trainer.fit(model)
```
## Training Script
If you have NeMo installed locally, you can also train the model with `examples/nlp/text_classification/text_classification_with_bert.py.`
To run training script, use:
`python text_classification_with_bert.py \
model.dataset.data_dir=PATH_TO_DATA_DIR \
model.task_name=TASK`
The training could take several minutes and the results should look something like:
```
precision recall f1-score support
0 0.7328 0.8348 0.7805 115
1 0.9402 0.9291 0.9346 7950
2 0.8311 0.9146 0.8708 199
3 0.6400 0.6302 0.6351 457
4 0.8002 0.8317 0.8156 1093
5 0.7228 0.7518 0.7370 548
accuracy 0.8949 10362
macro avg 0.7778 0.8153 0.7956 10362
weighted avg 0.8963 0.8949 0.8954 10362
```
| true |
code
| 0.693291 | null | null | null | null |
|
```
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
matplotlib.__version__, np.__version__, pd.__version__
```
## 2 Plots side by side
```
plt.clf()
# sample data
x = np.linspace(0.0,100,50)
y = np.random.uniform(low=0,high=10,size=50)
# create figure and axes
fig, axes = plt.subplots(1,2)
ax1 = axes[0]
ax2 = axes[1]
# just plot things on each individual axes
ax1.scatter(x,y,c='red',marker='+')
ax2.bar(x,y)
plt.gcf().set_size_inches(10,5)
plt.show()
```
## 2 plots one on top of the other
```
plt.clf()
# sample data
x = np.linspace(0.0,100,50)
y = np.random.uniform(low=0,high=10,size=50)
# create figure and axes
fig, axes = plt.subplots(2,1)
ax1 = axes[0]
ax2 = axes[1]
# just plot things on each individual axes
ax1.scatter(x,y,c='red',marker='+')
ax2.bar(x,y)
plt.gcf().set_size_inches(5,5)
plt.show()
```
## 4 plots in a grid
```
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.0,100,50)
y = np.random.uniform(low=0,high=10,size=50)
# plt.subplots returns an array of arrays. We can
# directly assign those to variables directly
# like this
fig, ((ax1,ax2),(ax3,ax4)) = plt.subplots(2,2)
# just plot things on each individual axes
ax1.scatter(x,y,c='red',marker='+')
ax2.bar(x,y)
ax3.scatter(x,y,marker='x')
ax4.barh(x,y)
plt.gcf().set_size_inches(5,5)
plt.show()
```
## Pandas plots
```
import matplotlib.pyplot as plt
import pandas as pd
df = pd.DataFrame({
'string_col':['foo','bar','baz','quux'],
'x':[10,20,30,40],
'y':[1,2,3,4]
})
df
plt.clf()
# plt.subplots returns an array of arrays. We can
# directly assign those to variables directly
fig, ((ax1,ax2),(ax3,ax4)) = plt.subplots(2,2)
# bar plot for column 'x'
df.plot(y='x', kind='bar', ax=ax1)
ax1.set_xlabel('index')
# horizontal bar plot for column 'y'
df.plot(y='y', kind='bar', ax=ax2, color='orange')
ax2.set_xlabel('index')
# both columns in a scatter plot
df.plot('x','y', kind='scatter', ax=ax3)
# to have two lines, plot twice in the same axis
df.plot(y='x', kind='line', ax=ax4)
df.plot(y='y', kind='line', ax=ax4)
ax4.set_xlabel('index')
plt.subplots_adjust(wspace=0.3, hspace=0.5)
plt.show()
```
## Set subplot title
```
plt.clf()
# plt.subplots returns an array of arrays. We can
# directly assign those to variables directly
fig, ((ax1,ax2),(ax3,ax4)) = plt.subplots(2,2)
# sample data
x = np.linspace(0.0,100,50)
y = np.random.uniform(low=0,high=10,size=50)
# plot individual subplots
ax1.bar(x,y)
ax2.bar(x,y)
ax3.scatter(x,y)
ax4.plot(x)
ax4.set_title('This is Plot 4',size=14)
plt.subplots_adjust(wspace=0.3, hspace=0.5)
plt.show()
```
## Padding
```
import numpy as np
import matplotlib.pyplot as plt
# sample data
x = np.linspace(0.0,100,50)
y = np.random.uniform(low=0,high=10,size=50)
# plt.subplots returns an array of arrays. We can
# directly assign those to variables directly
fig, ((ax1,ax2),(ax3,ax4)) = plt.subplots(2,2)
# just plot things on each individual axes
ax1.scatter(x,y,c='red',marker='+')
ax2.bar(x,y)
ax3.scatter(x,y,marker='x')
ax4.barh(x,y)
# here, set the width and the height between the subplots
# the default value is 0.2 for each
plt.subplots_adjust(wspace=0.50, hspace=1.0)
plt.show()
```
## Align axes
```
import numpy as np
import matplotlib.pyplot as plt
plt.clf()
# plt.subplots returns an array of arrays. We can
# directly assign those to variables directly
fig, ((ax1,ax2)) = plt.subplots(1,2)
np.random.seed(42)
x = np.linspace(0.0,100,50)
# sample data in different magnitudes
y1 = np.random.normal(loc=10, scale=2, size=10)
y2 = np.random.normal(loc=20, scale=2, size=10)
ax1.plot(y1)
ax2.plot(y2)
ax1.grid(True,alpha=0.3)
ax2.grid(True,alpha=0.3)
ax1.set_ylim(0,25)
ax2.set_ylim(0,25)
plt.subplots_adjust(wspace=0.3, hspace=0.5)
plt.show()
```
| true |
code
| 0.723138 | null | null | null | null |
|
## widgets.image_cleaner
fastai offers several widgets to support the workflow of a deep learning practitioner. The purpose of the widgets are to help you organize, clean, and prepare your data for your model. Widgets are separated by data type.
```
from fastai.vision import *
from fastai.widgets import DatasetFormatter, ImageCleaner, ImageDownloader, download_google_images
from fastai.gen_doc.nbdoc import *
%reload_ext autoreload
%autoreload 2
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
learn = create_cnn(data, models.resnet18, metrics=error_rate)
learn.fit_one_cycle(2)
learn.save('stage-1')
```
We create a databunch with all the data in the training set and no validation set (DatasetFormatter uses only the training set)
```
db = (ImageList.from_folder(path)
.no_split()
.label_from_folder()
.databunch())
learn = create_cnn(db, models.resnet18, metrics=[accuracy])
learn.load('stage-1');
show_doc(DatasetFormatter)
```
The [`DatasetFormatter`](/widgets.image_cleaner.html#DatasetFormatter) class prepares your image dataset for widgets by returning a formatted [`DatasetTfm`](/vision.data.html#DatasetTfm) based on the [`DatasetType`](/basic_data.html#DatasetType) specified. Use `from_toplosses` to grab the most problematic images directly from your learner. Optionally, you can restrict the formatted dataset returned to `n_imgs`.
```
show_doc(DatasetFormatter.from_similars)
from fastai.gen_doc.nbdoc import *
from fastai.widgets.image_cleaner import *
show_doc(DatasetFormatter.from_toplosses)
show_doc(ImageCleaner)
```
[`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) is for cleaning up images that don't belong in your dataset. It renders images in a row and gives you the opportunity to delete the file from your file system. To use [`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) we must first use `DatasetFormatter().from_toplosses` to get the suggested indices for misclassified images.
```
ds, idxs = DatasetFormatter().from_toplosses(learn)
ImageCleaner(ds, idxs, path)
```
[`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) does not change anything on disk (neither labels or existence of images). Instead, it creates a 'cleaned.csv' file in your data path from which you need to load your new databunch for the files to changes to be applied.
```
df = pd.read_csv(path/'cleaned.csv', header='infer')
# We create a databunch from our csv. We include the data in the training set and we don't use a validation set (DatasetFormatter uses only the training set)
np.random.seed(42)
db = (ImageList.from_df(df, path)
.no_split()
.label_from_df()
.databunch(bs=64))
learn = create_cnn(db, models.resnet18, metrics=error_rate)
learn = learn.load('stage-1')
```
You can then use [`ImageCleaner`](/widgets.image_cleaner.html#ImageCleaner) again to find duplicates in the dataset. To do this, you can specify `duplicates=True` while calling ImageCleaner after getting the indices and dataset from `.from_similars`. Note that if you are using a layer's output which has dimensions <code>(n_batches, n_features, 1, 1)</code> then you don't need any pooling (this is the case with the last layer). The suggested use of `.from_similars()` with resnets is using the last layer and no pooling, like in the following cell.
```
ds, idxs = DatasetFormatter().from_similars(learn, layer_ls=[0,7,1], pool=None)
ImageCleaner(ds, idxs, path, duplicates=True)
show_doc(ImageDownloader)
```
[`ImageDownloader`](/widgets.image_downloader.html#ImageDownloader) widget gives you a way to quickly bootstrap your image dataset without leaving the notebook. It searches and downloads images that match the search criteria and resolution / quality requirements and stores them on your filesystem within the provided `path`.
Images for each search query (or label) are stored in a separate folder within `path`. For example, if you pupulate `tiger` with a `path` setup to `./data`, you'll get a folder `./data/tiger/` with the tiger images in it.
[`ImageDownloader`](/widgets.image_downloader.html#ImageDownloader) will automatically clean up and verify the downloaded images with [`verify_images()`](/vision.data.html#verify_images) after downloading them.
```
path = Config.data_path()/'image_downloader'
os.makedirs(path, exist_ok=True)
ImageDownloader(path)
```
#### Downloading images in python scripts outside Jupyter notebooks
```
path = Config.data_path()/'image_downloader'
files = download_google_images(path, 'aussie shepherd', size='>1024*768', n_images=30)
len(files)
show_doc(download_google_images)
```
After populating images with [`ImageDownloader`](/widgets.image_downloader.html#ImageDownloader), you can get a an [`ImageDataBunch`](/vision.data.html#ImageDataBunch) by calling `ImageDataBunch.from_folder(path, size=size)`, or using the data block API.
```
# Setup path and labels to search for
path = Config.data_path()/'image_downloader'
labels = ['boston terrier', 'french bulldog']
# Download images
for label in labels:
download_google_images(path, label, size='>400*300', n_images=50)
# Build a databunch and train!
src = (ImageList.from_folder(path)
.random_split_by_pct()
.label_from_folder()
.transform(get_transforms(), size=224))
db = src.databunch(bs=16, num_workers=0)
learn = create_cnn(db, models.resnet34, metrics=[accuracy])
learn.fit_one_cycle(3)
```
#### Downloading more than a hundred images
To fetch more than a hundred images, [`ImageDownloader`](/widgets.image_downloader.html#ImageDownloader) uses `selenium` and `chromedriver` to scroll through the Google Images search results page and scrape image URLs. They're not required as dependencies by default. If you don't have them installed on your system, the widget will show you an error message.
To install `selenium`, just `pip install selenium` in your fastai environment.
**On a mac**, you can install `chromedriver` with `brew cask install chromedriver`.
**On Ubuntu**
Take a look at the latest Chromedriver version available, then something like:
```
wget https://chromedriver.storage.googleapis.com/2.45/chromedriver_linux64.zip
unzip chromedriver_linux64.zip
```
Note that downloading under 100 images doesn't require any dependencies other than fastai itself, however downloading more than a hundred images [uses `selenium` and `chromedriver`](/widgets.image_cleaner.html#Downloading-more-than-a-hundred-images).
`size` can be one of:
```
'>400*300'
'>640*480'
'>800*600'
'>1024*768'
'>2MP'
'>4MP'
'>6MP'
'>8MP'
'>10MP'
'>12MP'
'>15MP'
'>20MP'
'>40MP'
'>70MP'
```
## Methods
## Undocumented Methods - Methods moved below this line will intentionally be hidden
```
show_doc(ImageCleaner.make_dropdown_widget)
show_doc(ImageCleaner.next_batch)
show_doc(DatasetFormatter.sort_idxs)
show_doc(ImageCleaner.make_vertical_box)
show_doc(ImageCleaner.relabel)
show_doc(DatasetFormatter.largest_indices)
show_doc(ImageCleaner.delete_image)
show_doc(ImageCleaner.empty)
show_doc(ImageCleaner.empty_batch)
show_doc(DatasetFormatter.comb_similarity)
show_doc(ImageCleaner.get_widgets)
show_doc(ImageCleaner.write_csv)
show_doc(ImageCleaner.create_image_list)
show_doc(ImageCleaner.render)
show_doc(DatasetFormatter.get_similars_idxs)
show_doc(ImageCleaner.on_delete)
show_doc(ImageCleaner.make_button_widget)
show_doc(ImageCleaner.make_img_widget)
show_doc(DatasetFormatter.get_actns)
show_doc(ImageCleaner.batch_contains_deleted)
show_doc(ImageCleaner.make_horizontal_box)
show_doc(DatasetFormatter.get_toplosses_idxs)
show_doc(DatasetFormatter.padded_ds)
```
## New Methods - Please document or move to the undocumented section
| true |
code
| 0.692122 | null | null | null | null |
|
# Masked vs cropped implementation for Gated PixelCNN
Hi all, in this notebook we will compare the masked implemntation of the convolutions from the Gated PixelCNN versus the alternative sugexted in the paper, the use of convolutions operaritions with appropriate croppings and padding to achieve the same result.
Let's check out!
First, we willcheck if both implementation create the same result. For this we will create a 5x5 matrix filled with ones as our input example.
```
import math
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow import nn
from tensorflow.keras import initializers
test_ones_2d = np.ones([1, 5, 5, 1], dtype='float32')
print(test_ones_2d[0,:,:,0].squeeze())
```
Now, let's copy themasked implementation that we have been using for our Gated PixelCNN models.
# Masked convolutions
```
class MaskedConv2D(keras.layers.Layer):
"""Convolutional layers with masks extended to work with Gated PixelCNN.
Convolutional layers with simple implementation of masks type A and B for
autoregressive models. Extended version to work with the verticala and horizontal
stacks from the Gated PixelCNN model.
Arguments:
mask_type: one of `"V"`, `"A"` or `"B".`
filters: Integer, the dimensionality of the output space (i.e. the number of output
filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the height and width
of the 2D convolution window.
Can be a single integer to specify the same value for all spatial dimensions.
strides: An integer or tuple/list of 2 integers, specifying the strides of the
convolution along the height and width.
Can be a single integer to specify the same value for all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying any
`dilation_rate` value != 1.
padding: one of `"valid"` or `"same"` (case-insensitive).
kernel_initializer: Initializer for the `kernel` weights matrix.
bias_initializer: Initializer for the bias vector.
"""
def __init__(self,
mask_type,
filters,
kernel_size,
strides=1,
padding='same',
kernel_initializer='glorot_uniform',
bias_initializer='zeros'):
super(MaskedConv2D, self).__init__()
assert mask_type in {'A', 'B', 'V'}
self.mask_type = mask_type
self.filters = filters
if isinstance(kernel_size, int):
kernel_size = (kernel_size, kernel_size)
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding.upper()
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
def build(self, input_shape):
kernel_h, kernel_w = self.kernel_size
self.kernel = self.add_weight('kernel',
shape=(kernel_h,
kernel_w,
int(input_shape[-1]),
self.filters),
initializer=self.kernel_initializer,
trainable=True)
self.bias = self.add_weight('bias',
shape=(self.filters,),
initializer=self.bias_initializer,
trainable=True)
mask = np.ones(self.kernel.shape, dtype=np.float32)
# Get centre of the filter for even or odd dimensions
if kernel_h % 2 != 0:
center_h = kernel_h // 2
else:
center_h = (kernel_h - 1) // 2
if kernel_w % 2 != 0:
center_w = kernel_w // 2
else:
center_w = (kernel_w - 1) // 2
if self.mask_type == 'V':
mask[center_h + 1:, :, :, :] = 0.
else:
mask[:center_h, :, :] = 0.
mask[center_h, center_w + (self.mask_type == 'B'):, :, :] = 0.
mask[center_h + 1:, :, :] = 0.
self.mask = tf.constant(mask, dtype=tf.float32, name='mask')
def call(self, input):
masked_kernel = tf.math.multiply(self.mask, self.kernel)
x = nn.conv2d(input,
masked_kernel,
strides=[1, self.strides, self.strides, 1],
padding=self.padding)
x = nn.bias_add(x, self.bias)
return x
```
With this implementation, we will recreate all convolutional operation that occur inside of the Gated Block. These operations are:
- Vertical stack
- Vertical to horizontal stack
- Horizontal stack - convolution layer with mask type "A"
- Horizontal stack - convolution layer with mask type "B"
IMAGE GATED BLOCK
## Vertical stack
```
mask_type = 'V'
kernel_size = (3, 3)
conv = MaskedConv2D(mask_type=mask_type,
filters=1,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
result_v = conv(test_ones_2d)
print('MASK')
print(conv.mask.numpy().squeeze())
print('')
print('OUTPUT')
print(result_v.numpy().squeeze())
```
## Vertical to horizontal stack
```
padding = keras.layers.ZeroPadding2D(padding=((1, 0), 0))
cropping = keras.layers.Cropping2D(cropping=((0, 1), 0))
x = padding(result_v)
result = cropping(x)
print('INPUT')
print(result_v.numpy().squeeze())
print('')
print('OUTPUT')
print(result.numpy().squeeze())
```
## Horizontal stack - convolution layer with mask type "A"
```
mask_type = 'A'
kernel_size = (1, 3)
conv = MaskedConv2D(mask_type=mask_type,
filters=1,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
result = conv(test_ones_2d)
print('MASK')
print(conv.mask.numpy().squeeze())
print('')
print('OUTPUT')
print(result.numpy().squeeze())
```
## Horizontal stack - convolution layer with mask type "B"
```
mask_type = 'B'
kernel_size = (1, 3)
conv = MaskedConv2D(mask_type=mask_type,
filters=1,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
result = conv(test_ones_2d)
print('MASK')
print(conv.mask.numpy().squeeze())
print('')
print('OUTPUT')
print(result.numpy().squeeze())
```
Using the results of the masked approach as reference, let's check the cropped method.
# Cropped and padded convolutions
## Vertical stack
First, let's checkout this operation that some strategic padding and applying the convolution in "valid" mode to achieve the same result from the masked version.
```
kernel_h = 2
kernel_w = 3
kernel_size = (kernel_h, kernel_w)
padding = keras.layers.ZeroPadding2D(padding=((kernel_h - 1, 0), (int((kernel_w - 1) / 2), int((kernel_w - 1) / 2))))
res = padding(test_ones_2d)
conv = keras.layers.Conv2D(filters=1,
kernel_size=kernel_size,
strides=1,
padding='valid',
kernel_initializer='ones',
bias_initializer='zeros')
result_v = conv(res)
print('INPUT')
print(test_ones_2d.squeeze())
print('')
print('PADDED INPUT')
print(res.numpy().squeeze())
print('')
print('CONV FILTER')
print(conv.weights[0].numpy().squeeze())
print('')
print('OUTPUT')
print(result_v.numpy().squeeze())
```
Now, let's implement a layer that we will include all the previous operations.
```
class VerticalConv2D(keras.layers.Conv2D):
"""https://github.com/JesseFarebro/PixelCNNPP/blob/master/layers/VerticalConv2D.py"""
def __init__(self,
filters,
kernel_size,
**kwargs):
if not isinstance(kernel_size, tuple):
kernel_size = (kernel_size // 2 + 1, kernel_size)
super(VerticalConv2D, self).__init__(filters, kernel_size, **kwargs)
self.pad = tf.keras.layers.ZeroPadding2D(
(
(kernel_size[0] - 1, 0), # Top, Bottom
(kernel_size[1] // 2, kernel_size[1] // 2), # Left, Right
)
)
def call(self, inputs):
inputs = self.pad(inputs)
output = super(VerticalConv2D, self).call(inputs)
return output
kernel_h = 2
kernel_w = 3
kernel_size = (kernel_h, kernel_w)
conv = VerticalConv2D(filters=1,
kernel_size=kernel_size,
strides=1,
padding='valid',
kernel_initializer='ones',
bias_initializer='zeros')
result_v = conv(test_ones_2d)
print('INPUT')
print(test_ones_2d.squeeze())
print('')
print('CONV FILTER')
print(conv.weights[0].numpy().squeeze())
print('')
print('OUTPUT')
print(result_v.numpy().squeeze())
```
## Vertical to horizontal stack
In this operation, the implementation continue the same.
```
padding = keras.layers.ZeroPadding2D(padding=((1, 0), 0))
cropping = keras.layers.Cropping2D(cropping=((0, 1), 0))
x = padding(result_v)
result = cropping(x)
print('INPUT')
print(result_v.numpy().squeeze())
print('')
print('OUTPUT')
print(result.numpy().squeeze())
```
## Horizontal stack - convolution layer with mask type "A"
Again, let's check each operation step by step.
```
kernel_size = (1, 1)
conv = keras.layers.Conv2D(filters=1,
kernel_size=kernel_size,
strides=1,
kernel_initializer='ones',
bias_initializer='zeros')
padding = keras.layers.ZeroPadding2D(padding=(0, (1, 0)))
cropping = keras.layers.Cropping2D(cropping=(0, (0, 1)))
res = conv(test_ones_2d)
res_2 = padding(res)
res_3 = cropping(res_2)
print('INPUT')
print(test_ones_2d.squeeze())
print('')
print('CONV FILTER')
print(conv.weights[0].numpy().squeeze())
print('')
print('CONVOLUTION RESULT')
print(res.numpy().squeeze())
print('')
print('PADDED RESULT')
print(res_2.numpy().squeeze())
print('')
print('CROPPED RESULT')
print(res_3.numpy().squeeze())
```
Note: Since our input test just have one channel, the convolution 1x1 looks like did not perform any change.
## Horizontal stack - convolution layer with mask type "B"
The step by step of the mask type "B" convolution layer is a little different.
```
kernel_size = (1, 2)
kernel_h, kernel_w = kernel_size
padding = keras.layers.ZeroPadding2D(padding=((int((kernel_h - 1) / 2), int((kernel_h - 1) / 2)), (kernel_w - 1, 0)))
conv = keras.layers.Conv2D(filters=1,
kernel_size=kernel_size,
strides=1,
padding='valid',
kernel_initializer='ones',
bias_initializer='zeros')
res = padding(test_ones_2d)
result = conv(res)
print('INPUT')
print(test_ones_2d.squeeze())
print('')
print('PADDED INPUT')
print(res.numpy().squeeze())
print('')
print('CONV FILTER')
print(conv.weights[0].numpy().squeeze())
print('')
print('RESULT')
print(result.numpy().squeeze())
```
In this case, we also implemented a layer version encapsulation these operations
```
class HorizontalConv2D(keras.layers.Conv2D):
def __init__(self,
filters,
kernel_size,
**kwargs):
if not isinstance(kernel_size, tuple):
kernel_size = (kernel_size // 2 + 1,) * 2
super(HorizontalConv2D, self).__init__(filters, kernel_size, **kwargs)
self.pad = tf.keras.layers.ZeroPadding2D(
(
(kernel_size[0] - 1, 0), # (Top, Bottom)
(kernel_size[1] - 1, 0), # (Left, Right)
)
)
def call(self, inputs):
inputs = self.pad(inputs)
outputs = super(HorizontalConv2D, self).call(inputs)
return outputs
kernel_size = (1, 2)
conv = HorizontalConv2D(filters=1,
kernel_size=kernel_size,
strides=1,
kernel_initializer='ones',
bias_initializer='zeros')
result = conv(test_ones_2d)
print('INPUT')
print(test_ones_2d.squeeze())
print('')
print('CONV FILTER')
print(conv.weights[0].numpy().squeeze())
print('')
print('RESULT')
print(result.numpy().squeeze())
```
# Execution time
Now we will compare the time that takes to perform each convolutional operation.
```
import time
def measure_time(conv_fn):
exec_time = []
n_iter = 100
for _ in range(n_iter):
test_input = np.random.rand(128, 256, 256, 1).astype('float32')
start = time.time()
conv_fn(test_input)
exec_time.append(time.time() - start)
exec_time = np.array(exec_time, dtype='float32')
return exec_time.mean(), exec_time.std()
```
## Vertical stack
```
mask_type = 'V'
kernel_size = (3, 3)
masked_conv = MaskedConv2D(mask_type=mask_type,
filters=32,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
@tf.function
def test_masked_fn(x):
_ = masked_conv(x)
masked_time = measure_time(test_masked_fn)
# ----------------------------------------------------------------
kernel_size = (2, 3)
cropped_conv = VerticalConv2D(filters=32,
kernel_size=kernel_size,
strides=1,
padding='valid',
kernel_initializer='ones',
bias_initializer='zeros')
@tf.function
def test_cropped_fn(x):
_ = cropped_conv(x)
cropped_time = measure_time(test_cropped_fn)
# ----------------------------------------------------------------
print("Vertical stack")
print(f"Masked convolution: {masked_time[0]:.8f} +- {masked_time[1]:.8f} seconds")
print(f"Cropped padded convolution: {cropped_time[0]:.8f} +- {cropped_time[1]:.8f} seconds")
```
## Horizontal stack - convolution layer with mask type "A"
```
mask_type = 'A'
kernel_size = (1, 3)
masked_conv = MaskedConv2D(mask_type=mask_type,
filters=1,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
@tf.function
def test_masked_fn(x):
_ = masked_conv(x)
masked_time = measure_time(test_masked_fn)
# ----------------------------------------------------------------
kernel_size = (1, 1)
conv = keras.layers.Conv2D(filters=1,
kernel_size=kernel_size,
strides=1,
kernel_initializer='ones',
bias_initializer='zeros')
padding = keras.layers.ZeroPadding2D(padding=(0, (1, 0)))
cropping = keras.layers.Cropping2D(cropping=(0, (0, 1)))
@tf.function
def test_cropped_fn(x):
x = conv(x)
x = padding(x)
x = cropping(x)
cropped_time = measure_time(test_cropped_fn)
# ----------------------------------------------------------------
print("Horizontal stack - convolution layer with mask type 'A'")
print(f"Masked convolution: {masked_time[0]:.8f} +- {masked_time[1]:.8f} seconds")
print(f"Cropped padded convolution: {cropped_time[0]:.8f} +- {cropped_time[1]:.8f} seconds")
```
## Horizontal stack - convolution layer with mask type "B"
```
mask_type = 'B'
kernel_size = (1, 3)
masked_conv = MaskedConv2D(mask_type=mask_type,
filters=1,
kernel_size=kernel_size,
padding='same',
kernel_initializer='ones',
bias_initializer='zeros')
@tf.function
def test_masked_fn(x):
_ = masked_conv(x)
masked_time = measure_time(test_masked_fn)
# ----------------------------------------------------------------
kernel_size = (1, 2)
cropped_conv = HorizontalConv2D(filters=1,
kernel_size=kernel_size,
strides=1,
kernel_initializer='ones',
bias_initializer='zeros')
@tf.function
def test_cropped_fn(x):
_ = cropped_conv(x)
cropped_time = measure_time(test_cropped_fn)
# ----------------------------------------------------------------
print("Horizontal stack - convolution layer with mask type 'B'")
print(f"Masked convolution: {masked_time[0]:.8f} +- {masked_time[1]:.8f} seconds")
print(f"Cropped padded convolution: {cropped_time[0]:.8f} +- {cropped_time[1]:.8f} seconds")
```
Altough its looks like cropped is better in the vertical convolution, the difference does not to look very significant.
# REFERENCES
https://wiki.math.uwaterloo.ca/statwiki/index.php?title=STAT946F17/Conditional_Image_Generation_with_PixelCNN_Decoders#Gated_PixelCNN
https://www.slideshare.net/suga93/conditional-image-generation-with-pixelcnn-decoders
https://www.youtube.com/watch?v=1BURwCCYNEI
| true |
code
| 0.765221 | null | null | null | null |
|
# Comparing two Counters
Today we will look at a way of scoring the significance of differences between frequency distributions, based on a method called "Fightin' Words" by Monroe, Colaresi, and Quinn.
```
import re, sys, glob, math
import numpy
from collections import Counter
from matplotlib import pyplot
```
1. What is the encoding of the files? How are they structured? What do we need to do to separate text from non-textual words like speakers and stage directions?
2. Look at the most frequent words in the counters for comedy and tragedy. What is different? Is this view informative about differences between these two genres?
3. There is a problem calculating `log_rank`. What is it, and how can we fix it?
4. What does the `generate_scores` function do? What is the effect of the `smoothing` parameter?
5. Look at the plot showing "Fightin' Words" scores for comedy vs. tragedy. What stands out? What does this tell you about these genres in Shakespeare? What if any changes might you make to how we tokenize or otherwise pre-process the documents?
6. Create the same plot for tragedy vs. history and comedy vs. history. What is different? What words would you want to look at in their original context and why?
```
genre_directories = { "tragedy" : "shakespeare/tragedies", "comedy" : "shakespeare/comedies", "history" : "shakespeare/historical" }
word_pattern = re.compile("\w[\w\-\'’]*\w|\w")
# This counter will store the total frequency of each word type across all plays
all_counts = Counter()
# This dictionary will have one counter for each genre
genre_counts = {}
# This dictionary will have one dictionary for each genre, each containing one Counter for each play in that genre
genre_play_counts = {}
# Read the plays from files
for genre in genre_directories.keys():
genre_play_counts[genre] = {}
genre_counts[genre] = Counter()
for filename in glob.glob("{}/*.txt".format(genre_directories[genre])):
play_counter = Counter()
genre_play_counts[genre][filename] = play_counter
with open(filename, encoding="utf-8") as file: ## What encoding?
## This block reads a file line by line.
for line in file:
line = line.rstrip()
tokens = word_pattern.findall(line)
play_counter.update(tokens)
genre_counts[genre] += play_counter
all_counts += play_counter
genre_counts.keys()
genre_play_counts.keys()
genre_play_counts["comedy"].keys()
genre_play_counts["comedy"]["shakespeare/comedies/The Merry Wives of Windsor.txt"].most_common(30)
genre_counts["comedy"].most_common(15)
genre_counts["tragedy"].most_common(15)
vocabulary = [w for w, c in all_counts.most_common()]
vocabulary_size = len(vocabulary)
total_word_counts = numpy.array([all_counts[w] for w in vocabulary])
log_counts = numpy.log(total_word_counts)
word_ranks = numpy.arange(len(vocabulary))
log_ranks = numpy.log(word_ranks)
genres = genre_play_counts.keys()
pyplot.scatter(log_ranks, log_counts, alpha = 0.2)
pyplot.show()
def generate_scores(counter, smoothing = 0.0):
scores = numpy.zeros(vocabulary_size)
for word_id, word in enumerate(vocabulary):
scores[word_id] = counter[word] + smoothing
return scores
def count_difference(counter_a, counter_b, smoothing):
scores_a = generate_scores(counter_a, smoothing)
scores_b = generate_scores(counter_b, smoothing)
ratio_a = scores_a / (numpy.sum(scores_a) - scores_a)
ratio_b = scores_b / (numpy.sum(scores_b) - scores_b)
variances = (1.0/scores_a) + (1.0/scores_b)
return numpy.log(ratio_a / ratio_b) / numpy.sqrt(variances)
comedy_tragedy_scores = count_difference(genre_counts["comedy"], genre_counts["tragedy"], 0.0)
sorted_words = sorted(zip(comedy_tragedy_scores, vocabulary))
print(sorted_words[:10])
print(sorted_words[-10:])
pyplot.figure(figsize=(20, 20))
pyplot.xlim(3, 11)
pyplot.scatter(log_counts, comedy_tragedy_scores, alpha = 0.2)
for word_id, word in enumerate(vocabulary):
if numpy.abs(comedy_tragedy_scores[word_id]) + log_counts[word_id] > 7.5:
pyplot.text(log_counts[word_id], comedy_tragedy_scores[word_id], word)
pyplot.show()
```
| true |
code
| 0.445952 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.