prompt
stringlengths 501
4.98M
| target
stringclasses 1
value | chunk_prompt
bool 1
class | kind
stringclasses 2
values | prob
float64 0.2
0.97
⌀ | path
stringlengths 10
394
⌀ | quality_prob
float64 0.4
0.99
⌀ | learning_prob
float64 0.15
1
⌀ | filename
stringlengths 4
221
⌀ |
|---|---|---|---|---|---|---|---|---|
# Road Follower - Train Model
In this notebook we will train a neural network to take an input image, and output a set of x, y values corresponding to a target.
We will be using PyTorch deep learning framework to train ResNet18 neural network architecture model for road follower application.
```
import torch
import torch.optim as optim
import torch.nn.functional as F
import torchvision
import torchvision.datasets as datasets
import torchvision.models as models
import torchvision.transforms as transforms
import glob
import PIL.Image
import os
import numpy as np
```
### Download and extract data
Before you start, you should upload the ``road_following_<Date&Time>.zip`` file that you created in the ``data_collection.ipynb`` notebook on the robot.
> If you're training on the JetBot you collected data on, you can skip this!
You should then extract this dataset by calling the command below:
```
!unzip -q road_following.zip
```
You should see a folder named ``dataset_all`` appear in the file browser.
### Create Dataset Instance
Here we create a custom ``torch.utils.data.Dataset`` implementation, which implements the ``__len__`` and ``__getitem__`` functions. This class
is responsible for loading images and parsing the x, y values from the image filenames. Because we implement the ``torch.utils.data.Dataset`` class,
we can use all of the torch data utilities :)
We hard coded some transformations (like color jitter) into our dataset. We made random horizontal flips optional (in case you want to follow a non-symmetric path, like a road
where we need to 'stay right'). If it doesn't matter whether your robot follows some convention, you could enable flips to augment the dataset.
```
def get_x(path):
"""Gets the x value from the image filename"""
return (float(int(path[3:6])) - 50.0) / 50.0
def get_y(path):
"""Gets the y value from the image filename"""
return (float(int(path[7:10])) - 50.0) / 50.0
class XYDataset(torch.utils.data.Dataset):
def __init__(self, directory, random_hflips=False):
self.directory = directory
self.random_hflips = random_hflips
self.image_paths = glob.glob(os.path.join(self.directory, '*.jpg'))
self.color_jitter = transforms.ColorJitter(0.3, 0.3, 0.3, 0.3)
def __len__(self):
return len(self.image_paths)
def __getitem__(self, idx):
image_path = self.image_paths[idx]
image = PIL.Image.open(image_path)
x = float(get_x(os.path.basename(image_path)))
y = float(get_y(os.path.basename(image_path)))
if float(np.random.rand(1)) > 0.5:
image = transforms.functional.hflip(image)
x = -x
image = self.color_jitter(image)
image = transforms.functional.resize(image, (224, 224))
image = transforms.functional.to_tensor(image)
image = image.numpy()[::-1].copy()
image = torch.from_numpy(image)
image = transforms.functional.normalize(image, [0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
return image, torch.tensor([x, y]).float()
dataset = XYDataset('dataset_xy', random_hflips=False)
```
### Split dataset into train and test sets
Once we read dataset, we will split data set in train and test sets. In this example we split train and test a 90%-10%. The test set will be used to verify the accuracy of the model we train.
```
test_percent = 0.1
num_test = int(test_percent * len(dataset))
train_dataset, test_dataset = torch.utils.data.random_split(dataset, [len(dataset) - num_test, num_test])
```
### Create data loaders to load data in batches
We use ``DataLoader`` class to load data in batches, shuffle data and allow using multi-subprocesses. In this example we use batch size of 64. Batch size will be based on memory available with your GPU and it can impact accuracy of the model.
```
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=8,
shuffle=True,
num_workers=0
)
test_loader = torch.utils.data.DataLoader(
test_dataset,
batch_size=8,
shuffle=True,
num_workers=0
)
```
### Define Neural Network Model
We use ResNet-18 model available on PyTorch TorchVision.
In a process called transfer learning, we can repurpose a pre-trained model (trained on millions of images) for a new task that has possibly much less data available.
More details on ResNet-18 : https://github.com/pytorch/vision/blob/master/torchvision/models/resnet.py
More Details on Transfer Learning: https://www.youtube.com/watch?v=yofjFQddwHE
```
model = models.resnet18(pretrained=True)
```
ResNet model has fully connect (fc) final layer with 512 as ``in_features`` and we will be training for regression thus ``out_features`` as 1
Finally, we transfer our model for execution on the GPU
```
model.fc = torch.nn.Linear(512, 2)
device = torch.device('cuda')
model = model.to(device)
```
### Train Regression:
We train for 50 epochs and save best model if the loss is reduced.
```
NUM_EPOCHS = 70
BEST_MODEL_PATH = 'best_steering_model_xy.pth'
best_loss = 1e9
optimizer = optim.Adam(model.parameters())
for epoch in range(NUM_EPOCHS):
model.train()
train_loss = 0.0
for images, labels in iter(train_loader):
images = images.to(device)
labels = labels.to(device)
optimizer.zero_grad()
outputs = model(images)
loss = F.mse_loss(outputs, labels)
train_loss += float(loss)
loss.backward()
optimizer.step()
train_loss /= len(train_loader)
model.eval()
test_loss = 0.0
for images, labels in iter(test_loader):
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss = F.mse_loss(outputs, labels)
test_loss += float(loss)
test_loss /= len(test_loader)
print('%f, %f' % (train_loss, test_loss))
if test_loss < best_loss:
torch.save(model.state_dict(), BEST_MODEL_PATH)
best_loss = test_loss
```
Once the model is trained, it will generate ``best_steering_model_xy.pth`` file which you can use for inferencing in the live demo notebook.
If you trained on a different machine other than JetBot, you'll need to upload this to the JetBot to the ``road_following`` example folder.
| true |
code
| 0.802401 | null | null | null | null |
|
<h1 align="center"> Logistic Regression (Preloaded Dataset) </h1>
scikit-learn comes with a few small datasets that do not require to download any file from some external website. The digits dataset we will use is one of these small standard datasets. These datasets are useful to quickly illustrate the behavior of the various algorithms implemented in the scikit. They are however often too small to be representative of real world machine learning tasks. After learning the basics of logisitic regression, we will use the MNIST Handwritten digit database
<b>Each datapoint is a 8x8 image of a digit.</b>
Parameters | Number
--- | ---
Classes | 10
Samples per class | ~180
Samples total | 1797
Dimensionality | 64
Features | integers 0-16
```
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Used for Confusion Matrix
from sklearn import metrics
%matplotlib inline
digits = load_digits()
digits.data.shape
digits.target.shape
```
## Showing the Images and Labels
```
plt.figure(figsize=(20,4))
for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
plt.subplot(1, 5, index + 1)
plt.imshow(np.reshape(image, (8,8)), cmap=plt.cm.gray)
plt.title('Training: %i\n' % label, fontsize = 20)
```
## Splitting Data into Training and Test Sets
```
# test_size: what proportion of original data is used for test set
x_train, x_test, y_train, y_test = train_test_split(
digits.data, digits.target, test_size=0.25, random_state=0)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
```
## Scikit-learn 4-Step Modeling Pattern
<b>Step 1: </b> Import the model you want to use
In sklearn, all machine learning models are implemented as Python classes
```
from sklearn.linear_model import LogisticRegression
```
<b>Step 2:</b> Make an instance of the Model
```
logisticRegr = LogisticRegression()
```
<b>Step 3:</b> Training the model on the data, storing the information learned from the data
Model is learning the relationship between x (digits) and y (labels)
```
logisticRegr.fit(x_train, y_train)
```
<b>Step 4</b>: Predict the labels of new data (new images)
Uses the information the model learned during the model training process
```
# Returns a NumPy Array
# Predict for One Observation (image)
logisticRegr.predict(x_test[0].reshape(1,-1))
# Predict for Multiple Observations (images) at Once
logisticRegr.predict(x_test[0:10])
# Make predictions on entire test data
predictions = logisticRegr.predict(x_test)
predictions.shape
```
## Measuring Model Performance
accuracy (fraction of correct predictions): correct predictions / total number of data points
Basically, how the model performs on new data (test set)
```
# Use score method to get accuracy of model
score = logisticRegr.score(x_test, y_test)
print(score)
```
## Confusion Matrix (Matplotlib)
A confusion matrix is a table that is often used to describe the performance of a classification model (or "classifier") on a set of test data for which the true values are known.
```
def plot_confusion_matrix(cm, title='Confusion matrix', cmap='Pastel1'):
plt.figure(figsize=(9,9))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title, size = 15)
plt.colorbar()
tick_marks = np.arange(10)
plt.xticks(tick_marks, ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"], rotation=45, size = 10)
plt.yticks(tick_marks, ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"], size = 10)
plt.tight_layout()
plt.ylabel('Actual label', size = 15)
plt.xlabel('Predicted label', size = 15)
width, height = cm.shape
for x in xrange(width):
for y in xrange(height):
plt.annotate(str(cm[x][y]), xy=(y, x),
horizontalalignment='center',
verticalalignment='center')
# confusion matrix
confusion = metrics.confusion_matrix(y_test, predictions)
print('Confusion matrix')
print(confusion)
plt.figure()
plot_confusion_matrix(confusion);
plt.show();
```
## Confusion Matrix (Seaborn)
<b>Note: Seaborn needs to be installed for this portion </b>
```
# !conda install seaborn -y
# Make predictions on test data
predictions = logisticRegr.predict(x_test)
cm = metrics.confusion_matrix(y_test, predictions)
#cm_normalized = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
plt.figure(figsize=(9,9))
sns.heatmap(cm, annot=True, fmt=".3f", linewidths=.5, square = True, cmap = 'Blues_r');
plt.ylabel('Actual label');
plt.xlabel('Predicted label');
all_sample_title = 'Accuracy Score: {0}'.format(score)
plt.title(all_sample_title, size = 15);
```
## Display Misclassified images with Predicted Labels
```
index = 0
misclassifiedIndex = []
for predict, actual in zip(predictions, y_test):
if predict != actual:
misclassifiedIndex.append(index)
index +=1
plt.figure(figsize=(20,4))
for plotIndex, wrong in enumerate(misclassifiedIndex[10:15]):
plt.subplot(1, 5, plotIndex + 1)
plt.imshow(np.reshape(x_test[wrong], (8,8)), cmap=plt.cm.gray)
plt.title('Predicted: {}, Actual: {}'.format(predictions[wrong], y_test[wrong]), fontsize = 20)
```
Part 2 of the tutorial is located here: [MNIST Logistic Regression](https://github.com/mGalarnyk/Python_Tutorials/blob/master/Sklearn/Logistic_Regression/LogisticRegression_MNIST.ipynb)
<b>if this tutorial doesn't cover what you are looking for, please leave a comment on the youtube video and I will try to cover what you are interested in. </b>
[youtube video](https://www.youtube.com/watch?v=71iXeuKFcQM)
| true |
code
| 0.695603 | null | null | null | null |
|
SD211 TP2: Régression logistique
*<p>Author: Pengfei Mi</p>*
*<p>Date: 12/05/2017</p>*
```
import numpy as np
import matplotlib.pyplot as plt
from cervicalcancerutils import load_cervical_cancer
from scipy.optimize import check_grad
from time import time
from sklearn.metrics import classification_report
```
## Partie 1: Régularisation de Tikhonov
$\textbf{Question 1.1}\quad\text{Calculer le gradient et la matrice hessienne.}$
<div class="alert alert-success">
<p>
Notons $\tilde{X} = (\tilde{\mathbf{x}}_1,...,\tilde{\mathbf{ x}}_n)^T$, où $\tilde{\mathbf{x}}_i = \begin{pmatrix}1\\
\mathbf{x}_i\end{pmatrix}\in \mathbb{R}^{p+1}$, $\tilde{\mathbf{\omega}} = \begin{pmatrix}
\omega_0\\\mathbf{\omega}\end{pmatrix}\in \mathbb{R}^{p+1}$, et la matrice
$$A = diag(0,1,...,1) =
\begin{pmatrix}
0&0&\cdots&0\\
0&1&&0\\
\vdots&&\ddots&\vdots\\
0&0&\cdots&1
\end{pmatrix}
$$
</p>
<p>
On a:
$$
\begin{aligned}
f_1(\omega_0, \omega) &= \frac{1}{n}\sum_{i=1}^{n}\text{log}\big(1+e^{-y_i(x_i^T\omega+\omega_0)}\big)+\frac{\rho}{2}\|\omega\|_2^2 \\
& = \frac{1}{n}\sum_{i=1}^{n}\text{log}\big(1+e^{-y_i\tilde x_i^T \tilde \omega}\big)+\frac{\rho}{2}\tilde{\omega}^TA\tilde{\omega}
\end{aligned}
$$
</p>
<p>
Ainsi on obtient le gradient:
$$
\begin{aligned}
\nabla{f_1}(\omega_0, \omega) &= \frac{1}{n}\sum_{i=1}^{n}\frac{-e^{-y_i\tilde x_i^T \tilde \omega}y_i\tilde{\mathbf{x}}_i}{1+e^{-y_i\tilde x_i^T \tilde \omega}} + \rho A\tilde{\mathbf{\omega}} \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{-y_i\tilde{\mathbf{x}}_i}{1+e^{y_i\tilde x_i^T \tilde \omega}} +
\rho A\tilde{\mathbf{\omega}}
\end{aligned}
$$
</p>
<p>
et la matrice hessienne:
$$
\begin{aligned}
\mathbf{H} = \nabla^2f_1(\omega_0, \omega) &= \frac{1}{n}\sum_{i=1}^{n}\frac{e^{y_i\tilde x_i^T \tilde \omega}(y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})^2} + \rho A \\
& = \frac{1}{n}\sum_{i=1}^{n}\frac{(y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} + \rho A
\end{aligned}
$$
</p>
</div>
<div class="alert alert-success">
<p>
Soient $\omega \in \mathbb{R}^{p+1}$, on a:
$$
\begin{aligned}
\omega^TH\omega &= \frac{1}{n}\sum_{i=1}^{n}\frac{\omega^T (y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T \omega}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} + \rho \omega^T A \omega \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{(\omega^T y_i\tilde{\mathbf{x}}_i)(\omega^T y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} + \rho \omega^T A^2 \omega \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{\|\omega^T y_i\tilde{\mathbf{x}}_i\|_2^2}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} + \rho \|A\omega\|_2^2 \geq 0
\end{aligned}
$$
</p>
<p>Donc, la matrice hessienne est semi-définie positive, la fonction $f_1$ est convexe.</p>
</div>
$\textbf{Question 1.2}\quad\text{Coder une fonction qui retourne la valeur de la fonction, son gradient et sa hessienne.}$
<div class="alert alert-success">
<p>On insère une colonne de $1$ à gauche de $X$ pour simplifier le calcul.</p>
</div>
```
X, y = load_cervical_cancer("riskfactorscervicalcancer.csv")
print "Before the insertion:"
print X.shape, y.shape
n, p = X.shape
X = np.c_[np.ones(n), X]
print "After the insertion:"
print X.shape, y.shape
def objective(w_, X, y, rho, return_grad=True, return_H=True):
"""
X: matrix of size n*(p+1)
y: vector of size n
w0: real number
w: vector of size p
"""
# Initialize elementary intermediate variables;
n, p = X.shape
w = w_[1:]
y_x = np.array([y[i] * X[i, :] for i in range(n)])
yx_w = np.array([np.sum(y_x[i, :]*w_) for i in range(n)])
exp_yxw_1 = np.array([np.exp(yx_w[i]) for i in range(n)]) + 1
exp_neg_yxw_1 = np.array([np.exp(-yx_w[i]) for i in range(n)]) + 1
# Compute function value
val = np.mean(np.log(exp_neg_yxw_1)) + np.sum(w**2)*rho/2.
if return_grad == False:
return val
else:
# Compute gradient
grad = np.mean(-np.array([y_x[i]/exp_yxw_1[i] for i in range(n)]), axis=0) + rho*np.r_[0, w]
if return_H == False:
return val, grad
else:
# Compute the Hessian matrix
H = np.mean(np.array([y_x[i].reshape(-1, 1).dot(y_x[i].reshape(1, -1) / (exp_yxw_1[i]*exp_neg_yxw_1[i])) for i in range(n)]), axis=0) + rho*np.diag(np.r_[0, np.ones(p-1)])
return val, grad, H
def funcMask(w_, X, y, rho):
val, grad = objective(w_, X, y, rho, return_H=False)
return val
def gradMask(w_, X, y, rho):
val, grad = objective(w_, X, y, rho, return_H=False)
return grad
rho = 1./n
t0 = time()
print "The difference of gradient is: %0.12f" % check_grad(funcMask, gradMask, np.zeros(p+1), X, y, rho)
print "Done in %0.3fs." % (time()-t0)
def gradMask(w_, X, y, rho):
val, grad = objective(w_, X, y, rho, return_H=False)
return grad.sum()
def hessianMask(w_, X, y, rho):
val, grad, H = objective(w_, X, y, rho)
return np.sum(H, axis=1)
t0 = time()
rho = 1./n
print "The difference of Hessian matrix is: %0.12f" % check_grad(gradMask, hessianMask, np.zeros(p+1), X, y, rho)
print "Done in %0.3fs." % (time()-t0)
```
<div class="alert alert-success">
<p>On a vérifié le calcul de gradient et de matrice hessienne.</p>
</div>
$\textbf{Question 1.3}\quad\text{Coder la méthode de Newton.}$
<div class="alert alert-success">
<p>
Selon la définition de méthode de Newton, on a:
$$\omega^{k+1} = \omega^k - (\nabla^2f_1(\omega^k))^{-1}\nabla f_1(\omega^k)$$
</p>
</div>
```
def minimize_Newton(func, w_, X, y, rho, tol=1e-10):
n, p = X.shape
val, grad, H = func(w_, X, y, rho)
grad_norm = np.sqrt(np.sum(grad**2))
norms = [grad_norm]
cnt = 0
while (grad_norm > tol):
w_ = w_ - np.linalg.solve(H, np.identity(p)).dot(grad)
val, grad, H = func(w_, X, y, rho)
grad_norm = np.sqrt(np.sum(grad**2))
norms.append(grad_norm)
cnt = cnt + 1
return val, w_, cnt, norms
t0 = time()
rho = 1./n
val, w, cnt, grad_norms = minimize_Newton(objective, np.zeros(p+1), X, y, rho, tol=1e-10)
print "The value minimal of the objective function is: %0.12f" % val
print "Done in %0.3fs, number of iterations: %d" % (time()-t0, cnt)
print w
plt.figure(1, figsize=(8,6))
plt.title("The norm of gradient, $\omega^0 = 0$")
plt.semilogy(range(0, len(grad_norms)), grad_norms)
plt.xlabel("Number of iteration")
plt.ylabel("Norm of gradient")
plt.xlim(0, len(grad_norms))
plt.show()
```
$\textbf{Question 1.4}\quad\text{Lancer avec comme condition initiale }(\omega_0^0,\omega^0) = 0.3e\text{, où }e_i=0\text{ pour tout }i.$
```
t0 = time()
val, grad, H, cnt, grad_norms = minimize_Newton(objective, 0.3*np.ones(p+1), X, y, rho, tol=1e-10)
print "The value minimal of the objective function is: %0.12f" % val
print "Done in %0.3fs, number of iterations: %d" % (time()-t0, cnt)
```
<div class="alert alert-success">
<p>On a vu que avec cette condition initiale, la fonction objectif ne converge pas. C'est à cause de le point initiale est hors le domaine de convergence.</p>
</div>
$\textbf{Question 1.5}\quad\text{Coder la méthode de recherche linéaire d'Armijo.}$
<div class="alert alert-success">
<p>Notons $\omega^+(\gamma_k)=\omega^k - \gamma_k(\nabla^2 f_1(\omega^k))^{-1}\nabla f_1(\omega^k)$, soient $a \in (0,1)$, $b>0$ et $\beta \in (0,1)$, on cherche le premier entier $l$ non-négatif tel que:</p>
$$f_1(\omega^+(ba^l)) \leq f_1(\omega^k) + \beta\langle\nabla_{f_1}(\omega^k),\,\omega^+(ba^l)-\omega^k\rangle$$
</div>
<div class="alert alert-success">
<p>Ici, on prend $\beta = 0.5$, ainsi que la recherche linéaire d'Armijo devient équicalente à la recherche linéaire de Taylor.</p>
<p> On fixe $b_0 = 1$ et $b_k = 2\gamma_{k-1}$, c'est un choix classique.</p>
<p> On fixe $a = 0.5$, c'est pour faire un compromis entre la précision de recherche et la vitesse de convergence.</p>
</div>
```
def minimize_Newton_Armijo(func, w_, X, y, rho, a, b, beta, tol=1e-10, max_iter=500):
n, p = X.shape
val, grad, H = func(w_, X, y, rho)
grad_norm = np.sqrt(np.sum(grad**2))
norms = [grad_norm]
d = np.linalg.solve(H, np.identity(p)).dot(grad)
gamma = b / 2.
cnt = 0
while (grad_norm > tol and cnt < max_iter):
gamma = 2*gamma
val_ = func(w_ - gamma*d, X, y, rho, return_grad=False)
while (val_ > val - beta*gamma*np.sum(d*grad)):
gamma = gamma*a
val_ = func(w_ - gamma*d, X, y, rho, return_grad=False)
w_ = w_ - gamma*d
val, grad, H = func(w_, X, y, rho)
d = np.linalg.solve(H, np.identity(p)).dot(grad)
grad_norm = np.sqrt(np.sum(grad**2))
norms.append(grad_norm)
cnt = cnt + 1
return val, w_, cnt, norms
t0 = time()
rho = 1./n
a = 0.5
b = 1
beta = 0.5
val_nls, w_nls, cnt_nls, grad_norms_nls = minimize_Newton_Armijo(objective, 0.3*np.ones(p+1), X, y, rho, a, b, beta, tol=1e-10, max_iter=500)
print "The value minimal of the objective function is: %0.12f" % val_nls
t_nls = time()-t0
print "Done in %0.3fs, number of iterations: %d" % (t_nls, cnt_nls)
print w_nls
plt.figure(2, figsize=(8,6))
plt.title("The norm of gradient by Newton with linear search")
plt.semilogy(range(0, len(grad_norms_nls)), grad_norms_nls)
plt.xlabel("Number of iteration")
plt.ylabel("Norm of gradient")
plt.xlim(0, len(grad_norms_nls))
plt.show()
```
## Partie 2: Régularisation pour la parcimoine
$\textbf{Question 2.1}\quad\text{Pourquoi ne peut-on pas utiliser la méthode de Newton pour résoudre ce problème?}$
<div class="alert alert-success">
<p>Parce que la fonction objectif ici n'est pas différentiable, on ne peut pas utiliser le gradient et la matrice hessienne.</p>
</div>
$\textbf{Question 2.2}\quad\text{Écrire la fonction objectif sous la forme }F_2 = f_2 + g_2\text{ où }f_2\text{ est dérivable et l’opérateur proximal de }g_2\text{ est simple.}$
<div class="alert alert-success">
<p>
$$
\begin{aligned}
F_2(\omega_0,\omega) &= \frac{1}{n}\sum_{i=1}^{n}\text{log}\big(1+e^{-y_i(x_i^T\omega+\omega_0)}\big)+\rho\|\omega\|_1 \\
&= f_2+g_2
\end{aligned}
$$
où $f_2 = \frac{1}{n}\sum_{i=1}^{n}\text{log}\big(1+e^{-y_i(x_i^T\omega+\omega_0)}\big)$ est dérivable, $g_2 = \rho\|\omega\|_1$ de laquelle l'opérateur proximal est simple.
</p>
</div>
<div class="alert alert-success">
<p>
On a le gradient de $f_2$:
$$
\begin{aligned}
\nabla{f_2}(\omega_0, \omega) &= \frac{1}{n}\sum_{i=1}^{n}\frac{-e^{-y_i\tilde x_i^T \tilde \omega}y_i\tilde{\mathbf{x}}_i}{1+e^{-y_i\tilde x_i^T \tilde \omega}} \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{-y_i\tilde{\mathbf{x}}_i}{1+e^{y_i\tilde x_i^T \tilde \omega}}
\end{aligned}
$$
</p>
<p>
et l'opérateur proximal de $g_2$:
$$
\begin{aligned}
\text{prox}_{g_2}(x) &= \text{arg}\,\underset{y \in \mathbb{R}^p}{\text{min}}\, \big(g_2(y) + \frac{1}{2}\|y-x\|^2 \big) \\
&= \text{arg}\,\underset{y \in \mathbb{R}^p}{\text{min}}\, \big(\rho\|y\|_1 + \frac{1}{2}\|y-x\|^2 \big) \\
&= \text{arg}\,\underset{y \in \mathbb{R}^p}{\text{min}}\, \sum_{i=1}^{p}\big(\rho |y_i| + \frac{1}{2}(y_i-x_i)^2\big)
\end{aligned}
$$
</p>
<p>
pour $1 \leq i \leq n$, on obtient la solution:
$$
y_i^* = \left\{
\begin{align}
x_i - \rho, &\text{ si } x_i > \rho \\
x_i + \rho, &\text{ si } x_i < -\rho \\
0, &\text{ si } -\rho \leq x_i \leq \rho
\end{align}
\right.
$$
</p>
</div>
<div class="alert alert-success">
<p>
$$
\begin{aligned}
\mathbf{H_2} = \nabla^2f_2(\omega_0, \omega) &= \frac{1}{n}\sum_{i=1}^{n}\frac{e^{y_i\tilde x_i^T \tilde \omega}(y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})^2} \\
& = \frac{1}{n}\sum_{i=1}^{n}\frac{(y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})}
\end{aligned}
$$
</p>
<p>
Soient $\omega \in \mathbb{R}^{p+1}$, on a:
$$
\begin{aligned}
\omega^TH_2\omega &= \frac{1}{n}\sum_{i=1}^{n}\frac{\omega^T (y_i\tilde{\mathbf{x}}_i)(y_i\tilde{\mathbf{x}}_i)^T \omega}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{(\omega^T y_i\tilde{\mathbf{x}}_i)(\omega^T y_i\tilde{\mathbf{x}}_i)^T}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} \\
&= \frac{1}{n}\sum_{i=1}^{n}\frac{\|\omega^T y_i\tilde{\mathbf{x}}_i\|_2^2}{(1+e^{y_i\tilde x_i^T \tilde \omega})(1+e^{-y_i\tilde x_i^T \tilde \omega})} \geq 0
\end{aligned}
$$
</p>
<p>Donc, la matrice hessienne de $f_2$ est semi-définie positive, la fonction $f_2$ est convexe.</p>
<p>
$$
\begin{aligned}
g_2(\omega_0, \omega) &= \rho\|\omega\|_1 \\
&= \rho \sum_{i=1}^{n}|\omega_i|
\end{aligned}
$$
</p>
<p>La fonction de valeur absolue est convexe pour chaque élément de $\omega$, pour $\rho \geq 0$, $g_2$ est aussi convexe.</p>
<p>Donc $F_2 = f_2 + g_2$ est convexe pour $\rho \geq 0$.</p>
</div>
$\textbf{Question 2.3}\quad\text{Coder le gradient proximal avec recherche linéaire.}$
<div class="alert alert-success">
<p>On rajoute la recherche linéaire de Taylor.</p>
<p>On prend $a = 0.5$, $b_0 = 1b$ et $b = 2\gamma_{k-1}$. On cherche le premier entier $l$ non-négatif tel que:</p>
$$f_2(\omega^+(ba^l)) \leq f_2(\omega^k) + \langle\nabla_{f_2}(\omega^k),\,\omega^+(ba^l)-\omega^k\rangle + \frac{1}{2ba^l}\|\omega^k - \omega^+(ba^l)\|^2$$
</div>
<div class="alert alert-success">
On peut utiliser un seuillage pour la valeur de fonction objectif évaluée dans une itération comme test d'arrêt.
</div>
```
def objective_proximal(w_, X, y, rho):
"""
X: matrix of size n*(p+1)
y: vector of size n
w0: real number
w: vector of size p
"""
# Initialize elementary intermediate variables;
n, p = X.shape
w = w_[1:]
y_x = np.array([y[i] * X[i, :] for i in range(n)])
yx_w = np.array([np.sum(y_x[i, :]*w_) for i in range(n)])
exp_neg_yxw_1 = np.array([np.exp(-yx_w[i]) for i in range(n)]) + 1
# Compute function value
val = np.mean(np.log(exp_neg_yxw_1)) + rho*np.sum(np.fabs(w))
return val
def f(w_, X, y, return_grad=True):
"""
X: matrix of size n*(p+1)
y: vector of size n
w0: real number
w: vector of size p
"""
# Initialize elementary intermediate variables;
n, p = X.shape
w = w_[1:]
y_x = np.array([y[i] * X[i, :] for i in range(n)])
yx_w = np.array([np.sum(y_x[i, :]*w_) for i in range(n)])
exp_yxw_1 = np.array([np.exp(yx_w[i]) for i in range(n)]) + 1
exp_neg_yxw_1 = np.array([np.exp(-yx_w[i]) for i in range(n)]) + 1
# Compute function value
val = np.mean(np.log(exp_neg_yxw_1))
if return_grad == False:
return val
else:
# Compute gradient
grad = np.mean(-np.array([y_x[i]/exp_yxw_1[i] for i in range(n)]), axis=0)
return val, grad
def Soft_Threshold(w, rho):
w_ = np.zeros_like(w)
w_[w > rho] = w[w > rho] - rho
w_[w < -rho] = w[w < -rho] + rho
w_[0] = w[0]
return w_
def minimize_prox_grad_Taylor(func, f, w_, X, y, rho, a, b, tol=1e-10, max_iter=500):
n, p = X.shape
val = func(w_, X, y, rho)
val_f, grad_f = f(w_, X, y)
gamma = b / 2.
delta_val = tol*2
cnt = 0
while (delta_val > tol and cnt < max_iter):
gamma = 2*gamma
w_new = Soft_Threshold(w_ - gamma*grad_f, gamma*rho)
val_f_ = f(w_new, X, y, return_grad=False)
#while (val_f_ > val_f + beta*np.sum(grad_f*(w_new - w_))):
while (val_f_ > val_f + np.sum(grad_f*(w_new-w_)) + np.sum((w_new-w_)**2)/gamma):
#print val_
gamma = gamma*a
w_new = Soft_Threshold(w_ - gamma*grad_f, gamma*rho)
val_f_ = f(w_new, X, y, return_grad=False)
w_ = w_new
val_f, grad_f = f(w_, X, y)
val_ = func(w_, X, y, rho)
delta_val = val - val_
val = val_
cnt = cnt + 1
return func(w_, X, y, rho), w_, cnt
t0 = time()
rho = 0.1
a = 0.5
b = 1
val_pgls, w_pgls, cnt_pgls = minimize_prox_grad_Taylor(objective_proximal, f, 0.3*np.ones(p+1), X, y, rho, a, b, tol=1e-8, max_iter=500)
print "The value minimal of the objective function is: %0.12f" % val_pgls
t_pgls = time()-t0
print "Done in %0.3fs, number of iterations: %d" % (t_pgls, cnt_pgls)
print w_pgls
```
## Partie 3: Comparaison
$\textbf{Question 3.1}\quad\text{Comparer les propriétés des deux problèmes d’optimisation.}$
<div class="alert alert-success">
<p>1. Toutes les deux fonctions objectifs sont convexes, laquelle de régularisation de Tikhonov est différentible, l'autre n'est pas différentiable.</p>
<p>2. Selon les deux $\omega$ qu'on obtient, la régularisation de Tiknonov utilise tous les variables explicatives, la régularisation pour la parcimoine en utilise une partie.</p>
</div>
$\textbf{Question 3.2}\quad\text{Comparer les solutions obtenues avec les deux types de régularisation.}$
```
y_pred_nls = np.sign(X.dot(w_nls))
y_pred_pgls = np.sign(X.dot(w_pgls))
print "The chance level is: %f" % max(np.mean(y == 1), 1-np.mean(y == 1))
print "The score by Newton method with line search is: %f" % np.mean(y == y_pred_nls)
print "The score by proximal gradient method with line search is: %f" % np.mean(y == y_pred_pgls)
print "-"*60
print "Classification report for Newton method"
print classification_report(y, y_pred_nls)
print "-"*60
print "Classification report for proximal gradient method"
print classification_report(y, y_pred_pgls)
```
<div class="alert alert-success">
<p>En comparant les scores et les rapports de classification:</p>
<p>1. Le score obtenu par la méthode de Newton est meilleur que celui de la méthode de gradient proximal.</p>
<p>2. Selon le f1-score, la méthode de Newton est aussi meilleur.</p>
<p>3. Dans la méthode de gradient proximal, la «precision» pour class 1 est 1.0, de plus, la «recall» est 0.1. On peut conclure que cette méthode avandage la class 1.</p>
</div>
| true |
code
| 0.497315 | null | null | null | null |
|
# Aim of this notebook
* To construct the singular curve of universal type to finalize the solution of the optimal control problem
# Preamble
```
from sympy import *
init_printing(use_latex='mathjax')
# Plotting
%matplotlib inline
## Make inline plots raster graphics
from IPython.display import set_matplotlib_formats
## Import modules for plotting and data analysis
import matplotlib.pyplot as plt
from matplotlib import gridspec,rc,colors
import matplotlib.ticker as plticker
## Parameters for seaborn plots
import seaborn as sns
sns.set(style='white',font_scale=1.25,
rc={"xtick.major.size": 6, "ytick.major.size": 6,
'text.usetex': False, 'font.family': 'serif', 'font.serif': ['Times']})
import pandas as pd
pd.set_option('mode.chained_assignment',None)
import numpy as np
from scipy.optimize import fsolve, root
from scipy.integrate import ode
backend = 'dopri5'
import warnings
# Timer
import time
from copy import deepcopy
from itertools import cycle
palette_size = 10;
clrs = sns.color_palette("Reds",palette_size)
iclrs = cycle(clrs) # iterated colors
# Suppress warnings
import warnings
warnings.filterwarnings("ignore")
```
# Parameter values
* Birth rate and const of downregulation are defined below in order to fit some experim. data
```
d = .13 # death rate
c = .04 # cost of resistance
α = .3 # low equilibrium point at expression of the main pathway (high equilibrium is at one)
θ = .45 # threshold value for the expression of the main pathway
κ = 40 # robustness parameter
L = .2 # parameter used to model the effect of treatment (see the line below)
```
* Symbolic variables - the list insludes μ & μbar, because they will be varied later
```
σ, φ0, φ, x, μ, μbar = symbols('sigma, phi0, phi, x, mu, mubar')
```
* Main functions
```
A = 1-σ*(1-θ)*(1-L)
Θ = θ+σ*(1-θ)*L
Eminus = (α*A-Θ)**2/2
ΔE = A*(1-α)*((1+α)*A/2-Θ)
ΔEf = lambdify(σ,ΔE)
```
* Birth rate and cost of downregulation
```
b = (0.1*(exp(κ*(ΔEf(1)))+1)-0.14*(exp(κ*ΔEf(0))+1))/(exp(κ*ΔEf(1))-exp(κ*ΔEf(0))) # birth rate
χ = 1-(0.14*(exp(κ*ΔEf(0))+1)-b*exp(κ*ΔEf(0)))/b
b, χ
```
* Hamiltonian *H* and a part of it ρ that includes the control variable σ
```
h = b*(χ/(exp(κ*ΔE)+1)*(1-x)+c*x)
H = -φ0 + φ*(b*(χ/(exp(κ*ΔE)+1)-c)*x*(1-x)+μ*(1-x)/(exp(κ*ΔE)+1)-μbar*exp(-κ*Eminus)*x) + h
ρ = (φ*(b*χ*x+μ)+b*χ)/(exp(κ*ΔE)+1)*(1-x)-φ*μbar*exp(-κ*Eminus)*x
H, ρ
```
* Same but for no treatment (σ = 0)
```
h0 = h.subs(σ,0)
H0 = H.subs(σ,0)
ρ0 = ρ.subs(σ,0)
H0, ρ0
```
* Machinery: definition of the Poisson brackets
```
PoissonBrackets = lambda H1, H2: diff(H1,x)*diff(H2,φ)-diff(H1,φ)*diff(H2,x)
```
* Necessary functions and defining the right hand side of dynamical equations
```
ρf = lambdify((x,φ,σ,μ,μbar),ρ)
ρ0f = lambdify((x,φ,μ,μbar),ρ0)
dxdτ = lambdify((x,φ,σ,μ,μbar),-diff(H,φ))
dφdτ = lambdify((x,φ,σ,μ,μbar),diff(H,x))
dVdτ = lambdify((x,σ),h)
dρdσ = lambdify((σ,x,φ,μ,μbar),diff(ρ,σ))
dδρdτ = lambdify((x,φ,σ,μ,μbar),-PoissonBrackets(ρ0-ρ,H))
def ode_rhs(t,state,μ,μbar):
x, φ, V, δρ = state
σs = [0,1]
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σstar = 1.;
if ρf(x,φ,σstar,μ,μbar) < ρ0f(x,φ,μ,μbar):
sgm = 0
else:
sgm = σstar
return [dxdτ(x,φ,sgm,μ,μbar),dφdτ(x,φ,sgm,μ,μbar),dVdτ(x,sgm),dδρdτ(x,φ,σstar,μ,μbar)]
def σstarf(x,φ,μ,μbar):
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σstar = 1.;
if ρf(x,φ,σstar,μ,μbar) < ρ0f(x,φ,μ,μbar):
sgm = 0
else:
sgm = σstar
return sgm
def get_primary_field(name, experiment,μ,μbar):
solutions = {}
solver = ode(ode_rhs).set_integrator(backend)
τ0 = experiment['τ0']
tms = np.linspace(τ0,experiment['T_end'],1e3+1)
for x0 in experiment['x0']:
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
sol = []; k = 0;
while (solver.t < experiment['T_end']) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[k])
sol.append([solver.t]+list(solver.y))
k += 1
solutions[x0] = {'solution': sol}
for x0, entry in solutions.items():
entry['τ'] = [entry['solution'][j][0] for j in range(len(entry['solution']))]
entry['x'] = [entry['solution'][j][1] for j in range(len(entry['solution']))]
entry['φ'] = [entry['solution'][j][2] for j in range(len(entry['solution']))]
entry['V'] = [entry['solution'][j][3] for j in range(len(entry['solution']))]
entry['δρ'] = [entry['solution'][j][4] for j in range(len(entry['solution']))]
return solutions
def get_δρ_value(tme,x0,μ,μbar):
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
while (solver.t < tme) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tme)
sol = [solver.t]+list(solver.y)
return solver.y[3]
def get_δρ_ending(params,μ,μbar):
tme, x0 = params
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
δτ = 1.0e-8; tms = [tme,tme+δτ]
_k = 0; sol = []
while (_k<len(tms)):# and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append(solver.y)
_k += 1
#print(sol)
return(sol[0][3],(sol[1][3]-sol[0][3])/δτ)
def get_state(tme,x0,μ,μbar):
solver = ode(ode_rhs).set_integrator(backend)
δρ0 = ρ0.subs(x,x0).subs(φ,0)-ρ.subs(x,x0).subs(φ,0).subs(σ,1.)
solver.set_initial_value([x0,0,0,δρ0],0.).set_f_params(μ,μbar)
δτ = 1.0e-8; tms = [tme,tme+δτ]
_k = 0; sol = []
while (solver.t < tms[-1]) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append(solver.y)
_k += 1
return(list(sol[0])+[(sol[1][3]-sol[0][3])/δτ])
```
# Machinery for the universal line
* To find the universal singular curve we need to define two parameters
```
γ0 = PoissonBrackets(PoissonBrackets(H,H0),H)
γ1 = PoissonBrackets(PoissonBrackets(H0,H),H0)
```
* The dynamics
```
dxdτSingExpr = -(γ0*diff(H0,φ)+γ1*diff(H,φ))/(γ0+γ1)
dφdτSingExpr = (γ0*diff(H0,x)+γ1*diff(H,x))/(γ0+γ1)
dVdτSingExpr = (γ0*h0+γ1*h)/(γ0+γ1)
σSingExpr = γ1*σ/(γ0+γ1)
```
* Machinery for Python: lambdify the functions above
```
dxdτSing = lambdify((x,φ,σ,μ,μbar),dxdτSingExpr)
dφdτSing = lambdify((x,φ,σ,μ,μbar),dφdτSingExpr)
dVdτSing = lambdify((x,φ,σ,μ,μbar),dVdτSingExpr)
σSing = lambdify((x,φ,σ,μ,μbar),σSingExpr)
def ode_rhs_Sing(t,state,μ,μbar):
x, φ, V = state
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σstar = 1.;
#print([σstar,σSing(x,φ,σstar,μ,μbar)])
return [dxdτSing(x,φ,σstar,μ,μbar),dφdτSing(x,φ,σstar,μ,μbar),dVdτSing(x,φ,σstar,μ,μbar)]
# def ode_rhs_Sing(t,state,μ,μbar):
# x, φ, V = state
# if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
# σstar = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
# else:
# σstar = 1.;
# σTrav = fsolve(lambda σ: dxdτ(x,φ,σ,μ,μbar)-dxdτSing(x,φ,σstar,μ,μbar),.6)[0]
# print([σstar,σTrav])
# return [dxdτSing(x,φ,σstar,μ,μbar),dφdτSing(x,φ,σstar,μ,μbar),dVdτ(x,σTrav)]
def get_universal_curve(end_point,tmax,Nsteps,μ,μbar):
tms = np.linspace(end_point[0],tmax,Nsteps);
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
_k = 0; sol = []
while (solver.t < tms[-1]):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_σ_universal(tme,end_point,μ,μbar):
δτ = 1.0e-8; tms = [tme,tme+δτ]
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
_k = 0; sol = []
while (solver.t < tme+δτ):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
x, φ = sol[0][:2]
sgm = fsolve(lambda σ: dxdτ(x,φ,σ,μ,μbar)-(sol[1][0]-sol[0][0])/δτ,θ/2)[0]
return sgm
def get_state_universal(tme,end_point,μ,μbar):
solver = ode(ode_rhs_Sing).set_integrator(backend)
solver.set_initial_value(end_point[1:4],end_point[0]).set_f_params(μ,μbar)
solver.integrate(tme)
return [solver.t]+list(solver.y)
def ode_rhs_with_σstar(t,state,μ,μbar):
x, φ, V = state
if (dρdσ(1.,x,φ,μ,μbar)<0) and (dρdσ(θ,x,φ,μ,μbar)>0):
σ = fsolve(dρdσ,.8,args=(x,φ,μ,μbar,))[0]
else:
σ = 1.;
return [dxdτ(x,φ,σ,μ,μbar),dφdτ(x,φ,σ,μ,μbar),dVdτ(x,σ)]
def ode_rhs_with_given_σ(t,state,σ,μ,μbar):
x, φ, V = state
return [dxdτ(x,φ,σ,μ,μbar),dφdτ(x,φ,σ,μ,μbar),dVdτ(x,σ)]
def get_trajectory_with_σstar(starting_point,tmax,Nsteps,μ,μbar):
tms = np.linspace(starting_point[0],tmax,Nsteps)
solver = ode(ode_rhs_with_σstar).set_integrator(backend)
solver.set_initial_value(starting_point[1:],starting_point[0]).set_f_params(μ,μbar)
sol = []; _k = 0;
while solver.t < max(tms) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_trajectory_with_given_σ(starting_point,tmax,Nsteps,σ,μ,μbar):
tms = np.linspace(starting_point[0],tmax,100)
solver = ode(ode_rhs_with_given_σ).set_integrator(backend)
solver.set_initial_value(starting_point[1:],starting_point[0]).set_f_params(σ,μ,μbar)
sol = []; _k = 0;
while solver.t < max(tms) and (solver.y[0]<=1.) and (solver.y[0]>=0.):
solver.integrate(tms[_k])
sol.append([solver.t]+list(solver.y))
_k += 1
return sol
def get_state_with_σstar(tme,starting_point,μ,μbar):
solver = ode(ode_rhs_with_σstar).set_integrator(backend)
solver.set_initial_value(starting_point[1:4],starting_point[0]).set_f_params(μ,μbar)
solver.integrate(tme)
return [solver.t]+list(solver.y)
def get_finalizing_point_from_universal_curve(tme,tmx,end_point,μ,μbar):
unv_point = get_state_universal(tme,end_point,μ,μbar)
return get_state_with_σstar(tmx,unv_point,μ,μbar)[1]
```
# Field of optimal trajectories as the solution of the Bellman equation
* μ & μbar are varied by *T* and *T*bar ($\mu=1/T$ and $\bar\mu=1/\bar{T}$)
```
tmx = 720.
end_switching_curve = {'t': 24., 'x': .9/.8}
# for Τ, Τbar in zip([28]*5,[14,21,28,35,60]):
for Τ, Τbar in zip([28],[60]):
μ = 1./Τ; μbar = 1./Τbar
print("Parameters: μ = %.5f, μbar = %.5f"%(μ,μbar))
end_switching_curve['t'], end_switching_curve['x'] = fsolve(get_δρ_ending,(end_switching_curve['t'],.8*end_switching_curve['x']),args=(μ,μbar),xtol=1.0e-12)
end_point = [end_switching_curve['t']]+get_state(end_switching_curve['t'],end_switching_curve['x'],μ,μbar)
print("Ending point for the switching line: τ = %.1f days, x = %.1f%%" % (end_point[0], end_point[1]*100))
print("Checking the solution - should give zero values: ")
print(get_δρ_ending([end_switching_curve['t'],end_switching_curve['x']],μ,μbar))
print("* Constructing the primary field")
experiments = {
'sol1': { 'T_end': tmx, 'τ0': 0., 'x0': list(np.linspace(0,end_switching_curve['x']-(1e-3),10))+
list(np.linspace(end_switching_curve['x']+(1e-6),1.,10)) } }
primary_field = []
for name, values in experiments.items():
primary_field.append(get_primary_field(name,values,μ,μbar))
print("* Constructing the switching curve")
switching_curve = []
x0s = np.linspace(end_switching_curve['x'],1,21); _y = end_switching_curve['t']
for x0 in x0s:
tme = fsolve(get_δρ_value,_y,args=(x0,μ,μbar))[0]
if (tme>0):
switching_curve = switching_curve+[[tme,get_state(tme,x0,μ,μbar)[0]]]
_y = tme
print("* Constructing the universal curve")
universal_curve = get_universal_curve(end_point,tmx,25,μ,μbar)
print("* Finding the last characteristic")
#time0 = time.time()
tuniv = fsolve(get_finalizing_point_from_universal_curve,tmx-40.,args=(tmx,end_point,μ,μbar,))[0]
#print("The proccess to find the last characteristic took %0.1f minutes" % ((time.time()-time0)/60.))
univ_point = get_state_universal(tuniv,end_point,μ,μbar)
print("The last point on the universal line:")
print(univ_point)
last_trajectory = get_trajectory_with_σstar(univ_point,tmx,50,μ,μbar)
print("Final state:")
final_state = get_state_with_σstar(tmx,univ_point,μ,μbar)
print(final_state)
print("Fold-change in tumor size: %.2f"%(exp((b-d)*tmx-final_state[-1])))
# Plotting
plt.rcParams['figure.figsize'] = (6.75, 4)
_k = 0
for solutions in primary_field:
for x0, entry in solutions.items():
plt.plot(entry['τ'], entry['x'], 'k-', linewidth=.9, color=clrs[_k%palette_size])
_k += 1
plt.plot([x[0] for x in switching_curve],[x[1] for x in switching_curve],linewidth=2,color="red")
plt.plot([end_point[0]],[end_point[1]],marker='o',color="red")
plt.plot([x[0] for x in universal_curve],[x[1] for x in universal_curve],linewidth=2,color="red")
plt.plot([x[0] for x in last_trajectory],[x[1] for x in last_trajectory],linewidth=.9,color="black")
plt.xlim([0,tmx]); plt.ylim([0,1]);
plt.xlabel("time, days"); plt.ylabel("fraction of resistant cells")
plt.show()
print()
import csv
from numpy.linalg import norm
File = open("../figures/draft/sensitivity_mu-example.csv", 'w')
File.write("T,Tbar,mu,mubar,sw_end_t,sw_end_x,univ_point_t,univ_point_x,outcome,err_sw_t,err_sw_x\n")
writer = csv.writer(File,lineterminator='\n')
tmx = 720.
end_switching_curve0 = {'t': 23.36, 'x': .9592}
end_switching_curve_prev_t = end_switching_curve['t']
tuniv = tmx-30.
Τbars = np.arange(120,110,-2) #need to change here if more
for Τ in Τbars:
μ = 1./Τ
end_switching_curve = deepcopy(end_switching_curve0)
for Τbar in Τbars:
μbar = 1./Τbar
print("* Parameters: T = %.1f, Tbar = %.1f (μ = %.5f, μbar = %.5f)"%(Τ,Τbar,μ,μbar))
success = False; err = 1.
while (not success)|(norm(err)>1e-6):
end_switching_curve = {'t': 2*end_switching_curve['t']-end_switching_curve_prev_t-.001,
'x': end_switching_curve['x']-0.002}
sol = root(get_δρ_ending,(end_switching_curve['t'],end_switching_curve['x']),args=(μ,μbar))
end_switching_curve_prev_t = end_switching_curve['t']
end_switching_curve_prev_x = end_switching_curve['x']
end_switching_curve['t'], end_switching_curve['x'] = sol.x
success = sol.success
err = get_δρ_ending([end_switching_curve['t'],end_switching_curve['x']],μ,μbar)
if (not success):
print("! Trying again...", sol.message)
elif (norm(err)>1e-6):
print("! Trying again... Convergence is not sufficient")
else:
end_point = [end_switching_curve['t']]+get_state(end_switching_curve['t'],end_switching_curve['x'],μ,μbar)
print("Ending point: t = %.2f, x = %.2f%%"%(end_switching_curve['t'],100*end_switching_curve['x'])," Checking the solution:",err)
universal_curve = get_universal_curve(end_point,tmx,25,μ,μbar)
tuniv = root(get_finalizing_point_from_universal_curve,tuniv,args=(tmx,end_point,μ,μbar)).x
err_tuniv = get_finalizing_point_from_universal_curve(tuniv,tmx,end_point,μ,μbar)
univ_point = get_state_universal(tuniv,end_point,μ,μbar)
print("tuniv = %.2f"%tuniv," Checking the solution: ",err_tuniv)
final_state = get_state_with_σstar(tmx,univ_point,μ,μbar)
outcome = exp((b-d)*tmx-final_state[-1])
print("Fold-change in tumor size: %.2f"%(outcome))
output = [Τ,Τbar,μ,μbar,end_switching_curve['t'],end_switching_curve['x']]+list(univ_point[0:2])+[outcome]+list(err)+[err_tuniv]
writer.writerow(output)
if (Τbar==Τ):
end_switching_curve0 = deepcopy(end_switching_curve)
File.close()
```
* Here I investigate the dependence of $\mathrm{FoldChange}(T,\bar T)$. I fix $T$ at 15,30,45,60 days, and then I vary $\bar T$ between zero and $4T$. The example below is just a simulation for only one given value of $T$.
```
import csv
from numpy.linalg import norm
File = open("../results/sensitivity1.csv", 'w')
File.write("T,Tbar,mu,mubar,sw_end_t,sw_end_x,univ_point_t,univ_point_x,outcome,err_sw_t,err_sw_x\n")
writer = csv.writer(File,lineterminator='\n')
tmx = 720.
end_switching_curve = {'t': 23.36, 'x': .9592}
end_switching_curve_prev_t = end_switching_curve['t']
tuniv = tmx-30.
Τ = 15
Τbars_step = .5; Tbars = np.arange(Τ*4,0,-Τbars_step)
for Τbar in Tbars:
μ = 1./Τ; μbar = 1./Τbar
print("* Parameters: T = %.1f, Tbar = %.1f (μ = %.5f, μbar = %.5f)"%(Τ,Τbar,μ,μbar))
success = False; err = 1.
while (not success)|(norm(err)>1e-6):
end_switching_curve = {'t': 2*end_switching_curve['t']-end_switching_curve_prev_t-.001,
'x': end_switching_curve['x']-0.002}
sol = root(get_δρ_ending,(end_switching_curve['t'],end_switching_curve['x']),args=(μ,μbar))
end_switching_curve_prev_t = end_switching_curve['t']
end_switching_curve_prev_x = end_switching_curve['x']
end_switching_curve['t'], end_switching_curve['x'] = sol.x
success = sol.success
err = get_δρ_ending([end_switching_curve['t'],end_switching_curve['x']],μ,μbar)
if (not success):
print("! Trying again...", sol.message)
elif (norm(err)>1e-6):
print("! Trying again... Convergence is not sufficient")
else:
end_point = [end_switching_curve['t']]+get_state(end_switching_curve['t'],end_switching_curve['x'],μ,μbar)
print("Ending point: t = %.2f, x = %.2f%%"%(end_switching_curve['t'],100*end_switching_curve['x'])," Checking the solution:",err)
universal_curve = get_universal_curve(end_point,tmx,25,μ,μbar)
tuniv = root(get_finalizing_point_from_universal_curve,tuniv,args=(tmx,end_point,μ,μbar)).x
err_tuniv = get_finalizing_point_from_universal_curve(tuniv,tmx,end_point,μ,μbar)
univ_point = get_state_universal(tuniv,end_point,μ,μbar)
print("tuniv = %.2f"%tuniv," Checking the solution: ",err_tuniv)
final_state = get_state_with_σstar(tmx,univ_point,μ,μbar)
outcome = exp((b-d)*tmx-final_state[-1])
print("Fold-change in tumor size: %.2f"%(outcome))
output = [Τ,Τbar,μ,μbar,end_switching_curve['t'],end_switching_curve['x']]+list(univ_point[0:2])+[outcome]+list(err)+[err_tuniv]
writer.writerow(output)
File.close()
```
* The results are aggregated in a file **sensitivity1_agg.csv**.
```
df = pd.DataFrame.from_csv("../figures/draft/sensitivity1_agg.csv").reset_index().drop(['err_sw_t','err_sw_x','err_tuniv'],1)
df['Tratio'] = df['Tbar']/df['T']
df.head()
```
| true |
code
| 0.361418 | null | null | null | null |
|
# Logistic Regression (scikit-learn) with HDFS/Spark Data Versioning
This example is based on our [basic census income classification example](census-end-to-end.ipynb), using local setups of ModelDB and its client, and [HDFS/Spark data versioning](https://docs.verta.ai/en/master/api/api/versioning.html#verta.dataset.HDFSPath).
```
!pip install /path/to/verta-0.15.10-py2.py3-none-any.whl
HOST = "localhost:8080"
PROJECT_NAME = "Census Income Classification - HDFS Data"
EXPERIMENT_NAME = "Logistic Regression"
```
## Imports
```
from __future__ import print_function
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings("ignore", category=ConvergenceWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
import itertools
import os
import numpy as np
import pandas as pd
import sklearn
from sklearn import model_selection
from sklearn import linear_model
```
---
# Log Workflow
This section demonstrates logging model metadata and training artifacts to ModelDB.
## Instantiate Client
```
from verta import Client
from verta.utils import ModelAPI
client = Client(HOST)
proj = client.set_project(PROJECT_NAME)
expt = client.set_experiment(EXPERIMENT_NAME)
```
<h2>Prepare Data</h2>
```
from pyspark import SparkContext
sc = SparkContext("local")
from verta.dataset import HDFSPath
hdfs = "hdfs://HOST:PORT"
dataset = client.set_dataset(name="Census Income S3")
blob = HDFSPath.with_spark(sc, "{}/data/census/*".format(hdfs))
version = dataset.create_version(blob)
version
csv = sc.textFile("{}/data/census/census-train.csv".format(hdfs)).collect()
from verta.external.six import StringIO
df_train = pd.read_csv(StringIO('\n'.join(csv)))
X_train = df_train.iloc[:,:-1]
y_train = df_train.iloc[:, -1]
df_train.head()
```
## Prepare Hyperparameters
```
hyperparam_candidates = {
'C': [1e-6, 1e-4],
'solver': ['lbfgs'],
'max_iter': [15, 28],
}
hyperparam_sets = [dict(zip(hyperparam_candidates.keys(), values))
for values
in itertools.product(*hyperparam_candidates.values())]
```
## Train Models
```
def run_experiment(hyperparams):
# create object to track experiment run
run = client.set_experiment_run()
# create validation split
(X_val_train, X_val_test,
y_val_train, y_val_test) = model_selection.train_test_split(X_train, y_train,
test_size=0.2,
shuffle=True)
# log hyperparameters
run.log_hyperparameters(hyperparams)
print(hyperparams, end=' ')
# create and train model
model = linear_model.LogisticRegression(**hyperparams)
model.fit(X_train, y_train)
# calculate and log validation accuracy
val_acc = model.score(X_val_test, y_val_test)
run.log_metric("val_acc", val_acc)
print("Validation accuracy: {:.4f}".format(val_acc))
# save and log model
run.log_model(model)
# log dataset snapshot as version
run.log_dataset_version("train", version)
for hyperparams in hyperparam_sets:
run_experiment(hyperparams)
```
---
# Revisit Workflow
This section demonstrates querying and retrieving runs via the Client.
## Retrieve Best Run
```
best_run = expt.expt_runs.sort("metrics.val_acc", descending=True)[0]
print("Validation Accuracy: {:.4f}".format(best_run.get_metric("val_acc")))
best_hyperparams = best_run.get_hyperparameters()
print("Hyperparameters: {}".format(best_hyperparams))
```
## Train on Full Dataset
```
model = linear_model.LogisticRegression(multi_class='auto', **best_hyperparams)
model.fit(X_train, y_train)
```
## Calculate Accuracy on Full Training Set
```
train_acc = model.score(X_train, y_train)
print("Training accuracy: {:.4f}".format(train_acc))
```
---
| true |
code
| 0.578627 | null | null | null | null |
|
Train a simple deep CNN on the CIFAR10 small images dataset.
It gets to 75% validation accuracy in 25 epochs, and 79% after 50 epochs.
(it's still underfitting at that point, though)
```
# https://gist.github.com/deep-diver
import warnings;warnings.filterwarnings('ignore')
from tensorflow import keras
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Activation, Flatten
from tensorflow.keras.layers import Conv2D, MaxPooling2D
from tensorflow.keras.optimizers import RMSprop
import os
batch_size = 32
num_classes = 10
epochs = 100
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models')
model_name = 'keras_cifar10_trained_model.h5'
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Convert class vectors to binary class matrices.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same',
input_shape=x_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# initiate RMSprop optimizer
opt = RMSprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
# Save model and weights
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# Score trained model.
scores = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', scores[0])
print('Test accuracy:', scores[1])
```
| true |
code
| 0.694575 | null | null | null | null |
|
### Neural Machine Translation by Jointly Learning to Align and Translate
In this notebook we will implement the model from [Neural Machine Translation by Jointly Learning to Align and Translate](https://arxiv.org/abs/1409.0473) that will improve PPL (**perplexity**) as compared to the previous notebook.
Here is a general encoder-decoder model that we have used from the past.
<p align="center"><img src="https://github.com/bentrevett/pytorch-seq2seq/raw/49df8404d938a6edbf729876405558cc2c2b3013/assets/seq2seq1.png"/></p>
In the previous model, our architecture was set-up in a way to reduce "information compression" by explicitly passing the context vector, $z$, to the decoder at every time-step and by passing both the context vector and embedded input word, $d(y_t)$, along with the hidden state, $s_t$, to the linear layer, $f$, to make a prediction.
<p align="center"><img src="https://github.com/bentrevett/pytorch-seq2seq/raw/49df8404d938a6edbf729876405558cc2c2b3013/assets/seq2seq7.png"/></p>
Even though we have reduced some of this compression, our context vector still needs to contain all of the information about the source sentence. The model implemented in this notebook avoids this compression by allowing the decoder to look at the entire source sentence (via its hidden states) at each decoding step! How does it do this? It uses **attention**.
### Attention.
Attention works by first, calculating an attention vector, $a$, that is the length of the source sentence. The attention vector has the property that each element is between 0 and 1, and the entire vector sums to 1. We then calculate a weighted sum of our source sentence hidden states, $H$, to get a weighted source vector, $w$.
$$w = \sum_{i}a_ih_i$$
We calculate a new weighted source vector every time-step when decoding, using it as input to our decoder RNN as well as the linear layer to make a prediction.
### Data Preparation
Again we still prepare the data just like from the previous notebooks.
```
import torch
from torch import nn
from torch.nn import functional as F
import spacy, math, random
import numpy as np
from torchtext.legacy import datasets, data
```
### Setting seeds
```
SEED = 42
np.random.seed(SEED)
torch.manual_seed(SEED)
random.seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deteministic = True
```
### Loading the German and English models.
```
import spacy
import spacy.cli
spacy.cli.download('de_core_news_sm')
import de_core_news_sm, en_core_web_sm
spacy_de = spacy.load('de_core_news_sm')
spacy_en = spacy.load('en_core_web_sm')
```
### Preprocessing function that tokenizes sentences.
```
def tokenize_de(sent):
return [tok.text for tok in spacy_de.tokenizer(sent)]
def tokenize_en(sent):
return [tok.text for tok in spacy_en.tokenizer(sent)]
```
### Creating the `Fields`
```
SRC = data.Field(
tokenize = tokenize_de,
lower= True,
init_token = "<sos>",
eos_token = "<eos>"
)
TRG = data.Field(
tokenize = tokenize_en,
lower= True,
init_token = "<sos>",
eos_token = "<eos>"
)
```
### Loading `Multi30k` dataset.
```
train_data, valid_data, test_data = datasets.Multi30k.splits(
exts=('.de', '.en'),
fields = (SRC, TRG)
)
```
### Checking if we have loaded the data corectly.
```
from prettytable import PrettyTable
def tabulate(column_names, data):
table = PrettyTable(column_names)
table.title= "VISUALIZING SETS EXAMPLES"
table.align[column_names[0]] = 'l'
table.align[column_names[1]] = 'r'
for row in data:
table.add_row(row)
print(table)
column_names = ["SUBSET", "EXAMPLE(s)"]
row_data = [
["training", len(train_data)],
['validation', len(valid_data)],
['test', len(test_data)]
]
tabulate(column_names, row_data)
```
### Checking a single example, of the `SRC` and the `TRG`.
```
print(vars(train_data[0]))
```
### Building the vocabulary.
Just like from the previous notebook all the tokens that apears less than 2, are automatically converted to unknown token `<unk>`.
```
SRC.build_vocab(train_data, min_freq=2)
TRG.build_vocab(train_data, min_freq=2)
```
### Device
```
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
```
### Creating Iterators.
Just like from the previous notebook we are going to use the BucketIterator to create the train, validation and test sets.
```
BATCH_SIZE = 128
train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
(train_data, valid_data, test_data),
device = device,
batch_size = BATCH_SIZE
)
```
### Encoder.
First, we'll build the encoder. Similar to the previous model, we only use a single layer GRU, however we now use a bidirectional RNN. With a bidirectional RNN, we have two RNNs in each layer. A forward RNN going over the embedded sentence from left to right (shown below in green), and a backward RNN going over the embedded sentence from right to left (teal). All we need to do in code is set bidirectional = True and then pass the embedded sentence to the RNN as before.
<p align="center">
<img src="https://github.com/bentrevett/pytorch-seq2seq/raw/49df8404d938a6edbf729876405558cc2c2b3013/assets/seq2seq8.png"/>
</p>
We now have:
$$\begin{align*}
h_t^\rightarrow &= \text{EncoderGRU}^\rightarrow(e(x_t^\rightarrow),h_{t-1}^\rightarrow)\\
h_t^\leftarrow &= \text{EncoderGRU}^\leftarrow(e(x_t^\leftarrow),h_{t-1}^\leftarrow)
\end{align*}$$
Where $x_0^\rightarrow = \text{<sos>}, x_1^\rightarrow = \text{guten}$ and $x_0^\leftarrow = \text{<eos>}, x_1^\leftarrow = \text{morgen}$.
As before, we only pass an input (embedded) to the RNN, which tells PyTorch to initialize both the forward and backward initial hidden states ($h_0^\rightarrow$ and $h_0^\leftarrow$, respectively) to a tensor of all zeros. We'll also get two context vectors, one from the forward RNN after it has seen the final word in the sentence, $z^\rightarrow=h_T^\rightarrow$, and one from the backward RNN after it has seen the first word in the sentence, $z^\leftarrow=h_T^\leftarrow$.
The RNN returns outputs and hidden.
outputs is of size [src len, batch size, hid dim * num directions] where the first hid_dim elements in the third axis are the hidden states from the top layer forward RNN, and the last hid_dim elements are hidden states from the top layer backward RNN. We can think of the third axis as being the forward and backward hidden states concatenated together other, i.e. $h_1 = [h_1^\rightarrow; h_{T}^\leftarrow]$, $h_2 = [h_2^\rightarrow; h_{T-1}^\leftarrow]$ and we can denote all encoder hidden states (forward and backwards concatenated together) as $H=\{ h_1, h_2, ..., h_T\}$.
hidden is of size [n layers * num directions, batch size, hid dim], where [-2, :, :] gives the top layer forward RNN hidden state after the final time-step (i.e. after it has seen the last word in the sentence) and [-1, :, :] gives the top layer backward RNN hidden state after the final time-step (i.e. after it has seen the first word in the sentence).
As the decoder is not bidirectional, it only needs a single context vector, $z$, to use as its initial hidden state, $s_0$, and we currently have two, a forward and a backward one ($z^\rightarrow=h_T^\rightarrow$ and $z^\leftarrow=h_T^\leftarrow$, respectively). We solve this by concatenating the two context vectors together, passing them through a linear layer, $g$, and applying the $\tanh$ activation function.
$$z=\tanh(g(h_T^\rightarrow, h_T^\leftarrow)) = \tanh(g(z^\rightarrow, z^\leftarrow)) = s_0$$
**Note:** this is actually a deviation from the paper. Instead, they feed only the first backward RNN hidden state through a linear layer to get the context vector/decoder initial hidden state. ***_This doesn't seem to make sense to me, so we have changed it._**
As we want our model to look back over the whole of the source sentence we return outputs, the stacked forward and backward hidden states for every token in the source sentence. We also return hidden, which acts as our initial hidden state in the decoder.
```
class Encoder(nn.Module):
def __init__(self, input_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout):
super(Encoder, self).__init__()
self.embedding = nn.Embedding(input_dim, embedding_dim=emb_dim)
self.gru = nn.GRU(emb_dim, enc_hid_dim, bidirectional = True)
self.fc = nn.Linear(enc_hid_dim * 2, dec_hid_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, src): # src = [src len, batch size]
embedded = self.dropout(self.embedding(src)) # embedded = [src len, batch size, emb dim]
outputs, hidden = self.gru(embedded)
"""
outputs = [src len, batch size, hid dim * num directions]
hidden = [n layers * num directions, batch size, hid dim]
hidden is stacked [forward_1, backward_1, forward_2, backward_2, ...]
outputs are always from the last layer
hidden [-2, :, : ] is the last of the forwards RNN
hidden [-1, :, : ] is the last of the backwards RNN
initial decoder hidden is final hidden state of the forwards and backwards
encoder RNNs fed through a linear layer
"""
hidden = torch.tanh(self.fc(torch.cat((hidden[-2, :, :], hidden[-1, :, :]), dim=1)))
"""
outputs = [src len, batch size, enc hid dim * 2]
hidden = [batch size, dec hid dim]
"""
return outputs, hidden
```
### Attention Layer
Next up is the attention layer. This will take in the previous hidden state of the decoder, $s_{t-1}$, and all of the stacked forward and backward hidden states from the encoder, $H$. The layer will output an attention vector, $a_t$, that is the length of the source sentence, each element is between 0 and 1 and the entire vector sums to 1.
Intuitively, this layer takes what we have decoded so far, $s_{t-1}$, and all of what we have encoded, $H$, to produce a vector, $a_t$, that represents which words in the source sentence we should pay the most attention to in order to correctly predict the next word to decode, $\hat{y}_{t+1}$.
First, we calculate the energy between the previous decoder hidden state and the encoder hidden states. As our encoder hidden states are a sequence of $T$ tensors, and our previous decoder hidden state is a single tensor, the first thing we do is repeat the previous decoder hidden state $T$ times. We then calculate the energy, $E_t$, between them by concatenating them together and passing them through a linear layer (attn) and a $\tanh$ activation function.
$$E_t = \tanh(\text{attn}(s_{t-1}, H))$$
This can be thought of as calculating how well each encoder hidden state "matches" the previous decoder hidden state.
We currently have a [dec hid dim, src len] tensor for each example in the batch. We want this to be [src len] for each example in the batch as the attention should be over the length of the source sentence. This is achieved by multiplying the energy by a [1, dec hid dim] tensor, $v$.
$$\hat{a}_t = v E_t$$
We can think of $v$ as the weights for a weighted sum of the energy across all encoder hidden states. These weights tell us how much we should attend to each token in the source sequence. The parameters of $v$ are initialized randomly, but learned with the rest of the model via backpropagation. Note how $v$ is not dependent on time, and the same $v$ is used for each time-step of the decoding. We implement $v$ as a linear layer without a bias.
Finally, we ensure the attention vector fits the constraints of having all elements between 0 and 1 and the vector summing to 1 by passing it through a $\text{softmax}$ layer.
$$a_t = \text{softmax}(\hat{a_t})$$
This gives us the attention over the source sentence!
Graphically, this looks something like below. This is for calculating the very first attention vector, where $s_{t-1} = s_0 = z$. The green/teal blocks represent the hidden states from both the forward and backward RNNs, and the attention computation is all done within the pink block.
<p align="center"><img src="https://github.com/bentrevett/pytorch-seq2seq/raw/49df8404d938a6edbf729876405558cc2c2b3013/assets/seq2seq9.png"/></p>
```
class Attention(nn.Module):
def __init__(self, enc_hid_dim, dec_hid_dim):
super(Attention, self).__init__()
self.attn = nn.Linear((enc_hid_dim * 2) + dec_hid_dim, dec_hid_dim)
self.v = nn.Linear(dec_hid_dim, 1, bias = False)
def forward(self, hidden, encoder_outputs):
"""
hidden = [batch size, dec hid dim]
encoder_outputs = [src len, batch size, enc hid dim * 2]
"""
batch_size = encoder_outputs.shape[1]
src_len = encoder_outputs.shape[0]
# repeat decoder hidden state src_len times
hidden = hidden.unsqueeze(1).repeat(1, src_len, 1)
encoder_outputs = encoder_outputs.permute(1, 0, 2)
"""
hidden = [batch size, src len, dec hid dim]
encoder_outputs = [batch size, src len, enc hid dim * 2]
"""
energy = torch.tanh(self.attn(torch.cat((hidden, encoder_outputs), dim = 2))) # energy = [batch size, src len, dec hid dim]
attention = self.v(energy).squeeze(2) # attention= [batch size, src len]
return F.softmax(attention, dim=1)
```
### Decoder.
The decoder contains the attention layer, attention, which takes the previous hidden state, $s_{t-1}$, all of the encoder hidden states, $H$, and returns the attention vector, $a_t$.
We then use this attention vector to create a weighted source vector, $w_t$, denoted by weighted, which is a weighted sum of the encoder hidden states, $H$, using $a_t$ as the weights.
$$w_t = a_t H$$
The embedded input word, $d(y_t)$, the weighted source vector, $w_t$, and the previous decoder hidden state, $s_{t-1}$, are then all passed into the decoder RNN, with $d(y_t)$ and $w_t$ being concatenated together.
$$s_t = \text{DecoderGRU}(d(y_t), w_t, s_{t-1})$$
We then pass $d(y_t)$, $w_t$ and $s_t$ through the linear layer, $f$, to make a prediction of the next word in the target sentence, $\hat{y}_{t+1}$. This is done by concatenating them all together.
$$\hat{y}_{t+1} = f(d(y_t), w_t, s_t)$$
The image below shows decoding the first word in an example translation.
<p align="center">
<img src="https://github.com/bentrevett/pytorch-seq2seq/raw/49df8404d938a6edbf729876405558cc2c2b3013/assets/seq2seq10.png"/>
</p>
The green/teal blocks show the forward/backward encoder RNNs which output $H$, the red block shows the context vector, $z = h_T = \tanh(g(h^\rightarrow_T,h^\leftarrow_T)) = \tanh(g(z^\rightarrow, z^\leftarrow)) = s_0$, the blue block shows the decoder RNN which outputs $s_t$, the purple block shows the linear layer, $f$, which outputs $\hat{y}_{t+1}$ and the orange block shows the calculation of the weighted sum over $H$ by $a_t$ and outputs $w_t$. Not shown is the calculation of $a_t$.
```
class Decoder(nn.Module):
def __init__(self, output_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout, attention):
super(Decoder, self).__init__()
self.output_dim = output_dim
self.attention = attention
self.embedding = nn.Embedding(output_dim, emb_dim)
self.gru = nn.GRU((enc_hid_dim * 2) + emb_dim, dec_hid_dim)
self.fc_out = nn.Linear((enc_hid_dim * 2) + dec_hid_dim + emb_dim, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, input, hidden, encoder_outputs):
"""
input = [batch size]
hidden = [batch size, dec hid dim]
encoder_outputs = [src len, batch size, enc hid dim * 2]
"""
input = input.unsqueeze(0) # input = [1, batch size]
embedded = self.dropout(self.embedding(input)) # embedded = [1, batch size, emb dim]
a = self.attention(hidden, encoder_outputs)# a = [batch size, src len]
a = a.unsqueeze(1) # a = [batch size, 1, src len]
encoder_outputs = encoder_outputs.permute(1, 0, 2) # encoder_outputs = [batch size, src len, enc hid dim * 2]
weighted = torch.bmm(a, encoder_outputs) # weighted = [batch size, 1, enc hid dim * 2]
weighted = weighted.permute(1, 0, 2) # weighted = [1, batch size, enc hid dim * 2]
rnn_input = torch.cat((embedded, weighted), dim = 2) # rnn_input = [1, batch size, (enc hid dim * 2) + emb dim]
output, hidden = self.gru(rnn_input, hidden.unsqueeze(0))
"""
output = [seq len, batch size, dec hid dim * n directions]
hidden = [n layers * n directions, batch size, dec hid dim]
seq len, n layers and n directions will always be 1 in this decoder, therefore:
output = [1, batch size, dec hid dim]
hidden = [1, batch size, dec hid dim]
this also means that output == hidden
"""
assert (output == hidden).all()
embedded = embedded.squeeze(0)
output = output.squeeze(0)
weighted = weighted.squeeze(0)
prediction = self.fc_out(torch.cat((output, weighted, embedded), dim = 1)) # prediction = [batch size, output dim]
return prediction, hidden.squeeze(0)
```
### Seq2Seq Model
This is the first model where we don't have to have the encoder RNN and decoder RNN have the same hidden dimensions, however the encoder has to be bidirectional. This requirement can be removed by changing all occurences of enc_dim * 2 to enc_dim * 2 if encoder_is_bidirectional else enc_dim.
This seq2seq encapsulator is similar to the last two. The only difference is that the encoder returns both the final hidden state (which is the final hidden state from both the forward and backward encoder RNNs passed through a linear layer) to be used as the initial hidden state for the decoder, as well as every hidden state (which are the forward and backward hidden states stacked on top of each other). We also need to ensure that hidden and encoder_outputs are passed to the decoder.
**Briefly going over all of the steps:**
* the outputs tensor is created to hold all predictions, $\hat{Y}$
* the source sequence, $X$, is fed into the encoder to receive $z$ and $H$
* the initial decoder hidden state is set to be the context vector, $s_0 = z = h_T$
* we use a batch of <sos> tokens as the first input, $y_1$
* **we then decode within a loop:**
* inserting the input token $y_t$, previous hidden state, $s_{t-1}$, and all encoder outputs, $H$, into the decoder
* receiving a prediction, $\hat{y}_{t+1}$, and a new hidden state, $s_t$
* we then decide if we are going to teacher force or not, setting the next input as appropriate
```
class Seq2Seq(nn.Module):
def __init__(self, encoder, decoder, device):
super().__init__()
self.encoder = encoder
self.decoder = decoder
self.device = device
def forward(self, src, trg, teacher_forcing_ratio = 0.5):
"""
src = [src len, batch size]
trg = [trg len, batch size]
teacher_forcing_ratio is probability to use teacher forcing
e.g. if teacher_forcing_ratio is 0.75 we use teacher forcing 75% of the time
"""
trg_len, batch_size = trg.shape
trg_vocab_size = self.decoder.output_dim
# tensor to store decoder outputs
outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device)
# encoder_outputs is all hidden states of the input sequence, back and forwards
# hidden is the final forward and backward hidden states, passed through a linear layer
encoder_outputs, hidden = self.encoder(src)
# first input to the decoder is the <sos> tokens
input = trg[0,:]
for t in range(1, trg_len):
# insert input token embedding, previous hidden state and all encoder hidden states
# receive output tensor (predictions) and new hidden state
output, hidden = self.decoder(input, hidden, encoder_outputs)
# place predictions in a tensor holding predictions for each token
outputs[t] = output
# decide if we are going to use teacher forcing or not
teacher_force = random.random() < teacher_forcing_ratio
# get the highest predicted token from our predictions
top1 = output.argmax(1)
# if teacher forcing, use actual next token as next input
# if not, use predicted token
input = trg[t] if teacher_force else top1
return outputs
```
### Training the Seq2Seq Model
The rest of the code is similar from the previous notebooks, where there's changes I will highlight.
### Hyper parameters
```
INPUT_DIM = len(SRC.vocab)
OUTPUT_DIM = len(TRG.vocab)
ENC_EMB_DIM = DEC_EMB_DIM = 256
ENC_HID_DIM = DEC_HID_DIM = 512
ENC_DROPOUT = DEC_DROPOUT = 0.5
attn = Attention(ENC_HID_DIM, DEC_HID_DIM)
enc = Encoder(INPUT_DIM, ENC_EMB_DIM, ENC_HID_DIM, DEC_HID_DIM, ENC_DROPOUT)
dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, ENC_HID_DIM, DEC_HID_DIM, DEC_DROPOUT, attn)
model = Seq2Seq(enc, dec, device).to(device)
model
```
### Initializing the weights
ere, we will initialize all biases to zero and all weights from $\mathcal{N}(0, 0.01)$.
```
def init_weights(m):
for name, param in m.named_parameters():
if 'weight' in name:
nn.init.normal_(param.data, mean=0, std=0.01)
else:
nn.init.constant_(param.data, 0)
model.apply(init_weights)
```
### Counting model parameters.
The model parameters has increased with `~50%` from the previous notebook.
```
def count_trainable_params(model):
return sum(p.numel() for p in model.parameters()), sum(p.numel() for p in model.parameters() if p.requires_grad)
n_params, trainable_params = count_trainable_params(model)
print(f"Total number of paramaters: {n_params:,}\nTotal tainable parameters: {trainable_params:,}")
```
### Optimizer
```
optimizer = torch.optim.Adam(model.parameters())
```
### Loss Function
Our loss function calculates the average loss per token, however by passing the index of the `<pad>` token as the `ignore_index` argument we ignore the loss whenever the target token is a padding token.
```
TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token]
criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX)
```
### Training and Evaluating Functions
```
def train(model, iterator, optimizer, criterion, clip):
model.train()
epoch_loss = 0
for i, batch in enumerate(iterator):
src = batch.src
trg = batch.trg
optimizer.zero_grad()
output = model(src, trg)
# trg = [trg len, batch size]
# output = [trg len, batch size, output dim]
output_dim = output.shape[-1]
output = output[1:].view(-1, output_dim)
trg = trg[1:].view(-1)
# trg = [(trg len - 1) * batch size]
# output = [(trg len - 1) * batch size, output dim]
loss = criterion(output, trg)
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), clip)
optimizer.step()
epoch_loss += loss.item()
return epoch_loss / len(iterator)
def evaluate(model, iterator, criterion):
model.eval()
epoch_loss = 0
with torch.no_grad():
for i, batch in enumerate(iterator):
src = batch.src
trg = batch.trg
output = model(src, trg, 0) # turn off teacher forcing
# trg = [trg len, batch size]
# output = [trg len, batch size, output dim]
output_dim = output.shape[-1]
output = output[1:].view(-1, output_dim)
trg = trg[1:].view(-1)
# trg = [(trg len - 1) * batch size]
# output = [(trg len - 1) * batch size, output dim]
loss = criterion(output, trg)
epoch_loss += loss.item()
return epoch_loss / len(iterator)
```
### Train Loop.
Bellow is a function that tells us how long each epoch took to complete.
```
import time
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
N_EPOCHS = 10
CLIP = 1
best_valid_loss = float('inf')
for epoch in range(N_EPOCHS):
start_time = time.time()
train_loss = train(model, train_iterator, optimizer, criterion, CLIP)
valid_loss = evaluate(model, valid_iterator, criterion)
end_time = time.time()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'best-model.pt')
print(f'Epoch: {epoch+1:02} | Time: {epoch_mins}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train PPL: {math.exp(train_loss):7.3f}')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. PPL: {math.exp(valid_loss):7.3f}')
```
### Evaluating the best model.
```
model.load_state_dict(torch.load('best-model.pt'))
test_loss = evaluate(model, test_iterator, criterion)
print(f'| Test Loss: {test_loss:.3f} | Test PPL: {math.exp(test_loss):7.3f} |')
```
We've improved on the previous model, but this came at the cost of `doubling` the training time.
In the next notebook, we'll be using the same architecture but using a few tricks that are applicable to all RNN architectures - **``packed padded``** sequences and **`masking`**. We'll also implement code which will allow us to look at what words in the input the RNN is paying attention to when decoding the output.
### Credits.
* [bentrevett](https://github.com/bentrevett/pytorch-seq2seq/blob/master/3%20-%20Neural%20Machine%20Translation%20by%20Jointly%20Learning%20to%20Align%20and%20Translate.ipynb)
| true |
code
| 0.809464 | null | null | null | null |
|
# Tutorial: DESI spectral fitting with `provabgs`
```
# lets install the python package `provabgs`, a python package for generating the PRObabilistic Value-Added BGS (PROVABGS)
!pip install git+https://github.com/changhoonhahn/provabgs.git --upgrade --user
!pip install zeus-mcmc --user
import numpy as np
from provabgs import infer as Infer
from provabgs import models as Models
from provabgs import flux_calib as FluxCalib
# -- plotting --
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['font.family'] = 'serif'
mpl.rcParams['axes.linewidth'] = 1.5
mpl.rcParams['axes.xmargin'] = 1
mpl.rcParams['xtick.labelsize'] = 'x-large'
mpl.rcParams['xtick.major.size'] = 5
mpl.rcParams['xtick.major.width'] = 1.5
mpl.rcParams['ytick.labelsize'] = 'x-large'
mpl.rcParams['ytick.major.size'] = 5
mpl.rcParams['ytick.major.width'] = 1.5
mpl.rcParams['legend.frameon'] = False
# read in DESI Cascades spectra from TILE 80612
from desispec.io import read_spectra
spectra = read_spectra('/global/cfs/cdirs/desi/spectro/redux/cascades/tiles/80612/deep/coadd-0-80612-deep.fits')
igal = 10
from astropy.table import Table
zbest = Table.read('/global/cfs/cdirs/desi/spectro/redux/cascades/tiles/80612/deep/zbest-0-80612-deep.fits', hdu=1)
zred = zbest['Z'][igal]
print('z=%f' % zred)
fig = plt.figure(figsize=(10,5))
sub = fig.add_subplot(111)
sub.plot(spectra.wave['b'], spectra.flux['b'][igal])
sub.plot(spectra.wave['r'], spectra.flux['r'][igal])
sub.plot(spectra.wave['z'], spectra.flux['z'][igal])
sub.set_xlim(spectra.wave['b'].min(), spectra.wave['z'].max())
sub.set_ylim(0, 5)
# declare prior
priors = Infer.load_priors([
Infer.UniformPrior(9., 12, label='sed'),
Infer.FlatDirichletPrior(4, label='sed'),
Infer.UniformPrior(np.array([6.9e-5, 6.9e-5, 0., 0., -2.2]), np.array([7.3e-3, 7.3e-3, 3., 4., 0.4]), label='sed'),
Infer.UniformPrior(np.array([0.9, 0.9, 0.9]), np.array([1.1, 1.1, 1.1]), label='flux_calib') # flux calibration variables
])
# declare model
m_nmf = Models.NMF(burst=False, emulator=True)
# declare flux calibration
fluxcalib = FluxCalib.constant_flux_DESI_arms
desi_mcmc = Infer.desiMCMC(
model=m_nmf,
flux_calib=fluxcalib,
prior=priors
)
mcmc = desi_mcmc.run(
wave_obs=[spectra.wave['b'], spectra.wave['r'], spectra.wave['z']],
flux_obs=[spectra.flux['b'][igal], spectra.flux['r'][igal], spectra.flux['z'][igal]],
flux_ivar_obs=[spectra.ivar['b'][igal], spectra.ivar['r'][igal], spectra.ivar['z'][igal]],
zred=zred,
sampler='zeus',
nwalkers=100,
burnin=100,
opt_maxiter=10000,
niter=1000,
debug=True)
fig = plt.figure(figsize=(10,5))
sub = fig.add_subplot(111)
sub.plot(spectra.wave['b'], spectra.flux['b'][igal])
sub.plot(spectra.wave['r'], spectra.flux['r'][igal])
sub.plot(spectra.wave['z'], spectra.flux['z'][igal])
sub.plot(mcmc['wavelength_obs'], mcmc['flux_spec_model'], c='k', ls='--')
sub.set_xlim(spectra.wave['b'].min(), spectra.wave['z'].max())
sub.set_ylim(0, 5)
```
| true |
code
| 0.625066 | null | null | null | null |
|
# Human Rights Considered NLP
### **Overview**
This notebook creates a training dataset using data sourced from the [Police Brutality 2020 API](https://github.com/2020PB/police-brutality) by adding category labels for types of force and the people involved in incidents using [Snorkel](https://www.snorkel.org/) for NLP.
Build on original notebook by [Axel Corro](https://github.com/axefx) sourced from the HRD Team C DS [repository](https://github.com/Lambda-School-Labs/Labs25-Human_Rights_First-TeamC-DS/blob/main/notebooks/snorkel_hrf.ipynb).
# Imports
```
!pip install snorkel
import pandas as pd
from snorkel.labeling import labeling_function
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
import sys
from google.colab import files
# using our cleaned processed data
df = pd.read_csv('https://raw.githubusercontent.com/Lambda-School-Labs/Labs25-Human_Rights_First-TeamC-DS/main/Data/pv_incidents.csv', na_values=False)
df2 = df.filter(['text'], axis=1)
df2['text'] = df2['text'].astype(str)
```
# Use of Force Tags
### Categories of force:
- **Presence**: Police show up and their presence is enough to de-escalate. This is ideal.
- **verbalization**: Police use voice commands, force is non-physical.
- **empty-hand control soft technique**: Officers use grabs, holds and joint locks to restrain an individual. shove, chase, spit, raid, push
- **empty-hand control hard technique**: Officers use punches and kicks to restrain an individual.
- **blunt impact**: Officers may use a baton to immobilize a combative person, struck, shield, beat
- **projectiles**: Projectiles shot or launched by police at civilians. Includes "less lethal" mutnitions such as rubber bullets, bean bag rounds, water hoses, and flash grenades, as well as deadly weapons such as firearms.
- **chemical**: Officers use chemical sprays or projectiles embedded with chemicals to restrain an individual (e.g., pepper spray).
- **conducted energy devices**: Officers may use CEDs to immobilize an individual. CEDs discharge a high-voltage, low-amperage jolt of electricity at a distance.
- **miscillaneous**: LRAD (long-range audio device), sound cannon, sonic weapon
## Presence category
Police presence is enough to de-escalate. This is ideal.
```
PRESENCE = 1
NOT_PRESENCE = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_swarm(x):
return PRESENCE if 'swarm' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_show(x):
return PRESENCE if 'show' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_arrive(x):
return PRESENCE if 'arrive' in x.text.lower() else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_swarm, lf_keyword_show, lf_keyword_arrive]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["presence_label"] = label_model.predict(L=L_train, tie_break_policy="abstain")
```
## Verbalization Category
police use voice commands, force is non-physical
```
VERBAL = 1
NOT_VERBAL = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_shout(x):
return VERBAL if 'shout' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_order(x):
return VERBAL if 'order' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_loudspeaker(x):
return VERBAL if 'loudspeaker' in x.text.lower() else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_shout, lf_keyword_order,lf_keyword_loudspeaker]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["verbal_label"] = label_model.predict(L=L_train, tie_break_policy="abstain")
lf_keyword_shout, lf_keyword_order, lf_keyword_loudspeaker = (L_train != ABSTAIN).mean(axis=0)
print(f"lf_keyword_shout coverage: {lf_keyword_shout * 100:.1f}%")
print(f"lf_keyword_order coverage: {lf_keyword_order * 100:.1f}%")
print(f"lf_keyword_loudspeaker coverage: {lf_keyword_loudspeaker * 100:.1f}%")
df2[df2['verbal_label']==1]
```
## Empty-hand Control - Soft Technique
Officers use grabs, holds and joint locks to restrain an individual. shove, chase, spit, raid, push
```
EHCSOFT = 1
NOT_EHCSOFT = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_shove(x):
return EHCSOFT if 'shove' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_grabs(x):
return EHCSOFT if 'grabs' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_holds(x):
return EHCSOFT if 'holds' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_arrest(x):
return EHCSOFT if 'arrest' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_spit(x):
return EHCSOFT if 'spit' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_raid(x):
return EHCSOFT if 'raid' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_push(x):
return EHCSOFT if 'push' in x.text.lower() else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_shove, lf_keyword_grabs, lf_keyword_spit, lf_keyword_raid,
lf_keyword_push, lf_keyword_holds, lf_keyword_arrest]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["ehc-soft_technique"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['ehc-soft_technique']==1]
```
## Empty-hand Control - Hard Technique
Officers use bodily force (punches and kicks or asphyxiation) to restrain an individual.
```
EHCHARD = 1
NOT_EHCHARD = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_beat(x):
return EHCHARD if 'beat' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_tackle(x):
return EHCHARD if 'tackle' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_punch(x):
return EHCHARD if 'punch' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_assault(x):
return EHCHARD if 'assault' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_choke(x):
return EHCHARD if 'choke' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_kick(x):
return EHCHARD if 'kick' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_kneel(x):
return EHCHARD if 'kneel' in x.text.lower() else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_beat, lf_keyword_tackle, lf_keyword_choke,
lf_keyword_kick, lf_keyword_punch, lf_keyword_assault,
lf_keyword_kneel]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["ehc-hard_technique"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['ehc-hard_technique']==1]
```
## Blunt Impact Category
Officers may use tools like batons to immobilize a person.
```
BLUNT = 1
NOT_BLUNT = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_baton(x):
return BLUNT if 'baton' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_club(x):
return BLUNT if 'club' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_shield(x):
return BLUNT if 'shield' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_bike(x):
return BLUNT if 'bike' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_horse(x):
return BLUNT if 'horse' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_vehicle(x):
return BLUNT if 'vehicle' in x.text.lower() else ABSTAIN
@labeling_function()
def lf_keyword_car(x):
return BLUNT if 'car' in x.text.lower() else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_baton, lf_keyword_club, lf_keyword_horse, lf_keyword_vehicle,
lf_keyword_car, lf_keyword_shield, lf_keyword_bike]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["blunt_impact"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['blunt_impact']==1]
```
## Projectiles category
Projectiles shot or launched by police at civilians. Includes "less lethal" mutnitions such as rubber bullets, bean bag rounds, water hoses, and flash grenades, as well as deadly weapons such as firearms.
```
PROJECTILE = 1
NOT_PROJECTILE = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_pepper(x):
return PROJECTILE if 'pepper' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_rubber(x):
return PROJECTILE if 'rubber' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_bean(x):
return PROJECTILE if 'bean' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_shoot(x):
return PROJECTILE if 'shoot' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_shot(x):
return PROJECTILE if 'shot' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_fire(x):
return PROJECTILE if 'fire' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_grenade(x):
return PROJECTILE if 'grenade' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_bullet(x):
return PROJECTILE if 'bullet' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_throw(x):
return PROJECTILE if 'throw' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_discharge(x):
return PROJECTILE if 'discharge' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_projectile(x):
return PROJECTILE if 'projectile' in x.text else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_pepper, lf_keyword_rubber, lf_keyword_bean,
lf_keyword_shoot, lf_keyword_shot, lf_keyword_fire, lf_keyword_grenade,
lf_keyword_bullet, lf_keyword_throw, lf_keyword_discharge,
lf_keyword_projectile]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["projectile"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['projectile'] == 1]
```
## Chemical Agents
Police use chemical agents including pepper pray, tear gas on civilians.
```
CHEMICAL = 1
NOT_CHEMICAL = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_pepper(x):
return CHEMICAL if 'pepper' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_gas(x):
return CHEMICAL if 'gas' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_smoke(x):
return CHEMICAL if 'smoke' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_mace(x):
return CHEMICAL if 'mace' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_spray(x):
return CHEMICAL if 'spray' in x.text else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_pepper, lf_keyword_gas, lf_keyword_smoke,
lf_keyword_spray, lf_keyword_mace]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["chemical"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['chemical']==1]
```
## Conducted energy devices
Officers may use CEDs to immobilize an individual. CEDs discharge a high-voltage, low-amperage jolt of electricity at a distance. Most commonly tasers.
```
CED = 1
NOT_CED = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_taser(x):
return CED if 'taser' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_stun(x):
return CED if 'stun' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_stungun(x):
return CED if 'stungun' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_taze(x):
return CED if 'taze' in x.text else ABSTAIN
from snorkel.labeling.model import LabelModel
from snorkel.labeling import PandasLFApplier
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_taser, lf_keyword_stun, lf_keyword_stungun, lf_keyword_taze]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2["ced_category"] = label_model.predict(L=L_train, tie_break_policy="abstain")
df2[df2['ced_category']==1]
```
# Add force tags to dataframe
```
df2.columns
def add_force_labels(row):
tags = []
if row['presence_label'] == 1:
tags.append('Presence')
if row['verbal_label'] == 1:
tags.append('Verbalization')
if row['ehc-soft_technique'] == 1:
tags.append('EHC Soft Technique')
if row['ehc-hard_technique'] == 1:
tags.append('EHC Hard Technique')
if row['blunt_impact'] == 1:
tags.append('Blunt Impact')
if row['projectile'] == 1 or row['projectile'] == 0:
tags.append('Projectiles')
if row['chemical'] == 1:
tags.append('Chemical')
if row['ced_category'] == 1:
tags.append('Conductive Energy')
if not tags:
tags.append('Other/Unknown')
return tags
# apply force tags to incident data
df2['force_tags'] = df2.apply(add_force_labels,axis=1)
# take a peek
df2[['text','force_tags']].head(3)
# clean the tags column by seperating tags
def join_tags(content):
return ', '.join(content)
# add column to main df
df['force_tags'] = df2['force_tags'].apply(join_tags)
df['force_tags'].value_counts()
```
# Human Categories
### Police Categories:
police, officer, deputy, PD, cop
federal, agent
```
POLICE = 1
NOT_POLICE = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_police(x):
return POLICE if 'police' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_officer(x):
return POLICE if 'officer' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_deputy(x):
return POLICE if 'deputy' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_pd(x):
return POLICE if 'PD' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_cop(x):
return POLICE if 'cop' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_enforcement(x):
return POLICE if 'enforcement' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_leo(x):
return POLICE if 'LEO' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_swat(x):
return POLICE if 'SWAT' in x.text else ABSTAIN
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_police, lf_keyword_officer, lf_keyword_deputy, lf_keyword_pd,
lf_keyword_cop, lf_keyword_enforcement, lf_keyword_swat, lf_keyword_leo]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2['police_label'] = label_model.predict(L=L_train, tie_break_policy='abstain')
df2[df2['police_label']==1]
```
### Federal Agent Category
```
FEDERAL = 1
NOT_FEDERAL = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_federal(x):
return FEDERAL if 'federal' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_feds(x):
return FEDERAL if 'feds' in x.text else ABSTAIN
# national guard
@labeling_function()
def lf_keyword_guard(x):
return FEDERAL if 'guard' in x.text else ABSTAIN
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_federal, lf_keyword_feds, lf_keyword_guard]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2['federal_label'] = label_model.predict(L=L_train, tie_break_policy='abstain')
df2[df2['federal_label']==1]
```
### Civilian Categories:
protesters, medic,
reporter, journalist,
minor, child
```
PROTESTER = 1
NOT_PROTESTER = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_protester(x):
return PROTESTER if 'protester' in x.text else ABSTAIN
# adding the mispelling 'protestor'
@labeling_function()
def lf_keyword_protestor(x):
return PROTESTER if 'protestor' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_medic(x):
return PROTESTER if 'medic' in x.text else ABSTAIN
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_protester, lf_keyword_protestor, lf_keyword_medic]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2['protester_label'] = label_model.predict(L=L_train, tie_break_policy='abstain')
df2[df2['protester_label']==1]
```
Press
```
PRESS = 1
NOT_PRESS = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_reporter(x):
return PRESS if 'reporter' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_press(x):
return PRESS if 'press' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_journalist(x):
return PRESS if 'journalist' in x.text else ABSTAIN
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_reporter, lf_keyword_press, lf_keyword_journalist]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2['press_label'] = label_model.predict(L=L_train, tie_break_policy='abstain')
df2[df2['press_label']==1]
```
Minors
```
MINOR = 1
NOT_MINOR = 0
ABSTAIN = -1
@labeling_function()
def lf_keyword_minor(x):
return MINOR if 'minor' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_underage(x):
return MINOR if 'underage' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_teen(x):
return MINOR if 'teen' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_child(x):
return MINOR if 'child' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_baby(x):
return MINOR if 'baby' in x.text else ABSTAIN
@labeling_function()
def lf_keyword_toddler(x):
return MINOR if 'toddler' in x.text else ABSTAIN
# Define the set of labeling functions (LFs)
lfs = [lf_keyword_minor, lf_keyword_child, lf_keyword_baby,
lf_keyword_underage, lf_keyword_teen, lf_keyword_toddler]
# Apply the LFs to the unlabeled training data
applier = PandasLFApplier(lfs)
L_train = applier.apply(df2)
# Train the label model and compute the training labels
label_model = LabelModel(cardinality=2, verbose=True)
label_model.fit(L_train, n_epochs=500, log_freq=50, seed=123)
df2['minor_label'] = label_model.predict(L=L_train, tie_break_policy='abstain')
df2[df2['minor_label']==1]
```
# Add human tags to Dataframe
```
df2.columns
def add_human_labels(row):
tags = []
if row['police_label'] == 1 or row['police_label'] == 0:
tags.append('Police')
if row['federal_label'] == 1:
tags.append('Federal')
if row['protester_label'] == 1:
tags.append('Protester')
if row['press_label'] == 1:
tags.append('Press')
if row['minor_label'] == 1:
tags.append('Minor')
if not tags:
tags.append('Other/Unknown')
return tags
# apply human tags to incident data
df2['human_tags'] = df2.apply(add_human_labels,axis=1)
# take a peek
df2[['text','force_tags', 'human_tags']].head(3)
# clean the tags column by seperating tags
def join_tags(content):
return ', '.join(content)
# add column to main df
df['human_tags'] = df2['human_tags'].apply(join_tags)
df['human_tags'].value_counts()
# last check
df = df.drop('date_text', axis=1)
df = df.drop('Unnamed: 0', axis=1)
df = df.drop_duplicates(subset=['id'], keep='last')
df.head(3)
print(df.shape)
# exporting the dataframe
df.to_csv('training_data.csv')
files.download('training_data.csv')
```
| true |
code
| 0.553204 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/patrickcgray/deep_learning_ecology/blob/master/basic_cnn_minst.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Training a Convolutional Neural Network on the MINST dataset.
### import all necessary python modules
```
'''Trains a simple convnet on the MNIST dataset.
Gets to 99.25% test accuracy after 12 epochs
(there is still a lot of margin for parameter tuning).
16 seconds per epoch on a GRID K520 GPU.
'''
from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
import tensorflow as tf
tf.compat.v1.disable_eager_execution()
import numpy as np # linear algebra
import os
import matplotlib.pyplot as plt
%matplotlib inline
```
### set hyperparameters and get training and testing data formatted
```
batch_size = 128
num_classes = 10
epochs = 12
# input image dimensions
img_rows, img_cols = 28, 28
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
```
### build the model and take a look at the model summary
```
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
```
### compile and train/fit the model
```
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
```
### evaluate the model on the testing dataset
```
score = model.evaluate(x_test, y_test, verbose=1)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
### compare predictions to the input data
```
w=10
h=10
fig=plt.figure(figsize=(8, 8))
columns = 9
rows = 1
indices = np.random.randint(len(x_test), size=(10))
labels = np.argmax(model.predict(x_test[indices]), axis=1)
for i in range(1, columns*rows+1):
fig.add_subplot(rows, columns, i)
plt.imshow(x_test[indices[i-1]].reshape((28, 28)), cmap = 'gray')
plt.axis('off')
plt.text(15,45, labels[i-1], horizontalalignment='center', verticalalignment='center')
plt.show()
```
### code that will allow us to visualize the convolutional filters
```
layer_dict = dict([(layer.name, layer) for layer in model.layers])
# util function to convert a tensor into a valid image
def deprocess_image(x):
# normalize tensor: center on 0., ensure std is 0.1
x -= x.mean()
x /= (x.std() + 1e-5)
x *= 0.1
# clip to [0, 1]
x += 0.5
x = np.clip(x, 0, 1)
# convert to RGB array
x *= 255
#x = x.transpose((1, 2, 0))
x = np.clip(x, 0, 255).astype('uint8')
return x
def vis_img_in_filter(img = np.array(x_train[0]).reshape((1, 28, 28, 1)).astype(np.float64),
layer_name = 'conv2d_2'):
layer_output = layer_dict[layer_name].output
img_ascs = list()
for filter_index in range(layer_output.shape[3]):
# build a loss function that maximizes the activation
# of the nth filter of the layer considered
loss = K.mean(layer_output[:, :, :, filter_index])
# compute the gradient of the input picture wrt this loss
grads = K.gradients(loss, model.input)[0]
# normalization trick: we normalize the gradient
grads /= (K.sqrt(K.mean(K.square(grads))) + 1e-5)
# this function returns the loss and grads given the input picture
iterate = K.function([model.input], [loss, grads])
# step size for gradient ascent
step = 5.
img_asc = np.array(img)
# run gradient ascent for 20 steps
for i in range(20):
loss_value, grads_value = iterate([img_asc])
img_asc += grads_value * step
img_asc = img_asc[0]
img_ascs.append(deprocess_image(img_asc).reshape((28, 28)))
if layer_output.shape[3] >= 35:
plot_x, plot_y = 6, 6
elif layer_output.shape[3] >= 23:
plot_x, plot_y = 4, 6
elif layer_output.shape[3] >= 11:
plot_x, plot_y = 2, 6
else:
plot_x, plot_y = 1, 2
fig, ax = plt.subplots(plot_x, plot_y, figsize = (12, 12))
ax[0, 0].imshow(img.reshape((28, 28)), cmap = 'gray')
ax[0, 0].set_title('Input image')
fig.suptitle('Input image and %s filters' % (layer_name,))
fig.tight_layout(pad = 0.3, rect = [0, 0, 0.9, 0.9])
for (x, y) in [(i, j) for i in range(plot_x) for j in range(plot_y)]:
if x == 0 and y == 0:
continue
ax[x, y].imshow(img_ascs[x * plot_y + y - 1], cmap = 'gray')
ax[x, y].set_title('filter %d' % (x * plot_y + y - 1))
ax[x, y].set_axis_off()
#plt.axis('off')
```
### convolutional filters for the first element in the training dataset for the first convolutional layer
```
vis_img_in_filter(img = np.array(x_train[0]).reshape((1, 28, 28, 1)).astype(np.float64), layer_name = 'conv2d')
```
### convolutional filters for the first element in the training dataset for the second convolutional layer
```
vis_img_in_filter(img = np.array(x_train[0]).reshape((1, 28, 28, 1)).astype(np.float64), layer_name = 'conv2d_1')
```
| true |
code
| 0.840946 | null | null | null | null |
|
# Vectors, Matrices, and Arrays
# Loading Data
## Loading a Sample Dataset
```
# Load scikit-learn's datasets
from sklearn import datasets
# Load digit dataset
digits = datasets.load_digits()
# Create features matrix
features = digits.data
# Create target matrix
target = digits.target
# View first observation
print(features[0])
```
## Creating a Simulated Dataset
```
# For Regression
# Load library
from sklearn.datasets import make_regression
# Generate features matrix, target vector, and the true coefficients
features, target, coefficients = make_regression(n_samples = 100,
n_features = 3,
n_informative = 3,
n_targets = 1,
noise = 0.0,
coef = True,
random_state = 1)
# View feature matrix and target vector
print("Feature Matrix\n",features[:3])
print("Target Vector\n",target[:3])
# For Classification
# Load library
from sklearn.datasets import make_classification
# Generate features matrix, target vector, and the true coefficients
features, target = make_classification(n_samples = 100,
n_features = 3,
n_informative = 3,
n_redundant = 0,
n_classes = 2,
weights = [.25, .75],
random_state = 1)
# View feature matrix and target vector
print("Feature Matrix\n",features[:3])
print("Target Vector\n",target[:3])
# For Clustering
# Load library
from sklearn.datasets import make_blobs
# Generate features matrix, target vector, and the true coefficients
features, target = make_blobs(n_samples = 100,
n_features = 2,
centers = 3,
cluster_std = 0.5,
shuffle = True,
random_state = 1)
# View feature matrix and target vector
print("Feature Matrix\n",features[:3])
print("Target Vector\n",target[:3])
# Load library
import matplotlib.pyplot as plt
%matplotlib inline
# View scatterplot
plt.scatter(features[:,0], features[:,1], c=target)
plt.show()
```
## Loading a CSV File
```
# Load a library
import pandas as pd
# Create URL
url = 'https://people.sc.fsu.edu/~jburkardt/data/csv/airtravel.csv'
# Load dataset
dataframe = pd.read_csv(url)
# View first two rows
dataframe.head(2)
```
## Loading an Excel File
```
# Load a library
import pandas as pd
# Create URL
url = 'https://dornsife.usc.edu/assets/sites/298/docs/ir211wk12sample.xls'
# Load dataset
dataframe = pd.read_excel(url, sheet_name=0, header=1)
# View first two rows
dataframe.head(2)
```
## Loading a JSON File
```
# Load a library
import pandas as pd
# Create URL
url = 'http://ergast.com/api/f1/2004/1/results.json'
# Load dataset
dataframe = pd.read_json(url, orient = 'columns')
# View first two rows
dataframe.head(2)
# semistructured JSON to a pandas DataFrame
#pd.json_normalize
```
## Queryin a SQL Database
```
# Load a library
import pandas as pd
from sqlalchemy import create_engine
# Create a connection to the database
database_connection = create_engine('sqlite://sample.db')
# Load dataset
dataframe = pd.read_sql_query('SELECT * FROM data', database_connectiona)
# View first two rows
dataframe.head(2)
```
| true |
code
| 0.642657 | null | null | null | null |
|

## Welcome to The QuantConnect Research Page
#### Refer to this page for documentation https://www.quantconnect.com/docs#Introduction-to-Jupyter
#### Contribute to this template file https://github.com/QuantConnect/Lean/blob/master/Jupyter/BasicQuantBookTemplate.ipynb
## QuantBook Basics
### Start QuantBook
- Add the references and imports
- Create a QuantBook instance
```
%matplotlib inline
# Imports
from clr import AddReference
AddReference("System")
AddReference("QuantConnect.Common")
AddReference("QuantConnect.Jupyter")
AddReference("QuantConnect.Indicators")
from System import *
from QuantConnect import *
from QuantConnect.Data.Market import TradeBar, QuoteBar
from QuantConnect.Jupyter import *
from QuantConnect.Indicators import *
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
import pandas as pd
# Create an instance
qb = QuantBook()
```
### Selecting Asset Data
Checkout the QuantConnect [docs](https://www.quantconnect.com/docs#Initializing-Algorithms-Selecting-Asset-Data) to learn how to select asset data.
```
spy = qb.AddEquity("SPY")
eur = qb.AddForex("EURUSD")
```
### Historical Data Requests
We can use the QuantConnect API to make Historical Data Requests. The data will be presented as multi-index pandas.DataFrame where the first index is the Symbol.
For more information, please follow the [link](https://www.quantconnect.com/docs#Historical-Data-Historical-Data-Requests).
```
# Gets historical data from the subscribed assets, the last 360 datapoints with daily resolution
h1 = qb.History(360, Resolution.Daily)
# Plot closing prices from "SPY"
h1.loc["SPY"]["close"].plot()
# Gets historical data from the subscribed assets, from the last 30 days with daily resolution
h2 = qb.History(timedelta(30), Resolution.Daily)
# Plot high prices from "EURUSD"
h2.loc["EURUSD"]["high"].plot()
# Gets historical data from the subscribed assets, between two dates with daily resolution
h3 = qb.History(spy.Symbol, datetime(2014,1,1), datetime.now(), Resolution.Daily)
# Only fetchs historical data from a desired symbol
h4 = qb.History(spy.Symbol, 360, Resolution.Daily)
# or qb.History("SPY", 360, Resolution.Daily)
# Only fetchs historical data from a desired symbol
# When we are not dealing with equity, we must use the generic method
h5 = qb.History[QuoteBar](eur.Symbol, timedelta(30), Resolution.Daily)
# or qb.History[QuoteBar]("EURUSD", timedelta(30), Resolution.Daily)
```
### Historical Options Data Requests
- Select the option data
- Sets the filter, otherwise the default will be used SetFilter(-1, 1, timedelta(0), timedelta(35))
- Get the OptionHistory, an object that has information about the historical options data
```
goog = qb.AddOption("GOOG")
goog.SetFilter(-2, 2, timedelta(0), timedelta(180))
option_history = qb.GetOptionHistory(goog.Symbol, datetime(2017, 1, 4))
print option_history.GetStrikes()
print option_history.GetExpiryDates()
h6 = option_history.GetAllData()
```
### Get Fundamental Data
- *GetFundamental([symbol], selector, start_date = datetime(1998,1,1), end_date = datetime.now())*
We will get a pandas.DataFrame with fundamental data.
```
data = qb.GetFundamental(["AAPL","AIG","BAC","GOOG","IBM"], "ValuationRatios.PERatio")
data
```
### Indicators
We can easily get the indicator of a given symbol with QuantBook.
For all indicators, please checkout QuantConnect Indicators [Reference Table](https://www.quantconnect.com/docs#Indicators-Reference-Table)
```
# Example with BB, it is a datapoint indicator
# Define the indicator
bb = BollingerBands(30, 2)
# Gets historical data of indicator
bbdf = qb.Indicator(bb, "SPY", 360, Resolution.Daily)
# drop undesired fields
bbdf = bbdf.drop('standarddeviation', 1)
# Plot
bbdf.plot()
# For EURUSD
bbdf = qb.Indicator(bb, "EURUSD", 360, Resolution.Daily)
bbdf = bbdf.drop('standarddeviation', 1)
bbdf.plot()
# Example with ADX, it is a bar indicator
adx = AverageDirectionalIndex("adx", 14)
adxdf = qb.Indicator(adx, "SPY", 360, Resolution.Daily)
adxdf.plot()
# For EURUSD
adxdf = qb.Indicator(adx, "EURUSD", 360, Resolution.Daily)
adxdf.plot()
# SMA cross:
symbol = "EURUSD"
# Get History
hist = qb.History[QuoteBar](symbol, 500, Resolution.Daily)
# Get the fast moving average
fast = qb.Indicator(SimpleMovingAverage(50), symbol, 500, Resolution.Daily)
# Get the fast moving average
slow = qb.Indicator(SimpleMovingAverage(200), symbol, 500, Resolution.Daily)
# Remove undesired columns and rename others
fast = fast.drop('rollingsum', 1).rename(columns={'simplemovingaverage': 'fast'})
slow = slow.drop('rollingsum', 1).rename(columns={'simplemovingaverage': 'slow'})
# Concatenate the information and plot
df = pd.concat([hist.loc[symbol]["close"], fast, slow], axis=1).dropna(axis=0)
df.plot()
# Get indicator defining a lookback period in terms of timedelta
ema1 = qb.Indicator(ExponentialMovingAverage(50), "SPY", timedelta(100), Resolution.Daily)
# Get indicator defining a start and end date
ema2 = qb.Indicator(ExponentialMovingAverage(50), "SPY", datetime(2016,1,1), datetime(2016,10,1), Resolution.Daily)
ema = pd.concat([ema1, ema2], axis=1)
ema.plot()
rsi = RelativeStrengthIndex(14)
# Selects which field we want to use in our indicator (default is Field.Close)
rsihi = qb.Indicator(rsi, "SPY", 360, Resolution.Daily, Field.High)
rsilo = qb.Indicator(rsi, "SPY", 360, Resolution.Daily, Field.Low)
rsihi = rsihi.rename(columns={'relativestrengthindex': 'high'})
rsilo = rsilo.rename(columns={'relativestrengthindex': 'low'})
rsi = pd.concat([rsihi['high'], rsilo['low']], axis=1)
rsi.plot()
```
| true |
code
| 0.602354 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/GuysBarash/ML_Workshop/blob/main/Bayesian_Agent.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
from scipy.optimize import minimize_scalar
from scipy.stats import beta
from scipy.stats import binom
from scipy.stats import bernoulli
from matplotlib import animation
from IPython.display import HTML, clear_output
from matplotlib import rc
matplotlib.use('Agg')
agent_truth_p = 0.8 #@param {type: "slider", min: 0.0, max: 1.0, step:0.01}
repeats = 700
starting_guess_for_b = 1 # Agent's correct answers
starting_guess_for_a = 1 # Agent's incorrect answers
```
# Example
```
def plotPrior(a, b):
fig = plt.figure()
ax = plt.axes()
plt.xlim(0, 1)
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, a, b)
x_guess = x[y.argmax()]
ax.plot(x, y);
maximal_point = ax.axvline(x=x_guess, label=f'Best guess for prior: {x_guess:>.2f}');
ax.legend();
return
```
The agent has a chance of "p" of telling the truth, and a chance of 1-p of randomly selecting an answer
```
def agentDecision(real_answer,options,agent_truth_p):
choice = bernoulli.rvs(agent_truth_p)
if choice == 1:
return real_answer
else:
choice = bernoulli.rvs(0.5)
if choice == 1:
return options[0]
else:
return options[1]
b = starting_guess_for_b
a = starting_guess_for_a
```
Prior before any testing takes place. You can see it's balanced.
```
print("p = ", a / (a + b))
plotPrior(a, b)
agent_log = pd.DataFrame(index=range(repeats),columns=['a','b','Real type','Agent answer','Agent is correct'])
data_validity_types = ["BAD","GOOD"]
for i in range(repeats):
data_is_valid = np.random.choice(data_validity_types)
agent_response_on_the_data = agentDecision(data_is_valid,data_validity_types,agent_truth_p)
agent_is_correct = data_is_valid == agent_response_on_the_data
agent_log.loc[i,['Real type','Agent answer','Agent is correct']] = data_is_valid, agent_response_on_the_data, agent_is_correct
# a and b update dynamically each step
a += int(agent_is_correct)
b += int(not agent_is_correct)
agent_log.loc[i,['a','b']] = a, b
correct_answers = agent_log['Agent is correct'].sum()
total_answers = agent_log['Agent is correct'].count()
percentage = 0
if total_answers > 0:
percentage = float(correct_answers) / total_answers
print(f"Agent was right {correct_answers}/{total_answers} ({100 * percentage:>.2f} %) of the times.")
plotPrior(a, b)
```
# Dynamic example
```
# create a figure and axes
fig = plt.figure(figsize=(12,5));
ax = plt.subplot(1,1,1);
# set up the subplots as needed
ax.set_xlim(( 0, 1));
ax.set_ylim((0, 10));
# create objects that will change in the animation. These are
# initially empty, and will be given new values for each frame
# in the animation.
txt_title = ax.set_title('');
maximal_point = ax.axvline(x=0, label='line at x = {}'.format(0));
line1, = ax.plot([], [], 'b', lw=2); # ax.plot returns a list of 2D line objects
clear_output()
plt.close('all')
def getPriorFrame(frame_n):
global agent_log
a = agent_log.loc[frame_n,'a']
b = agent_log.loc[frame_n,'b']
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, a, b)
x_guess = x[y.argmax()]
ax.legend()
maximal_point.set_xdata(x_guess)
maximal_point.set_label(f'Best guess for prior: {x_guess:>.2f}')
line1.set_data(x, y)
txt_title.set_text(f'Agent step = {frame_n:4d}, a = {a}, b= {b}')
return line1,
num_of_steps = 50
frames =[0]+ list(range(0, len(agent_log), int(len(agent_log) / num_of_steps))) + [agent_log.index[-1]]
ani = animation.FuncAnimation(fig, getPriorFrame, frames,
interval=100, blit=True)
rc('animation', html='html5')
ani
```
| true |
code
| 0.535098 | null | null | null | null |
|
```
%matplotlib inline
import pymc3 as pm
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
plt.style.use(['seaborn-colorblind', 'seaborn-darkgrid'])
```
#### Code 2.1
```
ways = np.array([0, 3, 8, 9, 0])
ways / ways.sum()
```
#### Code 2.2
$$Pr(w \mid n, p) = \frac{n!}{w!(n − w)!} p^w (1 − p)^{n−w}$$
The probability of observing six W’s in nine tosses—under a value of p=0.5
```
stats.binom.pmf(6, n=9, p=0.5)
```
#### Code 2.3 and 2.5
Computing the posterior using a grid approximation.
In the book the following code is not inside a function, but this way is easier to play with different parameters
```
def posterior_grid_approx(grid_points=5, success=6, tosses=9):
"""
"""
# define grid
p_grid = np.linspace(0, 1, grid_points)
# define prior
prior = np.repeat(5, grid_points) # uniform
#prior = (p_grid >= 0.5).astype(int) # truncated
#prior = np.exp(- 5 * abs(p_grid - 0.5)) # double exp
# compute likelihood at each point in the grid
likelihood = stats.binom.pmf(success, tosses, p_grid)
# compute product of likelihood and prior
unstd_posterior = likelihood * prior
# standardize the posterior, so it sums to 1
posterior = unstd_posterior / unstd_posterior.sum()
return p_grid, posterior
```
#### Code 2.3
```
points = 20
w, n = 6, 9
p_grid, posterior = posterior_grid_approx(points, w, n)
plt.plot(p_grid, posterior, 'o-', label='success = {}\ntosses = {}'.format(w, n))
plt.xlabel('probability of water', fontsize=14)
plt.ylabel('posterior probability', fontsize=14)
plt.title('{} points'.format(points))
plt.legend(loc=0);
```
#### Code 2.6
Computing the posterior using the quadratic aproximation
```
data = np.repeat((0, 1), (3, 6))
with pm.Model() as normal_aproximation:
p = pm.Uniform('p', 0, 1)
w = pm.Binomial('w', n=len(data), p=p, observed=data.sum())
mean_q = pm.find_MAP()
std_q = ((1/pm.find_hessian(mean_q, vars=[p]))**0.5)[0]
mean_q['p'], std_q
norm = stats.norm(mean_q, std_q)
prob = .89
z = stats.norm.ppf([(1-prob)/2, (1+prob)/2])
pi = mean_q['p'] + std_q * z
pi
```
#### Code 2.7
```
# analytical calculation
w, n = 6, 9
x = np.linspace(0, 1, 100)
plt.plot(x, stats.beta.pdf(x , w+1, n-w+1),
label='True posterior')
# quadratic approximation
plt.plot(x, stats.norm.pdf(x, mean_q['p'], std_q),
label='Quadratic approximation')
plt.legend(loc=0, fontsize=13)
plt.title('n = {}'.format(n), fontsize=14)
plt.xlabel('Proportion water', fontsize=14)
plt.ylabel('Density', fontsize=14);
import sys, IPython, scipy, matplotlib, platform
print("This notebook was createad on a computer %s running %s and using:\nPython %s\nIPython %s\nPyMC3 %s\nNumPy %s\nSciPy %s\nMatplotlib %s\n" % (platform.machine(), ' '.join(platform.linux_distribution()[:2]), sys.version[:5], IPython.__version__, pm.__version__, np.__version__, scipy.__version__, matplotlib.__version__))
```
| true |
code
| 0.735419 | null | null | null | null |
|
# Rolling Window Features
Following notebook showcases an example workflow of creating rolling window features and building a model to predict which customers will buy in next 4 weeks.
This uses dummy sales data but the idea can be implemented on actual sales data and can also be expanded to include other available data sources such as click-stream data, call center data, email contacts data, etc.
***
<b>Spark 3.1.2</b> (with Python 3.8) has been used for this notebook.<br>
Refer to [spark documentation](https://spark.apache.org/docs/3.1.2/api/sql/index.html) for help with <b>data ops functions</b>.<br>
Refer to [this article](https://medium.com/analytics-vidhya/installing-and-using-pyspark-on-windows-machine-59c2d64af76e) to <b>install and use PySpark on Windows machine</b>.
### Building a spark session
To create a SparkSession, use the following builder pattern:
`spark = SparkSession\
.builder\
.master("local")\
.appName("Word Count")\
.config("spark.some.config.option", "some-value")\
.getOrCreate()`
```
from pyspark.sql import SparkSession
from pyspark.sql import functions as F
from pyspark.sql import Window
from pyspark.sql.types import FloatType
#initiating spark session
spark.stop()
spark = SparkSession\
.builder\
.appName("rolling_window")\
.config("spark.executor.memory", "1536m")\
.config("spark.driver.memory", "2g")\
.getOrCreate()
spark
```
## Data prep
We will be using window functions to compute relative features for all dates. We will first aggregate the data to customer x week level so it is easier to handle.
<mark>The week level date that we create will serve as the 'reference date' from which everything will be relative.</mark>
All the required dimension tables have to be joined with the sales table prior to aggregation so that we can create all required features.
### Read input datasets
```
import pandas as pd
df_sales = spark.read.csv('./data/rw_sales.csv',inferSchema=True,header=True)
df_customer = spark.read.csv('./data/clustering_customer.csv',inferSchema=True,header=True)
df_product = spark.read.csv('./data/clustering_product.csv',inferSchema=True,header=True)
df_payment = spark.read.csv('./data/clustering_payment.csv',inferSchema=True,header=True)
```
<b>Quick exploration of the datasets:</b>
1. We have sales data that captures date, customer id, product, quantity, dollar amount & payment type at order x item level. `order_item_id` refers to each unique product in each order
2. We have corresponding dimension tables for customer info, product info, and payment tender info
```
df_sales.show(5)
# order_item_id is the primary key
(df_sales.count(),
df_sales.selectExpr('count(Distinct order_item_id)').collect()[0][0],
df_sales.selectExpr('count(Distinct order_id)').collect()[0][0])
df_sales.printSchema()
# fix date type for tran_dt
df_sales = df_sales.withColumn('tran_dt', F.to_date('tran_dt'))
df_customer.show(5)
# we have 1k unique customers in sales data with all their info in customer dimension table
(df_sales.selectExpr('count(Distinct customer_id)').collect()[0][0],
df_customer.count(),
df_customer.selectExpr('count(Distinct customer_id)').collect()[0][0])
# product dimension table provides category and price for each product
df_product.show(5)
(df_product.count(),
df_product.selectExpr('count(Distinct product_id)').collect()[0][0])
# payment type table maps the payment type id from sales table
df_payment.show(5)
```
### Join all dim tables and add week_end column
```
df_sales = df_sales.join(df_product.select('product_id','category'), on=['product_id'], how='left')
df_sales = df_sales.join(df_payment, on=['payment_type_id'], how='left')
```
<b>week_end column: Saturday of every week</b>
`dayofweek()` returns 1-7 corresponding to Sun-Sat for a date.
Using this, we will convert each date to the date corresponding to the Saturday of that week (week: Sun-Sat) using below logic:<br/>
`date + 7 - dayofweek()`
```
df_sales.printSchema()
df_sales = df_sales.withColumn('week_end',
F.col('tran_dt') + 7 - F.dayofweek('tran_dt'))
df_sales.show(5)
```
### customer_id x week_end aggregation
We will be creating following features at weekly level. These will then be aggregated for multiple time frames using window functions for the final dataset.
1. Sales
2. No. of orders
3. No. of units
4. Sales split by category
5. Sales split by payment type
```
df_sales_agg = df_sales.groupBy('customer_id','week_end').agg(
F.sum('dollars').alias('sales'),
F.countDistinct('order_id').alias('orders'),
F.sum('qty').alias('units'))
# category split pivot
df_sales_cat_agg = df_sales.withColumn('category', F.concat(F.lit('cat_'), F.col('category')))
df_sales_cat_agg = df_sales_cat_agg.groupBy('customer_id','week_end').pivot('category').agg(F.sum('dollars'))
# payment type split pivot
# clean-up values in payment type column
df_payment_agg = df_sales.withColumn(
'payment_type',
F.concat(F.lit('pay_'), F.regexp_replace(F.col('payment_type'),' ','_')))
df_payment_agg = df_payment_agg.groupby('customer_id','week_end').pivot('payment_type').agg(F.max('dollars'))
# join all together
df_sales_agg = df_sales_agg.join(df_sales_cat_agg, on=['customer_id','week_end'], how='left')
df_sales_agg = df_sales_agg.join(df_payment_agg, on=['customer_id','week_end'], how='left')
df_sales_agg = df_sales_agg.persist()
df_sales_agg.count()
df_sales_agg.show(5)
```
### Fill Missing weeks
```
# cust level min and max weeks
df_cust = df_sales_agg.groupBy('customer_id').agg(
F.min('week_end').alias('min_week'),
F.max('week_end').alias('max_week'))
# function to get a dataframe with 1 row per date in provided range
def pandas_date_range(start, end):
dt_rng = pd.date_range(start=start, end=end, freq='W-SAT') # W-SAT required as we want all Saturdays
df_date = pd.DataFrame(dt_rng, columns=['date'])
return df_date
# use the cust level table and create a df with all Saturdays in our range
date_list = df_cust.selectExpr('min(min_week)', 'max(max_week)').collect()[0]
min_date = date_list[0]
max_date = date_list[1]
# use the function and create df
df_date_range = spark.createDataFrame(pandas_date_range(min_date, max_date))
# date format
df_date_range = df_date_range.withColumn('date',F.to_date('date'))
df_date_range = df_date_range.repartition(1).persist()
df_date_range.count()
```
<b>Cross join date list df with cust table to create filled base table</b>
```
df_base = df_cust.crossJoin(F.broadcast(df_date_range))
# filter to keep only week_end since first week per customer
df_base = df_base.where(F.col('date')>=F.col('min_week'))
# rename date to week_end
df_base = df_base.withColumnRenamed('date','week_end')
```
<b>Join with the aggregated week level table to create full base table</b>
```
df_base = df_base.join(df_sales_agg, on=['customer_id','week_end'], how='left')
df_base = df_base.fillna(0)
df_base = df_base.persist()
df_base.count()
# write base table as parquet
df_base.repartition(8).write.parquet('./data/rw_base/', mode='overwrite')
df_base = spark.read.parquet('./data/rw_base/')
```
## y-variable
Determining whether a customer buys something in the next 4 weeks of current week.
```
# flag 1/0 for weeks with purchases
df_base = df_base.withColumn('purchase_flag', F.when(F.col('sales')>0,1).otherwise(0))
# window to aggregate the flag over next 4 weeks
df_base = df_base.withColumn(
'purchase_flag_next_4w',
F.max('purchase_flag').over(
Window.partitionBy('customer_id').orderBy('week_end').rowsBetween(1,4)))
```
## Features
We will be aggregating the features columns over various time intervals (1/4/13/26/52 weeks) to create a rich set of look-back features. We will also create derived features post aggregation.
```
# we can create and keep Window() objects that can be referenced in multiple formulas
# we don't need a window definition for 1w features as these are already present
window_4w = Window.partitionBy('customer_id').orderBy('week_end').rowsBetween(-3,Window.currentRow)
window_13w = Window.partitionBy('customer_id').orderBy('week_end').rowsBetween(-12,Window.currentRow)
window_26w = Window.partitionBy('customer_id').orderBy('week_end').rowsBetween(-25,Window.currentRow)
window_52w = Window.partitionBy('customer_id').orderBy('week_end').rowsBetween(-51,Window.currentRow)
df_base.columns
```
<b>Direct features</b>
```
cols_skip = ['customer_id','week_end','min_week','max_week','purchase_flag_next_4w']
for cols in df_base.drop(*cols_skip).columns:
df_base = df_base.withColumn(cols+'_4w', F.sum(F.col(cols)).over(window_4w))
df_base = df_base.withColumn(cols+'_13w', F.sum(F.col(cols)).over(window_13w))
df_base = df_base.withColumn(cols+'_26w', F.sum(F.col(cols)).over(window_26w))
df_base = df_base.withColumn(cols+'_52w', F.sum(F.col(cols)).over(window_52w))
```
<b>Derived features</b>
```
# aov, aur, upt at each time cut
for cols in ['sales','orders','units']:
for time_cuts in ['1w','_4w','_13w','_26w','_52w']:
if time_cuts=='1w': time_cuts=''
df_base = df_base.withColumn('aov'+time_cuts, F.col('sales'+time_cuts)/F.col('orders'+time_cuts))
df_base = df_base.withColumn('aur'+time_cuts, F.col('sales'+time_cuts)/F.col('units'+time_cuts))
df_base = df_base.withColumn('upt'+time_cuts, F.col('units'+time_cuts)/F.col('orders'+time_cuts))
# % split of category and payment type for 26w (can be extended to other time-frames as well)
for cat in ['A','B','C','D','E']:
df_base = df_base.withColumn('cat_'+cat+'_26w_perc', F.col('cat_'+cat+'_26w')/F.col('sales_26w'))
for pay in ['cash', 'credit_card', 'debit_card', 'gift_card', 'others']:
df_base = df_base.withColumn('pay_'+pay+'_26w_perc', F.col('pay_'+pay+'_26w')/F.col('sales_26w'))
# all columns
df_base.columns
```
<b>Derived features: trend vars</b>
```
# we will take ratio of sales for different time-frames to estimate trend features
# that depict whether a customer has an increasing trend or not
df_base = df_base.withColumn('sales_1w_over_4w', F.col('sales')/ F.col('sales_4w'))
df_base = df_base.withColumn('sales_4w_over_13w', F.col('sales_4w')/ F.col('sales_13w'))
df_base = df_base.withColumn('sales_13w_over_26w', F.col('sales_13w')/F.col('sales_26w'))
df_base = df_base.withColumn('sales_26w_over_52w', F.col('sales_26w')/F.col('sales_52w'))
```
<b>Time elements</b>
```
# extract year, month, and week of year from week_end to be used as features
df_base = df_base.withColumn('year', F.year('week_end'))
df_base = df_base.withColumn('month', F.month('week_end'))
df_base = df_base.withColumn('weekofyear', F.weekofyear('week_end'))
```
<b>More derived features</b>:<br/>
We can add many more derived features as well, as required.
e.g. lag variables of existing features, trend ratios for other features, % change (Q-o-Q, M-o-M type) using lag variables, etc.
```
# save sample rows to csv for checks
df_base.limit(50).toPandas().to_csv('./files/rw_features_qc.csv',index=False)
# save features dataset as parquet
df_base.repartition(8).write.parquet('./data/rw_features/', mode='overwrite')
df_features = spark.read.parquet('./data/rw_features/')
```
## Model Build
### Dataset for modeling
<b>Sample one week_end per month</b>
```
df_wk_sample = df_features.select('week_end').withColumn('month', F.substring(F.col('week_end'), 1,7))
df_wk_sample = df_wk_sample.groupBy('month').agg(F.max('week_end').alias('week_end'))
df_wk_sample = df_wk_sample.repartition(1).persist()
df_wk_sample.count()
df_wk_sample.sort('week_end').show(5)
count_features = df_features.count()
# join back to filer
df_model = df_features.join(F.broadcast(df_wk_sample.select('week_end')), on=['week_end'], how='inner')
count_wk_sample = df_model.count()
```
<b>Eligibility filter</b>: Customer should be active in last year w.r.t the reference date
```
# use sales_52w for elig. filter
df_model = df_model.where(F.col('sales_52w')>0)
count_elig = df_model.count()
# count of rows at each stage
print(count_features, count_wk_sample, count_elig)
```
<b>Removing latest 4 week_end dates</b>: As we have a look-forward period of 4 weeks, latest 4 week_end dates in the data cannot be used for our model as these do not have 4 weeks ahead of them for the y-variable.
```
# see latest week_end dates (in the dataframe prior to monthly sampling)
df_features.select('week_end').drop_duplicates().sort(F.col('week_end').desc()).show(5)
# filter
df_model = df_model.where(F.col('week_end')<'2020-11-14')
count_4w_rm = df_model.count()
# count of rows at each stage
print(count_features, count_wk_sample, count_elig, count_4w_rm)
```
### Model Dataset Summary
Let's look at event rate for our dataset and also get a quick summary of all features.
The y-variable is balanced here because it is a dummy dataset. <mark>In most actual scenarios, this will not be balanced and the model build exercise will involving sampling for balancing.</mark>
```
df_model.groupBy('purchase_flag_next_4w').count().sort('purchase_flag_next_4w').show()
df_model.groupBy().agg(F.avg('purchase_flag_next_4w').alias('event_rate'), F.avg('purchase_flag').alias('wk_evt_rt')).show()
```
<b>Saving summary of all numerical features as a csv</b>
```
summary_metrics =\
('count','mean','stddev','min','0.10%','1.00%','5.00%','10.00%','20.00%','25.00%','30.00%',
'40.00%','50.00%','60.00%','70.00%','75.00%','80.00%','90.00%','95.00%','99.00%','99.90%','max')
df_summary_numeric = df_model.summary(*summary_metrics)
df_summary_numeric.toPandas().T.to_csv('./files/rw_features_summary.csv')
# fillna
df_model = df_model.fillna(0)
```
### Train-Test Split
80-20 split
```
train, test = df_model.randomSplit([0.8, 0.2], seed=125)
train.columns
```
### Data Prep
Spark Models require a vector of features as input. Categorical columns also need to be String Indexed before they can be used.
As we don't have any categorical columns currently, we will directly go with VectorAssembler.
<b>We will add it to a pipeline model that can be saved to be used on test & scoring datasets.</b>
```
# model related imports (RF)
from pyspark.ml.classification import RandomForestClassifier, RandomForestClassificationModel
from pyspark.ml import Pipeline, PipelineModel
from pyspark.ml.feature import VectorAssembler, StringIndexer
from pyspark.ml.evaluation import BinaryClassificationEvaluator
# list of features: remove identifier columns and the y-var
col_list = df_model.drop('week_end','customer_id','min_week','max_week','purchase_flag_next_4w').columns
stages = []
assembler = VectorAssembler(inputCols=col_list, outputCol='features')
stages.append(assembler)
pipe = Pipeline(stages=stages)
pipe_model = pipe.fit(train)
pipe_model.write().overwrite().save('./files/model_objects/rw_pipe/')
pipe_model = PipelineModel.load('./files/model_objects/rw_pipe/')
```
<b>Apply the transformation pipeline</b>
Also keep the identifier columns and y-var in the transformed dataframe.
```
train_pr = pipe_model.transform(train)
train_pr = train_pr.select('customer_id','week_end','purchase_flag_next_4w','features')
train_pr = train_pr.persist()
train_pr.count()
test_pr = pipe_model.transform(test)
test_pr = test_pr.select('customer_id','week_end','purchase_flag_next_4w','features')
test_pr = test_pr.persist()
test_pr.count()
```
### Model Training
We will train one iteration of Random Forest model as showcase.
In actual scenario, you will have to iterate through the training step multiple times for feature selection, and model hyper parameter tuning to get a good final model.
```
train_pr.show(5)
model_params = {
'labelCol': 'purchase_flag_next_4w',
'numTrees': 128, # default: 128
'maxDepth': 12, # default: 12
'featuresCol': 'features',
'minInstancesPerNode': 25,
'maxBins': 128,
'minInfoGain': 0.0,
'subsamplingRate': 0.7,
'featureSubsetStrategy': '0.3',
'impurity': 'gini',
'seed': 125,
'cacheNodeIds': False,
'maxMemoryInMB': 256
}
clf = RandomForestClassifier(**model_params)
trained_clf = clf.fit(train_pr)
```
### Feature Importance
We will save feature importance as a csv.
```
# Feature importance
feature_importance_list = trained_clf.featureImportances
feature_list = pd.DataFrame(train_pr.schema['features'].metadata['ml_attr']['attrs']['numeric']).sort_values('idx')
feature_importance_list = pd.DataFrame(
data=feature_importance_list.toArray(),
columns=['relative_importance'],
index=feature_list['name'])
feature_importance_list = feature_importance_list.sort_values('relative_importance', ascending=False)
feature_importance_list.to_csv('./files/rw_rf_feat_imp.csv')
```
### Predict on train and test
```
secondelement = F.udf(lambda v: float(v[1]), FloatType())
train_pred = trained_clf.transform(train_pr).withColumn('score',secondelement(F.col('probability')))
test_pred = trained_clf.transform(test_pr).withColumn('score', secondelement(F.col('probability')))
test_pred.show(5)
```
### Test Set Evaluation
```
evaluator = BinaryClassificationEvaluator(
rawPredictionCol='rawPrediction',
labelCol='purchase_flag_next_4w',
metricName='areaUnderROC')
# areaUnderROC
evaluator.evaluate(train_pred)
evaluator.evaluate(test_pred)
# cm
test_pred.groupBy('purchase_flag_next_4w','prediction').count().sort('purchase_flag_next_4w','prediction').show()
# accuracy
test_pred.where(F.col('purchase_flag_next_4w')==F.col('prediction')).count()/test_pred.count()
```
### Save Model
```
trained_clf.write().overwrite().save('./files/model_objects/rw_rf_model/')
trained_clf = RandomForestClassificationModel.load('./files/model_objects/rw_rf_model/')
```
## Scoring
We will take the records for latest week_end from df_features and score it using our trained model.
```
df_features = spark.read.parquet('./data/rw_features/')
max_we = df_features.selectExpr('max(week_end)').collect()[0][0]
max_we
df_scoring = df_features.where(F.col('week_end')==max_we)
df_scoring.count()
# fillna
df_scoring = df_scoring.fillna(0)
# transformation pipeline
pipe_model = PipelineModel.load('./files/model_objects/rw_pipe/')
# apply
df_scoring = pipe_model.transform(df_scoring)
df_scoring = df_scoring.select('customer_id','week_end','features')
# rf model
trained_clf = RandomForestClassificationModel.load('./files/model_objects/rw_rf_model/')
#apply
secondelement = F.udf(lambda v: float(v[1]), FloatType())
df_scoring = trained_clf.transform(df_scoring).withColumn('score',secondelement(F.col('probability')))
df_scoring.show(5)
# save scored output
df_scoring.repartition(8).write.parquet('./data/rw_scored/', mode='overwrite')
```
| true |
code
| 0.265642 | null | null | null | null |
|
# Hyperparameter Tuning using Your Own Keras/Tensorflow Container
This notebook shows how to build your own Keras(Tensorflow) container, test it locally using SageMaker Python SDK local mode, and bring it to SageMaker for training, leveraging hyperparameter tuning.
The model used for this notebook is a ResNet model, trainer with the CIFAR-10 dataset. The example is based on https://github.com/keras-team/keras/blob/master/examples/cifar10_cnn.py
## Set up the notebook instance to support local mode
Currently you need to install docker-compose in order to use local mode (i.e., testing the container in the notebook instance without pushing it to ECR).
```
!/bin/bash setup.sh
```
## Permissions
Running this notebook requires permissions in addition to the normal `SageMakerFullAccess` permissions. This is because it creates new repositories in Amazon ECR. The easiest way to add these permissions is simply to add the managed policy `AmazonEC2ContainerRegistryFullAccess` to the role that you used to start your notebook instance. There's no need to restart your notebook instance when you do this, the new permissions will be available immediately.
## Set up the environment
We will set up a few things before starting the workflow.
1. get the execution role which will be passed to sagemaker for accessing your resources such as s3 bucket
2. specify the s3 bucket and prefix where training data set and model artifacts are stored
```
import os
import numpy as np
import tempfile
import tensorflow as tf
import sagemaker
import boto3
from sagemaker.estimator import Estimator
region = boto3.Session().region_name
sagemaker_session = sagemaker.Session()
smclient = boto3.client("sagemaker")
bucket = (
sagemaker.Session().default_bucket()
) # s3 bucket name, must be in the same region as the one specified above
prefix = "sagemaker/DEMO-hpo-keras-cifar10"
role = sagemaker.get_execution_role()
NUM_CLASSES = 10 # the data set has 10 categories of images
```
## Complete source code
- [trainer/start.py](trainer/start.py): Keras model
- [trainer/environment.py](trainer/environment.py): Contain information about the SageMaker environment
## Building the image
We will build the docker image using the Tensorflow versions on dockerhub. The full list of Tensorflow versions can be found at https://hub.docker.com/r/tensorflow/tensorflow/tags/
```
import shlex
import subprocess
def get_image_name(ecr_repository, tensorflow_version_tag):
return "%s:tensorflow-%s" % (ecr_repository, tensorflow_version_tag)
def build_image(name, version):
cmd = "docker build -t %s --build-arg VERSION=%s -f Dockerfile ." % (name, version)
subprocess.check_call(shlex.split(cmd))
# version tag can be found at https://hub.docker.com/r/tensorflow/tensorflow/tags/
# e.g., latest cpu version is 'latest', while latest gpu version is 'latest-gpu'
tensorflow_version_tag = "1.10.1"
account = boto3.client("sts").get_caller_identity()["Account"]
domain = "amazonaws.com"
if region == "cn-north-1" or region == "cn-northwest-1":
domain = "amazonaws.com.cn"
ecr_repository = "%s.dkr.ecr.%s.%s/test" % (
account,
region,
domain,
) # your ECR repository, which you should have been created before running the notebook
image_name = get_image_name(ecr_repository, tensorflow_version_tag)
print("building image:" + image_name)
build_image(image_name, tensorflow_version_tag)
```
## Prepare the data
```
def upload_channel(channel_name, x, y):
y = tf.keras.utils.to_categorical(y, NUM_CLASSES)
file_path = tempfile.mkdtemp()
np.savez_compressed(os.path.join(file_path, "cifar-10-npz-compressed.npz"), x=x, y=y)
return sagemaker_session.upload_data(
path=file_path, bucket=bucket, key_prefix="data/DEMO-keras-cifar10/%s" % channel_name
)
def upload_training_data():
# The data, split between train and test sets:
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
train_data_location = upload_channel("train", x_train, y_train)
test_data_location = upload_channel("test", x_test, y_test)
return {"train": train_data_location, "test": test_data_location}
channels = upload_training_data()
```
## Testing the container locally (optional)
You can test the container locally using local mode of SageMaker Python SDK. A training container will be created in the notebook instance based on the docker image you built. Note that we have not pushed the docker image to ECR yet since we are only running local mode here. You can skip to the tuning step if you want but testing the container locally can help you find issues quickly before kicking off the tuning job.
### Setting the hyperparameters
```
hyperparameters = dict(
batch_size=32,
data_augmentation=True,
learning_rate=0.0001,
width_shift_range=0.1,
height_shift_range=0.1,
epochs=1,
)
hyperparameters
```
### Create a training job using local mode
```
%%time
output_location = "s3://{}/{}/output".format(bucket, prefix)
estimator = Estimator(
image_name,
role=role,
output_path=output_location,
train_instance_count=1,
train_instance_type="local",
hyperparameters=hyperparameters,
)
estimator.fit(channels)
```
## Pushing the container to ECR
Now that we've tested the container locally and it works fine, we can move on to run the hyperparmeter tuning. Before kicking off the tuning job, you need to push the docker image to ECR first.
The cell below will create the ECR repository, if it does not exist yet, and push the image to ECR.
```
# The name of our algorithm
algorithm_name = 'test'
# If the repository doesn't exist in ECR, create it.
exist_repo = !aws ecr describe-repositories --repository-names {algorithm_name} > /dev/null 2>&1
if not exist_repo:
!aws ecr create-repository --repository-name {algorithm_name} > /dev/null
# Get the login command from ECR and execute it directly
!$(aws ecr get-login --region {region} --no-include-email)
!docker push {image_name}
```
## Specify hyperparameter tuning job configuration
*Note, with the default setting below, the hyperparameter tuning job can take 20~30 minutes to complete. You can customize the code in order to get better result, such as increasing the total number of training jobs, epochs, etc., with the understanding that the tuning time will be increased accordingly as well.*
Now you configure the tuning job by defining a JSON object that you pass as the value of the TuningJobConfig parameter to the create_tuning_job call. In this JSON object, you specify:
* The ranges of hyperparameters you want to tune
* The limits of the resource the tuning job can consume
* The objective metric for the tuning job
```
import json
from time import gmtime, strftime
tuning_job_name = "BYO-keras-tuningjob-" + strftime("%d-%H-%M-%S", gmtime())
print(tuning_job_name)
tuning_job_config = {
"ParameterRanges": {
"CategoricalParameterRanges": [],
"ContinuousParameterRanges": [
{
"MaxValue": "0.001",
"MinValue": "0.0001",
"Name": "learning_rate",
}
],
"IntegerParameterRanges": [],
},
"ResourceLimits": {"MaxNumberOfTrainingJobs": 9, "MaxParallelTrainingJobs": 3},
"Strategy": "Bayesian",
"HyperParameterTuningJobObjective": {"MetricName": "loss", "Type": "Minimize"},
}
```
## Specify training job configuration
Now you configure the training jobs the tuning job launches by defining a JSON object that you pass as the value of the TrainingJobDefinition parameter to the create_tuning_job call.
In this JSON object, you specify:
* Metrics that the training jobs emit
* The container image for the algorithm to train
* The input configuration for your training and test data
* Configuration for the output of the algorithm
* The values of any algorithm hyperparameters that are not tuned in the tuning job
* The type of instance to use for the training jobs
* The stopping condition for the training jobs
This example defines one metric that Tensorflow container emits: loss.
```
training_image = image_name
print("training artifacts will be uploaded to: {}".format(output_location))
training_job_definition = {
"AlgorithmSpecification": {
"MetricDefinitions": [{"Name": "loss", "Regex": "loss: ([0-9\\.]+)"}],
"TrainingImage": training_image,
"TrainingInputMode": "File",
},
"InputDataConfig": [
{
"ChannelName": "train",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": channels["train"],
"S3DataDistributionType": "FullyReplicated",
}
},
"CompressionType": "None",
"RecordWrapperType": "None",
},
{
"ChannelName": "test",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": channels["test"],
"S3DataDistributionType": "FullyReplicated",
}
},
"CompressionType": "None",
"RecordWrapperType": "None",
},
],
"OutputDataConfig": {"S3OutputPath": "s3://{}/{}/output".format(bucket, prefix)},
"ResourceConfig": {"InstanceCount": 1, "InstanceType": "ml.m4.xlarge", "VolumeSizeInGB": 50},
"RoleArn": role,
"StaticHyperParameters": {
"batch_size": "32",
"data_augmentation": "True",
"height_shift_range": "0.1",
"width_shift_range": "0.1",
"epochs": "1",
},
"StoppingCondition": {"MaxRuntimeInSeconds": 43200},
}
```
## Create and launch a hyperparameter tuning job
Now you can launch a hyperparameter tuning job by calling create_tuning_job API. Pass the name and JSON objects you created in previous steps as the values of the parameters. After the tuning job is created, you should be able to describe the tuning job to see its progress in the next step, and you can go to SageMaker console->Jobs to check out the progress of each training job that has been created.
```
smclient.create_hyper_parameter_tuning_job(
HyperParameterTuningJobName=tuning_job_name,
HyperParameterTuningJobConfig=tuning_job_config,
TrainingJobDefinition=training_job_definition,
)
```
Let's just run a quick check of the hyperparameter tuning jobs status to make sure it started successfully and is `InProgress`.
```
smclient.describe_hyper_parameter_tuning_job(HyperParameterTuningJobName=tuning_job_name)[
"HyperParameterTuningJobStatus"
]
```
## Analyze tuning job results - after tuning job is completed
Please refer to "HPO_Analyze_TuningJob_Results.ipynb" to see example code to analyze the tuning job results.
## Deploy the best model
Now that we have got the best model, we can deploy it to an endpoint. Please refer to other SageMaker sample notebooks or SageMaker documentation to see how to deploy a model.
| true |
code
| 0.550003 | null | null | null | null |
|
### Scroll Down Below to start from Exercise 8.04
```
# Removes Warnings
import warnings
warnings.filterwarnings('ignore')
#import the necessary packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
```
## Reading the data using pandas
```
data= pd.read_csv('Churn_Modelling.csv')
data.head(5)
len(data)
data.shape
```
## Scrubbing the data
```
data.isnull().values.any()
#It seems we have some missing values now let us explore what are the columns
#having missing values
data.isnull().any()
## it seems that we have missing values in Gender,age and EstimatedSalary
data[["EstimatedSalary","Age"]].describe()
data.describe()
#### It seems that HasCrCard has value as 0 and 1 hence needs to be changed to category
data['HasCrCard'].value_counts()
## No of missing Values present
data.isnull().sum()
## Percentage of missing Values present
round(data.isnull().sum()/len(data)*100,2)
## Checking the datatype of the missing columns
data[["Gender","Age","EstimatedSalary"]].dtypes
```
### There are three ways to impute missing values:
1. Droping the missing values rows
2. Fill missing values with a test stastics
3. Predict the missing values using ML algorithm
```
mean_value=data['EstimatedSalary'].mean()
data['EstimatedSalary']=data['EstimatedSalary']\
.fillna(mean_value)
data['Gender'].value_counts()
data['Gender']=data['Gender'].fillna(data['Gender']\
.value_counts().idxmax())
mode_value=data['Age'].mode()
data['Age']=data['Age'].fillna(mode_value[0])
##checking for any missing values
data.isnull().any()
```
### Renaming the columns
```
# We would want to rename some of the columns
data = data.rename(columns={'CredRate': 'CreditScore',\
'ActMem' : 'IsActiveMember',\
'Prod Number': 'NumOfProducts',\
'Exited':'Churn'})
data.columns
```
### We would also like to move the churn columnn to the extreme right and drop the customer ID
```
data.drop(labels=['CustomerId'], axis=1,inplace = True)
column_churn = data['Churn']
data.drop(labels=['Churn'], axis=1,inplace = True)
data.insert(len(data.columns), 'Churn', column_churn.values)
data.columns
```
### Changing the data type
```
data["Geography"] = data["Geography"].astype('category')
data["Gender"] = data["Gender"].astype('category')
data["HasCrCard"] = data["HasCrCard"].astype('category')
data["Churn"] = data["Churn"].astype('category')
data["IsActiveMember"] = data["IsActiveMember"]\
.astype('category')
data.dtypes
```
# Exploring the data
## Statistical Overview
```
data['Churn'].value_counts(0)
data['Churn'].value_counts(1)*100
data['IsActiveMember'].value_counts(1)*100
data.describe()
summary_churn = data.groupby('Churn')
summary_churn.mean()
summary_churn.median()
corr = data.corr()
plt.figure(figsize=(15,8))
sns.heatmap(corr, \
xticklabels=corr.columns.values,\
yticklabels=corr.columns.values,\
annot=True,cmap='Greys_r')
corr
```
## Visualization
```
f, axes = plt.subplots(ncols=3, figsize=(15, 6))
sns.distplot(data.EstimatedSalary, kde=True, color="gray", \
ax=axes[0]).set_title('EstimatedSalary')
axes[0].set_ylabel('No of Customers')
sns.distplot(data.Age, kde=True, color="gray", \
ax=axes[1]).set_title('Age')
axes[1].set_ylabel('No of Customers')
sns.distplot(data.Balance, kde=True, color="gray", \
ax=axes[2]).set_title('Balance')
axes[2].set_ylabel('No of Customers')
plt.figure(figsize=(15,4))
p=sns.countplot(y="Gender", hue='Churn', data=data,\
palette="Greys_r")
legend = p.get_legend()
legend_txt = legend.texts
legend_txt[0].set_text("No Churn")
legend_txt[1].set_text("Churn")
p.set_title('Customer Churn Distribution by Gender')
plt.figure(figsize=(15,4))
p=sns.countplot(x='Geography', hue='Churn', data=data, \
palette="Greys_r")
legend = p.get_legend()
legend_txt = legend.texts
legend_txt[0].set_text("No Churn")
legend_txt[1].set_text("Churn")
p.set_title('Customer Geography Distribution')
plt.figure(figsize=(15,4))
p=sns.countplot(x='NumOfProducts', hue='Churn', data=data, \
palette="Greys_r")
legend = p.get_legend()
legend_txt = legend.texts
legend_txt[0].set_text("No Churn")
legend_txt[1].set_text("Churn")
p.set_title('Customer Distribution by Product')
plt.figure(figsize=(15,4))
ax=sns.kdeplot(data.loc[(data['Churn'] == 0),'Age'] , \
color=sns.color_palette("Greys_r")[0],\
shade=True,label='no churn')
ax=sns.kdeplot(data.loc[(data['Churn'] == 1),'Age'] , \
color=sns.color_palette("Greys_r")[1],\
shade=True, label='churn')
ax.set(xlabel='Customer Age', ylabel='Frequency')
plt.title('Customer Age - churn vs no churn')
plt.figure(figsize=(15,4))
ax=sns.kdeplot(data.loc[(data['Churn'] == 0),'Balance'] , \
color=sns.color_palette("Greys_r")[0],\
shade=True,label='no churn')
ax=sns.kdeplot(data.loc[(data['Churn'] == 1),'Balance'] , \
color=sns.color_palette("Greys_r")[1],\
shade=True, label='churn')
ax.set(xlabel='Customer Balance', ylabel='Frequency')
plt.title('Customer Balance - churn vs no churn')
plt.figure(figsize=(15,4))
ax=sns.kdeplot(data.loc[(data['Churn'] == 0),'CreditScore'] , \
color=sns.color_palette("Greys_r")[0],\
shade=True,label='no churn')
ax=sns.kdeplot(data.loc[(data['Churn'] == 1),'CreditScore'] , \
color=sns.color_palette("Greys_r")[1],\
shade=True, label='churn')
ax.set(xlabel='CreditScore', ylabel='Frequency')
plt.title('Customer CreditScore - churn vs no churn')
plt.figure(figsize=(16,4))
p=sns.barplot(x='NumOfProducts',y='Balance',hue='Churn',\
data=data, palette="Greys_r")
p.legend(loc='upper right')
legend = p.get_legend()
legend_txt = legend.texts
legend_txt[0].set_text("No Churn")
legend_txt[1].set_text("Churn")
p.set_title('Number of Product VS Balance')
```
## Feature selection
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
data.dtypes
### Encoding the categorical variables
data["Geography"] = data["Geography"].astype('category')\
.cat.codes
data["Gender"] = data["Gender"].astype('category').cat.codes
data["HasCrCard"] = data["HasCrCard"].astype('category')\
.cat.codes
data["Churn"] = data["Churn"].astype('category').cat.codes
target = 'Churn'
X = data.drop('Churn', axis=1)
y=data[target]
X_train, X_test, y_train, y_test = train_test_split\
(X,y,test_size=0.15, \
random_state=123, \
stratify=y)
forest=RandomForestClassifier(n_estimators=500,random_state=1)
forest.fit(X_train,y_train)
importances=forest.feature_importances_
features = data.drop(['Churn'],axis=1).columns
indices = np.argsort(importances)[::-1]
plt.figure(figsize=(15,4))
plt.title("Feature importances using Random Forest")
plt.bar(range(X_train.shape[1]), importances[indices],\
color="gray", align="center")
plt.xticks(range(X_train.shape[1]), features[indices], \
rotation='vertical',fontsize=15)
plt.xlim([-1, X_train.shape[1]])
plt.show()
feature_importance_df = pd.DataFrame({"Feature":features,\
"Importance":importances})
print(feature_importance_df)
```
## Model Fitting
```
import statsmodels.api as sm
top5_features = ['Age','EstimatedSalary','CreditScore',\
'Balance','NumOfProducts']
logReg = sm.Logit(y_train, X_train[top5_features])
logistic_regression = logReg.fit()
logistic_regression.summary
logistic_regression.params
# Create function to compute coefficients
coef = logistic_regression.params
def y (coef, Age, EstimatedSalary, CreditScore, Balance, \
NumOfProducts) : return coef[0]*Age+ coef[1]\
*EstimatedSalary+coef[2]*CreditScore\
+coef[1]*Balance+coef[2]*NumOfProducts
import numpy as np
#A customer having below attributes
#Age: 50
#EstimatedSalary: 100,000
#CreditScore: 600
#Balance: 100,000
#NumOfProducts: 2
#would have 38% chance of churn
y1 = y(coef, 50, 100000, 600,100000,2)
p = np.exp(y1) / (1+np.exp(y1))
p
```
## Logistic regression using scikit-learn
```
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0, solver='lbfgs')\
.fit(X_train[top5_features], y_train)
clf.predict(X_test[top5_features])
clf.predict_proba(X_test[top5_features])
clf.score(X_test[top5_features], y_test)
```
## Exercise 8.04
# Performing standardization
```
from sklearn import preprocessing
X_train[top5_features].head()
scaler = preprocessing.StandardScaler().fit(X_train[top5_features])
scaler.mean_
scaler.scale_
X_train_scalar=scaler.transform(X_train[top5_features])
X_train_scalar
X_test_scalar=scaler.transform(X_test[top5_features])
```
## Exercise 8.05
# Performing Scaling
```
min_max = preprocessing.MinMaxScaler().fit(X_train[top5_features])
min_max.min_
min_max.scale_
X_train_min_max=min_max.transform(X_train[top5_features])
X_test_min_max=min_max.transform(X_test[top5_features])
```
## Exercise 8.06
# Normalization
```
normalize = preprocessing.Normalizer().fit(X_train[top5_features])
normalize
X_train_normalize=normalize.transform(X_train[top5_features])
X_test_normalize=normalize.transform(X_test[top5_features])
np.sqrt(np.sum(X_train_normalize**2, axis=1))
np.sqrt(np.sum(X_test_normalize**2, axis=1))
```
## Exercise 8.07
# Model Evaluation
```
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_splits=10)\
.split(X_train[top5_features].values,y_train.values)
results=[]
for i, (train,test) in enumerate(skf):
clf.fit(X_train[top5_features].values[train],\
y_train.values[train])
fit_result=clf.score(X_train[top5_features].values[test],\
y_train.values[test])
results.append(fit_result)
print('k-fold: %2d, Class Ratio: %s, Accuracy: %.4f'\
% (i,np.bincount(y_train.values[train]),fit_result))
print('accuracy for CV is:%.3f' % np.mean(results))
```
### Using Scikit Learn cross_val_score
```
from sklearn.model_selection import cross_val_score
results_cross_val_score=cross_val_score\
(estimator=clf,\
X=X_train[top5_features].values,\
y=y_train.values,cv=10,n_jobs=1)
print('accuracy for CV is:%.3f '\
% np.mean(results_cross_val_score))
results_cross_val_score
print('accuracy for CV is:%.3f' % np.mean(results_cross_val_score))
```
## Exercise 8.08
# Fine Tuning of Model Using Grid Search
```
from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import StratifiedKFold
parameters = [ {'kernel': ['linear'], 'C':[0.1, 1]}, \
{'kernel': ['rbf'], 'C':[0.1, 1]}]
clf = GridSearchCV(svm.SVC(), parameters, \
cv = StratifiedKFold(n_splits = 3),\
verbose=4,n_jobs=-1)
clf.fit(X_train[top5_features], y_train)
print('best score train:', clf.best_score_)
print('best parameters train: ', clf.best_params_)
```
| true |
code
| 0.58433 | null | null | null | null |
|
# Aproximações e Erros de Arredondamento
_Prof. Dr. Tito Dias Júnior_
## **Erros de Arredondamento**
### Épsilon de Máquina
```
#Calcula o épsilon de máquina
epsilon = 1
while (epsilon+1)>1:
epsilon = epsilon/2
epsilon = 2 * epsilon
print(epsilon)
```
Aproximação de uma função por Série de Taylor
```
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -0.1*x**4 -0.15*x**3 -0.5*x**2 -0.25*x +1.2
def df(x):
return -0.4*x**3 -0.45*x**2 -1.0*x -0.25
def ddf(x):
return -1.2*x**2 -0.9*x -1.0
def dddf(x):
return -2.4*x -0.9
def d4f(x):
return -2.4
x1 = 0
x2 = 1
# Aproximação de ordem zero
fO_0 = f(x1) # Valor previsto
erroO_0 = f(x2) - fO_0 # valor exato menos o valor previsto
# Aproximação de primeira ordem
fO_1 = f(x1) + df(x1)*(x2-x1) # Valor previsto
erroO_1 = f(x2) - fO_1 # valor exato menos o valor previsto
# Aproximação de segunda ordem
fO_2 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 # Valor previsto
erroO_2 = f(x2) - fO_2 # valor exato menos o valor previsto
# Aproximação de terceira ordem
fO_3 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 + (dddf(x1)/6)*(x2-x1)**3 # Valor previsto 3!=3*2*1=6
erroO_3 = f(x2) - fO_3 # valor exato menos o valor previsto
# Aproximação de quarta ordem
fO_4 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 + (dddf(x1)/6)*(x2-x1)**3 + (d4f(x1)/24)*(x2-x1)**4 # Valor previsto 4!=4*3*2*1=24
erroO_4 = f(x2) - fO_4 # valor exato menos o valor previsto
print('Ordem ~f(x) Erro')
print('0 {0:8f} {1:3f}'.format(fO_0, erroO_0))
print('1 {0:8f} {1:8f}'.format(fO_1, erroO_1))
print('2 {0:8f} {1:8f}'.format(fO_2, erroO_2))
print('3 {0:8f} {1:8f}'.format(fO_3, erroO_3))
print('4 {0:8f} {1:8f}'.format(fO_4, erroO_4))
# Plotagem dos gráficos
xx = np.linspace(-2,2.0,40)
yy = f(xx)
plt.plot(xx,yy,'b',x2,fO_0,'*',x2,fO_1,'*r', x2, fO_2, '*g', x2, fO_3,'*y', x2, fO_4, '*r')
plt.savefig('exemplo1.png')
plt.show()
# Exercício do dia 17/08/2020
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return np.sin(x)
def df(x):
return np.cos(x)
def ddf(x):
return -np.sin(x)
def dddf(x):
return -np.cos(x)
def d4f(x):
return np.sin(x)
x1 = np.pi/2
x2 = 3*np.pi/4 # igual a pi/2 +pi/4
# Aproximação de ordem zero
fO_0 = f(x1) # Valor previsto
erroO_0 = f(x2) - fO_0 # valor exato menos o valor previsto
# Aproximação de primeira ordem
fO_1 = f(x1) + df(x1)*(x2-x1) # Valor previsto
erroO_1 = f(x2) - fO_1 # valor exato menos o valor previsto
# Aproximação de segunda ordem
fO_2 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 # Valor previsto
erroO_2 = f(x2) - fO_2 # valor exato menos o valor previsto
# Aproximação de terceira ordem
fO_3 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 + (dddf(x1)/6)*(x2-x1)**3 # Valor previsto 3!=3*2*1=6
erroO_3 = f(x2) - fO_3 # valor exato menos o valor previsto
# Aproximação de quarta ordem
fO_4 = f(x1) + df(x1)*(x2-x1) + (ddf(x1)/2)*(x2-x1)**2 + (dddf(x1)/6)*(x2-x1)**3 + (d4f(x1)/24)*(x2-x1)**4 # Valor previsto 4!=4*3*2*1=24
erroO_4 = f(x2) - fO_4 # valor exato menos o valor previsto
print('Ordem ~f(x) Erro')
print('0 {0:8f} {1:3f}'.format(fO_0, erroO_0))
print('1 {0:8f} {1:8f}'.format(fO_1, erroO_1))
print('2 {0:8f} {1:8f}'.format(fO_2, erroO_2))
print('3 {0:8f} {1:8f}'.format(fO_3, erroO_3))
print('4 {0:8f} {1:8f}'.format(fO_4, erroO_4))
# Plotagem dos gráficos
xx = np.linspace(0,2.*np.pi,40)
yy = f(xx)
plt.plot(xx,yy,'b',x2,fO_0,'*',x2,fO_1,'*b', x2, fO_2, '*g', x2, fO_3,'*y', x2, fO_4, '*r')
plt.savefig('exemplo2.png')
plt.show()
```
### Exercício - Aula 17/08/2020
Utilizando o exemplo anterior faça expansões de Taylor para a função seno, de ordem zero até ordem 4, a partir de $x = \pi/2$ com $h = \pi/4$, ou seja, para estimar o valor da função em $x_{i+1} = 3 \pi/4$. E responda os check de verificação no AVA:
1. Check: Qual o erro da estimativa de ordem zero?
2. Check: Qual o erro da estimativa de quarta ordem?
### Exercício - Aula 24/08/2020
Utilizando os exemplo e exercícios anteriores faça os gráficos das expansões de Taylor para as funções estudadas, de ordem zero até ordem 4, salve o arquivo em formato png e faça o upload no AVA.
## Referências
Kiusalaas, J. (2013). **Numerical Methods in Engineering With Python 3**. Cambridge: Cambridge.<br>
Brasil, R.M.L.R.F, Balthazar, J.M., Góis, W. (2015) **Métodos Numéricos e Computacionais na Prática de Engenharias e Ciências**, São Paulo: Edgar Blucher
| true |
code
| 0.309206 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/partha1189/machine_learning/blob/master/CONV1D_LSTM_time_series.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5
# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=42)
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 20
batch_size = 32
shuffle_buffer_size = 1000
def windowed_dataset(series, window_size, batch_size, shuffle_buffer_size):
series = tf.expand_dims(series, axis=-1)
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift= 1, drop_remainder =True)
dataset = dataset.flat_map(lambda window:window.batch(window_size+1))
dataset = dataset.shuffle(shuffle_buffer_size)
dataset = dataset.map(lambda window: (window[:-1], window[-1:]))
return dataset.batch(batch_size).prefetch(1)
def model_forecast(model, series, window_size):
ds = tf.data.Dataset.from_tensor_slices(series)
ds = ds.window(window_size, shift=1, drop_remainder=True)
ds = ds.flat_map(lambda w: w.batch(window_size))
ds = ds.batch(32).prefetch(1)
forecast = model.predict(ds)
return forecast
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
window_size = 30
train_set = windowed_dataset(x_train, window_size, batch_size=128, shuffle_buffer_size=shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=32, kernel_size=5, strides=1, padding='causal', activation='relu', input_shape=[None, 1]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x : x * 200)
])
lr_schedule = tf.keras.callbacks.LearningRateScheduler(lambda epoch : 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss= tf.keras.losses.Huber(),
optimizer = optimizer,
metrics = ['mae'])
history = model.fit(train_set, epochs = 100, callbacks = [lr_schedule])
plt.semilogx(history.history['lr'], history.history['loss'])
plt.axis([1e-8, 1e-4, 0, 30])
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
#batch_size = 16
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv1D(filters=32, kernel_size=3,
strides=1, padding="causal",
activation="relu",
input_shape=[None, 1]),
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 200)
])
optimizer = tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(dataset,epochs=500)
rnn_forecast = model_forecast(model, series[..., np.newaxis], window_size)
rnn_forecast = rnn_forecast[split_time - window_size:-1, -1, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, rnn_forecast)
tf.keras.metrics.mean_absolute_error(x_valid, rnn_forecast).numpy()
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
mae=history.history['mae']
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot MAE and Loss
#------------------------------------------------
plt.plot(epochs, mae, 'r')
plt.plot(epochs, loss, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
epochs_zoom = epochs[200:]
mae_zoom = mae[200:]
loss_zoom = loss[200:]
#------------------------------------------------
# Plot Zoomed MAE and Loss
#------------------------------------------------
plt.plot(epochs_zoom, mae_zoom, 'r')
plt.plot(epochs_zoom, loss_zoom, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
```
| true |
code
| 0.81604 | null | null | null | null |
|
# Solution for Ex 5 of the ibmqc 2021
This solution is from the point of view from someone who has just started to explore Quantum Computing, but is familiar with the physics behind it and has some experience with programming and optimization problems.
So I did not create this solution entirely by myself, but altered the tutorial solution from the H-H molecule which was provided.
The goal was to create an ansatz with the lowest possible number of CNOT gates.
```
from qiskit_nature.drivers import PySCFDriver
molecule = 'Li 0.0 0.0 0.0; H 0.0 0.0 1.5474'
driver = PySCFDriver(atom=molecule)
qmolecule = driver.run()
```
There were many hints on how to reduce the problem to a manageable, in particular reducing the number of qubits, hence resulting in smaller circuits with fewer operations. A first hint was to freeze the core, since Li has the configuration of 2 electrons in the 1s orbital and 1 in the 2s orbital (which forms bonds with other atoms). The electrons in orbitals nearer the core can therefore be frozen.
Li : 1s, 2s, and px, py, pz orbitals --> 6 orbitals
H : 1s --> 1 orbital
```
from qiskit_nature.transformers import FreezeCoreTransformer
trafo = FreezeCoreTransformer(freeze_core=True)
q_molecule_reduced = trafo.transform(qmolecule)
```
There are 5 properties to consider to better understand the task. Note that there was already a transformation. Before this transformation the properties would have been (in this order: 4, 6, 12, 12, 1.0259348796432726)
```
n_el = q_molecule_reduced.num_alpha + q_molecule_reduced.num_beta
print("Number of electrons in the system: ", n_el)
n_mo = q_molecule_reduced.num_molecular_orbitals
print("Number of molecular orbitals: ", n_mo)
n_so = 2 * q_molecule_reduced.num_molecular_orbitals
print("Number of spin orbitals: ", n_so)
n_q = 2 * q_molecule_reduced.num_molecular_orbitals
print("Number of qubits one would need with Jordan-Wigner mapping:", n_q)
e_nn = q_molecule_reduced.nuclear_repulsion_energy
print("Nuclear repulsion energy", e_nn)
```
#### Electronic structure problem
One can then create an `ElectronicStructureProblem` that can produce the list of fermionic operators before mapping them to qubits (Pauli strings).
In the following cell on could also use a quantum molecule transformer to remove orbitals which would not contribute to the ground state - for example px and py in this problem. Why they correspond to orbitals 3 and 4 I'm not really sure, maybe one has to look through the documentation a bit better than I did, but since there were only very limited combinations I tried them at random and kept an eye on the ground state energy.
```
from qiskit_nature.problems.second_quantization.electronic import ElectronicStructureProblem
problem= ElectronicStructureProblem(driver, q_molecule_transformers=[FreezeCoreTransformer(freeze_core=True,
remove_orbitals=[3,4])])
second_q_ops = problem.second_q_ops()
# Hamiltonian
main_op = second_q_ops[0]
```
### QubitConverter
Allows to define the mapping that you will use in the simulation. For the LiH problem the Parity mapper is chosen, because it allows the "TwoQubitReduction" setting which will further simplify the problem.
If I understand the paper correctly - referenced as [Bravyi *et al*, 2017](https://arxiv.org/abs/1701.08213v1)- symmetries from particle number operators such eq 52 of the paper are used to reduce the number of qubits. The only challenging thing was to understand what [1] is meaning if you pass this as the z2symmetry-reduction parameter.
```
from qiskit_nature.mappers.second_quantization import ParityMapper, BravyiKitaevMapper, JordanWignerMapper
from qiskit_nature.converters.second_quantization.qubit_converter import QubitConverter
# Setup the mapper and qubit converter
mapper = ParityMapper()
converter = QubitConverter(mapper=mapper, two_qubit_reduction=True, z2symmetry_reduction=[1])
# The fermionic operators are mapped to qubit operators
num_particles = (problem.molecule_data_transformed.num_alpha,
problem.molecule_data_transformed.num_beta)
qubit_op = converter.convert(main_op, num_particles=num_particles)
```
#### Initial state
One has to chose an initial state for the system which is reduced to 4 qubits from 12 at the beginning. The initialisation may be chosen by you or you stick to the one proposed by the Hartree-Fock function (i.e. $|\Psi_{HF} \rangle = |1100 \rangle$). For the Exercise it is recommended to stick to stick to the function!
```
from qiskit_nature.circuit.library import HartreeFock
num_particles = (problem.molecule_data_transformed.num_alpha,
problem.molecule_data_transformed.num_beta)
num_spin_orbitals = 2 * problem.molecule_data_transformed.num_molecular_orbitals
init_state = HartreeFock(num_spin_orbitals, num_particles, converter)
init_state.draw('mpl')
```
5. Ansatz
Playing with the Ansatz was really fun. I found the TwoLocal Ansatz very interesting to gain some knowlegde and insight on how to compose an ansatz for the problem. Later on I tried to create my own Ansatz and converged to an Ansatz quite similiar to a TwoLocal one.
It's obvious you have to entangle the qubits somehow with CNOTs. But to give the optimization algorithm a chance to find a minimum, you have to make sure to change the states of the qubits before and afterwards independently of the other ones.
```
# Choose the ansatz
ansatz_type = "Custom"
# Parameters for q-UCC ansatz
num_particles = (problem.molecule_data_transformed.num_alpha,
problem.molecule_data_transformed.num_beta)
num_spin_orbitals = 2 * problem.molecule_data_transformed.num_molecular_orbitals
# Put arguments for twolocal
if ansatz_type == "TwoLocal":
# Single qubit rotations that are placed on all qubits with independent parameters
rotation_blocks = ['ry']
# Entangling gates
entanglement_blocks = ['cx']
# How the qubits are entangled
entanglement = 'linear'
# Repetitions of rotation_blocks + entanglement_blocks with independent parameters
repetitions = 1
# Skip the final rotation_blocks layer
skip_final_rotation_layer = False
ansatz = TwoLocal(qubit_op.num_qubits, rotation_blocks, entanglement_blocks, reps=repetitions,
entanglement=entanglement, skip_final_rotation_layer=skip_final_rotation_layer)
# Add the initial state
ansatz.compose(init_state, front=True, inplace=True)
elif ansatz_type == "UCCSD":
ansatz = UCCSD(converter,num_particles,num_spin_orbitals,initial_state = init_state)
elif ansatz_type == "PUCCD":
ansatz = PUCCD(converter,num_particles,num_spin_orbitals,initial_state = init_state)
elif ansatz_type == "SUCCD":
ansatz = SUCCD(converter,num_particles,num_spin_orbitals,initial_state = init_state)
elif ansatz_type == "Custom":
# Example of how to write your own circuit
from qiskit.circuit import Parameter, QuantumCircuit, QuantumRegister
from qiskit.circuit.random import random_circuit
# Define the variational parameter
param_names_theta = ['a', 'b', 'c', 'd']
thetas = [Parameter(param_names_theta[i]) for i in range(len(param_names_theta))]
param_names_eta = ['e', 'f', 'g', 'h']
etas = [Parameter(param_names_eta[i]) for i in range(len(param_names_eta))]
n = qubit_op.num_qubits
# Make an empty quantum circuit
qc = QuantumCircuit(qubit_op.num_qubits)
qubit_label = 0
# Place a CNOT ladder
for i in range(n):
qc.ry(thetas[i], i)
for i in range(n-1):
qc.cx(i, i+1)
for i in range(n):
qc.ry(etas[n-i-1], i)
# Visual separator
ansatz = qc
ansatz.compose(init_state, front=True, inplace=True)
ansatz.draw('mpl')
```
### Backend
This is where you specify the simulator or device where you want to run your algorithm.
We will focus on the `statevector_simulator` in this challenge.
```
from qiskit import Aer
backend = Aer.get_backend('statevector_simulator')
```
### Optimizer
The optimizer guides the evolution of the parameters of the ansatz so it is very important to investigate the energy convergence as it would define the number of measurements that have to be performed on the QPU.
A clever choice might reduce drastically the number of needed energy evaluations.
Some of the optimizer seem to not reach the minimum. So the choice of the optimizer and the parameters is important.
I did not get to the minimum with the other optimizers than SLSQP.
I found a very nice and short explanation of how the optimizer works on stackoverflow:
The algorithm described by Dieter Kraft is a quasi-Newton method (using BFGS) applied to a lagrange function consisting of loss function and equality- and inequality-constraints. Because at each iteration some of the inequality constraints are active, some not, the inactive inequalities are omitted for the next iteration. An equality constrained problem is solved at each step using the active subset of constraints in the lagrange function.
https://stackoverflow.com/questions/59808494/how-does-the-slsqp-optimization-algorithm-work
```
from qiskit.algorithms.optimizers import SLSQP
optimizer = SLSQP(maxiter=4000)
```
### Exact eigensolver
In the exercise we got the following exact diagonalizer function to compare the results.
```
from qiskit_nature.algorithms.ground_state_solvers.minimum_eigensolver_factories import NumPyMinimumEigensolverFactory
from qiskit_nature.algorithms.ground_state_solvers import GroundStateEigensolver
import numpy as np
def exact_diagonalizer(problem, converter):
solver = NumPyMinimumEigensolverFactory()
calc = GroundStateEigensolver(converter, solver)
result = calc.solve(problem)
return result
result_exact = exact_diagonalizer(problem, converter)
exact_energy = np.real(result_exact.eigenenergies[0])
print("Exact electronic energy", exact_energy)
```
### VQE and initial parameters for the ansatz
Now we can import the VQE class and run the algorithm. This code was also provided. Everything I have done so far is plugged in.
```
from qiskit.algorithms import VQE
from IPython.display import display, clear_output
def callback(eval_count, parameters, mean, std):
# Overwrites the same line when printing
display("Evaluation: {}, Energy: {}, Std: {}".format(eval_count, mean, std))
clear_output(wait=True)
counts.append(eval_count)
values.append(mean)
params.append(parameters)
deviation.append(std)
counts = []
values = []
params = []
deviation = []
# Set initial parameters of the ansatz
# We choose a fixed small displacement
# So all participants start from similar starting point
try:
initial_point = [0.01] * len(ansatz.ordered_parameters)
except:
initial_point = [0.01] * ansatz.num_parameters
algorithm = VQE(ansatz,
optimizer=optimizer,
quantum_instance=backend,
callback=callback,
initial_point=initial_point)
result = algorithm.compute_minimum_eigenvalue(qubit_op)
print(result)
# Store results in a dictionary
from qiskit.transpiler import PassManager
from qiskit.transpiler.passes import Unroller
# Unroller transpile your circuit into CNOTs and U gates
pass_ = Unroller(['u', 'cx'])
pm = PassManager(pass_)
ansatz_tp = pm.run(ansatz)
cnots = ansatz_tp.count_ops()['cx']
score = cnots
accuracy_threshold = 4.0 # in mHa
energy = result.optimal_value
if ansatz_type == "TwoLocal":
result_dict = {
'optimizer': optimizer.__class__.__name__,
'mapping': converter.mapper.__class__.__name__,
'ansatz': ansatz.__class__.__name__,
'rotation blocks': rotation_blocks,
'entanglement_blocks': entanglement_blocks,
'entanglement': entanglement,
'repetitions': repetitions,
'skip_final_rotation_layer': skip_final_rotation_layer,
'energy (Ha)': energy,
'error (mHa)': (energy-exact_energy)*1000,
'pass': (energy-exact_energy)*1000 <= accuracy_threshold,
'# of parameters': len(result.optimal_point),
'final parameters': result.optimal_point,
'# of evaluations': result.optimizer_evals,
'optimizer time': result.optimizer_time,
'# of qubits': int(qubit_op.num_qubits),
'# of CNOTs': cnots,
'score': score}
else:
result_dict = {
'optimizer': optimizer.__class__.__name__,
'mapping': converter.mapper.__class__.__name__,
'ansatz': ansatz.__class__.__name__,
'rotation blocks': None,
'entanglement_blocks': None,
'entanglement': None,
'repetitions': None,
'skip_final_rotation_layer': None,
'energy (Ha)': energy,
'error (mHa)': (energy-exact_energy)*1000,
'pass': (energy-exact_energy)*1000 <= accuracy_threshold,
'# of parameters': len(result.optimal_point),
'final parameters': result.optimal_point,
'# of evaluations': result.optimizer_evals,
'optimizer time': result.optimizer_time,
'# of qubits': int(qubit_op.num_qubits),
'# of CNOTs': cnots,
'score': score}
# Plot the results
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
ax.set_xlabel('Iterations')
ax.set_ylabel('Energy')
ax.grid()
fig.text(0.7, 0.75, f'Energy: {result.optimal_value:.3f}\nScore: {score:.0f}')
plt.title(f"{result_dict['optimizer']}-{result_dict['mapping']}\n{result_dict['ansatz']}")
ax.plot(counts, values)
ax.axhline(exact_energy, linestyle='--')
fig_title = f"\
{result_dict['optimizer']}-\
{result_dict['mapping']}-\
{result_dict['ansatz']}-\
Energy({result_dict['energy (Ha)']:.3f})-\
Score({result_dict['score']:.0f})\
.png"
fig.savefig(fig_title, dpi=300)
# Display and save the data
import pandas as pd
import os.path
filename = 'results_h2.csv'
if os.path.isfile(filename):
result_df = pd.read_csv(filename)
result_df = result_df.append([result_dict])
else:
result_df = pd.DataFrame.from_dict([result_dict])
result_df.to_csv(filename)
result_df[['optimizer','ansatz', '# of qubits', '# of parameters','rotation blocks', 'entanglement_blocks',
'entanglement', 'repetitions', 'error (mHa)', 'pass', 'score']]
# Check your answer using following code
from qc_grader import grade_ex5
freeze_core = True # change to True if you freezed core electrons
grade_ex5(ansatz,qubit_op,result,freeze_core)
```
Thank you very much for this awesome challenge. Without the outline, explanations, examples and hints I would have never been able to solve this in a reasonable time.
I will definitely save this Notebook along with the other exercises as a bluprint for the future.
| true |
code
| 0.637115 | null | null | null | null |
|
# Training Models
```
import numpy as np
import pandas as pd
import os
import sys
import matplotlib as mpl
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "training_linear_models"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
## Linear regression using the Normal Equation
```
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
save_fig("generated_data_plot")
plt.show()
X_b = np.c_[np.ones((100, 1)), X]
theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new] # add x0 = 1 to each instance
y_predict = X_new_b.dot(theta)
y_predict
plt.plot(X_new, y_predict, 'r-')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 15])
plt.show()
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
lin_reg.predict(X_new)
```
### Linear regression using batch gradient descent
```
eta = 0.1
n_iterations = 100
m = 100
theta = np.random.randn(2, 1)
for i in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta*gradients
theta
```
### Stochastic Gradient Descent
```
n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2*xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch*m+i)
theta = theta - eta * gradients
theta
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=1000, tol=1e-3, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
```
### Mini-batch Gradient Descent
```
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1) # random initialization
t0, t1 = 200, 1000
def learning_schedule(t):
return t0 / (t + t1)
t = 0
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, minibatch_size):
t += 1
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(t)
theta = theta - eta * gradients
theta_path_mgd.append(theta)
theta
```
### Polynomial Regression
```
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_data_plot")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
X_poly[0]
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_predictions_plot")
plt.show()
```
### Learning Curves
```
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
train_errors, val_errors = [], []
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_pred = model.predict(X_train[:m])
y_val_pred = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_pred))
val_errors.append(mean_squared_error(y_val, y_val_pred))
plt.plot(np.sqrt(train_errors), 'r-+', linewidth=2, label='train')
plt.plot(np.sqrt(val_errors), 'b-', linewidth=3, label='val')
plt.show()
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
```
### Ridge Regression
```
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver='cholesky')
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
```
### Lasso Regression
```
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
```
### Elastic Net
```
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
```
### Logistic Regression
```
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())
X = iris['data'][:, 3:]
y = (iris['target'] ==2).astype(np.int)
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X, y)
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
y_proba
plt.plot(X_new, y_proba[:,1], 'g-', label='Iris-Virginica')
plt.plot(X_new, y_proba[:,0], 'b--', label='Not Iris-Virginica')
plt.xlabel("Petal width", fontsize=18)
plt.ylabel("Probability", fontsize=18)
plt.legend()
plt.show()
```
### Softmax Regression
```
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)
softmax_reg.predict([[3, 4]])
softmax_reg.predict_proba([[3, 4]])
```
| true |
code
| 0.568775 | null | null | null | null |
|
## Convolutional Neural Network for MNIST image classficiation
```
import numpy as np
# from sklearn.utils.extmath import softmax
from matplotlib import pyplot as plt
import re
from tqdm import trange
from sklearn import metrics
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from mpl_toolkits.axes_grid1 import make_axes_locatable
import pandas as pd
from sklearn.datasets import fetch_openml
import matplotlib.gridspec as gridspec
from sklearn.decomposition import PCA
plt.rcParams['font.family'] = 'serif'
plt.rcParams['font.serif'] = ['Times New Roman'] + plt.rcParams['font.serif']
```
## Alternating Least Squares for Matrix Factorization
```
def coding_within_radius(X, W, H0,
r=None,
a1=0, #L1 regularizer
a2=0, #L2 regularizer
sub_iter=[5],
stopping_grad_ratio=0.0001,
nonnegativity=True,
subsample_ratio=1):
"""
Find \hat{H} = argmin_H ( || X - WH||_{F}^2 + a1*|H| + a2*|H|_{F}^{2} ) within radius r from H0
Use row-wise projected gradient descent
"""
H1 = H0.copy()
i = 0
dist = 1
idx = np.arange(X.shape[1])
if subsample_ratio>1: # subsample columns of X and solve reduced problem (like in SGD)
idx = np.random.randint(X.shape[1], size=X.shape[1]//subsample_ratio)
A = W.T @ W ## Needed for gradient computation
B = W.T @ X[:,idx]
while (i < np.random.choice(sub_iter)):
if_continue = np.ones(H0.shape[0]) # indexed by rows of H
H1_old = H1.copy()
for k in [k for k in np.arange(H0.shape[0])]:
grad = (np.dot(A[k, :], H1[:,idx]) - B[k,:] + a1 * np.ones(len(idx))) + a2 * 2 * np.sign(H1[k,idx])
grad_norm = np.linalg.norm(grad, 2)
step_size = (1 / (((i + 1) ** (1)) * (A[k, k] + 1)))
if r is not None: # usual sparse coding without radius restriction
d = step_size * grad_norm
step_size = (r / max(r, d)) * step_size
if step_size * grad_norm / np.linalg.norm(H1_old, 2) > stopping_grad_ratio:
H1[k, idx] = H1[k, idx] - step_size * grad
if nonnegativity:
H1[k,idx] = np.maximum(H1[k,idx], np.zeros(shape=(len(idx),))) # nonnegativity constraint
i = i + 1
return H1
def ALS(X,
n_components = 10, # number of columns in the dictionary matrix W
n_iter=100,
a0 = 0, # L1 regularizer for H
a1 = 0, # L1 regularizer for W
a12 = 0, # L2 regularizer for W
H_nonnegativity=True,
W_nonnegativity=True,
compute_recons_error=False,
subsample_ratio = 10):
'''
Given data matrix X, use alternating least squares to find factors W,H so that
|| X - WH ||_{F}^2 + a0*|H|_{1} + a1*|W|_{1} + a12 * |W|_{F}^{2}
is minimized (at least locally)
'''
d, n = X.shape
r = n_components
#normalization = np.linalg.norm(X.reshape(-1,1),1)/np.product(X.shape) # avg entry of X
#print('!!! avg entry of X', normalization)
#X = X/normalization
# Initialize factors
W = np.random.rand(d,r)
H = np.random.rand(r,n)
# H = H * np.linalg.norm(X) / np.linalg.norm(H)
for i in trange(n_iter):
H = coding_within_radius(X, W.copy(), H.copy(), a1=a0, nonnegativity=H_nonnegativity, subsample_ratio=subsample_ratio)
W = coding_within_radius(X.T, H.copy().T, W.copy().T, a1=a1, a2=a12, nonnegativity=W_nonnegativity, subsample_ratio=subsample_ratio).T
if compute_recons_error and (i % 10 == 0) :
print('iteration %i, reconstruction error %f' % (i, np.linalg.norm(X-W@H)**2))
return W, H
# Simulated Data and its factorization
W0 = np.random.rand(10,5)
H0 = np.random.rand(5,20)
X0 = W0 @ H0
W, H = ALS(X=X0,
n_components=5,
n_iter=100,
a0 = 0, # L1 regularizer for H
a1 = 1, # L1 regularizer for W
a12 = 0, # L2 regularizer for W
H_nonnegativity=True,
W_nonnegativity=True,
compute_recons_error=True,
subsample_ratio=1)
print('reconstruction error (relative) = %f' % (np.linalg.norm(X0-W@H)**2/np.linalg.norm(X0)**2))
print('Dictionary error (relative) = %f' % (np.linalg.norm(W0 - W)**2/np.linalg.norm(W0)**2))
print('Code error (relative) = %f' % (np.linalg.norm(H0-H)**2/np.linalg.norm(H0)**2))
```
# Learn dictionary of MNIST images
```
def display_dictionary(W, save_name=None, score=None, grid_shape=None):
k = int(np.sqrt(W.shape[0]))
rows = int(np.sqrt(W.shape[1]))
cols = int(np.sqrt(W.shape[1]))
if grid_shape is not None:
rows = grid_shape[0]
cols = grid_shape[1]
figsize0=(6, 6)
if (score is None) and (grid_shape is not None):
figsize0=(cols, rows)
if (score is not None) and (grid_shape is not None):
figsize0=(cols, rows+0.2)
fig, axs = plt.subplots(nrows=rows, ncols=cols, figsize=figsize0,
subplot_kw={'xticks': [], 'yticks': []})
for ax, i in zip(axs.flat, range(100)):
if score is not None:
idx = np.argsort(score)
idx = np.flip(idx)
ax.imshow(W.T[idx[i]].reshape(k, k), cmap="viridis", interpolation='nearest')
ax.set_xlabel('%1.2f' % score[i], fontsize=13) # get the largest first
ax.xaxis.set_label_coords(0.5, -0.05)
else:
ax.imshow(W.T[i].reshape(k, k), cmap="viridis", interpolation='nearest')
if score is not None:
ax.set_xlabel('%1.2f' % score[i], fontsize=13) # get the largest first
ax.xaxis.set_label_coords(0.5, -0.05)
plt.tight_layout()
# plt.suptitle('Dictionary learned from patches of size %d' % k, fontsize=16)
plt.subplots_adjust(0.08, 0.02, 0.92, 0.85, 0.08, 0.23)
if save_name is not None:
plt.savefig( save_name, bbox_inches='tight')
plt.show()
def display_dictionary_list(W_list, label_list, save_name=None, score_list=None):
# Make plot
# outer gridspec
nrows=1
ncols=len(W_list)
fig = plt.figure(figsize=(16, 5), constrained_layout=False)
outer_grid = gridspec.GridSpec(nrows=nrows, ncols=ncols, wspace=0.1, hspace=0.05)
# make nested gridspecs
for i in range(1 * ncols):
k = int(np.sqrt(W_list[i].shape[0]))
sub_rows = int(np.sqrt(W_list[i].shape[1]))
sub_cols = int(np.sqrt(W_list[i].shape[1]))
idx = np.arange(W_list[i].shape[1])
if score_list is not None:
idx = np.argsort(score_list[i])
idx = np.flip(idx)
inner_grid = outer_grid[i].subgridspec(sub_rows, sub_cols, wspace=0.05, hspace=0.05)
for j in range(sub_rows*sub_cols):
a = j // sub_cols
b = j % sub_cols #sub-lattice indices
ax = fig.add_subplot(inner_grid[a, b])
ax.imshow(W_list[i].T[idx[j]].reshape(k, k), cmap="viridis", interpolation='nearest')
ax.set_xticks([])
if (b>0):
ax.set_yticks([])
if (a < sub_rows-1):
ax.set_xticks([])
if (a == 0) and (b==2):
#ax.set_title("W_nonnegativity$=$ %s \n H_nonnegativity$=$ %s"
# % (str(nonnegativity_list[i][0]), str(nonnegativity_list[i][1])), y=1.2, fontsize=14)
ax.set_title(label_list[i], y=1.2, fontsize=14)
if (score_list is not None) and (score_list[i] is not None):
ax.set_xlabel('%1.2f' % score_list[i][idx[j]], fontsize=13) # get the largest first
ax.xaxis.set_label_coords(0.5, -0.07)
# plt.suptitle('Dictionary learned from patches of size %d' % k, fontsize=16)
plt.subplots_adjust(0.08, 0.02, 0.92, 0.85, 0.08, 0.23)
plt.savefig(save_name, bbox_inches='tight')
# Load data from https://www.openml.org/d/554
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
# X = X.values ### Uncomment this line if you are having type errors in plotting. It is loading as a pandas dataframe, but our indexing is for numpy array.
X = X / 255.
print('X.shape', X.shape)
print('y.shape', y.shape)
'''
Each row of X is a vectroization of an image of 28 x 28 = 784 pixels.
The corresponding row of y holds the true class label from {0,1, .. , 9}.
'''
# Unconstrained matrix factorization and dictionary images
idx = np.random.choice(np.arange(X.shape[1]), 100)
X0 = X[idx,:].T
W, H = ALS(X=X0,
n_components=25,
n_iter=50,
subsample_ratio=1,
W_nonnegativity=False,
H_nonnegativity=False,
compute_recons_error=True)
display_dictionary(W)
# PCA and dictionary images (principal components)
pca = PCA(n_components=24)
pca.fit(X)
W = pca.components_.T
s = pca.singular_values_
display_dictionary(W, score=s, save_name = "MNIST_PCA_ex1.pdf", grid_shape=[1,24])
idx = np.random.choice(np.arange(X.shape[1]), 100)
X0 = X[idx,:].T
n_iter = 10
W_list = []
nonnegativitiy = [[False, False], [False, True], [True, True]]
for i in np.arange(3):
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
label_list = []
for i in np.arange(len(nonnegativitiy)):
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
display_dictionary_list(W_list=W_list, label_list = label_list, save_name = "MNIST_NMF_ex1.pdf")
# MF and PCA on MNIST
idx = np.random.choice(np.arange(X.shape[1]), 100)
X0 = X[idx,:].T
n_iter = 100
W_list = []
H_list = []
nonnegativitiy = ['PCA', [False, False], [False, True], [True, True]]
#PCA
pca = PCA(n_components=25)
pca.fit(X)
W = pca.components_.T
s = pca.singular_values_
W_list.append(W)
H_list.append(s)
# MF
for i in np.arange(1,len(nonnegativitiy)):
print('!!! nonnegativitiy[i]', nonnegativitiy[i])
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
H_list.append(H)
label_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
label = nonnegativitiy[0]
else:
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
score_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
score_list.append(H_list[0])
else:
H = H_list[i]
score = np.sum(abs(H), axis=1) # sum of the coefficients of each columns of W = overall usage
score_list.append(score)
display_dictionary_list(W_list=W_list,
label_list = label_list,
score_list = score_list,
save_name = "MNIST_PCA_NMF_ex1.pdf")
def random_padding(img, thickness=1):
# img = a x b image
[a,b] = img.shape
Y = np.zeros(shape=[a+thickness, b+thickness])
r_loc = np.random.choice(np.arange(thickness+1))
c_loc = np.random.choice(np.arange(thickness+1))
Y[r_loc:r_loc+a, c_loc:c_loc+b] = img
return Y
def list2onehot(y, list_classes):
"""
y = list of class lables of length n
output = n x k array, i th row = one-hot encoding of y[i] (e.g., [0,0,1,0,0])
"""
Y = np.zeros(shape = [len(y), len(list_classes)], dtype=int)
for i in np.arange(Y.shape[0]):
for j in np.arange(len(list_classes)):
if y[i] == list_classes[j]:
Y[i,j] = 1
return Y
def onehot2list(y, list_classes=None):
"""
y = n x k array, i th row = one-hot encoding of y[i] (e.g., [0,0,1,0,0])
output = list of class lables of length n
"""
if list_classes is None:
list_classes = np.arange(y.shape[1])
y_list = []
for i in np.arange(y.shape[0]):
idx = np.where(y[i,:]==1)
idx = idx[0][0]
y_list.append(list_classes[idx])
return y_list
def sample_multiclass_MNIST_padding(list_digits=['0','1', '2'], full_MNIST=[X,y], padding_thickness=10):
# get train and test set from MNIST of given digits
# e.g., list_digits = ['0', '1', '2']
# pad each 28 x 28 image with zeros so that it has now "padding_thickness" more rows and columns
# The original image is superimposed at a uniformly chosen location
if full_MNIST is not None:
X, y = full_MNIST
else:
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
X = X / 255.
Y = list2onehot(y.tolist(), list_digits)
idx = [i for i in np.arange(len(y)) if y[i] in list_digits] # list of indices where the label y is in list_digits
X01 = X[idx,:]
y01 = Y[idx,:]
X_train = []
X_test = []
y_test = [] # list of one-hot encodings (indicator vectors) of each label
y_train = [] # list of one-hot encodings (indicator vectors) of each label
for i in trange(X01.shape[0]):
# for each example i, make it into train set with probabiliy 0.8 and into test set otherwise
U = np.random.rand() # Uniform([0,1]) variable
img_padded = random_padding(X01[i,:].reshape(28,28), thickness=padding_thickness)
img_padded_vec = img_padded.reshape(1,-1)
if U<0.8:
X_train.append(img_padded_vec[0,:].copy())
y_train.append(y01[i,:].copy())
else:
X_test.append(img_padded_vec[0,:].copy())
y_test.append(y01[i,:].copy())
X_train = np.asarray(X_train)
X_test = np.asarray(X_test)
y_train = np.asarray(y_train)
y_test = np.asarray(y_test)
return X_train, X_test, y_train, y_test
# Simple MNIST binary classification experiments
list_digits=['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
X_train, X_test, y_train, y_test = sample_multiclass_MNIST_padding(list_digits=list_digits,
full_MNIST=[X,y],
padding_thickness=20)
idx = np.random.choice(np.arange(X_train.shape[1]), 100)
X0 = X_train[idx,:].T
n_iter = 100
W_list = []
nonnegativitiy = [[False, False], [False, True], [True, True]]
for i in np.arange(3):
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
label_list = []
for i in np.arange(len(nonnegativitiy)):
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
display_dictionary_list(W_list=W_list, label_list = label_list, save_name = "MNIST_NMF_ex2.pdf")
# MF and PCA on MNIST + padding
list_digits=['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
X_train, X_test, y_train, y_test = sample_multiclass_MNIST_padding(list_digits=list_digits,
full_MNIST=[X,y],
padding_thickness=20)
idx = np.random.choice(np.arange(X.shape[1]), 100)
X0 = X_train[idx,:].T
n_iter = 100
W_list = []
H_list = []
nonnegativitiy = ['PCA', [False, False], [False, True], [True, True]]
#PCA
pca = PCA(n_components=25)
pca.fit(X)
W = pca.components_.T
s = pca.singular_values_
W_list.append(W)
H_list.append(s)
# MF
for i in np.arange(1,len(nonnegativitiy)):
print('!!! nonnegativitiy[i]', nonnegativitiy[i])
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
H_list.append(H)
label_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
label = nonnegativitiy[0]
else:
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
score_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
score_list.append(H_list[0])
else:
H = H_list[i]
score = np.sum(abs(H), axis=1) # sum of the coefficients of each columns of W = overall usage
score_list.append(score)
display_dictionary_list(W_list=W_list,
label_list = label_list,
score_list = score_list,
save_name = "MNIST_PCA_NMF_ex2.pdf")
```
## Dictionary Learing for Face datasets
```
from sklearn.datasets import fetch_olivetti_faces
faces, _ = fetch_olivetti_faces(return_X_y=True, shuffle=True,
random_state=np.random.seed(0))
n_samples, n_features = faces.shape
# global centering
#faces_centered = faces - faces.mean(axis=0)
# local centering
#faces_centered -= faces_centered.mean(axis=1).reshape(n_samples, -1)
print("Dataset consists of %d faces" % n_samples)
print("faces_centered.shape", faces.shape)
# Plot some sample images
ncols = 10
nrows = 4
fig, ax = plt.subplots(nrows=nrows, ncols=ncols, figsize=[15, 6.5])
for j in np.arange(ncols):
for i in np.arange(nrows):
ax[i,j].imshow(faces[i*ncols + j].reshape(64,64), cmap="gray")
#if i == 0:
# ax[i,j].set_title("label$=$%s" % y[idx_subsampled[i]], fontsize=14)
# ax[i].legend()
plt.subplots_adjust(wspace=0.3, hspace=-0.1)
plt.savefig('Faces_ex1.pdf', bbox_inches='tight')
# PCA and dictionary images (principal components)
X0 = faces.T
pca = PCA(n_components=24)
pca.fit(X0.T)
W = pca.components_.T
s = pca.singular_values_
display_dictionary(W, score=s, save_name = "Faces_PCA_ex1.pdf", grid_shape=[2,12])
# Variable nonnegativity constraints
X0 = faces.T
#X0 /= 100 * np.linalg.norm(X0)
n_iter = 200
W_list = []
nonnegativitiy = [[False, False], [False, True], [True, True]]
for i in np.arange(3):
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
label_list = []
for i in np.arange(len(nonnegativitiy)):
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
display_dictionary_list(W_list=W_list, label_list = label_list, save_name = "Face_NMF_ex1.pdf")
n_iter = 200
W_list = []
H_list = []
X0 = faces.T
#X0 /= 100 * np.linalg.norm(X0)
nonnegativitiy = ['PCA', [False, False], [False, True], [True, True]]
#PCA
pca = PCA(n_components=25)
pca.fit(X0.T)
W = pca.components_.T
s = pca.singular_values_
W_list.append(W)
H_list.append(s)
# MF
for i in np.arange(1,len(nonnegativitiy)):
print('!!! nonnegativitiy[i]', nonnegativitiy[i])
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
W_nonnegativity=nonnegativitiy[i][0],
H_nonnegativity=nonnegativitiy[i][1],
compute_recons_error=True)
W_list.append(W)
H_list.append(H)
label_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
label = nonnegativitiy[0]
else:
label = "W_nonnegativity = %s" % nonnegativitiy[i][0] + "\n" + "H_nonnegativity = %s" % nonnegativitiy[i][1]
label_list.append(label)
score_list = []
for i in np.arange(len(nonnegativitiy)):
if i == 0:
score_list.append(H_list[0])
else:
H = H_list[i]
score = np.sum(abs(H), axis=1) # sum of the coefficients of each columns of W = overall usage
score_list.append(score)
display_dictionary_list(W_list=W_list,
label_list = label_list,
score_list = score_list,
save_name = "Faces_PCA_NMF_ex1.pdf")
# Variable regularizer for W
X0 = faces.T
print('X0.shape', X0.shape)
n_iter = 200
W_list = []
W_sparsity = [[0, 0], [0.5, 0], [0, 3]]
for i in np.arange(3):
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
a1 = W_sparsity[i][0], # L1 regularizer for W
a12 = W_sparsity[i][1], # L2 regularizer for W
W_nonnegativity=True,
H_nonnegativity=True,
compute_recons_error=True)
W_list.append(W)
label_list = []
for i in np.arange(len(W_sparsity)):
label = "W_$L_{1}$-regularizer = %.2f" % W_sparsity[i][0] + "\n" + "W_$L_{2}$-regularizer = %.2f" % W_sparsity[i][1]
label_list.append(label)
display_dictionary_list(W_list=W_list, label_list = label_list, save_name = "Face_NMF_ex2.pdf")
n_iter = 200
W_list = []
H_list = []
X0 = faces.T
#X0 /= 100 * np.linalg.norm(X0)
W_sparsity = ['PCA', [0, 0], [0.5, 0], [0, 3]]
#PCA
pca = PCA(n_components=25)
pca.fit(X0.T)
W = pca.components_.T
s = pca.singular_values_
W_list.append(W)
H_list.append(s)
# MF
for i in np.arange(1,len(nonnegativitiy)):
print('!!! nonnegativitiy[i]', nonnegativitiy[i])
W, H = ALS(X=X0,
n_components=25,
n_iter=n_iter,
subsample_ratio=1,
a1 = W_sparsity[i][0], # L1 regularizer for W
a12 = W_sparsity[i][1], # L2 regularizer for W
W_nonnegativity=True,
H_nonnegativity=True,
compute_recons_error=True)
W_list.append(W)
H_list.append(H)
label_list = []
for i in np.arange(len(W_sparsity)):
if i == 0:
label = nonnegativitiy[0]
else:
label = "W_$L_{1}$-regularizer = %.2f" % W_sparsity[i][0] + "\n" + "W_$L_{2}$-regularizer = %.2f" % W_sparsity[i][1]
label_list.append(label)
score_list = []
for i in np.arange(len(W_sparsity)):
if i == 0:
score_list.append(H_list[0])
else:
H = H_list[i]
score = np.sum(abs(H), axis=1) # sum of the coefficients of each columns of W = overall usage
score_list.append(score)
display_dictionary_list(W_list=W_list,
label_list = label_list,
score_list = score_list,
save_name = "Faces_PCA_NMF_ex2.pdf")
```
## Topic modeling for 20Newsgroups dataset
```
from nltk.corpus import stopwords
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from wordcloud import WordCloud, STOPWORDS
from scipy.stats import entropy
import pandas as pd
def list2onehot(y, list_classes):
"""
y = list of class lables of length n
output = n x k array, i th row = one-hot encoding of y[i] (e.g., [0,0,1,0,0])
"""
Y = np.zeros(shape = [len(y), len(list_classes)], dtype=int)
for i in np.arange(Y.shape[0]):
for j in np.arange(len(list_classes)):
if y[i] == list_classes[j]:
Y[i,j] = 1
return Y
def onehot2list(y, list_classes=None):
"""
y = n x k array, i th row = one-hot encoding of y[i] (e.g., [0,0,1,0,0])
output = list of class lables of length n
"""
if list_classes is None:
list_classes = np.arange(y.shape[1])
y_list = []
for i in np.arange(y.shape[0]):
idx = np.where(y[i,:]==1)
idx = idx[0][0]
y_list.append(list_classes[idx])
return y_list
remove = ('headers','footers','quotes')
stopwords_list = stopwords.words('english')
stopwords_list.extend(['thanks','edu','also','would','one','could','please','really','many','anyone','good','right','get','even','want','must','something','well','much','still','said','stay','away','first','looking','things','try','take','look','make','may','include','thing','like','two','or','etc','phone','oh','email'])
categories = [
'comp.graphics',
'comp.sys.mac.hardware',
'misc.forsale',
'rec.motorcycles',
'rec.sport.baseball',
'sci.med',
'sci.space',
'talk.politics.guns',
'talk.politics.mideast',
'talk.religion.misc'
]
newsgroups_train = fetch_20newsgroups(subset='train', categories=categories, remove=remove)
newsgroups_labels = newsgroups_train.target
# remove numbers
data_cleaned = [re.sub(r'\d+','', file) for file in newsgroups_train.data]
# print 10 random documents
#for i in np.arange(10):
# idx = np.random.choice(len(data_cleaned))
# print('>>>> %i th doc \n\n %s \n\n' % (idx, data_cleaned[idx]))
print('len(newsgroups_labels)', len(newsgroups_labels))
print('newsgroups_labels', newsgroups_labels)
print('data_cleaned[1]', data_cleaned[1])
print('newsgroups_labels[1]', newsgroups_labels[1])
# vectorizer = TfidfVectorizer(stop_words=stopwords_list)
vectorizer_BOW = CountVectorizer(stop_words=stopwords_list)
vectors_BOW = vectorizer_BOW.fit_transform(data_cleaned).transpose() # words x docs # in the form of sparse matrix
vectorizer = TfidfVectorizer(stop_words=stopwords_list)
vectors = vectorizer.fit_transform(data_cleaned).transpose() # words x docs # in the form of sparse matrix
idx_to_word = np.array(vectorizer.get_feature_names()) # list of words that corresponds to feature coordinates
print('>>>> vectors.shape', vectors.shape)
i = 4257
print('newsgroups_labels[i]', newsgroups_labels[i])
print('>>>> data_cleaned[i]', data_cleaned[i])
# print('>>>> vectors[:,i] \n', vectors[:,i])
a = vectors[:,i].todense()
I = np.where(a>0)
count_list = []
word_list = []
for j in np.arange(len(I[0])):
# idx = np.random.choice(I[0])
idx = I[0][j]
# print('>>>> %i th coordinate <===> %s, count %i' % (idx, idx_to_word[idx], vectors[idx, i]))
count_list.append([idx, vectors_BOW[idx, i], vectors[idx, i]])
word_list.append(idx_to_word[idx])
d = pd.DataFrame(data=np.asarray(count_list).T, columns=word_list).T
d.columns = ['Coordinate', 'Bag-of-words', 'tf-idf']
cols = ['Coordinate', 'Bag-of-words']
d[cols] = d[cols].applymap(np.int64)
print(d)
def sample_multiclass_20NEWS(list_classes=[0, 1], full_data=None, vectorizer = 'tf-idf', verbose=True):
# get train and test set from 20NewsGroups of given categories
# vectorizer \in ['tf-idf', 'bag-of-words']
# documents are loaded up from the following 10 categories
categories = [
'comp.graphics',
'comp.sys.mac.hardware',
'misc.forsale',
'rec.motorcycles',
'rec.sport.baseball',
'sci.med',
'sci.space',
'talk.politics.guns',
'talk.politics.mideast',
'talk.religion.misc'
]
data_dict = {}
data_dict.update({'categories': categories})
if full_data is None:
remove = ('headers','footers','quotes')
stopwords_list = stopwords.words('english')
stopwords_list.extend(['thanks','edu','also','would','one','could','please','really','many','anyone','good','right','get','even','want','must','something','well','much','still','said','stay','away','first','looking','things','try','take','look','make','may','include','thing','like','two','or','etc','phone','oh','email'])
newsgroups_train_full = fetch_20newsgroups(subset='train', categories=categories, remove=remove) # raw documents
newsgroups_train = [re.sub(r'\d+','', file) for file in newsgroups_train_full.data] # remove numbers (we are only interested in words)
y = newsgroups_train_full.target # document class labels
Y = list2onehot(y.tolist(), list_classes)
if vectorizer == 'tfidf':
vectorizer = TfidfVectorizer(stop_words=stopwords_list)
else:
vectorizer = CountVectorizer(stop_words=stopwords_list)
X = vectorizer.fit_transform(newsgroups_train) # words x docs # in the form of sparse matrix
X = np.asarray(X.todense())
print('!! X.shape', X.shape)
idx2word = np.array(vectorizer.get_feature_names()) # list of words that corresponds to feature coordinates
data_dict.update({'newsgroups_train': data_cleaned})
data_dict.update({'newsgroups_labels': y})
data_dict.update({'feature_matrix': vectors})
data_dict.update({'idx2word': idx2word})
else:
X, y = full_data
idx = [i for i in np.arange(len(y)) if y[i] in list_classes] # list of indices where the label y is in list_classes
X01 = X[idx,:]
Y01 = Y[idx,:]
X_train = []
X_test = []
y_test = [] # list of one-hot encodings (indicator vectors) of each label
y_train = [] # list of one-hot encodings (indicator vectors) of each label
for i in np.arange(X01.shape[0]):
# for each example i, make it into train set with probabiliy 0.8 and into test set otherwise
U = np.random.rand() # Uniform([0,1]) variable
if U<0.8:
X_train.append(X01[i,:])
y_train.append(Y01[i,:].copy())
else:
X_test.append(X01[i,:])
y_test.append(Y01[i,:].copy())
X_train = np.asarray(X_train)
X_test = np.asarray(X_test)
y_train = np.asarray(y_train)
y_test = np.asarray(y_test)
data_dict.update({'X_train': X_train})
data_dict.update({'X_test': X_test})
data_dict.update({'y_train': y_train})
data_dict.update({'y_test': y_test})
return X_train, X_test, y_train, y_test, data_dict
# test
X_train, X_test, y_train, y_test, data_dict = sample_multiclass_20NEWS(list_classes=[0, 1, 2,3,4,5,6,7,8,9],
vectorizer = 'tf-idf',
full_data=None)
print('X_train.shape', X_train.shape)
print('X_test.shape', X_test.shape)
print('y_train.shape', y_train.shape)
print('y_test.shape', y_test.shape)
print('y_test', y_test)
#print('y_list', onehot2list(y_test))
idx2word = data_dict.get('idx2word')
categories = data_dict.get('categories')
import random
def grey_color_func(word, font_size, position, orientation, random_state=None,
**kwargs):
return "hsl(0, 0%%, %d%%)" % random.randint(60, 100)
def plot_topic_wordcloud(W, idx2word, num_keywords_in_topic=5, save_name=None, grid_shape = [2,5]):
# plot the class-conditioanl PMF as wordclouds
# W = (p x r) (words x topic)
# idx2words = list of words used in the vectorization of documents
# categories = list of class labels
# prior on class labels = empirical PMF = [ # class i examples / total ]
# class-conditional for class i = [ # word j in class i examples / # words in class i examples]
fig, axs = plt.subplots(nrows=grid_shape[0], ncols=grid_shape[1], figsize=(15, 6), subplot_kw={'xticks': [], 'yticks': []})
for ax, i in zip(axs.flat, np.arange(W.shape[1])):
# dist = W[:,i]/np.sum(W[:,i])
### Take top k keywords in each topic (top k coordinates in each column of W)
### to generate text data corresponding to the ith topic, and then generate its wordcloud
list_words = []
idx = np.argsort(W[:,i])
idx = np.flip(idx)
for j in range(num_keywords_in_topic):
list_words.append(idx2word[idx[j]])
Y = " ".join(list_words)
#stopwords = STOPWORDS
#stopwords.update(["’", "“", "”", "000", "000 000", "https", "co", "19", "2019", "coronavirus",
# "virus", "corona", "covid", "ncov", "covid19", "amp"])
wc = WordCloud(background_color="black",
relative_scaling=0,
width=400,
height=400).generate(Y)
ax.imshow(wc.recolor(color_func=grey_color_func, random_state=3),
interpolation="bilinear")
# ax.set_xlabel(categories[i], fontsize='20')
# ax.axis("off")
plt.tight_layout()
plt.subplots_adjust(0.08, 0.02, 0.92, 0.85, 0.08, 0.08)
if save_name is not None:
plt.savefig(save_name, bbox_inches='tight')
X0 = X_train.T
print('X0.shape', X0.shape)
W, H = ALS(X=X0,
n_components=10,
n_iter=20,
subsample_ratio=1,
a1 = 0, # L1 regularizer for W
a12 = 0, # L2 regularizer for W
W_nonnegativity=True,
H_nonnegativity=True,
compute_recons_error=True)
plot_topic_wordcloud(W, idx2word=idx2word, num_keywords_in_topic=7, grid_shape=[2,5], save_name="20NEWS_topic1.pdf")
# Topic modeling by NMF
X0 = X_train.T
W, H = ALS(X=X0,
n_components=10,
n_iter=20,
subsample_ratio=1,
a1 = 0, # L1 regularizer for W
a12 = 0, # L2 regularizer for W
W_nonnegativity=True,
H_nonnegativity=False,
compute_recons_error=True)
plot_topic_wordcloud(W, idx2word=idx2word, num_keywords_in_topic=7, grid_shape = [2,5], save_name="20NEWS_topic2.pdf")
```
## EM algorithm for PCA
```
# Gram-Schmidt Orthogonalization of a given matrix
def orthogonalize(U, eps=1e-15):
"""
Orthogonalizes the matrix U (d x n) using Gram-Schmidt Orthogonalization.
If the columns of U are linearly dependent with rank(U) = r, the last n-r columns
will be 0.
Args:
U (numpy.array): A d x n matrix with columns that need to be orthogonalized.
eps (float): Threshold value below which numbers are regarded as 0 (default=1e-15).
Returns:
(numpy.array): A d x n orthogonal matrix. If the input matrix U's cols were
not linearly independent, then the last n-r cols are zeros.
"""
n = len(U[0])
# numpy can readily reference rows using indices, but referencing full rows is a little
# dirty. So, work with transpose(U)
V = U.T
for i in range(n):
prev_basis = V[0:i] # orthonormal basis before V[i]
coeff_vec = np.dot(prev_basis, V[i].T) # each entry is np.dot(V[j], V[i]) for all j < i
# subtract projections of V[i] onto already determined basis V[0:i]
V[i] -= np.dot(coeff_vec, prev_basis).T
if np.linalg.norm(V[i]) < eps:
V[i][V[i] < eps] = 0. # set the small entries to 0
else:
V[i] /= np.linalg.norm(V[i])
return V.T
# Example:
A = np.random.rand(2,2)
print('A \n', A)
print('orthogonalize(A) \n', orthogonalize(A))
print('A.T @ A \n', A.T @ A)
def EM_PCA(X,
n_components = 10, # number of columns in the dictionary matrix W
n_iter=10,
W_ini=None,
subsample_ratio=1,
n_workers = 1):
'''
Given data matrix X of shape (d x n), compute its rank r=n_components PCA:
\hat{W} = \argmax_{W} var(Proj_{W}(X))
= \argmin_{W} || X - Proj_{W}(X) ||_{F}^{2}
where W is an (d x r) matrix of rank r.
'''
d, n = X.shape
r = n_components
X_mean = np.mean(X, axis=1).reshape(-1,1)
X_centered = X - np.repeat(X_mean, X0.shape[1], axis=1)
print('subsample_size:', n//subsample_ratio)
# Initialize factors
W_list = []
loss_list = []
for i in trange(n_workers):
W = np.random.rand(d,r)
if W_ini is not None:
W = W_ini
A = np.zeros(shape=[r, n//subsample_ratio]) # aggregate matrix for code H
# Perform EM updates
for j in np.arange(n_iter):
idx_data = np.random.choice(np.arange(X.shape[1]), X.shape[1]//subsample_ratio, replace=False)
X1 = X_centered[:,idx_data]
H = np.linalg.inv(W.T @ W) @ (W.T @ X1) # E-step
# A = (1-(1/(j+1)))*A + (1/(j+1))*H # Aggregation
W = X1 @ H.T @ np.linalg.inv(H @ H.T) # M-step
# W = X1 @ A.T @ np.linalg.inv(A @ A.T) # M-step
# W = orthogonalize(W)
#if compute_recons_error and (j > n_iter-2) :
# print('iteration %i, reconstruction error %f' % (j, np.linalg.norm(X_centered-W@(W.T @ X_centered))))
W_list.append(W.copy())
loss_list.append(np.linalg.norm(X_centered-W@(W.T @ X_centered)))
idx = np.argsort(loss_list)[0]
W = W_list[idx]
print('loss_list',np.asarray(loss_list)[np.argsort(loss_list)])
return orthogonalize(W)
# Load Olivetti Face dataset
from sklearn.datasets import fetch_olivetti_faces
faces, _ = fetch_olivetti_faces(return_X_y=True, shuffle=True,
random_state=np.random.seed(0))
n_samples, n_features = faces.shape
# global centering
#faces_centered = faces - faces.mean(axis=0)
# local centering
#faces_centered -= faces_centered.mean(axis=1).reshape(n_samples, -1)
print("Dataset consists of %d faces" % n_samples)
print("faces_centered.shape", faces.shape)
# EM_PCA and dictionary images (principal components)
X0 = faces.T
W = EM_PCA(X0, W_ini = None, n_workers=10, n_iter=200, subsample_ratio=2, n_components=24)
display_dictionary(W, score=None, save_name = "Faces_EM_PCA_ex1.pdf", grid_shape=[2,12])
cov = np.cov(X0)
print('(cov @ W)[:,0] / W[:,0]', (cov @ W)[:,0] / W0[:,0])
print('var coeff', np.std((cov @ W)[:,0] / W[:,0]))
print('var coeff exact', np.std((cov @ W0)[:,0] / W0[:,0]))
# plot coefficients of Cov @ W / W for exact PCA and EM PCA
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 3))
pca = PCA(n_components=24)
pca.fit(X0.T)
W0 = pca.components_.T
axs[0].plot((cov @ W0)[:,0] / W0[:,0], label='Exact PCA, 1st comp.')
axs[0].legend(fontsize=13)
axs[1].plot((cov @ W)[:,0] / W[:,0], label='EM PCA, 1st comp.')
axs[1].legend(fontsize=13)
plt.savefig("EM_PCA_coeff_plot1.pdf", bbox_inches='tight')
X0 = faces.T
pca = PCA(n_components=24)
pca.fit(X0.T)
W0 = pca.components_.T
s = pca.singular_values_
cov = np.cov(X0)
print('(cov @ W)[:,0] / W[:,0]', (cov @ W0)[:,0] / W0[:,0])
display_dictionary(W0, score=s, save_name = "Faces_PCA_ex1.pdf", grid_shape=[2,12])
X_mean = np.sum(X0, axis=1).reshape(-1,1)/X0.shape[1]
X_centered = X0 - np.repeat(X_mean, X0.shape[1], axis=1)
Cov = (X_centered @ X_centered.T) / X0.shape[1]
(Cov @ W)[:,0] / W[:,0]
cov = np.cov(X0)
(cov @ W0)[:,0] / W0[:,0]
np.real(eig_val[0])
np.sort(np.real(eig_val))
x = np.array([
[0.387,4878, 5.42],
[0.723,12104,5.25],
[1,12756,5.52],
[1.524,6787,3.94],
])
#centering the data
x0 = x - np.mean(x, axis = 0)
cov = np.cov(x0, rowvar = False)
print('cov', cov)
print('cov', np.cov(x, rowvar = False))
evals , evecs = np.linalg.eigh(cov)
evals
```
| true |
code
| 0.655364 | null | null | null | null |
|
# About Notebook
- [**Kaggle Housing Dataset**](https://www.kaggle.com/ananthreddy/housing)
- Implement linear regression using:
1. **Batch** Gradient Descent
2. **Stochastic** Gradient Descent
3. **Mini-batch** Gradient Descent
**Note**: _Trying to implement using **PyTorch** instead of numpy_
```
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import torch
def banner(msg, _verbose=1):
if not _verbose:
return
print("-"*80)
print(msg.upper())
print("-"*80)
```
# Data import and preprocessing
```
df = pd.read_csv('Housing.csv', index_col=0)
def convert_to_binary(string):
return int('yes' in string)
for col in df.columns:
if df[col].dtype == 'object':
df[col] = df[col].apply(convert_to_binary)
data = df.values
scaler = StandardScaler()
data = scaler.fit_transform(data)
X = data[:, 1:]
y = data[:, 0]
print("X: ", X.shape)
print("y: ", y.shape)
X_train, X_valid, y_train, y_valid = map(torch.from_numpy, train_test_split(X, y, test_size=0.2))
print("X_train: ", X_train.shape)
print("y_train: ", y_train.shape)
print("X_valid: ", X_valid.shape)
print("y_valid: ", y_valid.shape)
class LinearRegression:
def __init__(self, X_train, y_train, X_valid, y_valid):
self.X_train = X_train
self.y_train = y_train
self.X_valid = X_valid
self.y_valid = y_valid
self.Theta = torch.randn((X_train.shape[1]+1)).type(type(X_train))
def _add_bias(self, tensor):
bias = torch.ones((tensor.shape[0], 1)).type(type(tensor))
return torch.cat((bias, tensor), 1)
def _forward(self, tensor):
return torch.matmul(
self._add_bias(tensor),
self.Theta
).view(-1)
def forward(self, train=True):
if train:
return self._forward(self.X_train)
else:
return self._forward(self.X_valid)
def _cost(self, X, y):
y_hat = self._forward(X)
mse = torch.sum(torch.pow(y_hat - y, 2))/2/X.shape[0]
return mse
def cost(self, train=True):
if train:
return self._cost(self.X_train, self.y_train)
else:
return self._cost(self.X_valid, self.y_valid)
def batch_update_vectorized(self):
m, _ = self.X_train.size()
return torch.matmul(
self._add_bias(self.X_train).transpose(0, 1),
(self.forward() - self.y_train)
) / m
def batch_update_iterative(self):
m, _ = self.X_train.size()
update_theta = None
X = self._add_bias(self.X_train)
for i in range(m):
if type(update_theta) == torch.DoubleTensor:
update_theta += (self._forward(self.X_train[i].view(1, -1)) - self.y_train[i]) * X[i]
else:
update_theta = (self._forward(self.X_train[i].view(1, -1)) - self.y_train[i]) * X[i]
return update_theta/m
def batch_train(self, tolerance=0.01, alpha=0.01):
converged = False
prev_cost = self.cost()
init_cost = prev_cost
num_epochs = 0
while not converged:
self.Theta = self.Theta - alpha * self.batch_update_vectorized()
cost = self.cost()
if (prev_cost - cost) < tolerance:
converged = True
prev_cost = cost
num_epochs += 1
banner("Batch")
print("\tepochs: ", num_epochs)
print("\tcost before optim: ", init_cost)
print("\tcost after optim: ", cost)
print("\ttolerance: ", tolerance)
print("\talpha: ", alpha)
def stochastic_train(self, tolerance=0.01, alpha=0.01):
converged = False
m, _ = self.X_train.size()
X = self._add_bias(self.X_train)
init_cost = self.cost()
num_epochs=0
while not converged:
prev_cost = self.cost()
for i in range(m):
self.Theta = self.Theta - alpha * (self._forward(self.X_train[i].view(1, -1)) - self.y_train[i]) * X[i]
cost = self.cost()
if prev_cost-cost < tolerance:
converged=True
num_epochs += 1
banner("Stochastic")
print("\tepochs: ", num_epochs)
print("\tcost before optim: ", init_cost)
print("\tcost after optim: ", cost)
print("\ttolerance: ", tolerance)
print("\talpha: ", alpha)
def mini_batch_train(self, tolerance=0.01, alpha=0.01, batch_size=8):
converged = False
m, _ = self.X_train.size()
X = self._add_bias(self.X_train)
init_cost = self.cost()
num_epochs=0
while not converged:
prev_cost = self.cost()
for i in range(0, m, batch_size):
self.Theta = self.Theta - alpha / batch_size * torch.matmul(
X[i:i+batch_size].transpose(0, 1),
self._forward(self.X_train[i: i+batch_size]) - self.y_train[i: i+batch_size]
)
cost = self.cost()
if prev_cost-cost < tolerance:
converged=True
num_epochs += 1
banner("Stochastic")
print("\tepochs: ", num_epochs)
print("\tcost before optim: ", init_cost)
print("\tcost after optim: ", cost)
print("\ttolerance: ", tolerance)
print("\talpha: ", alpha)
%%time
l = LinearRegression(X_train, y_train, X_valid, y_valid)
l.mini_batch_train()
%%time
l = LinearRegression(X_train, y_train, X_valid, y_valid)
l.stochastic_train()
%%time
l = LinearRegression(X_train, y_train, X_valid, y_valid)
l.batch_train()
```
| true |
code
| 0.533458 | null | null | null | null |
|
# EXAMPLE: Personal Workout Tracking Data
This Notebook provides an example on how to import data downloaded from a specific service Apple Health.
NOTE: This is still a work-in-progress.
# Dependencies and Libraries
```
from datetime import date, datetime as dt, timedelta as td
import pytz
import numpy as np
import pandas as pd
# functions to convert UTC to Eastern time zone and extract date/time elements
convert_tz = lambda x: x.to_pydatetime().replace(tzinfo=pytz.utc).astimezone(pytz.timezone('US/Eastern'))
get_year = lambda x: convert_tz(x).year
get_month = lambda x: '{}-{:02}'.format(convert_tz(x).year, convert_tz(x).month) #inefficient
get_date = lambda x: '{}-{:02}-{:02}'.format(convert_tz(x).year, convert_tz(x).month, convert_tz(x).day) #inefficient
get_day = lambda x: convert_tz(x).day
get_hour = lambda x: convert_tz(x).hour
get_day_of_week = lambda x: convert_tz(x).weekday()
```
# Import Data
# Workouts
```
# apple health
workouts = pd.read_csv("C:/Users/brand/Desktop/Healthcare Info Systems/90day_workouts.csv")
workouts.head()
```
# Drop unwanted metrics
```
new_workouts = workouts.drop(['Average Pace','Average Speed','Average Cadence','Elevation Ascended','Elevation Descended','Weather Temperature','Weather Humidity'], axis=1)
new_workouts.head()
age = input("Enter your age: ")
print(new_workouts.dtypes)
#new_workouts["Duration"] = pd.to_numeric(new_workouts.Duration, errors='coerce')
display(new_workouts.describe())
```
# Create Avg HR Intesnity
```
new_workouts['Avg Heart Rate Intensity'] = new_workouts['Average Heart Rate'] / input().age
# other try- new_workouts['Average Heart Rate'].div(age)
workouts.tail()
```
# Exercise Guidelines
```
# Minutes of Weekly Exercise
def getExer():
global ex_time
ex_time = input("Enter weekly exercise time in minutes: ")
print("For more educational information on recommended daily exercise for adults, visit", "\nhttps://health.gov/paguidenes/second-edition/pdf/Physical_Activity_Guidelines_2nd_edition.pdf#page=55")
print()
if int(ex_time) <= 149:
print("Your daily exercise time of", ex_time, "is less than recommended. Consider increasing it to achieve at least 150 minutes per week to improve your health.")
elif int(ex_time) >= 150 and int(ex_time) <= 300:
print("Your daily exercise time of", ex_time, "is within the recommended amount. Achieving 150-300 minutes per week will continue to improve your health.")
elif int(ex_time) >= 301:
print("Your daily exercise time of", ex_time, "exceeds the recommended amount. Your weekly total should benefit your health.")
else:
print("Invalid entry for minutes of daily exercise")
getExer()
```
| true |
code
| 0.240953 | null | null | null | null |
|
# Granger Causality with Google Trends - Did `itaewon class` cause `โคชูจัง`?
We will give an example of Granger casuality test with interests over time of `itaewon class` and `โคชูจัง` in Thailand during 2020-01 to 2020-04. During the time, gochujang went out of stock in many supermarkets supposedly because people micking the show. We are examining the hypothesis that the interst over time of `itaewon class` Granger causes that of `โคชูจัง`.
$x_t$ Granger causes $y_t$ means that the past values of $x_t$ could contain information that is useful in predicting $y_t$.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tqdm
import warnings
warnings.filterwarnings('ignore')
import matplotlib
matplotlib.rc('font', family='Ayuthaya') # MacOS
```
## 1. Get Trend Objects with Thailand Offset
We can get interest over time of a keyword with the unofficial `pytrends` library.
```
from pytrends.request import TrendReq
#get trend objects with thailand offset 7*60 = 420 minutes
trend = TrendReq(hl='th-TH', tz=420)
#compare 2 keywords
kw_list = ['โคชูจัง','itaewon class']
trend.build_payload(kw_list, geo='TH',timeframe='2020-01-01 2020-04-30')
df = trend.interest_over_time().iloc[:,:2]
df.head()
df.plot()
```
## 2. Stationarity Check: Augmented Dickey-Fuller Test
Stationarity is a pre-requisite for Granger causality test. We first use [augmented Dickey-Fuller test](https://en.wikipedia.org/wiki/Augmented_Dickey%E2%80%93Fuller_test) to detect stationarity. For the following model:
$$\Delta y_t = \alpha + \beta t + \gamma y_{t-1} + \delta_1 \Delta y_{t-1} + \cdots + \delta_{p-1} \Delta y_{t-p+1} + \varepsilon_t$$
where $\alpha$ is a constant, $\beta$ the coefficient on a time trend and $p$ the lag order of the autoregressive process. The null hypothesis is that $\gamma$ is 0; that is, $y_{t-1}$ does not have any valuable contribution to predicting $y_t$. If we reject the null hypothesis, that means $y_t$ does not have a unit root.
```
from statsmodels.tsa.stattools import adfuller
#test for stationarity with augmented dickey fuller test
def unit_root(name,series):
signif=0.05
r = adfuller(series, autolag='AIC')
output = {'test_statistic':round(r[0],4),'pvalue':round(r[1],4),'n_lags':round(r[2],4),'n_obs':r[3]}
p_value = output['pvalue']
def adjust(val,lenght=6):
return str(val).ljust(lenght)
print(f'Augmented Dickey-Fuller Test on "{name}"')
print('-'*47)
print(f'Null Hypothesis: Data has unit root. Non-Stationary.')
print(f'Observation = {output["n_obs"]}')
print(f'Significance Level = {signif}')
print(f'Test Statistic = {output["test_statistic"]}')
print(f'No. Lags Chosen = {output["n_lags"]}')
for key,val in r[4].items():
print(f'Critical value {adjust(key)} = {round(val,3)}')
if p_value <= signif:
print(f'=> P-Value = {p_value}. Rejecting null hypothesis.')
print(f'=> Series is stationary.')
else:
print(f'=> P-Value = {p_value}. Cannot reject the null hypothesis.')
print(f'=> "{name}" is non-stationary.')
```
2.1. `โคชูจัง` unit root test
```
name = 'โคชูจัง'
series = df.iloc[:,0]
unit_root(name,series)
```
2.2. `itaewon class` unit root test
```
name = 'itaewon class'
series = df.iloc[:,1]
unit_root(name,series)
```
We could not reject the null hypothesis of augmented Dickey-Fuller test for both time series. This should be evident just by looking at the plot that they are not stationary (have stable same means, variances, autocorrelations over time).
## 3. Taking 1st Difference
Most commonly used methods to "stationarize" a time series is to take the first difference aka $\frac{y_t-y_{t-1}}{y_{t-1}}$ of the time series.
```
diff_df = df.diff(1).dropna()
```
3.1. 1st Difference of `โคชูจัง` unit root test
```
name = 'โคชูจัง'
series = diff_df.iloc[:,0]
unit_root(name,series)
```
3.2. 1st Difference of `itaewon class` unit root test
```
name = 'itaewon class'
series = diff_df.iloc[:,1]
unit_root(name,series)
diff_df.plot()
```
- 1st Difference of `itaewon class` is stationary at 5% significance.
- 1st Difference of `โคชูจัง` is not stationary but 0.0564 is close enough to 5% significance, we are making an exception for this example.
## 5. Find Lag Length
Note that `maxlag` is an important hyperparameter that determines if your Granger test is significant or not. There are some criteria you can you to find that lag but as with any frequentist statistical test, you need to understand what assumptions you are making.
```
import statsmodels.tsa.api as smt
df_test = diff_df.copy()
df_test.head()
# make a VAR model
model = smt.VAR(df_test)
res = model.select_order(maxlags=None)
print(res.summary())
```
One thing to note is that this hyperparameter affects the conclusion of the test and the best solution is to have a strong theoretical assumption but if not the empirical methods above could be the next best thing.
```
#find the optimal lag
lags = list(range(1,23))
res = grangercausalitytests(df_test, maxlag=lags, verbose=False)
p_values = []
for i in lags:
p_values.append({'maxlag':i,
'ftest':res[i][0]['ssr_ftest'][1],
'chi2':res[i][0]['ssr_chi2test'][1],
'lr':res[i][0]['lrtest'][1],
'params_ftest':res[i][0]['params_ftest'][1],})
p_df = pd.DataFrame(p_values)
p_df.iloc[:,1:].plot()
```
## 6. Granger Causality Test
The Granger causality test the null hypothesis that $x_t$ **DOES NOT** Granger cause $y_t$ with the following models:
$$y_{t}=a_{0}+a_{1}y_{t-1}+a_{2}y_{t-2}+\cdots +a_{m}y_{t-m}+{\text{error}}_{t}$$
and
$$y_{t}=a_{0}+a_{1}y_{t-1}+a_{2}y_{t-2}+\cdots +a_{m}y_{t-m}+b_{p}x_{t-p}+\cdots +b_{q}x_{t-q}+{\text{error}}_{t}$$
An F-statistic is then calculated by ratio of residual sums of squares of these two models.
```
from statsmodels.tsa.stattools import grangercausalitytests
def granger_causation_matrix(data, variables,test,verbose=False):
x = pd.DataFrame(np.zeros((len(variables),len(variables))), columns=variables,index=variables)
for c in x.columns:
for r in x.index:
test_result = grangercausalitytests(data[[r,c]], maxlag=maxlag, verbose=False)
p_values = [round(test_result[i+1][0][test][1],4) for i in range(maxlag)]
if verbose:
print(f'Y = {r}, X= {c},P Values = {p_values}')
min_p_value = np.min(p_values)
x.loc[r,c] = min_p_value
x.columns = [var + '_x' for var in variables]
x.index = [var + '_y' for var in variables]
return x
# maxlag is the maximum lag that is possible number by statsmodels default
nobs = len(df_test.index)
maxlag = round(12*(nobs/100.)**(1/4.))
maxlag
data = df_test
variables = df_test.columns
```
#### 6.1. SSR based F test
```
test = 'ssr_ftest'
ssr_ftest = granger_causation_matrix(data, variables, test)
ssr_ftest['test'] = 'ssr_ftest'
```
#### 6.2. SSR based chi2 test
```
test = 'ssr_chi2test'
ssr_chi2test = granger_causation_matrix(data, variables, test)
ssr_chi2test['test'] = 'ssr_chi2test'
```
#### 6.3. Likelihood ratio test
```
test = 'lrtest'
lrtest = granger_causation_matrix(data, variables, test)
lrtest['test'] = 'lrtest'
```
#### 6.4. Parameter F test
```
test = 'params_ftest'
params_ftest = granger_causation_matrix(data, variables, test)
params_ftest['test'] = 'params_ftest'
frames = [ssr_ftest, ssr_chi2test, lrtest, params_ftest]
all_test = pd.concat(frames)
all_test
```
We may conclude that `itaewon class` Granger caused `โคชูจัง`, but `โคชูจัง` did not Granger cause `itaewon class`.
# What About Chicken and Eggs?
We use the annual chicken and eggs data from [Thurman and Fisher (1988) hosted by UIUC](http://www.econ.uiuc.edu/~econ536/Data/).
## 1. Get data from csv file
```
#chicken and eggs
chickeggs = pd.read_csv('chickeggs.csv')
chickeggs
#normalize for 1930 to be 1
df = chickeggs.iloc[:,1:]
df['chic'] = df.chic / df.chic[0]
df['egg'] = df.egg / df.egg[0]
df = df[['chic','egg']]
df
df.plot()
```
## 2. Stationarity check: Augmented Dickey-Fuller Test
2.1. `egg` unit root test
```
name = 'egg'
series = df.iloc[:,0]
unit_root(name,series)
```
2.2. `chic` unit root test
```
name = 'chic'
series = df.iloc[:,1]
unit_root(name,series)
```
## 3. Taking 1st Difference
```
diff_df = df.diff(1).dropna()
diff_df
diff_df.plot()
```
3.1. 1st Difference of `egg` unit root test
```
name = 'egg'
series = diff_df.iloc[:,0]
unit_root(name,series)
```
3.2. 1st Difference of `chic` unit root test
```
name = 'chic'
series = diff_df.iloc[:,1]
unit_root(name,series)
```
## 4. Find Lag Length
```
# make a VAR model
model = smt.VAR(diff_df)
res = model.select_order(maxlags=None)
print(res.summary())
#find the optimal lag
lags = list(range(1,23))
res = grangercausalitytests(diff_df, maxlag=lags, verbose=False)
p_values = []
for i in lags:
p_values.append({'maxlag':i,
'ftest':res[i][0]['ssr_ftest'][1],
'chi2':res[i][0]['ssr_chi2test'][1],
'lr':res[i][0]['lrtest'][1],
'params_ftest':res[i][0]['params_ftest'][1],})
p_df = pd.DataFrame(p_values)
print('Eggs Granger cause Chickens')
p_df.iloc[:,1:].plot()
#find the optimal lag
lags = list(range(1,23))
res = grangercausalitytests(diff_df[['egg','chic']], maxlag=lags, verbose=False)
p_values = []
for i in lags:
p_values.append({'maxlag':i,
'ftest':res[i][0]['ssr_ftest'][1],
'chi2':res[i][0]['ssr_chi2test'][1],
'lr':res[i][0]['lrtest'][1],
'params_ftest':res[i][0]['params_ftest'][1],})
p_df = pd.DataFrame(p_values)
print('Chickens Granger cause Eggs')
p_df.iloc[:,1:].plot()
```
## 5. Granger Causality Test
```
# nobs is number of observation
nobs = len(diff_df.index)
# maxlag is the maximum lag that is possible number
maxlag = round(12*(nobs/100.)**(1/4.))
data = diff_df
variables = diff_df.columns
```
#### 5.1. SSR based F test
```
test = 'ssr_ftest'
ssr_ftest = granger_causation_matrix(data, variables, test)
ssr_ftest['test'] = 'ssr_ftest'
```
#### 5.2. SSR based chi2 test
```
test = 'ssr_chi2test'
ssr_chi2test = granger_causation_matrix(data, variables, test)
ssr_chi2test['test'] = 'ssr_chi2test'
```
#### 5.3. Likelihood ratio test
```
test = 'lrtest'
lrtest = granger_causation_matrix(data, variables, test)
lrtest['test'] = 'lrtest'
```
#### 5.4. Parameter F test
```
test = 'params_ftest'
params_ftest = granger_causation_matrix(data, variables, test)
params_ftest['test'] = 'params_ftest'
frames = [ssr_ftest, ssr_chi2test, lrtest, params_ftest]
all_test = pd.concat(frames)
all_test
```
With this we can conclude that eggs Granger cause chickens!
| true |
code
| 0.283856 | null | null | null | null |
|
<table width=60% >
<tr style="background-color: white;">
<td><img src='https://www.creativedestructionlab.com/wp-content/uploads/2018/05/xanadu.jpg'></td>></td>
</tr>
</table>
---
<img src='https://raw.githubusercontent.com/XanaduAI/strawberryfields/master/doc/_static/strawberry-fields-text.png'>
---
<br>
<center> <h1> Gaussian boson sampling tutorial </h1></center>
To get a feel for how Strawberry Fields works, let's try coding a quantum program, Gaussian boson sampling.
## Background information: Gaussian states
A Gaussian state is one that can be described by a [Gaussian function](https://en.wikipedia.org/wiki/Gaussian_function) in the phase space. For example, for a single mode Gaussian state, squeezed in the $x$ quadrature by squeezing operator $S(r)$, could be described by the following [Wigner quasiprobability distribution](Wigner quasiprobability distribution):
$$W(x,p) = \frac{2}{\pi}e^{-2\sigma^2(x-\bar{x})^2 - 2(p-\bar{p})^2/\sigma^2}$$
where $\sigma$ represents the **squeezing**, and $\bar{x}$ and $\bar{p}$ are the mean **displacement**, respectively. For multimode states containing $N$ modes, this can be generalised; Gaussian states are uniquely defined by a [multivariate Gaussian function](https://en.wikipedia.org/wiki/Multivariate_normal_distribution), defined in terms of the **vector of means** ${\mu}$ and a **covariance matrix** $\sigma$.
### The position and momentum basis
For example, consider a single mode in the position and momentum quadrature basis (the default for Strawberry Fields). Assuming a Gaussian state with displacement $\alpha = \bar{x}+i\bar{p}$ and squeezing $\xi = r e^{i\phi}$ in the phase space, it has a vector of means and a covariance matrix given by:
$$ \mu = (\bar{x},\bar{p}),~~~~~~\sigma = SS\dagger=R(\phi/2)\begin{bmatrix}e^{-2r} & 0 \\0 & e^{2r} \\\end{bmatrix}R(\phi/2)^T$$
where $S$ is the squeezing operator, and $R(\phi)$ is the standard two-dimensional rotation matrix. For multiple modes, in Strawberry Fields we use the convention
$$ \mu = (\bar{x}_1,\bar{x}_2,\dots,\bar{x}_N,\bar{p}_1,\bar{p}_2,\dots,\bar{p}_N)$$
and therefore, considering $\phi=0$ for convenience, the multimode covariance matrix is simply
$$\sigma = \text{diag}(e^{-2r_1},\dots,e^{-2r_N},e^{2r_1},\dots,e^{2r_N})\in\mathbb{C}^{2N\times 2N}$$
If a continuous-variable state *cannot* be represented in the above form (for example, a single photon Fock state or a cat state), then it is non-Gaussian.
### The annihilation and creation operator basis
If we are instead working in the creation and annihilation operator basis, we can use the transformation of the single mode squeezing operator
$$ S(\xi) \left[\begin{matrix}\hat{a}\\\hat{a}^\dagger\end{matrix}\right] = \left[\begin{matrix}\cosh(r)&-e^{i\phi}\sinh(r)\\-e^{-i\phi}\sinh(r)&\cosh(r)\end{matrix}\right] \left[\begin{matrix}\hat{a}\\\hat{a}^\dagger\end{matrix}\right]$$
resulting in
$$\sigma = SS^\dagger = \left[\begin{matrix}\cosh(2r)&-e^{i\phi}\sinh(2r)\\-e^{-i\phi}\sinh(2r)&\cosh(2r)\end{matrix}\right]$$
For multiple Gaussian states with non-zero squeezing, the covariance matrix in this basis simply generalises to
$$\sigma = \text{diag}(S_1S_1^\dagger,\dots,S_NS_N^\dagger)\in\mathbb{C}^{2N\times 2N}$$
## Introduction to Gaussian boson sampling
<div class="alert alert-info">
“If you need to wait exponential time for \[your single photon sources to emit simultaneously\], then there would seem to be no advantage over classical computation. This is the reason why so far, boson sampling has only been demonstrated with 3-4 photons. When faced with these problems, until recently, all we could do was shrug our shoulders.” - [Scott Aaronson](https://www.scottaaronson.com/blog/?p=1579)
</div>
While [boson sampling](https://en.wikipedia.org/wiki/Boson_sampling) allows the experimental implementation of a quantum sampling problem that it countably hard classically, one of the main issues it has in experimental setups is one of **scalability**, due to its dependence on an array of simultaneously emitting single photon sources.
Currently, most physical implementations of boson sampling make use of a process known as [Spontaneous Parametric Down-Conversion](http://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion) to generate the single photon source inputs. Unfortunately, this method is non-deterministic - as the number of modes in the apparatus increases, the average time required until every photon source emits a simultaneous photon increases *exponentially*.
In order to simulate a *deterministic* single photon source array, several variations on boson sampling have been proposed; the most well known being scattershot boson sampling ([Lund, 2014](https://link.aps.org/doi/10.1103/PhysRevLett.113.100502)). However, a recent boson sampling variation by [Hamilton et al.](https://link.aps.org/doi/10.1103/PhysRevLett.119.170501) negates the need for single photon Fock states altogether, by showing that **incident Gaussian states** - in this case, single mode squeezed states - can produce problems in the same computational complexity class as boson sampling. Even more significantly, this negates the scalability problem with single photon sources, as single mode squeezed states can be easily simultaneously generated experimentally.
Aside from changing the input states from single photon Fock states to Gaussian states, the Gaussian boson sampling scheme appears quite similar to that of boson sampling:
1. $N$ single mode squeezed states $\left|{\xi_i}\right\rangle$, with squeezing parameters $\xi_i=r_ie^{i\phi_i}$, enter an $N$ mode linear interferometer with unitary $U$.
<br>
2. The output of the interferometer is denoted $\left|{\psi'}\right\rangle$. Each output mode is then measured in the Fock basis, $\bigotimes_i n_i\left|{n_i}\middle\rangle\middle\langle{n_i}\right|$.
Without loss of generality, we can absorb the squeezing parameter $\phi$ into the interferometer, and set $\phi=0$ for convenience. The covariance matrix **in the creation and annihilation operator basis** at the output of the interferometer is then given by:
$$\sigma_{out} = \frac{1}{2} \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right]\sigma_{in} \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right]$$
Using phase space methods, [Hamilton et al.](https://link.aps.org/doi/10.1103/PhysRevLett.119.170501) showed that the probability of measuring a Fock state is given by
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(U\bigoplus_i\tanh(r_i)U^T)]_{st}\right|^2}{n_1!n_2!\cdots n_N!\sqrt{|\sigma_{out}+I/2|}},$$
i.e. the sampled single photon probability distribution is proportional to the **Hafnian** of a submatrix of $U\bigoplus_i\tanh(r_i)U^T$, dependent upon the output covariance matrix.
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**The Hafnian**</p>
The Hafnian of a matrix is defined by
<br><br>
$$\text{Haf}(A) = \frac{1}{n!2^n}\sum_{\sigma=S_{2N}}\prod_{i=1}^N A_{\sigma(2i-1)\sigma(2i)}$$
<br>
$S_{2N}$ is the set of all permutations of $2N$ elements. In graph theory, the Hafnian calculates the number of perfect <a href="https://en.wikipedia.org/wiki/Matching_(graph_theory)">matchings</a> in an **arbitrary graph** with adjacency matrix $A$.
<br>
Compare this to the permanent, which calculates the number of perfect matchings on a *bipartite* graph - the Hafnian turns out to be a generalisation of the permanent, with the relationship
$$\begin{align}
\text{Per(A)} = \text{Haf}\left(\left[\begin{matrix}
0&A\\
A^T&0
\end{matrix}\right]\right)
\end{align}$$
As any algorithm that could calculate (or even approximate) the Hafnian could also calculate the permanent - a #P problem - it follows that calculating or approximating the Hafnian must also be a classically hard problem.
</div>
### Equally squeezed input states
In the case where all the input states are squeezed equally with squeezing factor $\xi=r$ (i.e. so $\phi=0$), we can simplify the denominator into a much nicer form. It can be easily seen that, due to the unitarity of $U$,
$$\left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right] = \left[ \begin{matrix}UU^\dagger&0\\0&U^*U^T\end{matrix} \right] =I$$
Thus, we have
$$\begin{align}
\sigma_{out} +\frac{1}{2}I &= \sigma_{out} + \frac{1}{2} \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right] = \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \frac{1}{2} \left(\sigma_{in}+I\right) \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right]
\end{align}$$
where we have subtituted in the expression for $\sigma_{out}$. Taking the determinants of both sides, the two block diagonal matrices containing $U$ are unitary, and thus have determinant 1, resulting in
$$\left|\sigma_{out} +\frac{1}{2}I\right| =\left|\frac{1}{2}\left(\sigma_{in}+I\right)\right|=\left|\frac{1}{2}\left(SS^\dagger+I\right)\right| $$
By expanding out the right hand side, and using various trig identities, it is easy to see that this simply reduces to $\cosh^{2N}(r)$ where $N$ is the number of modes; thus the Gaussian boson sampling problem in the case of equally squeezed input modes reduces to
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(UU^T\tanh(r))]_{st}\right|^2}{n_1!n_2!\cdots n_N!\cosh^N(r)},$$
## The Gaussian boson sampling circuit
The multimode linear interferometer can be decomposed into two-mode beamsplitters (`BSgate`) and single-mode phase shifters (`Rgate`) (<a href="https://doi.org/10.1103/physrevlett.73.58">Reck, 1994</a>), allowing for an almost trivial translation into a continuous-variable quantum circuit.
For example, in the case of a 4 mode interferometer, with arbitrary $4\times 4$ unitary $U$, the continuous-variable quantum circuit for Gaussian boson sampling is given by
<img src="https://s3.amazonaws.com/xanadu-img/gaussian_boson_sampling.svg" width=70%/>
In the above,
* the single mode squeeze states all apply identical squeezing $\xi=r$,
* the detectors perform Fock state measurements (i.e. measuring the photon number of each mode),
* the parameters of the beamsplitters and the rotation gates determines the unitary $U$.
For $N$ input modes, we must have a minimum of $N$ columns in the beamsplitter array ([Clements, 2016](https://arxiv.org/abs/1603.08788)).
## Simulating boson sampling in Strawberry Fields
```
import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import random_interferometer
```
Strawberry Fields makes this easy; there is an `Interferometer` quantum operation, and a utility function that allows us to generate the matrix representing a random interferometer.
```
U = random_interferometer(4)
```
The lack of Fock states and non-linear operations means we can use the Gaussian backend to simulate Gaussian boson sampling. In this example program, we are using input states with squeezing parameter $\xi=1$, and the randomly chosen interferometer generated above.
```
eng, q = sf.Engine(4)
with eng:
# prepare the input squeezed states
S = Sgate(1)
All(S) | q
# interferometer
Interferometer(U) | q
state = eng.run('gaussian')
```
We can see the decomposed beamsplitters and rotation gates, by calling `eng.print_applied()`:
```
eng.print_applied()
```
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**Available decompositions**</p>
Check out our <a href="https://strawberryfields.readthedocs.io/en/stable/conventions/decompositions.html">documentation</a> to see the available CV decompositions available in Strawberry Fields.
</div>
## Analysis
Let's now verify the Gaussian boson sampling result, by comparing the output Fock state probabilities to the Hafnian, using the relationship
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(UU^T\tanh(r))]_{st}\right|^2}{n_1!n_2!\cdots n_N!\cosh^N(r)}$$
### Calculating the Hafnian
For the right hand side numerator, we first calculate the submatrix $[(UU^T\tanh(r))]_{st}$:
```
B = (np.dot(U, U.T) * np.tanh(1))
```
In Gaussian boson sampling, we determine the submatrix by taking the rows and columns corresponding to the measured Fock state. For example, to calculate the submatrix in the case of the output measurement $\left|{1,1,0,0}\right\rangle$,
```
B[:,[0,1]][[0,1]]
```
To calculate the Hafnian in Python, we can use the direct definition
$$\text{Haf}(A) = \frac{1}{n!2^n} \sum_{\sigma \in S_{2n}} \prod_{j=1}^n A_{\sigma(2j - 1), \sigma(2j)}$$
Notice that this function counts each term in the definition multiple times, and renormalizes to remove the multiple counts by dividing by a factor $\frac{1}{n!2^n}$. **This function is extremely slow!**
```
from itertools import permutations
from scipy.special import factorial
def Haf(M):
n=len(M)
m=int(n/2)
haf=0.0
for i in permutations(range(n)):
prod=1.0
for j in range(m):
prod*=M[i[2*j],i[2*j+1]]
haf+=prod
return haf/(factorial(m)*(2**m))
```
## Comparing to the SF result
In Strawberry Fields, both Fock and Gaussian states have the method `fock_prob()`, which returns the probability of measuring that particular Fock state.
#### Let's compare the case of measuring at the output state $\left|0,1,0,1\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [1,3]][[1,3]]
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([0,1,0,1])
```
#### For the measurement result $\left|2,0,0,0\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [0,0]][[0,0]]
np.abs(Haf(B))**2 / (2*np.cosh(1)**4)
state.fock_prob([2,0,0,0])
```
#### For the measurement result $\left|1,1,0,0\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [0,1]][[0,1]]
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([1,1,0,0])
```
#### For the measurement result $\left|1,1,1,1\right\rangle$, this corresponds to the full matrix $B$:
```
B = (np.dot(U,U.T) * np.tanh(1))
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([1,1,1,1])
```
#### For the measurement result $\left|0,0,0,0\right\rangle$, this corresponds to a **null** submatrix, which has a Hafnian of 1:
```
1/np.cosh(1)**4
state.fock_prob([0,0,0,0])
```
As you can see, like in the boson sampling tutorial, they agree with almost negligable difference.
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**Exercises**</p>
Repeat this notebook with
<ol>
<li> A Fock backend such as NumPy, instead of the Gaussian backend</li>
<li> Different beamsplitter and rotation parameters</li>
<li> Input states with *differing* squeezed values $r_i$. You will need to modify the code to take into account the fact that the output covariance matrix determinant must now be calculated!
</ol>
</div>
| true |
code
| 0.304688 | null | null | null | null |
|
# Dynamic factors and coincident indices
Factor models generally try to find a small number of unobserved "factors" that influence a subtantial portion of the variation in a larger number of observed variables, and they are related to dimension-reduction techniques such as principal components analysis. Dynamic factor models explicitly model the transition dynamics of the unobserved factors, and so are often applied to time-series data.
Macroeconomic coincident indices are designed to capture the common component of the "business cycle"; such a component is assumed to simultaneously affect many macroeconomic variables. Although the estimation and use of coincident indices (for example the [Index of Coincident Economic Indicators](http://www.newyorkfed.org/research/regional_economy/coincident_summary.html)) pre-dates dynamic factor models, in several influential papers Stock and Watson (1989, 1991) used a dynamic factor model to provide a theoretical foundation for them.
Below, we follow the treatment found in Kim and Nelson (1999), of the Stock and Watson (1991) model, to formulate a dynamic factor model, estimate its parameters via maximum likelihood, and create a coincident index.
## Macroeconomic data
The coincident index is created by considering the comovements in four macroeconomic variables (versions of thse variables are available on [FRED](https://research.stlouisfed.org/fred2/); the ID of the series used below is given in parentheses):
- Industrial production (IPMAN)
- Real aggregate income (excluding transfer payments) (W875RX1)
- Manufacturing and trade sales (CMRMTSPL)
- Employees on non-farm payrolls (PAYEMS)
In all cases, the data is at the monthly frequency and has been seasonally adjusted; the time-frame considered is 1972 - 2005.
```
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
np.set_printoptions(precision=4, suppress=True, linewidth=120)
from pandas_datareader.data import DataReader
# Get the datasets from FRED
start = '1979-01-01'
end = '2014-12-01'
indprod = DataReader('IPMAN', 'fred', start=start, end=end)
income = DataReader('W875RX1', 'fred', start=start, end=end)
sales = DataReader('CMRMTSPL', 'fred', start=start, end=end)
emp = DataReader('PAYEMS', 'fred', start=start, end=end)
# dta = pd.concat((indprod, income, sales, emp), axis=1)
# dta.columns = ['indprod', 'income', 'sales', 'emp']
```
**Note**: in a recent update on FRED (8/12/15) the time series CMRMTSPL was truncated to begin in 1997; this is probably a mistake due to the fact that CMRMTSPL is a spliced series, so the earlier period is from the series HMRMT and the latter period is defined by CMRMT.
This has since (02/11/16) been corrected, however the series could also be constructed by hand from HMRMT and CMRMT, as shown below (process taken from the notes in the Alfred xls file).
```
# HMRMT = DataReader('HMRMT', 'fred', start='1967-01-01', end=end)
# CMRMT = DataReader('CMRMT', 'fred', start='1997-01-01', end=end)
# HMRMT_growth = HMRMT.diff() / HMRMT.shift()
# sales = pd.Series(np.zeros(emp.shape[0]), index=emp.index)
# # Fill in the recent entries (1997 onwards)
# sales[CMRMT.index] = CMRMT
# # Backfill the previous entries (pre 1997)
# idx = sales.loc[:'1997-01-01'].index
# for t in range(len(idx)-1, 0, -1):
# month = idx[t]
# prev_month = idx[t-1]
# sales.loc[prev_month] = sales.loc[month] / (1 + HMRMT_growth.loc[prev_month].values)
dta = pd.concat((indprod, income, sales, emp), axis=1)
dta.columns = ['indprod', 'income', 'sales', 'emp']
dta.loc[:, 'indprod':'emp'].plot(subplots=True, layout=(2, 2), figsize=(15, 6));
```
Stock and Watson (1991) report that for their datasets, they could not reject the null hypothesis of a unit root in each series (so the series are integrated), but they did not find strong evidence that the series were co-integrated.
As a result, they suggest estimating the model using the first differences (of the logs) of the variables, demeaned and standardized.
```
# Create log-differenced series
dta['dln_indprod'] = (np.log(dta.indprod)).diff() * 100
dta['dln_income'] = (np.log(dta.income)).diff() * 100
dta['dln_sales'] = (np.log(dta.sales)).diff() * 100
dta['dln_emp'] = (np.log(dta.emp)).diff() * 100
# De-mean and standardize
dta['std_indprod'] = (dta['dln_indprod'] - dta['dln_indprod'].mean()) / dta['dln_indprod'].std()
dta['std_income'] = (dta['dln_income'] - dta['dln_income'].mean()) / dta['dln_income'].std()
dta['std_sales'] = (dta['dln_sales'] - dta['dln_sales'].mean()) / dta['dln_sales'].std()
dta['std_emp'] = (dta['dln_emp'] - dta['dln_emp'].mean()) / dta['dln_emp'].std()
```
## Dynamic factors
A general dynamic factor model is written as:
$$
\begin{align}
y_t & = \Lambda f_t + B x_t + u_t \\
f_t & = A_1 f_{t-1} + \dots + A_p f_{t-p} + \eta_t \qquad \eta_t \sim N(0, I)\\
u_t & = C_1 u_{t-1} + \dots + C_q u_{t-q} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \Sigma)
\end{align}
$$
where $y_t$ are observed data, $f_t$ are the unobserved factors (evolving as a vector autoregression), $x_t$ are (optional) exogenous variables, and $u_t$ is the error, or "idiosyncratic", process ($u_t$ is also optionally allowed to be autocorrelated). The $\Lambda$ matrix is often referred to as the matrix of "factor loadings". The variance of the factor error term is set to the identity matrix to ensure identification of the unobserved factors.
This model can be cast into state space form, and the unobserved factor estimated via the Kalman filter. The likelihood can be evaluated as a byproduct of the filtering recursions, and maximum likelihood estimation used to estimate the parameters.
## Model specification
The specific dynamic factor model in this application has 1 unobserved factor which is assumed to follow an AR(2) proces. The innovations $\varepsilon_t$ are assumed to be independent (so that $\Sigma$ is a diagonal matrix) and the error term associated with each equation, $u_{i,t}$ is assumed to follow an independent AR(2) process.
Thus the specification considered here is:
$$
\begin{align}
y_{i,t} & = \lambda_i f_t + u_{i,t} \\
u_{i,t} & = c_{i,1} u_{1,t-1} + c_{i,2} u_{i,t-2} + \varepsilon_{i,t} \qquad & \varepsilon_{i,t} \sim N(0, \sigma_i^2) \\
f_t & = a_1 f_{t-1} + a_2 f_{t-2} + \eta_t \qquad & \eta_t \sim N(0, I)\\
\end{align}
$$
where $i$ is one of: `[indprod, income, sales, emp ]`.
This model can be formulated using the `DynamicFactor` model built-in to Statsmodels. In particular, we have the following specification:
- `k_factors = 1` - (there is 1 unobserved factor)
- `factor_order = 2` - (it follows an AR(2) process)
- `error_var = False` - (the errors evolve as independent AR processes rather than jointly as a VAR - note that this is the default option, so it is not specified below)
- `error_order = 2` - (the errors are autocorrelated of order 2: i.e. AR(2) processes)
- `error_cov_type = 'diagonal'` - (the innovations are uncorrelated; this is again the default)
Once the model is created, the parameters can be estimated via maximum likelihood; this is done using the `fit()` method.
**Note**: recall that we have de-meaned and standardized the data; this will be important in interpreting the results that follow.
**Aside**: in their empirical example, Kim and Nelson (1999) actually consider a slightly different model in which the employment variable is allowed to also depend on lagged values of the factor - this model does not fit into the built-in `DynamicFactor` class, but can be accomodated by using a subclass to implement the required new parameters and restrictions - see Appendix A, below.
## Parameter estimation
Multivariate models can have a relatively large number of parameters, and it may be difficult to escape from local minima to find the maximized likelihood. In an attempt to mitigate this problem, I perform an initial maximization step (from the model-defined starting paramters) using the modified Powell method available in Scipy (see the minimize documentation for more information). The resulting parameters are then used as starting parameters in the standard LBFGS optimization method.
```
# Get the endogenous data
endog = dta.loc['1979-02-01':, 'std_indprod':'std_emp']
# Create the model
mod = sm.tsa.DynamicFactor(endog, k_factors=1, factor_order=2, error_order=2)
initial_res = mod.fit(method='powell', disp=False)
res = mod.fit(initial_res.params, disp=False)
```
## Estimates
Once the model has been estimated, there are two components that we can use for analysis or inference:
- The estimated parameters
- The estimated factor
### Parameters
The estimated parameters can be helpful in understanding the implications of the model, although in models with a larger number of observed variables and / or unobserved factors they can be difficult to interpret.
One reason for this difficulty is due to identification issues between the factor loadings and the unobserved factors. One easy-to-see identification issue is the sign of the loadings and the factors: an equivalent model to the one displayed below would result from reversing the signs of all factor loadings and the unobserved factor.
Here, one of the easy-to-interpret implications in this model is the persistence of the unobserved factor: we find that exhibits substantial persistence.
```
print(res.summary(separate_params=False))
```
### Estimated factors
While it can be useful to plot the unobserved factors, it is less useful here than one might think for two reasons:
1. The sign-related identification issue described above.
2. Since the data was differenced, the estimated factor explains the variation in the differenced data, not the original data.
It is for these reasons that the coincident index is created (see below).
With these reservations, the unobserved factor is plotted below, along with the NBER indicators for US recessions. It appears that the factor is successful at picking up some degree of business cycle activity.
```
fig, ax = plt.subplots(figsize=(13,3))
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, res.factors.filtered[0], label='Factor')
ax.legend()
# Retrieve and also plot the NBER recession indicators
rec = DataReader('USREC', 'fred', start=start, end=end)
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
```
## Post-estimation
Although here we will be able to interpret the results of the model by constructing the coincident index, there is a useful and generic approach for getting a sense for what is being captured by the estimated factor. By taking the estimated factors as given, regressing them (and a constant) each (one at a time) on each of the observed variables, and recording the coefficients of determination ($R^2$ values), we can get a sense of the variables for which each factor explains a substantial portion of the variance and the variables for which it does not.
In models with more variables and more factors, this can sometimes lend interpretation to the factors (for example sometimes one factor will load primarily on real variables and another on nominal variables).
In this model, with only four endogenous variables and one factor, it is easy to digest a simple table of the $R^2$ values, but in larger models it is not. For this reason, a bar plot is often employed; from the plot we can easily see that the factor explains most of the variation in industrial production index and a large portion of the variation in sales and employment, it is less helpful in explaining income.
```
res.plot_coefficients_of_determination(figsize=(8,2));
```
## Coincident Index
As described above, the goal of this model was to create an interpretable series which could be used to understand the current status of the macroeconomy. This is what the coincident index is designed to do. It is constructed below. For readers interested in an explanation of the construction, see Kim and Nelson (1999) or Stock and Watson (1991).
In essense, what is done is to reconstruct the mean of the (differenced) factor. We will compare it to the coincident index on published by the Federal Reserve Bank of Philadelphia (USPHCI on FRED).
```
usphci = DataReader('USPHCI', 'fred', start='1979-01-01', end='2014-12-01')['USPHCI']
usphci.plot(figsize=(13,3));
dusphci = usphci.diff()[1:].values
def compute_coincident_index(mod, res):
# Estimate W(1)
spec = res.specification
design = mod.ssm['design']
transition = mod.ssm['transition']
ss_kalman_gain = res.filter_results.kalman_gain[:,:,-1]
k_states = ss_kalman_gain.shape[0]
W1 = np.linalg.inv(np.eye(k_states) - np.dot(
np.eye(k_states) - np.dot(ss_kalman_gain, design),
transition
)).dot(ss_kalman_gain)[0]
# Compute the factor mean vector
factor_mean = np.dot(W1, dta.loc['1972-02-01':, 'dln_indprod':'dln_emp'].mean())
# Normalize the factors
factor = res.factors.filtered[0]
factor *= np.std(usphci.diff()[1:]) / np.std(factor)
# Compute the coincident index
coincident_index = np.zeros(mod.nobs+1)
# The initial value is arbitrary; here it is set to
# facilitate comparison
coincident_index[0] = usphci.iloc[0] * factor_mean / dusphci.mean()
for t in range(0, mod.nobs):
coincident_index[t+1] = coincident_index[t] + factor[t] + factor_mean
# Attach dates
coincident_index = pd.Series(coincident_index, index=dta.index).iloc[1:]
# Normalize to use the same base year as USPHCI
coincident_index *= (usphci.loc['1992-07-01'] / coincident_index.loc['1992-07-01'])
return coincident_index
```
Below we plot the calculated coincident index along with the US recessions and the comparison coincident index USPHCI.
```
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
coincident_index = compute_coincident_index(mod, res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, label='Coincident index')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
```
## Appendix 1: Extending the dynamic factor model
Recall that the previous specification was described by:
$$
\begin{align}
y_{i,t} & = \lambda_i f_t + u_{i,t} \\
u_{i,t} & = c_{i,1} u_{1,t-1} + c_{i,2} u_{i,t-2} + \varepsilon_{i,t} \qquad & \varepsilon_{i,t} \sim N(0, \sigma_i^2) \\
f_t & = a_1 f_{t-1} + a_2 f_{t-2} + \eta_t \qquad & \eta_t \sim N(0, I)\\
\end{align}
$$
Written in state space form, the previous specification of the model had the following observation equation:
$$
\begin{bmatrix}
y_{\text{indprod}, t} \\
y_{\text{income}, t} \\
y_{\text{sales}, t} \\
y_{\text{emp}, t} \\
\end{bmatrix} = \begin{bmatrix}
\lambda_\text{indprod} & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{income} & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{sales} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{emp} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
f_t \\
f_{t-1} \\
u_{\text{indprod}, t} \\
u_{\text{income}, t} \\
u_{\text{sales}, t} \\
u_{\text{emp}, t} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
\end{bmatrix}
$$
and transition equation:
$$
\begin{bmatrix}
f_t \\
f_{t-1} \\
u_{\text{indprod}, t} \\
u_{\text{income}, t} \\
u_{\text{sales}, t} \\
u_{\text{emp}, t} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
\end{bmatrix} = \begin{bmatrix}
a_1 & a_2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & c_{\text{indprod}, 1} & 0 & 0 & 0 & c_{\text{indprod}, 2} & 0 & 0 & 0 \\
0 & 0 & 0 & c_{\text{income}, 1} & 0 & 0 & 0 & c_{\text{income}, 2} & 0 & 0 \\
0 & 0 & 0 & 0 & c_{\text{sales}, 1} & 0 & 0 & 0 & c_{\text{sales}, 2} & 0 \\
0 & 0 & 0 & 0 & 0 & c_{\text{emp}, 1} & 0 & 0 & 0 & c_{\text{emp}, 2} \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
f_{t-1} \\
f_{t-2} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
u_{\text{indprod}, t-2} \\
u_{\text{income}, t-2} \\
u_{\text{sales}, t-2} \\
u_{\text{emp}, t-2} \\
\end{bmatrix}
+ R \begin{bmatrix}
\eta_t \\
\varepsilon_{t}
\end{bmatrix}
$$
the `DynamicFactor` model handles setting up the state space representation and, in the `DynamicFactor.update` method, it fills in the fitted parameter values into the appropriate locations.
The extended specification is the same as in the previous example, except that we also want to allow employment to depend on lagged values of the factor. This creates a change to the $y_{\text{emp},t}$ equation. Now we have:
$$
\begin{align}
y_{i,t} & = \lambda_i f_t + u_{i,t} \qquad & i \in \{\text{indprod}, \text{income}, \text{sales} \}\\
y_{i,t} & = \lambda_{i,0} f_t + \lambda_{i,1} f_{t-1} + \lambda_{i,2} f_{t-2} + \lambda_{i,2} f_{t-3} + u_{i,t} \qquad & i = \text{emp} \\
u_{i,t} & = c_{i,1} u_{i,t-1} + c_{i,2} u_{i,t-2} + \varepsilon_{i,t} \qquad & \varepsilon_{i,t} \sim N(0, \sigma_i^2) \\
f_t & = a_1 f_{t-1} + a_2 f_{t-2} + \eta_t \qquad & \eta_t \sim N(0, I)\\
\end{align}
$$
Now, the corresponding observation equation should look like the following:
$$
\begin{bmatrix}
y_{\text{indprod}, t} \\
y_{\text{income}, t} \\
y_{\text{sales}, t} \\
y_{\text{emp}, t} \\
\end{bmatrix} = \begin{bmatrix}
\lambda_\text{indprod} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{income} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{sales} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
\lambda_\text{emp,1} & \lambda_\text{emp,2} & \lambda_\text{emp,3} & \lambda_\text{emp,4} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
f_t \\
f_{t-1} \\
f_{t-2} \\
f_{t-3} \\
u_{\text{indprod}, t} \\
u_{\text{income}, t} \\
u_{\text{sales}, t} \\
u_{\text{emp}, t} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
\end{bmatrix}
$$
Notice that we have introduced two new state variables, $f_{t-2}$ and $f_{t-3}$, which means we need to update the transition equation:
$$
\begin{bmatrix}
f_t \\
f_{t-1} \\
f_{t-2} \\
f_{t-3} \\
u_{\text{indprod}, t} \\
u_{\text{income}, t} \\
u_{\text{sales}, t} \\
u_{\text{emp}, t} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
\end{bmatrix} = \begin{bmatrix}
a_1 & a_2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & c_{\text{indprod}, 1} & 0 & 0 & 0 & c_{\text{indprod}, 2} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & c_{\text{income}, 1} & 0 & 0 & 0 & c_{\text{income}, 2} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & c_{\text{sales}, 1} & 0 & 0 & 0 & c_{\text{sales}, 2} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & c_{\text{emp}, 1} & 0 & 0 & 0 & c_{\text{emp}, 2} \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
f_{t-1} \\
f_{t-2} \\
f_{t-3} \\
f_{t-4} \\
u_{\text{indprod}, t-1} \\
u_{\text{income}, t-1} \\
u_{\text{sales}, t-1} \\
u_{\text{emp}, t-1} \\
u_{\text{indprod}, t-2} \\
u_{\text{income}, t-2} \\
u_{\text{sales}, t-2} \\
u_{\text{emp}, t-2} \\
\end{bmatrix}
+ R \begin{bmatrix}
\eta_t \\
\varepsilon_{t}
\end{bmatrix}
$$
This model cannot be handled out-of-the-box by the `DynamicFactor` class, but it can be handled by creating a subclass when alters the state space representation in the appropriate way.
First, notice that if we had set `factor_order = 4`, we would almost have what we wanted. In that case, the last line of the observation equation would be:
$$
\begin{bmatrix}
\vdots \\
y_{\text{emp}, t} \\
\end{bmatrix} = \begin{bmatrix}
\vdots & & & & & & & & & & & \vdots \\
\lambda_\text{emp,1} & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
f_t \\
f_{t-1} \\
f_{t-2} \\
f_{t-3} \\
\vdots
\end{bmatrix}
$$
and the first line of the transition equation would be:
$$
\begin{bmatrix}
f_t \\
\vdots
\end{bmatrix} = \begin{bmatrix}
a_1 & a_2 & a_3 & a_4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\vdots & & & & & & & & & & & \vdots \\
\end{bmatrix}
\begin{bmatrix}
f_{t-1} \\
f_{t-2} \\
f_{t-3} \\
f_{t-4} \\
\vdots
\end{bmatrix}
+ R \begin{bmatrix}
\eta_t \\
\varepsilon_{t}
\end{bmatrix}
$$
Relative to what we want, we have the following differences:
1. In the above situation, the $\lambda_{\text{emp}, j}$ are forced to be zero for $j > 0$, and we want them to be estimated as parameters.
2. We only want the factor to transition according to an AR(2), but under the above situation it is an AR(4).
Our strategy will be to subclass `DynamicFactor`, and let it do most of the work (setting up the state space representation, etc.) where it assumes that `factor_order = 4`. The only things we will actually do in the subclass will be to fix those two issues.
First, here is the full code of the subclass; it is discussed below. It is important to note at the outset that none of the methods defined below could have been omitted. In fact, the methods `__init__`, `start_params`, `param_names`, `transform_params`, `untransform_params`, and `update` form the core of all state space models in Statsmodels, not just the `DynamicFactor` class.
```
from statsmodels.tsa.statespace import tools
class ExtendedDFM(sm.tsa.DynamicFactor):
def __init__(self, endog, **kwargs):
# Setup the model as if we had a factor order of 4
super(ExtendedDFM, self).__init__(
endog, k_factors=1, factor_order=4, error_order=2,
**kwargs)
# Note: `self.parameters` is an ordered dict with the
# keys corresponding to parameter types, and the values
# the number of parameters of that type.
# Add the new parameters
self.parameters['new_loadings'] = 3
# Cache a slice for the location of the 4 factor AR
# parameters (a_1, ..., a_4) in the full parameter vector
offset = (self.parameters['factor_loadings'] +
self.parameters['exog'] +
self.parameters['error_cov'])
self._params_factor_ar = np.s_[offset:offset+2]
self._params_factor_zero = np.s_[offset+2:offset+4]
@property
def start_params(self):
# Add three new loading parameters to the end of the parameter
# vector, initialized to zeros (for simplicity; they could
# be initialized any way you like)
return np.r_[super(ExtendedDFM, self).start_params, 0, 0, 0]
@property
def param_names(self):
# Add the corresponding names for the new loading parameters
# (the name can be anything you like)
return super(ExtendedDFM, self).param_names + [
'loading.L%d.f1.%s' % (i, self.endog_names[3]) for i in range(1,4)]
def transform_params(self, unconstrained):
# Perform the typical DFM transformation (w/o the new parameters)
constrained = super(ExtendedDFM, self).transform_params(
unconstrained[:-3])
# Redo the factor AR constraint, since we only want an AR(2),
# and the previous constraint was for an AR(4)
ar_params = unconstrained[self._params_factor_ar]
constrained[self._params_factor_ar] = (
tools.constrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[constrained, unconstrained[-3:]]
def untransform_params(self, constrained):
# Perform the typical DFM untransformation (w/o the new parameters)
unconstrained = super(ExtendedDFM, self).untransform_params(
constrained[:-3])
# Redo the factor AR unconstraint, since we only want an AR(2),
# and the previous unconstraint was for an AR(4)
ar_params = constrained[self._params_factor_ar]
unconstrained[self._params_factor_ar] = (
tools.unconstrain_stationary_univariate(ar_params))
# Return all the parameters
return np.r_[unconstrained, constrained[-3:]]
def update(self, params, transformed=True, complex_step=False):
# Peform the transformation, if required
if not transformed:
params = self.transform_params(params)
params[self._params_factor_zero] = 0
# Now perform the usual DFM update, but exclude our new parameters
super(ExtendedDFM, self).update(params[:-3], transformed=True, complex_step=complex_step)
# Finally, set our new parameters in the design matrix
self.ssm['design', 3, 1:4] = params[-3:]
```
So what did we just do?
#### `__init__`
The important step here was specifying the base dynamic factor model which we were operating with. In particular, as described above, we initialize with `factor_order=4`, even though we will only end up with an AR(2) model for the factor. We also performed some general setup-related tasks.
#### `start_params`
`start_params` are used as initial values in the optimizer. Since we are adding three new parameters, we need to pass those in. If we hadn't done this, the optimizer would use the default starting values, which would be three elements short.
#### `param_names`
`param_names` are used in a variety of places, but especially in the results class. Below we get a full result summary, which is only possible when all the parameters have associated names.
#### `transform_params` and `untransform_params`
The optimizer selects possibly parameter values in an unconstrained way. That's not usually desired (since variances can't be negative, for example), and `transform_params` is used to transform the unconstrained values used by the optimizer to constrained values appropriate to the model. Variances terms are typically squared (to force them to be positive), and AR lag coefficients are often constrained to lead to a stationary model. `untransform_params` is used for the reverse operation (and is important because starting parameters are usually specified in terms of values appropriate to the model, and we need to convert them to parameters appropriate to the optimizer before we can begin the optimization routine).
Even though we don't need to transform or untransform our new parameters (the loadings can in theory take on any values), we still need to modify this function for two reasons:
1. The version in the `DynamicFactor` class is expecting 3 fewer parameters than we have now. At a minimum, we need to handle the three new parameters.
2. The version in the `DynamicFactor` class constrains the factor lag coefficients to be stationary as though it was an AR(4) model. Since we actually have an AR(2) model, we need to re-do the constraint. We also set the last two autoregressive coefficients to be zero here.
#### `update`
The most important reason we need to specify a new `update` method is because we have three new parameters that we need to place into the state space formulation. In particular we let the parent `DynamicFactor.update` class handle placing all the parameters except the three new ones in to the state space representation, and then we put the last three in manually.
```
# Create the model
extended_mod = ExtendedDFM(endog)
initial_extended_res = extended_mod.fit(maxiter=1000, disp=False)
extended_res = extended_mod.fit(initial_extended_res.params, method='nm', maxiter=1000)
print(extended_res.summary(separate_params=False))
```
Although this model increases the likelihood, it is not preferred by the AIC and BIC mesaures which penalize the additional three parameters.
Furthermore, the qualitative results are unchanged, as we can see from the updated $R^2$ chart and the new coincident index, both of which are practically identical to the previous results.
```
extended_res.plot_coefficients_of_determination(figsize=(8,2));
fig, ax = plt.subplots(figsize=(13,3))
# Compute the index
extended_coincident_index = compute_coincident_index(extended_mod, extended_res)
# Plot the factor
dates = endog.index._mpl_repr()
ax.plot(dates, coincident_index, '-', linewidth=1, label='Basic model')
ax.plot(dates, extended_coincident_index, '--', linewidth=3, label='Extended model')
ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI')
ax.legend(loc='lower right')
ax.set(title='Coincident indices, comparison')
# Retrieve and also plot the NBER recession indicators
ylim = ax.get_ylim()
ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1);
```
| true |
code
| 0.651771 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# AutoML 02: Regression with local compute
In this example we use the scikit learn's [diabetes dataset](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html) to showcase how you can use AutoML for a simple regression problem.
Make sure you have executed the [00.configuration](00.configuration.ipynb) before running this notebook.
In this notebook you would see
1. Creating an Experiment using an existing Workspace
2. Instantiating AutoMLConfig
3. Training the Model using local compute
4. Exploring the results
5. Testing the fitted model
## Create Experiment
As part of the setup you have already created a <b>Workspace</b>. For AutoML you would need to create an <b>Experiment</b>. An <b>Experiment</b> is a named object in a <b>Workspace</b>, which is used to run experiments.
```
import logging
import os
import random
from matplotlib import pyplot as plt
from matplotlib.pyplot import imshow
import numpy as np
import pandas as pd
from sklearn import datasets
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.train.automl import AutoMLConfig
from azureml.train.automl.run import AutoMLRun
ws = Workspace.from_config()
# choose a name for the experiment
experiment_name = 'automl-local-regression'
# project folder
project_folder = './sample_projects/automl-local-regression'
experiment = Experiment(ws, experiment_name)
output = {}
output['SDK version'] = azureml.core.VERSION
output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Project Directory'] = project_folder
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
pd.DataFrame(data = output, index = ['']).T
```
## Diagnostics
Opt-in diagnostics for better experience, quality, and security of future releases
```
from azureml.telemetry import set_diagnostics_collection
set_diagnostics_collection(send_diagnostics=True)
```
### Read Data
```
# load diabetes dataset, a well-known built-in small dataset that comes with scikit-learn
from sklearn.datasets import load_diabetes
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
X, y = load_diabetes(return_X_y = True)
columns = ['age', 'gender', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
## Instantiate Auto ML Config
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|classification or regression|
|**primary_metric**|This is the metric that you want to optimize.<br> Regression supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i><br><i>normalized_root_mean_squared_log_error</i>|
|**max_time_sec**|Time limit in seconds for each iteration|
|**iterations**|Number of iterations. In each iteration Auto ML trains a specific pipeline with the data|
|**n_cross_validations**|Number of cross validation splits|
|**X**|(sparse) array-like, shape = [n_samples, n_features]|
|**y**|(sparse) array-like, shape = [n_samples, ], [n_samples, n_classes]<br>Multi-class targets. An indicator matrix turns on multilabel classification. This should be an array of integers. |
|**path**|Relative path to the project folder. AutoML stores configuration files for the experiment under this folder. You can specify a new empty folder.|
```
automl_config = AutoMLConfig(task='regression',
max_time_sec = 600,
iterations = 10,
primary_metric = 'spearman_correlation',
n_cross_validations = 5,
debug_log = 'automl.log',
verbosity = logging.INFO,
X = X_train,
y = y_train,
path=project_folder)
```
## Training the Model
You can call the submit method on the experiment object and pass the run configuration. For Local runs the execution is synchronous. Depending on the data and number of iterations this can run for while.
You will see the currently running iterations printing to the console.
```
local_run = experiment.submit(automl_config, show_output=True)
local_run
```
## Exploring the results
#### Widget for monitoring runs
The widget will sit on "loading" until the first iteration completed, then you will see an auto-updating graph and table show up. It refreshed once per minute, so you should see the graph update as child runs complete.
NOTE: The widget displays a link at the bottom. This links to a web-ui to explore the individual run details.
```
from azureml.train.widgets import RunDetails
RunDetails(local_run).show()
```
#### Retrieve All Child Runs
You can also use sdk methods to fetch all the child runs and see individual metrics that we log.
```
children = list(local_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata
```
### Retrieve the Best Model
Below we select the best pipeline from our iterations. The *get_output* method on automl_classifier returns the best run and the fitted model for the last *fit* invocation. There are overloads on *get_output* that allow you to retrieve the best run and fitted model for *any* logged metric or a particular *iteration*.
```
best_run, fitted_model = local_run.get_output()
print(best_run)
print(fitted_model)
```
#### Best Model based on any other metric
Show the run and model that has the smallest `root_mean_squared_error` (which turned out to be the same as the one with largest `spearman_correlation` value):
```
lookup_metric = "root_mean_squared_error"
best_run, fitted_model = local_run.get_output(metric=lookup_metric)
print(best_run)
print(fitted_model)
```
#### Model from a specific iteration
Simply show the run and model from the 3rd iteration:
```
iteration = 3
third_run, third_model = local_run.get_output(iteration = iteration)
print(third_run)
print(third_model)
```
### Testing the Fitted Model
Predict on training and test set, and calculate residual values.
```
y_pred_train = fitted_model.predict(X_train)
y_residual_train = y_train - y_pred_train
y_pred_test = fitted_model.predict(X_test)
y_residual_test = y_test - y_pred_test
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.metrics import mean_squared_error, r2_score
# set up a multi-plot chart
f, (a0, a1) = plt.subplots(1, 2, gridspec_kw = {'width_ratios':[1, 1], 'wspace':0, 'hspace': 0})
f.suptitle('Regression Residual Values', fontsize = 18)
f.set_figheight(6)
f.set_figwidth(16)
# plot residual values of training set
a0.axis([0, 360, -200, 200])
a0.plot(y_residual_train, 'bo', alpha = 0.5)
a0.plot([-10,360],[0,0], 'r-', lw = 3)
a0.text(16,170,'RMSE = {0:.2f}'.format(np.sqrt(mean_squared_error(y_train, y_pred_train))), fontsize = 12)
a0.text(16,140,'R2 score = {0:.2f}'.format(r2_score(y_train, y_pred_train)), fontsize = 12)
a0.set_xlabel('Training samples', fontsize = 12)
a0.set_ylabel('Residual Values', fontsize = 12)
# plot histogram
a0.hist(y_residual_train, orientation = 'horizontal', color = 'b', bins = 10, histtype = 'step');
a0.hist(y_residual_train, orientation = 'horizontal', color = 'b', alpha = 0.2, bins = 10);
# plot residual values of test set
a1.axis([0, 90, -200, 200])
a1.plot(y_residual_test, 'bo', alpha = 0.5)
a1.plot([-10,360],[0,0], 'r-', lw = 3)
a1.text(5,170,'RMSE = {0:.2f}'.format(np.sqrt(mean_squared_error(y_test, y_pred_test))), fontsize = 12)
a1.text(5,140,'R2 score = {0:.2f}'.format(r2_score(y_test, y_pred_test)), fontsize = 12)
a1.set_xlabel('Test samples', fontsize = 12)
a1.set_yticklabels([])
# plot histogram
a1.hist(y_residual_test, orientation = 'horizontal', color = 'b', bins = 10, histtype = 'step');
a1.hist(y_residual_test, orientation = 'horizontal', color = 'b', alpha = 0.2, bins = 10);
plt.show()
```
| true |
code
| 0.680574 | null | null | null | null |
|
# Линейная регрессия
https://jakevdp.github.io/PythonDataScienceHandbook/
полезная книга которую я забыл добавить в прошлый раз
# План на сегодня:
1. Как различать различные решения задачи регрессии?
2. Как подбирать параметры Линейной модели?
3. Как восстанавливать нелинейные модели с помощью Линейной модели?
4. Что делать если у нас много признаков?
5. Проблема переобучения
```
# Для начала я предлагаю посмотреть на простой пример
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
plt.rc('font', **{'size':18})
```
Сгенерим набор данных. В наших данных один признак $x$ и одна целевая переменная $y$,
следом добавим к целевой переменной немного шума распределенного по нормальному закону $N(0, 10)$:
$$y = f(x) = 3 x + 6 + N(0, 10), x \in [0, 30]$$
```
random = np.random.RandomState(4242)
X = np.linspace(0, 30, 60)
y = X * 3 + 6
y_noisy = y + random.normal(scale=10, size=X.shape)
plt.figure(figsize=(15,5))
plt.plot(X, y, label='Y = 3x + 6', color='tab:red', lw=0.5);
plt.scatter(X, y_noisy, label='Y + $\epsilon$', color='tab:blue', alpha=0.5, s=100)
plt.title('True law (red line) vs Observations (blue points)')
plt.xlabel('X, признак')
plt.ylabel('Y, target')
plt.legend();
```
Задачей регрессии называют задачу восстановления закона (функции) $f(x)$ по набору наблюдений $(x, y)$. Мне дали новое значение $x$ которого я раньше не встречал, могу ли я предсказать для него значение $y$?
```
plt.figure(figsize=(15,5))
plt.scatter(X, y_noisy, label='Y + $\epsilon$', color='tab:blue', alpha=0.5, s=100)
plt.scatter(40, -5, marker='x', s=200, label='(X=40, Y=?)', color='tab:red')
plt.plot([40,40], [-7, 250], ls='--', color='tab:red');
plt.text(35, 150, 'Y = ???');
plt.xlabel('X, признак')
plt.ylabel('Y, target')
plt.legend(loc=2);
```
Модель линейной регрессии предлагает построить через это облако точек - прямую,
то есть искать функцию $f(x)$ в виде $f(x) = ax + b$, что сводит задачу к поиску двух
коэффициентов $a$ и $b$. Здесь однако возникает два важных вопроса:
1. Предположим мы каким то образом нашли две прямые $(a_1, b_1)$ и $(a_2, b_2)$.
Как понять какая из этих двух прямых лучше? И что вообще значит, лучше?
2. Как найти эти коэффициенты `a` и `b`
## 1. Какая прямая лучше?
```
plt.figure(figsize=(20,20))
plot1(plt.subplot(221), 2, 4, 'tab:blue')
plot1(plt.subplot(222), 2.5, 15, 'tab:green')
plot1(plt.subplot(223), 3, 6, 'tab:orange')
axes = plt.subplot(224)
axes.scatter(X, y_noisy, c='tab:red', alpha=0.5, s=100)
y_hat = X * 2 + 4
axes.plot(X, y_hat, color='tab:blue', label='$f_1(x)=2x+4$')
y_hat = X * 2.5 + 15
axes.plot(X, y_hat, color='tab:green', label='$f_2(x)=2.5x+15$')
y_hat = X * 3 + 6
axes.plot(X, y_hat, color='tab:orange', label='$f_3(x)=3x+6$');
axes.legend();
```
Кажется что $f_1$ (синяя прямая) отпадает сразу, но как выбрать между оставшимися двумя?
Интуитивный ответ таков: надо посчитать ошибку предсказания. Это значит что для каждой точки из
набора $X$ (для которой нам известно значение $y$) мы можем воспользовавшись функцией $f(x)$
посчитать соответственное $y_{pred}$. И затем сравнить $y$ и $y_{pred}$.
```
plt.figure(figsize=(10,10))
plt.scatter(X, y_noisy, s=100, c='tab:blue', alpha=0.1)
y_hat = X * 3 + 6
plt.plot(X, y_hat, label='$y_{pred} = 3x+6$')
plt.scatter(X[2:12], y_noisy[2:12], s=100, c='tab:blue', label='y')
for _x, _y in zip(X[2:12], y_noisy[2:12]):
plt.plot([_x, _x], [_y, 3*_x+6], c='b')
plt.legend();
```
Как же считать эту разницу? Существует множество способов:
$$
MSE(\hat{f}, x) = \frac{1}{N} \sum_{i=1}^{N}\left(\ y_i - \hat{f}(x_i)\ \right) ^ 2
$$
$$
MAE(\hat{f}, x) = \frac{1}{N} \sum_{i=1}^{N}\left|\ y_i - \hat{f}(x_i)\ \right|
$$
$$
RMSLE(\hat{f}, x) = \sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(\ \log(y_i + 1) - \log(\hat{f}(x_i) + 1)\ \right)^2}
$$
$$
MAPE (\hat{f}, x) = \frac{100}{N} \sum_{i=1}^{N}\left| \frac{y_i - \hat{f}(x_i)}{y_i} \right|
$$
и другие.
---
**Вопрос 1.** Почему бы не считать ошибку вот так:
$$
ERROR(\hat{f}, x) = \frac{1}{N} \sum_{i=1}^{N}\left(\ y_i - \hat{f}(x_i)\ \right)
$$
---
**Вопрос 2.** Чем отличаются `MSE`, `MAE`, `RMSLE`, `MAPE`? Верно ли, что модель наилучшая с точки зрения одной меры, всегда будет лучше с точки зрения другой/остальных?
---
Пока что мы остановимся на MSE. Давайте теперь сравним наши прямые используя MSE
```
def mse(y1, y2, prec=2):
return np.round(np.mean((y1 - y2)**2),prec)
def plot2(axes, a, b, color='b', X=X, y=y_noisy):
axes.plot(X, y_noisy, 'r.')
y_hat = X * a + b
axes.plot(X, y_hat, color=color, label='y = {}x + {}'.format(a,b))
axes.set_title('MSE = {:.2f}'.format(mse(y_hat, y_noisy)));
axes.legend()
plt.figure(figsize=(20,12))
plot2(plt.subplot(221), 2.5, 15, 'g')
plot2(plt.subplot(222), 3, 6, 'orange')
plot2(plt.subplot(223), 2, 4, 'b')
```
Понятно что чем меньше значение MSE тем меньше ошибка предсказания, а значит выбирать нужно модель для которой MSE наименьшее. В нашем случае это $f_3(x) = 3x+6$. Отлично, мы ответили на первый вопрос, как из многих прямых выбрать одну, теперь попробуем ответить на второй.
# 2. Как найти параметры прямой?
Зафиксируем что нам на текущий момент известно.
1. У нас есть данные ввиде множества пар $X$ и $y$: $\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}$
2. Мы хотим найти такую функцию $\hat{f}(x)$ которая бы минимизировала
$$MSE(\hat{f}, x) = \frac{1}{N} \sum_{i=1}^{N}\left(\ y_i - \hat{f}(x_i)\ \right) ^ 2 \rightarrow \text{min}$$
3. Мы будем искать $\hat{f}(x)$ в предположении что это линейная функция:
$$\hat{f}(x) = ax + b$$
----
Подставив теперь $\hat{f}(x)$ в выражение для MSE получим:
$$
\frac{1}{N} \sum_{i=1}^{N}\left(\ y_i - ax_i - b\ \right) ^ 2 \rightarrow \text{min}_{a,b}
$$
Сделать это можно по-меньшей мере двумя способами:
1. Аналитически: переписать выражение в векторном виде, посчитать первую производную и приравнять ее к 0, откуда выразить значения для параметров.
2. Численно: посчитать частные производные по a и по b и воспользоваться методом градиентного спуска.
Подробный аналитический вывод можно посмотреть например здесь https://youtu.be/Y_Ac6KiQ1t0?list=PL221E2BBF13BECF6C
(после просмотра также станет откуда взялся MSE). Нам же на будущее будет полезно сделать это в лоб (не особо вдаваясь в причины)
-----
Вектор $y$ имеет размерность $n \times 1$ вектор $x$ так же $n \times 1$, применим следующий трюк: превратим вектор $x$ в матрицу $X$ размера $n \times 2$ в которой первый столбец будет целиком состоять из 1. Тогда обзначив за $\theta = [b, a]$ получим выражение для MSE в векторном виде:
$$
\frac{1}{n}(y - X \theta)^{T}(y - X \theta) \rightarrow min_{\theta}
$$
взяв производную по $\theta$ и приравняв ее к 0, получим:
$$
y = X \theta
$$
поскольку матрица $X$ не квадратная и не имеет обратной, домножим обе части на $X^T$ слева
$$
X^T y = X^T X \theta
$$
матрица X^T X, за редким исключением (каким?) обратима, в итоге получаем выражение для $\theta$:
$$
\theta = (X^T X)^{-1} X^T y
$$
проделаем теперь эти шаги с нашими данными (Формула дающая выражение для $\theta$ называется Normal equation)
```
print(X.shape, y.shape)
print('----------')
print('Несколько первых значений X: ', np.round(X[:5],2))
print('Несколько первых значений Y: ', np.round(y[:5],2))
X_new = np.ones((60, 2))
X_new[:, 1] = X
y_new = y.reshape(-1,1)
print(X_new.shape, y_new.shape)
print('----------')
print('Несколько первых значений X:\n', np.round(X_new[:5],2))
print('Несколько первых значений Y:\n', np.round(y_new[:5],2))
theta = np.linalg.inv((X_new.T.dot(X_new))).dot(X_new.T).dot(y_new)
print(theta)
```
Таким образом мы восстановили функцию $f(x) = 3 x + 6$ (что совершенно случайно совпало с $f_3(x)$)
Отлично, это была красивая победа! Что дальше?
А дальше нас интересуют два вопроса:
1. Что если первоначальная функция была взята из нелинейного источника (например $y = 3 x^2 +1$)
2. Что делать если у нас не один признак, а много? (т.е. матрица $X$ имеет размер не $n \times 2$, а $n \times m+1$, где $m$ - число признаков)
# 3. Что если нужно восстановить нелинейную зависимость?
```
plt.figure(figsize=(10,10))
x = np.linspace(-3, 5, 60).reshape(-1,1)
y = 3*x**2 + 1 + random.normal(scale=5, size=x.shape)
y_model = 3*x**2 + 1
plt.scatter(x, y, label='$y = 3x^2 + 1 +$ N(0,5)')
plt.plot(x, y_model, label='$y = 3x^2 + 1$')
plt.legend();
```
Давайте для этого воспользуемся реализацией линейной регрессии из **sklearn**
```
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x, y)
print('y = {} X + {}'.format(np.round(model.coef_[0][0],2), np.round(model.intercept_[0], 2)))
```
Обратите внимание, мы не добавляли столбец из 1 в матрицу X, поскольку в классе
LinearRegression есть параметр fit_intercept (по умолчанию он равен True)
Посмотрим теперь как это выглядит
```
plt.figure(figsize=(20,15))
ax1 = plt.subplot(221)
ax1.scatter(x, y, )
ax1.plot(x, y_model, label=f'True source: $y = 3x^2 + 1$\nMSE={mse(y, y_model)}')
ax1.legend();
y_pred = model.coef_[0][0] * x + model.intercept_[0]
ax2 = plt.subplot(222)
ax2.scatter(x, y,)
ax2.plot(x, y_pred, label='Predicted curve: $y = {} x + {}$\nMSE={}'.format(np.round(model.coef_[0][0],2),
np.round(model.intercept_[0],2),
mse(y, y_pred)), c='r')
ax2.legend();
```
Кажется что в данном случае предсказывать "прямой" не лучшая идея, что же делать?
Если линейные признаки не дают желаемого результата, надо добавлять нелинейные!
Давайте например искать параметры $a$ и $b$ для вот такой функции:
$$
f(x) = ax^2 + b
$$
```
x_new = x**2
model.fit(x_new, y)
print('y = {} x^2 + {}'.format(np.round(model.coef_[0][0],2), np.round(model.intercept_[0], 2)))
plt.figure(figsize=(20,15))
ax1 = plt.subplot(221)
ax1.scatter(x, y, )
ax1.plot(x, y_model, label='True source: $y = 3x^2 + 1$\nMSE={}'.format(mse(y, y_model)))
ax1.legend();
y_pred = model.coef_[0][0] * x_new + model.intercept_[0]
ax2 = plt.subplot(222)
ax2.scatter(x, y,)
ax2.plot(x, y_pred, label='Predicted curve: $y = {} x^2 + {}$\nMSE={}'.format(np.round(model.coef_[0][0],2),
np.round(model.intercept_[0],2),
mse(y, y_pred)), c='r')
ax2.legend();
```
Некоторые замечания
1. Результирующая функция даже лучше всмысле MSE чем источник (причина - шум)
2. Регрессия все еще называется линейной (собственно линейной она зовется не по признакам X, а по параметрам $\theta$). Регрессия называется линейной потому что предсказываемая величина это **линейная комбинация признаков**, алгоритму неизвестно что мы там что-то возвели в квадрат или другую степень.
3. Откуда я узнал что нужно добавить именно квадратичный признак? (ниоткуда, просто угадал, дальше увидим как это делать)
### 3.1 Задача: воспользуйтесь Normal equation для того чтобы подобрать параметры a и b
Normal equation:
$$
\theta = (X^T X)^{-1} X^T y
$$
Уточнение: подобрать параметры a и b нужно для функции вида $f(x) = ax^2 + b$
# 4. Что делать если у нас не один признак, а много?
Отлично, теперь мы знаем что делать если у нас есть один признак и одна целевая переменная (например предсказывать вес по росту или стоимость квартиры на основе ее площади, или время подъезда такси на основе времени суток). Но что же нам делать если факторов несколько? Для этого давайте еще раз посмотрим на Normal equation:
$$
\theta_{m\times 1} = (X^T_{m\times n} X_{n\times m})^{-1} X^T_{m\times n} y_{n\times 1}
$$
Посчитав $\theta$ как мы будем делать предсказания для нового наблюдения $x$?
$$
y = x_{1\times m} \times \theta_{m\times 1}
$$
А что если у нас теперь не один признак а несколько (например $m$), как изменятся размерности?
Размерность X станет равна $n\times (m+1)$: $n$ строк и $(m+1)$ столбец (размерность $y$ не изменится), подставив теперь это в Normal equation получим что размерность $\theta$ изменилась и стала равна $(m+1)\times 1$, а предсказания мы будем делать все так же:$y = x \times \theta$ или если раскрыть $\theta$:
$$
y = \theta_0 + x^{[1]}\theta_1 + x^{[2]}\theta_2 + \ldots + x^{[m]}\theta_m
$$
здесь верхние индексы это индекс признака, а не наблюдения (номер столбца в матрице $X$), и не арифмитическая степень.
-----
Отлично, значит мы можем и с несколькими признаками строить линейную регрессию, что же дальше?
А дальше нам надо ответить на (очередные) два вопроса:
1. Как же все-таки подбирать какие признаки генерировать?
2. Как это делать с помощью функций из **sklearn**
Мы ответим на оба вопроса, но сперва разберем пример для того чтобы продемонстрировать
**интерпретируемость** линейной модели
# Пример. Определение цен на недвижимость.
**Интерпретируемость** линейной модели заключается в том что **увеличение значение признака на 1** ведет к **увеличению целевой переменной** на соответствующее значение **theta** (у этого признака в линейной модели):
$$
f(x_i) = \theta_0 + \theta_1 x_i^{[1]} + \ldots + \theta_j x_i^{[j]} + \ldots + \theta_m x_i^{[m]}
$$
Увеличим значение признака $j$ у наблюдения $x_i$:
$$
\bar{x_i}^{[j]} = x_i^{[j]} + 1 = (x_i+1)^{[j]}
$$
изменение значения функции составит:
$$
\Delta(f(x)) = f(\bar{x}_i) - f(x_i) = \theta_j
$$
```
import pandas as pd
from sklearn.metrics import mean_squared_log_error
# данные можно взять отсюда ---> https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data
# house_data = pd.read_csv('train.csv', index_col=0)
# trunc_data = house_data[['LotArea', '1stFlrSF', 'BedroomAbvGr', 'SalePrice']]
# trunc_data.to_csv('train_house.csv')
house_data = pd.read_csv('train_house.csv', index_col=0)
house_data.head()
X = house_data[['LotArea', '1stFlrSF', 'BedroomAbvGr']].values
y = house_data['SalePrice'].values
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)
print('Linear coefficients: ', list(model.coef_), 'Intercept: ', model.intercept_)
print('MSLE: ', np.sqrt(mean_squared_log_error(y, y_pred)))
print('MSE: ', mse(y, y_pred))
for y_t, y_p in zip(y[:5], y_pred[:5]):
print(y_t, np.round(y_p, 3), np.round(mean_squared_log_error([y_t], [y_p]), 6))
plt.figure(figsize=(7,7))
plt.scatter(y, y_pred);
plt.plot([0, 600000], [0, 600000], c='r');
plt.text(200000, 500000, 'Overestimated\narea')
plt.text(450000, 350000, 'Underestimated\narea')
plt.xlabel('True value')
plt.ylabel('Predicted value');
```
Вернемся к нашим вопросам:
1. Как же все-таки подбирать какие признаки генерировать?
2. Как это делать с помощью функций из **sklearn**
## 5. Генерация признаков.
```
X = np.array([0.76923077, 1.12820513, 1.48717949, 1.84615385, 2.20512821,
2.56410256, 2.92307692, 3.28205128, 3.64102564, 4.]).reshape(-1,1)
y = np.array([9.84030322, 26.33596415, 16.68207941, 12.43191433, 28.76859577,
32.31335979, 35.26001044, 31.73889375, 45.28107096, 46.6252025]).reshape(-1,1)
plt.scatter(X, y);
```
Попробуем простую модель с 1 признаком:
$$
f(x) = ax + b
$$
```
lr = LinearRegression()
lr.fit(X, y)
y_pred = lr.predict(X)
plt.scatter(X, y);
plt.plot(X, y_pred);
plt.title('MSE: {}'.format(mse(y, y_pred)));
```
Добавим квадратичные признаки
```
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
poly = PolynomialFeatures(degree=2)
X_2 = poly.fit_transform(X)
print(X_2[:3])
lr = LinearRegression()
lr.fit(X_2, y)
y_pred_2 = lr.predict(X_2)
plt.scatter(X, y);
plt.plot(X, y_pred_2);
plt.title('MSE: {}'.format(mse(y, y_pred_2)));
```
Добавим кубические
```
poly = PolynomialFeatures(degree=3)
X_3 = poly.fit_transform(X)
print(X_3[:3])
lr = LinearRegression()
lr.fit(X_3, y)
y_pred_3 = lr.predict(X_3)
plt.scatter(X, y);
plt.plot(X, y_pred_3);
plt.title('MSE: {}'.format(mse(y, y_pred_3)));
```
We need to go deeper..
```
def plot3(ax, degree):
poly = PolynomialFeatures(degree=degree)
_X = poly.fit_transform(X)
lr = LinearRegression()
lr.fit(_X, y)
y_pred = lr.predict(_X)
ax.scatter(X, y);
ax.plot(X, y_pred, label='MSE={}'.format(mse(y,y_pred)));
ax.set_title('Polynom degree: {}'.format(degree));
ax.legend()
plt.figure(figsize=(30,15))
plot3(plt.subplot(231), 4)
plot3(plt.subplot(232), 5)
plot3(plt.subplot(233), 6)
plot3(plt.subplot(234), 7)
plot3(plt.subplot(235), 8)
plot3(plt.subplot(236), 9)
```
### Переход в многомерное нелинейное пространство
#### Как сделать регрессию линейной если зависимость нелинейная?
- $\mathbf{x}$ может зависеть не совсем линейно от $\mathbf{y}$.
- Перейдем в новое пространство - $\phi(\mathbf{x})$ где $\phi(\cdot)$ это нелинейная функция от $\mathbf{x}$.
- В наших примерах присутствуют только полиномы, вообще говоря нелинейо преобразование может быть любым: экспонента, логарифм, тригонометрические функции и пр.
- Возьмем линейную комбинацию этих нелинейных функций $$f(\mathbf{x}) = \sum_{j=1}^k w_j \phi_j(\mathbf{x}).$$
- Возьмем некотрый базис функций (например квадратичный базис)
$$\boldsymbol{\phi} = [1, x, x^2].$$
- Теперь наша функция имеет такой вид
$$f(\mathbf{x}_i) = \sum_{j=1}^m w_j \phi_{i, j} (x_i).$$
Ну чтож, выходит что полином 9 степени это лучшее что мы можем здесь сделать? или все-таки нет...
```
a = 5
b = 10
n_points = 40
x_min = 0.5
x_max = 4
x = np.linspace(x_min, x_max, n_points)[:, np.newaxis]
completely_random_number = 33
rs = np.random.RandomState(completely_random_number)
noise = rs.normal(0, 5, (n_points, 1))
y = a + b * x + noise
idx = np.arange(3,40,4)
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
plt.scatter(x,y, s=80, c ='tab:blue', edgecolors='k', linewidths=0.3);
plt.scatter(x[idx],y[idx], s=80, c='tab:red');
plt.subplot(1,2,2)
plt.scatter(x[idx],y[idx], s=80, c ='tab:red', edgecolors='k', linewidths=0.3);
x_train = x[idx]
y_train = y[idx]
lr_linear = LinearRegression(fit_intercept=True)
lr_linear.fit(x_train, y_train)
y_linear = lr_linear.predict(x_train)
# Cubic
cubic = PolynomialFeatures(degree=3)
x_cubic = cubic.fit_transform(x_train)
lr_3 = LinearRegression(fit_intercept=False)
lr_3.fit(x_cubic, y_train)
y_cubic = lr_3.predict(x_cubic)
# 9'th fit
poly = PolynomialFeatures(degree=9)
x_poly = poly.fit_transform(x_train)
lr_9 = LinearRegression(fit_intercept=False)
lr_9.fit(x_poly, y_train)
y_poly = lr_9.predict(x_poly)
xx = np.linspace(0.75,4,50).reshape(-1,1)
xx_poly = poly.fit_transform(xx)
yy_poly = lr_9.predict(xx_poly)
# PREDICTION ON WHOLE DATA
# linear prediction
y_pred_linear = lr_linear.predict(x)
# cubic prediction
x_cubic_test = cubic.transform(x)
y_pred_cubic = lr_3.predict(x_cubic_test)
# poly 9 prediction
x_poly_test = poly.transform(x)
y_pred_poly = lr_9.predict(x_poly_test)
def plot4(ax, x, y, y_regression, test_idx=None):
ax.scatter(x,y, s=80, c ='tab:red', edgecolors='k', linewidths=0.3, label='Test');
ax.plot(x,y_regression);
if test_idx is not None:
ax.scatter(x[test_idx], y[test_idx], s=80, c ='tab:blue',
edgecolors='k',
linewidths=0.3,
label ='Train');
ax.legend()
ax.set_title('MSE = {}'.format(np.round(mse(y, y_regression), 2)));
# PLOT PICTURES
plt.figure(figsize=(24,12))
plot4(plt.subplot(231), x_train,y_train,y_linear)
plot4(plt.subplot(232), x_train,y_train,y_cubic)
plot4(plt.subplot(233), x_train,y_train,y_poly)
plot4(plt.subplot(234), x,y,y_pred_linear, test_idx=idx)
plot4(plt.subplot(235), x,y,y_pred_cubic, test_idx=idx)
plot4(plt.subplot(236), x[3:],y[3:],y_pred_poly[3:], test_idx=idx-3)
print('FIRST ROW is TRAIN data set, SECOD ROW is WHOLE data')
```
#### Вопрос: Почему на графиках в последней колонке поведение функции отличается на TRAIN и TEST данных? (области возрастания, убывания и кривизна)
**Ответ:**
```
mse_train = []
mse_test = []
for degree in range(1,10):
idx_train = [3, 7, 11, 15, 19, 23, 27, 31, 35, 39]
idx_test = [ 0, 1, 2, 4, 5, 6, 8, 9, 10, 12, 13, 14,
16, 17, 18, 20, 21, 22, 24, 25, 26, 28,
29, 30, 32, 33, 34, 36, 38, 39]
x_train, x_test = x[idx_train], x[idx_test]
y_train, y_test = y[idx_train], y[idx_test]
poly = PolynomialFeatures(degree=degree)
lr = LinearRegression(fit_intercept=True)
x_train = poly.fit_transform(x_train)
x_test = poly.transform(x_test)
lr.fit(x_train, y_train)
y_pred_train = lr.predict(x_train)
y_pred_test = lr.predict(x_test)
mse_train.append(mse(y_train, y_pred_train))
mse_test.append(mse(y_test, y_pred_test))
plt.figure(figsize=(15,10))
plt.plot(list(range(1,6)), mse_train[:5], label='Train error')
plt.plot(list(range(1,6)), mse_test[:5], label='Test error')
plt.legend();
```

1. http://scott.fortmann-roe.com/docs/BiasVariance.html
2. http://www.inf.ed.ac.uk/teaching/courses/mlsc/Notes/Lecture4/BiasVariance.pdf
| true |
code
| 0.538073 | null | null | null | null |
|
```
import spacy
from IPython.display import SVG, YouTubeVideo
from spacy import displacy
```
# Intro to Clinical NLP
### Instructor: Alec Chapman
### Email: [email protected]
Welcome to the NLP module! We'll start this module by watching a short introduction of the instructor and of Natural Language Processing (NLP) in medicine. Then we'll learn how to perform clinical NLP in spaCy and will end by applying an NLP system to several clinical tasks and datasets.
### Introduction videos:
- [Meet the Instructor: Dr. Wendy Chapman](https://youtu.be/piJc8RXCZW4)
- [Intro to Clinical NLP / Meet the Instructor: Alec Chapman](https://youtu.be/suVOm0CFX7A)
Slides: [Intro-to-NLP.pdf](https://github.com/Melbourne-BMDS/mimic34md2020_materials/blob/master/slides/Intro-to-NLP.pdf)
```
# Introduction to the instructor: Wendy Chapman
YouTubeVideo("piJc8RXCZW4")
YouTubeVideo("suVOm0CFX7A")
```
# Intro to spaCy
```
YouTubeVideo("agmaqyUMAkI")
```
One very popular tool for NLP is [spaCy](https://spacy.io). SpaCy offers many out-of-the-box tools for processing and analyzing text, and the spaCy framework allows users to extend the models for their own purposes. SpaCy consists mostly of **statistical NLP** models. In statistical models, a large corpus of text is processed and mathematical methods are used to identify patterns in the corpus. This process is called **training**. Once a model has been trained, we can use it to analyze new text. But as we'll see, we can also use spaCy to implement sophisticated rules and custom logic.
SpaCy comes with several pre-trained models, meaning that we can quickly load a model which has been trained on large amounts of data. This way, we can take advantage of work which has already been done by spaCy developers and focus on our own NLP tasks. Additionally, members of the open-source spaCy community can train and publish their own models.
<img alt="SpaCy logo" height="100" width="250" src="https://spacy.io/static/social_default-1d3b50b1eba4c2b06244425ff0c49570.jpg">
# Agenda
- We'll start by looking at the basic usage of spaCy
- Next, we'll focus on specific NLP task, **named entity recognition (NER)**, and see how this works in spaCy, as well as some of the limitations with clinical data
- Since spaCy's built-in statistical models don't accomplish the tasks we need in clinical NLP, we'll use spaCy's pattern matchers to write rules to extract clinical concepts
- We will then download and use a statistical model to extract clinical concepts from text
- Some of these limitations can be addressed by writing our own rules for concept extraction, and we'll practice that with some clinical texts. We'll then go a little deeper into how spaCy's models are implemented and how we can modify them. Finally, we'll end the day by spaCy models which were designed specifically for use in the biomedical domain.
# spaCy documentation
spaCy has great documentation. As we're going along today, try browsing through their documentation to find examples and instructions. Start by opening up these two pages and navigating through the documentation:
[Basic spaCy usage](https://spacy.io/usage/models)
[API documentation](https://spacy.io/api)
spaCy also has a really good, free online class. If you want to dig deeper into spaCy after this class, it's a great resource for using this library:
https://course.spacy.io/
It's also available on DataCamp (the first two chapters will be assigned for homework): https://learn.datacamp.com/courses/advanced-nlp-with-spacy
# Basic usage of spaCy
In this notebook, we'll look at the basic fundamentals of spaCy:
- Main classes in spaCy
- Linguistic attributes
- Named entity recognition (NER)
## How to use spaCy
At a high-level, here are the steps for using spaCy:
- Start by loading a pre-trained NLP model
- Process a string of text with the model
- Use the attributes in our processed documents for downstream NLP tasks like NER or document classification
For example, here's a very short example of how this works. For the sake of demonstration, we'll use this snippet of a business news article:
```
# First, load a pre-trained model
nlp = spacy.load("en_core_web_sm")
# Process a string of text with the model
text = """Taco Bell’s latest marketing venture, a pop-up hotel, opened at 10 a.m. Pacific Time Thursday.
The rooms sold out within two minutes.
The resort has been called “The Bell: A Taco Bell Hotel and Resort.” It’s located in Palm Springs, California."""
doc = nlp(text)
doc
# Use the attributes in our processed documents for downstream NLP tasks
# Here, we'll visualize the entities in this text identified through NER
displacy.render(doc, style="ent")
```
Let's dive a little deeper into how spaCy is structured and what we have to work with.
## SpaCy Architecture
The [spaCy documentation](https://spacy.io/api) offers a detailed description of the package's architecture. In this notebook, we'll focus on these 5 classes:
- `Language`: The NLP model used to process text
- `Doc`: A sequence of text which has been processed by a `Language` object
- `Token`: A single word or symbol in a Doc
- `Span`: A slice from a Doc
- `EntityRecognizer`: A model which extracts mentions of **named entities** from text
# `nlp`
The `nlp` object in spaCy is the linguistic model which will be used for processing text. We instantiate a `Language` class by providing the name of a pre-trained model which we wish to use. We typically name this object `nlp`, and this will be our primary entry point.
```
nlp = spacy.load("en_core_web_sm")
nlp
```
The `nlp` model we instantiated above is a **small** ("sm"), **English** ("en")-language model trained on **web** ("web") data, but there are currently 16 different models from 9 different languages. See the [spaCy documentation](https://spacy.io/usage/models) for more information on each of the models.
# Documents, spans and tokens
The `nlp` object is what we'll be using to process text. The next few classes represent the output of our NLP model.
## `Doc` class
The `doc` object represents a single document of text. To create a `doc` object, we call `nlp` on a string of text. This runs that text through a spaCy pipeline, which we'll learn more about in a future notebook.
```
text = 'Taco Bell’s latest marketing venture, a pop-up hotel, opened at 10 a.m. Pacific Time Thursday.'
doc = nlp(text)
type(doc)
print(doc)
```
## Tokens and Spans
### Token
A `Token` is a single word, symbol, or whitespace in a `doc`. When we create a `doc` object, the text broken up into individual tokens. This is called **"tokenization"**.
**Discussion**: Look at the tokens generated from this text snippet. What can you say about the tokenization method? Is it as simple as splitting up into words every time we reach a whitespace?
```
token = doc[0]
token
type(token)
doc
for token in doc:
print(token)
```
### Span
A `Span` is a slice of a document, or a consecutive sequence of tokens.
```
span = doc[1:4]
span
type(span)
```
## Linguistic Attributes
Because spaCy comes with pre-trained linguistic models, when we call `nlp` on a text we have access to a number of linguistic attributes in the `doc` or `token` objects.
### POS Tagging
Parts of speech are categories of words. For example, "nouns", "verbs", and "adjectives" are all examples of parts of speech. Assigning parts of speech to words is useful for downstream NLP texts such as word sense disambiguation and named entity recognition.
**Discussion**: What to the POS tags below mean?
```
print(f"Token -> POS\n")
for token in doc:
print(f"{token.text} -> {token.pos_}")
spacy.explain("PROPN")
```
### Lemma
The **lemma** of a word refers to the **root form** of a word. For example, "eat", "eats", and "ate" are all different inflections of the lemma "eat".
```
print(f"Token -> Lemma\n")
for token in doc:
print(f"{token.text} -> {token.lemma_}")
```
### Dependency Parsing
In dependency parsing, we analyze the structure of a sentence. We won't spend too much time on this, but here is a nice visualization of dependency parse looks like. Take a minute to look at the arrows between words and try to figure out what they mean.
```
doc = nlp("The cat sat on the green mat")
displacy.render(doc, style='dep')
```
### Other attributes
Look at spaCy's [Token class documentation](https://spacy.io/api/token) for a full list of additional attributes available for each token in a document.
# NER with spaCy
**"Named Entity Recognition"** is a subtask of NLP where we extract specific named entities from the text. The definition of a "named entity" changes depending on the domain we're working on. We'll look at clinical NER later, but first we'll look at some examples in more general domains.
NER is often performed using news articles as source texts. In this case, named entities are typically proper nouns, such as:
- People
- Geopolitical entities, like countries
- Organizations
We won't go into the details of how NER is implemented in spaCy. If you want to learn more about NER and various way it's implemented, a great resource is [Chapter 17.1 of Jurafsky and Martin's textbook "Speech and Language Processing."](https://web.stanford.edu/~jurafsky/slp3/17.pdf)
Here is an excerpt from an article in the Guardian. We'll process this document with our nlp object and then look at what entities are extracted. One way to do this is using spaCy's `displacy` package, which visualizes the results of a spaCy pipeline.
```
text = """Germany will fight to the last hour to prevent the UK crashing out of the EU without a deal and is willing
to hear any fresh ideas for the Irish border backstop, the country’s ambassador to the UK has said.
Speaking at a car manufacturers’ summit in London, Peter Wittig said Germany cherished its relationship
with the UK and was ready to talk about solutions the new prime minister might have for the Irish border problem."""
doc = nlp(text)
displacy.render(doc, style="ent")
```
We can use spaCy's `explain` function to see definitions of what an entity type is. Look up any entity types that you're not familiar with:
```
spacy.explain("GPE")
```
The last example comes from a political news article, which is pretty typical for what NER is often trained on and used for. Let's look at another news article, this one with a business focus:
```
# Example 2
text = """Taco Bell’s latest marketing venture, a pop-up hotel, opened at 10 a.m. Pacific Time Thursday.
The rooms sold out within two minutes.
The resort has been called “The Bell: A Taco Bell Hotel and Resort.” It’s located in Palm Springs, California."""
doc = nlp(text)
displacy.render(doc, style="ent")
```
## Discussion
Compare how the NER performs on each of these texts. Can you see any errors? Why do you think it might make those errors?
Once we've processed a text with `nlp`, we can iterate through the entities through the `doc.ents` attribute. Each entity is a spaCy `Span`. You can see the label of the entity through `ent.label_`.
```
for ent in doc.ents:
print(ent, ent.label_)
```
# spaCy Processing Pipelines
How does spaCy generate information like POS tags and entities? Under the hood, the `nlp` object goes through a number of sequential steps to processt the text. This is called a **pipeline** and it allows us to create modular, independent processing steps when analyzing text. The model we loaded comes with a default **pipeline** which helps extract linguistic attributes from the text. We can see the names of our pipeline components through the `nlp.pipe_names` attribute:
```
nlp.pipe_names
```
The image below shows a visual representation of this. In this default spaCy pipeline,
- We pass the text into the pipeline by calling `nlp(text)`
- The text is split into **tokens** by the `tokenizer`
- POS tags are assigned by the `tagger`
- A dependency parse is generated by the `parser`
- Entities are extracted by the `ner`
- a `Doc` object is returned
These are the steps taken in the default pipeline. However, as we'll see later we can add our own processing **components** and add them to our pipeline to do additional analysis.
<img alt="SpaCy logo" src="https://d33wubrfki0l68.cloudfront.net/16b2ccafeefd6d547171afa23f9ac62f159e353d/48b91/pipeline-7a14d4edd18f3edfee8f34393bff2992.svg">
# Clinical Text
Let's now try using spaCy's built-in NER model on clinical text and see what information we can extract.
```
clinical_text = "76 year old man with hypotension, CKD Stage 3, status post RIJ line placement and Swan. "
doc = nlp(clinical_text)
displacy.render(doc, style="ent")
```
### Discussion
- How did spaCy do with this sentence?
- What do you think caused it to make errors in the classifications?
General purpose NER models are typically made for extracting entities out of news articles. As we saw before, this includes mainly people, organizations, and geopolitical entities. We can see which labels are available in spaCy's NER model by looking at the NER component. As you can see, not many of these are very useful for clinical text extraction.
### Discussion
- What are some entity types we are interested in in clinical domain?
- Does spaCy's out-of-the-box NER handle any of these types?
# Next Steps
Since spaCy's model doesn't extract the information we need by default, we'll need to do some additional work to extract clinical concepts. In the next notebook, we'll look at how spaCy allows **rule-based NLP** through **pattern matching**.
[nlp-02-medspacy-concept-extraction.ipynb](nlp-02-medspacy-concept-extraction.ipynb)
| true |
code
| 0.655612 | null | null | null | null |
|
# Pre-trained embeddings for Text
```
import gzip
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
glove_path = '../data/embeddings/glove.6B.50d.txt.gz'
with gzip.open(glove_path, 'r') as fin:
line = fin.readline().decode('utf-8')
line
def parse_line(line):
values = line.decode('utf-8').strip().split()
word = values[0]
vector = np.asarray(values[1:], dtype='float32')
return word, vector
embeddings = {}
word_index = {}
word_inverted_index = []
with gzip.open(glove_path, 'r') as fin:
for idx, line in enumerate(fin):
word, vector = parse_line(line) # parse a line
embeddings[word] = vector # add word vector
word_index[word] = idx # add idx
word_inverted_index.append(word) # append word
word_index['good']
word_inverted_index[219]
embeddings['good']
embedding_size = len(embeddings['good'])
embedding_size
plt.plot(embeddings['good']);
plt.subplot(211)
plt.plot(embeddings['two'])
plt.plot(embeddings['three'])
plt.plot(embeddings['four'])
plt.title("A few numbers")
plt.ylim(-2, 5)
plt.subplot(212)
plt.plot(embeddings['cat'])
plt.plot(embeddings['dog'])
plt.plot(embeddings['rabbit'])
plt.title("A few animals")
plt.ylim(-2, 5)
plt.tight_layout()
vocabulary_size = len(embeddings)
vocabulary_size
```
## Loading pre-trained embeddings in Keras
```
from keras.models import Sequential
from keras.layers import Embedding
embedding_weights = np.zeros((vocabulary_size,
embedding_size))
for word, index in word_index.items():
embedding_weights[index, :] = embeddings[word]
emb_layer = Embedding(input_dim=vocabulary_size,
output_dim=embedding_size,
weights=[embedding_weights],
mask_zero=False,
trainable=False)
word_inverted_index[0]
model = Sequential()
model.add(emb_layer)
embeddings['cat']
cat_index = word_index['cat']
cat_index
model.predict([[cat_index]])
```
## Gensim
```
import gensim
from gensim.scripts.glove2word2vec import glove2word2vec
glove_path = '../data/embeddings/glove.6B.50d.txt.gz'
glove_w2v_path = '../data/embeddings/glove.6B.50d.txt.vec'
glove2word2vec(glove_path, glove_w2v_path)
from gensim.models import KeyedVectors
glove_model = KeyedVectors.load_word2vec_format(
glove_w2v_path, binary=False)
glove_model.most_similar(positive=['good'], topn=5)
glove_model.most_similar(positive=['two'], topn=5)
glove_model.most_similar(positive=['king', 'woman'],
negative=['man'], topn=3)
```
## Visualization
```
import os
model_dir = '/tmp/ztdl_models/embeddings/'
from shutil import rmtree
rmtree(model_dir, ignore_errors=True)
os.makedirs(model_dir)
n_viz = 4000
emb_layer_viz = Embedding(n_viz,
embedding_size,
weights=[embedding_weights[:n_viz]],
mask_zero=False,
trainable=False)
model = Sequential([emb_layer_viz])
word_embeddings = emb_layer_viz.weights[0]
word_embeddings
import keras.backend as K
import tensorflow as tf
sess = K.get_session()
saver = tf.train.Saver([word_embeddings])
saver.save(sess, os.path.join(model_dir, 'model.ckpt'), 1)
os.listdir(model_dir)
fname = os.path.join(model_dir, 'metadata.tsv')
with open(fname, 'w', encoding="utf-8") as fout:
for index in range(0, n_viz):
word = word_inverted_index[index]
fout.write(word + '\n')
config = """embeddings {{
tensor_name: "{tensor}"
metadata_path: "{metadata}"
}}""".format(tensor=word_embeddings.name,
metadata='metadata.tsv')
print(config)
fname = os.path.join(model_dir, 'projector_config.pbtxt')
with open(fname, 'w', encoding="utf-8") as fout:
fout.write(config)
```
| true |
code
| 0.476701 | null | null | null | null |
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Model Development with Custom Weights
This example shows how to retrain a model with custom weights and fine-tune the model with quantization, then deploy the model running on FPGA. Only Windows is supported. We use TensorFlow and Keras to build our model. We are going to use transfer learning, with ResNet50 as a featurizer. We don't use the last layer of ResNet50 in this case and instead add our own classification layer using Keras.
The custom wegiths are trained with ImageNet on ResNet50. We will use the Kaggle Cats and Dogs dataset to retrain and fine-tune the model. The dataset can be downloaded [here](https://www.microsoft.com/en-us/download/details.aspx?id=54765). Download the zip and extract to a directory named 'catsanddogs' under your user directory ("~/catsanddogs").
Please set up your environment as described in the [quick start](project-brainwave-quickstart.ipynb).
```
import os
import sys
import tensorflow as tf
import numpy as np
from keras import backend as K
```
## Setup Environment
After you train your model in float32, you'll write the weights to a place on disk. We also need a location to store the models that get downloaded.
```
custom_weights_dir = os.path.expanduser("~/custom-weights")
saved_model_dir = os.path.expanduser("~/models")
```
## Prepare Data
Load the files we are going to use for training and testing. By default this notebook uses only a very small subset of the Cats and Dogs dataset. That makes it run relatively quickly.
```
import glob
import imghdr
datadir = os.path.expanduser("~/catsanddogs")
cat_files = glob.glob(os.path.join(datadir, 'PetImages', 'Cat', '*.jpg'))
dog_files = glob.glob(os.path.join(datadir, 'PetImages', 'Dog', '*.jpg'))
# Limit the data set to make the notebook execute quickly.
cat_files = cat_files[:64]
dog_files = dog_files[:64]
# The data set has a few images that are not jpeg. Remove them.
cat_files = [f for f in cat_files if imghdr.what(f) == 'jpeg']
dog_files = [f for f in dog_files if imghdr.what(f) == 'jpeg']
if(not len(cat_files) or not len(dog_files)):
print("Please download the Kaggle Cats and Dogs dataset form https://www.microsoft.com/en-us/download/details.aspx?id=54765 and extract the zip to " + datadir)
raise ValueError("Data not found")
else:
print(cat_files[0])
print(dog_files[0])
# Construct a numpy array as labels
image_paths = cat_files + dog_files
total_files = len(cat_files) + len(dog_files)
labels = np.zeros(total_files)
labels[len(cat_files):] = 1
# Split images data as training data and test data
from sklearn.model_selection import train_test_split
onehot_labels = np.array([[0,1] if i else [1,0] for i in labels])
img_train, img_test, label_train, label_test = train_test_split(image_paths, onehot_labels, random_state=42, shuffle=True)
print(len(img_train), len(img_test), label_train.shape, label_test.shape)
```
## Construct Model
We use ResNet50 for the featuirzer and build our own classifier using Keras layers. We train the featurizer and the classifier as one model. The weights trained on ImageNet are used as the starting point for the retraining of our featurizer. The weights are loaded from tensorflow chkeckpoint files.
Before passing image dataset to the ResNet50 featurizer, we need to preprocess the input file to get it into the form expected by ResNet50. ResNet50 expects float tensors representing the images in BGR, channel last order. We've provided a default implementation of the preprocessing that you can use.
```
import azureml.contrib.brainwave.models.utils as utils
def preprocess_images():
# Convert images to 3D tensors [width,height,channel] - channels are in BGR order.
in_images = tf.placeholder(tf.string)
image_tensors = utils.preprocess_array(in_images)
return in_images, image_tensors
```
We use Keras layer APIs to construct the classifier. Because we're using the tensorflow backend, we can train this classifier in one session with our Resnet50 model.
```
def construct_classifier(in_tensor):
from keras.layers import Dropout, Dense, Flatten
K.set_session(tf.get_default_session())
FC_SIZE = 1024
NUM_CLASSES = 2
x = Dropout(0.2, input_shape=(1, 1, 2048,))(in_tensor)
x = Dense(FC_SIZE, activation='relu', input_dim=(1, 1, 2048,))(x)
x = Flatten()(x)
preds = Dense(NUM_CLASSES, activation='softmax', input_dim=FC_SIZE, name='classifier_output')(x)
return preds
```
Now every component of the model is defined, we can construct the model. Constructing the model with the project brainwave models is two steps - first we import the graph definition, then we restore the weights of the model into a tensorflow session. Because the quantized graph defintion and the float32 graph defintion share the same node names in the graph definitions, we can initally train the weights in float32, and then reload them with the quantized operations (which take longer) to fine-tune the model.
```
def construct_model(quantized, starting_weights_directory = None):
from azureml.contrib.brainwave.models import Resnet50, QuantizedResnet50
# Convert images to 3D tensors [width,height,channel]
in_images, image_tensors = preprocess_images()
# Construct featurizer using quantized or unquantized ResNet50 model
if not quantized:
featurizer = Resnet50(saved_model_dir)
else:
featurizer = QuantizedResnet50(saved_model_dir, custom_weights_directory = starting_weights_directory)
features = featurizer.import_graph_def(input_tensor=image_tensors)
# Construct classifier
preds = construct_classifier(features)
# Initialize weights
sess = tf.get_default_session()
tf.global_variables_initializer().run()
featurizer.restore_weights(sess)
return in_images, image_tensors, features, preds, featurizer
```
## Train Model
First we train the model with custom weights but without quantization. Training is done with native float precision (32-bit floats). We load the traing data set and batch the training with 10 epochs. When the performance reaches desired level or starts decredation, we stop the training iteration and save the weights as tensorflow checkpoint files.
```
def read_files(files):
""" Read files to array"""
contents = []
for path in files:
with open(path, 'rb') as f:
contents.append(f.read())
return contents
def train_model(preds, in_images, img_train, label_train, is_retrain = False, train_epoch = 10):
""" training model """
from keras.objectives import binary_crossentropy
from tqdm import tqdm
learning_rate = 0.001 if is_retrain else 0.01
# Specify the loss function
in_labels = tf.placeholder(tf.float32, shape=(None, 2))
cross_entropy = tf.reduce_mean(binary_crossentropy(in_labels, preds))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
def chunks(a, b, n):
"""Yield successive n-sized chunks from a and b."""
if (len(a) != len(b)):
print("a and b are not equal in chunks(a,b,n)")
raise ValueError("Parameter error")
for i in range(0, len(a), n):
yield a[i:i + n], b[i:i + n]
chunk_size = 16
chunk_num = len(label_train) / chunk_size
sess = tf.get_default_session()
for epoch in range(train_epoch):
avg_loss = 0
for img_chunk, label_chunk in tqdm(chunks(img_train, label_train, chunk_size)):
contents = read_files(img_chunk)
_, loss = sess.run([optimizer, cross_entropy],
feed_dict={in_images: contents,
in_labels: label_chunk,
K.learning_phase(): 1})
avg_loss += loss / chunk_num
print("Epoch:", (epoch + 1), "loss = ", "{:.3f}".format(avg_loss))
# Reach desired performance
if (avg_loss < 0.001):
break
def test_model(preds, in_images, img_test, label_test):
"""Test the model"""
from keras.metrics import categorical_accuracy
in_labels = tf.placeholder(tf.float32, shape=(None, 2))
accuracy = tf.reduce_mean(categorical_accuracy(in_labels, preds))
contents = read_files(img_test)
accuracy = accuracy.eval(feed_dict={in_images: contents,
in_labels: label_test,
K.learning_phase(): 0})
return accuracy
# Launch the training
tf.reset_default_graph()
sess = tf.Session(graph=tf.get_default_graph())
with sess.as_default():
in_images, image_tensors, features, preds, featurizer = construct_model(quantized=False)
train_model(preds, in_images, img_train, label_train, is_retrain=False, train_epoch=10)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
featurizer.save_weights(custom_weights_dir + "/rn50", tf.get_default_session())
```
## Test Model
After training, we evaluate the trained model's accuracy on test dataset with quantization. So that we know the model's performance if it is deployed on the FPGA.
```
tf.reset_default_graph()
sess = tf.Session(graph=tf.get_default_graph())
with sess.as_default():
print("Testing trained model with quantization")
in_images, image_tensors, features, preds, quantized_featurizer = construct_model(quantized=True, starting_weights_directory=custom_weights_dir)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
```
## Fine-Tune Model
Sometimes, the model's accuracy can drop significantly after quantization. In those cases, we need to retrain the model enabled with quantization to get better model accuracy.
```
if (accuracy < 0.93):
with sess.as_default():
print("Fine-tuning model with quantization")
train_model(preds, in_images, img_train, label_train, is_retrain=True, train_epoch=10)
accuracy = test_model(preds, in_images, img_test, label_test)
print("Accuracy:", accuracy)
```
## Service Definition
Like in the QuickStart notebook our service definition pipeline consists of three stages.
```
from azureml.contrib.brainwave.pipeline import ModelDefinition, TensorflowStage, BrainWaveStage
model_def_path = os.path.join(saved_model_dir, 'model_def.zip')
model_def = ModelDefinition()
model_def.pipeline.append(TensorflowStage(sess, in_images, image_tensors))
model_def.pipeline.append(BrainWaveStage(sess, quantized_featurizer))
model_def.pipeline.append(TensorflowStage(sess, features, preds))
model_def.save(model_def_path)
print(model_def_path)
```
## Deploy
Go to our [GitHub repo](https://aka.ms/aml-real-time-ai) "docs" folder to learn how to create a Model Management Account and find the required information below.
```
from azureml.core import Workspace
ws = Workspace.from_config()
```
The first time the code below runs it will create a new service running your model. If you want to change the model you can make changes above in this notebook and save a new service definition. Then this code will update the running service in place to run the new model.
```
from azureml.core.model import Model
from azureml.core.image import Image
from azureml.core.webservice import Webservice
from azureml.contrib.brainwave import BrainwaveWebservice, BrainwaveImage
from azureml.exceptions import WebserviceException
model_name = "catsanddogs-resnet50-model"
image_name = "catsanddogs-resnet50-image"
service_name = "modelbuild-service"
registered_model = Model.register(ws, model_def_path, model_name)
image_config = BrainwaveImage.image_configuration()
deployment_config = BrainwaveWebservice.deploy_configuration()
try:
service = Webservice(ws, service_name)
service.delete()
service = Webservice.deploy_from_model(ws, service_name, [registered_model], image_config, deployment_config)
service.wait_for_deployment(True)
except WebserviceException:
service = Webservice.deploy_from_model(ws, service_name, [registered_model], image_config, deployment_config)
service.wait_for_deployment(True)
```
The service is now running in Azure and ready to serve requests. We can check the address and port.
```
print(service.ipAddress + ':' + str(service.port))
```
## Client
There is a simple test client at amlrealtimeai.PredictionClient which can be used for testing. We'll use this client to score an image with our new service.
```
from azureml.contrib.brainwave.client import PredictionClient
client = PredictionClient(service.ipAddress, service.port)
```
You can adapt the client [code](../../pythonlib/amlrealtimeai/client.py) to meet your needs. There is also an example C# [client](../../sample-clients/csharp).
The service provides an API that is compatible with TensorFlow Serving. There are instructions to download a sample client [here](https://www.tensorflow.org/serving/setup).
## Request
Let's see how our service does on a few images. It may get a few wrong.
```
# Specify an image to classify
print('CATS')
for image_file in cat_files[:8]:
results = client.score_image(image_file)
result = 'CORRECT ' if results[0] > results[1] else 'WRONG '
print(result + str(results))
print('DOGS')
for image_file in dog_files[:8]:
results = client.score_image(image_file)
result = 'CORRECT ' if results[1] > results[0] else 'WRONG '
print(result + str(results))
```
## Cleanup
Run the cell below to delete your service.
```
service.delete()
```
## Appendix
License for plot_confusion_matrix:
New BSD License
Copyright (c) 2007-2018 The scikit-learn developers.
All rights reserved.
Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:
a. Redistributions of source code must retain the above copyright notice,
this list of conditions and the following disclaimer.
b. Redistributions in binary form must reproduce the above copyright
notice, this list of conditions and the following disclaimer in the
documentation and/or other materials provided with the distribution.
c. Neither the name of the Scikit-learn Developers nor the names of
its contributors may be used to endorse or promote products
derived from this software without specific prior written
permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE
ARE DISCLAIMED. IN NO EVENT SHALL THE REGENTS OR CONTRIBUTORS BE LIABLE FOR
ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT
LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY
OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH
DAMAGE.
| true |
code
| 0.535159 | null | null | null | null |
|
This notebook is part of https://github.com/AudioSceneDescriptionFormat/splines, see also https://splines.readthedocs.io/.
[back to rotation splines](index.ipynb)
# Barry--Goldman Algorithm
We can try to use the
[Barry--Goldman algorithm for non-uniform Euclidean Catmull--Rom splines](../euclidean/catmull-rom-barry-goldman.ipynb)
using [Slerp](slerp.ipynb) instead of linear interpolations,
just as we have done with [De Casteljau's algorithm](de-casteljau.ipynb).
```
def slerp(one, two, t):
return (two * one.inverse())**t * one
def barry_goldman(rotations, times, t):
q0, q1, q2, q3 = rotations
t0, t1, t2, t3 = times
return slerp(
slerp(
slerp(q0, q1, (t - t0) / (t1 - t0)),
slerp(q1, q2, (t - t1) / (t2 - t1)),
(t - t0) / (t2 - t0)),
slerp(
slerp(q1, q2, (t - t1) / (t2 - t1)),
slerp(q2, q3, (t - t2) / (t3 - t2)),
(t - t1) / (t3 - t1)),
(t - t1) / (t2 - t1))
```
Example:
```
import numpy as np
```
[helper.py](helper.py)
```
from helper import angles2quat, animate_rotations, display_animation
q0 = angles2quat(0, 0, 0)
q1 = angles2quat(90, 0, 0)
q2 = angles2quat(90, 90, 0)
q3 = angles2quat(90, 90, 90)
t0 = 0
t1 = 1
t2 = 3
t3 = 3.5
frames = 50
ani = animate_rotations({
'Barry–Goldman (q0, q1, q2, q3)': [
barry_goldman([q0, q1, q2, q3], [t0, t1, t2, t3], t)
for t in np.linspace(t1, t2, frames)
],
'Slerp (q1, q2)': slerp(q1, q2, np.linspace(0, 1, frames)),
}, figsize=(5, 2))
display_animation(ani, default_mode='once')
```
[splines.quaternion.BarryGoldman](../python-module/splines.quaternion.rst#splines.quaternion.BarryGoldman) class
```
from splines.quaternion import BarryGoldman
import numpy as np
```
[helper.py](helper.py)
```
from helper import angles2quat, animate_rotations, display_animation
rotations = [
angles2quat(0, 0, 180),
angles2quat(0, 45, 90),
angles2quat(90, 45, 0),
angles2quat(90, 90, -90),
angles2quat(180, 0, -180),
angles2quat(-90, -45, 180),
]
grid = np.array([0, 0.5, 2, 5, 6, 7, 9])
bg = BarryGoldman(rotations, grid)
```
For comparison ... [Catmull--Rom-like quaternion spline](catmull-rom-non-uniform.ipynb)
[splines.quaternion.CatmullRom](../python-module/splines.quaternion.rst#splines.quaternion.CatmullRom) class
```
from splines.quaternion import CatmullRom
cr = CatmullRom(rotations, grid, endconditions='closed')
def evaluate(spline, samples=200):
times = np.linspace(spline.grid[0], spline.grid[-1], samples, endpoint=False)
return spline.evaluate(times)
ani = animate_rotations({
'Barry–Goldman': evaluate(bg),
'Catmull–Rom-like': evaluate(cr),
}, figsize=(5, 2))
display_animation(ani, default_mode='loop')
rotations = [
angles2quat(90, 0, -45),
angles2quat(179, 0, 0),
angles2quat(181, 0, 0),
angles2quat(270, 0, -45),
angles2quat(0, 90, 90),
]
s_uniform = BarryGoldman(rotations)
s_chordal = BarryGoldman(rotations, alpha=1)
s_centripetal = BarryGoldman(rotations, alpha=0.5)
ani = animate_rotations({
'uniform': evaluate(s_uniform, samples=300),
'chordal': evaluate(s_chordal, samples=300),
'centripetal': evaluate(s_centripetal, samples=300),
}, figsize=(7, 2))
display_animation(ani, default_mode='loop')
```
## Constant Angular Speed
Not very efficient,
De Casteljau's algorithm is faster because it directly provides the tangent.
```
from splines import ConstantSpeedAdapter
class BarryGoldmanWithDerivative(BarryGoldman):
delta_t = 0.000001
def evaluate(self, t, n=0):
"""Evaluate quaternion or angular velocity."""
if not np.isscalar(t):
return np.array([self.evaluate(t, n) for t in t])
if n == 0:
return super().evaluate(t)
elif n == 1:
# NB: We move the interval around because
# we cannot access times before and after
# the first and last time, respectively.
fraction = (t - self.grid[0]) / (self.grid[-1] - self.grid[0])
before = super().evaluate(t - fraction * self.delta_t)
after = super().evaluate(t + (1 - fraction) * self.delta_t)
# NB: Double angle
return (after * before.inverse()).log_map() * 2 / self.delta_t
else:
raise ValueError('Unsupported n: {!r}'.format(n))
s = ConstantSpeedAdapter(BarryGoldmanWithDerivative(rotations, alpha=0.5))
```
Takes a long time!
```
ani = animate_rotations({
'non-constant speed': evaluate(s_centripetal),
'constant speed': evaluate(s),
}, figsize=(5, 2))
display_animation(ani, default_mode='loop')
```
| true |
code
| 0.732776 | null | null | null | null |
|
<center>
<img src="../../img/ods_stickers.jpg">
## Открытый курс по машинному обучению. Сессия № 2
Автор материала: программист-исследователь Mail.ru Group, старший преподаватель Факультета Компьютерных Наук ВШЭ Юрий Кашницкий. Материал распространяется на условиях лицензии [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/). Можно использовать в любых целях (редактировать, поправлять и брать за основу), кроме коммерческих, но с обязательным упоминанием автора материала.
# <center> Тема 5. Композиции алгоритмов, случайный лес
## <center>Практика. Деревья решений и случайный лес в соревновании Kaggle Inclass по кредитному скорингу
Тут веб-формы для ответов нет, ориентируйтесь на рейтинг [соревнования](https://inclass.kaggle.com/c/beeline-credit-scoring-competition-2), [ссылка](https://www.kaggle.com/t/115237dd8c5e4092a219a0c12bf66fc6) для участия.
Решается задача кредитного скоринга.
Признаки клиентов банка:
- Age - возраст (вещественный)
- Income - месячный доход (вещественный)
- BalanceToCreditLimit - отношение баланса на кредитной карте к лимиту по кредиту (вещественный)
- DIR - Debt-to-income Ratio (вещественный)
- NumLoans - число заемов и кредитных линий
- NumRealEstateLoans - число ипотек и заемов, связанных с недвижимостью (натуральное число)
- NumDependents - число членов семьи, которых содержит клиент, исключая самого клиента (натуральное число)
- Num30-59Delinquencies - число просрочек выплат по кредиту от 30 до 59 дней (натуральное число)
- Num60-89Delinquencies - число просрочек выплат по кредиту от 60 до 89 дней (натуральное число)
- Delinquent90 - были ли просрочки выплат по кредиту более 90 дней (бинарный) - имеется только в обучающей выборке
```
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score
%matplotlib inline
```
**Загружаем данные.**
```
train_df = pd.read_csv('../../data/credit_scoring_train.csv', index_col='client_id')
test_df = pd.read_csv('../../data/credit_scoring_test.csv', index_col='client_id')
y = train_df['Delinquent90']
train_df.drop('Delinquent90', axis=1, inplace=True)
train_df.head()
```
**Посмотрим на число пропусков в каждом признаке.**
```
train_df.info()
test_df.info()
```
**Заменим пропуски медианными значениями.**
```
train_df['NumDependents'].fillna(train_df['NumDependents'].median(), inplace=True)
train_df['Income'].fillna(train_df['Income'].median(), inplace=True)
test_df['NumDependents'].fillna(test_df['NumDependents'].median(), inplace=True)
test_df['Income'].fillna(test_df['Income'].median(), inplace=True)
```
### Дерево решений без настройки параметров
**Обучите дерево решений максимальной глубины 3, используйте параметр random_state=17 для воспроизводимости результатов.**
```
first_tree = # Ваш код здесь
first_tree.fit # Ваш код здесь
```
**Сделайте прогноз для тестовой выборки.**
```
first_tree_pred = first_tree # Ваш код здесь
```
**Запишем прогноз в файл.**
```
def write_to_submission_file(predicted_labels, out_file,
target='Delinquent90', index_label="client_id"):
# turn predictions into data frame and save as csv file
predicted_df = pd.DataFrame(predicted_labels,
index = np.arange(75000,
predicted_labels.shape[0] + 75000),
columns=[target])
predicted_df.to_csv(out_file, index_label=index_label)
write_to_submission_file(first_tree_pred, 'credit_scoring_first_tree.csv')
```
**Если предсказывать вероятности дефолта для клиентов тестовой выборки, результат будет намного лучше.**
```
first_tree_pred_probs = first_tree.predict_proba(test_df)[:, 1]
write_to_submission_file # Ваш код здесь
```
## Дерево решений с настройкой параметров с помощью GridSearch
**Настройте параметры дерева с помощью `GridSearhCV`, посмотрите на лучшую комбинацию параметров и среднее качество на 5-кратной кросс-валидации. Используйте параметр `random_state=17` (для воспроизводимости результатов), не забывайте про распараллеливание (`n_jobs=-1`).**
```
tree_params = {'max_depth': list(range(3, 8)),
'min_samples_leaf': list(range(5, 13))}
locally_best_tree = GridSearchCV # Ваш код здесь
locally_best_tree.fit # Ваш код здесь
locally_best_tree.best_params_, round(locally_best_tree.best_score_, 3)
```
**Сделайте прогноз для тестовой выборки и пошлите решение на Kaggle.**
```
tuned_tree_pred_probs = locally_best_tree # Ваш код здесь
write_to_submission_file # Ваш код здесь
```
### Случайный лес без настройки параметров
**Обучите случайный лес из деревьев неограниченной глубины, используйте параметр `random_state=17` для воспроизводимости результатов.**
```
first_forest = # Ваш код здесь
first_forest.fit # Ваш код здесь
first_forest_pred = first_forest # Ваш код здесь
```
**Сделайте прогноз для тестовой выборки и пошлите решение на Kaggle.**
```
write_to_submission_file # Ваш код здесь
```
### Случайный лес c настройкой параметров
**Настройте параметр `max_features` леса с помощью `GridSearhCV`, посмотрите на лучшую комбинацию параметров и среднее качество на 5-кратной кросс-валидации. Используйте параметр random_state=17 (для воспроизводимости результатов), не забывайте про распараллеливание (n_jobs=-1).**
```
%%time
forest_params = {'max_features': np.linspace(.3, 1, 7)}
locally_best_forest = GridSearchCV # Ваш код здесь
locally_best_forest.fit # Ваш код здесь
locally_best_forest.best_params_, round(locally_best_forest.best_score_, 3)
tuned_forest_pred = locally_best_forest # Ваш код здесь
write_to_submission_file # Ваш код здесь
```
**Посмотрите, как настроенный случайный лес оценивает важность признаков по их влиянию на целевой. Представьте результаты в наглядном виде с помощью `DataFrame`.**
```
pd.DataFrame(locally_best_forest.best_estimator_.feature_importances_ # Ваш код здесь
```
**Обычно увеличение количества деревьев только улучшает результат. Так что напоследок обучите случайный лес из 300 деревьев с найденными лучшими параметрами. Это может занять несколько минут.**
```
%%time
final_forest = RandomForestClassifier # Ваш код здесь
final_forest.fit(train_df, y)
final_forest_pred = final_forest.predict_proba(test_df)[:, 1]
write_to_submission_file(final_forest_pred, 'credit_scoring_final_forest.csv')
```
**Сделайте посылку на Kaggle.**
| true |
code
| 0.275422 | null | null | null | null |
|
# Complex Graphs Metadata Example
## Prerequisites
* A kubernetes cluster with kubectl configured
* curl
* pygmentize
## Setup Seldon Core
Use the setup notebook to [Setup Cluster](https://docs.seldon.io/projects/seldon-core/en/latest/examples/seldon_core_setup.html) to setup Seldon Core with an ingress.
```
!kubectl create namespace seldon
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
```
## Used model
In this example notebook we will use a dummy node that can serve multiple purposes in the graph.
The model will read its metadata from environmental variable (this is done automatically).
Actual logic that happens on each of this endpoint is not subject of this notebook.
We will only concentrate on graph-level metadata that orchestrator constructs from metadata reported by each node.
```
%%writefile models/generic-node/Node.py
import logging
import random
import os
NUMBER_OF_ROUTES = int(os.environ.get("NUMBER_OF_ROUTES", "2"))
class Node:
def predict(self, features, names=[], meta=[]):
logging.info(f"model features: {features}")
logging.info(f"model names: {names}")
logging.info(f"model meta: {meta}")
return features.tolist()
def transform_input(self, features, names=[], meta=[]):
return self.predict(features, names, meta)
def transform_output(self, features, names=[], meta=[]):
return self.predict(features, names, meta)
def aggregate(self, features, names=[], meta=[]):
logging.info(f"model features: {features}")
logging.info(f"model names: {names}")
logging.info(f"model meta: {meta}")
return [x.tolist() for x in features]
def route(self, features, names=[], meta=[]):
logging.info(f"model features: {features}")
logging.info(f"model names: {names}")
logging.info(f"model meta: {meta}")
route = random.randint(0, NUMBER_OF_ROUTES)
logging.info(f"routing to: {route}")
return route
```
### Build image
build image using provided Makefile
```
cd models/generic-node
make build
```
If you are using `kind` you can use `kind_image_install` target to directly
load your image into your local cluster.
## Single Model
In case of single-node graph model-level `inputs` and `outputs`, `x` and `y`, will simply be also the deployment-level `graphinputs` and `graphoutputs`.

```
%%writefile graph-metadata/single.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-single
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: model
env:
- name: MODEL_METADATA
value: |
---
name: single-node
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [node-input]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [node-output]
shape: [ 1 ]
graph:
name: model
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/single.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-single -o jsonpath='{.items[0].metadata.name}')
```
### Graph Level
Graph level metadata is available at the `api/v1.0/metadata` endpoint of your deployment:
```
import requests
import time
def getWithRetry(url):
for i in range(3):
r = requests.get(url)
if r.status_code == requests.codes.ok:
meta = r.json()
return meta
else:
print("Failed request with status code ",r.status_code)
time.sleep(3)
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-single/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
"model": {
"name": "single-node",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["node-input"], "shape": [1]}}
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}}
],
}
},
"graphinputs": [
{"messagetype": "tensor", "schema": {"names": ["node-input"], "shape": [1]}}
],
"graphoutputs": [
{"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}}
],
}
meta
```
### Model Level
Compare with `model` metadata available at the `api/v1.0/metadata/model`:
```
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-single/api/v1.0/metadata/model")
assert meta == {
"custom": {},
"name": "single-node",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [{
"messagetype": "tensor", "schema": {"names": ["node-input"], "shape": [1]},
}],
"outputs": [{
"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]},
}],
}
meta
!kubectl delete -f graph-metadata/single.yaml
```
## Two-Level Graph
In two-level graph graph output of the first model is input of the second model, `x2=y1`.
The graph-level input `x` will be first model’s input `x1` and graph-level output `y` will be the last model’s output `y2`.

```
%%writefile graph-metadata/two-levels.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-two-levels
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: node-one
env:
- name: MODEL_METADATA
value: |
---
name: node-one
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [ a1, a2 ]
shape: [ 2 ]
outputs:
- messagetype: tensor
schema:
names: [ a3 ]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node-two
env:
- name: MODEL_METADATA
value: |
---
name: node-two
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [ a3 ]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [b1, b2]
shape: [ 2 ]
graph:
name: node-one
type: MODEL
children:
- name: node-two
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/two-levels.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-two-levels -o jsonpath='{.items[0].metadata.name}')
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-two-levels/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
"node-one": {
"name": "node-one",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a1", "a2"], "shape": [2]}}
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["a3"], "shape": [1]}}
],
},
"node-two": {
"name": "node-two",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a3"], "shape": [1]}}
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["b1", "b2"], "shape": [2]}}
],
}
},
"graphinputs": [
{"messagetype": "tensor", "schema": {"names": ["a1", "a2"], "shape": [2]}}
],
"graphoutputs": [
{"messagetype": "tensor", "schema": {"names": ["b1", "b2"], "shape": [2]}}
],
}
meta
!kubectl delete -f graph-metadata/two-levels.yaml
```
## Combiner of two models
In graph with the `combiner` request is first passed to combiner's children and before it gets aggregated by the `combiner` itself.
Input `x` is first passed to both models and their outputs `y1` and `y2` are passed to the combiner.
Combiner's output `y` is the final output of the graph.

```
%%writefile graph-metadata/combiner.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-combiner
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: node-combiner
env:
- name: MODEL_METADATA
value: |
---
name: node-combiner
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [ c1 ]
shape: [ 1 ]
- messagetype: tensor
schema:
names: [ c2 ]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [combiner-output]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node-one
env:
- name: MODEL_METADATA
value: |
---
name: node-one
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [a, b]
shape: [ 2 ]
outputs:
- messagetype: tensor
schema:
names: [ c1 ]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node-two
env:
- name: MODEL_METADATA
value: |
---
name: node-two
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [a, b]
shape: [ 2 ]
outputs:
- messagetype: tensor
schema:
names: [ c2 ]
shape: [ 1 ]
graph:
name: node-combiner
type: COMBINER
children:
- name: node-one
type: MODEL
children: []
- name: node-two
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/combiner.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-combiner -o jsonpath='{.items[0].metadata.name}')
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-combiner/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
"node-combiner": {
"name": "node-combiner",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["c1"], "shape": [1]}},
{"messagetype": "tensor", "schema": {"names": ["c2"], "shape": [1]}},
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["combiner-output"], "shape": [1]}}
],
},
"node-one": {
"name": "node-one",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}},
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["c1"], "shape": [1]}}
],
},
"node-two": {
"name": "node-two",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}},
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["c2"], "shape": [1]}}
],
}
},
"graphinputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}},
],
"graphoutputs": [
{"messagetype": "tensor", "schema": {"names": ["combiner-output"], "shape": [1]}}
],
}
meta
!kubectl delete -f graph-metadata/combiner.yaml
```
## Router with two models
In this example request `x` is passed by `router` to one of its children.
Router then returns children output `y1` or `y2` as graph's output `y`.
Here we assume that all children accepts similarly structured input and retun a similarly structured output.

```
%%writefile graph-metadata/router.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-router
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: node-router
- image: seldonio/metadata-generic-node:0.4
name: node-one
env:
- name: MODEL_METADATA
value: |
---
name: node-one
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [ a, b ]
shape: [ 2 ]
outputs:
- messagetype: tensor
schema:
names: [ node-output ]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node-two
env:
- name: MODEL_METADATA
value: |
---
name: node-two
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [ a, b ]
shape: [ 2 ]
outputs:
- messagetype: tensor
schema:
names: [ node-output ]
shape: [ 1 ]
graph:
name: node-router
type: ROUTER
children:
- name: node-one
type: MODEL
children: []
- name: node-two
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/router.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-router -o jsonpath='{.items[0].metadata.name}')
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-router/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
'node-router': {
'name': 'seldonio/metadata-generic-node',
'versions': ['0.4'],
'inputs': [],
'outputs': [],
},
"node-one": {
"name": "node-one",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}}
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}}
],
},
"node-two": {
"name": "node-two",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}}
],
"outputs": [
{"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}}
],
}
},
"graphinputs": [
{"messagetype": "tensor", "schema": {"names": ["a", "b"], "shape": [2]}}
],
"graphoutputs": [
{"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}}
],
}
meta
!kubectl delete -f graph-metadata/router.yaml
```
## Input Transformer
Input transformers work almost exactly the same as chained nodes, see two-level example above.
Following graph is presented in a way that is suppose to make next example (output transfomer) more intuitive.

```
%%writefile graph-metadata/input-transformer.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-input
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: node-input-transformer
env:
- name: MODEL_METADATA
value: |
---
name: node-input-transformer
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [transformer-input]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [transformer-output]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node
env:
- name: MODEL_METADATA
value: |
---
name: node
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [transformer-output]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [node-output]
shape: [ 1 ]
graph:
name: node-input-transformer
type: TRANSFORMER
children:
- name: node
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/input-transformer.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-input -o jsonpath='{.items[0].metadata.name}')
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-input/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
"node-input-transformer": {
"name": "node-input-transformer",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-input"], "shape": [1]},
}],
"outputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-output"], "shape": [1]},
}],
},
"node": {
"name": "node",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-output"], "shape": [1]},
}],
"outputs": [{
"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]},
}],
}
},
"graphinputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-input"], "shape": [1]}
}],
"graphoutputs": [{
"messagetype": "tensor", "schema": {"names": ["node-output"], "shape": [1]}
}],
}
meta
!kubectl delete -f graph-metadata/input-transformer.yaml
```
## Output Transformer
Output transformers work almost exactly opposite as chained nodes in the two-level example above.
Input `x` is first passed to the model that is child of the `output-transformer` before it is passed to it.

```
%%writefile graph-metadata/output-transformer.yaml
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: graph-metadata-output
spec:
name: test-deployment
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/metadata-generic-node:0.4
name: node-output-transformer
env:
- name: MODEL_METADATA
value: |
---
name: node-output-transformer
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [transformer-input]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [transformer-output]
shape: [ 1 ]
- image: seldonio/metadata-generic-node:0.4
name: node
env:
- name: MODEL_METADATA
value: |
---
name: node
versions: [ generic-node/v0.4 ]
platform: seldon
inputs:
- messagetype: tensor
schema:
names: [node-input]
shape: [ 1 ]
outputs:
- messagetype: tensor
schema:
names: [transformer-input]
shape: [ 1 ]
graph:
name: node-output-transformer
type: OUTPUT_TRANSFORMER
children:
- name: node
type: MODEL
children: []
name: example
replicas: 1
!kubectl apply -f graph-metadata/output-transformer.yaml
!kubectl rollout status deploy/$(kubectl get deploy -l seldon-deployment-id=graph-metadata-output -o jsonpath='{.items[0].metadata.name}')
import requests
meta = getWithRetry("http://localhost:8003/seldon/seldon/graph-metadata-output/api/v1.0/metadata")
assert meta == {
"name": "example",
"models": {
"node-output-transformer": {
"name": "node-output-transformer",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-input"], "shape": [1]},
}],
"outputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-output"], "shape": [1]},
}],
},
"node": {
"name": "node",
"platform": "seldon",
"versions": ["generic-node/v0.4"],
"inputs": [{
"messagetype": "tensor", "schema": {"names": ["node-input"], "shape": [1]},
}],
"outputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-input"], "shape": [1]},
}],
}
},
"graphinputs": [{
"messagetype": "tensor", "schema": {"names": ["node-input"], "shape": [1]}
}],
"graphoutputs": [{
"messagetype": "tensor", "schema": {"names": ["transformer-output"], "shape": [1]}
}],
}
meta
!kubectl delete -f graph-metadata/output-transformer.yaml
```
| true |
code
| 0.468061 | null | null | null | null |
|
# INFO
This is my solution for the fourth homework problem.
# **SOLUTION**
# Description
I will use network with:
- input layer with **2 neurons** (two input variables)
- **one** hidden layer with **2 neurons** (I need to split the plane in a nonlinear way, creating a U-shaped plane containing the diagonal points)
- output layer with 1 neuron (result - active or inactive)
Also, as an activation function I will use a sigmoid function - simple, values between (0, 1) and with simple derivative
# CODE
```
import numpy as np
```
Let's define our sigmoid function and its derivative
```
def sigmoid(x, derivative=False):
if derivative:
return x * (1 - x)
else:
return 1 / (1 + np.exp(-x))
```
Now, number of neurons per layer
```
layers_sizes = np.array([2, 2, 1])
```
And layers initialization function
```
def init_layers(sizes):
weights = [np.random.uniform(size=size) for size in zip(sizes[0:-1], sizes[1:])]
biases = [np.random.uniform(size=(size, 1)) for size in sizes[1:]]
return weights, biases
```
Function which execute network (forward propagation).
Takes input layer, following layers weights and biases and activation function. Returns layers outputs.
```
def execute(input, weights, biases, activation_f):
result = [input]
previous_layer = input
for weight, bias in zip(weights, biases):
executed_layer = execute_layer(previous_layer, weight, bias, activation_f)
previous_layer = executed_layer
result.append(executed_layer)
return result
def execute_layer(input_layer, weight, bias, activation_f):
layer_activation = np.dot(input_layer.T, weight).T + bias
return activation_f(layer_activation)
```
And time for the backpropagation function.
Function takes layers outputs, weights, biases and activation function, expected output and learning rate.
```
def backpropagation(layers_outputs,
weights,
biases,
activation_f,
expected_output,
learning_rate):
updated_weights = weights.copy()
updated_biases = biases.copy()
predicted_output = layers_outputs[-1]
output_error = 2 * (expected_output - predicted_output)
output_delta = output_error * activation_f(predicted_output, True)
updated_weights[-1] += layers_outputs[-2].dot(output_delta.T) * learning_rate
updated_biases[-1] += output_delta * learning_rate
next_layer_delta = output_delta
for layer_id in reversed(range(1, len(layers_outputs)-1)):
weight_id = layer_id - 1
error = np.dot(weights[weight_id+1], next_layer_delta)
delta = error * activation_f(layers_outputs[layer_id], True)
updated_weights[weight_id] += layers_outputs[layer_id-1].dot(delta.T) * learning_rate
updated_biases[weight_id] += delta * learning_rate
next_layer_delta = delta
return updated_weights, updated_biases
```
---
Create test set:
```
test_set_X = [np.array([[0], [0]]), np.array([[1], [0]]), np.array([[0], [1]]), np.array([[1], [1]])]
test_set_Y = [np.array([[0]]), np.array([[1]]), np.array([[1]]), np.array([[0]])]
```
And training parameters:
```
learning_rate = 0.07
number_of_iterations = 30000
```
And train out model:
```
weights, biases = init_layers(layers_sizes)
errors = []
for iteration in range(number_of_iterations):
error = 0
for test_x, test_y in zip(test_set_X, test_set_Y):
values = execute(test_x, weights, biases, sigmoid)
predicted_y = values[-1]
error += np.sum((predicted_y - test_y) ** 2) / len(test_y)
new_weights, new_biases = backpropagation(values, weights, biases, sigmoid, test_y, learning_rate)
weights = new_weights
biases = new_biases
print("iteration number {} done! Error: {}".format(iteration, error / len(test_set_X)))
errors.append(error / len(test_set_X))
```
And plot the error over iterations
```
import matplotlib.pyplot as plt
plt.plot(errors)
plt.ylabel('error vs iteration')
plt.show()
```
And print results
```
print("iterations: {}, learning rate: {}".format(number_of_iterations, learning_rate))
for test_x, test_y in zip(test_set_X, test_set_Y):
values = execute(test_x, weights, biases, sigmoid)
predicted_y = values[-1]
print("{} xor {} = {} ({} confidence)".format(test_x[0][0], test_x[1][0], round(predicted_y[0][0]), predicted_y))
```
| true |
code
| 0.532425 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/enakai00/rl_book_solutions/blob/master/Chapter06/SARSA_vs_Q_Learning_vs_MC.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import numpy as np
from numpy import random
from pandas import DataFrame
import copy
class Car:
def __init__(self):
self.path = []
self.actions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
self.episodes = [0]
self.q = {}
self.c ={}
self.restart()
def restart(self):
self.x, self.y = 0, 3
self.path = []
def get_state(self):
return self.x, self.y
def show_path(self):
result = [[' ' for x in range(10)] for y in range(7)]
for c, (x, y, a) in enumerate(self.path):
result[y][x] = str(c)[-1]
result[3][7] = 'G'
return result
def add_episode(self, c=0):
self.episodes.append(self.episodes[-1]+c)
def move(self, action):
self.path.append((self.x, self.y, action))
vx, vy = self.actions[action]
if self.x >= 3 and self.x <= 8:
vy -= 1
if self.x >= 6 and self.x <= 7:
vy -= 1
_x, _y = self.x + vx, self.y + vy
if _x < 0 or _x > 9:
_x = self.x
if _y < 0 or _y > 6:
_y = self.y
self.x, self.y = _x, _y
if (self.x, self.y) == (7, 3): # Finish
return True
return False
def get_action(car, epsilon, default_q=0):
if random.random() < epsilon:
a = random.randint(0, len(car.actions))
else:
a = optimal_action(car, default_q)
return a
def optimal_action(car, default_q=0):
optimal = 0
q_max = 0
initial = True
x, y = car.get_state()
for a in range(len(car.actions)):
sa = "{:02},{:02}:{:02}".format(x, y, a)
if sa not in car.q.keys():
car.q[sa] = default_q
if initial or car.q[sa] > q_max:
q_max = car.q[sa]
optimal = a
initial = False
return optimal
def update_q(car, x, y, a, epsilon, q_learning=False):
sa = "{:02},{:02}:{:02}".format(x, y, a)
if q_learning:
_a = optimal_action(car)
else:
_a = get_action(car, epsilon)
_x, _y = car.get_state()
sa_next = "{:02},{:02}:{:02}".format(_x, _y, _a)
if sa not in car.q.keys():
car.q[sa] = 0
if sa_next not in car.q.keys():
car.q[sa_next] = 0
car.q[sa] += 0.5 * (-1 + car.q[sa_next] - car.q[sa])
if q_learning:
_a = get_action(car, epsilon)
return _a
def trial(car, epsilon = 0.1, q_learning=False):
car.restart()
a = get_action(car, epsilon)
while True:
x, y = car.get_state()
finished = car.move(a)
if finished:
car.add_episode(1)
sa = "{:02},{:02}:{:02}".format(x, y, a)
if sa not in car.q.keys():
car.q[sa] = 0
car.q[sa] += 0.5 * (-1 + 0 - car.q[sa])
break
a = update_q(car, x, y, a, epsilon, q_learning)
car.add_episode(0)
def trial_mc(car, epsilon=0.1):
car.restart()
while True:
x, y = car.get_state()
state = "{:02},{:02}".format(x, y)
a = get_action(car, epsilon, default_q=-10**10)
finished = car.move(a)
if finished:
car.add_episode(1)
g = 0
w = 1
path = copy.copy(car.path)
path.reverse()
for x, y, a in path:
car.x, car.y = x, y
opt_a = optimal_action(car, default_q=-10**10)
sa = "{:02},{:02}:{:02}".format(x, y, a)
g += -1 # Reward = -1 for each step
if sa not in car.c.keys():
car.c[sa] = w
car.q[sa] = g
else:
car.c[sa] += w
car.q[sa] += w*(g-car.q[sa])/car.c[sa]
if opt_a != a:
break
w = w / (1 - epsilon + epsilon/len(car.actions))
break
car.add_episode(0)
car1, car2, car3 = Car(), Car(), Car()
while True:
trial(car1)
if len(car1.episodes) >= 10000:
break
print(car1.episodes[-1])
while True:
trial(car2, q_learning=True)
if len(car2.episodes) >= 10000:
break
print(car2.episodes[-1])
while True:
trial_mc(car3)
if len(car3.episodes) >= 200000:
break
print(car3.episodes[-1])
DataFrame({'SARSA': car1.episodes[:8001],
'Q-Learning': car2.episodes[:8001],
'MC': car3.episodes[:8001]}
).plot()
trial(car1, epsilon=0)
print('SARSA:', len(car1.path))
print ("#" * 12)
for _ in map(lambda lst: ''.join(lst), car1.show_path()):
print('#' + _ + '#')
print ("#" * 12)
print ()
trial(car2, epsilon=0)
print('Q-Learning:', len(car2.path))
print ("#" * 12)
for _ in map(lambda lst: ''.join(lst), car2.show_path()):
print('#' + _ + '#')
print ("#" * 12)
print ()
trial_mc(car3, epsilon=0)
print('MC:', len(car3.path))
print ("#" * 12)
for _ in map(lambda lst: ''.join(lst), car3.show_path()):
print('#' + _ + '#')
print ("#" * 12)
print ()
```
| true |
code
| 0.281208 | null | null | null | null |
|
# Model Centric Federated Learning - MNIST Example: Create Plan
This notebook is an example of creating a simple model and a training plan
for solving MNIST classification in model-centric (aka cross-device) federated learning fashion.
It consists of the following steps:
* Defining the model
* Defining the Training Plan
* Defining the Averaging Plan & FL configuration
* Hosting everything to PyGrid
* Extra: demonstration of PyGrid API
The process of training a hosted model using existing python FL worker is demonstrated in
the following "[MCFL - Execute Plan](mcfl_execute_plan.ipynb)" notebook.
```
# stdlib
import base64
import json
# third party
import jwt
import requests
import torch as th
from websocket import create_connection
# syft absolute
import syft as sy
from syft import deserialize
from syft import serialize
from syft.core.plan.plan_builder import ROOT_CLIENT
from syft.core.plan.plan_builder import make_plan
from syft.federated.model_centric_fl_client import ModelCentricFLClient
from syft.lib.python.int import Int
from syft.lib.python.list import List
from syft.proto.core.plan.plan_pb2 import Plan as PlanPB
from syft.proto.lib.python.list_pb2 import List as ListPB
th.random.manual_seed(42)
```
## Step 1: Define the model
This model will train on MNIST data, it's very simple yet can demonstrate learning process.
There're 2 linear layers:
* Linear 784x100
* ReLU
* Linear 100x10
```
class MLP(sy.Module):
def __init__(self, torch_ref):
super().__init__(torch_ref=torch_ref)
self.l1 = self.torch_ref.nn.Linear(784, 100)
self.a1 = self.torch_ref.nn.ReLU()
self.l2 = self.torch_ref.nn.Linear(100, 10)
def forward(self, x):
x_reshaped = x.view(-1, 28 * 28)
l1_out = self.a1(self.l1(x_reshaped))
l2_out = self.l2(l1_out)
return l2_out
```
## Step 2: Define Training Plan
```
def set_params(model, params):
for p, p_new in zip(model.parameters(), params):
p.data = p_new.data
def cross_entropy_loss(logits, targets, batch_size):
norm_logits = logits - logits.max()
log_probs = norm_logits - norm_logits.exp().sum(dim=1, keepdim=True).log()
return -(targets * log_probs).sum() / batch_size
def sgd_step(model, lr=0.1):
with ROOT_CLIENT.torch.no_grad():
for p in model.parameters():
p.data = p.data - lr * p.grad
p.grad = th.zeros_like(p.grad.get())
local_model = MLP(th)
@make_plan
def train(
xs=th.rand([64 * 3, 1, 28, 28]),
ys=th.randint(0, 10, [64 * 3, 10]),
params=List(local_model.parameters()),
):
model = local_model.send(ROOT_CLIENT)
set_params(model, params)
for i in range(1):
indices = th.tensor(range(64 * i, 64 * (i + 1)))
x, y = xs.index_select(0, indices), ys.index_select(0, indices)
out = model(x)
loss = cross_entropy_loss(out, y, 64)
loss.backward()
sgd_step(model)
return model.parameters()
```
## Step 3: Define Averaging Plan
Averaging Plan is executed by PyGrid at the end of the cycle,
to average _diffs_ submitted by workers and update the model
and create new checkpoint for the next cycle.
_Diff_ is the difference between client-trained
model params and original model params,
so it has same number of tensors and tensor's shapes
as the model parameters.
We define Plan that processes one diff at a time.
Such Plans require `iterative_plan` flag set to `True`
in `server_config` when hosting FL model to PyGrid.
Plan below will calculate simple mean of each parameter.
```
@make_plan
def avg_plan(
avg=List(local_model.parameters()), item=List(local_model.parameters()), num=Int(0)
):
new_avg = []
for i, param in enumerate(avg):
new_avg.append((avg[i] * num + item[i]) / (num + 1))
return new_avg
```
# Config & keys
```
name = "mnist"
version = "1.0"
client_config = {
"name": name,
"version": version,
"batch_size": 64,
"lr": 0.1,
"max_updates": 1, # custom syft.js option that limits number of training loops per worker
}
server_config = {
"min_workers": 2,
"max_workers": 2,
"pool_selection": "random",
"do_not_reuse_workers_until_cycle": 6,
"cycle_length": 28800, # max cycle length in seconds
"num_cycles": 30, # max number of cycles
"max_diffs": 1, # number of diffs to collect before avg
"minimum_upload_speed": 0,
"minimum_download_speed": 0,
"iterative_plan": True, # tells PyGrid that avg plan is executed per diff
}
def read_file(fname):
with open(fname, "r") as f:
return f.read()
private_key = read_file("example_rsa").strip()
public_key = read_file("example_rsa.pub").strip()
server_config["authentication"] = {
"type": "jwt",
"pub_key": public_key,
}
```
## Step 4: Host in PyGrid
Let's now host everything in PyGrid so that it can be accessed by worker libraries (syft.js, KotlinSyft, SwiftSyft, or even PySyft itself).
# Auth
```
grid_address = "localhost:7000"
grid = ModelCentricFLClient(address=grid_address, secure=False)
grid.connect()
```
# Host
If the process already exists, might you need to clear the db. To do that, set path below correctly and run:
```
# !rm PyGrid/apps/domain/src/nodedatabase.db
response = grid.host_federated_training(
model=local_model,
client_plans={"training_plan": train},
client_protocols={},
server_averaging_plan=avg_plan,
client_config=client_config,
server_config=server_config,
)
response
```
# Authenticate for cycle
```
# Helper function to make WS requests
def sendWsMessage(data):
ws = create_connection("ws://" + grid_address)
ws.send(json.dumps(data))
message = ws.recv()
return json.loads(message)
auth_token = jwt.encode({}, private_key, algorithm="RS256").decode("ascii")
auth_request = {
"type": "model-centric/authenticate",
"data": {
"model_name": name,
"model_version": version,
"auth_token": auth_token,
},
}
auth_response = sendWsMessage(auth_request)
auth_response
```
# Do cycle request
```
cycle_request = {
"type": "model-centric/cycle-request",
"data": {
"worker_id": auth_response["data"]["worker_id"],
"model": name,
"version": version,
"ping": 1,
"download": 10000,
"upload": 10000,
},
}
cycle_response = sendWsMessage(cycle_request)
print("Cycle response:", json.dumps(cycle_response, indent=2).replace("\\n", "\n"))
```
# Download model
```
worker_id = auth_response["data"]["worker_id"]
request_key = cycle_response["data"]["request_key"]
model_id = cycle_response["data"]["model_id"]
training_plan_id = cycle_response["data"]["plans"]["training_plan"]
def get_model(grid_address, worker_id, request_key, model_id):
req = requests.get(
f"http://{grid_address}/model-centric/get-model?worker_id={worker_id}&request_key={request_key}&model_id={model_id}"
)
model_data = req.content
pb = ListPB()
pb.ParseFromString(req.content)
return deserialize(pb)
# Model
model_params_downloaded = get_model(grid_address, worker_id, request_key, model_id)
print("Params shapes:", [p.shape for p in model_params_downloaded])
model_params_downloaded[0]
```
# Download & Execute Plan
```
req = requests.get(
f"http://{grid_address}/model-centric/get-plan?worker_id={worker_id}&request_key={request_key}&plan_id={training_plan_id}&receive_operations_as=list"
)
pb = PlanPB()
pb.ParseFromString(req.content)
plan = deserialize(pb)
xs = th.rand([64 * 3, 1, 28, 28])
ys = th.randint(0, 10, [64 * 3, 10])
(res,) = plan(xs=xs, ys=ys, params=model_params_downloaded)
```
# Report Model diff
```
diff = [orig - new for orig, new in zip(res, local_model.parameters())]
diff_serialized = serialize((List(diff))).SerializeToString()
params = {
"type": "model-centric/report",
"data": {
"worker_id": worker_id,
"request_key": request_key,
"diff": base64.b64encode(diff_serialized).decode("ascii"),
},
}
sendWsMessage(params)
```
# Check new model
```
req_params = {
"name": name,
"version": version,
"checkpoint": "latest",
}
res = requests.get(f"http://{grid_address}/model-centric/retrieve-model", req_params)
params_pb = ListPB()
params_pb.ParseFromString(res.content)
new_model_params = deserialize(params_pb)
new_model_params[0]
# !rm PyGrid/apps/domain/src/nodedatabase.db
```
## Step 5: Train
To train hosted model, you can use existing python FL worker.
See the "[MCFL - Execute Plan](mcfl_execute_plan.ipynb)" notebook that
has example of using Python FL worker.
To understand how to make similar model working for mobile FL workers,
see "[MCFL for Mobile - Create Plan](mcfl_execute_plan_mobile.ipynb)" notebook!
| true |
code
| 0.643301 | null | null | null | null |
|
# Malaria Detection
Malaria is a life-threatening disease caused by parasites that are transmitted to people through the bites of infected female Anopheles mosquitoes. It is preventable and curable.
In 2017, there were an estimated 219 million cases of malaria in 90 countries.
Malaria deaths reached 435 000 in 2017.
The WHO African Region carries a disproportionately high share of the global malaria burden. In 2017, the region was home to 92% of malaria cases and 93% of malaria deaths.
Malaria is caused by Plasmodium parasites. The parasites are spread to people through the bites of infected female Anopheles mosquitoes, called *"malaria vectors."* There are 5 parasite species that cause malaria in humans, and 2 of these species – P. falciparum and P. vivax – pose the greatest threat.
**Diagnosis of malaria can be difficult:**
Where malaria is not endemic any more (such as in the United States), health-care providers may not be familiar with the disease. Clinicians seeing a malaria patient may forget to consider malaria among the potential diagnoses and not order the needed diagnostic tests. Laboratorians may lack experience with malaria and fail to detect parasites when examining blood smears under the microscope.
Malaria is an acute febrile illness. In a non-immune individual, symptoms usually appear 10–15 days after the infective mosquito bite. The first symptoms – fever, headache, and chills – may be mild and difficult to recognize as malaria. If not treated within 24 hours, P. falciparum malaria can progress to severe illness, often leading to death.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fastai import *
from fastai.vision import *
from fastai.callbacks.hooks import *
import os
print(os.listdir("../input/cell-images-for-detecting-malaria/cell_images/cell_images/"))
```
**Dataset**
```
img_dir='../input/cell-images-for-detecting-malaria/cell_images/cell_images/'
path=Path(img_dir)
path
data = ImageDataBunch.from_folder(path, train=".",
valid_pct=0.2,
ds_tfms=get_transforms(flip_vert=True, max_warp=0),
size=224,bs=64,
num_workers=0).normalize(imagenet_stats)
print(f'Classes: \n {data.classes}')
data.show_batch(rows=3, figsize=(7,6))
```
## Model ResNet34
```
learn = cnn_learner(data, models.resnet34, metrics=accuracy, model_dir="/tmp/model/")
learn.lr_find()
learn.recorder.plot()
learn.fit_one_cycle(6,1e-2)
learn.save('stage-2')
learn.recorder.plot_losses()
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_top_losses(9, figsize=(15,11))
```
**Confusion Matrix**
```
interp.plot_confusion_matrix(figsize=(8,8), dpi=60)
interp.most_confused(min_val=2)
pred_data= ImageDataBunch.from_folder(path, train=".",
valid_pct=0.2,
ds_tfms=get_transforms(flip_vert=True, max_warp=0),
size=224,bs=64,
num_workers=0).normalize(imagenet_stats)
predictor=cnn_learner(data, models.resnet34, metrics=accuracy, model_dir="/tmp/model/").load('stage-2')
pred_data.single_from_classes(path, pred_data.classes)
x,y = data.valid_ds[3]
x.show()
data.valid_ds.y[3]
pred_class,pred_idx,outputs = predictor.predict(x)
pred_class
```
## Heatmaps
**The heatmap will help us identify were our model it's looking and it's really useful for decision making**
```
def heatMap(x,y,data, learner, size=(0,224,224,0)):
"""HeatMap"""
# Evaluation mode
m=learner.model.eval()
# Denormalize the image
xb,_ = data.one_item(x)
xb_im = Image(data.denorm(xb)[0])
xb = xb.cuda()
# hook the activations
with hook_output(m[0]) as hook_a:
with hook_output(m[0], grad=True) as hook_g:
preds = m(xb)
preds[0,int(y)].backward()
# Activations
acts=hook_a.stored[0].cpu()
# Avg of the activations
avg_acts=acts.mean(0)
# Show HeatMap
_,ax = plt.subplots()
xb_im.show(ax)
ax.imshow(avg_acts, alpha=0.5, extent=size,
interpolation='bilinear', cmap='magma')
heatMap(x,y,pred_data,learn)
```
***It is very hard to completely eliminate false positives and negatives (in a case like this, it could indicate overfitting, given the relatively small training dataset), but the metric for the suitability of a model for the real world is how the model's sensitivity and specificity compare to that of a group of actual pathologists with domain expertise, when both analyze an identical set of real world data that neither has prior exposure to.***
You might improve the accuracy if you artificially increase the size of the training dataset by changing orientations, mirroring, etc., assuming the orientation of the NIH images of the smears haven't been normalized (I would assume they haven't, but that's a dangerous assumption). I'm also curious if you compared ResNet-34 and -50, as 50 might help your specificity (or not).*
| true |
code
| 0.622086 | null | null | null | null |
|
# Moving Square Video Prediction
This is the third toy example from Jason Brownlee's [Long Short Term Memory Networks with Python](https://machinelearningmastery.com/lstms-with-python/). It illustrates using a CNN LSTM, ie, an LSTM with input from CNN. Per section 8.2 of the book:
> The moving square video prediction problem is contrived to demonstrate the CNN LSTM. The
problem involves the generation of a sequence of frames. In each image a line is drawn from left to right or right to left. Each frame shows the extension of the line by one pixel. The task is for the model to classify whether the line moved left or right in the sequence of frames. Technically, the problem is a sequence classification problem framed with a many-to-one prediction model.
```
from __future__ import division, print_function
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt
import os
import shutil
%matplotlib inline
DATA_DIR = "../../data"
MODEL_FILE = os.path.join(DATA_DIR, "torch-08-moving-square-{:d}.model")
TRAINING_SIZE = 5000
VALIDATION_SIZE = 100
TEST_SIZE = 500
SEQUENCE_LENGTH = 50
FRAME_SIZE = 50
BATCH_SIZE = 32
NUM_EPOCHS = 5
LEARNING_RATE = 1e-3
```
## Prepare Data
Our data is going to be batches of sequences of images. Each image will need to be in channel-first format, since Pytorch only supports that format. So our output data will be in the (batch_size, sequence_length, num_channels, height, width) format.
```
def next_frame(frame, x, y, move_right, upd_int):
frame_size = frame.shape[0]
if x is None and y is None:
x = 0 if (move_right == 1) else (frame_size - 1)
y = np.random.randint(0, frame_size, 1)[0]
else:
if y == 0:
y = np.random.randint(y, y + 1, 1)[0]
elif y == frame_size - 1:
y = np.random.randint(y - 1, y, 1)[0]
else:
y = np.random.randint(y - 1, y + 1, 1)[0]
if move_right:
x = x + 1
else:
x = x - 1
new_frame = frame.copy()
new_frame[y, x] = upd_int
return new_frame, x, y
row, col = None, None
frame = np.ones((5, 5))
move_right = 1 if np.random.random() < 0.5 else 0
for i in range(5):
frame, col, row = next_frame(frame, col, row, move_right, 0)
plt.subplot(1, 5, (i+1))
plt.xticks([])
plt.yticks([])
plt.title((col, row, "R" if (move_right==1) else "L"))
plt.imshow(frame, cmap="gray")
plt.tight_layout()
plt.show()
def generate_data(frame_size, sequence_length, num_samples):
assert(frame_size == sequence_length)
xs, ys = [], []
for bid in range(num_samples):
frame_seq = []
row, col = None, None
frame = np.ones((frame_size, frame_size))
move_right = 1 if np.random.random() < 0.5 else 0
for sid in range(sequence_length):
frm, col, row = next_frame(frame, col, row, move_right, 0)
frm = frm.reshape((1, frame_size, frame_size))
frame_seq.append(frm)
xs.append(np.array(frame_seq))
ys.append(move_right)
return np.array(xs), np.array(ys)
X, y = generate_data(FRAME_SIZE, SEQUENCE_LENGTH, 10)
print(X.shape, y.shape)
Xtrain, ytrain = generate_data(FRAME_SIZE, SEQUENCE_LENGTH, TRAINING_SIZE)
Xval, yval = generate_data(FRAME_SIZE, SEQUENCE_LENGTH, VALIDATION_SIZE)
Xtest, ytest = generate_data(FRAME_SIZE, SEQUENCE_LENGTH, TEST_SIZE)
print(Xtrain.shape, ytrain.shape, Xval.shape, yval.shape, Xtest.shape, ytest.shape)
```
## Define Network
We want to build a CNN-LSTM network. Each image in the sequence will be fed to a CNN which will learn to produce a feature vector for the image. The sequence of vectors will be fed into an LSTM and the LSTM will learn to generate a context vector that will be then fed into a FCN that will predict if the square is moving left or right.
<img src="08-network-design.png"/>
```
class CNN(nn.Module):
def __init__(self, input_height, input_width, input_channels,
output_channels,
conv_kernel_size, conv_stride, conv_padding,
pool_size):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(input_channels, output_channels,
kernel_size=conv_kernel_size,
stride=conv_stride,
padding=conv_padding)
self.relu1 = nn.ReLU()
self.output_height = input_height // pool_size
self.output_width = input_width // pool_size
self.output_channels = output_channels
self.pool_size = pool_size
def forward(self, x):
x = self.conv1(x)
x = self.relu1(x)
x = F.max_pool2d(x, self.pool_size)
x = x.view(x.size(0), self.output_channels * self.output_height * self.output_width)
return x
cnn = CNN(FRAME_SIZE, FRAME_SIZE, 1, 2, 2, 1, 1, 2)
print(cnn)
# size debugging
print("--- size debugging ---")
inp = Variable(torch.randn(BATCH_SIZE, 1, FRAME_SIZE, FRAME_SIZE))
out = cnn(inp)
print(out.size())
class CNNLSTM(nn.Module):
def __init__(self, image_size, input_channels, output_channels,
conv_kernel_size, conv_stride, conv_padding, pool_size,
seq_length, hidden_size, num_layers, output_size):
super(CNNLSTM, self).__init__()
# capture variables
self.num_layers = num_layers
self.seq_length = seq_length
self.image_size = image_size
self.output_channels = output_channels
self.hidden_size = hidden_size
self.lstm_input_size = output_channels * (image_size // pool_size) ** 2
# define network layers
self.cnn = CNN(image_size, image_size, input_channels, output_channels,
conv_kernel_size, conv_stride, conv_padding, pool_size)
self.lstm = nn.LSTM(self.lstm_input_size, hidden_size, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, output_size)
self.softmax = nn.Softmax()
def forward(self, x):
if torch.cuda.is_available():
h0 = (Variable(torch.randn(self.num_layers, x.size(0), self.hidden_size).cuda()),
Variable(torch.randn(self.num_layers, x.size(0), self.hidden_size).cuda()))
else:
h0 = (Variable(torch.randn(self.num_layers, x.size(0), self.hidden_size)),
Variable(torch.randn(self.num_layers, x.size(0), self.hidden_size)))
cnn_out = []
for i in range(self.seq_length):
cnn_out.append(self.cnn(x[:, i, :, :, :]))
x = torch.cat(cnn_out, dim=1).view(-1, self.seq_length, self.lstm_input_size)
x, h0 = self.lstm(x, h0)
x = self.fc(x[:, -1, :])
x = self.softmax(x)
return x
model = CNNLSTM(FRAME_SIZE, 1, 2, 2, 1, 1, 2, SEQUENCE_LENGTH, 50, 1, 2)
if torch.cuda.is_available():
model.cuda()
print(model)
# size debugging
print("--- size debugging ---")
inp = Variable(torch.randn(BATCH_SIZE, SEQUENCE_LENGTH, 1, FRAME_SIZE, FRAME_SIZE))
out = model(inp)
print(out.size())
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=LEARNING_RATE)
```
## Train Network
Training on GPU is probably preferable for this example, takes a long time on CPU. During some runs, the training and validation accuracies get stuck, possibly because of bad initializations, the fix appears to be to just retry the training until it results in good training and validation accuracies and use the resulting model.
```
def compute_accuracy(pred_var, true_var):
if torch.cuda.is_available():
ypred = pred_var.cpu().data.numpy()
ytrue = true_var.cpu().data.numpy()
else:
ypred = pred_var.data.numpy()
ytrue = true_var.data.numpy()
return accuracy_score(ypred, ytrue)
history = []
for epoch in range(NUM_EPOCHS):
num_batches = Xtrain.shape[0] // BATCH_SIZE
shuffled_indices = np.random.permutation(np.arange(Xtrain.shape[0]))
train_loss, train_acc = 0., 0.
for bid in range(num_batches):
Xbatch_data = Xtrain[shuffled_indices[bid * BATCH_SIZE : (bid+1) * BATCH_SIZE]]
ybatch_data = ytrain[shuffled_indices[bid * BATCH_SIZE : (bid+1) * BATCH_SIZE]]
Xbatch = Variable(torch.from_numpy(Xbatch_data).float())
ybatch = Variable(torch.from_numpy(ybatch_data).long())
if torch.cuda.is_available():
Xbatch = Xbatch.cuda()
ybatch = ybatch.cuda()
# initialize gradients
optimizer.zero_grad()
# forward
Ybatch_ = model(Xbatch)
loss = loss_fn(Ybatch_, ybatch)
# backward
loss.backward()
train_loss += loss.data[0]
_, ybatch_ = Ybatch_.max(1)
train_acc += compute_accuracy(ybatch_, ybatch)
optimizer.step()
# compute training loss and accuracy
train_loss /= num_batches
train_acc /= num_batches
# compute validation loss and accuracy
val_loss, val_acc = 0., 0.
num_val_batches = Xval.shape[0] // BATCH_SIZE
for bid in range(num_val_batches):
# data
Xbatch_data = Xval[bid * BATCH_SIZE : (bid + 1) * BATCH_SIZE]
ybatch_data = yval[bid * BATCH_SIZE : (bid + 1) * BATCH_SIZE]
Xbatch = Variable(torch.from_numpy(Xbatch_data).float())
ybatch = Variable(torch.from_numpy(ybatch_data).long())
if torch.cuda.is_available():
Xbatch = Xbatch.cuda()
ybatch = ybatch.cuda()
Ybatch_ = model(Xbatch)
loss = loss_fn(Ybatch_, ybatch)
val_loss += loss.data[0]
_, ybatch_ = Ybatch_.max(1)
val_acc += compute_accuracy(ybatch_, ybatch)
val_loss /= num_val_batches
val_acc /= num_val_batches
torch.save(model.state_dict(), MODEL_FILE.format(epoch+1))
print("Epoch {:2d}/{:d}: loss={:.3f}, acc={:.3f}, val_loss={:.3f}, val_acc={:.3f}"
.format((epoch+1), NUM_EPOCHS, train_loss, train_acc, val_loss, val_acc))
history.append((train_loss, val_loss, train_acc, val_acc))
losses = [x[0] for x in history]
val_losses = [x[1] for x in history]
accs = [x[2] for x in history]
val_accs = [x[3] for x in history]
plt.subplot(211)
plt.title("Accuracy")
plt.plot(accs, color="r", label="train")
plt.plot(val_accs, color="b", label="valid")
plt.legend(loc="best")
plt.subplot(212)
plt.title("Loss")
plt.plot(losses, color="r", label="train")
plt.plot(val_losses, color="b", label="valid")
plt.legend(loc="best")
plt.tight_layout()
plt.show()
```
## Test/Evaluate Network
```
saved_model = CNNLSTM(FRAME_SIZE, 1, 2, 2, 1, 1, 2, SEQUENCE_LENGTH, 50, 1, 2)
saved_model.load_state_dict(torch.load(MODEL_FILE.format(5)))
if torch.cuda.is_available():
saved_model.cuda()
ylabels, ypreds = [], []
num_test_batches = Xtest.shape[0] // BATCH_SIZE
for bid in range(num_test_batches):
Xbatch_data = Xtest[bid * BATCH_SIZE : (bid + 1) * BATCH_SIZE]
ybatch_data = ytest[bid * BATCH_SIZE : (bid + 1) * BATCH_SIZE]
Xbatch = Variable(torch.from_numpy(Xbatch_data).float())
ybatch = Variable(torch.from_numpy(ybatch_data).long())
if torch.cuda.is_available():
Xbatch = Xbatch.cuda()
ybatch = ybatch.cuda()
Ybatch_ = saved_model(Xbatch)
_, ybatch_ = Ybatch_.max(1)
if torch.cuda.is_available():
ylabels.extend(ybatch.cpu().data.numpy())
ypreds.extend(ybatch_.cpu().data.numpy())
else:
ylabels.extend(ybatch.data.numpy())
ypreds.extend(ybatch_.data.numpy())
print("Test accuracy: {:.3f}".format(accuracy_score(ylabels, ypreds)))
print("Confusion matrix")
print(confusion_matrix(ylabels, ypreds))
for i in range(NUM_EPOCHS):
os.remove(MODEL_FILE.format(i + 1))
```
| true |
code
| 0.708994 | null | null | null | null |
|
# MLP example using PySNN
```
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
from torchvision import transforms
from tqdm import tqdm
from pysnn.connection import Linear
from pysnn.neuron import LIFNeuron, Input
from pysnn.learning import MSTDPET
from pysnn.encoding import PoissonEncoder
from pysnn.network import SNNNetwork
from pysnn.datasets import AND, BooleanNoise, Intensity
```
## Parameter defintions
```
# Architecture
n_in = 10
n_hidden = 5
n_out = 1
# Data
duration = 200
intensity = 50
num_workers = 0
batch_size = 1
# Neuronal Dynamics
thresh = 1.0
v_rest = 0
alpha_v = 10
tau_v = 10
alpha_t = 10
tau_t = 10
duration_refrac = 2
dt = 1
delay = 2
i_dynamics = (dt, alpha_t, tau_t, "exponential")
n_dynamics = (thresh, v_rest, alpha_v, alpha_v, dt, duration_refrac, tau_v, tau_t, "exponential")
c_dynamics = (batch_size, dt, delay)
# Learning
epochs = 100
lr = 0.1
w_init = 0.8
a = 0.0
```
## Network definition
The API is mostly the same as for regular PyTorch. The main differences are that layers are composed of a `Neuron` and `Connection` type,
and the layer has to be added to the network by calling the `add_layer` method. Lastly, all objects return both a
spike (or activation potential) object and a trace object.
```
class Network(SNNNetwork):
def __init__(self):
super(Network, self).__init__()
# Input
self.input = Input((batch_size, 1, n_in), *i_dynamics)
# Layer 1
self.mlp1_c = Linear(n_in, n_hidden, *c_dynamics)
self.mlp1_c.reset_weights(distribution="uniform") # initialize uniform between 0 and 1
self.neuron1 = LIFNeuron((batch_size, 1, n_hidden), *n_dynamics)
self.add_layer("fc1", self.mlp1_c, self.neuron1)
# Layer 2
self.mlp2_c = Linear(n_hidden, n_out, *c_dynamics)
self.mlp2_c.reset_weights(distribution="uniform")
self.neuron2 = LIFNeuron((batch_size, 1, n_out), *n_dynamics)
self.add_layer("fc2", self.mlp2_c, self.neuron2)
def forward(self, input):
x, t = self.input(input)
# Layer 1
x, _ = self.mlp1_c(x, t)
x, t = self.neuron1(x)
# Layer out
x, _ = self.mlp2_c(x, t)
x, t = self.neuron2(x)
return x, t
```
## Dataset
Simple Boolean AND dataset, generated to match the input dimensions of the network.
```
data_transform = transforms.Compose(
[
# BooleanNoise(0.2, 0.8),
Intensity(intensity)
]
)
lbl_transform = transforms.Lambda(lambda x: x * intensity)
train_dataset = AND(
data_encoder=PoissonEncoder(duration, dt),
data_transform=data_transform,
lbl_transform=lbl_transform,
repeats=n_in / 2,
)
train_dataloader = DataLoader(
train_dataset, batch_size=batch_size, shuffle=False, num_workers=num_workers
)
# Visualize input samples
_, axes = plt.subplots(1, 4, sharey=True, figsize=(25, 8))
for s in range(len(train_dataset)):
sample = train_dataset[s][0] # Drop label
sample = sample.sum(-1).numpy() # Total spike by summing over time dimension
sample = np.squeeze(sample)
axes[s].bar(range(len(sample)), sample)
axes[s].set_ylabel("Total number of spikes")
axes[s].set_xlabel("Input neuron")
```
## Training
```
device = torch.device("cpu")
net = Network()
# Learning rule definition
layers = net.layer_state_dict()
learning_rule = MSTDPET(layers, 1, 1, lr, np.exp(-1/10))
# Training loop
for _ in tqdm(range(epochs)):
for batch in train_dataloader:
sample, label = batch
# Iterate over input's time dimension
for idx in range(sample.shape[-1]):
input = sample[:, :, :, idx]
spike_net, _ = net(input)
# Determine reward, provide reward of 1 for desired behaviour, 0 otherwise.
# For positive samples (simulating an AND gate) spike as often as possible, for negative samples spike as little as possible.
if spike_net.long().view(-1) == label:
reward = 1
else:
reward = 0
# Perform a single step of the learning rule
learning_rule.step(reward)
# Reset network state (e.g. voltage, trace, spikes)
net.reset_state()
```
## Generate Data for Visualization
```
out_spikes = []
out_voltage = []
out_trace = []
for batch in train_dataloader:
single_out_s = []
single_out_v = []
single_out_t = []
sample, _ = batch
# Iterate over input's time dimension
for idx in range(sample.shape[-1]):
input = sample[:, :, :, idx]
spike_net, trace_net = net(input)
# Single timestep results logging
single_out_s.append(spike_net.clone())
single_out_t.append(trace_net.clone())
single_out_v.append(net.neuron2.v_cell.clone()) # Clone the voltage to make a copy of the value instead of using a pointer to memory
# Store batch results
out_spikes.append(torch.stack(single_out_s, dim=-1).view(-1))
out_voltage.append(torch.stack(single_out_v, dim=-1).view(-1))
out_trace.append(torch.stack(single_out_t, dim=-1).view(-1))
# Reset network state (e.g. voltage, trace, spikes)
net.reset_state()
```
### Visualize output neuron state over time
In the voltage plots the peaks never reach the voltage of 1, this is because the network has already reset the voltage of the spiking neurons during the forward pass. Thus it is not possible to register the exact voltage surpassing the threshold.
```
_, axes = plt.subplots(3, 4, sharey="row", figsize=(25, 12))
# Process every sample separately
for s in range(len(out_spikes)):
ax_col = axes[:, s]
spikes = out_spikes[s]
voltage = out_voltage[s]
trace = out_trace[s]
data_combined = [spikes, trace, voltage]
names = ["Spikes", "Trace", "Voltage"]
# Set column titles
ax_col[0].set_title(f"Sample {s}")
# Plot all states
for ax, data, name in zip(ax_col, data_combined, names):
ax.plot(data, label=name)
ax.legend()
```
| true |
code
| 0.756891 | null | null | null | null |
|
```
from toolz import curry
import pandas as pd
import numpy as np
from scipy.special import expit
from linearmodels.panel import PanelOLS
import statsmodels.formula.api as smf
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import style
style.use("ggplot")
```
# Difference-in-Diferences: Death and Rebirth
## The Promise of Panel Data
Panel data is when we have multiple units `i` over multiple periods of time `t`. Think about a policy evaluation scenario in the US, where you want to check the effect of cannabis legalization on crime rate. You have crime rate data on multiple states `i` over multiple time perios `t`. You also observe at what point in time each state adopts legislation in the direction of canabis legalization. I hope you can see why this is incredibly powerfull for causal inference. Call canabis legalization the treatment `D` (since `T` is taken; it represents time). We can follow the trend on crime rates for a particular state that eventually gets treated and see if there are any disruptions in the trend at the treatment time. In a way, a state serves as its own control unit, in a sort of before and after comparisson. Furthermore, becase we have multiple states, we can also compare treated states to control states. When we put both comparissons toguether, treated vs control and before and after treatement, we end up with an incredibly powerfull tool to infer counterfactuals and, hence, causal effects.
Panel data methods are often used in govenment policy evaluation, but we can easily make an argument about why it is also incredibly usefull for the (tech) industry. Companies often track user data across multiple periods of time, which results in a rich panel data structure. To expore that idea further, let's consider a hypothetical example of a tech company that traked customers for multiple years. Along those years, it rolled out a new product for some of its customers. More specifically, some customers got acess to the new product in 1985, others in 1994 and others in the year 2000. In causal infererence terms, we can already see that the new product can be seen as a treatment. We call each of those **groups of customers that got treated at the same time a cohort**. In this hypothetical exemple, we want to figure out the impact of the new product on sales. The folowing image shows how sales evolve over time for each of the treated cohorts, plus a never treated group of customers.
```
time = range(1980, 2010)
cohorts = [1985,1994,2000,2011]
units = range(1, 100+1)
np.random.seed(1)
df_hom_effect = pd.DataFrame(dict(
year = np.tile(time, len(units)),
unit = np.repeat(units, len(time)),
cohort = np.repeat(np.random.choice(cohorts, len(units)), len(time)),
unit_fe = np.repeat(np.random.normal(0, 5, size=len(units)), len(time)),
time_fe = np.tile(np.random.normal(size=len(time)), len(units)),
)).assign(
trend = lambda d: (d["year"] - d["year"].min())/8,
post = lambda d: (d["year"] >= d["cohort"]).astype(int),
).assign(
treat = 1,
y0 = lambda d: 10 + d["trend"] + d["unit_fe"] + 0.1*d["time_fe"],
).assign(
treat_post = lambda d: d["treat"]*d["post"],
y1 = lambda d: d["y0"] + 1
).assign(
tau = lambda d: d["y1"] - d["y0"],
sales = lambda d: np.where(d["treat_post"] == 1, d["y1"], d["y0"])
).drop(columns=["unit_fe", "time_fe", "trend", "y0", "y1"])
plt.figure(figsize=(10,4))
[plt.vlines(x=c, ymin=9, ymax=15, color="black", ls="dashed") for c in cohorts[:-1]]
sns.lineplot(
data=(df_hom_effect
.replace({"cohort":{2011:"never-treated"}})
.groupby(["cohort", "year"])["sales"]
.mean()
.reset_index()),
x="year",
y = "sales",
hue="cohort",
);
```
Let's take a momen to appreciate the richness of the data depicted in the above plot. First, we can see that each cohorts have its own baseline level. Thats simply because different customers buy different ammounts. For instance, it looks like customers in the never treated cohort have a higher baseline (of about 11), compared to other cohorts. This means that simply comparing treated cohorts to control cohorts would yield a biased result, since $Y_{0}$ for the neve treated is higher than the $Y_{0}$ for the treated. Fortunatly, we can compare acorss units and time.
Speaking of time, notice how there is an overall upward trend with some wigles (for example, there is a dip in the year 1999). Since latter years have higher $Y_{0}$ than early years, simply comparing the same unit across time would also yield in biased results. Once again, we are fortunate that the pannel data structure allow us to compare not only across time, but also across units.
Another way to see the power of panel data structure in through the lens of linear models and linear regression. Let's say each of our customers `i` has a spend propensity $\gamma$. This is because of indosincasies due to stuff we can't observe, like customer's salary, family sinze and so on. Also, we can say that each year has an sales level $\theta$. Again, maibe because there is a crisis in one year, sales drop. If that is the case, a good way of modeling sales is to say it depends on the customer effect $\gamma$ and the time effect $\theta$, plus some random noise.
$$
Sales_{it} = \gamma_i + \theta_t + e_{it}
$$
To include the treatment in this picture, lets define a variable $D_{it}$ wich is 1 if the unit is treated. In our example, this variable would be always zero for the never treated cohort. It would also be zero for all the other cohorts at the begining, but it would turn into 1 at year 1985 for the cohort treated in 1985 and stay on after that. Same thing for other cohorts, it would turn into 1 at 1994 fot the cohort treated in 1994 and so on. We can include in our model of sales as follows:
$$
Sales_{it} = \tau D_{it} + \gamma_i + \theta_t + e_{it}
$$
Estimating the above model is OLS is what is called the Two-Way Fixed Effects Models (TWFE). Notice that $\tau$ would be the treatment effect, as it tells us how much sales changes once units are treated. Another way of looking at it is to invoke the "holding things constant" propriety of linear regression. If we estimate the above model, we could read the estimate of $\tau$ as how much sales would change if we flip the treatment from 0 to 1 while holding the unit `i` and time `t` fixed. Take a minute to appriciate how bold this is! To say we would hold each unit fixed while seeng how $D$ changes the outcome is to say we are controling for all unit specific characteristic, known and unknown. For example, we would be controling for customers past sales, wich we could measure, but also stuff we have no idea about, like how much the customer like our brand, his salary... The only requirement is that this caracteristic is fixed over the time of the analysis. Moreover, to say we would hold each time period fixed is to say we are controlling for all year specifit characteristic. For instance, since we are holding year fixed, while looking at the effect of $D$, that trend over there would vanish.
To see all this power in action all we have to do is run an OLS model with the treatment indicator $D$ (`treat_post` here), plut dummies for the units and time. In our particular example, I've generated data in such a way that the effect of the treatment (new product) is to increase sales by 1. Notice how TWFE nais in recovering that treatment effect
```
formula = f"""sales ~ treat_post + C(unit) + C(year)"""
mod = smf.ols(formula, data=df_hom_effect)
result = mod.fit()
result.params["treat_post"]
```
Since I've simulated the data above, I know exactly the true individual treatment effect, which is stored in the `tau` column. Since the TWFE recovers the treatment effect on the treated, we can verify that the true ATT matches the one estimated above.
```
df_hom_effect.query("treat_post==1")["tau"].mean()
```
Before anyone comes and say that generating one dummy column for each unit is impossible with big data, let me come foreward and tell you that, yes, that is true. But there is a easy work around. We can use the FWL theorem to partiall that single regression into two. In fact, runing the above model is numerically equivalent to estimating the following model
$$
\tilde{Sales}_{it} = \tau \tilde D_{it} + e_{it}
$$
where
$$
\tilde{Sales}_{it} = Sales_{it} - \underbrace{\frac{1}{T}\sum_{t=0}^T Sales_{it}}_\text{Time Average} - \underbrace{\frac{1}{N}\sum_{i=0}^N Sales_{it}}_\text{Unit Average}
$$
and
$$
\tilde{D}_{it} = D_{it} - \frac{1}{T}\sum_{t=0}^T D_{it} - \frac{1}{N}\sum_{i=0}^N D_{it}
$$
In words now, in case the math is too crowded, we subtract the unit average across time (first term) and the time average across units (second term) from both the treatment indicator and the outcome variable to constrict the residuals. This process is often times called de-meaning, since we subtract the mean from the outcome and treatment. Finally, here is the same exact thing, but in code:
```
@curry
def demean(df, col_to_demean):
return df.assign(**{col_to_demean: (df[col_to_demean]
- df.groupby("unit")[col_to_demean].transform("mean")
- df.groupby("year")[col_to_demean].transform("mean"))})
formula = f"""sales ~ treat_post"""
mod = smf.ols(formula,
data=df_hom_effect
.pipe(demean(col_to_demean="treat_post"))
.pipe(demean(col_to_demean="sales")))
result = mod.fit()
result.summary().tables[1]
```
As we can see, with the alternative implementation, TWFE is also able to perfectly recover the ATT of 1.
## Assuptions
Two
## Death
## Trend in the Effect
```
time = range(1980, 2010)
cohorts = [1985,1994,2000,2011]
units = range(1, 100+1)
np.random.seed(3)
df_trend_effect = pd.DataFrame(dict(
year = np.tile(time, len(units)),
unit = np.repeat(units, len(time)),
cohort = np.repeat(np.random.choice(cohorts, len(units)), len(time)),
unit_fe = np.repeat(np.random.normal(size=len(units)), len(time)),
time_fe = np.tile(np.random.normal(size=len(time)), len(units)),
)).assign(
relative_year = lambda d: d["year"] - d["cohort"],
trend = lambda d: (d["year"] - d["year"].min())/8,
post = lambda d: (d["year"] >= d["cohort"]).astype(int),
).assign(
treat = 1,
y0 = lambda d: 10 + d["unit_fe"] + 0.02*d["time_fe"],
).assign(
y1 = lambda d: d["y0"] + np.minimum(0.2*(np.maximum(0, d["year"] - d["cohort"])), 1)
).assign(
tau = lambda d: d["y1"] - d["y0"],
outcome = lambda d: np.where(d["treat"]*d["post"] == 1, d["y1"], d["y0"])
)
plt.figure(figsize=(10,4))
sns.lineplot(
data=df_trend_effect.groupby(["cohort", "year"])["outcome"].mean().reset_index(),
x="year",
y = "outcome",
hue="cohort",
);
formula = f"""outcome ~ treat:post + C(year) + C(unit)"""
mod = smf.ols(formula, data=df_trend_effect)
result = mod.fit()
result.params["treat:post"]
df_trend_effect.query("treat==1 & post==1")["tau"].mean()
```
### Event Study Desing
```
relative_years = range(-10,10+1)
formula = "outcome~"+"+".join([f'Q({c})' for c in relative_years]) + "+C(unit)+C(year)"
mod = smf.ols(formula,
data=(df_trend_effect.join(pd.get_dummies(df_trend_effect["relative_year"]))))
result = mod.fit()
ax = (df_trend_effect
.query("treat==1")
.query("relative_year>-10")
.query("relative_year<10")
.groupby("relative_year")["tau"].mean().plot())
ax.plot(relative_years, result.params[-len(relative_years):]);
```
## Covariates
## X-Specific Trends
```
time = range(1980, 2000)
cohorts = [1990]
units = range(1, 100+1)
np.random.seed(3)
x = np.random.choice(np.random.normal(size=len(units)//10), size=len(units))
df_cov_trend = pd.DataFrame(dict(
year = np.tile(time, len(units)),
unit = np.repeat(units, len(time)),
cohort = np.repeat(np.random.choice(cohorts, len(units)), len(time)),
unit_fe = np.repeat(np.random.normal(size=len(units)), len(time)),
time_fe = np.tile(np.random.normal(size=len(time)), len(units)),
x = np.repeat(x, len(time)),
)).assign(
trend = lambda d: d["x"]*(d["year"] - d["year"].min())/20,
post = lambda d: (d["year"] >= d["cohort"]).astype(int),
).assign(
treat = np.repeat(np.random.binomial(1, expit(x)), len(time)),
y0 = lambda d: 10 + d["trend"] + 0.5*d["unit_fe"] + 0.01*d["time_fe"],
).assign(
y1 = lambda d: d["y0"] + 1
).assign(
tau = lambda d: d["y1"] - d["y0"],
outcome = lambda d: np.where(d["treat"]*d["post"] == 1, d["y1"], d["y0"])
)
plt.figure(figsize=(10,4))
sns.lineplot(
data=df_cov_trend.groupby(["treat", "year"])["outcome"].mean().reset_index(),
x="year",
y = "outcome",
hue="treat",
);
facet_col = "x"
all_facet_values = sorted(df_cov_trend[facet_col].unique())
g = sns.FacetGrid(df_cov_trend, col=facet_col, sharey=False, sharex=False, col_wrap=4, height=5, aspect=1)
for x, ax in zip(all_facet_values, g.axes):
plot_df = df_cov_trend.query(f"{facet_col}=={x}")
sns.lineplot(
data=plot_df.groupby(["treat", "year"])["outcome"].mean().reset_index(),
x="year",
y = "outcome",
hue="treat",
ax=ax
)
ax.set_title(f"X = {round(x, 2)}")
plt.tight_layout()
formula = f"""outcome ~ treat:post + C(year) + C(unit)"""
mod = smf.ols(formula, data=df_cov_trend)
result = mod.fit()
result.params["treat:post"]
formula = f"""outcome ~ treat:post + x * C(year) + C(unit)"""
mod = smf.ols(formula, data=df_cov_trend)
result = mod.fit()
result.params["treat:post"]
df_cov_trend.query("treat==1 & post==1")["tau"].mean()
```
| true |
code
| 0.506713 | null | null | null | null |
|
# Adadelta
:label:`sec_adadelta`
Adadelta is yet another variant of AdaGrad (:numref:`sec_adagrad`). The main difference lies in the fact that it decreases the amount by which the learning rate is adaptive to coordinates. Moreover, traditionally it referred to as not having a learning rate since it uses the amount of change itself as calibration for future change. The algorithm was proposed in :cite:`Zeiler.2012`. It is fairly straightforward, given the discussion of previous algorithms so far.
## The Algorithm
In a nutshell, Adadelta uses two state variables, $\mathbf{s}_t$ to store a leaky average of the second moment of the gradient and $\Delta\mathbf{x}_t$ to store a leaky average of the second moment of the change of parameters in the model itself. Note that we use the original notation and naming of the authors for compatibility with other publications and implementations (there is no other real reason why one should use different Greek variables to indicate a parameter serving the same purpose in momentum, Adagrad, RMSProp, and Adadelta).
Here are the technical details of Adadelta. Given the parameter du jour is $\rho$, we obtain the following leaky updates similarly to :numref:`sec_rmsprop`:
$$\begin{aligned}
\mathbf{s}_t & = \rho \mathbf{s}_{t-1} + (1 - \rho) \mathbf{g}_t^2.
\end{aligned}$$
The difference to :numref:`sec_rmsprop` is that we perform updates with the rescaled gradient $\mathbf{g}_t'$, i.e.,
$$\begin{aligned}
\mathbf{x}_t & = \mathbf{x}_{t-1} - \mathbf{g}_t'. \\
\end{aligned}$$
So what is the rescaled gradient $\mathbf{g}_t'$? We can calculate it as follows:
$$\begin{aligned}
\mathbf{g}_t' & = \frac{\sqrt{\Delta\mathbf{x}_{t-1} + \epsilon}}{\sqrt{{\mathbf{s}_t + \epsilon}}} \odot \mathbf{g}_t, \\
\end{aligned}$$
where $\Delta \mathbf{x}_{t-1}$ is the leaky average of the squared rescaled gradients $\mathbf{g}_t'$. We initialize $\Delta \mathbf{x}_{0}$ to be $0$ and update it at each step with $\mathbf{g}_t'$, i.e.,
$$\begin{aligned}
\Delta \mathbf{x}_t & = \rho \Delta\mathbf{x}_{t-1} + (1 - \rho) {\mathbf{g}_t'}^2,
\end{aligned}$$
and $\epsilon$ (a small value such as $10^{-5}$) is added to maintain numerical stability.
## Implementation
Adadelta needs to maintain two state variables for each variable, $\mathbf{s}_t$ and $\Delta\mathbf{x}_t$. This yields the following implementation.
```
%matplotlib inline
from d2l import tensorflow as d2l
import tensorflow as tf
def init_adadelta_states(feature_dim):
s_w = tf.Variable(tf.zeros((feature_dim, 1)))
s_b = tf.Variable(tf.zeros(1))
delta_w = tf.Variable(tf.zeros((feature_dim, 1)))
delta_b = tf.Variable(tf.zeros(1))
return ((s_w, delta_w), (s_b, delta_b))
def adadelta(params, grads, states, hyperparams):
rho, eps = hyperparams['rho'], 1e-5
for p, (s, delta), grad in zip(params, states, grads):
s[:].assign(rho * s + (1 - rho) * tf.math.square(grad))
g = (tf.math.sqrt(delta + eps) / tf.math.sqrt(s + eps)) * grad
p[:].assign(p - g)
delta[:].assign(rho * delta + (1 - rho) * g * g)
```
Choosing $\rho = 0.9$ amounts to a half-life time of 10 for each parameter update. This tends to work quite well. We get the following behavior.
```
data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(adadelta, init_adadelta_states(feature_dim),
{'rho': 0.9}, data_iter, feature_dim);
```
For a concise implementation we simply use the `adadelta` algorithm from the `Trainer` class. This yields the following one-liner for a much more compact invocation.
```
# adadelta is not converging at default learning rate
# but it's converging at lr = 5.0
trainer = tf.keras.optimizers.Adadelta
d2l.train_concise_ch11(trainer, {'learning_rate':5.0, 'rho': 0.9}, data_iter)
```
## Summary
* Adadelta has no learning rate parameter. Instead, it uses the rate of change in the parameters itself to adapt the learning rate.
* Adadelta requires two state variables to store the second moments of gradient and the change in parameters.
* Adadelta uses leaky averages to keep a running estimate of the appropriate statistics.
## Exercises
1. Adjust the value of $\rho$. What happens?
1. Show how to implement the algorithm without the use of $\mathbf{g}_t'$. Why might this be a good idea?
1. Is Adadelta really learning rate free? Could you find optimization problems that break Adadelta?
1. Compare Adadelta to Adagrad and RMS prop to discuss their convergence behavior.
[Discussions](https://discuss.d2l.ai/t/1077)
| true |
code
| 0.624007 | null | null | null | null |
|
# Deep Learning and Transfer Learning with pre-trained models
This notebook uses a pretrained model to build a classifier (CNN)
```
# import required libs
import os
import keras
import numpy as np
from keras import backend as K
from keras import applications
from keras.datasets import cifar10
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
import matplotlib.pyplot as plt
params = {'legend.fontsize': 'x-large',
'figure.figsize': (15, 5),
'axes.labelsize': 'x-large',
'axes.titlesize':'x-large',
'xtick.labelsize':'x-large',
'ytick.labelsize':'x-large'}
plt.rcParams.update(params)
%matplotlib inline
```
## Load VGG
```
vgg_model = applications.VGG19(include_top=False, weights='imagenet')
vgg_model.summary()
```
Set Parameters
```
batch_size = 128
num_classes = 10
epochs = 50
bottleneck_path = r'F:\work\kaggle\cifar10_cnn\bottleneck_features_train_vgg19.npy'
```
## Get CIFAR10 Dataset
```
# the data, shuffled and split between train and test sets
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
y_train.shape
```
## Pretrained Model for Feature Extraction
```
if not os.path.exists(bottleneck_path):
bottleneck_features_train = vgg_model.predict(x_train,verbose=1)
np.save(open(bottleneck_path, 'wb'),
bottleneck_features_train)
else:
bottleneck_features_train = np.load(open(bottleneck_path,'rb'))
bottleneck_features_train[0].shape
bottleneck_features_test = vgg_model.predict(x_test,verbose=1)
```
## Custom Classifier
```
clf_model = Sequential()
clf_model.add(Flatten(input_shape=bottleneck_features_train.shape[1:]))
clf_model.add(Dense(512, activation='relu'))
clf_model.add(Dropout(0.5))
clf_model.add(Dense(256, activation='relu'))
clf_model.add(Dropout(0.5))
clf_model.add(Dense(num_classes, activation='softmax'))
```
## Visualize the network architecture
```
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
SVG(model_to_dot(clf_model, show_shapes=True,
show_layer_names=True, rankdir='TB').create(prog='dot', format='svg'))
```
## Compile the model
```
clf_model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
```
## Train the classifier
```
clf_model.fit(bottleneck_features_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1)
```
## Predict and test model performance
```
score = clf_model.evaluate(bottleneck_features_test, y_test, verbose=1)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
```
### Assign label to a test image
```
def predict_label(img_idx,show_proba=True):
plt.imshow(x_test[img_idx],aspect='auto')
plt.title("Image to be Labeled")
plt.show()
print("Actual Class:{}".format(np.nonzero(y_test[img_idx])[0][0]))
test_image =np.expand_dims(x_test[img_idx], axis=0)
bf = vgg_model.predict(test_image,verbose=0)
pred_label = clf_model.predict_classes(bf,batch_size=1,verbose=0)
print("Predicted Class:{}".format(pred_label[0]))
if show_proba:
print("Predicted Probabilities")
print(clf_model.predict_proba(bf))
img_idx = 3999 # sample indices : 999,1999 and 3999
for img_idx in [999,1999,3999]:
predict_label(img_idx)
```
| true |
code
| 0.716956 | null | null | null | null |
|
# Example 1b: Spin-Bath model (Underdamped Case)
### Introduction
The HEOM method solves the dynamics and steady state of a system and its environment, the latter of which is encoded in a set of auxiliary density matrices.
In this example we show the evolution of a single two-level system in contact with a single Bosonic environment. The properties of the system are encoded in Hamiltonian, and a coupling operator which describes how it is coupled to the environment.
The Bosonic environment is implicitly assumed to obey a particular Hamiltonian (see paper), the parameters of which are encoded in the spectral density, and subsequently the free-bath correlation functions.
In the example below we show how to model the underdamped Brownian motion Spectral Density.
### Drude-Lorentz (overdamped) spectral density
Note that in the above, and the following, we set $\hbar = k_\mathrm{B} = 1$.
### Brownian motion (underdamped) spectral density
The underdamped spectral density is:
$$J_U = \frac{\alpha^2 \Gamma \omega}{(\omega_c^2 - \omega^2)^2 + \Gamma^2 \omega^2)}.$$
Here $\alpha$ scales the coupling strength, $\Gamma$ is the cut-off frequency, and $\omega_c$ defines a resonance frequency. With the HEOM we must use an exponential decomposition:
The Matsubara decomposition of this spectral density is, in real and imaginary parts:
\begin{equation*}
c_k^R = \begin{cases}
\alpha^2 \coth(\beta( \Omega + i\Gamma/2)/2)/4\Omega & k = 0\\
\alpha^2 \coth(\beta( \Omega - i\Gamma/2)/2)/4\Omega & k = 0\\
-2\alpha^2\Gamma/\beta \frac{\epsilon_k }{((\Omega + i\Gamma/2)^2 + \epsilon_k^2)(\Omega - i\Gamma/2)^2 + \epsilon_k^2)} & k \geq 1\\
\end{cases}
\end{equation*}
\begin{equation*}
\nu_k^R = \begin{cases}
-i\Omega + \Gamma/2, i\Omega +\Gamma/2, & k = 0\\
{2 \pi k} / {\beta } & k \geq 1\\
\end{cases}
\end{equation*}
\begin{equation*}
c_k^I = \begin{cases}
i\alpha^2 /4\Omega & k = 0\\
-i\alpha^2 /4\Omega & k = 0\\
\end{cases}
\end{equation*}
\begin{equation*}
\nu_k^I = \begin{cases}
i\Omega + \Gamma/2, -i\Omega + \Gamma/2, & k = 0\\
\end{cases}
\end{equation*}
Note that in the above, and the following, we set $\hbar = k_\mathrm{B} = 1$.
```
%pylab inline
from qutip import *
%load_ext autoreload
%autoreload 2
from bofin.heom import BosonicHEOMSolver
def cot(x):
return 1./np.tan(x)
def coth(x):
"""
Calculates the coth function.
Parameters
----------
x: np.ndarray
Any numpy array or list like input.
Returns
-------
cothx: ndarray
The coth function applied to the input.
"""
return 1/np.tanh(x)
# Defining the system Hamiltonian
eps = .5 # Energy of the 2-level system.
Del = 1.0 # Tunnelling term
Hsys = 0.5 * eps * sigmaz() + 0.5 * Del* sigmax()
# Initial state of the system.
rho0 = basis(2,0) * basis(2,0).dag()
# System-bath coupling (Drude-Lorentz spectral density)
Q = sigmaz() # coupling operator
#solver time steps
nsteps = 1000
tlist = np.linspace(0, 50, nsteps)
#correlation function plotting time steps
tlist_corr = np.linspace(0, 20, 1000)
#Bath properties:
gamma = .1 # cut off frequency
lam = .5 # coupling strenght
w0 = 1 #resonance frequency
T = 1
beta = 1./T
#HEOM parameters
NC = 10 # cut off parameter for the bath
#Spectral Density
wlist = np.linspace(0, 5, 1000)
pref = 1.
J = [lam**2 * gamma * w / ((w0**2-w**2)**2 + (gamma**2)*(w**2)) for w in wlist]
# Plot the results
fig, axes = plt.subplots(1, 1, sharex=True, figsize=(8,8))
axes.plot(wlist, J, 'r', linewidth=2)
axes.set_xlabel(r'$\omega$', fontsize=28)
axes.set_ylabel(r'J', fontsize=28)
#first of all lets look athe correlation functions themselves
Nk = 3 # number of exponentials
Om = np.sqrt(w0**2 - (gamma/2)**2)
Gamma = gamma/2.
#mats
def Mk(t,k):
ek = 2*pi*k/beta
return (-2*lam**2*gamma/beta)*ek*exp(-ek*abs(t))/(((Om+1.0j*Gamma)**2+ek**2)*((Om-1.0j*Gamma)**2+ek**2))
def c(t):
Cr = coth(beta*(Om+1.0j*Gamma)/2)*exp(1.0j*Om*t)+coth(beta*(Om-1.0j*Gamma)/2)*exp(-1.0j*Om*t)
#Cr = coth(beta*(Om+1.0j*Gamma)/2)*exp(1.0j*Om*t)+conjugate(coth(beta*(Om+1.0j*Gamma)/2)*exp(1.0j*Om*t))
Ci = exp(-1.0j*Om*t)-exp(1.0j*Om*t)
return (lam**2/(4*Om))*exp(-Gamma*abs(t))*(Cr+Ci) + sum([Mk(t,k) for k in range(1,Nk+1)])
plt.figure(figsize=(8,8))
plt.plot(tlist_corr ,[real(c(t)) for t in tlist_corr ], '-', color="black", label="Re[C(t)]")
plt.plot(tlist_corr ,[imag(c(t)) for t in tlist_corr ], '-', color="red", label="Im[C(t)]")
plt.legend()
plt.show()
#The Matsubara terms modify the real part
Nk = 3# number of exponentials
Om = np.sqrt(w0**2 - (gamma/2)**2)
Gamma = gamma/2.
#mats
def Mk(t,k):
ek = 2*pi*k/beta
return (-2*lam**2*gamma/beta)*ek*exp(-ek*abs(t))/(((Om+1.0j*Gamma)**2+ek**2)*((Om-1.0j*Gamma)**2+ek**2))
plt.figure(figsize=(8,8))
plt.plot(tlist_corr ,[sum([real(Mk(t,k)) for k in range(1,4)]) for t in tlist_corr ], '-', color="black", label="Re[M(t)] Nk=3")
plt.plot(tlist_corr ,[sum([real(Mk(t,k)) for k in range(1,6)]) for t in tlist_corr ], '--', color="red", label="Re[M(t)] Nk=5")
plt.legend()
plt.show()
#Lets collate the parameters for the HEOM
ckAR = [(lam**2/(4*Om))*coth(beta*(Om+1.0j*Gamma)/2),(lam**2/(4*Om))*coth(beta*(Om-1.0j*Gamma)/2)]
ckAR.extend([(-2*lam**2*gamma/beta)*( 2*pi*k/beta)/(((Om+1.0j*Gamma)**2+ (2*pi*k/beta)**2)*((Om-1.0j*Gamma)**2+( 2*pi*k/beta)**2))+0.j for k in range(1,Nk+1)])
vkAR = [-1.0j*Om+Gamma,1.0j*Om+Gamma]
vkAR.extend([2 * np.pi * k * T + 0.j for k in range(1,Nk+1)])
factor=1./4.
ckAI =[-factor*lam**2*1.0j/(Om),factor*lam**2*1.0j/(Om)]
vkAI = [-(-1.0j*(Om) - Gamma),-(1.0j*(Om) - Gamma)]
NC=14
NR = len(ckAR)
NI = len(ckAI)
Q2 = [Q for kk in range(NR+NI)]
print(Q2)
options = Options(nsteps=15000, store_states=True, rtol=1e-14, atol=1e-14)
HEOM = BosonicHEOMSolver(Hsys, Q2, ckAR, ckAI, vkAR, vkAI, NC, options=options)
result = HEOM.run(rho0, tlist)
# Define some operators with which we will measure the system
# Define some operators with which we will measure the system
# 1,1 element of density matrix - corresonding to groundstate
P11p=basis(2,0) * basis(2,0).dag()
P22p=basis(2,1) * basis(2,1).dag()
# 1,2 element of density matrix - corresonding to coherence
P12p=basis(2,0) * basis(2,1).dag()
# Calculate expectation values in the bases
P11 = expect(result.states, P11p)
P22 = expect(result.states, P22p)
P12= expect(result.states, P12p)
#DL = " 2*pi* 2.0 * {lam} / (pi * {gamma} * {beta}) if (w==0) else 2*pi*(2.0*{lam}*{gamma} *w /(pi*(w**2+{gamma}**2))) * ((1/(exp((w) * {beta})-1))+1)".format(gamma=gamma, beta = beta, lam = lam)
UD = " 2* {lam}**2 * {gamma} / ( {w0}**4 * {beta}) if (w==0) else 2* ({lam}**2 * {gamma} * w /(({w0}**2 - w**2)**2 + {gamma}**2 * w**2)) * ((1/(exp((w) * {beta})-1))+1)".format(gamma = gamma, beta = beta, lam = lam, w0 = w0)
optionsODE = Options(nsteps=15000, store_states=True,rtol=1e-12,atol=1e-12)
outputBR = brmesolve(Hsys, rho0, tlist, a_ops=[[sigmaz(),UD]], options = optionsODE)
# Calculate expectation values in the bases
P11BR = expect(outputBR.states, P11p)
P22BR = expect(outputBR.states, P22p)
P12BR = expect(outputBR.states, P12p)
#Prho0BR = expect(outputBR.states,rho0)
#This Thermal state of a reaction coordinate should, at high temperatures and not to broad baths, tell us the steady-state
dot_energy, dot_state = Hsys.eigenstates()
deltaE = dot_energy[1] - dot_energy[0]
gamma2 = gamma
wa = w0 # reaction coordinate frequency
g = lam/sqrt(2*wa)
#nb = (1 / (np.exp(wa/w_th) - 1))
NRC = 10
Hsys_exp = tensor(qeye(NRC), Hsys)
Q_exp = tensor(qeye(NRC), Q)
a = tensor(destroy(NRC), qeye(2))
H0 = wa * a.dag() * a + Hsys_exp
# interaction
H1 = (g * (a.dag() + a) * Q_exp)
H = H0 + H1
#print(H.eigenstates())
energies, states = H.eigenstates()
rhoss = 0*states[0]*states[0].dag()
for kk, energ in enumerate(energies):
rhoss += (states[kk]*states[kk].dag()*exp(-beta*energies[kk]))
rhoss = rhoss/rhoss.norm()
P12RC = tensor(qeye(NRC), basis(2,0) * basis(2,1).dag())
P12RC = expect(rhoss,P12RC)
P11RC = tensor(qeye(NRC), basis(2,0) * basis(2,0).dag())
P11RC = expect(rhoss,P11RC)
matplotlib.rcParams['figure.figsize'] = (7, 5)
matplotlib.rcParams['axes.titlesize'] = 25
matplotlib.rcParams['axes.labelsize'] = 30
matplotlib.rcParams['xtick.labelsize'] = 28
matplotlib.rcParams['ytick.labelsize'] = 28
matplotlib.rcParams['legend.fontsize'] = 28
matplotlib.rcParams['axes.grid'] = False
matplotlib.rcParams['savefig.bbox'] = 'tight'
matplotlib.rcParams['lines.markersize'] = 5
matplotlib.rcParams['font.family'] = 'STIXgeneral'
matplotlib.rcParams['mathtext.fontset'] = 'stix'
matplotlib.rcParams["font.serif"] = "STIX"
matplotlib.rcParams['text.usetex'] = False
# Plot the results
fig, axes = plt.subplots(1, 1, sharex=True, figsize=(12,7))
plt.yticks([P11RC,0.6,1.0],[0.38,0.6,1])
axes.plot(tlist, np.real(P11BR), 'y--', linewidth=3, label="Bloch-Redfield")
axes.plot(tlist, np.real(P11), 'b', linewidth=3, label="Matsubara $N_k=3$")
axes.plot(tlist, [P11RC for t in tlist], color='black', linestyle="-.",linewidth=2, label="Thermal state")
axes.locator_params(axis='y', nbins=6)
axes.locator_params(axis='x', nbins=6)
axes.set_ylabel(r'$\rho_{11}$',fontsize=30)
axes.set_xlabel(r'$t \Delta$',fontsize=30)
axes.locator_params(axis='y', nbins=4)
axes.locator_params(axis='x', nbins=4)
axes.legend(loc=0)
fig.savefig("figures/fig3.pdf")
from qutip.ipynbtools import version_table
version_table()
```
| true |
code
| 0.668204 | null | null | null | null |
|
# Mask R-CNN
This notebook shows how to train a Mask R-CNN object detection and segementation model on a custom coco-style data set.
```
import os
import sys
import random
import math
import re
import time
import numpy as np
import cv2
import matplotlib
import matplotlib.pyplot as plt
sys.path.insert(0, '../libraries')
from mrcnn.config import Config
import mrcnn.utils as utils
import mrcnn.model as modellib
import mrcnn.visualize as visualize
from mrcnn.model import log
import mcoco.coco as coco
import mextra.utils as extra_utils
%matplotlib inline
%config IPCompleter.greedy=True
HOME_DIR = '/home/keras'
DATA_DIR = os.path.join(HOME_DIR, "data/shapes")
WEIGHTS_DIR = os.path.join(HOME_DIR, "data/weights")
MODEL_DIR = os.path.join(DATA_DIR, "logs")
# Local path to trained weights file
COCO_MODEL_PATH = os.path.join(WEIGHTS_DIR, "mask_rcnn_coco.h5")
# Download COCO trained weights from Releases if needed
if not os.path.exists(COCO_MODEL_PATH):
utils.download_trained_weights(COCO_MODEL_PATH)
def get_ax(rows=1, cols=1, size=8):
"""Return a Matplotlib Axes array to be used in
all visualizations in the notebook. Provide a
central point to control graph sizes.
Change the default size attribute to control the size
of rendered images
"""
_, ax = plt.subplots(rows, cols, figsize=(size*cols, size*rows))
return ax
```
# Dataset
Organize the dataset using the following structure:
```
DATA_DIR
│
└───annotations
│ │ instances_<subset><year>.json
│
└───<subset><year>
│ image021.jpeg
│ image022.jpeg
```
```
dataset_train = coco.CocoDataset()
dataset_train.load_coco(DATA_DIR, subset="shapes_train", year="2018")
dataset_train.prepare()
dataset_validate = coco.CocoDataset()
dataset_validate.load_coco(DATA_DIR, subset="shapes_validate", year="2018")
dataset_validate.prepare()
dataset_test = coco.CocoDataset()
dataset_test.load_coco(DATA_DIR, subset="shapes_test", year="2018")
dataset_test.prepare()
# Load and display random samples
image_ids = np.random.choice(dataset_train.image_ids, 4)
for image_id in image_ids:
image = dataset_train.load_image(image_id)
mask, class_ids = dataset_train.load_mask(image_id)
visualize.display_top_masks(image, mask, class_ids, dataset_train.class_names)
```
# Configuration
```
image_size = 64
rpn_anchor_template = (1, 2, 4, 8, 16) # anchor sizes in pixels
rpn_anchor_scales = tuple(i * (image_size // 16) for i in rpn_anchor_template)
class ShapesConfig(Config):
"""Configuration for training on the shapes dataset.
"""
NAME = "shapes"
# Train on 1 GPU and 2 images per GPU. Put multiple images on each
# GPU if the images are small. Batch size is 2 (GPUs * images/GPU).
GPU_COUNT = 1
IMAGES_PER_GPU = 1
# Number of classes (including background)
NUM_CLASSES = 1 + 3 # background + 3 shapes (triangles, circles, and squares)
# Use smaller images for faster training.
IMAGE_MAX_DIM = image_size
IMAGE_MIN_DIM = image_size
# Use smaller anchors because our image and objects are small
RPN_ANCHOR_SCALES = rpn_anchor_scales
# Aim to allow ROI sampling to pick 33% positive ROIs.
TRAIN_ROIS_PER_IMAGE = 32
STEPS_PER_EPOCH = 400
VALIDATION_STEPS = STEPS_PER_EPOCH / 20
config = ShapesConfig()
config.display()
```
# Model
```
model = modellib.MaskRCNN(mode="training", config=config, model_dir=MODEL_DIR)
inititalize_weights_with = "coco" # imagenet, coco, or last
if inititalize_weights_with == "imagenet":
model.load_weights(model.get_imagenet_weights(), by_name=True)
elif inititalize_weights_with == "coco":
model.load_weights(COCO_MODEL_PATH, by_name=True,
exclude=["mrcnn_class_logits", "mrcnn_bbox_fc",
"mrcnn_bbox", "mrcnn_mask"])
elif inititalize_weights_with == "last":
# Load the last model you trained and continue training
model.load_weights(model.find_last()[1], by_name=True)
```
# Training
Training in two stages
## Heads
Only the heads. Here we're freezing all the backbone layers and training only the randomly initialized layers (i.e. the ones that we didn't use pre-trained weights from MS COCO). To train only the head layers, pass layers='heads' to the train() function.
```
model.train(dataset_train, dataset_validate,
learning_rate=config.LEARNING_RATE,
epochs=2,
layers='heads')
```
## Fine-tuning
Fine-tune all layers. Pass layers="all to train all layers.
```
model.train(dataset_train, dataset_validate,
learning_rate=config.LEARNING_RATE / 10,
epochs=3, # starts from the previous epoch, so only 1 additional is trained
layers="all")
```
# Detection
```
class InferenceConfig(ShapesConfig):
GPU_COUNT = 1
IMAGES_PER_GPU = 1
inference_config = InferenceConfig()
# Recreate the model in inference mode
model = modellib.MaskRCNN(mode="inference",
config=inference_config,
model_dir=MODEL_DIR)
# Get path to saved weights
# Either set a specific path or find last trained weights
# model_path = os.path.join(ROOT_DIR, ".h5 file name here")
print(model.find_last()[1])
model_path = model.find_last()[1]
# Load trained weights (fill in path to trained weights here)
assert model_path != "", "Provide path to trained weights"
print("Loading weights from ", model_path)
model.load_weights(model_path, by_name=True)
```
### Test on a random image from the test set
First, show the ground truth of the image, then show detection results.
```
image_id = random.choice(dataset_test.image_ids)
original_image, image_meta, gt_class_id, gt_bbox, gt_mask =\
modellib.load_image_gt(dataset_test, inference_config,
image_id, use_mini_mask=False)
log("original_image", original_image)
log("image_meta", image_meta)
log("gt_class_id", gt_class_id)
log("gt_bbox", gt_bbox)
log("gt_mask", gt_mask)
visualize.display_instances(original_image, gt_bbox, gt_mask, gt_class_id,
dataset_train.class_names, figsize=(8, 8))
results = model.detect([original_image], verbose=1)
r = results[0]
visualize.display_instances(original_image, r['rois'], r['masks'], r['class_ids'],
dataset_test.class_names, r['scores'], ax=get_ax())
```
# Evaluation
Use the test dataset to evaluate the precision of the model on each class.
```
predictions =\
extra_utils.compute_multiple_per_class_precision(model, inference_config, dataset_test,
number_of_images=250, iou_threshold=0.5)
complete_predictions = []
for shape in predictions:
complete_predictions += predictions[shape]
print("{} ({}): {}".format(shape, len(predictions[shape]), np.mean(predictions[shape])))
print("--------")
print("average: {}".format(np.mean(complete_predictions)))
print(model.find_last()[1])
```
## Convert result to COCO
Converting the result back to a COCO-style format for further processing
```
import json
import pylab
import matplotlib.pyplot as plt
from tempfile import NamedTemporaryFile
from pycocotools.coco import COCO
coco_dict = extra_utils.result_to_coco(results[0], dataset_test.class_names,
np.shape(original_image)[0:2], tolerance=0)
with NamedTemporaryFile('w') as jsonfile:
json.dump(coco_dict, jsonfile)
jsonfile.flush()
coco_data = COCO(jsonfile.name)
category_ids = coco_data.getCatIds(catNms=['square', 'circle', 'triangle'])
image_data = coco_data.loadImgs(1)[0]
image = original_image
plt.imshow(image); plt.axis('off')
pylab.rcParams['figure.figsize'] = (8.0, 10.0)
annotation_ids = coco_data.getAnnIds(imgIds=image_data['id'], catIds=category_ids, iscrowd=None)
annotations = coco_data.loadAnns(annotation_ids)
coco_data.showAnns(annotations)
```
| true |
code
| 0.509642 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/mirianfsilva/The-Heat-Diffusion-Equation/blob/master/FiniteDiff_test.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### Implementation of schemes for the Heat Equation:
- Forward Time, Centered Space;
- Backward Time, Centered Space;
- Crank-Nicolson.
\begin{equation}
\partial_{t}u = \partial^2_{x}u , \quad 0 < x < 1, \quad t > 0 \\
\end{equation}
\begin{equation}
\partial_{x}u(0,t) = 0, \quad \partial_x{u}(1,t) = 0\\
\end{equation}
\begin{equation}
u(x, 0) = cos(\pi x)
\end{equation}
### Exact Solution:
\begin{equation}
u(x,t) = e^{-\pi^2t}cos(\pi x)
\end{equation}
```
#Numerical Differential Equations - Federal University of Minas Gerais
""" Utils """
import math, sys
import numpy as np
import sympy as sp
from scipy import sparse
from sympy import fourier_series, pi
from scipy.fftpack import *
from scipy.sparse import diags
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
from os import path
count = 0
#Heat Diffusion in one dimensional wire within the Explicit Method
"""
λ = 2, λ = 1/2 e λ = 1/6
M = 4, M = 8, M = 10, M = 12 e M = 14
"""
#Heat function exact solution
def Solution(x, t):
return np.exp((-np.pi**2)*t)*np.cos(np.pi*x)
# ---- Surface plot ----
def surfaceplot(U, Uexact, tspan, xspan, M):
N = M**2
#meshgrid : Return coordinate matrices from coordinate vectors
X, T = np.meshgrid(tspan, xspan)
fig = plt.figure(figsize=plt.figaspect(0.3))
#fig2 = plt.figure(figsize=plt.figaspect(0.5))
#fig3 = plt.figure(figsize=plt.figaspect(0.5))
# ---- Exact Solution ----
ax = fig.add_subplot(1, 4, 1,projection='3d')
surf = ax.plot_surface(X, T, Uexact, linewidth=0, cmap=cm.jet, antialiased=True)
ax.set_title('Exact Solution')
ax.set_xlabel('Time')
ax.set_ylabel('Space')
ax.set_zlabel('U')
# ---- Method Aproximation Solution ----
ax1 = fig.add_subplot(1, 4, 2,projection='3d')
surf = ax1.plot_surface(X, T, U, linewidth=0, cmap=cm.jet, antialiased=True)
ax1.set_title('Approximation')
ax1.set_xlabel('Time')
ax1.set_ylabel('Space')
ax1.set_zlabel('U')
plt.tight_layout()
ax.view_init(30,230)
ax1.view_init(30,230)
fig.savefig(path.join("plot_METHOD{0}.png".format(count)),dpi=600)
plt.draw()
'''
Exact Solution for 1D reaction-diffusion equation:
u_t = k * u_xx
with Neumann boundary conditions
at x=0: u_x(0,t) = 0
at x=L: u_x(L,t) = 0
with L = 1 and initial conditions:
u(x,0) = np.cos(np.pi*x)
'''
def ExactSolution(M, T = 0.5, L = 1):
N = (M**2) #GRID POINTS on time interval
xspan = np.linspace(0, L, M)
tspan = np.linspace(0, T, N)
Uexact = np.zeros((M, N))
for i in range(0, M):
for j in range(0, N):
Uexact[i][j] = Solution(xspan[i], tspan[j])
return (Uexact, tspan, xspan)
'''
Forward method to solve 1D reaction-diffusion equation:
u_t = k * u_xx
with Neumann boundary conditions
at x=0: u_x(0,t) = 0 = sin(2*np.pi)
at x=L: u_x(L,t) = 0 = sin(2*np.pi)
with L = 1 and initial conditions:
u(x,0) = (1.0/2.0)+ np.cos(2.0*np.pi*x) - (1.0/2.0)*np.cos(3*np.pi*x)
u_x(x,t) = (-4.0*(np.pi**2))np.exp(-4.0*(np.pi**2)*t)*np.cos(2.0*np.pi*x) +
(9.0/2.0)*(np.pi**2)*np.exp(-9.0*(np.pi**2)*t)*np.cos(3*np.pi*x))
'''
def ForwardEuler(M, lambd, T = 0.5, L = 1, k = 1):
#Parameters needed to solve the equation within the explicit method
#M = GRID POINTS on space interval
N = (M**2) #GRID POINTS on time interval
# ---- Length of the wire in x direction ----
x0, xL = 0, L
# ----- Spatial discretization step -----
dx = (xL - x0)/(M-1)
# ---- Final time ----
t0,tF = 0, T
# ----- Time step -----
dt = (tF - t0)/(N-1)
#lambd = dt*k/dx**2
# ----- Creates grids -----
xspan = np.linspace(x0, xL, M)
tspan = np.linspace(t0, tF, N)
# ----- Initializes matrix solution U -----
U = np.zeros((M, N))
# ----- Initial condition -----
U[:,0] = np.cos(np.pi*xspan)
# ----- Neumann boundary conditions -----
"""
To implement these boundary conditions, we again use “false points”, x_0 and x_N+1 which are external points.
We use a difference to approximate ∂u/∂x (xL,t) and set it equal to the desired boundary condition:
"""
f = np.arange(1, N+1)
f = (-3*U[0,:] + 4*U[1,:] - U[2,:])/2*dx
U[0,:] = (4*U[1,:] - U[2,:])/3
g = np.arange(1, N+1)
g = (-3*U[-1,:] + 4*U[-2,:] - U[-3,:])/2*dx
U[-1,:] = (4*U[-2,:] - U[-3,:])/3
# ----- ftcs -----
for k in range(0, N-1):
for i in range(1, M-1):
U[i, k+1] = lambd*U[i-1, k] + (1-2*lambd)*U[i,k] + lambd*U[i+1,k]
return (U, tspan, xspan)
U, tspan, xspan = ForwardEuler(M = 14, lambd = 1.0/6.0)
Uexact, x, t = ExactSolution(M = 14)
surfaceplot(U, Uexact, tspan, xspan, M = 14)
'''
Backward method to solve 1D reaction-diffusion equation:
u_t = k * u_xx
with Neumann boundary conditions
at x=0: u_x(0,t) = 0 = sin(2*np.pi)
at x=L: u_x(L,t) = 0 = sin(2*np.pi)
with L = 1 and initial conditions:
u(x,0) = (1.0/2.0)+ np.cos(2.0*np.pi*x) - (1.0/2.0)*np.cos(3*np.pi*x)
u_x(x,t) = (-4.0*(np.pi**2))np.exp(-4.0*(np.pi**2)*t)*np.cos(2.0*np.pi*x) +
(9.0/2.0)*(np.pi**2)*np.exp(-9.0*(np.pi**2)*t)*np.cos(3*np.pi*x))
'''
def BackwardEuler(M, lambd, T = 0.5, L = 1, k = 1):
#Parameters needed to solve the equation within the explicit method
# M = GRID POINTS on space interval
N = (M**2) #GRID POINTS on time interval
# ---- Length of the wire in x direction ----
x0, xL = 0, L
# ----- Spatial discretization step -----
dx = (xL - x0)/(M-1)
# ---- Final time ----
t0, tF = 0, T
# ----- Time step -----
dt = (tF - t0)/(N-1)
# k = 1.0 Diffusion coefficient
#lambd = dt*k/dx**2
a = 1 + 2*lambd
xspan = np.linspace(x0, xL, M)
tspan = np.linspace(t0, tF, N)
main_diag = (1 + 2*lambd)*np.ones((1,M))
off_diag = -lambd*np.ones((1, M-1))
a = main_diag.shape[1]
diagonals = [main_diag, off_diag, off_diag]
#Sparse Matrix diagonals
A = sparse.diags(diagonals, [0,-1,1], shape=(a,a)).toarray()
A[0,1] = -2*lambd
A[M-1,M-2] = -2*lambd
# --- Initializes matrix U -----
U = np.zeros((M, N))
# --- Initial condition -----
U[:,0] = np.cos(np.pi*xspan)
# ---- Neumann boundary conditions -----
f = np.arange(1, N+1) #LeftBC
#(-3*U[i,j] + 4*U[i-1,j] - U[i-2,j])/2*dx = 0
f = U[0,:] = (4*U[1,:] - U[2,:])/3
g = np.arange(1, N+1) #RightBC
#(-3*U[N,j] + 4*U[N-1,j] - U[N-2,j])/2*dx = 0
g = U[-1,:] = (4*U[-2,:] - U[-3,:])/3
for i in range(1, N):
c = np.zeros((M-2,1)).ravel()
b1 = np.asarray([2*lambd*dx*f[i], 2*lambd*dx*g[i]])
b1 = np.insert(b1, 1, c)
b2 = np.array(U[0:M, i-1])
b = b1 + b2 # Right hand side
U[0:M, i] = np.linalg.solve(A,b) # Solve x=A\b
return (U, tspan, xspan)
U, tspan, xspan = BackwardEuler(M = 14, lambd = 1.0/6.0)
Uexact, x, t = ExactSolution(M = 14)
surfaceplot(U, Uexact, tspan, xspan, M = 14)
'''
Crank-Nicolson method to solve 1D reaction-diffusion equation:
u_t = D * u_xx
with Neumann boundary conditions
at x=0: u_x = sin(2*pi)
at x=L: u_x = sin(2*pi)
with L=1 and initial condition:
u(x,0) = u(x,0) = (1.0/2.0)+ np.cos(2.0*np.pi*x) - (1.0/2.0)*np.cos(3*np.pi*x)
'''
def CrankNicolson(M, lambd, T = 0.5, L = 1, k = 1):
#Parameters needed to solve the equation within the explicit method
# M = GRID POINTS on space interval
N = (M**2) #GRID POINTS on time interval
# ---- Length of the wire in x direction ----
x0, xL = 0, L
# ----- Spatial discretization step -----
dx = (xL - x0)/(M-1)
# ---- Final time ----
t0, tF = 0, T
# ----- Time step -----
dt = (tF - t0)/(N-1)
#lambd = dt*k/(2.0*dx**2)
a0 = 1 + 2*lambd
c0 = 1 - 2*lambd
xspan = np.linspace(x0, xL, M)
tspan = np.linspace(t0, tF, N)
maindiag_a0 = a0*np.ones((1,M))
offdiag_a0 = (-lambd)*np.ones((1, M-1))
maindiag_c0 = c0*np.ones((1,M))
offdiag_c0 = lambd*np.ones((1, M-1))
#Left-hand side tri-diagonal matrix
a = maindiag_a0.shape[1]
diagonalsA = [maindiag_a0, offdiag_a0, offdiag_a0]
A = sparse.diags(diagonalsA, [0,-1,1], shape=(a,a)).toarray()
A[0,1] = (-2)*lambd
A[M-1,M-2] = (-2)*lambd
#Right-hand side tri-diagonal matrix
c = maindiag_c0.shape[1]
diagonalsC = [maindiag_c0, offdiag_c0, offdiag_c0]
Arhs = sparse.diags(diagonalsC, [0,-1,1], shape=(c,c)).toarray()
Arhs[0,1] = 2*lambd
Arhs[M-1,M-2] = 2*lambd
# ----- Initializes matrix U -----
U = np.zeros((M, N))
#----- Initial condition -----
U[:,0] = np.cos(np.pi*xspan)
#----- Neumann boundary conditions -----
#Add one line above and one line below using finit differences
f = np.arange(1, N+1) #LeftBC
#(-3*U[i,j] + 4*U[i-1,j] - U[i-2,j])/2*dx = 0
f = U[0,:] = (4*U[1,:] - U[2,:])/3
g = np.arange(1, N+1) #RightBC
#(-3*U[N,j] + 4*U[N-1,j] - U[N-2,j])/2*dx = 0
g = U[-1,:] = (4*U[-2,:] - U[-3,:])/3
for k in range(1, N):
ins = np.zeros((M-2,1)).ravel()
b1 = np.asarray([4*lambd*dx*f[k], 4*lambd*dx*g[k]])
b1 = np.insert(b1, 1, ins)
b2 = np.matmul(Arhs, np.array(U[0:M, k-1]))
b = b1 + b2 # Right hand side
U[0:M, k] = np.linalg.solve(A,b) # Solve x=A\b
return (U, tspan, xspan)
U, tspan, xspan = CrankNicolson(M = 14, lambd = 1.0/6.0)
Uexact, x, t = ExactSolution(M = 14)
surfaceplot(U, Uexact, tspan, xspan, M = 14)
```
| true |
code
| 0.795698 | null | null | null | null |
|
# PyStan: Golf case study
Source: https://mc-stan.org/users/documentation/case-studies/golf.html
```
import pystan
import numpy as np
import pandas as pd
from scipy.stats import norm
import requests
from lxml import html
from io import StringIO
from matplotlib import pyplot as plt
```
Aux functions for visualization
```
def stanplot_postetior_hist(stan_sample, params):
'''This function takes a PyStan posterior sample object and a touple of parameter names, and plots posterior dist histogram of named parameter'''
post_sample_params = {}
for p in params:
post_sample_params[p] = stan_sample.extract(p)[p]
fig, panes = plt.subplots(1,len(params))
fig.suptitle('Posterior Dist of Params')
for p,w in zip(params, panes):
w.hist(post_sample_params[p])
w.set_title(p)
fig.show()
def stanplot_posterior_lineplot(x, y, stan_sample, params, f, sample_size=100, alpha=0.05, color='green'):
'''Posterior dist line plot
params:
x: x-axis values from actual data used for training
y: y-axis values from actual data used for training
stan_sample: a fitted PyStan sample object
params: list of parameter names required for calculating the posterior curve
f: a function the describes the model. Should take as parameters `x` and `*params` as inputs and return a list (or list-coercable object) that will be used for plotting the sampled curves
sample_size: how many curves to draw from the posterior dist
alpha: transparency of drawn curves (from pyplot, default=0.05)
color: color of drawn curves (from pyplot. default='green')
'''
tmp = stan_sample.stan_args
total_samples = (tmp[0]['iter'] - tmp[0]['warmup']) * len(tmp)
sample_rows = np.random.choice(a=total_samples, size=sample_size, replace=False)
sampled_param_array = np.array(list(stan_sample.extract(params).values()))[:, sample_rows]
_ = plt.plot(x, y)
for param_touple in zip(*sampled_param_array):
plt.plot(x, f(x, *param_touple), color=color, alpha=alpha)
def sigmoid_linear_curve(x, a, b):
return 1 / (1 + np.exp(-1 * (a + b * x)))
def trig_curve(x, sigma, r=(1.68/2)/12, R=(4.25/2)/12):
return 2 * norm.cdf(np.arcsin((R - r) / x) / sigma) - 1
def overshot_curve(x, sigma_distance, sigma_angle, r=(1.68/2)/12, R=(4.25/2)/12, overshot=1., distance_tolerance=3.):
p_angle = 2 * norm.cdf(np.arcsin((R - r) / x) / sigma_angle) - 1
p_upper = norm.cdf((distance_tolerance - overshot) / ((x + overshot) * sigma_distance))
p_lower = norm.cdf((-1 * overshot) / ((x + overshot) * sigma_distance))
return p_angle * (p_upper - p_lower)
```
## Data
Scrape webpage
```
url = 'https://statmodeling.stat.columbia.edu/2019/03/21/new-golf-putting-data-and-a-new-golf-putting-model'
xpath = '/html/body/div/div[3]/div/div[1]/div[3]/div[2]/pre[1]'
header = {'User-Agent': 'Mozilla/5.0 (Macintosh; Intel Mac OS X 10_10_1) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/39.0.2171.95 Safari/537.36'}
r = requests.get(url, headers=header)
```
Parse HTML to string
```
html_table = html.fromstring(r.text).xpath(xpath)[0]
```
Rease data into a Pandas DF
```
with StringIO(html_table.text) as f:
df = pd.read_csv(f, sep = ' ')
df.head()
```
And finally add some columns
```
df['p'] = df['y'] / df['n']
df['sd'] = np.sqrt(df['p'] * (1 - df['p']) / df['n'])
stan_data = {'x': df['x'], 'y': df['y'], 'n': df['n'], 'N': df.shape[0]}
```
### Plot data
```
#_ = df.plot(x='x', y='p')
plt.plot(df['x'], df['p'])
plt.fill_between(x=df['x'], y1=df['p'] - 2 * df['sd'], y2=df['p'] + 2 * df['sd'], alpha=0.3)
plt.show()
```
## Models
### Logistic model
```
stan_logistic = pystan.StanModel(file='./logistic.stan')
post_sample_logistic = stan_logistic.sampling(data=stan_data)
print(post_sample_logistic)
stanplot_postetior_hist(post_sample_logistic, ('a', 'b'))
stanplot_posterior_lineplot(df['x'], df['p'], post_sample_logistic, ('a', 'b'), sigmoid_linear_curve)
```
### Simple triginometric model
```
stan_trig = pystan.StanModel(file='./trig.stan')
stan_data.update({'r': (1.68/2)/12, 'R': (4.25/2)/12})
post_sample_trig = stan_trig.sampling(data=stan_data)
print(post_sample_trig)
stanplot_postetior_hist(post_sample_trig, ('sigma', 'sigma_degrees'))
stanplot_posterior_lineplot(df['x'], df['p'], post_sample_trig, ('sigma'), trig_curve)
```
### Augmented trigonometric model
```
stan_overshot = pystan.StanModel(file='./trig_overshot.stan')
stan_data.update({'overshot': 1., 'distance_tolerance': 3.})
post_sample_overshot = stan_overshot.sampling(data=stan_data)
print(post_sample_overshot)
stanplot_postetior_hist(post_sample_overshot, ('sigma_distance', 'sigma_angle', 'sigma_y'))
stanplot_posterior_lineplot(
x=df['x'],
y=df['p'],
stan_sample=post_sample_overshot,
params=('sigma_distance', 'sigma_angle'),
f=overshot_curve
)
```
| true |
code
| 0.76986 | null | null | null | null |
|
## Stacking
### 參考資料:
[Kaggle ensembling guide](https://mlwave.com/kaggle-ensembling-guide/)
<p></p>
[Introduction to Ensembling/Stacking in Python](https://www.kaggle.com/arthurtok/introduction-to-ensembling-stacking-in-python)
#### 5-fold stacking
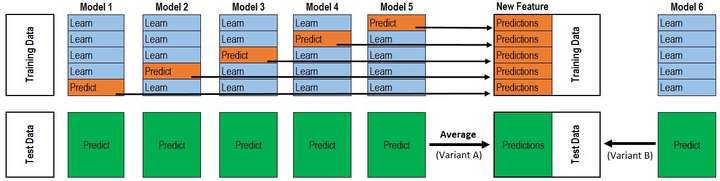
#### stacking network

```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
# Scikit-Learn 官網作圖函式
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure(figsize=(10,6)) #調整作圖大小
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
# Class to extend the Sklearn classifier
class SklearnHelper(object):
def __init__(self, clf, seed=0, params=None, seed_flag=False):
params['random_state'] = seed
if(seed_flag == False):
params.pop('random_state')
self.clf = clf(**params)
def train(self, x_train, y_train):
self.clf.fit(x_train, y_train)
def predict(self, x):
return self.clf.predict(x)
def fit(self,x,y):
return self.clf.fit(x,y)
def feature_importances(self,x,y):
print(self.clf.fit(x,y).feature_importances_)
return self.clf.fit(x,y).feature_importances_
#Out-of-Fold Predictions
def get_oof(clf, x_train, y_train, x_test):
oof_train = np.zeros((ntrain,))
oof_test = np.zeros((ntest,))
oof_test_skf = np.empty((NFOLDS, ntest))
for i, (train_index, test_index) in enumerate(kf): # kf:KFold(ntrain, n_folds= NFOLDS,...)
x_tr = x_train[train_index]
y_tr = y_train[train_index]
x_te = x_train[test_index]
clf.train(x_tr, y_tr)
oof_train[test_index] = clf.predict(x_te) # partial index from x_train
oof_test_skf[i, :] = clf.predict(x_test) # Row(n-Fold), Column(predict value)
#oof_test[:] = oof_test_skf.mean(axis=0) #predict value average by column, then output 1-row, ntest columns
#oof_test[:] = pd.DataFrame(oof_test_skf).mode(axis=0)[0]
#oof_test[:] = np.median(oof_test_skf, axis=0)
oof_test[:] = np.mean(oof_test_skf, axis=0)
return oof_train.reshape(-1, 1), oof_test.reshape(-1, 1) #make sure return n-rows, 1-column shape.
```
### Load Dataset
```
train = pd.read_csv('input/train.csv', encoding = "utf-8", dtype = {'type': np.int32})
test = pd.read_csv('input/test.csv', encoding = "utf-8")
#把示範用的 type 4, 資料去除, 以免干擾建模
train = train[train['type']!=4]
from sklearn.model_selection import train_test_split
X = train[['花瓣寬度','花瓣長度','花萼寬度','花萼長度']]
y = train['type']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state=100)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
test_std = sc.transform(test[['花瓣寬度','花瓣長度','花萼寬度','花萼長度']])
```
### Model Build
```
from sklearn.cross_validation import KFold
NFOLDS = 5 # set folds for out-of-fold prediction
SEED = 0 # for reproducibility
ntrain = X_train_std.shape[0] # X.shape[0]
ntest = test_std.shape[0] # test.shape[0]
kf = KFold(ntrain, n_folds= NFOLDS, random_state=SEED)
# Put in our parameters for said classifiers
# Decision Tree
dt_params = {
'criterion':'gini',
'max_depth':5
}
# KNN
knn_params = {
'n_neighbors':5
}
# Random Forest parameters
rf_params = {
'n_jobs': -1,
'n_estimators': 500,
'criterion': 'gini',
'max_depth': 4,
#'min_samples_leaf': 2,
'warm_start': True,
'oob_score': True,
'verbose': 0
}
# Extra Trees Parameters
et_params = {
'n_jobs': -1,
'n_estimators': 800,
'max_depth': 6,
'min_samples_leaf': 2,
'verbose': 0
}
# AdaBoost parameters
ada_params = {
'n_estimators': 800,
'learning_rate' : 0.75
}
# Gradient Boosting parameters
gb_params = {
'n_estimators': 500,
'max_depth': 5,
'min_samples_leaf': 2,
'verbose': 0
}
# Support Vector Classifier parameters
svc_params = {
'kernel' : 'linear',
'C' : 1.0,
'probability': True
}
# Support Vector Classifier parameters
svcr_params = {
'kernel' : 'rbf',
'C' : 1.0,
'probability': True
}
# Bagging Classifier
bag_params = {
'n_estimators' : 500,
'oob_score': True
}
#XGBoost Classifier
xgbc_params = {
'n_estimators': 500,
'max_depth': 4,
'learning_rate': 0.05,
'nthread': -1
}
#Linear Discriminant Analysis
lda_params = {}
#Quadratic Discriminant Analysis
qda1_params = {
'reg_param': 0.8,
'tol': 0.00001
}
#Quadratic Discriminant Analysis
qda2_params = {
'reg_param': 0.6,
'tol': 0.0001
}
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier, ExtraTreesClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from xgboost import XGBClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis, QuadraticDiscriminantAnalysis
dt = SklearnHelper(clf=DecisionTreeClassifier, seed=SEED, params=dt_params, seed_flag=True)
knn = SklearnHelper(clf=KNeighborsClassifier, seed=SEED, params=knn_params)
rf = SklearnHelper(clf=RandomForestClassifier, seed=SEED, params=rf_params, seed_flag=True)
et = SklearnHelper(clf=ExtraTreesClassifier, seed=SEED, params=et_params, seed_flag=True)
ada = SklearnHelper(clf=AdaBoostClassifier, seed=SEED, params=ada_params, seed_flag=True)
gb = SklearnHelper(clf=GradientBoostingClassifier, seed=SEED, params=gb_params, seed_flag=True)
svc = SklearnHelper(clf=SVC, seed=SEED, params=svc_params, seed_flag=True)
svcr = SklearnHelper(clf=SVC, seed=SEED, params=svcr_params, seed_flag=True)
bag = SklearnHelper(clf=BaggingClassifier, seed=SEED, params=bag_params, seed_flag=True)
xgbc = SklearnHelper(clf=XGBClassifier, seed=SEED, params=xgbc_params)
lda = SklearnHelper(clf=LinearDiscriminantAnalysis, seed=SEED, params=lda_params)
qda1 = SklearnHelper(clf=QuadraticDiscriminantAnalysis, seed=SEED, params=qda1_params)
qda2 = SklearnHelper(clf=QuadraticDiscriminantAnalysis, seed=SEED, params=qda2_params)
# Create Numpy arrays of train, test and target ( Survived) dataframes to feed into our models
y_train = y_train.ravel()
#y.ravel()
#x_train = X.values # Creates an array of the train data
#x_test = test.values # Creats an array of the test data
#STD dataset:
x_train = X_train_std
x_test = test_std
# Create our OOF train and test predictions. These base results will be used as new features
dt_oof_train, dt_oof_test = get_oof(dt, x_train, y_train, x_test) # Decision Tree
knn_oof_train, knn_oof_test = get_oof(knn, x_train, y_train, x_test) # KNeighbors
rf_oof_train, rf_oof_test = get_oof(rf, x_train, y_train, x_test) # Random Forest
et_oof_train, et_oof_test = get_oof(et, x_train, y_train, x_test) # Extra Trees
ada_oof_train, ada_oof_test = get_oof(ada, x_train, y_train, x_test) # AdaBoost
gb_oof_train, gb_oof_test = get_oof(gb, x_train, y_train, x_test) # Gradient Boost
svc_oof_train, svc_oof_test = get_oof(svc, x_train, y_train, x_test) # SVM-l
svcr_oof_train, svcr_oof_test = get_oof(svcr, x_train, y_train, x_test) # SVM-r
bag_oof_train, bag_oof_test = get_oof(bag, x_train, y_train, x_test) # Bagging
xgbc_oof_train, xgbc_oof_test = get_oof(xgbc, x_train, y_train, x_test) # XGBoost
lda_oof_train, lda_oof_test = get_oof(lda, x_train, y_train, x_test) # Linear Discriminant Analysis
qda1_oof_train, qda1_oof_test = get_oof(qda1, x_train, y_train, x_test) # Quadratic Discriminant Analysis
qda2_oof_train, qda2_oof_test = get_oof(qda2, x_train, y_train, x_test) # Quadratic Discriminant Analysis
dt_features = dt.feature_importances(x_train,y_train)
##knn_features = knn.feature_importances(x_train,y_train)
rf_features = rf.feature_importances(x_train,y_train)
et_features = et.feature_importances(x_train, y_train)
ada_features = ada.feature_importances(x_train, y_train)
gb_features = gb.feature_importances(x_train,y_train)
##svc_features = svc.feature_importances(x_train,y_train)
##svcr_features = svcr.feature_importances(x_train,y_train)
##bag_features = bag.feature_importances(x_train,y_train)
xgbc_features = xgbc.feature_importances(x_train,y_train)
##lda_features = lda.feature_importances(x_train,y_train)
##qda1_features = qda1.feature_importances(x_train,y_train)
##qda2_features = qda2.feature_importances(x_train,y_train)
cols = X.columns.values
# Create a dataframe with features
feature_dataframe = pd.DataFrame( {'features': cols,
'Decision Tree': dt_features,
'Random Forest': rf_features,
'Extra Trees': et_features,
'AdaBoost': ada_features,
'Gradient Boost': gb_features,
'XGBoost': xgbc_features
})
# Create the new column containing the average of values
feature_dataframe['mean'] = np.mean(feature_dataframe, axis= 1) # axis = 1 computes the mean row-wise
feature_dataframe
```
### First-Level Summary
```
#First-level output as new features
base_predictions_train = pd.DataFrame({
'DecisionTree': dt_oof_train.ravel(),
'KNeighbors': knn_oof_train.ravel(),
'RandomForest': rf_oof_train.ravel(),
'ExtraTrees': et_oof_train.ravel(),
'AdaBoost': ada_oof_train.ravel(),
'GradientBoost': gb_oof_train.ravel(),
'SVM-l': svc_oof_train.ravel(),
'SVM-r': svcr_oof_train.ravel(),
'Bagging': bag_oof_train.ravel(),
'XGBoost': xgbc_oof_train.ravel(),
'LDA': lda_oof_train.ravel(),
'QDA-1': qda1_oof_train.ravel(),
'QDA-2': qda2_oof_train.ravel(),
'type': y_train
})
base_predictions_train.head()
x_train = np.concatenate(( #dt_oof_train,
knn_oof_train,
rf_oof_train,
et_oof_train,
ada_oof_train,
gb_oof_train,
svc_oof_train,
#svcr_oof_train,
bag_oof_train,
xgbc_oof_train,
lda_oof_train,
#qda1_oof_train,
qda2_oof_train
), axis=1)
x_test = np.concatenate(( #dt_oof_test,
knn_oof_test,
rf_oof_test,
et_oof_test,
ada_oof_test,
gb_oof_test,
svc_oof_test,
#svcr_oof_test,
bag_oof_test,
xgbc_oof_test,
lda_oof_test,
#qda1_oof_test,
qda2_oof_test
), axis=1)
```
### Second Level Summary
### Level-2 XGBoost
```
#Second level learning model
import xgboost as xgb
l2_gbm = xgb.XGBClassifier(
learning_rate = 0.05,
n_estimators= 2000,
max_depth= 4,
#min_child_weight= 2,
gamma=0.9,
subsample=0.8,
colsample_bytree=0.8,
#scale_pos_weight=1,
objective= 'binary:logistic',
nthread= -1
).fit(x_train, y_train)
#level-2 CV: x_train, y_train
from sklearn import metrics
print(metrics.classification_report(y_train, l2_gbm.predict(x_train)))
from sklearn.model_selection import KFold
cv = KFold(n_splits=5, random_state=None, shuffle=True)
estimator = l2_gbm
plot_learning_curve(estimator, "level2 - XGBoost", x_train, y_train, cv=cv, train_sizes=np.linspace(0.2, 1.0, 8))
#level2 - XGB
l2_gbm_pred = l2_gbm.predict(x_test)
metrics.precision_recall_fscore_support(y_train, l2_gbm.predict(x_train), average='weighted')
print(l2_gbm_pred)
```
### Level-2 Linear Discriminant Analysis
```
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
l2_lda = LinearDiscriminantAnalysis()
l2_lda.fit(x_train, y_train)
print(metrics.classification_report(y_train, l2_lda.predict(x_train)))
from sklearn.model_selection import KFold
cv = KFold(n_splits=5, random_state=None, shuffle=True)
estimator = l2_lda
#plot_learning_curve(estimator, "lv2 Linear Discriminant Analysis", x_train, y_train, cv=cv, train_sizes=np.linspace(0.2, 1.0, 8))
#level2 - LDA
l2_lda_pred = l2_lda.predict(x_test)
metrics.precision_recall_fscore_support(y_train, l2_lda.predict(x_train), average='weighted')
print(l2_lda_pred)
```
### Level-2 Quadratic Discriminant Analysis
```
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
l2_qda = QuadraticDiscriminantAnalysis(reg_param=0.01, tol=0.001)
l2_qda.fit(x_train, y_train)
print(metrics.classification_report(y_train, l2_qda.predict(x_train)))
from sklearn.model_selection import KFold
cv = KFold(n_splits=5, random_state=None, shuffle=True)
estimator = l2_qda
plot_learning_curve(estimator, "Quadratic Discriminant Analysis", x_train, y_train, cv=cv, train_sizes=np.linspace(0.2, 1.0, 8))
#level2 - QDA
l2_qda_pred = l2_qda.predict(x_test)
metrics.precision_recall_fscore_support(y_train, l2_qda.predict(x_train), average='weighted')
print(l2_qda_pred)
```
| true |
code
| 0.581838 | null | null | null | null |
|
<img align="left" width="40%" src="http://www.lsce.ipsl.fr/Css/img/banniere_LSCE_75.png">
<br>Patrick BROCKMANN - LSCE (Climate and Environment Sciences Laboratory)
<hr>
### Discover Milankovitch Orbital Parameters over Time by reproducing figure from https://biocycle.atmos.colostate.edu/shiny/Milankovitch/
```
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.layouts import gridplot, column
from bokeh.models import CustomJS, Slider, RangeSlider
from bokeh.models import Span
output_notebook()
import ipywidgets as widgets
from ipywidgets import Layout
from ipywidgets import interact
import pandas as pd
import numpy as np
```
### Download files
Data files from http://vo.imcce.fr/insola/earth/online/earth/earth.html
```
! wget -nc http://vo.imcce.fr/insola/earth/online/earth/La2004/INSOLN.LA2004.BTL.100.ASC
! wget -nc http://vo.imcce.fr/insola/earth/online/earth/La2004/INSOLP.LA2004.BTL.ASC
```
### Read files
```
# t Time from J2000 in 1000 years
# e eccentricity
# eps obliquity (radians)
# pibar longitude of perihelion from moving equinox (radians)
df1 = pd.read_csv('INSOLN.LA2004.BTL.250.ASC', delim_whitespace=True, names=['t', 'e', 'eps', 'pibar'])
df1.set_index('t', inplace=True)
df2 = pd.read_csv('INSOLP.LA2004.BTL.ASC', delim_whitespace=True, names=['t', 'e', 'eps', 'pibar'])
df2.set_index('t', inplace=True)
#df = pd.read_csv('La2010a_ecc3.dat', delim_whitespace=True, names=['t', 'e'])
#df = pd.read_csv('La2010a_alkhqp3L.dat', delim_whitespace=True, names=['t','a','l','k','h','q','p'])
# INSOLP.LA2004.BTL.ASC has a FORTRAN DOUBLE notation D instead of E
df2['e'] = df2['e'].str.replace('D','E')
df2['e'] = df2['e'].astype(float)
df2['eps'] = df2['eps'].str.replace('D','E')
df2['eps'] = df2['eps'].astype(float)
df2['pibar'] = df2['pibar'].str.replace('D','E')
df2['pibar'] = df2['pibar'].astype(float)
df2['e'][0]
df = pd.concat([df1[::-1],df2[1:]])
df
# t Time from J2000 in 1000 years
# e eccentricity
# eps obliquity (radians)
# pibar longitude of perihelion from moving equinox (radians)
df['eccentricity'] = df['e']
df['perihelion'] = df['pibar']
df['obliquity'] = 180. * df['eps'] / np.pi
df['precession'] = df['eccentricity'] * np.sin(df['perihelion'])
#latitude <- 65. * pi / 180.
#Q.day <- S0*(1+eccentricity*sin(perihelion+pi))^2 *sin(latitude)*sin(obliquity)
latitude = 65. * np.pi / 180.
df['insolation'] = 1367 * ( 1 + df['eccentricity'] * np.sin(df['perihelion'] + np.pi))**2 * np.sin(latitude) * np.sin(df['eps'])
df
```
### Build plot
```
a = widgets.IntRangeSlider(
layout=Layout(width='600px'),
value=[-2000, 50],
min=-250000,
max=21000,
step=100,
disabled=False,
continuous_update=False,
orientation='horizontal',
description='-249Myr to +21Myr:',
)
def plot1(limits):
years = df[limits[0]:limits[1]].index
zeroSpan = Span(location=0, dimension='height', line_color='black',
line_dash='solid', line_width=1)
p1 = figure(title='Eccentricity', active_scroll="wheel_zoom")
p1.line(years, df[limits[0]:limits[1]]['eccentricity'], color='red')
p1.yaxis.axis_label = "Degrees"
p1.add_layout(zeroSpan)
p2 = figure(title='Obliquity', x_range=p1.x_range)
p2.line(years, df[limits[0]:limits[1]]['obliquity'], color='forestgreen')
p2.yaxis.axis_label = "Degrees"
p2.add_layout(zeroSpan)
p3 = figure(title='Precessional index', x_range=p1.x_range)
p3.line(years, df[limits[0]:limits[1]]['precession'], color='dodgerblue')
p3.yaxis.axis_label = "Degrees"
p3.add_layout(zeroSpan)
p4 = figure(title='Mean Daily Insolation at 65N on Summer Solstice', x_range=p1.x_range)
p4.line(years, df[limits[0]:limits[1]]['insolation'], color='#ffc125')
p4.yaxis.axis_label = "Watts/m2"
p4.add_layout(zeroSpan)
show(gridplot([p1,p2,p3,p4], ncols=1, plot_width=600, plot_height=200))
interact(plot1, limits=a)
# Merged tool of subfigures is not marked as active
# https://github.com/bokeh/bokeh/issues/10659
p1 = figure(title='Eccentricity', active_scroll="wheel_zoom")
years = df[0:2000].index
p1.line(years, df[0:2000]['eccentricity'], color='red')
p2 = figure(title='Obliquity', x_range=p1.x_range)
p2.line(years, df[0:2000]['obliquity'], color='forestgreen')
show(gridplot([p1,p2], ncols=1, plot_width=600, plot_height=200, merge_tools=True))
```
| true |
code
| 0.493531 | null | null | null | null |
|
# Tutorial 5: Inception, ResNet and DenseNet

**Filled notebook:**
[](https://github.com/phlippe/uvadlc_notebooks/blob/master/docs/tutorial_notebooks/tutorial5/Inception_ResNet_DenseNet.ipynb)
[](https://colab.research.google.com/github/phlippe/uvadlc_notebooks/blob/master/docs/tutorial_notebooks/tutorial5/Inception_ResNet_DenseNet.ipynb)
**Pre-trained models:**
[](https://github.com/phlippe/saved_models/tree/main/tutorial5)
[](https://drive.google.com/drive/folders/1zOgLKmYJ2V3uHz57nPUMY6tq15RmEtNg?usp=sharing)
In this tutorial, we will implement and discuss variants of modern CNN architectures. There have been many different architectures been proposed over the past few years. Some of the most impactful ones, and still relevant today, are the following: [GoogleNet](https://arxiv.org/abs/1409.4842)/Inception architecture (winner of ILSVRC 2014), [ResNet](https://arxiv.org/abs/1512.03385) (winner of ILSVRC 2015), and [DenseNet](https://arxiv.org/abs/1608.06993) (best paper award CVPR 2017). All of them were state-of-the-art models when being proposed, and the core ideas of these networks are the foundations for most current state-of-the-art architectures. Thus, it is important to understand these architectures in detail and learn how to implement them.
Let's start with importing our standard libraries here.
```
## Standard libraries
import os
import numpy as np
import random
from PIL import Image
from types import SimpleNamespace
## Imports for plotting
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('svg', 'pdf') # For export
from matplotlib.colors import to_rgb
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2.0
import seaborn as sns
sns.reset_orig()
## PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import torch.optim as optim
# Torchvision
import torchvision
from torchvision.datasets import CIFAR10
from torchvision import transforms
```
We will use the same `set_seed` function as in the previous tutorials, as well as the path variables `DATASET_PATH` and `CHECKPOINT_PATH`. Adjust the paths if necessary.
```
# Path to the folder where the datasets are/should be downloaded (e.g. CIFAR10)
DATASET_PATH = "../data"
# Path to the folder where the pretrained models are saved
CHECKPOINT_PATH = "../saved_models/tutorial5"
# Function for setting the seed
def set_seed(seed):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
set_seed(42)
# Ensure that all operations are deterministic on GPU (if used) for reproducibility
torch.backends.cudnn.determinstic = True
torch.backends.cudnn.benchmark = False
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
```
We also have pretrained models and Tensorboards (more on this later) for this tutorial, and download them below.
```
import urllib.request
from urllib.error import HTTPError
# Github URL where saved models are stored for this tutorial
base_url = "https://raw.githubusercontent.com/phlippe/saved_models/main/tutorial5/"
# Files to download
pretrained_files = ["GoogleNet.ckpt", "ResNet.ckpt", "ResNetPreAct.ckpt", "DenseNet.ckpt",
"tensorboards/GoogleNet/events.out.tfevents.googlenet",
"tensorboards/ResNet/events.out.tfevents.resnet",
"tensorboards/ResNetPreAct/events.out.tfevents.resnetpreact",
"tensorboards/DenseNet/events.out.tfevents.densenet"]
# Create checkpoint path if it doesn't exist yet
os.makedirs(CHECKPOINT_PATH, exist_ok=True)
# For each file, check whether it already exists. If not, try downloading it.
for file_name in pretrained_files:
file_path = os.path.join(CHECKPOINT_PATH, file_name)
if "/" in file_name:
os.makedirs(file_path.rsplit("/",1)[0], exist_ok=True)
if not os.path.isfile(file_path):
file_url = base_url + file_name
print("Downloading %s..." % file_url)
try:
urllib.request.urlretrieve(file_url, file_path)
except HTTPError as e:
print("Something went wrong. Please try to download the file from the GDrive folder, or contact the author with the full output including the following error:\n", e)
```
Throughout this tutorial, we will train and evaluate the models on the CIFAR10 dataset. This allows you to compare the results obtained here with the model you have implemented in the first assignment. As we have learned from the previous tutorial about initialization, it is important to have the data preprocessed with a zero mean. Therefore, as a first step, we will calculate the mean and standard deviation of the CIFAR dataset:
```
train_dataset = CIFAR10(root=DATASET_PATH, train=True, download=True)
DATA_MEANS = (train_dataset.data / 255.0).mean(axis=(0,1,2))
DATA_STD = (train_dataset.data / 255.0).std(axis=(0,1,2))
print("Data mean", DATA_MEANS)
print("Data std", DATA_STD)
```
We will use this information to define a `transforms.Normalize` module which will normalize our data accordingly. Additionally, we will use data augmentation during training. This reduces the risk of overfitting and helps CNNs to generalize better. Specifically, we will apply two random augmentations.
First, we will flip each image horizontally by a chance of 50% (`transforms.RandomHorizontalFlip`). The object class usually does not change when flipping an image, and we don't expect any image information to be dependent on the horizontal orientation. This would be however different if we would try to detect digits or letters in an image, as those have a certain orientation.
The second augmentation we use is called `transforms.RandomResizedCrop`. This transformation scales the image in a small range, while eventually changing the aspect ratio, and crops it afterward in the previous size. Therefore, the actual pixel values change while the content or overall semantics of the image stays the same.
We will randomly split the training dataset into a training and a validation set. The validation set will be used for determining early stopping. After finishing the training, we test the models on the CIFAR test set.
```
test_transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize(DATA_MEANS, DATA_STD)
])
# For training, we add some augmentation. Networks are too powerful and would overfit.
train_transform = transforms.Compose([transforms.RandomHorizontalFlip(),
transforms.RandomResizedCrop((32,32),scale=(0.8,1.0),ratio=(0.9,1.1)),
transforms.ToTensor(),
transforms.Normalize(DATA_MEANS, DATA_STD)
])
# Loading the training dataset. We need to split it into a training and validation part
# We need to do a little trick because the validation set should not use the augmentation.
train_dataset = CIFAR10(root=DATASET_PATH, train=True, transform=train_transform, download=True)
val_dataset = CIFAR10(root=DATASET_PATH, train=True, transform=test_transform, download=True)
set_seed(42)
train_set, _ = torch.utils.data.random_split(train_dataset, [45000, 5000])
set_seed(42)
_, val_set = torch.utils.data.random_split(val_dataset, [45000, 5000])
# Loading the test set
test_set = CIFAR10(root=DATASET_PATH, train=False, transform=test_transform, download=True)
# We define a set of data loaders that we can use for various purposes later.
train_loader = data.DataLoader(train_set, batch_size=128, shuffle=True, drop_last=True, pin_memory=True, num_workers=4)
val_loader = data.DataLoader(val_set, batch_size=128, shuffle=False, drop_last=False, num_workers=4)
test_loader = data.DataLoader(test_set, batch_size=128, shuffle=False, drop_last=False, num_workers=4)
```
To verify that our normalization works, we can print out the mean and standard deviation of the single batch. The mean should be close to 0 and the standard deviation close to 1 for each channel:
```
imgs, _ = next(iter(train_loader))
print("Batch mean", imgs.mean(dim=[0,2,3]))
print("Batch std", imgs.std(dim=[0,2,3]))
```
Finally, let's visualize a few images from the training set, and how they look like after random data augmentation:
```
NUM_IMAGES = 4
images = [train_dataset[idx][0] for idx in range(NUM_IMAGES)]
orig_images = [Image.fromarray(train_dataset.data[idx]) for idx in range(NUM_IMAGES)]
orig_images = [test_transform(img) for img in orig_images]
img_grid = torchvision.utils.make_grid(torch.stack(images + orig_images, dim=0), nrow=4, normalize=True, pad_value=0.5)
img_grid = img_grid.permute(1, 2, 0)
plt.figure(figsize=(8,8))
plt.title("Augmentation examples on CIFAR10")
plt.imshow(img_grid)
plt.axis('off')
plt.show()
plt.close()
```
## PyTorch Lightning
In this notebook and in many following ones, we will make use of the library [PyTorch Lightning](https://www.pytorchlightning.ai/). PyTorch Lightning is a framework that simplifies your code needed to train, evaluate, and test a model in PyTorch. It also handles logging into [TensorBoard](https://pytorch.org/tutorials/intermediate/tensorboard_tutorial.html), a visualization toolkit for ML experiments, and saving model checkpoints automatically with minimal code overhead from our side. This is extremely helpful for us as we want to focus on implementing different model architectures and spend little time on other code overhead. Note that at the time of writing/teaching, the framework has been released in version 1.0. Future versions might have a slightly changed interface and thus might not work perfectly with the code (we will try to keep it up-to-date as much as possible).
Now, we will take the first step in PyTorch Lightning, and continue to explore the framework in our other tutorials. First, we import the library:
```
# PyTorch Lightning
try:
import pytorch_lightning as pl
except ModuleNotFoundError: # Google Colab does not have PyTorch Lightning installed by default. Hence, we do it here if necessary
!pip install pytorch-lightning==1.0.3
import pytorch_lightning as pl
```
PyTorch Lightning comes with a lot of useful functions, such as one for setting the seed:
```
# Setting the seed
pl.seed_everything(42)
```
Thus, in the future, we don't have to define our own `set_seed` function anymore.
In PyTorch Lightning, we define `pl.LightningModule`'s (inheriting from `torch.nn.Module`) that organize our code into 5 main sections:
1. Initialization (`__init__`), where we create all necessary parameters/models
2. Optimizers (`configure_optimizers`) where we create the optimizers, learning rate scheduler, etc.
3. Training loop (`training_step`) where we only have to define the loss calculation for a single batch (the loop of optimizer.zero_grad(), loss.backward() and optimizer.step(), as well as any logging/saving operation, is done in the background)
4. Validation loop (`validation_step`) where similarly to the training, we only have to define what should happen per step
5. Test loop (`test_step`) which is the same as validation, only on a test set.
Therefore, we don't abstract the PyTorch code, but rather organize it and define some default operations that are commonly used. If you need to change something else in your training/validation/test loop, there are many possible functions you can overwrite (see the [docs](https://pytorch-lightning.readthedocs.io/en/stable/lightning_module.html) for details).
Now we can look at an example of how a Lightning Module for training a CNN looks like:
```
class CIFARTrainer(pl.LightningModule):
def __init__(self, model_name, model_hparams, optimizer_name, optimizer_hparams):
"""
Inputs:
model_name - Name of the model/CNN to run. Used for creating the model (see function below)
model_hparams - Hyperparameters for the model, as dictionary.
optimizer_name - Name of the optimizer to use. Currently supported: Adam, SGD
optimizer_hparams - Hyperparameters for the optimizer, as dictionary. This includes learning rate, weight decay, etc.
"""
super().__init__()
# Exports the hyperparameters to a YAML file, and create "self.hparams" namespace
self.save_hyperparameters()
# Create model
self.model = create_model(model_name, model_hparams)
# Create loss module
self.loss_module = nn.CrossEntropyLoss()
# Example input for visualizing the graph in Tensorboard
self.example_input_array = torch.zeros((1, 3, 32, 32), dtype=torch.float32)
def forward(self, imgs):
# Forward function that is run when visualizing the graph
return self.model(imgs)
def configure_optimizers(self):
# We will support Adam or SGD as optimizers.
if self.hparams.optimizer_name == "Adam":
# AdamW is Adam with a correct implementation of weight decay (see here for details: https://arxiv.org/pdf/1711.05101.pdf)
optimizer = optim.AdamW(self.parameters(), **self.hparams.optimizer_hparams)
elif self.hparams.optimizer_name == "SGD":
optimizer = optim.SGD(self.parameters(), **self.hparams.optimizer_hparams)
else:
assert False, "Unknown optimizer: \"%s\"" % self.hparams.optimizer_name
# We will reduce the learning rate by 0.1 after 100 and 150 epochs
scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[100,150], gamma=0.1)
return [optimizer], [scheduler]
def training_step(self, batch, batch_idx):
# "batch" is the output of the training data loader.
imgs, labels = batch
preds = self.model(imgs)
loss = self.loss_module(preds, labels)
acc = (preds.argmax(dim=-1) == labels).float().mean()
self.log('train_acc', acc, on_step=False, on_epoch=True) # Logs the accuracy per epoch to tensorboard (weighted average over batches)
self.log('train_loss', loss)
return loss # Return tensor to call ".backward" on
def validation_step(self, batch, batch_idx):
imgs, labels = batch
preds = self.model(imgs).argmax(dim=-1)
acc = (labels == preds).float().mean()
self.log('val_acc', acc) # By default logs it per epoch (weighted average over batches)
def test_step(self, batch, batch_idx):
imgs, labels = batch
preds = self.model(imgs).argmax(dim=-1)
acc = (labels == preds).float().mean()
self.log('test_acc', acc) # By default logs it per epoch (weighted average over batches), and returns it afterwards
```
We see that the code is organized and clear, which helps if someone else tries to understand your code.
Another important part of PyTorch Lightning is the concept of callbacks. Callbacks are self-contained functions that contain the non-essential logic of your Lightning Module. They are usually called after finishing a training epoch, but can also influence other parts of your training loop. For instance, we will use the following two pre-defined callbacks: `LearningRateMonitor` and `ModelCheckpoint`. The learning rate monitor adds the current learning rate to our TensorBoard, which helps to verify that our learning rate scheduler works correctly. The model checkpoint callback allows you to customize the saving routine of your checkpoints. For instance, how many checkpoints to keep, when to save, which metric to look out for, etc. We import them below:
```
# Callbacks
from pytorch_lightning.callbacks import LearningRateMonitor, ModelCheckpoint
```
To allow running multiple different models with the same Lightning module, we define a function below that maps a model name to the model class. At this stage, the dictionary `model_dict` is empty, but we will fill it throughout the notebook with our new models.
```
model_dict = {}
def create_model(model_name, model_hparams):
if model_name in model_dict:
return model_dict[model_name](**model_hparams)
else:
assert False, "Unknown model name \"%s\". Available models are: %s" % (model_name, str(model_dict.keys()))
```
Similarly, to use the activation function as another hyperparameter in our model, we define a "name to function" dict below:
```
act_fn_by_name = {
"tanh": nn.Tanh,
"relu": nn.ReLU,
"leakyrelu": nn.LeakyReLU,
"gelu": nn.GELU
}
```
If we pass the classes or objects directly as an argument to the Lightning module, we couldn't take advantage of PyTorch Lightning's automatically hyperparameter saving and loading.
Besides the Lightning module, the second most important module in PyTorch Lightning is the `Trainer`. The trainer is responsible to execute the training steps defined in the Lightning module and completes the framework. Similar to the Lightning module, you can override any key part that you don't want to be automated, but the default settings are often the best practice to do. For a full overview, see the [documentation](https://pytorch-lightning.readthedocs.io/en/stable/trainer.html). The most important functions we use below are:
* `trainer.fit`: Takes as input a lightning module, a training dataset, and an (optional) validation dataset. This function trains the given module on the training dataset with occasional validation (default once per epoch, can be changed)
* `trainer.test`: Takes as input a model and a dataset on which we want to test. It returns the test metric on the dataset.
For training and testing, we don't have to worry about things like setting the model to eval mode (`model.eval()`) as this is all done automatically. See below how we define a training function for our models:
```
def train_model(model_name, save_name=None, **kwargs):
"""
Inputs:
model_name - Name of the model you want to run. Is used to look up the class in "model_dict"
save_name (optional) - If specified, this name will be used for creating the checkpoint and logging directory.
"""
if save_name is None:
save_name = model_name
# Create a PyTorch Lightning trainer with the generation callback
trainer = pl.Trainer(default_root_dir=os.path.join(CHECKPOINT_PATH, save_name), # Where to save models
checkpoint_callback=ModelCheckpoint(save_weights_only=True, mode="max", monitor="val_acc"), # Save the best checkpoint based on the maximum val_acc recorded. Saves only weights and not optimizer
gpus=1 if str(device)=="cuda:0" else 0, # We run on a single GPU (if possible)
max_epochs=180, # How many epochs to train for if no patience is set
callbacks=[LearningRateMonitor("epoch")], # Log learning rate every epoch
progress_bar_refresh_rate=1) # In case your notebook crashes due to the progress bar, consider increasing the refresh rate
trainer.logger._log_graph = True # If True, we plot the computation graph in tensorboard
trainer.logger._default_hp_metric = None # Optional logging argument that we don't need
# Check whether pretrained model exists. If yes, load it and skip training
pretrained_filename = os.path.join(CHECKPOINT_PATH, save_name + ".ckpt")
if os.path.isfile(pretrained_filename):
print("Found pretrained model at %s, loading..." % pretrained_filename)
model = CIFARTrainer.load_from_checkpoint(pretrained_filename) # Automatically loads the model with the saved hyperparameters
else:
pl.seed_everything(42) # To be reproducable
model = CIFARTrainer(model_name=model_name, **kwargs)
trainer.fit(model, train_loader, val_loader)
model = CIFARTrainer.load_from_checkpoint(trainer.checkpoint_callback.best_model_path) # Load best checkpoint after training
# Test best model on validation and test set
val_result = trainer.test(model, test_dataloaders=val_loader, verbose=False)
test_result = trainer.test(model, test_dataloaders=test_loader, verbose=False)
result = {"test": test_result[0]["test_acc"], "val": val_result[0]["test_acc"]}
return model, result
```
Finally, we can focus on the Convolutional Neural Networks we want to implement today: GoogleNet, ResNet, and DenseNet.
## Inception
The [GoogleNet](https://arxiv.org/abs/1409.4842), proposed in 2014, won the ImageNet Challenge because of its usage of the Inception modules. In general, we will mainly focus on the concept of Inception in this tutorial instead of the specifics of the GoogleNet, as based on Inception, there have been many follow-up works ([Inception-v2](https://arxiv.org/abs/1512.00567), [Inception-v3](https://arxiv.org/abs/1512.00567), [Inception-v4](https://arxiv.org/abs/1602.07261), [Inception-ResNet](https://arxiv.org/abs/1602.07261),...). The follow-up works mainly focus on increasing efficiency and enabling very deep Inception networks. However, for a fundamental understanding, it is sufficient to look at the original Inception block.
An Inception block applies four convolution blocks separately on the same feature map: a 1x1, 3x3, and 5x5 convolution, and a max pool operation. This allows the network to look at the same data with different receptive fields. Of course, learning only 5x5 convolution would be theoretically more powerful. However, this is not only more computation and memory heavy but also tends to overfit much easier. The overall inception block looks like below (figure credit - [Szegedy et al.](https://arxiv.org/abs/1409.4842)):
<center width="100%"><img src="inception_block.svg" style="display: block; margin-left: auto; margin-right: auto;" width="500px"/></center>
The additional 1x1 convolutions before the 3x3 and 5x5 convolutions are used for dimensionality reduction. This is especially crucial as the feature maps of all branches are merged afterward, and we don't want any explosion of feature size. As 5x5 convolutions are 25 times more expensive than 1x1 convolutions, we can save a lot of computation and parameters by reducing the dimensionality before the large convolutions.
We can now try to implement the Inception Block ourselves:
```
class InceptionBlock(nn.Module):
def __init__(self, c_in, c_red : dict, c_out : dict, act_fn):
"""
Inputs:
c_in - Number of input feature maps from the previous layers
c_red - Dictionary with keys "3x3" and "5x5" specifying the output of the dimensionality reducing 1x1 convolutions
c_out - Dictionary with keys "1x1", "3x3", "5x5", and "max"
act_fn - Activation class constructor (e.g. nn.ReLU)
"""
super().__init__()
# 1x1 convolution branch
self.conv_1x1 = nn.Sequential(
nn.Conv2d(c_in, c_out["1x1"], kernel_size=1),
nn.BatchNorm2d(c_out["1x1"]),
act_fn()
)
# 3x3 convolution branch
self.conv_3x3 = nn.Sequential(
nn.Conv2d(c_in, c_red["3x3"], kernel_size=1),
nn.BatchNorm2d(c_red["3x3"]),
act_fn(),
nn.Conv2d(c_red["3x3"], c_out["3x3"], kernel_size=3, padding=1),
nn.BatchNorm2d(c_out["3x3"]),
act_fn()
)
# 5x5 convolution branch
self.conv_5x5 = nn.Sequential(
nn.Conv2d(c_in, c_red["5x5"], kernel_size=1),
nn.BatchNorm2d(c_red["5x5"]),
act_fn(),
nn.Conv2d(c_red["5x5"], c_out["5x5"], kernel_size=5, padding=2),
nn.BatchNorm2d(c_out["5x5"]),
act_fn()
)
# Max-pool branch
self.max_pool = nn.Sequential(
nn.MaxPool2d(kernel_size=3, padding=1, stride=1),
nn.Conv2d(c_in, c_out["max"], kernel_size=1),
nn.BatchNorm2d(c_out["max"]),
act_fn()
)
def forward(self, x):
x_1x1 = self.conv_1x1(x)
x_3x3 = self.conv_3x3(x)
x_5x5 = self.conv_5x5(x)
x_max = self.max_pool(x)
x_out = torch.cat([x_1x1, x_3x3, x_5x5, x_max], dim=1)
return x_out
```
The GoogleNet architecture consists of stacking multiple Inception blocks with occasional max pooling to reduce the height and width of the feature maps. The original GoogleNet was designed for image sizes of ImageNet (224x224 pixels) and had almost 7 million parameters. As we train on CIFAR10 with image sizes of 32x32, we don't require such a heavy architecture, and instead, apply a reduced version. The number of channels for dimensionality reduction and output per filter (1x1, 3x3, 5x5, and max pooling) need to be manually specified and can be changed if interested. The general intuition is to have the most filters for the 3x3 convolutions, as they are powerful enough to take the context into account while requiring almost a third of the parameters of the 5x5 convolution.
```
class GoogleNet(nn.Module):
def __init__(self, num_classes=10, act_fn_name="relu", **kwargs):
super().__init__()
self.hparams = SimpleNamespace(num_classes=num_classes,
act_fn_name=act_fn_name,
act_fn=act_fn_by_name[act_fn_name])
self._create_network()
self._init_params()
def _create_network(self):
# A first convolution on the original image to scale up the channel size
self.input_net = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=3, padding=1),
nn.BatchNorm2d(64),
self.hparams.act_fn()
)
# Stacking inception blocks
self.inception_blocks = nn.Sequential(
InceptionBlock(64, c_red={"3x3":32,"5x5":16}, c_out={"1x1":16,"3x3":32,"5x5":8,"max":8}, act_fn=self.hparams.act_fn),
InceptionBlock(64, c_red={"3x3":32,"5x5":16}, c_out={"1x1":24,"3x3":48,"5x5":12,"max":12}, act_fn=self.hparams.act_fn),
nn.MaxPool2d(3, stride=2, padding=1), # 32x32 => 16x16
InceptionBlock(96, c_red={"3x3":32,"5x5":16}, c_out={"1x1":24,"3x3":48,"5x5":12,"max":12}, act_fn=self.hparams.act_fn),
InceptionBlock(96, c_red={"3x3":32,"5x5":16}, c_out={"1x1":16,"3x3":48,"5x5":16,"max":16}, act_fn=self.hparams.act_fn),
InceptionBlock(96, c_red={"3x3":32,"5x5":16}, c_out={"1x1":16,"3x3":48,"5x5":16,"max":16}, act_fn=self.hparams.act_fn),
InceptionBlock(96, c_red={"3x3":32,"5x5":16}, c_out={"1x1":32,"3x3":48,"5x5":24,"max":24}, act_fn=self.hparams.act_fn),
nn.MaxPool2d(3, stride=2, padding=1), # 16x16 => 8x8
InceptionBlock(128, c_red={"3x3":48,"5x5":16}, c_out={"1x1":32,"3x3":64,"5x5":16,"max":16}, act_fn=self.hparams.act_fn),
InceptionBlock(128, c_red={"3x3":48,"5x5":16}, c_out={"1x1":32,"3x3":64,"5x5":16,"max":16}, act_fn=self.hparams.act_fn)
)
# Mapping to classification output
self.output_net = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(128, self.hparams.num_classes)
)
def _init_params(self):
# Based on our discussion in Tutorial 4, we should initialize the convolutions according to the activation function
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, nonlinearity=self.hparams.act_fn_name)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.input_net(x)
x = self.inception_blocks(x)
x = self.output_net(x)
return x
```
Now, we can integrate our model to the model dictionary we defined above:
```
model_dict["GoogleNet"] = GoogleNet
```
The training of the model is handled by PyTorch Lightning, and we just have to define the command to start. Note that we train for almost 200 epochs, which takes about an hour on Lisa's default GPUs (GTX1080Ti). We would recommend using the saved models and train your own model if you are interested.
```
googlenet_model, googlenet_results = train_model(model_name="GoogleNet",
model_hparams={"num_classes": 10,
"act_fn_name": "relu"},
optimizer_name="Adam",
optimizer_hparams={"lr": 1e-3,
"weight_decay": 1e-4})
```
We will compare the results later in the notebooks, but we can already print them here for a first glance:
```
print("GoogleNet Results", googlenet_results)
```
### Tensorboard log
A nice extra of PyTorch Lightning is the automatic logging into TensorBoard. To give you a better intuition of what TensorBoard can be used, we can look at the board that PyTorch Lightning has been generated when training the GoogleNet. TensorBoard provides an inline functionality for Jupyter notebooks, and we use it here:
```
# Import tensorboard
from torch.utils.tensorboard import SummaryWriter
%load_ext tensorboard
# Opens tensorboard in notebook. Adjust the path to your CHECKPOINT_PATH!
%tensorboard --logdir ../saved_models/tutorial5/tensorboards/GoogleNet/
```
<center width="100%"><img src="tensorboard_screenshot_GoogleNet.png" width="1000px"></center>
TensorBoard is organized in multiple tabs. The main tab is the scalar tab where we can log the development of single numbers. For example, we have plotted the training loss, accuracy, learning rate, etc. If we look at the training or validation accuracy, we can really see the impact of using a learning rate scheduler. Reducing the learning rate gives our model a nice increase in training performance. Similarly, when looking at the training loss, we see a sudden decrease at this point. However, the high numbers on the training set compared to validation indicate that our model was overfitting which is inevitable for such large networks.
Another interesting tab in TensorBoard is the graph tab. It shows us the network architecture organized by building blocks from the input to the output. It basically shows the operations taken in the forward step of `CIFARTrainer`. Double-click on a module to open it. Feel free to explore the architecture from a different perspective. The graph visualization can often help you to validate that your model is actually doing what it is supposed to do, and you don't miss any layers in the computation graph.
## ResNet
The [ResNet](https://arxiv.org/abs/1512.03385) paper is one of the [most cited AI papers](https://www.natureindex.com/news-blog/google-scholar-reveals-most-influential-papers-research-citations-twenty-twenty), and has been the foundation for neural networks with more than 1,000 layers. Despite its simplicity, the idea of residual connections is highly effective as it supports stable gradient propagation through the network. Instead of modeling $x_{l+1}=F(x_{l})$, we model $x_{l+1}=x_{l}+F(x_{l})$ where $F$ is a non-linear mapping (usually a sequence of NN modules likes convolutions, activation functions, and normalizations). If we do backpropagation on such residual connections, we obtain:
$$\frac{\partial x_{l+1}}{\partial x_{l}} = \mathbf{I} + \frac{\partial F(x_{l})}{\partial x_{l}}$$
The bias towards the identity matrix guarantees a stable gradient propagation being less effected by $F$ itself. There have been many variants of ResNet proposed, which mostly concern the function $F$, or operations applied on the sum. In this tutorial, we look at two of them: the original ResNet block, and the [Pre-Activation ResNet block](https://arxiv.org/abs/1603.05027). We visually compare the blocks below (figure credit - [He et al.](https://arxiv.org/abs/1603.05027)):
<center width="100%"><img src="resnet_block.svg" style="display: block; margin-left: auto; margin-right: auto;" width="300px"/></center>
The original ResNet block applies a non-linear activation function, usually ReLU, after the skip connection. In contrast, the pre-activation ResNet block applies the non-linearity at the beginning of $F$. Both have their advantages and disadvantages. For very deep network, however, the pre-activation ResNet has shown to perform better as the gradient flow is guaranteed to have the identity matrix as calculated above, and is not harmed by any non-linear activation applied to it. For comparison, in this notebook, we implement both ResNet types as shallow networks.
Let's start with the original ResNet block. The visualization above already shows what layers are included in $F$. One special case we have to handle is when we want to reduce the image dimensions in terms of width and height. The basic ResNet block requires $F(x_{l})$ to be of the same shape as $x_{l}$. Thus, we need to change the dimensionality of $x_{l}$ as well before adding to $F(x_{l})$. The original implementation used an identity mapping with stride 2 and padded additional feature dimensions with 0. However, the more common implementation is to use a 1x1 convolution with stride 2 as it allows us to change the feature dimensionality while being efficient in parameter and computation cost. The code for the ResNet block is relatively simple, and shown below:
```
class ResNetBlock(nn.Module):
def __init__(self, c_in, act_fn, subsample=False, c_out=-1):
"""
Inputs:
c_in - Number of input features
act_fn - Activation class constructor (e.g. nn.ReLU)
subsample - If True, we want to apply a stride inside the block and reduce the output shape by 2 in height and width
c_out - Number of output features. Note that this is only relevant if subsample is True, as otherwise, c_out = c_in
"""
super().__init__()
if not subsample:
c_out = c_in
# Network representing F
self.net = nn.Sequential(
nn.Conv2d(c_in, c_out, kernel_size=3, padding=1, stride=1 if not subsample else 2, bias=False), # No bias needed as the Batch Norm handles it
nn.BatchNorm2d(c_out),
act_fn(),
nn.Conv2d(c_out, c_out, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(c_out)
)
# 1x1 convolution with stride 2 means we take the upper left value, and transform it to new output size
self.downsample = nn.Conv2d(c_in, c_out, kernel_size=1, stride=2) if subsample else None
self.act_fn = act_fn()
def forward(self, x):
z = self.net(x)
if self.downsample is not None:
x = self.downsample(x)
out = z + x
out = self.act_fn(out)
return out
```
The second block we implement is the pre-activation ResNet block. For this, we have to change the order of layer in `self.net`, and do not apply an activation function on the output. Additionally, the downsampling operation has to apply a non-linearity as well as the input, $x_l$, has not been processed by a non-linearity yet. Hence, the block looks as follows:
```
class PreActResNetBlock(nn.Module):
def __init__(self, c_in, act_fn, subsample=False, c_out=-1):
"""
Inputs:
c_in - Number of input features
act_fn - Activation class constructor (e.g. nn.ReLU)
subsample - If True, we want to apply a stride inside the block and reduce the output shape by 2 in height and width
c_out - Number of output features. Note that this is only relevant if subsample is True, as otherwise, c_out = c_in
"""
super().__init__()
if not subsample:
c_out = c_in
# Network representing F
self.net = nn.Sequential(
nn.BatchNorm2d(c_in),
act_fn(),
nn.Conv2d(c_in, c_out, kernel_size=3, padding=1, stride=1 if not subsample else 2, bias=False),
nn.BatchNorm2d(c_out),
act_fn(),
nn.Conv2d(c_out, c_out, kernel_size=3, padding=1, bias=False)
)
# 1x1 convolution needs to apply non-linearity as well as not done on skip connection
self.downsample = nn.Sequential(
nn.BatchNorm2d(c_in),
act_fn(),
nn.Conv2d(c_in, c_out, kernel_size=1, stride=2, bias=False)
) if subsample else None
def forward(self, x):
z = self.net(x)
if self.downsample is not None:
x = self.downsample(x)
out = z + x
return out
```
Similarly to the model selection, we define a dictionary to create a mapping from string to block class. We will use the string name as hyperparameter value in our model to choose between the ResNet blocks. Feel free to implement any other ResNet block type and add it here as well.
```
resnet_blocks_by_name = {
"ResNetBlock": ResNetBlock,
"PreActResNetBlock": PreActResNetBlock
}
```
The overall ResNet architecture consists of stacking multiple ResNet blocks, of which some are downsampling the input. When talking about ResNet blocks in the whole network, we usually group them by the same output shape. Hence, if we say the ResNet has `[3,3,3]` blocks, it means that we have 3 times a group of 3 ResNet blocks, where a subsampling is taking place in the fourth and seventh block. The ResNet with `[3,3,3]` blocks on CIFAR10 is visualized below.
<center width="100%"><img src="resnet_notation.svg" width="500px"></center>
The three groups operate on the resolutions $32\times32$, $16\times16$ and $8\times8$ respectively. The blocks in orange denote ResNet blocks with downsampling. The same notation is used by many other implementations such as in the [torchvision library](https://pytorch.org/docs/stable/_modules/torchvision/models/resnet.html#resnet18) from PyTorch. Thus, our code looks as follows:
```
class ResNet(nn.Module):
def __init__(self, num_classes=10, num_blocks=[3,3,3], c_hidden=[16,32,64], act_fn_name="relu", block_name="ResNetBlock", **kwargs):
"""
Inputs:
num_classes - Number of classification outputs (10 for CIFAR10)
num_blocks - List with the number of ResNet blocks to use. The first block of each group uses downsampling, except the first.
c_hidden - List with the hidden dimensionalities in the different blocks. Usually multiplied by 2 the deeper we go.
act_fn_name - Name of the activation function to use, looked up in "act_fn_by_name"
block_name - Name of the ResNet block, looked up in "resnet_blocks_by_name"
"""
super().__init__()
assert block_name in resnet_blocks_by_name
self.hparams = SimpleNamespace(num_classes=num_classes,
c_hidden=c_hidden,
num_blocks=num_blocks,
act_fn_name=act_fn_name,
act_fn=act_fn_by_name[act_fn_name],
block_class=resnet_blocks_by_name[block_name])
self._create_network()
self._init_params()
def _create_network(self):
c_hidden = self.hparams.c_hidden
# A first convolution on the original image to scale up the channel size
if self.hparams.block_class == PreActResNetBlock: # => Don't apply non-linearity on output
self.input_net = nn.Sequential(
nn.Conv2d(3, c_hidden[0], kernel_size=3, padding=1, bias=False)
)
else:
self.input_net = nn.Sequential(
nn.Conv2d(3, c_hidden[0], kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(c_hidden[0]),
self.hparams.act_fn()
)
# Creating the ResNet blocks
blocks = []
for block_idx, block_count in enumerate(self.hparams.num_blocks):
for bc in range(block_count):
subsample = (bc == 0 and block_idx > 0) # Subsample the first block of each group, except the very first one.
blocks.append(
self.hparams.block_class(c_in=c_hidden[block_idx if not subsample else (block_idx-1)],
act_fn=self.hparams.act_fn,
subsample=subsample,
c_out=c_hidden[block_idx])
)
self.blocks = nn.Sequential(*blocks)
# Mapping to classification output
self.output_net = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(c_hidden[-1], self.hparams.num_classes)
)
def _init_params(self):
# Based on our discussion in Tutorial 4, we should initialize the convolutions according to the activation function
# Fan-out focuses on the gradient distribution, and is commonly used in ResNets
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity=self.hparams.act_fn_name)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.input_net(x)
x = self.blocks(x)
x = self.output_net(x)
return x
```
We also need to add the new ResNet class to our model dictionary:
```
model_dict["ResNet"] = ResNet
```
Finally, we can train our ResNet models. One difference to the GoogleNet training is that we explicitly use SGD with Momentum as optimizer instead of Adam. Adam often leads to a slightly worse accuracy on plain, shallow ResNets. It is not 100% clear why Adam performs worse in this context, but one possible explanation is related to ResNet's loss surface. ResNet has been shown to produce smoother loss surfaces than networks without skip connection (see [Li et al., 2018](https://arxiv.org/pdf/1712.09913.pdf) for details). A possible visualization of the loss surface with/out skip connections is below (figure credit - [Li et al.](https://arxiv.org/pdf/1712.09913.pdf)):
<center width="100%"><img src="resnet_loss_surface.svg" style="display: block; margin-left: auto; margin-right: auto;" width="600px"/></center>
The $x$ and $y$ axis shows a projection of the parameter space, and the $z$ axis shows the loss values achieved by different parameter values. On smooth surfaces like the one on the right, we might not require an adaptive learning rate as Adam provides. Instead, Adam can get stuck in local optima while SGD finds the wider minima that tend to generalize better.
However, to answer this question in detail, we would need an extra tutorial because it is not easy to answer. For now, we conclude: for ResNet architectures, consider the optimizer to be an important hyperparameter, and try training with both Adam and SGD. Let's train the model below with SGD:
```
resnet_model, resnet_results = train_model(model_name="ResNet",
model_hparams={"num_classes": 10,
"c_hidden": [16,32,64],
"num_blocks": [3,3,3],
"act_fn_name": "relu"},
optimizer_name="SGD",
optimizer_hparams={"lr": 0.1,
"momentum": 0.9,
"weight_decay": 1e-4})
```
Let's also train the pre-activation ResNet as comparison:
```
resnetpreact_model, resnetpreact_results = train_model(model_name="ResNet",
model_hparams={"num_classes": 10,
"c_hidden": [16,32,64],
"num_blocks": [3,3,3],
"act_fn_name": "relu",
"block_name": "PreActResNetBlock"},
optimizer_name="SGD",
optimizer_hparams={"lr": 0.1,
"momentum": 0.9,
"weight_decay": 1e-4},
save_name="ResNetPreAct")
```
### Tensorboard log
Similarly to our GoogleNet model, we also have a TensorBoard log for the ResNet model. We can open it below.
```
# Opens tensorboard in notebook. Adjust the path to your CHECKPOINT_PATH! Feel free to change "ResNet" to "ResNetPreAct"
%tensorboard --logdir ../saved_models/tutorial5/tensorboards/ResNet/
```
<center width="100%"><img src="tensorboard_screenshot_ResNet.png" width="1000px"></center>
Feel free to explore the TensorBoard yourself, including the computation graph. In general, we can see that with SGD, the ResNet has a higher training loss than the GoogleNet in the first stage of the training. After reducing the learning rate however, the model achieves even higher validation accuracies. We compare the precise scores at the end of the notebook.
## DenseNet
[DenseNet](https://arxiv.org/abs/1608.06993) is another architecture for enabling very deep neural networks and takes a slightly different perspective on residual connections. Instead of modeling the difference between layers, DenseNet considers residual connections as a possible way to reuse features across layers, removing any necessity to learn redundant feature maps. If we go deeper into the network, the model learns abstract features to recognize patterns. However, some complex patterns consist of a combination of abstract features (e.g. hand, face, etc.), and low-level features (e.g. edges, basic color, etc.). To find these low-level features in the deep layers, standard CNNs have to learn copy such feature maps, which wastes a lot of parameter complexity. DenseNet provides an efficient way of reusing features by having each convolution depends on all previous input features, but add only a small amount of filters to it. See the figure below for an illustration (figure credit - [Hu et al.](https://arxiv.org/abs/1608.06993)):
<center width="100%"><img src="densenet_block.svg" style="display: block; margin-left: auto; margin-right: auto;" width="500px"/></center>
The last layer, called the transition layer, is responsible for reducing the dimensionality of the feature maps in height, width, and channel size. Although those technically break the identity backpropagation, there are only a few in a network so that it doesn't affect the gradient flow much.
We split the implementation of the layers in DenseNet into three parts: a `DenseLayer`, and a `DenseBlock`, and a `TransitionLayer`. The module `DenseLayer` implements a single layer inside a dense block. It applies a 1x1 convolution for dimensionality reduction with a subsequential 3x3 convolution. The output channels are concatenated to the originals and returned. Note that we apply the Batch Normalization as the first layer of each block. This allows slightly different activations for the same features to different layers, depending on what is needed. Overall, we can implement it as follows:
```
class DenseLayer(nn.Module):
def __init__(self, c_in, bn_size, growth_rate, act_fn):
"""
Inputs:
c_in - Number of input channels
bn_size - Bottleneck size (factor of growth rate) for the output of the 1x1 convolution. Typically between 2 and 4.
growth_rate - Number of output channels of the 3x3 convolution
act_fn - Activation class constructor (e.g. nn.ReLU)
"""
super().__init__()
self.net = nn.Sequential(
nn.BatchNorm2d(c_in),
act_fn(),
nn.Conv2d(c_in, bn_size * growth_rate, kernel_size=1, bias=False),
nn.BatchNorm2d(bn_size * growth_rate),
act_fn(),
nn.Conv2d(bn_size * growth_rate, growth_rate, kernel_size=3, padding=1, bias=False)
)
def forward(self, x):
out = self.net(x)
out = torch.cat([out, x], dim=1)
return out
```
The module `DenseBlock` summarizes multiple dense layers applied in sequence. Each dense layer takes as input the original input concatenated with all previous layers' feature maps:
```
class DenseBlock(nn.Module):
def __init__(self, c_in, num_layers, bn_size, growth_rate, act_fn):
"""
Inputs:
c_in - Number of input channels
num_layers - Number of dense layers to apply in the block
bn_size - Bottleneck size to use in the dense layers
growth_rate - Growth rate to use in the dense layers
act_fn - Activation function to use in the dense layers
"""
super().__init__()
layers = []
for layer_idx in range(num_layers):
layers.append(
DenseLayer(c_in=c_in + layer_idx * growth_rate, # Input channels are original plus the feature maps from previous layers
bn_size=bn_size,
growth_rate=growth_rate,
act_fn=act_fn)
)
self.block = nn.Sequential(*layers)
def forward(self, x):
out = self.block(x)
return out
```
Finally, the `TransitionLayer` takes as input the final output of a dense block and reduces its channel dimensionality using a 1x1 convolution. To reduce the height and width dimension, we take a slightly different approach than in ResNet and apply an average pooling with kernel size 2 and stride 2. This is because we don't have an additional connection to the output that would consider the full 2x2 patch instead of a single value. Besides, it is more parameter efficient than using a 3x3 convolution with stride 2. Thus, the layer is implemented as follows:
```
class TransitionLayer(nn.Module):
def __init__(self, c_in, c_out, act_fn):
super().__init__()
self.transition = nn.Sequential(
nn.BatchNorm2d(c_in),
act_fn(),
nn.Conv2d(c_in, c_out, kernel_size=1, bias=False),
nn.AvgPool2d(kernel_size=2, stride=2) # Average the output for each 2x2 pixel group
)
def forward(self, x):
return self.transition(x)
```
Now we can put everything together and create our DenseNet. To specify the number of layers, we use a similar notation as in ResNets and pass on a list of ints representing the number of layers per block. After each dense block except the last one, we apply a transition layer to reduce the dimensionality by 2.
```
class DenseNet(nn.Module):
def __init__(self, num_classes=10, num_layers=[6,6,6,6], bn_size=2, growth_rate=16, act_fn_name="relu", **kwargs):
super().__init__()
self.hparams = SimpleNamespace(num_classes=num_classes,
num_layers=num_layers,
bn_size=bn_size,
growth_rate=growth_rate,
act_fn_name=act_fn_name,
act_fn=act_fn_by_name[act_fn_name])
self._create_network()
self._init_params()
def _create_network(self):
c_hidden = self.hparams.growth_rate * self.hparams.bn_size # The start number of hidden channels
# A first convolution on the original image to scale up the channel size
self.input_net = nn.Sequential(
nn.Conv2d(3, c_hidden, kernel_size=3, padding=1) # No batch norm or activation function as done inside the Dense layers
)
# Creating the dense blocks, eventually including transition layers
blocks = []
for block_idx, num_layers in enumerate(self.hparams.num_layers):
blocks.append(
DenseBlock(c_in=c_hidden,
num_layers=num_layers,
bn_size=self.hparams.bn_size,
growth_rate=self.hparams.growth_rate,
act_fn=self.hparams.act_fn)
)
c_hidden = c_hidden + num_layers * self.hparams.growth_rate # Overall output of the dense block
if block_idx < len(self.hparams.num_layers)-1: # Don't apply transition layer on last block
blocks.append(
TransitionLayer(c_in=c_hidden,
c_out=c_hidden // 2,
act_fn=self.hparams.act_fn))
c_hidden = c_hidden // 2
self.blocks = nn.Sequential(*blocks)
# Mapping to classification output
self.output_net = nn.Sequential(
nn.BatchNorm2d(c_hidden), # The features have not passed a non-linearity until here.
self.hparams.act_fn(),
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(c_hidden, self.hparams.num_classes)
)
def _init_params(self):
# Based on our discussion in Tutorial 4, we should initialize the convolutions according to the activation function
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, nonlinearity=self.hparams.act_fn_name)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.input_net(x)
x = self.blocks(x)
x = self.output_net(x)
return x
```
Let's also add the DenseNet to our model dictionary:
```
model_dict["DenseNet"] = DenseNet
```
Lastly, we train our network. In contrast to ResNet, DenseNet does not show any issues with Adam, and hence we train it with this optimizer. The other hyperparameters are chosen to result in a network with a similar parameter size as the ResNet and GoogleNet. Commonly, when designing very deep networks, DenseNet is more parameter efficient than ResNet while achieving a similar or even better performance.
```
densenet_model, densenet_results = train_model(model_name="DenseNet",
model_hparams={"num_classes": 10,
"num_layers": [6,6,6,6],
"bn_size": 2,
"growth_rate": 16,
"act_fn_name": "relu"},
optimizer_name="Adam",
optimizer_hparams={"lr": 1e-3,
"weight_decay": 1e-4})
```
### Tensorboard log
Finally, we also have another TensorBoard for the DenseNet training. We take a look at it below:
```
# Opens tensorboard in notebook. Adjust the path to your CHECKPOINT_PATH! Feel free to change "ResNet" to "ResNetPreAct"
%tensorboard --logdir ../saved_models/tutorial5/tensorboards/DenseNet/
```
<center width="100%"><img src="tensorboard_screenshot_DenseNet.png" width="1000px"></center>
The overall course of the validation accuracy and training loss resemble the training of GoogleNet, which is also related to training the network with Adam. Feel free to explore the training metrics yourself.
## Conclusion and Comparison
After discussing each model separately, and training all of them, we can finally compare them. First, let's organize the results of all models in a table:
```
%%html
<!-- Some HTML code to increase font size in the following table -->
<style>
th {font-size: 120%;}
td {font-size: 120%;}
</style>
import tabulate
from IPython.display import display, HTML
all_models = [
("GoogleNet", googlenet_results, googlenet_model),
("ResNet", resnet_results, resnet_model),
("ResNetPreAct", resnetpreact_results, resnetpreact_model),
("DenseNet", densenet_results, densenet_model)
]
table = [[model_name,
"%4.2f%%" % (100.0*model_results["val"]),
"%4.2f%%" % (100.0*model_results["test"]),
"{:,}".format(sum([np.prod(p.shape) for p in model.parameters()]))]
for model_name, model_results, model in all_models]
display(HTML(tabulate.tabulate(table, tablefmt='html', headers=["Model", "Val Accuracy", "Test Accuracy", "Num Parameters"])))
```
First of all, we see that all models are performing reasonably well. Simple models as you have implemented them in the practical achieve considerably lower performance, which is beside the lower number of parameters also attributed to the architecture design choice. GoogleNet is the model to obtain the lowest performance on the validation and test set, although it is very close to DenseNet. A proper hyperparameter search over all the channel sizes in GoogleNet would likely improve the accuracy of the model to a similar level, but this is also expensive given a large number of hyperparameters. ResNet outperforms both DenseNet and GoogleNet by more than 1% on the validation set, while there is a minor difference between both versions, original and pre-activation. We can conclude that for shallow networks, the place of the activation function does not seem to be crucial, although papers have reported the contrary for very deep networks (e.g. [He et al.](https://arxiv.org/abs/1603.05027)).
In general, we can conclude that ResNet is a simple, but powerful architecture. If we would apply the models on more complex tasks with larger images and more layers inside the networks, we would likely see a bigger gap between GoogleNet and skip-connection architectures like ResNet and DenseNet. A comparison with deeper models on CIFAR10 can be for example found [here](https://github.com/kuangliu/pytorch-cifar). Interestingly, DenseNet outperforms the original ResNet on their setup but comes closely behind the Pre-Activation ResNet. The best model, a Dual Path Network ([Chen et. al](https://arxiv.org/abs/1707.01629)), is actually a combination of ResNet and DenseNet showing that both offer different advantages.
### Which model should I choose for my task?
We have reviewed four different models. So, which one should we choose if have given a new task? Usually, starting with a ResNet is a good idea given the superior performance of the CIFAR dataset and its simple implementation. Besides, for the parameter number we have chosen here, ResNet is the fastest as DenseNet and GoogleNet have many more layers that are applied in sequence in our primitive implementation. However, if you have a really difficult task, such as semantic segmentation on HD images, more complex variants of ResNet and DenseNet are recommended.
| true |
code
| 0.80243 | null | null | null | null |
|
# Explorando Cartpole con Reinforcement Learning usando Deep Q-learning
Este cuaderno es una modificación del tutorial de [Pytorch RL DQN](https://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html)
Sigue la línea de clase de Reinforcement Learning, Q-learning & OpenAI de la RIIA 2019
```
# Veamos de qué se trata el ambiente de Cartpole:
import gym
env = gym.make('CartPole-v0')
env.reset()
for _ in range(30):
env.render()
env.step(env.action_space.sample()) # Toma acción aleatoria
env.close()
# Importamos las bibliotecas necesarias:
import gym
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from IPython import display
plt.ion()
from collections import namedtuple
from itertools import count
from PIL import Image
# Las soluciones usan pytorch, pueden usar keras y/o tensorflow si prefieren
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as T
# Ambiente de OpenAI "Cart pole"
enviroment = gym.make('CartPole-v0').unwrapped
enviroment.render()
# Revisa si hay GPU disponible y lo utiliza
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print('Número de acciones: {}'.format(enviroment.action_space.n))
print('Dimensión de estado: {}'.format(enviroment.observation_space))
# Factor de descuento temporal
gamma = 0.8
# Número de muestras que extraer del repositorio de experiencia para entrenar la red
No_grupo = 64
# Parámetros para la tasa de epsilon-gredy, ésta va cayendo exponencialmente
eps_inicial = 0.9
eps_final = 0.05
eps_tasa = 200
# Parámetro para el descenso por gradiente estocástico
lr = 0.001
# Cada cuanto actualizar la red de etiqueta
actualizar_red_med = 10
# Número de episodios para entrenar
No_episodios = 200
iters = 0
duracion_episodios = []
```
Define una función llamda `genera_accion` que reciba el vector del `estado` y tome la acción óptima o una acción aleatoria. La acción aleatoria la debe de tomar con una probabilidad que disminuya exponencialmente, de tal manera que en un principio se explore más.
Con probabilidad $$\epsilon_{final}+(\epsilon_{inicial}-\epsilon_{final})\times e^{-iters/tasa_{\epsilon}}$$ se escoge una acción aleatoria. En la siguiente gráfica se puede observar la tasa que cae exponencialmente.
```
plt.plot([eps_final + (eps_inicial - eps_final) * math.exp(-1. * iters / eps_tasa) for iters in range(1000)])
plt.title('Disminución exponencial de la tasa de exploración')
plt.xlabel('Iteración')
plt.ylabel('Probabilidad de explorar: $\epsilon$')
plt.show
def genera_accion(estado):
global iters
decimal = random.uniform(0, 1)
limite_epsilon = eps_final + (eps_inicial - eps_final) * math.exp(-1. * iters / eps_tasa)
iters += 1
if decimal > limite_epsilon:
with torch.no_grad():
return red_estrategia(estado).max(0)[1].view(1)
else:
return torch.tensor([random.randrange(2)], device=device, dtype=torch.long)
```
Genera una red neuronal que reciba el vector de estado y regrese un vector de dimensión igual al número de acciones
```
class red_N(nn.Module):
def __init__(self):
super(red_N, self).__init__()
# Capas densas
self.capa_densa1 = nn.Linear(4, 256)
self.capa_densa2 = nn.Linear(256, 128)
self.final = nn.Linear(128, 2)
def forward(self, x):
# Arquitectura de la red, con activación ReLU en las dos capas interiores
x = F.relu(self.capa_densa1(x))
x = F.relu(self.capa_densa2(x))
return self.final(x)
```
En a siguiente celda generamos una clase de repositorio de experiencia con diferentes atributos:
`guarda`: guarda la observación $(s_i,a_i,s_i',r_i)$
`muestra`: genera una muestra de tamaño No_gupo
`len`: función que regresa la cantidad de muestras en el repositorio
```
Transicion = namedtuple('Transicion',
('estado', 'accion', 'sig_estado', 'recompensa'))
class repositorioExperiencia(object):
def __init__(self, capacidad):
self.capacidad = capacidad
self.memoria = []
self.posicion = 0
def guarda(self, *args):
"""Guarda una transición."""
if len(self.memoria) < self.capacidad:
self.memoria.append(None)
self.memoria[self.posicion] = Transicion(*args)
self.posicion = (self.posicion + 1) % self.capacidad
def muestra(self, batch_size):
return random.sample(self.memoria, batch_size)
def __len__(self):
return len(self.memoria)
```
En la siguiente celda definimos una función llamda `actualiza_q` que implemente DQL:
1. Saque una muestra de tamaño `No_grupo`,
2. Usando la `red_estrategia`, calcule $Q_{\theta}(s_t,a_t)$ para la muestra
3. Calcula $V^*(s_{t+1})$ usando la `red_etiqueta`
4. Calcular la etiquetas $y_j=r_i+\max_aQ_{\theta'}(s_t,a)$
5. Calcula función de pérdida para $Q_{\theta}(s_t,a_t)-y_j$
6. Actualize $\theta$
```
def actualiza_q():
if len(memoria) < No_grupo:
return
transiciones = memoria.muestra(No_grupo)
# Transpose the batch (see http://stackoverflow.com/a/19343/3343043 for
# detailed explanation).
grupo = Transicion(*zip(*transiciones))
# Compute a mask of non-final states and concatenate the batch elements
estados_intermedios = torch.tensor(tuple(map(lambda s: s is not None,
grupo.sig_estado)), device=device, dtype=torch.uint8)
sig_estados_intermedios = torch.cat([s for s in grupo.sig_estado
if s is not None])
grupo_estado = torch.cat(grupo.estado)
accion_grupo = torch.cat(grupo.accion)
recompensa_grupo = torch.cat(grupo.recompensa)
# Calcula Q(s_t, a_t) - una manera es usar la red_estrategia para calcular Q(s_t),
# y seleccionar las columnas usando los índices de la acciones tomadas usando la función gather
q_actual = red_estrategia(grupo_estado).gather(1, accion_grupo.unsqueeze(1))
# Calcula V*(s_{t+1}) para todos los sig_estados en el grupo usando la red_etiqueta
valores_sig_estado = torch.zeros(No_grupo, device=device)
valores_sig_estado[estados_intermedios] = red_etiqueta(sig_estados_intermedios).max(1)[0].detach()
# Calcular las etiquetas
y_j = (valores_sig_estado * gamma) + recompensa_grupo
# Calcula función de pérdida de Huber
#perdida = F.smooth_l1_loss(q_actual, y_j.unsqueeze(1))
perdida = F.mse_loss(q_actual, y_j.unsqueeze(1))
# Optimizar el modelo
optimizador.zero_grad()
perdida.backward()
for param in red_estrategia.parameters():
param.grad.data.clamp_(-1, 1)
optimizador.step()
# Función para graficar la duración
def grafica_duracion(dur):
plt.figure(2)
plt.clf()
duracion_t = torch.tensor(duracion_episodios, dtype=torch.float)
plt.title('Entrenamiento...')
plt.xlabel('Episodio')
plt.ylabel('Duración')
plt.plot(duracion_t.numpy())
# Toma el promedio de duración d 100 episodios y los grafica
if len(duracion_t) >= 15:
media = duracion_t.unfold(0, 15, 1).mean(1).view(-1)
media = torch.cat((torch.zeros(14), media))
plt.plot(media.numpy())
plt.plot([200]*len(duracion_t))
plt.pause(dur) # Pausa un poco para poder veer las gráficas
display.clear_output(wait=True)
display.display(plt.gcf())
red_estrategia = red_N().to(device)
red_etiqueta = red_N().to(device)
red_etiqueta.load_state_dict(red_estrategia.state_dict())
red_etiqueta.eval()
#optimizador = optim.RMSprop(red_estrategia.parameters())
optimizador = optim.Adam(red_estrategia.parameters(),lr=lr)
memoria = repositorioExperiencia(10000)
# Entrenamiento
for episodio in range(0, No_episodios):
# Reset the enviroment
estado = enviroment.reset()
estado = torch.tensor(estado, dtype = torch.float)
# Initialize variables
recompensa = 0
termina = False
for t in count():
# Decide acción a tomar
accion = genera_accion(estado)
# Implementa la acción y recibe reacción del ambiente
sig_estado, recompensa, termina, _ = enviroment.step(accion.item())
# Convierte a observaciones a tensores
estado = torch.tensor(estado, dtype = torch.float)
sig_estado = torch.tensor(sig_estado, dtype = torch.float)
# Si acabó (Termina = True) el episodio la recompensa es negativa
if termina:
recompensa = -recompensa
recompensa = torch.tensor([recompensa], device=device)
# Guarda la transición en la memoria
memoria.guarda(estado.unsqueeze(0), accion, sig_estado.unsqueeze(0), recompensa)
# Actualiza valor q en la red de medida
actualiza_q()
## Moverse al siguiente estado
estado = sig_estado
# Grafica la duración de los episodios
if termina:
duracion_episodios.append(t + 1)
break
# Actualizar la red_etiqueta
if episodio % actualizar_red_med == 0:
red_etiqueta.load_state_dict(red_estrategia.state_dict())
grafica_duracion(0.3)
print("**********************************")
print("Entrenamiento finalizado!\n")
print("**********************************")
grafica_duracion(15)
grafica_duracion(15)
```
| true |
code
| 0.683195 | null | null | null | null |
|
```
import pandas as pd
import numpy as np
from boruta import BorutaPy
from IPython.display import display
```
### Data Prep
```
df = pd.read_csv('data/aml_df.csv')
df.drop(columns=['Unnamed: 0'], inplace=True)
display(df.info())
df.head()
#holdout validation set
final_val = df.sample(frac=0.2)
#X and y for holdout
final_X = final_val[model_columns]
final_y = final_val.iloc[:, -1]
# training data
data = df.drop(index= final_val.index)
X = data[model_columns]
y = data.iloc[:, -1]
display(X.info())
X.head()
```
# Feature Reduction
### Boruta
```
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=1000, max_depth=20, random_state=8, n_jobs=-1)
feat_selector = BorutaPy(rf, n_estimators='auto', verbose=2, max_iter = 200, random_state=8)
feat_selector.fit(X.values, y.values)
selected = X.values[:, feat_selector.support_]
print(selected.shape)
boruta_mask = feat_selector.support_
boruta_features = model_columns[boruta_mask]
boruta_df = df[model_columns[boruta_mask]]
```
### Lasso
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split, KFold
from sklearn.metrics import log_loss, accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
log_model = LogisticRegression(penalty='l1', solver='saga', max_iter=10000)
kf = KFold(n_splits=5, shuffle=True)
ll_performance = []
model_weights = []
for train_index, test_index in kf.split(X):
X_train, X_test = X.iloc[train_index], X.iloc[test_index]
y_train, y_test = y.iloc[train_index], y.iloc[test_index]
log_model.fit(X_train, y_train)
y_pred = log_model.predict_proba(X_test)
log_ll = log_loss(y_test, y_pred)
ll_performance.append(log_ll)
model_weights.append(log_model.coef_)
print(ll_performance)
average_weight = np.mean(model_weights, axis=0)[0]
def important_gene_mask(columns, coefs):
mask = coefs != 0
important_genes = columns[mask[0]]
print(len(important_genes))
return important_genes
lasso_k1 = set(important_gene_mask(model_columns, model_weights[0]))
lasso_k2 = set(important_gene_mask(model_columns, model_weights[1]))
lasso_k3 = set(important_gene_mask(model_columns, model_weights[2]))
lasso_k4 = set(important_gene_mask(model_columns, model_weights[3]))
lasso_k5 = set(important_gene_mask(model_columns, model_weights[4]))
lasso_gene_union = set.union(lasso_k1, lasso_k2, lasso_k3, lasso_k4, lasso_k5)
len(lasso_gene_union)
lasso_gene_intersection = set.intersection(lasso_k1, lasso_k2, lasso_k3, lasso_k4, lasso_k5)
len(lasso_gene_intersection)
lasso_columns = list(lasso_gene_union)
lasso_boruta_intersection = set.intersection(set(boruta_features), lasso_gene_intersection)
len(lasso_boruta_intersection)
lasso_boruta_intersection
gene_name = ['HOXA9', 'HOXA3', 'HOXA6', 'TPSG1', 'HOXA7', 'SPATA6', 'GPR12', 'LRP4',
'CPNE8', 'ST18', 'MPV17L', 'TRH', 'TPSAB1', 'GOLGA8M', 'GT2B11',
'ANKRD18B', 'AC055876.1', 'WHAMMP2', 'HOXA10-AS', 'HOXA10',
'HOXA-AS3', 'PDCD6IPP1', 'WHAMMP3']
gene_zip = list(zip(lasso_boruta_intersection, gene_name))
gene_zip
pd.DataFrame(gene_zip)
```
those are the feature deemed most important by both lasso rounds + boruta
```
boruta_not_lasso = set.difference(set(boruta_features), lasso_gene_union)
len(boruta_not_lasso)
```
25 features were considered important by boruta but not picked up by any of the lasso rounds...why?
| true |
code
| 0.325256 | null | null | null | null |
|
## Preamble
### Import libraries
```
import os, sys
# Import Pandas
import pandas as pd
# Import Plotly and Cufflinks
# Plotly username and API key should be set in environment variables
import plotly
plotly.tools.set_credentials_file(username=os.environ['PLOTLY_USERNAME'], api_key=os.environ['PLOTLY_KEY'])
import plotly.graph_objs as go
import cufflinks as cf
# Import numpy
import numpy as np
```
## Step 1:
### Import CSV containing photovoltaic performance of solar cells into Pandas Data Frame object
```
# Import module to read in secure data
sys.path.append('../data/NREL')
import retrieve_data as rd
solar = rd.retrieve_dirks_sheet()
```
## Step 2:
### Clean the data for inconsistencies
```
sys.path.append('utils')
import process_data as prd
prd.clean_data(solar)
```
## Step 3:
### Import functions from utils and define notebook-specific functions
```
import degradation_utils as du
def get_mode_correlation_percent(df, mode_1, mode_2, weighted):
"""
Return the percent of rows where two modes are seen together
Args:
df (DataFrame): Pandas DataFrame that has been cleaned using the clean_data function
mode_1 (string): Degradation mode to find in the DataFrame in pairing with mode_2
mode_2 (string): Degradation mode to find in the DataFrame in pairing with mode_1
weighted (bool): If true, count all modules in a system as degrading
If false, count a system as one degrading module
Returns:
float: The percentage of modules with both specified degradation modes
"""
# Calculate total number of modules
total_modules = du.get_total_modules(df, weighted)
if total_modules == 0:
return 0
if weighted:
single_modules = len(df[(df['System/module'] == 'Module') & (df[mode_1] == 1) & (df[mode_2] == 1)])
specified = df[(df['System/module'] != 'System') | (df['No.modules'].notnull())]
systems = specified[(specified['System/module'] != 'Module') &
(specified[mode_1] == 1) & (specified[mode_2] == 1)]['No.modules'].sum()
total = single_modules + systems
return float(total) / total_modules
else:
return float(len((df[(df[mode_1] == 1) & (df[mode_2] == 1)]))) / total_modules
def get_heatmap_data(df, modes, weighted):
"""
Returns a DataFrame used to construct a heatmap based on frequency of two degradation modes appearing together
Args:
df (DataFrame): A *cleaned* DataFrame containing the data entries to check modes from
modes (List of String): A list of all modes to check for in the DataFrame
weighted (bool): If true, count all modules in a system as degrading
If false, count a system as one degrading module
Returns:
heatmap (DataFrame): DataFrame containing all of degradation modes correlation frequency results
"""
# Initialize DataFrame to hold heatmap data
heatmap = pd.DataFrame(data=None, columns=modes, index=modes)
# Calculate all single mode percentages
mode_percentages = {}
for mode in modes:
mode_percentages[mode] = du.get_mode_percentage(df, mode, weighted)
# Iterate through every pair of modes
for mode_1 in modes:
for mode_2 in modes:
if mode_1 == mode_2:
heatmap.set_value(mode_1, mode_2, np.nan)
else:
print(mode_1 + " & " + mode_2)
heatmap_reflection = heatmap.at[mode_2, mode_1]
# If already calculated the reflection, save and skip
if (not pd.isnull(heatmap_reflection)):
heatmap.set_value(mode_1, mode_2, heatmap_reflection)
print('Skip, already calculated')
continue
percentage_1 = mode_percentages[mode_1]
percentage_2 = mode_percentages[mode_2]
print('Percentage 1: ' + str(percentage_1))
print('Percentage 2: ' + str(percentage_2))
if (percentage_1 == 0 or percentage_2 == 0):
heatmap.set_value(mode_1, mode_2, 0)
continue
percentage_both = get_mode_correlation_percent(df, mode_1, mode_2, weighted)
print('Percentage Both: ' + str(percentage_both))
result = float(percentage_both) / (percentage_1 * percentage_2)
print('Result: ' + str(result))
heatmap.set_value(mode_1, mode_2, result)
return heatmap
```
## Step 4: Generate heatmaps of correlation frequency between degradation modes
### Calculation
Find the correlation strength of all pairs of degradation modes by using the following formula:
P(Degradation mode A & Degradation mode B) / P(Degradation mode A)P(Degradation mode B)
### Weighted: Multiply data entries for module systems by number of modules
Number of degrading modules = # of degrading single modules + (# of degrading systems · # of modules per degrading system)
Total number of modules = # of single modules + (# of systems · # of modules per system)
P(Degradation mode X) = Number of degrading modules / Total number of modules
#### Generate heatmap for the entire dataset, regardless of time
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
sys_heatmap_all = get_heatmap_data(solar, modes, True)
sys_heatmap_all
sys_heatmap_all.iplot(kind='heatmap',colorscale='spectral',
filename='sys-heatmap-all', margin=(200,150,120,30))
```
#### Generate heatmap for the dataset of all modules installed before 2000
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
specified = solar[solar['Begin.Year'] < 2000]
sys_heatmap_pre_2000 = get_heatmap_data(specified, modes, True)
sys_heatmap_pre_2000
sys_heatmap_pre_2000.iplot(kind='heatmap',colorscale='spectral',
filename='sys-heatmap-pre-2000', margin=(200,150,120,30))
```
#### Generate heatmap for the dataset of all modules installed post 2000
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
specified = solar[solar['Begin.Year'] >= 2000]
sys_heatmap_post_2000 = get_heatmap_data(specified, modes, True)
sys_heatmap_post_2000
sys_heatmap_post_2000.iplot(kind='heatmap',colorscale='spectral',
filename='sys-heatmap-post-2000', margin=(200,150,120,30))
```
### Unweighted: Count module systems as single module
Number of degrading modules = # of degrading single modules + # of degrading systems
Total number of modules = # of single modules + # of systems
P(Degradation mode X) = Number of degrading modules / Total number of modules
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
modes_heatmap_all = get_heatmap_data(solar, modes, False)
modes_heatmap_all
modes_heatmap_all.iplot(kind='heatmap',colorscale='spectral',
filename='modes-heatmap-all', margin=(200,150,120,30))
```
#### Generate heatmap for the dataset of all modules installed before 2000
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
specified = solar[solar['Begin.Year'] < 2000]
modes_heatmap_pre_2000 = get_heatmap_data(specified, modes, False)
modes_heatmap_pre_2000
modes_heatmap_pre_2000.iplot(kind='heatmap',colorscale='spectral',
filename='modes-heatmap-pre-2000', margin=(200,150,120,30))
```
#### Generate heatmap for the dataset of all modules installed post 2000
```
modes = ['Encapsulant discoloration', 'Major delamination', 'Minor delamination',
'Backsheet other', 'Internal circuitry discoloration', 'Hot spots', 'Fractured cells',
'Diode/J-box problem', 'Glass breakage', 'Permanent soiling', 'Frame deformation']
specified = solar[solar['Begin.Year'] >= 2000]
modes_heatmap_post_2000 = get_heatmap_data(specified, modes, False)
modes_heatmap_post_2000
modes_heatmap_post_2000.iplot(kind='heatmap',colorscale='spectral',
filename='modes-heatmap-post-2000', margin=(200,150,120,30))
```
| true |
code
| 0.621254 | null | null | null | null |
|
# Task 9: Random Forests
_All credit for the code examples of this notebook goes to the book "Hands-On Machine Learning with Scikit-Learn & TensorFlow" by A. Geron. Modifications were made and text was added by K. Zoch in preparation for the hands-on sessions._
# Setup
First, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Function to save a figure. This also decides that all output files
# should stored in the subdirectorz 'classification'.
PROJECT_ROOT_DIR = "."
EXERCISE = "forests"
def save_fig(fig_id, tight_layout=True):
path = os.path.join(PROJECT_ROOT_DIR, "output", EXERCISE, fig_id + ".png")
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format='png', dpi=300)
```
# Bagging decision trees
First, let's create some half-moon data (as done in one of the earlier tasks).
```
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
```
This code example shows how "bagging" multiple decision trees can improve the classification performance, compared to a single decision tree. Notice how bias and variance change when combining 500 trees as in the example below (it can be seen very nicely in the plot). Please try the following:
1. How does the number of samples affect the performance of the ensemble classifier? Try changing it to the training size (m = 500), or go even higher.
2. How is the performance different when pasting is used instead of bagging (_no_ replacement of instances)?
3. How relevant is the number of trees in the ensemble?
```
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
# Create an instance of a bagging classifier, composed of
# 500 decision tree classifiers. bootstrap=True activates
# replacement when picking the random instances, i.e.
# turning it off will switch from bagging to pasting.
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
max_samples=100, bootstrap=True, n_jobs=-1, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
# Create an instance of a single decision tree to compare with.
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
# Now do the plotting of the two.
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[-1.5, 2.5, -1, 1.5], alpha=0.5, contour=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", alpha=alpha)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_decision_boundary(tree_clf, X, y)
plt.title("Decision Tree", fontsize=14)
plt.subplot(122)
plot_decision_boundary(bag_clf, X, y)
plt.title("Decision Trees with Bagging", fontsize=14)
save_fig("decision_tree_without_and_with_bagging_plot")
plt.show()
```
If you need an additional performance measure, you can use the accuracy score:
```
from sklearn.metrics import accuracy_score
print("Bagging ensemble: %s" % accuracy_score(y_test, y_pred))
print("Single tree: %s" % accuracy_score(y_test, y_pred_tree))
```
## Out-of-Bag evaluation
When a bagging classifier is used, evaluation of the performance can be performed _out-of-bag_. Remember what bagging does, and how many instances (on average) are picked from all training instances if the bag is chosen to be the same size as the number of training instances. The fraction of chosen instances should converge against something like
$$1 - \exp(-1) \approx 63.212\%$$
But that also means, that more than 35% of instances are _not seen_ in training. The [BaggingClassifier](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.BaggingClassifier.html) allows to set evaluation on out-of-bag instances automatically:
```
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42), n_estimators=500,
bootstrap=True, n_jobs=-1, oob_score=True, random_state=40)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_
```
# Boosting via AdaBoost
The performance of decision trees can be much improved through the procedure of _hypothesis boosting_. AdaBoost, probably the most popular algorithm, uses a very common technique: models are trained _sequentially_, where each model tries to correct for mistakes the previous model made. AdaBoost in particular _boosts_ the weights of those instances that were classified incorrectly. The next classifier will then be more sensitive to these instances and probably do an overall better job. In the end, the outputs of all sequential classifiers are combined into a prediction value. Each classifier enters this global value weighted according to its error rate. Please check/answer the following questions to familiarise yourself with AdaBoost:
1. What is the error rate of a predictor?
2. How is the weight for each predictor calculated?
3. How are weights of instances updated if they were classified correctly? How are they updated if classified incorrectly?
4. How is the final prediction made from an AdaBoost ensemble?
5. The [AdaBoostClassifier](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html) implements the AdaBoost algorithm in Scikit-Learn. The following bit of code implements AdaBoost with decision tree classifiers. Make yourself familiar with the class and its arguments, then try to tweak it to achieve better performance than in the example below!
```
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1), n_estimators=200,
algorithm="SAMME.R", learning_rate=0.5, random_state=42)
ada_clf.fit(X_train, y_train)
plot_decision_boundary(ada_clf, X, y)
```
The following bit of code is a visualisation of how the weight adjustment in AdaBoost works. While not relying on the above AdaBoostClassifier class, this implements a support vector machine classifier ([SVC](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html)) and boosts the weights of incorrectly classified instances by hand. With different learning rates, the "amount" of boosting can be controlled.
```
from sklearn.svm import SVC
m = len(X_train)
plt.figure(figsize=(11, 4))
for subplot, learning_rate in ((121, 1), (122, 0.5)):
# Start with equal weights for all instances.
sample_weights = np.ones(m)
plt.subplot(subplot)
# Now let's go through five iterations where the
# weights get adjusted based on the previous step.
for i in range(5):
# As an example, use SVM classifier with Gaussian kernel.
svm_clf = SVC(kernel="rbf", C=0.05, gamma="auto", random_state=42)
svm_clf.fit(X_train, y_train, sample_weight=sample_weights)
y_pred = svm_clf.predict(X_train)
# The most important step: increase the weights of
# incorrectly predicted instances according to the
# learning_rate parameter.
sample_weights[y_pred != y_train] *= (1 + learning_rate)
# And do the plotting.
plot_decision_boundary(svm_clf, X, y, alpha=0.2)
plt.title("learning_rate = {}".format(learning_rate), fontsize=16)
if subplot == 121:
plt.text(-0.7, -0.65, "1", fontsize=14)
plt.text(-0.6, -0.10, "2", fontsize=14)
plt.text(-0.5, 0.10, "3", fontsize=14)
plt.text(-0.4, 0.55, "4", fontsize=14)
plt.text(-0.3, 0.90, "5", fontsize=14)
save_fig("boosting_plot")
plt.show()
```
# Gradient Boosting
An alternative to AdaBoost is gradient boosting. Again, gradient boosting sequentially trains multiple predictors which are then combined for a global prediction in the end. Gradient boosting fits the new predictor to the _residual errors_ made by the previous predictor, but doesn't touch instance weights. This can be visualised very well with a regression problem (of course, classification can also be performed. Scikit-Learn comes with the two classes [GradientBoostingRegressor](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html) and [GradientBoostingClassifier](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html) for these tasks. As a first step, the following example implements regression with decision trees by hand.
First, generate our random data.
```
np.random.seed(42)
X = np.random.rand(100, 1) - 0.5
y = 3*X[:, 0]**2 + 0.05 * np.random.randn(100)
from sklearn.tree import DecisionTreeRegressor
# Start with the first tree and fit it to X, y.
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X, y)
# Calculate the residual errors the previous tree
# has made and fit a second tree to these.
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X, y2)
# Again, calculate the residual errors of the previous
# tree and fit a third tree.
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X, y3)
# And the rest is just plotting ...
def plot_predictions(regressors, X, y, axes, label=None, style="r-", data_style="b.", data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center", fontsize=16)
plt.axis(axes)
plt.figure(figsize=(11,11))
plt.subplot(321)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="g-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)
plt.subplot(322)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(323)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="g-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)
plt.subplot(324)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(325)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="g-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(326)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
save_fig("gradient_boosting_plot")
plt.show()
```
The following piece of code now uses the Scikit-Learn class for regression with gradient boosting. Two examples are given: (1) with a fast learning rate, but only very few predictors, (2) with a slower learning rate, but a high number of predictors. Clearly, the second ensemble overfits the problem. Can you try to tweak the parameters to get a model that generalises better?
```
from sklearn.ensemble import GradientBoostingRegressor
# First regression instance with only three estimaters,
# but a fast learning rate. The max_depth parameter
# controls the number of 'layers' in the decision
# tree estimators of the ensemble. Increase for stronger
# bias of the individual trees.
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=3, learning_rate=1.0, random_state=42)
gbrt.fit(X, y)
# Second instance with many estimators and slower
# learning rate.
gbrt_slow = GradientBoostingRegressor(max_depth=2, n_estimators=200, learning_rate=0.5, random_state=42)
gbrt_slow.fit(X, y)
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_predictions([gbrt], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="Ensemble predictions")
plt.title("learning_rate={}, n_estimators={}".format(gbrt.learning_rate, gbrt.n_estimators), fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_slow], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("learning_rate={}, n_estimators={}".format(gbrt_slow.learning_rate, gbrt_slow.n_estimators), fontsize=14)
save_fig("gbrt_learning_rate_plot")
plt.show()
```
One way to solve this overfitting is to use _early stopping_ to find the optimal number of iterations/predictors for this problem. For that, we first need to split the dataset into training and validation set, because of course we cannot evaluate performance on instances the predictor used in training. The following code implements the already known [model_selection.train_test_split](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) function. Then, train another ensemble (with a fixed number of 120 predictors), but this time only on the training set. Errors are calculated based on the validation set and the optimal number of iterations is extracted. The code also creates a plot of the performance on the validation set to point out the optimal iteration.
```
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Split dataset into training and validation set.
X_train, X_val, y_train, y_val = train_test_split(X, y, random_state=49)
# Fit an ensemble. Let's start with 120 estimators, which
# is probably too much (as we saw above).
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=120, random_state=42)
gbrt.fit(X_train, y_train)
# Calculate the errors for each iteration (on the validation set)
# and find the optimal iteration step.
errors = [mean_squared_error(y_val, y_pred)
for y_pred in gbrt.staged_predict(X_val)]
bst_n_estimators = np.argmin(errors)
min_error = np.min(errors)
# Retrain a new ensemble with those settings.
gbrt_best = GradientBoostingRegressor(max_depth=2,n_estimators=bst_n_estimators, random_state=42)
gbrt_best.fit(X_train, y_train)
# And do the plotting of validation error as well
# as the optimised ensemble.
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(errors, "b.-")
plt.plot([bst_n_estimators, bst_n_estimators], [0, min_error], "k--")
plt.plot([0, 120], [min_error, min_error], "k--")
plt.plot(bst_n_estimators, min_error, "ko")
plt.text(bst_n_estimators, min_error*1.2, "Minimum", ha="center", fontsize=14)
plt.axis([0, 120, 0, 0.01])
plt.xlabel("Number of trees")
plt.title("Validation error", fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_best], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("Best model (%d trees)" % bst_n_estimators, fontsize=14)
save_fig("early_stopping_gbrt_plot")
plt.show()
```
| true |
code
| 0.67346 | null | null | null | null |
|
<img src="https://github.com/pmservice/ai-openscale-tutorials/raw/master/notebooks/images/banner.png" align="left" alt="banner">
# Part 4: Drift Monitor
The notebook will train, create and deploy a Credit Risk model. It will then configure OpenScale to monitor drift in data and accuracy by injecting sample payloads for viewing in the OpenScale Insights dashboard.
### Contents
- [1. Setup](#setup)
- [2. Model building and deployment](#model)
- [3. OpenScale configuration](#openscale)
- [4. Generate drift model](#driftmodel)
- [5. Submit payload](#payload)
- [6. Enable drift monitoring](#monitor)
- [7. Run drift monitor](# )
# 1.0 Install Python Packages <a name="setup"></a>
```
import warnings
warnings.filterwarnings('ignore')
!rm -rf /home/spark/shared/user-libs/python3.6*
!pip install --upgrade ibm-ai-openscale==2.2.1 --no-cache --user | tail -n 1
!pip install --upgrade watson-machine-learning-client-V4==1.0.95 | tail -n 1
!pip install --upgrade pyspark==2.3 | tail -n 1
!pip install scikit-learn==0.20.2 | tail -n 1
```
### Action: restart the kernel!
```
import warnings
warnings.filterwarnings('ignore')
```
# 2.0 Configure credentials <a name="credentials"></a>
<font color=red>Replace the `username` and `password` values of `************` with your Cloud Pak for Data `username` and `password`. The value for `url` should match the `url` for your Cloud Pak for Data cluster, which you can get from the browser address bar (be sure to include the 'https://'.</font> The credentials should look something like this (these are example values, not the ones you will use):
```
WOS_CREDENTIALS = {
"url": "https://zen.clusterid.us-south.containers.appdomain.cloud",
"username": "cp4duser",
"password" : "cp4dpass"
}
```
**NOTE: Make sure that there is no trailing forward slash / in the url**
```
WOS_CREDENTIALS = {
"url": "************",
"username": "************",
"password": "************"
}
WML_CREDENTIALS = WOS_CREDENTIALS.copy()
WML_CREDENTIALS['instance_id']='openshift'
WML_CREDENTIALS['version']='3.0.0'
```
Lets retrieve the variables for the model and deployment we set up in the initial setup notebook. **If the output does not show any values, check to ensure you have completed the initial setup before continuing.**
```
%store -r MODEL_NAME
%store -r DEPLOYMENT_NAME
%store -r DEFAULT_SPACE
print("Model Name: ", MODEL_NAME, ". Deployment Name: ", DEPLOYMENT_NAME, ". Deployment Space: ", DEFAULT_SPACE)
```
# 3.0 Load the training data
```
!rm german_credit_data_biased_training.csv
!wget https://raw.githubusercontent.com/IBM/credit-risk-workshop-cpd/master/data/openscale/german_credit_data_biased_training.csv
import pandas as pd
data_df = pd.read_csv('german_credit_data_biased_training.csv', sep=",", header=0)
data_df.head()
```
# 4.0 Configure OpenScale <a name="openscale"></a>
The notebook will now import the necessary libraries and set up a Python OpenScale client.
```
from ibm_ai_openscale import APIClient4ICP
from ibm_ai_openscale.engines import *
from ibm_ai_openscale.utils import *
from ibm_ai_openscale.supporting_classes import PayloadRecord, Feature
from ibm_ai_openscale.supporting_classes.enums import *
from watson_machine_learning_client import WatsonMachineLearningAPIClient
import json
wml_client = WatsonMachineLearningAPIClient(WML_CREDENTIALS)
ai_client = APIClient4ICP(WOS_CREDENTIALS)
ai_client.version
subscription = None
if subscription is None:
subscriptions_uids = ai_client.data_mart.subscriptions.get_uids()
for sub in subscriptions_uids:
if ai_client.data_mart.subscriptions.get_details(sub)['entity']['asset']['name'] == MODEL_NAME:
print("Found existing subscription.")
subscription = ai_client.data_mart.subscriptions.get(sub)
if subscription is None:
print("No subscription found. Please run openscale-initial-setup.ipynb to configure.")
```
### Set Deployment UID
```
wml_client.set.default_space(DEFAULT_SPACE)
wml_deployments = wml_client.deployments.get_details()
deployment_uid = None
for deployment in wml_deployments['resources']:
print(deployment['entity']['name'])
if DEPLOYMENT_NAME == deployment['entity']['name']:
deployment_uid = deployment['metadata']['guid']
break
print(deployment_uid)
```
# 5.0 Generate drift model <a name="driftmodel"></a>
Drift requires a trained model to be uploaded manually for WML. You can train, create and download a drift detection model using the code below. The entire code can be found in the [training_statistics_notebook](https://github.com/IBM-Watson/aios-data-distribution/blob/master/training_statistics_notebook.ipynb) ( check for Drift detection model generation).
```
training_data_info = {
"class_label":'Risk',
"feature_columns":["CheckingStatus","LoanDuration","CreditHistory","LoanPurpose","LoanAmount","ExistingSavings","EmploymentDuration","InstallmentPercent","Sex","OthersOnLoan","CurrentResidenceDuration","OwnsProperty","Age","InstallmentPlans","Housing","ExistingCreditsCount","Job","Dependents","Telephone","ForeignWorker"],
"categorical_columns":["CheckingStatus","CreditHistory","LoanPurpose","ExistingSavings","EmploymentDuration","Sex","OthersOnLoan","OwnsProperty","InstallmentPlans","Housing","Job","Telephone","ForeignWorker"]
}
#Set model_type. Acceptable values are:["binary","multiclass","regression"]
model_type = "binary"
#model_type = "multiclass"
#model_type = "regression"
def score(training_data_frame):
WML_CREDENTAILS = WML_CREDENTIALS
#The data type of the label column and prediction column should be same .
#User needs to make sure that label column and prediction column array should have the same unique class labels
prediction_column_name = "predictedLabel"
probability_column_name = "probability"
feature_columns = list(training_data_frame.columns)
training_data_rows = training_data_frame[feature_columns].values.tolist()
#print(training_data_rows)
payload_scoring = {
wml_client.deployments.ScoringMetaNames.INPUT_DATA: [{
"fields": feature_columns,
"values": [x for x in training_data_rows]
}]
}
score = wml_client.deployments.score(deployment_uid, payload_scoring)
score_predictions = score.get('predictions')[0]
prob_col_index = list(score_predictions.get('fields')).index(probability_column_name)
predict_col_index = list(score_predictions.get('fields')).index(prediction_column_name)
if prob_col_index < 0 or predict_col_index < 0:
raise Exception("Missing prediction/probability column in the scoring response")
import numpy as np
probability_array = np.array([value[prob_col_index] for value in score_predictions.get('values')])
prediction_vector = np.array([value[predict_col_index] for value in score_predictions.get('values')])
return probability_array, prediction_vector
#Generate drift detection model
from ibm_wos_utils.drift.drift_trainer import DriftTrainer
drift_detection_input = {
"feature_columns":training_data_info.get('feature_columns'),
"categorical_columns":training_data_info.get('categorical_columns'),
"label_column": training_data_info.get('class_label'),
"problem_type": model_type
}
drift_trainer = DriftTrainer(data_df,drift_detection_input)
if model_type != "regression":
#Note: batch_size can be customized by user as per the training data size
drift_trainer.generate_drift_detection_model(score,batch_size=data_df.shape[0])
#Note: Two column constraints are not computed beyond two_column_learner_limit(default set to 200)
#User can adjust the value depending on the requirement
drift_trainer.learn_constraints(two_column_learner_limit=200)
drift_trainer.create_archive()
#Generate a download link for drift detection model
from IPython.display import HTML
import base64
import io
def create_download_link_for_ddm( title = "Download Drift detection model", filename = "drift_detection_model.tar.gz"):
#Retains stats information
with open(filename,'rb') as file:
ddm = file.read()
b64 = base64.b64encode(ddm)
payload = b64.decode()
html = '<a download="{filename}" href="data:text/json;base64,{payload}" target="_blank">{title}</a>'
html = html.format(payload=payload,title=title,filename=filename)
return HTML(html)
create_download_link_for_ddm()
```
# 6.0 Submit payload <a name="payload"></a>
### Score the model so we can configure monitors
Now that the WML service has been bound and the subscription has been created, we need to send a request to the model before we configure OpenScale. This allows OpenScale to create a payload log in the datamart with the correct schema, so it can capture data coming into and out of the model.
```
fields = ["CheckingStatus","LoanDuration","CreditHistory","LoanPurpose","LoanAmount","ExistingSavings","EmploymentDuration","InstallmentPercent","Sex","OthersOnLoan","CurrentResidenceDuration","OwnsProperty","Age","InstallmentPlans","Housing","ExistingCreditsCount","Job","Dependents","Telephone","ForeignWorker"]
values = [
["no_checking",13,"credits_paid_to_date","car_new",1343,"100_to_500","1_to_4",2,"female","none",3,"savings_insurance",46,"none","own",2,"skilled",1,"none","yes"],
["no_checking",24,"prior_payments_delayed","furniture",4567,"500_to_1000","1_to_4",4,"male","none",4,"savings_insurance",36,"none","free",2,"management_self-employed",1,"none","yes"],
["0_to_200",26,"all_credits_paid_back","car_new",863,"less_100","less_1",2,"female","co-applicant",2,"real_estate",38,"none","own",1,"skilled",1,"none","yes"],
["0_to_200",14,"no_credits","car_new",2368,"less_100","1_to_4",3,"female","none",3,"real_estate",29,"none","own",1,"skilled",1,"none","yes"],
["0_to_200",4,"no_credits","car_new",250,"less_100","unemployed",2,"female","none",3,"real_estate",23,"none","rent",1,"management_self-employed",1,"none","yes"],
["no_checking",17,"credits_paid_to_date","car_new",832,"100_to_500","1_to_4",2,"male","none",2,"real_estate",42,"none","own",1,"skilled",1,"none","yes"],
["no_checking",33,"outstanding_credit","appliances",5696,"unknown","greater_7",4,"male","co-applicant",4,"unknown",54,"none","free",2,"skilled",1,"yes","yes"],
["0_to_200",13,"prior_payments_delayed","retraining",1375,"100_to_500","4_to_7",3,"male","none",3,"real_estate",37,"none","own",2,"management_self-employed",1,"none","yes"]
]
payload_scoring = {"fields": fields,"values": values}
payload = {
wml_client.deployments.ScoringMetaNames.INPUT_DATA: [payload_scoring]
}
scoring_response = wml_client.deployments.score(deployment_uid, payload)
print('Single record scoring result:', '\n fields:', scoring_response['predictions'][0]['fields'], '\n values: ', scoring_response['predictions'][0]['values'][0])
```
# 7.0 Enable drift monitoring <a name="monitor"></a>
```
subscription.drift_monitoring.enable(threshold=0.05, min_records=10,model_path="./drift_detection_model.tar.gz")
```
# 8.0 Run Drift monitor on demand <a name="driftrun"></a>
```
!rm german_credit_feed.json
!wget https://raw.githubusercontent.com/IBM/credit-risk-workshop-cpd/master/data/openscale/german_credit_feed.json
import random
with open('german_credit_feed.json', 'r') as scoring_file:
scoring_data = json.load(scoring_file)
fields = scoring_data['fields']
values = []
for _ in range(10):
current = random.choice(scoring_data['values'])
#set age of all rows to 100 to increase drift values on dashboard
current[12] = 100
values.append(current)
payload_scoring = {"fields": fields, "values": values}
payload = {
wml_client.deployments.ScoringMetaNames.INPUT_DATA: [payload_scoring]
}
scoring_response = wml_client.deployments.score(deployment_uid, payload)
drift_run_details = subscription.drift_monitoring.run(background_mode=False)
subscription.drift_monitoring.get_table_content()
```
## Congratulations!
You have finished this section of the hands-on lab for IBM Watson OpenScale. You can now view the OpenScale dashboard by going to the Cloud Pak for Data `Home` page, and clicking `Services`. Choose the `OpenScale` tile and click the menu to `Open`. Click on the tile for the model you've created to see the monitors.
OpenScale shows model performance over time. You have two options to keep data flowing to your OpenScale graphs:
* Download, configure and schedule the [model feed notebook](https://raw.githubusercontent.com/emartensibm/german-credit/master/german_credit_scoring_feed.ipynb). This notebook can be set up with your WML credentials, and scheduled to provide a consistent flow of scoring requests to your model, which will appear in your OpenScale monitors.
* Re-run this notebook. Running this notebook from the beginning will delete and re-create the model and deployment, and re-create the historical data. Please note that the payload and measurement logs for the previous deployment will continue to be stored in your datamart, and can be deleted if necessary.
This notebook has been adapted from notebooks available at https://github.com/pmservice/ai-openscale-tutorials.
| true |
code
| 0.513668 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/TheoPantaz/Motor-Imagery-Classification-with-Tensorflow-and-MNE/blob/master/Motor_Imagery_clsf.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Install mne
```
!pip install mne
```
Import libraries
```
import scipy.io as sio
import sklearn.preprocessing as skpr
import mne
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
```
Import data
```
from google.colab import drive
drive.mount('/content/drive')
def import_from_mat(filename):
dataset = sio.loadmat(filename, chars_as_strings = True)
return dataset['EEG'], dataset['LABELS'].flatten(), dataset['Fs'][0][0], dataset['events'].T
filename = '/content/drive/My Drive/PANTAZ_s2'
EEG, LABELS, Fs, events = import_from_mat(filename)
```
Normalize data
```
def standardize(data):
scaler = skpr.StandardScaler()
return scaler.fit_transform(data)
EEG = standardize(EEG)
```
Create mne object
```
channel_names = ['c1', 'c2', 'c3', 'c4', 'cp1', 'cp2', 'cp3', 'cp4']
channel_type = 'eeg'
def create_mne_object(EEG, channel_names, channel_type):
info = mne.create_info(channel_names, Fs, ch_types = channel_type)
raw = mne.io.RawArray(EEG.T, info)
return raw
raw = create_mne_object(EEG, channel_names, channel_type)
```
filtering
```
def filtering(raw, low_freq, high_freq):
# Notch filtering
freqs = (50, 100)
raw = raw.notch_filter(freqs = freqs)
# Apply band-pass filter
raw.filter(low_freq, high_freq, fir_design = 'firwin', skip_by_annotation = 'edge')
return raw
low_freq = 7.
high_freq = 30.
filtered = filtering(raw, low_freq, high_freq)
```
Epoching the data
> IM_dur = duration of original epoch
> last_start_of_epoch : at what point(percentage) of the original epoch will the last new epoch start
```
def Epoch_Setup(events, IM_dur, step, last_start_of_epoch):
IM_dur = int(IM_dur * Fs)
step = int(step * IM_dur)
last_start_of_epoch = int(last_start_of_epoch * IM_dur)
print(last_start_of_epoch)
steps_sum = int(last_start_of_epoch / step)
new_events = [[],[],[]]
for index in events:
new_events[0].extend(np.arange(index[0], index[0] + last_start_of_epoch, step))
new_events[1].extend([0] * steps_sum)
new_events[2].extend([index[-1]] * steps_sum)
new_events = np.array(new_events).T
return new_events
def Epochs(data, events, tmin, tmax):
epochs = mne.Epochs(data, events=events, tmin=tmin, tmax=tmax, preload=True, baseline=None, proj=True)
epoched_data = epochs.get_data()
labels = epochs.events[:, -1]
return epoched_data, labels
IM_dur = 4
step = 1/250
last_start_of_epoch = 0.5
tmix = -1
tmax = 2
new_events = Epoch_Setup(events, IM_dur, step, last_start_of_epoch)
epoched_data, labels = Epochs(filtered, new_events, tmix, tmax)
```
Split training and testing data
```
def data_split(data, labels, split):
split = int(split * data.shape[0])
X_train = epoched_data[:split]
X_test = epoched_data[split:]
Y_train = labels[:split]
Y_test = labels[split:]
return X_train, X_test, Y_train, Y_test
split = 0.5
X_train, X_test, Y_train, Y_test = data_split(epoched_data, labels, split)
print(X_train.shape)
print(Y_train.shape)
```
CSP fit and transform
```
components = 8
csp = mne.decoding.CSP(n_components=components, reg='oas', log = None, norm_trace=True)
X_train = csp.fit_transform(X_train, Y_train)
X_test = csp.transform(X_test)
```
Data reshape for Tensorflow model
> Create batches for LSTM
```
def reshape_data(X_train, X_test, labels, final_reshape):
X_train = np.reshape(X_train, (int(X_train.shape[0]/final_reshape), final_reshape, X_train.shape[-1]))
X_test = np.reshape(X_test, (int(X_test.shape[0]/final_reshape), final_reshape, X_test.shape[-1]))
n_labels = []
for i in range(0,len(labels),final_reshape):
n_labels.append(labels[i])
Labels = np.array(n_labels)
Y_train = Labels[:X_train.shape[0]] - 1
Y_test = Labels[X_train.shape[0]:] - 1
return X_train, X_test, Y_train, Y_test
reshape_factor = int(last_start_of_epoch / step)
final_reshape = int(reshape_factor)
X_train, X_test, Y_train, Y_test = reshape_data(X_train, X_test, labels, final_reshape)
```
Create tensorflow model
```
model = tf.keras.Sequential([
tf.keras.layers.LSTM(128, input_shape = [None,X_train.shape[-1]], return_sequences = True),
tf.keras.layers.LSTM(256),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(64, activation = 'relu'),
tf.keras.layers.Dense(64, activation = 'relu'),
tf.keras.layers.Dense(1, activation = 'sigmoid')
])
model.compile(loss='binary_crossentropy',optimizer=tf.keras.optimizers.Adam(lr = 0.0001),metrics=['accuracy'])
model.summary()
```
Model fit
```
history = model.fit(X_train, Y_train, epochs= 50, batch_size = 25, validation_data=(X_test, Y_test), verbose=1)
```
Accuracy and plot loss
```
%matplotlib inline
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'r', label='Training Loss')
plt.plot(epochs, val_loss, 'b', label='Validation Loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
Running classifier
```
tmin = -1
tmax = 4
epoched_data_running, labels_running = Epochs(filtered, events, tmix, tmax)
split = 0.5
split = int(split * epoched_data_running.shape[0])
X_test_running = epoched_data_running[split:]
Y_test_running = LABELS[split:-1] - 1
w_length = int(Fs * 1.5) # running classifier: window length
w_step = int(Fs/250) # running classifier: window step size
w_start = np.arange(0, X_test_running.shape[2] - w_length, w_step)
final_reshape = int(reshape_factor/4)
scores = []
batch_data = []
for i, n in enumerate(w_start):
data = csp.transform(X_test_running[...,n:n+w_length])
batch_data.append(data)
if (i+1) % final_reshape == 0:
batch_data = np.transpose(np.array(batch_data), (1,0,2))
scores.append(model.evaluate(batch_data, Y_test_running))
batch_data = []
scores = np.array(scores)
w_times = (np.arange(0, X_test_running.shape[2] - w_length, final_reshape * w_step) + w_length / 2.) / Fs + tmin
w_times = w_times[:-1]
plt.figure()
plt.plot(w_times, scores[:,1], label='Score')
plt.axvline(0, linestyle='--', color='k', label='Onset')
plt.axhline(0.5, linestyle='-', color='k', label='Chance')
plt.xlabel('time (s)')
plt.ylabel('classification accuracy')
plt.title('Classification score over time')
plt.legend(loc='lower right')
plt.show()
```
| true |
code
| 0.659049 | null | null | null | null |
|
# Titanic Data Science Solutions
### This notebook is a companion to the book [Data Science Solutions](https://www.amazon.com/Data-Science-Solutions-Startup-Workflow/dp/1520545312).
The notebook walks us through a typical workflow for solving data science competitions at sites like Kaggle.
There are several excellent notebooks to study data science competition entries. However many will skip some of the explanation on how the solution is developed as these notebooks are developed by experts for experts. The objective of this notebook is to follow a step-by-step workflow, explaining each step and rationale for every decision we take during solution development.
## Workflow stages
The competition solution workflow goes through seven stages described in the Data Science Solutions book.
1. Question or problem definition.
2. Acquire training and testing data.
3. Wrangle, prepare, cleanse the data.
4. Analyze, identify patterns, and explore the data.
5. Model, predict and solve the problem.
6. Visualize, report, and present the problem solving steps and final solution.
7. Supply or submit the results.
The workflow indicates general sequence of how each stage may follow the other. However there are use cases with exceptions.
- We may combine mulitple workflow stages. We may analyze by visualizing data.
- Perform a stage earlier than indicated. We may analyze data before and after wrangling.
- Perform a stage multiple times in our workflow. Visualize stage may be used multiple times.
- Drop a stage altogether. We may not need supply stage to productize or service enable our dataset for a competition.
## Question and problem definition
Competition sites like Kaggle define the problem to solve or questions to ask while providing the datasets for training your data science model and testing the model results against a test dataset. The question or problem definition for Titanic Survival competition is [described here at Kaggle](https://www.kaggle.com/c/titanic).
> Knowing from a training set of samples listing passengers who survived or did not survive the Titanic disaster, can our model determine based on a given test dataset not containing the survival information, if these passengers in the test dataset survived or not.
We may also want to develop some early understanding about the domain of our problem. This is described on the [Kaggle competition description page here](https://www.kaggle.com/c/titanic). Here are the highlights to note.
- On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. Translated 32% survival rate.
- One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew.
- Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.
## Workflow goals
The data science solutions workflow solves for seven major goals.
**Classifying.** We may want to classify or categorize our samples. We may also want to understand the implications or correlation of different classes with our solution goal.
**Correlating.** One can approach the problem based on available features within the training dataset. Which features within the dataset contribute significantly to our solution goal? Statistically speaking is there a [correlation](https://en.wikiversity.org/wiki/Correlation) among a feature and solution goal? As the feature values change does the solution state change as well, and visa-versa? This can be tested both for numerical and categorical features in the given dataset. We may also want to determine correlation among features other than survival for subsequent goals and workflow stages. Correlating certain features may help in creating, completing, or correcting features.
**Converting.** For modeling stage, one needs to prepare the data. Depending on the choice of model algorithm one may require all features to be converted to numerical equivalent values. So for instance converting text categorical values to numeric values.
**Completing.** Data preparation may also require us to estimate any missing values within a feature. Model algorithms may work best when there are no missing values.
**Correcting.** We may also analyze the given training dataset for errors or possibly innacurate values within features and try to corrent these values or exclude the samples containing the errors. One way to do this is to detect any outliers among our samples or features. We may also completely discard a feature if it is not contribting to the analysis or may significantly skew the results.
**Creating.** Can we create new features based on an existing feature or a set of features, such that the new feature follows the correlation, conversion, completeness goals.
**Charting.** How to select the right visualization plots and charts depending on nature of the data and the solution goals.
## Refactor Release 2017-Jan-29
We are significantly refactoring the notebook based on (a) comments received by readers, (b) issues in porting notebook from Jupyter kernel (2.7) to Kaggle kernel (3.5), and (c) review of few more best practice kernels.
### User comments
- Combine training and test data for certain operations like converting titles across dataset to numerical values. (thanks @Sharan Naribole)
- Correct observation - nearly 30% of the passengers had siblings and/or spouses aboard. (thanks @Reinhard)
- Correctly interpreting logistic regresssion coefficients. (thanks @Reinhard)
### Porting issues
- Specify plot dimensions, bring legend into plot.
### Best practices
- Performing feature correlation analysis early in the project.
- Using multiple plots instead of overlays for readability.
```
# data analysis and wrangling
import pandas as pd
import numpy as np
import random as rnd
# visualization
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# machine learning
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
```
## Acquire data
The Python Pandas packages helps us work with our datasets. We start by acquiring the training and testing datasets into Pandas DataFrames. We also combine these datasets to run certain operations on both datasets together.
```
train_df = pd.read_csv('../input/train.csv')
test_df = pd.read_csv('../input/test.csv')
combine = [train_df, test_df]
```
## Analyze by describing data
Pandas also helps describe the datasets answering following questions early in our project.
**Which features are available in the dataset?**
Noting the feature names for directly manipulating or analyzing these. These feature names are described on the [Kaggle data page here](https://www.kaggle.com/c/titanic/data).
```
print(train_df.columns.values)
```
**Which features are categorical?**
These values classify the samples into sets of similar samples. Within categorical features are the values nominal, ordinal, ratio, or interval based? Among other things this helps us select the appropriate plots for visualization.
- Categorical: Survived, Sex, and Embarked. Ordinal: Pclass.
**Which features are numerical?**
Which features are numerical? These values change from sample to sample. Within numerical features are the values discrete, continuous, or timeseries based? Among other things this helps us select the appropriate plots for visualization.
- Continous: Age, Fare. Discrete: SibSp, Parch.
```
# preview the data
train_df.head()
```
**Which features are mixed data types?**
Numerical, alphanumeric data within same feature. These are candidates for correcting goal.
- Ticket is a mix of numeric and alphanumeric data types. Cabin is alphanumeric.
**Which features may contain errors or typos?**
This is harder to review for a large dataset, however reviewing a few samples from a smaller dataset may just tell us outright, which features may require correcting.
- Name feature may contain errors or typos as there are several ways used to describe a name including titles, round brackets, and quotes used for alternative or short names.
```
train_df.tail()
```
**Which features contain blank, null or empty values?**
These will require correcting.
- Cabin > Age > Embarked features contain a number of null values in that order for the training dataset.
- Cabin > Age are incomplete in case of test dataset.
**What are the data types for various features?**
Helping us during converting goal.
- Seven features are integer or floats. Six in case of test dataset.
- Five features are strings (object).
```
train_df.info()
print('_'*40)
test_df.info()
```
**What is the distribution of numerical feature values across the samples?**
This helps us determine, among other early insights, how representative is the training dataset of the actual problem domain.
- Total samples are 891 or 40% of the actual number of passengers on board the Titanic (2,224).
- Survived is a categorical feature with 0 or 1 values.
- Around 38% samples survived representative of the actual survival rate at 32%.
- Most passengers (> 75%) did not travel with parents or children.
- Nearly 30% of the passengers had siblings and/or spouse aboard.
- Fares varied significantly with few passengers (<1%) paying as high as $512.
- Few elderly passengers (<1%) within age range 65-80.
```
train_df.describe()
# Review survived rate using `percentiles=[.61, .62]` knowing our problem description mentions 38% survival rate.
# Review Parch distribution using `percentiles=[.75, .8]`
# SibSp distribution `[.68, .69]`
# Age and Fare `[.1, .2, .3, .4, .5, .6, .7, .8, .9, .99]`
```
**What is the distribution of categorical features?**
- Names are unique across the dataset (count=unique=891)
- Sex variable as two possible values with 65% male (top=male, freq=577/count=891).
- Cabin values have several dupicates across samples. Alternatively several passengers shared a cabin.
- Embarked takes three possible values. S port used by most passengers (top=S)
- Ticket feature has high ratio (22%) of duplicate values (unique=681).
```
train_df.describe(include=['O'])
```
### Assumtions based on data analysis
We arrive at following assumptions based on data analysis done so far. We may validate these assumptions further before taking appropriate actions.
**Correlating.**
We want to know how well does each feature correlate with Survival. We want to do this early in our project and match these quick correlations with modelled correlations later in the project.
**Completing.**
1. We may want to complete Age feature as it is definitely correlated to survival.
2. We may want to complete the Embarked feature as it may also correlate with survival or another important feature.
**Correcting.**
1. Ticket feature may be dropped from our analysis as it contains high ratio of duplicates (22%) and there may not be a correlation between Ticket and survival.
2. Cabin feature may be dropped as it is highly incomplete or contains many null values both in training and test dataset.
3. PassengerId may be dropped from training dataset as it does not contribute to survival.
4. Name feature is relatively non-standard, may not contribute directly to survival, so maybe dropped.
**Creating.**
1. We may want to create a new feature called Family based on Parch and SibSp to get total count of family members on board.
2. We may want to engineer the Name feature to extract Title as a new feature.
3. We may want to create new feature for Age bands. This turns a continous numerical feature into an ordinal categorical feature.
4. We may also want to create a Fare range feature if it helps our analysis.
**Classifying.**
We may also add to our assumptions based on the problem description noted earlier.
1. Women (Sex=female) were more likely to have survived.
2. Children (Age<?) were more likely to have survived.
3. The upper-class passengers (Pclass=1) were more likely to have survived.
## Analyze by pivoting features
To confirm some of our observations and assumptions, we can quickly analyze our feature correlations by pivoting features against each other. We can only do so at this stage for features which do not have any empty values. It also makes sense doing so only for features which are categorical (Sex), ordinal (Pclass) or discrete (SibSp, Parch) type.
- **Pclass** We observe significant correlation (>0.5) among Pclass=1 and Survived (classifying #3). We decide to include this feature in our model.
- **Sex** We confirm the observation during problem definition that Sex=female had very high survival rate at 74% (classifying #1).
- **SibSp and Parch** These features have zero correlation for certain values. It may be best to derive a feature or a set of features from these individual features (creating #1).
```
train_df[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean().sort_values(by='Survived', ascending=False)
train_df[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean().sort_values(by='Survived', ascending=False)
train_df[["SibSp", "Survived"]].groupby(['SibSp'], as_index=False).mean().sort_values(by='Survived', ascending=False)
train_df[["Parch", "Survived"]].groupby(['Parch'], as_index=False).mean().sort_values(by='Survived', ascending=False)
```
## Analyze by visualizing data
Now we can continue confirming some of our assumptions using visualizations for analyzing the data.
### Correlating numerical features
Let us start by understanding correlations between numerical features and our solution goal (Survived).
A histogram chart is useful for analyzing continous numerical variables like Age where banding or ranges will help identify useful patterns. The histogram can indicate distribution of samples using automatically defined bins or equally ranged bands. This helps us answer questions relating to specific bands (Did infants have better survival rate?)
Note that x-axis in historgram visualizations represents the count of samples or passengers.
**Observations.**
- Infants (Age <=4) had high survival rate.
- Oldest passengers (Age = 80) survived.
- Large number of 15-25 year olds did not survive.
- Most passengers are in 15-35 age range.
**Decisions.**
This simple analysis confirms our assumptions as decisions for subsequent workflow stages.
- We should consider Age (our assumption classifying #2) in our model training.
- Complete the Age feature for null values (completing #1).
- We should band age groups (creating #3).
```
g = sns.FacetGrid(train_df, col='Survived')
g.map(plt.hist, 'Age', bins=20)
```
### Correlating numerical and ordinal features
We can combine multiple features for identifying correlations using a single plot. This can be done with numerical and categorical features which have numeric values.
**Observations.**
- Pclass=3 had most passengers, however most did not survive. Confirms our classifying assumption #2.
- Infant passengers in Pclass=2 and Pclass=3 mostly survived. Further qualifies our classifying assumption #2.
- Most passengers in Pclass=1 survived. Confirms our classifying assumption #3.
- Pclass varies in terms of Age distribution of passengers.
**Decisions.**
- Consider Pclass for model training.
```
# grid = sns.FacetGrid(train_df, col='Pclass', hue='Survived')
grid = sns.FacetGrid(train_df, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend();
```
### Correlating categorical features
Now we can correlate categorical features with our solution goal.
**Observations.**
- Female passengers had much better survival rate than males. Confirms classifying (#1).
- Exception in Embarked=C where males had higher survival rate. This could be a correlation between Pclass and Embarked and in turn Pclass and Survived, not necessarily direct correlation between Embarked and Survived.
- Males had better survival rate in Pclass=3 when compared with Pclass=2 for C and Q ports. Completing (#2).
- Ports of embarkation have varying survival rates for Pclass=3 and among male passengers. Correlating (#1).
**Decisions.**
- Add Sex feature to model training.
- Complete and add Embarked feature to model training.
```
# grid = sns.FacetGrid(train_df, col='Embarked')
grid = sns.FacetGrid(train_df, row='Embarked', size=2.2, aspect=1.6)
grid.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', palette='deep')
grid.add_legend()
```
### Correlating categorical and numerical features
We may also want to correlate categorical features (with non-numeric values) and numeric features. We can consider correlating Embarked (Categorical non-numeric), Sex (Categorical non-numeric), Fare (Numeric continuous), with Survived (Categorical numeric).
**Observations.**
- Higher fare paying passengers had better survival. Confirms our assumption for creating (#4) fare ranges.
- Port of embarkation correlates with survival rates. Confirms correlating (#1) and completing (#2).
**Decisions.**
- Consider banding Fare feature.
```
# grid = sns.FacetGrid(train_df, col='Embarked', hue='Survived', palette={0: 'k', 1: 'w'})
grid = sns.FacetGrid(train_df, row='Embarked', col='Survived', size=2.2, aspect=1.6)
grid.map(sns.barplot, 'Sex', 'Fare', alpha=.5, ci=None)
grid.add_legend()
```
## Wrangle data
We have collected several assumptions and decisions regarding our datasets and solution requirements. So far we did not have to change a single feature or value to arrive at these. Let us now execute our decisions and assumptions for correcting, creating, and completing goals.
### Correcting by dropping features
This is a good starting goal to execute. By dropping features we are dealing with fewer data points. Speeds up our notebook and eases the analysis.
Based on our assumptions and decisions we want to drop the Cabin (correcting #2) and Ticket (correcting #1) features.
Note that where applicable we perform operations on both training and testing datasets together to stay consistent.
```
print("Before", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape)
train_df = train_df.drop(['Ticket', 'Cabin'], axis=1)
test_df = test_df.drop(['Ticket', 'Cabin'], axis=1)
combine = [train_df, test_df]
"After", train_df.shape, test_df.shape, combine[0].shape, combine[1].shape
```
### Creating new feature extracting from existing
We want to analyze if Name feature can be engineered to extract titles and test correlation between titles and survival, before dropping Name and PassengerId features.
In the following code we extract Title feature using regular expressions. The RegEx pattern `(\w+\.)` matches the first word which ends with a dot character within Name feature. The `expand=False` flag returns a DataFrame.
**Observations.**
When we plot Title, Age, and Survived, we note the following observations.
- Most titles band Age groups accurately. For example: Master title has Age mean of 5 years.
- Survival among Title Age bands varies slightly.
- Certain titles mostly survived (Mme, Lady, Sir) or did not (Don, Rev, Jonkheer).
**Decision.**
- We decide to retain the new Title feature for model training.
```
for dataset in combine:
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
pd.crosstab(train_df['Title'], train_df['Sex'])
```
We can replace many titles with a more common name or classify them as `Rare`.
```
for dataset in combine:
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
train_df[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
```
We can convert the categorical titles to ordinal.
```
title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Rare": 5}
for dataset in combine:
dataset['Title'] = dataset['Title'].map(title_mapping)
dataset['Title'] = dataset['Title'].fillna(0)
train_df.head()
```
Now we can safely drop the Name feature from training and testing datasets. We also do not need the PassengerId feature in the training dataset.
```
train_df = train_df.drop(['Name', 'PassengerId'], axis=1)
test_df = test_df.drop(['Name'], axis=1)
combine = [train_df, test_df]
train_df.shape, test_df.shape
```
### Converting a categorical feature
Now we can convert features which contain strings to numerical values. This is required by most model algorithms. Doing so will also help us in achieving the feature completing goal.
Let us start by converting Sex feature to a new feature called Gender where female=1 and male=0.
```
for dataset in combine:
dataset['Sex'] = dataset['Sex'].map( {'female': 1, 'male': 0} ).astype(int)
train_df.head()
```
### Completing a numerical continuous feature
Now we should start estimating and completing features with missing or null values. We will first do this for the Age feature.
We can consider three methods to complete a numerical continuous feature.
1. A simple way is to generate random numbers between mean and [standard deviation](https://en.wikipedia.org/wiki/Standard_deviation).
2. More accurate way of guessing missing values is to use other correlated features. In our case we note correlation among Age, Gender, and Pclass. Guess Age values using [median](https://en.wikipedia.org/wiki/Median) values for Age across sets of Pclass and Gender feature combinations. So, median Age for Pclass=1 and Gender=0, Pclass=1 and Gender=1, and so on...
3. Combine methods 1 and 2. So instead of guessing age values based on median, use random numbers between mean and standard deviation, based on sets of Pclass and Gender combinations.
Method 1 and 3 will introduce random noise into our models. The results from multiple executions might vary. We will prefer method 2.
```
# grid = sns.FacetGrid(train_df, col='Pclass', hue='Gender')
grid = sns.FacetGrid(train_df, row='Pclass', col='Sex', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend()
```
Let us start by preparing an empty array to contain guessed Age values based on Pclass x Gender combinations.
```
guess_ages = np.zeros((2,3))
guess_ages
```
Now we iterate over Sex (0 or 1) and Pclass (1, 2, 3) to calculate guessed values of Age for the six combinations.
```
for dataset in combine:
for i in range(0, 2):
for j in range(0, 3):
guess_df = dataset[(dataset['Sex'] == i) & \
(dataset['Pclass'] == j+1)]['Age'].dropna()
# age_mean = guess_df.mean()
# age_std = guess_df.std()
# age_guess = rnd.uniform(age_mean - age_std, age_mean + age_std)
age_guess = guess_df.median()
# Convert random age float to nearest .5 age
guess_ages[i,j] = int( age_guess/0.5 + 0.5 ) * 0.5
for i in range(0, 2):
for j in range(0, 3):
dataset.loc[ (dataset.Age.isnull()) & (dataset.Sex == i) & (dataset.Pclass == j+1),\
'Age'] = guess_ages[i,j]
dataset['Age'] = dataset['Age'].astype(int)
train_df.head()
```
Let us create Age bands and determine correlations with Survived.
```
train_df['AgeBand'] = pd.cut(train_df['Age'], 5)
train_df[['AgeBand', 'Survived']].groupby(['AgeBand'], as_index=False).mean().sort_values(by='AgeBand', ascending=True)
```
Let us replace Age with ordinals based on these bands.
```
for dataset in combine:
dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
dataset.loc[ dataset['Age'] > 64, 'Age']
train_df.head()
```
We can not remove the AgeBand feature.
```
train_df = train_df.drop(['AgeBand'], axis=1)
combine = [train_df, test_df]
train_df.head()
```
### Create new feature combining existing features
We can create a new feature for FamilySize which combines Parch and SibSp. This will enable us to drop Parch and SibSp from our datasets.
```
for dataset in combine:
dataset['FamilySize'] = dataset['SibSp'] + dataset['Parch'] + 1
train_df[['FamilySize', 'Survived']].groupby(['FamilySize'], as_index=False).mean().sort_values(by='Survived', ascending=False)
```
We can create another feature called IsAlone.
```
for dataset in combine:
dataset['IsAlone'] = 0
dataset.loc[dataset['FamilySize'] == 1, 'IsAlone'] = 1
train_df[['IsAlone', 'Survived']].groupby(['IsAlone'], as_index=False).mean()
```
Let us drop Parch, SibSp, and FamilySize features in favor of IsAlone.
```
train_df = train_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
test_df = test_df.drop(['Parch', 'SibSp', 'FamilySize'], axis=1)
combine = [train_df, test_df]
train_df.head()
```
We can also create an artificial feature combining Pclass and Age.
```
for dataset in combine:
dataset['Age*Class'] = dataset.Age * dataset.Pclass
train_df.loc[:, ['Age*Class', 'Age', 'Pclass']].head(10)
```
### Completing a categorical feature
Embarked feature takes S, Q, C values based on port of embarkation. Our training dataset has two missing values. We simply fill these with the most common occurance.
```
freq_port = train_df.Embarked.dropna().mode()[0]
freq_port
for dataset in combine:
dataset['Embarked'] = dataset['Embarked'].fillna(freq_port)
train_df[['Embarked', 'Survived']].groupby(['Embarked'], as_index=False).mean().sort_values(by='Survived', ascending=False)
```
### Converting categorical feature to numeric
We can now convert the EmbarkedFill feature by creating a new numeric Port feature.
```
for dataset in combine:
dataset['Embarked'] = dataset['Embarked'].map( {'S': 0, 'C': 1, 'Q': 2} ).astype(int)
train_df.head()
```
### Quick completing and converting a numeric feature
We can now complete the Fare feature for single missing value in test dataset using mode to get the value that occurs most frequently for this feature. We do this in a single line of code.
Note that we are not creating an intermediate new feature or doing any further analysis for correlation to guess missing feature as we are replacing only a single value. The completion goal achieves desired requirement for model algorithm to operate on non-null values.
We may also want round off the fare to two decimals as it represents currency.
```
test_df['Fare'].fillna(test_df['Fare'].dropna().median(), inplace=True)
test_df.head()
```
We can not create FareBand.
```
train_df['FareBand'] = pd.qcut(train_df['Fare'], 4)
train_df[['FareBand', 'Survived']].groupby(['FareBand'], as_index=False).mean().sort_values(by='FareBand', ascending=True)
```
Convert the Fare feature to ordinal values based on the FareBand.
```
for dataset in combine:
dataset.loc[ dataset['Fare'] <= 7.91, 'Fare'] = 0
dataset.loc[(dataset['Fare'] > 7.91) & (dataset['Fare'] <= 14.454), 'Fare'] = 1
dataset.loc[(dataset['Fare'] > 14.454) & (dataset['Fare'] <= 31), 'Fare'] = 2
dataset.loc[ dataset['Fare'] > 31, 'Fare'] = 3
dataset['Fare'] = dataset['Fare'].astype(int)
train_df = train_df.drop(['FareBand'], axis=1)
combine = [train_df, test_df]
train_df.head(10)
```
And the test dataset.
```
test_df.head(10)
```
## Model, predict and solve
Now we are ready to train a model and predict the required solution. There are 60+ predictive modelling algorithms to choose from. We must understand the type of problem and solution requirement to narrow down to a select few models which we can evaluate. Our problem is a classification and regression problem. We want to identify relationship between output (Survived or not) with other variables or features (Gender, Age, Port...). We are also perfoming a category of machine learning which is called supervised learning as we are training our model with a given dataset. With these two criteria - Supervised Learning plus Classification and Regression, we can narrow down our choice of models to a few. These include:
- Logistic Regression
- KNN or k-Nearest Neighbors
- Support Vector Machines
- Naive Bayes classifier
- Decision Tree
- Random Forrest
- Perceptron
- Artificial neural network
- RVM or Relevance Vector Machine
```
X_train = train_df.drop("Survived", axis=1)
Y_train = train_df["Survived"]
X_test = test_df.drop("PassengerId", axis=1).copy()
X_train.shape, Y_train.shape, X_test.shape
```
Logistic Regression is a useful model to run early in the workflow. Logistic regression measures the relationship between the categorical dependent variable (feature) and one or more independent variables (features) by estimating probabilities using a logistic function, which is the cumulative logistic distribution. Reference [Wikipedia](https://en.wikipedia.org/wiki/Logistic_regression).
Note the confidence score generated by the model based on our training dataset.
```
# Logistic Regression
logreg = LogisticRegression()
logreg.fit(X_train, Y_train)
Y_pred = logreg.predict(X_test)
acc_log = round(logreg.score(X_train, Y_train) * 100, 2)
acc_log
```
We can use Logistic Regression to validate our assumptions and decisions for feature creating and completing goals. This can be done by calculating the coefficient of the features in the decision function.
Positive coefficients increase the log-odds of the response (and thus increase the probability), and negative coefficients decrease the log-odds of the response (and thus decrease the probability).
- Sex is highest positivie coefficient, implying as the Sex value increases (male: 0 to female: 1), the probability of Survived=1 increases the most.
- Inversely as Pclass increases, probability of Survived=1 decreases the most.
- This way Age*Class is a good artificial feature to model as it has second highest negative correlation with Survived.
- So is Title as second highest positive correlation.
```
coeff_df = pd.DataFrame(train_df.columns.delete(0))
coeff_df.columns = ['Feature']
coeff_df["Correlation"] = pd.Series(logreg.coef_[0])
coeff_df.sort_values(by='Correlation', ascending=False)
```
Next we model using Support Vector Machines which are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis. Given a set of training samples, each marked as belonging to one or the other of **two categories**, an SVM training algorithm builds a model that assigns new test samples to one category or the other, making it a non-probabilistic binary linear classifier. Reference [Wikipedia](https://en.wikipedia.org/wiki/Support_vector_machine).
Note that the model generates a confidence score which is higher than Logistics Regression model.
```
# Support Vector Machines
svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
acc_svc = round(svc.score(X_train, Y_train) * 100, 2)
acc_svc
```
In pattern recognition, the k-Nearest Neighbors algorithm (or k-NN for short) is a non-parametric method used for classification and regression. A sample is classified by a majority vote of its neighbors, with the sample being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor. Reference [Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm).
KNN confidence score is better than Logistics Regression but worse than SVM.
```
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
acc_knn
```
In machine learning, naive Bayes classifiers are a family of simple probabilistic classifiers based on applying Bayes' theorem with strong (naive) independence assumptions between the features. Naive Bayes classifiers are highly scalable, requiring a number of parameters linear in the number of variables (features) in a learning problem. Reference [Wikipedia](https://en.wikipedia.org/wiki/Naive_Bayes_classifier).
The model generated confidence score is the lowest among the models evaluated so far.
```
# Gaussian Naive Bayes
gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
acc_gaussian
```
The perceptron is an algorithm for supervised learning of binary classifiers (functions that can decide whether an input, represented by a vector of numbers, belongs to some specific class or not). It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. The algorithm allows for online learning, in that it processes elements in the training set one at a time. Reference [Wikipedia](https://en.wikipedia.org/wiki/Perceptron).
```
# Perceptron
perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
acc_perceptron
# Linear SVC
linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
acc_linear_svc
# Stochastic Gradient Descent
sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
acc_sgd
```
This model uses a decision tree as a predictive model which maps features (tree branches) to conclusions about the target value (tree leaves). Tree models where the target variable can take a finite set of values are called classification trees; in these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values (typically real numbers) are called regression trees. Reference [Wikipedia](https://en.wikipedia.org/wiki/Decision_tree_learning).
The model confidence score is the highest among models evaluated so far.
```
# Decision Tree
decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
acc_decision_tree
```
The next model Random Forests is one of the most popular. Random forests or random decision forests are an ensemble learning method for classification, regression and other tasks, that operate by constructing a multitude of decision trees (n_estimators=100) at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees. Reference [Wikipedia](https://en.wikipedia.org/wiki/Random_forest).
The model confidence score is the highest among models evaluated so far. We decide to use this model's output (Y_pred) for creating our competition submission of results.
```
# Random Forest
random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
acc_random_forest
```
### Model evaluation
We can now rank our evaluation of all the models to choose the best one for our problem. While both Decision Tree and Random Forest score the same, we choose to use Random Forest as they correct for decision trees' habit of overfitting to their training set.
```
models = pd.DataFrame({
'Model': ['Support Vector Machines', 'KNN', 'Logistic Regression',
'Random Forest', 'Naive Bayes', 'Perceptron',
'Stochastic Gradient Decent', 'Linear SVC',
'Decision Tree'],
'Score': [acc_svc, acc_knn, acc_log,
acc_random_forest, acc_gaussian, acc_perceptron,
acc_sgd, acc_linear_svc, acc_decision_tree]})
models.sort_values(by='Score', ascending=False)
submission = pd.DataFrame({
"PassengerId": test_df["PassengerId"],
"Survived": Y_pred
})
# submission.to_csv('../output/submission.csv', index=False)
```
Our submission to the competition site Kaggle results in scoring 3,883 of 6,082 competition entries. This result is indicative while the competition is running. This result only accounts for part of the submission dataset. Not bad for our first attempt. Any suggestions to improve our score are most welcome.
## References
This notebook has been created based on great work done solving the Titanic competition and other sources.
- [A journey through Titanic](https://www.kaggle.com/omarelgabry/titanic/a-journey-through-titanic)
- [Getting Started with Pandas: Kaggle's Titanic Competition](https://www.kaggle.com/c/titanic/details/getting-started-with-random-forests)
- [Titanic Best Working Classifier](https://www.kaggle.com/sinakhorami/titanic/titanic-best-working-classifier)
| true |
code
| 0.604545 | null | null | null | null |
|
## First step in gap analysis is to determine the AEP based on operational data.
```
%load_ext autoreload
%autoreload 2
```
This notebook provides an overview and walk-through of the steps taken to produce a plant-level operational energy asssessment (OA) of a wind plant in the PRUF project. The La Haute-Borne wind farm is used here and throughout the example notebooks.
Uncertainty in the annual energy production (AEP) estimate is calculated through a Monte Carlo approach. Specifically, inputs into the OA code as well as intermediate calculations are randomly sampled based on their specified or calculated uncertainties. By performing the OA assessment thousands of times under different combinations of the random sampling, a distribution of AEP values results from which uncertainty can be deduced. Details on the Monte Carlo approach will be provided throughout this notebook.
### Step 1: Import plant data into notebook
A zip file included in the OpenOA 'examples/data' folder needs to be unzipped to run this step. Note that this zip file should be unzipped automatically as part of the project.prepare() function call below. Once unzipped, 4 CSV files will appear in the 'examples/data/la_haute_borne' folder.
```
# Import required packages
import os
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
import pandas as pd
import copy
from project_ENGIE import Project_Engie
from operational_analysis.methods import plant_analysis
```
In the call below, make sure the appropriate path to the CSV input files is specfied. In this example, the CSV files are located directly in the 'examples/data/la_haute_borne' folder
```
# Load plant object
project = Project_Engie('./data/la_haute_borne')
# Prepare data
project.prepare()
```
### Step 2: Review the data
Several Pandas data frames have now been loaded. Histograms showing the distribution of the plant-level metered energy, availability, and curtailment are shown below:
```
# Review plant data
fig, (ax1, ax2, ax3) = plt.subplots(ncols = 3, figsize = (15,5))
ax1.hist(project._meter.df['energy_kwh'], 40) # Metered energy data
ax2.hist(project._curtail.df['availability_kwh'], 40) # Curtailment and availability loss data
ax3.hist(project._curtail.df['curtailment_kwh'], 40) # Curtailment and availability loss data
plt.tight_layout()
plt.show()
```
### Step 3: Process the data into monthly averages and sums
The raw plant data can be in different time resolutions (in this case 10-minute periods). The following steps process the data into monthly averages and combine them into a single 'monthly' data frame to be used in the OA assessment.
```
project._meter.df.head()
```
First, we'll create a MonteCarloAEP object which is used to calculate long-term AEP. Two renalaysis products are specified as arguments.
```
pa = plant_analysis.MonteCarloAEP(project, reanal_products = ['era5', 'merra2'])
```
Let's view the result. Note the extra fields we've calculated that we'll use later for filtering:
- energy_nan_perc : the percentage of NaN values in the raw revenue meter data used in calculating the monthly sum. If this value is too large, we shouldn't include this month
- nan_flag : if too much energy, availability, or curtailment data was missing for a given month, flag the result
- num_days_expected : number of days in the month (useful for normalizing monthly gross energy later)
- num_days_actual : actual number of days per month as found in the data (used when trimming monthly data frame)
```
# View the monthly data frame
pa._aggregate.df.head()
```
### Step 4: Review reanalysis data
Reanalysis data will be used to long-term correct the operational energy over the plant period of operation to the long-term. It is important that we only use reanalysis data that show reasonable trends over time with no noticeable discontinuities. A plot like below, in which normalized annual wind speeds are shown from 1997 to present, provides a good first look at data quality.
The plot shows that both of the reanalysis products track each other reasonably well and seem well-suited for the analysis.
```
pa.plot_reanalysis_normalized_rolling_monthly_windspeed().show()
```
### Step 5: Review energy and loss data
It is useful to take a look at the energy data and make sure the values make sense. We begin with scatter plots of gross energy and wind speed for each reanalysis product. We also show a time series of gross energy, as well as availability and curtailment loss.
Let's start with the scatter plots of gross energy vs wind speed for each reanalysis product. Here we use the 'Robust Linear Model' (RLM) module of the Statsmodels package with the default Huber algorithm to produce a regression fit that excludes outliers. Data points in red show the outliers, and were excluded based on a Huber sensitivity factor of 3.0 (the factor is varied between 2.0 and 3.0 in the Monte Carlo simulation).
The plots below reveal that:
- there are some outliers
- Both renalysis products are strongly correlated with plant energy
```
pa.plot_reanalysis_gross_energy_data(outlier_thres=3).show()
```
Next we show time series plots of the monthly gross energy, availabilty, and curtialment. Note that the availability and curtailment data were estimated based on SCADA data from the plant.
Long-term availability and curtailment losses for the plant are calculated based on average percentage losses for each calendar month. Summing those average values weighted by the fraction of long-term gross energy generated in each month yields the long-term annual estimates. Weighting by monthly long-term gross energy helps account for potential correlation between losses and energy production (e.g., high availability losses in summer months with lower energy production). The long-term losses are calculated in Step 9.
```
pa.plot_aggregate_plant_data_timeseries().show()
```
### Step 6: Specify availabilty and curtailment data not represenative of actual plant performance
There may be anomalies in the reported availabilty that shouldn't be considered representative of actual plant performance. Force majeure events (e.g. lightning) are a good example. Such losses aren't typically considered in pre-construction AEP estimates; therefore, plant availablity loss reported in an operational AEP analysis should also not include such losses.
The 'availability_typical' and 'curtailment_typical' fields in the monthly data frame are initially set to True. Below, individual months can be set to 'False' if it is deemed those months are unrepresentative of long-term plant losses. By flagging these months as false, they will be omitted when assessing average availabilty and curtailment loss for the plant.
Justification for removing months from assessing average availabilty or curtailment should come from conversations with the owner/operator. For example, if a high-loss month is found, reasons for the high loss should be discussed with the owner/operator to determine if those losses can be considered representative of average plant operation.
```
# For illustrative purposes, let's suppose a few months aren't representative of long-term losses
pa._aggregate.df.loc['2014-11-01',['availability_typical','curtailment_typical']] = False
pa._aggregate.df.loc['2015-07-01',['availability_typical','curtailment_typical']] = False
```
### Step 7: Select reanalysis products to use
Based on the assessment of reanalysis products above (both long-tern trend and relationship with plant energy), we now set which reanalysis products we will include in the OA. For this particular case study, we use both products given the high regression relationships.
### Step 8: Set up Monte Carlo inputs
The next step is to set up the Monte Carlo framework for the analysis. Specifically, we identify each source of uncertainty in the OA estimate and use that uncertainty to create distributions of the input and intermediate variables from which we can sample for each iteration of the OA code. For input variables, we can create such distributions beforehand. For intermediate variables, we must sample separately for each iteration.
Detailed descriptions of the sampled Monte Carlo inputs, which can be specified when initializing the MonteCarloAEP object if values other than the defaults are desired, are provided below:
- slope, intercept, and num_outliers : These are intermediate variables that are calculated for each iteration of the code
- outlier_threshold : Sample values between 2 and 3 which set the Huber algorithm outlier detection parameter. Varying this threshold accounts for analyst subjectivity on what data points constitute outliers and which do not.
- metered_energy_fraction : Revenue meter energy measurements are associated with a measurement uncertainty of around 0.5%. This uncertainty is used to create a distribution centered at 1 (and with standard deviation therefore of 0.005). This column represents random samples from that distribution. For each iteration of the OA code, a value from this column is multiplied by the monthly revenue meter energy data before the data enter the OA code, thereby capturing the 0.5% uncertainty.
- loss_fraction : Reported availability and curtailment losses are estimates and are associated with uncertainty. For now, we assume the reported values are associated with an uncertainty of 5%. Similar to above, we therefore create a distribution centered at 1 (with std of 0.05) from which we sample for each iteration of the OA code. These sampled values are then multiplied by the availability and curtaiment data independently before entering the OA code to capture the 5% uncertainty in the reported values.
- num_years_windiness : This intends to capture the uncertainty associated with the number of historical years an analyst chooses to use in the windiness correction. The industry standard is typically 20 years and is based on the assumption that year-to-year wind speeds are uncorrelated. However, a growing body of research suggests that there is some correlation in year-to-year wind speeds and that there are trends in the resource on the decadal timescale. To capture this uncertainty both in the long-term trend of the resource and the analyst choice, we randomly sample integer values betweeen 10 and 20 as the number of years to use in the windiness correction.
- loss_threshold : Due to uncertainty in reported availability and curtailment estimates, months with high combined losses are associated with high uncertainty in the calculated gross energy. It is common to remove such data from analysis. For this analysis, we randomly sample float values between 0.1 and 0.2 (i.e. 10% and 20%) to serve as criteria for the combined availability and curtailment losses. Specifically, months are excluded from analysis if their combined losses exceeds that criteria for the given OA iteration.
- reanalyis_product : This captures the uncertainty of using different reanalysis products and, lacking a better method, is a proxy way of capturing uncertainty in the modelled monthly wind speeds. For each iteration of the OA code, one of the reanalysis products that we've already determined as valid (see the cells above) is selected.
### Step 9: Run the OA code
We're now ready to run the Monte-Carlo based OA code. We repeat the OA process "num_sim" times using different sampling combinations of the input and intermediate variables to produce a distribution of AEP values.
A single line of code here in the notebook performs this step, but below is more detail on what is being done.
Steps in OA process:
- Set the wind speed and gross energy data to be used in the regression based on i) the reanalysis product to be used (Monte-Carlo sampled); ii) the NaN energy data criteria (1%); iii) Combined availability and curtailment loss criteria (Monte-Carlo sampled); and iv) the outlier criteria (Monte-Carlo sampled)
- Normalize gross energy to 30-day months
- Perform linear regression and determine slope and intercept values, their standard errors, and the covariance between the two
- Use the information above to create distributions of possible slope and intercept values (e.g. mean equal to slope, std equal to the standard error) from which we randomly sample a slope and intercept value (note that slope and intercept values are highly negatively-correlated so the sampling from both distributions are constrained accordingly)
- to perform the long term correction, first determine the long-term monthly average wind speeds (i.e. average January wind speed, average Februrary wind speed, etc.) based on a 10-20 year historical period as determined by the Monte Carlo process.
- Apply the Monte-Carlo sampled slope and intercept values to the long-term monthly average wind speeds to calculate long-term monthly gross energy
- 'Denormalize' monthly long-term gross energy back to the normal number of days
- Calculate AEP by subtracting out the long-term avaiability loss (curtailment loss is left in as part of AEP)
```
# Run Monte-Carlo based OA
pa.run(num_sim=2000, reanal_subset=['era5', 'merra2'])
```
The key result is shown below: a distribution of AEP values from which uncertainty can be deduced. In this case, uncertainty is around 9%.
```
# Plot a distribution of AEP values from the Monte-Carlo OA method
pa.plot_result_aep_distributions().show()
```
### Step 10: Post-analysis visualization
Here we show some supplementary results of the Monte Carlo OA approach to help illustrate how it works.
First, it's worth looking at the Monte-Carlo tracker data frame again, now that the slope, intercept, and number of outlier fields have been completed. Note that for transparency, debugging, and analysis purposes, we've also included in the tracker data frame the number of data points used in the regression.
```
# Produce histograms of the various MC-parameters
mc_reg = pd.DataFrame(data = {'slope': pa._mc_slope.ravel(),
'intercept': pa._mc_intercept,
'num_points': pa._mc_num_points,
'metered_energy_fraction': pa._inputs.metered_energy_fraction,
'loss_fraction': pa._inputs.loss_fraction,
'num_years_windiness': pa._inputs.num_years_windiness,
'loss_threshold': pa._inputs.loss_threshold,
'reanalysis_product': pa._inputs.reanalysis_product})
```
It's useful to plot distributions of each variable to show what is happening in the Monte Carlo OA method. Based on the plot below, we observe the following:
- metered_energy_fraction, and loss_fraction sampling follow a normal distribution as expected
- The slope and intercept distributions appear normally distributed, even though different reanalysis products are considered, resulting in different regression relationships. This is likely because the reanalysis products agree with each other closely.
- 24 data points were used for all iterations, indicating that there was no variation in the number of outlier months removed
- We see approximately equal sampling of the num_years_windiness, loss_threshold, and reanalysis_product, as expected
```
plt.figure(figsize=(15,15))
for s in np.arange(mc_reg.shape[1]):
plt.subplot(4,3,s+1)
plt.hist(mc_reg.iloc[:,s],40)
plt.title(mc_reg.columns[s])
plt.show()
```
It's worth highlighting the inverse relationship between slope and intercept values under the Monte Carlo approach. As stated earlier, slope and intercept values are strongly negatively correlated (e.g. slope goes up, intercept goes down) which is captured by the covariance result when performing linear regression. By constrained random sampling of slope and intercept values based on this covariance, we assure we aren't sampling unrealisic combinations.
The plot below shows that the values are being sampled appropriately
```
# Produce scatter plots of slope and intercept values, and overlay the resulting line of best fits over the actual wind speed
# and gross energy data points. Here we focus on the ERA-5 data
plt.figure(figsize=(8,6))
plt.plot(mc_reg.intercept[mc_reg.reanalysis_product =='era5'],mc_reg.slope[mc_reg.reanalysis_product =='era5'],'.')
plt.xlabel('Intercept (GWh)')
plt.ylabel('Slope (GWh / (m/s))')
plt.show()
```
We can look further at the influence of certain Monte Carlo parameters on the AEP result. For example, let's see what effect the choice of reanalysis product has on the result:
```
# Boxplot of AEP based on choice of reanalysis product
tmp_df=pd.DataFrame(data={'aep':pa.results.aep_GWh,'reanalysis_product':mc_reg['reanalysis_product']})
tmp_df.boxplot(column='aep',by='reanalysis_product',figsize=(8,6))
plt.ylabel('AEP (GWh/yr)')
plt.xlabel('Reanalysis product')
plt.title('AEP estimates by reanalysis product')
plt.suptitle("")
plt.show()
```
In this case, the two reanalysis products lead to similar AEP estimates, although MERRA2 yields slightly higher uncertainty.
We can also look at the effect on the number of years used in the windiness correction:
```
# Boxplot of AEP based on number of years in windiness correction
tmp_df=pd.DataFrame(data={'aep':pa.results.aep_GWh,'num_years_windiness':mc_reg['num_years_windiness']})
tmp_df.boxplot(column='aep',by='num_years_windiness',figsize=(8,6))
plt.ylabel('AEP (GWh/yr)')
plt.xlabel('Number of years in windiness correction')
plt.title('AEP estimates by windiness years')
plt.suptitle("")
plt.show()
```
As seen above, the number of years used in the windiness correction does not significantly impact the AEP estimate.
| true |
code
| 0.714964 | null | null | null | null |
|
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base = automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
engine.execute('SELECT * FROM Measurement LIMIT 10').fetchall()
engine.execute('SELECT * FROM Station LIMIT 10').fetchall()
inspector = inspect(engine)
inspector.get_table_names()
measurement_columns = inspector.get_columns('measurement')
for m_c in measurement_columns:
print(m_c['name'], m_c["type"])
station_columns = inspector.get_columns('station')
for m_c in station_columns:
print(m_c['name'], m_c["type"])
```
# Exploratory Climate Analysis
```
# Design a query to retrieve the last 12 months of precipitation data and plot the results
Measurement = Base.classes.measurement
last_date = session.query(Measurement.date).order_by(Measurement.date.desc()).first()
# Calculate the date 1 year ago from today
last_year = dt.date(2017, 8, 23) - dt.timedelta(days=365)
# Perform a query to retrieve the data and precipitation scores
Precipitation = session.query(Measurement.date, Measurement.prcp).filter(Measurement.date > last_year).\
order_by(Measurement.date.desc()).all()
# Save the query results as a Pandas DataFrame and set the index to the date column
df = pd.DataFrame(Precipitation[:], columns=['date', 'prcp'])
df.set_index('date', inplace=True)
# Sort the dataframe by date
df = df.sort_index()
df.head()
# Use Pandas Plotting with Matplotlib to plot the data
df.plot(kind="line",linewidth=4,figsize=(15,10))
plt.style.use('fivethirtyeight')
plt.xlabel("Date")
plt.title("Precipitation Analysis (From 8/24/16 to 8/23/17)")
# Rotate the xticks for the dates
plt.xticks(rotation=45)
plt.legend(["Precipitation"])
plt.tight_layout()
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
df.describe()
# How many stations are available in this dataset?
stations_count = session.query(Measurement).group_by(Measurement.station).count()
print("There are {} stations.".format(stations_count))
# What are the most active stations?
# List the stations and the counts in descending order.
active_stations = session.query(Measurement.station, func.count(Measurement.tobs)).group_by(Measurement.station).\
order_by(func.count(Measurement.tobs).desc()).all()
active_stations
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature most active station?
most_active_station = 'USC00519281';
active_station_stat = session.query(Measurement.station, func.min(Measurement.tobs), func.max(Measurement.tobs), func.avg(Measurement.tobs)).\
filter(Measurement.station == most_active_station).all()
active_station_stat
# A query to retrieve the last 12 months of temperature observation data (tobs).
# Filter by the station with the highest number of observations.
temperature = session.query(Measurement.station, Measurement.date, Measurement.tobs).\
filter(Measurement.station == 'USC00519397').\
filter(Measurement.date > last_year).\
order_by(Measurement.date).all()
temperature
# Plot the results as a histogram with bins=12.
measure_df=pd.DataFrame(temperature)
hist_plot = measure_df['tobs'].hist(bins=12, figsize=(15,10))
plt.xlabel("Recorded Temperature")
plt.ylabel("Frequency")
plt.title("Last 12 Months Station Analysis for Most Active Station")
plt.show()
# Write a function called `calc_temps` that will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
print(calc_temps('2012-02-28', '2012-03-05'))
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
# for your trip using the previous year's data for those same dates.
trip_departure = dt.date(2018, 5, 1)
trip_arrival = dt.date(2018, 4, 2)
last_year = dt.timedelta(days=365)
trip_stat = (calc_temps((trip_arrival - last_year), (trip_departure - last_year)))
print(trip_stat)
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
average_temp = trip_stat[0][1]
minimum_temp = trip_stat[0][0]
maximum_temp = trip_stat[0][2]
peak_yerr = (maximum_temp - minimum_temp)/2
barvalue = [average_temp]
xvals = range(len(barvalue))
fig, ax = plt.subplots()
rects = ax.bar(xvals, barvalue, width, color='g', yerr=peak_yerr,
error_kw=dict(elinewidth=6, ecolor='black'))
def autolabel(rects):
# attach some text labels
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x()+rect.get_width()/2., .6*height, '%.2f'%float(height),
ha='left', va='top')
autolabel(rects)
plt.ylim(0, 100)
ax.set_xticks([1])
ax.set_xlabel("Trip")
ax.set_ylabel("Temp (F)")
ax.set_title("Trip Avg Temp")
fig.tight_layout()
plt.show()
#trip dates - last year
trip_arrival_date = trip_arrival - last_year
trip_departure_date = trip_departure - last_year
print(trip_arrival_date)
print(trip_departure_date)
# Calculate the rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
trip_arrival_date = trip_arrival - last_year
trip_departure_date = trip_departure - last_year
rainfall_trip_data = session.query(Measurement.station, Measurement.date, func.avg(Measurement.prcp), Measurement.tobs).\
filter(Measurement.date >= trip_arrival_date).\
filter(Measurement.date <= trip_departure_date).\
group_by(Measurement.station).\
order_by(Measurement.prcp.desc()).all()
rainfall_trip_data
df_rainfall_stations = session.query(Station.station, Station.name, Station.latitude, Station.longitude, Station.elevation).\
order_by(Station.station.desc()).all()
df_rainfall_stations
df_rainfall = pd.DataFrame(rainfall_trip_data[:], columns=['station','date','precipitation','temperature'])
df_station = pd.DataFrame(df_rainfall_stations[:], columns=['station', 'name', 'latitude', 'longitude', 'elevation'])
df_station
result = pd.merge(df_rainfall, df_station, on='station')
df_result = result.drop(['date','precipitation','temperature',], 1)
df_result
```
## Optional Challenge Assignment
```
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
# Use the start and end date to create a range of dates
# Stip off the year and save a list of %m-%d strings
# Loop through the list of %m-%d strings and calculate the normals for each date
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
# Plot the daily normals as an area plot with `stacked=False`
```
| true |
code
| 0.725016 | null | null | null | null |
|
# Experiments for ER Graph
## Imports
```
%load_ext autoreload
%autoreload 2
import os
import sys
from collections import OrderedDict
import logging
import math
from matplotlib import pyplot as plt
import networkx as nx
import numpy as np
import torch
from torchdiffeq import odeint, odeint_adjoint
sys.path.append('../')
# Baseline imports
from gd_controller import AdjointGD
from dynamics_driver import ForwardKuramotoDynamics, BackwardKuramotoDynamics
# Nodec imports
from neural_net import EluTimeControl, TrainingAlgorithm
# Various Utilities
from utilities import evaluate, calculate_critical_coupling_constant, comparison_plot, state_plot
from nnc.helpers.torch_utils.oscillators import order_parameter_cos
logging.getLogger().setLevel(logging.CRITICAL) # set to info to look at loss values etc.
```
## Load graph parameters
Basic setup for calculations, graph, number of nodes, etc.
```
dtype = torch.float32
device = 'cpu'
graph_type = 'erdos_renyi'
adjacency_matrix = torch.load('../../data/'+graph_type+'_adjacency.pt')
parameters = torch.load('../../data/parameters.pt')
# driver vector is a column vector with 1 value for driver nodes
# and 0 for non drivers.
result_folder = '../../results/' + graph_type + os.path.sep
os.makedirs(result_folder, exist_ok=True)
```
## Load dynamics parameters
Load natural frequencies and initial states which are common for all graphs and also calculate the coupling constant which is different per graph. We use a coupling constant value that is $10%$ of the critical coupling constant value.
```
total_time = parameters['total_time']
total_time = 5
natural_frequencies = parameters['natural_frequencies']
critical_coupling_constant = calculate_critical_coupling_constant(adjacency_matrix, natural_frequencies)
coupling_constant = 0.1*critical_coupling_constant
theta_0 = parameters['theta_0']
```
## NODEC
We now train NODEC with a shallow neural network. We initialize the parameters in a deterministic manner, and use stochastic gradient descent to train it. The learning rate, number of epochs and neural architecture may change per graph. We use different fractions of driver nodes.
```
fractions = np.linspace(0,1,10)
order_parameter_mean = []
order_parameter_std = []
samples = 1000
for p in fractions:
sample_arr = []
for i in range(samples):
print(p,i)
driver_nodes = int(p*adjacency_matrix.shape[0])
driver_vector = torch.zeros([adjacency_matrix.shape[0],1])
idx = torch.randperm(len(driver_vector))[:driver_nodes]
driver_vector[idx] = 1
forward_dynamics = ForwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
backward_dynamics = BackwardKuramotoDynamics(adjacency_matrix,
driver_vector,
coupling_constant,
natural_frequencies
)
neural_net = EluTimeControl([2])
for parameter in neural_net.parameters():
parameter.data = torch.ones_like(parameter.data)/1000 # deterministic init!
train_algo = TrainingAlgorithm(neural_net, forward_dynamics)
best_model = train_algo.train(theta_0, total_time, epochs=3, lr=0.3)
control_trajectory, state_trajectory =\
evaluate(forward_dynamics, theta_0, best_model, total_time, 100)
nn_control = torch.cat(control_trajectory).squeeze().cpu().detach().numpy()
nn_states = torch.cat(state_trajectory).cpu().detach().numpy()
nn_e = (nn_control**2).cumsum(-1)
nn_r = order_parameter_cos(torch.tensor(nn_states)).cpu().numpy()
sample_arr.append(nn_r[-1])
order_parameter_mean.append(np.mean(sample_arr))
order_parameter_std.append(np.std(sample_arr,ddof=1))
order_parameter_mean = np.array(order_parameter_mean)
order_parameter_std = np.array(order_parameter_std)
plt.figure()
plt.errorbar(fractions,order_parameter_mean,yerr=order_parameter_std/np.sqrt(samples),fmt="o")
plt.xlabel(r"fraction of controlled nodes")
plt.ylabel(r"$r(T)$")
plt.tight_layout()
plt.show()
np.savetxt("ER_drivers_K01.csv",np.c_[order_parameter_mean,order_parameter_std],header="order parameter mean\t order parameter std")
```
| true |
code
| 0.660556 | null | null | null | null |
|
Parallel Single-channel CSC
===========================
This example compares the use of [parcbpdn.ParConvBPDN](http://sporco.rtfd.org/en/latest/modules/sporco.admm.parcbpdn.html#sporco.admm.parcbpdn.ParConvBPDN) with [admm.cbpdn.ConvBPDN](http://sporco.rtfd.org/en/latest/modules/sporco.admm.cbpdn.html#sporco.admm.cbpdn.ConvBPDN) solving a convolutional sparse coding problem with a greyscale signal
$$\mathrm{argmin}_\mathbf{x} \; \frac{1}{2} \left\| \sum_m \mathbf{d}_m * \mathbf{x}_{m} - \mathbf{s} \right\|_2^2 + \lambda \sum_m \| \mathbf{x}_{m} \|_1 \;,$$
where $\mathbf{d}_{m}$ is the $m^{\text{th}}$ dictionary filter, $\mathbf{x}_{m}$ is the coefficient map corresponding to the $m^{\text{th}}$ dictionary filter, and $\mathbf{s}$ is the input image.
```
from __future__ import print_function
from builtins import input
import pyfftw # See https://github.com/pyFFTW/pyFFTW/issues/40
import numpy as np
from sporco import util
from sporco import signal
from sporco import plot
plot.config_notebook_plotting()
import sporco.metric as sm
from sporco.admm import cbpdn
from sporco.admm import parcbpdn
```
Load example image.
```
img = util.ExampleImages().image('kodim23.png', zoom=1.0, scaled=True,
gray=True, idxexp=np.s_[160:416, 60:316])
```
Highpass filter example image.
```
npd = 16
fltlmbd = 10
sl, sh = signal.tikhonov_filter(img, fltlmbd, npd)
```
Load dictionary and display it.
```
D = util.convdicts()['G:12x12x216']
plot.imview(util.tiledict(D), fgsz=(7, 7))
lmbda = 5e-2
```
The RelStopTol option was chosen for the two different methods to stop with similar functional values
Initialise and run standard serial CSC solver using ADMM with an equality constraint [[49]](http://sporco.rtfd.org/en/latest/zreferences.html#id51).
```
opt = cbpdn.ConvBPDN.Options({'Verbose': True, 'MaxMainIter': 200,
'RelStopTol': 5e-3, 'AuxVarObj': False,
'AutoRho': {'Enabled': False}})
b = cbpdn.ConvBPDN(D, sh, lmbda, opt=opt, dimK=0)
X = b.solve()
```
Initialise and run parallel CSC solver using ADMM dictionary partition method [[42]](http://sporco.rtfd.org/en/latest/zreferences.html#id43).
```
opt_par = parcbpdn.ParConvBPDN.Options({'Verbose': True, 'MaxMainIter': 200,
'RelStopTol': 1e-2, 'AuxVarObj': False, 'AutoRho':
{'Enabled': False}, 'alpha': 2.5})
b_par = parcbpdn.ParConvBPDN(D, sh, lmbda, opt=opt_par, dimK=0)
X_par = b_par.solve()
```
Report runtimes of different methods of solving the same problem.
```
print("ConvBPDN solve time: %.2fs" % b.timer.elapsed('solve_wo_rsdl'))
print("ParConvBPDN solve time: %.2fs" % b_par.timer.elapsed('solve_wo_rsdl'))
print("ParConvBPDN was %.2f times faster than ConvBPDN\n" %
(b.timer.elapsed('solve_wo_rsdl')/b_par.timer.elapsed('solve_wo_rsdl')))
```
Reconstruct images from sparse representations.
```
shr = b.reconstruct().squeeze()
imgr = sl + shr
shr_par = b_par.reconstruct().squeeze()
imgr_par = sl + shr_par
```
Report performances of different methods of solving the same problem.
```
print("Serial reconstruction PSNR: %.2fdB" % sm.psnr(img, imgr))
print("Parallel reconstruction PSNR: %.2fdB\n" % sm.psnr(img, imgr_par))
```
Display original and reconstructed images.
```
fig = plot.figure(figsize=(21, 7))
plot.subplot(1, 3, 1)
plot.imview(img, title='Original', fig=fig)
plot.subplot(1, 3, 2)
plot.imview(imgr, title=('Serial Reconstruction PSNR: %5.2f dB' %
sm.psnr(img, imgr)), fig=fig)
plot.subplot(1, 3, 3)
plot.imview(imgr_par, title=('Parallel Reconstruction PSNR: %5.2f dB' %
sm.psnr(img, imgr_par)), fig=fig)
fig.show()
```
Display low pass component and sum of absolute values of coefficient maps of highpass component.
```
fig = plot.figure(figsize=(21, 7))
plot.subplot(1, 3, 1)
plot.imview(sl, title='Lowpass component', fig=fig)
plot.subplot(1, 3, 2)
plot.imview(np.sum(abs(X), axis=b.cri.axisM).squeeze(),
cmap=plot.cm.Blues, title='Serial Sparse Representation',
fig=fig)
plot.subplot(1, 3, 3)
plot.imview(np.sum(abs(X_par), axis=b.cri.axisM).squeeze(),
cmap=plot.cm.Blues, title='Parallel Sparse Representation',
fig=fig)
fig.show()
```
| true |
code
| 0.784433 | null | null | null | null |
|
# Let's compare 4 different strategies to solve sentiment analysis:
1. **Custom model using open source package**. Build a custom model using scikit-learn and TF-IDF features on n-grams. This method is known to work well for English text.
2. **Integrate** a pre-built API. The "sentiment HQ" API provided by indico has been shown to achieve state-of-the-art accuracy, using a recurrent neural network.
3. **Word-level features**. A custom model, built from word-level text features from indico's "text features" API.
4. **RNN features**. A custom model, using transfer learning, using the recurrent features from indico's sentiment HQ model to train a new custom model.
Note: this notebook and the enclosed code snippets accompany the KDnuggets post:
### Semi-supervised feature transfer: the big practical benefit of deep learning today?
<img src="header.jpg">
### Download the data
1. Download the "Large Movie Review Dataset" from http://ai.stanford.edu/~amaas/data/sentiment/.
2. Decompress it.
3. Put it into some directory path that you define below.
Citation: Andrew L. Maas, Raymond E. Daly, Peter T. Pham, Dan Huang, Andrew Y. Ng, and Christopher Potts. (2011). Learning Word Vectors for Sentiment Analysis. The 49th Annual Meeting of the Association for Computational Linguistics (ACL 2011).
### User parameters
```
seed = 3 # for reproducibility across experiments, just pick something
train_num = 100 # number of training examples to use
test_num = 100 # number of examples to use for testing
base_model_name = "sentiment_train%s_test%s" % (train_num, test_num)
lab2bin = {'pos': 1, 'neg': 0} # label -> binary class
pos_path = "~DATASETS/aclImdb/train/pos/" # filepath to the positive examples
neg_path = "~DATASETS/aclImdb/train/neg/" # file path to the negative examples
output_path = "OUTPUT" # path where output file should go
batchsize = 25 # send this many requests at once
max_num_examples = 25000.0 # for making subsets below
```
### Setup and imports
Install modules as needed (for example: `pip install indicoio`)
```
import os, io, glob, random, time
# from itertools import islice, chain, izip_longest
import numpy as np
import pandas as pd
from tqdm import tqdm
import pprint
pp = pprint.PrettyPrinter(indent=4)
import indicoio
from indicoio.custom import Collection
from indicoio.custom import collections as check_status
import sklearn
from sklearn import metrics
from sklearn import linear_model
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt # for plotting results
%matplotlib inline
import seaborn # just for the colors
```
### Define your indico API key
If you don't have a (free) API key, you can [get one here](https://indico.io/pay-per-call). Your first 10,000 calls per months are free.
```
indicoio.config.api_key = "" # Add your API key here
```
### Convenience function for making batches of examples
```
def batcher(seq, stride = 4):
"""
Generator strides across the input sequence,
combining the elements between each stride.
"""
for pos in xrange(0, len(seq), stride):
yield seq[pos : pos + stride]
# for making subsets below
train_subset = (train_num / 25000.0)
test_subset = (test_num / 25000.0)
random.seed(seed)
np.random.seed(seed)
```
### Check that the requested paths exist
```
# check that paths exist
for p in [pos_path, neg_path]:
abs_path = os.path.abspath(p)
if not os.path.exists(abs_path):
os.makedirs(abs_path)
print(abs_path)
for p in [output_path]:
abs_path = os.path.abspath(p)
if not os.path.exists(abs_path): # and make output path if necessary
os.makedirs(abs_path)
print(abs_path)
```
### Query indico API to make sure everything is plumbed up correctly
```
# pre_status = check_status()
# pp.pprint(pre_status)
```
### Read data into a list of dictionary objects
where each dictionary object will be a single example. This makes it easy to manipulate later using dataframes, for cross-validation, visualization, etc.
### This dataset has pre-defined train/test splits
so rather than sampling our own, we'll use the existing splits to enable fair comparison with other published results.
```
train_data = [] # these lists will contain a bunch of little dictionaries, one for each example
test_data = []
# Positive examples (train)
examples = glob.glob(os.path.join(pos_path, "*")) # find all the positive examples, and read them
i = 0
for ex in examples:
d = {}
with open(ex, 'rb') as f:
d['label'] = 'pos' # label as "pos"
t = f.read().lower() # these files are already ascii text, so just lowercase them
d['text'] = t
d['pred_label'] = None # placeholder for predicted label
d['prob_pos'] = None # placeholder for predicted probability of a positive label
train_data.append(d) # add example to the list of training data
i +=1
print("Read %d positive training examples, of %d available (%.2f%%)" % (i, len(examples), (100.0*i)/len(examples)))
# Negative examples (train)
examples = glob.glob(os.path.join(neg_path, "*")) # find all the negative examples and read them
i = 0
for ex in examples:
d = {}
with open(ex, 'rb') as f:
d['label'] = 'neg'
t = f.read().lower()
d['text'] = t
d['pred_label'] = None
d['prob_pos'] = None
train_data.append(d)
i +=1
print("Read %d negative training examples, of %d available (%.2f%%)" % (i, len(examples), (100.0*i)/len(examples)))
# Positive examples (test)
examples = glob.glob(os.path.join(pos_path, "*"))
i = 0
for ex in examples:
d = {}
with open(ex, 'rb') as f:
d['label'] = 'pos'
t = f.read().lower() # these files are already ascii text
d['text'] = t
d['pred_label'] = None
d['prob_pos'] = None
test_data.append(d)
i +=1
print("Read %d positive test examples, of %d available (%.2f%%)" % (i, len(examples), (100.0*i)/len(examples)))
# Negative examples (test)
examples = glob.glob(os.path.join(neg_path, "*"))
i = 0
for ex in examples:
d = {}
with open(ex, 'rb') as f:
d['label'] = 'neg'
t = f.read().lower() # these files are already ascii text
d['text'] = t
d['pred_label'] = None
d['prob_pos'] = None
test_data.append(d)
i +=1
print("Read %d negative examples, of %d available (%.2f%%)" % (i, len(examples), (100.0*i)/len(examples)))
# Populate a dataframe, shuffle, and subset as required
df_train = pd.DataFrame(train_data)
df_train = df_train.sample(frac = train_subset) # shuffle (by sampling everything randomly)
print("After resampling, down to %d training records" % len(df_train))
df_test = pd.DataFrame(test_data)
df_test = df_test.sample(frac = test_subset) # shuffle (by sampling everything randomly)
print("After resampling, down to %d test records" % len(df_test))
```
### Quick sanity check on the data, is everything as expected?
```
df_train.head(10) # sanity check
df_train.tail(10)
df_test.tail(10)
```
# Strategy A: scikit-learn
Build a custom model from scratch using sklearn (ngrams -> TFIDF -> LR)
### Define the vectorizer, logistic regression model, and overall pipeline
```
vectorizer = sklearn.feature_extraction.text.TfidfVectorizer(
max_features = int(1e5), # max vocab size (pretty large)
max_df = 0.50,
sublinear_tf = True,
use_idf = True,
encoding = 'ascii',
decode_error = 'replace',
analyzer = 'word',
ngram_range = (1,3),
stop_words = 'english',
lowercase = True,
norm = 'l2',
smooth_idf = True,
)
lr = linear_model.SGDClassifier(
alpha = 1e-5,
average = 10,
class_weight = 'balanced',
epsilon = 0.15,
eta0 = 0.0,
fit_intercept = True,
l1_ratio = 0.15,
learning_rate = 'optimal',
loss = 'log',
n_iter = 5,
n_jobs = -1,
penalty = 'l2',
power_t = 0.5,
random_state = seed,
shuffle = True,
verbose = 0,
warm_start = False,
)
classifier = Pipeline([('vectorizer', vectorizer),
('logistic_regression', lr)
])
```
### Fit the classifier
```
_ = classifier.fit(df_train['text'], df_train['label'])
```
### Get predictions
```
pred_sk = classifier.predict(df_test['text'])
y_true_sk = [lab2bin[ex] for ex in df_test['label']]
proba_sk = classifier.predict_proba(df_test['text']) # also get probas
```
### Compute and plot ROC and AUC
```
cname = base_model_name + "_sklearn"
plt.figure(figsize=(8,8))
probas_sk = []
y_pred_labels_sk = []
y_pred_sk = []
# get predictions
for i, pred in enumerate(pred_sk):
proba_pos = proba_sk[i][1]
probas_sk.append(proba_pos)
if float(proba_pos) >= 0.50:
pred_label = "pos"
elif float(proba_pos) < 0.50:
pred_label = "neg"
else:
print("ERROR on example %d" % i) # if this happens, need to fix something
y_pred_labels_sk.append(pred_label)
y_pred_sk.append(lab2bin[pred_label])
# compute ROC
fpr, tpr, thresholds = metrics.roc_curve(y_true_sk, probas_sk)
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, lw = 1, label = "ROC area = %0.3f" % (roc_auc))
plt.plot([0, 1], [0, 1], '--', color=(0.5, 0.5, 0.5), label='random')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title("%d training examples" % len(examples))
plt.legend(loc="lower right")
plt.savefig(os.path.abspath(os.path.join(output_path, cname + "_ROC" + ".png")))
plt.show()
acc = metrics.accuracy_score(y_true_sk, y_pred_sk)
print("Accuracy: %.4f" % (acc))
```
# Put examples data into batches, for APIs
### Prepare batches of training examples
```
examples = [list(ex) for ex in zip(df_train['text'], df_train['label'])]
batches = [b for b in batcher(examples, batchsize)] # stores in memory, but the texts are small so no problem
```
### Prepare batches of test examples
```
test_examples = [list(ex) for ex in zip(df_test['text'], df_test['label'])] # test data
test_batches = [b for b in batcher(test_examples, batchsize)]
```
# Strategy B. Pre-trained sentiment HQ
```
# get predictions from sentiment-HQ API
cname = base_model_name + "hq"
predictions_hq = []
for batch in tqdm(test_batches):
labels = [x[1] for x in batch]
texts = [x[0] for x in batch]
results = indicoio.sentiment_hq(texts)
for i, result in enumerate(results):
r = {}
r['label'] = labels[i]
r['text'] = texts[i]
r['proba'] = result
predictions_hq.append(r)
cname = base_model_name + "_hq"
plt.figure(figsize=(8,8))
# y_true = [df_test['label']]
probas = []
y_true = []
y_pred_labels = []
y_pred = []
for i, pred in enumerate(predictions_hq):
y_true.append(lab2bin[pred['label']])
proba = pred['proba']
probas.append(proba)
if float(proba) >= 0.50:
pl = 'pos'
elif float(proba) < 0.50:
pl= 'neg'
else:
print("Error. Check proba value and y_true logic")
pred_label = pl # pick the most likely class by predicted proba
y_pred_labels.append(pred_label)
y_pred.append(lab2bin[pred_label])
fpr, tpr, thresholds = metrics.roc_curve(y_true, probas)
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, lw = 1, label = "ROC area = %0.3f" % (roc_auc))
plt.plot([0, 1], [0, 1], '--', color=(0.5, 0.5, 0.5), label='random')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
# plt.title("ROC plot model: '%s'" % cname)
plt.title("%d training examples" % len(examples))
plt.legend(loc="lower right")
# plt.savefig(os.path.abspath(cname + "_hq_ROC" + ".png"))
plt.savefig(os.path.abspath(os.path.join(output_path, cname + "_ROC" + ".png")))
plt.show()
acc = metrics.accuracy_score(y_true, y_pred)
print("Accuracy: %.4f" % (acc))
```
# Strategy C. Custom model using general text features.
### Create an indico custom collection using general (word-level) text features, and upload data
```
cname = base_model_name
print("This model will be cached as an indico custom collection using the name: '%s'" % cname)
collection = Collection(cname)
try:
collection.clear() # delete any previous data in this collection
collection.info()
collection = Collection(cname)
except:
print(" Error, probably because a collection with the given name didn't exist. Continuing...")
print(" Submitting %d training examples in %d batches..." % (len(examples), len(batches)))
for batch in tqdm(batches):
try:
collection.add_data(batch)
except Exception as e:
print("Exception: '%s' for batch:" % e)
pp.pprint(batch)
print(" training model: '%s'" % cname)
collection.train()
collection.wait() # blocks until the model is trained
# get predictions from the trained API model
predictions = []
cname = base_model_name
collection = Collection(cname)
for batch in tqdm(test_batches):
labels = [x[1] for x in batch]
texts = [x[0] for x in batch]
results = collection.predict(texts)
for i, result in enumerate(results):
r = {}
r['indico_result'] = result
r['label'] = labels[i]
r['text'] = texts[i]
r['proba'] = result['pos']
predictions.append(r)
pp.pprint(predictions[0]) # sanity check
```
### Draw ROC plot and compute metrics for the custom collection
```
plt.figure(figsize=(8,8))
probas = []
y_true = []
y_pred_labels = []
y_pred = []
for i, pred in enumerate(predictions):
y_true.append(lab2bin[pred['label']])
probas.append(pred['indico_result']['pos'])
pred_label = max(pred['indico_result'].keys(), key = (lambda x: pred['indico_result'][x])) # pick the most likely class by predicted proba
y_pred_labels.append(pred_label)
y_pred.append(lab2bin[pred_label])
fpr, tpr, thresholds = metrics.roc_curve(y_true, probas)
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, lw = 1, label = "ROC area = %0.3f" % (roc_auc))
plt.plot([0, 1], [0, 1], '--', color=(0.5, 0.5, 0.5), label='random')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title("%d training examples" % len(examples))
plt.legend(loc="lower right")
plt.savefig(os.path.abspath(os.path.join(output_path, cname + "_cc_ROC" + ".png")))
plt.show()
acc = metrics.accuracy_score(y_true, y_pred)
print("Accuracy: %.4f" % (acc))
```
# Strategy D. Custom model using sentiment features from the pretrained deep neural network.
```
cname = base_model_name + "_domain"
print("This model will be cached as an indico custom collection using the name: '%s'" % cname)
collection = Collection(cname, domain = "sentiment")
try:
collection.clear() # delete any previous data in this collection
collection.info()
collection = Collection(cname, domain = "sentiment")
except:
print(" Error, probably because a collection with the given name didn't exist. Continuing...")
print(" Submitting %d training examples in %d batches..." % (len(examples), len(batches)))
for batch in tqdm(batches):
try:
collection.add_data(batch, domain = "sentiment")
except Exception as e:
print("Exception: '%s' for batch:" % e)
pp.pprint(batch)
print(" training model: '%s'" % cname)
collection.train()
collection.wait()
```
### Get predictions for custom collection with sentiment domain text features
```
# get predictions from trained API
predictions_domain = []
cname = base_model_name + "_domain"
collection = Collection(cname, domain = "sentiment")
for batch in tqdm(test_batches):
labels = [x[1] for x in batch]
texts = [x[0] for x in batch]
results = collection.predict(texts, domain = "sentiment")
# batchsize = len(batch)
for i, result in enumerate(results):
r = {}
r['indico_result'] = result
r['label'] = labels[i]
r['text'] = texts[i]
r['proba'] = result['pos']
predictions_domain.append(r)
```
### Compute metrics and plot
```
cname = base_model_name + "_domain"
plt.figure(figsize=(8,8))
# y_true = [df_test['label']]
probas = []
y_true = []
y_pred_labels = []
y_pred = []
for i, pred in enumerate(predictions_domain):
y_true.append(lab2bin[pred['label']])
probas.append(pred['indico_result']['pos'])
pred_label = max(pred['indico_result'].keys(), key = (lambda x: pred['indico_result'][x])) # pick the most likely class by predicted proba
y_pred_labels.append(pred_label)
y_pred.append(lab2bin[pred_label])
fpr, tpr, thresholds = metrics.roc_curve(y_true, probas)
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, lw = 1, label = "ROC area = %0.3f" % (roc_auc))
plt.plot([0, 1], [0, 1], '--', color=(0.5, 0.5, 0.5), label='random')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
# plt.title("ROC plot model: '%s'" % cname)
plt.title("%d training examples" % len(examples))
plt.legend(loc="lower right")
# plt.savefig(os.path.abspath(cname + "_cc_domain_ROC" + ".png"))
plt.savefig(os.path.abspath(os.path.join(output_path, cname + "_ROC" + ".png")))
plt.show()
acc = metrics.accuracy_score(y_true, y_pred)
print("Accuracy: %.4f" % (acc))
```
# Sanity check on results for all 4 strategies
Compare the first prediction for each to make sure all the right stuff is there...
```
print("Strategy A. Custom sklearn model using n-grams, TFIDF, LR:")
print(y_true_sk[0])
print(pred_sk[0])
print(proba_sk[0])
print("")
print("Strategy B. Sentiment HQ:")
pp.pprint(predictions_hq[0])
print("Strategy C. Custom collection using general text features:")
pp.pprint(predictions[0])
print("")
print("Strategy D. Custom collection using sentiment features:")
pp.pprint(predictions_domain[0])
print("")
```
# Compute overall metrics and plot
```
plt.figure(figsize=(10,10))
cname = base_model_name
# compute and draw curve for sklearn LR built from scratch
probas_sk = []
y_pred_labels_sk = []
y_pred_sk = []
for i, pred in enumerate(pred_sk):
proba_pos = proba_sk[i][1]
probas_sk.append(proba_pos)
if float(proba_pos) >= 0.50:
pred_label = "pos"
elif float(proba_pos) < 0.50:
pred_label = "neg"
else:
print("ERROR on example %d" % i)
y_pred_labels_sk.append(pred_label)
y_pred_sk.append(lab2bin[pred_label])
fpr_sk, tpr_sk, thresholds_sk = metrics.roc_curve(y_true_sk, probas_sk)
roc_auc_sk = metrics.auc(fpr_sk, tpr_sk)
plt.plot(fpr_sk, tpr_sk, lw = 2, color = "#a5acaf", label = "A. Custom sklearn ngram LR model; area = %0.3f" % roc_auc_sk)
# compute and draw curve for sentimentHQ
probas_s = []
y_true_s = []
y_pred_labels_s = []
y_pred_s = []
for i, pred in enumerate(predictions_hq):
y_true_s.append(lab2bin[pred['label']])
probas_s.append(pred['proba'])
if float(pred['proba']) >= 0.50:
pred_label = "pos"
elif float(pred['proba']) < 0.50:
pred_label = "neg"
else:
print("ERROR on example %d" % i)
y_pred_labels_s.append(pred_label)
y_pred_s.append(lab2bin[pred_label])
fpr_s, tpr_s, thresholds_s = metrics.roc_curve(y_true_s, probas_s)
roc_auc_s = metrics.auc(fpr_s, tpr_s)
plt.plot(fpr_s, tpr_s, lw = 2, color = "#b05ecc", label = "B. Sentiment HQ model; area = %0.3f" % roc_auc_s)
# Compute and draw curve for the custom collection using general text features
probas = []
y_true = []
y_pred_labels = []
y_pred = []
lab2bin = {'pos': 1,
'neg': 0}
for i, pred in enumerate(predictions):
y_true.append(lab2bin[pred['label']])
probas.append(pred['indico_result']['pos'])
pred_label = max(pred['indico_result'].keys(), key = (lambda x: pred['indico_result'][x])) # pick the most likely class by predicted proba
y_pred_labels.append(pred_label)
y_pred.append(lab2bin[pred_label])
fpr, tpr, thresholds = metrics.roc_curve(y_true, probas)
roc_auc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, lw = 2, color = "#ffbb3b", label = "C. Custom IMDB model using general text features; area = %0.3f" % (roc_auc))
# now compute and draw curve for the CC using sentiment text features
probas_d = []
y_true_d = []
y_pred_labels_d = []
y_pred_d = []
for i, pred in enumerate(predictions_domain):
y_true_d.append(lab2bin[pred['label']])
probas_d.append(pred['indico_result']['pos'])
pred_label = max(pred['indico_result'].keys(), key = (lambda x: pred['indico_result'][x]))
y_pred_labels_d.append(pred_label)
y_pred_d.append(lab2bin[pred_label])
fpr_d, tpr_d, thresholds_d = metrics.roc_curve(y_true_d, probas_d)
roc_auc_d = metrics.auc(fpr_d, tpr_d)
plt.plot(fpr_d, tpr_d, lw = 2, color = "#43b9af", label = "D. Custom IMDB model using sentiment text features; area = %0.3f" % roc_auc_d)
# Add other stuff to figure
plt.plot([0, 1], [0, 1], '--', color=(0.5, 0.5, 0.5), label='random')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
# plt.title("ROC: %d training examples" % len(examples))
plt.title("%d training examples" % len(examples))
plt.legend(loc="lower right")
plt.savefig(os.path.abspath(os.path.join(output_path, cname + "_comparison_ROC" + ".png")), dpi = 300)
plt.show()
```
## Accuracy metrics
```
acc_sk = metrics.accuracy_score(y_true_sk, y_pred_sk)
print("A. Sklearn model from scratch (sklearn) : %.4f" % (acc_sk))
acc_s = metrics.accuracy_score(y_true_s, y_pred_s)
print("B. Sentiment HQ : %.4f" % (acc_s))
acc = metrics.accuracy_score(y_true, y_pred)
print("C. Custom model using general text features : %.4f" % (acc))
acc_d = metrics.accuracy_score(y_true_d, y_pred_d)
print("D. Custom model using sentiment text features : %.4f" % (acc_d))
# print("Using (%d, %d, %d, %d) examples" % (len(y_pred), len(y_pred_d), len(y_pred_s), len(y_pred_sk)))
```
| true |
code
| 0.44348 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/zaidalyafeai/Notebooks/blob/master/tf_Face_SSD.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Introduction
In this task we will detect faces in the wild using single shot detector (SSD) models. The SSD model is a bit complicated but will build a simple implmenetation that works for the current task. Basically, the SSD model is a basic model for object detection that uses full evaluation of the given image without using region proposals which was introduced in R-CNN. This makes SSD much faster. The basic architecture is using a CNN to extract the features and at the end we extract volumes of predictions in the shape $[w, h, c + 4]$ where $(w,h)$ is the size of prediction volume and the $c+5$ is the prediction of classes plus the bounding box offsets. Note that we add 1 for the background. Hence the size of the prediction module for one scale is $w \times h (c + 5)$. Note that we predict these valume at different scales and we use matching with IoU to infer the spatial location of the predicted boxes

# Download The Dataset
We use the dataset fromt his [project](http://vis-www.cs.umass.edu/fddb/). Each single frame frame is annotated by an ellpesioid around the faces that exist in that frame. This data set contains the annotations for 5171 faces in a set of 2845 images taken from the [Faces in the Wild data set](http://tamaraberg.com/faceDataset/index.html). Here is a sample 
```
!wget http://tamaraberg.com/faceDataset/originalPics.tar.gz
!wget http://vis-www.cs.umass.edu/fddb/FDDB-folds.tgz
!tar -xzvf originalPics.tar.gz >> tmp.txt
!tar -xzvf FDDB-folds.tgz >> tmp.txt
```
# Extract the Bounding Boxes
For each image we convert the ellipsoid annotation to a rectangluar region that frames the faces in the current image. Before that we need to explain the concept of anchor boxes. An **anchor box** that exists in a certain region of an image is a box that is responsible for predicting the box in that certain region. Given a certain set of boxes we could match these boxes to the corrospondant anchor box using the intersection over union metric IoU.

In the above example we see the anchor boxes with the associated true labels. If a certain anchor box has a maximum IoU overlap we consider that anchorbox responsible for that prediction. For simplicity we construct volumes of anchor boxes at only one scale.
```
from PIL import Image
import pickle
import os
import numpy as np
import cv2
import glob
```
Use anchors of size $(4,4)$
```
ANCHOR_SIZE = 4
def iou(boxA, boxB):
#evaluate the intersection points
xA = np.maximum(boxA[0], boxB[0])
yA = np.maximum(boxA[1], boxB[1])
xB = np.minimum(boxA[2], boxB[2])
yB = np.minimum(boxA[3], boxB[3])
# compute the area of intersection rectangle
interArea = np.maximum(0, xB - xA + 1) * np.maximum(0, yB - yA + 1)
# compute the area of both the prediction and ground-truth
# rectangles
boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
#compute the union
unionArea = (boxAArea + boxBArea - interArea)
# return the intersection over union value
return interArea / unionArea
#for a given box we predict the corrosponding bounding box
def get_anchor(box):
max_iou = 0.0
matching_anchor = [0, 0, 0, 0]
matching_index = (0, 0)
i = 0
j = 0
w , h = (1/ANCHOR_SIZE, 1/ANCHOR_SIZE)
for x in np.linspace(0, 1, ANCHOR_SIZE +1)[:-1]:
j = 0
for y in np.linspace(0, 1, ANCHOR_SIZE +1)[:-1]:
xmin = x
ymin = y
xmax = (x + w)
ymax = (y + h)
anchor_box = [xmin, ymin, xmax, ymax]
curr_iou = iou(box, anchor_box)
#choose the location with the highest overlap
if curr_iou > max_iou:
matching_anchor = anchor_box
max_iou = curr_iou
matching_index = (i, j)
j += 1
i+= 1
return matching_anchor, matching_index
```
For each image we output a volume of boxes where we map each true label to the corrosponindg location in the $(4, 4, 5)$ tenosr. Note that here we have only two lables 1 for face and 0 for background so we can use binary cross entropy
```
def create_volume(boxes):
output = np.zeros((ANCHOR_SIZE, ANCHOR_SIZE, 5))
for box in boxes:
if max(box) == 0:
continue
_, (i, j) = get_anchor(box)
output[i,j, :] = [1] + box
return output
#read all the files for annotation
annot_files = glob.glob('FDDB-folds/*ellipseList.txt')
data = {}
for file in annot_files:
with open(file, 'r') as f:
rows = f.readlines()
j = len(rows)
i = 0
while(i < j):
#get the file name
file_name = rows[i].replace('\n', '')+'.jpg'
#get the number of boxes
num_boxes = int(rows[i+1])
boxes = []
img = Image.open(file_name)
w, h = img.size
#get all the bounding boxes
for k in range(1, num_boxes+1):
box = rows[i+1+k]
box = box.split(' ')[0:5]
box = [float(x) for x in box]
#convert ellipse to a box
xmin = int(box[3]- box[1])
ymin = int(box[4]- box[0])
xmax = int(xmin + box[1]*2)
ymax = int(ymin + box[0]*2)
boxes.append([xmin/w, ymin/h, xmax/w, ymax/h])
#conver the boxes to a volume of fixed size
data[file_name] = create_volume(boxes)
i = i + num_boxes+2
```
# Imports
We use tensorflow with eager execution. Hence, eager execution allows immediate evaluation of tensors without instintiating graph.
```
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, MaxPooling2D, Dense, Input
from tensorflow.keras.layers import Flatten, Dropout, BatchNormalization, Concatenate, Reshape, GlobalAveragePooling2D, Reshape
from tensorflow.keras.applications.mobilenet_v2 import MobileNetV2, preprocess_input
import cv2
import matplotlib.pyplot as plt
import os
import numpy as np
from PIL import Image
from random import shuffle
import random
import tensorflow.contrib.eager as tfe
tf.enable_eager_execution()
```
#Create A Dataset
Here we use `tf.data` for manipulating the data and use them for training
```
def parse_training(filename, label):
image = tf.image.decode_jpeg(tf.read_file(filename), channels = 3)
image = tf.image.convert_image_dtype(image, tf.float32)
image = tf.image.resize(image, [IMG_SIZE, IMG_SIZE])
label = tf.cast(label, tf.float32)
return image, label
def parse_testing(filename, label):
image = tf.image.decode_jpeg(tf.read_file(filename), channels = 3)
image = tf.image.convert_image_dtype(image, tf.float32)
image = tf.image.resize_images(image, [IMG_SIZE, IMG_SIZE])
label = tf.cast(label, tf.float32)
return image, label
def create_dataset(ff, ll, training = True):
dataset = tf.data.Dataset.from_tensor_slices((ff, ll)).shuffle(len(ff) - 1)
if training:
dataset = dataset.map(parse_training, num_parallel_calls = 4)
else:
dataset = dataset.map(parse_testing, num_parallel_calls = 4)
dataset = dataset.batch(BATCH_SIZE)
return dataset
```
# Data Split
We create a 10% split for the test data to be used for validation
```
files = list(data.keys())
labels = list(data.values())
N = len(files)
M = int(0.9 * N)
#split files for images
train_files = files[:M]
test_files = files[M:]
#split labels
train_labels = labels[:M]
test_labels = labels[M:]
print('training', len(train_files))
print('testing' , len(test_files))
IMG_SIZE = 128
BATCH_SIZE = 32
train_dataset = create_dataset(train_files, train_labels)
test_dataset = create_dataset(test_files, test_labels, training = False)
```
# Visualization
```
def plot_annot(img, boxes):
img = img.numpy()
boxes = boxes.numpy()
for i in range(0, ANCHOR_SIZE):
for j in range(0, ANCHOR_SIZE):
box = boxes[i, j, 1:] * IMG_SIZE
label = boxes[i, j, 0]
if np.max(box) > 0:
img = cv2.rectangle(img, (int(box[0]), int(box[1])), (int(box[2]), int(box[3])), (1, 0, 0), 1)
plt.axis('off')
plt.imshow(img)
plt.show()
for x, y in train_dataset:
plot_annot(x[0], y[0])
break
```
# Create a model
We use a ResNet model with multiple blocks and at the end we use a conv volume with size (4, 4, 5) as a preciction.
```
def conv_block(fs, x, activation = 'relu'):
conv = Conv2D(fs, (3, 3), padding = 'same', activation = activation)(x)
bnrm = BatchNormalization()(conv)
drop = Dropout(0.5)(bnrm)
return drop
def residual_block(fs, x):
y = conv_block(fs, x)
y = conv_block(fs, y)
y = conv_block(fs, y)
return Concatenate(axis = -1)([x, y])
inp = Input(shape = (IMG_SIZE, IMG_SIZE, 3))
block1 = residual_block(16, inp)
pool1 = MaxPooling2D(pool_size = (2, 2))(block1)
block2 = residual_block(32, pool1)
pool2 = MaxPooling2D(pool_size = (2, 2))(block2)
block3 = residual_block(64, pool2)
pool3 = MaxPooling2D(pool_size = (2, 2))(block3)
block4 = residual_block(128, pool3)
pool4 = MaxPooling2D(pool_size = (2, 2))(block4)
block5 = residual_block(256, pool4)
pool5 = MaxPooling2D(pool_size = (2, 2))(block5)
out = Conv2D(5, (3, 3), padding = 'same', activation = 'sigmoid')(pool5)
#create a model with one input and two outputs
model = tf.keras.models.Model(inputs = inp, outputs = out)
model.summary()
```
# Loss and gradient
```
def loss(pred, y):
#extract the boxes that have values (i.e discard boxes that are zeros)
mask = y[...,0]
boxA = tf.boolean_mask(y, mask)
boxB = tf.boolean_mask(pred, mask)
prediction_error = tf.keras.losses.binary_crossentropy(y[...,0], pred[...,0])
detection_error = tf.losses.absolute_difference(boxA[...,1:], boxB[...,1:])
return tf.reduce_mean(prediction_error) + 10*detection_error
def grad(model, x, y):
#record the gradient
with tf.GradientTape() as tape:
pred = model(x)
value = loss(pred, y)
#return the gradient of the loss function with respect to the model variables
return tape.gradient(value, model.trainable_variables)
optimizer = tf.train.AdamOptimizer()
```
# Evaluation metric
```
epochs = 20
#initialize the history to record the metrics
train_loss_history = tfe.metrics.Mean('train_loss')
test_loss_history = tfe.metrics.Mean('test_loss')
best_loss = 1.0
for i in range(1, epochs + 1):
for x, y in train_dataset:
pred = model(x)
grads = grad(model, x, y)
#update the paramters of the model
optimizer.apply_gradients(zip(grads, model.trainable_variables), global_step = tf.train.get_or_create_global_step())
#record the metrics of the current batch
loss_value = loss(pred, y)
#calcualte the metrics of the current batch
train_loss_history(loss_value)
#loop over the test dataset
for x, y in test_dataset:
pred = model(x)
#calcualte the metrics of the current batch
loss_value = loss(pred, y)
#record the values of the metrics
test_loss_history(loss_value)
#print out the results
print("epoch: [{0:d}/{1:d}], Train: [loss: {2:0.4f}], Test: [loss: {3:0.4f}]".
format(i, epochs, train_loss_history.result(),
test_loss_history.result()))
current_loss = test_loss_history.result().numpy()
#save the best model
if current_loss < best_loss:
best_loss = current_loss
print('saving best model with loss ', current_loss)
model.save('keras.h5')
#clear the history after each epoch
train_loss_history.init_variables()
test_loss_history.init_variables()
from tensorflow.keras.models import load_model
best_model = load_model('keras.h5')
```
# Visualization
```
#visualize the predicted bounding box
def plot_pred(img_id):
font = cv2.FONT_HERSHEY_SIMPLEX
raw = cv2.imread(img_id)[:,:,::-1]
h, w = (512, 512)
img = cv2.resize(raw, (IMG_SIZE, IMG_SIZE)).astype('float32')
img = np.expand_dims(img, 0)/255.
boxes = best_model(img).numpy()[0]
raw = cv2.resize(raw, (w, h))
for i in range(0, ANCHOR_SIZE):
for j in range(0, ANCHOR_SIZE):
box = boxes[i, j, 1:] * w
lbl = round(boxes[i, j, 0], 2)
if lbl > 0.5:
color = [random.randint(0, 255) for _ in range(0, 3)]
raw = cv2.rectangle(raw, (int(box[0]), int(box[1])), (int(box[2]), int(box[3])), color, 3)
raw = cv2.rectangle(raw, (int(box[0]), int(box[1])-30), (int(box[0])+70, int(box[1])), color, cv2.FILLED)
raw = cv2.putText(raw, str(lbl), (int(box[0]), int(box[1])), font, 1, (255, 255, 255), 2)
plt.axis('off')
plt.imshow(raw)
plt.show()
img_id = np.random.choice(test_files)
plot_pred(img_id)
!wget https://pmctvline2.files.wordpress.com/2018/08/friends-revival-jennifer-aniston.jpg -O test.jpg
plot_pred('test.jpg')
```
| true |
code
| 0.519826 | null | null | null | null |
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/geemap/tree/master/examples/notebooks/geemap_and_earthengine.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/geemap/blob/master/examples/notebooks/geemap_and_earthengine.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/geemap/blob/master/examples/notebooks/geemap_and_earthengine.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
```
Map = emap.Map(center=(40, -100), zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
image = ee.Image('USGS/SRTMGL1_003')
# Set visualization parameters.
vis_params = {
'min': 0,
'max': 4000,
'palette': ['006633', 'E5FFCC', '662A00', 'D8D8D8', 'F5F5F5']}
# Print the elevation of Mount Everest.
xy = ee.Geometry.Point([86.9250, 27.9881])
elev = image.sample(xy, 30).first().get('elevation').getInfo()
print('Mount Everest elevation (m):', elev)
# Add Earth Engine layers to Map
Map.addLayer(image, vis_params, 'SRTM DEM', True, 0.5)
Map.addLayer(xy, {'color': 'red'}, 'Mount Everest')
```
## Change map positions
For example, center the map on an Earth Engine object:
```
Map.centerObject(ee_object=xy, zoom=13)
```
Set the map center using coordinates (longitude, latitude)
```
Map.setCenter(lon=-100, lat=40, zoom=4)
```
## Extract information from Earth Engine data based on user inputs
```
import ee
import geemap
from ipyleaflet import *
from ipywidgets import Label
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
Map = geemap.Map(center=(40, -100), zoom=4)
Map.default_style = {'cursor': 'crosshair'}
# Add Earth Engine dataset
image = ee.Image('USGS/SRTMGL1_003')
# Set visualization parameters.
vis_params = {
'min': 0,
'max': 4000,
'palette': ['006633', 'E5FFCC', '662A00', 'D8D8D8', 'F5F5F5']}
# Add Earth Eninge layers to Map
Map.addLayer(image, vis_params, 'STRM DEM', True, 0.5)
latlon_label = Label()
elev_label = Label()
display(latlon_label)
display(elev_label)
coordinates = []
markers = []
marker_cluster = MarkerCluster(name="Marker Cluster")
Map.add_layer(marker_cluster)
def handle_interaction(**kwargs):
latlon = kwargs.get('coordinates')
if kwargs.get('type') == 'mousemove':
latlon_label.value = "Coordinates: {}".format(str(latlon))
elif kwargs.get('type') == 'click':
coordinates.append(latlon)
# Map.add_layer(Marker(location=latlon))
markers.append(Marker(location=latlon))
marker_cluster.markers = markers
xy = ee.Geometry.Point(latlon[::-1])
elev = image.sample(xy, 30).first().get('elevation').getInfo()
elev_label.value = "Elevation of {}: {} m".format(latlon, elev)
Map.on_interaction(handle_interaction)
Map
import ee
import geemap
from ipyleaflet import *
from bqplot import pyplot as plt
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
Map = geemap.Map(center=(40, -100), zoom=4)
Map.default_style = {'cursor': 'crosshair'}
# Compute the trend of nighttime lights from DMSP.
# Add a band containing image date as years since 1990.
def createTimeBand(img):
year = img.date().difference(ee.Date('1991-01-01'), 'year')
return ee.Image(year).float().addBands(img)
NTL = ee.ImageCollection('NOAA/DMSP-OLS/NIGHTTIME_LIGHTS') \
.select('stable_lights')
# Fit a linear trend to the nighttime lights collection.
collection = NTL.map(createTimeBand)
fit = collection.reduce(ee.Reducer.linearFit())
image = NTL.toBands()
figure = plt.figure(1, title='Nighttime Light Trend', layout={'max_height': '250px', 'max_width': '400px'})
count = collection.size().getInfo()
start_year = 1992
end_year = 2013
x = range(1, count+1)
coordinates = []
markers = []
marker_cluster = MarkerCluster(name="Marker Cluster")
Map.add_layer(marker_cluster)
def handle_interaction(**kwargs):
latlon = kwargs.get('coordinates')
if kwargs.get('type') == 'click':
coordinates.append(latlon)
markers.append(Marker(location=latlon))
marker_cluster.markers = markers
xy = ee.Geometry.Point(latlon[::-1])
y = image.sample(xy, 500).first().toDictionary().values().getInfo()
plt.clear()
plt.plot(x, y)
# plt.xticks(range(start_year, end_year, 5))
Map.on_interaction(handle_interaction)
# Display a single image
Map.addLayer(ee.Image(collection.select('stable_lights').first()), {'min': 0, 'max': 63}, 'First image')
# Display trend in red/blue, brightness in green.
Map.setCenter(30, 45, 4)
Map.addLayer(fit,
{'min': 0, 'max': [0.18, 20, -0.18], 'bands': ['scale', 'offset', 'scale']},
'stable lights trend')
fig_control = WidgetControl(widget=figure, position='bottomright')
Map.add_control(fig_control)
Map
```
| true |
code
| 0.645958 | null | null | null | null |
|
```
# Ensure the scenepic library will auto reload
%load_ext autoreload
# Imports
import json
import math
import os
import numpy as np
import scenepic as sp
%autoreload
# Seed random number generator for consistency
np.random.seed(0)
ASSET_DIR = os.path.join("..", "ci", "assets")
def asset_path(filename):
return os.path.join(ASSET_DIR, filename)
```
# ScenePic Python Tutorials
These tutorials provide practical examples that highlight most of the functionality supported by ScenePic. While by no means exhaustive, they should give you a solid start towards building useful and insightful 3D visualizations of your own. If there is something you feel is missing from this tutorial, or if there is something you would like to contribute, please contact the maintainers via GitHub Issues.
```
# Tutorial 1 - Scene and Canvas basics
# Create a Scene, the top level container in ScenePic
scene = sp.Scene()
# A Scene can contain many Canvases
# For correct operation, you should create these using scene1.create_canvas() (rather than constructing directly using sp.Canvas(...))
canvas_1 = scene.create_canvas_3d(width = 300, height = 300)
canvas_2 = scene.create_canvas_3d(width = 100, height = 300)
# ScenePic has told Jupyter how to display scene objects
scene
# Tutorial 2 - Meshes and Frames
# Create a scene
scene = sp.Scene()
# A Mesh is a vertex/triangle/line buffer with convenience methods
# Meshes "belong to" the Scene, so should be created using create_mesh()
# Meshes can be re-used across multiple frames/canvases
my_first_mesh = scene.create_mesh(shared_color = sp.Color(1.0, 0.0, 1.0)) # If shared_color is not provided, you can use per-vertex coloring
my_first_mesh.add_cube(transform = sp.Transforms.Scale(0.1)) # Adds a unit cube centered at the origin
my_first_mesh.add_cube(transform = np.dot(sp.Transforms.Translate([-1.0, 1.0, -1.0]), sp.Transforms.Scale(0.5)))
my_first_mesh.add_sphere(transform = sp.Transforms.Translate([1.0, 1.0, 1.0]))
# A Canvas is a 3D rendering panel
canvas = scene.create_canvas_3d(width = 300, height = 300)
# Create an animation with multiple Frames
# A Frame references a set of Meshes
# Frames are created from the Canvas not the Scene
for i in range(10):
frame = canvas.create_frame()
frame.add_mesh(my_first_mesh, transform = sp.Transforms.Translate([i / 10.0, 0.0, 0.0])) # An arbitrary rigid transform can optionally be specified.
mesh2 = scene.create_mesh(shared_color = sp.Color(1.0,0.0,0.0),camera_space=True)
mesh2.add_cube(transform = np.dot(sp.Transforms.Translate([0.0, 0.0, -5.0]), sp.Transforms.Scale(0.5)))
frame.add_mesh(mesh2)
label = scene.create_label(text = "Hi", color = sp.Colors.White, size_in_pixels = 80, offset_distance = 0.6, camera_space = True)
frame.add_label(label = label, position = [0.0, 0.0, -5.0])
# Display the Scene in Jupyter
scene
# Tutorial 3 - Point clouds 1
# Create a scene
scene = sp.Scene()
# Create a mesh that we'll turn in to a point-cloud using enable_instancing()
mesh = scene.create_mesh(shared_color = sp.Color(0,1,0))
mesh.add_cube() # Unit diameter cube that will act as primitive
mesh.apply_transform(sp.Transforms.Scale(0.01)) # Scale the primitive
mesh.enable_instancing(positions = 2 * np.random.rand(10000, 3) - 1) # Cause the mesh to be replicated across many instances with the provided translations. You can optionally also provide per-instance colors and quaternion rotations.
# Create Canvas and Frame, and add Mesh to Frame
canvas = scene.create_canvas_3d(width = 300, height = 300, shading=sp.Shading(bg_color=sp.Colors.White))
frame = canvas.create_frame()
frame.add_mesh(mesh)
scene
# Tutorial 4 - Points clouds 2
# Note that the point cloud primitive can be arbitrarily complex.
# The primitive geometry will only be stored once for efficiency.
# Some parameters
disc_thickness = 0.2
normal_length = 1.5
point_size = 0.1
# A helper Mesh which we won't actually use for rendering - just to find the points and normals on a sphere to be used in mesh2 below
# NB this is created using the sp.Mesh() constructor directly so it doesn't get added automatically to the Scene
sphere_mesh = sp.Mesh()
sphere_mesh.add_sphere(transform = sp.Transforms.Scale(2.0), color = sp.Color(1.0, 0.0, 0.0))
N = sphere_mesh.count_vertices()
points = sphere_mesh.vertex_buffer['pos']
normals = sphere_mesh.vertex_buffer['norm']
# Convert the normals into quaternion rotations
rotations = np.zeros((N, 4))
for i in range(0, N):
rotations[i, :] = sp.Transforms.QuaternionToRotateXAxisToAlignWithAxis(normals[i, :])
# Generate some random colors
colors = np.random.rand(N,3)
# Create a scene
scene = sp.Scene()
# Create a mesh that we'll turn in to a point-cloud using enable_instancing()
mesh = scene.create_mesh(shared_color = sp.Color(0,1,0), double_sided = True) # shared_color will be overridden in a moment
# Add the primitive to the Mesh - a disc and a thickline showing the normal
mesh.add_disc(segment_count = 20, transform = sp.Transforms.Scale([disc_thickness, 1.0, 1.0]))
mesh.add_thickline(start_point = np.array([disc_thickness * 0.5, 0.0, 0.0]), end_point = np.array([normal_length, 0.0, 0.0]), start_thickness = 0.2, end_thickness = 0.1)
mesh.apply_transform(sp.Transforms.Scale(point_size))
# Now turn the mesh into a point-cloud
mesh.enable_instancing(positions = points, rotations = rotations, colors = colors) # Both rotations and colors are optional
# Create Canvas and Frame, and add Mesh to Frame
canvas = scene.create_canvas_3d(width = 300, height = 300)
frame = canvas.create_frame()
frame.add_mesh(mesh)
scene
# Tutorial 5 - Misc Meshes
# Scene is the top level container in ScenePic
scene = sp.Scene()
# Ok - let's start by creating some Mesh objects
# Mesh 1 - contains a cube and a sphere
# Mesh objects can contain arbitrary triangle mesh and line geometry
# Meshes can belong to "layers" which can be controlled by the user interactively
mesh1 = scene.create_mesh(layer_id = "Sphere+") # No shared_color provided, so per-vertex coloring enabled
mesh1.add_cylinder(color = sp.Color(1.0, 0.0, 0.0), transform = sp.Transforms.Translate([-2.0, 0.0, -2.0]))
mesh1.add_uv_sphere(color = sp.Color(0.0, 0.0, 1.0), transform = np.dot(sp.Transforms.Translate([-1.0, 1.0, 0.0]), sp.Transforms.Scale(1.8)), fill_triangles = False, add_wireframe = True)
mesh1.add_icosphere(color = sp.Color(0.0, 1.0, 1.0), transform = np.dot(sp.Transforms.Translate([2.0, 1.0, 0.0]), sp.Transforms.Scale(1.8)), fill_triangles = False, add_wireframe = True, steps = 2)
# Mesh 2 - coordinate axes
mesh2 = scene.create_mesh(layer_id = "Coords")
mesh2.add_coordinate_axes(transform = sp.Transforms.Translate([0.0, 0.0, 0.0]))
# Mesh 3 - example of Loop Subdivision on a cube
cube_verts = np.array([[-0.5, -0.5, -0.5], [+0.5, -0.5, -0.5], [-0.5, +0.5, -0.5], [+0.5, +0.5, -0.5], [-0.5, -0.5, +0.5], [+0.5, -0.5, +0.5], [-0.5, +0.5, +0.5], [+0.5, +0.5, +0.5]])
cube_tris = np.array([[0, 2, 3], [0, 3, 1], [1, 3, 7], [1, 7, 5], [4, 5, 7], [4, 7, 6], [4, 6, 2], [4, 2, 0], [2, 6, 7], [2, 7, 3], [4, 0, 1], [4, 1, 5]])
cube_verts_a, cube_tris_a = sp.LoopSubdivStencil(cube_tris, 2, False).apply(cube_verts) # Two steps of subdivision, no projection to limit surface. Stencils could be reused for efficiency for other meshes with same triangle topology.
cube_verts_b, cube_tris_b = sp.LoopSubdivStencil(cube_tris, 2, True).apply(cube_verts) # Two steps of subdivision, projection to limit surface. Stencils could be reused for efficiency for other meshes with same triangle topology.
mesh3 = scene.create_mesh(shared_color = sp.Color(1.0, 0.8, 0.8))
mesh3.add_mesh_without_normals(cube_verts, cube_tris, transform = sp.Transforms.Translate([-1.0, 0.0, 0.0])) # Add non-subdivided cube
mesh3.add_mesh_without_normals(cube_verts_a, cube_tris_a)
mesh3.add_mesh_without_normals(cube_verts_b, cube_tris_b, transform = sp.Transforms.Translate([+1.0, 0.0, 0.0]))
# Mesh 4 - line example
mesh4 = scene.create_mesh()
Nsegs = 7000
positions = np.cumsum(np.random.rand(Nsegs, 3) * 0.2, axis = 0)
colored_points = np.concatenate((positions, np.random.rand(Nsegs, 3)), axis = 1)
mesh4.add_lines(colored_points[0:-1, :], colored_points[1:, :])
mesh4.add_camera_frustum(color = sp.Color(1.0,1.0,0.0))
# Let's create two Canvases this time
canvas1 = scene.create_canvas_3d(width = 300, height = 300)
canvas2 = scene.create_canvas_3d(width = 300, height = 300)
# We can link their keyboard/mouse/etc. input events to keep the views in sync
scene.link_canvas_events(canvas1, canvas2)
# And we can specify that certain named "mesh collections" should have user-controlled visibility and opacity
# Meshs without mesh_collection set, or without specified visibilities will always be visible and opaque
canvas1.set_layer_settings({"Coords" : { "opacity" : 0 }, "Sphere+" : { "opacity" : 1 }})
# A Frame contains an array of meshes
frame11 = canvas1.create_frame(meshes = [mesh1, mesh2]) # Note that Frames are created from the Canvas not the Scene
frame21 = canvas2.create_frame(meshes = [mesh2, mesh3])
frame22 = canvas2.create_frame(meshes = [mesh4, mesh1])
# ScenePic has told Jupyter how to display scene objects
scene
# Tutorial 6 - Images and Textures
# Scene is the top level container in ScenePic
scene = sp.Scene()
# Create and populate an Image object
image1 = scene.create_image(image_id = "PolarBear")
image1.load(asset_path("PolarBear.png")) # This will preserve the image data in compressed PNG format
# Create a texture map
texture = scene.create_image(image_id = "texture")
texture.load(asset_path("uv.png")) # we can use this image to skin meshes
# Example of a mesh that is defined in camera space not world space
# This will not move as the virtual camera is moved with the mouse
cam_space_mesh = scene.create_mesh(shared_color = sp.Color(1.0, 0.0, 0.0), camera_space = True)
cam_space_mesh.add_sphere(transform = np.dot(sp.Transforms.Translate([10, -10, -20.0]), sp.Transforms.Scale(1.0)))
# Some textured primitives
sphere = scene.create_mesh(texture_id=texture.image_id, nn_texture = False)
sphere.add_icosphere(steps=4)
cube = scene.create_mesh(texture_id=texture.image_id)
transform = sp.Transforms.translate([-1, 0, 0]) @ sp.Transforms.scale(0.5)
cube.add_cube(transform=transform)
# Show images in 3D canvas
canvas = scene.create_canvas_3d(shading=sp.Shading(bg_color=sp.Colors.White))
mesh1 = scene.create_mesh(texture_id = "PolarBear")
mesh1.add_image() # Adds image in canonical position
# Add an animation that rigidly transforms each image
n_frames = 20
for i in range(n_frames):
angle = 2 * math.pi * i / n_frames
c, s = math.cos(angle), math.sin(angle)
# Create a focus point that allows you to "lock" the camera's translation and optionally orientation by pressing the "l" key
axis = np.array([1.0, 0.0, 1.0])
axis /= np.linalg.norm(axis)
focus_point = sp.FocusPoint([c,s,0], orientation_axis_angle = axis * angle)
mesh = scene.create_mesh()
mesh.add_coordinate_axes(transform = np.dot(sp.Transforms.Translate(focus_point.position), sp.Transforms.RotationMatrixFromAxisAngle(axis, angle)))
im_size = 15
im_data = np.random.rand(im_size, im_size, 4)
im_data[:,:,3] = 0.5 + 0.5 * im_data[:,:,3]
imageB = scene.create_image()
imageB.from_numpy(im_data) # Converts data to PNG format
meshB = scene.create_mesh(texture_id = imageB, is_billboard = True, use_texture_alpha=True)
meshB.add_image(transform = np.dot(sp.Transforms.Scale(2.0), sp.Transforms.Translate([0,0,-1])))
frame = canvas.create_frame(focus_point = focus_point)
frame.add_mesh(mesh1, transform = sp.Transforms.Translate([c,s,0]))
frame.add_mesh(meshB, transform = np.dot(sp.Transforms.Scale(i * 1.0 / n_frames), sp.Transforms.Translate([-c,-s,0])))
frame.add_mesh(cam_space_mesh)
frame.add_mesh(sphere, transform=sp.Transforms.rotation_about_y(np.pi * 2 * i / n_frames))
frame.add_mesh(cube, transform=sp.Transforms.rotation_about_y(-np.pi * 2 * i / n_frames))
frame.add_mesh(mesh)
# Show Scene
scene
# Tutorial 7 - 2D canvases
# Scene is the top level container in ScenePic
scene = sp.Scene()
# Load an image
image1 = scene.create_image(image_id = "PolarBear")
image1.load(asset_path("PolarBear.png")) # This will preserve the image data in compressed PNG format
# Create and populate an Image object
image2 = scene.create_image(image_id = "Random")
image2.from_numpy(np.random.rand(20, 30, 3) * 128 / 255.0) # Converts data to PNG format
# Create a 2D canvas demonstrating different image positioning options
canvas1 = scene.create_canvas_2d(width = 400, height = 300, background_color = sp.Colors.White)
canvas1.create_frame().add_image(image1, "fit")
canvas1.create_frame().add_image(image1, "fill")
canvas1.create_frame().add_image(image1, "stretch")
canvas1.create_frame().add_image(image1, "manual", x = 50, y= 50, scale = 0.3)
# You can composite images and primitives too
canvas2 = scene.create_canvas_2d(width = 300, height = 300)
f = canvas2.create_frame()
f.add_image(image2, "fit")
f.add_image(image1, "manual", x = 30, y= 30, scale = 0.2)
f.add_circle(200, 200, 40, fill_color = sp.Colors.Black, line_width = 10, line_color = sp.Colors.Blue)
f.add_rectangle(200, 100, 50, 25, fill_color = sp.Colors.Green, line_width = 0)
f.add_text("Hello World", 30, 100, sp.Colors.White, 100, "segoe ui light")
scene.framerate = 2
scene
# Tutorial 8 - a mix of transparent and opaque objects, with labels
np.random.seed(55)
scene = sp.Scene()
canvas = scene.create_canvas_3d(width = 700, height = 700)
frame = canvas.create_frame()
# Create a mesh that we'll turn in to a point-cloud using enable_instancing()
layer_settings = { "Labels" : { "opacity" : 1.0 }}
N = 20
for i in range(N):
# Sample object
geotype = np.random.randint(2)
color = np.random.rand(3)
size = 0.3 * np.random.rand() + 0.2
position = 3.0 * np.random.rand(3) - 1.5
opacity = 1.0 if np.random.randint(2) == 0 else np.random.uniform(0.45, 0.55)
# Generate geometry
layer_id = "Layer" + str(i)
mesh = scene.create_mesh(shared_color = color, layer_id = layer_id)
layer_settings[layer_id] = { "opacity" : opacity }
if geotype == 0:
mesh.add_cube()
elif geotype == 1:
mesh.add_sphere()
mesh.apply_transform(sp.Transforms.Scale(size)) # Scale the primitive
mesh.apply_transform(sp.Transforms.Translate(position))
frame.add_mesh(mesh)
# Add label
text = "{0:0.2f} {1:0.2f} {2:0.2f} {3:0.2f}".format(color[0], color[1], color[2], opacity)
horizontal_align = ["left", "center", "right"][np.random.randint(3)]
vertical_align = ["top", "middle", "bottom"][np.random.randint(3)]
if geotype == 0:
if horizontal_align != "center" and vertical_align != "middle":
offset_distance = size * 0.7
else:
offset_distance = size * 0.9
else:
if horizontal_align != "center" and vertical_align != "middle":
offset_distance = size * 0.5 * 0.8
else:
offset_distance = size * 0.6
label = scene.create_label(text = text, color = color, layer_id = "Labels", font_family = "consolas", size_in_pixels = 80 * size, offset_distance = offset_distance, vertical_align = vertical_align, horizontal_align = horizontal_align)
frame.add_label(label = label, position = position)
canvas.set_layer_settings(layer_settings)
scene
# Tutorial 9 - mesh animation
# let's create our mesh to get started
scene = sp.Scene()
canvas = scene.create_canvas_3d(width=700, height=700)
# Load a mesh to animate
jelly_mesh = sp.load_obj(asset_path("jelly.obj"))
texture = scene.create_image("texture")
texture.load(asset_path("jelly.png"))
# create a base mesh for the animation. The animation
# will only change the vertex positions, so this mesh
# is used to set everything else, e.g. textures.
base_mesh = scene.create_mesh("jelly_base")
base_mesh.texture_id = texture.image_id
base_mesh.use_texture_alpha = True
base_mesh.add_mesh(jelly_mesh)
def random_linspace(min_val, max_val, num_samples):
vals = np.linspace(min_val, max_val, num_samples)
np.random.shuffle(vals)
return vals
# this base mesh will be instanced, so we can animate each
# instance individual using rigid transforms, in this case
# just translation.
marbles = scene.create_mesh("marbles_base")
num_marbles = 10
marbles.add_sphere(sp.Colors.White, transform=sp.Transforms.Scale(0.2))
marble_positions = np.zeros((num_marbles, 3), np.float32)
marble_positions[:, 0] = random_linspace(-0.6, 0.6, num_marbles)
marble_positions[:, 2] = random_linspace(-1, 0.7, num_marbles)
marble_offsets = np.random.uniform(0, 2*np.pi, size=num_marbles).astype(np.float32)
marble_colors_start = np.random.uniform(0, 1, size=(num_marbles, 3)).astype(np.float32)
marble_colors_end = np.random.uniform(0, 1, size=(num_marbles, 3)).astype(np.float32)
marbles.enable_instancing(marble_positions, colors=marble_colors_start)
for i in range(60):
# animate the wave mesh by updating the vertex positions
positions = jelly_mesh.positions.copy()
delta_x = (positions[:, 0] + 0.0838 * i) * 10
delta_z = (positions[:, 2] + 0.0419 * i) * 10
positions[:, 1] = positions[:, 1] + 0.1 * (np.cos(delta_x) + np.sin(delta_z))
# we create a mesh update with the new posiitons. We can use this mesh update
# just like a new mesh, because it essentially is one, as ScenePic will create
# a new mesh from the old one using these new positions.
jelly_update = scene.update_mesh_positions("jelly_base", positions)
frame = canvas.create_frame(meshes=[jelly_update])
# this is a simpler form of animation in which we will change the position
# and colors of the marbles
marble_y = np.sin(0.105 * i + marble_offsets)
positions = np.stack([marble_positions[:, 0], marble_y, marble_positions[:, 2]], -1)
alpha = ((np.sin(marble_y) + 1) * 0.5).reshape(-1, 1)
beta = 1 - alpha
colors = alpha * marble_colors_start + beta * marble_colors_end
marbles_update = scene.update_instanced_mesh("marbles_base", positions, colors=colors)
frame.add_mesh(marbles_update)
scene.quantize_updates()
scene
# Tutorial 10 - Instanced Animation
# In this tutorial we will explore how we can use mesh updates on
# instanced meshes as well. We will begin by creating a simple primitive
# and use instancing to create a cloud of stylized butterflies. We will
# then using mesh updates on the instances to make the butterflies
# fly.
scene = sp.Scene()
butterflies = scene.create_mesh("butterflies", double_sided=True)
# the primitive will be a single wing, and we'll use instancing to create
# all the butterflies
butterflies.add_quad(sp.Colors.Blue, [0, 0, 0], [0.1, 0, 0.04], [0.08, 0, -0.06], [0.015, 0, -0.03])
rotate_back = sp.Transforms.quaternion_from_axis_angle([1, 0, 0], -np.pi / 6)
num_butterflies = 100
num_anim_frames = 20
# this will make them flap their wings independently
start_frames = np.random.randint(0, num_anim_frames, num_butterflies)
rot_angles = np.random.uniform(-1, 1, num_butterflies)
rotations = np.zeros((num_butterflies * 2, 4), np.float32)
positions = np.random.uniform(-1, 1, (num_butterflies * 2, 3))
colors = np.random.random((num_butterflies * 2, 3))
for b, angle in enumerate(rot_angles):
rot = sp.Transforms.quaternion_from_axis_angle([0, 1, 0], angle)
rotations[2 * b] = rotations[2 * b + 1] = rot
# we will use the second position per butterfly as a destination
dx = np.sin(angle) * 0.1
dy = positions[2 * b + 1, 1] - positions[2 * b, 1]
dy = np.sign(angle) * min(abs(angle), 0.1)
dz = np.cos(angle) * 0.1
positions[2 * b + 1] = positions[2 * b] + [dx, dy, dz]
butterflies.enable_instancing(positions, rotations, colors)
canvas = scene.create_canvas_3d("main", 700, 700)
canvas.shading = sp.Shading(sp.Colors.White)
start = -np.pi / 6
end = np.pi / 2
delta = (end - start) / (num_anim_frames // 2 - 1)
# let's construct the animation frame by frame
animation = []
for i in range(num_anim_frames):
frame_positions = np.zeros_like(positions)
frame_rotations = np.zeros_like(rotations)
frame_colors = np.zeros_like(colors)
for b, start_frame in enumerate(start_frames):
frame = (i + start_frame) % num_anim_frames
if frame < num_anim_frames // 2:
angle = start + delta * frame
else:
angle = end + delta * (frame - num_anim_frames // 2)
right = sp.Transforms.quaternion_from_axis_angle([0, 0, 1], angle)
right = sp.Transforms.quaternion_multiply(rotate_back, right)
right = sp.Transforms.quaternion_multiply(rotations[2 * b], right)
left = sp.Transforms.quaternion_from_axis_angle([0, 0, 1], np.pi - angle)
left = sp.Transforms.quaternion_multiply(rotate_back, left)
left = sp.Transforms.quaternion_multiply(rotations[2 * b + 1], left)
frame_rotations[2 * b] = right
frame_rotations[2 * b + 1] = left
progress = np.sin((frame * 2 * np.pi) / num_anim_frames)
progress = (progress + 1) * 0.5
# we move the butterfly along its path
pos = (1 - progress) * positions[2 * b] + progress * positions[2 * b + 1]
pos[1] -= np.sin(angle) * 0.02
frame_positions[2 * b : 2 * b + 2, :] = pos
# finally we alter the color
color = (1 - progress) * colors[2 * b] + progress * colors[2 * b + 1]
frame_colors[2 * b : 2 * b + 2, :] = color
# now we create the update. Here we update position, rotation,
# and color, but you can update them separately as well by passing
# the `*None()` versions of the buffers to this function.
update = scene.update_instanced_mesh("butterflies", frame_positions, frame_rotations, frame_colors)
animation.append(update)
# now we create the encapsulating animation which will move the camera
# around the butterflies. The inner animation will loop as the camera moves.
num_frames = 300
cameras = sp.Camera.orbit(num_frames, 3, 2)
for i, camera in enumerate(cameras):
frame = canvas.create_frame()
frame.add_mesh(animation[i % num_anim_frames])
frame.camera = camera
scene
# Tutorial 11 - camera movement
# in this tutorial we will show how to create per-frame camera movement.
# while the user can always choose to override this behavior, having a
# camera track specified can be helpful for demonstrating particular
# items in 3D. We will also show off the flexible GLCamera class.
scene = sp.Scene()
spin_canvas = scene.create_canvas_3d("spin")
spiral_canvas = scene.create_canvas_3d("spiral")
# let's create some items in the scene so we have a frame of reference
polar_bear = scene.create_image(image_id="polar_bear")
polar_bear.load(asset_path("PolarBear.png"))
uv_texture = scene.create_image(image_id = "texture")
uv_texture.load(asset_path("uv.png"))
cube = scene.create_mesh("cube", texture_id=polar_bear.image_id)
cube.add_cube()
sphere = scene.create_mesh("sphere", texture_id=uv_texture.image_id)
sphere.add_icosphere(steps=4, transform=sp.Transforms.translate([0, 1, 0]))
num_frames = 60
for i in range(num_frames):
angle = i*np.pi*2/num_frames
# for the first camera we will spin in place on the Z axis
rotation = sp.Transforms.rotation_about_z(angle)
spin_camera = sp.Camera(center=[0, 0, 4], rotation=rotation, fov_y_degrees=30.0)
# for the second camera, we will spin the camera in a spiral around the scene
# we can do this using the look-at initialization, which provides a straightforward
# "look at" interface for camera placement.
camera_center = [4*np.cos(angle), i*4/num_frames - 2, 4*np.sin(angle)]
spiral_camera = sp.Camera(camera_center, look_at=[0, 0.5, 0])
# we can add frustums directly using the ScenePic camera objects
frustums = scene.create_mesh()
frustums.add_camera_frustum(spin_camera, sp.Colors.Red)
frustums.add_camera_frustum(spiral_camera, sp.Colors.Green)
spin_frame = spin_canvas.create_frame()
spin_frame.camera = spin_camera # each frame can have its own camera object
spin_frame.add_meshes([cube, sphere, frustums])
spiral_frame = spiral_canvas.create_frame()
spiral_frame.camera = spiral_camera
spiral_frame.add_meshes([cube, sphere, frustums])
scene.link_canvas_events(spin_canvas, spiral_canvas)
scene
# Tutorial 12 - audio tracks
# in this tutorial we'll show how to attach audio tracks to canvases. ScenePic
# supports any audio file format supported by the browser.
def _set_audio(scene, canvas, path):
audio = scene.create_audio()
audio.load(path)
canvas.media_id = audio.audio_id
scene = sp.Scene()
names = ["red", "green", "blue"]
colors = [sp.Colors.Red, sp.Colors.Green, sp.Colors.Blue]
frequencies = [0, 1, 0.5]
graph = scene.create_graph("graph", width=900, height=150)
for name, color, frequency in zip(names, colors, frequencies):
mesh = scene.create_mesh()
mesh.add_cube(color)
canvas = scene.create_canvas_3d(name, width=300, height=300)
_set_audio(scene, canvas, asset_path(name + ".ogg"))
values = []
for j in range(60):
frame = canvas.create_frame()
scale = math.sin(j * 2 * math.pi * frequency / 30)
frame.add_mesh(mesh, sp.Transforms.scale((scale + 1) / 2 + 0.5))
values.append(scale)
graph.add_sparkline(name, values, color)
graph.media_id = canvas.media_id
names.append("graph")
scene.grid("600px", "1fr auto", "1fr 1fr 1fr")
scene.place("graph", "2", "1 / span 3")
scene.link_canvas_events(*names)
scene
# Tutorial 13 - video
# It is also possible to attach videos to ScenePic scenes. Once attached, you can draw the
# frames of those videos to canvases in the same way as images, and can draw the same
# video to multiple frames. Once a media file (video or audio) has been attached to a
# canvas, that file will be used to drive playback. In practical terms, this means that
# ScenePic will display frames such that they line up with the timestamps of the video
# working on the assumption that ScenePic frames are displayed at the framerate of the video.
def _angle_to_pos(angle, radius):
return np.cos(angle) * radius + 200, np.sin(angle) * radius + 200
scene = sp.Scene()
video = scene.create_video()
video.load(asset_path("circles.mp4"))
tracking = scene.create_canvas_2d("tracking", background_color=sp.Colors.White)
tracking.media_id = video.video_id
multi = scene.create_canvas_2d("multi", background_color=sp.Colors.White)
multi.media_id = video.video_id
angles = np.linspace(0, 2 * np.pi, 360, endpoint=False)
for angle in angles:
# if a 2D canvas has an associated video
# then a frame of that video can be added
# via the add_video method.
frame = tracking.create_frame()
frame.add_video(layer_id="video")
red_pos = _angle_to_pos(angle, 160)
frame.add_rectangle(red_pos[0] - 11, red_pos[1] - 11, 22, 22, [255, 0, 0], 2, layer_id="rect")
frame.add_circle(red_pos[0], red_pos[1], 10, fill_color=[255, 0, 0], layer_id="dot")
green_pos = _angle_to_pos(-2*angle, 80)
frame.add_rectangle(green_pos[0] - 11, green_pos[1] - 11, 22, 22, [0, 255, 0], 2, layer_id="rect")
frame.add_circle(green_pos[0], green_pos[1], 10, fill_color=[0, 255, 0], layer_id="dot")
blue_pos = _angle_to_pos(4*angle, 40)
frame.add_rectangle(blue_pos[0] - 11, blue_pos[1] - 11, 22, 22, [0, 0, 255], 2, layer_id="rect")
frame.add_circle(blue_pos[0], blue_pos[1], 10, fill_color=[0, 0, 255], layer_id="dot")
frame = multi.create_frame()
frame.add_video("manual", red_pos[0] - 40, red_pos[1] - 40, 0.2, layer_id="red")
frame.add_video("manual", green_pos[0] - 25, green_pos[1] - 25, 0.125, layer_id="green")
frame.add_video("manual", 160, 160, 0.2, layer_id="blue")
tracking.set_layer_settings({
"rect": {"render_order": 0},
"video": {"render_order": 1},
"dot": {"render_order": 2}
})
scene.link_canvas_events("tracking", "multi")
scene
# Tutorial 14 - Multiview Visualization
# One common and useful scenario for ScenePic is to visualize the result of multiview 3D reconstruction.
# In this tutorial we'll show how to load some geometry, assocaited camera calibration
# information, and images to create a visualization depicting the results.
def _load_camera(camera_info):
# this function loads an "OpenCV"-style camera representation
# and converts it to a GL style for use in ScenePic
location = np.array(camera_info["location"], np.float32)
euler_angles = np.array(camera_info["rotation"], np.float32)
rotation = sp.Transforms.euler_angles_to_matrix(euler_angles, "XYZ")
translation = sp.Transforms.translate(location)
extrinsics = translation @ rotation
world_to_camera = sp.Transforms.gl_world_to_camera(extrinsics)
aspect_ratio = camera_info["width"] / camera_info["height"]
projection = sp.Transforms.gl_projection(camera_info["fov"], aspect_ratio, 0.01, 100)
return sp.Camera(world_to_camera, projection)
def _load_cameras():
with open(asset_path("cameras.json")) as file:
cameras = json.load(file)
return [_load_camera(cameras[key])
for key in cameras]
scene = sp.Scene()
# load the fitted cameras
cameras = _load_cameras()
# this textured cube will stand in for a reconstructed mesh
texture = scene.create_image("texture")
texture.load(asset_path("PolarBear.png"))
cube = scene.create_mesh("cube")
cube.texture_id = texture.image_id
cube.add_cube(transform=sp.Transforms.scale(2))
# construct all of the frustums
# and camera images
frustums = scene.create_mesh("frustums", layer_id="frustums")
colors = [sp.Colors.Red, sp.Colors.Green, sp.Colors.Blue]
paths = [asset_path(name) for name in ["render0.png", "render1.png", "render2.png"]]
camera_images = []
images = []
for i, (color, path, camera) in enumerate(zip(colors, paths, cameras)):
image = scene.create_image(path)
image.load(path)
frustums.add_camera_frustum(camera, color)
image_mesh = scene.create_mesh("image{}".format(i),
layer_id="images",
shared_color=sp.Colors.Gray,
double_sided=True,
texture_id=image.image_id)
image_mesh.add_camera_image(camera)
images.append(image)
camera_images.append(image_mesh)
# create one canvas for each camera to show the scene from
# that camera's viewpoint
width = 640
for i, camera in enumerate(cameras):
height = width / camera.aspect_ratio
canvas = scene.create_canvas_3d("hand{}".format(i), width, height, camera=camera)
frame = canvas.create_frame()
frame.add_mesh(cube)
frame.add_mesh(frustums)
frame.camera = camera
for cam_mesh in camera_images:
frame.add_mesh(cam_mesh)
scene
# Tutorial 15 - Frame Layer Settings
# It is possible to use the per-frame layer settings to automatically
# change various layer properties, for example to fade meshes in and
# out of view. The user can still override this manually using the
# controls, of course, but this feature can help guide the user through
# more complex animations.
scene = sp.Scene()
# In this tutorial we will fade out one mesh (the cube) and fade
# another in (the sphere).
cube = scene.create_mesh(layer_id="cube")
cube.add_cube(sp.Colors.Green)
sphere = scene.create_mesh(layer_id="sphere")
sphere.add_sphere(sp.Colors.Red)
canvas = scene.create_canvas_3d()
for i in range(60):
sphere_opacity = i / 59
cube_opacity = 1 - sphere_opacity
frame = canvas.create_frame()
frame.add_mesh(cube)
frame.add_mesh(sphere)
# the interface here is the same as with how layer settings
# usually works at the canvas level.
frame.set_layer_settings({
"cube": {"opacity": cube_opacity},
"sphere": {"opacity": sphere_opacity}
})
scene
```
| true |
code
| 0.603873 | null | null | null | null |
|
# Under the Hood
*Modeling and Simulation in Python*
Copyright 2021 Allen Downey
License: [Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International](https://creativecommons.org/licenses/by-nc-sa/4.0/)
```
# download modsim.py if necessary
from os.path import basename, exists
def download(url):
filename = basename(url)
if not exists(filename):
from urllib.request import urlretrieve
local, _ = urlretrieve(url, filename)
print('Downloaded ' + local)
download('https://raw.githubusercontent.com/AllenDowney/' +
'ModSimPy/master/modsim.py')
# import functions from modsim
from modsim import *
```
In this chapter we "open the hood," looking more closely at how some of
the tools we have used---`run_solve_ivp`, `root_scalar`, and `maximize_scalar`---work.
Most of the time you don't need to know, which is why I left this chapter for last.
But you might be curious. And if nothing else, I have found that I can remember how to use these tools more easily because I know something about how they work.
## How run_solve_ivp Works
`run_solve_ivp` is a function in the ModSimPy library that checks for common errors in the parameters and then calls `solve_ip`, which is the function in the SciPy library that does the actual work.
By default, `solve_ivp` uses the Dormand-Prince method, which is a kind of Runge-Kutta method. You can read about it at
<https://en.wikipedia.org/wiki/Dormand-Prince_method>, but I'll give you a sense of
it here.
The key idea behind all Runge-Kutta methods is to evaluate the slope function several times at each time step and use a weighted average of the computed slopes to estimate the value at the next time step.
Different methods evaluate the slope function in different places and compute the average with different weights.
So let's see if we can figure out how `solve_ivp` works.
As an example, we'll solve the following differential equation:
$$\frac{dy}{dt}(t) = y \sin t$$
Here's the slope function we'll use:
```
import numpy as np
def slope_func(t, state, system):
y, = state
dydt = y * np.sin(t)
return dydt
```
I'll create a `State` object with the initial state and a `System` object with the end time.
```
init = State(y=1)
system = System(init=init, t_end=3)
```
Now we can call `run_solve_ivp`.
```
results, details = run_solve_ivp(system, slope_func)
details
```
One of the variables in `details` is `nfev`, which stands for "number of function evaluations", that is, the number of times `solve_ivp` called the slope function.
This example took 50 evaluations.
Keep that in mind.
Here are the first few time steps in `results`:
```
results.head()
```
And here is the number of time steps.
```
len(results)
```
`results` contains 101 points that are equally spaced in time.
Now you might wonder, if `solve_ivp` ran the slope function 50 times, how did we get 101 time steps?
To answer that question, we need to know more how the solver works.
There are actually three steps:
1. For each time step, `solve_ivp` evaluates the slope function seven times, with different values of `t` and `y`.
2. Using the results, it computes the best estimate for the value `y` at the next time step.
3. After computing all of the time steps, it uses interpolation to compute equally spaced points that connect the estimates from the previous step.
So we can see what's happening, I will run `run_solve_ivp` with the keyword argument `dense_output=False`, which skips the interpolation step and returns time steps that are not equally spaced (that is, not "dense").
While we're at it, I'll modify the slope function so that every time it runs, it adds the values of `t`, `y`, and `dydt` to a list called `evals`.
```
def slope_func(t, state, system):
y, = state
dydt = y * np.sin(t)
evals.append((t, y, dydt))
return dydt
```
Now, before we call `run_solve_ivp` again, I'll initialize `evals` with an empty list.
```
evals = []
results2, details = run_solve_ivp(system, slope_func, dense_output=False)
```
Here are the results:
```
results2
```
It turns out there are only eight time steps, and the first five of them only cover 0.11 seconds.
The time steps are not equal because the Dormand-Prince method is *adaptive*.
At each time step, it actually computes two estimates of the next
value. By comparing them, it can estimate the magnitude of the error,
which it uses to adjust the time step. If the error is too big, it uses
a smaller time step; if the error is small enough, it uses a bigger time
step. By adjusting the time step in this way, it minimizes the number
of times it calls the slope function to achieve a given level of
accuracy.
Because we saved the values of `y` and `t`, we can plot the locations where the slope function was evaluated.
I'll need to use a couple of features we have not seen before, if you don't mind.
First we'll unpack the values from `evals` using `np.transpose`.
Then we can use trigonometry to convert the slope, `dydt`, to components called `u` and `v`.
```
t, y, slope = np.transpose(evals)
theta = np.arctan(slope)
u = np.cos(theta)
v = np.sin(theta)
```
Using these values, we can generate a *quiver plot* that shows an arrow for each time the slope function ran.
The location of the each arrow represents the values of `t` and `y`; the orientation of the arrow shows the slope that was computed.
```
import matplotlib.pyplot as plt
plt.quiver(t, y, u, v, pivot='middle',
color='C1', alpha=0.4, label='evaluation points')
results2['y'].plot(style='o', color='C0', label='solution points')
results['y'].plot(lw=1, label='interpolation')
decorate(xlabel='Time (t)',
ylabel='Quantity (y)')
```
In this figure, the arrows show where the slope function was executed;
the dots show the best estimate of `y` for each time step; and the line shows the interpolation that connects the estimates.
Notice that many of the arrows do not fall on the line; `solve_ivp` evaluated the slope function at these locations in order to compute the solution, but as it turned out, they are not part of the solution.
This is good to know when you are writing a slope function; you should not assume that the time and state you get as input variables are correct.
## How root_scalar Works
`root_scalar` in the ModSim library is a wrapper for a function in the SciPy library with the same name.
Like `run_solve_ivp`, it checks for common errors and changes some of the parameters in a way that makes the SciPy function easier to use (I hope).
According to the documentation, `root_scalar` uses "a combination of bisection, secant, and inverse quadratic interpolation methods." (See
<https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.root_scalar.html>)
To understand what that means, suppose we're trying to find a root of a
function of one variable, $f(x)$, and assume we have evaluated the
function at two places, $x_1$ and $x_2$, and found that the results have
opposite signs. Specifically, assume $f(x_1) > 0$ and $f(x_2) < 0$, as
shown in the following diagram:

If $f$ is a continuous function, there must be at least one root in this
interval. In this case we would say that $x_1$ and $x_2$ *bracket* a
root.
If this were all you knew about $f$, where would you go looking for a
root? If you said "halfway between $x_1$ and $x_2$," congratulations!
`You just invented a numerical method called *bisection*!
If you said, "I would connect the dots with a straight line and compute
the zero of the line," congratulations! You just invented the *secant
method*!
And if you said, "I would evaluate $f$ at a third point, find the
parabola that passes through all three points, and compute the zeros of
the parabola," congratulations, you just invented *inverse quadratic
interpolation*!
That's most of how `root_scalar` works. The details of how these methods are
combined are interesting, but beyond the scope of this book. You can
read more at <https://en.wikipedia.org/wiki/Brents_method>.
## How maximize_scalar Works
`maximize_scalar` in the ModSim library is a wrapper for a function in the SciPy library called `minimize_scalar`.
You can read about it at <https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize_scalar.html>.
By default, it uses Brent's method, which is related to the method I described in the previous section for root-finding.
Brent's method for finding a maximum or minimum is based on a simpler algorithm:
the *golden-section search*, which I will explain.
Suppose we're trying to find the minimum of a function of a single variable, $f(x)$.
As a starting place, assume that we have evaluated the function at three
places, $x_1$, $x_2$, and $x_3$, and found that $x_2$ yields the lowest
value. The following diagram shows this initial state.

We will assume that $f(x)$ is continuous and *unimodal* in this range,
which means that there is exactly one minimum between $x_1$ and $x_3$.
The next step is to choose a fourth point, $x_4$, and evaluate $f(x_4)$.
There are two possible outcomes, depending on whether $f(x_4)$ is
greater than $f(x_2)$ or not.
The following figure shows the two possible states.

If $f(x_4)$ is less than $f(x_2)$ (shown on the left), the minimum must
be between $x_2$ and $x_3$, so we would discard $x_1$ and proceed with
the new bracket $(x_2, x_4, x_3)$.
If $f(x_4)$ is greater than $f(x_2)$ (shown on the right), the local
minimum must be between $x_1$ and $x_4$, so we would discard $x_3$ and
proceed with the new bracket $(x_1, x_2, x_4)$.
Either way, the range gets smaller and our estimate of the optimal value
of $x$ gets better.
This method works for almost any value of $x_4$, but some choices are
better than others. You might be tempted to bisect the interval between
$x_2$ and $x_3$, but that turns out not to be optimal. You can
read about a better option at <https://greenteapress.com/matlab/golden>.
## Chapter Review
The information in this chapter is not strictly necessary; you can use
these methods without knowing much about how they work. But there are
two reasons you might want to know.
One reason is pure curiosity. If you use these methods, and especially
if you come to rely on them, you might find it unsatisfying to treat
them as "black boxes." At the risk of mixing metaphors, I hope you
enjoyed opening the hood.
The other reason is that these methods are not infallible; sometimes
things go wrong. If you know how they work, at least in a general sense,
you might find it easier to debug them.
With that, you have reached the end of the book, so congratulations! I
hope you enjoyed it and learned a lot. I think the tools in this book
are useful, and the ways of thinking are important, not just in
engineering and science, but in practically every field of inquiry.
Models are the tools we use to understand the world: if you build good
models, you are more likely to get things right. Good luck!
| true |
code
| 0.453383 | null | null | null | null |
|
# What you will learn from this notebook
This notebook is supposed to demonstrate a simplified version of an actual analysis you might want to run. In the real world steps would be probably the same but the dataset itself would be much, much noisier (meaning it would take some effort to put it into the required shape) and much bigger (I mean, nowadays in the industry we are dealing with more than ~30 samples!).
```
# general packages
import pandas as pd
import numpy as np
# specialized stats packages
from lifelines import KaplanMeierFitter
# plotting
import matplotlib.pyplot as plt
import seaborn as sns
# preferences
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
```
# Data
I will use one of default datasets from lifetimes library. I don't know much about it and would prefer to avoid jumping to conclusions so I will pretend this data comes actually from a survey among 26 vampires collected a 100 years ago.
In that survey scientists collected information about how many years ago the vampire became un-dead (in other words was bitten by another vampire and turned into one), how old they were at the time of their transformation, whether they identified themselves as binary or non-binary and whether they have experienced depression symptoms yet.
```
# data
from lifelines.datasets import load_psychiatric_patients
df = load_psychiatric_patients()
df.head()
```
Alright, so we have vampires at different age when they tranformed (`Age` column), they reported how many years have passed since transformation (`T` column), whether they have experienced depression symptoms (`C` column) and what gender they identify with (`sex` column, I'm gonna assume `1` is binary and `2` is non-binary because why not).
# Plotting lifetimes and very basic data exploration
There aren't many variables to work with and I will first show you how to plot lifetimes (assuming *now* is at 25, change `current_time` to see how the plot changes):
```
current_time = 25
observed_lifetimes = df['T'].values
observed = observed_lifetimes < current_time
# I'm using slightly modified function from lifetimes library. See the end of this notebook for details.
# If you are running this notebook yourself first execute the cell with function definition at the bottom
# of this notebook
plot_lifetimes(observed_lifetimes, event_observed=observed, block=True)
```
Next I will see whether experiencing depression symptoms is somehow related to age at which the transformation into a vampire took place:
```
sns.catplot(x="C", y="Age", kind="boxen",
data=df.sort_values("C"));
plt.xlabel('Vampire experienced depression or not', size=18)
plt.ylabel('Age', size=18)
plt.title('Vampire survival as a function of age', size=18);
```
Looks like it does! Appears that vampires who have experienced depressive symptoms were on average older when they were bitten and consequently turned into vampires. This is very interesting! Let's look at Kaplan-Meier curves, and hazard curves to check whether gender has anything to do with depressive symptoms.
# Kaplan-Meier curve
```
kmf = KaplanMeierFitter()
T = df["T"] # time since vampire transformation
C = df["C"] # whether they experienced depression symptoms
kmf.fit(T,C);
kmf.survival_function_
kmf.median_
kmf.plot(figsize=[10,6])
```
## Kaplan-Meier curve plotted separately for vampires who define themselves as binary and non-binary
```
# plot both genders on the same plot
plt.figure(figsize=[10,6])
groups = df['sex']
ix = (groups == 1)
kmf.fit(T[~ix], C[~ix], label='binary vampires')
ax = kmf.plot(figsize=[10,10]);
kmf.fit(T[ix], C[ix], label='non-binary vampires')
kmf.plot(ax=ax);
```
Our sample size is small so error bars are relatively large. It looks like in the early years after vampire tranformation more binary (blue line) than non-binary (orange line) vampires experienced depressive symptoms. Maybe non-binary vampires were in a honeymoon stage with vampirism? However, the error bars are pretty much overlapping starting at 20 years past transformation so likely the differences are not statistically significant. But let's look at the hazard rate first.
# Hazard rate using Nelson-Aalen estimator
```
from lifelines import NelsonAalenFitter
naf = NelsonAalenFitter()
naf.fit(T,event_observed=C);
naf.plot(figsize=[10,6]);
naf.fit(T[~ix], C[~ix], label='binary vampires')
ax = naf.plot(figsize=[10,10])
naf.fit(T[ix], C[ix], label='non-binary vampires')
naf.plot(ax=ax);
```
Okay, so it looks like hazard rate increases with time for both groups which we could already deduce from survival curves. Interestingly, it seems that the hazard rate for non-binary vampires increases rapidly around 35 years compared to previous period (I'm ignoring error bars for the moment).
# Statistical analysis of differences
Is there a difference between hazard rate for binary and non-binary vampires? Let's run a log rank test. It will look at random combinations of samples from the two distributions and calculate how many times one had a higher value than the other.
A very important point to remember is that this analysis will not tell us anything about the hazard rates themselves but rather whether one is different from the other - so it signals only relative differences.
```
from lifelines.statistics import logrank_test
results = logrank_test(T[ix], T[~ix], event_observed_A=C[ix], event_observed_B=C[~ix])
results.print_summary()
```
Looks like indeed there are no significant differences between binary and non-binary vampires but for the sake of exercise let's see how to get from the test statistic to difference in hazard rate:
$$ log{\lambda} = Z \sqrt{ \frac{4}{D} } $$
```
Z = results.test_statistic
D = C.count()
log_lambda = Z * np.sqrt (D / 4)
log_lambda
```
Okay, so if the test was significant we could conclude that the hazard rate for binary versus non-binary vampires is roughly 4 times higher which means they are more likely to suffer from depressive symptoms
## What factors influence vampire's survival? Cox Proportional Hazards Model
Alright, and lets say now we want to look at how age and gender identity shape vampire's future. We want to train the model on one set of samples and then use it to predict relative hazard increases (it's always relative to other vampires, never absolute hazard!) during vampire's lifetime.
```
from lifelines import CoxPHFitter
cph = CoxPHFitter()
cph.fit(df, duration_col='T', event_col='C', show_progress=True)
cph.print_summary()
```
It looks like age is significantly related to the occurence of depressive symptoms, just like our EDA indicated at the beginning. If we had some new data we could use the beta values calculated in by fitting method in the previous step to predict relative changes in hazard rates of new vampires (using `cph.predict_cumulative_hazard(new_df)`. This is a semi-parametric model which means that it assumes the same constant rate of change during lifetime for all vampires. There are also models which take into account time covariates but they are beyond the scope of this short notebook. Thanks for reading and good luck with your own explorations!
## Helper function
```
# the function below is a modified version of plotting function from the lifetimes library. All credit should go to
# them and all faults are mine.
def plot_lifetimes(lifetimes, event_observed=None, birthtimes=None,
order=False, block=True):
"""
Parameters:
lifetimes: an (n,) numpy array of lifetimes.
event_observed: an (n,) numpy array of booleans: True if event observed, else False.
birthtimes: an (n,) numpy array offsetting the births away from t=0.
Creates a lifetime plot, see
examples:
"""
from matplotlib import pyplot as plt
N = lifetimes.shape[0]
if N > 100:
print("warning: you may want to subsample to less than 100 individuals.")
if event_observed is None:
event_observed = np.ones(N, dtype=bool)
if birthtimes is None:
birthtimes = np.zeros(N)
if order:
"""order by length of lifetimes; probably not very informative."""
ix = np.argsort(lifetimes, 0)
lifetimes = lifetimes[ix, 0]
event_observed = event_observed[ix, 0]
birthtimes = birthtimes[ix]
fig, ax = plt.subplots(figsize=[15,5], frameon=False)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
for i in range(N):
c = "#663366" if event_observed[i] else "green"
l = 'burned by the sun rays or an angry mob' if event_observed[i] else "alive"
plt.hlines(N - 1 - i, birthtimes[i], birthtimes[i] + lifetimes[i], color=c, lw=3, label=l if (i == 0) or (i==40) else "")
m = "|" if not event_observed[i] else 'o'
plt.scatter((birthtimes[i]) + lifetimes[i], N - 1 - i, color=c, s=30, marker=m)
plt.legend(fontsize=16)
plt.xlabel("Number of years since becoming a vampire", size=18)
plt.ylabel("Individual vampires", size=20)
plt.vlines(current_time, 0, N, lw=2, linestyles='--', alpha=0.5)
plt.xticks(fontsize=18)
plt.ylim(-0.5, N)
return
```
| true |
code
| 0.791388 | null | null | null | null |
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc" style="margin-top: 1em;"><ul class="toc-item"></ul></div>
# Saving TF Models with SavedModel for TF Serving <a class="tocSkip">
```
import math
import os
import numpy as np
np.random.seed(123)
print("NumPy:{}".format(np.__version__))
import tensorflow as tf
tf.set_random_seed(123)
print("TensorFlow:{}".format(tf.__version__))
DATASETSLIB_HOME = os.path.expanduser('~/dl-ts/datasetslib')
import sys
if not DATASETSLIB_HOME in sys.path:
sys.path.append(DATASETSLIB_HOME)
%reload_ext autoreload
%autoreload 2
import datasetslib
from datasetslib import util as dsu
datasetslib.datasets_root = os.path.join(os.path.expanduser('~'),'datasets')
models_root = os.path.join(os.path.expanduser('~'),'models')
```
# Serving Model in TensorFlow
# Saving model with SavedModel
```
# Restart kernel to run the flag setting again
#tf.flags.DEFINE_integer('model_version', 1, 'version number of the model.')
model_name = 'mnist'
model_version = '1'
model_dir = os.path.join(models_root,model_name,model_version)
# get the MNIST Data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets(os.path.join(datasetslib.datasets_root,'mnist'), one_hot=True)
x_train = mnist.train.images
x_test = mnist.test.images
y_train = mnist.train.labels
y_test = mnist.test.labels
# parameters
pixel_size = 28
num_outputs = 10 # 0-9 digits
num_inputs = 784 # total pixels
def mlp(x, num_inputs, num_outputs,num_layers,num_neurons):
w=[]
b=[]
for i in range(num_layers):
# weights
w.append(tf.Variable(tf.random_normal( \
[num_inputs if i==0 else num_neurons[i-1], \
num_neurons[i]]), \
name="w_{0:04d}".format(i) \
) \
)
# biases
b.append(tf.Variable(tf.random_normal( \
[num_neurons[i]]), \
name="b_{0:04d}".format(i) \
) \
)
w.append(tf.Variable(tf.random_normal(
[num_neurons[num_layers-1] if num_layers > 0 else num_inputs,
num_outputs]),name="w_out"))
b.append(tf.Variable(tf.random_normal([num_outputs]),name="b_out"))
# x is input layer
layer = x
# add hidden layers
for i in range(num_layers):
layer = tf.nn.relu(tf.matmul(layer, w[i]) + b[i])
# add output layer
layer = tf.matmul(layer, w[num_layers]) + b[num_layers]
model = layer
probs = tf.nn.softmax(model)
return model,probs
tf.reset_default_graph()
# input images
serialized_tf_example = tf.placeholder(tf.string, name='tf_example')
feature_configs = {'x': tf.FixedLenFeature(shape=[784], dtype=tf.float32),}
tf_example = tf.parse_example(serialized_tf_example, feature_configs)
x_p = tf.identity(tf_example['x'], name='x_p') # use tf.identity() to assign name
# target output
y_p = tf.placeholder(dtype=tf.float32, name="y_p", shape=[None, num_outputs])
num_layers = 2
num_neurons = []
for i in range(num_layers):
num_neurons.append(256)
learning_rate = 0.01
n_epochs = 50
batch_size = 100
n_batches = mnist.train.num_examples//batch_size
model,probs = mlp(x=x_p,
num_inputs=num_inputs,
num_outputs=num_outputs,
num_layers=num_layers,
num_neurons=num_neurons)
# loss function
#loss = tf.reduce_mean(-tf.reduce_sum(y * tf.log(model), axis=1))
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=model, labels=y_p))
# optimizer function
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss)
predictions_check = tf.equal(tf.argmax(probs,1), tf.argmax(y_p,1))
accuracy_function = tf.reduce_mean(tf.cast(predictions_check, tf.float32))
values, indices = tf.nn.top_k(probs, 10)
table = tf.contrib.lookup.index_to_string_table_from_tensor(
tf.constant([str(i) for i in range(10)]))
prediction_classes = table.lookup(tf.to_int64(indices))
with tf.Session() as tfs:
tfs.run(tf.global_variables_initializer())
for epoch in range(n_epochs):
epoch_loss = 0.0
for batch in range(n_batches):
x_batch, y_batch = mnist.train.next_batch(batch_size)
_,batch_loss = tfs.run([train_op,loss], feed_dict={x_p: x_batch, y_p: y_batch})
epoch_loss += batch_loss
average_loss = epoch_loss / n_batches
print("epoch: {0:04d} loss = {1:0.6f}".format(epoch,average_loss))
accuracy_score = tfs.run(accuracy_function, feed_dict={x_p: x_test, y_p: y_test })
print("accuracy={0:.8f}".format(accuracy_score))
# save the model
# definitions for saving the models
builder = tf.saved_model.builder.SavedModelBuilder(model_dir)
# build signature_def_map
classification_inputs = tf.saved_model.utils.build_tensor_info(
serialized_tf_example)
classification_outputs_classes = tf.saved_model.utils.build_tensor_info(
prediction_classes)
classification_outputs_scores = tf.saved_model.utils.build_tensor_info(values)
classification_signature = (
tf.saved_model.signature_def_utils.build_signature_def(
inputs={
tf.saved_model.signature_constants.CLASSIFY_INPUTS:
classification_inputs
},
outputs={
tf.saved_model.signature_constants.CLASSIFY_OUTPUT_CLASSES:
classification_outputs_classes,
tf.saved_model.signature_constants.CLASSIFY_OUTPUT_SCORES:
classification_outputs_scores
},
method_name=tf.saved_model.signature_constants.CLASSIFY_METHOD_NAME))
tensor_info_x = tf.saved_model.utils.build_tensor_info(x_p)
tensor_info_y = tf.saved_model.utils.build_tensor_info(probs)
prediction_signature = (
tf.saved_model.signature_def_utils.build_signature_def(
inputs={'inputs': tensor_info_x},
outputs={'outputs': tensor_info_y},
method_name=tf.saved_model.signature_constants.PREDICT_METHOD_NAME))
legacy_init_op = tf.group(tf.tables_initializer(), name='legacy_init_op')
builder.add_meta_graph_and_variables(
tfs, [tf.saved_model.tag_constants.SERVING],
signature_def_map={
'predict_images':
prediction_signature,
tf.saved_model.signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY:
classification_signature,
},
legacy_init_op=legacy_init_op)
builder.save()
print('Run following command:')
print('tensorflow_model_server --model_name=mnist --model_base_path={}'
.format(os.path.join(models_root,model_name)))
```
| true |
code
| 0.664976 | null | null | null | null |
|
# Face Recognition with SphereFace
Paper: https://arxiv.org/abs/1704.08063
Repo: https://github.com/wy1iu/sphereface
```
import cv2
import numpy as np
import pandas as pd
from tqdm import tqdm
import matplotlib.pyplot as plt
#We are going to use deepface to detect and align faces
#Repo: https://github.com/serengil/deepface
#!pip install deepface
from deepface.commons import functions
```
### Pre-trained model
```
#Structure: https://github.com/wy1iu/sphereface/blob/master/train/code/sphereface_deploy.prototxt
#Weights: https://drive.google.com/open?id=0B_geeR2lTMegb2F6dmlmOXhWaVk
model = cv2.dnn.readNetFromCaffe("sphereface_deploy.prototxt", "sphereface_model.caffemodel")
#SphereFace input shape. You can verify this in the prototxt.
input_shape = (112, 96)
```
### Common functions
```
#Similarity metrics tutorial: https://sefiks.com/2018/08/13/cosine-similarity-in-machine-learning/
def findCosineDistance(source_representation, test_representation):
a = np.matmul(np.transpose(source_representation), test_representation)
b = np.sum(np.multiply(source_representation, source_representation))
c = np.sum(np.multiply(test_representation, test_representation))
return 1 - (a / (np.sqrt(b) * np.sqrt(c)))
def findEuclideanDistance(source_representation, test_representation):
euclidean_distance = source_representation - test_representation
euclidean_distance = np.sum(np.multiply(euclidean_distance, euclidean_distance))
euclidean_distance = np.sqrt(euclidean_distance)
return euclidean_distance
```
### Data set
```
# Master.csv: https://github.com/serengil/deepface/blob/master/tests/dataset/master.csv
# Images: https://github.com/serengil/deepface/tree/master/tests/dataset
df = pd.read_csv("../deepface/tests/dataset/master.csv")
df.head()
euclidean_distances = []; cosine_distances = []
for index, instance in tqdm(df.iterrows(), total = df.shape[0]):
img1_path = instance["file_x"]
img2_path = instance["file_y"]
target_label = instance["Decision"]
#----------------------------------
#detect and align
img1 = functions.preprocess_face("../deepface/tests/dataset/%s" % (img1_path), target_size=input_shape)[0]
img2 = functions.preprocess_face("../deepface/tests/dataset/%s" % (img2_path), target_size=input_shape)[0]
#----------------------------------
#reshape images to expected shapes
img1_blob = cv2.dnn.blobFromImage(img1)
img2_blob = cv2.dnn.blobFromImage(img2)
if img1_blob.shape != (1, 3, 96, 112):
raise ValueError("img shape must be (1, 3, 96, 112) but it has a ", img1_blob.shape," shape")
#----------------------------------
#representation
model.setInput(img1_blob)
img1_representation = model.forward()[0]
model.setInput(img2_blob)
img2_representation = model.forward()[0]
#----------------------------------
euclidean_distance = findEuclideanDistance(img1_representation, img2_representation)
euclidean_distances.append(euclidean_distance)
cosine_distance = findCosineDistance(img1_representation, img2_representation)
cosine_distances.append(cosine_distance)
df['euclidean'] = euclidean_distances
df['cosine'] = cosine_distances
df.head()
```
### Visualize distributions
```
df[df.Decision == "Yes"]['euclidean'].plot(kind='kde', title = 'euclidean', label = 'Yes', legend = True)
df[df.Decision == "No"]['euclidean'].plot(kind='kde', title = 'euclidean', label = 'No', legend = True)
plt.show()
df[df.Decision == "Yes"]['cosine'].plot(kind='kde', title = 'cosine', label = 'Yes', legend = True)
df[df.Decision == "No"]['cosine'].plot(kind='kde', title = 'cosine', label = 'No', legend = True)
plt.show()
```
### Find the best threshold
```
#Repo: https://github.com/serengil/chefboost
#!pip install chefboost
from chefboost import Chefboost as chef
config = {'algorithm': 'C4.5'}
df[['euclidean', 'Decision']].head()
euclidean_tree = chef.fit(df[['euclidean', 'Decision']].copy(), config)
cosine_tree = chef.fit(df[['cosine', 'Decision']].copy(), config)
#stored in outputs/rules
euclidean_threshold = 17.212238311767578 #euclidean
cosine_threshold = 0.4668717384338379 #cosine
```
### Predictions
```
df['prediction_by_euclidean'] = 'No'
df['prediction_by_cosine'] = 'No'
df.loc[df[df['euclidean'] <= euclidean_threshold].index, 'prediction_by_euclidean'] = 'Yes'
df.loc[df[df['cosine'] <= cosine_threshold].index, 'prediction_by_cosine'] = 'Yes'
df.sample(5)
euclidean_positives = 0; cosine_positives = 0
for index, instance in df.iterrows():
target = instance['Decision']
prediction_by_euclidean = instance['prediction_by_euclidean']
prediction_by_cosine = instance['prediction_by_cosine']
if target == prediction_by_euclidean:
euclidean_positives = euclidean_positives + 1
if target == prediction_by_cosine:
cosine_positives = cosine_positives + 1
print("Accuracy (euclidean): ",round(100 * euclidean_positives/df.shape[0], 2))
print("Accuracy (cosine): ",round(100 * cosine_positives/df.shape[0], 2))
```
### Production
```
def verifyFaces(img1_path, img2_path):
print("Verify ",img1_path," and ",img2_path)
#------------------------------------
#detect and align
img1 = functions.preprocess_face(img1_path, target_size=input_shape)[0]
img2 = functions.preprocess_face(img2_path, target_size=input_shape)[0]
img1_blob = cv2.dnn.blobFromImage(img1)
img2_blob = cv2.dnn.blobFromImage(img2)
#------------------------------------
#representation
model.setInput(img1_blob)
img1_representation = model.forward()[0]
model.setInput(img2_blob)
img2_representation = model.forward()[0]
#------------------------------------
#verify
euclidean_distance = findEuclideanDistance(img1_representation, img2_representation)
print("Found euclidean distance is ",euclidean_distance," whereas required threshold is ",euclidean_threshold)
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
plt.imshow(img1[:,:,::-1])
plt.axis('off')
ax2 = fig.add_subplot(1,2,2)
plt.imshow(img2[:,:,::-1])
plt.axis('off')
plt.show()
if euclidean_distance <= euclidean_threshold:
print("they are same person")
else:
print("they are not same person")
```
### True positive examples
```
verifyFaces("../deepface/tests/dataset/img1.jpg", "../deepface/tests/dataset/img2.jpg")
verifyFaces("../deepface/tests/dataset/img54.jpg", "../deepface/tests/dataset/img3.jpg")
verifyFaces("../deepface/tests/dataset/img42.jpg", "../deepface/tests/dataset/img45.jpg")
verifyFaces("../deepface/tests/dataset/img9.jpg", "../deepface/tests/dataset/img49.jpg")
```
### True negative examples
```
verifyFaces("../deepface/tests/dataset/img1.jpg", "../deepface/tests/dataset/img3.jpg")
verifyFaces("../deepface/tests/dataset/img1.jpg", "../deepface/tests/dataset/img45.jpg")
verifyFaces("../deepface/tests/dataset/img1.jpg", "../deepface/tests/dataset/img49.jpg")
```
| true |
code
| 0.609524 | null | null | null | null |
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as st
import probability_kernels as pk
```
#### Note to users
This Jupyter Notebook is for creating the figures in the paper. It also demonstrates how percentile transition matrices can be calculatd using the python file `probability_kernels`.
```
save = True
```
### Figure of the Peason data
```
# Load the data frame (female) -> dff
dff = pd.read_csv('data/pearson-lee-mother-daughter.csv')
# x values (mothers)
xf = dff.Parent.to_numpy()
# y values (daughters)
yf = dff.Child.to_numpy()
# Load the data frame (male) -> dfm
dfm = pd.read_csv('data/pearson-lee-father-son.csv')
# x values (fathers)
xm = dfm.Parent.to_numpy()
# y values (sons)
ym = dfm.Child.to_numpy()
%%time
# Create an empty list of size three, that will store
matrices_p = [None] * 3
matrices_p[0] = pk.get_matrix_data(xf, yf)
matrices_p[1] = pk.get_matrix_data(xm, ym)
matrices_p[2] = pk.get_matrix(r=0.54, rs=0.96, num_iters=1_000_000, trim_score=6)
# Pearson male is exactly the same: pk.get_matrix(r=0.51, rs=0.89)
fig, axes = plt.subplots(3, 1, figsize=(13*1*0.95*0.75, 8*3/0.95*0.75))
titles_p = ['Pearson data, Mother-Daughter', 'Pearson data, Father-Son',
'Pearson data, simulation of estimated parameters']
for i in range(3):
pk.plot_ax(ax=axes.ravel()[i], matrix=matrices_p[i], i=0,
title=titles_p[i], title_loc='center', child=True)
plt.tight_layout()
legend = ['Descendant in\nTop Quintile', 'Fourth Quintile',
'Third Quintile', 'Second Quintile', 'Bottom Quintile']
fig.legend(legend, bbox_to_anchor=(1.27, 0.9805), fontsize=15)
if save:
plt.savefig('latex/figures/quintile-pearson.png', dpi=300)
plt.show()
```
### Figure for multigenerational mobility, standard parameters
```
r = 0.5
rs = pk.stable_rs(r)
num_steps = 6
matrices = [None] * num_steps
print('r_s =', round(rs, 5))
%%time
for i in range(num_steps):
matrices[i] = pk.get_matrix(r=r, rs=rs, n=i+1, num_iters=1_000_000, trim_score=6)
fig, axes = plt.subplots(3, 2, figsize=(13*2*0.95*0.75, 8*3/0.95*0.75))
for i in range(num_steps):
pk.plot_ax(ax=axes.ravel()[i], matrix=matrices[i], i=i, j=i,
title="$n = {}$".format(str(i+1)), title_loc='center', x_label=True, child=False)
plt.tight_layout()
if save:
plt.savefig('latex/figures/quintile-r=0.5-stable.png', dpi=300)
plt.show()
```
### Figure for the mobility measure
```
mv = np.array([12, 6, 3, 2, 1.4, 1])
m = mv.size
rv, rsv = pk.get_rv_rsv(mv)
matrices_m = [None] * m
%%time
for i in range(m):
matrices_m[i] = pk.get_matrix(r=rv[i], rs=rsv[i], n=1, num_iters=1_000_000, trim_score=6)
```
There are `num_iters` number of iterations over the simulated integral for each probability calculation. Therefore, $5\times 5 \times$ `num_iters` total for one quintile transition matrix. Here we make six matrices in 23 seconds. Therefore, about 6.5 million computations per second - due to vectorization.
```
fig, axes = plt.subplots(3, 2, figsize=(13*2*0.95*0.75, 8*3/0.95*0.75))
for i in range(m):
pk.plot_ax(ax=axes.ravel()[i], matrix=matrices_m[i], i=0, j=i,
title=pk.report_mobility(mv, rv, rsv, i), title_loc='center',
x_label=False, child=True)
plt.tight_layout()
if save:
plt.savefig('latex/figures/quintile-mobility.png', dpi=300)
plt.show()
```
### Figure for the Chetty data

```
chetty = np.array(
[[0.337, 0.242, 0.178, 0.134, 0.109],
[0.28, 0.242, 0.198, 0.16, 0.119],
[0.184, 0.217, 0.221, 0.209, 0.17],
[0.123, 0.176, 0.22, 0.244, 0.236],
[0.075, 0.123, 0.183, 0.254, 0.365]])
pk.plot_matrix(chetty, child=True, legend=False)
plt.tight_layout()
if save:
plt.savefig('latex/figures/quintile-chetty.png', dpi=300)
r_chetty = 0.31
pk.plot_matrix(
pk.get_matrix(r=r_chetty, rs=pk.stable_rs(r_chetty),
n=1, num_iters=100_000, trim_score=6))
pk.stable_rs(r_chetty) / r_chetty
```
### Reference
```
r_ref = 0.5
ref = pk.get_matrix(r=r_ref, rs=pk.stable_rs(r_ref), n=3, num_iters=1_000_000, trim_score=6)
fig, axes = plt.subplots(1, 1, figsize=(13*1*0.95*0.75, 8*1/0.95*0.75))
pk.plot_ax(axes, matrix=ref, i=2, j=2, x_label=True, child=False)
plt.tight_layout()
if save:
plt.savefig("latex/figures/quintile_reference.png", dpi=300)
```
#### Test symmetry (proof in paper)
```
def get_sigma(r, rs, n):
return np.sqrt((r**2+rs**2)**n)
def joint(v1, v2, r, rs, n):
return st.norm.pdf(v2,
scale=pk.get_sigma_tilda(1, r, rs, n),
loc=pk.get_mu_tilda(v1, r, n)) * st.norm.pdf(v1)
def check_vs(va, vb, r, rs, n):
va_vb = joint(va, vb, r, rs, n)
vb_va = joint(vb, va, r, rs, n)
return va_vb, vb_va
# Stable population variance
r_c = 0.3
check_vs(va=0.3, vb=0.7, r=r_c, rs=pk.stable_rs(r_c), n=3)
# (Not) stable population variance
check_vs(va=0.3, vb=0.7, r=r_c, rs=0.7, n=3)
pa = 0.17
pb = 0.64
def per_to_v1(p1):
return st.norm.ppf(p1)
def per_to_v2(p2, r, rs, n):
return st.norm.ppf(p2, scale=get_sigma(r, rs, n))
def check_ps(pa, pb, r, rs, n):
va_vb = joint(per_to_v1(pa), per_to_v2(pb, r, rs, n), r, rs, n)
vb_va = joint(per_to_v1(pb), per_to_v2(pa, r, rs, n), r, rs, n)
return va_vb, vb_va
# (Not) stable population variance, but index by percentile
check_ps(pa=0.17, pb=0.64, r=r_c, rs=0.7, n=3)
```
### Pearson summary stats
```
rawm = pk.get_matrix_data(xm, ym, return_raw=True)
rawf = pk.get_matrix_data(xf, yf, return_raw=True)
raws = np.ravel((rawm + rawf) / 2)
np.quantile(raws, (0.25, 0.5, 0.75))
min(np.min(rawm), np.min(rawf))
max(np.max(rawm), np.max(rawf))
np.mean(raws)
```
### Top two quintiles
```
# Stature
100-(25+25+43+25)/2
# Income
100-(25+24+36+24)/2
```
### Archive
```
# r2v = np.arange(0.05, 0.6, 0.1)
# rv = np.sqrt(r2v)
# rsv = pk.stable_rs(rv)
# mv = rsv / rv
# for r in np.arange(0.2, 0.9, 0.1):
# plot_matrix(get_matrix(r=r, rs=stable_rs(r)))
# plt.title(str(round(r, 2)) + ', ' + str(round(stable_rs(r), 2)) + ', ' + str(round(stable_rs(r) / r, 2)))
# plt.show()
```
| true |
code
| 0.607663 | null | null | null | null |
|
### Analyse node statistics for benchmark results
In this notebook we analyse the node statistics, such as e.g. average degree, for correctly and
misclassified nodes, given the benchmark results of any community detection method.
First, we import the necessary packages.
```
%reload_ext autoreload
%autoreload 2
import os
import matplotlib.pyplot as plt
import numpy as np
from clusim.clustering import Clustering
from src.utils.cluster_analysis import get_cluster_properties, get_node_properties
from src.utils.plotting import plot_histogram, init_plot_style
from src.wrappers.igraph import read_graph
%matplotlib
init_plot_style()
color_dict = {'infomap': 'tab:blue', 'synwalk': 'tab:orange', 'walktrap': 'tab:green', 'louvain': 'tab:red',
'graphtool': 'tab:purple'}
```
First, we specify the network to be analyzed, load the network and glance at its basic properties.
```
# select network
network = 'pennsylvania-roads'
# assemble paths
graph_file = '../data/empirical/clean/' + network + '.txt'
results_dir = '../results/empirical/' + network + '/'
os.makedirs(results_dir, exist_ok=True)
# output directory for storing generated figures
fig_dir = '../figures/'
os.makedirs(fig_dir, exist_ok=True)
# load network
graph = read_graph(graph_file)
node_degrees = graph.degree()
avg_degree = np.mean(node_degrees)
print(f'Network size is {len(graph.vs)} nodes, {len(graph.es)} edges')
print (f'Min/Max/Average degrees are {np.min(node_degrees)}, {np.max(node_degrees)}, {avg_degree}.')
```
Here we compute single-number characteristics of the detected clusters.
```
# methods = ['infomap', 'synwalk', 'walktrap']
methods = ['synwalk', 'louvain', 'graphtool']
colors = [color_dict[m] for m in methods]
graph = read_graph(graph_file)
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
trivial_clu_sizes = [len(cluster) for cluster in clu.to_cluster_list() if len(cluster) < 3]
num_trivial = len(trivial_clu_sizes)
num_non_trivial = clu.n_clusters - num_trivial
print ('\nCluster statistics for ' + method + ': ')
print (f'Number of detected clusters: {clu.n_clusters}')
# print (f'Number of trivial clusters: {clu.n_clusters - num_non_trivial}')
print (f'Number of non-trivial clusters: {num_non_trivial}')
print (f'Fraction of non-trivial clusters: {num_non_trivial/clu.n_clusters}')
print (f'Fraction of nodes in non-trivial clusters: {1.0 - sum(trivial_clu_sizes)/clu.n_elements}')
print (f'Modularity: {graph.modularity(clu.to_membership_list())}')
```
Here we plot the degree occurances of the network.
```
# plot parameters
bin_size = 1 # integer bin size for aggregating degrees
save_figure = False # if True, we save the figure as .pdf in ´fig_dir´
plt.close('all')
graph = read_graph(graph_file)
node_degrees = graph.degree()
avg_degree = np.mean(node_degrees)
# compute degree pmf
min_deg = np.min(node_degrees)
max_deg = np.max(node_degrees)
bin_edges = np.array(range(min_deg - 1, max_deg+1, bin_size)) + 0.5
bin_centers = bin_edges[:-1] + 0.5
occurances,_ = np.histogram(node_degrees, bins=bin_edges, density=True)
# plot the degree distribution
fig, ax = plt.subplots(figsize=(12,9))
ax.plot(bin_centers, occurances, 'x', label=f'Node Degrees')
ax.plot([avg_degree, avg_degree], [0, np.max(occurances)], color='crimson',
label=fr'Average Degree, $\bar{{k}} = {avg_degree:.2f}$')
ax.set_ylabel(r'Probability Mass, $p(k_\alpha)$')
ax.set_xlabel(r'Node Degree, $k_\alpha$')
ax.loglog()
ax.legend(loc='upper right')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + 'degrees_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of cluster sizes.
```
feature = 'size'
n_bins = 25
xmax = 1e3
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_cluster_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, xmax=xmax, colors=colors)
ax.set_xlabel(r'Cluster sizes, $|\mathcal{Y}_i|$')
ax.set_ylabel(r'Bin Probability Mass, $p(|\mathcal{Y}_i|)$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of cluster densities.
```
feature = 'density'
xmin=1e-2
n_bins = 25
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_cluster_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, xmin=xmin, colors=colors)
ax.set_xlabel(r'Cluster Density, $\rho(\mathcal{Y}_i)$')
ax.set_ylabel(r'Bin Probability Mass, $p(\rho(\mathcal{Y}_i))$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of clustering coefficients.
```
feature = 'clustering_coefficient'
n_bins = 25
xmin = 1e-2
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_cluster_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, xmin=xmin, colors=colors)
ax.set_xlabel(r'Clustering coefficient, $c(\mathcal{Y}_i)$')
ax.set_ylabel(r'Bin Probability Mass, $p(c(\mathcal{Y}_i))$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of cluster conductances.
```
feature = 'conductance'
n_bins = 25
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_cluster_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=False, colors=colors)
ax.set_xlabel(r'Conductance, $\kappa(\mathcal{Y}_i)$')
ax.set_ylabel(r'Bin Probability Mass, $p(\kappa(\mathcal{Y}_i))$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of cluster cut ratios.
```
feature = 'cut_ratio'
xmin = None
n_bins = 25
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_cluster_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, xmin=xmin, colors=colors)
ax.set_xlabel(r'Cut Ratio, $\xi(\mathcal{Y}_i)$')
ax.set_ylabel(r'Bin Probability Mass, $p(\xi(\mathcal{Y}_i))$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of node mixing parameters.
```
feature = 'mixing_parameter'
xmin = 1e-2
n_bins = 15
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_node_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, xmin=xmin, colors=colors)
ax.set_xlabel(r'Mixing parameter, $\mu_\alpha$')
ax.set_ylabel(r'Bin Probability Mass, $p(\mu_\alpha)$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
The next cell plots the histogram of normalized local degrees.
```
feature = 'nld'
n_bins = 25
plt.close('all')
save_figure = True # if True, we save the figure as .pdf in ´fig_dir´
# compute cluster properties
data = []
for method in methods:
clu = Clustering().load(results_dir + 'clustering_' + method + '.json')
data.append(get_node_properties(graph, clu, feature=feature))
# plot histogram
_, ax = plt.subplots(figsize=(12,9))
plot_histogram(ax, data, methods, n_bins, normalization = 'pmf', log_scale=True, colors=colors)
ax.set_xlabel(r'Normalized local degree, $\hat{k}_\alpha$')
ax.set_ylabel(r'Probability Mass, $p(\hat{k}_\alpha)$')
ax.legend(loc='best')
plt.tight_layout()
# save figure as .pdf
if save_figure:
fig_path = fig_dir + feature + '_' + network + '.pdf'
plt.savefig(fig_path, dpi=600, format='pdf')
plt.close()
```
| true |
code
| 0.722625 | null | null | null | null |
|
# Springboard Logistic Regression Advanced Case Study
$$
\renewcommand{\like}{{\cal L}}
\renewcommand{\loglike}{{\ell}}
\renewcommand{\err}{{\cal E}}
\renewcommand{\dat}{{\cal D}}
\renewcommand{\hyp}{{\cal H}}
\renewcommand{\Ex}[2]{E_{#1}[#2]}
\renewcommand{\x}{{\mathbf x}}
\renewcommand{\v}[1]{{\mathbf #1}}
$$
This case study delves into the math behind logistic regression in a Python environment. We've adapted this case study from [Lab 5 in the CS109](https://github.com/cs109/2015lab5) course. Please feel free to check out the original lab, both for more exercises, as well as solutions.
We turn our attention to **classification**. Classification tries to predict, which of a small set of classes, an observation belongs to. Mathematically, the aim is to find $y$, a **label** based on knowing a feature vector $\x$. For instance, consider predicting gender from seeing a person's face, something we do fairly well as humans. To have a machine do this well, we would typically feed the machine a bunch of images of people which have been labelled "male" or "female" (the training set), and have it learn the gender of the person in the image from the labels and the *features* used to determine gender. Then, given a new photo, the trained algorithm returns us the gender of the person in the photo.
There are different ways of making classifications. One idea is shown schematically in the image below, where we find a line that divides "things" of two different types in a 2-dimensional feature space. The classification show in the figure below is an example of a maximum-margin classifier where construct a decision boundary that is far as possible away from both classes of points. The fact that a line can be drawn to separate the two classes makes the problem *linearly separable*. Support Vector Machines (SVM) are an example of a maximum-margin classifier.
<img src="images/onelinesplit.png" width="400" height="200">
```
%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import pandas as pd
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")
import sklearn.model_selection
import warnings # For handling error messages.
# Don't worry about the following two instructions: they just suppress warnings that could occur later.
warnings.simplefilter(action="ignore", category=FutureWarning)
warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd")
c0=sns.color_palette()[0]
c1=sns.color_palette()[1]
c2=sns.color_palette()[2]
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
def points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=True, colorscale=cmap_light,
cdiscrete=cmap_bold, alpha=0.1, psize=10, zfunc=False, predicted=False):
h = .02
X=np.concatenate((Xtr, Xte))
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
#plt.figure(figsize=(10,6))
if zfunc:
p0 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 0]
p1 = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z=zfunc(p0, p1)
else:
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
ZZ = Z.reshape(xx.shape)
if mesh:
plt.pcolormesh(xx, yy, ZZ, cmap=cmap_light, alpha=alpha, axes=ax)
if predicted:
showtr = clf.predict(Xtr)
showte = clf.predict(Xte)
else:
showtr = ytr
showte = yte
ax.scatter(Xtr[:, 0], Xtr[:, 1], c=showtr-1, cmap=cmap_bold,
s=psize, alpha=alpha,edgecolor="k")
# and testing points
ax.scatter(Xte[:, 0], Xte[:, 1], c=showte-1, cmap=cmap_bold,
alpha=alpha, marker="s", s=psize+10)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
return ax,xx,yy
def points_plot_prob(ax, Xtr, Xte, ytr, yte, clf, colorscale=cmap_light,
cdiscrete=cmap_bold, ccolor=cm, psize=10, alpha=0.1):
ax,xx,yy = points_plot(ax, Xtr, Xte, ytr, yte, clf, mesh=False,
colorscale=colorscale, cdiscrete=cdiscrete,
psize=psize, alpha=alpha, predicted=True)
Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=ccolor, alpha=.2, axes=ax)
cs2 = plt.contour(xx, yy, Z, cmap=ccolor, alpha=.6, axes=ax)
#plt.clabel(cs2, fmt = '%2.1f', colors = 'k', fontsize=14, axes=ax)
return ax
```
## A Motivating Example Using `sklearn`: Heights and Weights
We'll use a dataset of heights and weights of males and females to hone our understanding of classifiers. We load the data into a dataframe and plot it.
```
dflog = pd.read_csv("data/01_heights_weights_genders.csv")
dflog.head()
```
Remember that the form of data we will use always is
<img src="images/dataform.jpg" width="400" height="200">
with the "response" or "label" $y$ as a plain array of 0s and 1s for binary classification. Sometimes we will also see -1 and +1 instead. There are also *multiclass* classifiers that can assign an observation to one of $K > 2$ classes and the labe may then be an integer, but we will not be discussing those here.
`y = [1,1,0,0,0,1,0,1,0....]`.
<div class="span5 alert alert-info">
<h3>Checkup Exercise Set I</h3>
<ul>
<li> <b>Exercise:</b> Create a scatter plot of Weight vs. Height
<li> <b>Exercise:</b> Color the points differently by Gender
</ul>
</div>
```
_ = sns.scatterplot(x='Weight', y='Height', hue='Gender', data=dflog, linestyle = 'None', color = 'blue', alpha=0.25)
```
### Training and Test Datasets
When fitting models, we would like to ensure two things:
* We have found the best model (in terms of model parameters).
* The model is highly likely to generalize i.e. perform well on unseen data.
<br/>
<div class="span5 alert alert-success">
<h4>Purpose of splitting data into Training/testing sets</h4>
<ul>
<li> We built our model with the requirement that the model fit the data well. </li>
<li> As a side-effect, the model will fit <b>THIS</b> dataset well. What about new data? </li>
<ul>
<li> We wanted the model for predictions, right?</li>
</ul>
<li> One simple solution, leave out some data (for <b>testing</b>) and <b>train</b> the model on the rest </li>
<li> This also leads directly to the idea of cross-validation, next section. </li>
</ul>
</div>
First, we try a basic Logistic Regression:
* Split the data into a training and test (hold-out) set
* Train on the training set, and test for accuracy on the testing set
```
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Split the data into a training and test set.
Xlr, Xtestlr, ylr, ytestlr = train_test_split(dflog[['Height','Weight']].values,
(dflog.Gender == "Male").values,random_state=5)
clf = LogisticRegression()
# Fit the model on the trainng data.
clf.fit(Xlr, ylr)
# Print the accuracy from the testing data.
print(accuracy_score(clf.predict(Xtestlr), ytestlr))
```
### Tuning the Model
The model has some hyperparameters we can tune for hopefully better performance. For tuning the parameters of your model, you will use a mix of *cross-validation* and *grid search*. In Logistic Regression, the most important parameter to tune is the *regularization parameter* `C`. Note that the regularization parameter is not always part of the logistic regression model.
The regularization parameter is used to control for unlikely high regression coefficients, and in other cases can be used when data is sparse, as a method of feature selection.
You will now implement some code to perform model tuning and selecting the regularization parameter $C$.
We use the following `cv_score` function to perform K-fold cross-validation and apply a scoring function to each test fold. In this incarnation we use accuracy score as the default scoring function.
```
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
def cv_score(clf, x, y, score_func=accuracy_score):
result = 0
nfold = 5
for train, test in KFold(nfold).split(x): # split data into train/test groups, 5 times
clf.fit(x[train], y[train]) # fit
result += score_func(clf.predict(x[test]), y[test]) # evaluate score function on held-out data
return result / nfold # average
```
Below is an example of using the `cv_score` function for a basic logistic regression model without regularization.
```
clf = LogisticRegression()
score = cv_score(clf, Xlr, ylr)
print(round(score,4))
```
<div class="span5 alert alert-info">
<h3>Checkup Exercise Set II</h3>
<b>Exercise:</b> Implement the following search procedure to find a good model
<ul>
<li> You are given a list of possible values of `C` below
<li> For each C:
<ol>
<li> Create a logistic regression model with that value of C
<li> Find the average score for this model using the `cv_score` function **only on the training set** `(Xlr, ylr)`
</ol>
<li> Pick the C with the highest average score
</ul>
Your goal is to find the best model parameters based *only* on the training set, without showing the model test set at all (which is why the test set is also called a *hold-out* set).
</div>
```
#the grid of parameters to search over
Cs = [0.001, 0.1, 1, 10, 100]
highest_score = 0
best_c = 0
for C in Cs:
clf = LogisticRegression(C=C)
score = cv_score(clf, Xlr, ylr)
if score > highest_score:
highest_score = score
best_c = C
print("Best score is {}".format(round(highest_score,4)))
```
<div class="span5 alert alert-info">
<h3>Checkup Exercise Set III</h3>
**Exercise:** Now you want to estimate how this model will predict on unseen data in the following way:
<ol>
<li> Use the C you obtained from the procedure earlier and train a Logistic Regression on the training data
<li> Calculate the accuracy on the test data
</ol>
<p>You may notice that this particular value of `C` may or may not do as well as simply running the default model on a random train-test split. </p>
<ul>
<li> Do you think that's a problem?
<li> Why do we need to do this whole cross-validation and grid search stuff anyway?
</ul>
</div>
```
clf = LogisticRegression(C=C)
clf.fit(Xlr, ylr)
ypredlr = clf.predict(Xtestlr)
print(accuracy_score(ypredlr, ytestlr))
```
### Black Box Grid Search in `sklearn`
Scikit-learn, as with many other Python packages, provides utilities to perform common operations so you do not have to do it manually. It is important to understand the mechanics of each operation, but at a certain point, you will want to use the utility instead to save time...
<div class="span5 alert alert-info">
<h3>Checkup Exercise Set IV</h3>
<b>Exercise:</b> Use scikit-learn's [GridSearchCV](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html) tool to perform cross validation and grid search.
* Instead of writing your own loops above to iterate over the model parameters, can you use GridSearchCV to find the best model over the training set?
* Does it give you the same best value of `C`?
* How does this model you've obtained perform on the test set?</div>
```
from sklearn.model_selection import GridSearchCV
parameters = {
'C': [0.001, 0.1, 1, 10, 100]
}
grid = GridSearchCV(clf, parameters)
grid.fit(Xlr, ylr)
ypredlr = grid.predict(Xtestlr)
print("Accuracy score is {}".format(accuracy_score(ypredlr, ytestlr)))
print("Best tuned parameters are {}".format(grid.best_params_))
print("Best score is {}".format(grid.best_score_))
print("Best estimator is {}".format(grid.best_estimator_))
```
## A Walkthrough of the Math Behind Logistic Regression
### Setting up Some Demo Code
Let's first set some code up for classification that we will need for further discussion on the math. We first set up a function `cv_optimize` which takes a classifier `clf`, a grid of hyperparameters (such as a complexity parameter or regularization parameter) implemented as a dictionary `parameters`, a training set (as a samples x features array) `Xtrain`, and a set of labels `ytrain`. The code takes the traning set, splits it into `n_folds` parts, sets up `n_folds` folds, and carries out a cross-validation by splitting the training set into a training and validation section for each foldfor us. It prints the best value of the parameters, and retuens the best classifier to us.
```
def cv_optimize(clf, parameters, Xtrain, ytrain, n_folds=5):
gs = sklearn.model_selection.GridSearchCV(clf, param_grid=parameters, cv=n_folds)
gs.fit(Xtrain, ytrain)
print("BEST PARAMS", gs.best_params_)
best = gs.best_estimator_
return best
```
We then use this best classifier to fit the entire training set. This is done inside the `do_classify` function which takes a dataframe `indf` as input. It takes the columns in the list `featurenames` as the features used to train the classifier. The column `targetname` sets the target. The classification is done by setting those samples for which `targetname` has value `target1val` to the value 1, and all others to 0. We split the dataframe into 80% training and 20% testing by default, standardizing the dataset if desired. (Standardizing a data set involves scaling the data so that it has 0 mean and is described in units of its standard deviation. We then train the model on the training set using cross-validation. Having obtained the best classifier using `cv_optimize`, we retrain on the entire training set and calculate the training and testing accuracy, which we print. We return the split data and the trained classifier.
```
from sklearn.model_selection import train_test_split
def do_classify(clf, parameters, indf, featurenames, targetname, target1val, standardize=False, train_size=0.8):
subdf=indf[featurenames]
if standardize:
subdfstd=(subdf - subdf.mean())/subdf.std()
else:
subdfstd=subdf
X=subdfstd.values
y=(indf[targetname].values==target1val)*1
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, train_size=train_size)
clf = cv_optimize(clf, parameters, Xtrain, ytrain)
clf=clf.fit(Xtrain, ytrain)
training_accuracy = clf.score(Xtrain, ytrain)
test_accuracy = clf.score(Xtest, ytest)
print("Accuracy on training data: {:0.2f}".format(training_accuracy))
print("Accuracy on test data: {:0.2f}".format(test_accuracy))
return clf, Xtrain, ytrain, Xtest, ytest
```
## Logistic Regression: The Math
We could approach classification as linear regression, there the class, 0 or 1, is the target variable $y$. But this ignores the fact that our output $y$ is discrete valued, and futhermore, the $y$ predicted by linear regression will in general take on values less than 0 and greater than 1. Additionally, the residuals from the linear regression model will *not* be normally distributed. This violation means we should not use linear regression.
But what if we could change the form of our hypotheses $h(x)$ instead?
The idea behind logistic regression is very simple. We want to draw a line in feature space that divides the '1' samples from the '0' samples, just like in the diagram above. In other words, we wish to find the "regression" line which divides the samples. Now, a line has the form $w_1 x_1 + w_2 x_2 + w_0 = 0$ in 2-dimensions. On one side of this line we have
$$w_1 x_1 + w_2 x_2 + w_0 \ge 0,$$
and on the other side we have
$$w_1 x_1 + w_2 x_2 + w_0 < 0.$$
Our classification rule then becomes:
\begin{eqnarray*}
y = 1 &\mbox{if}& \v{w}\cdot\v{x} \ge 0\\
y = 0 &\mbox{if}& \v{w}\cdot\v{x} < 0
\end{eqnarray*}
where $\v{x}$ is the vector $\{1,x_1, x_2,...,x_n\}$ where we have also generalized to more than 2 features.
What hypotheses $h$ can we use to achieve this? One way to do so is to use the **sigmoid** function:
$$h(z) = \frac{1}{1 + e^{-z}}.$$
Notice that at $z=0$ this function has the value 0.5. If $z > 0$, $h > 0.5$ and as $z \to \infty$, $h \to 1$. If $z < 0$, $h < 0.5$ and as $z \to -\infty$, $h \to 0$. As long as we identify any value of $y > 0.5$ as 1, and any $y < 0.5$ as 0, we can achieve what we wished above.
This function is plotted below:
```
h = lambda z: 1. / (1 + np.exp(-z))
zs=np.arange(-5, 5, 0.1)
plt.plot(zs, h(zs), alpha=0.5);
```
So we then come up with our rule by identifying:
$$z = \v{w}\cdot\v{x}.$$
Then $h(\v{w}\cdot\v{x}) \ge 0.5$ if $\v{w}\cdot\v{x} \ge 0$ and $h(\v{w}\cdot\v{x}) \lt 0.5$ if $\v{w}\cdot\v{x} \lt 0$, and:
\begin{eqnarray*}
y = 1 &if& h(\v{w}\cdot\v{x}) \ge 0.5\\
y = 0 &if& h(\v{w}\cdot\v{x}) \lt 0.5.
\end{eqnarray*}
We will show soon that this identification can be achieved by minimizing a loss in the ERM framework called the **log loss** :
$$ R_{\cal{D}}(\v{w}) = - \sum_{y_i \in \cal{D}} \left ( y_i \log(h(\v{w}\cdot\v{x})) + ( 1 - y_i) \log(1 - h(\v{w}\cdot\v{x})) \right )$$
We will also add a regularization term:
$$ R_{\cal{D}}(\v{w}) = - \sum_{y_i \in \cal{D}} \left ( y_i \log(h(\v{w}\cdot\v{x})) + ( 1 - y_i) \log(1 - h(\v{w}\cdot\v{x})) \right ) + \frac{1}{C} \v{w}\cdot\v{w},$$
where $C$ is the regularization strength (equivalent to $1/\alpha$ from the Ridge case), and smaller values of $C$ mean stronger regularization. As before, the regularization tries to prevent features from having terribly high weights, thus implementing a form of feature selection.
How did we come up with this loss? We'll come back to that, but let us see how logistic regression works out.
```
dflog.head()
clf_l, Xtrain_l, ytrain_l, Xtest_l, ytest_l = do_classify(LogisticRegression(),
{"C": [0.01, 0.1, 1, 10, 100]},
dflog, ['Weight', 'Height'], 'Gender','Male')
plt.figure()
ax=plt.gca()
points_plot(ax, Xtrain_l, Xtest_l, ytrain_l, ytest_l, clf_l, alpha=0.2);
```
In the figure here showing the results of the logistic regression, we plot the actual labels of both the training(circles) and test(squares) samples. The 0's (females) are plotted in red, the 1's (males) in blue. We also show the classification boundary, a line (to the resolution of a grid square). Every sample on the red background side of the line will be classified female, and every sample on the blue side, male. Notice that most of the samples are classified well, but there are misclassified people on both sides, as evidenced by leakage of dots or squares of one color ontothe side of the other color. Both test and traing accuracy are about 92%.
### The Probabilistic Interpretaion
Remember we said earlier that if $h > 0.5$ we ought to identify the sample with $y=1$? One way of thinking about this is to identify $h(\v{w}\cdot\v{x})$ with the probability that the sample is a '1' ($y=1$). Then we have the intuitive notion that lets identify a sample as 1 if we find that the probabilty of being a '1' is $\ge 0.5$.
So suppose we say then that the probability of $y=1$ for a given $\v{x}$ is given by $h(\v{w}\cdot\v{x})$?
Then, the conditional probabilities of $y=1$ or $y=0$ given a particular sample's features $\v{x}$ are:
\begin{eqnarray*}
P(y=1 | \v{x}) &=& h(\v{w}\cdot\v{x}) \\
P(y=0 | \v{x}) &=& 1 - h(\v{w}\cdot\v{x}).
\end{eqnarray*}
These two can be written together as
$$P(y|\v{x}, \v{w}) = h(\v{w}\cdot\v{x})^y \left(1 - h(\v{w}\cdot\v{x}) \right)^{(1-y)} $$
Then multiplying over the samples we get the probability of the training $y$ given $\v{w}$ and the $\v{x}$:
$$P(y|\v{x},\v{w}) = P(\{y_i\} | \{\v{x}_i\}, \v{w}) = \prod_{y_i \in \cal{D}} P(y_i|\v{x_i}, \v{w}) = \prod_{y_i \in \cal{D}} h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}$$
Why use probabilities? Earlier, we talked about how the regression function $f(x)$ never gives us the $y$ exactly, because of noise. This hold for classification too. Even with identical features, a different sample may be classified differently.
We said that another way to think about a noisy $y$ is to imagine that our data $\dat$ was generated from a joint probability distribution $P(x,y)$. Thus we need to model $y$ at a given $x$, written as $P(y|x)$, and since $P(x)$ is also a probability distribution, we have:
$$P(x,y) = P(y | x) P(x)$$
and can obtain our joint probability $P(x, y)$.
Indeed its important to realize that a particular training set can be thought of as a draw from some "true" probability distribution (just as we did when showing the hairy variance diagram). If for example the probability of classifying a test sample as a '0' was 0.1, and it turns out that the test sample was a '0', it does not mean that this model was necessarily wrong. After all, in roughly a 10th of the draws, this new sample would be classified as a '0'! But, of-course its more unlikely than its likely, and having good probabilities means that we'll be likely right most of the time, which is what we want to achieve in classification. And furthermore, we can quantify this accuracy.
Thus its desirable to have probabilistic, or at the very least, ranked models of classification where you can tell which sample is more likely to be classified as a '1'. There are business reasons for this too. Consider the example of customer "churn": you are a cell-phone company and want to know, based on some of my purchasing habit and characteristic "features" if I am a likely defector. If so, you'll offer me an incentive not to defect. In this scenario, you might want to know which customers are most likely to defect, or even more precisely, which are most likely to respond to incentives. Based on these probabilities, you could then spend a finite marketing budget wisely.
### Maximizing the Probability of the Training Set
Now if we maximize $P(y|\v{x},\v{w})$, we will maximize the chance that each point is classified correctly, which is what we want to do. While this is not exactly the same thing as maximizing the 1-0 training risk, it is a principled way of obtaining the highest probability classification. This process is called **maximum likelihood** estimation since we are maximising the **likelihood of the training data y**,
$$\like = P(y|\v{x},\v{w}).$$
Maximum likelihood is one of the corenerstone methods in statistics, and is used to estimate probabilities of data.
We can equivalently maximize
$$\loglike = \log{P(y|\v{x},\v{w})}$$
since the natural logarithm $\log$ is a monotonic function. This is known as maximizing the **log-likelihood**. Thus we can equivalently *minimize* a risk that is the negative of $\log(P(y|\v{x},\v{w}))$:
$$R_{\cal{D}}(h(x)) = -\loglike = -\log \like = -\log{P(y|\v{x},\v{w})}.$$
Thus
\begin{eqnarray*}
R_{\cal{D}}(h(x)) &=& -\log\left(\prod_{y_i \in \cal{D}} h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\right)\\
&=& -\sum_{y_i \in \cal{D}} \log\left(h(\v{w}\cdot\v{x_i})^{y_i} \left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\right)\\
&=& -\sum_{y_i \in \cal{D}} \log\,h(\v{w}\cdot\v{x_i})^{y_i} + \log\,\left(1 - h(\v{w}\cdot\v{x_i}) \right)^{(1-y_i)}\\
&=& - \sum_{y_i \in \cal{D}} \left ( y_i \log(h(\v{w}\cdot\v{x})) + ( 1 - y_i) \log(1 - h(\v{w}\cdot\v{x})) \right )
\end{eqnarray*}
This is exactly the risk we had above, leaving out the regularization term (which we shall return to later) and was the reason we chose it over the 1-0 risk.
Notice that this little process we carried out above tells us something very interesting: **Probabilistic estimation using maximum likelihood is equivalent to Empiricial Risk Minimization using the negative log-likelihood**, since all we did was to minimize the negative log-likelihood over the training samples.
`sklearn` will return the probabilities for our samples, or for that matter, for any input vector set $\{\v{x}_i\}$, i.e. $P(y_i | \v{x}_i, \v{w})$:
```
clf_l.predict_proba(Xtest_l)
```
### Discriminative vs Generative Classifier
Logistic regression is what is known as a **discriminative classifier** as we learn a soft boundary between/among classes. Another paradigm is the **generative classifier** where we learn the distribution of each class. For more examples of generative classifiers, look [here](https://en.wikipedia.org/wiki/Generative_model).
Let us plot the probabilities obtained from `predict_proba`, overlayed on the samples with their true labels:
```
plt.figure()
ax = plt.gca()
points_plot_prob(ax, Xtrain_l, Xtest_l, ytrain_l, ytest_l, clf_l, psize=20, alpha=0.1);
```
Notice that lines of equal probability, as might be expected are stright lines. What the classifier does is very intuitive: if the probability is greater than 0.5, it classifies the sample as type '1' (male), otherwise it classifies the sample to be class '0'. Thus in the diagram above, where we have plotted predicted values rather than actual labels of samples, there is a clear demarcation at the 0.5 probability line.
Again, this notion of trying to obtain the line or boundary of demarcation is what is called a **discriminative** classifier. The algorithm tries to find a decision boundary that separates the males from the females. To classify a new sample as male or female, it checks on which side of the decision boundary the sample falls, and makes a prediction. In other words we are asking, given $\v{x}$, what is the probability of a given $y$, or, what is the likelihood $P(y|\v{x},\v{w})$?
| true |
code
| 0.612889 | null | null | null | null |
|
# TensorFlow Lattice estimators
In this tutorial, we will cover basics of TensorFlow Lattice estimators.
```
# import libraries
!pip install tensorflow_lattice
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_lattice as tfl
import tempfile
from six.moves import urllib
```
# Synthetic dataset
Here we create a synthetic dataset.
```
%matplotlib inline
# Training dataset contains one feature, "distance".
train_features = {
'distance': np.array([1.0, 1.3, 1.5, 2.0, 2.1, 3.0,
4.0, 5.0, 1.3, 1.7, 2.5, 2.8,
4.7, 4.2, 3.5, 4.75, 5.2,
5.8, 5.9]) * 0.1,
}
train_labels = np.array([4.8, 4.9, 5.0, 5.0,
4.8, 3.3, 2.5, 2.0,
4.7, 4.6, 4.0, 3.2,
2.12, 2.1, 2.5, 2.2,
2.3, 2.34, 2.6])
plt.scatter(train_features['distance'], train_labels)
plt.xlabel('distance')
plt.ylabel('user hapiness')
# This function draws two plots.
# Firstly, we draw the scatter plot of `distance` vs. `label`.
# Secondly, we generate predictions from `estimator` distance ranges in
# [xmin, xmax].
def Plot(distance, label, estimator, xmin=0.0, xmax=10.0):
%matplotlib inline
test_features = {
'distance': np.linspace(xmin, xmax, num=100)
}
# Estimator accepts an input in the form of input_fn (callable).
# numpy_input_fn creates an input function that generates a dictionary where
# the key is a feaeture name ('distance'), and the value is a tensor with
# a shape [batch_size, 1].
test_input_fn = tf.estimator.inputs.numpy_input_fn(
x=test_features,
batch_size=1,
num_epochs=1,
shuffle=False)
# Estimator's prediction is 1d tensor with a shape [batch_size]. Since we
# set batch_size == 1 in the above, p['predictions'] will contain only one
# element in each batch, and we fetch this value by p['predictions'][0].
predictions = [p['predictions'][0]
for p in estimator.predict(input_fn=test_input_fn)]
# Plot estimator's response and (distance, label) scatter plot.
fig, ax = plt.subplots(1, 1)
ax.plot(test_features['distance'], predictions)
ax.scatter(distance, label)
plt.xlabel('distance')
plt.ylabel('user hapiness')
plt.legend(['prediction', 'data'])
```
# DNN Estimator
Now let us define feature columns and use DNN regressor to fit a model.
```
# Specify feature.
feature_columns = [
tf.feature_column.numeric_column('distance'),
]
# Define a neural network legressor.
# The first hidden layer contains 30 hidden units, and the second
# hidden layer contains 10 hidden units.
dnn_estimator = tf.estimator.DNNRegressor(
feature_columns=feature_columns,
hidden_units=[30, 10],
optimizer=tf.train.GradientDescentOptimizer(
learning_rate=0.01,
),
)
# Define training input function.
# mini-batch size is 10, and we iterate the dataset over
# 1000 times.
train_input_fn = tf.estimator.inputs.numpy_input_fn(
x=train_features,
y=train_labels,
batch_size=10,
num_epochs=1000,
shuffle=False)
tf.logging.set_verbosity(tf.logging.ERROR)
# Train this estimator
dnn_estimator.train(input_fn=train_input_fn)
# Response in [0.0, 1.0] range
Plot(train_features['distance'], train_labels, dnn_estimator, 0.0, 1.0)
# Now let's increase the prediction range to [0.0, 3.0]
# Note) In most machines, the prediction is going up.
# However, DNN training does not have a unique solution, so it's possible
# not to see this phenomenon.
Plot(train_features['distance'], train_labels, dnn_estimator, 0.0, 3.0)
```
# TensorFlow Lattice calibrated linear model
Let's use calibrated linear model to fit the data.
Since we only have one example, there's no reason to use a lattice.
```
# TensorFlow Lattice needs feature names to specify
# per-feature parameters.
feature_names = [fc.name for fc in feature_columns]
num_keypoints = 5
hparams = tfl.CalibratedLinearHParams(
feature_names=feature_names,
learning_rate=0.1,
num_keypoints=num_keypoints)
# input keypoint initializers.
# init_fns are dict of (feature_name, callable initializer).
keypoints_init_fns = {
'distance': lambda: tfl.uniform_keypoints_for_signal(num_keypoints,
input_min=0.0,
input_max=0.7,
output_min=-1.0,
output_max=1.0)}
non_monotnic_estimator = tfl.calibrated_linear_regressor(
feature_columns=feature_columns,
keypoints_initializers_fn=keypoints_init_fns,
hparams=hparams)
non_monotnic_estimator.train(input_fn=train_input_fn)
# The prediction goes up!
Plot(train_features['distance'], train_labels, non_monotnic_estimator, 0.0, 1.0)
# Declare distance as a decreasing monotonic input.
hparams.set_feature_param('distance', 'monotonicity', -1)
monotonic_estimator = tfl.calibrated_linear_regressor(
feature_columns=feature_columns,
keypoints_initializers_fn=keypoints_init_fns,
hparams=hparams)
monotonic_estimator.train(input_fn=train_input_fn)
# Now it's decreasing.
Plot(train_features['distance'], train_labels, monotonic_estimator, 0.0, 1.0)
# Even if the output range becomes larger, the prediction never goes up!
Plot(train_features['distance'], train_labels, monotonic_estimator, 0.0, 3.0)
```
| true |
code
| 0.822153 | null | null | null | null |
|

#Ejercicio: Algoritmo genético para optimizar un rotor o hélice, paso a paso
##El problema
A menudo, en ingeniería, cuando nos enfrentamos a un problema, no podemos resolver directamente o despejar la solución como en los problemas sencillos típicos de matemáticas o física clásica. Una manera muy típica en la que nos encontraremos los problemas es en la forma de simulación: tenemos una serie de parámetros y un modelo, y podemos simularlo para obtener sus características, pero sin tener ninguna fórmula explícita que relacione parámetros y resultados y que nos permita obtener una función inversa.
En este ejercicio, nos plantearemos un problema de ese tipo: tenemos una función que calcula las propiedades de una hélice en función de una serie de parámetros, pero no conocemos los cálculos que hace internamente. Para nosotros, es una caja negra.
Para optimizar, iremos recuperando las funciones del algoritmo genético que se vieron en la parte de teoría.
```
%matplotlib inline
import numpy as np # Trabajaremos con arrays
import matplotlib.pyplot as plt # Y vamos a pintar gráficos
from optrot.rotor import calcular_rotor # Esta función es la que vamos a usar para calcular el rotor
import random as random # Necesitaremos números aleatorios
```
Empecemos echando un ojo a la función del rotor, para ver qué vamos a necesitar y con qué parámetros vamos a trabajar.
```
help(calcular_rotor)
```
Podemos trazar unas cuantas curvas para observar qué pinta va a tener lo que saquemos. Por ejemplo, cómo cambian las características de la hélice dependiendo de la velocidad de vuelo, para una hélice de ejemplo que gira a uyna velocidad dada.
```
vel = np.linspace(0, 30, 100)
efic = np.zeros_like(vel)
T = np.zeros_like(vel)
P = np.zeros_like(vel)
mach = np.zeros_like(vel)
for i in range(len(vel)):
T[i], P[i], efic[i], mach[i] = calcular_rotor(130, vel[i], 0.5, 3)
plt.plot(vel, T)
plt.title('Tracción de la hélice')
plt.plot(vel, P)
plt.title('Potencia consumida')
plt.plot(vel, efic)
plt.title('Eficiencia de la hélice')
plt.plot(vel, mach)
plt.title('Mach en la punta de las palas')
```
##Definiendo el genoma
Definamos un individuo genérico: Cada individuo será un posible diseño del rotor, con unas características determinadas.
```
class Individual (object):
def __init__(self, genome):
self.genome = genome
self.traits = {}
self.performances = {}
self.fitness = 0
```
Nuestro rotor depende de varios parámetros, pero en general, buscaremos optimizar el valor de unos, mateniendo un valor controlado de otros. Por ejemplo, la velocidad de avance y la altitud normalmente las impondremos, ya que querremos optimizar para una velocidad y altura de vuelos dadas.
En nuestro algoritmo, usaremos como genoma los parámetros de optimización, y las variables circunstanciales las controlaremos a mano.
***Sugerencia*** (esta es una manera de organizar las variables, aunque puedes escoger otras)
Parámetros de optimización:
- omega (velocidad de rotación) (Entre 0 y 200 radianes/segundo)
- R (radio de la hélice) (Entre 0.1 y 2 metros)
- b (número de palas) (Entre 2 y 5 palas)
- theta0 (ángulo de paso colectivo) (Entre -0.26 y 0.26 radianes)(*se corresponde a -15 y 15 grados*)
- p (parámetro de torsión) (Entre -5 y 20 grados)
- cuerda (anchura de la pala) (Entre 0.01 y 0.2 metros)
Parámetros circunstanciales:
- vz (velocidad de vuelo)
- h (altura de vuelo)
Variables que se van a mantener
- ley de torsión (hiperbólica)
- formato de chord params: un solo número, para que la anchura sea constante a lo largo de la pala
```
15 * np.pi / 180
```
A continuación crearemos un diccionario de genes. En él iremos almacenando los nombres de los parámetros y la cantidad de bits que usaremos para definirlos. Cuantos más bits, más resolución
Ej: 1 bit : 2 valores, 2 bit : 4 valores, 10 bit : 1024 valores
```
#Completa este diccionario con las variables que hayas elegido y los bits que usarás
dict_genes = {
'omega' : 10,
'R': 10,
'b': 2
}
```
Ahora, crearemos una función que rellene estos genomas con datos aleatorios:
```
def generate_genome (dict_genes):
#Calculamos el número total de bits con un bucle que recorra el diccionario
n_bits = ?
#Generamos un array aletorio de 1 y 0 de esa longitud con numpy
genome = np.random.randint(0, 2, nbits)
#Transformamos el array en una lista antes de devolverlo
return list(genome)
# Podemos probar a usar nuestra función, para ver qué pinta tiene el ADN de un rotor:
generate_genome(dict_genes)
```
##Trabajando con el individuo
Ahora necesitamos una función que transforme esos genes a valores con sentido. Cada gen es un número binario cuyo valor estará entre 0 y 2 ^ n, siendo n el número de bits que hayamos escogido. Estas variables traducidas las guardaremos en otro diccionario, ya con su valor. Estos genes no están volando por ahí sueltos, sino que estarán guardados en el interior del individuo al que pertenezcan, por lo que la función deberá estar preparada para extraerlos del individuo, y guardar los resultados a su vez en el interior del individuo.
```
def calculate_traits (individual, dict_genes):
genome = individual.genome
integer_temporal_list = []
for gen in dict_genes: #Recorremos el diccionario de genes para ir traduciendo del binario
??? #Buscamos los bits que se corresponden al bit en cuestión
??? #Pasamos de lista binaria a número entero
integer_temporal_list.append(??) #Añadimos el entero a la lista
# Transformamos cada entero en una variable con sentido físico:
# Por ejemplo, si el entero de la variable Omega está entre 0 y 1023 (10bits),
# pero la variable Omega real estará entre 0 y 200 radianes por segundo:
omega = integer_temporal_list[0] * 200 / 1023
#del mismo modo, para R:
R = 0.1 + integer_temporal_list[1] * 1.9 / 1023 #Obtendremos un radio entre 0.1 y 2 metros
#El número de palas debe ser un entero, hay que tener cuidado:
b = integer_temporal_list[2] + 2 #(entre 2 y 5 palas)
#Continúa con el resto de variables que hayas elegido!
dict_traits = { #Aquí iremos guardando los traits, o parámetros
'omega' : omega,
'R': R
}
individual.traits = dict_traits #Por último, guardamos los traits en el individuo
```
El siguiente paso es usar estos traits(parámetros) para calcular las performances (características o desempeños) del motor. Aquí es donde entra el modelo del motor propiamente dicho.
```
def calculate_performances (individual):
dict_traits = individual.traits
#Nuestras circunstancias las podemos imponer aquí, o irlas pasando como argumento a la función
h = 2000 #Altitud de vuelo en metros
vz = 70 #velocidad de avance en m/s, unos 250 km/h
#Extraemos los traits del diccionario:
omega = dict_traits['omega']
R = dict_traits['R']
#... etc
T, P, efic, mach_punta = calcular_rotor(omega, vz, R, b, h...) #Introduce las variables que uses de parámetro.
# Consulta la ayuda para asegurarte de que usas el
# formato correcto!
dict_perfo = {
'T' : T, #Tracción de la hélice
'P' : P, #Potencia consumida por la hélice
'efic': efic, #Eficiencia propulsiva de la hélice
'mach_punta': mach_punta #Mach en la punta de las palas
}
individual.performances = dict_perfo
```
Comprobemos si todo funciona!
```
individuo = Individual(generate_genome(dict_genes))
calculate_traits(individuo, dict_genes)
calculate_performances(individuo)
print(individuo.traits)
print(individuo.performances)
```
El último paso que tenemos que realizar sobre el individuo es uno de los más críticos: Transformar las performances en un valor único (fitness) que con exprese cómo de bueno es con respecto al objetivo de optimización. La función de fitness puede ser función de parámetros(traits) y performances, dependiendo de qué queramos optimizar.
Por ejemplo, si buscáramos que tuviera la tracción máxima sin preocuparnos de nada más, el valor de fitnes sería simplemente igual al de T:
fitness = T
Si queremos imponer restricciones, por ejemplo, que la potencia sea menor a 1000 watios, se pueden añadir sentencias del tipo:
if P > 1000:
fitness -= 1000
Se puede hacer depender la fitness de varios parámetros de manera ponderada:
fitness = parámetro_importante * 10 + parámetro_poco_importante * 0.5
También se pueden combinar diferentes funciones no lineales:
fitness = parámetro_1 * parámetro_2 - parámetro_3 **2 * log(parámetro_4)
Ahora te toca ser creativo! Elige con qué objetivo quieres optimizar la hélice!
Sugerencias de posibles objetivos de optimización:
- Mínimo radio posible, manteniendo una tracción mínima de 30 Newtons
- Mínima potencia posible, máxima eficiencia, y mínimo radio posible en menor medida, manteniendo una tracción mínima de 40 Newtons y un mach en la punta de las palas de como mucho 0.7
- Mínima potencia posible y máxima eficiencia cuando vuela a 70 m/s, tracción mayor a 50 Newtons en el despegue (vz = 0), mínimo peso posible (calculado a partir del radio, número y anchura de las palas) (Puede que tengas que reescribir la función y el diccionario de performances!)
```
def calculate_fitness (individual):
dict_traits = individuo.traits
dict_performances = individuo.performances
fitness = ????? #Be Creative!
individual.fitness = fitness
```
Ya tenemos terminado todo lo que necesitamos a nivel de individuo!
## Que comiencen los Juegos!
Es hora de trabajar a nivel de algoritmo, y para ello, lo primero es crear una sociedad compuesta de individuos aleatorios. Definamos una función para ello.
```
def immigration (society, target_population, dict_genes):
while len(society) < target_population:
new_individual = Individual (generate_genome (dict_genes)) # Generamos un individuo aleatorio
calculate_traits (new_individual, dict_genes) # Calculamos sus traits
calculate_performances (new_individual) # Calculamos sus performances
calculate_fitness (new_individual) # Calculamos su fitness
society.append (new_individual) # Nuestro nuevo ciudadano está listo para unirse al grupo!
```
Ahora podemos crear nuestra sociedad:
```
society = []
immigration (society, 12, dict_genes) #12 por ejemplo, pueden ser los que sean
#Veamos qué pinta tienen los genes de la población
plt.matshow([individual.genome for individual in society], cmap=plt.cm.gray)
```
Ya tenemos nuestra pequeña sociedad, aumentémosla un poco más mezclando entre sí a los ciudadanos con mejores fitness! Vamos a extender nuestra población mezclando los genomas de otros individuos. Los individuos con mejor fitness es más probable que se reproduzcan. Además, en los nuevos individuos produciremos ligeras mutaciones aleatorias.
```
#This function was taken from Eli Bendersky's website
#It returns an index of a list called "weights",
#where the content of each element in "weights" is the probability of this index to be returned.
#For this function to be as fast as possible we need to pass it a list of weights in descending order.
def weighted_choice_sub(weights):
rnd = random.random() * sum(weights)
for i, w in enumerate(weights):
rnd -= w
if rnd < 0:
return i
def crossover (society, reproduction_rate, mutation_rate):
#First we create a list with the fitness values of every individual in the society
fitness_list = [individual.fitness for individual in society]
#We sort the individuals in the society in descending order of fitness.
society_sorted = [x for (y, x) in sorted(zip(fitness_list, society), key=lambda x: x[0], reverse=True)]
#We then create a list of relative probabilities in descending order,
#so that the fittest individual in the society has N times more chances to reproduce than the least fit,
#where N is the number of individuals in the society.
probability = [i for i in reversed(range(1,len(society_sorted)+1))]
#We create a list of weights with the probabilities of non-mutation and mutation
mutation = [1 - mutation_rate, mutation_rate]
#For every new individual to be created through reproduction:
for i in range (int(len(society) * reproduction_rate)):
#We select two parents randomly, using the list of probabilities in "probability".
father, mother = society_sorted[weighted_choice_sub(probability)], society_sorted[weighted_choice_sub(probability)]
#We randomly select two cutting points for the genome.
a, b = random.randrange(0, len(father.genome)), random.randrange(0, len(father.genome))
#And we create the genome of the child putting together the genome slices of the parents in the cutting points.
child_genome = father.genome[0:min(a,b)]+mother.genome[min(a,b):max(a,b)]+father.genome[max(a,b):]
#For every bit in the not-yet-born child, we generate a list containing
#1's in the positions where the genome must mutate (i.e. the bit must switch its value)
#and 0's in the positions where the genome must stay the same.
n = [weighted_choice_sub(mutation) for ii in range(len(child_genome))]
#This line switches the bits of the genome of the child that must mutate.
mutant_child_genome = [abs(n[i] - child_genome[i]) for i in range(len(child_genome))]
#We finally append the newborn individual to the society
newborn = Individual(mutant_child_genome)
calculate_traits (newborn, dict_genes)
calculate_performances (newborn)
calculate_fitness (newborn)
society.append(newborn)
```
Ahora que tenemos una sociedad extensa, es el momento de que actúe la selección "natural": Eliminaremos de la sociedad a los individuos con peor fitness hasta llegar a una población objetivo.
```
def tournament(society, target_population):
while len(society) > target_population:
fitness_list = [individual.fitness for individual in society]
society.pop(fitness_list.index(min(fitness_list)))
```
Ya tenemos nuestro algoritmo prácticamente terminado!
```
society = []
fitness_max = []
for generation in range(30):
immigration (society, 100, dict_genes) #Añade individuos aleatorios a la sociedad hasta tener 100
fitness_max += [max([individual.fitness for individual in society])]
tournament (society, 15) #Los hace competir hasta que quedan 15
crossover(society, 5, 0.05) #Los ganadores se reproducen hasta tener 75
plt.plot(fitness_max)
plt.title('Evolución del valor de fitness')
tournament (society, 1) #Buscamos el mejor de todos
winner = society[0]
print(winner.traits) #Comprobamos sus características
print(winner.performances)
```
Siro Moreno y Carlos Dorado, Aeropython, 20 de Noviembre de 2015
| true |
code
| 0.424233 | null | null | null | null |
|
The following additional libraries are needed to run this
notebook. Note that running on Colab is experimental, please report a Github
issue if you have any problem.
```
!pip install d2l==0.14.3
```
# Deep Convolutional Neural Networks (AlexNet)
:label:`sec_alexnet`
Although CNNs were well known
in the computer vision and machine learning communities
following the introduction of LeNet,
they did not immediately dominate the field.
Although LeNet achieved good results on early small datasets,
the performance and feasibility of training CNNs
on larger, more realistic datasets had yet to be established.
In fact, for much of the intervening time between the early 1990s
and the watershed results of 2012,
neural networks were often surpassed by other machine learning methods,
such as support vector machines.
For computer vision, this comparison is perhaps not fair.
That is although the inputs to convolutional networks
consist of raw or lightly-processed (e.g., by centering) pixel values, practitioners would never feed raw pixels into traditional models.
Instead, typical computer vision pipelines
consisted of manually engineering feature extraction pipelines.
Rather than *learn the features*, the features were *crafted*.
Most of the progress came from having more clever ideas for features,
and the learning algorithm was often relegated to an afterthought.
Although some neural network accelerators were available in the 1990s,
they were not yet sufficiently powerful to make
deep multichannel, multilayer CNNs
with a large number of parameters.
Moreover, datasets were still relatively small.
Added to these obstacles, key tricks for training neural networks
including parameter initialization heuristics,
clever variants of stochastic gradient descent,
non-squashing activation functions,
and effective regularization techniques were still missing.
Thus, rather than training *end-to-end* (pixel to classification) systems,
classical pipelines looked more like this:
1. Obtain an interesting dataset. In early days, these datasets required expensive sensors (at the time, 1 megapixel images were state-of-the-art).
2. Preprocess the dataset with hand-crafted features based on some knowledge of optics, geometry, other analytic tools, and occasionally on the serendipitous discoveries of lucky graduate students.
3. Feed the data through a standard set of feature extractors such as the SIFT (scale-invariant feature transform) :cite:`Lowe.2004`, the SURF (speeded up robust features) :cite:`Bay.Tuytelaars.Van-Gool.2006`, or any number of other hand-tuned pipelines.
4. Dump the resulting representations into your favorite classifier, likely a linear model or kernel method, to train a classifier.
If you spoke to machine learning researchers,
they believed that machine learning was both important and beautiful.
Elegant theories proved the properties of various classifiers.
The field of machine learning was thriving, rigorous, and eminently useful. However, if you spoke to a computer vision researcher,
you would hear a very different story.
The dirty truth of image recognition, they would tell you,
is that features, not learning algorithms, drove progress.
Computer vision researchers justifiably believed
that a slightly bigger or cleaner dataset
or a slightly improved feature-extraction pipeline
mattered far more to the final accuracy than any learning algorithm.
## Learning Representations
Another way to cast the state of affairs is that
the most important part of the pipeline was the representation.
And up until 2012 the representation was calculated mechanically.
In fact, engineering a new set of feature functions, improving results, and writing up the method was a prominent genre of paper.
SIFT :cite:`Lowe.2004`,
SURF :cite:`Bay.Tuytelaars.Van-Gool.2006`,
HOG (histograms of oriented gradient) :cite:`Dalal.Triggs.2005`,
[bags of visual words](https://en.wikipedia.org/wiki/Bag-of-words_model_in_computer_vision)
and similar feature extractors ruled the roost.
Another group of researchers,
including Yann LeCun, Geoff Hinton, Yoshua Bengio,
Andrew Ng, Shun-ichi Amari, and Juergen Schmidhuber,
had different plans.
They believed that features themselves ought to be learned.
Moreover, they believed that to be reasonably complex,
the features ought to be hierarchically composed
with multiple jointly learned layers, each with learnable parameters.
In the case of an image, the lowest layers might come
to detect edges, colors, and textures.
Indeed,
Alex Krizhevsky, Ilya Sutskever, and Geoff Hinton
proposed a new variant of a CNN,
*AlexNet*,
that achieved excellent performance in the 2012 ImageNet challenge.
AlexNet was named after Alex Krizhevsky,
the first author of the breakthrough ImageNet classification paper :cite:`Krizhevsky.Sutskever.Hinton.2012`.
Interestingly in the lowest layers of the network,
the model learned feature extractors that resembled some traditional filters.
:numref:`fig_filters` is reproduced from the AlexNet paper :cite:`Krizhevsky.Sutskever.Hinton.2012`
and describes lower-level image descriptors.

:width:`400px`
:label:`fig_filters`
Higher layers in the network might build upon these representations
to represent larger structures, like eyes, noses, blades of grass, and so on.
Even higher layers might represent whole objects
like people, airplanes, dogs, or frisbees.
Ultimately, the final hidden state learns a compact representation
of the image that summarizes its contents
such that data belonging to different categories be separated easily.
While the ultimate breakthrough for many-layered CNNs
came in 2012, a core group of researchers had dedicated themselves
to this idea, attempting to learn hierarchical representations of visual data
for many years.
The ultimate breakthrough in 2012 can be attributed to two key factors.
### Missing Ingredient: Data
Deep models with many layers require large amounts of data
in order to enter the regime
where they significantly outperform traditional methods
based on convex optimizations (e.g., linear and kernel methods).
However, given the limited storage capacity of computers,
the relative expense of sensors,
and the comparatively tighter research budgets in the 1990s,
most research relied on tiny datasets.
Numerous papers addressed the UCI collection of datasets,
many of which contained only hundreds or (a few) thousands of images
captured in unnatural settings with low resolution.
In 2009, the ImageNet dataset was released,
challenging researchers to learn models from 1 million examples,
1000 each from 1000 distinct categories of objects.
The researchers, led by Fei-Fei Li, who introduced this dataset
leveraged Google Image Search to prefilter large candidate sets
for each category and employed
the Amazon Mechanical Turk crowdsourcing pipeline
to confirm for each image whether it belonged to the associated category.
This scale was unprecedented.
The associated competition, dubbed the ImageNet Challenge
pushed computer vision and machine learning research forward,
challenging researchers to identify which models performed best
at a greater scale than academics had previously considered.
### Missing Ingredient: Hardware
Deep learning models are voracious consumers of compute cycles.
Training can take hundreds of epochs, and each iteration
requires passing data through many layers of computationally-expensive
linear algebra operations.
This is one of the main reasons why in the 1990s and early 2000s,
simple algorithms based on the more-efficiently optimized
convex objectives were preferred.
*Graphical processing units* (GPUs) proved to be a game changer
in making deep learning feasible.
These chips had long been developed for accelerating
graphics processing to benefit computer games.
In particular, they were optimized for high throughput $4 \times 4$ matrix-vector products, which are needed for many computer graphics tasks.
Fortunately, this math is strikingly similar
to that required to calculate convolutional layers.
Around that time, NVIDIA and ATI had begun optimizing GPUs
for general computing operations,
going as far as to market them as *general-purpose GPUs* (GPGPU).
To provide some intuition, consider the cores of a modern microprocessor
(CPU).
Each of the cores is fairly powerful running at a high clock frequency
and sporting large caches (up to several megabytes of L3).
Each core is well-suited to executing a wide range of instructions,
with branch predictors, a deep pipeline, and other bells and whistles
that enable it to run a large variety of programs.
This apparent strength, however, is also its Achilles heel:
general-purpose cores are very expensive to build.
They require lots of chip area,
a sophisticated support structure
(memory interfaces, caching logic between cores,
high-speed interconnects, and so on),
and they are comparatively bad at any single task.
Modern laptops have up to 4 cores,
and even high-end servers rarely exceed 64 cores,
simply because it is not cost effective.
By comparison, GPUs consist of $100 \sim 1000$ small processing elements
(the details differ somewhat between NVIDIA, ATI, ARM and other chip vendors),
often grouped into larger groups (NVIDIA calls them warps).
While each core is relatively weak,
sometimes even running at sub-1GHz clock frequency,
it is the total number of such cores that makes GPUs orders of magnitude faster than CPUs.
For instance, NVIDIA's recent Volta generation offers up to 120 TFlops per chip for specialized instructions
(and up to 24 TFlops for more general-purpose ones),
while floating point performance of CPUs has not exceeded 1 TFlop to date.
The reason for why this is possible is actually quite simple:
first, power consumption tends to grow *quadratically* with clock frequency.
Hence, for the power budget of a CPU core that runs 4 times faster (a typical number),
you can use 16 GPU cores at $1/4$ the speed,
which yields $16 \times 1/4 = 4$ times the performance.
Furthermore, GPU cores are much simpler
(in fact, for a long time they were not even *able*
to execute general-purpose code),
which makes them more energy efficient.
Last, many operations in deep learning require high memory bandwidth.
Again, GPUs shine here with buses that are at least 10 times as wide as many CPUs.
Back to 2012. A major breakthrough came
when Alex Krizhevsky and Ilya Sutskever
implemented a deep CNN
that could run on GPU hardware.
They realized that the computational bottlenecks in CNNs,
convolutions and matrix multiplications,
are all operations that could be parallelized in hardware.
Using two NVIDIA GTX 580s with 3GB of memory,
they implemented fast convolutions.
The code [cuda-convnet](https://code.google.com/archive/p/cuda-convnet/)
was good enough that for several years
it was the industry standard and powered
the first couple years of the deep learning boom.
## AlexNet
AlexNet, which employed an 8-layer CNN,
won the ImageNet Large Scale Visual Recognition Challenge 2012
by a phenomenally large margin.
This network showed, for the first time,
that the features obtained by learning can transcend manually-designed features, breaking the previous paradigm in computer vision.
The architectures of AlexNet and LeNet are very similar,
as :numref:`fig_alexnet` illustrates.
Note that we provide a slightly streamlined version of AlexNet
removing some of the design quirks that were needed in 2012
to make the model fit on two small GPUs.

:label:`fig_alexnet`
The design philosophies of AlexNet and LeNet are very similar,
but there are also significant differences.
First, AlexNet is much deeper than the comparatively small LeNet5.
AlexNet consists of eight layers: five convolutional layers,
two fully-connected hidden layers, and one fully-connected output layer. Second, AlexNet used the ReLU instead of the sigmoid
as its activation function.
Let us delve into the details below.
### Architecture
In AlexNet's first layer, the convolution window shape is $11\times11$.
Since most images in ImageNet are more than ten times higher and wider
than the MNIST images,
objects in ImageNet data tend to occupy more pixels.
Consequently, a larger convolution window is needed to capture the object.
The convolution window shape in the second layer
is reduced to $5\times5$, followed by $3\times3$.
In addition, after the first, second, and fifth convolutional layers,
the network adds maximum pooling layers
with a window shape of $3\times3$ and a stride of 2.
Moreover, AlexNet has ten times more convolution channels than LeNet.
After the last convolutional layer there are two fully-connected layers
with 4096 outputs.
These two huge fully-connected layers produce model parameters of nearly 1 GB.
Due to the limited memory in early GPUs,
the original AlexNet used a dual data stream design,
so that each of their two GPUs could be responsible
for storing and computing only its half of the model.
Fortunately, GPU memory is comparatively abundant now,
so we rarely need to break up models across GPUs these days
(our version of the AlexNet model deviates
from the original paper in this aspect).
### Activation Functions
Besides, AlexNet changed the sigmoid activation function to a simpler ReLU activation function. On one hand, the computation of the ReLU activation function is simpler. For example, it does not have the exponentiation operation found in the sigmoid activation function.
On the other hand, the ReLU activation function makes model training easier when using different parameter initialization methods. This is because, when the output of the sigmoid activation function is very close to 0 or 1, the gradient of these regions is almost 0, so that backpropagation cannot continue to update some of the model parameters. In contrast, the gradient of the ReLU activation function in the positive interval is always 1. Therefore, if the model parameters are not properly initialized, the sigmoid function may obtain a gradient of almost 0 in the positive interval, so that the model cannot be effectively trained.
### Capacity Control and Preprocessing
AlexNet controls the model complexity of the fully-connected layer
by dropout (:numref:`sec_dropout`),
while LeNet only uses weight decay.
To augment the data even further, the training loop of AlexNet
added a great deal of image augmentation,
such as flipping, clipping, and color changes.
This makes the model more robust and the larger sample size effectively reduces overfitting.
We will discuss data augmentation in greater detail in :numref:`sec_image_augmentation`.
```
from d2l import torch as d2l
import torch
from torch import nn
net = nn.Sequential(
# Here, we use a larger 11 x 11 window to capture objects. At the same
# time, we use a stride of 4 to greatly reduce the height and width of the
# output. Here, the number of output channels is much larger than that in
# LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# Make the convolution window smaller, set padding to 2 for consistent
# height and width across the input and output, and increase the number of
# output channels
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# Use three successive convolutional layers and a smaller convolution
# window. Except for the final convolutional layer, the number of output
# channels is further increased. Pooling layers are not used to reduce the
# height and width of input after the first two convolutional layers
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# Here, the number of outputs of the fully-connected layer is several
# times larger than that in LeNet. Use the dropout layer to mitigate
# overfitting
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# Output layer. Since we are using Fashion-MNIST, the number of classes is
# 10, instead of 1000 as in the paper
nn.Linear(4096, 10))
```
We construct a single-channel data example with both height and width of 224 to observe the output shape of each layer. It matches the AlexNet architecture in :numref:`fig_alexnet`.
```
X = torch.randn(1, 1, 224, 224)
for layer in net:
X=layer(X)
print(layer.__class__.__name__,'Output shape:\t',X.shape)
```
## Reading the Dataset
Although AlexNet is trained on ImageNet in the paper, we use Fashion-MNIST here
since training an ImageNet model to convergence could take hours or days
even on a modern GPU.
One of the problems with applying AlexNet directly on Fashion-MNIST
is that its images have lower resolution ($28 \times 28$ pixels)
than ImageNet images.
To make things work, we upsample them to $224 \times 224$
(generally not a smart practice,
but we do it here to be faithful to the AlexNet architecture).
We perform this resizing with the `resize` argument in the `d2l.load_data_fashion_mnist` function.
```
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
```
## Training
Now, we can start training AlexNet.
Compared with LeNet in :numref:`sec_lenet`,
the main change here is the use of a smaller learning rate
and much slower training due to the deeper and wider network,
the higher image resolution, and the more costly convolutions.
```
lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr)
```
## Summary
* AlexNet has a similar structure to that of LeNet, but uses more convolutional layers and a larger parameter space to fit the large-scale ImageNet dataset.
* Today AlexNet has been surpassed by much more effective architectures but it is a key step from shallow to deep networks that are used nowadays.
* Although it seems that there are only a few more lines in AlexNet's implementation than in LeNet, it took the academic community many years to embrace this conceptual change and take advantage of its excellent experimental results. This was also due to the lack of efficient computational tools.
* Dropout, ReLU, and preprocessing were the other key steps in achieving excellent performance in computer vision tasks.
## Exercises
1. Try increasing the number of epochs. Compared with LeNet, how are the results different? Why?
1. AlexNet may be too complex for the Fashion-MNIST dataset.
1. Try simplifying the model to make the training faster, while ensuring that the accuracy does not drop significantly.
1. Design a better model that works directly on $28 \times 28$ images.
1. Modify the batch size, and observe the changes in accuracy and GPU memory.
1. Analyze computational performance of AlexNet.
1. What is the dominant part for the memory footprint of AlexNet?
1. What is the dominant part for computation in AlexNet?
1. How about memory bandwidth when computing the results?
1. Apply dropout and ReLU to LeNet-5. Does it improve? How about preprocessing?
[Discussions](https://discuss.d2l.ai/t/76)
| true |
code
| 0.798501 | null | null | null | null |
|
<a id="topD"></a>
# Downloading COS Data
# Learning Goals
<font size="5"> This Notebook is designed to walk the user (<em>you</em>) through: <b>Downloading existing Cosmic Origins Spectrograph (<em>COS</em>) data from the online archive</b></font>
**1. [Using the web browser interface](#mastD)**
\- 1.1. [The Classic HST Web Search](#mastD)
\- 1.2. [Searching for a Series of Observations on the Classic Web Search](#WebSearchSeriesD)
\- 1.3. [The MAST Portal](#mastportD)
\- 1.4. [Searching for a Series of Observations on the MAST Portal](#mastportSeriesD)
**2. [Using the `Python` module `Astroquery`](#astroqueryD)**
\- 2.1. [Searching for a single source with Astroquery](#Astroquery1D)
\- 2.2. [Narrowing Search with Observational Parameters](#NarrowSearchD)
\- 2.3. [Choosing and Downloading Data Products](#dataprodsD)
\- 2.4. [Using astroquery to find data on a series of sources](#Astroquery2D)
## Choosing how to access the data
**This Notebook explains three methods of accessing COS data hosted by the STScI Mikulski Archive for Space Telescopes (MAST).**
You may read through all three, or you may wish to focus on a particular method which best suits your needs.
**Please use the table below to determine which section on which to focus.**
||The [Classic HST Search (Web Interface)](https://archive.stsci.edu/hst/search.php)|The [MAST Portal (Web Interface)](https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html)|The [`Astroquery` (`Python` Interface)](http://astroquery.readthedocs.io/)|
|-|-|-|-|
||- User-friendly point-and-click searching|- Very user-friendly point-and-click searching|- Requires a bit of `Python` experience|
||- Advanced **mission-specific** search parameters, including: central wavelength, detector, etc.|- Lacks some mission-specific search parameters|- Allows for programmatic searching and downloads|
||- Can be difficult to download the data if not on the STScI network|- Easy to download selected data|- Best for large datasets|
|||||
|***Use this method if...*** |*...You're unfamiliar with `Python` and need to search for data by cenwave*|*...You're exploring the data and you don't need to search by cenwave*|*...You know `Python` and have an idea of what data you're looking for, or you have a lot of data*|
|***Described in...***|*[Section 1.1](#mastD)*|*[Section 1.3](#mastportD)*|*[Section 2.1](#astroqueryD)*|
*Note* that these are only recommendations, and you may prefer another option. For most purposes, the writer of this tutorial recommends the `Astroquery` `Python` interface, unless you are not at all comfortable using python or doing purely exploratory work.
<!-- *You may review Section 1 or 2 independently or together.* -->
<!-- *The web search (Section 1) is generally better for introductory users and exploratory use, while the `astroquery` method (Section 2) is easier for those with some `python` experience.* -->
# 0. Introduction
**The Cosmic Origins Spectrograph ([*COS*](https://www.nasa.gov/content/hubble-space-telescope-cosmic-origins-spectrograph)) is an ultraviolet spectrograph on-board the Hubble Space Telescope([*HST*](https://www.stsci.edu/hst/about)) with capabilities in the near ultraviolet (*NUV*) and far ultraviolet (*FUV*).**
**This tutorial aims to prepare you to access the existing COS data of your choice by walking you through downloading a processed spectrum, as well as various calibration files obtained with COS.**
- For an in-depth manual to working with COS data and a discussion of caveats and user tips, see the [COS Data Handbook](https://hst-docs.stsci.edu/display/COSDHB/).
- For a detailed overview of the COS instrument, see the [COS Instrument Handbook](https://hst-docs.stsci.edu/display/COSIHB/).
<font size="5"> We will define a few directories in which to place our data.</font>
And to create new directories, we'll import `pathlib.Path`:
```
#Import for: working with system paths
from pathlib import Path
# This will be an important directory for the Notebook, where we save data
data_dir = Path('./data/')
data_dir.mkdir(exist_ok=True)
```
<a id="downloadD"></a>
# 1. Downloading the data through the browser interface
One can search for COS data from both a browser-based Graphical User Interface (*gui*) and a `Python` interface. This Section (1) will examine two web interfaces. [Section 2](#astroqueryD) will explain the `Python` interface.
*Note, there are other, more specialized ways to query the mast API not discussed in this Notebook. An in-depth MAST API tutorial can be found [here](https://mast.stsci.edu/api/v0/MastApiTutorial.html).*
<a id="mastD"></a>
## 1.1 The Classic HST Web Search
**A browser gui for searching *specifically* through [HST archival data can be found here](http://archive.stsci.edu/hst/search.php). We will be discussing *this* HST search in the section below.**
As of September, 2021, two other portals also allow access to the same data:
* A newer HST-specific search page ([here](https://mast.stsci.edu/search/hst/ui/#/)). Most downloading difficulties have been solved with this new site, and upcoming versions of this tutorial will focus on its use.
* A more general MAST gui, which also allows access to data from other telescopes such as TESS, but does not offer all HST-specific search parameters. We will discuss this interface in [Section 1.3](#mastportD).
The search page of the HST interface is laid out as in fig. 1.1:
### Fig 1.1
<center><img src=./figures/Mast_hst_searchformQSO.png width ="900" title="MAST Archive search form for a COS data query"> </center>
where here we have indicated we would like to find all archival science data from the **COS far-ultraviolet (FUV) configuration**, taken with any grating while looking at Quasi-Stellar Objects (QSO) within a 3 arcminute radius of (1hr:37':40", +33d 09m 32s). The output columns we have selected to see are visible in the bottom left of Fig 1.1.
Note that if you have a list of coordinates, Observation ID(s), etc. for a series of targets you can click on the "File Upload Form" and attach your list of OBSIDs or identifying features. Then specify which type of data your list contains using the "File Contents" drop-down menu.
Figure 1.2 shows the results of our search shown in Fig 1.1.
### Fig 1.2
<center><img src=figures/QSO_MastSearchRes.png width ="900" title="MAST Archive search results for a COS data query"> </center>
**We now choose our dataset.**
We rather arbitrarily select **`LCXV13050`** because of its long exposure time, taken under an observing program described as:
> "Project AMIGA: Mapping the Circumgalactic Medium of Andromeda"
This is a Quasar known as [3C48](http://simbad.u-strasbg.fr/simbad/sim-basic?Ident=3c48&submit=SIMBAD+search), one of the first quasars discovered.
Clicking on the dataset, we are taken to a page displaying a preview spectrum (Fig 1.3).
### Fig 1.3
<center><img src=./figures/QSOPreviewSpec.png width ="900" title="MAST Archive preview spectrum of LCXV13050"> </center>
We now return to the [search page](http://archive.stsci.edu/hst/search.php) and enter in LCXV13050 under "Dataset" with no other parameters set. Clicking "search", now we see a single-rowed table with *just* our dataset, and the option to download datasets. We mark the row we wish to download and click "Submit marked data for retrieval from STDADS". See Fig 1.4.
### Fig 1.4
<center><img src =figures/LCXV13050_res.png width ="900" title="MAST Archive dataset overview of LCXV13050"> </center>
Now we see a page like in Fig 1.5,
where we can either sign in with STScI credentials, or simply provide our email to proceed without credentials. Generally, you may proceed anonymously, unless you are retrieving proprietary data to which you have access. Next, make sure to select "Deliver the data to the Archive staging area". Click "Send Retrieval Request to ST-DADS" and you will receive an email with instructions on downloading the data.
### Fig 1.5
<center><img src =figures/DownloadOptions.png width ="900" title="Download Options for LCXV13050"> </center>
Now the data is "staged" on a MAST server, and you need to download it to your local computer.
### Downloading the staged data
We demonstrate three methods of downloading your staged data:
1. If your terminal supports it, you may [use the `wget` tool](#wgetDLD).
2. However if that does not work, we recommend [using a secure ftp client application](#download_ftps_cyduckD).
3. Finally, if you would instead like to download *staged data* programmatically, you may [use the Python `ftplib` package](#download_ftps_funcD), as described [here](https://archive.stsci.edu/ftp.html) in STScI's documentation of the MAST FTP Service. For your convenience, we have built the `download_anonymous_staged_data` function below, which will download anonymously staged data via ftps.
<a id=wgetDLD></a>
#### Downloading the staged data with `wget`
**If you are connected to the STScI network, either in-person or via a virtual private network (VPN), you should use the `wget` command as in the example below:**
`wget -r --ftp-user=anonymous --ask-password ftps://archive.stsci.edu/stage/anonymous/anonymous<directory_number> --directory-prefix=<data_dir>`
where `directory_number` is the number at the end of the anonymous path specified in the email you received from MAST and `data_dir` is the local directory where you want the downloaded data.
You will be prompted for a password. Type in the email address you used, then press enter/return.
Now all the data will be downloaded into a subdirectory of data_dir: `"./archive.stsci.edu/stage/anonymous/anonymous<directory_number>/"`
<a id=download_ftps_cyduckD></a>
#### Downloading the staged data with a secure ftp client application (`CyberDuck`)
CyberDuck is an application which allows you to securely access data stored on another machine using ftps. To download your staged data using Cyberduck, first download the [Cyberduck](https://cyberduck.io) application (*free, with a recommended donation*). Next, open a new browser window (Safari, Firefox, and Google Chrome have all been shown to work,) and type in the following web address: `ftps://archive.stsci.edu/stage/anonymous<directory_number>`, where `directory_number` is the number at the end of the anonymous path specified in the email you received from MAST. For example, if the email specifies:
> "The data can be found in the directory... /stage/anonymous/anonymous42822"
then this number is **42822**
Your browser will attempt to redirect to the CyberDuck application. Allow it to "Open CyberDuck.app", and CyberDuck should open a finder window displaying your files. Select whichever files you want to download by highlighting them (command-click or control-click) then right click one of the highlighted files, and select "Download To". This will bring up a file browser allowing you to save the selected files to wherever you wish on your local computer.
<a id=download_ftps_funcD></a>
#### Downloading the staged data with `ftps`
To download anonymously staged data programmatically with ftps, you may run the `download_anonymous_staged_data` function as shown here:
```python
download_anonymous_staged_data(email_used="[email protected]", directory_number=80552, outdir="./here_is_where_I_want_the_data")
```
Which results in:
```
Downloading lcxv13050_x1dsum1.fits
Done
...
...
Downloading lcxv13gxq_flt_b.fits
Done
```
```
import ftplib
def download_anonymous_staged_data(email_used, directory_number, outdir = "./data/ftps_download/", verbose=True):
"""
A direct implementation of the MAST FTP Service webpage's ftplib example code.
Downloads anonymously staged data from the MAST servers via ftps.
Inputs:
email_used (str): the email address used to stage the data
directory_number (str or int): The number at the end of the anonymous filepath. i.e. if the email you received includes:
"The data can be found in the directory... /stage/anonymous/anonymous42822",
then this number is 42822
outdir (str): Path to where the file will download locally.
verbose (bool): If True, prints name of each file downloaded.
"""
ftps = ftplib.FTP_TLS('archive.stsci.edu') # Set up connection
ftps.login(user="anonymous", passwd=email_used) # Login with anonymous credentials
ftps.prot_p() # Add protection to the connection
ftps.cwd(f"stage/anonymous/anonymous{directory_number}")
filenames = ftps.nlst()
outdir = Path(outdir) # Set up the output directory as a path
outdir.mkdir(exist_ok=True)
for filename in filenames: # Loop through all the staged files
if verbose:
print("Downloading " + filename)
with open(outdir / filename, 'wb') as fp: # Download each file locally
ftps.retrbinary('RETR {}'.format(filename), fp.write)
if verbose:
print(" Done")
```
<font size="5"> <b>Well Done making it this far!</b></font>
Attempt the exercise below for some extra practice.
### Exercise 1: *Searching the archive for TRAPPIST-1 data*
[TRAPPIST-1](https://en.wikipedia.org/wiki/TRAPPIST-1) is a cool red dwarf with a multiple-exoplanet system.
- Find its coordinates using the [SIMBAD Basic Search](http://simbad.u-strasbg.fr/simbad/sim-fbasic).
- Use those coordinates in the [HST web search](https://archive.stsci.edu/hst/search.php) or the [MAST portal](https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html) to find all COS exposures of the system.
- Limit the search terms to find the COS dataset taken in the COS far-UV configuration with the grating G130M.
**What is the dataset ID, and how long was the exposure?**
Place your answer in the cell below.
```
# Your answer here
```
<a id=WebSearchSeriesD></a>
## 1.2. Searching for a Series of Observations on the Classic HST Web Search
Now let's try using the web interface's [file upload form](http://archive.stsci.edu/hst/search.php?form=fuf) to search for a series of observations by their dataset IDs. We're going to look for three observations of the same object, the white dwarf WD1057+719, taken with three different COS gratings. Two are in the FUV and one in the NUV. The dataset IDs are
- LDYR52010
- LBNM01040
- LBBD04040
So that we have an example list of datasets to input to the web search, we make a comma-separated-value txt file with these three obs_ids, and save it as `obsId_list.txt`.
```
obsIdList = ['LDYR52010','LBNM01040','LBBD04040'] # The three observation IDs we want to gather
obsIdList_length = len(obsIdList)
with open('./obsId_list.txt', 'w') as f: # Open up this new file in "write" mode
for i, item in enumerate(obsIdList): # We want a newline after each obs_id except the last one
if i < obsIdList_length - 1:
f.writelines(item + "," + '\n')
if i == obsIdList_length - 1: # Make sure we don't end the file with a blank line (below)
f.writelines(item)
```
Then we link to this file under the **Local File Name** browse menu on the file upload form. We must set the **File Contents** term to Data ID, as that is the identifier we have provided in our file, and we change the **delimiter** to a comma.
Because we are searching by Dataset ID, we don't need to specify any additional parameters to narrow down the data.
### Fig 1.6
<center><img src =figures/FUF_search.png width ="900" title="File Upload Search Form"> </center>
**We now can access all the datasets, as shown in Fig. 1.7:**
### Fig 1.7
<center><img src =figures/FUF_res.png width ="900" title="File Upload Search Results"> </center>
Now, to download all of the relevant files, we can check the **mark** box for all of them, and again hit "Submit marked data for retrieval from STDADS". This time, we want to retrieve **all the calibration files** associated with each dataset, so we check the following boxes:
- Uncalibrated
- Calibrated
- Used Reference Files
(*See Fig. 1.8*)
### Fig 1.8
<center><img src =./figures/DownloadOptions_FUF.png width ="900" title="Download Options for multiple datasets"> </center>
The procedure from here is the same described above in Section 1.1. Now, when we download the staged data, we obtain multiple subdirectories with each dataset separated.
<a id = mastportD></a>
## 1.3. The MAST Portal
STScI hosts another web-based gui for accessing data, the [MAST Portal](https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html). This is a newer interface which hosts data from across many missions and allows the user to visualize the target in survey images, take quick looks at spectra or lightcurves, and manage multiple search tabs at once. Additionally, it handles downloads in a slightly more beginner-friendly manner than the current implementation of the Classic HST Search. This guide will only cover the basics of accessing COS data through the MAST Portal; you can find more in-depth documentation in the form of helpful video guides on the [MAST YouTube Channel](https://www.youtube.com/user/STScIMAST).
**Let's find the same data we found in Section 1.1, on the QSO 3C48:**
Navigate to the MAST Portal at <https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html>, and you will be greeted by a screen where the top looks like Fig. 1.9.
### Fig 1.9
<center><img src =figures/mastp_top.png width ="900" title="Top of MAST Portal Home"> </center>
Click on "Advanced Search" (boxed in red in Fig. 1.9). This will open up a new search tab, as shown in Fig. 1.10:
### Fig 1.10
<center><img src =figures/mastp_adv.png width ="900" title="The advanced search tab"> </center>
Fig 1.10 (above) shows the default search fields which appear. Depending on what you are looking for, these may or may not be the most helpful search fields. By unchecking some of the fields which we are not interested in searching by right now (boxed in green), and then entering the parameter values by which to narrow the search into each parameter's box, we generate Fig. 1.11 (below). One of the six fields (Mission) by which we are narrowing is boxed in a dashed blue line. The list of applied filters is boxed in red. A dashed pink box at the top left indicates that 2 records were found matching all of these parameters. To its left is an orange box around the "Search" button to press to bring up the list of results
Here we are searching by:
|**Search Parameter**|**Value**|
|-|-|
|Mission|HST|
|Instrument|COS/FUV|
|Filters|G160M|
|Target Name|3C48|
|Observation ID|LCXV\* (*the star is a "wild card" value, so the search will find any file whose `obs_id` begins with LCXV*)|
|Product Type|spectrum|
### Fig 1.11
<center><img src =figures/mastp_adv_2.png width ="900" title="The advanced search tab with some selections"> </center>
Click the "Search" button (boxed in orange), and you will be brought to a page resembling Fig. 1.12.
### Fig 1.12
<center><img src =figures/mastp_res1.png width ="900" title="Results of MAST Portal search"> </center>
<font size="4"> <b>Above, in Fig 1.12</b>:</font>
- The yellow box to the right shows the AstroView panel, where you can interactively explore the area around your target:
- click and drag to pan around
- scroll to zoom in/out
- The dashed-blue box highlights additional filters you can use to narrow your search results.
- The red box highlights a button you can click with *some* spectral datasets to pull up an interactive spectrum.
- The green box highlights the "Mark" checkboxes for each dataset.
- The black circle highlights the single dataset download button:
- **If you only need to download one or two datasets, you may simply click this button for each dataset**
- Clicking the single dataset download button will attempt to open a "pop-up" window, which you must allow in order to download the file. Some browsers will require you to manually allow pop-ups.
<a id="mastportSeriesD"></a>
## 1.4. Searching for a Series of Observations on the MAST Portal
<font size="4"> <b>To download multiple datasets</b>:</font>
The MAST portal acts a bit like an online shopping website, where you add your *data products* to the checkout *cart*/*basket*, then open up your cart to *checkout* and download the files.
Using the checkboxes, mark all the datasets you wish to download (in this case, we'll download both LCXV13040 and LCXV13050). Then, click the "Add data products to Download Basket" button (circled in a dashed-purple line), which will take you to a "Download Basket" screen resembling Fig 1.13:
### Fig 1.13
<center><img src =figures/mastp_cart2.png width ="900" title="MAST Portal Download Basket"> </center>
Each dataset contains *many* files, most of which are calibration files or intermediate processing files. You may or may not want some of these intermediate files in addition to the final product file.
In the leftmost "Filters" section of the Download Basket page, you can narrow which files will be downloaded (boxed in red).
By default, only the **minimum recommended products** (*mrp*) will be selected. In the case of most COS data, this will be the final spectrum `x1dsum` file and association `asn` file for each dataset. The mrp files for the first dataset (`LCXV13040`) are highlighted in yellow. These two mrp filetypes are fine for our purposes here; however if you want to download files associated with specific exposures, or any calibration files or intermediate files, you can select those you wish to download with the checkboxes in the file tree system (boxed in dashed-green).
**For this tutorial, we simply select "Minimum Recommended Products" at the top left. With this box checked, all of the folders representing individual exposures are no longer visible.**
Check the box labelled "HST" to select all files included by the filters, and click the "Download Selected Items" button at the top right (dashed-black circle). This will bring up a small window asking you what format to download your files as. For datasets smaller than several Gigabytes, the `Zip` format will do fine. Click Download, and a pop-up window will try to open to download the files. If no download begins, make sure to enable this particular pop-up, or allow pop-ups on the MAST page.
**Your files should now be downloaded as a compressed `Zip` folder.**
If you need help uncompressing the `Zip`ped files, check out these links for: [Windows](https://support.microsoft.com/en-us/windows/zip-and-unzip-files-8d28fa72-f2f9-712f-67df-f80cf89fd4e5) and [Mac](https://support.apple.com/guide/mac-help/zip-and-unzip-files-and-folders-on-mac-mchlp2528/mac). There are numerous ways to do this on Linux, however we have not vetted them.
<a id = astroqueryD></a>
# 2. The Python Package `astroquery.mast`
Another way to search for and download archived datasets is from within `Python` using the module [`astroquery.mast`](https://astroquery.readthedocs.io/en/latest/mast/mast.html). We will import one of this module's key submodules: `Observations`.
*Please note* that the canonical source of information on this package is the [`astroquery` docs](https://astroquery.readthedocs.io/en/latest/) - please look there for the most up-to-date instructions.
## We will import the following packages:
- `astroquery.mast`'s submodule `Observations` for finding and downloading data from the [MAST](https://mast.stsci.edu/portal/Mashup/Clients/Mast/Portal.html) archive
- `csv`'s submodule `reader` for reading in/out from a csv file of source names.
```
# Downloading data from archive
from astroquery.mast import Observations
# Reading in multiple source names from a csv file
from csv import reader
```
<a id=Astroquery1D></a>
## 2.1. Searching for a single source with Astroquery
There are *many* options for searching the archive with astroquery, but we will begin with a very general search using the coordinates we found for WD1057+719 in the last section to find the dataset with the longest exposure time using the COS/FUV mode through the G160M filter. We could also search by object name to have it resolved to a set of coordinates, with the function `Observations.query_object(objectname = '3C48')`.
- Our coordinates were: (11:00:34.126 +71:38:02.80).
- We can search these coordinates as sexagesimal coordinates, or convert them to decimal degrees.
```
query_1 = Observations.query_object("11:00:34.126 +71:38:02.80", radius="5 sec")
```
This command has generated a table of objects called **"query_1"**. We can see what information we have on the objects in the table by printing its *`keys`*, and see how many objects are in the table with `len(query_1)`.
```
print(f"We have table information on {len(query_1)} observations in the following categories/columns:\n")
q1_keys = (query_1.keys())
q1_keys
```
<a id=NarrowSearchD></a>
## 2.2. Narrowing Search with Observational Parameters
Now we narrow down a bit with some additional parameters and sort by exposure time.
The parameter limits we add to the search are:
- *Only look for sources in the coordinate range between right ascension 165 to 166 degrees and declination +71 to +72 degrees*
- *Only find observations in the UV*
- *Only find observations taken with the COS instrument (either in its FUV or NUV configuration).*
- *Only find spectrographic observations*
- *Only find observations made using the COS grating "G160M"*
```
query_2 = Observations.query_criteria(s_ra=[165., 166.], s_dec=[+71.,+72.],
wavelength_region="UV", instrument_name=["COS/NUV","COS/FUV"],
dataproduct_type = "spectrum", filters = 'G160M')
# Next lines simplifies the columns of data we see to some useful data we will look at right now
limq2 = query_2['obsid','obs_id', 'target_name', 'dataproduct_type', 'instrument_name',
'project', 'filters', 'wavelength_region', 't_exptime']
sort_order = query_2.argsort('t_exptime') # This is the index list in order of exposure time, increasing
print(limq2[sort_order])
chosenObs = limq2[sort_order][-1] # Grab the last value of the sorted list
print(f"\n\nThe longest COS/FUV exposure with the G160M filter is: \n\n{chosenObs}")
```
<font size="5">Caution! </font>
<img src=./figures/warning.png width ="60" title="CAUTION">
Please note that these queries are `Astropy` tables and do not always respond as expected for other data structures like `Pandas DataFrames`. For instance, the first way of filtering a table shown below is correct, but the second will consistently produce the *wrong result*. You *must* search and filter these tables by masking them, as in the first example below.
```
# Searching a table generated with a query
## First, correct way using masking
mask = (query_1['obs_id'] == 'lbbd01020') # NOTE, obs_id must be lower-case
print("Correct way yields: \n" , query_1[mask]['obs_id'],"\n\n")
# Second INCORRECT way
print("Incorrect way yields: \n" , query_1['obs_id' == 'LBBD01020']['obs_id'], "\nwhich is NOT what we're looking for!")
```
<a id=dataprodsD></a>
## 2.3. Choosing and Downloading Data Products
**Now we can choose and download our data products from the archive dataset.**
We will first generate a list of data products in the dataset: `product_list`. This will generate a large list, but we will only show the first 10 values.
```
product_list = Observations.get_product_list(chosenObs)
product_list[:10] #Not the whole dataset, just first 10 lines/observations
```
Now, we will download *just the* **minimum recommended products** (*mrp*) which are the fully calibrated spectrum (denoted by the suffix `_x1d` or here `x1dsum`) and the association file (denoted by the suffix `_asn`). We do this by setting the parameter `mrp_only` to True. The association file contains no data, but rather the metadata explaining which exposures produced the `x1dsum` dataset. The `x1dsum` file is the final product summed across all of the [fixed pattern noise positions](https://hst-docs.stsci.edu/cosdhb/chapter-1-cos-overview/1-1-instrument-capabilities-and-design#id-1.1InstrumentCapabilitiesandDesign-GratingOffset(FP-POS)GratingOffsetPositions(FP-POS)) (`FP-POS`). The `x1d` and `x1dsum<n>` files are intermediate spectra. Much more information can be found in the [COS Instrument Handbook](https://hst-docs.stsci.edu/display/COSIHB/).
We would set `mrp_only` to False, if we wanted to download ***all*** the data from the observation, including:
- support files such as the spacecraft's pointing data over time (`jit` files).
- intermediate data products such as calibrated TIME-TAG data (`corrtag` or `corrtag_a`/`corrtag_b` files) and extracted 1-dimensional spectra averaged over exposures with a specific `FP-POS` value (`x1dsum<n>` files).
<img src=./figures/warning.png width ="60" title="CAUTION">
However, use caution with downloading all files, as in this case, setting `mrp_only` to False results in the transfer of **7 Gigabytes** of data, which can take a long time to transfer and eat away at your computer's storage! In general, only download the files you need. On the other hand, often researchers will download only the raw data, so that they can process it for themselves. Since here we only need the final `x1dsum` and `asn` files, we only need to download 2 Megabytes.
```
downloads = Observations.download_products(product_list, download_dir=str(data_dir) , extension='fits', mrp_only=True, cache=False)
```
### Exercise 2: *Download the raw counts data on TRAPPIST-1*
In the previous exercise, we found an observation COS took on TRAPPIST-1 system. In case you skipped Exercise 1, the observation's Dataset ID is `LDLM40010`.
Use `Astroquery.mast` to download the raw `TIME-TAG` data, rather than the x1d spectra files. See the [COS Data Handbook Ch. 2](https://hst-docs.stsci.edu/cosdhb/chapter-2-cos-data-files/2-4-cos-data-products) for details on TIME-TAG data files. Make sure to get the data from both segments of the FUV detector (i.e. both `RAWTAG_A` and `RAWTAG_B` files). If you do this correctly, there should be five data files for each detector segment.
*Note that some of the obs_id may appear in the table as slightly different, i.e.: ldlm40alq and ldlm40axq, rather than ldlm40010. The main obs_id they fall under is still ldlm40010, and this will still work as a search term. They are linked together by the association file described here in section 2.3.*
```
# Your answer here
```
<a id=Astroquery2D></a>
## 2.4. Using astroquery to find data on a series of sources
In this case, we'll look for COS data around several bright globular clusters:
- Omega Centauri
- M5
- M13
- M15
- M53
We will first write a comma-separated-value (csv) file `objectname_list.csv` listing these sources by their common name. This is a bit redundant here, as we will immediately read back in what we have written; however it is done here to deliberately teach both sides of the writing/reading process, and as many users will find themselves with a csv sourcelist they must search.
```
sourcelist = ['omega Centauri', 'M5', 'M13', 'M15', 'M53'] # The 5 sources we want to look for
sourcelist_length = len(sourcelist) # measures the length of the list for if statements below
with open('./objectname_list.csv', 'w') as f: # Open this new file in "write" mode
for i, item in enumerate(sourcelist): # We want a comma after each source name except the last one
if i < sourcelist_length - 1:
f.writelines(item + ",")
if i == sourcelist_length - 1: # No comma after the last entry
f.writelines(item)
with open('./objectname_list.csv', 'r', newline = '') as csvFile: # Open the file we just wrote in "read" mode
objList = list(reader(csvFile, delimiter = ','))[0] # This is the exact same list as `sourcelist`!
print("The input csv file contained the following sources:\n", objList)
globular_cluster_queries = {} # Make a dictionary, where each source name (i.e. "M15") corresponds to a list of its observations with COS
for obj in objList: # each "obj" is a source name
query_x = Observations.query_criteria(objectname = obj, radius = "5 min", instrument_name=['COS/FUV', 'COS/NUV']) # query the area in +/- 5 arcminutes
globular_cluster_queries[obj] = (query_x) # add this entry to the dictionary
globular_cluster_queries # show the dictionary
```
**Excellent! You've now done the hardest part - finding and downloading the right data.** From here, it's generally straightforward to read in and plot the spectrum. We recommend you look into our tutorial on [Viewing a COS Spectrum](https://github.com/spacetelescope/notebooks/blob/master/notebooks/COS/ViewData/ViewData.ipynb).
## Congratulations! You finished this Notebook!
### There are more COS data walkthrough Notebooks on different topics. You can find them [here](https://spacetelescope.github.io/COS-Notebooks/).
---
## About this Notebook
**Author:** Nat Kerman <[email protected]>
**Updated On:** 2021-10-29
> *This tutorial was generated to be in compliance with the [STScI style guides](https://github.com/spacetelescope/style-guides) and would like to cite the [Jupyter guide](https://github.com/spacetelescope/style-guides/blob/master/templates/example_notebook.ipynb) in particular.*
## Citations
If you use `astropy`, `matplotlib`, `astroquery`, or `numpy` for published research, please cite the
authors. Follow these links for more information about citations:
* [Citing `astropy`/`numpy`/`matplotlib`](https://www.scipy.org/citing.html)
* [Citing `astroquery`](https://astroquery.readthedocs.io/en/latest/)
---
[Top of Page](#topD)
<img style="float: right;" src="https://raw.githubusercontent.com/spacetelescope/notebooks/master/assets/stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="Space Telescope Logo" width="200px"/>
<br></br>
<br></br>
<br></br>
## Exercise Solutions:
Note, that for many of these, there are multiple ways to get an answer.
**We will import:**
- numpy to handle array functions
- astropy.table Table for creating tidy tables of the data
```
# Manipulating arrays
import numpy as np
# Reading in data
from astropy.table import Table
## Ex. 1 solution:
dataset_id_ = 'LDLM40010'
exptime_ = 12403.904
print(f"The TRAPPIST-1 COS data is in dataset {dataset_id_}, taken with an exosure time of {exptime_}")
## Ex. 2 solution:
query_3 = Observations.query_criteria(obs_id = 'LDLM40010',
wavelength_region="UV", instrument_name="COS/FUV", filters = 'G130M')
product_list2 = Observations.get_product_list(query_3)
rawRowsA = np.where(product_list2['productSubGroupDescription'] == "RAWTAG_A")
rawRowsB = np.where(product_list2['productSubGroupDescription'] == "RAWTAG_B")
rawRows = np.append(rawRowsA,rawRowsB)
!mkdir ./data/Ex2/
downloads2 = Observations.download_products(product_list2[rawRows], download_dir=str(data_dir/'Ex2/') , extension='fits', mrp_only=False, cache=True)
downloads3 = Observations.download_products(product_list2, download_dir=str(data_dir/'Ex2/') , extension='fits', mrp_only=True, cache=True)
asn_data = Table.read('./data/Ex2/mastDownload/HST/ldlm40010/ldlm40010_asn.fits', hdu = 1)
print(asn_data)
```
| true |
code
| 0.432303 | null | null | null | null |
|
# Train a CNN Model for MNIST
This script here is to train a CNN model with 2 convolutional layers each with a pooling layer and a 2 fully-connected layers. The variables that would be needed for inference later have been added to tensorflow collections in this script.
- The MNIST dataset should be placed under a folder named 'MNIST_data' in the same directory as this script.
- The outputs of this script are tensorflow checkpoint models in a folder called 'models' in the same directory.
```
import tensorflow as tf
import numpy as np
import os
#import MNIST dataset
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
sess = tf.InteractiveSession() #initialize session
#input placeholders
with tf.name_scope('x'):
x = tf.placeholder(tf.float32, shape=[None, 784], name='x')
y_ = tf.placeholder(tf.float32, shape=[None, 10])
#function definitions
def weight_variable(shape, name):
initial = tf.truncated_normal(shape, stddev=0.1, name=name)
return tf.Variable(initial)
def bias_variable(shape, name):
initial = tf.constant(0.1, shape=shape, name=name)
return tf.Variable(initial)
def conv2d(x, W, name):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME', name=name)
def max_pool_2x2(x,name):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME', name=name)
W_conv1 = weight_variable([5, 5, 1, 32], name='W_C1')
b_conv1 = bias_variable([32], name='B_C1')
x_image = tf.reshape(x, [-1,28,28,1]) #vectorize the image
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1 , name='conv_1') + b_conv1)
h_pool1 = max_pool_2x2(h_conv1, name='pool_1')
W_conv2 = weight_variable([5, 5, 32, 64], name='W_C2')
b_conv2 = bias_variable([64], name='B_C2')
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2, name='conv_2') + b_conv2)
h_pool2 = max_pool_2x2(h_conv2, name='pool_2')
W_fc1 = weight_variable([7 * 7 * 64, 1024], name='W_FC1')
b_fc1 = bias_variable([1024], name='B_FC1')
feature_vector = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(feature_vector, W_fc1) + b_fc1, name='FC_1')
W_fc2 = weight_variable([1024, 10], name='W_FC2')
b_fc2 = bias_variable([10], name='B_FC2')
with tf.name_scope('logits'):
logits = tf.add(tf.matmul(h_fc1, W_fc2), b_fc2, name='logits')
y = tf.nn.softmax(logits, name='softmax_prediction')
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=logits))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(logits,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name='accuracy')
# we only need these two to make inference using the trained model
tf.add_to_collection("logits", logits)
tf.add_to_collection("x", x)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver(tf.global_variables())
for i in range(500):
batch = mnist.train.next_batch(100)
if i%100 == 0:
train_acc = accuracy.eval(feed_dict={
x:batch[0], y_:batch[1]
})
print("Step %d, training accuracy %g"%(i, train_acc))
train_step.run(feed_dict={x:batch[0], y_:batch[1]})
current_dir = os.getcwd() #get the current working directory
saver.save(sess, current_dir + '/model/mnist.ckpt') #save the model in the specified directory
print("Training is finished.")
```
| true |
code
| 0.651992 | null | null | null | null |
|

> **Copyright (c) 2021 CertifAI Sdn. Bhd.**<br>
<br>
This program is part of OSRFramework. You can redistribute it and/or modify
<br>it under the terms of the GNU Affero General Public License as published by
<br>the Free Software Foundation, either version 3 of the License, or
<br>(at your option) any later version.
<br>
<br>This program is distributed in the hope that it will be useful
<br>but WITHOUT ANY WARRANTY; without even the implied warranty of
<br>MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
<br>GNU Affero General Public License for more details.
<br>
<br>You should have received a copy of the GNU Affero General Public License
<br>along with this program. If not, see <http://www.gnu.org/licenses/>.
<br>
# Introduction
In this notebook, we are going to build neural machine translation (NMT) using Transformer with pytorch. This NMT could translate English to French.
Let's get started.

# What will we accomplish?
Steps to implement neural machine translation using Transformer with Pytorch:
> Step 1: Load and preprocess dataset
> Step 2: Building transformer architecture
> Step 3: Train the transformer model
> Step 4: Test the trained model
# Notebook Content
* [Load Dataset](#Load-Dataset)
* [Tokenization](#Tokenization)
* [Preprocessing](#Preprocessing)
* [Train-Test Split](#Train-Test-Split)
* [TabularDataset](#TabularDataset)
* [BucketIterator](#BucketIterator)
* [Custom Iterator](#Custom-Iterator)
* [Dive Deep into Transformer](#Dive-Deep-into-Transformer)
* [Embedding](#Embedding)
* [Positional Encoding](#Positional-Encoding)
* [Masking](#Masking)
* [Input Masks](#Input-Masks)
* [Target Sequence Masks](#Target-Sequence-Masks)
* [Multi-Headed Attention](#Multi-Headed-Attention)
* [Attention](#Attention)
* [Feed-Forward Network](#Feed-Forward-Network)
* [Normalisation](#Normalisation)
* [Building Transformer](#Building-Transformer)
* [EncoderLayer](#EncoderLayer)
* [DecoderLayer](#DecoderLayer)
* [Encoder](#Encoder)
* [Decoder](#Decoder)
* [Transformer](#Transformer)
* [Training the Model](#Training-the-Model)
* [Testing the Model](#Testing-the-Model)
# Load Dataset
The dataset we used is [parallel corpus French-English](http://www.statmt.org/europarl/v7/fr-en.tgz) dataset from [European Parliament Proceedings Parallel Corpus (1996–2011)](http://www.statmt.org/europarl/). This dataset contains 15 years of write-ups from E.U. proceedings, weighing in at 2,007,724 sentences, and 50,265,039 words. You should found the dataset in the `datasets` folder, else you may download it [here](http://www.statmt.org/europarl/v7/fr-en.tgz). You will have the following files after unzipping the downloaded file:
1. europarl-v7.fr-en.en
2. europarl-v7.fr-en.fr

Now we are going to load the dataset for preprocessing.
```
europarl_en = open('../../../resources/day_11/fr-en/europarl-v7.fr-en.en', encoding='utf-8').read().split('\n')
europarl_fr = open('../../../resources/day_11/fr-en/europarl-v7.fr-en.fr', encoding='utf-8').read().split('\n')
```
# Tokenization
The first job we need done is to **create a tokenizer for each language**. This is a function that will split the text into separate words and assign them unique numbers (indexes). This number will come into play later when we discuss embeddings.

He we will tokenize the text using **Torchtext** and **Spacy** together. Spacy is a library that has been specifically built to take sentences in various languages and split them into different tokens (see [here](https://spacy.io/) for more information). Without Spacy, Torchtext defaults to a simple .split(' ') method for tokenization. This is much less nuanced than Spacy’s approach, which will also split words like “don’t” into “do” and “n’t”, and much more.
```
import spacy
import torchtext
import torch
import numpy as np
from torchtext.legacy.data import Field, BucketIterator, TabularDataset
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# !python -m spacy download fr_core_news_lg
# !python -m spacy download en_core_web_lg
en = spacy.load('en_core_web_lg')
fr = spacy.load('fr_core_news_lg')
def tokenize_en(sentence):
return [tok.text for tok in en.tokenizer(sentence)]
def tokenize_fr(sentence):
return [tok.text for tok in fr.tokenizer(sentence)]
EN_TEXT = Field(tokenize=tokenize_en)
FR_TEXT = Field(tokenize=tokenize_fr, init_token = "<sos>", eos_token = "<eos>")
```
# Preprocessing
The best way to work with Torchtext is to turn your data into **spreadsheet format**, no matter the original format of your data file. This is due to the incredible versatility of the **Torchtext TabularDataset** function, which creates datasets from spreadsheet formats. So first to turn our data into an appropriate CSV file.
```
import pandas as pd
raw_data = {'English' : [line for line in europarl_en], 'French': [line for line in europarl_fr]}
df = pd.DataFrame(raw_data, columns=["English", "French"])
# Remove very long sentences and sentences where translations are not of roughly equal length
df['eng_len'] = df['English'].str.count(' ')
df['fr_len'] = df['French'].str.count(' ')
df = df.query('fr_len < 80 & eng_len < 80')
df = df.query('fr_len < eng_len * 1.5 & fr_len * 1.5 > eng_len')
```
## Train-Test Split
Now we are going to split the data into train set and test set. Fortunately Sklearn and Torchtext together make this process incredibly easy.
```
from sklearn.model_selection import train_test_split
# Create train and validation set
train, test = train_test_split(df, test_size=0.1)
train.to_csv("../../../resources/day_11/train.csv", index=False)
test.to_csv("../../../resources/day_11/test.csv", index=False)
```
This creates a train and test csv each with two columns (English, French), where each row contains an English sentence in the 'English' column, and its French translation in the 'French' column.
## TabularDataset
Calling the magic `TabularDataset.splits` then returns a train and test dataset with the respective data loaded into them, processed(/tokenized) according to the fields we defined earlier.
```
# Associate the text in the 'English' column with the EN_TEXT field, # and 'French' with FR_TEXT
data_fields = [('English', EN_TEXT), ('French', FR_TEXT)]
train, test = TabularDataset.splits(path='../../../resources/day_11', train='train.csv', validation='test.csv',
format='csv', fields=data_fields)
```
Processing a few million words can take a while so grab a cup of tea here…
```
FR_TEXT.build_vocab(train, test)
EN_TEXT.build_vocab(train, test)
```
To see what numbers the tokens have been assigned and vice versa in each field, we can use `self.vocab.stoi` and `self.vocab.itos`.
```
print(EN_TEXT.vocab.stoi['the'])
print(EN_TEXT.vocab.itos[11])
```
## BucketIterator
**BucketIterator** Defines an iterator that batches examples of similar lengths together.
It minimizes amount of padding needed while producing freshly shuffled batches for each new epoch. See pool for the bucketing procedure used.
```
train_iter = BucketIterator(train, batch_size=20, sort_key=lambda x: len(x.French), shuffle=True)
```
The `sort_key` dictates how to form each batch. The lambda function tells the iterator to try and find sentences of the **same length** (meaning more of the matrix is filled with useful data and less with padding).
```
batch = next(iter(train_iter))
print(batch.English)
print("Number of columns:", len(batch))
```
In each batch, sentences have been transposed so they are descending vertically (important: we will need to transpose these again to work with transformer). **Each index represents a token (word)**, and **each column represents a sentence**. We have 20 columns, as 20 was the batch_size we specified.
You might notice all the ‘1’s and think which incredibly common word is this the index for? Well the ‘1’ is not of course a word, but purely **padding**. While Torchtext is brilliant, it’s `sort_key` based batching leaves a little to be desired. Often the sentences aren’t of the same length at all, and you end up feeding a lot of padding into your network (as you can see with all the 1s in the last figure). We will solve this by implementing our own iterator.
## Custom Iterator
The custom iterator is built in reference to the code from http://nlp.seas.harvard.edu/2018/04/03/attention.html. Feel free to explore yourself to have more understanding about `MyIterator` class.
```
from torchtext.legacy import data
global max_src_in_batch, max_tgt_in_batch
def batch_size_fn(new, count, sofar):
"Keep augmenting batch and calculate total number of tokens + padding."
global max_src_in_batch, max_tgt_in_batch
if count == 1:
max_src_in_batch = 0
max_tgt_in_batch = 0
max_src_in_batch = max(max_src_in_batch, len(new.English))
max_tgt_in_batch = max(max_tgt_in_batch, len(new.French) + 2)
src_elements = count * max_src_in_batch
tgt_elements = count * max_tgt_in_batch
return max(src_elements, tgt_elements)
class MyIterator(data.Iterator):
def create_batches(self):
if self.train:
def pool(d, random_shuffler):
for p in data.batch(d, self.batch_size * 100):
p_batch = data.batch(
sorted(p, key=self.sort_key),
self.batch_size, self.batch_size_fn)
for b in random_shuffler(list(p_batch)):
yield b
self.batches = pool(self.data(), self.random_shuffler)
else:
self.batches = []
for b in data.batch(self.data(), self.batch_size, self.batch_size_fn):
self.batches.append(sorted(b, key=self.sort_key))
train_iter = MyIterator(train, batch_size= 64, device=device, repeat=False,
sort_key= lambda x: (len(x.English), len(x.French)),
batch_size_fn=batch_size_fn, train=True, shuffle=True)
```
# Dive Deep into Transformer

The diagram above shows the overview of the Transformer model. The inputs to the encoder will be the **English** sentence, and the 'Outputs' from the decoder will be the **French** sentence.
## Embedding
Embedding words has become standard practice in NMT, feeding the network with far more information about words than a one hot encoding would.

```
from torch import nn
class Embedder(nn.Module):
def __init__(self, vocab_size, embedding_dimension):
super().__init__()
self.embed = nn.Embedding(vocab_size, embedding_dimension)
def forward(self, x):
return self.embed(x)
```
When each word is fed into the network, this code will perform a look-up and retrieve its embedding vector. These vectors will then be learnt as a parameters by the model, adjusted with each iteration of gradient descent.
## Positional Encoding
In order for the model to make sense of a sentence, it needs to know two things about each word: what does the **word mean**? And what is its **position** in the sentence?
The embedding vector for each word will **learn the meaning**, so now we need to input something that tells the network about the word’s position.
*Vasmari et al* answered this problem by using these functions to create a constant of position-specific values:


This constant is a 2D matrix. Pos refers to the order in the sentence, and $i$ refers to the position along the embedding vector dimension. Each value in the pos/i matrix is then worked out using the equations above.

```
import math
class PositionalEncoder(nn.Module):
def __init__(self, d_model, max_seq_len = 200, dropout = 0.1):
super().__init__()
self.d_model = d_model
self.dropout = nn.Dropout(dropout)
# Create constant 'pe' matrix with values dependant on pos and i
pe = torch.zeros(max_seq_len, d_model)
for pos in range(max_seq_len):
for i in range(0, d_model, 2):
pe[pos, i] = \
math.sin(pos / (10000 ** ((2 * i)/d_model)))
pe[pos, i + 1] = \
math.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
# Make embeddings relatively larger
x = x * math.sqrt(self.d_model)
# Add constant to embedding
seq_len = x.size(1)
pe = Variable(self.pe[:,:seq_len], requires_grad=False)
if x.is_cuda:
pe.cuda()
x = x + pe
return self.dropout(x)
```
`PositionalEncoder` lets us add the **positional encoding to the embedding vector**, providing information about structure to the model.
The reason we increase the embedding values before addition is to make the positional encoding relatively smaller. This means the original meaning in the embedding vector won’t be lost when we add them together.
## Masking
Masking plays an important role in the transformer. It serves two purposes:
* In the encoder and decoder: To zero attention outputs wherever there is just padding in the input sentences.
* In the decoder: To prevent the decoder ‘peaking’ ahead at the rest of the translated sentence when predicting the next word.

### Input Masks
```
batch = next(iter(train_iter))
input_seq = batch.English.transpose(0,1)
input_pad = EN_TEXT.vocab.stoi['<pad>']
# creates mask with 0s wherever there is padding in the input
input_msk = (input_seq != input_pad).unsqueeze(1)
```
### Target Sequence Masks
```
from torch.autograd import Variable
target_seq = batch.French.transpose(0,1)
target_pad = FR_TEXT.vocab.stoi['<pad>']
target_msk = (target_seq != target_pad).unsqueeze(1)
```
The initial input into the decoder will be the **target sequence** (the French translation). The way the decoder predicts each output word is by making use of all the encoder outputs and the French sentence only up until the point of each word its predicting.
Therefore we need to prevent the first output predictions from being able to see later into the sentence. For this we use the `nopeak_mask`.
```
# Get seq_len for matrix
size = target_seq.size(1)
nopeak_mask = np.triu(np.ones((1, size, size)), k=1).astype('uint8')
nopeak_mask = Variable(torch.from_numpy(nopeak_mask) == 0).cuda()
print(nopeak_mask)
target_msk = target_msk & nopeak_mask
def create_masks(src, trg):
src_pad = EN_TEXT.vocab.stoi['<pad>']
trg_pad = FR_TEXT.vocab.stoi['<pad>']
src_mask = (src != src_pad).unsqueeze(-2)
if trg is not None:
trg_mask = (trg != trg_pad).unsqueeze(-2)
# Get seq_len for matrix
size = trg.size(1)
np_mask = nopeak_mask(size)
if device.type == 'cuda':
np_mask = np_mask.cuda()
trg_mask = trg_mask & np_mask
else:
trg_mask = None
return src_mask, trg_mask
def nopeak_mask(size):
np_mask = np.triu(np.ones((1, size, size)), k=1).astype('uint8')
np_mask = Variable(torch.from_numpy(np_mask) == 0)
return np_mask
```
If we later apply this mask to the attention scores, the values wherever the input is ahead will not be able to contribute when calculating the outputs.
## Multi-Headed Attention
Once we have our embedded values (with positional encodings) and our masks, we can start building the layers of our model.
Here is an overview of the multi-headed attention layer:

In multi-headed attention layer, each **input is split into multiple heads** which allows the network to simultaneously attend to different subsections of each embedding.
$V$, $K$ and $Q$ stand for ***key***, ***value*** and ***query***. These are terms used in attention functions. In the case of the Encoder, $V$, $K$ and $Q$ will simply be identical copies of the embedding vector (plus positional encoding). They will have the dimensions `Batch_size` * `seq_len` * `embedding_dimension`.
In multi-head attention we split the embedding vector into $N$ heads, so they will then have the dimensions `batch_size` * `N` * `seq_len` * (`embedding_dimension` / `N`).
This final dimension (`embedding_dimension` / `N`) we will refer to as $d_k$.
```
class MultiHeadAttention(nn.Module):
def __init__(self, heads, d_model, dropout = 0.1):
super().__init__()
self.d_model = d_model
self.d_k = d_model // heads
self.h = heads
self.q_linear = nn.Linear(d_model, d_model)
self.v_linear = nn.Linear(d_model, d_model)
self.k_linear = nn.Linear(d_model, d_model)
self.dropout = nn.Dropout(dropout)
self.out = nn.Linear(d_model, d_model)
def forward(self, q, k, v, mask=None):
bs = q.size(0)
# Perform linear operation and split into h heads
k = self.k_linear(k).view(bs, -1, self.h, self.d_k)
q = self.q_linear(q).view(bs, -1, self.h, self.d_k)
v = self.v_linear(v).view(bs, -1, self.h, self.d_k)
# Transpose to get dimensions bs * h * sl * d_model
k = k.transpose(1,2)
q = q.transpose(1,2)
v = v.transpose(1,2)
# Calculate attention using function we will define next
scores = attention(q, k, v, self.d_k, mask, self.dropout)
# Concatenate heads and put through final linear layer
concat = scores.transpose(1,2).contiguous()\
.view(bs, -1, self.d_model)
output = self.out(concat)
return output
```
## Attention
The equation below is the attention formula with retrieved from [Attention is All You Need](https://arxiv.org/abs/1706.03762) paper and it does a good job at explaining each step.


Each arrow in the diagram reflects a part of the equation.
Initially we must **multiply** $Q$ by the transpose of $K$. This is then scaled by **dividing the output by the square root** of $d_k$.
A step that’s not shown in the equation is the masking operation. Before we perform **Softmax**, we apply our mask and hence reduce values where the input is padding (or in the decoder, also where the input is ahead of the current word). Another step not shown is **dropout**, which we will apply after Softmax.
Finally, the last step is doing a **dot product** between the result so far and $V$.
```
import torch.nn.functional as F
def attention(q, k, v, d_k, mask=None, dropout=None):
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)
if mask is not None:
mask = mask.unsqueeze(1)
scores = scores.masked_fill(mask == 0, -1e9)
scores = F.softmax(scores, dim=-1)
if dropout is not None:
scores = dropout(scores)
output = torch.matmul(scores, v)
return output
```
## Feed-Forward Network
The feed-forward layer just consists of two linear operations, with a **relu** and **dropout** operation in between them. It simply deepens our network, employing linear layers to **analyse patterns** in the attention layers output.

```
class FeedForward(nn.Module):
def __init__(self, d_model, d_ff=2048, dropout = 0.1):
super().__init__()
# We set d_ff as a default to 2048
self.linear_1 = nn.Linear(d_model, d_ff)
self.dropout = nn.Dropout(dropout)
self.linear_2 = nn.Linear(d_ff, d_model)
def forward(self, x):
x = self.dropout(F.relu(self.linear_1(x)))
x = self.linear_2(x)
return x
```
## Normalisation
Normalisation is highly important in deep neural networks. It prevents the range of values in the layers changing too much, meaning the model **trains faster** and has **better ability to generalise**.

We will be normalising our results between each layer in the encoder/decoder.
```
class Norm(nn.Module):
def __init__(self, d_model, eps = 1e-6):
super().__init__()
self.size = d_model
# create two learnable parameters to calibrate normalisation
self.alpha = nn.Parameter(torch.ones(self.size))
self.bias = nn.Parameter(torch.zeros(self.size))
self.eps = eps
def forward(self, x):
norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
return norm
```
# Building Transformer
Let’s have another look at the over-all architecture and start building:

**One last Variable**: If you look at the diagram closely you can see a $N_x$ next to the encoder and decoder architectures. In reality, the encoder and decoder in the diagram above represent one layer of an encoder and one of the decoder. $N$ is the variable for the **number of layers** there will be. Eg. if `N=6`, the data goes through six encoder layers (with the architecture seen above), then these outputs are passed to the decoder which also consists of six repeating decoder layers.
We will now build `EncoderLayer` and `DecoderLayer` modules with the architecture shown in the model above. Then when we build the encoder and decoder we can define how many of these layers to have.
## EncoderLayer
```
# build an encoder layer with one multi-head attention layer and one feed-forward layer
class EncoderLayer(nn.Module):
def __init__(self, d_model, heads, dropout = 0.1):
super().__init__()
self.norm_1 = Norm(d_model)
self.norm_2 = Norm(d_model)
self.attn = MultiHeadAttention(heads, d_model)
self.ff = FeedForward(d_model)
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
def forward(self, x, mask):
x2 = self.norm_1(x)
x = x + self.dropout_1(self.attn(x2,x2,x2,mask))
x2 = self.norm_2(x)
x = x + self.dropout_2(self.ff(x2))
return x
```
## DecoderLayer
```
# build a decoder layer with two multi-head attention layers and one feed-forward layer
class DecoderLayer(nn.Module):
def __init__(self, d_model, heads, dropout=0.1):
super().__init__()
self.norm_1 = Norm(d_model)
self.norm_2 = Norm(d_model)
self.norm_3 = Norm(d_model)
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
self.dropout_3 = nn.Dropout(dropout)
self.attn_1 = MultiHeadAttention(heads, d_model)
self.attn_2 = MultiHeadAttention(heads, d_model)
self.ff = FeedForward(d_model).cuda()
def forward(self, x, e_outputs, src_mask, trg_mask):
x2 = self.norm_1(x)
x = x + self.dropout_1(self.attn_1(x2, x2, x2, trg_mask))
x2 = self.norm_2(x)
x = x + self.dropout_2(self.attn_2(x2, e_outputs, e_outputs, src_mask))
x2 = self.norm_3(x)
x = x + self.dropout_3(self.ff(x2))
return x
```
We can then build a convenient cloning function that can generate multiple layers:
```
import copy
def get_clones(module, N):
return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
```
## Encoder
```
class Encoder(nn.Module):
def __init__(self, vocab_size, d_model, N, heads):
super().__init__()
self.N = N
self.embed = Embedder(vocab_size, d_model)
self.pe = PositionalEncoder(d_model)
self.layers = get_clones(EncoderLayer(d_model, heads), N)
self.norm = Norm(d_model)
def forward(self, src, mask):
x = self.embed(src)
x = self.pe(x)
for i in range(N):
x = self.layers[i](x, mask)
return self.norm(x)
```
## Decoder
```
class Decoder(nn.Module):
def __init__(self, vocab_size, d_model, N, heads):
super().__init__()
self.N = N
self.embed = Embedder(vocab_size, d_model)
self.pe = PositionalEncoder(d_model)
self.layers = get_clones(DecoderLayer(d_model, heads), N)
self.norm = Norm(d_model)
def forward(self, trg, e_outputs, src_mask, trg_mask):
x = self.embed(trg)
x = self.pe(x)
for i in range(self.N):
x = self.layers[i](x, e_outputs, src_mask, trg_mask)
return self.norm(x)
```
## Transformer
```
class Transformer(nn.Module):
def __init__(self, src_vocab, trg_vocab, d_model, N, heads):
super().__init__()
self.encoder = Encoder(src_vocab, d_model, N, heads)
self.decoder = Decoder(trg_vocab, d_model, N, heads)
self.out = nn.Linear(d_model, trg_vocab)
def forward(self, src, trg, src_mask, trg_mask):
e_outputs = self.encoder(src, src_mask)
d_output = self.decoder(trg, e_outputs, src_mask, trg_mask)
output = self.out(d_output)
return output
```
**Note**: We don't perform softmax on the output as this will be handled automatically by our loss function.
# Training the Model
With the transformer built, all that remains is to train on the dataset. The coding part is done, but be prepared to wait for about 2 days for this model to start converging! However, in this session, we only perform minimal epoch to train the model and you may try to use more epoch during your self-study.
Let’s define some parameters first:
```
embedding_dimension = 512
heads = 4
N = 6
src_vocab = len(EN_TEXT.vocab)
trg_vocab = len(FR_TEXT.vocab)
model = Transformer(src_vocab, trg_vocab, embedding_dimension, N, heads)
if device.type == 'cuda':
model.cuda()
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
# This code is very important! It initialises the parameters with a
# range of values that stops the signal fading or getting too big.
optim = torch.optim.Adam(model.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-9)
```
Now we’re good to train the transformer model
```
import time
import torch
def train_model(epochs, print_every=100, timelimit=None):
model.train()
start = time.time()
temp = start
total_loss = 0
min_loss = float('inf')
for epoch in range(epochs):
for i, batch in enumerate(train_iter):
src = batch.English.transpose(0,1)
trg = batch.French.transpose(0,1)
# the French sentence we input has all words except
# the last, as it is using each word to predict the next
trg_input = trg[:, :-1]
# the words we are trying to predict
targets = trg[:, 1:].contiguous().view(-1)
# create function to make masks using mask code above
src_mask, trg_mask = create_masks(src, trg_input)
preds = model(src, trg_input, src_mask, trg_mask)
ys = trg[:, 1:].contiguous().view(-1)
optim.zero_grad()
loss = F.cross_entropy(preds.view(-1, preds.size(-1)), ys, ignore_index=target_pad)
loss.backward()
optim.step()
total_loss += loss.data.item()
if (i + 1) % print_every == 0:
loss_avg = total_loss / print_every
duration = (time.time() - start) // 60
print("time = %dm, epoch %d, iter = %d, loss = %.3f, %ds per %d iters" %
(duration, epoch + 1, i + 1, loss_avg, time.time() - temp, print_every))
if loss_avg < min_loss:
min_loss = loss_avg
torch.save(model, "model/training.model")
print("Current best model saved", "loss =", loss_avg)
if (timelimit and duration >= timelimit):
break
total_loss = 0
temp = time.time()
# train_model(1, timelimit=300)
torch.load("model/pretrained.model")
```
# Testing the Model
We can use the below function to translate sentences. We can feed it sentences directly from our batches, or input custom strings.
The translator works by running a loop. We start off by encoding the English sentence. We then feed the decoder the `<sos>` token index and the encoder outputs. The decoder makes a prediction for the first word, and we add this to our decoder input with the sos token. We rerun the loop, getting the next prediction and adding this to the decoder input, until we reach the `<eos>` token letting us know it has finished translating.
```
def translate(model, src, max_len = 80, custom_string=False):
model.eval()
if custom_string == True:
src = tokenize_en(src)
src = Variable(torch.LongTensor([[EN_TEXT.vocab.stoi[tok] for tok in src]])).cuda()
src_mask = (src != input_pad).unsqueeze(-2)
e_outputs = model.encoder(src, src_mask)
outputs = torch.zeros(max_len).type_as(src.data)
outputs[0] = torch.LongTensor([FR_TEXT.vocab.stoi['<sos>']])
for i in range(1, max_len):
trg_mask = np.triu(np.ones((1, i, i)), k=1).astype('uint8')
trg_mask = Variable(torch.from_numpy(trg_mask) == 0).cuda()
out = model.out(model.decoder(outputs[:i].unsqueeze(0), e_outputs, src_mask, trg_mask))
out = F.softmax(out, dim=-1)
val, ix = out[:, -1].data.topk(1)
outputs[i] = ix[0][0]
if ix[0][0] == FR_TEXT.vocab.stoi['<eos>']:
break
return ' '.join([FR_TEXT.vocab.itos[ix] for ix in outputs[:i]])
translate(model, "How're you my friend?", custom_string=True)
```
# Contributors
**Author**
<br>Chee Lam
# References
1. [How to Code The Transformer in Pytorch](https://towardsdatascience.com/how-to-code-the-transformer-in-pytorch-24db27c8f9ec#b0ed)
2. [How to Use TorchText for Neural Machine Translation](https://towardsdatascience.com/how-to-use-torchtext-for-neural-machine-translation-plus-hack-to-make-it-5x-faster-77f3884d95)
| true |
code
| 0.645707 | null | null | null | null |
|
# Circuit Basics
Here, we provide an overview of working with Qiskit. Qiskit provides the basic building blocks necessary to program quantum computers. The fundamental unit of Qiskit is the [quantum circuit](https://en.wikipedia.org/wiki/Quantum_circuit). A basic workflow using Qiskit consists of two stages: **Build** and **Run**. **Build** allows you to make different quantum circuits that represent the problem you are solving, and **Run** that allows you to run them on different backends. After the jobs have been run, the data is collected and postprocessed depending on the desired output.
```
import numpy as np
from qiskit import QuantumCircuit
%matplotlib inline
```
## Building the circuit <a name='basics'></a>
The basic element needed for your first program is the QuantumCircuit. We begin by creating a `QuantumCircuit` comprised of three qubits.
```
# Create a Quantum Circuit acting on a quantum register of three qubits
circ = QuantumCircuit(3)
```
After you create the circuit with its registers, you can add gates ("operations") to manipulate the registers. As you proceed through the tutorials you will find more gates and circuits; below is an example of a quantum circuit that makes a three-qubit GHZ state
$$|\psi\rangle = \left(|000\rangle+|111\rangle\right)/\sqrt{2}.$$
To create such a state, we start with a three-qubit quantum register. By default, each qubit in the register is initialized to $|0\rangle$. To make the GHZ state, we apply the following gates:
- A Hadamard gate $H$ on qubit 0, which puts it into the superposition state $\left(|0\rangle+|1\rangle\right)/\sqrt{2}$.
- A controlled-Not operation ($C_{X}$) between qubit 0 and qubit 1.
- A controlled-Not operation between qubit 0 and qubit 2.
On an ideal quantum computer, the state produced by running this circuit would be the GHZ state above.
In Qiskit, operations can be added to the circuit one by one, as shown below.
```
# Add a H gate on qubit 0, putting this qubit in superposition.
circ.h(0)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 1, putting
# the qubits in a Bell state.
circ.cx(0, 1)
# Add a CX (CNOT) gate on control qubit 0 and target qubit 2, putting
# the qubits in a GHZ state.
circ.cx(0, 2)
```
## Visualize Circuit <a name='visualize'></a>
You can visualize your circuit using Qiskit `QuantumCircuit.draw()`, which plots the circuit in the form found in many textbooks.
```
circ.draw('mpl')
```
In this circuit, the qubits are put in order, with qubit zero at the top and qubit two at the bottom. The circuit is read left to right (meaning that gates that are applied earlier in the circuit show up further to the left).
<div class="alert alert-block alert-info">
When representing the state of a multi-qubit system, the tensor order used in Qiskit is different than that used in most physics textbooks. Suppose there are $n$ qubits, and qubit $j$ is labeled as $Q_{j}$. Qiskit uses an ordering in which the $n^{\mathrm{th}}$ qubit is on the <em><strong>left</strong></em> side of the tensor product, so that the basis vectors are labeled as $Q_{n-1}\otimes \cdots \otimes Q_1\otimes Q_0$.
For example, if qubit zero is in state 0, qubit 1 is in state 0, and qubit 2 is in state 1, Qiskit would represent this state as $|100\rangle$, whereas many physics textbooks would represent it as $|001\rangle$.
This difference in labeling affects the way multi-qubit operations are represented as matrices. For example, Qiskit represents a controlled-X ($C_{X}$) operation with qubit 0 being the control and qubit 1 being the target as
$$C_X = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\\end{pmatrix}.$$
</div>
## Simulating circuits <a name='simulation'></a>
To simulate a circuit we use the quant-info module in Qiskit. This simulator returns the quantum state, which is a complex vector of dimensions $2^n$, where $n$ is the number of qubits
(so be careful using this as it will quickly get too large to run on your machine).
There are two stages to the simulator. The fist is to set the input state and the second to evolve the state by the quantum circuit.
```
from qiskit.quantum_info import Statevector
# Set the intial state of the simulator to the ground state using from_int
state = Statevector.from_int(0, 2**3)
# Evolve the state by the quantum circuit
state = state.evolve(circ)
#draw using latex
state.draw('latex')
```
Qiskit also provides a visualization toolbox to allow you to view the state.
Below, we use the visualization function to plot the qsphere and a hinton representing the real and imaginary components of the state density matrix $\rho$.
```
state.draw('qsphere')
state.draw('hinton')
```
## Unitary representation of a circuit
Qiskit's quant_info module also has an operator method which can be used to make a unitary operator for the circuit. This calculates the $2^n \times 2^n$ matrix representing the quantum circuit.
```
from qiskit.quantum_info import Operator
U = Operator(circ)
# Show the results
U.data
```
## OpenQASM backend
The simulators above are useful because they provide information about the state output by the ideal circuit and the matrix representation of the circuit. However, a real experiment terminates by _measuring_ each qubit (usually in the computational $|0\rangle, |1\rangle$ basis). Without measurement, we cannot gain information about the state. Measurements cause the quantum system to collapse into classical bits.
For example, suppose we make independent measurements on each qubit of the three-qubit GHZ state
$$|\psi\rangle = (|000\rangle +|111\rangle)/\sqrt{2},$$
and let $xyz$ denote the bitstring that results. Recall that, under the qubit labeling used by Qiskit, $x$ would correspond to the outcome on qubit 2, $y$ to the outcome on qubit 1, and $z$ to the outcome on qubit 0.
<div class="alert alert-block alert-info">
<b>Note:</b> This representation of the bitstring puts the most significant bit (MSB) on the left, and the least significant bit (LSB) on the right. This is the standard ordering of binary bitstrings. We order the qubits in the same way (qubit representing the MSB has index 0), which is why Qiskit uses a non-standard tensor product order.
</div>
Recall the probability of obtaining outcome $xyz$ is given by
$$\mathrm{Pr}(xyz) = |\langle xyz | \psi \rangle |^{2}$$
and as such for the GHZ state probability of obtaining 000 or 111 are both 1/2.
To simulate a circuit that includes measurement, we need to add measurements to the original circuit above, and use a different Aer backend.
```
# Create a Quantum Circuit
meas = QuantumCircuit(3, 3)
meas.barrier(range(3))
# map the quantum measurement to the classical bits
meas.measure(range(3), range(3))
# The Qiskit circuit object supports composition.
# Here the meas has to be first and front=True (putting it before)
# as compose must put a smaller circuit into a larger one.
qc = meas.compose(circ, range(3), front=True)
#drawing the circuit
qc.draw('mpl')
```
This circuit adds a classical register, and three measurements that are used to map the outcome of qubits to the classical bits.
To simulate this circuit, we use the ``qasm_simulator`` in Qiskit Aer. Each run of this circuit will yield either the bitstring 000 or 111. To build up statistics about the distribution of the bitstrings (to, e.g., estimate $\mathrm{Pr}(000)$), we need to repeat the circuit many times. The number of times the circuit is repeated can be specified in the ``execute`` function, via the ``shots`` keyword.
```
# Adding the transpiler to reduce the circuit to QASM instructions
# supported by the backend
from qiskit import transpile
# Use Aer's qasm_simulator
from qiskit.providers.aer import QasmSimulator
backend = QasmSimulator()
# First we have to transpile the quantum circuit
# to the low-level QASM instructions used by the
# backend
qc_compiled = transpile(qc, backend)
# Execute the circuit on the qasm simulator.
# We've set the number of repeats of the circuit
# to be 1024, which is the default.
job_sim = backend.run(qc_compiled, shots=1024)
# Grab the results from the job.
result_sim = job_sim.result()
```
Once you have a result object, you can access the counts via the function `get_counts(circuit)`. This gives you the _aggregated_ binary outcomes of the circuit you submitted.
```
counts = result_sim.get_counts(qc_compiled)
print(counts)
```
Approximately 50 percent of the time, the output bitstring is 000. Qiskit also provides a function `plot_histogram`, which allows you to view the outcomes.
```
from qiskit.visualization import plot_histogram
plot_histogram(counts)
```
The estimated outcome probabilities $\mathrm{Pr}(000)$ and $\mathrm{Pr}(111)$ are computed by taking the aggregate counts and dividing by the number of shots (times the circuit was repeated). Try changing the ``shots`` keyword in the ``execute`` function and see how the estimated probabilities change.
```
import qiskit.tools.jupyter
%qiskit_version_table
%qiskit_copyright
```
| true |
code
| 0.655171 | null | null | null | null |
|
## Deep face recognition with Keras, Dlib and OpenCV
Face recognition identifies persons on face images or video frames. In a nutshell, a face recognition system extracts features from an input face image and compares them to the features of labeled faces in a database. Comparison is based on a feature similarity metric and the label of the most similar database entry is used to label the input image. If the similarity value is below a certain threshold the input image is labeled as *unknown*. Comparing two face images to determine if they show the same person is known as face verification.
This notebook uses a deep convolutional neural network (CNN) to extract features from input images. It follows the approach described in [[1]](https://arxiv.org/abs/1503.03832) with modifications inspired by the [OpenFace](http://cmusatyalab.github.io/openface/) project. [Keras](https://keras.io/) is used for implementing the CNN, [Dlib](http://dlib.net/) and [OpenCV](https://opencv.org/) for aligning faces on input images. Face recognition performance is evaluated on a small subset of the [LFW](http://vis-www.cs.umass.edu/lfw/) dataset which you can replace with your own custom dataset e.g. with images of your family and friends if you want to further experiment with this notebook. After an overview of the CNN architecure and how the model can be trained, it is demonstrated how to:
- Detect, transform, and crop faces on input images. This ensures that faces are aligned before feeding them into the CNN. This preprocessing step is very important for the performance of the neural network.
- Use the CNN to extract 128-dimensional representations, or *embeddings*, of faces from the aligned input images. In embedding space, Euclidean distance directly corresponds to a measure of face similarity.
- Compare input embedding vectors to labeled embedding vectors in a database. Here, a support vector machine (SVM) and a KNN classifier, trained on labeled embedding vectors, play the role of a database. Face recognition in this context means using these classifiers to predict the labels i.e. identities of new inputs.
### Environment setup
For running this notebook, create and activate a new [virtual environment](https://docs.python.org/3/tutorial/venv.html) and install the packages listed in [requirements.txt](requirements.txt) with `pip install -r requirements.txt`. Furthermore, you'll need a local copy of Dlib's face landmarks data file for running face alignment:
```
import bz2
import os
from urllib.request import urlopen
def download_landmarks(dst_file):
url = 'http://dlib.net/files/shape_predictor_68_face_landmarks.dat.bz2'
decompressor = bz2.BZ2Decompressor()
with urlopen(url) as src, open(dst_file, 'wb') as dst:
data = src.read(1024)
while len(data) > 0:
dst.write(decompressor.decompress(data))
data = src.read(1024)
dst_dir = 'models'
dst_file = os.path.join(dst_dir, 'landmarks.dat')
if not os.path.exists(dst_file):
os.makedirs(dst_dir)
download_landmarks(dst_file)
```
### CNN architecture and training
The CNN architecture used here is a variant of the inception architecture [[2]](https://arxiv.org/abs/1409.4842). More precisely, it is a variant of the NN4 architecture described in [[1]](https://arxiv.org/abs/1503.03832) and identified as [nn4.small2](https://cmusatyalab.github.io/openface/models-and-accuracies/#model-definitions) model in the OpenFace project. This notebook uses a Keras implementation of that model whose definition was taken from the [Keras-OpenFace](https://github.com/iwantooxxoox/Keras-OpenFace) project. The architecture details aren't too important here, it's only useful to know that there is a fully connected layer with 128 hidden units followed by an L2 normalization layer on top of the convolutional base. These two top layers are referred to as the *embedding layer* from which the 128-dimensional embedding vectors can be obtained. The complete model is defined in [model.py](model.py) and a graphical overview is given in [model.png](model.png). A Keras version of the nn4.small2 model can be created with `create_model()`.
```
from model import create_model
nn4_small2 = create_model()
```
Model training aims to learn an embedding $f(x)$ of image $x$ such that the squared L2 distance between all faces of the same identity is small and the distance between a pair of faces from different identities is large. This can be achieved with a *triplet loss* $L$ that is minimized when the distance between an anchor image $x^a_i$ and a positive image $x^p_i$ (same identity) in embedding space is smaller than the distance between that anchor image and a negative image $x^n_i$ (different identity) by at least a margin $\alpha$.
$$L = \sum^{m}_{i=1} \large[ \small {\mid \mid f(x_{i}^{a}) - f(x_{i}^{p})) \mid \mid_2^2} - {\mid \mid f(x_{i}^{a}) - f(x_{i}^{n})) \mid \mid_2^2} + \alpha \large ] \small_+$$
$[z]_+$ means $max(z,0)$ and $m$ is the number of triplets in the training set. The triplet loss in Keras is best implemented with a custom layer as the loss function doesn't follow the usual `loss(input, target)` pattern. This layer calls `self.add_loss` to install the triplet loss:
```
from keras import backend as K
from keras.models import Model
from keras.layers import Input, Layer
# Input for anchor, positive and negative images
in_a = Input(shape=(96, 96, 3))
in_p = Input(shape=(96, 96, 3))
in_n = Input(shape=(96, 96, 3))
# Output for anchor, positive and negative embedding vectors
# The nn4_small model instance is shared (Siamese network)
emb_a = nn4_small2(in_a)
emb_p = nn4_small2(in_p)
emb_n = nn4_small2(in_n)
class TripletLossLayer(Layer):
def __init__(self, alpha, **kwargs):
self.alpha = alpha
super(TripletLossLayer, self).__init__(**kwargs)
def triplet_loss(self, inputs):
a, p, n = inputs
p_dist = K.sum(K.square(a-p), axis=-1)
n_dist = K.sum(K.square(a-n), axis=-1)
return K.sum(K.maximum(p_dist - n_dist + self.alpha, 0), axis=0)
def call(self, inputs):
loss = self.triplet_loss(inputs)
self.add_loss(loss)
return loss
# Layer that computes the triplet loss from anchor, positive and negative embedding vectors
triplet_loss_layer = TripletLossLayer(alpha=0.2, name='triplet_loss_layer')([emb_a, emb_p, emb_n])
# Model that can be trained with anchor, positive negative images
nn4_small2_train = Model([in_a, in_p, in_n], triplet_loss_layer)
```
During training, it is important to select triplets whose positive pairs $(x^a_i, x^p_i)$ and negative pairs $(x^a_i, x^n_i)$ are hard to discriminate i.e. their distance difference in embedding space should be less than margin $\alpha$, otherwise, the network is unable to learn a useful embedding. Therefore, each training iteration should select a new batch of triplets based on the embeddings learned in the previous iteration. Assuming that a generator returned from a `triplet_generator()` call can generate triplets under these constraints, the network can be trained with:
```
from data import triplet_generator
# triplet_generator() creates a generator that continuously returns
# ([a_batch, p_batch, n_batch], None) tuples where a_batch, p_batch
# and n_batch are batches of anchor, positive and negative RGB images
# each having a shape of (batch_size, 96, 96, 3).
generator = triplet_generator()
nn4_small2_train.compile(loss=None, optimizer='adam')
nn4_small2_train.fit_generator(generator, epochs=10, steps_per_epoch=100)
# Please note that the current implementation of the generator only generates
# random image data. The main goal of this code snippet is to demonstrate
# the general setup for model training. In the following, we will anyway
# use a pre-trained model so we don't need a generator here that operates
# on real training data. I'll maybe provide a fully functional generator
# later.
```
The above code snippet should merely demonstrate how to setup model training. But instead of actually training a model from scratch we will now use a pre-trained model as training from scratch is very expensive and requires huge datasets to achieve good generalization performance. For example, [[1]](https://arxiv.org/abs/1503.03832) uses a dataset of 200M images consisting of about 8M identities.
The OpenFace project provides [pre-trained models](https://cmusatyalab.github.io/openface/models-and-accuracies/#pre-trained-models) that were trained with the public face recognition datasets [FaceScrub](http://vintage.winklerbros.net/facescrub.html) and [CASIA-WebFace](http://arxiv.org/abs/1411.7923). The Keras-OpenFace project converted the weights of the pre-trained nn4.small2.v1 model to [CSV files](https://github.com/iwantooxxoox/Keras-OpenFace/tree/master/weights) which were then [converted here](face-recognition-convert.ipynb) to a binary format that can be loaded by Keras with `load_weights`:
```
nn4_small2_pretrained = create_model()
nn4_small2_pretrained.load_weights('weights/nn4.small2.v1.h5')
```
### Custom dataset
To demonstrate face recognition on a custom dataset, a small subset of the [LFW](http://vis-www.cs.umass.edu/lfw/) dataset is used. It consists of 100 face images of [10 identities](images). The metadata for each image (file and identity name) are loaded into memory for later processing.
```
import numpy as np
import os.path
class IdentityMetadata():
def __init__(self, base, name, file):
# dataset base directory
self.base = base
# identity name
self.name = name
# image file name
self.file = file
def __repr__(self):
return self.image_path()
def image_path(self):
return os.path.join(self.base, self.name, self.file)
def load_metadata(path):
metadata = []
for i in os.listdir(path):
for f in os.listdir(os.path.join(path, i)):
# Check file extension. Allow only jpg/jpeg' files.
ext = os.path.splitext(f)[1]
if ext == '.jpg' or ext == '.jpeg':
metadata.append(IdentityMetadata(path, i, f))
return np.array(metadata)
metadata = load_metadata('images')
```
### Face alignment
The nn4.small2.v1 model was trained with aligned face images, therefore, the face images from the custom dataset must be aligned too. Here, we use [Dlib](http://dlib.net/) for face detection and [OpenCV](https://opencv.org/) for image transformation and cropping to produce aligned 96x96 RGB face images. By using the [AlignDlib](align.py) utility from the OpenFace project this is straightforward:
```
import cv2
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from align import AlignDlib
%matplotlib inline
def load_image(path):
img = cv2.imread(path, 1)
# OpenCV loads images with color channels
# in BGR order. So we need to reverse them
return img[...,::-1]
# Initialize the OpenFace face alignment utility
alignment = AlignDlib('models/landmarks.dat')
# Load an image of Jacques Chirac
jc_orig = load_image(metadata[2].image_path())
# Detect face and return bounding box
bb = alignment.getLargestFaceBoundingBox(jc_orig)
# Transform image using specified face landmark indices and crop image to 96x96
jc_aligned = alignment.align(96, jc_orig, bb, landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)
# Show original image
plt.subplot(131)
plt.imshow(jc_orig)
# Show original image with bounding box
plt.subplot(132)
plt.imshow(jc_orig)
plt.gca().add_patch(patches.Rectangle((bb.left(), bb.top()), bb.width(), bb.height(), fill=False, color='red'))
# Show aligned image
plt.subplot(133)
plt.imshow(jc_aligned);
```
As described in the OpenFace [pre-trained models](https://cmusatyalab.github.io/openface/models-and-accuracies/#pre-trained-models) section, landmark indices `OUTER_EYES_AND_NOSE` are required for model nn4.small2.v1. Let's implement face detection, transformation and cropping as `align_image` function for later reuse.
```
def align_image(img):
return alignment.align(96, img, alignment.getLargestFaceBoundingBox(img),
landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)
```
### Embedding vectors
Embedding vectors can now be calculated by feeding the aligned and scaled images into the pre-trained network.
```
embedded = np.zeros((metadata.shape[0], 128))
for i, m in enumerate(metadata):
img = load_image(m.image_path())
img = align_image(img)
# scale RGB values to interval [0,1]
img = (img / 255.).astype(np.float32)
# obtain embedding vector for image
embedded[i] = nn4_small2_pretrained.predict(np.expand_dims(img, axis=0))[0]
```
Let's verify on a single triplet example that the squared L2 distance between its anchor-positive pair is smaller than the distance between its anchor-negative pair.
```
def distance(emb1, emb2):
return np.sum(np.square(emb1 - emb2))
def show_pair(idx1, idx2):
plt.figure(figsize=(8,3))
plt.suptitle(f'Distance = {distance(embedded[idx1], embedded[idx2]):.2f}')
plt.subplot(121)
plt.imshow(load_image(metadata[idx1].image_path()))
plt.subplot(122)
plt.imshow(load_image(metadata[idx2].image_path()));
show_pair(2, 3)
show_pair(2, 12)
```
As expected, the distance between the two images of Jacques Chirac is smaller than the distance between an image of Jacques Chirac and an image of Gerhard Schröder (0.30 < 1.12). But we still do not know what distance threshold $\tau$ is the best boundary for making a decision between *same identity* and *different identity*.
### Distance threshold
To find the optimal value for $\tau$, the face verification performance must be evaluated on a range of distance threshold values. At a given threshold, all possible embedding vector pairs are classified as either *same identity* or *different identity* and compared to the ground truth. Since we're dealing with skewed classes (much more negative pairs than positive pairs), we use the [F1 score](https://en.wikipedia.org/wiki/F1_score) as evaluation metric instead of [accuracy](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html).
```
from sklearn.metrics import f1_score, accuracy_score
distances = [] # squared L2 distance between pairs
identical = [] # 1 if same identity, 0 otherwise
num = len(metadata)
for i in range(num - 1):
for j in range(1, num):
distances.append(distance(embedded[i], embedded[j]))
identical.append(1 if metadata[i].name == metadata[j].name else 0)
distances = np.array(distances)
identical = np.array(identical)
thresholds = np.arange(0.3, 1.0, 0.01)
f1_scores = [f1_score(identical, distances < t) for t in thresholds]
acc_scores = [accuracy_score(identical, distances < t) for t in thresholds]
opt_idx = np.argmax(f1_scores)
# Threshold at maximal F1 score
opt_tau = thresholds[opt_idx]
# Accuracy at maximal F1 score
opt_acc = accuracy_score(identical, distances < opt_tau)
# Plot F1 score and accuracy as function of distance threshold
plt.plot(thresholds, f1_scores, label='F1 score');
plt.plot(thresholds, acc_scores, label='Accuracy');
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title(f'Accuracy at threshold {opt_tau:.2f} = {opt_acc:.3f}');
plt.xlabel('Distance threshold')
plt.legend();
```
The face verification accuracy at $\tau$ = 0.56 is 95.7%. This is not bad given a baseline of 89% for a classifier that always predicts *different identity* (there are 980 pos. pairs and 8821 neg. pairs) but since nn4.small2.v1 is a relatively small model it is still less than what can be achieved by state-of-the-art models (> 99%).
The following two histograms show the distance distributions of positive and negative pairs and the location of the decision boundary. There is a clear separation of these distributions which explains the discriminative performance of the network. One can also spot some strong outliers in the positive pairs class but these are not further analyzed here.
```
dist_pos = distances[identical == 1]
dist_neg = distances[identical == 0]
plt.figure(figsize=(12,4))
plt.subplot(121)
plt.hist(dist_pos)
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title('Distances (pos. pairs)')
plt.legend();
plt.subplot(122)
plt.hist(dist_neg)
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title('Distances (neg. pairs)')
plt.legend();
```
### Face recognition
Given an estimate of the distance threshold $\tau$, face recognition is now as simple as calculating the distances between an input embedding vector and all embedding vectors in a database. The input is assigned the label (i.e. identity) of the database entry with the smallest distance if it is less than $\tau$ or label *unknown* otherwise. This procedure can also scale to large databases as it can be easily parallelized. It also supports one-shot learning, as adding only a single entry of a new identity might be sufficient to recognize new examples of that identity.
A more robust approach is to label the input using the top $k$ scoring entries in the database which is essentially [KNN classification](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm) with a Euclidean distance metric. Alternatively, a linear [support vector machine](https://en.wikipedia.org/wiki/Support_vector_machine) (SVM) can be trained with the database entries and used to classify i.e. identify new inputs. For training these classifiers we use 50% of the dataset, for evaluation the other 50%.
```
from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import LinearSVC
targets = np.array([m.name for m in metadata])
encoder = LabelEncoder()
encoder.fit(targets)
# Numerical encoding of identities
y = encoder.transform(targets)
train_idx = np.arange(metadata.shape[0]) % 2 != 0
test_idx = np.arange(metadata.shape[0]) % 2 == 0
# 50 train examples of 10 identities (5 examples each)
X_train = embedded[train_idx]
# 50 test examples of 10 identities (5 examples each)
X_test = embedded[test_idx]
y_train = y[train_idx]
y_test = y[test_idx]
knn = KNeighborsClassifier(n_neighbors=1, metric='euclidean')
svc = LinearSVC()
knn.fit(X_train, y_train)
svc.fit(X_train, y_train)
acc_knn = accuracy_score(y_test, knn.predict(X_test))
acc_svc = accuracy_score(y_test, svc.predict(X_test))
print(f'KNN accuracy = {acc_knn}, SVM accuracy = {acc_svc}')
```
The KNN classifier achieves an accuracy of 96% on the test set, the SVM classifier 98%. Let's use the SVM classifier to illustrate face recognition on a single example.
```
import warnings
# Suppress LabelEncoder warning
warnings.filterwarnings('ignore')
example_idx = 29
example_image = load_image(metadata[test_idx][example_idx].image_path())
example_prediction = svc.predict([embedded[test_idx][example_idx]])
example_identity = encoder.inverse_transform(example_prediction)[0]
plt.imshow(example_image)
plt.title(f'Recognized as {example_identity}');
```
Seems reasonable :-) Classification results should actually be checked whether (a subset of) the database entries of the predicted identity have a distance less than $\tau$, otherwise one should assign an *unknown* label. This step is skipped here but can be easily added.
### Dataset visualization
To embed the dataset into 2D space for displaying identity clusters, [t-distributed Stochastic Neighbor Embedding](https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding) (t-SNE) is applied to the 128-dimensional embedding vectors. Except from a few outliers, identity clusters are well separated.
```
from sklearn.manifold import TSNE
X_embedded = TSNE(n_components=2).fit_transform(embedded)
for i, t in enumerate(set(targets)):
idx = targets == t
plt.scatter(X_embedded[idx, 0], X_embedded[idx, 1], label=t)
plt.legend(bbox_to_anchor=(1, 1));
```
### References
- [1] [FaceNet: A Unified Embedding for Face Recognition and Clustering](https://arxiv.org/abs/1503.03832)
- [2] [Going Deeper with Convolutions](https://arxiv.org/abs/1409.4842)
| true |
code
| 0.697596 | null | null | null | null |
|
# Parameter estimation and hypothesis testing
```
#Import packages
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import pymc3 as pm
from ipywidgets import interact
import arviz as az
%matplotlib inline
sns.set()
```
## Learning Objectives of Part 2
1. Understand what priors, likelihoods and posteriors are;
2. Use random sampling for parameter estimation to appreciate the relationship between sample size & the posterior distribution, along with the effect of the prior;
3. Use probabilistic programming for parameter estimation;
4. Use probabilistic programming for hypothesis testing.
## 1. From Bayes Theorem to Bayesian Inference
Let's say that we flip a biased coin several times and we want to estimate the probability of heads from the number of heads we saw. Statistical intuition tells us that our best estimate of $p(heads)=$ number of heads divided by total number of flips.
However,
1. It doesn't tell us how certain we can be of that estimate and
2. This type of intuition doesn't extend to even slightly more complex examples.
Bayesian inference helps us here. We can calculate the probability of a particular $p=p(H)$ given data $D$ by setting $A$ in Bayes Theorem equal to $p$ and $B$ equal to $D$.
$$P(p|D) = \frac{P(D|p)P(p)}{P(D)} $$
In this equation, we call $P(p)$ the prior (distribution), $P(D|p)$ the likelihood and $P(p|D)$ the posterior (distribution). The intuition behind the nomenclature is as follows: the prior is the distribution containing our knowledge about $p$ prior to the introduction of the data $D$ & the posterior is the distribution containing our knowledge about $p$ after considering the data $D$.
**Note** that we're _overloading_ the term _probability_ here. In fact, we have 3 distinct usages of the word:
- The probability $p$ of seeing a head when flipping a coin;
- The resulting binomial probability distribution $P(D|p)$ of seeing the data $D$, given $p$;
- The prior & posterior probability distributions of $p$, encoding our _uncertainty_ about the value of $p$.
**Key concept:** We only need to know the posterior distribution $P(p|D)$ up to multiplication by a constant at the moment: this is because we really only care about the values of $P(p|D)$ relative to each other – for example, what is the most likely value of $p$? To answer such questions, we only need to know what $P(p|D)$ is proportional to, as a function of $p$. Thus we don’t currently need to worry about the term $P(D)$. In fact,
$$P(p|D) \propto P(D|p)P(p) $$
**Note:** What is the prior? Really, what do we know about $p$ before we see any data? Well, as it is a probability, we know that $0\leq p \leq1$. If we haven’t flipped any coins yet, we don’t know much else: so it seems logical that all values of $p$ within this interval are equally likely, i.e., $P(p)=1$, for $0\leq p \leq1$. This is known as an uninformative prior because it contains little information (there are other uninformative priors we may use in this situation, such as the Jeffreys prior, to be discussed later). People who like to hate on Bayesian inference tend to claim that the need to choose a prior makes Bayesian methods somewhat arbitrary, but as we’ll now see, if you have enough data, the likelihood dominates over the prior and the latter doesn’t matter so much.
**Essential remark:** we get the whole distribution of $P(p|D)$, not merely a point estimate plus errors bars, such as [95% confidence intervals](http://andrewgelman.com/2018/07/04/4th-july-lets-declare-independence-95/).
## 2. Bayesian parameter estimation I: flip those coins
Now let's generate some coin flips and try to estimate $p(H)$. Two notes:
- given data $D$ consisting of $n$ coin tosses & $k$ heads, the likelihood function is given by $L:=P(D|p) \propto p^k(1-p)^{n-k}$;
- given a uniform prior, the posterior is proportional to the likelihood.
```
def plot_posterior(p=0.6, N=0):
"""Plot the posterior given a uniform prior; Bernoulli trials
with probability p; sample size N"""
np.random.seed(42)
# Flip coins
n_successes = np.random.binomial(N, p)
# X-axis for PDF
x = np.linspace(0, 1, 100)
# Prior
prior = 1
# Compute posterior, given the likelihood (analytic form)
posterior = x**n_successes*(1-x)**(N-n_successes)*prior
posterior /= np.max(posterior) # so that peak always at 1
plt.plot(x, posterior)
plt.show()
plot_posterior(N=10)
```
* Now use the great ipywidget interact to check out the posterior as you generate more and more data (you can also vary $p$):
```
interact(plot_posterior, p=(0, 1, 0.01), N=(0, 1500));
```
**Notes for discussion:**
* as you generate more and more data, your posterior gets narrower, i.e. you get more and more certain of your estimate.
* you need more data to be certain of your estimate when $p=0.5$, as opposed to when $p=0$ or $p=1$.
### The choice of the prior
You may have noticed that we needed to choose a prior and that, in the small to medium data limit, this choice can affect the posterior. We'll briefly introduce several types of priors and then you'll use one of them for the example above to see the effect of the prior:
- **Informative priors** express specific, definite information about a variable, for example, if we got a coin from the mint, we may use an informative prior with a peak at $p=0.5$ and small variance.
- **Weakly informative priors** express partial information about a variable, such as a peak at $p=0.5$ (if we have no reason to believe the coin is biased), with a larger variance.
- **Uninformative priors** express no information about a variable, except what we know for sure, such as knowing that $0\leq p \leq1$.
Now you may think that the _uniform distribution_ is uninformative, however, what if I am thinking about this question in terms of the probability $p$ and Eric Ma is thinking about it in terms of the _odds ratio_ $r=\frac{p}{1-p}$? Eric rightly feels that he has no prior knowledge as to what this $r$ is and thus chooses the uniform prior on $r$.
With a bit of algebra (transformation of variables), we can show that choosing the uniform prior on $p$ amounts to choosing a decidedly non-uniform prior on $r$ and vice versa. So Eric and I have actually chosen different priors, using the same philosophy. How do we avoid this happening? Enter the **Jeffreys prior**, which is an uninformative prior that solves this problem. You can read more about the Jeffreys prior [here](https://en.wikipedia.org/wiki/Jeffreys_prior) & in your favourite Bayesian text book (Sivia gives a nice treatment).
In the binomial (coin flip) case, the Jeffreys prior is given by $P(p) = \frac{1}{\sqrt{p(1-p)}}$.
#### Hands-on
* Create an interactive plot like the one above, except that it has two posteriors on it: one for the uniform prior, another for the Jeffries prior.
```
# Solution
def plot_posteriors(p=0.6, N=0):
np.random.seed(42)
n_successes = np.random.binomial(N, p)
x = np.linspace(0.01, 0.99, 100)
posterior1 = x**n_successes*(1-x)**(N-n_successes) # w/ uniform prior
posterior1 /= np.max(posterior1) # so that peak always at 1
plt.plot(x, posterior1, label='Uniform prior')
jp = np.sqrt(x*(1-x))**(-1) # Jeffreys prior
posterior2 = posterior1*jp # w/ Jeffreys prior
posterior2 /= np.max(posterior2) # so that peak always at 1 (not quite correct to do; see below)
plt.plot(x, posterior2, label='Jeffreys prior')
plt.legend()
plt.show()
interact(plot_posteriors, p=(0, 1, 0.01), N=(0, 100));
```
**Question:** What happens to the posteriors as you generate more and more data?
## 3. Bayesian parameter estimation using PyMC3
Well done! You've learnt the basics of Bayesian model building. The steps are
1. To completely specify the model in terms of _probability distributions_. This includes specifying
- what the form of the sampling distribution of the data is _and_
- what form describes our _uncertainty_ in the unknown parameters (This formulation is adapted from [Fonnesbeck's workshop](https://github.com/fonnesbeck/intro_stat_modeling_2017/blob/master/notebooks/2.%20Basic%20Bayesian%20Inference.ipynb) as Chris said it so well there).
2. Calculate the _posterior distribution_.
In the above, the form of the sampling distribution of the data was Binomial (described by the likelihood) and the uncertainty around the unknown parameter $p$ captured by the prior.
Now it is time to do the same using the **probabilistic programming language** PyMC3. There's _loads_ about PyMC3 and this paradigm, two of which are
- _probabililty distributions_ are first class citizens, in that we can assign them to variables and use them intuitively to mirror how we think about priors, likelihoods & posteriors.
- PyMC3 calculates the posterior for us!
Under the hood, PyMC3 will compute the posterior using a sampling based approach called Markov Chain Monte Carlo (MCMC) or Variational Inference. Check the [PyMC3 docs](https://docs.pymc.io/) for more on these.
But now, it's time to bust out some MCMC and get sampling!
### Parameter estimation I: click-through rate
A common experiment in tech data science is to test a product change and see how it affects a metric that you're interested in. Say that I don't think enough people are clicking a button on my website & I hypothesize that it's because the button is a similar color to the background of the page. Then I can set up two pages and send some people to each: the first the original page, the second a page that is identical, except that it has a button that is of higher contrast and see if more people click through. This is commonly referred to as an A/B test and the metric of interest is click-through rate (CTR), what proportion of people click through. Before even looking at two rates, let's use PyMC3 to estimate one.
First generate click-through data, given a CTR $p_a=0.15$.
```
# click-through rates
p_a = 0.15
N = 150
n_successes_a = np.sum(np.random.binomial(N, p_a))
```
Now it's time to build your probability model. Noticing that our model of having a constant CTR resulting in click or not is a biased coin flip,
- the sampling distribution is binomial and we need to encode this in the likelihood;
- there is a single parameter $p$ that we need to describe the uncertainty around, using a prior and we'll use a uniform prior for this.
These are the ingredients for the model so let's now build it:
```
# Build model of p_a
with pm.Model() as Model:
# Prior on p
prob = pm.Uniform('p')
# Binomial Likelihood
y = pm.Binomial('y', n=N, p=prob, observed=n_successes_a)
```
**Discussion:**
- What do you think of the API for PyMC3. Does it reflect how we think about model building?
It's now time to sample from the posterior using PyMC3. You'll also plot the posterior:
```
with Model:
samples = pm.sample(2000, njobs=1)
az.plot_posterior(samples, kind='hist');
```
**For discussion:** Interpret the posterior ditribution. What would your tell the non-technical manager of your growth team about the CTR?
### Hands-on: Parameter estimation II -- the mean of a population
In this exercise, you'll calculate the posterior mean beak depth of Galapagos finches in a given species. First you'll load the data and subset wrt species:
```
# Import and view head of data
df_12 = pd.read_csv('../data/finch_beaks_2012.csv')
df_fortis = df_12.loc[df_12['species'] == 'fortis']
df_scandens = df_12.loc[df_12['species'] == 'scandens']
```
To specify the full probabilty model, you need
- a likelihood function for the data &
- priors for all unknowns.
What is the likelihood here? Let's plot the measurements below and see that they look approximately Gaussian/normal so you'll use a normal likelihood $y_i\sim \mathcal{N}(\mu, \sigma^2)$. The unknowns here are the mean $\mu$ and standard deviation $\sigma$ and we'll use weakly informative priors on both
- a normal prior for $\mu$ with mean $10$ and standard deviation $5$;
- a uniform prior for $\sigma$ bounded between $0$ and $10$.
We can discuss biological reasons for these priors also but you can also test that the posteriors are relativelyt robust to the choice of prior here due to the amount of data.
```
sns.distplot(df_fortis['blength']);
with pm.Model() as model:
# Prior for mean & standard deviation
μ_1 = pm.Normal('μ_1', mu=10, sd=5)
σ_1 = pm.Lognormal('σ_1', 0, 10)
# Gaussian Likelihood
y_1 = pm.Normal('y_1', mu=μ_1, sd=σ_1, observed=df_fortis['blength'])
# bust it out & sample
with model:
samples = pm.sample(2000, njobs=1)
az.plot_posterior(samples);
```
## 4. Bayesian Hypothesis testing
### Bayesian Hypothesis testing I: A/B tests on click through rates
Assume we have a website and want to redesign the layout (*A*) and test whether the new layout (*B*) results in a higher click through rate. When people come to our website we randomly show them layout *A* or *B* and see how many people click through for each. First let's generate the data we need:
```
# click-through rates
p_a = 0.15
p_b = 0.20
N = 1000
n_successes_a = np.sum(np.random.uniform(size=N) <= p_a)
n_successes_b = np.sum(np.random.uniform(size=N) <= p_b)
```
Once again, we need to specify our models for $p_a$ and $p_b$. Each will be the same as the CTR example above
- Binomial likelihoods
- uniform priors on $p_a$ and $_p$.
We also want to calculate the posterior of the difference $p_a-p_b$ and we do so using `pm.Deterministic()`, which specifies a deterministic random variable, i.e., one that is completely determined by the values it references, in the case $p_a$ & $p_b$.
We'll now build the model:
```
with pm.Model() as Model:
# Prior on p
prob_a = pm.Uniform('p_a')
prob_b = pm.Uniform('p_b')
# Binomial Likelihood
y_a = pm.Binomial('y_a', n=N, p=prob_a, observed=n_successes_a)
y_b = pm.Binomial('y_b', n=N, p=prob_b, observed=n_successes_b)
diff_clicks = pm.Deterministic('diff_clicks', prob_a-prob_b)
```
Sample from the posterior and plot them:
```
with Model:
samples = pm.sample(2000, njobs=1)
az.plot_posterior(samples, kind='hist');
```
### Hands-on: Bayesian Hypothesis testing II -- beak lengths difference between species
**Task**: Determine whether the mean beak length of the Galapogas finches differs between species. For the mean of each species, use the same model as in previous hand-on section:
- Gaussian likelihood;
- Normal prior for the means;
- Uniform prior for the variances.
Also calculate the difference between the means and, for bonus points, the _effect size_, which is the difference between the means divided by the pooled standard deviations = $\sqrt{(\sigma_1^2+\sigma_2^2)/2}$. Hugo will talk through the importance of the _effect size_.
Don't forget to sample from the posteriors and plot them!
```
with pm.Model() as model:
# Priors for means and variances
μ_1 = pm.Normal('μ_1', mu=10, sd=5)
σ_1 = pm.Uniform('σ_1', 0, 10)
μ_2 = pm.Normal('μ_2', mu=10, sd=5)
σ_2 = pm.Uniform('σ_2', 0, 10)
# Gaussian Likelihoods
y_1 = pm.Normal('y_1', mu=μ_1, sd=σ_1, observed=df_fortis['blength'])
y_2 = pm.Normal('y_2', mu=μ_2, sd=σ_2, observed=df_scandens['blength'])
# Calculate the effect size and its uncertainty.
diff_means = pm.Deterministic('diff_means', μ_1 - μ_2)
pooled_sd = pm.Deterministic('pooled_sd',
np.sqrt(np.power(σ_1, 2) +
np.power(σ_2, 2)) / 2)
effect_size = pm.Deterministic('effect_size',
diff_means / pooled_sd)
# bust it out & sample
with model:
samples = pm.sample(2000, njobs=1)
az.plot_posterior(samples, var_names=['μ_1', 'μ_2', 'diff_means', 'effect_size'], kind='hist');
```
| true |
code
| 0.647241 | null | null | null | null |
|
# Clonotype and sequence deduplication
Starting with annotated sequence data (in AbStar's `minimal` output format), reduces sequences to clonotypes and collapses dupicate clonotypes.
The [`abutils`](https://www.github.com/briney/abutils) Python package is required, and can be installed by running `pip install abutils`
*NOTE: this notebook requires the use of the Unix command line tool `sort`. Thus, it requires a Unix-based operating system to run correctly (MacOS and most flavors of Linux should be fine). Running this notebook on Windows 10 may be possible using the [Windows Subsystem for Linux](https://docs.microsoft.com/en-us/windows/wsl/about) but we have not tested this.*
```
from __future__ import print_function, division
import itertools
import multiprocessing as mp
import os
import subprocess as sp
import sys
import tempfile
from abutils.utils.jobs import monitor_mp_jobs
from abutils.utils.pipeline import list_files, make_dir
from abutils.utils.progbar import progress_bar
```
### Subjects, directories and data fields
The input data (annotated sequences in [abstar's](https://github.com/briney/abstar) `minimal` format) is too large to be stored in a Github repository. A compressed archive of the data can be downloaded [**here**](http://burtonlab.s3.amazonaws.com/GRP_github_data/techrep-merged_minimal_no-header.tar.gz). The data file is fairly large (about 400GB uncompressed), so make sure you have enough space before downloading. Decompressing the archive from within the `data` directory (located in the same parent directory as this notebook) will allow the code in this notebook to run without modification. If you would prefer to store the input data somewhere else, be sure to modify the `raw_input_dir` path below.
The data fields defined below correspond to the prosition in abstar's `minimal` format. If for some reason you have a differently formatted annotation file, change the field positions to suit your annotation file.
```
# subjects
with open('./data/subjects.txt') as f:
subjects = sorted(f.read().split())
# directories
raw_input_dir = './data/techrep-merged_minimal_no-header/'
raw_clonotype_dir = './data/techrep-merged_vj-aa/'
dedup_clonotype_dir = './data/dedup_techrep-merged_vj-aa/'
dedup_sequence_dir = './data/dedup_techrep-merged_nt-seq/'
logfile = './data/dedup.log'
# data fields
prod_field = 3
v_field = 5
j_field = 9
cdr3aa_field = 12
vdjnt_field = 14
```
## Deduplication (biological replicates)
```
def dedup_bioreps(files, raw_clonotype_dir, unique_clonotype_dir,
raw_sequence_dir, unique_sequence_dir, log_file=None):
# set up output directories
make_dir(raw_clonotype_dir)
make_dir(unique_clonotype_dir)
make_dir(raw_sequence_dir)
make_dir(unique_sequence_dir)
# process minimal output files
for _f in files:
print(os.path.basename(_f))
clonotype_output_data = []
sequence_output_data = []
raw_clonotype_file = os.path.join(raw_clonotype_dir, os.path.basename(_f))
unique_clonotype_file = os.path.join(unique_clonotype_dir, os.path.basename(_f))
raw_sequence_file = os.path.join(raw_sequence_dir, os.path.basename(_f))
unique_sequence_file = os.path.join(unique_sequence_dir, os.path.basename(_f))
# collect clonotype/sequence information
with open(_f) as f:
for line in f:
data = line.strip().split(',')
if data[prod_field] == 'no':
continue
v_gene = data[v_field]
j_gene = data[j_field]
cdr3_aa = data[cdr3aa_field]
vdj_nt = data[vdjnt_field]
clonotype_output_data.append(' '.join([v_gene, j_gene, cdr3_aa]))
sequence_output_data.append(' '.join([v_gene, j_gene, vdj_nt]))
# write raw clonotype info to file
raw_clontype_string = '\n'.join(clonotype_output_data)
with open(raw_clonotype_file, 'w') as rf:
rf.write(raw_clontype_string)
raw_clonotype_count = len(clonotype_output_data)
print('raw clonotypes:', raw_clonotype_count)
# collapse duplicate clonotypes (without counts)
uniq_cmd = 'sort -u -o {} -'.format(unique_clonotype_file)
p = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, stdin=sp.PIPE, shell=True)
stdout, stderr = p.communicate(input=raw_clonotype_string)
# count the number of unique clonotypes
wc_cmd = 'wc -l {}'.format(unique_clonotype_file)
q = sp.Popen(wc_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
_count, _ = q.communicate()
unique_clonotype_count = int(_count.split()[0])
print('unique clonotypes:', unique_clonotype_count)
if log_file is not None:
with open(log_file, 'a') as f:
f.write('CLONOTYPES: {} {}\n'.format(raw_clonotype_count, unique_clonotype_count))
# write raw sequence info to file
raw_sequence_string = '\n'.join(sequence_output_data)
with open(raw_sequence_file, 'w') as rf:
rf.write(raw_sequence_string)
raw_sequence_count = len(sequence_output_data)
print('raw sequences:', raw_sequence_count)
# collapse duplicate sequences (without counts)
uniq_cmd = 'sort -u -o {} -'.format(unique_sequence_file)
p = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, stdin=sp.PIPE, shell=True)
stdout, stderr = p.communicate(input=raw_sequence_string)
# count the number of unique sequences
wc_cmd = 'wc -l {}'.format(unique_sequence_file)
q = sp.Popen(wc_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
_count, _ = q.communicate()
unique_sequence_count = int(_count.split()[0])
print('unique sequences:', unique_sequence_count)
if log_file is not None:
with open(log_file, 'a') as f:
f.write('SEQUENCES: {} {}\n'.format(raw_sequence_count, unique_sequence_count))
print('')
# clear the logfile
with open(logfile, 'w') as f:
f.write('')
# iteratively process each subject
for subject in subjects:
print(subject)
with open(logfile, 'a') as f:
f.write('#' + subject + '\n')
files = list_files('./data/techrep-merged_minimal_no-header/{}'.format(subject))
raw_clonotype_dir = './data/techrep-merged_vj-aa/{}'.format(subject)
unique_clonptype_dir = './data/dedup_techrep-merged_vj-aa/{}'.format(subject)
raw_sequence_dir = './data/techrep-merged_vdj-nt/{}'.format(subject)
unique_sequence_dir = './data/dedup_techrep-merged_vdj-nt/{}'.format(subject)
dedup_bioreps(files, raw_clonotype_dir, unique_clonptype_dir,
raw_sequence_dir, unique_sequence_dir, log_file=logfile)
print('')
```
## Deduplication (subject pools)
In the previous blocks of code, we created a unique clonotype file for each biological replicate for each subject. Here, we'd like to create a single file for each subject containing only unique clonotypes (regardless of which biological replicate they came from).
```
dedup_clonotype_subject_pool_dir = './data/dedup_subject_clonotype_pools/'
dedup_sequence_subject_pool_dir = './data/dedup_subject_sequence_pools/'
make_dir(dedup_clonotype_subject_pool_dir)
make_dir(dedup_sequence_subject_pool_dir)
```
First we want to create a unique clonotype file for each subject that also contains the number of times we saw each clonotype (using the deduplicated biological replicates, so the clonotype count essentially tallies the number of biological replicates in which we observed each clonotype)
```
for subject in subjects:
print(subject)
# clonotypes
input_clonotype_files = list_files(os.path.join(dedup_clonotype_dir, subject))
ofile = os.path.join(dedup_clonotype_subject_pool_dir, '{}_dedup_pool_vj-aa_with-counts.txt'.format(subject))
uniq_cmd = 'cat {} | sort | uniq -c > {}'.format(' '.join(input_clonotype_files), ofile)
c = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
stdout, stderr = c.communicate()
# sequences
input_sequence_files = list_files(os.path.join(dedup_sequence_dir, subject))
ofile = os.path.join(dedup_sequence_subject_pool_dir, '{}_dedup_pool_vdj-nt_with-counts.txt'.format(subject))
uniq_cmd = 'cat {} | sort | uniq -c > {}'.format(' '.join(input_sequence_files), ofile)
s = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
stdout, stderr = s.communicate()
```
Now the same process, but without counts:
```
for subject in subjects:
print(subject)
# clonotypes
input_clonotype_files = list_files(os.path.join(dedup_clonotype_dir, subject))
ofile = os.path.join(dedup_clonotype_subject_pool_dir, '{}_dedup_pool_vj-aa.txt'.format(subject))
uniq_cmd = 'cat {} | sort | uniq > {}'.format(' '.join(input_clonotype_files), ofile)
c = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
stdout, stderr = c.communicate()
# sequences
input_sequence_files = list_files(os.path.join(dedup_sequence_dir, subject))
ofile = os.path.join(dedup_sequence_subject_pool_dir, '{}_dedup_pool_vdj-nt.txt'.format(subject))
uniq_cmd = 'cat {} | sort | uniq > {}'.format(' '.join(input_sequence_files), ofile)
s = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
stdout, stderr = s.communicate()
```
## Deduplication (cross-subject pools)
Finally, we'd like to create unique clonotype files (with counts) for every groupwise combination of our 10 subjects. Each group can contain two or more subjects, meaning the total number of possible groupwise combinations is quite large. We'll use the `multiprocessing` package to parallelize the process which should speed things up substantially, although even with parallelization, this will take some time.
***NOTE:*** *The output from the following code blocks will be quite large (deduplicated clonotype files are >2TB in total, deduplicated sequence files are >20TB in total). Make sure you have sufficient storage and that the output paths below (`dedup_cross_subject_clonotype_pool_dir` and `dedup_cross_subject_sequence_pool_dir` are correct before starting.*
```
# directories
dedup_cross_subject_clonotype_pool_dir = './data/dedup_cross-subject_clonotype_pools/'
dedup_cross_subject_sequence_pool_dir = './data/dedup_cross-subject_sequence_pools/'
make_dir(dedup_cross_subject_clonotype_pool_dir)
make_dir(dedup_cross_subject_sequence_pool_dir)
# deduplicated subject pool files
dedup_clonotype_subject_files = [f for f in list_files(dedup_clonotype_subject_pool_dir) if '_dedup_pool_vj-aa.txt' in f]
dedup_sequence_subject_files = [f for f in list_files(dedup_sequence_subject_pool_dir) if '_dedup_pool_vdj-nt.txt' in f]
# every possible groupwise combination of subjects (2 or more subjects per group)
subject_combinations_by_size = {}
for size in range(2, 11):
subject_combinations_by_size[size] = [sorted(c) for c in itertools.combinations(subjects, size)]
def dedup_cross_subject_pool(subjects, files, output_dir):
files = sorted(list(set([f for f in dedup_subject_files if os.path.basename(f).split('_')[0] in subjects])))
output_file = os.path.join(output_dir, '{}_dedup_pool_vj-aa_with-counts.txt'.format('-'.join(subjects)))
uniq_cmd = 'cat {} | sort -T {} | uniq -c > {}'.format(' '.join(files), temp_dir, output_file)
p = sp.Popen(uniq_cmd, stdout=sp.PIPE, stderr=sp.PIPE, shell=True)
stdout, stderr = p.communicate()
```
### Clonotypes
```
p = mp.Pool(maxtasksperchild=1)
for size in sorted(subject_combinations_by_size.keys()):
subject_combinations = subject_combinations_by_size[size]
async_results = []
print('{}-subject pools:'.format(size))
progress_bar(0, len(subject_combinations))
for sub_comb in subject_combinations:
files = sorted(list(set([f for f in dedup_clonotype_subject_files if os.path.basename(f).split('_')[0] in sub_comb])))
async_results.append(p.apply_async(dedup_cross_subject_pool,
args=(sub_comb, files, dedup_cross_subject_clonotype_pool_dir)))
monitor_mp_jobs(async_results)
print('\n')
p.close()
p.join()
```
### Sequences
Just one more warning that the following code block will produce a very large amount of data (>20TB) and will take many hours to run even on a fairly robust server (an `m4.16xlarge` AWS EC2 instance, for example).
```
p = mp.Pool(maxtasksperchild=1)
for size in sorted(subject_combinations_by_size.keys()):
subject_combinations = subject_combinations_by_size[size]
async_results = []
print('{}-subject pools:'.format(size))
progress_bar(0, len(subject_combinations))
for sub_comb in subject_combinations:
files = sorted(list(set([f for f in dedup_sequence_subject_files if os.path.basename(f).split('_')[0] in sub_comb])))
async_results.append(p.apply_async(dedup_cross_subject_pool,
args=(sub_comb, files, dedup_cross_subject_sequence_pool_dir)))
monitor_mp_jobs(async_results)
print('\n')
p.close()
p.join()
```
| true |
code
| 0.258209 | null | null | null | null |
|
## In this Ipnyb , I'm going to build a model that can classify the Clothing Attribute Dataset which can be found at https://purl.stanford.edu/tb980qz1002 by the Category label. This is an image recognition and classification task . This dataset has only 1800 samples , out of which around 1100 samples have non - Nan values .
## ->Therefore , the approach to be followed will be :
## Use Transfer learning ( in this case VGGNet16 trained on Imagenet data ) to learn weights for our features
## -> Train our features against a classifier . Our choice of classifier here is SVM
```
import keras
import scipy.io as sio
import os
from keras.applications import imagenet_utils
from keras.preprocessing.image import img_to_array
from keras.preprocessing.image import load_img
import numpy as np
import h5py
from keras.utils.np_utils import to_categorical
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential
from keras.layers import Dropout, Flatten, Dense, Conv2D, MaxPooling2D
from keras import applications
from keras.optimizers import Adam
# Plot images
from keras.datasets import mnist
from matplotlib import pyplot
import pickle
#import cv2
image_dir = "/images"
label_file = "/labels/category_GT.mat"
```
## The first step is to load our data and labels . The data is stored in the images folder as folders. The label is stored in a matlab file . The name of the file , corresponds to its label index (plus 1 as image names start from 1) .
## To fix this , we first read all image file names in a list , sort the list and then parse files in ascending order, matching with the order of their labels¶
```
#get labels from the category label file for the task
mat_contents = sio.loadmat(os.getcwd() + label_file)['GT']
train_labels=np.array(mat_contents)
print "training labels loaded"
#print train_labels.shape
file_list = [f for f in os.listdir(os.getcwd() + image_dir) if os.path.isfile(os.path.join(os.getcwd() + image_dir, f))]
file_list.sort()
#get train data
inputShape = (150, 150)
img_list =[]
# for filename in os.listdir(os.getcwd() + image_dir):
for filename in file_list:
qualified_filename = os.getcwd() + image_dir + "/" + filename
#print filename
#print("[INFO] loading and pre-processing image...")
image = load_img(qualified_filename, target_size=inputShape)
#print (image.size)
image = img_to_array(image)
# our input image is now represented as a NumPy array of shape
# (inputShape[0], inputShape[1], 3)
pos = filename.split(".")[0]
pos = int(pos)
#print pos
#inserting the image at correct index that matches its label
img_list.insert(pos -1 , image)
print pos -1
print "training data loaded"
train_data = np.array(img_list)
print "shape of training data is " + str(train_data.shape)
#print img_list[0]
```
#### We'll do some EDA now. Because this data is labeled for multiple categories, we will explicitly look for Nan labels and filter them out . This reduces the number of available samples to 1104
```
#removing nan values
def get_filtered_data(train_data, train_labels):
print "in Filter Data method"
bool_label_array = np.isfinite(np.ravel(train_labels))
# print bool_label_array
train_data_filter = train_data[bool_label_array]
print train_data_filter.shape
train_labels_filter = train_labels[np.isfinite(train_labels)]
print train_labels_filter.shape
return (train_data_filter, train_labels_filter)
(train_data_filter, train_labels_filter) = get_filtered_data(train_data, train_labels)
print train_data.shape
```
#### It is important to see how the labels are distributed. If the data is biased towards one class, we might have to resample
```
# now let's see the distribution of classes
from collections import Counter
print Counter(train_labels_filter)
```
### The data seems to be distributed fairly , therefore we don't need to do class balancing . Now we'll write a function that shuffles our data , whilst maintaining the relative indexes of data and labels
```
def shuffle_data(x_train, y_train_zero):
idx = np.random.randint(len(y_train_zero), size=int(len(y_train_zero)))
y_train_zero = y_train_zero[idx]
x_train = x_train[idx, :]
return x_train, y_train_zero
```
### Before we start training our model , it is important to split our data into training and testing (eval) data . This enforces that the model never sees the test data before we start evaluation and helps us measure the effectiveness of our models .
### Since the size of out dataset is 1104, we're splitting it roughly into 75 - 25 ratio of train and test data . After splitting the data , we also write these to numpy files which can be loaded into memory using auxillary methods provided at the end of the notebook
### we shall use VGG16 to learn weights from the 16th layer of VGGNet for our images. Finally we'll save these features to a file
```
#load images
# dimensions of our images.
top_model_weights_path = 'bottleneck_fc_model.h5'
epochs = 5
batch_size = 16
train_data_filter = train_data_filter/255
def save_bottleneck_features_without_augmentation():
train_data_aug=[]
train_labels_aug=[]
model = applications.VGG16(include_top=False, weights='imagenet')
print "loading gen on training data"
print "generating augmentations of data"
bottleneck_features_train =model.predict(
train_data_filter, verbose =1)
return bottleneck_features_train, train_labels_filter
print "saving bottleneck features"
train_data_aug, train_labels_aug = save_bottleneck_features_without_augmentation()
#Compute one level accuaracy
def accuracy(matrix):
return (np.trace(matrix)) * 1.0 / np.sum(matrix)
print train_data_aug.shape
print train_labels_aug.shape
```
#### Visualizing our data : Let's see the first 9 images from the consolidated , as well as the evaluation and training datasets
```
def plot_first_n_images(img_list=img_list,n=9):
# load data
# create a grid of 3x3 images
for i in range(0, n):
pyplot.subplot(330 + 1 + i)
pyplot.imshow(img_list[i])
# show the plot
pyplot.show()
plot_first_n_images(train_data_filter)
```
### The features from VGGNet are very rich, but also very high in dimension ( 8192) . Since the size of our data is small, we shall be applying PCA to get the first 1000 more discriminative features. We chose the value 1000, after running hit and trial on a number of feature sizes to see which one produced the best evaluation metrics
```
#train_data_flat = np.reshape(train_data_aug,(8848, 67500) )
#print train_data_flat.shape
import numpy as np
import pandas as pd
import sklearn
from sklearn.model_selection import KFold, cross_val_score, GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
import pickle
# PCA
def pca(train_data_flat, num_features):
import numpy as np
from sklearn.decomposition import PCA
pca = PCA(n_components=num_features)
pca.fit(train_data_flat)
# print(pca.explained_variance_ratio_)
# print(pca.singular_values_)
train_data_flat_pca = pca.transform(train_data_flat)
print train_data_flat_pca.shape
return train_data_flat_pca
train_data_flat = np.reshape(train_data_aug, (1104, 8192))
train_data_flat_pca = pca(train_data_flat, 1000)
print train_data_aug.shape
print train_data_flat.shape
print train_data_flat_pca.shape
print train_labels_filter.shape
```
### We will now use the model with pre-trained weights and train them with a linear classifier . Since we've used augmentation with zero mean and PCA, we can't use Naive Bayes (doesn't take negative values) . The algorithms we'll test against are :
#### 1. Logistic Regression
#### 2. SVM ( Use grid search to find the best params and predict with the given parameters)
#### 3. Random Forest
```
#logistic regression
from sklearn import linear_model
from sklearn.metrics import f1_score
def lr(train_data, label, split):
logistic_clf = linear_model.LogisticRegression(penalty="l2", class_weight="balanced", max_iter=100, verbose=1)
logistic_clf.fit(train_data[:split], label[:split])
pred = logistic_clf.predict(train_data[split:])
print confusion_matrix(label[split:], pred)
print accuracy(confusion_matrix(label[split:], pred))
print f1_score(label[split:], pred, average= 'micro')
print f1_score(label[split:], pred, average= 'macro')
print f1_score(label[split:], pred, average= 'weighted')
# lr(train_data_flat, train_labels_aug, 850)
```
#### Running logistic Regression
```
train_data_flat_pca = pca(train_data_flat, 1000)
lr(train_data_flat_pca2, train_labels_aug2, 900)
train_data_flat_pca = pca(train_data_flat, 1104)
lr(train_data_flat_pca2, train_labels_aug2, 900)
```
#### running SVM, first selecting the best parameters using Grid Search then using those params to evaluate results
```
from sklearn.grid_search import GridSearchCV
def svm(train_data, train_labels_augmented):
from sklearn import svm
svc = svm.SVC(C=0.5, kernel='linear')
param_grid = [
{'C': [0.1, 0.5, 1, 5], 'kernel': ['linear']},
{'C': [0.1, 0.5, 1, 5], 'gamma': [0.001, 0.0001], 'kernel': ['rbf']},
]
kernel = ['linear', 'rbf']
Cs = [0.1, 0.3, 1]
clf = GridSearchCV(estimator=svc, param_grid=param_grid, cv=10, n_jobs=-1,)
clf.fit(train_data, train_labels_augmented)
print(clf.best_score_)
print(clf.best_estimator_.C)
print(clf.best_estimator_.kernel)
print(clf.best_params_)
return clf.cv_results_
# train_data_flat_pca = pca(train_data_flat, 1000)
cv_results_ = svm(train_data_flat_pca, train_labels_aug)
# train_data_flat_pca = pca(train_data_flat, 1104)
# lr(train_data_flat_pca, train_labels_aug, 850)
def svm_best(train_data, label, split):
from sklearn import svm
clf = svm.SVC(C=5, kernel='rbf', gamma = 0.001)
clf.fit(train_data[:split], label[:split])
pred = clf.predict(train_data[split:])
print confusion_matrix(label[split:], pred)
print accuracy(confusion_matrix(label[split:], pred))
print f1_score(label[split:], pred, average= 'micro')
print f1_score(label[split:], pred, average= 'macro')
print f1_score(label[split:], pred, average= 'weighted')
train_data_flat_pca2, train_labels_aug2 = shuffle_data(train_data_flat_pca, train_labels_aug)
svm_best(train_data_flat_pca2, train_labels_aug2, 900)
```
#### Running Random Forest using Grid Search to get classifier with best performance. Since the outputs in grid search don't do better than LR and SVM , we don't go forward with evaluation
```
def random_forest(X, y, split):
k_fold = 10
kf_total = KFold(n_splits=k_fold)
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=250,
random_state=0)
#estimators_list = [50, 100, 150, 250, 500, 800, 1000]
estimators_list = [50, 150, 500]
clf_forest = GridSearchCV(estimator=forest, param_grid=dict(n_estimators=estimators_list, warm_start=[True, False]), cv=k_fold, n_jobs=-1)
cms = [confusion_matrix(y[split:], clf_forest.fit(X[:split],y[:split]).predict(X[split:])) for train, test in kf_total.split(X)]
accuracies = []
for cm in cms:
accuracies.append(accuracy(cm))
print(accuracies)
print(np.mean(accuracies))
random_forest(train_data_flat_pca2, train_labels_aug2, 900)
```
# End of code in notebook
Auxillary methods to load data from pickle files
```
import pickle
file = open('train_data_1044.pkl', 'wb')
# Pickle dictionary using protocol 0.
pickle.dump(train_data_aug, file)
file.close()
file = open('train_label_v16_1044.pkl', 'wb')
# # Pickle dictionary using protocol 0.
pickle.dump(train_labels_filter, file)
file.close()
def plot_contours(ax, clf, xx, yy, **params):
"""Plot the decision boundaries for a classifier.
Parameters
----------
ax: matplotlib axes object
clf: a classifier
xx: meshgrid ndarray
yy: meshgrid ndarray
params: dictionary of params to pass to contourf, optional
"""
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
with open('train_data.pkl', 'rb') as f:
train_data_augmented = pickle.load(f)
train_data_augmented.shape,
with open('train_label.pkl', 'rb') as f:
train_labels_augmented = pickle.load(f)
train_labels_augmented.shape
```
| true |
code
| 0.606557 | null | null | null | null |
|
# Write summaries
TensorBoard helps us to summerize important parameters (such as wieghts, biases, activations, accuracy, loss, ...) to see how each parameter changes in each iteration of the training.
We can also see the images using TensorBoard
## Imports:
We will start with importing the needed libraries for our code.
```
# imports
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
```
## Input data:
For this tutorial we use the MNIST dataset. MNIST is a dataset of handwritten digits. If you are into machine learning, you might have heard of this dataset by now. MNIST is kind of benchmark of datasets for deep learning. One other reason that we use the MNIST is that it is easily accesible through Tensorflow. If you want to know more about the MNIST dataset you can check Yann Lecun's website.
We can easily import the dataset and see the size of training, test and validation set:
```
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
print("Size of:")
print("- Training-set:\t\t{}".format(len(mnist.train.labels)))
print("- Test-set:\t\t{}".format(len(mnist.test.labels)))
print("- Validation-set:\t{}".format(len(mnist.validation.labels)))
```
## Hyper-parameters:
Hyper-parameters are important parameters which are not learned by the network. So, we have to specify them externally. These parameters are constant and they are not learnable.
```
# hyper-parameters
logs_path = "./logs/write_summaries" # path to the folder that we want to save the logs for TensorBoard
learning_rate = 0.001 # The optimization learning rate
epochs = 10 # Total number of training epochs
batch_size = 100 # Training batch size
display_freq = 100 # Frequency of displaying the training results
# Network Parameters
# We know that MNIST images are 28 pixels in each dimension.
img_h = img_w = 28
# Images are stored in one-dimensional arrays of this length.
img_size_flat = img_h * img_w
# Number of classes, one class for each of 10 digits.
n_classes = 10
# number of units in the first hidden layer
h1 = 200
```
## Graph:
Like before, we start by constructing the graph. But, we need to define some functions that we need rapidly in our code.
To visualize the parameters, we will use ```tf.summary``` class to write the summaries of parameters.
Notice ```tf.summary.histogram()```__ functions added to the code.
```
# weight and bais wrappers
def weight_variable(name, shape):
"""
Create a weight variable with appropriate initialization
:param name: weight name
:param shape: weight shape
:return: initialized weight variable
"""
initer = tf.truncated_normal_initializer(stddev=0.01)
return tf.get_variable('W_' + name,
dtype=tf.float32,
shape=shape,
initializer=initer)
def bias_variable(name, shape):
"""
Create a bias variable with appropriate initialization
:param name: bias variable name
:param shape: bias variable shape
:return: initialized bias variable
"""
initial = tf.constant(0., shape=shape, dtype=tf.float32)
return tf.get_variable('b_' + name,
dtype=tf.float32,
initializer=initial)
def fc_layer(x, num_units, name, use_relu=True):
"""
Create a fully-connected layer
:param x: input from previous layer
:param num_units: number of hidden units in the fully-connected layer
:param name: layer name
:param use_relu: boolean to add ReLU non-linearity (or not)
:return: The output array
"""
with tf.variable_scope(name):
in_dim = x.get_shape()[1]
W = weight_variable(name, shape=[in_dim, num_units])
tf.summary.histogram('W', W)
b = bias_variable(name, [num_units])
tf.summary.histogram('b', b)
layer = tf.matmul(x, W)
layer += b
if use_relu:
layer = tf.nn.relu(layer)
return layer
```
Now that we have our helper functions we can create our graph.
To visualize some scalar values (such as loss and accuracy) we will use __```tf.summary.scalar()```__.
To visualize some images we will use __```tf.summary.image()```__.
Finally, to merge all the summeries, we will use __```tf.summary.merge_all()```__ function.
```
# Create graph
# Placeholders for inputs (x), outputs(y)
with tf.variable_scope('Input'):
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='X')
tf.summary.image('input_image', tf.reshape(x, (-1, img_w, img_h, 1)), max_outputs=5)
y = tf.placeholder(tf.float32, shape=[None, n_classes], name='Y')
fc1 = fc_layer(x, h1, 'Hidden_layer', use_relu=True)
output_logits = fc_layer(fc1, n_classes, 'Output_layer', use_relu=False)
# Define the loss function, optimizer, and accuracy
with tf.variable_scope('Train'):
with tf.variable_scope('Loss'):
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=output_logits), name='loss')
tf.summary.scalar('loss', loss)
with tf.variable_scope('Optimizer'):
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate, name='Adam-op').minimize(loss)
with tf.variable_scope('Accuracy'):
correct_prediction = tf.equal(tf.argmax(output_logits, 1), tf.argmax(y, 1), name='correct_pred')
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32), name='accuracy')
tf.summary.scalar('accuracy', accuracy)
# Network predictions
cls_prediction = tf.argmax(output_logits, axis=1, name='predictions')
# Initializing the variables
init = tf.global_variables_initializer()
merged = tf.summary.merge_all()
```
## Train:
As soon as the graph is created, we can run it on a session.
A ```tf.Session()``` is as good as it's runtime. As soon as the cell is run, the session will be ended and we will loose all the information. So. we will define an _InteractiveSession_ to keep the parameters for testing.
__NOTE:__ Each time that we run our session, we have to pass the _```merged```_ variable (which we merged all the summerize in) and we have to add the summaries in our __```tf.summary.FileWriter```__ class using __```add_summary```__ method in our class.
__NOTE:__ We can let the summary writer class know that these summaries are for which step by passing the _```step```_ which we are in.
```
# Launch the graph (session)
sess = tf.InteractiveSession() # using InteractiveSession instead of Session to test network in separate cell
sess.run(init)
train_writer = tf.summary.FileWriter(logs_path, sess.graph)
num_tr_iter = int(mnist.train.num_examples / batch_size)
global_step = 0
for epoch in range(epochs):
print('Training epoch: {}'.format(epoch + 1))
for iteration in range(num_tr_iter):
batch_x, batch_y = mnist.train.next_batch(batch_size)
global_step += 1
# Run optimization op (backprop)
feed_dict_batch = {x: batch_x, y: batch_y}
_, summary_tr = sess.run([optimizer, merged], feed_dict=feed_dict_batch)
train_writer.add_summary(summary_tr, global_step)
if iteration % display_freq == 0:
# Calculate and display the batch loss and accuracy
loss_batch, acc_batch = sess.run([loss, accuracy],
feed_dict=feed_dict_batch)
print("iter {0:3d}:\t Loss={1:.2f},\tTraining Accuracy={2:.01%}".
format(iteration, loss_batch, acc_batch))
# Run validation after every epoch
feed_dict_valid = {x: mnist.validation.images, y: mnist.validation.labels}
loss_valid, acc_valid = sess.run([loss, accuracy], feed_dict=feed_dict_valid)
print('---------------------------------------------------------')
print("Epoch: {0}, validation loss: {1:.2f}, validation accuracy: {2:.01%}".
format(epoch + 1, loss_valid, acc_valid))
print('---------------------------------------------------------')
```
## Test:
Now that the model is trained. It is time to test our model.
We will define some helper functions to plot some of the images and their corresponding predicted and true classes. We will also visualize some of the misclassified samples to see why the Neural Net failed to classify them correctly.
```
def plot_images(images, cls_true, cls_pred=None, title=None):
"""
Create figure with 3x3 sub-plots.
:param images: array of images to be plotted, (9, img_h*img_w)
:param cls_true: corresponding true labels (9,)
:param cls_pred: corresponding true labels (9,)
"""
fig, axes = plt.subplots(3, 3, figsize=(9, 9))
fig.subplots_adjust(hspace=0.3, wspace=0.3)
img_h = img_w = np.sqrt(images.shape[-1]).astype(int)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(images[i].reshape((img_h, img_w)), cmap='binary')
# Show true and predicted classes.
if cls_pred is None:
ax_title = "True: {0}".format(cls_true[i])
else:
ax_title = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
ax.set_title(ax_title)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
if title:
plt.suptitle(title, size=20)
plt.show()
def plot_example_errors(images, cls_true, cls_pred, title=None):
"""
Function for plotting examples of images that have been mis-classified
:param images: array of all images, (#imgs, img_h*img_w)
:param cls_true: corresponding true labels, (#imgs,)
:param cls_pred: corresponding predicted labels, (#imgs,)
"""
# Negate the boolean array.
incorrect = np.logical_not(np.equal(cls_pred, cls_true))
# Get the images from the test-set that have been
# incorrectly classified.
incorrect_images = images[incorrect]
# Get the true and predicted classes for those images.
cls_pred = cls_pred[incorrect]
cls_true = cls_true[incorrect]
# Plot the first 9 images.
plot_images(images=incorrect_images[0:9],
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9],
title=title)
# Test the network after training
# Accuracy
feed_dict_test = {x: mnist.test.images, y: mnist.test.labels}
loss_test, acc_test = sess.run([loss, accuracy], feed_dict=feed_dict_test)
print('---------------------------------------------------------')
print("Test loss: {0:.2f}, test accuracy: {1:.01%}".format(loss_test, acc_test))
print('---------------------------------------------------------')
# Plot some of the correct and misclassified examples
cls_pred = sess.run(cls_prediction, feed_dict=feed_dict_test)
cls_true = np.argmax(mnist.test.labels, axis=1)
plot_images(mnist.test.images, cls_true, cls_pred, title='Correct Examples')
plot_example_errors(mnist.test.images, cls_true, cls_pred, title='Misclassified Examples')
```
After we are finished the testing, we will close the session to free the memory.
```
# close the session after you are done with testing
sess.close()
```
At this step our coding is done. We have also plotted the accuarcy and some examples. But to inspect more in our network, we can run the __Tensorboard__. Open your terminal and type:
```bash
tensorboard --logdir=logs/write_summaries --host localhost
```
and Open the generated link in your browser.
__NOTE:__ Don't forget to activate your environment !!!
You can see the images, scalars and histograms in added tabs:
__Image summaries:__
<img src="https://github.com/easy-tensorflow/easy-tensorflow/raw/master/4_Tensorboard/Tutorials/files/image_summaries.png">
__Scalar summaries:__
<img src="https://github.com/easy-tensorflow/easy-tensorflow/raw/master/4_Tensorboard/Tutorials/files/scalar_summaries.png">
__Histogram summaries:__
<img src="https://github.com/easy-tensorflow/easy-tensorflow/raw/master/4_Tensorboard/Tutorials/files/hist_summaries.png">
Thanks for reading! If you have any question or doubt, feel free to leave a comment in our [website](http://easy-tensorflow.com/).
| true |
code
| 0.759415 | null | null | null | null |
|
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
```
## Sigmoid function
```
def sigmoid(x):
return 1 / (1+np.exp(-x))
x = np.linspace(-10,10,100)
plt.plot(x, sigmoid(x), 'r', label='linspace(-10,10,10)')
plt.grid()
plt.title('Sigmoid Function')
plt.text(4, 0.8, r'$\sigma(x)=\frac{1}{1+e^{-x}}$', fontsize=15)
plt.xlabel('X')
plt.ylabel(r'$\sigma(x)$')
bx = [-10,10]
by = [.5, .5]
plt.plot(x, sigmoid(x), 'r', label='sigmoid function')
plt.plot(bx, by, 'b', label='boundary')
plt.grid()
plt.title('Sigmoid function with threshold')
plt.text(4, 0.8, r'$\sigma(x)=\frac{1}{1+e^{-x}}$', fontsize=15)
plt.xlabel('X')
plt.ylabel(r'$\sigma(x)$')
```
## Logistic Regression
```
import sklearn
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
```
## We only consider 2 classes here, so we need to drop one class. We can use pandas to do that
```
iris = datasets.load_iris()
iris_df = pd.DataFrame(data= np.c_[iris['data'], iris['target']], columns= iris['feature_names'] + ['target'])
iris_df = iris_df.astype({'target': int})
iris_df = iris_df[iris_df['target'] != 2]
iris_df.head()
iris_df['target'].value_counts()
X = iris_df.drop(iris_df.columns[[4]], axis=1)
y = iris_df.drop(iris_df.columns[[0,1,2,3]], axis=1)
X.head()
y.head()
def intialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w, b
def sigmoid(x):
return 1 / (1+np.exp(-x))
def trainModel(w, b, X, Y, learning_rate=0.0001, no_iterations=5001):
costs = []
m = X.shape[0]
for i in range(no_iterations):
# map the result to probability by sigmoid function
a = sigmoid(np.dot(w,X.T)+b)
# compute the neg log-likelihood
cost = (-1/m)*(np.sum((Y.T*np.log(a)) + ((1-Y.T)*(np.log(1-a)))))
# calculate the gradient
dw = (1/m)*(np.dot(X.T, (a-Y.T).T))
db = (1/m)*(np.sum(a-Y.T))
# update w, b
w = w - learning_rate*dw.T
b = b - learning_rate*db
if i%100==0:
costs.append(cost)
if i%500==0:
print("%i iteration cost: %f" %(i, cost))
# final result
coef = {"w": w, "b": b}
return coef, costs
def runModel(X_tr, y_tr, X_te, y_te, thershold=0.5):
n_features = X_tr.shape[1]
w, b = intialization(n_features)
coef, costs = trainModel(w, b, X_tr, y_tr)
w = coef['w']
b = coef['b']
y_tr_hat = np.array(sigmoid(np.dot(w,X_tr.T)+b)>thershold).astype(int)
y_te_hat = np.array(sigmoid(np.dot(w,X_te.T)+b)>thershold).astype(int)
print('Optimized weights:', w)
print('Optimized intercept (b):',b)
print('Training Accuracy',accuracy_score(y_tr_hat.T, y_tr))
print('Test Accuracy',accuracy_score(y_te_hat.T, y_te))
return costs
X_tr, X_te, y_tr, y_te = train_test_split(X, y, test_size=0.2, random_state=2018)
y_tr = y_tr.as_matrix()
y_ts = y_te.as_matrix()
costs = runModel(X_tr, y_tr, X_te, y_te)
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title('Cost reduction over time')
```
| true |
code
| 0.464659 | null | null | null | null |
|
```
# HIDDEN
from datascience import *
import numpy as np
path_data = '../../../../data/'
import matplotlib
matplotlib.use('Agg', warn=False)
%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import warnings
warnings.simplefilter(action="ignore", category=FutureWarning)
from urllib.request import urlopen
import re
def read_url(url):
return re.sub('\\s+', ' ', urlopen(url).read().decode())
# HIDDEN
# Read two books, fast (again)!
huck_finn_url = 'https://www.inferentialthinking.com/chapters/01/3/huck_finn.txt'
huck_finn_text = read_url(huck_finn_url)
huck_finn_chapters = huck_finn_text.split('CHAPTER ')[44:]
little_women_url = 'https://www.inferentialthinking.com/chapters/01/3/little_women.txt'
little_women_text = read_url(little_women_url)
little_women_chapters = little_women_text.split('CHAPTER ')[1:]
```
In some situations, the relationships between quantities allow us to make predictions. This text will explore how to make accurate predictions based on incomplete information and develop methods for combining multiple sources of uncertain information to make decisions.
As an example of visualizing information derived from multiple sources, let us first use the computer to get some information that would be tedious to acquire by hand. In the context of novels, the word "character" has a second meaning: a printed symbol such as a letter or number or punctuation symbol. Here, we ask the computer to count the number of characters and the number of periods in each chapter of both *Huckleberry Finn* and *Little Women*.
```
# In each chapter, count the number of all characters;
# call this the "length" of the chapter.
# Also count the number of periods.
chars_periods_huck_finn = Table().with_columns([
'Huck Finn Chapter Length', [len(s) for s in huck_finn_chapters],
'Number of Periods', np.char.count(huck_finn_chapters, '.')
])
chars_periods_little_women = Table().with_columns([
'Little Women Chapter Length', [len(s) for s in little_women_chapters],
'Number of Periods', np.char.count(little_women_chapters, '.')
])
```
Here are the data for *Huckleberry Finn*. Each row of the table corresponds to one chapter of the novel and displays the number of characters as well as the number of periods in the chapter. Not surprisingly, chapters with fewer characters also tend to have fewer periods, in general – the shorter the chapter, the fewer sentences there tend to be, and vice versa. The relation is not entirely predictable, however, as sentences are of varying lengths and can involve other punctuation such as question marks.
```
chars_periods_huck_finn
```
Here are the corresponding data for *Little Women*.
```
chars_periods_little_women
```
You can see that the chapters of *Little Women* are in general longer than those of *Huckleberry Finn*. Let us see if these two simple variables – the length and number of periods in each chapter – can tell us anything more about the two books. One way for us to do this is to plot both sets of data on the same axes.
In the plot below, there is a dot for each chapter in each book. Blue dots correspond to *Huckleberry Finn* and gold dots to *Little Women*. The horizontal axis represents the number of periods and the vertical axis represents the number of characters.
```
plots.figure(figsize=(6, 6))
plots.scatter(chars_periods_huck_finn.column(1),
chars_periods_huck_finn.column(0),
color='darkblue')
plots.scatter(chars_periods_little_women.column(1),
chars_periods_little_women.column(0),
color='gold')
plots.xlabel('Number of periods in chapter')
plots.ylabel('Number of characters in chapter');
```
The plot shows us that many but not all of the chapters of *Little Women* are longer than those of *Huckleberry Finn*, as we had observed by just looking at the numbers. But it also shows us something more. Notice how the blue points are roughly clustered around a straight line, as are the yellow points. Moreover, it looks as though both colors of points might be clustered around the *same* straight line.
Now look at all the chapters that contain about 100 periods. The plot shows that those chapters contain about 10,000 characters to about 15,000 characters, roughly. That's about 100 to 150 characters per period.
Indeed, it appears from looking at the plot that on average both books tend to have somewhere between 100 and 150 characters between periods, as a very rough estimate. Perhaps these two great 19th century novels were signaling something so very familiar us now: the 140-character limit of Twitter.
| true |
code
| 0.435121 | null | null | null | null |
|
# Understanding Structured Point Clouds (SPCs)
Structured Point Clouds (SPC) is a differentiable, GPU-compatible, spatial-data structure which efficiently organizes 3D geometrically sparse information in a very compressed manner.

<b> When should you use it? </b>
* The SPC data structure is very general, which makes it <mark>a suitable building block for a variety of applications</mark>.
* Examples include:
* [Representation & rendering of implicit 3D surfaces](https://nv-tlabs.github.io/nglod/)
* Convolutions on voxels, meshes and point clouds
* and more..
SPCs are easily convertible from point clouds and meshes, and can be optimized to represent encoded neural implicit fields.
<b> In this tutorial you will learn to: </b>
1. Construct a SPC from triangular meshes and point clouds.
2. Visualize the SPC using ray-tracing functionality.
3. Become familiar with the internals of kaolin's SPC data structure
Practitioners are encouraged to view the [documentation](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.spc.html?highlight=spc#kaolin-ops-spc) for additional details about the internal workings of this data structure. <br>
This tutorial is best run locally to observe the full output.
## Setup
This tutorial assumes a minimal version of [kaolin v0.10.0](https://kaolin.readthedocs.io/en/latest/notes/installation.html). <br>
In addition, the following libraries are required for this tutorial:
```
!pip install -q matplotlib
!pip install -q termcolor
!pip install -q ipywidgets
from PIL import Image
import torch
import torch.nn.functional as F
import numpy as np
from matplotlib import pyplot as plt
import ipywidgets as widgets
from termcolor import colored
import kaolin as kal
from spc_formatting import describe_octree, color_by_level
```
To study the mechanics of the SPC structure, we'll need some auxilary functions (you may skip for now): <br>
```
def describe_tensor(torch_tensor, tensor_label, with_shape, with_content):
if with_shape:
print(f'"{tensor_label}" is a {torch_tensor.dtype} tensor of size {tuple(torch_tensor.shape)}')
if with_content:
print(f'Raw Content: \n{torch_tensor.cpu().numpy()}')
def convert_texture_to_torch_sample_format(texture):
""" Convert to (1, C, Tex-H, Tex-W) format """
return texture.unsqueeze(0).type(sampled_uvs.dtype).permute(0, 3, 1, 2)
```
### Preliminaries: Load Mesh and sample as Point Cloud
Throughout this tutorial we'll be using a triangular mesh as an example. <br>
First, we import the mesh using kaolin:
```
# Path to some .obj file with textures
mesh_path = "../samples/colored_sphere.obj"
mesh = kal.io.obj.import_mesh(mesh_path, with_materials=True)
print(f'Loaded mesh with {len(mesh.vertices)} vertices, {len(mesh.faces)} faces and {len(mesh.materials)} materials.')
```
Next, we'll oversample the mesh faces to make sure our SPC structure is densely populated and avoids "holes"
at the highest resolution level.
Note that our mesh face-vertices are mapped to some texture coordinates.
Luckily, kaolin has a `sample_points` function that will take care of interpolating these coordinates for us.
The sampled vertices will be returned along with the interpolated uv coordinates as well:
```
# Sample points over the mesh surface
num_samples = 1000000
# Load the uv coordinates per face-vertex like "features" per face-vertex,
# which sample_points will interpolate for new sample points.
# mesh.uvs is a tensor of uv coordinates of shape (#num_uvs, 2), which we consider as "features" here
# mesh.face_uvs_idx is a tensor of shape (#faces, 3), indexing which feature to use per-face-per-vertex
# Therefore, face_features will be of shape (#faces, 3, 2)
face_features = mesh.uvs[mesh.face_uvs_idx]
# Kaolin assumes an exact batch format, we make sure to convert from:
# (V, 3) to (1, V, 3)
# (F, 3, 2) to (1, F, 3, 2)
# where 1 is the batch size
batched_vertices = mesh.vertices.unsqueeze(0)
batched_face_features = face_features.unsqueeze(0)
# sample_points is faster on cuda device
batched_vertices = batched_vertices.cuda()
faces = mesh.faces.cuda()
batched_face_features = batched_face_features.cuda()
sampled_verts, _, sampled_uvs = kal.ops.mesh.trianglemesh.sample_points(batched_vertices,
faces,
num_samples=num_samples,
face_features=batched_face_features)
print(f'Sampled {sampled_verts.shape[1]} points over the mesh surface:')
print(f'sampled_verts is a tensor with batch size {sampled_verts.shape[0]},',
f'with {sampled_verts.shape[1]} points of {sampled_verts.shape[2]}D coordinates.')
print(f'sampled_uvs is a tensor with batch size {sampled_uvs.shape[0]},',
f'representing the corresponding {sampled_uvs.shape[1]} {sampled_uvs.shape[2]}D UV coordinates.')
```
To finish our setup, we'll want to use the UV coordinates to perform texture sampling and obtain the RGB color of each point we have:
```
# Convert texture to sample-compatible format
diffuse_color = mesh.materials[0]['map_Kd'] # Assumes a shape with a single material
texture_maps = convert_texture_to_torch_sample_format(diffuse_color) # (1, C, Th, Tw)
texture_maps = texture_maps.cuda()
# Sample colors according to uv-coordinates
sampled_uvs = kal.render.mesh.utils.texture_mapping(texture_coordinates=sampled_uvs,
texture_maps=texture_maps,
mode='nearest')
# Unbatch
vertices = sampled_verts.squeeze(0)
vertex_colors = sampled_uvs.squeeze(0)
# Normalize to [0,1]
vertex_colors /= 255
print(f'vertices is a tensor of {vertices.shape}')
print(f'vertex_colors is a tensor of {vertices.shape}')
```
## 1. Create & Visualize SPC
### Create the SPC
We start by converting our Point Cloud of continuous 3D coordinates to a Structured Point Cloud. <br>
`unbatched_pointcloud_to_spc` will return a `Spc` object, a data class holding all Structured Point Cloud related information. <br>
At the core of this object, points are kept in quantized coordinates using a compressed octree. <br>
The returned object contains multiple low-level data structures which we'll explore in details in the next section.
For now keep in mind that its important fields: `octree`, `features`, `point_hierarchy`, `pyramid` and `prefix`, represent our data structure.
When constructing a `Spc` object, the resolution of quantized coordinates can be controlled by the octree `level` arg, such that: $resolution=2^{level}$
```
# Our SPC will contain a hierarchy of multiple levels
level = 3
spc = kal.ops.conversions.pointcloud.unbatched_pointcloud_to_spc(vertices, level, features=vertex_colors)
```
### Set-up the camera
The SPC data structure can be efficiently visualized using ray-tracing ops. <br>
Note that SPC also supports differentiable rendering. In this tutorial we'll limit our demonstration to rendering this data structure efficiently. <br>
Differentiable ray-tracing is beyond the scope of this guide, and will be covered in future tutorials.
To begin our ray tracing implementation, we'll first need to set up our camera view and [generate some rays](https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-generating-camera-rays). <br>
We'll assume a pinhole camera model, and use the `look_at` function, which sets up a camera view originating at position `camera_from`, looking towards `camera_to`. <br>
`width`, `height`, `mode` and `fov` will determine the dimensions of our view.
```
def _normalized_grid(width, height, device='cuda'):
"""Returns grid[x,y] -> coordinates for a normalized window.
Args:
width, height (int): grid resolution
"""
# These are normalized coordinates
# i.e. equivalent to 2.0 * (fragCoord / iResolution.xy) - 1.0
window_x = torch.linspace(-1, 1, steps=width, device=device) * (width / height)
window_y = torch.linspace(1,- 1, steps=height, device=device)
coord = torch.stack(torch.meshgrid(window_x, window_y)).permute(1,2,0)
return coord
def look_at(camera_from, camera_to, width, height, mode='persp', fov=90.0, device='cuda'):
"""Vectorized look-at function, returns an array of ray origins and directions
URL: https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/lookat-function
"""
camera_origin = torch.FloatTensor(camera_from).to(device)
camera_view = F.normalize(torch.FloatTensor(camera_to).to(device) - camera_origin, dim=0)
camera_right = F.normalize(torch.cross(camera_view, torch.FloatTensor([0,1,0]).to(device)), dim=0)
camera_up = F.normalize(torch.cross(camera_right, camera_view), dim=0)
coord = _normalized_grid(width, height, device=device)
ray_origin = camera_right * coord[...,0,np.newaxis] * np.tan(np.radians(fov/2)) + \
camera_up * coord[...,1,np.newaxis] * np.tan(np.radians(fov/2)) + \
camera_origin + camera_view
ray_origin = ray_origin.reshape(-1, 3)
ray_offset = camera_view.unsqueeze(0).repeat(ray_origin.shape[0], 1)
if mode == 'ortho': # Orthographic camera
ray_dir = F.normalize(ray_offset, dim=-1)
elif mode == 'persp': # Perspective camera
ray_dir = F.normalize(ray_origin - camera_origin, dim=-1)
ray_origin = camera_origin.repeat(ray_dir.shape[0], 1)
else:
raise ValueError('Invalid camera mode!')
return ray_origin, ray_dir
```
Now generate some rays using the functions we've just created:
```
# ray_o and ray_d ~ torch.Tensor (width x height, 3)
# represent rays origin and direction vectors
ray_o, ray_d = look_at(camera_from=[-2.5,2.5,-2.5],
camera_to=[0,0,0],
width=1024,
height=1024,
mode='persp',
fov=30,
device='cuda')
print(f'Total of {ray_o.shape[0]} rays generated.')
```
### Render
We're now ready to perform the actual ray tracing. <br>
kaolin will "shoot" the rays for us, and perform an efficient intersection test between each ray and cell within the SPC structure. <br>
In kaolin terminology, <b>nuggets</b> are "ray-cell intersections" (or rather "ray-point" intersections).
<b>nuggets </b> are of represented by a structure of two tensors: `nugs_ridx` and `nugs_pidx`, <br>which form together pairs of `(index_to_ray, index_to_points)`. <br>
Both tensors are 1-dimensional tensors of shape (`#num_intersection`,).
```
octree, features = spc.octrees, spc.features
point_hierarchy, pyramid, prefix = spc.point_hierarchies, spc.pyramids[0], spc.exsum
nugs_ridx, nugs_pidx, depth = kal.render.spc.unbatched_raytrace(octree, point_hierarchy, pyramid, prefix, ray_o, ray_d, level)
print(f'Total of {nugs_ridx.shape[0]} nuggets were traced.\n')
```
Since we're assuming here our surface is opaque, for each ray, we only care about the <b>nugget</b>
closest to the camera. <br>
Note that per "ray-pack", the returned <b>nuggets</b> are already sorted by depth. <br>
The method below returns a boolean mask which specifies which <b>nuggets</b> represent a "first-hit".
```
masked_nugs = kal.render.spc.mark_pack_boundaries(nugs_ridx)
nugs_ridx = nugs_ridx[masked_nugs]
nugs_pidx = nugs_pidx[masked_nugs]
```
Finally, for each ray that hit the surface, a corresponding "first-hit" nugget exists. <br>
```
# 1. We initialize an empty canvas.
image = torch.ones_like(ray_o)
# 2. We'll query all first-hit nuggets to obtain their corresponding point-id (which cell they hit in the SPC).
ridx = nugs_ridx.long()
pidx = nugs_pidx.long() - pyramid[1,level]
# 3. We'll query the features auxilary structure to obtain the color.
# 4. We set each ray value as the corresponding nugget color.
image[ridx] = features[pidx]
image = image.reshape(1024, 1024, 3)
```
Putting it all together, we write our complete `render()` function and display the trace using matplotlib:
```
import matplotlib.pyplot as plt
def render(level):
""" Create & render an image """
spc = kal.ops.conversions.pointcloud.unbatched_pointcloud_to_spc(vertices, level, vertex_colors)
octree, features, point_hierarchy, pyramid, prefix = spc.octrees, spc.features, spc.point_hierarchies, spc.pyramids[0], spc.exsum
nugs_ridx, nugs_pidx, depth = kal.render.spc.unbatched_raytrace(octree, point_hierarchy, pyramid, prefix, ray_o, ray_d, level)
masked_nugs = kal.render.spc.mark_pack_boundaries(nugs_ridx)
nugs_ridx = nugs_ridx[masked_nugs]
nugs_pidx = nugs_pidx[masked_nugs]
ridx = nugs_ridx.long()
pidx = nugs_pidx.long() - pyramid[1,level]
image = torch.ones_like(ray_o)
image[ridx] = features[pidx]
image = image.reshape(1024, 1024, 3)
return image
fig = plt.figure(figsize=(20,10))
# Render left image of level 3 SPC
image1 = render(level=3)
image1 = image1.cpu().numpy().transpose(1,0,2)
ax = fig.add_subplot(1, 2, 1)
ax.set_title("level 3", fontsize=26)
ax.axis('off')
plt.imshow(image1)
# Render right image of level 5 SPC
image2 = render(level=8)
image2 = image2.cpu().numpy().transpose(1,0,2)
ax = fig.add_subplot(1, 2, 2)
ax.set_title("level 5", fontsize=26)
ax.axis('off')
plt.imshow(image2)
plt.show()
```
Finally, putting it all together, we may also construct the following interactive demo:
```
def update_demo(widget_spc_level):
image = render(widget_spc_level)
plt.figure(figsize=(10,10))
plt.axis('off')
plt.imshow(image.cpu().numpy().transpose(1,0,2))
plt.show()
def show_interactive_demo(max_level=10):
start_value = min(7, max_level)
widget_spc_level = widgets.IntSlider(value=start_value, min=1, max=max_level, step=1, orientation='vertical',
description='<h5>SPC Level:</h5>', disabled=False,
layout=widgets.Layout(height='100%',))
out = widgets.interactive_output(update_demo, {'widget_spc_level': widget_spc_level})
display(widgets.HBox([widgets.VBox([widget_spc_level]), out]))
show_interactive_demo()
```
## 2. SPC internals
In this section we'll explore the various components that make up the [SPC](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.spc.html?highlight=spc#structured-point-clouds) we've just created. <br>
We'll learn how data is stored, and how to view stored data.
### Boilerplate code
Let's rebuild our SPC object with fewer levels, that will make the internals easier to study. <br>
You may customize the number of levels and compare how the output changes.
```
level = 3
spc = kal.ops.conversions.pointcloud.unbatched_pointcloud_to_spc(vertices, level, features=vertex_colors)
```
Ok, let's see what we've got.
### octree
The first field we'll look into, `octrees`, keeps the entire geometric structure in a compressed manner. <br>
This is a huge advantage, as this structure is now small enough to fit our sparse data, which makes it very efficient.
```
octree = spc.octrees
describe_tensor(torch_tensor=octree, tensor_label='octree', with_shape=True, with_content=True)
print(f'\n"octrees" represents a hierarchy of {len(octree)} octree nodes.')
print(f"Let's have a look at the binary representation and what it means:\n")
describe_octree(octree, level)
text_out = widgets.Output(layout={'border': '0.2px dashed black'})
with text_out:
print('How to read the content of octrees?')
print('- Each entry represents a single octree of 8 cells --> 8 bits.')
print('- The bit position determines the cell index, in Morton Order.')
print('- The bit value determines if the cell is occupied or not.')
print(f'- If a cell is occupied, an additional octree may be generated in the next level, up till level {level}.')
print('For example, an entry of 00000001 is a single level octree, where only the bottom-left most cell is occupied.')
display(widgets.HBox([text_out]))
```
##### Order of octants within partitioned cells

Notice the field is named in plural.
That's because kaolin can batch multiple instances of octrees together within the same object. <br>
```
print(spc.batch_size)
```
Pay attention that `octrees` uses [packed representation](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.batch.html?highlight=packed#packed), meaning, there is no explicit batch dimension. <br>
Instead, we track the length of each octree instance in a separate field:
```
octrees_lengths = spc.lengths
describe_tensor(torch_tensor=octrees_lengths, tensor_label='lengths', with_shape=True, with_content=True)
text_out = widgets.Output(layout={'border': '0.2px dashed black'})
with text_out:
print('How to read the content of lengths?')
print(f'- This Spc stores a batch of {len(spc.lengths)} octrees.')
print(f'- The first octree is represented by {spc.lengths[0]} non-leaf cells.')
print(f'- Therefore the information of the first octree is kept in bytes 0-{spc.lengths[0]-1} of the octrees field.')
display(widgets.HBox([text_out]))
```
Advanced users who prefer a non object-oriented lower-level api can also use the following functionality which `kal.ops.conversions.pointcloud.unbatched_pointcloud_to_spc` employs under the hood:
```
from kaolin.ops.spc.points import quantize_points, points_to_morton, morton_to_points, unbatched_points_to_octree
# Construct a batch of 2 octrees. For brevity, we'll use the same ocuupancy data for both.
# 1. Convert continous to quantized coordinates
# 2. Build the octrees
points1 = quantize_points(vertices.contiguous(), level=2)
octree1 = unbatched_points_to_octree(points1, level=2)
points2 = quantize_points(vertices.contiguous(), level=3)
octree2 = unbatched_points_to_octree(points2, level=3)
# Batch 2 octrees together. For packed representations, this is just concatenation.
octrees = torch.cat((octree1, octree2), dim=0)
lengths = torch.tensor([len(octree1), len(octree2)], dtype=torch.int32)
describe_tensor(torch_tensor=octrees, tensor_label='octrees', with_shape=True, with_content=True)
print('')
describe_tensor(torch_tensor=lengths, tensor_label='lengths', with_shape=True, with_content=True)
```
These structures form the bare minimum required to shift back to high-level api and construct a Spc object:
```
kal.rep.spc.Spc(octrees, lengths)
```
### features
So far we've lookied into how Structured Point Clouds keep track of occupancy. <br>
Next we'll study how they keep track of features.
The `features` field contains features information per cell.
```
features = spc.features
def paint_features(features):
plt.figure(figsize=(10,10))
plt.axis('off')
plt.imshow(features.cpu().numpy()[None])
plt.show()
print('In this tutorial, cell features are RGB colors:')
describe_tensor(torch_tensor=features, tensor_label='features', with_shape=True, with_content=False)
paint_features(features)
text_out = widgets.Output(layout={'border': '0.2px dashed black'})
with text_out:
print('How to read the content of features?')
print(f'- We keep features only for leaf cells, a total of {features.shape[0]}.')
print(f'- The number of leaf cells can be obtained by summarizing the "1" bits at level {spc.max_level},\n' \
' the last level of the octree.')
print(f'- The dimensionality of each attribute is {features.shape[1]} (e.g: RGB channels)')
print('\nReminder - the highest level of occupancy octree is:')
describe_octree(spc.octrees, level, limit_levels=[spc.max_level])
display(widgets.HBox([text_out]))
```
### pyramid & exsum
Since the occupancy information is [compressed](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.spc.html?highlight=spc#octree) and [packed](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.batch.html?highlight=packed#packed), accessing level-specific information consistently involves
cumulative summarization of the number of "1" bits. <br>
It makes sense to calculate this information once and then cache it. <br>
The `pyramid` field does exactly that: it keeps summarizes the number of occupied cells per level, and their cumsum, for fast level-indexing.
```
# A pyramid is kept per octree in the batch.
# We'll study the pyramid of the first and only entry in the batch.
pyramid = spc.pyramids[0]
describe_tensor(torch_tensor=pyramid, tensor_label='pyramid', with_shape=True, with_content=True)
out_left = widgets.Output(layout={'border': '0.2px dashed black'})
out_right = widgets.Output(layout={'border': '0.2px dashed black'})
print('\nHow to read the content of pyramids?')
with out_left:
print('"pyramid" summarizes the number of occupied \ncells per level, and their cumulative sum:\n')
for i in range(pyramid.shape[-1]):
if i ==0:
print(f'Root node (implicitly defined):')
elif i+1 < pyramid.shape[-1]:
print(f'Level #{i}:')
else:
print(f'Final entry for total cumsum:')
print(f'\thas {pyramid[0,i]} occupied cells')
print(f'\tstart idx (cumsum excluding current level): {pyramid[1,i]}')
with out_right:
print(f'"octrees" represents a hierarchy of {len(spc.octrees)} octree nodes.')
print(f"Each bit represents a cell occupancy:\n")
describe_octree(octree, level)
display(widgets.HBox([out_left, out_right]))
```
Similarly, kaolin keeps a complementary field, `exsum`, which tracks the cumulative summarization of bits per-octree to fast access parent-child information between levels:
```
exsum = spc.exsum
describe_tensor(torch_tensor=exsum, tensor_label='exsum', with_shape=True, with_content=True)
out_left = widgets.Output(layout={'border': '0.2px dashed black'})
out_right = widgets.Output(layout={'border': '0.2px dashed black'})
print('\nHow to read the content of exsum?')
with out_left:
print('"exsum" summarizes the cumulative number of occupied \ncells per octree, e.g: exclusive sum of "1" bits:\n')
for i in range(exsum.shape[-1]):
print(f'Cells in Octree #{i} start from cell idx: {exsum[i]}')
with out_right:
print(f'"octrees" represents a hierarchy of {len(octree)} octree nodes.')
print(f"Each bit represents a cell occupancy:\n")
describe_octree(octree, level)
display(widgets.HBox([out_left, out_right]))
```
When using Spc objects, pyramids are implicitly created the first time they are needed so you don't have to worry about them. <br>
For advanced users, the low-level api allows their explicit creation through `scan_octrees`:
```
lengths = torch.tensor([len(octrees)], dtype=torch.int32)
max_level, pyramid, exsum = kal.ops.spc.spc.scan_octrees(octree, lengths)
print('max_level:')
print(max_level)
print('\npyramid:')
print(pyramid)
print('\nexsum:')
print(exsum)
```
### point_hierarchies
`point_hierarchies` is an auxilary field, which holds the *sparse* coordinates of each point / occupied cell within the octree, for easier access.
Sparse coordinates are packed for all cells on all levels combined.
```
describe_tensor(torch_tensor=spc.point_hierarchies, tensor_label='point_hierarchies', with_shape=True, with_content=False)
```
We can use the information stored in the pyramids field to color the coordinates by level:
```
out_left = widgets.Output(layout={'border': '0.2px dashed black'})
out_right = widgets.Output(layout={'border': '0.2px dashed black', 'width': '60%'})
max_points_to_display = 17 # To avoid clutter
with out_left:
level_idx =0
point_idx = 0
remaining_cells_per_level = spc.pyramids[0,0].cpu().numpy().tolist()
for coord in spc.point_hierarchies:
if not remaining_cells_per_level[level_idx]:
level_idx += 1
point_idx = 0
else:
remaining_cells_per_level[level_idx] -= 1
if point_idx == max_points_to_display:
print(colored(f'skipping more..', level_color))
elif point_idx < max_points_to_display:
level_color = color_by_level(level_idx - 1)
print(colored(f'Level #{level_idx}, Point #{point_idx}, ' \
f'Coords: {coord.cpu().numpy().tolist()}', level_color))
point_idx += 1
with out_right:
print('How to read the content of point_hierarchies?')
print(f'- Each cell / point is represented by {spc.point_hierarchies.shape[-1]} indices (xyz).')
print('- Sparse coordinates are absolute: \n they are defined relative to the octree origin.')
print('- Compare the point coordinates with the demo below.\n\n Remember: unoccupied cells are not displayed!')
show_interactive_demo(max_level=spc.max_level)
display(widgets.HBox([out_left, out_right]))
```
## Where to go from here
Structured Point Clouds support other useful operators which were not covered by this tutorial:
1. [Convolutions](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.spc.html?highlight=SPC#kaolin.ops.spc.Conv3d)
2. [Querying points by location](https://kaolin.readthedocs.io/en/latest/modules/kaolin.ops.spc.html?highlight=SPC#kaolin.ops.spc.unbatched_query)
3. [Differential ray-tracing ops](https://kaolin.readthedocs.io/en/latest/modules/kaolin.render.spc.html#kaolin-render-spc)
| true |
code
| 0.679631 | null | null | null | null |
|
# T81-558: Applications of Deep Neural Networks
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), School of Engineering and Applied Science, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
**Module 9 Assignment: Kaggle Submission**
**Student Name: Your Name**
# Assignment Instructions
For this assignment you will begin by loading a pretrained neural network that I provide here: [transfer_9.h5](https://data.heatonresearch.com/data/t81-558/networks/transfer_9.h5). You will demonstrate your ability to transfer several layers from this neural network to create a new neural network to be used for feature engineering.
The **transfer_9.h5** neural network is composed of the following four layers:
```
Model: "sequential_7"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_11 (Dense) (None, 25) 225
_________________________________________________________________
dense_12 (Dense) (None, 10) 260
_________________________________________________________________
dense_13 (Dense) (None, 3) 33
_________________________________________________________________
dense_14 (Dense) (None, 1) 4
=================================================================
Total params: 522
Trainable params: 522
Non-trainable params: 0
```
You should only use the first three layers. The final dense layer should be removed, exposing the (None, 3) shaped layer as the new output layer. This is a 3-neuron layer. The output from these 3 layers will become your 3 engineered features.
Complete the following tasks:
* Load the Keras neural network **transfer_9.h5**. Note that you will need to download it to either your hard drive or GDrive (if you're using Google CoLab). Keras does not allow loading of a neural network across HTTP.
* Create a new neural network with only the first 3 layers, drop the (None, 1) shaped layer.
* Load the dataset [transfer_data.csv](https://data.heatonresearch.com/data/t81-558/datasets/transfer_data.csv).
* Use all columns as input, but do not use *id* as input. You will need to save the *id* column to build your submission.
* Do not zscore or transform the input columns.
* Submit the output from the (None, 3) shaped layer, along with the corresponding *id* column. The three output neurons should create columns named *a*, *b*, and *c*.
The submit file will look something like:
|id|a|b|c|
|-|-|-|-|
|1|2.3602087|1.4411213|0|
|2|0.067718446|1.0037427|0.52129996|
|3|0.74778837|1.0647631|0.052594826|
|4|1.0594225|1.1211816|0|
|...|...|...|...|
# Assignment Submit Function
You will submit the 10 programming assignments electronically. The following submit function can be used to do this. My server will perform a basic check of each assignment and let you know if it sees any basic problems.
**It is unlikely that should need to modify this function.**
```
import base64
import os
import numpy as np
import pandas as pd
import requests
# This function submits an assignment. You can submit an assignment as much as you like, only the final
# submission counts. The paramaters are as follows:
# data - Pandas dataframe output.
# key - Your student key that was emailed to you.
# no - The assignment class number, should be 1 through 1.
# source_file - The full path to your Python or IPYNB file. This must have "_class1" as part of its name.
# . The number must match your assignment number. For example "_class2" for class assignment #2.
def submit(data,key,no,source_file=None):
if source_file is None and '__file__' not in globals(): raise Exception('Must specify a filename when a Jupyter notebook.')
if source_file is None: source_file = __file__
suffix = '_class{}'.format(no)
if suffix not in source_file: raise Exception('{} must be part of the filename.'.format(suffix))
with open(source_file, "rb") as image_file:
encoded_python = base64.b64encode(image_file.read()).decode('ascii')
ext = os.path.splitext(source_file)[-1].lower()
if ext not in ['.ipynb','.py']: raise Exception("Source file is {} must be .py or .ipynb".format(ext))
r = requests.post("https://api.heatonresearch.com/assignment-submit",
headers={'x-api-key':key}, json={'csv':base64.b64encode(data.to_csv(index=False).encode('ascii')).decode("ascii"),
'assignment': no, 'ext':ext, 'py':encoded_python})
if r.status_code == 200:
print("Success: {}".format(r.text))
else: print("Failure: {}".format(r.text))
```
# Google CoLab Instructions
If you are using Google CoLab, it will be necessary to mount your GDrive so that you can send your notebook during the submit process. Running the following code will map your GDrive to /content/drive.
```
from google.colab import drive
drive.mount('/content/drive')
!ls /content/drive/My\ Drive/Colab\ Notebooks
```
# Assignment #9 Sample Code
The following code provides a starting point for this assignment.
```
import os
import pandas as pd
from scipy.stats import zscore
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout
from tensorflow.keras.models import load_model
import pandas as pd
import io
import requests
import numpy as np
from sklearn import metrics
from sklearn.model_selection import KFold
import sklearn
from sklearn.linear_model import Lasso
# This is your student key that I emailed to you at the beginnning of the semester.
key = "PPboscDL2M94HCbkbvfOLakXXNy3dh5x2VV1Mlpm" # This is an example key and will not work.
# You must also identify your source file. (modify for your local setup)
# file='/content/drive/My Drive/Colab Notebooks/assignment_yourname_class9.ipynb' # Google CoLab
# file='C:\\Users\\jeffh\\projects\\t81_558_deep_learning\\assignments\\assignment_yourname_class9.ipynb' # Windows
file='/Users/jheaton/projects/t81_558_deep_learning/assignments/assignment_yourname_class9.ipynb' # Mac/Linux
# Begin assignment
model = load_model("/Users/jheaton/Downloads/transfer_9.h5") # modify to where you stored it
df = pd.read_csv("https://data.heatonresearch.com/data/t81-558/datasets/transfer_data.csv")
submit(source_file=file,data=df_submit,key=key,no=9)
```
| true |
code
| 0.555073 | null | null | null | null |
|
# "[ALGO&DS] Reverse a Linked List"
> "How to reverse a linked list both iteratively and recursively?"
- toc:false
- branch: master
- badges: false
- comments: true
- author: Peiyi Hung
- categories: [category, learning, algorithms]
# Introduction
Reversing a linked list is a classic problem by solving which we can get familiar with basic operations about a linked list. I got a hard time understanding this problem at first, so I decide to write a blog post explaining how this problem can be addressed to really understand it.
This problem can be solved recursively and iteratively. I will explain how to solve this problem in these two ways and give Python implementaion of them. You can try on the codes in this post on [Leetcode](https://leetcode.com/problems/reverse-linked-list/).
# The Problem
The problem we want to solve is reserving a lined list. Here's it:
> Given the head of a singly linked list, reverse the list, and return the reversed list.
If you want to reverse a array, you can just use two pointers and keep swapping values in these pointers. However, you do not have the ability to access an element by its index using linked list, so we can not use the same strategy to reverse a linked list.
A naive method to solve this problem is:
1. Find the last element of a linked list by scan the whole list, store this node to another list, and remove this node.
2. Keep doing this until the linked list is empty, and we can get a reversed linked list.
Tis method takes $O(n^2)$ time and $O(n)$ extra space, which is inefficient.
In the next two section, I will explain two method taking $O(n)$ time.
# Recursively
First, Let's solve this problem recursively. I will present the entire code and explain each step in detail.
```
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def reverseList(head: ListNode) -> ListNode:
# base case
if head is None or head.next is None:
return head
# revursive case
p = reverseList(head.next)
head.next.next = head
head.next = None
return p
```
A linked list is linked `ListNode`. We can access the value in a node by `ListNode.val` and the next node by `ListNode.next`. So there's a custom class in the code:
```
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
```
Since we want to solve this problem recursively, we have to discuss the base case and the recurrence relation.
The base case is that your linked list is empty or only contains one node. If this is the case, you could just return the `head` because they are reversed. This is done in this code:
```
if head is None or head.next is None:
return head
```
In the recursive case, we can first revserve the linked list after `head`:
```
p = reverseList(head.next)
```
assuming `reverseList` can really do that. Now `p` points to the last element of this linked list, the whole list except `head` is reversed and the next element of `head` is the last element of this reversed linked list. What we should do is to set the next element of `head.next` to `head` and chop off the "next" element of `head`. Here's the code:
```
head.next.next = head
head.next = None
```
By doing this, we can reverse a linked list recursively.
# Iteratively
We can reverse a linked list iteratively by this code:
```
def reverseList(head: ListNode) -> ListNode:
prev = None
curr = head
while curr:
temp = curr.next
curr.next = prev
prev = curr
curr = temp
return prev
```
In the iterative case, we keep reverse one node in the linked list. `prev` points to the head of the reversed part, and `curr` refers to the one of the part that have not been reversed.
How do we reverse a node? If we want to reverse a node `curr`, we have to set the next of `curr` to `prev` and the new `prev` to `curr`. We do this by:
```
curr.next = prev
prev = curr
```
However, if we do this, we would lost the pointer to the next element that has not been reversed. Thus, before we reverse `curr`, we should temperarily store where `curr.next` is. After we reversed a node, the "unreversed" part would be `temp`, so we assign `temp` to curr. That is, `temp = curr.next` and `curr = temp`.
If `curr` reach the end of a linked list, then we have reversed all elements and we should return `prev` which points to the head of the reversed list.
| true |
code
| 0.589421 | null | null | null | null |
|
# Analysis of TRPO
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as sts
plt.close('all')
delta = 0.2
def read_data(path):
df = pd.read_csv(path + 'progress.csv')
iterations = len(df)
batch_size = df['EpLenMean']
sigma_1 = []
sigma_2 = []
theta = []
for i in range(iterations):
policy_params = np.load(path + 'weights_' + str(i) + '.npy')
#iws = np.load(path + 'iws_' + str(i) + '.npy')
sigma_1.append(np.exp(policy_params[-2]))
sigma_2.append(np.exp(policy_params[-1]))
theta.append(policy_params[0])
df['Sigma1'] = sigma_1
df['Sigma2'] = sigma_2
df['Theta'] = theta
df['CumAvgRew'] = np.cumsum(df['EpRewMean'])/iterations
return df
def plot_data(dfs, columns, bottom=-np.infty, top=np.infty, rng=None):
fig = plt.figure()
ax = fig.add_subplot(111)
if type(dfs) is not list:
dfs = [dfs]
n_subplots = len(dfs)
for i in range(n_subplots):
df = dfs[i]
if rng is not None:
df = df[rng]
ax.set_xlabel('Iteration')
x = range(len(df))
for col in columns:
y = np.clip(df[col], bottom, top)
ax.plot(x, y, label=col)
ax.legend()
return fig
def plot_ci(mean, std, conf, n_runs):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(mean.index, mean)
interval = sts.t.interval(conf, n_runs-1,loc=mean,scale=std/np.sqrt(n_runs))
ax.fill_between(mean.index, interval[0], interval[1], alpha=0.3)
return fig
```
# LQG
## Setting:
* Policy mean: linear w/o bias
* Policy std: one logstd parameter
* Available random seeds: 0, 27, 62, 315, 640
* Batch size: 100
* delta = 0.2
* Implementation: baselines
* Task variant: ifqi
* Horizon: 200
### Performance (undiscounted) on 5 different random seeds
**Available data**
```
common_path = '../results/trpo/lqg/seed_'
seeds = [0, 27, 62, 315, 640]
dfs = []
for s in seeds:
dfs.append(read_data(common_path + str(s) + '/'))
plot_data(dfs, ['EpRewMean'])
plot_data(dfs, ['Theta'])
n_iter = min(len(df) for df in dfs)
n_runs = len(dfs)
print('Number of runs:', n_runs)
print('Number of iterations per run:', n_iter)
print('Columns:', list(dfs[0]))
concat_df = pd.concat(dfs, axis=1)
mean_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).mean()
std_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).std()
conf = 0.95
print('Average performance with %i%% confidence intervals:' % (conf*100))
mean = mean_df['EpRewMean']
std = std_df['EpRewMean']
plot_ci(mean, std, conf, n_runs)
cum_mean = mean_df['CumAvgRew'][len(mean_df)-1]
cum_std = std_df['CumAvgRew'][len(mean_df)-1]
interval = sts.t.interval(conf, n_runs-1,loc=cum_mean,scale=cum_std/np.sqrt(n_runs))
print('Average cumulative reward: %f, c.i. %s' % (cum_mean, interval))
```
# Cartpole
## Setting:
* Policy mean: linear with bias
* Policy std: one logstd parameter for each action dimension
* Available random seeds: 0, 27, 62, 315
* Batch size: 100
* delta = 0.2
* Implementation: baselines
* Task variant: gym
* Horizon: 200
### Performance (undiscounted) on 4 different random seeds
**Available data**
```
common_path = '../results/trpo/cartpole/seed_'
seeds = [0, 27, 62, 315]
dfs = []
for s in seeds:
dfs.append(read_data(common_path + str(s) + '/'))
plot_data(dfs, ['EpRewMean'])
n_iter = min(len(df) for df in dfs)
n_runs = len(dfs)
print('Number of runs:', n_runs)
print('Number of iterations per run:', n_iter)
print('Columns:', list(dfs[0]))
concat_df = pd.concat(dfs, axis=1)
mean_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).mean()
std_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).std()
conf = 0.95
print('Average performance with %i%% confidence intervals:' % (conf*100))
mean = mean_df['EpRewMean']
std = std_df['EpRewMean']
plot_ci(mean, std, conf, n_runs)
cum_mean = mean_df['CumAvgRew'][len(mean_df)-1]
cum_std = std_df['CumAvgRew'][len(mean_df)-1]
interval = sts.t.interval(conf, n_runs-1,loc=cum_mean,scale=cum_std/np.sqrt(n_runs))
print('Average cumulative reward: %f, c.i. %s' % (cum_mean, interval))
```
# Swimmer
## Setting:
* Policy mean: 64x64 tanh with biases
* Policy std: one logstd parameter for each action dimension
* Available random seeds: 0, 27, 62, 315, 640
* Batch size: 100
* delta = 0.2
* Implementation: baselines
* Task variant: gym
* Horizon: 500
### Performance (undiscounted) on 5 different random seeds
**Available data**
```
common_path = '../results/trpo/swimmer/seed_'
seeds = [0, 27, 62, 315, 640]
dfs = []
for s in seeds:
dfs.append(read_data(common_path + str(s) + '/'))
plot_data(dfs, ['EpRewMean'])
n_iter = min(len(df) for df in dfs)
n_runs = len(dfs)
print('Number of runs:', n_runs)
print('Number of iterations per run:', n_iter)
print('Columns:', list(dfs[0]))
concat_df = pd.concat(dfs, axis=1)
mean_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).mean()
std_df = pd.concat(dfs, axis=1).groupby(by=concat_df.columns, axis=1).std()
conf = 0.95
print('Average performance with %i%% confidence intervals:' % (conf*100))
mean = mean_df['EpRewMean']
std = std_df['EpRewMean']
plot_ci(mean, std, conf, n_runs)
cum_mean = mean_df['CumAvgRew'][len(mean_df)-1]
cum_std = std_df['CumAvgRew'][len(mean_df)-1]
interval = sts.t.interval(conf, n_runs-1,loc=cum_mean,scale=cum_std/np.sqrt(n_runs))
print('Average cumulative reward: %f, c.i. %s' % (cum_mean, interval))
```
| true |
code
| 0.504639 | null | null | null | null |
|
# 準備
```
# バージョン指定時にコメントアウト
#!pip install torch==1.7.0
#!pip install torchvision==0.8.1
import torch
import torchvision
# バージョンの確認
print(torch.__version__)
print(torchvision.__version__)
# Google ドライブにマウント
from google.colab import drive
drive.mount('/content/gdrive')
%cd '/content/gdrive/MyDrive/Colab Notebooks/gan_sample/chapter2'
import os
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizers
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import torchvision
import torchvision.transforms as transforms
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
```
# データセットの作成
```
np.random.seed(1234)
torch.manual_seed(1234)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# データの取得
root = os.path.join('data', 'mnist')
transform = transforms.Compose([transforms.ToTensor(),
lambda x: x.view(-1)])
mnist_train = \
torchvision.datasets.MNIST(root=root,
download=True,
train=True,
transform=transform)
mnist_test = \
torchvision.datasets.MNIST(root=root,
download=True,
train=False,
transform=transform)
train_dataloader = DataLoader(mnist_train,
batch_size=100,
shuffle=True)
test_dataloader = DataLoader(mnist_test,
batch_size=100,
shuffle=False)
```
# ネットワークの定義
```
class VAE(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.encoder = Encoder(device=device)
self.decoder = Decoder(device=device)
def forward(self, x):
# エンコーダ
mean, var = self.encoder(x)
# 潜在変数の作成
z = self.reparameterize(mean, var)
# デコーダ
y = self.decoder(z)
#生成画像yと潜在変数zが返り値
return y, z
# 潜在変数zの作成
def reparameterize(self, mean, var):
# 標準正規分布の作成
eps = torch.randn(mean.size()).to(self.device)
# 再パラメータ化トリック
z = mean + torch.sqrt(var) * eps
return z
# 誤差の計算
def lower_bound(self, x):
# 平均と分散のベクトルを計算
mean, var = self.encoder(x)
# 平均と分散から潜在変数zを作成
z = self.reparameterize(mean, var)
# 潜在変数zから生成画像を作成
y = self.decoder(z)
# 再構成誤差
reconst = - torch.mean(torch.sum(x * torch.log(y)
+ (1 - x) * torch.log(1 - y),
dim=1))
# 正則化
kl = - 1/2 * torch.mean(torch.sum(1
+ torch.log(var)
- mean**2
- var, dim=1))
# 再構成誤差 + 正則化
L = reconst + kl
return L
class Encoder(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.l1 = nn.Linear(784, 200)
self.l_mean = nn.Linear(200, 10)
self.l_var = nn.Linear(200, 10)
def forward(self, x):
# 784次元から200次元
h = self.l1(x)
# 活性化関数
h = torch.relu(h)
# 200次元から10次元の平均
mean = self.l_mean(h)
# 200次元から10次元の分散
var = self.l_var(h)
# 活性化関数softplus
var = F.softplus(var)
return mean, var
class Decoder(nn.Module):
def __init__(self, device='cpu'):
super().__init__()
self.device = device
self.l1 = nn.Linear(10, 200)
self.out = nn.Linear(200, 784)
def forward(self, x):
# 10次元から200次元
h = self.l1(x)
# 活性化関数
h = torch.relu(h)
# 200次元から784次元
h = self.out(h)
# シグモイド関数
y = torch.sigmoid(h)
return y
```
# 学習の実行
```
# モデルの設定
model = VAE(device=device).to(device)
# 損失関数の設定
criterion = model.lower_bound
# 最適化関数の設定
optimizer = optimizers.Adam(model.parameters())
print(model)
epochs = 10
# エポックのループ
for epoch in range(epochs):
train_loss = 0.
# バッチサイズのループ
for (x, _) in train_dataloader:
x = x.to(device)
# 訓練モードへの切替
model.train()
# 本物画像と生成画像の誤差計算
loss = criterion(x)
# 勾配の初期化
optimizer.zero_grad()
# 誤差の勾配計算
loss.backward()
# パラメータの更新
optimizer.step()
# 訓練誤差の更新
train_loss += loss.item()
train_loss /= len(train_dataloader)
print('Epoch: {}, Loss: {:.3f}'.format(
epoch+1,
train_loss
))
```
# 画像の生成
```
# ノイズの作成数
batch_size=8
# デコーダ入力用に標準正規分布に従う10次元のノイズを作成
z = torch.randn(batch_size, 10, device = device)
# 評価モードへの切替
model.eval()
# デコーダにノイズzを入力
images = model.decoder(z)
images = images.view(-1, 28, 28)
images = images.squeeze().detach().cpu().numpy()
for i, image in enumerate(images):
plt.subplot(2, 4, i+1)
plt.imshow(image, cmap='binary_r')
plt.axis('off')
plt.tight_layout()
plt.show()
fig = plt.figure(figsize=(10, 3))
model.eval()
for x, t in test_dataloader:
# 本物画像
for i, im in enumerate(x.view(-1, 28, 28).detach().numpy()[:10]):
ax = fig.add_subplot(3, 10, i+1, xticks=[], yticks=[])
ax.imshow(im, 'gray')
x = x.to(device)
# 本物画像から生成画像
y, z = model(x)
y = y.view(-1, 28, 28)
for i, im in enumerate(y.cpu().detach().numpy()[:10]):
ax = fig.add_subplot(3, 10, i+11, xticks=[], yticks=[])
ax.imshow(im, 'gray')
# 1つ目の画像と2つ目の画像の潜在変数を連続的に変化
z1to0 = torch.cat([z[1] * (i * 0.1) + z[0] * ((9 - i) * 0.1) for i in range(10)]).reshape(10,10)
y2 = model.decoder(z1to0).view(-1, 28, 28)
for i, im in enumerate(y2.cpu().detach().numpy()):
ax = fig.add_subplot(3, 10, i+21, xticks=[], yticks=[])
ax.imshow(im, 'gray')
break
```
| true |
code
| 0.769892 | null | null | null | null |
|
# Plotting kde objects
```
import scipy.stats as stats
import matplotlib.pyplot as plt
%matplotlib inline
```
# 1d kde
```
kde = stats.gaussian_kde(np.random.normal(loc=50, scale=5, size=100000))
x = np.arange(0, 100, 1)
plt.plot(x, kde(x))
plt.show()
```
## 2d kde
```
from scipy import stats
def measure(n):
"Measurement model, return two coupled measurements."
m1 = np.random.normal(size=n)
m2 = np.random.normal(scale=0.5, size=n)
return m1+m2, m1-m2
m1, m2 = measure(2000)
xmin = m1.min()
xmax = m1.max()
ymin = m2.min()
ymax = m2.max()
X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
positions = np.vstack([X.ravel(), Y.ravel()])
values = np.vstack([m1, m2])
kernel = stats.gaussian_kde(values)
Z = np.reshape(kernel(positions).T, X.shape)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import kde
np.random.seed(1977)
# Generate 200 correlated x,y points
data = np.random.multivariate_normal([0, 0], [[1, 0.5], [0.5, 3]], 200)
x, y = data.T
nbins = 20
fig, axes = plt.subplots(ncols=2, nrows=2, sharex=True, sharey=True)
axes[0, 0].set_title('Scatterplot')
axes[0, 0].plot(x, y, 'ko')
axes[0, 1].set_title('Hexbin plot')
axes[0, 1].hexbin(x, y, gridsize=nbins)
axes[1, 0].set_title('2D Histogram')
axes[1, 0].hist2d(x, y, bins=nbins)
# Evaluate a gaussian kde on a regular grid of nbins x nbins over data extents
k = kde.gaussian_kde(data.T)
xi, yi = np.mgrid[x.min():x.max():nbins*1j, y.min():y.max():nbins*1j]
zi = k(np.vstack([xi.flatten(), yi.flatten()]))
axes[1, 1].set_title('Gaussian KDE')
axes[1, 1].pcolormesh(xi, yi, zi.reshape(xi.shape))
fig.tight_layout()
plt.show()
size = 1000
kde = stats.gaussian_kde(
[np.random.normal(loc=40, scale=10, size=size),
np.random.normal(loc=55, scale=3, size=size)]
)
font = {'family' : 'normal',
'size' : 14}
plt.rc('font', **font)
start = 0
end = 100
step = 1
i = np.arange(start, end, step)
nbins = len(i)
xi,yi = np.mgrid[i.min():i.max():nbins*1j, i.min():i.max():nbins*1j]
zi = kde(np.vstack([xi.flatten(), yi.flatten()]))
fig = plt.figure(1)
plt.pcolormesh(xi, yi, zi.reshape(xi.shape))
plt.title('2d-KDE')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
#fig.savefig('/home/nick/test.png', bbox_inches='tight')
size = 1000
kde = stats.gaussian_kde(
[np.random.normal(loc=40, scale=10, size=size),
np.random.normal(loc=55, scale=3, size=size)]
)
f, axarr = plt.subplots(2)
start = 0
end = 100
step = 1
i = np.arange(start, end, step)
nbins = len(i)
xi,yi = np.mgrid[i.min():i.max():nbins*1j, i.min():i.max():nbins*1j]
zi = kde(np.vstack([xi.flatten(), yi.flatten()]))
#fig = plt.figure(1)
axarr[0].pcolormesh(xi, yi, zi.reshape(xi.shape))
#plt.title('2d-KDE')
#plt.xlabel('x')
#plt.ylabel('y')
#plt.show()
#fig.savefig('/home/nick/test.png', bbox_inches='tight')
```
# Plotting sandbox
```
plt.figure(1)
plt.subplot(211)
plt.plot(range(10), lw=10, alpha=0.1)
plt.subplot(212)
plt.plot(range(10), 'ro', alpha=0.5)
plt.show()
plt.subplot?
x = np.arange(0, 10, 0.1)
vals = kde.resample(size=100)
plt.figure(1)
plt.hist(vals[0,], 30)
plt.plot(x, kde(x))
plt.show()
```
# KDE intersection
```
size = 1000
kde1 = stats.gaussian_kde(
[np.random.normal(loc=40, scale=10, size=size),
np.random.normal(loc=55, scale=3, size=size)]
)
kde2 = stats.gaussian_kde(
[np.random.normal(loc=55, scale=10, size=size),
np.random.normal(loc=70, scale=3, size=size)]
)
kde3 = stats.gaussian_kde(
[np.random.normal(loc=40, scale=10, size=size),
np.random.normal(loc=55, scale=3, size=size)]
)
print kde1.integrate_kde(kde2)
print kde1.integrate_kde(kde3)
kde1 = stats.gaussian_kde(np.random.normal(loc=30, scale=10, size=size))
kde2 = stats.gaussian_kde(np.random.normal(loc=70, scale=10, size=size))
print kde1.integrate_kde(kde1)
print kde1.integrate_kde(kde2)
# calculating intersection
def kde_intersect(kde1, kde2, start=0, end=100, step=0.1):
# evalution grid
x = np.arange(start,end,step)
# calculate intersection densities
pmin = np.min(np.c_[kde1(x),kde2(x)], axis=1)
# integrate areas under curves
total = kde1.integrate_box_1d(start,end) + kde2.integrate_box_1d(start,end)
#total = np.trapz(y=kde1(x), x=x) + np.trapz(y=kde2(x), x=x)
intersection = np.trapz(y=pmin,x=x)
print 'kde1 max: {}'.format(np.max(kde1(x)))
print 'kde2 max: {}'.format(np.max(kde2(x)))
print 'pmin max: {}'.format(np.max(pmin))
print 'total: {}'.format(total)
print 'int: {}'.format(intersection)
# overlap coefficient
return 2 * intersection / float(total)
kde1 = stats.gaussian_kde(np.random.normal(loc=1.67, scale=0.01, size=size))
kde2 = stats.gaussian_kde(np.random.normal(loc=1.68, scale=0.01, size=size))
print kde_intersect(kde1, kde1)
#print kde_intersect(kde1, kde2)
# calculating intersection
def kde_intersect(kde1, kde2, start=0, end=100, step=0.1):
# evalution grid
x = np.arange(start,end,step)
# kde integrations
int1 = kde1.integrate_box_1d(start,end)
int2 = kde2.integrate_box_1d(start,end)
# kde scaled evaluated values
s1 = int1 / np.max(kde1(x)) * kde1(x)
s2 = int2 / np.max(kde2(x)) * kde2(x)
# calculate intersection densities
pmin = np.min(np.c_[s1,s2], axis=1)
# integrate areas under curves
total = kde1.integrate_box_1d(start,end) + kde2.integrate_box_1d(start,end)
intersection = np.trapz(y=pmin,x=x)
print 'kde1 max: {}'.format(np.max(kde1(x)))
print 'kde2 max: {}'.format(np.max(kde2(x)))
print 'pmin max: {}'.format(np.max(pmin))
print 'total: {}'.format(total)
print 'inter: {}'.format(intersection)
# overlap coefficient
return 2 * intersection / float(total)
kde1 = stats.gaussian_kde(np.random.normal(loc=1.67, scale=0.01, size=size))
kde2 = stats.gaussian_kde(np.random.normal(loc=1.68, scale=0.01, size=size))
print kde_intersect(kde1, kde1)
#print kde_intersect(kde1, kde2)
# calculating BD shift as 1 - kde_intersection
kde1 = stats.gaussian_kde(np.random.normal(loc=1.67, scale=0.01, size=size))
kde2 = stats.gaussian_kde(np.random.normal(loc=1.68, scale=0.01, size=size))
x = np.arange(1.6,1.76,0.001)
plt.figure(1)
plt.fill_between(x, kde1(x), color='b', alpha=0.3)
plt.fill_between(x, kde2(x), color='r', alpha=0.3)
plt.show()
BD_shift = 1 - kde_intersect(kde1, kde2, start=0, end=2, step=0.01)
print 'BD shift (1 - kde_intersection): {0:.3f}'.format(BD_shift)
# calculating BD shift as 1 - kde_intersection
kde1 = stats.gaussian_kde(np.random.normal(loc=1.67, scale=0.01, size=size))
kde2 = stats.gaussian_kde(np.random.normal(loc=1.695, scale=0.01, size=size))
x = np.arange(1.6,1.76,0.001)
plt.figure(1)
plt.fill_between(x, kde1(x), color='b', alpha=0.3)
plt.fill_between(x, kde2(x), color='r', alpha=0.3)
plt.show()
BD_shift = 1 - kde_intersect(kde1, kde2, start=0, end=2, step=0.01)
print 'BD shift (1 - kde_intersection): {0:.3f}'.format(BD_shift)
KernelDensity(kernel='gaussian').fit(vals)
```
| true |
code
| 0.672977 | null | null | null | null |
|
# Hierarchical Clustering
**Hierarchical clustering** refers to a class of clustering methods that seek to build a **hierarchy** of clusters, in which some clusters contain others. In this assignment, we will explore a top-down approach, recursively bipartitioning the data using k-means.
**Note to Amazon EC2 users**: To conserve memory, make sure to stop all the other notebooks before running this notebook.
## Import packages
The following code block will check if you have the correct version of GraphLab Create. Any version later than 1.8.5 will do. To upgrade, read [this page](https://turi.com/download/upgrade-graphlab-create.html).
```
import graphlab
import matplotlib.pyplot as plt
import numpy as np
import sys
import os
import time
from scipy.sparse import csr_matrix
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances
%matplotlib inline
'''Check GraphLab Create version'''
from distutils.version import StrictVersion
assert (StrictVersion(graphlab.version) >= StrictVersion('1.8.5')), 'GraphLab Create must be version 1.8.5 or later.'
```
## Load the Wikipedia dataset
```
wiki = graphlab.SFrame('people_wiki.gl/')
```
As we did in previous assignments, let's extract the TF-IDF features:
```
wiki['tf_idf'] = graphlab.text_analytics.tf_idf(wiki['text'])
```
To run k-means on this dataset, we should convert the data matrix into a sparse matrix.
```
from em_utilities import sframe_to_scipy # converter
# This will take about a minute or two.
tf_idf, map_index_to_word = sframe_to_scipy(wiki, 'tf_idf')
```
To be consistent with the k-means assignment, let's normalize all vectors to have unit norm.
```
from sklearn.preprocessing import normalize
tf_idf = normalize(tf_idf)
```
## Bipartition the Wikipedia dataset using k-means
Recall our workflow for clustering text data with k-means:
1. Load the dataframe containing a dataset, such as the Wikipedia text dataset.
2. Extract the data matrix from the dataframe.
3. Run k-means on the data matrix with some value of k.
4. Visualize the clustering results using the centroids, cluster assignments, and the original dataframe. We keep the original dataframe around because the data matrix does not keep auxiliary information (in the case of the text dataset, the title of each article).
Let us modify the workflow to perform bipartitioning:
1. Load the dataframe containing a dataset, such as the Wikipedia text dataset.
2. Extract the data matrix from the dataframe.
3. Run k-means on the data matrix with k=2.
4. Divide the data matrix into two parts using the cluster assignments.
5. Divide the dataframe into two parts, again using the cluster assignments. This step is necessary to allow for visualization.
6. Visualize the bipartition of data.
We'd like to be able to repeat Steps 3-6 multiple times to produce a **hierarchy** of clusters such as the following:
```
(root)
|
+------------+-------------+
| |
Cluster Cluster
+------+-----+ +------+-----+
| | | |
Cluster Cluster Cluster Cluster
```
Each **parent cluster** is bipartitioned to produce two **child clusters**. At the very top is the **root cluster**, which consists of the entire dataset.
Now we write a wrapper function to bipartition a given cluster using k-means. There are three variables that together comprise the cluster:
* `dataframe`: a subset of the original dataframe that correspond to member rows of the cluster
* `matrix`: same set of rows, stored in sparse matrix format
* `centroid`: the centroid of the cluster (not applicable for the root cluster)
Rather than passing around the three variables separately, we package them into a Python dictionary. The wrapper function takes a single dictionary (representing a parent cluster) and returns two dictionaries (representing the child clusters).
```
def bipartition(cluster, maxiter=400, num_runs=4, seed=None):
'''cluster: should be a dictionary containing the following keys
* dataframe: original dataframe
* matrix: same data, in matrix format
* centroid: centroid for this particular cluster'''
data_matrix = cluster['matrix']
dataframe = cluster['dataframe']
# Run k-means on the data matrix with k=2. We use scikit-learn here to simplify workflow.
kmeans_model = KMeans(n_clusters=2, max_iter=maxiter, n_init=num_runs, random_state=seed, n_jobs=1)
kmeans_model.fit(data_matrix)
centroids, cluster_assignment = kmeans_model.cluster_centers_, kmeans_model.labels_
# Divide the data matrix into two parts using the cluster assignments.
data_matrix_left_child, data_matrix_right_child = data_matrix[cluster_assignment==0], \
data_matrix[cluster_assignment==1]
# Divide the dataframe into two parts, again using the cluster assignments.
cluster_assignment_sa = graphlab.SArray(cluster_assignment) # minor format conversion
dataframe_left_child, dataframe_right_child = dataframe[cluster_assignment_sa==0], \
dataframe[cluster_assignment_sa==1]
# Package relevant variables for the child clusters
cluster_left_child = {'matrix': data_matrix_left_child,
'dataframe': dataframe_left_child,
'centroid': centroids[0]}
cluster_right_child = {'matrix': data_matrix_right_child,
'dataframe': dataframe_right_child,
'centroid': centroids[1]}
return (cluster_left_child, cluster_right_child)
```
The following cell performs bipartitioning of the Wikipedia dataset. Allow 20-60 seconds to finish.
Note. For the purpose of the assignment, we set an explicit seed (`seed=1`) to produce identical outputs for every run. In pratical applications, you might want to use different random seeds for all runs.
```
wiki_data = {'matrix': tf_idf, 'dataframe': wiki} # no 'centroid' for the root cluster
left_child, right_child = bipartition(wiki_data, maxiter=100, num_runs=6, seed=1)
```
Let's examine the contents of one of the two clusters, which we call the `left_child`, referring to the tree visualization above.
```
left_child
```
And here is the content of the other cluster we named `right_child`.
```
right_child
```
## Visualize the bipartition
We provide you with a modified version of the visualization function from the k-means assignment. For each cluster, we print the top 5 words with highest TF-IDF weights in the centroid and display excerpts for the 8 nearest neighbors of the centroid.
```
def display_single_tf_idf_cluster(cluster, map_index_to_word):
'''map_index_to_word: SFrame specifying the mapping betweeen words and column indices'''
wiki_subset = cluster['dataframe']
tf_idf_subset = cluster['matrix']
centroid = cluster['centroid']
# Print top 5 words with largest TF-IDF weights in the cluster
idx = centroid.argsort()[::-1]
for i in xrange(5):
print('{0:s}:{1:.3f}'.format(map_index_to_word['category'][idx[i]], centroid[idx[i]])),
print('')
# Compute distances from the centroid to all data points in the cluster.
distances = pairwise_distances(tf_idf_subset, [centroid], metric='euclidean').flatten()
# compute nearest neighbors of the centroid within the cluster.
nearest_neighbors = distances.argsort()
# For 8 nearest neighbors, print the title as well as first 180 characters of text.
# Wrap the text at 80-character mark.
for i in xrange(8):
text = ' '.join(wiki_subset[nearest_neighbors[i]]['text'].split(None, 25)[0:25])
print('* {0:50s} {1:.5f}\n {2:s}\n {3:s}'.format(wiki_subset[nearest_neighbors[i]]['name'],
distances[nearest_neighbors[i]], text[:90], text[90:180] if len(text) > 90 else ''))
print('')
```
Let's visualize the two child clusters:
```
display_single_tf_idf_cluster(left_child, map_index_to_word)
display_single_tf_idf_cluster(right_child, map_index_to_word)
```
The left cluster consists of athletes, whereas the right cluster consists of non-athletes. So far, we have a single-level hierarchy consisting of two clusters, as follows:
```
Wikipedia
+
|
+--------------------------+--------------------+
| |
+ +
Athletes Non-athletes
```
Is this hierarchy good enough? **When building a hierarchy of clusters, we must keep our particular application in mind.** For instance, we might want to build a **directory** for Wikipedia articles. A good directory would let you quickly narrow down your search to a small set of related articles. The categories of athletes and non-athletes are too general to facilitate efficient search. For this reason, we decide to build another level into our hierarchy of clusters with the goal of getting more specific cluster structure at the lower level. To that end, we subdivide both the `athletes` and `non-athletes` clusters.
## Perform recursive bipartitioning
### Cluster of athletes
To help identify the clusters we've built so far, let's give them easy-to-read aliases:
```
athletes = left_child
non_athletes = right_child
```
Using the bipartition function, we produce two child clusters of the athlete cluster:
```
# Bipartition the cluster of athletes
left_child_athletes, right_child_athletes = bipartition(athletes, maxiter=100, num_runs=6, seed=1)
```
The left child cluster mainly consists of baseball players:
```
display_single_tf_idf_cluster(left_child_athletes, map_index_to_word)
```
On the other hand, the right child cluster is a mix of players in association football, Austrailian rules football and ice hockey:
```
display_single_tf_idf_cluster(right_child_athletes, map_index_to_word)
```
Our hierarchy of clusters now looks like this:
```
Wikipedia
+
|
+--------------------------+--------------------+
| |
+ +
Athletes Non-athletes
+
|
+-----------+--------+
| |
| association football/
+ Austrailian rules football/
baseball ice hockey
```
Should we keep subdividing the clusters? If so, which cluster should we subdivide? To answer this question, we again think about our application. Since we organize our directory by topics, it would be nice to have topics that are about as coarse as each other. For instance, if one cluster is about baseball, we expect some other clusters about football, basketball, volleyball, and so forth. That is, **we would like to achieve similar level of granularity for all clusters.**
Notice that the right child cluster is more coarse than the left child cluster. The right cluster posseses a greater variety of topics than the left (ice hockey/association football/Austrialian football vs. baseball). So the right child cluster should be subdivided further to produce finer child clusters.
Let's give the clusters aliases as well:
```
baseball = left_child_athletes
ice_hockey_football = right_child_athletes
```
### Cluster of ice hockey players and football players
In answering the following quiz question, take a look at the topics represented in the top documents (those closest to the centroid), as well as the list of words with highest TF-IDF weights.
Let us bipartition the cluster of ice hockey and football players.
```
left_child_ihs, right_child_ihs = bipartition(ice_hockey_football, maxiter=100, num_runs=6, seed=1)
display_single_tf_idf_cluster(left_child_ihs, map_index_to_word)
display_single_tf_idf_cluster(right_child_ihs, map_index_to_word)
```
### 2. Which diagram best describes the hierarchy right after splitting the `ice_hockey_football` cluster? Refer to the quiz form for the diagrams.
**Caution**. The granularity criteria is an imperfect heuristic and must be taken with a grain of salt. It takes a lot of manual intervention to obtain a good hierarchy of clusters.
* **If a cluster is highly mixed, the top articles and words may not convey the full picture of the cluster.** Thus, we may be misled if we judge the purity of clusters solely by their top documents and words.
* **Many interesting topics are hidden somewhere inside the clusters but do not appear in the visualization.** We may need to subdivide further to discover new topics. For instance, subdividing the `ice_hockey_football` cluster led to the appearance of runners and golfers.
### Cluster of non-athletes
Now let us subdivide the cluster of non-athletes.
```
# Bipartition the cluster of non-athletes
left_child_non_athletes, right_child_non_athletes = bipartition(non_athletes, maxiter=100, num_runs=6, seed=1)
display_single_tf_idf_cluster(left_child_non_athletes, map_index_to_word)
display_single_tf_idf_cluster(right_child_non_athletes, map_index_to_word)
```
Neither of the clusters show clear topics, apart from the genders. Let us divide them further.
```
male_non_athletes = left_child_non_athletes
female_non_athletes = right_child_non_athletes
```
### 3. Let us bipartition the clusters `male_non_athletes` and `female_non_athletes`. Which diagram best describes the resulting hierarchy of clusters for the non-athletes? Refer to the quiz for the diagrams.
**Note**. Use `maxiter=100, num_runs=6, seed=1` for consistency of output.
| true |
code
| 0.570511 | null | null | null | null |
|
# How to create gates from physical processes
This tutorial shows how to use the `InterpolatedDenseOp` and `InterpolatedOpFactory` to create quick-to-evaluate operations by interpolating between the discrete points at quick a more computationally-intensive process is performed. Often the computationally intensive process simulates the physics of a qubit gate, and would not practially work as a custom model operation because of the time required to evaluate it.
In order to turn such physical processes into gates, you should implement a custom `PhysicalProcess` object and then use the `InterpolatedDenseOp` or `InterpolatedOpFactory` class to interpolate the values of the custom process on a set of pre-defined points. All the physics simulation is then done at the time of creating the interpolated operation (or factory), after which the object can be saved for later use. An `InterpolatedDenseOp` or `InterpolatedOpFactory` object can be evaluated at any parameter-space point within the ranges over which the initial interpolation was performed.
All of this functionality is currently provided within the `pygsti.extras.interpygate` sub-package. This tutorial demonstrates how to setup a custom physical process and create an interpolated gate and factory object from it.
We'll begin by some standard imports and by importing the `interpygate` sub-package. We get a MPI communicator if we can, as usually the physical simulation is performed using multiple processors.
```
import numpy as np
from scipy.linalg import expm
import pygsti
import pygsti.extras.interpygate as interp
try:
from mpi4py import MPI
comm = MPI.COMM_WORLD
except ImportError:
comm = None
```
## Defining a physical process
We create a physical process simulator by deriving from the `PhysicalProcess` class and implementing its `create_process_matrix` function. This is the computationally intensive method that generates a process matrix based on some set of parameters. Every physical process has a fixed number of parameters that define the space that will be interpolated over. The generated process matrix is expected to be in whatever basis the ultimate `Model` operations will be in - usually the Pauli-product basis specified by `"pp"` - and have a fixed shape. This shape, given by `process_shape` below, is almost always a square matrix of dimension $4^n$ where $n$ is the number of qubits. Specifying an auxiliary information shape (`aux_shape` below) and implementing the `create_aux_info` will allow additional (floating point) values that describe the process to be interpolated.
Below we create a physical process that evolves a quantum state for some time (also a parameter) using a parameterized Lindbladian. Process tomography is used to construct a process matrix from the state evolution. The process has 6 parameters.
```
class ExampleProcess(interp.PhysicalProcess):
def __init__(self):
self.Hx = np.array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, -1],
[0, 0, 1, 0]], dtype='float')
self.Hy = np.array([[0, 0, 0, 0],
[0, 0, 0, 1],
[0, 0, 0, 0],
[0, -1, 0, 0]], dtype='float')
self.Hz = np.array([[0, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 0],
[0, 0, 0, 0]], dtype='float')
self.dephasing_generator = np.diag([0, -1, -1, 0])
self.decoherence_generator = np.diag([0, -1, -1, -1])
num_params = 6 # omega (0), phase (1), detuning (2), dephasing (3), decoherence (4), time (5)
process_shape = (4, 4)
super().__init__(num_params, process_shape,
aux_shape=()) # our auxiliary information is a single float (None means no info)
def advance(self, state, v):
""" Evolves `state` in time """
state = np.array(state, dtype='complex')
omega, phase, detuning, dephasing, decoherence, t = v #Here are all our parameters
H = (omega * np.cos(phase) * self.Hx + omega * np.sin(phase) * self.Hy + detuning * self.Hz)
L = dephasing * self.dephasing_generator + decoherence * self.decoherence_generator
process = pygsti.tools.change_basis(expm((H + L) * t),'pp', 'col')
state = interp.unvec(np.dot(process, interp.vec(np.outer(state, state.conj()))))
return state
def create_process_matrix(self, v, comm=None):
def state_to_process_mxs(state):
return self.advance(state, v)
processes = interp.run_process_tomography(state_to_process_mxs, n_qubits=1,
basis='pp', comm=comm) # returns None on all but root processor
return np.array(processes) if (processes is not None) else None
def create_aux_info(self, v, comm=None):
omega, phase, detuning, dephasing, decoherence, t = v
return t*omega # matches aux_shape=() above
```
We can call `create_process_matrix` to generate a process matrix at a given set of parameters. Below we compute the ideal "target" operation by choosing the parameters corresponding to no errors.
```
example_process = ExampleProcess()
target_mx = example_process.create_process_matrix(np.array([1.0, 0.0, 0.0, 0.0, 0.0, np.pi/2]), comm=comm)
target_op = pygsti.modelmembers.operations.StaticArbitraryOp(target_mx)
print(target_op)
```
### Making things more efficient
We note that since our physical process is just an evolution in time, process matrices corresponding to different values of (just) the *time* parameter are especially easy to compute - a single evolution could compute, in one shot, the process matrices for an entire range of times.
The `PhysicalProcess` class contains support for such "easy-to-compute" parameters via the `num_params_evaluated_as_group` argument to its constructor. This argument defaults to 0, and specifies how many of the parameters, starting with the last one and working backward, should be evaluated within the same function call. If `num_params_evaluated_as_group` is set higher than 0, the derived class must implement the `create_process_matrices` and (optionally) `create_aux_infos` methods instead of `create_process_matrix` and `create_aux_info`. These methods take an additional `grouped_v` argument that contains *arrays* of values for the final `num_params_evaluated_as_group` parameters, and are expected return arrays of process matrices with corresponding shape (i.e., there is a leading index in the retured values for each "grouped" parameter).
We demonstrate this more complex usage below, where values for our final *time* argument are handled all at once.
```
class ExampleProcess_GroupTime(interp.PhysicalProcess):
def __init__(self):
self.Hx = np.array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, -1],
[0, 0, 1, 0]], dtype='float')
self.Hy = np.array([[0, 0, 0, 0],
[0, 0, 0, 1],
[0, 0, 0, 0],
[0, -1, 0, 0]], dtype='float')
self.Hz = np.array([[0, 0, 0, 0],
[0, 0, -1, 0],
[0, 1, 0, 0],
[0, 0, 0, 0]], dtype='float')
self.dephasing_generator = np.diag([0, -1, -1, 0])
self.decoherence_generator = np.diag([0, -1, -1, -1])
num_params = 6 # omega (0), phase (1), detuning (2), dephasing (3), decoherence (4), time (5)
process_shape = (4, 4)
super().__init__(num_params, process_shape,
aux_shape=(), # a single float
num_params_evaluated_as_group=1) # time values can be evaluated all at once
def advance(self, state, v, times):
state = np.array(state, dtype='complex')
omega, phase, detuning, dephasing, decoherence = v
H = (omega * np.cos(phase) * self.Hx + omega * np.sin(phase) * self.Hy + detuning * self.Hz)
L = dephasing * self.dephasing_generator + decoherence * self.decoherence_generator
processes = [pygsti.tools.change_basis(expm((H + L) * t),'pp', 'col') for t in times]
states = [interp.unvec(np.dot(process, interp.vec(np.outer(state, state.conj())))) for process in processes]
return states
def create_process_matrices(self, v, grouped_v, comm=None):
assert(len(grouped_v) == 1) # we expect a single "grouped" parameter
times = grouped_v[0]
def state_to_process_mxs(state):
return self.advance(state, v, times)
processes = interp.run_process_tomography(state_to_process_mxs, n_qubits=1,
basis='pp', time_dependent=True, comm=comm)
return np.array(processes) if (processes is not None) else None
def create_aux_infos(self, v, grouped_v, comm=None):
omega, phase, detuning, dephasing, decoherence = v
times = grouped_v[0]
return np.array([t*omega for t in times], 'd')
```
We can similarly create a target operation from this physical process, but now we must specify a list of times.
```
example_process = ExampleProcess_GroupTime()
target_mx = example_process.create_process_matrices(np.array([1.0, 0.0, 0.0, 0.0, 0.0]), [[np.pi/2]], comm=comm)[0]
target_op = pygsti.modelmembers.operations.StaticArbitraryOp(target_mx)
print(target_op)
```
## Creating an interpolated operation (gate)
Now that we've done the hard work of creating the physical process, it's easy to create an operator that evaluates the physical process on a grid of points and interpolates between them. The resulting `InterpolatedDenseOp` can be evaluated (i.e. `from_vector` can be invoked) at any point within the range being interpolated.
The parameters of the resulting `InterpolatedDenseOp` are the same as those of the underlying `PhysicalProcess`, and ranges are specified using either a *(min, max, num_points)* tuple or an array of values. Below we use only 2 points in most directions so it doesn't take too long to run.
Creating the object also requires a target operation, for which we use `target_op` as defined above. This is required because internally it is the *error generator* rather than the process matrix itself that is interpolated. The target operation can be parameterized by any contiguous subset of the physical process's parameters, starting with the first one. In our example, `target_op` is a `StaticArbitraryOp` and so takes 0 parameters. This should be interpreted as the "first 0 parameters of our example process".
```
param_ranges = ([(0.9, 1.1, 2), # omega
(-.1, .1, 2), # phase
(-.1, .1, 2), # detuning
(0, 0.1, 2), # dephasing
(0, 0.1, 2), # decoherence
np.linspace(np.pi / 2, np.pi / 2 + .5, 10) # time
])
interp_op = interp.InterpolatedDenseOp.create_by_interpolating_physical_process(
target_op, example_process, param_ranges, comm=comm)
```
The created `interp_op` can then be evaluated (quickly) at points in parameter space.
```
interp_op.from_vector([1.1, 0.01, 0.01, 0.055, 0.055, 1.59])
interp_op.to_dense()
```
The auxiliary information can be retrieved from any interpolated operator via its `aux_info` attribute.
```
interp_op.aux_info
```
## Creating an interpolated operation factory
Operation factories in pyGSTi take "arguments" provided by in-circuit labels and produce operations. For example, the value of the rotation angle might be specified over a continuous interval by the algorithm being run, rather than being noise parameter that is fit to data when a model is optimized (e.g. in GST).
The `InterpolatedOpFactory` object interpolates a physical process, similar to `InterpolatedDenseOp`, but allows the user to divide the parameters of the physical process into *factory arguments* and *operation parameters*. The first group is meant to range over different intended (target) operations, and the latter group is meant to be unkonwn quantities determined by fitting a model to data. To create an `InterpolatedOpFactory`, we must first create a custom factory class that creates the target operation corresponding to a given set of arguments. As in the case of `InterpolatedDenseOp`, the target operations can be parameterized by any contiguous subset of the factory's parameters, starting with the first one.
We choose to make a factory that takes as arguments the *time* and *omega* physical process parameters.
```
class TargetOpFactory(pygsti.modelmembers.operations.OpFactory):
def __init__(self):
self.process = ExampleProcess_GroupTime()
pygsti.modelmembers.operations.OpFactory.__init__(self, state_space=1, evotype="densitymx")
def create_object(self, args=None, sslbls=None):
assert(sslbls is None)
assert(len(args) == 2) # t (time), omega
t, omega = args
mx = self.process.create_process_matrices(np.array([omega, 0.0, 0.0, 0.0, 0.0]), [[t]], comm=None)[0]
#mx = self.process.create_process_matrix(np.array([omega, 0.0, 0.0, 0.0, 0.0, t]), comm=None) # Use this if using our initial ExampleProcess above.
return pygsti.modelmembers.operations.StaticArbitraryOp(mx)
```
We can then create an `InterpolatedOpFactory` similarly to how we created an `InterpolatedDenseOp` except now we separately specify factory argument and optimization parameter ranges, and specify which of the underlying physical process's parameters are turned into factory arguments (`arg_indices` below).
```
arg_ranges = [np.linspace(np.pi / 2, np.pi / 2 + .5, 10), # time
(0.9, 1.1, 2) # omega
]
param_ranges = [(-.1, .1, 2), # phase
(-.1, .1, 2), # detuning
(0, 0.1, 2), # dephasing
(0, 0.1, 2) # decoherence
]
arg_indices = [5, 0] #indices for time and omega within ExampleProcess_GroupTime's parameters
opfactory = interp.InterpolatedOpFactory.create_by_interpolating_physical_process(
TargetOpFactory(), example_process, arg_ranges, param_ranges, arg_indices, comm=comm)
```
Note that the factory has only 4 parameters (whereas the physical process and the interpolated operator we made above have 6). This is because 2 of the physical process parameters have been turned into factory arguments.
```
print(opfactory.num_params)
print(interp_op.num_params)
print(example_process.num_params)
```
We can use the factory to create an `InterpolatedDenseOp` operation at a given *time* and *omega* pair:
```
opfactory.from_vector(np.array([0.01, 0.01, 0.055, 0.055]))
op = opfactory.create_op((1.59, 1.1))
op.to_dense()
op.aux_info
```
| true |
code
| 0.637003 | null | null | null | null |
|
# PIO Programming
Resources:
* [RP2040 Datasheet Section 3.4](https://datasheets.raspberrypi.com/rp2040/rp2040-datasheet.pdf)
Life with David
## Setting multiple pins from Python
```
%serialconnect
from machine import Pin
import time
from rp2 import PIO, StateMachine, asm_pio
# decorator to translate to PIO machine code
@asm_pio(
out_init = (rp2.PIO.OUT_LOW,) * 8, # initialize 8 consecutive pins
out_shiftdir = rp2.PIO.SHIFT_RIGHT) # output lsb bits first
def parallel_prog():
pull(block) # pull data from Tx FIFO. Wait for data
out(pins, 8) # send 8 bits from OSR to pins
# create an instance of the state machine
sm = StateMachine(0, parallel_prog, freq=1000000, out_base=Pin(0))
# start the state machine
sm.active(1)
for n in range(256):
sm.put(n)
time.sleep(0.01)
```
## Writing Stepper Steps to pins
```
%serialconnect
from machine import Pin
import time
from rp2 import PIO, StateMachine, asm_pio
# decorator to translate to PIO machine code
@asm_pio(
out_init = (rp2.PIO.OUT_LOW,) * 4, # initialize 8 consecutive pins
out_shiftdir = rp2.PIO.SHIFT_RIGHT) # output lsb bits first
def stepper_step():
pull(block) # pull data from Tx FIFO. Wait for data
out(pins, 4) # send 8 bits from OSR to pins
# create an instance of the state machine
sm = StateMachine(0, stepper_step, freq=1000000, out_base=Pin(0))
# start the state machine
sm.active(1)
step_sequence = [8, 12, 4, 6, 2, 3, 1, 9]
for n in range(500):
sm.put(step_sequence[n % len(step_sequence)])
time.sleep(0.01)
%serialconnect
from machine import Pin
import time
from rp2 import PIO, StateMachine, asm_pio
# decorator to translate to PIO machine code
@asm_pio(
set_init = rp2.PIO.OUT_LOW)
def count_blink():
pull()
mov(x, osr)
label("count")
set(pins, 1)
set(y, 100)
label("on")
nop() [1]
jmp(y_dec, "on")
set(pins, 0)
nop() [19]
nop() [19]
nop() [19]
nop() [19]
jmp(x_dec, "count")
# create an instance of the state machine
sm = StateMachine(0, count_blink, freq=2000, set_base=Pin(25))
# start the state machine
sm.active(1)
sm.put(20)
%serialconnect
from machine import Pin
import time
from rp2 import PIO, StateMachine, asm_pio
# decorator to translate to PIO machine code
@asm_pio(
out_init = (rp2.PIO.OUT_LOW,) * 4, # initialize 8 consecutive pins
out_shiftdir = rp2.PIO.SHIFT_RIGHT) # output lsb bits first
def stepper_step():
pull(block) # pull data from Tx FIFO. Wait for data
out(pins, 4) # send 8 bits from OSR to pins
# create an instance of the state machine
sm = StateMachine(0, stepper_step, freq=1000000, out_base=Pin(0))
# start the state machine
sm.active(1)
step_sequence = [8, 12, 4, 6, 2, 3, 1, 9]
def step():
pos = 0
while True:
coils = step_sequence[pos % len(step_sequence)]
yield coils
pos += 1
stepper = step()
for k in range(10):
c = next(stepper)
print(c)
#for n in range(100):
# for step in step_sequence:
# sm.put(step)
# time.sleep(0.01)
```
## Interacting PIO programs
Section 3.2.7 of the RP2040 data sheet describes how interactions between state machines on the same PIO processor can be managed. Here will demonstrate this in a few steps. For the first step, we create a counter that accepts an integer from the FIFO buffer, then blinks an led a fixed number of times.
```
%serialconnect
from machine import Pin
import time
import rp2
from rp2 import PIO, StateMachine, asm_pio
@asm_pio(out_init = rp2.PIO.OUT_LOW)
def count_blink():
pull(block) # wait for data on Tx FIFO
set(pins, 1)
set(x, osr)
# create an instance of the state machine
sm0 = StateMachine(0, count_blink, freq=2000, out_base=Pin(25))
# start the state machine
sm0.active(1)
sm0.put(1)
time.sleep(2)
sm0.active(0)
%serialconnect
from machine import Pin
import time
from rp2 import PIO, StateMachine, asm_pio
# decorator to translate to PIO machine code
@asm_pio(
out_init = (rp2.PIO.OUT_LOW,) * 4, # initialize 8 consecutive pins
out_shiftdir = rp2.PIO.SHIFT_RIGHT) # output lsb bits first
def stepper_step():
pull(block) # pull data from Tx FIFO. Wait for data
out(pins, 4) # send 8 bits from OSR to pins
# create an instance of the state machine
sm = StateMachine(0, stepper_step, freq=1000000, out_base=Pin(0))
# start the state machine
sm.active(1)
step_sequence = [8, 12, 4, 6, 2, 3, 1, 9]
for n in range(1000):
sm.put(step_sequence[n % len(step_sequence)])
time.sleep(0.01)
```
| true |
code
| 0.232397 | null | null | null | null |
|
# Plot3D Python Tutorial
In this tutorial you will learn about the Plot3D NASA Standard and how to use NASA's Plot3D python library to read, write, find connectivity, split blocks, and find periodicity.
## About Plot3D
Plot3D is a standard for defining a simple structured grid. This standard was developed in the 1980's [User Manual](https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwiLm_2Q8JjzAhUCB50JHTfFCM4QFnoECAMQAQ&url=https%3A%2F%2Fwww.grc.nasa.gov%2Fwww%2Fwinddocs%2Ftowne%2Fplotc%2Fplotc_p3d.html&usg=AOvVaw0iKPGjnhjiQA9AFZcFhkEE)
To understand the plot3D standard, we must first start with the definition of an array. The figure below shows a box with 6 faces and 8 verticies represented by black dots. Now if you were to discretize a geometry into many of these boxes all connected to each other. You would have many x,y,z points. To organize things we arrange all this points into an array of x's, y'z, z's and we label them as capital X, Y, Z.
So what does this mean? how is this helpful. It depends on how to arrange the array. If you have a single dimensional array of x like x<sub>1</sub>,x<sub>2</sub>,x<sub>3</sub>, ..., x<sub>n</sub>. This isn't particularly useful because it's hard to split it in to faces - just try it with the simple box above. So what we do instead is represent x as a 3-dimensional array instead of a single dimension. For example x[0,0,0] or x<sub>0,0,0</sub> = some value.
The image below shows how we arrange the x values of each of the vertices.
With this new arrangement of x into a 3-dimensional array, x[i,j,k]. We can easily extract a face. For example the front face is defined by x[0,0,0] x[1,0,0], x[0,1,0], x[1,1,0]. Do you notice anything interesting from this array? The third index "k" is 0. **To define a face you simply set either i, j, or k to be a constant value.** For outer faces you would use KMIN or KMAX. Depending on the programming language the indicies may start at 1 or 0. In python we start at 0 and end at n-1. [More info on Python Arrays](https://www.w3schools.com/python/python_arrays.asp)
# Environment Setup
This step is relatively short. Run the code below to install plot3d
```
!pip install plot3d
```
# Reading and Writing a mesh file
In simple words, a mesh is a collection of boxes arranged to form a shape. In this example we will explore reading a mesh in ASCII and saving it into a binary format.
## Step 1: Load the functions from the library
```
from plot3d import read_plot3D, write_plot3D,Block
import pickle
import pprint
```
## Step 2: Download and read the mesh file
The code below reads the plot3D into a variable called blocks. "blocks" is a variable representing an array of plot3D blocks. You can think of a block as a 6 sided cube but inside the cube you have multiple smaller cubes. Cubes can be stretched and wrapped such that two ends are connected. This is called an o-mesh. We will plot this in a later step.
```
!wget https://nasa-public-data.s3.amazonaws.com/plot3d_utilities/PahtCascade-ASCII.xyz
blocks = read_plot3D('PahtCascade-ASCII.xyz',binary=False) # Reading plot3D
write_plot3D('PahtCascade-binary.xyz',blocks,binary=True) # Writing plot3D to binary file
```
### Plotting the Mesh
The function below shows how we can plot an outline of the mesh
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
import numpy as np
def plot_block_outline(block:Block,ax:axes3d):
IMAX,JMAX,KMAX = block.X.shape
X = block.X
Y = block.Y
Z = block.Z
for i in [0,IMAX-1]: # Plots curves at constant I bounds
for j in [0,JMAX-1]:
x = X[i,j,:]
y = Y[i,j,:]
z = Z[i,j,:]
ax.plot3D(x,y,z)
for j in [0,JMAX-1]: # Plots curves at constant I bounds
for k in [0,KMAX-1]:
x = X[:,j,k]
y = Y[:,j,k]
z = Z[:,j,k]
ax.plot3D(x,y,z)
for i in [0,IMAX-1]: # Plots curves at constant I bounds
for k in [0,KMAX-1]:
x = X[i,:,k]
y = Y[i,:,k]
z = Z[i,:,k]
ax.plot3D(x,y,z)
```
Try playing with this code to see if you can plot one block at a time. Also try changing the rotation
```
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
plot_block_outline(blocks[0],ax)
plot_block_outline(blocks[1],ax)
ax.view_init(30,45)
print("we have " + str(len(blocks)) + " blocks")
```
# Finding Connectivity
Connectivity tells the solver how information should transfer between Faces. For example, lets look at the example above. We have 2 blocks `blocks[0]` and `blocks[1]` These are connected via the pressure side of the blade. One of the features of the plot3d library is the ability to find connected faces between blocks as well as all the connected points.
## Finding Connected Faces
The function `connectivity` takes in a parameter for blocks. The output is a list of face matches between blocks along with the outer faces which are faces that do not have a connection to another block.
```
from plot3d import connectivity, connectivity_fast
face_matches, outer_faces_formatted = connectivity_fast(blocks) # Running this code will take a while depending on how fast google colab is on a given day.
# or you can call `face_matches, outer_faces_formatted = connectivity_fast(blocks)` which works too but might be slower
# Saving the results
with open('connectivity.pickle','wb') as f:
pickle.dump({"face_matches":face_matches, "outer_faces":outer_faces_formatted},f)
```
### Representing connected faces
`face_matches` contains matching face diagonals. The simpliest way to represent a face match is to use the following standard:
Block[0]-Face lower corner represented as [IMIN,JMIN,KMIN] and Face Upper corner represented as [IMAX,JMAX,KMAX] **is matched to** Block[1]-Face lower corner represented as [IMIN,JMIN,KMIN] and Face Upper corner represented as [IMAX,JMAX,KMAX].

`face_matches[0]['match']` is a dataframe of connected points. This is available to you in case you want to use it.
You can see that below when we print out the dictionary
```
with open('connectivity.pickle','rb') as f:
data = pickle.load(f)
face_matches = data['face_matches']
outer_faces = data['outer_faces']
face_matches
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(face_matches[0])
```
## Plotting Connected Faces
```
from matplotlib import cm
import numpy as np
def select_multi_dimensional(T:np.ndarray,dim1:tuple,dim2:tuple, dim3:tuple):
"""Takes a block (T) and selects X,Y,Z from the block given a face's dimensions
theres really no good way to do this in python
Args:
T (np.ndarray): arbitrary array so say a full matrix containing X
dim1 (tuple): 20,50 this selects X in the i direction from i=20 to 50
dim2 (tuple): 40,60 this selects X in the j direction from j=40 to 60
dim3 (tuple): 10,20 this selects X in the k direction from k=10 to 20
Returns:
np.ndarray: returns X or Y or Z given some range of I,J,K
"""
if dim1[0] == dim1[1]:
return T[ dim1[0], dim2[0]:dim2[1]+1, dim3[0]:dim3[1]+1 ]
if dim2[0] == dim2[1]:
return T[ dim1[0]:dim1[1]+1, dim2[0], dim3[0]:dim3[1]+1 ]
if dim3[0] == dim3[1]:
return T[ dim1[0]:dim1[1]+1, dim2[0]:dim2[1]+1, dim3[0] ]
return T[dim1[0]:dim1[1], dim2[0]:dim2[1], dim3[0]:dim3[1]]
def plot_face(face_matches,blocks):
for fm in face_matches:
block_index1 = fm['block1']['block_index']
I1 = [fm['block1']['IMIN'],fm['block1']['IMAX']] # [ IMIN IMAX ]
J1 = [fm['block1']['JMIN'],fm['block1']['JMAX']] # [ JMIN JMAX ]
K1 = [fm['block1']['KMIN'],fm['block1']['KMAX']] # [ KMIN KMAX ]
block_index2 = fm['block2']['block_index']
I2 = [fm['block2']['IMIN'],fm['block2']['IMAX']] # [ IMIN IMAX ]
J2 = [fm['block2']['JMIN'],fm['block2']['JMAX']] # [ JMIN JMAX ]
K2 = [fm['block2']['KMIN'],fm['block2']['KMAX']] # [ KMIN KMAX ]
X1 = select_multi_dimensional(blocks[block_index1].X, (I1[0],I1[1]), (J1[0],J1[1]), (K1[0],K1[1]))
Y1 = select_multi_dimensional(blocks[block_index1].Y, (I1[0],I1[1]), (J1[0],J1[1]), (K1[0],K1[1]))
Z1 = select_multi_dimensional(blocks[block_index1].Z, (I1[0],I1[1]), (J1[0],J1[1]), (K1[0],K1[1]))
X2 = select_multi_dimensional(blocks[block_index2].X, (I2[0],I2[1]), (J2[0],J2[1]), (K2[0],K2[1]))
Y2 = select_multi_dimensional(blocks[block_index2].Y, (I2[0],I2[1]), (J2[0],J2[1]), (K2[0],K2[1]))
Z2 = select_multi_dimensional(blocks[block_index2].Z, (I2[0],I2[1]), (J2[0],J2[1]), (K2[0],K2[1]))
# return X1
surf1 = ax.plot_surface(X1, Y1, Z1, cmap=cm.coolwarm, linewidth=0, antialiased=True)
surf2 = ax.plot_surface(X2, Y2, Z2, cmap=cm.coolwarm, linewidth=0, antialiased=True)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
plot_block_outline(blocks[0],ax)
plot_block_outline(blocks[1],ax)
plot_face(face_matches,blocks)
ax.view_init(30,45)
```
## Periodic Faces
Perodicity is a subset of connectivity. **It relates to how Faces of blocks are connected when rotated by an angle.** You can think of an apple pie and slice it up into equal slices. Say you put in a filling into one of those slices. The filling will splurge over to the other slices. This is kind of what perodicity means. Data goes into one slice, it is transfered into other slices. You can also think of the game Portal.
In turbomachinery, simulating an entire turbine wheel requires many points, it is easier to break it into pie slices and apply periodicity/connectivity to the sides.
```
from plot3d import periodicity, Face
# This step may take a while. It is looking for periodicity for all surfaces that have constant "k"
periodic_surfaces, outer_faces_to_keep,periodic_faces,outer_faces = periodicity(blocks,outer_faces,face_matches,periodic_direction='k',rotation_axis='x',nblades=55)
with open('connectivity-periodic.pickle','wb') as f:
[m.pop('match',None) for m in face_matches] # Remove the dataframe
pickle.dump({"face_matches":face_matches, "outer_faces":outer_faces_to_keep, "periodic_surfaces":periodic_surfaces},f)
```
## Plotting Periodic Faces
This function outputs 4 things
1. periodic_surfaces - this is list of all the surfaces/faces that match when rotated by an angle formatted as a dictionary.
2. outer_faces_to_keep - These are the list of outer faces that are not periodic formatted as a dictionary.
3. periodic_faces - is a list of `Face` objects that are connected to each other organized as a list of tuples: [Face1, Face2] where Face 1 will contain the block number and the diagonals [IMIN,JMIN,KMIN,IMAX,JMAX,KMAX]. Example: blk: 1 [168,0,0,268,100,0].
4. outer_faces - This is a list of outer faces save as a list of Faces
Try running the codes below to see how each of the variables is structured
```
periodic_faces
outer_faces
```
Code below shows how to plot all the periodic surfaces. Matplotlib is not easy to use in colab environment. You can't really zoom or rotate. It is encouraged for you to use paraview to plot. There is a tutorial and examples in the docs https://nasa.github.io/Plot3D_utilities/docs/build/html/index.html
```
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
plot_block_outline(blocks[0],ax)
plot_block_outline(blocks[1],ax)
plot_face(periodic_surfaces[0:1],blocks)
ax.view_init(30,45)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
plot_block_outline(blocks[0],ax)
plot_block_outline(blocks[1],ax)
plot_face(periodic_surfaces[2:],blocks)
ax.view_init(30,45)
```
# Advance Topics
## Splitting the Blocks for Computational Efficiency
When solving a plot3D block it is often useful to break it into smaller blocks of a certain size. This will improve the speed by splitting the blocks and allowing each CPU core to solve a part of the mesh. BUT we also need to maintain something called multi-grid.
### Multi-grid concept
Mulit-grid is a concept where you take a gird say 4x4 and you solve it as a 2x2 then interpolate the results on to the larger grid. The idea of solving a coarse grid and translating the solution onto a finer grid allows you to reach a converged solution much faster. So that's the benefits, what are the requirements?
To achieve multi-grid you need to have something called GCD - greatest common divisor. What does this even mean? If your grid/block is 257 x 101 x 33 in size this means that the largest divisor is 4. This means we can reduce the mesh about 2 times
257x101x33 (Fine)
129x51x17 (Coarse) (Coarse)/2
65x26x9 (Coarser) (fine)/4
Try to example below to find GCD of a grid
```
from math import gcd
grid_size = [257,101,33]
grid_size = [g-1 for g in grid_size]
temp = gcd(grid_size[0],gcd(grid_size[1],grid_size[2]))
print("Greatest common divisor is " + str(temp))
```
## Block split example
```
from plot3d import split_blocks, Direction
blocks = read_plot3D('PahtCascade-ASCII.xyz',binary=False) # Reading plot3D
blocks_split = split_blocks(blocks,300000, direction=Direction.i)
write_plot3D('PahtCascade-Split.xyz',blocks_split,binary=True)
```
### Connectivity using split blocks
```
face_matches, outer_faces_formatted = connectivity(blocks_split)
with open('connectivity-block-split.pickle','wb') as f:
pickle.dump({"face_matches":face_matches, "outer_faces":outer_faces_formatted},f)
print("There are {0} face matches".format(len(face_matches)))
print("There are {0} outer faces".format(len(outer_faces_formatted)))
# Displaying face matches
face_matches
# Displaying outer_faces
outer_faces_formatted
```
Plotting the Connectivity example
```
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
[plot_block_outline(block,ax) for block in blocks_split]
plot_face(face_matches,blocks_split)
ax.view_init(30,45)
```
### Periodicity using split blocks
Periodicity using split blocks is a bit interesting. There's lots of partial face matches etc. Again, it's really helpful to visualize using paraview than python, but I'll try to plot it for you anyways
```
with open('connectivity-block-split.pickle','rb') as f:
data = pickle.load(f)
face_matches = data['face_matches']
outer_faces = data['outer_faces']
blocks_split = read_plot3D('PahtCascade-Split.xyz', binary = True, big_endian=True)
periodic_surfaces, outer_faces_to_keep,periodic_faces,outer_faces = find_periodicity(blocks_split,outer_faces,periodic_direction='k',rotation_axis='x',nblades=55)
with open('connectivity-block-split_v02.pickle','wb') as f:
[m.pop('match',None) for m in face_matches] # Remove the dataframe
pickle.dump({"face_matches":face_matches, "outer_faces":outer_faces_to_keep, "periodic_surfaces":periodic_surfaces},f)
# Append periodic surfaces to face_matches
face_matches.extend(periodic_surfaces)
# Displaying periodic surfaces
periodic_surfaces
# Displaying face matches
face_matches
```
| true |
code
| 0.731832 | null | null | null | null |
|
<small><small><i>
All the IPython Notebooks in **[Python Natural Language Processing](https://github.com/milaan9/Python_Python_Natural_Language_Processing)** lecture series by **[Dr. Milaan Parmar](https://www.linkedin.com/in/milaanparmar/)** are available @ **[GitHub](https://github.com/milaan9)**
</i></small></small>
<a href="https://colab.research.google.com/github/milaan9/Python_Python_Natural_Language_Processing/blob/main/06_Named_Entity_Recognition.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 06 Named Entity Recognition (NER)
(also known as entity identification, entity chunking and entity extraction) is a subtask of information extraction that seeks to locate and classify named entities mentioned in unstructured text into pre-defined categories such as person names, organizations, locations, medical codes
spaCy has an **'ner'** pipeline component that identifies token spans fitting a predetermined set of named entities. These are available as the **`ents`** property of a **`Doc`** object.
https://spacy.io/usage/training#ner
```
# Perform standard imports
import spacy
nlp = spacy.load('en_core_web_sm')
# Write a function to display basic entity info:
def show_ents(doc):
if doc.ents:
for ent in doc.ents:
print(ent.text+' - '+ent.label_+' - '+str(spacy.explain(ent.label_)))
else:
print('No named entities found.')
doc = nlp(u'Hi, everyone welcome to Milaan Parmar CS tutorial on NPL')
show_ents(doc)
doc = nlp(u'May I go to England or Canada, next month to see the virus report?')
show_ents(doc)
```
## Entity annotations
`Doc.ents` are token spans with their own set of annotations.
<table>
<tr><td>`ent.text`</td><td>The original entity text</td></tr>
<tr><td>`ent.label`</td><td>The entity type's hash value</td></tr>
<tr><td>`ent.label_`</td><td>The entity type's string description</td></tr>
<tr><td>`ent.start`</td><td>The token span's *start* index position in the Doc</td></tr>
<tr><td>`ent.end`</td><td>The token span's *stop* index position in the Doc</td></tr>
<tr><td>`ent.start_char`</td><td>The entity text's *start* index position in the Doc</td></tr>
<tr><td>`ent.end_char`</td><td>The entity text's *stop* index position in the Doc</td></tr>
</table>
```
doc = nlp(u'Can I please borrow 500 dollars from Blake to buy some Microsoft stock?')
for ent in doc.ents:
print(ent.text, ent.start, ent.end, ent.start_char, ent.end_char, ent.label_)
```
## NER Tags
Tags are accessible through the `.label_` property of an entity.
<table>
<tr><th>TYPE</th><th>DESCRIPTION</th><th>EXAMPLE</th></tr>
<tr><td>`PERSON`</td><td>People, including fictional.</td><td>*Fred Flintstone*</td></tr>
<tr><td>`NORP`</td><td>Nationalities or religious or political groups.</td><td>*The Republican Party*</td></tr>
<tr><td>`FAC`</td><td>Buildings, airports, highways, bridges, etc.</td><td>*Logan International Airport, The Golden Gate*</td></tr>
<tr><td>`ORG`</td><td>Companies, agencies, institutions, etc.</td><td>*Microsoft, FBI, MIT*</td></tr>
<tr><td>`GPE`</td><td>Countries, cities, states.</td><td>*France, UAR, Chicago, Idaho*</td></tr>
<tr><td>`LOC`</td><td>Non-GPE locations, mountain ranges, bodies of water.</td><td>*Europe, Nile River, Midwest*</td></tr>
<tr><td>`PRODUCT`</td><td>Objects, vehicles, foods, etc. (Not services.)</td><td>*Formula 1*</td></tr>
<tr><td>`EVENT`</td><td>Named hurricanes, battles, wars, sports events, etc.</td><td>*Olympic Games*</td></tr>
<tr><td>`WORK_OF_ART`</td><td>Titles of books, songs, etc.</td><td>*The Mona Lisa*</td></tr>
<tr><td>`LAW`</td><td>Named documents made into laws.</td><td>*Roe v. Wade*</td></tr>
<tr><td>`LANGUAGE`</td><td>Any named language.</td><td>*English*</td></tr>
<tr><td>`DATE`</td><td>Absolute or relative dates or periods.</td><td>*20 July 1969*</td></tr>
<tr><td>`TIME`</td><td>Times smaller than a day.</td><td>*Four hours*</td></tr>
<tr><td>`PERCENT`</td><td>Percentage, including "%".</td><td>*Eighty percent*</td></tr>
<tr><td>`MONEY`</td><td>Monetary values, including unit.</td><td>*Twenty Cents*</td></tr>
<tr><td>`QUANTITY`</td><td>Measurements, as of weight or distance.</td><td>*Several kilometers, 55kg*</td></tr>
<tr><td>`ORDINAL`</td><td>"first", "second", etc.</td><td>*9th, Ninth*</td></tr>
<tr><td>`CARDINAL`</td><td>Numerals that do not fall under another type.</td><td>*2, Two, Fifty-two*</td></tr>
</table>
___
### **Adding a Named Entity to a Span**
Normally we would have spaCy build a library of named entities by training it on several samples of text.<br>In this case, we only want to add one value:
```
doc = nlp(u'Arthur to build a U.K. factory for $6 million')
show_ents(doc)
```
Add **Milaan** as **PERSON**
```
from spacy.tokens import Span
# Get the hash value of the ORG entity label
ORG = doc.vocab.strings[u'PERSON']
# Create a Span for the new entity
new_ent = Span(doc, 0, 1, label=ORG)
# Add the entity to the existing Doc object
doc.ents = list(doc.ents) + [new_ent]
```
<font color=green>In the code above, the arguments passed to `Span()` are:</font>
- `doc` - the name of the Doc object
- `0` - the *start* index position of the span
- `1` - the *stop* index position (exclusive)
- `label=PERSON` - the label assigned to our entity
```
show_ents(doc)
```
___
## Adding Named Entities to All Matching Spans
What if we want to tag *all* occurrences of "WORDS"? WE NEED TO use the PhraseMatcher to identify a series of spans in the Doc:
```
doc = nlp(u'Our company plans to introduce a new vacuum cleaner. '
u'If successful, the vacuum cleaner will be our first product.')
show_ents(doc)
# Import PhraseMatcher and create a matcher object:
from spacy.matcher import PhraseMatcher
matcher = PhraseMatcher(nlp.vocab)
# Create the desired phrase patterns:
phrase_list = ['vacuum cleaner', 'vacuum-cleaner']
phrase_patterns = [nlp(text) for text in phrase_list]
# Apply the patterns to our matcher object:
matcher.add('newproduct', None, *phrase_patterns)
# Apply the matcher to our Doc object:
matches = matcher(doc)
# See what matches occur:
matches
# Here we create Spans from each match, and create named entities from them:
from spacy.tokens import Span
PROD = doc.vocab.strings[u'PRODUCT']
new_ents = [Span(doc, match[1],match[2],label=PROD) for match in matches]
doc.ents = list(doc.ents) + new_ents
show_ents(doc)
```
___
## Counting Entities
While spaCy may not have a built-in tool for counting entities, we can pass a conditional statement into a list comprehension:
```
doc = nlp(u'Originally priced at $29.50, the sweater was marked down to five dollars.')
show_ents(doc)
len([ent for ent in doc.ents if ent.label_=='MONEY'])
spacy.__version__
doc = nlp(u'Originally priced at $29.50,\nthe sweater was marked down to five dollars.')
show_ents(doc)
```
### <font color=blue>However, there is a simple fix that can be added to the nlp pipeline:</font>
https://spacy.io/usage/processing-pipelines
```
# Quick function to remove ents formed on whitespace:
def remove_whitespace_entities(doc):
doc.ents = [e for e in doc.ents if not e.text.isspace()]
return doc
# Insert this into the pipeline AFTER the ner component:
nlp.add_pipe(remove_whitespace_entities, after='ner')
# Rerun nlp on the text above, and show ents:
doc = nlp(u'Originally priced at $29.50,\nthe sweater was marked down to five dollars.')
show_ents(doc)
```
For more on **Named Entity Recognition** visit https://spacy.io/usage/linguistic-features#101
___
## Noun Chunks
`Doc.noun_chunks` are *base noun phrases*: token spans that include the noun and words describing the noun. Noun chunks cannot be nested, cannot overlap, and do not involve prepositional phrases or relative clauses.<br>
Where `Doc.ents` rely on the **ner** pipeline component, `Doc.noun_chunks` are provided by the **parser**.
### `noun_chunks` components:
<table>
<tr><td>`.text`</td><td>The original noun chunk text.</td></tr>
<tr><td>`.root.text`</td><td>The original text of the word connecting the noun chunk to the rest of the parse.</td></tr>
<tr><td>`.root.dep_`</td><td>Dependency relation connecting the root to its head.</td></tr>
<tr><td>`.root.head.text`</td><td>The text of the root token's head.</td></tr>
</table>
```
doc = nlp(u"Autonomous cars shift insurance liability toward manufacturers.")
for chunk in doc.noun_chunks:
print(chunk.text+' - '+chunk.root.text+' - '+chunk.root.dep_+' - '+chunk.root.head.text)
```
### `Doc.noun_chunks` is a generator function
Previously we mentioned that `Doc` objects do not retain a list of sentences, but they're available through the `Doc.sents` generator.<br>It's the same with `Doc.noun_chunks` - lists can be created if needed:
```
len(doc.noun_chunks)
len(list(doc.noun_chunks))
```
For more on **noun_chunks** visit https://spacy.io/usage/linguistic-features#noun-chunks
| true |
code
| 0.317823 | null | null | null | null |
|
<a href="https://colab.research.google.com/github/lululxvi/deepxde/blob/master/examples/Lorenz_inverse_forced_Colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Description
This notebook aims at the identification of the parameters of the modified Lorenz attractor (with exogenous input)
Built upon:
* Lorenz attractor example from DeepXDE (Lu's code)
* https://github.com/lululxvi/deepxde/issues/79
* kind help from Lu, greatly acknowledged
# Install lib and imports
```
!pip install deepxde
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import re
import numpy as np
import requests
import io
import matplotlib.pyplot as plt
import deepxde as dde
from deepxde.backend import tf
import scipy as sp
import scipy.interpolate as interp
from scipy.integrate import odeint
```
# Generate data
```
# true values, see p. 15 in https://arxiv.org/abs/1907.04502
C1true = 10
C2true = 15
C3true = 8 / 3
# time points
maxtime = 3
time = np.linspace(0, maxtime, 200)
ex_input = 10 * np.sin(2 * np.pi * time) # exogenous input
# interpolate time / lift vectors (for using exogenous variable without fixed time stamps)
def ex_func(t):
spline = sp.interpolate.Rbf(
time, ex_input, function="thin_plate", smooth=0, episilon=0
)
# return spline(t[:,0:])
return spline(t)
# function that returns dy/dt
def LorezODE(x, t): # Modified Lorenz system (with exogenous input).
x1, x2, x3 = x
dxdt = [
C1true * (x2 - x1),
x1 * (C2true - x3) - x2,
x1 * x2 - C3true * x3 + ex_func(t),
]
return dxdt
# initial condition
x0 = [-8, 7, 27]
# solve ODE
x = odeint(LorezODE, x0, time)
# plot results
plt.plot(time, x, time, ex_input)
plt.xlabel("time")
plt.ylabel("x(t)")
plt.show()
time = time.reshape(-1, 1)
time.shape
```
# Perform identification
```
# parameters to be identified
C1 = tf.Variable(1.0)
C2 = tf.Variable(1.0)
C3 = tf.Variable(1.0)
# interpolate time / lift vectors (for using exogenous variable without fixed time stamps)
def ex_func2(t):
spline = sp.interpolate.Rbf(
time, ex_input, function="thin_plate", smooth=0, episilon=0
)
return spline(t[:, 0:])
# return spline(t)
# define system ODEs
def Lorenz_system(x, y, ex):
"""Modified Lorenz system (with exogenous input).
dy1/dx = 10 * (y2 - y1)
dy2/dx = y1 * (28 - y3) - y2
dy3/dx = y1 * y2 - 8/3 * y3 + u
"""
y1, y2, y3 = y[:, 0:1], y[:, 1:2], y[:, 2:]
dy1_x = dde.grad.jacobian(y, x, i=0)
dy2_x = dde.grad.jacobian(y, x, i=1)
dy3_x = dde.grad.jacobian(y, x, i=2)
return [
dy1_x - C1 * (y2 - y1),
dy2_x - y1 * (C2 - y3) + y2,
dy3_x - y1 * y2 + C3 * y3 - ex,
# dy3_x - y1 * y2 + C3 * y3 - 10*tf.math.sin(2*np.pi*x),
]
def boundary(_, on_initial):
return on_initial
# define time domain
geom = dde.geometry.TimeDomain(0, maxtime)
# Initial conditions
ic1 = dde.IC(geom, lambda X: x0[0], boundary, component=0)
ic2 = dde.IC(geom, lambda X: x0[1], boundary, component=1)
ic3 = dde.IC(geom, lambda X: x0[2], boundary, component=2)
# Get the training data
observe_t, ob_y = time, x
# boundary conditions
observe_y0 = dde.PointSetBC(observe_t, ob_y[:, 0:1], component=0)
observe_y1 = dde.PointSetBC(observe_t, ob_y[:, 1:2], component=1)
observe_y2 = dde.PointSetBC(observe_t, ob_y[:, 2:3], component=2)
# define data object
data = dde.data.PDE(
geom,
Lorenz_system,
[ic1, ic2, ic3, observe_y0, observe_y1, observe_y2],
num_domain=400,
num_boundary=2,
anchors=observe_t,
auxiliary_var_function=ex_func2,
)
plt.plot(observe_t, ob_y)
plt.xlabel("Time")
plt.legend(["x", "y", "z"])
plt.title("Training data")
plt.show()
# define FNN architecture and compile
net = dde.maps.FNN([1] + [40] * 3 + [3], "tanh", "Glorot uniform")
model = dde.Model(data, net)
model.compile("adam", lr=0.001)
# callbacks for storing results
fnamevar = "variables.dat"
variable = dde.callbacks.VariableValue([C1, C2, C3], period=1, filename=fnamevar)
losshistory, train_state = model.train(epochs=60000, callbacks=[variable])
```
Plots
```
# reopen saved data using callbacks in fnamevar
lines = open(fnamevar, "r").readlines()
# read output data in fnamevar (this line is a long story...)
Chat = np.array(
[
np.fromstring(
min(re.findall(re.escape("[") + "(.*?)" + re.escape("]"), line), key=len),
sep=",",
)
for line in lines
]
)
l, c = Chat.shape
plt.plot(range(l), Chat[:, 0], "r-")
plt.plot(range(l), Chat[:, 1], "k-")
plt.plot(range(l), Chat[:, 2], "g-")
plt.plot(range(l), np.ones(Chat[:, 0].shape) * C1true, "r--")
plt.plot(range(l), np.ones(Chat[:, 1].shape) * C2true, "k--")
plt.plot(range(l), np.ones(Chat[:, 2].shape) * C3true, "g--")
plt.legend(["C1hat", "C2hat", "C3hat", "True C1", "True C2", "True C3"], loc="right")
plt.xlabel("Epoch")
plt.show()
yhat = model.predict(observe_t)
plt.plot(observe_t, ob_y, "-", observe_t, yhat, "--")
plt.xlabel("Time")
plt.legend(["x", "y", "z", "xh", "yh", "zh"])
plt.title("Training data")
plt.show()
```
| true |
code
| 0.761195 | null | null | null | null |
|
# Lambda distribution (Vs Reff)
```
import matplotlib.pyplot as plt
import pickle
import numpy as np
## fucntions
def load_pickle(fname):
with open(fname, 'rb') as f:
return pickle.load(f)
def plot_lambda(catalog, i_early, i_late, i_bad, fn_out='./'):
import matplotlib.pyplot as plt
plt.ioff()
f = plt.figure()
ax = f.add_subplot(111)
#for i, val in enumerate(lambdar_arr):
for i in i_early:
a = np.asarray(catalog['lambda_arr'][i])
ax.plot(a, 'r-', alpha=0.5) # Red = Early
for i in i_late:
ax.plot(catalog['lambda_arr'][i], 'b-', alpha=0.3) # Red = Early
#plt.xlabel() # in the unit of Reff
ax.set_title(r"$\lambda _{R}$")
ax.set_ylabel(r"$\lambda _{R}$")
ax.set_xlabel("["+ r'$R/R_{eff}$'+"]")
ax.set_xlim(right=9)
ax.set_ylim([0,1])
ax.set_xticks([0, 4.5, 9])
ax.set_xticklabels(["0", "0.5", "1"])
plt.savefig(fn_out)
plt.close()
def aexp2zred(aexp):
return [1.0/a - 1.0 for a in aexp]
def zred2aexp(zred):
return [1.0/(1.0 + z) for z in zred]
def lbt2aexp(lts):
import astropy.units as u
from astropy.cosmology import WMAP7, z_at_value
zreds = [z_at_value(WMAP7.lookback_time, ll * u.Gyr) for ll in lts]
return [1.0/(1+z) for z in zreds]
def density_map(x, y, sort=True):
from scipy.stats import gaussian_kde
xy = np.vstack([x,y])
z = gaussian_kde(xy)(xy)
z /= max(z)
idx = z.argsort()
xx, yy = x[idx], y[idx]
z = z[idx]
return xx, yy, z
```
## I like this!
```
clusters = ['05427', '36413', '39990', '01605', '10002', '36415', '04466', '74010'][0:5]
lr_points = 5 # number of points int 1 Reff.
nreff = 3
nbins = 20
def lambda_den_map(clusters, exclude, nout=187, lr_points = 5, nreff=3, nbins=20,
density_kernel=False):
print(" nout:", nout, "lr_points:", lr_points, "nreff:", nreff, "nbins:", nbins)
points = np.arange(lr_points * nreff)
x_ticks_label = ["0", "1", "2", "3", "4"][0:nreff]
x_tick_pos = [0]
[x_tick_pos.append((i+1)*lr_points) for i in range(nreff)]
# Need a compiled array of lambda_arr
fig, axs = plt.subplots(2,2, sharey=True)#, sharex=True)
mass_cut_l = [2e9, 2e9, 1e10, 1e11]
mass_cut_r = [1e13,1e10, 1e11, 1e13]
yticks_ok=[0.0, 0.2, 0.4, 0.6, 0.8]
lambda_range=[0.0, 0.8]
snout = str(nout)
for imass in range(4):
# Count number of galaxies
ngood=0
for iclu, cluster in enumerate(clusters):
wdir = '/home/hoseung/Work/data/' + cluster
catalog = load_pickle(wdir + '/catalog_GM/' + 'catalog' + snout + '.pickle')
#i_good = np.where((catalog['mstar'] > mass_cut_l[imass]) & (catalog['mstar'] < mass_cut_r[imass]))[0]
i_good = (catalog['mstar'] > mass_cut_l[imass]) & (catalog['mstar'] < mass_cut_r[imass])
for i, gal in enumerate(catalog['id']):
if gal in exclude[iclu]: i_good[i] = False
#ngood += len(i_good)
ngood += sum(i_good)
ax = axs.ravel()[imass]
all_lr = np.zeros((len(points), ngood))
# compile data
ngood=0
for iclu, cluster in enumerate(clusters):
wdir = '/home/hoseung/Work/data/' + cluster
catalog = load_pickle(wdir + '/catalog_GM/' + 'catalog' + snout + '.pickle')
#i_good = np.where((catalog['mstar'] > mass_cut_l[imass]) & (catalog['mstar'] < mass_cut_r[imass]))[0]
i_good = (catalog['mstar'] > mass_cut_l[imass]) & (catalog['mstar'] < mass_cut_r[imass])
for i, gal in enumerate(catalog['id']):
if gal in exclude[iclu]: i_good[i] = False
ind_good = np.arange(len(i_good))[i_good]
for i, i_gal in enumerate(ind_good):
all_lr[:,ngood + i] = catalog['lambda_arr'][i_gal][:len(points)]
#ngood +=len(i_good)
ngood += sum(i_good)
# Draw density maps
if density_kernel:
xpoints = np.tile(points, ngood)
xx,yy,z = density_map(xpoints,all_lr.transpose().ravel())
im = ax.scatter(xx, yy, c=z, s=150, edgecolor='')
ax.set_xlim([-0.5, nreff*lr_points])
ax.set_ylim([-0.1,0.9])
#x_tick_pos = ""
#ax.set_xticks([0,lr_points-1,2*lr_points - 1])
#x_ticks_label = ["0", "1", "2"] # Correct. by default, rscale_lambda = 2.0
#ax.set_xticklabels(labels = [z for z in x_ticks_label])
#ax.set_xlabel(r"$R/R_{eff}$")
ax.set_title(r"{:.1e} $< M_\ast <$ {:.1e}".format(mass_cut_l[imass], mass_cut_r[imass]))
ax.text(1,0.65, "# gals:" + str(ngood)) # data coordinates
else:
den_map = np.zeros((nbins, len(points)))
for i in range(len(points)):
den_map[:,i], ypoints = np.histogram(all_lr[i,:], bins=nbins, range=lambda_range)
#den_map[:,i] /= den_map[:,i].max() # normalize each bin.
den_map /= den_map.max()
im = ax.imshow(den_map, origin="lower", cmap="Blues", interpolation="none"
, extent=[0,lr_points * nreff,0,nbins], aspect='auto')
#ax.set_xlim([-1.5, lr_points*nreff])
ax.set_ylim([-0.5,nbins])
ax.set_title(r"{:.1e} $< M_\ast <$ {:.1e}".format(mass_cut_l[imass], mass_cut_r[imass]))
ax.text(2,17, "# gals:" + str(ngood)) # data coordinates
#ax.set_yticks([np.where(ypoints == yy)[0] for yy in [0.0, 0.2, 0.4, 0.6, 0.8]]) # 0.0, 0.2, 0.4, 0.6, 0.8
#ax.set_yticklabels([str(yy) for yy in yticks_ok])
if density_kernel:
for j in range(2):
for i in range(2):
axs[j,i].set_xticks(x_tick_pos)
axs[j,i].set_xticklabels(labels = [z for z in x_ticks_label])
axs[1,i].set_xlabel(r"$R/R_{eff}$")
axs[i,0].set_ylabel("$\lambda _R$")
#axs[i,j].set_yticks([np.where(ypoints == yy)[0] for yy in np.arange(lambda_range[0], lambda_range[1])]) # 0.0, 0.2, 0.4, 0.6, 0.8
axs[i,j].set_yticks([ly for ly in [0.0, 0.2, 0.4, 0.6, 0.8]])
axs[i,j].set_yticklabels([str(yy) for yy in yticks_ok])
else:
for j in range(2):
for i in range(2):
axs[j,i].set_xticks(x_tick_pos)
axs[j,i].set_xticklabels(labels = [z for z in x_ticks_label])
axs[1,i].set_xlabel(r"$R/R_{eff}$")
axs[i,0].set_ylabel("$\lambda _R$")
#axs[i,j].set_yticks([np.where(ypoints == yy)[0] for yy in np.arange(lambda_range[0], lambda_range[1])]) # 0.0, 0.2, 0.4, 0.6, 0.8
axs[i,j].set_yticks([ nbins * ly for ly in [0.0, 0.2, 0.4, 0.6, 0.8]])
axs[i,j].set_yticklabels([str(yy) for yy in yticks_ok])
# Add + mark at 0.5, 1.0, 2.0Reff
#fig.tight_layout()
cax = fig.add_axes([0.86, 0.1, 0.03, 0.8]) # [left corner x, left corner y, x width, y width]
plt.colorbar(im, cax=cax, label='normalized denisty')
plt.subplots_adjust(left=0.1, bottom=None, right=0.8, top=None, wspace=0.05, hspace=0.22)
#left = 0.125 # the left side of the subplots of the figure
#right = 0.9 # the right side of the subplots of the figure
#bottom = 0.1 # the bottom of the subplots of the figure
#top = 0.9 # the top of the subplots of the figure
#wspace = 0.2 # the amount of width reserved for blank space between subplots
#hspace = 0.5 # the amount of height reserved for white space between subplots
plt.show()
#lambda_den_map(clusters)
exclude=[[],[],[],[],[1],[],[]]
lambda_den_map(["05427", "36413", "39990", "28928", "01605", "36415", "10002"], exclude, nout=187, lr_points = lr_points, density_kernel=True)
```
High resolution run seems to have more galaxies.
check mass function.
```
a=np.array([])
clusters = [5427, 36415, 39990, 1605, 10002, 36413, 4466, 74010][0:5]
# 74010 is unreliable.
# 36413 왜 안 돌아가나..?
#exclude_gals = [[],
# [],
# [],
# [123,155,],
# [2694,4684,5448,5885,5906,6967,6981,7047,7072,7151,7612],
# []]
lr_points = 10 # number of points int 1 Reff.
nreff = 3
points = np.arange(lr_points * nreff)
x_ticks_label = ["0", "1", "2", "3", "4"][0:nreff]
x_tick_pos = [0]
[x_tick_pos.append((i+1)*lr_points) for i in range(nreff)]
# Need a compiled array of lambda_arr
fig, axs = plt.subplots(2,2, sharey=True, sharex=True)
mass_cut_l = [0, 5e9, 1e10, 1e11, 1e12]
mass_cut_r = [1e13,1e10, 1e11, 1e12, 1e13]
#titles = #["All galaxies from all clusters",
# " {} $< M_{*} <$ {}".format(mass_cut_l[imass], mass_cut_r[imass])]
for imass in range(4):
ax = axs.ravel()[imass]
all_lr = np.zeros(0)
xpos = [] # why list??
ypos = []
zpos = []
clur = []
for i, cluster in enumerate(clusters):
wdir = '/home/hoseung/Work/data/' + str(cluster).zfill(5)
catalog = load_pickle(wdir + '/catalog_GM/' + 'catalog187.pickle')
i_good = np.where((catalog['mstar'] > mass_cut_l[imass]) & (catalog['mstar'] < mass_cut_r[imass]))[0]
for ij, j in enumerate(i_good):
all_lr = np.concatenate((all_lr, catalog['lambda_r'][j])) # some catalog has L_arr up to 2Rvir.
# Draw density maps
# x values
xpoints = np.tile(points, len(all_lr))
# Gaussian_kde measures 2D density. But in this case x-axis and y-axis are two independent parameters
#(not like x position and y position). So instead, measure 1-D histogram at each x point (R/Reff).
xx, yy, z = density_map(xpoints[:all_lr.shape[0]], all_lr.ravel(), ax)
ax.scatter(xx, yy, c=z, s=50, edgecolor='')
ax.set_xlim([-0.5,2*lr_points])
ax.set_ylim([0,0.8])
ax.set_title(r"{:.1e} $< M_\ast <$ {:.1e}".format(mass_cut_l[imass], mass_cut_r[imass]))
axs[1,0].set_xticks(x_tick_pos)#[0,lr_points-1,2*lr_points - 1])
axs[1,0].set_xticklabels(labels = [z for z in x_ticks_label])
axs[1,0].set_xlabel(r"$R/R_{eff}$")
axs[1,1].set_xticks(x_tick_pos)#[0,lr_points-1,2*lr_points - 1])
axs[1,1].set_xticklabels(labels = [z for z in x_ticks_label])
axs[1,1].set_xlabel(r"$R/R_{eff}$")
axs[0,0].set_ylabel("$\lambda _R$")
axs[1,0].set_ylabel("$\lambda _R$")
# Add + mark at 0.5, 1.0, 2.0Reff
plt.show()
plt.close()
```
#### Seaborn heat map
looks better than imshow. (BTW, you can use pcolomesh (X,Y,Z) instead of imshow(map))
Choose a suitable color map from Seaborn color map templates.
```
#plt.clf()
fig, ax = plt.subplots(1)
import seaborn.apionly as sns
# reset rc params to defaults
sns.reset_orig()
#cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(den_map, cmap="Blues", square=True, xticklabels=5, yticklabels=5,
linewidths=.2, cbar_kws={"shrink": .5}, ax=ax)
plt.gca().invert_yaxis()
plt.show()
# as a line
plt.close()
fig, ax = plt.subplots(len(clusters))
for i, cluster in enumerate(clusters):
wdir = '/home/hoseung/Work/data/' + str(cluster).zfill(5)
catalog = load_pickle(wdir + '/catalog_GM/' + 'catalog187.pickle')
#i_early = np.where(catalog['mstar'] > 5e11)[0]
i_early = np.where((catalog['mstar'] > 1e10) & (catalog['mstar'] < 1e11))[0]
for j in i_early:
ax[i].plot(points, catalog['lambda_arr'][j][:2 *lr_points], c='grey', alpha=0.3)
ax[i].set_xlim([-0.5,2*lr_points])
ax[i].set_ylim([0,0.8])
x_tick_pos = ""
ax[i].set_xticks([0,lr_points -1, 2*lr_points - 1])
x_ticks_label = ["0", "1", "2"] # Correct. by default, rscale_lambda = 2.0
ax[i].set_xticklabels(labels = [z for z in x_ticks_label])
ax[i].set_xlabel(r"$R/R_{eff}$")
plt.show()
len(catalog['lambda_arr'][j])
final_gals = list(cat['final_gal'])
# exclude disky galaxies
for bad_gal in exclude_gals[i]:
final_gals.remove(bad_gal)
ngals = len(final_gals)
mstar = np.zeros((ngals, nnouts))
l_r = np.zeros((ngals, nnouts))
```
| true |
code
| 0.405096 | null | null | null | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.