code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
#
#
#
# ## Cleaning the dataset
import geopy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
pd.options.mode.chained_assignment = None
# %matplotlib inline
from geopy.geocoders import Nominatim
geolocator = Nominatim(user_agent="app.py")
# Read the csv file
data = pd.read_csv('data.csv', encoding= 'unicode_escape')
data.head(10)
# ## Previewing the dataset
data.columns
data.shape
data.info
# +
data.describe()
## Notes
# Negative values in [UnitPrice], [Quantity],
# CustomerID missing ~ 100.000 entries/nulls
# Someone bought ~ 81.000 of an item
# -
# ## Processing the dataset
# +
# Converting [InvoiceDate] to datetime type
data['InvoiceDate'] = pd.to_datetime(data['InvoiceDate'])
# Creating Year, Month, Month/Year, Profit columns
data['Year'] = data['InvoiceDate'].dt.year.astype('str')
data['Month'] = data['InvoiceDate'].dt.month.astype('str')
data['MonthYear'] = data['Month'] + '/' + data['Year']
data['Profit'] = data.Quantity * data.UnitPrice
data.head()
# -
# ## Rearranging the columns
#
#
# Creating columns list
cols = list(data.columns.values)
cols
# Making a new dataframe with the correct order of columns
new_cols = ( 'Description', 'Quantity','UnitPrice','Profit','MonthYear','Year','Month',
'Country', 'StockCode','InvoiceNo','InvoiceDate', 'CustomerID'
)
data = pd.DataFrame(data, columns= new_cols)
# ## Inspecting negative values in :
# ### [UnitPrice]
# +
# 1A) Creating a new dataframe with only the filtered negative values in [UnitPrice]
unit_price_negatives = data[data['UnitPrice']< 0]
unit_price_negatives.head(5)
# -
# ### Notes
#
# - Notes for entries regarding negative price value :
# - Stock Code = B
# - Description = Adjust bad debt -> Refunds? (Keep negative value for accuracy reasons)
# - The invoices are chronologically related
# - UnitPrice for both = -11062.06 $
# - CustomerID = null
# - Null in CustomerID noted -> Bad debt
# +
# 1B) Searching for other stock codes = B
data[data['StockCode'] == 'B']
# -
# # Notes for entries regarding stockcode = B :
#
# - There is one more previous invoice (Possibly the price of the product before the refund)
# - Description = Adjust bad debt
# - Null in CustomerID noted -> Bad debt
#
# Conclusion :
# Possible Refund
#
# ### [Quantity]
# +
# 2A) Filtering negative values in [Quantity]
quantity_negatives = data[data['Quantity'] < 0]
quantity_negatives.head(20)
# Notes
# Stock Code = D
# Description = Discount
# +
# 2B) Searching for other stock codes = D
data[data['StockCode'] == 'D'].head(20)
# Notes
# There are 77 discounts in total
# -
# ## Non numerical-entries [Stockcode]
# +
# 3) Getting all non-numerical StockCode entries
# 3A) Filtering based on nun-numerical [StockCode] -> created new df
data_stock_code_non_num = data[data['StockCode'].str.contains('^[^0-9]', regex = True)]
len(data_stock_code_non_num)
# 2995 rows - > Roughly 3000 rows
# +
# NFX1) -> Descending
# 3B) Charting frequency of all non-numerical Stock-codes
plt.figure(figsize=(8, 8))
df_stock_code_non_num['StockCode'].value_counts().plot(kind = 'barh')
plt.xlabel('StockCode')
plt.ylabel('Count')
# +
# NFX1
# 3C) Charting frequency of products(description) with non-numerical Stock-codes
plt.figure(figsize=(10,10))
df_stock_code_non_num['Description'].value_counts().plot(kind = 'barh')
plt.xlabel('Description')
plt.ylabel('Count')
# -
# ### Notes
#
#
# - Only 3 products have a relatively large count of non numerical stock codes
# - The codes M,C2,D in the first chart refers to the manual, carriage and discount entries in the second chart.
# - Given that the total amount of non-numerical stock-code entries = ~ 2100 rows :
# - eg 2.100/540.000 -> ~ 1/250 of the dataset, we don't need (it is of trivial consequence) to remove them.
#
# ## Checking for null values
# +
# Finding total number of nulls for each column
data.isnull().sum()
# Found 1454 nulls in Description and 135080 in CustomerID
# -
# ### [Description] = null
# +
# Creating filtered dataframe -> [Description] = null
null_prod_df = data[data['Description'].isnull()].head(30)
null_prod_df
# +
data.dropna(subset=['Description'], inplace=True)
data.isnull().sum()
# Nulls in [Description] are 1454/541908 -> 1/500 -> Remove them as they wont affect the results significantly
# -
# ## [CustomerID] = null
# +
# Creating filtered dataframe -> [CustomerID] = null
null_cust_df = data[data['CustomerID'].isnull()]
null_cust_df.head(30)
# +
# Percentage of nulls[CustomerID]/total
round(len(null_cust_df) / len(data) * 100, 2)
# The percentage is around 1/4 of the dataset, should not hastily delete them.
# -
# ## Handling [CustomerID] nulls
# +
# Trying to find if there is a pattern depending on the month
# Plottting number on null entries for every month
null_cust_df['MonthYear'].value_counts().plot(kind = 'bar')
plt.xlabel('MonthYear')
plt.ylabel('Count')
# The highest count of missing CustomerID nulls is on 11/2011 and 12/2010 -> Server maintenance?
# +
# Trying to find if there is a pattern depending on the product
# We dont use a chart because there are too many products
null_cust_df['Description'].value_counts()
#Notes -> Null custIDs for dotcom-postage and some jumbo products
# Due to low number of rows, there is no need to remove them (They don't affect the general results of the dataset)
# -
# ## Checking for dupes
# +
# Showing all dupes
data[data.duplicated()]
# +
# Counting all dupes
len(data[data.duplicated()])
# +
# Removing all dupes
data = data.drop_duplicates()
data[data.duplicated()].sum()
# -
# ## Replacing illegal values
# +
# Replacing negative values in Quantity with 0\
data['Quantity'] = data['Quantity'].mask(data['Quantity'] < 0, 0)
data['Quantity'].describe()
# NFX2) -> Should I maintain negative values to reflect changes in quantity by returns?
# -
# Replacing null CustomerIDs with 0
data['CustomerID'].fillna(0, inplace = True)
data['CustomerID'].isnull().sum()
# ## Getting latitude and longitude for each country
#
# +
# Creating a dictionary{'geo'} having Country, Latitude and Longitude as keys, based on the list of unique Countries in the store dataset (data).
geo = {}
keys = ['Country', 'lat', 'long']
key1 = 'Country'
key2 = 'lat'
key3 = 'long'
geo.setdefault(key1, [])
geo.setdefault(key2, [])
geo.setdefault(key3, [])
for c in data['Country'].unique() :
location = geolocator.geocode(c)
geo['Country'].append(location[0])
geo['lat'].append(location.latitude)
geo['long'].append(location.longitude)
print(location, 'done!')
print('Finished!')
# +
# Converting to dataframe, in order to merge it with default store dataset (data).
geo_data = pd.DataFrame.from_dict(geo)
geo_data.head(20)
# +
# Merging geo_data and data to get lat and long for each country
mapped_data = data.merge(geo_data, how = 'left')
mapped_data.head(100)
# +
export = mapped_data.to_csv(r'C:\Users\Θοδωρής\clean_geo_data.csv')
| Sales_Analysis_2/Cleaning_Store_Dataset.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="https://raw.githubusercontent.com/melipass/umayor-ui-proyectos/main/logo-escuela.png" width="400" align="left" style="margin-bottom:20px;margin-right:20px;margin-top:25px">
#
# # Inteligencia Artificial
# ## Experiencia de Laboratorio 6: Perceptrón simple
#
# ## Objetivo del laboratorio
# Comprobar el funcionamiento de los modelos de redes neuronales correspondientes al perceptrón simple.
# ## Conceptos
# ### Perceptrón
# El perceptrón es la red neuronal más básica, de una sola capa y con una función de activación de escalón. El perceptrón se utiliza para la clasificación binaria de datos.
# ## Desarrollo
# ### 1. Implementar el perceptrón
#
# >Implementar un perceptrón simple y genérico en Python con una función de activación. Ajustar los pesos en cada iteración según corresponda, y entregar una salida acorde a la entrada recibida.
#
# Como primer paso, inicializamos el notebook con las librerías requeridas para trabajar. De ser necesario, hay que instalarlas.
# +
# #!pip install seaborn
# #!pip install numpy
# #!pip install matplotlib
# #!pip install pandas
# #!pip install graphviz
import seaborn as sn
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
plt.rcParams['figure.figsize'] = [6, 4]
plt.rcParams['figure.dpi'] = 100
import pandas as pd
import itertools
from graphviz import Digraph
from IPython.core.display import HTML
HTML("""
<style>
.output_png {
display: table-cell;
text-align: center;
vertical-align: middle;
}
</style>
""")
# -
# Según lo visto en clases, la función de activación del perceptrón es la de escalón, y será la utilizada en este notebook. Esta está definida de la siguiente manera:
#
# $$ \theta(z)= \left\{
# \begin{array}{ll}
# 1 & z \geq 0 \\
# 0 & z < 0 \\
# \end{array}
# \right. $$
#
# En donde el valor de $z$ corresponde a el valor ingresado en la función de activación $\theta$, y la salida de la función solo tiene dos posibles valores: $0$ y $1$.
# Función de activación del perceptrón
def theta(z):
return 1.0 if (z > 0) else 0.0
# Gráfico que representa la función de activación anterior
x = [-10,0,1,10]
y = [0,0,1,1]
plt.step(x, y)
plt.show()
# Usando esta función de activación, definiremos nuestro perceptrón como:
#
# $$
# y(\boldsymbol{x},\boldsymbol{w},b) = \theta(\boldsymbol{w}\cdot\boldsymbol{x}+b) = \theta(w_1x_1+w_2x_2+\dots+w_nx_n+b)
# $$
#
#
# Donde el vector $\boldsymbol{x}$ corresponde a las entradas del perceptrón y el vector $\boldsymbol{w}$ corresponde al peso asignado a cada uno. Esto se suma para después aplicar la función de activación, y queda nuestro perceptrón de la siguiente manera:
def perceptron(x,w,b):
entrada_theta = np.dot(w,x)+b
return theta(entrada_theta)
# El código de arriba contiene una función de producto punto que suma la multiplicación de cada elemento de los vectores, agregando el valor $b$ al final y almacenando el resultado en la variable ```entrada_theta```:
#
# $$\text{entrada_theta} = \left(\Sigma w_ix_i\right)+b$$
#
# Ese resultado se ingresa en la función de activación que definimos como $\theta$, la que luego nos devolverá el resultado del perceptrón. Visualmente, esto fluye así:
# +
nodos = ['x_1','x_2','⋮','x_n','w_1','w_2','⋮ ', 'w_n','Σ','θ','y']
vertices = {('x_1','w_1'),
('x_2','w_2'),
('⋮','⋮ '),
('x_n','w_n'),
('w_1','Σ'),
('w_2','Σ'),
('⋮ ','Σ'),
('w_n','Σ'),
('Σ','θ'),
('θ','y')}
dot = Digraph(node_attr={'shape':'circle','fixedsize':'true'},
graph_attr={'rankdir':'LR','label':'Perceptrón genérico','labelloc':'t','fontsize':'20'})
for nodo in nodos:
dot.node(nodo)
for vertice in vertices:
dot.edge(vertice[0],vertice[1])
dot
# -
# ### 2. Probar el perceptrón en AND, OR y XOR
# >Probar el perceptrón implementado para una compuerta lógica $\text{AND}$, $\text{OR}$ y $\text{XOR}$ con una entrada de tamaño 4.
#
# Para implementar perceptrones que simulen las compuertas lógicas $\text{AND}$, $\text{OR}$ y $\text{XOR}$ y que tengan cuatro entradas $x_1$, $x_2$, $x_3$ y $x_4$, debemos tomar el perceptrón y ajustarlo para que quede de la siguiente manera:
# $$
# y(\boldsymbol{x},\boldsymbol{w},b)=\theta(w_1x_1+w_2x_2+w_3x_3+w_4x_4+b)
# $$
#
# También, sabemos que existe un total de 16 posibles combinaciones de entradas para las compuertras con cuatro entradas, así que las dejaremos codificadas en un arreglo para probar en la parte 4:
l = [0,1]
x = [list(i) for i in itertools.product(l, repeat=4)]
print(x)
# #### 2.1. Compuerta AND
#
# La compuerta lógica $\text{AND}$ entrega el valor $1$ solo cuando todas sus entradas son $1$. Para que el perceptrón nos entregue el valor $1$ solo cuando todos los valores son $1$, debemos asignar valores a cada peso $w$ y al valor $b$, quedando así:
#
# $$
# \text{AND}(\text{x})=\theta(x_1+x_2+x_3+x_4-3.9)
# $$
#
# Donde decidimos dejar cada uno de los pesos $w_i = 1$ y el valor $b=-3.9$ para que la salida del perceptrón sea mayor a $0$ solo cuando todas las entradas valen $1$, teniendo que $1\cdot4-3.9=0.1$, y que $0.1>0 \Rightarrow y=1$.
def compuerta_AND(x):
w = [1,1,1,1]
b = -3.9
return perceptron(x,w,b)
# #### 2.2. Compuerta OR
# La compuerta lógica $\text{OR}$ también obtiene cuatro valores binarios y devuelve $1$ cuando existe al menos una entrada con valor $1$. El perceptrón queda así:
#
# $$
# \text{OR}(\text{x})=\theta(x_1+x_2+x_3+x_4-0.9)
# $$
#
# Donde decidimos dejar cada uno de los pesos $w_i = 1$ y el valor $b=-0.9$. Así, el perceptrón devolverá $1$ cuando exista al menos una entrada con valor $1$, ya que $1-0.9=0.1$ y sabemos que $0.1>0\Rightarrow y=1$.
def compuerta_OR(x):
w = [1,1,1,1]
b = -0.9
return perceptron(x,w,b)
# #### 2.3. Compuerta XOR
# En el caso de la compuerta $\text{XOR}$, sabemos que es necesario que nuestra compuerta devuelva el valor $0$ cuando todas las entradas son $0$ o $1$. Para ello, tuvimos que codificar la siguiente situación:
#
# - Encontrar la función que nos de $0$ solo cuando $\text{AND}$ nos devuelve $1$ (en otras palabras, hacer la compuerta $\text{NAND}$).
# - Poder combinar el resultado de la compuerta $\text{NAND}$ con el de la compuerta $\text{OR}$, es decir, crear un $\text{AND}$ con dos entradas.
#
# Una vez que identificamos esos dos requisitos creamos una función para cada uno, y así pudimos crear la compuerta $\text{XOR}$ que funciona satisfactoriamente. De esta forma, nos quedó la función $\text{XOR}$ como:
#
# $$
# \text{XOR}(\text{x})=\text{AND}(\text{NAND}(\text{x}),\text{OR}(\text{x})) = \text{AND}(\text{NAND}(x_1,x_2,x_3,x_4),\text{OR}(x_1,x_2,x_3,x_4))
# $$
# +
def compuerta_AND_2_entradas(x):
w = [1,1]
b = -1.9
return perceptron(x,w,b)
def compuerta_NAND(x):
w = [-1,-1,-1,-1]
b = 3.9
return perceptron(x,w,b)
def compuerta_XOR(x):
compuerta_1 = compuerta_NAND(x)
compuerta_2 = compuerta_OR(x)
return compuerta_AND_2_entradas([compuerta_1,compuerta_2])
# -
# Visualmente, las entradas pasan por las compuertas de la siguiente manera:
# +
nodos = ['x_1','x_2','Perceptrón NAND','Perceptrón OR','Perceptrón AND','y']
vertices = {('x_1','Perceptrón NAND'),
('x_2','Perceptrón NAND'),
('x_1','Perceptrón OR'),
('x_2','Perceptrón OR'),
('Perceptrón NAND','Perceptrón AND'),
('Perceptrón OR','Perceptrón AND'),
('Perceptrón AND','y')}
dot = Digraph(node_attr={'fixedsize':'true','width':'1.6'},
graph_attr={'rankdir':'LR','label':'Perceptrón XOR','labelloc':'t','fontsize':'20'})
for nodo in nodos:
dot.node(nodo)
for vertice in vertices:
dot.edge(vertice[0],vertice[1])
dot
# -
# ### 3. Probar el perceptrón con un dataset
# >Probar el perceptrón implementado para clasificar las entradas del dataset "letters.csv" determinando a qué letra corresponde cada entrada según las características recibidas.
#
# Primero que nada, cargamos los datos para ver con qué estamos trabajando.
df = pd.read_csv('letters.csv', header=None)
df
df[2].unique()
plt.scatter(df[0], df[1])#, color="orchid", marker="x", s=50)
plt.title("Dataset 'letters.csv'")
plt.xlabel('Valores $x_1$')
plt.ylabel('Valores $x_2$')
plt.xlim([-0.2, 1.2])
plt.ylim([-0.2, 1.2])
plt.show()
# Todos los valores numéricos de la tabla son positivos y no tenemos información de qué significa cada uno de ellos. Asumiremos que las dos primeras columnas de cada fila $i$ corresponderán a valores de entrada $x_1$ y $x_2$ y la tercera columna será la letra a clasificar, con valor ``o`` o ``l``.
# A continuación pasamos los datos del dataframe a un array:
datos = np.copy(df)
datos = np.array(datos)
# Creamos una función que nos devuelva un dataframe con la letra y la salida del perceptrón. Al perceptrón le daremos las dos columnas numéricas como entradas, un peso $\text{w}$ y un valor $b$ como variables para optimizar la clasificación en la sección 4.
def perceptron_datos(x,w,b):
df_datos = []
for valor in x:
df_datos.append([valor[2],perceptron([valor[0],valor[1]],w,b),valor[0],valor[1]])
return df_datos
# ### 4. Cálculo de error
# >Calcular el error obtenido en los pasos 2 y 3 durante el entrenamiento del perceptrón y expresarlo a través de un gráfico Iteración vs. Error.
# #### 4.1. Perceptrones de compuertas lógicas
# Para poder confirmar visualmente la existencia de un error dentro de nuestros perceptrones que implementan compuertas lógicas, decidimos hacer una función genérica para crear gráficos estilo 'serie de tiempo', donde podemos ver cómo va variando entre $0$ y $1$ el resultado de nuestros perceptrones a medida que vamos ingresando una lista de entradas. De esta manera, tendremos una guía visual de cuándo un perceptrón devuelve $0$ y cuándo devuelve $1$, y le entregaremos una función que marca el momento en el que se detecta un error para cada uno de los perceptrones.
def graficar_compuerta(x,compuerta,detector_error,titulo):
h = [0]
v = [0]
i = 1
error_en_titulo = ""
for posible_valor in x:
h.append(i)
i += 1
v.append(compuerta(posible_valor))
plt.plot(h, v)
plt.scatter(h, v, color="orchid", marker="x", s=50)
plt.xticks(h)
plt.yticks(v)
if detector_error(x,compuerta) != 1:
x_error = int(detector_error(x,compuerta))
plt.axvline(x = x_error+1, color = 'red')
error_en_titulo = " (Error)"
plt.title(titulo+error_en_titulo)
plt.show()
df = pd.DataFrame({'Entrada': x, 'Salida': v[1:]})
print(df)
# ##### 4.1.1. Prueba AND
#
# Sabemos que para un conjunto de entradas $x_n$, donde ninguna combinación de entradas se repite, la suma de todas las posibles salidas de la compuerta $\text{AND}$ jamás superará el valor $1$, cualquiera sea su dimensión. Teniendo esto presente, creamos la siguiente función:
# +
def error_compuerta_AND(x,compuerta):
i = 0
for posible_valor in x:
i += compuerta(posible_valor)
if i > 1:
print('Error: Existen entradas incorrectas o la lógica de la compuerta AND no es la correcta.')
return i
print("No se detectaron errores.")
return 1
error_compuerta_AND(x,compuerta_AND)
# -
# Tomando los valores que asignamos en la sección 2, obtenemos el siguiente gráfico y la siguiente tabla, donde en el eje x tendremos el índice de la combinación de entradas y en el eje y si esta corresponde a 0 o a 1, lo que nos permitirá confirmar si hay o no hay errores.
graficar_compuerta(x,compuerta_AND,error_compuerta_AND,'Salida del perceptrón para la compuerta AND')
# Para poner a prueba nuestro perceptrón que implementa una compuerta, usaremos dos conjuntos: uno con valores que no deberían ser aceptados, y otro con valores repetidos. La línea roja representará la iteración desde la cual comienza a estar erróneo nuestro perceptrón bajo las reglas establecidas de no repetición y admisión exclusiva de entradas $0$ y $1$, teniendo que los valores a la derecha de la línea ya no son correctos pues harán que la suma de todas las salidas sea mayor a $1$.
x_2_3 = [[2,3,3,2],[2,2,2,2],[3,3,3,3]]
x_repetido = [[1,1,1,1],[0,1,1,1],[1,1,1,1],[1,1,0,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]]
error_compuerta_AND(x_2_3,compuerta_AND)
graficar_compuerta(x_2_3,compuerta_AND,error_compuerta_AND,'Salida del perceptrón para la compuerta AND')
error_compuerta_AND(x_repetido,compuerta_AND)
graficar_compuerta(x_repetido,compuerta_AND,error_compuerta_AND,'Salida del perceptrón para la compuerta AND')
# ##### 4.1.2. Prueba OR
# Para la prueba en el caso de la compuerta OR, sabemos que si existen $x^2$ posibles combinaciones de entradas (donde $x$ es la cantidad de entradas), siempre existirá una salida que jamás tendrá el valor $1$. Por lo tanto, haremos un chequeo para detectar un error cuando la suma de los resultados de $\text{OR}(x)$ sea igual o mayor que $x^2$, teniendo la misma regla del caso anterior en la que cada combinación solo puede existir una vez en nuestro arreglo.
#
# En el caso específico del perceptrón donde implementamos la compuerta $\text{OR}$, sabemos que hay cuatro entradas, por lo tanto la cantidad de salidas será $4^2=4\times4=16$.
def error_compuerta_OR(x,compuerta):
i = 0
for posible_valor in x:
i += compuerta(posible_valor)
if i >= (len(x[0])*len(x[0])):
print('Error: Existen entradas incorrectas o la lógica de la compuerta OR no es la correcta.')
return i
print("No se detectaron errores.")
return 1
graficar_compuerta(x,compuerta_OR,error_compuerta_OR,'Salida del perceptrón para la compuerta OR')
# En el ejemplo de arriba, la suma total da 15. Sin embargo, en el ejemplo de abajo, la suma total supera el valor de 15 y nuestro código insertará una línea roja desde el punto en el que el error aparece, considerando incorrecto el gráfico desde esa línea vertical hacia la derecha.
x_error_or = np.copy(x)
x_error_or = x_error_or.tolist()
x_error_or.append([1,2,1,1])
x_error_or.append([1,2,5,1])
graficar_compuerta(x_error_or,compuerta_OR,error_compuerta_OR,'Salida del perceptrón para la compuerta OR')
# ##### 4.1.3. Prueba XOR
# Bajo la misma lógica que la prueba anterior, sabemos que la suma de todas las salidas de $\text{XOR}$ siempre será $x^2-2$, donde $x$ corresponde a la cantidad de entradas. Teniendo esto presente, tomaremos el código para validar $\text{OR}$ y lo ajustaremos a $\text{XOR}$, mostrándonos un error cuando la suma de las salidas supera $x^2-2$.
def error_compuerta_XOR(x,compuerta):
i = 0
for posible_valor in x:
i += compuerta(posible_valor)
if i >= (len(x[0])*len(x[0])-1):
print('Error: Existen entradas incorrectas o la lógica de la compuerta XOR no es la correcta.')
return i
print("No se detectaron errores.")
return 1
graficar_compuerta(x,compuerta_XOR,error_compuerta_XOR,'Salida del perceptrón para la compuerta XOR')
# Si repetimos algunas combinaciones, nos encontraremos con que la suma de todas las salidas superará $x^2-2$ y nos dará error:
x_error_xor = np.copy(x)
x_error_xor = x_error_xor.tolist()
x_error_xor.remove([1,1,1,1])
x_error_xor.append([1,0,1,1])
x_error_xor.append([1,0,0,1])
x_error_xor.append([1,0,1,0])
x_error_xor.append([1,1,1,1])
graficar_compuerta(x_error_xor,compuerta_XOR,error_compuerta_XOR,'Salida del perceptrón para la compuerta XOR')
# #### 4.2. Perceptrón con el dataset 'letters.csv'
# Para trabajar con el perceptrón, usaremos la función definida en la sección 3 para poder armar un dataframe que contenga dos columnas: la letra clasificada, y la salida del perceptrón.
#
# En esa función debemos ingresar el conjunto de datos a usar, los pesos $\text{w}$ y también un valor $b$. Para sistematizar la búsqueda de valores óptimos para los pesos y para el valor $b$, sabemos que idealmente tendremos una clasificación 100% correcta para la letra ``o`` y la letra ``l``, lo que llevado a números equivale a $1.0$ para cada una, por lo tanto, si sumamos esto, sabemos que el valor ideal de la suma de los valores óptimos de ``o`` y ``l`` será $2.0$, e iremos probando con números cercanos a esa cifra:
def evaluacion_perceptron_datos(suma_optima_a_buscar):
for i in range(1,11):
for j in range(1,11):
for k in range(1,11):
for l in [-1,1]:
df_salida = pd.DataFrame(perceptron_datos(datos,[1/i,1/j],l*1/k), columns=['Letra','Salida','x_1','x_2'])
o_en_cero = 0
o_en_uno = 0
l_en_cero = 0
l_en_uno = 0
for valor in df_salida.values:
if (valor[0] == 'o'):
if valor[1] == 0.0:
o_en_cero += 1
else:
o_en_uno += 1
else:
if valor[1] == 0.0:
l_en_cero += 1
else:
l_en_uno += 1
if o_en_cero/(o_en_cero+o_en_uno) + l_en_uno/(l_en_cero+l_en_uno) > suma_optima_a_buscar:
print("¡Valores encontrados!")
print("Peso w_1: " + str(1/i))
print("Peso w_2: " + str(1/j))
print("Valor b: " + str(l*1/k))
# Buscamos primero si existen valores que nos entreguen la clasificación perfecta, es decir, sin errores:
evaluacion_perceptron_datos(2.0)
# Y al no recibir valores de vuelta, bajamos la cifra a $1.8$:
evaluacion_perceptron_datos(1.8)
# Sigue muy alto, así que probaremos con $1.7$:
evaluacion_perceptron_datos(1.7)
# Y en esta ocasión sí encontramos valores que nos darán muy poco error. Revisamos si podemos discriminar entre cuál de las dos combinaciones de valores del perceptrón será mejor y subimos un poco hasta $1.73$:
evaluacion_perceptron_datos(1.73)
# Y ahora que solo tenemos una única combinación de valores, los ingresaremos en nuestro perceptrón para obtener los mejores resultados posibles según los datos y el trabajo previo:
# +
peso_w_1 = 0.3333333333333333
peso_w_2 = 0.1
valor_b = -0.25
df_salida = perceptron_datos(datos,[peso_w_1,peso_w_2],valor_b)
# -
# Creamos la siguiente función para encontrar todos los valores importantes en la evaluación de nuestro modelo:
def checkearErrores(df_salida):
o_en_cero = 0
o_en_uno = 0
l_en_cero = 0
l_en_uno = 0
for valor in df_salida:
if (valor[0] == 'o'):
if valor[1] == 0.0:
o_en_cero += 1
else:
o_en_uno += 1
else:
if valor[1] == 0.0:
l_en_cero += 1
else:
l_en_uno += 1
print('La cantidad de letras "o" clasificadas como 0 es: ' + str(o_en_cero))
print('La cantidad de letras "o" clasificadas como 1 es: ' + str(o_en_uno))
print('La cantidad de letras "l" clasificadas como 0 es: ' + str(l_en_cero))
print('La cantidad de letras "l" clasificadas como 1 es: ' + str(l_en_uno))
precision_o = o_en_cero/(o_en_cero+o_en_uno)
print('La precisión para clasificar "o" como 0 es: ' + str(precision_o))
precision_l = l_en_uno/(l_en_cero+l_en_uno)
print('La precisión para clasificar "l" como 1 es: ' + str(precision_l))
error_o = 1-o_en_cero/(o_en_cero+o_en_uno)
print('El error para clasificar "o" como 0 es: ' + str(error_o))
error_l = 1-l_en_uno/(l_en_cero+l_en_uno)
print('El error para clasificar "l" como 1 es: ' + str(error_l))
return precision_o, precision_l, error_o, error_l
precision_o, precision_l, error_o, error_l = checkearErrores(df_salida)
# Y así obtuvimos que el error para clasificar la letra ``o`` como $0$ es $0.26\dots$, mientras que clasificar ``l`` como $1$ no entrega ningún error, por lo tanto es una clasificación perfecta en base a los datos usados. Gráficamente, podemos ver esto en una matriz de confusión:
array = [[precision_o,error_o],[error_l,precision_l]]
df_cm = pd.DataFrame(array, index = [i for i in "ol"],
columns = [i for i in "01"])
sn.heatmap(df_cm, annot=True, cmap="OrRd")
# Finalmente, graficándo esto en un plano, tenemos:
# +
df_salida = pd.DataFrame(df_salida)
y = df_salida[1]
x1 = df_salida[2]
x2 = df_salida[3]
color = ['r' if value == 1 else 'b' for value in y]
label = [['l'],['o']]
plt.scatter(x1, x2, marker='o', color=color)
plt.xlabel('Valores $x_1$')
plt.ylabel('Valores $x_2$')
plt.title('Clasificación dada por el perceptrón')
a = -peso_w_1/peso_w_2
xx = np.linspace(-5, 5)
yy = a * xx - valor_b/peso_w_2
plt.xlim([-0.2, 1.2])
plt.ylim([-0.2, 1.2])
plt.plot(xx,yy)
plt.show()
# -
# Donde para generar la línea divisora entre los dos tipos de valores clasificados, hubo que hacer el siguiente cálculo en base a los pesos $\text{w}$ y el valor $b$:
#
# $$
# y(x) = \frac{w_1 \cdot b \cdot x}{w_2^2} = \frac{-0.\bar{3}\cdot0.25\cdot x}{0.01}
# $$
#
#
# En base a estos resultados, queremos tener un perceptrón que se auto-corrija iterativamente. El objetivo es tener un algoritmo que encuentre los mismos pesos óptimos que identificamos en los pasos anteriores. Para ello, definiremos una nueva función con *hiperparámetros*. Un hiperparámetro es un parámetro usado para controlar el perceptrón, y que no ingresa en él. En este caso, entregaremos la razón de aprendizaje y la cantidad de iteraciones en las que el perceptrón se irá ajustando:
# +
datos = np.copy(df)
datos = np.array(datos)
def perceptron_iterativo_datos(datos,aprendizaje,iteraciones):
valores = datos[:,:-1]
letras = datos[:,-1]
m, n = valores.shape
w = np.zeros(shape=(n+1,1),dtype=float)
lista_errores = []
for iteracion in range(iteraciones):
numero_errores = 0
for indice, x_i in enumerate(valores):
#insertando 1 para hacer x_0 = 1 como en varios modelos
x_i = np.insert(x_i,0,1).reshape(-1,1)
# llamamos la función de inicialización del principio del cuaderno
y = theta(np.dot(x_i.T, w))
# transformamos las letras a valores numéricos para comparar
letras[indice] = 1.0 if (letras[indice] == 'l') else 0.0
# en caso de haber diferencia entre el valor entregado por la función
# de inicialización y el valor esperado, registramos el error
if(np.squeeze(y) - letras[indice]) != 0:
w += (aprendizaje*(letras[indice] - y*x_i)).astype(np.float64)
numero_errores += 1
lista_errores.append(numero_errores)
return w, lista_errores
# -
w, lista_errores = perceptron_iterativo_datos(datos,0.5,10)
print(w)
print(lista_errores)
# Arriba podemos ver los resultados entregados por el código, que nos entrega los pesos correspondientes a cada entrada (en este caso, también agregamos una columna $x_0 = 1$ y así pudimos encontrar un nuevo $b$). No son los mismos valores que en el método que usamos anteriormente, sin embargo, podemos ver a continuación cómo este nuevo método iterativo comienza en un valor por defecto que da bastantes errores, y con el paso de las iteraciones va acercándose más a cero errores en la clasificación de las letras ```l``` y ```o```, llegando a cero en la tercera iteración.
lista_iteraciones = np.arange(1, 11)
plt.plot(lista_iteraciones, lista_errores)
plt.xlabel('Iteraciones')
plt.ylabel('Errores')
plt.show()
# +
valores = datos[:,:-1]
x1 = np.linspace(-5, 5)
m = -w[1]*3.33333/(w[2])
c = -w[0]/(w[2])
x2 = m*x1 + c*0.906
plt.scatter(valores[:, 0][y==0], valores[:, 1][y==0])
plt.scatter(valores[:, 0][y==1], valores[:, 1][y==1])
plt.xlabel("Valores $x_1$")
plt.ylabel("Valores $x_2$")
plt.title('Clasificación dada por el perceptrón entrenado')
plt.xlim([-0.2, 1.2])
plt.ylim([-0.2, 1.2])
plt.plot(x1, x2, 'y-')
plt.show()
# -
# ### 5. Análisis
# >Analizar y concluír sobre los resultados obtenidos en los pasos 2, 3 y 4.
# <!-- Respecto a la compuerta AND y OR, sabemos que el perceptrón devolverá $1$ para cualquier valor entrante mayor o igual que $0$, así que decidimos asignarle el valor $-1.9$ a $b$ para que el resultado de la suma $x_1w_1+x_2w_2+b$ sea $0.1$ solo cuando se cumpla simultáneamente que $x_1=1$ y $x_2=1$. Al analizarlo con el código dentro del $\text{for}$ en la misma celda donde definimos la función, pudimos comprobar que la compuerta funciona correctamente. -->
# Al realizar cada uno de los pasos anteriores fuimos aprendiendo diferentes características de los perceptrones, y consideramos que tras realizar este laboratorio pudimos entender correctamente su funcionamiento y el porqué es importante que auto-ajuste sus hiperparámetros.
#
# Esta importancia la demostramos al intentar encontrar los pesos $w$ utilizando iteraciones ```for``` en Python para cada uno de los posibles valores que varían dentro de la función de nuestro perceptrón, y luego irnos por el camino correcto de generar un perceptrón que vaya ajustando por sí mismo estos valores en la función ```perceptron_iterativo_datos```, basándonos en información del sitio web *Towards Data Science*. Esta última función tiene muchísimas menos iteraciones para encontrar valores óptimos para una correcta clasificación en comparación con la cantidad de iteraciones que debimos ejecutar en un principio, siendo computacionalmente muy beneficiosa a pesar de llegar al mismo resultado. Eso sí, la función auto-ajustada nos generó una recta que no se condice adecuadamente con lo que realmente debería mostrar, ya que a pesar de obtener una clasificación adecuada tuvimos que realizar un pequeño ajuste para mostrar esa recta en el gráfico, multiplicando por 3.333 el $w_1$. No logramos identificar exactamente por qué ocurre esto, pero al menos identificamos qué pasaba y lo corregimos con el fin de una buena visualización de los resultados.
#
# Un desafío que tuvimos fue interpretar correctamente el conjunto de datos ```letters.csv```, y tras explorar un poco los datos identificamos a qué correspondía cada columna. Esto lo pudimos manejar correctamente en el perceptrón y los resultados van acorde a esos datos.
#
# Por otro lado, para las compuertas lógicas razonamos tal como si hubieramos realizado un circuito en la vida real, donde las entradas y las salidas son binarias y ninguna 'cuenta' más que otra, así que desde un principio tomamos la decisión de dar peso $1$ y un límite específico que debiera ser superado para devolver un $1$. Esto, basándonos en nuestro conocimiento previo adquirido en la asignatura *Arquitectura de Computadoras* de nuestra escuela. Decidimos identificar errores como una serie de entradas de posibles combinaciones porque se nos volvió más práctico de representar visualmente, y estamos muy satisfechos con las gráficas generadas pues conseguimos codificar funciones genéricas para encontrar perturbaciones en nuestro perceptrón que no deberían existir bajo las reglas que definimos.
#
# Para finalizar, nos gustaría mucho implementar varias mejoras y lograr optimizar el código para el siguiente laboratorio en base a lo aprendido en esta experiencia, que sin duda fue muy positiva para complementar con la práctica lo visto en clases y en donde logramos probar nuestras propias teorías e investigar lo que es aceptado por la comunidad y la academia.
| lab-6-perceptron.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Find the best adversary
#
# - the idea is to train the best possible classifier of MNIST digits
# - and use it's 2nd most probable class as the adversarial choice for pre-commit
# +
import numpy as np
from precommit_analysis.keras_mnist_example import prepare_data, create_mnist_cnn_model
from precommit_analysis.generators import sparse_mnist_generator_nonzero, eval_precommit_adversarial_generator
batch_size = 128
num_classes = 10
epochs = 12
# -
x_train, y_train, x_test, y_test, input_shape = prepare_data(num_classes)
val_data_generator = sparse_mnist_generator_nonzero(
x_test,
y_test,
batch_size=x_test.shape[0],
sparsity=6,
shuffle=False
)
# load the judge 5k batches
judge = create_mnist_cnn_model(num_classes, input_shape)
judge.load_weights('models/model_sparse_mnist_generator_nonzero_5k.h5py')
# load the judge 30k batches
judge = create_mnist_cnn_model(num_classes, input_shape)
judge.load_weights('models/model_sparse_mnist_generator_nonzero_30k.h5py')
# ## The best possible classifier
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('models/model_mnist_12epochs.h5py')
# # This adversary works (87.36% -> 79.43%)
#
# - but couldn't we make a stronger adversary?
# - I realized that the probability distribution over classes is really sharp as this is a well trained classifier
# - which means that the 2nd most probable class is not the best adversarial choice (or as good as any other of the 8 remaining classes)
# - let's try to use an underfit model and see if it can be a better adversary
# ## Train a worse model - 30k samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:30000], y_train[:30000],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('models/model_mnist_30ksamples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# # Ok, this works even better! (77.73%)
#
# - let's try to limit the training even more
# - note: the following search was done manually, because I didn't originally know how much time I can spend searching for the best adversary
# - note 2: the search I did by hand was a binary search, but I reordered the cells for a better organization
# ## Train a worse model 15k samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:15000], y_train[:15000],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_15ksamples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversarial_model_1epoch, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model - 10k samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:10000], y_train[:10000],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_10ksamples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model 7.5k samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:7500], y_train[:7500],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_7500samples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model - 5k samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:5000], y_train[:5000],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_5ksamples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model - 500 samples
adversary = create_mnist_cnn_model(num_classes, input_shape)
adversary.fit(x_train[:500], y_train[:500],
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_500samples.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# # Ok, the idea with limited training worked
#
# - but limiting the number of samples is probably suboptimal with respect to our goal of finding the best adversarial choice
# - let's try to train the model on all training samples (1 full epoch)
# - but achieve the underfit by decreasing the learning rate
# ## Train a worse model - adam 1e-6
adversary = create_mnist_cnn_model(num_classes, input_shape, lr=1e-6)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_1epoch_adam1e-6.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model - adam 1e-5
adversary = create_mnist_cnn_model(num_classes, input_shape, lr=1e-5)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_1epoch_adam1e-5.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ## Train a worse model - adam 5e-5
adversary = create_mnist_cnn_model(num_classes, input_shape, lr=5e-5)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_1epoch_adam5e-5.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Train another one with a different seed
adversary = create_mnist_cnn_model(num_classes, input_shape, lr=5e-5)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_1epoch_adam5e-5_2.h5py')
# ## Train a worse model - adam 1e-4
adversary = create_mnist_cnn_model(num_classes, input_shape, lr=1e-4)
adversary.fit(x_train, y_train,
batch_size=batch_size,
epochs=1,
verbose=1,
validation_data=(x_test, y_test))
adversary.save('model_mnist_1epoch_adam1e-4.h5py')
# ### Judge - 5k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
# ### Better judge - 30k batches
accuracies = eval_precommit_adversarial_generator(x_test, val_data_generator, judge, adversary, num_repetitions=10)
print('accuracy: %.2f%%' % (100 * np.mean(accuracies)))
print('variance: %E' % np.var(accuracies))
| train_adversary.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# cd ..
# +
import numpy as np
import util.io
# -
image_data = util.io.load_json('./exp-visgeno-rel/visgeno-dataset/image_data.json')
objects = util.io.load_json('./exp-visgeno-rel/visgeno-dataset/objects.json')
relationships = util.io.load_json('./exp-visgeno-rel/visgeno-dataset/relationships.json')
# +
# compute average object number per image
count = 0
for obj in objects:
count += len(obj['objects'])
print('average objects per image:', count / len(objects))
# +
# compute average relationship number per image
count = 0
for rel in relationships:
count += len(rel['relationships'])
print('average relationships per image:', count / len(relationships))
# -
# collect a list of objects per image (turn into bbox format)
# (obj_idx_map, bboxes)
imdb = [None for _ in range(len(objects))]
# +
def _convert_bbox(obj):
x, y, w, h = obj['x'], obj['y'], obj['w'], obj['h']
bbox = [x, y, x+w-1, y+h-1]
return bbox
for n_im in range(len(objects)):
img_info = image_data[n_im]
assert(img_info['image_id'] == objects[n_im]['image_id'])
objs = objects[n_im]['objects']
# a dict mapping object_id to index in the list
obj_idx_map = {objs[n_obj]['object_id']: n_obj for n_obj in range(len(objs))}
# bounding box of each object
obj_bboxes = [_convert_bbox(obj) for obj in objs]
im_name = img_info['url'].replace('https://cs.stanford.edu/people/rak248/', '')
im_path = './exp-visgeno-rel/visgeno-dataset/' + im_name
imdb[n_im] = dict(image_id=img_info['image_id'],
obj_idx_map=obj_idx_map,
bboxes=obj_bboxes,
im_path=im_path)
# -
# match the relationships to objects
for n_im in range(len(relationships)):
img_info = image_data[n_im]
assert(img_info['image_id'] == relationships[n_im]['image_id'])
rels = relationships[n_im]['relationships']
obj_idx_map = imdb[n_im]['obj_idx_map']
mapped_rels = []
for rel in rels:
subj_name = rel['subject']['name']
obj_name = rel['object']['name']
predcate_name = rel['predicate']
subj_idx = obj_idx_map[rel['subject']['object_id']]
obj_idx = obj_idx_map[rel['object']['object_id']]
mapped_rels.append((subj_idx, obj_idx, subj_name, predcate_name, obj_name))
imdb[n_im]['mapped_rels'] = mapped_rels
partition_file = './exp-visgeno-rel/data/densecap_splits.json'
splits = util.io.load_json(partition_file)
rel_data_trn = [rel for rel in imdb if rel['image_id'] in splits['train']]
rel_data_val = [rel for rel in imdb if rel['image_id'] in splits['val']]
rel_data_tst = [rel for rel in imdb if rel['image_id'] in splits['test']]
util.io.save_numpy_obj(rel_data_trn, './exp-visgeno-rel/data/imdb/imdb_trn.npy')
util.io.save_numpy_obj(rel_data_val, './exp-visgeno-rel/data/imdb/imdb_val.npy')
util.io.save_numpy_obj(rel_data_tst, './exp-visgeno-rel/data/imdb/imdb_tst.npy')
| exp-visgeno-rel/build_visgeno_imdb.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"} tags=[] toc-hr-collapsed=false
# # Fuzzing with Grammars
#
# In the chapter on ["Mutation-Based Fuzzing"](MutationFuzzer.ipynb), we have seen how to use extra hints – such as sample input files – to speed up test generation. In this chapter, we take this idea one step further, by providing a _specification_ of the legal inputs to a program. Specifying inputs via a _grammar_ allows for very systematic and efficient test generation, in particular for complex input formats. Grammars also serve as the base for configuration fuzzing, API fuzzing, GUI fuzzing, and many more.
# + slideshow={"slide_type": "skip"}
from bookutils import YouTubeVideo
YouTubeVideo('Jc8Whz0W41o')
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
# **Prerequisites**
#
# * You should know how basic fuzzing works, e.g. from the [Chapter introducing fuzzing](Fuzzer.ipynb).
# * Knowledge on [mutation-based fuzzing](MutationFuzzer.ipynb) and [coverage](Coverage.ipynb) is _not_ required yet, but still recommended.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import bookutils
# + slideshow={"slide_type": "skip"}
from typing import List, Dict, Union, Any, Tuple, Optional
# + slideshow={"slide_type": "skip"}
import Fuzzer
# + [markdown] slideshow={"slide_type": "skip"}
# ## Synopsis
# <!-- Automatically generated. Do not edit. -->
#
# To [use the code provided in this chapter](Importing.ipynb), write
#
# ```python
# >>> from fuzzingbook.Grammars import <identifier>
# ```
#
# and then make use of the following features.
#
#
# This chapter introduces _grammars_ as a simple means to specify input languages, and to use them for testing programs with syntactically valid inputs. A grammar is defined as a mapping of nonterminal symbols to lists of alternative expansions, as in the following example:
#
# ```python
# >>> US_PHONE_GRAMMAR: Grammar = {
# >>> "<start>": ["<phone-number>"],
# >>> "<phone-number>": ["(<area>)<exchange>-<line>"],
# >>> "<area>": ["<lead-digit><digit><digit>"],
# >>> "<exchange>": ["<lead-digit><digit><digit>"],
# >>> "<line>": ["<digit><digit><digit><digit>"],
# >>> "<lead-digit>": ["2", "3", "4", "5", "6", "7", "8", "9"],
# >>> "<digit>": ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
# >>> }
# >>>
# >>> assert is_valid_grammar(US_PHONE_GRAMMAR)
# ```
# Nonterminal symbols are enclosed in angle brackets (say, `<digit>`). To generate an input string from a grammar, a _producer_ starts with the start symbol (`<start>`) and randomly chooses a random expansion for this symbol. It continues the process until all nonterminal symbols are expanded. The function `simple_grammar_fuzzer()` does just that:
#
# ```python
# >>> [simple_grammar_fuzzer(US_PHONE_GRAMMAR) for i in range(5)]
# ['(692)449-5179',
# '(519)230-7422',
# '(613)761-0853',
# '(979)881-3858',
# '(810)914-5475']
# ```
# In practice, though, instead of `simple_grammar_fuzzer()`, you should use [the `GrammarFuzzer` class](GrammarFuzzer.ipynb) or one of its [coverage-based](GrammarCoverageFuzzer.ipynb), [probabilistic-based](ProbabilisticGrammarFuzzer.ipynb), or [generator-based](GeneratorGrammarFuzzer.ipynb) derivatives; these are more efficient, protect against infinite growth, and provide several additional features.
#
# This chapter also introduces a [grammar toolbox](#A-Grammar-Toolbox) with several helper functions that ease the writing of grammars, such as using shortcut notations for character classes and repetitions, or extending grammars
#
#
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Input Languages
#
# All possible behaviors of a program can be triggered by its input. "Input" here can be a wide range of possible sources: We are talking about data that is read from files, from the environment, or over the network, data input by the user, or data acquired from interaction with other resources. The set of all these inputs determines how the program will behave – including its failures. When testing, it is thus very helpful to think about possible input sources, how to get them under control, and _how to systematically test them_.
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# For the sake of simplicity, we will assume for now that the program has only one source of inputs; this is the same assumption we have been using in the previous chapters, too. The set of valid inputs to a program is called a _language_. Languages range from the simple to the complex: the CSV language denotes the set of valid comma-separated inputs, whereas the Python language denotes the set of valid Python programs. We commonly separate data languages and programming languages, although any program can also be treated as input data (say, to a compiler). The [Wikipedia page on file formats](https://en.wikipedia.org/wiki/List_of_file_formats) lists more than 1,000 different file formats, each of which is its own language.
# + [markdown] slideshow={"slide_type": "subslide"}
# To formally describe languages, the field of *formal languages* has devised a number of *language specifications* that describe a language. *Regular expressions* represent the simplest class of these languages to denote sets of strings: The regular expression `[a-z]*`, for instance, denotes a (possibly empty) sequence of lowercase letters. *Automata theory* connects these languages to automata that accept these inputs; *finite state machines*, for instance, can be used to specify the language of regular expressions.
# + [markdown] slideshow={"slide_type": "subslide"}
# Regular expressions are great for not-too-complex input formats, and the associated finite state machines have many properties that make them great for reasoning. To specify more complex inputs, though, they quickly encounter limitations. At the other end of the language spectrum, we have *universal grammars* that denote the language accepted by *Turing machines*. A Turing machine can compute anything that can be computed; and with Python being Turing-complete, this means that we can also use a Python program $p$ to specify or even enumerate legal inputs. But then, computer science theory also tells us that each such testing program has to be written specifically for the program to be tested, which is not the level of automation we want.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} toc-hr-collapsed=true toc-nb-collapsed=true
# ## Grammars
#
# The middle ground between regular expressions and Turing machines is covered by *grammars*. Grammars are among the most popular (and best understood) formalisms to formally specify input languages. Using a grammar, one can express a wide range of the properties of an input language. Grammars are particularly great for expressing the *syntactical structure* of an input, and are the formalism of choice to express nested or recursive inputs. The grammars we use are so-called *context-free grammars*, one of the easiest and most popular grammar formalisms.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Rules and Expansions
#
# A grammar consists of a *start symbol* and a set of *expansion rules* (or simply *rules*) which indicate how the start symbol (and other symbols) can be expanded. As an example, consider the following grammar, denoting a sequence of two digits:
#
# ```
# <start> ::= <digit><digit>
# <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
# ```
#
# To read such a grammar, start with the start symbol (`<start>`). An expansion rule `<A> ::= <B>` means that the symbol on the left side (`<A>`) can be replaced by the string on the right side (`<B>`). In the above grammar, `<start>` would be replaced by `<digit><digit>`.
#
# In this string again, `<digit>` would be replaced by the string on the right side of the `<digit>` rule. The special operator `|` denotes *expansion alternatives* (or simply *alternatives*), meaning that any of the digits can be chosen for an expansion. Each `<digit>` thus would be expanded into one of the given digits, eventually yielding a string between `00` and `99`. There are no further expansions for `0` to `9`, so we are all set.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# The interesting thing about grammars is that they can be *recursive*. That is, expansions can make use of symbols expanded earlier – which would then be expanded again. As an example, consider a grammar that describes integers:
#
# ```
# <start> ::= <integer>
# <integer> ::= <digit> | <digit><integer>
# <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
# ```
#
# Here, a `<integer>` is either a single digit, or a digit followed by another integer. The number `1234` thus would be represented as a single digit `1`, followed by the integer `234`, which in turn is a digit `2`, followed by the integer `34`.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# If we wanted to express that an integer can be preceded by a sign (`+` or `-`), we would write the grammar as
#
# ```
# <start> ::= <number>
# <number> ::= <integer> | +<integer> | -<integer>
# <integer> ::= <digit> | <digit><integer>
# <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
# ```
#
# These rules formally define the language: Anything that can be derived from the start symbol is part of the language; anything that cannot is not.
# + slideshow={"slide_type": "skip"}
from bookutils import quiz
# + slideshow={"slide_type": "subslide"}
quiz("Which of these strings cannot be produced "
"from the above `<start>` symbol?",
[
"`007`",
"`-42`",
"`++1`",
"`3.14`"
], "[27 ** (1/3), 256 ** (1/4)]")
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Arithmetic Expressions
#
# Let us expand our grammar to cover full *arithmetic expressions* – a poster child example for a grammar. We see that an expression (`<expr>`) is either a sum, or a difference, or a term; a term is either a product or a division, or a factor; and a factor is either a number or a parenthesized expression. Almost all rules can have recursion, and thus allow arbitrary complex expressions such as `(1 + 2) * (3.4 / 5.6 - 789)`.
#
# ```
# <start> ::= <expr>
# <expr> ::= <term> + <expr> | <term> - <expr> | <term>
# <term> ::= <term> * <factor> | <term> / <factor> | <factor>
# <factor> ::= +<factor> | -<factor> | (<expr>) | <integer> | <integer>.<integer>
# <integer> ::= <digit><integer> | <digit>
# <digit> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
# ```
#
# In such a grammar, if we start with `<start>` and then expand one symbol after another, randomly choosing alternatives, we can quickly produce one valid arithmetic expression after another. Such *grammar fuzzing* is highly effective as it comes to produce complex inputs, and this is what we will implement in this chapter.
# + slideshow={"slide_type": "subslide"}
quiz("Which of these strings cannot be produced "
"from the above `<start>` symbol?",
[
"`1 + 1`",
"`1+1`",
"`+1`",
"`+(1)`",
], "4 ** 0.5")
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Representing Grammars in Python
#
# Our first step in building a grammar fuzzer is to find an appropriate format for grammars. To make the writing of grammars as simple as possible, we use a format that is based on strings and lists. Our grammars in Python take the format of a _mapping_ between symbol names and expansions, where expansions are _lists_ of alternatives. A one-rule grammar for digits thus takes the form
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
DIGIT_GRAMMAR = {
"<start>":
["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Excursion: A `Grammar` Type
# + [markdown] slideshow={"slide_type": "fragment"}
# Let us define a type for grammars, such that we can check grammar types statically.
# + [markdown] slideshow={"slide_type": "fragment"}
# A first attempt at a grammar type would be that each symbol (a string) is mapped to a list of expansions (strings):
# + slideshow={"slide_type": "fragment"}
SimpleGrammar = Dict[str, List[str]]
# + [markdown] slideshow={"slide_type": "fragment"}
# However, our `opts()` feature for adding optional attributes, which we will introduce later in this chapter, also allows expansions to be _pairs_ that consist of strings and options, where options are mappings of strings to values:
# + slideshow={"slide_type": "fragment"}
Option = Dict[str, Any]
# + [markdown] slideshow={"slide_type": "fragment"}
# Hence, an expansion is either a string – or a pair of a string and an option.
# + slideshow={"slide_type": "fragment"}
Expansion = Union[str, Tuple[str, Option]]
# + [markdown] slideshow={"slide_type": "subslide"}
# With this, we can now define a `Grammar` as a mapping of strings to `Expansion` lists.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### End of Excursion
# + [markdown] slideshow={"slide_type": "fragment"}
# We can capture the grammar structure in a _`Grammar`_ type, in which each symbol (a string) is mapped to a list of expansions (strings):
# + slideshow={"slide_type": "fragment"}
Grammar = Dict[str, List[Expansion]]
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# With this `Grammar` type, the full grammar for arithmetic expressions looks like this:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
EXPR_GRAMMAR: Grammar = {
"<start>":
["<expr>"],
"<expr>":
["<term> + <expr>", "<term> - <expr>", "<term>"],
"<term>":
["<factor> * <term>", "<factor> / <term>", "<factor>"],
"<factor>":
["+<factor>",
"-<factor>",
"(<expr>)",
"<integer>.<integer>",
"<integer>"],
"<integer>":
["<digit><integer>", "<digit>"],
"<digit>":
["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# In the grammar, every symbol can be defined exactly once. We can access any rule by its symbol...
# + button=false code_folding=[] new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
EXPR_GRAMMAR["<digit>"]
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# ....and we can check whether a symbol is in the grammar:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
"<identifier>" in EXPR_GRAMMAR
# + [markdown] slideshow={"slide_type": "fragment"}
# Note that we assume that on the left hand side of a rule (i.e., the key in the mapping) is always a single symbol. This is the property that gives our grammars the characterization of _context-free_.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Some Definitions
# + [markdown] slideshow={"slide_type": "fragment"}
# We assume that the canonical start symbol is `<start>`:
# + slideshow={"slide_type": "fragment"}
START_SYMBOL = "<start>"
# + [markdown] slideshow={"slide_type": "subslide"}
# The handy `nonterminals()` function extracts the list of nonterminal symbols (i.e., anything between `<` and `>`, except spaces) from an expansion.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import re
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
RE_NONTERMINAL = re.compile(r'(<[^<> ]*>)')
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
def nonterminals(expansion):
# In later chapters, we allow expansions to be tuples,
# with the expansion being the first element
if isinstance(expansion, tuple):
expansion = expansion[0]
return RE_NONTERMINAL.findall(expansion)
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert nonterminals("<term> * <factor>") == ["<term>", "<factor>"]
assert nonterminals("<digit><integer>") == ["<digit>", "<integer>"]
assert nonterminals("1 < 3 > 2") == []
assert nonterminals("1 <3> 2") == ["<3>"]
assert nonterminals("1 + 2") == []
assert nonterminals(("<1>", {'option': 'value'})) == ["<1>"]
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# Likewise, `is_nonterminal()` checks whether some symbol is a nonterminal:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
def is_nonterminal(s):
return RE_NONTERMINAL.match(s)
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert is_nonterminal("<abc>")
assert is_nonterminal("<symbol-1>")
assert not is_nonterminal("+")
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## A Simple Grammar Fuzzer
#
# Let us now put the above grammars to use. We will build a very simple grammar fuzzer that starts with a start symbol (`<start>`) and then keeps on expanding it. To avoid expansion to infinite inputs, we place a limit (`max_nonterminals`) on the number of nonterminals. Furthermore, to avoid being stuck in a situation where we cannot reduce the number of symbols any further, we also limit the total number of expansion steps.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import random
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
class ExpansionError(Exception):
pass
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
def simple_grammar_fuzzer(grammar: Grammar,
start_symbol: str = START_SYMBOL,
max_nonterminals: int = 10,
max_expansion_trials: int = 100,
log: bool = False) -> str:
"""Produce a string from `grammar`.
`start_symbol`: use a start symbol other than `<start>` (default).
`max_nonterminals`: the maximum number of nonterminals
still left for expansion
`max_expansion_trials`: maximum # of attempts to produce a string
`log`: print expansion progress if True"""
term = start_symbol
expansion_trials = 0
while len(nonterminals(term)) > 0:
symbol_to_expand = random.choice(nonterminals(term))
expansions = grammar[symbol_to_expand]
expansion = random.choice(expansions)
# In later chapters, we allow expansions to be tuples,
# with the expansion being the first element
if isinstance(expansion, tuple):
expansion = expansion[0]
new_term = term.replace(symbol_to_expand, expansion, 1)
if len(nonterminals(new_term)) < max_nonterminals:
term = new_term
if log:
print("%-40s" % (symbol_to_expand + " -> " + expansion), term)
expansion_trials = 0
else:
expansion_trials += 1
if expansion_trials >= max_expansion_trials:
raise ExpansionError("Cannot expand " + repr(term))
return term
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# Let us see how this simple grammar fuzzer obtains an arithmetic expression from the start symbol:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
simple_grammar_fuzzer(grammar=EXPR_GRAMMAR, max_nonterminals=3, log=True)
# + [markdown] slideshow={"slide_type": "subslide"}
# By increasing the limit of nonterminals, we can quickly get much longer productions:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
for i in range(10):
print(simple_grammar_fuzzer(grammar=EXPR_GRAMMAR, max_nonterminals=5))
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# Note that while fuzzer does the job in most cases, it has a number of drawbacks.
# + slideshow={"slide_type": "fragment"}
quiz("What drawbacks does `simple_grammar_fuzzer()` have?",
[
"It has a large number of string search and replace operations",
"It may fail to produce a string (`ExpansionError`)",
"It often picks some symbol to expand "
"that does not even occur in the string",
"All of the above"
], "1 << 2")
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# Indeed, `simple_grammar_fuzzer()` is rather inefficient due to the large number of search and replace operations, and it may even fail to produce a string. On the other hand, the implementation is straightforward and does the job in most cases. For this chapter, we'll stick to it; in the [next chapter](GrammarFuzzer.ipynb), we'll show how to build a more efficient one.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Visualizing Grammars as Railroad Diagrams
# + [markdown] slideshow={"slide_type": "fragment"}
# With grammars, we can easily specify the format for several of the examples we discussed earlier. The above arithmetic expressions, for instance, can be directly sent into `bc` (or any other program that takes arithmetic expressions). Before we introduce a few additional grammars, let us give a means to _visualize_ them, giving an alternate view to aid their understanding.
# + [markdown] slideshow={"slide_type": "fragment"}
# _Railroad diagrams_, also called _syntax diagrams_, are a graphical representation of context-free grammars. They are read left to right, following possible "rail" tracks; the sequence of symbols encountered on the track defines the language. To produce railroad diagrams, we implement a function `syntax_diagram()`.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Excursion: Implementing `syntax_diagram()`
# + [markdown] slideshow={"slide_type": "fragment"}
# We use [RailroadDiagrams](RailroadDiagrams.ipynb), an external library for visualization.
# + slideshow={"slide_type": "skip"}
from RailroadDiagrams import NonTerminal, Terminal, Choice, HorizontalChoice, Sequence
from RailroadDiagrams import show_diagram
# + slideshow={"slide_type": "skip"}
from IPython.display import SVG
# + [markdown] slideshow={"slide_type": "fragment"}
# We first define the method `syntax_diagram_symbol()` to visualize a given symbol. Terminal symbols are denoted as ovals, whereas nonterminal symbols (such as `<term>`) are denoted as rectangles.
# + slideshow={"slide_type": "fragment"}
def syntax_diagram_symbol(symbol: str) -> Any:
if is_nonterminal(symbol):
return NonTerminal(symbol[1:-1])
else:
return Terminal(symbol)
# + slideshow={"slide_type": "fragment"}
SVG(show_diagram(syntax_diagram_symbol('<term>')))
# + [markdown] slideshow={"slide_type": "fragment"}
# We define `syntax_diagram_expr()` to visualize expansion alternatives.
# + slideshow={"slide_type": "subslide"}
def syntax_diagram_expr(expansion: Expansion) -> Any:
# In later chapters, we allow expansions to be tuples,
# with the expansion being the first element
if isinstance(expansion, tuple):
expansion = expansion[0]
symbols = [sym for sym in re.split(RE_NONTERMINAL, expansion) if sym != ""]
if len(symbols) == 0:
symbols = [""] # special case: empty expansion
return Sequence(*[syntax_diagram_symbol(sym) for sym in symbols])
# + slideshow={"slide_type": "fragment"}
SVG(show_diagram(syntax_diagram_expr(EXPR_GRAMMAR['<term>'][0])))
# + [markdown] slideshow={"slide_type": "fragment"}
# This is the first alternative of `<term>` – a `<factor>` followed by `*` and a `<term>`.
# + [markdown] slideshow={"slide_type": "subslide"}
# Next, we define `syntax_diagram_alt()` for displaying alternate expressions.
# + slideshow={"slide_type": "skip"}
from itertools import zip_longest
# + slideshow={"slide_type": "fragment"}
def syntax_diagram_alt(alt: List[Expansion]) -> Any:
max_len = 5
alt_len = len(alt)
if alt_len > max_len:
iter_len = alt_len // max_len
alts = list(zip_longest(*[alt[i::iter_len] for i in range(iter_len)]))
exprs = [[syntax_diagram_expr(expr) for expr in alt
if expr is not None] for alt in alts]
choices = [Choice(len(expr) // 2, *expr) for expr in exprs]
return HorizontalChoice(*choices)
else:
return Choice(alt_len // 2, *[syntax_diagram_expr(expr) for expr in alt])
# + slideshow={"slide_type": "subslide"}
SVG(show_diagram(syntax_diagram_alt(EXPR_GRAMMAR['<digit>'])))
# + [markdown] slideshow={"slide_type": "fragment"}
# We see that a `<digit>` can be any single digit from `0` to `9`.
# + [markdown] slideshow={"slide_type": "fragment"}
# Finally, we define `syntax_diagram()` which given a grammar, displays the syntax diagram of its rules.
# + slideshow={"slide_type": "fragment"}
def syntax_diagram(grammar: Grammar) -> None:
from IPython.display import SVG, display
for key in grammar:
print("%s" % key[1:-1])
display(SVG(show_diagram(syntax_diagram_alt(grammar[key]))))
# + [markdown] slideshow={"slide_type": "subslide"}
# ### End of Excursion
# + [markdown] slideshow={"slide_type": "fragment"}
# Let us use `syntax_diagram()` to produce a railroad diagram of our expression grammar:
# + slideshow={"slide_type": "subslide"}
syntax_diagram(EXPR_GRAMMAR)
# + [markdown] slideshow={"slide_type": "subslide"}
# This railroad representation will come in handy as it comes to visualizing the structure of grammars – especially for more complex grammars.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} toc-hr-collapsed=false
# ## Some Grammars
#
# Let us create (and visualize) some more grammars and use them for fuzzing.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### A CGI Grammar
#
# Here's a grammar for `cgi_decode()` introduced in the [chapter on coverage](Coverage.ipynb).
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
CGI_GRAMMAR: Grammar = {
"<start>":
["<string>"],
"<string>":
["<letter>", "<letter><string>"],
"<letter>":
["<plus>", "<percent>", "<other>"],
"<plus>":
["+"],
"<percent>":
["%<hexdigit><hexdigit>"],
"<hexdigit>":
["0", "1", "2", "3", "4", "5", "6", "7",
"8", "9", "a", "b", "c", "d", "e", "f"],
"<other>": # Actually, could be _all_ letters
["0", "1", "2", "3", "4", "5", "a", "b", "c", "d", "e", "-", "_"],
}
# + slideshow={"slide_type": "subslide"}
syntax_diagram(CGI_GRAMMAR)
# + [markdown] slideshow={"slide_type": "subslide"}
# In contrast to [basic fuzzing](Fuzzer.ipynb) or [mutation-based fuzzing](MutationFuzzer.ipynb), the grammar quickly produces all sorts of combinations:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
for i in range(10):
print(simple_grammar_fuzzer(grammar=CGI_GRAMMAR, max_nonterminals=10))
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### A URL Grammar
#
# The same properties we have seen for CGI input also hold for more complex inputs. Let us use a grammar to produce a large number of valid URLs:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
URL_GRAMMAR: Grammar = {
"<start>":
["<url>"],
"<url>":
["<scheme>://<authority><path><query>"],
"<scheme>":
["http", "https", "ftp", "ftps"],
"<authority>":
["<host>", "<host>:<port>", "<userinfo>@<host>", "<userinfo>@<host>:<port>"],
"<host>": # Just a few
["cispa.saarland", "www.google.com", "fuzzingbook.com"],
"<port>":
["80", "8080", "<nat>"],
"<nat>":
["<digit>", "<digit><digit>"],
"<digit>":
["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"],
"<userinfo>": # Just one
["user:password"],
"<path>": # Just a few
["", "/", "/<id>"],
"<id>": # Just a few
["abc", "def", "x<digit><digit>"],
"<query>":
["", "?<params>"],
"<params>":
["<param>", "<param>&<params>"],
"<param>": # Just a few
["<id>=<id>", "<id>=<nat>"],
}
# + slideshow={"slide_type": "subslide"}
syntax_diagram(URL_GRAMMAR)
# + [markdown] slideshow={"slide_type": "subslide"}
# Again, within milliseconds, we can produce plenty of valid inputs.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
for i in range(10):
print(simple_grammar_fuzzer(grammar=URL_GRAMMAR, max_nonterminals=10))
# + [markdown] slideshow={"slide_type": "subslide"}
# ### A Natural Language Grammar
#
# Finally, grammars are not limited to *formal languages* such as computer inputs, but can also be used to produce *natural language*. This is the grammar we used to pick a title for this book:
# + slideshow={"slide_type": "subslide"}
TITLE_GRAMMAR: Grammar = {
"<start>": ["<title>"],
"<title>": ["<topic>: <subtopic>"],
"<topic>": ["Generating Software Tests", "<fuzzing-prefix>Fuzzing", "The Fuzzing Book"],
"<fuzzing-prefix>": ["", "The Art of ", "The Joy of "],
"<subtopic>": ["<subtopic-main>",
"<subtopic-prefix><subtopic-main>",
"<subtopic-main><subtopic-suffix>"],
"<subtopic-main>": ["Breaking Software",
"Generating Software Tests",
"Principles, Techniques and Tools"],
"<subtopic-prefix>": ["", "Tools and Techniques for "],
"<subtopic-suffix>": [" for <reader-property> and <reader-property>",
" for <software-property> and <software-property>"],
"<reader-property>": ["Fun", "Profit"],
"<software-property>": ["Robustness", "Reliability", "Security"],
}
# + slideshow={"slide_type": "subslide"}
syntax_diagram(TITLE_GRAMMAR)
# + slideshow={"slide_type": "skip"}
from typing import Set
# + slideshow={"slide_type": "subslide"}
titles: Set[str] = set()
while len(titles) < 10:
titles.add(simple_grammar_fuzzer(
grammar=TITLE_GRAMMAR, max_nonterminals=10))
titles
# + [markdown] slideshow={"slide_type": "subslide"}
# (If you find that there is redundancy ("Robustness and Robustness") in here: In [our chapter on coverage-based fuzzing](GrammarCoverageFuzzer.ipynb), we will show how to cover each expansion only once. And if you like some alternatives more than others, [probabilistic grammar fuzzing](ProbabilisticGrammarFuzzer.ipynb) will be there for you.)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Grammars as Mutation Seeds
# + [markdown] slideshow={"slide_type": "slide"}
# One very useful property of grammars is that they produce mostly valid inputs. From a syntactical standpoint, the inputs are actually _always_ valid, as they satisfy the constraints of the given grammar. (Of course, one needs a valid grammar in the first place.) However, there are also _semantical_ properties that cannot be easily expressed in a grammar. If, say, for a URL, the port range is supposed to be between 1024 and 2048, this is hard to write in a grammar. If one has to satisfy more complex constraints, one quickly reaches the limits of what a grammar can express.
# + [markdown] slideshow={"slide_type": "fragment"}
# One way around this is to attach constraints to grammars, as we will discuss [later in this book](ConstraintFuzzer.ipynb). Another possibility is to put together the strengths of grammar-based fuzzing and [mutation-based fuzzing](MutationFuzzer.ipynb). The idea is to use the grammar-generated inputs as *seeds* for further mutation-based fuzzing. This way, we can explore not only _valid_ inputs, but also check out the _boundaries_ between valid and invalid inputs. This is particularly interesting as slightly invalid inputs allow to find parser errors (which are often abundant). As with fuzzing in general, it is the unexpected which reveals errors in programs.
# + [markdown] slideshow={"slide_type": "subslide"}
# To use our generated inputs as seeds, we can feed them directly into the mutation fuzzers introduced earlier:
# + slideshow={"slide_type": "skip"}
from MutationFuzzer import MutationFuzzer # minor dependency
# + slideshow={"slide_type": "fragment"}
number_of_seeds = 10
seeds = [
simple_grammar_fuzzer(
grammar=URL_GRAMMAR,
max_nonterminals=10) for i in range(number_of_seeds)]
seeds
# + slideshow={"slide_type": "subslide"}
m = MutationFuzzer(seeds)
# + slideshow={"slide_type": "fragment"}
[m.fuzz() for i in range(20)]
# + [markdown] slideshow={"slide_type": "subslide"}
# While the first 10 `fuzz()` calls return the seeded inputs (as designed), the later ones again create arbitrary mutations. Using `MutationCoverageFuzzer` instead of `MutationFuzzer`, we could again have our search guided by coverage – and thus bring together the best of multiple worlds.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} toc-hr-collapsed=false
# ## A Grammar Toolbox
#
# Let us now introduce a few techniques that help us writing grammars.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# ### Escapes
#
# With `<` and `>` delimiting nonterminals in our grammars, how can we actually express that some input should contain `<` and `>`? The answer is simple: Just introduce a symbol for them.
# + slideshow={"slide_type": "fragment"}
simple_nonterminal_grammar: Grammar = {
"<start>": ["<nonterminal>"],
"<nonterminal>": ["<left-angle><identifier><right-angle>"],
"<left-angle>": ["<"],
"<right-angle>": [">"],
"<identifier>": ["id"] # for now
}
# + [markdown] slideshow={"slide_type": "fragment"}
# In `simple_nonterminal_grammar`, neither the expansion for `<left-angle>` nor the expansion for `<right-angle>` can be mistaken as a nonterminal. Hence, we can produce as many as we want.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Extending Grammars
#
# In the course of this book, we frequently run into the issue of creating a grammar by _extending_ an existing grammar with new features. Such an extension is very much like subclassing in object-oriented programming.
# + [markdown] slideshow={"slide_type": "fragment"}
# To create a new grammar $g'$ from an existing grammar $g$, we first copy $g$ into $g'$, and then go and extend existing rules with new alternatives and/or add new symbols. Here's an example, extending the above `nonterminal` grammar with a better rule for identifiers:
# + slideshow={"slide_type": "skip"}
import copy
# + slideshow={"slide_type": "fragment"}
nonterminal_grammar = copy.deepcopy(simple_nonterminal_grammar)
nonterminal_grammar["<identifier>"] = ["<idchar>", "<identifier><idchar>"]
nonterminal_grammar["<idchar>"] = ['a', 'b', 'c', 'd'] # for now
# + slideshow={"slide_type": "subslide"}
nonterminal_grammar
# + [markdown] slideshow={"slide_type": "fragment"}
# Since such an extension of grammars is a common operation, we introduce a custom function `extend_grammar()` which first copies the given grammar and then updates it from a dictionary, using the Python dictionary `update()` method:
# + slideshow={"slide_type": "fragment"}
def extend_grammar(grammar: Grammar, extension: Grammar = {}) -> Grammar:
new_grammar = copy.deepcopy(grammar)
new_grammar.update(extension)
return new_grammar
# + [markdown] slideshow={"slide_type": "subslide"}
# This call to `extend_grammar()` extends `simple_nonterminal_grammar` to `nonterminal_grammar` just like the "manual" example above:
# + slideshow={"slide_type": "fragment"}
nonterminal_grammar = extend_grammar(simple_nonterminal_grammar,
{
"<identifier>": ["<idchar>", "<identifier><idchar>"],
# for now
"<idchar>": ['a', 'b', 'c', 'd']
}
)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Character Classes
# + [markdown] slideshow={"slide_type": "fragment"}
# In the above `nonterminal_grammar`, we have enumerated only the first few letters; indeed, enumerating all letters or digits in a grammar manually, as in `<idchar> ::= 'a' | 'b' | 'c' ...` is a bit painful.
# + [markdown] slideshow={"slide_type": "fragment"}
# However, remember that grammars are part of a program, and can thus also be constructed programmatically. We introduce a function `srange()` which constructs a list of characters in a string:
# + slideshow={"slide_type": "fragment"}
import string
# + slideshow={"slide_type": "fragment"}
def srange(characters: str) -> List[Expansion]:
"""Construct a list with all characters in the string"""
return [c for c in characters]
# + [markdown] slideshow={"slide_type": "fragment"}
# If we pass it the constant `string.ascii_letters`, which holds all ASCII letters, `srange()` returns a list of all ASCII letters:
# + slideshow={"slide_type": "fragment"}
string.ascii_letters
# + slideshow={"slide_type": "fragment"}
srange(string.ascii_letters)[:10]
# + [markdown] slideshow={"slide_type": "subslide"}
# We can use such constants in our grammar to quickly define identifiers:
# + slideshow={"slide_type": "fragment"}
nonterminal_grammar = extend_grammar(nonterminal_grammar,
{
"<idchar>": (srange(string.ascii_letters) +
srange(string.digits) +
srange("-_"))
}
)
# + slideshow={"slide_type": "fragment"}
[simple_grammar_fuzzer(nonterminal_grammar, "<identifier>") for i in range(10)]
# + [markdown] slideshow={"slide_type": "subslide"}
# The shortcut `crange(start, end)` returns a list of all characters in the ASCII range of `start` to (including) `end`:
# + slideshow={"slide_type": "fragment"}
def crange(character_start: str, character_end: str) -> List[Expansion]:
return [chr(i)
for i in range(ord(character_start), ord(character_end) + 1)]
# + [markdown] slideshow={"slide_type": "fragment"}
# We can use this to express ranges of characters:
# + slideshow={"slide_type": "fragment"}
crange('0', '9')
# + slideshow={"slide_type": "fragment"}
assert crange('a', 'z') == srange(string.ascii_lowercase)
# + [markdown] slideshow={"slide_type": "subslide"} toc-hr-collapsed=false
# ### Grammar Shortcuts
# + [markdown] slideshow={"slide_type": "fragment"}
# In the above `nonterminal_grammar`, as in other grammars, we have to express repetitions of characters using _recursion_, that is, by referring to the original definition:
# + slideshow={"slide_type": "fragment"}
nonterminal_grammar["<identifier>"]
# + [markdown] slideshow={"slide_type": "fragment"}
# It could be a bit easier if we simply could state that a nonterminal should be a non-empty sequence of letters – for instance, as in
#
# ```
# <identifier> = <idchar>+
# ```
#
# where `+` denotes a non-empty repetition of the symbol it follows.
# + [markdown] slideshow={"slide_type": "subslide"}
# Operators such as `+` are frequently introduced as handy _shortcuts_ in grammars. Formally, our grammars come in the so-called [Backus-Naur form](https://en.wikipedia.org/wiki/Backus-Naur_form), or *BNF* for short. Operators _extend_ BNF to so-called _extended BNF*, or *EBNF* for short:
#
# * The form `<symbol>?` indicates that `<symbol>` is optional – that is, it can occur 0 or 1 times.
# * The form `<symbol>+` indicates that `<symbol>` can occur 1 or more times repeatedly.
# * The form `<symbol>*` indicates that `<symbol>` can occur 0 or more times. (In other words, it is an optional repetition.)
#
# To make matters even more interesting, we would like to use _parentheses_ with the above shortcuts. Thus, `(<foo><bar>)?` indicates that the sequence of `<foo>` and `<bar>` is optional.
# + [markdown] slideshow={"slide_type": "subslide"}
# Using such operators, we can define the identifier rule in a simpler way. To this end, let us create a copy of the original grammar and modify the `<identifier>` rule:
# + slideshow={"slide_type": "fragment"}
nonterminal_ebnf_grammar = extend_grammar(nonterminal_grammar,
{
"<identifier>": ["<idchar>+"]
}
)
# + [markdown] slideshow={"slide_type": "subslide"}
# Likewise, we can simplify the expression grammar. Consider how signs are optional, and how integers can be expressed as sequences of digits.
# + slideshow={"slide_type": "fragment"}
EXPR_EBNF_GRAMMAR: Grammar = {
"<start>":
["<expr>"],
"<expr>":
["<term> + <expr>", "<term> - <expr>", "<term>"],
"<term>":
["<factor> * <term>", "<factor> / <term>", "<factor>"],
"<factor>":
["<sign>?<factor>", "(<expr>)", "<integer>(.<integer>)?"],
"<sign>":
["+", "-"],
"<integer>":
["<digit>+"],
"<digit>":
srange(string.digits)
}
# + [markdown] slideshow={"slide_type": "subslide"}
# Let us implement a function `convert_ebnf_grammar()` that takes such an EBNF grammar and automatically translates it into a BNF grammar.
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Excursion: Implementing `convert_ebnf_grammar()`
# + [markdown] slideshow={"slide_type": "subslide"}
# Our aim is to convert EBNF grammars such as the ones above into a regular BNF grammar. This is done by four rules:
#
# 1. An expression `(content)op`, where `op` is one of `?`, `+`, `*`, becomes `<new-symbol>op`, with a new rule `<new-symbol> ::= content`.
# 2. An expression `<symbol>?` becomes `<new-symbol>`, where `<new-symbol> ::= <empty> | <symbol>`.
# 3. An expression `<symbol>+` becomes `<new-symbol>`, where `<new-symbol> ::= <symbol> | <symbol><new-symbol>`.
# 4. An expression `<symbol>*` becomes `<new-symbol>`, where `<new-symbol> ::= <empty> | <symbol><new-symbol>`.
#
# Here, `<empty>` expands to the empty string, as in `<empty> ::= `. (This is also called an *epsilon expansion*.)
# + [markdown] slideshow={"slide_type": "fragment"}
# If these operators remind you of _regular expressions_, this is not by accident: Actually, any basic regular expression can be converted into a grammar using the above rules (and character classes with `crange()`, as defined above).
# + [markdown] slideshow={"slide_type": "subslide"}
# Applying these rules on the examples above yields the following results:
#
# * `<idchar>+` becomes `<idchar><new-symbol>` with `<new-symbol> ::= <idchar> | <idchar><new-symbol>`.
# * `<integer>(.<integer>)?` becomes `<integer><new-symbol>` with `<new-symbol> ::= <empty> | .<integer>`.
# + [markdown] slideshow={"slide_type": "skip"}
# Let us implement these rules in three steps.
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Creating New Symbols
#
# First, we need a mechanism to create new symbols. This is fairly straightforward.
# + slideshow={"slide_type": "fragment"}
def new_symbol(grammar: Grammar, symbol_name: str = "<symbol>") -> str:
"""Return a new symbol for `grammar` based on `symbol_name`"""
if symbol_name not in grammar:
return symbol_name
count = 1
while True:
tentative_symbol_name = symbol_name[:-1] + "-" + repr(count) + ">"
if tentative_symbol_name not in grammar:
return tentative_symbol_name
count += 1
# + slideshow={"slide_type": "fragment"}
assert new_symbol(EXPR_EBNF_GRAMMAR, '<expr>') == '<expr-1>'
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Expanding Parenthesized Expressions
# + [markdown] slideshow={"slide_type": "fragment"}
# Next, we need a means to extract parenthesized expressions from our expansions and expand them according to the rules above. Let's start with extracting expressions:
# + slideshow={"slide_type": "fragment"}
RE_PARENTHESIZED_EXPR = re.compile(r'\([^()]*\)[?+*]')
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
def parenthesized_expressions(expansion: Expansion) -> List[str]:
# In later chapters, we allow expansions to be tuples,
# with the expansion being the first element
if isinstance(expansion, tuple):
expansion = expansion[0]
return re.findall(RE_PARENTHESIZED_EXPR, expansion)
# + slideshow={"slide_type": "fragment"}
assert parenthesized_expressions("(<foo>)* (<foo><bar>)+ (+<foo>)? <integer>(.<integer>)?") == [
'(<foo>)*', '(<foo><bar>)+', '(+<foo>)?', '(.<integer>)?']
# + [markdown] slideshow={"slide_type": "subslide"}
# We can now use these to apply rule number 1, above, introducing new symbols for expressions in parentheses.
# + slideshow={"slide_type": "fragment"}
def convert_ebnf_parentheses(ebnf_grammar: Grammar) -> Grammar:
"""Convert a grammar in extended BNF to BNF"""
grammar = extend_grammar(ebnf_grammar)
for nonterminal in ebnf_grammar:
expansions = ebnf_grammar[nonterminal]
for i in range(len(expansions)):
expansion = expansions[i]
if not isinstance(expansion, str):
expansion = expansion[0]
while True:
parenthesized_exprs = parenthesized_expressions(expansion)
if len(parenthesized_exprs) == 0:
break
for expr in parenthesized_exprs:
operator = expr[-1:]
contents = expr[1:-2]
new_sym = new_symbol(grammar)
exp = grammar[nonterminal][i]
opts = None
if isinstance(exp, tuple):
(exp, opts) = exp
assert isinstance(exp, str)
expansion = exp.replace(expr, new_sym + operator, 1)
if opts:
grammar[nonterminal][i] = (expansion, opts)
else:
grammar[nonterminal][i] = expansion
grammar[new_sym] = [contents]
return grammar
# + [markdown] slideshow={"slide_type": "subslide"}
# This does the conversion as sketched above:
# + slideshow={"slide_type": "fragment"}
convert_ebnf_parentheses({"<number>": ["<integer>(.<integer>)?"]})
# + [markdown] slideshow={"slide_type": "fragment"}
# It even works for nested parenthesized expressions:
# + slideshow={"slide_type": "fragment"}
convert_ebnf_parentheses({"<foo>": ["((<foo>)?)+"]})
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Expanding Operators
#
# After expanding parenthesized expressions, we now need to take care of symbols followed by operators (`?`, `*`, `+`). As with `convert_ebnf_parentheses()`, above, we first extract all symbols followed by an operator.
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
RE_EXTENDED_NONTERMINAL = re.compile(r'(<[^<> ]*>[?+*])')
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
def extended_nonterminals(expansion: Expansion) -> List[str]:
# In later chapters, we allow expansions to be tuples,
# with the expansion being the first element
if isinstance(expansion, tuple):
expansion = expansion[0]
return re.findall(RE_EXTENDED_NONTERMINAL, expansion)
# + slideshow={"slide_type": "fragment"}
assert extended_nonterminals(
"<foo>* <bar>+ <elem>? <none>") == ['<foo>*', '<bar>+', '<elem>?']
# + [markdown] slideshow={"slide_type": "subslide"}
# Our converter extracts the symbol and the operator, and adds new symbols according to the rules laid out above.
# + slideshow={"slide_type": "fragment"}
def convert_ebnf_operators(ebnf_grammar: Grammar) -> Grammar:
"""Convert a grammar in extended BNF to BNF"""
grammar = extend_grammar(ebnf_grammar)
for nonterminal in ebnf_grammar:
expansions = ebnf_grammar[nonterminal]
for i in range(len(expansions)):
expansion = expansions[i]
extended_symbols = extended_nonterminals(expansion)
for extended_symbol in extended_symbols:
operator = extended_symbol[-1:]
original_symbol = extended_symbol[:-1]
assert original_symbol in ebnf_grammar, \
f"{original_symbol} is not defined in grammar"
new_sym = new_symbol(grammar, original_symbol)
exp = grammar[nonterminal][i]
opts = None
if isinstance(exp, tuple):
(exp, opts) = exp
assert isinstance(exp, str)
new_exp = exp.replace(extended_symbol, new_sym, 1)
if opts:
grammar[nonterminal][i] = (new_exp, opts)
else:
grammar[nonterminal][i] = new_exp
if operator == '?':
grammar[new_sym] = ["", original_symbol]
elif operator == '*':
grammar[new_sym] = ["", original_symbol + new_sym]
elif operator == '+':
grammar[new_sym] = [
original_symbol, original_symbol + new_sym]
return grammar
# + slideshow={"slide_type": "subslide"}
convert_ebnf_operators({"<integer>": ["<digit>+"], "<digit>": ["0"]})
# + [markdown] slideshow={"slide_type": "subslide"} tags=[]
# ##### All Together
#
# We can combine the two, first extending parentheses and then operators:
# + slideshow={"slide_type": "fragment"}
def convert_ebnf_grammar(ebnf_grammar: Grammar) -> Grammar:
return convert_ebnf_operators(convert_ebnf_parentheses(ebnf_grammar))
# + [markdown] slideshow={"slide_type": "subslide"}
# #### End of Excursion
# + [markdown] slideshow={"slide_type": "fragment"}
# Here's an example of using `convert_ebnf_grammar()`:
# + slideshow={"slide_type": "fragment"}
convert_ebnf_grammar({"<authority>": ["(<userinfo>@)?<host>(:<port>)?"]})
# + slideshow={"slide_type": "subslide"}
expr_grammar = convert_ebnf_grammar(EXPR_EBNF_GRAMMAR)
expr_grammar
# + [markdown] slideshow={"slide_type": "fragment"}
# Success! We have nicely converted the EBNF grammar into BNF.
# + [markdown] slideshow={"slide_type": "fragment"}
# With character classes and EBNF grammar conversion, we have two powerful tools that make the writing of grammars easier. We will use these again and again as it comes to working with grammars.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Grammar Extensions
# + [markdown] slideshow={"slide_type": "fragment"}
# During the course of this book, we frequently want to specify _additional information_ for grammars, such as [_probabilities_](ProbabilisticGrammarFuzzer.ipynb) or [_constraints_](GeneratorGrammarFuzzer.ipynb). To support these extensions, as well as possibly others, we define an _annotation_ mechanism.
# + [markdown] slideshow={"slide_type": "subslide"}
# Our concept for annotating grammars is to add _annotations_ to individual expansions. To this end, we allow that an expansion cannot only be a string, but also a _pair_ of a string and a set of attributes, as in
#
# ```python
# "<expr>":
# [("<term> + <expr>", opts(min_depth=10)),
# ("<term> - <expr>", opts(max_depth=2)),
# "<term>"]
# ```
#
# Here, the `opts()` function would allow us to express annotations that apply to the individual expansions; in this case, the addition would be annotated with a `min_depth` value of 10, and the subtraction with a `max_depth` value of 2. The meaning of these annotations is left to the individual algorithms dealing with the grammars; the general idea, though, is that they can be ignored.
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Excursion: Implementing `opts()`
# + [markdown] slideshow={"slide_type": "fragment"}
# Our `opts()` helper function returns a mapping of its arguments to values:
# + slideshow={"slide_type": "fragment"}
def opts(**kwargs: Any) -> Dict[str, Any]:
return kwargs
# + slideshow={"slide_type": "fragment"}
opts(min_depth=10)
# + [markdown] slideshow={"slide_type": "fragment"}
# To deal with both expansion strings and pairs of expansions and annotations, we access the expansion string and the associated annotations via designated helper functions, `exp_string()` and `exp_opts()`:
# + slideshow={"slide_type": "fragment"}
def exp_string(expansion: Expansion) -> str:
"""Return the string to be expanded"""
if isinstance(expansion, str):
return expansion
return expansion[0]
# + slideshow={"slide_type": "subslide"}
exp_string(("<term> + <expr>", opts(min_depth=10)))
# + slideshow={"slide_type": "fragment"}
def exp_opts(expansion: Expansion) -> Dict[str, Any]:
"""Return the options of an expansion. If options are not defined, return {}"""
if isinstance(expansion, str):
return {}
return expansion[1]
# + slideshow={"slide_type": "fragment"}
def exp_opt(expansion: Expansion, attribute: str) -> Any:
"""Return the given attribution of an expansion.
If attribute is not defined, return None"""
return exp_opts(expansion).get(attribute, None)
# + slideshow={"slide_type": "fragment"}
exp_opts(("<term> + <expr>", opts(min_depth=10)))
# + slideshow={"slide_type": "fragment"}
exp_opt(("<term> - <expr>", opts(max_depth=2)), 'max_depth')
# + [markdown] slideshow={"slide_type": "subslide"}
# Finally, we define a helper function that sets a particular option:
# + slideshow={"slide_type": "subslide"}
def set_opts(grammar: Grammar, symbol: str, expansion: Expansion,
opts: Option = {}) -> None:
"""Set the options of the given expansion of grammar[symbol] to opts"""
expansions = grammar[symbol]
for i, exp in enumerate(expansions):
if exp_string(exp) != exp_string(expansion):
continue
new_opts = exp_opts(exp)
if opts == {} or new_opts == {}:
new_opts = opts
else:
for key in opts:
new_opts[key] = opts[key]
if new_opts == {}:
grammar[symbol][i] = exp_string(exp)
else:
grammar[symbol][i] = (exp_string(exp), new_opts)
return
raise KeyError(
"no expansion " +
repr(symbol) +
" -> " +
repr(
exp_string(expansion)))
# + [markdown] slideshow={"slide_type": "subslide"}
# #### End of Excursion
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Checking Grammars
#
# Since grammars are represented as strings, it is fairly easy to introduce errors. So let us introduce a helper function that checks a grammar for consistency.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# The helper function `is_valid_grammar()` iterates over a grammar to check whether all used symbols are defined, and vice versa, which is very useful for debugging; it also checks whether all symbols are reachable from the start symbol. You don't have to delve into details here, but as always, it is important to get the input data straight before we make use of it.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Excursion: Implementing `is_valid_grammar()`
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "skip"}
import sys
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
def def_used_nonterminals(grammar: Grammar, start_symbol:
str = START_SYMBOL) -> Tuple[Optional[Set[str]],
Optional[Set[str]]]:
"""Return a pair (`defined_nonterminals`, `used_nonterminals`) in `grammar`.
In case of error, return (`None`, `None`)."""
defined_nonterminals = set()
used_nonterminals = {start_symbol}
for defined_nonterminal in grammar:
defined_nonterminals.add(defined_nonterminal)
expansions = grammar[defined_nonterminal]
if not isinstance(expansions, list):
print(repr(defined_nonterminal) + ": expansion is not a list",
file=sys.stderr)
return None, None
if len(expansions) == 0:
print(repr(defined_nonterminal) + ": expansion list empty",
file=sys.stderr)
return None, None
for expansion in expansions:
if isinstance(expansion, tuple):
expansion = expansion[0]
if not isinstance(expansion, str):
print(repr(defined_nonterminal) + ": "
+ repr(expansion) + ": not a string",
file=sys.stderr)
return None, None
for used_nonterminal in nonterminals(expansion):
used_nonterminals.add(used_nonterminal)
return defined_nonterminals, used_nonterminals
# + slideshow={"slide_type": "fragment"}
def reachable_nonterminals(grammar: Grammar,
start_symbol: str = START_SYMBOL) -> Set[str]:
reachable = set()
def _find_reachable_nonterminals(grammar, symbol):
nonlocal reachable
reachable.add(symbol)
for expansion in grammar.get(symbol, []):
for nonterminal in nonterminals(expansion):
if nonterminal not in reachable:
_find_reachable_nonterminals(grammar, nonterminal)
_find_reachable_nonterminals(grammar, start_symbol)
return reachable
# + slideshow={"slide_type": "fragment"}
def unreachable_nonterminals(grammar: Grammar,
start_symbol=START_SYMBOL) -> Set[str]:
return grammar.keys() - reachable_nonterminals(grammar, start_symbol)
# + slideshow={"slide_type": "fragment"}
def opts_used(grammar: Grammar) -> Set[str]:
used_opts = set()
for symbol in grammar:
for expansion in grammar[symbol]:
used_opts |= set(exp_opts(expansion).keys())
return used_opts
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
def is_valid_grammar(grammar: Grammar,
start_symbol: str = START_SYMBOL,
supported_opts: Set[str] = set()) -> bool:
"""Check if the given `grammar` is valid.
`start_symbol`: optional start symbol (default: `<start>`)
`supported_opts`: options supported (default: none)"""
defined_nonterminals, used_nonterminals = \
def_used_nonterminals(grammar, start_symbol)
if defined_nonterminals is None or used_nonterminals is None:
return False
# Do not complain about '<start>' being not used,
# even if start_symbol is different
if START_SYMBOL in grammar:
used_nonterminals.add(START_SYMBOL)
for unused_nonterminal in defined_nonterminals - used_nonterminals:
print(repr(unused_nonterminal) + ": defined, but not used",
file=sys.stderr)
for undefined_nonterminal in used_nonterminals - defined_nonterminals:
print(repr(undefined_nonterminal) + ": used, but not defined",
file=sys.stderr)
# Symbols must be reachable either from <start> or given start symbol
unreachable = unreachable_nonterminals(grammar, start_symbol)
msg_start_symbol = start_symbol
if START_SYMBOL in grammar:
unreachable = unreachable - \
reachable_nonterminals(grammar, START_SYMBOL)
if start_symbol != START_SYMBOL:
msg_start_symbol += " or " + START_SYMBOL
for unreachable_nonterminal in unreachable:
print(repr(unreachable_nonterminal) + ": unreachable from " + msg_start_symbol,
file=sys.stderr)
used_but_not_supported_opts = set()
if len(supported_opts) > 0:
used_but_not_supported_opts = opts_used(
grammar).difference(supported_opts)
for opt in used_but_not_supported_opts:
print(
"warning: option " +
repr(opt) +
" is not supported",
file=sys.stderr)
return used_nonterminals == defined_nonterminals and len(unreachable) == 0
# + [markdown] slideshow={"slide_type": "subslide"}
# ### End of Excursion
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# Let us make use of `is_valid_grammar()`. Our grammars defined above pass the test:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert is_valid_grammar(EXPR_GRAMMAR)
assert is_valid_grammar(CGI_GRAMMAR)
assert is_valid_grammar(URL_GRAMMAR)
# + [markdown] slideshow={"slide_type": "fragment"}
# The check can also be applied to EBNF grammars:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert is_valid_grammar(EXPR_EBNF_GRAMMAR)
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# These ones do not pass the test, though:
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert not is_valid_grammar({"<start>": ["<x>"], "<y>": ["1"]}) # type: ignore
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert not is_valid_grammar({"<start>": "123"}) # type: ignore
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert not is_valid_grammar({"<start>": []}) # type: ignore
# + button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
assert not is_valid_grammar({"<start>": [1, 2, 3]}) # type: ignore
# + [markdown] slideshow={"slide_type": "fragment"}
# (The `#type: ignore` annotations avoid static checkers flagging the above as errors).
# + [markdown] slideshow={"slide_type": "fragment"}
# From here on, we will always use `is_valid_grammar()` when defining a grammar.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Synopsis
#
# This chapter introduces _grammars_ as a simple means to specify input languages, and to use them for testing programs with syntactically valid inputs. A grammar is defined as a mapping of nonterminal symbols to lists of alternative expansions, as in the following example:
# + slideshow={"slide_type": "subslide"}
US_PHONE_GRAMMAR: Grammar = {
"<start>": ["<phone-number>"],
"<phone-number>": ["(<area>)<exchange>-<line>"],
"<area>": ["<lead-digit><digit><digit>"],
"<exchange>": ["<lead-digit><digit><digit>"],
"<line>": ["<digit><digit><digit><digit>"],
"<lead-digit>": ["2", "3", "4", "5", "6", "7", "8", "9"],
"<digit>": ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
assert is_valid_grammar(US_PHONE_GRAMMAR)
# + [markdown] slideshow={"slide_type": "subslide"}
# Nonterminal symbols are enclosed in angle brackets (say, `<digit>`). To generate an input string from a grammar, a _producer_ starts with the start symbol (`<start>`) and randomly chooses a random expansion for this symbol. It continues the process until all nonterminal symbols are expanded. The function `simple_grammar_fuzzer()` does just that:
# + slideshow={"slide_type": "fragment"}
[simple_grammar_fuzzer(US_PHONE_GRAMMAR) for i in range(5)]
# + [markdown] slideshow={"slide_type": "subslide"}
# In practice, though, instead of `simple_grammar_fuzzer()`, you should use [the `GrammarFuzzer` class](GrammarFuzzer.ipynb) or one of its [coverage-based](GrammarCoverageFuzzer.ipynb), [probabilistic-based](ProbabilisticGrammarFuzzer.ipynb), or [generator-based](GeneratorGrammarFuzzer.ipynb) derivatives; these are more efficient, protect against infinite growth, and provide several additional features.
# + [markdown] slideshow={"slide_type": "fragment"}
# This chapter also introduces a [grammar toolbox](#A-Grammar-Toolbox) with several helper functions that ease the writing of grammars, such as using shortcut notations for character classes and repetitions, or extending grammars
# + [markdown] button=false new_sheet=true run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Lessons Learned
#
# * Grammars are powerful tools to express and produce syntactically valid inputs.
# * Inputs produced from grammars can be used as is, or used as seeds for mutation-based fuzzing.
# * Grammars can be extended with character classes and operators to make writing easier.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"}
# ## Next Steps
#
# As they make a great foundation for generating software tests, we use grammars again and again in this book. As a sneak preview, we can use grammars to [fuzz configurations](ConfigurationFuzzer.ipynb):
#
# ```
# <options> ::= <option>*
# <option> ::= -h | --version | -v | -d | -i | --global-config <filename>
# ```
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# We can use grammars for [fuzzing functions and APIs](APIFuzzer.ipynb) and [fuzzing graphical user interfaces](WebFuzzer.ipynb):
#
# ```
# <call-sequence> ::= <call>*
# <call> ::= urlparse(<url>) | urlsplit(<url>)
# ```
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# We can assign [probabilities](ProbabilisticGrammarFuzzer.ipynb) and [constraints](GeneratorGrammarFuzzer.ipynb) to individual expansions:
#
# ```
# <term>: 50% <factor> * <term> | 30% <factor> / <term> | 20% <factor>
# <integer>: <digit>+ { <integer> >= 100 }
# ```
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"}
# All these extras become especially valuable as we can
#
# 1. _infer grammars automatically_, dropping the need to specify them manually, and
# 2. _guide them towards specific goals_ such as coverage or critical functions;
#
# which we also discuss for all techniques in this book.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"}
# To get there, however, we still have bit of homework to do. In particular, we first have to learn how to
#
# * [create an efficient grammar fuzzer](GrammarFuzzer.ipynb)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Background
#
# As one of the foundations of human language, grammars have been around as long as human language existed. The first _formalization_ of generative grammars was by <NAME> in 350 BC \cite{Panini350bce}. As a general means to express formal languages for both data and programs, their role in computer science cannot be overstated. The seminal work by Chomsky \cite{Chomsky1956} introduced the central models of regular languages, context-free grammars, context-sensitive grammars, and universal grammars as they are used (and taught) in computer science as a means to specify input and programming languages ever since.
# + [markdown] slideshow={"slide_type": "subslide"}
# The use of grammars for _producing_ test inputs goes back to Burkhardt \cite{Burkhardt1967}, to be later rediscovered and applied by Hanford \cite{Hanford1970} and Purdom \cite{Purdom1972}. The most important use of grammar testing since then has been *compiler testing*. Actually, grammar-based testing is one important reason why compilers and Web browsers work as they should:
#
# * The [CSmith](https://embed.cs.utah.edu/csmith/) tool \cite{Yang2011} specifically targets C programs, starting with a C grammar and then applying additional steps, such as referring to variables and functions defined earlier or ensuring integer and type safety. Their authors have used it "to find and report more than 400 previously unknown compiler bugs."
#
# * The [LangFuzz](http://issta2016.cispa.saarland/interview-with-christian-holler/) work \cite{Holler2012}, which shares two authors with this book, uses a generic grammar to produce outputs, and is used day and night to generate JavaScript programs and test their interpreters; as of today, it has found more than 2,600 bugs in browsers such as Mozilla Firefox, Google Chrome, and Microsoft Edge.
#
# * The [EMI Project](http://web.cs.ucdavis.edu/~su/emi-project/) \cite{Le2014} uses grammars to stress-test C compilers, transforming known tests into alternative programs that should be semantically equivalent over all inputs. Again, this has led to more than 100 bugs in C compilers being fixed.
#
# * [Grammarinator](https://github.com/renatahodovan/grammarinator) \cite{Hodovan2018} is an open-source grammar fuzzer (written in Python!), using the popular ANTLR format as grammar specification. Like LangFuzz, it uses the grammar for both parsing and producing, and has found more than 100 issues in the *JerryScript* lightweight JavaScript engine and an associated platform.
#
# * [Domato](https://github.com/googleprojectzero/domato) is a generic grammar generation engine that is specifically used for fuzzing DOM input. It has revealed a number of security issues in popular Web browsers.
# + [markdown] slideshow={"slide_type": "subslide"}
# Compilers and Web browsers, of course, are not only domains where grammars are needed for testing, but also domains where grammars are well-known. Our claim in this book is that grammars can be used to generate almost _any_ input, and our aim is to empower you to do precisely that.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "slide"} toc-hr-collapsed=true toc-nb-collapsed=true
# ## Exercises
# + [markdown] slideshow={"slide_type": "subslide"} solution2="hidden" solution2_first=true
# ### Exercise 1: A JSON Grammar
#
# Take a look at the [JSON specification](http://www.json.org) and derive a grammar from it:
#
# * Use _character classes_ to express valid characters
# * Use EBNF to express repetitions and optional parts
# * Assume that
# - a string is a sequence of digits, ASCII letters, punctuation and space characters without quotes or escapes
# - whitespace is just a single space.
# * Use `is_valid_grammar()` to ensure the grammar is valid.
#
# Feed the grammar into `simple_grammar_fuzzer()`. Do you encounter any errors, and why?
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution.** This is a fairly straightforward translation:
# + slideshow={"slide_type": "skip"} solution2="hidden"
CHARACTERS_WITHOUT_QUOTE = (string.digits
+ string.ascii_letters
+ string.punctuation.replace('"', '').replace('\\', '')
+ ' ')
# + slideshow={"slide_type": "skip"} solution2="hidden"
JSON_EBNF_GRAMMAR: Grammar = {
"<start>": ["<json>"],
"<json>": ["<element>"],
"<element>": ["<ws><value><ws>"],
"<value>": ["<object>", "<array>", "<string>", "<number>",
"true", "false", "null", "'; DROP TABLE STUDENTS"],
"<object>": ["{<ws>}", "{<members>}"],
"<members>": ["<member>(,<members>)*"],
"<member>": ["<ws><string><ws>:<element>"],
"<array>": ["[<ws>]", "[<elements>]"],
"<elements>": ["<element>(,<elements>)*"],
"<element>": ["<ws><value><ws>"],
"<string>": ['"' + "<characters>" + '"'],
"<characters>": ["<character>*"],
"<character>": srange(CHARACTERS_WITHOUT_QUOTE),
"<number>": ["<int><frac><exp>"],
"<int>": ["<digit>", "<onenine><digits>", "-<digit>", "-<onenine><digits>"],
"<digits>": ["<digit>+"],
"<digit>": ['0', "<onenine>"],
"<onenine>": crange('1', '9'),
"<frac>": ["", ".<digits>"],
"<exp>": ["", "E<sign><digits>", "e<sign><digits>"],
"<sign>": ["", '+', '-'],
# "<ws>": srange(string.whitespace)
"<ws>": [" "]
}
assert is_valid_grammar(JSON_EBNF_GRAMMAR)
# + slideshow={"slide_type": "skip"} solution2="hidden"
JSON_GRAMMAR = convert_ebnf_grammar(JSON_EBNF_GRAMMAR)
# + slideshow={"slide_type": "skip"} solution2="hidden"
from ExpectError import ExpectError
# + slideshow={"slide_type": "skip"} solution2="hidden"
for i in range(50):
with ExpectError():
print(simple_grammar_fuzzer(JSON_GRAMMAR, '<object>'))
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# We get these errors because `simple_grammar_fuzzer()` first expands to a maximum number of elements, and then is limited because every further expansion would _increase_ the number of nonterminals, even though these may eventually reduce the string length. This issue is addressed in the [next chapter](GrammarFuzzer.ipynb), introducing a more solid algorithm for producing strings from grammars.
# + [markdown] slideshow={"slide_type": "subslide"} solution2="hidden" solution2_first=true
# ### Exercise 2: Finding Bugs
#
# The name `simple_grammar_fuzzer()` does not come by accident: The way it expands grammars is limited in several ways. What happens if you apply `simple_grammar_fuzzer()` on `nonterminal_grammar` and `expr_grammar`, as defined above, and why?
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution**. `nonterminal_grammar` does not work because `simple_grammar_fuzzer()` eventually tries to expand the just generated nonterminal:
# + slideshow={"slide_type": "skip"} solution2="hidden"
from ExpectError import ExpectError, ExpectTimeout
# + slideshow={"slide_type": "skip"} solution2="hidden"
with ExpectError():
simple_grammar_fuzzer(nonterminal_grammar, log=True)
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# For `expr_grammar`, things are even worse, as `simple_grammar_fuzzer()` can start a series of infinite expansions:
# + slideshow={"slide_type": "skip"} solution2="hidden"
with ExpectTimeout(1):
for i in range(10):
print(simple_grammar_fuzzer(expr_grammar))
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# Both issues are addressed and discussed in the [next chapter](GrammarFuzzer.ipynb), introducing a more solid algorithm for producing strings from grammars.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Exercise 3: Grammars with Regular Expressions
#
# In a _grammar extended with regular expressions_, we can use the special form
# ```
# /regex/
# ```
# to include regular expressions in expansions. For instance, we can have a rule
# ```
# <integer> ::= /[+-]?[0-9]+/
# ```
# to quickly express that an integer is an optional sign, followed by a sequence of digits.
# + [markdown] slideshow={"slide_type": "subslide"} solution2="hidden" solution2_first=true
# #### Part 1: Convert regular expressions
#
# Write a converter `convert_regex(r)` that takes a regular expression `r` and creates an equivalent grammar. Support the following regular expression constructs:
#
# * `*`, `+`, `?`, `()` should work just in EBNFs, above.
# * `a|b` should translate into a list of alternatives `[a, b]`.
# * `.` should match any character except newline.
# * `[abc]` should translate into `srange("abc")`
# * `[^abc]` should translate into the set of ASCII characters _except_ `srange("abc")`.
# * `[a-b]` should translate into `crange(a, b)`
# * `[^a-b]` should translate into the set of ASCII characters _except_ `crange(a, b)`.
#
# Example: `convert_regex(r"[0-9]+")` should yield a grammar such as
# ```python
# {
# "<start>": ["<s1>"],
# "<s1>": [ "<s2>", "<s1><s2>" ],
# "<s2>": crange('0', '9')
# }
# ```
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution.** Left as exercise to the reader.
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Part 2: Identify and expand regular expressions
#
# Write a converter `convert_regex_grammar(g)` that takes a EBNF grammar `g` containing regular expressions in the form `/.../` and creates an equivalent BNF grammar. Support the regular expression constructs as above.
#
# Example: `convert_regex_grammar({ "<integer>" : "/[+-]?[0-9]+/" })` should yield a grammar such as
# ```python
# {
# "<integer>": ["<s1><s3>"],
# "<s1>": [ "", "<s2>" ],
# "<s2>": srange("+-"),
# "<s3>": [ "<s4>", "<s4><s3>" ],
# "<s4>": crange('0', '9')
# }
# ```
# + [markdown] slideshow={"slide_type": "fragment"} solution2="hidden" solution2_first=true
# Optional: Support _escapes_ in regular expressions: `\c` translates to the literal character `c`; `\/` translates to `/` (and thus does not end the regular expression); `\\` translates to `\`.
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution.** Left as exercise to the reader.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "subslide"} solution="hidden" solution2="hidden" solution2_first=true solution_first=true
# ### Exercise 4: Defining Grammars as Functions (Advanced)
#
# To obtain a nicer syntax for specifying grammars, one can make use of Python constructs which then will be _parsed_ by an additional function. For instance, we can imagine a grammar definition which uses `|` as a means to separate alternatives:
# + slideshow={"slide_type": "fragment"}
def expression_grammar_fn():
start = "<expr>"
expr = "<term> + <expr>" | "<term> - <expr>"
term = "<factor> * <term>" | "<factor> / <term>" | "<factor>"
factor = "+<factor>" | "-<factor>" | "(<expr>)" | "<integer>.<integer>" | "<integer>"
integer = "<digit><integer>" | "<digit>"
digit = '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
# + [markdown] slideshow={"slide_type": "subslide"}
# If we execute `expression_grammar_fn()`, this will yield an error. Yet, the purpose of `expression_grammar_fn()` is not to be executed, but to be used as _data_ from which the grammar will be constructed.
# + slideshow={"slide_type": "fragment"}
with ExpectError():
expression_grammar_fn()
# + [markdown] slideshow={"slide_type": "fragment"}
# To this end, we make use of the `ast` (abstract syntax tree) and `inspect` (code inspection) modules.
# + slideshow={"slide_type": "skip"}
import ast
import inspect
# + [markdown] slideshow={"slide_type": "fragment"}
# First, we obtain the source code of `expression_grammar_fn()`...
# + slideshow={"slide_type": "subslide"}
source = inspect.getsource(expression_grammar_fn)
source
# + [markdown] slideshow={"slide_type": "fragment"}
# ... which we then parse into an abstract syntax tree:
# + slideshow={"slide_type": "fragment"}
tree = ast.parse(source)
# + [markdown] slideshow={"slide_type": "fragment"}
# We can now parse the tree to find operators and alternatives. `get_alternatives()` iterates over all nodes `op` of the tree; If the node looks like a binary _or_ (`|` ) operation, we drill deeper and recurse. If not, we have reached a single production, and we try to get the expression from the production. We define the `to_expr` parameter depending on how we want to represent the production. In this case, we represent a single production by a single string.
# + slideshow={"slide_type": "subslide"}
def get_alternatives(op, to_expr=lambda o: o.s):
if isinstance(op, ast.BinOp) and isinstance(op.op, ast.BitOr):
return get_alternatives(op.left, to_expr) + [to_expr(op.right)]
return [to_expr(op)]
# + [markdown] slideshow={"slide_type": "fragment"}
# `funct_parser()` takes the abstract syntax tree of a function (say, `expression_grammar_fn()`) and iterates over all assignments:
# + slideshow={"slide_type": "fragment"}
def funct_parser(tree, to_expr=lambda o: o.s):
return {assign.targets[0].id: get_alternatives(assign.value, to_expr)
for assign in tree.body[0].body}
# + [markdown] slideshow={"slide_type": "fragment"}
# The result is a grammar in our regular format:
# + slideshow={"slide_type": "subslide"}
grammar = funct_parser(tree)
for symbol in grammar:
print(symbol, "::=", grammar[symbol])
# + [markdown] slideshow={"slide_type": "subslide"} solution2="hidden" solution2_first=true
# #### Part 1 (a): One Single Function
#
# Write a single function `define_grammar(fn)` that takes a grammar defined as function (such as `expression_grammar_fn()`) and returns a regular grammar.
# + [markdown] button=false new_sheet=false run_control={"read_only": false} slideshow={"slide_type": "fragment"} solution="hidden" solution2="hidden"
# **Solution**. This is straightforward:
# + slideshow={"slide_type": "skip"} solution2="hidden"
def define_grammar(fn, to_expr=lambda o: o.s):
source = inspect.getsource(fn)
tree = ast.parse(source)
grammar = funct_parser(tree, to_expr)
return grammar
# + slideshow={"slide_type": "skip"} solution2="hidden"
define_grammar(expression_grammar_fn)
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Note.** Python allows us to directly bind the generated grammar to the name `expression_grammar_fn` using function decorators. This can be used to ensure that we do not have a faulty function lying around:
#
# ```python
# @define_grammar
# def expression_grammar():
# start = "<expr>"
# expr = "<term> + <expr>" | "<term> - <expr>"
# #...
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Part 1 (b): Alternative representations
# + [markdown] slideshow={"slide_type": "fragment"}
# We note that the grammar representation we designed previously does not allow simple generation of alternatives such as `srange()` and `crange()`. Further, one may find the string representation of expressions limiting. It turns out that it is simple to extend our grammar definition to support grammars such as below:
# + slideshow={"slide_type": "subslide"}
def define_name(o):
return o.id if isinstance(o, ast.Name) else o.s
# + slideshow={"slide_type": "subslide"}
def define_expr(op):
if isinstance(op, ast.BinOp) and isinstance(op.op, ast.Add):
return (*define_expr(op.left), define_name(op.right))
return (define_name(op),)
# + slideshow={"slide_type": "subslide"}
def define_ex_grammar(fn):
return define_grammar(fn, define_expr)
# + [markdown] slideshow={"slide_type": "subslide"}
# The grammar:
#
# ```python
# @define_ex_grammar
# def expression_grammar():
# start = expr
# expr = (term + '+' + expr
# | term + '-' + expr)
# term = (factor + '*' + term
# | factor + '/' + term
# | factor)
# factor = ('+' + factor
# | '-' + factor
# | '(' + expr + ')'
# | integer + '.' + integer
# | integer)
# integer = (digit + integer
# | digit)
# digit = '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
#
# for symbol in expression_grammar:
# print(symbol, "::=", expression_grammar[symbol])
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# **Note.** The grammar data structure thus obtained is a little more detailed than the standard data structure. It represents each production as a tuple.
# + [markdown] slideshow={"slide_type": "fragment"}
# We note that we have not enabled `srange()` or `crange()` in the above grammar. How would you go about adding these? (*Hint:* wrap `define_expr()` to look for `ast.Call`)
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Part 2: Extended Grammars
#
# Introduce an operator `*` that takes a pair `(min, max)` where `min` and `max` are the minimum and maximum number of repetitions, respectively. A missing value `min` stands for zero; a missing value `max` for infinity.
# + slideshow={"slide_type": "fragment"}
def identifier_grammar_fn():
identifier = idchar * (1,)
# + [markdown] slideshow={"slide_type": "fragment"} solution2="hidden" solution2_first=true
# With the `*` operator, we can generalize the EBNF operators – `?` becomes (0,1), `*` becomes (0,), and `+` becomes (1,). Write a converter that takes an extended grammar defined using `*`, parse it, and convert it into BNF.
# + [markdown] slideshow={"slide_type": "skip"} solution2="hidden"
# **Solution.** No solution yet :-)
| docs/notebooks/Grammars.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] nbgrader={}
# # Project Euler: Problem 1
# + [markdown] nbgrader={}
# If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
#
# Find the sum of all the multiples of 3 or 5 below 1000.
# + deletable=false nbgrader={"checksum": "6cff4e8e53b15273846c3aecaea84a3d", "solution": true}
numbers = [] # create an empty list to store all my numbers in
for i in range(1000): #this give me i values from 0 to 999
if i % 3 == 0 or i % 5 == 0: # if i divided by 3 or 5 yields a remainder of 0
numbers.append(i) # then that number is a multiple of 3 or 5 and is added to the list 'numbers'
answer = sum(numbers) # let the variable 'answer' equal the sum of the numbers in 'numbers'
print(answer) # and finally print the answer
# + deletable=false nbgrader={"checksum": "6e498cbe102f8b3c1bc4ebd777bcc952", "grade": true, "grade_id": "projecteuler1", "points": 10}
# This cell will be used for grading, leave it at the end of the notebook.
| assignments/assignment01/ProjectEuler1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# In this last part of the dissertation, we will price an Interest rate swap (IRS), a Credit default swap (CDS), CVA and Credit Insurance in Python.
import numpy as np
import pandas as pd
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import math
import unittest
# First, we start by writing a code to find the present value of an Interest rate swap.
#
# By defintion, an IRS is an agreement between two parties to exchange future interest rate payments of a set period of time. In this case we will consider Vanilla IRS which involves exchange of a fixed rate for a floating rate or viceversa.
# In order to find the present value of an IRS, we start with a set of data $years1$ which is a set of matuirties and $zero$_$rates1$ which are the zero rates at each maturity date. Then we use this data set to construct a zero yield curve ($zero$ _$yield$ _$curve$) using linear interpolation.
years1 = np.array([0, 1, 2, 4, 5, 10, 20])
zero_rates1 = np.array([0.01, 0.01, 0.011, 0.012, 0.012, 0.015, 0.015])
zero_yield_curve = interp1d(years1, zero_rates1)
xnew = np.linspace(0, 20, num=21, endpoint=True)
plt.title('Zero yield curve through linear interpolation.')
plt.xlabel('maturities')
plt.ylabel('zero rates')
plt.plot(years1, zero_rates1, 'o', xnew, zero_yield_curve(xnew))
plt.legend(['data', 'linear'], loc='best')
plt.show()
# A vanilla IRS is made of a fixed and a floating leg.
#
# The present value of a fixed rate leg is given by:
# $$PV_{fixed}(t)=RN \sum^{n}_{i=1} \tau_i D_i$$
# and the present value of a floating leg is given by:
# $$PV_{float}(t)=N \sum^{n}_{i=1} (F_i +s) \tau_i D_i$$
# where:
#
# $D_i=D(t,T_i)$ is the discount factor,
#
# $s$ is the floating spread,
#
# $N$ is the notional,
#
# $\tau_i$ is $(T_i-T_{i-1})$,
#
# $R$ is the fixed rate,and
#
# $F_i$ is the forward rate.
# In order the evaluate the present value of the fixed leg, we start by computing the discount factor $D_i=D(t,T_i)= e^{-(T_i-t)*zero \_ yield \_ curve(i)}$. We then use some known results and the unittest to check the code.
# +
def discount_factor1(t, Ti, zero_yield_curve):
return np.exp(-(Ti - t) * zero_yield_curve(Ti))
class TestDiscountFactor(unittest.TestCase):
def test_discountfactor(self):
self.assertAlmostEqual(discount_factor1(0, years1[1], zero_yield_curve), np.exp(-0.01))
self.assertAlmostEqual(discount_factor1(0, years1[2], zero_yield_curve), np.exp(-0.022))
unittest.main(argv=[''], verbosity=2, exit=False)
# -
# Next we compute the forward rate $F_i=\frac{(\frac{D_{i-1}}{D_i}-1)}{\tau_i}$.
# +
def forward_rates(
t, time1, time2, zero_yield_curve):
#time1 is the time used to evalaute D_{i-1} whilst time2 is used to evaluate D_i or viceversa
if time1 == time2:
tau = 0
elif time1 > time2:
tau = (time1 - time2)
else:
tau = (time2 - time1)
y1 = discount_factor1(t, time1, zero_yield_curve)
y2 = discount_factor1(t, time2, zero_yield_curve)
if time1 == time2:
forward_rate = zero_yield_curve(time1)
elif time1 > time2:
forward_rate = ((y2 / y1) - 1) / tau
else:
forward_rate = ((y1 / y2) - 1) / tau
return forward_rate
class TestForwardRates(unittest.TestCase):
def test_forwardrates(self):
self.assertAlmostEqual(forward_rates(0, years1[2], years1[1], zero_yield_curve), np.exp(-0.01) / np.exp(-0.022) - 1)
unittest.main(argv=[''], verbosity=2, exit=False)
# -
# We evaluate the present value of the fixed leg by using the formula we stated above. The variables in the formula below are:
#
# $t:$ time at which the fixed leg is evaluated,
#
# $coupon:$ coupon rate, frequency of payments in a year,
#
# $end\_ date:$ maturity of the swap,
#
# $k:$ fixed rate,
#
# $n:$ notional.
#
#
#
#
def fixed_leg(t, coupon, end_date, k, n, zero_yield_curve):
q = end_date * coupon #number of payments until end_date of the swap
s = 0
times = [0] * (q + 1)
tau = 1 / coupon
df = [0] * (q + 1)
for i in range(1, q + 1):
times[i] += (t + (1 / coupon) * i)
df[i] += discount_factor1(t, times[i], zero_yield_curve)
s += tau * df[i]
return s * n * k
fixed_leg(0, 2, 5, 0.05, 100, zero_yield_curve)
# We now evaluate the floating leg using the formula stated above. The variables used are the same as for the fixed leg.
def floating_leg(t, n, coupon, end_date, zero_yield_curve, forward_rates, spread):
s1 = 0
q = end_date *coupon
times = [0] * (q + 1)
tau = 1 / coupon
y = [0] * (q + 1)
z = [0] * (q + 1)
for k in range(1, q + 1):
times[k] += (t + (1 / coupon) * k)
y[k] += discount_factor1(t, times[k], zero_yield_curve)
z[k] += forward_rates(t, times[k - 1], times[k], zero_yield_curve)
s1 += (z[k]+ spread) * tau * y[k]
return n * s1
floating_leg(0, 100, 2, 5, zero_yield_curve, forward_rates,0.01)
# The present value of IRS from the fixed rate receiver perspective = Present value of the fixed leg - Present value of the floating leg.
def IRS(coupon, end_date, n, t, zero_yield_curve, k,spread):
return fixed_leg(t, coupon, end_date, k, n, zero_yield_curve) - floating_leg(t, n, coupon, end_date, zero_yield_curve, forward_rates,spread)
IRS(2, 5, 100, 0, zero_yield_curve, 0.05, 0.01)
# The present value of an interest rate swap from the fixed rate payer perspective is equal to the present value of the floating leg - present value of the fixed leg.
def IRS1(coupon, end_date, n, t, zero_yield_curve, k,spread):
return floating_leg(t, n, coupon, end_date, zero_yield_curve, forward_rates,spread)-fixed_leg(t, coupon, end_date, k, n, zero_yield_curve)
IRS1(2, 5, 100, 0, zero_yield_curve, 0.05, 0.01)
# We can now compute the Par swap rate, which is the value of the fixed rate that, at time $t$, makes the present value of the interest rate swap equal to $0$.
# $$par\_ rate(t)=\frac{\sum^{n}_{i=1}(F_i +s)D_i \tau_i}{\sum^{n}_{i=1}D_i \tau_i}$$
def par_rate(coupon,end_date, t,zero_yield_curve, spread):
q = coupon * end_date
df = [0] * (q + 1)
fr = [0] * (q + 1)
times = [0] * (q + 1)
tau = 1 / coupon
s = 0
k = 0
for i in range(1, q + 1):
times[i] = (t + (1 / coupon) * i)
df[i] += discount_factor1(t, times[i], zero_yield_curve)
fr[i] += forward_rates(t, times[i], times[i - 1], zero_yield_curve)
s += (fr[i]+spread) * df[i] * tau
k += df[i] * tau
return s / k
par_rate(2, 5, 0, zero_yield_curve, 0.01)
# We can also compute the annuity $$A(t)=\sum^{n}_{i=1}D_i \tau_i$$
def annuity(coupon, end_date, t, zero_yield_curve):
q = coupon * end_date
df = [0] * (q + 1)
times = [0] * (q + 1)
tau = 1 / coupon
s1 = 0
for i in range(1, q + 1):
times[i] = (t + (1 / coupon) * i)
df[i] += discount_factor1(t, times[i], zero_yield_curve)
s1 += df[i] * tau
return s1
annuity(2, 5, 0, zero_yield_curve)
# Then, the present value of the interest rate swap in terms of the annuity is given by:
# $$IRS(t)=notional*(fixed\_ rate - par\; swap\; rate(t))* A(t)$$
# $$=n*(k - par\; swap\; rate(t))*A(t)$$
def pv_swap(n, coupon, end_date, t, zero_yield_curve, k, par_rate,annuity,spread):
a = par_rate(coupon, end_date, t, zero_yield_curve, spread)
b = annuity(coupon, end_date, t, zero_yield_curve)
return n * (k - a) * b
# +
class TestIRS(unittest.TestCase):
def test_IRS(self):
self.assertAlmostEqual(pv_swap(100, 1, 5, 0, zero_yield_curve, 0.05, par_rate,annuity,0.01), IRS(1, 5, 100, 0, zero_yield_curve, 0.05, 0.01))
unittest.main(argv=[''], verbosity=2, exit=False)
# -
# The present value of the interest rate calculated using the annuity agrees with the present value of the interest rate swap calculated using the fixed and the floating leg.
# We want to price a CDS which is also made of two legs:
#
# The premium leg which can be calculated as follows:
# $$R \sum^{b}_{i=a+1} P(0,T_i) \alpha_i Q(\tau \geq T_i),$$
# and the floating leg which can be calculated as:
# $$LGD \int^{T_b}_{T_a} P(0,t) d_t Q(\tau \geq t)$$
# where:
#
# $\alpha_i= T_{i}-T_{i-1}$,
#
# $R$ is the fixed rate,and
#
# $LGD=(1-Recovery\; rate)$ loss-given-default.
#
# The premium leg does include another term, called the accrual term (see Equation 90 in the dissertation), however for simplicity, we are going to ignore it.
#
#
# Our set of data in this case consists of: maturities $y$, hazard rates $hazardrates$, and zero rates $zerorates$ at each maturity date.
# +
y = [0, 1, 3, 5, 7, 10]
hazardrates = [0.03199, 0.03199, 0.03780, 0.04033, 0.04458, 0.03891]
zerorates = [0.01, 0.014, 0.011, 0.01, 0.001, 0.012]
# -
# We use the $hazardrates$ and $y$ to write a function for the hazard rate using constant interpolation.
#
# +
def hazard_curve(x, years, hazard_rates):
hz_rate = 0
if years[0] <= x < years[1]:
hz_rate += hazard_rates[1]
elif years[1] <= x < years[2]:
hz_rate += hazard_rates[2]
elif years[2] <= x < years[3]:
hz_rate += hazard_rates[3]
elif years[3] <= x < years[4]:
hz_rate += hazard_rates[4]
else:
hz_rate += hazard_rates[5]
return hz_rate
class Testhazardratecurve(unittest.TestCase):
def test_hzrates(self):
self.assertAlmostEqual(hazard_curve(1.5, y, hazardrates), 0.0378)
unittest.main(argv=[''], verbosity=2, exit=False)
# -
plt.title('Constant interpolation')
plt.xlabel('years')
plt.ylabel('hazard rates')
plt.step(y, hazardrates)
plt.show()
print(y)
print(hazardrates)
# Next, we write a function to evaluate the survival probability $Q(\tau \geq t)$ and we check the results by using a unittest and the data in table 22.1 and 22.3 in Brigo Mercurio's book.
# +
def survival_probability(t, years, hazard_rates, hazard_curve):
y = np.linspace(0, t, 1000)
d = 0
for j in range(0, len(y)):
if j == 0:
d += 0
else:
d += (y[j] - y[j - 1]) * hazard_curve(y[j], years, hazard_rates)
return np.exp(-d)
class Testsurvivalprob(unittest.TestCase):
def test_survivalprob(self):
self.assertAlmostEqual(survival_probability(y[1],y, hazardrates, hazard_curve), 0.968, places=2)
unittest.main(argv=[''], verbosity=2, exit=False)
# -
# We use linear interpolation on $y$ and $zerorates$ to find the zero yield curve on this set of data.
zero_rate_curve = interp1d(y, zerorates)
# We now write a function to compute $P(0,t).$
def curve(t, years, zero_rates, zero_rate_curve):
z = np.linspace(0, t, 100)
d1 = 0
for j in range(0, len(z)):
if j == 0:
d1 += 0
else:
d1 += (z[j] - z[j - 1]) * zero_rate_curve(z[j])
return np.exp(-d1)
# Now, we write a function to compute the premium leg using the formula:
# $$Premium\_ Leg(t)=\sum^{b}_{i=a+1}(R*Q(t\geq T_i)*P(0,T_i)*(T_i -T_{i-1}))$$
def prem_leg(t, end_date,coupon, k, zero_rates, hazard_rates, years):
#end_date=maturity of the CDS
s2 = 0
q = (end_date-t) * coupon
times = [0] * (q + 1)
for i in range(1, q + 1):
times[i] += (t + (1 / coupon) * i)
s2 += (survival_probability(times[i], years, hazard_rates, hazard_curve)) * curve(times[i], years, zero_rates, zero_rate_curve) * (
times[i] - times[i - 1])
return k * s2
prem_leg(0, 3, 2, 0.05, zerorates, hazardrates, y)
# The formula to compute the protection leg is:
# $$LGD\sum^{n}_{i=a+1}\frac{1}{2} (Q(t \geq T_{i-1})-Q(\tau \geq T_i))*(P(0,T_{i-1})+ P(0,T_i))$$
def protect_leg(t, end_date,coupon, zero_rates, hazard_rates, years, LGD):
q = (end_date-t) * coupon
times = [0] * (q + 1)
s4 = 0
for i in range(1, (q + 1)):
times[i] += (t + (1 / coupon) * i)
s4 += (survival_probability(times[i - 1], years, hazard_rates, hazard_curve) - survival_probability(times[i], years, hazard_rates,
hazard_curve)) * (curve(times[i - 1], years, zero_rates, zero_rate_curve) + curve(times[i], years, zero_rates, zero_rate_curve)) / 2
return (LGD * s4)
protect_leg(0, 3, 2, zerorates, hazardrates, y, 0.6)
# Then the value of the CDS from the protection seller point of view= Premium leg - Protection leg.
def credit_default_swap(t, end_date, coupon, k, zero_rates, hazard_rates, years, LGD):
return prem_leg(t, end_date, coupon, k, zero_rates, hazard_rates, years) - protect_leg(t, end_date, coupon, zero_rates, hazard_rates, years, LGD)
credit_default_swap(0, 3, 2, 0.05, zerorates, hazardrates, y, 0.6)
# Premium leg(t)= $R*Risky\_ Annuity(t)$ where the $$Risky\_ Annuity(t)=\frac{1}{2}(T_i -T_{1-i})*(P(0,T_i))*(Q(\tau \geq T_{i-1})+Q(\tau \geq T_i)$$
def risky_annuity(t,end_date,coupon,years,hazard_rates,zero_rates):
q=(end_date-t)*coupon
z=[0]*(q+1)
summ=0
for i in range(1,(q+1)):
z[i]+=(t+(1/coupon)*i)
summ+=(z[i]-z[i-1])*curve(z[i],years,zero_rates,zero_rate_curve)*(survival_probability(z[i-1],years,hazard_rates,hazard_curve)+survival_probability(z[i],years,hazard_rates,hazard_curve))
return summ/2
risky_annuity(0, 3, 2, y, hazardrates, zerorates)
risky_annuity(0, 3, 2, y, hazardrates, zerorates) * 0.05
# $R*Risky\_ Annuity(t)= Premium\; Leg (t)$ is satisfied.
# The par credit swap for a CDS is defined as $\frac{Protect\; leg(t)}{Annuity(t)}$. We can compute it and then check the result using the test data in Brigo-Mercurio's book (Interest Rate Models Theory and Practice (2001, Springer)) and unittest. Here we did not use bootstrapping instead we are using the hazard rates in the book to show that we get the same CDS spreads.
def par_credit_swap(t, end_date, coupon, zero_rates, hazard_rates, years, LGD):
return protect_leg(t, end_date, coupon, zero_rates, hazard_rates, years, LGD) / risky_annuity(t, end_date, coupon, years, hazard_rates, zero_rates)
class Testparcreditswap(unittest.TestCase):
def test_parcreditswap(self):
self.assertAlmostEqual(par_credit_swap(0, 1, 2, zerorates, hazardrates, y, 0.6)
, 0.01925,places=3)
self.assertAlmostEqual(par_credit_swap(0, 3, 2, zerorates, hazardrates, y, 0.6)
, 0.0215,places=3)
self.assertAlmostEqual(par_credit_swap(0, 5, 2, zerorates, hazardrates, y, 0.6)
, 0.0225,places=3)
self.assertAlmostEqual(par_credit_swap(0, 10, 2, zerorates, hazardrates, y, 0.6)
, 0.0235,places=3)
unittest.main(argv=[''], verbosity=2, exit=False)
# Next, we want to price a CVA. From here on, no test data were available.
#
# In the dissertation, we have mentioned that CVA can be expressed as sum of swaptions. Here, we are going to use this fact, by evaluating first the price of the nromal swaption both from the payer and receiver perspectives.
# Then we use those to price the CVA.
from scipy.stats import norm
# $\text{Price of normal swaption payer at time 0} = \text{notional}* A(0) *\sigma *(T_0)^{1/2}(d_1*\Phi (d_1)+\phi(d_1))$
# $A(0)=\sum^{b}_{i=a}\tau_i P(0,T_i): annuity\; at\; time\; 0$,
#
# $\sigma:$ implied volatility,
# $d_1=\frac{s(0)-K}{\sigma * (T_0)^{1/2}}$,
# $s(0)=\frac{P(0,T_a)-P(0,T_b)}{A(0)}$,
#
# $K: fixed\; rate,$
#
# $T_0=T_a:$ maturity of the swaption,
#
# $T_b:$ maturity of the swap,
#
# $\Phi:$ cdf of standard normal distribution,and
#
# $\phi:$ pdf of standard normal distribution.
def annuity_0(end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
s5 = 0
q = (end_date-initial_date) * coupon
times = [0] * (q + 1)
for k in range(1, (q + 1)):
times[k] += initial_date + (1 / coupon) * k
s5 += (times[k] - times[k - 1]) * curve(times[k], years, zero_rates, zero_rate_curve)
return s5
annuity_0(8,1,zerorates,zero_rate_curve,5,y)
#s(0)
def rate(end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
return (curve(initial_date, years, zero_rates, zero_rate_curve) - curve(end_date, years, zero_rates,
zero_rate_curve)) / annuity_0(end_date,
coupon,
zero_rates,
zero_rate_curve,
initial_date,
years)
rate(8, 1, zerorates, zero_rate_curve, 5, y)
def d1(strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
return (rate(end_date, coupon, zero_rates, zero_rate_curve, initial_date, years) - strike) / (sigma * np.sqrt(
initial_date))
d1(0.01, 0.2, 8, 1, zerorates, zero_rate_curve, 5, y)
def d2(strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
return - d1(strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years)
d2(0.01, 0.2, 8, 1, zerorates, zero_rate_curve, 5, y)
# Now, using the above functions we can evaluate the price of a normal swaption from the payer perspective:
#the notional is taken to be 1
def norm_swaption_payer(notional, strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
d1_new = d1(strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years)
return notional * annuity_0(end_date, coupon, zero_rates, zero_rate_curve, initial_date, years)*sigma * np.sqrt(
initial_date) * (d1_new * norm.cdf(d1_new) + norm.pdf(d1_new))
norm_swaption_payer(1, 0.002, 0.02, 8, 1, zerorates, zero_rate_curve, 5, y)
# and also the price of the normal swaption from the receiver perspective:
def norm_swaption_receiver(notional, strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years):
d2_new = d2(strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years)
return notional * sigma *annuity_0(end_date, coupon, zero_rates, zero_rate_curve, initial_date, years)* np.sqrt(
initial_date) * (d2_new * norm.cdf(d2_new) + norm.pdf(d2_new))
norm_swaption_receiver(1, 0.002, 0.02, 8, 2, zerorates, zero_rate_curve,5, y)
# Then the CVA can be evaluated using the following formula:
#
# $CVA=LGD*\sum^{b}_{i=a+1}(Q(t_{i-1})-Q(t_i))*Swaption\; Payer_t$,
#
# where the $swaption\; payer_t$ is the price of a normal swaption with expiry $t$. In the case of CVA the strike of the swaption is taken to be $0$.
def cva(LGD, notional, strike, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years, hazard_rates, hazard_curve):
h = 0
q = (end_date-initial_date) * coupon
s=[0]*(q+1)
m = [0] * (q + 1)
for k in range(1, q + 1):
m[k] += initial_date +int(1/coupon)* k
s[k]+=norm_swaption_payer(notional, strike, sigma,m[k], coupon, zero_rates, zero_rate_curve,initial_date, years)
h += (survival_probability(m[k-1], years, hazard_rates, hazard_curve)-survival_probability(m[k], years, hazard_rates, hazard_curve)) * s[k]
return LGD * h
cva(0.6,1,0,0.02,8,1,zerorates,zero_rate_curve,5,y,hazardrates, hazard_curve)
# Lastly, we are going to price Credit Insurance.
#
# In Chapter 7, we found that the fair value of the price of Credit Insurance can be calculated as:
# $$CI= Premium\;Leg - Protection\;Leg$$
# $$=\sum^{b}_{i=a+1} \mathbb{E}[D(0, T_i) \cdot \alpha_i \cdot R ]-LGD \int_{t}^{T}\lambda_C(s) \cdot e^{-\int_{t}^{s}r_F(u)+\lambda_C(u) du}\mathbb{E}[min((1-p)V^+,K)]ds $$
#
# where:
#
# $(1-p)$ is the participation percentage,
#
# $\alpha_i=(T_i-T_{i-1})$, and the rest of the variables have already been defined above.
#
# $CI= \text{premium leg} - \left(CVA(\text{with strike 0})-CVA \left(\text{with strike} \frac{K}{1-p}\right)\right)$
def prem_leg_CI(end_date, coupon, initial_date, k, zero_rates, years):
s6 = 0
q = (end_date-initial_date) * coupon
times = [0] * (q + 1)
for i in range(1, q + 1):
times[i] += (initial_date + (1 / coupon) * i)
s6 += (times[i] - times[i - 1]) * curve(times[i], years, zero_rates, zero_rate_curve)
return k * s6
prem_leg_CI(8, 1, 5, 0.1, zerorates, y)
def ci_swaption(LGD, notional, strike, p, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years,hazard_rates,hazard_curve):
c = strike / (1 - p)
return cva(LGD, notional, 0, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years,hazard_rates, hazard_curve) - cva(LGD,notional,c,sigma,end_date,coupon, zero_rates,zero_rate_curve,initial_date,years,hazard_rates,hazard_curve)
ci_swaption(0.6,1,0.1,0.3,0.02,8,1,zerorates,zero_rate_curve,5,y,hazardrates, hazard_curve)
def ci(LGD, notional, strike, p, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years, k,hazard_rates,hazard_curve):
return prem_leg_CI(end_date, coupon, initial_date, k, zero_rates, years) - ci_swaption(LGD, notional, strike, p, sigma, end_date, coupon, zero_rates, zero_rate_curve, initial_date, years,hazard_rates,hazard_curve)
ci(0.6,1,0.1,0.4,0.02,8,1,zerorates,zero_rate_curve,1,y,0.1,hazardrates,hazard_curve)
| MSc Dissertation-UCL.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # [Assignment #2: NPFL067 Statistical NLP II](http://ufal.mff.cuni.cz/~hajic/courses/npfl067/assign2.html)
#
# ## Words and The Company They Keep
#
# ### Author: <NAME>
#
# ### March 28, 2018
#
# ---
# This Python notebook examines the role of mutual information in natural language processing.
#
# Code and explanation of results is fully viewable within this webpage.
#
# ## Files
#
# - [index.html](./index.html) - Contains all veiwable code and a summary of results
# - [README.md](./README.md) - Instructions on how to run the code with Python
# - [nlp-assignment-2.ipynb](./nlp-assignment-2.ipynb) - Jupyter notebook where code can be run
# - [brown_cluster.py](./brown_cluster.py) - Code defining the Brown clustering algorithm
# - [requirements.txt](./requirements.txt) - Required python packages for running
#
# - *.csv - CSV output of results
# ## 1. Best Friends
#
# #### Problem Statement
# > In this task you will do a simple exercise to find out the best word association pairs using the pointwise mutual information method.
#
# > First, you will have to prepare the data: take the same texts as in the previous assignment, i.e.
#
# > `TEXTEN1.txt` and `TEXTCZ1.txt`
#
# > (For this part of Assignment 2, there is no need to split the data in any way.)
#
# > Compute the pointwise mutual information for all the possible word pairs appearing consecutively in the data, **disregarding pairs in which one or both words appear less than 10 times in the corpus**, and sort the results from the best to the worst (did you get any negative values? Why?) Tabulate the results, and show the best 20 pairs for both data sets.
#
# > Do the same now but for distant words, i.e. words which are at least 1 word apart, but not farther than 50 words (both directions). Again, tabulate the results, and show the best 20 pairs for both data sets.
# ### Process Text
# The first step is to process the frequency distribution of the unigrams and bigrams and define a function to calculate the pointwise mutual information between two words. The class `LanguageModel` will handle this.
# +
# Import Python packages
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
# # %load_ext autoreload
# # %autoreload 2
from collections import defaultdict, Counter, Iterable
import itertools
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from tqdm import tqdm_notebook as tqdm, tnrange as trange
from scipy.special import comb
# Configure Plots
plt.rcParams['lines.linewidth'] = 4
pd.set_option('max_colwidth', 150)
np.random.seed(200) # Set a seed so that this notebook has the same output each time
# -
def open_text(filename):
"""Reads a text line by line, applies light preprocessing, and returns an array of words"""
with open(filename, encoding='iso-8859-2') as f:
content = f.readlines()
preprocess = lambda word: word.strip()
return np.array([preprocess(word) for word in content])
class LanguageModel:
"""Counts words and calculates the probabilities of a language model"""
def __init__(self, words, min_words=10):
self.min_words = min_words
# Unigrams
self.unigrams = words
self.unigram_set = list(set(self.unigrams))
self.total_unigram_count = len(self.unigrams)
self.unigram_dist = Counter(self.unigrams)
self.unigram_pdist = defaultdict(float)
for w in self.unigram_dist:
self.unigram_pdist[w] = self.unigram_dist[w] / self.total_unigram_count
# Bigrams
self.bigrams = list(zip(words, words[1:]))
self.bigram_set = list(set(self.bigrams))
self.total_bigram_count = len(self.bigrams)
self.bigram_dist = Counter(self.bigrams)
self.bigram_pdist = defaultdict(float)
for w in self.bigram_dist:
self.bigram_pdist[w] = self.bigram_dist[w] / self.total_bigram_count
def p_unigram(self, w):
"""Calculates the probability a unigram appears in the distribution"""
return self.unigram_pdist[w]
def p_bigram(self, wprev, w):
"""Calculates the probability a bigram appears in the distribution"""
return self.bigram_pdist[(wprev, w)]
def pointwise_mi(self, wprev, w, p_bigram_func=None):
"""Calculates the pointwise mutual information in a word pair"""
p_bigram_func = self.p_bigram if p_bigram_func is None else p_bigram_func
joint = p_bigram_func(wprev, w)
independent = self.p_unigram(wprev) * self.p_unigram(w)
return np.log2(joint / independent) if independent != 0 else 0
# +
# Read the texts into memory
english = './TEXTEN1.txt'
czech = './TEXTCZ1.txt'
words_en = open_text(english)
words_cz = open_text(czech)
# -
lm_en = LanguageModel(words_en)
lm_cz = LanguageModel(words_cz)
# Loop over all pairs of bigrams and calculate their pointwise mutual information, collecting them into a table.
def mutual_information(lm):
# Obtain all word pairs in the word list, disregarding pairs in which one or both words appear less than 10 times in the corpus
pairs = [pair for pair in lm.bigram_set
if lm.unigram_dist[pair[0]] >= lm.min_words
and lm.unigram_dist[pair[1]] >= lm.min_words]
mi = [(' '.join(pair), lm.pointwise_mi(*pair)) for pair in pairs]
return pd.DataFrame(mi, columns=['pair', 'mutual_information'])
mi_en = mutual_information(lm_en).sort_values(by='mutual_information', ascending=False)
mi_cz = mutual_information(lm_cz).sort_values(by='mutual_information', ascending=False)
# ### Results - Consecutive Pairs
# The two tables below show the pointwise mutual information (sorted descending) between pairs of words appearing consecutively in the English and Czech texts respectively.
#
# We see that proper names like Great Britain and Tomáš Ježek provide a lot of mutual information, as those words are frequently seen together and rarely seen apart from each other. However, some of these values are negative (see below).
mi_en[:20] # English
mi_cz[:20] # Czech
# Sorting in ascending order, there are pairs of words that provide negative mutual information. This can be explained by the definition of pointwise mutual information (PMI):
#
# $$PMI(w_t,w_{t+1}) = \log \frac{p(w_t,w_{t+1})}{p(w_t)p(w_{t+1})}$$
#
# where $w_t,w_{t+1}$ are consecutive words (in this instance). The `log` is negative when its input is less than 1, which is to say that
#
# $$p(w_t,w_{t+1}) < p(w_t)p(w_{t+1})$$
#
# i.e., the probability of the pair appearing consecutively in the text is less than the probability of them appearing independently from each other.
#
# This can be verified by the data below. For instance, '_the_' and '_,_' both appear very frequently in the text. However, they are unlikely to be seen consecutively, since 'the ,' is ungrammatical. Therefore, their pointwise mutual information must be negative.
mi_en[:-5:-1]
# Now define a function to calculate pointwise mutual information on all pairs of words a constant distance apart (up to 50) and store the results in a table.
def mutual_information_dist(lm):
def mi_step(distance):
# Get all pairs in the word list a certain distance apart
pair_list = list(zip(lm.unigrams, lm.unigrams[distance+1:]))
dist = Counter(pair_list)
# Obtain all word pairs in the word list, disregarding pairs in which one or both words appear less than 10 times in the corpus
pairs = [pair for pair in list(set(pair_list))
if lm.unigram_dist[pair[0]] >= lm.min_words
and lm.unigram_dist[pair[1]] >= lm.min_words]
p_bigram = lambda wprev, w: dist[(wprev, w)] / lm.total_bigram_count
yield ((distance, wprev, w, lm.pointwise_mi(wprev, w, p_bigram)) for wprev,w in pairs)
max_distance = 50
results = [m for distance in tqdm(range(1, max_distance+1)) for mi in mi_step(distance) for m in mi]
return pd.DataFrame(results, columns=['distance', 'word_1', 'word_2', 'mutual_information'])
mi_dist_en = mutual_information_dist(lm_en).sort_values(by='mutual_information', ascending=False)
mi_dist_cz = mutual_information_dist(lm_cz).sort_values(by='mutual_information', ascending=False)
# ### Results - Distant Pairs
# As before, the two tables below show the pointwise mutual information (sorted descending) between pairs of words appearing in the English and Czech texts. There is an added column called `distance` which indicates the number of words between the two words of interest.
#
# Expectedly, pairs of words with high pointwise mutual information appear close together. For example 'survival \_ \_ fittest' can be filled in as 'survival _of the_ fittest', which is a common phrase in the text. More surprisingly, some words appearing far apart from each other provide a lot of mutual information. It is likely pairs like 'Nastaseho \_ [x25] Newcomba' is a part of multiple quotations in the text such that the word pair appears infrequently outside of them.
mi_dist_en[:20] # English
mi_dist_cz[:20] # Czech
# ## 2. Best Friends
#
# #### Word Classes
#
# > **The Data**
#
# > Get `TEXTEN1.ptg`, `TEXTCZ1.ptg`. These are your data. They are almost the same as the .txt data you have used so far, except they now contain the part of speech tags in the following form:
#
# > `rady/NNFS2-----A----`
# `,/Z:-------------`
#
# > where the tag is separated from the word by a slash ('/'). Be careful: the tags might contain everything (including slashes, dollar signs and other weird characters). It is guaranteed however that there is no slash-word.
#
# > Similarly for the English texts (except the tags are shorter of course).
#
# > **The Task**
#
# > Compute a full class hierarchy of **words** using the first 8,000 words of those data, and only for words occurring 10 times or more (use the same setting for both languages). Ignore the other words for building the classes, but keep them in the data for the bigram counts. For details on the algorithm, use the Brown et al. paper distributed in the class; some formulas are wrong, however, so please see the corrections on the web (Class 12, formulas for Trick \#4). Note the history of the merges, and attach it to your homework. Now run the same algorithm again, but stop when reaching 15 classes. Print out all the members of your 15 classes and attach them too.
#
# > **Hints:**
#
# > The initial mutual information is (English, words, limit 8000):
#
# > `4.99726326162518` (if you add one extra word at the beginning of the data)
# > `4.99633675507535` (if you use the data as they are and are carefull at the beginning and end).
#
# > NB: the above numbers are finally confirmed from an independent source :-).
#
# > The first 5 merges you get on the English data should be:
#
# > `case subject`
# > `cannot may`
# > `individuals structure`
# > `It there`
# > `even less`
#
# > The loss of Mutual Information when merging the words "case" and "subject":
#
# > Minimal loss: `0.00219656653357569` for `case+subject`
# ### Process Text
# Process the text using the `LmCluster` class defined in `brown_cluster.py`. The code will perform the Brown clustering algorithm on the given texts.
from brown_cluster import LmCluster
def open_text(filename):
"""Reads a text line by line, applies light preprocessing, and returns an array of words and tags"""
with open(filename, encoding='iso-8859-2') as f:
content = f.readlines()
preprocess = lambda word: word.strip().rsplit('/', 1)
return [preprocess(word) for word in content]
# +
# Read the texts into memory
english = './TEXTEN1.ptg'
czech = './TEXTCZ1.ptg'
words_en, tags_en = zip(*open_text(english))
words_cz, tags_cz = zip(*open_text(czech))
# -
# ### Cluster the word classes
text_size = 8000
lm_en = LmCluster(words_en[:text_size])
lm_cz = LmCluster(words_cz[:text_size])
lm_en.cluster()
lm_cz.cluster()
def history(cluster):
return pd.DataFrame(cluster.merge_history, columns=['class 1', 'class 2', 'cluster id', 'mutual_information_loss'])
# ### History of Merges
# The tables below show the history of merges in the English and Czech texts respectively. The class (cluster) id is displayed by its corresponding word (if the class contains just one word).
#
# According to the Brown clustering algorithm, words appearing in the most similar contexts (and hence reducing the text's total mutual information the least) get clustered first. For instance, helper verbs 'may' and 'cannot' can be interchanged in the text without reducing the text's mutual information much.
history(lm_en) # English
history(lm_cz) # Czech
# As before, do the clustering, this time stopping at 15 clusters.
clusters = 15
lm_en_15 = LmCluster(words_en[:text_size])
lm_cz_15 = LmCluster(words_cz[:text_size])
lm_en_15.cluster(clusters)
lm_cz_15.cluster(clusters)
def class_cluster(lm):
classes = lm.get_classes()
return pd.DataFrame([(x, [lm.class_name(c) for c in classes[x] if c < len(lm.int2word)]) for x in classes], columns=['class', 'words'])
# ### Cluster Distribution with 15 Classes
# The tables below display the contents of each of the 15 classes merged with the clustering algorithm.
#
# Words that appear very frequently with other words like 'the' and 'of' will reduce the mutual information a lot if clustered with any other class, and so are left over. Class 1721 shows quantifiers like 'several' and 'one' are in similar contexts and hence in their own cluster. This is similar for articles in class 1758.
class_cluster(lm_en_15) # English
class_cluster(lm_cz_15) # Czech
# ## 3. Tag Classes
#
# > Use the same original data as above, but this time, you will compute the classes for tags (the strings after slashes). Compute tag classes for all tags appearing 5 times or more in the data. Use as much data as time allows. You will be graded relative to the other student's results. Again, note the full history of merges, and attach it to your homework. Pick three interesting classes as the algorithm goes (English data only; Czech optional), and comment on them (why you think you see those tags there together (or not), etc.).
cluster_en_tag = LmCluster(tags_en, word_cutoff=5)
cluster_en_tag.cluster()
# The tables below display the history of merges with regards to part-of-speech tags in the texts.
#
# Some interesting classes include:
#
# - 'JJ' (adjective) and 'JJR' (comparative adjective). These tags are both denote slightly different types of adjectives, so it makes sense that they would get merged into their own cluster.
# - 'TO' (to) and 'RBS' (superlative adverb). Likewise, the infinitive 'to' and adverbs like 'best' most frequently appear before a verb, and so get merged due to the similar context.
# - 'IN' (preposition), 'WP$' (posessive wh-pronoun), '(', and '"' all appear in a single class, likely due to the fact that all of these tags appear frequently at the beginning of a clause and break up sentences into phrases. For instance, 'the chair _which_ is ...' or 'the chair _in_ the ...'.
history(cluster_en_tag) # English
cluster_cz_tag = LmCluster(tags_cz, word_cutoff=5)
cluster_cz_tag.cluster()
history(cluster_cz_tag) # Czech
# #### Save all results to text files
history(lm_en).to_csv('merge_english.csv', index=False)
history(lm_cz).to_csv('merge_czech.csv', index=False)
class_cluster(lm_en_15).to_csv('classes_english_15.csv', index=False)
class_cluster(lm_cz_15).to_csv('classes_czech_15.csv', index=False)
history(cluster_en_tag).to_csv('cluster_english_tag.csv', index=False)
history(cluster_cz_tag).to_csv('cluster_czech_tag.csv', index=False)
| charles-university/statistical-nlp/assignment-2/kondrad.assign2/nlp-assignment-2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# ## Automated Snow Leopard Detection with Microsoft ML for Apache Spark
#
# <img src="https://mmlspark.blob.core.windows.net/graphics/SnowLeopardAD/SLTrust.PNG" width="900" style="float: right;"/>
# +
import os
# WARNING this notebook requires alot of memory.
# If you get a heap space error, try dropping the number of images bing returns
# or by writing out the images to parquet first
# Replace the following with a line like: BING_IMAGE_SEARCH_KEY = "hdwo2oyd3o928s....."
BING_IMAGE_SEARCH_KEY = os.environ["BING_IMAGE_SEARCH_KEY"] #please add your key here
# +
from mmlspark import *
from mmlspark import FluentAPI
import os
from pyspark.sql.functions import lit
def bingPhotoSearch(name, queries, pages):
offsets = [offset*10 for offset in range(0, pages)]
parameters = [(query, offset) for offset in offsets for query in queries]
return spark.createDataFrame(parameters, ("queries","offsets")) \
.mlTransform(
BingImageSearch() # Apply Bing Image Search
.setSubscriptionKey(BING_IMAGE_SEARCH_KEY) # Set the API Key
.setOffsetCol("offsets") # Specify a column containing the offsets
.setQueryCol("queries") # Specify a column containing the query words
.setCount(10) # Specify the number of images to return per offset
.setImageType("photo") # Specify a filter to ensure we get photos
.setOutputCol("images")) \
.mlTransform(BingImageSearch.getUrlTransformer("images", "urls")) \
.withColumn("labels", lit(name)) \
.limit(400)
# -
# <img src="https://mmlspark.blob.core.windows.net/graphics/SparkSummit2/cog_services.png" width="800" style="float: center;"/>
def displayDF(df, n=5, image_cols = set(["urls"])):
rows = df.take(n)
cols = df.columns
header = "".join(["<th>" + c + "</th>" for c in cols])
style = """
<!DOCTYPE html>
<html>
<head>
<style>
table {
font-family: arial, sans-serif;
border-collapse: collapse;
width: 300;
}
td, th {
border: 1px solid #dddddd;
text-align: left;
padding: 8px;
}
tr:nth-child(even) {
background-color: #dddddd;
}
</style>
</head>"""
table = []
for row in rows:
table.append("<tr>")
for col in cols:
if col in image_cols:
rep = '<img src="{}", width="100">'.format(row[col])
else:
rep = row[col]
table.append("<td>{}</td>".format(rep))
table.append("</tr>")
tableHTML = "".join(table)
body = """
<body>
<table>
<tr>
{}
</tr>
{}
</table>
</body>
</html>
""".format(header, tableHTML)
try:
displayHTML(style + body)
except:
pass
snowLeopardQueries = ["snow leopard"]
snowLeopardUrls = bingPhotoSearch("snow leopard", snowLeopardQueries, pages=100)
displayDF(snowLeopardUrls)
randomWords = spark.read.parquet("wasb://<EMAIL>/random_words.parquet").cache()
randomWords.show()
# +
randomLinks = randomWords \
.mlTransform(BingImageSearch()
.setSubscriptionKey(BING_IMAGE_SEARCH_KEY)
.setCount(10)
.setQueryCol("words")
.setOutputCol("images")) \
.mlTransform(BingImageSearch.getUrlTransformer("images", "urls")) \
.withColumn("label", lit("other")) \
.limit(400)
displayDF(randomLinks)
# +
images = snowLeopardUrls.union(randomLinks).repartition(100)\
.mlTransform(BingImageSearch.downloadFromUrls("urls", "image", concurrency=5, timeout=5000))\
.dropna()
train, test = images.randomSplit([.7,.3], seed=1)
# +
from pyspark.ml import Pipeline
from pyspark.ml.feature import StringIndexer
from pyspark.ml.classification import LogisticRegression
from pyspark.sql.functions import udf
def getIndex(row):
return float(row[1])
try:
network = ModelDownloader(spark, "Models/").downloadByName("ResNet50")
except:
network = ModelDownloader(spark, "dbfs:/Models/").downloadByName("ResNet50")
model = Pipeline(stages=[
StringIndexer(inputCol = "labels", outputCol="index"),
ImageFeaturizer(inputCol="image", outputCol="features", cutOutputLayers=2).setModel(network),
LogisticRegression(maxIter=5, labelCol="index", regParam=5.0),
UDFTransformer()\
.setUDF(udf(getIndex, DoubleType()))\
.setInputCol("probability")\
.setOutputCol("leopard_prob")
])
fitModel = model.fit(train)
# -
# <img src="https://mmlspark.blob.core.windows.net/graphics/SnowLeopardAD/SLPipeline.PNG" width="900" style="float: right;"/>
# +
def plotConfusionMatrix(df, label, prediction, classLabels):
from mmlspark.plot import confusionMatrix
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(4.5, 4.5))
confusionMatrix(df, label, prediction, classLabels)
display(fig)
plotConfusionMatrix(fitModel.transform(test), "index", "prediction", fitModel.stages[0].labels)
# +
import urllib.request
test_image_url = "https://mmlspark.blob.core.windows.net/graphics/SnowLeopardAD/snow_leopard1.jpg"
with urllib.request.urlopen(test_image_url) as url:
barr = url.read()
test_subsample = spark.createDataFrame([(bytearray(barr),)], ["image"])
lime = ImageLIME()\
.setModel(fitModel)\
.setLabelCol("leopard_prob")\
.setOutputCol("weights")\
.setInputCol("image")\
.setModelPartitions(50)\
.setCellSize(100.0)\
.setModifier(50.0)\
.setNSamples(300)
result = lime.transform(test_subsample)
# +
import matplotlib.pyplot as plt
import PIL
import io
def plot_superpixels(row):
image_bytes = row['image']
superpixels = row['superpixels']['clusters']
weights = list(row['weights'])
mean_weight = np.percentile(weights,90)
img = (PIL.Image.open(io.BytesIO(image_bytes))).convert('RGBA')
image_array = np.asarray(img).copy()
for (sp, w) in zip(superpixels, weights):
if w > mean_weight:
for (x, y) in sp:
image_array[y, x, 1] = 255
image_array[y, x, 3] = 200
plt.clf()
plt.imshow(image_array)
display()
# Gets first row from the LIME-transformed data frame
plot_superpixels(result.take(1)[0])
# -
# ### Your results will look like:
# <img src="https://mmlspark.blob.core.windows.net/graphics/SnowLeopardAD/lime_results.png" width="900" style="float: right;"/>
| notebooks/samples/ModelInterpretation - Snow Leopard Detection.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tensor images
# This notebook gives an overview of the concept of tensor images, and demonstrates how to use this feature.
import diplib as dip
# After reading the "*PyDIP* basics" notebook, you should be familiar with the concepts of scalar images and color images. We remind the reader that an image can have any number of values associated to each pixel. An image with a single value per pixel is a scalar image. Multiple values can be arranged in one or two dimensions, as a vector image or a matrix image. A color image is an example of a vector image, for example in the RGB color space the vector for each pixel has 3 values, it is a 3D vector.
#
# The generalization of vectors and matrices is a tensor. A rank 0 tensor is a scalar, a rank 1 tensor is a vector, and a rank 2 tensor is a matrix.
#
# This is a scalar image:
img = dip.ImageRead('../trui.ics')
img.Show()
# We can compute its gradient, which is a vector image:
g = dip.Gradient(img)
g.Show()
# The vector image is displayed by showing the first vector component in the red channel, and the second one in the green channel. `g` has two components:
print(g.TensorElements())
print(g.TensorShape())
# Multiplying a vector with its transposed leads to a symmetric matrix:
S = g * dip.Transpose(g)
print("Tensor size:", S.TensorSizes())
print("Tensor shape:", S.TensorShape())
print("Tensor elements:", S.TensorElements())
# Note how the 2x2 symmetric matrix stores only 3 elements per pixel. Because of the symmetry, the `[0,1]` and the `[1,0]` elements are identical, and need not be both stored. See [the documentation](https://diplib.org/diplib-docs/classdip_1_1Tensor.html#aa803a3cb47468de269ee5467f60af457) for details on how the individual elements are stored.
#
# Local averaging of this matrix image (i.e. applying a low-pass filter) leads to the structure tensor:
S = dip.Gauss(S, [5])
S.Show()
# We can still display this tensor image, because it has only 3 tensor elements, which can be mapped to the three RGB channels of the display.
#
# The structure tensor is one of the more important applications for the concept of the tensor image. In [this documentation page](https://diplib.org/diplib-docs/why_tensors.html) there are some example applications of the structure tensor. Here we show how to get the local orientation from it using the eigenvalue decomposition.
eigenvalues, eigenvectors = dip.EigenDecomposition(S)
print(eigenvalues.TensorShape())
print(eigenvectors.TensorShape())
# The eigendecomposition is such that `S * eigenvectors == eigenvectors * eigenvalues`. `eigenvectors` is a full 2x2 matrix, and hence has 4 tensor elements. These are stored in column-major order. The first column is the eigenvector that corresponds to the first eigenvalue. Eigenvalues are sorted in descending order, and hence the first eigenvector is perpendicular to the edges in the image.
v1 = eigenvectors.TensorColumn(0)
angle = dip.Angle(v1)
angle.Show('orientation')
# Note that extracting a column from the tensor yields a vector image, and that this vector image shares data with the column-major matrix image. Transposing a matrix is a cheap operation that just changes the storage order of the matrix, without a need to copy or reorder the data:
tmp = dip.Transpose(eigenvectors)
print(tmp.TensorShape())
print(tmp.SharesData(eigenvectors))
# A second important matrix image is the Hessian matrix, which contains all second order derivatives. Just like the strucutre tensor, it is a symmetric 2x2 matrix:
H = dip.Hessian(img)
print("Tensor size:", S.TensorSizes())
print("Tensor shape:", S.TensorShape())
print("Tensor elements:", S.TensorElements())
H.Show()
| examples/python/tensor_images.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# importing the required modules
import requests
from bs4 import BeautifulSoup
import pandas as pd
from selenium import webdriver
# +
# lets take the basic url
base_url = "https://m.kin.naver.com/mobile/expert/category/bridge?groupCategoryId=153"
# start web browser
driver = webdriver.Chrome(r'C:\Users\USER\chromedriver_win32\chromedriver.exe') # Optional argument, if not specified will search path.
# -
# get source code
driver.get(base_url)
# dir(driver)
elem = driver.find_element_by_xpath("//*")
source_code = elem.get_attribute("outerHTML")
type(source_code)
source_code
soup = BeautifulSoup(source_code, 'html.parser')
print(soup.prettify())
li = soup.find_all("li", class_ = "categoryItem--2egO7")
len(li)
a = []
for i in range(len(li)):
a.append(li[i].find('a', class_="categoryLink--ZUSGn").get("href"))
a
# +
bb = []
for j in range(len(a)):
if a[j] == "#":
continue
else:
l = len(a[j])
val = a[j]
newval = val[0:l]
bb.append(newval)
# -
len(bb)
len(set(bb))
df = pd.DataFrame(bb)
df
df.to_csv('Data/links.csv')
| Project01/Link_ETL/extract_url_korean.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Copyright 2020 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# -
# # Deploying NVIDIA Triton Inference Server in AI Platform Prediction Custom Container (Google Cloud SDK)
# In this notebook, we will walk through the process of deploying NVIDIA's Triton Inference Server into AI Platform Prediction Custom Container service in the Direct Model Server mode:
#
# 
#
PROJECT_ID='[Enter project name - REQUIRED]'
REPOSITORY='caipcustom'
REGION='us-central1'
TRITON_VERSION='20.06'
# +
import os
import random
import requests
import json
MODEL_BUCKET='gs://{}-{}'.format(PROJECT_ID,random.randint(10000,99999))
ENDPOINT='https://{}-ml.googleapis.com/v1'.format(REGION)
TRITON_IMAGE='tritonserver:{}-py3'.format(TRITON_VERSION)
CAIP_IMAGE='{}-docker.pkg.dev/{}/{}/{}'.format(REGION,PROJECT_ID,REPOSITORY,TRITON_IMAGE)
# -
'''
# Test values
PROJECT_ID='tsaikevin-1236'
REPOSITORY='caipcustom'
REGION='us-central1'
TRITON_VERSION='20.06'
import os
import random
import requests
import json
MODEL_BUCKET='gs://{}-{}'.format(PROJECT_ID,random.randint(10000,99999))
ENDPOINT='https://{}-ml.googleapis.com/v1'.format(REGION)
TRITON_IMAGE='tritonserver:{}-py3'.format(TRITON_VERSION)
CAIP_IMAGE='{}-docker.pkg.dev/{}/{}/{}'.format(REGION,PROJECT_ID,REPOSITORY,TRITON_IMAGE)
'''
# !gcloud config set project $PROJECT_ID
# ### Create the Artifact Registry
# This will be used to store the container image for the model server Triton.
# !gcloud beta artifacts repositories create $REPOSITORY --repository-format=docker --location=$REGION
# !gcloud beta auth configure-docker $REGION-docker.pkg.dev --quiet
# ### Prepare the container
# We will make a copy of the Triton container image into the Artifact Registry, where AI Platform Custom Container Prediction will only pull from during Model Version setup. The following steps will download the NVIDIA Triton Inference Server container to your VM, then upload it to your repo.
# !docker pull nvcr.io/nvidia/$TRITON_IMAGE && \
# docker tag nvcr.io/nvidia/$TRITON_IMAGE $CAIP_IMAGE && \
# docker push $CAIP_IMAGE
# ### Prepare model Artifacts
# Clone the NVIDIA Triton Inference Server repo.
# !git clone -b r$TRITON_VERSION https://github.com/triton-inference-server/server.git
# Create the GCS bucket where the model artifacts will be copied to.
# !gsutil mb $MODEL_BUCKET
# Stage model artifacts and copy to bucket.
# !mkdir model_repository
# !cp -R server/docs/examples/model_repository/* model_repository/
# !./server/docs/examples/fetch_models.sh
# !gsutil -m cp -R model_repository/ $MODEL_BUCKET
# !gsutil ls -RLl $MODEL_BUCKET/model_repository
# ### Prepare request payload
#
# To prepare the payload format, we have included a utility get_request_body_simple.py. To use this utility, install the following library:
# !pip3 install geventhttpclient
# #### Prepare non-binary request payload
#
# The first model will illustrate a non-binary payload. The following command will create a KF Serving v2 format non-binary payload to be used with the "simple" model:
# !python3 get_request_body_simple.py -m simple
# #### Prepare binary request payload
#
# Triton's implementation of KF Serving v2 protocol for binary data appends the binary data after the json body. Triton requires an additional header for offset:
#
# `Inference-Header-Content-Length: [offset]`
#
# We have provided a script that will automatically resize the image to the proper size for ResNet-50 [224, 224, 3] and calculate the proper offset. The following command takes an image file and outputs the necessary data structure to be use with the "resnet50_netdef" model. Please note down this offset as it will be used later.
# !python3 get_request_body_simple.py -m image -f server/qa/images/mug.jpg
# ## Create and deploy Model and Model Version
#
# In this section, we will deploy two models:
# 1. Simple model with non-binary data. KF Serving v2 protocol specifies a json format with non-binary data in the json body itself.
# 2. Binary data model with ResNet-50. Triton's implementation of binary data for KF Server v2 protocol.
#
# ### Simple model (non-binary data)
#
# #### Create Model
#
# AI Platform Prediction uses a Model/Model Version Hierarchy, where the Model is a logical grouping of Model Versions. We will first create the Model.
#
# Because the MODEL_NAME variable will be used later to specify the predict route, and Triton will use that route to run prediction on a specific model, we must set the value of this variable to a valid name of a model. For this section, will use the "simple" model.
MODEL_NAME='simple'
# !gcloud ai-platform models create $MODEL_NAME --region $REGION --enable-logging
# !gcloud ai-platform models list --region $REGION
# #### Create Model Version
#
# After the Model is created, we can now create a Model Version under this Model. Each Model Version will need a name that is unique within the Model. In AI Platform Prediction Custom Container, a {Project}/{Model}/{ModelVersion} uniquely identifies the specific container and model artifact used for inference.
VERSION_NAME='v01'
# The following config file will be used in the Model Version creation command.
# #### Command with YAML config file
# +
import yaml
config_simple={'deploymentUri': MODEL_BUCKET+'/model_repository', \
'container': {'image': CAIP_IMAGE, \
'args': ['tritonserver', '--model-repository=$(AIP_STORAGE_URI)'], \
'env': [], \
'ports': {'containerPort': 8000}}, \
'routes': {'predict': '/v2/models/'+MODEL_NAME+'/infer', \
'health': '/v2/models/'+MODEL_NAME}, \
'machineType': 'n1-standard-4', 'autoScaling': {'minNodes': 1}}
with open(r'config_simple.yaml', 'w') as file:
config = yaml.dump(config_simple, file)
# -
# !gcloud beta ai-platform versions create $VERSION_NAME \
# --model $MODEL_NAME \
# --accelerator count=1,type=nvidia-tesla-t4 \
# --config config_simple.yaml \
# --region=$REGION \
# --async
# #### To see details of the Model Version just created
# !gcloud ai-platform versions describe $VERSION_NAME --model=$MODEL_NAME --region=$REGION
# #### To list all Model Versions and their states in this Model
# !gcloud ai-platform versions list --model=$MODEL_NAME --region=$REGION
# #### Run prediction using `curl`
#
# The "simple" model takes two tensors with shape [1,16] and does a couple of basic arithmetic operation.
# !curl -X POST $ENDPOINT/projects/$PROJECT_ID/models/$MODEL_NAME/versions/$VERSION_NAME:predict \
# -k -H "Content-Type: application/json" \
# -H "Authorization: Bearer `gcloud auth print-access-token`" \
# -d @simple.json
# +
# this doesn't: gcloud auth application-default print-access-token
# !curl -X POST $ENDPOINT/projects/$PROJECT_ID/models/$MODEL_NAME/versions/$VERSION_NAME:predict \
# -k -H "Content-Type: application/json" \
# -H "Authorization: Bearer `gcloud auth application-default print-access-token`" \
# -d @simple.json
# -
# #### Run prediction using Using `requests` library
# +
with open('simple.json', 'r') as s:
data=s.read()
PREDICT_URL = "{}/projects/{}/models/{}/versions/{}:predict".format(ENDPOINT, PROJECT_ID, MODEL_NAME, VERSION_NAME)
HEADERS = {
'Content-Type': 'application/json',
'Authorization': 'Bearer {}'.format(os.popen('gcloud auth print-access-token').read().rstrip())
}
response = requests.request("POST", PREDICT_URL, headers=HEADERS, data = data).content.decode()
json.loads(response)
# +
# this doesn't work: gcloud auth application-default print-access-token
with open('simple.json', 'r') as s:
data=s.read()
PREDICT_URL = "https://us-central1-ml.googleapis.com/v1/projects/tsaikevin-1236/models/simple/versions/v01:predict"
HEADERS = {
'Content-Type': 'application/json',
'Authorization': 'Bearer {}'.format(os.popen('gcloud auth application-default print-access-token').read().rstrip())
}
response = requests.request("POST", PREDICT_URL, headers=HEADERS, data = data).content.decode()
json.loads(response)
# -
# ### ResNet-50 model (binary data)
#
# #### Create Model
BINARY_MODEL_NAME='resnet50_netdef'
# !gcloud ai-platform models create $BINARY_MODEL_NAME --region $REGION --enable-logging
# #### Create Model Version
BINARY_VERSION_NAME='v01'
# #### Command with YAML config file
# +
import yaml
config_binary={'deploymentUri': MODEL_BUCKET+'/model_repository', \
'container': {'image': CAIP_IMAGE, \
'args': ['tritonserver', '--model-repository=$(AIP_STORAGE_URI)'], \
'env': [], \
'ports': {'containerPort': 8000}}, \
'routes': {'predict': '/v2/models/'+BINARY_MODEL_NAME+'/infer', \
'health': '/v2/models/'+BINARY_MODEL_NAME}, \
'machineType': 'n1-standard-4', 'autoScaling': {'minNodes': 1}}
with open(r'config_binary.yaml', 'w') as file:
config_binary = yaml.dump(config_binary, file)
# -
# !gcloud beta ai-platform versions create $BINARY_VERSION_NAME \
# --model $BINARY_MODEL_NAME \
# --accelerator count=1,type=nvidia-tesla-t4 \
# --config config_binary.yaml \
# --region=$REGION \
# --async
# #### To see details of the Model Version just created
# !gcloud ai-platform versions describe $BINARY_VERSION_NAME --model=$BINARY_MODEL_NAME --region=$REGION
# #### To list all Model Versions and their states in this Model
# !gcloud ai-platform versions list --model=$BINARY_MODEL_NAME --region=$REGION
# #### Run prediction using `curl`
#
# Recall the offset value calcuated above. The binary case has an additional header:
#
# `Inference-Header-Content-Length: [offset]`
# !curl --request POST $ENDPOINT/projects/$PROJECT_ID/models/$BINARY_MODEL_NAME/versions/$BINARY_VERSION_NAME:predict \
# -k -H "Content-Type: application/octet-stream" \
# -H "Authorization: Bearer `gcloud auth print-access-token`" \
# -H "Inference-Header-Content-Length: 138" \
# --data-binary @payload.dat
# +
# this doesn't work: gcloud auth application-default print-access-token
# !curl --request POST $ENDPOINT/projects/$PROJECT_ID/models/$BINARY_MODEL_NAME/versions/$BINARY_VERSION_NAME:predict \
# -k -H "Content-Type: application/octet-stream" \
# -H "Authorization: Bearer `gcloud auth application-default print-access-token`" \
# -H "Inference-Header-Content-Length: 138" \
# --data-binary @payload.dat
# -
# #### Run prediction using Using `requests` library
# +
with open('payload.dat', 'rb') as s:
data=s.read()
PREDICT_URL = "{}/projects/{}/models/{}/versions/{}:predict".format(ENDPOINT, PROJECT_ID, BINARY_MODEL_NAME, BINARY_VERSION_NAME)
HEADERS = {
'Content-Type': 'application/octet-stream',
'Inference-Header-Content-Length': '138',
'Authorization': 'Bearer {}'.format(os.popen('gcloud auth print-access-token').read().rstrip())
}
response = requests.request("POST", PREDICT_URL, headers=HEADERS, data = data).content.decode()
json.loads(response)
# +
# this doesn't work: gcloud auth application-default print-access-token
with open('payload.dat', 'rb') as s:
data=s.read()
PREDICT_URL = "{}/projects/{}/models/{}/versions/{}:predict".format(ENDPOINT, PROJECT_ID, BINARY_MODEL_NAME, BINARY_VERSION_NAME)
HEADERS = {
'Content-Type': 'application/octet-stream',
'Inference-Header-Content-Length': '138',
'Authorization': 'Bearer {}'.format(os.popen('gcloud auth application-default print-access-token').read().rstrip())
}
response = requests.request("POST", PREDICT_URL, headers=HEADERS, data = data).content.decode()
json.loads(response)
# -
# ## Clean up
# !gcloud ai-platform versions delete $VERSION_NAME --model=$MODEL_NAME --region=$REGION --quiet
# !gcloud ai-platform models delete $MODEL_NAME --region=$REGION --quiet
# !gcloud ai-platform versions delete $BINARY_VERSION_NAME --model=$BINARY_MODEL_NAME --region=$REGION --quiet
# !gcloud ai-platform models delete $BINARY_MODEL_NAME --region=$REGION --quiet
# !gsutil -m rm -r -f $MODEL_BUCKET
# !rm -rf model_repository triton-inference-server server *.yaml *.dat *.json
| model_serving/caip-triton/direct-server/triton-simple-setup-sdk.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="ur8xi4C7S06n"
# Copyright 2022 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="JAPoU8Sm5E6e"
# <table align="left">
#
# <td>
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/official/ml_metadata/sdk-metric-parameter-tracking-for-custom-jobs.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
# </a>
# </td>
# <td>
# <a href="https://github.com/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/official/ml_metadata/sdk-metric-parameter-tracking-for-custom-jobs.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
# View on GitHub
# </a>
# </td>
# <td>
# <a href="https://console.cloud.google.com/vertex-ai/workbench/deploy-notebook?download_url=https://github.com/GoogleCloudPlatform/vertex-ai-samples/blob/main/notebooks/official/ml_metadata/sdk-metric-parameter-tracking-for-custom-jobs.ipynb">
# <img src="https://lh3.googleusercontent.com/UiNooY4LUgW_oTvpsNhPpQzsstV5W8F7rYgxgGBD85cWJoLmrOzhVs_ksK_vgx40SHs7jCqkTkCk=e14-rj-sc0xffffff-h130-w32" alt="Vertex AI logo">
# Open in Vertex AI Workbench
# </a>
# </td>
# </table>
# + [markdown] id="j9gUDU_3vV9d"
# # Vertex AI: Track parameters and metrics for custom training jobs
# + [markdown] id="tvgnzT1CKxrO"
# ## Overview
#
# This notebook demonstrates how to track metrics and parameters for Vertex AI custom training jobs, and how to perform detailed analysis using this data.
#
# ### Dataset
#
# This example uses the Abalone Dataset. For more information about this dataset please visit: https://archive.ics.uci.edu/ml/datasets/abalone
# ### Objective
#
# In this notebook, you will learn how to use Vertex AI SDK for Python to:
#
# * Track training parameters and prediction metrics for a custom training job.
# * Extract and perform analysis for all parameters and metrics within an Experiment.
#
# ### Costs
#
#
# This tutorial uses billable components of Google Cloud:
#
# * Vertex AI
# * Cloud Storage
#
# Learn about [Vertex AI
# pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
# pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
# Calculator](https://cloud.google.com/products/calculator/)
# to generate a cost estimate based on your projected usage.
# + [markdown] id="ze4-nDLfK4pw"
# ### Set up your local development environment
#
# **If you are using Colab or Vertex AI Workbench**, your environment already meets
# all the requirements to run this notebook. You can skip this step.
# + [markdown] id="gCuSR8GkAgzl"
# **Otherwise**, make sure your environment meets this notebook's requirements.
# You need the following:
#
# * The Google Cloud SDK
# * Git
# * Python 3
# * virtualenv
# * Jupyter notebook running in a virtual environment with Python 3
#
# The Google Cloud guide to [Setting up a Python development
# environment](https://cloud.google.com/python/setup) and the [Jupyter
# installation guide](https://jupyter.org/install) provide detailed instructions
# for meeting these requirements. The following steps provide a condensed set of
# instructions:
#
# 1. [Install and initialize the Cloud SDK.](https://cloud.google.com/sdk/docs/)
#
# 1. [Install Python 3.](https://cloud.google.com/python/setup#installing_python)
#
# 1. [Install
# virtualenv](https://cloud.google.com/python/setup#installing_and_using_virtualenv)
# and create a virtual environment that uses Python 3. Activate the virtual environment.
#
# 1. To install Jupyter, run `pip install jupyter` on the
# command-line in a terminal shell.
#
# 1. To launch Jupyter, run `jupyter notebook` on the command-line in a terminal shell.
#
# 1. Open this notebook in the Jupyter Notebook Dashboard.
# + [markdown] id="i7EUnXsZhAGF"
# ### Install additional packages
#
# Install additional package dependencies not installed in your notebook environment.
# + id="IaYsrh0Tc17L"
import os
# The Google Cloud Notebook product has specific requirements
IS_GOOGLE_CLOUD_NOTEBOOK = os.path.exists("/opt/deeplearning/metadata/env_version")
# Google Cloud Notebook requires dependencies to be installed with '--user'
USER_FLAG = ""
if IS_GOOGLE_CLOUD_NOTEBOOK:
USER_FLAG = "--user"
# + id="qblyW_dcyOQA"
# ! pip3 install -U tensorflow $USER_FLAG
# ! python3 -m pip install {USER_FLAG} google-cloud-aiplatform --upgrade
# ! pip3 install scikit-learn {USER_FLAG}
# + [markdown] id="hhq5zEbGg0XX"
# ### Restart the kernel
#
# After you install the additional packages, you need to restart the notebook kernel so it can find the packages.
# + id="EzrelQZ22IZj"
# Automatically restart kernel after installs
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
# + [markdown] id="lWEdiXsJg0XY"
# ## Before you begin
#
# ### Select a GPU runtime
#
# **Make sure you're running this notebook in a GPU runtime if you have that option. In Colab, select "Runtime --> Change runtime type > GPU"**
# + [markdown] id="BF1j6f9HApxa"
# ### Set up your Google Cloud project
#
# **The following steps are required, regardless of your notebook environment.**
#
# 1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
#
# 1. [Make sure that billing is enabled for your project](https://cloud.google.com/billing/docs/how-to/modify-project).
#
# 1. [Enable the Vertex AI API and Compute Engine API](https://console.cloud.google.com/flows/enableapi?apiid=aiplatform.googleapis.com,compute_component).
#
# 1. If you are running this notebook locally, you will need to install the [Cloud SDK](https://cloud.google.com/sdk).
#
# 1. Enter your project ID in the cell below. Then run the cell to make sure the
# Cloud SDK uses the right project for all the commands in this notebook.
#
# **Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$` into these commands.
# + [markdown] id="WReHDGG5g0XY"
# #### Set your project ID
#
# **If you don't know your project ID**, you may be able to get your project ID using `gcloud`.
# + id="oM1iC_MfAts1"
import os
PROJECT_ID = ""
# Get your Google Cloud project ID from gcloud
if not os.getenv("IS_TESTING"):
# shell_output = !gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID: ", PROJECT_ID)
# + [markdown] id="qJYoRfYng0XZ"
# Otherwise, set your project ID here.
# + id="riG_qUokg0XZ"
if PROJECT_ID == "" or PROJECT_ID is None:
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
# + [markdown] id="XsnuGoJM9mUw"
# Set gcloud config to your project ID.
# + id="TL9QIaVd9hvm"
# !gcloud config set project $PROJECT_ID
# + [markdown] id="06571eb4063b"
# #### Timestamp
#
# If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append it onto the name of resources you create in this tutorial.
# + id="697568e92bd6"
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
# + [markdown] id="dr--iN2kAylZ"
# ### Authenticate your Google Cloud account
#
# **If you are using Vertex AI Workbench**, your environment is already
# authenticated. Skip this step.
# + [markdown] id="sBCra4QMA2wR"
# **If you are using Colab**, run the cell below and follow the instructions
# when prompted to authenticate your account via oAuth.
#
# **Otherwise**, follow these steps:
#
# 1. In the Cloud Console, go to the [**Create service account key**
# page](https://console.cloud.google.com/apis/credentials/serviceaccountkey).
#
# 2. Click **Create service account**.
#
# 3. In the **Service account name** field, enter a name, and
# click **Create**.
#
# 4. In the **Grant this service account access to project** section, click the **Role** drop-down list. Type "Vertex AI"
# into the filter box, and select
# **Vertex AI Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
#
# 5. Click *Create*. A JSON file that contains your key downloads to your
# local environment.
#
# 6. Enter the path to your service account key as the
# `GOOGLE_APPLICATION_CREDENTIALS` variable in the cell below and run the cell.
# + id="PyQmSRbKA8r-"
import os
import sys
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
# If on Google Cloud Notebooks, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
# %env GOOGLE_APPLICATION_CREDENTIALS ''
# + [markdown] id="zgPO1eR3CYjk"
# ### Create a Cloud Storage bucket
#
# **The following steps are required, regardless of your notebook environment.**
#
#
# When you submit a training job using the Cloud SDK, you upload a Python package
# containing your training code to a Cloud Storage bucket. Vertex AI runs
# the code from this package. In this tutorial, Vertex AI also saves the
# trained model that results from your job in the same bucket. Using this model artifact, you can then
# create Vertex AI model and endpoint resources in order to serve
# online predictions.
#
# Set the name of your Cloud Storage bucket below. It must be unique across all
# Cloud Storage buckets.
#
# You may also change the `REGION` variable, which is used for operations
# throughout the rest of this notebook. Make sure to [choose a region where Vertex AI services are
# available](https://cloud.google.com/vertex-ai/docs/general/locations#available_regions). You may
# not use a Multi-Regional Storage bucket for training with Vertex AI.
# + id="MzGDU7TWdts_"
BUCKET_URI = "gs://[your-bucket-name]" # @param {type:"string"}
REGION = "[your-region]" # @param {type:"string"}
# + id="cf221059d072"
if BUCKET_URI == "" or BUCKET_URI is None or BUCKET_URI == "gs://[your-bucket-name]":
BUCKET_URI = "gs://" + PROJECT_ID + "-aip-" + TIMESTAMP
if REGION == "[your-region]":
REGION = "us-central1"
# + [markdown] id="-EcIXiGsCePi"
# **Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
# + id="NIq7R4HZCfIc"
# ! gsutil mb -l $REGION $BUCKET_URI
# + [markdown] id="ucvCsknMCims"
# Finally, validate access to your Cloud Storage bucket by examining its contents:
# + id="vhOb7YnwClBb"
# ! gsutil ls -al $BUCKET_URI
# + [markdown] id="XoEqT2Y4DJmf"
# ### Import libraries and define constants
# + [markdown] id="Y9Uo3tifg1kx"
# Import required libraries.
#
# + id="pRUOFELefqf1"
import pandas as pd
from google.cloud import aiplatform
from sklearn.metrics import mean_absolute_error, mean_squared_error
from tensorflow.python.keras.utils import data_utils
# + [markdown] id="O8XJZB3gR8eL"
# ## Initialize Vertex AI and set an _experiment_
#
# + [markdown] id="xtXZWmYqJ1bh"
# Define experiment name.
# + id="JIOrI-hoJ46P"
EXPERIMENT_NAME = "" # @param {type:"string"}
# + [markdown] id="jWQLXXNVN4Lv"
# If EXEPERIMENT_NAME is not set, set a default one below:
# + id="Q1QInYWOKsmo"
if EXPERIMENT_NAME == "" or EXPERIMENT_NAME is None:
EXPERIMENT_NAME = "my-experiment-" + TIMESTAMP
# + [markdown] id="DKIsYVjj56_X"
# Initialize the *client* for Vertex AI.
# + id="Wrlk2B2nJ7-X"
aiplatform.init(
project=PROJECT_ID,
location=REGION,
staging_bucket=BUCKET_URI,
experiment=EXPERIMENT_NAME,
)
# + [markdown] id="6PlilQPFeS_h"
# ## Tracking parameters and metrics in Vertex AI custom training jobs
# + [markdown] id="9nokDKBAxwV8"
# This example uses the Abalone Dataset. For more information about this dataset please visit: https://archive.ics.uci.edu/ml/datasets/abalone
# + id="V_T10yTTqcS_"
# !wget https://storage.googleapis.com/download.tensorflow.org/data/abalone_train.csv
# !gsutil cp abalone_train.csv {BUCKET_URI}/data/
gcs_csv_path = f"{BUCKET_URI}/data/abalone_train.csv"
# + [markdown] id="35QVNhACqcTJ"
# ### Create a managed tabular dataset from a CSV
#
# A Managed dataset can be used to create an AutoML model or a custom model.
# + id="4OfCqaYRqcTJ"
ds = aiplatform.TabularDataset.create(display_name="abalone", gcs_source=[gcs_csv_path])
ds.resource_name
# + [markdown] id="VcEOYYolqcTN"
# ### Write the training script
#
# Run the following cell to create the training script that is used in the sample custom training job.
# + id="OauJqJmJqcTO"
# %%writefile training_script.py
import pandas as pd
import argparse
import os
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
parser = argparse.ArgumentParser()
parser.add_argument('--epochs', dest='epochs',
default=10, type=int,
help='Number of epochs.')
parser.add_argument('--num_units', dest='num_units',
default=64, type=int,
help='Number of unit for first layer.')
args = parser.parse_args()
# uncomment and bump up replica_count for distributed training
# strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
# tf.distribute.experimental_set_strategy(strategy)
col_names = ["Length", "Diameter", "Height", "Whole weight", "Shucked weight", "Viscera weight", "Shell weight", "Age"]
target = "Age"
def aip_data_to_dataframe(wild_card_path):
return pd.concat([pd.read_csv(fp.numpy().decode(), names=col_names)
for fp in tf.data.Dataset.list_files([wild_card_path])])
def get_features_and_labels(df):
return df.drop(target, axis=1).values, df[target].values
def data_prep(wild_card_path):
return get_features_and_labels(aip_data_to_dataframe(wild_card_path))
model = tf.keras.Sequential([layers.Dense(args.num_units), layers.Dense(1)])
model.compile(loss='mse', optimizer='adam')
model.fit(*data_prep(os.environ["AIP_TRAINING_DATA_URI"]),
epochs=args.epochs ,
validation_data=data_prep(os.environ["AIP_VALIDATION_DATA_URI"]))
print(model.evaluate(*data_prep(os.environ["AIP_TEST_DATA_URI"])))
# save as Vertex AI Managed model
tf.saved_model.save(model, os.environ["AIP_MODEL_DIR"])
# + [markdown] id="Yp2clkOJSDhR"
# ### Launch a custom training job and track its trainig parameters on Vertex AI ML Metadata
# + id="btb6d48lqcTT"
job = aiplatform.CustomTrainingJob(
display_name="train-abalone-dist-1-replica",
script_path="training_script.py",
container_uri="us-docker.pkg.dev/vertex-ai/training/tf-cpu.2-8:latest",
requirements=["gcsfs==0.7.1"],
model_serving_container_image_uri="us-docker.pkg.dev/vertex-ai/prediction/tf2-cpu.2-8:latest",
)
# + [markdown] id="k_QorXXztzPH"
# Start a new experiment run to track training parameters and start the training job. Note that this operation will take around 10 mins.
# + id="oVTORjQpJ7-Y"
aiplatform.start_run("custom-training-run-1") # Change this to your desired run name
parameters = {"epochs": 10, "num_units": 64}
aiplatform.log_params(parameters)
model = job.run(
ds,
replica_count=1,
model_display_name="abalone-model",
args=[f"--epochs={parameters['epochs']}", f"--num_units={parameters['num_units']}"],
)
# + [markdown] id="5vhDsMJNqcTW"
# ### Deploy Model and calculate prediction metrics
# + [markdown] id="O-uCOL3Naap4"
# Deploy model to Google Cloud. This operation will take 10-20 mins.
# + id="Y9GH72wWqcTX"
endpoint = model.deploy(machine_type="n1-standard-4")
# + [markdown] id="JY-5skFhasWs"
# Once model is deployed, perform online prediction using the `abalone_test` dataset and calculate prediction metrics.
# + [markdown] id="saw50bqwa-dR"
# Prepare the prediction dataset.
# + id="ABZQmqsWISQv"
def read_data(uri):
dataset_path = data_utils.get_file("abalone_test.data", uri)
col_names = [
"Length",
"Diameter",
"Height",
"Whole weight",
"Shucked weight",
"Viscera weight",
"Shell weight",
"Age",
]
dataset = pd.read_csv(
dataset_path,
names=col_names,
na_values="?",
comment="\t",
sep=",",
skipinitialspace=True,
)
return dataset
def get_features_and_labels(df):
target = "Age"
return df.drop(target, axis=1).values, df[target].values
test_dataset, test_labels = get_features_and_labels(
read_data(
"https://storage.googleapis.com/download.tensorflow.org/data/abalone_test.csv"
)
)
# + [markdown] id="_HphZ38obJeB"
# Perform online prediction.
# + id="eXD-OvsrKmCt"
prediction = endpoint.predict(test_dataset.tolist())
prediction
# + [markdown] id="TDKiv_O7bNwE"
# Calculate and track prediction evaluation metrics.
# + id="cj0fHucbKopn"
mse = mean_squared_error(test_labels, prediction.predictions)
mae = mean_absolute_error(test_labels, prediction.predictions)
aiplatform.log_metrics({"mse": mse, "mae": mae})
# + [markdown] id="CCGmesdIbbHf"
# ### Extract all parameters and metrics created during this experiment.
# + id="KlcEBou-Pl4Z"
aiplatform.get_experiment_df()
# + [markdown] id="WTHvPMweMlP1"
# ### View data in the Cloud Console
# + [markdown] id="F19_5lw0MqXv"
# Parameters and metrics can also be viewed in the Cloud Console.
#
# + id="GmN9vE9pqqzt"
print("Vertex AI Experiments:")
print(
f"https://console.cloud.google.com/ai/platform/experiments/experiments?folder=&organizationId=&project={PROJECT_ID}"
)
# + [markdown] id="TpV-iwP9qw9c"
# ## Cleaning up
#
# To clean up all Google Cloud resources used in this project, you can [delete the Google Cloud
# project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
#
# Otherwise, you can delete the individual resources you created in this tutorial:
# Training Job
# Model
# Cloud Storage Bucket
#
# * Vertex AI Dataset
# * Training Job
# * Model
# * Endpoint
# * Cloud Storage Bucket
#
# + id="rwPZoZISHhaY"
# Warning: Setting this to true will delete everything in your bucket
delete_bucket = False
# Delete dataset
ds.delete()
# Delete the training job
job.delete()
# Undeploy model from endpoint
endpoint.undeploy_all()
# Delete the endpoint
endpoint.delete()
# Delete the model
model.delete()
if delete_bucket or os.getenv("IS_TESTING"):
# ! gsutil -m rm -r $BUCKET_URI
| notebooks/official/ml_metadata/sdk-metric-parameter-tracking-for-custom-jobs.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Import dependencies and file
# The dataset was obtained from CryptoCompare.
import numpy as np
import pandas as pd
from pathlib import Path
file_path = Path("crypto_data.csv")
# Read csv file in to dataframe
crypto_df = pd.read_csv(file_path)
crypto_df.head()
crypto_df.info()
# Rename Unnamed column
crypto_df.rename(columns={'Unnamed: 0': 'CryptoID'}, inplace=True)
crypto_df.head()
# Filter for currencies that are currently being traded
crypto_df = crypto_df[crypto_df["IsTrading"] == True]
crypto_df.info()
# Drop the IsTrading column from the dataframe
crypto_df.drop(['IsTrading'], axis=1, inplace=True)
crypto_df.info()
# Remove all rows that have at least one null value
crypto_df = crypto_df.dropna()
crypto_df.info()
# Filter for cryptocurrencies that have total coins mined 'greater than zero'
crypto_df = crypto_df[crypto_df["TotalCoinsMined"] > 0]
crypto_df.info()
# Data should be numeric, delete the CoinName from the original dataframe
crypto_data_df = crypto_df[["CryptoID","Algorithm","ProofType","TotalCoinsMined","TotalCoinSupply"]].copy()
crypto_data_df.head()
crypto_data_df=crypto_data_df.set_index("CryptoID")
crypto_data_df.head()
# View unique values in Algorithm column
crypto_data_df['Algorithm'].unique()
# View unique values in ProofType column
crypto_data_df['ProofType'].unique()
# +
# Import Dependencies to convert categorical data, Algorithm and ProofType, into numerica data
from sklearn.preprocessing import StandardScaler, MinMaxScaler, LabelEncoder
# Label encoding the 'Algorithm' column
crypto_data_df['Algorithm'] = LabelEncoder().fit_transform(crypto_data_df['Algorithm'])
crypto_data_df.head(10)
# -
# Label encoding the 'Algorithm' column
crypto_data_df['ProofType'] = LabelEncoder().fit_transform(crypto_data_df['ProofType'])
crypto_data_df.head(10)
crypto_data_df.info()
# Scale the data
scaler = StandardScaler()
scaled_data = scaler.fit_transform(crypto_data_df)
print(scaled_data[0:10])
# ### Dimensionality Reduction
# (1) Perform dimensionality reduction with PCA
# (2) Run t-SNE on the principal components: the output of the PCA transformation
# (3) Create a scatter plot of the t-SNE output
# +
# Perform dimensionality reduction with PCA
from sklearn.decomposition import PCA
# Initialize PCA model
pca = PCA(n_components=2)
# Get two principal components for the data.
crypto_pca = pca.fit_transform(crypto_data_df)
# -
# Transform PCA data to a DataFrame
crypto_data_df_pca = pd.DataFrame(
data=crypto_pca, index=crypto_data_df.index, columns=["principal component 1", "principal component 2"]
)
crypto_data_df_pca.head()
# Fetch the explained variance
pca.explained_variance_ratio_
# ### Sample Analysis
# The explained variance in the above sample states that the first principal component contains approximately 88% of the vaiance
# and the second principal component contains 12% of the variance. We have approximately 100% of the information in the
# original dataset.
# +
# Initialize PCA model for 3 principal components
pca = PCA(n_components=3)
# Get 3 principal components for data.
crypto_pca = pca.fit_transform(crypto_data_df)
# Transform PCA data to a DataFrame
crypto_data_df_pca = pd.DataFrame(
data=crypto_pca, index=crypto_data_df.index, columns=["principal component 1", "principal component 2", "principal component 3"]
)
crypto_data_df_pca.head()
# -
# Fetch the explained variance
pca.explained_variance_ratio_
# Run t-SNE on the principal components: the output of the PCA transformation
from sklearn.manifold import TSNE
tsne = TSNE(learning_rate =250)
tsne_features = tsne.fit_transform(crypto_data_df_pca)
tsne_features.shape
import matplotlib.pyplot as plt
plt.scatter(tsne_features[:,0], tsne_features[:,1])
plt.show()
# ### Cluster Analysis with k-Means
from sklearn.cluster import KMeans
# +
# Identify the best number of clusters using the elbow curve
inertia = []
k = list(range(1, 10))
# Same as k = [1,2,3,4,5,6,7,8,9,10]
# Looking for the best k
for i in k:
km = KMeans(n_clusters=i, random_state=0)
km.fit(crypto_data_df)
inertia.append(km.inertia_)
# Define a DataFrame to plot the Elbow Curve using hvPlot
elbow_data = {"k": k, "inertia": inertia}
df_elbow = pd.DataFrame(elbow_data)
df_elbow
# -
# Plot the elbow curve to find the best candidate(s) for k
plt.plot(df_elbow['k'], df_elbow['inertia'])
plt.xticks(range(1,10))
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()
# +
# Initializing model with K = 5
model = KMeans(n_clusters=5, random_state=5)
# Train the model
model.fit(crypto_data_df)
# Predict clusters
predictions = model.predict(crypto_data_df)
# Create return DataFrame with predicted clusters
crypto_data_df["class"] = model.labels_
crypto_data_df.head()
# -
plt.scatter(x=crypto_data_df["Algorithm"], y=crypto_data_df['ProofType'], c=crypto_data_df['class'])
plt.xlabel('Algorithm')
plt.ylabel('ProofType')
plt.show()
| .ipynb_checkpoints/Data_Preparation-checkpoint.ipynb |
# ### Creating multi-panel plots using `facets`.
#
# #### Problem
#
# You want to see more aspects of your data and it's not practcal to use the regular `aesthetics` approach for that.
#
# #### Solution - `facets`
#
# You can add one or more new dimentions to your plot using `faceting`.
#
# This approach allows you to split up your data by one or more variables and plot the subsets of data together.
#
#
# In this demo we will explore how various faceting functions work, as well as the built-in `sorting` and `formatting` options.
#
# To learn more about formatting templates see: [Formatting](https://github.com/JetBrains/lets-plot-kotlin/blob/master/docs/formats.md).
%useLatestDescriptors
%use lets-plot
%use krangl
var data = DataFrame.readCSV("https://raw.githubusercontent.com/JetBrains/lets-plot-kotlin/master/docs/examples/data/mpg2.csv")
data.head(3)
# ### One plot
#
# Create a scatter plot to show how `mpg` is related to a car's `engine horsepower`.
#
# Also use the `color` aesthetic to vizualise the region where a car was designed.
val p = (letsPlot(data.toMap()) {x="engine horsepower"; y="miles per gallon"} +
geomPoint {color="origin of car"})
p + ggsize(800, 350)
# ### More dimentions
#
# There are two functions for faceting:
#
# - facetGrid()
# - facetWrap()
#
# The former creates 2-D matrix of plot panels and latter creates 1-D strip of plot panels.
#
# We'll be using the `number of cylinders` variable as 1st fatceting variable, and sometimes the `origin of car` as a 2nd fatceting variable.
# ### facetGrid()
#
# The data can be split up by one or two variables that vary on the X and/or Y direction.
# #### One facet
#
# Let's split up the data by `number of cylinders`.
p + facetGrid(x="number of cylinders")
# #### Two facets
#
# Split up the data by two faceting variables: `number of cylinders` and `origin of car`.
p + facetGrid(x="number of cylinders", y="origin of car")
# #### Formatting and sorting.
#
# Apply a formatting template to the `number of cylinders` and
# sort the `origin of car` values in discending order.
#
# To learn more about formatting templates see: [Formatting](https://github.com/JetBrains/lets-plot-kotlin/blob/master/docs/formats.md).
p + facetGrid(x="number of cylinders", y="origin of car", xFormat="{d} cyl", yOrder=-1)
# ### facetWrap()
#
# The data can be split up by one or more variables.
# The panels layout is flexible and controlled by `ncol`, `nrow` and `dir` options.
# #### One facet
#
# Split data by the `number of cylinders` variable and arrange tiles in two rows.
p + facetWrap(facets="number of cylinders", nrow=2)
# #### Two facets
#
# Split data by `origin of car` and `number of cylinders` and arrange tiles in 5 columns.
p + facetWrap(facets=listOf("origin of car", "number of cylinders"), ncol=5)
# #### Arrange panels vertically.
#
# Use the `dir` parameter to arrange tiles by columns, in 3 columns (the default tile arrangment is "by row").
#
# Also, format `number of cylinders` labels and reverse the sorting direction for this facetting variable.
p + facetWrap(facets=listOf("origin of car", "number of cylinders"),
ncol=3,
format=listOf(null, "{} cyl"),
order=listOf(1, -1),
dir="v")
| docs/examples/jupyter-notebooks/facets.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: TensorFlow-GPU
# language: python
# name: tf-gpu
# ---
# +
import requests
from bs4 import BeautifulSoup
import os
import time
from keras.utils import get_file
try:
from urllib.request import urlretrieve
except ImportError:
from urllib import urlretrieve
import xml.sax
import subprocess
import mwparserfromhell
import json
import re
# -
index = requests.get('https://dumps.wikimedia.org/enwiki/').text
index
soup_index = BeautifulSoup(index, 'html.parser')
soup_index
dumps = [a['href'] for a in soup_index.find_all('a')
if a.has_attr('href') and a.text[:-1].isdigit()]
dumps
for dump_url in sorted(dumps, reverse=True):
print(dump_url)
dump_html = index = requests.get('https://dumps.wikimedia.org/enwiki/' + dump_url).text
soup_dump = BeautifulSoup(dump_html, 'html.parser')
pages_xml = [a['href'] for a in soup_dump.find_all('a')
if a.has_attr('href') and a['href'].endswith('-pages-articles.xml.bz2')]
if pages_xml:
break
time.sleep(0.8)
pages_xml
pages_xml[0]
wikipedia_dump = pages_xml[0].rsplit('/')[-1]
wikipedia_dump
wikipedia_dump = pages_xml[0].rsplit('/')[-1]
url = url = 'https://dumps.wikimedia.org/' + pages_xml[0]
path = get_file(wikipedia_dump, url)
url
path
def process_article(title, text):
rotten = [(re.findall('\d\d?\d?%', p), re.findall('\d\.\d\/\d+|$', p), p.lower().find('rotten tomatoes')) for p in text.split('\n\n')]
rating = next(((perc[0], rating[0]) for perc, rating, idx in rotten if len(perc) == 1 and idx > -1), (None, None))
wikicode = mwparserfromhell.parse(text)
film = next((template for template in wikicode.filter_templates()
if template.name.strip().lower() == 'infobox film'), None)
if film:
properties = {param.name.strip_code().strip(): param.value.strip_code().strip()
for param in film.params
if param.value.strip_code().strip()
}
links = [x.title.strip_code().strip() for x in wikicode.filter_wikilinks()]
return (title, properties, links) + rating
class WikiXmlHandler(xml.sax.handler.ContentHandler):
def __init__(self):
xml.sax.handler.ContentHandler.__init__(self)
self._buffer = None
self._values = {}
self._movies = []
self._curent_tag = None
def characters(self, content):
if self._curent_tag:
self._buffer.append(content)
def startElement(self, name, attrs):
if name in ('title', 'text'):
self._curent_tag = name
self._buffer = []
def endElement(self, name):
if name == self._curent_tag:
self._values[name] = ' '.join(self._buffer)
if name == 'page':
movie = process_article(**self._values)
if movie:
self._movies.append(movie)
import bz2
parser = xml.sax.make_parser()
handler = WikiXmlHandler()
parser.setContentHandler(handler)
with bz2.BZ2File(path, "r") as raw_data:
raw_data.seek(0, os.SEEK_END)
size = raw_data.tell()
size
with bz2.BZ2File(path, "r") as raw_data:
try:
for i, line in enumerate(raw_data):
#print(i)
parser.feed(line)
if i>1000000:
break
except KeyboardInterrupt:
print("Sorry")
with open('generated/wp_movies.ndjson', 'wt') as fout:
for movie in handler._movies:
fout.write(json.dumps(movie) + '\n')
| Collect Movie Data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="fTFj8ft5dlbS"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" id="lzyBOpYMdp3F"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + cellView="form" id="m_x4KfSJ7Vt7"
#@title MIT License
#
# Copyright (c) 2017 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a
# # copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
# + [markdown] id="C9HmC2T4ld5B"
# # Overfit and underfit
# + [markdown] id="kRTxFhXAlnl1"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/tutorials/keras/overfit_and_underfit"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="19rPukKZsPG6"
# As always, the code in this example will use the `tf.keras` API, which you can learn more about in the TensorFlow [Keras guide](https://www.tensorflow.org/guide/keras).
#
# In both of the previous examples—[classifying text](text_classification_with_hub.ipynb) and [predicting fuel efficiency](regression.ipynb)—the accuracy of models on the validation data would peak after training for a number of epochs and then stagnate or start decreasing.
#
# In other words, your model would *overfit* to the training data. Learning how to deal with overfitting is important. Although it's often possible to achieve high accuracy on the *training set*, what you really want is to develop models that generalize well to a *testing set* (or data they haven't seen before).
#
# The opposite of overfitting is *underfitting*. Underfitting occurs when there is still room for improvement on the train data. This can happen for a number of reasons: If the model is not powerful enough, is over-regularized, or has simply not been trained long enough. This means the network has not learned the relevant patterns in the training data.
#
# If you train for too long though, the model will start to overfit and learn patterns from the training data that don't generalize to the test data. You need to strike a balance. Understanding how to train for an appropriate number of epochs as you'll explore below is a useful skill.
#
# To prevent overfitting, the best solution is to use more complete training data. The dataset should cover the full range of inputs that the model is expected to handle. Additional data may only be useful if it covers new and interesting cases.
#
# A model trained on more complete data will naturally generalize better. When that is no longer possible, the next best solution is to use techniques like regularization. These place constraints on the quantity and type of information your model can store. If a network can only afford to memorize a small number of patterns, the optimization process will force it to focus on the most prominent patterns, which have a better chance of generalizing well.
#
# In this notebook, you'll explore several common regularization techniques, and use them to improve on a classification model.
# + [markdown] id="WL8UoOTmGGsL"
# ## Setup
# + [markdown] id="9FklhSI0Gg9R"
# Before getting started, import the necessary packages:
# + id="5pZ8A2liqvgk"
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import regularizers
print(tf.__version__)
# + id="QnAtAjqRYVXe"
# !pip install git+https://github.com/tensorflow/docs
import tensorflow_docs as tfdocs
import tensorflow_docs.modeling
import tensorflow_docs.plots
# + id="-pnOU-ctX27Q"
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import pathlib
import shutil
import tempfile
# + id="jj6I4dvTtbUe"
logdir = pathlib.Path(tempfile.mkdtemp())/"tensorboard_logs"
shutil.rmtree(logdir, ignore_errors=True)
# + [markdown] id="1cweoTiruj8O"
# ## The Higgs dataset
#
# The goal of this tutorial is not to do particle physics, so don't dwell on the details of the dataset. It contains 11,000,000 examples, each with 28 features, and a binary class label.
# + id="YPjAvwb-6dFd"
gz = tf.keras.utils.get_file('HIGGS.csv.gz', 'http://mlphysics.ics.uci.edu/data/higgs/HIGGS.csv.gz')
# + id="AkiyUdaWIrww"
FEATURES = 28
# + [markdown] id="SFggl9gYKKRJ"
# The `tf.data.experimental.CsvDataset` class can be used to read csv records directly from a gzip file with no intermediate decompression step.
# + id="QHz4sLVQEVIU"
ds = tf.data.experimental.CsvDataset(gz,[float(),]*(FEATURES+1), compression_type="GZIP")
# + [markdown] id="HzahEELTKlSV"
# That csv reader class returns a list of scalars for each record. The following function repacks that list of scalars into a (feature_vector, label) pair.
# + id="zPD6ICDlF6Wf"
def pack_row(*row):
label = row[0]
features = tf.stack(row[1:],1)
return features, label
# + [markdown] id="4oa8tLuwLsbO"
# TensorFlow is most efficient when operating on large batches of data.
#
# So, instead of repacking each row individually make a new `tf.data.Dataset` that takes batches of 10,000 examples, applies the `pack_row` function to each batch, and then splits the batches back up into individual records:
# + id="-w-VHTwwGVoZ"
packed_ds = ds.batch(10000).map(pack_row).unbatch()
# + [markdown] id="lUbxc5bxNSXV"
# Inspect some of the records from this new `packed_ds`.
#
# The features are not perfectly normalized, but this is sufficient for this tutorial.
# + id="TfcXuv33Fvka"
for features,label in packed_ds.batch(1000).take(1):
print(features[0])
plt.hist(features.numpy().flatten(), bins = 101)
# + [markdown] id="ICKZRY7gN-QM"
# To keep this tutorial relatively short, use just the first 1,000 samples for validation, and the next 10,000 for training:
# + id="hmk49OqZIFZP"
N_VALIDATION = int(1e3)
N_TRAIN = int(1e4)
BUFFER_SIZE = int(1e4)
BATCH_SIZE = 500
STEPS_PER_EPOCH = N_TRAIN//BATCH_SIZE
# + [markdown] id="FP3M9DmvON32"
# The `Dataset.skip` and `Dataset.take` methods make this easy.
#
# At the same time, use the `Dataset.cache` method to ensure that the loader doesn't need to re-read the data from the file on each epoch:
# + id="H8H_ZzpBOOk-"
validate_ds = packed_ds.take(N_VALIDATION).cache()
train_ds = packed_ds.skip(N_VALIDATION).take(N_TRAIN).cache()
# + id="9zAOqk2_Px7K"
train_ds
# + [markdown] id="6PMliHoVO3OL"
# These datasets return individual examples. Use the `Dataset.batch` method to create batches of an appropriate size for training. Before batching, also remember to use `Dataset.shuffle` and `Dataset.repeat` on the training set.
# + id="Y7I4J355O223"
validate_ds = validate_ds.batch(BATCH_SIZE)
train_ds = train_ds.shuffle(BUFFER_SIZE).repeat().batch(BATCH_SIZE)
# + [markdown] id="lglk41MwvU5o"
# ## Demonstrate overfitting
#
# The simplest way to prevent overfitting is to start with a small model: A model with a small number of learnable parameters (which is determined by the number of layers and the number of units per layer). In deep learning, the number of learnable parameters in a model is often referred to as the model's "capacity".
#
# Intuitively, a model with more parameters will have more "memorization capacity" and therefore will be able to easily learn a perfect dictionary-like mapping between training samples and their targets, a mapping without any generalization power, but this would be useless when making predictions on previously unseen data.
#
# Always keep this in mind: deep learning models tend to be good at fitting to the training data, but the real challenge is generalization, not fitting.
#
# On the other hand, if the network has limited memorization resources, it will not be able to learn the mapping as easily. To minimize its loss, it will have to learn compressed representations that have more predictive power. At the same time, if you make your model too small, it will have difficulty fitting to the training data. There is a balance between "too much capacity" and "not enough capacity".
#
# Unfortunately, there is no magical formula to determine the right size or architecture of your model (in terms of the number of layers, or the right size for each layer). You will have to experiment using a series of different architectures.
#
# To find an appropriate model size, it's best to start with relatively few layers and parameters, then begin increasing the size of the layers or adding new layers until you see diminishing returns on the validation loss.
#
# Start with a simple model using only densely-connected layers (`tf.keras.layers.Dense`) as a baseline, then create larger models, and compare them.
# + [markdown] id="_ReKHdC2EgVu"
# ### Training procedure
# + [markdown] id="pNzkSkkXSP5l"
# Many models train better if you gradually reduce the learning rate during training. Use `tf.keras.optimizers.schedules` to reduce the learning rate over time:
# + id="LwQp-ERhAD6F"
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
0.001,
decay_steps=STEPS_PER_EPOCH*1000,
decay_rate=1,
staircase=False)
def get_optimizer():
return tf.keras.optimizers.Adam(lr_schedule)
# + [markdown] id="kANLx6OYTQ8B"
# The code above sets a `tf.keras.optimizers.schedules.InverseTimeDecay` to hyperbolically decrease the learning rate to 1/2 of the base rate at 1,000 epochs, 1/3 at 2,000 epochs, and so on.
# + id="HIo_yPjEAFgn"
step = np.linspace(0,100000)
lr = lr_schedule(step)
plt.figure(figsize = (8,6))
plt.plot(step/STEPS_PER_EPOCH, lr)
plt.ylim([0,max(plt.ylim())])
plt.xlabel('Epoch')
_ = plt.ylabel('Learning Rate')
# + [markdown] id="ya7x7gr9UjU0"
# Each model in this tutorial will use the same training configuration. So set these up in a reusable way, starting with the list of callbacks.
#
# The training for this tutorial runs for many short epochs. To reduce the logging noise use the `tfdocs.EpochDots` which simply prints a `.` for each epoch, and a full set of metrics every 100 epochs.
#
# Next include `tf.keras.callbacks.EarlyStopping` to avoid long and unnecessary training times. Note that this callback is set to monitor the `val_binary_crossentropy`, not the `val_loss`. This difference will be important later.
#
# Use `callbacks.TensorBoard` to generate TensorBoard logs for the training.
#
# + id="vSv8rfw_T85n"
def get_callbacks(name):
return [
tfdocs.modeling.EpochDots(),
tf.keras.callbacks.EarlyStopping(monitor='val_binary_crossentropy', patience=200),
tf.keras.callbacks.TensorBoard(logdir/name),
]
# + [markdown] id="VhctzKhBWVDD"
# Similarly each model will use the same `Model.compile` and `Model.fit` settings:
# + id="xRCGwU3YH5sT"
def compile_and_fit(model, name, optimizer=None, max_epochs=10000):
if optimizer is None:
optimizer = get_optimizer()
model.compile(optimizer=optimizer,
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[
tf.keras.losses.BinaryCrossentropy(
from_logits=True, name='binary_crossentropy'),
'accuracy'])
model.summary()
history = model.fit(
train_ds,
steps_per_epoch = STEPS_PER_EPOCH,
epochs=max_epochs,
validation_data=validate_ds,
callbacks=get_callbacks(name),
verbose=0)
return history
# + [markdown] id="mxBeiLUiWHJV"
# ### Tiny model
# + [markdown] id="a6JDv12scLTI"
# Start by training a model:
# + id="EZh-QFjKHb70"
tiny_model = tf.keras.Sequential([
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(1)
])
# + id="X72IUdWYipIS"
size_histories = {}
# + id="bdOcJtPGHhJ5"
size_histories['Tiny'] = compile_and_fit(tiny_model, 'sizes/Tiny')
# + [markdown] id="rS_QGT6icwdI"
# Now check how the model did:
# + id="dkEvb2x5XsjE"
plotter = tfdocs.plots.HistoryPlotter(metric = 'binary_crossentropy', smoothing_std=10)
plotter.plot(size_histories)
plt.ylim([0.5, 0.7])
# + [markdown] id="LGxGzh_FWOJ8"
# ### Small model
# + [markdown] id="YjMb6E72f2pN"
# To check if you can beat the performance of the small model, progressively train some larger models.
#
# Try two hidden layers with 16 units each:
# + id="QKgdXPx9usBa"
small_model = tf.keras.Sequential([
# `input_shape` is only required here so that `.summary` works.
layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
layers.Dense(16, activation='elu'),
layers.Dense(1)
])
# + id="LqG3MXF5xSjR"
size_histories['Small'] = compile_and_fit(small_model, 'sizes/Small')
# + [markdown] id="L-DGRBbGxI6G"
# ### Medium model
# + [markdown] id="SrfoVQheYSO5"
# Now try three hidden layers with 64 units each:
# + id="jksi-XtaxDAh"
medium_model = tf.keras.Sequential([
layers.Dense(64, activation='elu', input_shape=(FEATURES,)),
layers.Dense(64, activation='elu'),
layers.Dense(64, activation='elu'),
layers.Dense(1)
])
# + [markdown] id="jbngCZliYdma"
# And train the model using the same data:
# + id="Ofn1AwDhx-Fe"
size_histories['Medium'] = compile_and_fit(medium_model, "sizes/Medium")
# + [markdown] id="vIPuf23FFaVn"
# ### Large model
#
# As an exercise, you can create an even larger model and check how quickly it begins overfitting. Next, add to this benchmark a network that has much more capacity, far more than the problem would warrant:
# + id="ghQwwqwqvQM9"
large_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(512, activation='elu'),
layers.Dense(1)
])
# + [markdown] id="D-d-i5DaYmr7"
# And, again, train the model using the same data:
# + id="U1A99dhqvepf"
size_histories['large'] = compile_and_fit(large_model, "sizes/large")
# + [markdown] id="Fy3CMUZpzH3d"
# ### Plot the training and validation losses
# + [markdown] id="HSlo1F4xHuuM"
# The solid lines show the training loss, and the dashed lines show the validation loss (remember: a lower validation loss indicates a better model).
# + [markdown] id="OLhL1AszdLfM"
# While building a larger model gives it more power, if this power is not constrained somehow it can easily overfit to the training set.
#
# In this example, typically, only the `"Tiny"` model manages to avoid overfitting altogether, and each of the larger models overfit the data more quickly. This becomes so severe for the `"large"` model that you need to switch the plot to a log-scale to really figure out what's happening.
#
# This is apparent if you plot and compare the validation metrics to the training metrics.
#
# * It's normal for there to be a small difference.
# * If both metrics are moving in the same direction, everything is fine.
# * If the validation metric begins to stagnate while the training metric continues to improve, you are probably close to overfitting.
# * If the validation metric is going in the wrong direction, the model is clearly overfitting.
# + id="0XmKDtOWzOpk"
plotter.plot(size_histories)
a = plt.xscale('log')
plt.xlim([5, max(plt.xlim())])
plt.ylim([0.5, 0.7])
plt.xlabel("Epochs [Log Scale]")
# + [markdown] id="UekcaQdmZxnW"
# Note: All the above training runs used the `callbacks.EarlyStopping` to end the training once it was clear the model was not making progress.
# + [markdown] id="DEQNKadHA0M3"
# ### View in TensorBoard
#
# These models all wrote TensorBoard logs during training.
#
# Open an embedded TensorBoard viewer inside a notebook:
# + id="6oa1lkJddZ-m"
#docs_infra: no_execute
# Load the TensorBoard notebook extension
# %load_ext tensorboard
# Open an embedded TensorBoard viewer
# %tensorboard --logdir {logdir}/sizes
# + [markdown] id="fjqx3bywDPjf"
# You can view the [results of a previous run](https://tensorboard.dev/experiment/vW7jmmF9TmKmy3rbheMQpw/#scalars&_smoothingWeight=0.97) of this notebook on [TensorBoard.dev](https://tensorboard.dev/).
#
# TensorBoard.dev is a managed experience for hosting, tracking, and sharing ML experiments with everyone.
#
# It's also included in an `<iframe>` for convenience:
# + id="dX5fcgrADwym"
display.IFrame(
src="https://tensorboard.dev/experiment/vW7jmmF9TmKmy3rbheMQpw/#scalars&_smoothingWeight=0.97",
width="100%", height="800px")
# + [markdown] id="RDQDBKYZBXF_"
# If you want to share TensorBoard results you can upload the logs to [TensorBoard.dev](https://tensorboard.dev/) by copying the following into a code-cell.
#
# Note: This step requires a Google account.
#
# ```
# # # !tensorboard dev upload --logdir {logdir}/sizes
# ```
#
# Caution: This command does not terminate. It's designed to continuously upload the results of long-running experiments. Once your data is uploaded you need to stop it using the "interrupt execution" option in your notebook tool.
# + [markdown] id="ASdv7nsgEFhx"
# ## Strategies to prevent overfitting
# + [markdown] id="YN512ksslaxJ"
# Before getting into the content of this section copy the training logs from the `"Tiny"` model above, to use as a baseline for comparison.
# + id="40k1eBtnQzNo"
shutil.rmtree(logdir/'regularizers/Tiny', ignore_errors=True)
shutil.copytree(logdir/'sizes/Tiny', logdir/'regularizers/Tiny')
# + id="vFWMeFo7jLpN"
regularizer_histories = {}
regularizer_histories['Tiny'] = size_histories['Tiny']
# + [markdown] id="4rHoVWcswFLa"
# ### Add weight regularization
#
# + [markdown] id="kRxWepNawbBK"
# You may be familiar with Occam's Razor principle: given two explanations for something, the explanation most likely to be correct is the "simplest" one, the one that makes the least amount of assumptions. This also applies to the models learned by neural networks: given some training data and a network architecture, there are multiple sets of weights values (multiple models) that could explain the data, and simpler models are less likely to overfit than complex ones.
#
# A "simple model" in this context is a model where the distribution of parameter values has less entropy (or a model with fewer parameters altogether, as demonstrated in the section above). Thus a common way to mitigate overfitting is to put constraints on the complexity of a network by forcing its weights only to take small values, which makes the distribution of weight values more "regular". This is called "weight regularization", and it is done by adding to the loss function of the network a cost associated with having large weights. This cost comes in two flavors:
#
# * [L1 regularization](https://developers.google.com/machine-learning/glossary/#L1_regularization), where the cost added is proportional to the absolute value of the weights coefficients (i.e. to what is called the "L1 norm" of the weights).
#
# * [L2 regularization](https://developers.google.com/machine-learning/glossary/#L2_regularization), where the cost added is proportional to the square of the value of the weights coefficients (i.e. to what is called the squared "L2 norm" of the weights). L2 regularization is also called weight decay in the context of neural networks. Don't let the different name confuse you: weight decay is mathematically the exact same as L2 regularization.
#
# L1 regularization pushes weights towards exactly zero, encouraging a sparse model. L2 regularization will penalize the weights parameters without making them sparse since the penalty goes to zero for small weights—one reason why L2 is more common.
#
# In `tf.keras`, weight regularization is added by passing weight regularizer instances to layers as keyword arguments. Add L2 weight regularization:
# + id="HFGmcwduwVyQ"
l2_model = tf.keras.Sequential([
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001),
input_shape=(FEATURES,)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(512, activation='elu',
kernel_regularizer=regularizers.l2(0.001)),
layers.Dense(1)
])
regularizer_histories['l2'] = compile_and_fit(l2_model, "regularizers/l2")
# + [markdown] id="bUUHoXb7w-_C"
# `l2(0.001)` means that every coefficient in the weight matrix of the layer will add `0.001 * weight_coefficient_value**2` to the total **loss** of the network.
#
# That is why we're monitoring the `binary_crossentropy` directly. Because it doesn't have this regularization component mixed in.
#
# So, that same `"Large"` model with an `L2` regularization penalty performs much better:
#
# + id="7wkfLyxBZdh_"
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
# + [markdown] id="Kx1YHMsVxWjP"
# As demonstrated in the diagram above, the `"L2"` regularized model is now much more competitive with the `"Tiny"` model. This `"L2"` model is also much more resistant to overfitting than the `"Large"` model it was based on despite having the same number of parameters.
# + [markdown] id="JheBk6f8jMQ7"
# #### More info
#
# There are two important things to note about this sort of regularization:
#
# 1. If you are writing your own training loop, then you need to be sure to ask the model for its regularization losses.
# + id="apDHQNybjaML"
result = l2_model(features)
regularization_loss=tf.add_n(l2_model.losses)
# + [markdown] id="MLhG6fMSjE-J"
# 2. This implementation works by adding the weight penalties to the model's loss, and then applying a standard optimization procedure after that.
#
# There is a second approach that instead only runs the optimizer on the raw loss, and then while applying the calculated step the optimizer also applies some weight decay. This "decoupled weight decay" is used in optimizers like `tf.keras.optimizers.Ftrl` and `tfa.optimizers.AdamW`.
# + [markdown] id="HmnBNOOVxiG8"
# ### Add dropout
#
# Dropout is one of the most effective and most commonly used regularization techniques for neural networks, developed by Hinton and his students at the University of Toronto.
#
# The intuitive explanation for dropout is that because individual nodes in the network cannot rely on the output of the others, each node must output features that are useful on their own.
#
# Dropout, applied to a layer, consists of randomly "dropping out" (i.e. set to zero) a number of output features of the layer during training. For example, a given layer would normally have returned a vector `[0.2, 0.5, 1.3, 0.8, 1.1]` for a given input sample during training; after applying dropout, this vector will have a few zero entries distributed at random, e.g. `[0, 0.5, 1.3, 0, 1.1]`.
#
# The "dropout rate" is the fraction of the features that are being zeroed-out; it is usually set between 0.2 and 0.5. At test time, no units are dropped out, and instead the layer's output values are scaled down by a factor equal to the dropout rate, so as to balance for the fact that more units are active than at training time.
#
# In Keras, you can introduce dropout in a network via the `tf.keras.layers.Dropout` layer, which gets applied to the output of layer right before.
#
# Add two dropout layers to your network to check how well they do at reducing overfitting:
# + id="OFEYvtrHxSWS"
dropout_model = tf.keras.Sequential([
layers.Dense(512, activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['dropout'] = compile_and_fit(dropout_model, "regularizers/dropout")
# + id="SPZqwVchx5xp"
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
# + [markdown] id="4zlHr4iaI1U6"
# It's clear from this plot that both of these regularization approaches improve the behavior of the `"Large"` model. But this still doesn't beat even the `"Tiny"` baseline.
#
# Next try them both, together, and see if that does better.
# + [markdown] id="u7qMg_7Nwy5t"
# ### Combined L2 + dropout
# + id="7zfs_qQIw1cz"
combined_model = tf.keras.Sequential([
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu', input_shape=(FEATURES,)),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(512, kernel_regularizer=regularizers.l2(0.0001),
activation='elu'),
layers.Dropout(0.5),
layers.Dense(1)
])
regularizer_histories['combined'] = compile_and_fit(combined_model, "regularizers/combined")
# + id="qDqBBxfI0Yd8"
plotter.plot(regularizer_histories)
plt.ylim([0.5, 0.7])
# + [markdown] id="tE0OoNCQNTJv"
# This model with the `"Combined"` regularization is obviously the best one so far.
# + [markdown] id="-dw23T03FEO1"
# ### View in TensorBoard
#
# These models also recorded TensorBoard logs.
#
# To open an embedded tensorboard viewer inside a notebook, copy the following into a code-cell:
#
# ```
# # # %tensorboard --logdir {logdir}/regularizers
# ```
# + [markdown] id="KX3Voac-FEO4"
# You can view the [results of a previous run](https://tensorboard.dev/experiment/fGInKDo8TXes1z7HQku9mw/#scalars&_smoothingWeight=0.97) of this notebook on [TensorBoard.dev](https://tensorboard.dev/).
#
# It's also included in an `<iframe>` for convenience:
# + id="doMtyYoqFEO5"
display.IFrame(
src="https://tensorboard.dev/experiment/fGInKDo8TXes1z7HQku9mw/#scalars&_smoothingWeight=0.97",
width = "100%",
height="800px")
# + [markdown] id="mds5RXGjIcSu"
# This was uploaded with:
#
# ```
# # # !tensorboard dev upload --logdir {logdir}/regularizers
# ```
# + [markdown] id="uXJxtwBWIhjG"
# ## Conclusions
# + [markdown] id="gjfnkEeQyAFG"
# To recap, here are the most common ways to prevent overfitting in neural networks:
#
# * Get more training data.
# * Reduce the capacity of the network.
# * Add weight regularization.
# * Add dropout.
#
# Two important approaches not covered in this guide are:
#
# * [Data augmentation](../images/data_augmentation.ipynb)
# * Batch normalization (`tf.keras.layers.BatchNormalization`)
#
# Remember that each method can help on its own, but often combining them can be even more effective.
| site/en/tutorials/keras/overfit_and_underfit.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Binary classification
# -----------------------
#
# This example shows how to use ATOM to solve a binary classification problem. Additonnaly, we'll perform a variety of data cleaning steps to prepare the data for modelling.
#
# The data used is a variation on the [Australian weather dataset](https://www.kaggle.com/jsphyg/weather-dataset-rattle-package) from Kaggle. You can download it from [here](https://github.com/tvdboom/ATOM/blob/master/examples/datasets/weatherAUS.csv). The goal of this dataset is to predict whether or not it will rain tomorrow training a binary classifier on target `RainTomorrow`.
# ## Load the data
# Import packages
import pandas as pd
from atom import ATOMClassifier
# +
# Load data
X = pd.read_csv("./datasets/weatherAUS.csv")
# Let's have a look
X.head()
# -
# ## Run the pipeline
# Call atom using only 5% of the complete dataset (for explanatory purposes)
atom = ATOMClassifier(X, "RainTomorrow", n_rows=0.05, n_jobs=8, warnings=False, verbose=2)
# Impute missing values
atom.impute(strat_num="median", strat_cat="drop", max_nan_rows=0.8)
# Encode the categorical features
atom.encode(strategy="Target", max_onehot=10, frac_to_other=0.04)
# Train an Extra-Trees and a Random Forest model
atom.run(models=["ET", "RF"], metric="f1", n_bootstrap=5)
# ## Analyze the results
# Let's have a look at the final results
atom.results
# Visualize the bootstrap results
atom.plot_results(title="RF vs ET performance")
# Print the results of some common metrics
atom.evaluate()
# The winner attribute calls the best model (atom.winner == atom.rf)
print(f"The winner is the {atom.winner.fullname} model!!")
# Visualize the distribution of predicted probabilities
atom.winner.plot_probabilities()
# + pycharm={"name": "#%%\n"}
# Compare how different metrics perform for different thresholds
atom.winner.plot_threshold(metric=["f1", "accuracy", "average_precision"], steps=50)
| docs_sources/examples/binary_classification.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
def times2(var):
return var*2
times2(5)
# # map()
seq=[1,2,3,4,5,6]
seq
list(map(times2,seq))
# # lambda
# +
t = lambda var : var*2
t(6)
# -
list(map(lambda num : num*3,seq))
# # filter
list(filter(lambda num:num%2==0,seq)) # chercher les valeur pair
s = " hello/my/name/is/ahmed "
s
s.lower()
s.upper()
s.split("/")[0]
d={"key1":1,"key2":2}
d.keys()
d.items()
d.values()
lst= [1,2,3]
lst
item = lst.pop()
item
lst
lst.pop(0)
lst
lst.append("new")
lst
"x" in lst
"new" in lst
x = [(1,2),(3,4),(5,6)]
x
x[1][1]
for a,b in x :
print(b)
for i in d.keys():
print(d[i]) #dictionary boucle
| python/python_part4.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.4 64-bit (''base'': conda)'
# language: python
# name: python37464bitbaseconda1aa5cdf7d7054eca93426f2a0775cc94
# ---
# +
import numpy as np
import sklearn as skl
import pandas as pd
import matplotlib as mat
wine_training = pd.read_csv('C:\\Users\\assharma\\Downloads\\winequality-red.csv')
wine_training.head(10)
# -
wine_training['Dummy']=wine_training['Dummy'].str.upper()
wine_training.columns=map(str.upper,wine_training.columns)
wine_training.rename(columns={'FREE SULFUR DIOXIDE':'FRF_SULF_DIX','TOTAL SULFUR DIOXIDE':'TOT_SULF_DIX'},inplace=True)
wine_training.head(10)
wine_training.drop(['DUMMY'],axis=1)
wine_training.info()
wine_training.describe()
wine_training.count()
wine_training.isnull().values.any()
wine_training.isnull().sum()
wine_training.isnull().values.sum()
wine_training=wine_training.dropna(axis=0)
wine_training.isnull().values.sum()
wine_training.drop()
| WINE_SELECTION_DROP_NA_VALUES.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
matrix = [[0,1,2],[3,4,5],[6,7,8]]
for row in range(len(matrix)):
for col in range(len(matrix)):
# if the condition is NOT satisfied: go to next iteration
if not (matrix[row][col] < 6 and row!=1): continue
print(row,col)
| leetcodes/tstcodes.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="vEO2FZbVMl4O"
# # Purpose
# This notebook is used to map note_number, velocity, instrument_source, qualities, z to f0_scaled and ld_scaled. It is composed of a LSTM layer, GRU layer and a dense layer
# + [markdown] id="byQTezEBbNRA"
# # Setup google drive
#
# + colab={"base_uri": "https://localhost:8080/"} id="seiaz41x00S_" outputId="1cac65ab-7931-4cd7-fa1b-53693412e8bb"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="JQ3HJu7_5cMK" outputId="c43ee3a1-f4c4-495a-cf12-6e7b1894a9b8"
# %tensorflow_version 2.x
# !pip install -qU ddsp[data_preparation]==1.0.1
# !pip install keras-tcn
# + [markdown] id="27LKzcK5d4ft"
# # Make directories to save model and data
# + colab={"base_uri": "https://localhost:8080/"} id="OspCTcni6bYE" outputId="4edb260a-943e-4157-ba41-be26091471a5"
import os
import datetime
from tcn import TCN, tcn_full_summary
drive_dir = '/content/drive/My Drive/Sound_generation'
checkpoint_dir = os.path.join(drive_dir, 'mapping/checkpoint')
assert os.path.exists(drive_dir)
print('Drive Directory Exists:', drive_dir)
# !mkdir -p "$checkpoint_dir"
# + [markdown] id="tlucbB8Hd27v"
# # Download Complete NSynth Guitar Subse
# + id="dW2CmoR77k0t" colab={"base_uri": "https://localhost:8080/"} outputId="3becb123-c1c0-40fc-9bf3-2d43661a2dca"
dataset_dir = '/content/complete'
train_dataset_dir = os.path.join(dataset_dir, 'train')
valid_dataset_dir = os.path.join(dataset_dir, 'valid')
test_dataset_dir = os.path.join(dataset_dir, 'test')
train_tfrecord_file = os.path.join(train_dataset_dir, 'complete.tfrecord')
valid_tfrecord_file = os.path.join(valid_dataset_dir, 'complete.tfrecord')
test_tfrecord_file = os.path.join(test_dataset_dir, 'complete.tfrecord')
if not os.path.exists(dataset_dir):
train = 'https://osr-tsoai.s3.amazonaws.com/complete/train/complete.tfrecord'
valid = 'https://osr-tsoai.s3.amazonaws.com/complete/valid/complete.tfrecord'
test = 'https://osr-tsoai.s3.amazonaws.com/complete/test/complete.tfrecord'
print("Downloading train dataset to {}\n".format(train_dataset_dir))
# !mkdir -p "$train_dataset_dir"
# !curl $train --output $train_tfrecord_file
print("\nDownloading valid dataset to {}\n".format(valid_dataset_dir))
# !mkdir -p "$valid_dataset_dir"
# !curl $valid --output $valid_tfrecord_file
print("\nDownloading test dataset to {}\n".format(test_dataset_dir))
# !mkdir -p "$test_dataset_dir"
# !curl $test --output $test_tfrecord_file
# + [markdown] id="EGVn7_Y7e7_O"
# # Copying data to drive or from drive
# + id="MuYlkUcDdyAa"
# # !cp -r /content/drive/MyDrive/Sound_generation/mapping/complete ./
# + [markdown] id="nFaepHvehLXC"
# # Defining Data class provider
#
# + id="wVqYQLJNgCdI" colab={"base_uri": "https://localhost:8080/"} outputId="09f30d94-a15a-4cd6-f5f5-1b0c95ce24e4"
import tensorflow as tf
import ddsp.training.data as data
class CompleteTFRecordProvider(data.RecordProvider):
def __init__(self,
file_pattern=None,
example_secs=4,
sample_rate=16000,
frame_rate=250,
map_func=None):
super().__init__(file_pattern, example_secs, sample_rate,
frame_rate, tf.data.TFRecordDataset)
self._map_func = map_func
def get_dataset(self, shuffle=True):
def parse_tfexample(record):
features = tf.io.parse_single_example(record, self.features_dict)
if self._map_func is not None:
return self._map_func(features)
else:
return features
filenames = tf.data.Dataset.list_files(self._file_pattern, shuffle=shuffle)
dataset = filenames.interleave(
map_func=self._data_format_map_fn,
cycle_length=40,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
dataset = dataset.map(parse_tfexample,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
return dataset
@property
def features_dict(self):
return {
'sample_name':
tf.io.FixedLenFeature([1], dtype=tf.string),
'note_number':
tf.io.FixedLenFeature([1], dtype=tf.int64),
'velocity':
tf.io.FixedLenFeature([1], dtype=tf.int64),
'instrument_source':
tf.io.FixedLenFeature([1], dtype=tf.int64),
'qualities':
tf.io.FixedLenFeature([10], dtype=tf.int64),
'audio':
tf.io.FixedLenFeature([self._audio_length], dtype=tf.float32),
'f0_hz':
tf.io.FixedLenFeature([self._feature_length], dtype=tf.float32),
'f0_confidence':
tf.io.FixedLenFeature([self._feature_length], dtype=tf.float32),
'loudness_db':
tf.io.FixedLenFeature([self._feature_length], dtype=tf.float32),
'f0_scaled':
tf.io.FixedLenFeature([self._feature_length], dtype=tf.float32),
'ld_scaled':
tf.io.FixedLenFeature([self._feature_length], dtype=tf.float32),
'z':
tf.io.FixedLenFeature([self._feature_length * 16], dtype=tf.float32),
}
# + [markdown] id="eyLOqJNBhwa-"
# # Defining feature mapping function
#
# + id="dJlzNevzhyul"
def features_map(features):
note_number = features['note_number']
velocity = features['velocity']
instrument_source = features['instrument_source']
qualities = features['qualities']
f0_scaled = features['f0_scaled']
ld_scaled = features['ld_scaled']
z = features['z']
sequence_length = f0_scaled.shape[0]
def convert_to_sequence(feature):
channels = feature.shape[0]
feature = tf.expand_dims(feature, axis=0)
feature = tf.broadcast_to(feature, shape=(sequence_length, channels))
feature = tf.cast(feature, dtype=tf.float32)
return feature
# Normalize data
# 0-127
note_number = note_number / 127
velocity = velocity / 127
# 0-2
# 0 acoustic, 1 electronic, 2 synthetic
instrument_source = instrument_source / 2
# Prepare dataset for a sequence to sequence mapping
note_number = convert_to_sequence(note_number)
velocity = convert_to_sequence(velocity)
instrument_source = convert_to_sequence(instrument_source)
qualities = convert_to_sequence(qualities)
f0_scaled = tf.expand_dims(f0_scaled, axis=-1)
f0_variation = f0_scaled * 127.0 - tf.cast(note_number, dtype=tf.float32)
f0_variation = tf.clip_by_value(f0_variation, -1.0, 1.0)
#f0_variation = tf.expand_dims(f0_variation, axis=-1)
ld_scaled = tf.expand_dims(ld_scaled, axis=-1)
z = tf.reshape(z, shape=(sequence_length, 16))
input = tf.concat(
[note_number, velocity, instrument_source, qualities, z],
axis=-1)
output = tf.concat(
[f0_variation, ld_scaled],
axis=-1)
# print(f'f0_variation shape: {f0_variation}' )
# print(f'f0_scaled shape: {f0_scaled}' )
return (input, output)
# + [markdown] id="cWeUD9z3nLAF"
# # Create Datasets
# + id="crbnUBoxnMY3"
batch_size = 16
example_secs = 4
sample_rate = 16000
frame_rate = 250
# Create train dataset
train_data_provider = CompleteTFRecordProvider(
file_pattern=train_tfrecord_file + '*',
example_secs=example_secs,
sample_rate=sample_rate,
frame_rate=frame_rate,
map_func=features_map)
train_dataset = train_data_provider.get_batch(
batch_size,
shuffle=True,
repeats=-1)
# Create valid dataset
valid_data_provider = CompleteTFRecordProvider(
file_pattern=valid_tfrecord_file + '*',
example_secs=example_secs,
sample_rate=sample_rate,
frame_rate=frame_rate,
map_func=features_map)
valid_dataset = valid_data_provider.get_batch(
batch_size,
shuffle=True,
repeats=-1)
# Create test dataset
test_data_provider = CompleteTFRecordProvider(
file_pattern=test_tfrecord_file + '*',
example_secs=example_secs,
sample_rate=sample_rate,
frame_rate=frame_rate,
map_func=features_map)
test_dataset = test_data_provider.get_batch(
batch_size,
shuffle=True,
repeats=-1)
# + colab={"base_uri": "https://localhost:8080/"} id="qI99UJes_RAd" outputId="f34641f0-f45c-4b5a-ea92-1ffac7809497"
tcn_layer = TCN(input_shape=(1000, 29), return_sequences=True, nb_filters=64, kernel_size=8,nb_stacks=2)
print('Receptive field size =', tcn_layer.receptive_field)
# + [markdown] id="00zdXuekoW0O"
# # Create and compile mapping model
#
# + id="mm3KlXvunN1n"
model = tf.keras.models.Sequential([
tcn_layer,
tf.keras.layers.LSTM(32, return_sequences=True),
tf.keras.layers.GRU(16, return_sequences=True),
tf.keras.layers.Dense(2, activation='tanh')
])
loss = tf.keras.losses.MeanSquaredError()
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.01),
loss=loss,
metrics=[tf.keras.losses.MeanSquaredError()])
log_dir = "logs/fit/loudness_f0_model/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
# + [markdown] id="4NG0o8Yzpvgf"
# # Building the model
# + colab={"base_uri": "https://localhost:8080/"} id="EvuUYIkhprsc" outputId="71f935cf-fe18-4cc2-e40a-17b9ebeca439"
x_train, y_train = next(iter(train_dataset))
out = model(x_train)
print(model.summary())
# + [markdown] id="2esZxKsEqU_f"
# # Load checkpoints
# + id="9KN7G6HFqWuR"
checkpoint_file = os.path.join(checkpoint_dir, 'cp.ckpt')
if os.path.isdir(checkpoint_dir) and os.listdir(checkpoint_dir):
model.load_weights(checkpoint_file)
# + [markdown] id="C_5Ytb13qkdf"
# # Create training callbacks
#
# + id="Z-W-3Q5tqXC8"
checkpoint = tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_file,
save_weights_only=True,
verbose=0,
save_freq='epoch')
early_stop = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)
def scheduler(epoch, lr):
if epoch < 10:
return lr
else:
return lr * 0.9
lr_scheduler = tf.keras.callbacks.LearningRateScheduler(scheduler)
# + [markdown] id="FhdPr24xquML"
# # Train the model
#
# + colab={"base_uri": "https://localhost:8080/"} id="vFzj98-eqvTB" outputId="f880e85f-123d-4242-a85d-3836e1774c18"
epochs = 100
steps_per_epoch = 100
validation_steps = 10
with tf.device('/device:GPU:0'):
model.fit(train_dataset,
epochs=epochs,
steps_per_epoch=steps_per_epoch,
validation_data=valid_dataset,
validation_steps=validation_steps,
callbacks=[lr_scheduler,tensorboard_callback,checkpoint])
# + [markdown] id="KgV7ETw-y1pD"
# # Evaluate the model
# + id="Pm0i1SoPrUXR" colab={"base_uri": "https://localhost:8080/"} outputId="4f6cdd94-6c56-4ef1-95f8-567f90899a5a"
model.evaluate(test_dataset,steps=500)
# + colab={"base_uri": "https://localhost:8080/"} id="SPoRpl8IFNOo" outputId="39c4b710-b139-40b0-ea09-708b8e773db2"
model.save('saved_model')
# + id="FDBPD3xYFu_U"
# + id="DNvw1hc1dNX8" colab={"base_uri": "https://localhost:8080/"} outputId="cd2ae1db-0c30-4970-ff8d-4a2995f42094"
# %load_ext tensorboard
# !tensorboard --logdir log_dir
# + colab={"base_uri": "https://localhost:8080/"} id="ggZ_G_4Z0Bg0" outputId="81ac8448-8eb0-4623-90ca-52097fa246d8"
# !tensorboard dev upload \
# --logdir logs/fit\
# --name "Mapping network for loudness and F0" \
# --description "Mapping of note_number, velocity, instrument_source, qualities, z to f0 scaled, and loudness scaled " \
# --one_shot
# + id="DzKFkTnQG7aZ" colab={"base_uri": "https://localhost:8080/"} outputId="56cf719b-79f7-4ee7-f34e-72d7943461fa"
# !cp -r saved_model
# + id="Q3S1x5axG8Ej"
| members/omar/Mapping_Network_TCN.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Relationships in Data pt.1
# ## Variance
# Measures how far a set of numbers is spread out from their average.
# ### Compute the variance of an array of numbers
# +
import numpy as np
data = np.array([1, 3, 5, 2, 3, 7, 8, 4, 10, 0, 6, 7, 3, 0, 3, 0, 5, 7, 10, 1, 4, 9, 3])
# first we have a function to calculate the mean
def mean(data):
return sum(data) / len(data)
def variance(data):
m = mean(data)
S = 0
for xi in data:
S += xi
return S / float(len(data) - 1)
print(variance(data))
print(mean(data))
#To check your work you can use the built in numpy variance method (np.var())
print(np.var(data, ddof=1))
# -
# ### Application of variance
# +
import numpy as np
import matplotlib.pyplot as plt
# Running Distance in Mile
X = np.array([3.3,4.4,5.5,6.71,6.93,4.168,9.779,6.182,7.59,2.167,
7.042,10.791,5.313,7.997,5.654,9.27,3.1])
# Water Drinks in Litre
Y = np.array([1.7,2.76,2.09,3.19,1.694,1.573,3.366,2.596,2.53,1.221,
2.827,3.465,1.65,2.904,2.42,2.94,1.3])
plt.scatter(X, Y)
plt.xlabel('Running Distance (Mile)')
plt.ylabel('Water Drinks (Litre)')
# -
predicted_y_values = list(map(lambda x: 0.7*x + 0.3, X))
plt.scatter(X, Y)
plt.plot(X, predicted_y_values, 'ro-')
# ## Percentile
# Percentile is defined as the value below which a percentage of the data falls. Percentiles can help us interpret the standing of a particular value within a data set. Given a dataset we can calculate the nth percentile using the steps below:
#
# * Arrange the data in ascending order
# * Find the index of the (ordinal rank) of the percentile value by calculating index = ceiling((percent/100) * len(data))
# * Find the value that is located at the index
#
# +
data = np.array([1, 3, 5, 2, 3, 7, 8, 4, 10, 0, 6, 7, 3, 0, 3, 0, 5, 7, 10, 1, 4, 9, 3])
def percentile(data, percent):
#first we want to sort the data in ascending order
data = np.sort(data)
#then we will get the index
index = (percent/100)*len(data) #TODO: finish this
#we will have to round up to the nearest whole number using the ceiling method and covert to an int
index = int(np.ceil(index))
return data[index-1] #adjust by -1 since indices start with 0
print(percentile(data, 44))
#check your work by comparing to numpy.percentile()
print(int(np.percentile(data, 44)))
# -
# ## Covariance and Correlation
# #### Obtain the correlation between two columns in Titanic, Fare and Siblings/Spouses Aboard
# * We want to know if we have large famility size then can we conclude we paid more
# +
import pandas as pd
import scipy.stats
df = pd.read_csv('titanic.csv')
#here is a function to calculate pearson's correlation coefficient
def pearson_corr(x, y):
x_mean = np.mean(x)
y_mean = np.mean(y)
num = [(i - x_mean)*(j - y_mean) for i,j in zip(x,y)]
den_1 = [(i - x_mean)**2 for i in x]
den_2 = [(j - y_mean)**2 for j in y]
correlation_x_y = np.sum(num)/np.sqrt(np.sum(den_1))/np.sqrt(np.sum(den_2))
return correlation_x_y
print(pearson_corr(df['Fare'])# , df['Siblings/Spouses Aboard']))
print(scipy.stats.pearsonr(df['Fare'])#, df['Siblings/Spouses Aboard']))
| Class 2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Part 3 Twitter Data Analysis
# ## Installing and importing R packages
# Inorder to help with the efficient running of our R scripts, it is essential to install the necessary packages to help support the corresponding functions that help with data manipulation. Here, the packages installed are:
# 1. rlang - Supports the basic R functionalities
# 2. usmap - Allows plotting the map of USA
# 3. dplyr - Helps with manipulation and working with dataframes i.e filter(), select()
# 4. tidyverse - Helps with the easy installation and loading of other 'tidyverse' packages
# 5. gridExtra - Aids to work with grid-based plots and drawing tables
# +
.libPaths()
#install.packages("rlang",repos='http://cran.us.r-project.org')
#install.packages('usmap',repos='http://cran.us.r-project.org')
#install.packages("dplyr",repos='http://cran.us.r-project.org',versions="0.3.1")
#install.packages("tidyverse",repos='http://cran.us.r-project.org',versions="0.3.1")
#install.packages("gridExtra",repos='http://cran.us.r-project.org')
library(gridExtra)
# -
library(usmap)
library(dplyr)
library(tidyverse)
library(rtweet)
# ## Tweet Collection
# Here, we have used the rtweet package to help with Twitter data collection and processing. It allows the use of functions which after the authentication of your twitter key credentials, helps collect streaming tweets using the Twitter Search API. Here, the process followed is,
# 1. Used 'search_tweets()' function is collect recent tweets. This is done using multiple keywords related to flu. One of the parameters we use while searching is lookup_coords()' which makes use of the Google API key; it basically helps getting the latitude/longitude coordinate information for the specified location.
# 2. Everytime, the tweets are collected and stored in dataframes. Now, all the dataframes are combined into one to hold all the data together. For this, we used the 'bind_rows()' function.
# 3. From the collected data, we select only the necessary fields using the 'select()' function.
# 4. From this dataframe, we retrieve the location of the tweets.
# 5. Now, we write the collected data into a CSV file for storage.
token <-create_token(
app = "InforRetrieve",
consumer_key = "-",
consumer_secret = "-",
access_token = "-",
access_secret = "-")
flu <- search_tweets("influenza", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
flu1 <- search_tweets("flu", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
dim(flu1)
dim(twt_df1)
flu2 <- search_tweets("flu shot", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
dim(twt_df2)
flu3 <- search_tweets("flu virus", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
flu4 <- search_tweets("flu virus", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
flu5 <- search_tweets("H1N1", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
flu6 <- search_tweets("#H1N1", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
flu7 <- search_tweets("flu awareness", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
combo = bind_rows(flu,flu1)
dim(combo)
combo = bind_rows(combo,flu2)
combo = bind_rows(combo,flu3)
combo = bind_rows(combo,flu4)
combo = bind_rows(combo,flu5)
combo = bind_rows(combo,flu6)
combo = bind_rows(combo,flu7)
combo = bind_rows(combo,flu8)
combo = bind_rows(combo,flu9)
head(combo)
colnames(combo)
tweets <-select(combo, user_id, status_id, created_at, screen_name, text, location ,source,retweet_count,lang, verified,country,country_code,url )
write.csv(tweets, file="dic_tweets_initial.csv")
locat <-select(combo, screen_name, text, location)
write.csv(locat, file="dic_tweets.csv")
# ## Tweet data Manipulation
# Now, we continute the procedure from above. The data stored in the CSV is read using the 'read.csv()'. Before moving ahead with the map creation, it is essential to clean the data. We first strip the data of retweets which is done by setting the 'include_rts' parameter to false. Then we check for duplicates. If duplicate tweets exist, we need to remove those data rows. Once data has been filtered and cleaned, we need to retrieve the states assigned to each tweet and the count from each state.
locat1 <- read.csv("tweets_with_location.csv", header=T)
head(locat1)
duplicated(locat1)
head(locat1[duplicated(locat1),])
dim(locat1)
# +
draw_map <- function(locat){
states <- c()
names(locat)
lst <- as.vector(locat$location)
for(i in lst){
x <- strsplit(i, "," )[[1]][2] #%>%
#sapply(tail, 1 )
states <- c(states,x)
}
rs <- as.data.frame(table(states))
class(rs)
names(rs)
#rs
result <- merge(x = statepop, y = rs, x.by = "abbr", y.by = "states", all.x = T)
result <- result[trimws(result$states) == trimws(result$abbr),]
#write.csv(result, file="flu_processed.csv")
#sum(result$Freq)
#print(result)
plt <- plot_usmap(data = result, values = "Freq", lines = "black") +
scale_fill_continuous(name = "Freq", label = scales::comma) +
theme(legend.position = "right")
return(plt)
}
# -
# ## Map Creation
# We now plot the graphs for the diffrent datasets. For plotting purposes , we use 'plot_usmap()'. We have three maps generated below:
# 1. Heatmap for the total number of tweets collected
# 2. Heatmap for the tweets collected corresponding to two specific keywords
total_plt <- draw_map(locat1)
total_plt + ggtitle("Twitter Data HeatChart")
search_flu <- locat1[grepl("flu",locat1$text),]
#write.csv(search_flu, file="flu_tweets.csv")
flu_plt <- draw_map(search_flu)
flu_plt + ggtitle("HeatMap for Keyword FLU")
search_hn <- locat1[grepl("H1N1",locat1$text),]
#write.csv(search_hn, file="hn_tweets.csv")
hn_plt <- draw_map(search_hn)
hn_plt + ggtitle("HeatMap for Keyword H1N1")
flu8 <- search_tweets("fight flu", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
dim(flu8)
flu9 <- search_tweets("flu 2019", geocode = lookup_coords("usa"), n = 1000, include_rts = FALSE)
dim(flu9)
# ## Compare Maps
# The next task is to compare the heatmap obtained in part 2 i.e the map generated from the CDC data and the heatmap generated in part 3 from the collected tweet data. To help with this, we use the 'grid.arrange()' function.
# +
library(ggplot2)
library(usmap)
data3 <- read.csv(file='StateDatabyWeekforMap_2018-19week40-8.csv', header=T)
colfunc <- colorRampPalette(c("red", "yellow", "green"))
usmapdata <- merge(x=data3, y=statepop, x.by=STATENAME, y.by=full, x.all= TRUE)
usmapdata <- usmapdata[ usmapdata$STATENAME == usmapdata$full & usmapdata$WEEK == 8,]
unique(usmapdata$ACTIVITY.LEVEL)
usmapdata$ACTIVITY.LEVEL <- factor(usmapdata$ACTIVITY.LEVEL, levels = c("Level 10", "Level 9", "Level 8", "Level 7", "Level 6", "Level 5", "Level 4", "Level 1"))
#write.csv(usmapdata,file="cdcshiny.csv")
part2_plt <- plot_usmap(data = usmapdata, values = "ACTIVITY.LEVEL", lines = "black") +
scale_fill_manual(values = c("#FF0000", "#FF3800" ,"#FF7100" ,"#FFAA00" ,"#FFE200" ,"#E2FF00" ,"#AAFF00", "#71FF00", "#38FF00" ,"#00FF00")) +
theme(legend.position = "right",
legend.title = element_text("ILI Activity Level", face = "bold"),
plot.title = element_text(hjust = 0.5, face="bold", size=6.5)) +
ggtitle("2018-19 Influenza Season Week 8 ending Feb 23, 2019")
# -
# ## Twitter Data VS CDC HeatMap
# We display the heatmap generated for the CDC data and the total collected tweets against each other. The graphs illustrate the intensity of the tweet count from each of the corresponding states. With respect to the Twitter Data HeatChart, the intensity goes lighter with increase in count whereas for the CDC chart, darker the color greater the count. Twitter Chart shows light blue for the state of California depicting that it contains the largest number of tweets i.e about 215; a slightly darker shade of blue for New York with about 150 tweets. With respect to the CDC graph, the red shades potray the greater count.
grid.arrange(total_plt + ggtitle("Twitter Data HeatChart"),part2_plt,nrow=1)
# ## CDC HeatMap VS Flu Data
# We display the heatmap generated for the CDC data and the tweets collected for the keyword 'flu' against each other. Similar to the previous depiction, for Flu keyword DataChart, the intensity goes lighter with increase in count whereas for the CDC chart, darker the color greater the count. Flu Chart shows light blue for the state of California depicting that it contains the largest number of tweets; a slightly darker shade of blue for the state of New York, Texas. With respect to the CDC graph, the red shades potray the greater count.
grid.arrange(flu_plt + ggtitle("HeatMap for Keyword FLU"),part2_plt,nrow=1)
# ## CDC HeatMap VS H1N1 Data
# We display the heatmap generated for the CDC data and the tweets collected for the keyword 'H1N1' against each other. H1N1 Chart shows light blue for the state of Kansas depicting that it contains the largest number of tweets; a slightly darker shade of blue for the state of Florida, California. With respect to the CDC graph, the red shades potray the greater count.
grid.arrange(hn_plt + ggtitle("HeatMap for Keyword H1N1"),part2_plt,nrow=1)
| part3 - Flu twitter data exploration/Part3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (scvi-env2)
# language: python
# name: scvi-env2
# ---
# # Benchmarking cell2location pyro model using softplus/exp for scales
# +
import sys, ast, os
#sys.path.insert(1, '/nfs/team205/vk7/sanger_projects/BayraktarLab/cell2location/')
sys.path.insert(1, '/nfs/team205/vk7/sanger_projects/BayraktarLab/scvi-tools/')
import scanpy as sc
import anndata
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import matplotlib as mpl
data_type='float32'
#import cell2location_model
#import cell2location_module_scvi
import scvi
import torch
from matplotlib import rcParams
rcParams['pdf.fonttype'] = 42 # enables correct plotting of text
import seaborn as sns
# -
# ### The purpose of the notebook is to benchmark several versions of the model using mouse brain data.
sc_data_folder = '/nfs/team205/vk7/sanger_projects/cell2location_paper/notebooks/selected_data/mouse_visium_snrna/'
sp_data_folder = '/nfs/team205/vk7/sanger_projects/cell2location_paper/notebooks/selected_results/benchmarking/with_tissue_zones/data/'
results_folder = '/nfs/team205/vk7/sanger_projects/cell2location_paper/notebooks/selected_results/benchmarking/with_tissue_zones/real_mg/pyro/'
# ## Read datasets and train cell2location
# Data can be downloaded as follows:
#
# ```bash
# wget https://cell2location.cog.sanger.ac.uk/paper/synthetic_with_tissue_zones/synth_adata_real_mg_20210131.h5ad
# wget https://cell2location.cog.sanger.ac.uk/paper/synthetic_with_tissue_zones/training_5705STDY8058280_5705STDY8058281_20210131.h5ad
# ```
# +
adata_vis = anndata.read(f'{sp_data_folder}synth_adata_real_mg_20210131.h5ad')
adata_vis.uns['spatial'] = {'x': 'y'}
#adata_vis = adata_vis[adata_vis.obs['sample'].isin([f'exper{i}' for i in range(5,10)]),:]
adata_snrna_raw = anndata.read(f'{sp_data_folder}training_5705STDY8058280_5705STDY8058281_20210131.h5ad')
# -
import scipy
adata_snrna_raw.X = scipy.sparse.csr_matrix(adata_snrna_raw.X)
# + active=""
# adata_vis.X = scipy.sparse.csr_matrix(adata_vis.X)
# -
# Add counts matrix as `adata.raw`
adata_snrna_raw.raw = adata_snrna_raw
adata_vis.raw = adata_vis
# +
# compute average for each cluster
aver = scvi.external.cell2location.compute_cluster_averages(adata_snrna_raw, 'annotation_1')
# make sure the order of gene matches between aver and x_data
aver = aver.loc[adata_vis.var_names,:]
# generate one-hot encoded matrix telling which obs belong to whic samples
obs2sample_df = pd.get_dummies(adata_vis.obs['sample'])
# + active=""
# adata_vis
# -
# ## Model training
adata_vis = scvi.external.cell2location.setup_anndata(adata=adata_vis, cell_state_df=aver, batch_key="sample")
adata_vis.uns['_scvi']
mod = scvi.external.Cell2location(adata_vis, batch_size=2500,
amortised=True,
encoder_kwargs={'n_layers': 1, 'n_hidden': 128,
'dropout_rate': 0.1,
'activation_fn': torch.nn.ReLU},
N_cells_per_location=8)
mod.train(max_epochs=1000, lr=0.01, use_gpu=True)
means = mod.posterior_median(use_gpu = True)
means['w_sf'].shape
mod_m = scvi.external.Cell2location(adata_vis, batch_size=1250,
amortised=True,
encoder_kwargs={'n_layers': 1, 'n_hidden': 128,
'dropout_rate': 0.1,
'activation_fn': torch.nn.ReLU},
N_cells_per_location=8)
mod_m.train(max_epochs=1000, lr=0.01, use_gpu=True)
means_m = mod_m.posterior_median(use_gpu = True)
# + active=""
# # test Predictive
# num_samples = 5
# predictive = mod_m.module.create_predictive(num_samples=num_samples, parallel=False)
#
# from scvi.dataloaders import AnnDataLoader
# train_dl = AnnDataLoader(adata_vis, shuffle=False, batch_size=500)
# for tensor_dict in train_dl:
# args, kwargs = mod_m.module._get_fn_args_from_batch(tensor_dict)
# samples = {
# k: v.detach().cpu().numpy()
# for k, v in predictive(*args, **kwargs).items()
# if k != "obs"
# }
# + active=""
# # save Pyro param state
# model_save_path = os.path.join(save_path, "model_params.pt")
# torch.save(model.state_dict(), model_save_path)
# + active=""
# amortised_plate_sites = {'name': "obs_plate",
# 'in': ['x_data'],
# 'sites': {
# "n_s_cells_per_location": 1,
# "y_s_groups_per_location": 1,
# "z_sr_groups_factors": 5,
# "w_sf": 4,
# "l_s_add": 1,
# }}
# np.sum([np.sum(amortised_plate_sites['sites'][k]) for k in amortised_plate_sites['sites'].keys()]) * 2
# + active=""
# # create indices for loc and scales of each site
# counter = 0
# indices = dict()
# for site, n_dim in amortised_plate_sites['sites'].items():
# indices[site] = {'locs': np.arange(counter, counter + n_dim),
# 'scales': np.arange(counter + n_dim, counter + n_dim * 2)}
# counter += n_dim * 2
#
# indices
# + active=""
# # save model
# mod_m.save(dir_path='./results/scvi/minibatch_1sample', overwrite=True, save_anndata=False)
#
# # load model
# mod_m.load(dir_path='./results/scvi/minibatch_1sample', adata=adata_vis, use_gpu=True)
# -
# ### Compare ELBO as training progresses
plt.plot(mod.module.history_['train_loss_epoch'].index[200:],
np.array(mod.module.history_['train_loss_epoch'].values.flatten())[200:]);
plt.plot(mod_m.module.history_['train_loss_epoch'].index[200:],
np.array(mod_m.module.history_['train_loss_epoch'].values.flatten())[200:]);
plt.legend(labels=['minibatch 2500/25000', 'minibatch 1250/25000']);
plt.xlim(0, len(mod_m.module.history_['train_loss_epoch']));
# + active=""
# plt.plot(mod.module.history_['train_loss_epoch'].index[10:],
# np.array(mod.module.history_['train_loss_epoch'].values.flatten())[10:]);
# plt.legend(labels=['minibatch 125/25000']);
# plt.xlim(0, len(mod_m.module.history_['train_loss_epoch']));
# + active=""
# plt.plot(mod_m.module.history_['train_loss_epoch'].index[40:],
# np.array(mod_m.module.history_['train_loss_epoch'].values.flatten())[40:]);
# plt.legend(labels=['minibatch 1250/25000']);
# plt.xlim(0, len(mod_m.module.history_['train_loss_epoch']));
# + active=""
# #plt.plot(range(1, 100), np.array(mod.module.history_)[1:100]);
# plt.plot(mod_m.module.history_['train_loss_epoch'].index[1:100],
# np.array(mod_m.module.history_['train_loss_epoch'].values.flatten())[1:100]);
# plt.legend(labels=['full data', 'minibatch 500/2500']);
# plt.xlim(0, 100);
# -
# ### Evaluate accuracy using $R^2$
# +
from re import sub
cell_count = adata_vis.obs.loc[:, ['cell_abundances_' in i for i in adata_vis.obs.columns]]
cell_count.columns = [sub('cell_abundances_', '', i) for i in cell_count.columns]
cell_count_columns = cell_count.columns
cell_proportions = (cell_count.T / cell_count.sum(1)).T
infer_cell_count = pd.DataFrame(means['w_sf'], index=adata_vis.obs_names,
columns=aver.columns)
infer_cell_count = infer_cell_count[cell_count.columns]
infer_cell_proportions = (infer_cell_count.T / infer_cell_count.sum(1)).T
infer_cell_count_m = pd.DataFrame(means_m['w_sf'], index=adata_vis.obs_names,
columns=aver.columns)
infer_cell_count_m = infer_cell_count_m[cell_count.columns]
infer_cell_proportions_m = (infer_cell_count_m.T / infer_cell_count_m.sum(1)).T
# -
infer_cell_count.iloc[0:5,0:5], infer_cell_count_m.iloc[0:5,0:5]
# +
rcParams['figure.figsize'] = 4, 4
rcParams["axes.facecolor"] = "white"
plt.hist2d(cell_count.values.flatten(),
infer_cell_count.values.flatten(),# / np.mean(adata_vis_res.var['gene_level'].values),
bins=[50, 50], norm=mpl.colors.LogNorm());
plt.xlabel('Simulated cell abundance');
plt.ylabel('Estimated cell abundance');
plt.title(r'minibatch 2500/25000, $R^2$: ' \
+ str(np.round(np.corrcoef(cell_count.values.flatten(),
infer_cell_count.values.flatten()), 3)[0,1]));
#plt.gca().set_aspect('equal', adjustable='box')
plt.tight_layout()
#plt.savefig(fig_path + '/Cell_density_cor.pdf')
# +
rcParams['figure.figsize'] = 4, 4
rcParams["axes.facecolor"] = "white"
plt.hist2d(cell_count.values.flatten(),
infer_cell_count_m.values.flatten(),# / np.mean(adata_vis_res.var['gene_level'].values),
bins=[50, 50], norm=mpl.colors.LogNorm());
plt.xlabel('Simulated cell abundance');
plt.ylabel('Estimated cell abundance');
plt.title(r'minibatch 1250/25000, $R^2$: ' \
+ str(np.round(np.corrcoef(cell_count.values.flatten(),
infer_cell_count_m.values.flatten()), 3)[0,1]));
#plt.gca().set_aspect('equal', adjustable='box')
plt.tight_layout()
#plt.savefig(fig_path + '/Cell_density_cor.pdf')
# -
# Original implementation of cell2location in pymc3 has $R^2 = 0.791$.
# ## Evaluate with PR curves
# +
import matplotlib as mpl
from matplotlib import pyplot as plt
import numpy as np
from scipy import interpolate
with plt.style.context('seaborn'):
seaborn_colors = mpl.rcParams['axes.prop_cycle'].by_key()['color']
def compute_precision_recall(pos_cell_count, infer_cell_proportions, mode='macro'):
r""" Plot precision-recall curves on average and for each cell type.
:param pos_cell_count: binary matrix showing which cell types are present in which locations
:param infer_cell_proportions: inferred locations (the higher the more cells)
"""
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
### calculating ###
predictor = infer_cell_proportions.values + np.random.gamma(20, 1e-12,
infer_cell_proportions.shape)
# For each cell type
precision = dict()
recall = dict()
average_precision = dict()
for i, c in enumerate(infer_cell_proportions.columns):
precision[c], recall[c], _ = precision_recall_curve(pos_cell_count[:, i],
predictor[:, i])
average_precision[c] = average_precision_score(pos_cell_count[:, i], predictor[:, i], average=mode)
average_precision["averaged"] = average_precision_score(pos_cell_count, predictor,
average=mode)
# A "micro-average": quantifying score on all classes jointly
if mode == 'micro':
precision_, recall_, threshold = precision_recall_curve(pos_cell_count.ravel(),
predictor.ravel())
#precision_[threshold < 0.1] = 0
precision["averaged"], recall["averaged"] = precision_, recall_
elif mode == 'macro':
precisions = []
recall_grid = np.linspace(0, 1, 2000)
for i, c in enumerate(infer_cell_proportions.columns):
f = interpolate.interp1d(recall[c], precision[c])
precision_interp = f(recall_grid)
precisions.append(precision_interp)
precision["averaged"] = np.mean(precisions, axis=0)
recall['averaged'] = recall_grid
return precision, recall, average_precision
def compare_precision_recall(pos_cell_count, infer_cell_proportions,
method_title, title='',
legend_loc=(0, -.37),
colors=sc.pl.palettes.default_102,
mode='macro', curve='PR'):
r""" Plot precision-recall curves on average and for each cell type.
:param pos_cell_count: binary matrix showing which cell types are present in which locations
:param infer_cell_proportions: inferred locations (the higher the more cells),
list of inferred parameters for several methods
:param method_title: title for each infer_cell_proportions
:param title: plot title
"""
# setup plot details
from itertools import cycle
colors = cycle(colors)
lines = []
labels = []
roc = {}
### plotting ###
for i, color in zip(range(len(infer_cell_proportions)), colors):
if curve == 'PR':
precision, recall, average_precision = compute_precision_recall(pos_cell_count,
infer_cell_proportions[i],
mode=mode)
xlabel = 'Recall'
ylabel = 'Precision'
l, = plt.plot(recall["averaged"], precision["averaged"], color=color, lw=3)
elif curve == 'ROC':
FPR, TPR, average_precision = compute_roc(pos_cell_count,
infer_cell_proportions[i],
mode=mode)
xlabel = 'FPR'
ylabel = 'TPR'
l, = plt.plot(FPR["averaged"], TPR["averaged"], color=color, lw=3)
lines.append(l)
labels.append(method_title[i] + '(' + curve + ' score = {0:0.2f})'
''.format(average_precision["averaged"]))
roc[method_title[i]] = average_precision["averaged"]
fig = plt.gcf()
fig.subplots_adjust(bottom=0.25)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel(xlabel)
plt.ylabel(ylabel)
plt.title(title)
if legend_loc is not None:
plt.legend(lines, labels, loc=legend_loc, prop=dict(size=8))
#plt.show()
return roc
# +
rcParams['figure.figsize'] = 6, 3
rcParams['font.size'] = 8
results = [
infer_cell_count,
infer_cell_count_m
]
results_proportion = [
infer_cell_proportions,
infer_cell_proportions_m
]
names = [
'minibatch 2500/25000 obs',
'minibatch 1250/25000 obs',
]
compare_precision_recall(cell_count.values > 0.1,
results,
method_title=names,
legend_loc=(1.1, 0.5))
plt.tight_layout();
plt.title('Absolute cell abundance');
plt.show();
compare_precision_recall(cell_count.values > 0.1,
results_proportion,
method_title=names,
legend_loc=(1.1, 0.5))
plt.tight_layout();
plt.title('Relative cell abundance');
plt.show();
# -
# Original implementation of cell2location in pymc3 has PR score = 0.66.
# ### $R^2$ stratified by abundance and regional pattern
# +
from scipy.spatial.distance import jensenshannon
def hist_obs_sim(cell_count, infer_cell_count,
xlab='Simulated cell proportion',
ylab='Estimated cell proportion',
title='', compute_kl=True, equal=True, max_val=1):
cor = np.round(np.corrcoef(cell_count.values.flatten(),
infer_cell_count.values.flatten()), 3)[0,1]
title = title +'\n'+ r'$R^2$: ' + str(cor)
if compute_kl:
js = np.array([jensenshannon(cell_count.values[r,:], infer_cell_count.values[r,:])
for r in range(cell_count.shape[0])])
js = np.mean(js[~np.isnan(js)])
title = title + '\nAverage JSD: ' + str(np.round(js, 2))
plt.hist2d(cell_count.values.flatten(),
infer_cell_count.values.flatten(),
bins=[35, 35], norm=mpl.colors.LogNorm());
plt.xlabel(xlab);
plt.ylabel(ylab);
if equal:
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(0, max_val);
plt.ylim(0, max_val);
plt.title(title);
def hist_by_category(cell_count, infer_cell_count, design,
xlab='Simulated cell proportion',
ylab='Estimated cell proportion',
nrow=1, ncol=4, compute_kl=True, equal=True):
design_loc = design.loc[cell_count.columns,:]
max_val = np.array([cell_count.values.max(), infer_cell_count.values.max()]).max()
if max_val < 1:
max_val = 1
plt.subplot(nrow, ncol, 1)
ind = (design_loc['is_uniform'] * design_loc['is_high_density']).values.astype(bool)
hist_obs_sim(cell_count.loc[:,ind], infer_cell_count.loc[:,ind],
xlab=xlab,
ylab=ylab,
title=f'Uniform & high abundance ({ind.sum()})',
compute_kl=compute_kl, equal=equal, max_val=max_val)
plt.subplot(nrow, ncol, 2)
ind = (design_loc['is_uniform'] * (1 - design_loc['is_high_density'])).values.astype(bool)
hist_obs_sim(cell_count.loc[:,ind], infer_cell_count.loc[:,ind],
xlab=xlab,
ylab=ylab,
title=f'Uniform & low abundance ({ind.sum()})',
compute_kl=compute_kl, equal=equal, max_val=max_val)
plt.subplot(nrow, ncol, 3)
ind = ((1 - design_loc['is_uniform']) * design_loc['is_high_density']).values.astype(bool)
hist_obs_sim(cell_count.loc[:,ind], infer_cell_count.loc[:,ind],
xlab=xlab,
ylab=ylab,
title=f'Sparse & high abundance ({ind.sum()})',
compute_kl=compute_kl, equal=equal, max_val=max_val)
plt.subplot(nrow, ncol, 4)
ind = ((1 - design_loc['is_uniform']) * (1 - design_loc['is_high_density'])).values.astype(bool)
hist_obs_sim(cell_count.loc[:,ind], infer_cell_count.loc[:,ind],
xlab=xlab,
ylab=ylab,
title=f'Sparse & low abundance ({ind.sum()})',
compute_kl=compute_kl, equal=equal, max_val=max_val)
rcParams['figure.figsize'] = 18,4.5
rcParams["axes.facecolor"] = "white"
hist_by_category(cell_proportions, infer_cell_proportions, adata_vis.uns['design']['cell_types2zones'],
xlab='Simulated cell proportion',
ylab='Estimated cell proportion',
nrow=1, ncol=4, equal=True)
plt.tight_layout();
plt.show();
hist_by_category(cell_proportions, infer_cell_proportions_m, adata_vis.uns['design']['cell_types2zones'],
xlab='Simulated cell proportion',
ylab='Estimated cell proportion',
nrow=1, ncol=4, equal=True)
plt.tight_layout();
plt.show();
# -
import sys
for module in sys.modules:
try:
print(module,sys.modules[module].__version__)
except:
try:
if type(modules[module].version) is str:
print(module,sys.modules[module].version)
else:
print(module,sys.modules[module].version())
except:
try:
print(module,sys.modules[module].VERSION)
except:
pass
| notebooks/scvi_amortised/cell2location_synthetic_data_scVI_amortised_10x_data_batch_1250_2500_dropout_rate01_n_hidden128.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (TRANSACT_figures)
# language: python
# name: transact_figures
# ---
# # Fig 2C-I : Drug response prediction from cell lines to PDX.
# This notebooks support Fig2 panel C to I and corresponds to the PDX prediction based on cell lines drug response.
# +
import os, sys
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from joblib import Parallel, delayed
import scipy
from copy import deepcopy
import uuid
from pickle import load, dump
import re
from datetime import date
sns.set_style("whitegrid")
sns.set_context('paper')
from matplotlib import font_manager as fm, rcParams
fpath = os.path.join(rcParams["datapath"], "fonts/ttf/arial.ttf")
prop_label = fm.FontProperties(fname=fpath)
prop_label.set_size(30)
prop_ticks = fm.FontProperties(fname=fpath)
prop_ticks.set_size(25)
fname = os.path.split(fpath)[1]
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import StratifiedKFold, KFold, GroupKFold, GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.linear_model import ElasticNet
from sklearn.metrics import mean_squared_error
from sklearn.pipeline import Pipeline
from sklearn.utils import shuffle, resample
from joblib import dump, load, Parallel, delayed
from statannot.statannot import add_stat_annotation
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import torch.utils.data as Data
from torch.utils.data import Dataset, TensorDataset, DataLoader
from torch.utils.data.dataset import random_split
from skorch import NeuralNetClassifier, NeuralNetRegressor
sys.path.insert(0, '../read_data/')
from read_data import read_data
from read_GDSC_response import read_GDSC_response
from read_PDXE_response import read_PDXE_response
from reformat_df import reformat_df
import library_size_normalization
sys.path.insert(0, '../src/')
from clf_utils import make_network
from transact.pv_computation import PVComputation
from transact.interpolation import Interpolation
from transact.matrix_operations import _center_kernel, _right_center_kernel, _left_center_kernel
from transact.kernel_computer import KernelComputer
from transact.TRANSACT import TRANSACT
from compute_proportion import compute_proportion
# +
# Normalization
with_mean = True
with_std = True
# domain adaptation
tissues = {
'PDXE': ['All'],
'GDSC': ['All']
}
projects = {
'PDXE':[None],
'GDSC': None
}
data_sources = ['GDSC', 'PDXE']
data_types = ['fpkm']
genes_filtering = 'mini'
data_normalization = 'library_size' # Can be TPM, "library_size" or "log". Else will not have any influence.
source = 'GDSC'
target = 'PDXE'
# Folder where CV has been saved
output_combat_cv_folder = ''
output_uncorrected_cv_folder = ''
random_state = 183627362
# -
# ## Read data
# +
data_df = read_data(tissues=tissues,
data_types=[e for e in data_types],
projects=projects,
data_sources=data_sources,
folder_basis='../data/')
source_data_key, target_data_key = reformat_df(data_df, source, target)
data_df_combat = deepcopy(data_df)
# -
# Library size normalization
average_depth_global = 10**5
for ds in list(data_df.keys()):
GE_normalized = library_size_normalization.TMM_normalization(data_df[ds].values.astype(float))
GE_normalized = np.array(GE_normalized)
average_depths = np.mean(np.sum(GE_normalized,1))
data_df_combat[ds] = pd.DataFrame(np.log(np.array(GE_normalized)+1),
columns=data_df_combat[ds].columns,
index=data_df_combat[ds].index)
GE_normalized = GE_normalized / average_depths * average_depth_global
GE_normalized = np.log(np.array(GE_normalized)+1)
data_df[ds] = pd.DataFrame(GE_normalized,
columns=data_df[ds].columns,
index=data_df[ds].index)
# +
# Reducing genes for ComBat
number_top_genes = 1700
top_source_variable_genes = pd.DataFrame(np.var(data_df[source_data_key]), columns=['variance'])
top_source_variable_genes = top_source_variable_genes.sort_values('variance', ascending=False)
top_source_variable_genes = top_source_variable_genes.head(number_top_genes).index
top_target_variable_genes = pd.DataFrame(np.var(data_df[target_data_key]), columns=['variance'])
top_target_variable_genes = top_target_variable_genes.sort_values('variance', ascending=False)
top_target_variable_genes = top_target_variable_genes.head(number_top_genes).index
top_variable_genes = np.intersect1d(top_source_variable_genes, top_target_variable_genes)
print(top_variable_genes.shape)
for d in data_df:
data_df_combat[d] = data_df_combat[d][top_variable_genes]
# +
normalized_data_df = {
ds : StandardScaler(with_mean=with_mean, with_std=with_std).fit_transform(data_df[ds])
for ds in data_df
}
for ds in normalized_data_df:
normalized_data_df[ds] = pd.DataFrame(normalized_data_df[ds],
index=data_df[ds].index,
columns=data_df[ds].columns)
# -
# ### Drug response
# GDSC
unique_drugs = None
GDSC_drug_response_frames = {}
for x in ['GDSC2', 'GDSC1']:
GDSC_drug_response_file = '../data/GDSC/response/%s_fitted_dose_response_25Feb20.xlsx'%(x)
GDSC_drug_response_frames[x] = pd.read_excel(GDSC_drug_response_file)
if unique_drugs is None:
unique_drugs = np.unique(GDSC_drug_response_frames[x]['DRUG_NAME'])
else:
unique_drugs = np.concatenate([unique_drugs, np.unique(GDSC_drug_response_frames[x]['DRUG_NAME'])])
# PDX
PDX_drug_response_df = pd.read_csv('../data/PDXE/response/response.csv', index_col=0)
# ## Alignment settings
# ### Different similarity functions to test
# +
kernel_surnames = ['linear_centered_standardized',
'rbf_gamma_1_centered_standardized',
'rbf_gamma_2_centered_standardized',
'rbf_gamma_3_centered_standardized',
'rbf_gamma_4_centered_standardized',
'rbf_gamma_5_centered_standardized',
'rbf_gamma_6_centered_standardized',
'rbf_gamma_7_centered_standardized'
]
order = [
'uncorrected_EN',
'uncorrected_network',
'combat_network',
'linear_centered_standardized',
'rbf_gamma_1_centered_standardized',
'rbf_gamma_2_centered_standardized',
'rbf_gamma_3_centered_standardized',
'rbf_gamma_4_centered_standardized',
'rbf_gamma_5_centered_standardized',
'rbf_gamma_6_centered_standardized',
'rbf_gamma_7_centered_standardized'
]
labels = [
'Elastic Net',
'DL',
'ComBat + DL',
'PRECISE',
r'$\gamma$=1$\times$$10^{-5}$',
r'$\gamma$=3$\times$$10^{-5}$',
r'$\gamma$=1$\times$$10^{-4}$',
r'$\gamma$=3$\times$$10^{-4}$',
r'$\gamma$=1$\times$$10^{-3}$',
r'$\gamma$=3$\times$$10^{-3}$',
r'$\gamma$=1$\times$$10^{-2}$',
]
kernel_names = ['linear', 'rbf', 'rbf', 'rbf', 'rbf', 'rbf', 'rbf', 'rbf']
kernel_param = [
{},
{'gamma': 10**(-5)},
{'gamma': 10**(-4.5)},
{'gamma': 10**(-4)},
{'gamma': 10**(-3.5)},
{'gamma': 10**(-3)},
{'gamma': 10**(-2.5)},
{'gamma': 10**(-2)}
]
kernel_param = {k:p for k,p in zip(kernel_surnames, kernel_param)}
number_pc = {
'source': 70,
'target': 50
}
n_pv = [20, 20, 20, 20, 20, 20, 20, 20]
n_pv = {k:p for k,p in zip(kernel_surnames, n_pv)}
n_interpolation = 100
# -
# ### Load drug data
# +
# Potential pairs:
# ('Erlotinib', 'erlotinib'),
# ('Cetuximab', 'cetuximab'),
# ('Gemcitabine', 'gemcitabine-50mpk'),
# ('Afatinib', 'trastuzumab'),
# ('Paclitaxel', 'paclitaxel'),
# ('Trametinib', 'trametinib'),
# ('Ruxolitinib', 'INC424'),
GDSC_drug_name, PDXE_drug_name = ('Ruxolitinib', 'INC424')
drug_folder_name = 'response_GDSC_%s_PDXE_%s'%(GDSC_drug_name, PDXE_drug_name)
if drug_folder_name not in os.listdir('./figures/'):
os.mkdir('./figures/'+drug_folder_name)
drug_folder_name = './figures/'+drug_folder_name
X_target_response, y_target = read_PDXE_response(PDX_drug_response_df,
PDXE_drug_name,
normalized_data_df[target_data_key])
X_source_response, y_source = read_GDSC_response(GDSC_drug_response_frames,
GDSC_drug_name,
normalized_data_df[source_data_key])
X_target_response_combat, y_target_combat = read_PDXE_response(PDX_drug_response_df,
PDXE_drug_name,
data_df_combat[target_data_key])
X_source_response_combat, y_source_combat = read_GDSC_response(GDSC_drug_response_frames,
GDSC_drug_name,
data_df_combat[source_data_key])
combat_cv_folder = output_combat_cv_folder + GDSC_drug_name
uncorrected_cv_folder = GDSC_drug_name + ('_centered' if with_mean else '') + ('_standardized' if with_std else '')
uncorrected_cv_folder = output_uncorrected_cv_folder + uncorrected_cv_folder
# -
# ## Test for various values of similarities and baselines
# ### Import CV deep network architecture
# +
param_names = ['hidden', 'input', 'activation', 'hiddenDO', 'inputDO', 'l2pen', 'lr']
def parse_folder_results(f, folder):
param = {}
for n in param_names:
param[n] = re.search('%s_([0-9A-Za-z-.]+)'%(n), f)
param[n] = [param[n].group(1)] if param[n] else ''
param['folder'] = f
param_df = pd.DataFrame.from_dict(param)
results_files = ['%s/%s/'%(folder, f) + e for e in os.listdir('%s/%s'%(folder, f))
if '.csv' in e and 'pred_perf' in e and (str(random_state) in e or random_state is None)]
if len(results_files) == 0:
return None
results_df = [pd.read_csv(r, header=0, index_col=0) for r in results_files]
results_df = pd.concat(results_df)
results_df.index = [f] * results_df.shape[0]
return results_df
def read_best_param(folder, output_fig=None):
relevant_subfolders = [e for e in os.listdir(folder)
if 'hidden' in e]
results_df = [parse_folder_results(f, folder)
for f in relevant_subfolders]
results_df = [df for df in results_df if df is not None]
results_df = pd.concat(results_df)
baseline_df = pd.read_csv('%s/baseline_pred_perf_random-state_%s.csv'%(folder,
random_state),
header=0, index_col=0)
results_df.columns = [('model', e) for e in results_df.columns]
for e in ['MSE', 'pred_perf']:
results_df[('baseline', e)] = baseline_df[e].values[0]
results_df.columns = pd.MultiIndex.from_tuples(results_df.columns)
if output_fig is not None:
results_df.to_csv('%s/%s'%(drug_folder_name, output_fig))
best_model = results_df.sort_values(('model', 'pred_perf'), ascending=False).index[0]
best_model_param = folder + '/' + best_model + '/param.pkl'
best_model_param = load(open(best_model_param, 'rb'))
return best_model_param
def make_skorch_network(net, param):
return NeuralNetRegressor(
net,
max_epochs=param['n_epochs'],
lr=param['learning_rate'],
batch_size=param['batch_size'],
device= 'cuda' if torch.cuda.is_available() else 'cpu',
optimizer=torch.optim.SGD,
optimizer__momentum=param['momentum'],
optimizer__weight_decay=param['l2_penalty'],
iterator_train__shuffle = True,
verbose=0
)
# +
uncorrected_param = read_best_param(uncorrected_cv_folder, 'uncorrected_cv_results.csv')
combat_param = read_best_param(combat_cv_folder, 'combat_cv_results.csv')
combat_param['n_input'] = data_df_combat[source_data_key].shape[1]
uncorrected_param['n_input'] = data_df[source_data_key].shape[1]
# +
uncorrected_network = make_network(uncorrected_param)
uncorrected_network = Pipeline([
('scaler', StandardScaler(with_mean=with_mean, with_std=with_std)),
('regression', make_skorch_network(uncorrected_network, uncorrected_param))
])
combat_network = make_network(combat_param)
combat_network = make_skorch_network(combat_network, combat_param)
# -
def predict_PDX_spearman_cor(n_jobs=20, verbose=0, return_clf=False):
target_spearman = {}
if return_clf:
classifiers = {}
for sim_surname, sim_name in zip(kernel_surnames, kernel_names):
#For each kernel:
# - compute consensus features and project bootstrapped data on them,
# - train predictive model based on bootstrapped labels,
# - predict on target and save spearman correlation.
print(sim_surname)
clf = TRANSACT(kernel=sim_name,
kernel_params=kernel_param[sim_surname],
n_components=number_pc,
n_jobs=n_jobs,
verbose=verbose)
clf.fit(normalized_data_df[source_data_key],
normalized_data_df[target_data_key],
n_pv=n_pv[sim_surname],
step=n_interpolation,
with_interpolation=True)
clf.fit_predictor(X_source_response, y_source.values.flatten(), l1_ratio=0.)
y_target_subsample_predicted = clf.predict(X_target_response)
target_spearman[sim_surname] = scipy.stats.spearmanr(y_target_subsample_predicted,
y_target['BestAvgResponse'])
if return_clf:
classifiers[sim_surname] = deepcopy(clf)
# Comparison to baseline
print('raw')
alpha_values = np.logspace(-5,10,16)
l1_ratio_values = np.linspace(1,10,11)/10
param_grid ={
'regression__alpha': alpha_values,
'regression__l1_ratio': l1_ratio_values
}
grid_raw = GridSearchCV(Pipeline([
('scaler', StandardScaler(with_mean=with_mean, with_std=with_std)),
('regression', ElasticNet())
]),
cv=10,
n_jobs=n_jobs,
param_grid=param_grid,
verbose=verbose,
scoring='neg_mean_squared_error')
grid_raw.fit(X_source_response, y_source.values.flatten())
y_target_subsample_predicted = grid_raw.predict(X_target_response)
target_spearman['uncorrected_EN'] = scipy.stats.spearmanr(y_target_subsample_predicted,
y_target['BestAvgResponse'])
classifiers['raw'] = grid_raw
# Neural network without correction
print('Neural network uncorrected')
uncorrected_network.fit(X_source_response.values.astype(np.float32), y_source.values.astype(np.float32))
y_target_subsample_predicted = uncorrected_network.predict(X_target_response.values.astype(np.float32)).flatten()
target_spearman['uncorrected_network'] = scipy.stats.spearmanr(y_target_subsample_predicted,
y_target['BestAvgResponse'].values.flatten())
classifiers['uncorrected_network'] = uncorrected_network
# Neural network without correction
print('Neural network with ComBat')
combat_network.fit(X_source_response_combat.values.astype(np.float32),
y_source_combat.values.astype(np.float32))
y_target_subsample_predicted = combat_network.predict(X_target_response_combat.values.astype(np.float32)).flatten()
target_spearman['combat_network'] = scipy.stats.spearmanr(y_target_subsample_predicted,
y_target['BestAvgResponse'].values.flatten())
classifiers['combat_network'] = combat_network
if return_clf:
return target_spearman, classifiers
return target_spearman
# +
n_jobs=30
correlations_per_sim, clfs = predict_PDX_spearman_cor(n_jobs=n_jobs, verbose=0, return_clf=True)
saving_id = str(uuid.uuid4())[:8]
dump(correlations_per_sim, '%s/prediction_%s.csv'%(drug_folder_name,
saving_id))
# -
potential_file = os.listdir(drug_folder_name)
potential_file = [p for p in potential_file if 'prediction' in p]
if len(potential_file) == 1:
file = potential_file[0]
else:
print('MORE THAN ONE FILE')
print(potential_file)
file = 'prediction_122e8b39.csv'
saving_id = re.search(r'_([0-9a-z]*).csv', file).group(1)
correlations_per_sim = load(open(drug_folder_name + '/' + file, 'rb'))
del file
# ## Plot results
to_plot_df = pd.DataFrame(correlations_per_sim)
to_plot_df = to_plot_df.T
to_plot_df.columns = ['cor', 'p-val']
to_plot_df = to_plot_df.loc[order]
to_plot_df.index = labels
# +
yticks = np.arange(0,8) / 10
yticks_labels = [str(y) for y in yticks]
colors = [mpl.colors.TABLEAU_COLORS['tab:gray']] * 4 + \
[mpl.colors.TABLEAU_COLORS['tab:olive']] * 20
plt.figure(figsize=(8,9))
bplot = sns.barplot(data=to_plot_df.reset_index(),
x='index',
y='cor',
order=labels,
palette=colors, alpha=1.)
plt.xlabel(None)
plt.xticks(fontsize=25, color='black', rotation=90, fontproperties=prop_label)
plt.ylim(0,0.7)
plt.yticks(yticks, yticks_labels, fontsize=25, fontproperties=prop_ticks, color='black')
plt.ylabel('Spearman correlation on PDXs', fontsize=25, color='black', fontproperties=prop_label)
plt.tight_layout()
plt.savefig('%s/results_%s.png'%(drug_folder_name, saving_id), dpi=300)
| figure_2/2C-I_PDX_predictions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/FinalModule_Coursera/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# <h1 align=center><font size = 5>Data Analysis with Python</font></h1>
#
# # House Sales in King County, USA
#
# This dataset contains house sale prices for King County, which includes Seattle. It includes homes sold between May 2014 and May 2015.
#
# | Variable | Description |
# | ------------- | ----------------------------------------------------------------------------------------------------------- |
# | id | A notation for a house |
# | date | Date house was sold |
# | price | Price is prediction target |
# | bedrooms | Number of bedrooms |
# | bathrooms | Number of bathrooms |
# | sqft_living | Square footage of the home |
# | sqft_lot | Square footage of the lot |
# | floors | Total floors (levels) in house |
# | waterfront | House which has a view to a waterfront |
# | view | Has been viewed |
# | condition | How good the condition is overall |
# | grade | overall grade given to the housing unit, based on King County grading system |
# | sqft_above | Square footage of house apart from basement |
# | sqft_basement | Square footage of the basement |
# | yr_built | Built Year |
# | yr_renovated | Year when house was renovated |
# | zipcode | Zip code |
# | lat | Latitude coordinate |
# | long | Longitude coordinate |
# | sqft_living15 | Living room area in 2015(implies-- some renovations) This might or might not have affected the lotsize area |
# | sqft_lot15 | LotSize area in 2015(implies-- some renovations) |
#
# You will require the following libraries:
#
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler,PolynomialFeatures
from sklearn.linear_model import LinearRegression
# %matplotlib inline
# # Module 1: Importing Data Sets
#
# Load the csv:
#
# + jupyter={"outputs_hidden": false}
file_name='https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/FinalModule_Coursera/data/kc_house_data_NaN.csv'
df=pd.read_csv(file_name)
# -
# We use the method <code>head</code> to display the first 5 columns of the dataframe.
#
df.head()
# ### Question 1
#
# Display the data types of each column using the function dtypes, then take a screenshot and submit it, include your code in the image.
#
# + jupyter={"outputs_hidden": false}
print(df.dtypes)
# -
# We use the method describe to obtain a statistical summary of the dataframe.
#
# + jupyter={"outputs_hidden": false}
df.describe()
# -
# # Module 2: Data Wrangling
#
# ### Question 2
#
# Drop the columns <code>"id"</code> and <code>"Unnamed: 0"</code> from axis 1 using the method <code>drop()</code>, then use the method <code>describe()</code> to obtain a statistical summary of the data. Take a screenshot and submit it, make sure the <code>inplace</code> parameter is set to <code>True</code>
#
# + jupyter={"outputs_hidden": false}
df1 = df[["id", "Unnamed: 0"]]
df.drop(df1, axis = 1, inplace =True)
df.describe()
# -
# We can see we have missing values for the columns <code> bedrooms</code> and <code> bathrooms </code>
#
# + jupyter={"outputs_hidden": false}
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
# -
# We can replace the missing values of the column <code>'bedrooms'</code> with the mean of the column <code>'bedrooms' </code> using the method <code>replace()</code>. Don't forget to set the <code>inplace</code> parameter to <code>True</code>
#
mean=df['bedrooms'].mean()
df['bedrooms'].replace(np.nan,mean, inplace=True)
# We also replace the missing values of the column <code>'bathrooms'</code> with the mean of the column <code>'bathrooms' </code> using the method <code>replace()</code>. Don't forget to set the <code> inplace </code> parameter top <code> True </code>
#
mean=df['bathrooms'].mean()
df['bathrooms'].replace(np.nan,mean, inplace=True)
# + jupyter={"outputs_hidden": false}
print("number of NaN values for the column bedrooms :", df['bedrooms'].isnull().sum())
print("number of NaN values for the column bathrooms :", df['bathrooms'].isnull().sum())
# -
# # Module 3: Exploratory Data Analysis
#
# ### Question 3
#
# Use the method <code>value_counts</code> to count the number of houses with unique floor values, use the method <code>.to_frame()</code> to convert it to a dataframe.
#
# + jupyter={"outputs_hidden": false}
df1 = df["floors"].value_counts()
df1.to_frame()
# -
# ### Question 4
#
# Use the function <code>boxplot</code> in the seaborn library to determine whether houses with a waterfront view or without a waterfront view have more price outliers.
#
# + jupyter={"outputs_hidden": false}
sns.boxplot(data = df, x = "waterfront", y = "price")
# -
# ### Question 5
#
# Use the function <code>regplot</code> in the seaborn library to determine if the feature <code>sqft_above</code> is negatively or positively correlated with price.
#
# + jupyter={"outputs_hidden": false}
sns.regplot(x="sqft_above",y="price",data=df)
# -
# We can use the Pandas method <code>corr()</code> to find the feature other than price that is most correlated with price.
#
# + jupyter={"outputs_hidden": false}
df.corr()['price'].sort_values()
# -
# # Module 4: Model Development
#
# We can Fit a linear regression model using the longitude feature <code>'long'</code> and caculate the R^2.
#
# + jupyter={"outputs_hidden": false}
X = df[['long']]
Y = df['price']
lm = LinearRegression()
lm.fit(X,Y)
lm.score(X, Y)
# -
# ### Question 6
#
# Fit a linear regression model to predict the <code>'price'</code> using the feature <code>'sqft_living'</code> then calculate the R^2. Take a screenshot of your code and the value of the R^2.
#
# + jupyter={"outputs_hidden": false}
X = df[["sqft_living"]]
Y = df[["price"]]
lm = LinearRegression()
lm.fit(X,Y)
lm.predict(X)
lm.score(X,Y)
# -
# ### Question 7
#
# Fit a linear regression model to predict the <code>'price'</code> using the list of features:
#
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
# Then calculate the R^2. Take a screenshot of your code.
#
# + jupyter={"outputs_hidden": false}
X = df[["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]]
Y = df[["price"]]
lm = LinearRegression()
lm.fit(X,Y)
lm.predict(X)
lm.score(X,Y)
# -
# ### This will help with Question 8
#
# Create a list of tuples, the first element in the tuple contains the name of the estimator:
#
# <code>'scale'</code>
#
# <code>'polynomial'</code>
#
# <code>'model'</code>
#
# The second element in the tuple contains the model constructor
#
# <code>StandardScaler()</code>
#
# <code>PolynomialFeatures(include_bias=False)</code>
#
# <code>LinearRegression()</code>
#
Input=[('scale',StandardScaler()),('polynomial', PolynomialFeatures(include_bias=False)),('model',LinearRegression())]
# ### Question 8
#
# Use the list to create a pipeline object to predict the 'price', fit the object using the features in the list <code>features</code>, and calculate the R^2.
#
# + jupyter={"outputs_hidden": false}
features = df[["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]]
pipe = Pipeline(Input)
features= features.astype(float)
pipe.fit(features, df["price"])
pipe.predict(features)
pipe.score(X, df[["price"]])
# -
# # Module 5: Model Evaluation and Refinement
#
# Import the necessary modules:
#
# + jupyter={"outputs_hidden": false}
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
print("done")
# -
# We will split the data into training and testing sets:
#
# + jupyter={"outputs_hidden": false}
features =["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]
X = df[features]
Y = df['price']
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.15, random_state=1)
print("number of test samples:", x_test.shape[0])
print("number of training samples:",x_train.shape[0])
# -
# ### Question 9
#
# Create and fit a Ridge regression object using the training data, set the regularization parameter to 0.1, and calculate the R^2 using the test data.
#
from sklearn.linear_model import Ridge
# + jupyter={"outputs_hidden": false}
Ridgemodel=Ridge(alpha=0.1)
Ridgemodel.fit(x_train,y_train)
yhat=Ridgemodel.predict(x_train)
Ridgemodel.score(x_test,y_test)
# -
# ### Question 10
#
# Perform a second order polynomial transform on both the training data and testing data. Create and fit a Ridge regression object using the training data, set the regularisation parameter to 0.1, and calculate the R^2 utilising the test data provided. Take a screenshot of your code and the R^2.
#
# + jupyter={"outputs_hidden": false}
pr=PolynomialFeatures(degree=2)
x_train_pr=pr.fit_transform(x_train[["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]])
x_test_pr=pr.fit_transform(x_test[["floors", "waterfront","lat" ,"bedrooms" ,"sqft_basement" ,"view" ,"bathrooms","sqft_living15","sqft_above","grade","sqft_living"]])
Ridgemodel=Ridge(alpha=0.1)
Ridgemodel.fit(x_train_pr,y_train)
yhat=Ridgemodel.predict(x_train_pr)
Ridgemodel.score(x_test_pr,y_test)
# -
# <p>Once you complete your notebook you will have to share it. Select the icon on the top right a marked in red in the image below, a dialogue box should open, and select the option all content excluding sensitive code cells.</p>
# <p><img width="600" src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/FinalModule_Coursera/images/share_notebook.png" alt="share notebook" style="display: block; margin-left: auto; margin-right: auto;"/></p>
# <p></p>
# <p>You can then share the notebook via a URL by scrolling down as shown in the following image:</p>
# <p style="text-align: center;"><img width="600" src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DA0101EN-SkillsNetwork/labs/FinalModule_Coursera/images/url_notebook.png" alt="HTML" style="display: block; margin-left: auto; margin-right: auto;" /></p>
# <p> </p>
#
# <h2>About the Authors:</h2>
#
# <a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDA0101ENSkillsNetwork20235326-2021-01-01"><NAME></a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
#
# Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDA0101ENSkillsNetwork20235326-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/jiahui-mavis-zhou-a4537814a?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDA0101ENSkillsNetwork20235326-2021-01-01"><NAME></a>
#
# ## Change Log
#
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# | ----------------- | ------- | --------------- | -------------------------------------------- |
# | 2020-12-01 | 2.2 | <NAME> | Coverted Data describtion from text to table |
# | 2020-10-06 | 2.1 | <NAME> | Changed markdown instruction of Question1 |
# | 2020-08-27 | 2.0 | <NAME> | Added lab to GitLab |
#
# <hr>
#
# ## <h3 align="center"> © IBM Corporation 2020. All rights reserved. <h3/>
#
# <p>
#
| House_Sales_in_King_Count_USA (1) (2).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h3>Simulación matemática 2018 </h3>
# <div style="background-color:#0099cc;">
# <font color = white>
# <ul>
# <li><NAME> </li>
# <li>Email: `<EMAIL>, <EMAIL>`</li>
# </ul>
# </font>
# </div>
# <!--NAVIGATION-->
# < [Programación Lineal](Clase5_ProgramacionLineal.ipynb) | [Guía](Clase0_GuiaSimulacionM.ipynb) | [Clasificación Binaria](Clase7_ClasificacionBinaria.ipynb) >
# ___
# # Ajuste de curvas
#
# <img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/a/a8/Regression_pic_assymetrique.gif" width="400px" height="125px" />
#
# > El **ajuste de curvas** es el proceso de construir una curva (función), que sea el mejor ajuste a una serie de puntos. Las curvas ajustadas pueden ser usadas como asistencia en la visualización de datos, para inferir valores de una función donde no hay datos disponibles, y para resumir la relación entre variables.
#
# **Referencia**:
# - https://en.wikipedia.org/wiki/Curve_fitting
# ___
# ## Introducción
#
# Consideremos un polinomio de grado uno:
#
# $$y = \beta_1 x + \beta_0.$$
#
# Esta es una **línea recta** que tiene pendiente $\beta_1$. Sabemos que habrá una línea conectando dos puntos cualesquiera. Por tanto, *una ecuación polinómica de primer grado es un ajuste perfecto entre dos puntos*.
#
# Si consideramos ahora un polinomio de segundo grado,
#
# $$y = \beta_2 x^2 + \beta_1 x + \beta_0,$$
#
# este se ajustará exactamente a tres puntos. Si aumentamos el grado de la función a la de un polinomio de tercer grado, obtenemos:
#
# $$y = \beta_3 x^3 + \beta_2 x^2 + \beta_1 x + \beta_0,$$
#
# que se ajustará a cuatro puntos.
#
# **Ejemplos**
# 1. Encontrar la línea recta que pasa exactamente por los puntos $(0,1)$ y $(1,0)$.
# 2. Encontrar la parábola que pasa exactamente por los puntos $(-1,1)$, $(0,0)$ y $(1,1)$.
#
# **Solución**
# 1. Consideramos $y=\beta_1 x + \beta_0$. Evaluando en el punto $(0,1)$, obtenemos $\beta_1(0) + \beta_0 = 1$. Ahora, evaluando en el punto $(1,0)$, obtenemos $\beta_1(1) + \beta_0 = 0$. De esta manera,
# $$\left[\begin{array}{cc} 1 & 0 \\ 1 & 1\end{array}\right]\left[\begin{array}{c} \beta_0 \\ \beta_1\end{array}\right]=\left[\begin{array}{c} 1 \\ 0\end{array}\right].$$
# Resolviendo, $\beta_0=-\beta_1=1$.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("darkgrid")
# %matplotlib inline
# +
P1 = [0, 1]
P2 = [1, 0]
X = np.array([[1, 0], [1, 1]])
y = np.array([1, 0])
b0, b1 = np.linalg.inv(X).dot(y)
b0, b1
# +
x = np.linspace(-0.2, 1.2, 100)
y = b1*x + b0
plt.figure(figsize=(6,6))
plt.scatter([0, 1], [1, 0], c = "r", s = 50);
plt.plot(x, y, 'b', label = 'recta ajustada')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend(loc = 'best')
plt.grid(True)
plt.show()
# -
# 2. Consideramos $y=\beta_2 x^2 + \beta_1 x + \beta_0$. Evaluando en el punto $(-1,1)$, obtenemos $\beta_2(-1)^2 + \beta_1(-1) + \beta_0 = 1$. Ahora, evaluando en el punto $(0,0)$, obtenemos $\beta_2(0)^2 + \beta_1(0) + \beta_0 = 0$. Finalmente, evaluando en el punto $(1,1)$, obtenemos $\beta_2(1)^2 + \beta_1(1) + \beta_0 = 1$. De esta manera,
# $$\left[\begin{array}{ccc} 1 & -1 & 1 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right]\left[\begin{array}{c} \beta_0 \\ \beta_1 \\ \beta_2 \end{array}\right]=\left[\begin{array}{c} 1 \\ 0 \\ 1 \end{array}\right].$$
# Resolviendo, $\beta_0=\beta_1=0$ y $\beta_2=1$.
# +
P1 = [-1, 1]
P2 = [0, 0]
P3 = [1, 1]
X = np.array([[1, -1, 1], [1, 0, 0], [1, 1, 1]])
y = np.array([1, 0, 1])
b0, b1, b2 = np.linalg.inv(X).dot(y)
b0, b1, b2
# +
x = np.linspace(-1.2, 1.2, 100)
y = b2*x**2+b1*x+b0
plt.figure(figsize=(6,6))
plt.scatter([-1,0,1],[1,0,1], s = 100, label = 'puntos')
plt.plot(x, y, 'b', label = 'parábola ajustada')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend(loc = 'best')
plt.grid(True)
plt.show()
# -
# ### ¿Qué tienen en común los anteriores problemas?
# Las curvas están completamente determinadas por los puntos (datos limpios, suficientes y necesarios).
#
# Esto se traduce en que, al llevar el problema a un sistema de ecuaciones lineales, existe una única solución: **no hay necesidad, ni se puede optimizar nada**.
#
# ¿Tendremos datos así de '*bonitos*' en la vida real?
#
# La realidad es que los datos que encontraremos en nuestra vida profesional se parecen más a esto...
# +
x = np.linspace(0, 1, 30)
y = 10*x + 2 + np.random.randn(30)
plt.figure(figsize=(6,6))
plt.scatter(x, y)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# ### ¿Cómo ajustamos una curva a esto?
# ## Problema básico
#
# <img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/3/3a/Linear_regression.svg" width="400px" height="125px" />
#
# Consideramos que tenemos un conjunto de n pares ordenados de datos $(x_i,y_i)$, para $i=1,2,3,\dots,n$.
#
# ### ¿Cuál es la recta que mejor se ajusta a estos datos?
# Consideramos entonces ajustes de la forma $\hat{f}(x) = \beta_0+\beta_1 x = \left[1 \quad x\right]\left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array}\right]=\left[1 \quad x\right]\boldsymbol{\beta}$ (lineas rectas).
#
# Para decir '*mejor*', tenemos que definir algún sentido en que una recta se ajuste *mejor* que otra.
#
# **Mínimos cuadrados**: el objetivo es seleccionar los coeficientes $\boldsymbol{\beta}=\left[\beta_0 \quad \beta_1 \right]^T$, de forma que la función evaluada en los puntos $x_i$ ($\hat{f}(x_i)$) aproxime los valores correspondientes $y_i$.
#
# La formulación por mínimos cuadrados, encuentra los $\boldsymbol{\beta}=\left[\beta_0 \quad \beta_1 \right]^T$ que minimiza
# $$\sum_{i=1}^{n}(y_i-\hat{f}(x_i))^2=\sum_{i=1}^{n}(y_i-\left[1 \quad x_i\right]\boldsymbol{\beta})^2=\left|\left|\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta}\right|\right|^2,$$
#
# donde $\boldsymbol{y}=\left[y_1\quad\dots\quad y_n\right]^T$, y $\boldsymbol{X}=\left[\begin{array}{ccc}1 & x_1\\ \vdots & \vdots \\ 1 & x_n\end{array}\right].$ Esto es,
#
# $$\boldsymbol{\beta}^{ls} = \arg \min_{\boldsymbol{\beta}} \left|\left|\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta}\right|\right|^2$$
# Para llevar a cabo la anterior minimización, la librería `SciPy` en su módulo `optimize` contiene la función `minimize`.
import scipy.optimize as opt
def fun_obj1(b, x, y):
return np.sum((y-b[0]-b[1]*x)**2)
b0 = np.array([1, 5])
res = opt.minimize(fun_obj1, b0, args = (x, y))
res
# +
yhat = res.x[0]+res.x[1]*x
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'Datos')
plt.plot(x, yhat, '-r', label = 'Ajuste')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# ### Ajuste polinomial
#
# Ahora, considere el siguiente conjunto de datos...
# +
n = 100
x = np.linspace(np.pi/6, 5*np.pi/3, n)
y = 4*np.sin(x) + 0.5*np.random.randn(n)
plt.figure(figsize=(6,6))
plt.scatter(x, y)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# #### Ajustando una línea recta ?
# +
def obj1(b, x, y):
return np.sum((y-b[0]-b[1]*x)**2)
b0 = np.random.random((2,))
# -
res = opt.minimize(obj1, b0, args=(x,y))
res
# +
yhat1 = res.x[0]+res.x[1]*x
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'datos')
plt.plot(x, yhat1, '-r', label = 'ajuste 1')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# #### Ajustando una parábola?
# +
def obj2(b, x, y):
return np.sum((y-b[0]-b[1]*x-b[2]*x**2)**2)
b0 = np.random.random((3,))
# +
res = opt.minimize(obj2, b0, args=(x,y))
yhat2 = res.x[0]+res.x[1]*x+res.x[2]*x**2
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'datos')
plt.plot(x, yhat1, '-r', label = 'ajuste 1')
plt.plot(x, yhat2, '-g', label = 'ajuste 2')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# #### Quizá un polinomio cúbico...
# +
def obj3(b, x, y):
return np.sum((y-b[0]-b[1]*x-b[2]*x**2-b[3]*x**3)**2)
b0 = np.random.random((4,))
# +
res = opt.minimize(obj3, b0, args=(x,y))
yhat3 = res.x[0]+res.x[1]*x+res.x[2]*x**2+res.x[3]*x**3
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'datos')
plt.plot(x, yhat1, '-r', label = 'ajuste 1')
plt.plot(x, yhat2, '-g', label = 'ajuste 2')
plt.plot(x, yhat3, '-k', label = 'ajuste 3')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# #### Entonces, ¿mientras más se suba el orden mejor la aproximación?
#
# ## <font color = red > ¡Cuidado! OVERFITTING... </font>
def obj7(b, x, y):
return np.sum((y-np.array([x**i for i in range(8)]).T.dot(b))**2)
b0 = np.random.random((8,))
res = opt.minimize(obj7, b0, args=(x,y))
yhat7 = np.array([x**i for i in range(8)]).T.dot(res.x)
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'datos')
plt.plot(x, yhat1, '-r', label = 'ajuste 1')
plt.plot(x, yhat2, '-g', label = 'ajuste 2')
plt.plot(x, yhat3, '-k', label = 'ajuste 3')
plt.plot(x, yhat7, '-c', label = 'ajuste 7')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# #### Es conveniente ver el error como función del orden del polinomio... <font color = red> selección de modelos </font>
# +
e_ms = []
def obj(b, x, y, n):
return np.sum((y - np.array([x**i for i in range(n + 1)]).T.dot(b))**2)
for i in range(7):
b0 = np.random.random((i + 2,))
res = opt.minimize(obj, b0, args=(x,y,i + 1))
yhat = np.array([x**j for j in range(i + 2)]).T.dot(res.x)
e_ms.append(sum((y - yhat)**2))
plt.figure(figsize=(6,6))
plt.plot(np.arange(7) + 1, e_ms, 'o')
plt.xlabel('orden', fontsize = 18)
plt.ylabel('error', fontsize = 18)
plt.show()
# -
# ### ¿Cómo prevenir el <font color = red > *overfitting* </font> sin importar el orden del modelo?
# ## Regularización
#
# Vimos que la solución de mínimos cuadrados es:
# $$\boldsymbol{\beta}^{ls} = \arg \min_{\boldsymbol{\beta}} \left|\left|\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta}\right|\right|^2.$$
#
# Sin embargo, si crecemos el orden del modelo hay overfitting y algunos coeficientes óptimos $\boldsymbol{\beta}$ crecen muchísimo. Que un coeficiente sea muy grande, significa que se le da mucha importancia a alguna característica (que quizá sea ruido... no sirve para predecir).
#
# La regularización consiste en penalizar la magnitud de los coeficientes $\boldsymbol{\beta}$ en el problema de optimización, para que no crezcan tanto.
# - [Ridge](Ridge.ipynb)
# - [Lasso](Lasso.ipynb)
# - [Ajuste robusto](Ajuste_robusto.ipynb)
#
# ___
# ### Actividad
#
# 1. Ajustar polinomios de grado 1 hasta grado 7 a los siguientes datos.
# 2. Graficar el error cuadrático acumulado contra el número de términos, y elegir un polinomio que ajuste bien y su grado no sea muy alto.
# 4. Comparar los beta.
#
# Abrir un nuevo notebook, llamado `ActividadClase6_nombreApellido`.
def f(x):
return np.exp(-x**2/2)/np.sqrt(2*np.pi)
# +
x = np.linspace(-3, 3)
y = f(x) + 0.04*np.random.randn(50)
plt.figure(figsize=(6,6))
plt.scatter(x, y, label = 'datos')
plt.legend(loc = 'best')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.show()
# -
# ___
# <!--NAVIGATION-->
# < [Programación Lineal](Clase5_ProgramacionLineal.ipynb) | [Guía](Clase0_GuiaSimulacionM.ipynb) | [Clasificación Binaria](Clase7_ClasificacionBinaria.ipynb) >
# <script>
# $(document).ready(function(){
# $('div.prompt').hide();
# $('div.back-to-top').hide();
# $('nav#menubar').hide();
# $('.breadcrumb').hide();
# $('.hidden-print').hide();
# });
# </script>
#
# <footer id="attribution" style="float:right; color:#808080; background:#fff;">
# Created with Jupyter by <NAME>.
# <Strong> Copyright: </Strong> Public Domain como en [CC](https://creativecommons.org/licenses/by/2.0/) (Exepto donde se indique lo contrario)
#
#
# </footer>
| Modulo1/Clase6_AjusteCurvas.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python3
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Foundations of Computational Economics #8
#
# by <NAME>, ANU
#
# <img src="_static/img/dag3logo.png" style="width:256px;">
# + [markdown] slideshow={"slide_type": "fragment"}
# ## Bundle goods market
#
# <img src="_static/img/lab.png" style="width:64px;">
# + [markdown] slideshow={"slide_type": "subslide"}
# <img src="_static/img/youtube.png" style="width:65px;">
#
# [https://youtu.be/Y6CtsI8X914](https://youtu.be/Y6CtsI8X914)
#
# Description: Object oriented programming in modeling consumer choice model.
# + [markdown] slideshow={"slide_type": "slide"}
# Consider the following model of a bundle goods market. A
# bundle of goods is a collection of particular items offered at a
# specified price. For example, Happy Meals at McDonalds is a set
# of items in a meal sold for a particular price.
#
# One other example of bundled goods - subscription packages in theaters,
# for example [La Scala in
# Milan](http://www.teatroallascala.org/en/box-office/subscriptions/types/subscription-types-2018-2019.html)
# or [Mariinsky in
# St.Petersburg](https://www.mariinsky.ru/playbill/subscriptions/2018_2019).
#
# In this task you will write code to implement and operationalize this
# setup.
# + [markdown] slideshow={"slide_type": "slide"}
# ### Bundle_good class
#
# Develop the Python class to represent a bundle good with the following specifications:
#
# - The class attribute (common to all objects of this class) is a
# list of goods
# - The public property is a vector of integers defining how many of each goods are in the bundle
# - The other property is the price for that bundle
#
#
# The following arithmetic operations are defined for the bungles:
#
# - addition:
# 1. sum of two bundles is a bundle with added up items and prices
# 1. sum of a bundle and a number (float or int) increases the price
# - subtraction:
# 1. difference between two bundles should produce a bundle with
# difference in items and difference in prices
# 1. subtracting a number (float or int) from a bundle should only
# decrease its price
# - multiplication is only defined for bundle and an integers, and results in the bundle with all items multiplied by this number, and price increased by the same number
# - devision is only defined for integers, and only such that the all quantities are divisible by this integer, the resulting bundle is a fraction of the original, with the price also decreased by the same number
#
#
# Complete the class definition code, and run the tests in the next cell.
# + hide-output=false slideshow={"slide_type": "slide"}
class bundle_good():
'''Class of bundled goods with well defined arithmetics'''
items = ('Opera A', 'Opera B', \
'Ballet A', 'Ballet B', \
'Symphonic orchestra concert', \
'Rock opera', \
'Operetta') # 7 different goods
def __init__(self,quantities=[0,],price=0.0):
'''Creates the bundle good object, empty by default'''
pass
# ignore extra quantities if passed
# add zeros for the unspecified items
# ensure all quantities are integers
def __repr__(@@@):
'''String representation of the object'''
pass
def __add__(self,other):
'''Addition for bundle goods'''
pass
# if wrong type pass, raise the TypeError
# raise TypeError('Can only add bundle to bundle, or number to bundle price')
def __sub__(self,other):
'''Subtraction for bundles: subtract items and prices, or decrease price'''
pass
def __mul__(self,num):
'''Multiplication for bundles: proportional increase in nomenclature and price'''
pass
def __truediv__(self,num):
'''Division for bundles: fraction of the original bundle, only if quantities are divisable'''
pass
# + [markdown] slideshow={"slide_type": "slide"}
# ### Tests
#
# To make sure the class is running as it is supposed to, run all the
# tests below and confirm that the output is as expected.
# + hide-output=false slideshow={"slide_type": "slide"}
# Tests
x=bundle_good([1,2,3,4,5,6,7],11.43)
print(x) #should print "Bundle object [1, 2, 3, 4, 5, 6, 7] with price 11.43"
# + hide-output=false slideshow={"slide_type": "slide"}
x=bundle_good([1,2])
print(x) #should print "Bundle object [1, 2, 0, 0, 0, 0, 0] with price 0.00"
# + hide-output=false slideshow={"slide_type": "slide"}
x=bundle_good(range(25),100.2)
print(x) #should print "Bundle object [0, 1, 2, 3, 4, 5, 6] with price 100.20"
# + hide-output=false slideshow={"slide_type": "slide"}
x=bundle_good([1.5,2.3,3.2,4.1,5.75,6.86,7.97],1.43)
print(x) #should print "Bundle object [1, 2, 3, 4, 5, 6, 7] with price 1.43"
# + hide-output=false slideshow={"slide_type": "slide"}
x=bundle_good([1,2,3,4,5,6,7],11.43)
y=bundle_good([7,6,5,4,3,2,1],77.45)
z=x+y
print(z) #should print "Bundle object [8, 8, 8, 8, 8, 8, 8] with price 88.88"
# + hide-output=false slideshow={"slide_type": "slide"}
z=y-x
print(z) #should print "Bundle object [6, 4, 2, 0, -2, -4, -6] with price 66.02"
# + hide-output=false slideshow={"slide_type": "slide"}
z=x+4.531
print(z) #should print "Bundle object [1, 2, 3, 4, 5, 6, 7] with price 15.96"
# + hide-output=false slideshow={"slide_type": "slide"}
z=y-77
print(z) #should print "Bundle object [7, 6, 5, 4, 3, 2, 1] with price 0.45"
# + hide-output=false slideshow={"slide_type": "slide"}
z=x*11
print(z) #should print "Bundle object [11, 22, 33, 44, 55, 66, 77] with price 125.73"
# + hide-output=false slideshow={"slide_type": "slide"}
try:
z=x*11.5 #should raise a TypeError
except TypeError:
print("Ok 1") #should print "Ok 1"
# + hide-output=false slideshow={"slide_type": "slide"}
try:
z=x*y #should raise a TypeError
except TypeError:
print("Ok 2") #should print "Ok 2"
# + hide-output=false slideshow={"slide_type": "slide"}
try:
z=x/y #should raise a TypeError
except TypeError:
print("Ok 3") #should print "Ok 3"
# + hide-output=false slideshow={"slide_type": "slide"}
z=(x+y)/8
print(z) #should print "Bundle object [1, 1, 1, 1, 1, 1, 1] with price 11.11"
# + hide-output=false slideshow={"slide_type": "slide"}
try:
(x+y)/7 #should raise a ValueError
except ValueError:
print("Ok 4") #should print "Ok 4"
# + hide-output=false slideshow={"slide_type": "slide"}
z=x*15-y*2
print(z) #should print "Bundle object [1, 18, 35, 52, 69, 86, 103] with price 16.55"
# + [markdown] slideshow={"slide_type": "slide"}
# ### Solution
# + hide-output=false slideshow={"slide_type": "slide"}
class bundle_good():
'''Class of bundled goods with well defined arithmetics'''
items = ('Opera A', 'Opera B', \
'Ballet A', 'Ballet B', \
'Symphonic orchestra concert', \
'Rock opera', \
'Operetta') # 7 different goods
def __init__(self,quantities=[0,],price=0.0):
'''Creates the bundle good object
'''
n = len(bundle_good.items) # number of available items
if len(quantities)<n:
# add zeros for the unspecified items
quantities += [0,]*(n-len(quantities))
elif len(quantities)>n:
# ignore extra numbers
quantities = quantities[0:n]
# create public attributes
# ensure the quantities in the object are integer
self.quantities=[int(x) for x in quantities]
self.price=price
def __repr__(self):
'''String representation of the object
'''
return 'Bundle object %r with price %1.2f' % (self.quantities,self.price)
def __add__(self,other):
'''Addition for bundles: add items and sum prices, or increase price
'''
if type(other) is bundle_good:
# add the quantities using list comprehension with one-to-one matching (zip)
q1 = [x+y for x,y in zip(self.quantities, other.quantities)]
# sum of the prices
p1 = self.price + other.price
# return new bundle
return bundle_good(quantities=q1,price=p1)
elif type(other) in (float,int):
# increase the price
p1 = self.price + other
# return new bundle
return bundle_good(quantities=self.quantities,price=p1)
else:
raise TypeError('Can only add bundle to bundle, or number to bundle price')
def __sub__(self,other):
'''Subtraction for bundles: subtract items and prices, or decrease price
'''
if type(other) is bundle_good:
# subtract the quantities using list comprehension with one-to-one matching (zip)
q1 = [x-y for x,y in zip(self.quantities, other.quantities)]
# sum of the prices
p1 = self.price - other.price
# return new bundle
return bundle_good(quantities=q1,price=p1)
elif type(other) in (float,int):
# decrease the price
p1 = self.price - other
# return new bundle
return bundle_good(quantities=self.quantities,price=p1)
else:
raise TypeError('Can only subtract bundle from bundle, or number from bundle price')
def __mul__(self,num):
'''Multiplication for bundles: repetition of the original bundle
'''
if type(num) is int:
# multiply quantities using list comprehension
q1 = [x * num for x in self.quantities]
# multiply the price
p1 = self.price * num
# return new bundle
return bundle_good(price=p1,quantities=q1)
else:
raise TypeError('Can only multiply bundle by an integer')
def __truediv__(self,num):
'''Division for bundles: fraction of the original bundle, only if quantities are devisable
'''
if type(num) is int:
# divide quantities and check for divisibility
q1 = [q//num for q in self.quantities]
if not all(q%num==0 for q in self.quantities):
# if can not be devided without a remainder, raise ValueError
raise ValueError('Can not divide bundle into fractional parts')
# divide the price
p1=self.price / num
# return new bundle
return bundle_good(price=p1,quantities=q1)
else:
raise TypeError('Can only divide bundle by an integer')
| 08_bundles_ex2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Let's draw a bar chart
# +
import numpy as np
import matplotlib.pyplot as plt
men_means, men_std = (20, 35, 30, 35, 27), (2, 3, 4, 1, 2)
women_means, women_std = (25, 32, 34, 20, 25), (3, 5, 2, 3, 3)
ind = np.arange(len(men_means)) # the x locations for the groups
width = 0.35 # the width of the bars
fig, ax = plt.subplots()
rects1 = ax.bar(ind - width/2, men_means, width, yerr=men_std,
color='SkyBlue', label='Men')
rects2 = ax.bar(ind + width/2, women_means, width, yerr=women_std,
color='IndianRed', label='Women')
# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Scores')
ax.set_title('Scores by group and gender')
ax.set_xticks(ind)
ax.set_xticklabels(('G1', 'G2', 'G3', 'G4', 'G5'))
ax.legend()
def autolabel(rects, xpos='center'):
"""
Attach a text label above each bar in *rects*, displaying its height.
*xpos* indicates which side to place the text w.r.t. the center of
the bar. It can be one of the following {'center', 'right', 'left'}.
"""
xpos = xpos.lower() # normalize the case of the parameter
ha = {'center': 'center', 'right': 'left', 'left': 'right'}
offset = {'center': 0.5, 'right': 0.57, 'left': 0.43} # x_txt = x + w*off
for rect in rects:
height = rect.get_height()
ax.text(rect.get_x() + rect.get_width()*offset[xpos], 1.01*height,
'{}'.format(height), ha=ha[xpos], va='bottom')
autolabel(rects1, "left")
autolabel(rects2, "right")
plt.show()
# -
| notebooks/Bar chart.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from collections import defaultdict
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
#import torch
#import torch.nn as nn
from pylab import *
from numpy import *
import numpy as np
from PIL import Image
import math
import time
from random import random
# -
from scipy.ndimage import geometric_transform
from scipy.ndimage import map_coordinates
def shift_func(coords,a,b,c,d):
""" Define the mobius transformation, though backwards """
#turn the first two coordinates into an imaginary number
z = coords[0] + 1j*coords[1]
w = (d*z-b)/(-c*z+a) #the inverse mobius transform
#take the color along for the ride
return real(w),imag(w),coords[2]
# +
# Image attributes
img_path='horse.png'
img = Image.open(img_path).convert('RGB')
image = np.array(img)
print(image.shape)
height=image.shape[0]
width=image.shape[1]
imshow(image)
# -
def drawpoints(image, point, color):
h = point[0]
w = point[1]
where_to_draw = []
where_to_draw.append(point)
where_to_draw.append([h-1,w])
where_to_draw.append([h+1,w])
where_to_draw.append([h,w-1])
where_to_draw.append([h,w+1])
new_where_to_draw=[]
for item in where_to_draw:
if item[0]>=0 and item[0]<height and item[1]>=0 and item[1]<width:
new_where_to_draw.append(item)
for item in new_where_to_draw:
if color == 'red':
image[item[0],item[1]]=[255,102,102]
elif color == 'green':
image[item[0],item[1]]=[0,204,0]
elif color == 'blue':
image[item[0],item[1]]=[0,128,255]
def get_images(original_image,a,b,c,d,new_points,original_points):
height=original_image.shape[0]
width=original_image.shape[1]
e=[complex(0,0)]*height*width
z=np.array(e).reshape(height,width)
for i in range(0,height):
for j in range(0,width):
z[i,j]=complex(i,j)
r = ones((height, width,3),dtype=uint8)*255
w = (a*z+b)/(c*z+d)
first=real(w)*1
second=imag(w)*1
first=first.astype(int)
second=second.astype(int)
f1=first>=0
f2=first<height
f= f1 & f2
s1=second>=0
s2=second<width
s= s1 & s2
combined = s&f
i=np.array(list(range(0,height))*width).reshape(width,height).T
j=np.array(list(range(0,width))*height).reshape(height,width)
r[first[combined],second[combined],:]=original_image[i[combined],j[combined],:]
start = time.time()
r2 = geometric_transform(original_image,shift_func,cval=0,order = 3,output_shape=(height,width,3),mode='constant',extra_arguments=(a,b,c,d))
end = time.time()
print('Time to get interpolation:', end - start)
drawpoints(r2, new_points[0], 'red')
drawpoints(r2, new_points[1], 'green')
drawpoints(r2, new_points[2], 'blue')
drawpoints(original_image, original_points[0], 'red')
drawpoints(original_image, original_points[1], 'green')
drawpoints(original_image, original_points[2], 'blue')
drawpoints(r, new_points[0], 'red')
drawpoints(r, new_points[1], 'green')
drawpoints(r, new_points[2], 'blue')
figure(figsize=(15, 10))
subplot(1,3,1)
title('Original')
imshow(original_image)
subplot(1,3,2)
title('No interpolation')
imshow(r)
subplot(1,3,3)
title('With interpolation')
imshow(r2)
# +
def M_admissable(a,b,c,d):
M=3
v1 = np.absolute(a) ** 2 / np.absolute(a*d - b*c)
if not (v1 < M and v1 > 1/M):
return False
v2 = np.absolute(a-32*c) ** 2 / (np.absolute(a*d -b*c))
if not (v2 < M and v2 > 1/M):
return False
v3 = np.absolute(complex(a,-32*c)) ** 2 / np.absolute(a*d-b*c)
if not (v3 < M and v3 > 1/M):
return False
v4 = np.absolute(complex(a-32*c,-32*c)) ** 2 / np.absolute(a*d-b*c)
if not (v4 < M and v4 > 1/M):
return False
v5 = np.absolute(complex(a-16*c,-16*c)) ** 2 / (np.absolute(a*d-b*c))
if not (v5 < M and v5 > 1/M):
return False
v6 = np.absolute(complex(16*d-b,16*d)/complex(a-16*c,-16*c)-complex(16,16))
if not( v6 < 8):
return False
return True
# +
zp=[complex(height*random(),width*random()), complex(height*random(),width*random()),complex(height*random(),width*random())]
wa=[complex(height*random(),width*random()), complex(height*random(),width*random()),complex(height*random(),width*random())]
original_points = np.array([[real(zp[0]),imag(zp[0])],
[real(zp[1]),imag(zp[1])],
[real(zp[2]),imag(zp[2])]],dtype=int)
new_points = np.array([[real(wa[0]),imag(wa[0])],
[real(wa[1]),imag(wa[1])],
[real(wa[2]),imag(wa[2])]],dtype=int)
# transformation parameters
a = linalg.det([[zp[0]*wa[0], wa[0], 1],
[zp[1]*wa[1], wa[1], 1],
[zp[2]*wa[2], wa[2], 1]]);
b = linalg.det([[zp[0]*wa[0], zp[0], wa[0]],
[zp[1]*wa[1], zp[1], wa[1]],
[zp[2]*wa[2], zp[2], wa[2]]]);
c = linalg.det([[zp[0], wa[0], 1],
[zp[1], wa[1], 1],
[zp[2], wa[2], 1]]);
d = linalg.det([[zp[0]*wa[0], zp[0], 1],
[zp[1]*wa[1], zp[1], 1],
[zp[2]*wa[2], zp[2], 1]]);
# -
oringial_image = image.copy()
get_images(oringial_image,a,b,c,d,new_points,original_points)
M_admissable(a,b,c,d)
test=False #finding true ones
while test==False:
zp=[complex(height*random(),width*random()), complex(height*random(),width*random()),complex(height*random(),width*random())]
wa=[complex(height*random(),width*random()), complex(height*random(),width*random()),complex(height*random(),width*random())]
original_points = np.array([[real(zp[0]),imag(zp[0])],
[real(zp[1]),imag(zp[1])],
[real(zp[2]),imag(zp[2])]],dtype=int)
new_points = np.array([[real(wa[0]),imag(wa[0])],
[real(wa[1]),imag(wa[1])],
[real(wa[2]),imag(wa[2])]],dtype=int)
# transformation parameters
a = linalg.det([[zp[0]*wa[0], wa[0], 1],
[zp[1]*wa[1], wa[1], 1],
[zp[2]*wa[2], wa[2], 1]]);
b = linalg.det([[zp[0]*wa[0], zp[0], wa[0]],
[zp[1]*wa[1], zp[1], wa[1]],
[zp[2]*wa[2], zp[2], wa[2]]]);
c = linalg.det([[zp[0], wa[0], 1],
[zp[1], wa[1], 1],
[zp[2], wa[2], 1]]);
d = linalg.det([[zp[0]*wa[0], zp[0], 1],
[zp[1]*wa[1], zp[1], 1],
[zp[2]*wa[2], zp[2], 1]]);
test=M_admissable(a,b,c,d)
oringial_image = image.copy()
get_images(oringial_image,a,b,c,d,new_points,original_points)
M_admissable(a,b,c,d)
# +
#trying to mimic the false negative
zp=[complex(height*0.8,width*0.5), complex(height*0.5,width*0.3), complex(height*0.25,width*0.5)]
wa=[complex(height*0.25,width*0.5), complex(height*0.5,width*0.75), complex(height*0.8,width*0.5)]
original_points = np.array([[real(zp[0]),imag(zp[0])],
[real(zp[1]),imag(zp[1])],
[real(zp[2]),imag(zp[2])]],dtype=int)
new_points = np.array([[real(wa[0]),imag(wa[0])],
[real(wa[1]),imag(wa[1])],
[real(wa[2]),imag(wa[2])]],dtype=int)
# transformation parameters
a = linalg.det([[zp[0]*wa[0], wa[0], 1],
[zp[1]*wa[1], wa[1], 1],
[zp[2]*wa[2], wa[2], 1]]);
b = linalg.det([[zp[0]*wa[0], zp[0], wa[0]],
[zp[1]*wa[1], zp[1], wa[1]],
[zp[2]*wa[2], zp[2], wa[2]]]);
c = linalg.det([[zp[0], wa[0], 1],
[zp[1], wa[1], 1],
[zp[2], wa[2], 1]]);
d = linalg.det([[zp[0]*wa[0], zp[0], 1],
[zp[1]*wa[1], zp[1], 1],
[zp[2]*wa[2], zp[2], 1]]);
oringial_image = image.copy()
get_images(oringial_image,a,b,c,d,new_points,original_points)
M_admissable(a,b,c,d)
# -
np.absolute(a-32*c) ** 2 / (np.absolute(a*d -b*c)) # just a bit complex syntax test below
a
np.absolute(complex(a,-32*c))
c
aa=complex(0,1)
cc=complex(2,3)
complex(0,cc)
np.absolute(32*c+a*complex(0,1))
| mobius_data_augmentation/notebooks/M-admissable-focused.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Omniglot symbol drawing speed exploration
# This notebook extracts the time taken to draw the symbol and the number of strokes (based on the pen up actions). But, only time is taken into consideration to find the easiest symbols.
# ## Find all stroke files
#
# Note that this algorithm expects all stroke files to be within the relative `../Datasets/omniglot_strokes` folder.
# +
import os
def list_files(dir, ext='txt'):
r = []
for root, dirs, files in os.walk(dir):
for name in files:
if name.endswith(ext):
r.append(os.path.join(root, name))
return r
# -
stroke_file_paths = list_files("../Datasets/omniglot_strokes")
print("{} characters found".format(len(stroke_file_paths)))
# ## Create a DataFrame with strokes and time
import pandas as pd
import numpy as np
df = pd.DataFrame(columns=['path', 'alphabet', 'character', 'strokes', 'time'])
for idx, stroke_file_path in enumerate(stroke_file_paths):
path_components = stroke_file_path.split("/")
character_nr = int(''.join(filter(str.isdigit, path_components[-2])))
alphabet = path_components[-3]
df.loc[idx] = (stroke_file_path, alphabet, character_nr, np.nan, np.nan)
for index, row in df.iterrows():
with open(row[0]) as fp:
lines = fp.readlines()
nr_strokes = sum([1 for line in lines if "BREAK" in line])
t = 0
for line in reversed(lines):
if "," in line:
t = int(line.split(",")[-1])
break
df.loc[index, "strokes"] = nr_strokes
df.loc[index, "time"] = t
df
# ## Find the characters that were written the fastest
fastest_symbols = df.groupby(['alphabet', 'character'])['time'].apply(np.median).sort_values()
for alphabet, char in fastest_symbols.index:
print(alphabet, char)
import ipyplot
from PIL import Image
images = []
labels = []
easy_symbols = df.groupby(['alphabet', 'character'])['time'].apply(np.median).sort_values().index[0:400]
for alphabet, char in easy_symbols:
char_row = df[(df.alphabet == alphabet) & (df.character == char)].iloc[0]
path = "../Datasets/omniglot_images/{}/character{:02d}/{}".format(char_row.alphabet, char_row.character, char_row.path.split("/")[-1][:-3]+"png")
labels.append(char_row.path.split("/")[-1].split("_")[0])
images.append(Image.open(path))
easy_symbols[9]
ipyplot.plot_images(images, labels, max_images=100, img_width=60)
ipyplot.plot_images(images, max_images=400, img_width=30)
# ## Time spent by number fo strokes
df.loc[28112]
med_strokes = df.groupby(['alphabet', 'character'])['strokes'].apply(np.median)
med_time = df.groupby(['alphabet', 'character'])['time'].apply(np.median)
strokes_time = pd.concat([med_strokes, med_time], axis=1)
strokes_time
median_by_strokes = strokes_time.groupby(['strokes'])['time'].apply(np.median)
median_by_strokes
# +
import matplotlib.pyplot as plt
# %matplotlib inline
x = median_by_strokes.index
y = median_by_strokes.values / 1000
plt.figure(figsize=(15,7))
plt.scatter(x, y)
plt.xlabel("Median Strokes")
plt.ylabel("Median Time (in seconds)")
plt.title("Median Speed Compared to Median Number of Strokes of Characters")
z = np.polyfit(x, y, 2)
p = np.poly1d(z)
plt.plot(x,p(x),"r--")
plt.show()
| Chapter2/Symbol Drawing Speed.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Face Operation Project
# * This is a simple `open-cv` face operation that creates a ghost image from another image
### Imports
import cv2
import numpy as np
from matplotlib import pyplot as plt
# ## Read an image and display It
# * The image we are going to read is in the `images` directory with name 'me.jpg'
# +
image = cv2.imread("me.jpg")
# imageRgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# imageGray = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
allImages = np.vstack([image])
plt.imshow(allImages)
plt.show()
# -
| beginner/Face-Operation-1-Open-CV-Py/.ipynb_checkpoints/ghost-image-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''zonmw'': conda)'
# language: python
# name: python3
# ---
# +
import pandas as pd
import matplotlib.pyplot as plt
import sys
sys.path.insert(0, '..')
from utils.config import PATHS
# -
# # Load data
# +
# all covid data with classifier predictions
path = PATHS.getpath('data_covid')
df = pd.read_pickle(path / 'covid_data.pkl').astype({'MDN': int})
df.Notitiedatum = pd.to_datetime(df.Notitiedatum)
# +
# time-series annotations of one patient (1165165)
path = PATHS.getpath('data_timeseries_annot')
pat = pd.read_excel(path / 'from_meskers/IAA-1165165-n.recs-43.xlsx')
pat.Notitiedatum = pd.to_datetime(pat.Notitiedatum)
# -
# # Process ADM levels
# +
# select the relevant patient from the classifier data
algo = df.loc[lambda df: df.MDN.isin(pat.MDN)].sort_values('Notitiedatum')
# +
# remove notes of type 'Brief' (n=6)
# align gold and predicted labels for ADM
get_dom = lambda df, dom: df.query("Typenotitie not in ['Brief']").set_index('Notitiedatum')[dom]
dom = 'ADM_lvl'
source = pd.concat([
get_dom(algo, dom).rename('classif'),
get_dom(pat, dom).rename('gold'),
], axis=1)
# -
source
# # Plot ADM levels
#
# The "broken axis" plot code is based on: [https://matplotlib.org/stable/gallery/subplots_axes_and_figures/broken_axis.html](https://matplotlib.org/stable/gallery/subplots_axes_and_figures/broken_axis.html)
# +
# if there are multiple notes on the same date, a mean level is plotted
data = source.resample('d').mean().interpolate()
fig, (ax1, ax2) = plt.subplots(1,2, sharey=True, tight_layout=True)
fig.subplots_adjust(wspace=0.05)
for ax in (ax1, ax2):
ax.plot(data.gold, label='gold')
ax.plot(data.classif, label='classifier')
ticks = source.dropna(subset=['gold']).index.unique()
ax.set_xticks(ticks)
ax.set_xticklabels([f"{i:%d-%m-%Y}" for i in ticks])
for label in ax.get_xticklabels():
label.set_rotation(90)
ax1.set_ylim(0, 4.5)
ax1.set_xlim(
pd.Timestamp('2020-03-24').to_pydatetime(),
pd.Timestamp('2020-04-02').to_pydatetime()
)
ax2.set_xlim(
pd.Timestamp('2020-06-01').to_pydatetime(),
pd.Timestamp('2020-10-01').to_pydatetime()
)
ax2.yaxis.set_ticks_position('none')
ax1.spines['right'].set_visible(False)
ax2.spines['left'].set_visible(False)
# add slanted lines where the axis breaks
d = 0.9
kwargs = dict(marker=[(-1, -d), (1, d)],
markersize=12,
linestyle="none", color='k', mec='k', mew=1, clip_on=False
)
ax1.plot([1, 1], [1, 0], transform=ax1.transAxes, **kwargs)
ax2.plot([0, 0], [0, 1], transform=ax2.transAxes, **kwargs)
ax2.legend(loc='lower right')
plt.savefig('figures/recpattern.png', dpi=300)
| nb_data_analysis/covid_rec_pattern_example.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="st0Rer20lXyu"
# # TP 2 : Computer Vision
#
# ## Part 3 : motion estimation
#
# In this part of the TP, we are going to look at the following method for estimating motion :
#
# - block matching
#
# First, let us again load some packages and define some helper functions
# + id="kQ2xEyMtlXy4" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="4ab624e3-426c-46ef-c4eb-5eb8a9196cce"
from matplotlib import pyplot as plt
import matplotlib as mpl
import numpy as np
import imageio
from skimage import color
from scipy import signal
from scipy.ndimage.morphology import binary_dilation
is_colab = True
def read_image(file_name):
img_color = imageio.imread(file_name)
img_gray = color.rgb2gray(img_color)
return img_gray,img_color
def write_image(img_in,file_name_out):
imageio.imwrite(file_name_out, np.uint8(255.0*img_in))
def display_image(img_in):
plt.figure(figsize=(10, 10))
if (img_in.ndim == 2):
plt.imshow(img_in,cmap='gray')
elif (img_in.ndim == 3):
# careful, in this case we supppose the pixel values are between 0 and 255
plt.imshow(np.uint8(img_in))
else:
print('Error, unknown number of dimensions in image')
return
def display_motion(img_1,img_2,key_pts,motion,file_save=''):
motion_x = motion[:,0]
motion_y = motion[:,1]
img_size = img_1.shape
head_width=2.0
head_length=3.0
fig = plt.figure()
plt.figure(figsize=(10, 10))
ax = plt.imshow(img_1,cmap='gray')
print(key_pts.shape[0])
for i in range(0,key_pts.shape[0]):
x = key_pts[i,0]
y = key_pts[i,1]
plt.arrow(x,y, motion_x[i],motion_y[i] , color='r',
head_width=head_width, head_length=head_length,)
plt.gca().set_axis_off()
fig.subplots_adjust(top = 1, bottom = 0, right = 1, left = 0,
hspace = 0, wspace = 0)
plt.margins(0,0)
plt.gca().xaxis.set_major_locator(mpl.ticker.NullLocator())
plt.gca().yaxis.set_major_locator(mpl.ticker.NullLocator())
if (file_save != ''):
plt.savefig(file_save, bbox_inches = 'tight', pad_inches = 0)
file_dir = 'images/'
file_name_1 = 'afgrunden_1'
file_name_2 = 'afgrunden_2'
file_ext = '.png'
if (is_colab == True):
# !wget "https://perso.telecom-paristech.fr/anewson/doc/images/afgrunden_1.png"
# !wget "https://perso.telecom-paristech.fr/anewson/doc/images/afgrunden_2.png"
img_1,_ = read_image(file_name_1+file_ext)
img_2,_ = read_image(file_name_2+file_ext)
else:
img_1,_ = read_image(file_dir+file_name_1+file_ext)
img_2,_ = read_image(file_dir+file_name_2+file_ext)
display_image(img_1)
display_image(img_2)
img_size = img_1.shape
img_size
# + [markdown] id="kYhm5AXhlXy7"
# __Question__ What sort of motion do you think is there between img_1 and img_2 ? You may want to flip between one image and another in an external viewer.
# + [markdown] id="N-y6YAUvlXy8"
# *__Answer__* A sort of rotatin of the camera
# + [markdown] id="lQr3Ly92lXy8"
# ## Block matching
#
# Block matching is a very intuitive algorithm for motion estimation. We choose a patch size, and for each patch $\Psi_p$ in the first frame, we look for the patch $\Psi_q$ which is the most similar, in a certain region around the original position. The motion $(\delta_x,\delta_y)$ is then defined as $(\delta_x,\delta_y) = q-p$, such that :
#
# $
# \begin{cases}
# q_x = p_x+\delta_x\\
# q_y = p_y+\delta_y
# \end{cases}
# $
#
# The ''similarity'' between two patches is the sum of squared differences (SSD) :
#
# $d(\Psi_p,\Psi_q) = \sum_{i \Psi} \left( I(p+i) - I(q+i) \right)^2,$
#
# where $\Psi$ is the patch neighbourhood (a square).
#
# We are going to be implementing block matching in a function called ``block_matching``. However, this can take a lot of time, so we only carry it out on a subset of the pixels, which we will call ``key_pts``. This will be a matrix of size $(N,2)$, where $N$ is the number of keypoints, and where each line has the following format :
#
# - $[x,y]$
#
# Create this function now, with the following parameters :
#
# - block_size = 7 (the patch size)
# - search_size = 15 (the maximum distance we search for the same patch in)
#
# You will have to deal with border conditions. There are two ways of doing this :
#
# - not allowing the patch search to go near to the borders (no closer than half the patch size)
# - making partial patch comparisons
#
# You can choose either method. The first is slightly easier to implement, but potentially incorrect near the borders. The second is more correct, but you have to make sure to make partial patch comparisons.
#
# Make sure you do __not__ carry out the patch distance calculation with a loop (which would not be very optimal). You can first create the patch neighbourhood $\Psi$ with
#
# - ``np.meshgrid``
#
# and then take the SSD of the two patches.
#
# Fill in the following function.
# + id="CcLqwf8GlXy9"
def block_matching(img_1,img_2,key_pts):
# FILL IN CODE HERE
motion = []
block_size = 7
search_size = 15
m, n =img_1.shape
for p in key_pts:
ssd_inf = np.inf
motion.append([0,0])
for dx in np.arange(-search_size,search_size+1):
for dy in np.arange(-search_size,search_size+1):
q = p + np.array([dx, dy])
if np.all(p!=q) and q[0] >= 0 and q[0] < n and q[1] >= 0 and q[1] < m:
min_depth_x = block_size - 1 if p[0] - block_size + 1 >= 0 else p[0]
max_depth_x = block_size - 1 if p[0] + block_size - 1 < n else n-1-p[0]
min_depth_y = block_size - 1 if p[1] - block_size + 1 >= 0 else p[1]
max_depth_y = block_size - 1 if p[1] + block_size - 1 < m else m-1-p[1]
min_patch_x = max([q[0] - min_depth_x, p[0] - search_size, 0])
max_patch_x = min([q[0] + max_depth_x, p[0] + search_size, n-1])
min_patch_y = max([q[1] - min_depth_y, p[1] - search_size, 0])
max_patch_y = min([q[1] + max_depth_y, p[1] + search_size, m-1])
patch_q = img_2[min_patch_y:(max_patch_y + 1)][:,min_patch_x:(max_patch_x + 1)]
patch_p = img_1[np.arange(min_patch_y, max_patch_y + 1) - q[1] + p[1]][:,np.arange(min_patch_x, max_patch_x + 1) - q[0] + p[0]]
ssd = np.sum(np.power((patch_p - patch_q),2))
if ssd < ssd_inf:
ssd_inf = ssd
motion[-1] = [dx, dy]
motion = np.asarray(motion)
return motion
# + [markdown] id="C4rYuO_tlXy-"
# We now draw some random keypoints to carry out the block matching on.
# + id="n_S_tE2SlXy-"
n_pts = 80
key_pts = np.zeros((n_pts,2)).astype(int)
# a random seed, if you want repeatability
np.random.seed(10)
pixel_list = np.asarray(range(0,img_size[0]*img_size[1]))
np.random.shuffle(pixel_list)
key_pts = np.zeros((n_pts,2)).astype(int)
key_pts[:,1],key_pts[:,0] = np.unravel_index(pixel_list[0:n_pts],img_size)
# + id="yXcawJ46lXy_" colab={"base_uri": "https://localhost:8080/"} outputId="a1fefa45-11ac-4b35-f989-8dce156f6bd8"
key_pts[:,0].max()
# + [markdown] id="QaMdiMEwlXy_"
# Carry out the block matching and display the result with the ``display_motion`` function.
# + id="OYx5Zb8ylXy_"
motion = block_matching(img_1,img_2,key_pts)
# + id="Bn6ZkaqXlXzA" colab={"base_uri": "https://localhost:8080/", "height": 918} outputId="41da890f-df62-4402-e8d7-c7557cb9db7a"
display_motion(img_1,img_2,key_pts,motion)
display_motion(img_1,img_2,key_pts,motion,file_name_1+'_motion_out.png')
# + [markdown] id="gUIqq2EblXzA"
# __Question__
# 1/ Does the previous visualisation confirm your hypothesis concerning the type of motion ?
# 2/ In what regions do you think the estimation might fail ?
#
# + [markdown] id="jVS4ieyjlXzB"
# __Answer__ : zones that look the same over a great surface tend to have flawd motion outputs. This being said the hypothesis of the slight rotation is confirmed.
# + id="iaAVnRAJlXzB"
| motion_estimation_for_students.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="XBa81egYhqvT"
# **Mount Google Drive**
# + colab={"base_uri": "https://localhost:8080/"} id="kbk9NiHIkYEk" outputId="1b8fe630-f8b4-498a-ec51-4fb72ff62e90"
from google.colab import drive
drive.mount('/content/gdrive',force_remount=True)
# + colab={"base_uri": "https://localhost:8080/"} id="-0xM3T51mbMQ" outputId="75fe8974-4e43-4fbc-8b01-995bf56412a8"
# !apt install libasound2-dev portaudio19-dev libportaudio2 libportaudiocpp0 ffmpeg
# + colab={"base_uri": "https://localhost:8080/"} id="BdtI8_pEmySG" outputId="3c62eea4-f2ae-4051-e130-ccdcafd04712"
# !pip install pyaudio
# + colab={"base_uri": "https://localhost:8080/"} id="PcWWwuTvnEa6" outputId="b89f04bd-9d3f-4494-b165-d67c5f0bd7b4"
# !pip install soundfile
# + id="hH6nQPSjlNZx"
import os
# + id="HvJNJkP9knpV" colab={"base_uri": "https://localhost:8080/"} outputId="cf0739d3-17b6-4a2d-88ff-9f4712bca243"
p="/content/gdrive/MyDrive/Colab Notebooks/audio_database"
os.chdir(p)
class_count = len(os.listdir(p))
print(class_count)
# + id="g18_nR9epGWX"
import librosa
from librosa import display
import matplotlib.pyplot as plt
# + [markdown] id="2i8xdE0Fr-dj"
# **Plotting the audio file which was just loaded by librosa using waveplot function of librosa.The Function librosa.display.waveplot plots the amplitude envelope of a waveform.**
# + id="Yft1bWf1qdTN"
#Neutral_Emotion
p="/content/gdrive/MyDrive/Colab Notebooks/audio_database/Actor_01/03-01-01-01-02-01-01.wav"
data, sr=librosa.load(p)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="BXODNOL7qEkP" outputId="89910d90-d256-4d57-a134-efeb639d6d1c"
plt.figure(figsize=(16, 4))
librosa.display.waveplot(data, sr=sr)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="ydel6Cx1qwHj" outputId="98eb5c79-2d55-4f5e-e9bd-03e3da08744e"
#Calm Emotion
p="/content/gdrive/MyDrive/Colab Notebooks/audio_database/Actor_01/03-01-02-01-02-01-01.wav"
data1, sr1=librosa.load(p)
plt.figure(figsize=(16, 4))
librosa.display.waveplot(data1, sr=sr1)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="6TZOctJFqwy2" outputId="b9a1e353-1a39-44e5-8800-705f4a04ec50"
#Sad Emotion
p="/content/gdrive/MyDrive/Colab Notebooks/audio_database/Actor_01/03-01-04-01-02-01-01.wav"
data2, sr2=librosa.load(p)
plt.figure(figsize=(16, 4))
librosa.display.waveplot(data2, sr=sr2)
# + id="b-SGB-_AnLNJ"
import soundfile
import glob
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
# + [markdown] id="bfTuVhGEsYjZ"
# ### Defining a Function extract_feature to extract features such as mfcc,chroma, mel from the audio file.
# + id="Se5OXft4njNg"
def extract_feature(file_name, mfcc, chroma, mel):
X, sample_rate = librosa.load(os.path.join(file_name), res_type='kaiser_fast')
if chroma:
stft=np.abs(librosa.stft(X))
result=np.array([])
if mfcc:
mfccs=np.mean(librosa.feature.mfcc(y=X, sr=sample_rate, n_mfcc=40).T, axis=0)
#n_mfcc - number of MFCCs to return
result=np.hstack((result, mfccs))
if chroma:
chroma=np.mean(librosa.feature.chroma_stft(S=stft, sr=sample_rate).T,axis=0)
result=np.hstack((result, chroma))
if mel:
mel=np.mean(librosa.feature.melspectrogram(X, sr=sample_rate).T,axis=0)
result=np.hstack((result, mel))
return result
# + id="7dQ1KFm4noiJ"
emotions={
'01':'neutral',
'02':'calm',
'03':'happy',
'04':'sad',
'05':'angry',
'06':'fearful',
'07':'disgust',
'08':'surprised'
}
# Emotions to observe
observed_emotions=['neutral','calm','happy','sad','angry','fearful', 'disgust','surprised']
# + [markdown] id="0w1GfByOvSl2"
# **Loading The Data and extracting features for each audio file**
# + id="ZOwfQOFznthW"
def load_data(test_size):
x,y=[],[]
for file in glob.glob('/content/gdrive/MyDrive/Colab Notebooks/audio_database/Actor_*/*.wav'):
file_name=os.path.basename(file)
emotion=emotions[file_name.split("-")[2]]
if emotion not in observed_emotions:
continue
feature=extract_feature(file, mfcc=True, chroma=True, mel=True)
x.append(feature)
y.append(emotion)
for file in glob.glob('/content/gdrive/MyDrive/Colab Notebooks/audio_song_database/Actor_*/*.wav'):
file_name=os.path.basename(file)
emotion=emotions[file_name.split("-")[2]]
if emotion not in observed_emotions:
continue
feature=extract_feature(file, mfcc=True, chroma=True, mel=True)
x.append(feature)
y.append(emotion)
return train_test_split(np.array(x), y, test_size=test_size, train_size= 0.75,random_state=9)
# + [markdown] id="w1z35-7lve9B"
# **Splitting The Data Into Training And Testing**
# + id="fS3F55uTn5CB"
x_train,x_test,y_train,y_test=load_data(test_size=0.25)
# + colab={"base_uri": "https://localhost:8080/"} id="r5o0uxWzsNRc" outputId="eb8e168e-a740-43ab-8c0c-659100d34c05"
#Observing the shape of the training and testing dataset
print((x_train.shape[0], x_test.shape[0]))
# + [markdown] id="OgkJKO9qv1Fk"
# #**MLP Classifier**
# + id="IYJBi5fxA6ot"
model=MLPClassifier(alpha=0.05, batch_size=20, epsilon=1e-07, hidden_layer_sizes=(200,), learning_rate='adaptive', max_iter=400)
# + id="lRiTWBOqsg9z" colab={"base_uri": "https://localhost:8080/"} outputId="443f21c2-4216-45cb-cb33-c94337343b4b"
# Train the model
model.fit(x_train,y_train)
# + [markdown] id="6smYESKSwMZ5"
# #**Predicting The Accuracy Of Model**
# + id="7V_Ti1HMsvmr" colab={"base_uri": "https://localhost:8080/"} outputId="28aeaa38-72fa-4b89-8e2b-e82f160484d3"
y_pred=model.predict(x_test)
accuracy=accuracy_score(y_true=y_test, y_pred=y_pred)
print("Accuracy: {:.2f}%".format(accuracy*100))
# + colab={"base_uri": "https://localhost:8080/"} id="r7XBR9MAPjqO" outputId="bcadfaa6-5a7c-4530-a4ed-ea93c4fe34f0"
y_pr_tr = model.predict(x_train)
tr_acc = float(accuracy_score(y_train,y_pr_tr))*100
print("----training accuracy score %s ----" % tr_acc)
# + [markdown] id="Yeoo_BqEwTxZ"
# #**Confusion Matrix**
# + colab={"base_uri": "https://localhost:8080/"} id="IL9wMWqtwbvi" outputId="90ebb671-7190-455b-8f75-980047dc4813"
from sklearn.metrics import confusion_matrix
matrix = confusion_matrix(y_test,y_pred)
print (matrix)
| MLPClassifier(Final).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Nibabel
#
# Nibabel is a low-level Python library that gives access to a variety of imaging formats, with a particular focus on providing a common interface to the various **volumetric** formats produced by scanners and used in common neuroimaging toolkits.
#
# - NIfTI-1
# - NIfTI-2
# - SPM Analyze
# - FreeSurfer .mgh/.mgz files
# - Philips PAR/REC
# - Siemens ECAT
# - DICOM (limited support)
#
# It also supports **surface** file formats
#
# - GIFTI
# - FreeSurfer surfaces, labels and annotations
#
# **Connectivity**
#
# - CIFTI-2
#
# **Tractocgraphy**
#
# - TrackViz .trk files
#
# And a number of related formats.
#
# **Note:** Almost all of these can be loaded through the `nibabel.load` interface.
# ## Setup
# +
# Image settings
import pylab as plt
# %matplotlib inline
import numpy as np
import nibabel as nb
# -
# ## Loading and inspecting images in `nibabel`
# Load a functional image of subject 01
img = nb.load('/data/ds000114/sub-02/ses-test/func/sub-02_ses-test_task-fingerfootlips_bold.nii.gz')
# Let's look at the header of this file
print(img)
# This data-affine-header structure is common to volumetric formats in nibabel, though the details of the header will vary from format to format.
#
# ### Access specific parameters
#
# If you're interested in specific parameters, you can access them very easily, as the following examples show.
data = img.get_data()
data.shape
affine = img.affine
affine
header = img.header['pixdim']
header
# Note that in the `'pixdim'` above contains the voxel resolution (`3.125., 3.125, 4.2`), as well as the TR (`2.`).
# ### Data
#
# The data is a simple numpy array. It has a shape, it can be sliced and generally manipulated as you would any array.
plt.imshow(data[:, :, data.shape[2] // 2, 0].T, cmap='Greys_r')
print(data.shape)
# + solution2="shown"
t1 = nb.load('/data/ds000114/sub-02/ses-test/anat/sub-02_ses-test_T1w.nii.gz')
data = t1.get_data()
plt.imshow(data[:, :, data.shape[2] // 2].T, cmap='Greys_r')
print(data.shape)
# -
# ## Creating and saving images
#
# Suppose we want to save space by rescaling our image to a smaller datatype, such as an unsigned byte. To do this, we first need to take the data, change it's datatype and save this new data in a new NIfTI image with the same header and affine as the original image.
# First, we need to load the image and get the data
img = nb.load('/data/ds000114/sub-02/ses-test/func/sub-02_ses-test_task-fingerfootlips_bold.nii.gz')
data = img.get_data()
# Now we force the values to be between 0 and 255
# and change the datatype to unsigned 8-bit
rescaled = ((data - data.min()) * 255. / (data.max() - data.min())).astype(np.uint8)
# Now we can save the changed data into a new NIfTI file
new_img = nb.Nifti1Image(rescaled, affine=img.affine, header=img.header)
nb.save(new_img, '/tmp/rescaled_image.nii.gz')
# # Nilearn
#
# [Nilearn](http://nilearn.github.io/index.html) labels itself as: *A Python module for fast and easy statistical learning on NeuroImaging data. It leverages the scikit-learn Python toolbox for multivariate statistics with applications such as predictive modelling, classification, decoding, or connectivity analysis.*
#
# But it's much more than that. It is also an excellent library to **manipulate** (e.g. resample images, smooth images, ROI extraction, etc.) and **visulaize** your neuroimages.
#
# So let's visit all three of those domains:
#
# 1. Image manipulation
# 2. Image visualization
# ## Setup
# +
# Image settings
from nilearn import plotting
import pylab as plt
# %matplotlib inline
import numpy as np
# -
# Throughout this tutorial we will be using the anatomical and functional image of subject 1. So let's load them already here that we have a quicker access later on:
from nilearn import image as nli
t1 = nli.load_img('/data/ds000114/sub-02/ses-test/anat/sub-02_ses-test_T1w.nii.gz')
bold = nli.load_img('/data/ds000114/sub-02/ses-test/func/sub-02_ses-test_task-fingerfootlips_bold.nii.gz')
# Because the bold image didn't reach steady-state at the beginning of the image, let's cut of the first 5 volumes, to be sure:
bold = bold.slicer[..., 5:]
# ## 1. Image manipulation with `nilearn`
#
# ### Let's create a mean image
#
# If you use nibabel to compute the mean image, you first need to load the img, get the data and then compute the mean thereof. With nilearn you can do all this in just one line with `mean image`.
from nilearn import image as nli
img = nli.mean_img(bold)
img.orthoview()
# Perfect! What else can we do with the `image` module?
# Let's see...
# ### Resample image to a template
# Using `resample_to_img`, we can resample one image to have the same dimensions as another one. For example, let's resample an anatomical T1 image to the computed mean image above.
mean = nli.mean_img(bold)
print([mean.shape, t1.shape])
# Let's resample the t1 image to the mean image.
resampled_t1 = nli.resample_to_img(t1, mean)
resampled_t1.shape
# The image size of the resampled t1 image seems to be right. But what does it look like?
from nilearn import plotting
plotting.plot_anat(t1, title='original t1', display_mode='z', dim=-1,
cut_coords=[-20, -10, 0, 10, 20, 30])
plotting.plot_anat(resampled_t1, title='resampled t1', display_mode='z', dim=-1,
cut_coords=[-20, -10, 0, 10, 20, 30])
# ### Smooth an image
# Using `smooth_img`, we can very quickly smooth any kind of MRI image. Let's for example take the mean image from above and smooth it with different FWHM values.
for fwhm in range(1, 12, 5):
smoothed_img = nli.smooth_img(mean, fwhm)
plotting.plot_epi(smoothed_img, title="Smoothing %imm" % fwhm,
display_mode='ortho', cmap='magma')
# ### Mask an image and extract an average signal of a region
#
# Thanks to nibabel and nilearn you can consider your images just a special kind of a numpy array. Which means that you have all the liberties that you are used to.
#
# For example, let's take a functional image, (1) create the mean image thereof, than we (2) threshold it to only keep the voxels that have a value that is higher than 95% of all voxels. Of this thresholded image, we only (3) keep those regions that are bigger than 1000mm^3. And finally, we (4) binarize those regions to create a mask image.
# So first, we load again a functional image and compute the mean thereof.
mean = nli.mean_img(bold)
# Use `threshold_img` to only keep voxels that have a value that is higher than 95% of all voxels.
thr = nli.threshold_img(mean, threshold='95%')
thr.orthoview()
# Now, let's only keep those voxels that are in regions/clusters that are bigger than 1000mm^3.
voxel_size = np.prod(thr.header['pixdim'][1:4]) # Size of 1 voxel in mm^3
voxel_size
# Let's create the mask that only keeps those big clusters.
from nilearn.regions import connected_regions
cluster = connected_regions(thr, min_region_size=1000. / voxel_size, smoothing_fwhm=1)[0]
# And finally, let's binarize this cluster file to create a mask.
mask = nli.math_img('np.mean(img,axis=3) > 0', img=cluster)
# Now let us investigate this mask by visualizing it on the subject specific anatomy:
from nilearn.plotting import plot_roi
plotting.plot_roi(mask, bg_img=t1, display_mode='ortho', dim=-.5, cmap='magma_r');
# Next step is now to take this mask, apply it to the original functional image and extract the mean of the temporal signal.
# +
# Apply mask to original functional image
from nilearn.masking import apply_mask
all_timecourses = apply_mask(bold, mask)
all_timecourses.shape
# -
# **Note:** You can bring the timecourses (or masked data) back into the original 3D/4D space with `unmask`:
from nilearn.masking import unmask
img_timecourse = unmask(all_timecourses, mask)
# Compute mean trace of all extractet timecourses and plot the mean signal.
mean_timecourse = all_timecourses.mean(axis=1)
plt.plot(mean_timecourse)
# ## 2. Image visualization with `nilearn`
#
# Above, we've already seen some ways on how to visualize brain images with `nilearn`. And there are many more. To keep this notebook short, we will only take a look at some of them. For a complete list, see [nilearn's plotting section](http://nilearn.github.io/plotting/index.html).
#
# **Note:** In most of the `nilearn`'s plotting functions, you can specify the value `output_file=example.png'`, to save the figure directly to a file.
| notebooks/03_nibabel_and_nilearn.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# %matplotlib inline
from tqdm import tqdm_notebook
import concurrent.futures
from multiprocessing import Pool
def mean_list(inp):
l = len(inp)
return sum(inp)/l
# # 梯度下降
# ## 各个损失函数的偏导
# ### **MSE (回归)**
# MSE计算公式:
# - $ MSE = (y-y_{true})^2 $
# - <font color=gray>[batch 累加形式] $ MSE = \frac{1}{m}\sum_{i=1}^{m}(y-y_i)^2$ </font>
#
# MSE偏导数:$\frac{\partial MSE}{\partial x} = 2(y-y_{true})\frac{\partial y}{\partial x}$
#
# 例如 $y=ax$ 带入到MSE计算**(a的)**偏导为 $\frac{\partial MSE}{\partial a} = 2(y-y_{true})\frac{\partial y}{\partial a} = 2(y-y_{true})x$
# ### Logloss (分类)
# - y、y_true 都是0、1类别(二分类)
# - 底数是e
#
# Logloss计算公式:
# - $ logloss = \frac{y_{true}}{n}log(y)+\frac{1-y_{true}}{n}log(1-y)$
# - <font color=gray>[batch 累加形式] $ logloss = -\sum_{i=1}^{n}(\frac{y_i}{n}log(p_i)+\frac{(1-y_i)}{n}log(1-p_i)) $ </font>
#
# Logloss偏导数:$\frac{\partial logloss}{\partial x} = \frac{y_{true}}{n}\frac{1}{y}\frac{\partial y}{\partial x}+\frac{1-y_{true}}{n}\frac{1}{1-y}(-\frac{\partial y}{\partial x})$
#
# 例如 $y=ax$ 带入到Logloss计算**(a的)**偏导为 $\frac{\partial MSE}{\partial a} = 2(y-y_{true})\frac{\partial y}{\partial a} = 2(y-y_{true})x$
# ### 直接误差
# 直接误差计算公式:$ Direct = y-y_{true} $
#
# 直接误差偏导数:$\frac{\partial Direct}{\partial x} = \frac{\partial y}{\partial x}$
#
# 例如 $y=ax$ 带入到直接误差计算**(a的)**偏导为 $\frac{\partial Direct}{\partial a} = \frac{\partial y}{\partial a} = x$
#
# ## 解一元一次方程(无常数项)
# ### SGD
# +
# 目标函数 y=ax,构造一批样本
import random
a_true=9
def y_true(x):
return a_true*x
allSamples = [[i,y_true(i)] for i in range(150)]
samples = allSamples[:100]
verify_samples = allSamples[100:]
a=0.05 # 初始化a
n = 0.001 # 定义学习率为0.01
# 损失函数设计为均方误差[mse = (y-y_true)^2]
# 参数更新方式为 param_new = param - 学习率*损失函数对param的(在x处的)偏导数
print(f"[true]: y={a_true}x")
print(f"[initial]: y={a}x")
it = 0
while it <= 2:
print(f"\n\n[第 {it} 次迭代]")
cnt = 0
for (x,y_true) in samples:
y = a*x
grad_a = (y-y_true)*x
a = a - n*grad_a #
verify_list = [pow((a*x-y_true),2) for (x,y_true) in verify_samples]
verify_mse = sum(verify_list)/len(verify_list)
if cnt%5==0:
print(f" x:{x}, y={a:.4f}x, verify_mse:{verify_mse:.4f}, grad_a:{grad_a:.4f}")
cnt += 1
if verify_mse<=0.001:
print(" [已完成]:")
print(f" x:{x}, y={a:.4f}x, verify_mse:{verify_mse:.4f}, grad_a:{grad_a:.4f}")
it = 2
break
it += 1
# assert False
# mse_list = [pow((a*x+b-y_true),2) for (x,y_true) in samples]
# new_mse = sum(mse_list)/len(mse_list)
# print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse}")
# -
# ### SGD (mini-batch)
# +
import itertools
# 目标函数 y=ax,构造一批样本
import random
a_true=9
def y_true(x):
return a_true*x
allSamples = [[i,y_true(i)] for i in range(150)]
samples = allSamples[:100]
verify_samples = allSamples[100:]
a=0.05 # 初始化a
n = 0.001 # 定义学习率为0.01
# 损失函数设计为均方误差[mse = (y-y_true)^2]
# 参数更新方式为 param_new = param - 学习率*损失函数对param的(在x处的)偏导数
print(f"[true]: y={a_true}x")
print(f"[initial]: y={a}x")
it = 0
while it <= 2:
print(f"\n\n[第 {it} 次迭代]")
cnt = 0
for (x,y_true) in samples:
y = a*x
grad_a = (y-y_true)*x
a = a - n*grad_a #
verify_list = [pow((a*x-y_true),2) for (x,y_true) in verify_samples]
verify_mse = sum(verify_list)/len(verify_list)
if cnt%5==0:
print(f" x:{x}, y={a:.4f}x, verify_mse:{verify_mse:.4f}, grad_a:{grad_a:.4f}")
cnt += 1
if verify_mse<=0.001:
print(" [已完成]:")
print(f" x:{x}, y={a:.4f}x, verify_mse:{verify_mse:.4f}, grad_a:{grad_a:.4f}")
it = 2
break
it += 1
# assert False
# mse_list = [pow((a*x+b-y_true),2) for (x,y_true) in samples]
# new_mse = sum(mse_list)/len(mse_list)
# print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse}")
# -
# ### GD
# # 二元一次
#
# +
# 目标函数 2x1+3x2+5,构造一批样本
import random
(a_true,b_true,c_true) = (2,3,0)
def y_true(x1,x2):
return a_true*x1+b_true*x2+c_true
samples = [[i,i+1,y_true(i,i+1)] for i in range(100)]
samples[:2]
(a,b,c) = (0.5,0.5,0) # 0.5初始化,或随机初始化a,b,c
n = 0.001 # 定义学习率为0.1
# 损失函数设计为均方误差
# 参数更新方式为 param_new = param - 学习率*损失函数对param的(在x处的)偏导数
print(f"[true]: y={a_true}x1+{b_true}x2+{c_true}")
print(f"[initial]: y={a}x1+{b}x2+{c}")
for _ in range(2):
print(f"第 {_} 次迭代")
for (x1,x2,y_true) in tqdm_notebook(samples):
y = a*x1+b*x2+c
grad_a = (y-y_true)*x1
grad_b = (y-y_true)*x2
grad_c = (y-y_true)*1
a = a - n*grad_a #
b = b - n*grad_b #
# c = c - n*grad_c
mse_list = [pow((a*x1+b*x2+c-y_true),2) for (x1,x2,y_true) in samples]
new_mse = sum(mse_list)/len(mse_list)
print(f"y={a:.4f}x1+{b:.4f}x2+{c:.4f}, new_mse:{new_mse:.2f}, x1:{x1},x2:{x2},grad_a:{grad_a:.4f},grad_b:{grad_b:.4f}")
if new_mse<=0.01:
break
print(f"y={a:.4f}x1+{b:.4f}x2+{c:.4f}, new_mse:{new_mse:.2f}")
# assert False
# mse_list = [pow((a*x+b-y_true),2) for (x,y_true) in samples]
# new_mse = sum(mse_list)/len(mse_list)
# print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse}")
# -
# # 一元二次方程
# +
# 目标函数 2x+5,构造一批样本
import random
(a_true,b_true) = (9,2)
def y_true(x):
return pow(a_true*x,2)+b_true
samples = [[i,y_true(i)] for i in range(100)]
samples[:2]
(a,b) = (0.5,0.5) # 0.5初始化,或随机初始化a,b
n = 0.001 # 定义学习率为0.1
# 损失函数设计为均方误差
# 参数更新方式为 param_new = param - 学习率*损失函数对param的(在x处的)偏导数
print(f"[true]: y={a_true}x+{b_true}")
print(f"[initial]: y={a}x+{b}")
for _ in range(10):
print(f"第 {_} 次迭代")
for (x,y_true) in tqdm_notebook(samples):
y = a*x+b
grad_a = (y-y_true)*x
grad_b = (y-y_true)*1
a = a - n*grad_a #
b = b - n*grad_b #
mse_list = [pow((a*x+b-y_true),2) for (x,y_true) in samples]
new_mse = sum(mse_list)/len(mse_list)
print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse:.2f}, grad_a:{grad_a:.4f},grad_b:{grad_b:.4f}")
if new_mse<=0.01:
break
print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse:.2f}")
# assert False
# mse_list = [pow((a*x+b-y_true),2) for (x,y_true) in samples]
# new_mse = sum(mse_list)/len(mse_list)
# print(f"y={a:.4f}x+{b:.4f}, new_mse:{new_mse}")
# -
| note_books/Basic.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.12 64-bit (''venv'': venv)'
# name: python3
# ---
# +
from __future__ import annotations
from dataclasses import dataclass, field
from typing import *
from collections import defaultdict
import graphlib
import statistics
from matplotlib import pyplot as plt
import timeit
import igraph
import functools
import graphlib2
import retworkx
# +
import platform
print(platform.platform())
print(platform.python_version())
# +
T = TypeVar("T", bound=Hashable)
Graph = Dict[T, List[T]]
# -
class RetworkXTopologicalSorter(Generic[T]):
def __init__(self, graph: Mapping[T, Iterable[T]]) -> None:
edge_list: List[Tuple[T, T]] = []
for node, children in graph.items():
for child in children:
edge_list.append((node, child))
rgraph = retworkx.PyDiGraph()
rgraph.extend_from_edge_list(edge_list)
self.ts = retworkx.TopologicalSorter(rgraph)
def is_active(self) -> bool:
return self.ts.is_active()
def get_ready(self) -> Iterable[T]:
return self.ts.get_ready()
def done(self, *nodes: T) -> None:
self.ts.done(list(nodes))
# +
@functools.cache
def get_linear_graph(n: int) -> Graph[int]:
g = igraph.Graph.Tree(n, 1)
res: Dict[int, List[int]] = defaultdict(list)
for source, dest in g.get_edgelist():
res[source].append(dest)
return res
@functools.cache
def get_branched_graph(n: int) -> Graph[int]:
g = igraph.Graph.Tree_Game(n, directed=True)
res: Dict[int, List[int]] = defaultdict(list)
for source, dest in g.get_edgelist():
res[source].append(dest)
return res
# +
def run(
t: Union[RetworkXTopologicalSorter[T], graphlib.TopologicalSorter[T]],
graph: Graph[T],
) -> None:
to_remove = t.get_ready()
while t.is_active():
t.done(*to_remove)
to_remove = t.get_ready()
def setup_retworkx(graph: Graph[T]) -> RetworkXTopologicalSorter[T]:
return RetworkXTopologicalSorter(graph)
def setup_graphlib(graph: Graph[T]) -> graphlib.TopologicalSorter[T]:
t: graphlib.TopologicalSorter[T] = graphlib.TopologicalSorter(graph)
t.prepare()
return t
def setup_graphlib2(graph: Graph[T]) -> graphlib2.TopologicalSorter[T]:
t: graphlib2.TopologicalSorter[T] = graphlib2.TopologicalSorter(graph)
t.prepare()
return t
def copy_retworkx(ts: RetworkXTopologicalSorter[T], graph: Graph[T]) -> None:
RetworkXTopologicalSorter(graph)
def copy_graphlib2(ts: graphlib2.TopologicalSorter[T], graph: Graph[T]) -> None:
ts.copy()
def copy_graphlib(ts: graphlib.TopologicalSorter[T], graph: Graph[T]) -> None:
setup_graphlib(graph)
# -
# ## Time individual methods
# These benchmarks are not a real Apples to Apples comparison since the methods do different amounts of work internally (even if it adds up the same total amount).
# +
@dataclass
class MethodTimings:
is_active: List[float] = field(default_factory=list)
done: List[float] = field(default_factory=list)
get_ready: List[float] = field(default_factory=list)
def bench_methods(ts: Union[RetworkXTopologicalSorter[T], graphlib.TopologicalSorter[T], graphlib2.TopologicalSorter[T]]) -> MethodTimings:
timings = MethodTimings()
while True:
start = timeit.default_timer()
is_active = ts.is_active()
timings.is_active.append(timeit.default_timer()-start)
if not is_active:
break
start = timeit.default_timer()
ready = ts.get_ready()
timings.get_ready.append(timeit.default_timer()-start)
start = timeit.default_timer()
ts.done(*ready)
timings.done.append(timeit.default_timer()-start)
return timings
# -
def plot_method_timings(
upper: int,
samples: int,
graph_factory: Callable[[int], Graph[T]],
lower: int = 0,
loops: int = 10,
) -> None:
samples = min(samples, upper-lower)
x = [round(lower + x*(upper-lower)/samples) for x in range(samples)]
graphlib_is_active: List[float] = []
graphlib_get_ready: List[float] = []
graphlib_done: List[float] = []
graphlib2_is_active: List[float] = []
graphlib2_get_ready: List[float] = []
graphlib2_done: List[float] = []
retworkx_is_active: List[float] = []
retworkx_get_ready: List[float] = []
retworkx_done: List[float] = []
for n in x:
graphlib: List[MethodTimings] = []
graphlib2: List[MethodTimings] = []
retworkx: List[MethodTimings] = []
graph = graph_factory(n)
for _ in range(loops):
graphlib.append(bench_methods(setup_graphlib(graph)))
graphlib2.append(bench_methods(setup_graphlib2(graph)))
retworkx.append(bench_methods(setup_retworkx(graph)))
graphlib_is_active.append(float(statistics.median([sum(t.is_active) for t in graphlib])))
graphlib_get_ready.append(float(statistics.median([sum(t.get_ready) for t in graphlib])))
graphlib_done.append(float(statistics.median([sum(t.done) for t in graphlib])))
graphlib2_is_active.append(float(statistics.median([sum(t.is_active) for t in graphlib2])))
graphlib2_get_ready.append(float(statistics.median([sum(t.get_ready) for t in graphlib2])))
graphlib2_done.append(float(statistics.median([sum(t.done) for t in graphlib2])))
retworkx_is_active.append(float(statistics.median([sum(t.is_active) for t in retworkx])))
retworkx_get_ready.append(float(statistics.median([sum(t.get_ready) for t in retworkx])))
retworkx_done.append(float(statistics.median([sum(t.done) for t in retworkx])))
fig, (is_active_ax, get_ready_ax, done_ax) = plt.subplots(1, 3)
fig.text(0.5, 0.04, "V (number of vertices)", ha='center')
fig.text(0.04, 0.5, "is_active()", va='center', rotation='vertical')
is_active_ax.set_yticklabels([])
is_active_ax.set_xticklabels([])
is_active_ax.plot(x, graphlib_is_active, label="graphlib")
is_active_ax.plot(x, graphlib2_is_active, label="graphlib2")
is_active_ax.plot(x, retworkx_is_active, label="retworkx")
is_active_ax.legend()
is_active_ax.title.set_text('is_active()')
get_ready_ax.set_yticklabels([])
get_ready_ax.set_xticklabels([])
get_ready_ax.plot(x, graphlib_get_ready, label="graphlib")
get_ready_ax.plot(x, graphlib2_get_ready, label="graphlib2")
get_ready_ax.plot(x, retworkx_get_ready, label="retworkx")
get_ready_ax.legend()
get_ready_ax.title.set_text('get_ready()')
done_ax.set_yticklabels([])
done_ax.set_xticklabels([])
done_ax.plot(x, graphlib_done, label="graphlib")
done_ax.plot(x, graphlib2_done, label="graphlib2")
done_ax.plot(x, retworkx_done, label="retworkx")
done_ax.legend()
done_ax.title.set_text('done()')
plot_method_timings(upper=500, samples=30, loops=20, graph_factory=get_branched_graph)
# ## Execution time benchmarks
# Benchmarks that test how long it takes to execute the graph assuming dependencies execute instantly.
# This does not count the time required to create the graph or prepare the toplogical sorter.
# +
@dataclass
class Target(Generic[T]):
retworkx: Callable[
[
Union[
RetworkXTopologicalSorter[T],
graphlib.TopologicalSorter[T],
graphlib2.TopologicalSorter[T],
],
Graph[T],
],
None,
]
graphlib: Callable[
[
Union[
RetworkXTopologicalSorter[T],
graphlib.TopologicalSorter[T],
graphlib2.TopologicalSorter[T],
],
Graph[T],
],
None,
]
graphlib2: Callable[
[
Union[
RetworkXTopologicalSorter[T],
graphlib.TopologicalSorter[T],
graphlib2.TopologicalSorter[T],
],
Graph[T],
],
None,
]
def plot(
upper: int,
samples: int,
graph_factory: Callable[[int], Graph[T]],
target: Target[T],
lower: int = 0,
loops: int = 10,
) -> None:
samples = min(samples, upper - lower)
x = [round(lower + x * (upper - lower) / samples) for x in range(samples)]
y_graphlib: List[float] = []
y_graphlib2: List[float] = []
y_retworkx: List[float] = []
for n in x:
graphlib: List[float] = []
graphlib2: List[float] = []
retworkx: List[float] = []
graph = graph_factory(n)
for _ in range(loops):
# graphlib
ts = setup_graphlib(graph)
start = timeit.default_timer()
target.graphlib(ts, graph)
graphlib.append(timeit.default_timer() - start)
# graphlib2
ts = setup_graphlib2(graph)
start = timeit.default_timer()
target.graphlib2(ts, graph)
graphlib2.append(timeit.default_timer() - start)
# retworkx
ts = setup_retworkx(graph)
start = timeit.default_timer()
target.retworkx(ts, graph)
retworkx.append(timeit.default_timer() - start)
y_graphlib.append(statistics.median(graphlib))
y_graphlib2.append(statistics.median(graphlib2))
y_retworkx.append(statistics.median(retworkx))
plt.plot(x, y_graphlib, label="graphlib")
plt.plot(x, y_graphlib2, label="graphlib2")
plt.plot(x, y_retworkx, label="retworkx")
plt.legend(loc="upper left")
plt.xlabel("V (number of vertices)")
plt.ylabel("Execution time (s)")
# -
# For a linear graph (`{"A": ["B"], "B": ["C"], "C": ["D"]}`):
plot(upper=50, samples=50, loops=30, graph_factory=get_linear_graph, target=Target(run, run, run))
# For a randomized branched graph (`{"A": ["B", "C"], "B": ["C"], "C": ["D", "E"]}`):
plot(upper=50, samples=50, loops=30, graph_factory=get_branched_graph, target=Target(run, run, run))
# Same benchmarks for much larger graphs
plot(upper=50_000, samples=50, loops=7, graph_factory=get_branched_graph, target=Target(run, run, run))
plot(upper=50_000, samples=50, loops=7, graph_factory=get_linear_graph, target=Target(run, run, run))
# ## Copy benchmarks
# Measure copying a `ToplogicalSorter` instance.
# The standard library does not have a `copy()` method, so we just re-create the `ToplogicalSorter`, which is inefficient but is the only option available.
target: Target[T] = Target(retworkx=copy_retworkx, graphlib=copy_graphlib, graphlib2=copy_graphlib2)
plot(upper=1_000, samples=35, loops=15, graph_factory=get_branched_graph, target=target)
plot(upper=50, samples=35, loops=15, graph_factory=get_branched_graph, target=target)
# Time copying a `graphlib2.ToplogicalSorter` so it can be compared against itself
# %%timeit ts = setup_graphlib2(get_branched_graph(100))
ts.copy()
| bench.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lesson 1 Exercise 1: Creating a Table with PostgreSQL
#
# <img src="images/postgresSQLlogo.png" width="250" height="250">
# ### Walk through the basics of PostgreSQL. You will need to complete the following tasks:
# <li>Create a table in PostgreSQL,<li>Insert rows of data<li>Run a simple SQL query to validate the information.
# #### Import the library
# *Note:* An error might popup after this command has executed. If it does read it careful before ignoring.
import psycopg2
# !echo "alter user student createdb;" | sudo -u postgres psql
# ### Create a connection to the database
try:
conn = psycopg2.connect("host=127.0.0.1 dbname=studentdb user=student password=<PASSWORD>")
except psycopg2.Error as e:
print("Error: Could not make connection to the Postgres database")
print(e)
# ### Use the connection to get a cursor that can be used to execute queries.
try:
cur = conn.cursor()
except psycopg2.Error as e:
print("Error: Could not get curser to the Database")
print(e)
# ### Set automatic commit to be true so that each action is committed without having to call conn.commit() after each command.
conn.set_session(autocommit=True)
# ### Create a database to do the work in.
try:
cur.execute("create database udacity")
except psycopg2.Error as e:
print(e)
# #### Add the database name in the connect statement. Let's close our connection to the default database, reconnect to the Udacity database, and get a new cursor.
# +
try:
conn.close()
except psycopg2.Error as e:
print(e)
try:
conn = psycopg2.connect("dbname=udacity")
except psycopg2.Error as e:
print("Error: Could not make connection to the Postgres database")
print(e)
try:
cur = conn.cursor()
except psycopg2.Error as e:
print("Error: Could not get curser to the Database")
print(e)
conn.set_session(autocommit=True)
# -
# ### Create a Song Library that contains a list of songs, including the song name, artist name, year, album it was from, and if it was a single.
#
# `song title
# artist
# year
# album
# single`
#
try:
cur.execute("CREATE TABLE IF NOT EXISTS songs (song_title varchar, artist_name varchar, year int, album_name varchar, single Boolean);")
except psycopg2.Error as e:
print("Error: Issue creating table")
print (e)
# ### Insert the following two rows in the table
# `First Row: "Across The Universe", "The Beatles", "1970", "False", "Let It Be"`
#
# `Second Row: "The Beatles", "Think For Yourself", "False", "1965", "Rubber Soul"`
# +
try:
cur.execute("INSERT INTO songs (song_title, artist_name, year, album_name, single) \
VALUES (%s, %s, %s, %s, %s)", \
("Across The Universe", "The Beatles", 1970, "Let It Be", False))
except psycopg2.Error as e:
print("Error: Inserting Rows")
print (e)
try:
cur.execute("INSERT INTO songs (song_title, artist_name, year, album_name, single) \
VALUES (%s, %s, %s, %s, %s)",
("Think For Yourself", "The Beatles", 1965, "Rubber Soul", False))
except psycopg2.Error as e:
print("Error: Inserting Rows")
print (e)
# -
# ### Validate your data was inserted into the table.
#
# +
try:
cur.execute("SELECT * FROM songs;")
except psycopg2.Error as e:
print("Error: select *")
print (e)
row = cur.fetchone()
while row:
print(row)
row = cur.fetchone()
# -
# ### And finally close your cursor and connection.
cur.close()
conn.close()
| L1_Introduction to Data Modeling /L1_Exercise_1_Solution_Creating_a_Table_with_Postgres.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Voorbereiding: Jupyter Notebook initialiseren**
import sys
sys.path.append('D:/Python/Projecten/pypv')
sys.path.append('D:/Python/Projecten/pypv/lib') # add my own lib folder to Python's search path
sys.path.append('D:/Python/Projecten/pypv/datafiles') # also add the folder with the data files
sys.path.append('D:/Python/Projecten/pypv/scripts') # and the folder that contains the script with the configuration of the PV system
from IPython.display import Image, HTML
import sun
import photovoltaic as pv
from quantities.date_time import Date, ANY_YEAR
# `sun`, `photovoltaic` en `quantities` zijn drie zelf geschreven Python *packages* (*libraries*) die alle programmatuur bevatten om de computer de berekeningen te laten uitvoeren.
# * `sun` bevat onder meer de programmacode om horizonprofielen, zonnebaandiagrammen en de zonnebestralingssterkte (irradiantie) op een oppervlak te berekenen.
# * `photovoltaic` modelleert de componenten van een fotovoltaïsche installatie (o.a. zonnepaneel, zonnepanelenmatrix, omvormer) en de programmcode om een energieanalyse te maken.
# * `quantities` is een secundaire *package* waarin fysische grootheden worden gemodelleerd (o.a. tijd, datum).
# # DEEL 3 | ENERGIEANALYSE
# In deze *notebook* zal een schatting worden gemaakt van de hoeveelheid 'groene' elektrische energie die op jaarbasis kan verwacht worden van de FV installatie, rekening houdend met de horizonprofielen van de twee FV matrices op het platte dak van de woning en het rendement van de samenstellende onderdelen: zonnepanelen, bekabeling en omvormer.<br>
# Vervolgens zal de zelfvoorzieningsgraad en de benuttingsgraad geëvalueerd worden. De zelfvoorzieningsgraad drukt uit hoeveel procent van het jaarlijks elektriciteitsverbruik geleverd wordt door de zonnepanelen. De benuttingsgraad drukt uit hoeveel procent van de jaarlijkse zonneopbrengst door de eigen elektrische installatie wordt verbruikt. De analyse wordt gemaakt, zowel zonder, als met opslagbatterij.<br>
# Tot slot wordt nagegaan wat de financiële consequenties kunnen zijn als men opteert voor, ofwel een (digitale) energiemeter volgens het principe van de terugdraaiende teller en de betaling van een prosumententarief (de zgn. 'compensatieregeling'), ofwel een digitale energiemeter waarbij het distributienettarief wordt aangerekend op basis van de werkelijke hoeveelheid van het openbare net afgenomen elektriciteit.
# De omvormer (`inverter`) die in deel 2, basisontwerp werd geconfigureerd en waaraan de FV matrices werden verbonden, moet in de werkomgeving van dit *notebook* opnieuw worden geïmporteerd. Ook de geografische locatie (`loc`) is opnieuw nodig.
from energy_analysis_02 import inverter, loc
# De energieanalyse wordt uitgevoerd door een `EnergyAnalyzer`-object. In de constructor wordt het pad opgegeven naar het bestand met de klimaatdata (`TMY_file`) en het pad naar het bestand met data over het elektriciteitsverbruik (`CLP_file`, *Consumer Load Profile*). Deze *csv*-bestanden moeten door de gebruiker voorbereid worden, zodat de `EnergyAnalyzer`deze correct zou interpreteren en kunnen verwerken.<br>
# Een FV installatie kan meer dan één omvormer omvatten. De parameter `pv_inverters`verwacht daarom een lijst van minstens 1 of meer `Inverter` objecten.
ea = pv.EnergyAnalyzer(
TMY_file='../datafiles/tmy.csv',
CLP_file='../datafiles/mlp.csv',
location=loc,
pv_inverters=[inverter]
)
# Het databestand <a href="/static/datafiles/tmy.csv" download="tmy.csv">tmy.csv</a> bevat de klimaatdata die afkomstig is uit de PVGIS 5 database. Het databestand <a href="/static/datafiles/mlp.csv" download="mlp.csv">mlp.csv</a> bevat de 'kwartierverbruiken' over een gans jaar. De vermelde tijdstippen zijn in de beide databestanden in UTC uitgedrukt. De verbruiken werden met een power analyzer gemeten. De meetcampagne duurde een drietal weken. De verzamelde data werd geëxtrapoleerd over een gans jaar, waarbij werd aangenomen dat het opgemeten weekprofiel zich zonder noemenswaardige variaties herhaalt.
# **Energieanalyse laten uitvoeren...**
# %time ea.analyze()
# ## Analyseresultaat 1: Opbrengst en Verbruik
# ### Geschatte Jaarlijkse Opbrengst van de FV Installatie
display(HTML(f'Geschatte jaarlijkse opbrengst = <b>{ea.get_annual_yield():.0f}</b> kWh'))
# ### Geschat Jaarlijks Verbruik van de Verbruikersinstallatie
display(HTML(f'Geschat jaarlijks verbruik = <b>{ea.get_annual_load():.0f}</b> kWh'))
# ### Opbrengst- en Verbruiksprofiel
graph = ea.plot_profiles(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ## Analyseresultaat 2: Energiestromen Zonder Batterijopslagsysteem
# In een fotovoltaïsche installatie kunnen de volgende energiestromen (eenheid: kWh) onderscheiden worden:
# * een energiestroom `Egtl` (*Grid to Load*) vanuit het net naar de verbruikersinstallatie (belasting) = netvoeding
# * een energiestroom `Eptg` (*PV to Grid*) vanuit de FV installatie naar het net = netinjectie
# * een energiestroom `Eptl` (*PV to Load*) vanuit de FV installatie naar de belasting = eigenverbruik
# * in het geval van een batterijopslagsysteem: een energiestroom `Eptb` (*PV to Battery*) vanuit de FV installatie naar de batterij
# * in het geval van een batterijopslagsysteem: een energiestroom `Ebtl` (*Battery to Load*) vanuit de batterij naar de belasting
# Een energiestroom vanuit het net naar de batterij (*Grid to Battery*) wordt niet toegelaten. Doel van het batterijopslagsysteem dient om momentaan productieoverschot van de zonnepanelen op te slaan in de batterij voor later eigenverbruik i.p.v. het productieoverschot in het net te injecteren. Het kan evenwel niet de bedoeling zijn dat de batterij wordt bijgeladen vanuit het net.
# ### Maandelijks Overzicht van de Energiestromen
# In het geval van een FV installatie zonder batterijopslagsysteem, bekomt het computerprogramma de volgende maandelijkse energiestromen:
display(HTML(ea.get_monthly_overview().to_html()))
# Dit kan ook overzichtelijk in een grafiek worden weergegeven:
graph = ea.plot_monthly_overview(fig_size=(14, 8), dpi=96)
# ## Analyseresultaat 3: Zelfvoorziening en Zelfconsumptie Zonder Batterijopslagsysteem
# * **Zelfvoorziening**: het elektrisch verbruik dat gedekt wordt door de eigen FV installatie. De *zelfvoorzieningsgraad* is het percentage van het jaarlijks verbruik dat geleverd wordt door de eigen FV installatie.
# * **Zelfconsumptie** of **eigenverbruik**: de energieopbrengst van de FV installatie die door de eigen verbruikersinstallatie wordt benut. De *benuttingsgraad* van de FV installatie is het percentage van de jaarlijkse opbrengst dat door de eigen verbruikerinstallatie wordt benut.
# ### Zelfvoorzieningsgraad
display(HTML(f'Zelfvoorzieningsgraad op jaarbasis = <b>{ea.get_self_sufficiency():.2f}</b> %'))
# *Maandelijks overzicht van de zelfvoorzieningsgraad*
graph = ea.plot_self_sufficiency(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ### Benuttingsgraad
display(HTML(f'Benuttingsgraad op jaarbasis = <b>{ea.get_self_consumption():.2f}</b> %'))
# *Maandelijks overzicht van de benuttingsgraad*
graph = ea.plot_self_consumption(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ### Netto Netverbruik
# In het geval van een terugdraaiende teller wordt het jaarlijks netto netverbruik aangerekend samen met een prosumententarief, dat afhangt van het nominaal AC-vermogen van de omvormer. Het netto netverbruik is het verschil tussen de hoeveelheid elektriciteit afgenomen van het net en de hoeveelheid elektriciteit die in het net werd geïnjecteerd.
display(HTML(f'Netto netverbruik = <b>{ea.get_net_consumption():.0f}</b> kWh'))
# ## Analyseresultaat 4: Energiestromen Met Batterijopslagsysteem
# ### Configuratie opslagbatterij
# Een batterijopslagsysteem dient om energieopbrengsten die niet momentaan verbruikt kunnen worden in een batterij op te slaan voor later verbruik, m.n. vóór zonsopgang en na zonsondergang, wanneer er geen FV productie mogelijk is, vermits er dan geen zonnestraling is. Om de benodigde batterijcapaciteit te bepalen, zou men zich daarom kunnen baseren op verbruiksgegevens vóór zonsopgang en na zonsondergang.<br>
# Aan het computerprogramma kan informatie worden opgevraagd over het dagelijks verbruik vóór zonsopgang en na zonsondergang (nachttijdverbruik): totaal jaarlijks nachttijdverbruik, het minimaal nachttijdverbruik dat voorkwam in het jaar, het gemiddeld nachttijdverbruik en het maximaal nachttijdverbruik.
nighttime_load_stats = ea.get_nighttime_load_stats()
display(HTML(
'<ul>'
f'<li>totaal jaarlijks nachttijdverbruik = <b>{nighttime_load_stats["sum"]:.0f}</b> kWh</li>'
f'<li>minimum nachttijdverbruik = <b>{nighttime_load_stats["min"]:.0f}</b> kWh</li>'
f'<li>gemiddeld nachttijdverbruik = <b>{nighttime_load_stats["avg"]:.0f}</b> kWh</li>'
f'<li>maximum nachttijdverbruik = <b>{nighttime_load_stats["max"]:.0f}</b> kWh</li>'
'</ul>'
))
# Op basis van deze data kan een opslagbatterij geselecteerd worden. Als we ons baseren op het gemiddeld nachttijdverbruik, hebben we een batterij nodig met een benutbare batterijcapaciteit van ca. 5 kWh.<br>
# <br>
# De benutbare batterijcapaciteit zal evenwel afhangen van de ontlaad- en laadstroom van de batterij. Hiernavolgend is een zoutwaterbatterij GREENROCK in aanmerking genomen. Eén *stack* heeft volgens de datasheet bij een laadstroom van 10 A (ca. 560 W bij laadspanning 56 V) en een ontlaadstroom van 15 A (ca. 720 W bij een ontlaadspanning van 48 V) een beschikbare capaciteit van 1,676 kWh. We zullen daarom 3 *stacks* nemen.<br>
# Indien het momentaan vermogen van de FV installatie groter zou zijn dan het vermogen dat de batterij kan accepteren, wordt het geaccepteerd vermogen begrensd tot wat de batterij aankan. Evenzo, indien het momentaan vermogen dat de verbruikersinstallatie vraagt, groter zou zijn dan hetgeen de batterij kan leveren, wordt het aan de batterij onttrokken vermogen eveneens begrensd tot wat de batterij aankan.
# **Configuratie opslagbatterij**
ea.battery = pv.Battery(battery_capacity=3 * 1.676) # available battery capacity depending on load and unload current (see battery specs)
ea.battery.set_loading_params(Idc=10.0, Vdc=56.0, eff=0.9) # battery current, load voltage and efficiency when loading
ea.battery.set_unloading_params(Idc=15.0, Vdc=48.0, eff=0.9) # battery current, load voltage and efficiency when unloading
# ### Maandelijks Overzicht van de Energiestromen
Eflow_stats = ea.analyze_energy_flows()
display(HTML(ea.get_monthly_overview().to_html()))
graph = ea.plot_monthly_overview(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ## Analyseresultaat 5: Zelfvoorziening en Zelfconsumptie Met Batterijopslagsysteem
# ### Zelfvoorzieningsgraad
display(HTML(f'Zelfvoorzieningsgraad op jaarbasis = <b>{ea.get_self_sufficiency():.2f}</b> %'))
# *Maandelijks overzicht van de zelfvoorzieningsgraad*
graph = ea.plot_self_sufficiency(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ### Benuttingsgraad
display(HTML(f'Benuttingsgraad op jaarbasis = <b>{ea.get_self_consumption():.2f}</b> %'))
# *Maandelijks overzicht van de benuttingsgraad*
graph = ea.plot_self_consumption(fig_size=(14, 8), dpi=96)
graph.show_graph()
# ### Zelfvoorzieningsgraad i.f.v. Batterijcapaciteit
# Men zou aannemen dat de zelfvoorzieningsgraad van een private elektrische installatie met zonnepanelen zal toenemen naarmate de batterijcapaciteit groter wordt gekozen.<br>
# Hieronder wordt de zelfvoorzieningsgraad van de desbetreffende installatie berekend voor verschillende batterijcapaciteiten gaande van 1 kWh tot 25 kWh en weergegeven in een grafiek.
# +
from nummath import graphing
battery_capacities = [i for i in range(1, 26)]
self_sufficiency = []
for battery_capacity in battery_capacities:
ea.battery = pv.Battery(battery_capacity)
ea.analyze_energy_flows()
self_sufficiency.append(ea.get_self_sufficiency())
graph = graphing.Graph(fig_size=(8, 6), dpi=96)
graph.add_data_set(name='none', x=battery_capacities, y=self_sufficiency, marker='o')
graph.set_axis_titles(x_title='battery capacity [kWh]', y_title='self-sufficiency [%]')
graph.turn_grid_on()
graph.draw_graph()
graph.show_graph()
# -
# Men constateert dat de curve een verzadigend verloop vertoont. Aanvankelijk neemt de zelfvoorzieningsgraad steil toe, maar vanaf een batterijcapaciteit van ca. 5 kWh buigt deze tendens zich om en vanaf ca. 10 kWh wordt de curve nagenoeg vlak. Het heeft bijgevolg geen zin om batterijen te installeren met een beschikbare batterijcapaciteit die groter is dan 10 kWh.
| pypv/notebooks/03_energieanalyse.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="A2mlp-BLpqPf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="d7446d21-0f68-4125-ace2-8963f4042250"
# Importing libraries we need for NLP
import nltk
nltk.download('punkt')
from nltk.stem.lancaster import LancasterStemmer
stemmer = LancasterStemmer()
import numpy as np
import random
from tensorflow import keras
from keras.models import load_model
# + id="GVNdkmgOpqPo" colab_type="code" colab={}
# import our chat-bot intents file
import json
with open('intents.json') as json_data:
intents = json.load(json_data)
# + id="smORE4tHpqPs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 88} outputId="5583629d-1f5e-406b-8e68-3168910d887a"
words = []
classes = []
documents = []
ignore_words = ['?']
# loop through each sentence in our intents patterns
for intent in intents['intents']:
for pattern in intent['patterns']:
# tokenize each word in the sentence
w = nltk.word_tokenize(pattern)
# add to our words list
words.extend(w)
# add to documents in our corpus
documents.append((w, intent['tag']))
# add to our classes list
if intent['tag'] not in classes:
classes.append(intent['tag'])
# stem and lower each word and remove duplicates
words = [stemmer.stem(w.lower()) for w in words if w not in ignore_words]
words = sorted(list(set(words)))
# remove duplicates
classes = sorted(list(set(classes)))
print (len(documents), "documents")
print (len(classes), "classes", classes)
print (len(words), "unique stemmed words", words)
# + id="Cx4NK4u9pqPx" colab_type="code" colab={}
model = load_model('model_ChatBot.h5')
# + id="6pf3d6s3pqP0" colab_type="code" colab={}
def clean_up_sentence(sentence):
# tokenize the pattern
sentence_words = nltk.word_tokenize(sentence)
# stem each word
sentence_words = [stemmer.stem(word.lower()) for word in sentence_words]
return sentence_words
# return bag of words array: 0 or 1 for each word in the bag that exists in the sentence
def bow(sentence, words, show_details=False):
# tokenize the pattern
sentence_words = clean_up_sentence(sentence)
# bag of words
bag = [0]*len(words)
for s in sentence_words:
for i,w in enumerate(words):
if w == s:
bag[i] = 1
if show_details:
print ("found in bag: %s" % w)
return(np.array(bag))
# + id="sl94UEj4pqP4" colab_type="code" colab={}
# create a data structure to hold user context
context = {}
ERROR_THRESHOLD = 0.65
def classify(sentence):
# generate probabilities from the model
p = bow(sentence, words)
d = len(p)
f = len(documents)-2
a = np.zeros([f, d])
tot = np.vstack((p,a))
results = model.predict(tot)[0]
# filter out predictions below a threshold
results = [[i,r] for i,r in enumerate(results) if r>ERROR_THRESHOLD]
# sort by strength of probability
results.sort(key=lambda x: x[1], reverse=True)
return_list = []
for r in results:
return_list.append((classes[r[0]], r[1]))
# return tuple of intent and probability
return return_list
def response(sentence, userID, show_details=False):
results = classify(sentence)
print('Result:',results)
# if we have a classification then find the matching intent tag
if results:
# loop as long as there are matches to process
while results:
for i in intents['intents']:
# find a tag matching the first result
if i['tag'] == results[0][0]:
# set context for this intent if necessary
#print(i)
if 'context_set' in i:
if show_details: print ('context:', i['context_set'])
context[userID] = i['context_set']
# check if this intent is contextual and applies to this user's conversation
if not 'context_filter' in i or \
(userID in context and 'context_filter' in i and i['context_filter'] == context[userID]):
if show_details: print ('tag:', i['tag'])
# a random response from the intent
return (random.choice(i['responses']))
results.pop(0)
# + id="PELH8pCnpqP7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 103} outputId="6081e748-0765-4da5-ea93-446e2a10df39"
response('the symptoms of heart disease?', '123', show_details=True)
# + id="T8UrQfT2pqQA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e23d6db7-09ea-4d0b-fd39-eb1b2e454625"
context
# + id="EGgs9ckkpqQF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 86} outputId="be47cad5-77cc-4b54-fd5f-765f22c6ed43"
response('hello there', '123', show_details=True)
# + id="CJL1sr_CpqQK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 120} outputId="a0b7e27a-f547-4b58-a200-1a4ecadaa0c0"
response('calculate heart rates', '123', show_details=True)
# + id="s9vmo0LCpqQN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="33a646aa-239b-499d-cc86-31904058d026"
context
# + id="nBFIJYQgpqQR" colab_type="code" colab={}
| ChatBotResponse.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/kageyama-xebec/data_science/blob/master/timeseries.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Qo2-NbW7fJSR" colab_type="code" colab={}
import os
import IPython
import IPython.display
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
mpl.rcParams['figure.figsize'] = (8,6)
mpl.rcParams['axes.grid'] = False
# + id="zmtSbjQcoFOv" colab_type="code" colab={}
| timeseries.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# PyGSLIB
# ========
#
# Probplot
# ---------------
#
#
#
#
# +
#general imports
import matplotlib.pyplot as plt
import pygslib
import numpy as np
#make the plots inline
# %matplotlib inline
# -
# Getting the data ready for work
# ---------
# If the data is in GSLIB format you can use the function `pygslib.gslib.read_gslib_file(filename)` to import the data into a Pandas DataFrame.
#
#get the data in gslib format into a pandas Dataframe
mydata= pygslib.gslib.read_gslib_file('../datasets/cluster.dat')
true= pygslib.gslib.read_gslib_file('../datasets/true.dat')
# +
# This is a 2D file, in this GSLIB version we require 3D data and drillhole name or domain code
# so, we are adding constant elevation = 0 and a dummy BHID = 1
mydata['Zlocation']=0
mydata['bhid']=1
true['Declustering Weight']=1
# printing to verify results
print ' \n **** 5 first rows in my datafile \n\n ', mydata.head(n=5)
print ' \n **** 5 first rows in my datafile \n\n ', true.head(n=5)
# -
#view data in a 2D projection
plt.scatter(mydata['Xlocation'],mydata['Ylocation'], c=mydata['Primary'])
plt.colorbar()
plt.grid(True)
plt.show()
# ## Testing probplot
# This is not plotting results but is handy to get declustered bins for plots
#
#
print pygslib.gslib.__plot.probplt.__doc__
mydata['Declustering Weight'].sum()
# +
parameters_probplt = {
'iwt' : 0, #int, 1 use declustering weight
'va' : mydata['Primary'], # array('d') with bounds (nd)
'wt' : mydata['Declustering Weight']} # array('d') with bounds (nd), wight variable (obtained with declust?)
parameters_probpltl = {
'iwt' : 1, #int, 1 use declustering weight
'va' : mydata['Primary'], # array('d') with bounds (nd)
'wt' : mydata['Declustering Weight']} # array('d') with bounds (nd), wight variable (obtained with declust?)
parameters_probpltt = {
'iwt' : 0, #int, 1 use declustering weight
'va' : true['Primary'], # array('d') with bounds (nd)
'wt' : true['Declustering Weight']} # array('d') with bounds (nd), wight variable (obtained with declust?)
binval,cl,xpt025,xlqt,xmed,xuqt,xpt975,xmin,xmax, \
xcvr,xmen,xvar,error = pygslib.gslib.__plot.probplt(**parameters_probplt)
binvall,cll,xpt025l,xlqtl,xmedl,xuqtl,xpt975l,xminl, \
xmaxl,xcvrl,xmenl,xvarl,errorl = pygslib.gslib.__plot.probplt(**parameters_probpltl)
binvalt,clt,xpt025t,xlqtt,xmedt,xuqtt,xpt975t,xmint, \
xmaxt,xcvrt,xment,xvart,errort = pygslib.gslib.__plot.probplt(**parameters_probpltt)
# -
print cl
print binvall
# +
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.plot (clt, binvalt, label = 'true')
plt.plot (cl, binval, label = 'raw')
plt.plot (cll, binvall, label = 'declustered')
plt.grid(True)
plt.legend()
fig.show
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.plot (clt, binvalt, label = 'true')
plt.plot (cl, binval, label = 'raw')
plt.plot (cll, binvall, label = 'declustered')
ax.set_xscale('log')
plt.grid(True)
plt.legend()
fig.show
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.plot (clt, binvalt, label = 'true')
plt.plot (cl, binval, label = 'raw')
plt.plot (cll, binvall, label = 'declustered')
ax.set_yscale('log')
plt.grid(True)
plt.legend()
fig.show
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
plt.plot (clt, binvalt, label = 'true')
plt.plot (cl, binval, label = 'raw')
plt.plot (cll, binvall, label = 'declustered')
ax.set_xscale('log')
ax.set_yscale('log')
plt.grid(True)
plt.legend()
fig.show
# -
print 'data min, max: ', xmin, xmax
print 'data quantile 2.5%, 25%, 50%, 75%, 97.75%: ' , xpt025,xlqt,xmed,xuqt,xpt975
print 'data cv, mean, variance : ', xcvr,xmen,xvar
print 'error <> 0? Then all ok?' , error==0
| pygslib/Ipython_templates/deprecated/probplt_raw.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Binary classification single feature
#
# Classification using "raw" python or libraries (SciKit Learn, Tensorflow).
#
# The classification is first on a single boundary defined by a continuous univariate function and added white noise
# +
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as pltcolors
from sklearn import metrics as metrics
from sklearn.linear_model import LogisticRegression as SkLinReg
import scipy as sy
import seaborn as sns
import pandas
import tensorflow as tf
# -
# ## Model
#
# We want to measure or predict a value y to be above a threshold. E.g.: y is a temperature.
#
# We know a feature x, y is related to x through a quadratic function we do not a priori know and some unknown
#
# This unknown is modeled by a Gaussian noise
# Single feature, Gaussian noise
nFeatures = 1
def generateBatch(N):
#
xMin = 0
xMax = 1
b = 0.2
std = 0.2
# Threshold from 0 to 1
threshold = 1
#
x = np.random.uniform(xMin, xMax, N)
# 4th degree relation between y and x
yClean = 2*(x**4 + (x-0.3)**3 + b)
labels = yClean + np.random.normal(0, std, N) > threshold
return (x, yClean, labels)
# The values of X are uniformly distributed and independent
# +
N = 2000
# x and y have 1 dim in R, label has 1 dim in B
xTrain, yCleanTrain, labelTrain = generateBatch(N)
colors = ['blue','red']
fig = plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plt.scatter(xTrain, yCleanTrain, c=labelTrain, cmap=pltcolors.ListedColormap(colors), marker=',', alpha=0.01)
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.subplot(1,2,2)
plt.scatter(xTrain, labelTrain, marker=',', alpha=0.01)
plt.xlabel('x')
plt.ylabel('label')
plt.grid()
# -
count, bins, ignored = plt.hist(labelTrain*1.0, 10, density=True, alpha=0.5)
p = np.mean(labelTrain)
print('Bernouilli parameter of the distribution:', p)
# Note: The two values are not a priori equi probable. In theory, ressampling of the training values would be required to balance the a priori distribution.
xTest, yTest, labelTest = generateBatch(N)
# ## Helpers
# +
def plotHeatMap(X, classes, title=None, fmt='.2g', ax=None, xlabel=None, ylabel=None):
""" Fix heatmap plot from Seaborn with pyplot 3.1.0, 3.1.1
https://stackoverflow.com/questions/56942670/matplotlib-seaborn-first-and-last-row-cut-in-half-of-heatmap-plot
"""
ax = sns.heatmap(X, xticklabels=classes, yticklabels=classes, annot=True, fmt=fmt, cmap=plt.cm.Blues, ax=ax) #notation: "annot" not "annote"
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)
if title:
ax.set_title(title)
if xlabel:
ax.set_xlabel(xlabel)
if ylabel:
ax.set_ylabel(ylabel)
def plotConfusionMatrix(yTrue, yEst, classes, title=None, fmt='.2g', ax=None):
plotHeatMap(metrics.confusion_matrix(yTrue, yEst), classes, title, fmt, ax, xlabel='Estimations', \
ylabel='True values');
# -
# ### Logistic and log of Logistic functions
def logistic(X):
return (1+(np.exp(-(X))))**-1
xx = np.linspace(-10, 10)
xlogistic = logistic(xx)
plt.figure(figsize=(10,5))
plt.subplot(1, 2, 1)
plt.plot(xx, xlogistic)
plt.grid()
plt.subplot(1, 2, 2)
plt.plot(xx, np.log(xlogistic))
plt.grid()
# # Logistic regression
#
# \begin{align}
# y \in \left\{ 0, 1 \right\}
# \end{align}
#
# \begin{align}
# p(Y=1 \mid x) & = \frac{1}{1+e^{-f_\theta(x)}} \\
# f_\theta(x) & = b + w x \\
# \theta &= \{b, w\}
# \end{align}
#
# We are looking for the value of w that maximize the likelyhood:
# \begin{align}
# \hat{\theta} & = \max_{\theta}{\prod_{i=0}^N{p(y_i \mid x_i, w)}} \\
# & = \max_{\theta}{\sum_{i=0}^N{log \left(p(y_i \mid x_i, w)\right)} } \\
# & = \max_{\theta}{\sum_{i=0}^N{log \left(\left(\frac{1}{1+e^{-f_\theta(x_i)}}\right)^{y_i}\left(1-\frac{1}{1+e^{-f_\theta(x_i)}}\right)^{1-y_i}\right)} } \\
# & = \max_{\theta}{\sum_{i=0}^N{log \left(y_i * \left(\frac{1}{1+e^{-f_\theta(x_i)}}\right) + \left(1-y_i\right) * \left(1-\frac{1}{1+e^{-f_\theta(x_I)}}\right) \right)} } \\
# \end{align}
#
# Using the fact that $y_i$ is either 0 or 1. The last formulation is avoiding logarithm of zero as one of the two terms within the sum is null.
#
# Since the number of classes is 2, the maximum log likelyhood is also called binary cross entropy.
#
# Reference:
# - https://en.wikipedia.org/wiki/Logistic_regression
#
# ## Fitting of $b$ and then $w$
#
#
# Suboptimal fitting:
# - Taking some assumption on $w$ to fit $b$ as $\hat{b}$
# - and then fitting $w$ with the $\hat{b}$ estimate
b = np.linspace(-5, 5)
w = 1
px = np.zeros(len(b))
for i in range(len(b)):
fx = logistic(b[i] + w*xTrain)
px[i] = 1/N * np.sum(np.log(labelTrain*fx + (1-labelTrain)*(1-fx)))
plt.plot(b, px);
plt.xlabel('$b$')
plt.ylabel('l(b, X)')
plt.grid()
bHat = b[np.argmax(px)]
print('Estimate b =', bHat)
w = np.linspace(-20, 20)
px = np.zeros(len(w))
for i in range(len(w)):
fx = logistic(bHat + w[i]*xTrain)
px[i] = 1/N * np.sum(np.log(labelTrain*fx + (1-labelTrain)*(1-fx)))
plt.plot(w, px);
plt.xlabel('w')
plt.ylabel('l(w, X)')
plt.grid()
wHat = w[np.argmax(px)]
print('Estimate w =', wHat)
pXTest0 = logistic(bHat + wHat * xTest)
labelEst0 = pXTest0 > 0.5
plt.scatter(xTest, pXTest0, c=labelEst0, cmap=pltcolors.ListedColormap(colors), marker=',', alpha=0.01);
plt.scatter(xTest, yTest/np.max(yTest), c = labelTest, cmap=pltcolors.ListedColormap(colors), marker='x', alpha=0.01);
plt.xlabel('x')
plt.legend(('Estimated probability', 'Normalized model'));
plt.hist(labelEst0*1.0, 10, density=True)
print('Bernouilli parameter =', np.mean(labelEst0))
accuracy0 = np.sum(labelTest == labelEst0)/N
print('Accuracy =', accuracy0)
# ### Precision
# $p(y = 1 \mid \hat{y} = 1)$
print('Precision =', np.sum(labelTest[labelEst0 == 1])/np.sum(labelEst0))
# ### Recall
# $p(\hat{y} = 1 \mid y = 1)$
print('Recall =', np.sum(labelTest[labelEst0 == 1])/np.sum(labelTest))
# ### Confusion matrix
plotConfusionMatrix(labelTest, labelEst0, np.array(['Blue', 'Red']));
print(metrics.classification_report(labelTest, labelEst0))
# # SciKit Learn
#
# References:
# - SciKit documentation
# - https://www.geeksforgeeks.org/ml-logistic-regression-using-python/
model1 = SkLinReg(solver='lbfgs')
model1.fit(xTrain.reshape(-1,1), labelTrain)
model1.coef_
labelEst1 = model1.predict(xTest.reshape(-1,1))
print('Accuracy =',model1.score(xTest.reshape(-1,1), labelTest))
plt.hist(labelEst1*1.0, 10, density=True)
print('Bernouilli parameter =', np.mean(labelEst1))
# ### Confusion matrix (plot)
plotConfusionMatrix(labelTest, labelEst1, np.array(['Blue', 'Red']))
# ### Classification report
print(metrics.classification_report(labelTest, labelEst1))
# References :
# - https://towardsdatascience.com/building-a-logistic-regression-in-python-step-by-step-becd4d56c9c8
# - https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression.get_params
# ### ROC curve
logit_roc_auc = metrics.roc_auc_score(labelTest, labelEst1)
fpr, tpr, thresholds = metrics.roc_curve(labelTest, model1.predict_proba(xTest.reshape(-1,1))[:,1])
plt.plot(fpr, tpr, label='Logistic Regression (area = %0.2f)' % logit_roc_auc)
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right");
# # Using TensorFlow 2.0
#
# In TensorFlow 2.0 many possibilities are available to design a sequential layer. It could be based on high level API using Keras, down to function code close to the syntax of Tensorflow 1.0.
#
# Following design is showing how to implement a custom layer within a Sequential pipeline of Keras, and how to implement a custom metric. This is the favoured method to implement custom code in TensorFlow 2.0.
# Labels as floats {0., 1.}
labelTrainF = np.multiply(labelTrain, 1.0)
labelTrainF.dtype, labelTrainF.shape
# (Mini) Batch size
nBatch = 100
# Number of batches per Epoch
nBatchPerEpoch =20
# Number of epochs
nEpochMax = 1000
# Simple custom layer exposing the linear regression model
class MyLogisticRegressionLayer(tf.keras.layers.Layer):
def __init__(self, *args, **kwargs):
super(MyLogisticRegressionLayer, self).__init__(*args, **kwargs)
def build(self, input_shape):
self.w = self.add_weight(
shape=input_shape[0],
dtype=self.dtype,
initializer=tf.keras.initializers.ones(),
#regularizer=tf.keras.regularizers.l2(0.02),
trainable=True)
self.b = self.add_weight(
shape=1,
dtype=self.dtype,
initializer=tf.keras.initializers.ones(),
#regularizer=tf.keras.regularizers.l2(0.02),
trainable=True)
@tf.function
def call(self, x, training=None):
return tf.math.sigmoid(tf.math.add(tf.math.multiply(x, self.w), self.b))
# Using TensorFlow 2.0 style of metrics to implement accuracy
class MyBinaryAccuracy(tf.keras.metrics.Metric):
def __init__(self, name='my_accuracy', **kwargs):
super(MyBinaryAccuracy, self).__init__(name=name, **kwargs)
self.accuracySum = self.add_weight(name='accuracySum',
initializer='zeros')
self.accuracyCount = self.add_weight(name='accuracyCount',
initializer='zeros')
def update_state(self, labels, yEst):
labels = tf.cast(labels, tf.bool)
labelEst = tf.greater(yEst, 0.5)
values = tf.cast(tf.equal(labels, labelEst), self.dtype)
self.accuracySum.assign_add(tf.reduce_sum(values))
self.accuracyCount.assign_add(values.get_shape()[0])
def result(self):
return self.accuracySum / self.accuracyCount
# +
# Model 1, instantiate the custom layer
model1 = tf.keras.Sequential([MyLogisticRegressionLayer(input_shape=[nFeatures], dtype="float64")])
# Stochastic Gradient Descent Optimizer
optim1 = tf.keras.optimizers.SGD(0.01)
# Perform a train step on a mini-batch
# This function's code is rewritten by TensorFlow 2.0 and shall be compiled at every execution of the optimizer
@tf.function
def trainStep1(x, labels):
with tf.GradientTape() as tape:
predictions = model1(x, training=True)
loss = -tf.reduce_sum(tf.math.log((labels * predictions) + ((1 - labels) * (1 - predictions))))
#loss = tf.keras.losses.categorical_crossentropy(labels, predictions)
gradients = tape.gradient(loss, model1.trainable_variables)
optim1.apply_gradients(zip(gradients, model1.trainable_variables))
return loss, predictions
# Initialize values and loop on epochs and mini batch
epoch = 0
cost_epoch = 1
histo = []
accuracy = MyBinaryAccuracy()
for epoch in range(nEpochMax):
cost_cumul = 0
accuracy.reset_states()
for b in range(0, nBatchPerEpoch*nBatch, nBatch):
cost, predictions = trainStep1(xTrain[b : b + nBatch], labelTrainF[b : b + nBatch])
cost_cumul += cost
accuracy.update_state(labelTrainF[b : b + nBatch], predictions)
cost_epoch = cost_cumul / nBatchPerEpoch
W = model1.get_weights()
histo.append((cost_epoch.numpy(), accuracy.result().numpy(), W[1][0], W[0]))
print("Predicted model: {b:.3f} + {w:.3f} x, num epochs={c}".format(w=W[0], b=W[1][0], c=len(histo)))
# Save history as a Panda Data Frame
df = pandas.DataFrame(histo, columns = ('cost', 'accuracy', 'b', 'w0'))
# -
# SGD shows that there is not a single optimal value for b+w (intercept + slope) but a straight line as shown on the graph below.
# This is explained by the single feature: the decision boundary does not need to be a straight line, a single intercept point would be enough.
plt.scatter(df['b'], df['w0'], marker='.', alpha=0.2);
plt.xlabel('intercept')
plt.ylabel('weight');
fig, ax = plt.subplots(1,2, figsize=(16, 4))
ax[0].plot(df['cost'])
ax[0].grid()
ax[1].plot(df['accuracy'])
ax[1].grid()
# # Where to go from here ?
#
# __More complex models__ with the 2 feature [binary classification](ClassificationContinuous2Features.html) ([Notebook](ClassificationContinuous2Features.ipynb)) or the [K Nearest Neighbors classifier](ClassificationContinuous2Features-KNN.html) ([Notebook](ClassificationContinuous2Features-KNN.ipynb))
#
# __Compare with the single feature linear regression__ [using simple algorithms](../linear/LinearRegressionUnivariate.html) ([Notebook](LinearRegressionUnivariate.ipynb])), [or using Tensorflow](LinearRegressionUnivariate-TensorFlow.html) ([Notebook](LinearRegressionUnivariate-TensorFlow.ipynb))
| classification/ClassificationContinuousSingleFeature.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# hide
# %load_ext autoreload
# %autoreload 2
# ! rm -rf ../data/projects/bbox/voila_results
# # Voila - Using Ipyannotator as a standalone web application
#
# [Voila](https://github.com/voila-dashboards/voila) is a library that turns jupyter notebooks into standalone web applications.
#
# Voila can be used alongside with Ipyannotator. This allows professional annotators to create annotations without even running a jupyter notebook.
#
# This notebook displays a bounding box annotator to exemplify how an organization can use Voila to allow external professional annotators to create datasets.
#
# To run this example use `voila nbs/09_voila_example.ipynb --enable_nbextensions=True`
from pathlib import Path
from ipyannotator.storage import construct_annotation_path
from ipyannotator.mltypes import InputImage, OutputImageBbox
from ipyannotator.bbox_annotator import BBoxAnnotator
input_item = InputImage(image_dir='pics', image_width=640, image_height=400)
output_item = OutputImageBbox(classes=['Label 01', 'Label 02'])
project_path = Path('../data/projects/bbox')
annotation_file_path = construct_annotation_path(project_path, results_dir='voila_results')
BBoxAnnotator(
project_path=project_path,
input_item=input_item,
output_item=output_item,
annotation_file_path=annotation_file_path
)
| nbs/09_voila_example.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="LHfPLGkqe-Jx" outputId="6d32f44e-3814-4b1d-a9dd-fde87461525e" colab={"base_uri": "https://localhost:8080/"}
# Clone the repo
# !git clone https://github.com/as-ideas/DeepForcedAligner
# + id="4mozuFkefE41" outputId="e40874c9-f497-40ff-ad4c-fb031bf742b4" colab={"base_uri": "https://localhost:8080/"}
# Install requirements
# %cd DeepForcedAligner/
# !pip install -r requirements.txt
# + id="N6FFe4g2fuBZ" outputId="810485f9-cb9f-4a07-b066-d89d4caec021" colab={"base_uri": "https://localhost:8080/"}
# Download and extract data (this may take a while)
# !wget http://data.keithito.com/data/speech/LJSpeech-1.1.tar.bz2
# !tar -xf LJSpeech-1.1.tar.bz2
# + id="fqYAxOsQtAxp"
# Update config with paths and settings for speedup
from dfa.utils import read_config, save_config
config = read_config('config.yaml')
config['paths']['dataset_dir'] = 'LJSpeech-1.1'
config['paths']['metadata_path'] = 'LJSpeech-1.1/metadata.csv'
config['training']['epochs'] = 4 # for speedup
config['durations']['method'] = 'beam' # for speedup
save_config(config, 'config.yaml')
# Preprocess data (tokenize text and convert wavs to mels)
# !python preprocess.py --num_workers 2
# + id="PpRQ1usSySaq"
# Start tensorboard
# %load_ext tensorboard
# %tensorboard --logdir dfa_checkpoints
# + id="NGh7XVhByTCX"
# Train speech-to-text model
# !python train.py
# + id="fuozwPCx0Qi6"
# Load latest model and extract char durations
# !python extract_durations.py --num_workers 2
# + id="0vlau7hm1nFi"
# Load and print example durations in mel steps and milliseconds
import numpy as np
durations = np.load('output/durations/LJ001-0002.npy')
mel_step_ms = 1000. * config['audio']['hop_length'] / config['audio']['sample_rate']
text = 'in being comparatively modern.'
print('ind char dur dur in ms')
for i, (t, dur) in enumerate(zip(text, durations)):
print(f'{i:#2} {t} {dur:#2} {dur * mel_step_ms:#.4}')
# + id="r34aJDkJEzEw"
# For comparison listen to the wav
import librosa
import IPython.display as ipd
sample_rate = config['audio']['sample_rate']
hop_len = config['audio']['hop_length']
wav, _ = librosa.load('LJSpeech-1.1/wavs/LJ001-0002.wav', sr=sample_rate)
ipd.Audio(wav, rate=sample_rate)
# + id="VE2kYwP0RKKo"
# Cut word out of wav
print(text[9:22])
char_time = np.cumsum(np.pad(durations, (1, 0))) * hop_len
wav_start, wav_end = char_time[9], char_time[22]
wav_cut = wav[wav_start: wav_end]
ipd.Audio(wav_cut, rate=sample_rate)
| notebooks/train.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["pdf-title"]
# # Multiclass Support Vector Machine exercise
#
# *Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the [assignments page](http://vision.stanford.edu/teaching/cs231n/assignments.html) on the course website.*
#
# In this exercise you will:
#
# - implement a fully-vectorized **loss function** for the SVM
# - implement the fully-vectorized expression for its **analytic gradient**
# - **check your implementation** using numerical gradient
# - use a validation set to **tune the learning rate and regularization** strength
# - **optimize** the loss function with **SGD**
# - **visualize** the final learned weights
#
# + tags=["pdf-ignore"]
# Run some setup code for this notebook.
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
# This is a bit of magic to make matplotlib figures appear inline in the
# notebook rather than in a new window.
# %matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
# %load_ext autoreload
# %autoreload 2
# + [markdown] tags=["pdf-ignore"]
# ## CIFAR-10 Data Loading and Preprocessing
# + tags=["pdf-ignore"]
# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
del X_train, y_train
del X_test, y_test
print('Clear previously loaded data.')
except:
pass
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
# + tags=["pdf-ignore"]
# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
# + tags=["pdf-ignore"]
# Split the data into train, val, and test sets. In addition we will
# create a small development set as a subset of the training data;
# we can use this for development so our code runs faster.
num_training = 49000
num_validation = 1000
num_test = 1000
num_dev = 500
# Our validation set will be num_validation points from the original
# training set.
mask = range(num_training, num_training + num_validation)
X_val = X_train[mask]
y_val = y_train[mask]
# Our training set will be the first num_train points from the original
# training set.
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
# We will also make a development set, which is a small subset of
# the training set.
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]
# We use the first num_test points of the original test set as our
# test set.
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
# + tags=["pdf-ignore"]
# Preprocessing: reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))
# As a sanity check, print out the shapes of the data
print('Training data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
print('dev data shape: ', X_dev.shape)
# + tags=["pdf-ignore-input"]
# Preprocessing: subtract the mean image
# first: compute the image mean based on the training data
mean_image = np.mean(X_train, axis=0)
print(mean_image[:10]) # print a few of the elements
plt.figure(figsize=(4,4))
plt.imshow(mean_image.reshape((32,32,3)).astype('uint8')) # visualize the mean image
plt.show()
# second: subtract the mean image from train and test data
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
X_dev -= mean_image
# third: append the bias dimension of ones (i.e. bias trick) so that our SVM
# only has to worry about optimizing a single weight matrix W.
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
print(X_train.shape, X_val.shape, X_test.shape, X_dev.shape)
# -
# ## SVM Classifier
#
# Your code for this section will all be written inside `cs231n/classifiers/linear_svm.py`.
#
# As you can see, we have prefilled the function `svm_loss_naive` which uses for loops to evaluate the multiclass SVM loss function.
# +
# Evaluate the naive implementation of the loss we provided for you:
from cs231n.classifiers.linear_svm import svm_loss_naive
import time
# generate a random SVM weight matrix of small numbers
W = np.random.randn(3073, 10) * 0.0001
loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.000005)
print('loss: %f' % (loss, ))
# -
# The `grad` returned from the function above is right now all zero. Derive and implement the gradient for the SVM cost function and implement it inline inside the function `svm_loss_naive`. You will find it helpful to interleave your new code inside the existing function.
#
# To check that you have correctly implemented the gradient correctly, you can numerically estimate the gradient of the loss function and compare the numeric estimate to the gradient that you computed. We have provided code that does this for you:
# +
# Once you've implemented the gradient, recompute it with the code below
# and gradient check it with the function we provided for you
# Compute the loss and its gradient at W.
loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.0)
# Numerically compute the gradient along several randomly chosen dimensions, and
# compare them with your analytically computed gradient. The numbers should match
# almost exactly along all dimensions.
from cs231n.gradient_check import grad_check_sparse
f = lambda w: svm_loss_naive(w, X_dev, y_dev, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad)
# do the gradient check once again with regularization turned on
# you didn't forget the regularization gra|ient did you?
loss, grad = svm_loss_naive(W, X_dev, y_dev, 5e1)
f = lambda w: svm_loss_naive(w, X_dev, y_dev, 5e1)[0]
grad_numerical = grad_check_sparse(f, W, grad)
# + [markdown] tags=["pdf-inline"]
# **Inline Question 1**
#
# It is possible that once in a while a dimension in the gradcheck will not match exactly. What could such a discrepancy be caused by? Is it a reason for concern? What is a simple example in one dimension where a gradient check could fail? How would change the margin affect of the frequency of this happening? *Hint: the SVM loss function is not strictly speaking differentiable*
#
# $\color{blue}{\textit Your Answer:}$ Non-linear function, e.g. max() has some kink points. No. y=max(0, x) when x = -1e-10, and step = 1e-4. Use only a few datapoints.
#
# + id="vectorized_time_1"
# Next implement the function svm_loss_vectorized; for now only compute the loss;
# we will implement the gradient in a moment.
tic = time.time()
loss_naive, grad_naive = svm_loss_naive(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Naive loss: %e computed in %fs' % (loss_naive, toc - tic))
from cs231n.classifiers.linear_svm import svm_loss_vectorized
tic = time.time()
loss_vectorized, _ = svm_loss_vectorized(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic))
# The losses should match but your vectorized implementation should be much faster.
print('difference: %f' % (loss_naive - loss_vectorized))
# + id="vectorized_time_2"
# Complete the implementation of svm_loss_vectorized, and compute the gradient
# of the loss function in a vectorized way.
# The naive implementation and the vectorized implementation should match, but
# the vectorized version should still be much faster.
tic = time.time()
_, grad_naive = svm_loss_naive(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Naive loss and gradient: computed in %fs' % (toc - tic))
tic = time.time()
_, grad_vectorized = svm_loss_vectorized(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Vectorized loss and gradient: computed in %fs' % (toc - tic))
# The loss is a single number, so it is easy to compare the values computed
# by the two implementations. The gradient on the other hand is a matrix, so
# we use the Frobenius norm to compare them.
difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('difference: %f' % difference)
# -
# ### Stochastic Gradient Descent
#
# We now have vectorized and efficient expressions for the loss, the gradient and our gradient matches the numerical gradient. We are therefore ready to do SGD to minimize the loss. Your code for this part will be written inside `cs231n/classifiers/linear_classifier.py`.
# + id="sgd"
# In the file linear_classifier.py, implement SGD in the function
# LinearClassifier.train() and then run it with the code below.
from cs231n.classifiers import LinearSVM
svm = LinearSVM()
tic = time.time()
loss_hist = svm.train(X_train, y_train, learning_rate=1e-7, reg=2.5e4,
num_iters=1500, verbose=True)
toc = time.time()
print('That took %fs' % (toc - tic))
# -
# A useful debugging strategy is to plot the loss as a function of
# iteration number:
plt.plot(loss_hist)
plt.xlabel('Iteration number')
plt.ylabel('Loss value')
plt.show()
# + id="validate"
# Write the LinearSVM.predict function and evaluate the performance on both the
# training and validation set
y_train_pred = svm.predict(X_train)
print('training accuracy: %f' % (np.mean(y_train == y_train_pred), ))
y_val_pred = svm.predict(X_val)
print('validation accuracy: %f' % (np.mean(y_val == y_val_pred), ))
# + id="tuning" tags=["code"]
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of about 0.39 on the validation set.
# Note: you may see runtime/overflow warnings during hyper-parameter search.
# This may be caused by extreme values, and is not a bug.
# results is dictionary mapping tuples of the form
# (learning_rate, regularization_strength) to tuples of the form
# (training_accuracy, validation_accuracy). The accuracy is simply the fraction
# of data points that are correctly classified.
results = {}
best_val = -1 # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.
################################################################################
# TODO: #
# Write code that chooses the best hyperparameters by tuning on the validation #
# set. For each combination of hyperparameters, train a linear SVM on the #
# training set, compute its accuracy on the training and validation sets, and #
# store these numbers in the results dictionary. In addition, store the best #
# validation accuracy in best_val and the LinearSVM object that achieves this #
# accuracy in best_svm. #
# #
# Hint: You should use a small value for num_iters as you develop your #
# validation code so that the SVMs don't take much time to train; once you are #
# confident that your validation code works, you should rerun the validation #
# code with a larger value for num_iters. #
################################################################################
# Provided as a reference. You may or may not want to change these hyperparameters
# learning_rates = [1e-7, 5e-5]
# regularization_strengths = [2.5e4, 5e4]
# These settings comes from https://github.com/lightaime/cs231n/blob/master/assignment1/svm.ipynb.
learning_rates = [1.4e-7, 1.5e-7, 1.6e-7]
regularization_strengths = [(1+i*0.1)*1e4 for i in range(-3,3)] + [(2+0.1*i)*1e4 for i in range(-3,3)]
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for lr in learning_rates:
for reg in regularization_strengths:
svm = LinearSVM()
svm.train(X_train, y_train, learning_rate = lr, reg = reg, num_iters = 1500)
tr_acc, val_acc = np.mean(svm.predict(X_train)==y_train), np.mean(svm.predict(X_val)==y_val)
if(val_acc > best_val):
best_svm = svm
best_val = val_acc
results[(lr, reg)] = (tr_acc, val_acc)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
# + tags=["pdf-ignore-input"]
# Visualize the cross-validation results
import math
import pdb
# pdb.set_trace()
x_scatter = [math.log10(x[0]) for x in results]
y_scatter = [math.log10(x[1]) for x in results]
# plot training accuracy
marker_size = 100
colors = [results[x][0] for x in results]
plt.subplot(2, 1, 1)
plt.tight_layout(pad=3)
plt.scatter(x_scatter, y_scatter, marker_size, c=colors, cmap=plt.cm.coolwarm)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('CIFAR-10 training accuracy')
# plot validation accuracy
colors = [results[x][1] for x in results] # default size of markers is 20
plt.subplot(2, 1, 2)
plt.scatter(x_scatter, y_scatter, marker_size, c=colors, cmap=plt.cm.coolwarm)
plt.colorbar()
plt.xlabel('log learning rate')
plt.ylabel('log regularization strength')
plt.title('CIFAR-10 validation accuracy')
plt.show()
# + id="test"
# Evaluate the best svm on test set
y_test_pred = best_svm.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('linear SVM on raw pixels final test set accuracy: %f' % test_accuracy)
# + tags=["pdf-ignore-input"]
# Visualize the learned weights for each class.
# Depending on your choice of learning rate and regularization strength, these may
# or may not be nice to look at.
w = best_svm.W[:-1,:] # strip out the bias
w = w.reshape(32, 32, 3, 10)
w_min, w_max = np.min(w), np.max(w)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
plt.subplot(2, 5, i + 1)
# Rescale the weights to be between 0 and 255
wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min)
plt.imshow(wimg.astype('uint8'))
plt.axis('off')
plt.title(classes[i])
# + [markdown] tags=["pdf-inline"]
# **Inline question 2**
#
# Describe what your visualized SVM weights look like, and offer a brief explanation for why they look they way that they do.
#
# $\color{blue}{\textit Your Answer:}$ *The SVM weights look like random noise. However, with careful observation, we can know the weights at a certain point is relative to the average of the pixel value of the point. Since the goal of SVM is to minimize the loss, that is, maximize the score of the correct class, the picture of the weights must be as similar to all the pictures in that corresponing catagory as possible.*
#
| assignment1/svm.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (py39)
# language: python
# name: py39
# ---
import netCDF4 as nc
import datetime as dt
import subprocess
import requests
import matplotlib.pyplot as plt
import cmocean
import numpy as np
import os
import glob
import dateutil as dutil
from salishsea_tools import viz_tools, places
# %matplotlib inline
jS3,iS3=places.PLACES['S3']['NEMO grid ji']
jSI,iSI=[343,198]
# + jupyter={"outputs_hidden": false}
with nc.Dataset('/ocean/eolson/MEOPAR/NEMO-forcing/grid/mesh_mask201702_noLPE.nc') as fm:
tmask=np.copy(fm.variables['tmask'])
umask=np.copy(fm.variables['umask'])
vmask=np.copy(fm.variables['vmask'])
navlon=np.copy(fm.variables['nav_lon'])
navlat=np.copy(fm.variables['nav_lat'])
dept=np.copy(fm.variables['gdept_1d'])
e3t_0=np.copy(fm.variables['e3t_0'])
e3u_0=np.copy(fm.variables['e3u_0'])
e3v_0=np.copy(fm.variables['e3v_0'])
e1t=np.copy(fm.variables['e1t'])
e2t=np.copy(fm.variables['e2t'])
e1v=np.copy(fm.variables['e1v'])
e2u=np.copy(fm.variables['e2u'])
A=fm.variables['e1t'][0,:,:]*fm.variables['e2t'][0,:,:]*tmask[0,0,:,:]
# -
fig,ax=plt.subplots(1,1,figsize=(4,6))
ax.pcolormesh(tmask[0,0,:,:])
ax.plot(iS3,jS3,'r*')
ax.plot(iSI,jSI,'r*')
ax.set_aspect(1)
jpkup=0
for i in range(0,40):
if dept[0][i]<=15:
jpkup=i
print(jpkup)
jpkup=jpkup+1
print(jpkup)
jpkmid=0
for i in range(0,40):
if dept[0][i]>=15<=50:
jpkmid=i
print(jpkmid)
jpkmid=jpkmid+1
print(jpkmid)
jpklo=0
for i in range(0,40):
if dept[0][i]>=50<=100:
jpklo=i
print(jpklo)
jpklo=jpklo+1
print(jpklo)
koff=jpkup
koff2=jpkmid
koff3=jpklo
# + jupyter={"outputs_hidden": false}
t0=dt.datetime(2010,1,1) # 1st start date of run
#te=dt.datetime(2011,12,31)# last start date of runfnum=18
stm=np.shape(tmask)
#nlen=36*2
nlen=730
dlist=[t0+dt.timedelta(days=ii) for ii in range(0,nlen)]
# -
#sdir0='/results/SalishSea/nowcast-green/'
#sdir1='/results/SalishSea/hindcast/'
#sdir3='/data/eolson/MEOPAR/SS36runs/CedarRuns/spring2015_HCMZ/'
#sdir1='/results2/SalishSea/nowcast-green.201905/'
sdir1='/results2/SalishSea/nowcast-green.201905/'
tmaskC=np.copy(tmask)
tmaskC[:,koff:,:,:]=0
tmaskD=np.copy(tmask)
tmaskD[:,koff2:,:,:]=0
tmaskE=np.copy(tmask)
tmaskE[:,koff3:,:,:]=0
# + jupyter={"outputs_hidden": false}
tlist=dlist
idir=sdir1
fformat1='%d%b%y/'
fformatT='SalishSea_1d_%Y%m%d_%Y%m%d_dia2_T.nc'
fformatP='SalishSea_1d_%Y%m%d_%Y%m%d_carp_T.nc'
meanMESZDS3up=np.zeros((len(tlist),))
meanMESZDS3mid=np.zeros((len(tlist),))
meanMESZDS3lo=np.zeros((len(tlist),))
meanMESZDSIup=np.zeros((len(tlist),))
meanMESZDSImid=np.zeros((len(tlist),))
meanMESZDSIlo=np.zeros((len(tlist),))
ind=-1
for idt0 in tlist:
ind=ind+1
cdir=idt0.strftime(fformat1).lower()
iffT=idt0.strftime(fformatT)
iffP=idt0.strftime(fformatP)
sffT=idir+cdir+iffT
sffP=idir+cdir+iffP
f=nc.Dataset(glob.glob(sffT)[0])
if ind%15==0: print(sffT)
fP=nc.Dataset(glob.glob(sffP)[0])
#e3t=fP.variables['e3t'][:2,:,:,:]
Vol=A*e3t_0
meanMESZDS3up[ind]=np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZDIAT'][0,:,jS3,iS3])/\
np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZDS3mid[ind]=np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZDIAT'][0,:,jS3,iS3])/\
np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZDS3lo[ind]=np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZDIAT'][0,:,jS3,iS3])/\
np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZDSIup[ind]=np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZDIAT'][0,:,jSI,iSI])/\
np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZDSImid[ind]=np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZDIAT'][0,:,jSI,iSI])/\
np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZDSIlo[ind]=np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZDIAT'][0,:,jSI,iSI])/\
np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
f.close()
fP.close()
# -
tlist=dlist
idir=sdir1
fformat1='%d%b%y/'
fformatT='SalishSea_1d_%Y%m%d_%Y%m%d_dia2_T.nc'
fformatP='SalishSea_1d_%Y%m%d_%Y%m%d_carp_T.nc'
meanMESZFS3up=np.zeros((len(tlist),))
meanMESZFS3mid=np.zeros((len(tlist),))
meanMESZFS3lo=np.zeros((len(tlist),))
meanMESZFSIup=np.zeros((len(tlist),))
meanMESZFSImid=np.zeros((len(tlist),))
meanMESZFSIlo=np.zeros((len(tlist),))
ind=-1
for idt0 in tlist:
ind=ind+1
cdir=idt0.strftime(fformat1).lower()
iffT=idt0.strftime(fformatT)
iffP=idt0.strftime(fformatP)
sffT=idir+cdir+iffT
sffP=idir+cdir+iffP
f=nc.Dataset(glob.glob(sffT)[0])
if ind%15==0: print(sffT)
fP=nc.Dataset(glob.glob(sffP)[0])
#e3t=fP.variables['e3t'][:2,:,:,:]
Vol=A*e3t_0
meanMESZFS3up[ind]=np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPHY'][0,:,jS3,iS3])/\
np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZFS3mid[ind]=np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPHY'][0,:,jS3,iS3])/\
np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZFS3lo[ind]=np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPHY'][0,:,jS3,iS3])/\
np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZFSIup[ind]=np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPHY'][0,:,jSI,iSI])/\
np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZFSImid[ind]=np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPHY'][0,:,jSI,iSI])/\
np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZFSIlo[ind]=np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPHY'][0,:,jSI,iSI])/\
np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
f.close()
fP.close()
tlist=dlist
idir=sdir1
fformat1='%d%b%y/'
fformatT='SalishSea_1d_%Y%m%d_%Y%m%d_dia2_T.nc'
fformatP='SalishSea_1d_%Y%m%d_%Y%m%d_carp_T.nc'
meanMESZMS3up=np.zeros((len(tlist),))
meanMESZMS3mid=np.zeros((len(tlist),))
meanMESZMS3lo=np.zeros((len(tlist),))
meanMESZMSIup=np.zeros((len(tlist),))
meanMESZMSImid=np.zeros((len(tlist),))
meanMESZMSIlo=np.zeros((len(tlist),))
ind=-1
for idt0 in tlist:
ind=ind+1
cdir=idt0.strftime(fformat1).lower()
iffT=idt0.strftime(fformatT)
iffP=idt0.strftime(fformatP)
sffT=idir+cdir+iffT
sffP=idir+cdir+iffP
f=nc.Dataset(glob.glob(sffT)[0])
if ind%15==0: print(sffT)
fP=nc.Dataset(glob.glob(sffP)[0])
#e3t=fP.variables['e3t'][:2,:,:,:]
Vol=A*e3t_0
meanMESZMS3up[ind]=np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMICZ'][0,:,jS3,iS3])/\
np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZMS3mid[ind]=np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMICZ'][0,:,jS3,iS3])/\
np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZMS3lo[ind]=np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMICZ'][0,:,jS3,iS3])/\
np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZMSIup[ind]=np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMICZ'][0,:,jSI,iSI])/\
np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZMSImid[ind]=np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMICZ'][0,:,jSI,iSI])/\
np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZMSIlo[ind]=np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMICZ'][0,:,jSI,iSI])/\
np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
f.close()
fP.close()
tlist=dlist
idir=sdir1
fformat1='%d%b%y/'
fformatT='SalishSea_1d_%Y%m%d_%Y%m%d_dia2_T.nc'
fformatP='SalishSea_1d_%Y%m%d_%Y%m%d_carp_T.nc'
meanMESZCS3up=np.zeros((len(tlist),))
meanMESZCS3mid=np.zeros((len(tlist),))
meanMESZCS3lo=np.zeros((len(tlist),))
meanMESZCSIup=np.zeros((len(tlist),))
meanMESZCSImid=np.zeros((len(tlist),))
meanMESZCSIlo=np.zeros((len(tlist),))
ind=-1
for idt0 in tlist:
ind=ind+1
cdir=idt0.strftime(fformat1).lower()
iffT=idt0.strftime(fformatT)
iffP=idt0.strftime(fformatP)
sffT=idir+cdir+iffT
sffP=idir+cdir+iffP
f=nc.Dataset(glob.glob(sffT)[0])
if ind%15==0: print(sffT)
fP=nc.Dataset(glob.glob(sffP)[0])
#e3t=fP.variables['e3t'][:2,:,:,:]
Vol=A*e3t_0
meanMESZCS3up[ind]=np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMRUB'][0,:,jS3,iS3])/\
np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZCS3mid[ind]=np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMRUB'][0,:,jS3,iS3])/\
np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZCS3lo[ind]=np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZMRUB'][0,:,jS3,iS3])/\
np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZCSIup[ind]=np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMRUB'][0,:,jSI,iSI])/\
np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZCSImid[ind]=np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMRUB'][0,:,jSI,iSI])/\
np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZCSIlo[ind]=np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZMRUB'][0,:,jSI,iSI])/\
np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
f.close()
fP.close()
tlist=dlist
idir=sdir1
fformat1='%d%b%y/'
fformatT='SalishSea_1d_%Y%m%d_%Y%m%d_dia2_T.nc'
fformatP='SalishSea_1d_%Y%m%d_%Y%m%d_carp_T.nc'
meanMESZPS3up=np.zeros((len(tlist),))
meanMESZPS3mid=np.zeros((len(tlist),))
meanMESZPS3lo=np.zeros((len(tlist),))
meanMESZPSIup=np.zeros((len(tlist),))
meanMESZPSImid=np.zeros((len(tlist),))
meanMESZPSIlo=np.zeros((len(tlist),))
ind=-1
for idt0 in tlist:
ind=ind+1
cdir=idt0.strftime(fformat1).lower()
iffT=idt0.strftime(fformatT)
iffP=idt0.strftime(fformatP)
sffT=idir+cdir+iffT
sffP=idir+cdir+iffP
f=nc.Dataset(glob.glob(sffT)[0])
if ind%15==0: print(sffT)
fP=nc.Dataset(glob.glob(sffP)[0])
#e3t=fP.variables['e3t'][:2,:,:,:]
Vol=A*e3t_0
meanMESZPS3up[ind]=np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPON'][0,:,jS3,iS3])/\
np.sum(tmaskC[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZPS3mid[ind]=np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPON'][0,:,jS3,iS3])/\
np.sum(tmaskD[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZPS3lo[ind]=np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3]*f.variables['GRMESZPON'][0,:,jS3,iS3])/\
np.sum(tmaskE[0,:,jS3,iS3]*Vol[0,:,jS3,iS3])#mmol/m3
meanMESZPSIup[ind]=np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPON'][0,:,jSI,iSI])/\
np.sum(tmaskC[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZPSImid[ind]=np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPON'][0,:,jSI,iSI])/\
np.sum(tmaskD[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
meanMESZPSIlo[ind]=np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI]*f.variables['GRMESZPON'][0,:,jSI,iSI])/\
np.sum(tmaskE[0,:,jSI,iSI]*Vol[0,:,jSI,iSI])#mmol/m3
f.close()
fP.close()
meanMESZtotalS3up=meanMESZDS3up+meanMESZFS3up+meanMESZCS3up+meanMESZMS3up
meanMESZtotalS3mid=meanMESZDS3mid+meanMESZFS3mid+meanMESZCS3mid+meanMESZMS3mid
meanMESZtotalS3lo=meanMESZDS3lo+meanMESZFS3lo+meanMESZCS3lo+meanMESZMS3lo
meanMESZtotalSIup=meanMESZDSIup+meanMESZFSIup+meanMESZCSIup+meanMESZMSIup
meanMESZtotalSImid=meanMESZDSImid+meanMESZFSImid+meanMESZCSImid+meanMESZMSImid
meanMESZtotalSIlo=meanMESZDSIlo+meanMESZFSIlo+meanMESZCSIlo+meanMESZMSIlo
# +
fig,ax=plt.subplots(1,1,figsize=(12,2))
ax.plot(tlist,(meanMESZDSIup*86400),'-',color='darkgreen',label='Diatoms')
ax.plot(tlist,(meanMESZFSIup*86400),':',color='red',label='Flagellates')
ax.plot(tlist,(meanMESZCSIup*86400),'-',color='orange',label='Ciliates')
ax.plot(tlist,(meanMESZMSIup*86400),'--',color='purple',label='Microzoop')
ax.plot(tlist,(meanMESZPSIup*86400),':',color='blue',label='PON')
ax.legend(frameon=False)
ax.set_ylim((0,1.5))
ax.set_ylabel('Feeding Rate ($\mu$M N d-1)')
ax.set_title('Saanich Inlet Mesozooplankton Feeding (upper 15 m)')
fig,ax=plt.subplots(1,1,figsize=(12,2))
ax.plot(tlist,(meanMESZDSImid*86400),'-',color='darkgreen',label='Diatoms')
ax.plot(tlist,(meanMESZFSImid*86400),':',color='red',label='Flagellates')
ax.plot(tlist,(meanMESZCSImid*86400),'-',color='orange',label='Ciliates')
ax.plot(tlist,(meanMESZMSImid*86400),'--',color='purple',label='Microzoop')
ax.plot(tlist,(meanMESZPSImid*86400),':',color='blue',label='PON')
ax.legend(frameon=False)
ax.set_ylim((0,.2))
ax.set_ylabel('Feeding Rate ($\mu$M N d-1)')
ax.set_title('Saanich Inlet Mesozooplankton Feeding (15-50 m)')
fig,ax=plt.subplots(1,1,figsize=(12,2))
ax.plot(tlist,(meanMESZDSIlo*86400),'-',color='darkgreen',label='Diatoms')
ax.plot(tlist,(meanMESZFSIlo*86400),':',color='red',label='Flagellates')
ax.plot(tlist,(meanMESZCSIlo*86400),'-',color='orange',label='Ciliates')
ax.plot(tlist,(meanMESZMSIlo*86400),'--',color='purple',label='Microzoop')
ax.plot(tlist,(meanMESZPSIlo*86400),':',color='blue',label='PON')
ax.legend(frameon=False)
ax.set_ylim((0,.2))
ax.set_ylabel('Feeding Rate ($\mu$M N d-1)')
ax.set_title('Saanich Inlet Mesozooplankton Feeding (50-100 m)')
# -
| notebooks/plotExamples/SaanichInletDepthSpecificDiet.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1> Experimenting with different models </h1>
#
# In this notebook, we try out different ideas. The first thing we have to do is to create a validation set, so that we are not doing experimentation with our independent test dataset.
# +
BUCKET='cs358-bucket'
import os
os.environ['BUCKET'] = BUCKET
# -
from __future__ import print_function
from pyspark.mllib.classification import LogisticRegressionWithLBFGS
from pyspark.mllib.regression import LabeledPoint
from pyspark.sql.types import StringType, FloatType, StructType, StructField
# +
# Create spark session
from __future__ import print_function
from pyspark.sql import SparkSession
from pyspark import SparkContext
sc = SparkContext('local', 'experimentation')
spark = SparkSession \
.builder \
.appName("experimentation w/ Spark ML") \
.getOrCreate()
print(spark)
print(sc)
# -
# <h2> Read dataset </h2>
traindays = spark.read \
.option("header", "true") \
.csv('gs://{}/flights/trainday.csv'.format(BUCKET))
traindays.createOrReplaceTempView('traindays')
# +
header = 'FL_DATE,UNIQUE_CARRIER,AIRLINE_ID,CARRIER,FL_NUM,ORIGIN_AIRPORT_ID,ORIGIN_AIRPORT_SEQ_ID,ORIGIN_CITY_MARKET_ID,ORIGIN,DEST_AIRPORT_ID,DEST_AIRPORT_SEQ_ID,DEST_CITY_MARKET_ID,DEST,CRS_DEP_TIME,DEP_TIME,DEP_DELAY,TAXI_OUT,WHEELS_OFF,WHEELS_ON,TAXI_IN,CRS_ARR_TIME,ARR_TIME,ARR_DELAY,CANCELLED,CANCELLATION_CODE,DIVERTED,DISTANCE,DEP_AIRPORT_LAT,DEP_AIRPORT_LON,DEP_AIRPORT_TZOFFSET,ARR_AIRPORT_LAT,ARR_AIRPORT_LON,ARR_AIRPORT_TZOFFSET,EVENT,NOTIFY_TIME'
def get_structfield(colname):
if colname in ['ARR_DELAY', 'DEP_DELAY', 'DISTANCE', 'TAXI_OUT']:
return StructField(colname, FloatType(), True)
else:
return StructField(colname, StringType(), True)
schema = StructType([get_structfield(colname) for colname in header.split(',')])
# +
inputs = 'gs://{}/flights/tzcorr/all_flights-00000-*' # 1/30th
#inputs = 'gs://{}/flights/tzcorr/all_flights-*' # FULL
flights = spark.read\
.schema(schema)\
.csv(inputs.format(BUCKET))
# this view can now be queried ...
flights.createOrReplaceTempView('flights')
# -
# <h2> Create separate training and validation data </h2>
from pyspark.sql.functions import rand
SEED = 13
traindays = traindays.withColumn("holdout", rand(SEED) > 0.8) # 80% of data is for training
traindays.createOrReplaceTempView('traindays')
traindays.head(10)
# <h2> Logistic regression </h2>
trainquery = """
SELECT
*
FROM flights f
JOIN traindays t
ON f.FL_DATE == t.FL_DATE
WHERE
t.is_train_day == 'True' AND
t.holdout == False AND
f.CANCELLED == '0.00' AND
f.DIVERTED == '0.00'
"""
traindata = spark.sql(trainquery)
traindata.head()
def to_example(fields):
return LabeledPoint(\
float(fields['ARR_DELAY'] < 15), #ontime \
[ \
fields['DEP_DELAY'], # DEP_DELAY \
fields['TAXI_OUT'], # TAXI_OUT \
fields['DISTANCE'], # DISTANCE \
])
examples = traindata.rdd.map(to_example)
lrmodel = LogisticRegressionWithLBFGS.train(examples, intercept=True)
print(lrmodel.weights,lrmodel.intercept)
lrmodel.setThreshold(0.7) # cancel if prob-of-ontime < 0.7
# <h2> Evaluate model on the heldout data </h2>
#
evalquery = trainquery.replace("t.holdout == False","t.holdout == True")
print(evalquery)
evaldata = spark.sql(evalquery)
examples = evaldata.rdd.map(to_example)
def eval(labelpred):
'''
data = (label, pred)
data[0] = label
data[1] = pred
'''
cancel = labelpred.filter(lambda data: data[1] < 0.7)
nocancel = labelpred.filter(lambda data: data[1] >= 0.7)
corr_cancel = cancel.filter(lambda data: data[0] == int(data[1] >= 0.7)).count()
corr_nocancel = nocancel.filter(lambda data: data[0] == int(data[1] >= 0.7)).count()
cancel_denom = cancel.count()
nocancel_denom = nocancel.count()
if cancel_denom == 0:
cancel_denom = 1
if nocancel_denom == 0:
nocancel_denom = 1
return {'total_cancel': cancel.count(), \
'correct_cancel': float(corr_cancel)/cancel_denom, \
'total_noncancel': nocancel.count(), \
'correct_noncancel': float(corr_nocancel)/nocancel_denom \
}
labelpred = examples.map(lambda p: (p.label, lrmodel.predict(p.features)))
print(eval(labelpred))
# Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| quests/data-science-on-gcp-edition1_tf2/07_sparkml_and_bqml/experimentation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="qXwioNNgLMY3" colab_type="text"
# # Welcome to the matched filtering tutorial!
#
# ### Installation
#
# Make sure you have PyCBC and some basic lalsuite tools installed.
#
# **Only execute the below cell if you have not already installed `pycbc`**
#
# *Note* –– if you were not able to install pycbc, or you got errors preventing your from importing pycbc, please upload this notebook to [google collaboratory](https://colab.research.google.com/notebooks/welcome.ipynb#recent=true), where you can easily `pip install lalsuite pycbc` and run the entire notebook.
# + id="aATq0C4dLMY7" colab_type="code" outputId="3d71db64-2fc9-4c1c-a9b5-107a17c80f97" colab={"base_uri": "https://localhost:8080/", "height": 1270}
# ! pip install lalsuite pycbc
# + [markdown] id="hjxCXphvLMZE" colab_type="text"
# <span style="color:gray">Jess notes: this notebook was made with a PyCBC 1.8.0 kernel. </span>
#
# ### Learning goals
#
# With this tutorial, you learn how to:
#
# * Generate source waveforms detectable by LIGO, Virgo, KAGRA
# * Use PyCBC to run a matched filter search on gravitational wave detector data
# * Estimate the significance of a trigger given a background distribution
# * **Challenge**: Code up a trigger coincidence algorithm
#
# This tutorial borrows heavily from tutorials made for the [LIGO-Virgo Open Data Workshop](https://www.gw-openscience.org/static/workshop1/course.html) by <NAME>. You can find PyCBC documentation and additional examples [here](http://pycbc.org/pycbc/latest/html/py-modindex.html).
#
# Let's get started!
#
# ___
# + [markdown] id="irxmLPLuLMZF" colab_type="text"
# ## Generate a gravitational wave signal waveform
#
# We'll use a popular waveform approximant ([SOEBNRv4](https://arxiv.org/pdf/1611.03703.pdf)) to generate waveforms that would be detectable by LIGO, Virgo, or KAGRA.
#
# First we import the packages we'll need.
# + id="y2wM3M_NLMZI" colab_type="code" colab={}
from pycbc.waveform import get_td_waveform
import matplotlib.pyplot as plt
# + [markdown] id="pHz3BYloLMZO" colab_type="text"
# Let's see what these waveforms look like for different component masses. We'll assume the two compact object have masses equal to each other, and we'll set a lower frequency bound of 30 Hz (determined by the sensitivity of our detectors).
#
# We can also set a time sample rate with `get_td_waveform`. Let's try a rate of 4096 Hz.
#
# Let's make a plot of the plus polarization (`hp`) to get a feel for what the waveforms look like.
#
# *Hint* –– you may want to zoom in on the plot to see the waveforms in detail.
# + id="jQcS5WVxLMZQ" colab_type="code" outputId="df74f032-edf4-4615-d755-0e56fae8af17" colab={"base_uri": "https://localhost:8080/", "height": 290}
for m in [5, 10, 30, 100]:
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=m,
mass2=m,
delta_t=1.0/4096,
f_lower=30)
plt.plot(hp.sample_times, hp, label='$M_{\odot 1,2}=%s$' % m)
plt.legend(loc='upper left')
plt.ylabel('GW strain (plus polarization)')
plt.grid()
plt.xlabel('Time (s)')
plt.show()
# + [markdown] id="XYPB9Ra5LMZY" colab_type="text"
# Now let's see what happens if we decrease the lower frequency bound from 30 Hz to 15 Hz.
# + id="FHZ1ZgO_LMZY" colab_type="code" outputId="e2a3d11e-1ab0-4f3a-a8bc-920415bf85d7" colab={"base_uri": "https://localhost:8080/", "height": 290}
for m in [5, 10, 30, 100]:
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=m,
mass2=m,
delta_t=1.0/4096,
f_lower= 15)
plt.plot(hp.sample_times, hp, label='$M_{\odot 1,2}=%s$' % m)
plt.legend(loc='upper left')
plt.ylabel('GW strain (plus polarization)')
plt.grid()
plt.xlabel('Time (s)')
plt.show()
# + [markdown] id="Kf_uEH4HLMZg" colab_type="text"
# ---
#
# ### Exercise 1
#
# What happens to the waveform when the total mass (let's say 20 M<sub>sol</sub>) stays the same, but the mass ratio between the component masses changes?
#
# Compare the waveforms for a m<sub>1</sub> = m<sub>2</sub> = 10 M<sub>sol</sub> system, a m<sub>1</sub> = 5 M<sub>sol</sub>, m<sub>2</sub> = 15 M<sub>sol</sub>, and a m<sub>1</sub> = 2 M<sub>sol</sub>, m<sub>2</sub> = 18 M<sub>sol</sub> system. What do you notice?
#
#
# + id="StShV_MJLMZi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 290} outputId="100088e8-3f7c-4bbe-dae7-7ee20f819881"
for m1, m2 in zip([10, 5, 2], [10, 15, 18]):
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=m1,
mass2=m2,
delta_t=1.0/4096,
f_lower= 15)
ratio = m1 / m2
plt.plot(hp.sample_times, hp, label='q = %.2f' %ratio)
plt.legend(loc='upper left')
plt.ylabel('GW strain (plus polarization)')
plt.grid()
plt.xlabel('Time (s)')
plt.show()
# + [markdown] id="G1IZ1H7nLMZo" colab_type="text"
# ### Exercise 2
#
# How much longer (in signal duration) would LIGO and Virgo (and KAGRA) be able to detect a 1.4-1.4 M<sub>sol</sub> binary neutron star system if our detectors were sensitive down to 10 Hz instead of 30 Hz? ** Note you'll need to use a different waveform approximant here. Try TaylorF2.**
#
# <span style="color:gray">Jess notes: this would be a major benefit of next-generation ("3G") ground-based gravitational wave detectors.</span>
# + id="w741ZOT1LMZq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 290} outputId="ae464ba2-6530-4ffa-93b1-5c78c2531a5f"
for f_lower in [10, 30]:
hp, hc = get_td_waveform(approximant="TaylorF2",
mass1=1.4,
mass2=1.4,
delta_t=1.0/4096,
f_lower= f_lower)
plt.plot(hp.sample_times, hp, label='f_lower = %i' % f_lower)
plt.legend(loc='upper left')
plt.ylabel('GW strain (plus polarization)')
plt.grid()
plt.xlabel('Time (s)')
plt.show()
# + [markdown] id="Gt8GJdtFLMZw" colab_type="text"
# ---
#
# ### Distance vs. signal amplitude
#
# Let's see what happens when we scale the distance (in units of Megaparsecs) for a system with a total mass of 20 M<sub>sol</sub>.
#
# <span style="color:gray">Note: redshift effects are not included here.</span>
# + id="XRulioR2LMZx" colab_type="code" outputId="247caf01-ea69-4d33-f708-220382b6e419" colab={"base_uri": "https://localhost:8080/", "height": 290}
for d in [100, 500, 1000]:
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=10,
mass2=10,
delta_t=1.0/4096,
f_lower=30,
distance=d)
plt.plot(hp.sample_times, hp, label='Distance=%s Mpc' % d)
plt.grid()
plt.xlabel('Time (s)')
plt.ylabel('GW strain (plus polarization)')
plt.legend(loc='upper left')
plt.show()
# + [markdown] id="rzPWz1pjLMZ8" colab_type="text"
# ---
#
# ## Run a matched filter search on gravitational wave detector data
#
# PyCBC also maintains a catalog of open data as PyCBC time series objects, easy to manipulate with PyCBC tools. Let's try using that and importing the data around the first detection, GW150914.
#
# + id="0p7jrBGXLMZ-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="2c2af09d-94fe-40cb-d73c-853eb55d0208"
from pycbc.catalog import Merger
from pycbc.filter import resample_to_delta_t, highpass
merger = Merger("GW150914")
# Get the data from the Hanford detector
strain = merger.strain('H1')
# + [markdown] id="xPaz5ArVLMaD" colab_type="text"
# ### Data pre-conditioning
#
# Once we've imported the open data from this alternate source, the first thing we'll need to do is **pre-condition** the data. This serves a few purposes:
# * 1) reduces the dynamic range of the data
# * 2) supresses high amplitudes at low frequencies, which can introduce numerical artifacts
# * 3) if we don't need high frequency information, downsampling allows us to compute our matched filter result faster
#
# Let's try highpassing above 15 Hz and downsampling to 2048 Hz, and we'll make a plot to see what the result looks like:
# + id="5QvxGrtlLMaE" colab_type="code" outputId="8849da2a-f585-4741-b50c-8b233c6146d2" colab={"base_uri": "https://localhost:8080/", "height": 307}
# Remove the low frequency content and downsample the data to 2048Hz
strain = resample_to_delta_t(highpass(strain, 15.0), 1.0/2048)
plt.plot(strain.sample_times, strain)
plt.xlabel('Time (s)')
# + [markdown] id="gb35trtzLMaL" colab_type="text"
# Notice the large amplitude excursions in the data at the start and end of our data segment. This is **spectral leakage** caused by filters we applied to the boundaries ringing off the discontinuities where the data suddenly starts and ends (for a time up to the length of the filter).
#
# To avoid this we should trim the ends of the data in all steps of our filtering. Let's try cropping a couple seconds off of either side.
# + id="oz-v_p-YLMaM" colab_type="code" outputId="b6ff9428-bd61-43f3-8d45-3114c831a773" colab={"base_uri": "https://localhost:8080/", "height": 307}
# Remove 2 seconds of data from both the beginning and end
conditioned = strain.crop(2, 2)
plt.plot(conditioned.sample_times, conditioned)
plt.xlabel('Time (s)')
# + [markdown] id="BohMb2xrLMaS" colab_type="text"
# That's better.
#
# ### Calculating the spectral density of the data
#
# Optimal matched filtering requires *whitening*; weighting the frequency components of the potential signal and data by the estimated noise amplitude.
#
# Let's compute the power spectral density (PSD) of our conditioned data.
#
# + id="bB482KNoLMaT" colab_type="code" colab={}
from pycbc.psd import interpolate, inverse_spectrum_truncation
# Estimate the power spectral density
# We use 4 second samles of our time series in Welch method.
psd = conditioned.psd(4)
# Now that we have the psd we need to interpolate it to match our data
# and then limit the filter length of 1 / PSD. After this, we can
# directly use this PSD to filter the data in a controlled manner
psd = interpolate(psd, conditioned.delta_f)
# 1/PSD will now act as a filter with an effective length of 4 seconds
# Since the data has been highpassed above 15 Hz, and will have low values
# below this we need to informat the function to not include frequencies
# below this frequency.
psd = inverse_spectrum_truncation(psd, 4 * conditioned.sample_rate,
low_frequency_cutoff=15)
# + [markdown] id="D6aClmyRLMaX" colab_type="text"
#
# ----
#
# ### Define a signal model
#
# Recall that matched filtering is essentially integrating the inner product between your data and your signal model in frequency or time (after weighting frequencies correctly) as you slide your signal model over your data in time.
#
# If there is a signal in the data that matches your 'template', we will see a large value of this inner product (the SNR, or 'signal to noise ratio') at that time.
#
# In a full search, we would grid over the parameters and calculate the SNR time series for each template in our template bank
#
# Here we'll define just one template. Let's assume equal masses (which is within the posterior probability of GW150914). Because we want to match our signal model with each time sample in our data, let's also rescale our signal model vector to match the same number of time samples as our data vector (**<- very important!**).
#
# Let's also plot the output to see what it looks like.
# + id="g4ahXQ3-LMaZ" colab_type="code" outputId="b140bc2d-5371-4e47-ad09-1fc32a5c1662" colab={"base_uri": "https://localhost:8080/", "height": 307}
m = 36 # Solar masses
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=m,
mass2=m,
delta_t=conditioned.delta_t,
f_lower=20)
# We should resize the vector of our template to match our data
hp.resize(len(conditioned))
plt.plot(hp)
plt.xlabel('Time samples')
# + [markdown] id="W2ZQJGWOLMag" colab_type="text"
# Note that the waveform template currently begins at the start of the vector. However, we want our SNR time series (the inner product between our data and our template) to track with the approximate merger time. To do this, we need to shift our template so that the merger is approximately at the first bin of the data.
#
# For this reason, waveforms returned from `get_td_waveform` have their merger stamped with time zero, so we can easily shift the merger into the right position to compute our SNR time series.
#
# Let's try shifting our template time and plot the output.
# + id="FVJZN8yGLMag" colab_type="code" outputId="42122458-a416-41d6-e646-40a25bc048d8" colab={"base_uri": "https://localhost:8080/", "height": 307}
template = hp.cyclic_time_shift(hp.start_time)
plt.plot(template)
plt.xlabel('Time samples')
# + [markdown] id="bJmbQO4ILMap" colab_type="text"
# ---
#
# ### Calculate an SNR time series
#
# Now that we've pre-conditioned our data and defined a signal model, we can compute the output of our matched filter search.
# + id="AQBmpmXALMaq" colab_type="code" outputId="8ee98439-ef78-4b7e-f190-58d0739d8d1b" colab={"base_uri": "https://localhost:8080/", "height": 300}
from pycbc.filter import matched_filter
import numpy
snr = matched_filter(template, conditioned,
psd=psd, low_frequency_cutoff=20)
plt.figure(figsize=[10, 4])
plt.plot(snr.sample_times, abs(snr))
plt.xlabel('Time (s)')
plt.ylabel('SNR')
# + [markdown] id="fFrr443-LMa0" colab_type="text"
# Note that as we expect, there is some corruption at the start and end of our SNR time series by the template filter and the PSD filter.
#
# To account for this, we can smoothly zero out 4 seconds (the length of the PSD filter) at the beginning and end for the PSD filtering.
#
# We should remove an 4 additional seconds at the beginning to account for the template length, although this is somewhat generous for so short a template. A longer signal such as from a BNS, would require much more padding at the beginning of the vector.
# + id="IlA0arHaLMa1" colab_type="code" outputId="08f22e91-b13c-4fef-caf1-bac153783ee1" colab={"base_uri": "https://localhost:8080/", "height": 283}
snr = snr.crop(4 + 4, 4)
plt.figure(figsize=[10, 4])
plt.plot(snr.sample_times, abs(snr))
plt.ylabel('Signal-to-noise')
plt.xlabel('Time (s)')
plt.show()
# + [markdown] id="mxDRDN91LMa8" colab_type="text"
# Finally, now that the output is properly cropped, we can find the peak of our SNR time series and estimate the merger time and associated SNR of any event candidate within the data.
# + id="LqdgYOERLMa9" colab_type="code" outputId="338a9f53-1bce-4db9-a158-2d60d923ba5b" colab={"base_uri": "https://localhost:8080/", "height": 34}
peak = abs(snr).numpy().argmax()
snrp = snr[peak]
time = snr.sample_times[peak]
print("We found a signal at {}s with SNR {}".format(time,
abs(snrp)))
# + [markdown] id="rYHWGJvRLMbG" colab_type="text"
# You found the first gravitational wave detection in LIGO Hanford data! Nice work.
#
# ---
#
# ### Exercise 3
#
# How does the SNR change if you re-compute the matched filter result using a signal model with compenent masses that are closer to the current estimates for GW150914, say m<sub>1</sub> = 36 M<sub>sol</sub> and m<sub>2</sub> = 31 M<sub>sol</sub>?
#
# + id="RrlxipwoLMbI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="759c10c1-cdce-47e3-b344-eb42aca6fe85"
m1, m2 = 36, 31 # Solar masses
hp, hc = get_td_waveform(approximant="SEOBNRv4_opt",
mass1=m1,
mass2=m2,
delta_t=conditioned.delta_t,
f_lower=20)
# We should resize the vector of our template to match our data
hp.resize(len(conditioned))
template = hp.cyclic_time_shift(hp.start_time)
snr = matched_filter(template, conditioned, psd=psd, low_frequency_cutoff=20)
snr = snr.crop(4 + 4, 4)
peak = abs(snr).numpy().argmax()
h1_snrp = snr[peak]
time = snr.sample_times[peak]
print("We found a signal at {}s with SNR {}".format(time,
abs(h1_snrp)))
# + [markdown] id="ztQjd88fLMbN" colab_type="text"
# ### Exercise 4
#
# **Network SNR** is the quadrature sum of the single-detector SNR from each contributing detector. GW150914 was detected by H1 and L1. Try calculating the network SNR (you'll need to estimate the SNR in L1 first), and compare your answer to the network PyCBC SNR as reported in the [GWTC-1 catalog](https://arxiv.org/abs/1811.12907).
# + id="uIQDl5RELMbN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="8963e783-cb6e-4976-cdcb-f32102028883"
# We should resize the vector of our template to match our data
hc.resize(len(conditioned))
template = hc.cyclic_time_shift(hc.start_time)
snr = matched_filter(template, conditioned, psd=psd, low_frequency_cutoff=20)
snr = snr.crop(4 + 4, 4)
peak = abs(snr).numpy().argmax()
l1_snrp = snr[peak]
time = snr.sample_times[peak]
print("We found a signal at {}s with SNR {}".format(time,
abs(l1_snrp)))
# + id="Z9lqO6K7N8jc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="590f21df-94e7-433e-9229-52b552122abf"
network_snr = numpy.sqrt(abs(l1_snrp) ** 2 + abs(h1_snrp) ** 2)
network_snr
# + [markdown] id="gZMOYAmVLMbQ" colab_type="text"
# ---
#
# ## Estimate the single-detector significance of an event candidate
#
# Great, we found a large spike in SNR! What are the chances this is a real astrophysical signal? How often would detector noise produce this by chance?
#
# Let's plot a histogram of SNR values output by our matched filtering analysis for this time and see how much this trigger stands out.
#
# + id="o2tp4UyHLMbR" colab_type="code" outputId="49f02da9-74ee-4a0f-f332-602b3889f365" colab={"base_uri": "https://localhost:8080/", "height": 301}
# import what we need
from scipy.stats import norm
from math import pi
from math import exp
# make a histogram of SNR values
background = (abs(snr))
# plot the histogram to check out any other outliers
plt.hist(background, bins=50)
plt.xlabel('SNR')
plt.semilogy()
# use norm.fit to fit a normal (Gaussian) distribution
(mu, sigma) = norm.fit(background)
# print out the mean and standard deviation of the fit
print('The fit mean = %f and the fit std dev = %f' %(mu, sigma))
# + [markdown] id="w_P0-RS0LMba" colab_type="text"
# ### Exercise 5
#
# At what single-detector SNR is the significance of a trigger > 5 sigma?
#
# Remember that sigma is constant for a normal distribution (read: this should be simple multiplication now that we have estimated what 1 sigma is).
# + id="g4XwYKofLMbf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="010fb72f-f40f-4570-ef5d-ff7860a1a622"
sigma * 5
# + [markdown] id="vOfStxBDLMbj" colab_type="text"
# ---
#
# ## Challenge
#
# Our match filter analysis assumes the noise is *stationary* and *Gaussian*, which is not a good assumption, and this short data set isn't representative of all the various things that can go bump in the detector (remember the phone?).
#
# **The simple significance estimate above won't work as soon as we encounter a glitch!** We need a better noise background estimate, and we can leverage our detector network to help make our signals stand out from our background.
#
# Observing a gravitational wave signal between detectors is an important cross-check to minimize the impact of transient detector noise. Our strategy:
#
# * We look for loud triggers within a time window to identify foreground events that occur within the gravitational wave travel time (v=c) between detectors, but could come from any sky position.
# * We use time slides to estimate the noise background for a network of detectors.
#
# If you still have time, try coding up an algorithm that checks for time coincidence between triggers in different detectors. Remember that the maximum gravitational wave travel time between LIGO detectors is ~10 ms. Check your code with the GPS times for the H1 and L1 triggers you identified for GW150914.
# + id="uYng66Y4LMbk" colab_type="code" colab={}
# complete if time
# + [markdown] id="FN_iAgYuLMbo" colab_type="text"
# ---
#
# ## Challenge 2
#
# Could you use a matched filter to classify LSST time series observations?
#
# What would you need in order to accomplish this?
#
# *Hint* –– think about the ways in which LSST observations and LIGO observations differ.
#
# + [markdown] id="BywT5HzcLMbo" colab_type="text"
# You would also need to account for:
#
# Different color optical passbands
# Unevenly-sampled observations
# Photometric uncertainties
| Session9/Day4/Matched_filter_tutorial_mywork.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/horizontal-primary-light.png" alt="he-black-box" width="600"/>
#
#
# # Homomorphic Encryption using Duet: Data Owner
# ## Tutorial 1: Training and Evaluating a Logistic Regression over Encrypted Data
#
#
# Welcome!
# This tutorial will show you how to train and evaluate a Logistic Regression using Duet and TenSEAL. This notebook illustrates the Data Owner view on the operations.
#
# We recommend going through Tutorial 0 before trying this one.
# ### Setup
#
# All modules are imported here, make sure everything is installed by running the cell below.
# +
import os
import syft as sy
import tenseal as ts
import torch
import pandas as pd
import random
import numpy as np
import requests
import pytest
from time import time
import matplotlib.pyplot as plt
import sys
sy.load("tenseal")
sy.logger.add(sys.stdout)
# -
# ### Start Duet Data Owner instance
# Start Duet local instance
duet = sy.launch_duet(loopback=True)
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 1 : Now STOP and run the Data Scientist notebook until the same checkpoint.
# ## Scenario 1: Evaluation of the Logistic Regression on Encrypted Data
# ### Prepare the data
#
# We now prepare the training and test data, the dataset was downloaded from Kaggle [here](https://www.kaggle.com/dileep070/heart-disease-prediction-using-logistic-regression).
# T
# his dataset provides patients' information along with a 10-year risk of future coronary heart disease (CHD) as a label, and the goal is to build a model that can predict this 10-year CHD risk based on patients' information, you can read more about the dataset in the link provided.
# +
from syft.util import get_root_data_path
def split_train_test(x, y, test_ratio=0.3):
idxs = [i for i in range(len(x))]
random.shuffle(idxs)
# delimiter between test and train data
delim = int(len(x) * test_ratio)
test_idxs, train_idxs = idxs[:delim], idxs[delim:]
return x[train_idxs], y[train_idxs], x[test_idxs], y[test_idxs]
def download_dataset():
try:
os.makedirs(get_root_data_path(), exist_ok=True)
except BaseException as e:
print(e)
url = "https://raw.githubusercontent.com/OpenMined/TenSEAL/master/tutorials/data/framingham.csv"
path = f"{get_root_data_path()}/framingham.csv"
r = requests.get(url)
with open(path, 'wb') as f:
f.write(r.content)
def heart_disease_data():
download_dataset()
data = pd.read_csv(f"{get_root_data_path()}/framingham.csv")
# drop rows with missing values
data = data.dropna()
# drop some features
data = data.drop(columns=["education", "currentSmoker", "BPMeds", "diabetes", "diaBP", "BMI"])
# balance data
grouped = data.groupby('TenYearCHD')
data = grouped.apply(lambda x: x.sample(grouped.size().min(), random_state=73).reset_index(drop=True))
# extract labels
y = torch.tensor(data["TenYearCHD"].values).float().unsqueeze(1)
data = data.drop("TenYearCHD", 'columns')
# standardize data
data = (data - data.mean()) / data.std()
x = torch.tensor(data.values).float()
return split_train_test(x, y)
x_train, y_train, x_test, y_test = heart_disease_data()
# -
# ### Make Training data Referenceable over Duet
#
# In this scenario, we train over the plain data over Duet.
x_train_ptr = x_train.send(duet, pointable=True, tags=["x_train"])
y_train_ptr = y_train.send(duet, pointable=True, tags=["y_train"])
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 2 : Now STOP and run the Data Scientist notebook until the same checkpoint.
# ### Approve the requests
duet.requests[0].accept()
duet.requests[0].accept()
duet.requests.pandas
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 3 : Now STOP and run the Data Scientist notebook until the same checkpoint.
# ### TenSEAL Context
#
# The next step is to prepare the data for encrypted evaluation.
#
# As you may recall from the first tutorial, the first step for that is to create a __TenSEAL context__.
context = ts.Context(
ts.SCHEME_TYPE.CKKS,
poly_modulus_degree=8192,
coeff_mod_bit_sizes=[60, 40, 40, 60]
)
context.global_scale = 2**40
context.generate_galois_keys()
context
# ### Encrypt the data
#
t_start = time()
x_test = x_test[:10]
enc_x_test = sy.lib.python.List([ts.ckks_vector(context, x.tolist()) for x in x_test])
t_end = time()
print(f"Encryption of the test-set took {int(t_end - t_start)} seconds")
# ### Make Context and Encrypted Vectors Referenceable over Duet
# +
# tag them so our partner can easily reference it
ctx_ptr = context.send(duet, pointable=True, tags=["context"])
enc_x_test_ptr = enc_x_test.send(duet, pointable=True, tags=["enc_x_test"])
# -
# we can see that our three objects are now inside the store we control
duet.store.pandas
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 4 : Now STOP and run the Data Scientist notebook until the same checkpoint.
# We can see that there are two requests, for the context and for the encrypted data.
duet.requests.pandas
# ### Approve the requests
duet.requests[0].accept()
duet.requests[0].accept()
# The requests should have been handled
duet.requests.pandas
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 5 : Now STOP and run the Data Scientist notebook until the same checkpoint.
print(duet.store.pandas)
# +
# Test the accuracy
result_eval = duet.store["result_eval"].get(delete_obj=False)
correct = 0
for actual, expected in zip(result_eval, y_test):
actual.link_context(context)
actual = torch.tensor(actual.decrypt())
actual = torch.sigmoid(actual)
if torch.abs(actual - expected) < 0.5:
correct += 1
print(f"Evaluated test_set of {len(x_test)} entries. Accuracy: {correct}/{len(x_test)} = {correct / len(x_test)}")
# -
# ### <img src="https://github.com/OpenMined/design-assets/raw/master/logos/OM/mark-primary-light.png" alt="he-black-box" width="100"/> Checkpoint 6: Well Done!
# # Congratulations!!! - Time to Join the Community!
#
# Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the movement toward privacy preserving, decentralized ownership of AI and the AI supply chain (data), you can do so in the following ways!
#
# ### Star PySyft and TenSEAL on GitHub
#
# The easiest way to help our community is just by starring the Repos! This helps raise awareness of the cool tools we're building.
#
# - [Star PySyft](https://github.com/OpenMined/PySyft)
# - [Star TenSEAL](https://github.com/OpenMined/TenSEAL)
#
# ### Join our Slack!
#
# The best way to keep up to date on the latest advancements is to join our community! You can do so by filling out the form at [http://slack.openmined.org](http://slack.openmined.org). #lib_tenseal and #code_tenseal are the main channels for the TenSEAL project.
#
# ### Donate
#
# If you don't have time to contribute to our codebase, but would still like to lend support, you can also become a Backer on our Open Collective. All donations go toward our web hosting and other community expenses such as hackathons and meetups!
#
# [OpenMined's Open Collective Page](https://opencollective.com/openmined)
| examples/homomorphic-encryption/Tutorial_1_TenSEAL_Syft_Data_Owner.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2
import numpy as np
import sklearn
from random import shuffle
import scipy.misc
import matplotlib.pyplot as plt
def generator(samples, batch_size=32):
num_samples = len(samples)
print (num_samples)
correlation=0.1
while 1: # Loop forever so the generator never terminates
shuffle(samples)
for offset in range(0, num_samples, batch_size):
batch_samples = samples[offset:offset+batch_size]
images = []
angles = []
for batch_sample in batch_samples:
name = '.'+batch_sample[0]
# print(name)
center_image = cv2.imread(name)
center_image=cv2.cvtColor(center_image,cv2.COLOR_BGR2RGB)
# plt.imshow(center_image)
# plt.show()
center_angle = float(batch_sample[3])
images.append(center_image)
angles.append(center_angle)
# if center_angle!=0.0:
images.append(cv2.flip(center_image,1))
angles.append(center_angle*-1)
name = '.'+batch_sample[1]
# print(name)
left_image = cv2.imread(name)
# plt.imshow(left_image)
# plt.show()
left_image=cv2.cvtColor(left_image,cv2.COLOR_BGR2RGB)
left_angle = float(batch_sample[3])
if left_angle !=0.0:
# if left_angle >=-.2:
# left_angle=left_angle-correlation
images.append(left_image)
angles.append(left_angle)
images.append(cv2.flip(left_image,1))
angles.append(left_angle*-1)
name = '.'+batch_sample[2]
right_image = cv2.imread(name)
right_image=cv2.cvtColor(right_image,cv2.COLOR_BGR2RGB)
right_angle = float(batch_sample[3])
if right_angle!=0.0:
# if right_angle <=.2:
# right_angle=right_angle+correlation
images.append(right_image)
angles.append(right_angle)
images.append(cv2.flip(right_image,1))
angles.append(right_angle*-1)
# trim image to only see section with road
X_train = np.array(images)
y_train = np.array(angles)
# print(y_train)
sklearn.utils.shuffle(X_train, y_train)
yield (X_train, y_train)
# +
def layerIntermed_output(inputs,outputs,numch):
intermediate_layer_model= Model(inputs,outputs)
intermediate_output = intermediate_layer_model.predict(lst0)
print('in shape',intermediate_output.shape)
sampleI=intermediate_output[0]
print(sampleI.shape)
return sampleI[:,:,0]
# +
import itertools
from keras.utils import np_utils
import csv
from sklearn.model_selection import train_test_split
from random import randint
import tensorflow as tf
lines=[]
with open ('./testImages/testImages6/driving_log2.csv') as csvfile:
next(csvfile)
reader =csv.reader(csvfile)
for line in reader:
lines.append(line)
with open ('./testImages/testImages7/driving_log.csv') as csvfile:
next(csvfile)
reader =csv.reader(csvfile)
for line in reader:
lines.append(line)
with open ('./testImages/testmages12/driving_log.csv') as csvfile:
next(csvfile)
reader =csv.reader(csvfile)
for line in reader:
lines.append(line)
with open ('./testImages/testImages13/driving_log.csv') as csvfile:
next(csvfile)
reader =csv.reader(csvfile)
for line in reader:
lines.append(line)
with open ('./testImages/testImages14/driving_log.csv') as csvfile:
next(csvfile)
reader =csv.reader(csvfile)
for line in reader:
lines.append(line)
#### if didnt work multiply filters*2
print(len(lines))
images=[]
mesurements=[]
print(len(lines))
train_samples, validation_samples = train_test_split(lines, test_size=0.2)
# print("tran samples")
# print(len(train_samples))
ltrain=len(train_samples)
lval=len(validation_samples)
train_generator=generator(train_samples)
validation_generator = generator(validation_samples)
lst = list(itertools.islice(train_generator,1))[0]
lst0=lst[0]
from keras.models import Sequential, Model
from keras import backend as k
from keras.layers import Flatten, Dense, Lambda, Cropping2D,Convolution2D,Dropout,Activation, Reshape
from keras.layers.pooling import MaxPooling2D,AveragePooling2D
from keras.layers.normalization import BatchNormalization
from keras.regularizers import l2
import matplotlib
from keras import layers
embedding_size = 50
maxlen=10
r= (100, 100,3)
model= Sequential()
model.add(Lambda(lambda x: ((x/255)-0.5),input_shape=(160,320,3)))
model.add(Cropping2D(cropping=((60,20),(0,0))))
im = layerIntermed_output(model.input,model.layers[1].output,1)
print(im.shape)
plt.title("copped")
plt.imshow(im,cmap='gray')
plt.savefig("./out/cropped.png")
plt.show()
model.add(Convolution2D(24,(5,5),strides=3,border_mode='same',activation='elu'))
im = layerIntermed_output(model.input,model.layers[2].output,3)
print(im.shape)
plt.title("conv1")
plt.imshow(im)
plt.savefig("./out/conv1_1.png")
plt.show()
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.25))
model.add(Convolution2D(36,(5,5),strides=2,border_mode='same', activation='elu'))
im = layerIntermed_output(model.input,model.layers[5].output,3)
print(im.shape)
plt.title("conv2")
plt.imshow(im)
plt.savefig("./out/conv2_1.png")
plt.show()
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.25))
model.add(Convolution2D(48,(3,3),strides=2,border_mode='same',activation='elu'))
im = layerIntermed_output(model.input,model.layers[6].output,3)
print(im.shape)
plt.title("conv3")
plt.imshow(im)
plt.savefig("./out/conv3_1.png")
plt.show()
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.25))
model.add(Convolution2D(64,(5,5),border_mode='same'
,activation='elu'))
im = layerIntermed_output(model.input,model.layers[9].output,3)
print(im.shape)
plt.title("conv4")
plt.imshow(im)
plt.savefig("./out/conv4_1.png")
plt.show()
# model.add(MaxPooling2D((2, 2), strides=(1, 1)))
model.add(Dropout(0.5))
# model.add(Convolution2D(64,(5,5),border_mode='same',
# activation='elu'))
# im = layerIntermed_output(model.input,model.layers[10].output,3)
# print(im.shape)
# plt.title("conv6")
# plt.imshow(im)
# plt.savefig("./out/conv5_1.png")
# plt.show()
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(500))
model.add(Dense(100))
model.add(Dense(10))
model.add(Dense(1))
model.compile(loss='mse',optimizer='adam')
history_object= model.fit_generator(train_generator,
steps_per_epoch=ltrain,
nb_epoch=3,
validation_data=validation_generator,
nb_val_samples=lval)
model.summary()
model.save('modelf.h5')
### print the keys contained in the history object
print(history_object.history.keys())
### plot the training and validation loss for each epoch
plt.plot(history_object.history['loss'])
plt.plot(history_object.history['val_loss'])
plt.title('model mean squared error loss')
plt.ylabel('mean squared error loss')
plt.xlabel('epoch')
plt.legend(['training set', 'validation set'], loc='upper right')
plt.savefig("./out/data.png")
plt.show()
# +
# print the keys contained in the history object
print(history_object.history.keys())
### plot the training and validation loss for each epoch
plt.plot(history_object.history['loss'])
plt.plot(history_object.history['val_loss'])
plt.title('model mean squared error loss')
plt.ylabel('mean squared error loss')
plt.xlabel('epoch')
plt.legend(['training set', 'validation set'], loc='upper right')
plt.savefig("./out/history.png")
plt.show()
| model.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 제어문
# ## 주요 내용
# 프로그램 실행의 흐름을 제어하는 여러 종류의 제어문(제어 명령문)을 소개한다.
#
# * `if` 조건문
# * `for` 반복문
# * `while` 반복문
# * `pass`, `continue`, `break` 예약어
# ## `if` 조건문
# `if` 조건문의 기본 양식은 다음과 같으며,
# `if` 다음에 위치한 부울 표현식이 참이면 지정된 코드가 실행된다.
#
# ```python
# if 부울표현식:
# 코드
# ```
# #### 예제
# 하나의 문자열이 다른 문자열의 부분문자열일지를 아래와 가티 확인할 수 있다.
if 'bc' in 'abcde':
print("'bc'가 'abcde'의 부분문자열이다.")
# #### 예제
# +
x = -2
if x < 0:
print("'음수'입니다.")
# -
# __주의사항:__ `'음수'입니다.` 문자열 안에 작은따옴표가
# 사용되기 때문에 반드시 큰따옴표로 감싸야 한다.
# 조건식이 만족되지 않으면 지정된 코드는 건너뛴다.
# #### 예제
# +
if 'ac' in 'abcde':
print("'ac'가 'abcde'의 부분문자열이다.")
print("if문을 건너뛰었음!")
# -
# #### 예제
# +
x = 4
if x < 0:
print("'음수'입니다.")
print("if문을 건너뛰었음!")
# -
# `if ... else ...` 명령문은 `if`의 부울 표현식이 `False`일 때 수행할 코드를 지정한다.
# ```python
# if 부울표현식:
# 코드1
# else:
# 코드2
# ```
# #### 예제
# 예를 들어, 짝수는 반으로 나누고, 홀수는 3배한 후에 1을 더해고자 한다면 아래와 같이 작성한다.
# +
x = 2
if x % 2 == 0:
print(int(x/2)) # int() 함수를 이용하여 정수 자료형을 유지한다.
else:
print(3 * x + 1)
# +
x = 7
if x % 2 == 0:
print(int(x/2)) # int() 함수를 이용하여 정수 자료형을 유지한다.
else:
print(3 * x + 1)
# -
# ### 다중 조건문
# 경우에 따른 여러 조건을 사용할 경우 원하는 만큼의 `elif` 문을 사용하고
# 마지막에 `else` 문을 한 번 사용할 수 있다.
# 단, `else` 문은 생략될 수 있다.
# ```python
# if 부울표현식1:
# 코드1
# elif 부울표현식2:
# 코드2
# elif 부울표현식2:
# 코드2
# ,,,
#
# elif 부울표현식k:
# 코드k
# else:
# 코드
# ```
# 맨 위에 위치한 조건식의 만족 여부부터 차례대로 조사하며 한 곳에서 만족되면 그 아래에 위치한
# `elif`와 `else` 명령문과 해당 코드는 전부 무시된다.
# #### 예제
# +
x = 4
if x < 0:
print('음수')
elif x == 0:
print('숫자 0')
elif 0 < x < 5:
print('5 보다 작은 양수')
else:
print('5 보다 큰 양수')
# -
# ### 부울 연산자를 사용할 때 주의할 점
# 부울 연산자를 이용하여 정의된 조건식을 사용할 때 주의해야 할 사항이 있다.
# 예를 들어, 아래 코드에서 `a < b`가 참이기에 `c/d > 0` 은 아예 검사하지 않는다.
# #### 예제
# +
a, b, c, d = 5, 7, 8, 0
if a < b or c / d > 0:
print('"or" 연산자 오른편에 위치한 표현식은 검사하지 않아요!')
# -
# 하지만 `c/d > 0`을 검사한다면 오류가 발생한다.
# 이유는 0으로 나누는 일은 허용되지 않기 때문이다.
# 실제로 0으로 나눗셈을 시도하면 `ZeroDivisionError` 라는 오류가 발생한다.
c / d > 0
# #### 예제
# 아래의 경우처럼 오류가 발생하는 명령문이나 표현식이 `elif` 또는 `else` 표현식에 포함되더라도
# 오류가 발생하지 않을 수 있다.
# 이유는 앞서 설명한 대로 특정 조건이 만족되면 그 아래에 있는 다른 조건의 코드는 전부 무시되기 때문이다.
# +
a, b, c, d = 5, 7, 8, 0
if a < b:
print(b - a)
elif (c / d) > 0:
print('오류가 발생하지 않아요!')
# +
a, b, c, d = 5, 7, 8, 0
if a < b:
print(b - a)
else:
print(c / d)
# -
# ### 중첩 조건문
# 조건문 안에 조건문이 사용될 수 있으며, 중첩 조건문이라 한다.
# #### 예제
# +
num1 = 10
num2 = 10
if num1 < num2:
print("num1이 num2 보다 작다.")
else:
if num1 == num2:
print("num1이 num2와 같다.")
else:
print("num1이 num2 보다 크다.")
# -
# 그런데 경우에 따라 중첩 조건문이 굳이 사용될 필요가 없을 수도 있다.
# 예를 들어, 위 중첩 조건문은 아래 조건문과 동일하게 작동한다.
# +
num1 = 10
num2 = 10
if num1 < num2:
print("num1이 num2 보다 작다.")
elif num1 == num2:
print("num1이 num2와 같다.")
else:
print("num1이 num2 보다 크다.")
# -
# ### 삼항 표현식
# 삼항 표현식 `if ... else ...` 를 이용하여 지정된 값을 한 줄로 간단하게 표현할 수 있다.
# 예를 들어, 아래 코드를 살펴보자.
# +
x = 5
if x >= 0:
y = 'Non-negative'
else:
y = 'Negative'
print(y)
# -
# 변수 `y`를 아래와 같이 한 줄로 선언할 수 있다.
# +
y = 'Non-negative' if x >= 0 else 'Negative'
print(y)
# -
# ## `for` 반복문
# `for` 반복문은 문자열, 리스트, 튜플, 사전 등 처럼 여러 개의 값을 하나로 묶어 놓은 값(collections)의
# 항목들을 순회하는 데에 사용된다.
# 문자열을 제외한 리스트, 튜플, 사전은 아직 학습하지 않았기에 여기서는 문자열을 이용하여
# `for` 반복문의 활용 예제를 다룬다.
# 다른 자료형과 `for` 반복문을 함께 사용하는 예제는 이후에 많이 다룰 것이다.
#
# `for` 반복문의 사용 양식은 다음과 같다. 콜론 기호(`:`)와 들여쓰기에 주의해야 한다.
# ```python
# for 변수 in collection:
# 코드
# ```
# #### 예제
# 아래 코드는 문자열에 포함된 문자 각각을 출력한다.
for char in "python":
print(char)
# #### 예제
# 문자열에 있는 소문자 `a`를 대문자 `A`로 변경하여 새로운 문자열을 생성하는 코드를 작성하라.
#
# 예를 들어, "aardvarks"를 이용하여 "AArdvArks"를 생성하는 코드를 작성하라.
# +
a_word = 'aardvarks'
new_word = ''
for char in a_word:
if char == 'a':
new_word = new_word + 'A'
else:
new_word = new_word + char
print(new_word)
# -
# #### 예제
# 아래 문자열
#
# ' n o r t h w e s t e r n'
#
# 을 이용하여 아래 문자열을 생성하는 코드를 구현하라:
#
# 'Northwestern'
# +
a_word = ' n o r t h w e s t e r n'
temp_word = ''
for char in a_word:
if char != ' ':
temp_word = temp_word + char
new_word = temp_word.title()
print(new_word)
# -
# #### 예제
# 정수 모양의 문자열에 포함된 모든 숫자들의 합을 계산해보자.
#
# 힌트: `int()` 함수를 활용해야 한다.
# +
a_string = "12345"
total = 0
for char in a_string:
total = total + int(char)
print(total)
# -
# 아래와 같이 `+=` 연산을 사용할 수도 있다.
# +
a_string = "12345"
total = 0
for char in a_string:
total += int(char)
print(total)
# -
# ## `while` 반복문
# 지정된 조건이 만족되는 동안, 또는 실행 중에 `break` 명령문을 만날 때까
# 동일한 코드를 반복실행 시킬 때 `while` 반복문을 사용한다.
# #### 예제
# 아래 코드는 256부터 시작해서 계속 반으로 나눈 값을 더하는 코드이며,
# 나누어진 값이 0보다 작거나 같아지면, 또는 더한 합이 500보다 커지면 바로 실행을 멈춘다.
# +
x = 256
total = 0
while x > 0:
if total > 500:
break
total += x
x = x // 2
print(total)
# -
# #### 예제
# 정수들을 나누어 몫을 구하는 코드를 작성해보자.
# 몫을 어떻게 구현할까?
#
# * 먼저 몫이 어떤 의미인가를 알아야 한다.
# * 그 다음에 그 의미를 구현하는 코드를 작성한다.
#
# 어떤 정수 `a`를 다른 정수 `b`로 나누었을 때의 몫은 `a`에서 `b`를 몇 번 뺄 수 있는가와 동일한 의미를 갖는다.
# 즉, `a`에서 `b`를 반복해서 빼주는 과정이 필요하고 이 과정을 음수가 되지 않을 때까지만 반복해야 한다.
#
# 예를 들어 43을 7로 나누었을 때의 몫은 다음과 같이 구할 수 있다.
# +
number = 43
divisor = 7
answer = 0
# While 루프
while number > 0:
number = number - divisor
# 음수가 아니라면 빼주는 횟수를 1회 늘린다.
if number > 0:
answer += 1
# 이제 answer를 출력하면 된다.
print('몫은', answer, '이다')
# -
# #### 예제
# 두 정수의 최대공약수(gcd)를 계산하는 함수를 구현하라.
#
# 힌트: 유클리드 호제법을 활용하라. 아래 사이트 참조: http://tibyte.kr/224
# +
a, b = 14, 21
if a < b:
# 이 경우에는 a와 b의 값을 서로 바꾼다.
a, b = b, a
while b != 0:
a, b = b, a % b
print(a)
# +
a, b = 6, 8
if a < b:
# 이 경우에는 a와 b의 값을 서로 바꾼다.
a, b = b, a
while b != 0:
a, b = b, a % b
print(a)
# -
# #### 예제
# `while`문을 사용해서 다음을 출력하는 프로그램을 작성하여라.
#
# ```python
# 박수 1번 짝
# 박수 2번 짝짝
# 박수 3번 짝짝짝
# 박수 4번 짝짝짝짝
# 박수 5번 짝짝짝짝짝
# ```
# +
n = 1
while n < 6 :
print("박수 ", n, "번 " + "짝" * n)
n += 1
# -
# 문자열 템플릿을 이용할 수도 있다.
# +
n = 1
while n < 6 :
print(f'박수 {n} 번 {"짝" * n}') # 작은 따옴표로 감싸야 함에 주의하라.
n += 1
# -
# ## `pass`, `continue`, `break` 예약어
# 코드 실행의 흐름을 조금 다른 방식으로 제어하는 3 개의 예약어의 기능을 살펴본다.
# ### `pass` 예약어
# 아무 것도 하지 않고 다음으로 넘어가도는 하는 명령문 역할을 수행하는 예약어이다.
# 주로 앞으로 채워야 할 부분을 명시할 때 또는
# 무시해야 하는 경우를 다룰 때 사용한다.
#
# 아래 코드는 x가 0일 때 할 일을 추후에 지정하도록 `pass` 예약어를 사용한다.
# +
x = 0
if x < 0:
print('negative!')
elif x == 0:
# 할 일: 추후 지정
pass
else:
print('positive!')
# -
# ### `continue` 예약어
# `for` 또는 `while` 반복문이 실행되는 도중에
# `continue` 예약어를 만나는 순간 현재 실행되는 코드의 실행을 멈추고
# 반복문의 처음으로 돌아간다.
# `for` 반복문인 경우 다음 순번 항목을 대상으로 반복문을 이어간다.
# #### 예제: `for` 반복문
#
# 문자열에 포함된 숫자 중에서 3을 제외한 숫자들의 합을 구해보자.
# +
a_string = "12345"
total = 0
for char in a_string:
if char == '3':
continue
total += int(char)
print(total)
# -
# #### 예제: `for` 반복문
#
# 예를 들어, "aardvarks"에서 알파벳 `'a'`만 대문자 `'A'`로 변환하고
# 나머지 문자는 버리는 코드를 작성하라.
#
# 힌트: `continue` 활용
# +
a_word = 'a<PASSWORD>'
new_word = ''
for char in a_word:
if char == 'a':
new_word = new_word + 'A'
else:
continue
new_word = new_word + char # 이 줄은 무시된다.
print(new_word)
# -
# #### 예제: `while` 반복문
#
# 0부터 10까지의 정수 중에서 홀수만 출력해보자.
# +
i = 0
while i < 10:
i += 1
if i % 2 == 0:
continue
print(i)
# -
# ### `break` 예약어
# `for` 또는 `while` 반복문이 실행되는 도중에
# `break` 예약어를 만나는 순간 현재 실행되는 반복문 자체의 실행을 멈추고,
# 다음 명령을 실행한다.
# #### 예제
# 문자열에 포함된 숫자 중에서 4를 만나는 순간에 실행을 반복문의 실행을 멈추게 해보자.
# +
a_string = "12345"
total = 0
for char in a_string:
if char == '4':
break
total += int(char)
print(total)
# -
# #### 예제: `for` 반복문
#
# 예를 들어, "aardvarks"에서 알파벳 `'a'`는 대문자 `'A'`로 변환하고
# 나머지 문자를 만나는 순간 멈추게 하는 코드를 작성하라.
#
# 힌트: `break` 활용
# +
a_word = 'aardvarks'
new_word = ''
for char in a_word:
if char == 'a':
new_word = new_word + 'A'
else:
break
new_word = new_word + char # 이 줄은 무시된다.
print(new_word)
# -
# `break` 예약어는 자기를 감싸는 `for` 또는 `while` 반복문의 실행을 멈추게 한다.
# 하지만 다른 반복문에 의해 감싸져 있다면 해당 반복문을 이어서 실행한다.
#
# 예를 들어, 아래 코드는 0, 1, 2, 3으로 이루어진 순서쌍들을 출력한다.
# 그런데 둘째 항목이 첫째 항목보다 큰 경우는 제외시킨다.
#
# __참고:__ `range(4)`는 0, 1, 2, 3 네 개의 숫자를 담고 있다고 생각하면 된다.
# `range()` 함수에 대해서는 잠시 뒤에 살펴본다.
for i in range(4):
for j in range(4):
if j > i:
break
print((i, j))
# #### 예제
# 아래 코드는 사용자로부터 숫자를 입력 받아 짝수/홀수 여부를 판명해준다.
# +
while True:
x=int(input("정수를 입력하세요: ")) # 정수 하나 입력
if x%2==0: # 짝수인 경우
print(f"{x}는 짝수입니다.")
else: # 홀수인 경우
print(f"{x}는 홀수입니다.")
# 게임을 계속 진행할지 여부 묻기
a=int(input("프로그램을 끝내시겠습니까? YES=1, NO=0: "))
if a==0: # 게임 계속 진행
continue
else: # 게임 종료
break
print("종료합니다.")
# -
# __참고:__ 위 코드에서 사용된 `continue` 대신에 `pass` 사용해도 동일하게 작동한다.
# 이유는 `pass`를 사용하면 바로 아래에 있는 코드로 넘어가야 하는 데 더 이상 실행할 코드가 없다.
# 따라서 다시 `while` 반복문의 처음으로 돌아간다.
# 이제 위 코드를 수정해서 컴퓨터가 임의로 1부터 100 사이의 수를 생성하게 한 후에 맞추는 프로그램을 작성해보자.
# 단, 숫자를 맞추면 바로 멈추고, 그렇지 않으면 찍은 값에 대한 정보를 크다, 작다의 형태로 전달해야 한다.
#
# 힌트: `random` 모듈의 `randint()` 함수 활용
# +
import random
# 컴퓨터가 1에서 100사이의 값을 무작위로 선택
secret = random.randint(1, 100)
# secret을 맞출 때까지 반복해서 guess함.
while True:
guess = int(input("맞춰보세요: "))
if secret == guess:
print(f"정답입니다.")
break # 정답이면 게임 종료
else:
print(f"틀렸습니다.")
if guess < secret: # 오답이면 크기 비교 알려주기
print("너무 작아!")
else:
print("너무 커!")
print("종료합니다.")
| notebooks/python03.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# One of the things you learned about in this chapter is that not all iterables are actual lists. A couple of examples that we looked at are strings and the use of the range() function. In this exercise, we will focus on the range() function.
#
# You can use range() in a for loop as if it's a list to be iterated over:
#
# >for i in range(5):
# print(i)
#
# Recall that range() doesn't actually create the list; instead, it creates a range object with an iterator that produces the values until it reaches the limit (in the example, until the value 4). If range() created the actual list, calling it with a value of 10100 may not work, especially since a number as big as that may go over a regular computer's memory. The value 10100 is actually what's called a Googol which is a 1 followed by a hundred 0s. That's a huge number!
#
# Your task for this exercise is to show that calling range() with 10100 won't actually pre-create the list.
#
# Instructions
#
# - Create an iterator object small_value over range(3) using the function iter().
# - Using a for loop, iterate over range(3), printing the value for every iteration. Use num as the loop variable.
# - Create an iterator object googol over range(10 ** 100).
# +
# Create an iterator for range(3): small_value
small_value = iter(range(3))
# Print the values in small_value
print(next(small_value))
print(next(small_value))
print(next(small_value))
# Loop over range(3) and print the values
for num in range(3):
print(num)
# +
# Create an iterator for range(10 ** 100): googol
googol = iter(range(10**100))
# Print the first 5 values from googol
print(next(googol))
print(next(googol))
print(next(googol))
print(next(googol))
print(next(googol))
| Python Data Science Toolbox -Part 2/Using iterators in PythonLand/03.Iterating over iterables (2).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [anaconda3]
# language: python
# name: Python [anaconda3]
# ---
# # RHT example workflow
# ### by <NAME>
#
# Imports. Note we are importing `rht` and `RHT_tools` from this repo.
from astropy.io import fits
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import rht, RHT_tools
# %matplotlib inline
# Load some test data. Let's use a fits version of a tesla coil image from <a href="https://commons.wikimedia.org/wiki/File:225W_Zeus_Tesla_coil_-_arcs2_(cropped).jpg">Wikimedia commons</a>.
data_fn = "testim_tesla_small"
tesla_data = fits.getdata(data_fn+".fits")
# Let's take a look at the original image.
fig = plt.figure(figsize=(6,6))
plt.imshow(tesla_data, cmap="Greys")
# Run the RHT! It's as simple as this. Note that depending on your setup, this may run quite slowly in a Jupyter notebook. The following should only take a few seconds from the command line. From the command line, simply do
#
# ~~~
# python rht.py data_fn --wlen=21 --smr=2
# ~~~
#
# Where wlen is the window length and smr is the unsharp mask smoothing radius. For details please refer to <a href="http://adsabs.harvard.edu/abs/2014ApJ...789...82C">the RHT paper</a>.
rht.main(data_fn, smr=2, wlen=21)
# By default, the data are saved as a fits file of the same name, with "_xytNN" appended, where NN is the RHT run number.
rht_data_fn = data_fn+"_xyt01.fits"
rht_tesla = fits.getdata(rht_data_fn)
# The backprojection is stored as the first hdu. This is total RHT linear intensity integrated over orientation. More prominent features in the backprojection indicate regions with greater total linear power.
fig = plt.figure(figsize=(6,6))
plt.imshow(rht_tesla, cmap="Greys")
# Some helper functions are provided in `RHT_tools.py`. Let's use them to grab the total RHT output (pixel indices and R(x, y, theta)) from the second header object.
ipoints, jpoints, hthets, naxis1, naxis2, wlen, smr, thresh = RHT_tools.get_RHT_data(rht_data_fn)
# Just to demonstrate, let's grab a random point. We'll also get the array of theta bins using `RHT_tools`.
indx = 20000
ipoint_example = ipoints[indx]
jpoint_example = jpoints[indx]
hthets_example = hthets[indx]
thets_arr = RHT_tools.get_thets(wlen, save=False)
# Plot the RHT spectrum at this random point.
# +
fig=plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.plot(np.degrees(thets_arr), hthets_example)
ax1.set_xlabel("theta [degrees]")
ax1.set_ylabel("RHT intensity")
ax1.set_title("RHT spectrum at point ({}, {})".format(ipoint_example, jpoint_example))
ax2.imshow(rht_tesla, cmap="Greys")
ax2.plot(ipoint_example, jpoint_example, '+', color="pink", ms=15, mew=3)
# -
# Let's now plot all of the RHT spectra that lie in a given row in our image.
# +
row_js = jpoints[np.where(jpoints == 250)]
row_is = ipoints[np.where(jpoints == 250)]
row_hthets = hthets[np.where(jpoints == 250)]
cmap = matplotlib.cm.get_cmap('Reds_r')
fig=plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
for _i in range(len(row_js)):
ax1.plot(np.degrees(thets_arr), row_hthets[_i, :,], color=cmap(_i*1./len(row_js)))
ax1.set_xlabel("theta [degrees]")
ax1.set_ylabel("RHT intensity")
ax1.set_title("RHT spectra where jpoint = {}".format(250))
ax2.imshow(rht_tesla, cmap="Greys")
plt.scatter(row_is, row_js, color=cmap(np.arange(len(row_js)*1.)/len(row_js)))
# -
| .ipynb_checkpoints/RHT_example_workflow-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matemática Para Machine Learning
# ## Gradiente Descendente
#
# Aplicando Gradiente Descendente para localizar o Global Minimo de uma função.
#
# Em Machine Learning utiliza-se Gradiente Descendente para para localizar qual a menor função de custo de um modelo.
# Ou seja, encontrar a menor diferença entre valor conhecido e valor previsto.
from IPython.display import Image
Image("images/gradiente2.png")
# ## Função
# Utlizaremos a função y = (x+5)² como exemplo.
#
# Inicaremos do ponto x = 3.
#
# ## Aplicando Gradiente Descendente
# +
# Crinado o algoritmo
def gradiante_descendente(parametro, rate):
# parametro é o numéro corrente de x
# rate é o leraning rate (passada)
# Definindo qual será a precisão do algoritmo
precision = 0.000001
# Inicializa o contador do passo anterior
previous_step_size = 1
# Número máximo de iterações
max_iters = 10000
# Contador de iterações
iters = 0
# Gradiente da função
df = lambda x: 2*(x+5)
# Crinado o loop de interações
while previous_step_size > precision and iters < max_iters:
p_x = parametro
# Aplicando o Gradient descent
parametro = parametro - rate * df(p_x)
# Alterando o valor de c
previous_step_size = abs(parametro - p_x)
# Alimentando o número de interações
iters = iters + 1
# Print das interações
print("Iteration", iters,"\nValor de x igual a ", parametro)
return print("\nO mínimo local da função ocorre em: ", parametro)
# +
# Executando o algoritimo
#Paramentro = 3
#Rante = 0.01
gradiante_descendente(3,0.01)
| Gradiente_Descendente.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 02-1데이터 집합 불러오기
# ## 데이터 분석의 시작은 데이터 불러오기부터
# 데이터 분석을 위해 가장 먼저 해야 할 일은 무엇일까요? 바로 데이터를 불러오는 것입니다. 이때 불러오는 데이터를 '데이터 집합'이라고 합니다. 그러면 데이터 집합을 불러오는 방법과 데이터를 간단히 살펴보는 방법에 대해 알아보겠습니다. 우리가 처음 불러올 데이터 집합은 갭마인더입니다. '02_practice'를 주피터 노트북으로 열어 실습을 시작해 볼까요?
# ## 갭마인더 데이터 집합 불러오기
#
# 1. 판다스의 여러 기능을 사용하려면 판다스 라이브러리를 불러와야 합니다. 다음과 같이 입력하여 판다스 라이브러리를 불러오세요.
import pandas
# 2. 갭마인더 데이터 집합을 불러오려면 read_csv메서드를 사용해야 합니다. read_csv메서드는 기본적으로 쉽표(,)로 열어 구분되어 있는 데이터를 불러옵니다. 하지만 갭마인더는 열이 탭으로 구분되어 있기 때문에 read_csv 메서드를 호 출할 때 열이 탭으로 구분되어 있따고 미리 알려주어야 합니다. sep 속성값으로 \t를 지정하세요
df = pandas.read_csv('data/gapminder.tsv',sep='\t')
# 3. 판다스에 있는 메서드를 호출하려면 pandas와 점(.) 연산자를 사용해야 합니다. 그런데 매번 pandas라고 입력하려면 번거롭겠죠. 그래서 이를 해결하기 위해 관습적으로 pandas를 pd로 줄여 사용합니다. 다음과 같이 입력하면 pandas를 pd로 줄여 사용할 수 있습니다. 앞으로는 이 방법을 사용하겠습니다.
import pandas as pd
df = pd.read_csv('data/gapminder.tsv',sep='\t')
# ## 시리즈와 데이터프레임
# 갭마인더 데이터 집합을 잘 불러왔나요? 이번에는 판다스에서 사용되는 자료형을 알아볼 차례입니다. 판다스는 데이터를 효율적으로 다루기 위해 시리즈와 데이터프레임이라는 자료형을 사용합니다. 데이터프레임은 엑셀에서 볼 수 있는 시트와 동일한 개념이며 시리즈는 시트의 열 1개를 의미합니다. 파이썬으로 비유하여 설명하면 데이터프레임은 시리즈들이 각 요소가 되는 딕셔너리라고 생각하면 됩니다.
# ### 불러온 데이터 집합 살펴보기.
# 1. rdad_csv 메서드는 데이터 집합을 읽어 들여와 데이터프레임이라는 자료형으로 반환합니다. 데이터프레임에는 데이터 분석에 유용한 여러 메서드가 미리 정의되어 있습니다. 데이터 프레임의 데이터를 확인하는 용도로 자주 사용하는 head 메서드에 대해 먼저 알아보겠습니다. head 메서드는 데이터프레임에서 가장 앞에 있는 5개의 행을 출력하므로 내가 불러온 데이터가 어떤 값을 가지고 있는지 살펴보기에 안성맞춤이죠.
print(df.head())
# 2. 이번에는 df에 저장된 값이 정말 데이터프레임이라는 자료형인지 확인해 보겠습니다. 실행 결과를 보면 판다스의 데이터프레임이라는 것을 알 수 있습니다. type 메서드는 자료형을 출력해 줍니다. 앞으로 자주 사용할 메서드이므로 꼭 기억해 두기 바랍니다.
print(type(df))
# 3. 데이터프레임은 자신이 가지고 있는 데이터의 행과 열의 크기에 대한 정보를 shape라는 속성에 저장하고 있습니다. 다음을 입력하여 실행하면 갭마인더의 행과 열의 크기를 확인할 수 있습니다. 1번째 값은 행의 크기이고 2번째 값은 열의 크기 입니다.
print(df.shape)
# 4.이번에는 갭마인더에 어떤 정보가 들어 있는지 알아보겠습니다. 먼저 열을 살펴보겠습니다. 과정 3에서 shape 속성을 사용했던 것처럼 columns속성을 사용하면 데이터 프레임의 열 이름을 확인할 수 있습니다. 갭마인더를 구성하는 열 이름은 각각 country,continent,year,lifeExp,pop, gdpPercap 입니다.
print(df.columns)
# 5. 데이터프레임을 구성하는 값의 자료형은 데이터프레임의 dtypes 속성이나 info 메서드로 쉽게 확인할 수 있습니다.
print(df.dtypes)
print(df.info())
# ## 판다스와 파이썬 자료형 비교
# 다음 표에 앞으로 판다스를 공부하며 자주 다루게 될 자료형을 정리했습니다. 그런데 판다스와 파이썬은 같은 자료형도 다르게 인식합니다. 예를 들어 판다스는 문자열 자료형을 dbect라는 이름으로 인식하고 파이썬은 string이라는 이름으로 인식합니다. 같은 자료형이라도 판다스, 파이썬이 서로 다른 이름으로 인식한다는 점을 주의 깊게 살펴보고 다음으로 넘어가세요.
# 판다스 자료형$\qquad$파이썬 자료형$\qquad$$\qquad$설명<br>
# object$\qquad$$\qquad$$\quad$string$\qquad$$\qquad$$\qquad$문자열<br>
# int64$\qquad$$\qquad$$\quad$$\;$$\;$$\;$int$\qquad$$\qquad$$\qquad$$\;$$\;$정수<br>
# float64$\qquad$$\qquad$$\quad$float$\qquad$$\qquad$$\qquad$수소점을 가진숫자<br>
# datetime64$\qquad$$\;$$\;$$\;$$\;$datetime$\qquad$$\qquad$$\;$$\;$$\;$$\;$$\;$파이썬 표준 라이브러리인 datetime이 반환하는 자료형
# # 02-2 데이터 추출하기
# 지금까지 데이터프레임의 크기와 자료형을 살펴보는 방법에 대해 알아보았습니다. 앞에서 haed 메서드를 이용해 데이터프레임에서 가장 앞에 있는 5개의 데이터를 추출하여 출력했던 것을 기억하나요? 이번에는 데이터프레임에서 데이터를 열 단위로 추출하는 방법과 행 단위로 추출하는 방법을 알아보겠습니다. 먼저 열 단위로 데이터를 추출하는 방법을 알아보겠습니다.
# ### 열 단위 데이터 추출하기
# 데이터프레임에서 데이터를 열 단위로 추출하려면 대괄호와 열 이름을 사용해야 합니다. 이때 열 이름은 꼭 작은따옴표를 사용해서 지정해야 하고 추출한 열은 변수에 저장해서 사용할 수도 있습니다. 이때 1개의 열만 추출하면 시리즈를 얻을 수 있고 2개 이상의 열을 추출하면 데이터프레임을 얻을 수 있습니다.
# #### 열 단위로 데이터 추출하기
# 1. 다음은 데이터프레임에서 열 이름이 country인 열을 추출하여 country_df에 저장한 것입니다. type 메서드를 사용하면 country_df에 저장된 데이터의 자료형이 시리즈라는 것을 확인할 수 있습니다. 시리즈도 head,tail 메서드를 가지고 있기 때문에 gead,tail메서드로 가장 앞이나 뒤에 있는 5개의 데이터를 출력할 수 있습니다.
country_df=df['country']
print(type(country_df))
print(country_df.head())
print(country_df.tail())
# 2.리스트에 열 이름을 전달하면 여러 개의 열을 한 번에 추출할 수 있습니다. 다음은 열 이름이 country,continent,year인 열을 추출하여 변수 subset에 저장한 것입니다. 이때 1개의 열이 아니라 2개 이상의 열을 추출했기 때문에 시리즈가 아니라 데이터프레임을 얻을 수 있습니다.
subset=df[['country','continent','year']]
print(type(subset))
print(subset.head())
print(subset.tail)
# ## 행단위 데이터 추출하기
# 이번에는 데이터를 행 당위로 추출하는 방법에 대해 알아보겠습니다. 데이터를 행 단위로 추출하려면 loc,iloc 속성을 사용해야 합니다. 밑에 두 속성을 간단하게 정리한 표입니다.<br>
# 속성$\quad$$\quad$$\quad$설명<br>
# loc$\quad$$\quad$$\quad$인덱스를 기준으로 행 데이터 추출<br>
# iloc$\quad$$\quad$$\quad$행 번호를 기준으로 행 데이터 추출
# 표의 설명을 보면 인덱스와 행 번호라는 것이 있습니다. 파이썬을 공부한 독자라면 리스트같은 자료형에 저장된 데이터의 순서를 인덱스라고 알고 있을 것입니다. 하지만 판다스에서는 이런 개념을 행 번호라고 부릅니다. 다음예제를 실습하면서 판다스에서 말하는 인덱스와 행 번호가 무엇인지 알아보겠습니다.
# ## 인덱스와 행 번호 개념 알아보기
# 다음은 갭마인더 데이터 집합을 불러온 다음 head메서드를 실행한 결과입니다.
print(df.head())
# 왼쪽에 번호가 보이나요? 바로 이것이 인덱스입니다. 인덱스는 보통 0부터 시작하지만 행 데이터가 추가, 삭제되면 언제든지 변할 수 있으며 숫자가 아니라 문자열을 사용할 수도 있습니다. 즉, 인덱스는 first, second,third와 같은 문자열로 지정할 수도 있습니다. 반면에 행 번호는 데이터의 순서를 따라가기 때문에 정수만으로 데이터를 조회하거나 추출할 수 있으며 실제 데이터프레임에서는 확인할 수 없는 값입니다.
print(df.loc[0])
print(df.loc[99])
# 2. 만약 데이터프레임의 마지막 행 데이터를 추출하려면 어떻게 해야 할까요? 마지막 행데이터의 인덱스를 알아내야 합니다. shape[0]에 행 크기(1704)가 저장되어 있다는 점을 이용하여 마지막 행의 인덱스를 구하면 됩니다. 다음은 shape[0]에서 1을 뺀 값으로(1704-1=1703)마지막 행 데이터를 추출한 것입니다.
number_of_rows=df.shape[0]
last_row_index=number_of_rows -1
print(df.loc[last_row_index])
# 3. 데이터프레임의 마지막 행 데이터를 추출하는 또 다른 방법으로는 tail메서드를 사용하는 방법이 있습니다. 다음과 같이 tail 메서드의 인자 n에 1을 전달하면 마지막 행의 데이터를 출출할 수 있습니다. 이방법이 조금 더 유용하겠죠?
print(df.tail(n=1))
# 4. 만약 인덱스가 0,99,999인 데이터를 한 번에 추출하려면 리스트에 원하는 인덱스를 담아 loc 속성에 전달하면 됩니다.
print(df.loc[[0,99,999]])
# ### tail메서드와 loc 속성이 반환하는 자료형은 서로 달라요!
# tail 메서드와 loc 속성이 반환하는 데이터의 자료형은 다릅니다. 다음은 tail 메서드와 lic속성으로 추출한 데이터의 자료형을 type메서드로 확인한 것입니다. loc속성이 반환한 데이터 자료형은 시리즈이고 tail 메서드가 반환한 데이터 자료형은 데이터프레임입니다.
# +
subset_loc=df.loc[0]
subset_tail=df.tail(n=1)
print(type(subset_loc))
print(type(subset_tail))
# -
# ### iloc 속성으로 행 데이터 추출하기
# 1. 이번에는 iloc속성으로 행 데이터를 추출하는 방법에 대해 알아보겠습니다. loc속성은 데이터프레임의 인덱스를 사용하여 데이터를 추출했지만 iloc 속성은 데이터 순서를 의미하는 행 번호를 사용하여 데이터를 추출합니다.지금은 인덱스와 행 번호가 동일하여 동일한 결괏값이 출력됩니다. 다음은 iloc속성에 1을 전달하여 데이터를 추출한 것입니다.
print(df.iloc[1])
print(df.iloc[99])
# 2. iloc 속성은 음수를 사용해도 데이터를 추출할 수 있습니다. 다음은 -1을 전달하여 마지막 행 데이터를 추출한 것입니다. 하지만 데이터프레임에 아예 존재하지 않는 행 번호를 전달하면 오류가 발생합니다.
print(df.iloc[-1])
# 3. iloc 속성도 여러 데이터를 한 번에 추출할 수 있습니다. loc 속성을 사용했던 것처럼 원하는 데이터의 행 번호를 리스트에 담아 전달하면 됩니다.
print(df.iloc[[0,99,999]])
# ## loc, iloc 속성 자유자재로 사용하기
# loc, iloc속성을 좀더 자유자재로 사용하려면 추출할 데이터의 행과 열을 지정하는 방법을 알아야 합니다. 두속성 모두 추출할 데이터의 행을 먼저 지정하고 그런 다음 열을 지정하는 방법으로 데이터를 추출합니다. 즉 df.loc[[행],[열]]이나 df.iloc[[행],[열]]과 같은 방법으로 코드를 작성하면 됩니다. <br> 이때 행과 열을 지정하는 방법은 슬라이싱 구문을 사용하는 방법과 range 메서드를 사용하는 방법이 있습니다. 먼저 슬라이싱 구문으로 원하는 데이터를 추출하는 방법을 알아보겠습니다.
# ### 데이터 추출하기--슬라이싱 구문, range메서드
# #### 1.슬라이싱 구문으로 데이터 추출하기
# 다음은 모든 행(:)의 데이터에 대해 tear,pop열을 추출하는 방법입니다. 이때 loc와 iloc속성에 전달하는 열 지정값은 반드시 형식에 맞게 전달해야 합니다. 예를 들어 loc 속성의 열 지정값에 정수 리스트를 전달하면 오류가 발생합니다.
subset=df.loc[:,['year','pop']]
print(subset.head())
subset=df.iloc[:,[2,4,-1]]
print(subset.head())
# #### 2. range메서드로 데이터 추출하기
# 이번에는 iloc 속성과 파이썬 내장 메서드인 range를 응용하는 방법을 알아보겠습니다. range 메서드는 지정한 구간의 정수 리스트를 반환해 줍니다. iloc속성의 열 지정값에는 정수 리스트를 전달해야 한다는 점과 range메서드의 반환값이 정수 리스트인 점을 이용하여 원하는 데이터를 추출하는 것이죠<br> 그런데 range 메서드는 조금 더 정확하게 말하면 지정한 범위의 정수 리스트를 반환하는 것이 아니라 제네레이터를 반환합니다. iloc속성은 제네레이터로 데이터 추출을 할 수 없죠. 다행이 제네레이터는 간단하게 리스트로 변환할 수 있습니다. 다음은 range(5)가 반환한 제네레이터를 정숫값을 가진 리스트 [0,1,2,3,4]로 변환하여 iloc의 열 지정값에 전달한 것입니다. 자주 사용하는 방법은 아니지만 알아두면 유용할 것입니다.|
small_range=list(range(5))
print(small_range)
print(type(small_range))
subset=df.iloc[:,small_range]
print(subset.head())
small_range=list(range(3,6))
print(small_range)
subset=df.iloc[:,small_range]
print(subset.head())
# #### 3. range 메서드에 대해 조금 더 알아볼까요? range 메서드에 range(0,6,2)와 같은 방법으로 3개의 인자를 전달하면 어떻게 될까요? 0부터 5까지 2만큼 건너뛰는 제네레이터를 생성합니다. 이 네네레이터를 리스트로 변환하면 번위는 0~5이고 짝수로 된 정수 리스트를 얻을 수 있죠.
small_range=list(range(0,6,2))
subset=df.iloc[:,small_range]
print(subset.head())
# #### 4.슬라이싱 구문과 range 메서드 비교하기
# 그런데 실무에서는 range 메서드보다는 간편하게 사용할 수 있는 파이썬 슬라이싱 구문을 더 선호합니다. range메서드가 반환한 제네레이터를 리스트로 변환하는 등의 과정을 거치지 않아도 되기 때문이죠. 예를 들어 list(range(3))과 [:3]의 결괏값은 동일합니다.
subset=df.iloc[:,:3]
print(subset.head())
# #### 5. 0:6:2를 열징정값에 전달하면 과정 3에서 얻은 결괏값과 동일한 결괏값을 얻을수 있습니다. range메서드와 슬라이싱 구문을 비교해 보세요.
subset=df.iloc[:,0:6:2]
print(subset.head())
# #### 6. loc,iloc 속성 자유자재로 사용하기
# 만약 iloc 속성으로 0,99,999번째 행의 0,3,5번째 열 데이터를 추출하려면 다음과 같이 코드를 작성하면 됩니다.
print(df.iloc[[0,99,999],[0,3,5]])
# #### 7. iloc 속성의 열 지정값으로 정수 리스트를 전달하는 것이 간편해 보일 수 있지만 이렇게 작성한 코드는 나중에 어떤 데이터를 추출하기 위한 코드인지 파악하지 못 할 수도 있습니다. 그래서 보통은 다음과 같은 방법으로 loc 속성을 이용하여 열 지정값으로 열 이름을 전달합니다.
print(df.loc[[0,99,999],['country','lifeExp','gdpPercap']])
# #### 8. 앞에서 배운 내용을 모두 응용하여 데이터를 추출해 볼까요? 다음은 인덱스가 10인 행부터 13인 행의 country,lifeExp,gdpPercap열 데이터를 추출하는 코드입니다.
print(df.loc[10:13,['country','lifeExp','gdpPercap']])
# # 02-3 기초적인 통계 계산하기
# 지금까지는 데이터를 추출하는 방법에 대해 알아보았습니다. 이번에는 추출한 데이터를 가지고 몇 가지 기초적인 통계 계산을 해보겠습니다. 다음은 갭마인더 데이터 집합에서 0~9번째 데이터를 추출하여 출력한 것입니다.
print(df.head(n=10))
# ### 그룹화한 데이터의 평균 구하기
# #### 1. lifeExp열을 연도별로 그룹화하여 평균 계산하기
# 예를 들어 연도별 lifeExp 열의 평균을 계산하려면 어떻게 해야 할까요? 데이터를 year열로 그룹화하고 lifeExp 열의 평균을 구하면 됩니다. 다음은 데이터프레임의 groupby 메서드에 year 열을 전달하여 연도별로 그룹화한 다음 lifeExp 열을 지정하여 mean 메서드로 평균을 구한 것입니다.
print(df.groupby('year')['lifeExp'].mean())
# #### 2. 과정 1에서 작성한 코드가 조금 복잡해서 어리둥절할 수도 있을 것입니다. 어떤 일이 벌어진 것일까요? 과정 1에서 작성한 코드를 작은 단위로 나누어 살펴보겠습니다. 먼저 데이터프레임을 연도별로 그룹화한 결과를 살펴보겠습니다. groupby 메서드에 year열 이름을 전달하면 연도별로 그룹화한 country, continent,.....gdpPercap 열을 모은 데이터프레임을 얻을 수 있습니다.
grouped_year_df=df.groupby('year')
print(type(grouped_year_df))
# #### 3. groupde_year_df를 출력하면 과정 2에서 얻은 데이터프레임이 저장된 메모리의 위치를 알수 있습니다. 이결과를 통해 연도별로 그룹화한 데이터는 데이터프레임 형태로 현재 메모리의 0x7fa9f012e700이라는 위치에 저장되어 있음을 알 수 있습니다.
print(grouped_year_df)
# #### 4. 이어서 lifeExp 열을 추출한 결과를 살펴보겠습니다. 그룹화한 데이터프레임에서 lifeExp 열을 추출하면 그룹화한 시리즈를 얻을 수 있습니다. 즉, 연도별로 그룹화한 lifeExp 열을 얻을 수 있습니다.
grouped_year_df_lifeExp=grouped_year_df['lifeExp']
print(type(grouped_year_df_lifeExp))
# #### 5. 마지막으로 평군을 구하는 mean 메서드를 사용한 결과를 살펴보겠습니다. 과정 4에서 연도별로 그룹화한 lifeExp에 mean 메서드를 사용했기 때문에 각 연도별 lifeExp 열의 평균값을 얻을 수 있습니다.
mean_lifeExp_by_year=grouped_year_df_lifeExp.mean()
print(mean_lifeExp_by_year)
# #### 6. lifeExpm gdpPercap 열의 평균값을 연도, 지역별로 그룹화하여 한 번에 계산하기.
# 다음은 과정 1~4를 응용한 코드입니다. year, continent 열로 그룹화한 그룹 데이터프레임에서 lifeExp, gdpPercap 열만 추출하여 평균값을 구한 것입니다.
multi_group_var=df.groupby(['year','continent'])[['lifeExp','gdpPercap']].mean()
print(multi_group_var)
print(type(multi_group_var))
# #### 7. 그룹화한 데이터 개수 세기
# 이번에는 그룹화한 데이터의 개수가 몇 개인지 알아보겠습니다. 이를 통계에서는 '빈도수'라고 부릅니다. 데이터의 빈도수는 nunique 메서드를 사용하면 쉽게 구할 수 있습니다. 다음은 continent를 기준으로 데이터프레임을 만들고 country 열만 추출하여 데이터의 빈도수를 계산할 것입니다.
print(df.groupby('continent')['country'].nunique())
# # 02-4 그래프 그리기
# 그래프와 같은 데이터의 시각화는 데이터 분석 과정에서 가장 중요한 요소입니다. 데이터를 시각화하면 데이터를 이해하거나 추이를 파악하는 등의 작업을 할 때 많은 도움이 됩니다. 여기에서는 간단한 그래프를 그려보고 데이터 시각화가 무엇인지 알아보겠습니다. 자세한 내용은 04장에서 더 자세히 설명하겠습니다.
# ### 그래프 그리기
# #### 1.먼저 그래프와 연관된 라이브러리를 불러옵니다.
# %matplotlib inline
import matplotlib.pyplot as plt
# #### 2. 그런 다음 year 열을 기준으로 그릅화한 데이터프레임에서 lifeExp 열만 추출하여 평균 값을 구합니다.
global_yearly_life_expectancy=df.groupby('year')['lifeExp'].mean()
print(global_yearly_life_expectancy)
# #### 3. 과정 2에서 구한 값에 plot메서드를 사용하면 다음과 같은 그래프가 그려집니다.
global_yearly_life_expectancy.plot()
# ### 마무리하며
# 이 장에서는 데이터 집합을 불러오는 방법과 데이터를 추출하는 방법 등을 알아보았습니다. 판다스가 무엇인지 감이 좀 잡혔나요? 다음 장에서는 판다스의 기본 자료형인 데이터프레임과 시리즈를 좀 더 자세히 알아보겠습니다.
# 출처 : "판다스"
| chapter_02-1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import json
from datasets import load_dataset
### json file format change to text file format for training and testing
### assume train.json, dev.json, test.json, labels.json in data path
dataset = load_dataset('json', data_files={
'train':'THUCNews/data'+"/train.json",
'validation':'THUCNews/data'+"/dev.json"
})
classes = {}
with open('THUCNews/data'+'/labels.json', encoding='utf-8') as f:
for i, line in enumerate(f):
classes[str(i)] = json.loads(line)['label_des']
# -
# # pd classes
dataset['train']['label']
from pylab import *
import matplotlib as mp
mp.rcParams['font.family'] = 'Microsoft YaHei'
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']
mpl.rcParams['font.size'] = 7
from matplotlib import pyplot as plt
from matplotlib.pyplot import figure
figure(figsize=(16,12), dpi=320)
train_set = pd.DataFrame({'id': dataset['train']['label'],
'class': [classes[l] for l in dataset['train']['label']]})
train_set['class'].value_counts(ascending=True).plot(kind='barh')
plt.show()
train_set
| basicEDA.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6.9 64-bit
# language: python
# name: python36964bit38de1cc02df948d3b9a63469152fc45c
# ---
import numpy as np
import matplotlib.pyplot as plt
import pyroomacoustics as pra
from pyroomacoustics.doa import circ_dist
# from scipy.io import wavfile
# +
# f2m = 1/3.2808
def f2m(x):
return x*(1/3.2808)
roomX = f2m(52/3)
roomY = f2m(49/2)
roomZ = f2m(7) #not sure about this
# -
m = pra.make_materials(
ceiling="hard_surface",
floor="hard_surface",
east="brickwork",
west="brickwork",
north="brickwork",
south="brickwork",
)
# Use this in lab to figure out the reflection order, you'll need to guess a reverberation time
rt60_tgt = 0.3 # seconds
room_dim = [10, 7.5, 3.5] # meters
fs, audio = wavfile.read("examples/samples/guitar_16k.wav")
# We invert Sabine's formula to obtain the parameters for the ISM simulator
e_absorption, max_order = pra.inverse_sabine(rt60_tgt, room_dim)
# Create the room
room = pra.ShoeBox(
room_dim, fs=fs, materials=pra.Material(e_absorption), max_order=max_order
)
# The desired reverberation time and dimensions of the room
# rt60_tgt = 0.3 # seconds
room_dim = [roomX, roomY, roomZ] # meters
room = pra.ShoeBox(
room_dim, fs=48000, materials=m, max_order=17, air_absorption=True, ray_tracing=True
)
# +
azimuth = 61.0 / 180.0 * np.pi # 60 degrees
# distance = 3.0 # 3 meters
# algorithms parameters
SNR = 0.0 # signal-to-noise ratio
c = 343.0 # speed of sound
fs = 16000 # sampling frequency
nfft = 256 # FFT size
freq_bins = np.arange(5, 60) # FFT bins to use for estimation
# compute the noise variance
# sigma2 = 10 ** (-SNR / 10) / (4.0 * np.pi * distance) ** 2
# Create an anechoic room
# room_dim = np.r_[roomX, roomY, roomZ] # meters
room_dim = np.r_[roomX, roomY] # meters
room = pra.ShoeBox(room_dim, fs=fs, max_order=17) #Assume no noise
sourceX = roomX/2
sourceY = roomY/3
h = roomY - 2*sourceY
b = h/np.tan(azimuth)
print(f'b: {b}')
distance = np.sqrt((b**2)+(h**2))
print(f'distance: {distance}')
# add the source
# source_location = room_dim / 2 + distance * \
# np.r_[np.cos(azimuth), np.sin(azimuth)]
source_location = np.r_[sourceX, sourceY]
print(f'source loc: {source_location}')
source_signal = np.random.randn((nfft // 2 + 1) * nfft)
room.add_source(source_location, signal=source_signal)
in_mic = 0.15
#Mics will be 0.14 m apart
mic_locs = np.c_[
[(roomX/2)+b+(in_mic/2), roomY-sourceY], # mic 1
[(roomX/2)+b-(in_mic/2), roomY-sourceY], # mic 2
]
# print(mic_locs)
print(f'In mic dist: {mic_locs[0][0] - mic_locs[0][1]}')
print(f'Mics loc:\n{mic_locs.T}')
room.add_microphone_array(mic_locs)
room.simulate()
# room.add_microphone_array(mic_locs)
# +
# Compute the STFT frames needed
X = np.array(
[
pra.transform.stft.analysis(signal, nfft, nfft // 2).T
for signal in room.mic_array.signals
]
)
##############################################
# Now we can test all the algorithms available
algo_names = sorted(pra.doa.algorithms.keys())
for algo_name in algo_names:
# Construct the new DOA object
# the max_four parameter is necessary for FRIDA only
# doa = pra.doa.algorithms[algo_name](R, fs, nfft, c=c, max_four=4)
doa = pra.doa.algorithms[algo_name](mic_locs, fs, nfft, c=c, max_four=4)
# this call here perform localization on the frames in X
doa.locate_sources(X, freq_bins=freq_bins)
doa.polar_plt_dirac()
plt.title(algo_name)
# doa.azimuth_recon contains the reconstructed location of the source
print(algo_name)
print(" Recovered azimuth:", doa.azimuth_recon / np.pi * 180.0, "degrees")
print(" Error:", circ_dist(azimuth, doa.azimuth_recon) /
np.pi * 180.0, "degrees")
plt.show()
# +
import numpy as np
from scipy.signal import fftconvolve
import matplotlib.pyplot as plt
import pyroomacoustics as pra
from pyroomacoustics.doa import circ_dist
######
# We define a meaningful distance measure on the circle
# Location of original source
# azimuth = 61.0 / 180.0 * np.pi # 60 degrees
azimuth = 1 / 180.0 * np.pi # 60 degrees
distance = 3.0 # 3 meters
#######################
# algorithms parameters
SNR = 0.0 # signal-to-noise ratio
c = 343.0 # speed of sound
fs = 16000 # sampling frequency
nfft = 256 # FFT size
freq_bins = np.arange(5, 60) # FFT bins to use for estimation
# compute the noise variance
sigma2 = 10 ** (-SNR / 10) / (4.0 * np.pi * distance) ** 2
roomX = f2m(52/3)
roomY = f2m(49/2)
# Create an anechoic room
room_dim = np.r_[roomX, roomY]
aroom = pra.ShoeBox(room_dim, fs=fs, max_order=0, sigma2_awgn=sigma2)
# add the source
# source_location = room_dim / 2 + distance * np.r_[np.cos(azimuth), np.sin(azimuth)]
# source_signal = np.random.randn((nfft // 2 + 1) * nfft)
# aroom.add_source(source_location, signal=source_signal)
source_location = np.r_[sourceX, sourceY]
print(f'source loc: {source_location}')
source_signal = np.random.randn((nfft // 2 + 1) * nfft)
aroom.add_source(source_location, signal=source_signal)
# We use a circular array with radius 15 cm # and 12 microphones
R = pra.circular_2D_array(room_dim / 2, 12, 0.0, 0.15)
print(f'R:\n{R}')
aroom.add_microphone_array(pra.MicrophoneArray(R, fs=aroom.fs))
# run the simulation
aroom.simulate()
################################
# Compute the STFT frames needed
X = np.array(
[
pra.transform.stft.analysis(signal, nfft, nfft // 2).T
for signal in aroom.mic_array.signals
]
)
##############################################
# Now we can test all the algorithms available
algo_names = sorted(pra.doa.algorithms.keys())
for algo_name in algo_names:
# Construct the new DOA object
# the max_four parameter is necessary for FRIDA only
doa = pra.doa.algorithms[algo_name](R, fs, nfft, c=c, max_four=4)
# this call here perform localization on the frames in X
doa.locate_sources(X, freq_bins=freq_bins)
doa.polar_plt_dirac()
plt.title(algo_name)
# doa.azimuth_recon contains the reconstructed location of the source
print(algo_name)
print(" Recovered azimuth:", doa.azimuth_recon / np.pi * 180.0, "degrees")
print(" Error:", circ_dist(azimuth, doa.azimuth_recon) /
np.pi * 180.0, "degrees")
plt.show()
| examples/doa_inlab.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Как писать быстрый код на Python
# ## <NAME>
# Язык Python обладает многими необходимыми для вычислений функциями.
# Целые числа хранятся со знаком и имеют произвольную длину
n = 1 # Целое число
for _ in range(500):
n *= 10
print(n)
print(type(n))
# Арифметика на целых определенна обычным образом.
print(f"1+2={1+2}")
print(f"1-2={1-2}")
print(f"1*2={1*2}")
# Обратите однако внимание, что целочисленное деление обозначается //
print(f"1/2={1/2}")
print(f"1//2={1//2}")
# Часто бывает полезен остаток от деления.
print(f"4%3={4%3}")
# Обратете внимание, что остаток от отрицательного числа положителен.
# Остаток определен таким образом, чтобы согласовываться с арифметикой по данному модулю.
print(f"(-1)%3={(-1)%3}")
assert ((-1)%3 + 1%3)%3 == (1-1)%3
# Вещественные числа имеют в своей записи точку или экспоненту
print(f"type(1)={type(1)}")
print(f"type(1.0)={type(1.0)}")
print(f"type(1e1)={type(1e1)}")
# Научная форма записи чисел указывает показатель после символа `e`:
# $$\textrm{314e-2}=e14\cdot 10^{-2}=3.14.$$
# Вещественные числа хранятся в виде чисел с плавающей запятой двойной точности.
print(f"1.0 + 1e-15 = {1.0 + 1e-15}")
print(f"1.0 + 1e-16 = {1.0 + 1e-16}")
print(f"1e307 * 10 = {1e307 * 10}")
print(f"1e308 * 10 = {1e308 * 10}")
print(f"1e309 = {1e309}")
print(f"1e-323 = {1e-323}")
print(f"1e-324 = {1e-324}")
# Также питон ествественно поддерживает комплексные числа.
# Чисто мнимое число получается добавлением символа j после вещественного числа.
print(f"1+2i = {1+2j}")
print(f"i*(1+2i) = {1j*(1+2j)}")
# Не во всех языках общего назначения в стандартной библиотеке есть рациональные числа, но в питоне они есть.
from fractions import Fraction
pi = Fraction(355, 113)
print(f"pi ~ {pi} ~ {float(pi)}")
print(f"pi*2/5 = {pi*2/5}")
# Обратите внимание, что типы конвертируются между собой вызовом конструктора.
print(f"int(3.14) = {int(3.14)}")
print(f"float('3.14') = {float('3.14')}")
# +
# Для хранения векторов на питоне есть две возможности: списки и кортежи.
a = [1,2,3] # Список
print(f"a = {a}")
a[1] = 5 # Списки можно изменять.
print(f"a[1]=5; a = {a}")
a.insert(1, 6) # Можно даже менять длину списка.
print(f"a.insert(1, 5); a = {a}")
b = (1,2,3) # Кортеж
print(f"b = {b}")
# b[1] = 5 # Кортежи нельзя изменять.
# И списки, и кортежи могут содержать любые объекты.
a1 = [1, 1.0, 'a']
b1 = (1, 1.0, 'a')
# -
# Универсальность списков и кортежей не позволяет хранить в них вектора чисел максимально плотно,
# и работать с ними максимально быстро.
# Магия IPython/Jupyter позволяет нам измерить время выполнения команды.
# В данном случае мы создаем список чисел до 1 000 000
# %timeit a = list(x for x in range(1000000))
# %%timeit
# Аналогично можно было создать список в цикле
a = []
for x in range(1000000):
a.append(x)
# В этом варианте несколько большие затраты на интерпретацию.
# Однако оба этих варианта работают слишком медленно.
# Кортежи дают аналогичный результат.
# %timeit a = tuple(x for x in range(1000000))
# В таком духе можно делать операции над векторами, но это медленно.
# Например, сложим два вектора.
# %time a = list(x for x in range(1000000))
# %time b = list(x*x for x in range(1000000))
# Интересно, что хотя во втором случае мы возвели числа в квадрат, на скорость вычислений это не повлияло.
# В данном случае основные расходы на интерпретацию, а остальное на выделение памяти, сами вычисления на этом фоне теряются.
# Правда можно сделать еще хуже, если добавить вызов функции.
# %time b = list(x**2 for x in range(1000000))
# Складываем вектора, используя list comprehension.
# %time c = list(x+y for x,y in zip(a,b))
# %%time
# А теперь сложим вектора без выделения новой памяти, сохраняя результат в существующий вектор.
for n in range(len(a)):
c[n] = a[n] + b[n]
# ## NumPy
# Как мы видим, на питоне можно считать, но он плохо подходит для численного моделирования, так как
# 1. Мало типов данных, невозможно контролировать точность, нет поддержки массивов, матриц и т.п.
# 2. Слишком малая скорость вычислений из-за интерпретируемости языка.
#
# Проблемы с хранением могуть быть решены создания специального типа, в котором хранятся числа только одного типа,
# тогда их можно хранить подряд друг за другом, что уменьшает требуемый обьем памяти.
# Такой класс определен в пакете NumPy.
import numpy as np # Далее пакет NumPy доступен по сокращению np.
# Снова создадим вектор из 1 000 000 первых целых чисел, но теперь в типе numpy.NDArray
# %time a = np.arange(1000000)
print(f"type a = {type(a)}")
# Время выполнения на порядок сохранилось, для больших массивов разница будет еще больше.
# Также тип NDArray удобен для хранения многомерных массивов.
m = np.array([[1,2,3],[4,5,6]])
# Здесь мы преобразовали матрицу в виде списка списков в NDArray
print(f"m = {m}")
# Теперь матрицу можно транспонировать
print(f"m.T = {m.T}")
# В виде списков это было бы сделать гораздо сложнее.
# +
# Над массивами естественным образом определены арифметические операции
# %time b = a**2
# %time b = a*a
# %time b = a**2
# Теперь время работы гораздо более разумное, так как арифметика над массивами написана
# на низкоуровневых языках и использует векторные команды процессора.
# Иногда инструкции NumPy работают быстрее наивного кода на C.
# %time c=a+b
# %time c+=a
# %time c=a+b
# Обратите внимание, что вторая команда работает чуть быстрее первой,
# так как в ней не выделяется память.
# Интересная особенность Jupyter, что третья команда выполняется на порядок быстрее первой,
# хотя команды буквально совпадают.
# Видимо, если переменная уже существовала, она переиспользуется.
# -
# %%time
# Вычисления в цикле работают значительно медленнее.
for n in range(len(a)):
c[n] += a[n]
# +
# Главный вывод: если вы делает операции над многими элементами, то пусть цикл будет внутри функции numpy,
# а не в коде на python.
# -
# ## Numba
#
# Если вам привычнее думать в терминах циклов, то вам может помочь Numba.
# С помощью этой библиотеке функция на python компилируется во время выполнения в весьма эффективный код.
# +
import numba as nb # Теперь Numba доступна под именем nb
# Для примера создадим функцию, которая складывает вектора.
@nb.njit(nb.int64[:](nb.int64[:],nb.int64[:]))
def add(a, b):
c = np.empty_like(a)
for n in range(a.shape[0]):
c[n] = a[n] + b[n]
return c
# Декоратор @nb.njit говорит, что следующая функция должна быть откомпилирована.
# Здесь нам пришлось задать типы входных и выходных значений, чтобы компилятор мог заменить сложение
# на машинную инструкцию.
# %time c=add(a,b)
# Производительность почти как у функции из NumPy.
# Не все функции можно использовать из Numba, см. поддерживаемые команды в документации.
# +
# Кроме эффективного преобразования циклов, Numba может быть полезно, если над одним элементом
# массива производится много операций.
# Так как в наше время основные затраты при вычислениях приходятся на доступ к памяти,
# то выполняя больше операций над одним элементом сразу, мы значительно ускоряем работу программы.
# Создадим массив чисел с плавающей запятой двойной точности
a=np.arange(10000000,dtype=np.float64)
# # %timeit c=np.sin(a)
# # %timeit c=np.sin(np.sin(a))
# %timeit c=a*a
# %timeit c=(a+3.14)*a
# Две операции занимают в два раза больше времени, что кажется логичным.
# +
@nb.njit(nb.float64[:](nb.float64[:]))
def f1(x):
y = np.empty_like(x)
for n in nb.prange(x.shape[0]):
y[n] = x[n]*x[n]
return y
@nb.njit(nb.float64[:](nb.float64[:]))
def f2(x):
y = np.empty_like(x)
for n in range(x.shape[0]):
y[n] = (x[n]+3.14)*x[n]
return y
# %timeit c=f1(a)
# %timeit c=f2(a)
# Магическим образом получили время работы f2 почти идентичное f1, хотя операций делалось две, вместо одной.
# Видим, что основное время работы занимал доступ к памяти, а не арифметика.
# Для дорогих операций, вроде np.sin, такой разницы во времени не будет.
# +
# Функция f1 выше работала медленнее, чем умножение в Numpy, но мы можем ускорить функцию, использую несколько потоков.
# Обратите внимание на использование numba.prange вместо range.
@nb.njit(nb.float64[:](nb.float64[:]), parallel=True)
def f1(x):
y = np.empty_like(x)
for n in nb.prange(x.shape[0]):
y[n] = x[n]*x[n]
return y
@nb.njit(nb.float64[:](nb.float64[:]), parallel=True)
def f2(x):
y = np.empty_like(x)
for n in nb.prange(x.shape[0]):
y[n] = (x[n]+3.14)*x[n]
return y
# %timeit c=f1(a)
# %timeit c=f2(a)
# +
# Если массивы заведомо непрерывные (т.е. не результат индексации),
# то можно это явно указать, включив дополнительные оптимизации.
# @nb.njit(nb.float64[::1](nb.float64[::1]), parallel=True)
# +
# Еще сильнее можно ускорить вычисления, исключив проверки чисел с плавающей запятой на нечисловые значения,
# и разрешив оптимизации, которые могут незначительно повлиять на ответ.
# В большинстве случаев безопасно использовать
# @nb.njit(..., parallel=True, nogil=True, fastmath=True)
# +
# Для получения оптимальной производительности нужно всегда учитывать работу кеша.
# Сравним два варианта сложения матриц, отличающихся порядком суммирования элементов.
a = np.arange(9000000, dtype=np.float64).reshape((3000,3000))
b = a.copy() # Чтобы создать копию массива, мало сделать присваивание, нужно вызвать copy.
@nb.njit(nb.float64[:,:](nb.float64[:,:],nb.float64[:,:]))
def sum1(a,b):
c = np.empty_like(a)
for n in range(a.shape[0]):
for m in range(a.shape[1]):
c[n,m] = a[n,m]+b[n,m]
return c
@nb.njit(nb.float64[:,:](nb.float64[:,:],nb.float64[:,:]))
def sum2(a,b):
c = np.empty_like(a)
for m in range(a.shape[1]):
for n in range(a.shape[0]):
c[n,m] = a[n,m]+b[n,m]
return c
# %timeit c = sum1(a,b)
# %timeit c = sum2(a,b)
# Вариант с внутренним циклом по столбцам на порядок быстрее.
# Это объясняется тем, что при чтении одного значения из памяти сразу целый набор последовательных
# значений загружаются в кеш, из которого чтение затем идем на порядок быстрее.
# Для максимальной производительности нужно максимально использовать записанные в кеш значения.
# +
# Чтобы получить максимальную производительность, нужно четко представлять,
# во что преобразуется ваш код, что часто не очевидно.
# Например, сравним следующие коды, вычисляющие конечную разность.
@nb.njit(nb.float64[::1](nb.float64[::1]))
def f0(a):
c = np.empty_like(a)
for n in range(1,a.shape[0]):
c[n] = a[n]-a[n-1]
c[0] = a[0] - a[-1]
return c
@nb.njit(nb.void(nb.float64[::1], nb.float64[::1]))
def f1(a, c):
for n in range(1, a.shape[0]):
c[n] = a[n] - a[n-1]
c[0] = a[0] - a[-1]
@nb.njit(nb.void(nb.float64[::1], nb.float64[::1]))
def f2(a, c):
sx, = a.shape
for n in range(sx):
c[n] = a[n]-a[(n-1)%sx]
a = np.arange(10000000,dtype=np.float64)
c = np.empty_like(a)
# %timeit c=f0(a)
# %timeit f1(a, c)
# %timeit f2(a, c)
# Вариант f0 отличается от f1 только выделением памяти в f0, что делает этот вариант самым медленным.
# Варианты f1 и f2 не выделяют памяти, но время их выполнения отличается в разы.
# В варианте f2 вычисляется остаток от деления %, который компилятор не может эффективно векторизовать.
# -
| practice/FastPython.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python3.6
# language: python
# name: python3
# ---
# # Online Trading Customer Attrition Risk Prediction using SparkML
#
# There are many users of online trading platforms and these companies would like to run analytics on and predict churn based on user activity on the platform. Since competition is rife, keeping customers happy so they do not move their investments elsewhere is key to maintaining profitability.
#
# In this notebook, we will leverage IBM Cloud Private for Data to do the following:
#
# 1. Ingest merged customer demographics and trading activity data
# 2. Visualize the merged dataset to get a better understanding of the data and build hypotheses for prediction
# 3. Leverage the SparkML library to build a classification model that predicts whether a customer has a propensity to churn
# 4. Expose the SparkML classification model as a RESTful API endpoint for the end-to-end customer churn risk prediction and risk remediation application
#
# <a id="top"></a>
# ## Table of Contents
#
# 1. [Load the customer demographics and trading activity data](#load_data)
# 2. [Load libraries](#load_libraries)
# 3. [Visualize the customer demographics and trading activity data](#visualize)
# 4. [Prepare data for building SparkML classification model](#prepare_data)
# 5. [Train classification model and test model performance](#build_model)
# 6. [Save model to ML repository and expose it as REST API endpoint](#save_model)
# 7. [Summary](#summary)
# ### Quick set of instructions to work through the notebook
#
# If you are new to Notebooks, here's a quick overview of how to work in this environment.
#
# 1. The notebook has 2 types of cells - markdown (text) such as this and code such as the one below.
# 2. Each cell with code can be executed independently or together (see options under the Cell menu). When working in this notebook, we will be running one cell at a time because we need to make code changes to some of the cells.
# 3. To run the cell, position cursor in the code cell and click the Run (arrow) icon. The cell is running when you see the * next to it. Some cells have printable output.
# 4. Work through this notebook by reading the instructions and executing code cell by cell. Some cells will require modifications before you run them.
# <a id="load_data"></a>
# ## 1. Load the customer and trading activity data
# [Top](#top)
#
# Data can be easily loaded within IBM Cloud Private for Data using point-and-click functionality. The following image illustrates how to load the data from a database. The data set can be located by its name and inserted into the notebook as a Spark DataFrame as shown below.
#
# 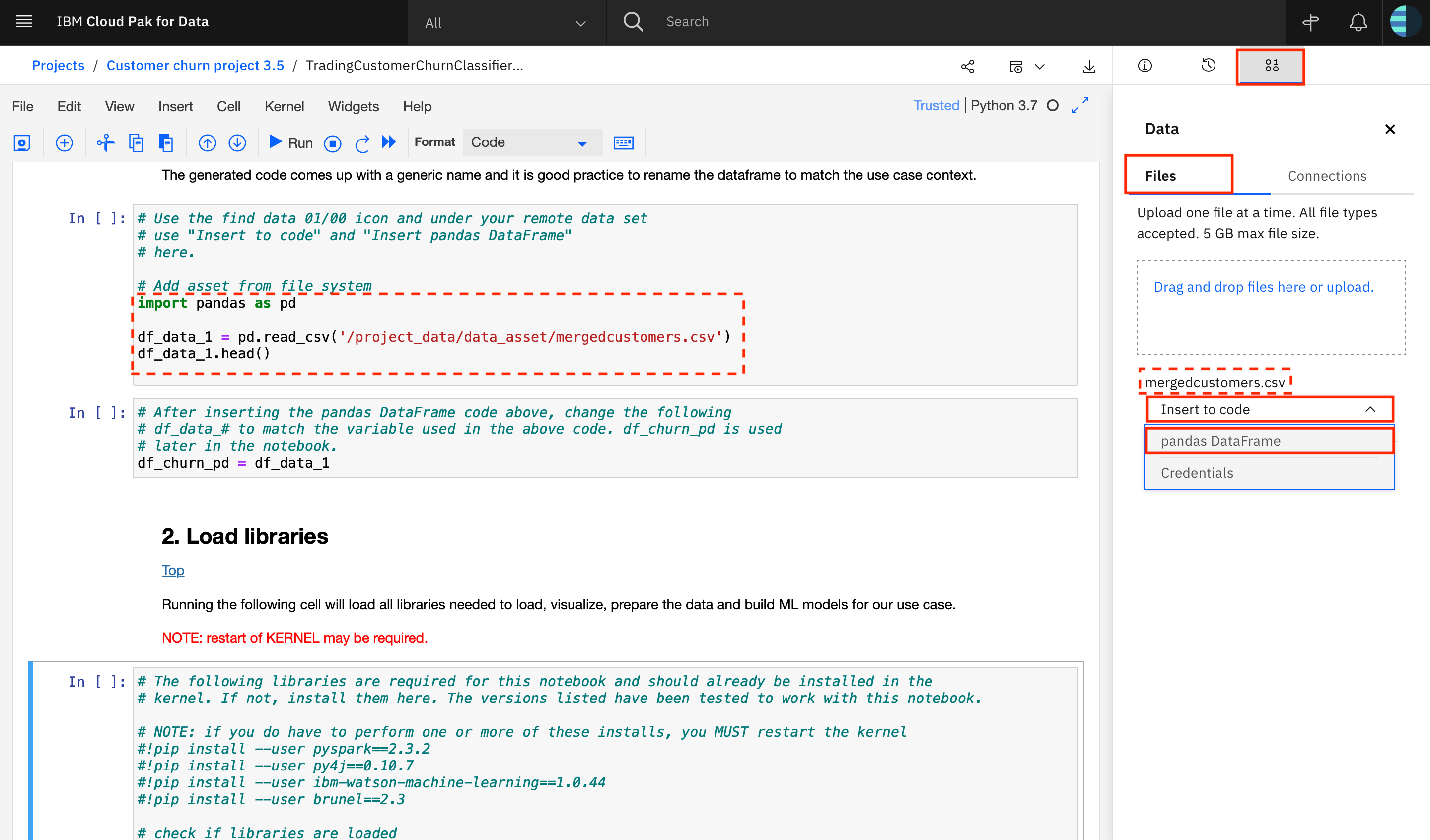
#
# The generated code comes up with a generic name and it is good practice to rename the dataframe to match the use case context.
# +
# Use the find data 10/01 icon and under your remote data set
# use "Insert to code" and "Insert Spark DataFrame in Python"
# here.
import dsx_core_utils, requests, os, io
from pyspark.sql import SparkSession
# Add asset from remote connection
df4 = None
dataSet = dsx_core_utils.get_remote_data_set_info('merge2')
dataSource = dsx_core_utils.get_data_source_info(dataSet['datasource'])
sparkSession = SparkSession(sc).builder.getOrCreate()
# Load JDBC data to Spark dataframe
dbTableOrQuery = ('"' + dataSet['schema'] + '"."' if(len(dataSet['schema'].strip()) != 0) else '') + dataSet['table'] + '"'
if (dataSet['query']):
dbTableOrQuery = "(" + dataSet['query'] + ") TBL"
df4 = sparkSession.read.format("jdbc").option("url", dataSource['URL']).option("dbtable", dbTableOrQuery).option("user",dataSource['user']).option("password",dataSource['password']).load()
df4.show(5)
# -
# After inserting the Spark DataFrame code above, change the following
# df# to match the variable used in the above code. df_churn is used
# later in the notebook.
#df_churn = df#
df_churn = df4
# <a id="load_libraries"></a>
# ## 2. Load libraries
# [Top](#top)
#
# Running the following cell will load all libraries needed to load, visualize, prepare the data and build ML models for our use case
import os
from pyspark.sql import SQLContext
from pyspark.sql.types import DoubleType
from pyspark.ml.feature import OneHotEncoder, StringIndexer, VectorIndexer, IndexToString
from pyspark.sql.types import IntegerType
from pyspark.ml import Pipeline
from pyspark.ml.feature import VectorAssembler
from pyspark.ml.classification import RandomForestClassifier, NaiveBayes
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.mllib.evaluation import MulticlassMetrics
import brunel
from dsx_ml.ml import save
import pandas as pd, numpy as np
import matplotlib.pyplot as plt
import dsx_core_utils, requests, os, io
from pyspark.sql import SparkSession
% matplotlib inline
# <a id="visualize"></a>
# ## 2. Visualize the customer demographics and trading activity data
# [Top](#top)
#
# Data visualization is a key step in the data mining process that helps to better understand the data before it can be prepared for building ML models.
#
# We will use the Brunel visualization which comes preloaded in IBM Cloud Private for Data analytics projects.
#
# The Brunel Visualization Language is a highly succinct and novel language that defines interactive data visualizations based on tabular data. The language is well suited for both data scientists and business users. More information about Brunel Visualization: https://github.com/Brunel-Visualization/Brunel/wiki
#
# Load the Spark DataFrame in to a pandas DataFrame
df_churn = df_churn.filter("ChurnRisk!='ChurnR'") # Filter out CSV header.
df_churn_pd = df_churn.toPandas()
df_churn_pd.head(5)
# %brunel data('df_churn_pd') stack polar bar x(CHURNRISK) y(#count) color(CHURNRISK) bar tooltip(#all)
# %brunel data('df_churn_pd') bar x(STATUS) y(#count) color(STATUS) tooltip(#all) | stack bar x(STATUS) y(#count) color(CHURNRISK: pink-orange-yellow) bin(STATUS) sort(STATUS) percent(#count) label(#count) tooltip(#all) :: width=1200, height=350
# %brunel data('df_churn_pd') bar x(TOTALUNITSTRADED) y(#count) color(CHURNRISK: pink-gray-orange) sort(STATUS) percent(#count) label(#count) tooltip(#all) :: width=1200, height=350
# %brunel data('df_churn_pd') bar x(DAYSSINCELASTTRADE) y(#count) color(CHURNRISK: pink-gray-orange) sort(STATUS) percent(#count) label(#count) tooltip(#all) :: width=1200, height=350
# <a id="prepare_data"></a>
# ## 3. Data preparation
# [Top](#top)
#
# Data preparation is a very important step in machine learning model building. This is because the model can perform well only when the data it is trained on is good and well prepared. Hence, this step consumes bulk of data scientist's time spent building models.
#
# During this process, we identify categorical columns in the dataset. Categories needed to be indexed, which means the string labels are converted to label indices. These label indices and encoded using One-hot encoding to a binary vector with at most a single one-value indicating the presence of a specific feature value from among the set of all feature values. This encoding allows algorithms which expect continuous features to use categorical features.
#
# Final step in the data preparation process is to assemble all the categorical and non-categorical columns into a feature vector. We use VectorAssembler for this. VectorAssembler is a transformer that combines a given list of columns into a single vector column. It is useful for combining raw features and features generated by different feature transformers into a single feature vector, in order to train ML models.
# Defining the categorical columns
categoricalColumns = ['Gender', 'Status', 'HomeOwner']
non_categoricalColumns = df_churn.select([c for c in df_churn.columns if c not in categoricalColumns]).columns
print(non_categoricalColumns)
non_categoricalColumns.remove('ChurnRisk')
stages = []
for categoricalCol in categoricalColumns:
# Category Indexing with StringIndexer
stringIndexer = StringIndexer(inputCol=categoricalCol, outputCol=categoricalCol + "Index")
#Use OneHotEncoder to convert categorical variables into binary SparseVectors
encoder = OneHotEncoder(inputCol=categoricalCol + "Index", outputCol=categoricalCol + "classVec")
stages += [stringIndexer, encoder]
labelIndexer = StringIndexer(inputCol='ChurnRisk', outputCol='label').fit(df_churn)
for colnum in non_categoricalColumns:
df_churn = df_churn.withColumn(colnum, df_churn[colnum].cast(IntegerType()))
# Transform all features into a vector using VectorAssembler
assemblerInputs = [c + "classVec" for c in categoricalColumns] + non_categoricalColumns
assembler = VectorAssembler(inputCols=assemblerInputs, outputCol="features")
# <a id="build_model"></a>
# ## 4. Build SparkML Random Forest classification model
# [Top](#top)
# We instantiate a decision-tree based classification algorithm, namely, RandomForestClassifier. Next we define a pipeline to chain together the various transformers and estimaters defined during the data preparation step before. MLlib standardizes APIs for machine learning algorithms to make it easier to combine multiple algorithms into a single pipeline, or workflow.
#
# We split original dataset into train and test datasets. We fit the pipeline to training data and apply the trained model to transform test data and generate churn risk class prediction
# +
# instantiate a random forest classifier, take the default settings
rf=RandomForestClassifier(labelCol="label", featuresCol="features")
# Convert indexed labels back to original labels.
labelConverter = IndexToString(inputCol="prediction", outputCol="predictedLabel", labels=labelIndexer.labels)
stages += [labelIndexer, assembler, rf, labelConverter]
pipeline = Pipeline(stages=stages)
# -
# Split data into train and test datasets
train, test = df_churn.randomSplit([0.7,0.3], seed=100)
train.cache()
test.cache()
print(train)
# Build models
model = pipeline.fit(train)
model.transform(test)
results = model.transform(test)
results=results.select(results["ID"],results["ChurnRisk"],results["label"],results["predictedLabel"],results["prediction"],results["probability"])
results.toPandas().head(6)
# ### Model results
#
# In a supervised classification problem such as churn risk classification, we have a true output and a model-generated predicted output for each data point. For this reason, the results for each data point can be assigned to one of four categories:
#
# 1. True Positive (TP) - label is positive and prediction is also positive
# 2. True Negative (TN) - label is negative and prediction is also negative
# 3. False Positive (FP) - label is negative but prediction is positive
# 4. False Negative (FN) - label is positive but prediction is negative
#
# These four numbers are the building blocks for most classifier evaluation metrics. A fundamental point when considering classifier evaluation is that pure accuracy (i.e. was the prediction correct or incorrect) is not generally a good metric. The reason for this is because a dataset may be highly unbalanced. For example, if a model is designed to predict fraud from a dataset where 95% of the data points are not fraud and 5% of the data points are fraud, then a naive classifier that predicts not fraud, regardless of input, will be 95% accurate. For this reason, metrics like precision and recall are typically used because they take into account the type of error. In most applications there is some desired balance between precision and recall, which can be captured by combining the two into a single metric, called the F-measure.
#
#
print('Model Precision = {:.2f}.'.format(results.filter(results.label == results.prediction).count() / float(results.count())))
# An added advantage of such tree-based classifiers is we can study feature importances and learn further about relative importances of features in the classification decision.
# +
# Evaluate model
# Compute raw scores on the test set
#predictionAndLabels = results.rdd.map(lambda lp: (results.prediction, results.label))
res = model.transform(test)
predictions = res.rdd.map(lambda pr: pr.prediction)
labels = res.rdd.map(lambda pr: pr.label)
predictionAndLabels = sc.parallelize(zip(predictions.collect(), labels.collect()))
# Instantiate metrics object
metrics = MulticlassMetrics(predictionAndLabels)
# Overall statistics
print("Overall Statistics")
f_measure = metrics.accuracy
print("Model F-measure = %s\n" % f_measure)
# statistics by class
print("Statistics by Class")
labels_itr = labels.distinct().collect()
for label in sorted(labels_itr):
print("Class %s F-Measure = %s" % (label, metrics.fMeasure(label)))
# +
# Feature importance
rfModel = model.stages[-2]
features = df_churn.columns
importances = rfModel.featureImportances.values
indices = np.argsort(importances)
# -
plt.figure(1)
plt.title('Feature Importances')
plt.barh(range(len(indices)), importances[indices], color='b',align='center')
plt.yticks(range(len(indices)), (np.array(features))[indices])
plt.xlabel('Relative Importance')
# Before we save the random forest classifier to repository, let us first evaluate the performance of a simple Naive Bayes classifier trained on the training dataset.
# +
nb = NaiveBayes(labelCol="label", featuresCol="features")
stages_nb = stages
stages_nb[-2] = nb
pipeline_nb = Pipeline(stages = stages_nb)
# Build models
model_nb = pipeline_nb.fit(train)
results_nb = model_nb.transform(test)
print('Naive Bayes Model Precision = {:.2f}.'.format(results_nb.filter(results_nb.label == results_nb.prediction).count() / float(results_nb.count())))
# -
# As you can see from the results above, Naive Bayes classifier does not perform well. Random forest classifier shows high F-measure upon evaluation and shows strong performance. Hence, we will save this model to the repository.
# <a id="save_model"></a>
# ## 5. Save the model into ML repository
# [Top](#top)
# +
# save(name='TradingChurnRiskClassificationSparkML',
# model=model,
# test_data = test,
# algorithm_type='Classification',
# description='This is a SparkML Model to Classify Trading Customer Churn Risk')
# -
# Write the test data without label to a .csv so that we can later use it for batch scoring
write_score_CSV=test.toPandas().drop(['ChurnRisk'], axis=1)
write_score_CSV.to_csv('../datasets/TradingCustomerSparkMLBatchScore.csv', sep=',', index=False)
# Write the test data to a .csv so that we can later use it for Evaluation
write_eval_CSV=test.toPandas()
write_eval_CSV.to_csv('../datasets/TradingCustomerSparkMLEval.csv', sep=',', index=False)
# <a id="summary"></a>
# ## 6. Summary
# [Top](#top)
# You have finished working on this hands-on lab. In this notebook you created a model using SparkML API, deployed it in Machine Learning service for online (real time) scoring and tested it using a test client.
# Created by **<NAME>** and **<NAME>**
#
# <EMAIL><br/>
# <EMAIL><br/>
#
# August 2018
| examples/TradingCustomerChurnClassifierSparkML.jupyter-py36.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="HKZ5o-QRJxlk" executionInfo={"status": "ok", "timestamp": 1607321417204, "user_tz": 300, "elapsed": 458, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
import pandas as pd
from matplotlib import style
style.use("ggplot")
import plotly.express as px
from pandas import DataFrame
from sklearn import neural_network
from sklearn.neural_network import MLPClassifier, MLPRegressor
from sklearn.metrics import classification_report,confusion_matrix
from sklearn.model_selection import cross_val_score
from sklearn.decomposition import PCA
# + id="7wlOM0zDtojd" executionInfo={"status": "ok", "timestamp": 1607321417387, "user_tz": 300, "elapsed": 631, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
features = [
"females",
"males",
"hispanic",
"not hispanic",
"White Alone",
"Black or African American Alone",
"American Indian or Alaska Native Alone",
"Asian Alone",
"Native Hawaiian and Other Pacific Islander Alone",
"Two or more races",
"Age: [0-10]",
"Age: [11-20]",
"Age: [21-30]",
"Age: [31-40]",
"Age: [41-50]",
"Age: [51-60]",
"Age: [61-70]",
"Age: [71-80]",
"Age: [81-84]",
"Age: [85]+",
"GDP Per Year (Normalized)",
"Personal income per capita (Normalized)",
"Personal Consumption expenditure per capita (Normalized)",
"Presidential Approval Rating",
"GOP/Total Senate Seats pre-election",
"GOP/Total House Seats pre-election"
]
# + id="Vu_G8FSStr5O" executionInfo={"status": "ok", "timestamp": 1607321417388, "user_tz": 300, "elapsed": 623, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
labels = [
"GOP Votes/Total Votes for Presidential Election",
"DNC Votes/Total Votes for Presidential Election",
"1 = Voted GOP, 0 = Voted DNC"
]
# + id="LOTReKM9tt5j" executionInfo={"status": "ok", "timestamp": 1607321417389, "user_tz": 300, "elapsed": 617, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
states = ["Alaska",
"Alabama",
"Arkansas",
"Arizona",
"California",
"Colorado",
"Connecticut",
"Delaware",
"Florida",
"Georgia",
"Hawaii",
"Iowa",
"Idaho",
"Illinois",
"Indiana",
"Kansas",
"Kentucky",
"Louisiana",
"Massachusetts",
"Maryland",
"Maine",
"Michigan",
"Minnesota",
"Missouri",
"Mississippi",
"Montana",
"North Carolina",
"North Dakota",
"Nebraska",
"New Hampshire",
"New Jersey",
"New Mexico",
"Nevada",
"New York",
"Ohio",
"Oklahoma",
"Oregon",
"Pennsylvania",
"Rhode Island",
"South Carolina",
"South Dakota",
"Tennessee",
"Texas",
"Utah",
"Virginia",
"Vermont",
"Washington",
"Wisconsin",
"West Virginia",
"Wyoming"
]
# + id="qQM-zDsOtunJ" executionInfo={"status": "ok", "timestamp": 1607321417389, "user_tz": 300, "elapsed": 608, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
states_abbrevs = ["AK", "AL", "AR", "AZ", "CA", "CO", "CT", "DE", "FL", "GA",
"HI", "IA", "ID", "IL", "IN", "KS", "KY", "LA", "MA", "MD",
"ME", "MI", "MN", "MO", "MS", "MT", "NC", "ND", "NE", "NH",
"NJ", "NM", "NV", "NY", "OH", "OK", "OR", "PA", "RI", "SC",
"SD", "TN", "TX", "UT", "VA", "VT", "WA", "WI", "WV", "WY"]
# + id="7fb2gTU7twb1" executionInfo={"status": "ok", "timestamp": 1607321417390, "user_tz": 300, "elapsed": 601, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
data_df_train = pd.read_csv("combined-data_no-states_train.csv")
# + id="28UqgDLVt0h5" executionInfo={"status": "ok", "timestamp": 1607321417390, "user_tz": 300, "elapsed": 592, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
data_df_test = pd.read_csv("combined-data_no-states_test.csv")
# + id="kUeqNGUIt1HA" executionInfo={"status": "ok", "timestamp": 1607321417548, "user_tz": 300, "elapsed": 745, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
X_train = np.array(data_df_train[features].values)
y_gop_train = (data_df_train[labels[0]].values.tolist())
# print(y_gop_train)
y_dnc_train = (data_df_train[labels[1]].values.tolist())
y_binary_train = (data_df_train[labels[2]].values.tolist())
# y_train = y_binary_train
y_binary_train = np.array(y_binary_train)
y_gop_train = np.array(y_gop_train)
y_dnc_train = np.array(y_dnc_train)
# + id="mTYugdcpt6jp" executionInfo={"status": "ok", "timestamp": 1607321417549, "user_tz": 300, "elapsed": 738, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
X_test = np.array(data_df_test[features].values)
y_gop_test = (data_df_test[labels[0]].values.tolist())
y_dnc_test = (data_df_test[labels[1]].values.tolist())
y_binary_test = (data_df_test[labels[2]].values.tolist())
# y_test = y_binary_test
y_binary_test = np.array(y_binary_test)
y_gop_test = np.array(y_gop_test)
y_dnc_test = np.array(y_dnc_test)
# + id="ZGl-dGNtt8ud" executionInfo={"status": "ok", "timestamp": 1607321417550, "user_tz": 300, "elapsed": 731, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}}
from sklearn import preprocessing
from sklearn import utils
lab_enc = preprocessing.LabelEncoder()
encoded_gop_train = lab_enc.fit_transform(y_gop_train)
encoded_dnc_train = lab_enc.fit_transform(y_dnc_train)
encoded_gop_test = lab_enc.fit_transform(y_gop_test)
encoded_dnc_test = lab_enc.fit_transform(y_dnc_test)
# + colab={"base_uri": "https://localhost:8080/", "height": 729} id="BbVtJEDt1pL0" executionInfo={"status": "ok", "timestamp": 1607322597818, "user_tz": 300, "elapsed": 1200, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}} outputId="f7e1c6c1-55a5-4667-e701-f6fff0881fc8"
# creating artifical neural network (ANN) for binary classifications
mlp = MLPClassifier(hidden_layer_sizes=(26,),max_iter=4000, solver = 'lbfgs', tol=.0000001)
mlp.fit(X_train,y_binary_train)
# print(y_binary_train)
predictions = mlp.predict(X_test) #generating predictions
df_states = DataFrame(states,columns=['State'])
df_y_pred = DataFrame(predictions, columns=['y_pred'])
df_y_binary_test = DataFrame(y_binary_test, columns=['y_binary_test'])
df_states_abbrevs = DataFrame(states_abbrevs, columns=['states_abbrevs'])
array5 = []
i = 0
while i < len(predictions):
if (int(df_y_pred._get_value(i, "y_pred")) != int(df_y_binary_test._get_value(i, "y_binary_test"))):
array5.append(0)
else:
array5.append(1)
i += 1
correct = pd.DataFrame(data=array5, columns=["correct"])
result = pd.concat([df_states, df_states_abbrevs, df_y_pred, df_y_binary_test, correct], axis=1)
fig2 = px.choropleth(
result,
locations=result['states_abbrevs'],
locationmode="USA-states",
color='correct',
color_continuous_scale="YlGn",
range_color=[0,1],
scope="usa",
hover_name="State")
# fig2.update_geos(fitbounds='locations', visible=False)
fig2.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig2.show()
print(confusion_matrix(y_binary_test,predictions))
print(classification_report(y_binary_test,predictions))
# + colab={"base_uri": "https://localhost:8080/"} id="7QNUyHLkzJJ9" executionInfo={"status": "ok", "timestamp": 1607324314044, "user_tz": 300, "elapsed": 4387, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}} outputId="a3b73cd9-5435-49e0-921e-8a82a1d9b92d"
# creating artificial neural network (ANN) for GOP percentages of vote
# mlp = MLPRegressor(hidden_layer_sizes=(26,),max_iter=1000000, solver = 'adam', tol=.0000001)
mlp = MLPRegressor(max_iter=10000, solver = 'sgd', activation = 'logistic', hidden_layer_sizes=(26,),
learning_rate = 'adaptive', momentum = .97,
nesterovs_momentum=True, learning_rate_init=.0001, shuffle = True)
# mlp = MLPRegressor()
mlp.fit(X_train,y_gop_train)
predictions = mlp.predict(X_test) #generating predictions
print(mlp.score(X_test, y_gop_test))
# + colab={"base_uri": "https://localhost:8080/"} id="R1tXJrB-zVhW" executionInfo={"status": "ok", "timestamp": 1607323728943, "user_tz": 300, "elapsed": 961, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}} outputId="da8d511f-301d-44b1-ee76-89ce497b14d7"
# creating artificial neural network (ANN) for DNC percentages of vote
mlp = MLPRegressor(hidden_layer_sizes=(26,26),max_iter=4000, alpha=1e-5, solver = 'lbfgs', tol=.000000001)
mlp.fit(X_train,y_dnc_train)
predictions = mlp.predict(X_test) #generating predictions
print(mlp.score(X_test, y_dnc_test))
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="txD1llRlj72X" executionInfo={"status": "ok", "timestamp": 1607321462949, "user_tz": 300, "elapsed": 8572, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}} outputId="1296d98a-7d1d-4965-adba-9c668f3b825f"
import warnings
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn import datasets
from sklearn.exceptions import ConvergenceWarning
# different learning rate schedules and momentum parameters
params = [
{'solver': 'sgd', 'hidden_layer_sizes':(26,), 'learning_rate': 'adaptive',
'power_t':0.2, 'momentum': .9},
{'solver': 'sgd', 'hidden_layer_sizes':(26,),'learning_rate': 'adaptive', 'momentum': .9,
'nesterovs_momentum': True, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'hidden_layer_sizes':(26,),'learning_rate': 'adaptive', 'momentum': 0,
'learning_rate_init': 0.2},
{'solver': 'sgd', 'hidden_layer_sizes':(26,),'learning_rate': 'adaptive', 'momentum': .97,
'nesterovs_momentum': True, 'learning_rate_init': 0.001},
{'solver': 'sgd', 'learning_rate': 'adaptive', 'momentum': .97,
'nesterovs_momentum': True, 'learning_rate_init': 0.001}
]
labels = [
"number1", "number2", "number3", "number4", "number5"
]
plot_args = [{'c': 'red', 'linestyle': '-'},
{'c': 'green', 'linestyle': '-'},
{'c': 'blue', 'linestyle': '-'},
{'c': 'red', 'linestyle': '--'},
{'c': 'green', 'linestyle': '--'}]
def plot_on_dataset(X, y, ax, name):
# for each dataset, plot learning for each learning strategy
print("\nlearning on dataset %s" % name)
ax.set_title(name)
X = MinMaxScaler().fit_transform(X)
mlps = []
if name == "digits":
# digits is larger but converges fairly quickly
max_iter = 15
else:
max_iter = 4000
for label, param in zip(labels, params):
print("training: %s" % label)
mlp = MLPClassifier(random_state=0,
max_iter=max_iter, **param)
# some parameter combinations will not converge as can be seen on the
# plots so they are ignored here
with warnings.catch_warnings():
warnings.filterwarnings("ignore", category=ConvergenceWarning,
module="sklearn")
mlp.fit(X, y)
if name == "loss curves":
predictions = mlp.predict(X_test) #generating predictions
print(confusion_matrix(y_binary_test,predictions))
print(classification_report(y_binary_test,predictions))
df_states = DataFrame(states,columns=['State'])
df_y_pred = DataFrame(predictions, columns=['y_pred'])
df_y_binary_test = DataFrame(y_binary_test, columns=['y_binary_test'])
df_states_abbrevs = DataFrame(states_abbrevs, columns=['states_abbrevs'])
array5 = []
i = 0
while i < len(predictions):
if (int(df_y_pred._get_value(i, "y_pred")) != int(df_y_binary_test._get_value(i, "y_binary_test"))):
array5.append(0)
else:
array5.append(1)
i += 1
correct = pd.DataFrame(data=array5, columns=["correct"])
result = pd.concat([df_states, df_states_abbrevs, df_y_pred, df_y_binary_test, correct], axis=1)
fig2 = px.choropleth(
result,
locations=result['states_abbrevs'],
locationmode="USA-states",
color='correct',
color_continuous_scale="YlGn",
range_color=[0,1],
scope="usa",
hover_name="State")
# fig2.update_geos(fitbounds='locations', visible=False)
fig2.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig2.show()
mlps.append(mlp)
print("Training set score: %f" % mlp.score(X, y))
print("Training set loss: %f" % mlp.loss_)
for mlp, label, args in zip(mlps, labels, plot_args):
ax.plot(mlp.loss_curve_, label=label, **args)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
data_sets = [(iris.data, iris.target),
(X_train, y_binary_train)]
for ax, data, name in zip(axes.ravel(), data_sets, ['iris','loss curves']):
plot_on_dataset(*data, ax=ax, name=name)
fig.legend(ax.get_lines(), labels, ncol=3, loc="upper center")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="6j97sZtYHrVj" executionInfo={"status": "ok", "timestamp": 1607321426934, "user_tz": 300, "elapsed": 10039, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07756857520123694370"}} outputId="cc824697-2c45-4309-b999-b96f7789c5f7"
#Graphing loss functions for the GOP Regressor
import warnings
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.preprocessing import MinMaxScaler
from sklearn import datasets
from sklearn.exceptions import ConvergenceWarning
# different learning rate schedules and momentum parameters
params = [{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': 0,
'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
'nesterovs_momentum': False, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
'nesterovs_momentum': True, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': 0,
'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
'nesterovs_momentum': True, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
'nesterovs_momentum': False, 'learning_rate_init': 0.2},
{'solver': 'adam', 'learning_rate_init': 0.01}]
labels = ["constant learning-rate", "constant with momentum",
"constant with Nesterov's momentum",
"inv-scaling learning-rate", "inv-scaling with momentum",
"inv-scaling with Nesterov's momentum", "adam"]
plot_args = [{'c': 'red', 'linestyle': '-'},
{'c': 'green', 'linestyle': '-'},
{'c': 'blue', 'linestyle': '-'},
{'c': 'red', 'linestyle': '--'},
{'c': 'green', 'linestyle': '--'},
{'c': 'blue', 'linestyle': '--'},
{'c': 'black', 'linestyle': '-'}]
def plot_on_dataset(X, y, ax, name):
# for each dataset, plot learning for each learning strategy
print("\nlearning on dataset %s" % name)
ax.set_title(name)
X = MinMaxScaler().fit_transform(X)
mlps = []
if name == "digits":
# digits is larger but converges fairly quickly
max_iter = 15
else:
max_iter = 4000
for label, param in zip(labels, params):
print("training: %s" % label)
mlp = MLPRegressor(random_state=0,
max_iter=max_iter, **param)
# some parameter combinations will not converge as can be seen on the
# plots so they are ignored here
with warnings.catch_warnings():
warnings.filterwarnings("ignore", category=ConvergenceWarning,
module="sklearn")
mlp.fit(X, y)
# if name == "election":
# predictions = mlp.predict(X_test) #generating predictions
# print(confusion_matrix(y_binary_test,predictions))
# print(classification_report(y_binary_test,predictions))
mlps.append(mlp)
print("Training set score: %f" % mlp.score(X, y))
print("Training set loss: %f" % mlp.loss_)
for mlp, label, args in zip(mlps, labels, plot_args):
ax.plot(mlp.loss_curve_, label=label, **args)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
data_sets = [(iris.data, iris.target),
(X_train, y_gop_train)]
for ax, data, name in zip(axes.ravel(), data_sets, ['iris','election']):
plot_on_dataset(*data, ax=ax, name=name)
fig.legend(ax.get_lines(), labels, ncol=3, loc="upper center")
plt.show()
| neuralNet.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/wizardcalidad/building_machine_learning_solutions/blob/indev/recommendars.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="XxQA3pYLRPTe"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import linear_kernel
# + [markdown] id="dn6cmjKWRdci"
# # Load Movies Metadata
#
# + colab={"base_uri": "https://localhost:8080/", "height": 434} id="ld7q-jUMRaJl" outputId="e85cb8cb-eee2-48b5-fce2-1499f1fff1da"
metadata = pd.read_csv('/content/drive/MyDrive/ml-latest-dataset/movies_metadata.csv', low_memory=False)
metadata.head(3)
# + [markdown] id="CO2TlJEI-sKq"
# # Simple Recommenders
#
# + [markdown] id="O0oierCU-wQ_"
# WeightedRating(WR)=(v/(v+m)R)+(m/(v+m)C)
#
# Calculate mean of vote average column
#
# + colab={"base_uri": "https://localhost:8080/"} id="ZtAzY108RjEA" outputId="ee8c1bbf-fe11-4081-dba3-865b23872313"
C = metadata['vote_average'].mean()
print(C)
# + [markdown] id="c9mK-R1E-6lM"
# calculate the number of votes, m, received by a movie in the 90th percentile.
#
# + colab={"base_uri": "https://localhost:8080/"} id="OZWhvj9b_CID" outputId="8fce6b97-d893-4219-c95c-5a9132a0eec1"
m = metadata['vote_count'].quantile(0.90)
print(m)
# + [markdown] id="KM74vfrj_M7V"
# Filter out all qualified movies into a new DataFrame
#
# + colab={"base_uri": "https://localhost:8080/"} id="8rLrZqT__Ojn" outputId="c755d74b-49f9-480e-b49b-f05e71af0854"
q_movies = metadata.copy().loc[metadata['vote_count'] >= m]
q_movies.shape
# + colab={"base_uri": "https://localhost:8080/"} id="GLFVm6ZI_X1h" outputId="3d2b5bce-19b5-45ba-d243-47de87231359"
metadata.shape
# + [markdown] id="j4j_UIMv_cdh"
# Function that computes the weighted rating of each movie
#
# + id="qTH7AgCX_Ya3"
def weighted_rating(x, m=m, C=C):
v = x['vote_count']
R = x['vote_average']
# Calculation based on the IMDB formula
return (v/(v+m) * R) + (m/(m+v) * C)
# + [markdown] id="zWFXpCQP_oZa"
# Define a new feature 'score' and calculate its value with `weighted_rating()`
# + id="aWqPGLn0_f7g"
q_movies['score'] = q_movies.apply(weighted_rating, axis=1)
# + colab={"base_uri": "https://localhost:8080/", "height": 417} id="dXsftKMG_wQF" outputId="5c6fcbc0-c4fe-41b8-bf5f-1b399aa1bb8a"
q_movies.head(3)
# + [markdown] id="MUTZGOtH__Nk"
# Sort movies based on score calculated above
# + colab={"base_uri": "https://localhost:8080/", "height": 669} id="HW8riv7B_zs8" outputId="9b4848a9-de08-4bca-f289-6bae83922d00"
q_movies = q_movies.sort_values('score', ascending=False)
q_movies[['title', 'vote_count', 'vote_average', 'score']].head(20)
# + [markdown] id="7Z5_8_9tAPYk"
# Simple recommenders: offer generalized recommendations to every user, based on movie popularity and/or genre. The basic idea behind this system is that movies that are more popular and critically acclaimed will have a higher probability of being liked by the average audience. An example could be IMDB Top 250.
# + [markdown] id="bxQu2Nw6ARea"
# # Content-Based Recommenders
# + [markdown] id="8F9E7CGoAVKY"
# We want to get to build a system that recommends movies that are similar to a particular movie, using `pairwise cosine similarity scores` for all movies based on their plot descriptions.
#
# + colab={"base_uri": "https://localhost:8080/"} id="RCrxfNUQAI75" outputId="f69ca589-9a00-44e8-ea24-d7ade58a1cf1"
metadata['overview'].head()
# + [markdown] id="aDifNOEUBCwB"
# ##### To get the similarities between our description we needs to run some jobs with NLP by computing the word vectors of each overview using `Term Frequency-Inverse Document Frequency` (TF-IDF)
#
# ###### 1. Define a TF-IDF Vectorizer Object. Remove all english stop words such as 'the', 'a'.
#
# ###### 2. Replace NaN with an empty string
#
# ###### 3. Construct the required TF-IDF matrix by fitting and transforming the data
#
# ###### 4. Output the shape of tfidf_matrix
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="790kuXX9Atbi" outputId="f8413e03-4dc6-441d-dec9-13c4dc0df916"
tfidf = TfidfVectorizer(stop_words='english')
metadata['overview'] = metadata['overview'].fillna('')
tfidf_matrix = tfidf.fit_transform(metadata['overview'])
tfidf_matrix.shape
# + [markdown] id="JZuZwQE9CFaH"
# Array mapping from feature integer indices to feature name.
#
# + colab={"base_uri": "https://localhost:8080/"} id="XBembiCJCF-i" outputId="0ab750d1-70f1-4aca-d6e9-527d455c5efb"
tfidf.get_feature_names()[5000:5010]
# + [markdown] id="WxxnbET6CTbH"
# With our matrix at hand, we can compute similarity score. There are several similarity metrics that you can use for this, such as the Manhattan, Euclidean, The Pearson and the Cosine Similarity scores. I will be using cosine similarity score here because it is fast and independent of magnitude and it works well in conjuction with TF-IDF.
#
# Since I have used the TF-IDF vectorizer, calculating the dot product between each vector will directly give the `cosine similarity score`. Therefore, I will use `sklearn's linear_kernel()` instead of `cosine_similarities()` since it is faster.
#
# + id="8czJj47oCMJV"
cosine_sim = linear_kernel(tfidf_matrix, tfidf_matrix, dense_output=False)
# + colab={"base_uri": "https://localhost:8080/"} id="zRjMsMV_iNzZ" outputId="cca7c3b1-949e-49fb-ae30-232d5988fb6d"
cosine_sim.shape
# + colab={"base_uri": "https://localhost:8080/"} id="iiA0apFJcipS" outputId="2b9d01ac-9cc6-4bcb-d9f9-2b3e1633f4ca"
list(enumerate(cosine_sim[0].toarray()[0]))[:10]
# + [markdown] id="9PWTV4UFkA11"
# Construct a reverse map of indices and movie titles
# + id="eP578DekiqpJ"
indices = pd.Series(metadata.index, index=metadata['title']).drop_duplicates()
# + colab={"base_uri": "https://localhost:8080/"} id="NpJlmpkOklnR" outputId="bf7ba4c9-0915-4133-9000-25e29b9b5d27"
indices[:10]
# + [markdown] id="W4nrJkkIntDc"
# Function that takes in movie title as input and outputs most similar movies
# + id="pHV4UF7alOnN"
def get_recommendations(title, cosine_sim=cosine_sim):
# Get the index of the movie that matches the title
idx = indices[title]
# Get the pairwsie similarity scores of all movies with that movie
sim_scores = list(enumerate(cosine_sim[idx].toarray()[0]))
# Sort the movies based on the similarity scores
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
# Get the scores of the 10 most similar movies
sim_scores = sim_scores[1:11]
# Get the movie indices
movie_indices = [sim_score[0] for sim_score in sim_scores]
# Return the top 10 most similar movies
return metadata['title'].iloc[movie_indices]
# + colab={"base_uri": "https://localhost:8080/"} id="qMREGiAJoEFW" outputId="c88ebd5a-df6e-4f83-8d86-b1d975f24ee3"
get_recommendations('The Champ')
# + id="iyzsXchg2nOu"
| recommendars.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ungraded lab 1: Linear algebra in Python with numpy
#
# *Copyrighted material*
#
# **Objectives:** Use numpy function to apply the most common linear algebra in Python
#
# **Steps:**
# * Create numpy arrays from lists
# * Create numpy matrix
# * Element wise multiplication
# * Transpose
# * The norm of a vector
# * All the dot products flavors
# * Sum by rows and sum by columns with numpy
# * Normalize
#
# In this ungraded lab, you will have the oportunity to remember somer basic concept abouts linear algebra and how use them in Python.
#
# Numpy is one of the most used libraries in Python for arrays manipulation. It adds to Python a set of functions that allows to operate on large multidimensional arrays with few lines. So forget about writing nested loops for adding matrices!. In numpy this is as simple as adding numbers.
#
# Let's start importing the numpy library and creating the alias np for it. You will see this line almost in every python code from here in advance.
import numpy as np # The swiss knife of the data scientist.
# ## Defining lists and numpy arrays
alist = [1, 2, 3, 4, 5] # Define a python list. It looks like an np array
narray = np.array([1, 2, 3, 4]) # Define a numpy array
# Note the difference between a python list and a numpy array
# +
print(alist)
print(narray)
print(type(alist))
print(type(narray))
# -
# ## Algebraic opertators on numpy arrays vs python lists
#
# One of the most common beginers mistakes in Python is mixing up the concepts of numpy array and python arrays. Just observe the next example, where you try to "add" two objects of different types. Note that the '+' operator on numpy arrays perform a sum element wise, while the same operator is used to apply a list concatenation. Be carefull while coding. Knowing this can save you a lot of headeachs.
print(narray + narray)
print(alist + alist)
# And the same with the product operator. In the first case you scale the vector and in the second case you concatenate the same list 3 times.
print(narray * 3)
print(alist * 3)
# Be aware of the difference, because within a function you can have both types.
# Nparrays are designed for numerical and matrix operations, while lists are for more general purposes.
# ## Matrix or Array of Arrays
#
# In linear algebra, a matrix is structure composed of n rows by m columns. That means each row, must have exactly the same number of columns. With Numpy, we have 2 ways to create a matrix:
# * Creating an array of arrays: This is the recomended way, although you cannot ensure that all the row has the same amount of columns
# * Creating a matrix using np.matrix. However this is not recomended since this class will desapear from numpy in the near future.
#
# You can use to initialize a matrix nparrays or lists, and the resulting matrix will contain only nparrays inside.
npmatrix1 = np.array([narray, narray, narray])
npmatrix2 = np.array([alist, alist, alist])
npmatrix3 = np.array([narray, [1, 1, 1, 1], narray])
print(npmatrix1)
print(npmatrix2)
print(npmatrix3)
# However, if you want to define a matrix be sure that all the rows contains the same number of elements. Otherwise you will end up with something that cannot be operated using the linear algebra operators. Analize the following 2 examples:
# +
# Example 1:
okmatrix = np.array([[1, 2], [3, 4]]) # Define a 2x2 matrix
print(okmatrix) # Print okmatrix
print(okmatrix * 2) # Print a scaled version of okmatrix
# +
# Example 2:
badmatrix = np.array([[1, 2], [3, 4], [5, 6, 7]]) # Define a matrix. Note the third row contains 3 elements
print(badmatrix) # Print the weird matrix
print(badmatrix * 2) # It is supposed to scale the whole matrix
# -
# ## Scaling and translating matrices
#
# So, now that you know how to build correct nparrays and matrices, let's see how easy is to operate with them in Python.
# Nparrays can be operated using the normal algebraic operator like '+-'. You can operate between nparrays and nparrays or between nparrays and scalars.
# Scale by 2 and translate 1 unit the matrix
result = okmatrix * 2 + 1 # For each element in the matrix, multiply by 2 and add 1
print(result)
# +
# Add two sum compatible matrices
result1 = okmatrix + okmatrix
print(result1)
# Substract two sum compatible matrices. This is called the difference vector
result2 = okmatrix - okmatrix
print(result2)
# -
# The product operator '*' when used on nparrays or matrices indicates element wise multiplications.
# Don't miss it with the dot product.
result = okmatrix * okmatrix # Multiply each element by itself
print(result)
# ## Transpose a matrix
#
# In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal, that is it switches the row and column indices of the matrix by producing another matrix. It original matrix dimension was n by m, the resulting transposed matrix will be m by n.
# With numpy matrices, the trasnpose operations is denoted by .T
matrix3x2 = np.array([[1, 2], [3, 4], [5, 6]]) # Define a 3x2 matrix
print('Original matrix 3 x 2')
print(matrix3x2)
print('Transposed matrix 2 x 3')
print(matrix3x2.T)
# However notice that the transpose operation does not have effect on 1D nparrays
nparray = np.array([1, 2, 3, 4]) # Define an array
print('Original array')
print(nparray)
print('Transposed array')
print(nparray.T)
# perhaps in this case you wanted to do:
nparray = np.array([[1, 2, 3, 4]]) # Define a 1 x 4 matrix. Note the 2 level of square brackets
print('Original array')
print(nparray)
print('Transposed array')
print(nparray.T)
# ## Get the norm of a nparray or matrix
#
# In linear algebra, the norm of a nD vector $\vec a$ is defined as:
#
# $$ norm(\vec a) = ||\vec a|| = \sqrt {\sum_{i=1}^{n} a_i ^ 2}$$
# Calculating the norm of vector or even of a matrix is a very common operation when dealing with data. Numpy has a set of functions for linear algebra in the subpackage linalg, including the norm function. Let's see how to get the norm a given nparray or matrix:
# +
nparray1 = np.array([1, 2, 3, 4]) # Define an array
norm1 = np.linalg.norm(nparray1)
nparray2 = np.array([[1, 2], [3, 4]]) # Define a 2 x 2 matrix. Note the 2 level of square brackets
norm2 = np.linalg.norm(nparray2)
print(norm1)
print(norm2)
# -
# Note that without any other parameter, the norm function assume you want treat your matrix as being just an array of numbers.
#
# But you can get the norm by rows or by columns. You control the dimension of the operation with the __axis__ parammeter. axis=0 means get the norm of each column. axis=1 means get the norm of each row. Let's see how
# +
nparray2 = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3 x 2 matrix.
normByCols = np.linalg.norm(nparray2, axis=0) # Get the norm for each column. Returns 2 elements
normByRows = np.linalg.norm(nparray2, axis=1) # get the norm for each row. Returns 3 elements
print(normByCols)
print(normByRows)
# -
# However, there is more ways to get the norm of matrix in Python.
# For that let's see all different ways as you can get the dot product between 2 nparrays
# ## Dot product between nparrays: All the flavors
#
# The dot product or scalar product or inner product between two vectors $\vec a$ and $\vec a$ of the same size is defined as:
# $$\vec a \cdot \vec b = \sum_{i=1}^{n} a_i b_i$$
#
# The dot product takes 2 vectors and returns a single number
# +
nparray1 = np.array([0, 1, 2, 3]) # Define an array
nparray2 = np.array([4, 5, 6, 7]) # Define an array
flavor1 = np.dot(nparray1, nparray2) # Recommended way
print(flavor1)
flavor2 = np.sum(nparray1 * nparray2) # Ok way
print(flavor2)
flavor3 = nparray1 @ nparray2 # Geeks way
print(flavor3)
# As you never should do: # Noobs way
flavor4 = 0
for a, b in zip(nparray1, nparray2):
flavor4 += a * b
print(flavor4)
# -
# **We strongly recommend you to use np.dot, since it is the only method that accepts nparrays and lists without problems**
# +
norm1 = np.dot(np.array([1, 2]), np.array([3, 4])) # Dot product on nparrays
norm2 = np.dot([1, 2], [3, 4]) # Dot product on python lists
print(norm1, '=', norm2 )
# -
# And finally note that the norm of a vector is defined as the dot product of the vector with it self. Thus, you can write the norm of a vector using any of the flavors of the dot product:
# $$ norm(\vec a) = ||\vec a|| = \sqrt {\sum_{i=1}^{n} a_i ^ 2} = \sqrt {a \cdot a}$$
#
# ## Sums by rows or columns
#
# Another very common operation that you must perform on data is to get the sum of the elements of the matrix by rows or columns.
#
# This is very similar as you already did for the norm function. You control the dimension of the operation with the axis parammeter. axis=0 means sum the elements of each column together. axis=1 means sum the elements of each row together.
# +
nparray2 = np.array([[1, -1], [2, -2], [3, -3]]) # Define a 3 x 2 matrix.
sumByCols = np.sum(nparray2, axis=0) # Get the sum for each column. Returns 2 elements
sumByRows = np.sum(nparray2, axis=1) # get the sum for each row. Returns 3 elements
print('Sum by columns: ')
print(sumByCols)
print('Sum by rows:')
print(sumByRows)
# -
# ## Get the mean by rows or columns
#
# As with the sums, you can use Numpy functions to get the mean of a vector or matrix. You can specify the axis of the operation as well. Just remember that the mean of a vector is the sum of its elements divided by the length of the vector
# $$ mean(\vec a) = \frac {\sqrt {\sum_{i=1}^{n} a_i }}{n}$$
# +
nparray2 = np.array([[1, -1], [2, -2], [3, -3]]) # Define a 3 x 2 matrix. Chosen to be a matrix with 0 mean
mean = np.mean(nparray2) # Get the mean for the whole matrix
meanByCols = np.mean(nparray2, axis=0) # Get the mean for each column. Returns 2 elements
meanByRows = np.mean(nparray2, axis=1) # get the mean for each row. Returns 3 elements
print('Matrix mean: ')
print(mean)
print('Mean by columns: ')
print(meanByCols)
print('Mean by rows:')
print(meanByRows)
# -
# ## Center the columns of a matrix
#
# Centering the attributes of a data matrix is a very important preprocessing step. Centering means removing the mean
# of each column of the matrix, such that the mean by columns of the resulting matrix is always 0.
#
# With numpy this process is as simple as this:
# +
nparray2 = np.array([[1, 1], [2, 2], [3, 3]]) # Define a 3 x 2 matrix.
nparrayCentered = nparray2 - np.mean(nparray2, axis=0) # Remove the mean for each column
print('Original matrix')
print(nparray2)
print('Centered by columns matrix')
print(nparrayCentered)
print('New mean by column')
print(nparrayCentered.mean(axis=0))
# -
# Warning!!. This process does not apply for centering rows. If you want to do so, consider trasposing the matrix, centering by columns and the transpose back the result.
# +
nparray2 = np.array([[1, 3], [2, 4], [3, 5]]) # Define a 3 x 2 matrix.
nparrayCentered = nparray2.T - np.mean(nparray2, axis=1) # Remove the mean for each row
nparrayCentered = nparrayCentered.T # Transpose back the result
print('Original matrix')
print(nparray2)
print('Centered by columns matrix')
print(nparrayCentered)
# -
# Note that some operations can be performed by the static function **np.sum** or **np.mean**, or rather by the inner function of the array
# +
nparray2 = np.array([[1, 3], [2, 4], [3, 5]]) # Define a 3 x 2 matrix.
mean1 = np.mean(nparray2) # Static way
mean2 = nparray2.mean() # Dinamic way
print(mean1, ' == ', mean2)
# -
# Even if they are equivalent, we encourage you to use the static way always.
#
#
# **Congratulations!!** you have now the tools to operate vector and matrices in Python with Numpy.
| Natural Language Processing with Classification and Vector Spaces/Week 3/NLP_C1_W3_lecture_nb_01.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import pandas as pd
if os.path.exists(html):
df = pd.read_html("http://isin.twse.com.tw/isin/C_public.jsp?strMode=4")
df = pd.DataFrame(df[0])
df_ = pd.DataFrame(columns=df.ix[0])
for i in range(2,len(df)):
df_ = df_.append({'有價證券代號及名稱' : df.ix[i][0]},ignore_index=True)
c = df_['有價證券代號及名稱']
n = pd.DataFrame({'Code' : []})
for i in c:
a = i.split()
n = n.append({'Code' : [a[0]]},ignore_index=True)
print(n)
n.to_pickle('Data/codelist_4.pkl')
# -
| codeParse.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + raw_mimetype="text/restructuredtext" active=""
# .. _nb_sres:
# -
# .. meta::
# :description: The stochastic ranking is based on bubble sort and provides infeasible solutions a chance to survive during the environment selection. Adding this selection to an evolution strategy method has shown to be an effective optimization method: Stochastic Ranking Evolutionary Strategy.
# .. meta::
# :keywords: Stochastic Ranking Evolutionary Strategy, SRES, Constrained Optimization, Real-Valued Optimization, Single-objective Optimization, Python
# # SRES: Stochastic Ranking Evolutionary Strategy
# Many different constrained handling methods have been proposed in the past. One way of addressing constraints in evolutionary strategy is to change the selection operator and give infeasible solutions a chance to survive.
# The survival is based on stochastic ranking, and thus the method is known as Stochastic Ranking Evolutionary Strategy <cite data-cite="sres"></cite>.
#
# The stochastic ranking is proposed as follows:
# <div style="display: block;margin-left: auto;margin-right: auto;width: 60%;">
# 
# </div>
# Together will the effective evolutionary strategy search algorithm, this provides a powerful method to optimize constrained problems.
# + tags=[]
from pymoo.algorithms.soo.nonconvex.sres import SRES
from pymoo.factory import get_problem
from pymoo.optimize import minimize
problem = get_problem("g01")
algorithm = SRES(n_offsprings=200, rule=1.0 / 7.0, gamma=0.85, alpha=0.2)
res = minimize(problem,
algorithm,
("n_gen", 200),
seed=1,
verbose=False)
print("Best solution found: \nX = %s\nF = %s\nCV = %s" % (res.X, res.F, res.CV))
# -
# An improved version of SRES, called ISRES, has been proposed to deal with dependent variables. The dependence has been addressed by using the differential between individuals as an alternative mutation.
# ### API
# + raw_mimetype="text/restructuredtext" active=""
# .. autoclass:: pymoo.algorithms.soo.nonconvex.sres.SRES
# :noindex:
| source/algorithms/soo/sres.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <NAME>
#
# ------------------------------------
# # Application of ontology embedding
#
# this is a simple implemantation that takes vectors of genes and diseases and positives dictionary
#
# then predict gene-disease association based on unsupervised and supervised methods
#
# unsupervised approach uses cosine similarity
#
# supervised method uses MLP with one hidden layer and does the training on 10-fold-cross validation
#
# using those methods, we can find the most similar gene or genes to diseases
#
# inputs :
#
# genes_vectors_filename : json dictionary {"gene_id":vector of real numbers as a list}
#
# diseases_vectors_filename : json dictionary {"disease_id":vector of real numbers as a list}
#
# positives_filename : json dictionary {"disease_id": list of gene ids}
#
# ------------------------------------------------------------------------
from sklearn.neural_network import MLPClassifier
from sklearn.metrics.pairwise import cosine_similarity
import json
import sys
import numpy as np
import random
import math
# Test files can be downloaded from here:
#
# https://drive.google.com/drive/folders/1_z3-7dhZdF7MbIqDa2T1q4wMzZ809Db_?usp=sharing
#
# These are embeddings generated using DL2Vec tool, on mouse phenotypes
genes_vectors_filename = "mouse_genes_embedding.json"
diseases_vectors_filename = "human_diseases_embedding.json"
positives_filename = "mouse_positives.json"
# 1- Unsupervised Analysis
#
# in this section we calculate the cosine similarity of genes and diseases, then we evaluate the prediction of gene-disease association
# +
with open(genes_vectors_filename,'r') as f:
genes_vectors = json.load(f)
with open(diseases_vectors_filename,'r') as f:
diseases_vectors = json.load(f)
with open(positives_filename,'r') as f:
positives = json.load(f)
human_disease_vectors=[]
human_disease_keys = list(diseases_vectors.keys())
for key in human_disease_keys:
human_disease_vectors.append(diseases_vectors[key])
mouse_genes_vectors=[]
mouse_genes_keys = list(genes_vectors.keys())
for key in mouse_genes_keys:
mouse_genes_vectors.append(genes_vectors[key])
Similarity_matrix = cosine_similarity(np.array(human_disease_vectors),np.array(mouse_genes_vectors))
print("the dimentions of this matrix is ", Similarity_matrix.shape)
# -
# After calculating cosine similarity between diseases and genes, we then can use these similarities to prdict gene-disease associations
#
# Here we define a function that returns the most similar gene to each disease:
# +
def find_most_similar_gene(disease_id, disease_genes_similarity_matrix, disease_keys, gene_keys):
disease_index = disease_keys.index(disease_id)
prediction_list = np.flip(np.argsort(disease_genes_similarity_matrix[disease_index]))
return gene_keys[prediction_list[0]]
def find_top_k_most_similar_genes(disease_id,k, disease_genes_similarity_matrix, disease_keys, gene_keys):
disease_index = disease_keys.index(disease_id)
prediction_list = np.flip(np.argsort(disease_genes_similarity_matrix[disease_index]))
return [gene_keys[prediction_list[x]] for x in range(k)]
print("Testing with the disease (OMIM:106190) Isolated anhidrosis with normal morphology and number sweat glands (ANHD)")
top = find_most_similar_gene("OMIM:106190", Similarity_matrix, human_disease_keys, mouse_genes_keys )
print("The most similar gene to disease OMIM:106190 is "+ top)
top_5 = find_top_k_most_similar_genes("OMIM:106190",5, Similarity_matrix, human_disease_keys, mouse_genes_keys )
print("The most similar genes to disease OMIM:106190 are "+ " ".join(top_5))
# -
# 2- Supervised Analysis
#
# In this section we test simple MLP model for the prediction task
# This method is used to generate negative samples
# input:
# # genes_keys: list of genes identifiers "must match the identifiers in the embeddings files"
# # diseases_keys: list of disease identifiers "must match the identifiers in the embeddings files"
# # positives: in a dictionary form
# # hard: binary setting for the split (if hard then negative genes are only sampled from the gene associated diseases)
# output:
# # negatives: in a dictionary, set of genes for each disease is sampled (ratio * number of positive genes)
# # new_positives: returns clean dictionary of positives diseases and genes where only those with representaions are retrived
# # pos_count
# # neg_count
#
# When data are generated the negative genes are selected in 2 ways: hard choise will select the negative genes from the disease associated genes only,
# not hard when the selection of the genes are from associated and non associated genes.
def generate_negatives(genes_keys, diseases_keys, positives, hard):
negatives = {}
new_positives = {}
pos_count = 0
neg_count = 0
disease_associated_genes = set([])
for disease in positives:
if (disease in diseases_keys):
for gene in positives[disease]:
if(gene in genes_keys):
if(disease not in new_positives):
new_positives[disease]=set([])
pos_count+=1
disease_associated_genes.add(gene)
new_positives[disease].add(gene)
non_disease_associated_genes = set([])
for gene in genes_keys:
if gene not in disease_associated_genes:
non_disease_associated_genes.add(gene)
#genes can be associated or non associated genes
if not hard:
for disease in diseases_keys:
if disease in positives:
negatives[disease] = set([])
for gene in genes_keys:
neg_count+=1
negatives[disease].add(gene)
#genes are only the associated genes
if hard:
for disease in diseases_keys:
if disease in positives:
negatives[disease] = set([])
for gene in genes_keys:
if (gene not in positives[disease]) and gene not in non_disease_associated_genes:
neg_count+=1
negatives[disease].add(gene)
break
return negatives,new_positives, pos_count, neg_count
def get_input_analysis(genes_vectors_filename, diseases_vectors_filename, positives_filename):
genes_vectors = {}
with open(genes_vectors_filename,'r') as f:
genes_vectors = json.load(f)
diseases_vectors = {}
with open(diseases_vectors_filename,'r') as f:
diseases_vectors = json.load(f)
positives = {}
with open(positives_filename,'r') as f:
positives = json.load(f)
diseases_keys = list(diseases_vectors.keys())
genes_keys = list(genes_vectors.keys())
new_positives={}
for disease in positives:
if (disease in diseases_keys):
for gene in positives[disease]:
if(gene in genes_keys):
if(disease not in new_positives):
new_positives[disease]=set([])
new_positives[disease].add(gene)
new_disease_keys = [x for x in diseases_keys if x in new_positives]
print(len(new_disease_keys), len(genes_keys) , len(new_positives.keys()))
return new_disease_keys,genes_keys,new_positives
def get_input(genes_vectors_filename, diseases_vectors_filename ,positives_filename, ratio):
genes_vectors = {}
with open(genes_vectors_filename,'r') as f:
genes_vectors = json.load(f)
diseases_vectors = {}
with open(diseases_vectors_filename,'r') as f:
diseases_vectors = json.load(f)
positives = {}
with open(positives_filename,'r') as f:
positives = json.load(f)
diseases_keys = list(diseases_vectors.keys())
genes_keys = list(genes_vectors.keys())
negatives, new_positives, pos_count, neg_count = generate_negatives(genes_keys, diseases_keys, positives, hard)
# Defining Feature Matrex
X= np.empty(((ratio+1)*pos_count,Vector_size*2))
y= np.empty((ratio+1)*pos_count)
negative_diseases = list(negatives.keys())
sample_number=0
for disease in new_positives:
for gene in new_positives[disease]:
x = np.concatenate((diseases_vectors[disease],genes_vectors[gene]),axis=0)
X[sample_number]=x
y[sample_number]=1
sample_number+=1
for i in range(ratio):
n = random.randint(0,len(negative_diseases))
n_disease = negative_diseases[n-1]
n = random.randint(0,len(negatives[n_disease]))
n_gene = list(negatives[n_disease])[n-1]
x = np.concatenate((diseases_vectors[n_disease],genes_vectors[n_gene]),axis=0)
X[sample_number]=x
y[sample_number]=0
sample_number+=1
return X,y
def get_training_folds(genes_vectors_filename, diseases_vectors_filename ,positives,diseases_keys,genes_keys, ratio, fold):
genes_vectors = {}
with open(genes_vectors_filename,'r') as f:
genes_vectors = json.load(f)
diseases_vectors = {}
with open(diseases_vectors_filename,'r') as f:
diseases_vectors = json.load(f)
start = int(len(diseases_keys)*fold/10)
end = int(len(diseases_keys)*(fold+1)/10) - 1
testing_disease_keys = diseases_keys[start:end]
training_disease_keys = [x for x in diseases_keys if x not in testing_disease_keys]
print(start,end,len(testing_disease_keys),len(training_disease_keys))
negatives, new_positives, pos_count, neg_count = generate_negatives(genes_keys, training_disease_keys, positives, hard)
# Defining Feature Matrex
X= np.empty(((ratio+1)*pos_count,Vector_size*2))
y= np.empty((ratio+1)*pos_count)
negative_diseases = list(negatives.keys())
sample_number=0
for disease in new_positives:
for gene in new_positives[disease]:
x = np.concatenate((diseases_vectors[disease],genes_vectors[gene]),axis=0)
X[sample_number]=x
y[sample_number]=1
sample_number+=1
for i in range(ratio):
n = random.randint(1,len(negative_diseases))
n_disease = negative_diseases[n-1]
n = random.randint(1,len(negatives[n_disease]))
n_gene = list(negatives[n_disease])[n-1]
x = np.concatenate((diseases_vectors[n_disease],genes_vectors[n_gene]),axis=0)
X[sample_number]=x
y[sample_number]=0
sample_number+=1
index = 0
X_test= np.empty((len(testing_disease_keys)*len(genes_keys),Vector_size*2))
y_test= np.empty(len(testing_disease_keys)*len(genes_keys))
test_guide = {}
for disease in testing_disease_keys:
test_guide[disease] = {}
for gene in genes_keys:
test_guide[disease][gene] = index
x = np.concatenate((diseases_vectors[disease],genes_vectors[gene]),axis=0)
X_test[index]=x
if(disease in new_positives):
if(gene in new_positives[disease]):
y_test[index]=1
else:
y_test[index]=0
else:
y_test[index]=0
index+=1
return X,y , X_test, y_test, test_guide
# +
hard = False
ratio = 5
Vector_size = 100
disease = []
genes = []
HDs_keys,OGs_keys,positives = get_input_analysis(genes_vectors_filename, diseases_vectors_filename, positives_filename)
OGs_HDs_sim = np.empty((len(HDs_keys),len(OGs_keys)))
for fold in range(10):
print("-------------statring fold--------------")
print(fold)
X_train, y_train, X_test, y_test, test_guid = get_training_folds(genes_vectors_filename, diseases_vectors_filename, positives,HDs_keys, OGs_keys, ratio, fold)
clf = MLPClassifier(hidden_layer_sizes=(Vector_size,), activation= "logistic", solver = "adam", alpha=0.0001, learning_rate= 'constant',learning_rate_init=0.001, random_state=42, max_iter=500, early_stopping=True).fit(X_train, y_train)
result = clf.predict_proba(X_test)
print("filling the results")
for d in range(0,len(HDs_keys)):
disease = HDs_keys[d]
if disease in test_guid:
for g in range(len(OGs_keys)):
gene=OGs_keys[g]
index = test_guid[disease][gene]
OGs_HDs_sim[d][g] = result[index][1]
print("matrix is ready!")
# -
# Lets now test the supervised prediction
# +
print("Testing with the disease (OMIM:106190) Isolated anhidrosis with normal morphology and number sweat glands (ANHD)")
top = find_most_similar_gene("OMIM:106190", OGs_HDs_sim, HDs_keys, OGs_keys )
print("The most similar gene to disease OMIM:106190 is "+ top)
top_5 = find_top_k_most_similar_genes("OMIM:106190",5, OGs_HDs_sim, HDs_keys, OGs_keys )
print("The most similar genes to disease OMIM:106190 are "+ " ".join(top_5))
# -
| mowl/examples/Application_of_ontology_embedding.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + jupyter={"outputs_hidden": false}
# %matplotlib inline
# -
# Matplotlib requires dates in float format for surface plots.
def convert_yyyymmdd_to_float(date_string_array):
import datetime
import matplotlib.dates as dates
date_float_array = []
for date_string in date_string_array:
if len(date_string)==10:
date_float = dates.date2num(datetime.datetime.strptime(date_string, '%Y-%m-%d'))
else:
date_float = dates.date2num(datetime.datetime.strptime(date_string, '%Y-%m-%dT%H:%M:%SZ'))
date_float_array.append(date_float)
return date_float_array
# Convert float date back to Y-m-d for the Surface y axis tick labels
def format_date(x, pos=None):
import matplotlib.dates as dates
return dates.num2date(x).strftime('%Y-%m-%d') #use FuncFormatter to format dates
def plot_surface(surfaces, surfaceTag,delta_plot=False):
# This import registers the 3D projection, but is otherwise unused.
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import matplotlib.ticker as ticker # import LinearLocator, FormatStrFormatter
surfaces = pd.DataFrame(data=surfaces)
surfaces.set_index('surfaceTag', inplace=True)
surface = surfaces[surfaces.index == surfaceTag]['surface'][0]
strike_axis = surface[0][1:]
surface = surface[1:]
time_axis = []
surface_grid = []
for line in surface:
time_axis.append(line[0])
surface_grid_line = line[1:]
surface_grid.append(surface_grid_line)
time_axis = convert_yyyymmdd_to_float(time_axis)
if delta_plot:
# When plotting FX Delta rather than Strike
# I'm converting the x axis value from Delta to Put Delta
delta_axis = list(map(convert_delta, strike_axis))
x = np.array(delta_axis, dtype=float)
else:
x = np.array(strike_axis, dtype=float)
y = np.array(time_axis, dtype=float)
Z = np.array(surface_grid, dtype=float)
X,Y = np.meshgrid(x,y)
fig = plt.figure(figsize=[15,10])
ax = plt.axes(projection='3d')
ax.set_facecolor('0.25')
ax.set_xlabel('Delta' if delta_plot else 'Moneyness',color='y',labelpad=10)
ax.set_ylabel('Expiry',color='y',labelpad=15)
ax.set_zlabel('Volatilities',color='y')
ax.tick_params(axis='both', colors='w')
ax.w_yaxis.set_major_formatter(ticker.FuncFormatter(format_date))
title = 'Vol Surface for : ' + str(surfaceTag)
ax.set_title(title,color='w')
surf = ax.plot_surface(X,Y,Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)
plt.show()
def convert_delta(delta):
if (delta<0):
return -delta
elif (delta>0):
return 1-delta
else:
return 0.5
def plot_smile(surfaces, maturity, delta_plot=False):
import pandas as pd
import matplotlib.pyplot as plt
import math
#fig = plt.figure(figsize=[15,5])
plt.rcParams["figure.figsize"] = (20,5)
fig, ax = plt.subplots(facecolor='0.25')
ax.set_facecolor('0.25')
ax.tick_params(axis='both', colors='w')
ax.set_xlabel('Delta' if delta_plot else 'Moneyness',color='y')
ax.set_ylabel('Volatility',color='y')
#fig.layout.update(xaxis_type = 'category')
surfaces = pd.DataFrame(data=surfaces)
for i in range(0,surfaces.shape[0]):
label = surfaces.loc[i,['surfaceTag']]['surfaceTag']
surface = surfaces.loc[i,['surface']]['surface']
error = surfaces.loc[i,['error']]['error'] if 'error' in surfaces else 0.0
x=[]
y=[]
if (type(error) is float):
x = surface[0][1:]
y = surface[maturity][1:]
title = 'Smile ' + str(surface[maturity][0])
ax.set_title(title,color='w')
# When plotting FX Delta rather than Strike
# I'm transforming the delta axis value delta call to make the chart easier to plot
if delta_plot:
delta_axis = list(map(convert_delta, x))
ax.plot(delta_axis,y,label=label)
else:
ax.plot(x,y,label=label)
plt.legend()
plt.show()
def plot_term_volatility (surfaces, strike):
import pandas as pd
import matplotlib.pyplot as plt
import math
import itertools
plt.rcParams["figure.figsize"] = (20,5)
fig, ax = plt.subplots(facecolor='0.25')
ax.set_facecolor('0.25')
ax.tick_params(axis='both', colors='w')
ax.set_xlabel('Time to expiry',color='y')
ax.set_ylabel('Volatility',color='y')
surfaces = pd.DataFrame(data=surfaces)
for i in range(0,surfaces.shape[0]):
error = surfaces.loc[i,['error']]['error'] if 'error' in surfaces else 0.0
label = surfaces.loc[i,['surfaceTag']]['surfaceTag']
x=[]
y=[]
if (type(error) is float):
title = 'Term Structure ' + str("{:.0%}".format(float(surfaces.loc[i,['surface']]['surface'][0][strike])))
surface = pd.DataFrame(surfaces.loc[i,['surface']]['surface'][1:])
dtx = surface[0]
# ETI and FX currently returning different datetime format
# so strip time from FX
x = dtx.str.slice(stop=10)
y = surface[strike]
ax.set_title(title,color='w')
ax.set_facecolor('0.25')
ax.plot(x,y,label=label)
plt.legend()
plt.show()
def plot_forward_curve(surfaces, surfaceTag):
# This import registers the 3D projection, but is otherwise unused.
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
plt.rcParams["figure.figsize"] = (15,5)
fig, ax = plt.subplots(facecolor='0.25')
ax.set_facecolor('0.25')
ax.set_xlabel('Time',color='y')
ax.set_ylabel('Price',color='y')
ax.set_title(surfaceTag,color='w')
ax.tick_params(axis='both', colors='w')
surfaces = pd.DataFrame(data=surfaces)
surfaces.set_index('surfaceTag', inplace=True)
fwd_curve = surfaces[surfaces.index == surfaceTag]['forwardCurve'][0]['dataPoints']
x=[]
y=[]
for key in fwd_curve.keys():
x.append(key)
y.append(fwd_curve[key])
ax.set_facecolor('0.25')
ax.plot(x,y)
def smooth_line(x, y, nb_data_points, smoothing_factor=None):
import scipy.interpolate as interpolate
import numpy as np
import math as math
s = 0.0 if (smoothing_factor==0.0) else len(x) + (2 * smoothing_factor - 1) * math.sqrt(2*len(x))
t,c,k = interpolate.splrep(x,y,k=3,s=s)
xnew = np.linspace(x[0], x[-1], nb_data_points)
spline = interpolate.BSpline(t, c, k, extrapolate=False)
xnew = np.linspace(x[0], x[-1], nb_data_points)
ynew = spline(xnew)
return xnew, ynew
def convert_ISODate_to_float(date_string_array):
import datetime
import matplotlib.dates as dates
date_float_array = []
for date_string in date_string_array:
date_float = dates.date2num(datetime.datetime.strptime(date_string, '%Y-%m-%d'))
date_float_array.append(date_float)
return date_float_array
def plot_zc_curves(curves, curve_tenors=None, smoothingfactor=None):
import pandas as pd
import matplotlib.pyplot as plt
tenors = curve_tenors if curve_tenors!=None else curves['description']['curveDefinition']['availableTenors'][:-1]
s = smoothingfactor if smoothingfactor != None else 0.0
plt.rcParams["figure.figsize"] = (20,5)
fig, ax = plt.subplots(facecolor='0.25')
ax.set_facecolor('0.25')
ax.tick_params(axis='both', colors='w')
ax.set_xlabel('Time')
ax.set_ylabel('ZC Rate')
ax.set_title(response.data.raw['data'][0]['curveDefinition']['name'],color='w')
for tenor in tenors:
curve = pd.DataFrame(data=curves['curves'][tenor]['curvePoints'])
x = convert_ISODate_to_float(curve['endDate'])
y = curve['ratePercent']
xnew, ynew = smooth_line(x,y,100,s)
ax.plot(xnew,ynew,label=tenor)
plt.xticks(rotation='vertical')
plt.legend(loc='upper left',fontsize='x-large')
plt.show()
| plotting_helper.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Our First CNN in Keras
# ### Creating a model based on the MNIST Dataset of Handwrittent Digits
# ### Step 1: Lets load our dataset
# +
from keras.datasets import mnist
# loads the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print (x_train.shape)
# -
# ### Step 2A: Examine the size and image dimenions (not required but good practice)
# - Check the number of samples, dimenions and whether images are color or grayscale
# - We see that our training data consist of **60,000** samples of training data, **10,000** samples of test data
# - Our labels are appropriately sized as well
# - Our Image dimenions are **28 x 28**, with **no color channels** (i.e. they are grayscale, so no BGR channels)
# +
# printing the number of samples in x_train, x_test, y_train, y_test
print("Initial shape or dimensions of x_train", str(x_train.shape))
print ("Number of samples in our training data: " + str(len(x_train)))
print ("Number of labels in our training data: " + str(len(y_train)))
print ("Number of samples in our test data: " + str(len(x_test)))
print ("Number of labels in our test data: " + str(len(y_test)))
print()
print ("Dimensions of x_train:" + str(x_train[0].shape))
print ("Labels in x_train:" + str(y_train.shape))
print()
print ("Dimensions of x_test:" + str(x_test[0].shape))
print ("Labels in y_test:" + str(y_test.shape))
# -
# ### Step 2B - Let's take a look at some of images in this dataset
# - Using OpenCV
# - Using Matplotlib
# +
# Using OpenCV
# import opencv and numpy
import cv2
import numpy as np
# Use OpenCV to display 6 random images from our dataset
for i in range(0,6):
random_num = np.random.randint(0, len(x_train))
img = x_train[random_num]
window_name = 'Random Sample #' + str(i)
cv2.imshow(window_name, img)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# ### Let's do the same thing but using matplotlib to plot 6 images
# +
# importing matplot lib
import matplotlib.pyplot as plt
# Plots 6 images, note subplot's arugments are nrows,ncols,index
# we set the color map to grey since our image dataset is grayscale
plt.subplot(331)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
plt.subplot(332)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
plt.subplot(333)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
plt.subplot(334)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
plt.subplot(335)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
plt.subplot(336)
random_num = np.random.randint(0,len(x_train))
plt.imshow(x_train[random_num], cmap=plt.get_cmap('gray'))
# Display out plots
plt.show()
# -
# ### Step 3A - Prepare our dataset for training
# +
# Lets store the number of rows and columns
img_rows = x_train[0].shape[0]
img_cols = x_train[0].shape[1]
# Getting our date in the right 'shape' needed for Keras
# We need to add a 4th dimenion to our date thereby changing our
# Our original image shape of (60000,28,28) to (60000,28,28,1)
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
# store the shape of a single image
input_shape = (img_rows, img_cols, 1)
# change our image type to float32 data type
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# Normalize our data by changing the range from (0 to 255) to (0 to 1)
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# -
# ### Step 3B - One Hot Encode Our Labels (Y)
# +
from keras.utils import np_utils
# Now we one hot encode outputs
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
# Let's count the number columns in our hot encoded matrix
print ("Number of Classes: " + str(y_test.shape[1]))
num_classes = y_test.shape[1]
num_pixels = x_train.shape[1] * x_train.shape[2]
# -
y_train[0]
# ### Step 4 - Create Our Model
# - We're constructing a simple but effective CNN that uses 32 filters of size 3x3
# - We've added a 2nd CONV layer of 64 filters of the same size 3x2
# - We then downsample our data to 2x2, here he apply a dropout where p is set to 0.25
# - We then flatten our Max Pool output that is connected to a Dense/FC layer that has an output size of 128
# - How we apply a dropout where P is set to 0.5
# - Thus 128 output is connected to another FC/Dense layer that outputs to the 10 categorical units
# +
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras.optimizers import SGD
# create model
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss = 'categorical_crossentropy',
optimizer = SGD(0.01),
metrics = ['accuracy'])
print(model.summary())
# -
# ### Step 5 - Train our Model
# - We place our formatted data as the inputs and set the batch size, number of epochs
# - We store our model's training results for plotting in future
# - We then use Kera's molel.evaluate function to output the model's fina performance. Here we are examing Test Loss and Test Accuracy
# +
batch_size = 32
epochs = 10
history = model.fit(x_train,
y_train,
batch_size = batch_size,
epochs = epochs,
verbose = 1,
validation_data = (x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# -
# ### Step 6 - Ploting our Loss and Accuracy Charts
# +
# Plotting our loss charts
import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
line1 = plt.plot(epochs, val_loss_values, label='Validation/Test Loss')
line2 = plt.plot(epochs, loss_values, label='Training Loss')
plt.setp(line1, linewidth=2.0, marker = '+', markersize=10.0)
plt.setp(line2, linewidth=2.0, marker = '4', markersize=10.0)
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.grid(True)
plt.legend()
plt.show()
# +
# Plotting our accuracy charts
import matplotlib.pyplot as plt
history_dict = history.history
acc_values = history_dict['acc']
val_acc_values = history_dict['val_acc']
epochs = range(1, len(loss_values) + 1)
line1 = plt.plot(epochs, val_acc_values, label='Validation/Test Accuracy')
line2 = plt.plot(epochs, acc_values, label='Training Accuracy')
plt.setp(line1, linewidth=2.0, marker = '+', markersize=10.0)
plt.setp(line2, linewidth=2.0, marker = '4', markersize=10.0)
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.grid(True)
plt.legend()
plt.show()
# -
# ### Step 7A - Saving our Model
model.save("/home/deeplearningcv/DeepLearningCV/Trained Models/8_mnist_simple_cnn_10_Epochs.h5")
print("Model Saved")
# ### Step 7B - Loading our Model
# +
from keras.models import load_model
classifier = load_model('/home/deeplearningcv/DeepLearningCV/Trained Models/8_mnist_simple_cnn_10_Epochs.h5')
# -
# ### Step 8 - Lets input some of our test data into our classifer
# +
import cv2
import numpy as np
def draw_test(name, pred, input_im):
BLACK = [0,0,0]
expanded_image = cv2.copyMakeBorder(input_im, 0, 0, 0, imageL.shape[0] ,cv2.BORDER_CONSTANT,value=BLACK)
expanded_image = cv2.cvtColor(expanded_image, cv2.COLOR_GRAY2BGR)
cv2.putText(expanded_image, str(pred), (152, 70) , cv2.FONT_HERSHEY_COMPLEX_SMALL,4, (0,255,0), 2)
cv2.imshow(name, expanded_image)
for i in range(0,10):
rand = np.random.randint(0,len(x_test))
input_im = x_test[rand]
imageL = cv2.resize(input_im, None, fx=4, fy=4, interpolation = cv2.INTER_CUBIC)
input_im = input_im.reshape(1,28,28,1)
## Get Prediction
res = str(classifier.predict_classes(input_im, 1, verbose = 0)[0])
draw_test("Prediction", res, imageL)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# ### Putting All Together!
# We don't need to run each section of code separately. Once we know it all works as it's supposed to, we can put all te pieces together and start training our model
# +
from keras.datasets import mnist
from keras.utils import np_utils
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras.optimizers import SGD
# Training Parameters
batch_size = 128
epochs = 10
# loads the MNIST dataset
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Lets store the number of rows and columns
img_rows = x_train[0].shape[0]
img_cols = x_train[1].shape[0]
# Getting our date in the right 'shape' needed for Keras
# We need to add a 4th dimenion to our date thereby changing our
# Our original image shape of (60000,28,28) to (60000,28,28,1)
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
# store the shape of a single image
input_shape = (img_rows, img_cols, 1)
# change our image type to float32 data type
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# Normalize our data by changing the range from (0 to 255) to (0 to 1)
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# Now we one hot encode outputs
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
# Let's count the number columns in our hot encoded matrix
print ("Number of Classes: " + str(y_test.shape[1]))
num_classes = y_test.shape[1]
num_pixels = x_train.shape[1] * x_train.shape[2]
# create model
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss = 'categorical_crossentropy',
optimizer = SGD(0.01),
metrics = ['accuracy'])
print(model.summary())
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# -
# ### Visualizing Our Model
# - First let's re-create our model
# +
# %matplotlib inline
import keras
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
from keras.utils import np_utils
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
input_shape = (28,28,1)
num_classes = 10
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=keras.optimizers.Adadelta(),
metrics=['accuracy'])
print(model.summary())
# -
# ### Generating the diagram of the model architecture
# +
# Save our model diagrams to this path
model_diagrams_path = '/home/deeplearningcv/DeeplearningCV/Trained Models/'
# Generate the plot
plot_model(model, to_file = model_diagrams_path + 'model_plot.png',
show_shapes = True,
show_layer_names = True)
# Show the plot here
img = mpimg.imread(model_diagrams_path + 'model_plot.png')
plt.figure(figsize=(30,15))
imgplot = plt.imshow(img)
| 8. Making a CNN in Keras/8.3 to 8.10 - Building a CNN for handwritten digits - MNIST.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## 중첩조건문
# - nested conditional
# - if 블록 안에 또다른 if 블록이 있는 경우
# - 들어쓰기로 논리를 구분한다.
# - (지양할 것)
# +
x = 0
y = 1
if x == y:
print('Block A')
else:
if x < y:
print('Block B')
elif x > y:
print('Block C')
# 안 좋은 예시 1
# +
if x > 0:
if x < 10:
print('Block A')
else:
print('Block B')
else:
print('Block C')
# 안 좋은 예시 2
# 0 < x < 10
# +
x = 0
y = 1
if x == y:
print('Block A')
elif x > y:
print('Block B')
elif x < y:
print('Block C')
# +
# 방법 1
if (x > 0) and (x < 10):
print('Block A')
else:
print('Block B')
# +
# 방법 2
if 0 < x < 10:
print('Block A')
else:
print('Block B')
# -
# ### 논리연산자
# - 비교연산자가 여러번 사용될 때 사용하는 것
# - and, or, not
# - A and B: A도 참이고, B도 참일때 True
# - 예: A & B
# - A or B: A 혹은 B, 둘 중 하나만 참이면 True
# - 예: A | B
# - not(A): A가 False -> True, True -> False
# - 비교연산자의 괄호는 가독성을 위해 (optional)
# - 파이썬에서만 가능한 표현: 0 < x < 10
# ### True, False
# - '만약 a가 참이라면, ...'
# - a = True
# +
a = True
if a == True:
print() # 틀림
if a:
print()
# -
# ### in
# - membership operator
# - 어떤 요소가 그 안에 있는지 확인하고 싶다
# - 비슷한 조건이 여러번 반복될 때 사용 가능
# +
character = 'k'
# character가 모음인지 확인하고 싶다: a, e, i, o, u
# if character == 'a' or character =='e' ...
if character in ['a', 'e', 'i', 'o', 'u']: # 리스트 요소에 character와 일치하는 것이 있는가
print('yes')
else:
print('no')
# +
word = 'abcde'
# word에 모음이 있는지 확인
for i in ['a', 'e', 'i', 'o', 'u']:
if i in word:
print('yes')
break
else:
continue
print('no')
# 또다른 방법
if ('a' or 'e' or 'i' or 'o' or 'u') in word:
print('yes')
else:
print('no')
# -
# ### 바다코끼리 연산자
# - walrus operator
# - 할당과 테스트를 동시에 하는 기능
# - :=
# +
tweet_limit = 200
tweet_string = 'blah' * 50 # 공백없이 스트링
tweet_string
# -
diff = tweet_limit - len(tweet_string)
if diff > 0:
print('it\'s ok')
else: print('it\'s too long')
if diff := tweet_limit - len(tweet_string) > 0:
print('able')
# ### Quiz
# - 윤년을 구하는 코드를 짜보자
# - 연도가 4로 나눠떨어지면 윤년
# - 100으로 나눠떨어지면 안된다
# - 400으로 나눠떨어지면 된다
#
# - year을 입력받는다.
# - 출력 = '{}년은 윤년입니다' / '{}년은 윤년이 아닙니다.'
# +
year = int(input('input the year: '))
if year % 400 == 0:
print(f'{year}년은 윤년입니다')
elif year % 100 == 0:
print(f'{year}년은 윤년이 아닙니다')
elif year % 4 == 0:
print(f'{year}년은 윤년입니다')
else:
print(f'{year}년은 윤년이 아닙니다')
# -
| lectures/wk3_lec1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''base'': conda)'
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/JonasRigo/AD-Numerical-Renormalization-Group/blob/main/dNRG.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="x_2eVyMfIjgS"
# # Differentiable Numerical Renormalization Group for a single Anderson impurity model
# by <NAME> and <NAME>
#
# In this notebook we follow the implementation of NRG for a single Anderson Impurity Model (siAM) laid out by *<NAME>, <NAME> and <NAME>* in *PRB 21, 3 1980*.
#
# ## Libraries
#
# We use the `jax` library for efficient GPU backed implementation and easy automatic differentiation.
# + id="bar_ONbWIjgW"
from jax.config import config # enable for 64 precision
config.update("jax_enable_x64",True)
import jax
import jax.numpy as jp
from jax import ops as jops
import jax.scipy.linalg as la
from jax import jacrev, grad, jacfwd
from jax import make_jaxpr
from jax import custom_vjp
from jax import custom_jvp
from functools import partial
# + [markdown] id="Nfjqr_9IIujW"
# # Global variables
#
# The NRG solver is based on iteratively expanding the Hilbert space of the Hamiltonian and then diagonalizing the grown Hamiltonian. The Hilbert space of the Hamiltonain at a step $N$ is always multiplied by the same $4$ dimensional Hilbert space of an $\uparrow$ and a $\downarrow$ flavoured fermions. The matrix elements of the grown Hamailtonian can be obtained as follows:
#
# $\langle i',l',N,\vert H_{N+1}\vert i,l,N\rangle = \Lambda^{1/2} E(l,N)\delta_{i i'}\delta_{l l'}+ t_N(\langle l',N\vert f^\dagger_{N\sigma}\vert l,N\rangle \langle i' \vert f_{N+1\sigma}\vert i\rangle + \rm h.c. )$
#
# where $l$ enumerates the eigenbasis of $H_N$ at iteration $N$ and $i$ enumerates the basis of a single Wilson chain site in the following way
#
# $\vert i = 0 \rangle = \vert vac \rangle \\ \vert i = 1 \rangle = f^{\dagger}_{\uparrow}\vert vac\rangle \\
# \vert i = 2 \rangle = f^{\dagger}_{\uparrow}f^{\dagger}_{\downarrow}\vert vac\rangle \\
# \vert i = 3 \rangle = f^{\dagger}_{\downarrow}\vert vac\rangle $
#
# Since the basis of a single Wilson chain site never changes, we can introduce
#
# $\eta_{\sigma i i’} = \langle i' \vert f_{N+1\sigma}\vert i\rangle$,
#
# which is saved as a global tensor called `elemaddedsite`. In the following we refer to `elemaddedsite` as “transfer tensor”.
#
# + colab={"base_uri": "https://localhost:8080/"} id="KlZkBkT8T0fq" outputId="602d51ce-6161-4d30-869d-ada0bf398956"
elemaddedsite = jp.zeros((2,4,4))
elemaddedsite = jops.index_update(elemaddedsite,jops.index[0,0,3],1.)
elemaddedsite = jops.index_update(elemaddedsite,jops.index[0,1,2],-1.)
elemaddedsite = jops.index_update(elemaddedsite,jops.index[1,0,1],1.)
elemaddedsite = jops.index_update(elemaddedsite,jops.index[1,3,2],1.)
elemaddedsite_index = [[1,3,2],[1,0,1],[0,1,2],[0,0,3]]
print("elemaddedsite: \n", elemaddedsite)
# + [markdown] id="6WeWzBsWp1pd"
# # Hamiltonian class
#
# The Hamiltonain has to undergo two important steps:
#
# * Initialize: set up $H_{-1} = H_{imp}$
# * Grow: $H_N \rightarrow H_{N+1}$
#
# For the *initialization* we need to define the impurity Hamiltonian (includes no bath or hybridization) and bring it in diagonal form. For the siAM the occupation basis is already an eigenbasis.
#
# To *grow* the Hamiltonian means to add a Wilson chain site to the Hamiltonian
# $\langle i',l',N,\vert H_{N+1}\vert i,l,N\rangle = \Lambda^{1/2} E(l,N)\delta_{i i'}\delta_{l l'}+ t_N(\langle l',N\vert f^\dagger_{N\sigma}\vert l,N\rangle \langle i' \vert f_{N+1\sigma}\vert i\rangle + \rm h.c. )$,
#
# where $t_N$ is the Wislon chain hopping and $\vert i,l,N\rangle$ an eigenvector of $H_N$. This equation can be rewritten as
# $\langle i',l',N,\vert H_{N+1}\vert i,l,N\rangle = \Lambda^{1/2} E(l,N)\delta_{i i'}\delta_{l l'}+ t_N((-1)^{l'}\eta^{N+1}_{\sigma l l’} \eta_{\sigma i’ i} + \rm h.c. )$,
#
# where $\eta^{N+1}_{\sigma l l’}$ is the complex transposed transfer tensor in the eigenbasis of $H_N$. How to obtain the transfer tensor in the basis of $H_N$ will be explained in detail later. The last crucial step performed in `grow` is to truncate the eigenbasis of $H_N$. No more than `rlim` states are kept.
# + id="fdWlYwgcgJt0"
class Hamiltonian(object):
def __init__(self, eps, U, V,lmax=40,rlim=200,Lam=3.,Himp_dim=4):
"""
Initialize the Hamiltonian class with all impurity couplings and the
parameters required by the NRG.
===========================================================
input:
eps: on-site energy
U: on-site interaction
V: hybridization strength
lmax: chain length
rlim: maximum number of kept states
Lam: discretization parameter
Himp_dim: dimension of a Wilson chain site
"""
print("Anderson impurity model")
print("Lambda = ",Lam)
print("max number of states kept at each iteration = ",rlim)
print("\n")
self.Lam = Lam
self.rlim = rlim
self.dim = Himp_dim
self.aux_dim = 4
self.eps = eps
self.U = U
self.V = V
def initialize(self):
"""
Create the `-1` Hamiltonian, it contains only the impurity without hybridization.
"""
print("U/D = ", self.U)
print("epsilon/D = ",self.eps)
print("V/D = ",self.V)
print("\n")
"""Renormalize the impurity parameters"""
alambda = (self.Lam + 1.)/(self.Lam - 1.)*jp.log(self.Lam)/2. # this factor accounts for the discretation
self.eps /= self.Lam
self.U /= self.Lam
"""
The impurity Hamiltonian is diagonal in the occupation basis.
We exploit that to write it in terms of its eigenvalues and use the occupation
basis as eigenbasis.
"""
energies = jp.zeros(self.dim)
energies = jops.index_update(energies,jp.array([0,1,2,3]),[0.,self.eps,(2.*self.eps + self.U),self.eps])
"""
The first hopping term is the hybridization between impurity and bath.
"""
self.wilson_t = jp.sqrt(alambda/self.Lam) * self.V # * we account for the descrete bath
"""
The transfer tensor in the basis of H_N becomes `elemlastsite`.
"""
elemlastsite = jp.zeros((2,self.aux_dim,self.aux_dim))
elemlastsite = jops.index_update(elemlastsite,0,jp.transpose(elemaddedsite[0]))
elemlastsite = jops.index_update(elemlastsite,1,jp.transpose(elemaddedsite[1]))
return energies, elemlastsite
def grow(self,wilson_site,energies,elemlastsite):
"""
The Hilbert space grows by an up and a down spin. We keep the
old dimension locally in `dim` and update the dimension in `self` by
multiplying it with the dimension of the added Hilbert space
===========================================================
input:
wilson_site: integer number defining the number of sites attached to the impurity
energies: array containing eigenvalues of the Hamiltonian
"""
dim = self.dim
"""
This step is crucial: we limit the maximum amount of states by truncating the
dimension of the Hilbert space.
"""
self.dim = self.dim*self.aux_dim
H = jp.zeros((self.dim,self.dim))
"""
The diagonal consists only of the beforehand calculated energies. Mind the
tesnor product! The factor `0.5` accounts for a factor `2` that the diagonal acquires
after summing up the trasnpose of `H`
"""
id = lambda x: dim*x
for i in jp.arange(4):
H = jops.index_update(H,jops.index[id(i):id(i+1),id(i):id(i+1)], 0.5 * jp.diag(jp.sqrt(self.Lam) * energies[0:dim]))
"""
We exploit the tensor nature of of `elementlastside` and `elementaddedstite` and
express the sum over the flavour (in this case spin) as a scalar product. Note that
this corresponds to taking a kronecker tensorproduct of the type: |N,l> x |i>.
"""
for idx in elemaddedsite_index:
sign, k, kp = idx
H = jops.index_update(H,jops.index[id(k):id(k+1),id(kp):id(kp+1)],self.wilson_t * elemlastsite[sign]*elemaddedsite[sign,k,kp] * (-1.)**(k))
"""
Add the hermitian conjugate that was neglected earlier
"""
H += H.T
"""
The wilson chain has now grown, so we calculate the next hoping paramter that links the
new Hamiltonian to next Hilbert space in the following iteration.
"""
self.wilson_t = .5*(1.+self.Lam**(-1.))*(1.-self.Lam**(-wilson_site-1.))*((1.-self.Lam**(-2.*wilson_site-1.))*(1.-self.Lam**(-2.*wilson_site-3.)))**(-.5)
return H
# + [markdown] id="FBuipGFokGuq"
# ## Differentiable Hamiltonian class
#
# Also the differentiable Hamitlonian has two functions
#
# * Initialize
# * Grow
#
# For the initialization we need to define the derivative of the impurity Hamiltonian with respect to a coupling parameter.
#
# To grow the Hamiltonian means in this case to propagate it forward. Where in the `Hamiltonian` routine we add sites to Hamiltonian, here we simply expand the Hilbert space and transform the differentiated Hamiltonian in the eigenbasis of the Hamiltonian obtained in `Hamiltonian`.
# + id="bGO2BVxCtSNX"
class dHamiltonian(object):
def __init__(self, eps, U, V,lmax=40,rlim=200,Lam=3.,Himp_dim=4):
"""
Initialize the Hamiltonian class with all impurity couplings and the
parameters required by the NRG.
===========================================================
input:
eps: on-site energy
U: on-site interaction
V: hybridization strength
lmax: chain length
rlim: maximum number of kept states
Lam: discretization parameter
Himp_dim: dimension of a Wilson chain site
"""
print("Anderson impurity model")
print("Lambda = ",Lam)
print("max number of states kept at each iteration = ",rlim)
print("\n")
self.Lam = Lam
self.rlim = rlim
self.dim = Himp_dim
self.aux_dim = 4
self.eps = eps
self.U = U
self.V = V
self.lmax = lmax
def initialize(self):
"""
Here we create the derivitative of the `-1` Hamiltonian.
"""
print("U/D = ", self.U)
print("epsilon/D = ",self.eps)
print("V/D = ",self.V)
print("\n")
"""Renormalize the impurity parameters"""
alambda = (self.Lam + 1.)/(self.Lam - 1.)*jp.log(self.Lam)/2. # this factor accounts for the discretation error
self.eps /= self.Lam
self.U /= self.Lam
"""
The impurity Hamiltonian is diagonal in the occupation basis.
We exploit that to write it in terms of its eigenvalues and use the occupation
basis as eigenbasis.
"""
energies = jp.zeros(self.dim)
energies = jops.index_update(energies,jp.array([0,1,2,3]),[0.,self.eps,(2.*self.eps + self.U),self.eps])
self.ham = jp.diag(energies)
"""
The first hopping term is the hybridization between impurity and bath:
"""
self.wilson_t = jp.sqrt(alambda/self.Lam) * self.V
def grow(self,eigsrset,rkept,trafoset):
"""
The Hilbert space grows now for an up and a down spin. We keep the
old dimension locally in `dim` and update the dimension in `self` by
multiplying it with the dimension of the added Hilbert space
===========================================================
input:
eigsrset: list of oll eigenstates of all iterative diagonalization of the
Hamiltonian.
rkept: number of kept states in every iteration
trafoset: list containing the `elemaddedsite` tensor in the eigenbasis of
of all iterations of the Hamiltonian.
"""
for i in range(self.lmax):
print("i: ", i)
eigs = eigsrset[i]
dim = rkept[i]
elemlastsite = trafoset[i]
print("dim: ",dim)
self.dim = rkept[i]*self.aux_dim
H = jp.zeros((self.dim,self.dim))
id = lambda x: dim*x
self.ham = jp.dot(eigs.T,jp.dot(self.ham,eigs))
for i in jp.arange(4):
H = jops.index_update(H,jops.index[id(i):id(i+1),id(i):id(i+1)], 0.5 * jp.sqrt(self.Lam) * self.ham[0:dim,0:dim])
for idx in elemaddedsite_index:
sign, k, kp = idx
H = jops.index_update(H,jops.index[id(k):id(k+1),id(kp):id(kp+1)],self.wilson_t * elemlastsite[sign]*elemaddedsite[sign,k,kp] * (-1.)**(k))
H += H.T
self.ham = H
"""
The wilson chain paramter is set to 0 becuase it vanishes through the derivative.
"""
self.wilson_t = 0.
return H
# + [markdown] id="x5hB6MOgsyCQ"
# ## Solver
#
# The solver handles two main routines
#
#
# * Basis change of the transfer tensor
# * Diagonalization of the Hamiltonian
# * Computing the thermodynamics
#
# ### Transfer tensor
#
# The basis change of the transfer tensor is a clever way to avoid high computational cost. We wrote the transfer tensor as follows
# $ \eta_{\sigma i j} = \langle j \vert f_\sigma\vert i\rangle $, now we express it in the basis of $H_N$. Let $\vert i \rangle \otimes \vert l, N \rangle$ be the basis of $H_N$ and $U$ the unitary transformation that diagonalizes $H_{N+1}$. Then
#
# $ \eta^{N+1}_{\sigma i j} = \sum_{l,l'}\sum_{k,k'}[U(i;lk)]^\dagger U(j;l'k')\eta_{\sigma k k'}$
# + id="PpqKQ6PF1Tfb"
def transfertensor(eigen_system,dim,trunc_dim):
"""
We use the knowledge about the transfer tensor `elemaddedsite` and calculate it
in the eigenbasis of the Hamitlonian. Thus, conceptually we transform
`elemaddesite` into `elemlastsite`.
"""
id = lambda x: dim*x
elemlastsite = jp.zeros((2,trunc_dim,trunc_dim))
for idx in elemaddedsite_index:
sigma, k, kp = idx
elemlastsite = jops.index_add(elemlastsite,jops.index[sigma],elemaddedsite[sigma,k,kp]*jp.matmul(jp.transpose(eigen_system[id(k):id(k)+dim,0:trunc_dim]),eigen_system[id(kp):id(kp)+dim,0:trunc_dim]))
return elemlastsite
# + [markdown] id="r-HtJ0FONROU"
# ### Thermodynamics
#
# To extract some physical insight from the simulation we compute thermodynamic quantities. Since we have the diagonalized Hamiltonian from NRG it is straightforward to calculate the full density matrix
#
# $\rho = \frac{1}{Z}e^{-\beta H_N},~Z=\sum_i e^{-\beta \lambda_i}$,
#
# where $\lambda_i$ are the eigenvalues of $H_N$. The temperature in this definition comes from the Hamiltonian itself. In the NRG scheme one can relate a certain chain length $N$ to a temperature $T$. The inverse temperature is given defined as
# $ \beta_N = 1/T_N$
#
# $\beta_N \Lambda^{-(N-1)/2} = \bar{\beta},~\bar{\beta} \propto \mathcal{O}(1)$
#
# For $\bar{\beta}$ we choose $\bar{\beta} = 0.9$. With this we know at which temperature the density matrix is calculated. Now we can compute is the system entropy
#
# $F = -T \ln(Z) \\
# S = - \frac{\partial F}{\partial T} \\
# \Rightarrow S = \bar{\beta}\langle H_N \rangle + \ln(Z),~\rm{with}~\langle H_N \rangle = \rm{tr}[\rho H ]$
# + id="G1wueUMT1b0t"
def thermo(i,energies,Lam):
"""
We calculate the density matrix for the momentary temperature
=====================================================
input:
i: wilson chain length
energies: eigen energies of the Hamiltonian
Lam: discretization parameter
"""
beta_bar = 0.9
"""the temperature is realted to the lenght of the wilson chain"""
temperature = np.power(Lam,-0.5*(i - 1.))/beta_bar
print("Temperature = ", temperature)
"""
from the diagonal hamiltonian we can directly calcualte the
partition funciton, desnity matrix and entropy
"""
rho = np.exp(-beta_bar*energies) # desnity vector -> diagonal only
exp_H = beta_bar*np.dot(energies,rho) # expectation value of the Hamiltonian
Z = np.sum(rho) # partition function
entropy = exp_H/Z + np.log(Z) # entropy
return temperature, entropy
# + [markdown] id="LVxKTAsT1czU"
# ### Solver class
#
# The iterative diagonalization routine.
# + id="JJj78PwPd3dK"
class Solver(object):
def __init__(self,ham,lmax):
"""
input:
ham: initialized hamiltonian of class type `Hamiltonian`
lmax: maximum chain length
"""
self.ham = ham
self.lmax = lmax
self.eigsrset = []
self.rkept = []
self.trafoset = []
self.rseed = rseed
def solve(self):
energies, elemlastsite = self.ham.initialize()
eigs = jp.eye(4,dtype=float)
entropy = []
for i in jp.arange(self.lmax):
"""
We save the dimension before growing, then pass it to the
trans fertensor and truncating:
"""
dim = self.ham.dim
self.eigsrset += [eigs]
self.trafoset += [elemlastsite]
self.rkept += [self.ham.dim]
""" Update for user: """
print("Interation: ", i)
print("States kept at this iteration = ", dim)
""" iterate the wilson chain and diagonalize the Hamiltonian"""
ham = self.ham.grow(i,energies,elemlastsite)
energies, eigs = la.eigh(ham,turbo=True)
""" set the groundstate to zero energy with a variable shift """
#energies -= energies[0]
""" update dimension and truncate """
self.ham.dim = jp.minimum(self.ham.dim, self.ham.rlim)
elemlastsite = transfertensor(eigs,dim,self.ham.dim)
print("\n")
self.eigsrset += [eigs]
self.trafoset += [elemlastsite]
self.rkept += [self.ham.dim]
print("Calculation complete.")
return energies, eigs
# + [markdown] id="daTybADwkT-3"
# ## Differentiable Solver Routine
#
# Other than the non-differentiable solver routine `Solver` the differentiable solver routine does not return the eigenstates and eigenenergies. The `dSolver` routine returns the final Hamiltonian matrix $H_N$.
# + id="3SfVggJ1kTFb"
class dSolver(object):
def __init__(self,ham,lmax,rseed):
"""
input:
ham: initialized hamiltonian of class type Hamiltonian
lmax: maximum chain length
rseed: numpy array containing ranodm values
"""
self.ham = ham
self.lmax = lmax
self.eigsrset = []
self.rkept = []
self.trafoset = []
self.rseed = rseed
def solve(self):
energies, elemlastsite = self.ham.initialize()
eigs = jp.eye(4,dtype=float)
entropy = []
for i in jp.arange(self.lmax):
dim = self.ham.dim
"""
Saving the eigensystem, the `elemaddedsite` tensor in the Hamiltonian
eigenbasis and the number of kept states.
"""
self.eigsrset += [eigs]
self.trafoset += [elemlastsite]
self.rkept += [self.ham.dim]
""" Update for user:"""
print("Interation: ", i)
print("States kept at this iteration = ", dim)
""" iterate the wilson chain and diagonalize the Hamiltonian"""
ham = self.ham.grow(i,energies,elemlastsite)
""" we add random noise to the diagonal to lift the degeneracy of eigenvalues """
energies, eigs = la.eigh(ham+jp.diag(rseed[:ham.shape[0]]),turbo=True)
""" set the groundstate to zero energy with a variable shift """
#energies -= energies[0]
""" updated dimension and truncate """
self.ham.dim = jp.minimum(self.ham.dim, self.ham.rlim)
elemlastsite = transfertensor(eigs,dim,self.ham.dim)
print("\n")
self.eigsrset += [eigs]
self.trafoset += [elemlastsite]
self.rkept += [self.ham.dim]
print("Calculation complete.")
return ham
# + [markdown] id="jLSV4SKHxzwp"
# ## Automatic Differentiation
#
# ### Differentiable `jax` NRG primitive
#
# The derivative of the whole NRG code with respect to impurity coupling constants, is given through the derivative of the Hamiltonian $H_N$. The the derivative of $H_N$ with respect to impurity coupling constants can be obtained through propagating forward $\text{d} H_{\rm imp}$, such that it can act on the $N^{\rm th}$ Hilbert space associated to $H_N$.
# + id="fz6EMfcrps8l"
@custom_jvp
def dH(eps,U,V,l,rlim,Lam):
"""
Initialize the Hamiltonian and obtain the Hamiltonian matrix
of maximal length.
Note: Derivatives can only be obtained with resepect to
eps, U or V.
===========================================================
input:
eps: on-site energy
U: on-site interaction
V: hybridization strength
l: chain length
rlim: maximum number of kept states
Lam: discretization parameter
"""
H1 = Hamiltonian(eps,U,V,l,rlim,Lam)
S = dSolver(H1,l,rseed)
return S.solve()
@dH.defjvp
def dH_jvp(primals, tangents):
"""
Returns the derivative of the Hamiltonian with respect to the
input parameters `eps`, `U` or `V`.
"""
eps_dot, U_dot, V_dot,adot,bdot,cdot = tangents
eps,U,V,l,rlim,Lam = primals
H1 = Hamiltonian(eps,U,V,l,rlim,Lam)
S = dSolver(H1,l,rseed)
ham = S.solve()
"""derivative wrt eps """
H = dHamiltonian(1.,0.,0.,l,rlim,Lam)
H.initialize()
dH1 = H.grow(S.eigsrset,S.rkept,S.trafoset)
"""derivative wrt U """
H = dHamiltonian(0.,1.,0.,l,rlim,Lam)
H.initialize()
dH2 = H.grow(S.eigsrset,S.rkept,S.trafoset)
"""derivative wrt V """
H = dHamiltonian(0.,0.,1.,l,rlim,Lam)
H.initialize()
dH3 = H.grow(S.eigsrset,S.rkept,S.trafoset)
""" accumulating derivative """
primal_out = ham
tangent_out = dH1*eps_dot + U_dot*dH2 + V_dot*dH3 + 0.*adot+0.*bdot+0.*cdot
return primal_out, tangent_out
# + [markdown] id="vLa2bgQzisqM"
# ### Examples of possible derivatives
# + id="mouTE36ySXTl"
import numpy as np
"""
The random values generated here are used the lift the
degeneracies of the Hamiltonian. This allows the computation of the
derivatives of the eigenvalues and eigenvectors.
"""
rseed = np.random.randn(4000)*1e-12
# + id="OvIABiaouxuD"
def free_energy(eps,U,V,l,rlim,Lam):
"""
Calculate the free energy of an Anderson impurity model
===========================================================
input:
eps: on-site energy
U: on-site interaction
V: hybridization strength
l: chain length
rlim: maximum number of kept states
Lam: discretization parameter
"""
ham = dH(eps,U,V,l,rlim,Lam)
energies, eivecs = la.eigh(ham + jp.diag(rseed[:ham.shape[0]]),turbo=True)
gs = energies[0]
energies -= energies[0]
beta_bar = 0.9
rho = jp.exp(-energies*beta_bar)
F = -(jp.log(jp.sum(rho))-beta_bar*gs)/(beta_bar*Lam**((l-2.)/2.))
return F
def nexp(eps,U,V,l,rlim,Lam):
"""
Calculate the occupation of an Anderson impurity model.
===========================================================
input:
eps: on-site energy
U: on-site interaction
V: hybridization strength
l: chain length
rlim: maximum number of kept states
Lam: discretization parameter
"""
H1 = Hamiltonian(eps,U,V,l,rlim,Lam)
S = Solver(H1,l)
eivals, eivecs = S.solve()
eivals -= eivals[0]
""" obtaining the occupation operator """
H = dHamiltonian(1.,0.,0.,l,rlim,Lam)
H.initialize()
dH1 = H.grow(S.eigsrset,S.rkept,S.trafoset)
beta_bar = 0.9
""" constructing the density matrix """
rho = np.dot(eivecs,np.dot(np.diag(np.exp(-eivals*beta_bar)),eivecs.conj().T))
""" calculating the thermodynamic expectation value """
nrho = np.trace(np.dot(rho,dH1))/jp.trace(rho)
return Lam**(-(l-2.)/2.)*nrho
""" backwards derivative of the free energy with respect to eps and U """
dFde = jacrev(free_energy,[0,1])
# + [markdown] id="JQZEeA16ZYbR"
# Here we calculate $\partial_\epsilon F$, where $F$ is the free energy and $\epsilon$ the on-site energy.
# + colab={"base_uri": "https://localhost:8080/"} id="jSMSgcubuxuE" outputId="fd3df802-9cb8-481d-891c-b958f63c7827"
eps,U,V,l,rlim,Lam = -0.15,0.3,0.1,2,200,3.
""" finite difference value to approximate the derivative """
dfs = 1e-6
""" finite difference derivative """
a = (free_energy(eps+dfs,U,V,l,rlim,Lam)/dfs-free_energy(eps,U,V,l,rlim,Lam)/dfs)
""" forward pass of the free energy """
b = free_energy(eps,U,V,l,rlim,Lam)
""" backward pass of the free energy """
c = dFde(eps,U,V,l,rlim,Lam)[0]
""" thermodynamic expectation value of the occupation """
d = nexp(eps,U,V,l,rlim,Lam)
print("\n")
print("free energy: ",b)
print("\n")
print("automatic derivative: ",c)
print("\n")
print("finite difference derivative: ",a)
print("\n")
print("expectation value: ",d)
# + [markdown] id="WpW1lAiaZtif"
# Here we calculate $\frac{\partial^2}{\partial\epsilon \partial U} F$, where $F$ is the free energy and $\epsilon$ the on-site energy and $U$ the on-site interaction.
# + id="6_N1WgtZuxuE"
""" calculating the second order derivative of the free energy"""
dFdedU = jacrev(jacfwd(free_energy,[0]),[1])
# + colab={"base_uri": "https://localhost:8080/"} id="UJpaJlPEuxuF" outputId="62eb6108-4798-4c23-ab19-f084ee10849a"
""" finite difference value to approximate derivative """
dfs = 0.00390625
print("AD")
a = dFdedU(eps,U,V,l,rlim,Lam)
print("\n")
print("FD")
""" finite difference derivative """
b = nexp(eps,U+dfs,V,l,rlim,Lam)/dfs-nexp(eps,U,V,l,rlim,Lam)/dfs
print("\n")
print("automatic derivative: ",a[0][0])
print("finite difference derivative: ",b)
# + id="PGC5RmbIfWN1"
| dNRG.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# # !wget https://malaya-dataset.s3-ap-southeast-1.amazonaws.com/crawler/academia/academia-pdf.json
# -
import json
import cleaning
from tqdm import tqdm
# +
with open('academia-pdf.json') as fopen:
pdf = json.load(fopen)
len(pdf)
# +
from unidecode import unidecode
def clean(string):
string = [cleaning.cleaning(s) for s in string]
string = [s.strip() for s in string if 'tarikh' not in s.lower() and 'soalan no' not in s.lower()]
string = [s for s in string if not ''.join(s.split()[:1]).isdigit() and '.soalan' not in s.lower() and 'jum ' not in s.lower()]
string = [s for s in string if not s[:3].isdigit() and not s[-3:].isdigit()]
return string
# +
outer = []
for k in tqdm(range(len(pdf))):
c = clean(pdf[k]['content']['content'].split('\n'))
t, last = [], 0
i = 0
while i < len(c):
text = c[i]
if len(text) > 5:
if len(text.split()) > 1:
t.append(text)
last = i
else:
if len(t) and (i - last) > 2:
t.append('')
outer.extend(t)
t = []
last = i
elif not len(t):
last = i
i += 1
if len(t):
t.append('')
outer.extend(t)
# -
len(outer)
# +
# %%time
temp_vocab = list(set(cleaning.multiprocessing(outer, cleaning.unique_words)))
# +
# %%time
# important
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.duplicate_dots_marks_exclamations, list_mode = False)
print(len(temp_dict))
# -
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# +
# %%time
# important
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.remove_underscore, list_mode = False)
print(len(temp_dict))
# -
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# +
# %%time
# important
temp_dict = cleaning.multiprocessing(outer, cleaning.isolate_spamchars, list_mode = False)
print(len(temp_dict))
# -
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.break_short_words, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.break_long_words, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.remove_ending_underscore, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.remove_starting_underscore, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.end_punct, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.start_punct, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
# %%time
temp_dict = cleaning.multiprocessing(temp_vocab, cleaning.join_dashes, list_mode = False)
print(len(temp_dict))
outer = cleaning.string_dict_cleaning(outer, temp_dict)
outer[-100:]
with open('dumping-pdf.txt', 'w') as fopen:
fopen.write('\n'.join(outer))
| pretrained-model/xlnet/tokenizer/preprocessing-pdf.ipynb |
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Q#
# language: qsharp
# name: iqsharp
# ---
# # Superdense Coding Kata
#
# **Superdense Coding** quantum kata is a series of exercises designed to get you familiar with programming in Q#.
#
# It covers the superdense coding protocol which allows us to transmit two bits of classical information by sending just one qubit using previously shared quantum entanglement.
#
# - A good description can be found in [the Wikipedia article](https://en.wikipedia.org/wiki/Superdense_coding).
# - A great interactive demonstration can be found [on the Wolfram Demonstrations Project](http://demonstrations.wolfram.com/SuperdenseCoding/).
# - Superdense coding protocol is described in Nielsen & Chuang, section 2.3 (pp. 97-98).
#
# Each task is wrapped in one operation preceded by the description of the task. Your goal is to fill in the blank (marked with `// ...` comment) with some Q# code that solves the task. To verify your answer, run the cell using Ctrl/⌘+Enter.
#
# Each task defines an operation that can be used in subsequent tasks to simplify implementations and build on existing code. We split the superdense coding protocol into several steps, following the description in the [Wikipedia article](https://en.wikipedia.org/wiki/Superdense_coding):
#
# * Preparation (creating the entangled pair of qubits that are sent to Alice and Bob).
# * Encoding the message (Alice's task): Encoding the classical bits of the message into the state of Alice's qubit which then is sent to Bob.
# * Decoding the message (Bob's task): Using Bob's original qubit and the qubit he received from Alice to decode the classical message sent.
# * Finally, we compose those steps into the complete superdense coding protocol.
# To begin, first prepare this notebook for execution (if you skip this step, you'll get "Syntax does not match any known patterns" error when you try to execute Q# code in the next cells):
%package Microsoft.Quantum.Katas::0.8.1907.1701
# > The package versions in the output of the cell above should always match. If you are running the Notebooks locally and the versions do not match, please install the IQ# version that matches the version of the `Microsoft.Quantum.Katas` package.
# > <details>
# > <summary><u>How to install the right IQ# version</u></summary>
# > For example, if the version of `Microsoft.Quantum.Katas` package above is 0.1.2.3, the installation steps are as follows:
# >
# > 1. Stop the kernel.
# > 2. Uninstall the existing version of IQ#:
# > dotnet tool uninstall microsoft.quantum.iqsharp -g
# > 3. Install the matching version:
# > dotnet tool install microsoft.quantum.iqsharp -g --version 0.1.2.3
# > 4. Reinstall the kernel:
# > dotnet iqsharp install
# > 5. Restart the Notebook.
# > </details>
#
# ### Task 1. Entangled pair
#
# **Input:** Two qubits, each in the $|0\rangle$ state.
#
# **Goal:** Prepare a Bell state $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$ on these qubits.
# +
%kata T1_CreateEntangledPair_Test
operation CreateEntangledPair (q1 : Qubit, q2 : Qubit) : Unit is Adj {
// ...
}
# -
# ### Task 2. Send the message (Alice's task)
#
# Encode the message (two classical bits) in the state of Alice's qubit.
#
# **Inputs**:
# 1. Alice's part of the entangled pair of qubits qAlice.
# 2. Two classical bits, stored as ProtocolMessage.
#
# **Goal**: Transform the input qubit to encode the two classical bits.
#
# >`ProtocolMessage` is a custom type that represents the message to be transmitted. It includes two items of type `Bool` called `Bit1` and `Bit2`.
#
# <br/>
# <details>
# <summary>Need a hint? Click here</summary>
# Manipulate Alice's half of the entangled pair to change the joint state of the two qubits to one of the following four states based on the value of message:
#
# * [0; 0]: $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$
# * [0; 1]: $|\Psi^{+}\rangle = \frac{1}{\sqrt{2}} (|01\rangle + |10\rangle)$
# * [1; 0]: $|\Phi^{-}\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$
# * [1; 1]: $|\Psi^{-}\rangle = \frac{1}{\sqrt{2}} (|01\rangle + |10\rangle)$
#
# </details>
# +
%kata T2_EncodeMessageInQubit_Test
open Quantum.Kata.SuperdenseCoding;
operation EncodeMessageInQubit (qAlice : Qubit, message : ProtocolMessage) : Unit {
if (message::Bit1) { // accesses the item 'Bit1' of 'message'
// ...
}
// ...
}
# -
# ### Task 3. Decode the message and reset the qubits (Bob's task)
#
# Decode the message using the qubit received from Alice and reset both qubits to a $|00\rangle$ state.
#
# **Inputs:**
#
# 1. Qubit received from Alice qAlice.
# 2. Bob's part of the entangled pair qBob.
#
# **Goal** : Retrieve two bits of classic data from the qubits and return them as `ProtocolMessage`. The state of the qubits in the end of the operation should be $|00\rangle$.
#
# > You can create an instance of `ProtocolMessage` as `ProtocolMessage(bit1value, bit2value)`.
# +
%kata T3_DecodeMessageFromQubits_Test
open Quantum.Kata.SuperdenseCoding;
operation DecodeMessageFromQubits (qAlice : Qubit, qBob : Qubit) : ProtocolMessage {
// ...
}
# -
# ### Task 4. Superdense coding protocol end-to-end:
#
# Put together the steps performed in tasks 1-3 to implement the full superdense coding protocol.
#
# **Input:** Two classical bits to be transmitted.
#
# **Goal:** Prepare an EPR Pair, encode the two classical bits in the state of the pair by applying quantum gates to one member of the pair, and decode the two classical bits from the state of the pair. Return the result of decoding.
# +
%kata T4_SuperdenseCodingProtocol_Test
open Quantum.Kata.SuperdenseCoding;
operation SuperdenseCodingProtocol (message : ProtocolMessage) : ProtocolMessage {
// ...
}
| SuperdenseCoding/SuperdenseCoding.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dressmaker - Medium
# Prerequesites
from pyhive import hive
# %load_ext sql
# %sql hive://[email protected]:10000/sqlzoo
# %config SqlMagic.displaylimit = 20
# ## 1.
# Assuming that any garment could be made in any of the available materials, list the garments (description, fabric, colour and pattern) which are expensive to make, that is, those for which the labour costs are 80% or more of the total cost.
# + language="sql"
# SELECT description, fabric, colour, pattern
# FROM garment, material
# WHERE garment.labour_cost/(garment.labour_cost+material.cost) > 0.8
# -
# ## 2.
# List the descriptions and the number of orders of the less popular garments, that is those for which less than the average number of orders per garment have been placed. Also print out the average number of orders per garment. When calculating the average, ignore any garments for which no orders have been made.
# + language="sql"
# WITH t AS (
# SELECT style_no, description, COUNT(order_ref) n_orders
# FROM garment JOIN order_line ON (garment.style_no=order_line.ol_style)
# GROUP BY style_no, description
# )
# SELECT description, n_orders, ROUND(avg_orders, 2) avg
# FROM t JOIN (
# SELECT AVG(n_orders) avg_orders FROM t WHERE n_orders>0
# ) a
# WHERE n_orders < avg_orders
# -
# ## 3.
# Which is the most popular line, that is, the garment with the highest number of orders. Bearing in mind the fact that there may be several such garments, list the garment description(s) and number(s) of orders.
# + language="sql"
# WITH t AS (
# SELECT style_no, description, COUNT(order_ref) n_orders
# FROM garment JOIN order_line ON (
# garment.style_no=order_line.ol_style)
# GROUP BY style_no, description
# )
# SELECT description, t.n_orders
# FROM t JOIN (
# SELECT DISTINCT n_orders FROM t
# ORDER BY n_orders DESC LIMIT 1) a ON (
# t.n_orders=a.n_orders)
# -
# ## 4.
# List the descriptions, and costs of the more expensive size 8, Cotton garments which might be ordered, that is those costing more than the average (labour costs + material costs) to make.
# + language="sql"
# WITH t AS (
# SELECT style_no, material_no, description, ol_size, fabric,
# labour_cost+quantity*cost tot_cost
# FROM garment JOIN order_line ON (
# order_line.ol_style=garment.style_no) JOIN
# material ON (
# material.material_no=order_line.ol_material) JOIN
# quantities ON (
# quantities.size_q=order_line.ol_size AND
# quantities.style_q=order_line.ol_style)
# )
# SELECT description, material_no, ROUND(tot_cost, 2) total_cost
# FROM t JOIN (SELECT AVG(tot_cost) avg_cost FROM t) a
# WHERE ol_size=8 AND LOWER(fabric)='cotton' AND
# tot_cost>avg_cost
# -
# ## 5.
# What is the most common size ordered for each garment type? List description, size and number of orders, assuming that there could be several equally popular sizes for each type.
# + language="sql"
# WITH t AS (
# SELECT style_no, description, ol_size, COUNT(*) n_orders,
# RANK() OVER (PARTITION BY style_no ORDER BY COUNT(*) DESC) rank
# FROM garment JOIN order_line ON (
# order_line.ol_style=garment.style_no)
# GROUP BY style_no, ol_size, description
# )
# SELECT description, ol_size, n_orders
# FROM t
# WHERE rank=1
# -
| Hive/17-2 Dressmaker - Medium.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Задание 1.2 - Линейный классификатор (Linear classifier)
#
# В этом задании мы реализуем другую модель машинного обучения - линейный классификатор. Линейный классификатор подбирает для каждого класса веса, на которые нужно умножить значение каждого признака и потом сложить вместе.
# Тот класс, у которого эта сумма больше, и является предсказанием модели.
#
# В этом задании вы:
# - потренируетесь считать градиенты различных многомерных функций
# - реализуете подсчет градиентов через линейную модель и функцию потерь softmax
# - реализуете процесс тренировки линейного классификатора
# - подберете параметры тренировки на практике
#
# На всякий случай, еще раз ссылка на туториал по numpy:
# http://cs231n.github.io/python-numpy-tutorial/
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
# -
from dataset import load_svhn, random_split_train_val
from gradient_check import check_gradient
from metrics import multiclass_accuracy
import linear_classifer
# # Как всегда, первым делом загружаем данные
#
# Мы будем использовать все тот же SVHN.
# +
def prepare_for_linear_classifier(train_X, test_X):
train_flat = train_X.reshape(train_X.shape[0], -1).astype(np.float) / 255.0
test_flat = test_X.reshape(test_X.shape[0], -1).astype(np.float) / 255.0
# Subtract mean
mean_image = np.mean(train_flat, axis = 0)
train_flat -= mean_image
test_flat -= mean_image
# Add another channel with ones as a bias term
train_flat_with_ones = np.hstack([train_flat, np.ones((train_X.shape[0], 1))])
test_flat_with_ones = np.hstack([test_flat, np.ones((test_X.shape[0], 1))])
return train_flat_with_ones, test_flat_with_ones
train_X, train_y, test_X, test_y = load_svhn("data", max_train=10000, max_test=1000)
train_X, test_X = prepare_for_linear_classifier(train_X, test_X)
# Split train into train and val
train_X, train_y, val_X, val_y = random_split_train_val(train_X, train_y, num_val = 1000)
# -
# # Играемся с градиентами!
#
# В этом курсе мы будем писать много функций, которые вычисляют градиенты аналитическим методом.
#
# Все функции, в которых мы будем вычислять градиенты, будут написаны по одной и той же схеме.
# Они будут получать на вход точку, где нужно вычислить значение и градиент функции, а на выходе будут выдавать кортеж (tuple) из двух значений - собственно значения функции в этой точке (всегда одно число) и аналитического значения градиента в той же точке (той же размерности, что и вход).
# ```
# def f(x):
# """
# Computes function and analytic gradient at x
#
# x: np array of float, input to the function
#
# Returns:
# value: float, value of the function
# grad: np array of float, same shape as x
# """
# ...
#
# return value, grad
# ```
#
# Необходимым инструментом во время реализации кода, вычисляющего градиенты, является функция его проверки. Эта функция вычисляет градиент численным методом и сверяет результат с градиентом, вычисленным аналитическим методом.
#
# Мы начнем с того, чтобы реализовать вычисление численного градиента (numeric gradient) в функции `check_gradient` в `gradient_check.py`. Эта функция будет принимать на вход функции формата, заданного выше, использовать значение `value` для вычисления численного градиента и сравнит его с аналитическим - они должны сходиться.
#
# Напишите часть функции, которая вычисляет градиент с помощью численной производной для каждой координаты. Для вычисления производной используйте так называемую two-point formula (https://en.wikipedia.org/wiki/Numerical_differentiation):
#
# 
#
# Все функции приведенные в следующей клетке должны проходить gradient check.
# +
# TODO: Implement check_gradient function in gradient_check.py
# All the functions below should pass the gradient check
def square(x):
return float(x*x), 2*x
check_gradient(square, np.array([3.0]))
def array_sum(x):
assert x.shape == (2,), x.shape
return np.sum(x), np.ones_like(x)
check_gradient(array_sum, np.array([3.0, 2.0]))
def array_2d_sum(x):
assert x.shape == (2,2)
return np.sum(x), np.ones_like(x)
check_gradient(array_2d_sum, np.array([[3.0, 2.0], [1.0, 0.0]]))
# -
# ## Начинаем писать свои функции, считающие аналитический градиент
#
# Теперь реализуем функцию softmax, которая получает на вход оценки для каждого класса и преобразует их в вероятности от 0 до 1:
# 
#
# **Важно:** Практический аспект вычисления этой функции заключается в том, что в ней учавствует вычисление экспоненты от потенциально очень больших чисел - это может привести к очень большим значениям в числителе и знаменателе за пределами диапазона float.
#
# К счастью, у этой проблемы есть простое решение -- перед вычислением softmax вычесть из всех оценок максимальное значение среди всех оценок:
# ```
# predictions -= np.max(predictions)
# ```
# (подробнее здесь - http://cs231n.github.io/linear-classify/#softmax, секция `Practical issues: Numeric stability`)
# +
# TODO Implement softmax and cross-entropy for single sample
probs = linear_classifer.softmax(np.array([-10, 0, 10]))
# Make sure it works for big numbers too!
probs = linear_classifer.softmax(np.array([1000, 0, 0]))
assert np.isclose(probs[0], 1.0)
# -
# Кроме этого, мы реализуем cross-entropy loss, которую мы будем использовать как функцию ошибки (error function).
# В общем виде cross-entropy определена следующим образом:
# 
#
# где x - все классы, p(x) - истинная вероятность принадлежности сэмпла классу x, а q(x) - вероятность принадлежности классу x, предсказанная моделью.
# В нашем случае сэмпл принадлежит только одному классу, индекс которого передается функции. Для него p(x) равна 1, а для остальных классов - 0.
#
# Это позволяет реализовать функцию проще!
probs = linear_classifer.softmax(np.array([-5, 0, 5]))
linear_classifer.cross_entropy_loss(probs, 1)
# После того как мы реализовали сами функции, мы можем реализовать градиент.
#
# Оказывается, что вычисление градиента становится гораздо проще, если объединить эти функции в одну, которая сначала вычисляет вероятности через softmax, а потом использует их для вычисления функции ошибки через cross-entropy loss.
#
# Эта функция `softmax_with_cross_entropy` будет возвращает и значение ошибки, и градиент по входным параметрам. Мы проверим корректность реализации с помощью `check_gradient`.
# TODO Implement combined function or softmax and cross entropy and produces gradient
loss, grad = linear_classifer.softmax_with_cross_entropy(np.array([1, 0, 0]), 1)
check_gradient(lambda x: linear_classifer.softmax_with_cross_entropy(x, 1), np.array([1, 0, 0], np.float))
# В качестве метода тренировки мы будем использовать стохастический градиентный спуск (stochastic gradient descent или SGD), который работает с батчами сэмплов.
#
# Поэтому все наши фукнции будут получать не один пример, а батч, то есть входом будет не вектор из `num_classes` оценок, а матрица размерности `batch_size, num_classes`. Индекс примера в батче всегда будет первым измерением.
#
# Следующий шаг - переписать наши функции так, чтобы они поддерживали батчи.
#
# Финальное значение функции ошибки должно остаться числом, и оно равно среднему значению ошибки среди всех примеров в батче.
# TODO Extend combined function so it can receive a 2d array with batch of samples
np.random.seed(42)
# Test batch_size = 1
num_classes = 4
batch_size = 1
predictions = np.random.randint(-1, 3, size=(batch_size, num_classes)).astype(np.float)
target_index = np.random.randint(0, num_classes, size=(batch_size, 1)).astype(np.int)
check_gradient(lambda x: linear_classifer.softmax_with_cross_entropy(x, target_index), predictions)
target_index
print(predictions)
linear_classifer.cross_entropy_loss(predictions, target_index)
predictions.shape[0]
# +
# Test batch_size = 3
num_classes = 4
batch_size = 3
predictions = np.random.randint(-1, 3, size=(batch_size, num_classes)).astype(np.float)
target_index = np.random.randint(0, num_classes, size=(batch_size, 1)).astype(np.int)
check_gradient(lambda x: linear_classifer.softmax_with_cross_entropy(x, target_index), predictions)
# Make sure maximum subtraction for numberic stability is done separately for every sample in the batch
probs = linear_classifer.softmax(np.array([[20,0,0], [1000, 0, 0]]))
assert np.all(np.isclose(probs[:, 0], 1.0))
# -
# ### Наконец, реализуем сам линейный классификатор!
#
# softmax и cross-entropy получают на вход оценки, которые выдает линейный классификатор.
#
# Он делает это очень просто: для каждого класса есть набор весов, на которые надо умножить пиксели картинки и сложить. Получившееся число и является оценкой класса, идущей на вход softmax.
#
# Таким образом, линейный классификатор можно представить как умножение вектора с пикселями на матрицу W размера `num_features, num_classes`. Такой подход легко расширяется на случай батча векторов с пикселями X размера `batch_size, num_features`:
#
# `predictions = X * W`, где `*` - матричное умножение.
#
# Реализуйте функцию подсчета линейного классификатора и градиентов по весам `linear_softmax` в файле `linear_classifer.py`
# +
# TODO Implement linear_softmax function that uses softmax with cross-entropy for linear classifier
batch_size = 2
num_classes = 2
num_features = 3
np.random.seed(42)
W = np.random.randint(-1, 3, size=(num_features, num_classes)).astype(np.float)
X = np.random.randint(-1, 3, size=(batch_size, num_features)).astype(np.float)
target_index = np.ones(batch_size, dtype=np.int)
loss, dW = linear_classifer.linear_softmax(X, W, target_index)
check_gradient(lambda w: linear_classifer.linear_softmax(X, w, target_index), W)
# -
# ### И теперь регуляризация
#
# Мы будем использовать L2 regularization для весов как часть общей функции ошибки.
#
# Напомним, L2 regularization определяется как
#
# l2_reg_loss = regularization_strength * sum<sub>ij</sub> W[i, j]<sup>2</sup>
#
# Реализуйте функцию для его вычисления и вычисления соотвествующих градиентов.
# TODO Implement l2_regularization function that implements loss for L2 regularization
linear_classifer.l2_regularization(W, 0.01)
check_gradient(lambda w: linear_classifer.l2_regularization(w, 0.01), W)
# # Тренировка!
# Градиенты в порядке, реализуем процесс тренировки!
# TODO: Implement LinearSoftmaxClassifier.fit function
classifier = linear_classifer.LinearSoftmaxClassifier()
loss_history = classifier.fit(train_X, train_y, epochs=10, learning_rate=1e-3, batch_size=300, reg=1e1)
# let's look at the loss history!
plt.plot(loss_history)
# +
# Let's check how it performs on validation set
pred = classifier.predict(val_X)
accuracy = multiclass_accuracy(pred, val_y)
print("Accuracy: ", accuracy)
# Now, let's train more and see if it performs better
classifier.fit(train_X, train_y, epochs=100, learning_rate=1e-3, batch_size=300, reg=1e1)
pred = classifier.predict(val_X)
accuracy = multiclass_accuracy(pred, val_y)
print("Accuracy after training for 100 epochs: ", accuracy)
# -
# ### Как и раньше, используем кросс-валидацию для подбора гиперпараметтов.
#
# В этот раз, чтобы тренировка занимала разумное время, мы будем использовать только одно разделение на тренировочные (training) и проверочные (validation) данные.
#
# Теперь нам нужно подобрать не один, а два гиперпараметра! Не ограничивайте себя изначальными значениями в коде.
# Добейтесь точности более чем **20%** на проверочных данных (validation data).
# +
num_epochs = 200
batch_size = 300
learning_rates = [1e-3, 1e-4, 1e-5]
reg_strengths = [1e-4, 1e-5, 1e-6]
best_classifier = None
best_val_accuracy = None
# TODO use validation set to find the best hyperparameters
# hint: for best results, you might need to try more values for learning rate and regularization strength
# than provided initially
print('best validation accuracy achieved: %f' % best_val_accuracy)
# -
# # Какой же точности мы добились на тестовых данных?
test_pred = best_classifier.predict(test_X)
test_accuracy = multiclass_accuracy(test_pred, test_y)
print('Linear softmax classifier test set accuracy: %f' % (test_accuracy, ))
| assignments/assignment1/Linear classifier.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import datetime
from imblearn.over_sampling import SMOTE
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from xgboost import XGBClassifier
from xgboost import plot_importance
import matplotlib.pyplot as plt
# -
# ## 1. Load data
# - I'm using the files that were updated at **April 21st**
# - ref : https://github.com/jihoo-kim/Data-Science-for-COVID-19
# +
# Prepare dataset
Region_df = pd.read_csv('../dataset/Region_sido_addPop_addHospital.csv')[['province', 'safe_hospitals_count', 'infection_hospitals_count', 'infection_hospitals_bed_num']]
PatientInfo_df = pd.read_csv('../dataset/Patient/PatientInfo.csv')
print(f'PatientInfo.csv shape : {PatientInfo_df.shape}')
PatientInfo_df = PatientInfo_df[PatientInfo_df.state.isin(['released', 'deceased'])]
PatientInfo_df['confirmed_date'] = pd.to_datetime(PatientInfo_df['confirmed_date']) # convert data type
print(f' → datset shape : {PatientInfo_df.shape}')
display(PatientInfo_df.head(3))
# Save patient_id list
present_patients = PatientInfo_df.patient_id.astype(str).tolist()
with open('patients_id_0421.txt', 'w') as fp:
fp.write('\n'.join(present_patients))
# -
# Check Null values
PatientInfo_df.contact_number.value_counts(dropna=False, normalize=True) * 100
PatientInfo_df.symptom_onset_date.value_counts(dropna=False, normalize=True) * 100
PatientInfo_df.infection_order.value_counts(dropna=False, normalize=True) * 100
PatientInfo_df.disease.value_counts(dropna=False, normalize=True) * 100
# ## 2. Preprocess data
# - selected features : 'sex', 'birth_year', 'age', 'country', 'province', 'infection_case', 'confirmed_date'
# - handling nan
# - drop nan from 'sex' & 'age'
# - replace with mean of same age group in birth_year
# - replace with 'not-reported' in infection_case
# - new features : 'years_after_birth', 'days_after_first_date'
# - (ohter new features were created but deleted after evaluation - 'days_after_first_date_province', 'province_safe_hospitals_count', 'province_infection_hospitals_count', 'province_infection_bed_count')
# - feature encoding
# - age : convert to integer (0~10) - label encoding
# - other columns : one-hot encoding
# +
# Select features
X_features = PatientInfo_df[['sex', 'birth_year', 'age', 'country', 'province', 'infection_case', 'confirmed_date']].copy()
y_target = PatientInfo_df[['state']].copy()
print(f'X_features.shape : {X_features.shape}')
print(f'y_target.shape : {y_target.shape}')
X_features.head(3)
# +
print('\n<< no of nan table (before handling) >>')
print(X_features.isna().sum())
# Handle nan - sex & age
y_target = y_target[~X_features.sex.isna() & ~X_features.age.isna()]
X_features = X_features[~X_features.sex.isna() & ~X_features.age.isna()]
# Handle nan - birth_year
mean_year_list = dict(X_features.groupby('age')['birth_year'].mean().round().reset_index().values)
X_features.loc[X_features.birth_year.isna(), 'birth_year'] = X_features.loc[X_features.birth_year.isna(), 'age'].map( lambda x : mean_year_list[ x ] )
# Handle nan - infection_case
X_features.loc[X_features.infection_case.isna(), 'infection_case'] = 'not-reported'
print('\n<< no of nan table (after handling) >>')
print(X_features.isna().sum())
print(f'\n\nX_features.shape : {X_features.shape}')
print(f'y_target.shape : {y_target.shape}')
# +
# Create new features
X_features['years_after_birth'] = (datetime.date.today().year - X_features['birth_year']).astype(int)
X_features['days_after_first_date'] = X_features['confirmed_date'] - X_features['confirmed_date'].min()
X_features['days_after_first_date'] = X_features['days_after_first_date'].dt.days
## deleted after evaluation - days_after_first_date_province
# first_date_province_dict = dict(PatientInfo_df.groupby('province')['confirmed_date'].min().reset_index().values)
# X_features['first_date_province'] = X_features['province'].map( lambda x : first_date_province_dict[x] )
# X_features['days_after_first_date_province'] = X_features['confirmed_date'] - X_features['first_date_province']
# X_features['days_after_first_date_province'] = X_features['days_after_first_date_province'].dt.days
## deleted after evaluation - province infomations
# province_info_dict = { item_list[0]:item_list[1:] for item_list in Region_df.values }
# X_features['province_safe_hospitals_count'] = X_features.province.map(lambda x : province_info_dict[x][0])
# X_features['province_infection_hospitals_count'] = X_features.province.map(lambda x : province_info_dict[x][1])
# X_features['province_infection_bed_count'] = X_features.province.map(lambda x : province_info_dict[x][2])
X_features = X_features.drop(columns=['birth_year', 'confirmed_date'])
X_features.head(3)
# +
# feature encoding - X_features
X_features_processed = X_features.copy()
X_features_processed = pd.concat([X_features_processed, pd.get_dummies(X_features_processed[['sex', 'country', 'province', 'infection_case']])],
axis=1) # one-hot encoding
X_features_processed = X_features_processed.drop(columns=['sex', 'country', 'province', 'infection_case'])
X_features_processed['age'] = X_features.age.str.replace('s','').astype(int)//10 # label encoding
display(X_features_processed.head(3))
print()
# feature encoding - y_target
y_target_processed = pd.get_dummies(y_target)['state_deceased']
display(y_target_processed.head(3))
# -
# ## 3. Split data into train, val, test
# - It's important that **labels are highly unbalanced** (only about 3% is deceased)
# - Since the dataset is quite small(1704 records), I will split the date into **6:3:1** for now (test data could be added from the next file update)
# - Since the labels are highly imbalanced, it's better to use **stratified random sampling**.
# +
# Get train dataset
X_train, X_val_test, y_train, y_val_test = train_test_split(X_features_processed, y_target_processed, test_size=0.4, random_state=0, stratify=y_target)
# Get val & test dataset
X_val, X_test, y_val, y_test = train_test_split(X_val_test, y_val_test, test_size=0.25, random_state=0, stratify=y_val_test)
# Check the labels of each dataset
print('< Percentage of each label (whole dataset) >')
print(y_target_processed.value_counts(normalize=True) * 100)
print('\n< Percentage of each label (Train dataset) > - size of dataset :', y_train.shape[0])
print(y_train.value_counts(normalize=True) * 100)
print('\n< Percentage of each label (Validation dataset) > - size of dataset :', y_val.shape[0])
print(y_val.value_counts(normalize=True) * 100)
print('\n< Percentage of each label (Test dataset) > - size of dataset :', y_test.shape[0])
print(y_test.value_counts(normalize=True) * 100)
# -
# ## 4. Oversampling in train dataset - SMOTE
# - The dataset is highly imbalanced and it's hard to acquire more data. Therefore, **we can consider using oversampling methods**.
# - I tried oversampling using SMOTE. usually, **using SMOTE increases recall but decreased precision in return**. What's more important in this project is recall(finding more people who are likely to decease), so it's a preferable option.
# +
print('>>> SMOTE 적용 전 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('>>> SMOTE 적용 전 레이블 분포:')
print(pd.Series(y_train).value_counts())
smote = SMOTE(random_state=0)
X_train, y_train = smote.fit_sample(X_train, y_train)
print('\n>>> SMOTE 적용 후 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('>>> SMOTE 적용 후 레이블 분포:')
print(pd.Series(y_train).value_counts())
# -
# ## 5. Train model - XGBoost
# +
# Train model
xgb_wrapper = XGBClassifier(random_state=0)
xgb_wrapper.fit(X_train, y_train)
# Evaluate model
def get_clf_eval(y_test , pred):
from sklearn.metrics import confusion_matrix, accuracy_score
from sklearn.metrics import precision_score, recall_score
from sklearn.metrics import f1_score, roc_auc_score
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
f1 = f1_score(y_test,pred)
roc_auc = roc_auc_score(y_test, pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
pass
xgb_preds = xgb_wrapper.predict(X_val)
get_clf_eval(y_val , xgb_preds)
# +
# Visualize the feature importance
fig, ax = plt.subplots(figsize=(10, 7))
plot_importance(xgb_wrapper, ax=ax)
ax.set_title('Feature importance', size=13)
ax.tick_params(axis='y', labelsize=15)
plt.show()
# -
| dacon_covid-19/ML/COVID_ML_03_XGBoost.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
from sklearn.metrics import roc_curve
from sklearn.neighbors import KNeighborsClassifier
import random
import matplotlib.patheffects as PathEffects
from keras.layers import Input, Conv2D, Lambda, Dense, Flatten,MaxPooling2D, concatenate
from keras.models import Model, Sequential
from keras.regularizers import l2
from keras import backend as K
from keras.optimizers import SGD,Adam
from keras.losses import binary_crossentropy
import os
import pickle
import matplotlib.pyplot as plt
from itertools import permutations
import seaborn as sns
from keras.datasets import mnist
from sklearn.manifold import TSNE
from sklearn.svm import SVC
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Define our own plot function
def scatter(x, labels, subtitle=None):
# We choose a color palette with seaborn.
palette = np.array(sns.color_palette("hls", 10))
# We create a scatter plot.
f = plt.figure(figsize=(8, 8))
ax = plt.subplot(aspect='equal')
sc = ax.scatter(x[:,0], x[:,1], lw=0, s=40,
c=palette[labels.astype(np.int)])
plt.xlim(-25, 25)
plt.ylim(-25, 25)
ax.axis('off')
ax.axis('tight')
# We add the labels for each digit.
txts = []
for i in range(10):
# Position of each label.
xtext, ytext = np.median(x[labels == i, :], axis=0)
txt = ax.text(xtext, ytext, str(i), fontsize=24)
txt.set_path_effects([
PathEffects.Stroke(linewidth=5, foreground="w"),
PathEffects.Normal()])
txts.append(txt)
if subtitle != None:
plt.suptitle(subtitle)
plt.savefig(subtitle)
x_train_flat = x_train.reshape(-1,784)
x_test_flat = x_test.reshape(-1,784)
# +
tsne = TSNE()
train_tsne_embeds = tsne.fit_transform(x_train_flat[:512])
scatter(train_tsne_embeds, y_train[:512], "Samples from Training Data")
eval_tsne_embeds = tsne.fit_transform(x_test_flat[:512])
scatter(eval_tsne_embeds, y_test[:512], "Samples from Validation Data")
# -
Classifier_input = Input((784,))
Classifier_output = Dense(10, activation='softmax')(Classifier_input)
Classifier_model = Model(Classifier_input, Classifier_output)
from sklearn.preprocessing import LabelBinarizer
le = LabelBinarizer()
y_train_onehot = le.fit_transform(y_train)
y_test_onehot = le.transform(y_test)
Classifier_model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
Classifier_model.fit(x_train_flat,y_train_onehot, validation_data=(x_test_flat,y_test_onehot),epochs=10)
def generate_triplet(x,y,testsize=0.3,ap_pairs=10,an_pairs=10):
data_xy = tuple([x,y])
trainsize = 1-testsize
triplet_train_pairs = []
triplet_test_pairs = []
for data_class in sorted(set(data_xy[1])):
same_class_idx = np.where((data_xy[1] == data_class))[0]
diff_class_idx = np.where(data_xy[1] != data_class)[0]
A_P_pairs = random.sample(list(permutations(same_class_idx,2)),k=ap_pairs) #Generating Anchor-Positive pairs
Neg_idx = random.sample(list(diff_class_idx),k=an_pairs)
#train
A_P_len = len(A_P_pairs)
Neg_len = len(Neg_idx)
for ap in A_P_pairs[:int(A_P_len*trainsize)]:
Anchor = data_xy[0][ap[0]]
Positive = data_xy[0][ap[1]]
for n in Neg_idx:
Negative = data_xy[0][n]
triplet_train_pairs.append([Anchor,Positive,Negative])
#test
for ap in A_P_pairs[int(A_P_len*trainsize):]:
Anchor = data_xy[0][ap[0]]
Positive = data_xy[0][ap[1]]
for n in Neg_idx:
Negative = data_xy[0][n]
triplet_test_pairs.append([Anchor,Positive,Negative])
return np.array(triplet_train_pairs), np.array(triplet_test_pairs)
X_train, X_test = generate_triplet(x_train_flat,y_train, ap_pairs=150, an_pairs=150,testsize=0.2)
# ## Triplet NN
def triplet_loss(y_true, y_pred, alpha = 0.4):
"""
Implementation of the triplet loss function
Arguments:
y_true -- true labels, required when you define a loss in Keras, you don't need it in this function.
y_pred -- python list containing three objects:
anchor -- the encodings for the anchor data
positive -- the encodings for the positive data (similar to anchor)
negative -- the encodings for the negative data (different from anchor)
Returns:
loss -- real number, value of the loss
"""
print('y_pred.shape = ',y_pred)
total_lenght = y_pred.shape.as_list()[-1]
# print('total_lenght=', total_lenght)
# total_lenght =12
anchor = y_pred[:,0:int(total_lenght*1/3)]
positive = y_pred[:,int(total_lenght*1/3):int(total_lenght*2/3)]
negative = y_pred[:,int(total_lenght*2/3):int(total_lenght*3/3)]
# distance between the anchor and the positive
pos_dist = K.sum(K.square(anchor-positive),axis=1)
# distance between the anchor and the negative
neg_dist = K.sum(K.square(anchor-negative),axis=1)
# compute loss
basic_loss = pos_dist-neg_dist+alpha
loss = K.maximum(basic_loss,0.0)
return loss
def create_base_network(in_dims):
"""
Base network to be shared.
"""
model = Sequential()
model.add(Conv2D(128,(7,7),padding='same',input_shape=(in_dims[0],in_dims[1],in_dims[2],),activation='relu',name='conv1'))
model.add(MaxPooling2D((2,2),(2,2),padding='same',name='pool1'))
model.add(Conv2D(256,(5,5),padding='same',activation='relu',name='conv2'))
model.add(MaxPooling2D((2,2),(2,2),padding='same',name='pool2'))
model.add(Flatten(name='flatten'))
model.add(Dense(4,name='embeddings'))
# model.add(Dense(600))
return model
adam_optim = Adam(lr=0.0001, beta_1=0.9, beta_2=0.999)
# +
anchor_input = Input((28,28,1, ), name='anchor_input')
positive_input = Input((28,28,1, ), name='positive_input')
negative_input = Input((28,28,1, ), name='negative_input')
# Shared embedding layer for positive and negative items
Shared_DNN = create_base_network([28,28,1,])
encoded_anchor = Shared_DNN(anchor_input)
encoded_positive = Shared_DNN(positive_input)
encoded_negative = Shared_DNN(negative_input)
merged_vector = concatenate([encoded_anchor, encoded_positive, encoded_negative], axis=-1, name='merged_layer')
model = Model(inputs=[anchor_input,positive_input, negative_input], outputs=merged_vector)
model.compile(loss=triplet_loss, optimizer=adam_optim)
# -
model.summary()
# +
Anchor = X_train[:,0,:].reshape(-1,28,28,1)
Positive = X_train[:,1,:].reshape(-1,28,28,1)
Negative = X_train[:,2,:].reshape(-1,28,28,1)
Anchor_test = X_test[:,0,:].reshape(-1,28,28,1)
Positive_test = X_test[:,1,:].reshape(-1,28,28,1)
Negative_test = X_test[:,2,:].reshape(-1,28,28,1)
Y_dummy = np.empty((Anchor.shape[0],300))
Y_dummy2 = np.empty((Anchor_test.shape[0],1))
model.fit([Anchor,Positive,Negative],y=Y_dummy,validation_data=([Anchor_test,Positive_test,Negative_test],Y_dummy2), batch_size=512, epochs=500)
# -
trained_model = Model(inputs=anchor_input, outputs=encoded_anchor)
trained_model.load_weights('triplet_model_MNIST.hdf5')
tsne = TSNE()
X_train_trm = trained_model.predict(x_train[:512].reshape(-1,28,28,1))
X_test_trm = trained_model.predict(x_test[:512].reshape(-1,28,28,1))
train_tsne_embeds = tsne.fit_transform(X_train_trm)
eval_tsne_embeds = tsne.fit_transform(X_test_trm)
scatter(train_tsne_embeds, y_train[:512], "Training Data After TNN")
scatter(eval_tsne_embeds, y_test[:512], "Validation Data After TNN")
# +
X_train_trm = trained_model.predict(x_train.reshape(-1,28,28,1))
X_test_trm = trained_model.predict(x_test.reshape(-1,28,28,1))
Classifier_input = Input((4,))
Classifier_output = Dense(10, activation='softmax')(Classifier_input)
Classifier_model = Model(Classifier_input, Classifier_output)
Classifier_model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
Classifier_model.fit(X_train_trm,y_train_onehot, validation_data=(X_test_trm,y_test_onehot),epochs=10)
# -
| site/public/courses/DS-2.4/Notebooks/Advanced_Keras/Triplet NN Test on MNIST.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:data science]
# language: python
# name: conda-env-data_science-py
# ---
print("Hello, my friends!")
# +
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# -
away_dog_wins = pd.read_csv("../groupscores/awaydogswin.csv")
away_dog_wins
home_dog_wins = pd.read_csv("../groupscores/homedogswin.csv")
home_dog_wins
# +
plt.figure(figsize=(6, 6))
plt.subplot(2, 1, 1)
home_dog_scores = np.array(home_dog_wins['dogscore'])
home_dog_scores.sort()
plt.hist(home_dog_scores, bins = 30, edgecolor="black")
plt.title("Home Dog wins")
plt.ylabel("counts")
plt.xlabel("dog score")
away_dog_scores = np.array(away_dog_wins['dogscore'])
away_dog_scores.sort()
plt.subplot(2, 1, 2)
plt.hist(away_dog_scores, bins = 30, edgecolor="black")
plt.title("away dog wins")
plt.xlabel("dog score")
plt.ylabel("counts")
plt.tight_layout()
plt.show()
# -
| src/test.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DL Deep Dive - Training
# In this section, we will be using Keras (https://keras.io/) to build a TensorFlow-based model for recognizing handwritten digits. This walkthough builds the most basic type of deep nerual network, a mulit-layer perceptron (MLP), consisting of:
# * 1 input layer of 784 neurons
# * 2 hidden layers of 512 neurons each, with randomized dropout
# * 1 output layer of 10 neurons
#
# ## Preamble
# The first step will be to load all of the appropriate Python libraries. Keras provides classes and helper functions for building layered neural networks and loading standard datasets, such as the MNIST dataset of handwritten digits. For this exercise, we will be importing keras, the mnist dataset, and the Dense and Dropout layers, as well as the RMSProp optimizer. The optimizer is the function used to update the gradients during backpropagation (when training actually occurs).
# +
from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
# -
# ## Hyperparameter selection
# Next, we will select hyperparameter values, such as the number of output classes (in our case 10, 1 for each digit), the batch size, and the number of epochs.
#
# The **batch size** is the number of images to pass through the network simultaneously. This adds an extra dimension to the matrix of stored activations for each layer, which has dimensions corresponding to the width of the prior dimension, the width of the current dimension, and the batch size.
#
# The **epochs** is the number of times we will repeat the entire training dataset. For neural networks, seeing an image once is not enough. Fine tuning of the weights and bias values is slow, and seeing the same images many times can help to fine-tune the model.
num_classes = 10
batch_size = 128
epochs = 20
# ## Collecting the Training and Testing data
# Next, we will use Keras built-in dataset helper functions to download the training and testing datasets. The MNIST dataset consists of 70,000 images, split into 60,000 training images and 10,000 testing images. We will use the testing images to evaluate the performance of the model after each epoch, but we will **not** allow the network to learn from the testing images.
# +
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# -
# ## Set the labels to binary classification
# Since each category is a yes or no (a digit is not part 3, part 6, for example) we use the to_categorical utility function to specify that each category (num_classes) is a binary classification.
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# ## Build the Neural Network
# Now we will actually build the neural network. As we mentioned above, the architecure we are using is a multi-layer perceptron (MLP). Keras calls perceptron (or fully-connected) layers Dense layers.
#
# Each neruon in the Dense layers will be activated by the Rectified Linear Unit (ReLU) function. The ReLU function is a more computationally efficient variant of other traditional non-linear activation functions, such as hyperbolic tangent (tanh) and sigmoid:
#
# 
#
# We will also use a virtual layer after each Dense layer called Dropout. The Dropout layer will periodically zero out the output of a neuron in the preceeding Dense layer. This adds non-linearity to the network, and allows it to explore the function space for more optimal solutions.
#
# The network layout is:
# * *784 input neruons*, corresponding to an image which is 28 x 28 x 1. MNIST images are grayscale, so they contain only 1 color channel. A color (RGB) image would contain 3 channels.
# * 2 *512 neuron* hidden layers, each followed by a virtual layer of *512 Dropout* neurons
# * *10 output neurons*, corresponding to the 10 different digit classifications (0..10). This layer will be activated by the softmax function in order to provide percentage likelihood that an image falls into a particular category.
# +
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# -
# As we can see from the summary above, the network has 669,706 total parameters, all of which are trainable. The number of parameters for the first dense layer is larger because the number of inputs is larger (784 vs 512).
#
# The number of parameters in a layer is the number of neurons in the previous layer, times the number of neurons in the current layer (the connectivity matrix from the previous layer to the current layer), plus the number of neurons in the current layer (the bias values of the current layer).
#
# So for our example:
# * The number of parameters in hidden layer 1 is $(784 \times 512) + 512 = 401,920$.
# * The number of parameters in hidden layer 2 is $(512 \times 512) + 512 = 262,656$.
# * The number of parameters in the output layer is $(512 \times 10) + 10 = 5,130$.
#
# ## Compiling the Model
# The next step is to compile the model. Compilation requires setting:
# * The loss function to optimize
# * The optimization function to be used (RMSProp in this case)
# * The metrics to report (accuracy in this case)
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
# ## Training the Model (finally!)
# Finally, we can fit the model to the training data. the fit() function will allow us to pass the training data to the model, in batches of size batch_size, for a certain number of epochs. We will also provide the validation data (test data), which is the data for which accuracy will be reported.
#
# As the model trains, it will show the progress of each epoch (because verbose is set to 1). It will report the time required per epoch, the time per step (a step is a single batch of images), the loss and accuracy of the last batch, as well as the validation loss and accuracy for that epoch (since we will run the validation after each epoch).
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(x_test, y_test))
# ## Scoring the final model
# Once the model is trained, we can evaluate its performance by using the evaluate function. The evaluate function takes in the evaluation dataset and provides the accuracy and loss for inference on that dataset. In our case, the evaluation set will be the same as a test set, but in a production environment you would likely want a completely separate dataset for final evaluation vs validation.
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# ## Let's Predict Some Digits!
# Let's play around with different images in the test dataset and see just how accurate our neural network is. In order to look at one of the images in the dataset, let's first pick an image from the dataset. Just grab any range of length 1 from the x_test set ([0:1] ... [9999:10000]).
image = x_test[400:401]
# ## Display the Image of the Handwritten Digit
# Now that we have set the image we want to predict, let's take a look at the actual image. We will use the image object and reshape it as a 28 x 28 grayscale image. MatPlotLib will allow us to do this with the pyplot class.
import matplotlib.pyplot as plt
pixels = image.reshape((28, 28))
plt.imshow(pixels, cmap='gray')
plt.show()
# ## Make the Prediction
# Now we will see if our neural network accurately predicts this digit. First, we get the prediction using model.predict, then we will display the prediction using a bar chart.
# +
prediction = model.predict(image)
print(prediction[0])
plt.bar(range(10),prediction[0])
plt.show()
# -
# ## Try it Out!
# Feel free to change the number of neurons, the dropout rate, the number of epochs, and other parameters and see if you can build a better digit predictor!
| DL_Deep_Dive-Training-keras_mnist_MLP.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## SCOTUS justices voting pattern
#
# Here I compare the voting pattern of justices in the Roberts court (2005 to the 2017 term). Note that the 2017 term ends in June 2018. This data is publicly available at [SCOTUS database](http://scdb.wustl.edu/) provided by the Washington University of Law. Specifically, I looked at the [Modern Database:2018 Release 2--Justice Centered data](http://scdb.wustl.edu/_brickFiles/2018_02/SCDB_2018_02_justiceCentered_LegalProvision.csv.zip). For the purpose of this analysis, I only pay attention to the following attributes:
# ## Key attributes
#
# ### Chief justice:
# The variable *chief* identifies the chief justice during whose tenure the case was decided. The chief justices documented in this datasets are:
# * 1 Jay
# * 2 Rutledge
# * 3 Ellsworth
# * 4 Marshall
# * 5 Taney
# * 6 Chase
# * 7 Waite
# * 8 Fuller
# * 9 White
# * 10 Taft
# * 11 Hughes
# * 12 Stone
# * 13 Vinson
# * 14 Warren
# * 15 Burger
# * 16 Rehnquist
# * 17 Roberts
#
# ### Vote
# Encoded in the variable named *vote* that takes value between 1 and 8 with the following meaning.
# * 1: voted with majority or plurality
# * 2: dissent
# * 3: regular concurrence
# * 4: special concurrence
# * 5: judgment of the Court
# * 6: dissent from a denial or dismissal of certiorari , or dissent from summary affirmation of an appeal
# * 7: jurisdictional dissent
# * 8: justice participated in an equally divided vote
#
# Note that for the purpose the following anaysis, I aggregated case 1, 3, 4, 5 into a single variable *1* indicating majority while 2,6,7 into *2* indicating dissent. I left case 8 unspecified due to the ambiguity detailed in the documentation of this database. Note that a regular concurrence is when the justice agrees with the Court's opinion as well as its disposition. A special concurence (i.e., a concurence in the judgment) is when the justice agrees with the Court's disposition but not its opinion. A jurisdictional dissent is when the justice disagrees with the Court's assertion or denial of jurisdiction. Such votes are counted as nonparticipations.
#
# ### Case name:
# Encoded in the variable named *caseName* which is of string type.
#
#
# ### Justice name:
# Encoded in the variable named *justiceName*. In the following analysis, I focused on the Roberts' court (2005 to present). Although some currently sitting justices were also part of Rehnquist's count, those tend to have less overlap with others on the Robert's court. For this reason, I choose Robert's court for the analysis. Among these, I purged <NAME> and <NAME> since they have little overlap with currently sitting ones. This boils down to the following justices:
#
# 'AScalia', 'AMKennedy', 'DHSouter',
# 'CThomas', 'RBGinsburg', 'SGBreyer', 'JGRoberts', 'SAAlito',
# 'SSotomayor', 'EKagan', 'NMGorsuch'
#
# Note that just<NAME> is not included in this dataset since it only contains up to the 2017-2018 term, with the last case named *<NAME>* decided on June 28, 2018
#
# ### Case area:
#
# Vaiable *issueArea* categorizes the case into the following sometime over- and under-specified areas.
#
# * 1: Criminal procedure
# * 2: Civil rights
# * 3: First Amendment
# * 4: Due process
# * 5: Privacy
# * 6: Attorneys' or governmental officials' fees or compensation
# * 7: Unions
# * 8: Economic activity
# * 9: Judicial power
# * 10: Federalism
# * 11: Interstate relation
# * 12: Federal taxation
# * 13: Miscellaneous
# * 14: Private law
# By trimming the dataset down to the Roberts count and keep only attributes mentioned above plus some metadata (e.g. case decision date, whether the case declared the case being heard unconstitutional etc.), I got the dataset named *SCDB_2018_02_Roberts_new.csv*. You can download this trimmed dataset from my [Dropbox](https://www.dropbox.com/s/0makeeadk3pwvdh/SCDB_2018_02_Roberts_new.csv?dl=0).
# +
import pandas as pd
import seaborn as sns
import chardet
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
dfr = pd.read_csv('SCDB_2018_02_Roberts_new.csv', encoding = 'Latin-1')
def make_fig(df, area):
corr = df.corr()
fig = plt.figure()
if area == 1:
title_str = 'Criminal_Procedure'
elif area == 2:
title_str = 'Civil_Rights'
elif area == 3:
title_str = '1st_Amendment'
elif area == 4:
title_str = 'Due_Process'
elif area == 5:
title_str = 'Privacy'
elif area == 6:
title_str = 'Attorneys'
elif area == 7:
title_str = 'Unions'
elif area == 8:
title_str = 'Economic_Activity'
elif area == 9:
title_str = 'Judicial_Power'
elif area == 10:
title_str = 'Federalism'
elif area == 11:
title_str = 'Interstate_Relations'
elif area == 12:
title_str = 'Federal_Taxation'
elif area == 13:
title_str = 'Miscellaneous'
elif area == 14:
title_str = 'Private_action'
else:
title_str = 'Others'
title_str = 'corr_' + title_str
sns.heatmap(corr,
xticklabels=corr.columns,
yticklabels=corr.columns, cmap="YlGnBu")
plt.title(title_str, fontsize = 14)
fig.savefig(title_str + '.pdf',bbox_inches='tight')
fig.savefig(title_str + '.png',bbox_inches='tight')
# -
justice = dfr.justiceName.unique()
justice
#Here purge JPStevens and SDOConnor
justice = np.array(['AScalia', 'AMKennedy','CThomas', 'RBGinsburg', 'SGBreyer',
'JGRoberts', 'SAAlito','SSotomayor', 'EKagan', 'NMGorsuch'], dtype=object)
case = dfr.caseName.unique()
area = dfr.issueArea.unique()
area
# To choose one particular area, one can just specify it as an array: e.g. civial rights
area = np.array([2])
for are in area:
df = pd.DataFrame(np.zeros([case.shape[0], justice.shape[0]]), columns=list(justice), index = list(case))
for jus in justice:
for cas in case:
entry = (dfr['justiceName'] == jus) & (dfr['caseName'] == cas) & (dfr['issueArea'] == are)
s= dfr.loc[entry,'vote']
if s.shape[0] == 0:
df.loc[cas, jus] = float('nan')
else:
if s.iloc[0] == 1 or s.iloc[0] ==3 or s.iloc[0] ==4 or s.iloc[0] ==5:
df.loc[cas, jus] = 1
elif s.iloc[0] == 2 or s.iloc[0] == 6 or s.iloc[0] == 7:
df.loc[cas, jus] = 2
else:
df.loc[cas, jus] = float('nan')
make_fig(df, are)
# One can also show the aggregated result by not specifying the issueArea:
# +
for jus in justice:
for cas in case:
entry = (dfr['justiceName'] == jus) & (dfr['caseName'] == cas)
s= dfr.loc[entry,'vote']
if s.shape[0] == 0:
df.loc[cas, jus] = float('nan')
else:
if s.iloc[0] == 1 or s.iloc[0] ==3 or s.iloc[0] ==4 or s.iloc[0] ==5:
df.loc[cas, jus] = 1
elif s.iloc[0] == 2 or s.iloc[0] == 6 or s.iloc[0] == 7:
df.loc[cas, jus] = 2
else:
df.loc[cas, jus] = float('nan')
corr = df.corr()
fig = plt.figure()
sns.heatmap(corr,
xticklabels=corr.columns,
yticklabels=corr.columns, cmap="YlGnBu")
plt.title('All areas', fontsize = 14)
fig.savefig('corr.pdf',bbox_inches='tight')
fig.savefig('corr.png',bbox_inches='tight')
# -
# One can also visualize the dataset used to calculate the correlation matrix and save it as an csv file for future convenience:
df
df.to_csv('SCDB_2018_02_Roberts_vote.csv', index=False)
| SCOTUS/notebooks/SCOTUS-voting-correlation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Logistic Regression with a Neural Network mindset
#
# Welcome to your first (required) programming assignment! You will build a logistic regression classifier to recognize cats. This assignment will step you through how to do this with a Neural Network mindset, and so will also hone your intuitions about deep learning.
#
# **Instructions:**
# - Do not use loops (for/while) in your code, unless the instructions explicitly ask you to do so.
#
# **You will learn to:**
# - Build the general architecture of a learning algorithm, including:
# - Initializing parameters
# - Calculating the cost function and its gradient
# - Using an optimization algorithm (gradient descent)
# - Gather all three functions above into a main model function, in the right order.
# ## 1 - Packages ##
#
# First, let's run the cell below to import all the packages that you will need during this assignment.
# - [numpy](www.numpy.org) is the fundamental package for scientific computing with Python.
# - [h5py](http://www.h5py.org) is a common package to interact with a dataset that is stored on an H5 file.
# - [matplotlib](http://matplotlib.org) is a famous library to plot graphs in Python.
# - [PIL](http://www.pythonware.com/products/pil/) and [scipy](https://www.scipy.org/) are used here to test your model with your own picture at the end.
# +
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from skimage.transform import resize
from lr_utils import load_dataset
# %matplotlib inline
# -
# ## 2 - Overview of the Problem set ##
#
# **Problem Statement**: You are given a dataset ("data.h5") containing:
# - a training set of m_train images labeled as cat (y=1) or non-cat (y=0)
# - a test set of m_test images labeled as cat or non-cat
# - each image is of shape (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
#
# You will build a simple image-recognition algorithm that can correctly classify pictures as cat or non-cat.
#
# Let's get more familiar with the dataset. Load the data by running the following code.
# Loading the data (cat/non-cat)
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
# We added "_orig" at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don't need any preprocessing).
#
# Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the `index` value and re-run to see other images.
# Example of a picture
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture.")
# Many software bugs in deep learning come from having matrix/vector dimensions that don't fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
#
# **Exercise:** Find the values for:
# - m_train (number of training examples)
# - m_test (number of test examples)
# - num_px (= height = width of a training image)
# Remember that `train_set_x_orig` is a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can access `m_train` by writing `train_set_x_orig.shape[0]`.
# +
### START CODE HERE ### (≈ 3 lines of code)
m_train = len(train_set_x_orig)
m_test = len(test_set_x_orig)
num_px = train_set_x_orig[0].shape[0]
### END CODE HERE ###
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
# -
# **Expected Output for m_train, m_test and num_px**:
# <table style="width:15%">
# <tr>
# <td>**m_train**</td>
# <td> 209 </td>
# </tr>
#
# <tr>
# <td>**m_test**</td>
# <td> 50 </td>
# </tr>
#
# <tr>
# <td>**num_px**</td>
# <td> 64 </td>
# </tr>
#
# </table>
#
# For convenience, you should now reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px $*$ num_px $*$ 3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
#
# **Exercise:** Reshape the training and test data sets so that images of size (num_px, num_px, 3) are flattened into single vectors of shape (num\_px $*$ num\_px $*$ 3, 1).
#
# A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b$*$c$*$d, a) is to use:
# ```python
# X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
# ```
# +
# Reshape the training and test examples
### START CODE HERE ### (≈ 2 lines of code)
image_shape = num_px * num_px * 3
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
### END CODE HERE ###
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
# -
# **Expected Output**:
#
# <table style="width:35%">
# <tr>
# <td>**train_set_x_flatten shape**</td>
# <td> (12288, 209)</td>
# </tr>
# <tr>
# <td>**train_set_y shape**</td>
# <td>(1, 209)</td>
# </tr>
# <tr>
# <td>**test_set_x_flatten shape**</td>
# <td>(12288, 50)</td>
# </tr>
# <tr>
# <td>**test_set_y shape**</td>
# <td>(1, 50)</td>
# </tr>
# <tr>
# <td>**sanity check after reshaping**</td>
# <td>[17 31 56 22 33]</td>
# </tr>
# </table>
# To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
#
# One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
#
# <!-- During the training of your model, you're going to multiply weights and add biases to some initial inputs in order to observe neuron activations. Then you backpropogate with the gradients to train the model. But, it is extremely important for each feature to have a similar range such that our gradients don't explode. You will see that more in detail later in the lectures. !-->
#
# Let's standardize our dataset.
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
# <font color='blue'>
# **What you need to remember:**
#
# Common steps for pre-processing a new dataset are:
# - Figure out the dimensions and shapes of the problem (m_train, m_test, num_px, ...)
# - Reshape the datasets such that each example is now a vector of size (num_px \* num_px \* 3, 1)
# - "Standardize" the data
# ## 3 - General Architecture of the learning algorithm ##
#
# It's time to design a simple algorithm to distinguish cat images from non-cat images.
#
# You will build a Logistic Regression, using a Neural Network mindset. The following Figure explains why **Logistic Regression is actually a very simple Neural Network!**
#
# <img src="images/LogReg_kiank.png" style="width:650px;height:400px;">
#
# **Mathematical expression of the algorithm**:
#
# For one example $x^{(i)}$:
# $$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
# $$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
# $$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
#
# The cost is then computed by summing over all training examples:
# $$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
#
# **Key steps**:
# In this exercise, you will carry out the following steps:
# - Initialize the parameters of the model
# - Learn the parameters for the model by minimizing the cost
# - Use the learned parameters to make predictions (on the test set)
# - Analyse the results and conclude
# ## 4 - Building the parts of our algorithm ##
#
# The main steps for building a Neural Network are:
# 1. Define the model structure (such as number of input features)
# 2. Initialize the model's parameters
# 3. Loop:
# - Calculate current loss (forward propagation)
# - Calculate current gradient (backward propagation)
# - Update parameters (gradient descent)
#
# You often build 1-3 separately and integrate them into one function we call `model()`.
#
# ### 4.1 - Helper functions
#
# **Exercise**: Using your code from "Python Basics", implement `sigmoid()`. As you've seen in the figure above, you need to compute $sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$ to make predictions. Use np.exp().
# +
# GRADED FUNCTION: sigmoid
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1 / (1 + np.exp(-z))
### END CODE HERE ###
return s
# -
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
# **Expected Output**:
#
# <table>
# <tr>
# <td>**sigmoid([0, 2])**</td>
# <td> [ 0.5 0.88079708]</td>
# </tr>
# </table>
# ### 4.2 - Initializing parameters
#
# **Exercise:** Implement parameter initialization in the cell below. You have to initialize w as a vector of zeros. If you don't know what numpy function to use, look up np.zeros() in the Numpy library's documentation.
# +
# GRADED FUNCTION: initialize_with_zeros
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
### START CODE HERE ### (≈ 1 line of code)
w = np.zeros((dim, 1))
b = 0
### END CODE HERE ###
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
# -
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
# **Expected Output**:
#
#
# <table style="width:15%">
# <tr>
# <td> ** w ** </td>
# <td> [[ 0.]
# [ 0.]] </td>
# </tr>
# <tr>
# <td> ** b ** </td>
# <td> 0 </td>
# </tr>
# </table>
#
# For image inputs, w will be of shape (num_px $\times$ num_px $\times$ 3, 1).
# ### 4.3 - Forward and Backward propagation
#
# Now that your parameters are initialized, you can do the "forward" and "backward" propagation steps for learning the parameters.
#
# **Exercise:** Implement a function `propagate()` that computes the cost function and its gradient.
#
# **Hints**:
#
# Forward Propagation:
# - You get X
# - You compute $A = \sigma(w^T X + b) = (a^{(1)}, a^{(2)}, ..., a^{(m-1)}, a^{(m)})$
# - You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
#
# Here are the two formulas you will be using:
#
# $$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
# $$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$
# +
# GRADED FUNCTION: propagate
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
Tips:
- Write your code step by step for the propagation. np.log(), np.dot()
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
### START CODE HERE ### (≈ 2 lines of code)
# compute activation
A = sigmoid(np.dot(np.transpose(w), X) + b)
# compute cost
cost = -1/m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
### END CODE HERE ###
# BACKWARD PROPAGATION (TO FIND GRAD)
### START CODE HERE ### (≈ 2 lines of code)
dw = 1/m * np.dot(X, np.transpose(A - Y))
db = 1/m * np.sum(A - Y)
### END CODE HERE ###
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
# -
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
# **Expected Output**:
#
# <table style="width:50%">
# <tr>
# <td> ** dw ** </td>
# <td> [[ 0.99845601]
# [ 2.39507239]]</td>
# </tr>
# <tr>
# <td> ** db ** </td>
# <td> 0.00145557813678 </td>
# </tr>
# <tr>
# <td> ** cost ** </td>
# <td> 5.801545319394553 </td>
# </tr>
#
# </table>
# ### 4.4 - Optimization
# - You have initialized your parameters.
# - You are also able to compute a cost function and its gradient.
# - Now, you want to update the parameters using gradient descent.
#
# **Exercise:** Write down the optimization function. The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $ \theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.
# +
# GRADED FUNCTION: optimize
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation (≈ 1-4 lines of code)
### START CODE HERE ###
grads, cost = propagate(w, b, X, Y)
### END CODE HERE ###
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule (≈ 2 lines of code)
### START CODE HERE ###
w = w - learning_rate * dw
b = b - learning_rate * db
### END CODE HERE ###
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training iterations
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
# +
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
# -
# **Expected Output**:
#
# <table style="width:40%">
# <tr>
# <td> **w** </td>
# <td>[[ 0.19033591]
# [ 0.12259159]] </td>
# </tr>
#
# <tr>
# <td> **b** </td>
# <td> 1.92535983008 </td>
# </tr>
# <tr>
# <td> **dw** </td>
# <td> [[ 0.67752042]
# [ 1.41625495]] </td>
# </tr>
# <tr>
# <td> **db** </td>
# <td> 0.219194504541 </td>
# </tr>
#
# </table>
# **Exercise:** The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the `predict()` function. There are two steps to computing predictions:
#
# 1. Calculate $\hat{Y} = A = \sigma(w^T X + b)$
#
# 2. Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5), stores the predictions in a vector `Y_prediction`. If you wish, you can use an `if`/`else` statement in a `for` loop (though there is also a way to vectorize this).
# +
# GRADED FUNCTION: predict
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat being present in the picture
### START CODE HERE ### (≈ 1 line of code)
A = sigmoid(np.dot(np.transpose(w), X) + b)
### END CODE HERE ###
Y_prediction = np.vectorize(lambda x: 1 if x > 0.5 else 0)(A)
return Y_prediction
# -
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]])
print ("predictions = " + str(predict(w, b, X)))
# **Expected Output**:
#
# <table style="width:30%">
# <tr>
# <td>
# **predictions**
# </td>
# <td>
# [[ 1. 1. 0.]]
# </td>
# </tr>
#
# </table>
#
# <font color='blue'>
# **What to remember:**
# You've implemented several functions that:
# - Initialize (w,b)
# - Optimize the loss iteratively to learn parameters (w,b):
# - computing the cost and its gradient
# - updating the parameters using gradient descent
# - Use the learned (w,b) to predict the labels for a given set of examples
# ## 5 - Merge all functions into a model ##
#
# You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
#
# **Exercise:** Implement the model function. Use the following notation:
# - Y_prediction_test for your predictions on the test set
# - Y_prediction_train for your predictions on the train set
# - w, costs, grads for the outputs of optimize()
# +
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
### START CODE HERE ###
dim = X_train.shape[0]
# initialize parameters with zeros (≈ 1 line of code)
w, b = initialize_with_zeros(dim)
# Gradient descent (≈ 1 line of code)
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples (≈ 2 lines of code)
Y_prediction_test = predict(w, b, X_test)
Y_prediction_train = predict(w, b, X_train)
### END CODE HERE ###
# Print train/test Errors
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
# -
# Run the following cell to train your model.
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
# **Expected Output**:
#
# <table style="width:40%">
#
# <tr>
# <td> **Cost after iteration 0 ** </td>
# <td> 0.693147 </td>
# </tr>
# <tr>
# <td> <center> $\vdots$ </center> </td>
# <td> <center> $\vdots$ </center> </td>
# </tr>
# <tr>
# <td> **Train Accuracy** </td>
# <td> 99.04306220095694 % </td>
# </tr>
#
# <tr>
# <td>**Test Accuracy** </td>
# <td> 70.0 % </td>
# </tr>
# </table>
#
#
#
# **Comment**: Training accuracy is close to 100%. This is a good sanity check: your model is working and has high enough capacity to fit the training data. Test error is 68%. It is actually not bad for this simple model, given the small dataset we used and that logistic regression is a linear classifier. But no worries, you'll build an even better classifier next week!
#
# Also, you see that the model is clearly overfitting the training data. Later in this specialization you will learn how to reduce overfitting, for example by using regularization. Using the code below (and changing the `index` variable) you can look at predictions on pictures of the test set.
# Example of a picture that was wrongly classified.
index = 1
plt.imshow(test_set_x[:,index].reshape((num_px, num_px, 3)))
print ("y = " + str(test_set_y[0,index]) + ", you predicted that it is a \"" + classes[d["Y_prediction_test"][0,index]].decode("utf-8") + "\" picture.")
# Let's also plot the cost function and the gradients.
# Plot learning curve (with costs)
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
# **Interpretation**:
# You can see the cost decreasing. It shows that the parameters are being learned. However, you see that you could train the model even more on the training set. Try to increase the number of iterations in the cell above and rerun the cells. You might see that the training set accuracy goes up, but the test set accuracy goes down. This is called overfitting.
# ## 6 - Further analysis (optional/ungraded exercise) ##
#
# Congratulations on building your first image classification model. Let's analyze it further, and examine possible choices for the learning rate $\alpha$.
# #### Choice of learning rate ####
#
# **Reminder**:
# In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate $\alpha$ determines how rapidly we update the parameters. If the learning rate is too large we may "overshoot" the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.
#
# Let's compare the learning curve of our model with several choices of learning rates. Run the cell below. This should take about 1 minute. Feel free also to try different values than the three we have initialized the `learning_rates` variable to contain, and see what happens.
# +
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
# -
# **Interpretation**:
# - Different learning rates give different costs and thus different predictions results.
# - If the learning rate is too large (0.01), the cost may oscillate up and down. It may even diverge (though in this example, using 0.01 still eventually ends up at a good value for the cost).
# - A lower cost doesn't mean a better model. You have to check if there is possibly overfitting. It happens when the training accuracy is a lot higher than the test accuracy.
# - In deep learning, we usually recommend that you:
# - Choose the learning rate that better minimizes the cost function.
# - If your model overfits, use other techniques to reduce overfitting. (We'll talk about this in later videos.)
#
# ## 7 - Test with your own image (optional/ungraded exercise) ##
#
# Congratulations on finishing this assignment. You can use your own image and see the output of your model. To do that:
# 1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
# 2. Add your image to this Jupyter Notebook's directory, in the "images" folder
# 3. Change your image's name in the following code
# 4. Run the code and check if the algorithm is right (1 = cat, 0 = non-cat)!
# +
## START CODE HERE ## (PUT YOUR IMAGE NAME)
my_image = "la_defense.jpg" # change this to the name of your image file
## END CODE HERE ##
# We preprocess the image to fit your algorithm.
fname = "images/" + my_image
image = np.array(plt.imread(fname))
my_image = resize(image, output_shape=(num_px,num_px), mode='constant').reshape((1, num_px*num_px*3)).T
my_predicted_image = predict(d["w"], d["b"], my_image)
plt.imshow(image)
print("y = " + str(np.squeeze(my_predicted_image)) + ", your algorithm predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
# -
# <font color='blue'>
# **What to remember from this assignment:**
# 1. Preprocessing the dataset is important.
# 2. You implemented each function separately: initialize(), propagate(), optimize(). Then you built a model().
# 3. Tuning the learning rate (which is an example of a "hyperparameter") can make a big difference to the algorithm. You will see more examples of this later in this course!
# Finally, if you'd like, we invite you to try different things on this Notebook. Make sure you submit before trying anything. Once you submit, things you can play with include:
# - Play with the learning rate and the number of iterations
# - Try different initialization methods and compare the results
# - Test other preprocessings (center the data, or divide each row by its standard deviation)
# Bibliography:
# - http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/
# - https://stats.stackexchange.com/questions/211436/why-do-we-normalize-images-by-subtracting-the-datasets-image-mean-and-not-the-c
| 2. Coursera - Neural Networks and Deep Learning/Week 2/Logistic Regression as a Neural Network/2. Logistic+Regression+with+a+Neural+Network+mindset+v5.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="KWEGFZRvFniW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 658} outputId="4895c628-1694-40b2-a372-9b787abfeed2" executionInfo={"status": "ok", "timestamp": 1583502407537, "user_tz": -60, "elapsed": 20260, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
# !pip install --upgrade tables
# !pip install eli5
# !pip install xgboost
# !pip install hyperopt
# + id="jEEeyBwpGOcM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 183} outputId="10a05703-64ab-40ff-a7da-a0529d08d2fd" executionInfo={"status": "ok", "timestamp": 1583502437573, "user_tz": -60, "elapsed": 3482, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
import pandas as pd
import numpy as np
from sklearn.dummy import DummyRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score, KFold
from hyperopt import hp, fmin, tpe, STATUS_OK
import eli5
from eli5.sklearn import PermutationImportance
# + id="OYTlCYvWGZ7D" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="5a28275c-b791-4a03-87f1-fbc16e329669" executionInfo={"status": "ok", "timestamp": 1583502493774, "user_tz": -60, "elapsed": 1614, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
# cd "drive/My Drive/Colab Notebooks/matrix/matrix_two/dw_matrix_car"
# + id="32p6CegKGn6L" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="d39f4a6a-bd3e-4987-a209-c3f40b6d7c94" executionInfo={"status": "ok", "timestamp": 1583502515726, "user_tz": -60, "elapsed": 12379, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
df = pd.read_hdf('data/car.h5')
df.shape
# + id="LRdbA1U_Gqqt" colab_type="code" colab={}
SUFFIX_CAT = '__cat'
for feat in df.columns:
if isinstance(df[feat][0], list): continue
factorized_values = df[feat].factorize()[0]
if SUFFIX_CAT in feat:
df[feat] = factorized_values
else:
df[feat + SUFFIX_CAT] = factorized_values
# + id="2vLIT0C6GtxW" colab_type="code" colab={}
df['param_rok-produkcji'] = df['param_rok-produkcji'].map(lambda x: -1 if str(x) == 'None' else int(x))
df['param_moc'] = df['param_moc'].map(lambda x: -1 if str(x) == 'None' else int(x.split(' ')[0]) )
df['param_pojemność-skokowa'] = df['param_pojemność-skokowa'].map(lambda x: -1 if str(x) == 'None' else int(x.split('cm')[0].replace(' ', '')) )
# + id="J6FCd7_kG6I8" colab_type="code" colab={}
def run_model(model, feats):
X = df[feats].values
y = df['price_value'].values
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
# + id="45j4MkajHEKM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 104} outputId="7ac0a1b9-fdd9-426e-d78f-b98aca80d2eb" executionInfo={"status": "ok", "timestamp": 1583502676827, "user_tz": -60, "elapsed": 12057, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
feats = ['param_napęd__cat',
'param_rok-produkcji',
'param_stan__cat',
'param_skrzynia-biegów__cat',
'param_faktura-vat__cat',
'param_moc',
'param_marka-pojazdu__cat',
'feature_kamera-cofania__cat',
'param_typ__cat',
'param_pojemność-skokowa',
'seller_name__cat',
'feature_wspomaganie-kierownicy__cat',
'param_model-pojazdu__cat',
'param_wersja__cat',
'param_kod-silnika__cat',
'feature_system-start-stop__cat',
'feature_asystent-pasa-ruchu__cat',
'feature_czujniki-parkowania-przednie__cat',
'feature_łopatki-zmiany-biegów__cat',
'feature_regulowane-zawieszenie__cat']
xgb_params = {
'max_depth':5,
'n_estimators': 50,
'learning_rate':0.1,
'seed':0
}
model = xgb.XGBRegressor(**xgb_params)
run_model(model, feats)
# + id="COAfpCaNHQUf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 961} outputId="331249ed-c48a-420e-bae8-01f758270d78" executionInfo={"status": "ok", "timestamp": 1583505010256, "user_tz": -60, "elapsed": 1379518, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "07993273702187826689"}}
def obj_func(params):
print("Training with params: ")
print(params)
mean_mae, score_std = run_model(xgb.XGBRegressor(**params), feats)
return {'loss': np.abs(mean_mae), 'status': STATUS_OK}
xgb_reg_params = {
'learning_rate': hp.choice('learning_rate', np.arange(0.05, 0.31, 0.05)),
'max_depth': hp.choice('max_depth', np.arange(5, 16, 1, dtype=int)),
'subsample': hp.quniform('subsample', 0.5, 1, 0.05),
'colsample_bytree': hp.quniform('colsample_bytree', 0.5, 1, 0.05),
'objective': 'reg:squarederror',
'n_estimators': 100,
'seed': 0,
}
best = fmin(obj_func, xgb_reg_params, algo=tpe.suggest, max_evals=25)
best
# + id="qD5kM1TsKrv_" colab_type="code" colab={}
# !git config --global user.email "<EMAIL>"
# !git config --global user.name "Hubert"
# + id="ifE3YuhRRZnU" colab_type="code" colab={}
| day5.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python ml
# language: python
# name: ml
# ---
#cell-width control
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:80% !important; }</style>"))
# # Imports
# +
#packages
import numpy
import tensorflow as tf
from tensorflow.core.example import example_pb2
#utils
import os
import random
import pickle
import struct
import time
from generators import *
#keras
import keras
from keras.preprocessing import text, sequence
from keras.preprocessing.text import Tokenizer
from keras.models import Model, Sequential
from keras.models import load_model
from keras.layers import Dense, Dropout, Activation, Concatenate, Dot, Embedding, LSTM, Conv1D, MaxPooling1D, Input, Lambda
#callbacks
from keras.callbacks import TensorBoard, ModelCheckpoint, Callback
# -
# # Seed
sd = 6
from numpy.random import seed
seed(sd)
from tensorflow import set_random_seed
set_random_seed(sd)
# # CPU usage
# +
#os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID" # see issue #152
#os.environ["CUDA_VISIBLE_DEVICES"] = ""
# -
# # Global parameters
# +
# Embedding
max_features = 400000
maxlen_text = 400
maxlen_summ = 80
embedding_size = 100 #128
# Convolution
kernel_size = 5
filters = 64
pool_size = 4
# LSTM
lstm_output_size = 70
# Training
batch_size = 32
epochs = 20
# -
# # Load data
# +
data_dir = '/mnt/disks/500gb/experimental-data-mini/experimental-data-mini/pseudorandom-dist-1to1/1to1/'
processing_dir = '/mnt/disks/500gb/stats-and-meta-data/400000/'
with open(data_dir+'partition.pickle', 'rb') as handle: partition = pickle.load(handle)
with open(data_dir+'labels.pickle', 'rb') as handle: labels = pickle.load(handle)
with open(processing_dir+'tokenizer.pickle', 'rb') as handle: tokenizer = pickle.load(handle)
embedding_matrix = numpy.load(processing_dir+'embedding_matrix.npy')
#the p_n constant
c = 80000
#stats
maxi = numpy.load(processing_dir+'training-stats-all/maxi.npy')
mini = numpy.load(processing_dir+'training-stats-all/mini.npy')
sample_info = (numpy.random.uniform, mini,maxi)
# -
# # Model
# +
#2way input
text_input = Input(shape=(maxlen_text,embedding_size), dtype='float32')
summ_input = Input(shape=(maxlen_summ,embedding_size), dtype='float32')
#1way dropout
#text_route = Dropout(0.25)(text_input)
summ_route = Dropout(0.25)(summ_input)
#1way conv
#text_route = Conv1D(filters,
#kernel_size,
#padding='valid',
#activation='relu',
#strides=1)(text_route)
summ_route = Conv1D(filters,
kernel_size,
padding='valid',
activation='relu',
strides=1)(summ_route)
#1way max pool
#text_route = MaxPooling1D(pool_size=pool_size)(text_route)
summ_route = MaxPooling1D(pool_size=pool_size)(summ_route)
#1way lstm
#text_route = LSTM(lstm_output_size)(text_route)
summ_route = LSTM(lstm_output_size)(summ_route)
#negate results
#merged = Lambda(lambda x: -1*x)(merged)
#add p_n constant
#merged = Lambda(lambda x: x + c)(merged)
#output
output = Dense(1, activation='sigmoid')(summ_route)
#define model
model = Model(inputs=[text_input, summ_input], outputs=[output])
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
# -
print(model.summary())
# # Train model
# +
#callbacks
class BatchHistory(keras.callbacks.Callback):
def on_train_begin(self, logs={}):
self.losses = []
self.accs = []
def on_batch_end(self, batch, logs={}):
self.losses.append(logs.get('loss'))
self.accs.append(logs.get('acc'))
history = BatchHistory()
tensorboard = TensorBoard(log_dir='./logs', histogram_freq=0, batch_size=batch_size, write_graph=True, write_grads=True)
modelcheckpoint = ModelCheckpoint('best.h5', monitor='val_loss', verbose=0, save_best_only=True, mode='min', period=1)
#batch generator parameters
params = {'dim': [(maxlen_text,embedding_size),(maxlen_summ,embedding_size)],
'batch_size': batch_size,
'shuffle': True,
'tokenizer':tokenizer,
'embedding_matrix':embedding_matrix,
'maxlen_text':maxlen_text,
'maxlen_summ':maxlen_summ,
'data_dir':data_dir,
'sample_info':sample_info}
#generators
training_generator = ContAllGenerator(partition['train'], labels, **params)
validation_generator = ContAllGenerator(partition['validation'], labels, **params)
# Train model on dataset
model.fit_generator(generator=training_generator,
validation_data=validation_generator,
use_multiprocessing=True,
workers=5,
epochs=epochs,
callbacks=[tensorboard, modelcheckpoint, history])
# -
with open('losses.pickle', 'wb') as handle: pickle.dump(history.losses, handle, protocol=pickle.HIGHEST_PROTOCOL)
with open('accs.pickle', 'wb') as handle: pickle.dump(history.accs, handle, protocol=pickle.HIGHEST_PROTOCOL)
| experiments/ow-on-pseudorandom/6/.ipynb_checkpoints/ow_template-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Ex2 - Filtering and Sorting Data
# This time we are going to pull data directly from the internet.
#
# ### Step 1. Import the necessary libraries
import pandas as pd
# ### Step 2. Import the dataset from this [address](https://raw.githubusercontent.com/jokecamp/FootballData/master/Euro%202012/Euro%202012%20stats%20TEAM.csv).
# ### Step 3. Assign it to a variable called euro12.
euro12 = pd.read_csv('https://raw.githubusercontent.com/jokecamp/FootballData/master/Euro%202012/Euro%202012%20stats%20TEAM.csv')
euro12
# ### Step 4. Select only the Goal column.
euro12.Goals
# ### Step 5. How many team participated in the Euro2012?
euro12.shape[0]
# ### Step 6. What is the number of columns in the dataset?
euro12.info()
# ### Step 7. View only the columns Team, Yellow Cards and Red Cards and assign them to a dataframe called discipline
# +
# filter only giving the column names
discipline = euro12[['Team', 'Yellow Cards', 'Red Cards']]
discipline
# -
# ### Step 8. Sort the teams by Red Cards, then to Yellow Cards
discipline.sort_values(['Red Cards', 'Yellow Cards'], ascending = False)
# ### Step 9. Calculate the mean Yellow Cards given per Team
round(discipline['Yellow Cards'].mean())
# ### Step 10. Filter teams that scored more than 6 goals
euro12[euro12.Goals > 6]
# ### Step 11. Select the teams that start with G
euro12[euro12.Team.str.startswith('G')]
# ### Step 12. Select the first 7 columns
# +
# use .iloc to slices via the position of the passed integers
# : means all, 0:7 means from 0 to 7
euro.iloc[: , 0:7]
# -
# ### Step 13. Select all columns except the last 3.
# +
# use negative to exclude the last 3 columns
euro.iloc[: , :-3]
# -
# ### Step 14. Present only the Shooting Accuracy from England, Italy and Russia
# +
# .loc is another way to slice, using the labels of the columns and indexes
euro12.loc[euro12.Team.isin(['England', 'Italy', 'Russia']), ['Team','Shooting Accuracy']]
| pandas/02_Filtering_&_Sorting/Euro12/Exercises_with_Solutions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import importlib
import os, sys
sys.path.insert(1, os.path.join(sys.path[0], '..'))
from dsm import datasets, DeepSurvivalMachines, DeepConvolutionalSurvivalMachines
import numpy as np
from sksurv.metrics import concordance_index_ipcw, brier_score
# +
# self.cnn = torchvision.models.resnet18(pretrained=True).float()
# self.cnn.conv1 = torch.nn.Conv1d(1, 64, (7, 7), (2, 2), (3, 3), bias=False)
# self.linear = torch.nn.Linear(1000, hidden_dim)
# +
import torchvision
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
train = torchvision.datasets.MNIST(root='../datasets/', train=True, download=True)
x = train.data.numpy()
x = np.expand_dims(x, 1)
t = train.targets.numpy() + 1
# print(x.shape, t.shape)
# test = torchvision.datasets.MNIST(root='../datasets/', train=False, download=True)
# x = test.data.numpy()
# x = np.expand_dims(x, 1)
# t = test.targets.numpy() + 1
e, t = datasets.increase_censoring(np.ones(t.shape),t,.5)
plt.scatter(train.targets.numpy(),t)
print(x.shape, t.shape, e.shape)
# +
from matplotlib import pyplot as plt
plt.hist(t[e==1])
# +
# x, t, e = datasets.load_dataset('SUPPORT')
# print(x.shape, t.shape, e.shape)
# x = np.random.random((9105,1,100,100))
# times = np.quantile(t[e==1], [0.25, 0.5, 0.75]).tolist()
# cv_folds = 5
# folds = list(range(cv_folds))*10000
# folds = np.array(folds[:len(x)])
# +
def avg(marks):
print (np.min(marks))
assert np.min(marks) > 0
return marks
marks = [[1, 10], [10, 20, 5]]
print("Average of mark1:",avg(marks))
# +
x.shape[0]
# +
# import importlib
# import os, sys
# sys.path.insert(1, os.path.join(sys.path[0], '..'))
from dsm import datasets, DeepSurvivalMachines, DeepConvolutionalSurvivalMachines
import numpy as np
from sksurv.metrics import concordance_index_ipcw, brier_score
x, t, e = datasets.load_dataset('MNIST')
# x = np.random.random((9105,1,100,100))
x = x.reshape(x.shape[0], -1)
print(x.shape, t.shape, e.shape)
times = np.quantile(t[e==1], [0.25, 0.5, 0.75]).tolist()
cv_folds = 6
folds = list(range(cv_folds))*10000
folds = np.array(folds[:len(x)])
cis = []
brs = []
for fold in range(cv_folds):
print ("On Fold:", fold)
x_train, t_train, e_train = x[folds!=fold], t[folds!=fold], e[folds!=fold]
x_test, t_test, e_test = x[folds==fold], t[folds==fold], e[folds==fold]
print (x_train.shape)
model = DeepSurvivalMachines(distribution='Weibull', layers=[100, 100])
#model = DeepConvolutionalSurvivalMachines(distribution='Weibull', hidden=100)
model.fit(x_train, t_train, e_train, iters=100, learning_rate=1e-3, batch_size=1000)
et_train = np.array([(e_train[i], t_train[i]) for i in range(len(e_train))],
dtype=[('e', bool), ('t', float)])
et_test = np.array([(e_test[i], t_test[i]) for i in range(len(e_test))],
dtype=[('e', bool), ('t', float)])
out_risk = model.predict_risk(x_test, times)
out_survival = model.predict_survival(x_test, times)
cis_ = []
for i in range(len(times)):
cis_.append(concordance_index_ipcw(et_train, et_test, out_risk[:,i], times[i])[0])
cis.append(cis_)
brs.append(brier_score(et_train, et_test, out_survival, times )[1])
break
print ("Concordance Index:", np.mean(cis,axis=0))
print ("Brier Score:", np.mean(brs,axis=0))
# -
cis
# +
# import importlib
# import os, sys
# sys.path.insert(1, os.path.join(sys.path[0], '..'))
from dsm import datasets, DeepSurvivalMachines, DeepConvolutionalSurvivalMachines
import numpy as np
from sksurv.metrics import concordance_index_ipcw, brier_score
x, t, e = datasets.load_dataset('MNIST')
print(x.shape, t.shape, e.shape)
# x = np.random.random((9105,1,100,100))
# x = x[:10000]
# t = t[:10000]
# e = e[:10000]
times = np.quantile(t[e==1], [0.25, 0.5, 0.75]).tolist()
cv_folds = 5
folds = list(range(cv_folds))*100000
folds = np.array(folds[:len(x)])
cis = []
brs = []
for fold in range(cv_folds):
print ("On Fold:", fold)
x_train, t_train, e_train = x[folds!=fold], t[folds!=fold], e[folds!=fold]
x_test, t_test, e_test = x[folds==fold], t[folds==fold], e[folds==fold]
print (x_train.shape)
# model = DeepSurvivalMachines(distribution='Weibull', layers=[100])
model = DeepConvolutionalSurvivalMachines(distribution='Weibull', hidden=100)
model.fit(x_train, t_train, e_train, iters=10, learning_rate=1e-3, batch_size=1000)
et_train = np.array([(e_train[i], t_train[i]) for i in range(len(e_train))],
dtype=[('e', bool), ('t', float)])
et_test = np.array([(e_test[i], t_test[i]) for i in range(len(e_test))],
dtype=[('e', bool), ('t', float)])
out_risk = model.predict_risk(x_test, times)
out_survival = model.predict_survival(x_test, times)
cis_ = []
for i in range(len(times)):
cis_.append(concordance_index_ipcw(et_train, et_test, out_risk[:,i], times[i])[0])
cis.append(cis_)
brs.append(brier_score(et_train, et_test, out_survival, times )[1])
print ("Concordance Index:", np.mean(cis,axis=0))
print ("Brier Score:", np.mean(brs,axis=0))
# -
cis
import torch
# +
x_train_ = torch.from_numpy(x_train)
# -
model.torch_model.embedding(x_train_).shape
x.shape
cis
model.predict_survival(x_test, times)
print ("Concordance Index:", np.mean(cis,axis=0))
print ("Brier Score:", np.mean(brs,axis=0))
from sksurv.linear_model import CoxPHSurvivalAnalysis
cis = []
for fold in range(cv_folds):
print ("On Fold:", fold)
x_train, t_train, e_train = x[folds!=fold], t[folds!=fold], e[folds!=fold]
x_test, t_test, e_test = x[folds==fold], t[folds==fold], e[folds==fold]
et_train = np.array([(e_train[i], t_train[i]) for i in range(len(e_train))],
dtype=[('e', bool), ('t', int)])
et_test = np.array([(e_test[i], t_test[i]) for i in range(len(e_test))],
dtype=[('e', bool), ('t', int)])
model = CoxPHSurvivalAnalysis(alpha=1e-3)
model.fit(x_test, et_test)
out_risk = model.predict_survival_function(x_test)
cis_ = []
for i in range(len(times)):
cis_.append(concordance_index_ipcw(et_train, et_test, out_risk, times[i])[0])
cis.append(cis_)
time = 6
int(np.where(out_risk[0].x == time)[0])
out_risk[0].x
model = CoxPHSurvivalAnalysis(alpha=1e-3)
model.fit(x_test, et_test)
np.mean(cis,axis=0)
out_risk = model.predict_risk(x, times)
model.torch_model.eval()
out_survival = model.predict_survival(x, times)
# +
from matplotlib import pyplot as plt
# -
from sksurv.metrics import brier_score, concordance_index_ipcw
# +
import numpy as np
et = np.array([(e[i], t[i]) for i in range(len(e))],
dtype=[('e', bool), ('t', int)])
# -
brier_score(et, et, out_survival, times )
for i in range(len(times)):
print(concordance_index_ipcw(et, et, out_risk[:,i], times[i])[0])
# +
from sksurv.linear_model import CoxPHSurvivalAnalysis
estimator = CoxPHSurvivalAnalysis(alpha=1e-3).fit(x, et,)
# -
surv_funcs = estimator.predict(x)
surv_funcs
for i in range(len(times)):
print(concordance_index_ipcw(et, et, surv_funcs, times[i])[0])
| examples/conv_example.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# First, we wanted a map of ICD (International Classification of Diseases) codes to general disease states. We can read the long descriptions, but they are generally categorized by where they focus. The ink is [here](https://icd.codes/icd9cm) and as a reminder, neoplasms are cancers (new, unplanned cells, in a sense.)
# read in ICD diagnostic codes, notice these are latin-1 encooded, not standard utf. Drop the short description, since it doesn't help identification/is redundant to long description that is helpful.
import pandas as pd
procedure_codes = pd.read_csv('CMS27_DESC_LONG_SHORT_SG_092709.csv', encoding='latin-1')
diag_codes = pd.read_csv('V27LONG_SHORT_DX_110909u021012.csv', encoding='latin-1')
procedure_codes = procedure_codes.set_index('PROCEDURE CODE').drop('SHORT DESCRIPTION', axis=1)
procedure_codes
diag_codes = diag_codes.set_index('DIAGNOSIS CODE').drop('SHORT DESCRIPTION', axis=1)
diag_codes
# turn ICD dataframes into dictionaries
procedure_dict = procedure_codes['LONG DESCRIPTION'].to_dict()
procedure_dict
diag_dict = diag_codes['LONG DESCRIPTION'].to_dict()
diag_dict
# read in in-patient data, set claimID as index to make easier to specify in location in creating within-frame dictionaries
in_patient_train = pd.read_csv('Train_Inpatientdata-1542865627584.csv')
in_patient_train = in_patient_train.set_index('ClaimID')
# define the diagnostic code columns to make our diagnostic dictionary for each claim. Then do a dictionary comprehension for the diagnostic columns so you have ICD code and long description for each, then wrap that inside a list comprehension to write the diagnostic dictionary column in the dataframe. Command took 170 sec to run on my computer, so slow.
# +
diag_codes = ['ClmDiagnosisCode_1', 'ClmDiagnosisCode_2', 'ClmDiagnosisCode_3',
'ClmDiagnosisCode_4', 'ClmDiagnosisCode_5', 'ClmDiagnosisCode_6',
'ClmDiagnosisCode_7', 'ClmDiagnosisCode_8', 'ClmDiagnosisCode_9',
'ClmDiagnosisCode_10']
in_patient_train['diag_dict'] = [{in_patient_train.loc[clm][diagcol]:diag_dict[in_patient_train.loc[clm][diagcol].lstrip('0')] for diagcol in diag_codes \
if (in_patient_train.loc[clm][diagcol] in diag_dict.keys())} for clm in in_patient_train.index]
# -
# do the same thing with the diagnostic procedure codes. These seem to be all numerics, so it is a little faster.
import numpy as np
proc_codes = ['ClmProcedureCode_1', 'ClmProcedureCode_2',
'ClmProcedureCode_3', 'ClmProcedureCode_4', 'ClmProcedureCode_5',
'ClmProcedureCode_6']
in_patient_train['proc_dict'] = [{in_patient_train.loc[clm][proccol]:procedure_dict[in_patient_train.loc[clm][proccol]] for proccol in proc_codes \
if ~np.isnan(in_patient_train.loc[clm][proccol])} for clm in in_patient_train.index]
in_patient_train
| .ipynb_checkpoints/ICD_Diagnostic_and_Procedure_dictionary columns-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Quiz #0204 (Solution)
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
# %matplotlib inline
# #### Read in the data.
# !wget --no-clobber https://raw.githubusercontent.com/stefannae/SIC-Artificial-Intelligence/main/SIC_AI_Quizzes/SIC_AI_Chapter_03_Quiz/data_coffeeshop.csv
df = pd.read_csv('data_coffeeshop.csv', header='infer',na_values=[' '])
df.shape
df.head(5)
# #### Answer the following questions.
# 1). Make a frequency table of 'yearOfStart' and visualize by year.
# - Sort by the year.
# - Draw a line plot from 1997 to 2014. <= Hint: plt.xlim()
table = df.yearOfStart.value_counts()
table = table.sort_index()
plt.plot(table.index, table.values, color='blue', alpha=0.5, linewidth=2, linestyle='--')
plt.xlim([1997, 2014])
plt.show()
# 2). Now, split the data by the current state of business ('In' or 'Out' of business). Then, visualize the yearly trend of the 'yearOfStart' frequencies.
# - Sort by the year.
# - Draw two overlapping line plots from 1997 to 2014.
# - Use the 'figure' object.
# Split the data by the current state of business.
df_in = df[df.CurrentState == 'In'] # In business.
df_out = df[df.CurrentState == 'Out'] # Out of business.
# Frequency tables.
table_in = df_in.yearOfStart.value_counts()
table_in = table_in.sort_index()
table_out = df_out.yearOfStart.value_counts()
table_out = table_out.sort_index()
# Visualize as two overlapping line plots.
fig = plt.figure(figsize=[5,3])
my_axes = fig.add_axes([0,0,1,1])
my_axes.plot(table_in.index, table_in.values, color = 'blue', linestyle='--',label='In Business')
my_axes.plot(table_out.index, table_out.values,color = 'red', linestyle='-.', label='Out of Business')
my_axes.legend(loc=0)
my_axes.set_xlim([1997, 2014])
plt.show()
# 3). From the results of 1) and 2), how can you describe the trend in general?
# - Around the year 2008, began a steep increase in the number of new coffee shops.
# - As of the year 2014, more coffee shops opened in the past 5 years are still in business rather than going out of business.
| SIC_AI_Quizzes/SIC_AI_Chapter_03_Quiz/sol_0204.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <!-- dom:TITLE: Day 3: Homework 2 -->
# # Day 3: Homework 2
# <!-- dom:AUTHOR: Data Analysis and Machine Learning -->
# <!-- Author: -->
# **Data Analysis and Machine Learning**
#
# Date: **May 22, 2020**
#
# ## Day three exercises
#
#
# ### Exercise 1
#
# This exercise is a continuation of exercise 3 from homework 1. We will
# use the same function to generate our data set, still staying with a
# simple function $y(x)$ which we want to fit using linear regression,
# but now extending the analysis to include the Ridge and the Lasso
# regression methods. You can use the code under the Regression as an example on how to use the Ridge and the Lasso methods, see the [regression slides](https://compphysics.github.io/MachineLearning/doc/pub/Regression/html/Regression-bs.html)).
#
# We will thus again generate our own dataset for a function $y(x)$ where
# $x \in [0,1]$ and defined by random numbers computed with the uniform
# distribution. The function $y$ is a quadratic polynomial in $x$ with
# added stochastic noise according to the normal distribution $\cal{N}(0,1)$.
#
# The following simple Python instructions define our $x$ and $y$ values (with 100 data points).
x = np.random.rand(100,1)
y = 5*x*x+0.1*np.random.randn(100,1)
# 1. (1a) Write your own code for the Ridge method (see chapter 3.4 of Hastie *et al.*, equations (3.43) and (3.44)) and compute the parametrization for different values of $\lambda$. Compare and analyze your results with those from exercise 2. Study the dependence on $\lambda$ while also varying the strength of the noise in your expression for $y(x)$.
#
# 2. (1b) Repeat the above but using the functionality of **Scikit-Learn**. Compare your code with the results from **Scikit-Learn**. Remember to run with the same random numbers for generating $x$ and $y$.
#
# 3. (1c) Our next step is to study the variance of the parameters $\beta_1$ and $\beta_2$ (assuming that we are parameterizing our function with a second-order polynomial). We will use standard linear regression and the Ridge regression. You can now opt for either writing your own function or using **Scikit-Learn** to find the parameters $\beta$. From your results calculate the variance of these paramaters (recall that this is equal to the diagonal elements of the matrix $(\hat{X}^T\hat{X})+\lambda\hat{I})^{-1}$). Discuss the results of these variances as functions of $\lambda$. In particular, try to link your discussion with the discussion in Hastie *et al.* and their figure 3.11.
#
# 4. (1d) Repeat the previous step but add now the Lasso method, see equation (3.53) of Hastie *et al.*. Discuss your results and compare with standard regression and the Ridge regression results. You can write your own code or use the functionality of **scikit-learn**. We recommend the latter since we have not yet discussed how to solve the Lasso equations numerically.
#
# 5. (1e) Finally, using **Scikit-Learn** or your own code, compute also the mean square error, a risk metric corresponding to the expected value of the squared (quadratic) error defined as
# $$
# MSE(\hat{y},\hat{\tilde{y}}) = \frac{1}{n}
# \sum_{i=0}^{n-1}(y_i-\tilde{y}_i)^2,
# $$
# and the $R^2$ score function.
# If $\tilde{\hat{y}}_i$ is the predicted value of the $i-th$ sample and $y_i$ is the corresponding true value, then the score $R^2$ is defined as
# $$
# R^2(\hat{y}, \tilde{\hat{y}}) = 1 - \frac{\sum_{i=0}^{n - 1} (y_i - \tilde{y}_i)^2}{\sum_{i=0}^{n - 1} (y_i - \bar{y})^2},
# $$
# where we have defined the mean value of $\hat{y}$ as
# $$
# \bar{y} = \frac{1}{n} \sum_{i=0}^{n - 1} y_i.
# $$
# Discuss these quantities as functions of the variable $\lambda$ in the Ridge and Lasso regression methods.
#
# ## Exercise 2
#
#
# A much used approach before starting to train the data is to preprocess our
# data. Normally the data may need a rescaling and/or may be sensitive
# to extreme values. Scaling the data renders our inputs much more
# suitable for the algorithms we want to employ.
#
# **Scikit-Learn** has several functions which allow us to rescale the
# data, normally resulting in much better results in terms of various
# accuracy scores. The **StandardScaler** function in **Scikit-Learn**
# ensures that for each feature/predictor we study the mean value is
# zero and the variance is one (every column in the design/feature
# matrix). This scaling has the drawback that it does not ensure that
# we have a particular maximum or minimum in our data set. Another
# function included in **Scikit-Learn** is the **MinMaxScaler** which
# ensures that all features are exactly between $0$ and $1$. The
#
#
# The **Normalizer** scales each data
# point such that the feature vector has a euclidean length of one. In other words, it
# projects a data point on the circle (or sphere in the case of higher dimensions) with a
# radius of 1. This means every data point is scaled by a different number (by the
# inverse of it’s length).
# This normalization is often used when only the direction (or angle) of the data matters,
# not the length of the feature vector.
#
# The **RobustScaler** works similarly to the StandardScaler in that it
# ensures statistical properties for each feature that guarantee that
# they are on the same scale. However, the RobustScaler uses the median
# and quartiles, instead of mean and variance. This makes the
# RobustScaler ignore data points that are very different from the rest
# (like measurement errors). These odd data points are also called
# outliers, and might often lead to trouble for other scaling
# techniques.
#
#
# It also common to split the data in a **training** set and a **testing** set. A typical split is to use $80\%$ of the data for training and the rest
# for testing. This can be done as follows with our design matrix $\boldsymbol{X}$ and data $\boldsymbol{y}$ (remember to import **scikit-learn**)
# split in training and test data
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2)
# Then we can use the stadndard scale to scale our data as
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# In this exercise we want you to to compute the MSE for the training
# data and the test data as function of the complexity of a polynomial,
# that is the degree of a given polynomial. We want you also to compute the $R2$ score as function of the complexity of the model for both training data and test data. You should also run the calculation with and without scaling.
#
# One of
# the aims is to reproduce Figure 2.11 of [Hastie et al](https://github.com/CompPhysics/MLErasmus/blob/master/doc/Textbooks/elementsstat.pdf).
# We will also use Ridge and Lasso regression.
#
#
# Our data is defined by $x\in [-3,3]$ with a total of for example $100$ data points.
np.random.seed()
n = 100
maxdegree = 14
# Make data set.
x = np.linspace(-3, 3, n).reshape(-1, 1)
y = np.exp(-x**2) + 1.5 * np.exp(-(x-2)**2)+ np.random.normal(0, 0.1, x.shape)
# where $y$ is the function we want to fit with a given polynomial.
#
# 1. (2a) Write a first code which sets up a design matrix $X$ defined by a fifth-order polynomial. Scale your data and split it in training and test data.
#
# 2. (2b) Perform an ordinary least squares and compute the means squared error and the $R2$ factor for the training data and the test data, with and without scaling.
#
# 3. (2c) Add now a model which allows you to make polynomials up to degree $15$. Perform a standard OLS fitting of the training data and compute the MSE and $R2$ for the training and test data and plot both test and training data MSE and $R2$ as functions of the polynomial degree. Compare what you see with Figure 2.11 of Hastie et al. Comment your results. For which polynomial degree do you find an optimal MSE (smallest value)?
#
# 4. (2d) Repeat part (2c) but now using Ridge regressions with various hyperparameters $\lambda$. Make the same plots for the optimal $\lambda$ value for each polynomial degree. Compare these results with those from the standard OLS approach.
#
# ## Example of how to solve the previous exercise
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
n = 100
# Make data set.
x = np.linspace(-3, 3, n).reshape(-1, 1)
y = np.exp(-x**2) + 1.5 * np.exp(-(x-2)**2)+ np.random.normal(0, 0.1, x.shape)
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Decide which values of lambda to use
nlambdas = 500
lambdas = np.logspace(-3, 5, nlambdas)
estimated_mse_sklearn = np.zeros(nlambdas)
i = 0
for lmb in lambdas:
clf_ridge = Ridge(alpha=lmb).fit(X_train_scaled, y_train)
yridge = clf_ridge.predict(X_test_scaled)
estimated_mse_sklearn[i] = mean_squared_error(y_test, yridge)
i += 1
plt.figure()
plt.plot(np.log10(lambdas), estimated_mse_sklearn, label = 'Ridge MSE')
plt.xlabel('log10(lambda)')
plt.ylabel('MSE')
plt.legend()
plt.show()
# -
# ## And now with OLS only and Bootstrap
# +
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.utils import resample
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
n = 100
n_boostraps = 100
maxdegree = 14
# Make data set.
x = np.linspace(-3, 3, n).reshape(-1, 1)
y = np.exp(-x**2) + 1.5 * np.exp(-(x-2)**2)+ np.random.normal(0, 0.1, x.shape)
error = np.zeros(maxdegree)
bias = np.zeros(maxdegree)
variance = np.zeros(maxdegree)
polydegree = np.zeros(maxdegree)
# Make data set.
x = np.linspace(-3, 3, n).reshape(-1, 1)
y = np.exp(-x**2) + 1.5 * np.exp(-(x-2)**2)+ np.random.normal(0, 0.1, x.shape)
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
for degree in range(maxdegree):
model = make_pipeline(PolynomialFeatures(degree=degree), LinearRegression(fit_intercept=False))
y_pred = np.empty((y_test.shape[0], n_boostraps))
for i in range(n_boostraps):
x_, y_ = resample(X_train_scaled, y_train)
y_pred[:, i] = model.fit(x_, y_).predict(X_test_scaled).ravel()
polydegree[degree] = degree
error[degree] = np.mean( np.mean((y_test - y_pred)**2, axis=1, keepdims=True) )
bias[degree] = np.mean( (y_test - np.mean(y_pred, axis=1, keepdims=True))**2 )
variance[degree] = np.mean( np.var(y_pred, axis=1, keepdims=True) )
print('Polynomial degree:', degree)
print('Error:', error[degree])
print('Bias^2:', bias[degree])
print('Var:', variance[degree])
print('{} >= {} + {} = {}'.format(error[degree], bias[degree], variance[degree], bias[degree]+variance[degree]))
plt.plot(polydegree, error, label='Error')
plt.plot(polydegree, bias, label='bias')
plt.plot(polydegree, variance, label='Variance')
plt.legend()
plt.show()
| doc/ProjectsExercises/2020/hw2/ipynb/.ipynb_checkpoints/hw2-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + hide_input=true inputHidden=true language="html"
# <span style="color:red; font-family:Helvetica Neue, Helvetica, Arial, sans-serif; font-size:2em;">An Exception was encountered at 'In [12]'.</span>
# + papermill={"duration": 0.039307, "end_time": "2019-11-25T14:46:10.563644", "exception": false, "start_time": "2019-11-25T14:46:10.524337", "status": "completed"} tags=[]
# %load_ext autoreload
# %autoreload 2
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" executionInfo={"elapsed": 48054, "status": "ok", "timestamp": 1573636583219, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDViwxKXBjVKZfXMWGuXrQ48D62bye6HNutAOX0=s64", "userId": "06737229821528734971"}, "user_tz": -60} id="2mU_ZLUH5jz4" outputId="c4cbc445-56dd-49df-de87-c34e18da5f6c" papermill={"duration": 4.83916, "end_time": "2019-11-25T14:46:15.421072", "exception": false, "start_time": "2019-11-25T14:46:10.581912", "status": "completed"} tags=[]
import glob
import nibabel as nib
import os
import time
import pandas as pd
import numpy as np
import cv2
from skimage.transform import resize
from mricode.utils import log_textfile, createPath, data_generator
from mricode.utils import copy_colab
from mricode.utils import return_iter
from mricode.utils import return_csv
from mricode.config import config
from mricode.models.DenseNet_normal_hierach import MyDenseNet
import tensorflow as tf
from tensorflow.keras.layers import Conv3D
from tensorflow import nn
from tensorflow.python.ops import nn_ops
from tensorflow.python.framework import tensor_shape
from tensorflow.python.keras.engine.base_layer import InputSpec
from tensorflow.python.keras.utils import conv_utils
tf.__version__
# + papermill={"duration": 0.070823, "end_time": "2019-11-25T14:46:15.514360", "exception": false, "start_time": "2019-11-25T14:46:15.443537", "status": "completed"} tags=[]
tf.test.is_gpu_available()
# + colab={} colab_type="code" id="nH4XzW8C5yhH" papermill={"duration": 0.069196, "end_time": "2019-11-25T14:46:15.605052", "exception": false, "start_time": "2019-11-25T14:46:15.535856", "status": "completed"} tags=[]
path_output = './output/'
path_tfrecords = '/data2/res64/down/'
path_csv = '/data2/csv/'
filename_res = {'train': 'intell_residual_train.csv', 'val': 'intell_residual_valid.csv', 'test': 'intell_residual_test.csv'}
filename_final = filename_res
sample_size = 'site16_allimages'
batch_size = 8
onlyt1 = False
Model = MyDenseNet
versionkey = 'down64' #down256, cropped128, cropped64, down64
modelname = 'new_hiearch_densenet_allimages_' + versionkey
# + papermill={"duration": 0.068397, "end_time": "2019-11-25T14:46:15.695439", "exception": false, "start_time": "2019-11-25T14:46:15.627042", "status": "completed"} tags=[]
createPath(path_output + modelname)
# + papermill={"duration": 0.336485, "end_time": "2019-11-25T14:46:16.053138", "exception": false, "start_time": "2019-11-25T14:46:15.716653", "status": "completed"} tags=[]
train_df, val_df, test_df, norm_dict = return_csv(path_csv, filename_final, False)
# + papermill={"duration": 0.070739, "end_time": "2019-11-25T14:46:16.145531", "exception": false, "start_time": "2019-11-25T14:46:16.074792", "status": "completed"} tags=[]
train_iter = config[versionkey]['iter_train']
val_iter = config[versionkey]['iter_val']
test_iter = config[versionkey]['iter_test']
t1_mean = config[versionkey]['norm']['t1'][0]
t1_std= config[versionkey]['norm']['t1'][1]
t2_mean=config[versionkey]['norm']['t2'][0]
t2_std=config[versionkey]['norm']['t2'][1]
ad_mean=config[versionkey]['norm']['ad'][0]
ad_std=config[versionkey]['norm']['ad'][1]
fa_mean=config[versionkey]['norm']['fa'][0]
fa_std=config[versionkey]['norm']['fa'][1]
md_mean=config[versionkey]['norm']['md'][0]
md_std=config[versionkey]['norm']['md'][1]
rd_mean=config[versionkey]['norm']['rd'][0]
rd_std=config[versionkey]['norm']['rd'][1]
# + colab={"base_uri": "https://localhost:8080/", "height": 442} colab_type="code" executionInfo={"elapsed": 3147, "status": "ok", "timestamp": 1573636641787, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDViwxKXBjVKZfXMWGuXrQ48D62bye6HNutAOX0=s64", "userId": "06737229821528734971"}, "user_tz": -60} id="0xYy4XUyVBeC" outputId="a6a19d59-31ff-4064-f1dc-952befcce4b3" papermill={"duration": 0.0706, "end_time": "2019-11-25T14:46:16.237345", "exception": false, "start_time": "2019-11-25T14:46:16.166745", "status": "completed"} tags=[]
norm_dict
# + colab={} colab_type="code" id="eTk95ptFV5oN" papermill={"duration": 0.065871, "end_time": "2019-11-25T14:46:16.325682", "exception": false, "start_time": "2019-11-25T14:46:16.259811", "status": "completed"} tags=[]
cat_cols = {'female': 2, 'race.ethnicity': 5, 'high.educ_group': 4, 'income_group': 8, 'married': 6}
num_cols = [x for x in list(val_df.columns) if '_norm' in x]
# + colab={} colab_type="code" id="hROMApYiDagm" papermill={"duration": 0.232552, "end_time": "2019-11-25T14:46:16.580084", "exception": false, "start_time": "2019-11-25T14:46:16.347532", "status": "completed"} tags=[]
def calc_loss_acc(out_loss, out_acc, y_true, y_pred, cat_cols, num_cols, norm_dict):
for col in num_cols:
tmp_col = col
tmp_std = norm_dict[tmp_col.replace('_norm','')]['std']
tmp_y_true = tf.cast(y_true[col], tf.float32).numpy()
tmp_y_pred = np.squeeze(y_pred[col].numpy())
if not(tmp_col in out_loss):
out_loss[tmp_col] = np.sum(np.square(tmp_y_true-tmp_y_pred))
else:
out_loss[tmp_col] += np.sum(np.square(tmp_y_true-tmp_y_pred))
if not(tmp_col in out_acc):
out_acc[tmp_col] = np.sum(np.square((tmp_y_true-tmp_y_pred)*tmp_std))
else:
out_acc[tmp_col] += np.sum(np.square((tmp_y_true-tmp_y_pred)*tmp_std))
for col in list(cat_cols.keys()):
tmp_col = col
if not(tmp_col in out_loss):
out_loss[tmp_col] = tf.keras.losses.SparseCategoricalCrossentropy()(tf.squeeze(y_true[col]), tf.squeeze(y_pred[col])).numpy()
else:
out_loss[tmp_col] += tf.keras.losses.SparseCategoricalCrossentropy()(tf.squeeze(y_true[col]), tf.squeeze(y_pred[col])).numpy()
if not(tmp_col in out_acc):
out_acc[tmp_col] = tf.reduce_sum(tf.dtypes.cast((y_true[col] == tf.argmax(y_pred[col], axis=-1)), tf.float32)).numpy()
else:
out_acc[tmp_col] += tf.reduce_sum(tf.dtypes.cast((y_true[col] == tf.argmax(y_pred[col], axis=-1)), tf.float32)).numpy()
return(out_loss, out_acc)
def format_output(out_loss, out_acc, n, cols, print_bl=False):
loss = 0
acc = 0
output = []
for col in cols:
output.append([col, out_loss[col]/n, out_acc[col]/n])
loss += out_loss[col]/n
acc += out_acc[col]/n
df = pd.DataFrame(output)
df.columns = ['name', 'loss', 'acc']
if print_bl:
print(df)
return(loss, acc, df)
@tf.function
def train_step(X, y, model, optimizer, cat_cols, num_cols):
with tf.GradientTape() as tape:
predictions = model(X)
i = 0
loss = tf.keras.losses.MSE(tf.cast(y[num_cols[i]], tf.float32), tf.squeeze(predictions[num_cols[i]]))
for i in range(1,len(num_cols)):
loss += tf.keras.losses.MSE(tf.cast(y[num_cols[i]], tf.float32), tf.squeeze(predictions[num_cols[i]]))
for col in list(cat_cols.keys()):
loss += tf.keras.losses.SparseCategoricalCrossentropy()(tf.squeeze(y[col]), tf.squeeze(predictions[col]))
gradients = tape.gradient(loss, model.trainable_variables)
mean_std = [x.name for x in model.non_trainable_variables if ('batch_norm') in x.name and ('mean' in x.name or 'variance' in x.name)]
with tf.control_dependencies(mean_std):
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
return(y, predictions, loss)
@tf.function
def test_step(X, y, model):
predictions = model(X)
return(y, predictions)
def epoch(data_iter, df, model, optimizer, cat_cols, num_cols, norm_dict):
out_loss = {}
out_acc = {}
n = 0.
n_batch = 0.
total_time_dataload = 0.
total_time_model = 0.
start_time = time.time()
for batch in data_iter:
total_time_dataload += time.time() - start_time
start_time = time.time()
t1 = (tf.cast(batch['t1'], tf.float32)-t1_mean)/t1_std
t2 = (batch['t2']-t2_mean)/t2_std
if False:
ad = batch['ad']
ad = tf.where(tf.math.is_nan(ad), tf.zeros_like(ad), ad)
ad = (ad-ad_mean)/ad_std
fa = batch['fa']
fa = tf.where(tf.math.is_nan(fa), tf.zeros_like(fa), fa)
fa = (fa-fa_mean)/fa_std
md = batch['md']
md = tf.where(tf.math.is_nan(md), tf.zeros_like(md), md)
md = (md-md_mean)/md_std
rd = batch['rd']
rd = tf.where(tf.math.is_nan(rd), tf.zeros_like(rd), rd)
rd = (rd-rd_mean)/rd_std
subjectid = decoder(batch['subjectid'])
y = get_labels(df, subjectid, list(cat_cols.keys())+num_cols)
#X = tf.concat([t1], axis=4)
X = tf.concat([t1, t2], axis=4)
if optimizer != None:
y_true, y_pred, loss = train_step(X, y, model, optimizer, cat_cols, num_cols)
else:
y_true, y_pred = test_step(X, y, model)
out_loss, out_acc = calc_loss_acc(out_loss, out_acc, y_true, y_pred, cat_cols, num_cols, norm_dict)
n += X.shape[0]
n_batch += 1
if (n_batch % 10) == 0:
log_textfile(path_output + modelname + '/log' + '.log', str(n_batch))
total_time_model += time.time() - start_time
start_time = time.time()
return (out_loss, out_acc, n, total_time_model, total_time_dataload)
def get_labels(df, subjectid, cols = ['nihtbx_fluidcomp_uncorrected_norm']):
subjects_df = pd.DataFrame(subjectid)
result_df = pd.merge(subjects_df, df, left_on=0, right_on='subjectkey', how='left')
output = {}
for col in cols:
output[col] = np.asarray(result_df[col].values)
return output
def best_val(df_best, df_val, df_test, e):
df_best = pd.merge(df_best, df_val, how='left', left_on='name', right_on='name')
df_best = pd.merge(df_best, df_test, how='left', left_on='name', right_on='name')
df_best.loc[df_best['best_loss_val']>=df_best['cur_loss_val'], 'best_loss_epochs'] = e
df_best.loc[(df_best['best_acc_val']<=df_best['cur_acc_val'])&(df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'best_acc_epochs'] = e
df_best.loc[df_best['best_loss_val']>=df_best['cur_loss_val'], 'best_loss_test'] = df_best.loc[df_best['best_loss_val']>=df_best['cur_loss_val'], 'cur_loss_test']
df_best.loc[df_best['best_loss_val']>=df_best['cur_loss_val'], 'best_loss_val'] = df_best.loc[df_best['best_loss_val']>=df_best['cur_loss_val'], 'cur_loss_val']
df_best.loc[(df_best['best_acc_val']<=df_best['cur_acc_val'])&(df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'best_acc_test'] = df_best.loc[(df_best['best_acc_val']<=df_best['cur_acc_val'])&(df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'cur_acc_test']
df_best.loc[(df_best['best_acc_val']<=df_best['cur_acc_val'])&(df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'best_acc_val'] = df_best.loc[(df_best['best_acc_val']<=df_best['cur_acc_val'])&(df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'cur_acc_val']
df_best.loc[(df_best['best_acc_val']>=df_best['cur_acc_val'])&(~df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'best_acc_test'] = df_best.loc[(df_best['best_acc_val']>=df_best['cur_acc_val'])&(~df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'cur_acc_test']
df_best.loc[(df_best['best_acc_val']>=df_best['cur_acc_val'])&(~df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'best_acc_val'] = df_best.loc[(df_best['best_acc_val']>=df_best['cur_acc_val'])&(~df_best['name'].isin(['female', 'race.ethnicity', 'high.educ_group', 'income_group', 'married'])), 'cur_acc_val']
df_best = df_best.drop(['cur_loss_val', 'cur_acc_val', 'cur_loss_test', 'cur_acc_test'], axis=1)
return(df_best)
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" executionInfo={"elapsed": 46355, "status": "ok", "timestamp": 1573636701683, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mDViwxKXBjVKZfXMWGuXrQ48D62bye6HNutAOX0=s64", "userId": "06737229821528734971"}, "user_tz": -60} id="RV24LE3k-00n" outputId="067125be-6ce2-40c9-998e-62f800ccb2f1" papermill={"duration": 11975.3067, "end_time": "2019-11-25T18:05:51.909540", "exception": false, "start_time": "2019-11-25T14:46:16.602840", "status": "completed"} tags=[]
decoder = np.vectorize(lambda x: x.decode('UTF-8'))
template = 'Epoch {0}, Loss: {1:.3f}, Accuracy: {2:.3f}, Val Loss: {3:.3f}, Val Accuracy: {4:.3f}, Time Model: {5:.3f}, Time Data: {6:.3f}'
for col in [0]:
log_textfile(path_output + modelname + '/log' + '.log', cat_cols)
log_textfile(path_output + modelname + '/log' + '.log', num_cols)
loss_object = tf.keras.losses.SparseCategoricalCrossentropy()
optimizer = tf.keras.optimizers.Adam(lr = 0.001)
model = Model(cat_cols, num_cols)
df_best = None
for e in range(20):
log_textfile(path_output + modelname + '/log' + '.log', 'Epochs: ' + str(e))
loss = tf.Variable(0.)
acc = tf.Variable(0.)
val_loss = tf.Variable(0.)
val_acc = tf.Variable(0.)
test_loss = tf.Variable(0.)
test_acc = tf.Variable(0.)
tf.keras.backend.set_learning_phase(True)
train_out_loss, train_out_acc, n, time_model, time_data = epoch(train_iter, train_df, model, optimizer, cat_cols, num_cols, norm_dict)
tf.keras.backend.set_learning_phase(False)
val_out_loss, val_out_acc, n, _, _ = epoch(val_iter, val_df, model, None, cat_cols, num_cols, norm_dict)
test_out_loss, test_out_acc, n, _, _ = epoch(test_iter, test_df, model, None, cat_cols, num_cols, norm_dict)
loss, acc, _ = format_output(train_out_loss, train_out_acc, n, list(cat_cols.keys())+num_cols)
val_loss, val_acc, df_val = format_output(val_out_loss, val_out_acc, n, list(cat_cols.keys())+num_cols, print_bl=False)
test_loss, test_acc, df_test = format_output(test_out_loss, test_out_acc, n, list(cat_cols.keys())+num_cols, print_bl=False)
df_val.columns = ['name', 'cur_loss_val', 'cur_acc_val']
df_test.columns = ['name', 'cur_loss_test', 'cur_acc_test']
if e == 0:
df_best = pd.merge(df_test, df_val, how='left', left_on='name', right_on='name')
df_best['best_acc_epochs'] = 0
df_best['best_loss_epochs'] = 0
df_best.columns = ['name', 'best_loss_test', 'best_acc_test', 'best_loss_val', 'best_acc_val', 'best_acc_epochs', 'best_loss_epochs']
df_best = best_val(df_best, df_val, df_test, e)
print(df_best[['name', 'best_loss_test', 'best_acc_test']])
print(df_best[['name', 'best_loss_val', 'best_acc_val']])
log_textfile(path_output + modelname + '/log' + '.log', template.format(e, loss, acc, val_loss, val_acc, time_model, time_data))
if e in [10, 15]:
optimizer.lr = optimizer.lr/3
log_textfile(path_output + modelname + '/log' + '.log', 'Learning rate: ' + str(optimizer.lr))
df_best.to_csv(path_output + modelname + '/df_best' + str(e) + '.csv')
df_best.to_csv(path_output + modelname + '/df_best' + '.csv')
#model.save_weights(path_output + modelname + '/checkpoints/' + str(e) + '/')
# + papermill={"duration": 0.892812, "end_time": "2019-11-25T18:05:53.390033", "exception": true, "start_time": "2019-11-25T18:05:52.497221", "status": "failed"} tags=[]
error
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
test_loss, test_acc, df_test = format_output(test_out_loss, test_out_acc, n, list(cat_cols.keys())+num_cols, print_bl=False)
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
df_test.to_csv('final_output_all.csv')
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
inputs = tf.keras.Input(shape=(64,64,64,2), name='inputlayer123')
a = model(inputs)['female']
mm = tf.keras.models.Model(inputs=inputs, outputs=a)
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
from tf_explain.core.smoothgrad import SmoothGrad
import pickle
explainer = SmoothGrad()
output_grid = {}
output_n = {}
for i in range(2):
output_grid[i] = np.zeros((64,64,64))
output_n[i] = 0
counter = 0
for batch in test_iter:
counter+=1
print(counter)
t1 = (tf.cast(batch['t1'], tf.float32)-t1_mean)/t1_std
t2 = (batch['t2']-t2_mean)/t2_std
X = tf.concat([t1, t2], axis=4)
subjectid = decoder(batch['subjectid'])
y = get_labels(test_df, subjectid, list(cat_cols.keys())+num_cols)
y_list = list(y['female'])
for i in range(X.shape[0]):
X_i = X[i]
X_i = tf.expand_dims(X_i, axis=0)
y_i = y_list[i]
grid = explainer.explain((X_i, _), mm, y_i, 20, 1.)
output_grid[y_i] += grid
output_n[y_i] += 1
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
pickle.dump([output_grid, output_n], open( "smoothgrad_female_all.p", "wb" ) )
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
#output_grid, output_n = pickle.load(open( "smoothgrad_female.p", "rb" ))
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
def apply_grey_patch(image, top_left_x, top_left_y, top_left_z, patch_size):
"""
Replace a part of the image with a grey patch.
Args:
image (numpy.ndarray): Input image
top_left_x (int): Top Left X position of the applied box
top_left_y (int): Top Left Y position of the applied box
patch_size (int): Size of patch to apply
Returns:
numpy.ndarray: Patched image
"""
patched_image = np.array(image, copy=True)
patched_image[
top_left_x : top_left_x + patch_size, top_left_y : top_left_y + patch_size, top_left_z : top_left_z + patch_size, :
] = 0
return patched_image
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
import math
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
def get_sensgrid(image, mm, class_index, patch_size):
sensitivity_map = np.zeros((
math.ceil(image.shape[0] / patch_size),
math.ceil(image.shape[1] / patch_size),
math.ceil(image.shape[2] / patch_size)
))
for index_z, top_left_z in enumerate(range(0, image.shape[2], patch_size)):
patches = [
apply_grey_patch(image, top_left_x, top_left_y, top_left_z, patch_size)
for index_x, top_left_x in enumerate(range(0, image.shape[0], patch_size))
for index_y, top_left_y in enumerate(range(0, image.shape[1], patch_size))
]
coordinates = [
(index_y, index_x)
for index_x, _ in enumerate(range(0, image.shape[0], patch_size))
for index_y, _ in enumerate(range(0, image.shape[1], patch_size))
]
predictions = mm.predict(np.array(patches), batch_size=1)
target_class_predictions = [prediction[class_index] for prediction in predictions]
for (index_y, index_x), confidence in zip(coordinates, target_class_predictions):
sensitivity_map[index_y, index_x, index_z] = 1 - confidence
sm = resize(sensitivity_map, (64,64,64))
heatmap = (sm - np.min(sm)) / (sm.max() - sm.min())
return(heatmap)
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
output_grid = {}
output_n = {}
for i in range(2):
output_grid[i] = np.zeros((64,64,64))
output_n[i] = 0
counter = 0
for batch in test_iter:
counter+=1
print(counter)
t1 = (tf.cast(batch['t1'], tf.float32)-t1_mean)/t1_std
t2 = (batch['t2']-t2_mean)/t2_std
X = tf.concat([t1, t2], axis=4)
subjectid = decoder(batch['subjectid'])
y = get_labels(test_df, subjectid, list(cat_cols.keys())+num_cols)
y_list = list(y['female'])
for i in range(X.shape[0]):
print(i)
X_i = X[i]
y_i = y_list[i]
grid = get_sensgrid(X_i, mm, y_i, 4)
output_grid[y_i] += grid
output_n[y_i] += 1
if counter==6:
break
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
pickle.dump([output_grid, output_n], open( "heatmap_female_all.p", "wb" ) )
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
error
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
batch = next(iter(train_iter))
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
t1 = (tf.cast(batch['t1'], tf.float32)-t1_mean)/t1_std
t2 = (batch['t2']-t2_mean)/t2_std
ad = batch['ad']
ad = tf.where(tf.math.is_nan(ad), tf.zeros_like(ad), ad)
ad = (ad-ad_mean)/ad_std
fa = batch['fa']
fa = tf.where(tf.math.is_nan(fa), tf.zeros_like(fa), fa)
fa = (fa-fa_mean)/fa_std
md = batch['md']
md = tf.where(tf.math.is_nan(md), tf.zeros_like(md), md)
md = (md-md_mean)/md_std
rd = batch['rd']
rd = tf.where(tf.math.is_nan(rd), tf.zeros_like(rd), rd)
rd = (rd-rd_mean)/rd_std
#subjectid = decoder(batch['subjectid'])
#y = get_labels(df, subjectid, list(cat_cols.keys())+num_cols)
#X = tf.concat([t1, t2, ad, fa, md, rd], axis=4)
X = tf.concat([t1, t2], axis=4)
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
tf.keras.backend.set_learning_phase(True)
model(X)['female']
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
tf.keras.backend.set_learning_phase(False)
model(X)['female']
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
mean_std = [x.name for x in model.non_trainable_variables if ('batch_norm') in x.name and ('mean' in x.name or 'variance' in x.name)]
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
model = Model(cat_cols, num_cols)
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
model.non_trainable_variables
# + papermill={"duration": null, "end_time": null, "exception": null, "start_time": null, "status": "pending"} tags=[]
| mirimages-master/oldjupyter/xxx_hiearchdensenet.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Limits
# + slideshow={"slide_type": "slide"}
# Load module
from sympy import *
# + slideshow={"slide_type": "slide"}
# Define variable
x = symbols('x')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Define Function $$f(x) = \frac{x^2}{x} - 1$$
# + slideshow={"slide_type": "slide"}
# Function f(x) = x^2 / x - 1
def f(x):
return x**2 / x - 1
# + [markdown] slideshow={"slide_type": "slide"}
# ## Calculate $$\lim_{x \to 0} f(x)$$ $$=\lim_{x \to 0^+} (x-1)$$
# + slideshow={"slide_type": "slide"}
# Limit of f(x)
lim = Limit(f(x), x, 0)
lim
# + slideshow={"slide_type": "slide"}
# Do the limit
lim.doit()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Define Function $$g(x) = \frac{1}{x}$$
# + slideshow={"slide_type": "slide"}
# Function g(x) = 1/x
def g(x):
return 1/x
# + [markdown] slideshow={"slide_type": "slide"}
# ## Calculate $$\lim_{x \to 0^+} g(x)$$
# + slideshow={"slide_type": "slide"}
# Do the limit at positive side
limit(g(x), x, 0, '+')
# + [markdown] slideshow={"slide_type": "slide"}
# ## Calculate $$\lim_{x \to 0^-} g(x)$$
# + slideshow={"slide_type": "slide"}
# Do the limit at negative side
limit(g(x), x, 0, '-')
| limits.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introdução à Ciência de Dados - UFPB
# Professor: <NAME>
#
# ## NumPy
# Implemente a função `distance` abaixo. Ela deve receber dois pontos e retornar a distância euclidiana entre eles. Cada ponto é representado por um array do NumPy, por exemplo, `p1 = np.array([2,4])` representa o ponto com coordenadas x=2 e y=2.
# +
import numpy as np
def distance(p1, p2):
"""
>>> distance(np.array([0,0]), np.array([1,1]))
1.4142135623730951
>>> distance(np.array([1,2]), np.array([3,4]))
2.8284271247461903
>>> distance(np.array([5,2]), np.array([-2,-1]))
7.615773105863909
"""
# ADICIONE O SEU CÓDIGO AQUI
return ((p2[0]-p1[0])**2 + (p2[1]-p1[1])**2) ** (1/2) #Fórmula distância entre 2 pontos.
# -
distance(np.array([1,2]), np.array([3,4]))
# Implemente a função `n_distances` abaixo. Ela recebe um ponto (`p1`), como um array do NumPy, e uma lista de pontos (`points`), uma matriz do NumPy, onde cada linha representa um ponto.
#
# Esta função deve retornar a distância de `p1` para todos os pontos da matriz `points`. O retorno também é uma matriz, onde cada linha tem a distância de `p1` para o ponto daquela linha.
def n_distances(p1, points):
"""
>>> n_distances(np.array([0,0]), np.array([[1,1]]))
array([1.41421356])
>>> n_distances(np.array([0,0]), np.array([[1,1], [2,2]]))
array([1.41421356, 2.82842712])
>>> n_distances(np.array([1,2]), np.array([[3,-1], [2,1], [5, 2], [10, 1], [-2, -5]]))
array([3.60555128, 1.41421356, 4. , 9.05538514, 7.61577311])
"""
# ADICIONE O SEU CÓDIGO AQUI
z = np.zeros((points.shape[0])) #Criei um array de 0 de acordo com a quantidade de pontos da matriz points.
for i in range(len(points)):
z[i] = distance(p1,points[i]) #For para preencher o array com os resultados da chamada da primeira função.
return z
n_distances(np.array([0,0]), np.array([[1,1], [2,2]]))
# ## Teste
# +
import doctest
doctest.testmod(verbose=True)
# -
| 03.Dist_2_pontos_NumPy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Match Zeta Identities
# The goal of this notebook is to attempt to create links between different datasets to see what the current situation is regarding identity resolution. Thoughts: 20%
# ## Import and Initialize
# + tags=[]
import networkx as nx
import numpy as np
import pandas as pd
# -
# ## Load Data
# Load the datasets with 10,000 rows each.
# + tags=[]
dsp = pd.read_csv("data/dsp_cookies_export_20210625_10k.csv")
print(f"DSP data shape: {dsp.shape}")
sizmek = pd.read_csv("data/sizmek_bidstream_raw_20210625_10k.csv")
print(f"Sizmek data shape: {sizmek.shape}")
# Fix column headers
dsp.columns = [i.split(".")[1] for i in dsp.columns]
sizmek.columns = [i.split(".")[1] for i in sizmek.columns]
# -
# We can use any of the three columns below to create graph connections with.
# + tags=[]
print("Common columns:", set(dsp.columns).intersection(set(sizmek.columns)))
# -
# ## Match Data
# We first see that there are no direct matches of the `zeta_user_id` between datasets.
# + tags=[]
dsp[["zeta_user_id"]].merge(sizmek[["zeta_user_id"]], on="zeta_user_id")
# -
# This is because the DSP dataset has them formatted as a list for each row.
# + tags=[]
dsp["zeta_user_id"].head(3)
# -
# While Sizmek has single ids with some amount of NaNs.
# + tags=[]
sizmek["zeta_user_id"].sample(3)
# + tags=[]
print(f"Avg length of DSP user ids: {np.mean([len(i) for i in dsp['zeta_user_id']])}")
# -
# So now I wonder **why** are there around 54 ids in each row?
# First I would like to see the proportion of NaNs in the Sizmek dataset.
# + tags=[]
print(f"Percent of NaNs: {sizmek['zeta_user_id'].isna().sum() / len(sizmek):.2%}")
# -
| match_data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: U4S1DS10 (Python 3.7)
# language: python
# name: u4-s1-nlp-ds10
# ---
# Lambda School Data Science
#
# *Unit 4, Sprint 3, Module 2*
#
# ---
# # Convolutional Neural Networks (Prepare)
#
# > Convolutional networks are simply neural networks that use convolution in place of general matrix multiplication in at least one of their layers. *Goodfellow, et al.*
# ## Learning Objectives
# - <a href="#p1">Part 1: </a>Describe convolution and pooling
# - <a href="#p2">Part 2: </a>Apply a convolutional neural network to a classification task
# - <a href="#p3">Part 3: </a>Use a pre-trained convolution neural network for image classification
#
# Modern __computer vision__ approaches rely heavily on convolutions as both a dimensionality reduction and feature extraction method. Before we dive into convolutions, let's talk about some of the common computer vision applications:
# * Classification [(Hot Dog or Not Dog)](https://www.youtube.com/watch?v=ACmydtFDTGs)
# * Object Detection [(YOLO)](https://www.youtube.com/watch?v=MPU2HistivI)
# * Pose Estimation [(PoseNet)](https://ai.googleblog.com/2019/08/on-device-real-time-hand-tracking-with.html)
# * Facial Recognition [Emotion Detection](https://www.cbronline.com/wp-content/uploads/2018/05/Mona-lIsa-test-570x300.jpg)
# * and *countless* more
#
# We are going to focus on classification and pre-trained classification today. What are some of the applications of image classification?
from IPython.display import YouTubeVideo
YouTubeVideo('MPU2HistivI', width=600, height=400)
# + [markdown] toc-hr-collapsed=false
# # Convolution & Pooling (Learn)
# <a id="p1"></a>
# + [markdown] toc-hr-collapsed=true
# ## Overview
#
# Like neural networks themselves, CNNs are inspired by biology - specifically, the receptive fields of the visual cortex.
#
# Put roughly, in a real brain the neurons in the visual cortex *specialize* to be receptive to certain regions, shapes, colors, orientations, and other common visual features. In a sense, the very structure of our cognitive system transforms raw visual input, and sends it to neurons that specialize in handling particular subsets of it.
#
# CNNs imitate this approach by applying a convolution. A convolution is an operation on two functions that produces a third function, showing how one function modifies another. Convolutions have a [variety of nice mathematical properties](https://en.wikipedia.org/wiki/Convolution#Properties) - commutativity, associativity, distributivity, and more. Applying a convolution effectively transforms the "shape" of the input.
#
# One common confusion - the term "convolution" is used to refer to both the process of computing the third (joint) function and the process of applying it. In our context, it's more useful to think of it as an application, again loosely analogous to the mapping from visual field to receptive areas of the cortex in a real animal.
# -
from IPython.display import YouTubeVideo
YouTubeVideo('IOHayh06LJ4', width=600, height=400)
# + [markdown] toc-hr-collapsed=false
# ## Follow Along
#
# Let's try to do some convolutions and pooling
# -
# ### Convolution
#
# Consider blurring an image - assume the image is represented as a matrix of numbers, where each number corresponds to the color value of a pixel.
#
# 
#
# *Image Credits from __Hands on Machine Learning with Sckit-Learn, Keras & TensorFlow__*
#
#
# Helpful Terms:
# - __Filter__: The weights (parameters) we will apply to our input image.
# - __Stride__: How the filter moves across the image
# - __Padding__: Zeros (or other values) around the the input image border (kind of like a frame of zeros).
# + colab={"base_uri": "https://localhost:8080/", "height": 243} colab_type="code" id="OsAcbKvoeaqU" outputId="dbb28705-36c7-4691-f7df-e9f82e3ee91e"
import imageio
import matplotlib.pyplot as plt
from skimage import color, io
from skimage.exposure import rescale_intensity
austen = io.imread('https://dl.airtable.com/S1InFmIhQBypHBL0BICi_austen.jpg')
austen_grayscale = rescale_intensity(color.rgb2gray(austen))
austen_grayscale.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 351} colab_type="code" id="KN-ibr_DhyaV" outputId="241716ac-3415-4cfd-9602-0dd59a80ed47"
plt.imshow(austen_grayscale, cmap="gray");
# -
austen_grayscale.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 243} colab_type="code" id="QopB0uo6lNxq" outputId="2364bf3d-8fb9-487a-d2db-eb794939c77a"
import numpy as np
import scipy.ndimage as nd
horizontal_edge_convolution = np.array([[1,1,1,1,1],
[0,0,0,0,0],
[-1,-1,-1,-1,-1]])
vertical_edge_convolution = np.array([[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1]])
austen_edges = nd.convolve(austen_grayscale, vertical_edge_convolution)#horizontal_edge_convolution)
austen_edges.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 368} colab_type="code" id="-LwEpFW1l-6b" outputId="51b9bdf4-dab6-406a-f98b-fd0a7b480859"
plt.imshow(austen_edges, cmap="gray");
# -
# ### Pooling Layer
#
# 
#
# *Image Credits from __Hands on Machine Learning with Sckit-Learn, Keras & TensorFlow__*
#
# We use Pooling Layers to reduce the dimensionality of the feature maps. We get smaller and smaller feature set by apply convolutions and then pooling layers.
#
# Let's take a look very simple example using Austen's pic.
# +
from skimage.measure import block_reduce
reduced = block_reduce(austen_edges,(2,2), np.max) #austen_grayscale, (2,2), np.max)
plt.imshow(reduced, cmap="gray");
# -
reduced.shape
# ## Challenge
#
# You will be expected to be able to describe convolution.
# # CNNs for Classification (Learn)
# + [markdown] toc-hr-collapsed=true
# ## Overview
# + [markdown] colab_type="text" id="OOep4ugw8coa"
# ### Typical CNN Architecture
#
# 
#
# The first stage of a CNN is, unsurprisingly, a convolution - specifically, a transformation that maps regions of the input image to neurons responsible for receiving them. The convolutional layer can be visualized as follows:
#
# 
#
# The red represents the original input image, and the blue the neurons that correspond.
#
# As shown in the first image, a CNN can have multiple rounds of convolutions, [downsampling](https://en.wikipedia.org/wiki/Downsampling_(signal_processing)) (a digital signal processing technique that effectively reduces the information by passing through a filter), and then eventually a fully connected neural network and output layer. Typical output layers for a CNN would be oriented towards classification or detection problems - e.g. "does this picture contain a cat, a dog, or some other animal?"
#
#
# #### A Convolution in Action
#
# 
#
#
#
# Why are CNNs so popular?
# 1. Compared to prior image learning techniques, they require relatively little image preprocessing (cropping/centering, normalizing, etc.)
# 2. Relatedly, they are *robust* to all sorts of common problems in images (shifts, lighting, etc.)
#
# Actually training a cutting edge image classification CNN is nontrivial computationally - the good news is, with transfer learning, we can get one "off-the-shelf"!
# -
# ## Follow Along
from tensorflow.keras import datasets
from tensorflow.keras.models import Sequential, Model # <- May Use
from tensorflow.keras.layers import Dense, Conv2D, MaxPooling2D, Flatten
# +
(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()
# Normalize pixel values to be between 0 and 1
train_images, test_images = train_images / 255.0, test_images / 255.0
# +
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(class_names[train_labels[i][0]])
plt.show()
# -
train_images[0].shape
train_labels[1]
32*32*3
# +
# Setup Architecture
model = Sequential()
model.add(Conv2D(32, (3,3), activation='relu', input_shape=(32,32,3)))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3,3), activation='relu'))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3,3), activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.summary()
# +
# Compile Model
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# -
# Fit Model
model.fit(train_images, train_labels, epochs=10, validation_data=(test_images, test_labels))
# +
# Evaluate Model
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
# -
# ## Challenge
#
# You will apply CNNs to a classification task in the module project.
# # Transfer Learning for Image Classification (Learn)
# + [markdown] toc-hr-collapsed=true
# ## Overview
# + [markdown] colab_type="text" id="ic_wzFnprwXI"
# ### Transfer Learning Repositories
#
# #### TensorFlow Hub
#
# "A library for reusable machine learning modules"
#
# This lets you quickly take advantage of a model that was trained with thousands of GPU hours. It also enables transfer learning - reusing a part of a trained model (called a module) that includes weights and assets, but also training the overall model some yourself with your own data. The advantages are fairly clear - you can use less training data, have faster training, and have a model that generalizes better.
#
# https://www.tensorflow.org/hub/
#
# TensorFlow Hub is very bleeding edge, and while there's a good amount of documentation out there, it's not always updated or consistent. You'll have to use your problem-solving skills if you want to use it!
#
# #### Keras API - Applications
#
# > Keras Applications are deep learning models that are made available alongside pre-trained weights. These models can be used for prediction, feature extraction, and fine-tuning.
#
# There is a decent selection of important benchmark models. We'll focus on an image classifier: ResNet50.
# -
# ## Follow Along
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="FM_ApKbGYM9S" outputId="4bfd7ce4-47e5-4320-d1b8-2b20e9f66416"
import numpy as np
from tensorflow.keras.applications.resnet50 import ResNet50
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications.resnet50 import preprocess_input, decode_predictions
def process_img_path(img_path):
return image.load_img(img_path, target_size=(224, 224))
def img_contains_banana(img):
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
model = ResNet50(weights='imagenet')
features = model.predict(x)
results = decode_predictions(features, top=3)[0]
print(results)
for entry in results:
if entry[1] == 'banana':
return entry[2]
return 0.0
# + colab={"base_uri": "https://localhost:8080/", "height": 593} colab_type="code" id="_cQ8ZsJF_Z3B" outputId="02545656-8773-4bb2-9ff5-36d8c658dc00"
import requests
image_urls = ["https://github.com/LambdaSchool/ML-YouOnlyLookOnce/raw/master/sample_data/negative_examples/example11.jpeg",
"https://github.com/LambdaSchool/ML-YouOnlyLookOnce/raw/master/sample_data/positive_examples/example0.jpeg"]
for _id,img in enumerate(image_urls):
r = requests.get(img)
with open(f'example{_id}.jpg', 'wb') as f:
f.write(r.content)
# + colab={"base_uri": "https://localhost:8080/", "height": 417} colab_type="code" id="Gxzkai0q_d-4" outputId="a6bd9b95-9665-4df0-c74d-3d4e876eaf48"
from IPython.display import Image
Image(filename='./example0.jpg', width=600)
# + colab={"base_uri": "https://localhost:8080/", "height": 141} colab_type="code" id="X8NIlClb_n8s" outputId="7c9b9f98-073e-4ab0-a336-e3fc89fa8439"
img_contains_banana(process_img_path('example0.jpg'))
# + colab={"base_uri": "https://localhost:8080/", "height": 417} colab_type="code" id="YIwtRazQ_tQr" outputId="7be6599b-253d-4600-e1f5-ac0ab0f2dfbc"
Image(filename='example1.jpg', width=600)
# + colab={"base_uri": "https://localhost:8080/", "height": 52} colab_type="code" id="GDXwkPWOAB14" outputId="6493a0cb-b57b-43be-8a4e-ac06e51bdada"
img_contains_banana(process_img_path('example1.jpg'))
# + [markdown] colab_type="text" id="CdF5A88oPYvX"
# Notice that, while it gets it right, the confidence for the banana image is fairly low. That's because so much of the image is "not-banana"! How can this be improved? Bounding boxes to center on items of interest.
# -
# ## Challenge
#
# You will be expected to apply a pretrained model to a classificaiton problem today.
# # Review
#
# - <a href="#p1">Part 1: </a>Describe convolution and pooling
# * A Convolution is a function applied to another function to produce a third function
# * Convolutional Kernels are typically 'learned' during the process of training a Convolution Neural Network
# * Pooling is a dimensionality reduction technique that uses either Max or Average of a feature map region to downsample data
# - <a href="#p2">Part 2: </a>Apply a convolutional neural network to a classification task
# * Keras has layers for convolutions :)
# - <a href="#p3">Part 3: </a>Transfer Learning for Image Classification
# * Check out both pretinaed models available in Keras & TensorFlow Hub
# # Sources
#
# - *_Deep Learning_*. Goodfellow *et al.*
# - *Hands-on Machine Learnign with Scikit-Learn, Keras & Tensorflow*
# - [Keras CNN Tutorial](https://www.tensorflow.org/tutorials/images/cnn)
# - [Tensorflow + Keras](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Conv2D)
# - [Convolution Wiki](https://en.wikipedia.org/wiki/Convolution)
# - [Keras Conv2D: Working with CNN 2D Convolutions in Keras](https://missinglink.ai/guides/keras/keras-conv2d-working-cnn-2d-convolutions-keras/)
# - [Intuitively Understanding Convolutions for Deep Learning](https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1)
# - [A Beginner's Guide to Understanding Convolutional Neural Networks Part 2](https://adeshpande3.github.io/A-Beginner%27s-Guide-To-Understanding-Convolutional-Neural-Networks-Part-2/)
| module2-convolutional-neural-networks/LS_DS_432_Convolutional_Neural_Networks_Lecture.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
#
# The :term:`Events <events>` and :class:`~mne.Annotations` data structures
# =========================================================================
#
# :term:`Events <events>` and :term:`annotations` are quite similar.
# This tutorial highlights their differences and similarities, and tries to shed
# some light on which one is preferred to use in different situations when using
# MNE.
#
# Both events and :class:`~mne.Annotations` can be seen as triplets
# where the first element answers to **when** something happens and the last
# element refers to **what** it is.
# The main difference is that events represent the onset in samples taking into
# account the first sample value
# (:attr:`raw.first_samp <mne.io.Raw.first_samp>`), and the description is
# an integer value.
# In contrast, :class:`~mne.Annotations` represents the
# ``onset`` in seconds (relative to the reference ``orig_time``),
# and the ``description`` is an arbitrary string.
# There is no correspondence between the second element of events and
# :class:`~mne.Annotations`.
# For events, the second element corresponds to the previous value on the
# stimulus channel from which events are extracted. In practice, the second
# element is therefore in most cases zero.
# The second element of :class:`~mne.Annotations` is a float
# indicating its duration in seconds.
#
# See `ex-read-events`
# for a complete example of how to read, select, and visualize **events**;
# and `tut-artifact-rejection` to
# learn how :class:`~mne.Annotations` are used to mark bad segments
# of data.
#
# An example of events and annotations
# ------------------------------------
#
# The following example shows the recorded events in `sample_audvis_raw.fif` and
# marks bad segments due to eye blinks.
#
# +
import os.path as op
import numpy as np
import mne
# Load the data
data_path = mne.datasets.sample.data_path()
fname = op.join(data_path, 'MEG', 'sample', 'sample_audvis_raw.fif')
raw = mne.io.read_raw_fif(fname)
# -
# First we'll create and plot events associated with the experimental paradigm:
#
#
# +
# extract the events array from the stim channel
events = mne.find_events(raw)
# Specify event_id dictionary based on the meaning of experimental triggers
event_id = {'Auditory/Left': 1, 'Auditory/Right': 2,
'Visual/Left': 3, 'Visual/Right': 4,
'smiley': 5, 'button': 32}
color = {1: 'green', 2: 'yellow', 3: 'red', 4: 'c', 5: 'black', 32: 'blue'}
mne.viz.plot_events(events, raw.info['sfreq'], raw.first_samp, color=color,
event_id=event_id)
# -
# Next, we're going to detect eye blinks and turn them into
# :class:`~mne.Annotations`:
#
#
# +
# find blinks
annotated_blink_raw = raw.copy()
eog_events = mne.preprocessing.find_eog_events(raw)
n_blinks = len(eog_events)
# Turn blink events into Annotations of 0.5 seconds duration,
# each centered on the blink event:
onset = eog_events[:, 0] / raw.info['sfreq'] - 0.25
duration = np.repeat(0.5, n_blinks)
description = ['bad blink'] * n_blinks
annot = mne.Annotations(onset, duration, description,
orig_time=raw.info['meas_date'])
annotated_blink_raw.set_annotations(annot)
# plot the annotated raw
annotated_blink_raw.plot()
# -
# Add :term:`annotations` to :term:`raw` objects
# ----------------------------------------------
#
# An important element of :class:`~mne.Annotations` is
# ``orig_time`` which is the time reference for the ``onset``.
# It is key to understand that when calling
# :func:`raw.set_annotations <mne.io.Raw.set_annotations>`, given
# annotations are copied and transformed so that
# :class:`raw.annotations.orig_time <mne.Annotations>`
# matches the recording time of the raw object.
# Refer to the documentation of :class:`~mne.Annotations` to see
# the expected behavior depending on ``meas_date`` and ``orig_time``.
# Where ``meas_date`` is the recording time stored in
# :class:`Info <mne.Info>`.
# You can find more information about :class:`Info <mne.Info>` in
# `tut-info-class`.
#
# We'll now manipulate some simulated annotations.
# The first annotations has ``orig_time`` set to ``None`` while the
# second is set to a chosen POSIX timestamp for illustration purposes.
# Note that both annotations have different ``onset`` values.
#
#
# +
# Create an annotation object with orig_time undefined (default)
annot_none = mne.Annotations(onset=[0, 2, 9], duration=[0.5, 4, 0],
description=['foo', 'bar', 'foo'],
orig_time=None)
print(annot_none)
# Create an annotation object with orig_time
orig_time = '2002-12-03 19:01:31.676071'
annot_orig = mne.Annotations(onset=[22, 24, 31], duration=[0.5, 4, 0],
description=['foo', 'bar', 'foo'],
orig_time=orig_time)
print(annot_orig)
# -
# Now we create two raw objects and set each with different annotations.
# Then we plot both raw objects to compare the annotations.
#
#
# +
# Create two cropped copies of raw with the two previous annotations
raw_a = raw.copy().crop(tmax=12).set_annotations(annot_none)
raw_b = raw.copy().crop(tmax=12).set_annotations(annot_orig)
# Plot the raw objects
raw_a.plot()
raw_b.plot()
# -
# Note that although the ``onset`` values of both annotations were different,
# due to complementary ``orig_time`` they are now identical. This is because
# the first one (``annot_none``), once set in raw, adopted its ``orig_time``.
# The second one (``annot_orig``) already had an ``orig_time``, so its
# ``orig_time`` was changed to match the onset time of the raw. Changing an
# already defined ``orig_time`` of annotations caused its ``onset`` to be
# recalibrated with respect to the new ``orig_time``. As a result both
# annotations have now identical ``onset`` and identical ``orig_time``:
#
#
# +
# Show the annotations in the raw objects
print(raw_a.annotations)
print(raw_b.annotations)
# Show that the onsets are the same
np.set_printoptions(precision=6)
print(raw_a.annotations.onset)
print(raw_b.annotations.onset)
# -
# Notice again that for the case where ``orig_time`` is ``None``,
# it is assumed that the ``orig_time`` is the time of the first sample of data.
#
#
raw_delta = (1 / raw.info['sfreq'])
print('raw.first_sample is {}'.format(raw.first_samp * raw_delta))
print('annot_none.onset[0] is {}'.format(annot_none.onset[0]))
print('raw_a.annotations.onset[0] is {}'.format(raw_a.annotations.onset[0]))
# Valid operations in :class:`mne.Annotations`
# --------------------------------------------
#
# Concatenate
# ~~~~~~~~~~~
#
# It is possible to concatenate two annotations with the + operator (just like
# lists) if both share the same ``orig_time``
#
#
annot = mne.Annotations(onset=[10], duration=[0.5],
description=['foobar'],
orig_time=orig_time)
annot = annot_orig + annot # concatenation
print(annot)
# Iterating, Indexing and Slicing :class:`mne.Annotations`
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#
# :class:`~mne.Annotations` supports iterating, indexing and slicing.
# Iterating over :class:`~mne.Annotations` and indexing with an integer returns
# a dictionary. While slicing returns a new :class:`~mne.Annotations` instance.
#
# See the following examples and usages:
#
#
# difference between indexing and slicing a single element
print(annot[0]) # indexing
print(annot[:1]) # slicing
# How about iterations?
#
#
for key, val in annot[0].items(): # iterate on one element which is dictionary
print(key, val)
for idx, my_annot in enumerate(annot): # iterate on the Annotations object
print('annot #{0}: onset={1}'.format(idx, my_annot['onset']))
print('annot #{0}: duration={1}'.format(idx, my_annot['duration']))
print('annot #{0}: description={1}'.format(idx, my_annot['description']))
for idx, my_annot in enumerate(annot[:1]):
for key, val in my_annot.items():
print('annot #{0}: {1} = {2}'.format(idx, key, val))
# Iterating, indexing and slicing return a copy. This has implications like the
# fact that changes are not kept.
#
#
# +
# this change is not kept
annot[0]['onset'] = 42
print(annot[0])
# this change is kept
annot.onset[0] = 42
print(annot[0])
# -
# Save
# ~~~~
#
# Note that you can also save annotations to disk in FIF format::
#
# >>> annot.save('my-annot.fif')
#
# Or as CSV with onsets in (absolute) ISO timestamps::
#
# >>> annot.save('my-annot.csv')
#
# Or in plain text with onsets relative to ``orig_time``::
#
# >>> annot.save('my-annot.txt')
#
#
#
| stable/_downloads/a663da19dfef335563cab63585276d60/plot_object_annotations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Wide and Deep on TensorFlow (notebook style)
# Copyright 2016 Google Inc. All Rights Reserved. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
# # Introduction
#
# This notebook uses the tf.learn API in TensorFlow to answer a yes/no question. This is called a binary classification problem: Given census data about a person such as age, gender, education and occupation (the features), we will try to predict whether or not the person earns more than 50,000 dollars a year (the target label).
#
# Given an individual's information our model will output a number between 0 and 1, which can be interpreted as the model's certainty that the individual has an annual income of over 50,000 dollars, (1=True, 0=False)
#
# # Imports and constants
# First we'll import our libraries and set up some strings for column names. We also print out the version of TensorFlow we are running.
# +
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import time
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.ERROR) # Set to INFO for tracking training, default is WARN
from tensorflow.contrib.learn.python.learn.datasets import base
print("Using TensorFlow version %s" % (tf.__version__))
CATEGORICAL_COLUMNS = ["workclass", "education", "marital_status", "occupation",
"relationship", "race", "gender", "native_country"]
# Columns of the input csv file
COLUMNS = ["age", "workclass", "fnlwgt", "education", "education_num", "marital_status",
"occupation", "relationship", "race", "gender", "capital_gain", "capital_loss",
"hours_per_week", "native_country", "income_bracket"]
# Feature columns for input into the model
FEATURE_COLUMNS = ["age", "workclass", "education", "education_num", "marital_status",
"occupation", "relationship", "race", "gender", "capital_gain", "capital_loss",
"hours_per_week", "native_country"]
# -
# # Input file parsing
#
# This section puts the file into a `Reader` which reads from the file one batch at a time.
#
# We set up the Tensors to be a dictionary of features mapping from their string name to the tensor value.
#
# Note that the `_input_fn()` function is wrapped, enabling it to be used for different files.
#
# NOTE: This reads from the input file directly via TensorFlow, rather than using an intermediate tool such as pandas to load the entire dataset into memory first. This is done to enable the system to scale to large inputs.
# ## More about input functions
#
# The input function is how we will feed the input data into the model during training and evaluation.
# The structure that must be returned is a pair, where the first element is a dict of the column names (features) mapped to a tensor of values, and the 2nd element is a tensor of values representing the answers (labels). Recall that a tensor is just a general term for an n-dimensional array.
#
# This could be represented as: `map(column_name => [Tensor of values]) , [Tensor of labels])`
#
# More concretely, for this particular dataset, something like this:
#
# {
# 'age': [ 39, 50, 38, 53, 28, … ],
# 'marital_status': [ 'Married-civ-spouse', 'Never-married', 'Widowed', 'Widowed' … ],
# ...
# 'gender': ['Male', 'Female', 'Male', 'Male', 'Female',, … ],
# } ,
# [ 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1]
#
# Additionally, we define which columns of the input data we will treat as categorical vs continuous, using the global `CATEGORICAL_COLUMNS`.
#
# You can try different values for `BATCH_SIZE` to see how they impact your results
# +
BATCH_SIZE = 40
def generate_input_fn(filename, batch_size=BATCH_SIZE):
def _input_fn():
filename_queue = tf.train.string_input_producer([filename])
reader = tf.TextLineReader()
# Reads out batch_size number of lines
key, value = reader.read_up_to(filename_queue, num_records=batch_size)
# record_defaults should match the datatypes of each respective column.
record_defaults = [[0], [" "], [0], [" "], [0],
[" "], [" "], [" "], [" "], [" "],
[0], [0], [0], [" "], [" "]]
# Decode CSV data that was just read out.
columns = tf.decode_csv(
value, record_defaults=record_defaults)
# features is a dictionary that maps from column names to tensors of the data.
# income_bracket is the last column of the data. Note that this is NOT a dict.
all_columns = dict(zip(COLUMNS, columns))
# Save the income_bracket column as our labels
# dict.pop() returns the popped array of income_bracket values
income_bracket = all_columns.pop('income_bracket')
# remove the fnlwgt key, which is not used
all_columns.pop('fnlwgt', 'fnlwgt key not found')
# the remaining columns are our features
features = all_columns
# Sparse categorical features must be represented with an additional dimension.
# There is no additional work needed for the Continuous columns; they are the unaltered columns.
# See docs for tf.SparseTensor for more info
for feature_name in CATEGORICAL_COLUMNS:
# Requires tensorflow >= 0.12
features[feature_name] = tf.expand_dims(features[feature_name], -1)
# Convert ">50K" to 1, and "<=50K" to 0
labels = tf.to_int32(tf.equal(income_bracket, " >50K"))
return features, labels
return _input_fn
print('input function configured')
# -
# # Create Feature Columns
# This section configures the model with the information about the model. There are many parameters here to experiment with to see how they affect the accuracy.
#
# This is the bulk of the time and energy that is often spent on making a machine learning model work, called *feature selection* or *feature engineering*. We choose the features (columns) we will use for training, and apply any additional transformations to them as needed.
# ### Sparse Columns
# First we build the sparse columns.
#
# Use `sparse_column_with_keys()` for columns that we know all possible values for.
#
# Use `sparse_column_with_hash_bucket()` for columns that we want the the library to automatically map values for us.
# +
# Sparse base columns.
gender = tf.contrib.layers.sparse_column_with_keys(column_name="gender",
keys=["female", "male"])
race = tf.contrib.layers.sparse_column_with_keys(column_name="race",
keys=["Amer-Indian-Eskimo",
"Asian-Pac-Islander",
"Black", "Other",
"White"])
education = tf.contrib.layers.sparse_column_with_hash_bucket(
"education", hash_bucket_size=1000)
marital_status = tf.contrib.layers.sparse_column_with_hash_bucket(
"marital_status", hash_bucket_size=100)
relationship = tf.contrib.layers.sparse_column_with_hash_bucket(
"relationship", hash_bucket_size=100)
workclass = tf.contrib.layers.sparse_column_with_hash_bucket(
"workclass", hash_bucket_size=100)
occupation = tf.contrib.layers.sparse_column_with_hash_bucket(
"occupation", hash_bucket_size=1000)
native_country = tf.contrib.layers.sparse_column_with_hash_bucket(
"native_country", hash_bucket_size=1000)
print('Sparse columns configured')
# -
# ### Continuous columns
# Second, configure the real-valued columns using `real_valued_column()`.
# +
# Continuous base columns.
age = tf.contrib.layers.real_valued_column("age")
education_num = tf.contrib.layers.real_valued_column("education_num")
capital_gain = tf.contrib.layers.real_valued_column("capital_gain")
capital_loss = tf.contrib.layers.real_valued_column("capital_loss")
hours_per_week = tf.contrib.layers.real_valued_column("hours_per_week")
print('continuous columns configured')
# -
# ### Transformations
# Now for the interesting stuff. We will employ a couple of techniques to get even more out of the data.
#
# * **bucketizing** turns what would have otherwise been a continuous feature into a categorical one.
# * **feature crossing** allows us to compute a model weight for specific pairings across columns, rather than learning them as independently. This essentially encodes related columns together, for situations where having 2 (or more) columns being certain values is meaningful.
#
# Only categorical features can be crossed. This is one reason why age has been bucketized.
#
# For example, crossing education and occupation would enable the model to learn about:
#
# education="Bachelors" AND occupation="Exec-managerial"
#
# or perhaps
#
# education="Bachelors" AND occupation="Craft-repair"
#
# We do a few combined features (feature crosses) here.
#
# Add your own, based on your intuitions about the dataset, to try to improve on the model!
# +
# Transformations.
age_buckets = tf.contrib.layers.bucketized_column(age,
boundaries=[ 18, 25, 30, 35, 40, 45, 50, 55, 60, 65 ])
education_occupation = tf.contrib.layers.crossed_column([education, occupation],
hash_bucket_size=int(1e4))
age_race_occupation = tf.contrib.layers.crossed_column([age_buckets, race, occupation],
hash_bucket_size=int(1e6))
country_occupation = tf.contrib.layers.crossed_column([native_country, occupation],
hash_bucket_size=int(1e4))
print('Transformations complete')
# -
# ### Group feature columns into 2 objects
#
# The wide columns are the sparse, categorical columns that we specified, as well as our hashed, bucket, and feature crossed columns.
#
# The deep columns are composed of embedded categorical columns along with the continuous real-valued columns. **Column embeddings** transform a sparse, categorical tensor into a low-dimensional and dense real-valued vector. The embedding values are also trained along with the rest of the model. For more information about embeddings, see the TensorFlow tutorial on [Vector Representations Words](https://www.tensorflow.org/tutorials/word2vec/), or [Word Embedding](https://en.wikipedia.org/wiki/Word_embedding) on Wikipedia.
#
# The higher the dimension of the embedding is, the more degrees of freedom the model will have to learn the representations of the features. We are starting with an 8-dimension embedding for simplicity, but later you can come back and increase the dimensionality if you wish.
#
#
# +
# Wide columns and deep columns.
wide_columns = [gender, race, native_country,
education, occupation, workclass,
marital_status, relationship,
age_buckets, education_occupation,
age_race_occupation, country_occupation]
deep_columns = [
tf.contrib.layers.embedding_column(workclass, dimension=8),
tf.contrib.layers.embedding_column(education, dimension=8),
tf.contrib.layers.embedding_column(marital_status, dimension=8),
tf.contrib.layers.embedding_column(gender, dimension=8),
tf.contrib.layers.embedding_column(relationship, dimension=8),
tf.contrib.layers.embedding_column(race, dimension=8),
tf.contrib.layers.embedding_column(native_country, dimension=8),
tf.contrib.layers.embedding_column(occupation, dimension=8),
age,
education_num,
capital_gain,
capital_loss,
hours_per_week,
]
print('wide and deep columns configured')
# -
# # Create the model
#
# You can train either a "wide" model, a "deep" model, or a "wide and deep" model, using the classifiers below. Try each one and see what kind of results you get.
#
# * **Wide**: Linear Classifier
# * **Deep**: Deep Neural Net Classifier
# * **Wide & Deep**: Combined Linear and Deep Classifier
#
# The `hidden_units` or `dnn_hidden_units` argument is to specify the size of each layer of the deep portion of the network. For example, `[12, 20, 15]` would create a network with the first layer of size 12, the second layer of size 20, and a third layer of size 15.
# +
def create_model_dir(model_type):
return 'models/model_' + model_type + '_' + str(int(time.time()))
# If new_model=False, pass in the desired model_dir
def get_model(model_type, new_model=True, model_dir=None):
if new_model or model_dir is None:
model_dir = create_model_dir(model_type) # Comment out this line to continue training a existing model
print("Model directory = %s" % model_dir)
m = None
# Linear Classifier
if model_type == 'WIDE':
m = tf.contrib.learn.LinearClassifier(
model_dir=model_dir,
feature_columns=wide_columns)
# Deep Neural Net Classifier
if model_type == 'DEEP':
m = tf.contrib.learn.DNNClassifier(
model_dir=model_dir,
feature_columns=deep_columns,
hidden_units=[100, 50])
# Combined Linear and Deep Classifier
if model_type == 'WIDE_AND_DEEP':
m = tf.contrib.learn.DNNLinearCombinedClassifier(
model_dir=model_dir,
linear_feature_columns=wide_columns,
dnn_feature_columns=deep_columns,
dnn_hidden_units=[100, 70, 50, 25])
print('estimator built')
return m, model_dir
m, model_dir = get_model(model_type = 'WIDE_AND_DEEP')
# -
# # Fit the model (train it)
#
# Run `fit()` to train the model. You can experiment with the `train_steps` and `BATCH_SIZE` parameters.
#
# This can take some time, depending on the values chosen for `train_steps` and `BATCH_SIZE`.
#
# Our datafile is hosted on Google Cloud Storage; the reader we created at the beginning knows how to read from it.
#
# If you don't want to download a new copy of the dataset each time your script runs, you can download it locally using
#
# gsutil cp gs://cloudml-public/census/data/adult.data.csv .
# gsutil cp gs://cloudml-public/census/data/adult.test.csv .
# +
train_file = "adult.data.csv" # "gs://cloudml-public/census/data/adult.data.csv"
test_file = "adult.test.csv" # "gs://cloudml-public/census/data/adult.test.csv"
train_steps = 1000
m.fit(input_fn=generate_input_fn(train_file, BATCH_SIZE), steps=train_steps)
print('fit done')
# -
# # Evaluate the accuracy of the model
# Let's see how the model did. We will evaluate all the test data.
# +
results = m.evaluate(input_fn=generate_input_fn(test_file), steps=100)
print('evaluate done')
print('Accuracy: %s' % results['accuracy'])
# -
# # Export model
# We can upload our trained model to the Cloud Machine Learning Engine's Prediction Service, which will take care of serving our model and scaling it. The code below exports our trained model to a `saved_model.pb` file and a `variables` folder where the trained weights are stored.
#
# The `export_savedmodel()` function expects a `serving_input_fn()`, which returns the mapping from the data that the Prediction Service passes in to the data that should be fed into the trained TensorFlow prediction graph.
# +
from tensorflow.contrib.learn.python.learn.utils import input_fn_utils
def column_to_dtype(column):
if column in CATEGORICAL_COLUMNS:
return tf.string
else:
return tf.float32
def serving_input_fn():
feature_placeholders = {
column: tf.placeholder(column_to_dtype(column), [None])
for column in FEATURE_COLUMNS
}
# DNNCombinedLinearClassifier expects rank 2 Tensors, but inputs should be
# rank 1, so that we can provide scalars to the server
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return input_fn_utils.InputFnOps(
features, # input into graph
None,
feature_placeholders # tensor input converted from request
)
export_folder = m.export_savedmodel(
export_dir_base = model_dir + '/exports',
input_fn=serving_input_fn
)
print('model exported successfully to {}'.format(export_folder))
# -
# # Conclusions
#
# In this Juypter notebook, we have configured, created, and evaluated a Wide & Deep machine learning model, that combines the powers of a Linear Classifier with a Deep Neural Network, using TensorFlow's tf.learn module.
#
# Upon completing training, you exported the trained classifier to a format suitable for running predictions.
#
# With this working example in your toolbelt, you are ready to explore the wide (and deep) world of machine learning with TensorFlow! Some ideas to help you get going:
# * Change the features we used today. Which columns do you think are correlated and should be crossed? Which ones do you think are just adding noise and could be removed to clean up the model?
# * Swap in an entirely new dataset! There are many dataset available on the web, or use a dataset you possess! Check out https://archive.ics.uci.edu/ml to find your own dataset.
| workshop_sections/wide_n_deep/wide_n_deep_flow.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import random
import sys
from termcolor import colored
def print_menu():
print("Let's Play Wordle:")
print("Type a 5 letter word and hit enter!")
def read_random_word():
with open("wordsp.txt") as f:
words = f.read().splitlines()
return random.choice(words)
print_menu()
word = read_random_word()
for attempt in range(1,7):
guess = input().lower()
for i in range(min(len(guess),5)):
if guess[i] == word[i]:
print(colored(guess[i],"green"),end = " ")
elif guess[i] in word:
print(colored(guess[i],"yellow"),end = " ")
else:
print(guess[i],end=" ")
if guess == word :
print(colored(f"Congrats! You got the words in {attempt} guesses" , "red"))
break
print(f"Sorry!, you could not guess the word!! , the word was {word}")
# -
pip install termcolor
| Wordle_clone.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Vanilla RNNs, GRUs and the `scan` function
# In this notebook, you will learn how to define the forward method for vanilla RNNs and GRUs. Additionally, you will see how to define and use the function `scan` to compute forward propagation for RNNs.
#
# By completing this notebook, you will:
#
# - Be able to define the forward method for vanilla RNNs and GRUs
# - Be able to define the `scan` function to perform forward propagation for RNNs
# - Understand how forward propagation is implemented for RNNs.
import numpy as np
from numpy import random
from time import perf_counter
# An implementation of the `sigmoid` function is provided below so you can use it in this notebook.
def sigmoid(x): # Sigmoid function
return 1.0 / (1.0 + np.exp(-x))
# # Part 1: Forward method for vanilla RNNs and GRUs
# In this part of the notebook, you'll see the implementation of the forward method for a vanilla RNN and you'll implement that same method for a GRU. For this excersice you'll use a set of random weights and variables with the following dimensions:
#
# - Embedding size (`emb`) : 128
# - Hidden state size (`h_dim`) : (16,1)
#
# The weights `w_` and biases `b_` are initialized with dimensions (`h_dim`, `emb + h_dim`) and (`h_dim`, 1). We expect the hidden state `h_t` to be a column vector with size (`h_dim`,1) and the initial hidden state `h_0` is a vector of zeros.
random.seed(10) # Random seed, so your results match ours
emb = 128 # Embedding size
T = 256 # Number of variables in the sequences
h_dim = 16 # Hidden state dimension
h_0 = np.zeros((h_dim, 1)) # Initial hidden state
# Random initialization of weights and biases
w1 = random.standard_normal((h_dim, emb+h_dim))
w2 = random.standard_normal((h_dim, emb+h_dim))
w3 = random.standard_normal((h_dim, emb+h_dim))
b1 = random.standard_normal((h_dim, 1))
b2 = random.standard_normal((h_dim, 1))
b3 = random.standard_normal((h_dim, 1))
X = random.standard_normal((T, emb, 1))
weights = [w1, w2, w3, b1, b2, b3]
# ## 1.1 Forward method for vanilla RNNs
# The vanilla RNN cell is quite straight forward. Its most general structure is presented in the next figure:
#
# <img src="RNN.PNG" width="400"/>
#
# As you saw in the lecture videos, the computations made in a vanilla RNN cell are equivalent to the following equations:
#
# \begin{equation}
# h^{<t>}=g(W_{h}[h^{<t-1>},x^{<t>}] + b_h)
# \label{eq: htRNN}
# \end{equation}
#
# \begin{equation}
# \hat{y}^{<t>}=g(W_{yh}h^{<t>} + b_y)
# \label{eq: ytRNN}
# \end{equation}
#
# where $[h^{<t-1>},x^{<t>}]$ means that $h^{<t-1>}$ and $x^{<t>}$ are concatenated together. In the next cell we provide the implementation of the forward method for a vanilla RNN.
def forward_V_RNN(inputs, weights): # Forward propagation for a a single vanilla RNN cell
x, h_t = inputs
# weights.
wh, _, _, bh, _, _ = weights
# new hidden state
h_t = np.dot(wh, np.concatenate([h_t, x])) + bh
h_t = sigmoid(h_t)
return h_t, h_t
# As you can see, we omitted the computation of $\hat{y}^{<t>}$. This was done for the sake of simplicity, so you can focus on the way that hidden states are updated here and in the GRU cell.
# ## 1.2 Forward method for GRUs
# A GRU cell have more computations than the ones that vanilla RNNs have. You can see this visually in the following diagram:
#
# <img src="GRU.PNG" width="400"/>
#
# As you saw in the lecture videos, GRUs have relevance $\Gamma_r$ and update $\Gamma_u$ gates that control how the hidden state $h^{<t>}$ is updated on every time step. With these gates, GRUs are capable of keeping relevant information in the hidden state even for long sequences. The equations needed for the forward method in GRUs are provided below:
#
# \begin{equation}
# \Gamma_r=\sigma{(W_r[h^{<t-1>}, x^{<t>}]+b_r)}
# \end{equation}
#
# \begin{equation}
# \Gamma_u=\sigma{(W_u[h^{<t-1>}, x^{<t>}]+b_u)}
# \end{equation}
#
# \begin{equation}
# c^{<t>}=\tanh{(W_h[\Gamma_r*h^{<t-1>},x^{<t>}]+b_h)}
# \end{equation}
#
# \begin{equation}
# h^{<t>}=\Gamma_u*c^{<t>}+(1-\Gamma_u)*h^{<t-1>}
# \end{equation}
#
# In the next cell, please implement the forward method for a GRU cell by computing the update `u` and relevance `r` gates, and the candidate hidden state `c`.
def forward_GRU(inputs, weights): # Forward propagation for a single GRU cell
x, h_t = inputs
# weights.
wu, wr, wc, bu, br, bc = weights
# Update gate
### START CODE HERE (1-2 lINES) ###
u = np.dot(wu, np.concatenate([h_t, x])) + bu
u = sigmoid(u)
### END CODE HERE ###
# Relevance gate
### START CODE HERE (1-2 lINES) ###
r = np.dot(wr, np.concatenate([h_t, x])) + br
r = sigmoid(u)
### END CODE HERE ###
# Candidate hidden state
### START CODE HERE (1-2 lINES) ###
c = np.dot(wc, np.concatenate([r * h_t, x])) + bc
c = np.tanh(c)
### END CODE HERE ###
# New Hidden state h_t
h_t = u* c + (1 - u)* h_t
return h_t, h_t
# Run the following cell to check your implementation.
forward_GRU([X[1],h_0], weights)[0]
# Expected output:
# <pre>
# array([[ 9.77779014e-01],
# [-9.97986240e-01],
# [-5.19958083e-01],
# [-9.99999886e-01],
# [-9.99707004e-01],
# [-3.02197037e-04],
# [-9.58733503e-01],
# [ 2.10804828e-02],
# [ 9.77365398e-05],
# [ 9.99833090e-01],
# [ 1.63200940e-08],
# [ 8.51874303e-01],
# [ 5.21399924e-02],
# [ 2.15495959e-02],
# [ 9.99878828e-01],
# [ 9.77165472e-01]])
# </pre>
# # Part 2: Implementation of the `scan` function
# In the lectures you saw how the `scan` function is used for forward propagation in RNNs. It takes as inputs:
#
# - `fn` : the function to be called recurrently (i.e. `forward_GRU`)
# - `elems` : the list of inputs for each time step (`X`)
# - `weights` : the parameters needed to compute `fn`
# - `h_0` : the initial hidden state
#
# `scan` goes through all the elements `x` in `elems`, calls the function `fn` with arguments ([`x`, `h_t`],`weights`), stores the computed hidden state `h_t` and appends the result to a list `ys`. Complete the following cell by calling `fn` with arguments ([`x`, `h_t`],`weights`).
def scan(fn, elems, weights, h_0=None): # Forward propagation for RNNs
h_t = h_0
ys = []
for x in elems:
### START CODE HERE (1 lINE) ###
y, h_t = fn([x, h_t], weights)
### END CODE HERE ###
ys.append(y)
return ys, h_t
# # Part 3: Comparison between vanilla RNNs and GRUs
# You have already seen how forward propagation is computed for vanilla RNNs and GRUs. As a quick recap, you need to have a forward method for the recurrent cell and a function like `scan` to go through all the elements from a sequence using a forward method. You saw that GRUs performed more computations than vanilla RNNs, and you can check that they have 3 times more parameters. In the next two cells, we compute forward propagation for a sequence with 256 time steps (`T`) for an RNN and a GRU with the same hidden state `h_t` size (`h_dim`=16).
# vanilla RNNs
tic = perf_counter()
ys, h_T = scan(forward_V_RNN, X, weights, h_0)
toc = perf_counter()
RNN_time=(toc-tic)*1000
print (f"It took {RNN_time:.2f}ms to run the forward method for the vanilla RNN.")
# GRUs
tic = perf_counter()
ys, h_T = scan(forward_GRU, X, weights, h_0)
toc = perf_counter()
GRU_time=(toc-tic)*1000
print (f"It took {GRU_time:.2f}ms to run the forward method for the GRU.")
# As you were told in the lectures, GRUs take more time to compute (However, sometimes, although a rare occurrence, Vanilla RNNs take more time. Can you figure out what might cause this ?). This means that training and prediction would take more time for a GRU than for a vanilla RNN. However, GRUs allow you to propagate relevant information even for long sequences, so when selecting an architecture for NLP you should assess the tradeoff between computational time and performance.
# <b>Congratulations!</b> Now you know how the forward method is implemented for vanilla RNNs and GRUs, and you know how the scan function provides an abstraction for forward propagation in RNNs.
| Natural Language Processing/Course 3 - Natural Language Processing with Sequence Models/Labs/Week 2/Vanilla RNNs, GRUs and the scan function.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # Celeribity Recognition using Amazon Rekognition
#
# This notebook provides a walkthrough of [celebrity recognition API](https://docs.aws.amazon.com/rekognition/latest/dg/celebrities.html) in Amazon Rekognition. You can quickly identify well known people in your video and image libraries to catalog footage and photos for marketing, advertising, and media industry use cases.
# # Initialize stuff
# Initialise Notebook
import boto3
from IPython.display import HTML, display, Image as IImage
from PIL import Image, ImageDraw, ImageFont
import time
import os
# +
import sagemaker
sagemaker_session = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = sagemaker_session.default_bucket()
# +
# Curent AWS Region. Use this to choose corresponding S3 bucket with sample content
mySession = boto3.session.Session()
awsRegion = mySession.region_name
# -
# Init clients
rekognition = boto3.client("rekognition")
s3 = boto3.client("s3")
# +
# S3 bucket that contains sample images and videos
# We are providing sample images and videos in this bucket so
# you do not have to manually download/upload test images and videos.
bucketName = bucket
# +
# Create temporary directory
# This directory is not needed to call Rekognition APIs.
# We will only use this directory to download images from S3 bucket and draw bounding boxes
# around recognized celebrities to show them here in the notebook.
# !mkdir -p m1tmp
tempFolder = "m1tmp/"
# -
# # Recognize celebrities in image
# ***
imageName = "content-moderation/media/GrandTourjc.png"
display(IImage(url=s3.generate_presigned_url("get_object", Params={"Bucket": bucketName, "Key": imageName})))
# #### Call Rekognition to recognize celebrities in the image
# +
# Call Amazon Rekognition to recognize celebrities in the image
# https://docs.aws.amazon.com/rekognition/latest/dg/API_RecognizeCelebrities.html
recognizeCelebritiesResponse = rekognition.recognize_celebrities(
Image={
"S3Object": {
"Bucket": bucketName,
"Name": imageName,
}
}
)
# -
# #### Review the raw JSON reponse from Rekognition
# +
# Show JSON response returned by Rekognition Celebrity Recognition API
# In the JSON response below, you will see CelebrityFaces which contains information about recognized celebrities.
# For each recognized celebrity, you will see information like Name, Id, Urls and additional information about
# their facial attributes.
display(recognizeCelebritiesResponse)
# -
# #### Show image with bounding boxes around recognized celebrities
# +
# Define a function that will display image with bounded boxes around recognized celebrites
# We will call this function in next step
def drawBoundingBoxes(sourceImage, boxes):
# blue, green, red, grey
colors = ((255, 255, 255), (255, 255, 255), (76, 182, 252), (52, 194, 123))
# Download image locally
imageLocation = tempFolder + os.path.basename(sourceImage)
s3.download_file(bucketName, sourceImage, imageLocation)
# Draws BB on Image
bbImage = Image.open(imageLocation)
draw = ImageDraw.Draw(bbImage)
width, height = bbImage.size
col = 0
maxcol = len(colors)
line = 3
for box in boxes:
x1 = int(box[1]["Left"] * width)
y1 = int(box[1]["Top"] * height)
x2 = int(box[1]["Left"] * width + box[1]["Width"] * width)
y2 = int(box[1]["Top"] * height + box[1]["Height"] * height)
draw.text((x1, y1), box[0], colors[col])
for l in range(line):
draw.rectangle((x1 - l, y1 - l, x2 + l, y2 + l), outline=colors[col])
col = (col + 1) % maxcol
imageFormat = "PNG"
ext = sourceImage.lower()
if ext.endswith("jpg") or ext.endswith("jpeg"):
imageFormat = "JPEG"
bbImage.save(imageLocation, format=imageFormat)
display(bbImage)
# +
# Extract bounding box information from JSON response above and display image with bounding boxes around celebrites.
boxes = []
celebrities = recognizeCelebritiesResponse["CelebrityFaces"]
for celebrity in celebrities:
boxes.append((celebrity["Name"], celebrity["Face"]["BoundingBox"]))
drawBoundingBoxes(imageName, boxes)
# -
# # Recognize celebrities in video
# Celebrity recognition in video is an async operation.
# https://docs.aws.amazon.com/rekognition/latest/dg/API_StartCelebrityRecognition.html
# - We first start celebrity recognition job which returns a Job Id.
# - We can then call `get_celebrity_recognition` to get the job status and after job is complete, we can get celebrity metadata.
# - In production use cases, you would usually use StepFucntion or SNS topic to get notified when job is complete.
# ***
videoName = "content-moderation/media/GrandTour720.mp4"
# #### Call Rekognition to start a job for celebrity rekognition
# +
# Start celebrity recognition job
startCelebrityRekognition = rekognition.start_celebrity_recognition(
Video={
"S3Object": {
"Bucket": bucketName,
"Name": videoName,
}
},
)
celebrityJobId = startCelebrityRekognition["JobId"]
display("Job Id: {0}".format(celebrityJobId))
# -
# #### Wait for celebrity rekognition job to complete
# +
# %%time
# Wait for celebrity recognition job to complete
# In production use cases, you would usually use StepFucntion or SNS topic to get notified when job is complete.
getCelebrityRecognition = rekognition.get_celebrity_recognition(JobId=celebrityJobId, SortBy="TIMESTAMP")
while getCelebrityRecognition["JobStatus"] == "IN_PROGRESS":
time.sleep(5)
print(".", end="")
getCelebrityRecognition = rekognition.get_celebrity_recognition(JobId=celebrityJobId, SortBy="TIMESTAMP")
display(getCelebrityRecognition["JobStatus"])
# -
# #### Review raw JSON reponse from Rekognition
# +
# Show JSON response returned by Rekognition Celebrity Recognition API
# In the JSON response below, you will see list Celebrities which contains information about recognized celebrities.
# For each recognized celebrity, you will see information like Timestamp, Name, Id, Urls
# and additional information about their facial attributes.
display(getCelebrityRecognition)
# -
# #### Dislpay names of recognized celebrities in the video
# +
theCelebs = {}
# Display timestamps and celebrites detected at that time
strDetail = "Celebrites detected in video<br>=======================================<br>"
strOverall = "Celebrities in the overall video:<br>=======================================<br>"
# Celebrities detected in each frame
for celebrity in getCelebrityRecognition["Celebrities"]:
if "Celebrity" in celebrity:
cconfidence = celebrity["Celebrity"]["Confidence"]
if cconfidence > 95:
ts = celebrity["Timestamp"]
cname = celebrity["Celebrity"]["Name"]
strDetail = strDetail + "At {} ms: {} (Confidence: {})<br>".format(ts, cname, round(cconfidence, 2))
if not cname in theCelebs:
theCelebs[cname] = cname
# Unique faces detected in video
for theCeleb in theCelebs:
strOverall = strOverall + "Name: {}<br>".format(theCeleb)
# Display results
display(HTML(strOverall))
# display(HTML(strDetail))
# -
# #### Show video in the player
# +
# Show video in a player
s3FilePrefix = "https://s3.amazonaws.com"
if not awsRegion == "us-east-1":
s3FilePrefix = "https://s3-{}.amazonaws.com".format(awsRegion)
s3VideoUrl = "{0}/{1}/{2}".format(s3FilePrefix, bucketName, videoName)
videoTag = "<video controls='controls' autoplay width='640' height='360' name='Video' src='{0}'></video>".format(
s3VideoUrl
)
videoui = "<table><tr><td style='vertical-align: top'>{}</td><td>{}</td></tr></table>".format(videoTag, strDetail)
display(HTML(videoui))
# -
# ## Try recognizing custom celebrities
# ***
# +
# Now let us try an image with non-celebrities in the image.
customCelebrityImageName = "content-moderation/media/serverless-bytes.png"
# -
display(
IImage(url=s3.generate_presigned_url("get_object", Params={"Bucket": bucketName, "Key": customCelebrityImageName}))
)
# +
# Call Amazon Rekognition to recognize celebrities in the image
customCelebrityResponse = rekognition.recognize_celebrities(
Image={
"S3Object": {
"Bucket": bucketName,
"Name": customCelebrityImageName,
}
}
)
# +
# Display Rekognition response
# You will see Rekognition return an empty list for CelebrityFaces and
# UnrecognizedFaces list with unrecognized faces that were detected in the image.
# In the next module you will learn how to get custom-celebrity faces recognized.
display(customCelebrityResponse)
# +
# Show image and bounded boxes around detected faces
# Extract BB info from response
cboxes = []
faces = customCelebrityResponse["UnrecognizedFaces"]
for face in faces:
cboxes.append(("Unrecognized Face", face["BoundingBox"]))
drawBoundingBoxes(customCelebrityImageName, cboxes)
# -
# ***
# ### References
# - https://docs.aws.amazon.com/rekognition/latest/dg/celebrities.html
# - https://docs.aws.amazon.com/rekognition/latest/dg/API_RecognizeCelebrities.html
# - https://docs.aws.amazon.com/rekognition/latest/dg/API_StartCelebrityRecognition.html
# - https://docs.aws.amazon.com/rekognition/latest/dg/API_GetCelebrityRecognition.html
#
# ***
# You have successfully used Amazon Rekognition to identify celebrities in images an videos. In the next module, Recognize Custom Celebrities, you will learn how to recognize your custom celebrities in the images and videos.
| 02_usecases/archive/05_Celebrity_Detection.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# .. _registrikood_userguide:
#
# Registrikood Strings
# ============
# + active=""
# Introduction
# ------------
#
# The function :func:`clean_ee_registrikood() <dataprep.clean.clean_ee_registrikood.clean_ee_registrikood>` cleans a column containing Estonian organisation registration code (Registrikood) strings, and standardizes them in a given format. The function :func:`validate_ee_registrikood() <dataprep.clean.clean_ee_registrikood.validate_ee_registrikood>` validates either a single Registrikood strings, a column of Registrikood strings or a DataFrame of Registrikood strings, returning `True` if the value is valid, and `False` otherwise.
# -
# Registrikood strings can be converted to the following formats via the `output_format` parameter:
#
# * `compact`: only number strings without any seperators or whitespace, like "12345678"
# * `standard`: Registrikood strings with proper whitespace in the proper places. Note that in the case of Registrikood, the compact format is the same as the standard one.
#
# Invalid parsing is handled with the `errors` parameter:
#
# * `coerce` (default): invalid parsing will be set to NaN
# * `ignore`: invalid parsing will return the input
# * `raise`: invalid parsing will raise an exception
#
# The following sections demonstrate the functionality of `clean_ee_registrikood()` and `validate_ee_registrikood()`.
# ### An example dataset containing Registrikood strings
import pandas as pd
import numpy as np
df = pd.DataFrame(
{
"registrikood": [
'12345678',
'12345679',
'BE 428759497',
'BE431150351',
"002 724 334",
"hello",
np.nan,
"NULL",
],
"address": [
"123 Pine Ave.",
"main st",
"1234 west main heights 57033",
"apt 1 789 s maple rd manhattan",
"robie house, 789 north main street",
"1111 S Figueroa St, Los Angeles, CA 90015",
"(staples center) 1111 S Figueroa St, Los Angeles",
"hello",
]
}
)
df
# ## 1. Default `clean_ee_registrikood`
#
# By default, `clean_ee_registrikood` will clean registrikood strings and output them in the standard format with proper separators.
from dataprep.clean import clean_ee_registrikood
clean_ee_registrikood(df, column = "registrikood")
# ## 2. Output formats
# This section demonstrates the output parameter.
# ### `standard` (default)
clean_ee_registrikood(df, column = "registrikood", output_format="standard")
# ### `compact`
clean_ee_registrikood(df, column = "registrikood", output_format="compact")
# ## 3. `inplace` parameter
#
# This deletes the given column from the returned DataFrame.
# A new column containing cleaned Registrikood strings is added with a title in the format `"{original title}_clean"`.
clean_ee_registrikood(df, column="registrikood", inplace=True)
# ## 4. `errors` parameter
# ### `coerce` (default)
clean_ee_registrikood(df, "registrikood", errors="coerce")
# ### `ignore`
clean_ee_registrikood(df, "registrikood", errors="ignore")
# ## 4. `validate_ee_registrikood()`
# `validate_ee_registrikood()` returns `True` when the input is a valid Registrikood. Otherwise it returns `False`.
#
# The input of `validate_ee_registrikood()` can be a string, a Pandas DataSeries, a Dask DataSeries, a Pandas DataFrame and a dask DataFrame.
#
# When the input is a string, a Pandas DataSeries or a Dask DataSeries, user doesn't need to specify a column name to be validated.
#
# When the input is a Pandas DataFrame or a dask DataFrame, user can both specify or not specify a column name to be validated. If user specify the column name, `validate_ee_registrikood()` only returns the validation result for the specified column. If user doesn't specify the column name, `validate_ee_registrikood()` returns the validation result for the whole DataFrame.
from dataprep.clean import validate_ee_registrikood
print(validate_ee_registrikood("12345678"))
print(validate_ee_registrikood("12345679"))
print(validate_ee_registrikood('BE 428759497'))
print(validate_ee_registrikood('BE431150351'))
print(validate_ee_registrikood("004085616"))
print(validate_ee_registrikood("hello"))
print(validate_ee_registrikood(np.nan))
print(validate_ee_registrikood("NULL"))
# ### Series
validate_ee_registrikood(df["registrikood"])
# ### DataFrame + Specify Column
validate_ee_registrikood(df, column="registrikood")
# ### Only DataFrame
validate_ee_registrikood(df)
| docs/source/user_guide/clean/clean_ee_registrikood.ipynb |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.