code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !python -mpip install --quiet fitparse==1.2.0
# +
from fitparse import FitFile
def to_deg(semicircles):
return semicircles * (180 / 2 ** 31)
fitfile = FitFile("5006234923.fit")
positions = [
(
to_deg(record.get_value("position_lat")),
to_deg(record.get_value("position_long")),
)
for record in fitfile.get_messages("record")
]
session = next(fitfile.get_messages(name="session"))
timestamp = session.get_value("timestamp")
start_position = (
to_deg(session.get_value("start_position_lat")),
to_deg(session.get_value("start_position_long")),
)
total_distance = session.get_value("total_distance")
print("timestamp", timestamp)
print("start_position", start_position)
print("total_distance", total_distance)
# +
from statistics import mean
lats, longs = zip(*positions)
mean_position = (mean(lats), mean(longs))
# +
import folium
m = folium.Map(mean_position, zoom_start=14)
for position in positions:
folium.Circle(position, radius=1).add_to(m)
m
# +
import altair as alt
import pandas as pd
data = pd.DataFrame(
(
(record.get_value("timestamp"), record.get_value("speed"))
for record in fitfile.get_messages("record")
),
columns=["timestamp", "speed"],
)
alt.Chart(data).mark_line().encode(
x="timestamp", y="speed",
)
| fitparse-visualisation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
import re
plt.close('all')
from evaluate import *
# +
examplesDf = getExamplesDf('../../datasets/test.csv')
examplesSize = examplesDf.shape[0]
print('examplesDf ', examplesDf.shape)
mfogDF = getMatchesDf('../../out/ond-1matches.csv')
print('mfogDF ', mfogDF.shape)
# minasDF = getMatchesDf('../../out/minas-og/2020-07-20T18-36-59.803/matches.csv')
minasDF = getMatchesDf('../../out/revised-java.log')
print('minasDF ', minasDF.shape)
# ogdf = getOriginalMatchesDf('../../out/minas-og/2020-07-20T12-21-54.755/results')
# print('ogdf ', ogdf.shape)
# newMatDF = getMatchesDf('../../out/minas-og/2020-07-22T21-46-01.167/matches.csv')
# diffMinasMfog(examplesDf, minasDF, newMatDF)
# +
mfogCF = confusionMatrix(examplesDf, mfogDF)
print('mfog hits', mfogCF[0]['hits'].sum())
minasCF = confusionMatrix(examplesDf, minasDF)
print('minas hits', minasCF[0]['hits'].sum())
# printEval(examplesDf, mfogDF)
# printEval(examplesDf, ogdf)
# printEval(examplesDf, ogndDf)
# diffMinasMfog(examplesDf, minasDF, mfogDF)
type(mfogCF)
# -
off = mfogCF[4]
merged = pd.merge(examplesDf[['id', 'class']], mfogDF[['id', 'label']], on='id', how='left')
cf = pd.crosstab(merged['class'], merged['label'], rownames=['Classes'], colnames=['Labels'])
cf
cf[sorted(list(cf.columns), key=lambda x: int(x) if x.isnumeric() else -1)]
# cf = cf.transpose()
# cf['Assigned'] = [l if l in off else c for l, c in zip(cf.index.to_list(), cf.idxmax(axis='columns'))]
# cf['Hits'] = [0 if l == '-' else cf.at[i, l] for i, l in cf['Assigned'].iteritems()]
# cf
tm = getTimeFromLog('../../experiments/online-nd.log')
resume = pd.DataFrame({
'Metric': ['Hits', 'Misses', 'Unknowns', 'Time', 'System', 'Elapsed' ],
'Value': [0.1, 0.2, 0.3, tm['user'], tm['system'], tm['elapsed'] ],
}).set_index('Metric')
tex = fixTex(resume.to_latex()).replace('{}', 'Metric').replace('Metric & \\\\\hline\n', '')
tex = tex
print(tex)
resume
# +
tex = mfogCF[0].T.to_latex()
rep = {'\\midrule': '\\hline', '\\toprule': '', '\\\\\n\\bottomrule': '', '\\\\': '\\\\\hline',}
for a in rep:
tex = tex.replace(a, rep[a])
r = re.compile(r'\{l(l+)\}')
ma = r.search(tex)
if ma:
a = ma.group(1)
b = a.replace('l', '|r')
(ma, a, b)
tex = tex.replace(ma.group(0), '{l'+b+'}')
# r.sub(, '/{id}',)
# print(tex)
print(tex)
mfogCF[0].T
# +
modelDF = getModelDf('../../datasets/model-clean.csv')
print('modelDF', modelDF.shape)
# minasFiModDF = getModelDf('../../out/minas-og/2020-07-22T01-19-11.984/model/653457_final.csv')
mfogModelDF = getModelDf('../../out/model.csv')
print('mfogModelDF', mfogModelDF.shape)
d = compareModelDf(modelDF, mfogModelDF)
print('model diff min', d.min().min())
print('model diff meanDistance', d['meanDistance'].abs().sum())
# newIni = getModelDf('../../out/minas-og/2020-07-22T21-46-01.167/model/0_initial.csv')
# newFin = getModelDf('../../out/minas-og/2020-07-22T21-46-01.167/model/653457_final.csv')
# compareModelDf(modelDF, newIni)
# compareModelDf(newIni, newFin)
# compareModelDf(mfogModelDF, newIni)
# +
# # %history -g -f ../../ref/jupyter_hist.py
# -
df = merge(examplesDf, mfogDF)
cf, classes, labels, off, assignment = confusionMatrix(df)
#
title='mfog'
df = plotHitMissUnkRate(df, assignment, off, path=None, title='mfog')
# forgotten 546
# forgotten 171
# forgotten 853
# forgotten 217
sum([546, 171, 853, 217])
# Total 665107 (100.000000%)
# ### Mfog
# Total 659249 (100.000000%)
653457 - 665107
df = getOriginalMatchesDf('../../out/og/clustream-nd/results')
df = merge(examplesDf, df)
cf, classes, labels, off, assignment = confusionMatrix(df)
df = plotHitMissUnkRate(df, assignment, off, path=None, title='Minas Clustream ND Original')
# cf
df = getMatchesDf('../../out/og/clustream-nd/matches.csv')
df = merge(examplesDf, df)
cf, classes, labels, off, assignment = confusionMatrix(df)
df = plotHitMissUnkRate(df, assignment, off, path='None', title='Minas Clustream ND Mathces')
cf
# %matplotlib widget
clustreamDfPath = '/home/puhl/project/minas-flink/mfog-mpi/out/minas-og/2020-07-27T17-13-24.304/matches.csv'
df = getMatchesDf(clustreamDfPath)
df = merge(examplesDf, df)
cf, classes, labels, off, assignment = confusionMatrix(df)
df = plotHitMissUnkRate(df, assignment, off, path=None, title='Minas Clustream ND Mathces')
labelSet = set()
xcoords = []
prevLen = len(off)
for i, l in zip(df.index, df['label']):
labelSet.add(l)
if len(labelSet) > prevLen:
prevLen = len(labelSet)
xcoords += [i]
#
if (title is not None):
title += ' Hit Miss Unk'
else:
title = 'Hit Miss Unk'
ax = df[['d_hit', 'd_mis', 'd_unk' ]].plot(title=title, figsize=figsize)
ax.vlines(x=xcoords, ymin=-0.05, ymax=1.05, colors='gray', ls='--', lw=0.5, label='vline_multiple')
ax.get_xaxis().set_major_formatter(matplotlib.ticker.EngFormatter())
# '/home/puhl/project/minas-flink/mfog-mpi/out/minas-og/2020-07-27T17-13-24.304/hits.png'
plt.show()
# +
examplesDf = getExamplesDf('../../datasets/test.csv')
countPerClass = examplesDf.groupby('class').count()[['id']]
print("Count per class")
print(countPerClass)
matchesDf = getMatchesDf('../../out/ond-1matches.csv')
assert pd.Series(['id', 'class']).isin(examplesDf.columns).all()
assert pd.Series(['id', 'label']).isin(matchesDf.columns).all()
#
merged = pd.merge(examplesDf[['id', 'class']], matchesDf[['id', 'label']], on='id', how='left')
print('NaN labels:', merged['label'].isna().sum())
# merged['label'] = merged['label'].fillna('N')
# merged
cf = pd.crosstab(merged['class'], merged['label'], rownames=['Classes (act)'], colnames=['Labels (pred)']).transpose()
classes = cf.columns.values
labels = cf.index.to_list()
off = ['-'] + [c for c in classes if c in labels]
cf['assigned'] = [l if l in off else c for l, c in zip(labels, cf.idxmax(axis='columns'))]
cf['hits'] = [0 if l == '-' else cf.at[i, l] for i, l in cf['assigned'].iteritems()]
assignment = dict([ v for v in cf['assigned'].iteritems()])
df = merged
df['assigned'] = df['label'].map(assignment)
df['hit'] = (df['assigned'] == df['class']).map({False: 0, True: 1})
df['miss'] = (df['assigned'] != df['class']).map({False: 0, True: 1})
df['unk'] = (df['assigned'] == '-').map({False: 0, True: 1})
df['miss'] = df['miss'] - df['unk']
df['hits'] = df['hit'].cumsum()
df['misses'] = df['miss'].cumsum()
df['unks'] = df['unk'].cumsum()
df['tot'] = df['hits'] + df['misses'] + df['unks']
df['d_hit'] = df['hits'] / df['tot']
df['d_mis'] = df['misses'] / df['tot']
df['d_unk'] = df['unks'] / df['tot']
last = df['d_hit'].tail(1).index.item()
hits = df['d_hit'][last]
misses = df['d_mis'][last]
unks = df['d_unk'][last]
print((('hits', hits), ('misses', misses), ('unks', unks)))
# + tags=[]
df['d_hit'][df['d_hit'].tail(1).index.item()]
# -
mfogDF = getMatchesDf('../../out/ond-1matches.csv')
# + tags=[]
mfogDF['label'].unique()
# -
| src/evaluation/evaluate.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Project 3 - Single Inheritance - Solution
# You are writing an inventory application for a budding tech guy who has a video channel featuring computer builds.
# Basically they have a pool of inventory, (for example 5 x AMD Ryzen 2-2700 CPUs) that they use for builds. When they take a CPU from the pool, they will indicate this using the object that tracks that sepcific type of CPU. They may also purchase additional CPUs, or retire some (because they overclocked it too much and burnt them out!).
# Technically we would want a database to back all this data, but here we're just going to build the classes we'll use while our program is running and not worry about retrieving or saving the state of the inventory.
# The base class is going to be a general `Resource`. This class should provide functionality common to all the actual resources (CPU, GPU, Memory, HDD, SSD) - for this exercise we're only going to implement CPU, HDD and SSD.
# It should provide this at a minimum:
# - `name` : user-friendly name of resource instance (e.g.` Intel Core i9-9900K`)
# - `manufacturer` - resource instance manufacturer (e.g. `Nvidia`)
# - `total` : inventory total (how many are in the inventory pool)
# - `allocated` : number allocated (how many are already in use)
# - a `__str__` representation that just returns the resource name
# - a mode detailed `__repr__` implementation
# - `claim(n)` : method to take n resources from the pool (as long as inventory is available)
# - `freeup(n)` : method to return n resources to the pool (e.g. disassembled some builds)
# - `died(n)` : method to return and permanently remove inventory from the pool (e.g. they broke something) - as long as total available allows it
# - `purchased(n)` - method to add inventory to the pool (e.g. they purchased a new CPU)
# - `category` - computed property that returns a lower case version of the class name
# Next we are going to define child classes for each of CPU, HDD and SDD.
# For the `CPU` class:
# - `cores` (e.g. `8`)
# - `socket` (e.g. `AM4`)
# - `power_watts` (e.g. `94`)
# For the HDD and SDD classes, we're going to create an intermediate class called `Storage` with these additional properties:
# - `capacity_GB` (e.g. `120`)
# The `HDD` class extends `Storage` and has these additional properties:
# - `size` (e.g. ``2.5"``)
# - `rpm` (e.g. `7000`)
# The `SSD` class extends `Storage` and has these additional properties:
# - `interface` (e.g. `PCIe NVMe 3.0 x4`)
# For all your classes, implement a full constructor that can be used to initialize all the properties, some form of validation on numeric types, as well as customized `__repr__` as you see fit.
# For the `total` and `allocated` values in the `Resource` init, think of the arguments there as the **current** total and allocated counts. Those `total` and `allocated` attributes should be private **read-only** properties, but they are modifiable through the various methods such as `claim`, `return`, `died` and `purchased`. Other attributes like `name`, `manufacturer_name`, etc should be read-only.
| dd_1/Part 4/Section 07 - Project 3/Project 3 - Description.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/m-aliabbas/EvolutionaryComputing/blob/master/Resnet18LastLayerPretrainTuned.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="gBB3Ll-njzgm" colab_type="code" outputId="b7de43ba-a45e-4ba8-aa06-916dd058e46f" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Load the Drive helper and mount
from google.colab import drive
# This will prompt for authorization.
drive.mount('/content/drive')
# + id="MruWNMl5kcTj" colab_type="code" colab={}
import fastai
from fastai.vision import *
import os
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# + id="VRU9HPbYkmqM" colab_type="code" colab={}
from zipfile import ZipFile
def unZip(file_name):
with ZipFile(file_name, 'r') as zip:
zip.extractall()
print('Done!')
# + id="-vBi93P3koL8" colab_type="code" colab={}
file_name = '/content/drive/chestXRay.zip'
# + id="AD77rju9kpWJ" colab_type="code" colab={}
path="/content/drive/My Drive/"
file_name=path+'chestXRay.zip'
# + id="JgaJJIBrks8H" colab_type="code" outputId="99a9d6e9-2193-4a6e-f99c-0b31ecd864e1" colab={"base_uri": "https://localhost:8080/", "height": 34}
unZip(file_name)
# + id="N9xrHB2fkudz" colab_type="code" outputId="02aba26c-eb5e-4a96-9ed9-d5e8d3930eb0" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls chest_xray
# + id="2eDHntzblbVu" colab_type="code" outputId="9f5b0be8-7b2a-44ab-d7d4-adf93ac0e053" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls
# + id="p-Eu3yZzlc2q" colab_type="code" outputId="759b95e3-c464-4539-dc25-0b0106ad07e5" colab={"base_uri": "https://localhost:8080/", "height": 34}
unZip('chest_xray.zip')
# + id="Gjm5P0h-lhra" colab_type="code" outputId="d06b9ac3-0352-4029-b3e9-b894bf41f3db" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls chest_xray
# + id="VA1uq7KUl5TN" colab_type="code" colab={}
import glob
import cv2
import numpy as np
# %matplotlib inline
filesPos= sorted(glob.glob('chest_xray/train/NORMAL/*.jpeg'))
filesNeg=sorted(glob.glob('chest_xray/train/PNEUMONIA/*.jpeg'))
# + id="G9emPBEYmCov" colab_type="code" outputId="57d93047-b428-48bc-b6f6-874e3d92a28f" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(len(filesPos),len(filesNeg))
# + id="6lAhEsxGmEbW" colab_type="code" colab={}
from fastai import *
import shutil
def copyfiles(filesName,dest):
c=0
for file in filesName:
shutil.copy(file, dest)
c+=1
print("Copied "+str(c))
# + id="rcOIZ4GfmNcg" colab_type="code" colab={}
# !mkdir dataset1
# + id="Z7fjTJp34uMl" colab_type="code" colab={}
# !mkdir dataset1/train
# + id="mRULkoAu4_FI" colab_type="code" outputId="95e02eff-50dc-46e8-e69c-218e269b334a" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls dataset1
# + id="SJqJvZDj4y8H" colab_type="code" colab={}
# !mkdir dataset1/train/PNEUMONIA
# !mkdir dataset1/train/NORMAL
# + id="fBU9J0NFmPaN" colab_type="code" outputId="5f37731a-9026-486e-c0ea-687350075120" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls dataset1/train/
# + id="NGuWNiPosuPE" colab_type="code" colab={}
filesNeg=filesNeg[:1340]
# + id="UHu4RizZYPyK" colab_type="code" colab={}
# + id="4BUii-2WoiIU" colab_type="code" colab={}
import random
random.seed(3000)
random.shuffle(filesNeg)
random.shuffle(filesPos)
# + id="vIXci3av7XDu" colab_type="code" outputId="fbdd2cb4-fae4-4893-f801-73902b276a31" colab={"base_uri": "https://localhost:8080/", "height": 34}
# !ls chest_xray
# + id="elm_4HZCsJHg" colab_type="code" outputId="d0972238-a3b1-4af1-af2e-d5b6366c7576" colab={"base_uri": "https://localhost:8080/", "height": 34}
copyfiles(filesPos,'dataset1/train/NORMAL')
# + id="ljrkYc4x7Lzz" colab_type="code" outputId="900fe042-2c45-4052-b8df-e709b0c7f3e1" colab={"base_uri": "https://localhost:8080/", "height": 34}
copyfiles(filesNeg,'dataset1/train/PNEUMONIA')
# + id="MkfLAQHu7YEb" colab_type="code" colab={}
# !mkdir dataset1/valid
# + id="w7D2OS6t7pKs" colab_type="code" colab={}
# !mkdir dataset1/test
# + id="0GJkGQ3g7tCB" colab_type="code" colab={}
# !cp -r chest_xray/val dataset1/
# + id="HX4vRhC48GTr" colab_type="code" colab={}
# !cp -r chest_xray/test dataset1/
# + id="fg54q0Ke8cTf" colab_type="code" colab={}
# !rm -rf dataset1/valid
# + id="gXqRlYPX8mpJ" colab_type="code" colab={}
# !mv dataset1/val dataset1/valid
# + id="mgtrgE6O-Pds" colab_type="code" colab={}
# + id="ukBQGPJSsZWO" colab_type="code" colab={}
np.random.seed(1234)
path='dataset1'
data = ImageDataBunch.from_folder(path,
ds_tfms=get_transforms(do_flip=True,max_lighting=0.1),
seed=1234,
valid_pct=0.2,
size=224,
num_workers=8,
bs=32,
test="test")
# + id="dYUszAmctZ2_" colab_type="code" outputId="80233003-630b-4612-fe3d-8dbef5cb10cf" colab={"base_uri": "https://localhost:8080/", "height": 34}
data.classes
# + id="UR7RePYIuTqo" colab_type="code" outputId="8db48c24-4cc4-44fc-f31a-545d0b6872d2" colab={"base_uri": "https://localhost:8080/", "height": 441}
data.show_batch(rows=3, figsize=(10,6), hide_axis=False)
# + id="rVckscFkuXBs" colab_type="code" outputId="2b93ee0d-66b8-4393-dea5-41212836c209" colab={"base_uri": "https://localhost:8080/", "height": 391}
data
# + id="L-0NDob8u2dV" colab_type="code" colab={}
import torch
import torchvision
resnet18PT = torchvision.models.resnet18(pretrained=True)
# + [markdown] id="4Jye0gkA6Lbh" colab_type="text"
#
# + id="w8pLlwoOzONl" colab_type="code" colab={}
num_ftrs = resnet18PT.fc.in_features
resnet18PT.fc=nn.Sequential(
nn.Dropout(0.5),
nn.Linear(num_ftrs, 128),
nn.Dropout(0.5),
nn.Linear(128, 2),
)
# + id="0EKgGpOvMTgd" colab_type="code" colab={}
resnet18PT=resnet18PT.cuda()
# + id="EBQIa6MtwLuM" colab_type="code" colab={}
learn = Learner(data, resnet18PT, metrics=[error_rate, accuracy,])
# + id="M3NohgGf6V1u" colab_type="code" outputId="25fb7a94-415d-4537-d010-c1b74305b447" colab={"base_uri": "https://localhost:8080/", "height": 1000}
learn
# + id="0Tf9gpUYwah2" colab_type="code" colab={}
learn.freeze_to(40)
# + id="o4cvo0JrxB-L" colab_type="code" outputId="79d029ce-be8d-4787-90aa-741be45b63fb" colab={"base_uri": "https://localhost:8080/", "height": 565}
from fastai.callbacks import *
learn.fit_one_cycle(15,0.0003,callbacks=[SaveModelCallback(learn, every='imrpovement', monitor='error_rate')])
# + id="E7VRrmyn-p1r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 832} outputId="03413b1e-1441-431a-efa9-d1be0f4ec758"
learn.recorder.plot_losses()
learn.recorder.plot(show_momentum=True)
learn.lr_find()
learn.recorder.plot()
# + id="iA4ZFvuz_mff" colab_type="code" colab={}
learn.save('resnet18LastLayer')
# + id="0RB9lztN_mb7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="cf1aae28-4dc2-42d4-efdd-370c417803b7"
learn.load('resnet18LastLayer')
# + id="9HshLoI0_wy1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 444} outputId="10bcc67d-0214-444a-c1a8-cc8c97b54f60"
learn.fit_one_cycle(10,0.1,callbacks=[SaveModelCallback(learn, every='imrpovement', monitor='error_rate')])
# + id="2Uhj49gNEH18" colab_type="code" colab={}
# + id="N2UrcVhSC5LX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 549} outputId="ae8ac0e2-8f47-4608-e8c4-cb5be670d473"
learn.recorder.plot_losses()
learn.recorder.plot()
# + id="ckdOFQTnDGlq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 300} outputId="b44ade88-8ba4-4dc5-80f0-fa870b1a550a"
learn.lr_find()
learn.recorder.plot()
# + id="Y9KjC1d4GGi5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 311} outputId="3a667cf1-e857-4895-c77b-64878a44a01c"
learn.save('model1Resnet')
learn.load('model1Resnet')
learn.unfreeze()
learn.fit_one_cycle(12,max_lr=1e-06,callbacks=[SaveModelCallback(learn, every='imrpovement', monitor='error_rate')])
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
# + id="8niUygaWFEn_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 421} outputId="72e9f382-bca2-4767-ad94-d3c3c237a971"
learn.fit_one_cycle(12,max_lr=1e-06)
# + id="FLJrxm1B2SA-" colab_type="code" colab={}
learn.save('Res')
# + id="IVlaieLv2Z3y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="6be94544-e5a7-4b01-f0d0-e3da943117a4"
learn.load('Res')
# + id="9CuP8nOk2djq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 300} outputId="285b67f1-7480-4bc7-97ad-843c9a808684"
learn.lr_find()
learn.recorder.plot()
# + id="ckcUFTzR20Tf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 669} outputId="dd7b05c8-ed22-4b19-8128-619df01cbbc7"
learn.fit_one_cycle(20,max_lr=(1e-07),wd=0.25)
# + id="wJ9g8LJ4FE7F" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 311} outputId="7064097f-12b6-4460-c2f2-42c2ebf38f46"
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
# + id="IgCu_etdCpaV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 255} outputId="fb583881-737b-4bca-f7d3-ef9c12de2864"
learn.lr_find()
# + id="cnnPIgNlCvhP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 283} outputId="685b3c65-714f-425e-bffa-8dde35876de0"
learn.recorder.plot()
# + id="RqOD5wcgH9Mg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="d6131349-f95e-486a-e69d-49666cffefc9"
conf=interp.confusion_matrix()
TrueNagitive=conf[0][0]
FalseNegative=conf[0][1]
TruePositive=conf[1][1]
FalsePositive=conf[1][0]
recal=TruePositive/(TruePositive+FalseNegative)
precision=TruePositive/(TruePositive+FalsePositive)
print("Precision of Model =",precision,"Recall of Model ", recal)
f1=2*((precision*recal)/(precision+recal))
print('F1 Score of Model =',f1)
# + id="Fh4fPAsfDbhY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 266} outputId="5e605b35-a768-4d36-aa70-d8238ee29238"
learn.fit(7,1e-06)
# + id="m2-F3aPMSPUN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 566} outputId="3811c3e5-d43f-4bf9-8e8b-4c1054d48c7d"
learn.recorder.plot_losses()
learn.lr_find()
learn.recorder.plot()
# + id="QrXld42oHe30" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 311} outputId="fb7d57bf-b665-41d7-96c8-a47c6f05eed2"
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
# + id="42sYYqK4IF6u" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="df0b430b-36bc-4b91-d12a-484860526a9a"
conf=interp.confusion_matrix()
TrueNagitive=conf[0][0]
FalseNegative=conf[0][1]
TruePositive=conf[1][1]
FalsePositive=conf[1][0]
recal=TruePositive/(TruePositive+FalseNegative)
precision=TruePositive/(TruePositive+FalsePositive)
print("Precision of Model =",precision,"Recall of Model ", recal)
f1=2*((precision*recal)/(precision+recal))
print('F1 Score of Model =',f1)
# + id="nNgBUAFaIPZG" colab_type="code" colab={}
| Resnet18LastLayerPretrainTuned.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/tf-estimator-tutorials/blob/master/00_Miscellaneous/text-similarity-analysis/bqml/classification_with_embeddings.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="u9cD843d8k8L" colab_type="code" colab={}
from google.colab import auth
auth.authenticate_user()
# + id="XqYlHNGi8mV0" colab_type="code" colab={}
from google.cloud import bigquery
client = bigquery.Client(project='YOUR-PROJECT-NAME')
# + [markdown] id="aieSw_8QA007" colab_type="text"
# ## Table Schema
# + id="jwJgzeAkAxTW" colab_type="code" outputId="5bc60584-2f77-47f8-c364-34da60fdbbab" colab={"base_uri": "https://localhost:8080/", "height": 107}
dataset_id = 'YOUR-DATASET-NAME'
table_id = 'YOUR-TABLE-NAME'
dataset_ref = client.dataset(dataset_id)
table_ref = dataset_ref.table(table_id)
table = client.get_table(table_ref)
# View table properties
for e in table.schema:
print(e)
# + [markdown] id="VBWxKdVk9B9n" colab_type="text"
# ##Create Features
# + id="jubsR5FI9EOQ" colab_type="code" colab={}
def get_flattened_embeddings(input_column='content_embed', n=512):
L = []
for i in range(n):
L.append("{0}[OFFSET({1})] AS {0}_{1}".format(input_column, i))
return (',').join(L)
def get_one_hot_vectors(input_column='topics', categories=['acl','gas']):
L = []
for cat in categories:
L.append(
"CASE WHEN '{1}' in UNNEST(SPLIT({0})) THEN 1 ELSE 0 END as {1}".format(
input_column, cat))
return (',').join(L)
def get_number(input_column='topics', categories=['acl','gas']):
L = []
for cat in categories:
L.append(
"(CASE WHEN '{1}' in UNNEST(SPLIT({0})) THEN 1 ELSE 0 END)".format(
input_column, cat))
return ('+').join(L)
# + id="ZMLe79r2CZ_n" colab_type="code" colab={}
def get_topics_and_count(dataset_id, table_id):
sql = """
WITH topics_flatten AS
(
SELECT topic FROM
(
SELECT
SPLIT(topics, ',') AS topic
FROM
`{0}.{1}`
WHERE
topics != ''
),
unnest(topic) topic
)
SELECT
REPLACE(topic, '-', '_') AS topic,
count(*) AS count
FROM
topics_flatten
GROUP BY
topic
""".format(dataset_id, table_id)
return sql
df = client.query(get_topics_and_count(dataset_id, table_id)).to_dataframe()
# + id="IcNHFq-jDY7J" colab_type="code" outputId="a083e9f3-551b-42db-89d2-aa7201b2e0e0" colab={"base_uri": "https://localhost:8080/", "height": 317}
df.hist(bins=100)
# + id="dFqK5QPQDiZj" colab_type="code" outputId="41ff3d5c-a399-4f55-e0bd-9ab3d0f418e2" colab={"base_uri": "https://localhost:8080/", "height": 35}
target_categories = list(df[df['count'] >= 100].topic)
target_categories[:2]
# + id="DAQIYAKo9zDA" colab_type="code" outputId="a4dbbc02-3916-4cae-dd3a-8e29fd304ebb" colab={"base_uri": "https://localhost:8080/", "height": 35}
def create_dataset(
dataset_id, table_id, categories=['acq'], embed='content_embed', n=512):
sql = """
CREATE OR REPLACE TABLE `{0}.input_data`
AS
(
SELECT
STRUCT( {2} ) AS label,
STRUCT( {3} ) AS feature
FROM
`{0}.{1}`
WHERE
{4} > 0
)
""".format(
dataset_id, table_id,
get_one_hot_vectors(input_column='topics', categories=categories),
get_flattened_embeddings(input_column=embed, n=n),
get_number(input_column='topics', categories=categories))
return sql
sql = create_dataset(
dataset_id, table_id,
categories=target_categories, embed='content_embed', n = 512)
client.query(sql)
# + [markdown] id="jOSrAqrT-SkN" colab_type="text"
# ## Create Models
# + id="Mc2aON2f-Ojz" colab_type="code" outputId="3cd4971a-62ba-43f0-e67e-a42b5fe2614c" colab={"base_uri": "https://localhost:8080/", "height": 35}
def create_model(dataset_id, target='acq'):
sql = """
CREATE OR REPLACE MODEL `{0}.model_{1}`
OPTIONS (
model_type='logistic_reg',
input_label_cols=['label']) AS
SELECT
label.{1} as label,
feature.*
FROM
`{0}.input_data`
""".format(dataset_id, target)
return sql
sql = create_model(dataset_id, target='acq')
client.query(sql)
# + [markdown] id="_QfdyOGa-f9f" colab_type="text"
# ## Evaluate Models
# + id="qVCysT6g-Y9m" colab_type="code" outputId="8c71cf7b-b03c-4640-96cc-0d82a365afbe" colab={"base_uri": "https://localhost:8080/", "height": 80}
def evaluate_model(dataset_id, target='acq', threshold=0.55):
sql = """
SELECT
*
FROM
ML.EVALUATE(MODEL `{0}.model_{1}`,
(
SELECT
label.{1} as label,
feature.*
FROM
`{0}.input_data`),
STRUCT({2} AS threshold))
""".format(dataset_id, target, threshold)
return sql
sql = evaluate_model(dataset_id, target='acq', threshold=0.55)
client.query(sql).to_dataframe()
# + id="6Rq8LkEN-lBp" colab_type="code" colab={}
def evaluate_model_roc(dataset_id, target='acq'):
sql = """
SELECT
*
FROM
ML.ROC_CURVE
(
MODEL `{0}.model_{1}`,
(
SELECT
label.{1} as label,
feature.*
FROM
`{0}.input_data`
)
)
""".format(dataset_id, target)
return sql
sql = evaluate_model_roc(dataset_id, target='acq')
df = client.query(sql).to_dataframe()
# + id="_2xdr1i3-pLb" colab_type="code" outputId="ac5a897f-af2d-48ab-8eb4-b9927375bdcd" colab={"base_uri": "https://localhost:8080/", "height": 314}
df.plot(x='false_positive_rate', y='recall', grid=True, title='roc curve')
# + id="jqxoMHiz-rwa" colab_type="code" colab={}
def evaluate_model_pr(target='acq'):
sql = """
SELECT
recall,
true_positives / (true_positives + false_positives) AS precision
FROM
ML.ROC_CURVE(
MODEL `{0}.model_{1}`,
(SELECT label.{1} as label, feature.* FROM `{0}.input_data`))
""".format(dataset_id, target)
return sql
sql = evaluate_model_pr(target='acq')
df = client.query(sql).to_dataframe()
# + id="KBJP_mwM_lQ7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 313} outputId="8523cdfd-7fe9-4e1d-99e8-7186d2200501"
df.plot(x='precision', y='recall', grid=True, title='precision recall curve')
# + id="JPTHEt7M-xaG" colab_type="code" outputId="55906bae-cd81-4bdd-9477-49aa575181c0" colab={"base_uri": "https://localhost:8080/", "height": 111}
def evaluate_model_confusion_matrix(target='acq'):
sql = """
SELECT
*
FROM
ML.CONFUSION_MATRIX(MODEL `{0}.model_{1}`,
(
SELECT
label.{1} as label,
feature.*
FROM
`{0}.input_data`))
""".format(dataset_id, target)
return sql
sql = evaluate_model_confusion_matrix(target='acq')
client.query(sql).to_dataframe()
# + [markdown] id="LeO9Afw1-47G" colab_type="text"
# ## Multi-Class Logistic Regression
# + id="b730TAUs_CDF" colab_type="code" outputId="09415e1c-668f-4399-f6e7-7eea5bd5c11f" colab={"base_uri": "https://localhost:8080/", "height": 71}
for target_category in target_categories[:3]:
print("Creating a model for {0}...".format(target_category))
client.query(create_model(dataset_id, target=target_category))
# + id="_23cHG33_Fb0" colab_type="code" outputId="946e1c16-3ca3-407b-baf0-28080cca33e2" colab={"base_uri": "https://localhost:8080/", "height": 71}
d_cat_to_eval = {}
for target_category in target_categories[:3]:
print("Evaluating a model for {0}...".format(target_category))
sql = evaluate_model_roc(dataset_id, target=target_category)
d_cat_to_eval[target_category] = client.query(sql).to_dataframe()
# + id="GzoiciOj_J4r" colab_type="code" outputId="cab69f53-3ebe-4e41-e8cb-4126a19cc7c6" colab={"base_uri": "https://localhost:8080/", "height": 314}
d_cat_to_eval['acq'].plot(x='false_positive_rate', y='recall', grid=True, title='roc curve')
# + id="-BRvczlA_L_i" colab_type="code" outputId="aa81e88b-6d90-4bd8-cf0d-b3c88c798c32" colab={"base_uri": "https://localhost:8080/", "height": 314}
d_cat_to_eval['bop'].plot(x='false_positive_rate', y='recall', grid=True, title='roc curve')
# + id="6IQ37Nfc_Nff" colab_type="code" outputId="f22ac616-5db4-4b05-abb7-d076123e2948" colab={"base_uri": "https://localhost:8080/", "height": 314}
d_cat_to_eval['cpi'].plot(x='false_positive_rate', y='recall', grid=True, title='roc curve')
| 00_Miscellaneous/text-similarity-analysis/bqml/classification_with_embeddings.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Load data
# +
import pickle
training_file = 'traffic-signs-data/train.p'
validation_file = 'traffic-signs-data/valid.p'
testing_file = 'traffic-signs-data/test.p'
with open(training_file, mode='rb') as f:
train = pickle.load(f)
with open(validation_file, mode='rb') as f:
valid = pickle.load(f)
with open(testing_file, mode='rb') as f:
test = pickle.load(f)
X_train, y_train = train['features'], train['labels']
X_valid, y_valid = valid['features'], valid['labels']
X_test, y_test = test['features'], test['labels']
# -
# ## Data set summary
# +
import numpy as np
n_train = y_train.shape[0]
n_validation = y_valid.shape[0]
n_test = y_test.shape[0]
image_shape = X_train.shape[1:]
n_classes = len(np.unique(y_train))
print("Number of training examples =", n_train)
print("Number of validation examples =", n_validation)
print("Number of testing examples =", n_test)
print("Image data shape =", image_shape)
print("Number of classes =", n_classes)
# -
# ## Data visualization
# +
import matplotlib.pyplot as plt
import random
# %matplotlib inline
fig, ax = plt.subplots(1, 5, figsize=(20,4))
indices = []
for i in range(5):
index = random.randint(0, n_train)
indices.append(index)
image = X_train[index].squeeze()
ax[i].imshow(image, cmap="gray")
ax[i].set_title(y_train[index])
# -
plt.hist(y_train, bins=np.arange(0,n_classes))
plt.show()
# ## Data preprocessing
# +
X_train = np.mean(X_train, axis=3, keepdims=True)
X_valid = np.mean(X_valid, axis=3, keepdims=True)
X_test = np.mean(X_test, axis=3, keepdims=True)
X_train = (X_train - 128) / 128
X_valid = (X_valid - 128) / 128
X_test = (X_test - 128) / 128
# +
fig, ax = plt.subplots(1, 5, figsize=(20,4))
for i, index in enumerate(indices):
image = X_train[index].squeeze()
ax[i].imshow(image, cmap="gray")
ax[i].set_title(y_train[index])
# -
# ## Model Architecture
# +
import tensorflow as tf
from tensorflow.contrib.layers import flatten
def Inception(x):
mu = 0
sigma = 0.1
# Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x32.
w1 = tf.Variable(tf.truncated_normal(shape=(5,5,1,32), mean=mu, stddev=sigma), name='w1')
b1 = tf.Variable(tf.zeros(32), name='b1')
layer1 = tf.nn.conv2d(x, w1, strides=[1,1,1,1], padding='VALID') + b1
# Activation & Max pool. Output = 14x14x32.
layer1 = tf.nn.relu(layer1)
layer1 = tf.nn.max_pool(layer1, ksize=[1,2,2,1], strides=[1,2,2,1], padding='VALID')
# Layer 2: Convolutional. Input = 14x14x32. Output = 10x10x64.
w2 = tf.Variable(tf.truncated_normal(shape=(5,5,32,64), mean=mu, stddev=sigma), name='w2')
b2 = tf.Variable(tf.zeros(64), name='b2')
layer2 = tf.nn.conv2d(layer1, w2, strides=[1,1,1,1], padding='VALID') + b2
# Activation & Max pool. Output = 5x5x64.
layer2 = tf.nn.relu(layer2)
layer2 = tf.nn.max_pool(layer2, ksize=[1,2,2,1], strides=[1,2,2,1], padding='VALID')
# Layer 3: Convolutional. Input = 5x5x64. Output = 3x3x128.
w3 = tf.Variable(tf.truncated_normal(shape=(3,3,64,128), mean=mu, stddev=sigma), name='w3')
b3 = tf.Variable(tf.zeros(128), name='b3')
layer3 = tf.nn.conv2d(layer2, w3, strides=[1,1,1,1], padding='VALID') + b3
# Activation & Max pool. Output = 2x2x128.
layer3 = tf.nn.relu(layer3)
layer3 = tf.nn.max_pool(layer3, ksize=[1,2,2,1], strides=[1,1,1,1], padding='VALID')
# Max pool, Flatten, Concat, & Dropout. Output = 1920
layer1 = tf.nn.max_pool(layer1, ksize=[1,4,4,1], strides=[1,2,2,1], padding='VALID')
layer2 = tf.nn.max_pool(layer2, ksize=[1,2,2,1], strides=[1,2,2,1], padding='VALID')
fc0 = tf.concat([flatten(layer1), flatten(layer2), flatten(layer3)], 1)
fc0 = tf.nn.dropout(fc0, keep_prob)
# Layer 4: Fully connected layer. Input = 1920. Output = 800.
w4 = tf.Variable(tf.truncated_normal(shape=(1920,800), mean=mu, stddev=sigma), name='w4')
b4 = tf.Variable(tf.zeros(800), name='b4')
layer4 = tf.matmul(fc0, w4) + b4
layer4 = tf.nn.relu(layer4)
# Layer 5: Fully connected layer. Input = 800. Output = 43.
w5 = tf.Variable(tf.truncated_normal(shape=(800,43), mean=mu, stddev=sigma), name='w5')
b5 = tf.Variable(tf.zeros(43), name='b5')
logits = tf.matmul(layer4, w5) + b5
return logits
# -
# ## Train, validate and test model
# +
from sklearn.utils import shuffle
EPOCHS = 20
BATCH_SIZE = 128
rate = 0.0005
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, n_classes)
keep_prob = tf.placeholder(tf.float32)
# -
logits = Inception(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
# +
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y, keep_prob: 1.0})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
# -
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train)
print("Training...")
print()
for i in range(EPOCHS):
X_train, y_train = shuffle(X_train, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y, keep_prob: 0.5})
validation_accuracy = evaluate(X_valid, y_valid)
print("EPOCH {} ...".format(i+1))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './lenet')
print("Model saved")
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
train_accuracy = evaluate(X_train, y_train)
valid_accuracy = evaluate(X_valid, y_valid)
test_accuracy = evaluate(X_test, y_test)
print("Training Accuracy = {:.3f}".format(train_accuracy))
print("Validation Accuracy = {:.3f}".format(valid_accuracy))
print("Test Accuracy = {:.3f}".format(test_accuracy))
# ## Test images
# +
import matplotlib.image as mpimg
import cv2
import os
path = 'test_images/'
images = []
labels = [37, 31, 40, 11, 28]
for image_name in os.listdir(path):
image = mpimg.imread(path + image_name)
image = cv2.resize(image, (32, 32))
images.append(image)
fig, ax = plt.subplots(1, 5, figsize=(20,4))
for i in range(5):
ax[i].imshow(images[i], cmap="gray")
ax[i].set_title(labels[i])
# -
# ### Predictions
# +
images = np.mean(images, axis=3, keepdims=True)
images = (images - 128) / 128
predict = tf.argmax(logits, 1)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
prediction = sess.run(predict, feed_dict={x: images, y: labels, keep_prob: 1.0})
print(prediction)
# -
# ### Accuracy
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
test_accuracy = evaluate(images, labels)
print("Test Accuracy = {:.3f}".format(test_accuracy))
# ### Top 5 softmax probabilities
# +
top_k = tf.nn.top_k(tf.nn.softmax(logits), k=5)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
top_5 = sess.run(top_k, feed_dict={x: images, y: labels, keep_prob: 1.0})
for i in range(5):
print(['%.3f' % j for j in top_5[0][i]])
for i in range(5):
print(top_5[1][i])
| data_exploration.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/drewamorbordelon/DS-Unit-2-Applied-Modeling/blob/master/module2-wrangle-ml-datasets/232_assignment_monthly_10yrTreasuryModel.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="WX7_F3-iEkBI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 352} outputId="0441d909-6647-40ab-8ada-86efdcdbff1f"
# %matplotlib inline
import sys
# !pip install category_encoders==2.*
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from category_encoders import OneHotEncoder, OrdinalEncoder
from sklearn.ensemble import RandomForestRegressor
from sklearn.impute import SimpleImputer
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import make_pipeline
from sklearn.metrics import accuracy_score
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import RandomForestClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import SelectKBest
# + id="B-QU3XPoEsDu" colab_type="code" colab={}
df = pd.read_csv('/content/MoM_Unit2ProjectDataFrame.csv', parse_dates=['date'], skipfooter=1, engine='python')
# + id="q10gIRWKGsS0" colab_type="code" colab={}
df['vix_basket'] = df['vix']
df = df.iloc[217:]
# + id="9JFLrshhLxOT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 244} outputId="1be81548-4070-4d53-f003-6a86b7abe316"
df.head()
# + id="vnyoEgDbMk39" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 244} outputId="9fe8b801-bb53-412b-fb2a-137fadd7d118"
df['vix_basket'].value_counts()
df.head()
# + id="uBpxSeZpPWvo" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 629} outputId="11897e71-9134-493d-ef5a-079d8a79a2f7"
df.info()
# + [markdown] id="LvbDjpqPFHFS" colab_type="text"
# #Wrangle Function
# + id="Ucr90wIUFCqk" colab_type="code" colab={}
def wrangle (df):
df = df.copy()
# NEW FEATURES = Creating baskets for VIX levels
# create baskets for VIX
# >= 30
# 30-18
# < 18
# Creating a new column with categories
defensive = (df['vix_basket'] >= 30.00)
tradable = (df['vix_basket'] < 30.00) & (df['vix_basket'] >= 16.00)
investable = (df['vix_basket'] < 16.00)
# unknown = (df['vix_basket'] < 30.00) & (df['vix_basket'] > 27.00) & (df['vix_basket'] < 18.00) & (df(['vix_basket'] >= 15.00)
# NEW Category Features
df.loc[defensive, 'vix_basket'] = 'defensive'
df.loc[tradable, 'vix_basket'] = 'tradable'
df.loc[investable, 'vix_basket'] = 'investable'
# df.loc[unknown, 'vix_basket'] = 'unknown'
# NEW FEATURES = Creating conditional statement for the `Regime`
condition1 = (df['roccpi_bps'] < 0.00)
regime1 = df[condition1]
regime1_date = regime1[['date']]
regime1_date['regime'] = 'regime 1,3'
condition2 = (df['roccpi_bps'] > 0.00)
regime2 = df[condition2]
regime2_date = regime2[['date']]
regime2_date['regime'] = 'regime 2,4'
by_row_1 = pd.concat([regime1_date, regime2_date])
df = pd.merge(df, by_row_1, on='date', how='inner')
# Drop recorded_by (never varies) and id (always varies, random)
# unusable_variance = ['10y2yr', 'roc10_2', '10y2y_bps', 'roc10y', '10y_bps']
# df = df.drop(columns=unusable_variance, axis=1) #'cpi', 'gdp', 'rocgdp_bps', 'rocgdp', 'roccpi_bps', 'roccpi','vehicle_sales', 'conjob_claims', 'Indust Prod Index', 'm2vel',, '10y2yr', '10y', 'wti','dxy'
return df
# + id="VIFOw0peIF4d" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 222} outputId="748b452c-b1eb-4660-a6d6-cf6f3f16d3ab"
df = wrangle(df).sort_index()
# + id="CfKRQqSaU4h1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 330} outputId="b19ef6ac-c1bb-4e8e-b275-713c80931ff7"
df.tail()
# + id="v-7ArV9qJSoo" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 554} outputId="f4cc465b-0927-4cab-bf5b-fb0d800bf4f0"
df.info()
# + id="M0MlprioxzMk" colab_type="code" colab={}
# Set `date` as index
df = df.set_index('date')
# + [markdown] id="MTf-dAtIVYqa" colab_type="text"
# #Split TV from FM
# + id="mPAtMToxVUym" colab_type="code" colab={}
# target is the regime column
# categorical
target = '10y'
y = df[target]
X = df.drop(target , axis=1)
# + id="FzEkXV1IVe0x" colab_type="code" colab={}
cutoff1 = '2018-01-01'
# cutoff2 = '2010-01-01'
# mask1 = df.index < cutoff2
mask1 = (df.index <= cutoff1)
# mask2 = (df.index >= cutoff1) & (df.index < cutoff2)
# mask3 = df.index >= cutoff2
train = df[mask1]
val = df[~mask1]
# val = df[mask2]
# test = df[mask3]
# + id="nZiquQD7eAkY" colab_type="code" colab={}
y_train = train[target]
X_train = train.drop([target], axis=1)
y_val = val[target]
X_val = val.drop(target, axis=1)
# y_test = test[target]
# X_test = test.drop(target, axis=1)
# + [markdown] id="_2rQ7m7heGZ-" colab_type="text"
# ###Test with assert
# + id="mg6i2YqkeBbs" colab_type="code" colab={}
assert df.shape[0] == train.shape[0] + val.shape[0]
# assert df.shape[0] == train.shape[0] + val.shape[0] + test.shape[0]
# + id="EewgiwWVe3Zj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="c46b010f-5e75-48b6-ebe5-e876ec698590"
print(train.shape)
print(val.shape)
# print(test.shape)
# + id="R14Jh_hQtfeR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 536} outputId="0090073f-18aa-4b37-e836-0b1f98efb636"
train.info()
# + id="61l3Cd6moLKc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 536} outputId="1193e608-2967-4b2d-a786-3d5971f490ad"
val.info()
# + [markdown] id="pDjusrtxfBo0" colab_type="text"
# #Establish Baseline
# + id="UBo5D3toe9R5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="51a07143-16c3-4402-ae31-3fbb90ce4338"
# Regression --> mean absolute error
from sklearn.metrics import mean_absolute_error
print('Baseline MAE:')
print(mean_absolute_error(y_train, [y_train.mean()]*len(y_train)))
# + [markdown] id="-0k_GiLzfPdM" colab_type="text"
# #Build Model
# + id="FSyeku1PfAhb" colab_type="code" colab={}
model = make_pipeline(
OneHotEncoder(use_cat_names=True),
SelectKBest(k=6),
LinearRegression() #LinearRegression() RandomForestRegressor(random_state=42)
)
model.fit(X_train, y_train);
# + id="I8XmQDxdfTrg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="fae5a68b-3d2a-4335-a07f-a3d993a129e4"
print('Training MAE:', mean_absolute_error(y_train, model.predict(X_train)))
print('Validation MAE:', mean_absolute_error(y_val, model.predict(X_val)))
# print('Test MAE:', mean_absolute_error(y_test, model.predict(X_test)))
# + id="E_WpyHQRsYwF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="f16ac268-ad2f-4058-af87-81d5c39b9058"
from sklearn.metrics import r2_score
print("Training R2:", model.score(X_train, y_train))
print("Validation R2:", model.score(X_val, y_val))
# print("Test R2:", model.score(X_test, y_test))
# + id="G-t38AFPobro" colab_type="code" colab={}
model_rfr = make_pipeline(
OneHotEncoder(use_cat_names=True),
SimpleImputer(),
SelectKBest(k=6), # <-- Hyperparameter
RandomForestRegressor(n_estimators=10000, n_jobs=-1, random_state=42) # <-- max_depth, n_estimators
)
model_rfr.fit(X_train, y_train);
# + id="DVe9-o8yo8uZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="cf63335b-c604-4cc0-d5c8-3250a0566120"
print('Training MAE:', mean_absolute_error(y_train, model_rfr.predict(X_train)))
print('Validation MAE:', mean_absolute_error(y_val, model_rfr.predict(X_val)))
# print('Test MAE:', mean_absolute_error(y_test, model_rfr.predict(X_test)))
# + id="z24tkPvppO1_" colab_type="code" colab={}
rfr_model = make_pipeline(
OneHotEncoder(use_cat_names=True),
SimpleImputer(strategy='mean'),
SelectKBest(k=8),
RandomForestRegressor(random_state=42)
)
# The ranges I want to test as dictionary
params= {'randomforestregressor__n_estimators': range(50, 801, 50),
'randomforestregressor__max_depth': range(5, 501, 10)}
# Create Grid Search
gs = GridSearchCV(rfr_model,
param_grid = params,
n_jobs=-1,
verbose=1,
cv=10
)
# + id="23N53ND8pR9U" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="455e86a3-7cc8-4ca1-f048-9bc4307722e0"
gs.fit(X_train, y_train);
# + id="tVEoOTMqpowN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="57caa71f-9e08-4558-982f-9a1bc1d0e85a"
# # What are the best set of hyperparameters?
gs.best_params_
# + id="E5SwJY8OprJk" colab_type="code" colab={}
# What if I want to save my best model?
best_model = gs.best_estimator_
# + id="y_sy5dyEptIf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="6c998f1e-c946-4fb6-bddc-58a9d20bf3be"
print('Tuned training MAE:', mean_absolute_error(y_train, gs.predict(X_train)))
print('Tuned validation MAE:', mean_absolute_error(y_val, gs.predict(X_val)))
# print('Tuned test MAE:', mean_absolute_error(y_test, gs.predict(X_test)))
# + id="2ggm4t8clUC9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 247} outputId="bc192794-e620-495c-f78f-8b5f62272f99"
# # Multiple Linear Regression
from sklearn.metrics import r2_score
print("Training R2:", model_1.score(X_train, y_train))
print("Validation R2:", model_1.score(X_val, y_val))
# print("Test R2:", model_1.score(X_test, y_test))
# + id="wTtFBz67jP6h" colab_type="code" colab={}
from sklearn.datasets import make_classification
from sklearn.ensemble import ExtraTreesClassifier
# + id="CwyAl3hZjRXu" colab_type="code" colab={}
X, y = make_classification(n_samples=1000,
n_features=10,
n_informative=3,
n_redundant=0,
n_repeated=0,
n_classes=2,
random_state=0,
shuffle=False)
# + id="1sgek60_jwmv" colab_type="code" colab={}
forest = ExtraTreesClassifier(n_estimators=250,
random_state=0)
# + id="Rn1F9DLRjz2y" colab_type="code" colab={}
# forest.fit(X, y)
# importances = forest.feature_importances_
# std = np.std([tree.feature_importances_ for tree in forest.estimators_],
# axis=0)
# indices = np.argsort(importances)[::-1]
# + id="J60b65NUj5CX" colab_type="code" colab={}
# Print the feature ranking
# print("Feature ranking:")
# for f in range(X.shape[1]):
# print("%d. feature %d (%f)" % (f + 1, indices[f], importances[indices[f]]))
# # Plot the impurity-based feature importances of the forest
# plt.figure()
# plt.title("Feature importances")
# plt.bar(range(X.shape[1]), importances[indices],
# color="r", yerr=std[indices], align="center")
# plt.xticks(range(X.shape[1]), indices)
# plt.xlim([-1, X.shape[1]])
# plt.show()
# + id="rnCBbp0zkUgq" colab_type="code" colab={}
# plot feature importance using built-in function
# from numpy import loadtxt
# from xgboost import XGBRegressor
# from xgboost import plot_importance
# # fit model no training data
# model = XGBRegressor()
# model.fit(X, y)
# # plot feature importance
# plot_importance(model)
# plt.show()
# + id="wcxUn8OwkJzZ" colab_type="code" colab={}
| module2-wrangle-ml-datasets/232_assignment_monthly_10yrTreasuryModel.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: ibaio_dev39
# language: python
# name: ibaio_dev39
# ---
# # Section 3: Homework Exercises
#
# This material provides some hands-on experience using the methods learned from the third day's material.
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
import scipy.stats as st
import pymc3 as pm
import theano.tensor as tt
import arviz as az
# ## Exercise: Effects of coaching on SAT scores
#
# This example was taken from Gelman *et al.* (2013):
#
# > A study was performed for the Educational Testing Service to analyze the effects of special coaching programs on test scores. Separate randomized experiments were performed to estimate the effects of coaching programs for the SAT-V (Scholastic Aptitude Test- Verbal) in each of eight high schools. The outcome variable in each study was the score on a special administration of the SAT-V, a standardized multiple choice test administered by the Educational Testing Service and used to help colleges make admissions decisions; the scores can vary between 200 and 800, with mean about 500 and standard deviation about 100. The SAT examinations are designed to be resistant to short-term efforts directed specifically toward improving performance on the test; instead they are designed to reflect knowledge acquired and abilities developed over many years of education. Nevertheless, each of the eight schools in this study considered its short-term coaching program to be successful at increasing SAT scores. Also, there was no prior reason to believe that any of the eight programs was more effective than any other or that some were more similar in effect to each other than to any other.
#
# You are given the estimated coaching effects (`d`) and their sampling variances (`s`). The estimates were obtained by independent experiments, with relatively large sample sizes (over thirty students in each school), so you can assume that they have approximately normal sampling distributions with known variances variances.
#
# Here are the data:
J = 8
d = np.array([28., 8., -3., 7., -1., 1., 18., 12.])
s = np.array([15., 10., 16., 11., 9., 11., 10., 18.])
# Construct an appropriate model for estimating whether coaching effects are positive, using a **centered parameterization**, and then compare the diagnostics for this model to that from an **uncentered parameterization**.
#
# Finally, perform goodness-of-fit diagnostics on the better model.
with pm.Model() as centered_schools:
mu = pm.Normal('mu', mu=0, sigma=5)
tau = pm.HalfCauchy('tau', beta=5)
theta = pm.Normal('theta', mu=mu, sigma=tau, shape=J)
effects = pm.Normal('effects', mu=theta, sigma=s, observed=d)
with centered_schools:
trace_centered = pm.sample(1000, tune=1000)
az.plot_trace(trace_centered, var_names=['mu', 'tau']);
az.plot_energy(trace_centered);
# +
def pairplot_divergence(trace, ax=None, divergence=True, color='C3', divergence_color='C2'):
theta = trace.get_values(varname='theta', combine=True)[:, 0]
logtau = trace.get_values(varname='tau_log__', combine=True)
if not ax:
_, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(theta, logtau, 'o', color=color, alpha=.5)
if divergence:
divergent = trace['diverging']
ax.plot(theta[divergent], logtau[divergent], 'o', color=divergence_color)
ax.set_xlabel('theta[0]')
ax.set_ylabel('log(tau)')
ax.set_title('scatter plot between log(tau) and theta[0]');
return ax
pairplot_divergence(trace_centered);
# -
az.plot_parallel(trace_centered);
with pm.Model() as noncentered_schools:
mu = pm.Normal('mu', mu=0, sigma=5)
tau = pm.HalfCauchy('tau', beta=5)
theta_tilde = pm.Normal('theta_t', mu=0, sigma=1, shape=J)
theta = pm.Deterministic('theta', mu + tau * theta_tilde)
effects = pm.Normal('effects', mu=theta, sigma=s, observed=d)
with noncentered_schools:
trace_noncentered = pm.sample(1000, tune=1000)
az.plot_trace(trace_noncentered, var_names=['mu', 'tau']);
az.plot_energy(trace_noncentered);
pairplot_divergence(trace_noncentered);
| solutions/Section3-Homework.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This notebook applies SPARQL query to retrieve and download biomedically relevant edge category types from Wikidata to be utilized by the downstream drug repurposing algorithm. The nodes.csv from the previous notebook is utilized here.
#
# I. [Load Packages](#Load) [clicking on phrase will take you directly to section] <br>
# II. [Identification and Filtering of Infectious Taxa as Part of Network](#Taxa) <br>
# III. [Mapping Edges to Node Types](#Map)<br>
# IV. [Concatenate and View Updated Node and Edge Results, Save as .csv files](#Concatenate) <br>
# ## Load
# Packages and modules with relevant functions
# +
# %matplotlib inline
# Above line visualizes plots, cannot put note on side because of %
import pandas as pd
import time
from datetime import datetime
import functools
from pathlib import Path
from itertools import chain
from tqdm.autonotebook import tqdm
from data_tools.df_processing import char_combine_iter, add_curi
from data_tools.plotting import count_plot_h
from data_tools.wiki import execute_sparql_query, node_query_pipeline, standardize_nodes, standardize_edges
# -
def process_taxa(edges):
nodes = edges.drop_duplicates(subset=['taxon', 'tax_id'])[['taxon', 'taxonLabel', 'tax_id']]
nodes = add_curi(nodes, {'tax_id': 'NCBITaxon'})
return standardize_nodes(nodes, 'taxon')
# Connects path, irrespective of OS
prev_dir = Path('../results/').resolve()
prev_nodes = pd.read_csv(prev_dir.joinpath('01a_nodes.csv'))
nodes = []
edges = []
# ## Taxa
# Account for the various taxa involved in or related to disease. This will include 2 types of syntax, and 2 approaches.
#
# #### Syntax in the Wikidata data model
#
# 1. Direct statements:
# Taxon has-effect Disease... or Disease has-cause Taxon
#
#
# 2. Qualifier Statements:
# Disease has-cause infection (qual: of Taxon)
#
# #### Approaches in the Wikidata data model
# 1. Direct links:
# Taxon has-effect Disease
#
#
# 2. Punning down to a specific taxonomic level:
# Partent_taxon has-effect Disease
# Taxon has-parent* Parent_taxon
# Taxon has-rank Species
# +
# Create time stamp
timeStringNow = datetime.now().strftime("+%Y-%m-%dT00:00:00Z")
start_time = time.time()
# Approach 1
## Syntax 1 -- Direct statement: Disease causes infection
q = """SELECT DISTINCT ?disease ?taxon ?taxonLabel ?tax_id
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?disease p:P828 [ps:P828 wd:Q166231;pq:P642 ?taxon;].
OPTIONAL{?taxon wdt:P685 ?tax_id}.
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGUAGE],en". }}"""
qr = execute_sparql_query(q) # Query
tax_nodes = process_taxa(qr) # Query by taxa
edge_res = standardize_edges(qr, 'taxon', 'disease', 'causes') # Standardize taxon, disease, and causes
nodes.append(tax_nodes) # Update nodes
edges.append(edge_res) # Update edges
## Syntax 2 -- Qualifier statements
### a. disease has-cause TAXON
q = """SELECT DISTINCT ?disease ?diseaseLabel ?doid ?taxon ?taxonLabel ?tax_id
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?taxon wdt:P685 ?tax_id.
{?disease wdt:P828 ?taxon}UNION{?taxon wdt:P1542 ?disease}.
OPTIONAL {?disease wdt:P699 ?doid.}
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGUAGE],en". }}"""
qr = execute_sparql_query(q)
tax_nodes = process_taxa(qr)
edge_res = standardize_edges(qr, 'taxon', 'disease', 'causes')
nodes.append(tax_nodes)
edges.append(edge_res)
### b. TAXON has-effect Disease
q = """SELECT DISTINCT ?disease ?diseaseLabel ?doid ?taxon ?taxonLabel ?tax_id
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?taxon wdt:P685 ?tax_id.
{?disease wdt:P828 ?taxon}UNION{?taxon wdt:P1542 ?disease}.
OPTIONAL {?disease wdt:P699 ?doid.}
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGUAGE],en". }}"""
qr = execute_sparql_query(q)
tax_nodes = process_taxa(qr)
edge_res = standardize_edges(qr, 'taxon', 'disease', 'causes')
nodes.append(tax_nodes)
edges.append(edge_res)
# Approach 2
## Syntax 1
q = """SELECT DISTINCT ?disease ?diseaseLabel ?doid ?parent_tax ?parent_taxLabel ?par_taxid ?taxon ?taxonLabel ?tax_id
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?disease p:P828 [ps:P828 wd:Q166231;
pq:P642 ?parent_tax;].
OPTIONAL{?disease wdt:P699 ?doid}.
OPTIONAL{?parent_tax wdt:P685 ?par_taxid}.
FILTER NOT EXISTS {?parent_tax wdt:P105 wd:Q36732}.
FILTER NOT EXISTS {?parent_tax wdt:P105 wd:Q3978005}.
{?taxon wdt:P171+ ?parent_tax}UNION{?parent_tax wdt:P171+ ?taxon}
?taxon wdt:P105 wd:Q7432 .
?taxon wdt:P685 ?tax_id
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGUAGE],en". }}"""
qr = execute_sparql_query(q)
tax_nodes = process_taxa(qr)
edge_res = standardize_edges(qr, 'taxon', 'disease', 'causes', 'computed')
edge_res['comp_type'] = 'punning' # What does this do? What is meant by 'punning'?
nodes.append(tax_nodes)
edges.append(edge_res)
## Syntax 2
q = """SELECT DISTINCT ?disease ?diseaseLabel ?doid ?parent_tax ?parent_taxLabel ?parent_tax_id ?taxon ?taxonLabel ?tax_id
WHERE
{{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?parent_tax wdt:P685 ?parent_tax_id.
FILTER NOT EXISTS {?parent_tax wdt:P105 wd:Q36732}.
FILTER NOT EXISTS {?parent_tax wdt:P105 wd:Q3978005}.
{?disease wdt:P828 ?parent_tax}UNION{?parent_tax wdt:P1542 ?disease}.
OPTIONAL {?disease wdt:P699 ?doid.}
{?taxon wdt:P171+ ?parent_tax}UNION{?parent_tax wdt:P171+ ?taxon}
?taxon wdt:P685 ?tax_id .
?taxon wdt:P105 wd:Q7432 .
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGUAGE],en". }}
limit 48000"""
qr = execute_sparql_query(q)
tax_nodes = process_taxa(qr)
edge_res = standardize_edges(qr, 'taxon', 'disease', 'causes', 'computed')
edge_res['comp_type'] = 'punning'
nodes.append(tax_nodes)
edges.append(edge_res)
# Output and print when query is complete
end_time = time.time()
print("The total time of this query is:", (end_time - start_time)/60, "minutes")
# -
# Remove duplicates
tax_nodes = pd.concat(nodes, sort=False, ignore_index=True).drop_duplicates(subset=['id'])
nodes = [tax_nodes]
# ## Map
# Here we use SPARQL to map node types via edges in Wikidata (ordered *almost* alphabetically) <br>
# To affirm a edge type category has been added, move it to its own cell and view separately using the 'print' function.
# +
# Create time stamp
timeStringNow = datetime.now().strftime("+%Y-%m-%dT00:00:00Z")
start_time = time.time()
# IN TAXON (needs to come first for ENCODES)
## Focuses on taxa with annotations to genes or proteins in Wikidata
### Genes
q = """SELECT DISTINCT ?taxon
WHERE {?gene wdt:P31 wd:Q7187.
?gene wdt:P703 ?taxon.}"""
qr = execute_sparql_query(q)
gene_taxa = set(qr['taxon'])
q = """SELECT DISTINCT ?gene ?geneLabel ?entrez ?symbol ?hgnc ?omim ?ensembl
WHERE {{
?gene wdt:P31 wd:Q7187.
?gene wdt:P703 wd:{tax}.
OPTIONAL{{?gene wdt:P351 ?entrez .}}
OPTIONAL{{?gene wdt:P353 ?symbol .}}
OPTIONAL{{?gene wdt:P354 ?hgnc .}}
OPTIONAL{{?gene wdt:P492 ?omim .}}
OPTIONAL{{?gene wdt:P594 ?ensembl .}}
SERVICE wikibase:label {{ bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}}}"""
tax_gene_edges = []
gene_curi_map = {'entrez': 'NCBIGene', 'symbol': 'SYM', 'hgnc':'HGNC', 'omim':'OMIM', 'ensembl':'ENSG'}
for tax_id in gene_taxa & set(tax_nodes['id']):
this_q = q.format(tax=tax_id)
res = node_query_pipeline(this_q, gene_curi_map, 'gene')
if res is None:
continue
nodes.append(res[['id', 'name', 'label', 'xrefs']].copy())
res['tax'] = tax_id
res_edges = standardize_edges(res, 'id', 'tax', 'in_taxon')
tax_gene_edges.append(res_edges)
gene_tax = pd.concat(tax_gene_edges, sort=False, ignore_index=True)
edges.append(gene_tax)
q = """SELECT DISTINCT ?taxon
WHERE {?gene wdt:P31 wd:Q7187.
?gene wdt:P703 ?taxon.}"""
qr = execute_sparql_query(q)
gene_taxa = set(qr['taxon'])
q = """SELECT DISTINCT ?gene ?geneLabel ?entrez ?symbol ?hgnc ?omim ?ensembl
WHERE {{
?gene wdt:P31 wd:Q7187.
?gene wdt:P703 wd:{tax}.
OPTIONAL{{?gene wdt:P351 ?entrez .}}
OPTIONAL{{?gene wdt:P353 ?symbol .}}
OPTIONAL{{?gene wdt:P354 ?hgnc .}}
OPTIONAL{{?gene wdt:P492 ?omim .}}
OPTIONAL{{?gene wdt:P594 ?ensembl .}}
SERVICE wikibase:label {{ bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}}}"""
tax_gene_edges = []
gene_curi_map = {'entrez': 'NCBIGene', 'symbol': 'SYM', 'hgnc':'HGNC', 'omim':'OMIM', 'ensembl':'ENSG'}
for tax_id in gene_taxa & set(tax_nodes['id']):
this_q = q.format(tax=tax_id)
res = node_query_pipeline(this_q, gene_curi_map, 'gene')
if res is None:
continue
nodes.append(res[['id', 'name', 'label', 'xrefs']].copy())
res['tax'] = tax_id
res_edges = standardize_edges(res, 'id', 'tax', 'in_taxon')
tax_gene_edges.append(res_edges)
gene_tax = pd.concat(tax_gene_edges, sort=False, ignore_index=True)
edges.append(gene_tax)
### Proteins
q = """SELECT DISTINCT ?taxon
WHERE {?protein wdt:P31 wd:Q8054.
?protein wdt:P703 ?taxon.}"""
qr = execute_sparql_query(q)
prot_taxa = set(qr['taxon'])
q = """SELECT DISTINCT ?protein ?proteinLabel ?uniprot
WHERE {{
?protein wdt:P31 wd:Q8054.
?protein wdt:P703 wd:{tax}.
OPTIONAL{{?protein wdt:P352 ?uniprot .}}
SERVICE wikibase:label {{ bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}}}"""
tax_prot_edges = []
for tax_id in prot_taxa & set(tax_nodes['id']):
this_q = q.format(tax=tax_id)
res = node_query_pipeline(this_q, {'uniprot':'UniProt'}, 'protein')
if res is None:
continue
nodes.append(res[['id', 'name', 'label', 'xrefs']].copy())
res['tax'] = tax_id
res_edges = standardize_edges(res, 'id', 'tax', 'in_taxon')
tax_prot_edges.append(res_edges)
prot_tax = pd.concat(tax_prot_edges, sort=False, ignore_index=True)
edges.append(prot_tax)
# ASSOCIATED WITH
## Gene ASSOCIATED WITH Disease
q = """SELECT DISTINCT ?disease ?diseaseLabel ?gene ?geneLabel
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
?gene wdt:P31 wd:Q7187 .
?disease wdt:P2293 ?gene
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'gene', 'disease', 'associated_with')
edges.append(edge_res)
## Pathway ASSOCIATED WITH Disease
q = """SELECT DISTINCT ?pathway ?disease
WHERE {
?pathway wdt:P31 wd:Q4915012 .
FILTER NOT EXISTS{?pathway wdt:P686 ?goid}
{?disease wdt:P31 wd:Q12136 .}UNION{?disease wdt:P699 ?doid}
{?pathway wdt:P1050 ?disease}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'pathway', 'disease', 'associated_with')
edges.append(edge_res)
# ENABLES
## Protein ENABLES Molecular Function
q = """SELECT DISTINCT ?protein ?molecular_function
WHERE {?protein wdt:P31 wd:Q8054.
?molecular_function wdt:P686 ?goid.
{?protein wdt:P680 ?molecular_function}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'protein', 'molecular_function', 'enables')
edges.append(edge_res)
# ENCODES
## Gene ENCODES Protein (note focus on Homo sapiens)
q = """SELECT DISTINCT ?gene ?protein
WHERE {{
?gene wdt:P31 wd:Q7187.
?gene wdt:P703 wd:{tax}.
?protein wdt:P31 wd:Q8054.
?protein wdt:P703 wd:{tax}.
{{?gene wdt:P688 ?protein}}UNION{{?protein wdt:P702 ?gene}}}}"""
human_tax_id = 'Q15978631'
encodes_edges = []
infectious_tax = list(set(gene_tax['end_id']) & set(prot_tax['end_id']))
for tax in infectious_tax + [human_tax_id]:
this_q = q.format(tax=tax)
qr = execute_sparql_query(this_q)
if qr is not None:
this_edge = standardize_edges(qr, 'gene', 'protein', 'encodes')
encodes_edges.append(this_edge)
encodes_edges = pd.concat(encodes_edges, sort=False, ignore_index=True)
edges.append(encodes_edges)
# HAS PART
## Pathway HAS PART Compoound
q = """SELECT DISTINCT ?pathway ?compound
WHERE {
?pathway wdt:P31 wd:Q4915012 .
FILTER NOT EXISTS{?pathway wdt:P686 ?goid}
?compound wdt:P31 wd:Q11173 .
?pathway wdt:P527 ?compound}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'pathway', 'compound', 'has_part')
edges.append(edge_res)
## Pathway HAS PART Gene
q = """SELECT DISTINCT ?pathway ?gene
WHERE {?pathway wdt:P31 wd:Q4915012 .
FILTER NOT EXISTS{?pathway wdt:P686 ?goid}
?gene wdt:P31 wd:Q7187 .
?pathway wdt:P527 ?gene}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'pathway', 'gene', 'has_part')
edges.append(edge_res)
# INVOLVED IN
## Pathway INVOLVED IN Biological Process
q = """SELECT DISTINCT ?pathway ?bio_process
WHERE {
?pathway wdt:P31 wd:Q4915012 .
FILTER NOT EXISTS{?pathway wdt:P686 ?goid}
?bio_process wdt:P31 wd:Q2996394 .
?bio_process wdt:P686 ?goid .
{?pathway wdt:P31 ?bio_process}UNION{?bio_process wdt:P31 ?pathway}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'pathway', 'bio_process', 'involved_in')
edges.append(edge_res)
## Protein INVOLVED IN Biological Process
q = """SELECT DISTINCT ?protein ?biological_process
WHERE {?protein wdt:P31 wd:Q8054.
?biological_process wdt:P686 ?goid.
{?protein wdt:P682 ?biological_process}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'protein', 'biological_process', 'involved_in')
edges.append(edge_res)
# INTERACTS WITH
## Compound INTERACTS WITH Protein
q = """SELECT DISTINCT ?compound ?compoundLabel ?qualifier ?qualifierLabel ?protein ?proteinLabel
WHERE {
?compound wdt:P31 wd:Q11173 .
?protein wdt:P31 wd:Q8054 .
{ ?compound p:P129 [ps:P129 ?protein;
pq:P2868 ?qualifier] }
UNION { ?protein p:P129 [ps:P129 ?compound;
pq:P366 ?qualifier] }
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'compound', 'protein', 'qualifierLabel')
edges.append(edge_res)
# PART OF
## Protein PART OF Cellular Component
q = """SELECT DISTINCT ?protein ?cell_component
WHERE {?protein wdt:P31 wd:Q8054.
?cell_component wdt:P686 ?goid.
{?protein wdt:P681 ?cell_component}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'protein', 'cell_component', 'part_of')
edges.append(edge_res)
# SITE OF
## Anatomy SITE OF Disease
q = """SELECT DISTINCT ?disease ?diseaseLabel ?anatomy ?anatomyLabel
WHERE {
{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
{?disease1 wdt:P31 wd:Q12136}UNION{?disease1 wdt:P699 ?doid1}.
?anatomy wdt:P1554 ?uberon .
{?disease1 wdt:P927 ?anatomy} {?disease wdt:P279? ?disease1}
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'anatomy', 'disease', 'site_of')
edges.append(edge_res)
# # ? Presents ? is this an edge..?
## Disease to Phenotype
q = """SELECT DISTINCT ?disease ?pheno
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}
{?pheno wdt:P31 wd:Q169872.}UNION{?pheno wdt:P3841 ?hpo}
{?pheno wdt:P780 ?disease}UNION{?disease wdt:P780 ?pheno}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'disease', 'pheno', 'presents')
edges.append(edge_res)
# ?? SUBCLASS OF ?? What is the purpose of this 'later punning' meaning...?
## Anatomy SUBCLASS OF Anatomy
q = """SELECT DISTINCT ?anatomy ?anatomyLabel ?anatomy1 ?anatomy1Label
WHERE {
?anatomy wdt:P1554 ?uberon .
?anatomy1 wdt:P1554 ?uberon1 .
?anatomy wdt:P279? ?anatomy1
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'anatomy', 'anatomy1', 'subclass_of')
edges.append(edge_res)
## Disease SUBCLASS OF Disease
q = """SELECT DISTINCT ?disease ?diseaseLabel ?disease1 ?disease1Label
WHERE {{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
{?disease1 wdt:P31 wd:Q12136}UNION{?disease1 wdt:P699 ?doid1}.
?disease wdt:P279? ?disease1
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'disease', 'disease1', 'subclass_of')
edges.append(edge_res)
# TREATS
## Compound TREATS Disease
q = """SELECT DISTINCT ?compound ?compoundLabel ?disease ?diseaseLabel
WHERE {
?compound wdt:P31 wd:Q11173 .
{?disease wdt:P31 wd:Q12136}UNION{?disease wdt:P699 ?doid}.
{?compound wdt:P2175 ?disease}UNION{?disease wdt:P2176 ?compound}
SERVICE wikibase:label { bd:serviceParam wikibase:language "[AUTO_LANGAGE],en" }}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'compound', 'disease', 'treats')
edges.append(edge_res)
## Compound TREATS Phenotype
q = """SELECT DISTINCT ?compound ?pheno
WHERE {?compound wdt:P31 wd:Q11173 .
{?pheno wdt:P31 wd:Q169872.}UNION{?pheno wdt:P3841 ?hpo}
{?pheno wdt:P2176 ?compound}UNION{?compound wdt:P2175 ?pheno}}"""
qr = execute_sparql_query(q)
edge_res = standardize_edges(qr, 'compound', 'pheno', 'treats')
edges.append(edge_res)
# Output and print when query is complete
end_time = time.time()
print("The total time of this query is:", (end_time - start_time)/60, "minutes")
# -
# ## Concatenate
# Affirm queries and compile into a csv (2 total)
nodes.append(prev_nodes)
nodes = pd.concat(nodes, sort=False, ignore_index=True)
edges = pd.concat(edges, sort=False, ignore_index=True)
len(nodes) # 781096 (previously 1074047 with 150,000 Compound limit)
nodes['id'].nunique() # 570592
nodes.head()
count_plot_h(nodes['label']) # Graph form of value counts from nodes file
len(edges) # 3988081 (edges go down by about 100000 with new limit)
edges['start_id'].append(edges['end_id']).nunique() # 902743 (where the row is unique for both columns) right?
edges.head() # comp_type NaN???
count_plot_h(edges['type'].value_counts().head(10)) # note there are more after this if you remove .head(10)
# +
out_dir = Path('../results/')
out_dir.mkdir(parents=True, exist_ok=True)
nodes.to_csv(out_dir.joinpath('01b_nodes.csv'), index=False)
edges.to_csv(out_dir.joinpath('01b_edges.csv'), index=False)
| src/archive/01b_Wikidata-Edges.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Percentiles
# +
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
vals = np.random.normal(0, 0.5, 10000)
plt.hist(vals, 50)
plt.show()
# -
np.percentile(vals, 50)
#median is equal to 50º percentile
np.median(vals)
np.percentile(vals, 90)
np.percentile(vals, 99)
# ## Activity
# Experiment with different parameters when creating the test data. What effect does it have on the percentiles?
| other ideas/percentiles.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Logistic Regression Baseline, Numeric Features Only
# +
import sys
import os
sys.path.append(os.path.abspath('../data'))
import pathlib
import json
from datetime import datetime
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
# -
# # 1. Loading
data_root = pathlib.Path('../data')
all_json_paths = list(data_root.glob('*.json'))
all_json_paths = [str(path) for path in all_json_paths]
all_json_paths
# +
data = []
for line in open(all_json_paths[0], 'r', encoding='utf8'):
data.append(json.loads(line))
data = [record['data'] for record in data]
raw = pd.DataFrame.from_records(data)
# -
# # 2. Preprocessing
def preproc(df: pd.DataFrame) -> pd.DataFrame:
"""
Naive preprocessing the input data by dropping samples that still have the campaign running,
impute durations and categories, dropping unnecessary features, and one-hot encoding for
training.
Parameters
----------
df : pandas.DataFrame
Returns
----------
df : pandas.DataFrame
"""
# get durations by taking the difference between launch and deadline and transform
# the seconds integer into days.
df['durations'] = round((df.deadline - df.launched_at)/(60*60*24))
# parse the category feature's json format and extract the first level categories
df['cat_slug'] = df.category.apply(lambda x: x['slug'].split('/')[0])
# map states to 1 for success and 0 for others. Also will drop all 'live' records.
state_dict = {'successful':1, 'failed':0, 'canceled':0, 'suspended':0}
df = df.replace({"state": state_dict})
df = df[df.state != 'live']
# drop unused features
df = df[['name', 'blurb', 'goal', 'country', 'durations', 'cat_slug', 'state']]
return df
cols_names = raw.columns.to_list()
X_col = ['goal', 'durations']
df = raw.copy()
df = preproc(df)
X = df[X_col]
# need to add .astype('int') to turn it y into int from object. otherise sklearn wont work
# https://stackoverflow.com/questions/45346550/valueerror-unknown-label-type-unknown
y = df.state.astype('int')
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=45)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# %time clf = LogisticRegression(random_state=45, solver='lbfgs', multi_class='ovr').fit(X_train, y_train)
clf.score(X_test, y_test)
X_test.iloc[0]
clf.predict(X_test.iloc[0].to_numpy().reshape(1, -1))
# Since our target is (0, 1), the classifier would output a probability matrix of dimension (N, 2). The first index refers to the probability of belonging to class 0, the second index refers to the probability of belonging to class 1. The two will sum to one.
#
# https://datascience.stackexchange.com/questions/22762/understanding-predict-proba-from-multioutputclassifier
#
# Thus, the 'chance' of success (1) will be the second component of predict_proba.
clf.predict_proba(X_test.iloc[0].to_numpy().reshape(1, -1))[:, 1]
| notebooks/2_han_model_logreg_numeric_only.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:ds]
# language: python
# name: conda-env-ds-py
# ---
# # Visualizing datasets larger than memory using Datashader with Dask
#
# ## Datashading a 2.7-billion-point Open Street Map database
#
# Most [datashader](https://github.com/bokeh/datashader) examples use "medium-sized" datasets, because they need to be small enough to be distributed over the internet without racking up huge bandwidth charges for the project maintainers. Even though these datasets can be relatively large (such as the [1-billion point Open Street Map example](https://anaconda.org/jbednar/osm-1billion)), they still fit into memory on a 16GB laptop.
#
# Because Datashader supports [Dask](http://dask.pydata.org) dataframes, it also works well with truly large datasets, much bigger than will fit in any one machine's physical memory. On a single machine, Dask will automatically and efficiently page in the data as needed, and you can also easily distribute the data and computation across multiple machines. Here we illustrate how to work "out of core" on a single machine using a 22GB OSM dataset containing 2.7 billion points.
#
# The data is taken from Open Street Map's (OSM) [bulk GPS point data](https://blog.openstreetmap.org/2012/04/01/bulk-gps-point-data/), and is unfortunately too large to distribute with Datashader (7GB compressed). The data was collected by OSM contributors' GPS devices, and was provided as a CSV file of `latitude,longitude` coordinates. The data was downloaded from their website, extracted, converted to use positions in Web Mercator format using `datashader.utils.lnglat_to_meters()`, and then stored in a [parquet](https://github.com/dask/fastparquet) file for [faster disk access](https://github.com/bokeh/datashader/issues/129#issuecomment-300515690). To run this notebook, you would need to do the same process yourself to obtain `osm.snappy.parq`. Once you have it, you can follow the steps below to load and plot the data.
import dask.dataframe as dd
import dask.diagnostics as diag
import datashader as ds
import datashader.transfer_functions as tf
df = dd.io.parquet.read_parquet('data/osm.snappy.parq')
df.head()
# ### Aggregation
#
# First, we create a canvas to provide pixel-shaped bins in which points can be aggregated, and then aggregate the data to produce a fixed-size aggregate array. This process may take up to a minute, so we provide a progress bar using dask:
# +
bound = 20026376.39
bounds = dict(x_range = (-bound, bound), y_range = (int(-bound*0.4), int(bound*0.6)))
plot_width = 1000
plot_height = int(plot_width*0.5)
cvs = ds.Canvas(plot_width=plot_width, plot_height=plot_height, **bounds)
with diag.ProgressBar(), diag.Profiler() as prof, diag.ResourceProfiler(0.5) as rprof:
agg = cvs.points(df, 'x', 'y', ds.count())
# -
# We can now visualize this data very quickly, ignoring low-count noise as described in the [1-billion point OSM version](https://anaconda.org/jbednar/osm-1billion):
tf.shade(agg.where(agg > 15), cmap=["lightblue", "darkblue"])
# ### Performance Profile
#
# Dask offers some tools to visualize how memory and processing power are being used during these calculations:
from bokeh.io import output_notebook
from bokeh.resources import CDN
output_notebook(CDN, hide_banner=True)
diag.visualize([prof, rprof])
None
# Performance notes:
# - On a 16GB machine, most of the time is spent reading the data from disk (the purple rectangles)
# - Reading time includes not just disk I/O, but decompressing chunks of data
# - The disk reads don't release the [Global Interpreter Lock](https://wiki.python.org/moin/GlobalInterpreterLock) (GIL), and so CPU usage (see second chart above) drops to only one core during those periods.
# - During the aggregation steps (the green rectangles), CPU usage on this machine with 8 hyperthreaded cores (4 full cores) spikes to nearly 800%, because the aggregation function is implemented in parallel.
# - The data takes up 22 GB uncompressed, but only a peak of around 6 GB of physical memory is ever used because the data is paged in as needed.
| examples/osm.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="kP0yBzqJINf0" outputId="f6ad3b18-49d5-4a91-a705-6a0021371f7b"
# !pip install tensorflow-gpu==2.0.0
# + id="G_kOtg5tsveL"
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import tensorflow as tf
from tensorflow.keras import backend as K
from tensorflow.keras.layers import Input, Dense, Lambda, Layer, Add, Multiply, add, Activation
from tensorflow.keras.models import Model, Sequential
import tensorflow.keras.optimizers as optimizers
from tensorflow.keras.callbacks import Callback
#tf.debugging.set_log_device_placement(True)
# + id="2q1wPC6itNUv"
'''
Functions for residual modules which have identity and shortcut projections.
And convolutional layers with batch normalization and ReLu activation
'''
def conv2d_bn(x,
filters,
strides,
padding='same'
):
x = tf.keras.layers.Conv2D(filters, (3, 3),
strides=strides,
padding=padding, kernel_initializer='he_normal',
use_bias=False)(x)
bn_axis = -1
x = tf.keras.layers.BatchNormalization(axis=bn_axis, scale=False)(x)
x = tf.keras.layers.Activation('relu')(x)
return x
def conv2d_bn_1x1(x,
filters,
strides,
padding='same'
):
x = tf.keras.layers.Conv2D(filters, (1, 1),
strides=strides,
padding=padding, kernel_initializer='he_normal',
use_bias=False)(x)
bn_axis = -1
x = tf.keras.layers.BatchNormalization(axis=bn_axis, scale=False)(x)
x = tf.keras.layers.Activation('relu')(x)
return x
def conv2d_trans(x,
filters,
strides,
padding='same'
):
x = tf.keras.layers.Conv2DTranspose(filters, (3,3), strides=strides,
padding='same',
kernel_initializer='he_normal')(x)
bn_axis = -1
x = tf.keras.layers.BatchNormalization(axis=bn_axis, scale=False)(x)
x = tf.keras.layers.Activation('relu')(x)
return x
def conv2d_trans_sigmoid(x,
filters,
strides,
padding='same'
):
x = tf.keras.layers.Conv2DTranspose(filters, (3,3), strides=strides,
padding='same',
kernel_initializer='he_normal')(x)
bn_axis = -1
x = tf.keras.layers.BatchNormalization(axis=bn_axis, scale=False)(x)
x = tf.keras.layers.Activation('sigmoid')(x)
return x
def residual_module1(layer_in, n_filters):
# conv1
x = conv2d_bn(layer_in, n_filters, strides=(1, 1), padding='same')
# conv2
conv2 = conv2d_bn(x, n_filters, strides=(1, 1), padding='same')
# add filters, assumes filters/channels last
layer_out = add([conv2, layer_in])
# activation function
layer_out = Activation('relu')(layer_out)
return layer_out
def residual_module2(layer_in, n_filters):
# conv1
x = conv2d_bn(layer_in, n_filters, strides=(2, 2), padding='same')
# conv2
conv2 = conv2d_bn(x, n_filters, strides=(1, 1), padding='same')
#projection shortcut for mismatch in number of channels
y = conv2d_bn_1x1(layer_in, n_filters, strides=(2, 2), padding='same')
# add filters, assumes filters/channels last
layer_out = add([conv2, y])
# activation function
layer_out = Activation('relu')(layer_out)
return layer_out
# + id="5C88lBAbCt26"
epochs = 100
latent_dim = 2
def inference_net(x):
#x = tf.keras.layers.InputLayer(input_shape=(32,32,3))(x)
x = tf.keras.layers.InputLayer(input_shape=(28, 28, 1))(x)
x = conv2d_bn(x, filters=32, strides=(2, 2))
x = conv2d_bn(x, filters=64, strides=(2, 2))
x = tf.keras.layers.Flatten()(x)
# No activation outputs
z_mu = tf.keras.layers.Dense(units = latent_dim)(x)
z_logvar = tf.keras.layers.Dense(units = latent_dim)(x)
return z_mu, z_logvar
def generative_net(z):
x = tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu)(z)
x = tf.keras.layers.Reshape(target_shape=(7, 7, 32))(x)
x = conv2d_trans(x, filters=64, strides=(2,2))
x = conv2d_trans(x, filters=32,strides=(2,2))
# No activation
x = tf.keras.layers.Conv2DTranspose(filters=1, kernel_size=3,
strides=1, padding='same')(x)
return x
# + id="teaxqluItgt-"
'''
Creating the encoder-decoder model for VAE
'''
def VAE_Model():
# defining input shape
x = Input(shape=(28,28,1))
z_mu, z_log_var = inference_net(x)
# splitting the output from encoder into two equal dimension tensors of mean
# and variance
#= tf.split(z1, num_or_size_splits=2, axis=1)
# reparameterization
eps = K.random_normal(stddev=1.0,shape=(K.shape(x)[0], latent_dim))
z = eps * tf.exp(z_log_var * .5) + z_mu
encoder = Model(inputs=x, outputs=[z, z_mu, z_log_var], name='Encoder')
print(encoder.summary())
#defining decoder model
z_s = Input(shape=(latent_dim,), name='z_sampling')
decoded = generative_net(z_s)
decoder = Model(inputs = z_s, outputs =decoded, name='decoder')
print(decoder.summary())
# decoder invoke
x_pred = decoder(encoder(x)[2])
learning_rate = 0.0001
adm = optimizers.Adam(lr=learning_rate)
vae = Model(inputs=x, outputs=[x_pred, z_mu, z_log_var], name='VAE')
#vae.compile(optimizer= adm, loss= vae_loss(z, z_mu, z_log_var, weight),experimental_run_tf_function=False)
print(vae.summary())
return vae, encoder, decoder
# + colab={"base_uri": "https://localhost:8080/"} id="4Xu_YdXGvSnc" outputId="c49533d4-1cdb-4f41-cf59-4efc8fca5077"
'''
Loading data and normalizing it
'''
# write code for training data, validation and test data
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() #tf.keras.datasets.cifar10.load_data()
print(type(x_train), x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
def norm_images(images):
images = np.asarray(images, dtype='f').reshape(images.shape[0], 28, 28, 1) /255.0
return images
x_train = norm_images(x_train)
x_test = norm_images(x_test)
train_dataset = (tf.data.Dataset.from_tensor_slices(x_train)
.shuffle(50000).batch(128))
test_dataset = (tf.data.Dataset.from_tensor_slices(x_test)
.shuffle(10000).batch(128))
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="ks9iSJaPswjI" outputId="d212f74f-d58a-45cd-ea37-989a5ed04a43"
import time
epochs = 100
# Create the model with the shape of the input
vae, encoder, decoder = VAE_Model()
learning_rate = 0.0001
optimizer = tf.keras.optimizers.Adam(lr=learning_rate)
# the starting value of weight is 0
# define it as a keras backend variable
weight = tf.Variable(0.)
# The number of epochs at which KL loss should be included
klstart = 19 # 7
# number of epochs over which KL scaling is increased from 0 to 1
kl_annealtime = 10 # 10
batch_size = 32
steps_per_epoch = 50000/batch_size
@tf.function
def compute_loss(vae_v, x, wi):
x_pred, mean, logvar = vae_v(x)
# reconstruction_loss
reconstruction_loss = tf.reduce_sum(tf.keras.losses.MSE(x, x_pred), axis=(1,2))
reconstruction_loss = tf.reduce_mean(reconstruction_loss)
# kl loss
kl_loss = -0.5 * (1 + logvar - tf.square(mean) - tf.exp(logvar))
kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))
#kl_loss *= -0.5
#reconstruction_loss = tf.reduce_mean(tf.square(x+0.0 - x_pred))
#print('recon')
#print(reconstruction_loss)
#kl_l = - 0.5 * K.mean(1 + logvar - K.square(mean) - K.exp(logvar))
return reconstruction_loss + (weight * kl_loss), reconstruction_loss, kl_loss
@tf.function
def compute_apply_gradients(vae_model, x, optimizer, w):
with tf.GradientTape() as tape:
final_loss, recon_loss, klloss = compute_loss(vae_model, x, w)
gradients = tape.gradient(final_loss, vae_model.trainable_variables)
optimizer.apply_gradients(zip(gradients, vae_model.trainable_variables))
return final_loss, recon_loss, klloss
for epoch in range(1, epochs + 1):
start_time = time.time()
print('epoch start ' + str(epoch))
print(start_time)
if epoch > klstart:
weight.assign(min(((1. / kl_annealtime)*(epoch-klstart)), 1.))
print(kl_annealtime)
print("Current KL Weight is " + str(weight.read_value()))
step = 0
for train_x in train_dataset:
#step = step+1
#if step == steps_per_epoch:
#print('step broken at' + str(step))
#break
if (epoch) == 1:
global_step = step + 1
else:
global_step = (epoch * steps_per_epoch) + (step + 1)
loss, reloss, kl_loss = compute_apply_gradients(vae, train_x, optimizer, weight)
x_dash,_,_ = vae(train_x)
if step % 300 == 0:
print('in step' + str(step))
print('loss per 200 batches')
tf.print(reloss)
tf.print(kl_loss)
tf.print(loss)
#tf.summary.scalar('train_reconstruction_loss', data=reloss, step=global_step)
#tf.summary.scalar('train_kl_loss', data=kl_loss, step=global_step)
#tf.summary.scalar('train_loss', data=loss, step=global_step)
#x_dash = x_dash.numpy()
#x_dash = np.reshape(x_dash, (batch_size, 32, 32, 3))
#tf.summary.image('reconstructed image slice1', x_dash, max_outputs=batch_size, step=global_step)
#ip_plt = np.reshape(train_x, (batch_size, 32, 32, 3))
#tf.summary.image('ip image slice1', ip_plt, max_outputs=batch_size, step=global_step)
step = step+1
end_time = time.time()
step = 0
if epoch % 1 == 0:
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
#step = step + 1
#if step == validata_steps:
#print('step broken at' + str(step))
#break
loss(compute_loss(vae, test_x, weight)[0])
if step % 200 == 0:
print('in validation step' + str(step))
step = step+1
elbo = loss.result()
print('Epoch: {}, Test set loss: {}, '
'time elapse for current epoch {}'.format(epoch,
elbo,
end_time - start_time))
# display a 2D plot of the digit classes in the latent space
z_test, z_mu_test , z_log_var_test = encoder.predict(x_test, batch_size=batch_size)
from sklearn.decomposition import PCA
X = PCA(n_components=2).fit_transform(z_test)
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_test,
alpha=.4, s=3**2, cmap='viridis')
plt.colorbar()
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 378} id="kOtl3HJBEqSF" outputId="cf5a58e5-9998-43bc-9111-eca125ef9bc9"
# display a 2D plot of the digit classes in the latent space
z_test, z_mu_test , z_log_var_test = encoder.predict(x_test, batch_size=batch_size)
from sklearn.decomposition import PCA
#X = PCA(n_components=2).fit_transform(z_test)
plt.figure(figsize=(6, 6))
plt.scatter(z_test[:, 0], z_test[:, 1], c=y_test,
alpha=.4, s=3**2, cmap='viridis')
plt.colorbar()
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 332} id="vs9QrazRH6iC" outputId="ab29113f-2d75-4e45-94ba-4486da001548"
print(z_test.shape)
print(z_test[0].shape)
x_testhat0 = decoder(z_test[0:32])
print(x_testhat0.shape)
plt.imshow(x_testhat0[12].numpy().reshape(28,28))
# + colab={"base_uri": "https://localhost:8080/", "height": 575} id="ZDSFMjmaW59n" outputId="4340200b-d2bb-475d-a57c-05e<PASSWORD>62454"
import tensorflow_probability as tfp
def plot_latent_images(decoder, n, digit_size=28):
"""Plots n x n digit images decoded from the latent space."""
norm = tfp.distributions.Normal(0, 1)
grid_x = norm.quantile(np.linspace(0.05, 0.95, n))
grid_y = norm.quantile(np.linspace(0.05, 0.95, n))
image_width = digit_size*n
image_height = image_width
image = np.zeros((image_height, image_width))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z = np.array([[xi, yi]])
x_decoded = decoder(z)
digit = tf.reshape(x_decoded[0], (digit_size, digit_size))
image[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit.numpy()
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='Greys_r')
plt.axis('Off')
plt.show()
plot_latent_images(decoder, 20)
# + id="eyBEaLiPFUBl"
| VAE_TF.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div style="width:1000 px">
#
# <div style="float:right; width:98 px; height:98px;">
# <img src="https://raw.githubusercontent.com/Unidata/MetPy/master/metpy/plots/_static/unidata_150x150.png" alt="Unidata Logo" style="height: 98px;">
# </div>
#
# <h1>Introduction to MetPy</h1>
# <h3>Unidata Python Workshop</h3>
#
# <div style="clear:both"></div>
# </div>
#
# <hr style="height:2px;">
#
#
# ## Overview:
#
# * **Teaching:** 15 minutes
# * **Exercises:** 15 minutes
#
# ### Questions
# 1. What is MetPy?
# 1. How is MetPy structured?
# 1. How are units handled in MetPy?
#
# ### Objectives
# 1. <a href="#whatis">What is MetPy?</a>
# 1. <a href="#units">Units and MetPy</a>
# 1. <a href="#constants">MetPy Constants</a>
# 1. <a href="#calculations">MetPy Calculations</a>
# <a name="whatis"></a>
# ## What is MetPy?
# MetPy is a modern meteorological toolkit for Python. It is now a maintained project of [Unidata](http://www.unidata.ucar.edu) to serve the academic meteorological community. MetPy consists of three major areas of functionality:
#
# 
#
# ### Plots
# As meteorologists, we have many field specific plots that we make. Some of these, such as the Skew-T Log-p require non-standard axes and are difficult to plot in most plotting software. In MetPy we've baked in a lot of this specialized functionality to help you get your plots made and get back to doing science. We will go over making different kinds of plots during the workshop.
#
#
# ### Calculations
# Meteorology also has a common set of calculations that everyone ends up programming themselves. This is error-prone and a huge duplication of work! MetPy contains a set of well tested calculations that is continually growing in an effort to be at feature parity with other legacy packages such as GEMPAK.
#
# ### File I/O
# Finally, there are a number of odd file formats in the meteorological community. MetPy has incorporated a set of readers to help you deal with file formats that you may encounter during your research.
# <a name="units"></a>
# ## Units and MetPy
# Early in our scientific careers we all learn about the importance of paying attention to units in our calculations. Unit conversions can still get the best of us and have caused more than one major technical disaster, including the crash and complete loss of the $327 million [Mars Climate Orbiter](https://en.wikipedia.org/wiki/Mars_Climate_Orbiter).
#
# In MetPy, we use the [pint](https://pint.readthedocs.io/en/latest/) library and a custom unit registry to help prevent unit mistakes in calculations. That means that every quantity you pass to MetPy should have units attached, just like if you were doing the calculation on paper! Attaching units is easy:
# Import the MetPy unit registry
from metpy.units import units
length = 10.4 * units.inches
width = 20 * units.meters
print(length, width)
# Don't forget that you can use tab completion to see what units are available! Just about every imaginable quantity is there, but if you find one that isn't, we're happy to talk about adding it.
#
# While it may seem like a lot of trouble, let's compute the area of a rectangle defined by our length and width variables above. Without units attached, you'd need to remember to perform a unit conversion before multiplying or you would end up with an area in inch-meters and likely forget about it. With units attached, the units are tracked for you.
area = length * width
print(area)
# That's great, now we have an area, but it is not in a very useful unit still. Units can be converted using the `.to()` method. While you won't see m$^2$ in the units list, we can parse complex/compound units as strings:
area.to('m^2')
# ### Exercise
# * Create a variable named `speed` with a value of 25 knots.
# * Create a variable named `time` with a value of 1 fortnight.
# * Calculate how many furlongs you would travel in `time` at `speed`.
# Your code goes here
# #### Solution
# # %load solutions/distance.py
# ### Temperature
# Temperature units are actually relatively tricky (more like absolutely tricky as you'll see). Temperature is a non-multiplicative unit - they are in a system with a reference point. That means that not only is there a scaling factor, but also an offset. This makes the math and unit book-keeping a little more complex. Imagine adding 10 degrees Celsius to 100 degrees Celsius. Is the answer 110 degrees Celsius or 383.15 degrees Celsius (283.15 K + 373.15 K)? That's why there are delta degrees units in the unit registry for offset units. For more examples and explanation you can watch [MetPy Monday #13](https://www.youtube.com/watch?v=iveJCqxe3Z4).
#
# Let's take a look at how this works and fails:
# We would expect this to fail because we cannot add two offset units (and it does fail as an "Ambiguous operation with offset unit").
#
# <pre style='color:#000000;background:#ffffff;'><span style='color:#008c00; '>10</span> <span style='color:#44aadd; '>*</span> units<span style='color:#808030; '>.</span>degC <span style='color:#44aadd; '>+</span> <span style='color:#008c00; '>5</span> <span style='color:#44aadd; '>*</span> units<span style='color:#808030; '>.</span>degC
# </pre>
#
# On the other hand, we can subtract two offset quantities and get a delta:
10 * units.degC - 5 * units.degC
# We can add a delta to an offset unit as well:
25 * units.degC + 5 * units.delta_degF
# Absolute temperature scales like Kelvin and Rankine do not have an offset and therefore can be used in addition/subtraction without the need for a delta verion of the unit.
273 * units.kelvin + 10 * units.kelvin
273 * units.kelvin - 10 * units.kelvin
# ### Exercise
# A cold front is moving through, decreasing the ambient temperature of 25 degC at a rate of 2.3 degF every 10 minutes. What is the temperature after 1.5 hours?
# +
# Your code goes here
# -
# #### Solution
# # %load solutions/temperature_change.py
# <a href="#top">Top</a>
# <hr style="height:2px;">
# <a name="constants"></a>
# ## MetPy Constants
# Another common place that problems creep into scientific code is the value of constants. Can you reproduce someone else's computations from their paper? Probably not unless you know the value of all of their constants. Was the radius of the earth 6000 km, 6300km, 6371 km, or was it actually latitude dependent?
#
# MetPy has a set of constants that can be easily accessed and make your calculations reproducible. You can view a [full table](https://unidata.github.io/MetPy/latest/api/generated/metpy.constants.html#module-metpy.constants) in the docs, look at the module docstring with `metpy.constants?` or checkout what's available with tab completion.
import metpy.constants as mpconst
mpconst.earth_avg_radius
mpconst.dry_air_molecular_weight
# You may also notice in the table that most constants have a short name as well that can be used:
mpconst.Re
mpconst.Md
# <a href="#top">Top</a>
# <hr style="height:2px;">
# <a name="calculations"></a>
# ## MetPy Calculations
# MetPy also encompasses a set of calculations that are common in meteorology (with the goal of have all of the functionality of legacy software like GEMPAK and more). The [calculations documentation](https://unidata.github.io/MetPy/latest/api/generated/metpy.calc.html) has a complete list of the calculations in MetPy.
#
# We'll scratch the surface and show off a few simple calculations here, but will be using many during the workshop.
import metpy.calc as mpcalc
import numpy as np
# +
# Make some fake data for us to work with
np.random.seed(19990503) # So we all have the same data
u = np.random.randint(0, 15, 10) * units('m/s')
v = np.random.randint(0, 15, 10) * units('m/s')
print(u)
print(v)
# -
# Let's use the `wind_direction` function from MetPy to calculate wind direction from these values. Remember you can look at the docstring or the website for help.
direction = mpcalc.wind_direction(u, v)
print(direction)
# ### Exercise
# * Calculate the wind speed using the `wind_speed` function.
# * Print the wind speed in m/s and mph.
# Your code goes here
# #### Solution
# # %load solutions/wind_speed.py
# As one final demonstration, we will calculation the dewpoint given the temperature and relative humidity:
mpcalc.dewpoint_rh(25 * units.degC, 75 * units.percent)
# <a href="#top">Top</a>
# <hr style="height:2px;">
| metpy/Introduction to MetPy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Group assignment
# The group assignment is to write a Psychopy script for a psychological experiment.
#
# In the first lesson, you will meet in groups to decide which experiment to code.
#
# It should be an experiment in which:
#
# - participants have to give responses in several trials (e.g., decide between options)
# - there should be some sort of randomization across trials/within block (e.g., options are presented left vs. right)
# - there are at least 2 blocks of trials in which some factor is manipulated (e.g., easy vs. hard block)
# - there are at least 2 between subjects conditions (e.g., one group of subjects sees one set of stimuli and the other group sees another one)
#
# **By the 28th May**, send me one google document per group in which you wrote a detailed plan for the experiment you want to write.
#
# In the second lesson, we are going to start the actual coding. You can start in class, and ask me questions, and then finish on your own. The final deadline for the script is the **20th June**. The final product should be a working script (that gives no errors) and that does what was described in the google document.
import os
os.path.join(os.getcwd())
os.path.join(os.getcwd(), 'stimuli')
os.path.join(os.getcwd(), 'stimuli', 'A.png')
# +
path_to_check = os.path.join(os.getcwd(), 'stimuli', 'A.png')
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img = mpimg.imread(path_to_check)
imgplot = plt.imshow(img)
plt.show()
# -
| notebooks/wpa_7.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Simple linear regression
# ## Import the relevant libraries
# +
# For these lessons we will need NumPy, pandas, matplotlib and seaborn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# and of course the actual regression (machine learning) module
from sklearn.linear_model import LinearRegression
# -
# ## Load the data
# +
# We start by loading the data
data = pd.read_csv('1.01. Simple linear regression.csv')
# Let's explore the top 5 rows of the df
data.head()
# -
# ## Create the regression
# ### Declare the dependent and independent variables
# +
# There is a single independent variable: 'SAT' called input or feature
x = data['SAT']
# and a single depended variable: 'GPA' called output or target
y = data['GPA']
# -
# Often it is useful to check the shapes of the features
x.shape
y.shape
# +
# In order to feed x to sklearn, it should be a 2D array (a matrix)
# Therefore, we must reshape it
# Note that this will not be needed when we've got more than 1 feature (as the inputs will be a 2D array by default)
# x_matrix = x.values.reshape(84,1)
x_matrix = x.values.reshape(-1,1)
# Check the shape just in case
x_matrix.shape
# -
# ### Regression itself
# Full documentation: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
# We start by creating a linear regression object
reg = LinearRegression()
# The whole learning process boils down to fitting the regression
# Note that the first argument is the independent variable, while the second - the dependent (unlike with StatsModels)
reg.fit(x_matrix,y)
# ### R-Sqaured
reg.score(x_matrix,y)
# ### Coefficients
reg.coef_
# ### Intercepts
reg.intercept_
# ### Making Predictions
reg.predict([[1740]])
new_data = pd.DataFrame(data=[1740,1760], columns=['SAT'])
new_data
reg.predict(new_data)
new_data['Predicted GPA'] = reg.predict(new_data)
new_data
# Create a scatter plot
plt.scatter(x_matrix,y)
# Define the regression equation, so we can plot it later
y_hat = reg.coef_*x_matrix + reg.intercept_ #formula from above
# Plot the regression line against the independent variable (SAT)
fig = plt.plot(x_matrix,y_hat, lw=4, c='red', label ='regression line')
# Label the axes
plt.xlabel('SAT', fontsize = 25)
plt.ylabel('GPA', fontsize = 25)
plt.show()
# #### Information on Feature Scaling: https://en.wikipedia.org/wiki/Feature_scaling
# #### Information on L1 and L2 Norm: http://www.chioka.in/differences-between-the-l1-norm-and-the-l2-norm-least-absolute-deviations-and-least-squares/
| Part_5_Advanced_Statistical_Methods_(Machine_Learning)/Linear Regression/Sklearn/sklearn - Simple Linear Regression - GPA Problem.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Calculate Changes in Water Levels #
# ---
#
# ## Overview ##
# ---
# The purpose of this tutorial is to use Planet imagery to calculate an approximate percentage change in reservoir water levels.
# ## Table of Contents
#
# ---
#
# * **[How to Get Started](#how-to-get-started)**
# * Requirements
# * Software & Modules
# * How to Export Planet API Key and Install Packages
# * Download Images at Two Time Points
# * Download Images with Planet CLI
# * Use QGIS to Select Common Window to Compare
# * Crop Images With GDAL Warp Command
#
# * **[Find the Water](#find-the-water)**
# * Create a Mask Using Threshold
# * Clean up Mask With Erosion and Dilation
#
# * **[Watershed Algorithm](#watershed-algorithm)**
# * How to segment image using watershed
#
# * **[Get Contours and Area](#contour-area)**
# * Apply Function to Calculate Area and Water Change
# * Output
#
#
# * **[Data Visualization](#data-viz)**
#
#
# * **[Conclusion](#conclusion)**
# <a name="how-to-get-started"></a>
# ## How To Get Started
# ---
# Before we start our analysis we need to ensure we have the required packages and Planet satellite images.
# ### Requirements
# ---
# #### Software & Python Libraries
# You will need:
#
# * Python 3
# * GDAL
# * scipy & numpy
# * skimage
# * requests
# * OpenCV
# * imutils
# * The Planet CLI _(optional)_
# * Your Planet API Key
# #### How to Export Planet API Key and Install Packages
# ---
# To export your Planet API Key to your environment:
# ```bash
# export PLANET_API_KEY=a3a64774d30c4749826b6be445489d3b # (not a real key)
# ```
# You can find GDAL installation instructions [here](https://trac.osgeo.org/gdal/wiki/DownloadingGdalBinaries). For installation of scipy & numpy, [see this page](https://www.scipy.org/install.html).
#
# To install the Python libraries, do:
#
# ```bash
# $ python -m pip install requests
# $ python -m pip install opencv-python
# $ python -m pip install scikit-image
# $ python -m pip install imutils
#
# # optionally:
# $ python -m pip install planet
# ```
# Once installation is complete, you're ready to start with Step 1 below.
#
# A note about Planet Imagery Product Compatability: this tutorial is compatable with all ItemTypes & Asset Types.
# ### Download Images at Two Time Points
# ---
# First, let's download images of the same Reservoir in California, 2 weeks apart.
#
# You can use the [Data API](https://developers.planet.com/docs/data/) to search for, activate & download these images, or optionally you can use the planet CLI.
#
# #### How to Download Images with Planet CLI
#
# To use the CLI, do:
# ```bash
# $ planet data download --item-type REOrthoTile --asset-type visual --string-in id 20160707_195146_1057917_RapidEye-1
# $ planet data download --item-type REOrthoTile --asset-type visual --string-in id 20160722_194930_1057917_RapidEye-2
# ```
#
# You now have the two Planet 'visual' GeoTIFF format images in your current directory.
#
# N.B.: As this is just an example, we are using Planet's 'visual' asset type. If we wanted a more accurate measurement we would use the higher bit-depth 'analytic' product.
# ### Use QGIS to Select Common Window to Compare
# ---
# Our scenes don't overlap perfectly, and for the calculation to be accurate we'd prefer they did. The GDAL Warp command enables us to do this crop.
#
# With QGIS we can find the overlapping rectangle between the two scenes. Move your mouse to where you estimate the corners might be, and take note of the numbers from the 'coordinates' box on the bottom menu bar.
# <div>
# <img src="images/qgis_bounds.png" width="900"/>
# </div>
# ### Crop Images With GDAL Warp Command
# ---
# We then run the following bash commands:
# ```bash
# gdalwarp -te 547500 4511500 556702 4527000 1057917_2016-07-07_RE1_3A_Visual.tif 20160707.tif
# ```
# ```bash
# gdalwarp -te 547500 4511500 556702 4527000 1057917_2016-07-22_RE2_3A_Visual.tif 20160722.tif
# ```
# <div>
# <img src="images/20160707.png"/>
# <img src="images/20160722.png"/>
# </div>
# <a name="find-the-water"></a>
# ## Find the Water
# ---
# In order to find the water we want to extract the blue hues within the image. Using OpenCV, we convert the BGR colorspace to HSV and create a threshold to extract the blue water. As you can see below, the mask we created differentiates the water from the land.
#
# ### Create a Mask Using Threshold
# ---
# ```python
#
# import cv2 as cv
#
# a = cv.imread('20160707.tif')
# b = cv.imread('20160722.tif')
#
# hsv_a = cv.cvtColor(a, cv.COLOR_BGR2HSV)
# hsv_b = cv.cvtColor(b, cv.COLOR_BGR2HSV)
#
# low = np.array([55, 0, 0])
# high = np.array([118, 255, 255])
#
# inner_a = cv.inRange(hsv_a, low, high)
# inner_b = cv.inRange(hsv_b, low, high
#
# cv.imwrite('inner_a.png', inner_a)
# cv.imwrite('inner_b.png', inner_b)
# ```
# <div>
# <h1><center>Mask A</center></h1>
# <img src="images/inner_a.png" width="500"/>
# <h1><center>Mask B</center></h1>
# <img src="images/inner_b.png" width="500"/>
# </div>
# ### Cleaning up the Mask Using Erosion and Dilation
# ---
#
# We currently have some noise in our mask that we can eliminate using two morphological operations, erosion and dilation. The purpose of these operations to ensure we have a clear separation between the background and foreground, or land and water.
#
# ```python
#
# kernel = np.ones((5,5),np.uint8)
#
# erosion_a = cv.erode(inner_a,kernel,iterations = 2)
# erosion_b = cv.erode(inner_b,kernel,iterations = 2)
#
# innerA = cv.dilate(erosion_a,kernel,iterations = 1)
# innerB = cv.dilate(erosion_b,kernel,iterations = 1)
#
# cv.imwrite('innerA.png', innerA)
# cv.imwrite('innerB.png', innerB)
# ```
# <div>
# <h1><center>Mask A</center></h1>
# <img src="images/innerA.png" width="500"/>
# <h1><center>Mask B</center></h1>
# <img src="images/innerB.png" width="500"/>
# </div>
# <a name="watershed-algorithm"></a>
# ## Watershed Algorithm
# ---
# In order to calculate the changes in water levels we need to know the area of the water in the image. We will use a segmentation technique so we only focus on the water and ignore everything else. The watershed algorithm returns a numpy array of labels with unique values corresponding to the pixel value.
#
# ```python
#
# from scipy import ndimage
# from skimage.feature import peak_local_max
# from skimage.segmentation import watershed
# import numpy as np
#
# eucl_a = ndimage.distance_transform_edt(innerA)
# eucl_b = ndimage.distance_transform_edt(innerB)
#
# localMaxA = peak_local_max(eucl_a, indices=False, labels=innerA)
# localMaxB = peak_local_max(eucl_b, indices=False, labels=innerB)
#
# markers_a = ndimage.label(localMaxA, structure=np.ones((3, 3)))[0]
# markers_b = ndimage.label(localMaxB, structure=np.ones((3, 3)))[0]
#
# labels_a = watershed(-eucl_a, markers_a, mask=innerA)
# labels_b = watershed(-eucl_b, markers_b, mask=innerB)
# ```
#
# <a name="contour-area"></a>
# ## Calculating Area Using Contours and Overlaying Mask##
# ---
# Once we have our labels, we loop over each unique label and look for the values that correspond with the foreground, or water. After applying those values to our mask, we then grab the contour of each object in our mask in order to perform our calculations on it. By adding the area of each individual contour to the total area, we are able to approximate the area of the water in our image.
#
# **Note**: I added lines to fill the contours and save the image for visualization purposes but this isn't necessary for our calculation.
#
# ### Python Function to Find Area
# ---
# ```python
# def get_area(labels, inner_mask, img):
# area = 0
# for label in np.unique(labels):
#
# if label== 0:
# continue
#
# mask = np.zeros(inner_mask.shape, dtype="uint8")
# mask[labels == label] = 255
#
# contours = cv.findContours(mask, cv.RETR_EXTERNAL, cv.CHAIN_APPROX_SIMPLE)
# contours = imutils.grab_contours(contours)
# cv.fillPoly(img, pts=contours, color=(0,255,255))
#
# a = cv.contourArea(contours[0])
# area+=a
#
# cv.imwrite('mask.png', img)
#
# return area
#
# area_a = get_area(labels_a, innerA, a)
# area_b = get_area(labels_b, innerB, b)
# ```
# <div>
# <h1><center>Image A</center></h1>
# <img src="images/a_mask.png" width="500"/>
# <h2><center>Image B</center></h2>
# <img src="images/b_mask.png" width="500"/>
# </div>
# ### Apply Function to get Area and Water Change
# ---
# After we apply our function to both planet images, we now know the approximate change in water reservoir water levels between the times both these images were captured.
#
# ```python
# area_a = mask_img(labels_a, innerA, a)
# area_b = mask_img(labels_b, innerB, b)
# water_level_diff = area_b/float(area_a)
# ```
#
# ### Output
# ---
# ```
# Area A = 1164765.0
# Area B = 1120738.5
# Water Level Difference = 0.9622013882628685
# Percent change = -3.7798611737131504%
# ```
# <a name="data-viz"></a>
# ## Data Visualization Section ##
# ---
# Our last step is to plot a bar chart to represent the difference in water levels.
#
# ```python
# from bokeh.io import output_file, show
# from bokeh.plotting import figure
# import bokeh.plotting as bk
#
# dates = ['2016-07-13', '2016-09-10']
# pixels = [area_a, area_b]
#
# plt = figure(x_range=dates, plot_height=275, title="Reservoir Pixels",
# toolbar_location=None, tools="")
#
# plt.vbar(x=dates, top=pixels, width=0.3, fill_color="#cfe31e")
#
# plt.xgrid.grid_line_color = None
# plt.y_range.start = 0
# plt.xaxis.axis_label = "Date"
# plt.yaxis.axis_label = "Sum(Pixels)"
#
# #saves as a html file
# bk.save(plt)
# show(plt)
# ```
# <div>
# <h1><center>Water Changes</center></h1>
# <img src="images/water_change.png"/>
# </div>
# Questions or comments about this guide? Join the conversation at [Planet Community](https://support.planet.com/hc/en-us/community/topics).
| jupyter-notebooks/water_change/water-level-changes-notebook/calculate_changes.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:notebook] *
# language: python
# name: conda-env-notebook-py
# ---
# # Landsat-8
#
#
# <div class="alert-info">
#
# ### Overview
#
# * **teaching:** 30 minutes
# * **exercises:** 0
# * **questions:**
# * How can I find, anaylize, and visualize Landsat8 satellite imagery for an area of interest using Python?
#
# </div>
#
#
# This notebook will focus on accessing public datasets on AWS for a target area affected by Cyclone Kenneth (2019-04-25). Read more about this event and its impact at the [Humanitarian Open Street Map website](https://tasks.hotosm.org/project/5977). We will use a bounding box we will work with covers the island of Nagazidja, including the captial [city of Moroni](https://en.wikipedia.org/wiki/Moroni,_Comoros) - Union of the Comoros, a sovereign archipelago nation in the Indian Ocean.
#
# We will examine raster images from the [Landsat-8 instrument](https://www.usgs.gov/land-resources/nli/landsat). The Landsat program is the longest-running civilian satellite imagery program, with the first satellite launched in 1972 by the US Geological Survey. Landsat 8 is the latest satellite in this program, and was launched in 2013. Landsat observations are processed into “scenes”, each of which is approximately 183 km x 170 km, with a spatial resolution of 30 meters and a temporal resolution of 16 days. The duration of the landsat program makes it an attractive source of medium-scale imagery for land surface change analyses.
#
# Additional code examples for Landsat-8 can be found in Geohackweek 2018 content: https://geohackweek.github.io/raster/04-workingwithrasters/
# ## Table of contents
#
# 1. [**Sat-search**](#Sat-search)
# 1. [**Holoviz visualization**](#Holoviz)
# 1. [**Rasterio and xarray**](#Rasterio-and-xarray)
# +
# Import libraries
import geopandas as gpd
import pandas as pd
import satsearch
from satstac import Items
import holoviews as hv
import hvplot.xarray
import hvplot.pandas
import geoviews as gv
import ipywidgets
import datetime
from ipywidgets import interact
from IPython.display import display, Image
import json
from cartopy import crs as ccrs
import rasterio
import rasterio.mask
from rasterio.session import AWSSession
import xarray as xr
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
# %matplotlib inline
# -
# Set up our bounding box
bbox = [43.16, -11.32, 43.54, -11.96]
west, north, east, south = bbox
bbox_ctr = [0.5*(north+south), 0.5*(west+east)]
# ## Sat-search
#
# [Sat-search](https://github.com/sat-utils/sat-search) is open-source software designed to easily discover public imagery on AWS. It depends upon metadata called Spatio-Temporal Asset Catalogs [STAC catalogs](https://stacspec.org/) to filter scenes. We will use it to search for Landsat-8 data covering our area of interest
# +
# bbox as a python list is great for use in python, but we can instead save to a more interoperable format (GeoJSON)
# Here is a great website for creating and visualizing geojson on a map: http://geojson.io
aoi = { "type": "Polygon",
"coordinates": [[[west, south], [west, north], [east, north], [east, south], [west, south]]]
}
# pretty print formatting
print(json.dumps(aoi, sort_keys=False, indent=2))
# save to file for future use
with open('aoi-5977.geojson', 'w') as f:
json.dump(aoi, f)
# -
# Load results to pandas geodataframe
# now other packages such as geojson can read this file
gfa = gpd.read_file('aoi-5977.geojson')
gfa
# Get results for bbox and time range
results = satsearch.Search(bbox=bbox, datetime='2019-02-01/2019-06-01')
print('%s items' % results.found())
items = results.items()
print('%s collections:' % len(items._collections))
print(items._collections)
# +
# If you are unfamiliar with one of these satellites, we can look at stored metadata
col = items._collections[1]
print('Title:', col.title)
print('Collection Version:', col.version)
print('Keywords: ', col.keywords)
print('License:', col.license)
print('Providers:', col.providers)
print('Extent', col.extent)
# -
# We can delve deeper to see what kind of metadata is available at the scene level
for key in col.properties:
if key == 'eo:bands':
[print(band) for band in col[key]]
else:
print('%s: %s' % (key, col[key]))
# +
# Search for just tier1 Landsat8 scenes, all dates
properties = ["landsat:tier=T1"]
bbox = (west, south, east, north) #(min lon, min lat, max lon, max lat)
results = satsearch.Search.search(collection='landsat-8-l1',
bbox=bbox,
sort=['<datetime'], #earliest scene first
property=properties)
print('%s items' % results.found())
# -
# Save search results for later or to share with others
items = results.items()
items.save('items-landsat8.json')
items = Items.load('items-landsat8.json')
# # Assets correspond to actual images related to a STAC metadata item
# Use pandas to better display python dictionaries!
pd.DataFrame(items[0].assets).T.reset_index()
# Read results into a geopandas GeoDataFrame
gfl = gpd.read_file('items-landsat8.json')
gfl = gfl.sort_values('datetime').reset_index(drop=True)
print('records:', len(gfl))
gfl.head()
# Hack for neat display of band information
import ast
band_info = pd.DataFrame(ast.literal_eval(gfl.iloc[0]['eo:bands']))
band_info
# +
# Note the cloud_cover column, we can narrow our search by any of these properties
properties.extend(["eo:cloud_cover<10"])
test = satsearch.Search.search(collection='landsat-8-l1',
bbox=bbox,
sort=['<datetime'], #earliest scene first
property=properties)
print('%s items' % test.found())
# -
# Or since we can just use geopandas to filter results
subset = gfl[gfl['eo:cloud_cover'] < 10]
print('%s items' % len(subset))
# ## Holoviz
#
# [Holoviz](https://holoviz.org/) is a set of Python visualization libraries that simplify interactive visualizations of data in a web-browser. We'll use several of these libraries including hvplot and geoviews to visualize both vector data (such as image footprints) and raster data (actual raster values).
#
# <div class="alert-warning">
#
# #### Note
#
# the toolbars on the right and side of these plots. We are using a library called Bokeh that gives interactive widgets to zoom in and pan around on maps.
# </div>
# +
# Plot search AOI and frames on a map using Holoviz Libraries
cols = gfl.loc[:,('id','geometry')]
footprints = cols.hvplot(geo=True, line_color='k', alpha=0.1, title='Landsat 8 T1')
aoi = gfa.hvplot(geo=True, line_color='b', fill_color=None)
tiles = gv.tile_sources.CartoEco.options(width=700, height=500)
labels = gv.tile_sources.StamenLabels.options(level='annotation')
tiles * footprints * aoi * labels
# -
# ## ipywidgets
#
# [ipywidgets](https://ipywidgets.readthedocs.io/en/latest/) provide another convenient approach to custom visualizations. The function below allows us to browse through all the image thumbnails for a group of images (more specifically a specific Landsat8 path and row).
def browse_images(items):
n = len(items)
def view_image(i=0):
item = items[i]
print(f"id={item.id}\tdate={item.datetime}\tcloud%={item['eo:cloud_cover']}")
display(Image(item.asset('thumbnail')['href']))
interact(view_image, i=(0,n-1))
# Custom syntax (additional fields, query strings instead of query dict)
properties = ["eo:row=068",
"eo:column=162",
"landsat:tier=T1"]
results = satsearch.Search.search(collection='landsat-8-l1',
bbox=bbox,
sort=['<datetime'], #earliest scene first
property=properties)
print('%s items' % results.found())
items = results.items()
# May not work on Chrome currently, does work on Safari
browse_images(items)
# ## Rasterio and xarray
#
# To actually load full resolution data from a particular Landsat-8 band we'll use rasterio and xarray libraries.
# These are environmnent variable settings for efficiently reading data on AWS S3
env = rasterio.Env(GDAL_DISABLE_READDIR_ON_OPEN='EMPTY_DIR',
CPL_VSIL_CURL_ALLOWED_EXTENSIONS='TIF',
)
item = items[0]
band = 'red'
url = item.asset(band)['href']
print(url)
with env:
with rasterio.open(url) as src:
print(src.profile) # image metadata
width = src.width
blockx = src.profile['blockxsize']
blocky = src.profile['blockysize']
xchunk = int(width/blockx)*blockx
ychunk = blocky
da = xr.open_rasterio(src, chunks={'band': 1, 'x': xchunk, 'y': ychunk})
da
# Nice dask array visualization
da.data
# This will pull raster data over network. if operating in the same AWS region, should be very fast!
# NOTE: seems there is a bug currently with 'logz' for a log-scale colorbar
img = da.hvplot.image(rasterize=True, logz=True, width=700, height=500, cmap='reds', title=f'{item.id} ({band})')
img
# ### Visualize with on-the-fly reprojection
# Display image in latitute, longitude coordinates instead of EPSG:32638 (UTM 38N)
crs = ccrs.UTM(zone='38N')
img = da.hvplot.image(crs=crs, rasterize=True, width=700, height=500, cmap='reds', alpha=0.8, title=f'{item.id} ({band})') # , logz=True not working
aoi = gfa.hvplot(geo=True, line_color='b', fill_color=None)
img * aoi
# ### Image subsets and crop by shapefile
#
# Often we are only interested in small regions of full images. One of the killer features of cloud-optimized data formats stored on the cloud is that we can efficiently pull subsets of an image rather than the whole thing. Here we'll pull only the pixels within a vector polygon in our area of interest.
#
# <div class="alert-warning">
#
# #### Note
#
# It's up to you to make sure the vector and raster CRS's match!
# </div>
gfa
with rasterio.open(url) as src:
# re-project vector to match raster CRS
print(src.meta)
shape = gfa.to_crs(epsg=src.crs.to_epsg())
out_image, out_transform = rasterio.mask.mask(src, shape.geometry.values, crop=True)
out_meta = src.meta
out_meta.update({
"height": out_image.shape[1],
"width": out_image.shape[2],
"transform": out_transform})
print(out_meta)
# write small image to local Geotiff file
with rasterio.open('subset.tif', 'w', **out_meta) as dst:
dst.write(out_image)
# Plot just the subset
import rasterio.plot
with rasterio.open('subset.tif') as src:
rasterio.plot.show(src, cmap='Reds')
# +
# Excercise 1) Load and visualize the highest-resolution 15m pancromatic band instead of the red band
# Excercise 2) Calculate a band ratio between any two bands
# -
# # Xarray DataArray
#
# The xarray multidimensional data model works well if you want to perform computations on multiple bands for a single image, and to utilize dask for distributed computations
# Use just 30 meter bands for simplicity
bands = band_info.query('gsd == 30').common_name.to_list()
bands
def load_dataarray(item, bands):
''' Load STAC item into an xarray DataSet '''
data_arrays = []
for band in bands:
url = item.asset(band)['href']
da = xr.open_rasterio(url, chunks={'band': 1, 'x': 1024, 'y': 1024})
data_arrays.append(da.assign_coords(band=[band]))
return xr.concat(data_arrays, dim='band')
da = load_dataarray(item, bands)
da
img = da.hvplot.image(groupby='band', rasterize=True, width=700, height=500, alpha=0.8, title=f'{item.id}') # , logz=True not working
img
# # Xarray DataSets
#
# It is arguable better to think of image bands as observational variables rather than a dimension of the dataset. DataSets are meant for storing multiple variables. This data structure is also useful for timeseries of multiple images.
def load_dataset(item, bands):
''' Load STAC item into an xarray DataSet '''
data_arrays = []
for band in bands:
url = item.asset(band)['href']
da = xr.open_rasterio(url, chunks={'band': 1, 'x': 1024, 'y': 1024})
da = da.expand_dims(time=[pd.to_datetime(item.date)])
ds = da.to_dataset(name=band)
data_arrays.append(ds)
ds = xr.combine_by_coords(data_arrays)
return ds
ds = load_dataset(item, bands)
ds
print(ds)
print('Dataset size (Gb): ', ds.nbytes/1e9)
ds['blue'].hvplot.image(rasterize=True, logz=True, width=700, height=500, cmap='blues', title=f'{item.id} (blue)')
# Lazy computation with dask
NDVI = (ds['nir'] - ds['red']) / (ds['nir'] + ds['red'])
NDVI
# Compute and store in local memory
ndvi = NDVI.compute()
ndvi
# Put together a larger dataset
results = satsearch.Search.search(collection='landsat-8-l1',
bbox=bbox,
datetime='2019-08-15/2019-09-30',
sort=['<datetime']) #earliest scene first
print('%s items' % results.found())
items = results.items()
items.save('set.geojson')
gf = gpd.read_file('set.geojson')
gf
# +
# Plot search AOI and frames on a map using Holoviz Libraries
cols = gf.loc[:,('id','geometry')]
footprints = cols.hvplot(geo=True, line_color='k', alpha=0.1, title='Landsat 8 T1')
tiles = gv.tile_sources.CartoEco.options(width=700, height=500)
labels = gv.tile_sources.StamenLabels.options(level='annotation')
tiles * footprints * labels
# -
# NOTE: this is not a very efficient bit of code, but it works
datasets = []
for item in items:
datasets.append(load_dataset(item, bands))
DS = xr.concat(datasets, dim='band')
print('Dataset size (Gb): ', DS.nbytes/1e9)
DS
# +
from dask.distributed import Client
client = Client("tcp://192.168.14.160:39645")
client
# -
DS = DS.assign_coords(band=range(len(datasets)))
DS
bounds = gfa.to_crs(epsg=32638).bounds #32638 UTM 38N #32738 UTM 38S
bounds
print(bounds.minx[0], bounds.maxx[0], bounds.miny[0], bounds.maxy[0])
DS.sel(x=slice(bounds.minx[0], bounds.maxx[0]), y=slice(bounds.miny[0], bounds.maxy[0]))
mosaic = DS.sel(x=slice(bounds.minx[0], bounds.maxx[0]), y=slice(bounds.miny[0], bounds.maxy[0])).mean(dim='band')
# Can change chunks before computing at dask
mosaic.chunk(chunks=dict(time=3,x=1395,y=2368))
mosaic['nir'].hvplot.image(x='x',y='y',groupby='time', rasterize=True, width=700, height=500)
| notebooks/amazon-web-services/landsat8.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="ADKY4re5Kx-5"
# ##### Copyright 2019 The TensorFlow Probability Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# + cellView="form" id="S2AOrHzjK0_L"
#@title Licensed under the Apache License, Version 2.0 (the "License"); { display-mode: "form" }
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="56dF5DnkKx0a"
# # Approximate inference for STS models with non-Gaussian observations
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/probability/examples/STS_approximate_inference_for_models_with_non_Gaussian_observations"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/probability/blob/master/tensorflow_probability/examples/jupyter_notebooks/STS_approximate_inference_for_models_with_non_Gaussian_observations.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/probability/blob/master/tensorflow_probability/examples/jupyter_notebooks/STS_approximate_inference_for_models_with_non_Gaussian_observations.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/probability/tensorflow_probability/examples/jupyter_notebooks/STS_approximate_inference_for_models_with_non_Gaussian_observations.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="laPe5xoS42ob"
# This notebook demonstrates the use of TFP approximate inference tools to incorporate a (non-Gaussian) observation model when fitting and forecasting with structural time series (STS) models. In this example, we'll use a Poisson observation model to work with discrete count data.
# + id="4YJz-JDu0X9E"
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v2 as tf
import tensorflow_probability as tfp
from tensorflow_probability import bijectors as tfb
from tensorflow_probability import distributions as tfd
tf.enable_v2_behavior()
# + [markdown] id="YagBskFAO34k"
# ## Synthetic Data
#
# First we'll generate some synthetic count data:
# + id="OKgRbodJ4EuU"
num_timesteps = 30
observed_counts = np.round(3 + np.random.lognormal(np.log(np.linspace(
num_timesteps, 5, num=num_timesteps)), 0.20, size=num_timesteps))
observed_counts = observed_counts.astype(np.float32)
plt.plot(observed_counts)
# + [markdown] id="OH2nvBuOxDrd"
# ## Model
#
# We'll specify a simple model with a randomly walking linear trend:
# + id="hSsekKzIwsg6"
def build_model(approximate_unconstrained_rates):
trend = tfp.sts.LocalLinearTrend(
observed_time_series=approximate_unconstrained_rates)
return tfp.sts.Sum([trend],
observed_time_series=approximate_unconstrained_rates)
# + [markdown] id="iY-pH3hQz0Vp"
# Instead of operating on the observed time series, this model will operate on the series of Poisson rate parameters that govern the observations.
#
# Since Poisson rates must be positive, we'll use a bijector to transform the
# real-valued STS model into a distribution over positive values. The `Softplus`
# transformation $y = \log(1 + \exp(x))$ is a natural choice, since it is nearly linear for positive values, but other choices such as `Exp` (which transforms the normal random walk into a lognormal random walk) are also possible.
# + id="Hg_B4tofzxgc"
positive_bijector = tfb.Softplus() # Or tfb.Exp()
# Approximate the unconstrained Poisson rate just to set heuristic priors.
# We could avoid this by passing explicit priors on all model params.
approximate_unconstrained_rates = positive_bijector.inverse(
tf.convert_to_tensor(observed_counts) + 0.01)
sts_model = build_model(approximate_unconstrained_rates)
# + [markdown] id="Pxua5B2wxIMz"
# To use approximate inference for a non-Gaussian observation model,
# we'll encode the STS model as a TFP JointDistribution. The random variables in this joint distribution are the parameters of the STS model, the time series of latent Poisson rates, and the observed counts.
#
# + id="vquh2LxgBjfy"
Root = tfd.JointDistributionCoroutine.Root
def sts_with_poisson_likelihood_model():
# Encode the parameters of the STS model as random variables.
param_vals = []
for param in sts_model.parameters:
param_val = yield Root(param.prior)
param_vals.append(param_val)
# Use the STS model to encode the log- (or inverse-softplus)
# rate of a Poisson.
unconstrained_rate = yield sts_model.make_state_space_model(
num_timesteps, param_vals)
rate = positive_bijector.forward(unconstrained_rate[..., 0])
observed_counts = yield tfd.Independent(tfd.Poisson(rate),
reinterpreted_batch_ndims=1)
model = tfd.JointDistributionCoroutine(sts_with_poisson_likelihood_model)
# + [markdown] id="R-3amgmKhYn1"
# ### Preparation for inference
#
# We want to infer the unobserved quantities in the model, given the observed counts. First, we condition the joint log density on the observed counts.
# + id="rSj7blvWh1w8"
# Condition a joint log-prob on the observed counts.
target_log_prob_fn = lambda *args: model.log_prob(args + (observed_counts,))
# + [markdown] id="RFeZ7NYt1qnw"
# HMC and VI inference also like to operate over unconstrained real-valued spaces, so we'll construct the list of bijectors that constrains each of the parameters to their respective supports.
# + id="Dyhb06i41qIg"
constraining_bijectors = ([param.bijector for param in sts_model.parameters] +
# `unconstrained_rate` is already unconstrained, but
# we can speed up inference by rescaling it.
[tfb.Scale(positive_bijector.inverse(
np.float32(np.max(observed_counts / 5.))))])
# + [markdown] id="25nJYyx-nW2T"
# ## Inference with HMC
#
# We'll use HMC (specifically, NUTS) to sample from the joint posterior over model parameters and latent rates.
#
# This will be significantly slower than fitting a standard STS model with HMC, since in addition to the model's (relatively small number of) parameters we also have to infer the entire series of Poisson rates. So we'll run for a relatively small number of steps; for applications where inference quality is critical it might make sense to increase these values or to run multiple chains.
# + id="NMPlVBk6PcpT"
#@title Sampler configuration
# Allow external control of sampling to reduce test runtimes.
num_results = 100 # @param { isTemplate: true}
num_results = int(num_results)
num_burnin_steps = 50 # @param { isTemplate: true}
num_burnin_steps = int(num_burnin_steps)
# + [markdown] id="mhSe-GFDPg9o"
# First we specify a sampler, and then use `sample_chain` to run that sampling
# kernel to produce samples.
# + id="15ue-mBGdcmh"
sampler = tfp.mcmc.TransformedTransitionKernel(
tfp.mcmc.NoUTurnSampler(
target_log_prob_fn=target_log_prob_fn,
step_size=0.1),
bijector=constraining_bijectors)
adaptive_sampler = tfp.mcmc.DualAveragingStepSizeAdaptation(
inner_kernel=sampler,
num_adaptation_steps=int(0.8 * num_burnin_steps),
target_accept_prob=0.75,
# NUTS inside of a TTK requires custom getter/setter functions.
step_size_setter_fn=lambda pkr, new_step_size: pkr._replace(
inner_results=pkr.inner_results._replace(step_size=new_step_size)
),
step_size_getter_fn=lambda pkr: pkr.inner_results.step_size,
log_accept_prob_getter_fn=lambda pkr: pkr.inner_results.log_accept_ratio,
)
initial_state = [b.forward(tf.random.normal(part_shape))
for (b, part_shape) in zip(
constraining_bijectors, model.event_shape[:-1])]
# + id="jvriVTPlih3B"
# Speed up sampling by tracing with `tf.function`.
@tf.function(autograph=False, experimental_compile=True)
def do_sampling():
return tfp.mcmc.sample_chain(
kernel=adaptive_sampler,
current_state=initial_state,
num_results=num_results,
num_burnin_steps=num_burnin_steps)
t0 = time.time()
samples, kernel_results = do_sampling()
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
# + [markdown] id="FwE0yWm_2_kE"
# We can sanity-check the inference by examining the parameter traces. In this case they appear to have explored multiple explanations for the data, which is good, although more samples would be helpful to judge how well the chain is mixing.
# + id="LPOVTbboAtGr"
f = plt.figure(figsize=(12, 4))
for i, param in enumerate(sts_model.parameters):
ax = f.add_subplot(1, len(sts_model.parameters), i + 1)
ax.plot(samples[i])
ax.set_title("{} samples".format(param.name))
# + [markdown] id="tZOydxU53oE9"
# Now for the payoff: let's see the posterior over Poisson rates! We'll also plot the 80% predictive interval over observed counts, and can check that this interval appears to contain about 80% of the counts we actually observed.
# + id="56rIH8MCeU9F"
param_samples = samples[:-1]
unconstrained_rate_samples = samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(np.random.poisson(rate_samples),
[10, 90], axis=0)
_ = plt.plot(observed_counts, color="blue", ls='--', marker='o', label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color="green", ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey', label='counts', alpha=0.2)
plt.xlabel("Day")
plt.ylabel("Daily Sample Size")
plt.title("Posterior Mean")
plt.legend()
# + [markdown] id="GuBYar27YZf6"
# ## Forecasting
#
# To forecast the observed counts, we'll use the standard STS tools to build a forecast distribution over the latent rates (in unconstrained space, again since STS is designed to model real-valued data), then pass the sampled forecasts through a Poisson observation model:
# + id="v1HuVuk6Qocm"
def sample_forecasted_counts(sts_model, posterior_latent_rates,
posterior_params, num_steps_forecast,
num_sampled_forecasts):
# Forecast the future latent unconstrained rates, given the inferred latent
# unconstrained rates and parameters.
unconstrained_rates_forecast_dist = tfp.sts.forecast(sts_model,
observed_time_series=unconstrained_rate_samples,
parameter_samples=posterior_params,
num_steps_forecast=num_steps_forecast)
# Transform the forecast to positive-valued Poisson rates.
rates_forecast_dist = tfd.TransformedDistribution(
unconstrained_rates_forecast_dist,
positive_bijector)
# Sample from the forecast model following the chain rule:
# P(counts) = P(counts | latent_rates)P(latent_rates)
sampled_latent_rates = rates_forecast_dist.sample(num_sampled_forecasts)
sampled_forecast_counts = tfd.Poisson(rate=sampled_latent_rates).sample()
return sampled_forecast_counts, sampled_latent_rates
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
# + id="MyPFQzV8SOSs"
forecast_samples = np.squeeze(forecast_samples)
# + id="iD_kLwF1V3m-"
def plot_forecast_helper(data, forecast_samples, CI=90):
"""Plot the observed time series alongside the forecast."""
plt.figure(figsize=(10, 4))
forecast_median = np.median(forecast_samples, axis=0)
num_steps = len(data)
num_steps_forecast = forecast_median.shape[-1]
plt.plot(np.arange(num_steps), data, lw=2, color='blue', linestyle='--', marker='o',
label='Observed Data', alpha=0.7)
forecast_steps = np.arange(num_steps, num_steps+num_steps_forecast)
CI_interval = [(100 - CI)/2, 100 - (100 - CI)/2]
lower, upper = np.percentile(forecast_samples, CI_interval, axis=0)
plt.plot(forecast_steps, forecast_median, lw=2, ls='--', marker='o', color='orange',
label=str(CI) + '% Forecast Interval', alpha=0.7)
plt.fill_between(forecast_steps,
lower,
upper, color='orange', alpha=0.2)
plt.xlim([0, num_steps+num_steps_forecast])
ymin, ymax = min(np.min(forecast_samples), np.min(data)), max(np.max(forecast_samples), np.max(data))
yrange = ymax-ymin
plt.title("{}".format('Observed time series with ' + str(num_steps_forecast) + ' Day Forecast'))
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.legend()
# + id="IyUp4NnzWOcs"
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
# + [markdown] id="QmS-ybPM903-"
# ## VI inference
#
# Variational inference can be problematic when inferring a full time series, like our approximate counts (as opposed to just
# the *parameters* of a time series, as in standard STS models). The standard assumption that variables have independent posteriors is quite wrong, since each timestep is correlated with its neighbors, which can lead to underestimating uncertainty. For this reason, HMC may be a better choice for approximate inference over full time series. However, VI can be quite a bit faster, and may be useful for model prototyping or in cases where its performance can be empirically shown to be 'good enough'.
#
# To fit our model with VI, we simply build and optimize a surrogate posterior:
# + id="7aZQEnTThgMT"
surrogate_posterior = tfp.experimental.vi.build_factored_surrogate_posterior(
event_shape=model.event_shape[:-1], # Infer everything but the observed counts.
constraining_bijectors=constraining_bijectors)
# + id="65cf0_EiimGq"
# Allow external control of optimization to reduce test runtimes.
num_variational_steps = 200 # @param { isTemplate: true}
num_variational_steps = int(num_variational_steps)
t0 = time.time()
losses = tfp.vi.fit_surrogate_posterior(target_log_prob_fn,
surrogate_posterior,
optimizer=tf.optimizers.Adam(0.1),
num_steps=num_variational_steps)
t1 = time.time()
print("Inference ran in {:.2f}s.".format(t1-t0))
# + id="zX8WtcLmk2mj"
plt.plot(losses)
plt.title("Variational loss")
_ = plt.xlabel("Steps")
# + id="kQoUExeBkpC0"
posterior_samples = surrogate_posterior.sample(50)
param_samples = posterior_samples[:-1]
unconstrained_rate_samples = posterior_samples[-1][..., 0]
rate_samples = positive_bijector.forward(unconstrained_rate_samples)
plt.figure(figsize=(10, 4))
mean_lower, mean_upper = np.percentile(rate_samples, [10, 90], axis=0)
pred_lower, pred_upper = np.percentile(
np.random.poisson(rate_samples), [10, 90], axis=0)
_ = plt.plot(observed_counts, color='blue', ls='--', marker='o',
label='observed', alpha=0.7)
_ = plt.plot(np.mean(rate_samples, axis=0), label='rate', color='green',
ls='dashed', lw=2, alpha=0.7)
_ = plt.fill_between(
np.arange(0, 30), mean_lower, mean_upper, color='green', alpha=0.2)
_ = plt.fill_between(np.arange(0, 30), pred_lower, pred_upper, color='grey',
label='counts', alpha=0.2)
plt.xlabel('Day')
plt.ylabel('Daily Sample Size')
plt.title('Posterior Mean')
plt.legend()
# + id="0aoMoQyf_fWC"
forecast_samples, rate_samples = sample_forecasted_counts(
sts_model,
posterior_latent_rates=unconstrained_rate_samples,
posterior_params=param_samples,
# Days to forecast:
num_steps_forecast=30,
num_sampled_forecasts=100)
# + id="eQ7zJpEr_hHU"
forecast_samples = np.squeeze(forecast_samples)
# + id="lcEpkAEi_jcn"
plot_forecast_helper(observed_counts, forecast_samples, CI=80)
| site/en-snapshot/probability/examples/STS_approximate_inference_for_models_with_non_Gaussian_observations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Okfr_uhwhS1X" colab_type="text"
# # Lambda School Data Science - A First Look at Data
#
#
# + [markdown] id="9dtJETFRhnOG" colab_type="text"
# ## Lecture - let's explore Python DS libraries and examples!
#
# The Python Data Science ecosystem is huge. You've seen some of the big pieces - pandas, scikit-learn, matplotlib. What parts do you want to see more of?
# + id="WiBkgmPJhmhE" colab_type="code" outputId="b091ab3d-db11-4548-c390-36e25da84017" colab={"base_uri": "https://localhost:8080/", "height": 34}
2 + 2
# + [markdown] id="lOqaPds9huME" colab_type="text"
# ## Assignment - now it's your turn
#
# Pick at least one Python DS library, and using documentation/examples reproduce in this notebook something cool. It's OK if you don't fully understand it or get it 100% working, but do put in effort and look things up.
# + id="TGUS79cOhPWj" colab_type="code" outputId="11d12134-40ef-44ec-d50f-cfb66f3d724b" colab={"base_uri": "https://localhost:8080/", "height": 204}
#I am trying to set up an experimental GANS network
#step 1: import pygan library
pip install pygan
# + id="5bVnYXYnGDKs" colab_type="code" outputId="7bf5e0e7-c76f-4e54-922e-bd322cc42782" colab={"base_uri": "https://localhost:8080/", "height": 850}
pip install jupyterlab
# + id="E4cqvusbIYEk" colab_type="code" outputId="85fd9ad8-7409-42d1-d6b7-3c5e1b321bc3" colab={"base_uri": "https://localhost:8080/", "height": 221}
pip install pydbm
# + id="84QercR3I93K" colab_type="code" outputId="1f22c6c4-266b-4e68-c49d-ab7978c4757f" colab={"base_uri": "https://localhost:8080/", "height": 136}
pip install CNTK
# + id="HzOA8oeQIc9C" colab_type="code" colab={}
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tensorflow import keras
# + id="HNusR_ijIhWy" colab_type="code" outputId="65c03870-7639-47fb-e717-3d12543fa0a8" colab={"base_uri": "https://localhost:8080/", "height": 34}
from keras.layers.recurrent import LSTM
# + id="N04tI_ijIimi" colab_type="code" colab={}
#Step 1: set hyperparameters
# Batch Size
batch_size = 20
# The lenght of sequences
seq_len = 30
# The dimension of observed or feature points
dim = 5
# + id="VEDe-b29IlS_" colab_type="code" outputId="b1b8d4a0-d0bb-4526-da5e-0d62cdbc4c98" colab={"base_uri": "https://localhost:8080/", "height": 486}
# Step 2: Import Python modules
# is-a 'TrueSampler'
from pygan.truesampler.sine_wave_true_sampler import SineWaveTrueSampler
# is-a 'NoiseSampler'
from pygan.noisesampler.uniform_noise_sampler import UniformNoiseSampler
# is-a 'GenerativeModel'
from pygan.generativemodel.lstm_model import LSTMModel
# is-a 'DiscriminativeModel'
from pygan.discriminativemodel.nn_model import NNModel
# is-a 'GANValueFunction'
from pygan.gansvaluefunction.mini_max import MiniMax
# GANs framework
from pygan.generative_adversarial_networks import GenerativeAdversarialNetworks
# + id="iQYOc10OL4ht" colab_type="code" colab={}
# I am trying to solve the error above but could not figure out the solution out despite importing pydbm, will work with TL and instructor regarding that. I am using a CPU, so not sure if I need a GPU for running this deep learning library.
# Meanwhile I am trying to create a sine wave using GAN, source github code from accel_brain_code
batch_size = 20
seq_len = 30
dim = 5
from logging import getLogger, StreamHandler, NullHandler, DEBUG, ERROR
logger = getLogger("pygan")
handler = StreamHandler()
handler.setLevel(DEBUG)
logger.addHandler(handler)
# + id="UPtOz63RNGqy" colab_type="code" colab={}
from pygan.truesampler.sine_wave_true_sampler import SineWaveTrueSampler
# + id="OOjqlWjkNPrd" colab_type="code" colab={}
true_sampler = SineWaveTrueSampler(
batch_size=batch_size,
seq_len=seq_len,
dim=dim
)
# + id="iHdcoOPwNiTa" colab_type="code" outputId="d78ff23b-e828-4eb1-b0ee-b1768d801d28" colab={"base_uri": "https://localhost:8080/", "height": 34}
true_sampler.draw().shape
# + id="M9xliA2YNo2M" colab_type="code" colab={}
true_arr = true_sampler.draw()
# + id="KIaBIrPCNxbb" colab_type="code" outputId="1d55d396-0ba7-4d6d-deb1-fe226b77bb2f" colab={"base_uri": "https://localhost:8080/", "height": 632}
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# %config InlineBackend.figure_format = "png"
plt.style.use("fivethirtyeight")
plt.figure(figsize=(15,10))
plt.plot(true_arr[0])
plt.show()
#The sine wave was successfully created as shown below
# + id="ZBdC_QvtOcJD" colab_type="code" colab={}
from pygan.noisesampler.uniform_noise_sampler import UniformNoiseSampler
# + id="-2_JSgbPOoUr" colab_type="code" colab={}
noise_sampler = UniformNoiseSampler(low= -1, high=1, output_shape=(batch_size, 1, dim))
# + id="iDsDYPvyO3es" colab_type="code" outputId="42a4639a-05da-464a-f7dd-4cb5b7802c6b" colab={"base_uri": "https://localhost:8080/", "height": 34}
noise_sampler.generate().shape
# + id="PMcPPvlqQSAj" colab_type="code" outputId="529b6a46-3f94-44a8-dbcb-5fb23bb55519" colab={"base_uri": "https://localhost:8080/", "height": 153}
pip install keras
# + id="j1i-XtyDRuy0" colab_type="code" outputId="1a99ea8f-dd0f-4a05-bcd5-0264ba17e02c" colab={"base_uri": "https://localhost:8080/", "height": 68}
pip install pydbm
# + id="DVIaHNzX8OI4" colab_type="code" outputId="f576b690-a4e5-4753-823c-c88f58bf0531" colab={"base_uri": "https://localhost:8080/", "height": 207}
pip install pytorch
# + id="MpWWq7ZuO_vL" colab_type="code" outputId="eb7a7e4e-5285-4a75-b65a-33868b57e00d" colab={"base_uri": "https://localhost:8080/", "height": 299}
from keras.generativemodel.lstm_model import LSTMModel
# + id="_V48MTaVPPBt" colab_type="code" colab={}
# This is the same LSTM model import error which was I was getting while running the above GAN experiment too
# + [markdown] id="BT9gdS7viJZa" colab_type="text"
# ### Assignment questions
#
# After you've worked on some code, answer the following questions in this text block:
#
# 1. Describe in a paragraph of text what you did and why, as if you were writing an email to somebody interested but nontechnical.
#
# 2. What was the most challenging part of what you did?
#
# 3. What was the most interesting thing you learned?
#
# 4. What area would you like to explore with more time?
#
#
#
# + [markdown] id="_D5ZbD7ZUOHQ" colab_type="text"
# I tried to set up a GANS network to analyze data, which is a depp learning technology. I was able to create a sine wave. I am having some trouble importing LSTM library to complete my experiment. One way to do it is keras but pygan should have the LSTM librarty installed. I would like to work further on GANS and look forward to solving the problems that I am facing like installing LSTM libratry with TL/instructor.
# + [markdown] id="_XXg2crAipwP" colab_type="text"
# ## Stretch goals and resources
#
# Following are *optional* things for you to take a look at. Focus on the above assignment first, and make sure to commit and push your changes to GitHub (and since this is the first assignment of the sprint, open a PR as well).
#
# - [pandas documentation](https://pandas.pydata.org/pandas-docs/stable/)
# - [scikit-learn documentation](http://scikit-learn.org/stable/documentation.html)
# - [matplotlib documentation](https://matplotlib.org/contents.html)
# - [Awesome Data Science](https://github.com/bulutyazilim/awesome-datascience) - a list of many types of DS resources
#
# Stretch goals:
#
# - Find and read blogs, walkthroughs, and other examples of people working through cool things with data science - and share with your classmates!
# - Write a blog post (Medium is a popular place to publish) introducing yourself as somebody learning data science, and talking about what you've learned already and what you're excited to learn more about.
| module1-afirstlookatdata/Bhav_sample_GANS.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Sample CNN for MNIST handwriting recognition
import tensorflow as tf
mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Loand and process MNIST data
# reshape and rescale data for the CNN
train_images = train_images.reshape(60000, 28, 28, 1)
test_images = test_images.reshape(10000, 28, 28, 1)
train_images, test_images = train_images/255, test_images/255
# Create LeNet-5 CNN
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Dropout(0.25),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(10, activation='softmax')
])
# Compile
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
print('Compile complete')
# +
# Set log data to feed to TensorBoard for visual analysis
tensor_board = tf.keras.callbacks.TensorBoard('./logs/sample-LeNet-MNIST-1')
# Train model (with timing)
import time
start_time=time.time()
model.fit(train_images, train_labels, batch_size=128, epochs=15, verbose=1,
validation_data=(test_images, test_labels), callbacks=[tensor_board])
print('Training took {} seconds'.format(time.time()-start_time))
# -
| notebooks/00-sample.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction
#
# #Introduce the concept of sorting and sorting algorithms, discuss the
# relevance of concepts such as complexity (time and space), performance, in-place sorting,
# stable sorting, comparator functions, comparison-based and non-comparison-based sorts,
# etc.
# Sorting algorithms vary greatly in their performance. This benchmarking project is to find out which algorithms will perform the best.
# n
# # Sorting Algorithms
#
# Introduce each of your chosen algorithms in turn,
# discuss their space and time complexity, and explain how each algorithm works using your
# own diagrams and different example input instances.
# ## 1. Bubble Sort (A simple comparison-based sort)
#
# Bubble sort is a simple sorting algorithm. https://en.wikipedia.org/wiki/Bubble_sort
#
# How it works:
# 1. It starts at the beginning of the dataset and compares the first two elements and if the first is greater it will swap them.
# 2. It will continue doing this until no swaps are needed.
#
# #### Performance
# Bubble sort has a worst-case and average complexity of О(n2), where n is the number of items being sorted.
# When the list is already sorted (best-case), the complexity of bubble sort is only O(n).
# In the case of a large dataset, Bubble sort should be avoided. It is not very practical or efficient and rarely used in the real world.
#
# Bubble sort in action https://www.youtube.com/watch?v=lyZQPjUT5B4&feature=youtu.be
#
# #insert a diagram
# +
# code sourced from http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBubbleSort.html
def bubbleSort(alist):
for passnum in range(len(alist)-1,0,-1):
for i in range(passnum):
if alist[i]>alist[i+1]:
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
alist = [54,26,93,17,77,31,44,55,20]
bubbleSort(alist)
print(alist)
# +
# import time module
import time
# start timer
start_time = time.time()
# bubble sort function, use the numbers from alist
def bubbleSort(alist):
for passnum in range(len(alist)-1,0,-1):
for i in range(passnum):
if alist[i]>alist[i+1]:
temp = alist[i]
alist[i] = alist[i+1]
alist[i+1] = temp
print(bubbleSort(alist))
#print(bubbleSort(alist1))
# end timer
end_time = time.time()
# calculate time
time_elapsed= end_time - start_time
print(bubbleSort(alist), "alist time: ", time_elapsed)
# -
# ## 2. Merge Sort (An efficient comparison-based sort)
#
# Merge sort is a recursive divide and conquer algorithm that was invented by <NAME> in 1945.(https://en.wikipedia.org/wiki/Merge_sort)
#
# How it works:
# 1. It starts by breaking down the list into sublists until each sublists contains just one element.
# 2. Repeatedly merging the sublists to produce new sorted sublists until there is only one sublist remaining.
#
# #### Performance
# In sorting n objects, merge sort has an average and worst-case performance of O(n log n). It's best, worst and average cases are very similar, making it a good choice for predictable running behaviour. (source from lecture notes)
#
# Merge sort in action:
# https://www.youtube.com/watch?v=XaqR3G_NVoo
#
#
# An efficient sorting algorithm??
#
# ### insert a diagram
# +
# code sourced from http://interactivepython.org/runestone/static/pythonds/SortSearch/TheMergeSort.html
def mergeSort(alist):
#print("Splitting ",alist)
if len(alist)>1:
mid = len(alist)//2
lefthalf = alist[:mid]
righthalf = alist[mid:]
mergeSort(lefthalf)
mergeSort(righthalf)
i=0
j=0
k=0
while i < len(lefthalf) and j < len(righthalf):
if lefthalf[i] < righthalf[j]:
alist[k]=lefthalf[i]
i=i+1
else:
alist[k]=righthalf[j]
j=j+1
k=k+1
while i < len(lefthalf):
alist[k]=lefthalf[i]
i=i+1
k=k+1
while j < len(righthalf):
alist[k]=righthalf[j]
j=j+1
k=k+1
#print("Merging ",alist)
alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)
# -
# ## 3. Counting Sort (A non-comparison sort)
# +
# code sourced http://www.learntosolveit.com/python/algorithm_countingsort.html
def counting_sort(array, maxval):
"""in-place counting sort"""
n = len(array)
m = maxval + 1
count = [0] * m # init with zeros
for a in array:
count[a] += 1 # count occurences
i = 0
for a in range(m): # emit
for c in range(count[a]): # - emit 'count[a]' copies of 'a'
array[i] = a
i += 1
return array
print(counting_sort( alist, 93 ))
# -
# ## 4. Quick Sort
#
# Quicksort was developed by British computer scientist <NAME> in 1959. It is a recursive divide and conquer algorithm. Due to it's efficiency, it is still a commonly used algorithm for sorting.(https://en.wikipedia.org/wiki/Quicksort)
#
# How it works (lecture notes referenced):
# 1. Pivot selection: Pick an element, called a “pivot” from the array
# 2. Partioning: reorder the array elements with values < the pivot come beofre it, which all elements the values ≥ than the pivot come after it. After this partioining, the pivot is in its final position.
# 3. Recursion: apply steps 1 and 2 above recursively to each of the two subarrays
#
# #### Performance
# +
# http://interactivepython.org/runestone/static/pythonds/SortSearch/TheQuickSort.html
def quickSort(alist):
quickSortHelper(alist,0,len(alist)-1)
def quickSortHelper(alist,first,last):
if first<last:
splitpoint = partition(alist,first,last)
quickSortHelper(alist,first,splitpoint-1)
quickSortHelper(alist,splitpoint+1,last)
def partition(alist,first,last):
pivotvalue = alist[first]
leftmark = first+1
rightmark = last
done = False
while not done:
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
rightmark = rightmark -1
if rightmark < leftmark:
done = True
else:
temp = alist[leftmark]
alist[leftmark] = alist[rightmark]
alist[rightmark] = temp
temp = alist[first]
alist[first] = alist[rightmark]
alist[rightmark] = temp
return rightmark
# alist = [54,26,93,17,77,31,44,55,20]
quickSort(alist)
print(alist)
# -
# ## 5. Insertion Sort
# +
def insertionSort(alist):
for index in range(1,len(alist)):
currentvalue = alist[index]
position = index
while position>0 and alist[position-1]>currentvalue:
alist[position]=alist[position-1]
position = position-1
alist[position]=currentvalue
alist = [54,26,93,17,77,31,44,55,20]
insertionSort(alist)
print(alist)
# -
# # Implementation & Benchmarking
# For this section, a function will be definied to call each sorting function defined above
# 1. Bubble Sort
# 2. Merge Sort
# 3. Counting Sort
# 4. Quick Sort
# 5. Insertion Sort
#
# Firstly, arrays are generated with random numbers using randint from the python's random library (https://docs.python.org/2/library/random.html). These will be used to test the speed of efficiency of the algorithms.
# +
# Creating an array using randint
from random import *
# creating a random array, function takes in n numbers
def random_array(n):
# create an array variable
array = []
# if n = 5, 0,1,2,3,4
for i in range(0,n, 1):
# add to the array random integers between 0 and 100
array.append(randint(0,100))
return array
# assign the random array to alist
alist = random_array(100)
alist1 = random_array(1000)
alist2 = random_array(10000)
# -
# Using the time module (https://docs.python.org/3/library/time.html), a start time and end time for each function will be noted and the elapsed time is what will be noted.
# Above a random arrays were defined. They will be used to test the performance of the
# +
# import time module
import time
# function to call sort functions and time each individually
def callsorts():
# start timer
start_time = time.time()
######## bubblesort
bubbleSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist), "Bubble Sort: ", time_elapsed)
# start timer
start_time = time.time()
bubbleSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist1), "Bubble Sort: ", time_elapsed)
# start timer
start_time = time.time()
bubbleSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist2), "Bubble Sort: ", time_elapsed)
##### Merge Sort
#start timer
start_time = time.time()
mergeSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist), "Merge Sort: ", time_elapsed)
# start timer
start_time = time.time()
mergeSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist1), "Merge Sort: ", time_elapsed)
# start timer
start_time = time.time()
mergeSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist2), "Merge Sort: ", time_elapsed)
##### counting_sort
start_time = time.time()
counting_sort(alist, 100)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
# start timer
start_time = time.time()
counting_sort(alist1, 1000)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
# start timer
start_time = time.time()
counting_sort(alist2, 10000)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
##### quick sort
start_time = time.time()
quickSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
# start timer
start_time = time.time()
quickSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
# start timer
start_time = time.time()
quickSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
##### insertionSort
start_time = time.time()
insertionSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
# start timer
start_time = time.time()
insertionSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
# start timer
start_time = time.time()
insertionSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
callsorts()
# +
# import time module
import time
import pandas as pd
import numpy as np
df = pd.DataFrame(index = ['Bubble Sort', 'Merge Sort', 'Counting sort', 'Quick sort', 'Insertion sort'])
# function to call sort functions and time each individually
def callsorts():
# start timer
start_time = time.time()
######## bubblesort
bubbleSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist), "Bubble Sort: ", time_elapsed)
df.insert(0,'100', time_elapsed)
# start timer
start_time = time.time()
bubbleSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist1), "Bubble Sort: ", time_elapsed)
# start timer
start_time = time.time()
bubbleSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print(bubbleSort(alist2), "Bubble Sort: ", time_elapsed)
##### Merge Sort
#start timer
start_time = time.time()
mergeSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist), "Merge Sort: ", time_elapsed)
df.insert(1,'100', time_elapsed)
# start timer
start_time = time.time()
mergeSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist1), "Merge Sort: ", time_elapsed)
# start timer
start_time = time.time()
mergeSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print(mergeSort(alist2), "Merge Sort: ", time_elapsed)
##### counting_sort
start_time = time.time()
counting_sort(alist, 100)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
# start timer
start_time = time.time()
counting_sort(alist1, 1000)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
# start timer
start_time = time.time()
counting_sort(alist2, 10000)
end_time = time.time()
time_elapsed= end_time - start_time
print("Counting sort: ", time_elapsed)
##### quick sort
start_time = time.time()
quickSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
# start timer
start_time = time.time()
quickSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
# start timer
start_time = time.time()
quickSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print("Quick sort: ", time_elapsed)
##### insertionSort
start_time = time.time()
insertionSort(alist)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
# start timer
start_time = time.time()
insertionSort(alist1)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
# start timer
start_time = time.time()
insertionSort(alist2)
end_time = time.time()
time_elapsed= end_time - start_time
print("Insertion sort: ", time_elapsed)
callsorts()
df
# -
df[2]=2
df
print("Size", '\t', "100") #table column headings
print("---", '\t', "-----")
# generate values for columns
print("Bubble Sort", '\t', bubbleSort(alist2), "BubbleSort: ", time_elapsed)
| Algorithms_problems/Sorting Project/Benchmarking Sorting Algorithms.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "5266166b-6758-4bd7-b469-565830f7cca5", "showTitle": true, "title": "Get this from documentation"}
#change jdbc url username password
jdbcUrl = "jdbc:sqlserver://sbsqlcon.database.windows.net:1433;database=pknt"
connectionProperties = {
"user" : 'praveen',
"password" : '********',
"driver" : "com.microsoft.sqlserver.jdbc.SQLServerDriver"
}
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "940c6190-c0e7-42e1-9519-6dd7e5e6d63b", "showTitle": false, "title": ""}
pushdown_query = "(select * from saleslt.customer) cust"
df = spark.read.jdbc(url=jdbcUrl, table=pushdown_query, properties=connectionProperties)
display(df)
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "b9f779a1-cc5c-4a63-954e-1e087ed83c59", "showTitle": false, "title": ""}
df.write.jdbc(url = jdbcUrl,table = 'customerpk', mode = 'append', properties=connectionProperties)
# + application/vnd.databricks.v1+cell={"inputWidgets": {}, "nuid": "02cae812-a60f-4239-b45e-34695aadb934", "showTitle": false, "title": ""}
| Data Extraction/6. Azure SQL to db.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Basically mapping ( it stores key value objects )
#
# The format is
#
#
# 'key1':'value1','key2':'value2'
my_dictionary={'key1':'value1','key2':'value2'}
my_dictionary
my_dictionary['key1']
prices={'apples':100,'oranges':200,'chocolate':500}
prices['apples']
prices['apples']*prices['oranges']
d={'k1':123,'k2':[0,1,2],'k3':[100,200,300]}
d['k2']
d['k3'][0]
d1={'key1':['a','b','candidate']}
mylist=d1['key1']
letter=mylist[2]
letter
letter.upper()
letter.upper()
d1['key1'].upper()
d={'k1':100,'k2':200}
d['k3']=300
d
d['k1']='new_value'
d
d
d.keys()
d.values()
d.items()
m={'apples':[100,200,300,400],'oranges':300,'apple cider vinegar':400}
m['apples'][3]*100
| trial scripts/dictionaries.ipynb |
# ##### Copyright 2020 Google LLC.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#
# # integer_programming_example
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/google/or-tools/blob/master/examples/notebook/linear_solver/integer_programming_example.ipynb"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/colab_32px.png"/>Run in Google Colab</a>
# </td>
# <td>
# <a href="https://github.com/google/or-tools/blob/master/ortools/linear_solver/samples/integer_programming_example.py"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/github_32px.png"/>View source on GitHub</a>
# </td>
# </table>
# First, you must install [ortools](https://pypi.org/project/ortools/) package in this colab.
# !pip install ortools
# +
# Copyright 2010-2018 Google LLC
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Small example to illustrate solving a MIP problem."""
# [START program]
# [START import]
from ortools.linear_solver import pywraplp
# [END import]
def IntegerProgrammingExample():
"""Integer programming sample."""
# [START solver]
# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver('SCIP')
# [END solver]
# [START variables]
# x, y, and z are non-negative integer variables.
x = solver.IntVar(0.0, solver.infinity(), 'x')
y = solver.IntVar(0.0, solver.infinity(), 'y')
z = solver.IntVar(0.0, solver.infinity(), 'z')
# [END variables]
# [START constraints]
# 2*x + 7*y + 3*z <= 50
constraint0 = solver.Constraint(-solver.infinity(), 50)
constraint0.SetCoefficient(x, 2)
constraint0.SetCoefficient(y, 7)
constraint0.SetCoefficient(z, 3)
# 3*x - 5*y + 7*z <= 45
constraint1 = solver.Constraint(-solver.infinity(), 45)
constraint1.SetCoefficient(x, 3)
constraint1.SetCoefficient(y, -5)
constraint1.SetCoefficient(z, 7)
# 5*x + 2*y - 6*z <= 37
constraint2 = solver.Constraint(-solver.infinity(), 37)
constraint2.SetCoefficient(x, 5)
constraint2.SetCoefficient(y, 2)
constraint2.SetCoefficient(z, -6)
# [END constraints]
# [START objective]
# Maximize 2*x + 2*y + 3*z
objective = solver.Objective()
objective.SetCoefficient(x, 2)
objective.SetCoefficient(y, 2)
objective.SetCoefficient(z, 3)
objective.SetMaximization()
# [END objective]
# Solve the problem and print the solution.
# [START print_solution]
solver.Solve()
# Print the objective value of the solution.
print('Maximum objective function value = %d' % solver.Objective().Value())
print()
# Print the value of each variable in the solution.
for variable in [x, y, z]:
print('%s = %d' % (variable.name(), variable.solution_value()))
# [END print_solution]
IntegerProgrammingExample()
# [END program]
| examples/notebook/linear_solver/integer_programming_example.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import matplotlib.pyplot as plt
from halotools.mock_observables import delta_sigma, return_xyz_formatted_array
from halotools.utils import randomly_downsample_data
import time
# +
# halo_directory = '/Users/fardila/Documents/GitHub/baryonic_effects/sample_data/'
halo_directory = '/Users/fardila/Documents/Data/baryonic_effects/input/halo_catalogs/'
# particle_directory = '/Users/fardila/Documents/GitHub/baryonic_effects/sample_data/'
particle_directory = '/Users/fardila/Documents/Data/baryonic_effects/input/particle_catalogs/'
halo_file_all = 'um_smdpl_insitu_exsitu_0.7124_basic_logmp_11.5.npy'
halo_file_Mpeak13 = 'um_smdpl_insitu_exsitu_0.7124_basic_logmp_11.5_cutMpeak13.npy'
particle_file_50M = 'um_smdpl_particles_0.7124_50m.npy'
particle_file_10M = 'um_smdpl_particles_0.7124_10m.npy'
# +
def DS_from_catalog_files(halo_cat_file, particle_cat_file):
print('loading catalogs!')
halo_cat = np.load(halo_cat_file)
particle_cat = np.load(particle_cat_file)
print('formatting positions!')
halo_cat_positions = return_xyz_formatted_array(halo_cat['x'], halo_cat['y'], halo_cat['z'])
particle_cat_positions = return_xyz_formatted_array([particle[0] for particle in particle_cat],
[particle[1] for particle in particle_cat],
[particle[2] for particle in particle_cat])
n_particles_per_dim=3840
n_particles_tot = (n_particles_per_dim ** 3)
downsampling_factor = (n_particles_tot / float(len(particle_cat)))
m_particle=9.63E7 #Msun/h
box_size=400 #Mpc/h
wl_min_r=0.08
wl_max_r=50.0
wl_n_bins=22
rp_bins = np.logspace(np.log10(wl_min_r), np.log10(wl_max_r), wl_n_bins)
print('calculating DS!')
rp_mids, ds = delta_sigma(galaxies=halo_cat_positions,
particles=particle_cat_positions, particle_masses=m_particle,
downsampling_factor=downsampling_factor,
rp_bins=rp_bins, period=box_size,
num_threads = 'max')
return rp_mids, ds
def DS_from_catalogs(halo_cat, particle_cat):
print('formatting positions!')
halo_cat_positions = return_xyz_formatted_array(halo_cat['x'], halo_cat['y'], halo_cat['z'])
particle_cat_positions = return_xyz_formatted_array([particle[0] for particle in particle_cat],
[particle[1] for particle in particle_cat],
[particle[2] for particle in particle_cat])
n_particles_per_dim=3840
n_particles_tot = (n_particles_per_dim ** 3)
downsampling_factor = (n_particles_tot / float(len(particle_cat)))
m_particle=9.63E7 #Msun/h
box_size=400 #Mpc/h
wl_min_r=0.08
wl_max_r=50.0
wl_n_bins=22
rp_bins = np.logspace(np.log10(wl_min_r), np.log10(wl_max_r), wl_n_bins)
print('calculating DS!')
rp_mids, ds = delta_sigma(galaxies=halo_cat_positions,
particles=particle_cat_positions, particle_masses=m_particle,
downsampling_factor=downsampling_factor,
rp_bins=rp_bins, period=box_size,
num_threads = 'max')
return rp_mids, ds
# -
time_i = time.time()
rp_mids_Mpeak13_10M, ds_Mpeak13_10M = DS_from_catalog_files(halo_directory+halo_file_Mpeak13,
particle_directory+particle_file_10M)
print('{0} seconds to run'.format(time.time()-time_i))
time_i = time.time()
rp_mids_all_halo_50M, ds_all_halo_50M = DS_from_catalog_files(halo_directory+halo_file_all,
particle_directory+particle_file_50M)
print('{0} seconds to run'.format(time.time()-time_i))
time_i = time.time()
rp_mids_all_halo_10M, ds_all_halo_10M = DS_from_catalog_files(halo_directory+halo_file_all,
particle_directory+particle_file_10M)
print('{0} seconds to run'.format(time.time()-time_i))
time_i = time.time()
rp_mids_Mpeak13_50M, ds_Mpeak13_50M = DS_from_catalog_files(halo_directory+halo_file_Mpeak13,
particle_directory+particle_file_50M)
print('{0} seconds to run'.format(time.time()-time_i))
# +
plt.loglog(rp_mids_all_halo_50M, ds_all_halo_50M, label='All halos, 50M particles')
plt.loglog(rp_mids_Mpeak13_10M,ds_Mpeak13_10M, label='Mpeak > 13 halos, 10M particles')
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.show()
# +
plt.loglog(rp_mids_all_halo_50M, ds_all_halo_50M, label='All halos, 50M particles')
plt.loglog(rp_mids_Mpeak13_10M,ds_Mpeak13_10M, label='Mpeak > 13 halos, 10M particles')
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.show()
# +
plt.loglog(rp_mids_all_halo_10M, ds_all_halo_10M, label='All halos, 10M particles')
plt.loglog(rp_mids_Mpeak13_50M,ds_Mpeak13_50M, label='Mpeak > 13 halos, 50M particles')
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.show()
# +
plt.loglog(rp_mids_all_halo_50M, ds_all_halo_50M, label='All halos, 50M particles')
plt.loglog(rp_mids_all_halo_10M, ds_all_halo_10M, linestyle='--', label='All halos, 10M particles')
plt.loglog(rp_mids_Mpeak13_50M,ds_Mpeak13_50M, label='Mpeak > 13 halos, 50M particles')
plt.loglog(rp_mids_Mpeak13_10M,ds_Mpeak13_10M, linestyle='--', label='Mpeak > 13 halos, 10M particles')
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.legend()
plt.show()
# -
wl_min_r=0.08
wl_max_r=50.0
wl_n_bins=22
np.log(np.logspace(np.log10(wl_min_r), np.log10(wl_max_r), wl_n_bins))
# ## check even fewer particles
halo_cat = np.load(halo_directory+halo_file_Mpeak13)
particle_cat = np.load(particle_directory+particle_file_50M)
# +
for num_ptcls_to_use in [5e7, 1e7, 5e6, 1e6, 5e5, 1e5]:
particle_cat_reduced = randomly_downsample_data(particle_cat, int(num_ptcls_to_use))
rp_mids, ds = DS_from_catalogs(halo_cat, particle_cat_reduced)
plt.loglog(rp_mids,ds, linestyle='-', label='{0} particles'.format(str(num_ptcls_to_use)))
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.legend()
plt.show()
# -
halo_cat_cut13 = halo_cat[(halo_cat['logmh_peak']>13.2) & (halo_cat['logmh_peak']<13.3)]
halo_cat_cut14 = halo_cat[(halo_cat['logmh_peak']>14.2) & (halo_cat['logmh_peak']<14.3)]
print(len(halo_cat_cut13), len(halo_cat_cut14))
# +
for num_ptcls_to_use in [5e7, 1e7, 5e6, 1e6, 5e5, 1e5]:
particle_cat_reduced = randomly_downsample_data(particle_cat, int(num_ptcls_to_use))
rp_mids, ds = DS_from_catalogs(halo_cat_cut, particle_cat_reduced)
plt.loglog(rp_mids,ds, linestyle='-', label='{0} particles'.format(str(num_ptcls_to_use)))
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.legend()
plt.show()
# -
# +
plt.figure(figsize=[12,10])
for num_ptcls_to_use, label in zip([5e7, 1e7, 1e6, 1e5],['5e7', '1e7', '1e6', '1e5']):
particle_cat_reduced = randomly_downsample_data(particle_cat, int(num_ptcls_to_use))
rp_mids, ds = DS_from_catalogs(halo_cat_cut13, particle_cat_reduced)
plt.loglog(rp_mids,ds, linestyle='-', label='{0} particles'.format(label))
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.legend()
plt.title('13.2 < logMpeak < 13.3')
plt.show()
# +
plt.figure(figsize=[12,10])
for num_ptcls_to_use, label in zip([5e7, 1e7, 1e6, 1e5],['5e7', '1e7', '1e6', '1e5']):
particle_cat_reduced = randomly_downsample_data(particle_cat, int(num_ptcls_to_use))
rp_mids, ds = DS_from_catalogs(halo_cat_cut14, particle_cat_reduced)
plt.loglog(rp_mids,ds, linestyle='-', label='{0} particles'.format(label))
plt.xlabel(r'$r_{\rm p}$', fontsize=30)
# plt.xlabel(r'$r_{\rm p}$ ${\rm [Mpc]}$', fontsize=30)
plt.ylabel(r'$\Delta \Sigma$', fontsize=30)
# plt.ylabel(r'$\Delta\Sigma$ $[M_{\odot}/{\rm pc}^2]$', fontsize=30)
plt.legend()
plt.title('14.2 < logMpeak < 14.3')
plt.show()
# -
| tests/testing_DS_with_reduced_catalogs.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Generating Normally Distributed Random Numbers in Power Query
# > Custom function to generate a column with normally distributed random numbers with specified mean and standard deviation
#
# - toc: true
# - badges: true
# - comments: true
# - categories: [Power BI, random number, M, Power Query]
# - hide: false
# ## Power Query Doesn't Have NORMINV()
# In Excel, if you want to generate a column with random numbers that are normally distributed, you can use the `NORMINV()` function like [this](https://support.microsoft.com/en-us/office/norminv-function-87981ab8-2de0-4cb0-b1aa-e21d4cb879b8). You can specify the probability (which is usually a random number drawn from uniform distribution), mean and standard deviation. While DAX has the `NORM.INV()` [function](https://docs.microsoft.com/en-us/dax/norm-inv-dax), M does not. If you create simulations, what-if scenario analyses etc., more than likely you will need to generate a column with random numbers that follow the Gaussian distribution. I have written a blog post on how to generate various distributions using DAX, you can read it [here](https://pawarbi.github.io/blog/power%20bi/statistics/distribution/pert/beta/normal/uniform/lognormal/logistic/weibull/2020/12/24/Statistical-distributions-powerbi.html).
#
# In this blog, I will share a simple formula to generate the normally distributed random numbers using M. It uses the Box-Muller transform to generate the inverse distribution. I won't go into the theory and math, but if you are interested you can read it [here](https://medium.com/mti-technology/how-to-generate-gaussian-samples-3951f2203ab0).
#
# 
# ## Custom Function
# +
#hide-output
// Gaussian Random Number Generator with mean =mean and standard number as sd using Box-Mueller Transform
// Add an index column to the table before invoking this function.
let
gaussianrandom = (mean as number, sd as number) as number=>
(
sd
* (
Number.Sqrt(- 2 * Number.Ln(Number.Random())
)
* Number.Cos( 2.0 * 3.14159265358979323846
* Number.Random()
)
)
+ mean
)
in
gaussianrandom
# -
# ## Steps
#
# - Create a Power Query function using the formula above. In the below example, I named the function `_NormalDist`
#
# 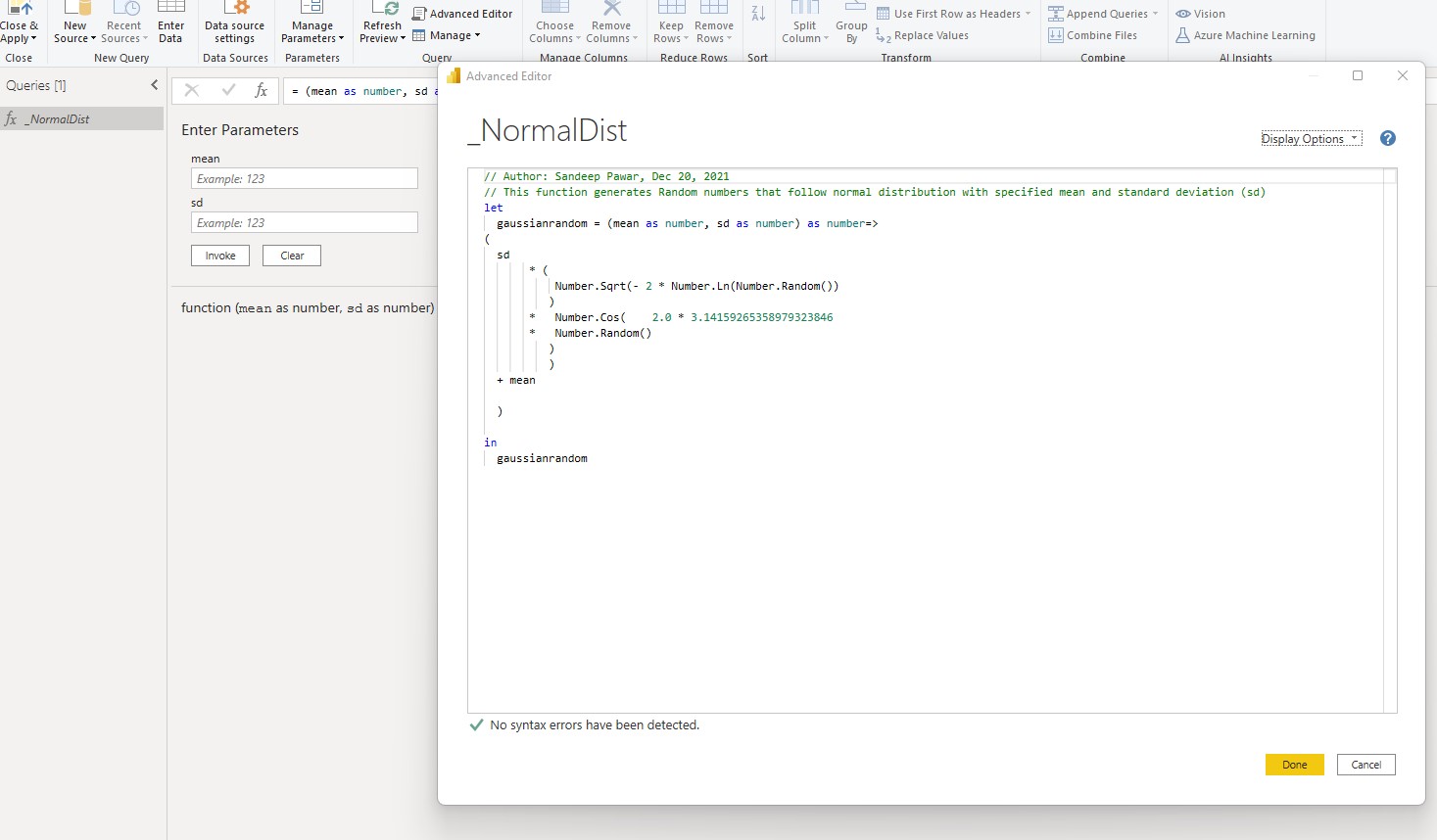
#
# - You will need to have unique rows. If you don't, create an index column (Add Column > Index Column).
# - To create a new column that follows the Gaussian distribution using the above function, go to Add Column and use the above function. In the example below, I created a new column that has mean of 10 and standard deviation of 0.25
#
# 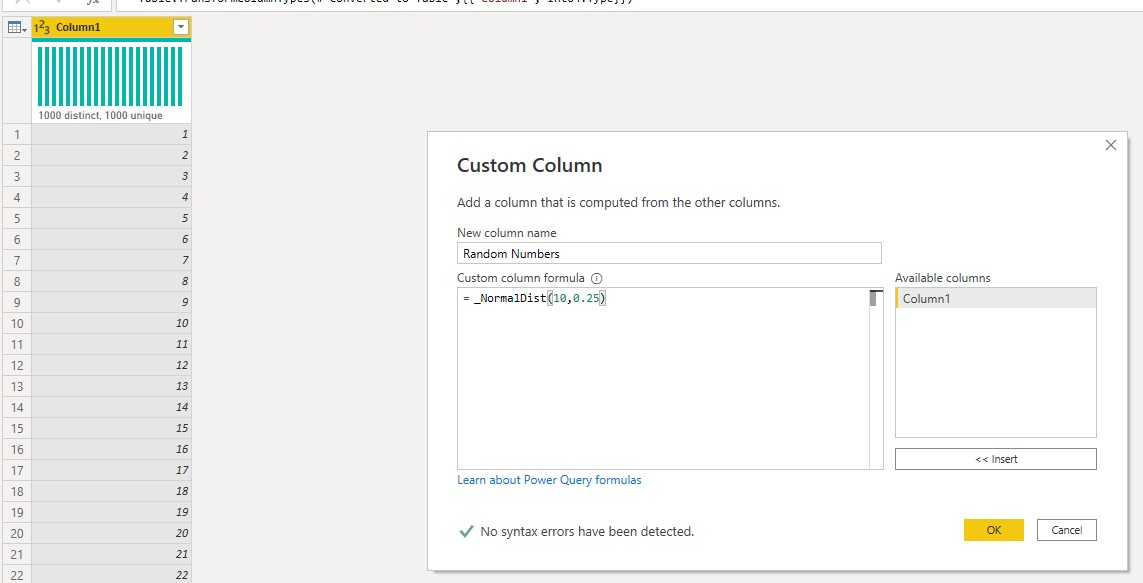
#
#
# - Here is the result:
# 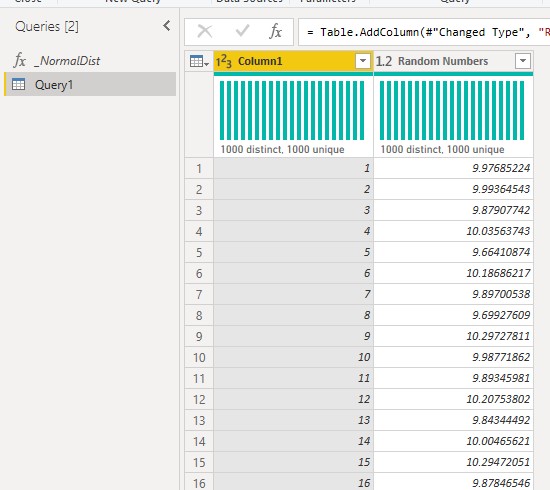
#
#
# Refresh the report and you will see the numbers in your table. If you see same number on all rows, just add another index column and remove it again.
#
# `NORM.INV()` in DAX generates new numbers every time the report is refreshed. In Power Query you can disable the refresh for this table, and hence generated numbers will stay the same even after refreshing the report. If you open the PowerQuery, however, it will generate new numbers. You can use `Table.Buffer()` to freeze it but I haven't had luck with that. If you know how to do it, please let me know.
# Here is the resulting distribution:
#
#hide-input
import pandas as pd
import seaborn as sns
df = pd.read_clipboard().set_index('Column1')
df.head(5)
sns.displot(df['Random Numbers'], rug=True, kde=True);
print("The mean and standard deviation of random numbers : ", round(df['Random Numbers'].mean(),2), round(df['Random Numbers'].std(),2))
# I also wrote another function to generate Traingular Distribution,which is very common to simulate risk profiles. Hope to share that soon.
| _notebooks/2021-12-22-PowerQuery-Normal-distribution.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Preparing the dataset for hippocampus segmentation
#
# In this notebook you will use the skills and methods that we have talked about during our EDA Lesson to prepare the hippocampus dataset using Python. Follow the Notebook, writing snippets of code where directed so using Task comments, similar to the one below, which expects you to put the proper imports in place. Write your code directly in the cell with TASK comment. Feel free to add cells as you see fit, but please make sure that code that performs that tasked activity sits in the same cell as the Task comment.
#
# TASK: Import the following libraries that we will use: nibabel, matplotlib, numpy
import nibabel as nib
import numpy as np
import matplotlib.pyplot as plt
import os
import shutil
from glob import glob
import scipy.ndimage as nd
# It will help your understanding of the data a lot if you were able to use a tool that allows you to view NIFTI volumes, like [3D Slicer](https://www.slicer.org/). I will refer to Slicer throughout this Notebook and will be pasting some images showing what your output might look like.
# ## Loading NIFTI images using NiBabel
#
# NiBabel is a python library for working with neuro-imaging formats (including NIFTI) that we have used in some of the exercises throughout the course. Our volumes and labels are in NIFTI format, so we will use nibabel to load and inspect them.
#
# NiBabel documentation could be found here: https://nipy.org/nibabel/
#
# Our dataset sits in two directories - *images* and *labels*. Each image is represented by a single file (we are fortunate to have our data converted to NIFTI) and has a corresponding label file which is named the same as the image file.
#
# Note that our dataset is "dirty". There are a few images and labels that are not quite right. They should be quite obvious to notice, though. The dataset contains an equal amount of "correct" volumes and corresponding labels, and you don't need to alter values of any samples in order to get the clean dataset.
# +
# TASK: Your data sits in directory /data/TrainingSet.
# Load an image and a segmentation mask into variables called image and label
images = glob("/data/TrainingSet/images/*")
labels = glob("/data/TrainingSet/labels/*")
image = nib.load(images[0])
label = nib.load(labels[0])
# +
# Nibabel can present your image data as a Numpy array by calling the method get_fdata()
# The array will contain a multi-dimensional Numpy array with numerical values representing voxel intensities.
# In our case, images and labels are 3-dimensional, so get_fdata will return a 3-dimensional array. You can verify this
# by accessing the .shape attribute. What are the dimensions of the input arrays?
# TASK: using matplotlib, visualize a few slices from the dataset, along with their labels.
# You can adjust plot sizes like so if you find them too small:
# plt.rcParams["figure.figsize"] = (10,10)
image_arr = image.get_fdata()
label_arr = label.get_fdata()
image_arr.shape #3 dimensionsal with dimensions (35, 55, 37)
label_arr.shape #3 dimensionsal with dimensions (35, 55, 37)
#Another volume from the dataset
image2 = nib.load(images[2])
label2 = nib.load(labels[2])
image_arr2 = image2.get_fdata()
label_arr2 = label2.get_fdata()
image_arr2.shape #3 dimensrional with dimensions (37, 45, 46)
label_arr2.shape #3 dimensrional with dimensions (37, 45, 46)
#Another volume from the dataset
image3 = nib.load(images[4])
label3 = nib.load(labels[4])
image_arr3 = image3.get_fdata()
label_arr3 = image3.get_fdata()
image_arr3.shape #3 dimensrional with dimensions (35, 50, 36)
label_arr3.shape #3 dimensrional with dimensions (35, 50, 36)
#Plot of three image slices from image and label loaded
plt.rcParams["figure.figsize"] = (16,16)
plt.subplot(131)
plt.imshow(image_arr[2,:,:] + label_arr[2,:,:], cmap= "gray")
plt.subplot(132)
plt.imshow(image_arr2[4,:,:] + label_arr2[4,:,:], cmap= "gray")
plt.subplot(133)
plt.imshow(image_arr3[6,:,:] + label_arr3[6,:,:], cmap= "gray")
# -
# Load volume into 3D Slicer to validate that your visualization is correct and get a feel for the shape of structures.Try to get a visualization like the one below (hint: while Slicer documentation is not particularly great, there are plenty of YouTube videos available! Just look it up on YouTube if you are not sure how to do something)
#
# 
# Stand out suggestion: use one of the simple Volume Rendering algorithms that we've
# implemented in one of our earlier lessons to visualize some of these volumes
#Plot volumetric rendering using maximum intensity projection for second image
mip = np.zeros((image_arr2.shape[0], image_arr2.shape[2]))
for y in range (image_arr2.shape[1]):
mip = np.maximum(mip,image_arr2[:,y,:])
plt.imshow(nd.rotate(mip, 90), cmap="gray")
# ## Looking at single image data
# In this section we will look closer at the NIFTI representation of our volumes. In order to measure the physical volume of hippocampi, we need to understand the relationship between the sizes of our voxels and the physical world.
# Nibabel supports many imaging formats, NIFTI being just one of them. I told you that our images
# are in NIFTI, but you should confirm if this is indeed the format that we are dealing with
# TASK: using .header_class attribute - what is the format of our images?
img1_type = image.header
img2_type = image2.header
img3_type = image3.header
print("Image type for first image:" + str(img1_type))
print("Image type for second image:" + str(img2_type))
print("Image type for third image:" + str(img3_type))
# Further down we will be inspecting .header attribute that provides access to NIFTI metadata. You can use this resource as a reference for various fields: https://brainder.org/2012/09/23/the-nifti-file-format/
# TASK: How many bits per pixel are used?
'''The first and third images have 32 bits per pixel which can be
inferred from the bitpix field, the seond image has 8 bit per pixel.'''
# +
# TASK: What are the units of measurement?
img1_type.get_xyzt_units() # Units of measurements are millimeters and seconds
img2_type.get_xyzt_units() # Units of measurements are millimeters and seconds
img3_type.get_xyzt_units() # Units of measurements are millimeters and seconds
'''Units of measurement for all three images are millimeters and seconds.'''
# -
# TASK: Do we have a regular grid? What are grid spacings?
'''The pixdim field in the NIFTI header stores an array of spatial and temporal measurements.
The first three bits of the pixdim array indicate spatial measurements or grid spacing in the x, y and z directions,
for all three images the grid spacing is 1, and since it is 1 in the x, y and z directions we have a
regular grid'''
# TASK: What dimensions represent axial, sagittal, and coronal slices? How do you know?
'''The dim field in the NIFTI file header contains an array of dimensions for the given NIFTI volume
,elements 1, 2, 3 in the dim field array contain information on the x, y, z dimensions which would correspond
to the sagittal, coronal, and axial slices in the volume'''
# By now you should have enough information to decide what are dimensions of a single voxel
# TASK: Compute the volume (in mm³) of a hippocampus using one of the labels you've loaded.
# You should get a number between ~2200 and ~4500
# since the grid spacing is 1x1x1 we can simply sum up the number of voxels in the volume
vol = np.sum(label_arr2 > 0)
vol
# ## Plotting some charts
# +
def calc_vol(label_in):
return np.sum(nib.load(label_in).get_fdata() > 0)
volumes = []
def cal_vols(labels):
for label in labels:
vol = calc_vol(label)
volumes.append(vol)
# -
# TASK: Plot a histogram of all volumes that we have in our dataset and see how
# our dataset measures against a slice of a normal population represented by the chart below.
plt.figure(figsize=(16,16))
cal_vols(labels)
plt.hist(volumes)
plt.xlabel('volume mm^3')
plt.ylabel('Number of Images')
#Most hippocampus volumes are between the 2200 mm^3 and 4500 mm^3 range except for the two outliers
# <img src="img/nomogram_fem_right.svg" width=400 align=left>
# Do you see any outliers? Why do you think it's so (might be not immediately obvious, but it's always a good idea to inspect) outliers closer. If you haven't found the images that do not belong, the histogram may help you.
# In the real world we would have precise information about the ages and conditions of our patients, and understanding how our dataset measures against population norm would be the integral part of clinical validation that we talked about in last lesson. Unfortunately, we do not have this information about this dataset, so we can only guess why it measures the way it is. If you would like to explore further, you can use the [calculator from HippoFit project](http://www.smanohar.com/biobank/calculator.html) to see how our dataset compares against different population slices
# Did you notice anything odd about the label files? We hope you did! The mask seems to have two classes, labeled with values `1` and `2` respectively. If you visualized sagittal or axial views, you might have gotten a good guess of what those are. Class 1 is the anterior segment of the hippocampus and class 2 is the posterior one.
#
# For the purpose of volume calculation we do not care about the distinction, however we will still train our network to differentiate between these two classes and the background
def copy_files(labels, images):
for label, image in zip(labels,images):
label_file_name = label[-22:]
image_file_name = label[-22:]
vol = calc_vol(label)
if vol >= 2200 and vol <= 4500:
shutil.copy(label, "/home/workspace/out/labels/"+str(label_file_name))
shutil.copy(label, "/home/workspace/out/images/"+str(image_file_name))
# TASK: Copy the clean dataset to the output folder inside section1/out. You will use it in the next Section
copy_files(labels,images)
# ## Final remarks
#
# Congratulations! You have finished Section 1.
#
# In this section you have inspected a dataset of MRI scans and related segmentations, represented as NIFTI files. We have visualized some slices, and understood the layout of the data. We have inspected file headers to understand what how the image dimensions relate to the physical world and we have understood how to measure our volume. We have then inspected dataset for outliers, and have created a clean set that is ready for consumption by our ML algorithm.
#
# In the next section you will create training and testing pipelines for a UNet-based machine learning model, run and monitor the execution, and will produce test metrics. This will arm you with all you need to use the model in the clinical context and reason about its performance!
| section1/out/Final Project EDA-completed.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#code to model the motion of a damped harmonic oscillator
#<NAME>
#<EMAIL>
#June 24 2020
#bring in numerical functions and plotting utilities
import numpy as np
import matplotlib.pyplot as plt
###################################
## begin function definitions ##
###################################
#each function definition contains general information about what the function accomplishes
#it also contains information about inputs and outputs in the form:
# - variable_name; data_type; information about the variable
#if the return is just returned without being named, the variable name will be listed as N/A
#purpose:
# - determine the sign of a number, used to orient drag forces in the correct direction
#input(s):
# - x; number; any number, positive, nevative, or zero
#output:
# - N/A; number; -1 if x is negative, +1 if x is positive, and 0 if x is 0
def sign(x):
if(x<0):
return -1.0
elif(x>0):
return 1.0
return 0.0
#purpose:
# - perform one step of 4th order Runge-Kutta integration
#input(s):
# - x0; rank 1 Python list; vector of (time,position,velocity) at start of step
# - fit_parameters; rank 1 Python list; vector of fit parameters
# - dt; number; duration of this step
#output:
# - N/A; rank 1 Python list; vector of (time,position,velocity) at end of step
def take_step(x0,fit_parameters,dt):
k1=dt*get_derivatives(x0,fit_parameters)
k2=dt*get_derivatives(x0+k1/2.0,fit_parameters)
k3=dt*get_derivatives(x0+k2/2.0,fit_parameters)
k4=dt*get_derivatives(x0+k3,fit_parameters)
return x0+(k1+2.0*k2+2.0*k3+k4)/6.0
#purpose:
# - perform numerical integration (via 4th order Runge-Kutta) to determine the best-fit function
#input(s):
# - fit_parameters; rank 1 Python list; vector of fit parameters
# - dt; number; duration of this step
# - imax; integer; length of the data set, this tells the Runge-Kutta method how many points to output
# - rk_substeps; integer; how many Runge-Kutta steps to take between each data point
# (i.e., divide the data set's dt by this...more iterations means better resolution)
#output:
# - f; rank 2 Python list; (time,position,velocity) at each time-step (corresponding to the time steps of data),
# first index selects timestep number, second index selects from (time,position,velocity) at that timestep
def fit_function(fit_parameters,dt,imax,rk_substeps):
step_dt=dt/rk_substeps
i=1
f=[[0,fit_parameters[0],fit_parameters[1]]]
while (i<imax):
new_f=take_step(f[-1],fit_parameters,step_dt)
j=1
while (j<rk_substeps):
new_f=take_step(new_f,fit_parameters,step_dt)
j+=1
f.append([i*dt,new_f[1],new_f[2]])
i+=1
return f
#purpose:
# - compute the gradient of the fit function with respect to fit parameters using finite differencing
#input(s):
# - f; rank 2 Python list; (time,position,velocity) at each time-step (see fit_function)
# - fit_parameters; rank 1 Python list; vector of fit parameters
# - dt; number; time between data points
# - imax; integer; the number of data points
# - rk_substeps; integer; number of numerical integration steps between data points (see fit_function)
# - fd_scale; number; controls size of finite differencing (see grad_fit_function)
#output:
# - N/A; rank 2 Python list; derivative of the fit function with respect to fit parameter at each timestep
# first index selects fit parameter, second index selects timestep
def grad_fit_function(f,fit_parameters,dt,imax,rk_substeps,fd_scale):
#rename fit_parameters, otherwise the expresssions get way too long
a=fit_parameters
f0=fit_function([a[0]*(1+fd_scale),a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f1=fit_function([a[0],a[1]*(1+fd_scale),a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f2=fit_function([a[0],a[1],a[2]*(1+fd_scale),a[3],a[4],a[5],a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f3=fit_function([a[0],a[1],a[2],a[3]*(1+fd_scale),a[4],a[5],a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f4=fit_function([a[0],a[1],a[2],a[3],a[4]*(1+fd_scale),a[5],a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f5=fit_function([a[0],a[1],a[2],a[3],a[4],a[5]*(1+fd_scale),a[6],a[7],a[8],a[9]],dt,imax,rk_substeps)
f6=fit_function([a[0],a[1],a[2],a[3],a[4],a[5],a[6]*(1+fd_scale),a[7],a[8],a[9]],dt,imax,rk_substeps)
f7=fit_function([a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7]*(1+fd_scale),a[8],a[9]],dt,imax,rk_substeps)
f8=fit_function([a[0],a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8]*(1+fd_scale),a[9]],dt,imax,rk_substeps)
dfd0=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[0]),f,f0))
dfd1=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[1]),f,f1))
dfd2=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[2]),f,f2))
dfd3=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[3]),f,f3))
dfd4=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[4]),f,f4))
dfd5=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[5]),f,f5))
dfd6=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[6]),f,f6))
dfd7=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[7]),f,f7))
dfd8=list(map(lambda foo0,foo1: (foo1[1]-foo0[1])/(fd_scale*a[8]),f,f8))
return [dfd0,dfd1,dfd2,dfd3,dfd4,dfd5,dfd6,dfd7,dfd8]
#purpose:
# - compute the gradient of chi^2 with respect to fit parameters, given the gradient of the fit function
# (essentially implementing the chain rule)
#input(s):
# - f; rank 2 Python list; (time,position,velocity) at each time-step (see fit_function)
# - fit_parameters; rank 1 Python list; vector of fit parameters
# - data; rank 2 numpy array; fit data, first index is data point number, second index selects (time,position)
# - rk_substeps; integer; number of numerical integration steps between data points (see fit_function)
# - fd_scale; number; controls size of finite differencing (see grad_fit_function)
#output:
# - N/A; rank 2 Python list; gradient of fit function, first index selects gradient component (derivative
# with respect to which fit parameter), second index selects time
def grad_chi2(f,fit_parameters,data,rk_substeps,fd_scale):
imax=len(data)
dt=(data[-1][0]-data[0][0])/(imax-1)
[dfd0,dfd1,dfd2,dfd3,dfd4,dfd5,dfd6,dfd7,dfd8]=grad_fit_function(f,fit_parameters,dt,imax,rk_substeps,fd_scale)
dcd0=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd0,data))))
dcd1=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd1,data))))
dcd2=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd2,data))))
dcd3=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd3,data))))
dcd4=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd4,data))))
dcd5=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd5,data))))
dcd6=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd6,data))))
dcd7=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd7,data))))
dcd8=2*np.sum(np.array(list(map(lambda foo0,foo1,foo2: foo1*(foo0[1]-foo2[1]),f,dfd8,data))))
return np.array([dcd0,dcd1,dcd2,dcd3,dcd4,dcd5,dcd6,dcd7,dcd8])
#purpose:
# - compute chi^2, the sum of the square of the residuals between the fit and data
#input(s):
# - data; rank 2 numpy array; fit data, first index is data point number, second index selects (time,position)
# - f; rank 2 Python list; (time,position,velocity) at each time-step (see fit_function)
#output:
# - N/A; number; the value of chi^2 for the given fit f
def chi2(data,f):
return np.sum(np.array(list(map(lambda foo0,foo1: (foo0[1]-foo1[1])**2,f,data))))
#purpose:
# - perform a gradient descent search for fit parameters which minimize chi^2
#input(s):
# - gd_iterations; integer; how many steps of gradient descent to do
# - alpha; number; parameter controlling the size of each gradient descent step
# - data; rank 2 numpy array; fit data, first index is data point number, second index selects (time,position)
# - initial_fit_parameters; rank 1 Python list; vector of fit parameters before fit (initial guess)
# - rk_substeps; integer; number of numerical integration steps between data points (see fit_function)
# - fd_scale; number; controls size of finite differencing (see grad_fit_function)
#output:
# - fit_parameters; rank 1 Python list; vector of fit parameters after fit
# - chi2s; rank 2 numpy array; the value of chi^2 at each gradient descent iteration, first index is iteration number,
# second index selects (iteration #,chi^2)
# - note that these returns are grouped together in a ragged Python list to make one output
def gradient_descent(gd_iterations,alpha,data,initial_fit_parameters,rk_substeps,fd_scale):
imax=len(data)
dt=(data[-1][0]-data[0][0])/(imax-1)
fit_parameters = np.array(initial_fit_parameters)
f=fit_function(fit_parameters,dt,imax,rk_substeps)
chi2s=[[0,chi2(data,f)]]
i=1
while (i<=gd_iterations):
print("gradient_descent iteration: " + str(i) + "/" + str(gd_iterations), end="\r")
fit_parameters -= alpha * np.append(np.array(grad_chi2(f,fit_parameters.tolist(),data,rk_substeps,fd_scale)),0.0)
f=fit_function(fit_parameters,dt,imax,rk_substeps)
chi2s.append([i,chi2(data,f)])
i+=1
print("\n")
print("final chi2=" + str(chi2s[-1][1]))
print("final Delta chi2=" + str(np.abs(chi2s[-1][1]/chi2s[-2][1]-1.0)))
print("\n")
return [fit_parameters,np.array(chi2s)]
#purpose:
# - display data about the fit which was determined
#input(s):
# - fit_parameters; rank 1 Python list; vector of fit parameters
# - data; rank 2 numpy array; fit data, first index is data point number, second index selects (time,position)
# - f; rank 2 Python list; (time,position,velocity) at each time-step (see fit_function)
# - chi2s; rank 2 Python list; the value of chi^2 throughout the fit (see gradient_descent)
#output:
# - no formal return, prints new values of parameters to screen and saves plots showing fit, residuals,
# and learning to the code's directory
def output_info(fit_parameters,data,f,chi2s):
#print out the new fit parameters in a form which can easily be copied over to use as initial guesses on the next fit
print("\n")
print("updated fit parameters:")
print("x0=" + str(fit_parameters[0]))
print("v0=" + str(fit_parameters[1]))
print("m=" + str(fit_parameters[2]))
print("xeq=" + str(fit_parameters[3]))
print("c0=" + str(fit_parameters[4]))
print("c1=" + str(fit_parameters[5]))
print("c2=" + str(fit_parameters[6]))
print("cn=" + str(fit_parameters[7]))
print("n=" + str(fit_parameters[8]))
print("k=" + str(fit_parameters[9]))
print("\n")
#plot the data along with the fit determined
plt.figure(figsize=(16, 12), dpi=300)
plt.plot(data[:,0],data[:,1],marker='.',linestyle='')
plt.plot(np.array(f)[:,0],np.array(f)[:,1])
plt.xlabel("Time (s)")
plt.ylabel("Position (m)")
plt.savefig('fit.png')
#plot the residuals
plt.figure(figsize=(16, 12), dpi=300)
plt.plot(data[:,0],np.array(f)[:,1]-data[:,1])
plt.xlabel("Time (s)")
plt.ylabel("Residuals (m)")
plt.savefig('residuals.png')
#plot the learning curve, chi^2 throughout the gradient descent
plt.figure(figsize=(16, 12), dpi=300)
plt.semilogy(chi2s[:,0],chi2s[:,1],marker='.',linestyle='')
plt.xlabel("Iteration")
plt.ylabel("chi^2 (m^2)")
plt.savefig('learning.png')
output=np.array(list(map(lambda foo0,foo1: [foo0[0],foo0[1],foo1[1],foo0[1]-foo1[1]],data,f)))
np.savetxt('c0_c1_c2_cn_data_fit_residuals.csv',output,delimiter=',')
#purpose:
# - compute the value of the derivatives at each timestep in the numerical integration,
# note that this is where the physics comes in and is also where the differential equation is communicated
# to the code
#input(s):
# - x0; rank 1 Python list; vector of (time,position,velocity) at start of step
# - fit_parameters; rank 1 Python list; vector of fit parameters
#output:
# - N/A; rank 1 Python list; vector of (dt/dt,dx/dt,dv/dt)
def get_derivatives(x,fit_parameters):
[time,position,velocity]=x
[x0,v0,m,xeq,c0,c1,c2,cn,n,k]=fit_parameters
force=-(k*(position-xeq)+c1*velocity+(c0+c2*velocity**2+cn*np.abs(velocity)**n)*sign(velocity))
return np.array([1.0,velocity,force/m])
##############################################################################
## definitions done; this is where the code begins its thought process ##
##############################################################################
#read in the data, skip the first line because it should contain column titles
data=(np.genfromtxt('20cmTrial1.csv',delimiter=','))[1:]
#initial guesses for fit parameters, collected into a list
x0=-0.18693030855815537
v0=-0.3051726546250762
m=1.1466645537288631
xeq=-0.0015746613895467575
c0=0.022089169719687676
c1=0.007436547041692171
c2=0.005139077158679122
cn=0.0282202394837076
n=1.4999047900466689
k=48.84
fit_parameters=[x0,v0,m,xeq,c0,c1,c2,cn,n,k]
#set some paramters for the fit
# gd_iterations controls how many steps of gradient descent the fitter does
# alpha controls the alpha parameter in the gradient descent method
# rk_substeps controls the number of numerical integration steps between data points
# fd_scale controls the size of the difference when doing finite differencing in computing the gradient of the fit function
gd_iterations=2
alpha=1.0e-6
rk_substeps=128
fd_scale=1.0e-9
#do the fit
# fit_parameters is the updated set of fit parameters after doing the fit
# chi2s is a list of chi^2 values throughout the gradient descent (a "learning curve")
[fit_parameters,chi2s]=gradient_descent(gd_iterations,alpha,data,fit_parameters,rk_substeps,fd_scale)
#compute the best fit line
#need to know how many data points there are and the time between them
imax=len(data)
dt=(data[-1][0]-data[0][0])/(imax-1)
f=fit_function(fit_parameters,dt,imax,rk_substeps)
#output new fit parameters and graphs
output_info(fit_parameters,data,f,chi2s)
# -
| damped_oscillation_fitting/damped_oscillation_fitting.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import seaborn as sns
dados = np.array([
126. , 129.5, 133. , 133. , 136.5, 136.5, 140. , 140. , 140. ,
140. , 143.5, 143.5, 143.5, 143.5, 143.5, 143.5, 147. , 147. ,
147. , 147. , 147. , 147. , 147. , 150.5, 150.5, 150.5, 150.5,
150.5, 150.5, 150.5, 150.5, 154. , 154. , 154. , 154. , 154. ,
154. , 154. , 154. , 154. , 157.5, 157.5, 157.5, 157.5, 157.5,
157.5, 157.5, 157.5, 157.5, 157.5, 161. , 161. , 161. , 161. ,
161. , 161. , 161. , 161. , 161. , 161. , 164.5, 164.5, 164.5,
164.5, 164.5, 164.5, 164.5, 164.5, 164.5, 168. , 168. , 168. ,
168. , 168. , 168. , 168. , 168. , 171.5, 171.5, 171.5, 171.5,
171.5, 171.5, 171.5, 175. , 175. , 175. , 175. , 175. , 175. ,
178.5, 178.5, 178.5, 178.5, 182. , 182. , 185.5, 185.5, 189. , 192.5
])
sns.histplot(dados, kde=True)
media = np.mean(dados)
desvio_padrao = np.std(dados)
media, desvio_padrao
np.quantile(dados, [0.25,0.5,0.75])
# ### Probabilidade de selecionar uma pessoa no Q1
# z-score
(150.5 - media)/desvio_padrao
0.26109
# Como pode ser observado na tabela Z:
# * 0.26109 é a probabilidade de selecionar qualquer pessoa antes do primeiro quartil.
# ### Probabilidade de selecionar uma pessoa no Q3
# z-score
(168. - media)/desvio_padrao
0.73891, 1-0.73891
# Como pode ser observado na tabela Z:
# * 0.73891 é a probabilidade de selecionar qualquer pessoa antes do terceiro quartil.
# * 0.26109 é a probabilidade de selecionar qualquer pessoa depois do terceiro quartil.
# ### Probabilidade de selecionar uma pessoa entre Q2 e Q3
(159.25-media)/desvio_padrao
0.5
# Como pode ser observado na tabela Z:
# * 0.5 é a pobabilidade de selecionar uma pessoa a direita ou a esquerda do segundo quartil.
# * O fato é que o segundo quartil corresponde extamente a média.
0.73891-0.5
# Pela subtração, 0.23891 é a pobabilidade de selecionar uma pessoa entre o segundo e o terceiro quartil.
# ### Probabilidade de selecionar uma pessoa em Q1 e Q3
0.26109+0.26109
# Pela soma, 0.52218 é a pobabilidade de selecionar uma pessoa no primeiro e no terceiro quartil.
# ### Probabilidade de não selecionar uma pessoa em Q1 e Q3
1-0.52218
# Pela subtração, 0.47782 é a pobabilidade de não selecionar uma pessoa no primeiro e no terceiro quartil.
# ## Bibliotecas (Scipy)
from scipy import stats
media = np.mean(dados)
desvio_padrao = np.std(dados)
media, desvio_padrao, np.quantile(dados, [0.25,0.5,0.75])
# Probabilidade de selecionar uma pessoa no Q1.
stats.norm.cdf(150.5, media, desvio_padrao)
# Probabilidade de selecionar uma pessoa até o Q3.
stats.norm.cdf(168, media, desvio_padrao)
# Probabilidade de selecionar uma pessoa depois do Q3.
stats.norm.sf(168, media, desvio_padrao)
# Probabilidade de selecionar uma pessoa entre Q2 e Q3.
q2 = stats.norm.cdf(159.25, media, desvio_padrao)
q3 = stats.norm.cdf(168, media, desvio_padrao)
q3-q2
# # Testes
# #### Teste do aluno
x = 40
media = 24
desvio_padrao = 8
padronizacao = (X-media)/desvio_padrao
padronizacao
stats.norm.cdf(2.0) # retorna a probabilidade: 97,72%
stats.norm.ppf(0.9772498680518208) # retorna o valor padronizado.
# #### Teste do pneu
# +
media_pneus = 38000
desvio_padrao_pneus = 3000
pneu1 = 35000 # dure igual
pneu2 = 44000 # dure mais
# -
stats.norm.sf(pneu1, media_pneus, desvio_padrao_pneus)
stats.norm.sf(pneu2, media_pneus, desvio_padrao_pneus)
| 7_probabilidades/probabilidade_distribuicao_normal.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import pandas as pd
import numpy as np
from statsmodels.tsa import stattools
# %matplotlib inline
from matplotlib import pyplot as plt
from pandas.plotting import autocorrelation_plot
djia_df = pd.read_excel('datasets/DJIA_Jan2016_Dec2016.xlsx')
djia_df.head(10)
#Let us parse the Date column and use as row index for the DataFrame and drop it as a column
djia_df['Date'] = pd.to_datetime(djia_df['Date'], '%Y-%m-%d')
djia_df.index = djia_df['Date']
djia_df.drop('Date', axis=1, inplace=True)
#Let us see first few rows of the modified DataFrame
djia_df.head(10)
#We would be using the 'Close' values of the DJIA to illustrate Differencing
first_order_diff = djia_df['Close'].diff(1)
#Let us plot the original time series and first-differences
fig, ax = plt.subplots(2, sharex=True)
fig.set_size_inches(5.5, 5.5)
djia_df['Close'].plot(ax=ax[0], color='b')
ax[0].set_title('Close values of DJIA during Jan 2016-Dec 2016')
first_order_diff.plot(ax=ax[1], color='r')
ax[1].set_title('First-order differences of DJIA during Jan 2016-Dec 2016')
#plt.savefig('plots/ch2/B07887_02_06.png', format='png', dpi=300)
#Let us plot the ACFs of original time series and first-differences
fig, ax = plt.subplots(2, sharex=True)
fig.set_size_inches(5.5, 5.5)
autocorrelation_plot(djia_df['Close'], color='b', ax=ax[0])
ax[0].set_title('ACF of DJIA Close values')
autocorrelation_plot(first_order_diff.iloc[1:], color='r', ax=ax[1])
ax[1].set_title('ACF of first differences of DJIA Close values')
plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=2.0)
plt.savefig('plots/ch2/B07887_02_07.png', format='png', dpi=300)
"""
Now we will perform the Ljung-Box test on the ACFs
of the original time series and the first-differences.
For running the test we will limit upto 20 lags
"""
"""
Let us obtain the confidence intervls, Ljung-Box Q-statistics and p-values
for the original DJIA Close values
"""
acf_djia, confint_djia, qstat_djia, pvalues_djia = stattools.acf(djia_df['Close'],
unbiased=True,
nlags=20,
qstat=True,
alpha=0.05)
"""Let us check if at confidence level 95% (alpha=0.05)
if the null hypothesis is rejected at any of the lags
"""
alpha = 0.05
for l, p_val in enumerate(pvalues_djia):
if p_val > alpha:
print('Null hypothesis is accepted at lag = {} for p-val = {}'.format(l, p_val))
else:
print('Null hypothesis is rejected at lag = {} for p-val = {}'.format(l, p_val))
"""
The above results show statistically significant ACF in the original DJIA Close values
"""
"""
Let us obtain the confidence intervls, Ljung-Box Q-statistics and p-values
for the differenced DJIA Close values
"""
acf_first_diff, confint_first_diff,\
qstat_first_diff, pvalues_first_diff = stattools.acf(first_order_diff.iloc[1:],
unbiased=True,
nlags=20,
qstat=True,
alpha=0.05)
"""Let us check if at confidence level of 95% (alpha = 0.05)
if the null hypothesis is rejected at any of the lags
"""
alpha = 0.05
for l, p_val in enumerate(pvalues_first_diff):
if p_val > alpha:
print('Null hypothesis is accepted at lag = {} for p-val = {}'.format(l, p_val))
else:
print('Null hypothesis is rejected at lag = {} for p-val = {}'.format(l, p_val))
"""
The above results show that ACF is essentially random in the differenced DJIA Close values
"""
| time series regression/autocorelation, mov avg etc/First_Order_Differencing.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Discretization
#
# ---
#
# In this notebook, you will deal with continuous state and action spaces by discretizing them. This will enable you to apply reinforcement learning algorithms that are only designed to work with discrete spaces.
#
# ### 1. Import the Necessary Packages
# +
import sys
import gym
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Set plotting options
# %matplotlib inline
plt.style.use('ggplot')
np.set_printoptions(precision=3, linewidth=120)
# -
# ### 2. Specify the Environment, and Explore the State and Action Spaces
#
# We'll use [OpenAI Gym](https://gym.openai.com/) environments to test and develop our algorithms. These simulate a variety of classic as well as contemporary reinforcement learning tasks. Let's use an environment that has a continuous state space, but a discrete action space.
# Create an environment and set random seed
env = gym.make('MountainCar-v0')
env.seed(505);
# Run the next code cell to watch a random agent.
state = env.reset()
score = 0
for t in range(200):
action = env.action_space.sample()
env.render()
state, reward, done, _ = env.step(action)
score += reward
if done:
break
print('Final score:', score)
env.close()
# In this notebook, you will train an agent to perform much better! For now, we can explore the state and action spaces, as well as sample them.
# Explore state (observation) space
print("State space:", env.observation_space)
print("- low:", env.observation_space.low)
print("- high:", env.observation_space.high)
# Generate some samples from the state space
print("State space samples:")
print(np.array([env.observation_space.sample() for i in range(10)]))
# +
# Explore the action space
print("Action space:", env.action_space)
# Generate some samples from the action space
print("Action space samples:")
print(np.array([env.action_space.sample() for i in range(10)]))
# -
# ### 3. Discretize the State Space with a Uniform Grid
#
# We will discretize the space using a uniformly-spaced grid. Implement the following function to create such a grid, given the lower bounds (`low`), upper bounds (`high`), and number of desired `bins` along each dimension. It should return the split points for each dimension, which will be 1 less than the number of bins.
#
# For instance, if `low = [-1.0, -5.0]`, `high = [1.0, 5.0]`, and `bins = (10, 10)`, then your function should return the following list of 2 NumPy arrays:
#
# ```
# [array([-0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8]),
# array([-4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0, 4.0])]
# ```
#
# Note that the ends of `low` and `high` are **not** included in these split points. It is assumed that any value below the lowest split point maps to index `0` and any value above the highest split point maps to index `n-1`, where `n` is the number of bins along that dimension.
# +
def create_uniform_grid(low, high, bins=(10, 10)):
"""Define a uniformly-spaced grid that can be used to discretize a space.
Parameters
----------
low : array_like
Lower bounds for each dimension of the continuous space.
high : array_like
Upper bounds for each dimension of the continuous space.
bins : tuple
Number of bins along each corresponding dimension.
Returns
-------
grid : list of array_like
A list of arrays containing split points for each dimension.
"""
# TODO: Implement this
low_offset = (high[0] - low[0])/bins[0]
high_offset = (high[1] - low[1])/bins[1]
start = low[0] + low_offset
result = list()
result_low = list()
result_high = list()
for i in np.arange(low[0] + low_offset, high[0], low_offset):
result_low.append(round(i, 1))
for i in np.arange(low[1] + high_offset, high[1], high_offset):
result_high.append(round(i, 1))
result.append(result_low)
result.append(result_high)
return result
low = [-1.0, -5.0]
high = [1.0, 5.0]
create_uniform_grid(low, high) # [test]
# -
# Now write a function that can convert samples from a continuous space into its equivalent discretized representation, given a grid like the one you created above. You can use the [`numpy.digitize()`](https://docs.scipy.org/doc/numpy-1.9.3/reference/generated/numpy.digitize.html) function for this purpose.
#
# Assume the grid is a list of NumPy arrays containing the following split points:
# ```
# [array([-0.8, -0.6, -0.4, -0.2, 0.0, 0.2, 0.4, 0.6, 0.8]),
# array([-4.0, -3.0, -2.0, -1.0, 0.0, 1.0, 2.0, 3.0, 4.0])]
# ```
#
# Here are some potential samples and their corresponding discretized representations:
# ```
# [-1.0 , -5.0] => [0, 0]
# [-0.81, -4.1] => [0, 0]
# [-0.8 , -4.0] => [1, 1]
# [-0.5 , 0.0] => [2, 5]
# [ 0.2 , -1.9] => [6, 3]
# [ 0.8 , 4.0] => [9, 9]
# [ 0.81, 4.1] => [9, 9]
# [ 1.0 , 5.0] => [9, 9]
# ```
#
# **Note**: There may be one-off differences in binning due to floating-point inaccuracies when samples are close to grid boundaries, but that is alright.
# +
def discretize(sample, grid):
"""Discretize a sample as per given grid.
Parameters
----------
sample : array_like
A single sample from the (original) continuous space.
grid : list of array_like
A list of arrays containing split points for each dimension.
Returns
-------
discretized_sample : array_like
A sequence of integers with the same number of dimensions as sample.
"""
# TODO: Implement this
return list(int(np.digitize(s, g)) for s, g in zip(sample, grid))
# Test with a simple grid and some samples
grid = create_uniform_grid([-1.0, -5.0], [1.0, 5.0])
samples = np.array(
[[-1.0 , -5.0],
[-0.81, -4.1],
[-0.8 , -4.0],
[-0.5 , 0.0],
[ 0.2 , -1.9],
[ 0.8 , 4.0],
[ 0.81, 4.1],
[ 1.0 , 5.0]])
discretized_samples = np.array([discretize(sample, grid) for sample in samples])
print("\nSamples:", repr(samples), sep="\n")
print("\nDiscretized samples:", repr(discretized_samples), sep="\n")
# -
# ### 4. Visualization
#
# It might be helpful to visualize the original and discretized samples to get a sense of how much error you are introducing.
# +
import matplotlib.collections as mc
def visualize_samples(samples, discretized_samples, grid, low=None, high=None):
"""Visualize original and discretized samples on a given 2-dimensional grid."""
fig, ax = plt.subplots(figsize=(10, 10))
# Show grid
ax.xaxis.set_major_locator(plt.FixedLocator(grid[0]))
ax.yaxis.set_major_locator(plt.FixedLocator(grid[1]))
ax.grid(True)
# If bounds (low, high) are specified, use them to set axis limits
if low is not None and high is not None:
ax.set_xlim(low[0], high[0])
ax.set_ylim(low[1], high[1])
else:
# Otherwise use first, last grid locations as low, high (for further mapping discretized samples)
low = [splits[0] for splits in grid]
high = [splits[-1] for splits in grid]
# Map each discretized sample (which is really an index) to the center of corresponding grid cell
grid_extended = np.hstack((np.array([low]).T, grid, np.array([high]).T)) # add low and high ends
grid_centers = (grid_extended[:, 1:] + grid_extended[:, :-1]) / 2 # compute center of each grid cell
locs = np.stack(grid_centers[i, discretized_samples[:, i]] for i in range(len(grid))).T # map discretized samples
ax.plot(samples[:, 0], samples[:, 1], 'o') # plot original samples
ax.plot(locs[:, 0], locs[:, 1], 's') # plot discretized samples in mapped locations
ax.add_collection(mc.LineCollection(list(zip(samples, locs)), colors='orange')) # add a line connecting each original-discretized sample
ax.legend(['original', 'discretized'])
visualize_samples(samples, discretized_samples, grid, low, high)
# -
# Now that we have a way to discretize a state space, let's apply it to our reinforcement learning environment.
# Create a grid to discretize the state space
state_grid = create_uniform_grid(env.observation_space.low, env.observation_space.high, bins=(10, 10))
state_grid
# Obtain some samples from the space, discretize them, and then visualize them
state_samples = np.array([env.observation_space.sample() for i in range(10)])
discretized_state_samples = np.array([discretize(sample, state_grid) for sample in state_samples])
visualize_samples(state_samples, discretized_state_samples, state_grid,
env.observation_space.low, env.observation_space.high)
plt.xlabel('position'); plt.ylabel('velocity'); # axis labels for MountainCar-v0 state space
# You might notice that if you have enough bins, the discretization doesn't introduce too much error into your representation. So we may be able to now apply a reinforcement learning algorithm (like Q-Learning) that operates on discrete spaces. Give it a shot to see how well it works!
#
# ### 5. Q-Learning
#
# Provided below is a simple Q-Learning agent. Implement the `preprocess_state()` method to convert each continuous state sample to its corresponding discretized representation.
# +
class QLearningAgent:
"""Q-Learning agent that can act on a continuous state space by discretizing it."""
def __init__(self, env, state_grid, alpha=0.02, gamma=0.99,
epsilon=1.0, epsilon_decay_rate=0.9995, min_epsilon=.01, seed=505):
"""Initialize variables, create grid for discretization."""
# Environment info
self.env = env
self.state_grid = state_grid
self.state_size = tuple(len(splits) + 1 for splits in self.state_grid) # n-dimensional state space
self.action_size = self.env.action_space.n # 1-dimensional discrete action space
self.seed = np.random.seed(seed)
print("Environment:", self.env)
print("State space size:", self.state_size)
print("Action space size:", self.action_size)
# Learning parameters
self.alpha = alpha # learning rate
self.gamma = gamma # discount factor
self.epsilon = self.initial_epsilon = epsilon # initial exploration rate
self.epsilon_decay_rate = epsilon_decay_rate # how quickly should we decrease epsilon
self.min_epsilon = min_epsilon
# Create Q-table
self.q_table = np.zeros(shape=(self.state_size + (self.action_size,)))
print("Q table size:", self.q_table.shape)
def preprocess_state(self, state):
"""Map a continuous state to its discretized representation."""
# TODO: Implement this
pass
def reset_episode(self, state):
"""Reset variables for a new episode."""
# Gradually decrease exploration rate
self.epsilon *= self.epsilon_decay_rate
self.epsilon = max(self.epsilon, self.min_epsilon)
# Decide initial action
self.last_state = self.preprocess_state(state)
self.last_action = np.argmax(self.q_table[self.last_state])
return self.last_action
def reset_exploration(self, epsilon=None):
"""Reset exploration rate used when training."""
self.epsilon = epsilon if epsilon is not None else self.initial_epsilon
def act(self, state, reward=None, done=None, mode='train'):
"""Pick next action and update internal Q table (when mode != 'test')."""
state = self.preprocess_state(state)
if mode == 'test':
# Test mode: Simply produce an action
action = np.argmax(self.q_table[state])
else:
# Train mode (default): Update Q table, pick next action
# Note: We update the Q table entry for the *last* (state, action) pair with current state, reward
self.q_table[self.last_state + (self.last_action,)] += self.alpha * \
(reward + self.gamma * max(self.q_table[state]) - self.q_table[self.last_state + (self.last_action,)])
# Exploration vs. exploitation
do_exploration = np.random.uniform(0, 1) < self.epsilon
if do_exploration:
# Pick a random action
action = np.random.randint(0, self.action_size)
else:
# Pick the best action from Q table
action = np.argmax(self.q_table[state])
# Roll over current state, action for next step
self.last_state = state
self.last_action = action
return action
q_agent = QLearningAgent(env, state_grid)
# -
# Let's also define a convenience function to run an agent on a given environment. When calling this function, you can pass in `mode='test'` to tell the agent not to learn.
# +
def run(agent, env, num_episodes=20000, mode='train'):
"""Run agent in given reinforcement learning environment and return scores."""
scores = []
max_avg_score = -np.inf
for i_episode in range(1, num_episodes+1):
# Initialize episode
state = env.reset()
action = agent.reset_episode(state)
total_reward = 0
done = False
# Roll out steps until done
while not done:
state, reward, done, info = env.step(action)
total_reward += reward
action = agent.act(state, reward, done, mode)
# Save final score
scores.append(total_reward)
# Print episode stats
if mode == 'train':
if len(scores) > 100:
avg_score = np.mean(scores[-100:])
if avg_score > max_avg_score:
max_avg_score = avg_score
if i_episode % 100 == 0:
print("\rEpisode {}/{} | Max Average Score: {}".format(i_episode, num_episodes, max_avg_score), end="")
sys.stdout.flush()
return scores
scores = run(q_agent, env)
# -
# The best way to analyze if your agent was learning the task is to plot the scores. It should generally increase as the agent goes through more episodes.
# Plot scores obtained per episode
plt.plot(scores); plt.title("Scores");
# If the scores are noisy, it might be difficult to tell whether your agent is actually learning. To find the underlying trend, you may want to plot a rolling mean of the scores. Let's write a convenience function to plot both raw scores as well as a rolling mean.
# +
def plot_scores(scores, rolling_window=100):
"""Plot scores and optional rolling mean using specified window."""
plt.plot(scores); plt.title("Scores");
rolling_mean = pd.Series(scores).rolling(rolling_window).mean()
plt.plot(rolling_mean);
return rolling_mean
rolling_mean = plot_scores(scores)
# -
# You should observe the mean episode scores go up over time. Next, you can freeze learning and run the agent in test mode to see how well it performs.
# Run in test mode and analyze scores obtained
test_scores = run(q_agent, env, num_episodes=100, mode='test')
print("[TEST] Completed {} episodes with avg. score = {}".format(len(test_scores), np.mean(test_scores)))
_ = plot_scores(test_scores, rolling_window=10)
# It's also interesting to look at the final Q-table that is learned by the agent. Note that the Q-table is of size MxNxA, where (M, N) is the size of the state space, and A is the size of the action space. We are interested in the maximum Q-value for each state, and the corresponding (best) action associated with that value.
# +
def plot_q_table(q_table):
"""Visualize max Q-value for each state and corresponding action."""
q_image = np.max(q_table, axis=2) # max Q-value for each state
q_actions = np.argmax(q_table, axis=2) # best action for each state
fig, ax = plt.subplots(figsize=(10, 10))
cax = ax.imshow(q_image, cmap='jet');
cbar = fig.colorbar(cax)
for x in range(q_image.shape[0]):
for y in range(q_image.shape[1]):
ax.text(x, y, q_actions[x, y], color='white',
horizontalalignment='center', verticalalignment='center')
ax.grid(False)
ax.set_title("Q-table, size: {}".format(q_table.shape))
ax.set_xlabel('position')
ax.set_ylabel('velocity')
plot_q_table(q_agent.q_table)
# -
# ### 6. Modify the Grid
#
# Now it's your turn to play with the grid definition and see what gives you optimal results. Your agent's final performance is likely to get better if you use a finer grid, with more bins per dimension, at the cost of higher model complexity (more parameters to learn).
# TODO: Create a new agent with a different state space grid
state_grid_new = create_uniform_grid(?, ?, bins=(?, ?))
q_agent_new = QLearningAgent(env, state_grid_new)
q_agent_new.scores = [] # initialize a list to store scores for this agent
# Train it over a desired number of episodes and analyze scores
# Note: This cell can be run multiple times, and scores will get accumulated
q_agent_new.scores += run(q_agent_new, env, num_episodes=50000) # accumulate scores
rolling_mean_new = plot_scores(q_agent_new.scores)
# Run in test mode and analyze scores obtained
test_scores = run(q_agent_new, env, num_episodes=100, mode='test')
print("[TEST] Completed {} episodes with avg. score = {}".format(len(test_scores), np.mean(test_scores)))
_ = plot_scores(test_scores)
# Visualize the learned Q-table
plot_q_table(q_agent_new.q_table)
# ### 7. Watch a Smart Agent
state = env.reset()
score = 0
for t in range(200):
action = q_agent_new.act(state, mode='test')
env.render()
state, reward, done, _ = env.step(action)
score += reward
if done:
break
print('Final score:', score)
env.close()
| discretization/Discretization.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Gaussian Mixture Model Sine Curve
#
#
# This example demonstrates the behavior of Gaussian mixture models fit on data
# that was not sampled from a mixture of Gaussian random variables. The dataset
# is formed by 100 points loosely spaced following a noisy sine curve. There is
# therefore no ground truth value for the number of Gaussian components.
#
# The first model is a classical Gaussian Mixture Model with 10 components fit
# with the Expectation-Maximization algorithm.
#
# The second model is a Bayesian Gaussian Mixture Model with a Dirichlet process
# prior fit with variational inference. The low value of the concentration prior
# makes the model favor a lower number of active components. This models
# "decides" to focus its modeling power on the big picture of the structure of
# the dataset: groups of points with alternating directions modeled by
# non-diagonal covariance matrices. Those alternating directions roughly capture
# the alternating nature of the original sine signal.
#
# The third model is also a Bayesian Gaussian mixture model with a Dirichlet
# process prior but this time the value of the concentration prior is higher
# giving the model more liberty to model the fine-grained structure of the data.
# The result is a mixture with a larger number of active components that is
# similar to the first model where we arbitrarily decided to fix the number of
# components to 10.
#
# Which model is the best is a matter of subjective judgement: do we want to
# favor models that only capture the big picture to summarize and explain most of
# the structure of the data while ignoring the details or do we prefer models
# that closely follow the high density regions of the signal?
#
# The last two panels show how we can sample from the last two models. The
# resulting samples distributions do not look exactly like the original data
# distribution. The difference primarily stems from the approximation error we
# made by using a model that assumes that the data was generated by a finite
# number of Gaussian components instead of a continuous noisy sine curve.
#
# +
import itertools
import numpy as np
from scipy import linalg
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import mixture
print(__doc__)
color_iter = itertools.cycle(['navy', 'c', 'cornflowerblue', 'gold',
'darkorange'])
def plot_results(X, Y, means, covariances, index, title):
splot = plt.subplot(5, 1, 1 + index)
for i, (mean, covar, color) in enumerate(zip(
means, covariances, color_iter)):
v, w = linalg.eigh(covar)
v = 2. * np.sqrt(2.) * np.sqrt(v)
u = w[0] / linalg.norm(w[0])
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)
# Plot an ellipse to show the Gaussian component
angle = np.arctan(u[1] / u[0])
angle = 180. * angle / np.pi # convert to degrees
ell = mpl.patches.Ellipse(mean, v[0], v[1], 180. + angle, color=color)
ell.set_clip_box(splot.bbox)
ell.set_alpha(0.5)
splot.add_artist(ell)
plt.xlim(-6., 4. * np.pi - 6.)
plt.ylim(-5., 5.)
plt.title(title)
plt.xticks(())
plt.yticks(())
def plot_samples(X, Y, n_components, index, title):
plt.subplot(5, 1, 4 + index)
for i, color in zip(range(n_components), color_iter):
# as the DP will not use every component it has access to
# unless it needs it, we shouldn't plot the redundant
# components.
if not np.any(Y == i):
continue
plt.scatter(X[Y == i, 0], X[Y == i, 1], .8, color=color)
plt.xlim(-6., 4. * np.pi - 6.)
plt.ylim(-5., 5.)
plt.title(title)
plt.xticks(())
plt.yticks(())
# Parameters
n_samples = 100
# Generate random sample following a sine curve
np.random.seed(0)
X = np.zeros((n_samples, 2))
step = 4. * np.pi / n_samples
for i in range(X.shape[0]):
x = i * step - 6.
X[i, 0] = x + np.random.normal(0, 0.1)
X[i, 1] = 3. * (np.sin(x) + np.random.normal(0, .2))
plt.figure(figsize=(10, 10))
plt.subplots_adjust(bottom=.04, top=0.95, hspace=.2, wspace=.05,
left=.03, right=.97)
# Fit a Gaussian mixture with EM using ten components
gmm = mixture.GaussianMixture(n_components=10, covariance_type='full',
max_iter=100).fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0,
'Expectation-maximization')
dpgmm = mixture.BayesianGaussianMixture(
n_components=10, covariance_type='full', weight_concentration_prior=1e-2,
weight_concentration_prior_type='dirichlet_process',
mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
init_params="random", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 1,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=0.01$.")
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 0,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=0.01$ sampled with $2000$ samples.")
dpgmm = mixture.BayesianGaussianMixture(
n_components=10, covariance_type='full', weight_concentration_prior=1e+2,
weight_concentration_prior_type='dirichlet_process',
mean_precision_prior=1e-2, covariance_prior=1e0 * np.eye(2),
init_params="kmeans", max_iter=100, random_state=2).fit(X)
plot_results(X, dpgmm.predict(X), dpgmm.means_, dpgmm.covariances_, 2,
"Bayesian Gaussian mixture models with a Dirichlet process prior "
r"for $\gamma_0=100$")
X_s, y_s = dpgmm.sample(n_samples=2000)
plot_samples(X_s, y_s, dpgmm.n_components, 1,
"Gaussian mixture with a Dirichlet process prior "
r"for $\gamma_0=100$ sampled with $2000$ samples.")
plt.show()
| sklearn/sklearn learning/demonstration/auto_examples_jupyter/mixture/plot_gmm_sin.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: TensorFlow 2.4 on Python 3.8 & CUDA 11.1
# language: python
# name: python3
# ---
# **12장 – 텐서플로를 사용한 사용자 정의 모델과 훈련**
# _이 노트북은 12장에 있는 모든 샘플 코드와 연습문제 해답을 가지고 있습니다._
# <table align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/rickiepark/handson-ml2/blob/master/12_custom_models_and_training_with_tensorflow.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩에서 실행하기</a>
# </td>
# </table>
# # 설정
# 먼저 몇 개의 모듈을 임포트합니다. 맷플롯립 그래프를 인라인으로 출력하도록 만들고 그림을 저장하는 함수를 준비합니다. 또한 파이썬 버전이 3.5 이상인지 확인합니다(파이썬 2.x에서도 동작하지만 곧 지원이 중단되므로 파이썬 3을 사용하는 것이 좋습니다). 사이킷런 버전이 0.20 이상인지와 텐서플로 버전이 2.0 이상인지 확인합니다.
# +
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# # %tensorflow_version은 코랩 명령입니다.
# %tensorflow_version 2.x
except Exception:
pass
# 이 노트북은 텐서플로 ≥2.4이 필요합니다
# 2.x 버전은 대부분 동일한 결과를 만들지만 몇 가지 버그가 있습니다.
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.4"
# 공통 모듈 임포트
import numpy as np
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
tf.random.set_seed(42)
# 깔끔한 그래프 출력을 위해
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "deep"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# -
# ## 텐서와 연산
# ### 텐서
tf.constant([[1., 2., 3.], [4., 5., 6.]]) # 행렬
tf.constant(42) # 스칼라
t = tf.constant([[1., 2., 3.], [4., 5., 6.]])
t
t.shape
t.dtype
# ### 인덱싱
t[:, 1:]
t[..., 1, tf.newaxis]
# ### 연산
t + 10
tf.square(t)
t @ tf.transpose(t)
# ### `keras.backend` 사용하기
from tensorflow import keras
K = keras.backend
K.square(K.transpose(t)) + 10
# ### 넘파이 변환
a = np.array([2., 4., 5.])
tf.constant(a)
t.numpy()
np.array(t)
tf.square(a)
np.square(t)
# ### 타입 변환
try:
tf.constant(2.0) + tf.constant(40)
except tf.errors.InvalidArgumentError as ex:
print(ex)
try:
tf.constant(2.0) + tf.constant(40., dtype=tf.float64)
except tf.errors.InvalidArgumentError as ex:
print(ex)
t2 = tf.constant(40., dtype=tf.float64)
tf.constant(2.0) + tf.cast(t2, tf.float32)
# ### 문자열
tf.constant(b"hello world")
tf.constant("café")
u = tf.constant([ord(c) for c in "café"])
u
b = tf.strings.unicode_encode(u, "UTF-8")
tf.strings.length(b, unit="UTF8_CHAR")
tf.strings.unicode_decode(b, "UTF-8")
# ### 문자열 배열
p = tf.constant(["Café", "Coffee", "caffè", "咖啡"])
tf.strings.length(p, unit="UTF8_CHAR")
r = tf.strings.unicode_decode(p, "UTF8")
r
print(r)
# ### 래그드 텐서
print(r[1])
print(r[1:3])
r2 = tf.ragged.constant([[65, 66], [], [67]])
print(tf.concat([r, r2], axis=0))
r3 = tf.ragged.constant([[68, 69, 70], [71], [], [72, 73]])
print(tf.concat([r, r3], axis=1))
tf.strings.unicode_encode(r3, "UTF-8")
r.to_tensor()
# ### 희소 텐서
s = tf.SparseTensor(indices=[[0, 1], [1, 0], [2, 3]],
values=[1., 2., 3.],
dense_shape=[3, 4])
print(s)
tf.sparse.to_dense(s)
s2 = s * 2.0
try:
s3 = s + 1.
except TypeError as ex:
print(ex)
s4 = tf.constant([[10., 20.], [30., 40.], [50., 60.], [70., 80.]])
tf.sparse.sparse_dense_matmul(s, s4)
s5 = tf.SparseTensor(indices=[[0, 2], [0, 1]],
values=[1., 2.],
dense_shape=[3, 4])
print(s5)
try:
tf.sparse.to_dense(s5)
except tf.errors.InvalidArgumentError as ex:
print(ex)
s6 = tf.sparse.reorder(s5)
tf.sparse.to_dense(s6)
# ### 집합
set1 = tf.constant([[2, 3, 5, 7], [7, 9, 0, 0]])
set2 = tf.constant([[4, 5, 6], [9, 10, 0]])
tf.sparse.to_dense(tf.sets.union(set1, set2))
tf.sparse.to_dense(tf.sets.difference(set1, set2))
tf.sparse.to_dense(tf.sets.intersection(set1, set2))
# ### 변수
v = tf.Variable([[1., 2., 3.], [4., 5., 6.]])
v.assign(2 * v)
v[0, 1].assign(42)
v[:, 2].assign([0., 1.])
try:
v[1] = [7., 8., 9.]
except TypeError as ex:
print(ex)
v.scatter_nd_update(indices=[[0, 0], [1, 2]],
updates=[100., 200.])
sparse_delta = tf.IndexedSlices(values=[[1., 2., 3.], [4., 5., 6.]],
indices=[1, 0])
v.scatter_update(sparse_delta)
# ### 텐서 배열
array = tf.TensorArray(dtype=tf.float32, size=3)
array = array.write(0, tf.constant([1., 2.]))
array = array.write(1, tf.constant([3., 10.]))
array = array.write(2, tf.constant([5., 7.]))
array.read(1)
array.stack()
mean, variance = tf.nn.moments(array.stack(), axes=0)
mean
variance
# ## 사용자 정의 손실 함수
# 캘리포니아 주택 데이터셋을 로드하여 준비해 보겠습니다. 먼저 이 데이터셋을 로드한 다음 훈련 세트, 검증 세트, 테스트 세트로 나눕니다. 마지막으로 스케일을 변경합니다:
# +
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
housing = fetch_california_housing()
X_train_full, X_test, y_train_full, y_test = train_test_split(
housing.data, housing.target.reshape(-1, 1), random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(
X_train_full, y_train_full, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
X_test_scaled = scaler.transform(X_test)
# -
def huber_fn(y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < 1
squared_loss = tf.square(error) / 2
linear_loss = tf.abs(error) - 0.5
return tf.where(is_small_error, squared_loss, linear_loss)
plt.figure(figsize=(8, 3.5))
z = np.linspace(-4, 4, 200)
plt.plot(z, huber_fn(0, z), "b-", linewidth=2, label="huber($z$)")
plt.plot(z, z**2 / 2, "b:", linewidth=1, label=r"$\frac{1}{2}z^2$")
plt.plot([-1, -1], [0, huber_fn(0., -1.)], "r--")
plt.plot([1, 1], [0, huber_fn(0., 1.)], "r--")
plt.gca().axhline(y=0, color='k')
plt.gca().axvline(x=0, color='k')
plt.axis([-4, 4, 0, 4])
plt.grid(True)
plt.xlabel("$z$")
plt.legend(fontsize=14)
plt.title("Huber loss", fontsize=14)
plt.show()
# +
input_shape = X_train.shape[1:]
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1),
])
# -
model.compile(loss=huber_fn, optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
# ## 사용자 정의 요소를 가진 모델을 저장하고 로드하기
model.save("my_model_with_a_custom_loss.h5")
model = keras.models.load_model("my_model_with_a_custom_loss.h5",
custom_objects={"huber_fn": huber_fn})
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
def create_huber(threshold=1.0):
def huber_fn(y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < threshold
squared_loss = tf.square(error) / 2
linear_loss = threshold * tf.abs(error) - threshold**2 / 2
return tf.where(is_small_error, squared_loss, linear_loss)
return huber_fn
model.compile(loss=create_huber(2.0), optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save("my_model_with_a_custom_loss_threshold_2.h5")
model = keras.models.load_model("my_model_with_a_custom_loss_threshold_2.h5",
custom_objects={"huber_fn": create_huber(2.0)})
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
class HuberLoss(keras.losses.Loss):
def __init__(self, threshold=1.0, **kwargs):
self.threshold = threshold
super().__init__(**kwargs)
def call(self, y_true, y_pred):
error = y_true - y_pred
is_small_error = tf.abs(error) < self.threshold
squared_loss = tf.square(error) / 2
linear_loss = self.threshold * tf.abs(error) - self.threshold**2 / 2
return tf.where(is_small_error, squared_loss, linear_loss)
def get_config(self):
base_config = super().get_config()
return {**base_config, "threshold": self.threshold}
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1),
])
model.compile(loss=HuberLoss(2.), optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save("my_model_with_a_custom_loss_class.h5")
model = keras.models.load_model("my_model_with_a_custom_loss_class.h5",
custom_objects={"HuberLoss": HuberLoss})
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.loss.threshold
# ## 그외 사용자 정의 함수
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
# +
def my_softplus(z): # tf.nn.softplus(z) 값을 반환합니다
return tf.math.log(tf.exp(z) + 1.0)
def my_glorot_initializer(shape, dtype=tf.float32):
stddev = tf.sqrt(2. / (shape[0] + shape[1]))
return tf.random.normal(shape, stddev=stddev, dtype=dtype)
def my_l1_regularizer(weights):
return tf.reduce_sum(tf.abs(0.01 * weights))
def my_positive_weights(weights): # tf.nn.relu(weights) 값을 반환합니다
return tf.where(weights < 0., tf.zeros_like(weights), weights)
# -
layer = keras.layers.Dense(1, activation=my_softplus,
kernel_initializer=my_glorot_initializer,
kernel_regularizer=my_l1_regularizer,
kernel_constraint=my_positive_weights)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1, activation=my_softplus,
kernel_regularizer=my_l1_regularizer,
kernel_constraint=my_positive_weights,
kernel_initializer=my_glorot_initializer),
])
model.compile(loss="mse", optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save("my_model_with_many_custom_parts.h5")
model = keras.models.load_model(
"my_model_with_many_custom_parts.h5",
custom_objects={
"my_l1_regularizer": my_l1_regularizer,
"my_positive_weights": my_positive_weights,
"my_glorot_initializer": my_glorot_initializer,
"my_softplus": my_softplus,
})
class MyL1Regularizer(keras.regularizers.Regularizer):
def __init__(self, factor):
self.factor = factor
def __call__(self, weights):
return tf.reduce_sum(tf.abs(self.factor * weights))
def get_config(self):
return {"factor": self.factor}
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1, activation=my_softplus,
kernel_regularizer=MyL1Regularizer(0.01),
kernel_constraint=my_positive_weights,
kernel_initializer=my_glorot_initializer),
])
model.compile(loss="mse", optimizer="nadam", metrics=["mae"])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.save("my_model_with_many_custom_parts.h5")
model = keras.models.load_model(
"my_model_with_many_custom_parts.h5",
custom_objects={
"MyL1Regularizer": MyL1Regularizer,
"my_positive_weights": my_positive_weights,
"my_glorot_initializer": my_glorot_initializer,
"my_softplus": my_softplus,
})
# ## 사용자 정의 지표
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1),
])
model.compile(loss="mse", optimizer="nadam", metrics=[create_huber(2.0)])
model.fit(X_train_scaled, y_train, epochs=2)
# **노트**: 손실과 지표에 같은 함수를 사용하면 다른 결과가 나올 수 있습니다. 이는 일반적으로 부동 소수점 정밀도 오차 때문입니다. 수학 식이 동일하더라도 연산은 동일한 순서대로 실행되지 않습니다. 이로 인해 작은 차이가 발생합니다. 또한 샘플 가중치를 사용하면 정밀도보다 더 큰 오차가 생깁니다:
#
# * 에포크에서 손실은 지금까지 본 모든 배치 손실의 평균입니다. 각 배치 손실은 가중치가 적용된 샘플 손실의 합을 _배치 크기_ 로 나눈 것입니다(샘플 가중치의 합으로 나눈 것이 아닙니다. 따라서 배치 손실은 손실의 가중 평균이 아닙니다).
# * 에포크에서 지표는 가중치가 적용된 샘플 손실의 합을 지금까지 본 모든 샘플 가중치의 합으로 나눈 것입니다. 다른 말로하면 모든 샘플 손실의 가중 평균입니다. 따라서 위와 같지 않습니다.
#
# 수학적으로 말하면 손실 = 지표 * 샘플 가중치의 평균(더하기 약간의 부동 소수점 정밀도 오차)입니다.
model.compile(loss=create_huber(2.0), optimizer="nadam", metrics=[create_huber(2.0)])
sample_weight = np.random.rand(len(y_train))
history = model.fit(X_train_scaled, y_train, epochs=2, sample_weight=sample_weight)
history.history["loss"][0], history.history["huber_fn"][0] * sample_weight.mean()
# ### 스트리밍 지표
precision = keras.metrics.Precision()
precision([0, 1, 1, 1, 0, 1, 0, 1], [1, 1, 0, 1, 0, 1, 0, 1])
precision([0, 1, 0, 0, 1, 0, 1, 1], [1, 0, 1, 1, 0, 0, 0, 0])
precision.result()
precision.variables
precision.reset_states()
# 스트리밍 지표 만들기:
class HuberMetric(keras.metrics.Metric):
def __init__(self, threshold=1.0, **kwargs):
super().__init__(**kwargs) # 기본 매개변수 처리 (예를 들면, dtype)
self.threshold = threshold
self.huber_fn = create_huber(threshold)
self.total = self.add_weight("total", initializer="zeros")
self.count = self.add_weight("count", initializer="zeros")
def update_state(self, y_true, y_pred, sample_weight=None):
metric = self.huber_fn(y_true, y_pred)
self.total.assign_add(tf.reduce_sum(metric))
self.count.assign_add(tf.cast(tf.size(y_true), tf.float32))
def result(self):
return self.total / self.count
def get_config(self):
base_config = super().get_config()
return {**base_config, "threshold": self.threshold}
# +
m = HuberMetric(2.)
# total = 2 * |10 - 2| - 2²/2 = 14
# count = 1
# result = 14 / 1 = 14
m(tf.constant([[2.]]), tf.constant([[10.]]))
# +
# total = total + (|1 - 0|² / 2) + (2 * |9.25 - 5| - 2² / 2) = 14 + 7 = 21
# count = count + 2 = 3
# result = total / count = 21 / 3 = 7
m(tf.constant([[0.], [5.]]), tf.constant([[1.], [9.25]]))
m.result()
# -
m.variables
m.reset_states()
m.variables
# `HuberMetric` 클래스가 잘 동작하는지 확인해 보죠:
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1),
])
model.compile(loss=create_huber(2.0), optimizer="nadam", metrics=[HuberMetric(2.0)])
model.fit(X_train_scaled.astype(np.float32), y_train.astype(np.float32), epochs=2)
model.save("my_model_with_a_custom_metric.h5")
model = keras.models.load_model("my_model_with_a_custom_metric.h5",
custom_objects={"huber_fn": create_huber(2.0),
"HuberMetric": HuberMetric})
model.fit(X_train_scaled.astype(np.float32), y_train.astype(np.float32), epochs=2)
# **경고**: 텐서플로 2.2에서 tf.keras가 `model.metrics`의 0번째 위치에 지표를 추가합니다([텐서플로 이슈 #38150](https://github.com/tensorflow/tensorflow/issues/38150) 참조). 따라서 `HuberMetric`에 접근하려면 `model.metrics[0]` 대신 `model.metrics[-1]`를 사용해야 합니다.
model.metrics[-1].threshold
# 잘 동작하는군요! 다음처럼 더 간단하게 클래스를 만들 수 있습니다:
class HuberMetric(keras.metrics.Mean):
def __init__(self, threshold=1.0, name='HuberMetric', dtype=None):
self.threshold = threshold
self.huber_fn = create_huber(threshold)
super().__init__(name=name, dtype=dtype)
def update_state(self, y_true, y_pred, sample_weight=None):
metric = self.huber_fn(y_true, y_pred)
super(HuberMetric, self).update_state(metric, sample_weight)
def get_config(self):
base_config = super().get_config()
return {**base_config, "threshold": self.threshold}
# 이 클래스는 크기를 잘 처리하고 샘플 가중치도 지원합니다.
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="selu", kernel_initializer="lecun_normal",
input_shape=input_shape),
keras.layers.Dense(1),
])
model.compile(loss=keras.losses.Huber(2.0), optimizer="nadam", weighted_metrics=[HuberMetric(2.0)])
sample_weight = np.random.rand(len(y_train))
history = model.fit(X_train_scaled.astype(np.float32), y_train.astype(np.float32),
epochs=2, sample_weight=sample_weight)
history.history["loss"][0], history.history["HuberMetric"][0] * sample_weight.mean()
model.save("my_model_with_a_custom_metric_v2.h5")
model = keras.models.load_model("my_model_with_a_custom_metric_v2.h5",
custom_objects={"HuberMetric": HuberMetric})
model.fit(X_train_scaled.astype(np.float32), y_train.astype(np.float32), epochs=2)
model.metrics[-1].threshold
# ## 사용자 정의 층
exponential_layer = keras.layers.Lambda(lambda x: tf.exp(x))
exponential_layer([-1., 0., 1.])
# 회귀 모델이 예측할 값이 양수이고 스케일이 매우 다른 경우 (예를 들어, 0.001, 10., 10000) 출력층에 지수 함수를 추가하면 유용할 수 있습니다:
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu", input_shape=input_shape),
keras.layers.Dense(1),
exponential_layer
])
model.compile(loss="mse", optimizer="sgd")
model.fit(X_train_scaled, y_train, epochs=5,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
class MyDense(keras.layers.Layer):
def __init__(self, units, activation=None, **kwargs):
super().__init__(**kwargs)
self.units = units
self.activation = keras.activations.get(activation)
def build(self, batch_input_shape):
self.kernel = self.add_weight(
name="kernel", shape=[batch_input_shape[-1], self.units],
initializer="glorot_normal")
self.bias = self.add_weight(
name="bias", shape=[self.units], initializer="zeros")
super().build(batch_input_shape) # must be at the end
def call(self, X):
return self.activation(X @ self.kernel + self.bias)
def compute_output_shape(self, batch_input_shape):
return tf.TensorShape(batch_input_shape.as_list()[:-1] + [self.units])
def get_config(self):
base_config = super().get_config()
return {**base_config, "units": self.units,
"activation": keras.activations.serialize(self.activation)}
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
MyDense(30, activation="relu", input_shape=input_shape),
MyDense(1)
])
model.compile(loss="mse", optimizer="nadam")
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
model.save("my_model_with_a_custom_layer.h5")
model = keras.models.load_model("my_model_with_a_custom_layer.h5",
custom_objects={"MyDense": MyDense})
class MyMultiLayer(keras.layers.Layer):
def call(self, X):
X1, X2 = X
print("X1.shape: ", X1.shape ," X2.shape: ", X2.shape) # 사용자 정의 층 디버깅
return X1 + X2, X1 * X2
def compute_output_shape(self, batch_input_shape):
batch_input_shape1, batch_input_shape2 = batch_input_shape
return [batch_input_shape1, batch_input_shape2]
# 사용자 정의 층은 다음처럼 함수형 API를 사용해 호출할 수 있습니다:
inputs1 = keras.layers.Input(shape=[2])
inputs2 = keras.layers.Input(shape=[2])
outputs1, outputs2 = MyMultiLayer()((inputs1, inputs2))
# `call()` 메서드는 심볼릭 입력을 받습니다. 이 입력의 크기는 부분적으로만 지정되어 있습니다(이 시점에서는 배치 크기를 모릅니다. 그래서 첫 번째 차원이 None입니다):
#
# 사용자 층에 실제 데이터를 전달할 수도 있습니다. 이를 테스트하기 위해 각 데이터셋의 입력을 각각 네 개의 특성을 가진 두 부분으로 나누겠습니다:
# +
def split_data(data):
columns_count = data.shape[-1]
half = columns_count // 2
return data[:, :half], data[:, half:]
X_train_scaled_A, X_train_scaled_B = split_data(X_train_scaled)
X_valid_scaled_A, X_valid_scaled_B = split_data(X_valid_scaled)
X_test_scaled_A, X_test_scaled_B = split_data(X_test_scaled)
# 분할된 데이터 크기 출력
X_train_scaled_A.shape, X_train_scaled_B.shape
# -
# 크기가 완전하게 지정된 것을 볼 수 있습니다:
outputs1, outputs2 = MyMultiLayer()((X_train_scaled_A, X_train_scaled_B))
# 함수형 API를 사용해 완전한 모델을 만들어 보겠습니다(이 모델은 간단한 예제이므로 놀라운 성능을 기대하지 마세요):
# +
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
input_A = keras.layers.Input(shape=X_train_scaled_A.shape[-1])
input_B = keras.layers.Input(shape=X_train_scaled_B.shape[-1])
hidden_A, hidden_B = MyMultiLayer()((input_A, input_B))
hidden_A = keras.layers.Dense(30, activation='selu')(hidden_A)
hidden_B = keras.layers.Dense(30, activation='selu')(hidden_B)
concat = keras.layers.Concatenate()((hidden_A, hidden_B))
output = keras.layers.Dense(1)(concat)
model = keras.models.Model(inputs=[input_A, input_B], outputs=[output])
# -
model.compile(loss='mse', optimizer='nadam')
model.fit((X_train_scaled_A, X_train_scaled_B), y_train, epochs=2,
validation_data=((X_valid_scaled_A, X_valid_scaled_B), y_valid))
# 훈련과 테스트에서 다르게 동작하는 층을 만들어 보죠:
class AddGaussianNoise(keras.layers.Layer):
def __init__(self, stddev, **kwargs):
super().__init__(**kwargs)
self.stddev = stddev
def call(self, X, training=None):
if training:
noise = tf.random.normal(tf.shape(X), stddev=self.stddev)
return X + noise
else:
return X
def compute_output_shape(self, batch_input_shape):
return batch_input_shape
# 다음은 사용자 정의 층을 사용하는 간단한 모델입니다:
# +
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
AddGaussianNoise(stddev=1.0),
keras.layers.Dense(30, activation="selu"),
keras.layers.Dense(1)
])
# -
model.compile(loss="mse", optimizer="nadam")
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
# ## 사용자 정의 모델
X_new_scaled = X_test_scaled
class ResidualBlock(keras.layers.Layer):
def __init__(self, n_layers, n_neurons, **kwargs):
super().__init__(**kwargs)
self.hidden = [keras.layers.Dense(n_neurons, activation="elu",
kernel_initializer="he_normal")
for _ in range(n_layers)]
def call(self, inputs):
Z = inputs
for layer in self.hidden:
Z = layer(Z)
return inputs + Z
class ResidualRegressor(keras.models.Model):
def __init__(self, output_dim, **kwargs):
super().__init__(**kwargs)
self.hidden1 = keras.layers.Dense(30, activation="elu",
kernel_initializer="he_normal")
self.block1 = ResidualBlock(2, 30)
self.block2 = ResidualBlock(2, 30)
self.out = keras.layers.Dense(output_dim)
def call(self, inputs):
Z = self.hidden1(inputs)
for _ in range(1 + 3):
Z = self.block1(Z)
Z = self.block2(Z)
return self.out(Z)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = ResidualRegressor(1)
model.compile(loss="mse", optimizer="nadam")
history = model.fit(X_train_scaled, y_train, epochs=5)
score = model.evaluate(X_test_scaled, y_test)
y_pred = model.predict(X_new_scaled)
model.save("my_custom_model.ckpt")
model = keras.models.load_model("my_custom_model.ckpt")
history = model.fit(X_train_scaled, y_train, epochs=5)
# 대신 시퀀셜 API를 사용하는 모델을 정의할 수 있습니다:
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
block1 = ResidualBlock(2, 30)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="elu", kernel_initializer="he_normal"),
block1, block1, block1, block1,
ResidualBlock(2, 30),
keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer="nadam")
history = model.fit(X_train_scaled, y_train, epochs=5)
score = model.evaluate(X_test_scaled, y_test)
y_pred = model.predict(X_new_scaled)
# ## 모델 구성 요소에 기반한 손실과 지표
# **노트**: TF 2.2에 있는 이슈([#46858](https://github.com/tensorflow/tensorflow/issues/46858)) 때문에 `build()` 메서드와 함께 `add_loss()`를 사용할 수 없습니다. 따라서 다음 코드는 책과 다릅니다. `build()` 메서드 대신 생성자에 `reconstruct` 층을 만듭니다. 이 때문에 이 층의 유닛 개수를 하드코딩해야 합니다(또는 생성자 매개변수로 전달해야 합니다).
# +
class ReconstructingRegressor(keras.models.Model):
def __init__(self, output_dim, **kwargs):
super().__init__(**kwargs)
self.hidden = [keras.layers.Dense(30, activation="selu",
kernel_initializer="lecun_normal")
for _ in range(5)]
self.out = keras.layers.Dense(output_dim)
self.reconstruct = keras.layers.Dense(8) # TF 이슈 #46858에 대한 대책
self.reconstruction_mean = keras.metrics.Mean(name="reconstruction_error")
# TF 이슈 #46858 때문에 주석 처리
# def build(self, batch_input_shape):
# n_inputs = batch_input_shape[-1]
# self.reconstruct = keras.layers.Dense(n_inputs, name='recon')
# super().build(batch_input_shape)
def call(self, inputs, training=None):
Z = inputs
for layer in self.hidden:
Z = layer(Z)
reconstruction = self.reconstruct(Z)
self.recon_loss = 0.05 * tf.reduce_mean(tf.square(reconstruction - inputs))
if training:
result = self.reconstruction_mean(recon_loss)
self.add_metric(result)
return self.out(Z)
def train_step(self, data):
x, y = data
with tf.GradientTape() as tape:
y_pred = self(x)
loss = self.compiled_loss(y, y_pred, regularization_losses=[self.recon_loss])
gradients = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
return {m.name: m.result() for m in self.metrics}
# -
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = ReconstructingRegressor(1)
model.compile(loss="mse", optimizer="nadam")
history = model.fit(X_train_scaled, y_train, epochs=2)
y_pred = model.predict(X_test_scaled)
# ## 자동 미분을 사용하여 그레이디언트 계산하기
def f(w1, w2):
return 3 * w1 ** 2 + 2 * w1 * w2
w1, w2 = 5, 3
eps = 1e-6
(f(w1 + eps, w2) - f(w1, w2)) / eps
(f(w1, w2 + eps) - f(w1, w2)) / eps
# +
w1, w2 = tf.Variable(5.), tf.Variable(3.)
with tf.GradientTape() as tape:
z = f(w1, w2)
gradients = tape.gradient(z, [w1, w2])
# -
gradients
# +
with tf.GradientTape() as tape:
z = f(w1, w2)
dz_dw1 = tape.gradient(z, w1)
try:
dz_dw2 = tape.gradient(z, w2)
except RuntimeError as ex:
print(ex)
# +
with tf.GradientTape(persistent=True) as tape:
z = f(w1, w2)
dz_dw1 = tape.gradient(z, w1)
dz_dw2 = tape.gradient(z, w2) # works now!
del tape
# -
dz_dw1, dz_dw2
# +
c1, c2 = tf.constant(5.), tf.constant(3.)
with tf.GradientTape() as tape:
z = f(c1, c2)
gradients = tape.gradient(z, [c1, c2])
# -
gradients
# +
with tf.GradientTape() as tape:
tape.watch(c1)
tape.watch(c2)
z = f(c1, c2)
gradients = tape.gradient(z, [c1, c2])
# -
gradients
# +
with tf.GradientTape() as tape:
z1 = f(w1, w2 + 2.)
z2 = f(w1, w2 + 5.)
z3 = f(w1, w2 + 7.)
tape.gradient([z1, z2, z3], [w1, w2])
# +
with tf.GradientTape(persistent=True) as tape:
z1 = f(w1, w2 + 2.)
z2 = f(w1, w2 + 5.)
z3 = f(w1, w2 + 7.)
tf.reduce_sum(tf.stack([tape.gradient(z, [w1, w2]) for z in (z1, z2, z3)]), axis=0)
del tape
# -
with tf.GradientTape(persistent=True) as hessian_tape:
with tf.GradientTape() as jacobian_tape:
z = f(w1, w2)
jacobians = jacobian_tape.gradient(z, [w1, w2])
hessians = [hessian_tape.gradient(jacobian, [w1, w2])
for jacobian in jacobians]
del hessian_tape
jacobians
hessians
# +
def f(w1, w2):
return 3 * w1 ** 2 + tf.stop_gradient(2 * w1 * w2)
with tf.GradientTape() as tape:
z = f(w1, w2)
tape.gradient(z, [w1, w2])
# +
x = tf.Variable(100.)
with tf.GradientTape() as tape:
z = my_softplus(x)
tape.gradient(z, [x])
# -
tf.math.log(tf.exp(tf.constant(30., dtype=tf.float32)) + 1.)
# +
x = tf.Variable([100.])
with tf.GradientTape() as tape:
z = my_softplus(x)
tape.gradient(z, [x])
# -
@tf.custom_gradient
def my_better_softplus(z):
exp = tf.exp(z)
def my_softplus_gradients(grad):
return grad / (1 + 1 / exp)
return tf.math.log(exp + 1), my_softplus_gradients
def my_better_softplus(z):
return tf.where(z > 30., z, tf.math.log(tf.exp(z) + 1.))
# +
x = tf.Variable([1000.])
with tf.GradientTape() as tape:
z = my_better_softplus(x)
z, tape.gradient(z, [x])
# -
# # 사용자 정의 훈련 반복
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
l2_reg = keras.regularizers.l2(0.05)
model = keras.models.Sequential([
keras.layers.Dense(30, activation="elu", kernel_initializer="he_normal",
kernel_regularizer=l2_reg),
keras.layers.Dense(1, kernel_regularizer=l2_reg)
])
def random_batch(X, y, batch_size=32):
idx = np.random.randint(len(X), size=batch_size)
return X[idx], y[idx]
def print_status_bar(iteration, total, loss, metrics=None):
metrics = " - ".join(["{}: {:.4f}".format(m.name, m.result())
for m in [loss] + (metrics or [])])
end = "" if iteration < total else "\n"
print("\r{}/{} - ".format(iteration, total) + metrics,
end=end)
# +
import time
mean_loss = keras.metrics.Mean(name="loss")
mean_square = keras.metrics.Mean(name="mean_square")
for i in range(1, 50 + 1):
loss = 1 / i
mean_loss(loss)
mean_square(i ** 2)
print_status_bar(i, 50, mean_loss, [mean_square])
time.sleep(0.05)
# -
# A fancier version with a progress bar:
def progress_bar(iteration, total, size=30):
running = iteration < total
c = ">" if running else "="
p = (size - 1) * iteration // total
fmt = "{{:-{}d}}/{{}} [{{}}]".format(len(str(total)))
params = [iteration, total, "=" * p + c + "." * (size - p - 1)]
return fmt.format(*params)
progress_bar(3500, 10000, size=6)
def print_status_bar(iteration, total, loss, metrics=None, size=30):
metrics = " - ".join(["{}: {:.4f}".format(m.name, m.result())
for m in [loss] + (metrics or [])])
end = "" if iteration < total else "\n"
print("\r{} - {}".format(progress_bar(iteration, total), metrics), end=end)
mean_loss = keras.metrics.Mean(name="loss")
mean_square = keras.metrics.Mean(name="mean_square")
for i in range(1, 50 + 1):
loss = 1 / i
mean_loss(loss)
mean_square(i ** 2)
print_status_bar(i, 50, mean_loss, [mean_square])
time.sleep(0.05)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
n_epochs = 5
batch_size = 32
n_steps = len(X_train) // batch_size
optimizer = keras.optimizers.Nadam(lr=0.01)
loss_fn = keras.losses.mean_squared_error
mean_loss = keras.metrics.Mean()
metrics = [keras.metrics.MeanAbsoluteError()]
for epoch in range(1, n_epochs + 1):
print("Epoch {}/{}".format(epoch, n_epochs))
for step in range(1, n_steps + 1):
X_batch, y_batch = random_batch(X_train_scaled, y_train)
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
for variable in model.variables:
if variable.constraint is not None:
variable.assign(variable.constraint(variable))
mean_loss(loss)
for metric in metrics:
metric(y_batch, y_pred)
print_status_bar(step * batch_size, len(y_train), mean_loss, metrics)
print_status_bar(len(y_train), len(y_train), mean_loss, metrics)
for metric in [mean_loss] + metrics:
metric.reset_states()
try:
from tqdm.notebook import trange
from collections import OrderedDict
with trange(1, n_epochs + 1, desc="All epochs") as epochs:
for epoch in epochs:
with trange(1, n_steps + 1, desc="Epoch {}/{}".format(epoch, n_epochs)) as steps:
for step in steps:
X_batch, y_batch = random_batch(X_train_scaled, y_train)
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
for variable in model.variables:
if variable.constraint is not None:
variable.assign(variable.constraint(variable))
status = OrderedDict()
mean_loss(loss)
status["loss"] = mean_loss.result().numpy()
for metric in metrics:
metric(y_batch, y_pred)
status[metric.name] = metric.result().numpy()
steps.set_postfix(status)
for metric in [mean_loss] + metrics:
metric.reset_states()
except ImportError as ex:
print("To run this cell, please install tqdm, ipywidgets and restart Jupyter")
# ## 텐서플로 함수
def cube(x):
return x ** 3
cube(2)
cube(tf.constant(2.0))
tf_cube = tf.function(cube)
tf_cube
tf_cube(2)
tf_cube(tf.constant(2.0))
# ### TF 함수와 콘크리트 함수
concrete_function = tf_cube.get_concrete_function(tf.constant(2.0))
concrete_function.graph
concrete_function(tf.constant(2.0))
concrete_function is tf_cube.get_concrete_function(tf.constant(2.0))
# ### 함수 정의와 그래프
concrete_function.graph
ops = concrete_function.graph.get_operations()
ops
pow_op = ops[2]
list(pow_op.inputs)
pow_op.outputs
concrete_function.graph.get_operation_by_name('x')
concrete_function.graph.get_tensor_by_name('Identity:0')
concrete_function.function_def.signature
# ### TF 함수가 계산 그래프를 추출하기 위해 파이썬 함수를 트레이싱하는 방법
@tf.function
def tf_cube(x):
print("print:", x)
return x ** 3
result = tf_cube(tf.constant(2.0))
result
result = tf_cube(2)
result = tf_cube(3)
result = tf_cube(tf.constant([[1., 2.]])) # New shape: trace!
result = tf_cube(tf.constant([[3., 4.], [5., 6.]])) # New shape: trace!
result = tf_cube(tf.constant([[7., 8.], [9., 10.], [11., 12.]])) # New shape: trace!
# 특정 입력 시그니처를 지정하는 것도 가능합니다:
@tf.function(input_signature=[tf.TensorSpec([None, 28, 28], tf.float32)])
def shrink(images):
print("트레이싱", images)
return images[:, fd00:c2b6:b24b:be67:2827:688d:e6a1:6a3b, ::2] # 행과 열의 절반을 버립니다
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
img_batch_1 = tf.random.uniform(shape=[100, 28, 28])
img_batch_2 = tf.random.uniform(shape=[50, 28, 28])
preprocessed_images = shrink(img_batch_1) # 함수 트레이싱
preprocessed_images = shrink(img_batch_2) # 동일한 콘크리트 함수 재사용
img_batch_3 = tf.random.uniform(shape=[2, 2, 2])
try:
preprocessed_images = shrink(img_batch_3) # 다른 타입이나 크기 거부
except ValueError as ex:
print(ex)
# ### 오토그래프를 사용해 제어 흐름 나타내기
# `range()`를 사용한 정적인 `for` 반복:
@tf.function
def add_10(x):
for i in range(10):
x += 1
return x
add_10(tf.constant(5))
add_10.get_concrete_function(tf.constant(5)).graph.get_operations()
# `tf.while_loop()`를 사용한 동적인 반복:
@tf.function
def add_10(x):
condition = lambda i, x: tf.less(i, 10)
body = lambda i, x: (tf.add(i, 1), tf.add(x, 1))
final_i, final_x = tf.while_loop(condition, body, [tf.constant(0), x])
return final_x
add_10(tf.constant(5))
add_10.get_concrete_function(tf.constant(5)).graph.get_operations()
# (오토그래프에 의한) `tf.range()`를 사용한 동적인 `for` 반복:
@tf.function
def add_10(x):
for i in tf.range(10):
x = x + 1
return x
add_10.get_concrete_function(tf.constant(0)).graph.get_operations()
# ### TF 함수에서 변수와 다른 자원 다루기
# +
counter = tf.Variable(0)
@tf.function
def increment(counter, c=1):
return counter.assign_add(c)
# -
increment(counter)
increment(counter)
function_def = increment.get_concrete_function(counter).function_def
function_def.signature.input_arg[0]
# +
counter = tf.Variable(0)
@tf.function
def increment(c=1):
return counter.assign_add(c)
# -
increment()
increment()
function_def = increment.get_concrete_function().function_def
function_def.signature.input_arg[0]
class Counter:
def __init__(self):
self.counter = tf.Variable(0)
@tf.function
def increment(self, c=1):
return self.counter.assign_add(c)
c = Counter()
c.increment()
c.increment()
# +
@tf.function
def add_10(x):
for i in tf.range(10):
x += 1
return x
print(tf.autograph.to_code(add_10.python_function))
# -
def display_tf_code(func):
from IPython.display import display, Markdown
if hasattr(func, "python_function"):
func = func.python_function
code = tf.autograph.to_code(func)
display(Markdown('```python\n{}\n```'.format(code)))
display_tf_code(add_10)
# ## tf.keras와 TF 함수를 함께 사용하거나 사용하지 않기
# 기본적으로 tf.keras는 자동으로 사용자 정의 코드를 TF 함수로 변환하기 때문에 `tf.function()`을 사용할 필요가 없습니다:
# 사용자 손실 함수
def my_mse(y_true, y_pred):
print("my_mse() 손실 트레이싱")
return tf.reduce_mean(tf.square(y_pred - y_true))
# 사용자 지표 함수
def my_mae(y_true, y_pred):
print("my_mae() 지표 트레이싱")
return tf.reduce_mean(tf.abs(y_pred - y_true))
# 사용자 정의 층
class MyDense(keras.layers.Layer):
def __init__(self, units, activation=None, **kwargs):
super().__init__(**kwargs)
self.units = units
self.activation = keras.activations.get(activation)
def build(self, input_shape):
self.kernel = self.add_weight(name='kernel',
shape=(input_shape[1], self.units),
initializer='uniform',
trainable=True)
self.biases = self.add_weight(name='bias',
shape=(self.units,),
initializer='zeros',
trainable=True)
super().build(input_shape)
def call(self, X):
print("MyDense.call() 트레이싱")
return self.activation(X @ self.kernel + self.biases)
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
# +
# 사용자 정의 모델
class MyModel(keras.models.Model):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.hidden1 = MyDense(30, activation="relu")
self.hidden2 = MyDense(30, activation="relu")
self.output_ = MyDense(1)
def call(self, input):
print("MyModel.call() 트레이싱")
hidden1 = self.hidden1(input)
hidden2 = self.hidden2(hidden1)
concat = keras.layers.concatenate([input, hidden2])
output = self.output_(concat)
return output
model = MyModel()
# -
model.compile(loss=my_mse, optimizer="nadam", metrics=[my_mae])
model.fit(X_train_scaled, y_train, epochs=2,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
# `dynamic=True`로 모델을 만들어 이 기능을 끌 수 있습니다(또는 모델의 생성자에서 `super().__init__(dynamic=True, **kwargs)`를 호출합니다):
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = MyModel(dynamic=True)
model.compile(loss=my_mse, optimizer="nadam", metrics=[my_mae])
# 사용자 정의 코드는 반복마다 호출됩니다. 너무 많이 출력되는 것을 피하기 위해 작은 데이터셋으로 훈련, 검증, 평가해 보겠습니다:
model.fit(X_train_scaled[:64], y_train[:64], epochs=1,
validation_data=(X_valid_scaled[:64], y_valid[:64]), verbose=0)
model.evaluate(X_test_scaled[:64], y_test[:64], verbose=0)
# 또는 모델을 컴파일할 때 `run_eagerly=True`를 지정합니다:
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = MyModel()
model.compile(loss=my_mse, optimizer="nadam", metrics=[my_mae], run_eagerly=True)
model.fit(X_train_scaled[:64], y_train[:64], epochs=1,
validation_data=(X_valid_scaled[:64], y_valid[:64]), verbose=0)
model.evaluate(X_test_scaled[:64], y_test[:64], verbose=0)
# ## 사용자 정의 옵티마이저
# 사용자 정의 옵티마이저를 정의하는 것은 일반적이지 않습니다. 하지만 어쩔 수 없이 만들어야 하는 상황이라면 다음 예를 참고하세요:
class MyMomentumOptimizer(keras.optimizers.Optimizer):
def __init__(self, learning_rate=0.001, momentum=0.9, name="MyMomentumOptimizer", **kwargs):
"""super().__init__()를 호출하고 _set_hyper()를 사용해 하이퍼파라미터를 저장합니다"""
super().__init__(name, **kwargs)
self._set_hyper("learning_rate", kwargs.get("lr", learning_rate)) # lr=learning_rate을 처리
self._set_hyper("decay", self._initial_decay) #
self._set_hyper("momentum", momentum)
def _create_slots(self, var_list):
"""모델 파라미터마다 연관된 옵티마이저 변수를 만듭니다.
텐서플로는 이런 옵티마이저 변수를 '슬롯'이라고 부릅니다.
모멘텀 옵티마이저에서는 모델 파라미터마다 하나의 모멘텀 슬롯이 필요합니다.
"""
for var in var_list:
self.add_slot(var, "momentum")
@tf.function
def _resource_apply_dense(self, grad, var):
"""슬롯을 업데이트하고 모델 파라미터에 대한 옵티마이저 스텝을 수행합니다.
"""
var_dtype = var.dtype.base_dtype
lr_t = self._decayed_lr(var_dtype) # 학습률 감쇠 처리
momentum_var = self.get_slot(var, "momentum")
momentum_hyper = self._get_hyper("momentum", var_dtype)
momentum_var.assign(momentum_var * momentum_hyper - (1. - momentum_hyper)* grad)
var.assign_add(momentum_var * lr_t)
def _resource_apply_sparse(self, grad, var):
raise NotImplementedError
def get_config(self):
base_config = super().get_config()
return {
**base_config,
"learning_rate": self._serialize_hyperparameter("learning_rate"),
"decay": self._serialize_hyperparameter("decay"),
"momentum": self._serialize_hyperparameter("momentum"),
}
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([keras.layers.Dense(1, input_shape=[8])])
model.compile(loss="mse", optimizer=MyMomentumOptimizer())
model.fit(X_train_scaled, y_train, epochs=5)
# # 연습문제
# ## 1. to 11.
# 부록 A 참조.
# # 12. _층 정규화_ 를 수행하는 사용자 정의 층을 구현하세요.
#
# _15장에서 순환 신경망을 사용할 때 이런 종류의 층을 사용합니다._
# ### a.
# _문제: `build()` 메서드에서 두 개의 훈련 가능한 가중치 *α*와 *β*를 정의합니다. 두 가중치 모두 크기가 `input_shape[-1:]`이고 데이터 타입은 `tf.float32`입니다. *α*는 1로 초기화되고 *β*는 0으로 초기화되어야 합니다._
# 솔루션: 아래 참조.
# ### b.
# _문제: `call()` 메서드는 샘플의 특성마다 평균 μ와 표준편차 σ를 계산해야 합니다. 이를 위해 전체 샘플의 평균 μ와 분산 σ<sup>2</sup>을 반환하는 `tf.nn.moments(inputs, axes=-1, keepdims=True)`을 사용할 수 있습니다(분산의 제곱근으로 표준편차를 계산합니다). 그다음 *α*⊗(*X* - μ)/(σ + ε) + *β*를 계산하여 반환합니다. 여기에서 ⊗는 원소별
# 곱셈(`*`)을 나타냅니다. ε은 안전을 위한 항입니다(0으로 나누어지는 것을 막기 위한 작은 상수. 예를 들면 0.001)._
class LayerNormalization(keras.layers.Layer):
def __init__(self, eps=0.001, **kwargs):
super().__init__(**kwargs)
self.eps = eps
def build(self, batch_input_shape):
self.alpha = self.add_weight(
name="alpha", shape=batch_input_shape[-1:],
initializer="ones")
self.beta = self.add_weight(
name="beta", shape=batch_input_shape[-1:],
initializer="zeros")
super().build(batch_input_shape) # 반드시 끝에 와야 합니다
def call(self, X):
mean, variance = tf.nn.moments(X, axes=-1, keepdims=True)
return self.alpha * (X - mean) / (tf.sqrt(variance + self.eps)) + self.beta
def compute_output_shape(self, batch_input_shape):
return batch_input_shape
def get_config(self):
base_config = super().get_config()
return {**base_config, "eps": self.eps}
# _ε_ 하이퍼파라미터(`eps`)는 필수가 아닙니다. 또한 `tf.sqrt(variance) + self.eps` 보다 `tf.sqrt(variance + self.eps)`를 계산하는 것이 좋습니다. sqrt(z)의 도함수는 z=0에서 정의되지 않기 때문에 분산 벡터의 한 원소가 0에 가까우면 훈련이 이리저리 널뜁니다. 제곱근 안에 _ε_를 넣으면 이런 현상을 방지할 수 있습니다.
# ### c.
# _문제: 사용자 정의 층이 `keras.layers.LayerNormalization` 층과 동일한(또는 거의 동일한) 출력을 만드는지 확인하세요._
# 각 클래스의 객체를 만들고 데이터(예를 들면, 훈련 세트)를 적용해 보죠. 차이는 무시할 수 있는 수준입니다.
# +
X = X_train.astype(np.float32)
custom_layer_norm = LayerNormalization()
keras_layer_norm = keras.layers.LayerNormalization()
tf.reduce_mean(keras.losses.mean_absolute_error(
keras_layer_norm(X), custom_layer_norm(X)))
# -
# 네 충분히 가깝네요. 조금 더 확실하게 알파와 베타를 완전히 랜덤하게 지정하고 다시 비교해 보죠:
# +
random_alpha = np.random.rand(X.shape[-1])
random_beta = np.random.rand(X.shape[-1])
custom_layer_norm.set_weights([random_alpha, random_beta])
keras_layer_norm.set_weights([random_alpha, random_beta])
tf.reduce_mean(keras.losses.mean_absolute_error(
keras_layer_norm(X), custom_layer_norm(X)))
# -
# 여전히 무시할 수 있는 수준입니다! 사용자 정의 층이 잘 동작합니다.
# ## 13. 사용자 정의 훈련 반복을 사용해 패션 MNIST 데이터셋으로 모델을 훈련해보세요.
#
# _패션 MNIST 데이터셋은 10장에서 소개했습니다._
# ### a.
# _문제: 에포크, 반복, 평균 훈련 손실, (반복마다 업데이트되는) 에포크의 평균 정확도는 물론 에포크 끝에서 검증 손실과 정확도를 출력하세요._
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full.astype(np.float32) / 255.
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test.astype(np.float32) / 255.
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation="relu"),
keras.layers.Dense(10, activation="softmax"),
])
n_epochs = 5
batch_size = 32
n_steps = len(X_train) // batch_size
optimizer = keras.optimizers.Nadam(lr=0.01)
loss_fn = keras.losses.sparse_categorical_crossentropy
mean_loss = keras.metrics.Mean()
metrics = [keras.metrics.SparseCategoricalAccuracy()]
with trange(1, n_epochs + 1, desc="All epochs") as epochs:
for epoch in epochs:
with trange(1, n_steps + 1, desc="Epoch {}/{}".format(epoch, n_epochs)) as steps:
for step in steps:
X_batch, y_batch = random_batch(X_train, y_train)
with tf.GradientTape() as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
for variable in model.variables:
if variable.constraint is not None:
variable.assign(variable.constraint(variable))
status = OrderedDict()
mean_loss(loss)
status["loss"] = mean_loss.result().numpy()
for metric in metrics:
metric(y_batch, y_pred)
status[metric.name] = metric.result().numpy()
steps.set_postfix(status)
y_pred = model(X_valid)
status["val_loss"] = np.mean(loss_fn(y_valid, y_pred))
status["val_accuracy"] = np.mean(keras.metrics.sparse_categorical_accuracy(
tf.constant(y_valid, dtype=np.float32), y_pred))
steps.set_postfix(status)
for metric in [mean_loss] + metrics:
metric.reset_states()
# ### b.
# _문제: 상위 층과 하위 층에 학습률이 다른 옵티마이저를 따로 사용해보세요._
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
lower_layers = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation="relu"),
])
upper_layers = keras.models.Sequential([
keras.layers.Dense(10, activation="softmax"),
])
model = keras.models.Sequential([
lower_layers, upper_layers
])
lower_optimizer = keras.optimizers.SGD(lr=1e-4)
upper_optimizer = keras.optimizers.Nadam(lr=1e-3)
n_epochs = 5
batch_size = 32
n_steps = len(X_train) // batch_size
loss_fn = keras.losses.sparse_categorical_crossentropy
mean_loss = keras.metrics.Mean()
metrics = [keras.metrics.SparseCategoricalAccuracy()]
with trange(1, n_epochs + 1, desc="All epochs") as epochs:
for epoch in epochs:
with trange(1, n_steps + 1, desc="Epoch {}/{}".format(epoch, n_epochs)) as steps:
for step in steps:
X_batch, y_batch = random_batch(X_train, y_train)
with tf.GradientTape(persistent=True) as tape:
y_pred = model(X_batch)
main_loss = tf.reduce_mean(loss_fn(y_batch, y_pred))
loss = tf.add_n([main_loss] + model.losses)
for layers, optimizer in ((lower_layers, lower_optimizer),
(upper_layers, upper_optimizer)):
gradients = tape.gradient(loss, layers.trainable_variables)
optimizer.apply_gradients(zip(gradients, layers.trainable_variables))
del tape
for variable in model.variables:
if variable.constraint is not None:
variable.assign(variable.constraint(variable))
status = OrderedDict()
mean_loss(loss)
status["loss"] = mean_loss.result().numpy()
for metric in metrics:
metric(y_batch, y_pred)
status[metric.name] = metric.result().numpy()
steps.set_postfix(status)
y_pred = model(X_valid)
status["val_loss"] = np.mean(loss_fn(y_valid, y_pred))
status["val_accuracy"] = np.mean(keras.metrics.sparse_categorical_accuracy(
tf.constant(y_valid, dtype=np.float32), y_pred))
steps.set_postfix(status)
for metric in [mean_loss] + metrics:
metric.reset_states()
| 12_custom_models_and_training_with_tensorflow.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
# %matplotlib inline
import scipy.stats as stats
plt.rcParams.update({'font.size': 22})
plt.rcParams['figure.figsize'] = (12, 5)
# The data for this visualizations project comes from Kaggle https://www.kaggle.com/unsdsn/world-happiness. It features World Happinesss Report 2017 which was released at the United Nations International Day of Happiness on March 20, 2017.
#
# The report mentions *Dystopia*, an imaginary world's least happy country, which was introduced for the purpose of providing a benchmark for comparison.'The Dystopia Residual metric actually is the Dystopia Happiness Score (1.85) + the Residual value or the unexplained value for each country."
happiness = pd.read_csv('C:\Inna\'s files\data\Happiness\Happiness.csv')
happiness.columns
happiness.rename(columns={'Country':'Country'}, inplace = True)
happiness.rename(columns={'Happiness.Rank': 'Happiness Rank'}, inplace = True)
happiness.rename(columns={'Happiness.Score': 'Happiness Score'}, inplace = True)
happiness.rename(columns={'Whisker.high': 'Whisker high'}, inplace = True)
happiness.rename(columns={'Whisker.low': 'Whisker low'}, inplace = True)
happiness.rename(columns={'Economy..GDP.per.Capita.': 'Economy. GDP per Capita.'}, inplace = True)
happiness.rename(columns={'Family': 'Family'}, inplace = True)
happiness.rename(columns={'Health..Life.Expectancy.': 'Health. Life Expectancy'}, inplace = True)
happiness.rename(columns={'Freedom.': 'Freedom'}, inplace = True)
happiness.rename(columns={'Generosity': 'Generosity'}, inplace = True)
happiness.rename(columns={'Trust..Government.Corruption.': 'Trust. Government. Corruption'}, inplace = True)
happiness.rename(columns={'Dystopia.Residual': 'Dystopia Residual'}, inplace = True)
happiness.head()
happiness.describe()
# Which countries are the happiest in the world? The following bar chart shows world's **top twenty** happiest countries.
# +
top_twenty = happiness.loc[:, ['Country', 'Happiness Score']].head(20)
plt.figure(figsize=(12,5))
plt.bar(top_twenty['Country'],top_twenty['Happiness Score'], color=['red', 'orange', 'yellow', 'green', 'blue', 'purple'])
plt.xticks(rotation=90)
plt.title('Top Twenty \nHappiest Countries In The World')
plt.ylabel('Happiness Scores')
plt.show()
# -
# The distribution of the happiness scores is approximately normal. The Shaprio-Wilk test for normality gives us the p-value of approximately 0.052229.
# +
happiness_score = happiness.loc[:, 'Happiness Score']
plt.hist(happiness_score, color='blue')
plt.title('Happiness Scores Distribution')
plt.xlabel('Happiness Scores')
plt.ylabel('Number of Countries')
plt.axvline(happiness_score.mean(), color='r')
plt.show()
print(stats.shapiro(happiness_score))
print('Mean happiness score is {}.'.format(np.mean(happiness_score)))
# -
# Another question to investigate is how different factors are correlated with the final happiness score.
# +
plt.figure(figsize=(15,5))
plt.subplot(131)
economic_factor = happiness.loc[:, ['Happiness Score', 'Economy. GDP per Capita.']]
plt.scatter(x=economic_factor['Happiness Score'], y=economic_factor['Economy. GDP per Capita.'])
plt.title('Happiness and Economy')
plt.ylabel('GDP per Capita')
plt.xlabel('Happiness Score')
plt.subplot(132)
family_factor = happiness.loc[:, ['Happiness Score', 'Family']]
plt.scatter(x=family_factor['Happiness Score'], y=family_factor['Family'])
plt.title('Happiness and Family')
plt.xlabel('Happiness Score')
plt.ylabel('Family Score')
plt.subplot(133)
health_factor=happiness.loc[:, ['Happiness Score','Health. Life Expectancy']]
plt.scatter(x=health_factor['Happiness Score'], y=health_factor['Health. Life Expectancy'])
plt.title('Happiness and Health')
plt.ylabel('Health Score')
plt.xlabel('Happiness Score')
plt.tight_layout()
plt.show()
plt.figure(figsize=(15,5))
plt.subplot(131)
freedom_factor = happiness.loc[:, ['Happiness Score', 'Freedom']]
plt.scatter(x=freedom_factor['Happiness Score'], y=freedom_factor['Freedom'])
plt.title('Happiness and Freedom')
plt.xlabel('Happiness Score')
plt.ylabel('Freedom Score')
plt.subplot(132)
generosity_factor = happiness.loc[:, ['Happiness Score', 'Generosity']]
plt.scatter(x=generosity_factor['Happiness Score'], y=generosity_factor['Generosity'])
plt.title('Happiness and Generosity')
plt.xlabel('Happiness Score')
plt.ylabel('Generosity Score')
plt.subplot(133)
government_factor = happiness.loc[:, ['Happiness Score', 'Trust. Government. Corruption']]
plt.scatter(x=government_factor['Happiness Score'], y=government_factor['Trust. Government. Corruption'])
plt.title('Happiness and Government')
plt.xlabel('Happiness Score')
plt.ylabel('Government Score')
plt.tight_layout()
plt.show()
#lineplot would suggest continuity which I don't want to do
# -
happiness.drop(columns=['Whisker high', 'Whisker low', 'Dystopia Residual', 'Happiness Rank']).corr()
# Economy, health, and family are much stronger correlated with happiness than freedom, generosity, and confidence in the government. Unexpected insight from the data is that generosity does not seem to contribute much to happiness. This could be a further point of investigation.
# Another intersting category to look at is Trust in the Government. Here, we analyze Trust in the Government depending on whether GPD per capita is above the medium.
happiness['Economy'] = np.where (happiness['Economy. GDP per Capita.'] >= 1.064578, True,False)
plt.figure(figsize=(12, 5))
happiness.boxplot(column = 'Trust. Government. Corruption', by = 'Economy')
plt.xlabel('GDP above median')
plt.ylabel('Trust in the Government')
plt.title('Trust in the Govertment \n Grouped by GDP')
plt.suptitle("")
# Not surprisingly, countries with higher GDP tend to have more trust in their government. However, it is worth mentioning that the low GPD category has a few outliers: some countries trust their governments despite their economy is weak.
| Happiness.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import k3d
import numpy as np
N = 100
theta = np.linspace(0, 2.0 * np.pi, N)
phi = np.linspace(0, 2.0 * np.pi, N)
theta, phi = np.meshgrid(theta, phi)
c, a = 2, 1
x = (c + a * np.cos(theta)) * np.cos(phi)
y = (c + a * np.cos(theta)) * np.sin(phi)
z = a * np.sin(theta)
vertices = np.dstack([x, y, z]).astype(np.float32)
indices = (np.stack([
np.arange(N*N) + 0, np.arange(N*N) + N, np.arange(N*N) + N + 1,
np.arange(N*N) + 0, np.arange(N*N) + N + 1, np.arange(N*N) + 1
]).T % (N * N)).astype(np.uint32)
plot = k3d.plot()
plot += k3d.points(vertices, point_size=0.05, shader='3d', color=0)
mesh = k3d.mesh(vertices, indices, flat_shading=False,
attribute=phi,
color_map=k3d.matplotlib_color_maps.twilight)
plot += mesh
plot.display()
# -
mesh.attribute = []
plot.colorbar_object_id = -1
mesh.colors = np.random.randint(0, 0xFFFFFF, N * N).astype(np.uint32)
| examples/mesh_custom.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # GPU-Jupyter
#
# This Jupyterlab Instance is connected to the GPU via CUDA drivers. In this notebook, we test the installation and perform some basic operations on the GPU.
# ## Test GPU connection
#
# #### Using the following command, your GPU type and its NVIDIA-SMI driver version should be listed:
# !nvcc -V
# !nvidia-smi
# #### Now, test if PyTorch can access the GPU via CUDA:
# !pip install torch
import torch
torch.cuda.is_available()
torch.__version__
from __future__ import print_function
import numpy as np
import torch
a = torch.rand(5, 3)
a
# #### Now, test if Tensorflow can access the GPU via CUDA:
# !pip install tensorflow
import tensorflow as tf
tf.test.is_built_with_cuda()
tf.__version__
gpus = tf.config.experimental.list_physical_devices('GPU')
print(f'Num GPUs Available: {len(gpus)}')
for gpu in gpus:
print(f'Name: {gpu.name} Type: {gpu.device_type}')
tf.config.list_physical_devices()
tf.config.get_visible_devices()
# ## Performance test
#
# #### Now we want to know how much faster a typical operation is using GPU. Therefore we do the same operation in numpy, PyTorch and PyTorch with CUDA. The test operation is the calculation of the prediction matrix that is done in a linear regression.
# ### 1) Numpy
x = np.random.rand(10000, 256)
# %%timeit
H = x.dot(np.linalg.inv(x.transpose().dot(x))).dot(x.transpose())
# ### 2) PyTorch
x = torch.rand(10000, 256)
# %%timeit
# Calculate the projection matrix of x on the CPU
H = x.mm( (x.t().mm(x)).inverse() ).mm(x.t())
# ### 3) PyTorch on GPU via CUDA
# let us run this cell only if CUDA is available
# We will use ``torch.device`` objects to move tensors in and out of GPU
if torch.cuda.is_available():
device = torch.device("cuda") # a CUDA device object
x = torch.rand(10000, 256, device=device) # directly create a tensor on GPU
y = x.to(device) # or just use strings ``.to("cuda")``
print(x[0:5, 0:5])
print(y.to("cpu", torch.double)[0:5, 0:5])
# %%timeit
# Calculate the projection matrix of x on the GPU
H = x.mm( (x.t().mm(x)).inverse() ).mm(x.t())
# ### 4) Tensorflow
with tf.device("/cpu:0"):
x = tf.random.uniform(shape=(10000, 256), minval=0, maxval=1)
print(x[0:5, 0:5])
# %%timeit
with tf.device("/cpu:0"):
op = tf.matmul(tf.matmul(x, tf.linalg.inv(tf.matmul(tf.transpose(x), x))), tf.transpose(x))
#tf.print(op)
# ### 5) Tensorflow on GPU via CUDA
with tf.device("/gpu:0"):
x = tf.random.uniform(shape=(10000, 256), minval=0, maxval=1)
print(x[0:5, 0:5])
# %%timeit
with tf.device("/gpu:0"):
op = tf.matmul(tf.matmul(x, tf.linalg.inv(tf.matmul(tf.transpose(x), x))), tf.transpose(x))
#tf.print(op)
| test/gpu.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 머신 러닝 교과서 3판
# # 4장 - 좋은 훈련 데이터셋 만들기 – 데이터 전처리
# **아래 링크를 통해 이 노트북을 주피터 노트북 뷰어(nbviewer.jupyter.org)로 보거나 구글 코랩(colab.research.google.com)에서 실행할 수 있습니다.**
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://nbviewer.jupyter.org/github/rickiepark/python-machine-learning-book-3rd-edition/blob/master/ch04/SequentialFeatureSelector.ipynb"><img src="https://jupyter.org/assets/main-logo.svg" width="28" />주피터 노트북 뷰어로 보기</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/rickiepark/python-machine-learning-book-3rd-edition/blob/master/ch04/SequentialFeatureSelector.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
# </td>
# </table>
# + [markdown] id="8Os-4JDvScgV"
# ## 4.5.4 순차 특성 선택 알고리즘
# + colab={"base_uri": "https://localhost:8080/"} id="1KNgp1IyScgZ" outputId="b9e09add-044a-48e1-c0d7-12040d113b0a"
# 이 노트북은 사이킷런 0.24 이상에서 실행할 수 있습니다.
# 코랩에서 실행할 경우 최신 버전의 사이킷런을 설치하세요.
# !pip install --upgrade scikit-learn
# + [markdown] id="B2ogTR9QScgZ"
# 4.5절에서 사용하는 데이터셋을 로드합니다.
# + id="LKqSVFwhScga"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# + id="l6Z2jGnUScga"
df_wine = pd.read_csv('https://archive.ics.uci.edu/'
'ml/machine-learning-databases/wine/wine.data',
header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue', 'OD280/OD315 of diluted wines',
'Proline']
# + id="-drOG_MMScga"
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test =\
train_test_split(X, y,
test_size=0.3,
random_state=0,
stratify=y)
stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
# + [markdown] id="Gj1VsXpgScga"
# `SequentialFeatureSelector`를 임포트하고 최근접 이웃 분류기 객체를 준비합니다.
# + id="vGEcLkkUScgb"
from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5)
# + [markdown] id="0ghi7Y2DScgb"
# 사용할 모델 객체를 첫 번째 매개변수로 전달합니다. 선택할 특성의 개수는 `n_features_to_select`에서 지정합니다. 기본값은 입력 특성의 절반입니다. 0~1 사이 실수를 지정하면 선택할 특성의 비율로 인식합니다.
#
# `direction` 매개변수로 특성 선택 방향(전진 또는 후진)을 선택합니다. 기본값은 전진을 의미하는 `'forward'`이고 후진을 선택하려면 `'backward'`로 지정합니다.
#
# 이 클래스는 특성을 선택하기 위해 교차 검증을 사용합니다. `cv` 매개변수에서 교차 검증 횟수를 지정할 수 있습니다. 기본값은 5입니다. 회귀 모델일 경우 `KFold`, 분류 모델일 경우 `StratifiedKFold`를 사용하여 폴드를 나눕니다.
#
# 이 클래스는 하나의 특성을 선택할 때마다 현재 남은 특성 개수(m)에 대해 교차 검증을 수행하므로 `m * cv`개의 모델을 만듭니다. 이렇게 단계마다 많은 모델을 만들기 때문에 일반적으로 `RFE`나 `SelectFromModel`보다 느립니다. `n_jobs` 매개변수를 1 이상으로 지정하여 여러 코어를 사용하는 것이 좋습니다.
# + id="SPaLDZt6Scgb"
scores = []
for n_features in range(1, 13):
sfs = SequentialFeatureSelector(knn, n_features_to_select=n_features, n_jobs=-1)
sfs.fit(X_train_std, y_train)
f_mask = sfs.support_
knn.fit(X_train_std[:, f_mask], y_train)
scores.append(knn.score(X_train_std[:, f_mask], y_train))
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="o7y0RoNAScgb" outputId="235b0195-8f90-40cc-a030-474fc22976ba"
plt.plot(range(1, 13), scores, marker='o')
plt.ylim([0.7, 1.02])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.tight_layout()
# plt.savefig('images/04_sfs.png', dpi=300)
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="0Bt-QBgtScgc" outputId="e523911a-cc8e-4d21-de1b-3479213c75c6"
sfs = SequentialFeatureSelector(knn, n_features_to_select=7, n_jobs=-1)
sfs.fit(X_train_std, y_train)
# + colab={"base_uri": "https://localhost:8080/"} id="xHezF2ZrScgd" outputId="a19cdd1c-64d3-43cc-dca6-e90e2eb393d2"
print(sfs.n_features_to_select_)
f_mask = sfs.support_
df_wine.columns[1:][f_mask]
# + colab={"base_uri": "https://localhost:8080/"} id="76DLeStyScgd" outputId="216e01d3-7ea7-470f-865b-ddfeeeafa1d3"
knn.fit(X_train_std[:, f_mask], y_train)
print('훈련 정확도:', knn.score(X_train_std[:, f_mask], y_train))
print('테스트 정확도:', knn.score(X_test_std[:, f_mask], y_test))
| ch04/SequentialFeatureSelector.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Session 5: Generative Networks
# ## Assignment: Generative Adversarial Networks, Variational Autoencoders, and Recurrent Neural Networks
# <p class="lead">
# <a href="https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info">Creative Applications of Deep Learning with Google's Tensorflow</a><br />
# <a href="http://pkmital.com"><NAME></a><br />
# <a href="https://www.kadenze.com">Kadenze, Inc.</a>
# </p>
#
# Continued from [session-5-part-1.ipynb](session-5-part-1.ipynb)...
#
# # Table of Contents
#
# <!-- MarkdownTOC autolink="true" autoanchor="true" bracket="round" -->
# - [Overview](session-5-part-1.ipynb#overview)
# - [Learning Goals](session-5-part-1.ipynb#learning-goals)
# - [Part 1 - Generative Adversarial Networks \(GAN\) / Deep Convolutional GAN \(DCGAN\)](#part-1---generative-adversarial-networks-gan--deep-convolutional-gan-dcgan)
# - [Introduction](session-5-part-1.ipynb#introduction)
# - [Building the Encoder](session-5-part-1.ipynb#building-the-encoder)
# - [Building the Discriminator for the Training Samples](session-5-part-1.ipynb#building-the-discriminator-for-the-training-samples)
# - [Building the Decoder](session-5-part-1.ipynb#building-the-decoder)
# - [Building the Generator](session-5-part-1.ipynb#building-the-generator)
# - [Building the Discriminator for the Generated Samples](session-5-part-1.ipynb#building-the-discriminator-for-the-generated-samples)
# - [GAN Loss Functions](session-5-part-1.ipynb#gan-loss-functions)
# - [Building the Optimizers w/ Regularization](session-5-part-1.ipynb#building-the-optimizers-w-regularization)
# - [Loading a Dataset](session-5-part-1.ipynb#loading-a-dataset)
# - [Training](session-5-part-1.ipynb#training)
# - [Equilibrium](session-5-part-1.ipynb#equilibrium)
# - [Part 2 - Variational Auto-Encoding Generative Adversarial Network \(VAEGAN\)](#part-2---variational-auto-encoding-generative-adversarial-network-vaegan)
# - [Batch Normalization](session-5-part-1.ipynb#batch-normalization)
# - [Building the Encoder](session-5-part-1.ipynb#building-the-encoder-1)
# - [Building the Variational Layer](session-5-part-1.ipynb#building-the-variational-layer)
# - [Building the Decoder](session-5-part-1.ipynb#building-the-decoder-1)
# - [Building VAE/GAN Loss Functions](session-5-part-1.ipynb#building-vaegan-loss-functions)
# - [Creating the Optimizers](session-5-part-1.ipynb#creating-the-optimizers)
# - [Loading the Dataset](session-5-part-1.ipynb#loading-the-dataset)
# - [Training](session-5-part-1.ipynb#training-1)
# - [Part 3 - Latent-Space Arithmetic](session-5-part-1.ipynb#part-3---latent-space-arithmetic)
# - [Loading the Pre-Trained Model](session-5-part-1.ipynb#loading-the-pre-trained-model)
# - [Exploring the Celeb Net Attributes](session-5-part-1.ipynb#exploring-the-celeb-net-attributes)
# - [Find the Latent Encoding for an Attribute](session-5-part-1.ipynb#find-the-latent-encoding-for-an-attribute)
# - [Latent Feature Arithmetic](session-5-part-1.ipynb#latent-feature-arithmetic)
# - [Extensions](session-5-part-1.ipynb#extensions)
# - [Part 4 - Character-Level Language Model](session-5-part-2.ipynb#part-4---character-level-language-model)
# - [Part 5 - Pretrained Char-RNN of Donald Trump](session-5-part-2.ipynb#part-5---pretrained-char-rnn-of-donald-trump)
# - [Getting the Trump Data](session-5-part-2.ipynb#getting-the-trump-data)
# - [Basic Text Analysis](session-5-part-2.ipynb#basic-text-analysis)
# - [Loading the Pre-trained Trump Model](session-5-part-2.ipynb#loading-the-pre-trained-trump-model)
# - [Inference: Keeping Track of the State](session-5-part-2.ipynb#inference-keeping-track-of-the-state)
# - [Probabilistic Sampling](session-5-part-2.ipynb#probabilistic-sampling)
# - [Inference: Temperature](session-5-part-2.ipynb#inference-temperature)
# - [Inference: Priming](session-5-part-2.ipynb#inference-priming)
# - [Assignment Submission](session-5-part-2.ipynb#assignment-submission)
#
# <!-- /MarkdownTOC -->
#
# +
# First check the Python version
import sys
if sys.version_info < (3,4):
print('You are running an older version of Python!\n\n',
'You should consider updating to Python 3.4.0 or',
'higher as the libraries built for this course',
'have only been tested in Python 3.4 and higher.\n')
print('Try installing the Python 3.5 version of anaconda'
'and then restart `jupyter notebook`:\n',
'https://www.continuum.io/downloads\n\n')
# Now get necessary libraries
try:
import os
import numpy as np
import matplotlib.pyplot as plt
from skimage.transform import resize
from skimage import data
from scipy.misc import imresize
from scipy.ndimage.filters import gaussian_filter
import IPython.display as ipyd
import tensorflow as tf
from libs import utils, gif, datasets, dataset_utils, nb_utils
except ImportError as e:
print("Make sure you have started notebook in the same directory",
"as the provided zip file which includes the 'libs' folder",
"and the file 'utils.py' inside of it. You will NOT be able",
"to complete this assignment unless you restart jupyter",
"notebook inside the directory created by extracting",
"the zip file or cloning the github repo.")
print(e)
# We'll tell matplotlib to inline any drawn figures like so:
# %matplotlib inline
plt.style.use('ggplot')
# -
# Bit of formatting because I don't like the default inline code style:
from IPython.core.display import HTML
HTML("""<style> .rendered_html code {
padding: 2px 4px;
color: #c7254e;
background-color: #f9f2f4;
border-radius: 4px;
} </style>""")
# <style> .rendered_html code {
# padding: 2px 4px;
# color: #c7254e;
# background-color: #f9f2f4;
# border-radius: 4px;
# } </style>
#
#
#
# <a name="part-4---character-level-language-model"></a>
# # Part 4 - Character-Level Language Model
#
# We'll now continue onto the second half of the homework and explore recurrent neural networks. We saw one potential application of a recurrent neural network which learns letter by letter the content of a text file. We were then able to synthesize from the model to produce new phrases. Let's try to build one. Replace the code below with something that loads your own text file or one from the internet. Be creative with this!
#
# <h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
import tensorflow as tf
from six.moves import urllib
script = 'http://www.awesomefilm.com/script/biglebowski.txt'
txts = []
f, _ = urllib.request.urlretrieve(script, script.split('/')[-1])
with open(f, 'r') as fp:
txt = fp.read()
# Let's take a look at the first part of this:
txt[:100]
# We'll just clean up the text a little. This isn't necessary, but can help the training along a little. In the example text I provided, there is a lot of white space (those \t's are tabs). I'll remove them. There are also repetitions of \n, new lines, which are not necessary. The code below will remove the tabs, ending whitespace, and any repeating newlines. Replace this with any preprocessing that makes sense for your dataset. Try to boil it down to just the possible letters for what you want to learn/synthesize while retaining any meaningful patterns:
txt = "\n".join([txt_i.strip()
for txt_i in txt.replace('\t', '').split('\n')
if len(txt_i)])
# Now we can see how much text we have:
len(txt)
# In general, we'll want as much text as possible. But I'm including this just as a minimal example so you can explore your own. Try making a text file and seeing the size of it. You'll want about 1 MB at least.
#
# Let's now take a look at the different characters we have in our file:
vocab = list(set(txt))
vocab.sort()
print(len(vocab))
print(vocab)
# And then create a mapping which can take us from the letter to an integer look up table of that letter (and vice-versa). To do this, we'll use an `OrderedDict` from the `collections` library. In Python 3.6, this is the default behavior of dict, but in earlier versions of Python, we'll need to be explicit by using OrderedDict.
# +
from collections import OrderedDict
encoder = OrderedDict(zip(vocab, range(len(vocab))))
decoder = OrderedDict(zip(range(len(vocab)), vocab))
# -
encoder
# We'll store a few variables that will determine the size of our network. First, `batch_size` determines how many sequences at a time we'll train on. The `seqence_length` parameter defines the maximum length to unroll our recurrent network for. This is effectively the depth of our network during training to help guide gradients along. Within each layer, we'll have `n_cell` LSTM units, and `n_layers` layers worth of LSTM units. Finally, we'll store the total number of possible characters in our data, which will determine the size of our one hot encoding (like we had for MNIST in Session 3).
# +
# Number of sequences in a mini batch
batch_size = 100
# Number of characters in a sequence
sequence_length = 50
# Number of cells in our LSTM layer
n_cells = 128
# Number of LSTM layers
n_layers = 3
# Total number of characters in the one-hot encoding
n_chars = len(vocab)
# -
# Let's now create the input and output to our network. We'll use placeholders and feed these in later. The size of these need to be [`batch_size`, `sequence_length`]. We'll then see how to build the network in between.
#
# <h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
# +
X = tf.placeholder(tf.int32, shape=..., name='X')
# We'll have a placeholder for our true outputs
Y = tf.placeholder(tf.int32, shape=..., name='Y')
# -
# The first thing we need to do is convert each of our `sequence_length` vectors in our batch to `n_cells` LSTM cells. We use a lookup table to find the value in `X` and use this as the input to `n_cells` LSTM cells. Our lookup table has `n_chars` possible elements and connects each character to `n_cells` cells. We create our lookup table using `tf.get_variable` and then the function `tf.nn.embedding_lookup` to connect our `X` placeholder to `n_cells` number of neurons.
# +
# we first create a variable to take us from our one-hot representation to our LSTM cells
embedding = tf.get_variable("embedding", [n_chars, n_cells])
# And then use tensorflow's embedding lookup to look up the ids in X
Xs = tf.nn.embedding_lookup(embedding, X)
# The resulting lookups are concatenated into a dense tensor
print(Xs.get_shape().as_list())
# -
# Now recall from the lecture that recurrent neural networks share their weights across timesteps. So we don't want to have one large matrix with every timestep, but instead separate them. We'll use `tf.split` to split our `[batch_size, sequence_length, n_cells]` array in `Xs` into a list of `sequence_length` elements each composed of `[batch_size, n_cells]` arrays. This gives us `sequence_length` number of arrays of `[batch_size, 1, n_cells]`. We then use `tf.squeeze` to remove the 1st index corresponding to the singleton `sequence_length` index, resulting in simply `[batch_size, n_cells]`.
with tf.name_scope('reslice'):
Xs = [tf.squeeze(seq, [1])
for seq in tf.split(Xs, sequence_length, 1)]
# With each of our timesteps split up, we can now connect them to a set of LSTM recurrent cells. We tell the `tf.contrib.rnn.BasicLSTMCell` method how many cells we want, i.e. how many neurons there are, and we also specify that our state will be stored as a tuple. This state defines the internal state of the cells as well as the connection from the previous timestep. We can also pass a value for the `forget_bias`. Be sure to experiment with this parameter as it can significantly effect performance (e.g. Gers, <NAME>, Schmidhuber, Jurgen, and Cummins, Fred. Learning to forget: Continual prediction with lstm. Neural computation, 12(10):2451–2471, 2000).
cells = tf.contrib.rnn.BasicLSTMCell(num_units=n_cells, state_is_tuple=True, forget_bias=1.0)
# Let's take a look at the cell's state size:
cells.state_size
# `c` defines the internal memory and `h` the output. We'll have as part of our `cells`, both an `initial_state` and a `final_state`. These will become important during inference and we'll see how these work more then. For now, we'll set the `initial_state` to all zeros using the convenience function provided inside our `cells` object, `zero_state`:
initial_state = cells.zero_state(tf.shape(X)[0], tf.float32)
# Looking at what this does, we can see that it creates a `tf.Tensor` of zeros for our `c` and `h` states for each of our `n_cells` and stores this as a tuple inside the `LSTMStateTuple` object:
initial_state
# So far, we have created a single layer of LSTM cells composed of `n_cells` number of cells. If we want another layer, we can use the `tf.contrib.rnn.MultiRNNCell` method, giving it our current cells, and a bit of pythonery to multiply our cells by the number of layers we want. We'll then update our `initial_state` variable to include the additional cells:
cells = tf.contrib.rnn.MultiRNNCell(
[cells] * n_layers, state_is_tuple=True)
initial_state = cells.zero_state(tf.shape(X)[0], tf.float32)
# Now if we take a look at our `initial_state`, we should see one `LSTMStateTuple` for each of our layers:
initial_state
# So far, we haven't connected our recurrent cells to anything. Let's do this now using the `tf.contrib.rnn.static_rnn` method. We also pass it our `initial_state` variables. It gives us the `outputs` of the rnn, as well as their states after having been computed. Contrast that with the `initial_state`, which set the LSTM cells to zeros. After having computed something, the cells will all have a different value somehow reflecting the temporal dynamics and expectations of the next input. These will be stored in the `state` tensors for each of our LSTM layers inside a `LSTMStateTuple` just like the `initial_state` variable.
# ```python
# help(tf.contrib.rnn.static_rnn)
#
# Help on function static_rnn in module tensorflow.contrib.rnn.python.ops.core_rnn:
#
# static_rnn(cell, inputs, initial_state=None, dtype=None, sequence_length=None, scope=None)
# Creates a recurrent neural network specified by RNNCell `cell`.
#
# The simplest form of RNN network generated is:
#
# state = cell.zero_state(...)
# outputs = []
# for input_ in inputs:
# output, state = cell(input_, state)
# outputs.append(output)
# return (outputs, state)
#
# However, a few other options are available:
#
# An initial state can be provided.
# If the sequence_length vector is provided, dynamic calculation is performed.
# This method of calculation does not compute the RNN steps past the maximum
# sequence length of the minibatch (thus saving computational time),
# and properly propagates the state at an example's sequence length
# to the final state output.
#
# The dynamic calculation performed is, at time t for batch row b,
# (output, state)(b, t) =
# (t >= sequence_length(b))
# ? (zeros(cell.output_size), states(b, sequence_length(b) - 1))
# : cell(input(b, t), state(b, t - 1))
#
# Args:
# cell: An instance of RNNCell.
# inputs: A length T list of inputs, each a `Tensor` of shape
# `[batch_size, input_size]`, or a nested tuple of such elements.
# initial_state: (optional) An initial state for the RNN.
# If `cell.state_size` is an integer, this must be
# a `Tensor` of appropriate type and shape `[batch_size, cell.state_size]`.
# If `cell.state_size` is a tuple, this should be a tuple of
# tensors having shapes `[batch_size, s] for s in cell.state_size`.
# dtype: (optional) The data type for the initial state and expected output.
# Required if initial_state is not provided or RNN state has a heterogeneous
# dtype.
# sequence_length: Specifies the length of each sequence in inputs.
# An int32 or int64 vector (tensor) size `[batch_size]`, values in `[0, T)`.
# scope: VariableScope for the created subgraph; defaults to "RNN".
#
# Returns:
# A pair (outputs, state) where:
# - outputs is a length T list of outputs (one for each input), or a nested
# tuple of such elements.
# - state is the final state
#
# Raises:
# TypeError: If `cell` is not an instance of RNNCell.
# ValueError: If `inputs` is `None` or an empty list, or if the input depth
# (column size) cannot be inferred from inputs via shape inference.
# ```
# Use the help on the function `tf.contrib.rnn.static_rnn` to create the `outputs` and `states` variable as below. We've already created each of the variable you need to use:
#
# <h3><font color='red'>TODO! COMPLETE THIS SECTION!</font></h3>
outputs, state = tf.contrib.rnn.static_rnn(cell=..., inputs=..., initial_state=...)
# Let's take a look at the state now:
state
# Our outputs are returned as a list for each of our timesteps:
outputs
# We'll now stack all our outputs for every timestep. We can treat every observation at each timestep and for each batch using the same weight matrices going forward, since these should all have shared weights. Each timstep for each batch is its own observation. So we'll stack these in a 2d matrix so that we can create our softmax layer:
outputs_flat = tf.reshape(tf.concat(values=outputs, axis=1), [-1, n_cells])
# Our outputs are now concatenated so that we have [`batch_size * timesteps`, `n_cells`]
outputs_flat
# We now create a softmax layer just like we did in Session 3 and in Session 3's homework. We multiply our final LSTM layer's `n_cells` outputs by a weight matrix to give us `n_chars` outputs. We then scale this output using a `tf.nn.softmax` layer so that they become a probability by exponentially scaling its value and dividing by its sum. We store the softmax probabilities in `probs` as well as keep track of the maximum index in `Y_pred`:
with tf.variable_scope('prediction'):
W = tf.get_variable(
"W",
shape=[n_cells, n_chars],
initializer=tf.random_normal_initializer(stddev=0.1))
b = tf.get_variable(
"b",
shape=[n_chars],
initializer=tf.random_normal_initializer(stddev=0.1))
# Find the output prediction of every single character in our minibatch
# we denote the pre-activation prediction, logits.
logits = tf.matmul(outputs_flat, W) + b
# We get the probabilistic version by calculating the softmax of this
probs = tf.nn.softmax(logits)
# And then we can find the index of maximum probability
Y_pred = tf.argmax(probs, 1)
# To train the network, we'll measure the loss between our predicted outputs and true outputs. We could use the `probs` variable, but we can also make use of `tf.nn.softmax_cross_entropy_with_logits` which will compute the softmax for us. We therefore need to pass in the variable just before the softmax layer, denoted as `logits` (unscaled values). This takes our variable `logits`, the unscaled predicted outputs, as well as our true outputs, `Y`. Before we give it `Y`, we'll need to reshape our true outputs in the same way, [`batch_size` x `timesteps`, `n_chars`]. Luckily, tensorflow provides a convenience for doing this, the `tf.nn.sparse_softmax_cross_entropy_with_logits` function:
# ```python
# help(tf.nn.sparse_softmax_cross_entropy_with_logits)
#
# Help on function sparse_softmax_cross_entropy_with_logits in module tensorflow.python.ops.nn_ops:
#
# sparse_softmax_cross_entropy_with_logits(logits, labels, name=None)
# Computes sparse softmax cross entropy between `logits` and `labels`.
#
# Measures the probability error in discrete classification tasks in which the
# classes are mutually exclusive (each entry is in exactly one class). For
# example, each CIFAR-10 image is labeled with one and only one label: an image
# can be a dog or a truck, but not both.
#
# **NOTE:** For this operation, the probability of a given label is considered
# exclusive. That is, soft classes are not allowed, and the `labels` vector
# must provide a single specific index for the true class for each row of
# `logits` (each minibatch entry). For soft softmax classification with
# a probability distribution for each entry, see
# `softmax_cross_entropy_with_logits`.
#
# **WARNING:** This op expects unscaled logits, since it performs a softmax
# on `logits` internally for efficiency. Do not call this op with the
# output of `softmax`, as it will produce incorrect results.
#
# A common use case is to have logits of shape `[batch_size, num_classes]` and
# labels of shape `[batch_size]`. But higher dimensions are supported.
#
# Args:
# logits: Unscaled log probabilities of rank `r` and shape
# `[d_0, d_1, ..., d_{r-2}, num_classes]` and dtype `float32` or `float64`.
# labels: `Tensor` of shape `[d_0, d_1, ..., d_{r-2}]` and dtype `int32` or
# `int64`. Each entry in `labels` must be an index in `[0, num_classes)`.
# Other values will result in a loss of 0, but incorrect gradient
# computations.
# name: A name for the operation (optional).
#
# Returns:
# A `Tensor` of the same shape as `labels` and of the same type as `logits`
# with the softmax cross entropy loss.
#
# Raises:
# ValueError: If logits are scalars (need to have rank >= 1) or if the rank
# of the labels is not equal to the rank of the labels minus one.
# ```
with tf.variable_scope('loss'):
# Compute mean cross entropy loss for each output.
Y_true_flat = tf.reshape(tf.concat(values=Y, axis=1), [-1])
# logits are [batch_size x timesteps, n_chars] and
# Y_true_flat are [batch_size x timesteps]
loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=Y_true_flat, logits=logits)
# Compute the mean over our `batch_size` x `timesteps` number of observations
mean_loss = tf.reduce_mean(loss)
# Finally, we can create an optimizer in much the same way as we've done with every other network. Except, we will also "clip" the gradients of every trainable parameter. This is a hacky way to ensure that the gradients do not grow too large (the literature calls this the "exploding gradient problem"). However, note that the LSTM is built to help ensure this does not happen by allowing the gradient to be "gated". To learn more about this, please consider reading the following material:
#
# http://www.felixgers.de/papers/phd.pdf
# https://colah.github.io/posts/2015-08-Understanding-LSTMs/
with tf.name_scope('optimizer'):
optimizer = tf.train.AdamOptimizer(learning_rate=0.001)
gradients = []
clip = tf.constant(5.0, name="clip")
for grad, var in optimizer.compute_gradients(mean_loss):
gradients.append((tf.clip_by_value(grad, -clip, clip), var))
updates = optimizer.apply_gradients(gradients)
# Let's take a look at the graph:
nb_utils.show_graph(tf.get_default_graph().as_graph_def())
# Below is the rest of code we'll need to train the network. I do not recommend running this inside Jupyter Notebook for the entire length of the training because the network can take 1-2 days at least to train, and your browser may very likely complain. Instead, you should write a python script containing the necessary bits of code and run it using the Terminal. We didn't go over how to do this, so I'll leave it for you as an exercise. The next part of this notebook will have you load a pre-trained network.
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
cursor = 0
it_i = 0
while it_i < 500:
Xs, Ys = [], []
for batch_i in range(batch_size):
if (cursor + sequence_length) >= len(txt) - sequence_length - 1:
cursor = 0
Xs.append([encoder[ch]
for ch in txt[cursor:cursor + sequence_length]])
Ys.append([encoder[ch]
for ch in txt[cursor + 1: cursor + sequence_length + 1]])
cursor = (cursor + sequence_length)
Xs = np.array(Xs).astype(np.int32)
Ys = np.array(Ys).astype(np.int32)
loss_val, _ = sess.run([mean_loss, updates],
feed_dict={X: Xs, Y: Ys})
if it_i % 100 == 0:
print(it_i, loss_val)
if it_i % 500 == 0:
p = sess.run(probs, feed_dict={X: np.array(Xs[-1])[np.newaxis]})
ps = [np.random.choice(range(n_chars), p=p_i.ravel())
for p_i in p]
p = [np.argmax(p_i) for p_i in p]
if isinstance(txt[0], str):
print('original:', "".join(
[decoder[ch] for ch in Xs[-1]]))
print('synth(samp):', "".join(
[decoder[ch] for ch in ps]))
print('synth(amax):', "".join(
[decoder[ch] for ch in p]))
else:
print([decoder[ch] for ch in ps])
it_i += 1
# <a name="part-5---pretrained-char-rnn-of-donald-trump"></a>
# # Part 5 - Pretrained Char-RNN of Donald Trump
#
# Rather than stick around to let a model train, let's now explore one I've trained for you Donald Trump. If you've trained your own model on your own text corpus then great! You should be able to use that in place of the one I've provided and still continue with the rest of the notebook.
#
# For the Donald Trump corpus, there are a lot of video transcripts that you can find online. I've searched for a few of these, put them in a giant text file, made everything lowercase, and removed any extraneous letters/symbols to help reduce the vocabulary (not that it's not very large to begin with, ha).
#
# I used the code exactly as above to train on the text I gathered and left it to train for about 2 days. The only modification is that I also used "dropout" which you can see in the libs/charrnn.py file. Let's explore it now and we'll see how we can play with "sampling" the model to generate new phrases, and how to "prime" the model (a psychological term referring to when someone is exposed to something shortly before another event).
#
# First, let's clean up any existing graph:
tf.reset_default_graph()
# <a name="getting-the-trump-data"></a>
# ## Getting the Trump Data
#
# Now let's load the text. This is included in the repo or can be downloaded from:
with open('trump.txt', 'r') as fp:
txt = fp.read()
# Let's take a look at what's going on in here:
txt[:100]
# <a name="basic-text-analysis"></a>
# ## Basic Text Analysis
#
# We can do some basic data analysis to get a sense of what kind of vocabulary we're working with. It's really important to look at your data in as many ways as possible. This helps ensure there isn't anything unexpected going on. Let's find every unique word he uses:
words = set(txt.split(' '))
words
# Now let's count their occurrences:
counts = {word_i: 0 for word_i in words}
for word_i in txt.split(' '):
counts[word_i] += 1
counts
# We can sort this like so:
[(word_i, counts[word_i]) for word_i in sorted(counts, key=counts.get, reverse=True)]
# As we should expect, "the" is the most common word, as it is in the English language: https://en.wikipedia.org/wiki/Most_common_words_in_English
#
# <a name="loading-the-pre-trained-trump-model"></a>
# ## Loading the Pre-trained Trump Model
#
# Let's load the pretrained model. Rather than provide a tfmodel export, I've provided the checkpoint so you can also experiment with training it more if you wish. We'll rebuild the graph using the `charrnn` module in the `libs` directory:
from libs import charrnn
# Let's get the checkpoint and build the model then restore the variables from the checkpoint. The only parameters of consequence are `n_layers` and `n_cells` which define the total size and layout of the model. The rest are flexible. We'll set the `batch_size` and `sequence_length` to 1, meaning we can feed in a single character at a time only, and get back 1 character denoting the very next character's prediction.
ckpt_name = './trump.ckpt'
g = tf.Graph()
n_layers = 3
n_cells = 512
with tf.Session(graph=g) as sess:
model = charrnn.build_model(txt=txt,
batch_size=1,
sequence_length=1,
n_layers=n_layers,
n_cells=n_cells,
gradient_clip=10.0)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
if os.path.exists(ckpt_name):
saver.restore(sess, ckpt_name)
print("Model restored.")
# Let's now take a look at the model:
nb_utils.show_graph(g.as_graph_def())
n_iterations = 100
# <a name="inference-keeping-track-of-the-state"></a>
# ## Inference: Keeping Track of the State
#
# Now recall from Part 4 when we created our LSTM network, we had an `initial_state` variable which would set the LSTM's `c` and `h` state vectors, as well as the final output state which was the output of the `c` and `h` state vectors after having passed through the network. When we input to the network some letter, say 'n', we can set the `initial_state` to zeros, but then after having input the letter `n`, we'll have as output a new state vector for `c` and `h`. On the next letter, we'll then want to set the `initial_state` to this new state, and set the input to the previous letter's output. That is how we ensure the network keeps track of time and knows what has happened in the past, and let it continually generate.
curr_states = None
g = tf.Graph()
with tf.Session(graph=g) as sess:
model = charrnn.build_model(txt=txt,
batch_size=1,
sequence_length=1,
n_layers=n_layers,
n_cells=n_cells,
gradient_clip=10.0)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
if os.path.exists(ckpt_name):
saver.restore(sess, ckpt_name)
print("Model restored.")
# Get every tf.Tensor for the initial state
init_states = []
for s_i in model['initial_state']:
init_states.append(s_i.c)
init_states.append(s_i.h)
# Similarly, for every state after inference
final_states = []
for s_i in model['final_state']:
final_states.append(s_i.c)
final_states.append(s_i.h)
# Let's start with the letter 't' and see what comes out:
synth = [[encoder[' ']]]
for i in range(n_iterations):
# We'll create a feed_dict parameter which includes what to
# input to the network, model['X'], as well as setting
# dropout to 1.0, meaning no dropout.
feed_dict = {model['X']: [synth[-1]],
model['keep_prob']: 1.0}
# Now we'll check if we currently have a state as a result
# of a previous inference, and if so, add to our feed_dict
# parameter the mapping of the init_state to the previous
# output state stored in "curr_states".
if curr_states:
feed_dict.update(
{init_state_i: curr_state_i
for (init_state_i, curr_state_i) in
zip(init_states, curr_states)})
# Now we can infer and see what letter we get
p = sess.run(model['probs'], feed_dict=feed_dict)[0]
# And make sure we also keep track of the new state
curr_states = sess.run(final_states, feed_dict=feed_dict)
# Find the most likely character
p = np.argmax(p)
# Append to string
synth.append([p])
# Print out the decoded letter
print(model['decoder'][p], end='')
sys.stdout.flush()
# <a name="probabilistic-sampling"></a>
# ## Probabilistic Sampling
#
# Run the above cell a couple times. What you should find is that it is deterministic. We always pick *the* most likely character. But we can do something else which will make things less deterministic and a bit more interesting: we can sample from our probabilistic measure from our softmax layer. This means if we have the letter 'a' as 0.4, and the letter 'o' as 0.2, we'll have a 40% chance of picking the letter 'a', and 20% chance of picking the letter 'o', rather than simply always picking the letter 'a' since it is the most probable.
curr_states = None
g = tf.Graph()
with tf.Session(graph=g) as sess:
model = charrnn.build_model(txt=txt,
batch_size=1,
sequence_length=1,
n_layers=n_layers,
n_cells=n_cells,
gradient_clip=10.0)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
if os.path.exists(ckpt_name):
saver.restore(sess, ckpt_name)
print("Model restored.")
# Get every tf.Tensor for the initial state
init_states = []
for s_i in model['initial_state']:
init_states.append(s_i.c)
init_states.append(s_i.h)
# Similarly, for every state after inference
final_states = []
for s_i in model['final_state']:
final_states.append(s_i.c)
final_states.append(s_i.h)
# Let's start with the letter 't' and see what comes out:
synth = [[encoder[' ']]]
for i in range(n_iterations):
# We'll create a feed_dict parameter which includes what to
# input to the network, model['X'], as well as setting
# dropout to 1.0, meaning no dropout.
feed_dict = {model['X']: [synth[-1]],
model['keep_prob']: 1.0}
# Now we'll check if we currently have a state as a result
# of a previous inference, and if so, add to our feed_dict
# parameter the mapping of the init_state to the previous
# output state stored in "curr_states".
if curr_states:
feed_dict.update(
{init_state_i: curr_state_i
for (init_state_i, curr_state_i) in
zip(init_states, curr_states)})
# Now we can infer and see what letter we get
p = sess.run(model['probs'], feed_dict=feed_dict)[0]
# And make sure we also keep track of the new state
curr_states = sess.run(final_states, feed_dict=feed_dict)
# Now instead of finding the most likely character,
# we'll sample with the probabilities of each letter
p = p.astype(np.float64)
p = np.random.multinomial(1, p.ravel() / p.sum())
p = np.argmax(p)
# Append to string
synth.append([p])
# Print out the decoded letter
print(model['decoder'][p], end='')
sys.stdout.flush()
# <a name="inference-temperature"></a>
# ## Inference: Temperature
#
# When performing probabilistic sampling, we can also use a parameter known as temperature which comes from simulated annealing. The basic idea is that as the temperature is high and very hot, we have a lot more free energy to use to jump around more, and as we cool down, we have less energy and then become more deterministic. We can use temperature by scaling our log probabilities like so:
temperature = 0.5
curr_states = None
g = tf.Graph()
with tf.Session(graph=g) as sess:
model = charrnn.build_model(txt=txt,
batch_size=1,
sequence_length=1,
n_layers=n_layers,
n_cells=n_cells,
gradient_clip=10.0)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
if os.path.exists(ckpt_name):
saver.restore(sess, ckpt_name)
print("Model restored.")
# Get every tf.Tensor for the initial state
init_states = []
for s_i in model['initial_state']:
init_states.append(s_i.c)
init_states.append(s_i.h)
# Similarly, for every state after inference
final_states = []
for s_i in model['final_state']:
final_states.append(s_i.c)
final_states.append(s_i.h)
# Let's start with the letter 't' and see what comes out:
synth = [[encoder[' ']]]
for i in range(n_iterations):
# We'll create a feed_dict parameter which includes what to
# input to the network, model['X'], as well as setting
# dropout to 1.0, meaning no dropout.
feed_dict = {model['X']: [synth[-1]],
model['keep_prob']: 1.0}
# Now we'll check if we currently have a state as a result
# of a previous inference, and if so, add to our feed_dict
# parameter the mapping of the init_state to the previous
# output state stored in "curr_states".
if curr_states:
feed_dict.update(
{init_state_i: curr_state_i
for (init_state_i, curr_state_i) in
zip(init_states, curr_states)})
# Now we can infer and see what letter we get
p = sess.run(model['probs'], feed_dict=feed_dict)[0]
# And make sure we also keep track of the new state
curr_states = sess.run(final_states, feed_dict=feed_dict)
# Now instead of finding the most likely character,
# we'll sample with the probabilities of each letter
p = p.astype(np.float64)
p = np.log(p) / temperature
p = np.exp(p) / np.sum(np.exp(p))
p = np.random.multinomial(1, p.ravel() / p.sum())
p = np.argmax(p)
# Append to string
synth.append([p])
# Print out the decoded letter
print(model['decoder'][p], end='')
sys.stdout.flush()
# <a name="inference-priming"></a>
# ## Inference: Priming
#
# Let's now work on "priming" the model with some text, and see what kind of state it is in and leave it to synthesize from there. We'll do more or less what we did before, but feed in our own text instead of the last letter of the synthesis from the model.
prime = "obama"
temperature = 1.0
curr_states = None
n_iterations = 500
g = tf.Graph()
with tf.Session(graph=g) as sess:
model = charrnn.build_model(txt=txt,
batch_size=1,
sequence_length=1,
n_layers=n_layers,
n_cells=n_cells,
gradient_clip=10.0)
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver()
if os.path.exists(ckpt_name):
saver.restore(sess, ckpt_name)
print("Model restored.")
# Get every tf.Tensor for the initial state
init_states = []
for s_i in model['initial_state']:
init_states.append(s_i.c)
init_states.append(s_i.h)
# Similarly, for every state after inference
final_states = []
for s_i in model['final_state']:
final_states.append(s_i.c)
final_states.append(s_i.h)
# Now we'll keep track of the state as we feed it one
# letter at a time.
curr_states = None
for ch in prime:
feed_dict = {model['X']: [[model['encoder'][ch]]],
model['keep_prob']: 1.0}
if curr_states:
feed_dict.update(
{init_state_i: curr_state_i
for (init_state_i, curr_state_i) in
zip(init_states, curr_states)})
# Now we can infer and see what letter we get
p = sess.run(model['probs'], feed_dict=feed_dict)[0]
p = p.astype(np.float64)
p = np.log(p) / temperature
p = np.exp(p) / np.sum(np.exp(p))
p = np.random.multinomial(1, p.ravel() / p.sum())
p = np.argmax(p)
# And make sure we also keep track of the new state
curr_states = sess.run(final_states, feed_dict=feed_dict)
# Now we're ready to do what we were doing before but with the
# last predicted output stored in `p`, and the current state of
# the model.
synth = [[p]]
print(prime + model['decoder'][p], end='')
for i in range(n_iterations):
# Input to the network
feed_dict = {model['X']: [synth[-1]],
model['keep_prob']: 1.0}
# Also feed our current state
feed_dict.update(
{init_state_i: curr_state_i
for (init_state_i, curr_state_i) in
zip(init_states, curr_states)})
# Inference
p = sess.run(model['probs'], feed_dict=feed_dict)[0]
# Keep track of the new state
curr_states = sess.run(final_states, feed_dict=feed_dict)
# Sample
p = p.astype(np.float64)
p = np.log(p) / temperature
p = np.exp(p) / np.sum(np.exp(p))
p = np.random.multinomial(1, p.ravel() / p.sum())
p = np.argmax(p)
# Append to string
synth.append([p])
# Print out the decoded letter
print(model['decoder'][p], end='')
sys.stdout.flush()
# <a name="assignment-submission"></a>
# # Assignment Submission
# After you've completed both notebooks, create a zip file of the current directory using the code below. This code will make sure you have included this completed ipython notebook and the following files named exactly as:
#
# session-5/
# session-5-part-1.ipynb
# session-5-part-2.ipynb
# vaegan.gif
# You'll then submit this zip file for your third assignment on Kadenze for "Assignment 5: Generative Adversarial Networks and Recurrent Neural Networks"! If you have any questions, remember to reach out on the forums and connect with your peers or with me.
#
# To get assessed, you'll need to be a premium student! This will allow you to build an online portfolio of all of your work and receive grades. If you aren't already enrolled as a student, register now at http://www.kadenze.com/ and join the #CADL community to see what your peers are doing! https://www.kadenze.com/courses/creative-applications-of-deep-learning-with-tensorflow/info
#
# Also, if you share any of the GIFs on Facebook/Twitter/Instagram/etc..., be sure to use the #CADL hashtag so that other students can find your work!
utils.build_submission('session-5.zip',
('vaegan.gif',
'session-5-part-1.ipynb',
'session-5-part-2.ipynb'))
| session-5/session-5-part-2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="copyright"
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="title"
# # Vertex AI client library: Custom training tabular regression model for online prediction
#
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/ai-platform-samples/blob/master/ai-platform-unified/notebooks/community/gapic/custom/showcase_custom_tabular_regression_online.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
# </a>
# </td>
# <td>
# <a href="https://github.com/GoogleCloudPlatform/ai-platform-samples/blob/master/ai-platform-unified/notebooks/community/gapic/custom/showcase_custom_tabular_regression_online.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
# View on GitHub
# </a>
# </td>
# </table>
# <br/><br/><br/>
# + [markdown] id="overview:custom"
# ## Overview
#
#
# This tutorial demonstrates how to use the Vertex AI Python client library to train and deploy a custom tabular regression model for online prediction.
# + [markdown] id="dataset:custom,boston,lrg"
# ### Dataset
#
# The dataset used for this tutorial is the [Boston Housing Prices dataset](https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html). The version of the dataset you will use in this tutorial is built into TensorFlow. The trained model predicts the median price of a house in units of 1K USD.
# + [markdown] id="objective:custom,training,online_prediction"
# ### Objective
#
# In this tutorial, you create a custom model from a Python script in a Google prebuilt Docker container using the Vertex AI client library, and then do a prediction on the deployed model by sending data. You can alternatively create custom models using `gcloud` command-line tool or online using Google Cloud Console.
#
# The steps performed include:
#
# - Create a Vertex AI custom job for training a model.
# - Train a TensorFlow model.
# - Retrieve and load the model artifacts.
# - View the model evaluation.
# - Upload the model as a Vertex AI `Model` resource.
# - Deploy the `Model` resource to a serving `Endpoint` resource.
# - Make a prediction.
# - Undeploy the `Model` resource.
# + [markdown] id="costs"
# ### Costs
#
# This tutorial uses billable components of Google Cloud (GCP):
#
# * Vertex AI
# * Cloud Storage
#
# Learn about [Vertex AI
# pricing](https://cloud.google.com/ai-platform-unified/pricing) and [Cloud Storage
# pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
# Calculator](https://cloud.google.com/products/calculator/)
# to generate a cost estimate based on your projected usage.
# + [markdown] id="install_aip"
# ## Installation
#
# Install the latest version of Vertex AI client library.
# + id="install_aip"
import sys
if "google.colab" in sys.modules:
USER_FLAG = ""
else:
USER_FLAG = "--user"
# ! pip3 install -U google-cloud-aiplatform $USER_FLAG
# + [markdown] id="install_storage"
# Install the latest GA version of *google-cloud-storage* library as well.
# + id="install_storage"
# ! pip3 install -U google-cloud-storage $USER_FLAG
# + [markdown] id="restart"
# ### Restart the kernel
#
# Once you've installed the Vertex AI client library and Google *cloud-storage*, you need to restart the notebook kernel so it can find the packages.
# + id="restart"
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
# + [markdown] id="before_you_begin"
# ## Before you begin
#
# ### GPU runtime
#
# *Make sure you're running this notebook in a GPU runtime if you have that option. In Colab, select* **Runtime > Change Runtime Type > GPU**
#
# ### Set up your Google Cloud project
#
# **The following steps are required, regardless of your notebook environment.**
#
# 1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
#
# 2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
#
# 3. [Enable the Vertex AI APIs and Compute Engine APIs.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component)
#
# 4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Vertex AI Notebooks.
#
# 5. Enter your project ID in the cell below. Then run the cell to make sure the
# Cloud SDK uses the right project for all the commands in this notebook.
#
# **Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$` into these commands.
# + id="set_project_id"
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
# + id="autoset_project_id"
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
# shell_output = !gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
# + id="set_gcloud_project_id"
# ! gcloud config set project $PROJECT_ID
# + [markdown] id="region"
# #### Region
#
# You can also change the `REGION` variable, which is used for operations
# throughout the rest of this notebook. Below are regions supported for Vertex AI. We recommend that you choose the region closest to you.
#
# - Americas: `us-central1`
# - Europe: `europe-west4`
# - Asia Pacific: `asia-east1`
#
# You may not use a multi-regional bucket for training with Vertex AI. Not all regions provide support for all Vertex AI services. For the latest support per region, see the [Vertex AI locations documentation](https://cloud.google.com/ai-platform-unified/docs/general/locations)
# + id="region"
REGION = "us-central1" # @param {type: "string"}
# + [markdown] id="timestamp"
# #### Timestamp
#
# If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append onto the name of resources which will be created in this tutorial.
# + id="timestamp"
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
# + [markdown] id="gcp_authenticate"
# ### Authenticate your Google Cloud account
#
# **If you are using Vertex AI Notebooks**, your environment is already authenticated. Skip this step.
#
# **If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
#
# **Otherwise**, follow these steps:
#
# In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
#
# **Click Create service account**.
#
# In the **Service account name** field, enter a name, and click **Create**.
#
# In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex AI" into the filter box, and select **Vertex AI Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
#
# Click Create. A JSON file that contains your key downloads to your local environment.
#
# Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
# + id="gcp_authenticate"
import os
import sys
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
# If on AI Platform, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
# %env GOOGLE_APPLICATION_CREDENTIALS ''
# + [markdown] id="bucket:custom"
# ### Create a Cloud Storage bucket
#
# **The following steps are required, regardless of your notebook environment.**
#
# When you submit a custom training job using the Vertex AI client library, you upload a Python package
# containing your training code to a Cloud Storage bucket. Vertex AI runs
# the code from this package. In this tutorial, Vertex AI also saves the
# trained model that results from your job in the same bucket. You can then
# create an `Endpoint` resource based on this output in order to serve
# online predictions.
#
# Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
# + id="bucket"
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
# + id="autoset_bucket"
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
# + [markdown] id="create_bucket"
# **Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
# + id="create_bucket"
# ! gsutil mb -l $REGION $BUCKET_NAME
# + [markdown] id="validate_bucket"
# Finally, validate access to your Cloud Storage bucket by examining its contents:
# + id="validate_bucket"
# ! gsutil ls -al $BUCKET_NAME
# + [markdown] id="setup_vars"
# ### Set up variables
#
# Next, set up some variables used throughout the tutorial.
# ### Import libraries and define constants
# + [markdown] id="import_aip"
# #### Import Vertex AI client library
#
# Import the Vertex AI client library into our Python environment.
# + id="import_aip"
import os
import sys
import time
import google.cloud.aiplatform_v1 as aip
from google.protobuf import json_format
from google.protobuf.json_format import MessageToJson, ParseDict
from google.protobuf.struct_pb2 import Struct, Value
# + [markdown] id="aip_constants"
# #### Vertex AI constants
#
# Setup up the following constants for Vertex AI:
#
# - `API_ENDPOINT`: The Vertex AI API service endpoint for dataset, model, job, pipeline and endpoint services.
# - `PARENT`: The Vertex AI location root path for dataset, model, job, pipeline and endpoint resources.
# + id="aip_constants"
# API service endpoint
API_ENDPOINT = "{}-aiplatform.googleapis.com".format(REGION)
# Vertex AI location root path for your dataset, model and endpoint resources
PARENT = "projects/" + PROJECT_ID + "/locations/" + REGION
# + [markdown] id="accelerators:training,prediction,cpu"
# #### Hardware Accelerators
#
# Set the hardware accelerators (e.g., GPU), if any, for training and prediction.
#
# Set the variables `TRAIN_GPU/TRAIN_NGPU` and `DEPLOY_GPU/DEPLOY_NGPU` to use a container image supporting a GPU and the number of GPUs allocated to the virtual machine (VM) instance. For example, to use a GPU container image with 4 Nvidia Telsa K80 GPUs allocated to each VM, you would specify:
#
# (aip.AcceleratorType.NVIDIA_TESLA_K80, 4)
#
# For GPU, available accelerators include:
# - aip.AcceleratorType.NVIDIA_TESLA_K80
# - aip.AcceleratorType.NVIDIA_TESLA_P100
# - aip.AcceleratorType.NVIDIA_TESLA_P4
# - aip.AcceleratorType.NVIDIA_TESLA_T4
# - aip.AcceleratorType.NVIDIA_TESLA_V100
#
#
# Otherwise specify `(None, None)` to use a container image to run on a CPU.
#
# *Note*: TF releases before 2.3 for GPU support will fail to load the custom model in this tutorial. It is a known issue and fixed in TF 2.3 -- which is caused by static graph ops that are generated in the serving function. If you encounter this issue on your own custom models, use a container image for TF 2.3 with GPU support.
# + id="accelerators:training,prediction,cpu"
if os.getenv("IS_TESTING_TRAIN_GPU"):
TRAIN_GPU, TRAIN_NGPU = (
aip.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_TRAIN_GPU")),
)
else:
TRAIN_GPU, TRAIN_NGPU = (aip.AcceleratorType.NVIDIA_TESLA_K80, 1)
if os.getenv("IS_TESTING_DEPOLY_GPU"):
DEPLOY_GPU, DEPLOY_NGPU = (
aip.AcceleratorType.NVIDIA_TESLA_K80,
int(os.getenv("IS_TESTING_DEPOLY_GPU")),
)
else:
DEPLOY_GPU, DEPLOY_NGPU = (None, None)
# + [markdown] id="container:training,prediction"
# #### Container (Docker) image
#
# Next, we will set the Docker container images for training and prediction
#
# - TensorFlow 1.15
# - `gcr.io/cloud-aiplatform/training/tf-cpu.1-15:latest`
# - `gcr.io/cloud-aiplatform/training/tf-gpu.1-15:latest`
# - TensorFlow 2.1
# - `gcr.io/cloud-aiplatform/training/tf-cpu.2-1:latest`
# - `gcr.io/cloud-aiplatform/training/tf-gpu.2-1:latest`
# - TensorFlow 2.2
# - `gcr.io/cloud-aiplatform/training/tf-cpu.2-2:latest`
# - `gcr.io/cloud-aiplatform/training/tf-gpu.2-2:latest`
# - TensorFlow 2.3
# - `gcr.io/cloud-aiplatform/training/tf-cpu.2-3:latest`
# - `gcr.io/cloud-aiplatform/training/tf-gpu.2-3:latest`
# - TensorFlow 2.4
# - `gcr.io/cloud-aiplatform/training/tf-cpu.2-4:latest`
# - `gcr.io/cloud-aiplatform/training/tf-gpu.2-4:latest`
# - XGBoost
# - `gcr.io/cloud-aiplatform/training/xgboost-cpu.1-1`
# - Scikit-learn
# - `gcr.io/cloud-aiplatform/training/scikit-learn-cpu.0-23:latest`
# - Pytorch
# - `gcr.io/cloud-aiplatform/training/pytorch-cpu.1-4:latest`
# - `gcr.io/cloud-aiplatform/training/pytorch-cpu.1-5:latest`
# - `gcr.io/cloud-aiplatform/training/pytorch-cpu.1-6:latest`
# - `gcr.io/cloud-aiplatform/training/pytorch-cpu.1-7:latest`
#
# For the latest list, see [Pre-built containers for training](https://cloud.google.com/ai-platform-unified/docs/training/pre-built-containers).
#
# - TensorFlow 1.15
# - `gcr.io/cloud-aiplatform/prediction/tf-cpu.1-15:latest`
# - `gcr.io/cloud-aiplatform/prediction/tf-gpu.1-15:latest`
# - TensorFlow 2.1
# - `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-1:latest`
# - `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-1:latest`
# - TensorFlow 2.2
# - `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-2:latest`
# - `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-2:latest`
# - TensorFlow 2.3
# - `gcr.io/cloud-aiplatform/prediction/tf2-cpu.2-3:latest`
# - `gcr.io/cloud-aiplatform/prediction/tf2-gpu.2-3:latest`
# - XGBoost
# - `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.1-2:latest`
# - `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.1-1:latest`
# - `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.0-90:latest`
# - `gcr.io/cloud-aiplatform/prediction/xgboost-cpu.0-82:latest`
# - Scikit-learn
# - `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-23:latest`
# - `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-22:latest`
# - `gcr.io/cloud-aiplatform/prediction/sklearn-cpu.0-20:latest`
#
# For the latest list, see [Pre-built containers for prediction](https://cloud.google.com/ai-platform-unified/docs/predictions/pre-built-containers)
# + id="container:training,prediction"
if os.getenv("IS_TESTING_TF"):
TF = os.getenv("IS_TESTING_TF")
else:
TF = "2-1"
if TF[0] == "2":
if TRAIN_GPU:
TRAIN_VERSION = "tf-gpu.{}".format(TF)
else:
TRAIN_VERSION = "tf-cpu.{}".format(TF)
if DEPLOY_GPU:
DEPLOY_VERSION = "tf2-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf2-cpu.{}".format(TF)
else:
if TRAIN_GPU:
TRAIN_VERSION = "tf-gpu.{}".format(TF)
else:
TRAIN_VERSION = "tf-cpu.{}".format(TF)
if DEPLOY_GPU:
DEPLOY_VERSION = "tf-gpu.{}".format(TF)
else:
DEPLOY_VERSION = "tf-cpu.{}".format(TF)
TRAIN_IMAGE = "gcr.io/cloud-aiplatform/training/{}:latest".format(TRAIN_VERSION)
DEPLOY_IMAGE = "gcr.io/cloud-aiplatform/prediction/{}:latest".format(DEPLOY_VERSION)
print("Training:", TRAIN_IMAGE, TRAIN_GPU, TRAIN_NGPU)
print("Deployment:", DEPLOY_IMAGE, DEPLOY_GPU, DEPLOY_NGPU)
# + [markdown] id="machine:training,prediction"
# #### Machine Type
#
# Next, set the machine type to use for training and prediction.
#
# - Set the variables `TRAIN_COMPUTE` and `DEPLOY_COMPUTE` to configure the compute resources for the VMs you will use for for training and prediction.
# - `machine type`
# - `n1-standard`: 3.75GB of memory per vCPU.
# - `n1-highmem`: 6.5GB of memory per vCPU
# - `n1-highcpu`: 0.9 GB of memory per vCPU
# - `vCPUs`: number of \[2, 4, 8, 16, 32, 64, 96 \]
#
# *Note: The following is not supported for training:*
#
# - `standard`: 2 vCPUs
# - `highcpu`: 2, 4 and 8 vCPUs
#
# *Note: You may also use n2 and e2 machine types for training and deployment, but they do not support GPUs*.
# + id="machine:training,prediction"
if os.getenv("IS_TESTING_TRAIN_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_TRAIN_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
TRAIN_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Train machine type", TRAIN_COMPUTE)
if os.getenv("IS_TESTING_DEPLOY_MACHINE"):
MACHINE_TYPE = os.getenv("IS_TESTING_DEPLOY_MACHINE")
else:
MACHINE_TYPE = "n1-standard"
VCPU = "4"
DEPLOY_COMPUTE = MACHINE_TYPE + "-" + VCPU
print("Deploy machine type", DEPLOY_COMPUTE)
# + [markdown] id="tutorial_start:custom"
# # Tutorial
#
# Now you are ready to start creating your own custom model and training for Boston Housing.
# + [markdown] id="clients:custom"
# ## Set up clients
#
# The Vertex AI client library works as a client/server model. On your side (the Python script) you will create a client that sends requests and receives responses from the Vertex AI server.
#
# You will use different clients in this tutorial for different steps in the workflow. So set them all up upfront.
#
# - Model Service for `Model` resources.
# - Endpoint Service for deployment.
# - Job Service for batch jobs and custom training.
# - Prediction Service for serving.
# + id="clients:custom"
# client options same for all services
client_options = {"api_endpoint": API_ENDPOINT}
def create_job_client():
client = aip.JobServiceClient(client_options=client_options)
return client
def create_model_client():
client = aip.ModelServiceClient(client_options=client_options)
return client
def create_endpoint_client():
client = aip.EndpointServiceClient(client_options=client_options)
return client
def create_prediction_client():
client = aip.PredictionServiceClient(client_options=client_options)
return client
clients = {}
clients["job"] = create_job_client()
clients["model"] = create_model_client()
clients["endpoint"] = create_endpoint_client()
clients["prediction"] = create_prediction_client()
for client in clients.items():
print(client)
# + [markdown] id="train_custom_model"
# ## Train a model
#
# There are two ways you can train a custom model using a container image:
#
# - **Use a Google Cloud prebuilt container**. If you use a prebuilt container, you will additionally specify a Python package to install into the container image. This Python package contains your code for training a custom model.
#
# - **Use your own custom container image**. If you use your own container, the container needs to contain your code for training a custom model.
# + [markdown] id="train_custom_job_specification:prebuilt_container"
# ## Prepare your custom job specification
#
# Now that your clients are ready, your first step is to create a Job Specification for your custom training job. The job specification will consist of the following:
#
# - `worker_pool_spec` : The specification of the type of machine(s) you will use for training and how many (single or distributed)
# - `python_package_spec` : The specification of the Python package to be installed with the pre-built container.
# + [markdown] id="train_custom_job_machine_specification"
# ### Prepare your machine specification
#
# Now define the machine specification for your custom training job. This tells Vertex AI what type of machine instance to provision for the training.
# - `machine_type`: The type of GCP instance to provision -- e.g., n1-standard-8.
# - `accelerator_type`: The type, if any, of hardware accelerator. In this tutorial if you previously set the variable `TRAIN_GPU != None`, you are using a GPU; otherwise you will use a CPU.
# - `accelerator_count`: The number of accelerators.
# + id="train_custom_job_machine_specification"
if TRAIN_GPU:
machine_spec = {
"machine_type": TRAIN_COMPUTE,
"accelerator_type": TRAIN_GPU,
"accelerator_count": TRAIN_NGPU,
}
else:
machine_spec = {"machine_type": TRAIN_COMPUTE, "accelerator_count": 0}
# + [markdown] id="train_custom_job_disk_specification"
# ### Prepare your disk specification
#
# (optional) Now define the disk specification for your custom training job. This tells Vertex AI what type and size of disk to provision in each machine instance for the training.
#
# - `boot_disk_type`: Either SSD or Standard. SSD is faster, and Standard is less expensive. Defaults to SSD.
# - `boot_disk_size_gb`: Size of disk in GB.
# + id="train_custom_job_disk_specification"
DISK_TYPE = "pd-ssd" # [ pd-ssd, pd-standard]
DISK_SIZE = 200 # GB
disk_spec = {"boot_disk_type": DISK_TYPE, "boot_disk_size_gb": DISK_SIZE}
# + [markdown] id="train_custom_job_worker_pool_specification:prebuilt_container,tabular"
# ### Define the worker pool specification
#
# Next, you define the worker pool specification for your custom training job. The worker pool specification will consist of the following:
#
# - `replica_count`: The number of instances to provision of this machine type.
# - `machine_spec`: The hardware specification.
# - `disk_spec` : (optional) The disk storage specification.
#
# - `python_package`: The Python training package to install on the VM instance(s) and which Python module to invoke, along with command line arguments for the Python module.
#
# Let's dive deeper now into the python package specification:
#
# -`executor_image_spec`: This is the docker image which is configured for your custom training job.
#
# -`package_uris`: This is a list of the locations (URIs) of your python training packages to install on the provisioned instance. The locations need to be in a Cloud Storage bucket. These can be either individual python files or a zip (archive) of an entire package. In the later case, the job service will unzip (unarchive) the contents into the docker image.
#
# -`python_module`: The Python module (script) to invoke for running the custom training job. In this example, you will be invoking `trainer.task.py` -- note that it was not neccessary to append the `.py` suffix.
#
# -`args`: The command line arguments to pass to the corresponding Pythom module. In this example, you will be setting:
# - `"--model-dir=" + MODEL_DIR` : The Cloud Storage location where to store the model artifacts. There are two ways to tell the training script where to save the model artifacts:
# - direct: You pass the Cloud Storage location as a command line argument to your training script (set variable `DIRECT = True`), or
# - indirect: The service passes the Cloud Storage location as the environment variable `AIP_MODEL_DIR` to your training script (set variable `DIRECT = False`). In this case, you tell the service the model artifact location in the job specification.
# - `"--epochs=" + EPOCHS`: The number of epochs for training.
# - `"--steps=" + STEPS`: The number of steps (batches) per epoch.
# - `"--distribute=" + TRAIN_STRATEGY"` : The training distribution strategy to use for single or distributed training.
# - `"single"`: single device.
# - `"mirror"`: all GPU devices on a single compute instance.
# - `"multi"`: all GPU devices on all compute instances.
# - `"--param-file=" + PARAM_FILE`: The Cloud Storage location for storing feature normalization values.
# + id="train_custom_job_worker_pool_specification:prebuilt_container,tabular"
JOB_NAME = "custom_job_" + TIMESTAMP
MODEL_DIR = "{}/{}".format(BUCKET_NAME, JOB_NAME)
if not TRAIN_NGPU or TRAIN_NGPU < 2:
TRAIN_STRATEGY = "single"
else:
TRAIN_STRATEGY = "mirror"
EPOCHS = 20
STEPS = 100
PARAM_FILE = BUCKET_NAME + "/params.txt"
DIRECT = True
if DIRECT:
CMDARGS = [
"--model-dir=" + MODEL_DIR,
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
"--distribute=" + TRAIN_STRATEGY,
"--param-file=" + PARAM_FILE,
]
else:
CMDARGS = [
"--epochs=" + str(EPOCHS),
"--steps=" + str(STEPS),
"--distribute=" + TRAIN_STRATEGY,
"--param-file=" + PARAM_FILE,
]
worker_pool_spec = [
{
"replica_count": 1,
"machine_spec": machine_spec,
"disk_spec": disk_spec,
"python_package_spec": {
"executor_image_uri": TRAIN_IMAGE,
"package_uris": [BUCKET_NAME + "/trainer_boston.tar.gz"],
"python_module": "trainer.task",
"args": CMDARGS,
},
}
]
# + [markdown] id="assemble_custom_job_specification"
# ### Assemble a job specification
#
# Now assemble the complete description for the custom job specification:
#
# - `display_name`: The human readable name you assign to this custom job.
# - `job_spec`: The specification for the custom job.
# - `worker_pool_specs`: The specification for the machine VM instances.
# - `base_output_directory`: This tells the service the Cloud Storage location where to save the model artifacts (when variable `DIRECT = False`). The service will then pass the location to the training script as the environment variable `AIP_MODEL_DIR`, and the path will be of the form:
#
# <output_uri_prefix>/model
# + id="assemble_custom_job_specification"
if DIRECT:
job_spec = {"worker_pool_specs": worker_pool_spec}
else:
job_spec = {
"worker_pool_specs": worker_pool_spec,
"base_output_directory": {"output_uri_prefix": MODEL_DIR},
}
custom_job = {"display_name": JOB_NAME, "job_spec": job_spec}
# + [markdown] id="examine_training_package"
# ### Examine the training package
#
# #### Package layout
#
# Before you start the training, you will look at how a Python package is assembled for a custom training job. When unarchived, the package contains the following directory/file layout.
#
# - PKG-INFO
# - README.md
# - setup.cfg
# - setup.py
# - trainer
# - \_\_init\_\_.py
# - task.py
#
# The files `setup.cfg` and `setup.py` are the instructions for installing the package into the operating environment of the Docker image.
#
# The file `trainer/task.py` is the Python script for executing the custom training job. *Note*, when we referred to it in the worker pool specification, we replace the directory slash with a dot (`trainer.task`) and dropped the file suffix (`.py`).
#
# #### Package Assembly
#
# In the following cells, you will assemble the training package.
# + id="examine_training_package"
# Make folder for Python training script
# ! rm -rf custom
# ! mkdir custom
# Add package information
# ! touch custom/README.md
setup_cfg = "[egg_info]\n\ntag_build =\n\ntag_date = 0"
# ! echo "$setup_cfg" > custom/setup.cfg
setup_py = "import setuptools\n\nsetuptools.setup(\n\n install_requires=[\n\n 'tensorflow_datasets==1.3.0',\n\n ],\n\n packages=setuptools.find_packages())"
# ! echo "$setup_py" > custom/setup.py
pkg_info = "Metadata-Version: 1.0\n\nName: Boston Housing tabular regression\n\nVersion: 0.0.0\n\nSummary: Demostration training script\n\nHome-page: www.google.com\n\nAuthor: Google\n\nAuthor-email: <EMAIL>\n\nLicense: Public\n\nDescription: Demo\n\nPlatform: Vertex AI"
# ! echo "$pkg_info" > custom/PKG-INFO
# Make the training subfolder
# ! mkdir custom/trainer
# ! touch custom/trainer/__init__.py
# + [markdown] id="taskpy_contents:boston"
# #### Task.py contents
#
# In the next cell, you write the contents of the training script task.py. I won't go into detail, it's just there for you to browse. In summary:
#
# - Get the directory where to save the model artifacts from the command line (`--model_dir`), and if not specified, then from the environment variable `AIP_MODEL_DIR`.
# - Loads Boston Housing dataset from TF.Keras builtin datasets
# - Builds a simple deep neural network model using TF.Keras model API.
# - Compiles the model (`compile()`).
# - Sets a training distribution strategy according to the argument `args.distribute`.
# - Trains the model (`fit()`) with epochs specified by `args.epochs`.
# - Saves the trained model (`save(args.model_dir)`) to the specified model directory.
# - Saves the maximum value for each feature `f.write(str(params))` to the specified parameters file.
# + id="taskpy_contents:boston"
# %%writefile custom/trainer/task.py
# Single, Mirror and Multi-Machine Distributed Training for Boston Housing
import tensorflow_datasets as tfds
import tensorflow as tf
from tensorflow.python.client import device_lib
import numpy as np
import argparse
import os
import sys
tfds.disable_progress_bar()
parser = argparse.ArgumentParser()
parser.add_argument('--model-dir', dest='model_dir',
default=os.getenv('AIP_MODEL_DIR'), type=str, help='Model dir.')
parser.add_argument('--lr', dest='lr',
default=0.001, type=float,
help='Learning rate.')
parser.add_argument('--epochs', dest='epochs',
default=20, type=int,
help='Number of epochs.')
parser.add_argument('--steps', dest='steps',
default=100, type=int,
help='Number of steps per epoch.')
parser.add_argument('--distribute', dest='distribute', type=str, default='single',
help='distributed training strategy')
parser.add_argument('--param-file', dest='param_file',
default='/tmp/param.txt', type=str,
help='Output file for parameters')
args = parser.parse_args()
print('Python Version = {}'.format(sys.version))
print('TensorFlow Version = {}'.format(tf.__version__))
print('TF_CONFIG = {}'.format(os.environ.get('TF_CONFIG', 'Not found')))
# Single Machine, single compute device
if args.distribute == 'single':
if tf.test.is_gpu_available():
strategy = tf.distribute.OneDeviceStrategy(device="/gpu:0")
else:
strategy = tf.distribute.OneDeviceStrategy(device="/cpu:0")
# Single Machine, multiple compute device
elif args.distribute == 'mirror':
strategy = tf.distribute.MirroredStrategy()
# Multiple Machine, multiple compute device
elif args.distribute == 'multi':
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy()
# Multi-worker configuration
print('num_replicas_in_sync = {}'.format(strategy.num_replicas_in_sync))
def make_dataset():
# Scaling Boston Housing data features
def scale(feature):
max = np.max(feature)
feature = (feature / max).astype(np.float)
return feature, max
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.boston_housing.load_data(
path="boston_housing.npz", test_split=0.2, seed=113
)
params = []
for _ in range(13):
x_train[_], max = scale(x_train[_])
x_test[_], _ = scale(x_test[_])
params.append(max)
# store the normalization (max) value for each feature
with tf.io.gfile.GFile(args.param_file, 'w') as f:
f.write(str(params))
return (x_train, y_train), (x_test, y_test)
# Build the Keras model
def build_and_compile_dnn_model():
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu', input_shape=(13,)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(1, activation='linear')
])
model.compile(
loss='mse',
optimizer=tf.keras.optimizers.RMSprop(learning_rate=args.lr))
return model
NUM_WORKERS = strategy.num_replicas_in_sync
# Here the batch size scales up by number of workers since
# `tf.data.Dataset.batch` expects the global batch size.
BATCH_SIZE = 16
GLOBAL_BATCH_SIZE = BATCH_SIZE * NUM_WORKERS
with strategy.scope():
# Creation of dataset, and model building/compiling need to be within
# `strategy.scope()`.
model = build_and_compile_dnn_model()
# Train the model
(x_train, y_train), (x_test, y_test) = make_dataset()
model.fit(x_train, y_train, epochs=args.epochs, batch_size=GLOBAL_BATCH_SIZE)
model.save(args.model_dir)
# + [markdown] id="tarball_training_script"
# #### Store training script on your Cloud Storage bucket
#
# Next, you package the training folder into a compressed tar ball, and then store it in your Cloud Storage bucket.
# + id="tarball_training_script"
# ! rm -f custom.tar custom.tar.gz
# ! tar cvf custom.tar custom
# ! gzip custom.tar
# ! gsutil cp custom.tar.gz $BUCKET_NAME/trainer_boston.tar.gz
# + [markdown] id="train_custom_job"
# ### Train the model
#
#
# Now start the training of your custom training job on Vertex AI. Use this helper function `create_custom_job`, which takes the following parameter:
#
# -`custom_job`: The specification for the custom job.
#
# The helper function calls job client service's `create_custom_job` method, with the following parameters:
#
# -`parent`: The Vertex AI location path to `Dataset`, `Model` and `Endpoint` resources.
# -`custom_job`: The specification for the custom job.
#
# You will display a handful of the fields returned in `response` object, with the two that are of most interest are:
#
# `response.name`: The Vertex AI fully qualified identifier assigned to this custom training job. You save this identifier for using in subsequent steps.
#
# `response.state`: The current state of the custom training job.
# + id="train_custom_job"
def create_custom_job(custom_job):
response = clients["job"].create_custom_job(parent=PARENT, custom_job=custom_job)
print("name:", response.name)
print("display_name:", response.display_name)
print("state:", response.state)
print("create_time:", response.create_time)
print("update_time:", response.update_time)
return response
response = create_custom_job(custom_job)
# + [markdown] id="job_id:response"
# Now get the unique identifier for the custom job you created.
# + id="job_id:response"
# The full unique ID for the custom job
job_id = response.name
# The short numeric ID for the custom job
job_short_id = job_id.split("/")[-1]
print(job_id)
# + [markdown] id="get_custom_job"
# ### Get information on a custom job
#
# Next, use this helper function `get_custom_job`, which takes the following parameter:
#
# - `name`: The Vertex AI fully qualified identifier for the custom job.
#
# The helper function calls the job client service's`get_custom_job` method, with the following parameter:
#
# - `name`: The Vertex AI fully qualified identifier for the custom job.
#
# If you recall, you got the Vertex AI fully qualified identifier for the custom job in the `response.name` field when you called the `create_custom_job` method, and saved the identifier in the variable `job_id`.
# + id="get_custom_job"
def get_custom_job(name, silent=False):
response = clients["job"].get_custom_job(name=name)
if silent:
return response
print("name:", response.name)
print("display_name:", response.display_name)
print("state:", response.state)
print("create_time:", response.create_time)
print("update_time:", response.update_time)
return response
response = get_custom_job(job_id)
# + [markdown] id="wait_training_complete:custom"
# # Deployment
#
# Training the above model may take upwards of 20 minutes time.
#
# Once your model is done training, you can calculate the actual time it took to train the model by subtracting `end_time` from `start_time`. For your model, we will need to know the location of the saved model, which the Python script saved in your local Cloud Storage bucket at `MODEL_DIR + '/saved_model.pb'`.
# + id="wait_training_complete:custom"
while True:
response = get_custom_job(job_id, True)
if response.state != aip.JobState.JOB_STATE_SUCCEEDED:
print("Training job has not completed:", response.state)
model_path_to_deploy = None
if response.state == aip.JobState.JOB_STATE_FAILED:
break
else:
if not DIRECT:
MODEL_DIR = MODEL_DIR + "/model"
model_path_to_deploy = MODEL_DIR
print("Training Time:", response.update_time - response.create_time)
break
time.sleep(60)
print("model_to_deploy:", model_path_to_deploy)
# + [markdown] id="load_saved_model"
# ## Load the saved model
#
# Your model is stored in a TensorFlow SavedModel format in a Cloud Storage bucket. Now load it from the Cloud Storage bucket, and then you can do some things, like evaluate the model, and do a prediction.
#
# To load, you use the TF.Keras `model.load_model()` method passing it the Cloud Storage path where the model is saved -- specified by `MODEL_DIR`.
# + id="load_saved_model"
import tensorflow as tf
model = tf.keras.models.load_model(MODEL_DIR)
# + [markdown] id="evaluate_custom_model:tabular"
# ## Evaluate the model
#
# Now let's find out how good the model is.
#
# ### Load evaluation data
#
# You will load the Boston Housing test (holdout) data from `tf.keras.datasets`, using the method `load_data()`. This will return the dataset as a tuple of two elements. The first element is the training data and the second is the test data. Each element is also a tuple of two elements: the feature data, and the corresponding labels (median value of owner-occupied home).
#
# You don't need the training data, and hence why we loaded it as `(_, _)`.
#
# Before you can run the data through evaluation, you need to preprocess it:
#
# x_test:
# 1. Normalize (rescaling) the data in each column by dividing each value by the maximum value of that column. This will replace each single value with a 32-bit floating point number between 0 and 1.
# + id="evaluate_custom_model:tabular,boston"
import numpy as np
from tensorflow.keras.datasets import boston_housing
(_, _), (x_test, y_test) = boston_housing.load_data(
path="boston_housing.npz", test_split=0.2, seed=113
)
def scale(feature):
max = np.max(feature)
feature = (feature / max).astype(np.float32)
return feature
# Let's save one data item that has not been scaled
x_test_notscaled = x_test[0:1].copy()
for _ in range(13):
x_test[_] = scale(x_test[_])
x_test = x_test.astype(np.float32)
print(x_test.shape, x_test.dtype, y_test.shape)
print("scaled", x_test[0])
print("unscaled", x_test_notscaled)
# + [markdown] id="perform_evaluation_custom"
# ### Perform the model evaluation
#
# Now evaluate how well the model in the custom job did.
# + id="perform_evaluation_custom"
model.evaluate(x_test, y_test)
# + [markdown] id="get_dataset_ststistics"
# ### Get dataset statistics
#
# The training script is designed to return dataset statistics you will need for serving predictions on data items that have not otherwise been preprocessed -- feature normalization, which is also referred to as rescaling. *Note*, that the `x_test` data was already preprocessed, so we don't need to do additional feature normalization if we use that data from `x_test`.
#
# Instead, we set aside a copy of one data item that was not feature normalized. We will use this subsequently when doing a prediction.
# + id="get_dataset_ststistics"
# Get the rescaling values,.
with tf.io.gfile.GFile(PARAM_FILE, "r") as f:
rescale = f.read()
# Convert string to floating point list
rescale = rescale.replace("[", "").replace("]", "")
rescale = [float(val) for val in rescale.split(",")]
print(rescale)
# + [markdown] id="serving_function_signature"
# ## Get the serving function signature
#
# You can get the signatures of your model's input and output layers by reloading the model into memory, and querying it for the signatures corresponding to each layer.
#
# When making a prediction request, you need to route the request to the serving function instead of the model, so you need to know the input layer name of the serving function -- which you will use later when you make a prediction request.
# + id="serving_function_signature"
loaded = tf.saved_model.load(model_path_to_deploy)
serving_input = list(
loaded.signatures["serving_default"].structured_input_signature[1].keys()
)[0]
print("Serving function input:", serving_input)
# + [markdown] id="upload_the_model"
# ### Upload the model
#
# Use this helper function `upload_model` to upload your model, stored in SavedModel format, up to the `Model` service, which will instantiate a Vertex AI `Model` resource instance for your model. Once you've done that, you can use the `Model` resource instance in the same way as any other Vertex AI `Model` resource instance, such as deploying to an `Endpoint` resource for serving predictions.
#
# The helper function takes the following parameters:
#
# - `display_name`: A human readable name for the `Endpoint` service.
# - `image_uri`: The container image for the model deployment.
# - `model_uri`: The Cloud Storage path to our SavedModel artificat. For this tutorial, this is the Cloud Storage location where the `trainer/task.py` saved the model artifacts, which we specified in the variable `MODEL_DIR`.
#
# The helper function calls the `Model` client service's method `upload_model`, which takes the following parameters:
#
# - `parent`: The Vertex AI location root path for `Dataset`, `Model` and `Endpoint` resources.
# - `model`: The specification for the Vertex AI `Model` resource instance.
#
# Let's now dive deeper into the Vertex AI model specification `model`. This is a dictionary object that consists of the following fields:
#
# - `display_name`: A human readable name for the `Model` resource.
# - `metadata_schema_uri`: Since your model was built without an Vertex AI `Dataset` resource, you will leave this blank (`''`).
# - `artificat_uri`: The Cloud Storage path where the model is stored in SavedModel format.
# - `container_spec`: This is the specification for the Docker container that will be installed on the `Endpoint` resource, from which the `Model` resource will serve predictions. Use the variable you set earlier `DEPLOY_GPU != None` to use a GPU; otherwise only a CPU is allocated.
#
# Uploading a model into a Vertex AI Model resource returns a long running operation, since it may take a few moments. You call response.result(), which is a synchronous call and will return when the Vertex AI Model resource is ready.
#
# The helper function returns the Vertex AI fully qualified identifier for the corresponding Vertex AI Model instance upload_model_response.model. You will save the identifier for subsequent steps in the variable model_to_deploy_id.
# + id="upload_the_model"
IMAGE_URI = DEPLOY_IMAGE
def upload_model(display_name, image_uri, model_uri):
model = {
"display_name": display_name,
"metadata_schema_uri": "",
"artifact_uri": model_uri,
"container_spec": {
"image_uri": image_uri,
"command": [],
"args": [],
"env": [{"name": "env_name", "value": "env_value"}],
"ports": [{"container_port": 8080}],
"predict_route": "",
"health_route": "",
},
}
response = clients["model"].upload_model(parent=PARENT, model=model)
print("Long running operation:", response.operation.name)
upload_model_response = response.result(timeout=180)
print("upload_model_response")
print(" model:", upload_model_response.model)
return upload_model_response.model
model_to_deploy_id = upload_model(
"boston-" + TIMESTAMP, IMAGE_URI, model_path_to_deploy
)
# + [markdown] id="get_model"
# ### Get `Model` resource information
#
# Now let's get the model information for just your model. Use this helper function `get_model`, with the following parameter:
#
# - `name`: The Vertex AI unique identifier for the `Model` resource.
#
# This helper function calls the Vertex AI `Model` client service's method `get_model`, with the following parameter:
#
# - `name`: The Vertex AI unique identifier for the `Model` resource.
# + id="get_model"
def get_model(name):
response = clients["model"].get_model(name=name)
print(response)
get_model(model_to_deploy_id)
# + [markdown] id="create_endpoint:custom"
# ## Deploy the `Model` resource
#
# Now deploy the trained Vertex AI custom `Model` resource. This requires two steps:
#
# 1. Create an `Endpoint` resource for deploying the `Model` resource to.
#
# 2. Deploy the `Model` resource to the `Endpoint` resource.
# + [markdown] id="create_endpoint"
# ### Create an `Endpoint` resource
#
# Use this helper function `create_endpoint` to create an endpoint to deploy the model to for serving predictions, with the following parameter:
#
# - `display_name`: A human readable name for the `Endpoint` resource.
#
# The helper function uses the endpoint client service's `create_endpoint` method, which takes the following parameter:
#
# - `display_name`: A human readable name for the `Endpoint` resource.
#
# Creating an `Endpoint` resource returns a long running operation, since it may take a few moments to provision the `Endpoint` resource for serving. You call `response.result()`, which is a synchronous call and will return when the Endpoint resource is ready. The helper function returns the Vertex AI fully qualified identifier for the `Endpoint` resource: `response.name`.
# + id="create_endpoint"
ENDPOINT_NAME = "boston_endpoint-" + TIMESTAMP
def create_endpoint(display_name):
endpoint = {"display_name": display_name}
response = clients["endpoint"].create_endpoint(parent=PARENT, endpoint=endpoint)
print("Long running operation:", response.operation.name)
result = response.result(timeout=300)
print("result")
print(" name:", result.name)
print(" display_name:", result.display_name)
print(" description:", result.description)
print(" labels:", result.labels)
print(" create_time:", result.create_time)
print(" update_time:", result.update_time)
return result
result = create_endpoint(ENDPOINT_NAME)
# + [markdown] id="endpoint_id:result"
# Now get the unique identifier for the `Endpoint` resource you created.
# + id="endpoint_id:result"
# The full unique ID for the endpoint
endpoint_id = result.name
# The short numeric ID for the endpoint
endpoint_short_id = endpoint_id.split("/")[-1]
print(endpoint_id)
# + [markdown] id="instance_scaling"
# ### Compute instance scaling
#
# You have several choices on scaling the compute instances for handling your online prediction requests:
#
# - Single Instance: The online prediction requests are processed on a single compute instance.
# - Set the minimum (`MIN_NODES`) and maximum (`MAX_NODES`) number of compute instances to one.
#
# - Manual Scaling: The online prediction requests are split across a fixed number of compute instances that you manually specified.
# - Set the minimum (`MIN_NODES`) and maximum (`MAX_NODES`) number of compute instances to the same number of nodes. When a model is first deployed to the instance, the fixed number of compute instances are provisioned and online prediction requests are evenly distributed across them.
#
# - Auto Scaling: The online prediction requests are split across a scaleable number of compute instances.
# - Set the minimum (`MIN_NODES`) number of compute instances to provision when a model is first deployed and to de-provision, and set the maximum (`MAX_NODES) number of compute instances to provision, depending on load conditions.
#
# The minimum number of compute instances corresponds to the field `min_replica_count` and the maximum number of compute instances corresponds to the field `max_replica_count`, in your subsequent deployment request.
# + id="instance_scaling"
MIN_NODES = 1
MAX_NODES = 1
# + [markdown] id="deploy_model:dedicated"
# ### Deploy `Model` resource to the `Endpoint` resource
#
# Use this helper function `deploy_model` to deploy the `Model` resource to the `Endpoint` resource you created for serving predictions, with the following parameters:
#
# - `model`: The Vertex AI fully qualified model identifier of the model to upload (deploy) from the training pipeline.
# - `deploy_model_display_name`: A human readable name for the deployed model.
# - `endpoint`: The Vertex AI fully qualified endpoint identifier to deploy the model to.
#
# The helper function calls the `Endpoint` client service's method `deploy_model`, which takes the following parameters:
#
# - `endpoint`: The Vertex AI fully qualified `Endpoint` resource identifier to deploy the `Model` resource to.
# - `deployed_model`: The requirements specification for deploying the model.
# - `traffic_split`: Percent of traffic at the endpoint that goes to this model, which is specified as a dictionary of one or more key/value pairs.
# - If only one model, then specify as **{ "0": 100 }**, where "0" refers to this model being uploaded and 100 means 100% of the traffic.
# - If there are existing models on the endpoint, for which the traffic will be split, then use `model_id` to specify as **{ "0": percent, model_id: percent, ... }**, where `model_id` is the model id of an existing model to the deployed endpoint. The percents must add up to 100.
#
# Let's now dive deeper into the `deployed_model` parameter. This parameter is specified as a Python dictionary with the minimum required fields:
#
# - `model`: The Vertex AI fully qualified model identifier of the (upload) model to deploy.
# - `display_name`: A human readable name for the deployed model.
# - `disable_container_logging`: This disables logging of container events, such as execution failures (default is container logging is enabled). Container logging is typically enabled when debugging the deployment and then disabled when deployed for production.
# - `dedicated_resources`: This refers to how many compute instances (replicas) that are scaled for serving prediction requests.
# - `machine_spec`: The compute instance to provision. Use the variable you set earlier `DEPLOY_GPU != None` to use a GPU; otherwise only a CPU is allocated.
# - `min_replica_count`: The number of compute instances to initially provision, which you set earlier as the variable `MIN_NODES`.
# - `max_replica_count`: The maximum number of compute instances to scale to, which you set earlier as the variable `MAX_NODES`.
#
# #### Traffic Split
#
# Let's now dive deeper into the `traffic_split` parameter. This parameter is specified as a Python dictionary. This might at first be a tad bit confusing. Let me explain, you can deploy more than one instance of your model to an endpoint, and then set how much (percent) goes to each instance.
#
# Why would you do that? Perhaps you already have a previous version deployed in production -- let's call that v1. You got better model evaluation on v2, but you don't know for certain that it is really better until you deploy to production. So in the case of traffic split, you might want to deploy v2 to the same endpoint as v1, but it only get's say 10% of the traffic. That way, you can monitor how well it does without disrupting the majority of users -- until you make a final decision.
#
# #### Response
#
# The method returns a long running operation `response`. We will wait sychronously for the operation to complete by calling the `response.result()`, which will block until the model is deployed. If this is the first time a model is deployed to the endpoint, it may take a few additional minutes to complete provisioning of resources.
# + id="deploy_model:dedicated"
DEPLOYED_NAME = "boston_deployed-" + TIMESTAMP
def deploy_model(
model, deployed_model_display_name, endpoint, traffic_split={"0": 100}
):
if DEPLOY_GPU:
machine_spec = {
"machine_type": DEPLOY_COMPUTE,
"accelerator_type": DEPLOY_GPU,
"accelerator_count": DEPLOY_NGPU,
}
else:
machine_spec = {
"machine_type": DEPLOY_COMPUTE,
"accelerator_count": 0,
}
deployed_model = {
"model": model,
"display_name": deployed_model_display_name,
"dedicated_resources": {
"min_replica_count": MIN_NODES,
"max_replica_count": MAX_NODES,
"machine_spec": machine_spec,
},
"disable_container_logging": False,
}
response = clients["endpoint"].deploy_model(
endpoint=endpoint, deployed_model=deployed_model, traffic_split=traffic_split
)
print("Long running operation:", response.operation.name)
result = response.result()
print("result")
deployed_model = result.deployed_model
print(" deployed_model")
print(" id:", deployed_model.id)
print(" model:", deployed_model.model)
print(" display_name:", deployed_model.display_name)
print(" create_time:", deployed_model.create_time)
return deployed_model.id
deployed_model_id = deploy_model(model_to_deploy_id, DEPLOYED_NAME, endpoint_id)
# + [markdown] id="make_prediction"
# ## Make a online prediction request
#
# Now do a online prediction to your deployed model.
# + [markdown] id="get_test_item:test"
# ### Get test item
#
# You will use an example out of the test (holdout) portion of the dataset as a test item.
# + id="get_test_item:test,tabular"
test_item = x_test[0]
test_label = y_test[0]
print(test_item.shape)
# + [markdown] id="send_prediction_request:tabular"
# ### Send the prediction request
#
# Ok, now you have a test data item. Use this helper function `predict_data`, which takes the parameters:
#
# - `data`: The test data item as a numpy 1D array of floating point values.
# - `endpoint`: The Vertex AI fully qualified identifier for the `Endpoint` resource where the `Model` resource was deployed.
# - `parameters_dict`: Additional parameters for serving.
#
# This function uses the prediction client service and calls the `predict` method with the parameters:
#
# - `endpoint`: The Vertex AI fully qualified identifier for the `Endpoint` resource where the `Model` resource was deployed.
# - `instances`: A list of instances (data items) to predict.
# - `parameters`: Additional parameters for serving.
#
# To pass the test data to the prediction service, you package it for transmission to the serving binary as follows:
#
# 1. Convert the data item from a 1D numpy array to a 1D Python list.
# 2. Convert the prediction request to a serialized Google protobuf (`json_format.ParseDict()`)
#
#
# Each instance in the prediction request is a dictionary entry of the form:
#
# {input_name: content}
#
# - `input_name`: the name of the input layer of the underlying model.
# - `content`: The data item as a 1D Python list.
#
# Since the `predict()` service can take multiple data items (instances), you will send your single data item as a list of one data item. As a final step, you package the instances list into Google's protobuf format -- which is what we pass to the `predict()` service.
#
# The `response` object returns a list, where each element in the list corresponds to the corresponding image in the request. You will see in the output for each prediction:
#
# - `predictions` -- the predicated median value of a house in units of 1K USD.
# + id="send_prediction_request:tabular"
def predict_data(data, endpoint, parameters_dict):
parameters = json_format.ParseDict(parameters_dict, Value())
# The format of each instance should conform to the deployed model's prediction input schema.
instances_list = [{serving_input: data.tolist()}]
instances = [json_format.ParseDict(s, Value()) for s in instances_list]
response = clients["prediction"].predict(
endpoint=endpoint, instances=instances, parameters=parameters
)
print("response")
print(" deployed_model_id:", response.deployed_model_id)
predictions = response.predictions
print("predictions")
for prediction in predictions:
print(" prediction:", prediction)
predict_data(test_item, endpoint_id, None)
# + [markdown] id="undeploy_model"
# ## Undeploy the `Model` resource
#
# Now undeploy your `Model` resource from the serving `Endpoint` resoure. Use this helper function `undeploy_model`, which takes the following parameters:
#
# - `deployed_model_id`: The model deployment identifier returned by the endpoint service when the `Model` resource was deployed to.
# - `endpoint`: The Vertex AI fully qualified identifier for the `Endpoint` resource where the `Model` is deployed to.
#
# This function calls the endpoint client service's method `undeploy_model`, with the following parameters:
#
# - `deployed_model_id`: The model deployment identifier returned by the endpoint service when the `Model` resource was deployed.
# - `endpoint`: The Vertex AI fully qualified identifier for the `Endpoint` resource where the `Model` resource is deployed.
# - `traffic_split`: How to split traffic among the remaining deployed models on the `Endpoint` resource.
#
# Since this is the only deployed model on the `Endpoint` resource, you simply can leave `traffic_split` empty by setting it to {}.
# + id="undeploy_model"
def undeploy_model(deployed_model_id, endpoint):
response = clients["endpoint"].undeploy_model(
endpoint=endpoint, deployed_model_id=deployed_model_id, traffic_split={}
)
print(response)
undeploy_model(deployed_model_id, endpoint_id)
# + [markdown] id="cleanup"
# # Cleaning up
#
# To clean up all GCP resources used in this project, you can [delete the GCP
# project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
#
# Otherwise, you can delete the individual resources you created in this tutorial:
#
# - Dataset
# - Pipeline
# - Model
# - Endpoint
# - Batch Job
# - Custom Job
# - Hyperparameter Tuning Job
# - Cloud Storage Bucket
# + id="cleanup"
delete_dataset = True
delete_pipeline = True
delete_model = True
delete_endpoint = True
delete_batchjob = True
delete_customjob = True
delete_hptjob = True
delete_bucket = True
# Delete the dataset using the Vertex AI fully qualified identifier for the dataset
try:
if delete_dataset and "dataset_id" in globals():
clients["dataset"].delete_dataset(name=dataset_id)
except Exception as e:
print(e)
# Delete the training pipeline using the Vertex AI fully qualified identifier for the pipeline
try:
if delete_pipeline and "pipeline_id" in globals():
clients["pipeline"].delete_training_pipeline(name=pipeline_id)
except Exception as e:
print(e)
# Delete the model using the Vertex AI fully qualified identifier for the model
try:
if delete_model and "model_to_deploy_id" in globals():
clients["model"].delete_model(name=model_to_deploy_id)
except Exception as e:
print(e)
# Delete the endpoint using the Vertex AI fully qualified identifier for the endpoint
try:
if delete_endpoint and "endpoint_id" in globals():
clients["endpoint"].delete_endpoint(name=endpoint_id)
except Exception as e:
print(e)
# Delete the batch job using the Vertex AI fully qualified identifier for the batch job
try:
if delete_batchjob and "batch_job_id" in globals():
clients["job"].delete_batch_prediction_job(name=batch_job_id)
except Exception as e:
print(e)
# Delete the custom job using the Vertex AI fully qualified identifier for the custom job
try:
if delete_customjob and "job_id" in globals():
clients["job"].delete_custom_job(name=job_id)
except Exception as e:
print(e)
# Delete the hyperparameter tuning job using the Vertex AI fully qualified identifier for the hyperparameter tuning job
try:
if delete_hptjob and "hpt_job_id" in globals():
clients["job"].delete_hyperparameter_tuning_job(name=hpt_job_id)
except Exception as e:
print(e)
if delete_bucket and "BUCKET_NAME" in globals():
# ! gsutil rm -r $BUCKET_NAME
| ai-platform-unified/notebooks/unofficial/gapic/custom/showcase_custom_tabular_regression_online.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Splitting the katakana from romaji in Japanese name
# import library
import pandas as pd
import re
# load dataset
df = pd.read_csv('./pokemon.csv')
# excerpt the column
jpn = df.japanese_name
# + tags=[]
# select japanese character substrings
jpn_1 = []
for i in jpn:
jpn_1.append(re.split('[a-zA-Z]+', i))
jpn_2 = []
for i in jpn_1:
jpn_2.append(i[-1])
katakana = []
for i in jpn_2:
if re.match('\W', i):
i = i[1:]
katakana.append(i)
else:
katakana.append(i)
# + tags=[]
# remove the japanese character substrings = romaji
romaji = []
for i in range(len(jpn)):
romaji.append(jpn[i].replace(katakana[i], ''))
# +
# combine the 2 lists to be a dataframe
dic = {
'id': [i for i in range(1, len(df)+1)],
'pokedex_no': df.pokedex_number,
'katakana': katakana,
'romaji': romaji
}
df = pd.DataFrame(dic)
# export as csv
df.to_csv(path_or_buf='jpn_name.csv', index=False)
# -
df.head()
| pokemon/pokemon_jpn.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/matonima/Simple-codes/blob/main/power.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="ee2262a9cO_9" outputId="c2103477-66a2-44f1-e9ce-15dc61d49af1"
import numpy as np
def power(x, n):
if n==0:
y=1
elif n<0:
n=n*(-1)
z=[x]*n
print(z)
y=np.prod(z)
y=1/y
else:
z=[x]*n
print(z)
y=np.prod(z)
return y
power(2,-5)
| power.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from my_functions1 import extractor, extractorAurora
# ## Extraction ##
qw_str = "What is better bread or pizza ?"
# +
import torch
my_extractor = extractor(model_name = 'bertttt.hdf5', my_device = 7)
print ("loaded extractor")
my_extractor_aurora = extractorAurora(model_name = 'Aurora.hdf5', my_device = 7)
print ("loaded extractor")
# -
import nltk
def create_sequence_from_sentence(str_sentences):
return [nltk.word_tokenize(str_sentence) for str_sentence in str_sentences]
words = create_sequence_from_sentence([qw_str])
tags = my_extractor.model.predict_tags_from_words(words)
words, tags
words = create_sequence_from_sentence([qw_str])
tags = my_extractor_aurora.model.predict_tags_from_words(words)
words, tags
# ## Or
my_extractor.from_string(qw_str)
obj1, obj2, pred = my_extractor.get_params()
my_extractor_aurora.from_string(qw_str)
obj1, obj2, pred = my_extractor_aurora.get_params()
obj1, obj2, pred
# ## Evaluation ##
from src.evaluators.evaluator_base import EvaluatorBase
from src.evaluators.evaluator_f1_macro_token_level import EvaluatorF1MacroTokenLevel # choose evaluator type
# +
from src.classes.datasets_bank import DatasetsBank, DatasetsBankSorted
from src.data_io.data_io_connl_ner_2003 import DataIOConnlNer2003
data_io = DataIOConnlNer2003()
word_sequences_test, tag_sequences_test = data_io.read_data(fn='your_connll_targets.tsv', verbose=True)
datasets_bank = DatasetsBank(verbose=True)
#datasets_bank.add_train_sequences(word_sequences_train, tag_sequences_train)
#datasets_bank.add_dev_sequences(word_sequences_dev, tag_sequences_dev)
datasets_bank.add_test_sequences(word_sequences_test, tag_sequences_test)
# -
word_sequences=datasets_bank.word_sequences_test
targets_tag_sequences=datasets_bank.tag_sequences_test
with open('your_predicted_tags.txt') as lines:
outputs_tag_sequences = []
for line in lines:
outputs_tag_sequences.append(line.strip().split(', '))
new_ts = []
for line in tag_sequences_test:
for ind, elem in enumerate(line):
if (elem == 'NONE'):
line[ind] = 'O'
new_ts.append(line)
tag_sequences_test=new_ts
evaluator = EvaluatorF1MacroTokenLevel()
evaluator.get_evaluation_score(tag_sequences_test, outputs_tag_sequences, word_sequences)
| object_extraction_evaluation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# orphan: true
# ---
# # Examples
#
# This document is intended to show run files that provide
# techniques for using certain features in combination, or examples of solving canonical problems in OpenMDAO.
# If you need to learn the basics of how things work, please see the :ref:`User Guide <UserGuide>`.
#
# - [Optimizing a Paraboloid – The TL;DR Version](tldr_paraboloid.ipynb)
# - [Optimizing a Paraboloid](paraboloid.ipynb)
# - [Optimizing an Actuator Disk Model to Find Betz Limit for Wind Turbines](betz_limit.ipynb)
# - [Hohmann Transfer Example - Optimizing a Spacecraft Manuever](hohmann_transfer/hohmann_transfer.ipynb)
# - [Kepler’s Equation Example - Solving an Implicit Equation](keplers_equation.ipynb)
# - [Converging an Implicit Model: Nonlinear circuit analysis](circuit_analysis_examples.ipynb)
# - [Optimizing the Thickness Distribution of a Cantilever Beam Using the Adjoint Method](beam_optimization_example.ipynb)
# - [Revisiting the Beam Problem - Minimizing Stress with KS Constraints and BSplines](beam_optimization_example_part_2.ipynb)
# - [Simple Optimization using Simultaneous Derivatives](simul_deriv_example.ipynb)
#
| openmdao/docs/openmdao_book/examples/examples.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. Convolution and Blurring
# +
import cv2 # importing the opencv module
import numpy as np
# -
# Now reading the image that we have
img=cv2.imread("obama.jpg")
print(img) # Now we can see that by using opencv.imread function we can read the images
# +
# Now let us view the image by using imshow function
cv2.imshow("img",img) # This will display the image
cv2.waitKey() # This function will hold the screen/display like we use getch() in c/c++ language
cv2.destroyAllWindows() # This function is very important to use because this function will close/shut down all the display screen
# we cam also say that cv2.destroyAllWindows will act like closing all opened files
# -
# # the snapshot of the above output
# 
# # Now lets do Convolution on our image
# ### A Convolution is a mathematical operation performed on two functions producing a third function which is typically a modified version of one of the original function
#
# output_image(modified image) = original_image x kernel_function
#
# Where kernel_function is a matrix of our choice which have shape of any (2x3 or 5x5 or 7x7 and so on )
# Now for performing convolution operation we have to change our 3d image to 2d image ie from colored image to black n white
#
#
#
img=cv2.imread("obama.jpg",0) # by putting 0 in imread function we can see black n white output of our colored image
img.shape # lets us see shape of img and we find that ys its actually 2d
cv2.imshow("img",img)
cv2.waitKey()
cv2.destroyAllWindows()
# # This is the snapshot of above code's output
# 
# +
# lets do convolution
# Here the img is our original image and kernel is kernel function and the ouput image will be modified version of original image
# +
# Creating our 3 x 3 kernel/filter
kernel_3x3 = np.ones((3, 3), np.float32) / 9 # we divide out kernel matrix with 9 so that we can normalized our kernel ( scaled)
# We use the cv2.fitler2D to convolve the kernal with an image
blurred = cv2.filter2D(img, -1, kernel_3x3)
cv2.imshow('3x3 Kernel Blurring', blurred)
cv2.waitKey(0)
# Creating our 7 x 7 kernel
kernel_7x7 = np.ones((7, 7), np.float32) / 49 # normalized by dividing the kernel with 49 so that there elements summed up to 1
# We use the cv2.fitler2D to convolve the kernal with an image
blurred2 = cv2.filter2D(img, -1, kernel_7x7)
cv2.imshow('7x7 Kernel Blurring', blurred2)
cv2.waitKey(0)
# Creating our 11 x 11 kernel
kernel_11x11=np.ones((11,11),np.float32)/121 # normalized by dividing kernel by 121
# We use the cv2.fitler2D to convolve the kernal with an image
blurred3= cv2.filter2D(img, -1, kernel_11x11)
cv2.imshow('11x11 Kernel Blurring', blurred3)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# # Snapshot of above cell's output
# 
# # Blurring by using cv2 functions and the convolution concept
# Now above we make our kernel/filter and then do convolution by using filter2d function. And there are various kernels that are designed for some specific purpose like blurring, sharpening, detecting edges and so on
#
# Now we use the inbuilt cv2 function that has built in kernel and will automatically perform convolution. Such functions are :
# blur(), GaussianBlur(), medianBlur(), bilateralFilter(). Lets use all and see the result
# +
# Averaging done by convolving the image with a normalized box filter(ie kernel that designed for this bluring purpose)
# This takes the pixels under the box(kernel) and replaces the central element
# Box(kernel) size needs to odd and positive
blur = cv2.blur(img, (3,3))
cv2.imshow('Averaging', blur)
cv2.waitKey(0)
# Instead of box filter, gaussian kernel
Gaussian = cv2.GaussianBlur(img, (7,7), 0)
cv2.imshow('Gaussian Blurring', Gaussian)
cv2.waitKey(0)
# Takes median of all the pixels under kernel area and central
# element is replaced with this median value
median = cv2.medianBlur(img, 5)
cv2.imshow('Median Blurring', median)
cv2.waitKey(0)
# Bilateral is very effective in noise removal while keeping edges sharp
bilateral = cv2.bilateralFilter(img, 9, 75, 75)
cv2.imshow('Bilateral Blurring', bilateral)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# # Snapshot of above ouput
# 
# # 2. Sharpening
# ### By altering our kernels we can implement sharpening, which has the effects of in strengthening or emphasizing edges in an image.
# +
# Create our shapening kernel, we don't normalize since the
# the values in the matrix sum to 1
kernel_sharpening = np.array([[-1,-1,-1],
[-1,9,-1],
[-1,-1,-1]])
# applying different kernels to the input image
sharpened = cv2.filter2D(img, -1, kernel_sharpening)
cv2.imshow('Image Sharpening', sharpened)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# # Snapshot of output
# 
# +
# Thanks
# for any query u can dm me on linkedin : https://www.linkedin.com/in/gurdeep-singh-bhatia-319441171/
| gurdeepsingh_openCV_blurring_and_sharpening.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Repositorio GCM-TFG
# ## Problemas de optimización en el modelado de materia oscura galáctica
#
# En este repositorio se implementan las funciones necesarias para tratar el problema de modelado de componentes galácticas, en particular el de la componente de materia oscura.
# A continuación se detallan los ficheros y sus respectivas funciones, así como los tipos y estructuras de datos que usan.
# ### `data.py`
# Contiene la lista `galaxlist` de galaxias a explorar. Para cada galaxia se abre y lee su respectivo archivo `.arff`, en el que cada fila corresponde a una partícula que se ha observado que gira en torno a la galaxia. Para cada una de estas partículas se tienen los siguientes datos:
# * Radio de giro en torno a la galaxia
# * Velocidad rotacional de la partícula
# * Errores
# * Velocidad debida a la materia bariónica bariónica
#
# A partir de estos datos construye el diccionario `galaxies` donde se asocia cada galaxia con los datos que se tienen de ella:
# * `R`: Vector de radios de giro de las diferentes partículas observadas
# * `vrot`: Vector de velocidades rotacionales
# * `errs`: Vector de errores
# * `vbary`: Vector de velocidades debidas a la materia bariónica
#
# A continuación se muestra un ejemplo de lectura y recogida de datos de una de las 23 galaxias estudiadas.
# +
from scipy.io import arff
import numpy as np
galaxlist = ["DDO43"]
galaxies = {}
for i in galaxlist:
fp = open("galaxies/"+i+".arff")
dt, metadt = arff.loadarff(fp)
data = []
for d in dt.tolist():
data.append(np.asarray(d))
data = np.asarray(data)
galaxies[i] = {
"R": data[:, 0] * 1000,
"vrot": abs(data[:, 1]),
"errs": data[:, 3],
"vbary": np.sqrt(data[:, 4] ** 2 + data[:, 5] ** 2)
}
fp.close()
# -
# Vector de radios de la galaxia DDO43:
print(galaxies["DDO43"]["R"])
# Vector de velocidades rotacionales de la galaxia DDO43:
print(galaxies["DDO43"]["vrot"])
# Vector de errores de la galaxia DDO43:
print(galaxies["DDO43"]["errs"])
# Vector de velocidades debidas a la materia bariónica de la galaxia DDO43:
print(galaxies["DDO43"]["vbary"])
# En `data.py` también se declaran las constantes $\nu$ (número de parámetros libres) y $CteDim$ (constante de adimensionalización).
# * Puesto que sólo trabajaremos con los perfiles ISO, BUR y NFW, $\nu = 2$.
# * $CteDim = \frac{10000}{4.51697\times3.0856776^ 2}$.
#
# A continuación creamos el diccionario `galaxdata`, donde almacenaremos los datos que más usaremos, en este caso de la galaxia DDO43.
# +
import commonFunctions as cf
import data as dt
galaxdata = {
"radii": np.array([]),
"vrot": np.array([]),
"vbary": np.array([]),
"weights": np.array([]),
"CteDim": dt.CteDim,
"totalnullvbary": False,
"somenullvbary": False,
"vones": np.array([]),
"vv": np.array([]),
"vvbary": np.array([]),
"profile": '',
"graphic": False
}
for i in galaxlist:
radii = galaxies[i]["R"]
galaxdata["radii"] = radii
vrot = galaxies[i]["vrot"]
galaxdata["vrot"] = vrot
vbary = galaxies[i]["vbary"]
galaxdata["vbary"] = vbary
n = len(radii)
vones = np.ones(n)
galaxdata["vones"] = vones
weights = 1 / ((n - dt.nu) * galaxies[i]["errs"] ** 2)
galaxdata["weights"] = weights
totalnullvbary = np.sum(vbary) == 0
galaxdata["totalnullvbary"] = totalnullvbary
somenullvbary = round(np.prod(vbary)) == 0
galaxdata["somenullvbary"] = somenullvbary
vv = cf.vv(galaxdata)
galaxdata["vv"] = vv
vvbary = cf.vvbary(galaxdata)
galaxdata["vvbary"] = vvbary
# galaxdata["graphic"] = True
# -
# ### `commonFunctions.py`
# Aquí se definen algunas funciones comunes a todas las galaxias y para cualquiera de los perfiles ISO, BUR y NFW.
# * `WeighProd(x, y, sigmas)`: Dados los arrays `x` e `y`, y los pesos `sigmas` devuelve el producto escalar pesado definido en (15).
# * `ginf(x, model)`: Dados un array `x` y un perfil de densidad `model`, devuelve el valor de g cuando s tiende a infinito, definida en la Tabla 2.
# * `eqVLimInf(t, ginf, galaxdata)`: Dados el parámetro `t`, el valor de g definida en la Tabla 2 cuando s tiende a infinito y el diccionario `galaxdata` de datos de la galaxia, devuelve la ecuación definida en (33).
# * `g0(x, model)`: Dado un array `x` y un perfil de densidad `model`, devuelve el valor de g cuando s tiende a cero, definida en la Tabla 2.
# * `eqVLim0(t, g0, galaxdata)`: Dados el parámetro `t`, el valor de g definida en la Tabla 2 cuando s tiende a cero y el diccionario `galaxdata` de datos de la galaxia, devuelve la ecuación definida en (35).
# * `v(r, s, model)`: Dado un array de radios `r`, un array de inversos de parámetros de escalas `s` y un perfil de densidad de materia oscura `model`, devuelve el valor de la ecuación definida en (18) para estos parámetros.
# * `chiquad(rho, s, galaxdata)`: Dados un array de parámetro de densidad central `rho`, un array de de inversos de parámetros de escala `s` y un diccionario de datos de una galaxia `galaxdata`, devuelve el valor de la ecuación definida en (16) para estos parámetros.
# * `rho(s, galaxdata)`: Dados un array de inversos de parámetros de escala `s` y un diccionario de datos de una galaxia `galaxdata`, devuelve el valor de rho estudiado en la Proposición 1.
# * `alphaMV(s, galaxdata)`: Dados un array de inversos de parámetros de escala `s` y un diccionario de datos de una galaxia `galaxdata`, devuelve el valor de la ecuación (24) para estos parámetros.
# * `vv(galaxdata)`: Dado un diccionario de datos de una galaxia `galaxdata`, devuelve el producto escalar pesado de la velocidad rotacional.
# * `vvbary(galaxdata)`: Dado un diccionario de datos de una galaxia `galaxdata`, devuelve el el producto escalar pesado de la velocidad debida a la materia bariónica.
# * `phi(s, galaxdata)`: Dados un array de inversos de parámetros de escala `s` y un diccionario de datos de una galaxia `galaxdata`, devuelve el valor de la función varphi y el valor de la función rho para estos parámetros.
#
# ### `calLimits.py`
# Aquí se define la función que calcula los límites de varphi en cero y en infinito, usando el Lema 1.
# * `calLimits(galaxdata)`: Dado un diccionario de datos de una galaxia `galaxdata`, devuelve un array con los valores de los límites de varphi en cero y en infinito.
# Calculamos los límites para la galaxia DDO43 con el perfil ISO.
# +
from calLimits import *
galaxdata["profile"] = "ISO"
varphiLim0, varphiLimInf = calLimits(galaxdata)
# -
# El límite de varphi cuando s tiende a 0 para la galaxia DDO43 con el perfil ISO es
print(varphiLim0)
# El límite de varphi cuando s tiende a infinito para la galaxia DDO43 con el perfil ISO es
print(varphiLimInf)
# Calculamos los límites para la galaxia DDO43 con el perfil BUR.
galaxdata["profile"] = "BUR"
varphiLim0, varphiLimInf = calLimits(galaxdata)
# El límite de varphi cuando s tiende a 0 para la galaxia DDO43 con el perfil BUR es
print(varphiLim0)
# El límite de varphi cuando s tiende a infinito para la galaxia DDO43 con el perfil BUR es
print(varphiLimInf)
# Calculamos los límites para la galaxia DDO43 con el perfil NFW.
galaxdata["profile"] = "NFW"
varphiLim0, varphiLimInf = calLimits(galaxdata)
# El límite de varphi cuando s tiende a 0 para la galaxia DDO43 con el perfil NFW es
print(varphiLim0)
# + active=""
# El límite de varphi cuando s tiende a infinito para la galaxia DDO43 con el perfil NFW es
# -
print(varphiLimInf)
# ### `intervalMinim.py`
# Aquí se definen las distintas funciones que forman el algoritmo de reducción del intervalo de búsqueda. Se especifica una tolerancia `tol`$=10^{-2}$ y se fija la semilla del random a 1.
# * `inftestElementwise(eval)`: Dado un array de puntos vecinos al candidato a extremo inferior del intervalo `eval`, devuelve dos booleanos. El primero indica si los puntos vecinos de la derecha cumplen la ecuación (40) y el segundo indica si la cumplen los vecinos de la izquierda.
# * `suptestElementwise(eval)`: Dado un array de puntos vecinos al candidato a extremo superior del intervalo `eval`, devuelve dos booleanos. El primero indica si los puntos vecinos de la izquierda cumplen la ecuación (39) y el segundo indica si la cumplen los vecinos de la derecha.
# * `inftestElementsum(eval)`: Dado un array de puntos vecinos al candidato a extremo inferior del intervalo `eval`, devuelve dos booleanos. El primero indica si la suma de los puntos vecinos de la derecha cumplen la ecuación (40) y el segundo indica si la cumple la suma de los vecinos de la izquierda.
# * `suptestElementsum(eval)`: Dado un array de puntos vecinos al candidato a extremo superior del intervalo `eval`, devuelve dos booleanos. El primero indica si la suma de los puntos vecinos de la izquierda cumplen la ecuación (39) y el segundo indica si la cumple la suma de los vecinos de la derecha.
# * `infConditions(test1, test2, intervalinf, stop, i)`: Dados un booleano `test1` indicando si los puntos de la derecha (o su suma) cumplen (40), un booleano `test2` indicando si los puntos de la izquierda (o su suma) cumplen (40), un candidato a extremo inferior del intervalo `intervalinf`, un parámetro que controla la condición de parada del algoritmo `stop` y un parámetro `i` que almacena el anterior candidato a extremo inferior en caso de que estemos acercándonos a estar en condición de parada, la función decide si el candidato cumple la condición óptima y en qué dirección moverse.
#
# Supongamos que estamos evaluando la situación de un candidato `intervalinf = 1.5` a extremo inferior. Sus vecinos de la derecha no cumplen (40), y sus vecinos de la izquierda tampoco, es decir, `test1 = False` y `test2 = False`. No estamos en condición de parada, `stop = False`, y el candidato anterior a extremo inferior `i` es cualquiera, supongamos `i=2.0`.
# +
from intervalMinim import *
test1 = False
test2 = False
stop = False
i = 2.0
intervalinf = 1.5
new_intervalinf, direction, stop, i = infConditions(test1, test2, intervalinf, stop, i)
# -
# ¿En qué dirección debemos movernos?
print(direction)
# El nuevo candidato a extremo inferior es
print(new_intervalinf)
# ¿Estamos en condición de parada?
print(stop)
# El candidato anterior no ha cambiado, el valor de i sigue siendo
print(i)
# Supongamos ahora que estamos evaluando la situación de un candidato `intervalinf = 1.2` a extremo inferior que no está en condición de parada, `stop = False`. Sus vecinos de la izquierda cumplen (40), pero sus vecinos de la derecha no, es decir, `test2 = True` y `test1 = False`. El candidato anterior a extremo inferior `i`es cualquiera, supongamos `i=1.25`.
# +
test1 = False
test2 = True
stop = False
i = 1.28
intervalinf = 1.2
new_intervalinf, direction, stop, i = infConditions(test1, test2, intervalinf, stop, i)
# -
# ¿En qué dirección debemos movernos?
print(direction)
# Nos movemos para comprobar en la siguiente iteración que los puntos en esta dirección siguen cumpliendo (40). En la siguiente iteración estudiaremos el punto
print(new_intervalinf)
# ¿Estamos en condición de parada?
print(stop)
# El candidato anterior ha cambiado, ahora el valor de i es
print(i)
# Ahora, para alcanzar por completo la condicón óptima, los valores a la izquierda del candidato `i = 1.2` deberían cumplir (40). Supongamos que sí: `test1 = True` y `test2 = True`.
# +
test1 = True
test2 = True
intervalinf, direction, stop, i = infConditions(test1, test2, new_intervalinf, stop, i)
# -
# Ahora la dirección es
print(direction)
# Esta dirección indica que hemos alcanzaco la condición de parada. Recuperamos de i el que era nuestro candidato. Ahora intervalinf tiene el valor
print(intervalinf)
# * `supConditions(test1, test2, intervalsup, stop, i)`: Dados un booleano `test1` indicando si los puntos de la izquierda (o su suma) cumplen (39), un booleano `test2` indicando si los puntos de la derecha (o su suma) cumplen (39), un candidato a extremo superior del intervalo `intervalsup`, un parámetro que controla la condición de parada del algoritmo `stop` y un parámetro `i` que almacena el anterior candidato a extremo superior, la función decide si el candidato cumple la condición óptima y en qué dirección moverse.
# * `jumpCondition(twoclosevar, varLimdistance, interval, direction, k)`: Dados un booleano `twoclosevar` indicando si los dos últimos candidatos están "cerca", un valor `varLimdistance` indicando a qué distancia está el candidato del valor del límite, un candidato `interval`, una dirección (-1, 0 o 1) `direction` y un contador de la condición de salto `k`, la función devuelve si ha habido salto y, en caso de que sí, cuál es el nuevo candidato.
# * `intervalMin(varphiLim0, varphiLimInf, galaxdata)`: Dados el valor del límite de varphi en cero `varphiLim0`, el valor del límite de varphi en infinito `varphiLimInf` y un diccionario de datos de una galaxia `galaxdata`, la función realiza la reducción del intervalo de búsqueda. Primero busca el extremo inferior que cumple alguna condición satisfactoria y luego el extremo superior, análogamente. Finalmente devuelve los valores propuestos como extremos, el valor mínimo de varphi encontrado en la búsqueda del extremo inferior y el valor mínimo de varphi encontrado en la búsqueda del extremo superior. También puede devolver datos para la elaboración de gráficas.
#
# A continuación hacemos la minimización del intervalo de búsqueda para la galaxia DDO43 con el perfil ISO.
# +
galaxdata["profile"] = "ISO"
varphiLim0, varphiLimInf = calLimits(galaxdata)
interval, intinfmin, intsupmin = intervalMin(varphiLim0, varphiLimInf, galaxdata)
intervalinf = interval[0]
intervalsup = interval[1]
# -
# Así, el extremo inferior del intervalo de búsqueda tras su exploración es
print(intervalinf)
# El extremo superior del intervalo de búsqueda tras su exploración es
print(intervalsup)
# El valor mínimo de varphi encontrado en la exploración del extremo inferior es
print(intinfmin[1])
# para el valor de s
print(intinfmin[0])
# El valor mínimo de varphi encontrado en la exploración del extremo superior es
print(intsupmin[1])
# para el valor de s
print(intsupmin[0])
# A continuación se muestra la exploración del intervalo de búsqueda para su reducción para la galaxia DDO43 con perfil ISO. Los puntos rojos representan los puntos explorados y la línea negra el intervalo deducido en el algoritmo.
# +
import matplotlib.pyplot as plt
# %matplotlib inline
galaxdata["graphic"] = True
res = intervalMin(varphiLim0, varphiLimInf, galaxdata)
intervalinf = res[0][0]
intervalsup = res[0][1]
Xi = res[1]
Yi = res[2]
intinfmin = res[3]
intsupmin = res[4]
plt.semilogx()
plt.title("Galaxia DDO43 con perfil ISO")
plt.xlabel("s (parámetro de escala)")
plt.ylabel(r"$\varphi(s)$")
plt.scatter(intervalinf, 0, c='black', marker=3)
plt.scatter(intervalsup, 0, c='black', marker=3)
plt.hlines(0, intervalinf, intervalsup)
plt.scatter(Xi, Yi, c='r', marker='.')
plt.show()
# -
# ### `varphiMinim.py`
# Aquí se definen las distintas funciones que forman el algoritmo de minimización de la función varphi.
# * `getIMD(intizq, intder, galaxdata)`: Dados el extremo inferior del intervalo `intizq`, el extremo superior del intervalo `intder`y un diccionario de datos de una galaxia `galaxdata`, la función devuelve el valor medio `m`y su evaluación en varphi, así como un punto aleatorio a la derecha y otro a la izquierda, con sus respectivas evaluaciones en varphi.
# * `reductionInterval(varphiLim0, varphiLimInf, intinfmin, intsupmin, intervalinf, intervalsup)`: Realiza la mejora propuesta en la memoria para el algoritmo de minimización de varphi. Dados el límite de varphi en 0 `varphiLim0`, el límite de varphi en infinito `varphiLimInf`, el punto mínimo encontrado en la exploración del intervalo inferior `intinfmin`, el punto mínimo encontrado en la exploración del intervalo superior `intsupmin`, el extremo inferior del intervalo calculado en intervalMinim.py `intervalinf` y el extremo superior del intervalo calculado en intervalMinim.py `intervalsup`, la función devuelve el intervalo de búsqueda nuevamente reducido (en caso de que haya sido posible reducirlo).
# * `varphiMin(varphiLim0, varphiLimInf, intinfmin, intsupmin, intervalinf, intervalsup, galaxdata)`: Dados el límite de varphi cuando s tiende a 0 `varphiLim0`, el límite de varphi cuando s tiende a infinito `varphiLimInf`, el punto mínimo encontrado en la exploración del intervalo inferior `intinfmin`, el punto mínimo encontrado en la exploración del intervalo superior `intsupmin`, el extremo inferior del intervalo calculado en intervalMinim.py `intervalinf`, el extremo superior del intervalo calculado en intervalMinim.py `intervalsup` y el diccionario de datos de una galaxia `galaxdata`, la función realiza la exploración de varphi y devuelve el mínimo valor encontrado.
#
# A continuación realizamos la minimización de varphi para la galaxia DDO43 con el perfil ISO.
# +
from varphiMinim import *
res = varphiMin(varphiLim0, varphiLimInf, intinfmin, intsupmin, intervalinf, intervalsup, galaxdata)
minvarphi = res[0]
minrho = res[1]
minvarphiX = res[2]
Xj = res[3]
Yj = res[4]
forkpoints = res[5]
X = res[6]
intervalinf = res[7]
intervalsup = res[8]
# -
# Así, el intervalo de búsqueda tras aplicar la mejora propuesta en el algoritmo de minimización de varphi es
print("[", intervalinf, ", ", intervalsup, "]")
# El valor mínimo de varphi encontrado es
print(minvarphi)
# para el valor de s
print(minvarphiX)
# Mientras que el valor de la función rho (para este valor de s) definida en la Proposición 1 es
print(minrho)
# A continuación se muestra la exploración del intervalo de búsqueda para la minimización de varphi para la galaxia DDO43 con perfil ISO. Los puntos rojos representan los puntos explorados en el algoritmo de reducción del intervalo, la línea negra el intervalo deducido en el algoritmo y los puntos azules los puntos explorados en la minimización de varphi.
plt.semilogx()
plt.title("Galaxia DDO43 con perfil ISO")
plt.xlabel("s (parámetro de escala)")
plt.ylabel(r"$\varphi(s)$")
plt.scatter(intervalinf, 0, c='black', marker=3)
plt.scatter(intervalsup, 0, c='black', marker=3)
plt.hlines(0, intervalinf, intervalsup)
plt.scatter(Xi, Yi, c='r', marker='.')
plt.scatter(X, np.zeros(len(X)), color='black', marker=3)
plt.scatter(Xj, Yj, c='b', marker='.', linewidths=0.01)
plt.show()
# ### `redMethRotCurveFitting.py`
# Aquí es donde se realiza todo el proceso de ajuste de curvas de rotación, acudiendo a las funciones mencionadas anteriormente. Consta de tres partes: cálculo de límites, reducción del intervalo de búsqueda y minimización de la función varphi. A continuación, incluimos una galaxia más en nuestro conjunto de galaxias y repetimos el proceso desarrollado anteriormente para los perfiles ISO, BUR y NFW, a modo de ejemplo.
# +
import data as dt
galaxlist = ["DDO43", "DDO46"]
fp = open("galaxies/DDO46.arff")
dat, metadt = arff.loadarff(fp)
data = []
for d in dat.tolist():
data.append(np.asarray(d))
data = np.asarray(data)
galaxies["DDO46"] = {
"R": data[:, 0] * 1000,
"vrot": abs(data[:, 1]),
"errs": data[:, 3],
"vbary": np.sqrt(data[:, 4] ** 2 + data[:, 5] ** 2)
}
fp.close()
radii = galaxies["DDO46"]["R"]
galaxdata["radii"] = radii
vrot = galaxies["DDO46"]["vrot"]
galaxdata["vrot"] = vrot
vbary = galaxies["DDO46"]["vbary"]
galaxdata["vbary"] = vbary
n = len(radii)
vones = np.ones(n)
galaxdata["vones"] = vones
weights = 1 / ((n - dt.nu) * galaxies["DDO46"]["errs"] ** 2)
galaxdata["weights"] = weights
totalnullvbary = np.sum(vbary) == 0
galaxdata["totalnullvbary"] = totalnullvbary
somenullvbary = round(np.prod(vbary)) == 0
galaxdata["somenullvbary"] = somenullvbary
vv = cf.vv(galaxdata)
galaxdata["vv"] = vv
vvbary = cf.vvbary(galaxdata)
galaxdata["vvbary"] = vvbary
galaxdata["graphic"] = False
profiles = ["ISO", "BUR", "NFW"]
for g in galaxies:
print("\n")
print("GALAXIA ", g)
for p in profiles:
galaxdata["profile"] = p
print("Para el perfil ", p)
"""
Cálculo de límites
"""
limits = calLimits(galaxdata)
varphiLim0 = limits[0]
varphiLimInf = limits[1]
print("El límite de varphi cuando s tiende a cero es ", varphiLim0)
print("El límite de varphi cuando s tiende a infinito es ", varphiLimInf)
"""
Minimización del intervalo de búsqueda
"""
interval = intervalMin(varphiLim0, varphiLimInf, galaxdata)
intervalinf = interval[0][0]
intervalsup = interval[0][1]
print("El intervalo de búsqueda deducido es [", intervalinf, ", ", intervalsup, "]")
intinfmin = interval[1]
intsupmin = interval[2]
print("Mínimo encontrado en la exploración del intervalo inferior: ", intinfmin)
print("Mínimo encontrado en la exploración del intervalo superior: ", intsupmin)
"""
Minimización de la función varphi
"""
pmin = varphiMin(varphiLim0, varphiLimInf, intinfmin, intsupmin, intervalinf, intervalsup, galaxdata)
minvarphi = pmin[0]
minrho = pmin[1]
minvarphiX = pmin[2]
intervalinf = pmin[5]
intervalsup = pmin[6]
print("Tras la mejora propuesta en. el algoritmo de minimización de varphi, el intervalo de búsqueda es [", intervalinf, ", ", intervalsup, "]")
print("El intervalo de búsqueda tras aplicar la mejora propuesta en el algoritmo de minimización de varphi es [", intervalinf, ", ", intervalsup, "]")
print("El valor mínimo de varphi encontrado es ", minvarphi, ", para s = ", minvarphiX)
print("El valor de rho(", minvarphiX, ") = ", minrho)
# -
| Tutorial.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# ## All event Data meta
# +
library(ggplot2)
library(plyr)
library(scales)
library(dplyr)
library(stringr)
library(RColorBrewer)
library(httr)
library(tidyr)
library(psych)
# -
# subject,year,count,percentage,sum
# copper,2006,32,79,5255
# silver,2006,4176,79,5255
#
# +
load("../data/2018-10-08_all_meta.Rda",verbose=TRUE)
print((meta$registrants$years[1]))
registrants <- meta$registrants
citation_types <- meta$`citation-types`
relation_types <- meta$`relation-types`
pairings <- meta$pairings
# -
# # Types Distribution
hundred_plot<-function(types){
print(summary(types$count))
print(describe(types$count))
fill <- c("#5F9EA0", "#E1B372", "#E1B373", "#E1B374", "#E1B375", "#E1B376", "#E1B377", "#E1B379", "#E1B379", "#E1B379")
p4 <- ggplot() + geom_bar(aes(y = percentage, x = column, fill = type), data = (types),
stat="identity", colour="white") + labs(x="Type", y="Percentage") +
scale_y_continuous(labels = dollar_format(suffix = "%", prefix = "")) +
ggtitle("DOI-DOI Links by Type (%)")
p4 + coord_flip() + theme(
plot.margin = unit(c(5,0,5,2), "cm"))
#https://stackoverflow.com/questions/34399760/change-color-for-specific-variable-r-ggplot-stacked-bar-chart
}
# +
types <- relation_types %>%
mutate(total = sum(count), percentage = (count/total)*100, type=title, column="Type") %>%
arrange(desc(total))
hundred_plot(types)
# +
citation_types_ss <- citation_types %>%
mutate(total = sum(count), percentage = (count/total)*100, type=title, column="Type") %>%
arrange(desc(total))
hundred_plot(citation_types_ss)
# -
| mimolette/visualisation/All eventdata meta.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import matplotlib.pyplot as plt
import os
import glob
import pathlib
import numpy as np
from PIL import Image
plt.style.use('seaborn')
plt.rcParams['font.sans-serif']=['SimHei']
# -
data_dir = './data/character/'
character_csv = './data/label_character.csv'
# +
images_list = glob.glob(str(pathlib.Path(data_dir)/'**/*.jpg'), recursive=True)
characters = {}
f = open(character_csv, 'r', encoding='utf-8')
for line in f.readlines():
characters[line.split(',')[0]] = int(line.split(',')[1])
# -
print('Total number of images: %d' % len(images_list))
print('Total number of characters: %d' % len(characters))
# +
character_number = {}
for item in characters.keys():
character_number[item] = 0
for idx, file_path in enumerate(images_list):
temp_char = file_path.split(os.sep)[-2]
character_number[temp_char] += 1
# -
plt.figure()
plt.title('Distribution of the number of images')
plt.hist(list(character_number.values()), bins=150)
plt.xlabel('number of images')
plt.ylabel('number of characters')
plt.show()
# +
more_than_20 = 0
more_than_30 = 0
more_than_40 = 0
more_than_50 = 0
more_than_60 = 0
for item in character_number.values():
if item >= 60:
more_than_60 += 1
if item >= 50:
more_than_50 += 1
if item >= 40:
more_than_40 += 1
if item >= 30:
more_than_30 += 1
if item >= 20:
more_than_20 += 1
print('Characters with more than 60 images: %d' % more_than_60)
print('Characters with more than 50 images: %d' % more_than_50)
print('Characters with more than 40 images: %d' % more_than_40)
print('Characters with more than 30 images: %d' % more_than_30)
print('Characters with more than 20 images: %d' % more_than_20)
# +
# sort the dict by value
character_number_sorted = sorted(character_number.items(), key=lambda d: d[1],reverse=True)
character_number_sorted = np.array(character_number_sorted)
# we use first 2000 characters to show the results
character_number_2000 = character_number_sorted[:2000]
plt.figure(figsize=(24, 6))
plt.title('Distribution of the number of images owned by each character')
plt.bar(character_number_2000[:, 0], character_number_2000[:, 1].astype(np.int))
plt.xlabel('characters')
plt.ylabel('number of images')
plt.vlines(1000, 0, 75, colors='r')
plt.text(1005, 60, '1000 characters')
plt.show()
# +
image_size = []
for item in images_list:
img = Image.open(item)
image_size.append(img.size)
# +
image_size = np.array(image_size)
plt.figure()
plt.title('Distribution of the size of images')
plt.xlabel('width')
plt.ylabel('height')
plt.scatter(image_size[:, 1], image_size[:, 0])
plt.show()
# -
| eda.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jorgejosht/daa_2021_1/blob/master/02Diciembre.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="cWWtSB7X_6RK"
def fnRecInfinita():
print("Hola")
fnRecInfinita()
fnRecInfinita()
# + colab={"base_uri": "https://localhost:8080/"} id="T6aaZiwIAR6z" outputId="1f132327-7b0d-4343-8455-8fff0d001e36"
def fnRec(x):
if x==0:
print("Stop")
else:
fnRec(x-1)
print(x)
def main():
print("inicio del programa")
fnRec(5)
print("final del programa")
main()
# + colab={"base_uri": "https://localhost:8080/"} id="tLtd6sD7Bbu1" outputId="eb3b1455-ab8b-46a8-a70a-fe5b260bc73f"
def printRev(x):
if x>0:
print(x)
printRev(x-1)
printRev(3)
# + colab={"base_uri": "https://localhost:8080/"} id="Mqohsj0EHPUK" outputId="f7539de3-529d-459a-e167-347996e71161"
def fibonacci(n):
if n < 2:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
fibonacci(8)
| 02Diciembre.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="MhoQ0WE77laV"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab_type="code" id="_ckMIh7O7s6D" colab={}
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + cellView="form" colab_type="code" id="vasWnqRgy1H4" colab={}
#@title MIT License
#
# Copyright (c) 2017 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a
# # copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
# + [markdown] colab_type="text" id="jYysdyb-CaWM"
# # はじめてのニューラルネットワーク:分類問題の初歩
# + [markdown] colab_type="text" id="S5Uhzt6vVIB2"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/beta/tutorials/keras/basic_classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ja/beta/tutorials/keras/basic_classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ja/beta/tutorials/keras/basic_classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] id="EQ4yfFQxW7by" colab_type="text"
# Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [<EMAIL> メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
# + [markdown] colab_type="text" id="FbVhjPpzn6BM"
# このガイドでは、スニーカーやシャツなど、身に着けるものの写真を分類するニューラルネットワークのモデルを訓練します。すべての詳細を理解できなくても問題ありません。TensorFlowの全体を早足で掴むためのもので、詳細についてはあとから見ていくことになります。
#
# このガイドでは、TensorFlowのモデルを構築し訓練するためのハイレベルのAPIである [tf.keras](https://www.tensorflow.org/guide/keras)を使用します。
# + colab_type="code" id="jL3OqFKZ9dFg" colab={}
# !pip install tensorflow==2.0.0-beta0
# + colab_type="code" id="dzLKpmZICaWN" colab={}
from __future__ import absolute_import, division, print_function, unicode_literals
# TensorFlow と tf.keras のインポート
import tensorflow as tf
from tensorflow import keras
# ヘルパーライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
# + [markdown] colab_type="text" id="yR0EdgrLCaWR"
# ## ファッションMNISTデータセットのロード
# + [markdown] colab_type="text" id="DLdCchMdCaWQ"
# このガイドでは、[Fashion MNIST](https://github.com/zalandoresearch/fashion-mnist)を使用します。Fashion MNISTには10カテゴリーの白黒画像70,000枚が含まれています。それぞれは下図のような1枚に付き1種類の衣料品が写っている低解像度(28×28ピクセル)の画像です。
#
# <table>
# <tr><td>
# <img src="https://tensorflow.org/images/fashion-mnist-sprite.png"
# alt="Fashion MNIST sprite" width="600">
# </td></tr>
# <tr><td align="center">
# <b>Figure 1.</b> <a href="https://github.com/zalandoresearch/fashion-mnist">Fashion-MNIST samples</a> (by Zalando, MIT License).<br/>
# </td></tr>
# </table>
#
# Fashion MNISTは、画像処理のための機械学習での"Hello, World"としてしばしば登場する[MNIST](http://yann.lecun.com/exdb/mnist/) データセットの代替として開発されたものです。MNISTデータセットは手書きの数字(0, 1, 2 など)から構成されており、そのフォーマットはこれから使うFashion MNISTと全く同じです。
#
# Fashion MNISTを使うのは、目先を変える意味もありますが、普通のMNISTよりも少しだけ手応えがあるからでもあります。どちらのデータセットも比較的小さく、アルゴリズムが期待したとおりに機能するかどうかを確かめるために使われます。プログラムのテストやデバッグのためには、よい出発点になります。
#
# ここでは、60,000枚の画像を訓練に、10,000枚の画像を、ネットワークが学習した画像分類の正確性を評価するのに使います。TensorFlowを使うと、下記のようにFashion MNISTのデータを簡単にインポートし、ロードすることが出来ます。
# + colab_type="code" id="7MqDQO0KCaWS" colab={}
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# + [markdown] colab_type="text" id="t9FDsUlxCaWW"
# ロードしたデータセットは、NumPy配列になります。
#
# * `train_images` と `train_labels` の2つの配列は、モデルの訓練に使用される**訓練用データセット**です。
# * 訓練されたモデルは、 `test_images` と `test_labels` 配列からなる**テスト用データセット**を使ってテストします。
#
# 画像は28×28のNumPy配列から構成されています。それぞれのピクセルの値は0から255の間の整数です。**ラベル**(label)は、0から9までの整数の配列です。それぞれの数字が下表のように、衣料品の**クラス**(class)に対応しています。
#
# <table>
# <tr>
# <th>Label</th>
# <th>Class</th>
# </tr>
# <tr>
# <td>0</td>
# <td>T-shirt/top</td>
# </tr>
# <tr>
# <td>1</td>
# <td>Trouser</td>
# </tr>
# <tr>
# <td>2</td>
# <td>Pullover</td>
# </tr>
# <tr>
# <td>3</td>
# <td>Dress</td>
# </tr>
# <tr>
# <td>4</td>
# <td>Coat</td>
# </tr>
# <tr>
# <td>5</td>
# <td>Sandal</td>
# </tr>
# <tr>
# <td>6</td>
# <td>Shirt</td>
# </tr>
# <tr>
# <td>7</td>
# <td>Sneaker</td>
# </tr>
# <tr>
# <td>8</td>
# <td>Bag</td>
# </tr>
# <tr>
# <td>9</td>
# <td>Ankle boot</td>
# </tr>
# </table>
#
# 画像はそれぞれ単一のラベルに分類されます。データセットには上記の**クラス名**が含まれていないため、後ほど画像を出力するときのために、クラス名を保存しておきます。
# + colab_type="code" id="IjnLH5S2CaWx" colab={}
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
# + [markdown] colab_type="text" id="Brm0b_KACaWX"
# ## データの観察
#
# モデルの訓練を行う前に、データセットのフォーマットを見てみましょう。下記のように、訓練用データセットには28×28ピクセルの画像が60,000枚含まれています。
# + colab_type="code" id="zW5k_xz1CaWX" colab={}
train_images.shape
# + [markdown] colab_type="text" id="cIAcvQqMCaWf"
# 同様に、訓練用データセットには60,000個のラベルが含まれます。
# + colab_type="code" id="TRFYHB2mCaWb" colab={}
len(train_labels)
# + [markdown] colab_type="text" id="YSlYxFuRCaWk"
# ラベルはそれぞれ、0から9までの間の整数です。
# + colab_type="code" id="XKnCTHz4CaWg" colab={}
train_labels
# + [markdown] colab_type="text" id="TMPI88iZpO2T"
# テスト用データセットには、10,000枚の画像が含まれます。画像は28×28ピクセルで構成されています。
# + colab_type="code" id="2KFnYlcwCaWl" colab={}
test_images.shape
# + [markdown] colab_type="text" id="rd0A0Iu0CaWq"
# テスト用データセットには10,000個のラベルが含まれます。
# + colab_type="code" id="iJmPr5-ACaWn" colab={}
len(test_labels)
# + [markdown] colab_type="text" id="ES6uQoLKCaWr"
# ## データの前処理
#
# ネットワークを訓練する前に、データを前処理する必要があります。最初の画像を調べてみればわかるように、ピクセルの値は0から255の間の数値です。
# + colab_type="code" id="m4VEw8Ud9Quh" colab={}
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
# + [markdown] colab_type="text" id="3jCZdQNNCaWv"
# ニューラルネットワークにデータを投入する前に、これらの値を0から1までの範囲にスケールします。そのためには、画素の値を255で割ります。
#
# **訓練用データセット**と**テスト用データセット**は、同じように前処理することが重要です。
# + colab_type="code" id="bW5WzIPlCaWv" colab={}
train_images = train_images / 255.0
test_images = test_images / 255.0
# + [markdown] colab_type="text" id="Ee638AlnCaWz"
# **訓練用データセット**の最初の25枚の画像を、クラス名付きで表示してみましょう。ネットワークを構築・訓練する前に、データが正しいフォーマットになっていることを確認します。
# + colab_type="code" id="oZTImqg_CaW1" colab={}
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
# + [markdown] colab_type="text" id="59veuiEZCaW4"
# ## モデルの構築
#
# ニューラルネットワークを構築するには、まずモデルの階層を定義し、その後モデルをコンパイルします。
# + [markdown] colab_type="text" id="Gxg1XGm0eOBy"
# ### 層の設定
#
# ニューラルネットワークを形作る基本的な構成要素は**層**(layer)です。層は、入力されたデータから「表現」を抽出します。それらの「表現」は、今取り組もうとしている問題に対して、より「意味のある」ものであることが期待されます。
#
# ディープラーニングモデルのほとんどは、単純な層の積み重ねで構成されています。`tf.keras.layers.Dense` のような層のほとんどには、訓練中に学習されるパラメータが存在します。
# + colab_type="code" id="9ODch-OFCaW4" colab={}
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
# + [markdown] colab_type="text" id="gut8A_7rCaW6"
# このネットワークの最初の層は、`tf.keras.layers.Flatten` です。この層は、画像を(28×28ピクセルの)2次元配列から、28×28=784ピクセルの、1次元配列に変換します。この層が、画像の中に積まれているピクセルの行を取り崩し、横に並べると考えてください。この層には学習すべきパラメータはなく、ただデータのフォーマット変換を行うだけです。
#
# ピクセルが1次元化されたあと、ネットワークは2つの `tf.keras.layers.Dense` 層となります。これらの層は、密結合あるいは全結合されたニューロンの層となります。最初の `Dense` 層には、128個のノード(あるはニューロン)があります。最後の層でもある2番めの層は、10ノードの**softmax**層です。この層は、合計が1になる10個の確率の配列を返します。それぞれのノードは、今見ている画像が10個のクラスのひとつひとつに属する確率を出力します。
#
# ### モデルのコンパイル
#
# モデルが訓練できるようになるには、いくつかの設定を追加する必要があります。それらの設定は、モデルの**コンパイル**(compile)時に追加されます。
#
# * **損失関数**(loss function) —訓練中にモデルがどれくらい正確かを測定します。この関数の値を最小化することにより、訓練中のモデルを正しい方向に向かわせようというわけです。
# * **オプティマイザ**(optimizer)—モデルが見ているデータと、損失関数の値から、どのようにモデルを更新するかを決定します。
# * **メトリクス**(metrics) —訓練とテストのステップを監視するのに使用します。下記の例では*accuracy* (正解率)、つまり、画像が正しく分類された比率を使用しています。
# + colab_type="code" id="Lhan11blCaW7" colab={}
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# + [markdown] colab_type="text" id="qKF6uW-BCaW-"
# ## モデルの訓練
#
# ニューラルネットワークの訓練には次のようなステップが必要です。
#
# 1. モデルに訓練用データを投入します—この例では `train_images` と `train_labels` の2つの配列です。
# 2. モデルは、画像とラベルの対応関係を学習します。
# 3. モデルにテスト用データセットの予測(分類)を行わせます—この例では `test_images` 配列です。その後、予測結果と `test_labels` 配列を照合します。
#
# 訓練を開始するには、`model.fit` メソッドを呼び出します。モデルを訓練用データに "fit"(適合)させるという意味です。
# + colab_type="code" id="xvwvpA64CaW_" colab={}
model.fit(train_images, train_labels, epochs=5)
# + [markdown] colab_type="text" id="W3ZVOhugCaXA"
# モデルの訓練の進行とともに、損失値と正解率が表示されます。このモデルの場合、訓練用データでは0.88(すなわち88%)の正解率に達します。
# + [markdown] colab_type="text" id="oEw4bZgGCaXB"
# ## 正解率の評価
#
# 次に、テスト用データセットに対するモデルの性能を比較します。
# + colab_type="code" id="VflXLEeECaXC" colab={}
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('\nTest accuracy:', test_acc)
# + [markdown] colab_type="text" id="yWfgsmVXCaXG"
# ご覧の通り、テスト用データセットでの正解率は、訓練用データセットでの正解率よりも少し低くなります。この訓練時の正解率とテスト時の正解率の差は、**過学習**(over fitting)の一例です。過学習とは、新しいデータに対する機械学習モデルの性能が、訓練時と比較して低下する現象です。
# + [markdown] colab_type="text" id="xsoS7CPDCaXH"
# ## 予測する
#
# モデルの訓練が終わったら、そのモデルを使って画像の分類予測を行うことが出来ます。
# + colab_type="code" id="Gl91RPhdCaXI" colab={}
predictions = model.predict(test_images)
# + [markdown] colab_type="text" id="x9Kk1voUCaXJ"
# これは、モデルがテスト用データセットの画像のひとつひとつを分類予測した結果です。最初の予測を見てみましょう。
# + colab_type="code" id="3DmJEUinCaXK" colab={}
predictions[0]
# + [markdown] colab_type="text" id="-hw1hgeSCaXN"
# 予測結果は、10個の数字の配列です。これは、その画像が10の衣料品の種類のそれぞれに該当するかの「確信度」を表しています。どのラベルが一番確信度が高いかを見てみましょう。
# + colab_type="code" id="qsqenuPnCaXO" colab={}
np.argmax(predictions[0])
# + [markdown] colab_type="text" id="E51yS7iCCaXO"
# というわけで、このモデルは、この画像が、アンクルブーツ、`class_names[9]` である可能性が最も高いと判断したことになります。これが正しいかどうか、テスト用ラベルを見てみましょう。
# + colab_type="code" id="Sd7Pgsu6CaXP" colab={}
test_labels[0]
# + [markdown] colab_type="text" id="kgdvGD52CaXR"
# 10チャンネルすべてをグラフ化してみることができます。
# + colab_type="code" id="VsRq6uZiG7eT" colab={}
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array[i], true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array[i], true_label[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
# + [markdown] colab_type="text" id="aZ_jDyLZG7eW"
# 0番目の画像と、予測、予測配列を見てみましょう。
# + colab_type="code" id="UH_jgCxEG7eW" colab={}
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
# + colab_type="code" id="5_7K0ZL7G7eY" colab={}
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions, test_labels)
plt.show()
# + [markdown] colab_type="text" id="Lduh0pbfG7eb"
# 予測の中のいくつかの画像を、予測値とともに表示してみましょう。正しい予測は青で、誤っている予測は赤でラベルを表示します。数字は予測したラベルのパーセント(100分率)を示します。自信があるように見えても間違っていることがあることに注意してください。
# + colab_type="code" id="YGBDAiziCaXR" colab={}
# X個のテスト画像、予測されたラベル、正解ラベルを表示します。
# 正しい予測は青で、間違った予測は赤で表示しています。
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions, test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions, test_labels)
plt.show()
# + [markdown] colab_type="text" id="R32zteKHCaXT"
# 最後に、訓練済みモデルを使って1枚の画像に対する予測を行います。
# + colab_type="code" id="yRJ7JU7JCaXT" colab={}
# テスト用データセットから画像を1枚取り出す
img = test_images[0]
print(img.shape)
# + [markdown] colab_type="text" id="vz3bVp21CaXV"
# `tf.keras` モデルは、サンプルの中の**バッチ**(batch)あるいは「集まり」について予測を行うように作られています。そのため、1枚の画像を使う場合でも、リスト化する必要があります。
# + colab_type="code" id="lDFh5yF_CaXW" colab={}
# 画像を1枚だけのバッチのメンバーにする
img = (np.expand_dims(img,0))
print(img.shape)
# + [markdown] colab_type="text" id="EQ5wLTkcCaXY"
# そして、予測を行います。
# + colab_type="code" id="o_rzNSdrCaXY" colab={}
predictions_single = model.predict(img)
print(predictions_single)
# + colab_type="code" id="6o3nwO-KG7ex" colab={}
plot_value_array(0, predictions_single, test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
# + [markdown] colab_type="text" id="cU1Y2OAMCaXb"
# `model.predict` メソッドの戻り値は、リストのリストです。リストの要素のそれぞれが、バッチの中の画像に対応します。バッチの中から、(といってもバッチの中身は1つだけですが)予測を取り出します。
# + colab_type="code" id="2tRmdq_8CaXb" colab={}
np.argmax(predictions_single[0])
# + [markdown] colab_type="text" id="YFc2HbEVCaXd"
# というわけで、モデルは9というラベルを予測しました。
| site/ja/beta/tutorials/keras/basic_classification.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Emojify!
#
# Welcome to the second assignment of Week 2. You are going to use word vector representations to build an Emojifier.
#
# Have you ever wanted to make your text messages more expressive? Your emojifier app will help you do that. So rather than writing "Congratulations on the promotion! Lets get coffee and talk. Love you!" the emojifier can automatically turn this into "Congratulations on the promotion! 👍 Lets get coffee and talk. ☕️ Love you! ❤️"
#
# You will implement a model which inputs a sentence (such as "Let's go see the baseball game tonight!") and finds the most appropriate emoji to be used with this sentence (⚾️). In many emoji interfaces, you need to remember that ❤️ is the "heart" symbol rather than the "love" symbol. But using word vectors, you'll see that even if your training set explicitly relates only a few words to a particular emoji, your algorithm will be able to generalize and associate words in the test set to the same emoji even if those words don't even appear in the training set. This allows you to build an accurate classifier mapping from sentences to emojis, even using a small training set.
#
# In this exercise, you'll start with a baseline model (Emojifier-V1) using word embeddings, then build a more sophisticated model (Emojifier-V2) that further incorporates an LSTM.
#
# Lets get started! Run the following cell to load the package you are going to use.
# +
import numpy as np
from emo_utils import *
import emoji
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# ## 1 - Baseline model: Emojifier-V1
#
# ### 1.1 - Dataset EMOJISET
#
# Let's start by building a simple baseline classifier.
#
# You have a tiny dataset (X, Y) where:
# - X contains 127 sentences (strings)
# - Y contains a integer label between 0 and 4 corresponding to an emoji for each sentence
#
# <img src="images/data_set.png" style="width:700px;height:300px;">
# <caption><center> **Figure 1**: EMOJISET - a classification problem with 5 classes. A few examples of sentences are given here. </center></caption>
#
# Let's load the dataset using the code below. We split the dataset between training (127 examples) and testing (56 examples).
X_train, Y_train = read_csv('data/train_emoji.csv')
X_test, Y_test = read_csv('data/tesss.csv')
maxLen = len(max(X_train, key=len).split())
# Run the following cell to print sentences from X_train and corresponding labels from Y_train. Change `index` to see different examples. Because of the font the iPython notebook uses, the heart emoji may be colored black rather than red.
index = 18
print(X_train[index], label_to_emoji(Y_train[index]))
# ### 1.2 - Overview of the Emojifier-V1
#
# In this part, you are going to implement a baseline model called "Emojifier-v1".
#
# <center>
# <img src="images/image_1.png" style="width:900px;height:300px;">
# <caption><center> **Figure 2**: Baseline model (Emojifier-V1).</center></caption>
# </center>
#
# The input of the model is a string corresponding to a sentence (e.g. "I love you). In the code, the output will be a probability vector of shape (1,5), that you then pass in an argmax layer to extract the index of the most likely emoji output.
# To get our labels into a format suitable for training a softmax classifier, lets convert $Y$ from its current shape current shape $(m, 1)$ into a "one-hot representation" $(m, 5)$, where each row is a one-hot vector giving the label of one example, You can do so using this next code snipper. Here, `Y_oh` stands for "Y-one-hot" in the variable names `Y_oh_train` and `Y_oh_test`:
#
Y_oh_train = convert_to_one_hot(Y_train, C = 5)
Y_oh_test = convert_to_one_hot(Y_test, C = 5)
# Let's see what `convert_to_one_hot()` did. Feel free to change `index` to print out different values.
index = 50
print(Y_train[index], "is converted into one hot", Y_oh_train[index])
# All the data is now ready to be fed into the Emojify-V1 model. Let's implement the model!
# ### 1.3 - Implementing Emojifier-V1
#
# As shown in Figure (2), the first step is to convert an input sentence into the word vector representation, which then get averaged together. Similar to the previous exercise, we will use pretrained 50-dimensional GloVe embeddings. Run the following cell to load the `word_to_vec_map`, which contains all the vector representations.
word_to_index, index_to_word, word_to_vec_map = read_glove_vecs('../../readonly/glove.6B.50d.txt')
# You've loaded:
# - `word_to_index`: dictionary mapping from words to their indices in the vocabulary (400,001 words, with the valid indices ranging from 0 to 400,000)
# - `index_to_word`: dictionary mapping from indices to their corresponding words in the vocabulary
# - `word_to_vec_map`: dictionary mapping words to their GloVe vector representation.
#
# Run the following cell to check if it works.
word = "cucumber"
index = 289846
print("the index of", word, "in the vocabulary is", word_to_index[word])
print("the", str(index) + "th word in the vocabulary is", index_to_word[index])
# **Exercise**: Implement `sentence_to_avg()`. You will need to carry out two steps:
# 1. Convert every sentence to lower-case, then split the sentence into a list of words. `X.lower()` and `X.split()` might be useful.
# 2. For each word in the sentence, access its GloVe representation. Then, average all these values.
# +
# GRADED FUNCTION: sentence_to_avg
def sentence_to_avg(sentence, word_to_vec_map):
"""
Converts a sentence (string) into a list of words (strings). Extracts the GloVe representation of each word
and averages its value into a single vector encoding the meaning of the sentence.
Arguments:
sentence -- string, one training example from X
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
Returns:
avg -- average vector encoding information about the sentence, numpy-array of shape (50,)
"""
### START CODE HERE ###
# Step 1: Split sentence into list of lower case words (≈ 1 line)
words = (sentence.lower()).split()
# Initialize the average word vector, should have the same shape as your word vectors.
avg = np.zeros((50, ))
# Step 2: average the word vectors. You can loop over the words in the list "words".
for w in words:
avg += word_to_vec_map[w]
avg = avg / len(words)
### END CODE HERE ###
return avg
# -
avg = sentence_to_avg("Morrocan couscous is my favorite dish", word_to_vec_map)
print("avg = ", avg)
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **avg= **
# </td>
# <td>
# [-0.008005 0.56370833 -0.50427333 0.258865 0.55131103 0.03104983
# -0.21013718 0.16893933 -0.09590267 0.141784 -0.15708967 0.18525867
# 0.6495785 0.38371117 0.21102167 0.11301667 0.02613967 0.26037767
# 0.05820667 -0.01578167 -0.12078833 -0.02471267 0.4128455 0.5152061
# 0.38756167 -0.898661 -0.535145 0.33501167 0.68806933 -0.2156265
# 1.797155 0.10476933 -0.36775333 0.750785 0.10282583 0.348925
# -0.27262833 0.66768 -0.10706167 -0.283635 0.59580117 0.28747333
# -0.3366635 0.23393817 0.34349183 0.178405 0.1166155 -0.076433
# 0.1445417 0.09808667]
# </td>
# </tr>
# </table>
# #### Model
#
# You now have all the pieces to finish implementing the `model()` function. After using `sentence_to_avg()` you need to pass the average through forward propagation, compute the cost, and then backpropagate to update the softmax's parameters.
#
# **Exercise**: Implement the `model()` function described in Figure (2). Assuming here that $Yoh$ ("Y one hot") is the one-hot encoding of the output labels, the equations you need to implement in the forward pass and to compute the cross-entropy cost are:
# $$ z^{(i)} = W . avg^{(i)} + b$$
# $$ a^{(i)} = softmax(z^{(i)})$$
# $$ \mathcal{L}^{(i)} = - \sum_{k = 0}^{n_y - 1} Yoh^{(i)}_k * log(a^{(i)}_k)$$
#
# It is possible to come up with a more efficient vectorized implementation. But since we are using a for-loop to convert the sentences one at a time into the avg^{(i)} representation anyway, let's not bother this time.
#
# We provided you a function `softmax()`.
# +
# GRADED FUNCTION: model
def model(X, Y, word_to_vec_map, learning_rate = 0.01, num_iterations = 400):
"""
Model to train word vector representations in numpy.
Arguments:
X -- input data, numpy array of sentences as strings, of shape (m, 1)
Y -- labels, numpy array of integers between 0 and 7, numpy-array of shape (m, 1)
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
learning_rate -- learning_rate for the stochastic gradient descent algorithm
num_iterations -- number of iterations
Returns:
pred -- vector of predictions, numpy-array of shape (m, 1)
W -- weight matrix of the softmax layer, of shape (n_y, n_h)
b -- bias of the softmax layer, of shape (n_y,)
"""
np.random.seed(1)
# Define number of training examples
m = Y.shape[0] # number of training examples
n_y = 5 # number of classes
n_h = 50 # dimensions of the GloVe vectors
# Initialize parameters using Xavier initialization
W = np.random.randn(n_y, n_h) / np.sqrt(n_h)
b = np.zeros((n_y,))
# Convert Y to Y_onehot with n_y classes
Y_oh = convert_to_one_hot(Y, C = n_y)
# Optimization loop
for t in range(num_iterations): # Loop over the number of iterations
for i in range(m): # Loop over the training examples
### START CODE HERE ### (≈ 4 lines of code)
# Average the word vectors of the words from the i'th training example
avg = sentence_to_avg(X[i], word_to_vec_map)
# Forward propagate the avg through the softmax layer
z = np.dot(W, avg) + b
a = softmax(z)
# Compute cost using the i'th training label's one hot representation and "A" (the output of the softmax)
cost = -np.sum(Y_oh[i] * np.log(a))
### END CODE HERE ###
# Compute gradients
dz = a - Y_oh[i]
dW = np.dot(dz.reshape(n_y,1), avg.reshape(1, n_h))
db = dz
# Update parameters with Stochastic Gradient Descent
W = W - learning_rate * dW
b = b - learning_rate * db
if t % 100 == 0:
print("Epoch: " + str(t) + " --- cost = " + str(cost))
pred = predict(X, Y, W, b, word_to_vec_map)
return pred, W, b
# +
print(X_train.shape)
print(Y_train.shape)
print(np.eye(5)[Y_train.reshape(-1)].shape)
print(X_train[0])
print(type(X_train))
Y = np.asarray([5,0,0,5, 4, 4, 4, 6, 6, 4, 1, 1, 5, 6, 6, 3, 6, 3, 4, 4])
print(Y.shape)
X = np.asarray(['I am going to the bar tonight', 'I love you', 'miss you my dear',
'Lets go party and drinks','Congrats on the new job','Congratulations',
'I am so happy for you', 'Why are you feeling bad', 'What is wrong with you',
'You totally deserve this prize', 'Let us go play football',
'Are you down for football this afternoon', 'Work hard play harder',
'It is suprising how people can be dumb sometimes',
'I am very disappointed','It is the best day in my life',
'I think I will end up alone','My life is so boring','Good job',
'Great so awesome'])
print(X.shape)
print(np.eye(5)[Y_train.reshape(-1)].shape)
print(type(X_train))
# -
# Run the next cell to train your model and learn the softmax parameters (W,b).
pred, W, b = model(X_train, Y_train, word_to_vec_map)
print(pred)
# **Expected Output** (on a subset of iterations):
#
# <table>
# <tr>
# <td>
# **Epoch: 0**
# </td>
# <td>
# cost = 1.95204988128
# </td>
# <td>
# Accuracy: 0.348484848485
# </td>
# </tr>
#
#
# <tr>
# <td>
# **Epoch: 100**
# </td>
# <td>
# cost = 0.0797181872601
# </td>
# <td>
# Accuracy: 0.931818181818
# </td>
# </tr>
#
# <tr>
# <td>
# **Epoch: 200**
# </td>
# <td>
# cost = 0.0445636924368
# </td>
# <td>
# Accuracy: 0.954545454545
# </td>
# </tr>
#
# <tr>
# <td>
# **Epoch: 300**
# </td>
# <td>
# cost = 0.0343226737879
# </td>
# <td>
# Accuracy: 0.969696969697
# </td>
# </tr>
# </table>
# Great! Your model has pretty high accuracy on the training set. Lets now see how it does on the test set.
# ### 1.4 - Examining test set performance
#
print("Training set:")
pred_train = predict(X_train, Y_train, W, b, word_to_vec_map)
print('Test set:')
pred_test = predict(X_test, Y_test, W, b, word_to_vec_map)
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **Train set accuracy**
# </td>
# <td>
# 97.7
# </td>
# </tr>
# <tr>
# <td>
# **Test set accuracy**
# </td>
# <td>
# 85.7
# </td>
# </tr>
# </table>
# Random guessing would have had 20% accuracy given that there are 5 classes. This is pretty good performance after training on only 127 examples.
#
# In the training set, the algorithm saw the sentence "*I love you*" with the label ❤️. You can check however that the word "adore" does not appear in the training set. Nonetheless, lets see what happens if you write "*I adore you*."
#
#
# +
X_my_sentences = np.array(["i adore you", "i love you", "funny lol", "lets play with a ball", "food is ready", "not feeling happy"])
Y_my_labels = np.array([[0], [0], [2], [1], [4],[3]])
pred = predict(X_my_sentences, Y_my_labels , W, b, word_to_vec_map)
print_predictions(X_my_sentences, pred)
# -
# Amazing! Because *adore* has a similar embedding as *love*, the algorithm has generalized correctly even to a word it has never seen before. Words such as *heart*, *dear*, *beloved* or *adore* have embedding vectors similar to *love*, and so might work too---feel free to modify the inputs above and try out a variety of input sentences. How well does it work?
#
# Note though that it doesn't get "not feeling happy" correct. This algorithm ignores word ordering, so is not good at understanding phrases like "not happy."
#
# Printing the confusion matrix can also help understand which classes are more difficult for your model. A confusion matrix shows how often an example whose label is one class ("actual" class) is mislabeled by the algorithm with a different class ("predicted" class).
#
#
#
print(Y_test.shape)
print(' '+ label_to_emoji(0)+ ' ' + label_to_emoji(1) + ' ' + label_to_emoji(2)+ ' ' + label_to_emoji(3)+' ' + label_to_emoji(4))
print(pd.crosstab(Y_test, pred_test.reshape(56,), rownames=['Actual'], colnames=['Predicted'], margins=True))
plot_confusion_matrix(Y_test, pred_test)
# <font color='blue'>
# **What you should remember from this part**:
# - Even with a 127 training examples, you can get a reasonably good model for Emojifying. This is due to the generalization power word vectors gives you.
# - Emojify-V1 will perform poorly on sentences such as *"This movie is not good and not enjoyable"* because it doesn't understand combinations of words--it just averages all the words' embedding vectors together, without paying attention to the ordering of words. You will build a better algorithm in the next part.
#
# ## 2 - Emojifier-V2: Using LSTMs in Keras:
#
# Let's build an LSTM model that takes as input word sequences. This model will be able to take word ordering into account. Emojifier-V2 will continue to use pre-trained word embeddings to represent words, but will feed them into an LSTM, whose job it is to predict the most appropriate emoji.
#
# Run the following cell to load the Keras packages.
import numpy as np
np.random.seed(0)
from keras.models import Model
from keras.layers import Dense, Input, Dropout, LSTM, Activation
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
from keras.initializers import glorot_uniform
np.random.seed(1)
# ### 2.1 - Overview of the model
#
# Here is the Emojifier-v2 you will implement:
#
# <img src="images/emojifier-v2.png" style="width:700px;height:400px;"> <br>
# <caption><center> **Figure 3**: Emojifier-V2. A 2-layer LSTM sequence classifier. </center></caption>
#
#
# ### 2.2 Keras and mini-batching
#
# In this exercise, we want to train Keras using mini-batches. However, most deep learning frameworks require that all sequences in the same mini-batch have the same length. This is what allows vectorization to work: If you had a 3-word sentence and a 4-word sentence, then the computations needed for them are different (one takes 3 steps of an LSTM, one takes 4 steps) so it's just not possible to do them both at the same time.
#
# The common solution to this is to use padding. Specifically, set a maximum sequence length, and pad all sequences to the same length. For example, of the maximum sequence length is 20, we could pad every sentence with "0"s so that each input sentence is of length 20. Thus, a sentence "i love you" would be represented as $(e_{i}, e_{love}, e_{you}, \vec{0}, \vec{0}, \ldots, \vec{0})$. In this example, any sentences longer than 20 words would have to be truncated. One simple way to choose the maximum sequence length is to just pick the length of the longest sentence in the training set.
#
# ### 2.3 - The Embedding layer
#
# In Keras, the embedding matrix is represented as a "layer", and maps positive integers (indices corresponding to words) into dense vectors of fixed size (the embedding vectors). It can be trained or initialized with a pretrained embedding. In this part, you will learn how to create an [Embedding()](https://keras.io/layers/embeddings/) layer in Keras, initialize it with the GloVe 50-dimensional vectors loaded earlier in the notebook. Because our training set is quite small, we will not update the word embeddings but will instead leave their values fixed. But in the code below, we'll show you how Keras allows you to either train or leave fixed this layer.
#
# The `Embedding()` layer takes an integer matrix of size (batch size, max input length) as input. This corresponds to sentences converted into lists of indices (integers), as shown in the figure below.
#
# <img src="images/embedding1.png" style="width:700px;height:250px;">
# <caption><center> **Figure 4**: Embedding layer. This example shows the propagation of two examples through the embedding layer. Both have been zero-padded to a length of `max_len=5`. The final dimension of the representation is `(2,max_len,50)` because the word embeddings we are using are 50 dimensional. </center></caption>
#
# The largest integer (i.e. word index) in the input should be no larger than the vocabulary size. The layer outputs an array of shape (batch size, max input length, dimension of word vectors).
#
# The first step is to convert all your training sentences into lists of indices, and then zero-pad all these lists so that their length is the length of the longest sentence.
#
# **Exercise**: Implement the function below to convert X (array of sentences as strings) into an array of indices corresponding to words in the sentences. The output shape should be such that it can be given to `Embedding()` (described in Figure 4).
# +
# GRADED FUNCTION: sentences_to_indices
def sentences_to_indices(X, word_to_index, max_len):
"""
Converts an array of sentences (strings) into an array of indices corresponding to words in the sentences.
The output shape should be such that it can be given to `Embedding()` (described in Figure 4).
Arguments:
X -- array of sentences (strings), of shape (m, 1)
word_to_index -- a dictionary containing the each word mapped to its index
max_len -- maximum number of words in a sentence. You can assume every sentence in X is no longer than this.
Returns:
X_indices -- array of indices corresponding to words in the sentences from X, of shape (m, max_len)
"""
m = X.shape[0] # number of training examples
### START CODE HERE ###
# Initialize X_indices as a numpy matrix of zeros and the correct shape (≈ 1 line)
X_indices = np.zeros((m, max_len))
for i in range(m): # loop over training examples
# Convert the ith training sentence in lower case and split is into words. You should get a list of words.
sentence_words = (X[i].lower()).split()
# Initialize j to 0
j = 0
# Loop over the words of sentence_words
for w in sentence_words:
# Set the (i,j)th entry of X_indices to the index of the correct word.
X_indices[i, j] = word_to_index[w]
# Increment j to j + 1
j = j + 1
### END CODE HERE ###
return X_indices
# -
# Run the following cell to check what `sentences_to_indices()` does, and check your results.
X1 = np.array(["funny lol", "lets play baseball", "food is ready for you"])
X1_indices = sentences_to_indices(X1,word_to_index, max_len = 5)
print("X1 =", X1)
print("X1_indices =", X1_indices)
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **X1 =**
# </td>
# <td>
# ['funny lol' 'lets play football' 'food is ready for you']
# </td>
# </tr>
# <tr>
# <td>
# **X1_indices =**
# </td>
# <td>
# [[ 155345. 225122. 0. 0. 0.] <br>
# [ 220930. 286375. 151266. 0. 0.] <br>
# [ 151204. 192973. 302254. 151349. 394475.]]
# </td>
# </tr>
# </table>
# Let's build the `Embedding()` layer in Keras, using pre-trained word vectors. After this layer is built, you will pass the output of `sentences_to_indices()` to it as an input, and the `Embedding()` layer will return the word embeddings for a sentence.
#
# **Exercise**: Implement `pretrained_embedding_layer()`. You will need to carry out the following steps:
# 1. Initialize the embedding matrix as a numpy array of zeroes with the correct shape.
# 2. Fill in the embedding matrix with all the word embeddings extracted from `word_to_vec_map`.
# 3. Define Keras embedding layer. Use [Embedding()](https://keras.io/layers/embeddings/). Be sure to make this layer non-trainable, by setting `trainable = False` when calling `Embedding()`. If you were to set `trainable = True`, then it will allow the optimization algorithm to modify the values of the word embeddings.
# 4. Set the embedding weights to be equal to the embedding matrix
# +
# GRADED FUNCTION: pretrained_embedding_layer
def pretrained_embedding_layer(word_to_vec_map, word_to_index):
"""
Creates a Keras Embedding() layer and loads in pre-trained GloVe 50-dimensional vectors.
Arguments:
word_to_vec_map -- dictionary mapping words to their GloVe vector representation.
word_to_index -- dictionary mapping from words to their indices in the vocabulary (400,001 words)
Returns:
embedding_layer -- pretrained layer Keras instance
"""
vocab_len = len(word_to_index) + 1 # adding 1 to fit Keras embedding (requirement)
emb_dim = word_to_vec_map["cucumber"].shape[0] # define dimensionality of your GloVe word vectors (= 50)
### START CODE HERE ###
# Initialize the embedding matrix as a numpy array of zeros of shape (vocab_len, dimensions of word vectors = emb_dim)
emb_matrix = np.zeros((vocab_len, emb_dim))
# Set each row "index" of the embedding matrix to be the word vector representation of the "index"th word of the vocabulary
for word, index in word_to_index.items():
emb_matrix[index, :] = word_to_vec_map[word]
# Define Keras embedding layer with the correct output/input sizes, make it trainable. Use Embedding(...). Make sure to set trainable=False.
embedding_layer = Embedding(vocab_len, emb_dim, trainable = False)
### END CODE HERE ###
# Build the embedding layer, it is required before setting the weights of the embedding layer. Do not modify the "None".
embedding_layer.build((None,))
# Set the weights of the embedding layer to the embedding matrix. Your layer is now pretrained.
embedding_layer.set_weights([emb_matrix])
return embedding_layer
# -
embedding_layer = pretrained_embedding_layer(word_to_vec_map, word_to_index)
print("weights[0][1][3] =", embedding_layer.get_weights()[0][1][3])
# **Expected Output**:
#
# <table>
# <tr>
# <td>
# **weights[0][1][3] =**
# </td>
# <td>
# -0.3403
# </td>
# </tr>
# </table>
# ## 2.3 Building the Emojifier-V2
#
# Lets now build the Emojifier-V2 model. You will do so using the embedding layer you have built, and feed its output to an LSTM network.
#
# <img src="images/emojifier-v2.png" style="width:700px;height:400px;"> <br>
# <caption><center> **Figure 3**: Emojifier-v2. A 2-layer LSTM sequence classifier. </center></caption>
#
#
# **Exercise:** Implement `Emojify_V2()`, which builds a Keras graph of the architecture shown in Figure 3. The model takes as input an array of sentences of shape (`m`, `max_len`, ) defined by `input_shape`. It should output a softmax probability vector of shape (`m`, `C = 5`). You may need `Input(shape = ..., dtype = '...')`, [LSTM()](https://keras.io/layers/recurrent/#lstm), [Dropout()](https://keras.io/layers/core/#dropout), [Dense()](https://keras.io/layers/core/#dense), and [Activation()](https://keras.io/activations/).
# +
# GRADED FUNCTION: Emojify_V2
def Emojify_V2(input_shape, word_to_vec_map, word_to_index):
"""
Function creating the Emojify-v2 model's graph.
Arguments:
input_shape -- shape of the input, usually (max_len,)
word_to_vec_map -- dictionary mapping every word in a vocabulary into its 50-dimensional vector representation
word_to_index -- dictionary mapping from words to their indices in the vocabulary (400,001 words)
Returns:
model -- a model instance in Keras
"""
### START CODE HERE ###
# Define sentence_indices as the input of the graph, it should be of shape input_shape and dtype 'int32' (as it contains indices).
sentence_indices = Input(shape = input_shape, dtype = 'int32')
# Create the embedding layer pretrained with GloVe Vectors (≈1 line)
embedding_layer = pretrained_embedding_layer(word_to_vec_map, word_to_index)
# Propagate sentence_indices through your embedding layer, you get back the embeddings
embeddings = embedding_layer(sentence_indices)
# Propagate the embeddings through an LSTM layer with 128-dimensional hidden state
# Be careful, the returned output should be a batch of sequences.
X = LSTM(units = 128, return_sequences = True)(embeddings)
# Add dropout with a probability of 0.5
X = Dropout(0.5)(X)
# Propagate X trough another LSTM layer with 128-dimensional hidden state
# Be careful, the returned output should be a single hidden state, not a batch of sequences.
X = LSTM(units = 128)(X)
# Add dropout with a probability of 0.5
X = Dropout(0.5)(X)
# Propagate X through a Dense layer with softmax activation to get back a batch of 5-dimensional vectors.
X = Dense(5)(X)
# Add a softmax activation
X = Activation('softmax')(X)
# Create Model instance which converts sentence_indices into X.
model = Model(inputs = sentence_indices, outputs = X)
### END CODE HERE ###
return model
# -
# Run the following cell to create your model and check its summary. Because all sentences in the dataset are less than 10 words, we chose `max_len = 10`. You should see your architecture, it uses "20,223,927" parameters, of which 20,000,050 (the word embeddings) are non-trainable, and the remaining 223,877 are. Because our vocabulary size has 400,001 words (with valid indices from 0 to 400,000) there are 400,001\*50 = 20,000,050 non-trainable parameters.
model = Emojify_V2((maxLen,), word_to_vec_map, word_to_index)
model.summary()
# As usual, after creating your model in Keras, you need to compile it and define what loss, optimizer and metrics your are want to use. Compile your model using `categorical_crossentropy` loss, `adam` optimizer and `['accuracy']` metrics:
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# It's time to train your model. Your Emojifier-V2 `model` takes as input an array of shape (`m`, `max_len`) and outputs probability vectors of shape (`m`, `number of classes`). We thus have to convert X_train (array of sentences as strings) to X_train_indices (array of sentences as list of word indices), and Y_train (labels as indices) to Y_train_oh (labels as one-hot vectors).
X_train_indices = sentences_to_indices(X_train, word_to_index, maxLen)
Y_train_oh = convert_to_one_hot(Y_train, C = 5)
# Fit the Keras model on `X_train_indices` and `Y_train_oh`. We will use `epochs = 50` and `batch_size = 32`.
model.fit(X_train_indices, Y_train_oh, epochs = 50, batch_size = 32, shuffle=True)
# Your model should perform close to **100% accuracy** on the training set. The exact accuracy you get may be a little different. Run the following cell to evaluate your model on the test set.
X_test_indices = sentences_to_indices(X_test, word_to_index, max_len = maxLen)
Y_test_oh = convert_to_one_hot(Y_test, C = 5)
loss, acc = model.evaluate(X_test_indices, Y_test_oh)
print()
print("Test accuracy = ", acc)
# You should get a test accuracy between 80% and 95%. Run the cell below to see the mislabelled examples.
# This code allows you to see the mislabelled examples
C = 5
y_test_oh = np.eye(C)[Y_test.reshape(-1)]
X_test_indices = sentences_to_indices(X_test, word_to_index, maxLen)
pred = model.predict(X_test_indices)
for i in range(len(X_test)):
x = X_test_indices
num = np.argmax(pred[i])
if(num != Y_test[i]):
print('Expected emoji:'+ label_to_emoji(Y_test[i]) + ' prediction: '+ X_test[i] + label_to_emoji(num).strip())
# Now you can try it on your own example. Write your own sentence below.
# Change the sentence below to see your prediction. Make sure all the words are in the Glove embeddings.
x_test = np.array(['not feeling happy'])
X_test_indices = sentences_to_indices(x_test, word_to_index, maxLen)
print(x_test[0] +' '+ label_to_emoji(np.argmax(model.predict(X_test_indices))))
# Previously, Emojify-V1 model did not correctly label "not feeling happy," but our implementation of Emojiy-V2 got it right. (Keras' outputs are slightly random each time, so you may not have obtained the same result.) The current model still isn't very robust at understanding negation (like "not happy") because the training set is small and so doesn't have a lot of examples of negation. But if the training set were larger, the LSTM model would be much better than the Emojify-V1 model at understanding such complex sentences.
#
# ### Congratulations!
#
# You have completed this notebook! ❤️❤️❤️
#
# <font color='blue'>
# **What you should remember**:
# - If you have an NLP task where the training set is small, using word embeddings can help your algorithm significantly. Word embeddings allow your model to work on words in the test set that may not even have appeared in your training set.
# - Training sequence models in Keras (and in most other deep learning frameworks) requires a few important details:
# - To use mini-batches, the sequences need to be padded so that all the examples in a mini-batch have the same length.
# - An `Embedding()` layer can be initialized with pretrained values. These values can be either fixed or trained further on your dataset. If however your labeled dataset is small, it's usually not worth trying to train a large pre-trained set of embeddings.
# - `LSTM()` has a flag called `return_sequences` to decide if you would like to return every hidden states or only the last one.
# - You can use `Dropout()` right after `LSTM()` to regularize your network.
#
# Congratulations on finishing this assignment and building an Emojifier. We hope you're happy with what you've accomplished in this notebook!
#
# # 😀😀😀😀😀😀
#
#
#
# ## Acknowledgments
#
# Thanks to <NAME> and the Woebot team for their advice on the creation of this assignment. Woebot is a chatbot friend that is ready to speak with you 24/7. As part of Woebot's technology, it uses word embeddings to understand the emotions of what you say. You can play with it by going to http://woebot.io
#
# <img src="images/woebot.png" style="width:600px;height:300px;">
#
#
#
| Emojify - v2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/uzmakhan7/uk/blob/master/numpy.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="kITdEQ8fBnz6" colab_type="code" colab={}
import numpy
# + id="sKQLkd2SBtpx" colab_type="code" colab={}
import numpy as np
# + id="Q0O2FkklCuvy" colab_type="code" colab={}
a=np.array([2,7,1,99,4])
# + id="HmNACPGOC_LJ" colab_type="code" outputId="67f92674-6ab4-4f2d-ff72-30e6b68b23ae" colab={"base_uri": "https://localhost:8080/", "height": 34}
type(a)
# + id="XEWTiOlvDLAk" colab_type="code" colab={}
b=np.array([12,17,11,199,14])
# + id="K7FqfZKADYZq" colab_type="code" outputId="e5f881f1-bc36-4d51-bbbe-e55364ef7cba" colab={"base_uri": "https://localhost:8080/", "height": 34}
a
# + id="9X2V4eecDaTy" colab_type="code" outputId="2644f860-0270-44ad-d4ba-0fca49951845" colab={"base_uri": "https://localhost:8080/", "height": 34}
b
# + id="DZ-rElGpDcP0" colab_type="code" outputId="cdd99a46-f17b-4a89-f7bf-d5bf1f0f10b3" colab={"base_uri": "https://localhost:8080/", "height": 34}
a[0]
# + id="nS7TfVgEDehi" colab_type="code" outputId="c02b3dba-88d8-447d-8a4a-04a10a1033b0" colab={"base_uri": "https://localhost:8080/", "height": 34}
b[0]
# + id="07IRRtW0DkdO" colab_type="code" outputId="00ab234c-e031-4deb-e4e4-9e170638404f" colab={"base_uri": "https://localhost:8080/", "height": 34}
a+b
# + id="-DNr-wxrDq1c" colab_type="code" outputId="4d579c22-2e87-4d1c-e308-72de7f876a73" colab={"base_uri": "https://localhost:8080/", "height": 34}
a+2
# + id="GBwnhHpDDvxK" colab_type="code" outputId="2c842f58-244f-42eb-858e-4684d7d95d2b" colab={"base_uri": "https://localhost:8080/", "height": 34}
a*2
# + id="OinA-Tg0Dy3P" colab_type="code" outputId="1ed9e2c5-9ebb-4003-c94e-f5fd99d1a4b6" colab={"base_uri": "https://localhost:8080/", "height": 34}
a**2
# + id="IHtvCu2AD2ec" colab_type="code" colab={}
x=np.array([[2,5,8],[3,6,1]])
# + id="j1KG5iBoF2ga" colab_type="code" outputId="688cca59-18d9-4864-b95b-0b61982804c4" colab={"base_uri": "https://localhost:8080/", "height": 34}
x[0][0]
# + id="dSB1PChmGmew" colab_type="code" colab={}
y=x+7
# + id="HtrF939tGsnt" colab_type="code" colab={}
z=np.array([[2,7],[3,8],[2,9],[9,4]])
# + id="uFD_CosAHquC" colab_type="code" outputId="4c976b98-ef46-44ed-db8a-ae405c20ff9f" colab={"base_uri": "https://localhost:8080/", "height": 85}
z
# + id="wtIHKcRUHszu" colab_type="code" outputId="fea02596-a4cc-4e02-a7f4-3184c7d38909" colab={"base_uri": "https://localhost:8080/", "height": 34}
z.shape
# + id="c5-T8bTRHx5U" colab_type="code" outputId="7674daf6-8e3c-46fa-d2b9-7c039c4a8970" colab={"base_uri": "https://localhost:8080/", "height": 51}
z[0:2]
# + id="PL0klluBIJNe" colab_type="code" outputId="2cbcc0f6-4f54-44ba-cf05-5b6d8c18cdf0" colab={"base_uri": "https://localhost:8080/", "height": 85}
z[0:]
# + id="5LNkRmx8IYS6" colab_type="code" outputId="bcb63a49-d048-40fa-8a13-434d02c16379" colab={"base_uri": "https://localhost:8080/", "height": 34}
z[0:,0]
# + id="Ckscr1MjItLv" colab_type="code" outputId="1ec91326-379e-4116-ac30-d912add15f9d" colab={"base_uri": "https://localhost:8080/", "height": 34}
z[0:2,0]
# + id="6kv90ExJJDOv" colab_type="code" outputId="c7139bf7-9e32-49bc-af9e-397e4803ca5c" colab={"base_uri": "https://localhost:8080/", "height": 34}
z[0:,1]
# + id="GSH6Utz0JNum" colab_type="code" outputId="8d7a0b28-57f5-4e88-8d55-fed0dbb7c153" colab={"base_uri": "https://localhost:8080/", "height": 85}
z[0:,0:2]
# + id="i9ZiLjy6Jp_3" colab_type="code" outputId="68191140-fe7b-4d3e-c1e3-23557880b2a3" colab={"base_uri": "https://localhost:8080/", "height": 85}
z[0:,[0,1]]
# + id="YqZDU7ihJ2ZB" colab_type="code" outputId="dffecb99-177d-414c-9925-8a42599c3e4d" colab={"base_uri": "https://localhost:8080/", "height": 51}
z[[0,2]]
# + id="FJ6OZyugKpLC" colab_type="code" outputId="d8fb17f8-1514-460f-a27d-3d4e667fb697" colab={"base_uri": "https://localhost:8080/", "height": 34}
z[[0,3],1]
# + id="tAC-aw-vLIsS" colab_type="code" outputId="8464eae9-83ec-4106-c665-e228e275d321" colab={"base_uri": "https://localhost:8080/", "height": 163}
b=np.array[[1,9,7],[3,2,8],[4,5,6],[2,9,0]]
# + id="HhSi4rKyNkOH" colab_type="code" colab={}
x1=x.reshape(3,2)
# + id="uF7wbsiXORpi" colab_type="code" outputId="a98ef02f-ff8d-4289-849d-000c8f5db365" colab={"base_uri": "https://localhost:8080/", "height": 68}
np.zeros((3,6))
# + id="aAJ2crGFP0rd" colab_type="code" outputId="2e4dcd29-0903-4b33-f091-e4a7293b2044" colab={"base_uri": "https://localhost:8080/", "height": 163}
np.ones((3,4),dtype=int32)
# + id="CuMdZGxjQMHx" colab_type="code" outputId="9039ecd7-a330-4192-8ccd-8d769dc4da20" colab={"base_uri": "https://localhost:8080/", "height": 85}
np.full((4,5),9)
# + id="zh8TGsjvQbab" colab_type="code" colab={}
| numpy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Exploration of RISE with mnist binary
#
# Function : Exploration of RISE mnist binary
# Author : Team DIANNA
# Contributor :
# First Built : 2021.08.25
# Last Update : 2021.08.25
# Note : We ran the method using the our own trained model on mnist and various instances from mnist dataset. Results look random. There is no sense that we can make of the heatmaps.
import dianna
import onnx
import onnxruntime
import numpy as np
# %matplotlib inline
from matplotlib import pyplot as plt
from scipy.special import softmax
import pandas as pd
from dianna.methods import RISE
from dianna import visualization
data = np.load('./binary-mnist.npz')
X_test = data['X_test'].astype(np.float32).reshape([-1, 28, 28, 1])/255
y_test = data['y_test']
# # Predict classes for test data
# +
def run_model(data):
data = data.reshape([-1, 1, 28, 28]).astype(np.float32)*255
fname = './mnist_model.onnx'
# get ONNX predictions
sess = onnxruntime.InferenceSession(fname)
input_name = sess.get_inputs()[0].name
output_name = sess.get_outputs()[0].name
onnx_input = {input_name: data}
pred_onnx = sess.run([output_name], onnx_input)
return softmax(pred_onnx[0], axis=1)
pred_onnx = run_model(X_test)
# -
# Print class and image of a single instance in the test data
i_instance = 3
print(pred_onnx[i_instance])
plt.imshow(X_test[i_instance][...,0]) # 0 for channel
# +
# heatmaps = dianna.explain(run_model, X_test[[i_instance]], method="RISE", n_masks=2000, feature_res=8, p_keep=0.5)
# +
# investigate which value for p_keep works best by looking at the stddev of the probabilities for the target class,
def print_stats(p_keep):
n_masks = 500
feature_res = 8
explainer = RISE(n_masks=n_masks, feature_res=feature_res, p_keep=p_keep)
explainer(run_model, X_test[[i_instance]])
preds = explainer.predictions[:, y_test[i_instance]]
df = pd.DataFrame(preds)
display(df.describe())
# print_stats(.5) # stddev = .006 -> too low
# print_stats(.3) # .1 -> still a bit low
print_stats(.1) # .26, with minimum probability of .56 and max of 1.0. This may be ok
# -
explainer = RISE(n_masks=5000, feature_res=8, p_keep=.1)
heatmaps = explainer(run_model, X_test[[i_instance]])
visualization.plot_image(heatmaps[0], X_test[i_instance], data_cmap='gray', heatmap_cmap='bwr')
visualization.plot_image(heatmaps[0], heatmap_cmap='gray')
visualization.plot_image(heatmaps[1])
# # Conclusion
# We see that for this zero, the left and right parts of it are most important to determine the class. This makes sense, as a one would not have signal in those regions. For higher values of p_keep, the probability does not change enough for RISE to give sensible results, so this parameter needs to be checked/tuned. With proper values for p_keep, RISE thus seems to work.
# +
def describe(arr):
print('shape:',arr.shape, 'min:',np.min(arr), 'max:',np.max(arr), 'std:',np.std(arr))
describe(heatmaps[0])
describe(heatmaps[1])
# -
for i in range(10):
plt.imshow(explainer.masks[i])
plt.show()
| example_data/xai_method_study/RISE/rise_mnist.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: lexgen
# language: python
# name: lexgen
# ---
# # Clean Corpora - One Off
# ## Imports and Settings
from nate_givens_toolkit import cloud_io as cloud
import pandas as pd
from datetime import datetime
# ## Global Variables
RAW_CORPORA_DIR = 'raw_corpora/'
CLEAN_CORPORA_DIR = 'clean_corpora/'
DATA_DIR = 'data_files/'
BUCKET = 'lexgen'
# ## Functions
def is_invalid_word(word, valid_chars):
# take a word and list of valid chars
# return true if the word contains any chars *not* in valid_chars
# otherwise return false
return any([x not in valid_chars for x in str(word)])
# ## Logic
# ### Specify Clean Corpus Variables
raw_corpus_filename = 'af_full_2018.txt'
clean_corpus_filename = 'af_full_2018_A.txt'
clean_corpus_note = 'Cleaned version of af_full_2018 with top 200 words having frequency reset to exclusive mean'
# ### Read in Data Tables
# #### Raw Corpora
raw_corpora = cloud.read_csv_from_s3('raw_corpora_inventory.dat', DATA_DIR, BUCKET, sep='|')
raw_corpora.head()
# #### Clean Corpora
clean_corpora = cloud.read_csv_from_s3('clean_corpora_inventory.dat', DATA_DIR, BUCKET, sep='|')
clean_corpora.head()
# #### Valid Characters
valid_chars_table = cloud.read_csv_from_s3('valid_chars.dat', DATA_DIR, BUCKET, sep='|')
valid_chars_table.head()
# ## Populate Secondary Variables
# #### Use raw_corpus_filename to get lang_code
lang_code = raw_corpora.loc[raw_corpora['filename'] == raw_corpus_filename]['lang_code'].values[0]
# #### Use lang_code to get clean_chars
valid_chars = valid_chars_table.loc[valid_chars_table['lang_code'] == lang_code]['valid_chars'].values[0].split(',')
# ### Read in Raw Corpus
raw_corpus = cloud.read_csv_from_s3(raw_corpus_filename, RAW_CORPORA_DIR, BUCKET, sep=' ', header = None, names = ['word', 'freq'])
raw_corpus.head()
# ### Clean Raw Corpus
# #### Flag and then remove words that contain invalid characters
raw_corpus['invalid'] = raw_corpus['word'].apply(is_invalid_word, valid_chars=valid_chars)
valid_corpus = raw_corpus.copy(deep=True)
valid_corpus = valid_corpus[raw_corpus['invalid'] == False]
valid_corpus.drop(labels='invalid', axis=1, inplace=True)
valid_corpus.reset_index
# #### Replace the frequency of the top-200 words with the average frequency
mean_freq = valid_corpus.loc[200:, 'freq'].mean()
valid_corpus.loc[:199, 'freq'] = mean_freq
# ### Write Clean Corpora to S3
cloud.write_csv_to_s3(clean_corpus_filename, CLEAN_CORPORA_DIR, BUCKET, valid_corpus, sep='|', index=False)
# ### Update Clean Corpora Inventory
new_row = {
'filename': clean_corpus_filename
,'raw_corpora_filename': raw_corpus_filename
,'last_load_dtime': str(datetime.utcnow())
,'note': clean_corpus_note
}
clean_corpora = clean_corpora.append(new_row, ignore_index=True)
cloud.write_csv_to_s3('clean_corpora_inventory.dat', DATA_DIR, BUCKET, clean_corpora, sep='|', index=False)
| .ipynb_checkpoints/Clean_Corpora_OneOff-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="W_USwZH65G6x"
# # Sample script to create data for the NLI Data Sanity Check
# https://github.com/Helsinki-NLP/nli-data-sanity-check
#
# + colab={"base_uri": "https://localhost:8080/"} id="p7rN3VGSOrHt" outputId="ea094316-1c01-4ba8-bd5f-f415e786171b"
# !pip install datasets
# + id="dwVNtbFGOz2L"
import datasets
# + colab={"base_uri": "https://localhost:8080/"} id="WFEqr7BdPEaI" outputId="520ceb4c-ec78-4e21-8cc4-cbd504e4d8ea"
nli_data = datasets.load_dataset('multi_nli')
# + id="xOPNYzmBPeGm"
train_data = nli_data['train']
dev = nli_data['validation_matched']
test = nli_data['validation_matched']
# + id="Gx_8s4UwgqXO"
train_hypothesis = train_data['hypothesis']
train_premise = train_data['premise']
train_label = train_data['label']
# + id="tFM15QK1PxBN"
dev_hypothesis = dev['hypothesis']
dev_premise = dev['premise']
dev_label = dev['label']
# + colab={"base_uri": "https://localhost:8080/"} id="IrC3DWTeXitZ" outputId="4e915f0c-67ca-4978-d1f2-b33a780b35c9"
import nltk
nltk.download(['universal_tagset', 'punkt','averaged_perceptron_tagger'])
# + [markdown] id="8OlVj7Kw5bcR"
# ###Define whether to corrupt the test data or train data.
# + id="XvCei1nr2z8y"
dataset = 'train'
# + id="XkmSEVMz4nb7"
if dataset == 'dev':
premise = test['premise']
hypothesis = test['hypothesis']
goldlabels = test['label']
else:
premise = train_data['premise']
hypothesis = train_data['hypothesis']
goldlabels = train_data['label']
# + id="Bk3UUnW-g4js" colab={"base_uri": "https://localhost:8080/"} outputId="71857102-b5de-4553-b023-dfd6ffd8166d"
from tqdm import tqdm
tokenized_prem = []
prem_labels = []
for sentence in tqdm(premise):
text = nltk.word_tokenize(sentence)
tagged = nltk.pos_tag(text, tagset='universal')
sent = []
lab = []
for pair in tagged:
sent.append(pair[0])
lab.append(pair[1])
tokenized_prem.append(sent)
prem_labels.append(lab)
# + id="aT0ZqJTuhXHD" colab={"base_uri": "https://localhost:8080/"} outputId="d4d95e45-6ab1-4c31-c6a3-68bed04dcd50"
tokenized_hypo = []
hypo_labels = []
for sentence in tqdm(hypothesis):
text = nltk.word_tokenize(sentence)
tagged = nltk.pos_tag(text, tagset='universal')
sent = []
lab = []
for pair in tagged:
sent.append(pair[0])
lab.append(pair[1])
tokenized_hypo.append(sent)
hypo_labels.append(lab)
# + id="9Bk-IrbHhepf"
def corrupt(POS, tokenized_hypo, hypo_labels, tokenized_prem, prem_labels):
prem_list = []
hypo_list = []
count_prem = 0
count_hypo = 0
for h, l in zip(tokenized_hypo, hypo_labels):
sent = []
for word, label in zip(h, l):
if label not in [POS]:
sent.append(word)
else:
count_hypo = count_hypo + 1
hypo_list.append(sent)
for h, l in zip(tokenized_prem, prem_labels):
sent = []
for word, label in zip(h, l):
if label not in [POS]:
sent.append(word)
else:
count_prem = count_prem + 1
prem_list.append(sent)
print(f'TOKENS REMOVED ({POS}):')
print('prem: ' + str(count_prem))
print('hypo: ' + str(count_hypo))
return prem_list, hypo_list
# + id="TVtRHvo9hXAi"
def write_file(POS, prem_list, hypo_list, goldlabels):
filename = 'MNLI-'+ POS + '.tsv'
with open(filename, 'w') as adjfile:
i=0
adjfile.write('index\tsentence1\tsentence2\tgold_label\n')
for pre, hyp, lab in zip(prem_list, hypo_list, goldlabels):
if str(lab) == '0':
lab = 'entailment'
elif str(lab) == '1':
lab = 'neutral'
else:
lab = 'contradiction'
if len(hyp) != 0 and len(pre) != 0:
adjfile.write(str(i) + "\t" + ' '.join(pre) + "\t" + ' '.join(hyp) + '\t' + lab + '\n')
i = i+1
# + colab={"base_uri": "https://localhost:8080/"} id="4QeYCbfI6xR4" outputId="6aeda806-6c99-4a19-809f-d2998079ae36"
for pos in ['NOUN', 'VERB', 'PRON', 'ADJ', 'ADV', 'CONJ', 'NUM', 'DET']:
prem_list, hypo_list = corrupt(pos, tokenized_hypo, hypo_labels, tokenized_prem, prem_labels)
write_file(pos, prem_list, hypo_list, goldlabels)
# + id="Lznfoz0_AYDj"
| corrupt_mnli_datasets.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
# +
from sklearn.linear_model import LinearRegression
import pandas as pd
import numpy as np
bmi_life_data = pd.read_csv('bmi_and_life_expectancy.csv')
model = LinearRegression()
bmi_life_data.head()
# -
model.fit(bmi_life_data[['BMI']], bmi_life_data[['Life expectancy']])
laos_life_exp = model.predict([21.07931])
print(laos_life_exp)
| week_1/linear_regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # GDC June 2021 Webinar: GDC Data Submission Overview
#
# ### Monday, June 28, 2021<br>2:00 PM - 3:00 PM (EST)<br><NAME>, Lead for GDC User Services <br>University of Chicago
#
#
# # <a id='overview'>Notebook Overview</a>
#
#
# ### <a id='about_notebook'>About this notebook</a>
#
# - This notebook functions as a step-by-step set of instructions to submit a BAM file to the GDC using Python. Submitters who have a completely empty project or who have just started submitting with python might find this useful.
#
# - Commands and functions in this notebook will rely on the following Python packages:
# - `requests` - if not already installed on your system, can install with command `pip install requests` from command line or using a new code cell in this notebook
# - `json` - part of Python standard library, should already be installed on system
# - To execute code in a code cell, press either 'Cmd + Enter' or 'Control + Enter' depending on operating system and keyboard layout
# - A token file will need to be downloaded from the [GDC Submission Portal](https://docs.gdc.cancer.gov/Data_Submission_Portal/Users_Guide/Data_Submission_Process/#authentication)
# ### Overview
#
# - For projects that have been approved to be included in the GDC, submitters can make use of the `submission` GDC API endpoint to submit node entities to submission projects
# - Submission will require a token downloaded from the [GDC Submission Portal](https://docs.gdc.cancer.gov/Data_Submission_Portal/Users_Guide/Data_Submission_Process/#authentication)
# - Data can be submitted in `JSON` or `TSV` format; depending on the data format, users will need to edit the `"Content-Type"` in the request command (see below)
# - Additionally, `JSON` and `TSV` templates for nodes to be submitted can be downloaded from the GDC Data Dictionary Viewer webpage: https://docs.gdc.cancer.gov/Data_Dictionary/viewer/#?_top=1
# - Submittable files (such as FASTQ or BAM files) should be uploaded with the [GDC Data Transfer Tool](https://gdc.cancer.gov/access-data/gdc-data-transfer-tool)
# - Additional features and more information regarding submission using the GDC API can be found here: https://docs.gdc.cancer.gov/API/Users_Guide/Submission/
# - [Strategies for Submitting in Bulk](https://docs.gdc.cancer.gov/Data_Submission_Portal/Users_Guide/Data_Submission_Walkthrough/#strategies-for-submitting-in-bulk)
#
# ### Endpoint
#
# - The format for using the GDC API Submission endpoint uses the project information, i.e. `https://api.gdc.cancer.gov/submission/<program_name>/<project_code>`
# - For example: https://api.gdc.cancer.gov/submission/TCGA/LUAD or https://api.gdc.cancer.gov/submission/CPTAC/3
#
# ### Steps
#
# 1. Read in token file
# 2. Read in submission file
# 3. Edit endpoint with project ID information and submit data using `POST` (JSON file submission) or `PUT` (TSV file submission) request
#
# ### 1. Submitting a Case (JSON)
# +
#1. Import Python packages and read in token file
import json
import requests
token = open("../gdc-user-token.txt").read().strip()
# +
#2. Read in submission file
case_json = json.load(open("case.json"))
print(json.dumps(case_json, indent=4))
# +
#3. Edit endpoint and submit data using PUT request
ENDPT = "https://api.gdc.cancer.gov/submission/GDC/INTERNAL/_dry_run"
#submission request if data is in JSON format
response = requests.put(url = ENDPT, json = case_json, headers={'X-Auth-Token': token, "Content-Type": "application/json"})
print(json.dumps(json.loads(response.text), indent = 4))
# -
# ### 2: Submitting a Sample
# +
#1. Read in submission file
sample_tsv = open("sample.tsv", "rb")
sample_tsv_display = open("sample.tsv", "r")
for x in sample_tsv_display.readlines():
print(x.strip().split("\t"))
# +
#2. Edit endpoint and submit data using PUT request
ENDPT = "https://api.gdc.cancer.gov/submission/GDC/INTERNAL/"
#submission request if data is in TSV format
response = requests.put(url = ENDPT, data = sample_tsv, headers={'X-Auth-Token': token, "Content-Type": "text/tsv"})
print(json.dumps(json.loads(response.text), indent = 4))
# -
# ### 3: Submitting the Aliquot and Read_Group
# +
#1. Read in submission file
aliquot_rg_json = json.load(open("aliquot_readgroup.json"))
print(json.dumps(aliquot_rg_json, indent=4))
# +
#2. Submit data using PUT request
ENDPT = "https://api.gdc.cancer.gov/submission/GDC/INTERNAL"
#submission request if data is in JSON format
response = requests.put(url = ENDPT, json = aliquot_rg_json, headers={'X-Auth-Token': token, "Content-Type": "application/json"})
print(json.dumps(json.loads(response.text), indent = 4))
# -
# ### 4: Register the Submitted Aligned Reads File
# +
#1. Read in submission file
sar_json = json.load(open("SAR.json"))
print(json.dumps(sar_json, indent=4))
# +
#2. Submit data using PUT request
ENDPT = "https://api.gdc.cancer.gov/submission/GDC/INTERNAL"
#submission request if data is in JSON format
response = requests.put(url = ENDPT, json = sar_json, headers={'X-Auth-Token': token, "Content-Type": "application/json"})
print(json.dumps(json.loads(response.text), indent = 4))
# -
# ### 5: Upload the Submitted Aligned Reads Data File Using Data Transfer Tool
#
# +
## ./gdc-client upload <UUID> -t token_file.txt
| Notebooks/Submission_June_2021/Webinar_June_2021.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Intro to Models
# ## Lecture 5, EM212: Applied Data Science
# + [markdown] slideshow={"slide_type": "slide"}
# # This lecture will introduce:
#
# 1. A public dataset
# 2. Exploratory analysis
# 3. Linear models
# 4. Performing 1-3 using Python
#
# We will be taking time at the end of class to play with the tools we just used.
# + [markdown] slideshow={"slide_type": "slide"}
# # Let's pretend you're Ariana Grande
#
# 
# photo: <NAME>
# + [markdown] slideshow={"slide_type": "slide"}
# # How would you use data on this shopping expedition?
#
# 
# photo: <NAME>
# + [markdown] slideshow={"slide_type": "fragment"}
# A data frame with 53940 rows and 10 variables:
#
# price: price in US dollars (326--18,823)
#
# carat: weight of the diamond (0.2--5.01)
#
# cut: quality of the cut (Fair, Good, Very Good, Premium, Ideal)
#
# color: diamond colour, from J (worst) to D (best)
#
# clarity: a measurement of how clear the diamond is (I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best))
#
# x: length in mm (0--10.74)
#
# y: width in mm (0--58.9)
#
# z: depth in mm (0--31.8)
#
# depth: total depth percentage = z / mean(x, y) = 2 * z / (x + y) (43--79)
#
# table: width of top of diamond relative to widest point (43--95)
# + slideshow={"slide_type": "fragment"}
import pandas as pd
import numpy as np
import seaborn as sns
import warnings
import statsmodels.formula.api as smf
from sklearn.linear_model import Lasso
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
sns.set_context('talk')
sns.set_style('darkgrid')
sns.set_palette('colorblind')
# + slideshow={"slide_type": "slide"}
diamonds = sns.load_dataset("diamonds")
diamonds.head()
# + [markdown] slideshow={"slide_type": "fragment"}
# cut: quality of the cut (Fair, Good, Very Good, Premium, Ideal)
#
# color: diamond colour, from J (worst) to D (best)
#
# clarity: a measurement of how clear the diamond is (I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best))
# + [markdown] slideshow={"slide_type": "slide"}
# We'll be using Python. For a good intro to the language, try https://www.codecademy.com/learn/learn-python
#
# The lines below setup the tools we'll be using:
| Lecture 5- FillIn.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# ***
# ***
# # 数据清洗之推特数据
# ***
# ***
#
# 王成军
#
# <EMAIL>
#
# 计算传播网 http://computational-communication.com
# + [markdown] slideshow={"slide_type": "slide"}
# ## 数据清洗(data cleaning)
# 是数据分析的重要步骤,其主要目标是将混杂的数据清洗为可以被直接分析的数据,一般需要将数据转化为数据框(data frame)的样式。
#
# 本章将以推特文本的清洗作为例子,介绍数据清洗的基本逻辑。
#
# - 清洗错误行
# - 正确分列
# - 提取所要分析的内容
# - 介绍通过按行、chunk的方式对大规模数据进行预处理
#
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# # 1. 抽取tweets样本做实验
# 此节学生略过
# + slideshow={"slide_type": "fragment"}
bigfile = open('/Users/chengjun/百度云同步盘/Writing/OWS/ows-raw.txt', 'rb')
chunkSize = 1000000
chunk = bigfile.readlines(chunkSize)
print len(chunk)
with open("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample.txt", 'w') as f:
for i in chunk:
f.write(i)
# + [markdown] slideshow={"slide_type": "slide"}
# # 2. 清洗错行的情况
# + slideshow={"slide_type": "subslide"}
with open("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample.txt", 'rb') as f:
lines = f.readlines()
# + slideshow={"slide_type": "subslide"}
# 总行数
len(lines)
# + slideshow={"slide_type": "subslide"}
# 查看第一行
lines[0]
# + [markdown] slideshow={"slide_type": "subslide"}
# # 问题: 第一行是变量名
# > ## 1. 如何去掉换行符?
# > ## 2. 如何获取每一个变量名?
#
# + slideshow={"slide_type": "subslide"}
varNames = lines[0].replace('\n', '').split(',')
varNames
# + slideshow={"slide_type": "subslide"}
len(varNames)
# -
lines[1344]
# + [markdown] slideshow={"slide_type": "subslide"}
# # 如何来处理错误换行情况?
# + slideshow={"slide_type": "subslide"}
with open("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample_clean.txt", 'w') as f:
right_line = '' # 正确的行,它是一个空字符串
blocks = [] # 确认为正确的行会被添加到blocks里面
for line in lines:
right_line += line.replace('\n', ' ')
line_length = len(right_line.split(','))
if line_length >= 14:
blocks.append(right_line)
right_line = ''
for i in blocks:
f.write(i + '\n')
# + slideshow={"slide_type": "subslide"}
len(blocks)
# + slideshow={"slide_type": "subslide"}
blocks[1344]
# + slideshow={"slide_type": "subslide"}
with open("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample_clean4.txt", 'w') as f:
right_line = '' # 正确的行,它是一个空字符串
blocks = [] # 确认为正确的行会被添加到blocks里面
for line in lines:
right_line += line.replace('\n', ' ').replace('\r', ' ')
line_length = len(right_line.split(','))
if line_length >= 14:
blocks.append(right_line)
right_line = ''
for i in blocks:
f.write(i + '\n')
# + slideshow={"slide_type": "subslide"}
blocks[1344]
# + [markdown] slideshow={"slide_type": "slide"}
# # 3. 读取数据、正确分列
# + slideshow={"slide_type": "fragment"}
# 提示:你可能需要修改以下路径名
with open("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample_clean.txt", 'rb') as f:
chunk = f.readlines()
# + slideshow={"slide_type": "subslide"}
len(chunk)
# + slideshow={"slide_type": "fragment"}
chunk[:3]
# + slideshow={"slide_type": "slide"}
import csv
clean_lines = (line.replace('\x00','') \
for line in chunk[1:])
lines = csv.reader(clean_lines, delimiter=',', \
quotechar='"')
# + slideshow={"slide_type": "slide"}
import pandas as pd
df = pd.read_csv("/Users/chengjun/GitHub/cjc/data/ows_tweets_sample_clean.txt",\
sep = ',', quotechar='"')
df[:3]
# + slideshow={"slide_type": "subslide"}
df.Text[1]
# + slideshow={"slide_type": "subslide"}
df['From User']
# + [markdown] slideshow={"slide_type": "slide"}
# # 4. 统计数量
# ### 统计发帖数量所对应的人数的分布
# > 人数在发帖数量方面的分布情况
# + slideshow={"slide_type": "fragment"}
from collections import defaultdict
data_dict = defaultdict(int)
line_num = 0
lines = csv.reader((line.replace('\x00','') for line in chunk[1:]), delimiter=',', quotechar='"')
for i in lines:
line_num +=1
data_dict[i[8]] +=1 # i[8] 是user
# + slideshow={"slide_type": "subslide"}
data_dict.items()[:5]
# + slideshow={"slide_type": "fragment"}
print line_num
# + slideshow={"slide_type": "slide"}
# %matplotlib inline
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import matplotlib
#matplotlib.rcParams['font.sans-serif'] = ['Microsoft YaHei'] #指定默认字体
matplotlib.rc("savefig", dpi=100)
font = FontProperties(fname=r'/Users/chengjun/github/cjc/data/msyh.ttf', size=14) # 注意:修改这里的路径名
# + slideshow={"slide_type": "slide"}
plt.hist(data_dict.values())
#plt.yscale('log')
#plt.xscale('log')
plt.xlabel(u'发帖数', fontproperties=font)
plt.ylabel(u'人数', fontproperties=font)
plt.show()
# + slideshow={"slide_type": "slide"}
tweet_dict = defaultdict(int)
for i in data_dict.values():
tweet_dict[i] += 1
plt.loglog(tweet_dict.keys(), tweet_dict.values(), 'ro',linewidth=2)
plt.xlabel(u'推特数', fontproperties=font)
plt.ylabel(u'人数', fontproperties=font )
plt.show()
# + slideshow={"slide_type": "slide"}
import numpy as np
import statsmodels.api as sm
def powerPlot(d_value, d_freq, color, marker):
d_freq = [i + 1 for i in d_freq]
d_prob = [float(i)/sum(d_freq) for i in d_freq]
#d_rank = ss.rankdata(d_value).astype(int)
x = np.log(d_value)
y = np.log(d_prob)
xx = sm.add_constant(x, prepend=True)
res = sm.OLS(y,xx).fit()
constant,beta = res.params
r2 = res.rsquared
plt.plot(d_value, d_prob, linestyle = '', color = color, marker = marker)
plt.plot(d_value, np.exp(constant+x*beta),"red")
plt.xscale('log'); plt.yscale('log')
plt.text(max(d_value)/2,max(d_prob)/10,
r'$\beta$ = ' + str(round(beta,2)) +'\n' + r'$R^2$ = ' + str(round(r2, 2)))
# -
histo, bin_edges = np.histogram(data_dict.values(), 15)
bin_center = 0.5*(bin_edges[1:] + bin_edges[:-1])
powerPlot(bin_center,histo, 'r', 'o')
#lg=plt.legend(labels = [u'Tweets', u'Fit'], loc=3, fontsize=20)
plt.ylabel(u'概率', fontproperties=font)
plt.xlabel(u'推特数', fontproperties=font)
plt.show()
# + slideshow={"slide_type": "slide"}
import statsmodels.api as sm
from collections import defaultdict
import numpy as np
def powerPlot(data):
d = sorted(data, reverse = True )
d_table = defaultdict(int)
for k in d:
d_table[k] += 1
d_value = sorted(d_table)
d_value = [i+1 for i in d_value]
d_freq = [d_table[i]+1 for i in d_value]
d_prob = [float(i)/sum(d_freq) for i in d_freq]
#d_rank = ss.rankdata(d_value).astype(int)
x = np.log(d_value)
y = np.log(d_prob)
xx = sm.add_constant(x, prepend=True)
res = sm.OLS(y,xx).fit()
constant,beta = res.params
r2 = res.rsquared
plt.plot(d_value, d_prob, 'ro')
plt.plot(d_value, np.exp(constant+x*beta),"red")
plt.xscale('log'); plt.yscale('log')
plt.text(max(d_value)/2,max(d_prob)/5,
'Beta = ' + str(round(beta,2)) +'\n' + 'R squared = ' + str(round(r2, 2)))
plt.title('Distribution')
plt.ylabel('P(K)')
plt.xlabel('K')
plt.show()
# + slideshow={"slide_type": "subslide"}
powerPlot(data_dict.values())
# -
import powerlaw
def plotPowerlaw(data,ax,col,xlab):
fit = powerlaw.Fit(data,xmin=2)
#fit = powerlaw.Fit(data)
fit.plot_pdf(color = col, linewidth = 2)
a,x = (fit.power_law.alpha,fit.power_law.xmin)
fit.power_law.plot_pdf(color = col, linestyle = 'dotted', ax = ax, \
label = r"$\alpha = %d \:\:, x_{min} = %d$" % (a,x))
ax.set_xlabel(xlab, fontsize = 20)
ax.set_ylabel('$Probability$', fontsize = 20)
plt.legend(loc = 0, frameon = False)
# +
from collections import defaultdict
data_dict = defaultdict(int)
for i in df['From User']:
data_dict[i] += 1
# +
import matplotlib.cm as cm
cmap = cm.get_cmap('rainbow_r',6)
fig = plt.figure(figsize=(6, 4),facecolor='white')
ax = fig.add_subplot(1, 1, 1)
plotPowerlaw(data_dict.values(), ax,cmap(1), '$Gold\;Metals$')
# + [markdown] slideshow={"slide_type": "slide"}
# # 5. 清洗tweets文本
# + slideshow={"slide_type": "subslide"}
tweet = '''RT @AnonKitsu: ALERT!!!!!!!!!!COPS ARE KETTLING PROTESTERS IN PARK W HELICOPTERS AND PADDYWAGONS!!!!
#OCCUPYWALLSTREET #OWS #OCCUPYNY PLEASE @chengjun @mili http://computational-communication.com
http://ccc.nju.edu.cn RT !!HELP!!!!'''
# + slideshow={"slide_type": "subslide"}
import re
import twitter_text
# + [markdown] slideshow={"slide_type": "subslide"}
# # 安装twitter_text
# > ## pip install twitter-text-py
#
# + [markdown] slideshow={"slide_type": "subslide"}
# # 无法正常安装的同学
# ## 可以在spyder中打开terminal安装
# + slideshow={"slide_type": "subslide"}
import re
tweet = '''RT @AnonKitsu: ALERT!!!!!!!!!!COPS ARE KETTLING PROTESTERS IN PARK W HELICOPTERS AND PADDYWAGONS!!!!
#OCCUPYWALLSTREET #OWS #OCCUPYNY PLEASE @chengjun @mili http://computational-communication.com
http://ccc.nju.edu.cn RT !!HELP!!!!'''
rt_patterns = re.compile(r"(RT|via)((?:\b\W*@\w+)+)", \
re.IGNORECASE)
rt_user_name = rt_patterns.findall(tweet)[0][1].strip(' @')
rt_user_name
# + slideshow={"slide_type": "subslide"}
import re
tweet = '''@AnonKitsu: ALERT!!!!!!!!!!COPS ARE KETTLING PROTESTERS IN PARK W HELICOPTERS AND PADDYWAGONS!!!!
#OCCUPYWALLSTREET #OWS #OCCUPYNY PLEASE @chengjun @mili http://computational-communication.com
http://ccc.nju.edu.cn RT !!HELP!!!!'''
rt_patterns = re.compile(r"(RT|via)((?:\b\W*@\w+)+)", re.IGNORECASE)
rt_user_name = rt_patterns.findall(tweet)
print rt_user_name
if rt_user_name:
print 'it exits.'
else:
print 'None'
# + slideshow={"slide_type": "subslide"}
import re
def extract_rt_user(tweet):
rt_patterns = re.compile(r"(RT|via)((?:\b\W*@\w+)+)", re.IGNORECASE)
rt_user_name = rt_patterns.findall(tweet)
if rt_user_name:
rt_user_name = rt_user_name[0][1].strip(' @')
else:
rt_user_name = None
return rt_user_name
# + slideshow={"slide_type": "subslide"}
tweet = '''@AnonKitsu: ALERT!!!!!!!!!!COPS ARE KETTLING PROTESTERS IN PARK W HELICOPTERS AND PADDYWAGONS!!!!
#OCCUPYWALLSTREET #OWS #OCCUPYNY PLEASE @chengjun @mili http://computational-communication.com
http://ccc.nju.edu.cn RT !!HELP!!!!'''
print extract_rt_user(tweet)
# + [markdown] slideshow={"slide_type": "subslide"}
# # 获得清洗过的推特文本
#
# 不含人名、url、各种符号(如RT @等)
# + slideshow={"slide_type": "fragment"}
def extract_tweet_text(tweet, at_names, urls):
for i in at_names:
tweet = tweet.replace(i, '')
for j in urls:
tweet = tweet.replace(j, '')
marks = ['RT @', '@', '"', '#', '\n', '\t', ' ']
for k in marks:
tweet = tweet.replace(k, '')
return tweet
# + slideshow={"slide_type": "subslide"}
import twitter_text
tweet = '''RT @AnonKitsu: ALERT!!!!!!!!!!COPS ARE KETTLING PROTESTERS IN PARK W HELICOPTERS AND PADDYWAGONS!!!!
#OCCUPYWALLSTREET #OWS #OCCUPYNY PLEASE @chengjun @mili http://computational-communication.com
http://ccc.nju.edu.cn RT !!HELP!!!!'''
ex = twitter_text.Extractor(tweet)
at_names = ex.extract_mentioned_screen_names()
urls = ex.extract_urls()
hashtags = ex.extract_hashtags()
rt_user = extract_rt_user(tweet)
tweet_text = extract_tweet_text(tweet, at_names, urls)
print at_names, urls, hashtags, rt_user,'-------->', tweet_text
# + slideshow={"slide_type": "subslide"}
import csv
lines = csv.reader((line.replace('\x00','') for line in chunk[1:]), delimiter=',', quotechar='"')
tweets = [i[1] for i in lines]
# + slideshow={"slide_type": "subslide"}
for tweet in tweets[:5]:
ex = twitter_text.Extractor(tweet)
at_names = ex.extract_mentioned_screen_names()
urls = ex.extract_urls()
hashtags = ex.extract_hashtags()
rt_user = extract_rt_user(tweet)
tweet_text = extract_tweet_text(tweet, at_names, urls)
print at_names, urls, hashtags, rt_user,
print tweet_text
# + [markdown] slideshow={"slide_type": "slide"}
# # 思考:
#
# ### 提取出tweets中的rtuser与user的转发网络
#
# ## 格式:
# rt_user1, user1
#
# rt_user2, user3
#
# rt_user2, user4
#
# ...
#
# 数据保存为csv格式
# + slideshow={"slide_type": "notes"}
import csv
lines = csv.reader((line.replace('\x00','') \
for line in chunk[1:]), \
delimiter=',', quotechar='"')
tweet_user_data = [(i[1], i[8]) for i in lines]
for tweet,user in tweet_user_data:
rt_user = extract_rt_user(tweet)
if rt_user:
print rt_user, ',', user
# + [markdown] slideshow={"slide_type": "subslide"}
# # 阅读文献
# -
| data/06.data_cleaning_Tweets.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Projeto de portfólio - Health Insurance Cross Sell
# # 0.0 Imports
# +
import pandas as pd
import inflection
import numpy as np
import seaborn as sns
import random
import json
import requests
from scipy import stats as ss
import scikitplot as skplt
import matplotlib.pyplot as plt
from sklearn import preprocessing as pp
from sklearn import model_selection as ms
from sklearn import ensemble as en
from sklearn import neighbors as nh
from sklearn import linear_model as lm
from sklearn import metrics as m
from sklearn.ensemble import RandomForestClassifier
from skopt import forest_minimize
import xgboost as xgb
import pickle
# -
from IPython.display import Image
from IPython.core.display import HTML
# + [markdown] heading_collapsed=true
# ## 0.1 Loading Datasets
# + hidden=true
df_raw = pd.read_csv("data/train.csv")
# + hidden=true
df_raw.head()
# -
# ## 0.2 Helper Functions
# +
def cramer_v(x, y):
cm = pd.crosstab(x, y).to_numpy()
n = cm.sum()
r, k = cm.shape
chi2 = ss.chi2_contingency(cm)[0]
chi2corr = max(0, chi2 - (k-1)*(r-1)/(n-1))
kcorr = k - (k-1)**2/(n-1)
rcorr = r - (r-1)**2/(n-1)
return np.sqrt((chi2corr/n) / (min(kcorr-1, rcorr-1)))
def jupyter_settings():
# %matplotlib inline
# %pylab inline
plt.style.use('bmh')
plt.rcParams['figure.figsize'] = [12, 8]
plt.rcParams['font.size'] = 24
display( HTML( '<style>.container{width:100% !important;}</style>') )
pd.options.display.max_columns = None
pd.options.display.max_rows = None
pd.set_option('display.expand_frame_repr', False)
sns.set()
def topK_performance(df,probas,response,perc):
df_final_performance=pd.DataFrame()
for i in probas:
for j in perc:
k=int(np.floor(len(df_mp)*j))
df_tg=df.copy()
target_total=df_tg[response].sum()
df_tg['score']= i[:,1].tolist()
df_tg=df_tg.sort_values('score',ascending=False)
target_at_k=df_tg[response][:k].sum()
target_perc=target_at_k/target_total
df_final_performance=df_final_performance.append({'Model':'Model','perc':j, 'perc_target':target_perc, 'target_at_k':target_at_k, 'target_total':target_total},ignore_index=True)
return df_final_performance
def precision_at_k(x_val, yhat_model, k=2000):
# propensity score
x_val['score'] = yhat_model[:,1].tolist()
# sorted clients by score
x_val = x_val.sort_values('score', ascending=False)
x_val = x_val.reset_index(drop=True)
# create ranking order
x_val['ranking'] = x_val.index+1
x_val['precision_at_k'] = x_val['response'].cumsum()/x_val['ranking']
return x_val.loc[k, 'precision_at_k']
def recall_at_k(x_val, yhat_model, k=2000):
# propensity score
x_val['score'] = yhat_model[:,1].tolist()
# sorted clients by score
x_val = x_val.sort_values('score', ascending=False)
x_val = x_val.reset_index(drop=True)
# creaate ranking order
x_val['ranking'] = x_val.index+1
x_val['recall_at_k'] = x_val['response'].cumsum()/x_val['response'].sum()
return x_val.loc[k, 'recall_at_k']
def ml_metrics(model_name, y_val, x_val, yhat_model, k=2000):
rec = recall_at_k(x_val, yhat_model, k=k)
prec = precision_at_k(x_val, yhat_model, k=k)
f1 = 2*(prec*rec)/(prec+rec)
roc = m.roc_auc_score(y_val,yhat_model[:,1])
return pd.DataFrame({'Model Name': model_name,
'Recall_at_K': rec,
'Precision_at_K': prec,
'F1_score:':f1,
'Roc_score': roc
}, index=[0])
def cross_validation(models_performance, num_folds, modelName, model, x_train, y_train):
kfold=ms.StratifiedKFold(n_splits = num_folds, shuffle=True, random_state=42)
precision_list = []
recall_list = []
f1_list = []
roc_list = []
i=1
for train_cv,val_cv in kfold.split(x_train,y_train):
x_train_fold = x_train.iloc[train_cv]
y_train_fold = y_train.iloc[train_cv]
x_val_fold = x_train.iloc[val_cv]
y_val_fold = y_train.iloc[val_cv]
model_fit = model.fit(x_train_fold,y_train_fold)
yhat_model = model_fit.predict_proba(x_val_fold)
x_val_fold['response'] = y_val_fold
precision = round(precision_at_k(x_val_fold, yhat_model),3)
recall= round(recall_at_k(x_val_fold, yhat_model),3)
f1 = round(2*(precision*recall)/(precision+recall),3)
roc = round(m.roc_auc_score(y_val_fold,yhat_model[:,1]),3)
precision_list.append(precision)
recall_list.append(recall)
f1_list.append(f1)
roc_list.append(roc)
i+=1
precision_str = np.round(np.mean(precision_list),4).astype(str) + ' +/- ' + np.round(np.std(precision_list),4).astype(str)
recall_str = np.round(np.mean(recall_list),4).astype(str) + ' +/- ' + np.round(np.std(recall_list),4).astype(str)
f1_str = np.round(np.mean(f1_list),4).astype(str) + ' +/- ' + np.round(np.std(f1_list),4).astype(str)
auc_str = np.round(np.mean(roc_list),4).astype(str) + ' +/- ' + np.round(np.std(roc_list),4).astype(str)
models_performance = models_performance.append(pd.Series([modelName, precision_str, recall_str, f1_str, auc_str], index=models_performance.columns), ignore_index=True)
return models_performance
# -
jupyter_settings()
# + [markdown] heading_collapsed=true
# # 1.0 Data description
# + hidden=true
X_raw = df_raw.drop(['Response'], axis = 1)
y_raw = df_raw['Response'].copy()
x_train, x_test, y_train, y_test = ms.train_test_split(X_raw, y_raw, test_size=0.10)
df1 = pd.concat([x_train, y_train], axis = 1)
# + [markdown] hidden=true
# ## Columns Description
# + [markdown] hidden=true
# - Id: Customer identifier
# - Gender: Gender of customer
# - Age: Age of customer
# - Driving License: 0 if customer does not have the permission for drive; 1 if customer has the permission for drive
# - Region Code: Region code of customer
# - Previously Insured: 0 if customer does not have a vehicle insurance; 1 if customer already has a vehicle insurance.
# - Vehicle Age: Age of vehicle
# - Vehicle Damage: 0 if customer never got involved in a previous vehicle damage; 1 if customer already had a vehicle damage
# - Annual Premium: amount paid for health insurance to the company anualy.
# - Policy sales channel: anonymous code for contact with customer.
# - Vintage: time (in days) that customer bought his health assurance.
# - Response: 0 if customer has no interest in product; 1 if customer has interest in product
# + [markdown] heading_collapsed=true hidden=true
# ## 1.1 Rename columns
# + hidden=true
cols_old = ['id', 'Gender', 'Age', 'Driving_License', 'Region_Code',
'Previously_Insured', 'Vehicle_Age', 'Vehicle_Damage', 'Annual_Premium',
'Policy_Sales_Channel', 'Vintage', 'Response']
snakecase = lambda x: inflection.underscore(x)
cols_new = list(map(snakecase, cols_old))
# rename
df1.columns = cols_new
# + [markdown] heading_collapsed=true hidden=true
# ## 1.2 Data dimensions
# + hidden=true
print('Number of rows: {}'.format(df1.shape[0]))
print('Number of columns: {}'.format(df1.shape[1]))
# + [markdown] heading_collapsed=true hidden=true
# ## 1.3 Data types
# + hidden=true
df1.dtypes
# + [markdown] heading_collapsed=true hidden=true
# ## 1.4 Check NA
# + hidden=true
df1.isna().sum()
# + [markdown] heading_collapsed=true hidden=true
# ## 1.5 Fillout NA
# + hidden=true
# + [markdown] heading_collapsed=true hidden=true
# ## 1.6 Change types
# + hidden=true
# + [markdown] heading_collapsed=true hidden=true
# ## 1.7 Descriptive statistical
# + hidden=true
num_attr = df1[['age', 'annual_premium', 'vintage']]
cat_attr = df1[['driving_license', 'previously_insured', 'vehicle_damage', 'vehicle_age', 'gender', 'region_code', 'policy_sales_channel' ]]
target_attr = df1['response']
# + [markdown] heading_collapsed=true hidden=true
# ### 1.7.1 Numerical Attributes
# + hidden=true
# Central tendency - mean, median
ct1 = pd.DataFrame(num_attr.apply(np.mean)).T
ct2 = pd.DataFrame(num_attr.apply(np.median)).T
# Dispersion - std, min, max, range, skew e kurtosis
d1 = pd.DataFrame(num_attr.apply(np.std)).T
d2 = pd.DataFrame(num_attr.apply(min)).T
d3 = pd.DataFrame(num_attr.apply(max)).T
d4 = pd.DataFrame(num_attr.apply(lambda x: x.max() - x.min())).T
d5 = pd.DataFrame(num_attr.apply(lambda x: x.skew())).T
d6 = pd.DataFrame(num_attr.apply(lambda x: x.kurtosis())).T
# concatenate
m = pd.concat([d2, d3, d4, d1, ct1, ct2, d5, d6]).T.reset_index()
m.columns = ['attributes', 'min', 'max', 'range', 'std', 'mean', 'median', 'skew', 'kurtosis']
# + hidden=true
m
# + hidden=true
fig, axs = plt.subplots(3, figsize = (8,10))
sns.distplot(df1['age'], ax=axs[0], bins = 6)
sns.distplot(df1[df1['annual_premium']<100000]['annual_premium'], ax=axs[1])
sns.distplot(df1['vintage'], ax=axs[2]);
# + [markdown] heading_collapsed=true hidden=true
# ### 1.7.2 Categorical Attributes
# + hidden=true
cat_attr.apply(lambda x: x.unique().shape[0])
# + hidden=true
fig, axs = plt.subplots(ncols = 3, nrows = 2, figsize = (16,8))
sns.countplot(x ='driving_license', data= df1, ax=axs[0][0])
sns.countplot(x = 'previously_insured', data=df1, ax=axs[0][1])
sns.countplot(x = 'vehicle_damage', data=df1, ax=axs[0][2])
sns.countplot(x = 'vehicle_age', data=df1,ax=axs[1][0])
sns.countplot(x = 'gender', data=df1,ax=axs[1][1])
# + [markdown] heading_collapsed=true hidden=true
# ### 1.7.3 Target Attribute
# + hidden=true
sns.countplot(x = 'response', data=df1)
# + [markdown] heading_collapsed=true
# # 2.0 Feature Engineering
# + hidden=true
df2 = df1.copy()
# + [markdown] hidden=true
# ## 2.1 Criação de hipótesis
# + [markdown] hidden=true
# ## 2.2 Lista final de hipotesis
# + [markdown] hidden=true
# ## 2.3 Feature engineering
# + hidden=true
# vehicle age
df2['vehicle_age'] = df2['vehicle_age'].apply(lambda x: 'over_2_years' if x == '> 2 Years' else 'between_1_and_2_year' if x == '1-2 Year' else 'below_1_year')
# vehicle demage
df2['vehicle_damage'] = df2['vehicle_damage'].apply(lambda x: 1 if x == 'Yes' else 0)
# + [markdown] heading_collapsed=true
# # 3.0 Variables filtering
# + hidden=true
df3 = df2.copy()
# + [markdown] heading_collapsed=true
# # 4.0 Exploratory Analysis
# + hidden=true
df4 = df3.copy()
# + [markdown] hidden=true
# ## 4.1 Univariate Analysis
# + [markdown] hidden=true
# ### 4.1.1 Numerical Attributes
# + hidden=true
num_attr.hist(bins=25)
# + [markdown] hidden=true
# ### 4.1.2 Categorical Attributes
# + hidden=true
plt.subplot(3, 2, 1)
sns.countplot(df4['gender'])
plt.subplot(3, 2, 2)
sns.kdeplot(df4[df4['gender'] == 'Male']['response'], label='gender', shade=True)
sns.kdeplot(df4[df4['gender'] == 'Female']['response'], label='gender', shade=True)
plt.subplot(3, 2, 3)
sns.countplot(df4['vehicle_age'])
plt.subplot(3, 2, 4)
sns.kdeplot(df4[df4['vehicle_age'] == 'over_2_years']['response'], label='vehicle_age', shade=True)
sns.kdeplot(df4[df4['vehicle_age'] == 'between_1_and_2_year']['response'], label='vehicle_age', shade=True)
sns.kdeplot(df4[df4['vehicle_age'] == 'below_1_year']['response'], label='vehicle_age', shade=True)
plt.subplot(3, 2, 5)
sns.countplot(df4['vehicle_damage'])
plt.subplot(3, 2, 6)
sns.kdeplot(df4[df4['vehicle_damage'] == 0]['response'], label='vehicle_damage', shade=True)
sns.kdeplot(df4[df4['vehicle_damage'] == 1]['response'], label='vehicle_damage', shade=True)
# + [markdown] hidden=true
# ## 4.2 Bivariete Analysis
# + hidden=true
# age
plt.subplot(2, 2, 1)
sns.boxplot(x='response', y='age', data=df4)
plt.subplot(2, 2, 3)
aux0 = df4.loc[df4['response'] == 0, 'age']
sns.histplot(aux0)
plt.subplot(2, 2, 4)
aux0 = df4.loc[df4['response'] == 1, 'age']
sns.histplot(aux0)
# + hidden=true
# driving_license
aux = df4[['response', 'driving_license']].groupby('response').sum().reset_index()
aux['driving_license_perc'] = aux['driving_license'] / aux['driving_license'].sum()
aux
#sns.barplot(x='response', y='driving_license_perc', data=aux)
# + hidden=true
# region_code
aux = df4[['id', 'region_code', 'response']].groupby(['region_code', 'response']).count().reset_index()
sns.scatterplot(x='region_code', y='id', hue='response', data=aux)
# + hidden=true
# previously_insured
pd.crosstab(df4['previously_insured'], df4['response']).apply(lambda x: x/x.sum(), axis=1)
# + hidden=true
# vehicle_age
df4[['vehicle_age', 'response']].value_counts(normalize=True).reset_index()
# + hidden=true
# vehicle_damage
pd.crosstab(df4['vehicle_damage'], df4['response']).apply(lambda x: x/x.sum(), axis=1)
# + hidden=true
# annual_premium
plt.subplot(2, 2, 1)
aux = df4[(df4['annual_premium']<70000) & (df4['annual_premium'] > 10000)]
sns.boxplot(x='response', y='annual_premium', data=aux)
plt.subplot(2, 2, 3)
aux0 = aux.loc[aux['response'] == 0, 'annual_premium']
sns.histplot(aux0)
plt.subplot(2, 2, 4)
aux0 = aux.loc[aux['response'] == 1, 'annual_premium']
sns.histplot(aux0)
# + hidden=true
# policy_sales_channel
aux = df4[['policy_sales_channel', 'response']].groupby('policy_sales_channel').sum().reset_index()
#aux.set_index('policy_sales_channel').plot(kind='bar', stacked=True, color=['steelblue', 'red'])
aux.sample(10)
# + hidden=true
# vintage
plt.subplot(2, 2, 1)
sns.boxplot(x='response', y='vintage', data=df4)
plt.subplot(2, 2, 3)
aux0 = df4.loc[df4['response'] == 0, 'vintage']
sns.histplot(aux0)
plt.subplot(2, 2, 4)
aux0 = df4.loc[df4['response'] == 1, 'vintage']
sns.histplot(aux0)
# + [markdown] hidden=true
# ## 4.3 Multivariate Analysis
# + [markdown] hidden=true
# ### 4.2.1 Numerical attributes
# + hidden=true
correlation = num_attr.corr(method='pearson')
sns.heatmap(correlation, annot=True)
# + [markdown] hidden=true
# ### 4.2.2 Categorical attributes
# + hidden=true
cat_attr.columns
# + hidden=true
# only categorical data
a = cat_attr
# Calculate cramver_v
a1 = cramer_v(a['gender'], a['gender'])
a2 = cramer_v(a['gender'], a['vehicle_age'])
a3 = cramer_v(a['gender'], a['vehicle_damage'])
a4 = cramer_v(a['vehicle_age'], a['gender'])
a5 = cramer_v(a['vehicle_age'], a['vehicle_age'])
a6 = cramer_v(a['vehicle_age'], a['vehicle_damage'])
a7 = cramer_v(a['vehicle_damage'], a['gender'])
a8 = cramer_v(a['vehicle_damage'], a['vehicle_age'])
a9 = cramer_v(a['vehicle_damage'], a['vehicle_damage'])
# Final dataset
d = pd.DataFrame( {'gender': [a1, a2, a3],
'vehicle_age': [a4, a5, a6],
'vehicle_damage': [a7, a8, a9]
} )
d = d.set_index(d.columns)
# + hidden=true
sns.heatmap(d, annot=True)
# + [markdown] hidden=true
# *vhicle_age tem uma correlação positiva interessante com vehicle_damage*
# - *ou seja, quanto mais velho o veículo cresce a chance de ter sofrido danos*
# + [markdown] heading_collapsed=true
# # 5.0 Data preparation
# + hidden=true
X = df4.drop('response', axis=1)
y = df4['response'].copy()
x_train, x_val, y_train, y_val = ms.train_test_split(X, y, test_size=0.20)
#x_val_api = x_val.copy()
df5 = pd.concat([x_train, y_train], axis=1)
# + [markdown] hidden=true
# ## 5.1 Standardization
# + hidden=true
ss = pp.StandardScaler()
# annual_premium
df5['annual_premium'] = ss.fit_transform(df5[['annual_premium']].values)
pickle.dump(ss, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/annual_premium_scaler.pkl', 'wb'))
# + [markdown] hidden=true
# ## 5.2 Rescaling
# + hidden=true
mms_age = pp.MinMaxScaler()
mms_vintage = pp.MinMaxScaler()
# age
df5['age'] = mms_age.fit_transform(df5[['age']].values)
pickle.dump(mms_age, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/age_scaler.pkl', 'wb'))
# vintage
df5['vintage'] = mms_vintage.fit_transform(df5[['vintage']].values)
pickle.dump(mms_vintage, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/vintage_scaler.pkl', 'wb'))
# + [markdown] hidden=true
# ## 5.3 Transformation
# + [markdown] hidden=true
# ### 5.3.1 Encoding
# + hidden=true
# driving_license -- Label encoding -- Já esta no formato
# vehicle_damage -- Label encoding -- Já esta no formato
# previously_insured -- Label encoding -- Já esta no formato
# gender -- Target Encoding
target_encode_gender = df5.groupby('gender')['response'].mean()
df5.loc[:,'gender'] = df5['gender'].map(target_encode_gender)
pickle.dump(target_encode_gender, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/gender_scaler.pkl', 'wb'))
# region_code -- Target encoding
target_encode_region_code = df5.groupby('region_code')['response'].mean()
df5.loc[:, 'region_code'] = df5['region_code'].map(target_encode_region_code)
pickle.dump(target_encode_region_code, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/region_code_scaler.pkl', 'wb'))
# vehicle_age -- One Hot Encoding / Order Encoding
df5 = pd.get_dummies(df5, prefix='vehicle_age', columns=['vehicle_age'])
# policy_sales_channel -- Frequency encoding
fe_policy_sales_channel = df5.groupby('policy_sales_channel').size() / len(df5)
df5.loc[:, 'policy_sales_channel'] = df5['policy_sales_channel'].map(fe_policy_sales_channel)
pickle.dump(fe_policy_sales_channel, open('/home/romulo/Documentos/health_insurance/health_insurance/src/features/policy_sales_channel_scaler.pkl', 'wb'))
# + [markdown] heading_collapsed=true hidden=true
# ## 5.4 Validation Preparation
# + hidden=true
# annual_premium
x_val.loc[:,'annual_premium'] = ss.fit_transform(x_val[['annual_premium']].values)
# age
x_val.loc[:, 'age'] = mms_age.fit_transform(x_val[['age']].values)
# vintage
x_val.loc[:,'vintage'] = mms_vintage.fit_transform(x_val[['vintage']].values)
# gender
x_val.loc[:, 'gender'] = x_val.loc[:,'gender'].map(target_encode_gender)
# region_code
x_val.loc[:, 'region_code'] = x_val.loc[:,'region_code'].map(target_encode_region_code)
# vehicle_age
x_val = pd.get_dummies(x_val, prefix='vehicle_age', columns=['vehicle_age'])
# policy_sales_channel
x_val.loc[:, 'policy_sales_channel'] = x_val.loc[:,'policy_sales_channel'].map(fe_policy_sales_channel)
# fillna
x_val = x_val.fillna(0)
# + [markdown] heading_collapsed=true
# # 6.0 Feature selection
# + [markdown] hidden=true
# ## 6.1 Features Importance
# + hidden=true
# model definition
forest = en.ExtraTreesClassifier(n_estimators = 250, random_state=0, n_jobs=-1)
#data preparation
x_train_n = df5.drop(['id','response'], axis=1)
y_train_n = y_train.values
forest.fit(x_train_n, y_train_n)
# + hidden=true
importances = forest.feature_importances_
std = np.std([tree.feature_importances_ for tree in forest.estimators_], axis=0)
indices = np.argsort(importances)[::-1]
# print the feature ranking
print("Feature Ranking:")
df = pd.DataFrame()
for i, j in zip(x_train_n, forest.feature_importances_):
aux=pd.DataFrame({'feature':i, 'importance':j}, index=[0])
df = pd.concat([df, aux], axis=0)
print(df.sort_values('importance', ascending=False))
# Plot the impurity-based feature importances of the forest
plt.figure()
plt.title("Feature_importances")
plt.bar(range(x_train_n.shape[1]), importances[indices], color='r', yerr=std[indices], align='center')
plt.xticks(range(x_train_n.shape[1]), indices)
plt.xlim((-1, x_train_n.shape[1]))
plt.show()
# -
# # 7.0 Machine learning modeling
# +
cols_selected = ['vintage','annual_premium','age','region_code','vehicle_damage', 'policy_sales_channel', 'previously_insured']
x_train = df5[cols_selected]
x_validation = x_val[cols_selected]
y_validation = y_val.copy()
# + [markdown] heading_collapsed=true
# ## 7.1 KNN Model
# + hidden=true
#model definition
knn_model = nh.KNeighborsClassifier(n_neighbors=7)
# model training
model_knn = knn_model.fit( x_train, y_train)
# model prediction - Poder de Generalização
yhat_knn = model_knn.predict_proba(x_validation)
# + hidden=true
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
# Accumulative Gain
skplt.metrics.plot_cumulative_gain(y_validation, yhat_knn, ax=axs[0], title='Cumulative Gain KNN')
# Lift Curve
skplt.metrics.plot_lift_curve(y_validation, yhat_knn, ax=axs[1], title='Lift Curve KNN')
# + [markdown] heading_collapsed=true
# ## 7.2 Logistic Regression Model
# + hidden=true
# model definition
lr_model = lm.LogisticRegression(random_state=42)
# model training
lr_model.fit(x_train, y_train)
# model prediction
yhat_lr = lr_model.predict_proba(x_validation)
# + hidden=true
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
# Accumulative Gain
skplt.metrics.plot_cumulative_gain(y_validation, yhat_lr, ax=axs[0], title='Cumulative Gain Logistic Regressor')
# Lift Curve
skplt.metrics.plot_lift_curve(y_validation, yhat_lr, ax=axs[1], title='Lift Curve Logistic Regressor')
# + [markdown] heading_collapsed=true
# ## 7.3 XGBoost Classifier Model
# + hidden=true
# model definition
xgb_model = xgb.XGBClassifier(objective='binary:logistic', eval_metric='error')
# model training
model_xgb = xgb_model.fit(x_train,y_train)
# model prediction
yhat_xgb = model_xgb.predict_proba(x_validation)
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
# Accumulative Gain
skplt.metrics.plot_cumulative_gain(y_validation, yhat_xgb, ax=axs[0],title='Cumulative Gain xgb')
# Lift Curve
skplt.metrics.plot_lift_curve(y_validation, yhat_xgb,ax=axs[1],title='Lift Curve xgb')
# + [markdown] heading_collapsed=true
# ## 7.4 Random Forest Classifier model
# + hidden=true
# model definition
rf_model = RandomForestClassifier(n_estimators=100,random_state=42)
# model training
model_rf = rf_model.fit(x_train,y_train)
# model prediction
yhat_rf = model_rf.predict_proba(x_validation)
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
# Accumulative Gain
skplt.metrics.plot_cumulative_gain(y_validation, yhat_rf, ax=axs[0],title='Cumulative Gain Random Forest')
# Lift Curve
skplt.metrics.plot_lift_curve(y_validation, yhat_rf,ax=axs[1],title='Lift Curve Random Forest')
# -
# # 8.0 Model Performance
df8 = x_validation.copy()
df8['response'] = y_validation.copy()
# + [markdown] heading_collapsed=true
# ## 8.1 KNN
# + hidden=true
df8_knn.head()
# + hidden=true
df8_knn = df8.copy()
knn_result = ml_metrics('KNN', df8_knn, yhat_knn, k=2000)
knn_result
# + [markdown] heading_collapsed=true
# ## 8.2 Logistic Regression
# + hidden=true
df8_lr = df8.copy()
lr_result = ml_metrics('Logistic Regression', df8_lr, yhat_lr, k=2000)
lr_result
# + [markdown] heading_collapsed=true
# ## 8.3 XGBoost
# + hidden=true
df8_xgb = df8.copy()
xgb_result = ml_metrics('XGBoost Classifier', df8_xgb, yhat_xgb, k=2000)
xgb_result
# + [markdown] heading_collapsed=true
# ## 8.4 Random Forest
# + hidden=true
df8_rf = df8.copy()
rf_result = ml_metrics('Random Forest Classifier', df8_rf, yhat_rf, k=2000)
rf_result
# + [markdown] heading_collapsed=true
# ## 8.5 Cross Validation
# + hidden=true
models_performance_cv = pd.DataFrame({'Model':[], "Precision_at_k": [], "Recall_at_k": [], "F1-Score_at_k": [], "ROC_AUC_Score": []})
# + hidden=true
models_performance_cv = cross_validation(models_performance_cv, 5 , 'Logistic Regression CV', lr_model, x_train, y_train)
models_performance_cv = cross_validation(models_performance_cv, 5 , 'K Neighbors Classifier CV', knn_model, x_train, y_train)
models_performance_cv = cross_validation(models_performance_cv, 5 , 'Random Forest Classifier CV', rf_model, x_train, y_train)
models_performance_cv = cross_validation(models_performance_cv, 5 , 'XGBoost Classifier CV', xgb_model, x_train, y_train)
# + hidden=true
models_performance_cv.sort_values('F1-Score_at_k', ascending=False)
# + [markdown] heading_collapsed=true
# ## 8.6. Hyperparameter Fine Tuning
# + [markdown] heading_collapsed=true hidden=true
# ### 8.6.1 XGBoost
# + hidden=true
models_performance_xgboost = pd.DataFrame({'Model':[], "Precision_at_k": [], "Recall_at_k": [], "F1-Score_at_k": [], "ROC_AUC_Score": []})
# + hidden=true
param = {
'n_estimators': [1500, 1700, 2500, 3000, 3500],
'eta': [0.01, 0.03],
'max_depth': [3, 5, 9],
'subsample': [0.1, 0.5, 0.7],
'colsample_bytree': [0.3, 0.7, 0.9],
'min_child_weight': [3, 8, 15]
}
MAX_EVAL = 5
# + hidden=true
final_result = pd.DataFrame()
for i in range (MAX_EVAL):
# choose values for parameters randomly
hp = { k: random.sample( v, 1 )[0] for k, v in param.items() }
print(hp)
# model
model_xgb = xgb.XGBClassifier(objective='reg:squarederror',
n_estimators=hp['n_estimators'],
eta=hp['eta'],
max_depth=hp['max_depth'],
subsample=hp['subsample'],
colsample_bytee=hp['colsample_bytree'],
min_child_weight=hp['min_child_weight'], n_jobs=-1)
# performance
# cross_validation(models_performance, num_folds, modelName, model, x_train, y_train)
result = cross_validation(models_performance, 5, 'XGBoost Regressor', model_xgb, x_train, y_train)
final_result = pd.concat([final_result, result])
final_result
# + [markdown] heading_collapsed=true
# ## 8.7 Final Model XGBoost Classifier
# + hidden=true
param_tuned = {'n_estimators': 3000, 'eta': 0.01, 'max_depth': 3, 'subsample': 0.5, 'colsample_bytree': 0.9, 'min_child_weight': 8}
# model
model_xgb_tuned = xgb.XGBClassifier(objective='reg:squarederror',
n_estimators=param_tuned['n_estimators'],
eta=param_tuned['eta'],
max_depth=param_tuned['max_depth'],
subsample=param_tuned['subsample'],
colsample_bytee=param_tuned['colsample_bytree'],
min_child_weight=param_tuned['min_child_weight']).fit(x_train, y_train)
# + hidden=true
models_performance_xgboost_tunned = pd.DataFrame({'Model':[], "Precision_at_k": [], "Recall_at_k": [], "F1-Score_at_k": [], "ROC_AUC_Score": []})
# + hidden=true
result = cross_validation(models_performance_xgboost_tunned, 5, 'XGBoost Regressor', model_xgb_tuned, x_train, y_train)
result
# + hidden=true
yhat_proba_val = model_xgb_tuned.predict_proba(x_validation)
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
skplt.metrics.plot_cumulative_gain(y_val, yhat_proba_val, ax=axs[0],title='Cumulative Gain Validation');
skplt.metrics.plot_lift_curve(y_val, yhat_proba_val,ax=axs[1],title='Lift Curve Validation')
# -
# ## 8.8 Model Performance in Test Data
# + [markdown] heading_collapsed=true
# ### 8.8.1 Preparation Pipeline
# + hidden=true
def preparation_pipeline(x_test, y_test):
df8 = pd.concat([x_test, y_test], axis=1)
# Rename Columns
cols_old = ['id', 'Gender', 'Age', 'Driving_License', 'Region_Code',
'Previously_Insured', 'Vehicle_Age', 'Vehicle_Damage', 'Annual_Premium',
'Policy_Sales_Channel', 'Vintage', 'Response']
snakecase = lambda x: inflection.underscore(x)
cols_new = list(map(snakecase, cols_old))
df8.columns = cols_new
# vehicle age
df8['vehicle_age'] = df8['vehicle_age'].apply(lambda x: 'over_2_years' if x == '> 2 Years' else 'between_1_and_2_year' if x == '1-2 Year' else 'below_1_year')
# vehicle demage
df8['vehicle_damage'] = df8['vehicle_damage'].apply(lambda x: 1 if x == 'Yes' else 0)
### Standardization
ss = pp.StandardScaler()
# annual_premium
df8['annual_premium'] = ss.fit_transform(df8[['annual_premium']].values)
### Rescaling
mms_age = pp.MinMaxScaler()
mms_vintage = pp.MinMaxScaler()
# age
df8['age'] = mms_age.fit_transform(df8[['age']].values)
# vintage
df8['vintage'] = mms_vintage.fit_transform(df8[['vintage']].values)
### Encoding
# gender -- Target Encoding
target_encode_gender = df8.groupby('gender')['response'].mean()
df8.loc[:,'gender'] = df8['gender'].map(target_encode_gender)
# region_code -- Target encoding
target_encode_region_code = df8.groupby('region_code')['response'].mean()
df8.loc[:, 'region_code'] = df8['region_code'].map(target_encode_region_code)
# vehicle_age -- One Hot Encoding / Order Encoding
df8 = pd.get_dummies(df8, prefix='vehicle_age', columns=['vehicle_age'])
# policy_sales_channel -- Frequency encoding
fe_policy_sales_channel = df8.groupby('policy_sales_channel').size() / len(df8)
df8.loc[:, 'policy_sales_channel'] = df8['policy_sales_channel'].map(fe_policy_sales_channel)
# Split features and target
x_test_df8 = df8.drop('response', axis=1)
y_test_df8 = df8['response'].copy()
x_test_df8 = x_test_df8[cols_selected]
return x_test_df8, y_test_df8
# -
# ### 8.8.2 Model Performance
x_test_df8, y_test_df8 = preparation_pipeline(x_test, y_test)
# +
yhat_xgb_tuned = model_xgb_tuned.predict_proba(x_test_df8)
fig, axs = plt.subplots(ncols= 2, figsize = (12,6))
skplt.metrics.plot_cumulative_gain(y_test_df8, yhat_xgb_tuned, ax=axs[0],title='Cumulative Gain Test');
skplt.metrics.plot_lift_curve(y_test_df8, yhat_xgb_tuned,ax=axs[1],title='Lift Curve Test')
# -
ml_metrics('XGBoost Classifier Tuned', y_test_df8, df8, yhat_xgb_tuned, k=2000)
# # 9.0 Model Performance in Business Value
df_test = pd.read_csv("data/test.csv")
def perc_target(x_test, y_test, yhat_xgb_tuned, percCalls):
customerInteresting=pd.DataFrame()
df_mp = x_test.copy()
df_mp['response'] = y_test
probas = [yhat_xgb_tuned]
customerInteresting = topK_performance(df_mp,probas,'response',[percCalls])
return customerInteresting
# **1.** **Com a capacidade de 5 mil ligações, qual % dos clientes mais interessados a empresa poderá contactar?**
calls = 5000
totalClientes = x_test.shape[0]
percCalls = calls/totalClientes
print("Total de clientes: ", totalClientes)
print("% de clientes contactados: {0:.2f}".format(percCalls*100))
customerInteresting = perc_target(x_test, y_test, yhat_xgb_tuned, percCalls)
customerInteresting
# Logo para 5 mil ligações, que representam 13,12% dos clientes, conseguimos atingir 41,2% dos clientes interessados.
# ____________________________________________________________________________________________________________
# **2.** **Com a capacidade dobrada para 10 mil ligações, qual % dos clientes mais interessados a empresa poderá contactar?**
calls = 10000
totalClientes = x_test.shape[0]
percCalls = calls/totalClientes
print("Total de clientes: ", totalClientes)
print("% de clientes contactados: {0:.2f}".format(percCalls*100))
customerInteresting = perc_target(x_test, y_test, yhat_xgb_tuned, percCalls)
customerInteresting
# Logo para 10 mil ligações, que representam 26,24% dos clientes, conseguimos atingir 71,13% dos clientes interessados.
# ## 9.1 Random Model
# +
from sklearn.dummy import DummyClassifier
dummy_clf = DummyClassifier(strategy="most_frequent")
dummy_clf.fit(x_test_df8, y_test_df8)
yhat_dummy = dummy_clf.predict_proba(x_test_df8)
# -
calls = 5000
totalClientes = x_test.shape[0]
percCalls = calls/totalClientes
print("Total de clientes: ", totalClientes)
print("% de clientes contactados: {0:.2f}".format(percCalls*100))
customerInteresting = perc_target(x_test, y_test, yhat_dummy, percCalls)
customerInteresting
# Logo para 5 mil ligações com um modelo randômico, que representam 13,12% dos clientes, conseguimos atingir apenas 13,01% dos clientes interessados.
# ## 9.2 Result
# **A cerca do modelo de machine learning aplicado:**
# **5 mil ligações abrange 1877 interessados.**
# - A um custo hipotético de 10,00 reais por ligação e retorno de 1.000,00 reais por seguro vendido, logo:
# - Custo de ligações = 50.000,00 reais
# - Retorno por vendas = 1877 * 1.000,00 reais = 1.877.000,00 reais
# - *Lucro = 1.827.000 reais*
# **A cerca do modelo randômico. que significa fazer ligações aleatórias:**
# **5 mil ligações abrange 593 interessados.**
# - A um custo hipotético de 10,00 reais por ligação e retorno de 1.000,00 reais por seguro vendido, logo:
# - Custo de ligações = 50.000,00 reais
# - Retorno por vendas = 593 * 1.000,00 reais = 593.000,00 reais
# - *Lucro = 543.000,00 reais*
# **Logo, o modelo de machine learning aumenta o faturamento em 3,36 vezes**
# # 10.0 Deploy to production
# + [markdown] heading_collapsed=true
# ## 10.1 Saving Model
# + hidden=true
pickle.dump(model_xgb_tuned, open('/home/romulo/Documentos/health_insurance/health_insurance/src/models/model_xgb_tuned.pkl','wb'))
# -
# ## 10.2 API Tester
# loading test dataset
#x_val_api = x_val_api.drop(['response'], axis=1)
df_test = x_val_api
df_test = df_test.sample(10)
# convert dataframe to json
data = json.dumps( df_test.to_dict( orient='records' ) )
data
# +
# save json in file
with open('data.json', 'w') as o:
o.write(data)
# save json file in csv
data_json = pd.read_json('data.json')
data_json.to_csv('data.csv')
# +
# API Call
#url = 'http://0.0.0.0:5000/predict'
url = 'https://health-insurance-model-rf.herokuapp.com/predict'
header = {'Content-type': 'application/json' }
r = requests.post( url, data=data, headers=header )
print( 'Status Code {}'.format( r.status_code ) )
# -
d1 = pd.DataFrame( r.json(), columns=r.json()[0].keys() )
d1.sort_values( 'prediction', ascending=False )
# ## 10.3 Saving Client's List in CSV
| v1.0-Health_insurance_cross_sell.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sys
# sys.path.insert(0,'../prada_bayes_opt/')
sys.path.insert(0,'../')
from prada_bayes_opt import PradaBayOptBatch
from prada_bayes_opt import functions
from prada_bayes_opt import auxiliary_functions
import numpy as np
import matplotlib.pyplot as plt
from auxiliary_functions import *
from prada_bayes_opt import *
import visualization
import ppo_functions as pfunctions
import real_experiment_function
import random
import warnings
warnings.filterwarnings("ignore")
random.seed('6789')
# saveGraphPath = ('./graphs/')
# plt.savefig('books_read.png')
# +
# please select one of the functions / exepriments below
#myfunction=functions.forrester() #1D
# myfunction=functions.branin() #2D
#myfunction=functions.dropwave() #2D
# myfunction=functions.hartman_3d() #3D
# myfunction=real_experiment_function.SVR_function() #4D Real Experiment with SVR
#myfunction=functions.gSobol(a=np.array([1,1,1,1,1])) #5D
#myfunction=functions.alpine2(input_dim=5) #5D
#myfunction=functions.hartman_6d() #6D
# myfunction=real_experiment_function.DeepLearning_MLP_MNIST() #7D Real Experiment with SV
#myfunction=functions.gSobol(a=np.array([1,1,1,1,1,1,1,1,1,1])) #10D
#myfunction=functions.alpine2(input_dim=10) #10D
myfunction = pfunctions.PpoImport()
# +
print ("=======================================================================")
print ("You are selecting function {:s} D={:d}".format(myfunction.name, myfunction.input_dim))
# if myfunction.input_dim<=2:
# visualization.plot_original_function(myfunction)
# create an empty object for BO
bo=PradaBayOptBatch(f=myfunction.func, pbounds=myfunction.bounds, acq='ucb',opt='scipy')
# parameter for Gaussian Process
gp_params = {'theta':0.1*bo.dim,'noise_delta':0.1}
# -
# init Bayesian Optimization
print ("=======================================================================")
print ("Start Initialization")
bo.init(n_init_points=3*bo.dim)
# +
print ("=======================================================================")
print ("\nRunning Budgeted Batch Bayesian Optimization")
# number of iteration
TT=5*myfunction.input_dim
print ("TT: ", TT)
for index in range(0,TT):
print ("index: ", index)
bo.maximize_batch_B3O(gp_params,kappa=2,IsPlot=1)
sys.stdout.write("\nIter={:d} Optimization Time={:.2f} sec ".format(index,bo.opt_time[index]))
# +
print ("=======================================================================")
print ("\nB3O #TotalPoints={:.0f} Best-found-value={:.3f}".format(np.sum(bo.NumPoints),bo.Y.max()))
idxMax=np.argmax(bo.Y)
print ("X_optimal ")
print (bo.X_original[idxMax])
NumPoints = np.asarray(bo.NumPoints, dtype = 'int')
# plot the best-found-value
# my_yBest=auxiliary_functions.yBest_Iteration(bo.Y,bo.NumPoints,IsPradaBO=1)
my_yBest=auxiliary_functions.yBest_Iteration(bo.Y,NumPoints,IsPradaBO=1)
plt.plot(range(0,TT+1),my_yBest,linewidth=2,color='r',linestyle='-', marker='s',label='B3O')
plt.ylabel('Best-found-value',fontdict={'size':18})
plt.xlabel('Iteration',fontdict={'size':18})
plt.legend(loc=1,prop={'size':18})
#plt.ylim([np.min(my_yBest)*0.7,np.max(my_yBest)*1.2])
strTitle="{:s} D={:d}".format(myfunction.name,myfunction.input_dim)
plt.title(strTitle,fontdict={'size':20})
# plot the batch size per iteration
fig=plt.figure(figsize=(9, 4.5))
strNTotal="B3O (N={:.0f})".format(np.sum(bo.NumPoints))
plt.plot(range(1,TT+1),bo.NumPoints[1:],linewidth=2,color='r',linestyle='-',marker='s', label=strNTotal)
plt.ylabel('# BatchSize per Iter',fontdict={'size':18})
plt.xlabel('Iteration',fontdict={'size':18})
plt.legend(loc=1,prop={'size':18})
plt.ylim([np.min(bo.NumPoints[1:])-1,np.max(bo.NumPoints[1:])+1])
plt.title(strTitle,fontdict={'size':20})
# +
# my_yBest=auxiliary_functions.yBest_Iteration(bo.Y,bo.NumPoints,IsPradaBO=1)
print (bo.Y)
print (bo.NumPoints)
NumPoints = np.asarray(bo.NumPoints, dtype = 'int')
print (NumPoints)
# -
| ICDM2016_B3O/run_batch/runningForPPO.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import torch
from torch import nn, optim
from torch.utils.data import DataLoader
import torch.nn.functional as F
# for loading MNIST data
from torchvision import transforms, datasets
# -
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm_notebook as tqdm
# %matplotlib inline
# +
# if cuda device is available then run model on gpu
if torch.cuda.is_available():
cuda_flag=True
else:
cuda_flag=False
torch.manual_seed(3120)
# -
# ### Setting up data loader
# +
batch_size=64
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5], std=[0.5])])
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('./dataset/', train=True, download=True,transform=transforms.ToTensor()),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('./dataset/', train=False, download=True, transform=transforms.ToTensor()),
batch_size=batch_size)
# -
# ### Class definition for encoder decoder networks
# +
class Encoder(nn.Module):
def __init__(self, input_dim, z_dim):
super(Encoder, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, padding=1)
self.conv2 = nn.Conv2d(in_channels=16, out_channels=32, kernel_size=3, padding=1)
self.shared_fc1 = nn.Linear(in_features=2*input_dim, out_features=z_dim*8)
self.shared_fc2 = nn.Linear(in_features=z_dim*8, out_features=z_dim*4)
self.pool = nn.MaxPool2d(kernel_size=2)
self.mu = nn.Linear(z_dim*4, z_dim)
self.var = nn.Linear(z_dim*4, z_dim)
def forward(self, x):
x = x.view(len(x),1,28,28)
x = torch.relu(self.conv1(x))
x = self.pool(x)
x = torch.relu(self.conv2(x))
x = self.pool(x)
x = x.view(len(x),-1)
x = F.relu(self.shared_fc1(x))
x = F.relu(self.shared_fc2(x))
z_mu = self.mu(x)
z_var = self.var(x)
return z_mu, z_var
class Decoder(nn.Module):
def __init__(self, output_dim, z_dim):
super(Decoder, self).__init__()
self.fc1 = nn.Linear(in_features=z_dim, out_features=z_dim*4)
self.fc2 = nn.Linear(in_features=z_dim*4, out_features=z_dim*16)
self.fc3 = nn.Linear(in_features=z_dim*16, out_features=output_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = torch.sigmoid(self.fc3(x))
return x
# -
class VAE(nn.Module):
def __init__(self, enc, dec, z_dim):
super(VAE, self).__init__()
self.enc = enc
self.dec = dec
def forward(self,x):
z_mu,z_logvar = self.enc(x)
# sample z using the mean and variance obtained from encoder
std = torch.exp(0.5*z_logvar)
eps = torch.randn_like(std)
z = z_mu + eps*std
predicted = self.dec(z)
return predicted, z_mu, z_logvar
def crit(y_pred, y, z_mu, z_logvar):
reconstruction_loss = F.binary_cross_entropy(y_pred, y, reduction='sum')
kl_divergence = -0.5 * torch.sum(1 + z_logvar - z_mu.pow(2) - z_logvar.exp())
return reconstruction_loss+kl_divergence
def plot_tensor_img(x):
fig = plt.figure(figsize=(10,1))
generated_images = x.detach().cpu().numpy().reshape(len(x),28,28)
for i in range(10):
plt.subplot(1,10,i+1)
plt.imshow(generated_images[i])
plt.show()
# +
# instantiate the models
enc = Encoder(input_dim=784, z_dim=32)
dec = Decoder(output_dim=784, z_dim=32)
model = VAE(enc, dec, 32)
if cuda_flag:
model = model.cuda()
# -
lr = 1e-3
opt = optim.Adam(model.parameters(), lr=lr)
# +
epochs = 15
loss_history = []
sample_images = next(iter(test_loader))[0]
# +
print("True Images")
plot_tensor_img(sample_images)
for epoch in tqdm(range(epochs)):
train_loss=0
# iterate over dataset
for x,_ in train_loader:
x = x.view(len(x),-1)
# move data to gpu if cuda_flag is set
if cuda_flag:
x = x.cuda()
# zero_grad to ensure no unaccounted calculation creeps in while calculating gradients
opt.zero_grad()
# forward propogation and loss computation
x_gen, z_mu, z_logvar = model(x)
loss = crit(x_gen,x, z_mu, z_logvar)
train_loss+=loss.item()
# backpropogate gradients
loss.backward()
# update weights
opt.step()
train_loss/=len(train_loader)*batch_size
print ("Epoch:{} Train Loss:{:.6}".format(epoch,train_loss))
loss_history.append(train_loss)
if epoch%3==0:
print("Reconstructed Images after Epoch ",epoch)
with torch.no_grad():
x = sample_images.view(len(sample_images),-1)
# move data to gpu if cuda_flag is set
if cuda_flag:
x = x.cuda()
# forward propogation and loss computation
x_gen, _, _ = model(x)
plot_tensor_img(x_gen)
# -
# ### New Image Generation using Decoder
# +
# sample random tensors using standard multivariate normal distribution
z = torch.randn(64,32)
if cuda_flag:
z = z.cuda()
# pass the random tensors through decoder to generate the new images
with torch.no_grad():
generated_images = model.dec(z).cpu().numpy().reshape(len(z),28,28)
fig = plt.figure(figsize=(10,10))
for i in range(64):
plt.subplot(8,8,i+1)
plt.imshow(generated_images[i])
plt.show()
# -
| vision/VAE.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. REPL (Read Evaluation Print Loop)
# +
# /* Enter REPL */
# >python
# /* Exit REPL */
# >>>exit()
# -
# > special _ variable to store the latest calculation result
# # 2. Run Python Script
# +
# >python script.py
# -
# # 3. Snake Case for Variable Name
# # 4. Ada Lovelace
# [Wikipedia](https://en.wikipedia.org/wiki/Ada_Lovelace)
# # 5. Input from User
help(input)
name = input("What's your name? ")
print(name)
# ## === END ===
| python_basics/Section1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day and Night Image Classifier
# ---
#
# The day/night image dataset consists of 200 RGB color images in two categories: day and night. There are equal numbers of each example: 100 day images and 100 night images.
#
# We'd like to build a classifier that can accurately label these images as day or night, and that relies on finding distinguishing features between the two types of images!
#
# *Note: All images come from the [AMOS dataset](http://cs.uky.edu/~jacobs/datasets/amos/) (Archive of Many Outdoor Scenes).*
#
# ### Import resources
#
# Before you get started on the project code, import the libraries and resources that you'll need.
# +
import cv2 # computer vision library
import helpers
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# %matplotlib inline
# -
# ## Training and Testing Data
# The 200 day/night images are separated into training and testing datasets.
#
# * 60% of these images are training images, for you to use as you create a classifier.
# * 40% are test images, which will be used to test the accuracy of your classifier.
#
# First, we set some variables to keep track of some where our images are stored:
#
# image_dir_training: the directory where our training image data is stored
# image_dir_test: the directory where our test image data is stored
# Image data directories
image_dir_training = "day_night_images/training/"
image_dir_test = "day_night_images/test/"
# ## Load the datasets
#
# These first few lines of code will load the training day/night images and store all of them in a variable, `IMAGE_LIST`. This list contains the images and their associated label ("day" or "night").
#
# For example, the first image-label pair in `IMAGE_LIST` can be accessed by index:
# ``` IMAGE_LIST[0][:]```.
#
# Using the load_dataset function in helpers.py
# Load training data
IMAGE_LIST = helpers.load_dataset(image_dir_training)
# ## Construct a `STANDARDIZED_LIST` of input images and output labels.
#
# This function takes in a list of image-label pairs and outputs a **standardized** list of resized images and numerical labels.
# Standardize all training images
STANDARDIZED_LIST = helpers.standardize(IMAGE_LIST)
# ## Visualize the standardized data
#
# Display a standardized image from STANDARDIZED_LIST.
# +
# Display a standardized image and its label
# Select an image by index
image_num = 0
selected_image = STANDARDIZED_LIST[image_num][0]
selected_label = STANDARDIZED_LIST[image_num][1]
# Display image and data about it
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label [1 = day, 0 = night]: " + str(selected_label))
# -
# # Feature Extraction
#
# Create a feature that represents the brightness in an image. We'll be extracting the **average brightness** using HSV colorspace. Specifically, we'll use the V channel (a measure of brightness), add up the pixel values in the V channel, then divide that sum by the area of the image to get the average Value of the image.
#
# ---
# ### Find the average brightness using the V channel
#
# This function takes in a **standardized** RGB image and returns a feature (a single value) that represent the average level of brightness in the image. We'll use this value to classify the image as day or night.
# Find the average Value or brightness of an image
def avg_brightness(rgb_image):
# Convert image to HSV
hsv = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2HSV)
# Add up all the pixel values in the V channel
sum_brightness = np.sum(hsv[:,:,2])
area = 600*1100.0 # pixels
# find the avg
avg = sum_brightness/area
return avg
# +
# Testing average brightness levels
# Look at a number of different day and night images and think about
# what average brightness value separates the two types of images
# As an example, a "night" image is loaded in and its avg brightness is displayed
image_num = 200
test_im = STANDARDIZED_LIST[image_num][0]
avg = avg_brightness(test_im)
print('Avg brightness: ' + str(avg))
plt.imshow(test_im)
# -
# # Classification and Visualizing Error
#
# In this section, we'll turn our average brightness feature into a classifier that takes in a standardized image and returns a `predicted_label` for that image. This `estimate_label` function should return a value: 0 or 1 (night or day, respectively).
# ---
# ### TODO: Build a complete classifier
#
# Set a threshold that you think will separate the day and night images by average brightness.
# This function should take in RGB image input
def estimate_label(rgb_image):
## TODO: extract average brightness feature from an RGB image
# Use the avg brightness feature to predict a label (0, 1)
avg = avg_brightness(rgb_image)
## TODO: set the value of a threshold that will separate day and night images
threshold = 108.5
## TODO: Return the predicted_label (0 or 1) based on whether the avg is
# above or below the threshold
predicted_label = 0
if(avg > threshold):
predicted_label = 1
return predicted_label
## Test out your code by calling the above function and seeing
# how some of your training data is classified
estimate_label(test_im)
| 1_1_Image_Representation/6_4. Classification.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ###### Текст распространяется на условиях лицензии Creative Commons Attribution license CC-BY 4.0, код — на условиях лицензии MIT license. (c)2015 <NAME>, <NAME>.
# # Упражнение: Вывод панельного метода вихрей-источников
# Потенциал в точке $(x, y)$, создаваемый равномерным потоком, слоем источников и вихревым слоем, может быть записан в виде:
# \begin{equation}
# \begin{split}
# \phi(x, y)
# &= \phi_{uniform\ flow}(x, y) \\
# &+ \phi_{source\ sheet}(x, y) + \phi_{vortex\ sheet}(x, y)
# \end{split}
# \end{equation}
# То есть
# \begin{equation}
# \begin{split}
# \phi(x, y) &= xU_{\infty}\cos(\alpha) + yU_{\infty}\sin(\alpha) \\
# &+
# \frac{1}{2\pi} \int_{sheet} \sigma(s)\ln\left[(x-\xi(s))^2+(y-\eta(s))^2\right]^{\frac{1}{2}}ds \\
# &-
# \frac{1}{2\pi} \int_{sheet} \gamma(s)\tan^{-1} \frac{y-\eta(s)}{x-\xi(s)}ds
# \end{split}
# \end{equation}
# где $s$ — локальная координата слоя, а $\xi(s)$ и $\eta(s)$ — координаты бесконечного ряда источников и вихрей, из которых состоят слои. В записанном выше уравнении мы предполагаем, что слои источников и вихрей пересекаются.
# ------------------------------------------------------
# ### Вопрос 1:
# Пусть слой разбит на $N$ панелей, перепешите уравнение, полученное выше, в дискретном виде. Предположим, что $l_j$ — длина панели $j$. И что
#
# \begin{equation}
# \left\{
# \begin{array}{l}
# \xi_j(s)=x_j-s\sin\beta_j \\
# \eta_j(s)=y_j+s\cos\beta_j
# \end{array}
# ,\ \ \
# 0\le s \le l_j
# \right.
# \end{equation}
#
# На следующей картинке показана панель $j$:
#
# <center> <img src="resources/Lesson11_Exercise_Fig.1.png" width=360> </center>
#
# Подсказка: например, рассмотрим интеграл $\int_0^L f(x) dx$. Если разбить отрезок $0\sim L$ на три панели, его можно записать в виде:
# $$\int_0^L f(x) dx = \int_0^{L/3} f(x)dx+\int_{L/3}^{2L/3} f(x)dx+\int_{2L/3}^{L} f(x)dx \\=
# \sum_{j=1}^3 \int_{l_j}f(x)dx$$
# ----------------------------
# Теперь предположим, что
#
# 1. $\sigma_j(s) = constant = \sigma_j$
# 2. $\gamma_1(s) = \gamma_2(s) = ... = \gamma_N(s) = \gamma$
# ------------------------------------------------
# ### Вопрос 2:
# Примените изложенные выше предположения к уравнению для $\phi(x, y)$, полученному в Вопросе 1.
# ---------------------------
# Нормальную компоненту скорости $U_n$ можно получить, воспользовавшись правилом дифференцирования сложной функции:
# \begin{equation}
# \begin{split}
# U_n &= \frac{\partial \phi}{\partial \vec{n}} \\
# &=
# \frac{\partial \phi}{\partial x}\frac{\partial x}{\partial \vec{n}}
# +
# \frac{\partial \phi}{\partial y}\frac{\partial y}{\partial \vec{n}} \\
# &=
# \frac{\partial \phi}{\partial x}\nabla x\cdot \vec{n}
# +
# \frac{\partial \phi}{\partial y}\nabla y\cdot \vec{n} \\
# &=
# \frac{\partial \phi}{\partial x}n_x
# +
# \frac{\partial \phi}{\partial y}n_y
# \end{split}
# \end{equation}
# Касательную компоненту можно получить, используя тот же подход. Таким образом, в точке $(x, y)$ можно записать выражения для компонент скорости:
# \begin{equation}
# \left\{
# \begin{array}{l}
# U_n(x, y)=\frac{\partial \phi}{\partial x}(x, y) n_x(x, y)+\frac{\partial \phi}{\partial y}(x, y) n_y(x, y) \\
# U_t(x, y)=\frac{\partial \phi}{\partial x}(x, y) t_x(x, y)+\frac{\partial \phi}{\partial y}(x, y) t_y(x, y)
# \end{array}
# \right.
# \end{equation}
# -------------------------------------
# ### Вопрос 3:
# Используя выписанные выше уравнения, выведите соотношения для $U_n(x,y)$ и $U_t(x,y)$ из уравнения, полученного в Вопросе 2.
# -----------------------------------------
# ### Вопрос 4:
# Рассмотрим нормальную компоненту скорости в центре $i$-ой панели, то есть в точке $(x_{c,i}, y_{c,i})$. Подставив $(x_{c,i}, y_{c,i})$ вместо $(x, y)$ в уравнении, выведенном в Вопросе 3, можно переписать его в матричном виде:
# \begin{equation}
# \begin{split}
# U_n(x_{c,i}, y_{c,i}) &= U_{n,i} \\
# &=
# b^n_i
# +
# \left[\begin{matrix} A^n_{i1} && A^n_{i2} && ... && A^n_{iN}\end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \end{matrix}\right]
# +
# \left(\sum_{j=1}^N B^n_{ij}\right)\gamma \\
# &=
# b^n_i
# +
# \left[\begin{matrix} A^n_{i1} && A^n_{i2} && ... && A^n_{iN} && \left(\sum_{j=1}^N B^n_{ij}\right) \end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \\ \gamma \end{matrix}\right]
# \end{split}
# \end{equation}
# \begin{equation}
# \begin{split}
# U_t(x_{c,i}, y_{c,i}) &= U_{t,i} \\
# &=
# b^t_i
# +
# \left[\begin{matrix} A^t_{i1} && A^t_{i2} && ... && A^t_{iN}\end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \end{matrix}\right]
# +
# \left(\sum_{j=1}^N B^t_{ij}\right)\gamma \\
# &=
# b^t_i
# +
# \left[\begin{matrix} A^t_{i1} && A^t_{i2} && ... && A^t_{iN} && \left(\sum_{j=1}^N B^t_{ij}\right) \end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \\ \gamma \end{matrix}\right]
# \end{split}
# \end{equation}
# Чему равны $b^n_i$, $A^n_{ij}$, $B^n_{ij}$, $b^t_i$, $A^t_{ij}$ и $B^t_{ij}$?
# -----------------------
# Учитывая, что (согласно Рис. 1)
#
# \begin{equation}
# \left\{\begin{matrix} \vec{n}_i=n_{x,i}\vec{i}+n_{y,i}\vec{j} = \cos(\beta_i)\vec{i}+\sin(\beta_i)\vec{j} \\ \vec{t}_i=t_{x,i}\vec{i}+t_{y,i}\vec{j} = -\sin(\beta_i)\vec{i}+\cos(\beta_i)\vec{j} \end{matrix}\right.
# \end{equation}
#
# получим
#
# \begin{equation}
# \left\{
# \begin{matrix}
# n_{x,i}=t_{y,i} \\
# n_{y,i}=-t_{x,i}
# \end{matrix}
# \right.
# ,\ or\
# \left\{
# \begin{matrix}
# t_{x,i}=-n_{y,i} \\
# t_{y,i}=n_{x,i}
# \end{matrix}
# \right.
# \end{equation}
# -----------------------
# ### Вопрос 5:
# Применив вышеуказанные соотношения между $\vec{n}_i$ и $\vec{t}_i$ к ответу на Вопрос 4, найдите соотношения между $B^n_{ij}$ и $A^t_{ij}$, а также между $B^t_{ij}$ и $A^n_{ij}$. Наличие таких связей означает, что в коде не нужно вычислять значения $B^n_{ij}$ и $B^t_{ij}$. Какие это соотношения?
# -------------------------
# Теперь, обратите внимание, что при $i=j$, в области интегрирования имеется особенность при вычислении $A^n_{ii}$ и $A^t_{ii}$. Эта особенность возникает при $s=l_i/2$, то есть при $\xi_i(l_i/2)=x_{c,i}$ и $\eta_i(l_i/2)=y_{c,i}$. Это означает, что нужно вывести $A^n_{ii}$ и $A^t_{ii}$ аналитически.
# --------------------------
# ### Вопрос 6:
# Каковы точные значения $A^n_{ii}$ и $A^t_{ii}$?
# ------------------------------
# В нашей задаче есть $N+1$ неизвестных, то есть $\sigma_1, \sigma_2, ..., \sigma_N, \gamma$. Нам понадобится $N+1$ линейных уравнений для определения неизвестных. Первые $N$ уравнений можно получить из условия непротекания на каждой панели. То есть
#
# \begin{equation}
# \begin{split}
# U_{n,i} &= 0 \\
# &=
# b^n_i
# +
# \left[\begin{matrix} A^n_{i1} && A^n_{i2} && ... && A^n_{iN} && \left(\sum_{j=1}^N B^n_{ij}\right) \end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \\ \gamma \end{matrix}\right] \\
# &,\ \ for\
# i=1\sim N
# \end{split}
# \end{equation}
#
# или
#
# \begin{equation}
# \begin{split}
# &\left[\begin{matrix} A^n_{i1} && A^n_{i2} && ... && A^n_{iN} && \left(\sum_{j=1}^N B^n_{ij}\right) \end{matrix}\right]\left[\begin{matrix} \sigma_1 \\ \sigma_2 \\ \vdots \\ \sigma_N \\ \gamma \end{matrix}\right]
# =-b^n_i \\
# &,\ \ for\
# i=1\sim N
# \end{split}
# \end{equation}
# Для последнего уравнения воспользуемся условием Кутты-Жуковского.
#
# \begin{equation}
# U_{t,1} = - U_{t,N}
# \end{equation}
# ----------------------
# ### Вопрос 7:
# Используйте матрицы из соотношений для $U_{t,i}$ и $U_{t,N}$ для записи условия Кутты-Жуковского и получите последнее линейное уравнение. Перегруппируйте уравнения так, чтобы неизвестные оказались в левой части, а известные величины — в правой.
# ---------------------
# ### Вопрос 8:
# Теперь у вас есть $N+1$ линейных уравнений для нахождения $N+1$ неизвестной. Попробуйте скомбинировать первые $N$ линейных уравнений и последнее (то, что получилось при наложении условия Кутты-Жуковского) из ответа на Вопрос 7, чтобы получить полную систему линейных уравнений в матричной форме.
# ----------------------------
# Теперь можно решать уравнения! Это и есть панельный метод вихрей и источников.
# --------------------
# + active=""
# Пожалуйста, не обращайте внимания на ячейку ниже. При её исполнении загружаются стили для отображения блокнота.
# -
from IPython.core.display import HTML
def css_styling():
styles = open('../styles/custom.css', 'r').read()
return HTML(styles)
css_styling()
| lessons/11_Lesson11_Exercise.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pySpark (Spark 1.6.0)
# language: python
# name: pyspark1.6
# ---
#SKIP_COMPARE_OUTPUT
import pixiedust
# +
data = [(2010, 'Camping Equipment', 3),
(2010, 'Golf Equipment', 1),
(2010, 'Mountaineering Equipment', 1),
(2010, 'Outdoor Protection', 2),
(2010, 'Personal Accessories', 2),
(2011, 'Camping Equipment', 4),
(2011, 'Golf Equipment', 5),
(2011, 'Mountaineering Equipment',2),
(2011, 'Outdoor Protection', 4),
(2011, 'Personal Accessories', 2),
(2012, 'Camping Equipment', 5),
(2012, 'Golf Equipment', 5),
(2012, 'Mountaineering Equipment', 3),
(2012, 'Outdoor Protection', 5),
(2012, 'Personal Accessories', 3),
(2013, 'Camping Equipment', 8),
(2013, 'Golf Equipment', 5),
(2013, 'Mountaineering Equipment', 3),
(2013, 'Outdoor Protection', 8),
(2013, 'Personal Accessories', 4)]
columns = ["year","zone","unique_customers"]
# -
#TARGET=SPARK
dd = sqlContext.createDataFrame( data, columns)
dd.count()
#TARGET=PLAIN
import pandas
dd = pandas.DataFrame( data, columns=columns )
# + pixiedust={"displayParams": {"aggregation": "SUM", "handlerId": "dataframe", "keyFields": "zone", "rendererId": "matplotlib", "rowCount": "100", "showLegend": "true", "stacked": "true", "staticFigure": "false", "valueFields": "unique_customers"}}
#SKIP_COMPARE_OUTPUT
display(dd, no_gen_tests='true')
# -
display(dd,cell_id='2850507A33444756801B43A74E3E6A56',no_gen_tests='true',showLegend='true',staticFigure='false',aggregation='SUM',rowCount='100',handlerId='pieChart',valueFields='unique_customers',rendererId='matplotlib',stacked='true',keyFields='zone',nostore_cw='1098',nostore_pixiedust='true',nostore_bokeh='false',prefix='ae087e77')
display(dd,cell_id='2850507A33444756801B43A74E3E6A56',no_gen_tests='true',showLegend='true',staticFigure='false',aggregation='SUM',rowCount='100',handlerId='barChart',valueFields='unique_customers',rendererId='matplotlib',stacked='true',keyFields='zone',nostore_cw='1098',nostore_pixiedust='true',nostore_bokeh='false',prefix='2e7ed979')
display(dd,cell_id='2850507A33444756801B43A74E3E6A56',no_gen_tests='true',showLegend='true',staticFigure='false',aggregation='SUM',rowCount='100',handlerId='dataframe',valueFields='unique_customers',rendererId='matplotlib',stacked='true',keyFields='zone',nostore_cw='1098',nostore_pixiedust='true',nostore_bokeh='false',prefix='09810fd8')
| tests/TestDisplay-BarPieTable.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # VacationPy
# ----
#
# #### Note
# * Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
# +
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
# from api_key import g_key
g_key="<KEY>"
# -
# ### Store Part I results into DataFrame
# * Load the csv exported in Part I to a DataFrame
weather_df=pd.read_csv("../output_data/weather_check_output.csv")
del weather_df["Unnamed: 0"]
weather_df.head()
# +
# # remove rows with blank ('') values
# weather_df=weather_df[weather_df['Humidity(%)']!='']
# weather_df
# -
# ### Humidity Heatmap
# * Configure gmaps.
# * Use the Lat and Lng as locations and Humidity as the weight.
# * Add Heatmap layer to map.
# +
#access maps with unique API key
gmaps.configure(api_key=g_key)
#handle NaN values
weather_df = weather_df.dropna()
#Store Lat and Lng as locations
locations= weather_df[["Lat", "Lng"]].astype(float)
locations
#Humidty
humidity= weather_df['Humidity(%)'].astype(float)
humidity
# Create the size of the figure
# figure_layout = {
# 'width': '900px',
# 'height': '600px',
# 'border': '1px solid black',
# 'padding': '1px',
# 'margin': '0 auto 0 auto'
# }
fig = gmaps.figure(center=(0,10),zoom_level=1.75)
# markers = gmaps.marker_layer(locations)
# fig.add_layer(markers)
fig
# Heatmap layer to map
humidity_layer = gmaps.heatmap_layer(locations, weights=humidity,
dissipating=False, max_intensity=max(weather_df["Humidity(%)"]),
point_radius = 3)
fig.add_layer(humidity_layer)
fig
# -
# ### Create new DataFrame fitting weather criteria
# * Narrow down the cities to fit weather conditions.
# * Drop any rows will null values.
#Narrow data to my ideal weather conditions
#Max temperature between 70-85 degF, Wind speed less than 10mph, Cloudiness between 10-50%
ideal_df = weather_df.loc[(weather_df["Wind Speed (mph)"]<10) & (weather_df["Max Temp"]>70) & \
(weather_df["Max Temp"]<85) & (weather_df["Cloudiness(%)"]<51) & (weather_df["Cloudiness(%)"]>9)].dropna()
ideal_df
# ### Hotel Map
# * Store into variable named `hotel_df`.
# * Add a "Hotel Name" column to the DataFrame.
# * Set parameters to search for hotels with 5000 meters.
# * Hit the Google Places API for each city's coordinates.
# * Store the first Hotel result into the DataFrame.
# * Plot markers on top of the heatmap.
# +
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# +
# Add marker layer ontop of heat map
# Display figure
# -
| .ipynb_checkpoints/VacationPy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from dask_kubernetes import KubeCluster
from dask.distributed import Client, progress
import dask.array as da
import numpy as np
import pandas as pd
import zarr
import allel
import sys
import ag3
import psutil
from humanize import naturalsize
import numba
# +
# set up a method to call ktypes based on SVM or KNN.
# +
# Data storage, uses about 34 MB
pca_cloud_zarr_path_template = 'vo_agam_production/ag3_data_paper/{}.pca_output.zarr'
# Writing the PCA data to the cloud will require the appropriate authentication and authorization.
import gcsfs
# UNCOMMENT THIS TO AUTHENTICATE. YOU ONLY NEED TO RUN THIS ONCE.
# After running this once, your authentication token should then be cached in `~/.gcs_tokens`
# Once you have authenticated, you should comment this out again to avoid re-authenticating.
# gcs_browser = gcsfs.GCSFileSystem(project='malariagen-jupyterhub', token='browser')
# Use `cache_timeout=0` to prevent object list cache, to avoid recreating map for Zarr consolidated metadata
auth_fs = gcsfs.GCSFileSystem(project='malariagen-jupyterhub', token='cache', cache_timeout=0)
# +
pca_cloud_zarr_path = pca_cloud_zarr_path_template.format('gamb_colu_arab_pca')
pca_cloud_zarr_path
# +
# Sometimes errors with `overwrite=True`, sometimes errors without, when dir not exist
# Keep the zarr_store for zarr.consolidate_metadata(zarr_store)
zarr_store = auth_fs.get_mapper(pca_cloud_zarr_path)
zarr_group = zarr.group(zarr_store)
# -
sample_names = zarr_group["sample_names"][:]
sample_names = [s.decode() for s in sample_names]
pca_coordinates = zarr_group["coords"]
pca_components = zarr_group["components"]
pca_pve = zarr_group["explained_variance_ratio"]
from ag3 import release_data
v3 = release_data()
all_meta = v3.load_sample_set_metadata(v3.all_wild_sample_sets)
import matplotlib.pyplot as plt
# %matplotlib inline
cdict = {"gamb_colu": "orange", "arabiensis": "blue", "intermediate":"green"}
all_meta["species_colours"] = all_meta.species_gambcolu_arabiensis.map(cdict)
import seaborn as sns
f, ax = plt.subplots(ncols=1, nrows=1, figsize=(12, 12))
ax.scatter(pca_coordinates[:, 0], pca_coordinates[:, 1], c=all_meta["species_colours"], edgecolor='k', lw=0.5)
ax.grid(True)
ax.set_xlabel(f"PC1")
ax.set_ylabel(f"PC2")
sns.despine(ax=ax)
#f.savefig("../content/images/pca/2La_karyotypes.svg", dpi=200)
def call_inversion_status(v):
if v < -20:
return 2
elif v > 35:
return 1
else:
return 0
# +
pca1 = pd.Series(pca_coordinates[:, 0], sample_names)
call_2La = pca1.map(call_inversion_status)
call_2La.name = "kt_2La"
# -
import yaml
with open("../content/population_definitions.yml") as f:
definitions = yaml.load(f, Loader=yaml.Loader)
# +
sample_ids = []
grouping = []
for k, v in definitions.items():
for x in v:
sample_ids.append(x)
grouping.append(k)
population_definitions = pd.Series(grouping, index=sample_ids, name="sampling_group").reindex(all_meta.index)
# -
all_meta["population_definitions"] = population_definitions
all_meta["2La_kt"] = call_2La
x = pd.crosstab(all_meta["population_definitions"], all_meta["2La_kt"])
x["n_samples"] = x.sum(axis=1)
x["frac_2La"] = (x[1] + 2*x[2]) / (2 * x["n_samples"])
x.head()
summary_2la = x.sort_values("frac_2La", ascending=False)
summary_2la.to_csv("../content/tables/karotype_summary_2La.csv")
summary_2la.head()
# Given arabiensis is fixed for the inverted form... we can assume PC1 < -20 is
call_2La.to_csv("../content/tables/karyotype_status_2La.csv")
| notebooks/karyotype_infer-using-pca.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Text models, data, and training
# + hide_input=true
from fastai.gen_doc.nbdoc import *
# -
# The [`text`](/text.html#text) module of the fastai library contains all the necessary functions to define a Dataset suitable for the various NLP (Natural Language Processing) tasks and quickly generate models you can use for them. Specifically:
# - [`text.transform`](/text.transform.html#text.transform) contains all the scripts to preprocess your data, from raw text to token ids,
# - [`text.data`](/text.data.html#text.data) contains the definition of [`TextDataset`](/text.data.html#TextDataset), which the main class you'll need in NLP,
# - [`text.learner`](/text.learner.html#text.learner) contains helper functions to quickly create a language model or an RNN classifier.
#
# Have a look at the links above for full details of the API of each module, of read on for a quick overview.
# ## Quick Start: Training an IMDb sentiment model with *ULMFiT*
# Let's start with a quick end-to-end example of training a model. We'll train a sentiment classifier on a sample of the popular IMDb data, showing 4 steps:
#
# 1. Reading and viewing the IMDb data
# 1. Getting your data ready for modeling
# 1. Fine-tuning a language model
# 1. Building a classifier
# ### Reading and viewing the IMDb data
# First let's import everything we need for text.
from fastai.text import *
# Contrary to images in Computer Vision, text can't directly be transformed into numbers to be fed into a model. The first thing we need to do is to preprocess our data so that we change the raw texts to lists of words, or tokens (a step that is called tokenization) then transform these tokens into numbers (a step that is called numericalization). These numbers are then passed to embedding layers that will convert them in arrays of floats before passing them through a model.
#
# You can find on the web plenty of [Word Embeddings](https://en.wikipedia.org/wiki/Word_embedding) to directly convert your tokens into floats. Those word embeddings have generally be trained on a large corpus such as wikipedia. Following the work of [ULMFiT](https://arxiv.org/abs/1801.06146), the fastai library is more focused on using pre-trained Language Models and fine-tuning them. Word embeddings are just vectors of 300 or 400 floats that represent different words, but a pretrained language model not only has those, but has also been trained to get a representation of full sentences and documents.
#
# That's why the library is structured around three steps:
#
# 1. Get your data preprocessed and ready to use in a minimum amount of code,
# 1. Create a language model with pretrained weights that you can fine-tune to your dataset,
# 1. Create other models such as classifiers on top of the encoder of the language model.
#
# To show examples, we have provided a small sample of the [IMDB dataset](https://www.imdb.com/interfaces/) which contains 1,000 reviews of movies with labels (positive or negative).
path = untar_data(URLs.IMDB_SAMPLE)
path
# Creating a dataset from your raw texts is very simple if you have it in one of those ways
# - organized it in folders in an ImageNet style
# - organized in a csv file with labels columns and a text columns
#
# Here, the sample from imdb is in a texts csv files that looks like this:
df = pd.read_csv(path/'texts.csv')
df.head()
# ### Getting your data ready for modeling
# + hide_input=true
for file in ['train_tok.npy', 'valid_tok.npy']:
if os.path.exists(path/'tmp'/file): os.remove(path/'tmp'/file)
# -
# To get a [`DataBunch`](/basic_data.html#DataBunch) quickly, there are also several factory methods depending on how our data is structured. They are all detailed in [`text.data`](/text.data.html#text.data), here we'll use the method <code>from_csv</code> of the [`TextLMDataBunch`](/text.data.html#TextLMDataBunch) (to get the data ready for a language model) and [`TextClasDataBunch`](/text.data.html#TextClasDataBunch) (to get the data ready for a text classifier) classes.
# Language model data
data_lm = TextLMDataBunch.from_csv(path, 'texts.csv')
# Classifier model data
data_clas = TextClasDataBunch.from_csv(path, 'texts.csv', vocab=data_lm.train_ds.vocab, bs=32)
# This does all the necessary preprocessing behind the scene. For the classifier, we also pass the vocabulary (mapping from ids to words) that we want to use: this is to ensure that `data_clas` will use the same dictionary as `data_lm`.
#
# Since this step can be a bit time-consuming, it's best to save the result with:
data_lm.save()
data_clas.save()
# This will create a 'tmp' directory where all the computed stuff will be stored. You can then reload those results with:
data_lm = TextLMDataBunch.load(path)
data_clas = TextClasDataBunch.load(path, bs=32)
# Note that you can load the data with different [`DataBunch`](/basic_data.html#DataBunch) parameters (batch size, `bptt`,...)
# ### Fine-tuning a language model
# We can use the `data_lm` object we created earlier to fine-tune a pretrained language model. [fast.ai](http://www.fast.ai/) has an English model available that we can download. We can create a learner object that will directly create a model, download the pretrained weights and be ready for fine-tuning.
learn = language_model_learner(data_lm, AWD_LSTM, drop_mult=0.5)
learn.fit_one_cycle(1, 1e-2)
# Like a computer vision model, we can then unfreeze the model and fine-tune it.
learn.unfreeze()
learn.fit_one_cycle(1, 1e-3)
# To evaluate your language model, you can run the [`Learner.predict`](/basic_train.html#Learner.predict) method and specify the number of words you want it to guess.
learn.predict("This is a review about", n_words=10)
# It doesn't make much sense (we have a tiny vocabulary here and didn't train much on it) but note that it respects basic grammar (which comes from the pretrained model).
#
# Finally we save the encoder to be able to use it for classification in the next section.
learn.save_encoder('ft_enc')
# ### Building a classifier
# We now use the `data_clas` object we created earlier to build a classifier with our fine-tuned encoder. The learner object can be done in a single line.
learn = text_classifier_learner(data_clas, AWD_LSTM, drop_mult=0.5)
learn.load_encoder('ft_enc')
data_clas.show_batch()
learn.fit_one_cycle(1, 1e-2)
# Again, we can unfreeze the model and fine-tune it.
learn.freeze_to(-2)
learn.fit_one_cycle(1, slice(5e-3/2., 5e-3))
learn.unfreeze()
learn.fit_one_cycle(1, slice(2e-3/100, 2e-3))
# Again, we can predict on a raw text by using the [`Learner.predict`](/basic_train.html#Learner.predict) method.
learn.predict("This was a great movie!")
| docs_src/text.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
beis_2013 = pd.read_csv('~/Documents/PhD/Projects/10-ELECSIM/run/beis_case_study/data/reference_run/2013_projection_1.csv')
beis_2013
# +
beis_2013_long = pd.melt(beis_2013, id_vars='fuel_type')
beis_2013_long.loc[:,'variable'] = beis_2013_long.variable.astype(np.float)
beis_2013_long.head()
# -
sns.lineplot(data=beis_2013_long, x='variable', y='value', hue='fuel_type')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
# +
elecsim_run = pd.read_csv('~/Documents/PhD/Projects/10-ELECSIM/run/beis_case_study/data/reference_run/elecsim_projections_coal_dropout.csv')
elecsim_run = elecsim_run[['year','type','run_id','value_perc','Technology','value']]
elecsim_run['type']=elecsim_run['type'].str.replace("Predicted","ElecSim")
elecsim_run = elecsim_run.dropna()
elecsim_run
# +
elecsim_run_wide = pd.pivot_table(elecsim_run.drop('value', axis=1), index=['year','type','run_id'], columns='Technology')
elecsim_run_wide.columns= elecsim_run_wide.columns.droplevel(0)
elecsim_run_wide = elecsim_run_wide.reset_index()
elecsim_run_wide['Renewables'] = elecsim_run_wide.Wind + elecsim_run_wide.Solar
elecsim_run_wide = elecsim_run_wide.drop(['Solar', 'Wind'], axis=1)
elecsim_renewables_long = pd.melt(elecsim_run_wide, id_vars=['year','type','run_id'])
elecsim_renewables_long = elecsim_renewables_long.rename(columns={'value': 'value_perc'})
elecsim_renewables_long.head()
# +
def get_value_perc(df):
df['value_perc'] = 100*df.value/df.value.sum()
return df
beis_2013_long = beis_2013_long.rename(columns={"fuel_type":"Technology",'variable':'year'})
beis_2013_long = beis_2013_long.groupby('year').apply(get_value_perc)
beis_2013_long['type'] = "BEIS"
beis_2013_long['run_id'] = -2
# beis_2013_long = beis_2013_long.drop("value", axis=1)
beis_2013_long.to_csv('/Users/b1017579/Documents/PhD/Projects/10-ELECSIM/notebooks/validation-optimisation/data/results/beis_forecasts.csv')
beis_2013_long
# +
# all_projections['Technology'] = all_projections['Technology'].str.replace("Gas","CCGT")
all_projections = beis_2013_long.append(elecsim_renewables_long)
all_projections.to_csv('/Users/b1017579/Documents/PhD/Projects/10-ELECSIM/notebooks/validation-optimisation/data/results/predictions_actuals_all_data_coal_dropout.csv')
all_projections = all_projections.rename(columns = {"type":'Type'})
sns.set(font_scale=1)
sns.set_style("whitegrid")
g = sns.lineplot(data=all_projections, x='year', y='value_perc', style='Type', hue='Technology')
# lgd = plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
lgd = plt.legend(bbox_to_anchor=(1,-0.17), borderaxespad=0., ncol=3)
g.set(xlabel='Year', ylabel='Electricity Mix (%)')
plt.savefig('/Users/b1017579/Documents/PhD/Projects/10-ELECSIM/notebooks/validation-optimisation/figures/results/throughout_years_beis_elecsim_comparison_coal_dropout_leg_below.pdf',dpi=1000, bbox_extra_artists=(lgd,), bbox_inches='tight')
# -
all_projections
# +
sns.set(font_scale=1.5)
sns.set_style("whitegrid")
g = sns.barplot(data=all_projections[(all_projections.year==2018) & (all_projections.Type!='BEIS') & (all_projections.run_id<=40)], x='Technology', y='value_perc', hue='Type', capsize = 0.2, saturation = 8, errwidth = 2)
lgd = plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
g.set(xlabel='Technology', ylabel='Electricity Mix (%)')
plt.savefig('/Users/b1017579/Documents/PhD/Projects/10-ELECSIM/notebooks/validation-optimisation/figures/introduction/best_run_coal_dropout_95_ci.pdf',dpi=1000, bbox_extra_artists=(lgd,), bbox_inches='tight')
# -
# +
all_projections.reset_index(drop=True).groupby(['Type','Technology','year'])['value_perc'].mean().to_csv('/Users/b1017579/Documents/PhD/Projects/10-ELECSIM/notebooks/validation-optimisation/data/results/predictions_actuals_coal_dropout1.csv')
# +
def get_relative_error(x):
x['relative_error'] = (x.value_perc - x[x.Type=="Actual"].value_perc.values)
x['type'] = x.Type
return x
# all_projections
all_projections = beis_2013_long.append(elecsim_renewables_long)
to_plot = all_projections[~all_projections["Technology"].str.contains('Coal and gas CCS|Oil')]
to_plot['relative_error'] = to_plot.groupby(['year', "Technology"], as_index=False).apply(lambda x: x.value_perc - x[x.type=="Actual"].value_perc.values).reset_index().value_perc
to_plot
sns.set(font_scale=1.5)
sns.set_style("whitegrid")
g = sns.lineplot(data=to_plot, x='year', y='relative_error', style='type', hue='Technology')
lgd = plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
g.set(xlabel='Year', ylabel='Electricity Mix (%)')
# plt.savefig('/Users/b1017579/Documents/PhD/Projects/10. ELECSIM/notebooks/validation-optimisation/figures/results/throughout_years_beis_elecsim_comparison.pdf',dpi=500, bbox_extra_artists=(lgd,), bbox_inches='tight')
# +
best_mix_year = pd.read_csv('~/Documents/PhD/Projects/10. ELECSIM/run/beis_case_study/data/reference_run/elecsim_projections_total')
contributed_results = best_mix_year.filter(regex='contributed_')
contributed_results['year'] = best_mix_year['year']
contributed_results['run_id'] = best_mix_year['run_id']
contributed_results = contributed_results.rename(columns={'contributed_PV': "contributed_solar"})
# contributed_results
cluster_size = pd.Series([22.0, 30.0, 32.0, 35.0, 43.0, 53.0, 68.0, 82.0])
contributed_results['contributed_Wind'] = contributed_results['contributed_Offshore'] + contributed_results['contributed_Onshore']
contributed_results = contributed_results.drop(['contributed_Offshore', 'contributed_Onshore'], axis=1)
contributed_results
# +
def get_weighted_average(df):
# print(df)
year = df['year']
run_id = df['run_id']
df.apply(lambda x: x*cluster_size.values)
df['run_id'] = run_id
df['year'] = year
return df
# return df.apply(lambda x: np.average(x, weights=cluster_size.values))
results_wa = contributed_results.groupby(['run_id','year']).apply(lambda x: get_weighted_average(x)).reset_index(drop=True)
results_wa
# +
def sum_years(df):
year = df['year'].iloc[0]
run_id = df['run_id'].iloc[0]
sum_df = df.sum()
sum_df.year=year
sum_df.run_id=run_id
return sum_df
elecsim_summed = results_wa.groupby(["year",'run_id']).apply(sum_years)
elecsim_summed
# +
hist_long = pd.melt(elecsim_summed, id_vars=["run_id", "year"])
hist_long
# -
hist_long['variable'] = hist_long.variable.str.split("_").str[-1].str.lower()
hist_long['year'] = hist_long['year'] + 2013
# +
def get_mix(df):
df['value_perc'] = df['value']/sum(df['value'])*100
return df
hist_long_perc = hist_long.groupby(['year','run_id']).apply(lambda x: get_mix(x))
hist_long_perc = hist_long_perc.rename(columns={"type":"Type", "variable":'Technology'})
hist_long_perc['Technology'] = hist_long_perc['Technology'].map({'coal': "Coal", 'ccgt': "CCGT", 'nuclear':"Nuclear", "wind":"Wind","solar":"Solar", "gas":"Recip_gas"})
hist_long_perc
# -
hist_long_perc = hist_long_perc.dropna()
# hist_long_perc = hist_long_perc.drop('index', axis=1)
hist_long_perc['type']='ElecSim'
hist_long_perc
both = hist_long_perc.append(elecsim_run[elecsim_run.type=="Actual"])
both = both.reset_index(drop=True)
both
# +
# both.year = both.year.astype(int)
# -
sns.lineplot(data=both, x='year', y='value_perc', hue='Technology', style='type')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
beis_2013_long.loc[:,"value"] = beis_2013_long.loc[:,"value"]*100
beis_2013_long
beis_actual = beis_2013_long.append(elecsim_run[elecsim_run.type=="Actual"])
beis_actual
sns.lineplot(data=beis_actual, x='year', y='value', style="type", hue='Technology')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
# # 2018-2035 Projections
beis_2035 = pd.read_csv('~/Documents/PhD/Projects/10. ELECSIM/run/beis_case_study/data/reference_run/2018-2035-beis.csv')
beis_2035.head()
beis_2035_long = pd.melt(beis_2035, id_vars='fuel_type')
beis_2035_long.head()
sns.lineplot(data=beis_2035_long, x='variable', y='value', hue='fuel_type')
| notebooks/forward_scenario/2.0-ajmk-comparison-of-projections 3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Named Tuples - Application - Returning Multiple Values
# We already know that we can easily return multiple values from a function by using a tuple:
# +
from random import randint, random
def random_color():
red = randint(0, 255)
green = randint(0,255)
blue = randint(0, 255)
alpha = round(random(), 2)
return red, green, blue, alpha
# -
random_color()
# So of course, we could call the function this and unpack the results at the same time:
red, green, blue, alpha = random_color()
print(f'red={red}, green={green}, blue={blue}, alpha={alpha}')
# But it might be nicer to use a named tuple:
from collections import namedtuple
# +
Color = namedtuple('Color', 'red green blue alpha')
def random_color():
red = randint(0, 255)
green = randint(0,255)
blue = randint(0, 255)
alpha = round(random(), 2)
return Color(red, green, blue, alpha)
# -
color = random_color()
color.red
color
| python-tuts/0-beginner/7-Tuples Data Records/06 - Named Tuples - Application - Returning Multiple Values.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Deep Recurrent Q-Network
# ## Setup
# +
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
# !apt update && apt install -y libpq-dev libsdl2-dev swig xorg-dev xvfb
# !pip install -q -U tf-agents pyvirtualdisplay gym[atari,box2d]
IS_COLAB = True
except Exception:
IS_COLAB = False
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
gpus = tf.config.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
else:
print("No GPU was detected. CNNs can be very slow without a GPU.")
if IS_COLAB:
print("Go to Runtime > Change runtime and select a GPU hardware accelerator.")
# Common imports
import numpy as np
import random
import os
import functools
import time
import gin
import PIL
import imageio
from absl import app
from absl import flags
from absl import logging
import gym
from gym.envs.registration import register
from collections import deque
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Input, Dense, LSTM, Activation, Flatten, Conv2D, MaxPooling2D
from tensorflow.keras.optimizers import Adam
from IPython import display
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# To get smooth animations
import matplotlib.animation as animation
mpl.rc('animation', html='jshtml')
# -
# ## Environment Setup
# +
env_name = 'LunarLander-v2'
#env_name = 'CartPole-v1'
random_seed = 42
ROOT_DIR = "."
IMAGES_PATH = os.path.join(ROOT_DIR, "images")
os.makedirs(IMAGES_PATH, exist_ok=True)
# Params for train
max_episodes = 500
max_replay = 10
batch_size = 32
gamma = 0.99
epsilon_min = 0.01
learning_rate = 0.005
target_update_rate = 2
time_steps = 4
#loss_fn = keras.losses.sparse_categorical_crossentropy
#loss_fn = keras.losses.mean_squared_error
loss_fn = keras.losses.MeanSquaredError()
#activation_fn = "softmax"
activation_fn = "linear"
keras.backend.clear_session()
tf.random.set_seed(random_seed)
np.random.seed(random_seed)
# -
# ## Replay Buffer
class ReplayBuffer:
def __init__(self, time_steps, batch_size=32, capacity=10000):
self.time_steps = time_steps
self.batch_size = batch_size
self.buffer = deque(maxlen=capacity)
def put(self, state, action, reward, next_state, done):
self.buffer.append([state, action, reward, next_state, done])
def sample(self):
minibatch = random.sample(self.buffer, self.batch_size)
states, actions, rewards, next_states, done = map(np.asarray, zip(*minibatch))
states = np.array(states).reshape(self.batch_size, self.time_steps, -1)
next_states = np.array(next_states).reshape(self.batch_size, self.time_steps, -1)
return states, actions, rewards, next_states, done
def size(self):
return len(self.buffer)
# ## Deep Recurrent Q-Network
class DRQN:
def __init__(self, network_name, state_dim, action_dim, time_steps=4, loss_fn=keras.losses.MeanSquaredError(), gamma=0.99, learning_rate=0.005, max_episodes=500, eps_min=0.01):
self.network_name = network_name
self.state_dim = state_dim
self.action_dim = action_dim
self.gamma = gamma
self.lr = learning_rate
self.eps_den = (max_episodes * 0.85)
self.eps_min = eps_min
self.time_steps = time_steps
self.loss_fn = loss_fn
self.optimizer = Adam(lr=self.lr)
self.checkpoint_folder = os.path.join(ROOT_DIR, "training/" + self.network_name)
os.makedirs(self.checkpoint_folder, exist_ok=True)
self.checkpoint_path = os.path.join(self.checkpoint_folder, 'cp-{epoch:04d}.ckpt')
self.checkpoint_dir = os.path.dirname(self.checkpoint_path)
self.model = self.create_model()
def create_model(self):
model = tf.keras.Sequential([
Input((self.time_steps, self.state_dim)),
LSTM(32, activation='tanh'),
Dense(16, activation='relu'),
Dense(self.action_dim)
])
return model
def epsilon(self, episode):
eps = max(1 - episode / self.eps_den, self.eps_min)
return eps
def epsilon_greedy(self, state, episode):
if random.uniform(0,1) < self.epsilon(episode):
action = np.random.randint(self.action_dim)
else:
Q_value = self.predict(state)[0]
action = np.argmax(Q_value)
return action
def predict(self, state):
return self.model.predict(state)
def get_action(self, state, episode):
state = np.reshape(state, [1, self.time_steps, self.state_dim])
return self.epsilon_greedy(state, episode)
def train(self, states, targets):
targets = tf.stop_gradient(targets)
with tf.GradientTape() as tape:
logits = self.model(states, training=True)
assert targets.shape == logits.shape
loss = self.loss_fn(targets, logits)
grads = tape.gradient(loss, self.model.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.model.trainable_variables))
def load(self, weights=''):
if weights:
self.model.load_weights(weights)
else:
latest = tf.train.latest_checkpoint(self.checkpoint_dir)
if latest is not None:
self.model.load_weights(latest)
def save(self, e):
self.model.save_weights(self.checkpoint_path.format(epoch=e))
def clean(self):
for f in os.listdir(self.checkpoint_folder):
os.remove(os.path.join(self.checkpoint_folder, f))
# ## Agent Class
class Agent:
def __init__(self, env_name, random_seed=42, time_steps=4, loss_fn=keras.losses.MeanSquaredError(), gamma=0.95, learning_rate=0.005, max_episodes=500, eps_min=0.01, batch_size=32, max_replay=10, target_update_rate=50):
self.env = gym.make(env_name)
self.env.seed(random_seed)
self.state_dim = self.env.observation_space.shape[0]
self.action_dim = self.env.action_space.n
self.gamma = gamma
self.batch_size = batch_size
self.target_update_rate = target_update_rate
self.time_steps = time_steps
self.states = np.zeros([self.time_steps, self.state_dim])
self.frames = []
self.rewards = []
self.image_name = env_name + ".gif"
self.image_path = os.path.join(IMAGES_PATH, self.image_name)
self.main_model = DRQN("main", self.state_dim, self.action_dim, self.time_steps, loss_fn, self.gamma, learning_rate, max_episodes, eps_min)
self.target_model = DRQN("target", self.state_dim, self.action_dim, self.time_steps, loss_fn, self.gamma, learning_rate, max_episodes, eps_min)
self.target_update()
self.buffer = ReplayBuffer(self.time_steps, self.batch_size)
def cp_init(self):
self.main_model.clean()
self.target_model.clean()
def convert_time(self, t):
hours, rem = divmod(t, 3600)
minutes, seconds = divmod(rem, 60)
return hours, minutes, seconds
def make_gif(self):
frame_images = [PIL.Image.fromarray(frame) for frame in self.frames]
frame_images[0].save(self.image_path, format='GIF', append_images=frame_images[1:], save_all=True, duration=120, loop=0)
def show_gif(self):
html_img = '<img src=' + self.image_path + ' />'
display.HTML(html_img)
def plot_rewards(self):
plt.figure(figsize=(8, 4))
plt.plot(self.rewards)
plt.xlabel("Episode", fontsize=14)
plt.ylabel("Reward", fontsize=14)
plt.grid()
plt.show()
def target_update(self):
weights = self.main_model.model.get_weights()
self.target_model.model.set_weights(weights)
def replay(self, max_replay=10):
for _ in range(max_replay):
states, actions, rewards, next_states, done = self.buffer.sample()
next_q_values = self.target_model.predict(next_states).max(axis=1)
q_values = self.main_model.predict(states)
q_values[range(self.batch_size), actions] = rewards + (1-done) * next_q_values * self.gamma
self.main_model.train(states, q_values)
def update_states(self, next_state):
self.states = np.roll(self.states, -1, axis=0)
self.states[-1] = next_state
def train(self, max_episodes=1000, max_replay=10):
train_time, best_reward = 0, -1000
self.rewards = []
avg_rewards = []
self.main_model.load()
self.main_model.clean()
for ep in range(max_episodes):
done, total_reward, time_step = False, 0, 0
self.states = np.zeros([self.time_steps, self.state_dim])
self.update_states(self.env.reset())
while not done:
action = self.main_model.get_action(self.states, ep)
next_state, reward, done, _ = self.env.step(action)
prev_states = self.states
self.update_states(next_state)
self.buffer.put(prev_states, action, reward, self.states, done)
total_reward += reward
time_step += 1
self.rewards.append(total_reward)
avg_reward = np.mean(self.rewards[-100:])
avg_rewards.append(avg_reward)
if total_reward >= best_reward:
best_weights = self.main_model.model.get_weights()
best_reward = total_reward
self.main_model.save(ep)
if self.buffer.size() >= self.batch_size:
start_time = time.time()
self.replay(max_replay)
train_time += time.time() - start_time
if ep % self.target_update_rate:
self.target_update()
hours, minutes, seconds = self.convert_time(train_time)
print("\rEpisode: {}, Timestep: {}, Current Reward: {:.5f}, Best Reward: {:.5f}, Avg. Reward: {:.5f}, Train Time: {:0>2}:{:0>2}:{:05.2f}".format(ep, time_step, total_reward, best_reward, avg_reward, int(hours), int(minutes), seconds), end="")
self.main_model.model.set_weights(best_weights)
self.main_model.save(ep)
def play(self):
self.states = np.zeros([self.time_steps, self.state_dim])
self.update_states(self.env.reset())
self.frames = []
total_reward, step_indx = 0, 0
while True:
self.frames.append(self.env.render(mode="rgb_array"))
action_state = np.reshape(self.states, [1, self.time_steps, self.state_dim])
Q_value = self.main_model.predict(action_state)[0]
action = np.argmax(Q_value)
state, reward, done, _ = self.env.step(action)
self.update_states(state)
total_reward += reward
step_indx += 1
print("\rTimestep: {}, Reward: {:.5f}".format(step_indx, total_reward), end="")
if done:
break
self.env.close()
# ## Train
agent = Agent(env_name, random_seed, time_steps, loss_fn, gamma, learning_rate, max_episodes, epsilon_min, batch_size, max_replay, target_update_rate)
agent.cp_init()
agent.train(max_episodes, max_replay)
agent.train(max_episodes, max_replay)
# ## Display Results
agent.plot_rewards()
# ## Play
agent.play()
agent.make_gif()
agent.show_gif()
display.HTML("<img src='images/LunarLander-v2.gif' />")
| DRQN/DRQN.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Innarticles/Data-Science-Resources/blob/master/Copy_of_S%2BP_Week_2_Exercise_Answer.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="D1J15Vh_1Jih" colab_type="code" cellView="both" colab={}
# !pip install tf-nightly-2.0-preview
# + id="BOjujz601HcS" colab_type="code" colab={}
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
# + colab_type="code" id="Zswl7jRtGzkk" colab={}
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(False)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.1,
np.cos(season_time * 6 * np.pi),
2 / np.exp(9 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(10 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.005
noise_level = 3
# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=51)
split_time = 3000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 20
batch_size = 32
shuffle_buffer_size = 1000
plot_series(time, series)
# + id="4sTTIOCbyShY" colab_type="code" colab={}
def windowed_dataset(series, window_size, batch_size, shuffle_buffer):
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer).map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
# + id="TW-vT7eLYAdb" colab_type="code" colab={}
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(100, input_shape=[window_size], activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9))
model.fit(dataset,epochs=100,verbose=0)
# + id="efhco2rYyIFF" colab_type="code" colab={}
forecast = []
for time in range(len(series) - window_size):
forecast.append(model.predict(series[time:time + window_size][np.newaxis]))
forecast = forecast[split_time-window_size:]
results = np.array(forecast)[:, 0, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, results)
# + id="-kT6j186YO6K" colab_type="code" colab={}
tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()
| Copy_of_S+P_Week_2_Exercise_Answer.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center>
# <a href="https://uv.bf/" target="_parent"><img src="logo.png" alt="" width="200" height="240"/></a>
# </center>
# ### Mini Projet – Traitement de Données avec Python - Pandas
# #### Le but de cet exercice est d'extraire un sous-ensemble de données à partir d'une base de données existantes
# Supposons que vous ayez besoin de réaliser une application qui prend en entrée, des noms
# de lieux du Burkina Faso, avec des informations telles que la latitude/longitude.
# Pour ce faire, nous décidons d'extraire ces informations à partir du server de référencement
# géoname (http://www.geonames.org/). Vous allez procéder de la façon suivante :
# ##### 1. Exporter la base de données qui recense les informations sur le Burkina Faso
# (https://download.geonames.org/export/dump/).
# ##### ◦ Pour ce faire, reférez-vous au Readme, décrit à la fin de la page pour identifier le code iso correspondant à celui du Burkina Faso
# ##### 2. Télécharger le fichier zip correspondant
# ##### 3. Appliquer les opérations de prétraitement et filtres nécessaires à ce fichier, pour ne garder que les colonnes correspondantes :
import numpy as np
import pandas as pd
path=""
data = pd.read_csv(path+"BF.txt", sep="\t", header = None)
print(data)
# ###### ◦ Identifiants, Noms de lieux, latitudes, longitudes
data1=data.iloc[:,[0,1,4,5]]
data1
data1.columns = ['Identifiants', 'Noms de lieux', 'latitudes', 'longitudes']
data1
# ###### ◦ Renommez les avec les noms suivants : 'ID', 'location_name', 'lat', 'long'
data2=data1.iloc[:,[0,1,2,3]]
data2.columns = ['ID', 'location_name', 'lat', 'long']
data2
# ###### ◦ Sauvegarder ces données dans un fichier CSV, nommez-le burkina_location.csv
data2.to_csv('burkina_location.csv', index=False)
# ##### 4. Opérations sur le fichier CSV burkina_location.csv.
burkina_location=pd.read_csv('burkina_location.csv')
burkina_location.head()
burkina_location.set_index(keys = 'location_name', inplace = True)
burkina_location.head()
# ##### ◦ Extraire les données contenant le nom 'gounghin', enregistrez-le sous le fichier gounghin.csv
burkina_location1 = burkina_location.loc['Gounghin']
burkina_location1
# ##### ◦ Extraire la sous-partie de la base de données (fichier burkina_location.csv), dont les premières lettres des noms de lieux sont compris entre 'A' et 'P' (ordre alphabétique).
burkina_location=burkina_location.reset_index().head()
burkina_location
burkina_location.set_index(keys = 'ID', inplace = True)
burkina_location.head()
# +
req1 = burkina_location['location_name'][0: ]=="A"
req2 = burkina_location['location_name'][0: ]=="P"
burkina_location2 = burkina_location[req1 & req2]
# +
# Create a Pandas Excel writer using XlsxWriter as the engine.
writer = pd.ExcelWriter('mini_projet.xlsx', engine='xlsxwriter')
# Write each dataframe to a different worksheet.
burkina_location1.to_excel(writer, sheet_name='Gounghin')
burkina_location2.to_excel(writer, sheet_name='A_to_P')
# Close the Pandas Excel writer and output the Excel file.
writer.save()
# -
# ##### ◦ Identifiez respectivement, la latitude, la longitude minimale et les noms de lieux correspondants dans le fichier burkina_location.csv.
req3 = burkina_location['lat'].min()
req3
req4 = burkina_location['long'].min()
req4
tmp1 = burkina_location['lat']==12.36667
tmp2 = burkina_location['long']==-2.73333
burkina_location[tmp1 | tmp2]
# ##### ◦ Quels sont les lieux dont les coordonnées sont comprises entre (lat >= 11 et lon <= 0.5)
tmp3 = burkina_location['lat']>=11
tmp4 = burkina_location['long']<=0.5
burkina_location[tmp3 & tmp4]
| mini_projet_uvbf.ipynb |
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # DJL BERT Inference Demo
//
// ## Introduction
//
// In this tutorial, you walk through running inference using DJL on a [BERT](https://towardsdatascience.com/bert-explained-state-of-the-art-language-model-for-nlp-f8b21a9b6270) QA model trained with MXNet and PyTorch.
// You can provide a question and a paragraph containing the answer to the model. The model is then able to find the best answer from the answer paragraph.
//
// Example:
// ```text
// Q: When did BBC Japan start broadcasting?
// ```
//
// Answer paragraph:
// ```text
// BBC Japan was a general entertainment channel, which operated between December 2004 and April 2006.
// It ceased operations after its Japanese distributor folded.
// ```
// And it picked the right answer:
// ```text
// A: December 2004
// ```
//
// One of the most powerful features of DJL is that it's engine agnostic. Because of this, you can run different backend engines seamlessly. We showcase BERT QA first with an MXNet pre-trained model, then with a PyTorch model.
// ## Preparation
//
// This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/deepjavalibrary/djl/blob/master/jupyter/README.md).
// +
// // %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
// %maven ai.djl:api:0.15.0
// %maven ai.djl.mxnet:mxnet-engine:0.15.0
// %maven ai.djl.mxnet:mxnet-model-zoo:0.15.0
// %maven ai.djl.pytorch:pytorch-engine:0.15.0
// %maven ai.djl.pytorch:pytorch-model-zoo:0.15.0
// %maven org.slf4j:slf4j-simple:1.7.32
// -
// ### Import java packages by running the following:
import ai.djl.*;
import ai.djl.engine.*;
import ai.djl.modality.nlp.qa.*;
import ai.djl.repository.zoo.*;
import ai.djl.training.util.*;
import ai.djl.inference.*;
import ai.djl.repository.zoo.*;
// Now that all of the prerequisites are complete, start writing code to run inference with this example.
//
//
// ## Load the model and input
//
// **First, load the input**
// +
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
// -
// Then load the model and vocabulary. Create a variable `model` by using the `ModelZoo` as shown in the following code.
Criteria<QAInput, String> criteria = Criteria.builder()
.optApplication(Application.NLP.QUESTION_ANSWER)
.setTypes(QAInput.class, String.class)
.optEngine("MXNet") // For DJL to use MXNet engine
.optProgress(new ProgressBar()).build();
ZooModel<QAInput, String> model = criteria.loadModel();
// ## Run inference
// Once the model is loaded, you can call `Predictor` and run inference as follows
Predictor<QAInput, String> predictor = model.newPredictor();
String answer = predictor.predict(input);
answer
// Running inference on DJL is that easy. Now, let's try the PyTorch engine by specifying PyTorch engine in Criteria.optEngine("PyTorch"). Let's rerun the inference code.
// +
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
Criteria<QAInput, String> criteria = Criteria.builder()
.optApplication(Application.NLP.QUESTION_ANSWER)
.setTypes(QAInput.class, String.class)
.optFilter("modelType", "distilbert")
.optEngine("PyTorch") // Use PyTorch engine
.optProgress(new ProgressBar()).build();
ZooModel<QAInput, String> model = criteria.loadModel();
Predictor<QAInput, String> predictor = model.newPredictor();
String answer = predictor.predict(input);
answer
// -
// ## Summary
// Suprisingly, there are no differences between the PyTorch code snippet and MXNet code snippet.
// This is power of DJL. We define a unified API where you can switch to different backend engines on the fly.
// Next chapter: Inference with your own BERT: [MXNet](mxnet/load_your_own_mxnet_bert.ipynb) [PyTorch](pytorch/load_your_own_pytorch_bert.ipynb).
| jupyter/BERTQA.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
# +
data = pd.read_csv('Dataset.csv')
data['value'] = data['sentiment'].map({'positive': 1, 'negative': 0})
data = data.drop(['sentiment'],axis=1)
print(data.head())
# -
p = data.head(25000)
p.head()
X = p.review
y = p.value
def drawrocSVM(y_test, y_pred):
fpr, tpr, threshold = roc_curve(y_test, y_pred)
print("Drawing")
roc_auc = auc(fpr, tpr)
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b', label='SVM AUC = %0.2f' % roc_auc, color='b')
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([-0.1, 1.2])
plt.ylim([-0.1, 1.2])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
svm = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()),
('svm', SVC(kernel="linear", C=1))])
svm = svm.fit(X_train, y_train)
ypred = svm.predict(X_test)
print("SVM metrics")
print(metrics.accuracy_score(y_test, ypred))
print(metrics.classification_report(y_test, ypred))
drawrocSVM(y_test, ypred)
a = svm.predict(["i love the show"])
print(a)
a2 = svm.predict(["the show is boring"])
a2
| models/svm/SVM.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introducción a Jupyter
# ## Expresiones aritmeticas y algebraicas
# Empezaremos esta práctica con algo de conocimientos previos de programación. Se que muchos de ustedes no han tenido la oportunidad de utilizar Python como lenguaje de programación y mucho menos Jupyter como ambiente de desarrollo para computo cientifico, asi que el primer objetivo de esta práctica será acostumbrarnos a la sintaxis del lenguaje y a las funciones que hacen especial a Jupyter.
#
# Primero tratemos de evaluar una expresión aritmetica. Para correr el código en la siguiente celda, tan solo tienes que hacer clic en cualquier punto de ella y presionar las teclas Shift + Return.
2 + 3
2*3
2**3
sin(pi)
# Sin embargo no existen funciones trigonométricas cargadas por default. Para esto tenemos que importarlas de la libreria ```math```:
from math import sin, pi
sin(pi)
# ## Variables
# Las variables pueden ser utilizadas en cualquier momento, sin necesidad de declararlas, tan solo usalas!
a = 10
a
# ### Ejercicio
# Ejecuta el siguiente calculo y guardalo en una variable:
#
# $$
# c = \pi *10^2
# $$
#
# > Nota: Una vez que hayas concluido el calculo y guardado el valor en una variable, puedes desplegar el valor de cualquier variable al ejecutar en una celda el nombre de la variable
c =
# Ejecuta la prueba de abajo para saber si has creado el codigo correcto
from pruebas_1 import prueba_1_1
prueba_1_1(_, c)
# ## Listas
# Las listas son una manera de guardar varios datos en un mismo arreglo. Podemos tener por ejemplo:
A = [2, 4, 8, 10]
A
# Pero si intentamos multiplicar estos datos por un numero, no tendrá el comportamiento esperado.
A*2
# ## Funciones
# Podemos definir funciones propias de la siguiente manera:
f = lambda x: x**2 + 1
# Esta linea de codigo es equivalente a definir una función matemática de la siguiente manera:
#
# $$
# f(x) = x^2 + 1
# $$
#
# Por lo que si la evaluamos con $x = 2$, obviamente obtendremos como resultado $5$.
f(2)
# Esta notación que introducimos es muy util para funciones matemáticas, pero esto nos obliga a pensar en las definiciones de una manera funcional, lo cual no siempre es la solución (sobre todo en un lenguaje con un paradigma de programación orientado a objetos).
#
# Esta función tambien puede ser escrita de la siguiente manera:
def g(x):
y = x**2 + 1
return y
# Con los mismos resultados:
g(2)
# ### Ejercicio
# Define una función que convierta grados Celsius a grados Farenheit, de acuerdo a la siguiente formula:
#
# $$
# F = \frac{9}{5} C + 32
# $$
def cel_a_faren(grados_cel):
grados_faren = # Escribe el codigo para hacer el calculo aqui
return grados_faren
# Y para probar trata de convertir algunos datos:
cel_a_faren(10)
cel_a_faren(50)
# ## Ciclos de control
# Cuando queremos ejecutar código varias veces tenemos varias opciones, vamos a explorar rapidamente el ciclo for.
# ```python
# for paso in pasos:
# ...
# codigo_a_ejecutar(paso)
# ...
# ```
# En este caso el codigo se ejecutará tantas veces sean necesarias para usar todos los elementos que hay en pasos.
#
# Por ejemplo, pordemos ejecutar la multiplicacion por 2 en cada uno de los datos:
for dato in A:
print dato*2
# ó agregarlo en una lista nueva:
# +
B = []
for dato in A:
B.append(dato*2)
B
# -
# y aun muchas cosas mas, pero por ahora es momento de empezar con la práctica.
# ### Ejercicio
# * Crea una lista ```C``` con los enteros positivos de un solo digito, es decir: $\left\{ x \in \mathbb{Z} \mid 0 \leq x < 10\right\}$
# * Crea una segunda lista ```D``` con los cuadrados de cada elemento de ```C```
# +
C = [] # Escribe el codigo para declarar el primer arreglo adentro de los corchetes
C
# +
D = []
# Escribe el codigo de tu ciclo for aqui
D
# -
# Ejecuta las pruebas de abajo
from pruebas_1 import prueba_1_3
prueba_1_3(C, D)
# ## Método de bisección
# Para obtener una raiz real de un polinomio $f(x) = x^3 + 2 x^2 + 10 x - 20$ por el metodo de bisección, tenemos que primero definir dos puntos, uno que evaluado en el polinomio nos de positivo, y otro que nos de negativo. Propondremos $x_1 = 1$ y $x_2 = 2$, y los evaluaremos para asegurarnos de que cumplan lo que acabamos de pedir.
f = lambda x: x**3 + 2*x**2 + 10*x - 20
f(1.0)
f(2.0)
# Una vez que tenemos dos puntos de los que sabemos que definen el intervalo donde se encuetra una raiz, podemos empezar a iterar para descubrir el punto medio.
#
# $$x_M = \frac{x_1 + x_2}{2}$$
#
# Si hacemos esto ingenuamente y lo evaluamos en la función, podremos iterar manualmente:
x_1, x_2 = 1.0, 2.0
xm1 = (x_1 + x_2)/2.0
f(xm1)
# Y de aqui podemos notar que el resultado que nos dio esto es positivo, es decir que la raiz tiene que estar entre $x_1$ y $x_M$. Por lo que para nuestra siguiente iteración usaremos el nuevo intervalo $x_1 = 1$ y $x_2 = 2.875$, es decir que ahora asignaremos el valor de $x_M$ a $x_2$.
x_1, x_2 = x_1, xm1
xm2 = (x_1 + x_2)/2.0
f(xm2)
# Y podriamos seguir haciendo esto hasta que tengamos la exactitud que queremos, pero esa no seria una manera muy inteligente de hacerlo (tenemos una maquina a la que le gusta hacer tareas repetitivas y no la aprovechamos?).
#
# En vez de eso, notemos que la formula no cambia absolutamente en nada, por lo que la podemos hacer una funcion y olvidarnos de ella.
def biseccion(x1, x2):
return (x1 + x2)/2.0
# Si volvemos a ejecutar el codigo que teniamos, sustituyendo esta función, obtendremos exactamente el mismo resultado:
x_1, x_2 = x_1, xm1
xm2 = biseccion(x_1, x_2)
f(xm2)
# Y ahora lo que tenemos que hacer es poner una condicion para que $x_M$ se intercambie con $x_1$ ó $x_2$ dependiendo del signo.
x_1, x_2 = 1.0, 2.0
xm1 = biseccion(x_1, x_2)
f(xm1)
# +
if x_2*xm1 > 0:
x_2 = xm1
else:
x_1 = xm1
xm2 = biseccion(x_1, x_2)
f(xm2)
# +
if x_2*xm2 > 0:
x_2 = xm2
else:
x_1 = xm2
xm3 = biseccion(x_1, x_2)
f(xm3)
# -
# Si, yo se que parece raro, pero si lo revisas con calma te daras cuenta que funciona.
#
# Ya casi llegamos, tan solo tenemos que ir guardando cada una de las aproximaciones en un arreglo, y calcularemos el numero de aproximaciones necesarias para llegar a la precisión requerida. Tomemos en cuenta $\varepsilon = 0.001$. La formula para el numero de aproximaciones necesarias es:
#
# $$n = \frac{\ln{a} - \ln{\varepsilon}}{\ln{2}}$$
#
# donde $a$ es el tamaño del intervalo original.
n = (log(1) - log(0.001))/(log(2))
n
# Es decir, $n = 10$.
def metodo_biseccion(funcion, x1, x2, n):
xs = []
for i in range(n):
xs.append(biseccion(x1, x2))
if funcion(x2)*funcion(xs[-1]) > 0:
x2 = xs[-1]
else:
x1 = xs[-1]
return xs[-1]
metodo_biseccion(f, 1.0, 2.0, 10)
# Y asi obtenemos la aproximación de nuestro ejemplo.
# ## Problemas
# 1. Copia y pega el codigo necesario (no mas, no menos) para calcular una raiz real de un polinomio en el reporte de practica.
# 2. Calcule por el metodo de bisección la raiz real del siguiente polinomio (se espera un error no mayor a $0.001$) $f(x) = x^5 + 4 x^4 + 10 x^3 + x^2 + 20 x - 10$.
# 3. Modifique el codigo para que en lugar de aceptar el numero de iteraciones ($n$), acepte el error maximo ($\varepsilon$).
| Practicas/P1/.ipynb_checkpoints/Practica 1 - Introduccion a Jupyter-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# I use this notebook to automatically label image overlap pairs that I haven't seen yet with pairs that I have seen (See [tile_cliques_poc.ipynb](notebooks/eda/tile_cliques_poc.ipynb), and [tile_dicts_vs_cliques.ipynb](notebooks/eda/tile_dicts_vs_cliques.ipynb)).
# +
from collections import Counter
import numpy as np
import networkx as nx
from tqdm import tqdm_notebook
from sdcdup.utils import generate_tag_pair_lookup
from sdcdup.utils import load_duplicate_truth
from sdcdup.utils import update_duplicate_truth
from sdcdup.utils import update_tile_cliques
from sdcdup.features import SDCImageContainer
# %reload_ext autoreload
# %autoreload 2
tag_pair_lookup = generate_tag_pair_lookup()
# -
matches_files = ['matches_bmh96_0.9.csv']
sdcic = SDCImageContainer()
overlap_image_maps = sdcic.load_image_overlap_properties(matches_files, score_types=['bmh96'])
print(len(overlap_image_maps))
dup_truth = load_duplicate_truth(chunk_type='both')
print(len(dup_truth))
# ## Get all the overlap_image_maps that are not in dup_truth.
# + code_folding=[]
overlap_candidates = []
for (img1_id, img2_id, img1_overlap_tag) in tqdm_notebook(overlap_image_maps):
if (img1_id, img2_id, img1_overlap_tag) in dup_truth:
continue
overlap_candidates.append((img1_id, img2_id, img1_overlap_tag))
print(len(overlap_candidates))
# -
# ## Create list of flat hashes.
# (i.e. hashes for tiles where every pixel is the same color)
# +
solid_hashes = set()
for img_id, tile_issolid_grid in sdcic.img_metrics['sol'].items():
idxs = set(np.where(tile_issolid_grid >= 0)[0])
for idx in idxs:
if np.all(tile_issolid_grid[idx] >= 0):
solid_hashes.add(sdcic.img_metrics['md5'][img_id][idx])
print(solid_hashes)
# -
# ### Using cliques (networkx)
# +
tile_hash_dup_cliques = nx.Graph()
tile_hash_dif_cliques = nx.Graph()
for (img1_id, img2_id, img1_overlap_tag), is_dup in dup_truth.items():
for idx1, idx2 in tag_pair_lookup[img1_overlap_tag]:
tile1_hash = sdcic.img_metrics['md5'][img1_id][idx1]
tile2_hash = sdcic.img_metrics['md5'][img2_id][idx2]
if is_dup:
if tile1_hash in solid_hashes or tile2_hash in solid_hashes:
continue
update_tile_cliques(tile_hash_dup_cliques, tile1_hash, tile2_hash)
else:
if tile1_hash == tile2_hash:
continue
tile_hash_dif_cliques.add_edge(tile1_hash, tile2_hash)
print(tile_hash_dup_cliques.number_of_nodes(), tile_hash_dif_cliques.number_of_nodes())
neighbor_counts = Counter()
for tile_hashes in nx.connected_components(tile_hash_dup_cliques):
neighbor_counts[len(tile_hashes)] += 1
list(sorted(neighbor_counts.items()))
# +
auto_overlap_labels = {}
for img1_id, img2_id, img1_overlap_tag in overlap_candidates:
if (img1_id, img2_id, img1_overlap_tag) in auto_overlap_labels:
continue
is_dup = 1
for idx1, idx2 in tag_pair_lookup[img1_overlap_tag]:
tile1_hash = sdcic.img_metrics['md5'][img1_id][idx1]
tile2_hash = sdcic.img_metrics['md5'][img2_id][idx2]
if tile1_hash in tile_hash_dif_cliques and tile2_hash in set(nx.neighbors(tile_hash_dif_cliques, tile1_hash)):
is_dup = 0
break
elif tile1_hash in tile_hash_dup_cliques and tile2_hash in set(nx.neighbors(tile_hash_dup_cliques, tile1_hash)):
continue
else:
is_dup = -1
if is_dup == -1:
continue
auto_overlap_labels[(img1_id, img2_id, img1_overlap_tag)] = is_dup
print(len(auto_overlap_labels))
# -
# This will create a new txt file with the prefix `chunk_auto`, and then the date, followed by `len(auto_overlap_labels)`. The new file will be saved to [data/processed/](data/processed/). TODO: example.
dup_truth = update_duplicate_truth(auto_overlap_labels)
len(dup_truth)
| notebooks/auto_truth_from_cliques.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# import sys
# sys.path.insert(0,'/home/nigam/librascal_cs/librascal/build/')
# +
from ase.io import read, write
import ase
import json
from tqdm.notebook import tqdm
class tqdm_reusable:
def __init__(self, *args, **kwargs):
self._args = args
self._kwargs = kwargs
def __iter__(self):
return tqdm(*self._args, **self._kwargs).__iter__()
from copy import deepcopy
import numpy as np
import matplotlib.pyplot as plt
from rascal.representations import SphericalExpansion, SphericalInvariants
from rascal.utils import (get_radial_basis_covariance, get_radial_basis_pca,
get_radial_basis_projections, get_optimal_radial_basis_hypers )
from rascal.utils import radial_basis
from rascal.utils import WignerDReal, ClebschGordanReal, spherical_expansion_reshape, lm_slice, real2complex_matrix, compute_lambda_soap
# -
# a library of utilities and wrapper to compute pair features and manipulate a Hamiltonian-like target
from ncnice import *
# # Check Bispectrum
from ncnice.representations import *#compute_rho3i_lambda
# +
spherical_expansion_hypers = {
"interaction_cutoff": 4,
"max_radial": 8,
"max_angular": 6,
"gaussian_sigma_constant": 0.3,
"gaussian_sigma_type": "Constant",
"cutoff_smooth_width": 0.5,
"radial_basis": "GTO",
}
spex = SphericalExpansion(**spherical_expansion_hypers)
mycg = ClebschGordanReal(spherical_expansion_hypers["max_angular"])
# +
frames = read('data/ethanol-structures.xyz', ':')
# frames = read('water/water_randomized_1000.xyz', ':')
# for f in frames:
# f.cell=[100,100,100]
# f.positions+=50
# # use same specie for all atoms so we get a single projection matrix
# f.numbers = f.numbers*0+1
# spherical_expansion_hypers = get_optimal_radial_basis_hypers(spherical_expansion_hypers, frames, expanded_max_radial=12)
# # ... and we replicate it
# pm = spherical_expansion_hypers['optimization']['RadialDimReduction']['projection_matrices'][1]
# spherical_expansion_hypers['optimization']['RadialDimReduction']['projection_matrices'] = { i: pm for i in range(1000) }
spex = SphericalExpansion(**spherical_expansion_hypers)
# -
frames = read('data/ethanol-structures.xyz', ':')
# frames = read('/water_randomized_1000.xyz', ':')
for f in frames:
f.cell=[100,100,100]
f.positions+=50
rhoi = compute_rhoi(frames[:1], spex, spherical_expansion_hypers)*1e0
rho2i_l, prho2i_l = compute_all_rho2i_lambda(rhoi, mycg, rho2i_pca=None)
rho3ilambda, prho3 = compute_rho3i_lambda(rho2i_l,rhoi, 0, mycg, prho2i_l)
# +
#MANUAL computation of bispectrum from librascal/nice_demo.ipynb
selframe = frames[:1]; # frame used for the test
feat_scaling = 1e0
feats = spex.transform(selframe).get_features(spex)
ref_feats = feat_scaling*spherical_expansion_reshape(feats, **spherical_expansion_hypers)
nice2_full = mycg.combine_nice(ref_feats, ref_feats)
bisp_nice = np.zeros(ref_feats.shape[:3] + (spherical_expansion_hypers["max_angular"]+1,) +
ref_feats.shape[1:3] + (spherical_expansion_hypers["max_angular"]+1,) +
ref_feats.shape[1:3] + (spherical_expansion_hypers["max_angular"]+1,) )
for l in range(spherical_expansion_hypers["max_angular"]+1):
# while we are at it, we also reorder the indices in a bispectrum-like way
bisp_nice[...,l] = mycg.combine_einsum(nice2_full[...,lm_slice(l)],
ref_feats[...,lm_slice(l)],
L=0,
combination_string="ianANlL,ibp->ianlANLbp" )[...,0]
# -
bisp_nice[0,0,1,:,0,2,:,0,2,0]
rho3ilambda[0,0,1,0,2,0,2,:,0]
# they are the **same** modulo noise. because we dont account for sorting l's in the manual computation and the storage format is inefficient, the shapes of the matrices are different
# # rho2iP
def compute_rho1ijp_species(rho1ijp, frame, cg):
"""groups neighbors j by species"""
species = frame.numbers
nspecies = len(set(species))
shape = rho1ijp.shape[:2]+(nspecies,) +rho1ijp.shape[2:]
rho1ijp_spec = np.zeros(shape)
for ispe, spe in enumerate(sorted(set(species))):
idx_spe = np.where(species==spe)[0]
# print(spe, idx_spe)
for j in range(rho1ijp.shape[1]):
if j in idx_spe:
rho1ijp_spec[:,j,ispe, ...]= rho1ijp[:,j,...]
return rho1ijp_spec
# +
hypers_ij = deepcopy(spherical_expansion_hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
frame = frames[0]
fgij = compute_gij(frame, spex_ij, hypers_ij)
rhoi = compute_rhoi(frame, spex, spherical_expansion_hypers)
rho1ijp, prhoijp = compute_rho1ijp_lambda(rhoi, fgij,0, mycg)
rho1ij, prhoij = compute_rho1ij_lambda(rhoi, fgij,0, mycg)
# -
rho1ijp_l, prho1ijp_l = compute_all_rho1ijp_lambda(rhoi, fgij, mycg)
def compute_rho1ip_lambda(rhoi, rho1ijp_l, fgij, frame, L, cg, prho1ijp_l):
"""compute combined rhoi and rhoi-MP"""
rho1ijp_spec = {}
prhoijp_spec = {}
rho1ip_lambda = {}
lmax = int(np.sqrt(rhoi.shape[-1])) -1
for l in range(lmax+1):
rho1ijp_spec[l] = compute_rho1ijp_species(rho1ijp_l[l], frame, cg)
rho1ip_lambda[l] = np.sum(rho1ijp_spec[l], axis=1) # MP - atom density
# do the usual gig of angular coupling
nl=0
for l1 in range(lmax+1):
for l2 in range(lmax+1):
if abs(l2 - l1) > L or l2 + l1 < L:
continue
nl += 1*rho1ip_lambda[l2].shape[4]
# multiplication above to account for (l1,l2,l3) combinations. rho1ip_lambda[L].shape[4] accounts for l1,l2
# combinations of g(rij) and rhoj
shape = rhoi.shape[:3] + rho1ip_lambda[L].shape[1:4] +(nl, 2*L+1,)
rho_combined_lam = np.zeros(shape)
prho_combined_lam = np.ones(nl, dtype = int)*(1-2*(L%2))
il=0
for l1 in range(lmax+1):
for l2 in range(lmax+1):
if abs(l2 - l1) > L or l2 + l1 < L:
continue
rho_combined_lam[...,il:il+rho1ip_lambda[l2].shape[4],:] = cg.combine_einsum(rhoi[...,lm_slice(l1)], rho1ip_lambda[l2],
L, combination_string="ian,ibNMl->ianbNMl")
prho_combined_lam[il:il+rho1ip_lambda[l2].shape[4]] = (1-2*(l1%2)) * prho1ijp_l[l2]
il+=rho1ip_lambda[l2].shape[4]
return rho_combined_lam, prho_combined_lam
rho_combined_lam, prho_combined_lam = compute_rho1ip_lambda(rhoi, rho1ijp_l, fgij, frame, 1, mycg, prho1ijp_l)
rho_combined_lam.shape
def compute_hamiltonian_representations(frames, orbs, hypers, lmax, nu, cg, scale=1,
select_feats = None, half_hete = True, mp_feats = False,
rhoi_pca = None, rho2i_pca = None,
rhoij_rho2i_pca = None, rhoij_pca = None,
verbose = False
):
"""
Computes the full set of features needed to learn matrix elements up to lmax.
Options are fluid, but here are some that need an explanation:
select_feats = dict(type=["diag", "offd_m", "offd_p", "hete"], block = ('el1', ['el2',] L, pi) )
does the minimal amount of calculation to evaluate the selected block. other terms might be computed as well if they come for free.
"""
spex = SphericalExpansion(**hypers)
rhoi = compute_rhoi(frames, spex, hypers)
# compresses further the spherical expansion features across species
if rhoi_pca is not None:
rhoi = apply_rhoi_pca(rhoi, rhoi_pca)
# makes sure that the spex used for the pair terms uses adaptive species
hypers_ij = deepcopy(hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
tnat = 0
els = list(orbs.keys())
nel = len(els)
# prepare storage
elL = list(itertools.product(els,range(lmax+1),[-1,1]))
hetL = [ (els[i1], els[i2], L, pi) for i1 in range(nel) for i2 in range((i1+1 if half_hete else 0), nel) for L in range(lmax+1) for pi in [-1,1] ]
feats = dict(diag = { L: [] for L in elL },
offd_p = { L: [] for L in elL },
offd_m = { L: [] for L in elL },
hete = { L: [] for L in hetL },)
if rhoij_rho2i_pca is None and rho2i_pca is not None:
rhoij_rho2i_pca = rho2i_pca
#before = tracemalloc.take_snapshot()
for f in frames:
fnat = len(f.numbers)
frhoi = rhoi[tnat:tnat+fnat]*scale
fgij = compute_gij(f, spex_ij, hypers_ij)*scale
if (select_feats is None or select_feats["type"]!="diag") and nu == 2:
rhonui, prhonui = compute_all_rho2i_lambda(frhoi, cg, rhoij_rho2i_pca)
else:
rhonui, prhonui = frhoi, None
for L in range(lmax+1):
if select_feats is not None and L>0 and select_feats["block"][-2] != L:
continue
if nu==0:
lrhonui, lprhonui = np.ones((fnat, 1, 2*L+1)), np.ones((1))
elif nu==1:
lrhonui, lprhonui = compute_rho1i_lambda(frhoi, L, cg)
else:
if mp_feats:
frho1ijp_l, fprho1ijp_l = compute_all_rho1ijp_lambda(frhoi, fgij, mycg)
lrhonui, lprhonui = compute_rho1ip_lambda(frhoi, frho1ijp_l, fgij, frame, L, cg, fprho1ijp_l)
# lrhonui, lprhonui = compute_rho1ip_lambda(frhoi, L, cg)
else:
frho2i_l,fprho2i_l = compute_all_rho2i_lambda(frhoi, cg, rho2i_pca=None)
lrhonui, lprhonui = compute_rho3i_lambda(frho2i_l, frhoi, L, cg,fprho2i_l )
#lrhonui, lprhonui = compute_rho2i_lambda(frhoi, L, cg)
#if rho2i_pca is not None:
# lrhonui, lprhonui = apply_rho2i_pca(lrhonui, lprhonui, rho2i_pca)
if select_feats is None or select_feats["type"]!="diag":
if nu==0:
lrhoij, prhoij = compute_rho0ij_lambda(rhonui, fgij, L, cg, prhonui)
elif nu==1:
if mp_feats:
lrhoij, prhoij = compute_rho1ijp_lambda(rhonui, fgij, L, cg, prhonui)
else:
lrhoij, prhoij = compute_rho1ij_lambda(rhonui, fgij, L, cg, prhonui)
else:
lrhoij, prhoij = compute_rho2ij_lambda(rhonui, fgij, L, cg, prhonui)
if rhoij_pca is not None:
lrhoij, prhoij = apply_rhoij_pca(lrhoij, prhoij, rhoij_pca)
for i, el in enumerate(els):
iel = np.where(f.symbols==el)[0]
if len(iel) == 0:
continue
if select_feats is not None and el != select_feats["block"][0]:
continue
for pi in [-1,1]:
wherepi = np.where(lprhonui==pi)[0]
if len(wherepi)==0:
# add a vector of zeros
feats['diag'][(el, L, pi)].append(np.zeros(shape=(len(iel), 1, 2*L+1)))
continue
feats['diag'][(el, L, pi)].append(lrhonui[...,wherepi,:][iel].reshape((len(iel), -1, 2*L+1) ) )
if select_feats is not None and select_feats["type"]=="diag":
continue
triu = np.triu_indices(len(iel), 1)
ij_up = (iel[triu[0]],iel[triu[1]]) # ij indices, i>j
ij_lw = (ij_up[1], ij_up[0]) # ij indices, i<j
lrhoij_p = (lrhoij[ij_up] + lrhoij[ij_lw])/np.sqrt(2)
lrhoij_m = (lrhoij[ij_up] - lrhoij[ij_lw])/np.sqrt(2)
for pi in [-1,1]:
if len(ij_up[0])==0:
continue
wherepi = np.where(prhoij==pi)[0];
if len(wherepi)==0:
feats['offd_p'][(el, L, pi)].append( np.zeros((lrhoij_p.shape[0], 1, 2*L+1)) )
feats['offd_m'][(el, L, pi)].append( np.zeros((lrhoij_p.shape[0], 1, 2*L+1)) )
continue
feats['offd_p'][(el, L, pi)].append(lrhoij_p[...,wherepi,:].reshape(lrhoij_p.shape[0], -1, 2*L+1))
feats['offd_m'][(el, L, pi)].append(lrhoij_m[...,wherepi,:].reshape(lrhoij_m.shape[0], -1, 2*L+1))
if select_feats is not None and select_feats["type"]!="hete":
continue
for elb in els[i+1:]:
ielb = np.where(f.symbols==elb)[0]
if len(ielb) == 0:
continue
if select_feats is not None and elb != select_feats["block"][1]:
continue
# combines rho_ij and rho_ji
lrhoij_het = lrhoij[iel][:,ielb]
lrhoij_het_rev = np.swapaxes(lrhoij[ielb][:,iel],1,0)
# make a copy and not a slice, so we keep better track
for pi in [-1,1]:
wherepi = np.where(prhoij==pi)[0];
if len(wherepi)==0:
feats['hete'][(el, elb, L, pi)].append(np.zeros((lrhoij_het.shape[0]*lrhoij_het.shape[1],1,2*L+1)))
continue
lrhoij_het_pi = lrhoij_het[...,wherepi,:]
lrhoij_het_rev_pi = lrhoij_het_rev[...,wherepi,:]
feats['hete'][(el, elb, L, pi)].append(
np.concatenate([
lrhoij_het_pi.reshape(
(lrhoij_het.shape[0]*lrhoij_het.shape[1],-1,2*L+1) )
,
lrhoij_het_rev_pi.reshape(
(lrhoij_het_rev.shape[0]*lrhoij_het_rev.shape[1],-1,2*L+1) )
], axis=-2)
)
#del(lrhoij_het)
#del(lrhoij_p, lrhoij_m)
#del(lrhoij, lrho2)
tnat+=fnat
# cleans up combining frames blocks into single vectors - splitting also odd and even blocks
for k in feats.keys():
for b in list(feats[k].keys()):
if len(feats[k][b]) == 0:
continue
block = np.vstack(feats[k][b])
feats[k].pop(b)
if len(block) == 0:
continue
feats[k][b] = block.reshape((block.shape[0], -1, 1+2*b[-2]))
return feats
# # Regression Test
# +
nframes = 50
frames = read('data/ethanol-structures.xyz',':')[:nframes]
for f in frames:
f.cell=[100,100,100]
f.positions+=50
# use same specie for all atoms so we get a single projection matrix,
# which we can apply throughout. a bit less efficient but much more practical
f.numbers = f.numbers*0+1
spherical_expansion_hypers = get_optimal_radial_basis_hypers(spherical_expansion_hypers, frames, expanded_max_radial=16)
# ... and we replicate it
pm = spherical_expansion_hypers['optimization']['RadialDimReduction']['projection_matrices'][1]
spherical_expansion_hypers['optimization']['RadialDimReduction']['projection_matrices'] = { i: pm for i in range(99) }
spex = SphericalExpansion(**spherical_expansion_hypers)
hypers_ij = deepcopy(spherical_expansion_hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_gij = SphericalExpansion(**hypers_ij)
orbs = json.load(open('data/ethanol-saph-orbs.json', "r"))
frames = read('data/ethanol-structures.xyz', ':')[:nframes]
ofocks = np.load('data/ethanol-saph-ofock.npy', allow_pickle=True)[:nframes]
# hamiltonian to block coupling
ofock_blocks, slices_idx = matrix_list_to_blocks(ofocks, frames, orbs, mycg)
# training settings
train_fraction = 0.5
itrain = np.arange(len(frames))
np.random.seed(12345)
np.random.shuffle(itrain)
ntrain = int(len(itrain)*train_fraction)
itest = itrain[ntrain:]; itrain=itrain[:ntrain]
train_slices = get_block_idx(itrain, slices_idx)
print(itrain)
FR = FockRegression(orbs, alpha = 1e-6, #alphas=np.geomspace(1e-8, 1e4, 7),
fit_intercept="auto")
for f in frames:
f.cell=[100,100,100]
f.positions+=50
print("Calling all representation subroutines (no PCA)")
rhoi = compute_rhoi(frames[0], spex, spherical_expansion_hypers)
# -
import itertools
# +
feats_nu1 = compute_hamiltonian_representations(tqdm_reusable(frames, desc="features", leave=False),
orbs, spherical_expansion_hypers, 2, nu=1, cg=mycg, scale=1e3, mp_feats = True)
FR.fit(feats_nu1, ofock_blocks, train_slices, progress=tqdm)
pred_blocks = FR.predict(feats_nu1, progress=tqdm)
pred_ofocks = blocks_to_matrix_list(pred_blocks, frames, slices_idx, orbs, mycg)
mse_train = 0
for i in itrain:
mse_train += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itrain)
mse_test = 0
for i in itest:
mse_test += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itest)
print("Model size: ", len(FR.cv_stats_))
print("Train RMSE: ", np.sqrt(mse_train))
print("Test RMSE: ", np.sqrt(mse_test))
# +
blocks_c = ofock_blocks
tblock = 'diag'
sel_type = list(blocks_c[tblock].keys())
fblock=[]
for i in range(len(sel_type)):
kblock = sel_type[i]
lblock = list(blocks_c['diag'][sel_type[i]].keys())
for l in lblock:
fblock.append(block_to_feat_index(tblock, kblock, l, orbs))
fblock = list(set(fblock))
for j in fblock:
print(j)
feats_nu1['diag'][j] = compute_hamiltonian_representations(tqdm_reusable(frames, desc="features", leave=False),
orbs, spherical_expansion_hypers, 2, nu=2, cg=mycg, scale=1e3, mp_feats = False, select_feats =dict(block=j, type=tblock))[tblock][j]
# +
FR.fit(feats_nu1, ofock_blocks, train_slices, progress=tqdm)
pred_blocks = FR.predict(feats_nu1, progress=tqdm)
pred_ofocks = blocks_to_matrix_list(pred_blocks, frames, slices_idx, orbs, mycg)
mse_train = 0
for i in itrain:
mse_train += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itrain)
mse_test = 0
for i in itest:
mse_test += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itest)
print("Model size: ", len(FR.cv_stats_))
print("Train RMSE: ", np.sqrt(mse_train))
print("Test RMSE: ", np.sqrt(mse_test))
# +
blocks_c = ofock_blocks
tblock = 'diag'
sel_type = list(blocks_c[tblock].keys())
fblock=[]
for i in range(len(sel_type)):
kblock = sel_type[i]
lblock = list(blocks_c['diag'][sel_type[i]].keys())
for l in lblock:
fblock.append(block_to_feat_index(tblock, kblock, l, orbs))
fblock = list(set(fblock))
for j in fblock:
print(j)
feats_nu1['diag'][j] = compute_hamiltonian_representations(tqdm_reusable(frames, desc="features", leave=False),
orbs, spherical_expansion_hypers, 2, nu=2, cg=mycg, scale=1e3, mp_feats = True, select_feats =dict(block=j, type=tblock))[tblock][j]
# +
FR.fit(feats_nu1, ofock_blocks, train_slices, progress=tqdm)
pred_blocks = FR.predict(feats_nu1, progress=tqdm)
pred_ofocks = blocks_to_matrix_list(pred_blocks, frames, slices_idx, orbs, mycg)
mse_train = 0
for i in itrain:
mse_train += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itrain)
mse_test = 0
for i in itest:
mse_test += np.sum((pred_ofocks[i] - ofocks[i])**2)/len(ofocks[i])/len(itest)
print("Model size: ", len(FR.cv_stats_))
print("Train RMSE: ", np.sqrt(mse_train))
print("Test RMSE: ", np.sqrt(mse_test))
# -
# + [markdown] heading_collapsed=true
# # Compute bispectrum as sum over rho2ij lambda - NOT RIGHT
# + hidden=true
hypers_ij = deepcopy(spherical_expansion_hypers)
# hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
scale=1e3
for f in frames[:1]:
fgij = compute_gij(f, spex_ij, hypers_ij)
rhoi = compute_rhoi(f, spex, spherical_expansion_hypers)
rho2i_l, prho2i_l = compute_all_rho2i_lambda(rhoi, mycg, rho2i_pca=None)
rho2ij, prho2ij = compute_rho2ij_lambda(rho2i_l, fgij, 0, mycg, prho2i_l)
# + hidden=true
shape = (rho2ij.shape[0],
rhoi.shape[1],rho2ij.shape[2],
rho2ij.shape[3], rho2ij.shape[4],
rho2ij.shape[5], rho2ij.shape[6],
rho2ij.shape[7], rho2ij.shape[8]
)
bisp_gij = np.zeros(shape)
# parity = np.ones(nl, dtype = int)*(1-2*(L%2))
# + hidden=true
rho2ij.shape
# + hidden=true
for f in frames[:1]:
fgij = compute_gij(f, spex_ij, hypers_ij)
rhoi = compute_rhoi(f, spex, spherical_expansion_hypers)
rho2i_l, prho2i_l = compute_all_rho2i_lambda(rhoi, mycg, rho2i_pca=None)
rho2ij, prho2ij = compute_rho2ij_lambda(rho2i_l, fgij, 0, mycg, prho2i_l)
shape = (rho2ij.shape[0],
rhoi.shape[1],rho2ij.shape[2],
rho2ij.shape[3], rho2ij.shape[4],
rho2ij.shape[5], rho2ij.shape[6],
rho2ij.shape[7], rho2ij.shape[8]
)
bisp_gij = np.zeros(shape)
# parity = np.ones(nl, dtype = int)*(1-2*(L%2))
species = f.numbers
nspecies = rhoi.shape[1]
for ispe, spe in enumerate(set(species)):
idx_spe = np.where(species==spe)[0]
print(spe, idx_spe)
bisp_gij[:,ispe, ...]= np.sum(rho2ij[:,idx_spe,...],axis =1)
# + hidden=true
bisp_gij.shape
# + hidden=true
bisp_gij[0,0,1,0,2,0,2,:,0][np.where(bisp_gij[0,0,1,0,2,0,2,:,0])]
# + hidden=true
rho3ilambda[0,0,1,0,2,0,2,:,0][np.where(rho3ilambda[0,0,1,0,2,0,2,:,0])]
# + hidden=true
rho3ilambda[0][np.where(rho3ilambda[0])]
# + hidden=true
bisp_gij[0][np.where(bisp_gij[0])]*2.14dd
# + hidden=true
bisp_gij.shape
# + hidden=true
# + hidden=true
def compute_mp(frames,hypers, lmax, nui, nuj, cg, rhoi_pca=None, rhoij_rho2i_pca=None,rho2i_pca=None, scale=1):
spex = SphericalExpansion(**hypers)
rhoi = compute_rhoi(frames, spex, hypers)
# compresses further the spherical expansion features across species
if rhoi_pca is not None:
rhoi = apply_rhoi_pca(rhoi, rhoi_pca)
# makes sure that the spex used for the pair terms uses adaptive species
hypers_ij = deepcopy(hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
tnat = 0
els = list(orbs.keys())
nel = len(els)
# prepare storage
# elL = list(itertools.product(els,range(lmax+1),[-1,1]))
# hetL = [ (els[i1], els[i2], L, pi) for i1 in range(nel) for i2 in range((i1+1 if half_hete else 0), nel) for L in range(lmax+1) for pi in [-1,1] ]
# feats = dict(diag = { L: [] for L in elL },
# offd_p = { L: [] for L in elL },
# offd_m = { L: [] for L in elL },
# hete = { L: [] for L in hetL },)
if rhoij_rho2i_pca is None and rho2i_pca is not None:
rhoij_rho2i_pca = rho2i_pca
#before = tracemalloc.take_snapshot()
for f in frames:
fnat = len(f.numbers)
frhoi = rhoi[tnat:tnat+fnat]*scale
fgij = compute_gij(f, spex_ij, hypers_ij)*scale
for L in range(lmax+1):
if nu==0:
lrhonui, lprhonui = np.ones((fnat, 1, 2*L+1)), np.ones((1))
elif nui==1 or nuj==1:
lrhonui, lprhonui = compute_rho1i_lambda(frhoi, L, cg)
rho_mp =
# + hidden=true
frames,hypers, lmax, nui, nuj, cg = frames, spherical_expansion_hypers, 2, 1, 1, mycg
rhoi_pca=None
rhoij_rho2i_pca=None
rho2i_pca=None
scale=1
tnat = 0
hypers_ij = deepcopy(hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
rhoi = compute_rhoi(frames[:1], spex, hypers)
# els = list(orbs.keys())
# nel = len(els)
for f in frames[:1]:
fnat = len(f.numbers)
frhoi = rhoi[tnat:tnat+fnat]*scale
rhonui, prhonui = frhoi, None
fgij = compute_gij(f, spex_ij, hypers_ij)*scale
for L in range(lmax+1):
#lrho0i, lprho0i = np.ones((fnat, 1, 2*L+1)), np.ones((1))
lrho1i, lprho1i = compute_rho1i_lambda(frhoi, L, cg)
lrho0ij, prho0ij = compute_rho0ij_lambda(rhonui, fgij, L, cg, prhonui)
# + hidden=true
np.where(rhonui[:,0,:, lm_slice(2)]-lrho1i)
# + hidden=true
lrho0ij
# + hidden=true
# ?compute_rho0ij_lambda
# + hidden=true
def compute_rho0ij_lambda(rhoi, gij, L, cg, prfeats = None): # prfeats is (in analogy with rho2ijlambda) the parity, but is not really necessary)
""" computes |rho^0_{ij}; lm> """
rho0ij = gij[..., lm_slice(L)].reshape((gij.shape[0], gij.shape[1], -1, 2*L+1))
return rho0ij, np.ones(rho0ij.shape[2])
def compute_rho1ij_lambda(rhoj, gij, L, cg, prfeats = None):
""" computes |rho^1_{ij}; lm> """
lmax = int(np.sqrt(gij.shape[-1])) -1
# can't work out analytically how many terms we have, so we precompute it here
nl = 0
for l1 in range(lmax + 1):
for l2 in range(lmax + 1): # |rho_i> and |rho_ij; g> are not symmetric so we need all l2
if abs(l2 - l1) > L or l2 + l1 < L:
continue
nl += 1
rhoj = rhoj.reshape((rhoj.shape[0], -1, rhoj.shape[-1]))
# natom, natom, nel*nmax, nmax, lmax+1, lmax+1, M
shape = (rhoj.shape[0], rhoj.shape[0],
rhoj.shape[1] , gij.shape[2], nl, 2*L+1)
rho1jilambda = np.zeros(shape)
parity = np.ones(nl, dtype = int)*(1-2*(L%2))
il = 0
for l1 in range(lmax+1):
for l2 in range(lmax+1):
if abs(l2 - l1) > L or l2 + l1 < L:
continue
rho1jilambda[:,:,:,:,il] = cg.combine_einsum(rhoj[...,lm_slice(l1)], gij[...,lm_slice(l2)],
L, combination_string="in,ijN->ijnN")
parity[il] *= (1-2*(l1%2)) * (1-2*(l2%2))
il+=1
return rho1jilambda, parity
# + hidden=true
spex = SphericalExpansion(**hypers)
rhoi = compute_rhoi(frames, spex, hypers)
hypers_ij = deepcopy(hypers)
hypers_ij["expansion_by_species_method"] = "structure wise"
spex_ij = SphericalExpansion(**hypers_ij)
# + [markdown] heading_collapsed=true
# # Test features and Hamiltonian transformation
# + hidden=true
import re
from ase.data import atomic_numbers
import json
class NpEncoder(json.JSONEncoder):
def default(self, obj):
if isinstance(obj, np.integer):
return int(obj)
elif isinstance(obj, np.floating):
return float(obj)
elif isinstance(obj, np.ndarray):
return obj.tolist()
else:
return super(NpEncoder, self).default(obj)
# + hidden=true
# frames = read('qm7/qm7b-chno.xyz', ':100')
# fock = np.load('qm7/qm7-chno-fock.npy', allow_pickle=True)
frames = read('water_random/water_randomized_1000.xyz',':')
for f in frames:
f.pbc=False
focks = np.load('water/water-fock.npy', allow_pickle=True)
orbs = json.loads(json.load(open('water/orbs.json', "r")))
# + [markdown] hidden=true
# we have to fix the L=1 terms that are stored in a weird order. we do this as post-processing
# and one should undo the change if the matrix is to be read back into pyscf
# + hidden=true
for i in range(len(focks)):
focks[i] = pyscf_fix_l1(focks[i], frames[i], orbs)
# + [markdown] heading_collapsed=true hidden=true
# ## Rotational behavior of features
# + hidden=true
from rascal.representations import SphericalExpansion, SphericalInvariants
from rascal.utils import (get_radial_basis_covariance, get_radial_basis_pca,
get_radial_basis_projections, get_optimal_radial_basis_hypers )
from rascal.utils import radial_basis
from rascal.utils import (WignerDReal, ClebschGordanReal,
spherical_expansion_reshape,
lm_slice, real2complex_matrix, xyz_to_spherical, spherical_to_xyz)
from rascal.utils.cg_utils import _r2c as r2c
from rascal.utils.cg_utils import _c2r as c2r
from rascal.utils.cg_utils import _cg as clebsch_gordan
from rascal.utils.cg_utils import _rotation as rotation
from rascal.utils.cg_utils import _wigner_d as wigner_d
# + [markdown] hidden=true
# ### Rotation of features
# + hidden=true
frame = frames[90]
frame.cell = [100,100,100]
frame.positions += 50
rotframe = frame.copy()
rotframe.positions = rotframe.positions @ mrot.T
rotframe.cell = rotframe.cell @ mrot.T # rotate also the cell
feats = spex.transform(frame).get_features(spex)
feats *= 1e6
rfeats = spherical_expansion_reshape(feats, **spherical_expansion_hypers)
g= get_gij_fast(frame, spex,spherical_expansion_hypers)
# + hidden=true
rotfeats = spex.transform(rotframe).get_features(spex)
rotfeats *= 1e6
rotfeats = spherical_expansion_reshape(rotfeats, **spherical_expansion_hypers)
rotg = get_gij_fast(rotframe, spex,spherical_expansion_hypers)
# + [markdown] hidden=true
# Check rotation of $| \overline{\rho_{ij}^0; \lambda \mu} \rangle \equiv \langle n | g; \lambda \mu\rangle $
# + hidden=true
np.linalg.norm(WD.rotate(mk_rho0ijlambda_fast(g, 4, mycg)) - mk_rho0ijlambda_fast(rotg, 4, mycg))/np.linalg.norm(mk_rho0ijlambda_fast(g, 4, mycg))
# + [markdown] hidden=true
# Check rotation of $| \overline{\rho_{i}^1; \lambda \mu} \rangle $
# + hidden=true
(np.linalg.norm(WD.rotate(rfeats[...,lm_slice(3)]) - rotfeats[...,lm_slice(3)]))/np.linalg.norm(rfeats[...,lm_slice(3)])
# + [markdown] hidden=true
# Check $| \overline{\rho_{i}^2; \lambda \mu} \rangle $
# + hidden=true
lsoap=mk_rho2ilambda_fast(rfeats, 1, mycg)
# + hidden=true
rotlsoap = mk_rho2ilambda_fast(rotfeats, 1, mycg)
np.linalg.norm(WD.rotate(lsoap) -rotlsoap)/np.linalg.norm(lsoap)
# + [markdown] hidden=true
# Check rotation of $| \overline{\rho_{ij}^1; 00} \rangle $
# + hidden=true
rhoij = mk_rho1ij_fast(rfeats, g, mycg)
rhoij_rot = mk_rho1ij_fast(rotfeats, rotg, mycg)
# + hidden=true
np.linalg.norm(WD.rotate(rhoij[...,np.newaxis]) - rhoij_rot[...,np.newaxis])/np.linalg.norm(rhoij)
# + [markdown] hidden=true
# Check rotation of $| \overline{\rho_{ij}^1; \lambda \mu} \rangle $
# + hidden=true
rhoijlm= mk_rho1ijlambda_fast(rfeats, g, 3, mycg)
rhoijlm_rot = mk_rho1ijlambda_fast(rotfeats, rotg, 3, mycg)
np.linalg.norm(WD.rotate(rhoijlm) - rhoijlm_rot)/np.linalg.norm(rhoijlm)
# + [markdown] heading_collapsed=true
# # Simple regression test
# + hidden=true
iwater = 99
fock = np.load('water/water-fock.npy', allow_pickle=True)[iwater]
orbs = json.loads(json.load(open("water/orbs.json", "r")))
# + [markdown] hidden=true
# there has to be a model for each (n1,l1,n2,l2,L) entry in the coupled representation of the Fock matrix
# + hidden=true
frame = read('water/water_coords_1000.xyz',':')[iwater]
frame.cell = [100,100,100]
frame.positions += 50
frame.symbols
# + hidden=true
fock = pyscf_fix_l1(fock, frame, orbs)
fock_blocks = pyscf_to_blocks(fock, frame, orbs)
fock_blocks_c = to_coupled(fock_blocks, mycg)
# + hidden=true
ffeats = do_full_features([frame], orbs, spherical_expansion_hypers, 4, mycg, scale=1e3)
# + hidden=true
FR = FockRegression(orbs, alpha=1e-18, solver='svd')
# + hidden=true
FR.fit(ffeats, fock_blocks_c)
# + hidden=true
fpred = FR.predict(ffeats)
# + hidden=true
fpred['diag'][(2,1,2,1)]
# + hidden=true
fock_blocks_c['diag'][(2,1,2,1)]
# + hidden=true
unfock = blocks_to_pyscf(to_decoupled(fpred, mycg), frame, orbs)
# + hidden=true
plt.matshow((unfock-fock).astype(float))
np.linalg.norm(unfock-fock) # bingo!
# + hidden=true
np.mean(np.abs(np.linalg.eigvalsh(fock.astype(float))-np.linalg.eigvalsh(unfock)))
# + hidden=true
plt.plot(np.linalg.eigvalsh(fock.astype(float)), 'b.')
plt.plot(np.linalg.eigvalsh(unfock.astype(float)), 'r--')
# + [markdown] hidden=true
# #### Rotation and permutation
# + hidden=true
iwater = 99
frame = read('water/water_coords_1000.xyz',':')[iwater]
frame.cell = [100,100,100]
frame.positions += 50
print(frame.symbols)
fock = np.load('water/water-fock.npy', allow_pickle=True)[iwater]
orbs = json.loads(json.load(open("water/orbs.json", "r")))
# + hidden=true
fock = pyscf_fix_l1(fock, frame, orbs)
fock_blocks = pyscf_to_blocks(fock, frame, orbs)
fock_blocks_c = to_coupled(fock_blocks, mycg)
feats = do_full_features([frame], orbs, spherical_expansion_hypers, 4, mycg, scale=1e3)
# + hidden=true
FR = FockRegression(orbs, alpha=1e-18, solver='svd')
FR.fit(feats, fock_blocks_c)
fpred = FR.predict(feats)
# + hidden=true
fock_original = blocks_to_pyscf(to_decoupled(fpred, mycg), frame, orbs)
# + hidden=true
frame_rotperm = frame.copy()
iperm = np.arange(len(frame.numbers), dtype=int)
np.random.shuffle(iperm)
frame_rotperm.numbers = frame_rotperm.numbers[iperm]
frame_rotperm.positions = frame_rotperm.positions[iperm]
print(frame_rotperm.symbols)
abc = np.random.uniform(size=(3))*np.pi
WD = WignerDReal(spherical_expansion_hypers["max_angular"], *abc)
WD.rotate_frame(frame_rotperm)
# + hidden=true
feat_rotperm = do_full_features([frame_rotperm], orbs, spherical_expansion_hypers, 4, mycg, scale=1e3)
# + hidden=true
pred_rotperm = FR.predict(feat_rotperm)
# + hidden=true
fock_rotperm = blocks_to_pyscf(to_decoupled(pred_rotperm, mycg), frame_rotperm, orbs)
# + hidden=true
plt.matshow((fock_rotperm-fock_original).astype(float))
np.linalg.norm(fock_rotperm-fock_original)
# + hidden=true
plt.plot(np.linalg.eigvalsh(fock_original.astype(float)), 'b.')
plt.plot(np.linalg.eigvalsh(fock_rotperm.astype(float)), 'r--')
print(np.mean(np.abs(np.linalg.eigvalsh(fock_original)-np.linalg.eigvalsh(fock_rotperm))))
# + hidden=true
| MP_tests.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#导入package
import pandas as pd
import numpy as np
#读取数据
data = pd.read_csv("poj_question_text.csv")
data.head()
# # 数据清洗
data.info()
# ## 去除空值
data = data.dropna(how="any")
data.info(verbose=True)
# ## 中文/乱码处理
def check_cn(check_str):
for ch in check_str:
if u'\u4e00' <= ch <= u'\u9fff':
return True
return False
#取出带有中文的数据(这里的中文大部分都是乱码)
data_zh = data[data['q_text'].map(lambda x:check_cn(x))]
data_zh.info() #可以看到中文的有50个
#选出英文数据
data_en = data[data['q_text'].map(lambda x:not check_cn(x))]
data_en.info()
# ## 观察文字长度信息
#去掉英文数据中的回车符号
data_en['q_text'] = data_en['q_text'].apply(lambda x:x.strip())
word_length = data_en['q_text'].map(lambda x:len(x.split()))
count_data = word_length>510
count_data.value_counts() # 大于510的有116个,比较少,选择去除这些数据
#去除大于510的文本数据
data_en = data_en[data_en['q_text'].map(lambda x:len(x.split())<510)]
data_en.info() # 现在就剩下2832个数据
data_en
data_en.to_csv("post_poj_text.csv",index=False)
# # 处理JUNYI数据
junyi = pd.read_csv("junyi_question_text.txt",sep='#') #由于文本中有颜色属性也是用#号表示的
junyi = junyi.loc[:,['question_name','chinese_question']]
junyi['q_index'] = [i for i in range(1,841)] #加入索引列,题目序号从1开始
junyi.head()
junyi.info() #可以看到是有空值存在的,所以要去掉空值
# ## 去除TIMEOUT_ISSUE和NAN数据
#去除空值
junyi.dropna(how="any",inplace=True)
junyi.info()
# 去除 TIMEOUT_ISSUE and LINK_ISSUE
junyi = junyi[junyi['chinese_question'].map(lambda x:'TIMEOUT_ISSUE' not in x)]
junyi = junyi[junyi['chinese_question'].map(lambda x:'LINK_ISSUE' not in x)]
junyi
junyi.info()
# ## 去除回车符号
junyi['chinese_question'] = junyi['chinese_question'].apply(lambda x:x.strip())
# ## 观察长度信息
length_info = junyi['chinese_question'].map(lambda x:len(x.split(" ")) > 510)
length_info.value_counts() # 说明长度还可以,不需要做过多处理
# 保存
junyi.to_csv("post_junyi_text.csv",index=False)
# ## 确认下name是否有重复的
check = junyi[junyi['question_name'].duplicated()]
check #419 和 629 应该要删掉
junyi.drop([419,629],axis=0,inplace=True)
check = junyi[junyi['question_name'].duplicated()]
check
junyi.to_csv("post_junyi_text.csv",index=False)
| data_process/process poj data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import scipy.optimize as op
import scipy.stats as ss
import matplotlib.pyplot as plt
# %matplotlib inline
#Test which optimizers return the hessian automatically
mu = np.array([0.1, 3])
variances = np.array([0.3, 2.])**2
corr = 0.3
Sigma = np.diag(variances)
Sigma[0, 1] = Sigma[1, 0] = corr * np.sqrt(variances.prod())
Sigma
# a posterior
def neg_lnpost(x):
return -ss.multivariate_normal.logpdf(x, mean=mu, cov=Sigma)
result = op.minimize(neg_lnpost, x0=[0,0], method="BFGS")
print(result)
| notebooks/dev_work.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Word2Vec model widgets
#
# This notebook introduces several examples of linking word2vec model in `ml5_ipynb` with jupyter widget `ipywidgets` to produce outputs.
# The model used contains 300-dimension embeddings for 10000 most common English words. There are smaller models in data folder.
#
# This example can refer to an word2vec [example](https://github.com/ml5js/ml5-library/tree/main/examples/p5js/Word2Vec/Word2Vec_Interactive/data) in ml5.js
#
# **Note:** Using words not in the model embeddings will result in errors.
from ml5_ipynb import ml5_text
import ipywidgets as widgets
w2v = ml5_text.word2Vec('data/wordvecs10000.json')
# ## What are the Top 3 nearest words?
#
# The following uses `nearest(word)` function to calculate the cosine distance and output the top 3 words with smallest distance.
nearest = widgets.Textarea(
value='',
placeholder='Type a word',
# description='Please type a word',
disabled=False
)
nearest_output = widgets.HTML(
value="",
# placeholder='Some HTML',
# description='Some HTML',
)
nearest_button = widgets.ToggleButton(
value=False,
description='is nearest to',
disabled=False,
button_style='', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
# icon='check'
)
def get_nearest(val):
if val:
word = nearest.value
if not word:
print('Empty word!')
return
w2v.nearest(word)
nearest_list = w2v.nearest_results[-1]
if not nearest_list:
print('No nearest word!')
return
nearest_words = [i['word'] for i in nearest_list[:3]]
w_str = '<br>'.join(nearest_words)
nearest_output.value = w_str
nearest_button.value = False
out = widgets.interactive_output(get_nearest,{'val':nearest_button})
widgets.VBox([nearest,nearest_button,nearest_output,out])
# ## What's the Top 3 words between two words?
#
# The following uses `average([word1,word2])` function to calculate the average of embedding of two words and output the top 3 words similar to the average embedding.
w1 = widgets.Text(
value='',
placeholder='Type a word',
disabled=False
)
w2 = widgets.Text(
value='',
placeholder='Type a word',
disabled=False
)
btw_output = widgets.HTML(
value="",
)
btw_button = widgets.ToggleButton(
value=False,
description='is',
disabled=False,
button_style='', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
)
def get_btw(val):
if val:
word1 = w1.value
word2 = w2.value
if not word1 or not word2:
print('Please type in both!')
return
w2v.average([word1,word2])
btw_list = w2v.average_results[-1]
if not btw_list:
print('No between word!')
return
btw_words = [i['word'] for i in btw_list[:3]]
w_str = '<br>'.join(btw_words)
btw_output.value = w_str
btw_button.value = False
btw_out = widgets.interactive_output(get_btw,{'val':btw_button})
widgets.VBox([widgets.HBox([widgets.HTML(value="Between "),
w1,
widgets.HTML(value=" and "),
w2,btw_button]),
btw_output,btw_out])
# ## Analogy
#
# Analogy is to show how two things are similar to each other. Analogy of word embedding can refer to element-wise addition and subtraction. It is a "word algebra".
# For example, king is to queen as man is to woman. The resulting word is determined by the following formula.
# ```
# vector('queen') - vector('king') + vector('man')
# ```
is_word = widgets.Text(
value='',
placeholder='Type a word',
disabled=False
)
to_word = widgets.Text(
value='',
placeholder='Type a word',
disabled=False
)
is_word2 = widgets.Text(
value='',
placeholder='Type a word',
disabled=False
)
analogy_output = widgets.HTML(
value="",
)
analogy_button = widgets.ToggleButton(
value=False,
description='is to',
disabled=False,
button_style='', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
)
def get_analogy(val):
if val:
iw = is_word.value
tw = to_word.value
iw2 = is_word2.value
if not iw or not tw or not iw2:
print('Please finish typing!')
return
w2v.subtract([tw,iw])
sub_list = w2v.subtract_results[-1]
if not sub_list:
print('Oops! Please type in other words!')
return
sub_w = sub_list[0]['word']
w2v.add([sub_w,iw2])
add_list = w2v.add_results[-1]
if not add_list:
print('Oops! No analogy for this example!')
add_word = [i['word']+"("+ str(round(i['distance'],2))+")" for i in add_list[:3]]
analogy_output.value = " , ".join(add_word)
analogy_button.value = False
analogy_out = widgets.interactive_output(get_analogy,{'val':analogy_button})
widgets.VBox([widgets.HBox([is_word,
widgets.HTML(value=" is to "),
to_word,
widgets.HTML(value=" as "),
is_word2,analogy_button]),
analogy_output,analogy_out])
| examples/Word2vec widget.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PythonData
# language: python
# name: pythondata
# ---
# ## Deliverable 2. Create a Customer Travel Destinations Map.
# +
# Dependencies and Setup
import pandas as pd
import requests
import gmaps
import numpy as np
# Import API key
from config import g_key
# Configure gmaps API key
gmaps.configure(api_key=g_key)
# -
# 1. Import the WeatherPy_database.csv file.
city_data_df = pd.read_csv ("C:/Users/betti/Desktop/World_weather_analysis/Weather_Database/WeatherPy_Database.csv")
city_data_df.head()
# 2. Prompt the user to enter minimum and maximum temperature criteria
min_temp = float(input("What is the minimum temperature you would like for your trip? "))
max_temp = float(input("What is the maximum temperature you would like for your trip? "))
# 3. Filter the city_data_df DataFrame using the input statements to create a new DataFrame using the loc method.
preferred_cities_df = city_data_df.loc[(city_data_df["Max Temp"] <= max_temp) & \
(city_data_df["Max Temp"] >= min_temp)]
preferred_cities_df.head(10)
# 4a. Determine if there are any empty rows.
preferred_cities_df.count()
# 4b. Drop any empty rows and create a new DataFrame that doesn’t have empty rows.
preferred_cities_df=preferred_cities_df.dropna()
len(preferred_cities_df)
# +
# 5a. Create DataFrame called hotel_df to store hotel names along with city, country, max temp, and coordinates.
hotel_df = preferred_cities_df[["City", "Country", "Max Temp", "Current Description", "Lat", "Lng"]].copy()
# 5b. Create a new column "Hotel Name"
hotel_df["Hotel Name"] = ""
hotel_df.head(10)
# +
# 6a. Set parameters to search for hotels with 5000 meters.
params = {
"radius": 5000,
"type": "lodging",
"key": g_key
}
# 6b. Iterate through the hotel DataFrame.
for index,row in hotel_df.iterrows():
# 6c. Get latitude and longitude from DataFrame
lat = row["Lat"]
lng = row["Lng"]
params["location"] = f"{lat},{lng}"
# 6d. Set up the base URL for the Google Directions API to get JSON data.
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json"
# 6e. Make request and retrieve the JSON data from the search.
hotels = requests.get(base_url, params=params).json()
# 6f. Get the first hotel from the results and store the name, if a hotel isn't found skip the city.
try:
hotel_df.loc[index, "Hotel Name"] = hotels["results"][0]["name"]
except (IndexError):
print("Hotel not found... skipping.")
# -
# 7. Drop the rows where there is no Hotel Name.
hotel_df = hotel_df.replace(r'^\s*$', np.NaN, regex=True)
hotel_df = hotel_df.dropna()
hotel_df
hotel_df.count()
# 8a. Create the output File (CSV)
output_data_file = "C:/Users/betti/Desktop/World_weather_analysis/Vacation_Search/WeatherPy_Vacation.csv"
# 8b. Export the City_Data into a csv
hotel_df.to_csv(output_data_file, index_label="City_ID")
# +
# 9. Using the template add city name, the country code, the weather description and maximum temperature for the city.
info_box_template = """
<dl>
<dt>Hotel Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
<dt>Weather Description</dt><dd>{Current Description} at {Max Temp}°F</dd>
</dl>
"""
# 10a. Get the data from each row and add it to the formatting template and store the data in a list.
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
# 10b. Get the latitude and longitude from each row and store in a new DataFrame.
locations = hotel_df[["Lat", "Lng"]]
# +
# 11a. Add a marker layer for each city to the map.
marker_layer = gmaps.marker_layer(locations, info_box_content=hotel_info)
# 11b. Display the figure
fig = gmaps.figure()
fig.add_layer(marker_layer)
fig
# -
| Vacation_Search/Vacation_Search.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### Parallel Cluster Initialization with MPI4py: This could only be run on a HPC cluster
# The is only relevant to running mpi4py in a Jupyter notebook.
import ipyparallel
cluster=ipyparallel.Client(profile='mpi_tutorial')
print("IDs:",cluster.ids)
# %%px
from mpi4py import MPI
# %%px
comm = MPI.COMM_WORLD
rank = comm.Get_rank()
size = comm.Get_size()
print ("I'm rank %d of %d on %s" %(rank,size,MPI.Get_processor_name()))
# #### Packages Import
# %%px
import numpy as np
from numpy import math
from scipy.stats import norm
from scipy import stats
import matplotlib.pyplot as plt
import progressbar
import time
import datetime
# #### Model Specification: OU Process
# 1. $dX_{t} = \theta_{1}(\theta_{2} - X_{t})dt + \sigma dW_{t}$, $Y_{t}|X_{t} \sim \mathcal{N}(X_{t}, \theta_{3}^2)$
# 2. $\mathbb{E}[X_{t}] = x_{0} e^{-\theta_1t} + \theta_{2} (1-e^{-\theta_{1}t})$, $Var[X_{t}] = \frac{\sigma^{2}}{2\theta_{1}}(1-e^{-2t\theta_1})$
# 3. $Y_{1},Y_{2},...$ mutually independent, $Y_{t} \sim_{i.i.d.} \mathcal{N}(\mathbb{E}[X_{t}], \theta_{3}^2 + Var[X_{t}])$, for $t \in \mathbb{N}_{0}$
# + jupyter={"source_hidden": true}
# %%px
initial_val = 1
sigma = 0.5
theta = np.array([1,0,np.sqrt(0.2)])
def diff_coef(x, dt, dw):
return sigma*np.math.sqrt(dt)*dw
def drift_coef(x, dt):
return theta[0]*(theta[1]-x)*dt
# Log-scaled unnormalized likelihood function p(y|x)
def likelihood_logscale(y, x):
d = (y-x)
gn = -1/2*(d**2/(theta[2]**2))
return gn
def likelihood_update(y,un,unormal_weight):
gamma = math.sqrt(0.2)
d = (y-un)
gn1 = -1/2*(d**2/(theta[2]**2)) + unormal_weight
return gn1
def sig_mean(t,theta):
return initial_val*np.exp(-theta[0]*t) + theta[1]*(1-np.exp(-theta[0]*t))
## Used only when theta[0] != 0
def sig_var(t,theta):
return (sigma**2 / (2*theta[0])) * (1-np.exp(-2*theta[0]*t))
def gen_data(T):
Y = np.zeros(T+1)
for t in range(T+1):
std = np.sqrt(sig_var(t,theta) + theta[2]**2)
Y[t] = sig_mean(t,theta) + std * np.random.randn(1)
return Y
def Kalmanfilter(T,Y):
m = np.zeros((T+1))
mhat = np.zeros((T+1))
c = np.zeros((T+1))
a = theta[0]
s = sigma
# observational noise variance is gam^2*I
gam = theta[2]
# dynamics noise variance is sig^2*I
sig = np.sqrt(s**2/2/a*(1-np.exp(-2*a)))
# dynamics determined by A
A = np.exp(-a)
# initial mean&covariance
m[0] = initial_val
c[0] = 0
H = 1
# solution & assimilate!
for t in range(T):
mhat[t] = A*m[t] + theta[1]*(1-A)
chat = A*c[t]*A + sig**2
########################
d = Y[t+1] - H*mhat[t]
# Kalmab Gain
K = (chat*H) / (H*chat*H + gam**2)
# Mean Update
m[t+1] = mhat[t] + K*d
# Covariance update
c[t+1] = (1-K*H)*chat
tv = m[T]
return tv
def Kalmanfilter_path(T,Y):
m = np.zeros((T+1))
mhat = np.zeros((T+1))
c = np.zeros((T+1))
a = theta[0]
s = sigma
# observational noise variance is gam^2*I
gam = theta[2]
# dynamics noise variance is sig^2*I
sig = np.sqrt(s**2/2/a*(1-np.exp(-2*a)))
# dynamics determined by A
A = np.exp(-a)
# initial mean&covariance
m[0] = initial_val
c[0] = 0
H = 1
# solution & assimilate!
for t in range(T):
mhat[t] = A*m[t] + theta[1]*(1-A)
chat = A*c[t]*A + sig**2
########################
d = Y[t+1] - H*mhat[t]
# Kalmab Gain
K = (chat*H) / (H*chat*H + gam**2)
# Mean Update
m[t+1] = mhat[t] + K*d
# Covariance update
c[t+1] = (1-K*H)*chat
return m
# -
# #### Main Function
# + jupyter={"source_hidden": true}
# %%px
# Resampling - input one-dimensional particle x
def resampling(weight, gn, x, N):
ess = 1/((weight**2).sum())
if ess <= (N/2):
## Sample with uniform dice
dice = np.random.random_sample(N)
## np.cumsum obtains CDF out of PMF
bins = np.cumsum(weight)
## np.digitize gets the indice of the bins where the dice belongs to
x_hat = x[np.digitize(dice,bins)]
## after resampling we reset the accumulating weight
gn = np.zeros(N)
if ess > (N/2):
x_hat = x
return x_hat, gn
# Coupled Wasserstein Resampling
def coupled_wasserstein(fine_weight, coarse_weight, gn, gc, fine_par, coarse_par, N):
ess = 1/((fine_weight**2).sum())
fine_hat = fine_par
coarse_hat = coarse_par
if ess <= (N/2):
# Sort in ascending order of particles
ind = np.argsort(fine_par[:])
inc = np.argsort(coarse_par[:])
fine_par = fine_par[ind]
fine_weight = fine_weight[ind]
coarse_par = coarse_par[inc]
coarse_weight = coarse_weight[inc]
# Sample with uniform dice
dice = np.random.random_sample(N)
# CDF
bins = np.cumsum(fine_weight)
bins1 = np.cumsum(coarse_weight)
# get the indices of the bins where the dice belongs to
fine_hat = fine_par[np.digitize(dice, bins)]
coarse_hat = coarse_par[np.digitize(dice, bins1)]
# reset accumulating weight after resampling
gn = np.zeros(N)
gc = np.zeros(N)
if ess > (N/2):
fine_hat = fine_par
coarse_hat = coarse_par
return fine_hat, gn, coarse_hat, gc
# Maixmally Coupled Resampling
def coupled_maximal(fine_weight, coarse_weight, gn, gc, fine_par, coarse_par, N):
ess = 1/((fine_weight**2).sum())
if ess <= (N/2):
# Maximal coupled resampling
fine_hat, coarse_hat = maximal_resample(fine_weight, coarse_weight, fine_par, coarse_par, N)
# reset accumulating weight after resampling
gn = np.zeros(N)
gc = np.zeros(N)
if ess > (N/2):
fine_hat = fine_par
coarse_hat = coarse_par
return fine_hat, gn, coarse_hat, gc
def maximal_resample(weight1,weight2,x1,x2,N):
# Initialize
x1_hat = np.zeros(N)
x2_hat = np.zeros(N)
# Calculating many weights
unormal_min_weight = np.minimum(weight1, weight2)
min_weight_sum = np.sum(unormal_min_weight)
min_weight = unormal_min_weight / min_weight_sum
unormal_reduce_weight1 = weight1 - unormal_min_weight
unormal_reduce_weight2 = weight2 - unormal_min_weight
## Sample with uniform dice
dice = np.random.random_sample(N)
## [0] takes out the numpy array which is suitable afterwards
coupled = np.where(dice <= min_weight_sum)[0]
independ = np.where(dice > min_weight_sum)[0]
ncoupled = np.sum(dice <= min_weight_sum)
nindepend = np.sum(dice > min_weight_sum)
if ncoupled>=0:
dice1 = np.random.random_sample(ncoupled)
bins = np.cumsum(min_weight)
x1_hat[coupled] = x1[np.digitize(dice1,bins)]
x2_hat[coupled] = x2[np.digitize(dice1,bins)]
## nindepend>0 implies min_weight_sum>0 imples np.sum(unormal_reduce_weight*) is positive, thus the division won't report error
if nindepend>0:
reduce_weight1 = unormal_reduce_weight1 / np.sum(unormal_reduce_weight1)
reduce_weight2 = unormal_reduce_weight2 / np.sum(unormal_reduce_weight2)
dice2 = np.random.random_sample(nindepend)
bins1 = np.cumsum(reduce_weight1)
bins2 = np.cumsum(reduce_weight2)
x1_hat[independ] = x1[np.digitize(dice2,bins1)]
x2_hat[independ] = x2[np.digitize(dice2,bins2)]
return x1_hat, x2_hat
def Particle_filter(l,T,N,Y):
hl = 2**(-l)
un = np.zeros(N)+initial_val
un_hat = un
gn = np.zeros(N)
for t in range(T):
un_hat = un
for dt in range(2**l):
dw = np.random.randn(N)
un = un + drift_coef(un, hl) + diff_coef(un, hl, dw)
# Cumulating weight function
gn = likelihood_logscale(Y[t+1], un) + gn
what = np.exp(gn-np.max(gn))
wn = what/np.sum(what)
# Wasserstein resampling
un_hat, gn = resampling(wn, gn, un, N)
return(np.sum(un*wn))
def Coupled_particle_filter_wasserstein(l,T,N,Y):
hl = 2**(-l)
## Initial value
un1 = np.zeros(N) + initial_val
cn1 = np.zeros(N) + initial_val
gn = np.ones(N)
gc = np.ones(N)
for t in range(T):
un = un1
cn = cn1
for dt in range(2**(l-1)):
dw = np.random.randn(2,N)
for s in range(2):
un = un + drift_coef(un, hl) + diff_coef(un, hl, dw[s,:])
cn = cn + drift_coef(cn, hl*2) + diff_coef(cn, hl, (dw[0,:] + dw[1,:]))
## Accumulating Weight Function
gn = likelihood_update(Y[t+1], un, gn)
what = np.exp(gn-np.max(gn))
wn = what/np.sum(what)
gc = likelihood_update(Y[t+1], cn, gc)
wchat = np.exp(gc-np.max(gc))
wc = wchat/np.sum(wchat)
## Wassersteing Resampling
un1, gn, cn1, gc = coupled_wasserstein(wn,wc,gn,gc,un,cn,N)
return(np.sum(un*wn-cn*wc))
def Coupled_particle_filter_maximal(l,T,N,Y):
hl = 2**(-l)
## Initial value
un1 = np.zeros(N) + initial_val
cn1 = np.zeros(N) + initial_val
gn = np.ones(N)
gc = np.ones(N)
for t in range(T):
un = un1
cn = cn1
for dt in range(2**(l-1)):
dw = np.random.randn(2,N)
for s in range(2):
un = un + drift_coef(un, hl) + diff_coef(un, hl, dw[s,:])
cn = cn + drift_coef(cn, hl*2) + diff_coef(cn, hl, (dw[0,:] + dw[1,:]))
## Accumulating Weight Function
gn = likelihood_update(Y[t+1], un, gn)
what = np.exp(gn-np.max(gn))
wn = what/np.sum(what)
gc = likelihood_update(Y[t+1], cn, gc)
wchat = np.exp(gc-np.max(gc))
wc = wchat/np.sum(wchat)
## Wassersteing Resampling
un1, gn, cn1, gc = coupled_maximal(wn,wc,gn,gc,un,cn,N)
return(np.sum(un*wn-cn*wc))
def coef(x, y):
# number of observations/points
n = np.size(x)
# mean of x and y vector
m_x, m_y = np.mean(x), np.mean(y)
# calculating cross-deviation and deviation about x
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x
# calculating regression coefficients
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)
def num_coupled_par(p, p_max, const):
return int(2**(p+2*p_max) * (p_max**2) * const * c3)
def num_par(p, p_max, const):
return int(2**(p+2*p_max) * (p_max**2) * const * c2)
def prob_l_func(max_val):
prob = np.zeros(max_val)
for l in range(max_val):
prob[l] = 2**(-l*beta)
prob = prob / np.sum(prob)
return prob
def prob_p_func(max_val):
prob = np.zeros(max_val)
for p in range(max_val):
prob[p] = 2**(-p)
prob = prob / np.sum(prob)
return prob
def Xi_zero(T,p_prob,p_max,const,Y):
# sample the variable P
p = int(np.random.choice(p_max, 1, p=p_prob)[0])
#print('p_val is',p)
# construct the estimator
Xi_zero = (Particle_filter(0,T,num_par(p, p_max, const),Y) - Particle_filter(0,T,num_par(p-1, p_max, const),Y)) / p_prob[p]
return Xi_zero
def Xi_nonzero(l,T,p_prob,p_max,const,Y):
# sample the variable P
p = int(np.random.choice(p_max, 1, p=p_prob)[0])
#print('p_val is',p)
# construct the estimator
Xi = (Coupled_particle_filter_maximal(l,T,num_coupled_par(p,p_max,const),Y) - Coupled_particle_filter_maximal(l,T,num_coupled_par(p-1,p_max,const),Y)) / p_prob[p]
return Xi
def Xi(T,l_prob,l_max,p_prob,p_max,const,Y):
l = int(np.random.choice(l_max, 1, p=l_prob)[0])
#print('value of l is',l)
if l==0:
Xi = Xi_zero(T,p_prob,p_max,const,Y)
if l!=0:
Xi = Xi_nonzero(l,T,p_prob,p_max,const,Y)
est = Xi / l_prob[l]
return est
def parallel_particle_filter(M,T,max_val,const,Y):
l_max = max_val
p_max = max_val
l_prob = prob_l_func(l_max)
p_prob = prob_p_func(p_max)
est_summand = np.zeros(M)
for m in range(M):
est_summand[m] = Xi(T,l_prob,l_max,p_prob,p_max,const,Y)
return (np.mean(est_summand))
def parallel_particle_filter_record_progbar(M,T,max_val,const,Y):
l_max = max_val
p_max = max_val
l_prob = prob_l_func(l_max)
p_prob = prob_p_func(p_max)
est_summand = np.zeros(M)
pr = progressbar.ProgressBar(max_value=M).start()
for m in range(M):
est_summand[m] = Xi(T,l_prob,l_max,p_prob,p_max,const,Y)
pr.update(m+1)
pr.finish()
return est_summand
def parallel_particle_filter_record(M,T,max_val,const,Y):
l_max = max_val
p_max = max_val
l_prob = prob_l_func(l_max)
p_prob = prob_p_func(p_max)
est_summand = np.zeros(M)
for m in range(M):
est_summand[m] = Xi(T,l_prob,l_max,p_prob,p_max,const,Y)
return est_summand
# For OU process, beta=2
def num_ml_coupled(l,lmax,const):
return 2**(2*lmax-1.5*l) * const * c3
def num_ml_single(l,lmax,const):
return 2**(2*lmax-1.5*l) * const * c2
def mlpf(T,max_val,const,Y):
L = max_val
level_est = np.zeros(L)
level_est[0] = Particle_filter(0,T,int(num_ml_single(0,L,const)),Y)
for l in range(1,L):
level_est[l] = Coupled_particle_filter_maximal(l,T,int(num_ml_coupled(l,L,const)),Y)
return np.sum(level_est)
# -
# #### Simulation Setup Example
# 1. At discretization level $l=2$, aim at variance level of 10^{-7} for ppf (parallel particle filter), this is so that the variance is banlanced with the square bias, which we have already obtained. This is done by using $C=10^6$ on a single processor, with $M=1$.
#
# 2. Note that the PPF estimator has variance $Var(\sum_{i=1}^{M}\Xi_{i}) = \mathcal{O}(C^{-1}M^{-1})$, this means we can achieve the same variance level by using $C=10^3$ and $M=10^3$. We use $10^3$ parallel cores to obtain $i.i.d.$ realizations of $\Xi$ at the same time, this will give us a giant speed up. The simulation is set out to find how much is the speed up, at the same time ensuring $Var(\sum_{i=1}^{M}\Xi_{i}) \approx Bias(\sum_{i=1}^{M}\Xi_{i}) \approx 10^{-7}$.
# + jupyter={"source_hidden": true}
# %%px
T = 100
data_path = np.load('ou_model_data_path.npy')
c2, c3, beta = np.load('ou_fit_values.npy')
max_val=2
M=1000
const=1000
true_val = Kalmanfilter(T,data_path)
# -
# #### Parallel Implementaion of PPF
# 1. We need to parallel compute the $M$ realizations. We record the time needed for such one parallel realization.
# 2. We check the MSE of such PPF with $M$ values, this can be done in any fashion.
# 3. We can then compare MLPF with PPF 's cost for similar MSE targets.
# + jupyter={"source_hidden": true}
# %%px
# Used to construct a parallel - PPF: evaluate the cost of it
# Use M cores to get M repe of it and record the time
def multi_xi(seed_val):
l_max = max_val
np.random.seed(seed_val)
l = int(np.random.choice(l_max, 1, p=l_prob)[0])
#print('value of l is',l)
if l==0:
Xi = Xi_zero(T,p_prob,p_max,const,Y)
if l!=0:
Xi = Xi_nonzero(l,T,p_prob,p_max,const,Y)
est = Xi / l_prob[l]
return est
# Used to obtain MSE of PPF with M.
# Use Rep_num of cores to get repetition of it and compute the (sample) MSE.
def multi_ppf(seed_val):
np.random.seed(seed_val)
l_max = max_val
p_max = max_val
l_prob = prob_l_func(l_max)
p_prob = prob_p_func(p_max)
est_summand = np.zeros(M)
for m in range(M):
est_summand[m] = Xi(T,l_prob,l_max,p_prob,p_max,const,Y)
return (np.mean(est_summand))
# -
# #### MPI4py HPC Implementation
# + jupyter={"source_hidden": true}
# %%px
iter_num = 0
rank = comm.Get_rank()
size = comm.Get_size()
## Every iteration should have different initial_seed values
initial_seed = iter_num*(size)
seed_val_rankwise = initial_seed + rank
# -
# #### (I) Cost record of M parallel implementations for PPF estimate
# + jupyter={"source_hidden": true}
# %%px
stime = time.time()
xi_reptition = np.zeros(1)
xi_reptition = multi_xi(seed_val_rankwise)
result = np.zeros(size)
comm.Gather(xi_reptition,result,root=0)
if rank == 0 :
x = np.asarray(result)
ppf_estimate = np.mean(x)
print('HPC-PPF outputs:',ppf_estimate)
etime = time.time()
time_len = str(datetime.timedelta(seconds=etime-stime))
print("Time cost for HPC-PPF is:",time_len)
# -
# #### (II) MSE compuation for PPF estimate
# + jupyter={"source_hidden": true}
# %%px
ppf_reptition = np.zeros(1)
ppf_reptition = multi_ppf(seed_val_rankwise)
result = np.zeros(size)
comm.Gather(xi_reptition,result,root=0)
if rank == 0 :
x = np.asarray(result)
mse_ppf = np.mean((x-true_val)**2)
var_ppf = np.var(x)
square_bias_ppf = mse_ppf - var_ppf
print('HPC-PPF has MSE:',mse_ppf, 'Variance:',var_ppf, 'Square Bias:',square_bias_ppf)
| HPC UPF.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Line Fitting
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# Get random data about a trend line
# +
#set random number seed
np.random.seed(119)
#set number of data points
npoints = 50
#set x
x = np.linspace(0, 10., npoints)
#set slope, intercept, and scatter rms
m = 2.0
b = 1.0
sigma = 2.0
#generate y points
y = m*x + b + np.random.normal(scale = sigma, size = npoints)
y_err = np.full(npoints,sigma) #generate array full with a single value (2), 50 elements of the number 2
# -
# We plot the data
f = plt.figure(figsize = (7,7))
plt.errorbar(x,y,sigma,fmt='o')
plt.xlabel('x')
plt.ylabel('y')
# ## Line Fitting Methods
# #### Method 1: polyfit()
# +
m_fit, b_fit = np.poly1d(np.polyfit(x,y,1, w=1./y_err)) #weight with uncertainty
y_fit = m_fit*x + b_fit #equation for straight best fit line
f = plt.figure(figsize=(7,7))
plt.errorbar(x,y,yerr=y_err, fmt='o', label = 'data')
plt.plot(x,y_fit,label='fit')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2, frameon = False)
# -
| line_fitting.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Beautiful is better than ugly.
#Explicit is better than implicit.
#Simple better than complex
#Complex is better than complicated.
# Flat is better than nested.
# Sparse is better than dense.
# Readability counts.
# Special cases aren't special enough to break the rules.
# Practicality beats purity.
# Errors should never pass silently.
# Unless explicitly silenced.
# In the face of ambiguity, refuse the temptation to guess.
# there should be one - and preferably only one - obvious way to do it.
# Although that way may not beobvious at first unless unless you're Dutch.
# Now is better than never, but never is often better than *right* now.
# Implementation should be easy to explain.
# Namespaces are a great idea! Use them!
# +
# Quick Refresher on Python.
# Be aware of Python's type hierarchy, variables, conditionals, functions, loops, break, countinue and try.
# Classes. Quick Refresher Basic.
# -
# Variables are symbols for memory addresses.
# Memory
# Python memory management --> reference counting, garbage colleciton
# Mutability --> function arguments, shared refrences
# What is equality of two objects?
# Python memory optimizations (optimize for memory/speed
# +
#Numeric Types (integers, rationals, floats --> binary represenations)
# Floats (Exactness, binary representations, rounding, equality, measures of closeness (approximate equality))
# Decimals --> alternative to floats (exactness, precision, rounding, complex numbers)
# Complex Numbers with cmath standard library
# -
# Numeric Types (Booleans)
# Associated with Truth values. Everything in Python is object.
# Precedence and short-circuiting. Boolean operators (what they really do, using oin context of associated truth values
# Comparison operators (identity, value equalities, ordering)
# +
# Functions (higher-order functions, can take in and return functions)
# Docstrings and annotations, lambdas, introspection, fun ctional programming
# Functional Programming (map, filter, zip, reducing functions, partial functions)
# Functions (Positional arguments, keyword-only arguments, default values, packing and unpacking of iterables/arguments)
# Variable positional arguments, variable keyword-only arguments.
# +
# Global and local copes, nested scopes, closures, nested closures
# +
#Decorators
# (nested decorators)
# Parameterized decorators
# stacked decorators
# class decorators
# decorator classes
# applications (memoriztion, single dispatch, logging, timing)
#
# -
# Tuples as Data Structures
# tuples are not just read-only lists
# data structure as well!
# packing and unpacking of tuples
# named tuples
# augmenting named tuples
# +
# Modules, packages and namespaces
# what are modules?
# what are packages?
# how do the various imports work?
# how to manipulate namespaces using packages.
# zip archives
# __ main __
# -
#Extras section
# important new features of python 3.6 and later.
# best practices.
# random collection of interesting stuff.
# additional resources
# send me your suggestions!!!
# +
# Python Type Hierarchy, multline statements and strings, naming conventions, conditionals, functions, loops (while, for, break, continue, try)
# +
# Python type hierachy is a subset of the Python type hierarchy that we will cover in this course:
# Numbers (integral, non-integral)
# Integrals (Integers, Booleans)
# Non-integral (Floats, Complex, Decimals, Fractions
# +
# Collections
# Sequences (mutable, immutable)
# Mutable (lists)
# Immutable (Tuples, strings)
# Sets (Mutable, Immutable)
# Sets, Frozen Sets
# Mappings --> Dictionaries
# CAllables (anything that is invokable, or callable like a fuction)
# +
# Callables
# User-Defined Functions
# Generators
# Classes
# Instance Methods
# Class Instances (__call__())
# Built-in Functions (e.g. len(), open())
# Built-In Methods (e.g. my_list.append(x))
# -
# Singletons
# None (same memory address)
# Notimplemented
# Ellipsis (...)
# +
# Multi-line statements and strings
# Python Program --> physical lines of code (uses enter line to create new line)
# Logical Lines of code -- > Tokenized to interpret the code
# Physical lines of code end with aphysical newline character
# Logical lines of code end with a logical NEWLINE token
# Physical newline vs. logical newline (sometimes, physical newlines are ignored to in order to combine multiople physical lines into a single logical line of code. terminated by a logical NEWLINE token.
# Python interpreter doesn't really care. It doesn't care about human readability.
# Other people might be reading our code. Readability helps everybody to understand what the code is doing.
# Conversion can be implicit or explicit.
# +
# Implicit expressions in:
# list literals: []
# tuple literals: ()
# dictionary literals: {}
# set literals: {}
# function arguments/parameters (supports inline comments.)
# can include inline comments.
# functions can be written over multiple lines
# my_func (10, #comment, 20, 30)
# +
# Multi-LIne statements and strings
# Explicit (you can break up statements over multiple lines explicitly by using the backslash character.)
# Multi-line statements are not implicitly converted to a single logical line.
# if a \ and b \ and c:
# Comments cannot be part of a statement, not even a multi-line statements.
# Mult-string literals can be created using triple delimiters.
# Be aware that non-visible characters such as newlines, tabs, etc are part of the string -- basically anything you type
# Can use escape d characters (e.g. \n, \t), use string formatting, etc.
# Amulti-line string is just a regular string.
# Multi-line strings are not comments, although they can be used as such.
# -
a = [1,2,3]
a = [1,2,
3,4,5]
a
a = [1 #item 1
,2]
a
a = (1,
2, #comment
3)
a
a = {'key1' : 1 #values for key 1
,'key2': 2 #value for key 2
}
a
def my_func(a, #this is used to indicate...
b, # this is used to
c):
print(a,b,c)
my_func(1,4,5)
my_func(10,
20,
30)
my_func(10, #comment
20, #comment
30 #comment
)
a= 10
b = 20
c=30
if a>5 and b>10 and c>15:
print('yes')
if a>5 \
and b>10 \
and c>20:
print('yes')
a = '''this is a string'''
a
a = '''this
is
a
string'''
a
print(a)
a = '''this
is a string
that is created over
multiple lines'''
a
print(a)
a = '''some items:
1. item 1
2. item 2'''
a
print(a)
def my_func():
a = '''a multi-line string
that is indented in the second line'''
return a
print(my_func())
# # Identifier Names
# +
# Identifier names are case-sensitive my_var, my_Var, ham, Ham are different identifiers.
# -
#identifiers must follow certain rules
#identifiers must start with underscore (_) or letter (a-z, A-Z)
# followed by any number of underscores, letters or digits. identifiers cannot be started with digits.
# var, my_var, index1, index_1, _var, __var, __lt__ have a specific meaning attached to them
# identifiers cannot be reserved standard words (none, true, false, etc.)
#_my_var, or a single underscore.
# This is a convention to indicate "internal use" or "private" objects.
# objects named this way will not get imported by a statement such as: from module import *.
# double underscore used to "mangle" class attributes -- useful in inheritance chains.
# the double underscored to help in inheritance chains.
# the ones that start and end with double underscore are used for system-defined names that have a special meaning to the interpreter.
# don't invent them, stick to the ones pre-defined by Python!
# __init__ method helps initiate a class. it will look for this ~init~~ funciton when called.
# x<y, is doing a x.__lt__(y)
# Other naming conventions include the following from the PEP8 Style Guide.
# Packages are short names, all-lowercase names. Preferably no underscores. utilities is a package.
# Modules are short, all-lowercase names. Can have underscores.
# Classes using CapWords (upper camel case) convention. Upper case letter typically
# Functions (lowercase, words separated by underscores (snake_case))
# variables are lowercase, words separated by underscores.
# Constants are all-uppercase, words separated by underscores.
# Can find style guide at pep 008, this is a should-read. A foolish consistency is the hobgoblin of little minds (Emerson)
# Conditionals
a=6
if a<5:
print('a<5')
else:
print('a>=5')
a = 5
if a <5:
print('a<5')
else:
if a<10:
print('5<= a<10')
else:
print('a>=10')
a = 25
if a<5:
print('a<5')
elif a<10:
print('5 <=a<10')
elif a<15:
print('10<=a<15')
elif a<20:
print('15<=a<20')
else:
print('a>=20')
# +
#X if (condition is true) else Y
# +
a = 25
if a<5:
b= 'a<5'
else:
b='a>=5'
print(b)
# -
b = 'a<5' if a<5 else 'a>=5'
b
print(b)
a=4
print(b)
# Functions
s = [1,2,3]
len(s)
from math import sqrt
sqrt(4)
import math
math.pi
math.exp(1)
def func_1():
print('running func_1')
func_1
func_1()
def func_2(a: int,b: int):
return a*b
func_2(2,3)
func_2('a',3)
func_2([1,2],3)
func_2('a',7)
# +
#polymorphism can go across several types.
# -
func_2
# +
#can call functions inside this that haven't been defined eyt.
# +
def func_3():
return func_4()
def func_4():
return 'running func_4'
# -
func_3()
# +
def func_5():
return func_6()
def func_6():
print('running_func_6')
# -
func_5
func_5()
#lambda allows you to create a function without the syntax above. allows for quicker definitions.
type(func_5)
# +
#can assign this funciton to another function
# -
my_func = func_4
func_4()
my_func()
#can assign a funciton to a variable name.
lambda x: x**2
fn1 = lambda x: x**2
fn1
fn1(2)
fn1
# +
#While Loop
# +
i = 5
while True:
if i>=5:
print(i)
break
else:
i+=1
break
# +
min_length = 2
name = input("Please enter your name:")
while not(len(name)>=min_length and name.isprintable() and name.isalpha()):
name = input("Try again. Please enter your name:")
print("Hello, {}".format(name))
#always best to write code only one time instead of twice.
# -
min_length = 2
while True:
name = input("Please enter your name: ")
if len(name)>=min_length and name.isprintable() and name.isalpha():
break
print("Hello {}".format(name))
# +
a=0
while a<10:
a +=1
if a%2 != 0:
continue
print(a)
# +
# the else clause of a while loop will execute iff the while loop did not encounter a break statement. If it ran normally, then it iwll execute the ELSE statement. For example
# +
l = [1,2,10,3]
val = 10
found = False
idx = 0
while idx < len(l):
if l[idx] == val:
found = True
break
idx += 1
if not found:
l.append(val)
print(l)
# +
l = [1,2,3,45,45]
val = 45
idx = 0
while idx < len(l):
if l[idx] == val:
break
idx += 1
else:
l.append(val)
print(l)
# +
# try...except...finally
# -
a = 10
b=0
try:
a/b
except ZeroDivisionError:
print('division by 0')
finally:
print('this always executes')
# +
a=0
b=10
while a <4:
print('------')
a += 1
b -= 1
try:
a/b
except ZeroDivisionError:
print("(0),{1} - division by 0".format(a,b))
break
finally:
print("{0},{1} - this always executes".format(a,b))
print("{0},{1} - main loop".format(a,b))
else:
print('Code executed without a zero division error')
# -
#The For Loop
#In Python, an iterable is an object capable of returning values one at a time.
# A lot of objects are iterables in Python (strings, tuples, etc.)
# The For Loop lets you iterate over an interable.
# The While Loop is probably the closest to a For Loop.
i=0
while i<5:
print(i)
i += 1
#in this instance, i gets discounted
i = None
# a very simple iterable is via the range function.
for i in range(5):
print(i)
#these two are not the same. range(5) is iterable, it asks the objects for the next value.
# java
for i in [1,2,3,4]:
print(i)
for c in 'hello':
print(c)
for x in ('a','b','c',4):
print(x)
for i,j in [(1,2),(3,4),(5,6)]:
print(i)
# the break and the continue statement work the same
for i in range(5):
if i == 3:
break
print(i)
for i in range(1,10):
print(i)
if i % 7 ==0:
print('multiple of 7 found')
break
else: print('no multiples of 7 in the range')
# the try-catch works the same as in the where clause. The finally will still execute if it's encountered
for i in range(5):
print('-----------')
try:
x = 10/(i-3)
except ZeroDivisionError:
print('divided by 0')
finally:
print('always run')
print('i={} and x ={}'.format(i,x))
s= 'hello'
for c in s:
print(c)
#Dictionaries, or sets, cannot reference a specific an order in a set. In a dictionary, cannot call a specific one with a set or a dictionary. The keys and the values are iterable. Can iterate over key-value pairs. An index is useful, can get the index back
s = ' hello'
i=0
for c in s:
print(i,c)
i+=1
s = 'hello'
for i in range(len(s)):
print(i,s[i])
s = 'hello'
for i, c in enumerate(s):
print(i,c)
# # Classes
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
r1 = Rectangle(10,20)
r1.width
r1.width =100
r1.width
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
def area(self):
return self.width * self.height
def perimeter(self):
return 2*(self.width + self.height)
r1 = Rectangle(10,20)
r1.area()
r1.perimeter()
# +
#using self makes the most amount of sense. It helps keep everything clarified within itself. The Self is an instance attribute in this example.
# -
str(r1)
hex(id(r1))
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
def area(self):
return self.width * self.height
def perimeter(self):
return 2*(self.width + self.height)
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
r1 = Rectangle(10,20)
str(r1)
r1.to_string()
# these are not necessarily magical.
r1
l = [1,2,3]
str(l)
r1
r2 = Rectangle(10,20)
r1 is not r2
r1 == r2
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
def area(self):
return self.width * self.height
def perimeter(self):
return 2*(self.width + self.height)
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
def __eq__(self,other):
return self.width == other.width and self.height == other.height
r1 = Rectangle(10,20)
r2= Rectangle(10,20)
r1 is not r2
r1 == r2
r1 == 100
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
def area(self):
return self.width * self.height
def perimeter(self):
return 2*(self.width + self.height)
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
def __eq__(self,other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
r1 = Rectangle(10,20)
r2 = Rectangle(10,20)
r1==r2
r1 == 100
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#the class is created
def area(self):
return self.width * self.height
def perimeter(self):
return 2*(self.width + self.height)
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
def __eq__(self,other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
def __lt__(self,other):
if isinstance(other, Rectangle):
return self.area() < other.area()
else:
return NotImplemented
r1 = Rectangle(10,20)
r2 = Rectangle(50,20)
r1 < r2
r2 > r1
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
def __eq__(self,other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
def __lt__(self,other):
if isinstance(other, Rectangle):
return self.area() < other.area()
else:
return NotImplemented
r1 = Rectangle(10,20)
r1.width
r1.width = -100
r1
# +
# might want to restrict the properties allowed for a rectangle. You don't want a negative value in here.
# -
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self._width = width
self._height = height
#this means don't mess around with it.
def get_width(self):
return self._width
def set_width(self, width):
if width <= 0:
raise ValueError('Width must be positive.')
else:
self._width = width
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self._width,self._height)
def __repr__(self):
return 'Rectangle({},{})'.format(self._width,self._height)
def __eq__(self,other):
if isinstance(other, Rectangle):
return self._width == other._width and self._height == other._height
else:
return False
r1 = Rectangle(10,20)
r1.width
r1.width = -100
r1._width
r1.get_width()
r1.set_width(-10)
r1.set_width(100)
r1
#The Dunder EQ method allows us to specify and define how we compare objects to eachother.
# Classes, should know some basic ideas with Classes. Should know how to do it in Python
class Rectangle:
def __init__(self, width, height):
self.width = width
self.height = height
#this means don't mess around with it.
# going to get all of the logic required for the getter in the same block.
@property
def width(self):
return self._width
@width.setter
# this is how we create a width setter.
def width(self, width):
if width <= 0:
raise ValueError('Width must be positive.')
else:
self._width = width
@property
def height(self):
return self._height
@height.setter
# this is how we create a width setter.
def height(self, width):
if height <= 0:
raise ValueError('Height must be positive.')
else:
self._height = height
def __str__(self):
return 'Rectangle: width={}, height ={}'.format(self.width,self.height)
def __repr__(self):
return 'Rectangle({},{})'.format(self.width,self.height)
def __eq__(self,other):
if isinstance(other, Rectangle):
return self.width == other.width and self.height == other.height
else:
return False
r1 = Rectangle(10,20)
r1.width
r1.width = 100
r1
# +
#No Reason to create a getter or setter with these Classes in Python. Do not need to create a getter or setter in Python, it's going to be transparent in Python.
# -
r1 = Rectangle(-100,20)
r1
# # Variables
# memory references
# what variables really are
# memory management
# reference counting vs garbage collection
# dynamic vs static typing
# mutability and immutability
# shared references
# variable equality
# everything is an object
# # Variables are Memory References
# +
# see paper notebook
# -
my_var = 10
print(my_var)
my_var
print(id(my_var))
print(hex(id(my_var)))
greeting = 'hello'
print(greeting)
print(id(greeting))
print(hex(id(greeting)))
#my_var is the memory address of the variable. It is a reference.
#Can keep track of the memory address and knowing how many variables are pointing to them.
my_var = 10
other_var = my_var
#now other_var is pointing to the same address as my_var. now sharing the reference
# now the reference_counter is 2.
# now suppose it goes away. if other_var and my_var go away, at that point the Python memory manager recognizes that and decides to throw away the object. That space is now freed up.
# # Reference Counting
import sys
import ctypes
#finding the reference count...
sys.getrefcount(my_var)
#passing my_var to getrefcount creates an extra reference.
ctypes.c_long.from_address(address).value
#Here, we just pass the memory address (an integer) not a reference.
import sys
a = [1,2,3]
id(a)
sys.getrefcount(a)
#subtract 1 because you are referencing it with the query.
import ctypes
def ref_count(address: int):
return ctypes.c_long.from_address(address).value
ref_count(id(a))
# it has released the pointer because id(a) has already been calculated
ref_count(4369341832)
b=a
ref_count(4369341832)
id(b)
ref_count(id(a))
c=a
ref_count(id(c))
c=10
ref_count(id(a))
b = None
ref_count(id(a))
a_id = id(a)
a= None
ref_count(a_id)
a_id
id(a)
ref_count(a_id)
ref_count(a_id)
# # Garbage Collection
# +
#Circular References
# if you have a variable, my_var, that points to Object A.
# The reference count can go from 1 to 0.
# However, let's suppose that Object A that points to Object B.
# if Object A reference count goes to 0, then Object B's reference count goes to 0 as well.
# By destroying the first reference, it destroys A and B.
# Suppose that var_2 points to var_1. Or B --> A.
# The reference count goes to A, not 0. Reference Counting will not destroy either A or B. They cannot be destroyed.
# A Circular Reference would generate a memory leak.
# No way that A and B will get destroyed.
# +
#The Garbage Collector can identify the circular references
# can be controlled programatically using the gc module.
# by default the gc is turned on.
# you may turn off the gc if you're sure your code does not create circular references.
# you might want to turn it off for performance reasons. it tries to identify the circular references.
# runs periodically on its own
# can call the garbage collector manually, and even do your own cleanup.
# In general, the Garbage Collector works just find (but not always)
# for Python <3.4. If even one of the objects in the circular references has a destructor [e.g. __del__()]
# the destruction order of the objects may be important for Python <3.4
# but the GC does not know what the order should be. so the object is marked as uncollectable and the objects in the circular reference are not cleaned up.
# in Python 3.4 and up, does not matter
# -
import ctypes
import gc
def ref_count(address):
return ctypes.c_long.from_address(address).value
def object_by_id(object_id):
for obj in gc.get_objects():
if id(obj) == object_id:
return "Object Exists"
return "Not Found"
class A:
def __init__(self):
self.b = B(self)
print('A: self: {}, b: {}'.format(hex(id(self)), hex(id(self.b))))
class B:
def __init__(self,a):
self.a = a
print('B: self: {}, a: {}'.format(hex(id(self)), hex(id(self.a))))
gc.disable()
my_var = A()
hex(id(my_var))
print(hex(id(my_var.b)))
print(hex(id(my_var.b.a)))
a_id = id(my_var)
b_id = id(my_var.b)
print(hex(a_id))
print(hex(b_id))
ref_count(a_id)
ref_count(b_id)
object_by_id(a_id)
object_by_id(b_id)
my_var = None
ref_count(a_id)
ref_count(b_id)
object_by_id(a_id)
object_by_id(b_id)
gc.collect()
object_by_id(a_id)
object_by_id(b_id)
ref_count(a_id)
ref_count(a_id)
ref_count(b_id)
ref_count(b_id)
ref_count(b_id)
ref_count(a_id)
ref_count(a_id)
object_by_id(a_id)
ref_count(a_id)
# # Static Typing
# +
#don't use memory addresses unless trying to debug items.
#keep the garbage collector in. the memory space can be reclaimed, used for something else
#Some languages are statically typed
#String myVar = "hello";
#data_type, variable_name, value.
#the memory object is typed
# Some languages are statically typed.
# String myvar = "hello"
# the datatype is associated with the variable name.
#myVar has been declared as a String, and cannot be assigned the integer value 10 later.
# myVar ="abc" --> this is okay
#Python, in contrast, is dynamically typed.
#my_var = 'hello' the variable my_var is purely a reference to a string object with value hello.
# no type is 'attached' to my_var
my_var =10
# the variable my_var is now pointing to an integer object with value 10. myVar has never changed.
# we can use the built-in type() function to determine the type of the object currently referenced by a variable.
# variables in Python do no thave an inherent static type.
# -
a = "hello"
type(a)
a = 10
# it is the type of the object a is referencing.
type(a)
a = lambda x: x**2
a(2)
type(a)
a = 3 + 4J
type(a)
# +
# the type is fungible for the reference of a variable.
# -
# # Variable Re-Assignment
my_var = 10
my_var = 15
# +
#the reference of the new object changes. new object at new memory address
# -
my_var = my_var +5
my_var
# +
# did not change the contents of the address before.
# +
# the value inside the int objects can never be changecd
# -
a = 10
hex(id(a))
type(a)
a = 15
hex(id(a))
a = a + 1
hex(id(a))
a
a = 10
b = 10
hex(id(a))
hex(id(b))
# +
#both a and b are pointing to the same object.
#mutability and immutability, allows for safety surrounding this idea
# +
# consider an object in memory, has a type, state. Changing the data inside the object is called modifyiing the internal state of the object.
#my_account has two instance properties (Bank Account, Balance). Now suppose we modify the balance, so now the balance is 500.
# the internal state of the data has changed, but the memory address has not changed (same id)
# internal state (data) has changed. Here we are modifying the internal state of the same object. The data has changed, but the memory address has not changed.
#The object was mutated
# +
# An object whose internal state can be changed is called mutable.
# An object whose internal state cannot be changed is called immutable.
# We need to know if objects are mutable or immutable at times.
# Immutable objects include numbers (integers, floats, booleans, etc. are immutable. they get created in memory, but we can never change the internal value of that number. MyVar = 10 and MyVar = 15, we were changing it from one to another. Never modified the internal state. Integers are immutable)
# Strings are also immutable (once a string is created, cannot change the internal state of that string)
# Tuples are also immutable (container type of object with elements. cannot add/remove/replace elements in that space)
# Frozen sets are also an immutable type of object
# User defined classes are also immutable by definition
# lists, sets, dictionaries and user-defined classes are mutable objects.
# -
t = (1,2,3) #tuples are immutable: elements cannot be deleted, inserts or replaced. Both this container (tuple) and its elements (ints) are immutable
a = [1,2]
b = [3,4]
t = (a,b)
# +
#lists are mutable: elements can be deleted, inserted or replaced
# -
t
a.append(3)
b.append(5)
t
#the tuple is immutable, we did not change the elements that were referenced in those positions; however, we were able to add elements to the lists.
# t changed from our perspective even though it was immutable. Need to be careful about what mutability means.
t =(1,2,3)
# these are references to immutable objects (integer)
# however, the tuple can reference a mutable object
my_list = [1,2,3]
type(my_list)
id(my_list)
my_list.append(4)
my_list
id(my_list)
# +
# the memory list has not changed even though we have added elements.
# -
my_list_1 = [1,2,3]
id(my_list_1)
my_list_1 = my_list_1 + [4]
my_list_1
my_list_1.append(5)
my_list_1
my_dict = dict(key1 = 1, key2='a')
my_dict
id(my_dict)
my_dict['key3'] = 10.5
my_dict
id(my_dict)
t = (1,2,3)
id(t)
t[0]
id(t[0])
id(t[1])
t = ([1,2],[3,4])
id(t)
t[0]
t[1]
t[0].append(3)
t
# +
# In Python, STrings are immutable objects.
# once a string has been created, the contents of the object can never be changed.
# In this code, my_var = 'hello'
# the only way to modify the valuke of my_var is to re-assign my_var.
# immutable objects are safe from unintended side-effects.
# -
def process(s):
s= s+ ' world'
return s
my_var = 'hello'
process(my_var)
# +
# Scopes (a module scope and and a process() scope). When we run my_var = ' hello' it points to an object in memory.
# When we run process(my_var)..
# my_var's reference is passed to process(). The process scope now stores that reference in the variable s. It points to the same object in memory.
# WE are not modifying the contents of this object. S is no longer pointing to hello, it is pointing to new object hello world.
# in the process scope, it has now changed from hello to hello world. When we print my_var, we actually print out hello.
# Because the string is immutable, s has now changed from s to hello world. A new address. when we print out my_var.
# The function can never change the value of the string. Immutable objects are safe from unintended consequences.
# Even though tuples are immutable, they can still change. They still have safety in that scenario.
def process(lst):
lst.append(100)
return lst
my_list = [1,2,3]
process(my_list)
# the list's reference is passed to process(). We are appending 100 to what it currently points to.
# The contents of the list have changed. We have changed its state. my_list is still referencing the same.
# The list was modified by the function. The process method changed the state of the variable.
# Mutable objects are not safe from unintended side effects.
# -
# Immutable collection objects that contain mutable objects
def process(t):
t[0].append(3)
return t
my_tuple = ([1,2],'a')
process(my_tuple)
# when we call process(my_tuple), we have simply modified the three to that list. The memory address has stayed the same. The content of the first object has changed.
def process(s):
print('Initial s #: = {}'.format(id(s)))
s = s + ' world'
print('Final s #: = {}'.format(id(s)))
# since s is a string, it must be pointed to a new object
my_var = 'hello'
print('my_var # = {}'.format(id(my_var)))
process(my_var)
id(my_var)
# +
# id of my var is still the original version. It hasn't changed and therefore the value of my_var has not changed.
# -
my_var
def modify_list(lst):
print('Initial s #: = {}'.format(id(lst)))
lst.append(100)
print('Final s #: = {}'.format(id(lst)))
my_list = [1,2,3]
id(my_list)
modify_list(my_list)
# +
# the memory address does not change after appending an object to a list.
# the id of my_list, dealing with the same object
# -
id(my_list)
my_list
# +
#because lists are mutable objects, we can modify. mutable objects do not have the safety. Immutable objects are safe to a certain degree.
# -
def modify_tuple(t):
print('Initial t #: = {}'.format(id(t)))
t[0].append(100)
print('Final t #: = {}'.format(id(t)))
my_tuple = ([1,2],'a')
id(my_tuple)
modify_tuple(my_tuple)
# +
# the tuples memory address has not changed. If we print my_tuple out, it is stil the same.
# +
#Immutable object cannot change. Cannot modify the containment of elements in the tuple. However, the element in a tuple is mutable.
#The tuple's value has changed. Immutable means things can still change.
# -
# # Shared References and Mutability
# The term shared reference is the concept of two variables referencing the same object in memory (i.e. having the same memory address)
a = 10
b=a
def my_func(v):
t=20
my_func(t)
id(a)
id(b)
s1 = 'hello'
s2 = 'hello'
id(s1)
# +
# in both these cases, Python's memory manager decides to automatically re-use the memory references.
# Yes, this is safe because it is immutable.
# When working with mutable objects, have to be more careful
# -
a = [1,2,3]
b=a
b.append(100)
id(a)
id(b)
a
# +
# with mutable objects, the Python memory manager will never create shared references.
# -
a = [1,2,3]
b = [1,2,3]
id(a)
id(b)
a = "hello"
b = a
hex(id(a))
hex(id(b))
#they are pointing to the same memory address due to immutability.
a = "hello"
b = "hello"
hex(id(a))
hex(id(b))
#here we will understand why it is doing that and if it's safe to do.
b = "hello world"
hex(id(b))
b=a
hex(id(a))
a
b
a = [1,2,3]
b = a
hex(id(a))
hex(id(b))
hex(id(a))
b.append(100)
a
b
a = [1,2,3]
b=a
hex(id(a))
hex(id(b))
# +
# need to be careful with mutable objects
# shared reference that Python does automatically
# -
a=10
b=10
id(a)
id(b)
a = 500
b=500
id(a)
id(b)
# +
# it is not always a shared reference for integers. weird
# -
# # Variable Equality
# We can think of variabile equality in two fundamental ways (memory address, or object state/data)
# Might not have same memory address
# The memory address is an identity operator.
# var_1 is var_2. this compares memory addresses.
# use the equality operator, ==, to see if the data is the same, var_1 == var_2
# negation is not. var_1 is not var_2. not(var_1 is var_2)
# != is not equal to in Python. var_1 != var_2.
# not(var_1 == var_2)
a=10
b=a
a is b
a ==b
#they both have same values and same memory address.
a= 'hello'
b= 'hello'
a is b
# as we'll see later, don't count on it. is compares memory addresses.
a == b
a = [1,2]
b = [1,2]
a is b
a == b
a = 10
b= 10.0
a is b
a ==b
# +
#floats versus integers. The two values are still equal despite different types.
# -
# The None Object can be assigned to variables to indicate that they are not set (in the way we would expect to be), i.e. an "empty" value (or null pointer)
# The none object is a real objectr managed by Python memory manager
# The memory manager will always use a shared reference when assigning a variable to None.
a = None
b= None
c=None
a is b
a == b
# +
#We can test if a variable is "not set" or "empty" by comparing it's memory address to the memory address of None using the is operator
# -
a is None
b is None
x = 10
x is None
x is not None
a = 10
b = 10
id(a)
id(b)
a is b
a==b
a = 500
b = 500
id(a)
id(b)
a is b
a ==b
a = [1,2,3]
b=[1,2,3]
a is b
a ==b
a =10
b = 10.0
a is b
a ==b
a = 10+0j
type(a)
type(b)
a is b
a==b
id(None)
type(None)
a = None
b=None
a is b
a is c
a is None
b is None
id(c)
a ==c
# # Everything is an Object
# +
# Everything is an object.
# Functions (function) is an object
# Classes (class) is an object
# Types (type)
# This means all of these have memory addresses.
# -
def my_func(x):
print(x)
#my_func points to a memory address with a function and a state
id(my_func)
# Any object can be assigned to a variable (ncluding functions)
# Any object can be passed to a function (including functions)
# Any object can be returned from a function (including functions)
# +
#my_func is the name of the function.
#my_func() with parantheses invokes the function
# +
#the function name excludes the parantheses, which means we are calling the function
# -
a=10
print(type(a))
b = int(10)
b
print(type(b))
#classes can have built in documentation.
help(int)
c = int()
c
c = int('101', base=2)
c
def square(a):
return a **2
type(square)
print(type(square))
f = square
id(square)
id(f)
f is square
square(2)
f(2)
def cube(a):
return a **3
def select_function(fn_id):
if fn_id == 1:
return square
else:
return cube
select_function(1)
f = select_function(0)
f is square
f is cube
f is cube
f(3)
select_function(1)(3)
# +
#function can be passed to a function
# -
def exec_function(fn, n):
return fn(n)
exec_function(square,3)
exec_function(square,3)
# # Python Optimizations (Interning)
# +
# we are using cPython, the standard Python implementation
#Jython (written in Java)
# IronPython targets .net CLR
# PyPy written in RPython which is a statically-typed subset of Python written in C that is specifically designed to write interpreters.
# There are multiple versions
# -
a = 10
b = 10
a is b
a = 500
b =500
a is b
#why different addresses? Interning is reusing objects on-demand.
#at startup, Python caches a global list of integers in the range [-5,256]
# any time an integer is referenced in that range, Python will use the cached version of that object.
# Singleton objects are in the [-5,256] integer range. They can only be instantiated once.
# Optimization strategy - small integers show up often.
# Do not want to create memory overhead. Just cache a certain number.
a = 10
#Python has to point to the existing reference for 10
a =257
#Python does not use the global list and a new object is created every time.
a = 257
b=257
id(a) == id(b)
#only way to change a is to change a's reference.
a = -5
b=-5
id(a) == id(b)
a is b
a = 256
b=256
a is b
a = 10
b = int(10)
c = int('10')
d = int('1010',2)
id(a) == id(b) == id(c) == id(d)
a is b is c is d
# +
# the memory addresses are all the same.
# -
# # String Interning
# +
# Some strings are cached, or interned, by Python.
# as the python code is compiled, identifiers are cached.
# variable names, function names, class names, etc. Identifiers must with _ or a letter
# Some string literals may also be automatically interned.
# string literals that look like identifiers (e.g. 'hello_world')
# Python is all about speed and memory optimization
# -
# Python, both internally and in the code you write, deals with lots of dictionary type lookups on string keys, which means a lot of string equality testing.
a = 'some_long_string'
b = 'some_long_string'
a == b
# +
#if we know that some_long_string has been interned, then a and b are the same strings if they both point to the same memory address.
# -
a is b #compares two integers. this is much faster.
# +
#Not all strings are automatically interned by python.
# can force strings to be interned by using the sys.intern() method.
import sys
a= sys.intern('the quick brown fox')
b = sys.intern('the quick brown fox')
# this allows for quick caching
# -
a is b
# +
#should do this when dealing with a large amount of string that could have high repetition. e.g. tokenizing a large corpus of text (NLP)
# every string could reduce memory overhead using string interning.
# this can also allow for quick string comparisons.
# can have lots of string comparisons with this methodology.
# in general, until you find that you need it, don't use string interning until you need to do it.
# -
a = 'hello'
b = 'hello'
id(a) == id(b)
a = 'hello world'
b = 'hello world'
id(a) == id(b)
# do not assume string interning will happen.
a == b
a = 'hello'
b = 'hello'
a is b
# +
#when strings are interne, they share the same memory addresses.
# -
a = '_this_is_a_long_string_that_could_be_used_as_identifier'
b = '_this_is_a_long_string_that_could_be_used_as_identifier'
a is b
# +
# as long as it looks like an identifier, it will be stringed automatically.
# +
# it will intern strings with the underscoring. do not have to rely on it.
# -
import sys
a = sys.intern('hello world')
b = sys.intern('hello world')
c = 'hello world'
id(a) == id(b)
id(a) == id(c)
# +
# if you are going to intern the string, you need to intern all of the strings. if I know a and b are interned strings, can compare the values
# -
a == b
a is b
a is c
a == c
def compare_using_equals(n):
a = 'a long string that is not interned' * 200
b = 'a long string that is not interned' * 200
for i in range(n):
if a == b:
pass
def compare_using_interning(n):
a = sys.intern('a long string that is not interned' * 200)
b = sys.intern('a long string that is not interned' * 200)
for i in range(n):
if a is b:
pass
import time
start = time.perf_counter()
compare_using_equals(10000000)
end = time.perf_counter()
print('equality', end - start)
start = time.perf_counter()
compare_using_interning(10000000)
end = time.perf_counter()
print('equality', end - start)
# +
#faster to do interning, but it takes more effort.
# -
# # Python Optimizations Peepholes
# +
# this is another variety of optimizations that can occur at compile time.
# every time you restart application, code might recompile.
# Constant expressions sometimes get optimized.
# numberic calculations 24*60. It might have to re-calculate 24*60 each time.
# Python will actually pre-calculate 24*60 --> 1440
# When Python compiles this code, it will pre-calculate.
# Constant expression
# -
# Short sequences length < 20
(1,2)*5
# this gets precalculated
'abc'*3
'hello' + ' world' # will also use pre-calculated values
# +
#however, if it's greater than 20 characters, it does not get stored. How much overhead do we want versus the speed?
# -
# Membership Tests: Mutables are replaced by immutables.
# When membership tests such as:
#are encoutered, the constant is replaced by its immutable counterpart
# +
# lists change to tuples
# sets change to frozensets.
# set membership is much faster than list of tuple membership (sets are basically like dictionaries)
# it is much faster to do a set lookup in a dictionary; a list is much slower because you have to go through it sequentially.
# hashmaps much faster that lists.
# if e in [1,2,3]: or if e in (1,2,3):
# best to write if e in {1,2,3}:
# consider using sets instead of lists or tupl;es
# -
def my_func():
a = 24*60
b = (1,2)*5
c = 'abc'*3
d = 'ab'*11
e = 'the quick brown fox' * 5
f = ['a','b'] * 3 #will be a list with 6 elements in that list.
# a# li
my_func.__code__.co_consts
# +
# lots of the answers are pre-calculated. they are new constants. some did not get pre-calculated.
# -
def my_func(e):
if e in [1,2,3]:
pass
my_func.__code__.co_consts
# +
# the list transitioned over to a tuple of (1,2,3) transitioned to an immutable object.
# -
def my_func(e):
if e in {1,2,3}:
pass
my_func.__code__.co_consts
#this turns into a frozen set.
# want to compare mutable versus immutable membership and performance
# set membership is much more efficient than strings or tuples.
import string
import time
string.ascii_letters
# +
#contains lower and upper case letters.
# -
char_list = list(string.ascii_letters)
char_tuple = tuple(string.ascii_letters)
char_set = set(string.ascii_letters)
# the set constructor creates a set out of characters. Sets ignore repeating characters
print(char_list)
print(char_tuple)
print(char_set)
# +
#lists and tuples are ordered sequences
# sets are not ordered sequences, it can be random order.
# in no particular order, like a dictionary
# -
def membership_test(n, container):
for i in range(n):
if 'z' in container:
#python is highly polymorphic. more interested in a type that has certain properties
pass
start = time.perf_counter()
membership_test(10000000, char_list)
end = time.perf_counter()
print('list: ', end-start)
start = time.perf_counter()
membership_test(10000000, char_tuple)
end = time.perf_counter()
print('tuple: ', end-start)
start = time.perf_counter()
membership_test(10000000, char_set)
end = time.perf_counter()
print('set: ', end-start)
# +
# set membership is way faster. whenever possible, use set membership
# -
| udemycoursework/Python 3 Deep Dive (Part 1 Function Notes).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Presidential Races Analysis
# ## 2020 Trump/Biden Election
# +
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from tabulate import tabulate
# processing data
def clean_data(filename): # removes any lines with nan values
df = pd.read_csv(filename)
#replacing empty entries with nan
df.replace(r'', np.nan)
#cleaning data
cleaned_df = df[~pd.isnull(df).any(axis = 1)]
return cleaned_df
df = clean_data("2020_President_General_Election_including_precincts_and_demographics.csv")
f = sns.lmplot(x="Black Percentage", y="Biden Percentage", data=df, height = 4, aspect = 2.5);
plt.title("2020 Biden Percentage of Votes by Black Percentage")
f.savefig('2020_BPBiden.png', dpi=300)
# -
BP_Biden = df[["Black Percentage", "Biden Percentage"]]
correlation = BP_Biden.corr(method='pearson')
print(correlation)
from IPython.display import display, HTML
df = df.sort_values(by='Black Percentage', ascending=False)[["Ward", "Pct", "Biden Percentage", "Trump Percentage", "Black Percentage"]]
display(HTML(df.to_html()))
g = sns.lmplot(x="Black Percentage", y="Trump Percentage", data=df, height = 4, aspect = 2.5);
plt.title("2020 Trump Percentage of Votes by Black Percentage")
g.savefig('2020_BPTrump.png', dpi=300)
BP_Trump = df[["Black Percentage", "Trump Percentage"]]
correlation2 = BP_Trump.corr(method='pearson')
print(correlation2)
# ## 2016 Trump/Clinton Election
df2 = clean_data("2016_President_General_Election_including_precincts_and_demographics.csv")
m = sns.lmplot(x="Black Percentage", y="Clinton Percentage", data=df2, height = 4, aspect = 2.5);
plt.title("2016 Clinton Percentage of Votes by Black Percentage")
m.savefig('2016_BPClinton.png', dpi=300)
BP_Clinton = df2[["Black Percentage", "Clinton Percentage"]]
correlation3 = BP_Clinton.corr(method='pearson')
print(correlation3)
n = sns.lmplot(x="Black Percentage", y="Trump Percentage", data=df2, height = 4, aspect = 2.5);
plt.title("2016 Trump Percentage of Votes by Black Percentage")
n.savefig('2016_BPTrump.png', dpi=300)
BP_Trump2016 = df2[["Black Percentage", "Trump Percentage"]]
correlation4 = BP_Trump2016.corr(method='pearson')
print(correlation4)
| Write-up - Code/Presidential Races/PresidentialAnalysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Iris Data Visualizations
#
#
#
#
# +
#Importing necessary libraries for Data presentation and visualization.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
# -
#Reading csv file downloaded from kaggle in a data frame presentation.
Iris=pd.read_csv('iris.data.csv',header=None)
# +
#Exploring top 5 row of Data.
Iris.columns=['Sepal_L_cm','Sepal_W_cm','Petal_L_cm','Petal_W_cm','Species']
# -
Iris.head()
Iris.shape
# +
Iris.describe()
# -
Iris.info()
Iris.groupby('Species').size()
Iris.isnull().sum()
Iris.plot(kind='box', subplots=True, layout=(2,2),figsize=(10,10),grid=True)
plt.show()
Iris.hist(figsize=(10,10))
plt.show()
# +
sns.pairplot(Iris,hue='Species',diag_kind='hist')
sns.set_style('dark')
# -
Iris.head()
sns.jointplot(x=['Sepal_L_cm'],y=['Sepal_W_cm'],data=Iris,kind="reg")
sns.set_style(style='darkgrid')
sns.jointplot(x=['Petal_L_cm'],y=['Petal_W_cm'],data=Iris,kind="reg")
sns.set_style(style='darkgrid')
| Iris Visuals.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Poission GLM (Attempt 1)
#
# Below are the different GLM methods possible. Initially we take Xell's code and clean it a little.
#
# First all package imports have been collated for ease.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
import seaborn as sns
from sklearn.linear_model import PoissonRegressor
from sklearn.model_selection import train_test_split
# Next we simply import our data and get it into the format required. We are firslty looking to tackle the 31-day data to start off with.
# +
#Read the data into the file.
fullData = pd.read_csv("31DayDataUpdate.csv")
#Create a dataframe from the relevant columns.
df = fullData[['Quarter', 'HB', 'CancerType','NumberOfEligibleReferrals31DayStandard','NumberOfEligibleReferralsTreatedWithin31Days']]
#Remove the 'all cancer types' rows from the dataframe.
df = df[df['CancerType'] != 'All Cancer Types']
df = df[df['NumberOfEligibleReferrals31DayStandard'].notna()]
# -
# The following may be of use when looking at the correlation between the two sets of numerical values which we have here. We can also identify all the data types within our frame.
# +
#Correlation of the Eligible Referrals with the Eligible Referalls Treated.
rho = df.corr()
#print(rho)
#View of the whole data frame.
types = df.dtypes
#print(types)
# -
# Next we take an overview of the different cancers within the data we have in our set. We firstly achieve four different graphs which are explained below the output, before also looking at the boxplot in the situation.
sns.pairplot(df, hue='CancerType', height=2.5, aspect=1)
sns.boxplot(y='NumberOfEligibleReferrals31DayStandard', x='CancerType',data=df)
# Next we look to form the variables in the correct way. This is the first part of building our GLM.
#
# ## 0. Correct form of data for a GLM
# +
# choose explanatory variables - note we can also include 'Quarter', 'CancerType' and 'Sex' here.
X = df[['HB', 'CancerType']]
# turn our catergories into dummies.
X = pd.get_dummies(data=X, drop_first=True)
#X.head()
# choose which column is the targeted output data.
Y = df['NumberOfEligibleReferrals31DayStandard']
#Y.head()
# -
# ## 1. SKLearn
# Below we create our GLM model using the SKLearn method.
# +
#Build the model using SKLearn.
prSKLearn = PoissonRegressor(alpha=0, fit_intercept=True)
#Fit the model using the build above.
prSKLearn.fit(X, Y)
parameters = prSKLearn.get_params()
score = prSKLearn.score(X, Y)
#Should we want to see the values of each of the intercepts we can do so by uncommenting the below.
#print(prSKLearn.intercept_)
print(score)
#I need to check what the below actually does...
coeff_parameter = pd.DataFrame(prSKLearn.coef_, X.columns,columns=['Coefficient'])
# -
# Next we use instead use our data in a split manner in order to try and see whether the GLM achieves a suitable outcome (from https://medium.com/analytics-vidhya/implementing-linear-regression-using-sklearn-76264a3c073c).
#
# +
#Split our data into test and train.
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.5)
#Use our training data to let the SKLearn model learn
prSKLearn.fit(X_train, y_train)
#Get predictions for the test data using the SKLearn model.
predictions = prSKLearn.predict(X_test)
# -
#Quantify the useful nature of the model using the R2 value.
print(prSKLearn.score(X_train, y_train))
#Create a regressional plot to show
sns.regplot(y_test, predictions)
# ## 2. StatsModels
# Next we use the StatsModels package to create the GLM.
# +
#Add the X to the constants.
XSM = sm.add_constant(X)
#Create the model.
ls=sm.OLS(Y,XSM).fit()
#Print the summary of the model.
print(ls.summary())
# -
# ----------------------------------------------------------------------
#
# # Poisson GLM (Attempt 2)
# Firstly below we read our data in different ways, and furthermore edit the data to a certain extent to make it easier for handling. We also then provide some summary statistics and graphs.
# +
#Import the 31 day standard data.
Data31Read = pd.read_csv("31DayDataUpdate.csv")
Data31 = Data31Read[['Quarter', 'HB', 'CancerType','NumberOfEligibleReferrals31DayStandard','NumberOfEligibleReferralsTreatedWithin31Days']]
#Import the 62 day standard data.
Data62Read = pd.read_csv("62DayDataUpdate.csv")
Data62 = Data62Read[['Quarter', 'HB', 'CancerType','NumberOfEligibleReferrals62DayStandard','NumberOfEligibleReferralsTreatedWithin62Days']]
#Import the weekly cancer data.
WeekData = pd.read_csv("cancerdata.csv")
# +
#Make edits to the data
##31Day Edits start here.
df31 = Data31
#Remove NaNs and 'all cancer types'
df31 = df31[df31['NumberOfEligibleReferrals31DayStandard'].notna()]
df31 = df31[df31['NumberOfEligibleReferralsTreatedWithin31Days'].notna()]
df31 = df31[df31['CancerType'] != 'All Cancer Types']
# add a numerical variable 1-1 to quarters and an index variable before/after pandemic
quarters = df31['Quarter']
date = np.zeros(len(quarters))
quars = df31['Quarter'].unique()
dates = np.arange(len(quars))
pandemic = np.zeros(len(quarters))
x = np.where(quars == '2020Q2') # change to decide in which quarter the pandemic begins
pandemic = np.zeros(len(quarters))
x = np.where(quars == '2020Q2')
j=0
for i in np.arange(len(quarters)):
y = np.where(quars == quarters[i])
date[i] = dates[y]
if dates[y] > x:
pandemic[i] = dates[y]-x
df31['Date'] = date.tolist()
df31['Pandemic'] = pandemic.tolist()
##Do the same with 62 days data
df62 = Data62
#Remove NaNs and 'all cancer types'
df62 = df62[df62['NumberOfEligibleReferrals62DayStandard'].notna()]
df62 = df62[df62['NumberOfEligibleReferralsTreatedWithin62Days'].notna()]
df62 = df62[df62['CancerType'] != 'All Cancer Types']
# add a numerical variable 1-1 to quarters and an index variable before/after pandemic
quarters = df62['Quarter']
date = np.zeros(len(quarters))
quars = df62['Quarter'].unique()
dates = np.arange(len(quars))
pandemic = np.zeros(len(quarters))
x = np.where(quars == '2020Q2') # change to decide in which quarter the pandemic begins
pandemic = np.zeros(len(quarters))
x = np.where(quars == '2020Q2')
j=0
for i in np.arange(len(quarters)):
y = np.where(quars == quarters[i])
date[i] = dates[y]
if dates[y] > x:
pandemic[i] = dates[y]-x
df62['Date'] = date.tolist()
df62['Pandemic'] = pandemic.tolist()
#Edit weekly data
dfW = WeekData
#Remove NaNs and cumulative data.
dfW = dfW[dfW['CancerType'] != 'All Cancers']
dfW = dfW[dfW['Age Group'] != 'All Ages']
dfW = dfW[dfW['Sex'] != 'All']
dfW = dfW[dfW['Count'].notna()]
months = np.asarray(dfW['Month'])
date = np.zeros(len(months))
quars = dfW['Month'].unique()
dates = np.arange(len(quars))
pandemic = np.zeros(len(months))
x = np.where(quars == 202003)
for i in np.arange(len(months)):
y = np.where(quars == months[i])
date[i] = dates[y]
if dates[y] > x:
pandemic[i] = dates[y]-x
dfW['Date'] = date.tolist()
dfW['Pandemic'] = pandemic.tolist()
# +
# take a look at what we have
Cor31 = df31.corr()
Cor62 = df62.corr()
CorW = dfW.corr()
# plot eligibles per cancer type
plt.figure(figsize=(15,8))
ax =sns.boxplot(y='NumberOfEligibleReferrals31DayStandard', x='CancerType', data=df31)
plt.show()
plt.figure(figsize=(15,8))
ax =sns.boxplot(y='NumberOfEligibleReferrals62DayStandard', x='CancerType', data=df62)
plt.show()
plt.figure(figsize=(15,8))
ax =sns.boxplot(y='Count', x='CancerType', data=dfW)
plt.show()
# -
# ## 3. Hybrid Inputs
# Next we take Xell's code which is in more of a functional mode.
#Define a function that fits poisson regression.
def poissonGLM(X, Y, Train):
'''
inputs:
X: explanatory variables (dataframe)
Y: output variable (dataframe)
train: do training or not (boolean)
outputs:
parameters: possion regressor parameters
intercept: value of independetn term (y intercept),
coefficients: coefficients of explanatory vairables (all linera)
y_test: testing data
predictions: predicted data
stats : summary of statistics of the predictive power of the model
'''
#Turn categorical into dummies.
X = pd.get_dummies(data=X, drop_first=True)
#Build model.
prFunction = PoissonRegressor(alpha=0, fit_intercept=True, max_iter = 10000)
#Fit model.
prFunction.fit(X, Y)
#Recover model information.
parameters = prFunction.get_params()
intercept = prFunction.intercept_
coefficients = pd.DataFrame(prFunction.coef_,X.columns, columns=['Coefficient'])
#Initialise training parameters.
y_train = 0
predictions = 0
stats = 0
if Train==1:
#Split data into train and test (test_size specifies %).
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2)
#Fit training data.
prFunction.fit(X_train, y_train)
#Use model to predict test data outputs.
predictions = prFunction.predict(X_test)
#Also now run the Statsmodels version of prediction.
XSM = sm.add_constant(X)
ls = sm.OLS(Y, X).fit()
stats = ls.summary()
return parameters, intercept, coefficients, y_test, predictions, stats
# +
#Create the options for explanatory and output data.
#FOR 31 DAYS DATA
#Choose explanatory variables
X31 = df31[['Date','CancerType','HB']] #no pandemic
X31_p = df31[['Pandemic','CancerType','HB']] #pandemic, no date
X31_dp = df31[['Date','Pandemic','CancerType','HB']] #both
#Choose output data
Y31 = df31['NumberOfEligibleReferrals31DayStandard']
Y31t = df31['NumberOfEligibleReferralsTreatedWithin31Days']
#FOR 62 DAYS DATA
#Choose explanatory variables
X62 = df62[['Date','HB','CancerType']] #no pandemic
X62_p = df62[['Pandemic','CancerType','HB']] #pandemic, no date
X62_dp = df62[['Date','Pandemic','CancerType','HB']] #both
#Choose output data
Y62 = df62['NumberOfEligibleReferrals62DayStandard']
Y62t = df62['NumberOfEligibleReferralsTreatedWithin62Days']
## FOR WEEKLY DIAGNOSIS DATA
XW = dfW[['Date','HB', 'Sex','Age Group']]
XW_p = dfW[['Pandemic','HB', 'Sex','Age Group']]
XW_dp = dfW[['Pandemic','Date','HB', 'Sex','Age Group']]
#Choose output data
YW = dfW['Count']
# +
#Choose explanatory and output variables from above sets.
X=X31_dp
Y=Y31
#Run Poisson regression for chosen data
parameters, intercept, coefficients, y_test, predictions, stats = poissonGLM(X, Y, 1)
# +
# take a look at results of Poisson Regressor
print(intercept)
print(coefficients[1:2])
# check predictive power
sns.regplot(y_test,predictions)
# take a look at results of Statsmodels
print(stats)
# -
# -----------
# # Analysis of vartiation of $\epsilon$
#
# +
##31Day Edits start here.
df31e = Data31
#Remove NaNs and 'all cancer types' and add a numerical variable 1-1 to quarters
df31e = df31e[df31e['NumberOfEligibleReferrals31DayStandard'].notna()]
df31e = df31e[df31e['NumberOfEligibleReferralsTreatedWithin31Days'].notna()]
df31e = df31e[df31e['CancerType'] != 'All Cancer Types']
quarters = df31e['Quarter']
date = np.zeros(len(quarters))
quars = df31e['Quarter'].unique()
dates = np.arange(len(quars))
CovQuarters = ['2020Q1', '2020Q2', '2020Q3', '2020Q4']
CoefHold = []
for i in CovQuarters:
#index variable before/after pandemic
pandemic = np.zeros(len(quarters))
x = np.where(quars == i) # change to decide in which quarter the pandemic begins
pandemic = np.zeros(len(quarters))
x = np.where(quars == i)
j=0
for j in np.arange(len(quarters)):
y = np.where(quars == quarters[j])
date[j] = dates[y]
if dates[y] > x:
pandemic[j] = dates[y]-x
df31e['Date'] = date.tolist()
df31e['Pandemic'] = pandemic.tolist()
X31_dpe = df31e[['Date','Pandemic','CancerType','HB']]
Y31e = df31e['NumberOfEligibleReferrals31DayStandard']
X=X31_dpe
Y=Y31e
parameters, intercept, coefficients, y_test, predictions, stats = poissonGLM(X, Y, 1)
newCoef = coefficients[1:2].to_numpy()
CoefHold.append(newCoef[0][0])
print(CoefHold)
# +
##31Day Edits start here.
df62e = Data62
#Remove NaNs and 'all cancer types' and add a numerical variable 1-1 to quarters
df62e = df62e[df62e['NumberOfEligibleReferrals62DayStandard'].notna()]
df62e = df62e[df62e['NumberOfEligibleReferralsTreatedWithin62Days'].notna()]
df62e = df62e[df62e['CancerType'] != 'All Cancer Types']
quarters = df62e['Quarter']
date = np.zeros(len(quarters))
quars = df62e['Quarter'].unique()
dates = np.arange(len(quars))
CovQuarters = ['2020Q1', '2020Q2', '2020Q3', '2020Q4']
CoefHold = []
for i in CovQuarters:
#index variable before/after pandemic
pandemic = np.zeros(len(quarters))
x = np.where(quars == i) # change to decide in which quarter the pandemic begins
pandemic = np.zeros(len(quarters))
x = np.where(quars == i)
j=0
for j in np.arange(len(quarters)):
y = np.where(quars == quarters[j])
date[j] = dates[y]
if dates[y] > x:
pandemic[j] = dates[y]-x
df62e['Date'] = date.tolist()
df62e['Pandemic'] = pandemic.tolist()
X62_dpe = df62e[['Date','Pandemic','CancerType','HB']]
Y62e = df62e['NumberOfEligibleReferrals62DayStandard']
X=X62_dpe
Y=Y62e
parameters, intercept, coefficients, y_test, predictions, stats = poissonGLM(X, Y, 1)
newCoef = coefficients[1:2].to_numpy()
CoefHold.append(newCoef[0][0])
print(CoefHold)
| .ipynb_checkpoints/COPoissionGLM-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # params
# +
PRFX = 'CVKfld0920-1'
p_o = '../output/{PRFX}'
from pathlib import Path
Path(p_o).mkdir(exist_ok=True)
SEED = 111
K = 5
BS = 40
SZ = 512
FP16 = True
DO_TTA = False
epochs_freeze = 14
epochs_unfreeze = 2
dbg = False
if dbg: dbgsz = 500
# +
'''
get_transforms(do_flip:bool=True, flip_vert:bool=False, max_rotate:float=10.0, max_zoom:float=1.1,
max_lighting:float=0.2, max_warp:float=0.2, p_affine:float=0.75, p_lighting:float=0.75,
xtra_tfms:Optional[Collection[Transform]]=None) → Collection[Transform]
'''
from fastai.vision import *
params_tfms = dict(
max_lighting=0.1,
max_warp=0,
max_rotate=0,
max_zoom=0,)
resize_method = ResizeMethod.PAD
padding_mode = 'zeros'
# -
# # setup
# +
from fastai.vision import *
from torchvision.models.resnet import ResNet, Bottleneck
import cv2
from sklearn.model_selection import StratifiedKFold
from fastai.utils.mod_display import *
import random
import numpy as np
import torch
import os
def set_torch_seed(seed=SEED):
os.environ['PYTHONHASHSEED'] = str(seed)
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
set_torch_seed()
from fastai import *
from fastai.vision import *
from fastai.callbacks import *
import scipy as sp
from sklearn.metrics import cohen_kappa_score
def quadratic_weighted_kappa(y1, y2):
return cohen_kappa_score(y1, y2, weights='quadratic')
import datetime
def timestr(): return datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
# -
# ## crop
# +
def crop_margin(image, keep_less=0.83):
output = image.copy()
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
ret,gray = cv2.threshold(gray,10,255,cv2.THRESH_BINARY)
contours,hierarchy = cv2.findContours(gray,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
if not contours:
#print('no contours!')
flag = 0
return image, flag
cnt = max(contours, key=cv2.contourArea)
((x, y), r) = cv2.minEnclosingCircle(cnt)
r = r*keep_less
x = int(x); y = int(y); r = int(r)
flag = 1
#print(x,y,r)
if r > 100:
return output[0 + (y-r)*int(r<y):-1 + (y+r+1)*int(r<y),0 + (x-r)*int(r<x):-1 + (x+r+1)*int(r<x)], flag
else:
#print('none!')
flag = 0
return image,flag
# https://stackoverflow.com/questions/16646183/crop-an-image-in-the-centre-using-pil
def center_crop(img):
h0, w0 = 480, 640 #most common in test
ratio = h0/w0 #most common in test
height, width, _= img.shape
new_width, new_height = width, math.ceil(width*ratio)
width = img.shape[1]
height = img.shape[0]
if new_width is None:
new_width = min(width, height)
if new_height is None:
new_height = min(width, height)
left = int(np.ceil((width - new_width) / 2))
right = width - int(np.floor((width - new_width) / 2))
top = int(np.ceil((height - new_height) / 2))
bottom = height - int(np.floor((height - new_height) / 2))
if len(img.shape) == 2:
center_cropped_img = img[top:bottom, left:right]
else:
center_cropped_img = img[top:bottom, left:right, ...]
return center_cropped_img
def open_yz(fn, convert_mode, after_open)->Image:
image = cv2.imread(fn)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image, _ = crop_margin(image)
image = center_crop(image)
image = cv2.resize(image, (640, 480))
image = cv2.addWeighted ( image,4, cv2.GaussianBlur( image , (0,0) , sigmaX=10) ,-4 ,128)
return Image(pil2tensor(image, np.float32).div_(255))
vision.data.open_image = open_yz
# -
# ## TTTA
# +
from fastai.core import *
from fastai.basic_data import *
from fastai.basic_train import *
from fastai.torch_core import *
def _tta_only(learn:Learner, ds_type:DatasetType=DatasetType.Valid, num_pred:int=5) -> Iterator[List[Tensor]]:
"Computes the outputs for several augmented inputs for TTA"
dl = learn.dl(ds_type)
ds = dl.dataset
old = ds.tfms
aug_tfms = [o for o in learn.data.train_ds.tfms if o.tfm !=zoom]
try:
pbar = master_bar(range(num_pred))
for i in pbar:
ds.tfms = aug_tfms
yield get_preds(learn.model, dl, pbar=pbar)[0]
finally: ds.tfms = old
Learner.tta_only = _tta_only
def _TTA(learn:Learner, beta:float=0, ds_type:DatasetType=DatasetType.Valid, num_pred:int=5, with_loss:bool=False) -> Tensors:
"Applies TTA to predict on `ds_type` dataset."
preds,y = learn.get_preds(ds_type)
all_preds = list(learn.tta_only(ds_type=ds_type, num_pred=num_pred))
avg_preds = torch.stack(all_preds).mean(0)
if beta is None: return preds,avg_preds,y
else:
final_preds = preds*beta + avg_preds*(1-beta)
if with_loss:
with NoneReduceOnCPU(learn.loss_func) as lf: loss = lf(final_preds, y)
return final_preds, y, loss
return final_preds, y
Learner.TTA = _TTA
# + [markdown] _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
# # prep
# +
img2grd = []
p = '../input/aptos2019-blindness-detection'
pp = Path(p)
train = pd.read_csv(pp/'train.csv')
test = pd.read_csv(pp/'test.csv')
len_blnd = len(train)
len_blnd_test = len(test)
img2grd_blnd = [(f'{p}/train_images/{o[0]}.png',o[1]) for o in train.values]
len_blnd, len_blnd_test
# -
img2grd += img2grd_blnd
display(len(img2grd))
display(Counter(o[1] for o in img2grd).most_common())
if not np.all([Path(o[0]).exists() for o in img2grd]): print('Some files are missing!!!')
df = pd.DataFrame(img2grd)
df.columns = ['fnm', 'target']
display(df.shape)
df.target.value_counts()
# https://www.kaggle.com/chanhu/eye-inference-num-class-1-ver3 LB 0.77
#
# [0.57, 1.37, 2.57, 3.57]
# 2 1226
# 0 326
# 3 200
# 1 152
# 4 24
if dbg:
df = df.head(dbgsz)
set_torch_seed()
idx_blnd_train = np.where(df.fnm.str.contains('aptos2019-blindness-detection/train_images'))[0]
idx_val = np.random.choice(idx_blnd_train, int(len_blnd*0.10), replace=False)
df['is_val']=False
df.loc[idx_val, 'is_val']=True
# +
# %%time
tfms = get_transforms(**params_tfms)
def get_data(sz, bs):
src = (ImageList.from_df(df=df,path='./',cols='fnm')
.split_from_df(col='is_val')
.label_from_df(cols='target',
label_cls=FloatList)
)
data= (src.transform(tfms, size=sz,
resize_method=resize_method,
padding_mode=padding_mode) #Data augmentation
.databunch(bs=bs) #DataBunch
.normalize(imagenet_stats) #Normalize
)
return data
bs = BS
sz = SZ
set_torch_seed()
data = get_data(sz, bs)
# -
# %%time
data.show_batch(rows=3, figsize=(7,6))
# ## test set
learn = cnn_learner(data,
base_arch = models.resnet50,
path=p_o)
learn.loss = MSELossFlat
if FP16: learn = learn.to_fp16()
df_test = pd.read_csv('../input/aptos2019-blindness-detection/test.csv')
df_test.head()
if dbg:
df_test = df_test.head(dbgsz)
learn.data.add_test(
ImageList.from_df(df_test,
'../input/aptos2019-blindness-detection',
folder='test_images',
suffix='.png'))
# %%time
data.show_batch(rows=3, figsize=(7,6), ds_type=DatasetType.Test)
# # model
# +
# %%time
# Downloading: "https://download.pytorch.org/models/resnet50-19c8e357.pth" to /tmp/.cache/torch/checkpoints/resnet50-19c8e357.pth
# Making pretrained weights work without needing to find the default filename
if not os.path.exists('/tmp/.cache/torch/checkpoints/'):
os.makedirs('/tmp/.cache/torch/checkpoints/')
# !cp '../input/pytorch-vision-pretrained-models/resnet50-19c8e357.pth' '/tmp/.cache/torch/checkpoints/resnet50-19c8e357.pth'
# +
learn = cnn_learner(data,
base_arch = models.resnet50,
path=p_o)
learn.loss = MSELossFlat
if FP16: learn = learn.to_fp16()
# -
# # train
# + active=""
# learn.freeze()
# + active=""
# %%time
# learn.lr_find(start_lr=1e-5)
# + active=""
# !nvidia-smi
# + active=""
# learn.recorder.plot(suggestion=True)
# -
# ## Kfold
skf = StratifiedKFold(n_splits=K)
# for trn_idx, val_idx in skf.split(df, df.target):
# print(df.target[trn_idx].value_counts())
# for trn_idx, val_idx in skf.split(df, df.target):
# print(df.target[val_idx].value_counts())
# for trn_idx, val_idx in skf.split(df, df.target):
# print(val_idx[:10])
# for trn_idx, val_idx in skf.split(df, df.target):
# print(len(trn_idx), len(val_idx))
# +
# %%time
set_torch_seed()
pred_val = np.zeros(len(df))
y_val = np.zeros(len(df))
preds_tst = np.zeros((K, len(df_test)))
for k, (trn_idx, val_idx) in enumerate(skf.split(df, df.target)):
print(f'[{timestr()}] k:', k)
df['is_val'] = 0
df.loc[val_idx, 'is_val']=1
data = get_data(sz, bs)
learn = cnn_learner(data,
base_arch = models.resnet50,
path=p_o)
learn.loss = MSELossFlat
if FP16: learn = learn.to_fp16()
print(f'[{timestr()}] train freeze')
set_torch_seed()
with progress_disabled_ctx(learn) as learn:
learn.fit_one_cycle(epochs_freeze, max_lr=1e-2,
callbacks=[SaveModelCallback(learn, name=f'bestmodel_frozen_{PRFX}_fld_{k}')])
print(f'[{timestr()}] train unfreeze')
learn.unfreeze()
with progress_disabled_ctx(learn) as learn:
learn.fit_one_cycle(epochs_unfreeze, max_lr=slice(1e-7, 1e-5),
callbacks=[SaveModelCallback(learn, name=f'bestmodel_finetune_{PRFX}_fld_{k}')])
print(f'[{timestr()}] inference val set')
learn = learn.load('bestmodel_finetune')
if FP16: learn = learn.to_fp32()
set_torch_seed()
with progress_disabled_ctx(learn) as learn:
pred_val_k, y_val_k = (learn.TTA(ds_type=DatasetType.Valid) if DO_TTA else
learn.get_preds(ds_type=DatasetType.Valid))
pred_val_k = pred_val_k.numpy().squeeze()
y_val_k= y_val_k.numpy()
pred_val[val_idx]=pred_val_k
y_val[val_idx]=y_val_k
print(f'[{timestr()}] inference test set')
set_torch_seed()
learn.data.add_test(
ImageList.from_df(df_test,
'../input/aptos2019-blindness-detection',
folder='test_images',
suffix='.png'))
with progress_disabled_ctx(learn) as learn:
pred_tst_k, _ = (learn.TTA(ds_type=DatasetType.Test) if DO_TTA else
learn.get_preds(ds_type=DatasetType.Test))
pred_tst_k = pred_tst_k.numpy().squeeze()
preds_tst[k] = pred_tst_k
del learn
gc.collect()
# -
pred_tst = preds_tst.mean(0)
# # rounder
# +
# https://www.kaggle.com/c/petfinder-adoption-prediction/discussion/88773#latest-515044
# We used OptimizedRounder given by hocop1. https://www.kaggle.com/c/petfinder-adoption-prediction/discussion/76107#480970
# put numerical value to one of bins
def to_bins(x, borders):
for i in range(len(borders)):
if x <= borders[i]:
return i
return len(borders)
class Hocop1OptimizedRounder(object):
def __init__(self):
self.coef_ = 0
def _loss(self, coef, X, y, idx):
X_p = np.array([to_bins(pred, coef) for pred in X])
ll = -quadratic_weighted_kappa(y, X_p)
return ll
def fit(self, X, y):
coef = [1.5, 2.0, 2.5, 3.0]
golden1 = 0.618
golden2 = 1 - golden1
ab_start = [(1, 2), (1.5, 2.5), (2, 3), (2.5, 3.5)]
for it1 in range(10):
for idx in range(4):
# golden section search
a, b = ab_start[idx]
# calc losses
coef[idx] = a
la = self._loss(coef, X, y, idx)
coef[idx] = b
lb = self._loss(coef, X, y, idx)
for it in range(20):
# choose value
if la > lb:
a = b - (b - a) * golden1
coef[idx] = a
la = self._loss(coef, X, y, idx)
else:
b = b - (b - a) * golden2
coef[idx] = b
lb = self._loss(coef, X, y, idx)
self.coef_ = {'x': coef}
def predict(self, X, coef):
X_p = np.array([to_bins(pred, coef) for pred in X])
return X_p
def coefficients(self):
return self.coef_['x']
# -
# https://www.kaggle.com/c/petfinder-adoption-prediction/discussion/76107#480970
class AbhishekOptimizedRounder(object):
def __init__(self):
self.coef_ = 0
def _kappa_loss(self, coef, X, y):
X_p = np.copy(X)
for i, pred in enumerate(X_p):
if pred < coef[0]:
X_p[i] = 0
elif pred >= coef[0] and pred < coef[1]:
X_p[i] = 1
elif pred >= coef[1] and pred < coef[2]:
X_p[i] = 2
elif pred >= coef[2] and pred < coef[3]:
X_p[i] = 3
else:
X_p[i] = 4
ll = quadratic_weighted_kappa(y, X_p)
return -ll
def fit(self, X, y):
loss_partial = partial(self._kappa_loss, X=X, y=y)
initial_coef = [0.5, 1.5, 2.5, 3.5]
self.coef_ = sp.optimize.minimize(loss_partial, initial_coef, method='nelder-mead')
def predict(self, X, coef):
X_p = np.copy(X)
for i, pred in enumerate(X_p):
if pred < coef[0]:
X_p[i] = 0
elif pred >= coef[0] and pred < coef[1]:
X_p[i] = 1
elif pred >= coef[1] and pred < coef[2]:
X_p[i] = 2
elif pred >= coef[2] and pred < coef[3]:
X_p[i] = 3
else:
X_p[i] = 4
return X_p
def coefficients(self):
return self.coef_['x']
def bucket(preds_raw, coef = [0.5, 1.5, 2.5, 3.5]):
preds = np.zeros(preds_raw.shape)
for i, pred in enumerate(preds_raw):
if pred < coef[0]:
preds[i] = 0
elif pred >= coef[0] and pred < coef[1]:
preds[i] = 1
elif pred >= coef[1] and pred < coef[2]:
preds[i] = 2
elif pred >= coef[2] and pred < coef[3]:
preds[i] = 3
else:
preds[i] = 4
return preds
optnm2coefs = {'simple': [0.5, 1.5, 2.5, 3.5]}
# %%time
set_torch_seed()
optR = Hocop1OptimizedRounder()
optR.fit(pred_val, y_val)
optnm2coefs['hocop1'] = optR.coefficients()
# %%time
set_torch_seed()
optR = AbhishekOptimizedRounder()
optR.fit(pred_val, y_val)
optnm2coefs['abhishek'] = optR.coefficients()
optnm2coefs
optnm2preds_val_grd = {k: bucket(pred_val, coef) for k,coef in optnm2coefs.items()}
optnm2qwk = {k: quadratic_weighted_kappa(y_val, preds) for k,preds in optnm2preds_val_grd.items()}
optnm2qwk
Counter(y_val).most_common()
pred_val_grd = optnm2preds_val_grd['simple'].squeeze()
pred_val_grd.mean()
Counter(pred_val_grd).most_common()
list(zip(pred_val_grd, y_val))[:10]
(pred_val_grd== y_val.squeeze()).mean()
pickle.dump(optnm2qwk, open(f'{p_o}/optnm2qwk.p', 'wb'))
pickle.dump(optnm2preds_val_grd, open(f'{p_o}/optnm2preds_val_grd.p', 'wb'))
pickle.dump(optnm2coefs, open(f'{p_o}/optnm2coefs.p', 'wb'))
for optnm, coef in optnm2coefs.items():
print(optnm, optnm2qwk[optnm], coef)
pred_val_grd = bucket(pred_val, coef)
display(pd.Series(pred_val_grd.squeeze().astype(int)).value_counts())
# # testing
for optnm, coef in optnm2coefs.items():
print(optnm, optnm2qwk[optnm], coef)
pred_tst_grd = bucket(pred_tst, coef)
display(pd.Series(pred_tst_grd.squeeze().astype(int)).value_counts())
coef = optnm2coefs['simple']
pred_tst_grd = bucket(pred_tst, coef)
pd.Series(pred_tst_grd.squeeze().astype(int)).value_counts()
# ## submit
subm = pd.read_csv("../input/aptos2019-blindness-detection/test.csv")
subm['diagnosis'] = pred_tst_grd.squeeze().astype(int)
subm.head()
subm.diagnosis.value_counts()
subm.to_csv(f"{p_o}/submission.csv", index=False)
| nbs/CVKfld0920-1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ex08 Aplicações da DFT
#
# ## Parte 1 - Filtragem no Domínio da Frequência
#
# Dos itens abaixo *a*, *b* e *c* você deve fazer obrigatoriamente o item *a* e no mínimo mais um item: *b* ou *c*. Nada impede você de fazer os 3 itens: *a*, *b* e *c*.
#
# ### a. Projetando filtros no domínio da frequência
#
# Para projetar os filtros no domínio da frequência, utilize imagens sintéticas, como círculo ou quadrado ou retângulo (filtros ideais), tomando-se o cuidado para verificar se estes filtros são complexos-conjugados. Se preciso, crie uma função que retorne *True*, caso a imagem seja complexa conjugada e *False*, caso contrário. Lembre-se também que o projeto do filtro é normalmente feito no espectro ótico de Fourier, mas sua aplicação é feita com coordenadas 0 a N-1.
#
# Teste os filtros projetados filtrando alguma imagem.
#
# ### b. Filtro Butterworth
#
# Crie uma função para projetar um filtro passa-baixas Butterworth. A função de transferência do filtro passa-baixas de Butterworth de ordem $n$ e com posição da frequência de corte a uma distância $D_0$ da origem é definida pela relação $$ H(u,v) = \frac{1}{1 + [\frac{D(u,v)}{D_0}]^{2n}}, $$ onde $n$ é a ordem do filtro. Para facilitar a implementação, podemos usar a seguinte expressão: $$ H(u,v) = \frac{1}{1 + (\sqrt{2} - 1)(\sqrt{(\frac{u}{N})^2 + (\frac{v}{M})^2)}.t_c)^{2n}}$$ com $$ u \in{[-\frac{N}{2},N - \frac{N}{2} -1]}$$ $$ v \in{[-\frac{M}{2},M - \frac{M}{2} -1]}$$ $$ t_c \in{[2, max\{N,M\}]}$$
#
# Compare o resultado da filtragem de uma imagem usando um filtro ideal e o filtro de Butterworth.
#
# ### c. Filtrando uma imagem com textura
#
# Veja que a imagem do código de barras a seguir possui uma textura no fundo. Projete um filtro (em frequencia) que elimine esta textura, sem borrar demais a imagem.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
f = mpimg.imread('../data/barcode.tif')
plt.figure(figsize=(8,8))
plt.imshow(f,cmap='gray');
plt.show()
# -
# ## Parte 2 - Identificando Translação/Rotação por Correlação de Fase
#
# Dos itens abaixo *a*, *b* e *c* você deve fazer obrigatoriamente o item *a* e no mínimo mais um item: *b* ou *c*. Nada impede você de fazer os 3 itens: *a*, *b* e *c*.
#
# Através da Correlação de fase é possível identificar uma translação ou uma rotação sofrida por uma imagem (veja o notebook [Correlação de Fase](13 Correlacao de fase.ipynb)).
#
# ### a. Coordenada polar da imagem ou da DFT?
#
# Para identificar a rotação, a imagem é transformada para coordenadas polares, para depois ser aplicada a Transformada de Fourier e então calculada a correlação de fase. Verifique se é equivalente fazer a transformada de Fourier e só depois fazer a conversão para coordenadas polares no domínio da frequência para então computar a correlação de fase;
#
# ### b. Rotação e translação simultaneas
#
# Imagine agora que uma imagem tenha sofrido rotação e translação simultaneamente. Tente agora identificar ambas transformações com esta mesma técnica. (DICA: Tente resolver o problema em 2 etapas, ou seja, aplicando 2 vezes os passos para a correlação de fase);
# c. (Opcional) Identifique o quão robusta é esta técnica, com relação a: ruído, variação de contraste, escala
#
# ### c. *Template Matching*
#
# Experimente resolver um problema de *Template Matching* usando correlação fase. Ou seja, recorte um pedaço de uma imagem e tente encontrar este pedaço na imagem original maior.
| 2S2018/Ex08 Aplicacoes da DFT.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # _*Pricing Asian Barrier Spreads*_
# ### Introduction
# <br>
# An Asian barrier spread is a combination of 3 different option types, and as such, combines multiple possible features that the Qiskit Finance option pricing framework supports:
#
# - <a href="https://www.investopedia.com/terms/a/asianoption.asp">Asian option</a>: The payoff depends on the average price over the considered time horizon.
# - <a href="https://www.investopedia.com/terms/b/barrieroption.asp">Barrier Option</a>: The payoff is zero if a certain threshold is exceeded at any time within the considered time horizon.
# - <a href="https://www.investopedia.com/terms/b/bullspread.asp">(Bull) Spread</a>: The payoff follows a piecewise linear function (depending on the average price) starting at zero, increasing linear, staying constant.
#
# Suppose strike prices $K_1 < K_2$ and time periods $t=1,2$, with corresponding spot prices $(S_1, S_2)$ following a given multivariate distribution (e.g. generated by some stochastic process), and a barrier threshold $B>0$.
# The corresponding payoff function is defined as
#
#
# $$
# P(S_1, S_2) =
# \begin{cases}
# \min\left\{\max\left\{\frac{1}{2}(S_1 + S_2) - K_1, 0\right\}, K_2 - K_1\right\}, & \text{ if } S_1, S_2 \leq B \\
# 0, & \text{otherwise.}
# \end{cases}
# $$
#
#
# In the following, a quantum algorithm based on amplitude estimation is used to estimate the expected payoff, i.e., the fair price before discounting, for the option
#
#
# $$\mathbb{E}\left[ P(S_1, S_2) \right].$$
#
#
# The approximation of the objective function and a general introduction to option pricing and risk analysis on quantum computers are given in the following papers:
#
# - <a href="https://arxiv.org/abs/1806.06893">Quantum Risk Analysis. Woerner, Egger. 2018.</a>
# - <a href="https://arxiv.org/abs/1905.02666">Option Pricing using Quantum Computers. Stamatopoulos et al. 2019.</a>
# +
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import griddata
# %matplotlib inline
import numpy as np
from qiskit import QuantumRegister, QuantumCircuit, Aer, execute
from qiskit.circuit.library import IntegerComparator
from qiskit.aqua.algorithms import IterativeAmplitudeEstimation
from qiskit.aqua.circuits import WeightedSumOperator
from qiskit.aqua.components.uncertainty_problems import UnivariatePiecewiseLinearObjective as PwlObjective
from qiskit.aqua.components.uncertainty_problems import MultivariateProblem
from qiskit.aqua.components.uncertainty_models import MultivariateLogNormalDistribution
# MultivariateProblem internally still needs the methods in the Comparator custom class below.
# The code will be changed so that an IntegerComparator can be passed directly without the need
# of a custom class. Until it happens the custom class is necessary.
class Comparator(IntegerComparator):
def required_ancillas(self):
return self.num_ancilla_qubits
def build(self, qc, q, q_ancillas=None, params=None):
i_state = range(self.num_state_qubits)
i_target = self.num_state_qubits
instr = self.to_instruction()
qr = [q[i] for i in i_state] + [q[i_target]]
if q_ancillas:
qr += [qi for qi in q_ancillas[:self.required_ancillas()]]
qc.append(instr, qr)
def build_inverse(self, qc, q, q_ancillas=None):
qc_ = QuantumCircuit(*qc.qregs)
self.build(qc_, q, q_ancillas)
qc.extend(qc_.inverse())
# -
# ### Uncertainty Model
#
# We construct a circuit factory to load a multivariate log-normal random distribution into a quantum state on $n$ qubits.
# For every dimension $j = 1,\ldots,d$, the distribution is truncated to a given interval $[low_j, high_j]$ and discretized using $2^{n_j}$ grid points, where $n_j$ denotes the number of qubits used to represent dimension $j$, i.e., $n_1+\ldots+n_d = n$.
# The unitary operator corresponding to the circuit factory implements the following:
#
# $$\big|0\rangle_{n} \mapsto \big|\psi\rangle_{n} = \sum_{i_1,\ldots,i_d} \sqrt{p_{i_1\ldots i_d}}\big|i_1\rangle_{n_1}\ldots\big|i_d\rangle_{n_d},$$
#
# where $p_{i_1\ldots i_d}$ denote the probabilities corresponding to the truncated and discretized distribution and where $i_j$ is mapped to the right interval using the affine map:
#
# $$ \{0, \ldots, 2^{n_j}-1\} \ni i_j \mapsto \frac{high_j - low_j}{2^{n_j} - 1} * i_j + low_j \in [low_j, high_j].$$
#
# For simplicity, we assume both stock prices are independent and identically distributed.
# This assumption just simplifies the parametrization below and can be easily relaxed to more complex and also correlated multivariate distributions.
# The only important assumption for the current implementation is that the discretization grid of the different dimensions has the same step size.
# +
# number of qubits per dimension to represent the uncertainty
num_uncertainty_qubits = 2
# parameters for considered random distribution
S = 2.0 # initial spot price
vol = 0.4 # volatility of 40%
r = 0.05 # annual interest rate of 4%
T = 40 / 365 # 40 days to maturity
# resulting parameters for log-normal distribution
mu = ((r - 0.5 * vol**2) * T + np.log(S))
sigma = vol * np.sqrt(T)
mean = np.exp(mu + sigma**2/2)
variance = (np.exp(sigma**2) - 1) * np.exp(2*mu + sigma**2)
stddev = np.sqrt(variance)
# lowest and highest value considered for the spot price; in between, an equidistant discretization is considered.
low = np.maximum(0, mean - 3*stddev)
high = mean + 3*stddev
# map to higher dimensional distribution
# for simplicity assuming dimensions are independent and identically distributed)
dimension = 2
num_qubits=[num_uncertainty_qubits]*dimension
low=low*np.ones(dimension)
high=high*np.ones(dimension)
mu=mu*np.ones(dimension)
cov=sigma**2*np.eye(dimension)
# construct circuit factory
u = MultivariateLogNormalDistribution(num_qubits=num_qubits, low=low, high=high, mu=mu, cov=cov)
# -
# plot PDF of uncertainty model
x = [ v[0] for v in u.values ]
y = [ v[1] for v in u.values ]
z = u.probabilities
#z = map(float, z)
#z = list(map(float, z))
resolution = np.array([2**n for n in num_qubits])*1j
grid_x, grid_y = np.mgrid[min(x):max(x):resolution[0], min(y):max(y):resolution[1]]
grid_z = griddata((x, y), z, (grid_x, grid_y))
fig = plt.figure(figsize=(10, 8))
ax = fig.gca(projection='3d')
ax.plot_surface(grid_x, grid_y, grid_z, cmap=plt.cm.Spectral)
ax.set_xlabel('Spot Price $S_1$ (\$)', size=15)
ax.set_ylabel('Spot Price $S_2$ (\$)', size=15)
ax.set_zlabel('Probability (\%)', size=15)
plt.show()
# ### Payoff Function
#
# For simplicity, we consider the sum of the spot prices instead of their average.
# The result can be transformed to the average by just dividing it by 2.
#
# The payoff function equals zero as long as the sum of the spot prices $(S_1 + S_2)$ is less than the strike price $K_1$ and then increases linearly until the sum of the spot prices reaches $K_2$.
# Then payoff stays constant to $K_2 - K_1$ unless any of the two spot prices exceeds the barrier threshold $B$, then the payoff goes immediately down to zero.
# The implementation first uses a weighted sum operator to compute the sum of the spot prices into an ancilla register, and then uses a comparator, that flips an ancilla qubit from $\big|0\rangle$ to $\big|1\rangle$ if $(S_1 + S_2) \geq K_1$ and another comparator/ancilla to capture the case that $(S_1 + S_2) \geq K_2$.
# These ancillas are used to control the linear part of the payoff function.
#
# In addition, we add another ancilla variable for each time step and use additional comparators to check whether $S_1$, respectively $S_2$, exceed the barrier threshold $B$. The payoff function is only applied if $S_1, S_2 \leq B$.
#
# The linear part itself is approximated as follows.
# We exploit the fact that $\sin^2(y + \pi/4) \approx y + 1/2$ for small $|y|$.
# Thus, for a given approximation scaling factor $c_{approx} \in [0, 1]$ and $x \in [0, 1]$ we consider
#
# $$ \sin^2( \pi/2 * c_{approx} * ( x - 1/2 ) + \pi/4) \approx \pi/2 * c_{approx} * ( x - 1/2 ) + 1/2 $$ for small $c_{approx}$.
#
# We can easily construct an operator that acts as
#
# $$\big|x\rangle \big|0\rangle \mapsto \big|x\rangle \left( \cos(a*x+b) \big|0\rangle + \sin(a*x+b) \big|1\rangle \right),$$
#
# using controlled Y-rotations.
#
# Eventually, we are interested in the probability of measuring $\big|1\rangle$ in the last qubit, which corresponds to
# $\sin^2(a*x+b)$.
# Together with the approximation above, this allows to approximate the values of interest.
# The smaller we choose $c_{approx}$, the better the approximation.
# However, since we are then estimating a property scaled by $c_{approx}$, the number of evaluation qubits $m$ needs to be adjusted accordingly.
#
# For more details on the approximation, we refer to:
# <a href="https://arxiv.org/abs/1806.06893">Quantum Risk Analysis. <NAME>. 2018.</a>
#
# Since the weighted sum operator (in its current implementation) can only sum up integers, we need to map from the original ranges to the representable range to estimate the result, and reverse this mapping before interpreting the result. The mapping essentially corresponds to the affine mapping described in the context of the uncertainty model above.
# +
# determine number of qubits required to represent total loss
weights = []
for n in num_qubits:
for i in range(n):
weights += [2**i]
n_s = WeightedSumOperator.get_required_sum_qubits(weights)
# create circuit factory
agg = WeightedSumOperator(sum(num_qubits), weights)
# +
# set the strike price (should be within the low and the high value of the uncertainty)
strike_price_1 = 3
strike_price_2 = 4
# set the barrier threshold
barrier = 2.5
# map strike prices and barrier threshold from [low, high] to {0, ..., 2^n-1}
max_value = 2**n_s - 1
low_ = low[0]
high_ = high[0]
mapped_strike_price_1 = (strike_price_1 - dimension*low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
mapped_strike_price_2 = (strike_price_2 - dimension*low_) / (high_ - low_) * (2**num_uncertainty_qubits - 1)
mapped_barrier = (barrier - low) / (high - low) * (2**num_uncertainty_qubits - 1)
# -
# condition and condition result
conditions = []
barrier_thresholds = [2]*dimension
for i in range(dimension):
# target dimension of random distribution and corresponding condition (which is required to be True)
conditions += [(i, Comparator(num_qubits[i], mapped_barrier[i] + 1, geq=False))]
# +
# set the approximation scaling for the payoff function
c_approx = 0.25
# setup piecewise linear objective fcuntion
breakpoints = [0, mapped_strike_price_1, mapped_strike_price_2]
slopes = [0, 1, 0]
offsets = [0, 0, mapped_strike_price_2 - mapped_strike_price_1]
f_min = 0
f_max = mapped_strike_price_2 - mapped_strike_price_1
bull_spread_objective = PwlObjective(
n_s,
0,
max_value,
breakpoints,
slopes,
offsets,
f_min,
f_max,
c_approx
)
# define overall multivariate problem
asian_barrier_spread = MultivariateProblem(u, agg, bull_spread_objective, conditions=conditions)
# -
# plot exact payoff function
plt.figure(figsize=(7,5))
x = np.linspace(sum(low), sum(high))
y = (x <= 5)*np.minimum(np.maximum(0, x - strike_price_1), strike_price_2 - strike_price_1)
plt.plot(x, y, 'r-')
plt.grid()
plt.title('Payoff Function (for $S_1 = S_2$)', size=15)
plt.xlabel('Sum of Spot Prices ($S_1 + S_2)$', size=15)
plt.ylabel('Payoff', size=15)
plt.xticks(size=15, rotation=90)
plt.yticks(size=15)
plt.show()
# + tags=["nbsphinx-thumbnail"]
# plot contour of payoff function with respect to both time steps, including barrier
plt.figure(figsize=(7,5))
z = np.zeros((17, 17))
x = np.linspace(low[0], high[0], 17)
y = np.linspace(low[1], high[1], 17)
for i, x_ in enumerate(x):
for j, y_ in enumerate(y):
z[i, j] = np.minimum(np.maximum(0, x_ + y_ - strike_price_1), strike_price_2 - strike_price_1)
if x_ > barrier or y_ > barrier:
z[i, j] = 0
plt.title('Payoff Function', size=15)
plt.contourf(x, y, z)
plt.colorbar()
plt.xlabel('Spot Price $S_1$', size=15)
plt.ylabel('Spot Price $S_2$', size=15)
plt.xticks(size=15)
plt.yticks(size=15)
plt.show()
# -
# evaluate exact expected value
sum_values = np.sum(u.values, axis=1)
payoff = np.minimum(np.maximum(sum_values - strike_price_1, 0), strike_price_2 - strike_price_1)
leq_barrier = [ np.max(v) <= barrier for v in u.values ]
exact_value = np.dot(u.probabilities[leq_barrier], payoff[leq_barrier])
print('exact expected value:\t%.4f' % exact_value)
# ### Evaluate Expected Payoff
#
# We first verify the quantum circuit by simulating it and analyzing the resulting probability to measure the $|1\rangle$ state in the objective qubit.
# +
num_req_qubits = asian_barrier_spread.num_target_qubits
num_req_ancillas = asian_barrier_spread.required_ancillas()
q = QuantumRegister(num_req_qubits, name='q')
q_a = QuantumRegister(num_req_ancillas, name='q_a')
qc = QuantumCircuit(q, q_a)
asian_barrier_spread.build(qc, q, q_a)
print('state qubits: ', num_req_qubits)
print('circuit width:', qc.width())
print('circuit depth:', qc.depth())
# -
job = execute(qc, backend=Aer.get_backend('statevector_simulator'))
# +
# evaluate resulting statevector
value = 0
for i, a in enumerate(job.result().get_statevector()):
b = ('{0:0%sb}' % asian_barrier_spread.num_target_qubits).format(i)[-asian_barrier_spread.num_target_qubits:]
prob = np.abs(a)**2
if prob > 1e-4 and b[0] == '1':
value += prob
# all other states should have zero probability due to ancilla qubits
if i > 2**num_req_qubits:
break
# map value to original range
mapped_value = asian_barrier_spread.value_to_estimation(value) / (2**num_uncertainty_qubits - 1) * (high_ - low_)
print('Exact Operator Value: %.4f' % value)
print('Mapped Operator value: %.4f' % mapped_value)
print('Exact Expected Payoff: %.4f' % exact_value)
# -
# Next we use amplitude estimation to estimate the expected payoff.
# Note that this can take a while since we are simulating a large number of qubits. The way we designed the operator (asian_barrier_spread) implies that the number of actual state qubits is significantly smaller, thus, helping to reduce the overall simulation time a bit.
# +
# set target precision and confidence level
epsilon = 0.01
alpha = 0.05
# construct amplitude estimation
ae = IterativeAmplitudeEstimation(epsilon=epsilon, alpha=alpha, a_factory=asian_barrier_spread)
# -
result = ae.run(quantum_instance=Aer.get_backend('qasm_simulator'), shots=100)
conf_int = np.array(result['confidence_interval']) / (2**num_uncertainty_qubits - 1) * (high_ - low_)
print('Exact value: \t%.4f' % exact_value)
print('Estimated value:\t%.4f' % (result['estimation'] / (2**num_uncertainty_qubits - 1) * (high_ - low_)))
print('Confidence interval: \t[%.4f, %.4f]' % tuple(conf_int))
import qiskit.tools.jupyter
# %qiskit_version_table
# %qiskit_copyright
| tutorials/finance/07_asian_barrier_spread_pricing.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Feature Selection
# <NAME>
#
# GEIA - Grupo de estudos em Inteligência Aritificial
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Content:
# <br>
#
# 1. The context;
# 2. The problem;
# 3. Possible solutions;
# 4. Feature selection approaches: Filter, Wrapper and Embedded methods;
# + [markdown] slideshow={"slide_type": "notes"}
# Occam's razor (law of parsimony)
#
# _"Entities should not be multiplied without necessity."_
#
# When presented with competing hypotheses that make the same predictions, one should select the solution with the fewest assumptions
# + [markdown] slideshow={"slide_type": "slide"}
# # 1. Context
# -
# <h3>What is a feature</h3>
#
# <i>In machine learning and pattern recognition, a **feature** (or an attribute) is an individual measurable property or characteristic of a phenomenon being observed. <a href="#References">[1]</a></i>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">1. The context</p>
# <p style="font-size:0.8em;">
# 1997: very few domains operated with more than 40 features <a style="font-size:0.6em;" href="#References">[1]</a></p>
# <ul style="margin:0">
# <li style="font-size:0.6em;">Soybean - 1988 (35 features)</li>
# <li style="font-size:0.6em;">Letter Recognition - 1991 (16 features)</li>
# <li style="font-size:0.6em;">Lung Cancer - 1992 (32 features)</li>
# </ul>
# + [markdown] slideshow={"slide_type": "fragment"}
# <p style="font-size:0.8em;">2009: ImageNet - 14 million images with 256x256 pixels (+196k features) each, and more than 20,000 categories <a style="font-size:0.6em;" href="#References">[2]</a></p>
# <p style="font-size:0.8em;">2010: The Wikipedia Corpus - almost 1.9 billion words from more than 4 million articles <a style="font-size:0.6em;" href="#References">[3]</a></p>
# <p style="font-size:0.8em;">2011: Cancer detection based on gene expression (e.g.: Colon dataset - 2,000 features) <a style="font-size:0.6em;" href="#References">[4]</a></p>
# <br>
# <center><img width="800" src="./figures/number_of_attributes_growth.png"/></center>
# <p style="font-size:0.6em; text-align:right">Source: <a href="#References">[5]</a></p>
# + [markdown] slideshow={"slide_type": "notes"}
# ImageNet: 256x256x3 = 196608
#
# Wikipedia: 1.9 billion words, not distinct, of course - the Second Edition of the 20-volume Oxford English Dictionary, published in 1989, contains full entries for 171,476 words in current use, and 47,156 obsolete words.
# + [markdown] slideshow={"slide_type": "slide"}
# # 2. The problem
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2. The problem</p>
# <h3>Too many features, too many problems</h3>
# <p style="font-size:0.8em"><i>What problems arise with too many features?</i></p>
#
# ---
#
# 1. require longer training times*
#
# 2. jeopardize human interpretability*
#
# 3. worsen prediction quality due to sample size effects
#
# 4. potentially increase overfitting
#
# <p style="font-size:0.6em; text-align:right">* Considered self-explainatory, will not be explained below</p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2. The problem</p>
# <h4>3. Worsen prediction quality due to sample size effects</h4>
# <p style="font-size:0.8em"><i>Couldn't a predictor simply disregard irrelevant features?</i></p>
# + [markdown] slideshow={"slide_type": "fragment"}
# ---
#
# To answer this, we will have to resort to some statistical learning theory, exploring the ways of estimating functional dependency from a given collection of data.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2.3. The problem: Worsen accuracy due to sample size effects</p>
# <h5>Statistical Learning Theory</h5>
# + [markdown] slideshow={"slide_type": "fragment"}
# Let $X \in \mathbb R^p$ be a input random vector and $Y\in \mathbb R$ be an output random variable, with joint distribution $P(X,Y)$.
#
# The task of learning aims at finding a function $f(X)$ for predicting $Y$ given values of input $X$. This structure requires a *loss function* $L(Y, f(X))$ for identifying and penalizing errors in prediction. With this structure, we can define a criterion for choosing a suitable $f$ known as the *Statistical Risk ($R$)*.
#
# $$
# \begin{equation}
# \begin{split}
# \text{R}(f) & = \mathbb{E} \thinspace L(Y, f(X)) \\
# & = \int L(y, f(x))\thinspace P(dx,dy) \\
# & = \mathbb{E}_{X}\mathbb{E}_{Y|X} [L(Y, f(X))|X]
# \end{split}
# \end{equation}
# $$
# <p style="text-align:right;">Source: <a href="#References">[5]</a></p>
#
# This criterion tells us how well, on average, the predictor $f$ performs with respect to the chosen loss function
# + [markdown] slideshow={"slide_type": "skip"}
# Instead of working with the joint distribution, we can condition the Statistical Risk on $X$
# $$
# \begin{equation}
# \begin{split}
# \text{R}(f) & = \int\int [L(y, f(x))|x]\thinspace P(dy)\thinspace P(dx) \\
# & = \mathbb{E}_{X}\mathbb{E}_{Y|X} [L(Y, f(X))|X]
# \end{split}
# \end{equation}
# $$
# + [markdown] slideshow={"slide_type": "subslide"}
# Finally, what we seek is a $f(X)$ which minimizes the the Risk:
# <br><br>
# $$f(X)_{opt}= argmin_c \mathbb{E}_{X}\mathbb{E}_{Y|X}[L(Y,c)|X]$$
# + [markdown] slideshow={"slide_type": "skip"}
# <p style="font-size:0.6em; text-align:right">2.3. The problem: Worsen accuracy due to sample size effects</p>
# The optimal solution will be different depending on the metric used
#
# <h5>Regression</h5>
# <h6>Mean Squared Error (MSE)</h6>
# <br>
# $$
# \begin{equation}
# \begin{split}
# f(X)_{opt} & = argmin_c \mathbb{E}_{X}\mathbb{E}_{Y|X}[(Y-c)^2|X] \\
# & = \mathbb{E}(Y|X=x)
# \end{split}
# \end{equation}
# $$
# known as the conditional mean or expectation - the "average" value over an arbitrarily large number of occurrences
# <h6>Mean Absolute Error (MAP)</h6>
# <br>
# $$
# \begin{equation}
# \begin{split}
# f(X)_{opt} & = argmin_c \mathbb{E}_{X}\mathbb{E}_{Y|X}[|Y-c|\thinspace|X] \\
# & = median(Y|X=x)
# \end{split}
# \end{equation}
# $$
# or the conditional median of the distribution
#
# + [markdown] slideshow={"slide_type": "skip"}
# <h3>Regression loss functions for SLT</h3>
#
# **MSE**: the most preferable option, due to its ease of computation of minimum, since it is differentiable. However it is more sensitive to outliers as a big difference becomes even larger by squaring them.
#
# **MAP**: its optimal estimates are more robust than those for the conditional mean. However, MAP has discontinuities in their derivatives, which have hindered their widespread use.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2.3. The problem: Worsen accuracy due to sample size effects</p>
# <h5>Classification</h5>
# <h6>0-1 loss</h6>
# $$
# \begin{equation}
# \begin{split}
# f(X)_{opt} & = argmin_c \mathbb{E}_{X}\mathbb{E}_{Y|X}[I(f(X),Y)] \\
# & = \underset{y \in Y}{\max}P(y|X)
# \end{split}
# \end{equation}
# $$
# where ${\displaystyle I}$ is the indicator function:
#
# $$I :=\begin{cases}
# 0\text{, if } f(X) = Y\\
# 1\text{, otherwise}\\
# \end{cases}$$
#
# The decider is also known as the *Optimal Bayes classifier*.
# + [markdown] slideshow={"slide_type": "subslide"}
# If the joint probability $P(X,Y)$ is known and the classification decision is optimal.
# <center><img src="./figures/bayes_error.svg" width="900" align="center"/></center>
# This doesn't mean that there are no errors, rather than the lowest error achievable, resulted by noise among distributions.
#
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2.3. The problem: Worsen accuracy due to sample size effects</p>
# If the probability distribution for the problem was known, the classifier wouldn't be affected by adding more of features.
#
# If such features carried the slightest contributions, it is shown that the Bayes optimal classifier tends to zero as the number of features approach infinity.
# + [markdown] slideshow={"slide_type": "fragment"}
# <center><img src='./figures/trunk.png' width="800"/></center>
#
# However, the probability distribution used is an estimation, based on the finite set of samples, causing a **peaking phenomenon**: the prediction accuracy increases with the number of features, but soon reaches a peak, in which the noise becomes larger than the separability increase caused by the new feature.
# <p style="font-size:0.6em; text-align:right;">Source: <a href="#References">[6]</a></p>
# + [markdown] slideshow={"slide_type": "notes"}
# This is often called the peaking phenomenon. Some ideas evolved around it are discussed in the great pattern recognition blog by <NAME> and <NAME> called [37steps](http://37steps.com/about/):
# - [Peaking summarized](http://37steps.com/2545/peaking-summarized/)
# - [Peaking paradox](http://37steps.com/2279/the-peaking-paradox/)
# - [Trunk’s example of the peaking phenomenond](http://37steps.com/2448/trunks-example/)
# - [The curse of dimensionality](http://37steps.com/2349/curse-of-dimensionality/)
#
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2. The problem</p>
# <h4> 4. potentially increase overfitting</h4>
# + [markdown] slideshow={"slide_type": "fragment"}
# <p>As the number of features increase, the observations become more sparse within the feature space.</p>
# + [markdown] slideshow={"slide_type": "fragment"}
# <br>
# <table>
# <tr>
# <td>
# <img src='./figures/exp_curse_of_overfitting.svg' width="1500"/>
# </td>
# <td style="font-size:3em; width: 700px; word-wrap: break-word;">
# <p>Having the observations further apart makes it difficult for the estimator to generalize, increasing its variance, i.e. relying on the specific observations to produce new predictions, causing overfitting.</p>
# </td>
# </tr>
# </table>
# + [markdown] slideshow={"slide_type": "notes"}
# Consequences for classical:
#
# **Non-parametric (Local methods)**: methods such as the $k$ *nearest neighboors*, as the examples become increasingly sparse, the approximation of the conditional expectation by taking the average of its nearest neighboors becomes correspondingly worse as the query point distance itself from the known examples. Additionally, in high dimensions, as the datapoints become more spread apart, their distances become more uniform, making it dificult for the algorithm to decide which data points are more relevant to region of interest [Source](https://www.youtube.com/watch?v=dZrGXYty3qc&list=PLXP3p2MXX_ahmhsMiP5YWtc7IcABeFOGH&index=2)
#
# **Parametric methods**: In very high dimensional spaces, there is more than one plane that can be fitted to your data, and without proper type of regularization can cause the model to behave very poorly. . Collinearity often results in overfitting, i.e. in a too efficient modelling of learning samples without model generalization ability. [[7]]()
#
# More examples on check the answer on [stackexchange](https://stats.stackexchange.com/questions/186184/does-dimensionality-curse-effect-some-models-more-than-others)
# + [markdown] slideshow={"slide_type": "subslide"}
# What causes these problems?
# + [markdown] slideshow={"slide_type": "fragment"}
# <p style="font-size:0.8em; text-align:right"><i>The curse of dimensionality</i></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">2. The problem</p>
# <h3>The curse of dimensionality</h3>
# <br>
# <table>
# <tr>
# <td>
# <img src='./figures/exp_curse_of_dimensionality.svg' width="700"/>
# </td>
# <td style="font-size:3em; width: 700px; word-wrap: break-word;">
# <p>Increasing the number of factors to be taken into consideration requires an exponential growth of observations <a href="#References">[5]</a><br><br>
# However, having a small number of samples means that many regions of the feature space are never observed</p>
# </td>
# </tr>
# </table>
# + [markdown] slideshow={"slide_type": "slide"}
# # 3. How to overcome this problem?
# + [markdown] slideshow={"slide_type": "fragment"}
# <p style="font-size:0.8em; text-align:right"><i>Ans.: Dimensionality reduction</i></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <h2>Dimensionality reduction</h2>
#
# The process of reducing the number attributes under consideration by obtaining a set of principal variables.
#
# It can be carried out through two distinct techniques: feature *extraction* and *selection*
# + [markdown] slideshow={"slide_type": "subslide"}
# <h2>Feature extraction</h2>
#
# Feature extraction projects the original high-dimensional features to a new feature space with low dimensionality through a combination of the original features.
#
# - **Advantages**: It can generate meaning with incomprehensible features
# - **Disavantages**: It may lose physical meanings of comprehensible features
#
# <br>
#
# **Types:**
# 1. Ad hoc techniques;
# 2. Data transformation techniques;
# 3. Deep learning techniques.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.1 Feature extraction</p>
#
# <h3>1. Ad hoc techniques</h3>
#
# Consists on relying on user expertise to derive meaningful relationship between features
# - **Advantages**: Interpretability
# - **Disavantages**: Time-consuption and prior knowledge
# + [markdown] slideshow={"slide_type": "fragment"}
# A fundamental step in this process is to perform an exploratory analysis - [*Facets*](https://ai.googleblog.com/2017/07/facets-open-source-visualization-tool.html) may be a helpful tool.
# <center><img src="https://2.bp.blogspot.com/-Kab341D9VYI/WWz0NrlzH_I/AAAAAAAAB5E/BkIxG4WnADgQTmAFxLSw2zoAuPvIRw6igCLcBGAs/s1600/image1.gif"/></center>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.1 Feature extraction</p>
#
# <h2>2. Data transformation and clustering techniques</h2>
#
# Instead of relying solely on the expert's knownledge on the data, several techniques have been already developed to for the purpose of reducing the dimensions of a problem
#
# <table>
# <tr>
# <td>
# <a href="https://lvdmaaten.github.io/tsne/">
# <img src="./figures/tsne.png" width="400">
# </a>
# </td>
# <td>
# <a href="https://commons.wikimedia.org/wiki/File:Classical_Multidimensional_Scaling_(MDS)_analysis_performed_on_the_1,719_samples.png">
# <img src="./figures/mds.png" width="400"/>
# </a>
# </td>
# <td>
# <a href="https://austingwalters.com/pca-principal-component-analysis/">
# <img src="./figures/pca.png" width="400">
# </a>
# </td>
# </tr>
# <tr>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://youtu.be/NEaUSP4YerM">
# t-SNE
# </a>
# </p>
# </td>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://youtu.be/GEn-_dAyYME">
# MDS
# </a>
# </p>
# </td>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://youtu.be/FgakZw6K1QQ">
# PCA
# </a>
# </p>
# </td>
# </tr>
# <tr>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html">
# scikit.learn
# </a>
# </p>
# </td>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html">
# scikit.learn
# </a>
# </p>
# </td>
# <td>
# <p style="font-size: 2em; text-align:center">
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html">
# scikit.learn
# </a>
# </p>
# </td>
# </tr>
# </table>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.1 Feature extraction</p>
# <h3>3. Deep learning techniques</h3>
#
# Deep learning architectures successively combine feature transformations in order to generate higher hierarchical representations that are more associated with the given task in hand.
# <p style="font-size:0.8em">Examples: Stacked autoenconders, Deep Belief Nets, Sparse filtering and Convolutional layers</p>
# + slideshow={"slide_type": "skip"}
from IPython.core.display import HTML
zoom = 0.9
width = 900
height = 800
url = "https://distill.pub/2018/building-blocks/#AttributionGroups"
html = (
'''
<style type="text/css">
#frame {
zoom: {zoom};
-moz-transform:scale({zoom});
-moz-transform-origin: 0 0;
-o-transform: scale({zoom});
-o-transform-origin: 0 0;
-webkit-transform: scale({zoom});
-webkit-transform-origin: 0 0;
}
</style>
<iframe
height={height}
width={width}
id="frame"
src={url}
scrolling="no"
></iframe>
<a style="font-size:0.6em" href="{url}">Source</a>
'''
.replace("{zoom}", str(zoom))
.replace("{width}", str(width))
.replace("{height}", str(height))
.replace("{url}", url)
)
# + slideshow={"slide_type": "fragment"}
HTML(html)
# + [markdown] slideshow={"slide_type": "subslide"}
# <h2>Feature selection</h2>
#
# Feature selection addresses the task of finding a subset of $M$ features from a set of $N$ features, $M < N$, such that the value of a criterion function is optimized over all subsets of size $M$ either:
# 1. improving prediction quality;
# 2. decreasing the size of the structure without significantly decreasing performance; or
# 3. maintaining the original distribution.
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[11]</a></p>
#
# ---
#
# - **Advantages**: It retains the physical meaning of features
# - **Disavantages**: It cannot generate new meaning using the original features
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2 Feature selection</p>
# <h2> What to select?</h2>
#
# A good subset of features should include a subset of the relevant features that optimizes some performance function. The relevance of features can be classified as:
#
# - Strongly relevant: those that if removed handicap the prediction quality of the feature set;
# - Weakly relevant: those that if removed handicap the prediction quality for a particular feature subset;
# - Irrelavant features: those that are not neither strongly or weakly relevant.
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[12]</a></p>
# + [markdown] slideshow={"slide_type": "slide"}
# <h1>4. Feature selection methods</h1>
# <br><br>
#
# 1. Filter methods;
# 2. Wrapper methods;
# 3. Embedded methods.
# + [markdown] slideshow={"slide_type": "subslide"}
# Disclaimer: This is just the tip of the iceberg
#
# - There are many more techniques than those here presented;
# - Feature selection methods shown are designed for the assumption that the features are independent (*Flat features*). For some cases (e.g. Image Recognition), this assumption does not hold. Check [[13]](#Reference) for a survey on *Strucutred Features* as well.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">4. Feature selection methods</p>
# <h3> Filter methods</h3>
#
# Filter methods are independent of any algorithms and are applied before learning. They rely on characteristics of data to assess feature importance thus discarding less relevant features.
#
# <br>
# <center><img src="./figures/filter_methods.svg"/></center>
# <br>
#
#
#
#
# - **Advantages**: Filter methods are typically computationally efficient
#
# - **Disavantages**: Due to the lack of a specific learning algorithm guiding the feature selection phase, the selected features may not be optimal; Univariate methods do not capture redundancy.
# + [markdown] slideshow={"slide_type": "subslide"}
# A typical filter method consists of two steps:
# 1. Feature importance is ranked according to some feature evaluation criteria
# 2. Lowly ranked features are filtered out either by a threshold of acceptance or by a limiting number of features to be selected.
#
# Some of the evaluation criteria are:
# 1. Correlation-based Criteria
# 2. Fisher Score
# 3. Information Gain
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.1 Filter methods</p>
#
# <h3>1. Correlation Criteria</h3>
#
# One of the simplest criteria used is the Pearson correlation coefficient:
#
# $$R(i) = \frac{cov(X_i, Y)}{\sqrt{var(X_i)var(Y)}}$$
#
# where $X_i$ is the $i_{th}$ feature.
#
# Although useful, the coefficient fails to detect important non-linear dependecies. To overcome this is the user may perform non-linear transformations onto the input, or use different correlation criteria, such as the [Spearman's rank correlation](https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient) or [Kendall's Tau](https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient).
#
# ---
#
# Python implementation: [`scikit-learn.feature_selection`](https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.f_regression.html#sklearn.feature_selection.f_regression) (Pearson) and [`microsoft azure`](https://docs.microsoft.com/en-us/azure/machine-learning/studio-module-reference/feature-selection-modules) (Pearson, Kendall and Spearman)
# + [markdown] slideshow={"slide_type": "subslide"}
# Additionally, the relationship described by such coefficients can be misleading, as demonstrated by [Anscombe's quartet](https://en.wikipedia.org/wiki/Anscombe's_quartet)
#
# <center><img width="900" src="https://upload.wikimedia.org/wikipedia/commons/e/ec/Anscombe%27s_quartet_3.svg"/></center>
# + [markdown] slideshow={"slide_type": "notes"}
# Here all of the relationships shown possess the same correlation coefficient, however, it is evident that they do not share the same relationship between variables. This is an important concept to exemplify the limitations of a coefficient and how far can we trust it
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.1 Filter methods</p>
#
# <h3>2. Fisher Score</h3>
#
# Features with high quality should assign similar values to instances in the same class and different values to instances from different classes. With this intuition, the score for the $i_{th}$ feature $S_i$ will be calculated by Fisher Score as,
# $$S_i = \frac{\sum^K_{j=0}n_j(\mu_{ij}-\mu_{i})^2}{\sum^K_{j=0}n_j\thinspace var(X_{ij})^2}$$
# where $\mu_{ij}$ and $\mu_{j}$ are the mean of the $i_{th}$ feature and the mean of the $j_{th}$ class of the $i_{th}$ feature, respectively, while $K$ is the total number of features and $n_j$ is the number of instances in the $j_{th}$ class on $X_i$.
#
# ---
#
# Python implementation: [`scikit-feature`](https://github.com/jundongl/scikit-feature)
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[13]</a></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.1 Filter methods</p>
#
# <h3>3. Information Gain (Mutual information)</h3>
#
# Information Gain expresses the dependence of one variable to another, quantifying how much knowing a feature reduces uncertainty about the outcome.
#
# $$I_i = \sum_{x_i}\sum_yP(X=x_i, Y=y)\thinspace log\frac{P(X=x_i,Y=y)}{P(X=x_i)P(Y=y)}$$
#
# where the probabilities used are an estimation derived from the training set.
#
# If X and Y were independent then MI would be zero and greater than zero if they were dependent.
#
# We can select our features from feature space by ranking their mutual information with the target variable.
#
# ---
#
# Python implementation: [`scikit-learn.feature_selection`](https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.mutual_info_classif.html#sklearn.feature_selection.mutual_info_classif)
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.1 Filter methods</p>
# <h4>Addendum: other relevant techniques</h4>
#
# When categorical data is used, other statistical tests are used in order to determine whether the a feature is independent or not from a desired variable. [Chi-Square](https://www.quora.com/How-is-chi-test-used-for-feature-selection-in-machine-learning) test, implemented under [`scikit-learn.feature_selection`](https://scikit-learn.org/stable/modules/feature_selection.html) module
#
# Alternatively, the [RELIEF](https://en.wikipedia.org/wiki/Relief_(feature_selection)) is used to determine consistent dependency between features and classes. Python implementation: [`scikit-rebate`](https://github.com/EpistasisLab/scikit-rebate)
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.1.1 Filter Methods </p>
#
# *Important:* Even though filter methods try to select useful features individually, [[2, pg. 1165]](#References) shows that a variable that is completely useless by itself can provide a significant performance improvement when taken with others.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2 Feature selection</p>
# <h3> Wrapper methods</h3>
#
# Wrapper methods rely on the predictive performance of a predefined learning algorithm to evaluate the quality of selected features.
#
# <br>
# <center><img src="./figures/wrapper_methods.svg"/></center>
# <br>
#
# - **Advantages**: Simplicity; Can in principle find the optimal set of features
#
# - **Disavantages**: Are prone to overfitting; Computationally expensive
# + [markdown] slideshow={"slide_type": "subslide"}
# A typical wrapper method consists of two steps:
# 1. search for a subset of features
# 2. evaluate the selected features.
# 3. Repeat *1.* and *2.* until some stopping criteria are satisfied.
#
#
# Finding the optimal set of features has been shown to be unable to solve in polynomial-time*. [[14]](#References), therefore using a exaustive search approach is intractable. Moreover, oftentimes the search space in too large ($2^n$) Therefore, different search strategies have been employed:
# 1. Sequential selection algorithms
# 2. Branch-and-bound
# 3. Metaheuristics
#
# <p style="text-align:right; font-size:0.6em"><b>*</b>Under the assumption that $P ≠ NP$. For more information on computational complexity theory check <a href="https://en.wikipedia.org/wiki/P_versus_NP_problem">this article</a></p>
#
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.2 Wrapper methods</p>
#
# <h3>1. Sequential Search</h3>
#
# 1. **Sequential Feature Selection (SFS)**<br>
# It Starts with an empty set and gradually adds the feature that most improved the subset predictive performance until it reaches a stopping criteria (predetermined number of features, or the *probing method*).<br><br>
# 2. **Sequential Backward Selection (SBS)**<br>
# Similar to SFS, but it starts with the complete set of features and gradually removes the feature that gives the lowest decrease in prediction performance.<br><br>
# 3. **Sequential Floating Forward Selection (SFFS)**<br>
# It starts with an empty number and iteratively adds a SFS step followed by a SBS step.<br><br>
# 4. **Sequential Backward Floating Selection (SBFS)**<br>
# It starts with the complete set and iteratively adds SBS step followed by a SFS step<br><br>
#
# The forward methods more efficient than their backward counterpart, as they start with smaller subsets.
#
# ---
#
# [Further reading](https://rasbt.github.io/mlxtend/user_guide/feature_selection/SequentialFeatureSelector/) and Python implementation: [`mlxtend.feature_selection`](https://rasbt.github.io/mlxtend/user_guide/feature_selection/SequentialFeatureSelector/#api)
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[15]</a></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.2 Wrapper methods</p>
#
# <h3>2. Branch-and-bound</h3>
#
# Developed in the 1960's the branch and bound is one of the most commonly known algorithms for solving NP-hard problems.
#
# The subset combinations are arranged in a tree-like structure and bounds on the prediction quality are established throughout the alogrithmic search in order to prevent the exploration of non-optimal candidates
#
# Narendra and Fukunaga (1977) [[16]](#Reference) proposed using branch and bound for feature selection problems. However, an optimal solution can only be guaranteed if monotonicity is satisfied (the addition of a feature to a subset can never decline the prediction quality). This assumption rarely holds in the real-world.
#
# ---
#
#
# Python implementation: [`enusearch`](https://github.com/artur-deluca/enusearch)
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[15]</a></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.2 Wrapper methods</p>
#
# <h3>3. Metaheuristics</h3>
#
# Metaheuristics are iterative techniques that use strategies for exploring and exploiting the search space in order to efficiently find near-optimal solutions. [[17]](#References)
#
# There is a plethora of metaheuristics, some of which have been successfully employed in feature selection:
#
#
#
# 1. Genetic algortihms (GA) [Kudo and Sklansky (2000)](http://www.sciencedirect.com/science/article/abs/pii/S0031320399000412)
# 2. Particle swarm optimization (PSO) ([Unler and Murat (2010)](http://www.sciencedirect.com/science/article/pii/S0377221710001633))
# 3. Tabu search (TS) ([<NAME> (2009)](https://www.sciencedirect.com/science/article/abs/pii/S037722170800828X), [Zhang and Sun (2002)](https://www.sciencedirect.com/science/article/abs/pii/S0031320301000462))
#
# As experimentally demonstrated in Unler and Kudo, metaheuristics find more satisfying results as Sequential search techniques oftentimes in less time. However, due to their stochastic nature, oftentimes the results are not consistent as the ones reproduce by the aforementioned techniques
#
# ---
# Python implementations: GA: [`gaft`](https://github.com/PytLab/gaft) and PSO:[`PSOpt`](https://github.com/artur-deluca/psopt/)
#
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[15]</a></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# Note: Performance assessments are usually done using a validation set or by cross-validation
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2 Feature selection</p>
# <h3> Embedded methods</h3>
#
# Embedded methods, are quite similar to wrapper methods since they are also used to optimize the objective function or performance of a learning algorithm or model. The difference to wrapper methods is that an intrinsic model building metric is used during learning
#
# Embedded methods perform variable selection in the process of training and are usually specific to given learning machines.
#
# <br>
# <center><img src="./figures/embedded_methods.svg"/></center>
# <br>
#
# - **Advantages**: Make better usage of data (doesn't split it for evaluation). It is less computationally expensive and less prone to overfitting than wrapper methods
#
# - **Disavantages**: More computationally expensive than filter methods.
# + [markdown] slideshow={"slide_type": "subslide"}
# Some of the embedded techniques are:
#
# 1. Built-in selectors
# 2. Prunning methods
# 3. Regularization methods
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.3 Embedded methods</p>
#
# <h3>1. Built-in selectors</h3>
#
# Decision tree (CART) algorithms such as the ID3 and C4.5 use feature selection methods in its operations.
#
# The algorithm iterates through every unused attribute of the dataset and calculates the information gain of that attribute. The set is then split by the attribute with highest information gain to produce subsets of data. The algorithm continues to recur on each subset, considering only attributes never selected before.
#
# The algorithm may stop if each example within a certain subset belongs to a class, or any other limitation (given by the number of splits allowed or available attributes)
#
# In these circumstances, these algorithms can sort through features and decide which are the most relevant among them as the model is being built.
#
# ---
# Python implementation: [`scikit-learn.tree`](https://scikit-learn.org/stable/modules/tree.html#tree-algorithms-id3-c4-5-c5-0-and-cart)
# <p style="text-align:right; font-size:0.6em"><a href="https://en.wikipedia.org/wiki/Decision_tree_learning">Further reading</a></p>
# + [markdown] slideshow={"slide_type": "notes"}
#
# C4.5 made a number of improvements to ID3. Some of these are:
#
# - Handling both continuous and discrete attributes
# - Handling training data with missing attribute values
# - Handling attributes with differing costs.
# - Pruning trees after creation - C4.5 goes back through the tree once it's been created and attempts to remove branches that do not help by replacing them with leaf nodes.
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.3 Embedded methods</p>
#
# <h3>2. Prunning methods</h3>
#
# <h4>Recursive feature elimination (RFE)</h4>
#
# Recursively eliminates one feature at iteration until predetermined number of features is reached.
#
# It differs from traditional wrapper methods because it uses internal information from the learning algorithm to endorse the elimination.
#
# For linear predictors, RFE eliminates the feature that carries the smallest weight as for decision trees and random forest classifiers, the concept feature importance is used, which can be defined by:
# - *Gini Importance or Mean Decrease in Impurity (MDI)*: the sum over the number of splits (accross all tress) that include the feature, proportionaly to the number of samples it splits.
# - *Permutation Importance or Mean Decrease in Accuracy (MDA)* is assessed for each feature by removing the association between that feature and the target. This is achieved by randomly permuting the values of the feature and measuring the resulting increase in error.
#
# ---
#
# Python implementation: [`scikit-learn.feature_selection`](https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.RFE.html)
#
# Under scikit-learn, only the Gini importance can used for RFE in tree-based classifiers.
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="https://alexisperrier.com/datascience/2015/08/27/feature-importance-random-forests-gini-accuracy.html">article</a> and <a href="#References">[13]</a></p>
# + [markdown] slideshow={"slide_type": "subslide"}
# <p style="font-size:0.6em; text-align:right">3.2.3 Embedded methods</p>
#
# <h3>3. Regularization methods</h3>
#
# Regularization methods introduce penalization into the loss function to balance the decision between accuracy and model simplicity. Models with too many parameters have higher penalties, and if a weight associated with a feature sinks below a certain threshold, its value goes to zero.
#
# - Lasso ($L_1$ Regularization)
# $$penalty\thinspace(w) = \sum^n_{i=1}\vert w_i\vert$$
#
# - Elastic-net regularization
# $$penalty\thinspace(w) = \lambda_1\sum^n_{i=1}\vert w_i\vert + \lambda_2(\sum^n_{i=1}w^2_i), \thinspace\lambda\ge0$$
#
# ---
#
# - Adpative Lasso regularization
# - Bridge regularization:
#
# ---
#
# Python implementation: [`sklearn.linear_model`](https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model)
#
#
# <p style="text-align:right; font-size:0.6em">Source: <a href="#References">[13]</a></p>
# + [markdown] slideshow={"slide_type": "notes"}
# - L2 regularization (Ridge regression) is not suitable for feature selection since its penalization doesn't reduce coefficients to zero
#
# L1:
# - L1 requires a higher coefficient for feature selection than for simple regularization
# - When p > n, L1 tends to select n variables before it saturates
# - Small nonzero parameters cannot be detected consistently
# - High correlations between predictors leads to poor selection performance
#
# Elastic-net:
#
# The quadratic penalty term makes the loss function strongly convex, and it therefore has a unique minimum.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Wrap up
#
# **1** *Do you have domain knowledge?*
# If yes, construct a better set of “ad hoc” features.
#
# **2** *Are your features commensurate?* If no, consider normalizing them.
#
# **3** *Do you suspect interdependence of features?* If yes, expand your feature set by constructing
# conjunctive features or products of features, as much as your computer resources allow you.
#
# **4** *Do you need to prune the input variables (e.g. for cost, speed or data understanding reasons)?* If no, construct disjunctive features or weighted sums of features (e.g. clustering or matrix factorization)
#
# **5** Do you need to assess features individually (e.g. to understand their influence on the system
# or because their number is so large that you need to do a first filtering)? If yes, use a variable
# ranking method; else, do it anyway to get baseline results.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Wrap up
#
# **6** Do you need a predictor? If no, stop.
#
# **7** Do you suspect your data is “dirty” (has a few meaningless input patterns and/or noisy
# outputs or wrong class labels)? If yes, detect the outlier examples using the top ranking
# variables obtained in step 5 as representation; check and/or discard them.
#
# **8** Do you know what to try first? If no:
# - Take a linear predictor and use a forward selection method with the “probe” method as a stopping criterion or use the 0-norm embedded method.
# - For comparison, following the ranking of step 5, construct a sequence of predictors of same nature using increasing subsets of features. Can you match
# or improve performance with a smaller subset? If yes, try a non-linear predictor with that subset.
#
# **9** Do you have new ideas, time, computational resources, and enough examples? If yes,
# compare several feature selection methods, including your new idea, correlation coefficients,
# backward selection and embedded methods. Use linear and non-linear predictors.
# Select the best approach with model selection.
#
# **10** Do you want a stable solution (to improve performance and/or understanding)? If yes, subsample your data and redo your analysis for several subsets.
# + [markdown] slideshow={"slide_type": "fragment"}
# For a more comprehensive survey on feature selection methods and their recommended applications see: [[18]](#References) and [[this article](http://featureselection.asu.edu/algorithms.php)]
# + [markdown] slideshow={"slide_type": "subslide"}
# # References
# <p style="font-size:0.6em;">
# <a href="https://www.amazon.com/Pattern-Recognition-Learning-Information-Statistics/dp/0387310738">[1]</a> : <NAME>. (2006). Pattern recognition and machine learning<br>
# <a href="http://jmlr.csail.mit.edu/papers/volume3/guyon03a/guyon03a.pdf">[2]</a> : <NAME>. and <NAME>. (2003). An Introduction to Variable and Feature Selection<br>
# <a href="http://image-net.org/challenges/LSVRC/">[3]</a>: <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>. and <NAME>. (2015) ImageNet Large Scale Visual Recognition Challenge. IJCV, 2015<br>
# <a href="https://snap.stanford.edu/data/wiki-meta.html">[4]</a>:<NAME>. (2010). Processed Wikipedia Edit History. Stanford large network dataset collection<br>
# <a href="https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3287491/">[5]</a>: <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>. (2011). Gene selection and classification for cancer microarray data based on machine learning and similarity measures.<br>
# <a href="https://www.springer.com/gp/book/9780387848570">[6]</a>: <NAME>., <NAME>., and <NAME>. H. (2009). The elements of Statistical learning: data mining, inference, and prediction.<br>
# <a href="https://ieeexplore.ieee.org/document/4766926">[7]</a>: <NAME>. (1979). A Problem of Dimensionality: A Simple Example<br>
# <a href="https://link.springer.com/chapter/10.1007/11494669_93">[8]</a>: <NAME>. and <NAME>. (2005). The Curse of Dimensionality in Data Mining and Time Series Prediction<br>
# <a href=" http://papers.nips.cc/paper/2020-on-discriminative-vs-generative-classifiers-a-comparison-of-logistic-regression-and-naive-bayes.pdf">[9]</a>: <NAME>. and <NAME>. (2001). On Discriminative vs. Generative Classifiers: A comparison of logistic regression and naive Bayes<br>
# <a href=" https://arxiv.org/abs/1601.07996">[10]</a>: <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., and <NAME>. (2017). Feature Selection: A Data Perspective<br>
# <a href=" https://www.sciencedirect.com/science/article/pii/S1088467X97000085">[11]</a>: <NAME>. and <NAME>. (1997). Feature selection for classification<br>
# <a href="https://www.researchgate.net/publication/2771488_Feature_Subset_Selection_as_Search_with_Probabilistic_Estimates">[12]</a>: <NAME>. (1994). Feature Subset Selection as Search with Probabilistic Estimates<br>
# <a href="https://www.researchgate.net/publication/288257551_Feature_selection_for_classification_A_review">[13]</a>: <NAME>., <NAME>., <NAME>. (2014). Feature selection for classification: A review<br>
# <a href="https://www.sciencedirect.com/science/article/pii/S0304397597001151">[14]</a>: Amaldi,E., <NAME>. (1998). On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems<br>
# <a href="https://dl.acm.org/citation.cfm?id=2577699">[15]</a>:<NAME>., <NAME>. (2014). A survey on feature selection methods<br>
# <a href="https://ieeexplore.ieee.org/document/1674939/">[16]</a>: <NAME>., <NAME>. (1977). A Branch and Bound Algorithm for Feature Subset Selection<br>
# <a href="https://www.amazon.com/Modern-Heuristic-Search-Methods-Rayward-Smith/dp/0471962805">[17]</a>: <NAME>., <NAME>., <NAME>., <NAME>. (1996). Modern Heuristic Search Methods<br>
# <a href="https://bib.irb.hr/datoteka/763354.MIPRO_2015_JovicBrkicBogunovic.pdf">[18]</a>: <NAME>., <NAME>., and <NAME>. (2015). A review of feature selection methods with applications<br>
#
# </p>
#
| content/work/feature_selection/presentation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Mini-Project 2: Source extraction
#
# **Context**
#
# This notebook illustrates the basics of distributing image data, and process them separately. In this notebook, we will load [MegaCam](https://www.cfht.hawaii.edu/Instruments/Imaging/Megacam/) data, and extract source positions in the images.
# + [markdown] slideshow={"slide_type": "slide"}
# **Learning objectives**
#
# After going through this notebook, you should be able to:
#
# - Load and efficiently access astronomical images with Apache Spark
# - Interface and use your favourite image processing package.
#
# For this project, you will use the data at `data/images` (see the `download_data_project.sh` script).
# + slideshow={"slide_type": "slide"}
# We use the custom spark-fits connector
df = spark.read.format("fits").option("hdu", 1).load("../data/images/*.fits")
# + slideshow={"slide_type": "fragment"}
df.show(3)
# + [markdown] slideshow={"slide_type": "subslide"}
# By default, spark-fits will assign one image line per row, without specifying the data provenance. But you can retrieve it easily:
# + slideshow={"slide_type": "fragment"}
from pyspark.sql.functions import input_file_name
df = df.withColumn('ImgIndex', input_file_name())
df.show(3)
# + [markdown] slideshow={"slide_type": "subslide"}
# We have 4 images with 4644 lines each:
# + slideshow={"slide_type": "fragment"}
df.groupBy('ImgIndex').count().show()
# + [markdown] slideshow={"slide_type": "subslide"}
# and for each image, we have 2112 columns:
# + slideshow={"slide_type": "fragment"}
import pandas as pd
from pyspark.sql.functions import pandas_udf
@pandas_udf('int')
def count_col(col: pd.Series) -> pd.Series:
return pd.Series(col.apply(lambda x: len(x)))
df.withColumn('ncolumns', count_col(df['Image'])).select('ncolumns').distinct().show()
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercise:** Using [photutils](https://photutils.readthedocs.io/en/stable/index.html) (or whatever you prefer), extract the position of sources in the images whose peak value is 50-sigma above the background.
# + slideshow={"slide_type": "subslide"}
from astropy.stats import sigma_clipped_stats
from astropy.visualization import SqrtStretch
from astropy.visualization.mpl_normalize import ImageNormalize
import numpy as np
import pandas as pd
from photutils import DAOStarFinder
from photutils import CircularAperture
from pyspark.sql.types import FloatType, ArrayType
from pyspark.sql.functions import pandas_udf, PandasUDFType
from typing import Iterator, Generator
def get_stat(data, sigma=3.0, iters=3):
""" Estimate the background and background noise using
sigma-clipped statistics.
Parameters
----------
data : 2D array
2d array containing the data.
sigma : float
sigma.
iters : int
Number of iteration to perform to get accurate estimate.
The higher the better, but it will be longer.
"""
mean, median, std = sigma_clipped_stats(data, sigma=sigma, maxiters=iters)
return mean, median, std
def extract_catalog(pdf: pd.DataFrame) -> pd.DataFrame:
""" Use photutils to extract source information
from image (one image per partition).
"""
# Reshape images for photutils
image = np.array(
[np.array(j, dtype=float) for j in pdf['Image'].values],
dtype=float
)
# Get background statistics
mean, median, std = get_stat(image)
# Use star finder
sf = DAOStarFinder(fwhm=10.0, threshold=50.*std)
cat = sf(image - median)
pdf_to_return = cat.to_pandas()
pdf_to_return['ImgIndex'] = pdf['ImgIndex'].values[0]
return pdf_to_return
# + slideshow={"slide_type": "subslide"}
from pyspark.sql.types import StructField, StructType, IntegerType, FloatType, StringType
# Define the output schema (catalog from photutils)
schema = StructType(
[
StructField('id', IntegerType(), True),
StructField('xcentroid', FloatType(), True),
StructField('ycentroid', FloatType(), True),
StructField('sharpness', FloatType(), True),
StructField('roundness1', FloatType(), True),
StructField('roundness2', FloatType(), True),
StructField('npix', IntegerType(), True),
StructField('sky', FloatType(), True),
StructField('peak', FloatType(), True),
StructField('flux', FloatType(), True),
StructField('mag', FloatType(), True),
StructField('ImgIndex', StringType(), True)
]
)
catalog = df.groupBy('ImgIndex').applyInPandas(extract_catalog, schema=schema)
# + slideshow={"slide_type": "subslide"}
catalog.show()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Plotting results
# + slideshow={"slide_type": "subslide"}
# retrieve image indices
indices = df.select('ImgIndex').distinct().collect()[0]
# retrieve the first image to the driver
first_image = df.filter(df['ImgIndex'] == indices[0]).select('Image').collect()
# retrieve the first catalog of sources to the driver
first_catalog = catalog.filter(catalog['ImgIndex'] == indices[0]).toPandas()
# + slideshow={"slide_type": "subslide"}
# Overplot detections on the images
from astropy.visualization import AsinhStretch
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('talk')
data = np.transpose(first_image).reshape((2112, 4644))
# only for visualisation purposes!
data = np.log(data)
norm = ImageNormalize(stretch=AsinhStretch())
fig = plt.figure(0, (15, 15))
plt.imshow(data, cmap='binary', origin="lower", norm=norm)
plt.show()
fig = plt.figure(0, (15, 15))
positions = [[y, x] for y, x in zip(first_catalog['ycentroid'].values, first_catalog['xcentroid'].values)]
apertures = CircularAperture(positions, r=30.)
plt.imshow(data, cmap='binary', origin="lower", norm=norm)
apertures.plot(color='blue', lw=1.0, alpha=0.5);
# -
| spark/notebooks/mini-projects-images.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Working with contexts using NLTK
#
# NLTK is a powerful tool to work on Natural Language Processing. Some interesting and usuful approaches are to search a word applied in contexts, understanding the author's intent with that word, search similar words application and search the application of two or more words in a same context, thus, you can understand how the author associate those two or more words.
#
# Below are examples of how to do that stated above.
#Importing libs
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import nltk
#Calling the texts
from nltk.book import *
#Testing the text display
text3
# # concordance, similar and common_contexts commands
# Let's start with concordance command. That command returns all contexts in which the selected word appears. From that, we can understand the connotation that an author assigns to a word.
#Searching context in which word "God" is inserted
text3.concordance('God')
# As you may see, the word "God" is inserted in a context where he is a creator.
# Another command is similar( ), which is applied to search similar words in terms of semantic.
#Searching words similar to good
text3.similar('good')
# The returned result shows how the author of Genesis associates the word "good". For him, it is related to creations of God and connotes a positive term.
# Using the common contexts command, we can observe two or more words sharing the same context, thus, we can understand common applications and how the author works those two or more words.
#Searching contexts where the word God is inserted with other words
text3.common_contexts(['God', 'he']) #God and he
text3.common_contexts(['God', 'pharaoh']) #God and Pharaoh
text3.common_contexts(['God', 'Abraham']) #God and Abraham
text3.common_contexts(['God', 'Judah']) #God and Judah
text3.common_contexts(['God', 'Sarah']) #God and Sarah
# Those responses show that God relates to those characters by saying them something or doing something into the men's direction.
# # Lexical dispersion plot
# An interesting approach is the use of a plot. Lexical Dispersion Plot (LDP) evidences the frequency of a word in a given text, as you can see below.
#Ploting Lexical Dispersion Plot
plt.figure(figsize=(16,8))
text3.dispersion_plot(['God', 'pharaoh', 'Abraham', 'Judah', 'Sarah', 'Adam', 'evil', 'iniquity', 'sin'])
# Between the words selected in the book of Genesis, the most frequent is God, followed by Abraham.
| NLTK_dealing_with_context_part1.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Dependencies
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _kg_hide-input=true _kg_hide-output=true _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import os
import sys
import cv2
import shutil
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from tensorflow import set_random_seed
from sklearn.utils import class_weight
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, cohen_kappa_score
from keras import backend as K
from keras.models import Model
from keras.utils import to_categorical
from keras import optimizers, applications
from keras.preprocessing.image import ImageDataGenerator
from keras.layers import Dense, Dropout, GlobalAveragePooling2D, Input
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, Callback, LearningRateScheduler
def seed_everything(seed=0):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
set_random_seed(0)
seed = 0
seed_everything(seed)
# %matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
sys.path.append(os.path.abspath('../input/efficientnet/efficientnet-master/efficientnet-master/'))
from efficientnet import *
# + [markdown] _kg_hide-output=true
# ## Load data
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _kg_hide-input=true _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
hold_out_set = pd.read_csv('../input/aptos-data-split/hold-out.csv')
X_train = hold_out_set[hold_out_set['set'] == 'train']
X_val = hold_out_set[hold_out_set['set'] == 'validation']
test = pd.read_csv('../input/aptos2019-blindness-detection/test.csv')
print('Number of train samples: ', X_train.shape[0])
print('Number of validation samples: ', X_val.shape[0])
print('Number of test samples: ', test.shape[0])
# Preprocecss data
X_train["id_code"] = X_train["id_code"].apply(lambda x: x + ".png")
X_val["id_code"] = X_val["id_code"].apply(lambda x: x + ".png")
test["id_code"] = test["id_code"].apply(lambda x: x + ".png")
display(X_train.head())
# -
# # Model parameters
# Model parameters
FACTOR = 4
BATCH_SIZE = 8 * FACTOR
EPOCHS = 20
WARMUP_EPOCHS = 5
LEARNING_RATE = 1e-4 * FACTOR
WARMUP_LEARNING_RATE = 1e-3 * FACTOR
HEIGHT = 224
WIDTH = 224
CHANNELS = 3
ES_PATIENCE = 5
RLROP_PATIENCE = 3
DECAY_DROP = 0.5
LR_WARMUP_EPOCHS_1st = 2
LR_WARMUP_EPOCHS_2nd = 5
STEP_SIZE = len(X_train) // BATCH_SIZE
TOTAL_STEPS_1st = WARMUP_EPOCHS * STEP_SIZE
TOTAL_STEPS_2nd = EPOCHS * STEP_SIZE
WARMUP_STEPS_1st = LR_WARMUP_EPOCHS_1st * STEP_SIZE
WARMUP_STEPS_2nd = LR_WARMUP_EPOCHS_2nd * STEP_SIZE
# # Pre-procecess images
# + _kg_hide-input=true
train_base_path = '../input/aptos2019-blindness-detection/train_images/'
test_base_path = '../input/aptos2019-blindness-detection/test_images/'
train_dest_path = 'base_dir/train_images/'
validation_dest_path = 'base_dir/validation_images/'
test_dest_path = 'base_dir/test_images/'
# Making sure directories don't exist
if os.path.exists(train_dest_path):
shutil.rmtree(train_dest_path)
if os.path.exists(validation_dest_path):
shutil.rmtree(validation_dest_path)
if os.path.exists(test_dest_path):
shutil.rmtree(test_dest_path)
# Creating train, validation and test directories
os.makedirs(train_dest_path)
os.makedirs(validation_dest_path)
os.makedirs(test_dest_path)
def crop_image(img, tol=7):
if img.ndim ==2:
mask = img>tol
return img[np.ix_(mask.any(1),mask.any(0))]
elif img.ndim==3:
gray_img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
mask = gray_img>tol
check_shape = img[:,:,0][np.ix_(mask.any(1),mask.any(0))].shape[0]
if (check_shape == 0): # image is too dark so that we crop out everything,
return img # return original image
else:
img1=img[:,:,0][np.ix_(mask.any(1),mask.any(0))]
img2=img[:,:,1][np.ix_(mask.any(1),mask.any(0))]
img3=img[:,:,2][np.ix_(mask.any(1),mask.any(0))]
img = np.stack([img1,img2,img3],axis=-1)
return img
def circle_crop(img):
img = crop_image(img)
height, width, depth = img.shape
largest_side = np.max((height, width))
img = cv2.resize(img, (largest_side, largest_side))
height, width, depth = img.shape
x = width//2
y = height//2
r = np.amin((x, y))
circle_img = np.zeros((height, width), np.uint8)
cv2.circle(circle_img, (x, y), int(r), 1, thickness=-1)
img = cv2.bitwise_and(img, img, mask=circle_img)
img = crop_image(img)
return img
def preprocess_image(base_path, save_path, image_id, HEIGHT, WIDTH, sigmaX=10):
image = cv2.imread(base_path + image_id)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image = circle_crop(image)
image = cv2.resize(image, (HEIGHT, WIDTH))
image = cv2.addWeighted(image, 4, cv2.GaussianBlur(image, (0,0), sigmaX), -4 , 128)
cv2.imwrite(save_path + image_id, image)
# Pre-procecss train set
for i, image_id in enumerate(X_train['id_code']):
preprocess_image(train_base_path, train_dest_path, image_id, HEIGHT, WIDTH)
# Pre-procecss validation set
for i, image_id in enumerate(X_val['id_code']):
preprocess_image(train_base_path, validation_dest_path, image_id, HEIGHT, WIDTH)
# Pre-procecss test set
for i, image_id in enumerate(test['id_code']):
preprocess_image(test_base_path, test_dest_path, image_id, HEIGHT, WIDTH)
# -
# # Data generator
# + _kg_hide-input=true
datagen=ImageDataGenerator(rescale=1./255,
rotation_range=360,
horizontal_flip=True,
vertical_flip=True)
train_generator=datagen.flow_from_dataframe(
dataframe=X_train,
directory=train_dest_path,
x_col="id_code",
y_col="diagnosis",
class_mode="raw",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
valid_generator=datagen.flow_from_dataframe(
dataframe=X_val,
directory=validation_dest_path,
x_col="id_code",
y_col="diagnosis",
class_mode="raw",
batch_size=BATCH_SIZE,
target_size=(HEIGHT, WIDTH),
seed=seed)
test_generator=datagen.flow_from_dataframe(
dataframe=test,
directory=test_dest_path,
x_col="id_code",
batch_size=1,
class_mode=None,
shuffle=False,
target_size=(HEIGHT, WIDTH),
seed=seed)
# + _kg_hide-input=true
def cosine_decay_with_warmup(global_step,
learning_rate_base,
total_steps,
warmup_learning_rate=0.0,
warmup_steps=0,
hold_base_rate_steps=0):
"""
Cosine decay schedule with warm up period.
In this schedule, the learning rate grows linearly from warmup_learning_rate
to learning_rate_base for warmup_steps, then transitions to a cosine decay
schedule.
:param global_step {int}: global step.
:param learning_rate_base {float}: base learning rate.
:param total_steps {int}: total number of training steps.
:param warmup_learning_rate {float}: initial learning rate for warm up. (default: {0.0}).
:param warmup_steps {int}: number of warmup steps. (default: {0}).
:param hold_base_rate_steps {int}: Optional number of steps to hold base learning rate before decaying. (default: {0}).
:param global_step {int}: global step.
:Returns : a float representing learning rate.
:Raises ValueError: if warmup_learning_rate is larger than learning_rate_base, or if warmup_steps is larger than total_steps.
"""
if total_steps < warmup_steps:
raise ValueError('total_steps must be larger or equal to warmup_steps.')
learning_rate = 0.5 * learning_rate_base * (1 + np.cos(
np.pi *
(global_step - warmup_steps - hold_base_rate_steps
) / float(total_steps - warmup_steps - hold_base_rate_steps)))
if hold_base_rate_steps > 0:
learning_rate = np.where(global_step > warmup_steps + hold_base_rate_steps,
learning_rate, learning_rate_base)
if warmup_steps > 0:
if learning_rate_base < warmup_learning_rate:
raise ValueError('learning_rate_base must be larger or equal to warmup_learning_rate.')
slope = (learning_rate_base - warmup_learning_rate) / warmup_steps
warmup_rate = slope * global_step + warmup_learning_rate
learning_rate = np.where(global_step < warmup_steps, warmup_rate,
learning_rate)
return np.where(global_step > total_steps, 0.0, learning_rate)
class WarmUpCosineDecayScheduler(Callback):
"""Cosine decay with warmup learning rate scheduler"""
def __init__(self,
learning_rate_base,
total_steps,
global_step_init=0,
warmup_learning_rate=0.0,
warmup_steps=0,
hold_base_rate_steps=0,
verbose=0):
"""
Constructor for cosine decay with warmup learning rate scheduler.
:param learning_rate_base {float}: base learning rate.
:param total_steps {int}: total number of training steps.
:param global_step_init {int}: initial global step, e.g. from previous checkpoint.
:param warmup_learning_rate {float}: initial learning rate for warm up. (default: {0.0}).
:param warmup_steps {int}: number of warmup steps. (default: {0}).
:param hold_base_rate_steps {int}: Optional number of steps to hold base learning rate before decaying. (default: {0}).
:param verbose {int}: quiet, 1: update messages. (default: {0}).
"""
super(WarmUpCosineDecayScheduler, self).__init__()
self.learning_rate_base = learning_rate_base
self.total_steps = total_steps
self.global_step = global_step_init
self.warmup_learning_rate = warmup_learning_rate
self.warmup_steps = warmup_steps
self.hold_base_rate_steps = hold_base_rate_steps
self.verbose = verbose
self.learning_rates = []
def on_batch_end(self, batch, logs=None):
self.global_step = self.global_step + 1
lr = K.get_value(self.model.optimizer.lr)
self.learning_rates.append(lr)
def on_batch_begin(self, batch, logs=None):
lr = cosine_decay_with_warmup(global_step=self.global_step,
learning_rate_base=self.learning_rate_base,
total_steps=self.total_steps,
warmup_learning_rate=self.warmup_learning_rate,
warmup_steps=self.warmup_steps,
hold_base_rate_steps=self.hold_base_rate_steps)
K.set_value(self.model.optimizer.lr, lr)
if self.verbose > 0:
print('\nBatch %02d: setting learning rate to %s.' % (self.global_step + 1, lr))
# -
# # Model
def create_model(input_shape):
input_tensor = Input(shape=input_shape)
base_model = EfficientNetB3(weights=None,
include_top=False,
input_tensor=input_tensor)
base_model.load_weights('../input/efficientnet-keras-weights-b0b5/efficientnet-b3_imagenet_1000_notop.h5')
x = GlobalAveragePooling2D()(base_model.output)
final_output = Dense(1, activation='linear', name='final_output')(x)
model = Model(input_tensor, final_output)
return model
# # Train top layers
# + _kg_hide-output=true
model = create_model(input_shape=(HEIGHT, WIDTH, CHANNELS))
for layer in model.layers:
layer.trainable = False
for i in range(-2, 0):
model.layers[i].trainable = True
cosine_lr_1st = WarmUpCosineDecayScheduler(learning_rate_base=WARMUP_LEARNING_RATE,
total_steps=TOTAL_STEPS_1st,
warmup_learning_rate=0.0,
warmup_steps=WARMUP_STEPS_1st,
hold_base_rate_steps=(2 * STEP_SIZE))
metric_list = ["accuracy"]
callback_list = [cosine_lr_1st]
optimizer = optimizers.Adam(lr=WARMUP_LEARNING_RATE)
model.compile(optimizer=optimizer, loss='mean_squared_error', metrics=metric_list)
model.summary()
# + _kg_hide-input=true _kg_hide-output=true
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history_warmup = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=WARMUP_EPOCHS,
callbacks=callback_list,
verbose=2).history
# -
# # Fine-tune the complete model
# + _kg_hide-input=false _kg_hide-output=true
for layer in model.layers:
layer.trainable = True
es = EarlyStopping(monitor='val_loss', mode='min', patience=ES_PATIENCE, restore_best_weights=True, verbose=1)
cosine_lr_2nd = WarmUpCosineDecayScheduler(learning_rate_base=LEARNING_RATE,
total_steps=TOTAL_STEPS_2nd,
warmup_learning_rate=0.0,
warmup_steps=WARMUP_STEPS_2nd,
hold_base_rate_steps=(3 * STEP_SIZE))
callback_list = [es, cosine_lr_2nd]
optimizer = optimizers.Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer, loss='mean_squared_error', metrics=metric_list)
model.summary()
# + _kg_hide-input=true _kg_hide-output=true
history = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=EPOCHS,
callbacks=callback_list,
verbose=2).history
# + _kg_hide-input=true
fig, (ax1, ax2) = plt.subplots(2, 1, sharex='col', figsize=(20, 6))
ax1.plot(cosine_lr_1st.learning_rates)
ax1.set_title('Warm up learning rates')
ax2.plot(cosine_lr_2nd.learning_rates)
ax2.set_title('Fine-tune learning rates')
plt.xlabel('Steps')
plt.ylabel('Learning rate')
sns.despine()
plt.show()
# -
# # Model loss graph
# + _kg_hide-input=true
fig, (ax1, ax2) = plt.subplots(2, 1, sharex='col', figsize=(20, 14))
ax1.plot(history['loss'], label='Train loss')
ax1.plot(history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history['acc'], label='Train accuracy')
ax2.plot(history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
plt.xlabel('Epochs')
sns.despine()
plt.show()
# + _kg_hide-input=true
# Create empty arays to keep the predictions and labels
df_preds = pd.DataFrame(columns=['label', 'pred', 'set'])
train_generator.reset()
valid_generator.reset()
# Add train predictions and labels
for i in range(STEP_SIZE_TRAIN + 1):
im, lbl = next(train_generator)
preds = model.predict(im, batch_size=train_generator.batch_size)
for index in range(len(preds)):
df_preds.loc[len(df_preds)] = [lbl[index], preds[index][0], 'train']
# Add validation predictions and labels
for i in range(STEP_SIZE_VALID + 1):
im, lbl = next(valid_generator)
preds = model.predict(im, batch_size=valid_generator.batch_size)
for index in range(len(preds)):
df_preds.loc[len(df_preds)] = [lbl[index], preds[index][0], 'validation']
df_preds['label'] = df_preds['label'].astype('int')
# + _kg_hide-input=true
def classify(x):
if x < 0.5:
return 0
elif x < 1.5:
return 1
elif x < 2.5:
return 2
elif x < 3.5:
return 3
return 4
# Classify predictions
df_preds['predictions'] = df_preds['pred'].apply(lambda x: classify(x))
train_preds = df_preds[df_preds['set'] == 'train']
validation_preds = df_preds[df_preds['set'] == 'validation']
# -
# # Model Evaluation
# ## Confusion Matrix
#
# ### Original thresholds
# + _kg_hide-input=true
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe', '4 - Proliferative DR']
def plot_confusion_matrix(train, validation, labels=labels):
train_labels, train_preds = train
validation_labels, validation_preds = validation
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
train_cnf_matrix = confusion_matrix(train_labels, train_preds)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap=sns.cubehelix_palette(8),ax=ax2).set_title('Validation')
plt.show()
plot_confusion_matrix((train_preds['label'], train_preds['predictions']), (validation_preds['label'], validation_preds['predictions']))
# -
# ## Quadratic Weighted Kappa
# + _kg_hide-input=true
def evaluate_model(train, validation):
train_labels, train_preds = train
validation_labels, validation_preds = validation
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(np.append(train_preds, validation_preds), np.append(train_labels, validation_labels), weights='quadratic'))
evaluate_model((train_preds['label'], train_preds['predictions']), (validation_preds['label'], validation_preds['predictions']))
# -
# ## Apply model to test set and output predictions
# + _kg_hide-input=true
def apply_tta(model, generator, steps=10):
step_size = generator.n//generator.batch_size
preds_tta = []
for i in range(steps):
generator.reset()
preds = model.predict_generator(generator, steps=step_size)
preds_tta.append(preds)
return np.mean(preds_tta, axis=0)
preds = apply_tta(model, test_generator)
predictions = [classify(x) for x in preds]
results = pd.DataFrame({'id_code':test['id_code'], 'diagnosis':predictions})
results['id_code'] = results['id_code'].map(lambda x: str(x)[:-4])
# + _kg_hide-input=true _kg_hide-output=false
# Cleaning created directories
if os.path.exists(train_dest_path):
shutil.rmtree(train_dest_path)
if os.path.exists(validation_dest_path):
shutil.rmtree(validation_dest_path)
if os.path.exists(test_dest_path):
shutil.rmtree(test_dest_path)
# -
# # Predictions class distribution
# + _kg_hide-input=true
fig = plt.subplots(sharex='col', figsize=(24, 8.7))
sns.countplot(x="diagnosis", data=results, palette="GnBu_d").set_title('Test')
sns.despine()
plt.show()
# + _kg_hide-input=true
results.to_csv('submission.csv', index=False)
display(results.head())
| Model backlog/EfficientNet/EfficientNetB3/172 - EfficientNetB3 - Reg - Batch 32, Img 224.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit
# language: python
# name: python385jvsc74a57bd031f2aee4e71d21fbe5cf8b01ff0e069b9275f58929596ceb00d14d90e3e16cd6
# ---
# +
import pandas as pd
from sklearn.datasets import load_breast_cancer
pd.set_option('display.max_columns', 30)
dados = load_breast_cancer()
x = pd.DataFrame(dados.data, columns = [dados.feature_names])
y = pd.Series(dados.target)
# -
x.head()
# +
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# Separando os dados entre treino e teste:
X_treino, X_teste, Y_treino, Y_teste = train_test_split(x, y, test_size = 0.3, random_state = 9)
modelo = LogisticRegression(solver='liblinear', C = 95, penalty = 'l1')
modelo.fit(X_treino, Y_treino)
resultado = modelo.score(X_teste, Y_teste)
print(resultado)
# -
predicoes = modelo.predict_proba(X_teste)
probs = predicoes[:, 1]
# +
from sklearn.metrics import roc_curve
fpr, tpr, threshholds = roc_curve(Y_teste, probs)
print('TPR:', tpr)
print('FPR:', fpr)
print('Threshholds:', threshholds)
# -
# ##### Onde
# $FPR = \frac{FP} {FP + TN}$
#
# $TPR = \frac{TP} {TP + FN}$
# +
import matplotlib.pyplot as plt
plt.scatter(fpr, tpr)
plt.show()
# +
from sklearn.metrics import roc_auc_score
# Score em relação à área da curva
print(roc_auc_score(Y_teste, probs))
| Normalizacoes/ROC_AUC.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <img style="float: left; padding-right: 10px; width: 45px" src="https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png"> CS109B Data Science 2: Advanced Topics in Data Science
# ## Lab 2 - Smoothers and Generalized Additive Models - Model Fitting
#
# <div class="discussion"><b>Spring 2020</b></div>
#
# **Harvard University**<br>
# **Spring 2020**<br>
# **Instructors:** <NAME>, <NAME>, and <NAME><br>
# **Lab Instructors:** <NAME> and <NAME><br>
# **Content:** <NAME> and <NAME>
#
# ---
## RUN THIS CELL TO PROPERLY HIGHLIGHT THE EXERCISES
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2019-CS109B/master/content/styles/cs109.css").text
HTML(styles)
# +
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import pandas as pd
# %matplotlib inline
# -
# ## Learning Goals
#
# By the end of this lab, you should be able to:
# * Understand how to implement GAMs with the Python package `pyGAM`
# * Learn about the practical aspects of Splines and how to use them.
#
# **This lab corresponds to lectures 1, 2, and 3 and maps to homework 1.**
# ## Table of Contents
#
# * 1 - Overview - A Top View of LMs, GLMs, and GAMs to set the stage
# * 2 - A review of Linear Regression with `statsmodels`. What are those weird formulas?
# * 3 - Splines
# * 4 - Generative Additive Models with pyGAM
# * 5 - Smooting Splines using pyGAM
# ## Overview
#
# Linear Models (LM), Generalized Linear Models (GLMs), Generalized Additive Models (GAMs), Splines, Natural Splines, Smoothing Splines! So many definitions. Let's try and work through an example for each of them so we can better understand them.
#
# 
# *image source: <NAME> (one of the developers of pyGAM)*
# ### A - Linear Models
#
# First we have the **Linear Models** which you know from 109a. These models are linear in the coefficients. Very *interpretable* but suffer from high bias because let's face it, few relationships in life are linear. Simple Linear Regression (defined as a model with one predictor) as well as Multiple Linear Regression (more than one predictors) are examples of LMs. Polynomial Regression extends the linear model by adding terms that are still linear for the coefficients but non-linear when it somes to the predictiors which are now raised in a power or multiplied between them.
#
# 
#
# $$
# \begin{aligned}
# y = \beta{_0} + \beta{_1}{x_1} & \mbox{(simple linear regression)}\\
# y = \beta{_0} + \beta{_1}{x_1} + \beta{_2}{x_2} + \beta{_3}{x_3} & \mbox{(multiple linear regression)}\\
# y = \beta{_0} + \beta{_1}{x_1} + \beta{_2}{x_1^2} + \beta{_3}{x_3^3} & \mbox{(polynomial regression)}\\
# \end{aligned}
# $$
# <div class="discussion"><b>Discussion</b></div>
#
# - What does it mean for a model to be **interpretable**?
# - Are linear regression models interpretable? Are random forests? What about Neural Networks such as FFNs and CNNs?
# - Do we always want interpretability? Describe cases where we do and cases where we do not care.
# - interpretable: easily understand how each predictors affect the response variable
# - linear models are more interpretable than NN
# - It depends on the context. We don't want interpretability when users don't care about how the model works.
# ### B - Generalized Linear Models (GLMs)
#
# 
#
# $$
# \begin{aligned}
# y = \beta{_0} + \beta{_1}{x_1} + \beta{_2}{x_2} + \beta{_3}{x_3}
# \end{aligned}
# $$
#
#
# **Generalized Linear Models** is a term coined in the early 1970s by Nelder and Wedderburn for a class of models that includes both Linear Regression and Logistic Regression. A GLM fits one coefficient per feature (predictor).
# ### C - Generalized Additive Models (GAMs)
#
# Hastie and Tidshirani coined the term **Generalized Additive Models** in 1986 for a class of non-linear extensions to Generalized Linear Models.
#
# 
#
# $$
# \begin{aligned}
# y = \beta{_0} + f_1\left(x_1\right) + f_2\left(x_2\right) + f_3\left(x_3\right) \\
# y = \beta{_0} + f_1\left(x_1\right) + f_2\left(x_2, x_3\right) + f_3\left(x_3\right) & \mbox{(with interaction terms)}
# \end{aligned}
# $$
#
# In practice we add splines and regularization via smoothing penalties to our GLMs. Decision Trees also fit in this category.
#
# *image source: <NAME>*
# ### D - Basis Functions
#
# In our models we can use various types of functions as "basis".
# - Monomials such as $x^2$, $x^4$ (**Polynomial Regression**)
# - Sigmoid functions (neural networks)
# - Fourier functions
# - Wavelets
# - **Regression splines** which we will look at shortly.
# <div class="discussion"><b>Discussion</b></div>
#
# - Where does polynomial regression fit in all this? Linear model: linear with respect to beta coefficients here
# Answer: GLMs include Polynomial Regression so the graphic above should really include curved lines, not just straight...
# ## Implementation
#
# ### 1 - Linear/Polynomial Regression
#
# We will use the `diabetes` dataset.
#
# Variables are:
# - subject: subject ID number
# - age: age diagnosed with diabetes
# - acidity: a measure of acidity called base deficit
# Response:
# - y: natural log of serum C-peptide concentration
#
# *Original source is Sockett et al. (1987) mentioned in Hastie and Tibshirani's book
# "Generalized Additive Models".*
#
#
#
# Reading data and (some) exploring in Pandas:
diab = pd.read_csv("../data/diabetes.csv")
diab.head()
diab.dtypes
diab.describe()
# Plotting with matplotlib:
ax0 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data") #plotting direclty from pandas!
ax0.set_xlabel("Age at Diagnosis")
ax0.set_ylabel("Log C-Peptide Concentration");
# ### Linear/Polynomial regression with statsmodels.
#
# As you remember from 109a, we have two tools for Linear Regression:
# - `statsmodels` [https://www.statsmodels.org/stable/regression.html](https://www.statsmodels.org/stable/regression.html), and
# - `sklearn`[https://scikit-learn.org/stable/index.html](https://scikit-learn.org/stable/index.html)
#
# Previously, we worked from a vector of target values and a design matrix we built ourself (e.g. using `sklearn`'s PolynomialFeatures). `statsmodels` allows users to fit statistical models using R-style **formulas**. They build the target value and design matrix for you.
#
# ```
# # our target variable is 'Lottery', while 'Region' is a categorical predictor
# df = dta.data[['Lottery', 'Literacy', 'Wealth', 'Region']]
#
# formula='Lottery ~ Literacy + Wealth + C(Region) + Literacy * Wealth'
# ```
#
# For more on these formulas see:
#
# - https://www.statsmodels.org/stable/examples/notebooks/generated/formulas.html
# - https://patsy.readthedocs.io/en/latest/overview.html
# +
import statsmodels.formula.api as sm
model1 = sm.ols('y ~ age',data=diab)
fit1_lm = model1.fit()
# -
# Let's build a dataframe to predict values on (sometimes this is just the test or validation set). Very useful for making pretty plots of the model predictions - predict for TONS of values, not just whatever's in the training set.
# +
x_pred = np.linspace(0,16,100)
predict_df = pd.DataFrame(data={"age":x_pred})
predict_df.head()
# -
# Use `get_prediction(<data>).summary_frame()` to get the model's prediction (and error bars!)
prediction_output = fit1_lm.get_prediction(predict_df).summary_frame()
prediction_output.head()
# Plot the model and error bars
# +
ax1 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data with least-squares linear fit")
ax1.set_xlabel("Age at Diagnosis")
ax1.set_ylabel("Log C-Peptide Concentration")
ax1.plot(predict_df.age, prediction_output['mean'],color="green")
ax1.plot(predict_df.age, prediction_output['mean_ci_lower'], color="blue",linestyle="dashed")
ax1.plot(predict_df.age, prediction_output['mean_ci_upper'], color="blue",linestyle="dashed");
# -
# <div class="exercise"><b>Exercise 1</b></div>
#
# - Fit a 3rd degree polynomial model and
# - plot the model+error bars.
#
# You can either take
# - **Route1**: Build a design df with a column for each of `age`, `age**2`, `age**3`, or
# - **Route2**: Just edit the formula
# your answer here
poly_model = sm.ols('y ~ age + I(age**2) + I(age**3)',data=diab).fit()
# +
# # %load ../solutions/exercise1-1.py
fit2_lm = sm.ols(formula="y ~ age + np.power(age, 2) + np.power(age, 3)",data=diab).fit()
poly_predictions = fit2_lm.get_prediction(predict_df).summary_frame()
poly_predictions.head()
# +
# # %load ../solutions/exercise1-2.py
ax2 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data with least-squares cubic fit")
ax2.set_xlabel("Age at Diagnosis")
ax2.set_ylabel("Log C-Peptide Concentration")
ax2.plot(predict_df.age, poly_predictions['mean'],color="green")
ax2.plot(predict_df.age, poly_predictions['mean_ci_lower'], color="blue",linestyle="dashed")
ax2.plot(predict_df.age, poly_predictions['mean_ci_upper'], color="blue",linestyle="dashed");
# -
# <div class="discussion"><b>Ed exercise</b></div>
#
# This example was similar with the Ed exercise. [Open it in Ed](https://us.edstem.org/courses/172/lessons/656/slides/2916) and let's go though it.
# ### 2 - Piecewise Polynomials a.k.a. Splines
#
# Splines are a type of piecewise polynomial interpolant. A spline of degree k is a piecewise polynomial that is continuously differentiable k − 1 times.
#
# Splines are the basis of CAD software and vector graphics including a lot of the fonts used in your computer. The name “spline” comes from a tool used by ship designers to draw smooth curves. Here is the letter $epsilon$ written with splines:
#
# 
#
# *font idea inspired by <NAME> (AM205)*
#
# If the degree is 1 then we have a Linear Spline. If it is 3 then we have a Cubic spline. It turns out that cubic splines because they have a continous 2nd derivative at the knots are very smoothly looking to the eye. We do not need higher order than that. The Cubic Splines are usually Natural Cubic Splines which means they have the added constrain of the end points' second derivative = 0.
#
# We will use the CubicSpline and the B-Spline as well as the Linear Spline.
#
# #### scipy.interpolate
#
# See all the different splines that scipy.interpolate has to offer: https://docs.scipy.org/doc/scipy/reference/interpolate.html
#
# Let's use the simplest form which is interpolate on a set of points and then find the points between them.
# +
from scipy.interpolate import splrep, splev
from scipy.interpolate import BSpline, CubicSpline
from scipy.interpolate import interp1d
# define the range of the function
a = -1
b = 1
# define the number of knots
num_knots = 10
x = np.linspace(a,b,num_knots)
# define the function we want to approximate
y = 1/(1+25*(x**2))
# make a linear spline
linspline = interp1d(x, y)
# sample at these points to plot
xx = np.linspace(a,b,1000)
yy = 1/(1+25*(xx**2))
plt.plot(x,y,'*')
plt.plot(xx, yy, label='true function')
plt.plot(xx, linspline(xx), label='linear spline');
plt.legend();
# -
# <div class="exercise"><b>Exercise 2</b></div>
#
# The Linear interpolation does not look very good. Fit a Cubic Spline and plot along the Linear to compare.
# +
# your answer here
cub_spline = CubicSpline(x, y)
plt.plot(x,y,'*')
plt.plot(xx, yy, label='true function')
plt.plot(xx, linspline(xx), label='linear spline');
plt.plot(xx, cub_spline(xx), label='cubic spline');
plt.legend();
# +
# # %load ../solutions/exercise2.py
# define the range of the function
a = -1
b = 1
# define the knots
num_knots = 10
x = np.linspace(a,b,num_knots)
# define the function we want to approximate
y = 1/(1+25*(x**2))
# make the Cubic spline
cubspline = CubicSpline(x, y)
# OR make a linear spline
linspline = interp1d(x, y)
# plot
xx = np.linspace(a,b,1000)
yy = 1/(1+25*(xx**2))
plt.plot(xx, yy, label='true function')
plt.plot(x,y,'*')
plt.plot(xx, linspline(xx), label='linear');
plt.plot(xx, cubspline(xx), label='cubic');
plt.legend();
# -
# <div class="discussion"><b>Discussion</b></div>
#
# - Change the number of knots to 100 and see what happens. What would happen if we run a polynomial model of degree equal to the number of knots (a global one as in polynomial regression, not a spline)?
# - What makes a spline 'Natural'?
# change num_knots to 100 will make the interpolation curve fit much better.
# #### B-Splines
#
# A B-splines (Basis Splines) is defined by a set of **control points** and a set of **basis functions** that intepolate (fit) the function between these points. By choosing to have no smoothing factor we forces the final B-spline to pass though all the points. If, on the other hand, we set a smothing factor, our function is more of an approximation with the control points as "guidance". The latter produced a smoother curve which is prefferable for drawing software. For more on Splines see: https://en.wikipedia.org/wiki/B-spline)
#
# 
#
# We will use [`scipy.splrep`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.splrep.html#scipy.interpolate.splrep) to calulate the coefficients for the B-Spline and draw it.
# #### B-Spline with no smooting
# +
from scipy.interpolate import splev, splrep
x = np.linspace(0, 10, 10)
y = np.sin(x)
t,c,k = splrep(x, y) # (tck) is a tuple containing the vector of knots, coefficients, degree of the spline
print(t,c,k)
# define the points to plot on (x2)
x2 = np.linspace(0, 10, 200)
y2 = BSpline(t, c, k)
plt.plot(x, y, 'o', x2, y2(x2))
plt.show()
# -
# #### B-Spline with smooting factor s
# +
from scipy.interpolate import splev, splrep
x = np.linspace(0, 10, 10)
y = np.sin(x)
s = 0.5 # add smooting factor
task = 0 # task needs to be set to 0, which represents:
# we are specifying a smoothing factor and thus only want
# splrep() to find the optimal t and c
t,c,k = splrep(x, y, task=task, s=s)
# define the points to plot on (x2)
x2 = np.linspace(0, 10, 200)
y2 = BSpline(t, c, k)
plt.plot(x, y, 'o', x2, y2(x2))
plt.show()
# -
# #### B-Spline with given knots
x = np.linspace(0, 10, 100)
y = np.sin(x)
knots = np.quantile(x, [0.25, 0.5, 0.75])
print(knots)
# calculate the B-Spline
t,c,k = splrep(x, y, t=knots)
curve = BSpline(t,c,k)
curve
plt.scatter(x=x,y=y,c='grey', alpha=0.4)
yknots = np.sin(knots)
plt.scatter(knots, yknots, c='r')
plt.plot(x,curve(x))
plt.show()
# <div class="discussion"><b>Ed exercise</b></div>
#
# This example was similar with the Ed exercise. [Open it in Ed](https://us.edstem.org/courses/172/lessons/656/slides/2917) and let's go though it.
# ### 3 - GAMs
#
# https://readthedocs.org/projects/pygam/downloads/pdf/latest/
#
# #### A - Classification in `pyGAM`
#
# Let's get our (multivariate!) data, the `kyphosis` dataset, and the `LogisticGAM` model from `pyGAM` to do binary classification.
#
# - kyphosis - wherther a particular deformation was present post-operation
# - age - patient's age in months
# - number - the number of vertebrae involved in the operation
# - start - the number of the topmost vertebrae operated on
# +
kyphosis = pd.read_csv("../data/kyphosis.csv")
display(kyphosis.head())
display(kyphosis.describe(include='all'))
display(kyphosis.dtypes)
# -
# convert the outcome in a binary form, 1 or 0
kyphosis = pd.read_csv("../data/kyphosis.csv")
kyphosis["outcome"] = 1*(kyphosis["Kyphosis"] == "present")
kyphosis.describe()
# +
from pygam import LogisticGAM, s, f, l
X = kyphosis[["Age","Number","Start"]]
y = kyphosis["outcome"]
kyph_gam = LogisticGAM().fit(X,y)
# -
# #### Outcome dependence on features
#
# To help us see how the outcome depends on each feature, `pyGAM` has the `partial_dependence()` function.
# ```
# pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
# ```
# For more on this see the : https://pygam.readthedocs.io/en/latest/api/logisticgam.html
#
res = kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(kyph_gam.terms):
if term.isintercept:
continue
XX = kyph_gam.generate_X_grid(term=i)
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
# Notice that we did not specify the basis functions in the .fit(). Cool. `pyGAM` figures them out for us by using $s()$ (splines) for numerical variables and $f()$ for categorical features. If this is not what we want we can manually specify the basis functions, as follows:
kyph_gam = LogisticGAM(s(0)+s(1)+s(2)).fit(X,y)
res = kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(kyph_gam.terms):
if term.isintercept:
continue
XX = kyph_gam.generate_X_grid(term=i)
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
# #### B - Regression in `pyGAM`
#
# For regression problems, we can use a `linearGAM` model. For this part we will use the `wages` dataset.
#
# https://pygam.readthedocs.io/en/latest/api/lineargam.html
# #### The `wages` dataset
#
# Let's inspect another dataset that is included in `pyGAM` that notes the wages of people based on their age, year of employment and education.
# +
# from the pyGAM documentation
from pygam import LinearGAM, s, f
from pygam.datasets import wage
X, y = wage(return_X_y=True)
## model
gam = LinearGAM(s(0) + s(1) + f(2))
gam.gridsearch(X, y)
## plotting
plt.figure();
fig, axs = plt.subplots(1,3);
titles = ['year', 'age', 'education']
for i, ax in enumerate(axs):
XX = gam.generate_X_grid(term=i)
ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX))
ax.plot(XX[:, i], gam.partial_dependence(term=i, X=XX, width=.95)[1], c='r', ls='--')
if i == 0:
ax.set_ylim(-30,30)
ax.set_title(titles[i]);
# -
# <div class="discussion"><b>Discussion</b></div>
#
# What are your observations from the plots above?
# ### 4 - Smoothing Splines using pyGAM
#
# For clarity: this is the fancy spline model that minimizes $MSE - \lambda\cdot\text{wiggle penalty}$ $=$ $\sum_{i=1}^N \left(y_i - f(x_i)\right)^2 - \lambda \int \left(f''(x)\right)^2$, across all possible functions $f$. The winner will always be a continuous, cubic polynomial with a knot at each data point.
# Let's see how this smoothing works in `pyGAM`. We start by creating some arbitrary data and fitting them with a GAM.
# +
X = np.linspace(0,10,500)
y = np.sin(X*2*np.pi)*X + np.random.randn(len(X))
plt.scatter(X,y);
# -
# let's try a large lambda first and lots of splines
gam = LinearGAM(lam=1e6, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
# We see that the large $\lambda$ forces a straight line, no flexibility. Let's see now what happens if we make it smaller.
# let's try a smaller lambda
gam = LinearGAM(lam=1e2, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
# There is some curvature there but still not a good fit. Let's try no penalty. That should have the line fit exactly.
# no penalty, let's try a 0 lambda
gam = LinearGAM(lam=0, n_splines=50). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3)
plt.plot(XX, gam.predict(XX))
# Yes, that is good. Now let's see what happens if we lessen the number of splines. The fit should not be as good.
# no penalty, let's try a 0 lambda
gam = LinearGAM(lam=0, n_splines=10). fit(X,y)
XX = gam.generate_X_grid(term=0)
plt.scatter(X,y,alpha=0.3);
plt.plot(XX, gam.predict(XX));
# Indeed.
| content/labs/lab2 smoothing/cs109b_lab2_smooths_and_GAMs.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] nbgrader={}
# # Interact Exercise 01
# + [markdown] nbgrader={}
# ## Import
# + nbgrader={}
# %matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
# + nbgrader={}
from IPython.html.widgets import interact, interactive, fixed
from IPython.display import display
# + [markdown] nbgrader={}
# ## Interact basics
# + [markdown] nbgrader={}
# Write a `print_sum` function that `prints` the sum of its arguments `a` and `b`.
# + nbgrader={"checksum": "4d7fa34d285413499aa7359dda2a2dcc", "solution": true}
def print_sum(a, b):
return (a+b)
# + [markdown] nbgrader={}
# Use the `interact` function to interact with the `print_sum` function.
#
# * `a` should be a floating point slider over the interval `[-10., 10.]` with step sizes of `0.1`
# * `b` should be an integer slider the interval [-8, 8] with step sizes of `2`.
# + deletable=false nbgrader={"checksum": "6cff4e8e53b15273846c3aecaea84a3d", "solution": true}
w = interactive(print_sum, a = (-10.0,10.0,0.1), b = (-8, 8, 2))
# -
display(w)
w.result
# + deletable=false nbgrader={"checksum": "42c776e2480b70e6a45ee325285f2977", "grade": true, "grade_id": "interactex01a", "points": 5}
assert True # leave this for grading the print_sum exercise
# + [markdown] nbgrader={}
# Write a function named `print_string` that prints a string and additionally prints the length of that string if a boolean parameter is `True`.
# + nbgrader={"checksum": "0a454725f1214af3f65e36c5bc4123e9", "solution": true}
def print_string(s, length=False):
print (s)
if length == True:
print(len(s))
# + [markdown] nbgrader={}
# Use the `interact` function to interact with the `print_string` function.
#
# * `s` should be a textbox with the initial value `"Hello World!"`.
# * `length` should be a checkbox with an initial value of `True`.
# + deletable=false nbgrader={"checksum": "6cff4e8e53b15273846c3aecaea84a3d", "solution": true}
w = interactive(print_string, s = "Hello, World!")
# -
w
# + deletable=false nbgrader={"checksum": "414350009853ea9cb00917ef3bec7b10", "grade": true, "grade_id": "interactex01b", "points": 5}
assert True # leave this for grading the print_string exercise
# -
| assignments/assignment05/InteractEx01.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (pytorch)
# language: python
# name: pytorch
# ---
# + [markdown] code_folding=[1] slideshow={"slide_type": "slide"}
# # Lecture 3: Matvecs and matmuls, memory hierarchy, Strassen algorithm
# + [markdown] slideshow={"slide_type": "slide"}
# ## Recap of the previous lectures
#
# - Floating point arithmetics and related issues
# - Stable algorithms: backward and forward stability
# - Most important matrix norms: spectral and Frobenius
# - Unitary matrices preserve these norms
# - There are two "basic" classes of unitary matrices: Householder and Givens matrices
# + [markdown] slideshow={"slide_type": "slide"}
# ## Examples of peak performance
#
# **Flops** –– floating point operations per second.
#
# Giga = $2^{30} \approx 10^9$,
# Tera = $2^{40} \approx 10^{12}$,
# Peta = $2^{50} \approx 10^{15}$,
# Exa = $2^{60} \approx 10^{18}$
#
# What is the **peak perfomance** of:
#
# 1. Modern CPU
# 2. Modern GPU
# 3. Largest supercomputer of the world?
# + [markdown] slideshow={"slide_type": "slide"}
# ### Clock frequency of CPU vs. performance in flops
#
# FLOPS = sockets * (cores per socket) * (number of clock cycles per second) * (number of floating point operations per cycle).
#
# - Typically sockets = 1
# - Number of cores is typically 2 or 4
# - Number of ticks per second is familiar clock frequency
# - Number of floating point operations per tick depends on the particular CPU
# + [markdown] slideshow={"slide_type": "slide"}
#
# 1. Modern CPU (Intel Core i7) –– 400 Gflops
# 2. Modern GPU (Nvidia Quadro RTX 8000) –– 16.3 Tflops single precision
# 3. [Largest supercomputer in the world](https://www.top500.org/lists/2019/06/) –– 513.85 Pflops –– peak performanse
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Matrix-by-vector multiplication (matvec)
#
# Multiplication of an $n\times n$ matrix $A$ by a vector $x$ of size $n\times 1$ ($y=Ax$):
#
# $$
# y_{i} = \sum_{i=1}^n a_{ij} x_j
# $$
#
# requires $n^2$ mutliplications and $n(n-1)$ additions. Thus, the overall complexity is $2n^2 - n =$ <font color='red'> $\mathcal{O}(n^2)$ </font>
# + [markdown] slideshow={"slide_type": "slide"}
# ## How bad is $\mathcal{O}(n^2)$?
#
# - Let $A$ be the matrix of pairwise gravitational interaction between planets in a galaxy.
#
# - The number of planets in an average galaxy is $10^{11}$, so the size of this matrix is $10^{11} \times 10^{11}$.
#
# - To model evolution in time we have to multiply this matrix by vector at each time step.
#
# - Top supercomputers do around $10^{16}$ floating point operations per second (flops), so the time required to multiply the matrix $A$ by a vector is approximately
#
# \begin{align*}
# \frac{(10^{11})^2 \text{ operations}}{10^{16} \text{ flops}} = 10^6 \text{ sec} \approx 11.5 \text{ days}
# \end{align*}
#
# for one time step. If we could multiply it with $\mathcal{O}(n)$ complexity, we would get
#
# \begin{align*}
# \frac{10^{11} \text{ operations}}{10^{16} \text{ flops}} = 10^{-5} \text{ sec}.
# \end{align*}
#
# Here is the YouTube video that illustrates collision of two galaxisies which was modelled by $\mathcal{O}(n \log n)$ algorithm:
# + slideshow={"slide_type": "slide"}
from IPython.display import YouTubeVideo
YouTubeVideo("7HF5Oy8IMoM")
# + [markdown] slideshow={"slide_type": "slide"}
# ## Can we beat $\mathcal{O}(n^2)$?
#
# - Generally speaking **NO**.
# - The point is that we have $\mathcal{O}(n^2)$ input data, so there is no way to be faster for a general matrix.
# - Fortunately, we can be faster <font color='red'>for certain types of matrices</font>.
# Here are some examples:
#
# * The simplest example may be a matrix of all ones, which can be easily multiplied with only $n-1$ additions. This matrix is of rank one. More generally we can multiply fast by <font color='red'>low-rank </font> matrices (or by matrices that have low-rank blocks)
#
# * <font color='red'>Sparse</font> matrices (contain $\mathcal{O}(n)$ nonzero elements)
#
# * <font color='red'>Structured</font> matrices:
# * Fourier
# * Circulant
# * Toeplitz
# * Hankel
# + [markdown] slideshow={"slide_type": "slide"}
# ## Matrix-by-matrix product
#
# Consider composition of two linear operators:
#
# 1. $y = Bx$
# 2. $z = Ay$
#
# Then, $z = Ay = A B x = C x$, where $C$ is the **matrix-by-matrix product**.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Matrix-by-matrix product (MM): classics
#
# **Definition**. A product of an $n \times k$ matrix $A$ and a $k \times m$ matrix $B$ is a $n \times m$ matrix $C$ with the elements
# $$
# c_{ij} = \sum_{s=1}^k a_{is} b_{sj}, \quad i = 1, \ldots, n, \quad j = 1, \ldots, m
# $$
#
# For $m=k=n$ complexity of a naïve algorithm is $2n^3 - n^2 =$ <font color='red'>$\mathcal{O}(n^3)$</font>.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Discussion of MM
#
# - Matrix-by-matrix product is the **core** for almost all efficient algorithms in numerical linear algebra.
#
# - Basically, all the dense NLA algorithms are reduced to a sequence of matrix-by-matrix products.
#
# - Efficient implementation of MM reduces the complexity of numerical algorithms by the same factor.
#
# - However, implementing MM is not easy at all!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Efficient implementation for MM
# **Q1**: Is it easy to multiply a matrix by a matrix in the most efficient way?
# + [markdown] slideshow={"slide_type": "slide"}
# ## Answer: no, it is not easy
#
# If you want it as fast as possible, using the computers that are at hand.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Demo
# Let us do a short demo and compare a `np.dot()` procedure which in my case uses MKL with a hand-written matrix-by-matrix routine in Python and also its numba version.
# + code_folding=[] slideshow={"slide_type": "slide"}
import numpy as np
def matmul(a, b):
n = a.shape[0]
k = a.shape[1]
m = b.shape[1]
c = np.zeros((n, m))
for i in range(n):
for j in range(m):
for s in range(k):
c[i, j] += a[i, s] * b[s, j]
return c
# + slideshow={"slide_type": "slide"}
import numpy as np
from numba import jit # Just-in-time compiler for Python, see http://numba.pydata.org
@jit(nopython=True)
def numba_matmul(a, b):
n = a.shape[0]
k = a.shape[1]
m = b.shape[1]
c = np.zeros((n, m))
for i in range(n):
for j in range(m):
for s in range(k):
c[i, j] += a[i, s] * b[s, j]
return c
# + [markdown] slideshow={"slide_type": "slide"}
# Then we just compare computational times.
#
# Guess the answer.
# + slideshow={"slide_type": "slide"}
import jax.numpy as jnp
from jax.config import config
config.update("jax_enable_x64", True)
n = 100
a = np.random.randn(n, n)
b = np.random.randn(n, n)
a_jax = jnp.array(a)
b_jax = jnp.array(b)
# %timeit matmul(a, b)
# %timeit numba_matmul(a, b)
# %timeit a @ b
# %timeit (a_jax @ b_jax).block_until_ready()
# + [markdown] slideshow={"slide_type": "slide"}
# Is this answer correct for any dimensions of matrices?
# + slideshow={"slide_type": "slide"}
import matplotlib.pyplot as plt
# %matplotlib inline
dim_range = [10*i for i in range(1, 11)]
time_range_matmul = []
time_range_numba_matmul = []
time_range_np = []
for n in dim_range:
print("Dimension = {}".format(n))
a = np.random.randn(n, n)
b = np.random.randn(n, n)
# t = %timeit -o -q matmul(a, b)
time_range_matmul.append(t.best)
# t = %timeit -o -q numba_matmul(a, b)
time_range_numba_matmul.append(t.best)
# t = %timeit -o -q np.dot(a, b)
time_range_np.append(t.best)
# + slideshow={"slide_type": "slide"}
plt.plot(dim_range, time_range_matmul, label="Matmul")
plt.plot(dim_range, time_range_numba_matmul, label="Matmul Numba")
plt.plot(dim_range, time_range_np, label="Numpy")
plt.legend(fontsize=18)
plt.xlabel("Dimension", fontsize=18)
plt.ylabel("Time", fontsize=18)
plt.yscale("log")
# + [markdown] slideshow={"slide_type": "slide"}
# ## Why is naïve implementation slow?
# It is slow due to two issues:
#
# - It does not use the benefits of fast memory (cache) and in general memory architecture
# - It does not use available parallelization ability (especially important for GPU)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Memory architecture
# <img width=80% src="Memory-Hierarchy.jpg">
#
# - Fast memory is small
# - Bigger memory is slow
# + [markdown] slideshow={"slide_type": "slide"}
# ## Making algorithms more computationally intensive
#
# <font color='red'>**Implementation in NLA**</font>: use block version of algorithms. <br>
#
# This approach is a core of **[BLAS (Basic Linear Algebra Subroutines)](http://www.netlib.org/blas/)**, written in Fortran many years ago, and still rules the computational world.
# + [markdown] slideshow={"slide_type": "slide"}
# Split the matrix into blocks! For illustration consider splitting in $2 \times 2$ block matrix:
#
# $$
# A = \begin{bmatrix}
# A_{11} & A_{12} \\
# A_{21} & A_{22}
# \end{bmatrix}, \quad B = \begin{bmatrix}
# B_{11} & B_{12} \\
# B_{21} & B_{22}
# \end{bmatrix}$$
#
# Then,
#
# $$AB = \begin{bmatrix}A_{11} B_{11} + A_{12} B_{21} & A_{11} B_{12} + A_{12} B_{22} \\
# A_{21} B_{11} + A_{22} B_{21} & A_{21} B_{12} + A_{22} B_{22}\end{bmatrix}.$$
# + [markdown] slideshow={"slide_type": "fragment"}
# If $A_{11}, B_{11}$ and their product fit into the cache memory (which is 12 Mb (L3) for the [recent Intel Chip](https://en.wikipedia.org/wiki/List_of_Intel_microprocessors#Desktop)), then we load them only once into the memory.
# + [markdown] slideshow={"slide_type": "slide"}
# ## BLAS
# BLAS has three levels:
# 1. BLAS-1, operations like $c = a + b$
# 2. BLAS-2, operations like matrix-by-vector product
# 3. BLAS-3, matrix-by-matrix product
#
# What is the principal differences between them?
# + [markdown] slideshow={"slide_type": "slide"}
# The main difference is the number of operations vs. the number of input data!
#
# 1. BLAS-1: $\mathcal{O}(n)$ data, $\mathcal{O}(n)$ operations
# 2. BLAS-2: $\mathcal{O}(n^2)$ data, $\mathcal{O}(n^2)$ operations
# 3. BLAS-3: $\mathcal{O}(n^2)$ data, $\mathcal{O}(n^3)$ operations
# + [markdown] slideshow={"slide_type": "slide"}
# ## Why BLAS is so important and actual?
#
# 1. The state-of-the-art implementation of the basic linear algebra operations
# 2. Provides standard names for operations in any new implementations (e.g. [ATLAS](https://www.netlib.org/atlas/), [OpenBLAS](https://www.openblas.net/), [MKL](https://software.intel.com/en-us/mkl)). You can call matrix-by-matrix multiplication function (GEMM), link your code with any BLAS implementation and it will work correctly
# 3. Formulate new algorithms in terms of BLAS operations
# 4. There are wrappers for the most popular languages
# + [markdown] slideshow={"slide_type": "slide"}
# ## Packages related to BLAS
#
# 1. [ATLAS](http://math-atlas.sourceforge.net) - Automatic Tuned Linear Algebra Software. It automatically adapts to a particular system architechture.
# 2. [LAPACK](http://www.netlib.org/lapack/) - Linear Algebra Package. It provides high-level linear algebra operations (e.g. matrix factorizations), which are based on calls of BLAS subroutines.
# 3. [Intel MKL](https://software.intel.com/en-us/intel-mkl) - Math Kernel Library. It provides re-implementation of BLAS and LAPACK, optimized for Intel processors. Available in Anaconda Python distribution:
# ```
# conda install mkl
# ```
# MATLAB uses Intel MKL by default.
#
# 4. OpenBLAS is an optimized BLAS library based on [GotoBLAS](https://en.wikipedia.org/wiki/GotoBLAS).
#
# 5. PyTorch [supports](https://pytorch.org/docs/stable/torch.html#blas-and-lapack-operations) some calls from BLAS and LAPACK
#
# 6. For GPU it was implemented special [cuBLAS](https://docs.nvidia.com/cuda/cublas/index.html).
#
#
# For comparison of OpenBLAS and Intel MKL, see this [review](https://software.intel.com/en-us/articles/performance-comparison-of-openblas-and-intel-math-kernel-library-in-r)
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Faster algorithms for matrix multiplication
#
# Recall that matrix-matrix multiplication costs $\mathcal{O}(n^3)$ operations.
# However, storage is $\mathcal{O}(n^2)$.
#
# **Question:** is it possible to reduce number operations down to $\mathcal{O}(n^2)$?
# + [markdown] slideshow={"slide_type": "fragment"}
# **Answer**: a quest for $\mathcal{O}(n^2)$ matrix-by-matrix multiplication algorithm is not yet done.
# + [markdown] slideshow={"slide_type": "slide"}
# * Strassen gives $\mathcal{O}(n^{2.807\dots})$ –– sometimes used in practice
#
# * [Current world record](http://arxiv.org/pdf/1401.7714v1.pdf) $\mathcal{O}(n^{2.37\dots})$ –– big constant, not practical, based on [Coppersmith-Winograd_algorithm](https://en.wikipedia.org/wiki/Coppersmith%E2%80%93Winograd_algorithm).
# - It improved the previous record (Williams 2012) by $3\cdot 10^{-7}$
# - The papers still study multiplication of $3 \times 3$ matrices and interpret it from different sides ([Heule, et. al. 2019](https://arxiv.org/pdf/1905.10192.pdf))
#
# Consider Strassen in more details.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Naïve multiplication
#
# Let $A$ and $B$ be two $2\times 2$ matrices. Naïve multiplication $C = AB$
#
# $$
# \begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix} =
# \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}
# \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} =
# \begin{bmatrix}
# a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{21} + a_{12}b_{22} \\
# a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{21} + a_{22}b_{22}
# \end{bmatrix}
# $$
#
# contains $8$ multiplications and $4$ additions.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Strassen algorithm
#
# In the work [Gaussian elimination is not optimal](http://link.springer.com/article/10.1007%2FBF02165411?LI=true) (1969) Strassen found that one can calculate $C$ using 18 additions and only 7 multiplications:
# $$
# \begin{split}
# c_{11} &= f_1 + f_4 - f_5 + f_7, \\
# c_{12} &= f_3 + f_5, \\
# c_{21} &= f_2 + f_4, \\
# c_{22} &= f_1 - f_2 + f_3 + f_6,
# \end{split}
# $$
# where
# $$
# \begin{split}
# f_1 &= (a_{11} + a_{22}) (b_{11} + b_{22}), \\
# f_2 &= (a_{21} + a_{22}) b_{11}, \\
# f_3 &= a_{11} (b_{12} - b_{22}), \\
# f_4 &= a_{22} (b_{21} - b_{11}), \\
# f_5 &= (a_{11} + a_{12}) b_{22}, \\
# f_6 &= (a_{21} - a_{11}) (b_{11} + b_{12}), \\
# f_7 &= (a_{12} - a_{22}) (b_{21} + b_{22}).
# \end{split}
# $$
#
# Fortunately, these formulas hold even if $a_{ij}$ and $b_{ij}$, $i,j=1,2$ are block matrices.
#
# Thus, Strassen algorithm looks as follows.
# - First of all we <font color='red'>split</font> matrices $A$ and $B$ of sizes $n\times n$, $n=2^d$ <font color='red'> into 4 blocks</font> of size $\frac{n}{2}\times \frac{n}{2}$
# - Then we <font color='red'>calculate multiplications</font> in the described formulas <font color='red'>recursively</font>
#
# This leads us again to the **divide and conquer** idea.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Complexity of the Strassen algorithm
#
# #### Number of multiplications
#
# Calculation of number of multiplications is a trivial task. Let us denote by $M(n)$ number of multiplications used to multiply 2 matrices of sizes $n\times n$ using the divide and conquer concept.
# Then for naïve algorithm we have number of multiplications
#
# $$ M_\text{naive}(n) = 8 M_\text{naive}\left(\frac{n}{2} \right) = 8^2 M_\text{naive}\left(\frac{n}{4} \right)
# = \dots = 8^{d-1} M(1) = 8^{d} = 8^{\log_2 n} = n^{\log_2 8} = n^3 $$
#
# So, even when using divide and coquer idea we can not be better than $n^3$.
#
# Let us calculate number of multiplications for the Strassen algorithm:
#
# $$ M_\text{strassen}(n) = 7 M_\text{strassen}\left(\frac{n}{2} \right) = 7^2 M_\text{strassen}\left(\frac{n}{4} \right)
# = \dots = 7^{d-1} M(1) = 7^{d} = 7^{\log_2 n} = n^{\log_2 7} $$
# + [markdown] slideshow={"slide_type": "slide"}
# #### Number of additions
#
# There is no point to estimate number of addtitions $A(n)$ for naive algorithm, as we already got $n^3$ multiplications.
# For the Strassen algorithm we have:
#
# $$ A_\text{strassen}(n) = 7 A_\text{strassen}\left( \frac{n}{2} \right) + 18 \left( \frac{n}{2} \right)^2 $$
#
# since on the first level we have to add $\frac{n}{2}\times \frac{n}{2}$ matrices 18 times and then go deeper for each of the 7 multiplications. Thus,
#
# <font size=2.0>
#
# $$
# \begin{split}
# A_\text{strassen}(n) =& 7 A_\text{strassen}\left( \frac{n}{2} \right) + 18 \left( \frac{n}{2} \right)^2 = 7 \left(7 A_\text{strassen}\left( \frac{n}{4} \right) + 18 \left( \frac{n}{4} \right)^2 \right) + 18 \left( \frac{n}{2} \right)^2 =
# 7^2 A_\text{strassen}\left( \frac{n}{4} \right) + 7\cdot 18 \left( \frac{n}{4} \right)^2 + 18 \left( \frac{n}{2} \right)^2 = \\
# =& \dots = 18 \sum_{k=1}^d 7^{k-1} \left( \frac{n}{2^k} \right)^2 = \frac{18}{4} n^2 \sum_{k=1}^d \left(\frac{7}{4} \right)^{k-1} = \frac{18}{4} n^2 \frac{\left(\frac{7}{4} \right)^d - 1}{\frac{7}{4} - 1} = 6 n^2 \left( \left(\frac{7}{4} \right)^d - 1\right) \leqslant 6 n^2 \left(\frac{7}{4} \right)^d = 6 n^{\log_2 7}
# \end{split}
# $$
# </font>
#
# (since $4^d = n^2$ and $7^d = n^{\log_2 7}$).
#
#
# Asymptotic behavior of $A(n)$ could be also found from the [master theorem](https://en.wikipedia.org/wiki/Master_theorem).
# + [markdown] slideshow={"slide_type": "slide"}
# #### Total complexity
#
# Total complexity is $M_\text{strassen}(n) + A_\text{strassen}(n)=$ <font color='red'>$7 n^{\log_2 7}$</font>. Strassen algorithm becomes faster
# when
#
# \begin{align*}
# 2n^3 &> 7 n^{\log_2 7}, \\
# n &> 667,
# \end{align*}
#
# so it is not a good idea to get to the bottom level of recursion.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Strassen algorithm reloaded
#
# - Recent paper [Strassen algorithm reloaded](http://jianyuhuang.com/papers/sc16.pdf)
# claim to **break conventional wisdom** that Strassen algorithm is not very practical.
# + [markdown] slideshow={"slide_type": "slide"}
# - Conventional wisdom: it is only
# practical for very large matrices. The proposed implementation is practical
# for small matrices.
# - Conventional wisdom: the matrices being
# multiplied should be relatively square. The proposed implementation is
# practical for rank-$k$ updates, where $k$ is relatively small (a shape
# of importance for libraries like LAPACK).
# - Conventional wisdom:
# it inherently requires substantial workspace. The proposed implementation
# requires no workspace beyond buffers already incorporated
# into conventional high-performance DGEMM implementations.
# - Conventional wisdom: a Strassen DGEMM interface must pass
# in workspace. The proposed implementation requires no such workspace
# and can be plug-compatible with the standard DGEMM interface.
# - Conventional wisdom: it is hard to demonstrate speedup
# on multi-core architectures. The proposed implementation demonstrates
# speedup over conventional DGEMM even on an IntelR Xeon
# PhiTM coprocessor utilizing 240 threads. It is shown how a distributed
# memory matrix-matrix multiplication also benefits from
# these advances.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Strassen algorithm and tensor rank (advanced topic)
#
# - It is not clear how Strassen found these formulas.
# - However, now we can see that they are not artificial.
# - There is a general approach based on the so-called tensor decomposition technique.
# - Here by tensor we imply a multidimensional array - generalization of the matrix concept to many dimensions.
#
# Let us enumerate elements in the $2\times 2$ matrices as follows
#
# $$
# \begin{bmatrix} c_{1} & c_{3} \\ c_{2} & c_{4} \end{bmatrix} =
# \begin{bmatrix} a_{1} & a_{3} \\ a_{2} & a_{4} \end{bmatrix}
# \begin{bmatrix} b_{1} & b_{3} \\ b_{2} & b_{4} \end{bmatrix}=
# \begin{bmatrix}
# a_{1}b_{1} + a_{3}b_{2} & a_{1}b_{3} + a_{3}b_{4} \\
# a_{2}b_{1} + a_{4}b_{2} & a_{2}b_{3} + a_{4}b_{4}
# \end{bmatrix}
# $$
#
# This can be written as
#
# $$ c_k = \sum_{i=1}^4 \sum_{j=1}^4 x_{ijk} a_i b_j, \quad k=1,2,3,4 $$
# + [markdown] slideshow={"slide_type": "slide"}
# $x_{ijk}$ is a 3-dimensional array, that consists of zeros and ones:
#
# $$
# \begin{split}
# x_{\ :,\ :,\ 1} =
# \begin{pmatrix}
# 1 & 0 & 0 & 0 \\
# 0 & 0 & 0 & 0 \\
# 0 & 1 & 0 & 0 \\
# 0 & 0 & 0 & 0 \\
# \end{pmatrix}
# \quad
# x_{\ :,\ :,\ 2} =
# \begin{pmatrix}
# 0 & 0 & 0 & 0 \\
# 1 & 0 & 0 & 0 \\
# 0 & 0 & 0 & 0 \\
# 0 & 1 & 0 & 0 \\
# \end{pmatrix} \\
# x_{\ :,\ :,\ 3} =
# \begin{pmatrix}
# 0 & 0 & 1 & 0 \\
# 0 & 0 & 0 & 0 \\
# 0 & 0 & 0 & 1 \\
# 0 & 0 & 0 & 0 \\
# \end{pmatrix}
# \quad
# x_{\ :,\ :,\ 4} =
# \begin{pmatrix}
# 0 & 0 & 1 & 0 \\
# 0 & 0 & 0 & 0 \\
# 0 & 0 & 0 & 0 \\
# 0 & 0 & 0 & 1 \\
# \end{pmatrix}
# \end{split}
# $$
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# #### Trilinear decomposition
#
# To get Strassen algorithm we should do the following trick –– decompose $x_{ijk}$ in the following way
#
# $$ x_{ijk} = \sum_{\alpha=1}^r u_{i\alpha} v_{j\alpha} w_{k\alpha}. $$
#
# This decomposition is called **trilinear tensor decomposition** and has a meaning of separation of variables: we have a sum of $r$ (called rank) summands with separated $i$, $j$ and $k$.
# + [markdown] slideshow={"slide_type": "slide"}
# #### Strassen via trilinear
#
# Now we have
#
# $$ c_k = \sum_{\alpha=1}^r w_{k\alpha} \left(\sum_{i=1}^4 u_{i\alpha} a_i \right) \left( \sum_{j=1}^4 v_{j\alpha} b_j\right), \quad k=1,2,3,4. $$
#
# Multiplications by $u_{i\alpha}$ or $v_{j\alpha}$ or $w_{k\alpha}$ do not require recursion since $u, v$ and $w$ are known precomputed matrices. Therefore, we have only $r$ multiplications of $\left(\sum_{i=1}^4 u_{i\alpha} a_i \right)$ $\left( \sum_{j=1}^4 v_{j\alpha} b_j\right)$ where both factors depend on the input data.
#
# As you might guess array $x_{ijk}$ has rank $r=7$, which leads us to $7$ multiplications and to the Strassen algorithm!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Summary of MM part
# - MM is the core of NLA. You have to think in block terms, if you want high efficiency
# - This is all about computer memory hierarchy
# - Concept of block algorithms
# - (Advanced topic) Strassen and trilinear form
# + slideshow={"slide_type": "skip"}
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
| lectures/lecture3/lecture-3.ipynb |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.