code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Mini project-------Analysis of student preference
#
# ### Data
#
# I use part of the [student preference](http://archive.ics.uci.edu/ml/datasets/Student+Performance) data from UCI ML repo.
#
# #### Data Set Information:
# This data approach student achievement in secondary education of two Portuguese schools. The data attributes include student grades, demographic, social and school related features) and it was collected by using school reports and questionnaires. Two datasets are provided regarding the performance in two distinct subjects: Mathematics (mat) and Portuguese language (por). In [Cortez and Silva, 2008], the two datasets were modeled under binary/five-level classification and regression tasks. Important note: the target attribute G3 has a strong correlation with attributes G2 and G1. This occurs because G3 is the final year grade (issued at the 3rd period), while G1 and G2 correspond to the 1st and 2nd period grades. It is more difficult to predict G3 without G2 and G1, but such prediction is much more useful (see paper source for more details).
#
#
# #### Attribute Information:
# Attributes for both student-mat.csv (Math course) and student-por.csv (Portuguese language course) datasets:
# 1. school - student's school (binary: 'GP' - Gabriel Pereira or 'MS' - Mousinho da Silveira)
# 2. sex - student's sex (binary: 'F' - female or 'M' - male)
# 3. age - student's age (numeric: from 15 to 22)
# 4. address - student's home address type (binary: 'U' - urban or 'R' - rural)
# 5. famsize - family size (binary: 'LE3' - less or equal to 3 or 'GT3' - greater than 3)
# 6. Pstatus - parent's cohabitation status (binary: 'T' - living together or 'A' - apart)
# 7. Medu - mother's education (numeric: 0 - none, 1 - primary education (4th grade), 2 – 5th to 9th grade, 3 – secondary education or 4 – higher education)
# 8. Fedu - father's education (numeric: 0 - none, 1 - primary education (4th grade), 2 – 5th to 9th grade, 3 – secondary education or 4 – higher education)
# 9. Mjob - mother's job (nominal: 'teacher', 'health' care related, civil 'services' (e.g. administrative or police), 'at_home' or 'other')
# 10. Fjob - father's job (nominal: 'teacher', 'health' care related, civil 'services' (e.g. administrative or police), 'at_home' or 'other')
# 11. reason - reason to choose this school (nominal: close to 'home', school 'reputation', 'course' preference or 'other')
# 12. guardian - student's guardian (nominal: 'mother', 'father' or 'other')
# 13. traveltime - home to school travel time (numeric: 1 - <15 min., 2 - 15 to 30 min., 3 - 30 min. to 1 hour, or 4 - >1 hour)
# 14. studytime - weekly study time (numeric: 1 - <2 hours, 2 - 2 to 5 hours, 3 - 5 to 10 hours, or 4 - >10 hours)
# 15. failures - number of past class failures (numeric: n if 1<=n<3, else 4)
# 16. schoolsup - extra educational support (binary: yes or no)
# 17. famsup - family educational support (binary: yes or no)
# 18. paid - extra paid classes within the course subject (Math or Portuguese) (binary: yes or no)
# 19. activities - extra-curricular activities (binary: yes or no)
# 20. nursery - attended nursery school (binary: yes or no)
# 21. higher - wants to take higher education (binary: yes or no)
# 22. internet - Internet access at home (binary: yes or no)
# 23. romantic - with a romantic relationship (binary: yes or no)
# 24. famrel - quality of family relationships (numeric: from 1 - very bad to 5 - excellent)
# 25. freetime - free time after school (numeric: from 1 - very low to 5 - very high)
# 26. goout - going out with friends (numeric: from 1 - very low to 5 - very high)
# 27. Dalc - workday alcohol consumption (numeric: from 1 - very low to 5 - very high)
# 28. Walc - weekend alcohol consumption (numeric: from 1 - very low to 5 - very high)
# 29. health - current health status (numeric: from 1 - very bad to 5 - very good)
# 30. absences - number of school absences (numeric: from 0 to 93)
#
# these grades are related with the course subject, Math or Portuguese:
# 31. G1 - first period grade (numeric: from 0 to 20)
# 31. G2 - second period grade (numeric: from 0 to 20)
# 32. G3 - final grade (numeric: from 0 to 20, output target)
#
#
# citation: <NAME> and <NAME>. Using Data Mining to Predict Secondary School Student Performance. In A. Brito and <NAME>., Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) pp. 5-12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978-9077381-39-7.
import os
import pickle
import numpy as np
import pandas as pd
import numpy.linalg as npla
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn.metrics import accuracy_score, log_loss
from sklearn.linear_model import LogisticRegression
from sklearn import linear_model
from sklearn.model_selection import train_test_split, GridSearchCV, RandomizedSearchCV, cross_val_score
from sklearn.linear_model import ElasticNet
from sklearn.datasets import make_regression
from sklearn.svm import SVR, LinearSVR
from collections import deque
from sklearn.datasets import load_boston
# %matplotlib inline
# ## Input data
#input raw data
#Due to the whole dataset is a zip file and have several csv file, i can't use URL to download it.
#So i directly download it by hand and put it to my data folder.
student=pd.read_csv('../data/student-mat.csv',sep=";")
student.head()
# Find percentage of missing data in each feature
for i in range(0,33):
if student.iloc[:,i].dtype == "O":
print(student.columns[i])
print(sum(student.iloc[:,i]=="?")/len(student.iloc[:,i]))
#all out put are 0, so there are no missing value
student.shape
# In this case, we want use some features to predict students final grade(G3), so i use G3 as response variable.
y=student["G3"]
X=student.drop(["G3","school"],axis=1)
# ## Data wrangled
# +
# recode all factors as numbers
X["sex"]=X["sex"].map({'F':0,'M':1})
X["address"]=X["address"].map({'U':0,'R':1})
X["famsize"]=X["famsize"].map({'LE3':0,'GT3':1})
X["Pstatus"]=X["Pstatus"].map({'T':0,'A':1})
X["Mjob"]=X["Mjob"].map({'teacher':0,'health':1,'services':2,'at_home':3,'other':4})
X["Fjob"]=X["Fjob"].map({'teacher':0,'health':1,'services':2,'at_home':3,'other':4})
X["reason"]=X["reason"].map({'home':0,'reputation':1,'course':2,'other':3})
X["guardian"]=X["guardian"].map({'mother':0,'father':1,'other':2})
X["schoolsup"]=X["schoolsup"].map({'yes':0,'no':1})
X["famsup"]=X["famsup"].map({'yes':0,'no':1})
X["paid"]=X["paid"].map({'yes':0,'no':1})
X["activities"]=X["activities"].map({'yes':0,'no':1})
X["nursery"]=X["nursery"].map({'yes':0,'no':1})
X["higher"]=X["higher"].map({'yes':0,'no':1})
X["romantic"]=X["romantic"].map({'yes':0,'no':1})
X["internet"]=X["internet"].map({'yes':0,'no':1})
X.head()
# -
#Set training data and test data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=12345)
X_train.shape
# ## EDA
X.describe()
import seaborn as sns
f,ax = plt.subplots(figsize=(18,18))
sns.heatmap(X.corr(), annot=True, linewidths=.5,ax=ax)
# +
# Plot travel time histogram
plt.hist(X["traveltime"])
plt.title("Frequency of traveltime")
plt.xlabel("traveltime")
plt.ylabel("Frequency")
plt.savefig("../results/traveltime.png")
plt.show()
# +
# Plot study time histogram
plt.hist(X["studytime"])
plt.title("Frequency of study time")
plt.xlabel("study time")
plt.ylabel("Frequency")
plt.savefig("../results/studytime.png")
plt.show()
# +
# Plot failures histogram
plt.hist(X["failures"])
plt.title("Frequency of failures")
plt.xlabel("failures")
plt.ylabel("Frequency")
plt.savefig("../results/failures.png")
plt.show()
# +
# Plot absences histogram
plt.hist(X["absences"])
plt.title("Frequency of absences")
plt.xlabel("absences")
plt.ylabel("Frequency")
plt.savefig("../results/absences.png")
plt.show()
# -
# ## feature selection
# +
#drop features with largr relation ship
#We can see from plot,Dalc(workday alcohol consumption) have large correlation with Walc(weekly alcohol consumption)
#So I delete the Wacl from X.
#G1 and G2 are highly correlated, so i delete G1.
#Mather job, father job, and father education are highly correlated, so I delete Fedu and Mjob.
drop_feature=['Fedu','Mjob','Walc','G1']
X_new=X.drop(drop_feature,axis=1)
X_new.shape
# -
X_new.describe()
#Set training data and test data
X_train, X_test, y_train, y_test = train_test_split(X_new, y, test_size=0.2, random_state=12345)
# ## Model selection
# +
# Model selection
method = {
'linearregression' : LinearRegression(),
'ridge' : Ridge(),
'log regression': LogisticRegression(),
'ElasticNet' : ElasticNet(),
'SVR' : SVR()
}
#MSE in regression
mean_squared_err = lambda y, yhat: np.mean((y-yhat)**2)
for c in method:
clf = method[c]
clf.fit(X_train, y_train)
print(c)
print("Training error: ", mean_squared_err(y_train,clf.predict(X_train)))
print("Validation error: ",mean_squared_err(y_test,clf.predict(X_test)))
print("\n")
# -
# The ridge classifier get small training error and validation error. The ElasticNet classifier can get the lowest validation error but the training error is large. So i choose Ridge method.
# +
#select the parameter
alpha = 10**np.arange(-3,4,0.01)
#L2
train_error=[]
validation_error=[]
for a in alpha:
l2 = Ridge(alpha=a)
l2.fit(X_train,y_train)
train_error.append( mean_squared_err(y_train, l2.predict(X_train)))
validation_error.append(mean_squared_err(y_test, l2.predict(X_test)))
print("Min L2 validation error: %f" % min(validation_error))
print("alpha that Minimun L2 validation error: %f" % alpha[validation_error.index(min(validation_error))])
plt.plot(alpha, validation_error,label='validation error')
plt.plot(alpha, train_error,label='training error')
plt.ylabel("error rate")
plt.xlabel("The value of alpha")
plt.xscale("log")
plt.legend(loc='upper right')
plt.savefig("../results/alpha.png")
plt.show()
# -
# ## Feature selection again (forward selection)
# +
# ForwardSelection
#Reference: lab1 solution in DSCI573
def fit_and_report(model, X, y, Xv, yv):
model.fit(X,y)
mean_squared_err = lambda y, yhat: np.mean((y-yhat)**2)
errors = [mean_squared_err(y, model.predict(X)), mean_squared_err(yv, model.predict(Xv))]
return errors
class ForwardSelection:
def __init__(self, model, min_features=None, max_features=None,
scoring=None, cv=None):
self.max_features = max_features
if min_features is None:
self.min_features = 1
else:
self.min_features = min_features
self.model = model
self.scoring = scoring
self.cv = cv
return
def fit(self, X, y):
if (self.max_features is None) or (self.max_features > X.shape[1]):
self.max_features = X.shape[1]
self.ftr_ = []
idx = np.setdiff1d(range(X.shape[1]), self.ftr_)
best_round_score = deque()
best_round_score.append(np.inf)
X_train, X_val, y_train, y_val = train_test_split(X, y,test_size=0.2,random_state=1245)
for j in range(self.max_features):
round_scores = np.zeros(idx.size)
for i, ii in enumerate(idx):
X_train_s = X_train.iloc[:, self.ftr_ + [ii]]
X_val_s = X_val.iloc[:, self.ftr_ + [ii]]
round_scores[i] = fit_and_report(self.model, X_train_s, y_train,
X_val_s, y_val)[1] # val error only
i_star = np.argmin(round_scores)
ii_star = idx[i_star]
best_round_score.append(round_scores[i_star])
if (len(self.ftr_) > self.min_features) and (best_round_score[-1] >= best_round_score[-2]):
print('found best subset.')
self.best_round_scores_ = np.array(best_round_score)[1:-1]
self.score_ = best_round_score[-2]
return
elif (len(self.ftr_) >= self.max_features):
print('reached max features.')
self.best_round_scores_ = np.array(best_round_score)[1:-1]
self.score_ = best_round_score[-2]
return
else:
self.ftr_ += [ii_star]
idx = np.setdiff1d(range(X.shape[1]), self.ftr_)
return
def transform(self, X, y=None):
return X.iloc[:, self.ftr_]
# +
fs = ForwardSelection(Ridge(alpha=125))
fs.fit(X_train,y_train)
print('features: {}'.format(fs.ftr_))
print('final mean xval error: {}'.format(fs.score_))
# -
#set new training data
X_new = X[X.columns[fs.ftr_]]
X_new
# ## Fit with model and feature i selected
# +
#new train and test set
X_train_new, X_test_new, y_train_new, y_test_new = train_test_split(X, y,test_size=0.2,random_state=1245)
##My best model
model = Ridge(alpha=125)
model.fit(X_train_new,y_train_new)
print("The MSE of train set ", mean_squared_err(y_train_new, model.predict(X_train_new)))
print("The MSE of test set", mean_squared_err(y_test_new, model.predict(X_test_new)))
# -
| src/Student_preference_analysis.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# In order to successfully complete this assignment you must do the required reading, watch the provided videos and complete all instructions. The embedded Google form must be entirely filled out and submitted on or before **11:59pm on Sunday February 16**. Students must come to class the next day prepared to discuss the material covered in this assignment. answer
# # Pre-class assignment: Unit Testing
#
# ### Goals for today's pre-class assignment
#
# </p>
#
#
#
# 2. [2D Array Indexing](#2D_Array_Indexing)
# 1. [Introduction to Unit Testing](#Introduction_to_Unit_Testing)
#
# ---
#
# <a name="2D_Array_Indexing"></a>
#
# # 1. 2D Array Indexing
#
# All memory in a computer is stored linearly with each location in memory given a sequential address. I want you to think for a moment to understand how we take a linear list of numbers and turn it into a 2D array:
#
# IN the following image you can see the relationship between a linear index and a imposed structure that we give it to represent the row and column of the array. We will set up the problem similar to a checker board, such that each grid has a linear label, an index of row, and an index of column.
#
# <img src="https://lh5.googleusercontent.com/tpc1tFPULkPDt1q03E1nPkllHRO60jYyL-rZWmiJLM0AQtVkm1-EF6Pf0yKrm6S5ifVxJ1knHLpVRv7Fsu_pP-rzrauVa2dp2DLrAx2iya9Jbqs2gRWJJ3J-uBqE=w740" alt = "Visual relationship between linear index and a 2D index" width=600 />
#
# First, we will make functions that convert the incremental label of a grid point to it's corresponding row and column index. For example, in the above ($99 \times 49$) grid the 99-th item is at row = 2 and col = 1 .
# ✅ **<font color=red>DO THIS:</font>** Write a function named ```LabelToIndex``` which takes in three arguments (Number of rows, Number of column and the linear index). The function should then return the row and column for that index. The following is a stub function to get you started:
def LabelToIndices(n_row, n_col, lab):
"""function for converting linear label of grid to indices of row and column
Run the function with number of rows, number of columns and the index as input:
>>> LabelToIndices(99, 49, 3675)
(75, 0)
"""
return 2,1
help(LabelToIndices)
# Let's test the ```LabelToIndices``` function for 3675-th grid. Print the index of row and column.
LabelToIndices(99, 49, 3675)
# ✅ **<font color=red>DO THIS:</font>** Using the following stub function as a guild write a function named ```LabelToIndex``` that converts the indices of row and column of a grid to the linear label. For example, the grid at row = 2 and col = 1 is labeled as the 99-th point.
def IndicesToLabel(n_row, n_col, row, col):
"""function for converting row and column indices of a grid to linear label
Usage:
>>> IndicesToLabel(99, 49, 2,1)
99
"""
return 42
IndicesToLabel(99, 49, 2, 1)
# ---
#
# <a name="Introduction_to_Unit_Testing"></a>
#
# # 2. Introduction to Unit Testing
#
# Unit tests are small tests of individual parts of your code. Effective unit testing is absolutely necessary to grow a project past a few developers. Ideally unit tests run after every major/minor change and provide a reality check that nothing is broken. Good unit tests are hard to do and can take practice and time (which is not often where you want to spend your time). That being said, if you know the basic format/syntax of some of the most common testing programs you can format your code to be ready for unit testing.
#
# ## unittest
# Lets start with the most basic unit test program built with python; ```unittest```.
import unittest
help(unittest)
from IPython.display import YouTubeVideo
YouTubeVideo("1Lfv5tUGsn8",width=640,height=360)
# The following are a couple of unit tests for the ```LabelToIndices``` and ```LabelToIndices``` functions. **Note:** It is standard practice to name a unit test ```test_ + <function being tested>```. This naming standard allows for automated test using some libraries.
#
#
# ✅ **<font color=red>DO THIS:</font>** Modify the code to add a few more tests.
#
#
# ✅ **<font color=red>DO THIS:</font>** Temporarily modify the code to make a test fail.
# +
import unittest
# Create a test case
class TestLableToIndeces(unittest.TestCase):
# Create the unit test
def test_LabelToIndices(self):
# Test if 122 equals the output of (6,2)
self.assertEqual((6,2), LabelToIndices(10, 20, 122))
def test_LabelToIndices(self):
# Test if 122 equals the output of (6,2)
self.assertEqual(3110, IndicesToLabel(99, 49, 63, 23))
# -
# We can run all of the unittests in a notebook using the following command:
# +
if __name__ == '__main__':
unittest.main(argv=['first-arg-is-ignored'], exit=False)
# -
# ## doctest
#
# Another type of unit tester is ```doctest```. This is a clever solution that includes the tests inside a function's docstring. See the docstrings for ```LabelToIndices``` and ```LabelToIndices``` and note the "usage" section is one such test.
#
# We can run all of the tests in a jupyter notebook using the following command:
import doctest
doctest.testmod(verbose=True)
# ✅ **<font color=red>DO THIS:</font>** Modify the docstrings for ```makeSchellingGrid``` and ```visualizeGrid``` functions to include some unit testing.
# ## pytest
#
# There are many (Many!) other unit testers out there. Fortunately, most of them work nicely together. One of the best is ```pytest```. Unfortunately, I have not found a clean way to get ```pytest``` to work inside a jupyter notebook. THe options include:
#
# - Export the ipynb as a py file and run pytest on the resulting file.
# - Use one of the many jupyter plug-ins to enable pytest in jupyter (requires an install).
#
# Here is an brief introduction video to ```pytest``` (included with anaconda) to give you a basic idea.
#
from IPython.display import YouTubeVideo
YouTubeVideo("_xoCujgdFgk",width=640,height=360, start=14)
# Although it dosn't work great with Jupyter notebooks PyTest is my prefered unit testing platform and should be used for your class projects.
# ----
# <a name="T5"></a>
# # 5. Assignment wrap-up
#
# Please fill out the form that appears when you run the code below. **You must completely fill this out in order to receive credit for the assignment!**
#
# [Direct Link to Google Form](https://cmse.msu.edu/cmse802-pc-survey)
#
#
# If you have trouble with the embedded form, please make sure you log on with your MSU google account at [googleapps.msu.edu](https://googleapps.msu.edu) and then click on the direct link above.
# ✅ **<font color=red>Assignment-Specific QUESTION:</font>** What are the pros/cons for using unittest, doctest and pytest? Does it make sense to use more than one in your project?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** Summarize what you did in this assignment.
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** What questions do you have, if any, about any of the topics discussed in this assignment after working through the jupyter notebook?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** How well do you feel this assignment helped you to achieve a better understanding of the above mentioned topic(s)?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** What was the **most** challenging part of this assignment for you?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** What was the **least** challenging part of this assignment for you?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** What kind of additional questions or support, if any, do you feel you need to have a better understanding of the content in this assignment?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** Do you have any further questions or comments about this material, or anything else that's going on in class?
# Put your answer to the above question here
# ✅ **<font color=red>QUESTION:</font>** Approximately how long did this pre-class assignment take?
# Put your answer to the above question here
from IPython.display import HTML
HTML(
"""
<iframe
src="https://cmse.msu.edu/cmse802-pc-survey?embedded=true"
width="100%"
height="1200px"
frameborder="0"
marginheight="0"
marginwidth="0">
Loading...
</iframe>
"""
)
# ---------
# ### Congratulations, we're done!
#
# To get credit for this assignment you must fill out and submit the above Google From on or before the assignment due date.
# ### Course Resources:
#
# - [Syllabus](https://docs.google.com/document/d/e/2PACX-1vTW4OzeUNhsuG_zvh06MT4r1tguxLFXGFCiMVN49XJJRYfekb7E6LyfGLP5tyLcHqcUNJjH2Vk-Isd8/pub)
# - [Preliminary Schedule](https://docs.google.com/spreadsheets/d/e/2PACX-1vRsQcyH1nlbSD4x7zvHWAbAcLrGWRo_RqeFyt2loQPgt3MxirrI5ADVFW9IoeLGSBSu_Uo6e8BE4IQc/pubhtml?gid=2142090757&single=true)
# - [Course D2L Page](https://d2l.msu.edu/d2l/home/912152)
# © Copyright 2020, Michigan State University Board of Trustees
| cmse802-s20/0216-Unit_Testing-pre-class-assignment.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text"
# This is a companion notebook for the book [Deep Learning with Python, Second Edition](https://www.manning.com/books/deep-learning-with-python-second-edition?a_aid=keras&a_bid=76564dff). For readability, it only contains runnable code blocks and section titles, and omits everything else in the book: text paragraphs, figures, and pseudocode.
#
# **If you want to be able to follow what's going on, I recommend reading the notebook side by side with your copy of the book.**
#
# This notebook was generated for TensorFlow 2.6.
# + [markdown] colab_type="text"
# ## Interpreting what convnets learn
# + [markdown] colab_type="text"
# ### Visualizing intermediate activations
# + colab_type="code"
# You can use this to load the file "convnet_from_scratch_with_augmentation.keras"
# you obtained in the last chapter.
from google.colab import files
files.upload()
# + colab_type="code"
from tensorflow import keras
model = keras.models.load_model("convnet_from_scratch_with_augmentation.keras")
model.summary()
# + [markdown] colab_type="text"
# **Preprocessing a single image**
# + colab_type="code"
from tensorflow import keras
import numpy as np
img_path = keras.utils.get_file(
fname="cat.jpg",
origin="https://img-datasets.s3.amazonaws.com/cat.jpg")
def get_img_array(img_path, target_size):
img = keras.utils.load_img(
img_path, target_size=target_size)
array = keras.utils.img_to_array(img)
array = np.expand_dims(array, axis=0)
return array
img_tensor = get_img_array(img_path, target_size=(180, 180))
# + [markdown] colab_type="text"
# **Displaying the test picture**
# + colab_type="code"
import matplotlib.pyplot as plt
plt.axis("off")
plt.imshow(img_tensor[0].astype("uint8"))
plt.show()
# + [markdown] colab_type="text"
# **Instantiating a model that returns layer activations**
# + colab_type="code"
from tensorflow.keras import layers
layer_outputs = []
layer_names = []
for layer in model.layers:
if isinstance(layer, (layers.Conv2D, layers.MaxPooling2D)):
layer_outputs.append(layer.output)
layer_names.append(layer.name)
activation_model = keras.Model(inputs=model.input, outputs=layer_outputs)
# + [markdown] colab_type="text"
# **Using the model to compute layer activations**
# + colab_type="code"
activations = activation_model.predict(img_tensor)
# + colab_type="code"
first_layer_activation = activations[0]
print(first_layer_activation.shape)
# + [markdown] colab_type="text"
# **Visualizing the fifth channel**
# + colab_type="code"
import matplotlib.pyplot as plt
plt.matshow(first_layer_activation[0, :, :, 5], cmap="viridis")
# + [markdown] colab_type="text"
# **Visualizing every channel in every intermediate activation**
# + colab_type="code"
images_per_row = 16
for layer_name, layer_activation in zip(layer_names, activations):
n_features = layer_activation.shape[-1]
size = layer_activation.shape[1]
n_cols = n_features // images_per_row
display_grid = np.zeros(((size + 1) * n_cols - 1,
images_per_row * (size + 1) - 1))
for col in range(n_cols):
for row in range(images_per_row):
channel_index = col * images_per_row + row
channel_image = layer_activation[0, :, :, channel_index].copy()
if channel_image.sum() != 0:
channel_image -= channel_image.mean()
channel_image /= channel_image.std()
channel_image *= 64
channel_image += 128
channel_image = np.clip(channel_image, 0, 255).astype("uint8")
display_grid[
col * (size + 1): (col + 1) * size + col,
row * (size + 1) : (row + 1) * size + row] = channel_image
scale = 1. / size
plt.figure(figsize=(scale * display_grid.shape[1],
scale * display_grid.shape[0]))
plt.title(layer_name)
plt.grid(False)
plt.axis("off")
plt.imshow(display_grid, aspect="auto", cmap="viridis")
# + [markdown] colab_type="text"
# ### Visualizing convnet filters
# + [markdown] colab_type="text"
# **Instantiating the Xception convolutional base**
# + colab_type="code"
model = keras.applications.xception.Xception(
weights="imagenet",
include_top=False)
# + [markdown] colab_type="text"
# **Printing the names of all convolutional layers in Xception**
# + colab_type="code"
for layer in model.layers:
if isinstance(layer, (keras.layers.Conv2D, keras.layers.SeparableConv2D)):
print(layer.name)
# + [markdown] colab_type="text"
# **Creating a "feature extractor" model that returns the output of a specific layer**
# + colab_type="code"
layer_name = "block3_sepconv1"
layer = model.get_layer(name=layer_name)
feature_extractor = keras.Model(inputs=model.input, outputs=layer.output)
# + [markdown] colab_type="text"
# **Using the feature extractor**
# + colab_type="code"
activation = feature_extractor(
keras.applications.xception.preprocess_input(img_tensor)
)
# + colab_type="code"
import tensorflow as tf
def compute_loss(image, filter_index):
activation = feature_extractor(image)
filter_activation = activation[:, 2:-2, 2:-2, filter_index]
return tf.reduce_mean(filter_activation)
# + [markdown] colab_type="text"
# **Loss maximization via stochastic gradient ascent**
# + colab_type="code"
@tf.function
def gradient_ascent_step(image, filter_index, learning_rate):
with tf.GradientTape() as tape:
tape.watch(image)
loss = compute_loss(image, filter_index)
grads = tape.gradient(loss, image)
grads = tf.math.l2_normalize(grads)
image += learning_rate * grads
return image
# + [markdown] colab_type="text"
# **Function to generate filter visualizations**
# + colab_type="code"
img_width = 200
img_height = 200
def generate_filter_pattern(filter_index):
iterations = 30
learning_rate = 10.
image = tf.random.uniform(
minval=0.4,
maxval=0.6,
shape=(1, img_width, img_height, 3))
for i in range(iterations):
image = gradient_ascent_step(image, filter_index, learning_rate)
return image[0].numpy()
# + [markdown] colab_type="text"
# **Utility function to convert a tensor into a valid image**
# + colab_type="code"
def deprocess_image(image):
image -= image.mean()
image /= image.std()
image *= 64
image += 128
image = np.clip(image, 0, 255).astype("uint8")
image = image[25:-25, 25:-25, :]
return image
# + colab_type="code"
plt.axis("off")
plt.imshow(deprocess_image(generate_filter_pattern(filter_index=2)))
# + [markdown] colab_type="text"
# **Generating a grid of all filter response patterns in a layer**
# + colab_type="code"
all_images = []
for filter_index in range(64):
print(f"Processing filter {filter_index}")
image = deprocess_image(
generate_filter_pattern(filter_index)
)
all_images.append(image)
margin = 5
n = 8
cropped_width = img_width - 25 * 2
cropped_height = img_height - 25 * 2
width = n * cropped_width + (n - 1) * margin
height = n * cropped_height + (n - 1) * margin
stitched_filters = np.zeros((width, height, 3))
for i in range(n):
for j in range(n):
image = all_images[i * n + j]
stitched_filters[
(cropped_width + margin) * i : (cropped_width + margin) * i + cropped_width,
(cropped_height + margin) * j : (cropped_height + margin) * j
+ cropped_height,
:,
] = image
keras.utils.save_img(
f"filters_for_layer_{layer_name}.png", stitched_filters)
# + [markdown] colab_type="text"
# ### Visualizing heatmaps of class activation
# + [markdown] colab_type="text"
# **Loading the Xception network with pretrained weights**
# + colab_type="code"
model = keras.applications.xception.Xception(weights="imagenet")
# + [markdown] colab_type="text"
# **Preprocessing an input image for Xception**
# + colab_type="code"
img_path = keras.utils.get_file(
fname="elephant.jpg",
origin="https://img-datasets.s3.amazonaws.com/elephant.jpg")
def get_img_array(img_path, target_size):
img = keras.utils.load_img(img_path, target_size=target_size)
array = keras.utils.img_to_array(img)
array = np.expand_dims(array, axis=0)
array = keras.applications.xception.preprocess_input(array)
return array
img_array = get_img_array(img_path, target_size=(299, 299))
# + colab_type="code"
preds = model.predict(img_array)
print(keras.applications.xception.decode_predictions(preds, top=3)[0])
# + colab_type="code"
np.argmax(preds[0])
# + [markdown] colab_type="text"
# **Setting up a model that returns the last convolutional output**
# + colab_type="code"
last_conv_layer_name = "block14_sepconv2_act"
classifier_layer_names = [
"avg_pool",
"predictions",
]
last_conv_layer = model.get_layer(last_conv_layer_name)
last_conv_layer_model = keras.Model(model.inputs, last_conv_layer.output)
# + [markdown] colab_type="text"
# **Setting up a model that goes from the last convolutional output to the final predictions**
# + colab_type="code"
classifier_input = keras.Input(shape=last_conv_layer.output.shape[1:])
x = classifier_input
for layer_name in classifier_layer_names:
x = model.get_layer(layer_name)(x)
classifier_model = keras.Model(classifier_input, x)
# + [markdown] colab_type="text"
# **Retrieving the gradients of the top predicted class with regard to the last convolutional output**
# + colab_type="code"
import tensorflow as tf
with tf.GradientTape() as tape:
last_conv_layer_output = last_conv_layer_model(img_array)
tape.watch(last_conv_layer_output)
preds = classifier_model(last_conv_layer_output)
top_pred_index = tf.argmax(preds[0])
top_class_channel = preds[:, top_pred_index]
grads = tape.gradient(top_class_channel, last_conv_layer_output)
# + [markdown] colab_type="text"
# **Gradient pooling and channel importance weighting**
# + colab_type="code"
pooled_grads = tf.reduce_mean(grads, axis=(0, 1, 2)).numpy()
last_conv_layer_output = last_conv_layer_output.numpy()[0]
for i in range(pooled_grads.shape[-1]):
last_conv_layer_output[:, :, i] *= pooled_grads[i]
heatmap = np.mean(last_conv_layer_output, axis=-1)
# + [markdown] colab_type="text"
# **Heatmap post-processing**
# + colab_type="code"
heatmap = np.maximum(heatmap, 0)
heatmap /= np.max(heatmap)
plt.matshow(heatmap)
# + [markdown] colab_type="text"
# **Superimposing the heatmap with the original picture**
# + colab_type="code"
import matplotlib.cm as cm
img = keras.utils.load_img(img_path)
img = keras.utils.img_to_array(img)
heatmap = np.uint8(255 * heatmap)
jet = cm.get_cmap("jet")
jet_colors = jet(np.arange(256))[:, :3]
jet_heatmap = jet_colors[heatmap]
jet_heatmap = keras.utils.array_to_img(jet_heatmap)
jet_heatmap = jet_heatmap.resize((img.shape[1], img.shape[0]))
jet_heatmap = keras.utils.img_to_array(jet_heatmap)
superimposed_img = jet_heatmap * 0.4 + img
superimposed_img = keras.utils.array_to_img(superimposed_img)
save_path = "elephant_cam.jpg"
superimposed_img.save(save_path)
# + [markdown] colab_type="text"
# ## Chapter summary
| notebooks/dlp09_part03_interpreting_what_convnets_learn.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# 
# # Account management
# Qiskit Runtime is available on both IBM Cloud and IBM Quantum. The former requires an IBM Cloud account and the latter an IBM Quantum account. If you don't have these accounts, please refer to [01_introduction_cloud_runtime.ipynb](01_introduction_cloud_runtime.ipynb) or [02_introduction_legacy_runtime.ipynb](02_introduction_legacy_runtime.ipynb) on how to set one up.
#
#
# There are a number of methods for handling account management. Your account credentials can be saved to disk, or used in a session and never saved.
#
# - `save_account()`: Save your account to disk for future use.
# - `delete_account()`: Delete the saved account from disk.
# - `active_account()`: List the account currently in the session.
# - `saved_account()`: List the account stored on disk.
# ## Storing credentials
# The [save_account()](https://qiskit.org/documentation/partners/qiskit_ibm_runtime/stubs/qiskit_ibm_runtime.IBMRuntimeService.html#qiskit_ibm_runtime.IBMRuntimeService.save_account) method can be used to store your account credentials on disk, in the `$HOME/.qiskit/qiskit-ibm.json` file. Once the credentials are saved, you will only need to use `IBMRuntimeService()` to initialize your account in the future.
# <div class="alert alert-block alert-info">
# <b>Note:</b> Account credentials are saved in plain text, so only do so if you are using a trusted device.
# </div>
# Below are examples of saving an IBM Cloud and an IBM Quantum accounts. The `auth` parameter indicates the authentication type of the account. If you are saving multiple account, consider using the `name` parameter to differentiate them.
#
# +
from qiskit_ibm_runtime import IBMRuntimeService
# Save an IBM Cloud account on disk.
# IBMRuntimeService.save_account(auth="cloud", token=<IBM Cloud API key>, instance=<IBM Cloud CRN> or <IBM Cloud service name>)
# Save an IBM Quantum account on disk.
# IBMRuntimeService.save_account(auth="legacy", token=<IBM Quantum API token>)
# -
# ## Initializing
# You need to initialize your account in a Python session before you can start using Qiskit Runtime. If you have the credentials already saved, you can initialize an `IBMRuntimeService` instance without additional parameters.
# Read default credentials from disk.
service = IBMRuntimeService()
# If you have both an IBM Cloud and an IBM Quantum accounts saved, `IBMRuntimeService()` by default will load the IBM Cloud account. To load the IBM Quantum account, you can specify `IBMRuntimeService(auth="legacy")` instead.
#
# Alternatively, if you specified a `name` for your account when saving it, you can also specify the name of the account to load.
# +
# Save an IBM Cloud account on disk and give it a name.
# IBMRuntimeService.save_account(auth="cloud", token=<IBM Cloud API key>, instance=<IBM Cloud CRN>, name="prod")
# service = IBMRuntimeService(name="prod")
# -
# If you want to use your credentials for just the session instead of saving it, you can pass the credentials in when initializing the `IBMRuntimeService` instance:
# +
# Initialize an IBM Cloud account without saving it.
# service = IBMRuntimeService(auth="cloud", token=<IBM Cloud API key>, instance=<IBM Cloud CRN>)
# +
from qiskit.tools.jupyter import *
# %qiskit_copyright
| docs/tutorials/04_account_management.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # FMAS_S_R
#
# This examples demonstrates photon number conservation for the simplified
# forward model for the analytic signal including the Raman effect (FMAS_S_R).
#
# The considered propagation model provides a proper conservation law as class
# method `claw`. However, for clarity, we here re-implement the conservation
# law and explicitly pass this user-defined function to the solver class upon
# initialization.
#
# As exemplary propagation scenario, the setup used in the step-by-step demo
#
# `sphx_glr_auto_tutorials_specific_g_spectrogram.py`
#
# is used.
#
# .. codeauthor:: <NAME> <<EMAIL>>
#
# +
import fmas
import numpy as np
from fmas.solver import IFM_RK4IP
from fmas.analytic_signal import AS
from fmas.grid import Grid
from fmas.propagation_constant import PropConst, define_beta_fun_ESM
from fmas.tools import sech, change_reference_frame, plot_claw
beta_fun = define_beta_fun_ESM()
pc = PropConst(beta_fun)
grid = Grid(t_max=5500.0, t_num=2 ** 14) # (fs) # (-)
Ns = 8.0 # (-)
t0 = 7.0 # (fs)
w0 = 1.7 # (rad/fs)
n2 = 3.0e-8 # (micron^2/W)
A0 = Ns * np.sqrt(abs(pc.beta2(w0)) * pc.c0 / w0 / n2) / t0
E_0t_fun = lambda t: np.real(A0 * sech(t / t0) * np.exp(1j * w0 * t))
Eps_0w = AS(E_0t_fun(grid.t)).w_rep
# -
# As model we here consider the simplified forward model for the analytic
# signal including the Raman effect (FMAS_S_R)
#
#
from fmas.models import FMAS_S_R
model = FMAS_S_R(w=grid.w, beta_w=pc.beta(grid.w), n2=n2)
# For the FMAS_S_R $z$-propagation model we consider a conserved quantity
# that is related to the classical analog of the photon number, see Eq. (24) of
# [AD2010] and the appendix of [BW1989]. In particular we here implement
#
# \begin{align}C_p(z) = \sum_{\omega>0} \omega^{-1} |u_\omega(z)|^,\end{align}
#
# which is, by default, provided as method `model.claw` .
#
#
def Cp(i, zi, w, uw):
_a2_w = np.divide(
np.abs(uw) ** 2, w, out=np.zeros(w.size, dtype="float"), where=w > 0.
)
return np.sum(_a2_w)
# As shown below, this conserved quantity can be provided when an instance of
# the desired solver is initialized. Here, for simply monitoring the
# conservation law we use the Runge-Kutta in the ineraction picture method.
# However, a proper conserved quantity is especially important when the
# conservation quantity error method (CQE) is used, see, e.g., demo
#
# `sphx_glr_auto_tutorials_tests_g_performance_CQE.py`
#
#
#
solver = IFM_RK4IP(model.Lw, model.Nw, user_action=Cp)
solver.set_initial_condition(grid.w, Eps_0w)
solver.propagate(z_range=0.01e6, n_steps=4000, n_skip=8) # (micron) # (-) # (-)
# The figure below shows the dynamic evolution of the pulse in the time domain
# (top subfigure) and in the frequency domain (center subfigure). The subfigure
# at the bottom shows the conservation law (c-law) given by the normalized
# photon number variation
#
# \begin{align}\delta_{\rm{Ph}}(z) = \frac{ C_p(z)-C_p(0)}{C_p(0)}\end{align}
#
# as function of the proapgation coordinate $z$. For the considered
# discretization of the computational domain the normalized photon number
# variation is of the order $\delta_{\rm{Ph}}\approx 10^{-7}$ and thus
# very small. The value can be still decreased by decreasing the stepsize
# $\Delta z$.
#
#
# +
utz = change_reference_frame(solver.w, solver.z, solver.uwz, pc.vg(w0))
plot_claw(
solver.z, grid.t, utz, solver.ua_vals, t_lim=(-25, 125), w_lim=(0.5, 4.5)
)
# -
# **References:**
#
# [AD2010] <NAME>, <NAME>, Hamiltonian structure of propagation
# equations for ultrashort optical pulses, Phys. Rev. E 10 (2010) 013812,
# http://dx.doi.org/10.1103/PhysRevA.82.013812.
#
# [BW1989] <NAME>, <NAME>, Theoretical description of transient stimulated
# Raman scattering in optical fibers. IEEE J. Quantum Electron., 25 (1989)
# 1159, https://doi.org/10.1109/3.40655.
#
#
| docs/_downloads/de56593fa622daeb829c84329a94b5bc/g_FMAS_S_R.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Training Models - Ch4
# We'll do more than just treat models as black boxes in this chapter.
#
#
# +
#Linear Algebra micro review
import pandas as pd
#Dot Product of vector
vec = pd.DataFrame([1,3,-5])
vec
# -
vec.T
vec.T.dot(pd.DataFrame([4,-2,-1]))
# ## Linear Regression
# Generalized, it is an equation for a line where the "mx" part (of y = mx + b) is a weighted sum of input features.
#
# To train a linear model, you find values of theta that minimize error metric. Most commonly for linear that is RMSE (root mean square error). Or use MSE, since it is easier.
#
# The **Normal Equation** is solved for theta^ directly, and is written in terms of X and y. It is "closed-form".
# We'll generate data to play with this idea.
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
X = 2 * np.random.rand(100,1)
y = 4 + 3 * X + np.random.randn(100,1)
# our random generated linear dataset.
X, y
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()
X_b = np.c_[np.ones((100,1)), X] #adds x0 = 1 to each instance, for dot product and matrix sizing i presume.
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
np.linalg.inv(X_b.T.dot(X_b))
X_b.T.dot(X_b)
# Here we used the normal equation to solve for theta. Ideally theta would be 4 and 3, since that is what we used to generate the noise.
#Make predictions against our model and plot.
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)), X_new]
y_predict = X_new_b.dot(theta_best)
y_predict
plt.plot(X_new, y_predict, "r-")
plt.plot(X,y, "b.")
plt.axis([0,2,0,15])
plt.show()
#Same regression with Sklearn
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
lin_reg.intercept_, lin_reg.coef_
lin_reg.predict(X_new)
# ## Gradient Descent
# Tweak parameters iteratively in order to minimize a cost function. (finds local/global mins)
#
# Practically speaking, you can fill theta (your model parameters) with random numbers and start changing them gradually to minimize the MSE. The number of steps you take is the learning rate hyperparam. learning rate too low and it takes too long, too high and you might jump across a valley and miss the minimum.
#
# ### Tip
# For gradient descent, ensure you've used something like `sklearn StandardScaler` to ensure features are similar scale. This helps speed up convergence.
#
# ### Batch Gradient Descent
# We are essentially computing partial derivatives with respect to each model parameter (thetas). AKA how much will the cost function change, if I change this input param just a little bit.
#
# It is called "Batch" because the entire training set is used in the computation for each gradient step. (to compute all the partial derivatives)
#
# The gradients point "up hill" which is why we subtract.
#Example gradient Descent.
eta = 0.1 #learning rate
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) #random initialization.
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients
theta # It worked!
# ### Stochastic Gradient Descent
# Much faster than batch since it doesn't use the entire traning set at each step. Once the algorithm stops, the parameter values it found are simply "good", but not guaranteed to be optimal. The randomness also helps it find the global minimum, if the cost function is not convex.
#
# This is also called "simulated annealing".
#
# The "learning schedule" determines what the learning rate will be at each iteration.
# +
n_epochs = 50
t0, t1 = 5, 50 #learning schedule hyperparams.
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) #random init
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_b[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
# -
theta
# Similar good results to batch but we only had to iterate 50 times (50 "epochs").
# Stochastic Gradient Descent using sklearn
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter=50, penalty=None, eta0=0.1)
sgd_reg.fit(X,y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
# ### Mini Batch
# sort of a combo of Batch and Stochastic. compute gradient at each step by randomly selecting small subset of instances from training set.
# ## Polynomial Regression
m = 100
X = 6 * np.random.rand(m,1) -3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.plot(X,y, "b.")
plt.show()
# A simple straight line won't fit this, so lets use PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
X_poly[0] #added the square of X to the dataset.
#Now we can fit a standard linear regression onto this polynomial data.
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
# Not too bad, since the original function was `y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)`
# ### Learning Curves
#
# How do you determine what type of curve to fit your data? (aka which degree polynomial).
#
# Another way to look at model performance is to look at the "learning curves". These are plots of the models performance on training and validation sets, as a fu nction of the training set size (aka training iteration). You train the model several times on different sized subsets of the training set. Aka how does the model respond as it gets more and more data to use?
# +
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, x, y, y_lim=False):
X_train, X_val, y_train, y_val = train_test_split(X,y, test_size=0.2)
train_errors, val_errors = [],[]
for m in range(1, len(X_train)):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train_predict, y_train[:m]))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
plt.legend(loc="upper right", fontsize=14) # not shown in the book
plt.xlabel("Training set size", fontsize=14) # not shown
plt.ylabel("RMSE", fontsize=14) # not shown
if y_lim:
plt.ylim((0, y_lim))
# -
lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X,y, 3)
# Tip: If your model is underfitting your model (such as this graph suggests) adding more training data will not help, you need a more complex model, or better features in your data.
# +
# Plot learning curves for complex 10th degree polynomial
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression())
])
plot_learning_curves(polynomial_regression, X,y, 2)
# -
# We notice that the error is lower than with the linear model.
# ## Regularized Linear Models
# To avoid overfitting a model (i.e. constrain it) you can limit the degrees of freedom. A way to do this for polynomial models is to limit the degree.
#
# For linear models, you can constrain the weights of the model. What follors is Ridge Regression, Lasso Regression, and Elastic Net, three weights of constraining linear weights.
# Ridge Regression is a "regularized" version of linear regression. A regularization term is added to the cost function. Hyperparameter alpha (a) controls how much to regularize. alpha of 0 is just plain linear regression.
# ## Logistic Regression
# Uses probablilities to determine if something is class 1 or 0 (aka binary classifier).
from sklearn import datasets
iris = datasets.load_iris() #Famous Iris flower data set.
list(iris.keys())
X = iris["data"][:, 3:] #petal width
y = (iris["target"] == 2).astype(np.int) #1 if Iris-Virginica, else 0
#train logistic regression model.
from sklearn.linear_model import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit(X,y)
#look at estimated probabilities for flowers with petal widths from 0 to 3cm
X_new = np.linspace(0,3,1000).reshape(-1,1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris Virginica")
# X axis is petal width in cm.
| handsOn/ch4/TrainingModels.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="kA4Pu2sPr_eG" colab_type="code" outputId="ba330d94-510d-41cf-a5a4-25fb5d4b78db" executionInfo={"status": "ok", "timestamp": 1590159303260, "user_tz": 180, "elapsed": 4010, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 318}
# !nvidia-smi
# + id="rOXNne0OoLTd" colab_type="code" outputId="20886340-bc20-4ce8-faa0-51e590c2a7d8" executionInfo={"status": "ok", "timestamp": 1590159347250, "user_tz": 180, "elapsed": 13309, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 105}
# !pip --quiet install transformers
# !pip --quiet install tokenizers
# + id="htKChfMHoYRb" colab_type="code" outputId="da83e53f-53d6-4db8-e828-accee6fae9a4" executionInfo={"status": "ok", "timestamp": 1590159373461, "user_tz": 180, "elapsed": 39135, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 125}
from google.colab import drive
drive.mount('/content/drive')
# + id="xtDZkoyzod_S" colab_type="code" colab={}
# !cp -r '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Scripts/.' .
# + id="38KKgQn7owCr" colab_type="code" colab={}
COLAB_BASE_PATH = '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/'
MODEL_BASE_PATH = COLAB_BASE_PATH + 'Models/Files/167-roBERTa_base/'
import os
os.mkdir(MODEL_BASE_PATH)
# + [markdown] id="MOE8CNSAnvq-" colab_type="text"
# ## Dependencies
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _kg_hide-input=true _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" id="x48gxo3vnvrA" colab_type="code" outputId="ef5f1248-4ef4-4de1-c6ac-854e458ee55e" executionInfo={"status": "ok", "timestamp": 1590159405850, "user_tz": 180, "elapsed": 6230, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.<KEY>", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 72}
import json, warnings, shutil
from scripts_step_lr_schedulers import *
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts_aux import *
import tweet_utility_preprocess_roberta_scripts_text as preprocess_text
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
# + [markdown] id="6HW0GQzPnvrF" colab_type="text"
# # Load data
# + id="jS858zlQNNCs" colab_type="code" colab={}
# Unzip files
# !tar -xf '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Data/complete_96/no_qa_fold_1.tar.gz'
# !tar -xf '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Data/complete_96/no_qa_fold_2.tar.gz'
# !tar -xf '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Data/complete_96/no_qa_fold_3.tar.gz'
# !tar -xf '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Data/complete_96/no_qa_fold_4.tar.gz'
# !tar -xf '/content/drive/My Drive/Colab Notebooks/Tweet Sentiment Extraction/Data/complete_96/no_qa_fold_5.tar.gz'
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _kg_hide-input=true _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a" id="hVhA98wenvrG" colab_type="code" outputId="45077f99-013d-43f2-d05a-236cfd1a1a1a" executionInfo={"status": "ok", "timestamp": 1590159423015, "user_tz": 180, "elapsed": 22488, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 501}
database_base_path = COLAB_BASE_PATH + 'Data/complete_96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# + [markdown] id="b0bUTMPynvrM" colab_type="text"
# # Model parameters
# + id="Paexn4ywnvrM" colab_type="code" colab={}
vocab_path = COLAB_BASE_PATH + 'qa-transformers/roberta/roberta-base-vocab.json'
merges_path = COLAB_BASE_PATH + 'qa-transformers/roberta/roberta-base-merges.txt'
base_path = COLAB_BASE_PATH + 'qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 5,
"question_size": 0,
"N_FOLDS": 5,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open(MODEL_BASE_PATH + 'config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
# + [markdown] id="D_8F5nxDnvrW" colab_type="text"
# # Tokenizer
# + _kg_hide-output=true id="6qeQlxrDnvrX" colab_type="code" colab={}
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
# + [markdown] id="S3FN1pb1nvrb" colab_type="text"
# ## Learning rate schedule
# + _kg_hide-input=true id="XUYfnwPRnvrc" colab_type="code" outputId="7d8d74f8-8712-4e29-8eb3-94ff4caf81a1" executionInfo={"status": "ok", "timestamp": 1590159435510, "user_tz": 180, "elapsed": 33303, "user": {"displayName": "Dimit<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 405}
lr_min = 1e-6
lr_max = config['LEARNING_RATE']
train_size = len(k_fold[k_fold['fold_1'] == 'train']) *2
step_size = train_size // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
decay = .9993
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [exponential_schedule_with_warmup(tf.cast(x, tf.float32), warmup_steps=1, lr_start=lr_max, lr_max=lr_max, lr_min=lr_min, decay=decay) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
# + [markdown] id="3aHwZDF9nvrR" colab_type="text"
# # Model
# + id="7gIO5wkQnvrS" colab_type="code" colab={}
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
x = layers.Dropout(.1)(last_hidden_state)
x_start = layers.Dense(1)(x)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Dense(1)(x)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
return model
# + [markdown] id="jy24FlCgnvrj" colab_type="text"
# # Train
# + _kg_hide-input=true _kg_hide-output=true id="RU2sa648nvrj" colab_type="code" outputId="a1de8f35-8ce1-40ca-df88-4dfc0f6bd748" executionInfo={"status": "ok", "timestamp": 1590167754144, "user_tz": 180, "elapsed": 371355, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
AUTO = tf.data.experimental.AUTOTUNE
strategy = tf.distribute.get_strategy()
k_fold_best = k_fold.copy()
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
base_data_path = 'fold_%d/' % (n_fold)
# Load data
x_train = np.load('no_qa_' + base_data_path + 'x_train.npy')
y_train = np.load('no_qa_' + base_data_path + 'y_train.npy')
x_valid = np.load('no_qa_' + base_data_path + 'x_valid.npy')
y_valid = np.load('no_qa_' + base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
valid_step_size = x_valid.shape[1] // config['BATCH_SIZE']
# Build TF datasets
train_dist_ds = strategy.experimental_distribute_dataset(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED))
valid_dist_ds = strategy.experimental_distribute_dataset(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=True, seed=SEED))
train_data_iter = iter(train_dist_ds)
valid_data_iter = iter(valid_dist_ds)
# Step functions
@tf.function
def train_step(data_iter):
def train_step_fn(x, y):
with tf.GradientTape() as tape:
probabilities = model(x, training=True)
loss_start = loss_fn(y['y_start'], probabilities[0])
loss_end = loss_fn(y['y_end'], probabilities[1])
loss = tf.math.add(loss_start, loss_end)
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# update metrics
train_loss.update_state(loss)
train_loss_start.update_state(loss_start)
train_loss_end.update_state(loss_end)
for _ in tf.range(step_size):
strategy.experimental_run_v2(train_step_fn, next(data_iter))
@tf.function
def valid_step(data_iter):
def valid_step_fn(x, y):
probabilities = model(x, training=False)
loss_start = loss_fn(y['y_start'], probabilities[0])
loss_end = loss_fn(y['y_end'], probabilities[1])
loss = tf.math.add(loss_start, loss_end)
# update metrics
valid_loss.update_state(loss)
valid_loss_start.update_state(loss_start)
valid_loss_end.update_state(loss_end)
for _ in tf.range(valid_step_size):
strategy.experimental_run_v2(valid_step_fn, next(data_iter))
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
optimizer = optimizers.Adam(learning_rate=lambda: exponential_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32)//step_size, warmup_steps=1,
lr_start=lr_max, lr_max=lr_max, lr_min=lr_min, decay=decay))
loss_fn = losses.categorical_crossentropy
train_loss = metrics.Sum()
valid_loss = metrics.Sum()
train_loss_start = metrics.Sum()
valid_loss_start = metrics.Sum()
train_loss_end = metrics.Sum()
valid_loss_end = metrics.Sum()
metrics_dict = {'loss': train_loss, 'loss_start': train_loss_start, 'loss_end': train_loss_end,
'val_loss': valid_loss, 'val_loss_start': valid_loss_start, 'val_loss_end': valid_loss_end}
history = custom_fit(model, metrics_dict, train_step, valid_step, train_data_iter, valid_data_iter,
step_size, valid_step_size, config['BATCH_SIZE'], config['EPOCHS'], config['ES_PATIENCE'],
(MODEL_BASE_PATH + model_path), save_last=False)
history_list.append(history)
model.save_weights(MODEL_BASE_PATH +'last_' + model_path)
# Make predictions (last model)
x_train = np.load('no_qa_' + base_data_path + 'x_train.npy')
x_valid = np.load('no_qa_' + base_data_path + 'x_valid.npy')
train_preds = model.predict(get_test_dataset(x_train, config['BATCH_SIZE']))
valid_preds = model.predict(get_test_dataset(x_valid, config['BATCH_SIZE']))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: preprocess_text.decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna(k_fold["text"], inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
# Make predictions (best model)
model.load_weights(MODEL_BASE_PATH + model_path)
train_preds = model.predict(get_test_dataset(x_train, config['BATCH_SIZE']))
valid_preds = model.predict(get_test_dataset(x_valid, config['BATCH_SIZE']))
k_fold_best.loc[k_fold_best['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold_best.loc[k_fold_best['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold_best.loc[k_fold_best['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold_best.loc[k_fold_best['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold_best['end_fold_%d' % (n_fold)] = k_fold_best['end_fold_%d' % (n_fold)].astype(int)
k_fold_best['start_fold_%d' % (n_fold)] = k_fold_best['start_fold_%d' % (n_fold)].astype(int)
k_fold_best['end_fold_%d' % (n_fold)].clip(0, k_fold_best['text_len'], inplace=True)
k_fold_best['start_fold_%d' % (n_fold)].clip(0, k_fold_best['end_fold_%d' % (n_fold)], inplace=True)
k_fold_best['prediction_fold_%d' % (n_fold)] = k_fold_best.apply(lambda x: preprocess_text.decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], tokenizer), axis=1)
k_fold_best['prediction_fold_%d' % (n_fold)].fillna(k_fold_best["text"], inplace=True)
k_fold_best['jaccard_fold_%d' % (n_fold)] = k_fold_best.apply(lambda x: jaccard(x['selected_text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
# + [markdown] id="_59x5WnGnvro" colab_type="text"
# # Model loss graph
# + _kg_hide-input=true id="Tlq60Zvenvro" colab_type="code" outputId="6a65b88c-d997-44b4-a17f-a818640ce0ae" executionInfo={"status": "ok", "timestamp": 1590167810182, "user_tz": 180, "elapsed": 6799, "user": {"displayName": "<NAME>", "photoUrl": "<KEY>", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
# + [markdown] id="MvzO_AjPnvrt" colab_type="text"
# # Model evaluation (last model)
# + _kg_hide-input=true id="ELe26ujlnvrt" colab_type="code" outputId="72e8b5e3-a567-4e54-b124-58b0bb08ada9" executionInfo={"status": "ok", "timestamp": 1590167815071, "user_tz": 180, "elapsed": 9285, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 266}
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
# + [markdown] id="xxbg-_R_p2dE" colab_type="text"
# # Model evaluation (best model)
# + id="KgsapEFup3zY" colab_type="code" outputId="2c3e25b6-ec5f-4900-e9b8-8ba333fb3b02" executionInfo={"status": "ok", "timestamp": 1590167820859, "user_tz": 180, "elapsed": 14086, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 266}
display(evaluate_model_kfold(k_fold_best, config['N_FOLDS']).style.applymap(color_map))
# + [markdown] id="yP3xG-Cenvry" colab_type="text"
# # Visualize predictions
# + _kg_hide-input=true id="cGxcMVRMnvrz" colab_type="code" outputId="9498421c-d321-4e57-b464-d25805cf48b2" executionInfo={"status": "ok", "timestamp": 1590167820860, "user_tz": 180, "elapsed": 12817, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjWI4QgYDUyC8ZcW5KHpuBwcY-MZWVqbPWcZSzxIg=s64", "userId": "06256612867315483887"}} colab={"base_uri": "https://localhost:8080/", "height": 767}
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
| Model backlog/Train/175-Tweet-Train-5Fold-roBERTa base no QA.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %run ../../common/import_all.py
from common.setup_notebook import set_css_style, setup_matplotlib, config_ipython
config_ipython()
setup_matplotlib()
set_css_style()
# -
# # Programming Languages
# ## A short and very non-comprehensive timeline of languages
#
# * 1949 Assembly: low-level, strong correspondence to machine code
# * 1957 Fortran
# * 1978 C, low-medium level
# * 1983 C++
# * 1991 Python
# * 1995 Java
#
# About Fortran, and why it still is so common within the scientific programming circles, have a read at this brilliant article [[2]](#fortran).
# ## Main programming paradigms
#
# A programming paradigm is a style of coding. The main ones are
#
# * imperative
# * declarative (of which functional is a subset)
# * object-oriented
#
# ### Imperative and declarative
#
# Are two opposing ones. In an *imperative* paradigm, algorithms are implemented in explicit steps and statements are used to change the state: statements are the smallest standalone instructions.
# In a *declarative* paradigm, algorithms are logically expressed without the explicit list of instructions (for example with the use of list comprehensions in Python).
#
# ### Object oriented
#
# In an *object-oriented* programming paradigm, objects are declared that contain attributes and methods.
#
# ### Functional
#
# The *functional* programming paradigm, belonging to the declarative class, treats computation as the evaluation of mathematical functions and is based on lambda calculus, avoiding statements. Examples of functional languages are Clojure, Haskell; other that support the functional paradigm are Python, R, Java, Scala.
#
# For example, in Clojure you'd get the square of integers until 25 as
#
# ```
# (take 25 (squares-of (integers)))
# ```
#
# where `take`, `squares-of` and `integers` are functions, as opposed to an explicit for loop you'd write in other languages.
#
# Scala is a functional programming language that runs on the JVM (Java virtual machine), meaning it gets compiled to Java bytecode, it is statically typed, object-oriented. The name stands for "scalable language" because it has been conceived to grow with demand of its users. The project started in 2001 at the E. Polytechnique de Lausanne by <NAME> and it is taking more and more interest in the data science community.
# ## Compiled and interpreted languages
#
# A *compiler* is something, like a parser, that transforms the source code the programmers uses into machine code (binary file with low-level instructions the machine understands). Compiled languages are for instance C, C++, Fortran.
#
# An *interpreter* interprets the language, in that when you write your high-level instructions it goes searching for the corresponding binary code, which is part of itself. The difference with a compiler is that this process is executed at run time, making interpreted code sensibly slower than compiled one. Examples are Python and Ruby.
# ## Statically and dynamically typed languages
#
# In a statically typed language, you cannot change the type of a variable after you've declared it. Python is a dynamically typed one as you can do things like
#
# ```
# a = 1
#
# ...
#
# a = "bla"
# ```
# ## References
#
# 1. <a name="book"></a> <NAME>, **An Introduction to Computer Organisation**, 2015
# 2. <a name="fortran"></a> [Scientific computing’s future: Can any coding language top a 1950s behemoth?](https://arstechnica.com/science/2014/05/scientific-computings-future-can-any-coding-language-top-a-1950s-behemoth/), an article abotu Fortran still being used today in numerical work, Ars Technica, 2014
| cs/foundations/programming-languages.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
N_trials = 100000
x = np.random.uniform(size=N_trials)
y = np.random.uniform(size=N_trials)
z = x+y
_ = plt.hist(z, bins=np.linspace(0,2,100), density=True)
plt.scatter(x,y)
import numpy as np
import matplotlib.pyplot as plt
N_trials = 100000
N_vars = 10
x_array = np.random.uniform(0,1, size=N_trials*N_vars).reshape(N_trials,N_vars)
z = np.sum(x_array,axis=1)
_ = plt.hist(z, bins=np.linspace(0,N_vars,100), density=True)
import numpy as np
import matplotlib.pyplot as plt
N_trials = 100000
def cos_conv(N_vars):
x_array = np.random.uniform(-np.pi,np.pi, size=N_trials*N_vars).reshape(N_trials,N_vars)
cos_array = np.cos(x_array)
z = np.sum(cos_array,axis=1)
return z
bins = np.linspace(-5,5,100)
_ = plt.hist(cos_conv(1), bins=bins, density=True, alpha=.2, label='N=1')
_ = plt.hist(cos_conv(2), bins=bins, density=True, alpha=.2, label='N=2')
_ = plt.hist(cos_conv(5), bins=bins, density=True, alpha=.2, label='N=5')
plt.legend();
| book/error-propagation/convolution-demo.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Recreating Ling _IMMI_ (2017)
# In this notebook, we will recreate some key results from [Ling et al. _IMMI_ (2017)](https://link.springer.com/article/10.1007/s40192-017-0098-z), which studied the application of random-forest-based uncertainties to materials design. We will show that the errors produced from the Random Forest implemented in lolo (the code used by Ling et al.) are well-calibrated and that the uncertainties can be used with Sequential Learning to quickly find optimal materials within a search space.
#
# Note: This notebook will require you to install [lolopy](https://pypi.org/project/lolopy/) and establish an account with Citrination to get an an API key (see [Quickstart](https://citrineinformatics.github.io/api-documentation/quickstart/index.html)), and set it as an environment variable named CITRINE_KEY. Also, the uncertainity calculations do not currently function on Windows.
#
# Last used with matminer version 0.4.5.
# %matplotlib inline
from matplotlib import pyplot as plt
from matminer.data_retrieval.retrieve_Citrine import CitrineDataRetrieval
from matminer.featurizers.conversions import StrToComposition
from matminer.featurizers.base import MultipleFeaturizer
from matminer.featurizers import composition as cf
from lolopy.learners import RandomForestRegressor
from sklearn.model_selection import KFold
from pymatgen import Composition
from scipy.stats import norm
import pandas as pd
import numpy as np
import os
# Set the random seed
np.random.seed(8)
# ## Get the Datasets
# The Ling Paper used 4 different datasets to test the uncertainty estimates
cdr = CitrineDataRetrieval()
data = cdr.get_dataframe(criteria={'data_set_id': 150888}, print_properties_options=False)
# Convert the composition and class variable from strings
data = StrToComposition(target_col_id='composition').featurize_dataframe(data, "chemicalFormula")
data['ZT'] = pd.to_numeric(data['ZT'], errors='coerce')
data.reset_index(drop=True, inplace=True)
# ## Compute Features
# Every dataset except the steel fatigue dataset uses the composition-based features of [Ward et al.](https://www.nature.com/articles/npjcompumats201628).
f = MultipleFeaturizer([cf.Stoichiometry(), cf.ElementProperty.from_preset("magpie"),
cf.ValenceOrbital(props=['avg']), cf.IonProperty(fast=True)])
X = np.array(f.featurize_many(data['composition']))
# ## Get the Residuals and RF Uncertainty
# As described in the Ling paper, ideally-calibrated uncertainty estimaes should have a particular relationship with the errors of a machine learning model. Specifically, the distribution of $r(x)/\sigma(x)$ where $r(x)$ is the residual of the prediction and $\sigma(x)$ is the uncertainty of the prediction for x should have a Gaussian distribution with zero mean and unit standard deviation.
model = RandomForestRegressor()
# Get the errors from 8-fold cross-validation
y = data['ZT'].values
y_resid = []
y_uncer = []
for train_id, test_id in KFold(8, shuffle=True).split(X):
model.fit(X[train_id], y[train_id])
yf_pred, yf_std = model.predict(X[test_id], return_std=True)
y_resid.extend(yf_pred - y[test_id])
y_uncer.extend(yf_std)
# Plot the normalized residuals ($r(x)/\sigma(x)$) against the normal distribution
# +
fig, axs = plt.subplots(1, 2, sharey=True)
x = np.linspace(-8, 8, 50)
# Plot the RF uncertainty
resid = np.divide(y_resid, y_uncer)
axs[0].hist(resid, x, density=True)
axs[0].set_title('With Lolo Uncertainty Estimates')
# Plot assuming constant errors
resid = np.divide(y_resid, np.sqrt(np.power(y_resid, 2).mean()))
axs[1].hist(resid, x, density=True)
axs[1].set_title('Assuming Constant Error')
for ax in axs:
ax.plot(x, norm.pdf(x), 'k--', lw=0.75)
ax.set_xlabel('Normalized Residual')
axs[0].set_ylabel('Probability Density')
fig.set_size_inches(6.5, 2)
fig.tight_layout()
# -
# Here, we compare the error distribution using the Lolo uncertainty estimates (_left_) and the assumption that all entries have the same error (_right_). The normalized residuals for the uncertainty estimates have a distribution closer to the unit normal distribution, which means - as expected - that it better captures which predictions will have a higher error.
# ## Sequential Learning
# One important use of model uncertainties is to employ them to guide which experiments to pick to find optimal materials with minimal experiments/computations. As described in the Ling paper (and [other](https://journals.aps.org/prb/abstract/10.1103/PhysRevB.89.054303) [nice](https://www.nature.com/articles/srep19660) [articles](https://link.springer.com/article/10.1007/s10822-015-9832-9)), it is not always best to pick the experiment that the model predicts to have the best properties if you can perform more than one experiment sequentially. Rather, it can be better to pick entries with large uncertainities that, when tested and added to the training set, can improve the models predictions for the next experiments.
#
# Here, we demonstrate one approach for picking experiments: Maximum Liklihood of Improvement (MLI). In contrast to picking the material with the best predicted properties (an approach we refer to Maximum Expected Improvment (MEI)), the MLI approach pickes the material with with the highest liklihood of being better than the best material in the training set - a measure that uses both the predicted value and the uncertainty. The MLI method is equivalent to the [Expected Improvement metric common in Bayesian Optimization](https://sigopt.com/blog/expected-improvement-vs-knowledge-gradient), and balances a tradeoff between picking entries with favorable predictions (*exploitation*) and those with high uncertainties (*exploration*).
# ### Step 1: Pick an initial training set
# We'll start with a small set of entries from the training set
in_train = np.zeros(len(data), dtype=np.bool)
in_train[np.random.choice(len(data), 10, replace=False)] = True
print('Picked {} training entries'.format(in_train.sum()))
assert not np.isclose(max(y), max(y[in_train]))
# ### Step 2: Demonstrate picking the entries based on MLI and MEI
# Just to give a visual of how the selection process works
# Make the predictions
model.fit(X[in_train], y[in_train])
y_pred, y_std = model.predict(X[~in_train], return_std=True)
# For MEI, we pick the highest predicted value. For MLI, we pick the material that has the highest probability of being better than any material in the training set. As we assume the predictions to be normally distributed, the probability of materials can be computed from the [Z-score](https://en.wikipedia.org/wiki/Standard_score) $Z = (y - y^*)/\sigma$ where $y^*$ is the maximum of the $y$ of the training set. Formally, the probability can be computed from the Z-score using the cumulative distribution function of the normal distribution. For our purposes, we can use the Z-score becuase the probability is a monotonic function of the Z-score (stated simply: the material with the highest probability will have the highest Z-score).
mei_selection = np.argmax(y_pred)
mli_selection = np.argmax(np.divide(y_pred - np.max(y[in_train]), y_std))
print('Predicted ZT of material #{} selected based on MEI: {:.2f} +/- {:.2f}'.format(mei_selection, y_pred[mei_selection], y_std[mei_selection]))
print('Predicted ZT of material #{} selected based on MLI: {:.2f} +/- {:.2f}'.format(mli_selection, y_pred[mli_selection], y_std[mli_selection]))
# For this particular iteration, the MEI and MLI strategies pick the same material. Depending on the random seed of this notebook and that used by lolo, you may see that the material picked by MLI has a lower predicted $ZT$ but a higher variance. According to the logic behind MLI, picking that entry will (1) yield a higher liklihood of finding a well-performing material and (2) lead to an improved model.
# ### Step 3: Run an iterative search
# Starting with the same 32 materials in the training set, we will iteratively pick materials, add them to the training set, and retrain the model using 3 different strategies for picking entries: MEI, MLI, and randomly.
n_steps = 32
all_inds = set(range(len(y)))
# #### Random Selection
# Just pick an entry at random, no need to train a model
random_train = [set(np.where(in_train)[0].tolist())]
for i in range(n_steps):
# Get the current train set and search space
train_inds = set(random_train[-1]) # Last iteration
search_inds = sorted(all_inds.difference(train_inds))
# Pick an entry at random
train_inds.add(np.random.choice(search_inds))
# Add it to the list of training sets
random_train.append(train_inds)
# #### Maximum Expected Improvement
# Pick the entry with the largest predicted value
mei_train = [set(np.where(in_train)[0].tolist())]
for i in range(n_steps):
# Get the current train set and search space
train_inds = sorted(set(mei_train[-1])) # Last iteration
search_inds = sorted(all_inds.difference(train_inds))
# Pick entry with the largest maximum value
model.fit(X[train_inds], y[train_inds])
y_pred = model.predict(X[search_inds])
train_inds.append(search_inds[np.argmax(y_pred)])
# Add it to the list of training sets
mei_train.append(set(train_inds))
# #### Maximum Likelihood of Improvement
# Pick the entry with the largest probability of improvement
mli_train = [set(np.where(in_train)[0].tolist())]
for i in range(n_steps):
# Get the current train set and search space
train_inds = sorted(set(mei_train[-1])) # Last iteration
search_inds = sorted(all_inds.difference(train_inds))
# Pick entry with the largest maximum value
model.fit(X[train_inds], y[train_inds])
y_pred, y_std = model.predict(X[search_inds], return_std=True)
train_inds.append(search_inds[np.argmax(np.divide(y_pred - np.max(y[train_inds]), y_std))])
# Add it to the list of training sets
mli_train.append(set(train_inds))
# Plot the results
# +
fig, ax = plt.subplots()
for train_inds, label in zip([random_train, mei_train, mli_train], ['Random', 'MEI', 'MLI']):
ax.plot(np.arange(len(train_inds)), [max(y[list(t)]) for t in train_inds], label=label)
ax.set_xlabel('Number of New Experiments')
ax.set_ylabel('Best $ZT$ Found')
fig.set_size_inches(3.5, 2)
ax.legend()
fig.tight_layout()
# -
# For this particular case, we find that the MLI strategy finds the best material more quickly than the Random or MEI approaches. In Ling 2017, they evaluate the performance of these strategies over many iterations and find that, on average, MLI finds the optimal materials as fast or better than any other approach.
| matminer_examples/machine_learning-nb/rf-with-uncertainty.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import re
text = open('Curriculum Detail for Explore.txt', encoding='utf-8').read()
for line in range(len(text.split('\n')))
re.search(r"Overview", text.split('\n')[line]) == 'Overview'
print(text)
text2 = open('Scoring at EXPLORE an explanation.txt', encoding='utf-8').read()
print(text2)
import PyPDF2
| resources/documents/Untitled.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pytorch
# language: python
# name: pytorch
# ---
# +
# # %load paperFigs_events.py
from hydroDL import pathSMAP, master, utils
from hydroDL.master import default
from hydroDL.post import plot, stat
import os
import matplotlib.pyplot as plt
import numpy as np
import torch
import pandas as pd
import matplotlib.gridspec as gridspec
import matplotlib
doLst = list()
# doLst.append('train')
doLst.append('test')
doLst.append('post')
saveDir = os.path.join(pathSMAP['dirResult'], 'DA')
# test
if 'test' in doLst:
torch.cuda.set_device(2)
subset = 'CONUSv2f1'
tRange = [20150402, 20180401]
yrStrLst = ['2015', '2016', '2017']
yfLst = list()
ypLst = list()
for yrStr in yrStrLst:
out = os.path.join(pathSMAP['Out_L3_NA'], 'DA', 'CONUSv2f1_DA' + yrStr)
df, yf, obs = master.test(
out, tRange=tRange, subset=subset, batchSize=100)
out = os.path.join(pathSMAP['Out_L3_NA'], 'DA',
'CONUSv2f1_LSTM' + yrStr)
df, yp, obs = master.test(out, tRange=tRange, subset=subset)
yf = yf.squeeze()
yp = yp.squeeze()
yfLst.append(yf)
ypLst.append(yp)
obs = obs.squeeze()
# figure out how many days observation lead
maskObs = 1 * ~np.isnan(obs.squeeze())
maskDay = np.zeros(maskObs.shape).astype(int)
ngrid, nt = maskObs.shape
for j in range(ngrid):
temp = 0
for i in range(nt):
maskDay[j, i] = temp
if maskObs[j, i] == 1:
temp = 1
else:
if temp != 0:
temp = temp + 1
ind = np.random.randint(0, ngrid)
maskObsDay = maskObs * maskDay
unique, counts = np.unique(maskObsDay, return_counts=True)
maskF = (maskDay >= 1) & (maskDay <= 3)
# # test error train on different year
trLst = [[20150402, 20160401], [20160401, 20170401], [20170401, 20180401]]
statPLst = list()
statFLst = list()
for k in range(3):
trTrain = trLst[k]
taTrain = utils.time.tRange2Array(trTrain)
taAll = utils.time.tRange2Array([20150402, 20180401])
indTrain, ind2 = utils.time.intersect(taAll, taTrain)
indTest = np.delete(np.arange(len(taAll)), indTrain)
tempYp = ypLst[k][:, indTest]
tempYf = yfLst[k][:, indTest]
tempMask = maskF[:, indTest]
tempObs = obs[:, indTest]
tempStatP = stat.statError(
utils.fillNan(tempYp, tempMask), utils.fillNan(tempObs, tempMask))
tempStatF = stat.statError(
utils.fillNan(tempYf, tempMask), utils.fillNan(tempObs, tempMask))
statPLst.append(tempStatP)
statFLst.append(tempStatF)
# +
# %matplotlib notebook
# plot map and time series
matplotlib.rcParams.update({'font.size': 10})
matplotlib.rcParams.update({'lines.linewidth': 0.8})
matplotlib.rcParams.update({'lines.markersize': 4})
matplotlib.rcParams.update({'legend.fontsize': 10})
import importlib
importlib.reload(plot)
dataGrid = [
statPLst[0]['RMSE'] - statFLst[0]['RMSE'],
statPLst[1]['RMSE'] - statFLst[1]['RMSE'],
statPLst[2]['RMSE'] - statFLst[2]['RMSE']
]
prcp = df.getDataTs('APCP_FORA').squeeze()
dataTs = [[obs, ypLst[0], yfLst[0]], [obs, ypLst[1], yfLst[1]],
[obs, ypLst[2], yfLst[2]], [prcp]]
crd = df.getGeo()
t = df.getT()
mapNameLst = ['dRMSE 2015', 'dRMSE 2016', 'dRMSE 2017']
tsNameLst = ['obs', 'prj', 'fore']
plot.plotTsMap(
dataGrid,
dataTs,
figsize=[10,6],
lat=crd[0],
lon=crd[1],
t=t,
tBar=[utils.time.t2dt(20160401),
utils.time.t2dt(20170401)],
mapNameLst=mapNameLst,
isGrid=True,
multiTS=True)
# +
# plot pixel time series
import importlib
importlib.reload(plot)
matplotlib.rcParams.update({'font.size': 12})
matplotlib.rcParams.update({'lines.linewidth': 1})
matplotlib.rcParams.update({'lines.markersize': 6})
matplotlib.rcParams.update({'legend.fontsize': 12})
indLst = [1442, 1023]
indYLst = [0, 2]
nts = len(indLst)
hrLst = list()
for i in range(nts):
hrLst = hrLst + [1, 0.7, 0.2]
del hrLst[-1]
gs = gridspec.GridSpec(nts * 3 - 1, 1, width_ratios=[1], height_ratios=hrLst)
fig = plt.figure(figsize=[12, 6])
plt.subplots_adjust(hspace=0)
plt.subplots_adjust(vspace=0)
t = df.getT()
prcp = df.getDataTs('APCP_FORA').squeeze()
tBarLst = [20160401, [20160401, 20170401], 20170401]
for k in range(nts):
ind = indLst[k]
indY = indYLst[k]
ax = fig.add_subplot(gs[k * 3, 0])
tBar = utils.time.t2dt(tBarLst[indY])
if k == 0:
legLst1 = ['project', 'forecast', 'SMAP']
legLst2 = ['prcp']
else:
legLst1 = None
legLst2 = None
plot.plotTS(
t, [ypLst[indY][ind, :], yfLst[indY][ind, :], obs[ind, :]],
ax=ax,
tBar=tBar,
legLst=legLst1,
linewidth=1)
ax.set_xticklabels([])
ax = fig.add_subplot(gs[k * 3 + 1, 0])
plot.plotTS(
t, [prcp[ind, :]],
ax=ax,
cLst='c',
legLst=legLst2,
tBar=tBar,
linewidth=1)
fig.show()
fig.savefig(os.path.join(saveDir, 'ts_extreme.eps'))
fig.savefig(os.path.join(saveDir, 'ts_extreme'))
| app/closeLoop/.ipynb_checkpoints/multiYear-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# In this notebook, we provide a sample test when applying fastMRI knee-trained (or -tuned) models to a sample brain image. We measure the performance loss by computing how the scores look like when evaluating brain-trained (or -tuned) models on the brain image.
# +
from __future__ import print_function
import matplotlib.pyplot as plt
# #%matplotlib notebook/
import os
import sys
sys.path.insert(0,'/root/bart-0.6.00/python/')
import bart
os.environ['TOOLBOX_PATH'] = "/root/bart-0.6.00/"
import sigpy.mri as mr
import sigpy as sp
import sigpy.mri as mr
from os import listdir
from os.path import isfile, join
import glob
import warnings
warnings.filterwarnings('ignore')
from include import *
from PIL import Image
import PIL
import h5py
#from skimage.metrics import structural_similarity as ssim
from common.evaluate import *
from pytorch_msssim import ms_ssim
import pickle
from common.subsample import RandomMaskFunc, EquispacedMaskFunc
from DIP_UNET_models.unet_and_tv.train_unet import UnetMRIModel
from DIP_UNET_models.unet_and_tv.varnet import VariationalNetworkModel
import numpy as np
import torch
import torch.optim
from torch.autograd import Variable
import torch.nn as nn
#from models import *
#from utils.denoising_utils import *
# from facebook MRI
#import transforms
from include import transforms as transform
GPU = True
if GPU == True:
torch.backends.cudnn.enabled = True
torch.backends.cudnn.benchmark = True
dtype = torch.cuda.FloatTensor
#os.environ['CUDA_VISIBLE_DEVICES'] = '0'
gpu = 3
torch.cuda.set_device(gpu)
print("num GPUs",torch.cuda.device_count())
else:
dtype = torch.FloatTensor
devices = [torch.device("cuda:3"),
torch.device("cuda:2"),
torch.device("cuda:1"),
torch.device("cuda:0"),]
# -
# # Load the data and create a mask
# +
datapath = '/data/brain/multicoil_val/' # change this to your data path
filename = datapath + 'file_brain_AXT1POST_207_2070067.h5'
f = h5py.File(filename, 'r') # contains a kspace measurement f['kspace'] and rss reconstruction f['reconstruction_rss']
print("Kspace shape (number slices, number coils, x, y):", f['kspace'].shape)
# which slice to consider in the following
slicenu = f["kspace"].shape[0]//2
slice_ksp = f['kspace'][slicenu]
slice_ksp_torchtensor = transform.to_tensor(slice_ksp) # Convert from numpy array to pytorch tensor
orig = f["reconstruction_rss"][slicenu]
print("Ground truth image shape (x,y):",orig.shape)# for soe brain images, this resolution is
# different, so remember to change the crop_size values for each reconstruction method accordingly
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111)
ax.imshow(orig,"gray")
ax.set(title="ground truth")
ax.axis("off")
plt.show()
ksp = slice_ksp_torchtensor.clone()
# +
try: # if the file already has a mask
temp = np.array([1 if e else 0 for e in f["mask"]])
temp = temp[np.newaxis].T
temp = np.array([[temp]])
mask = transform.to_tensor(temp).type(dtype).detach().cpu()
except: # if we need to create a mask
desired_factor = 4 # desired under-sampling factor
undersampling_factor = 0
tolerance = 0.03
while undersampling_factor < desired_factor - tolerance or undersampling_factor > desired_factor + tolerance:
mask_func = EquispacedMaskFunc(center_fractions=[0.07], accelerations=[desired_factor]) # Create the mask function object
masked_kspace, mask = transform.apply_mask(slice_ksp_torchtensor, mask_func=mask_func) # Apply the mask to k-space
mask1d = var_to_np(mask)[0,:,0]
undersampling_factor = len(mask1d) / sum(mask1d)
mask1d = var_to_np(mask)[0,:,0]
# The provided mask and data have last dim of 368, but the actual data is smaller.
# To prevent forcing the network to learn outside the data region, we force the mask to 0 there.
mask1d[:mask1d.shape[-1]//2-160] = 0
mask1d[mask1d.shape[-1]//2+160:] =0
mask2d = np.repeat(mask1d[None,:], slice_ksp.shape[1], axis=0).astype(int) # Turning 1D Mask into 2D that matches data dimensions
mask2d = np.pad(mask2d,((0,),((slice_ksp.shape[-1]-mask2d.shape[-1])//2,)),mode='constant') # Zero padding to make sure dimensions match up
mask = transform.to_tensor( np.array( [[mask2d[0][np.newaxis].T]] ) ).type(dtype).detach().cpu()
print("under-sampling factor:",round(len(mask1d)/sum(mask1d),2))
plt.imshow(mask2d,"gray")
plt.title("mask")
plt.axis("off")
plt.show()
# -
# # Evaluation and plot functions
def ssim2_(im1,im2):
# im1: ground truth
# im2: reconstruction
im2 = (im2-im2.mean()) / im2.std()
im2 *= im1.std()
im2 += im1.mean()
s = ssim(np.array([im1]),np.array([im2]))
return s
def plot_(results,f):
ctr = 1
fig = plt.figure(figsize=(16,10))
for key in results:
if ctr == 1:
ax = fig.add_subplot(2,3,ctr)
ax.imshow(np.flip(results[key][f]['original'],axis=0),'gray')
ax.set_title('ground truth')
ax.axis('off')
ctr += 1
ax = fig.add_subplot(2,3,ctr)
ax.imshow(np.flip(results[key][f]['reconstruction'],axis=0),'gray')
ax.set_title(key + ' SSIM: %0.4f'%(results[key][f]['score']))
ax.axis('off')
ctr += 1
plt.show()
# # Reconstruction functions
def varnet_reconstruction(vmdl, ksp, mask, orig):
masked_kspace, _ = transform.apply_mask(ksp.to(devices[0]), mask = mask.to(devices[0]))
inp = masked_kspace.clone()
with torch.no_grad():
out = vmdl(inp[None,:].type(dtype).to(devices[0]),mask.type(torch.cuda.ByteTensor).to(devices[0]))
rec = crop_center2(out[0].data.cpu().numpy(),320,320)
Ssim = ssim2_(orig,rec)
return rec, Ssim
def unet_reconstruction(umdl, ksp, mask, orig, need_crop=True):
masked_kspace, _ = transform.apply_mask(ksp.to(devices[0]), mask = mask.type(dtype).to(devices[0]))
### fixed reconstruction from non-perturbed data
sampled_image2 = transform.ifft2(masked_kspace)
if need_crop:
crop_size = (320, 320)
sampled_image = transform.complex_center_crop(sampled_image2, crop_size)
else:
sampled_image = sampled_image2
# Absolute value
sampled_image = transform.complex_abs(sampled_image)
# Apply Root-Sum-of-Squares if multicoil data
sampled_image = transform.root_sum_of_squares(sampled_image)
# Normalize input
sampled_image, mean, std = transform.normalize_instance(sampled_image, eps=1e-11)
sampled_image = sampled_image.clamp(-6, 6)
inp = sampled_image.unsqueeze(0)
out = umdl(inp.type(dtype).to(devices[0]))
rec = out.data.cpu().numpy()[0]
Ssim = ssim2_(orig,rec)
return rec, Ssim
from pytorch_wavelets import DWTForward, DWTInverse
xfm = DWTForward(J=3, mode='zero', wave='db3').cuda(gpu)
def l1_reconstruction(ksp, mask, orig, num_iters = 1000, lam=1e-2,LR=1e-1,):
unders, _ = transform.apply_mask(ksp, mask = mask)
mse = torch.nn.MSELoss()
x = Variable(torch.zeros(unders.shape[1:])).type(dtype).to(devices[0])
x.requires_grad = True
zpad = unders.data.cpu().numpy()
zpad_complex = []
for m in range(zpad.shape[0]):
zpad_complex += [zpad[m,:,:,0]+1j*zpad[m,:,:,1]]
zpad_complex = np.array(zpad_complex)
zpad_complex.shape
masked_complex_kspace = zpad_complex * np.array(ksp.shape[0]*[list(mask2d)]) # shape: (15, 640, 368)
sens_maps = bart.bart(1, f'ecalib -d0 -m1', np.array([np.moveaxis(masked_complex_kspace,0,2)]))
sens_maps = np.moveaxis(sens_maps[0],2,0)
optimizer = torch.optim.SGD([x], lr=LR)
S = transform.to_tensor(sens_maps).type(dtype).to(devices[0])
L = []
trL = []
for i in range(num_iters):
def closure():
imgs = torch.zeros(S.shape).type(dtype).to(devices[0])
for j,s in enumerate(S):
imgs[j,:,:,0] = x[:,:,0] * s[:,:,0] - x[:,:,1] * s[:,:,1]
imgs[j,:,:,1] = x[:,:,0] * s[:,:,1] + x[:,:,1] * s[:,:,0]
optimizer.zero_grad()
out,_ = transform.apply_mask(transform.fft2(imgs),mask=mask.to(devices[0]))
Rx, Ux = xfm(x[None,:].permute(0,3,1,2))
loss = mse( out , unders.type(dtype).to(devices[0]) ) + lam*torch.norm(Rx,p=1)
loss.backward(retain_graph=True)
if i % 100 == 0:
print("iteration{} -- fitting loss: {}".format(i,loss.data),"\r",end='')
L.append(loss.data.cpu().numpy()[np.newaxis][0])
return loss
loss = optimizer.step(closure)
rec = center_crop(transform.complex_abs(x).data.cpu().numpy(),(320,320))
Ssim = ssim2_(orig,rec)
return rec, Ssim
def get_scale_factor(net,num_channels,in_size,ksp_tt,scale_out=1,scale_type="norm"):
### get norm of deep decoder output
# get net input, scaling of that is irrelevant
shape = [1,num_channels, in_size[0], in_size[1]]
ni = Variable(torch.zeros(shape)).type(dtype).to(devices[0])
ni.data.uniform_()
# generate random image
try:
out_chs = net( ni.type(dtype).to(devices[0]),scale_out=scale_out ).data.cpu().numpy()[0]
except:
out_chs = net( ni.type(dtype).to(devices[0]) ).data.cpu().numpy()[0]
print(net(ni.type(dtype).to(devices[0])).shape)
out_imgs = channels2imgs(out_chs)
out_img_tt = transform.root_sum_of_squares( torch.tensor(out_imgs) , dim=0)
### get norm of least-squares reconstruction
orig_tt = transform.ifft2(ksp_tt) # Apply Inverse Fourier Transform to get the complex image
orig_imgs_tt = transform.complex_abs(orig_tt) # Compute absolute value to get a real image
orig_img_tt = transform.root_sum_of_squares(orig_imgs_tt, dim=0)
orig_img_np = orig_img_tt.cpu().numpy()
if scale_type == "norm":
s = np.linalg.norm(out_img_tt) / np.linalg.norm(orig_img_np)
if scale_type == "mean":
s = (out_img_tt.mean() / orig_img_np.mean()).numpy()[np.newaxis][0]
return s,ni
def convdecoder_reconstruction(net, slice_ksp, ksp, mask, mask1d, mask2d, orig, brain=False):
### fix scaling for ConvDecoder
scaling_factor,ni = get_scale_factor(net,
num_channels,
in_size,
ksp,)
slice_ksp1 = slice_ksp * scaling_factor
slice_ksp_torchtensor1 = ksp.type(dtype).to(devices[0]) * scaling_factor
masked_kspace, mask = transform.apply_mask(slice_ksp_torchtensor1, mask = mask.type(dtype).to(devices[0]))
unders_measurement = Variable(masked_kspace[None,:])
sampled_image2 = transform.ifft2(masked_kspace)
measurement = slice_ksp_torchtensor1.unsqueeze(0).type(dtype).to(devices[0])
lsimg = lsreconstruction(measurement)
out = []
for img in sampled_image2:
out += [ img[:,:,0].data.cpu().numpy() , img[:,:,1].data.cpu().numpy() ]
lsest = torch.tensor(np.array([out]))
num_iters =25000
LR = 0.008
import copy
if brain:
### fit with coil sensitivity map estimates
#########
zpad = masked_kspace.data.cpu().numpy()
zpad_complex = []
for i in range(zpad.shape[0]):
zpad_complex += [zpad[i,:,:,0]+1j*zpad[i,:,:,1]]
zpad_complex = np.array(zpad_complex)
masked_complex_kspace = zpad_complex * np.array(slice_ksp_torchtensor1.shape[0]*[list(mask2d)]) # shape: (15, 640, 368)
sens_maps = bart.bart(1, f'ecalib -d0 -m1', np.array([np.moveaxis(masked_complex_kspace,0,2)]))
sens_maps = np.moveaxis(sens_maps[0],2,0)
#print(sens_maps.shape,slice_ksp_torchtensor1.shape)
##########
scale_out,sover,pover,norm_ratio,mse_n, mse_t, parni, pert_net = fits( in_size = in_size,
num_channels=[num_channels]*(num_layers-1),
slice_ksp_torchtensor = slice_ksp_torchtensor1,
sens_maps = sens_maps,
num_iter=num_iters,
LR=LR,
mask = mask.type(dtype).to(devices[0]),
img_noisy_var=unders_measurement.to(devices[0]),
net=copy.deepcopy(net),
upsample_mode="free",
img_clean_var= transform.root_sum_of_squares(sampled_image2).permute(2,0,1)[None,:].type(dtype).to(devices[0]),#Variable(lsest1).type(dtype),
find_best=True,
devices=devices,
loss_type="MSE",
scale_out=1,
net_input = ni.data.cpu().type(dtype).to(devices[0]),
)
rec = data_consistency_sense(pert_net,parni,mask,mask1d,slice_ksp1,sens_maps,post_process=True)
else:
scale_out,sover,pover,par_mse_n, par_mse_t, parni, pert_net = fitr(copy.deepcopy(net),
unders_measurement.to(devices[0]),
Variable(lsest).type(dtype).to(devices[0]),
mask2d,
num_iter=num_iters,
LR=LR,
apply_f = forwardm,
lsimg = lsimg,
find_best=True,
net_input = ni.data.cpu().type(dtype).to(devices[0]),
OPTIMIZER = "adam"
)
rec = data_consistency(pert_net, parni, mask1d, slice_ksp_torchtensor1.data.cpu())
Ssim = ssim2_(orig,rec)
return rec, Ssim
# # Load pre-trained models
# ### trained on knee
# +
### Load a pre-trained varnet (trained on 4x accelerated multi-coil measurements of the FastMRI dataset)
class args():
def __init__(self):
self.num_cascades = 12
self.pools = 4
self.chans = 18
self.sens_pools = 4
self.sens_chans = 8
Args = args()
vmdl_knee = VariationalNetworkModel(Args)
checkpoint = torch.load('/data/trained_e2e/best.ckpt', map_location='cpu')
vmdl_knee.load_state_dict(checkpoint['state_dict'])
vmdl_knee.to(devices[0]);
for i,cas in enumerate(vmdl_knee.cascades):
vmdl_knee.cascades[i] = cas.to(devices[i//3])
# +
### Load a pre-trained unet (trained on 4x accelerated multi-coil measurements of the FastMRI dataset)
class args():
def __init__(self):
self.num_pools = 4
self.drop_prob = 0
self.num_chans = 32
args = args()
umdl_knee = UnetMRIModel(args)
checkpoint = torch.load('./UNET_trained/epoch=49.ckpt', map_location='cpu')
umdl_knee.load_state_dict(checkpoint['state_dict'])
umdl_knee.to(devices[0]);
# -
# ### trained on brain
# +
### Load a pre-trained varnet (trained on 4x accelerated multi-coil measurements of the FastMRI dataset)
class args():
def __init__(self):
self.num_cascades = 12
self.pools = 4
self.chans = 18
self.sens_pools = 4
self.sens_chans = 8
Args = args()
vmdl_brain = VariationalNetworkModel(Args)
checkpoint = torch.load('/root/convD_paper_works/brain/var_out/lightning_logs/version_0/checkpoints/epoch=42.ckpt', map_location='cpu')
vmdl_brain.load_state_dict(checkpoint['state_dict'])
vmdl_brain.to(devices[0]);
for i,cas in enumerate(vmdl_brain.cascades):
vmdl_brain.cascades[i] = cas.to(devices[i//3])
# +
### Load a pre-trained unet (trained on 4x accelerated multi-coil measurements of the FastMRI dataset)
class args():
def __init__(self):
self.num_pools = 4
self.drop_prob = 0
self.num_chans = 32
args = args()
umdl_brain = UnetMRIModel(args)
checkpoint = torch.load('/root/convD_paper_works/brain/output/100_percent/version_1/checkpoints/epoch=18.ckpt', map_location='cpu')
umdl_brain.load_state_dict(checkpoint['state_dict'])
umdl_brain.to(devices[0]);
# -
# # Sample test: Evaluate knee-trained (or knee-tuned) models on the loaded brain sample
# +
kresults = {'VarNet':{},'Unet':{},'l1':{},'ConvDecoder':{}}
f = 'file_brain_AXT1POST_207_2070067.h5'
### create a convdecoder
num_channels = 256 #256
num_layers = 8
strides = [1]*(num_layers-1)
in_size = [10,5]
kernel_size = 3
output_depth = slice_ksp_torchtensor.numpy().shape[0]*2
out_size =slice_ksp_torchtensor.numpy().shape[1:-1]
##### fit the network for reconstruction without perturbation #####
net = convdecoder(out_size,in_size,output_depth,
num_layers,strides,num_channels, act_fun = nn.ReLU(),
skips=False,need_sigmoid=False,bias=True, need_last = True,
kernel_size=kernel_size,upsample_mode="nearest").type(dtype).to(devices[0])
vrec, vs = varnet_reconstruction(vmdl_knee, slice_ksp_torchtensor, mask, orig)
urec, us = unet_reconstruction(umdl_knee, slice_ksp_torchtensor, mask, orig)
lrec, ls = l1_reconstruction(slice_ksp_torchtensor, mask, orig, num_iters=1000,lam=1e-12,LR=1e5)
crec, cs = convdecoder_reconstruction(net, slice_ksp, slice_ksp_torchtensor, mask, mask1d, mask2d, orig,brain=False)
kresults['VarNet'][f] = {}
kresults['VarNet'][f]['original'] = orig
kresults['VarNet'][f]['reconstruction'] = vrec
kresults['VarNet'][f]['score'] = vs
kresults['Unet'][f] = {}
kresults['Unet'][f]['original'] = orig
kresults['Unet'][f]['reconstruction'] = urec
kresults['Unet'][f]['score'] = us
kresults['l1'][f] = {}
kresults['l1'][f]['original'] = orig
kresults['l1'][f]['reconstruction'] = lrec
kresults['l1'][f]['score'] = ls
kresults['ConvDecoder'][f] = {}
kresults['ConvDecoder'][f]['original'] = orig
kresults['ConvDecoder'][f]['reconstruction'] = crec
kresults['ConvDecoder'][f]['score'] = cs
#with open('*****','wb') as fn:
# pickle.dump(results,fn)
# -
print('knee-trained (or -tuned) models lose performance on a sample brain image.')
plot_(kresults,f)
# We would like to also note that the artifacts for this specific sample are partly due to the mask change between knee to brain (random to equi-spaced). However, there exist other samples that even without a mask type change, we get these artifacts.
# # Sample test: Evaluate brain-trained (or brain-tuned) models on the loaded brain sample
# +
bresults = {'VarNet':{},'Unet':{},'l1':{},'ConvDecoder':{}}
f = 'file_brain_AXT1POST_207_2070067.h5'
### create a convdecoder
num_channels = 64
num_layers = 5
strides = [1]*(num_layers-1)
in_size = [10,5]
kernel_size = 3
output_depth = 2
out_size = slice_ksp.shape[1:]
net = convdecoder(out_size, in_size, output_depth,
num_layers, strides, num_channels, act_fun = nn.ReLU(),
skips=False, need_sigmoid=False, bias=True, need_last=True, need_lin_comb=False,
kernel_size=kernel_size,upsample_mode="nearest").type(dtype).to(devices[0])
vrec, vs = varnet_reconstruction(vmdl_brain, slice_ksp_torchtensor, mask, orig)
urec, us = unet_reconstruction(umdl_brain, slice_ksp_torchtensor, mask, orig)
lrec, ls = l1_reconstruction(slice_ksp_torchtensor, mask, orig, num_iters=200,lam=1e-11,LR=1e5)
crec, cs = convdecoder_reconstruction(net, slice_ksp, slice_ksp_torchtensor, mask, mask1d, mask2d, orig,brain=True)
bresults['VarNet'][f] = {}
bresults['VarNet'][f]['original'] = orig
bresults['VarNet'][f]['reconstruction'] = vrec
bresults['VarNet'][f]['score'] = vs
bresults['Unet'][f] = {}
bresults['Unet'][f]['original'] = orig
bresults['Unet'][f]['reconstruction'] = urec
bresults['Unet'][f]['score'] = us
bresults['l1'][f] = {}
bresults['l1'][f]['original'] = orig
bresults['l1'][f]['reconstruction'] = lrec
bresults['l1'][f]['score'] = ls
bresults['ConvDecoder'][f] = {}
bresults['ConvDecoder'][f]['original'] = orig
bresults['ConvDecoder'][f]['reconstruction'] = crec
bresults['ConvDecoder'][f]['score'] = cs
#with open('*****','wb') as fn:
# pickle.dump(results,fn)
# -
print('knee-trained (or -tuned) models lose performance on a sample brain image (compare to cell).')
plot_(bresults,f)
| distribution_shift_fastMRI_knee_to_brain.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# import seaborn as sns
# import metapack as mp
# import pandas as pd
# import numpy as np
# import matplotlib.pyplot as plt
# from IPython.display import display
# import sklearn
#
# %matplotlib inline
# sns.set_context('notebook')
# mp.jupyter.init()
#
# ! mp config
# -
pkg = mp.open_package('http://library.metatab.org/jhu.edu-covid19.csv')
pkg
confirmed_df = pkg.resource('confirmed').dataframe()
confirmed_df.head()
deaths_df = pkg.resource('deaths').dataframe()
deaths_df.head()
# +
fig, ax = plt.subplots(figsize=(15,8))
fig.suptitle('Number of Confirmed Cases By Country', fontsize=20)
t = confirmed_df
t = t[t.location.isin( ['Italy','US','Germany','France', 'United Kingdom','China'])]
display(t.head())
sns.lineplot(ax=ax, x='days_100',y='confirmed_log', data=t, hue='location', ci=None)
ax.set_xlabel('Days since first 100 cases', fontsize=18)
ax.set_ylabel('Log Number of Cases', fontsize=18)
# +
t = t[t.location.isin( ['Italy','US','Germany','France', 'United Kingdom', 'China'])]
fig, ax = plt.subplots(figsize=(12,8))
fig.suptitle('Growth Rate in Confirmed Cases\nComputed from trailing 5 days', fontsize=20)
sns.lineplot(ax=ax, x='days_100',y='rate_t5d', data=t, hue='location', ci=None)
ax.set_xlabel('Days Since 100 Cases', fontsize=18)
ax.set_ylabel('Rate of Growth', fontsize=18)
# +
confirmed_df['double_days'] = np.log(2)/np.log(1+confirmed_df.rate_t5d)
confirmed_df.sort_values('double_days', ascending=False)
t = confirmed_df[(confirmed_df.days_100 > 0) & (confirmed_df.days_100 < 30)
& (confirmed_df.double_days < 100) & (confirmed_df.double_days > 0)]
t = t[t.location.isin( ['Italy','Germany','France', 'United Kingdom'])]
fig, ax = plt.subplots(figsize=(12,8))
ax = sns.regplot(x=t.days_100, y=t.double_days, color="g", order=2, ax=ax)
fig.suptitle('Number of Days to Double Cases vs Days Since 100 Cases\n'
'For Italy, Germany, France and UK',
fontsize=20)
ax.set_xlabel('Days Since 100 Cases', fontsize=18)
ax.set_ylabel('Number of Days to Double', fontsize=18)
# +
from sklearn import linear_model
def plot_growth_reg_100(t, y_col, ax = None, subtitle=''):
x = t.days_100.values.reshape(len(t), 1)
y = t[y_col].values.reshape(len(t), 1)
regr = linear_model.LinearRegression()
regr.fit(x, y)
if not ax:
fig, ax = plt.subplots(figsize=(12,8))
fig.suptitle('Growth Rate in Confirmed Cases, Trailing 5 days' +("\n"+subtitle if subtitle else ''),
fontsize=20)
sns.scatterplot(ax=ax, x='days_100',y=y_col, data=t, hue='location', ci=None)
ax.plot(x, regr.predict(x), color='blue', linewidth=3)
ax.set_xlabel('Days Since 100 Cases', fontsize=18)
ax.set_ylabel('Rate of Growth', fontsize=18)
plt.gcf().text(.45,0, f"Source data : JHU CSSE, updated {pkg['Root'].find_first('root.modified').value} ", fontsize=14)
plt.show()
print('Coefficients:', regr.coef_, regr.intercept_)
print("Correlation:", t.days_100.corr(t.rate_t5d))
m = regr.coef_[0][0]
b = regr.intercept_[0]
print(f"Zero growth at {-b/m} days")
return fig, ax
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.confirmed>100)]
t = t[t.location.isin( ['Italy','Germany','France', 'United Kingdom'])]
plot_growth_reg_100(t,'rate_t5d')
# +
t = confirmed_df[(confirmed_df.days_10<30) & (confirmed_df.days_100>10)]
t = t[t.location.isin( ['Italy'])]
plot_growth_reg_100(t, 'rate_t5d', subtitle="Italy Only")
# +
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.days_100>0)]
t = t[t.location.isin([ 'US - California' ])]
t = t.dropna()
plot_growth_reg_100(t, 'rate_t5d', "California")
# +
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.days_100>0)]
t = t[t.location.isin([ 'China - Hubei' ])]
t = t.dropna()
plot_growth_reg_100(t, 'rate_t5d', "China")
# +
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.days_100>0)]
t = t[t.location.isin([ 'US - New York' ])]
t = t.dropna()
plot_growth_reg_100(t, 'rate_t5d', "New York")
# +
fig, ax = plt.subplots(figsize=(15,8))
fig.suptitle('Number of Confirmed Cases By US and US States', fontsize=20)
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.days_100>=5)]
t = t[t.country == 'US']
t = t[t.location.isin(['US','US - Washington', 'US - New York', 'US - California',
'US - Massachusetts', 'US - Colorado' ])]
sns.lineplot(ax=ax, x='days_100',y='confirmed', data=t, hue='location', palette='Set1', ci=None)
ax.set_xlabel('Days since first 100 cases', fontsize=18)
ax.set_ylabel('Log Number of Cases', fontsize=18)
ax.set_yscale('log')
rate_tab = t.groupby('location')[['location','rate_t5d']].mean().sort_values('rate_t5d', ascending=False)
display(rate_tab)
# +
t = confirmed_df[(confirmed_df.days_100<30) & (confirmed_df.days_100>=5)]
t = t[(t.country == 'US') & (~t.location.isin(['US', 'US - New York'])) ]
plot_growth_reg_100(t, 'rate_t5d', subtitle='US States, Excluding NY')
# +
fig, ax = plt.subplots(figsize=(15,8))
fig.suptitle('Number of Deaths By US and US States', fontsize=20)
t = death_df[(death_df.days_10<30) & (death_df.days_10>0)]
t = t[t.location.isin(['US','US - Washington', 'US - New York', 'US - California',
'US - Massachusetts' ])]
sns.lineplot(ax=ax, x='days_10',y='death', data=t, hue='location', palette='Set1', ci=None)
ax.set_xlabel('Days since first 10 cases', fontsize=18)
ax.set_ylabel('Log Number of Cases', fontsize=18)
ax.set_yscale('log')
rate_tab = t.groupby('location')[['location','rate_t5d']].mean().sort_values('rate_t5d', ascending=False)
display(rate_tab)
# +
def plot_growth_reg_10(t, y_col, subtitle=''):
t = t.dropna(subset=[y_col,'days_10'])
x = t.days_10.values.reshape(len(t), 1)
y = t[y_col].values.reshape(len(t), 1)
regr = linear_model.LinearRegression()
regr.fit(x, y)
fig, ax = plt.subplots(figsize=(12,8))
fig.suptitle('Growth Rate in Deaths\nComputed from trailing 5 days' +("\n"+subtitle if subtitle else ''),
fontsize=20)
sns.scatterplot(ax=ax, x='days_10',y=y_col, data=t, hue='location', ci=None)
ax.plot(x, regr.predict(x), color='blue', linewidth=3)
ax.set_xlabel('Days Since 10 Cases', fontsize=18)
ax.set_ylabel('Rate of Growth', fontsize=18)
plt.show()
print('Coefficients:', regr.coef_, regr.intercept_)
print("Correlation:", t.days_10.corr(t.rate_t5d))
m = regr.coef_[0][0]
b = regr.intercept_[0]
print(f"Zero growth at {-b/m} days")
death_df = pkg.resource('deaths').dataframe()
t = death_df[(death_df.days_10>2) & (death_df.days_10<30)]
t = t[t.location.isin( ['US'])]
plot_growth_reg_10(t,'rate_t5d')
# -
| jhu.edu-covid19/notebooks/ProcessTimeseriesCharts.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pymongo
# +
def execute_mongo(url):
myclient = pymongo.MongoClient(url)
db = myclient["sample_airbnb"]
collection = db["listingsAndReviews"]
# following 2 queries show simple filtering of data with OR condition
# match with logical operator and counting
# name contains beach or house type property or accomodates > 6
s = collection.aggregate([
{"$match" : {
"$or" : [
{"name": {"$regex":"Beach"} },
{"property_type":"House"}
]
}},
{ "$project": { "name": 1, "_id": 0} }
])
count = 0
for record in s:
print(record)
count = count + 1
print("#records: " + str(count))
print("----------")
# s = collection.aggregate([
# {
# "$match" : {
# "$or" : [
# {"property_type":"House"}
# ]
# },
# },
# { "$project": { "name": 1, "_id": 0} }
# ])
# count = 0
# for record in s:
# print(record)
# count = count + 1
# print("#records: " + str(count))
'''
# some more sample queries
# match with no logical operator - check for field
s = collection.aggregate([
{
"$match" : {
"name": {"$regex":"Beach"},
"property_type": {"$exists":True, "$eq": "House"},
"accommodates": {"$gt": 6 }
}
},
{
"$count": "number_of_records"
}
])
# find with logical operator, sort, selection , limit
s = collection.find( { "$or" : [ {"name":{"$regex":"Beach"} } , { "property_type":"House"} ] }, {"name":1,"_id":0} ).sort("name",-1).limit(10)
# text search
resp = collection.create_index([ ("name", "text")])
print("index creation response:", resp)
s = collection.find( { "$text" : { "$search" : "beach" } }, {"name":1,"accommodates":1,"_id":0}).sort("accommodates", -1).limit(10)
# count with group by with filtered rows
s = collection.aggregate([
{
"$match" : {
"$and" : [
{"name": {"$regex":"Beach"} },
{"accommodates": {"$gt": 6 }}
]
}
},
{
"$group" : {
"_id": {
"property_type": "$property_type"
},
"count": {"$sum":1}
}
},
{
"$sort" : {
"count" : -1
}
}
])
# sort search results by score
s = collection.aggregate([
{ "$match": { "$text": { "$search": "beach front" } } },
{ "$project": { "name": 1, "_id": 0, "score": { "$meta": "textScore" } } },
{ "$match": { "score": { "$gt": 1.0 } } },
{ "$sort": { "score": -1}},
{ "$limit": 10}
])
'''
# -
# take url from the mongoDB instance you create
if __name__ =='__main__':
url="mongodb+srv://admin:<EMAIL>/myFirstDatabase?retryWrites=true&w=majority"
execute_mongo(url)
url="mongodb+srv://admin:<EMAIL>@cluster0.mjug9.mongodb.net/myFirstDatabase?retryWrites=true&w=majority"
myclient = pymongo.MongoClient(url)
db = myclient["sample_airbnb"]
collection = db["listingsAndReviews"]
print(collection.count_documents({}))
s = collection.aggregate([
{"$match" : {
"$or" : [
{"name": {"$regex":"Beach"} },
{"property_type":"House"}
]
}},
{ "$project": { "name": 1, "_id": 0} }
])
count = 0
for record in s:
print(record)
count = count + 1
print("#records: " + str(count))
| notebooks/Untitled.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/hasnat2379/578-Data/blob/master/Data_578%20Kiavash_Hasnat_Douglas.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="9gUTkUsm_nhN"
# *****************************************
# * Course: NAME 578 *
# * Assignment: Data Analysis Assignment *
# * Date: December 18, 2020 *
# * *
# * Name ID# *
# * ------------------- -------- *
# * <NAME> 90774803 *
# * <NAME> 54688346 *
# * <NAME> 52216363 *
# *****************************************
# + id="wB4M8sxmLAtn"
# IMPORT AND FILTER DATA
# ----------------------
import pandas as pd
import numpy as np
# + id="Wg1-rFN3M_-D"
pd0 = 'out_0.csv'
pd1 = 'out_1.csv'
pd2 = 'out_2.csv'
pd3 = 'out_3.csv'
pd4 = 'out_4.csv'
pd5 = 'out_5.csv'
pd6 = 'out_6.csv'
# + id="gpDIGRdvSrd1"
import os
import glob
import pandas as pd
os = ("\Desktop\Data Analysis\Data")
# + id="Twifiva4T6Op"
extension = 'csv'
all_filenames = [i for i in glob.glob('*.{}'.format(extension))]
# + id="RaABY0gvUAtH" colab={"base_uri": "https://localhost:8080/"} outputId="4492f65f-5c80-4d9b-dc23-57684a0416f2"
combined_csv = pd.concat([pd.read_csv(f) for f in all_filenames ])
combined_csv.to_csv( "combined_csv.csv", index=False, encoding='utf-8-sig')
# + [markdown] id="WSzB2JLX9PO-"
#
# + colab={"base_uri": "https://localhost:8080/", "height": 596} id="FmCm_OEjUaV1" outputId="e1a7301b-a853-45dc-c5c5-b4012bc2d492"
import pandas
df = pandas.read_csv('out_com.csv')
display(df)
# + colab={"base_uri": "https://localhost:8080/"} id="JVIb3-FouhTt" outputId="e14de84d-8fae-41fc-ee7b-c7d98026861f"
import pandas
df = pandas.read_csv('out_com.csv')
df = df.dropna() # Drop NaN
df = df[
# Conditions
(df['Speed 1 (rpm)'] > 30) &
(df['Speed 1 (rpm)'] < 140)
]
# + colab={"base_uri": "https://localhost:8080/", "height": 626} id="7XG68XXrQXWA" outputId="c4f3050b-80c6-45b7-8b95-58dbae23a9d1"
display(df)
# + colab={"base_uri": "https://localhost:8080/", "height": 411} id="iNP0ZWVksyuK" outputId="341a0252-3f92-421e-cc4c-f119f5ebf77a"
display(df[['Datetime','Eng1 Tot1 Mass (kg)', 'Power1 (kW)']])
# + colab={"base_uri": "https://localhost:8080/", "height": 329} id="DEEoayh0-ama" outputId="a6c730e3-b697-41e4-c919-39ad534cea9a"
# VISUALIZE DATA
# --------------
# Import librairies
import matplotlib
import matplotlib.pyplot as plt
# Show stats for data
df.describe()
# + id="H4Dv2b_--4P2" colab={"base_uri": "https://localhost:8080/", "height": 409} outputId="1b1e6256-fda5-40de-fdd8-b8a5f6f5e73b"
# Plot histogram for torque
plt.figure(figsize=(10,6)) # Specify the size
plt.hist(df['Torque 1 (kNm)'], bins=25, facecolor=(0.1, 0.3, 0.5)) # Plot
plt.title('Torque 1 Histogram', fontsize=14)
plt.xlabel('Torque 1 [kNm]', fontsize=14)
plt.ylabel('Relative Frequency', fontsize=14)
plt.grid()
plt.savefig('torque-hist.png',dpi=150) # Saving options
plt.show()
# + id="jRaX5f5M1bgV" colab={"base_uri": "https://localhost:8080/", "height": 409} outputId="f054ed63-78ee-43bd-9bf3-4a1caac592b9"
# Plot histogram for consupmtion rate
plt.figure(figsize=(10,6)) # Specify the size
plt.hist(df['Consump2 Rate (kg/h)'], bins=25, facecolor=(0.1, 0.3, 0.5)) # Plot
plt.xlim(0, 300)
plt.title('Consumption Rate 2 Histogram', fontsize=14)
plt.xlabel('Consumption Rate 2 [kg/h]', fontsize=14)
plt.ylabel('Relative Frequency', fontsize=14)
plt.grid()
plt.savefig('consump-hist.png',dpi=150) # Saving options
plt.show()
# + id="KeRdbLYB92c_" colab={"base_uri": "https://localhost:8080/", "height": 409} outputId="63841999-f6ee-4fe9-81f6-60d25a6a47e0"
# Scatter plot speed versus torque
plt.figure(figsize=(10,6)) # Specify the size
plt.scatter(df['Speed 1 (rpm)'], df['Torque 1 (kNm)'], color=(0.1, 0.3, 0.5))
plt.title('Torque 1 versus Speed', fontsize=14)
plt.xlabel('Speed 1 [rpm]', fontsize=14)
plt.ylabel('Torque 1 [kNm]', fontsize=14)
plt.grid()
plt.savefig('torque-vs-speed.png',dpi=150) # Saving options
plt.show()
# + id="dohaz5ow_WT8" colab={"base_uri": "https://localhost:8080/", "height": 409} outputId="6e58c3f4-19a8-4cfb-e13b-279759f5fd4b"
# Scatter plot power versus speed
plt.figure(figsize=(10,6)) # Specify the size
plt.scatter(df['Speed 1 (rpm)'], df['SpeedlogSpeed (kn)'], color=(0.1, 0.3, 0.5))
plt.title('RPM versus KNOT ', fontsize=14)
plt.xlabel('Speed 1 [rpm]', fontsize=14)
plt.ylabel('Log Speed [Kn]', fontsize=14)
plt.grid()
plt.savefig('rpm-vs-speed.png',dpi=150) # Saving options
plt.show()
# + id="uAAj6OOH4HV4" colab={"base_uri": "https://localhost:8080/", "height": 409} outputId="156b407d-0f2c-4198-fad2-68e9508dcb2c"
# Scatter plot power versus ship speed
plt.figure(figsize=(10,6)) # Specify the size
plt.scatter(df['SpeedlogSpeed (kn)'], df['Consump2 Rate (kg/h)'], color=(0.1, 0.3, 0.5))
plt.ylim(0, 400)
plt.title('Power versus Speed', fontsize=14)
plt.xlabel('SpeedlogSpeed [kn]', fontsize=14)
plt.ylabel('Consumption Rate 2 [kg/h]', fontsize=14)
plt.grid()
plt.savefig('consump-vs-speed.png',dpi=150) # Saving options
plt.show()
# + id="0q8H_YUf_0iO"
# EXPORT DATA
# -----------
# Import libraries
import glob as glob
# + id="oJrH_xYG_4oP"
# Export to a csv file
compress_opts = dict(method='zip', archive_name = 'out-csv.csv')
df.to_csv('out-csv.zip', index = False, compression = compress_opts)
# + id="xjkG9bfL_5Ys"
# Export to an excel file
df.to_excel('out-excel.xlsx')
# + id="moWGQ54_DY3n" colab={"base_uri": "https://localhost:8080/"} outputId="d385347a-9775-480b-cbe9-442e34fcb6ba"
# MACHINE LEARNING
# ----------------
# Features are the colummns used to train the model (inputs)
# Label is what we are trying to predict (output)
# Create a list for all features
features = list(df)
features
# + id="An7t8mT8Da_b" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="af9141d9-355f-4d5e-9a1d-e9a1e7927403"
# Set label
label = features[8]
label
# + id="fRfLl9sMDepo" colab={"base_uri": "https://localhost:8080/"} outputId="14fb4367-abf7-44b4-d383-07d90a66912e"
# Create list for test features
test_features = [features[6],
features[7],
features[9]]
test_features
# + id="TYPB02dHDhOh" colab={"base_uri": "https://localhost:8080/", "height": 201} outputId="f056fa4a-a276-4b2b-9b64-518737f424eb"
# Create new dataframe for training
df_train = pd.DataFrame()
for n_ in test_features:
df_train[n_] = df[n_]
df_train.head()
# + id="f3z45_9lDkrx"
# Create arrays
X = np.array(df_train)
y = np.array(df[label])
# + id="OBoWy_dIDm75"
# Import librairies
import sklearn as sk
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# + id="QrWISr8gDp9L"
# Make a train/test split
# Don't use all the data for training the model
# Divide it into a train and test set (75 / 25 split)
# Split is created randomly - removed data is not seen by the model for training
# The removed data is used to test the model after being trained
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, test_size=0.25, random_state=42)
train_dataset = df_train.sample(frac=0.75,random_state=42)
test_dataset = df_train.drop(train_dataset.index)
# + id="wmPwnI8FDrpK" colab={"base_uri": "https://localhost:8080/"} outputId="ff34d6e8-2728-4b06-ec43-8ff4016d1648"
# Linear regression
m_linear = sk.linear_model.LinearRegression()
m_linear.fit(X_train, y_train.reshape(-1,))
R2_train = r2_score(m_linear.predict(X_test), y_test)
print('Linear R2 train', R2_train)
# + id="h1JQz4ZCDtb4" colab={"base_uri": "https://localhost:8080/", "height": 404} outputId="23409344-a850-41ee-ec65-7072e70d372f"
# Scatter plot
plt.figure(figsize=(10,6)) # Specify the size
plt.scatter(y, m_linear.predict(X))
plt.title('Power1')
plt.xlabel('True Value [kW]')
plt.ylabel('Predicted Value [kW]')
plt.grid()
plt.savefig('ml.png',dpi=150) # Saving options
plt.show()
| Data_578 Kiavash_Hasnat_Douglas.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="ur8xi4C7S06n" colab_type="code" colab={}
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="JAPoU8Sm5E6e" colab_type="text"
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/ai-platform-samples/blob/master/notebooks/templates/ai_platform_notebooks_template_hybrid.ipynb"">
# <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
# </a>
# </td>
# <td>
# <a href="https://github.com/GoogleCloudPlatform/ai-platform-samples/blob/master/notebooks/templates/ai_platform_notebooks_template_hybrid.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
# View on GitHub
# </a>
# </td>
# </table>
# + [markdown] id="tvgnzT1CKxrO" colab_type="text"
# ## Overview
# + [markdown] id="a2VgGzVIlLo2" colab_type="text"
# ### Objective
#
# Estimate how much an existing customer will spend in the future based on their historical orders to find similar new customers using lookalike features of advertising tools.
#
# In this tutorial, you will:
# - Define how far in the future you want to predict the monetary value of your customers (ex: 3 months)
# - Use a moving session concept to aggregate multiple inputs and targets per customer (For more details, see the *Create inputs and targets* section of this tutorial).
# - Use primarly inputs such as Recency, Frequency and Monetary which are common values to use in an LTV context, especially in statistical model due to their distribution patterns.
# - Accelerate model development by using AutoML from within BigQuery ML.
# - Predict the monetary value of all existing customers for a predefined period of time in the future.
# - Use first-party data to extract the most valuable customers email in order to run lookalike campaigns using the [Google Ads API][ads_api]. You can extend the concept to do the same using [Facebook API][fb_api].
#
# [ads_api]:https://developers.google.com/adwords/api/docs/samples/python/remarketing#create-and-populate-a-user-list
# [fb_api]:https://www.facebook.com/business/help/341425252616329?id=2469097953376494
#
#
# + [markdown] id="lAeYu9bBlLaZ" colab_type="text"
# ### Sales dataset
# Sales data can be of different forms but generally look like a list of transactions where each record contains at a minimum the following:
# - a customer reference
# - a transaction date
# - a transaction reference
# - a monetary value
#
# Each record usually represents one of the following:
# - An entire order which contains aggregated values across products for that order. You can find the total order value in the record.
# - A part of a transaction which contains a unique product, some of its characteristics including SKU and unit price and the quantity ordered.
#
# This tutorial uses the latter.
#
# You can run this tutorial with your own dataset. The dataset that you provide must meet the following requirements:
# 1. Each row represents a transaction related to a product item and linked to a transaction, a date and a customer. A row can be either a transaction (quantity is > 0) or a return (quantity is < 0)
# 1. Columns must include the following:
#
# | Field name | Type | Description |
# | :-|:-|:-|
# | customer_id | STRING | First party identifier of the customer. |
# | order_id | STRING | First party identitfier of the order. |
# | order_date | DATE | Date of the order. |
# | product_sku | STRING | First party identitifer of the product. |
# | qty | INTEGER | Quantity of the product either ordered or returned. |
# | unit_price | FLOAT | Unit price of the product. |
# + [markdown] id="__KXS_qcyNRK" colab_type="text"
# ### Customer dataset
# Customer data often resides in a Customer Relationship Management (CRM).
#
# This first party data is key for companies that want to provide a certain level of customer service.
#
# This tutorial only uses two columns of the customer dataset:
# - customer_id to join with the sales data
# - email to create a marketing list.
#
# The public dataset contains other fields that are not relevant for this tutorial and your data might have other fields. This tutorial focuses on an activation based on email addresses.
# + [markdown] id="LdyWWnIElL0C" colab_type="text"
# ### Costs
#
# This tutorial uses billable components of Google Cloud Platform (GCP):
#
# * BigQuery
# * BigQuery ML
# * Cloud Storage
#
# To learn more about pricing:
# - Read [BigQuery pricing](https://cloud.google.com/bigquery/docs/pricing)
# - Read [BigQuery ML pricing](https://cloud.google.com/bigquery-ml/pricing)
# - Read [Cloud Storage pricing](https://cloud.google.com/storage/pricing)
# - Use the [Pricing Calculator](https://cloud.google.com/products/calculator/)
# to generate a cost estimate based on your projected usage.
# + [markdown] id="UDn9SREOlXaN" colab_type="text"
# ### Terminology
# - **'Input' transactions**: The set of transactions that the training task uses to create inputs values for the model.
# - **'Target' transactions**: The set of transactions that the training task uses to create the target value to predict. The target value is an aggregated monetary value per customer for a defined timeline.
# - **Threshold date**: Date that separates 'Input' transactions from 'Target' transactions per customer.
# + [markdown] id="fmvu_N0ovY8N" colab_type="text"
# ## Setup
# This step sets up packages, variables, authentication, APIs clients and resources for Google Cloud and Adwords.
# + [markdown] id="i7EUnXsZhAGF" colab_type="text"
# ### Install packages and dependencies
# Installs libraries, packages and dependencies to run this tutorial
# + id="wyy5Lbnzg5fi" colab_type="code" colab={"base_uri": "https://localhost:8080/"} outputId="f5fa8b23-a707-4480-a170-061eaf260c01"
# Install libraries.
# The magic cells insures that those libraries can be part of a custom container
# if moving the code somewhere else.
# %pip install -q googleads
# %pip install -q -U kfp matplotlib Faker --user
# Automatically restart kernel after installs
# import IPython
# app = IPython.Application.instance()
# app.kernel.do_shutdown(True)
# + [markdown] id="vmSgVQ9x4aO0" colab_type="text"
# ### Import packages
# + id="ouL1aMrvVgnL" colab_type="code" colab={"base_uri": "https://localhost:8080/"} outputId="e9eac7e7-a422-4353-d06a-d8a69ec013a7"
# Import
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import os, json, random
import hashlib, uuid
import time, calendar, math
import pandas as pd, numpy as np
import matplotlib.pyplot as plt, seaborn as sns
from datetime import datetime
from google.cloud import bigquery
from googleads import adwords
# + [markdown] id="BF1j6f9HApxa" colab_type="text"
# ### Set up your GCP project
#
# **The following steps are required, regardless of your notebook environment.**
#
# 1. [Select or create a GCP project.](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
#
# 2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
#
# 3. [Enable the AI Platform APIs and Compute Engine APIs.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component)
#
# 4. If you are running this notebook locally, you will need to install [Google Cloud SDK](https://cloud.google.com/sdk).
#
# 5. Enter your project ID in the cell below. Then run the cell to make sure the
# Cloud SDK uses the right project for all the commands in this notebook.
# + id="oM1iC_MfAts1" colab_type="code" colab={"base_uri": "https://localhost:8080/"} outputId="fd734b46-80c3-4149-e48d-1b2d26ad0d6b"
PROJECT_ID = "[YOUR-PROJECT]" #@param {type:"string"}
REGION = "US"
# ! gcloud config set project $PROJECT_ID
# + [markdown] id="dr--iN2kAylZ" colab_type="text"
# ### Authenticate your GCP account
# If you are using AI Platform Notebooks, you are already authenticated so there is no need to run this step.
# + id="PyQmSRbKA8r-" colab_type="code" colab={}
import sys
if 'google.colab' in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# + [markdown] id="T4MuyozBoPv9" colab_type="text"
# ### Create a working dataset
# This tutorial mostly uses BigQuery magic cells where the --params field does not support variables for datasets, tables and column names.
#
# This steps hardcode the dataset where all the steps of this tutorial happens.
# + id="sGRa9QxXoZMO" colab_type="code" colab={}
# ! bq show $PROJECT_ID:ltv_ecommerce || bq mk $PROJECT_ID:ltv_ecommerce
# + [markdown] id="9i6ZRZgqCEPY" colab_type="text"
# ### Load example tables
# + id="pjc30TarCHSp" colab_type="code" colab={}
# Loads CRM data
# !bq load \
# --project_id $PROJECT_ID \
# --skip_leading_rows 1 \
# --max_bad_records 100000 \
# --replace \
# --field_delimiter "," \
# --autodetect \
# ltv_ecommerce.00_crm \
# gs://solutions-public-assets/analytics-componentized-patterns/ltv/crm.csv
# + id="Fe4GT-fWEcUt" colab_type="code" colab={}
# Loads Sales data
# !bq load \
# --project_id $PROJECT_ID \
# --skip_leading_rows 1 \
# --max_bad_records 100000 \
# --replace \
# --field_delimiter "," \
# --autodetect \
# ltv_ecommerce.10_orders \
# gs://solutions-public-assets/analytics-componentized-patterns/ltv/sales_*
# + [markdown] id="EVNkkGV8jUN6" colab_type="text"
# ### Create clients
# + id="amZzWHkjjWTi" colab_type="code" colab={}
# BigQuery client
bq_client = bigquery.Client(project=PROJECT_ID)
# + [markdown] id="TJB0PYUS7sYw" colab_type="text"
# ## [Optional] Match your dataset to template
# If you use the example data, you can skip this step.
#
# This tutorial assumes that you have a dump of your sales data already available in BigQuery located at `[YOUR_PROJECT].[YOUR_DATASET].[YOUR_SOURCE_TABLE]`
#
# You are free to adapt the SQL query in the next cell to a SQL statement that transforms your data according to the template.
# + id="NK_wCQt78JjO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 32} outputId="b1f6d49d-3d26-46e0-d753-f5b1e55f1a65"
# %%bigquery --params $MATCH_FIELDS --project $PROJECT_ID
CREATE OR REPLACE TABLE `ltv_ecommerce.10_orders` AS (
SELECT
CAST(customer_id AS STRING) AS customer_id,
order_id AS order_id,
transaction_date AS transaction_date,
product_sku AS product_sku,
qty AS qty,
unit_price AS unit_price
FROM
`[YOUR_PROJECT].[YOUR_DATASET].[YOUR_SOURCE_TABLE]`
);
# + [markdown] id="T9q6jKCM4-v8" colab_type="text"
# ## Analyze dataset
#
# **Some charts might use a log scale.**
#
#
# + [markdown] id="LEchqKz1HiOZ" colab_type="text"
# #### Quantity
# This sections shows how to use the BigQuery [ML BUCKETIZE][bucketize] preprocessing function to create buckets of data for quantity and display a log scaled distribution of the `qty` field.
#
# [bucketize]:https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-preprocessing-functions#bucketize
# + id="keis4kuj5A71" colab_type="code" colab={}
# %%bigquery df_histo_qty --project $PROJECT_ID
WITH
min_max AS (
SELECT
MIN(qty) min_qty,
MAX(qty) max_qty,
CEIL((MAX(qty) - MIN(qty)) / 100) step
FROM
`ltv_ecommerce.10_orders`
)
SELECT
COUNT(1) c,
bucket_same_size AS bucket
FROM (
SELECT
-- Creates (1000-100)/100 + 1 buckets of data.
ML.BUCKETIZE(qty, GENERATE_ARRAY(min_qty, max_qty, step)) AS bucket_same_size,
-- Creates custom ranges.
ML.BUCKETIZE(qty, [-1, -1, -2, -3, -4, -5, 0, 1, 2, 3, 4, 5]) AS bucket_specific,
FROM
`ltv_ecommerce.10_orders`, min_max )
# WHERE bucket != "bin_1" and bucket != "bin_2"
GROUP BY
bucket
-- Ohterwise, orders bin_10 before bin_2
ORDER BY CAST(SPLIT(bucket, "_")[OFFSET(1)] AS INT64)
# + id="O6JqHipXDPto" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 307} outputId="33d8e932-c3f9-4b1f-d3df-fcf8355bcb42"
# Uses a log scale for bucket_same_size.
# Can remove the log scale when using bucket_specific.
plt.figure(figsize=(12,5))
plt.title('Log scaled distribution for qty')
hqty = sns.barplot( x='bucket', y='c', data=df_histo_qty)
hqty.set_yscale("log")
# + [markdown] id="5v8wFktnHlA_" colab_type="text"
# #### Unit price
# + id="OFYqRpzLHnuE" colab_type="code" colab={}
# %%bigquery df_histo_unit_price --project $PROJECT_ID
WITH
min_max AS (
SELECT
MIN(unit_price) min_unit_price,
MAX(unit_price) max_unit_price,
CEIL((MAX(unit_price) - MIN(unit_price)) / 10) step
FROM
`ltv_ecommerce.10_orders`
)
SELECT
COUNT(1) c,
bucket_same_size AS bucket
FROM (
SELECT
-- Creates (1000-100)/100 + 1 buckets of data.
ML.BUCKETIZE(unit_price, GENERATE_ARRAY(min_unit_price, max_unit_price, step)) AS bucket_same_size,
-- Creates custom ranges.
ML.BUCKETIZE(unit_price, [10, 20, 30, 40, 50, 100, 200, 300, 400, 500, 1000]) AS bucket_specific,
FROM
`ltv_ecommerce.10_orders`, min_max )
# WHERE bucket != "bin_1" and bucket != "bin_2"
GROUP BY
bucket
-- Ohterwise, orders bin_10 before bin_2
ORDER BY CAST(SPLIT(bucket, "_")[OFFSET(1)] AS INT64)
# + id="02bF2qA7HuiU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 324} outputId="053433c5-b4f9-4ee9-b4f4-d1793d729900"
# Uses a log scale for bucket_same_size.
# Can remove the log scale when using bucket_specific.
plt.figure(figsize=(12,5))
q = sns.barplot( x='bucket', y='c', data=df_histo_unit_price)
q.set_yscale("log")
plt.title('Log scaled distribution for unit_price')
# + [markdown] id="K6Ih3v9D6ZGE" colab_type="text"
# ## Set parameters for LTV
# Some parameters useful to run some of the queries in this tutorial:
#
# 1. **WINDOW_STEP**: How many days between threshold dates.
# 1. **WINDOW_STEP_INITIAL**: How many days between the first order and the first threshold date. A threshold date is when BigQuery computes inputs and targets.
# 1. **WINDOW_LENGTH**: How many days back to use for input transactions. The default value is 0 which means that this tutorial takes all transactions before the threshold date.
# 1. **LENGTH_FUTURE**: How far in the future to predict the monetary value. At every threshold date, BigQuery calculate the target value for all orders that happen LENGTH_FUTURE after the threshold date.
# 1. **MAX_STDV_MONETARY**: Standard deviation of the monetary value per customer. Removes orders per customer that have order values with a greater standard deviation.
# 1. **MAX_STDV_QTY**: Standard deviation of the quantity of products per customer. Removes orders per customer that have product quantity with a greater standard deviation.
# 1. **TOP_LTV_RATIO**: Percentage of top customers that you want to keep for your lookalike activation.
#
# You can change those parameters to see how they impact the model especially the parameters related to the window. There is no obvious rule to set values as they depend on how data looks.
#
# For example:
# - If your customers buy multiple times a week, you could try to predict monetary value on a weekly basis.
# - If you have a lot of data, you can create more windows by decreasing their sizes and possibly the number of days between threshold dates.
#
# After multiple trials, this tutorial chose values that provides a decent result for the example dataset.
# + id="wZGi-Sm5suzM" colab_type="code" colab={"base_uri": "https://localhost:8080/"} outputId="00034056-2fca-4c73-a40d-1a050994810b"
LTV_PARAMS = {
'WINDOW_LENGTH': 0,
'WINDOW_STEP': 30,
'WINDOW_STEP_INITIAL': 90,
'LENGTH_FUTURE': 30,
'MAX_STDV_MONETARY': 500,
'MAX_STDV_QTY': 100,
'TOP_LTV_RATIO': 0.2
}
LTV_PARAMS
# + [markdown] id="mhOH4XM52otf" colab_type="text"
# ## Aggregate per day per customer
# This query aggregates all orders per day per customer. This is useful if:
# - Your database has multiple records for one order, for example if each record represent a product in a transaction, which is the case in this tutorial.
# - Customers bought multiple times during one day. This guide is based on LTV per day so no need to keep hourly records (unless you decided to use that data as a feature).
#
# This query also
# 1. Creates inputs related to returns.
# 1. Removes orders with outliers per customer. This means that high spending customers remain in the dataset but orders that seems unusual for a unique customers are filtered out.
# + id="r0sb0KFeik5M" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="c085dc6d-5dba-4641-cea9-d5980ccbc497"
# %%bigquery --params $LTV_PARAMS --project $PROJECT_ID
DECLARE MAX_STDV_MONETARY INT64 DEFAULT @MAX_STDV_MONETARY;
DECLARE MAX_STDV_QTY INT64 DEFAULT @MAX_STDV_QTY;
CREATE OR REPLACE TABLE `ltv_ecommerce.20_aggred` AS
SELECT
customer_id,
order_day,
ROUND(day_value_after_returns, 2) AS value,
day_qty_after_returns as qty_articles,
day_num_returns AS num_returns,
CEIL(avg_time_to_return) AS time_to_return
FROM (
SELECT
customer_id,
order_day,
SUM(order_value_after_returns) AS day_value_after_returns,
STDDEV(SUM(order_value_after_returns)) OVER(PARTITION BY customer_id ORDER BY SUM(order_value_after_returns)) AS stdv_value,
SUM(order_qty_after_returns) AS day_qty_after_returns,
STDDEV(SUM(order_qty_after_returns)) OVER(PARTITION BY customer_id ORDER BY SUM(order_qty_after_returns)) AS stdv_qty,
CASE
WHEN MIN(order_min_qty) < 0 THEN count(1)
ELSE 0
END AS day_num_returns,
CASE
WHEN MIN(order_min_qty) < 0 THEN AVG(time_to_return)
ELSE NULL
END AS avg_time_to_return
FROM (
SELECT
customer_id,
order_id,
-- Gives the order date vs return(s) dates.
MIN(transaction_date) AS order_day,
MAX(transaction_date) AS return_final_day,
DATE_DIFF(MAX(transaction_date), MIN(transaction_date), DAY) AS time_to_return,
-- Aggregates all products in the order
-- and all products returned later.
SUM(qty * unit_price) AS order_value_after_returns,
SUM(qty) AS order_qty_after_returns,
-- If negative, order has qty return(s).
MIN(qty) order_min_qty
FROM
`ltv_ecommerce.10_orders`
GROUP BY
customer_id,
order_id)
GROUP BY
customer_id,
order_day)
WHERE
-- [Optional] Remove dates with outliers per a customer.
(stdv_value < MAX_STDV_MONETARY
OR stdv_value IS NULL) AND
(stdv_qty < MAX_STDV_QTY
OR stdv_qty IS NULL);
SELECT * FROM `ltv_ecommerce.20_aggred` LIMIT 5;
# + [markdown] id="bq0WFrHqGgjE" colab_type="text"
# ## Check distributions
# This tutorial does minimum data cleansing and focuses mostly on transforming a list of transactions into workable inputs for the model.
#
# This section checks that data is generally usable.
# + [markdown] id="_cYheRxJIYjs" colab_type="text"
# ### Per date
# + id="ulyzgY2RGg0N" colab_type="code" colab={}
# %%bigquery df_dist_dates --project $PROJECT_ID
SELECT count(1) c, SUBSTR(CAST(order_day AS STRING), 0, 7) as yyyy_mm
FROM `ltv_ecommerce.20_aggred`
WHERE qty_articles > 0
GROUP BY yyyy_mm
ORDER BY yyyy_mm
# + id="sgSVTR0pIxpV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 351} outputId="8d014db8-e565-4d15-ce16-3b7b626260ba"
plt.figure(figsize=(12,5))
sns.barplot( x='yyyy_mm', y='c', data=df_dist_dates)
# + [markdown] id="_85oPxL4zqQF" colab_type="text"
# Orders are quite well distributed across the year despite a lower number in the early days of the dataset. You can keep this in mind when choosing a value for `WINDOW_STEP_INITIAL`.
# + [markdown] id="opxsPUhZJQtY" colab_type="text"
# ### Per customer
# + id="giPBoy4dJQ4O" colab_type="code" colab={}
# %%bigquery df_dist_customers --params $LTV_PARAMS --project $PROJECT_ID
SELECT customer_id, count(1) c
FROM `ltv_ecommerce.20_aggred`
GROUP BY customer_id
# + id="6jnDQRtiJQ7r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 306} outputId="3ed301a2-ff33-42ea-e3ce-c228a3626d72"
plt.figure(figsize=(12,4))
sns.distplot(df_dist_customers['c'], hist_kws=dict(ec="k"), kde=False)
# + [markdown] id="hzvPvPvl0WHD" colab_type="text"
# The number of transactions per customer is distributed across a few discrete values with no clear outliers.
# + [markdown] id="zEkWNb1Z11GE" colab_type="text"
# ### Per quantity
# This section looks at the general distribution of the number of articles per orders and check if there are some outliers.
# + id="7Ak9z1us2Da5" colab_type="code" colab={}
# %%bigquery df_dist_qty --params $LTV_PARAMS --project $PROJECT_ID
SELECT qty_articles, count(1) c
FROM `ltv_ecommerce.20_aggred`
GROUP BY qty_articles
# + id="MlF-3blV2M_N" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 309} outputId="e7a62f01-2b5e-4260-fc31-dacad3cabaed"
plt.figure(figsize=(12,4))
sns.distplot(df_dist_qty['qty_articles'], hist_kws=dict(ec="k"), kde=False)
# + [markdown] id="dK-0HMq63XZD" colab_type="text"
# A few customers seems to have quite large quantities in their orders but the distribution is generally healthy.
#
# They could be weird behavior for the same customers but the Standard Deviation filters should minimize the risk.
#
# Analyzing those few outliers can be part of additional data preparation work that can help improve your model.
# + [markdown] id="1pFm1_oKJkVZ" colab_type="text"
# ### Per value
# This section shows that there are quite a few outliers 'outliers' that spend way more than others. We want to ignore them when creating the RFM values.
# + id="xnMBqS7uhooL" colab_type="code" colab={}
# %%bigquery df_dist_values --params $LTV_PARAMS --project $PROJECT_ID
SELECT value
FROM `ltv_ecommerce.20_aggred`
# + id="6rO6XsZkd-bh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 296} outputId="18a93e73-ee34-4cec-d1e6-bdb38c8ed2ce"
axv = sns.violinplot(x=df_dist_values["value"])
axv.set_xlim(-200, 3500)
# + [markdown] id="2uY8l0Os51xW" colab_type="text"
# The distribution shows a few outliers that you could investigate to improve the base model that you create in this tutorial.
# + [markdown] id="UxrNfMNMUifK" colab_type="text"
# ## Create inputs and targets for the ML model
# The goal of this tutorial is to predict *How much each customer is going to spend in the next N days knowing their transactions history.*
#
# Because all customers have different buying behavior over a specific period of time, this tutorial create multiple records per customer by:
#
# 1. Moving a threshold date by `WINDOW_STEP` over the dataset to create input and targets.
# 1. Aggregates input data per customer using transactions between `WINDOW_START` and `THRESHOLD_DATE` threshold date.
# 1. Aggregates the monetary value of the target transactions whose dates are between `THRESHOLD_DATE` and `THRESHOLD_DATE + LENGTH_FUTURE`.
#
# Based on the size of your dataset and what you are trying to predict, you can update those values as needed in the *Set parameters for LTV* section.
#
# This tutorial uses all historical data to predict the monetary value of its customers in the next 30 (`LENGTH_FUTURE`) days with a dataset that contains inputs/target value calculated every 30 days (`WINDOW_STEP`).
# + [markdown] id="nFjSNi_lFgPc" colab_type="text"
# ### Query
# + id="2tY96qAzgXjh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 32} outputId="5d0da276-abf1-47d0-ae0e-48ea4c58d22f"
# %%bigquery --params $LTV_PARAMS --project $PROJECT_ID
-- Lenght are number of days
--
-- Date of the first order in the dataset.
DECLARE MIN_DATE DATE;
-- Date of the final order in the dataset.
DECLARE MAX_DATE DATE;
-- Date that separates inputs orders from target transactions.
DECLARE THRESHOLD_DATE DATE;
-- How many days back for inputs transactions. 0 means from the start.
DECLARE WINDOW_LENGTH INT64 DEFAULT @WINDOW_LENGTH;
-- Date at which an input transactions window starts.
DECLARE WINDOW_START DATE;
-- How many days between thresholds.
DECLARE WINDOW_STEP INT64 DEFAULT @WINDOW_STEP;
-- How many days for the first window.
DECLARE WINDOW_STEP_INITIAL INT64 DEFAULT @WINDOW_STEP_INITIAL;
-- Index of the window being run.
DECLARE STEP INT64 DEFAULT 1;
-- How many days to predict for.
DECLARE LENGTH_FUTURE INT64 DEFAULT @LENGTH_FUTURE;
SET (MIN_DATE, MAX_DATE) = (
SELECT AS STRUCT
MIN(order_day) AS min_days,
MAX(order_day) AS max_days
FROM
`ltv_ecommerce.20_aggred`
);
SET THRESHOLD_DATE = MIN_DATE;
-- For more information about the features of this table,
-- see https://github.com/CamDavidsonPilon/lifetimes/blob/master/lifetimes/utils.py#L246
-- and https://cloud.google.com/solutions/machine-learning/clv-prediction-with-offline-training-train#aggregating_data
CREATE OR REPLACE TABLE ltv_ecommerce.30_featured
(
-- dataset STRING,
customer_id STRING,
monetary FLOAT64,
frequency INT64,
recency INT64,
T INT64,
time_between FLOAT64,
avg_basket_value FLOAT64,
avg_basket_size FLOAT64,
has_returns STRING,
avg_time_to_return FLOAT64,
num_returns INT64,
-- threshold DATE,
-- step INT64,
target_monetary FLOAT64,
);
LOOP
-- Can choose a longer original window in case
-- there were not many orders in the early days.
IF STEP = 1 THEN
SET THRESHOLD_DATE = DATE_ADD(THRESHOLD_DATE, INTERVAL WINDOW_STEP_INITIAL DAY);
ELSE
SET THRESHOLD_DATE = DATE_ADD(THRESHOLD_DATE, INTERVAL WINDOW_STEP DAY);
END IF;
SET STEP = STEP + 1;
IF THRESHOLD_DATE >= DATE_SUB(MAX_DATE, INTERVAL (WINDOW_STEP) DAY) THEN
LEAVE;
END IF;
-- Takes all transactions before the threshold date unless you decide
-- to use a different window lenght to test model performance.
IF WINDOW_LENGTH != 0 THEN
SET WINDOW_START = DATE_SUB(THRESHOLD_DATE, INTERVAL WINDOW_LENGTH DAY);
ELSE
SET WINDOW_START = MIN_DATE;
END IF;
INSERT ltv_ecommerce.30_featured
SELECT
-- CASE
-- WHEN THRESHOLD_DATE <= DATE_SUB(MAX_DATE, INTERVAL LENGTH_FUTURE DAY) THEN 'UNASSIGNED'
-- ELSE 'TEST'
-- END AS dataset,
CAST(tf.customer_id AS STRING),
ROUND(tf.monetary_orders, 2) AS monetary,
tf.cnt_orders AS frequency,
tf.recency,
tf.T,
ROUND(tf.recency/cnt_orders, 2) AS time_between,
ROUND(tf.avg_basket_value, 2) AS avg_basket_value,
ROUND(tf.avg_basket_size, 2) AS avg_basket_size,
has_returns,
CEIL(avg_time_to_return) AS avg_time_to_return,
num_returns,
-- THRESHOLD_DATE AS threshold,
-- STEP - 1 AS step,
ROUND(tt.target_monetary, 2) AS target_monetary,
FROM (
-- This SELECT uses only data before THRESHOLD_DATE to make features.
SELECT
customer_id,
SUM(value) AS monetary_orders,
DATE_DIFF(MAX(order_day), MIN(order_day), DAY) AS recency,
DATE_DIFF(THRESHOLD_DATE, MIN(order_day), DAY) AS T,
COUNT(DISTINCT order_day) AS cnt_orders,
AVG(qty_articles) avg_basket_size,
AVG(value) avg_basket_value,
CASE
WHEN SUM(num_returns) > 0 THEN 'y'
ELSE 'n'
END AS has_returns,
AVG(time_to_return) avg_time_to_return,
THRESHOLD_DATE AS threshold,
SUM(num_returns) num_returns,
FROM
`ltv_ecommerce.20_aggred`
WHERE
order_day <= THRESHOLD_DATE AND
order_day >= WINDOW_START
GROUP BY
customer_id
) tf
INNER JOIN (
-- This SELECT uses all data after threshold as target.
SELECT
customer_id,
SUM(value) target_monetary
FROM
`ltv_ecommerce.20_aggred`
WHERE
order_day <= DATE_ADD(THRESHOLD_DATE, INTERVAL LENGTH_FUTURE DAY)
-- Overall value is similar to predicting only what's after threshold.
-- and the prediction performs better. We can substract later.
-- AND order_day > THRESHOLD_DATE
GROUP BY
customer_id) tt
ON
tf.customer_id = tt.customer_id;
END LOOP;
# + [markdown] id="JPwha05IFivK" colab_type="text"
# ### Dataset
# + id="1kNnLuWt-HBb" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 503} outputId="95530fe0-f56f-4929-ee07-fe44461d45f1"
# %%bigquery --project $PROJECT_ID
-- Shows all data for a specific customer and some other random records.
SELECT * FROM `ltv_ecommerce.30_featured` WHERE customer_id = "10"
UNION ALL
(SELECT * FROM `ltv_ecommerce.30_featured` LIMIT 5)
ORDER BY customer_id, frequency, T
# + colab_type="code" id="4qKPX7HV2VoP" colab={}
# %%bigquery df_featured --project $PROJECT_ID
ltv_ecommerce.30_featured
# + id="XuG-eO8qMJdo" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 317} outputId="64f8a981-6956-4ae6-cf31-c92b215e4c78"
df_featured.describe()
# + colab_type="code" id="TBr78kKG2j-3" colab={"base_uri": "https://localhost:8080/", "height": 387} outputId="2dfb9dda-0e2c-40ee-88cb-f9b2890f855b"
# Display distribution for all columns that are numerical (but will still ignore the categorical ones like day of the week)
valid_column_names = [key for key in dict(df_featured.dtypes) if dict(df_featured.dtypes)[key] in ['float64', 'int64']]
NUM_COLS = 5
NUM_ROWS = math.ceil(int(len(valid_column_names)) / NUM_COLS)
fig, axs = plt.subplots(nrows=NUM_ROWS, ncols=NUM_COLS, figsize=(25, 7))
for idx, cname in enumerate(valid_column_names):
x = int(idx/NUM_COLS)
y = idx % NUM_COLS
sns.violinplot(df_featured[cname], ax=axs[x, y], label=cname)
# + [markdown] id="w-vSwvNNBKgZ" colab_type="text"
# Seems like for most values, there is a long tail of records. This is something that might required additional feature preparation even if AutoML already provides some automatic engineering. You can investigate this if you want to improve the base model.
# + [markdown] id="6g8ZoZcJfxoJ" colab_type="text"
# ## Train the model
# This tutorial uses an AutoML regressor to predict the continuous value of target_monetary.
#
# With a non-AutoML model, you would generally need to:
# 1. Apply common ML patterns such as normalization or clipping.
# 1. Split data in two to three datasets for training, evaluating and testing.
#
# AutoML lets you split your data:
# - Manually using a column with a name for each split.
# - Manually using a column that defines a time
# - Automatically
#
# This tutorial uses the latter option where AutoML automatically assigns each row to a split.
# + id="VyjyGOicfx-L" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="38e4dc66-0234-4d34-898b-9c6ed82c0d57"
# You can run this query using the magic cell but the cell would run for hours.
# Although stopping the cell would not stop the query, using the Python client
# also enables you to add a custom parameter for the model name.
suffix_now = datetime.now().strftime("%Y%m%d_%H%M%S")
train_model_jobid = f'train_model_{suffix_now}'
train_model_sql = f'''
CREATE OR REPLACE MODEL `ltv_ecommerce.model_tutorial_{suffix_now}`
OPTIONS(MODEL_TYPE="AUTOML_REGRESSOR",
INPUT_LABEL_COLS=["target_monetary"],
OPTIMIZATION_OBJECTIVE="MINIMIZE_MAE")
AS SELECT
* EXCEPT(customer_id)
FROM
`ltv_ecommerce.30_featured`
'''
bq_client.query(train_model_sql, job_id=train_model_jobid)
# + [markdown] id="J1rW-h3wQW80" colab_type="text"
# This is an example of a model evaluation
#
# 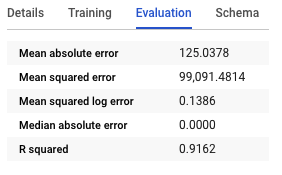
# + [markdown] id="IJnwrWjT_4W7" colab_type="text"
# ## Predict LTV
# Predicts LTV for all customers. It uses the overall monetary value for each customer to predict a future one.
# + id="6_nmt4DuIVzL" colab_type="code" colab={}
# %%bigquery --params $LTV_PARAMS --project $PROJECT_ID
-- TODO(developer):
-- 1. Update the model name to the one you want to use.
-- 2. Update the table where to output predictions.
-- How many days back for inputs transactions. 0 means from the start.
DECLARE WINDOW_LENGTH INT64 DEFAULT @WINDOW_LENGTH;
-- Date at which an input transactions window starts.
DECLARE WINDOW_START DATE;
-- Date of the first transaction in the dataset.
DECLARE MIN_DATE DATE;
-- Date of the final transaction in the dataset.
DECLARE MAX_DATE DATE;
-- Date from which you want to predict.
DECLARE PREDICT_FROM_DATE DATE;
SET (MIN_DATE, MAX_DATE) = (
SELECT AS STRUCT
MIN(order_day) AS min_days,
MAX(order_day) AS max_days
FROM
`ltv_ecommerce.20_aggred`
);
-- You can set any date here. In production, it is generally today.
SET PREDICT_FROM_DATE = MAX_DATE;
IF WINDOW_LENGTH != 0 THEN
SET WINDOW_START = DATE_SUB(PREDICT_FROM_DATE, INTERVAL WINDOW_LENGTH DAY);
ELSE
SET WINDOW_START = MIN_DATE;
END IF;
CREATE OR REPLACE TABLE `ltv_ecommerce.predictions_tutorial`
AS (
SELECT
customer_id,
monetary AS monetary_so_far,
ROUND(predicted_target_monetary, 2) AS monetary_predicted,
ROUND(predicted_target_monetary - monetary, 2) AS monetary_future
FROM
ML.PREDICT(
-- /!\ Set your model name here.
MODEL ltv_ecommerce.model_tutorial_YYYYMMDD,
(
SELECT
customer_id,
ROUND(monetary_orders, 2) AS monetary,
cnt_orders AS frequency,
recency,
T,
ROUND(recency/cnt_orders, 2) AS time_between,
ROUND(avg_basket_value, 2) AS avg_basket_value,
ROUND(avg_basket_size, 2) AS avg_basket_size,
has_returns,
CEIL(avg_time_to_return) AS avg_time_to_return,
num_returns
FROM (
SELECT
customer_id,
SUM(value) AS monetary_orders,
DATE_DIFF(MAX(order_day), MIN(order_day), DAY) AS recency,
DATE_DIFF(PREDICT_FROM_DATE, MIN(order_day), DAY) AS T,
COUNT(DISTINCT order_day) AS cnt_orders,
AVG(qty_articles) avg_basket_size,
AVG(value) avg_basket_value,
CASE
WHEN SUM(num_returns) > 0 THEN 'y'
ELSE 'n'
END AS has_returns,
AVG(time_to_return) avg_time_to_return,
SUM(num_returns) num_returns,
FROM
`ltv_ecommerce.20_aggred`
WHERE
order_day <= PREDICT_FROM_DATE AND
order_day >= WINDOW_START
GROUP BY
customer_id
)
)
)
)
# + id="XQVtTFK0Q7fF" colab_type="code" colab={}
# %%bigquery df_predictions --project $PROJECT_ID
ltv_ecommerce.predictions_windowed
# + id="MPSdMaTdRCzz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 297} outputId="22a6b85b-241c-4bed-aa00-8d330adec418"
df_predictions.describe()
# + id="Rhy9Sb2Hwmox" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="5af70098-494b-4577-ed89-6a11d3156258"
from matplotlib.gridspec import GridSpec
fig = plt.figure(constrained_layout=True, figsize=(15, 5))
gs = GridSpec(2, 2, figure=fig)
sns.set(font_scale = 1)
plt.tick_params(axis='x', labelsize=14)
ax0 = plt.subplot(gs.new_subplotspec((0, 0), colspan=1))
ax1 = plt.subplot(gs.new_subplotspec((0, 1), colspan=1))
ax2 = plt.subplot(gs.new_subplotspec((1, 0), colspan=2))
sns.violinplot(df_predictions['monetary_so_far'], ax=ax0, label='monetary_so_far')
sns.violinplot(df_predictions['monetary_predicted'], ax=ax1, label='monetary_predicted')
sns.violinplot(df_predictions['monetary_future'], ax=ax2, label='monetary_future')
# + [markdown] id="l6YQTMvX5Q08" colab_type="text"
# The monetary distribution analysis shows small monetary amounts for the next month compare to the overall historical value. The difference is about 3 to 4 orders of magnitude.
#
# One reason is that the model is trained to predict the value for the next month (LENGTH_FUTURE = 30).
#
# You can play around with that value to train and predict for the next quarter for example (LENGTH_FUTURE = 90)
# + [markdown] id="BD8paLvr7Kvb" colab_type="text"
# ## Activation
# This part shows how to activate on [Google Ads][lookalike_adwords] using similar audience.
#
# You can follow a similar process for [Facebook][lookalike_facebook] for example
#
# [lookalike_adwords]: https://developers.google.com/adwords/api/docs/guides/remarketing#customer_match_with_email_address_address_or_user_id
# [lookalike_facebook]: https://www.facebook.com/business/help/170456843145568?id=2469097953376494
# + [markdown] id="tmK61nL6_KbC" colab_type="text"
# ### Extract top customers
#
# This step extracts the top 20% customers with the highest **future** monetary value and join with a CRM table to get their email.
#
# The prediction used the overall monetary value but in this use case, we are looking at the most valuable in the future. You can modify the PERCENT_RANK to use another KPI.
# + id="r4QBQflQ_1NU" colab_type="code" colab={}
# %%bigquery df_top_ltv --params $LTV_PARAMS --project $PROJECT_ID
DECLARE TOP_LTV_RATIO FLOAT64 DEFAULT @TOP_LTV_RATIO;
SELECT
p.customer_id,
monetary_future,
c.email AS email
FROM (
SELECT
customer_id,
monetary_future,
PERCENT_RANK() OVER (ORDER BY monetary_future DESC) AS percent_rank_monetary
FROM
`ltv_ecommerce.predictions_windowed` ) p
-- This creates fake emails. You need to join with your own CRM table.
INNER JOIN (
SELECT
customer_id,
email
FROM
`ltv_ecommerce.00_crm` ) c
ON
p.customer_id = CAST(c.customer_id AS STRING)
WHERE
-- Decides the size of your list of emails. For similar-audience use cases
-- where you need to find a minimum of matching emails, 20% should provide
-- enough potential emails.
percent_rank_monetary <= TOP_LTV_RATIO
ORDER BY monetary_future DESC
# + id="BOlGSv1eHFGh" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="57a37ed8-de3e-42de-ce5b-7abe5aa82d40"
df_top_ltv.head(5)
# + id="0KtOjoRTkCjF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 459} outputId="860cce9e-0d11-43f4-8669-a233ed8d1b71"
# Shows distribution of the predicted monetary value for the top LTV customers.
print(df_top_ltv.describe())
fig, axs = plt.subplots()
sns.set(font_scale = 1.2)
sns.distplot(df_top_ltv['monetary_future'])
# + [markdown] id="y7yvUDKWgZ5_" colab_type="text"
# ### Setup Adwords client
# Creates the configuration YAML file for the Google Ads client. You need to:
# 1. Create Client ID and Secret using the Cloud Console
# 2. Follow [these steps](https://developers.google.com/google-ads/api/docs/client-libs/python/oauth-installed)
# + id="UVDjGJ87hhQG" colab_type="code" colab={}
# Sets your variables.
if 'google.colab' in sys.modules:
from google.colab import files
ADWORDS_FILE = "/tmp/adwords.yaml"
DEVELOPER_TOKEN = "[YOUR_DEVELOPER_TOKEN]"
OAUTH_2_CLIENT_ID = "[YOUR_OAUTH_2_CLIENT_ID]"
CLIENT_SECRET = "[YOUR_CLIENT_SECRET]"
REFRESH_TOKEN = "[YOUR_REFRESH_TOKEN]"
# + id="XIm9PUspgco4" colab_type="code" colab={}
# Creates a local YAML file
adwords_content = f"""
# AdWordsClient configurations
adwords:
#############################################################################
# Required Fields #
#############################################################################
developer_token: {DEVELOPER_TOKEN}
#############################################################################
# Optional Fields #
#############################################################################
# client_customer_id: INSERT_CLIENT_CUSTOMER_ID_HERE
# user_agent: INSERT_USER_AGENT_HERE
# partial_failure: True
# validate_only: True
#############################################################################
# OAuth2 Configuration #
# Below you may provide credentials for either the installed application or #
# service account flows. Remove or comment the lines for the flow you're #
# not using. #
#############################################################################
# The following values configure the client for the installed application
# flow.
client_id: {OAUTH_2_CLIENT_ID}
client_secret: {CLIENT_SECRET}
refresh_token: {REFRESH_TOKEN}
# The following values configure the client for the service account flow.
# path_to_private_key_file: INSERT_PATH_TO_JSON_KEY_FILE_HERE
# delegated_account: INSERT_DOMAIN_WIDE_DELEGATION_ACCOUNT
#############################################################################
# ReportDownloader Headers #
# Below you may specify boolean values for optional headers that will be #
# applied to all requests made by the ReportDownloader utility by default. #
#############################################################################
# report_downloader_headers:
# skip_report_header: False
# skip_column_header: False
# skip_report_summary: False
# use_raw_enum_values: False
# AdManagerClient configurations
ad_manager:
#############################################################################
# Required Fields #
#############################################################################
application_name: INSERT_APPLICATION_NAME_HERE
#############################################################################
# Optional Fields #
#############################################################################
# The network_code is required for all services except NetworkService:
# network_code: INSERT_NETWORK_CODE_HERE
# delegated_account: INSERT_DOMAIN_WIDE_DELEGATION_ACCOUNT
#############################################################################
# OAuth2 Configuration #
# Below you may provide credentials for either the installed application or #
# service account (recommended) flows. Remove or comment the lines for the #
# flow you're not using. #
#############################################################################
# The following values configure the client for the service account flow.
path_to_private_key_file: INSERT_PATH_TO_JSON_KEY_FILE_HERE
# delegated_account: INSERT_DOMAIN_WIDE_DELEGATION_ACCOUNT
# The following values configure the client for the installed application
# flow.
# client_id: INSERT_OAUTH_2_CLIENT_ID_HERE
# client_secret: INSERT_CLIENT_SECRET_HERE
# refresh_token: INSERT_REFRESH_TOKEN_HERE
# Common configurations:
###############################################################################
# Compression (optional) #
# Below you may specify whether to accept and automatically decompress gzip #
# encoded SOAP requests. By default, gzip compression is not enabled. #
###############################################################################
# enable_compression: False
###############################################################################
# Logging configuration (optional) #
# Below you may specify the logging configuration. This will be provided as #
# an input to logging.config.dictConfig. #
###############################################################################
# logging:
# version: 1
# disable_existing_loggers: False
# formatters:
# default_fmt:
# format: ext://googleads.util.LOGGER_FORMAT
# handlers:
# default_handler:
# class: logging.StreamHandler
# formatter: default_fmt
# level: INFO
# loggers:
# Configure root logger
# "":
# handlers: [default_handler]
# level: INFO
###############################################################################
# Proxy configurations (optional) #
# Below you may specify an HTTP or HTTPS Proxy to be used when making API #
# requests. Note: You must specify the scheme used for the proxy endpoint. #
# #
# For additional information on configuring these values, see: #
# http://docs.python-requests.org/en/master/user/advanced/#proxies #
###############################################################################
# proxy_config:
# http: INSERT_HTTP_PROXY_URI_HERE
# https: INSERT_HTTPS_PROXY_URI_HERE
# If specified, the given cafile will only be used if certificate validation
# is not disabled.
# cafile: INSERT_PATH_HERE
# disable_certificate_validation: False
################################################################################
# Utilities Included (optional) #
# Below you may specify whether the library will include utilities used in the #
# user agent. By default, the library will include utilities used in the user #
# agent. #
################################################################################
# include_utilities_in_user_agent: True
################################################################################
# Custom HTTP headers (optional) #
# Specify one or more custom headers to pass along with all requests to #
# the API. #
################################################################################
# custom_http_headers:
# X-My-Header: 'content'
"""
# + id="dX99FqKHh4gb" colab_type="code" colab={}
with open(ADWORDS_FILE, "w") as adwords_file:
print(adwords_content, file=adwords_file)
# + id="sDJ3_QYYS1Ua" colab_type="code" colab={}
# Google Ads client
# adwords_client = adwords.AdWordsClient.LoadFromStorage(ADWORDS_FILE)
# + [markdown] id="ObzXCrly_gZe" colab_type="text"
# ### Create an AdWords user list
# Using emails of the top LTV customers, you create an AdWords list. If more than 5000 of the users are matched with AdWords email, a similar audience list will be created.
#
# > Note that this guide uses fake emails so running these steps is not going to work but you can leverage this code with emails coming from your CRM.
# + id="BfBQWgj8HhQQ" colab_type="code" colab={}
ltv_emails = list(set(df_top_ltv['email']))
# + id="evaDxOKy7aos" colab_type="code" colab={}
# https://developers.google.com/adwords/api/docs/samples/python/remarketing#create-and-populate-a-user-list
# https://github.com/googleads/googleads-python-lib/blob/7c41584c65759b6860572a13bde65d7395c5b2d8/examples/adwords/v201809/remarketing/add_crm_based_user_list.py
# """Adds a user list and populates it with hashed email addresses.
# Note: It may take several hours for the list to be populated with members. Email
# addresses must be associated with a Google account. For privacy purposes, the
# user list size will show as zero until the list has at least 1000 members. After
# that, the size will be rounded to the two most significant digits.
# """
# def normalize_and_SHA256(s):
# """Normalizes (lowercase, remove whitespace) and hashes a string with SHA-256.
# Args:
# s: The string to perform this operation on.
# Returns:
# A normalized and SHA-256 hashed string.
# """
# return hashlib.sha256(s.strip().lower()).hexdigest()
# def create_user_list(client):
# # Initialize appropriate services.
# user_list_service = client.GetService('AdwordsUserListService', 'v201809')
# user_list = {
# 'xsi_type': 'CrmBasedUserList',
# 'name': f'Customer relationship management list #{uuid.uuid4()}',
# 'description': 'A list of customers that originated from email addresses',
# # CRM-based user lists can use a membershipLifeSpan of 10000 to indicate
# # unlimited; otherwise normal values apply.
# 'membershipLifeSpan': 30,
# 'uploadKeyType': 'CONTACT_INFO'
# }
# # Create an operation to add the user list.
# operations = [{
# 'operator': 'ADD',
# 'operand': user_list
# }]
# result = user_list_service.mutate(operations)
# user_list_id = result['value'][0]['id']
# emails = ltv_emails
# members = [{'hashedEmail': normalize_and_SHA256(email)} for email in emails]
# mutate_members_operation = {
# 'operand': {
# 'userListId': user_list_id,
# 'membersList': members
# },
# 'operator': 'ADD'
# }
# response = user_list_service.mutateMembers([mutate_members_operation])
# if 'userLists' in response:
# for user_list in response['userLists']:
# print('User list with name "%s" and ID "%d" was added.'
# % (user_list['name'], user_list['id']))
# create_user_list(adwords_client)
# + [markdown] id="Xcw1uVqmgdrG" colab_type="text"
# ## Thoughts
# As mentioned a few time, the goal of this tutorial is not to provide a state of the art model for predicting LTV but show a possible approach to create a base model for predicting future monetary value of your customers.
#
# If you decided to investigate more the approach, you could:
# - Do additional data engineering or find additional example when you see outliers.
# - Try a different approach to create inputs. For example, you could:
# - Use a ratio of transactions as *input transactions* and the rest as *target transactions*. An earlier version of this tutorial tried that but the current method led to better results for the problem at hand (predict value in the next X days).
# - Customize the time range for input transactions. This tutorial uses all orders that happened before a threshold but you could image to use 6 months before to predict one month after.
# - The data preparation creates several examples from a unique customer by using multiple threshold dates. The model can link those example with their original customer. A more advanced approach could try to treat those example as timeseries examples and use how the customer behavior evolve over time. Model might perform better...or not. As you noticed, the `T` value kind of contains that information already across examples that might seem random to the model. Let us know if you decide to try and find some great results.
# - When comparing models, make sure that you keep a unique test set to fairly compare the model's performance.
# - This tutorial prepares the data knowing that you want to predict the orders for the next 30 days. If you want a model to predict for the next quarter, you need to update `LENGTH_FUTURE` and prepare a new training dataset.
# - The original dataset uses a limited number of fields. If you have other dimensions such as product categories, regions or demographics, try to create additional inputs for your model.
# + [markdown] id="TpV-iwP9qw9c" colab_type="text"
# # Cleaning up
#
# To clean up all GCP resources used in this project, you can [delete the GCP
# project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
| retail/ltv/bqml/notebooks/bqml_automl_ltv_activate_lookalike.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This article explains Hopfield nets, simulates one and contains the relation to the Ising model.
#
# ## Hopfield Nets
#
# Let's assume you have a classification task for images where all images are known. The optimal solution would be to store all images and when you are given an image you compare all memory images to this one and get an exact match.
# But then you realize that this "look up" (comparing one image after another) becomes costly the more images you have to memorize.
# Even if you try to arange the images in a tree structure you will never be as fast as the following solution: store all images in **Content addressable memory (CAM)**.
# CAM is specialized hardware that is used in routers. Ternary-CAM additionally has a "Don't-Care" state ("?") with which parts of the pattern can be masked (this is useful for IP routing).
#
# In German CAMs are referred to as "Assoziativspeicher" (associative memory). Intuitively you don't use an address to access data but instead you use data to access the address of the data.
#
# Now imagine we had many pictures of dogs in our memorized array. And then comes a new image of a dog.
# Expect for the masking option ("?") we cannot perform any kind of fuzzy search on hardware CAM.
#
# As we will see in the following section, a Hopfield Network is a form of a recurrent artificial neural network and it serves as some kind of **associative memory**. It is interesting to analyse because we can model how neural networks store patterns.
#
# ### Binary Hopfield Networks
#
# A network with N binary units which are interconnected symmetrically (weight $T_{ij}=T_{ji}$) and without self-loops ($T_{ii} = 0$).
# Every unit can either be positive ("+1") or negative ("-1"). Therefore we can describe the state of the network with a vector U. For example U = (+,-,-,-,+...).
#
# Intuitively we initially set a state and wait until the network relaxes into another stable state. That means it does not change anymore once it reached that state. The reached state is the output value. For the associative memory example with images, the initial state is the image (black and white) and the stable state can also be interpreted as an image.
#
# Each of the units is a McCulloch-Pitts neuron with a step-function as non-linearity.
# That means if we only update a single unit ("neuron") then we calculate the weighted sum of the neighbours and set the neuron to "+" if the sum is greater or equals a threshold.
#
# - Weighted sum of neuron $x_j$: $g(x_j) = \sum_{i}{x_i \cdot T_{ji}}$
# - Step function: $x_j = \begin{cases}
# +1, g(x_j) \ge 0\\
# -1, else
# \end{cases}$
#
# **Update procedure**:
# - Synchronous update: A global clock tells all neurons at the same time to update. As a consequence all new states
# only depend on the old states
# - Asynchronous update: One unit is updated after another. This seems to be more plausible for biological neurons or
# ferro-magnets because they have no common clock. The order is random.
#
# **Learning** refers to finding apropriate weights. For the associative memory we want the connections between two neurons positive if they are often active together and we want the value to be negative if they are often different.
#
# ### Example
#
# The following example simulates a Hopfield network for noise reduction. The training patterns are eight times "+"/"-", six times "+"/"-" and six times the result of "+"/"-" AND "+"/"-".
# The reason for the redundancy will be explained later.
#
# The images of the simulations have the number of state at the x-axis and the time step as y-axis.
# +
import numpy as np
import random
import matplotlib.pyplot as plt
patterns = [
# Left variable | Right variable = Left AND Right
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[-1, -1, -1, -1, -1, -1, -1, -1, +1, +1, +1, +1, +1, +1, +1, +1, -1, -1, -1, -1, -1, -1],
[+1, +1, +1, +1, +1, +1, +1, +1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[+1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1, +1]
]
size = len(patterns[0])
weights = np.array([[0]*size]*size)
for pattern in patterns:
for i in range(0, size):
for j in range(0, size):
if j==i:
pass
else:
weights[i,j] += pattern[i] * pattern[j]
def simulate(x1, x2, eps=30, first_state=None, visualize=True):
number_of_iteration_unchanged = 0
if not first_state:
first_state = [x1]*8 + [x2]*8 + [+1, -1, +1, -1, +1, -1]
trace = [
first_state
]
while (number_of_iteration_unchanged < eps):
if len(trace) > 1 and trace[-1] == trace[-2]:
number_of_iteration_unchanged += 1
else:
number_of_iteration_unchanged = 0
random_unit = random.randint(0, size-1)
all_new_states = (np.array(np.dot(weights, trace[-1]) >= 0.0, dtype=np.int)*2) - 1
trace.append(trace[-1].copy())
trace[-1][random_unit] = all_new_states[random_unit].copy()
np_trace = np.array(trace)
if visualize:
plt.imshow(np_trace)
plt.show()
return trace[-1]
# -
simulate(-1,-1, eps=100);
simulate(1,1, eps=100)
simulate(-1,+1, eps=100);
simulate(+1,-1, eps=100);
# We see that all of the simulations "relaxed" to a solution which did not change for a long time (epsilon).
# Running the simulations multiple times showed that the (0,0) and (1,1) cases always converged to the correct pattern whereas the distinct cases were torn between the the correct state and its inverse.
#
# But why does the network converge at all?
#
# ### Stability theory
#
# In system theory there is the quest to prove the stability of different kind of systems (see [here](https://en.wikipedia.org/wiki/Lyapunov_stability)). A system is said to be stable if small perturbations of the input data lead to small variations of the output value.
#
# Stability can be intuitively grasped by imagining the velocity and phase of a pendulum.
# See the image by [Krishnavedala](https://commons.wikimedia.org/wiki/File:Pendulum_phase_portrait_illustration.svg).
#
# 
#
# If the pendulum was damped the phase portrait would look like a spiral.
# The center to which it converges over time is a of point of attraction which is called **equilibrium**.
# The circle in the diagram is called "orbit". An important question is for example: Will the trajectory of a given initial state converge to the point or will it diverge.
#
# And what happens if the system gets "pushed" a little bit. A pendulum would oscilate a little bit and converge back to the **equilibrium** but a football on a hill would roll down.
#
# For linear systems we can use the magnitude of the derivative of a point a. If it is less than one the system is said to be stable.
#
# For more information see [Stability theory](https://en.wikipedia.org/wiki/Stability_theory) on Wikipedia.
#
# The **Lyapunov Function** can be used to show asymptotic stability (it gets really close) or lyapunov stability (all points which were at time t in an orbit are at t+1 in a small neighbourhood). It works by choosing a Lyapunov function which has an analogy to the **potential function** of classical dynamics. In real physical systems a precise Energy function can be used. You can imagine a state x of pendulum. If the system loses energy the system will reach a final resting point. The final state is the attractor.
# Lyapunov showed that it is not necessary to know the energy function but it is enough to find a Lyapunov function V(x) with the following criteria:
#
# - $V(0) = 0$
# - $V(x) > 0$ if $x \ne 0$
# - $\dot{V}(x) = \frac{d}{dt}V(x) = \nabla V \cdot f(x) \le 0$ if $x \ne 0$
#
# [Lyapunov Stability](https://en.wikipedia.org/wiki/Lyapunov_stability)
#
# ### Energy function
#
# Let's apply this to Binary Hopfield Networks. We saw in the simulation that the Hopfield nets converge.
# Will this always be the case?
#
# We choose our Energy function: $E = -0.5 \sum_{j}{ \sum_{i \ne j}{u_i \cdot u_j \cdot T_{ji}} }$
#
# Actually we cannot assume to have a single global optimum on the surface of the energy function.
# At least every pattern we want to store should a local optimum. So we just show that the energy at t+1 is less or equal to t and therefore we always find a local optimum of the energy function.
#
# In our asynchronous, random update procedure we pick a unit u. It either has the state -1 and we change it to +1 or it has the state +1 and we change it to -1. In the first case the difference is "+2" and the the second one it is "-2". => $\Delta u_j \in \{ -2, +2 \}$
#
# How does the energie of unit j change?
#
# $\Delta E_j = E_{j_{new}} - E_{j_{old}} = $
#
# $ -0.5 \sum_{i \ne j}{u_{i} u_{j_{new}} T_{ji}} -0.5 \sum_{i \ne j}{u_i u_j T_{ji}} = $
#
# $ -0.5 \cdot (\sum_{i \ne j}{u_{i} u_{j_{new}} T_{ji}} -\sum_{i \ne j}{u_i u_j T_{ji}} ) = $
#
# $ -0.5 \cdot (\sum_{i \ne j}{u_{i} u_{j_{new}} T_{ji} -{u_i u_j T_{ji}}} ) = $
#
# $ -0.5 \cdot (\sum_{i \ne j}{u_{i} \cdot T_{ji} \cdot (u_{j_{new}} - u_j}) ) = $
#
# Define: $\Delta u_j = u_{j_{new}} - u_j$
#
# $ -0.5 \cdot (\sum_{i \ne j}{u_{i} \cdot T_{ji} \cdot \Delta u_j }) = $
#
# $ -0.5 \Delta u_j (\sum_{i \ne j}{u_{i} \cdot T_{ji} }) = $
#
#
# Two possible cases for the neuron j:
# - "+2" case: The weighted neighbours are greater equal zero ($\sum_{i \ne j}{u_{i} \cdot T_{ji} } >= 0$)
#
# $\Delta u_j=+2$
#
# $ \Delta E_j = -1 \cdot (\sum_{i \ne j}{u_{i} \cdot T_{ji} }) \le 0 $
#
#
# - "-2" case: The weighted neighbours are less than zero ($\sum_{i \ne j}{u_{i} \cdot T_{ji} } < 0$)
#
# $\Delta u_j=-2$
#
# $ \Delta E_j = +1 \cdot (\sum_{i \ne j}{u_{i} \cdot T_{ji} }) < 0 $
#
# **Conclusion:** In both cases the energy either reduces or stays the same. Every minimum of the energy function is a stable state.
#
# 
#
# In the example of the associative memory we see that a pattern (state) can only converge to the correct solution (pattern) if it is in its attractor region. Imagine a 2d hill. On which side of the hill we roll down is determined by the random sampling process. This explains why the "AND-simulation" from above can converge into different states.
#
# **Note:** Not all attractor regions have the same size. Therefore one state can attract more patterns than another. For the associative memory this leads to some kind of prior.
# Additionally mixture of an odd number of patterns cause **mixture states** which do not correspond to real patterns.
#
# If we try to store too many patterns so called **spin glass** states are generated. They are no linear combination of the original states. A network of N units has the capacity to store ~ 0.15N uncorrelated patterns.
#
# More math about Hopfield nets [here](https://page.mi.fu-berlin.de/rojas/neural/chapter/K13.pdf).
#
# ### Ising model
#
# Hopfield nets are isomorph to the **Ising model** in statistical physics which is used to model magnetism at low temperatures. Every neuron equals an atom in a solid body. The state of the unit coincides with the spin (the magnetic moment).
# In the **Heisenbergmodel** the spin can be multivariate. In the **Ising model** the spin is either parallel or antiparallel to a given axis z). The latter can be written as the Binary Hopfield Network.
#
# In physics the energy of the atoms is "measured" with the **Hamilton operator H**. It is the sum of the potential and kinetic energies in the system.
#
# $ H = -0.5 \sum_{ij} T_{ij} \cdot s_i \cdot s_j - H_z \sum_{i=1}{s_i} $
#
# - $s_i$ the spin of an atom
# - $T_{ij}$ the coupling constant between the spin of two atoms
# - $H$ is the strength of the magnetic field
#
# The critical temperature was calculated with this model. A system with less than its critical temperature is dominated by quantum mechanical effects.
#
| notebooks/06_boltzmann/.ipynb_checkpoints/Boltzmann-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Programming Bootcamp 2017
# # Lesson 2 Exercises
# ---
# **Earning points (optional)**
# - Enter your name below.
# - Email your `.ipynb` file to me (<EMAIL>) **before Monday 9:00 pm on 9/11**.
# - You do not need to complete all the problems to get points.
# - Points will be assigned based on participation.
# - Those who consistenly participate throughout bootcamp will get a prize (TBA).
# **Name**:
# ---
# ## 1. Guess the output: conditionals practice (1pt)
#
# For the following blocks of code, first try to guess what the output will be, and then run the code yourself. Points will be given for filling in the guesses; guessing wrong won't be penalized.
#
# **NOTE: The first cell below holds the variables that will be used in the problems. Since variables are shared across cells in Jupyter notebooks, you just need to run this cell once and then those variables can be used in any other code cell. **
#
# (However, remember that closing the notebook or restarting the kernel clears all the variables, so you will need to re-run the cell to re-populate those variables after doing that.)
# RUN THIS BLOCK FIRST TO SET UP VARIABLES!
a = True
b = False
x = 2
y = -2
cat = "Mittens"
# (^^ you might find it helpful to copy these variables somewhere you can easily see them when doing the problems. e.g. a piece of paper or a text file.)
print(a)
# Your guess:
#
print(not a)
# Your guess:
#
print (a == b)
# Your guess:
#
print (a != b)
# Your guess:
#
print (x == y)
# Your guess:
#
print (x > y)
# Your guess:
#
print (x = 2)
# A single = means assignment, and you can't do assignment within a print statement (assignments are always done on their own line). What we want here is: print (x == 2)
#
print (a and b)
# Your guess:
#
print (a and not b)
# Your guess:
#
print (a or b)
# Your guess:
#
print (not b or a)
# Your guess:
#
print (not (b or a))
# Your guess:
#
print (not b and a)
# Your guess:
#
print (not (b and a))
# Your guess:
#
print (x == abs(y))
# Your guess:
#
print (len(cat))
# Your guess:
#
print (cat + x)
# You cannot concatenate string and integer.
#
print (cat + str(x))
# Your guess:
#
print (float(x))
# Your guess:
#
print ("i" in cat)
# Your guess:
#
print ("g" in cat)
# Your guess:
#
print ("Mit" in cat)
# Your guess:
#
# > What is "`in`"? This is just another Python operator that you can use in your conditionals. As you may have guessed, `(x in y)` evaluates to `True` if `x` is found in `y`. This can be used to check if a string is contained in another string (e.g. `"Mit" in "Mittens"`).
# ---
# ## 2. Guess the output: if statement practice (1pt)
#
# Same directions as above.
# RUN THIS BLOCK FIRST TO SET UP VARIABLES!
x = 2
y = -2
cat = "Mittens"
if (x % 2) == 0:
print ("x is even")
else:
print ("x is odd")
# Your guess:
#
if (y - 4*x) < 0:
print (":)")
else:
print (":(")
# Your guess:
#
if "Mit" in cat:
print ("Hey Mit!")
else:
print ("Where's Mit?")
# Your guess:
#
x = "C"
if x == "A" or "B":
print ("yes")
else:
print ("no")
# Your guess:
#
x = "C"
if (x == "A") or (x == "B"):
print ("yes")
else:
print ("no")
# Your guess:
#
# > Surprised by the last two? It's important to note that when you want compare a variable against multiple things, you can only compare it to one thing at a time. Although it makes sense in English to say "is x equal to A or B?", in Python you must write: ((x == "A") or (x == "B")) to accomplish this. The same goes for e.g. ((x > 5) and (x < 10)) and anything along those lines.
#
# > So why does the first version give the answer "yes"? Basically, anything that isn't `False` or the literal number 0 is considered to be `True` in Python. When you say '`x == "A" or "B"`', Python reads it as '`(x == "A") or (B)`', which evaluates to '`(False) or (True)`', which is `True`!
# ---
# ## 3. On your own (2pts)
#
# Write code to accomplish the following tasks using the concepts we went over in the lecture.
#
# Use the following variables in your code. You must actually use the variables; pretend you don't know their values.
# RUN THIS BLOCK FIRST!
num1 = 3.14159
num2 = 6
num3 = 100
num4 = 6 * -5 - 4 * 2 + -7 * -8 + 3
motif = "GTAAGTCGGTAACGTAAGTCGGTAAC"
# **(A)** Check if `num3` is greater than `num4`. Print "yes" if it is, and "no" if it isn't.
# **(B)** Print a random integer between `num2` and `num3`.
# **(C)** Check if the length of the string stored in `motif` is less than or equal to 25. Print "yes" if it is, and "no" if it isn't.
# **(D)** Round `num1` to the nearest hundredth.
# **(E)** Check if num4 is positive or negative.
# ---
# ## 4. Quadratic formula: checking for negative roots (1pt)
#
# Recall that when calculating the quadratic formula, you will get an error if $b^2 - 4ac$ is negative, since you can't take the square root of a negative number.
#
# Edit the code below so that it checks for this potential error before it occurs:
# - If the error is going to occur, print a message saying "non-real answer" and **do not** calculate the values of x.
# - If the error is not going to occur, calculate and print the values of x.
#
# +
import sys
a = float(input("Enter value for a: "))
b = float(input("Enter value for b: "))
c = float(input("Enter value for c: "))
underRoot = (b**2 - 4*a*c)
print ("x =", x1, "or", x2)
# -
# **[ Check your answer ]**
# - If a=1, b=4, and c=1, expected output is:
# ```
# x = -0.267949192431 or -3.73205080757
# ```
# - If a=2, b=2, and c=2, expected output is:
# ```
# non-real answer
# ```
# ---
# ## 5. Motif checker (2pts)
#
# Using `input()`, prompt the user for a DNA sequence and a motif to search for (the sequence and motif can be any string of A/T/G/C's; see below for examples).
# **(A)** Find the length of the motif and length of the DNA sequence and check if the motif is longer than the sequence. If it is, print "Motif is too long".
# **(B)** Adding to your code from part (A): If and only if the motif is shorter than the sequence, go on to check if the motif can be found somewhere within the sequence (hint: use "`in`"). If it is found, print "Motif found". If it is not found, print "Motif not found".
# **[ Check your answer ]** Try running your code above using the following input and make sure your results match the expected output.
#
#
# > **Sequence:** `AGCTAGCCTGCTAGAAATCGATTGGCTAGCAATCTTATTGTGTTCTACG` <br>
# > **Motif:** `ATG` <br>
# > **Expected output:**
# > ```
# Motif not found
# ```
# >
# > **Sequence:** `AGCTAGCCTGCTAGAAATCGATTGGCTAGCAATCTTATTGTGTTCTACG` <br>
# > **Motif:** `ATCGA` <br>
# > **Expected output:**
# > ```
# Motif found
# ```
# >
# > **Sequence:** `CTAGCC` <br>
# > **Motif:** `ATGGCTAGCTA` <br>
# > **Expected output:**
# > ```
# Motif is too long
# ```
# ---
# ## 6. Password protection (3pts)
#
# Write code that prompts the user to guess a password and checks whether the password is correct.
#
# - First create a variable called `password` and set it equal to whatever you want the password to be (any string).
# - Then prompt the user to guess the password, and read their input from the terminal.
# - Check if what they entered matches your password, and print a message saying whether or not the guess was correct.
# **(A)** Do this giving the user only one chance to guess.
# **(B)** Do this giving the user 3 chances to guess. Only prompt for another guess if the previous guess was incorrect. When they guess correctly, print a confirmation message and end the program. If they don't guess correctly in 3 tries, print "Access denied!" and end the program.
# ---
# ## 7. Coin flip simulation (2pts)
# For this problem, we will simulate a coin flip using the random number generator in the `random` module.
#
# Try running the following code several times:
# +
import random
randNum = random.randint(0,1)
print (randNum)
# -
# You should see that you always get either 0 or 1. We will pretend that each time we run `random.randint(0,1)` we are flipping a coin, where 1 represents heads and 0 represents tails.
#
# **Write code that "flips a coin" 10 times and counts how many times it comes up heads. At the end, print how many of the flips were heads.**
# ---
#
# ---
# ## Extra problems (0pt)
#
# The following problems are for people who would like more practice. They will not be counted for points.
# **(A)** Following from the coin flip problem above:
#
# Change your code so that the coin is now "unfair" (i.e. the chance of heads is not equal to the chance of tails). See if you can make it so the probability of heads is 75%.
#
# *Hint: There are several ways to do this, but one simple way involves using a larger range of random ints and assigning heads/tails differently.*
# **(B)** Using `input()`, prompt the user for a number. Check if that number is between 50 and 100, and print different messages depending on the outcome.
# **(C)** Using `input()`, prompt the user for an integer. Check if the integer is a multiple of 7, and print different messages depending on the outcome.
| class_materials/Conditionals(If_Else)/2017/lab2_exercises.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: ibaio_dev39
# language: python
# name: ibaio_dev39
# ---
# # Markov chain Monte Carlo
#
# The main technical challenge in using Bayesian models resides in calculating the model's joint posterior distribution.
#
# Recall that we are interested in combining the information from our data, via the **likelihood** $Pr(y|\theta)$, and prior information, via the **prior distribution** $Pr(\theta)$, to produce a joint posterior distribution for the model of interest:
#
# $$Pr(\theta | y) \propto Pr(y|\theta) Pr(\theta)$$
#
# However, to guarantee that the posterior is itself a proper probability density (and not just proportional to one), it has to be normalized by dividing by the **marginal likelihood**:
#
# $$Pr(\theta | y) = \frac{Pr(y|\theta) Pr(\theta)}{Pr(y)}$$
#
# The marginal likelihood is the numerator, integrated over the parameters $\theta$:
#
# $$Pr(\theta | y) = \frac{Pr(y|\theta) Pr(\theta)}{\int_{\theta} Pr(y|\theta) Pr(\theta) d\theta}$$
#
# which, except for very simple (one- or two-parameter) models cannot be calculated analytically.
#
# The two alternative strategies to obtaining posteriors for moderate to large models involve either analytic **approximations** or stochastic **sampling**. Approximations are usually valid conditional on assumptions regarding the true posterior distribution, which are typically impossible to validate. Direct sampling strategies rely on our ability to sample from the posterior distribution, and this is frequently not possible. Indirect sampling methods, such as rejection sampling, can be plagued with sampling efficiency issues.
#
# The sampling approaches we have introduced so far have each attempted to obtain *independent* samples from the posterior distribution. It turns out, however, that it is possible to generate samples from the posterior distribution using a *dependent* sampling algorithm, and despite the dependence of the samples, one may extract valid inference from them. A class of algorithms called **Markov chain Monte Carlo** yields a Markovian sample (explained below) which, provided that certain conditions are satisfied, is guaranteed to be indistinguishable from a sample drawn from the true posterior itself.
# ## Markov Chains
#
# A Markov chain is a special type of **stochastic process**. The standard definition of a stochastic process is an ordered collection of random variables:
#
# $$\{X_t: t \in T\}$$
#
# where $t$ is frequently (but not necessarily) a time index. If we think of $X_t$ as a state $X$ at time $t$, and invoke the following dependence condition on each state:
#
# $$Pr(X_{t+1}=x_{t+1} | X_t=x_t, X_{t-1}=x_{t-1},\ldots,X_0=x_0) = Pr(X_{t+1}=x_{t+1} | X_t=x_t)$$
#
# then the stochastic process is known as a **Markov chain**. This conditioning specifies that the future depends on the current state, but not past states. Thus, the Markov chain wanders about the state space, remembering only where it has just been in the last time step. The collection of transition probabilities is sometimes called a **transition matrix** when dealing with discrete states, or more generally, a
# **kernel**.
#
# In the context of Markov chain Monte Carlo, it is useful to think of the Markovian property as “mild non-independence”. MCMC allows us to indirectly generate independent samples from a particular posterior distribution.
#
# ## Why MCMC Works: Reversible Markov Chains
#
# Markov chain Monte Carlo simulates a Markov chain for which some function of interest
# (*e.g.* the joint distribution of the parameters of some model) is the unique, invariant limiting distribution. An invariant distribution with respect to some Markov chain with transition kernel $Pr(y \mid x)$ implies that:
#
# $$\int_x Pr(y \mid x) \pi(x) dx = \pi(y).$$
#
# Invariance is guaranteed for any **reversible** Markov chain. Consider a Markov chain in reverse sequence:
# $\{\theta^{(n)},\theta^{(n-1)},...,\theta^{(0)}\}$. This sequence is still Markovian, because:
#
# $$Pr(\theta^{(k)}=y \mid \theta^{(k+1)}=x,\theta^{(k+2)}=x_1,\ldots ) = Pr(\theta^{(k)}=y \mid \theta^{(k+1)})=x$$
#
# Forward and reverse transition probabilities may be related through Bayes theorem:
#
# $$Pr(\theta^{(k)}=y \mid \theta^{(k+1)}=x) = \frac{Pr(\theta^{(k+1)}=x \mid \theta^{(k)}=y) \pi^{(k)}(y)}{\pi^{(k+1)}(x)}$$
#
# Though not homogeneous in general, $\pi$ becomes homogeneous if:
#
# - $n \rightarrow \infty$
#
# - $\pi^{(i)}=\pi$ for some $i < k$
#
# If this chain is homogeneous it is called reversible, because it satisfies the **detailed balance equation**:
#
# $$\pi(x)Pr(y \mid x) = \pi(y) Pr(x \mid y)$$
#
# Reversibility is important because it has the effect of balancing movement through the entire state space. When a Markov chain is reversible, $\pi$ is the unique, invariant, stationary distribution of that chain. Hence, if $\pi$ is of interest, we need only find the reversible Markov chain for which $\pi$ is the limiting distribution.
# This is what MCMC does!
# ## The Metropolis-Hastings Algorithm
#
# One of the simplest and most flexible algorithms for generating reversible Markov chains is the Metropolis-Hastings algorithm. Since we cannot sample directly from the (unknown) posterior distribution, this algorithm employs an **auxilliary distribution** that is easy to sample from. These samples generate candidate state transitions, which are accepted or rejected probabilistically.
#
# 
#
# Let us first consider a simple Metropolis-Hastings algorithm for a single parameter, $\theta$. We will use a well-known statistical distribution to produce candidate variables $q_t(\theta^{\prime} | \theta)$. Each generated value, $\theta^{\prime}$, is a *possible* next value for
# $\theta$ at step $t+1$.
#
# Whether or not $\theta^{\prime}$ is accepted depends on the relative probability of the new value versus the current value, weighted by the probabilities of the two values under the proposal distribution:
#
# $$a(\theta^{\prime},\theta) = \frac{q_t(\theta^{\prime} | \theta) \pi(\theta^{\prime})}{q_t(\theta | \theta^{\prime}) \pi(\theta)}$$
#
# This is the **acceptance ratio**, and is used as a threshold value for a uniform random draw that determines acceptance:
#
# $$
# \theta^{(t+1)} =
# \begin{cases}
# \theta^{\prime} & \text{with prob. } p = \min(a(\theta^{\prime},\theta^{(t)}),1)\cr
# \theta^{(t)} & \text{with prob } 1 - p
# \end{cases}
# $$
#
# This transition kernel implies that movement is not guaranteed at every step. It only occurs if the suggested transition is likely based on the acceptance ratio.
#
# A single iteration of the Metropolis-Hastings algorithm proceeds as follows:
#
# 1. Sample $\theta^{\prime}$ from $q(\theta^{\prime} | \theta^{(t)})$.
#
# 2. Generate a Uniform[0,1] random variate $u$.
#
# 3. If $a(\theta^{\prime},\theta) > u$ then
# $\theta^{(t+1)} = \theta^{\prime}$, otherwise
# $\theta^{(t+1)} = \theta^{(t)}$.
#
#
# ### Random-walk Metropolis-Hastings
#
# We still have not talked about how to choose the proposal $q$. In principle, it can be just about anything, but some choices are wiser than others. A practical implementation of the Metropolis-Hastings algorithm makes use of a **random-walk** proposal.
#
# A random walk is a Markov chain that evolves according to:
#
# $$\begin{aligned}
# \theta^{(t+1)} &= \theta^{(t)} + \epsilon_t \\
# \epsilon_t &\sim f(\phi)
# \end{aligned}$$
#
# As applied to the MCMC sampling, the random walk is used as a proposal distribution, whereby dependent proposals are generated according to:
#
# $$q(\theta^{\prime} | \theta^{(t)}) = f(\theta^{\prime} - \theta^{(t)}) = \theta^{(t)} + \epsilon_t$$
#
# Generally, the density generating $\epsilon_t$ is **symmetric** about zero,
# resulting in a symmetric chain. Chain symmetry implies that
# $q(\theta^{\prime} | \theta^{(t)}) = q(\theta^{(t)} | \theta^{\prime})$,
# which reduces the Metropolis-Hastings acceptance ratio to:
#
# $$a(\theta^{\prime},\theta) = \frac{\pi(\theta^{\prime})}{\pi(\theta)}$$
#
# The choice of the random walk distribution for $\epsilon_t$ is frequently a normal or Student’s $t$ density, but it may be any distribution that generates an irreducible proposal chain.
#
# An important consideration is the specification of the **scale parameter** for the random walk error distribution. Large values produce random walk steps that are highly exploratory, but tend to produce proposal values in the tails of the target distribution, potentially resulting in very small acceptance rates. Conversely, small values tend to be accepted more frequently, since they tend to produce proposals close to the current parameter value, but may result in chains that mix very slowly.
#
# Some simulation studies suggest optimal acceptance rates in the range of **20-50%**. It is often worthwhile to optimize the proposal variance by iteratively adjusting its value, according to observed acceptance rates early in the MCMC simulation .
# ## Example: Linear model estimation
#
# This very simple dataset is a selection of real estate prices, with the associated age of each house. We wish to estimate a simple linear relationship between the two variables, using the Metropolis-Hastings algorithm.
#
# $$\mu_i = \beta_0 + \beta_1 a_i$$
#
# $$p_i \sim N(\mu_i, \tau)$$
# +
# %matplotlib inline
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
age = np.array([13, 14, 14,12, 9, 15, 10, 14, 9, 14, 13, 12, 9, 10, 15, 11,
15, 11, 7, 13, 13, 10, 9, 6, 11, 15, 13, 10, 9, 9, 15, 14,
14, 10, 14, 11, 13, 14, 10])
price = np.array([2950, 2300, 3900, 2800, 5000, 2999, 3950, 2995, 4500, 2800,
1990, 3500, 5100, 3900, 2900, 4950, 2000, 3400, 8999, 4000,
2950, 3250, 3950, 4600, 4500, 1600, 3900, 4200, 6500, 3500,
2999, 2600, 3250, 2500, 2400, 3990, 4600, 450,4700])/1000.
# -
sns.scatterplot(age, price)
plt.xlabel('Age')
plt.ylabel('Price');
# This function calculates the joint log-posterior, conditional on values for each paramter:
# +
from scipy.stats import gamma, norm
dgamma = gamma.logpdf
dnorm = norm.logpdf
def calc_posterior(a, b, t, y=price, x=age):
# Calculate joint posterior, given values for a, b and t
# Priors on a,b
logp = dnorm(a, 0, 10000) + dnorm(b, 0, 10000)
# Prior on t
logp += dgamma(t, 0.001, 0.001)
# Calculate mu
mu = a + b*x
# Data likelihood
logp += sum(dnorm(y, mu, t**-0.5))
return logp
# +
rnorm = np.random.normal
runif = np.random.rand
np.random.seed(42)
def metropolis(n_iterations, initial_values, prop_var=1):
n_params = len(initial_values)
# Initial proposal standard deviations
prop_sd = [prop_var]*n_params
# Initialize trace for parameters
trace = np.empty((n_iterations+1, n_params))
# Set initial values
trace[0] = initial_values
# Calculate joint posterior for initial values
current_log_prob = calc_posterior(*trace[0])
# Initialize acceptance counts
accepted = [0]*n_params
for i in range(n_iterations):
if not i%1000: print('Iteration %i' % i)
# Grab current parameter values
current_params = trace[i]
for j in range(n_params):
# Get current value for parameter j
p = trace[i].copy()
# Propose new value
if j==2:
# Ensure tau is positive
theta = np.exp(rnorm(np.log(current_params[j]), prop_sd[j]))
else:
theta = rnorm(current_params[j], prop_sd[j])
# Insert new value
p[j] = theta
# Calculate log posterior with proposed value
proposed_log_prob = calc_posterior(*p)
# Log-acceptance rate
alpha = proposed_log_prob - current_log_prob
# Sample a uniform random variate
u = runif()
# Test proposed value
if np.log(u) < alpha:
# Accept
trace[i+1,j] = theta
current_log_prob = proposed_log_prob
accepted[j] += 1
else:
# Reject
trace[i+1,j] = trace[i,j]
return trace, accepted
# -
# Let's run the MH algorithm with a very small proposal variance:
n_iter = 5000
trace, acc = metropolis(n_iter, (1,0,1), 0.001)
# We can see that the acceptance rate is way too high:
np.array(acc, float)/n_iter
for param, samples in zip(['intercept', 'slope', 'precision'], trace.T):
fig, axes = plt.subplots(1, 2, figsize=(8, 2))
axes[0].plot(samples)
axes[0].set_ylabel(param)
axes[1].hist(samples[int(n_iter/2):])
# Now, with a very large proposal variance:
trace_hivar, acc = metropolis(n_iter, (1,0,1), 20)
np.array(acc, float)/n_iter
for param, samples in zip(['intercept', 'slope', 'precision'], trace_hivar.T):
fig, axes = plt.subplots(1, 2, figsize=(8, 2))
axes[0].plot(samples)
axes[0].set_ylabel(param)
axes[1].hist(samples[int(n_iter/2):])
# In order to avoid having to set the proposal variance by trial-and-error, we can add some tuning logic to the algorithm.
#
# ## Auto-tuning Metropolis-Hastings
#
# We can modify the Metropolis-Hastings algorithm above by adding logic to automatically change the proposal scale depending on the acceptance rate of the chain.
def metropolis_tuned(n_iterations, initial_values, prop_var=1,
tune_for=None, tune_interval=100):
n_params = len(initial_values)
# Initial proposal standard deviations
prop_sd = [prop_var] * n_params
# Initialize trace for parameters
trace = np.empty((n_iterations+1, n_params))
# Set initial values
trace[0] = initial_values
# Initialize acceptance counts
accepted = [0]*n_params
# Calculate joint posterior for initial values
current_log_prob = calc_posterior(*trace[0])
if tune_for is None:
tune_for = n_iterations/2
for i in range(n_iterations):
if not i%1000: print('Iteration %i' % i)
# Grab current parameter values
current_params = trace[i]
for j in range(n_params):
# Get current value for parameter j
p = trace[i].copy()
# Propose new value
if j==2:
# Ensure tau is positive
theta = np.exp(rnorm(np.log(current_params[j]), prop_sd[j]))
else:
theta = rnorm(current_params[j], prop_sd[j])
# Insert new value
p[j] = theta
# Calculate log posterior with proposed value
proposed_log_prob = calc_posterior(*p)
# Log-acceptance rate
alpha = proposed_log_prob - current_log_prob
# Sample a uniform random variate
u = runif()
# Test proposed value
if np.log(u) < alpha:
# Accept
trace[i+1,j] = theta
current_log_prob = proposed_log_prob
accepted[j] += 1
else:
# Reject
trace[i+1,j] = trace[i,j]
# Tune every 100 iterations
if (not (i+1) % tune_interval) and (i < tune_for):
# Calculate aceptance rate
acceptance_rate = (1.*accepted[j])/tune_interval
if acceptance_rate<0.2:
prop_sd[j] *= 0.9
elif acceptance_rate>0.4:
prop_sd[j] *= 1.1
accepted[j] = 0
return trace[tune_for:], accepted
trace_tuned, acc = metropolis_tuned(10000, (10,0,1), tune_for=5000)
np.array(acc, float)/5000
for param, samples in zip(['intercept', 'slope', 'precision'], trace_tuned.T):
fig, axes = plt.subplots(1, 2, figsize=(8, 2))
axes[0].plot(samples)
axes[0].set_ylabel(param)
axes[1].hist(samples[int(len(samples)/2):])
# A useful way to informally examine the fit of the model is to examine functions of the posterior distribution. For example, here are 50 random regression lines drawn from the posterior:
plt.plot(age, price, 'bo')
plt.xlabel('age (years)'); plt.ylabel('price ($1000\'s)')
xvals = np.linspace(age.min(), age.max())
for i in range(50):
b0,b1,tau = trace_tuned[np.random.randint(0, 1000)]
plt.plot(xvals, b0 + b1*xvals, 'r-', alpha=0.2)
# # Hamiltonian Monte Carlo
#
# While flexible and easy to implement, Metropolis-Hastings sampling is a random walk
# sampler that might not be statistically efficient for many models. Specifically, for models of high dimension, random walk jumping algorithms do not perform well. It is not enough to simply guess at the next sample location; we need to make each iteration a useful draw from the posterior whenever we can, in order to have an efficient sampler for bigger models.
#
# 
#
# (*image: Hoffman and Gelman, 2014*)
#
# Since Bayesian inference is all about calculating expectations over posteriors, what we seek is an algorithm that samples from the area of the parameter space that contains most of the non-zero probability. This region is called the **typical set**.
# ### What's a Typical Set?
#
# The typical set is where most of the probability lies in a particular volume associated with the distribution. As the dimension of a model increases, this set moves progressively further from the mode, and becomes more singular, as the result of concentration of measure.
#
# The typical set is a product of both the density, which is highest at the mode, and volume (that we integrate over), which increasingly becomes larger away from the mode as dimensionality increases. In fact, at high dimensions, the region around the mode contributes almost nothing to the expectation. We need an algorithm that will find this narrow region and explore it efficiently.
#
# 
#
# (image: Betancourt 2017)
#
# In this context, and when sampling from continuous variables, Hamiltonian (or Hybrid) Monte
# Carlo (HMC) can prove to be a powerful tool. It avoids
# random walk behavior by simulating a physical system governed by
# Hamiltonian dynamics, potentially avoiding tricky conditional
# distributions in the process.
# ### Simulating Hamiltonian Dynamics
#
# In HMC, model samples are obtained by simulating a physical system,
# where particles move about a high-dimensional landscape, subject to
# potential and kinetic energies. Adapting the notation from [Neal (1993)](http://www.cs.toronto.edu/~radford/review.abstract.html),
# particles are characterized by a position vector or state
# $s \in \mathcal{R}^D$ and velocity vector $\phi \in \mathcal{R}^D$. The
# combined state of a particle is denoted as $\chi=(s,\phi)$.
#
# The joint **canonical distribution** of the position and velocity can be expressed as a product of the marginal position (which is of interest) and the conditional distribution of the velocity:
#
# $$\pi(s, \phi) = \pi(\phi | s) \pi(s)$$
#
# This joint probability can also be written in terms of an invariant **Hamiltonian function**:
#
# $$\pi(s, \phi) \propto \exp(-H(s,\phi))$$
#
# The Hamiltonian is then defined as the sum of potential energy $E(s)$ and kinetic energy
# $K(\phi)$, as follows:
#
# $$\mathcal{H}(s,\phi) = E(s) + K(\phi)
# = E(s) + \frac{1}{2} \sum_i \phi_i^2$$
#
# Instead of sampling $p(s)$ directly, HMC operates by sampling from the canonical distribution.
#
# $$p(s,\phi) = \frac{1}{Z} \exp(-\mathcal{H}(s,\phi))=p(s)p(\phi)$$.
#
# If we choose a momentum that is independent of position, marginalizing over $\phi$ is
# trivial and recovers the original distribution of interest.
#
# The Hamiltonian $\mathcal{H}$ is independent of the parameterization of the model, and therefore, captures the geometry of the phase space distribution, including typical set.
# **Hamiltonian Dynamics**
#
# State $s$ and velocity $\phi$ are modified such that
# $\mathcal{H}(s,\phi)$ remains constant throughout the simulation. The
# differential equations are given by:
#
# $$\begin{aligned}\frac{ds_i}{dt} &= \frac{\partial \mathcal{H}}{\partial \phi_i} = \phi_i \\
# \frac{d\phi_i}{dt} &= - \frac{\partial \mathcal{H}}{\partial s_i}
# = - \frac{\partial E}{\partial s_i}
# \end{aligned}$$
#
# As shown in [Neal (1993)](http://www.cs.toronto.edu/~radford/review.abstract.html),
# the above transformation preserves volume and is
# reversible. The above dynamics can thus be used as transition operators
# of a Markov chain and will leave $p(s,\phi)$ invariant. That chain by
# itself is not ergodic however, since simulating the dynamics maintains a
# fixed Hamiltonian $\mathcal{H}(s,\phi)$. HMC thus alternates Hamiltonian
# dynamic steps, with Gibbs sampling of the velocity. Because $p(s)$ and
# $p(\phi)$ are independent, sampling $\phi_{new} \sim p(\phi|s)$ is
# trivial since $p(\phi|s)=p(\phi)$, where $p(\phi)$ is often taken to be
# the univariate Gaussian.
#
# 
#
# **The Leap-Frog Algorithm**
#
# In practice, we cannot simulate Hamiltonian dynamics exactly because of
# the problem of time discretization. There are several ways one can do
# this. To maintain invariance of the Markov chain however, care must be
# taken to preserve the properties of *volume conservation* and *time
# reversibility*. The **leap-frog algorithm** maintains these properties
# and operates in 3 steps:
#
# $$\begin{aligned}
# \phi_i(t + \epsilon/2) &= \phi_i(t) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t)) \\
# s_i(t + \epsilon) &= s_i(t) + \epsilon \phi_i(t + \epsilon/2) \\
# \phi_i(t + \epsilon) &= \phi_i(t + \epsilon/2) - \frac{\epsilon}{2} \frac{\partial{}}{\partial s_i} E(s(t + \epsilon))
# \end{aligned}$$
#
# We thus perform a half-step update of the velocity at time
# $t+\epsilon/2$, which is then used to compute $s(t + \epsilon)$ and
# $\phi(t + \epsilon)$.
#
# **Accept / Reject**
#
# In practice, using finite stepsizes $\epsilon$ will not preserve
# $\mathcal{H}(s,\phi)$ exactly and will introduce bias in the simulation.
# Also, rounding errors due to the use of floating point numbers means
# that the above transformation will not be perfectly reversible.
#
# HMC cancels these effects **exactly** by adding a Metropolis
# accept/reject stage, after $n$ leapfrog steps. The new state
# $\chi' = (s',\phi')$ is accepted with probability $p_{acc}(\chi,\chi')$,
# defined as:
#
# $$p_{acc}(\chi,\chi') = min \left( 1, \frac{\exp(-\mathcal{H}(s',\phi')}{\exp(-\mathcal{H}(s,\phi)} \right)$$
#
# **HMC Algorithm**
#
# We obtain a new HMC sample as follows:
#
# 1. sample a new velocity from a univariate Gaussian distribution
# 2. perform $n$ leapfrog steps to obtain the new state $\chi'$
# 3. perform accept/reject move of $\chi'$
# ## Example: Normal mixture
#
# HMC as implemented in PyMC3 is heavily automated. To provide some innsight into how the components of HMC work, let's look at a simpler implementation provided by [`minimc`](https://github.com/ColCarroll/minimc), a package created by <NAME>. This can be used to illustrate leapfrog integration and the paths taken for HMC sampling.
#
# The example we will employ here is a mixture of three bivariate normal distribution, each with its own location and covariance.
# +
from autograd import grad
import autograd.numpy as np
from minimc import mixture, neg_log_mvnormal
# Plotting helper function
def neg_log_p_to_img(neg_log_p, extent=None, num=100):
if extent is None:
extent = (-3, 3, -3, 3)
X, Y = np.meshgrid(np.linspace(*extent[:2], num), np.linspace(*extent[2:], num))
Z = np.array([np.exp(-neg_log_p(j)) for j in np.array((X.ravel(), Y.ravel())).T]).reshape(X.shape)
return Z, extent
np.random.seed(7)
mu1 = np.ones(2)
cov1 = 0.5 * np.array([[1., 0.7],
[0.7, 1.]])
mu2 = -mu1
cov2 = 0.2 * np.array([[1., -0.6],
[-0.6, 1.]])
mu3 = np.array([-1., 2.])
cov3 = 0.3 * np.eye(2)
neg_log_p = mixture([neg_log_mvnormal(mu1, cov1),
neg_log_mvnormal(mu2, cov2),
neg_log_mvnormal(mu3, cov3)], [0.3, 0.3, 0.4])
Z, extent = neg_log_p_to_img(neg_log_p, (-3, 4, -3, 4), num=200)
plt.imshow(Z, alpha=0.9, extent=extent, cmap='afmhot_r', origin='top')
# -
# Though simple, this would be very challenging for a Metropolis sampler, which would have a great deal of difficulty crossing the areas of low probabilities between the peaks. Most of the time, you would end up with an estimate of one of the three components, leaving the others entirely unexplored.
# ### Leapfrog Integration
#
# We can explore the paths taken by HMC samplers by simulating from a leapfrog integrator, which varies by the amount of momentum and the size and number of steps taken.
# +
from minimc.minimc_slow import leapfrog, hamiltonian_monte_carlo
from minimc import neg_log_mvnormal
dVdq = grad(neg_log_p)
steps = slice(None, None, 40)
positions, momentums = [], []
for _ in range(3):
q, p = np.random.randn(2, 2)
_, _, q, p = leapfrog(q, p, dVdq, 4 * np.pi, 0.01)
positions.append(q)
momentums.append(p)
# +
fig, axes = plt.subplots(ncols=len(positions), figsize=(7 * len(positions), 7))
steps = slice(None, None, 40)
Z, extent = neg_log_p_to_img(neg_log_p, (-3, 4, -3, 4), num=200)
for idx, (ax, q, p) in enumerate(zip(axes.ravel(), positions, momentums)):
ax.imshow(Z, alpha=0.9, extent=extent, cmap='afmhot_r', origin='top')
ax.quiver(q[steps, 0], q[steps, 1], p[steps, 0], p[steps, 1], headwidth=6,
scale=60, headlength=7, alpha=0.8, color='C0')
ax.plot(q[:, 0], q[:, 1], '-', lw=3, color='C0')
# -
# ## Hamiltonian Monte Carlo
#
# Rolling leapfrog integration into HMC requires additional choices concerning path length (how far to leapfrog).
np.random.seed(111)
ss, pp, mm, pl = [], [], [], [1, 2, 4]
for path_len in pl:
samples, positions, momentums, accepted = hamiltonian_monte_carlo(10,
neg_log_p,
np.random.randn(2),
path_len=path_len,
step_size=0.01)
ss.append(samples)
pp.append(positions)
mm.append(momentums)
# +
fig, axes = plt.subplots(ncols=len(ss), figsize=(7 * len(ss), 7))
Z, extent = neg_log_p_to_img(neg_log_p, (-3, 4, -3, 4), num=200)
steps = slice(None, None, 20)
for ax, samples, positions, momentums, path_len in zip(axes.ravel(), ss, pp, mm, pl):
ax.imshow(Z, alpha=0.9, extent=extent, cmap='afmhot_r', origin='top')
for q, p in zip(positions, momentums):
ax.quiver(q[steps, 0], q[steps, 1], p[steps, 0], p[steps, 1], headwidth=6,
scale=60, headlength=7, alpha=0.8)
ax.plot(q[:, 0], q[:, 1], 'k-', lw=3)
ax.plot(samples[:, 0], samples[:, 1], 'o', color='w', mfc='C1', ms=10)
ax.set_title(f'Path length of {path_len}')
# -
# ---
#
# ## To Learn More
#
# - **<NAME>. (2010)** [MCMC using Hamiltonian dynamics](http://www.mcmchandbook.net/HandbookChapter5.pdf), in the Handbook of Markov Chain Monte Carlo, <NAME>, <NAME>, <NAME>, and <NAME> (editors), Chapman & Hall / CRC Press, pp. 113-162.
# - **<NAME>'s "[A Conceptual Introduction to Hamiltonian Monte Carlo](https://arxiv.org/abs/1701.02434)"** A thorough, readable reference that is the main source here
# - **<NAME>., and <NAME>. (2014)**. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research: JMLR 15 (1): 1593–1623.
# - **[Hamiltonian Monte Carlo from Scratch](https://colindcarroll.com/2019/04/11/hamiltonian-monte-carlo-from-scratch/)**, by <NAME>, from which the HMC code was stolen.
| notebooks/2-Markov_chain_Monte_Carlo.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Reliability Requirements
#
# Grid operators must plan for resource adequacy. The typical metric for assuring this resource adequacy is the "planning reserve margin" (PRM). The North American Electric Reliability Corporation (NERC) [recommends](https://www.nerc.com/pa/RAPA/ra/Reliability%20Assessments%20DL/IVGTF1-2.pdf) around a 15% PRM.
#
# The planning reserve margin is defined as
#
#
# $$ PRM = \frac{ C_{\text{firm}} - D_{\text{peak}} }{ D_{\text{peak}} }\\
# C_{\text{firm}} = \text{The firm capacity [GW]}\\
# D_{\text{peak}} = \text{The peak demand [GW]}$$
#
#
# Firm capacity is sometimes considered the amount of power guaranteed to be available for the duration of a commitment. We consider firm capacity to be the amount of power that is available "on-demand." Thus, renewable energy sources do not contribute to firm capacity.
# Since we insist on carbon free electricity by 2030 in our simulations, the only technologies available to contribute to firm capacity are
# 1. Nuclear power
# 2. Battery or other kind of storage
#
# We can calculate the required battery storage for each year in the simulation with the following method:
# 1. Conduct Temoa simulation and observe the available capacity for both existing and advanced nuclear technologies.
# 2. Use the above equation to calculate the required battery storage
#
# Based on the HOMER simulation, we estimate the peak demand as 54.39 GW. Any year with zero nuclear capacity thus has a battery storage requirement of (to meet the NERC recommendation):
#
# $$
# PRM = \frac{C_{firm}}{D_{peak}} - 1 = \frac{C_{battery}+C_{nuclear}}{D_{peak}} - 1\\
# (PRM+1)\cdot D_{peak}-C_{nuclear} = C_{battery}\\
# C_{battery} = (0.15+1)\cdot 54.39 [GW]\\
# = 62.56 [GW]
# $$
# +
PRM = 0.15
nuclear_cap = 0.0 # GW
demand_peak = 54.39 # GW
battery_cap = (PRM+1)*demand_peak - nuclear_cap
print(f'Approximately {battery_cap} GW of battery capacity is required to meet NERC reliability recommendations.')
# -
| data/reliability_requirements.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercise 4 - Transmon qubit
#
# ## Historical background
#
# In quantum computing, a qubit is the basic unit of quantum information. It is essentially a two-level quantum mechanical system, can be implemented in many physical systems, including natural systems such as electron spins (spin qubit), atomic levels in ions (trapped ion qubits) or artificial systems such as states in a superconducting circuit (superconducting qubit).
#
# The original superconducting qubit was the Cooper Pair Box debuted in 1999[1], in which a well-defined number of Cooper pairs (bound electrons in a superconductor) occupy an island of superconductor weakly coupled to a lead by a Josephson junction. In Cooper pair box qubit, the energy difference between the $|0\rangle$ state (no Cooper Pairs) and $|1\rangle$ state (a single Cooper Pair)is strongly dependent on any stray or applied electrostatic charges in or around the system. This sensitivity to charge noise leads to qubit dephasing. The qubit dephasing time ($T_2$) for Cooper pair box qubit is typically limited to ~ 1$\mu s$.
#
# The key discovery behind the transmon qubit, first proposed in 2007[2], is that this energy dependence on voltage (known as dispersion) is periodic. By introducing a shunting capacitor, the ratio between the Josephson energy and charging energy $E_J/E_c$ become very large ~ 50, leading to a flat charge dispersion. While Cooper pair box is very sensitive to the charge noise (i.e. uncertainty in x axis position in Fig. 1a), it is largely suppressed in transmon qubit (Fig. 1d). The qubit dephasing time ($T_2$) for transmon qubit is improved significantly. In IBM Quantum systems, $T_2$ is typically ~ 100 $\mu s$. See [`ibmq_santiago`](https://quantum-computing.ibm.com/services?skip=0&systems=all&system=ibmq_santiago) for example.
#
# <figure>
# <img src="resources/transmon-charge-dispersion.png" alt="Transmon charge dispersion" style="width:50%">
# <center><figcaption><b>Fig. 1</b> Charge dispersion of qubit for different ratios $E_J/E_c$. (from Ref [2])</figcaption></center>
# </figure>
#
# In this exercise, you will investigate the characteristic energies of the transmon qubit by performing spectroscopy with a real IBM Quantum system. the ratio between the Josephson energy and charging energy $E_J/E_c$ is the key to solving the charge noise problem of its predecessor, the Cooper Pair Box qubit.
#
# ### References
#
# 1. Nakamura, Yasunobu, <NAME>, and <NAME>. "Coherent control of macroscopic quantum states in a single-Cooper-pair box." Nature 398.6730 (1999): 786-788.
# 2. <NAME>, et al. "Charge-insensitive qubit design derived from the Cooper pair box." Physical Review A 76.4 (2007): 042319.
# 3. <NAME>, et al. "A quantum engineer's guide to superconducting qubits." Applied Physics Reviews 6.2 (2019): 021318.
# ## Energy levels and characteristic energies of the transmon qubit
#
# The Hamiltonian of quantum harmonic oscillator (QHO) can be obtained by quantizing Hamiltonian of a linear LC circuit. Its energy levels are equally spaced (Fig. 2c). By introducing a non-linear circuit element, the Josephson junction, the energy levels of the transmon qubit is modified (Fig. 2d). The energy levels are no longer equally spaced. Higher energy level spacing is smaller than those of lower energies. The anharmonicity $\delta$ is defined as the energy difference between $|1\rangle \rightarrow |2\rangle$ and $|0\rangle \rightarrow |1\rangle$ transition: $\delta = \hbar \omega_{12} - \hbar \omega_{01}$ or simply $\omega_{12} - \omega_{01}$ (we'll set $\hbar \equiv 1$ for the remainder of this discussion). By tunning the microwave frequency to $\omega_{01}$, we can effectively address the multi-level transmon as a two-level system, i.e. a qubit.
#
# <figure>
# <img src="resources/transmon-energy-levels.png" alt="Transmon energy levels" style="width:50%">
# <center><figcaption><b>Fig. 2</b> Energy potential for a quantum harmonic oscillator and a trasmon qubit. (from Ref [3])</figcaption></center>
# </figure>
#
# In superconductors, electrons form Cooper pairs with the effective charge of $2e$, where $e$ is the charge of a single electron. The charging energy $E_c$ is the energy cost of adding a single Cooper pair to the qubit and is related to the capacitance of the superconducting circuit. The Josephson energy $E_J$ is the energy of the Cooper pairs tunneling through the Josephson junction. In transmon qubits, the inductive energy is wholly provided by the Josephson junction, but this is not true of other styles of superconducting qubit (for information on the design and analysis of superconducting qubits, [Qiskit Metal](https://qiskit.org/metal/) has recently been released!).
#
# By deriving the Duffing oscillator Hamiltonian from the Cooper Pair Box Hamiltonian, these energies can be related to the relevant transmon frequencies as
#
# $$
# f_{01} = \sqrt{8 E_c E_J} - E_c \qquad E_c = -\delta = f_{01} - f_{12},
# $$
#
# We will use $f$ to replace $\omega$ as the symbol for frequency for the rest of the notebook, because it is more commonly used for microwave. The anharmonicity $\delta$ is wholly provided by the charging energy $E_c$. Physically, this is incorporated as a large *shunting* (parallel) capacitor to the junction. This addition allows well-separated transmon levels while suppressing susceptibility to the charge noise.
# ## Qiskit Pulse overview
#
# So far, you have been playing with qubits in the abstract quantum circuit level. Physically the quantum gates in circuits are implemented as microwave pulses. Qiskit Pulse provides you pulse level access to manipulate the microwave pulses sending to IBM Quantum system.
#
# As a brief overview, Qiskit Pulse schedules (experiments) consist of Instructions (e.g., Play) acting on Channels (e.g., the drive channel). Here is a summary table of available Instructions and Channels:
#
# 
#
# For more details, this table summarizes the interaction of the channels with the actual quantum hardware:
#
# 
#
# You can learn more about Qiskit Pulse on [Qiskit documentation](https://qiskit.org/documentation/apidoc/pulse.html). However, we find it is more instructive to begin with guided programming in Pulse. Below you will learn how to create pulses, schedules, and run experiments on a real quantum system.
# ## Let's get started!
#
# <div class="alert alert-block alert-success">
#
# **Goal**
#
# Find $|1\rangle \rightarrow |2\rangle$ transition frequency $f_{12}$.
#
# **Plan**
#
# 1. **(Tutorial) Find $|0\rangle \rightarrow |1\rangle$ transition frequency $f_{01}$** using spectroscopy (sweeping frequency).
# 1. **(Tutorial) Calibrate X-180 pulse amplitude** using Rabi oscillation (sweeping amplitude).
# 1. **(Problem) Find $|1\rangle \rightarrow |2\rangle$ transition frequency $f_{12}$** using the calibrated X-180 pulse and spectroscopy (sweeping frequency).
#
# </div>
#
# <div class="alert alert-block alert-danger">
#
# **You will only need to <a href="#problem">modify one cell</a> within this notebook.** You may also need to <a href="#fit-f12">modify the fitting parameters</a> to get a good fit. But other than that, in rest of the cells, nothing needs to be modified. However, you will need to execute the cells by pressing `shift+Enter` in each code block.
#
# </div>
#
# In order to keep things tidy and focus on the important aspects of Qiskit Pulse, the following cells make use of methods from the `helper` module. For the gory details, please refer to the [Investigating Quantum Hardware Using Microwave Pulses
# ](https://qiskit.org/textbook/ch-quantum-hardware/index-pulses.html) chapter of the Qiskit Textbook and Lectures 16-21, Labs 6-7 of the [Qiskit Global Summer School](https://qiskit.org/learn/intro-qc-qh/).
# +
# Import helper module from local folder
import sys
import os
sys.path.append(os.getcwd())
from resources import helper
# Numerical and plotting tools
import numpy as np
import matplotlib.pyplot as plt
# Import SI unit conversion factors
from resources.helper import GHz, MHz, kHz, us, ns
# -
# <div class="alert alert-block alert-danger">
#
# **Special provider**
#
# We have reserved a brand new `ibmq_jakarta` quantum system for the challenge. Participants will have exclusive access to the system during the challenge period (May 20 - 26, 2021) through a special [provider](https://quantum-computing.ibm.com/composer/docs/iqx/manage/provider/#providers). You need to **complete at least one of the five exercises** in the challenge to get assigned to a special provider for the challenge. When you do, you will receive an email with header `You have been added to a new project in IBM Quantum` in the email address associated with your IBM Quantum account. If everything work properly, you should be able to see the information of the special provider in [your account details page](https://quantum-computing.ibm.com/account).
#
# Your IBM Quantum account needs to be associated with an IBMid. Otherwise, you will encounter this error `Login with some authorized required.`. Please [register a new IBMid](https://auth.quantum-computing.ibm.com/auth/idaas) using the SAME email address associated with your IBM Quantum account and login to [IBM Quantum](https://quantum-computing.ibm.com) again.
#
# **Note: It may take up to 12 hours to get assigned to the provider upon completion of other exercises.** If you face any issues, please reach out to us in [#iqc2021](https://qiskit.slack.com/archives/C021UTFN9GE) channel. Join the Qiskit Slack workspace [here](https://ibm.co/joinqiskitslack) if you haven't already.
#
# </div>
#
# Run the cell below to check if you have been assigned to a special provider. If you are added to a special provider, you should be able to see in the output a provider looks like this `<AccountProvider for IBMQ(hub='iqc2021-n', group='challenge-m', project='ex4')>` where `n` is a number goes from `1` to `10` and `m` is a number goes from `1` to `1000`. You will need this information to get access to `ibmq_jakarta` quantum system reserved for the challenge.
# +
# Importing standard Qiskit libraries
from qiskit import IBMQ
from qiskit.tools.jupyter import *
# Loading your IBM Quantum account
IBMQ.load_account()
IBMQ.providers() # see a list of providers you have access to
# +
# Get the special provider assigned to you using information from the output above
hub_name = 'iqc2021-1' # e.g. 'iqc2021-1'
group_name = 'challenge-123' # e.g. 'challenge-1'
project_name = 'ex4' # Your project name should be 'ex4'
provider = IBMQ.get_provider(hub=hub_name, group=group_name, project=project_name)
# Get `ibmq_jakarta` backend from the provider
backend_name = 'ibmq_jakarta'
backend = provider.get_backend(backend_name)
backend # See details of the `ibmq_jakarta` quantum system
# -
# ### Instantiate channels and retrieve measurement schedule
#
# We will use the same measurement schedule throughout, whereas the drive schedules will vary. For any backend, we can ask for its default measurement pulse instead of calibrating it separately.
# +
from qiskit import pulse
from qiskit.pulse import Play, Schedule, DriveChannel
# Please use qubit 0 throughout the notebook
qubit = 0
# -
# Next, save the backend configuration and the sampling time $dt$. We will exclude the `AcquireChannel`s when plotting for clarity.
backend_config = backend.configuration()
exc_chans = helper.get_exc_chans(globals())
dt = backend_config.dt
print(f"Sampling time: {dt*1e9} ns")
# The `instruction_schedule_map` provides the parameters of the default calibrated pulses used by the backend. In particular, we see that this "native gate set" consists of a subset of operations you can perform on a [`QuantumCircuit`](https://qiskit.org/documentation/apidoc/circuit.html#gates-and-instructions), and is the gate set that the `QuantumCircuit` is transpiled to by Qiskit.
backend_defaults = backend.defaults()
center_frequency = backend_defaults.qubit_freq_est
inst_sched_map = backend_defaults.instruction_schedule_map
inst_sched_map.instructions
# The instructions consist of the native gate set of the backend: single-qubit gates square-root of $X$, `sx`, and parameterized rotation about the $Z$-axis, `rz(θ)`, and the two-qubit controlled-NOT, `cx`. There are several other gates listed here, in particular the soon-to-be deprecated ["U-gates"](https://qiskit.org/textbook/ch-states/single-qubit-gates.html#generalU3) based on Euler angles, summarized below for completeness
#
# Basis Gate | Operation
# --- | ---
# `u1(λ)` | `rz(λ)`
# `u2(φ,λ)` | `rz(φ+π/2) sx rz(λ-π/2)`
# `u3(θ,φ,λ)` | `rz(φ+π) sx rz(θ+π) sx rz(λ)`
# `id` | identity
# `x` | $X$ for echoes in dynamical decoupling
# `measure` | measurement
#
# One thing to note is that each `sx` consists of one physical pulse and the `rz`s are implemented in software by [frame changes](https://arxiv.org/abs/1612.00858). From the `instruction_schedule_map` we can retrieve the default measurement pulse instead of building it from scratch. This also serves as a useful starting point from retrieving calibrated pulses and manipulating them further.
# Retrieve calibrated measurement pulse from backend
meas = inst_sched_map.get('measure', qubits=[qubit])
meas.exclude(channels=exc_chans).draw(time_range=[0,1000])
# <div class="alert alert-block alert-success">
#
# ## Step 1 (Tutorial): Find $|0\rangle \rightarrow |1\rangle$ transition
#
# You don't need to modify any code in this section. Just go through all the cells and make sure you understand the steps. Pay close attention to how `spec01_scheds` is built. You will need to build similar pulse schedules in <a href="#problem">the final problem</a>. You can learn more about how to build pulse schedule in [this tutorial](https://qiskit.org/documentation/tutorials/circuits_advanced/06_building_pulse_schedules.html).
#
# </div>
# +
from qiskit.pulse import DriveChannel, Gaussian
# The same spec pulse for both 01 and 12 spec
drive_amp = 0.25
drive_duration = inst_sched_map.get('x', qubits=[qubit]).duration
# Calibrated backend pulse use advanced DRAG pulse to reduce leakage to the |2> state.
# Here we will use simple Gaussian pulse
drive_sigma = drive_duration // 4 # DRAG pulses typically 4*sigma long.
spec_pulse = Gaussian(duration=drive_duration, amp=drive_amp,
sigma=drive_sigma, name=f"Spec drive amplitude = {drive_amp}")
# Construct an np array of the frequencies for our experiment
spec_freqs_GHz = helper.get_spec01_freqs(center_frequency, qubit)
# Create the base schedule
# Start with drive pulse acting on the drive channel
spec01_scheds = []
for freq in spec_freqs_GHz:
with pulse.build(name="Spec Pulse at %.3f GHz" % freq) as spec01_sched:
with pulse.align_sequential():
# Pay close attention to this part to solve the problem at the end
pulse.set_frequency(freq*GHz, DriveChannel(qubit))
pulse.play(spec_pulse, DriveChannel(qubit))
pulse.call(meas)
spec01_scheds.append(spec01_sched)
print("Number of schedules :",len(spec01_scheds))
# Draw spec01 schedule
spec01_scheds[-1].exclude(channels=exc_chans).draw(time_range=[0,1000])
# +
from qiskit.tools.monitor import job_monitor
# Run the job on a real backend
spec01_job = backend.run(spec01_scheds, job_name="Spec 01", **helper.job_params)
print(spec01_job.job_id())
job_monitor(spec01_job)
# -
# ### Fit the Spectroscopy Data
#
# We will fit the spectroscopy signal to a *Lorentzian* function of the form
#
# $$ \frac{AB}{\pi[(f-f_{01})^2 + B^2]} + C $$
#
# to find the qubit frequency $f_{01}$ with these fitting parameters:
#
#
# Parameter | Corresponds to
# --- | ---
# $A$ | amplitude
# $f_{01}$ | 01 frequency guess (GHz)
# $B$ | scale
# $C$ | offset
#
#
# We will use the `SpecFitter` from the `helper` module that is based on the fitters from `qiskit.ignis.characterization.fitters` library.
#
# <div class="alert alert-block alert-danger">
#
# **Note:** You may need to modify the fitting parameters below to get a good fit.
#
# </div>
# +
from resources.helper import SpecFitter
amp_guess = 5e6
f01_guess = 5
B = 1
C = 0
fit_guess = [amp_guess, f01_guess, B, C]
fit = SpecFitter(spec01_job.result(), spec_freqs_GHz, qubits=[qubit], fit_p0=fit_guess)
fit.plot(0, series='z')
f01 = fit.spec_freq(0, series='z')
print("Spec01 frequency is %.6f GHz" % f01)
# -
# Let's compare your result with the calibrated qubit frequency from the backend! If things are working properly, your result should be very close to the calibrated value ($\pm$1 MHz).
# Retrieve qubit frequency from backend properties
f01_calibrated = backend.properties().frequency(qubit) / GHz
f01_error = abs(f01-f01_calibrated) * 1000 # error in MHz
print("Qubit frequency error is %.6f MHz" % f01_error)
# 🎉 Congratulations! You have successfully ran your first pulse experiment on a real quantum system and analyzed the data. This was not possible without access to an advanced research lab before [less than two years ago](https://www.ibm.com/blogs/research/2019/12/qiskit-openpulse/), when we released Qiskit Pulse and provided pulse access in our open quantum system `ibmq_armonk`. Now you can do experimental quantum physics on your laptop in the comfort of your home. This is incredible!
# <div class="alert alert-block alert-success">
#
# ## Step 2 (Tutorial): Calibrate X-180 pulse amplitude using Rabi oscillation
#
# You don't need to modify any code in this section. Just go through all the cells and make sure you understand the steps.
# </div>
#
# ### Build Rabi schedule from measured frequency
# +
max_rabi_amp = 0.75
rabi_amps = helper.get_rabi_amps(max_rabi_amp)
#make the list for the schedule
rabi_scheds = []
for ridx, amp in enumerate(rabi_amps):
with pulse.build(name="rabisched_%d_0" % ridx) as sched: # '0' corresponds to Rabi
with pulse.align_sequential():
# set the frequency
pulse.set_frequency(f01*GHz, DriveChannel(qubit))
rabi_pulse = Gaussian(duration=drive_duration, amp=amp, \
sigma=drive_sigma, name=f"Rabi drive amplitude = {amp}")
pulse.play(rabi_pulse, DriveChannel(qubit))
pulse.call(meas)
rabi_scheds.append(sched)
# Draw rabi schedule
rabi_scheds[-1].exclude(channels=exc_chans).draw(time_range=[0,1000])
# +
# Run the job on a real device
rabi_job = backend.run(rabi_scheds, job_name="Rabi", **helper.job_params)
print(rabi_job.job_id())
job_monitor(rabi_job)
# -
# ### Fit the Rabi Data
#
# We will fit the Rabi signal to a sinusoidal function of the form
#
# $$ a \cos(2\pi f x + \phi) + c $$
#
# to find the Rabi period $T = 2\pi/f$ with these fitting parameters:
#
#
# Parameter | Corresponds to
# --- | ---
# $a$ | amplitude
# $f$ | Rabi drive frequency
# $\phi$ | phase offset
# $c$ | offset
#
#
# We will use the `RabiFitter` from the `qiskit.ignis.characterization.calibration.fitters` library.
#
# <div class="alert alert-block alert-danger">
#
# **Note:** You may need to modify the fitting parameters below to get a good fit.
#
# </div>
# +
from qiskit.ignis.characterization.calibrations.fitters import RabiFitter
amp_guess = 5e7
fRabi_guess = 3
phi_guess = 0.5
c_guess = 0
fit_guess = [amp_guess, fRabi_guess, phi_guess, c_guess]
fit = RabiFitter(rabi_job.result(), rabi_amps, qubits=[qubit], fit_p0=fit_guess)
fit.plot(qind=0, series='0')
x180_amp = fit.pi_amplitude()
print("Pi amplitude is %.3f" % x180_amp)
# -
# <div id='problem'></div>
# <div class="alert alert-block alert-success">
#
# ## Step 3 (Problem): Find $|1\rangle \rightarrow |2\rangle$ transition frequency
#
# In order to observe the transition between the $|1\rangle$ and $|2\rangle$ states of the transmon, you need to:
#
# 1. Apply an $X_\pi$ pulse to transition the qubit from $|0\rangle$ to $|1\rangle$.
# 1. Apply a second pulse with varying frequency to find the $|1\rangle \rightarrow |2\rangle$ transition.
#
# </div>
# <div class="alert alert-block alert-danger">
# The cell below is the only one you need to modify in the entire notebook.
# </div>
# +
# Define pi pulse
x_pulse = Gaussian(duration=drive_duration,
amp=x180_amp,
sigma=drive_sigma,
name='x_pulse')
# define gaussian
# The same spec pulse for both 01 and 12 spec
drive_amp = 0.25
drive_duration = inst_sched_map.get('x', qubits=[qubit]).duration
# Calibrated backend pulse use advanced DRAG pulse to reduce leakage to the |2> state.
# Here we will use simple Gaussian pulse
drive_sigma = drive_duration // 4 # DRAG pulses typically 4*sigma long.
spec_pulse = Gaussian(duration=drive_duration, amp=drive_amp,
sigma=drive_sigma, name=f"Spec drive amplitude = {drive_amp}")
def build_spec12_pulse_schedule(freq, anharm_guess_GHz):
with pulse.build(name="Spec Pulse at %.3f GHz" % (freq+anharm_guess_GHz)) as spec12_schedule:
with pulse.align_sequential():
# WRITE YOUR CODE BETWEEN THESE LINES - START
# first add x pi pulse
pulse.play(x_pulse, DriveChannel(qubit))
# now add the varying frequency pulse
pulse.set_frequency(freq*GHz + anharm_guess_GHz*GHz, DriveChannel(qubit))
pulse.play(spec_pulse,DriveChannel(qubit))
pulse.call(meas)
# WRITE YOUR CODE BETWEEN THESE LINES - END
return spec12_schedule
# -
# The anharmonicity of our transmon qubits is typically around $-300$ MHz, so we will sweep around that value.
# +
anharmonicity_guess_GHz = -0.28 # your anharmonicity guess
freqs_GHz = helper.get_spec12_freqs(f01, qubit)
# Now vary the sideband frequency for each spec pulse
spec12_scheds = []
for freq in freqs_GHz:
spec12_scheds.append(build_spec12_pulse_schedule(freq, anharmonicity_guess_GHz))
# Draw spec12 schedule
spec12_scheds[40].exclude(channels=exc_chans).draw(time_range=[0,1000])
# +
# Run the job on a real device
spec12_job = backend.run(spec12_scheds, job_name="Spec 12", **helper.job_params)
print(spec12_job.job_id())
job_monitor(spec12_job)
# If the queuing time is too long, you can save the job id
# And retrieve the job after it's done
# Replace 'JOB_ID' with the the your job id and uncomment to line below
#spec12_job = backend.retrieve_job('JOB_ID')
# -
# ### Fit the Spectroscopy Data
#
# <div id='fit-f12'></div>
#
# We will again fit the spectroscopy signal to a Lorentzian function of the form
#
# $$ \frac{AB}{\pi[(f-f_{12})^2 + B^2]} + C $$
#
# to find the frequency of the $|1\rangle \to |2\rangle$ transition $f_{12}$ with these fitting parameters:
#
# Parameter | Corresponds to
# --- | ---
# $A$ | amplitude
# $f_{12}$ | 12 frequency guess (GHz)
# $B$ | scale
# $C$ | offset
#
#
# <div class="alert alert-block alert-danger">
#
# **Note:** You may need to modify the fitting parameters below to get a good fit.
#
# </div>
# +
amp_guess = 2e7
f12_guess = f01 - 0.27
B = .1
C = 0
fit_guess = [amp_guess, f12_guess, B, C]
fit = SpecFitter(spec12_job.result(), freqs_GHz+anharmonicity_guess_GHz, qubits=[qubit], fit_p0=fit_guess)
fit.plot(0, series='z')
f12 = fit.spec_freq(0, series='z')
print("Spec12 frequency is %.6f GHz" % f12)
# -
# Check your answer using following code
from qc_grader import grade_ex4
grade_ex4(f12,qubit,backend_name)
# Submit your answer. You can re-submit at any time.
from qc_grader import submit_ex4
submit_ex4(f12,qubit,backend_name)
# ## Calculating $E_J/E_c$
#
# Modifying the equations in the introduction section, we can calculate $E_c$ and $E_J$ using $f_{01}$ and $f_{12}$ obtained from the pulse experiments:
#
# $$
# E_c = -\delta = f_{01} - f_{12} \qquad E_J = \frac{(2f_{01}-f_{12})^2}{8(f_{01}-f_{12})}
# $$
Ec = f01 - f12
Ej = (2*f01-f12)**2/(8*(f01-f12))
print(f"Ej/Ec: {Ej/Ec:.2f}") # This value is typically ~ 30
# ## Additional information
#
# **Created by:** <NAME>, <NAME>
#
# **Version:** 1.0.0
| solutions by participants/ex4/ex4-InnanNouhaila.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="lXToC5a2H6oi"
# #### TF-IDF
# + [markdown] id="jiJ_pvCgH9xE"
# $n_{\mathbb{d}\mathbb{w}}$ - term frequency - the number of times that word/term $\mathbb{w}$ occurs in document $\mathbb{d}$
# divided by the number of all words in the document;<br>
# $N_{\mathbb{w}}$ - the number of documents containing the term $\mathbb{w}$;<br>
# $N$ - total number of documents; <br><br>
#
# $p(\mathbb{w}, \mathbb{d}) = N_{\mathbb{w}} / N$ - probabilty of appearence of the term $\mathbb{w}$ in any document $\mathbb{d}$
# <br>
# $P(\mathbb{w}, \mathbb{d}, n_{\mathbb{d}\mathbb{w}}) = (N_{\mathbb{w}} / N)^{n_{\mathbb{d}\mathbb{w}}}$ - probability that the given term $\mathbb{w}$ appears $n_{\mathbb{d}\mathbb{w}}$ times in document $\mathbb{d}$<br><br>
#
# $-\log{P(\mathbb{w}, \mathbb{d}, n_{\mathbb{d}\mathbb{w}})} = n_{\mathbb{d}\mathbb{w}} \cdot \log{(N / N_{\mathbb{w}})} = TF(\mathbb{w}, \mathbb{d}) \cdot IDF(\mathbb{w})$<br><br>
#
# $TF(\mathbb{w}, \mathbb{d}) = n_{\mathbb{d}\mathbb{w}}$ - term frequency;<br>
# $IDF(\mathbb{w}) = \log{(N /N_{\mathbb{w}})}$ - inverted document frequency;
# + [markdown] id="iksete4U2e7W"
# ### Some parameters of TfidfVectorizer
#
# ##### input : string {‘filename’, ‘file’, ‘content’}
# ##### lowercase : boolean, default True
# ##### preprocessor : callable or None (default)
# ##### tokenizer : callable or None (default)
# ##### stop_words : string {‘english’}, list, or None (default)
# ##### ngram_range : tuple (min_n, max_n)
# ##### max_df : float in range [0.0, 1.0] or int, default=1.0
# ##### min_df : float in range [0.0, 1.0] or int, default=1
# ##### max_features : int or None, default=None
#
# + colab={"base_uri": "https://localhost:8080/"} id="5Ys0dV-RIDYz" outputId="1220540a-de11-4199-879a-369e2e786dbe"
from sklearn.datasets import fetch_20newsgroups
categories = ['alt.atheism', 'talk.religion.misc',
'comp.graphics', 'sci.space']
newsgroups_train = fetch_20newsgroups(subset='train',
categories=categories)
# + id="oR21XB3q3G0B"
newsgroups_train.data[:5]
# + colab={"base_uri": "https://localhost:8080/"} id="RdpDkFmL2YaJ" outputId="bb225c9d-d0f7-4981-84e0-a035afa07f5e"
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="i1KMtbec3AyP" outputId="56fe96ef-5a82-4a5b-ea1d-1668ebff0f45"
vectorizer = TfidfVectorizer(lowercase=False)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="z4Dq2d0I3Kct" outputId="23a39c73-4d72-4fc7-f71e-8244c837754f"
vectorizer.get_feature_names()[:10]
# + colab={"base_uri": "https://localhost:8080/"} id="R2YhUuzk3zG5" outputId="54302810-363d-4dee-acea-e1a6f3f6f30c"
vectorizer = TfidfVectorizer(min_df=0.8)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="sy1Tw_Cr32eB" outputId="0ee2fe0a-6368-490b-c9bd-215375a4260c"
vectorizer.get_feature_names()
# + colab={"base_uri": "https://localhost:8080/"} id="wby51AxC37L3" outputId="1bf50a2a-f3d4-4023-e03e-fecbcf2fcb68"
vectorizer = TfidfVectorizer(min_df=0.01, max_df=0.8)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="aE9iO5wC3_jc" outputId="0202441a-3ec9-41bc-daf7-0c7fda5fd0c8"
vectorizer = TfidfVectorizer(ngram_range=(1, 3), min_df=0.03, max_df=0.9)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="vrScK0Dj4DV1" outputId="1c036bdb-0b1e-4549-c9ef-6043c88520cd"
import nltk
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
nltk.download('punkt')
nltk.download('stopwords')
nltk.download('wordnet')
stopWords = set(stopwords.words('english'))
wnl = nltk.WordNetLemmatizer()
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="aPqUL9168CcJ" outputId="9769c7a7-ef27-42f1-fdf8-c172d7585b2c"
def preproc1(text):
return ' '.join([wnl.lemmatize(word) for word in word_tokenize(text.lower()) if word not in stopWords])
st = "The saddest aspect of life right now is that science gathers knowledge faster than society gathers wisdom."
preproc1(st)
# + colab={"base_uri": "https://localhost:8080/"} id="-WlFDLQ28ZaX" outputId="026f516c-5afe-47e9-f577-51339f3cb937"
vectorizer = TfidfVectorizer(preprocessor=preproc1)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + colab={"base_uri": "https://localhost:8080/"} id="dqq4uIP881kt" outputId="fa21f23e-1c51-4c2a-8dc7-a8ad82cbb3af"
#vectorizer = TfidfVectorizer(preprocessor=preproc1, ngram_range=(1, 3), max_df=0.5, max_features=1000)
vectorizer = TfidfVectorizer(preprocessor=preproc1, min_df = 0.001, max_df=0.9)
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
# + id="rolvaMuG-HoT"
vectorizer.get_feature_names()[::100]
# + id="orD9VhzJ-L1C"
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.linear_model import SGDClassifier
# + colab={"base_uri": "https://localhost:8080/"} id="SVdWw59C-QYd" outputId="b52b8349-adcb-4981-ae9a-07ccbf433aeb"
dense_vectors = vectors.todense()
X_train, X_test, y_train, y_test= train_test_split(dense_vectors, newsgroups_train.target, test_size=0.2, random_state=0)
y_train.shape, y_test.shape
# + colab={"base_uri": "https://localhost:8080/"} id="IVNCXqdmDww0" outputId="95d9c554-7264-4923-d9f8-80701005433c"
from sklearn.metrics import accuracy_score
svc = svm.SVC()
svc.fit(X_train, y_train)
accuracy_score(y_test, svc.predict(X_test))
# + colab={"base_uri": "https://localhost:8080/"} id="bAVoH12TEDUV" outputId="b1d77047-7dac-4951-9053-38a5d0876f56"
sgd = SGDClassifier()
sgd.fit(X_train, y_train)
accuracy_score(y_test, sgd.predict(X_test))
# + [markdown] id="QFJJ0sbyFwyI"
# ### Custom TF-IDF
# + id="XcGzYrBFENXb"
# just for practicing with unigrams
import math
from collections import Counter
class MyTfIdf():
def __init__(self, preprocessor=None, min_df = 0.001, max_df = 0.9):
self.preproc_func = preprocessor
self.vocab = []
self.idf = {}
self.term2id = {}
self.min_df = min_df
self.max_df = max_df
def __prepoc_data(self, data):
preproc_data = data
if self.preproc_func is not None:
preproc_data = list(map(self.preproc_func, preproc_data))
preproc_data = list(map(lambda x: x.split(), preproc_data))
return preproc_data
def fit(self, data):
preproc_data = self.__prepoc_data(data)
vocab_set = set()
for doc in preproc_data:
vocab_set.update(doc)
self.vocab = sorted(list(vocab_set))
df = dict(zip(self.vocab, [0]*len(self.vocab)))
for doc in preproc_data:
doc_vocab_set = set(doc)
for term in doc_vocab_set:
if term in df.keys():
df[term] += 1
for k, v in df.items():
df[k] = v / len(preproc_data)
df = {k: v for k, v in df.items() if v > self.min_df and v < self.max_df}
for k, v in df.items():
self.idf[k] = math.log(1 / v)
for i, val in enumerate(self.idf.keys()):
self.term2id[val] = i
def fit_transform(self, data):
self.fit(data)
preproc_data = self.__prepoc_data(data)
results = []
for doc in preproc_data:
doc_vector = [0]*len(self.idf.keys())
term_cnts = Counter(doc)
for term in term_cnts.keys():
if term in self.term2id.keys():
tf = term_cnts[term]/len(doc)
doc_vector[self.term2id[term]] = tf * self.idf[term]
results.append(doc_vector)
return results #self.idf #preproc_data#self.idf
# + id="CCEN3FRsF3TV"
my_vectorizer = MyTfIdf(preprocessor=preproc1)
my_vectors = my_vectorizer.fit_transform(newsgroups_train.data)
list(filter(lambda x: x!=0, my_vectors[0]))
# + colab={"base_uri": "https://localhost:8080/"} id="2isPalhJKHJt" outputId="323c5497-6609-4874-f754-2c2483226950"
X_train, X_test, y_train, y_test= train_test_split(my_vectors, newsgroups_train.target, test_size=0.2, random_state=0)
y_train.shape, y_test.shape
# + colab={"base_uri": "https://localhost:8080/"} id="XftrZwR5qtOb" outputId="5ebb8e9c-45ef-48d6-e502-e40c7a0c2890"
from sklearn.metrics import accuracy_score
svc = svm.SVC()
svc.fit(X_train, y_train)
accuracy_score(y_test, svc.predict(X_test))
# + colab={"base_uri": "https://localhost:8080/"} id="fZE8vHRqdFoG" outputId="58afe497-4d39-4a26-8d71-3f0442193b06"
sgd = SGDClassifier()
sgd.fit(X_train, y_train)
accuracy_score(y_test, sgd.predict(X_test))
# + id="TCX2djWudmjS"
| tf_idf_details/TF_IDF_details.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (spinningup)
# language: python
# name: spinningup
# ---
# + [markdown] colab_type="text" id="XT2oM6FHVJCf"
# ## Enviroment:
# Open AI gym [MountainCar-v0](https://github.com/openai/gym/wiki/MountainCar-v0)
#
# ### Observation
# Type: Box(2)
#
# | Num | Observation | Min | Max |
# | ---- | ----------- | ----- | ---- |
# | 0 | position | -1.2 | 0.6 |
# | 1 | velocity | -0.07 | 0.07 |
#
# ### Actions
#
# Type: Discrete(3)
#
# | Num | Action |
# | ---- | ---------- |
# | 0 | push left |
# | 1 | no push |
# | 2 | push right |
#
# ### Reward
#
# -1 for each time step, until the goal position of 0.5 is reached. As with MountainCarContinuous v0, there is no penalty for climbing the left hill, which upon reached acts as a wall.
#
# ### Starting State
#
# Random position from -0.6 to -0.4 with no velocity.
#
# ### Episode Termination
#
# The episode ends when you reach 0.5 position, or if 200 iterations are reached.
#
# + [markdown] colab_type="text" id="xzVWtGxJVJCh"
# ## 1. gym enviroment setup
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="G312rzBjVJCi" outputId="f24448be-40e1-4cdd-e008-15b2534e6d37"
import gym
import numpy as np
import matplotlib.pyplot as plt
env = gym.make("MountainCar-v0")
env.reset()
# + colab={} colab_type="code" id="80YCNcHUZYtI"
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import models
from tensorflow.keras import losses,optimizers,metrics
from tensorflow.keras.layers import Dense, Activation, Flatten
from tensorflow.keras.optimizers import Adam
from collections import deque
import random
from tqdm import tqdm
# + colab={} colab_type="code" id="IjkusASudj9W"
ACTION_SPACE_SIZE = env.action_space.n
REPLAY_MEMORY_SIZE = 50_000
MIN_REPLAY_MEMORY_SIZE = 1_000
MINIBATCH_SIZE = 64
UPDATE_TARGET_EVERY = 5
DISCOUNT = 0.99
EPISODES =1000
# Exploration settings
epsilon = 1 # not a constant, going to be decayed
EPSILON_DECAY = 0.995
MIN_EPSILON = 0.001
ep_rewards = []
AGGREGATE_STATS_EVERY = 50
MIN_EPSILON = 0.001
# + [markdown] colab_type="text" id="Gm5w81XdRgyz"
# ### Plot epsilon decay
# + colab={"base_uri": "https://localhost:8080/", "height": 286} colab_type="code" id="41yF0b4u46gb" outputId="03888fbc-7567-49b7-f190-4910f8c40816"
recorder = {"epsode":[],"epsilon":[]}
for epsode in range(EPISODES):
if epsilon > MIN_EPSILON:
epsilon *= EPSILON_DECAY
epsilon = max(MIN_EPSILON, epsilon)
recorder["epsode"].append(epsode)
recorder["epsilon"].append(epsilon)
plt.plot(recorder["epsode"], recorder["epsilon"])
# + [markdown] colab_type="text" id="fkddyPjSZOBU"
# ## 2. Create Model
# + colab={} colab_type="code" id="tlX30pzsZXOb"
def create_model():
model = models.Sequential()
model.add(Dense(16 ,input_shape=(env.observation_space.shape)))
model.add(Activation('relu'))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(ACTION_SPACE_SIZE))
model.add(Activation('linear'))
print(model.summary())
model.compile(loss = 'mse', optimizer=Adam(lr=0.001),metrics=['accuracy'])
return model
# + [markdown] colab_type="text" id="lTRr9PZPZ1-1"
# ## 2. Agent Class
# + colab={} colab_type="code" id="w_7sLLVzZ1Tj"
class DQNAgent:
def __init__(self):
# Replay memory
self.replay_memory = deque(maxlen=REPLAY_MEMORY_SIZE)
# Prediction Network (the main Model)
self.model_prediction = create_model()
# Target Network
self.model_target = create_model()
self.model_target.set_weights(self.model_prediction.get_weights())
# Used to count when to update target network with prediction network's weights
self.target_update_counter = 0
# Adds step's data to a memory replay array
# (current_state, action, reward, next_state, done)
def update_replay_memory(self, transition):
self.replay_memory.append(transition)
# Queries prediction network for Q values given current observation space (environment state)
def get_qs(self, state):
return self.model_prediction.predict(np.array(state).reshape(-1, *state.shape))[0]
def train(self, terminal_state, step):
if len(self.replay_memory) < MIN_REPLAY_MEMORY_SIZE:
return
minibatch = random.sample(self.replay_memory, MINIBATCH_SIZE)
# Get current states from minibatch, then query NN model_prediction for current Q values
current_states = np.array([transition[0] for transition in minibatch])
current_qs_list = self.model_prediction.predict(current_states)
# Get next_states from minibatch, then query NN model_target for target Q values
# When using target network, query it, otherwise main network should be queried
next_states = np.array([transition[3] for transition in minibatch])
target_qs_list = self.model_target.predict(next_states)
X = []
y = []
# Now we need to enumerate our batches
for index, (current_state, action, reward, next_state, done) in enumerate(minibatch):
# If not a terminal state, get new q from future states, otherwise set it to 0
# almost like with Q Learning, but we use just part of equation here
if not done:
max_target_q = np.max(target_qs_list[index])
new_q = reward + DISCOUNT * max_target_q
else:
new_q = reward
# Update Q value for given state
current_qs = current_qs_list[index]
current_qs[action] = new_q
# And append to our training data
X.append(current_state)
y.append(current_qs)
# Fit on all samples as one batch, log only on terminal state
self.model_prediction.fit(np.array(X), np.array(y), batch_size=MINIBATCH_SIZE, verbose=0, shuffle=False if terminal_state else None)
# Update target network counter every episode
if terminal_state:
self.target_update_counter +=1
# If counter reaches set value, update target network with weights of main network
if self.target_update_counter > UPDATE_TARGET_EVERY:
self.model_target.set_weights(self.model_prediction.get_weights())
self.target_update_counter = 0
# + colab={"base_uri": "https://localhost:8080/", "height": 874} colab_type="code" id="TUDDhaxOadLa" outputId="4b30291d-f387-435a-e011-fa542d80db43"
agent = DQNAgent()
# + [markdown] colab_type="text" id="EvjpcUbaR3EF"
# ## 3. Train the agent
# + colab={} colab_type="code" id="I7j_aM56tO2_"
aggr_ep_rewards = {'ep':[],'avg':[],'min':[],'max':[]}
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="Xmoxp-PEjN3s" outputId="d39fc30e-0129-4c0e-a845-907eed7aea69"
# Iterate over episodes
for episode in tqdm(range(1, EPISODES + 1), ascii=True, unit='episodes'):
# # Update tensorboard step every episode
# agent.tensorboard.step = episode
# Restarting episode - reset episode reward and step number
episode_reward = 0
step = 1
# Reset environment and get initial state
current_state = env.reset()
# Reset flag and start iterating until episode ends
done = False
while not done:
# This part stays mostly the same, the change is to query a model for Q values
if np.random.random() > epsilon:
# Get action from Q table
action = np.argmax(agent.get_qs(current_state))
else:
# Get random action
action = np.random.randint(0, ACTION_SPACE_SIZE)
next_state, reward, done, _ = env.step(action)
# Transform new continous state to new discrete state and count reward
episode_reward += reward
# if SHOW_PREVIEW and not episode % AGGREGATE_STATS_EVERY:
# env.render()
# Every step we update replay memory and train main network
agent.update_replay_memory((current_state, action, reward, next_state, done))
agent.train(done, step)
current_state = next_state
step += 1
# Append episode reward to a list and log stats (every given number of episodes)
ep_rewards.append(episode_reward)
if not episode % AGGREGATE_STATS_EVERY or episode == 1:
average_reward = sum(ep_rewards[-AGGREGATE_STATS_EVERY:])/len(ep_rewards[-AGGREGATE_STATS_EVERY:])
min_reward = min(ep_rewards[-AGGREGATE_STATS_EVERY:])
max_reward = max(ep_rewards[-AGGREGATE_STATS_EVERY:])
# rewards recording
aggr_ep_rewards['ep'].append(episode)
aggr_ep_rewards['avg'].append(average_reward)
aggr_ep_rewards['min'].append(min_reward)
aggr_ep_rewards['max'].append(max_reward)
# agent.tensorboard.update_stats(reward_avg=average_reward, reward_min=min_reward, reward_max=max_reward, epsilon=epsilon)
# Save model, but only when min reward is greater or equal a set value
# if min_reward >= MIN_REWARD:
# agent.model.save(f'models/{MODEL_NAME}__{max_reward:_>7.2f}max_{average_reward:_>7.2f}avg_{min_reward:_>7.2f}min__{int(time.time())}.model')
# Decay epsilon
if epsilon > MIN_EPSILON:
epsilon *= EPSILON_DECAY
epsilon = max(MIN_EPSILON, epsilon)
# + [markdown] colab_type="text" id="QQ22Ry_q4mQS"
# ## Plot episodes vs rewards
# + colab={"base_uri": "https://localhost:8080/", "height": 300} colab_type="code" id="G1TtpQaZVJDA" outputId="5119d0e5-ca00-4d78-d9d6-887c5c7d7904"
plt.plot(aggr_ep_rewards['ep'], aggr_ep_rewards['avg'], label = 'avg')
plt.plot(aggr_ep_rewards['ep'], aggr_ep_rewards['min'], label = 'min')
plt.plot(aggr_ep_rewards['ep'], aggr_ep_rewards['max'], label = 'max')
plt.legend(loc='upper left')
plt.xlabel('Episodes')
plt.ylabel('Rewards')
# + [markdown] colab_type="text" id="nwD41YstHyGx"
# ### Save model
# + colab={} colab_type="code" id="YU3N0zE_HxQb"
agent.model_prediction.save('dqn_1.model')
# + [markdown] colab_type="text" id="9ILbxFFfIckN"
# ### Rendering Test
# + colab={} colab_type="code" id="iFZ1eIgjHwXw"
done = False
state = env.reset()
while not done:
qs_list = agent.get_qs(state)
action = np.argmax(qs_list())
next_state, _, done, _ = env.step(action)
state = next_state
env.render()
env.close()
| 10_Renforcement_Learning_Moutain_Car/5_DQN_keras_mountain_car.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import findspark
findspark.init()
import pyspark
# +
import sys
from pyspark.context import SparkContext
from pyspark.sql.session import SparkSession
from pyspark.sql import SparkSession, functions, types, Window
from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorAssembler, StandardScaler
from pyspark.ml import Pipeline
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller, coint
#assert sys.version_info >= (3, 5) # make sure we have Python 3.5+
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# -
#remove null/nan or empty cell
def to_null(c):
return functions.when(~(functions.col(c).isNull() | functions.isnan(functions.col(c)) | (functions.trim(functions.col(c)) == "")), functions.col(c))
#clean inpou data and pivot table
def clean(minutedt):
minutedt=minutedt.select([to_null(c).alias(c) for c in minutedt.columns]).na.drop()
minutedt.createOrReplaceTempView('minutedt')
notnull = spark.sql(""" SELECT DateTime, SUBSTRING_INDEX(windcode, '.',1) AS symbol,close FROM minutedt """)
notnull.createOrReplaceTempView('notnull')
pivoted = spark.sql("""SELECT * FROM
(
SELECT DateTime, symbol, close
FROM notnull
)
PIVOT
(
SUM(close)
FOR symbol in ("000008" AS a, "000009" AS b, '000010' AS c, '000011' AS d, '000012' AS e, "000014" AS f, "000016" AS g, '000017' AS h, '000020' AS i, '000021' AS j)
)
ORDER BY DateTime """).cache()
pivoted.createOrReplaceTempView('pivoted')
dt = spark.sql("""SELECT DateTime, a,b,c,d,e,f,g,h ,i,j FROM pivoted """)
dt=dt.select([to_null(c).alias(c) for c in dt.columns]).na.drop()
dt.createOrReplaceTempView('dt')
return dt
#find all cointgration stock pair under threshodl, pvalue <0.02
def find_coint(regdt):
pvalue ={}
count =0
for i in regdt.columns:
count +=1
for j in regdt.columns[count:]:
if i != j:
#calculate slope, intercept using 2 year(2018-2019) window between two underlyers to determine their relationship
logdt = spark.sql(""" SELECT log({0}) AS y,log({1}) AS x FROM regdt""".format(i,j))
logdt.createOrReplaceTempView('logdt')
vectorAssembler = VectorAssembler(inputCols=['x'], outputCol="features")
lr = LinearRegression(featuresCol='features', labelCol= 'y')
stages = [vectorAssembler, lr]
pipeline = Pipeline(stages=stages)
model = pipeline.fit(logdt)
slope = model.stages[-1].coefficients[0]
intercept = model.stages[-1].intercept
spddt = spark.sql(""" SELECT (y - {0}* x - {1} )AS spread FROM logdt""".format(slope,intercept))
spddt.createOrReplaceTempView('spddt')
spddt = spddt.toPandas()
adfSpread = adfuller(spddt['spread'] , autolag ='AIC')
adf_pvalue = adfSpread[1]
print(i,j,'slope: ',slope,'intercept: ', intercept,'pvalue: ', adf_pvalue)
pvalue[(i,j)] = (adf_pvalue, intercept, slope)
#find pairs with pvalue under threshold 0.005
min_pvalue = 0.005
pv =0
slope =0
intercept = 0
pair1 = 0
pair2 = 0
result=[]
for k,v in pvalue.items():
if v[0] < min_pvalue:
pv= v[0]
slope = v[2]
intercept = v[1]
pair1 = k[0]
pair2 = k[1]
result.append([pair1,pair2, pv, slope, intercept])
return result
def training(coint_pair):
#get all valid pairs and trade each pair
for i in range(len(coint_pair)):
pair1 = coint_pair[i][0]
pair2 = coint_pair[i][1]
slope = coint_pair[i][3]
intercept = coint_pair[i][4]
#calculate spread of the train window for each valid pair
dt2 = spark.sql(""" SELECT DateTime, {0}, {1}, (log({0}) - log({1}) * {2} - {3}) AS spread FROM train """.format(pair1,pair2,slope,intercept))
dt2.createOrReplaceTempView('dt2')
mu = dt2.agg(functions.avg(dt2['spread'])).collect()[0][0]
std = dt2.agg(functions.stddev(dt2['spread'])).collect()[0][0]
#set trading signal boundries if the spread is 2 times standard deviation from spread mean
up = mu +std*1.8
down = mu - std*1.8
#set stop_loss point
upsl = mu +std*2.8
downsl = mu - std*2.8
#set take profit point
uptp = mu +std*0.2
downtp = mu - std*0.2
#simulate trade
test1 = spark.sql(""" SELECT DateTime, {0}, {1}, (log({0}) - log({1}) * {2} - {3}) AS spread FROM test """.format(pair1,pair2,slope,intercept))
test1.createOrReplaceTempView('test1')
test1.toPandas()
test3 = trade(test1,pair1,pair2, up, down, upsl,downsl,uptp,downtp, mu, slope)
#save trading history/result to csv
test3.to_csv('retcsv_{}_{}.csv'.format(pair1,pair2), index = True)
return 0
# +
#trade simulation
def trade(test1,pair1,pair2, up, down, upsl,downsl,uptp,downtp, mu ,slope):
#use up/down boundries to determine trade position in test dataset (2020)
test1 = test1.withColumn("up", functions.lit(up) )
test1 = test1.withColumn("down",functions.lit( down) )
test1 = test1.withColumn("upsl",functions.lit( upsl) )
test1 = test1.withColumn("downsl", functions.lit(downsl) )
test1 = test1.withColumn("uptp", functions.lit(uptp) )
test1 = test1.withColumn("downtp", functions.lit(downtp) )
test1 = test1.withColumn("mu",functions.lit( mu) )
test1.createOrReplaceTempView('test1')
#set trade positions based on signal
test1 = spark.sql(""" SELECT DateTime, {0}, {1}, spread,
CASE
WHEN spread >=upsl THEN 3
WHEN spread >=up AND spread <upsl THEN 2
WHEN spread >=uptp AND spread <up THEN 1
WHEN spread < downsl THEN -3
WHEN spread < down AND spread >=downsl THEN -2
WHEN spread < downtp AND spread >=down THEN -1
ELSE 0
END AS level FROM test1 """ .format(pair1,pair2))
test1.createOrReplaceTempView('test1')
test1 = test1.withColumn('position',functions.lit(0) )
test1 = test1.withColumn('signal',functions.lit(0) )
test1 = test1.toPandas()
#set trade signal
for i in range(1, len(test1)):
if test1['level'][i-1] ==1 and test1['level'][i] ==2: #open position -> short I, long J
test1.loc[i,'signal'] = -2
elif test1['level'][i-1] ==1 and test1['level'][i] ==0: #take profit -I+J -> long I, short J
test1.loc[i,'signal'] = 2
elif test1['level'][i-1] ==2 and test1['level'][i] ==3: #stop loss -I+J -> long I, short J
test1.loc[i,'signal'] = 3
elif test1['level'][i-1] == -1 and test1['level'][i] == -2: #open position -> long I, short J
test1.loc[i,'signal'] = 1
elif test1['level'][i-1] == -1 and test1['level'][i] ==0: #take profit +I-J -> short I, long J
test1.loc[i,'signal'] = -1
elif test1['level'][i-1] ==-2 and test1['level'][i] ==-3: #stop loss +I-J -> short I, long J
test1.loc[i,'signal'] = -3
#set trade position
for i in range(1,len(test1)):
test1.loc[i,'position'] = test1['position'][i-1]
if test1['signal'][i] == 1:
test1.loc[i,'position'] = 1
elif test1['signal'][i] == -2:
test1.loc[i,'position'] = -1
elif test1['signal'][i] == -1 and test1['position'][i-1] == 1:
test1.loc[i,'position'] = 0
elif test1['signal'][i] == 2 and test1['position'][i-1] == -1:
test1.loc[i,'position'] = 0
elif test1['signal'][i] == 3:
test1.loc[i,'position'] = 0
elif test1['signal'][i] == -3:
test1.loc[i,'position'] = 0
#initialize portfolio
size=1000
test1['pair1_share'] = test1['position']*size
test1['pair2_share'] = round( - test1['pair1_share'] *slope * test1[pair1]/ test1[pair2] )
test1['cash'] = 5000
test3 = test1
for i in range(1,len(test3)):
test3.loc[i,'pair2_share'] = test3['pair2_share'][i-1]
test3.loc[i,'cash'] = test3['cash'][i-1]
if test3['position'][i-1] == 0 and test3['position'][i] ==1:
test3.loc[i,'pair2_share'] = round( - test3['pair1_share'][i] *slope * test3[pair1][i]/ test3[pair2][i] )
test3.loc[i, 'cash'] = test3['cash'][i-1] - (test3['pair1_share'][i] * test3[pair1][i] + test3['pair2_share'][i] * test3[pair2][i] )
elif test3['position'][i-1] == 0 and test3['position'][i] == -1:
test3.loc[i,'pair2_share'] = round( - test3['pair1_share'][i] *slope * test3[pair1][i]/ test3[pair2][i] )
test3.loc[i, 'cash'] = test3['cash'][i-1] - (test3['pair1_share'][i] * test3[pair1][i] + test3['pair2_share'][i] * test3[pair2][i] )
elif test3['position'][i-1] == 1 and test3['position'][i] ==0:
test3.loc[i,'pair2_share'] = 0
test3.loc[i,'cash'] = test3['cash'][i-1] + (test3['pair1_share'][i-1] * test3[pair1][i] + test3['pair2_share'][i-1] * test3[pair2][i] )
elif test3['position'][i-1] == -1 and test3['position'][i] == 0:
test3.loc[i,'pair2_share'] = 0
test3.loc[i,'cash'] = test3['cash'][i-1] + (test3['pair1_share'][i-1] * test3[pair1][i] + test3['pair2_share'][i-1] * test3[pair2][i] )
test3['asset'] = test3['cash']+ test3['pair1_share']*test3[pair1] +test3['pair2_share']*test3[pair2]
return test3
# -
#import spark.sqlContext.implicits._
def main():
# main logic starts here
inputs = '15stock.csv'
minute_schema = types.StructType([
types.StructField('DateTime', types.StringType()),
types.StructField('windcode', types.StringType()),
types.StructField('close', types.DoubleType()),
])
minutedt = spark.read.csv(inputs, schema=minute_schema)
dt = clean(minutedt)
#training dataset
train = spark.sql(""" SELECT * FROM dt WHERE DateTime < '2019-10-01 08:00:00' """).cache()
train.createOrReplaceTempView('train')
#test dataset
test = spark.sql(""" SELECT * FROM dt WHERE DateTime > '2019-10-01 08:00:00'""").cache()
test.createOrReplaceTempView('test')
#select all time series other than time
#regdt = spark.sql(""" SELECT j,i,h,g,f,e,d,c,b,a FROM train""").cache()
regdt = spark.sql(""" SELECT j,i,h,g,f,e,d,c,b,a FROM train""").cache()
regdt.createOrReplaceTempView('regdt')
coint_pair = find_coint(regdt)
for i in coint_pair:
training(coint_pair)
return 0
if __name__ == '__main__':
spark = SparkSession.builder.appName('example code').getOrCreate()
#assert spark.version >= '2.4' # make sure we have Spark 2.4+
spark.sparkContext.setLogLevel('WARN')
sc = spark.sparkContext
main()
| pair_trading_stat_coint1-stock15_multiple.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
train=pd.read_csv('Train.csv')
test=pd.read_csv('test (2).csv')
train.head()
train.info()
train.describe()
null=dict(train.isnull().sum())
train.isnull().sum()
train.info()
new_col=train.select_dtypes(include=object).columns
new_col
for i in new_col:
print(train[i])
for i in (new_col):
print(i)
train[i]=train[i].fillna(train[i].mode()[0])
train.isnull().sum()
for i in ['auctioneerID','MachineHoursCurrentMeter']:
train[i]=train[i].mean()
train.isnull().sum()
test.info()
def preprocess(DF):
NULL=dict(DF.isnull().sum())
for i in DF.columns:
if (NULL[i])>0.70*len(DF):
DF=DF.drop(i,axis=1)
new_col=DF.select_dtypes(include=object).columns
new_col
for i in (new_col):
DF[i]=DF[i].fillna(DF[i].mode()[0])
new_col1=DF.select_dtypes(include=float).columns
for i in (new_col1):
DF[i]=DF[i].fillna(DF[i].mean())
return DF
test_new=preprocess(test)
train_new=preprocess(train)
print(len(test_new.columns))
print(len(train_new.columns))
test_new=test_new.drop('UsageBand',axis=1)
new_col=train_new.select_dtypes(include=object).columns
for i in new_col:
print(train_new[i].value_counts())
new_col=train_new.select_dtypes(include=object).columns
new_col1=test_new.select_dtypes(include=object).columns
print(len(new_col))
print(len(new_col1))
from sklearn.preprocessing import LabelEncoder
lr=LabelEncoder()
for i in new_col:
train_new[i]=lr.fit_transform(train_new[i])
test_new[i]=lr.fit_transform(test_new[i])
train_new.info()
test_new.info()
train_new.corr()
import seaborn as sns
import matplotlib.pyplot as plt
f,ax=plt.subplots(figsize=(20, 20))
sns.heatmap(train_new.corr(), annot=True,center=0, linewidths=.5, fmt='.2%',ax=ax)
import warnings
warnings.filterwarnings("ignore")
sns.pairplot(train_new,hue='SalePrice')
from sklearn import preprocessing
trainn=train_new.drop('SalePrice',axis=1)
r_scaler = preprocessing.MinMaxScaler()
r_scaler.fit(trainn)
train1 = pd.DataFrame(r_scaler.transform(trainn), index=trainn.index, columns=trainn.columns)
print(train1.head())
r_scaler1 = preprocessing.MinMaxScaler()
r_scaler1.fit(test_new)
test1 = pd.DataFrame(r_scaler1.transform(test_new), index=test_new.index, columns=test_new.columns)
test1.head()
from sklearn.feature_selection import SelectKBest, chi2
X = train1.loc[:,train1.columns!='SalePrice']
y = train_new[['SalePrice']]
selector = SelectKBest(chi2, k=10)
selector.fit(X, y)
X_new = selector.transform(X)
print(X.columns[selector.get_support(indices=True)])
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
X_train=train1[['ModelID','MachineID','auctioneerID', 'YearMade', 'MachineHoursCurrentMeter', 'Transmission','Coupler','fiProductClassDesc','ProductGroup', 'ProductGroupDesc', 'Enclosure', 'Forks','Ride_Control', 'Hydraulics']]
y_train=train_new['SalePrice']
X_test=test1[['ModelID','MachineID', 'auctioneerID', 'YearMade', 'MachineHoursCurrentMeter', 'Transmission','Coupler','fiProductClassDesc','ProductGroup', 'ProductGroupDesc', 'Enclosure', 'Forks','Ride_Control', 'Hydraulics']]
#X_train,y_train=nm.fit_resample(X_train,y_train)
print(X.shape)
print(y.shape)
gb=GradientBoostingRegressor()
gb.fit(X_train,y_train)
pred=gb.predict(X_test)
cm1=gb.score(X_train,y_train)
print(cm1)
print(pred)
# +
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
forest_model = RandomForestRegressor(random_state=1)
forest_model.fit(X_train, y_train)
y_pred = forest_model.predict(X_test)
print(y_pred)
print(round(forest_model.score(X_train, y_train)*100,2))
# -
print(y_pred)
# +
from sklearn.tree import DecisionTreeRegressor
dforest_model = DecisionTreeRegressor()
dforest_model.fit(X_train, y_train)
y_pred = dforest_model.predict(X_test)
print(y_pred)
print(round(dforest_model.score(X_train, y_train)*100,2))
# -
| manufacturing-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import math
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# %matplotlib inline
plt.rcParams["figure.figsize"] = (9,6)
# #%config InlineBackend.figure_format = 'retina' # Uncomment if using a retina display
plt.rc('pdf', fonttype=42)
plt.rcParams['ps.useafm'] = True
plt.rcParams['pdf.use14corefonts'] = True
#plt.rcParams['text.usetex'] = True # Uncomment if LaTeX installed to render plots in LaTeX
plt.rcParams['font.serif'] = 'Times'
plt.rcParams['font.family'] = 'serif'
df = pd.read_csv('../output/model_params_and_results.csv')
df['score'] = abs(df['mean_test_score'])
df['num_hidden_layers'] = df['param_num_hidden_layers']
df['hidden_layer_size'] = df['param_hidden_layer_size']
df['activation_function'] = df['param_activation_function']
df.head()
# # Plotting the results in a more interpretable fashion
# # Number of hidden layers
x = [0, 1, 2, 3]
y = [df.query('num_hidden_layers == 0')['score'].mean(),
df.query('num_hidden_layers == 1')['score'].mean(),
df.query('num_hidden_layers == 2')['score'].mean(),
df.query('num_hidden_layers == 3')['score'].mean()]
e = [df.query('num_hidden_layers == 0')['score'].sem(),
df.query('num_hidden_layers == 1')['score'].mean(),
df.query('num_hidden_layers == 2')['score'].sem(),
df.query('num_hidden_layers == 3')['score'].sem()]
plt.scatter(df['num_hidden_layers'], df['score'], alpha=0.4)
plt.xticks([0,1,2,3])
plt.xlabel("Number of hidden layers")
plt.ylabel("MSE")
plt.title('MSE by number of hidden layers')
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
# Some of these results are skewed due to outlier values with high MSE scores. Removing all values with MSE > 1 for a clearer picture of the results.
df_ = df[df['score'] <= 1.0]
x = [1, 2, 3]
y = [df_.query('num_hidden_layers == 1')['score'].mean(),
df_.query('num_hidden_layers == 2')['score'].mean(),
df_.query('num_hidden_layers == 3')['score'].mean()]
e = [df_.query('num_hidden_layers == 1')['score'].sem(),
df_.query('num_hidden_layers == 2')['score'].sem(),
df_.query('num_hidden_layers == 3')['score'].sem()]
plt.scatter(df_['num_hidden_layers'], df_['score'], alpha=0.4)
plt.xticks([1,2,3])
plt.xlabel("Number of hidden layers")
plt.ylabel("MSE")
plt.title('MSE by number of hidden layers')
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
# # Hidden layer size
# Without removing MSE > 1
hidden_layer_size_map = {0:0, 64:1, 128: 2, 256: 3}
df['hidden_layer_size_numeric'] = [hidden_layer_size_map[x] for x in list(df['hidden_layer_size'])]
#fig, ax = plt.subplots()
# zero is again omitted
x = [0, 1, 2, 3]
y = [df.query('hidden_layer_size == 0')['score'].mean(),
df.query('hidden_layer_size == 64')['score'].mean(),
df.query('hidden_layer_size == 128')['score'].mean(),
df.query('hidden_layer_size == 256')['score'].mean()]
e = [df.query('hidden_layer_size == 0')['score'].sem(),
df.query('hidden_layer_size == 64')['score'].sem(),
df.query('hidden_layer_size == 128')['score'].sem(),
df.query('hidden_layer_size == 256')['score'].sem()]
plt.scatter(df['hidden_layer_size_numeric'], df['score'], alpha=0.5)
plt.xticks( range(4), ('0','64','128', '256'))
plt.xlabel("Number of nodes in hidden layers")
plt.ylabel("MSE")
plt.title("MSE by number of hidden layer size")
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
hidden_layer_size_map = {64:0, 128: 1, 256: 2}
df_['hidden_layer_size_numeric'] = [hidden_layer_size_map[x] for x in list(df_['hidden_layer_size'])]
#fig, ax = plt.subplots()
# zero is again omitted
x = [0, 1, 2]
y = [df_.query('hidden_layer_size == 64')['score'].mean(),
df_.query('hidden_layer_size == 128')['score'].mean(),
df_.query('hidden_layer_size == 256')['score'].mean()]
e = [df_.query('hidden_layer_size == 64')['score'].sem(),
df_.query('hidden_layer_size == 128')['score'].sem(),
df_.query('hidden_layer_size == 256')['score'].sem()]
plt.scatter(df_['hidden_layer_size_numeric'], df_['score'], alpha=0.5)
plt.xticks( range(3), ('64','128', '256'))
plt.xlabel("Number of nodes in hidden layers")
plt.ylabel("MSE")
plt.title("MSE by number of hidden layer size")
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
# # Activation function
activation_function_map = {'linear':0, 'sigmoid': 1, 'tanh': 2, 'relu': 3}
df['activation_function_numeric'] = [activation_function_map[x] for x in list(df['activation_function'])]
df_['activation_function_numeric'] = [activation_function_map[x] for x in list(df_['activation_function'])]
# +
x = [0, 1, 2, 3]
y = [df.query('activation_function == "linear"')['score'].mean(),
df.query('activation_function == "sigmoid"')['score'].mean(),
df.query('activation_function == "tanh"')['score'].mean(),
df.query('activation_function == "relu"')['score'].mean()]
e = [df.query('activation_function == "linear"')['score'].sem(),
df.query('activation_function == "sigmoid"')['score'].sem(),
df.query('activation_function == "tanh"')['score'].sem(),
df.query('activation_function == "relu"')['score'].sem()]
plt.scatter(df['activation_function_numeric'], df['score'], alpha=0.5)
plt.scatter(pd.DataFrame([0,1,2,3]),
[df.query('activation_function == "linear"')['score'].mean(),
df.query('activation_function == "sigmoid"')['score'].mean(),
df.query('activation_function == "tanh"')['score'].mean(),
df.query('activation_function == "relu"')['score'].mean()])
plt.xticks( range(4), ('Linear','Sigmoid', 'Tanh', 'ReLU',''))
plt.xlabel("Number of nodes in hidden layers")
plt.xlabel("Activation function")
plt.ylabel("MSE")
plt.title("MSE by activation function")
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
# +
#fig, ax = plt.subplots()
# zero is again omitted
#fig, ax = plt.subplots()
# zero is again omitted
x = [0, 1, 2, 3]
y = [df_.query('activation_function == "linear"')['score'].mean(),
df_.query('activation_function == "sigmoid"')['score'].mean(),
df_.query('activation_function == "tanh"')['score'].mean(),
df_.query('activation_function == "relu"')['score'].mean()]
e = [df_.query('activation_function == "linear"')['score'].sem(),
df_.query('activation_function == "sigmoid"')['score'].sem(),
df_.query('activation_function == "tanh"')['score'].sem(),
df_.query('activation_function == "relu"')['score'].sem()]
plt.scatter(df_['activation_function_numeric'], df_['score'], alpha=0.5)
plt.scatter(pd.DataFrame([0,1,2,3]),
[df_.query('activation_function == "linear"')['score'].mean(),
df_.query('activation_function == "sigmoid"')['score'].mean(),
df_.query('activation_function == "tanh"')['score'].mean(),
df_.query('activation_function == "relu"')['score'].mean()])
plt.xticks( range(4), ('Linear','Sigmoid', 'Tanh', 'ReLU',''))
plt.xlabel("Number of nodes in hidden layers")
plt.xlabel("Activation function")
plt.ylabel("MSE")
plt.title("MSE by activation function")
plt.errorbar(x, y, yerr=e, fmt='o', color='black')
plt.show()
# -
# Overall we see much narrower error bars for the sigmoid and tanh activations, suggesting that they tend to perform much more consistently.
| code/supplementary/results_table_to_figures.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#Dependencies
import tweepy
import numpy as np
import json
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
#Import and Initialize Sentiment Analyzer
from vaderSentiment.vaderSentiment import SentimentIntensityAnalyzer
analyzer = SentimentIntensityAnalyzer()
# Twitter API Keys
from config import consumer_key, consumer_secret, access_token, access_token_secret
consumer_key = consumer_key
consumer_secret = consumer_secret
access_token = access_token
access_token_secret = access_token_secret
#Setup Tweepy API Authentication
auth = tweepy.OAuthHandler(consumer_key, consumer_secret)
auth.set_access_token(access_token, access_token_secret)
api = tweepy.API(auth, parser=tweepy.parsers.JSONParser())
# +
# Target Search Term
news_orgs = ["@BBC", "@CBS", "@CNN", "@FoxNews", "@nytimes"]
results_list = []
for org in news_orgs:
# Create empty sentiment lists
compound_list = []
positive_list = []
negative_list = []
neutral_list = []
index = []
count = 0
# Grab the most recent 100 tweets
public_tweets = api.search(org, count=100, result_type="recent")
# Loop
for tweet in public_tweets["statuses"]:
# Enable Vader Analyzer
compound = analyzer.polarity_scores(tweet["text"])["compound"]
pos = analyzer.polarity_scores(tweet["text"])["pos"]
neg = analyzer.polarity_scores(tweet["text"])["neg"]
neu = analyzer.polarity_scores(tweet["text"])["neu"]
# Adding to the sentiment list
compound_list.append(compound)
positive_list.append(pos)
negative_list.append(neg)
neutral_list.append(neu)
index.append(count)
count = count + 1
lgnd = plt.legend(news_orgs, title= 'News Organizations', bbox_to_anchor=(1, 0.75))
plt.scatter(index, compound_list, facecolors=['red','blue','purple','green','yellow'], edgecolors="black", linewidth=1, marker='o', alpha=0.8)
plt.title("Sentiment Analysis of Media Tweets")
plt.xlabel("Tweets Ago")
plt.ylabel("Tweet Polarity")
plt.legend
plt.xlim(len(compound_list), 0)
plt.yticks([-1, -.5, 0, .5, 1])
# Store the Average Sentiments
sentiment = {"News Organization": org,
"Compound": np.mean(compound_list),
"Positive": np.mean(positive_list),
"Negative": np.mean(negative_list),
"Neutral": np.mean(neutral_list)}
results_list.append(sentiment)
# Save the plot
plt.savefig("plot1.png")
#Show the plot
plt.show()
# +
compounds = []
for sentiment in results_list:
compounds.append(sentiment["Compound"])
plt.title("Overall Media Sentiment Based on Twitter")
plt.ylabel("Tweet Polarity")
plt.bar(news_orgs, compounds)
# Save the plot
plt.savefig("plot2.png")
#Show the plot
plt.show()
# -
news_orgs_df = pd.DataFrame(results_list).set_index('News Organization').round(3).reset_index()
news_orgs_df.head()
news_orgs_df.to_csv("NewsMood.csv", encoding='utf-8', index=False)
| News_Mood_.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# %load_ext autoreload
# %autoreload 2
# +
import pandas as pd
#md_file = '/home/jvdzwaan/data/adh-corpora/fiqh_corpus/Meta/Metadata_Fiqh.csv'
md_file = '/home/jvdzwaan/data/adh-corpora/dawa/DawaMetadata.csv'
#md_file = '/media/sf_VBox_Shared/Arabic/fiqh_corpus/Meta/Metadata_Fiqh.csv'
# -
md = pd.read_csv(md_file, sep=',', encoding='utf-8')
md = md.fillna(0)
md.head()
# +
from nlppln.utils import get_files
in_dir = '/home/jvdzwaan/data/adh-corpora/dawa/txt/'
corpus = get_files(in_dir)
print(len(corpus))
# +
from nlppln.utils import remove_ext
corpus = [remove_ext(b) for b in corpus]
print(corpus[0])
# -
corpus = set(corpus)
print(len(corpus))
md_corpus = set([str(int(val)) for val in md['BookURI']])
print(len(md_corpus))
# works we have files for, but no metadata
corpus.difference(md_corpus)
# works we have metadata for, but no files
md_corpus.difference(corpus)
md.query('BookURI == 0')
# +
# remove files that are not in the metadata
import os
import shutil
in_dir = '/home/jvdzwaan/data/tmp/adh/20190404-tmp-dawa'
for n in corpus.difference(md_corpus):
fname = os.path.join(in_dir, '{}.txt'.format(n))
if os.path.isfile(fname):
print(fname)
os.remove(fname)
| notebooks/dawa_match_files_to_metadata.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # JSON examples and exercise
# ****
# + get familiar with packages for dealing with JSON
# + study examples with JSON strings and files
# + work on exercise to be completed and submitted
# ****
# + reference: http://pandas.pydata.org/pandas-docs/stable/io.html#io-json-reader
# + data source: http://jsonstudio.com/resources/
# ****
import pandas as pd
# ## imports for Python, Pandas
import json
from pandas.io.json import json_normalize
# ## JSON example, with string
#
# + demonstrates creation of normalized dataframes (tables) from nested json string
# + source: http://pandas.pydata.org/pandas-docs/stable/io.html#normalization
# define json string
data = [{'state': 'Florida',
'shortname': 'FL',
'info': {'governor': '<NAME>'},
'counties': [{'name': 'Dade', 'population': 12345},
{'name': 'Broward', 'population': 40000},
{'name': '<NAME>', 'population': 60000}]},
{'state': 'Ohio',
'shortname': 'OH',
'info': {'governor': '<NAME>'},
'counties': [{'name': 'Summit', 'population': 1234},
{'name': 'Cuyahoga', 'population': 1337}]}]
# use normalization to create tables from nested element
json_normalize(data, 'counties')
# further populate tables created from nested element
json_normalize(data, 'counties', ['state', 'shortname', ['info','governor']])
# ****
# ## JSON example, with file
#
# + demonstrates reading in a json file as a string and as a table
# + uses small sample file containing data about projects funded by the World Bank
# + data source: http://jsonstudio.com/resources/
# load json as string
json.load((open('data/world_bank_projects_less.json')))
# load as Pandas dataframe
sample_json_df = pd.read_json('data/world_bank_projects_less.json')
# ****
# ## JSON exercise
#
# Using data in file 'data/world_bank_projects.json' and the techniques demonstrated above,
# 1. Find the 10 countries with most projects
# 2. Find the top 10 major project themes (using column 'mjtheme_namecode')
# 3. In 2. above you will notice that some entries have only the code and the name is missing. Create a dataframe with the missing names filled in.
# ## Solution:
#
# 1.To find the top 10 countries with most number of projects we need to first read the json string into a pandas dataframe and display the 10 countries with most projects.
json_df=pd.read_json('data/world_bank_projects.json')
top_countries=json_df['countryname'].value_counts().head(10)
top_countries
# 2.Use json_normalize to get a table of the mjtheme_namecode find the top 10 major project themes.
project_theme = json.load(open('data/world_bank_projects.json'))
project_theme_1 = json_normalize(project_theme, 'mjtheme_namecode')
count=project_theme_1.name.value_counts().head(10)
project_theme_2=json_normalize(project_theme, 'mjtheme_namecode')
project_theme_2
# Finding the missing values: In this approach of my problem, I have replaced the entire data frame where missing values are present with Null values and later dropped the null values because in pandas it is easier to drop null values. Next conver this data frame into a dictionary and assign the key(i.e the code) to the corresponding key in the missing dataframe to map the value(name) in both the dataframes.
# +
import numpy as np
project_theme_2['name'].replace('',np.nan,inplace=True)
project_theme_2.dropna(subset=['name'],inplace=True)
dict_=project_theme_2.set_index('code')['name'].to_dict()
for i in range(len(project_theme_1)):
if project_theme_1.loc[i, 'name'] == '':
project_theme_1.loc[i, 'name'] = dict_[project_theme_1.loc[i, 'code']]
project_theme_1['name'].value_counts().head(11)
| Json_World_Bank.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src='https://radiant-assets.s3-us-west-2.amazonaws.com/PrimaryRadiantMLHubLogo.png' alt='Radiant MLHub Logo' width='300'/>
#
# How to use the Radiant MLHub API
# =====
#
# The Radiant MLHub API gives access to open Earth imagery training data for machine learning applications. You can learn more about the repository at the [Radiant MLHub site](https://mlhub.earth) and about the organization behind it at the [Radiant Earth Foundation site](https://radiant.earth).
#
# This Jupyter notebook, which you may copy and adapt for any use, shows basic examples of how to use the API. Full documentation for the API is available at [docs.mlhub.earth](docs.mlhub.earth).
#
# We'll show you how to set up your authorization, see the list of available collections and datasets, and retrieve the items (the data contained within them) from those collections.
#
# Each item in our collection is explained in json format compliant with [STAC](https://stacspec.org/) [label extension](https://github.com/radiantearth/stac-spec/tree/master/extensions/label) definition.
# Authentication
# -----
#
# Access to the Radiant MLHub API requires an API key. To get your API key, go to [dashboard.mlhub.earth](https://dashboard.mlhub.earth). If you have not used Radiant MLHub before, you will need to sign up and create a new account. Otherwise, sign in. In the **API Keys** tab, you'll be able to create API key, which you will need. *Do not share* your API key with others: your usage may be limited and sharing your API key is a security risk.
#
# Copy the API key, and paste it in the box bellow.
#
# Click **Run** or press `SHIFT` + `ENTER` before moving on to run this first piece of code.
# +
# only the requests module is required to access the API
import requests
# # copy your API key from dashboard.mlhub.earth and paste it in the following
API_KEY = 'PASTE_YOUR_API_KEY_HERE'
API_BASE = 'https://api.radiant.earth/mlhub/v1'
# -
# Search for data collections
# -----
#
# To see what training data is available, you will want to see the collections available through the API.
#
# A collection represents the top-most data level. Typically this means the data comes from the same source for the same geography. It might include different years or sub-geographies.
#
# To find data with specific parameters, see the [API documentation](http://docs.mlhub.earth/?python#the-feature-collections-in-the-dataset).
#
# To see the list, simply run the following cell. The returned list shows the collection id values, collection license, and data source citation (if available).
# +
# get list of all collections
r = requests.get(f'{API_BASE}/collections?key={API_KEY}')
h = r.json()
collections = h['collections']
# print the list of collections
for c in collections:
print(f'ID: {c["id"]}\nLicense: {c.get("license", "N/A")}\nCitation: {c.get("sci:citation", "N/A")}\n')
# -
# Retrieve properties of a collection
# ----
#
# Once you have found the collection that you want to access, you can get its properties from the API.
#
# You can limit what data you get in the response using the optional parameters:
# * **Limit** limits how many items will be returned, with a minimum of 1 and maximum of 10000.
# * **Bounding box** limits the returned items to a specific geographic area.
# * **Date time** limits the returned items to those that fall within a specific time-frame.
#
# See the [get features](http://docs.mlhub.earth/#getfeatures) API documentation for more information.
#
# Paste the collection id below for `collectionId`, and enter any desired parameters, then run the cell.
# +
# paste the id of the collection you are interested in here:
collectionId = 'ref_african_crops_kenya_01_labels'
# retrieves the items and their metadata in the collection
r = requests.get(f'{API_BASE}/collections/{collectionId}/items?key={API_KEY}')
collection = r.json()
# -
# Selecting an Item to Download
# ---
#
# For the purposes of this demo we will only download the assets of one item. The next cell selects the first item in the collection. If you wish to download the assets for all of the items in the collection then the following cells should be repeated for every item in the collection.
#
selected_item = None
assets = None
for feature in collection.get('features', []):
selected_item = feature
assets = list(feature.get('assets').keys())
# For demo purposes we only want the first item
break
# Listing Available Assets
# ---
#
# Source imagery assets follow the pattern `year_month_day_type` so we'll loop through the list of assets and only print the ones which don't match that pattern.
# +
import re
# List all assets which don't match the pattern "year_month_day_*"
for asset in assets:
if not re.match('\d{4}_\d{2}_\d{2}_.*', asset):
print(asset)
# -
# As you can see, there are 3 assets which match this criteria: `labels`, `documentation`, and `property descriptions`.
#
# Downloading Assets
# ---
# We'll need to set up some functions to download assets first.
# +
from urllib.parse import urlparse
def get_download_url(item, asset_key):
asset = item.get('assets', {}).get(asset_key, None)
if asset is None:
print(f'Asset "{asset_key}" does not exist in this item')
return None
r = requests.get(asset.get('href'), allow_redirects=False)
return r.headers.get('Location')
def download_file(url):
filename = urlparse(url).path.split('/')[-1]
r = requests.get(url)
f = open(filename, 'wb')
for chunk in r.iter_content(chunk_size=512 * 1024):
if chunk:
f.write(chunk)
f.close()
print(f'Downloaded {filename}')
return
# -
# Downloading Labels
# ---
#
# We can download the `labels` asset of the `selected_item` by calling the following function:
download_file(get_download_url(selected_item, 'labels'))
# Downloading Metadata
# ---
#
# Likewise, we can download the documentation pdf and property description csv.
download_file(get_download_url(selected_item, 'documentation'))
download_file(get_download_url(selected_item, 'property_descriptions'))
# Downloading Source Imagery
# ---
#
# For this example, we'll query the API for the download url for three bands of a Sentinel 2 scene associated with this asset.
for link in selected_item['links']:
if link['rel'] == 'source':
r = requests.get(f'{link["href"]}?key={API_KEY}')
source_item = r.json()
break
download_file(get_download_url(source_item, 'B01'))
download_file(get_download_url(source_item, 'B02'))
download_file(get_download_url(source_item, 'B03'))
| notebooks/radiant-mlhub-api-know-how.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %matplotlib inline
#
# 如何在PyTorch中使用VisualDL
# =====================
#
# 下面我们演示一下如何在PyTorch中使用VisualDL,从而可以把PyTorch的训练过程以及最后的模型可视化出来。我们将以PyTorch用卷积神经网络(CNN, Convolutional Neural Network)来训练 [Cifar10](https://www.cs.toronto.edu/~kriz/cifar.html) 数据集作为例子。
#
# 程序的主体来自PyTorch的 [Tutorial](http://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html)
#
# +
import torch
import torchvision
import torchvision.transforms as transforms
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib
matplotlib.use('Agg')
from visualdl import LogWriter
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=500,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=500,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
import matplotlib.pyplot as plt
import numpy as np
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
fig, ax = plt.subplots()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# we can either show the image or save it locally
# plt.show()
fig.savefig('out' + str(np.random.randint(0, 10000)) + '.pdf')
# -
# 然后我们开始创建 VisualDL 的数据采集 loggers
#
# +
logdir = "/workspace"
logger = LogWriter(logdir, sync_cycle=100)
# mark the components with 'train' label.
with logger.mode("train"):
# create a scalar component called 'scalars/'
scalar_pytorch_train_loss = logger.scalar("scalars/scalar_pytorch_train_loss")
image1 = logger.image("images/image1", 1)
image2 = logger.image("images/image2", 1)
histogram0 = logger.histogram("histogram/histogram0", num_buckets=100)
# -
# Cifar10 中有 50000 个训练图像和 10000 个测试图像。我们每 500 个作为一个训练集,图片采样也选 500 。 每个训练集 (batch) 是如下的维度:
#
# 500 x 3 x 32 x 32
#
# 接下来我们开始创建 CNN 模型
#
# +
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
# Define a Convolution Neural Network
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
# -
# 接下来我们开始训练并且同时用 VisualDL 来采集相关数据
#
# +
# Train the network
for epoch in range(5): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
# wrap them in Variable
inputs, labels = Variable(inputs), Variable(labels)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# use VisualDL to retrieve metrics
# scalar
scalar_pytorch_train_loss.add_record(train_step, float(loss))
# histogram
weight_list = net.conv1.weight.view(6*3*5*5, -1)
histogram0.add_record(train_step, weight_list)
# image
image1.start_sampling()
image1.add_sample([96, 25], net.conv2.weight.view(16*6*5*5, -1))
image1.finish_sampling()
image2.start_sampling()
image2.add_sample([18, 25], net.conv1.weight.view(6*3*5*5, -1))
image2.finish_sampling()
train_step += 1
# print statistics
running_loss += loss.data[0]
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
# -
# 最后,因为 PyTorch 采用 Dynamic Computation Graphs,我们用一个 dummy 输入来空跑一下模型,以便产生图
# +
import torch.onnx
dummy_input = Variable(torch.randn(4, 3, 32, 32))
torch.onnx.export(net, dummy_input, "pytorch_cifar10.onnx")
print('Done')
| demo/pytorch/pytorch_cifar10.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sys
import pickle
from scipy import signal
from scipy import stats
import numpy as np
from sklearn.model_selection import ShuffleSplit
from sklearn.metrics import cohen_kappa_score
import math
from collections import OrderedDict
import matplotlib.pyplot as plt
sys.path.append('D:\Diamond\code')
from csp_james_2 import *
sys.path.append('D:\Diamond\code')
from thesis_funcs_19_03 import *
import torch
import torch.nn as nn
import torch.nn.functional as nnF
import torch.optim as optim
from torch.autograd import Variable
from torch.optim import lr_scheduler
import csv
import datetime
# +
meth = 'gold_stand' #gold_stand,tl_comp_csp_kld , tl_comp_csp_mi
#raw_data_root = 'E:\\Diamond\\bci_iv\\DATA\\2a\\extract_raw\\'
config_root= 'E:\\Diamond\\bci_iv\\MODELS\\fbcsp_mibif_cnn\\2a\\configs\\'
feature_root = 'E:\\Diamond\\own_expo\\pilot_test\\'
model_root = feature_root
save_root = model_root + 'eval\\'
#load in cv config grid
hp_names =[] #all the hyper-parameter names to be validated
with open(config_root +'cv_config.csv', mode = 'r') as csv_file:
csv_reader = csv.reader(csv_file, delimiter = ',')
for row in csv_reader:
hp_names.append((row[0]).strip())
with open(config_root +'_lambda_config.csv', mode = 'r') as csv_file:
csv_reader = csv.reader(csv_file, delimiter = ',')
for row in csv_reader:
hp_names.append((row[0]).strip())
csv_file.close()
num_inits = 5
k_fold = 5
# initialize csp
m = 2# m is Nw in the paper "learning temporal information for brain-copmuter interface, Sakhavi et.al"
n_components = 2 * m # pick some components
down_sample_step = 20 #Hilbert evelope
# select Ns pairs of csp filters
Ns = 4
CLASSES =[0,1]
C_OVR = [0,1]
balance_classes = 1
########################################################################################################################
# DEFINE FILTER BANK
########################################################################################################################
#Filter Bank
FB = [[4., 8.], [8., 12.], [12., 16.], [16., 20.], [20., 24.], [24., 28.], [28., 32.], [32., 36.], [36., 40.]]
FB = np.array(FB)
#argumaents for Chebyl II filtering
# Nyquist frequency
# min. attenuation in stop band
gstop = 45
# max. attenuation in passband
gpass= 5
EEG_PERIOD = [[0.5,4]]
FS = [512]
# -
to_save = 1
save_root
def seperate_train_eval_ind(sub_id):
EEG_MI_RAW_load = pickle.load(open( 'E:\\Diamond\\own_expo\\pilot_test\\' + sub_id + '\\signals\\' + sub_id + ".pickle", "rb" ) )
LABELS_load = pickle.load(open( 'E:\\Diamond\\own_expo\\pilot_test\\' + sub_id + '\\signals\\' + sub_id + "_LABELS.pickle", "rb" ) )
#fist half of recording is training, second half is evaluation
train_set_ind = np.arange(0, int(len(LABELS_load)/2))
eval_set_ind = np.arange(int(len(LABELS_load)/2), int(len(LABELS_load)))
EEG_MI_RAW_T = EEG_MI_RAW_load[train_set_ind]
EEG_MI_RAW_E = EEG_MI_RAW_load[eval_set_ind]
LABELS_load_T = LABELS_load[train_set_ind]
LABELS_load_E = LABELS_load[eval_set_ind]
return EEG_MI_RAW_T, LABELS_load_T, EEG_MI_RAW_E, LABELS_load_E
for portion_train in [1]:
if to_save == 1:
filewrite = open(save_root + '4s_' + str(int(portion_train*100))+'_best_config_eval_acc_all_subjects.txt', 'w')
filewrite.write('')
filewrite.close()
filewrite = open(save_root + '4s_' + str(int(portion_train*100))+'_best_config_eval_acc_all_subjects.txt', 'a')
filewrite.write('subject, ')
for f in range (0, len(C_OVR)-1):
filewrite.write('class '+ str(C_OVR[f]+1) + ', ')
filewrite.write('class ' + str(C_OVR[-1]+1) + ', average'+ ', best_model_init_fold\n')
for subject in range (3,4):
sub_id = 's' + str(subject)
eeg_period = EEG_PERIOD[0]
fs = FS[0]
for run_win in range (0,1):
if run_win == 0:
file_root_feature = feature_root + sub_id + '\\models\\4s\\' + 'pt_' + str(int(portion_train*100))
file_root_model = model_root + sub_id + '\\models\\4s\\' + 'pt_' + str(int(portion_train*100))
#file_root_save = save_root + filename_save[:-1] + '\\4s\\' + 'pt_' + str(int(portion_train*100))
#len_inp = 44
elif run_win == 1:
file_root_feature = feature_root + filename_save[:-1] + '\\2s\\' + 'pt_' + str(int(portion_train*100))
file_root_model = model_root + filename_save[:-1] + '\\2s\\' + 'pt_' + str(int(portion_train*100))
#file_root_save = save_root + filename_save[:-1] + '\\2s\\' + 'pt_' + str(int(portion_train*100))
#len_inp = 25
###################################################################################################################
#load best config
###################################################################################################################
#load in best config line
config_file = open(file_root_model + '\\ANN\\best_config_val.txt', 'r')
config_log= config_file.readlines()
config_file.close()
for i in range (0,len(config_log)):
line = config_log[(i + 1) * -1]
if '_act_fun_' in line: #and line.split(' ')[0].split('_lambda_')[1] == '0':
break
#extract best config values and make into dictionary
config = OrderedDict()
for hp_ind in range(0, len(hp_names)-1):
config[hp_names[hp_ind]] = (line.split(hp_names[hp_ind] + '_')[1].split('_'+hp_names[hp_ind+1]+'_')[0])
config[hp_names[-1]] = line.split(hp_names[-1]+'_')[1].split(' ')[0]
EEG_MI_RAW_T, LABELS_load_T, EEG_MI_RAW_E, LABELS_load_E= seperate_train_eval_ind(sub_id)
LABELS = LABELS_load_E - 1
EEG_extract_raw = EEG_MI_RAW_E
########################################################################################################################
#APPLY FILTER BANK
########################################################################################################################
#Store Filter bank filtered raw EEG data, in the shape of num_filter_bank X num_trials X num_chanl X num_samples
#initiate empty matrix
EEG_filt_FB_L = np.empty( [len(FB),
np.shape(EEG_extract_raw)[0], np.shape(EEG_extract_raw)[1],np.shape(EEG_extract_raw)[2]] )
Nf = fs / 2.
for fb in range (0, len(FB)):
passband = FB[fb]
stopband = FB[fb] + np.array([-2., +2.])
EEG_filt_FB_L[fb] = filter_signal(EEG_extract_raw, passband, stopband, Nf, gpass, gstop)
EEG_filt_FB = EEG_filt_FB_L
#trake only the MI 3.5 seconds
EEG_filt_FB_go = EEG_filt_FB[:,:,:,int(eeg_period[0]*fs):int(eeg_period[1]*fs)]
LABELS0_go = LABELS.copy()
LABELS0 = LABELS0_go
###########################################################################################################################
pred_indi = []
############################################################################################################################
OUT = 0
best_mod_acc_prod = 0 #initialise best model average class acc
best_mod_kappa = -2
best_model = [0,0] #which model performs the best? model id, init = best_model[0], fold = best_model[1]
for fold in range (0, k_fold):
#print ('fold', fold)
pred_indi.append([])
for c_ovr in C_OVR:
#print (c_ovr)
#load in csp filters and mutual informtaion ranked indicies
W_B = pickle.load(open( file_root_feature +'\\W_B_fold_' + str(fold) +
'_c_ovr_' + str(c_ovr) + '_lambda_' + str(float(config['_lambda'])) +
".pickle", 'rb'))
FB_FILTER_IND = pickle.load(open( file_root_feature + '\\FB_FILTER_IND_fold_' + str(fold) +
'_c_ovr_' + str(c_ovr) + '_lambda_' + str(float(config['_lambda'])) +
".pickle", 'rb'))
#find the selected csp filters indicies
FB_FILTER_IND_slt = find_selected_csp_filters(Ns, m, FB_FILTER_IND)
#construct selected csp filters, W_B_slt has shape (2*Ns, num_chls), (8,22) for example
W_B_slt = W_B[FB_FILTER_IND_slt[:,0], :, FB_FILTER_IND_slt[:,1]]
EEG_FB_slt = EEG_filt_FB_go[FB_FILTER_IND_slt[:,0],:]
#transform into z space, then take the hilbert envelope of the transformed signal
Z_env = calc_z_features(W_B_slt, EEG_FB_slt, Ns, down_sample_step)
#concatenate all classes
if c_ovr == C_OVR[0]:
Z_all_eval = Z_env
else:
Z_all_eval = np.concatenate((Z_all_eval, Z_env), axis = 0)
#reshape into ANN input size
Z_all_eval = np.transpose(Z_all_eval, [1,0,2])
X_eval = np.reshape(Z_all_eval, [np.shape(Z_all_eval)[0], 1, np.shape(Z_all_eval)[1], np.shape(Z_all_eval)[2]])
X_eval = torch.from_numpy(X_eval).float()
#initilize ANN model
model = Model_current(chn_inp = X_eval.size()[-2], len_inp = X_eval.size()[-1], nf = int(config['nf']), ks = int(config['ks']) ,
stride = int(config['stride']), act_f = config['act_fun'], nfc = int(config['nfc']))
for n_inits in range (0, num_inits):
save_path = file_root_model + '\\ANN\\model_config_'+ line.split(' ')[0] + '_n_inits_'+ str(n_inits) +'_fold_' + str(fold) + '.pt'
model.load_state_dict(torch.load(save_path))
model.eval()
#predictoin, sum up the output (probability of being class) predicted at each fold, tehn the class with the max probability if the class prediction
out = model(X_eval)
OUT = OUT + out
#print out class precition at each fold
pred = torch.argmax(out, dim = 1).numpy()
#print (str(n_inits), np.average(calc_class_acc(pred, LABELS0, C_OVR)))
if cohen_kappa_score(LABELS0, pred) > best_mod_kappa:
best_model = [n_inits, fold]
best_mod_acc_prod = np.average(calc_class_acc(pred, LABELS0, C_OVR))
best_mod_kappa = cohen_kappa_score(LABELS0, pred)
#pred_indi[fold].append(cohen_kappa_score(LABELS0, pred))
#final prediciotn using all trained ANNs
PRED = torch.argmax(OUT, dim = 1).numpy()
acc_c = calc_class_acc(PRED, LABELS0, C_OVR)
print(sub_id, acc_c, np.average(acc_c))
kappa = cohen_kappa_score(LABELS0, PRED)
if to_save == 1:
filewrite.write(str(subject) + ', ')
for a in acc_c:
filewrite.write(str(round(a*100,2)) + ', ')
filewrite.write(str(round(np.average(acc_c)*100, 2)) +' '+'('+str(round(kappa, 3))+')' +', ' + str(best_model[0])+'_'+str(best_model[1]) + '_'+ str(best_mod_acc_prod) + '(' + str(best_mod_kappa) + ')' +'\n')
if to_save == 1:
filewrite.close()
| eval_gtec.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="QAVqXpOE4QaM"
# # Personalized Counterfactual Fairness in Recommendation
# + [markdown] id="iVJdn7A33_bk"
# ## Setup
# + [markdown] id="BXJY8c9d4Xi5"
# ### Installations
# + id="TGJ5fBMK4Xgj"
# !pip install -q wget
# + [markdown] id="GB_yDppW3_Yt"
# ### Imports
# + id="yebvVSIT3_WD"
import sys
import os
import wget
import logging
import os.path as osp
from pathlib import Path
import zipfile
import numpy as np
import pandas as pd
from tqdm.notebook import tqdm
import pickle
from sklearn.metrics import *
from sklearn.preprocessing import LabelBinarizer
import itertools as it
from time import time
import gc
from collections import defaultdict, namedtuple, OrderedDict
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
# + [markdown] id="NyxCtlrJ3_Ta"
# ### Params
# + id="MXBwnUCD3_RD"
class Args:
path = '/content'
train_suffix = '.train.tsv' # train file suffix
validation_suffix = '.validation.tsv' # validation file suffix
test_suffix = '.test.tsv' # test file suffix
all_suffix = '.all.tsv' # all data file
feature_suffix = '.features.txt' # feature file
test_pkl_suffix = '.test.pkl' # prepared test data pickle file suffix
valid_pkl_suffix = '.validation.pkl' # prepared validation data pickle file suffix
USER = 'uid' # user column name
ITEM = 'iid' # item column name
LABEL = 'label' # label column name
RANK_FILE_NAME = 'rank.csv' # Trained model generated ranking list
SAMPLE_ID = 'sample_id' # sample id for each record
gpu ='0' # Set CUDA_VISIBLE_DEVICES
verbose = logging.INFO # Logging Level, 0, 10, ..., 50
log_file = 'log.txt' # Logging file path
result_file = 'result.npy' # Result file path
random_seed = 2020 # Random seed of numpy and tensorflow
train = 1 # To train the model or not
dataset = 'ml1M'
sep = '\t' # sep of csv file
label = 'label' # name of dataset label column
disc_batch_size = 7000 # discriminator train batch size
train_num_neg = 1 # Negative sample num for each instance in train set
vt_num_neg = -1 # Number of negative sample in validation/testing stage
model_path ='model.pt' # Model save path
u_vector_size = 64 # user vector size
i_vector_size = 64 # item vector size
filter_mode = 'combine' # combine for using one filter per sensitive feature, separate for using one filter per sensitive feature combination
load = 0 # Whether load model and continue to train
load_attack = False # Whether load attacker model and continue to train
epoch = 100 # Number of epochs
disc_epoch = 500 # Number of epochs for training extra discriminator
check_epoch = 1 # Check every epochs
early_stop = 1 # whether to early-stop
lr = 0.001 # Learning rate
lr_attack = 0.001 # attacker learning rate
batch_size = 128 # Batch size during training
vt_batch_size = 512 # Batch size during testing
dropout = 0.2 # Dropout probability for each deep layer
l2 = 1e-4 # Weight of l2_regularize in loss
l2_attack = 1e-4 # Weight of attacker l2_regularize in loss
no_filter = False # if or not use filters
reg_weight = 1 # Trade off for adversarial penalty
d_steps = 10 # the number of steps of updating discriminator
optimizer = 'GD' # 'optimizer: GD, Adam, Adagrad
metric = "RMSE" # metrics: RMSE, MAE, AUC, F1, Accuracy, Precision, Recall
skip_eval = 0 # number of epochs without evaluation
num_worker = 2 # number of processes for multi-processing data loading
fix_one = False # fix one feature for evaluation
eval_disc = False # train extra discriminator for evaluation
data_reader = 'RecDataReader' # Choose data_reader
data_processor = 'RecDataset' # Choose data_processor
model_name = 'BiasedMF' # Choose model to run
runner = 'RecRunner' # Choose runner
args = Args()
# + id="DSwbYFgC_6F0"
LOWER_METRIC_LIST = ["rmse", 'mae']
# + [markdown] id="Q40X4lHf4JHw"
# ### Logger
# + id="cibwpV5L4JFb"
logging.basicConfig(stream=sys.stdout,
level = logging.DEBUG,
format='%(asctime)s [%(levelname)s] : %(message)s',
datefmt='%d-%b-%y %H:%M:%S')
logger = logging.getLogger('T297944 Logger')
# + [markdown] id="yTA5LxDK4ES0"
# ## Utilities
# + [markdown] id="fznS-E31A53b"
# ### Dataset
# + id="fLUcWP4p4EQd"
def download_movielens():
download_link = 'https://github.com/sparsh-ai/fairness-recsys/raw/main/data/bronze/ml1m/ml1m_t297944.zip'
save_path = osp.join(args.path,args.dataset+'.zip')
save_path_extracted = osp.join(args.path,args.dataset)
Path(save_path_extracted).mkdir(parents=True, exist_ok=True)
if not os.listdir(save_path_extracted):
wget.download(download_link, out=save_path)
with zipfile.ZipFile(save_path, 'r') as zip_ref:
zip_ref.extractall(save_path_extracted)
logger.info('Files saved in {}'.format(save_path_extracted))
else:
logger.info('Files already exists in {}, skipping!'.format(save_path_extracted))
# + id="MxKtfPC1A7nD"
class DataReader:
def __init__(self, path, dataset_name, sep='\t', seq_sep=','):
self.path = osp.join(path, dataset_name)
self.dataset_name = dataset_name
self.sep = sep
self.seq_sep = seq_sep
self.train_file = osp.join(self.path, dataset_name + args.train_suffix)
self.validation_file = osp.join(self.path, dataset_name + args.validation_suffix)
self.test_file = osp.join(self.path, dataset_name + args.test_suffix)
self.all_file = osp.join(self.path, dataset_name + args.all_suffix)
self.feature_file = osp.join(self.path, dataset_name + args.feature_suffix)
self._load_data()
self.features = self._load_feature() if osp.exists(self.feature_file) else None
def _load_data(self):
if osp.exists(self.all_file):
logger.info("load all csv...")
self.all_df = pd.read_csv(self.all_file, sep=self.sep)
else:
raise FileNotFoundError('all file is not found.')
if osp.exists(self.train_file):
logger.info("load train csv...")
self.train_df = pd.read_csv(self.train_file, sep=self.sep)
logger.info("size of train: %d" % len(self.train_df))
else:
raise FileNotFoundError('train file is not found.')
if osp.exists(self.validation_file):
logger.info("load validation csv...")
self.validation_df = pd.read_csv(self.validation_file, sep=self.sep)
logger.info("size of validation: %d" % len(self.validation_df))
else:
raise FileNotFoundError('validation file is not found.')
if osp.exists(self.test_file):
logger.info("load test csv...")
self.test_df = pd.read_csv(self.test_file, sep=self.sep)
logger.info("size of test: %d" % len(self.test_df))
else:
raise FileNotFoundError('test file is not found.')
def _load_feature(self):
"""
load pre-trained/feature embeddings. It is saved as a numpy text file.
:return:
"""
return np.loadtxt(self.feature_file, dtype=np.float32)
# + id="hCqf2POUCoeQ"
class RecDataReader(DataReader):
def __init__(self, path, dataset_name, sep='\t', seq_sep=','):
super().__init__(path, dataset_name, sep, seq_sep)
self.user_ids_set = set(self.all_df[args.USER].tolist())
self.item_ids_set = set(self.all_df[args.ITEM].tolist())
self.num_nodes = len(self.user_ids_set) + len(self.item_ids_set)
self.train_item2users_dict = self._prepare_item2users_dict(self.train_df)
self.all_user2items_dict = self._prepare_user2items_dict(self.all_df)
self.train_user2items_dict = self._prepare_user2items_dict(self.train_df)
self.valid_user2items_dict = self._prepare_user2items_dict(self.validation_df)
self.test_user2items_dict = self._prepare_user2items_dict(self.test_df)
# add feature info for discriminator and filters
uid_iid_label = [args.USER, args.ITEM, args.LABEL]
self.feature_columns = [name for name in self.train_df.columns.tolist() if name not in uid_iid_label]
Feature = namedtuple('Feature', ['num_class', 'label_min', 'label_max', 'name'])
self.feature_info = \
OrderedDict({idx + 1: Feature(self.all_df[col].nunique(), self.all_df[col].min(), self.all_df[col].max(),
col) for idx, col in enumerate(self.feature_columns)})
self.num_features = len(self.feature_columns)
@staticmethod
def _prepare_user2items_dict(df):
df_groups = df.groupby(args.USER)
user_sample_dict = defaultdict(set)
for uid, group in df_groups:
user_sample_dict[uid] = set(group[args.ITEM].tolist())
return user_sample_dict
@staticmethod
def _prepare_item2users_dict(df):
df_groups = df.groupby(args.ITEM)
user_sample_dict = defaultdict(set)
for uid, group in df_groups:
user_sample_dict[uid] = set(group[args.USER].tolist())
return user_sample_dict
# + id="Q_wJAytIDRoB"
class DiscriminatorDataReader:
def __init__(self, path, dataset_name, sep='\t', seq_sep=',', test_ratio=0.1):
self.path = osp.join(path, dataset_name)
self.sep = sep
self.seq_sep = seq_sep
self.all_file = osp.join(self.path, dataset_name + args.all_suffix)
self.train_attacker_file = osp.join(self.path, dataset_name + '.attacker' + args.train_suffix)
self.test_attacker_file = osp.join(self.path, dataset_name + '.attacker' + args.test_suffix)
self.all_df = pd.read_csv(self.all_file, sep='\t')
# add feature info for discriminator and filters
uid_iid_label = [args.USER, args.ITEM, args.LABEL]
self.feature_columns = [name for name in self.all_df.columns.tolist() if name not in uid_iid_label]
Feature = namedtuple('Feature', ['num_class', 'label_min', 'label_max', 'name'])
self.feature_info = \
OrderedDict({idx + 1: Feature(self.all_df[col].nunique(), self.all_df[col].min(), self.all_df[col].max(),
col) for idx, col in enumerate(self.feature_columns)})
self.f_name_2_idx = {f_name: idx + 1 for idx, f_name in enumerate(self.feature_columns)}
self.num_features = len(self.feature_columns)
if osp.exists(self.train_attacker_file) and osp.exists(self.test_attacker_file):
self.train_df = pd.read_csv(self.train_attacker_file, sep='\t')
self.test_df = pd.read_csv(self.test_attacker_file, sep='\t')
else:
self.train_df, self.test_df = self._init_feature_df(self.all_df, test_ratio)
def _init_feature_df(self, all_df, test_ratio):
logger.info('Initializing attacker train/test file...')
feature_df = pd.DataFrame()
all_df = all_df.sort_values(by='uid')
all_group = all_df.groupby('uid')
uid_list = []
feature_list_dict = {key: [] for key in self.feature_columns}
for uid, group in all_group:
uid_list.append(uid)
for key in feature_list_dict:
feature_list_dict[key].append(group[key].tolist()[0])
feature_df[args.USER] = uid_list
for f in self.feature_columns:
feature_df[f] = feature_list_dict[f]
test_size = int(len(feature_df) * test_ratio)
sign = True
counter = 0
while sign:
test_set = feature_df.sample(n=test_size).sort_index()
for f in self.feature_columns:
num_class = self.feature_info[self.f_name_2_idx[f]].num_class
val_range = set([i for i in range(num_class)])
test_range = set(test_set[f].tolist())
if len(val_range) != len(test_range):
sign = True
break
else:
sign = False
print(counter)
counter += 1
train_set = feature_df.drop(test_set.index)
train_set.to_csv(self.train_attacker_file, sep='\t', index=False)
test_set.to_csv(self.test_attacker_file, sep='\t', index=False)
return train_set, test_set
# + id="XlYwe4eAD8yt"
class RecDataset:
def __init__(self, data_reader, stage, batch_size=128, num_neg=1):
self.data_reader = data_reader
self.num_user = len(data_reader.user_ids_set)
self.num_item = len(data_reader.item_ids_set)
self.batch_size = batch_size
self.stage = stage
self.num_neg = num_neg
# prepare test/validation dataset
valid_pkl_path = osp.join(self.data_reader.path, self.data_reader.dataset_name + args.valid_pkl_suffix)
test_pkl_path = osp.join(self.data_reader.path, self.data_reader.dataset_name + args.test_pkl_suffix)
if self.stage == 'valid':
if osp.exists(valid_pkl_path):
with open(valid_pkl_path, 'rb') as file:
logger.info('Load validation data from pickle file.')
self.data = pickle.load(file)
else:
self.data = self._get_data()
with open(valid_pkl_path, 'wb') as file:
pickle.dump(self.data, file)
elif self.stage == 'test':
if osp.exists(test_pkl_path):
with open(test_pkl_path, 'rb') as file:
logger.info('Load test data from pickle file.')
self.data = pickle.load(file)
else:
self.data = self._get_data()
with open(test_pkl_path, 'wb') as file:
pickle.dump(self.data, file)
else:
self.data = self._get_data()
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
def _get_data(self):
if self.stage == 'train':
return self._get_train_data()
else:
return self._get_vt_data()
def _get_train_data(self):
df = self.data_reader.train_df
df[args.SAMPLE_ID] = df.index
columns_order = [args.USER, args.ITEM, args.SAMPLE_ID, args.LABEL] + [f_col for f_col in self.data_reader.feature_columns]
data = df[columns_order].to_numpy()
return data
def _get_vt_data(self):
if self.stage == 'valid':
df = self.data_reader.validation_df
logger.info('Prepare validation data...')
elif self.stage == 'test':
df = self.data_reader.test_df
logger.info('Prepare test data...')
else:
raise ValueError('Wrong stage in dataset.')
df[args.SAMPLE_ID] = df.index
columns_order = [args.USER, args.ITEM, args.SAMPLE_ID, args.LABEL] + [f_col for f_col in self.data_reader.feature_columns]
data = df[columns_order].to_numpy()
total_batches = int((len(df) + self.batch_size - 1) / self.batch_size)
batches = []
for n_batch in tqdm(range(total_batches), leave=False, ncols=100, mininterval=1, desc='Prepare Batches'):
batch_start = n_batch * self.batch_size
batch_end = min(len(df), batch_start + self.batch_size)
real_batch_size = batch_end - batch_start
batch = data[batch_start:batch_start + real_batch_size, :]
inputs = np.asarray(batch)[:, 0:3]
labels = np.asarray(batch)[:, 3]
features = np.asarray(batch)[:, 4:]
inputs = np.concatenate((inputs, features), axis=1)
neg_samples = self._neg_samples_from_all(inputs, self.num_neg)
neg_labels = np.asarray([0] * neg_samples.shape[0])
tmp_sample = np.concatenate((inputs, neg_samples), axis=0)
samples = torch.from_numpy(tmp_sample[:, 0:3])
labels = torch.from_numpy(np.concatenate((labels, neg_labels), axis=0))
features = torch.from_numpy(tmp_sample[:, 3:])
feed_dict = {'X': samples, args.LABEL: labels, 'features': features}
batches.append(feed_dict)
gc.collect()
return batches
def collate_fn(self, batch):
if self.stage == 'train':
feed_dict = self._collate_train(batch)
else:
feed_dict = self._collate_vt(batch)
return feed_dict
def _collate_train(self, batch):
inputs = np.asarray(batch)[:, 0:3]
labels = np.asarray(batch)[:, 3]
features = np.asarray(batch)[:, 4:]
neg_samples = self._neg_sampler(inputs)
neg_samples = np.insert(neg_samples, 0, inputs[:, 0], axis=1)
neg_samples = np.insert(neg_samples, 2, inputs[:, 2], axis=1)
neg_labels = np.asarray([0] * neg_samples.shape[0])
neg_features = np.copy(features)
assert len(inputs) == len(neg_samples)
samples = torch.from_numpy(np.concatenate((inputs, neg_samples), axis=0))
labels = torch.from_numpy(np.concatenate((labels, neg_labels), axis=0))
features = torch.from_numpy((np.concatenate((features, neg_features), axis=0)))
feed_dict = {'X': samples, args.LABEL: labels, 'features': features}
return feed_dict
@staticmethod
def _collate_vt(data):
return data
def _neg_sampler(self, batch):
neg_items = np.random.randint(1, self.num_item, size=(len(batch), self.num_neg))
for i, (user, _, _) in enumerate(batch):
user_clicked_set = self.data_reader.all_user2items_dict[user]
for j in range(self.num_neg):
while neg_items[i][j] in user_clicked_set:
neg_items[i][j] = np.random.randint(1, self.num_item)
return neg_items
def _neg_samples_from_all(self, batch, num_neg=-1):
neg_items = None
for idx, data in enumerate(batch):
user = data[0]
sample_id = data[2]
features = data[3:]
neg_candidates = list(self.data_reader.item_ids_set - self.data_reader.all_user2items_dict[user])
if num_neg != -1:
if num_neg <= len(neg_candidates):
neg_candidates = np.random.choice(neg_candidates, num_neg, replace=False)
else:
neg_candidates = np.random.choice(neg_candidates, len(neg_candidates), replace=False)
user_arr = np.asarray([user] * len(neg_candidates))
id_arr = np.asarray([sample_id] * len(neg_candidates))
feature_arr = np.tile(features, (len(neg_candidates), 1))
neg_candidates = np.expand_dims(np.asarray(neg_candidates), axis=1)
neg_candidates = np.insert(neg_candidates, 0, user_arr, axis=1)
neg_candidates = np.insert(neg_candidates, 2, id_arr, axis=1)
neg_candidates = np.concatenate((neg_candidates, feature_arr), axis=1)
if neg_items is None:
neg_items = neg_candidates
else:
neg_items = np.concatenate((neg_items, neg_candidates), axis=0)
return neg_items
# + id="73FySA2dEOgn"
class DiscriminatorDataset:
def __init__(self, data_reader, stage, batch_size=1000):
self.data_reader = data_reader
self.stage = stage
self.batch_size = batch_size
self.data = self._get_data()
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
def _get_data(self):
if self.stage == 'train':
return self._get_train_data()
else:
return self._get_test_data()
def _get_train_data(self):
data = self.data_reader.train_df.to_numpy()
return data
def _get_test_data(self):
data = self.data_reader.test_df.to_numpy()
return data
@staticmethod
def collate_fn(data):
feed_dict = dict()
feed_dict['X'] = torch.from_numpy(np.asarray(data)[:, 0])
feed_dict['features'] = torch.from_numpy(np.asarray(data)[:, 1:])
return feed_dict
# + [markdown] id="3xeYrB4zLsZA"
# ### Models
# + id="EvGqNW4cL6Z7"
class BaseRecModel(nn.Module):
@staticmethod
def init_weights(m):
"""
initialize nn weights,called in main.py
:param m: parameter or the nn
:return:
"""
if type(m) == torch.nn.Linear:
torch.nn.init.normal_(m.weight, mean=0.0, std=0.01)
if m.bias is not None:
torch.nn.init.normal_(m.bias, mean=0.0, std=0.01)
elif type(m) == torch.nn.Embedding:
torch.nn.init.normal_(m.weight, mean=0.0, std=0.01)
def __init__(self, data_processor_dict, user_num, item_num, u_vector_size, i_vector_size,
random_seed=2020, dropout=0.2, model_path='../model/Model/Model.pt', filter_mode='combine'):
"""
:param data_processor_dict:
:param user_num:
:param item_num:
:param u_vector_size:
:param i_vector_size:
:param random_seed:
:param dropout:
:param model_path:
:param filter_mode: 'combine'-> for each combination train one filter;
'separate' -> one filter for one sensitive feature, do combination for complex case.
"""
super(BaseRecModel, self).__init__()
self.data_processor_dict = data_processor_dict
self.user_num = user_num
self.item_num = item_num
self.u_vector_size = u_vector_size
self.i_vector_size = i_vector_size
self.dropout = dropout
self.random_seed = random_seed
self.filter_mode = filter_mode
torch.manual_seed(self.random_seed)
torch.cuda.manual_seed(self.random_seed)
self.model_path = model_path
self._init_nn()
self._init_sensitive_filter()
logger.debug(list(self.parameters()))
self.total_parameters = self.count_variables()
logger.info('# of params: %d' % self.total_parameters)
# optimizer assigned by *_runner.py
self.optimizer = None
def _init_nn(self):
"""
Initialize neural networks
:return:
"""
raise NotImplementedError
def _init_sensitive_filter(self):
def get_sensitive_filter(embed_dim):
sequential = nn.Sequential(
nn.Linear(embed_dim, embed_dim * 2),
nn.LeakyReLU(),
nn.Linear(embed_dim * 2, embed_dim),
nn.LeakyReLU(),
nn.BatchNorm1d(embed_dim)
)
return sequential
num_features = len(self.data_processor_dict['train'].data_reader.feature_columns)
self.filter_num = num_features if self.filter_mode == 'combine' else 2**num_features
self.num_features = num_features
self.filter_dict = nn.ModuleDict(
{str(i + 1): get_sensitive_filter(self.u_vector_size) for i in range(self.filter_num)})
def apply_filter(self, vectors, filter_mask):
if self.filter_mode == 'separate' and np.sum(filter_mask) != 0:
filter_mask = np.asarray(filter_mask)
idx = filter_mask.dot(2**np.arange(filter_mask.size))
sens_filter = self.filter_dict[str(idx)]
result = sens_filter(vectors)
elif self.filter_mode == 'combine' and np.sum(filter_mask) != 0:
result = None
for idx, val in enumerate(filter_mask):
if val != 0:
sens_filter = self.filter_dict[str(idx + 1)]
result = sens_filter(vectors) if result is None else result + sens_filter(vectors)
result = result / np.sum(filter_mask) # average the embedding
else:
result = vectors
return result
def count_variables(self):
"""
Total number of parameters in the model
:return:
"""
total_parameters = sum(p.numel() for p in self.parameters() if p.requires_grad)
return total_parameters
def l2(self):
"""
calc the summation of l2 of all parameters
:return:
"""
l2 = 0
for p in self.parameters():
l2 += (p ** 2).sum()
return l2
def predict(self, feed_dict, filter_mask):
"""
prediction only without loss calculation
:param feed_dict: input dictionary
:param filter_mask: mask for filter selection
:return: output dictionary,with keys (at least)
"prediction": predicted values;
"check": intermediate results to be checked and printed out
"""
check_list = []
x = self.x_bn(feed_dict['X'].float())
x = torch.nn.Dropout(p=feed_dict['dropout'])(x)
prediction = F.relu(self.prediction(x)).view([-1])
out_dict = {'prediction': prediction,
'check': check_list}
return out_dict
def forward(self, feed_dict, filter_mask):
out_dict = self.predict(feed_dict, filter_mask)
batch_size = int(feed_dict[args.LABEL].shape[0] / 2)
pos, neg = out_dict['prediction'][:batch_size], out_dict['prediction'][batch_size:]
loss = -(pos - neg).sigmoid().log().sum()
out_dict['loss'] = loss
return out_dict
def save_model(self, model_path=None):
if model_path is None:
model_path = self.model_path
dir_path = osp.dirname(model_path)
if not osp.exists(dir_path):
os.mkdir(dir_path)
torch.save(self.state_dict(), model_path)
logger.info('Save model to ' + model_path)
def load_model(self, model_path=None):
if model_path is None:
model_path = self.model_path
self.load_state_dict(torch.load(model_path))
self.eval()
logger.info('Load model from ' + model_path)
def freeze_model(self):
self.eval()
for params in self.parameters():
params.requires_grad = False
# + id="tryT1aMRM_bh"
class PMF(BaseRecModel):
def _init_nn(self):
self.uid_embeddings = torch.nn.Embedding(self.user_num, self.u_vector_size)
self.iid_embeddings = torch.nn.Embedding(self.item_num, self.u_vector_size)
def predict(self, feed_dict, filter_mask):
check_list = []
u_ids = feed_dict['X'][:, 0] - 1
i_ids = feed_dict['X'][:, 1] - 1
pmf_u_vectors = self.uid_embeddings(u_ids)
pmf_i_vectors = self.iid_embeddings(i_ids)
pmf_u_vectors = self.apply_filter(pmf_u_vectors, filter_mask)
prediction = (pmf_u_vectors * pmf_i_vectors).sum(dim=1).view([-1])
out_dict = {'prediction': prediction,
'check': check_list,
'u_vectors': pmf_u_vectors}
return out_dict
# + id="JfnXVZLONt6h"
class RecRunner:
def __init__(self, optimizer='GD', learning_rate=0.01, epoch=100, batch_size=128, eval_batch_size=128 * 128,
dropout=0.2, l2=1e-5, metrics='RMSE', check_epoch=10, early_stop=1, num_worker=1, no_filter=False,
reg_weight=0.1, d_steps=100, disc_epoch=1000):
"""
初始化
:param optimizer: optimizer name
:param learning_rate: learning rate
:param epoch: total training epochs
:param batch_size: batch size for training
:param eval_batch_size: batch size for evaluation
:param dropout: dropout rate
:param l2: l2 weight
:param metrics: evaluation metrics list
:param check_epoch: check intermediate results in every n epochs
:param early_stop: 1 for early stop, 0 for not.
:param no_filter: if or not use filters
:param reg_weight: adversarial penalty weight
:param d_steps: the number of steps to optimize discriminator
:param disc_epoch: number of epoch for training extra discriminator
"""
self.optimizer_name = optimizer
self.learning_rate = learning_rate
self.epoch = epoch
self.batch_size = batch_size
self.eval_batch_size = eval_batch_size
self.dropout = dropout
self.no_dropout = 0.0
self.l2_weight = l2
self.reg_weight = reg_weight
self.d_steps = d_steps
self.no_filter = no_filter
self.disc_epoch = disc_epoch
# convert metrics to list of str
self.metrics = metrics.lower().split(',')
self.check_epoch = check_epoch
self.early_stop = early_stop
self.time = None
# record train, validation, test results
self.train_results, self.valid_results, self.test_results = [], [], []
self.disc_results = []
self.num_worker = num_worker
def _build_optimizer(self, model, lr=None, l2_weight=None):
optimizer_name = self.optimizer_name.lower()
if lr is None:
lr = self.learning_rate
if l2_weight is None:
l2_weight = self.l2_weight
if optimizer_name == 'gd':
logger.info("Optimizer: GD")
optimizer = torch.optim.SGD(model.parameters(), lr=lr, weight_decay=l2_weight)
elif optimizer_name == 'adagrad':
logger.info("Optimizer: Adagrad")
optimizer = torch.optim.Adagrad(model.parameters(), lr=lr, weight_decay=l2_weight)
elif optimizer_name == 'adam':
logger.info("Optimizer: Adam")
optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=l2_weight)
else:
logging.error("Unknown Optimizer: " + self.optimizer_name)
assert self.optimizer_name in ['GD', 'Adagrad', 'Adam']
optimizer = torch.optim.SGD(model.parameters(), lr=lr, weight_decay=l2_weight)
return optimizer
def _check_time(self, start=False):
if self.time is None or start:
self.time = [time()] * 2
return self.time[0]
tmp_time = self.time[1]
self.time[1] = time()
return self.time[1] - tmp_time
@staticmethod
def get_filter_mask(filter_num):
return np.random.choice([0, 1], size=(filter_num,))
@staticmethod
def _get_masked_disc(disc_dict, labels, mask):
if np.sum(mask) == 0:
return []
masked_disc_label = [(disc_dict[i + 1], labels[:, i]) for i, val in enumerate(mask) if val != 0]
return masked_disc_label
def fit(self, model, batches, fair_disc_dict, epoch=-1): # fit the results for an input set
"""
Train the model
:param model: model instance
:param batches: train data in batches
:param fair_disc_dict: fairness discriminator dictionary
:param epoch: epoch number
:return: return the output of the last round
"""
gc.collect()
torch.cuda.empty_cache()
if model.optimizer is None:
model.optimizer = self._build_optimizer(model)
model.train()
for idx in fair_disc_dict:
discriminator = fair_disc_dict[idx]
if discriminator.optimizer is None:
discriminator.optimizer = self._build_optimizer(discriminator)
discriminator.train()
loss_list = list()
output_dict = dict()
eval_dict = None
for batch in tqdm(batches, leave=False, desc='Epoch %5d' % (epoch + 1),
ncols=100, mininterval=1):
# step1: use filter mask select filters
# step2: use selected filter filter out the embeddings
# step3: use the filtered embeddings for recommendation task and get rec loss rec_loss
# step4: apply the discriminator with the filtered embeddings and get discriminator loss d_loss
# (use filter_mask to decide use which discriminator)
# step5: combine rec_loss and d_loss and do optimization (use filter and rec model optimizer)
# step6: use discriminator optimizer to optimize discriminator K times
if self.no_filter:
mask = [0] * model.num_features
mask = np.asarray(mask)
else:
mask = self.get_filter_mask(model.num_features)
batch = batch_to_gpu(batch)
model.optimizer.zero_grad()
labels = batch['features'][:len(batch['features'])//2, :]
if not self.no_filter:
masked_disc_label = \
self._get_masked_disc(fair_disc_dict, labels, mask)
else:
masked_disc_label = \
self._get_masked_disc(fair_disc_dict, labels, mask + 1)
# calculate recommendation loss + fair discriminator penalty
result_dict = model(batch, mask)
rec_loss = result_dict['loss']
vectors = result_dict['u_vectors']
vectors = vectors[:len(vectors) // 2, :]
fair_d_penalty = 0
if not self.no_filter:
for fair_disc, label in masked_disc_label:
fair_d_penalty += fair_disc(vectors, label)
fair_d_penalty *= -1
loss = rec_loss + self.reg_weight * fair_d_penalty
else:
loss = rec_loss
loss.backward()
model.optimizer.step()
loss_list.append(result_dict['loss'].detach().cpu().data.numpy())
output_dict['check'] = result_dict['check']
# update discriminator
if not self.no_filter:
if len(masked_disc_label) != 0:
for _ in range(self.d_steps):
for discriminator, label in masked_disc_label:
discriminator.optimizer.zero_grad()
disc_loss = discriminator(vectors.detach(), label)
disc_loss.backward(retain_graph=False)
discriminator.optimizer.step()
# collect discriminator evaluation results
if eval_dict is None:
eval_dict = self._eval_discriminator(model, labels, vectors.detach(), fair_disc_dict, len(mask))
else:
batch_eval_dict = self._eval_discriminator(model, labels, vectors.detach(), fair_disc_dict, len(mask))
for f_name in eval_dict:
new_label = batch_eval_dict[f_name]['label']
current_label = eval_dict[f_name]['label']
eval_dict[f_name]['label'] = torch.cat((current_label, new_label), dim=0)
new_prediction = batch_eval_dict[f_name]['prediction']
current_prediction = eval_dict[f_name]['prediction']
eval_dict[f_name]['prediction'] = torch.cat((current_prediction, new_prediction), dim=0)
# generate discriminator evaluation scores
d_score_dict = {}
if eval_dict is not None:
for f_name in eval_dict:
l = eval_dict[f_name]['label']
pred = eval_dict[f_name]['prediction']
n_class = eval_dict[f_name]['num_class']
d_score_dict[f_name] = self._disc_eval_method(l, pred, n_class)
output_dict['d_score'] = d_score_dict
output_dict['loss'] = np.mean(loss_list)
return output_dict
def train(self, model, dp_dict, fair_disc_dict, skip_eval=0, fix_one=False):
"""
Train model
:param model: model obj
:param dp_dict: Data processors for train valid and test
:param skip_eval: number of epochs to skip for evaluations
:param fair_disc_dict: fairness discriminator dictionary
:return:
"""
train_data = DataLoader(dp_dict['train'], batch_size=self.batch_size, num_workers=self.num_worker,
shuffle=True, collate_fn=dp_dict['train'].collate_fn)
validation_data = DataLoader(dp_dict['valid'], batch_size=None, num_workers=self.num_worker,
pin_memory=True, collate_fn=dp_dict['test'].collate_fn)
test_data = DataLoader(dp_dict['test'], batch_size=None, num_workers=self.num_worker,
pin_memory=True, collate_fn=dp_dict['test'].collate_fn)
self._check_time(start=True) # start time
try:
for epoch in range(self.epoch):
self._check_time()
output_dict = \
self.fit(model, train_data, fair_disc_dict, epoch=epoch)
if self.check_epoch > 0 and (epoch == 1 or epoch % self.check_epoch == 0):
self.check(model, output_dict)
training_time = self._check_time()
if epoch >= skip_eval:
valid_result_dict, test_result_dict = None, None
if self.no_filter:
valid_result = self.evaluate(model, validation_data) if \
validation_data is not None else [-1.0] * len(self.metrics)
test_result = self.evaluate(model, test_data) \
if test_data is not None else [-1.0] * len(self.metrics)
else:
valid_result, valid_result_dict = \
self.eval_multi_combination(model, validation_data, fix_one) \
if validation_data is not None else [-1.0] * len(self.metrics)
test_result, test_result_dict = self.eval_multi_combination(model, test_data, fix_one) \
if test_data is not None else [-1.0] * len(self.metrics)
testing_time = self._check_time()
# self.train_results.append(train_result)
self.valid_results.append(valid_result)
self.test_results.append(test_result)
self.disc_results.append(output_dict['d_score'])
if self.no_filter:
logger.info("Epoch %5d [%.1f s]\n validation= %s test= %s [%.1f s] "
% (epoch + 1, training_time,
format_metric(valid_result), format_metric(test_result),
testing_time) + ','.join(self.metrics))
else:
logger.info("Epoch %5d [%.1f s]\t Average: validation= %s test= %s [%.1f s] "
% (epoch + 1, training_time,
format_metric(valid_result), format_metric(test_result),
testing_time) + ','.join(self.metrics))
for key in valid_result_dict:
logger.info("validation= %s test= %s "
% (format_metric(valid_result_dict[key]),
format_metric(test_result_dict[key])) + ','.join(self.metrics) +
' (' + key + ') ')
if best_result(self.metrics[0], self.valid_results) == self.valid_results[-1]:
model.save_model()
for idx in fair_disc_dict:
fair_disc_dict[idx].save_model()
if self.eva_termination() and self.early_stop == 1:
logger.info("Early stop at %d based on validation result." % (epoch + 1))
break
if epoch < skip_eval:
logger.info("Epoch %5d [%.1f s]" % (epoch + 1, training_time))
except KeyboardInterrupt:
logger.info("Early stop manually")
save_here = input("Save here? (1/0) (default 0):")
if str(save_here).lower().startswith('1'):
model.save_model()
for idx in fair_disc_dict:
fair_disc_dict[idx].save_model()
# Find the best validation result across iterations
best_valid_score = best_result(self.metrics[0], self.valid_results)
best_epoch = self.valid_results.index(best_valid_score)
# prepare disc result string
disc_info = self.disc_results[best_epoch]
disc_info_str = ['{}={:.4f}'.format(key, disc_info[key]) for key in disc_info]
disc_info_str = ','.join(disc_info_str)
logger.info("Best Iter(validation)= %5d\t valid= %s test= %s [%.1f s] "
% (best_epoch + 1,
format_metric(self.valid_results[best_epoch]),
format_metric(self.test_results[best_epoch]),
self.time[1] - self.time[0]) + ','.join(self.metrics) + ' ' + disc_info_str +
' AUC')
best_test_score = best_result(self.metrics[0], self.test_results)
best_epoch = self.test_results.index(best_test_score)
disc_info = self.disc_results[best_epoch]
disc_info_str = ['{}={:.4f}'.format(key, disc_info[key]) for key in disc_info]
disc_info_str = ','.join(disc_info_str)
logger.info("Best Iter(test)= %5d\t valid= %s test= %s [%.1f s] "
% (best_epoch + 1,
format_metric(self.valid_results[best_epoch]),
format_metric(self.test_results[best_epoch]),
self.time[1] - self.time[0]) + ','.join(self.metrics) + ' ' + disc_info_str +
' AUC')
model.load_model()
for idx in fair_disc_dict:
fair_disc_dict[idx].load_model()
def eval_multi_combination(self, model, data, fix_one=False):
"""
Evaluate model on validation/test dataset under different filter combinations.
The output is the averaged result over all the possible combinations.
:param model: trained model
:param data: validation or test data (not train data)
:param fix_one: if true, only evaluate on one feature instead of all the combinations (save running time)
:return: averaged evaluated result on given dataset
"""
n_features = model.num_features
feature_info = model.data_processor_dict['train'].data_reader.feature_info
if not fix_one:
mask_list = [list(i) for i in it.product([0, 1], repeat=n_features)]
mask_list.pop(0)
# mask_list = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
else:
feature_range = np.arange(n_features)
shape = (feature_range.size, feature_range.max() + 1)
one_hot = np.zeros(shape).astype(int)
one_hot[feature_range, feature_range] = 1
mask_list = one_hot.tolist()
mask_list = [mask_list[1]]
result_dict = {}
acc_result = None
for mask in mask_list:
mask = np.asarray(mask)
feature_idx = np.where(mask == 1)[0]
f_name_list = [feature_info[i + 1].name for i in feature_idx]
f_name = ' '.join(f_name_list)
cur_result = self.evaluate(model, data, mask) if data is not None else [-1.0] * len(self.metrics)
acc_result = np.array(cur_result) if acc_result is None else acc_result + np.asarray(cur_result)
result_dict[f_name] = cur_result
if acc_result is not None:
acc_result /= len(mask_list)
return list(acc_result), result_dict
@torch.no_grad()
def evaluate(self, model, batches, mask=None, metrics=None):
"""
evaluate recommendation performance
:param model:
:param batches: data batches, each batch is a dict.
:param mask: filter mask
:param metrics: list of str
:return: list of float number for each metric
"""
if metrics is None:
metrics = self.metrics
model.eval()
if mask is None:
mask = [0] * model.filter_num
mask = np.asarray(mask)
result_dict = defaultdict(list)
for batch in tqdm(batches, leave=False, ncols=100, mininterval=1, desc='Predict'):
batch = batch_to_gpu(batch)
out_dict = model.predict(batch, mask)
prediction = out_dict['prediction']
labels = batch[args.LABEL].cpu()
sample_ids = batch['X'][:, 2].cpu()
assert len(labels) == len(prediction)
assert len(sample_ids == len(prediction))
prediction = prediction.cpu().numpy()
data_dict = {args.LABEL: labels, args.SAMPLE_ID: sample_ids}
results = self.evaluate_method(prediction, data_dict, metrics=metrics)
for key in results:
result_dict[key].extend(results[key])
evaluations = []
for metric in metrics:
evaluations.append(np.average(result_dict[metric]))
return evaluations
@staticmethod
def evaluate_method(p, data, metrics):
"""
Evaluate model predictions.
:param p: predicted values, np.array
:param data: data dictionary which include ground truth labels
:param metrics: metrics list
:return: a list of results. The order is consistent to metric list.
"""
label = data[args.LABEL]
evaluations = {}
for metric in metrics:
if metric == 'rmse':
evaluations[metric] = [np.sqrt(mean_squared_error(label, p))]
elif metric == 'mae':
evaluations[metric] = [mean_absolute_error(label, p)]
elif metric == 'auc':
evaluations[metric] = [roc_auc_score(label, p)]
else:
k = int(metric.split('@')[-1])
df = pd.DataFrame()
df[args.SAMPLE_ID] = data[args.SAMPLE_ID]
df['p'] = p
df['l'] = label
df = df.sort_values(by='p', ascending=False)
df_group = df.groupby(args.SAMPLE_ID)
if metric.startswith('ndcg@'):
ndcgs = []
for uid, group in df_group:
ndcgs.append(ndcg_at_k(group['l'].tolist()[:k], k=k, method=1))
evaluations[metric] = ndcgs
elif metric.startswith('hit@'):
hits = []
for uid, group in df_group:
hits.append(int(np.sum(group['l'][:k]) > 0))
evaluations[metric] = hits
elif metric.startswith('precision@'):
precisions = []
for uid, group in df_group:
precisions.append(precision_at_k(group['l'].tolist()[:k], k=k))
evaluations[metric] = precisions
elif metric.startswith('recall@'):
recalls = []
for uid, group in df_group:
recalls.append(1.0 * np.sum(group['l'][:k]) / np.sum(group['l']))
evaluations[metric] = recalls
elif metric.startswith('f1@'):
f1 = []
for uid, group in df_group:
num_overlap = 1.0 * np.sum(group['l'][:k])
f1.append(2 * num_overlap / (k + 1.0 * np.sum(group['l'])))
evaluations[metric] = f1
return evaluations
def eva_termination(self):
"""
Early stopper
:return:
"""
metric = self.metrics[0]
valid = self.valid_results
if len(valid) > 20 and metric in LOWER_METRIC_LIST and strictly_increasing(valid[-5:]):
return True
elif len(valid) > 20 and metric not in LOWER_METRIC_LIST and strictly_decreasing(valid[-5:]):
return True
elif len(valid) - valid.index(best_result(metric, valid)) > 20:
return True
return False
@torch.no_grad()
def _eval_discriminator(self, model, labels, u_vectors, fair_disc_dict, num_disc):
feature_info = model.data_processor_dict['train'].data_reader.feature_info
feature_eval_dict = {}
for i in range(num_disc):
discriminator = fair_disc_dict[i + 1]
label = labels[:, i]
# metric = 'auc' if feature_info[i + 1].num_class == 2 else 'f1'
feature_name = feature_info[i + 1].name
discriminator.eval()
if feature_info[i + 1].num_class == 2:
prediction = discriminator.predict(u_vectors)['prediction'].squeeze()
else:
prediction = discriminator.predict(u_vectors)['output']
feature_eval_dict[feature_name] = {'label': label.cpu(), 'prediction': prediction.detach().cpu(),
'num_class': feature_info[i + 1].num_class}
discriminator.train()
return feature_eval_dict
@staticmethod
def _disc_eval_method(label, prediction, num_class, metric='auc'):
if metric == 'auc':
if num_class == 2:
score = roc_auc_score(label, prediction, average='micro')
# score = roc_auc_score(label, prediction)
score = max(score, 1 - score)
return score
else:
lb = LabelBinarizer()
classes = [i for i in range(num_class)]
lb.fit(classes)
label = lb.transform(label)
# label = lb.fit_transform(label)
score = roc_auc_score(label, prediction, multi_class='ovo', average='macro')
score = max(score, 1 - score)
return score
else:
raise ValueError('Unknown evaluation metric in _disc_eval_method().')
def check(self, model, out_dict):
"""
Check intermediate results
:param model: model obj
:param out_dict: output dictionary
:return:
"""
check = out_dict
logger.info(os.linesep)
for i, t in enumerate(check['check']):
d = np.array(t[1].detach().cpu())
logger.info(os.linesep.join([t[0] + '\t' + str(d.shape), np.array2string(d, threshold=20)]) + os.linesep)
loss, l2 = check['loss'], model.l2()
l2 = l2 * self.l2_weight
l2 = l2.detach()
logger.info('loss = %.4f, l2 = %.4f' % (loss, l2))
if not (np.absolute(loss) * 0.005 < l2 < np.absolute(loss) * 0.1):
logging.warning('l2 inappropriate: loss = %.4f, l2 = %.4f' % (loss, l2))
# for discriminator
disc_score_dict = out_dict['d_score']
for feature in disc_score_dict:
logger.info('{} AUC = {:.4f}'.format(feature, disc_score_dict[feature]))
def train_discriminator(self, model, dp_dict, fair_disc_dict, lr_attack=None, l2_attack=None):
"""
Train discriminator to evaluate the quality of learned embeddings
:param model: trained model
:param dp_dict: Data processors for train valid and test
:param fair_disc_dict: fairness discriminator dictionary
:return:
"""
train_data = DataLoader(dp_dict['train'], batch_size=dp_dict['train'].batch_size, num_workers=self.num_worker,
shuffle=True, collate_fn=dp_dict['train'].collate_fn)
test_data = DataLoader(dp_dict['test'], batch_size=dp_dict['test'].batch_size, num_workers=self.num_worker,
pin_memory=True, collate_fn=dp_dict['test'].collate_fn)
self._check_time(start=True) # 记录初始时间s
feature_results = defaultdict(list)
best_results = dict()
try:
for epoch in range(self.disc_epoch):
self._check_time()
output_dict = \
self.fit_disc(model, train_data, fair_disc_dict, epoch=epoch,
lr_attack=lr_attack, l2_attack=l2_attack)
if self.check_epoch > 0 and (epoch == 1 or epoch % (self.disc_epoch // 4) == 0):
self.check_disc(output_dict)
training_time = self._check_time()
test_result_dict = \
self.evaluation_disc(model, fair_disc_dict, test_data, dp_dict['train'])
d_score_dict = test_result_dict['d_score']
# testing_time = self._check_time()
if epoch % (self.disc_epoch // 4) == 0:
logger.info("Epoch %5d [%.1f s]" % (epoch + 1, training_time))
for f_name in d_score_dict:
if epoch % (self.disc_epoch // 4) == 0:
logger.info("{} AUC= {:.4f}".format(f_name, d_score_dict[f_name]))
feature_results[f_name].append(d_score_dict[f_name])
if d_score_dict[f_name] == max(feature_results[f_name]):
best_results[f_name] = d_score_dict[f_name]
idx = dp_dict['train'].data_reader.f_name_2_idx[f_name]
fair_disc_dict[idx].save_model()
except KeyboardInterrupt:
logger.info("Early stop manually")
save_here = input("Save here? (1/0) (default 0):")
if str(save_here).lower().startswith('1'):
for idx in fair_disc_dict:
fair_disc_dict[idx].save_model()
for f_name in best_results:
logger.info("{} best AUC: {:.4f}".format(f_name, best_results[f_name]))
for idx in fair_disc_dict:
fair_disc_dict[idx].load_model()
def fit_disc(self, model, batches, fair_disc_dict, epoch=-1, lr_attack=None, l2_attack=None):
"""
Train the discriminator
:param model: model instance
:param batches: train data in batches
:param fair_disc_dict: fairness discriminator dictionary
:param epoch: epoch number
:param lr_attack: attacker learning rate
:param l2_attack: l2 regularization weight for attacker
:return: return the output of the last round
"""
gc.collect()
torch.cuda.empty_cache()
for idx in fair_disc_dict:
discriminator = fair_disc_dict[idx]
if discriminator.optimizer is None:
discriminator.optimizer = self._build_optimizer(discriminator, lr=lr_attack, l2_weight=l2_attack)
discriminator.train()
output_dict = dict()
loss_acc = defaultdict(list)
eval_dict = None
for batch in tqdm(batches, leave=False, desc='Epoch %5d' % (epoch + 1),
ncols=100, mininterval=1):
if self.no_filter:
mask = [0] * model.num_features
mask = np.asarray(mask)
else:
mask = self.get_filter_mask(model.num_features)
batch = batch_to_gpu(batch)
labels = batch['features']
if not self.no_filter:
masked_disc_label = \
self._get_masked_disc(fair_disc_dict, labels, mask)
else:
masked_disc_label = \
self._get_masked_disc(fair_disc_dict, labels, mask + 1)
# calculate recommendation loss + fair discriminator penalty
uids = batch['X'] - 1
vectors = model.apply_filter(model.uid_embeddings(uids), mask)
output_dict['check'] = []
# update discriminator
if len(masked_disc_label) != 0:
for idx, (discriminator, label) in enumerate(masked_disc_label):
discriminator.optimizer.zero_grad()
disc_loss = discriminator(vectors.detach(), label)
disc_loss.backward()
discriminator.optimizer.step()
loss_acc[discriminator.name].append(disc_loss.detach().cpu())
for key in loss_acc:
loss_acc[key] = np.mean(loss_acc[key])
output_dict['loss'] = loss_acc
return output_dict
@torch.no_grad()
def evaluation_disc(self, model, fair_disc_dict, test_data, dp):
num_features = dp.data_reader.num_features
def eval_disc(labels, u_vectors, fair_disc_dict, mask):
feature_info = dp.data_reader.feature_info
feature_eval_dict = {}
for i, val in enumerate(mask):
if val == 0:
continue
discriminator = fair_disc_dict[i + 1]
label = labels[:, i]
# metric = 'auc' if feature_info[i + 1].num_class == 2 else 'f1'
feature_name = feature_info[i + 1].name
discriminator.eval()
if feature_info[i + 1].num_class == 2:
prediction = discriminator.predict(u_vectors)['prediction'].squeeze()
else:
prediction = discriminator.predict(u_vectors)['output']
feature_eval_dict[feature_name] = {'label': label.cpu(), 'prediction': prediction.detach().cpu(),
'num_class': feature_info[i + 1].num_class}
discriminator.train()
return feature_eval_dict
eval_dict = {}
for batch in test_data:
# VERSION 1
# if self.no_filter:
# # mask = [0] * model.num_features
# feature_range = np.arange(num_features)
# shape = (feature_range.size, feature_range.max() + 1)
# one_hot = np.zeros(shape).astype(int)
# one_hot[feature_range, feature_range] = 1
# mask_list = one_hot.tolist()
# # if num_features == 3:
# # mask_list = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
# # elif num_features == 4:
# # mask_list = [[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]
# else:
# mask_list = [list(i) for i in it.product([0, 1], repeat=num_features)]
# mask_list.pop(0)
# VERSION 2
mask_list = [list(i) for i in it.product([0, 1], repeat=num_features)]
mask_list.pop(0)
batch = batch_to_gpu(batch)
labels = batch['features']
uids = batch['X'] - 1
for mask in mask_list:
if self.no_filter:
vectors = model.uid_embeddings(uids)
else:
vectors = model.apply_filter(model.uid_embeddings(uids), mask)
batch_eval_dict = eval_disc(labels, vectors.detach(), fair_disc_dict, mask)
for f_name in batch_eval_dict:
if f_name not in eval_dict:
eval_dict[f_name] = batch_eval_dict[f_name]
else:
new_label = batch_eval_dict[f_name]['label']
current_label = eval_dict[f_name]['label']
eval_dict[f_name]['label'] = torch.cat((current_label, new_label), dim=0)
new_prediction = batch_eval_dict[f_name]['prediction']
current_prediction = eval_dict[f_name]['prediction']
eval_dict[f_name]['prediction'] = torch.cat((current_prediction, new_prediction), dim=0)
# generate discriminator evaluation scores
d_score_dict = {}
if eval_dict is not None:
for f_name in eval_dict:
l = eval_dict[f_name]['label']
pred = eval_dict[f_name]['prediction']
n_class = eval_dict[f_name]['num_class']
d_score_dict[f_name] = self._disc_eval_method(l, pred, n_class)
output_dict = dict()
output_dict['d_score'] = d_score_dict
return output_dict
@staticmethod
def check_disc(out_dict):
check = out_dict
logger.info(os.linesep)
for i, t in enumerate(check['check']):
d = np.array(t[1].detach().cpu())
logger.info(os.linesep.join([t[0] + '\t' + str(d.shape), np.array2string(d, threshold=20)]) + os.linesep)
loss_dict = check['loss']
for disc_name, disc_loss in loss_dict.items():
logger.info('%s loss = %.4f' % (disc_name, disc_loss))
# for discriminator
if 'd_score' in out_dict:
disc_score_dict = out_dict['d_score']
for feature in disc_score_dict:
logger.info('{} AUC = {:.4f}'.format(feature, disc_score_dict[feature]))
# + [markdown] id="-mBpD_r2A37k"
# ### Utils
# + id="c5BXgA7TAa8s"
def balance_data(data):
pos_indexes = np.where(data['Y'] == 1)[0]
copy_num = int((len(data['Y']) - len(pos_indexes)) / len(pos_indexes))
if copy_num > 1:
copy_indexes = np.tile(pos_indexes, copy_num)
sample_index = np.concatenate([np.arange(0, len(data['Y'])), copy_indexes])
for k in data:
data[k] = data[k][sample_index]
return data
def input_data_is_list(data):
if type(data) is list or type(data) is tuple:
print("input_data_is_list")
new_data = {}
for k in data[0]:
new_data[k] = np.concatenate([d[k] for d in data])
return new_data
return data
def format_metric(metric):
# print(metric, type(metric))
if type(metric) is not tuple and type(metric) is not list:
metric = [metric]
format_str = []
if type(metric) is tuple or type(metric) is list:
for m in metric:
# print(type(m))
if type(m) is float or type(m) is np.float or type(m) is np.float32 or type(m) is np.float64:
format_str.append('%.4f' % m)
elif type(m) is int or type(m) is np.int or type(m) is np.int32 or type(m) is np.int64:
format_str.append('%d' % m)
return ','.join(format_str)
def shuffle_in_unison_scary(data):
"""
shuffle entire dataset
:param data:
:return:
"""
rng_state = np.random.get_state()
for d in data:
np.random.set_state(rng_state)
np.random.shuffle(data[d])
return data
def best_result(metric, results_list):
if type(metric) is list or type(metric) is tuple:
metric = metric[0]
if metric in LOWER_METRIC_LIST:
return min(results_list)
return max(results_list)
def strictly_increasing(l):
return all(x < y for x, y in zip(l, l[1:]))
def strictly_decreasing(l):
return all(x > y for x, y in zip(l, l[1:]))
def non_increasing(l):
return all(x >= y for x, y in zip(l, l[1:]))
def non_decreasing(l):
return all(x <= y for x, y in zip(l, l[1:]))
def monotonic(l):
return non_increasing(l) or non_decreasing(l)
def numpy_to_torch(d):
t = torch.from_numpy(d)
if torch.cuda.device_count() > 0:
t = t.cuda()
return t
def str2bool(v):
if isinstance(v, bool):
return v
if v.lower() in ('yes', 'true', 't', 'y', '1'):
return True
elif v.lower() in ('no', 'false', 'f', 'n', '0'):
return False
else:
raise argparse.ArgumentTypeError('Boolean value expected.')
def batch_to_gpu(batch):
if torch.cuda.device_count() > 0:
for c in batch:
if type(batch[c]) is torch.Tensor:
batch[c] = batch[c].cuda()
return batch
# + [markdown] id="jKJUMRk6Af0x"
# ### Metrics
# + id="yiC5cZjOAhD3"
def mean_reciprocal_rank(rs):
"""Score is reciprocal of the rank of the first relevant item
First element is 'rank 1'. Relevance is binary (nonzero is relevant).
Example from http://en.wikipedia.org/wiki/Mean_reciprocal_rank
>>> rs = [[0, 0, 1], [0, 1, 0], [1, 0, 0]]
>>> mean_reciprocal_rank(rs)
0.61111111111111105
>>> rs = np.array([[0, 0, 0], [0, 1, 0], [1, 0, 0]])
>>> mean_reciprocal_rank(rs)
0.5
>>> rs = [[0, 0, 0, 1], [1, 0, 0], [1, 0, 0]]
>>> mean_reciprocal_rank(rs)
0.75
Args:
rs: Iterator of relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
Mean reciprocal rank
"""
rs = (np.asarray(r).nonzero()[0] for r in rs)
return np.mean([1. / (r[0] + 1) if r.size else 0. for r in rs])
def reciprocal_rank(rs):
"""Score is reciprocal of the rank of the first relevant item
Args:
rs: Iterator of relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
reciprocal rank
"""
rs = np.asarray(rs).nonzero()[0]
return 1. / (rs[0] + 1) if rs.size else 0.
def r_precision(r):
"""Score is precision after all relevant documents have been retrieved
Relevance is binary (nonzero is relevant).
>>> r = [0, 0, 1]
>>> r_precision(r)
0.33333333333333331
>>> r = [0, 1, 0]
>>> r_precision(r)
0.5
>>> r = [1, 0, 0]
>>> r_precision(r)
1.0
Args:
r: Relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
R Precision
"""
r = np.asarray(r) != 0
z = r.nonzero()[0]
if not z.size:
return 0.
return np.mean(r[:z[-1] + 1])
def precision_at_k(r, k):
"""Score is precision @ k
Relevance is binary (nonzero is relevant).
>>> r = [0, 0, 1]
>>> precision_at_k(r, 1)
0.0
>>> precision_at_k(r, 2)
0.0
>>> precision_at_k(r, 3)
0.33333333333333331
>>> precision_at_k(r, 4)
Traceback (most recent call last):
File "<stdin>", line 1, in ?
ValueError: Relevance score length < k
Args:
r: Relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
Precision @ k
Raises:
ValueError: len(r) must be >= k
"""
assert k >= 1
r = np.asarray(r)[:k] != 0
if r.size != k:
raise ValueError('Relevance score length < k')
return np.mean(r)
def average_precision(r):
"""Score is average precision (area under PR curve)
Relevance is binary (nonzero is relevant).
>>> r = [1, 1, 0, 1, 0, 1, 0, 0, 0, 1]
>>> delta_r = 1. / sum(r)
>>> sum([sum(r[:x + 1]) / (x + 1.) * delta_r for x, y in enumerate(r) if y])
0.7833333333333333
>>> average_precision(r)
0.78333333333333333
Args:
r: Relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
Average precision
"""
r = np.asarray(r) != 0
out = [precision_at_k(r, k + 1) for k in range(r.size) if r[k]]
if not out:
return 0.
return np.mean(out)
def mean_average_precision(rs):
"""Score is mean average precision
Relevance is binary (nonzero is relevant).
>>> rs = [[1, 1, 0, 1, 0, 1, 0, 0, 0, 1]]
>>> mean_average_precision(rs)
0.78333333333333333
>>> rs = [[1, 1, 0, 1, 0, 1, 0, 0, 0, 1], [0]]
>>> mean_average_precision(rs)
0.39166666666666666
Args:
rs: Iterator of relevance scores (list or numpy) in rank order
(first element is the first item)
Returns:
Mean average precision
"""
return np.mean([average_precision(r) for r in rs])
def dcg_at_k(r, k, method=0):
"""Score is discounted cumulative gain (dcg)
Relevance is positive real values. Can use binary
as the previous methods.
Example from
http://www.stanford.edu/class/cs276/handouts/EvaluationNew-handout-6-per.pdf
>>> r = [3, 2, 3, 0, 0, 1, 2, 2, 3, 0]
>>> dcg_at_k(r, 1)
3.0
>>> dcg_at_k(r, 1, method=1)
3.0
>>> dcg_at_k(r, 2)
5.0
>>> dcg_at_k(r, 2, method=1)
4.2618595071429155
>>> dcg_at_k(r, 10)
9.6051177391888114
>>> dcg_at_k(r, 11)
9.6051177391888114
Args:
r: Relevance scores (list or numpy) in rank order
(first element is the first item)
k: Number of results to consider
method: If 0 then weights are [1.0, 1.0, 0.6309, 0.5, 0.4307, ...]
If 1 then weights are [1.0, 0.6309, 0.5, 0.4307, ...]
Returns:
Discounted cumulative gain
"""
r = np.asfarray(r)[:k]
if r.size:
if method == 0:
return r[0] + np.sum(r[1:] / np.log2(np.arange(2, r.size + 1)))
elif method == 1:
return np.sum(r / np.log2(np.arange(2, r.size + 2)))
else:
raise ValueError('method must be 0 or 1.')
return 0.
def ndcg_at_k(r, k, method=0):
"""Score is normalized discounted cumulative gain (ndcg)
Relevance is positive real values. Can use binary
as the previous methods.
Example from
http://www.stanford.edu/class/cs276/handouts/EvaluationNew-handout-6-per.pdf
>>> r = [3, 2, 3, 0, 0, 1, 2, 2, 3, 0]
>>> ndcg_at_k(r, 1)
1.0
>>> r = [2, 1, 2, 0]
>>> ndcg_at_k(r, 4)
0.9203032077642922
>>> ndcg_at_k(r, 4, method=1)
0.96519546960144276
>>> ndcg_at_k([0], 1)
0.0
>>> ndcg_at_k([1], 2)
1.0
Args:
r: Relevance scores (list or numpy) in rank order
(first element is the first item)
k: Number of results to consider
method: If 0 then weights are [1.0, 1.0, 0.6309, 0.5, 0.4307, ...]
If 1 then weights are [1.0, 0.6309, 0.5, 0.4307, ...]
Returns:
Normalized discounted cumulative gain
"""
dcg_max = dcg_at_k(sorted(r, reverse=True), k, method)
if not dcg_max:
return 0.
return dcg_at_k(r, k, method) / dcg_max
# + [markdown] id="YqvAt2nl4EOL"
# ## Jobs
# + id="nb4As1933lK_"
# # No filters
# python ./main.py --model_name BiasedMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/biasedMF_ml1m_no_filter_neg_sample=100/biasedMF_ml1m_l2=1e-4_dim=64_no_filter_neg_sample=100.pt" --runner RecRunner --d_step 10 --vt_num_neg 100 --vt_batch_size 1024 --no_filter --eval_dict
# python ./main.py --model_name PMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/PMF_ml1m_no_filter_neg_sample=100/PMF_ml1m_l2=1e-4_dim=64_no_filter_neg_sample=100.pt" --runner RecRunner --d_step 10 --vt_num_neg 100 --vt_batch_size 1024 --no_filter --eval_disc
# python ./main.py --model_name DMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/DMF_ml1m_no_filter_neg_sample=100/DMF_ml1m_l2=1e-4_dim=64_no_filter_neg_sample=100.pt" --runner RecRunner --d_step 10 --vt_num_neg 100 --vt_batch_size 1024 --no_filter --eval_disc
# python ./main.py --model_name MLP --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/MLP_ml1m_no_filter_neg_sample=100/MLP_ml1m_l2=1e-4_dim=64_no_filter_neg_sample=100.pt" --runner RecRunner --d_step 10 --vt_num_neg 100 --vt_batch_size 1024 --no_filter --eval_disc
# # Sample command for separate method
# python ./main.py --model_name BiasedMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/biasedMF_ml1m_neg_sample=100_reg_weight=20_separate/biasedMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_separate.pt" --runner RecRunner --d_step 10 --reg_weight 20 --epoch 200 --vt_num_neg 100 --vt_batch_size 1024 --filter_mode separate --fix_one --eval_disc
# python ./main.py --model_name PMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/PMF_ml1m_neg_sample=100_reg_weight=20_separate/PMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_separate.pt" --runner RecRunner --d_step 10 --reg_weight 20 --epoch 200 --vt_num_neg 100 --vt_batch_size 1024 --filter_mode separate --fix_one --eval_disc
# python ./main.py --model_name DMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/DMF_ml1m_neg_sample=100_reg_weight=20_separate/DMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_separate.pt" --runner RecRunner --d_step 10 --reg_weight 20 --epoch 200 --vt_num_neg 100 --vt_batch_size 1024 --filter_mode separate --fix_one --eval_disc
# python ./main.py --model_name MLP --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --u_vector_size 32 --batch_size 1024 --model_path "../model/MLP_ml1m_neg_sample=100_reg_weight=20_separate/MLP_ml1m_l2=1e-4_dim=32_reg_weight=20_neg_sample=100_separate.pt" --runner RecRunner --d_step 10 --reg_weight 20 --vt_num_neg 100 --vt_batch_size 1024 --fix_one --filter_mode separate --eval_disc
# # Sample command for combination method
# python ./main.py --model_name BiasedMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/biasedMF_ml1m_reg_weight=20_neg_sample=100_combine/biasedMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_combine.pt" --runner RecRunner --d_step 10 --reg_weight 20 --vt_num_neg 100 --vt_batch_size 1024 --fix_one --eval_disc
# python ./main.py --model_name PMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/PMF_ml1m_reg_weight=20_neg_sample=100_combine/PMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_combine.pt" --runner RecRunner --d_step 10 --reg_weight 20 --vt_num_neg 100 --vt_batch_size 1024 --fix_one --eval_disc
# python ./main.py --model_name DMF --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --batch_size 1024 --model_path "../model/DMF_ml1m_reg_weight=20_neg_sample=100_combine/DMF_ml1m_l2=1e-4_dim=64_reg_weight=20_neg_sample=100_combine.pt" --runner RecRunner --d_step 10 --reg_weight 20 --vt_num_neg 100 --vt_batch_size 1024 --fix_one --eval_disc
# python ./main.py --model_name MLP --optimizer Adam --dataset ml1M --data_processor RecDataset --metric ndcg@5,ndcg@10,hit@5,hit@10 --l2 1e-4 --u_vector_size 32 --batch_size 1024 --model_path "../model/MLP_ml1m_l2=1e-4_dim=32_reg_weight=20_neg_sample=100/MLP_ml1m_l2=1e-4_dim=32_reg_weight=20_neg_sample=100.pt" --runner RecRunner --d_step 10 --vt_num_neg 100 --vt_batch_size 1024 --reg_weight 20 --fix_one --eval_disc
# + colab={"base_uri": "https://localhost:8080/"} id="MmQfVXVf4EME" executionInfo={"status": "ok", "timestamp": 1636457007116, "user_tz": -330, "elapsed": 33, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "13037694610922482904"}} outputId="300d7bd7-e1e9-4975-94cc-fb9a3d3f4b32"
download_movielens()
# + id="d8Pks02yWPt8"
args.model_name = 'PMF'
# + colab={"base_uri": "https://localhost:8080/"} id="aOPPaVnacCDa" executionInfo={"status": "ok", "timestamp": 1636457009002, "user_tz": -330, "elapsed": 9, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "13037694610922482904"}} outputId="7576be4c-da64-477e-9f0f-37fa01e0d53f"
# choose data_reader
data_reader_name = eval(args.data_reader)
# choose model
model_name = eval(args.model_name)
runner_name = eval(args.runner)
# choose data_processor
data_processor_name = eval(args.data_processor)
# logging
logger.info('DataReader: ' + args.data_reader)
logger.info('Model: ' + args.model_name)
logger.info('Runner: ' + args.runner)
logger.info('DataProcessor: ' + args.data_processor)
# random seed
torch.manual_seed(args.random_seed)
torch.cuda.manual_seed_all(args.random_seed)
np.random.seed(args.random_seed)
# cuda
os.environ["CUDA_VISIBLE_DEVICES"] = args.gpu
logger.info("# cuda devices: %d" % torch.cuda.device_count())
# + colab={"base_uri": "https://localhost:8080/"} id="0WsqdYjkcEQP" executionInfo={"status": "ok", "timestamp": 1636457020721, "user_tz": -330, "elapsed": 5949, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a/default-user=s64", "userId": "13037694610922482904"}} outputId="395e7487-a552-422a-cd83-624b80e450e2"
# create data_reader
data_reader = data_reader_name(path=args.path, dataset_name=args.dataset, sep=args.sep)
# + colab={"base_uri": "https://localhost:8080/", "height": 214, "referenced_widgets": ["b5c1118b4bfb4f9fa0695e91163a1e47", "47532d7cbe0a4c5fb1f1b3575d836ea9", "32db06de410a4481a5ca0b75b42f7ec2", "f0c36db39c5746e79a5643c8dcb21abf", "2d8aeab54e2d4b0ab739c96445f91394", "a39ae408211c46bd95e4a333f2eabbff", "79f7f84ff4b640c7bc7c3cc40f161798", "62be46a350e846a5995ccad4fc4a5954", "b720c3aaf1644da789fdad2d70251972", "4a16f523a0ca4d83b0dd9ce12ff32e4e", "e02966e60c78464496a57d61417d7aa1"]} id="KZWHNAQWcThk" outputId="45d8f03e-f982-4cff-e242-bcb7ad499d21"
# create data processor
data_processor_dict = {}
for stage in ['train', 'valid', 'test']:
if stage == 'train':
if args.data_processor in ['RecDataset']:
data_processor_dict[stage] = data_processor_name(
data_reader, stage, batch_size=args.batch_size, num_neg=args.train_num_neg)
else:
raise ValueError('Unknown DataProcessor')
else:
if args.data_processor in ['RecDataset']:
data_processor_dict[stage] = data_processor_name(
data_reader, stage, batch_size=args.vt_batch_size, num_neg=args.vt_num_neg)
else:
raise ValueError('Unknown DataProcessor')
gc.collect()
# + id="4DT-IGUEiEMB"
# create model
if args.model_name in ['BiasedMF', 'PMF']:
model = model_name(data_processor_dict, user_num=len(data_reader.user_ids_set),
item_num=len(data_reader.item_ids_set), u_vector_size=args.u_vector_size,
i_vector_size=args.i_vector_size, random_seed=args.random_seed, dropout=args.dropout,
model_path=args.model_path, filter_mode=args.filter_mode)
elif args.model_name in ['DMF', 'MLP']:
model = model_name(data_processor_dict, user_num=len(data_reader.user_ids_set),
item_num=len(data_reader.item_ids_set), u_vector_size=args.u_vector_size,
i_vector_size=args.i_vector_size, num_layers=args.num_layers,
random_seed=args.random_seed, dropout=args.dropout,
model_path=args.model_path, filter_mode=args.filter_mode)
else:
logger.error('Unknown Model: ' + args.model_name)
# init model params
model.apply(model.init_weights)
# use gpu
if torch.cuda.device_count() > 0:
model = model.cuda()
# + id="GCxtyvnmibfE"
# create discriminators
fair_disc_dict = {}
for feat_idx in data_reader.feature_info:
fair_disc_dict[feat_idx] = \
Discriminator(args.u_vector_size, data_reader.feature_info[feat_idx],
random_seed=args.random_seed, dropout=args.dropout, neg_slope=args.neg_slope,
model_dir_path=os.path.dirname(args.model_path))
fair_disc_dict[feat_idx].apply(fair_disc_dict[feat_idx].init_weights)
if torch.cuda.device_count() > 0:
fair_disc_dict[feat_idx] = fair_disc_dict[feat_idx].cuda()
if args.runner in ['BaseRunner']:
runner = runner_name(
optimizer=args.optimizer, learning_rate=args.lr,
epoch=args.epoch, batch_size=args.batch_size, eval_batch_size=args.vt_batch_size,
dropout=args.dropout, l2=args.l2,
metrics=args.metric, check_epoch=args.check_epoch, early_stop=args.early_stop)
elif args.runner in ['RecRunner']:
runner = runner_name(
optimizer=args.optimizer, learning_rate=args.lr,
epoch=args.epoch, batch_size=args.batch_size, eval_batch_size=args.vt_batch_size,
dropout=args.dropout, l2=args.l2,
metrics=args.metric, check_epoch=args.check_epoch, early_stop=args.early_stop, num_worker=args.num_worker,
no_filter=args.no_filter, reg_weight=args.reg_weight, d_steps=args.d_steps, disc_epoch=args.disc_epoch)
else:
logger.error('Unknown Runner: ' + args.runner)
if args.load > 0:
model.load_model()
for idx in fair_disc_dict:
fair_disc_dict[idx].load_model()
if args.train > 0:
runner.train(model, data_processor_dict, fair_disc_dict, skip_eval=args.skip_eval, fix_one=args.fix_one)
# + id="ptjwSmJUih-h"
# reset seed
torch.manual_seed(args.random_seed)
torch.cuda.manual_seed_all(args.random_seed)
np.random.seed(args.random_seed)
if args.eval_disc:
# Train extra discriminator for evaluation
# create data reader
disc_data_reader = DiscriminatorDataReader(path=args.path, dataset_name=args.dataset, sep=args.sep)
# create data processor
extra_data_processor_dict = {}
for stage in ['train', 'test']:
extra_data_processor_dict[stage] = DiscriminatorDataset(disc_data_reader, stage, args.disc_batch_size)
# create discriminators
extra_fair_disc_dict = {}
for feat_idx in disc_data_reader.feature_info:
if disc_data_reader.feature_info[feat_idx].num_class == 2:
extra_fair_disc_dict[feat_idx] = \
BinaryAttacker(args.u_vector_size, disc_data_reader.feature_info[feat_idx],
random_seed=args.random_seed, dropout=args.dropout,
neg_slope=args.neg_slope, model_dir_path=os.path.dirname(args.model_path),
model_name='eval')
else:
extra_fair_disc_dict[feat_idx] = \
MultiClassAttacker(args.u_vector_size, disc_data_reader.feature_info[feat_idx],
random_seed=args.random_seed, dropout=args.dropout, neg_slope=args.neg_slope,
model_dir_path=os.path.dirname(args.model_path), model_name='eval')
extra_fair_disc_dict[feat_idx].apply(extra_fair_disc_dict[feat_idx].init_weights)
if torch.cuda.device_count() > 0:
extra_fair_disc_dict[feat_idx] = extra_fair_disc_dict[feat_idx].cuda()
if args.load_attack:
for idx in extra_fair_disc_dict:
logger.info('load attacker model...')
extra_fair_disc_dict[idx].load_model()
model.load_model()
model.freeze_model()
runner.train_discriminator(model, extra_data_processor_dict, extra_fair_disc_dict, args.lr_attack,
args.l2_attack)
# + id="IjNJ3ZmqikOC"
test_data = DataLoader(data_processor_dict['test'], batch_size=None, num_workers=args.num_worker,
pin_memory=True, collate_fn=data_processor_dict['test'].collate_fn)
test_result_dict = dict()
if args.no_filter:
test_result = runner.evaluate(model, test_data)
else:
test_result, test_result_dict = runner.eval_multi_combination(model, test_data, args.fix_one)
if args.no_filter:
logger.info("Test After Training = %s "
% (format_metric(test_result)) + ','.join(runner.metrics))
else:
logger.info("Test After Training:\t Average: %s "
% (format_metric(test_result)) + ','.join(runner.metrics))
for key in test_result_dict:
logger.info("test= %s "
% (format_metric(test_result_dict[key])) + ','.join(runner.metrics) +
' (' + key + ') ')
| _notebooks/2022-01-24-fairness.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from src.models.level_kv_div import binaryTrainer, utils, network
from torch.utils.data import DataLoader
import pandas as pd
import torch
# -
# # train_dataset = binaryTrainer.SparseDataset('../data/processed/sample/train.csv', '../data/processed/sample/train.level.grading', balanced=True, random_neg=False)
# # dev_dataset = binaryTrainer.SparseDataset('../data/processed/sample/dev.csv', '../data/processed/sample/dev.level.grading', balanced=True, random_neg=False)
# train_dataset = binaryTrainer.LargeSparseDataset('../data/sift/siftsmall/siftsmall_learn.csv', 100, balanced=True, random_neg=True)
# dev_dataset = binaryTrainer.LargeSparseDataset('../data/sift/siftsmall/siftsmall_base.csv', 100, balanced=True, random_neg=False)
# torch.save(train_dataset, '../data/sift/siftsmall/siftsmall_learn.binaryTrainer.LargeSparseDataset')
# torch.save(dev_dataset, '../data/sift/siftsmall/siftsmall_base.binaryTrainer.LargeSparseDataset')
train_dataset = torch.load('../data/sift/siftsmall/siftsmall_learn.binaryTrainer.LargeSparseDataset')
dev_dataset = torch.load('../data/sift/siftsmall/siftsmall_base.binaryTrainer.LargeSparseDataset')
# +
model = network.SiameseNet(network.EmbeddingNet())
learning_rate = 4e-3
batch_size = 32768
num_epoches = 3
verbose = True
device = 'cuda' if torch.cuda.is_available() else 'cpu'
weight_decay = 1e-6
log_epoch = 3
# +
# optimizer
no_decay = ['bias', 'LayerNorm.weight']
optimizer_grouped_parameters = [
{'params': [p for n, p in model.named_parameters() if not any(
nd in n for nd in no_decay) and p.requires_grad], 'weight_decay': weight_decay},
{'params': [p for n, p in model.named_parameters() if any(
nd in n for nd in no_decay) and p.requires_grad], 'weight_decay': 0.0}
]
optimizer = torch.optim.AdamW(params=optimizer_grouped_parameters, lr=learning_rate)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size, pin_memory=True)
dev_loader = DataLoader(dev_dataset, shuffle=False, batch_size=batch_size, pin_memory=True)
model = model.to(device)
# -
best_avg_val_kl_loss, best_model, model = binaryTrainer.train_with_eval(train_loader, dev_loader, model, optimizer, num_epoches, log_epoch, verbose, device)
best_avg_val_kl_loss
model = model.cpu()
x = torch.from_numpy(pd.read_csv('../data/sift/siftsmall/siftsmall_base.csv', header=None).to_numpy()).float()
loss_param = 1, 3, 4, 6
k = 100
(margin_res, margin_measure_confusion), (linear_search_res, linear_search_confusion), (pred_dist) = binaryTrainer.evaluate_results(x, best_model, k, loss_param, cache_dist=True)
margin_res
linear_search_res
| notebooks/level_grade_s2.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: bayesian
# language: python
# name: bayesian
# ---
# +
import pymc3 as pm
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import theano.tensor as tt
import theano
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
# +
df = pd.read_csv('../datasets/bikes/hour.csv')
df
feature_cols = ['workingday', 'holiday', 'temp', 'atemp', 'hum', 'windspeed']
out_col = ['cnt']
df[out_col]
# +
X = pm.floatX(df[feature_cols])
Y = pm.floatX(df[out_col].apply(np.log10))
n_hidden = X.shape[1]
with pm.Model() as nn_model:
w1 = pm.Normal('w1', mu=0, sd=1, shape=(X.shape[1], n_hidden))
w2 = pm.Normal('w2', mu=0, sd=1, shape=(n_hidden, 1))
b1 = pm.Normal('b1', mu=0, sd=1, shape=(n_hidden,))
b2 = pm.Normal('b2', mu=0, sd=1, shape=(1,))
a1 = pm.Deterministic('a1', tt.nnet.relu(tt.dot(X, w1) + b1))
a2 = pm.Deterministic('a2', tt.dot(a1, w2) + b2)
output = pm.Normal('likelihood', mu=a2, observed=Y)
# -
with pm.Model() as three_layer_model:
w1 = pm.Normal('w1', mu=0, sd=1, shape=(X.shape[1], n_hidden))
w2 = pm.Normal('w2', mu=0, sd=1, shape=(n_hidden, n_hidden))
w3 = pm.Normal('w3', mu=0, sd=1, shape=(n_hidden, 1))
b1 = pm.Normal('b1', mu=0, sd=1, shape=(n_hidden,))
b2 = pm.Normal('b2', mu=0, sd=1, shape=(n_hidden,))
b3 = pm.Normal('b3', mu=0, sd=1, shape=(1,))
a1 = pm.Deterministic('a1', tt.nnet.relu(tt.dot(X, w1) + b1))
a2 = pm.Deterministic('a2', tt.nnet.relu(tt.dot(a1, w2) + b2))
a3 = pm.Deterministic('a3', tt.dot(a2, w3) + b3)
sd = pm.HalfCauchy('sd', beta=1)
output = pm.Normal('likelihood', mu=a3, sd=sd, observed=Y)
with pm.Model() as linreg_model:
w1 = pm.Normal('w1', mu=0, sd=1, shape=(X.shape[1], 1))
b1 = pm.Normal('b1', mu=0, sd=1, shape=(1,))
a1 = pm.Deterministic('a1', tt.dot(X, w1) + b1)
sd = pm.HalfCauchy('sd', beta=1)
output = pm.Normal('likelihood', mu=a1, sd=sd, observed=Y)
with linreg_model:
s = theano.shared(pm.floatX(1.1))
inference = pm.ADVI(cost_part_grad_scale=s, learning_rate=.01)
approx = pm.fit(200000, method=inference)
plt.plot(inference.hist)
with linreg_model:
trace = approx.sample(2000)
pm.traceplot(trace, varnames=['w1', 'b1'])
with linreg_model:
samps = pm.sample_ppc(trace)
samps['likelihood'].std(axis=0)
samps['likelihood'].mean(axis=0)
# +
from sklearn.metrics import mean_squared_error as mse
mse(Y, samps['likelihood'].mean(axis=0))
# -
plt.scatter(samps['likelihood'].mean(axis=0).squeeze(), Y.values)
| notebooks/deep-regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ### Movies for vertical Flux
# +
#KRM
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib as mpl
# #%matplotlib inline
from math import *
import scipy.io
import scipy as spy
from netCDF4 import Dataset
import pylab as pl
import os
import sys
import seaborn as sns
# +
lib_path = os.path.abspath('../../Building_canyon/BuildCanyon/PythonModulesMITgcm') # Add absolute path to my python scripts
sys.path.append(lib_path)
import ReadOutTools_MITgcm as rout
# +
# Functions
def vertTracBox(Mask, W,zlim=30,ylim=230):
mask_expand = np.expand_dims(Mask[zlim,ylim:,:],0)
mask_expand = mask_expand + np.zeros(W[:,zlim,ylim:,:].shape)
vert = W[:,zlim,ylim:,:]
VertTrans= np.ma.masked_array(vert,mask = mask_expand)
return VertTrans
# Functions
def vertTracBoxDom(Mask, W,zlim=30):
mask_expand = np.expand_dims(Mask[zlim,:,:],0)
mask_expand = mask_expand + np.zeros(W[:,zlim,:,:].shape)
vert = W[:,zlim,:,:]
VertTrans= np.ma.masked_array(vert,mask = mask_expand)
return VertTrans
# +
NoCCanyonGrid='/ocean/kramosmu/MITgcm/TracerExperiments/3DDIFF/run06/gridGlob.nc'
NoCCanyonGridOut = Dataset(NoCCanyonGrid)
NoCCanyonState='/ocean/kramosmu/MITgcm/TracerExperiments/3DDIFF/run06/stateGlob.nc'
NoCCanyonStateOut = Dataset(NoCCanyonState)
FluxTR01NoC = '/ocean/kramosmu/MITgcm/TracerExperiments/3DDIFF/run06/FluxTR01Glob.nc'
NoCFluxOut = Dataset(FluxTR01NoC)
CanyonGrid='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/gridGlob.nc' # this has a canyon but calling it no canyon to use old code
CanyonGridOut = Dataset(CanyonGrid)
CanyonState='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/stateGlob.nc'
CanyonStateOut = Dataset(CanyonState)
FluxTR01 = '/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/FluxTR01Glob.nc'
FluxOut = Dataset(FluxTR01)
# +
#for dimobj in CanyonStateOut.variables.values():
# print dimobj
# +
# General input
nx = 360
ny = 360
nz = 90
nt = 19 # t dimension size
z = CanyonStateOut.variables['Z']
Time = CanyonStateOut.variables['T']
xc = rout.getField(CanyonGrid, 'XC') # x coords tracer cells
yc = rout.getField(CanyonGrid, 'YC') # y coords tracer cells
bathy = rout.getField(CanyonGrid, 'Depth')
hFacC = rout.getField(CanyonGrid, 'HFacC')
MaskC = rout.getMask(CanyonGrid, 'HFacC')
MaskCNoC = rout.getMask(NoCCanyonGrid, 'HFacC')
# +
WTRAC = rout.getField(FluxTR01,'ADVrTr01') #
WTRACNoC = rout.getField(FluxTR01NoC,'ADVrTr01') #
# +
#Vertbase = vertTracAlong(MaskC,VTRAC,zlim=30,ylim=230)*1000.0
#VertbaseNoC = vertTracAlong(MaskCNoC,VTRACNoC,zlim=30,ylim=230)*1000.0
#Anom = (Vertbase-VertbaseNoC)
Vertbase = vertTracBoxDom(MaskC, WTRAC,zlim=30)*1000.0
VertbaseNoC = vertTracBoxDom(MaskCNoC, WTRACNoC,zlim=30)*1000.0
Anom = (Vertbase-VertbaseNoC)
# +
minT = Vertbase.min()
maxT = Vertbase.max()
minTNoC = VertbaseNoC.min()
maxTNoC = VertbaseNoC.max()
minTAnom = Anom.min()
maxTAnom = Anom.max()
print(minT, maxT)
print(minTNoC, maxTNoC)
print(minTAnom,maxTAnom)
# -
import matplotlib.animation as animation
# +
sns.set()
sns.set_style('white')
sns.set_context("talk")
#divmap = sns.diverging_palette(255, 100, l=60, n=7, center="dark", as_cmap=True)
# +
def Plot1(t,ax1):
ax1.clear()
csU = np.linspace(minT,-minT,num=31)
Base = ax1.contourf(xc, yc,Vertbase[t,:,:],csU,cmap='RdYlGn')
if t == 1:
cbar=plt.colorbar(Base,ax=ax1,ticks=[np.arange(minT,-minT,100000)])
cbar.set_label(' mol/s')
#CS = ax1.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax1.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax1.set_xlabel('Along-shore distance [km]')
ax1.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax1.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax1.set_ylabel('Cross-shore distance [km]')
ax1.set_yticks([10000,20000,30000,40000,50000,60000,70000,80000,90000])
ax1.set_yticklabels(['10','20','30','40', '50', '60', '70', '80','90'])
ax1.set_title('Base case - %.1f m Vertical flux at day %0.1f' %(t/2.0+0.5, z[30]))
def Plot2(t,ax2):
ax2.clear()
csU = np.linspace(minTNoC,-minTNoC,num=31)
Base = ax2.contourf(xc, yc,VertbaseNoC[t,:,:],csU,cmap='RdYlGn')
if t == 1:
cbar=plt.colorbar(Base,ax=ax2,ticks=[np.arange(minTNoC,-minTNoC,100000)])
cbar.set_label('mol/s')
#CS = ax1.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax2.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax2.set_xlabel('Along-shore distance [km]')
ax2.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax2.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax2.set_ylabel('Cross-shore distance [km]')
ax2.set_yticks([10000,20000,30000,40000,50000,60000,70000,80000,90000])
ax2.set_yticklabels(['10','20','30','40', '50', '60', '70', '80','90'])
ax2.set_title('Enhanced $K_v$ ($10^{-3}m^2s^{-1}$) in within canyon')
def Plot3(t,ax3):
ax3.clear()
csU = np.linspace(-maxTAnom,maxTAnom,num=31)
Base = ax3.contourf(xc, yc,Anom[t,:,:],csU,cmap='RdYlBu')
if t == 1:
cbar=plt.colorbar(Base,ax=ax3,ticks=[np.arange(minTAnom,-minTAnom,10000)])
cbar.set_label('mol/s')
#CS = ax3.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax3.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax3.set_xlabel('Along-shore distance [km]')
ax3.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax3.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax3.set_ylabel('Cross-shore distance [km]')
ax3.set_yticks([10000,20000,30000,40000,50000,60000,70000,80000,90000])
ax3.set_yticklabels(['10','20','30','40', '50', '60', '70', '80','90'])
ax3.set_title('Difference')
def Plot4(t,ax4):
ax4.clear()
csU = np.linspace(minTNoC,-minTNoC,num=31)
Base = ax4.contourf(xc[100:-100,100:-100], yc[100:-100,100:-100],VertbaseNoC[t,100:-100,100:-100],csU,cmap='RdYlGn')
line = ax4.plot(xc[230,100:-100], yc[230,100:-100],'k',linewidth=2)
if t == 1:
cbar=plt.colorbar(Base,ax=ax4,ticks=[np.arange(minTNoC,-minTNoC,75000)])
cbar.set_label('mol/s')
#CS = ax3.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax4.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax4.set_xlabel('Along-shore distance [km]')
ax4.set_xticks([45000,55000,65000,75000])
ax4.set_xticklabels(['45', '55', '65', '75'])
ax4.set_ylabel('Cross-shore distance [km]')
ax4.set_yticks([40000,50000,60000])
ax4.set_yticklabels(['40', '50', '60'])
ax4.set_title('Zoom enhanced $K_v$')
# +
## Animation
#N=5
xslice=180
yslice=235
zslice= 29 # shelf break index
zslice2= 23
#Empty figures
fig,((ax1,ax2),(ax3,ax4)) = plt.subplots(2, 2,figsize=(30,30))
#Initial image
def init():
Plot1(0,ax1)
Plot2(0,ax2)
Plot3(0,ax3)
Plot4(0,ax4)
plt.tight_layout()
#return[ax1,ax2,ax3,ax4,ax5,ax6,ax7,ax8,ax9]
def animate(tt):
Plot1(tt,ax1)
Plot2(tt,ax2)
Plot3(tt,ax3)
Plot4(tt,ax4)
plt.tight_layout()
#The animation function (max frames=47)
anim = animation.FuncAnimation(fig, animate, init_func=init,frames=18, interval = 200,blit=False, repeat=False)
##A line that makes it all work
mywriter = animation.FFMpegWriter()
##Save in current folder
anim.save('FluxVert_Z30_Tr01_Base_and_3DDiffRun06.mp4',writer=mywriter,fps=0.2, dpi = 300, bitrate = 1000000, codec = "libx264")
plt.show()
# +
# -
| MoviesNotebooks/MoviesVerticalFlux.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to Access Control
#
# We can now start using CrypTen to carry out private computations in some common use cases. In this tutorial, we will demonstrate how CrypTen would apply for the scenarios described in the Introduction. In all scenarios, we'll use a simple two-party setting and demonstrate how we can learn a linear SVM. In the process, we will see how access control works in CrypTen.
#
# As usual, we'll begin by importing the `crypten` and `torch` libraries, and initialize `crypten` with `crypten.init()`.
# +
import crypten
import torch
crypten.init()
torch.set_num_threads(1)
# -
# ### Setup
# In this tutorial, we will train a Linear SVM to perform binary classification. We will first generate 1000 ground truth samples using 100 features and a randomly generated hyperplane to separate positive and negative examples.
#
# (Note: this will cause our classes to be linearly separable, so a linear SVM will be able to classify with perfect accuracy given the right parameters.)
#
# We will also include a test set of examples (that are also linearly separable by the same hyperplane) to show that the model learns a general hyperplane rather than memorizing the training data.
# +
num_features = 100
num_train_examples = 1000
num_test_examples = 100
epochs = 40
lr = 3.0
# Set random seed for reproducibility
torch.manual_seed(1)
features = torch.randn(num_features, num_train_examples)
w_true = torch.randn(1, num_features)
b_true = torch.randn(1)
labels = w_true.matmul(features).add(b_true).sign()
test_features = torch.randn(num_features, num_test_examples)
test_labels = w_true.matmul(test_features).add(b_true).sign()
# -
# Now that we have generated our dataset, we will train our SVM in four different access control scenarios across two parties, Alice and Bob:
#
# - Data Labeling: Alice has access to features, while Bob has access to labels
# - Feature Aggregation: Alice has access to the first 50 features, while Bob has access to the last 50 features
# - Data Augmentation: Alice has access to the first 500 examples, while Bob has access to the last 500 examples
# - Model Hiding: Alice has access to `w_true` and `b_true`, while Bob has access to data samples to be classified
#
# Throughout this tutorial, we will assume Alice is using the rank 0 process, while Bob is using the rank 1 process. Additionally we will initialize our weights using random values.
ALICE = 0
BOB = 1
# In each example, we will use the same code to train our linear SVM once the features and labels are properly encrypted. This code is contained in `examples/mpc_linear_svm`, but it is unnecessary to understand the training code to properly use access control. The training process itself is discussed in depth in later tutorials.
#
from examples.mpc_linear_svm.mpc_linear_svm import train_linear_svm, evaluate_linear_svm
# ## Saving / Loading Data
#
# We have now generated features and labels for our model to learn. In the scenarios we explore in this tutorial, we would like to ensure that each party only has access to some subset of the data we have generated. To do so, we will use special save / load methods that CrypTen provides to handle loading only to a specified party and synchronizing across processes.
#
# We will use `crypten.save_from_party()` here to save data from a particular source, then we will load using `crypten.load_from_party()` in each example to load on a particular source. The following code will save all data we will use to files, then each example will load its data as necessary.
#
# (Note that because we are operating on a single machine, all processes will have access to all of the files we are using. However, this still will work as expected when operating across machines.)
# +
from crypten import mpc
# Specify file locations to save each piece of data
filenames = {
"features": "/tmp/features.pth",
"labels": "/tmp/labels.pth",
"features_alice": "/tmp/features_alice.pth",
"features_bob": "/tmp/features_bob.pth",
"samples_alice": "/tmp/samples_alice.pth",
"samples_bob": "/tmp/samples_bob.pth",
"w_true": "/tmp/w_true.pth",
"b_true": "/tmp/b_true.pth",
"test_features": "/tmp/test_features.pth",
"test_labels": "/tmp/test_labels.pth",
}
@mpc.run_multiprocess(world_size=2)
def save_all_data():
# Save features, labels for Data Labeling example
crypten.save(features, filenames["features"])
crypten.save(labels, filenames["labels"])
# Save split features for Feature Aggregation example
features_alice = features[:50]
features_bob = features[50:]
crypten.save_from_party(features_alice, filenames["features_alice"], src=ALICE)
crypten.save_from_party(features_bob, filenames["features_bob"], src=BOB)
# Save split dataset for Dataset Aggregation example
samples_alice = features[:, :500]
samples_bob = features[:, 500:]
crypten.save_from_party(samples_alice, filenames["samples_alice"], src=ALICE)
crypten.save_from_party(samples_bob, filenames["samples_bob"], src=BOB)
# Save true model weights and biases for Model Hiding example
crypten.save_from_party(w_true, filenames["w_true"], src=ALICE)
crypten.save_from_party(b_true, filenames["b_true"], src=ALICE)
crypten.save_from_party(test_features, filenames["test_features"], src=BOB)
crypten.save_from_party(test_labels, filenames["test_labels"], src=BOB)
save_all_data()
# -
# ## Scenario 1: Data Labeling
#
# Our first example will focus on the <i>Data Labeling</i> scenario. In this example, Alice has access to features, while Bob has access to the labels. We will train our linear svm by encrypting the features from Alice and the labels from Bob, then training our SVM using an aggregation of the encrypted data.
#
# In order to indicate the source of a given encrypted tensor, we encrypt our tensor using `crypten.load()` (from a file) or `crypten.cryptensor()` (from a tensor) using a keyword argument `src`. This `src` argument takes the rank of the party we want to encrypt from (recall that ALICE is 0 and BOB is 1).
#
# (If the `src` is not specified, it will default to the rank 0 party. We will use the default when encrypting public values since the source is irrelevant in this case.)
# +
from crypten import mpc
@mpc.run_multiprocess(world_size=2)
def data_labeling_example():
"""Apply data labeling access control model"""
# Alice loads features, Bob loads labels
features_enc = crypten.load_from_party(filenames["features"], src=ALICE)
labels_enc = crypten.load_from_party(filenames["labels"], src=BOB)
# Execute training
w, b = train_linear_svm(features_enc, labels_enc, epochs=epochs, lr=lr)
# Evaluate model
evaluate_linear_svm(test_features, test_labels, w, b)
data_labeling_example()
# -
# ## Scenario 2: Feature Aggregation
#
# Next, we'll show how we can use CrypTen in the <i>Feature Aggregation</i> scenario. Here Alice and Bob each have 50 features for each sample, and would like to use their combined features to train a model. As before, Alice and Bob wish to keep their respective data private. This scenario can occur when multiple parties measure different features of a similar system, and their measurements may be proprietary or otherwise sensitive.
#
# Unlike the last scenario, one of our variables is split among two parties. This means we will have to concatenate the tensors encrypted from each party before passing them to the training code.
# +
@mpc.run_multiprocess(world_size=2)
def feature_aggregation_example():
"""Apply feature aggregation access control model"""
# Alice loads some features, Bob loads other features
features_alice_enc = crypten.load_from_party(filenames["features_alice"], src=ALICE)
features_bob_enc = crypten.load_from_party(filenames["features_bob"], src=BOB)
# Concatenate features
features_enc = crypten.cat([features_alice_enc, features_bob_enc], dim=0)
# Encrypt labels
labels_enc = crypten.cryptensor(labels)
# Execute training
w, b = train_linear_svm(features_enc, labels_enc, epochs=epochs, lr=lr)
# Evaluate model
evaluate_linear_svm(test_features, test_labels, w, b)
feature_aggregation_example()
# -
# ## Scenario 3: Dataset Augmentation
#
# The next example shows how we can use CrypTen in a <i>Data Augmentation</i> scenario. Here Alice and Bob each have 500 samples, and would like to learn a classifier over their combined sample data. This scenario can occur in applications where several parties may each have access to a small amount of sensitive data, where no individual party has enough data to train an accurate model.
#
# Like the last scenario, one of our variables is split amongst parties, so we will have to concatenate tensors from encrypted from different parties. The main difference from the last scenario is that we are concatenating over the other dimension (the sample dimension rather than the feature dimension).
# +
@mpc.run_multiprocess(world_size=2)
def dataset_augmentation_example():
"""Apply dataset augmentation access control model"""
# Alice loads some samples, Bob loads other samples
samples_alice_enc = crypten.load_from_party(filenames["samples_alice"], src=ALICE)
samples_bob_enc = crypten.load_from_party(filenames["samples_bob"], src=BOB)
# Concatenate features
samples_enc = crypten.cat([samples_alice_enc, samples_bob_enc], dim=1)
labels_enc = crypten.cryptensor(labels)
# Execute training
w, b = train_linear_svm(samples_enc, labels_enc, epochs=epochs, lr=lr)
# Evaluate model
evaluate_linear_svm(test_features, test_labels, w, b)
dataset_augmentation_example()
# -
# ## Scenario 4: Model Hiding
#
# The last scenario we will explore involves <i>model hiding</i>. Here, Alice has a pre-trained model that cannot be revealed, while Bob would like to use this model to evaluate on private data sample(s). This scenario can occur when a pre-trained model is proprietary or contains sensitive information, but can provide value to other parties with sensitive data.
#
# This scenario is somewhat different from the previous examples because we are not interested in training the model. Therefore, we do not need labels. Instead, we will demonstrate this example by encrypting the true model parameters (`w_true` and `b_true`) from Alice and encrypting the test set from Bob for evaluation.
#
# (Note: Because we are using the true weights and biases used to generate the test labels, we will get 100% accuracy.)
# +
@mpc.run_multiprocess(world_size=2)
def model_hiding_example():
"""Apply model hiding access control model"""
# Alice loads the model
w_true_enc = crypten.load_from_party(filenames["w_true"], src=ALICE)
b_true_enc = crypten.load_from_party(filenames["b_true"], src=ALICE)
# Bob loads the features to be evaluated
test_features_enc = crypten.load(filenames["test_features"], src=BOB)
# Evaluate model
evaluate_linear_svm(test_features_enc, test_labels, w_true_enc, b_true_enc)
model_hiding_example()
# -
# In this tutorial we have reviewed four techniques where CrypTen can be used to perform encrypted training / inference. Each of these techniques can be used to facilitate computations in different privacy-preserving scenarios. However, these techniques can also be combined to increase the amount of scenarios where CrypTen can maintain privacy.
#
# For example, we can combine feature aggregation and data labeling to train a model on data split between three parties, where two parties each have access to a subset of features, and the third party has access to labels.
#
# Before exiting this tutorial, please clean up the files generated using the following code.
# +
import os
for fn in filenames.values():
if os.path.exists(fn): os.remove(fn)
| tutorials/Tutorial_3_Introduction_to_Access_Control.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# + [markdown] origin_pos=0
# # 自注意力和位置编码
# :label:`sec_self-attention-and-positional-encoding`
#
# 在深度学习中,我们经常使用卷积神经网络(CNN)或循环神经网络(RNN)对序列进行编码。
# 想象一下,有了注意力机制之后,我们将词元序列输入注意力池化中,
# 以便同一组词元同时充当查询、键和值。
# 具体来说,每个查询都会关注所有的键-值对并生成一个注意力输出。
# 由于查询、键和值来自同一组输入,因此被称为
# *自注意力*(self-attention)
# :cite:`Lin.Feng.Santos.ea.2017,Vaswani.Shazeer.Parmar.ea.2017`,
# 也被称为*内部注意力*(intra-attention) :cite:`Cheng.Dong.Lapata.2016,Parikh.Tackstrom.Das.ea.2016,Paulus.Xiong.Socher.2017`。
# 在本节中,我们将使用自注意力进行序列编码,以及如何使用序列的顺序作为补充信息。
#
# + origin_pos=3 tab=["tensorflow"]
import numpy as np
import tensorflow as tf
from d2l import tensorflow as d2l
# + [markdown] origin_pos=4
# ## [**自注意力**]
#
# 给定一个由词元组成的输入序列$\mathbf{x}_1, \ldots, \mathbf{x}_n$,
# 其中任意$\mathbf{x}_i \in \mathbb{R}^d$($1 \leq i \leq n$)。
# 该序列的自注意力输出为一个长度相同的序列
# $\mathbf{y}_1, \ldots, \mathbf{y}_n$,其中:
#
# $$\mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \ldots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^d$$
#
# 根据 :eqref:`eq_attn-pooling`中定义的注意力池化函数$f$。
# 下面的代码片段是基于多头注意力对一个张量完成自注意力的计算,
# 张量的形状为(批量大小,时间步的数目或词元序列的长度,$d$)。
# 输出与输入的张量形状相同。
#
# + origin_pos=7 tab=["tensorflow"]
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
# + origin_pos=9 tab=["tensorflow"]
batch_size, num_queries, valid_lens = 2, 4, tf.constant([3, 2])
X = tf.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens, training=False).shape
# + [markdown] origin_pos=10
# ## 比较卷积神经网络、循环神经网络和自注意力
# :label:`subsec_cnn-rnn-self-attention`
#
# 让我们比较下面几个架构,目标都是将由$n$个词元组成的序列映射到另一个长度相等的序列,其中的每个输入词元或输出词元都由$d$维向量表示。具体来说,我们将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意,顺序操作会妨碍并行计算,而任意的序列位置组合之间的路径越短,则能更轻松地学习序列中的远距离依赖关系 :cite:`Hochreiter.Bengio.Frasconi.ea.2001`。
#
# 
# :label:`fig_cnn-rnn-self-attention`
#
# 考虑一个卷积核大小为$k$的卷积层。
# 我们将在后面的章节中提供关于使用卷积神经网络处理序列的更多详细信息。
# 目前,我们只需要知道,由于序列长度是$n$,输入和输出的通道数量都是$d$,
# 所以卷积层的计算复杂度为$\mathcal{O}(knd^2)$。
# 如 :numref:`fig_cnn-rnn-self-attention`所示,
# 卷积神经网络是分层的,因此为有$\mathcal{O}(1)$个顺序操作,
# 最大路径长度为$\mathcal{O}(n/k)$。
# 例如,$\mathbf{x}_1$和$\mathbf{x}_5$处于
# :numref:`fig_cnn-rnn-self-attention`中卷积核大小为3的双层卷积神经网络的感受野内。
#
# 当更新循环神经网络的隐状态时,
# $d \times d$权重矩阵和$d$维隐状态的乘法计算复杂度为$\mathcal{O}(d^2)$。
# 由于序列长度为$n$,因此循环神经网络层的计算复杂度为$\mathcal{O}(nd^2)$。
# 根据 :numref:`fig_cnn-rnn-self-attention`,
# 有$\mathcal{O}(n)$个顺序操作无法并行化,最大路径长度也是$\mathcal{O}(n)$。
#
# 在自注意力中,查询、键和值都是$n \times d$矩阵。
# 考虑 :eqref:`eq_softmax_QK_V`中缩放的”点-积“注意力,
# 其中$n \times d$矩阵乘以$d \times n$矩阵。
# 之后输出的$n \times n$矩阵乘以$n \times d$矩阵。
# 因此,自注意力具有$\mathcal{O}(n^2d)$计算复杂性。
# 正如我们在 :numref:`fig_cnn-rnn-self-attention`中看到的那样,
# 每个词元都通过自注意力直接连接到任何其他词元。
# 因此,有$\mathcal{O}(1)$个顺序操作可以并行计算,
# 最大路径长度也是$\mathcal{O}(1)$。
#
# 总而言之,卷积神经网络和自注意力都拥有并行计算的优势,
# 而且自注意力的最大路径长度最短。
# 但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
#
# ## [**位置编码**]
# :label:`subsec_positional-encoding`
#
# 在处理词元序列时,循环神经网络是逐个的重复地处理词元的,
# 而自注意力则因为并行计算而放弃了顺序操作。
# 为了使用序列的顺序信息,我们通过在输入表示中添加
# *位置编码*(positional encoding)来注入绝对的或相对的位置信息。
# 位置编码可以通过学习得到也可以直接固定得到。
# 接下来,我们描述的是基于正弦函数和余弦函数的固定位置编码
# :cite:`Vaswani.Shazeer.Parmar.ea.2017`。
#
# 假设输入表示$\mathbf{X} \in \mathbb{R}^{n \times d}$
# 包含一个序列中$n$个词元的$d$维嵌入表示。
# 位置编码使用相同形状的位置嵌入矩阵
# $\mathbf{P} \in \mathbb{R}^{n \times d}$输出$\mathbf{X} + \mathbf{P}$,
# 矩阵第$i$行、第$2j$列和$2j+1$列上的元素为:
#
# $$\begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned}$$
# :eqlabel:`eq_positional-encoding-def`
#
# 乍一看,这种基于三角函数的设计看起来很奇怪。
# 在解释这个设计之前,让我们先在下面的`PositionalEncoding`类中实现它。
#
# + origin_pos=13 tab=["tensorflow"]
#@save
class PositionalEncoding(tf.keras.layers.Layer):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super().__init__()
self.dropout = tf.keras.layers.Dropout(dropout)
# 创建一个足够长的P
self.P = np.zeros((1, max_len, num_hiddens))
X = np.arange(max_len, dtype=np.float32).reshape(
-1,1)/np.power(10000, np.arange(
0, num_hiddens, 2, dtype=np.float32) / num_hiddens)
self.P[:, :, 0::2] = np.sin(X)
self.P[:, :, 1::2] = np.cos(X)
def call(self, X, **kwargs):
X = X + self.P[:, :X.shape[1], :]
return self.dropout(X, **kwargs)
# + [markdown] origin_pos=14
# 在位置嵌入矩阵$\mathbf{P}$中,
# [**行代表词元在序列中的位置,列代表位置编码的不同维度**]。
# 在下面的例子中,我们可以看到位置嵌入矩阵的第$6$列和第$7$列的频率高于第$8$列和第$9$列。
# 第$6$列和第$7$列之间的偏移量(第$8$列和第$9$列相同)是由于正弦函数和余弦函数的交替。
#
# + origin_pos=17 tab=["tensorflow"]
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
X = pos_encoding(tf.zeros((1, num_steps, encoding_dim)), training=False)
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(np.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in np.arange(6, 10)])
# + [markdown] origin_pos=18
# ### 绝对位置信息
#
# 为了明白沿着编码维度单调降低的频率与绝对位置信息的关系,
# 让我们打印出$0, 1, \ldots, 7$的[**二进制表示**]形式。
# 正如我们所看到的,每个数字、每两个数字和每四个数字上的比特值
# 在第一个最低位、第二个最低位和第三个最低位上分别交替。
#
# + origin_pos=19 tab=["tensorflow"]
for i in range(8):
print(f'{i}的二进制是:{i:>03b}')
# + [markdown] origin_pos=20
# 在二进制表示中,较高比特位的交替频率低于较低比特位,
# 与下面的热图所示相似,只是位置编码通过使用三角函数[**在编码维度上降低频率**]。
# 由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。
#
# + origin_pos=23 tab=["tensorflow"]
P = tf.expand_dims(tf.expand_dims(P[0, :, :], axis=0), axis=0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')
# + [markdown] origin_pos=24
# ### 相对位置信息
#
# 除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。
# 这是因为对于任何确定的位置偏移$\delta$,位置$i + \delta$处
# 的位置编码可以线性投影位置$i$处的位置编码来表示。
#
# 这种投影的数学解释是,令$\omega_j = 1/10000^{2j/d}$,
# 对于任何确定的位置偏移$\delta$,
# :eqref:`eq_positional-encoding-def`中的任何一对
# $(p_{i, 2j}, p_{i, 2j+1})$都可以线性投影到
# $(p_{i+\delta, 2j}, p_{i+\delta, 2j+1})$:
#
# $$\begin{aligned}
# &\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix}
# \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\
# =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\
# =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\
# =&
# \begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix},
# \end{aligned}$$
#
# $2\times 2$投影矩阵不依赖于任何位置的索引$i$。
#
# ## 小结
#
# * 在自注意力中,查询、键和值都来自同一组输入。
# * 卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
# * 为了使用序列的顺序信息,我们可以通过在输入表示中添加位置编码,来注入绝对的或相对的位置信息。
#
# ## 练习
#
# 1. 假设我们设计一个深度架构,通过堆叠基于位置编码的自注意力层来表示序列。可能会存在什么问题?
# 1. 你能设计一种可学习的位置编码方法吗?
#
| tensorflow/chapter_attention-mechanisms/self-attention-and-positional-encoding.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 循环神经网络—TensorFlow
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
import matplotlib.pyplot as plt
# ## 导入 MNIST 数据集
mnist = input_data.read_data_sets('./datasets/ch08/tensorflow/MNIST',one_hot=True)
print(mnist.train.images.shape)
print(mnist.train.labels.shape)
print(mnist.validation.images.shape)
print(mnist.validation.labels.shape)
print(mnist.test.images.shape)
print(mnist.test.labels.shape)
# ## 定义占位符 placeholder
# +
# 参数设置
batch_size = 100 # BATCH 的大小,相当于一次处理100个image
time_step = 28 # 一个LSTM中,输入序列的长度Tx,image有28行
input_size = 28 # 单个x向量长度,image有28列
lr = 0.001 # 学习率
num_units = 100 # 隐藏层多少个LTSM单元
iterations =1000 # 迭代训练次数
classes =10 # 输出大小,0-9十个数字的概率
# 定义 placeholders
# 维度是[batch_size,time_step * input_size]
x = tf.placeholder(tf.float32, [None, time_step * input_size])
# 输入的是二维数据,将其还原为三维,维度是[batch_size, time_step, input_size]
x_image = tf.reshape(x, [-1, time_step, input_size])
y = tf.placeholder(tf.int32, [None, classes])
# -
# ## 定义RNN(LSTM)结构
rnn_cell = tf.contrib.rnn.BasicLSTMCell(num_units=num_units)
outputs,final_state = tf.nn.dynamic_rnn(
cell=rnn_cell, # 选择传入的cell
inputs=x_image, # 传入的数据
initial_state=None, # 初始状态
dtype=tf.float32, # 数据类型
time_major=False, # False: (batch, time_step, input); True: (time_step, batch, input),这里根据x_image结构选择False
)
output = tf.layers.dense(inputs=outputs[:, -1, :], units=classes)
# ## 定义损失函数与优化算法
cross_entropy = tf.losses.softmax_cross_entropy(onehot_labels=y, logits=output) # 计算loss
train_step = tf.train.AdamOptimizer(lr).minimize(cross_entropy) #选择优化方法
#判断预测标签和实际标签是否匹配
correct_prediction = tf.equal(tf.argmax(y, axis=1),tf.argmax(output, axis=1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction,'float')) #计算正确率
# ## 训练并验证准确率
# +
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
for i in range(iterations):
batch_x, batch_y = mnist.train.next_batch(batch_size)
sess.run(train_step, feed_dict={x: batch_x, y: batch_y})
if (i+1) % 50 == 0:
print("train accuracy %.3f" % accuracy.eval(session = sess,
feed_dict = {x:batch_x, y:batch_y}))
print("test accuracy %.3f" % accuracy.eval(session = sess,
feed_dict = {x:mnist.test.images, y:mnist.test.labels}))
# -
| 09_rnn_tensorflow.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# Reinforcement Learning (DQN) Tutorial
# =====================================
# **Author**: `<NAME> <https://github.com/apaszke>`_
#
#
# This tutorial shows how to use PyTorch to train a Deep Q Learning (DQN) agent
# on the CartPole-v0 task from the `OpenAI Gym <https://gym.openai.com/>`__.
#
# **Task**
#
# The agent has to decide between two actions - moving the cart left or
# right - so that the pole attached to it stays upright. You can find an
# official leaderboard with various algorithms and visualizations at the
# `Gym website <https://gym.openai.com/envs/CartPole-v0>`__.
#
# .. figure:: /_static/img/cartpole.gif
# :alt: cartpole
#
# cartpole
#
# As the agent observes the current state of the environment and chooses
# an action, the environment *transitions* to a new state, and also
# returns a reward that indicates the consequences of the action. In this
# task, rewards are +1 for every incremental timestep and the environment
# terminates if the pole falls over too far or the cart moves more then 2.4
# units away from center. This means better performing scenarios will run
# for longer duration, accumulating larger return.
#
# The CartPole task is designed so that the inputs to the agent are 4 real
# values representing the environment state (position, velocity, etc.).
# However, neural networks can solve the task purely by looking at the
# scene, so we'll use a patch of the screen centered on the cart as an
# input. Because of this, our results aren't directly comparable to the
# ones from the official leaderboard - our task is much harder.
# Unfortunately this does slow down the training, because we have to
# render all the frames.
#
# Strictly speaking, we will present the state as the difference between
# the current screen patch and the previous one. This will allow the agent
# to take the velocity of the pole into account from one image.
#
# **Packages**
#
#
# First, let's import needed packages. Firstly, we need
# `gym <https://gym.openai.com/docs>`__ for the environment
# (Install using `pip install gym`).
# We'll also use the following from PyTorch:
#
# - neural networks (``torch.nn``)
# - optimization (``torch.optim``)
# - automatic differentiation (``torch.autograd``)
# - utilities for vision tasks (``torchvision`` - `a separate
# package <https://github.com/pytorch/vision>`__).
#
#
#
# +
import gym
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple
from itertools import count
from PIL import Image
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as T
env = gym.make('CartPole-v0').unwrapped
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
# if gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# -
# Replay Memory
# -------------
#
# We'll be using experience replay memory for training our DQN. It stores
# the transitions that the agent observes, allowing us to reuse this data
# later. By sampling from it randomly, the transitions that build up a
# batch are decorrelated. It has been shown that this greatly stabilizes
# and improves the DQN training procedure.
#
# For this, we're going to need two classses:
#
# - ``Transition`` - a named tuple representing a single transition in
# our environment. It essentially maps (state, action) pairs
# to their (next_state, reward) result, with the state being the
# screen difference image as described later on.
# - ``ReplayMemory`` - a cyclic buffer of bounded size that holds the
# transitions observed recently. It also implements a ``.sample()``
# method for selecting a random batch of transitions for training.
#
#
#
# +
Transition = namedtuple('Transition',
('state', 'action', 'next_state', 'reward'))
class ReplayMemory(object):
def __init__(self, capacity):
self.capacity = capacity
self.memory = []
self.position = 0
def push(self, *args):
"""Saves a transition."""
if len(self.memory) < self.capacity:
self.memory.append(None)
self.memory[self.position] = Transition(*args)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
# -
# Now, let's define our model. But first, let quickly recap what a DQN is.
#
# DQN algorithm
# -------------
#
# Our environment is deterministic, so all equations presented here are
# also formulated deterministically for the sake of simplicity. In the
# reinforcement learning literature, they would also contain expectations
# over stochastic transitions in the environment.
#
# Our aim will be to train a policy that tries to maximize the discounted,
# cumulative reward
# $R_{t_0} = \sum_{t=t_0}^{\infty} \gamma^{t - t_0} r_t$, where
# $R_{t_0}$ is also known as the *return*. The discount,
# $\gamma$, should be a constant between $0$ and $1$
# that ensures the sum converges. It makes rewards from the uncertain far
# future less important for our agent than the ones in the near future
# that it can be fairly confident about.
#
# The main idea behind Q-learning is that if we had a function
# $Q^*: State \times Action \rightarrow \mathbb{R}$, that could tell
# us what our return would be, if we were to take an action in a given
# state, then we could easily construct a policy that maximizes our
# rewards:
#
# \begin{align}\pi^*(s) = \arg\!\max_a \ Q^*(s, a)\end{align}
#
# However, we don't know everything about the world, so we don't have
# access to $Q^*$. But, since neural networks are universal function
# approximators, we can simply create one and train it to resemble
# $Q^*$.
#
# For our training update rule, we'll use a fact that every $Q$
# function for some policy obeys the Bellman equation:
#
# \begin{align}Q^{\pi}(s, a) = r + \gamma Q^{\pi}(s', \pi(s'))\end{align}
#
# The difference between the two sides of the equality is known as the
# temporal difference error, $\delta$:
#
# \begin{align}\delta = Q(s, a) - (r + \gamma \max_a Q(s', a))\end{align}
#
# To minimise this error, we will use the `Huber
# loss <https://en.wikipedia.org/wiki/Huber_loss>`__. The Huber loss acts
# like the mean squared error when the error is small, but like the mean
# absolute error when the error is large - this makes it more robust to
# outliers when the estimates of $Q$ are very noisy. We calculate
# this over a batch of transitions, $B$, sampled from the replay
# memory:
#
# \begin{align}\mathcal{L} = \frac{1}{|B|}\sum_{(s, a, s', r) \ \in \ B} \mathcal{L}(\delta)\end{align}
#
# \begin{align}\text{where} \quad \mathcal{L}(\delta) = \begin{cases}
# \frac{1}{2}{\delta^2} & \text{for } |\delta| \le 1, \\
# |\delta| - \frac{1}{2} & \text{otherwise.}
# \end{cases}\end{align}
#
# Q-network
# ^^^^^^^^^
#
# Our model will be a convolutional neural network that takes in the
# difference between the current and previous screen patches. It has two
# outputs, representing $Q(s, \mathrm{left})$ and
# $Q(s, \mathrm{right})$ (where $s$ is the input to the
# network). In effect, the network is trying to predict the *expected return* of
# taking each action given the current input.
#
#
#
class DQN(nn.Module):
def __init__(self, h, w, outputs):
super(DQN, self).__init__()
self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=2)
self.bn1 = nn.BatchNorm2d(16)
self.conv2 = nn.Conv2d(16, 32, kernel_size=5, stride=2)
self.bn2 = nn.BatchNorm2d(32)
self.conv3 = nn.Conv2d(32, 32, kernel_size=5, stride=2)
self.bn3 = nn.BatchNorm2d(32)
# Number of Linear input connections depends on output of conv2d layers
# and therefore the input image size, so compute it.
def conv2d_size_out(size, kernel_size = 5, stride = 2):
return (size - (kernel_size - 1) - 1) // stride + 1
convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w)))
convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h)))
linear_input_size = convw * convh * 32
self.head = nn.Linear(linear_input_size, outputs)
# Called with either one element to determine next action, or a batch
# during optimization. Returns tensor([[left0exp,right0exp]...]).
def forward(self, x):
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
return self.head(x.view(x.size(0), -1))
# Input extraction
# ^^^^^^^^^^^^^^^^
#
# The code below are utilities for extracting and processing rendered
# images from the environment. It uses the ``torchvision`` package, which
# makes it easy to compose image transforms. Once you run the cell it will
# display an example patch that it extracted.
#
#
#
# +
resize = T.Compose([T.ToPILImage(),
T.Resize(40, interpolation=Image.CUBIC),
T.ToTensor()])
def get_cart_location(screen_width):
world_width = env.x_threshold * 2
scale = screen_width / world_width
return int(env.state[0] * scale + screen_width / 2.0) # MIDDLE OF CART
def get_screen():
# Returned screen requested by gym is 400x600x3, but is sometimes larger
# such as 800x1200x3. Transpose it into torch order (CHW).
screen = env.render(mode='rgb_array').transpose((2, 0, 1))
# Cart is in the lower half, so strip off the top and bottom of the screen
_, screen_height, screen_width = screen.shape
screen = screen[:, int(screen_height*0.4):int(screen_height * 0.8)]
view_width = int(screen_width * 0.6)
cart_location = get_cart_location(screen_width)
if cart_location < view_width // 2:
slice_range = slice(view_width)
elif cart_location > (screen_width - view_width // 2):
slice_range = slice(-view_width, None)
else:
slice_range = slice(cart_location - view_width // 2,
cart_location + view_width // 2)
# Strip off the edges, so that we have a square image centered on a cart
screen = screen[:, :, slice_range]
# Convert to float, rescale, convert to torch tensor
# (this doesn't require a copy)
screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
screen = torch.from_numpy(screen)
# Resize, and add a batch dimension (BCHW)
return resize(screen).unsqueeze(0).to(device)
env.reset()
plt.figure()
plt.imshow(get_screen().cpu().squeeze(0).permute(1, 2, 0).numpy(),
interpolation='none')
plt.title('Example extracted screen')
plt.show()
# -
# Training
# --------
#
# Hyperparameters and utilities
# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
# This cell instantiates our model and its optimizer, and defines some
# utilities:
#
# - ``select_action`` - will select an action accordingly to an epsilon
# greedy policy. Simply put, we'll sometimes use our model for choosing
# the action, and sometimes we'll just sample one uniformly. The
# probability of choosing a random action will start at ``EPS_START``
# and will decay exponentially towards ``EPS_END``. ``EPS_DECAY``
# controls the rate of the decay.
# - ``plot_durations`` - a helper for plotting the durations of episodes,
# along with an average over the last 100 episodes (the measure used in
# the official evaluations). The plot will be underneath the cell
# containing the main training loop, and will update after every
# episode.
#
#
#
# +
BATCH_SIZE = 128
GAMMA = 0.999
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 200
TARGET_UPDATE = 10
# Get screen size so that we can initialize layers correctly based on shape
# returned from AI gym. Typical dimensions at this point are close to 3x40x90
# which is the result of a clamped and down-scaled render buffer in get_screen()
init_screen = get_screen()
_, _, screen_height, screen_width = init_screen.shape
# Get number of actions from gym action space
n_actions = env.action_space.n
policy_net = DQN(screen_height, screen_width, n_actions).to(device)
target_net = DQN(screen_height, screen_width, n_actions).to(device)
target_net.load_state_dict(policy_net.state_dict())
target_net.eval()
optimizer = optim.RMSprop(policy_net.parameters())
memory = ReplayMemory(10000)
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * \
math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
with torch.no_grad():
# t.max(1) will return largest column value of each row.
# second column on max result is index of where max element was
# found, so we pick action with the larger expected reward.
return policy_net(state).max(1)[1].view(1, 1)
else:
return torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long)
episode_durations = []
def plot_durations():
plt.figure(2)
plt.clf()
durations_t = torch.tensor(episode_durations, dtype=torch.float)
plt.title('Training...')
plt.xlabel('Episode')
plt.ylabel('Duration')
plt.plot(durations_t.numpy())
# Take 100 episode averages and plot them too
if len(durations_t) >= 100:
means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
means = torch.cat((torch.zeros(99), means))
plt.plot(means.numpy())
plt.show()
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
# -
# Training loop
# ^^^^^^^^^^^^^
#
# Finally, the code for training our model.
#
# Here, you can find an ``optimize_model`` function that performs a
# single step of the optimization. It first samples a batch, concatenates
# all the tensors into a single one, computes $Q(s_t, a_t)$ and
# $V(s_{t+1}) = \max_a Q(s_{t+1}, a)$, and combines them into our
# loss. By defition we set $V(s) = 0$ if $s$ is a terminal
# state. We also use a target network to compute $V(s_{t+1})$ for
# added stability. The target network has its weights kept frozen most of
# the time, but is updated with the policy network's weights every so often.
# This is usually a set number of steps but we shall use episodes for
# simplicity.
#
#
#
def optimize_model():
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
# Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for
# detailed explanation). This converts batch-array of Transitions
# to Transition of batch-arrays.
batch = Transition(*zip(*transitions))
# Compute a mask of non-final states and concatenate the batch elements
# (a final state would've been the one after which simulation ended)
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), device=device, dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
# Compute Q(s_t, a) - the model computes Q(s_t), then we select the
# columns of actions taken. These are the actions which would've been taken
# for each batch state according to policy_net
state_action_values = policy_net(state_batch).gather(1, action_batch)
# Compute V(s_{t+1}) for all next states.
# Expected values of actions for non_final_next_states are computed based
# on the "older" target_net; selecting their best reward with max(1)[0].
# This is merged based on the mask, such that we'll have either the expected
# state value or 0 in case the state was final.
next_state_values = torch.zeros(BATCH_SIZE, device=device)
next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
# Compute the expected Q values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
# Compute Huber loss
loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
# Optimize the model
optimizer.zero_grad()
loss.backward()
for param in policy_net.parameters():
param.grad.data.clamp_(-1, 1)
optimizer.step()
# Below, you can find the main training loop. At the beginning we reset
# the environment and initialize the ``state`` Tensor. Then, we sample
# an action, execute it, observe the next screen and the reward (always
# 1), and optimize our model once. When the episode ends (our model
# fails), we restart the loop.
#
# Below, `num_episodes` is set small. You should download
# the notebook and run lot more epsiodes, such as 300+ for meaningful
# duration improvements.
#
#
#
# +
num_episodes = 50
for i_episode in range(num_episodes):
# Initialize the environment and state
env.reset()
last_screen = get_screen()
current_screen = get_screen()
state = current_screen - last_screen
for t in count():
# Select and perform an action
action = select_action(state)
_, reward, done, _ = env.step(action.item())
reward = torch.tensor([reward], device=device)
# Observe new state
last_screen = current_screen
current_screen = get_screen()
if not done:
next_state = current_screen - last_screen
else:
next_state = None
# Store the transition in memory
memory.push(state, action, next_state, reward)
# Move to the next state
state = next_state
# Perform one step of the optimization (on the target network)
optimize_model()
if done:
episode_durations.append(t + 1)
#plot_durations()
break
# Update the target network, copying all weights and biases in DQN
if i_episode % TARGET_UPDATE == 0:
target_net.load_state_dict(policy_net.state_dict())
print('Complete')
plot_durations()
env.render()
env.close()
plt.ioff()
plt.show()
# -
print(episode_durations)
plt.plot(episode_durations)
# Here is the diagram that illustrates the overall resulting data flow.
#
# .. figure:: /_static/img/reinforcement_learning_diagram.jpg
#
# Actions are chosen either randomly or based on a policy, getting the next
# step sample from the gym environment. We record the results in the
# replay memory and also run optimization step on every iteration.
# Optimization picks a random batch from the replay memory to do training of the
# new policy. "Older" target_net is also used in optimization to compute the
# expected Q values; it is updated occasionally to keep it current.
#
#
#
| dev/reinforcement_q_learning.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="2J1ZrS_WGVa_"
# ## Clonar repositório do github na máquina do Colab para ter acesso aos scripts
# + id="yzP1o6uCiHY0"
# !git clone https://github.com/aogdrummond/sound_field_sim_neural_net.git
# + [markdown] id="S-KIWoXtHowx"
# ## Instalação do miniconda
# (compreender os comandos conda e configurar versões apropriadas)
#
# + id="EQJP-wrDhc2w"
#Installing miniconda na pasta GitHub do drive if required
#Serve para compreender os comandos conda
# %%bash
MINICONDA_INSTALLER_SCRIPT=Miniconda3-4.5.4-Linux-x86_64.sh
MINICONDA_PREFIX=/usr/local
wget https://repo.continuum.io/miniconda/$MINICONDA_INSTALLER_SCRIPT
chmod +x $MINICONDA_INSTALLER_SCRIPT
./$MINICONDA_INSTALLER_SCRIPT -b -f -p $MINICONDA_PREFIX
# + [markdown] id="ADHCL1EMGxFO"
# ## Criar o ambiente necessário para a aplicação (versões, dependências...)
#
# (Essa etapa vai levar alguns minutos)
# + id="X7Bnu-ZErMgq"
# !conda install anaconda-client python=3.6.10 conda=4.8.3 --yes
# %cd /content/sound_field_sim_neural_net
# !conda install -c r openssl==1.1.1k conda=4.8.3 --yes
# !conda install -c r cudatoolkit conda=4.8.3 --yes
# !conda env create -f environment.yml
# !conda init bash
# !conda install -c anaconda scipy conda=4.8.3 --yes
# !conda install -c anaconda pandas conda=4.8.3 --yes
# !conda install -c conda-forge matplotlib conda=4.8.3 --yes
# !conda install -c anaconda scikit-image conda=4.8.3 --yes
# !conda install -c conda-forge keras==2.2.4 conda=4.8.3 --yes
# !conda install -c conda-forge opencv=4.4.0.46 conda=4.8.3 --yes
# !pip install tensorflow==1.12
# !python sfun.py
# !pip install ruamel_yaml==0.13.14
# !apt-get -qq install -y libsm6 libxext6 && pip install -q -U opencv-python
# !pip install setuptools==41.0.0
# !pip install ipykernel
# !cp /content/sound_field_sim_neural_net/bugfix/saving.py /usr/local/lib/python3.6/site-packages/keras/engine/saving.py
# + [markdown] id="QbATxbyrIFuF"
# ## Treinar modelo
#
# ---
#
#
#
# #### Para alterar as configurações de treinamento, assim como alguns hiperparâmetros (batch size, learning rate...) insira os valores desejados no campo apropriado no link abaixo:
#
# /content/sound_field_sim_neural_net/config/config.json
#
# Obs: é necessário clicar duas vezes na aba acima da janela, escrito "config.json", para que a alteração seja salva (o asterisco ao lado deve desaparecer para confirmar que a alteração foi salva)
#
# ####Sintaxe:
#
#
# * ! - declara se tratar de um comando shell
# * python main.py - declara que será executado o script .py "main.py"
# * --mode train - atribui globalmente o string "train" à variável "--mode"
# * -- config /content/sound_field_sim_neural_net/config/config.json - atribui globalmente o string contendo o caminho para o arquivo no .json contendo as configurações do modelo a ser executado
#
#
# ---
#
#
#
# #### Caso necessário, já existe um modelo treinado denomiado "session_0", podendo ser utilizado nas etapas seguintes sem exigir o treinamento.
#
# ---
#
#
#
#
#
#
#
# + id="yU_VRXa-sQSL"
# !python main.py --mode train --config /content/sound_field_sim_neural_net/config/config.json
# + [markdown] id="ir2ufmBzLVnm"
# ##Avaliar o desempenho do modelo na previsão do campo acústico em salas simuladas
#
# Obs: A sessão configurada antes de "\config.json" deve corresponder à do modelo treinado, em "session_id".
#
# Os resultados serão salvos nos arquivos "NMSE.svg" e "SSIM.svg", na pasta correspondente em "sessions"
# + id="vqLeBHs5scQa"
# !python main.py --mode sim-eval --config /content/sound_field_sim_neural_net/sessions/session_1/config.json
# + [markdown] id="_myDKsasLWSZ"
# ##Avaliar o desempenho do modelo na previsão do campos acústico de uma sala real
# + id="P0dphOCyscS0"
# !python main.py --mode real-eval --config /content/sound_field_sim_neural_net/sessions/session_1/config.json
# + [markdown] id="L7oiEtmYLXIp"
# ##Gerar imagens para visualizar o campo acústico previsto
#
# Obs: os arquivos png estarão disponíveis em na pasta "visualization" da sessão
# + id="Gir7KW_uscVK"
# !python main.py --mode visualize --config /content/sound_field_sim_neural_net/sessions/session_1/config.json
# + [markdown] id="VUdE4gXKPCM1"
# ### Visualizar avaliação de desempenho
#
#
# file_path : string com o caminho para o arquivo .csv contendo os resultados da etapa de avaliação, dentro da pasta da sessão correspondente
#
# num_mics : string contendo o número de microfones cuja curva de previsão será plotado (deve corresponder a alguns dos valores utilizados na etapa de simulação)
# + id="anoGMgE3GONw"
from util.eval_util import preprocess_df, plot_evaluation, db, columns_names
import pandas as pd
file_path = '/content/sound_field_sim_neural_net/sessions/session_1/simulated_data_evaluation/min_mics_5_max_mics_65_step_mics_5/results_file_number_1.csv'
eval_dataframe = pd.read_csv(file_path,names=columns_names)
dicts, freq, labels = preprocess_df(eval_dataframe)
num_mics = '5'.split(',')
plot_evaluation(dicts,freq,labels,num_mics=num_mics)
| Sound_Field_Neural_Network.ipynb |
# # Regression
#
# In this notebook, we will present the metrics that can be used in regression.
#
# A set of metrics are dedicated to regression. Indeed, classification metrics
# cannot be used to evaluate the statistical performance of regression models
# because there is a fundamental difference between their target type `target`:
# it is a continuous variable in regression, while a discrete variable in
# classification.
#
# We will use the Ames housing dataset. The goal is to predict the price
# of houses in the city of Ames, Iowa. As with classification, we will only use
# a single train-test split to focus solely on the regression metrics.
# +
import pandas as pd
import numpy as np
ames_housing = pd.read_csv("../datasets/house_prices.csv")
data = ames_housing.drop(columns="SalePrice")
target = ames_housing["SalePrice"]
data = data.select_dtypes(np.number)
target /= 1000
data
# -
# <div class="admonition note alert alert-info">
# <p class="first admonition-title" style="font-weight: bold;">Note</p>
# <p class="last">If you want a deeper overview regarding this dataset, you can refer to the
# Appendix - Datasets description section at the end of this MOOC.</p>
# </div>
# Let's start by splitting our dataset intro a train and test set.
# +
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = train_test_split(
data, target, shuffle=True, random_state=0
)
# -
# Some machine learning models are designed to be solved as an optimization
# problem: minimizing an error (also known as the loss function) using a
# training set.
# A basic loss function used in regression is the mean squared error (MSE).
# Thus, this metric is sometimes used to evaluate the model since it is
# optimized by said model.
#
# We will give an example using a linear regression model.
# +
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
regressor = LinearRegression()
regressor.fit(data_train, target_train)
target_predicted = regressor.predict(data_train)
print(f"Mean squared error on the training set: "
f"{mean_squared_error(target_train, target_predicted):.3f}")
# -
# Our linear regression model is minimizing the mean squared error on the
# training set. It means that there is no other set of coefficients which
# will decrease the error.
#
# Then, we can compute the mean squared error on the test set.
# +
target_predicted = regressor.predict(data_test)
print(f"Mean squared error on the testing set: "
f"{mean_squared_error(target_test, target_predicted):.3f}")
# -
# The raw MSE can be difficult to interpret. One way is to rescale the MSE
# by the variance of the target. This score is known as the $R^2$ also called
# the coefficient of determination. Indeed, this is the default score used
# in scikit-learn by calling the method `score`.
regressor.score(data_test, target_test)
# The $R^2$ score represents the proportion of variance of the target that is
# explained by the independent variables in the model. The best score possible
# is 1 but there is no lower bound. However, a model that predicts the expected
# value of the target would get a score of 0.
# +
from sklearn.dummy import DummyRegressor
dummy_regressor = DummyRegressor(strategy="mean")
dummy_regressor.fit(data_train, target_train)
print(f"R2 score for a regressor predicting the mean:"
f"{dummy_regressor.score(data_test, target_test):.3f}")
# -
# The $R^2$ score gives insight into the quality of the model's fit. However,
# this score cannot be compared from one dataset to another and the value
# obtained does not have a meaningful interpretation relative the original unit
# of the target. If we wanted to get an interpretable score, we would be
# interested in the median or mean absolute error.
# +
from sklearn.metrics import mean_absolute_error
target_predicted = regressor.predict(data_test)
print(f"Mean absolute error: "
f"{mean_absolute_error(target_test, target_predicted):.3f} k$")
# -
# By computing the mean absolute error, we can interpret that our model is
# predicting on average 22.6 k$ away from the true house price. A disadvantage
# of this metric is that the mean can be impacted by large error. For some
# applications, we might not want these large errors to have such a big
# influence on our metric. In this case we can use the median absolute error.
# +
from sklearn.metrics import median_absolute_error
print(f"Median absolute error: "
f"{median_absolute_error(target_test, target_predicted):.3f} k$")
# -
# The mean absolute error (or median absolute error) still have a known
# limitation: committing an error of 50 k$ for an house valued at 50 k$ has the
# same impact than committing an error of 50 k$ for an house valued at 500 k$.
# Indeed, the mean absolute error is not relative.
#
# The mean absolute percentage error introduce this relative scaling.
# +
from sklearn.metrics import mean_absolute_percentage_error
print(f"Mean absolute percentage error: "
f"{mean_absolute_percentage_error(target_test, target_predicted) * 100:.3f} %")
# -
# In addition of metrics, we can visually represent the results by plotting
# the predicted values versus the true values.
predicted_actual = {
"True values (k$)": target_test, "Predicted values (k$)": target_predicted}
predicted_actual = pd.DataFrame(predicted_actual)
predicted_actual
# +
import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(data=predicted_actual,
x="True values (k$)", y="Predicted values (k$)",
color="black", alpha=0.5)
plt.axline((0, 0), slope=1, label="Perfect fit")
plt.axis('square')
_ = plt.title("Regression using a model without \ntarget transformation")
# -
# On this plot, correct predictions would lie on the diagonal line. This plot
# allows us to detect if the model makes errors in a consistent way, i.e.
# has some bias.
#
# On this plot, we see that for the large True price values, our model tends to
# under-estimate the price of the house. Typically, this issue arises when the
# target to predict does not follow a normal distribution. In this case the
# model would benefit from target transformation.
# +
from sklearn.preprocessing import QuantileTransformer
from sklearn.compose import TransformedTargetRegressor
transformer = QuantileTransformer(
n_quantiles=900, output_distribution="normal")
model_transformed_target = TransformedTargetRegressor(
regressor=regressor, transformer=transformer)
model_transformed_target.fit(data_train, target_train)
target_predicted = model_transformed_target.predict(data_test)
# -
predicted_actual = {
"True values (k$)": target_test, "Predicted values (k$)": target_predicted}
predicted_actual = pd.DataFrame(predicted_actual)
predicted_actual
sns.scatterplot(data=predicted_actual,
x="True values (k$)", y="Predicted values (k$)",
color="black", alpha=0.5)
plt.axline((0, 0), slope=1, label="Perfect fit")
plt.axis('square')
plt.legend()
_ = plt.title("Regression using a model that\n transform the target before "
"fitting")
# Thus, once we transformed the target, we see that we corrected some of the
# high values.
| notebooks/metrics_regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
file = "WebVisualizations\Resources\cities.csv"
# Read our Kickstarter data into pandas
df = pd.read_csv(file)
df.head()
# -
html = df.to_html()
text_file = open("WebVisualizations\Resources\cities.html", "w")
text_file.write(html)
text_file.close()
| .ipynb_checkpoints/Untitled-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Part 4: 模型平均的联邦学习
#
# **概述:** 在本教程的第2部分中,我们使用了非常简单的联邦学习版本来训练模型。这要求每个数据所有者信任模型所有者才能看到其梯度。
#
# **说明:** 在本教程中,我们将展示如何使用第3部分中的高级聚合工具来允许参数由可信的“安全工作机”聚合,然后将最终结果模型发送回模型所有者(我们)。
#
# 这样,只有安全工作机才能看到谁的模型参数来自谁。我们也许能够知道模型的哪些部分发生了更改,但是我们**不**知道哪个工作人员(Bob或Alice)进行了哪些更改,从而创建了一层隐私。
#
# 作者:
# - <NAME> - Twitter: [@iamtrask](https://twitter.com/iamtrask)
# - <NAME> - Twitter: [@jvmancuso](https://twitter.com/jvmancuso)
#
# 中文版译者:
# - <NAME> - github:[@dljgs1](https://github.com/dljgs1)
import torch
import syft as sy
import copy
hook = sy.TorchHook(torch)
from torch import nn, optim
# # 第一步: 建立数据所有者
#
# 首先,我们将创建两个数据所有者(Bob和Alice),每个数据所有者拥有少量数据。 我们还将初始化一个名为“secure_worker”的安全机器。实际上,这可以是安全的硬件(例如英特尔的SGX),也可以只是受信任的中介。
# +
# 创建一对工作机
bob = sy.VirtualWorker(hook, id="bob")
alice = sy.VirtualWorker(hook, id="alice")
secure_worker = sy.VirtualWorker(hook, id="secure_worker")
# 玩具数据集
data = torch.tensor([[0,0],[0,1],[1,0],[1,1.]], requires_grad=True)
target = torch.tensor([[0],[0],[1],[1.]], requires_grad=True)
# 通过以下方式获取每个工作机的训练数据的指针
# 向bob和alice发送一些训练数据
bobs_data = data[0:2].send(bob)
bobs_target = target[0:2].send(bob)
alices_data = data[2:].send(alice)
alices_target = target[2:].send(alice)
# -
# # 第二步: 建立我们的模型
#
# 对于此示例,我们将使用简单的线性模型进行训练。 我们通常可以使用PyTorch的nn.Linear构造函数对其进行初始化。
# 初始化玩具模型
model = nn.Linear(2,1)
# # 第三步:发送模型的拷贝给Alice和Bob
#
# 接下来,我们需要将当前模型的副本发送给Alice和Bob,以便他们可以对自己的数据集执行学习步骤。
# +
bobs_model = model.copy().send(bob)
alices_model = model.copy().send(alice)
bobs_opt = optim.SGD(params=bobs_model.parameters(),lr=0.1)
alices_opt = optim.SGD(params=alices_model.parameters(),lr=0.1)
# -
# # 第4步:训练鲍勃和爱丽丝的模型(并行)
#
# 与通过安全平均进行联邦学习的常规做法一样,每个数据所有者首先在本地对模型进行几次迭代训练,然后再对模型进行平均。
for i in range(10):
# 训练Bob的模型
bobs_opt.zero_grad()
bobs_pred = bobs_model(bobs_data)
bobs_loss = ((bobs_pred - bobs_target)**2).sum()
bobs_loss.backward()
bobs_opt.step()
bobs_loss = bobs_loss.get().data
# 训练Alice的模型
alices_opt.zero_grad()
alices_pred = alices_model(alices_data)
alices_loss = ((alices_pred - alices_target)**2).sum()
alices_loss.backward()
alices_opt.step()
alices_loss = alices_loss.get().data
print("Bob:" + str(bobs_loss) + " Alice:" + str(alices_loss))
# # 第5步:将两个更新的模型发送到安全工作机
#
# 现在,每个数据所有者都拥有部分受过训练的模型,是时候以安全的方式将它们平均在一起了。我们通过指示Alice和Bob将其模型发送到安全(可信)服务器来实现这一目标。
#
# 请注意,这种使用我们的API的方式意味着每个模型都**直接**发送到secure_worker。我们从未见过。
alices_model.move(secure_worker)
bobs_model.move(secure_worker)
# # 第6步:模型平均
# 最后,此训练epoch(译者注:一个epoch表示全部训练数据完整训练一轮)的最后一步是将Bob和Alice的训练模型平均在一起,然后使用它来设置全局“模型”的值。
with torch.no_grad():
model.weight.set_(((alices_model.weight.data + bobs_model.weight.data) / 2).get())
model.bias.set_(((alices_model.bias.data + bobs_model.bias.data) / 2).get())
# # 冲洗并重复
#
# 现在,我们只需要对此进行多次迭代!
# +
iterations = 10
worker_iters = 5
for a_iter in range(iterations):
bobs_model = model.copy().send(bob)
alices_model = model.copy().send(alice)
bobs_opt = optim.SGD(params=bobs_model.parameters(),lr=0.1)
alices_opt = optim.SGD(params=alices_model.parameters(),lr=0.1)
for wi in range(worker_iters):
# 训练Bob的模型
bobs_opt.zero_grad()
bobs_pred = bobs_model(bobs_data)
bobs_loss = ((bobs_pred - bobs_target)**2).sum()
bobs_loss.backward()
bobs_opt.step()
bobs_loss = bobs_loss.get().data
# 训练Alice的模型
alices_opt.zero_grad()
alices_pred = alices_model(alices_data)
alices_loss = ((alices_pred - alices_target)**2).sum()
alices_loss.backward()
alices_opt.step()
alices_loss = alices_loss.get().data
alices_model.move(secure_worker)
bobs_model.move(secure_worker)
with torch.no_grad():
model.weight.set_(((alices_model.weight.data + bobs_model.weight.data) / 2).get())
model.bias.set_(((alices_model.bias.data + bobs_model.bias.data) / 2).get())
print("Bob:" + str(bobs_loss) + " Alice:" + str(alices_loss))
# -
# 最后,我们想确保我们得到的模型学习正确,因此我们将在测试数据集上对其进行评估。在这个玩具问题中,我们将使用原始数据,但在实践中,我们将希望使用新数据来了解模型对看不见的样本的泛化程度。
preds = model(data)
loss = ((preds - target) ** 2).sum()
print(preds)
print(target)
print(loss.data)
# 在这个玩具示例中,平均模型相对于本地训练的纯文本模型表现不佳,但是我们能够在不暴露每个工人的训练数据的情况下对其进行训练。我们还能够在可信任的聚合器上聚合每个工作人员的更新模型,以防止数据泄露给模型所有者。
#
# 在未来的教程中,我们的目标是直接使用梯度进行可信聚合,以便我们可以使用更好的梯度估计来更新模型并获得更强大的模型。
# # 恭喜!!! 是时候加入社区了!
#
# 祝贺您完成本笔记本教程! 如果您喜欢此方法,并希望加入保护隐私、去中心化AI和AI供应链(数据)所有权的运动,则可以通过以下方式做到这一点!
#
# ### 给 PySyft 加星
#
# 帮助我们的社区的最简单方法是仅通过给GitHub存储库加注星标! 这有助于提高人们对我们正在构建的出色工具的认识。
#
# - [Star PySyft](https://github.com/OpenMined/PySyft)
#
# ### 选择我们的教程
#
# 我们编写了非常不错的教程,以更好地了解联合学习和隐私保护学习的外观,以及我们如何为实现这一目标添砖加瓦。
#
# - [Checkout the PySyft tutorials](https://github.com/OpenMined/PySyft/tree/master/examples/tutorials)
#
#
# ### 加入我们的 Slack!
#
# 保持最新进展的最佳方法是加入我们的社区! 您可以通过填写以下表格来做到这一点[http://slack.openmined.org](http://slack.openmined.org)
#
# ### 加入代码项目!
#
# 对我们的社区做出贡献的最好方法是成为代码贡献者! 您随时可以转到PySyft GitHub的Issue页面并过滤“projects”。这将向您显示所有概述,选择您可以加入的项目!如果您不想加入项目,但是想做一些编码,则还可以通过搜索标记为“good first issue”的GitHub问题来寻找更多的“一次性”微型项目。
#
# - [PySyft Projects](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3AProject)
# - [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
#
# ### 捐赠
#
# 如果您没有时间为我们的代码库做贡献,但仍想提供支持,那么您也可以成为Open Collective的支持者。所有捐款都将用于我们的网络托管和其他社区支出,例如黑客马拉松和聚会!
#
# [OpenMined's Open Collective Page](https://opencollective.com/openmined)
| examples/tutorials/translations/chinese/Part 04 - Federated Learning via Trusted Aggregator.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python3.8 (tf2env)
# language: python
# name: tf2env
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/nyp-sit/it3103-tutors/blob/main/week3/multi_class_image_classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="0RZIgnFFEv5t"
# # Lab Exercise: Multi-class Image Classification
#
# Now that you have learnt how to train a model to do binary image classification of cats and dogs using Convolutional Neural Network.
#
# Modify the code to train a model to recognise whether a hand gesture is one of the gesture in the rock, paper and scissor game.
#
# The dataset of rock paper scissor can be downloaded from https://nypai.s3-ap-southeast-1.amazonaws.com/datasets/rps2.zip
# + [markdown] id="22qK2vQiEqgB"
# ### Step 1: Import the necessary packages
# + id="E0Widz3qoiVr"
import os
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras import layers
from tensorflow.keras import models
from tensorflow.keras import optimizers
import matplotlib.pyplot as plt
import numpy as np
# + [markdown] id="iKGTrOeiEzmP"
# ### Step 2: Download Datasets
#
# Download the dataset and unzip the file to a folder.
# + id="YH_eNtAbn78U"
dataset_URL = 'https://nypai.s3-ap-southeast-1.amazonaws.com/datasets/rps2.zip'
path_to_zip = tf.keras.utils.get_file('rps2.zip', origin=dataset_URL, extract=True, cache_dir='.')
print(path_to_zip)
PATH = os.path.join(os.path.dirname(path_to_zip), 'rps2')
# + [markdown] id="qcaiLftXEONn"
# ### Step 3: Set up your train and validation directory.
#
# Examine your dataset folder and set your train_dir and validation_dir to point to the correct directories.
# + id="9N0WuIbxwJGb"
train_dir = os.path.join(PATH, 'train')
validation_dir = os.path.join(PATH, 'validation')
# + [markdown] id="Jk2edwW2FJ1d"
# ### Step 4: Set up the ImageDataGenerator
#
# Set up the ImageDataGenerator for both train and validation set.
# + id="c5-bXiSWoFtW"
# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1./255)
validation_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# since our dataset has more than 3 classes, we will choose either categorical or sparse categorical
# this must match with the loss function we choose in our model
class_mode='sparse')
validation_generator = validation_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='sparse')
# + id="WqZmYV4VxLQ8"
for data_batch, labels_batch in train_generator:
print('data batch shape:', data_batch.shape)
print('labels batch shape:', labels_batch.shape)
break
# + [markdown] id="BpaO7BJVxkAO"
# You can see the labels is **NOT** one-hot-encoded. Try changing the class_mode to 'categorical' and observe that the label will be one-hot-encoded.
# + [markdown] id="IrSOVvwfFpcz"
# Print out the class indices so that you know what label is assigned to which class. Hint: use ``class_indices`` of the generator.
# + id="OPs--CSYvpmT"
train_generator.class_indices
# + [markdown] id="S4kbK7XpGLYc"
# ### Step 5: Create your model
# + id="8ZCiZLK9vupW"
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(3, activation='softmax'))
# + [markdown] id="G2It5kjbGZA0"
# ### Step 6: Compile and Train the Model
#
# Make sure you choose the correct loss function.
# + id="NTPLmxO5IvaD"
def create_tb_callback():
root_logdir = os.path.join(os.curdir, "tb_logs")
def get_run_logdir(): # use a new directory for each run
import time
run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S")
return os.path.join(root_logdir, run_id)
run_logdir = get_run_logdir()
tb_callback = tf.keras.callbacks.TensorBoard(run_logdir)
return tb_callback
# + id="JaTbltHQxCzq"
model.compile(loss='sparse_categorical_crossentropy',
optimizer=optimizers.RMSprop(learning_rate=1e-4),
metrics=['acc'])
tb_callback = create_tb_callback()
earlystop_callback = tf.keras.callbacks.EarlyStopping(
monitor='val_acc', patience=10, verbose=0,
mode='auto', restore_best_weights=True
)
history = model.fit(
train_generator,
steps_per_epoch=126,
epochs=30,
validation_data=validation_generator,
validation_steps=18, callbacks=[earlystop_callback, tb_callback])
# + id="vOXpmCBGI8Ql"
# %load_ext tensorboard
# %tensorboard --logdir tb_logs
# + [markdown] id="4i3Z8WIQJLi1"
# ### Step 7: Save your Model
#
# Save your model for use in inference later on.
# + id="PprYt9Sz0oUM"
model.save("rps_model")
# + [markdown] id="TkWGYOK4HGBE"
# ### Test your model
#
# The following code cells shows you how to set up Google Colab to take a picture using your webcam. Take a picture of your hand gesture (rock, paper or scissors) and infer using your saved model.
# + id="SWkCXDE70WiA"
from IPython.display import display, Javascript
from google.colab.output import eval_js
from base64 import b64decode
def take_photo(filename='photo.jpg', quality=0.8):
js = Javascript('''
async function takePhoto(quality) {
const div = document.createElement('div');
const capture = document.createElement('button');
capture.textContent = 'Capture';
div.appendChild(capture);
const video = document.createElement('video');
video.style.display = 'block';
const stream = await navigator.mediaDevices.getUserMedia({video: true});
document.body.appendChild(div);
div.appendChild(video);
video.srcObject = stream;
await video.play();
// Resize the output to fit the video element.
google.colab.output.setIframeHeight(document.documentElement.scrollHeight, true);
// Wait for Capture to be clicked.
await new Promise((resolve) => capture.onclick = resolve);
const canvas = document.createElement('canvas');
canvas.width = video.videoWidth;
canvas.height = video.videoHeight;
canvas.getContext('2d').drawImage(video, 0, 0);
stream.getVideoTracks()[0].stop();
div.remove();
return canvas.toDataURL('image/jpeg', quality);
}
''')
display(js)
data = eval_js('takePhoto({})'.format(quality))
binary = b64decode(data.split(',')[1])
with open(filename, 'wb') as f:
f.write(binary)
return filename
# + id="Qp5MYbtv0WiD"
from IPython.display import Image
try:
filename = take_photo()
print('Saved to {}'.format(filename))
# Show the image which was just taken.
display(Image(filename))
except Exception as err:
# Errors will be thrown if the user does not have a webcam or if they do not
# grant the page permission to access it.
print(str(err))
# + id="jm3XARik0eT_"
img = keras.preprocessing.image.load_img(
filename, target_size=(150, 150)
)
# we convert the image to numpy array
img_array = keras.preprocessing.image.img_to_array(img)
# Although we only have single image, however our model expected data in batches
# so we will need to add in the batch axis too
img_array = tf.expand_dims(img_array, 0) # Create a batch
# we load the model saved earlier and do the inference
model = tf.keras.models.load_model('rps_model')
predicted_label = model.predict(img_array)
# or predicted_label = model(img_array)
print(predicted_label)
# + id="JHvhn8Dk1zVF"
print(train_generator.class_indices)
| week3/multi_class_image_classification.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import altair.vega.v3 as vg
from altair.datasets import load_dataset
spec = {
"$schema": "https://vega.github.io/schema/vega/v3.0.json",
"width": 400,
"height": 200,
"padding": 5,
"data": [
{
"name": "table",
"values": [
{"category": "A", "amount": 28},
{"category": "B", "amount": 55},
{"category": "C", "amount": 43},
{"category": "D", "amount": 91},
{"category": "E", "amount": 81},
{"category": "F", "amount": 53},
{"category": "G", "amount": 19},
{"category": "H", "amount": 87}
]
}
],
"signals": [
{
"name": "tooltip",
"value": {},
"on": [
{"events": "rect:mouseover", "update": "datum"},
{"events": "rect:mouseout", "update": "{}"}
]
}
],
"scales": [
{
"name": "xscale",
"type": "band",
"domain": {"data": "table", "field": "category"},
"range": "width",
"padding": 0.05,
"round": True
},
{
"name": "yscale",
"domain": {"data": "table", "field": "amount"},
"nice": True,
"range": "height"
}
],
"axes": [
{ "orient": "bottom", "scale": "xscale" },
{ "orient": "left", "scale": "yscale" }
],
"marks": [
{
"type": "rect",
"from": {"data":"table"},
"encode": {
"enter": {
"x": {"scale": "xscale", "field": "category"},
"width": {"scale": "xscale", "band": 1},
"y": {"scale": "yscale", "field": "amount"},
"y2": {"scale": "yscale", "value": 0}
},
"update": {
"fill": {"value": "steelblue"}
},
"hover": {
"fill": {"value": "red"}
}
}
},
{
"type": "text",
"encode": {
"enter": {
"align": {"value": "center"},
"baseline": {"value": "bottom"},
"fill": {"value": "#333"}
},
"update": {
"x": {"scale": "xscale", "signal": "tooltip.category", "band": 0.5},
"y": {"scale": "yscale", "signal": "tooltip.amount", "offset": -2},
"text": {"signal": "tooltip.amount"},
"fillOpacity": [
{"test": "datum === tooltip", "value": 0},
{"value": 1}
]
}
}
}
]
}
# To render in the classic notebook run this line:
vg.renderers.enable('notebook')
# To render in JupyterLab and nteract, run this
vg.renderers.enable('default')
vg.renderers.get()(spec)
vg.vega(spec, validate=True)
vg.renderers.enable('json')
vg.vega(spec, validate=True)
| notebooks/Vega3Test.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# <center>
# <h1> Beyond Matplotlib: Building Interactive Climate Data Visualizations with Holoviews and Friends </h1>
#
# <br>
# <img src="./img/hv-gv-bk-hvplot.png" width="50%" style="margin: 0px 25%">
#
#
# <center>
#
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Getting Help with Holoviews, Geoviews, Bokeh, Hvplot
#
#
# Here are some important resources for learning more about Holoviews, Geoviews, Bokeh, Hvplot and getting help.
#
# - [Holoviews Documentation](http://holoviews.org/)
# - [Geoviews Documentation](http://geoviews.org/)
# - [Hvplot Documentation](https://hvplot.pyviz.org)
# - [Bokeh Documentation](https://bokeh.pydata.org/en/latest/)
# - [Xarray Documentation](http://xarray.pydata.org/en/latest/)
# - [NCAR Hackathons Visualization Guide](https://ncar-hackathons.github.io/visualization)
# - [Holoviews GitHub Issue Tracker](https://github.com/pyviz/holoviews/issues)
# - [Holoviews questions on StackOverflow](https://stackoverflow.com/questions/tagged/holoviews)
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Learning Objectives
#
# In this tutorial we will explore these newer tools for building interactive plots, supported by Anaconda:
#
# * [**Bokeh**](http://bokeh.pydata.org): Interactive plotting in web browsers, running JavaScript but controlled by Python
# * [**HoloViews**](http://holoviews.org): Declarative objects for instantly visualizable data, building Bokeh plots from convenient high-level specifications
# * [**GeoViews**](http://geo.holoviews.org): Visualizable geographic data that that can be mixed and matched with HoloViews objects
#
# * [**Hvplot**](https://hvplot.pyviz.org/index.html): A high-level plotting API for the PyData ecosystem built on HoloViews.
#
# This tutorial will introduce HoloViews and guide you through the process of building rich, deployable visualizations based on Bokeh, and (briefly) matplotlib.
#
# When using HoloViews, the focus is on bundling your data together with the appropriate metadata to support both analysis and plotting, making your raw data and its visualization equally accessible at all times.
#
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Workflow from data to decision
# <img src="./img/workflow.png" width=40% align="left" style="margin: 0px 20px">
# <br>
# If there's no visualization at any of these stages, you're flying blind.<br><br>
#
# What if it were simple to visualize anything, anywhere?
#
# <br><br><br><small>(adapted from <NAME>)
# + [markdown] slideshow={"slide_type": "subslide"}
# <img src="./img/landscape_hv_nx.png" width=65% align="left" style="margin: 0px 30px">
#
# ## Good news:<br><br>Lots of choices!
# <br><br><br><small>(adapted from Jake VanderPlas)
# + [markdown] slideshow={"slide_type": "subslide"}
# <img src="./img/landscape_hv_nx.png" width=65% align="left" style="margin: 0px 30px">
#
# ## Bad news:<br><br>Lots of choices = Choice Paralysis!
# <br><br>
# Too hard to
# try them all,
# learn them all, or
# get them to work together.
# + [markdown] slideshow={"slide_type": "subslide"}
# <img src="./img/landscape_hv_nx_pyviz.png" width=65% align="left" style="margin: 0px 30px">
#
# ## This Tutorial:
# <br><br>
# Explore seamless interoperability<br>for browser-based<br>viz tools
#
# + slideshow={"slide_type": "slide"}
import warnings
warnings.filterwarnings('ignore')
import xarray as xr
import numpy as np
import holoviews as hv
import geoviews as gv
import hvplot.xarray
hv.extension('bokeh')
# + [markdown] slideshow={"slide_type": "subslide"}
# Here we import the NumPy and Xarray libraries with their standard abbreviations, plus Geoviews, HoloViews with theri standard aliases. The line reading `hv.extension('bokeh')` loads and activates the bokeh plotting backend, so all visualizations will be generated using Bokeh.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## 0. Load Monthly Sea Surface Temperature
# + slideshow={"slide_type": "fragment"}
ds = xr.open_mfdataset("../../datasets/sst/*.nc").load()
sst = ds.sst
ds
# + [markdown] slideshow={"slide_type": "subslide"}
# ## 1. Create a Quick-look Contour-filled Plot with Hvplot
# + slideshow={"slide_type": "fragment"}
sst.hvplot(x='lon', y='lat', z='sst', kind='contourf', global_extent=True)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## 2. Customize Visual Appearance
#
# Let's
#
# - specificy projection
# - set levels for the contours
# - specify a custom colormap
# - create an overlay of a map plot with some features (grid, coastline)
# - Create a movie!!
# + slideshow={"slide_type": "subslide"}
levels = np.linspace(start=sst.min(), stop=sst.max(), num=15)
levels
# + slideshow={"slide_type": "fragment"}
import cartopy
import cartopy.crs as ccrs
import cmocean # For color maps
# + slideshow={"slide_type": "fragment"}
plot = sst.hvplot(x='lon', y='lat', z='sst', kind='contourf', levels=levels,
cmap=cmocean.cm.thermal,
projection=ccrs.Robinson(central_longitude=300.))
# + slideshow={"slide_type": "fragment"}
plot.opts(colorbar_position='right', colorbar_opts={'title': '°C'})
# + slideshow={"slide_type": "subslide"}
plot * gv.feature.grid
# + slideshow={"slide_type": "subslide"}
plot * gv.feature.coastline
# + slideshow={"slide_type": "subslide"}
plot * gv.feature.land(fill_color='green')
# + [markdown] slideshow={"slide_type": "subslide"}
# **Putting it all together…**
# + slideshow={"slide_type": "fragment"}
final_plot = plot * gv.feature.grid * gv.feature.coastline * gv.feature.land(fill_color='green')
final_plot
# + slideshow={"slide_type": "subslide"}
# %output holomap='scrubber' fps=11
final_plot
# -
| visualization/Holoviews-and-Friends/Introduction_to_interactive_viz.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Introduction to the Interstellar Medium
# ### <NAME>
# ### Figure 11.1: multi-wavelength montage of the spiral galaxy M51 (NGC 5194)
# #### UV/O/IR data are from from http://dustpedia.astro.noa.gr/
# #### HST Halpha data from https://archive.stsci.edu/prepds/m51/
# #### VLA/Effelsberg 3cm data from https://www.mpifr-bonn.mpg.de/3168319/m51
# #### VLA HI data from https://www2.mpia-hd.mpg.de/THINGS
# #### IRAM CO 2-1 data from https://www2.mpia-hd.mpg.de/PAWS
# #### most of the fits files are in the github repo except the very large ones (DSS_2, 2MASS_Ks, and Spitzer_24) which you have to download manually from the dustpedia website
import numpy as np
import matplotlib.pyplot as plt
from astropy.io import fits
from astropy.nddata import Cutout2D
from astropy.wcs import WCS
from astropy import units as u
from astropy.visualization import PercentileInterval
from astropy.visualization import ImageNormalize
from astropy.visualization import LinearStretch, SqrtStretch, LogStretch, AsinhStretch
# %matplotlib inline
# +
# SIMBAD center 13 29 52.698 +47 11 42.93
xcen, ycen = 202.469575, 47.19525833
# image size =
xbox, ybox = 0.22, 0.20
fig = plt.figure(figsize=(7.7,10))
files = ['GALEX_NUV', 'DSS2_R', '2MASS_Ks', 'Halpha', 'VLA_3cm', 'Spitzer_24', 'SPIRE_250', 'VLA_HI_mom0', 'IRAM_CO21_mom0']
label = ['NUV', 'Opt', 'NIR', r'H$\alpha$', '3cm', 'MIR', 'FIR', 'HI', 'CO']
stretch = ['Log','Asinh','Asinh','Asinh','Asinh','Asinh','Linear','Linear','Linear']
nfiles = len(files)
# note that there are various warnings that come up due to the range of fits file headers
# (there is no standard) but these are benign so no worries...
for i in range(nfiles):
f = files[i]
fitsfile = 'NGC5194_'+f+'.fits'
hdu = fits.open(fitsfile, ignore_missing_end=True)
if 'VLA' in f:
wcs = WCS(hdu[0].header, naxis=(1,2))
im = hdu[0].data.squeeze()
else:
wcs = WCS(hdu[0].header)
im = hdu[0].data
hdu.close()
# no distortion for drizzled images
# https://docs.astropy.org/en/stable/wcs/note_sip.html
if f=='Halpha':
wcs.sip = None
#print(f, im.min(), im.max())
world = np.array([[xcen+xbox/2, ycen-ybox/2], [xcen-xbox/2, ycen+ybox/2]])
pix = np.rint(wcs.wcs_world2pix(world, 1)).astype(int)
position = (0.5*(pix[0,0]+pix[1,0]), 0.5*(pix[0,1]+pix[1,1]))
size = (pix[1,1]-pix[0,1], pix[1,0]-pix[0,0])
crop = Cutout2D(im, position=position, size=size, wcs=wcs, mode='partial')
ax = fig.add_subplot(3, 3, i+1, projection=crop.wcs)
if stretch[i]=='Log':
norm = ImageNormalize(crop.data, stretch=LogStretch(), interval=PercentileInterval(99))
elif stretch[i]=='Asinh':
norm = ImageNormalize(crop.data, stretch=AsinhStretch(), interval=PercentileInterval(99))
elif stretch[i]=='Sqrt':
norm = ImageNormalize(crop.data, stretch=SqrtStretch(), interval=PercentileInterval(99))
else:
norm = ImageNormalize(crop.data, stretch=LinearStretch(), interval=PercentileInterval(99))
ax.imshow(crop.data, cmap='gray_r', origin='lower', norm=norm)
ax.text(0.9, 0.9, label[i], ha='right', transform=ax.transAxes)
#ax.axis('off')
for i in (0,1):
ax.coords[i].set_ticks_visible(False)
ax.coords[i].set_ticklabel_visible(False)
ax.coords[i].set_ticks_visible(False)
ax.coords[i].set_ticklabel_visible(False)
ax.coords[i].set_axislabel('')
ax.coords[i].set_axislabel('')
plt.tight_layout()
plt.savefig('M51_montage.pdf')
# -
| extragalactic/M51_montage.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
lower = 0
upper = 4
t = np.arange(lower, upper, 0.1)
v = 80 * np.ones(len(t), )
x = v * t
fig, ax = plt.subplots()
plt.plot(t, v, 'b', label='2.', linewidth=5)
plt.xlim((0, 4))
plt.ylim((0, 100))
plt.title('Velocity v.s. Time')
plt.xlabel("Time [s]")
plt.ylabel("Velocity [m/s]")
plt.grid(True)
plt.savefig('1.png')
fig, ax = plt.subplots()
plt.plot(t, x, 'b', label='2.', linewidth=5)
plt.xlim((0, 4))
plt.ylim((0, 350))
plt.title('Position v.s. Time')
plt.xlabel("Time [s]")
plt.ylabel("Position [m]")
plt.grid(True)
plt.savefig('2.png')
| asset/03.week/plotter.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dependencies
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _kg_hide-input=true _kg_hide-output=true _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import gc
import os
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from gensim.models import KeyedVectors
from sklearn import metrics
from sklearn.model_selection import train_test_split
from keras import optimizers
from keras.models import Model
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, LearningRateScheduler
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.layers import Dense, Input, Embedding, Dropout, Activation, CuDNNGRU, Conv1D, Bidirectional, GlobalMaxPool1D, GlobalAveragePooling1D, SpatialDropout1D
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
def seed_everything(seed=0):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
set_random_seed(0)
seed_everything()
# %matplotlib inline
sns.set_style("whitegrid")
pd.set_option('display.float_format', lambda x: '%.4f' % x)
warnings.filterwarnings("ignore")
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _kg_hide-input=true _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
train = pd.read_csv("../input/jigsaw-unintended-bias-in-toxicity-classification/train.csv")
test = pd.read_csv("../input/jigsaw-unintended-bias-in-toxicity-classification/test.csv")
print("Train shape : ", train.shape)
print("Test shape : ", test.shape)
# -
# # Preprocess
# + _kg_hide-input=true
train['target'] = np.where(train['target'] >= 0.5, 1, 0)
train['comment_text'] = train['comment_text'].astype(str)
X_test = test['comment_text'].astype(str)
# + _kg_hide-input=true _kg_hide-output=true
# Lower comments
train['comment_text'] = train['comment_text'].apply(lambda x: x.lower())
X_test = X_test.apply(lambda x: x.lower())
# + _kg_hide-input=true _kg_hide-output=true
# Mapping Punctuation
def map_punctuation(data):
punct_mapping = {"_":" ", "`":" ",
"‘": "'", "₹": "e", "´": "'", "°": "", "€": "e", "™": "tm", "√": " sqrt ", "×": "x", "²": "2", "—": "-", "–": "-",
"’": "'", "_": "-", "`": "'", '“': '"', '”': '"', '“': '"', "£": "e", '∞': 'infinity', 'θ': 'theta', '÷': '/',
'α': 'alpha', '•': '.', 'à': 'a', '−': '-', 'β': 'beta', '∅': '', '³': '3', 'π': 'pi'}
def clean_special_chars(text, mapping):
for p in mapping:
text = text.replace(p, mapping[p])
return text
return data.apply(lambda x: clean_special_chars(x, punct_mapping))
train['comment_text'] = map_punctuation(train['comment_text'])
X_test = map_punctuation(X_test)
# + _kg_hide-input=true _kg_hide-output=true
# Removing Punctuation
def remove_punctuation(data):
punct = "/-'?!.,#$%\'()*+-/:;<=>@[\\]^_`{|}~`" + '""“”’' + '∞θ÷α•à−β∅³π‘₹´°£€\×™√²—–&'
def clean_special_chars(text, punct):
for p in punct:
text = text.replace(p, ' ')
return text
return data.apply(lambda x: clean_special_chars(x, punct))
train['comment_text'] = remove_punctuation(train['comment_text'])
X_test = remove_punctuation(X_test)
# + _kg_hide-input=true _kg_hide-output=true
# Clean contractions
def clean_contractions(text):
specials = ["’", "‘", "´", "`"]
for s in specials:
text = text.replace(s, "'")
return text
train['comment_text'] = train['comment_text'].apply(lambda x: clean_contractions(x))
X_test = X_test.apply(lambda x: clean_contractions(x))
# + _kg_hide-input=true _kg_hide-output=true
# Mapping contraction
def map_contraction(data):
contraction_mapping = {"trump's": 'trump is', "'cause": 'because', ',cause': 'because', ';cause': 'because', "ain't": 'am not', 'ain,t': 'am not', 'ain;t': 'am not',
'ain´t': 'am not', 'ain’t': 'am not', "aren't": 'are not', 'aren,t': 'are not', 'aren;t': 'are not', 'aren´t': 'are not', 'aren’t': 'are not',
"can't": 'cannot', "can't've": 'cannot have', 'can,t': 'cannot', 'can,t,ve': 'cannot have', 'can;t': 'cannot', 'can;t;ve': 'cannot have',
'can´t': 'cannot', 'can´t´ve': 'cannot have', 'can’t': 'cannot', 'can’t’ve': 'cannot have', "could've": 'could have', 'could,ve': 'could have',
'could;ve': 'could have', "couldn't": 'could not', "couldn't've": 'could not have', 'couldn,t': 'could not', 'couldn,t,ve': 'could not have',
'couldn;t': 'could not', 'couldn;t;ve': 'could not have', 'couldn´t': 'could not', 'couldn´t´ve': 'could not have', 'couldn’t': 'could not',
'couldn’t’ve': 'could not have', 'could´ve': 'could have', 'could’ve': 'could have', "didn't": 'did not', 'didn,t': 'did not', 'didn;t': 'did not',
'didn´t': 'did not', 'didn’t': 'did not', "doesn't": 'does not', 'doesn,t': 'does not', 'doesn;t': 'does not', 'doesn´t': 'does not', 'doesn’t': 'does not',
"don't": 'do not', 'don,t': 'do not', 'don;t': 'do not', 'don´t': 'do not', 'don’t': 'do not', "hadn't": 'had not', "hadn't've": 'had not have',
'hadn,t': 'had not', 'hadn,t,ve': 'had not have', 'hadn;t': 'had not', 'hadn;t;ve': 'had not have', 'hadn´t': 'had not', 'hadn´t´ve': 'had not have',
'hadn’t': 'had not', 'hadn’t’ve': 'had not have', "hasn't": 'has not', 'hasn,t': 'has not', 'hasn;t': 'has not', 'hasn´t': 'has not', 'hasn’t': 'has not',
"haven't": 'have not', 'haven,t': 'have not', 'haven;t': 'have not', 'haven´t': 'have not', 'haven’t': 'have not', "he'd": 'he would', "he'd've": 'he would have',
"he'll": 'he will', "he's": 'he is', 'he,d': 'he would', 'he,d,ve': 'he would have', 'he,ll': 'he will', 'he,s': 'he is', 'he;d': 'he would',
'he;d;ve': 'he would have', 'he;ll': 'he will', 'he;s': 'he is', 'he´d': 'he would', 'he´d´ve': 'he would have', 'he´ll': 'he will', 'he´s': 'he is',
'he’d': 'he would', 'he’d’ve': 'he would have', 'he’ll': 'he will', 'he’s': 'he is', "how'd": 'how did', "how'll": 'how will', "how's": 'how is',
'how,d': 'how did', 'how,ll': 'how will', 'how,s': 'how is', 'how;d': 'how did', 'how;ll': 'how will', 'how;s': 'how is', 'how´d': 'how did', 'how´ll':
'how will', 'how´s': 'how is', 'how’d': 'how did', 'how’ll': 'how will', 'how’s': 'how is', "i'd": 'i would', "i'll": 'i will', "i'm": 'i am', "i've":
'i have', 'i,d': 'i would', 'i,ll': 'i will', 'i,m': 'i am', 'i,ve': 'i have', 'i;d': 'i would', 'i;ll': 'i will', 'i;m': 'i am', 'i;ve': 'i have',
"isn't": 'is not', 'isn,t': 'is not', 'isn;t': 'is not', 'isn´t': 'is not', 'isn’t': 'is not', "it'd": 'it would', "it'll": 'it will', "it's": 'it is',
'it,d': 'it would', 'it,ll': 'it will', 'it,s': 'it is', 'it;d': 'it would', 'it;ll': 'it will', 'it;s': 'it is', 'it´d': 'it would', 'it´ll': 'it will',
'it´s': 'it is', 'it’d': 'it would', 'it’ll': 'it will', 'it’s': 'it is', 'i´d': 'i would', 'i´ll': 'i will', 'i´m': 'i am', 'i´ve': 'i have', 'i’d': 'i would',
'i’ll': 'i will', 'i’m': 'i am', 'i’ve': 'i have', "let's": 'let us', 'let,s': 'let us', 'let;s': 'let us', 'let´s': 'let us', 'let’s': 'let us', "ma'am": 'madam',
'ma,am': 'madam', 'ma;am': 'madam', "mayn't": 'may not', 'mayn,t': 'may not', 'mayn;t': 'may not', 'mayn´t': 'may not', 'mayn’t': 'may not', 'ma´am': 'madam',
'ma’am': 'madam', "might've": 'might have', 'might,ve': 'might have', 'might;ve': 'might have', "mightn't": 'might not', 'mightn,t': 'might not',
'mightn;t': 'might not', 'mightn´t': 'might not', 'mightn’t': 'might not', 'might´ve': 'might have', 'might’ve': 'might have', "must've": 'must have',
'must,ve': 'must have', 'must;ve': 'must have', "mustn't": 'must not', 'mustn,t': 'must not', 'mustn;t': 'must not', 'mustn´t': 'must not',
'mustn’t': 'must not', 'must´ve': 'must have', 'must’ve': 'must have', "needn't": 'need not', 'needn,t': 'need not', 'needn;t': 'need not', 'needn´t': 'need not',
'needn’t': 'need not', "oughtn't": 'ought not', 'oughtn,t': 'ought not', 'oughtn;t': 'ought not', 'oughtn´t': 'ought not', 'oughtn’t': 'ought not',
"sha'n't": 'shall not', 'sha,n,t': 'shall not', 'sha;n;t': 'shall not', "shan't": 'shall not', 'shan,t': 'shall not', 'shan;t': 'shall not', 'shan´t': 'shall not',
'shan’t': 'shall not', 'sha´n´t': 'shall not', 'sha’n’t': 'shall not', "she'd": 'she would', "she'll": 'she will', "she's": 'she is', 'she,d': 'she would',
'she,ll': 'she will', 'she,s': 'she is', 'she;d': 'she would', 'she;ll': 'she will', 'she;s': 'she is', 'she´d': 'she would', 'she´ll': 'she will',
'she´s': 'she is', 'she’d': 'she would', 'she’ll': 'she will', 'she’s': 'she is', "should've": 'should have', 'should,ve': 'should have',
'should;ve': 'should have', "shouldn't": 'should not', 'shouldn,t': 'should not', 'shouldn;t': 'should not', 'shouldn´t': 'should not', 'shouldn’t': 'should not',
'should´ve': 'should have', 'should’ve': 'should have', "that'd": 'that would', "that's": 'that is', 'that,d': 'that would', 'that,s': 'that is',
'that;d': 'that would', 'that;s': 'that is', 'that´d': 'that would', 'that´s': 'that is', 'that’d': 'that would', 'that’s': 'that is', "there'd": 'there had',
"there's": 'there is', 'there,d': 'there had', 'there,s': 'there is', 'there;d': 'there had', 'there;s': 'there is', 'there´d': 'there had', 'there´s': 'there is',
'there’d': 'there had', 'there’s': 'there is', "they'd": 'they would', "they'll": 'they will', "they're": 'they are', "they've": 'they have',
'they,d': 'they would', 'they,ll': 'they will', 'they,re': 'they are', 'they,ve': 'they have', 'they;d': 'they would', 'they;ll': 'they will',
'they;re': 'they are', 'they;ve': 'they have', 'they´d': 'they would', 'they´ll': 'they will', 'they´re': 'they are', 'they´ve': 'they have',
'they’d': 'they would', 'they’ll': 'they will', 'they’re': 'they are', 'they’ve': 'they have', "wasn't": 'was not', 'wasn,t': 'was not', 'wasn;t': 'was not',
'wasn´t': 'was not', 'wasn’t': 'was not', "we'd": 'we would', "we'll": 'we will', "we're": 'we are', "we've": 'we have', 'we,d': 'we would', 'we,ll': 'we will',
'we,re': 'we are', 'we,ve': 'we have', 'we;d': 'we would', 'we;ll': 'we will', 'we;re': 'we are', 'we;ve': 'we have', "weren't": 'were not', 'weren,t': 'were not',
'weren;t': 'were not', 'weren´t': 'were not', 'weren’t': 'were not', 'we´d': 'we would', 'we´ll': 'we will', 'we´re': 'we are', 'we´ve': 'we have',
'we’d': 'we would', 'we’ll': 'we will', 'we’re': 'we are', 'we’ve': 'we have', "what'll": 'what will', "what're": 'what are', "what's": 'what is',
"what've": 'what have', 'what,ll': 'what will', 'what,re': 'what are', 'what,s': 'what is', 'what,ve': 'what have', 'what;ll': 'what will', 'what;re': 'what are',
'what;s': 'what is', 'what;ve': 'what have', 'what´ll': 'what will', 'what´re': 'what are', 'what´s': 'what is', 'what´ve': 'what have', 'what’ll': 'what will',
'what’re': 'what are', 'what’s': 'what is', 'what’ve': 'what have', "where'd": 'where did', "where's": 'where is', 'where,d': 'where did', 'where,s': 'where is',
'where;d': 'where did', 'where;s': 'where is', 'where´d': 'where did', 'where´s': 'where is', 'where’d': 'where did', 'where’s': 'where is', "who'll": 'who will',
"who's": 'who is', 'who,ll': 'who will', 'who,s': 'who is', 'who;ll': 'who will', 'who;s': 'who is', 'who´ll': 'who will', 'who´s': 'who is', 'who’ll': 'who will',
'who’s': 'who is', "won't": 'will not', 'won,t': 'will not', 'won;t': 'will not', 'won´t': 'will not', 'won’t': 'will not', "wouldn't": 'would not',
'wouldn,t': 'would not', 'wouldn;t': 'would not', 'wouldn´t': 'would not', 'wouldn’t': 'would not', "you'd": 'you would', "you'll": 'you will',
"you're": 'you are', 'you,d': 'you would', 'you,ll': 'you will', 'you,re': 'you are', 'you;d': 'you would', 'you;ll': 'you will', 'you;re': 'you are',
'you´d': 'you would', 'you´ll': 'you will', 'you´re': 'you are', 'you’d': 'you would', 'you’ll': 'you will', 'you’re': 'you are', '´cause': 'because',
'’cause': 'because', "you've": 'you have', "could'nt": 'could not', "havn't": 'have not', 'here’s': 'here is', 'i""m': 'i am', "i'am": 'i am', "i'l": 'i will',
"i'v": 'i have', "wan't": 'want', "was'nt": 'was not', "who'd": 'who would', "who're": 'who are', "who've": 'who have', "why'd": 'why would',
"would've": 'would have', "y'all": 'you all', "y'know": 'you know', 'you.i': 'you i', "your'e": 'you are', "arn't": 'are not', "agains't": 'against',
"c'mon": 'common', "doens't": 'does not', 'don""t': 'do not', "dosen't": 'does not', "dosn't": 'does not', "shoudn't": 'should not', "that'll": 'that will',
"there'll": 'there will', "there're": 'there are', "this'll": 'this all', "u're": 'you are', "ya'll": 'you all', "you'r": 'you are', 'you’ve': 'you have',
"d'int": 'did not', "did'nt": 'did not', "din't": 'did not', "dont't": 'do not', "gov't": 'government', "i'ma": 'i am', "is'nt": 'is not', '‘i': 'i',
'ᴀɴᴅ': 'and', 'ᴛʜᴇ': 'the', 'ʜᴏᴍᴇ': 'home', 'ᴜᴘ': 'up', 'ʙʏ': 'by', 'ᴀᴛ': 'at', '…and': 'and', 'civilbeat': 'civil beat', 'trumpcare': 'trump care',
'obamacare': 'obama care', 'ᴄʜᴇᴄᴋ': 'check', 'ғᴏʀ': 'for', 'ᴛʜɪs': 'this', 'ᴄᴏᴍᴘᴜᴛᴇʀ': 'computer', 'ᴍᴏɴᴛʜ': 'month', 'ᴡᴏʀᴋɪɴɢ': 'working', 'ᴊᴏʙ': 'job',
'ғʀᴏᴍ': 'from', 'sᴛᴀʀᴛ': 'start', 'gubmit': 'submit', 'co₂': 'carbon dioxide', 'ғɪʀsᴛ': 'first', 'ᴇɴᴅ': 'end', 'ᴄᴀɴ': 'can', 'ʜᴀᴠᴇ': 'have', 'ᴛᴏ': 'to',
'ʟɪɴᴋ': 'link', 'ᴏғ': 'of', 'ʜᴏᴜʀʟʏ': 'hourly', 'ᴡᴇᴇᴋ': 'week', 'ᴇxᴛʀᴀ': 'extra', 'gʀᴇᴀᴛ': 'great', 'sᴛᴜᴅᴇɴᴛs': 'student', 'sᴛᴀʏ': 'stay', 'ᴍᴏᴍs': 'mother',
'ᴏʀ': 'or', 'ᴀɴʏᴏɴᴇ': 'anyone', 'ɴᴇᴇᴅɪɴɢ': 'needing', 'ᴀɴ': 'an', 'ɪɴᴄᴏᴍᴇ': 'income', 'ʀᴇʟɪᴀʙʟᴇ': 'reliable', 'ʏᴏᴜʀ': 'your', 'sɪɢɴɪɴɢ': 'signing',
'ʙᴏᴛᴛᴏᴍ': 'bottom', 'ғᴏʟʟᴏᴡɪɴɢ': 'following', 'mᴀᴋᴇ': 'make', 'ᴄᴏɴɴᴇᴄᴛɪᴏɴ': 'connection', 'ɪɴᴛᴇʀɴᴇᴛ': 'internet', 'financialpost': 'financial post',
'ʜaᴠᴇ': ' have ', 'ᴄaɴ': ' can ', 'maᴋᴇ': ' make ', 'ʀᴇʟɪaʙʟᴇ': ' reliable ', 'ɴᴇᴇᴅ': ' need ', 'ᴏɴʟʏ': ' only ', 'ᴇxᴛʀa': ' extra ', 'aɴ': ' an ',
'aɴʏᴏɴᴇ': ' anyone ', 'sᴛaʏ': ' stay ', 'sᴛaʀᴛ': ' start', 'shopo': 'shop'}
def clean_special_chars(text, mapping):
for p in mapping:
text = text.replace(p, mapping[p])
return text
return data.apply(lambda x: clean_special_chars(x, contraction_mapping))
train['comment_text'] = map_contraction(train['comment_text'])
X_test = map_contraction(X_test)
# + _kg_hide-input=true _kg_hide-output=true
# Mapping misspelling
def map_misspelling(data):
misspelling_mapping = {'sb91': 'senate bill', 'trump': 'trump', 'utmterm': 'utm term', 'fakenews': 'fake news', 'gʀᴇat': 'great', 'ʙᴏᴛtoᴍ': 'bottom',
'washingtontimes': 'washington times', 'garycrum': 'gary crum', 'htmlutmterm': 'html utm term', 'rangermc': 'car', 'tfws': 'tuition fee waiver',
'sjws': 'social justice warrior', 'koncerned': 'concerned', 'vinis': 'vinys', 'yᴏᴜ': 'you', 'trumpsters': 'trump', 'trumpian': 'trump', 'bigly': 'big league',
'trumpism': 'trump', 'yoyou': 'you', 'auwe': 'wonder', 'drumpf': 'trump', 'brexit': 'british exit', 'utilitas': 'utilities', 'ᴀ': 'a', '😉': 'wink',
'😂': 'joy', '😀': 'stuck out tongue', 'theguardian': 'the guardian', 'deplorables': 'deplorable', 'theglobeandmail': 'the globe and mail',
'justiciaries': 'justiciary', 'creditdation': 'accreditation', 'doctrne': 'doctrine', 'fentayal': 'fentanyl', 'designation-': 'designation',
'conartist': 'con-artist', 'mutilitated': 'mutilated', 'obumblers': 'bumblers', 'negotiatiations': 'negotiations', 'dood-': 'dood', 'irakis': 'iraki',
'cooerate': 'cooperate', 'cox': 'cox', 'racistcomments': 'racist comments', 'envirnmetalists': 'environmentalists'}
def clean_special_chars(text, mapping):
for p in mapping:
text = text.replace(p, mapping[p])
return text
return data.apply(lambda x: clean_special_chars(x, misspelling_mapping))
train['comment_text'] = map_misspelling(train['comment_text'])
X_test = map_misspelling(X_test)
# + _kg_hide-input=true
# Train/validation split
train_ids, val_ids = train_test_split(train['id'], test_size=0.2, random_state=2019)
train_df = pd.merge(train_ids.to_frame(), train)
validate_df = pd.merge(val_ids.to_frame(), train)
Y_train = train_df['target'].values
Y_val = validate_df['target'].values
X_train = train_df['comment_text']
X_val = validate_df['comment_text']
# -
# Hyper parameters
maxlen = 220 # max number of words in a question to use
embed_size = 250 # how big is each word vector
max_features = 410047 # how many unique words to use (i.e num rows in embedding vector)
learning_rate = 0.001
decay_factor = 0.25
epochs = 6
batch_size = 512
# + _kg_hide-input=true
# Fill missing values
X_train = X_train.fillna("_na_").values
X_val = X_val.fillna("_na_").values
X_test = X_test.fillna("_na_").values
# + _kg_hide-input=true
# Tokenize the sentences
tokenizer = Tokenizer(num_words=max_features)
tokenizer.fit_on_texts(list(X_train))
X_train = tokenizer.texts_to_sequences(X_train)
X_val = tokenizer.texts_to_sequences(X_val)
X_test = tokenizer.texts_to_sequences(X_test)
# + _kg_hide-input=true
# Pad the sentences
X_train = pad_sequences(X_train, maxlen=maxlen)
X_val = pad_sequences(X_val, maxlen=maxlen)
X_test = pad_sequences(X_test, maxlen=maxlen)
# -
# # Loading Embedding
# + _kg_hide-input=true _kg_hide-output=true
def get_coefs(word, *arr):
return word, np.asarray(arr, dtype='float32')
def load_embeddings(path):
emb_arr = KeyedVectors.load(path)
return emb_arr
def build_matrix(word_index, path):
embedding_index = load_embeddings(path)
embedding_matrix = np.zeros((len(word_index) + 1, 300))
unknown_words = []
for word, i in word_index.items():
if i <= max_features:
try:
embedding_matrix[i] = embedding_index[word]
except KeyError:
try:
embedding_matrix[i] = embedding_index[word.lower()]
except KeyError:
try:
embedding_matrix[i] = embedding_index[word.title()]
except KeyError:
unknown_words.append(word)
return embedding_matrix, unknown_words
glove_path = '../input/gensim-embeddings-dataset/glove.840B.300d.gensim'
craw_path = '../input/gensim-embeddings-dataset/crawl-300d-2M.gensim'
glove_embedding_matrix, glove_unknown_words = build_matrix(tokenizer.word_index, glove_path)
print('n unknown words (GloVe): ', len(glove_unknown_words))
craw_embedding_matrix, craw_unknown_words = build_matrix(tokenizer.word_index, craw_path)
print('n unknown words (Crawl): ', len(craw_unknown_words))
embedding_matrix = np.concatenate([glove_embedding_matrix, craw_embedding_matrix], axis=-1)
del glove_embedding_matrix, craw_embedding_matrix
gc.collect()
# -
# # Model
# + _kg_hide-output=true
inp = Input(shape=(maxlen,))
x = Embedding(*embedding_matrix.shape, weights=[embedding_matrix], trainable=False)(inp)
x = SpatialDropout1D(0.3)(x)
x = Bidirectional(CuDNNGRU(128, return_sequences=True))(x)
x = Bidirectional(CuDNNGRU(256, return_sequences=True))(x)
x = GlobalAveragePooling1D()(x)
# x = GlobalMaxPool1D()(x)
x = Dense(512, activation="relu")(x)
x = Dense(512, activation="relu")(x)
x = Dense(1, activation="sigmoid")(x)
model = Model(inputs=inp, outputs=x)
optimizer = optimizers.SGD(lr=learning_rate, momentum=0.9, nesterov='true')
model.compile(loss='binary_crossentropy', optimizer=optimizer, metrics=['accuracy'])
model.summary()
# + _kg_hide-input=true _kg_hide-output=true
es = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=5)
rlrop = ReduceLROnPlateau(monitor='val_loss', factor=decay_factor, patience=3)
history = model.fit(X_train, Y_train, batch_size=batch_size, epochs=epochs, validation_data=(X_val, Y_val), callbacks=[es, rlrop])
# + _kg_hide-input=true
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(20, 8))
ax1.plot(history.history['acc'], label='Train Accuracy')
ax1.plot(history.history['val_acc'], label='Validation accuracy')
ax1.legend(loc='best')
ax1.set_title('Accuracy')
ax2.plot(history.history['loss'], label='Train loss')
ax2.plot(history.history['val_loss'], label='Validation loss')
ax2.legend(loc='best')
ax2.set_title('Loss')
plt.xlabel('Epochs')
sns.despine()
plt.show()
# -
# # Model evaluation
# + _kg_hide-input=true
identity_columns = [
'male', 'female', 'homosexual_gay_or_lesbian', 'christian', 'jewish',
'muslim', 'black', 'white', 'psychiatric_or_mental_illness']
# Convert taget and identity columns to booleans
def convert_to_bool(df, col_name):
df[col_name] = np.where(df[col_name] >= 0.5, True, False)
def convert_dataframe_to_bool(df):
bool_df = df.copy()
for col in ['target'] + identity_columns:
convert_to_bool(bool_df, col)
return bool_df
SUBGROUP_AUC = 'subgroup_auc'
BPSN_AUC = 'bpsn_auc' # stands for background positive, subgroup negative
BNSP_AUC = 'bnsp_auc' # stands for background negative, subgroup positive
def compute_auc(y_true, y_pred):
try:
return metrics.roc_auc_score(y_true, y_pred)
except ValueError:
return np.nan
def compute_subgroup_auc(df, subgroup, label, model_name):
subgroup_examples = df[df[subgroup]]
return compute_auc(subgroup_examples[label], subgroup_examples[model_name])
def compute_bpsn_auc(df, subgroup, label, model_name):
"""Computes the AUC of the within-subgroup negative examples and the background positive examples."""
subgroup_negative_examples = df[df[subgroup] & ~df[label]]
non_subgroup_positive_examples = df[~df[subgroup] & df[label]]
examples = subgroup_negative_examples.append(non_subgroup_positive_examples)
return compute_auc(examples[label], examples[model_name])
def compute_bnsp_auc(df, subgroup, label, model_name):
"""Computes the AUC of the within-subgroup positive examples and the background negative examples."""
subgroup_positive_examples = df[df[subgroup] & df[label]]
non_subgroup_negative_examples = df[~df[subgroup] & ~df[label]]
examples = subgroup_positive_examples.append(non_subgroup_negative_examples)
return compute_auc(examples[label], examples[model_name])
def compute_bias_metrics_for_model(dataset, subgroups, model, label_col, include_asegs=False):
"""Computes per-subgroup metrics for all subgroups and one model."""
records = []
for subgroup in subgroups:
record = {
'subgroup': subgroup,
'subgroup_size': len(dataset[dataset[subgroup]])
}
record[SUBGROUP_AUC] = compute_subgroup_auc(dataset, subgroup, label_col, model)
record[BPSN_AUC] = compute_bpsn_auc(dataset, subgroup, label_col, model)
record[BNSP_AUC] = compute_bnsp_auc(dataset, subgroup, label_col, model)
records.append(record)
return pd.DataFrame(records).sort_values('subgroup_auc', ascending=True)
# validate_df = pd.merge(val_ids.to_frame(), train)
validate_df['preds'] = model.predict(X_val)
validate_df = convert_dataframe_to_bool(validate_df)
bias_metrics_df = compute_bias_metrics_for_model(validate_df, identity_columns, 'preds', 'target')
print('Validation bias metric by group')
display(bias_metrics_df)
# + _kg_hide-input=true
def power_mean(series, p):
total = sum(np.power(series, p))
return np.power(total / len(series), 1 / p)
def get_final_metric(bias_df, overall_auc, POWER=-5, OVERALL_MODEL_WEIGHT=0.25):
bias_score = np.average([
power_mean(bias_df[SUBGROUP_AUC], POWER),
power_mean(bias_df[BPSN_AUC], POWER),
power_mean(bias_df[BNSP_AUC], POWER)
])
return (OVERALL_MODEL_WEIGHT * overall_auc) + ((1 - OVERALL_MODEL_WEIGHT) * bias_score)
# train_df = pd.merge(train_ids.to_frame(), train)
train_df['preds'] = model.predict(X_train)
train_df = convert_dataframe_to_bool(train_df)
print('Train ROC AUC: %.4f' % get_final_metric(bias_metrics_df, metrics.roc_auc_score(train_df['target'].values, train_df['preds'].values)))
print('Validation ROC AUC: %.4f' % get_final_metric(bias_metrics_df, metrics.roc_auc_score(validate_df['target'].values, validate_df['preds'].values)))
# -
# # Predictions
Y_test = model.predict(X_test)
# + _kg_hide-input=true
submission = pd.read_csv('../input/jigsaw-unintended-bias-in-toxicity-classification/sample_submission.csv')
submission['prediction'] = Y_test
submission.to_csv('submission.csv', index=False)
submission.head(10)
| Model backlog/Deep Learning/[36th] Bi GRU - Craw, GloVe - Model tunning.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
from IPython.display import Image
from IPython.core.display import HTML
from sympy import *
Image(url= "https://i.imgur.com/wo5OwkX.png")
f = Function("f")
x,y = symbols("x y")
e0 = Integral(f(x),(x,-pi,pi))
e0
a = 2*x**3
b = 5*sin(x)
e3 = Piecewise((a, ((x < 0)) & ((x >= -pi))),(b,((x<=pi))& ((x >= 0))))
e4 = Eq(f(x),e3)
e4
e5 = Integral(e4,(x,-pi,pi))
e5
e5.doit()
print(e5.doit().rhs)
Image(url= "https://i.imgur.com/XAC2vgG.png")
Image(url= "https://i.imgur.com/z77oGr5.png")
e6 = 1/(cos(x)**2)
e7 = Integral(e6,(x,-pi/4,0))
e7
e7.doit()
Image(url= "https://i.imgur.com/F7HIMOE.png")
Image(url= "https://i.imgur.com/30ggSC2.png")
e8 = x*(x+2)*(1-x)
e9 = Integral(e8,(x,-2,1))
e9
e9.doit()
Image(url= "https://i.imgur.com/hyJJz6w.png")
Image(url= "https://i.imgur.com/xUGdasC.png")
e10 = abs(x**3)
e11 = Integral(e10,(x,-2,1))
e11
e11.doit()
Image(url= "https://i.imgur.com/rYiDqF4.png")
Image(url= "https://i.imgur.com/vnZPXrc.png")
t = symbols('t')
e12 = sqrt(t)*(5+t)
e13 = Integral(e12,(t,1,4))
e13
e13.doit()
Image(url= "https://i.imgur.com/RPOvgy8.png")
Image(url= "https://i.imgur.com/vmAzFRJ.png")
e14= sqrt(2/x)
e15 = Integral(e14,(x,1,4))
e15
e15.doit()
Image(url= "https://i.imgur.com/hcQlywf.png")
Image(url= "https://i.imgur.com/iyZsZHs.png")
e15= t**3 - 4*t**2
e16 = Integral(e15,(t,-1,5))
e16
e16.doit()
e17 = abs(e15)
e18 = Integral(e17,(t,-1,5))
e18
e18.doit()
Image(url= "https://i.imgur.com/7uplphF.png")
Image(url= "https://i.imgur.com/d9Fbxag.png")
e20 = t**Rational(1,2)+3
e21 = Integral(e20,(t,5,9))
e21
a = e21.doit().evalf()
a
a/4
Image(url= "https://i.imgur.com/kG9utPJ.png")
Image(url= "https://i.imgur.com/1jAeHgI.png")
v = Function("v")
r,n,l,R,P = symbols('r n l R P')
v(r)
e22 = (P/(4*n*l) )*(R**2-r**2)
e23 = Eq(v(r),e22)
e23
e24 = Integral(e23.rhs,(r,0,R))
e24
e24.doit()/R
print(e24.doit()/R)
e40 = P*R**2/(6*l*n)
e40
# source 06-05-018_Average_Value_of_a_Function.pdf
Image(url= "https://i.imgur.com/3c17nUy.png")
Image(url= "https://i.imgur.com/psTFm7P.png")
e30 = x**2
e31 = Integral(e30,(x,3,6))
e31
e31.doit()
63/3
Image(url= "https://i.imgur.com/CeUw8Mi.png")
Image(url= "https://i.imgur.com/af7s3HK.png")
e32 = 0.2*x**2+130*x+200
e33 = Integral(e32,(x,0,450))
e33
e33.doit()/450
Image(url= "https://i.imgur.com/xII0vO4.png")
| Calculus_Homework/WWB19.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# Optional: Data Parallelism
# ==========================
# **Authors**: `<NAME> <https://github.com/hunkim>`_ and `<NAME> <https://github.com/jennykang>`_
#
# In this tutorial, we will learn how to use multiple GPUs using ``DataParallel``.
#
# It's very easy to use GPUs with PyTorch. You can put the model on a GPU:
#
# .. code:: python
#
# device = torch.device("cuda:0")
# model.to(device)
#
# Then, you can copy all your tensors to the GPU:
#
# .. code:: python
#
# mytensor = my_tensor.to(device)
#
# Please note that just calling ``my_tensor.to(device)`` returns a new copy of
# ``my_tensor`` on GPU instead of rewriting ``my_tensor``. You need to assign it to
# a new tensor and use that tensor on the GPU.
#
# It's natural to execute your forward, backward propagations on multiple GPUs.
# However, Pytorch will only use one GPU by default. You can easily run your
# operations on multiple GPUs by making your model run parallelly using
# ``DataParallel``:
#
# .. code:: python
#
# model = nn.DataParallel(model)
#
# That's the core behind this tutorial. We will explore it in more detail below.
#
#
# Imports and parameters
# ----------------------
#
# Import PyTorch modules and define parameters.
#
#
#
# +
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
# Parameters and DataLoaders
input_size = 5
output_size = 2
batch_size = 30
data_size = 100
# -
# Device
#
#
#
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Dummy DataSet
# -------------
#
# Make a dummy (random) dataset. You just need to implement the
# getitem
#
#
#
# +
class RandomDataset(Dataset):
def __init__(self, size, length):
self.len = length
self.data = torch.randn(length, size)
def __getitem__(self, index):
return self.data[index]
def __len__(self):
return self.len
rand_loader = DataLoader(dataset=RandomDataset(input_size, data_size),
batch_size=batch_size, shuffle=True)
# -
# Simple Model
# ------------
#
# For the demo, our model just gets an input, performs a linear operation, and
# gives an output. However, you can use ``DataParallel`` on any model (CNN, RNN,
# Capsule Net etc.)
#
# We've placed a print statement inside the model to monitor the size of input
# and output tensors.
# Please pay attention to what is printed at batch rank 0.
#
#
#
class Model(nn.Module):
# Our model
def __init__(self, input_size, output_size):
super(Model, self).__init__()
self.fc = nn.Linear(input_size, output_size)
def forward(self, input):
output = self.fc(input)
print("\tIn Model: input size", input.size(),
"output size", output.size())
return output
# Create Model and DataParallel
# -----------------------------
#
# This is the core part of the tutorial. First, we need to make a model instance
# and check if we have multiple GPUs. If we have multiple GPUs, we can wrap
# our model using ``nn.DataParallel``. Then we can put our model on GPUs by
# ``model.to(device)``
#
#
#
# +
model = Model(input_size, output_size)
if torch.cuda.device_count() > 1:
print("Let's use", torch.cuda.device_count(), "GPUs!")
# dim = 0 [30, xxx] -> [10, ...], [10, ...], [10, ...] on 3 GPUs
model = nn.DataParallel(model)
model.to(device)
# -
# Run the Model
# -------------
#
# Now we can see the sizes of input and output tensors.
#
#
#
for data in rand_loader:
input = data.to(device)
output = model(input)
print("Outside: input size", input.size(),
"output_size", output.size())
# Results
# -------
#
# If you have no GPU or one GPU, when we batch 30 inputs and 30 outputs, the model gets 30 and outputs 30 as
# expected. But if you have multiple GPUs, then you can get results like this.
#
# 2 GPUs
# ~~~~~~
#
# If you have 2, you will see:
#
# .. code:: bash
#
# # on 2 GPUs
# Let's use 2 GPUs!
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# In Model: input size torch.Size([15, 5]) output size torch.Size([15, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
# In Model: input size torch.Size([5, 5]) output size torch.Size([5, 2])
# Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])
#
# 3 GPUs
# ~~~~~~
#
# If you have 3 GPUs, you will see:
#
# .. code:: bash
#
# Let's use 3 GPUs!
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# In Model: input size torch.Size([10, 5]) output size torch.Size([10, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])
#
# 8 GPUs
# ~~~~~~~~~~~~~~
#
# If you have 8, you will see:
#
# .. code:: bash
#
# Let's use 8 GPUs!
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([4, 5]) output size torch.Size([4, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# Outside: input size torch.Size([30, 5]) output_size torch.Size([30, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# In Model: input size torch.Size([2, 5]) output size torch.Size([2, 2])
# Outside: input size torch.Size([10, 5]) output_size torch.Size([10, 2])
#
#
#
# Summary
# -------
#
# DataParallel splits your data automatically and sends job orders to multiple
# models on several GPUs. After each model finishes their job, DataParallel
# collects and merges the results before returning it to you.
#
# For more information, please check out
# https://pytorch.org/tutorials/beginner/former\_torchies/parallelism\_tutorial.html.
#
#
#
| official_tutorial/data_parallel_tutorial.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Workshop 3 - Quality control for sequencing data
#
# Suppose you had a biological question of interest that could be solved by sequencing. You've received some funding to perform a sequencing run (lucky you!). The sample is run in a sequencing machine (you know a few kinds of sequencers from the sequencing technologies lecture) and you are delivered a file containing all of your reads. It's possible that there were problems, either with the sequencing reaction or with the starting materials. Before you perform your analysis and report your findings, you want to be sure that the data you have is of good quality. This is where quality control (QC) comes in.
#
# This week you will write your own code to perform QC on some real sequencing data.
#
# <br>
#
# ## Task 0 - Getting set up for plotting in python
#
# There are three python libraries that we will be using to produce figures - `numpy`, `pandas` and `matplotlib`.
#
# All three are already installed on SWAN. `numpy` and `pandas` are used for data manipulation and processing, while `matplotlib` is used to plot and visualise your data.
#
# Check that they are installed by importing them.
#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# +
# You can install them on your personal machine with the following conda or pip commands.
# conda install numpy pandas
# pip install numpy pandas
# pip install matplotlib
# conda install -c conda-forge matplotlib
# -
# <br>
#
# If you are new to `pandas`, this tutorial below will help. It is also available under the additional resources module on the LMS.
# > http://pandas.pydata.org/pandas-docs/stable/getting_started/10min.html
#
# We use the `matplotlib` library to create simple plots. You can learn more about `matplotlib` using the link below. The link is also available on the additional resources module on the LMS.
# >https://matplotlib.org/tutorials/introductory/usage.html#sphx-glr-tutorials-introductory-usage-py
#
# The following tutorial shows how `pandas`, `numpy` and `matplotlib` can be used together.
# > https://www.kaggle.com/chats351/introduction-to-numpy-pandas-and-matplotlib
# <br>
#
# ## Task 1 - Reading in the read set
#
# First, we read in some sample reads. The reads in `ERR024571_selected.fastq` are a selection of 800 reads from the ERR024571 read set.
#
# Note that converting a readset into a list of `skbio` objects makes it easier to handle.
#
# The data originates from a *Yersinia enterocolitica* sample, a bacterial species that causes yersiniosis in humans.
#
# <br>
#
import skbio
# +
fname = 'ERR024571_selected.fastq'
registry = skbio.io.read(fname, format = 'fastq', phred_offset = 33)
readset = list(registry)
# -
# <br>
# We can use the len function to find the number of reads in the readset.
len(readset)
# And to find the length of the first read in the readset.
len(readset[0])
#
# More can be read about these skbio objects here:
# > http://scikit-bio.org/docs/0.5.0/generated/skbio.sequence.DNA.html#skbio.sequence.DNA
# <br>
#
# ## Task 2 - Compute per-sequence quality scores
#
# The per-sequence quality is simply the average of the base quality scores in a sequence.
# Display the quality scores for the first 10 bases of the first read.
r1_meta = readset[0].positional_metadata
r1_meta.head(10)
# ### Crash course on `pandas` and `numpy`
#
# The output of the code above is a data frame object. Most data can be stored in data frames and there are many functions to process them available in the `pandas` library.
#
# The `numpy` library stores data in `numpy` arrays, which can range from being one-dimensional vectors or multi-dimensional matrices. A `pandas` data frame is equivalent to a 2-dimensional `numpy` array with named rows and columns. While `numpy` arrays are more memory efficient, `pandas` dataframes have other advantages such as named rows and columns.
#
# We will first try out a few indexing operations.
#
# +
import pandas as pd
import numpy as np
# All of these indexes give the same results. Think of the data frame as a 2-D matrix.
# Here we retrieve data using .iloc
print(r1_meta.iloc[:3,])
print(r1_meta.iloc[0:3, 0:1])
print(r1_meta.iloc[0:3, :])
print(r1_meta.iloc[0:3,])
# -
# Above we use positional information along the data frame (i.e. rows 0:3 and column 0:1).
#
# Instead, we can index rows and columns using *row names* and *column names* with `pandas`.
# In the example below, 0:2 refers to the rows with names '0', '1', and '2' and the column with the name 'quality'.
#
#
# Here we retrieve data using names with loc. 0, 1, and 2 are row names rather than indexes.
print(r1_meta.loc[0:2, 'quality'])
# Because we selected just one column a one-dimensional vector was returned.
#
# When using `pandas` this object is called a `pandas` series, which is equivalent to a one-dimensional `numpy` array.
print(type(r1_meta.loc[0:2, 'quality']))
print(type(np.asarray(r1_meta.loc[0:2, 'quality'])))
# <br>
#
# If we retrieve the entire `quality` column, we can subset it obtain the base quality at any position.
# Retrieve the base quality at position 3. Remember that Python is zero indexed!
r1_qualities = r1_meta.loc[:, 'quality']
r1_qualities[2]
# <br>
#
# ### Now to compute the quality of a sequence
#
# We can now write a function to compute the sequence quality of a given sequence using a for loop and the `.positional_metadata` method.
# +
def read_quality_with_loop(read):
"""
Compute the quality of a given read (DNA sequence).
This is the average of base qualities.
Return a single floating point number.
"""
# -
print(read_quality_with_loop(readset[0])) # should give 27.36
print(read_quality_with_loop(readset[2])) # should give 26.35
# <br>
#
# Using functions from within the `numpy` library can be simpler to write and run considerably faster.
#
# Try computing the sequence quality of a given sequence **without** a for loop, using the `np.mean()` function.
def read_quality(read):
"""
Compute the quality of a given read (DNA sequence).
This is the average of base qualities.
Return a single number representing the quality
"""
print(read_quality(readset[0])) # should also give 27.36
# <br>
#
# ## Task 3 - Compute and visualise the per-sequence quality distribution
#
# We will compute per-sequence qualities for all reads and compute a sequence quality histogram. A histogram visualises the distribution of data by binning the data values into intervals of equal widths and visualising the frequency of values in each bin.
#
# First, you should divide the range of values into equal intervals. These intervals should be non-overlapping integers. Here we would like bins with a width of 1.
# i.e. For a given integer \$i\$, the interval (bin) should be \$[i, i + 1)\$. This means including \$i\$ but excluding \$i + 1\$.
#
#
# Second, you need to count up the frequency of values that fall into each bin. We can represent this histogram data as a dictionary. Keys in the dictionary will be \$i\$ and the values will be the total number of quality scores that fall in the interval \$[i, i + 1)\$.
#
#
# When defining your bins, the `np.floor()` function can be be used to round down quality scores to the nearest integer.
print(np.floor(30.01))
print(np.floor(30.99))
def read_histogram_dict(reads):
"""
Compute a dictionary representing the histogram
Keys are the starting point of the interval
Values are the number of items in the interval
"""
read_histogram_dict(readset[0:4]) # should give {27.0: 2, 28.0: 1, 26.0: 1}
# <br>
#
# Now that we have the histogram data as a dictionary, let's get to plotting!
#
# +
# %matplotlib inline
import matplotlib.pyplot as plt
hist_data = read_histogram_dict(readset)
plt.scatter(hist_data.keys(), hist_data.values())
plt.xlabel('Phred quality score')
plt.ylabel('Frequency')
plt.show()
# -
# <br>
#
# Alternatively, you could directly use the `plt.hist()` function in `matplotlib`.
#
# This function takes the data values you want to bin, and the intervals you want to put them in. But you should provide the bins in order with `sorted()`.
#
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# Get the read qualities
read_qualities = [read_quality(r) for r in readset]
# Define the intervals [i,i+1)
distribution_keys = [np.floor(r) for r in read_qualities]
# Include the upper bound of the last interval
# distribution_keys.append(max(sorted(distribution_keys))+1)
# Plot
plt.hist(read_qualities, sorted(distribution_keys))
plt.xlabel('Phred quality score')
plt.ylabel('Frequency')
plt.show()
# -
# <br>
#
# We can also change the colour, overlay lines, and edit the appearance of the plot.
#
# Change some of the arguments (`fontsize`, `labelpad` or `color`) below to see what effect they have.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# Plot
plt.hist(read_qualities, sorted(distribution_keys), color="skyblue")
plt.xlabel('Phred quality score', fontsize=14)
plt.ylabel('Frequency', fontsize=14, labelpad=12)
plt.axvline(x=20,linewidth=1, color='r')
plt.show()
# -
# <br>
#
# You can also make other plot types, like boxplots.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# Plot
plt.boxplot(read_qualities, vert=False)
plt.xlabel('Phred quality score', fontsize=14, labelpad=12)
plt.yticks([])
plt.show()
# -
# <br>
#
# The documentation for these functions can be found here:
# > https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.scatter.html
#
# > https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.hist.html
#
# > https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.boxplot.html
#
# A list of colour names can be found here:
# > https://matplotlib.org/stable/gallery/color/named_colors.html
# <br>
#
# ## Task 4 - Using FastQC for quality control
#
# The above analysis and more can be performed using the FastQC tool.
#
# FastQC is installed on SWAN.
# If you wish to install FastQC on a (Mac or Linux) personal device, use the conda command `conda install -c bioconda fastqc`.
#
#
# The documentation for FastQC can be found here:
# > https://www.bioinformatics.babraham.ac.uk/projects/fastqc/
# **Please execute the command below to run FastQC.**
# Run FastQC on the ERR024571_1 dataset.
# !fastqc -o ./ ERR024571_1.fastq.gz
# Open the ERR024571_1_fastqc.html file to see the FastQC report.
#
# ### What does this all mean?
#
# The report provides information about several QC metrics.
#
# You should refer to this documentation to help you figure out what some of the metrics mean:
# >https://dnacore.missouri.edu/PDF/FastQC_Manual.pdf
#
#
# There is also a FastQC report explanation video on the LMS in the week 3 module.
#
# <br>
#
#
# ### Try answering some of these questions:
#
# <br>
#
# 1. How many reads are in the read set?
#
# 2. How long are the reads?
#
# 3. Are all the reads the same length?
#
# 4. How are the quality scores distributed across the length of the reads?
#
# 5. Are there any overrepresented sequences?
#
# 6. What is the likely source of the overrepresented sequences?
#
# 7. Overall, is this read set of acceptable quality?
#
# <br>
#
# ### Some comments about quality control
#
# <br>
# What we have covered in this workshop is just one layer of quality control.
#
# Further QC would need to be done, depending on the type of analysis. QC should form an important component of all analyses. Ultimately, it can save a lot of time and effort!
#
#
# FastQC outputs a report for an individual FASTQ file. If you are dealing with multiple read sets in your own projects, MultiQC provides a summary of all FastQC reports. See https://multiqc.info/ and have a look at the example reports.
# <br>
#
# `Workshop developed by <NAME>, Dr <NAME>, <NAME> and <NAME>.`
| workshop_3.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Laboratorio 7
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import altair as alt
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
alt.themes.enable('opaque')
# %matplotlib inline
# -
# En este laboratorio utilizaremos los mismos datos de diabetes vistos en la clase
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True, as_frame=True)
diabetes = pd.concat([diabetes_X, diabetes_y], axis=1)
diabetes.head()
diabetes_y
# ## Pregunta 1
#
# (1 pto)
#
# * ¿Por qué la columna de sexo tiene esos valores?
# * ¿Cuál es la columna a predecir?
# * ¿Crees que es necesario escalar o transformar los datos antes de comenzar el modelamiento?
# __Respuesta:__
#
# * Porque los valores no estan normalizados
# * La columna "target"
# * No
# ## Pregunta 2
#
# (1 pto)
#
# Realiza dos regresiones lineales con todas las _features_, el primer caso incluyendo intercepto y el segundo sin intercepto. Luego obtén la predicción para así calcular el error cuadrático medio y coeficiente de determinación de cada uno de ellos.
regr_with_incerpet = linear_model.LinearRegression(fit_intercept=True)
regr_with_incerpet.fit(diabetes_X, diabetes_y)
diabetes_y_pred_with_intercept = regr_with_incerpet.predict(diabetes_X)
# Coeficientes
print(f"Coefficients: \n{regr_with_incerpet.coef_}\n")
# Intercepto
print(f"Intercept: \n{regr_with_incerpet.intercept_}\n")
# Error cuadrático medio
print(f"Mean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_with_intercept):.2f}\n")
# Coeficiente de determinación
print(f"Coefficient of determination: {r2_score(diabetes_y, diabetes_y_pred_with_intercept):.2f}\n")
regr_without_incerpet = linear_model.LinearRegression(fit_intercept=False)
regr_without_incerpet.fit(diabetes_X, diabetes_y)
diabetes_y_pred_without_intercept = regr_without_incerpet.predict(diabetes_X)
# Coeficientes
print(f"Coefficients: \n{regr_without_incerpet.coef_}\n")
# Error cuadrático medio
print(f"Mean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_without_intercept):.2f}\n")
# Coeficiente de determinación
print(f"Coefficient of determination: {r2_score(diabetes_y, diabetes_y_pred_without_intercept):.2f}")
# **Pregunta: ¿Qué tan bueno fue el ajuste del modelo?**
# __Respuesta:__ La regresion lineal con el intercepto no es mala, pero tampoco es muy buena, ya que, el error es alto, pero el coeficiente de determinacion es 0,52, o sea, el modelo es decente. Por otro lado, la segunda regresion lineal sin intercepto es muy mala porque el error es altisimo y el coeficiente de determinacion es -3.39.
# ## Pregunta 3
#
# (1 pto)
#
# Realizar multiples regresiones lineales utilizando una sola _feature_ a la vez.
#
# En cada iteración:
#
# - Crea un arreglo `X`con solo una feature filtrando `X`.
# - Crea un modelo de regresión lineal con intercepto.
# - Ajusta el modelo anterior.
# - Genera una predicción con el modelo.
# - Calcula e imprime las métricas de la pregunta anterior.
for col in diabetes_X:
X_i = diabetes_X[col].to_frame()
regr_i = linear_model.LinearRegression()
regr_i.fit(X_i, diabetes_y)
diabetes_y_pred_i = regr_i.predict(X_i)
print(f"Feature: {col}")
print(f"\tCoefficients: {regr_i.coef_}")
print(f"\tIntercept: {regr_i.intercept_}")
print(f"\tMean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_i):.2f}")
print(f"\tCoefficient of determination: {r2_score(diabetes_y,diabetes_y_pred_i):.2f}\n")
# **Pregunta: Si tuvieras que escoger una sola _feauture_, ¿Cuál sería? ¿Por qué?**
# **Respuesta:** El feature "bmi", porque es el que tiene el menor error cuadratico medio y el mayor coeficiente de determinacion, es decir, de todas las feature, tiene la relacion mas cercana a ser lineal con target.
# ## Ejercicio 4
#
# (1 pto)
#
# Con la feature escogida en el ejercicio 3 realiza el siguiente gráfico:
#
# - Scatter Plot
# - Eje X: Valores de la feature escogida.
# - Eje Y: Valores de la columna a predecir (target).
# - En color rojo dibuja la recta correspondiente a la regresión lineal (utilizando `intercept_`y `coefs_`).
# - Coloca un título adecuado, nombre de los ejes, etc.
#
# Puedes utilizar `matplotlib` o `altair`, el que prefieras.
regr = linear_model.LinearRegression().fit(diabetes_X["bmi"].to_frame(), diabetes_y)
# +
line_values=regr.coef_ * diabetes_X["bmi"] + regr.intercept_ #Se crea una serie con los valores de la recta
line_values=line_values.rename("valores")
diabetes_df=pd.concat([diabetes,line_values],axis=1) #Se agrega la serie al dataframe como columna para graficar con altair
points=alt.Chart(diabetes_df).mark_point().encode(
x="bmi",
y=alt.Y("target", axis=alt.Axis(title="target"))
).properties(
title="Regresion Lineal en bmi")
line=alt.Chart(diabetes_df).mark_line(
color="red",
size=2
).encode(
x="bmi",
y="valores"
)
points + line
| labs/lab07.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
def mean_value(arr):
sum=0
length=len(arr)
for i in arr:
sum=sum+i
mean=sum/length
return mean
def variance_value(arr,mean_value,var_list):
for i in arr:
diff=i-mean_value
var_list.append(diff)
def theta_1(var1,var2):
sum_theta1_numerator=0
sum_theta1_denominator=0
for i,j in zip(var1,var2):
sum_theta1_numerator=sum_theta1_numerator+i*j
for i in var1:
sum_theta1_denominator=sum_theta1_denominator+i*i
theta1=sum_theta1_numerator/sum_theta1_denominator
return theta1
def theta_0(x_mean,y_mean,theta1):
theta0=y_mean-x_mean*theta1
return theta0
def Predicted_value(arr):
for i in arr:
y=theta0+theta1*i
predicted.append(y)
def Error_values(y,predicted):
for i,j in zip(y,predicted):
err=i-j
errors.append(err)
def R_square(predicted,y):
numerator_list=[]
denomenator_list=[]
numerator=0
denomenator=0
j=0
k=0
for i in predicted:
j=i-y_mean
j=j*j
numerator_list.append(j)
for i in y:
k=i-y_mean
k=k*k
denomenator_list.append(k)
#print(numerator_list)
#print(denomenator_list)
for p in numerator_list:
numerator=numerator+p
for q in denomenator_list:
denomenator=denomenator+q
r_square=numerator/denomenator
return r_square
x=np.array([2,3,5,7,9])
x_mean=mean_value(x)
y=np.array([4,5,7,10,15])
y_mean=mean_value(y)
print("mean value of x and y {0},{1} respectively".format(x_mean,y_mean))
x_var_list=[]
variance_value(x,x_mean,x_var_list)
print(x_var_list)
y_var_list=[]
variance_value(y,y_mean,y_var_list)
print(y_var_list)
theta1=0
theta1=theta_1(x_var_list,y_var_list)
print(theta1)
theta0=0
theta0=theta_0(x_mean,y_mean,theta1)
print(theta0)
predicted=[]
Predicted_value(x)
print(predicted)
#absolute errors between actual and predicted values
errors=[]
Error_values(y,predicted)
print(errors)
#accuracy measurement using R square value
r_square=R_square(predicted,y)
print(r_square)
if(r_square>0.9):
print("It is a good dataset for predction")
# -
| ML Concepts Coding/Linear_Regression.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <font size="+5">#05 | Cluster Analysis con k-Means</font>
# - Subscribe to my [Blog ↗](https://blog.pythonassembly.com/)
# - Let's keep in touch on [LinkedIn ↗](www.linkedin.com/in/jsulopz) 😄
# # Discipline to Search Solutions in Google
# > Apply the following steps when **looking for solutions in Google**:
# >
# > 1. **Necesity**: How to load an Excel in Python?
# > 2. **Search in Google**: by keywords
# > - `load excel python`
# > - ~~how to load excel in python~~
# > 3. **Solution**: What's the `function()` that loads an Excel in Python?
# > - A Function to Programming is what the Atom to Phisics.
# > - Every time you want to do something in programming
# > - **You will need a `function()`** to make it
# > - Theferore, you must **detect parenthesis `()`**
# > - Out of all the words that you see in a website
# > - Because they indicate the presence of a `function()`.
# # Machine Learning Review
# - **Supervised Learning:**
# - Regression → Predicting a Numerical Variable
# - Classification → Predicting a Categorical Variable
#
#
# - **Unsupervised Learning:**
# - Cluster Analysis → Groups based on Explanatory Variables
# # Load the Data
# > - Simply execute the following lines of code to load the data.
# > - This dataset contains **statistics about Car Accidents** (columns)
# > - In each one of **USA States** (rows)
# https://www.kaggle.com/fivethirtyeight/fivethirtyeight-bad-drivers-dataset/
# +
import seaborn as sns
df = sns.load_dataset(name='car_crashes', index_col='abbrev')
df.sample(5)
# -
# # `KMeans()` Model in Python
# ## Build the Model
# > 1. **Necesity**: Build Model
# > 2. **Google**: How do you search for the solution?
# > 3. **Solution**: Find the `function()` that makes it happen
# ## Code Thinking
#
# > Which function computes the Model?
# > - `fit()`
# >
# > How could can you **import the function in Python**?
fit()
model.fit()
# `model = ?`
model = KMeans()
from sklearn.cluster import KMeans
model = KMeans()
model.fit(X=)
# + [markdown] tags=[]
# ### Separate Variables for the Model
#
# > Regarding their role:
# > 1. **Target Variable `y`**
# >
# > - [ ] What would you like **to predict**?
# >
# > The group to which each row belongs to
# >
# > 2. **Explanatory Variable `X`**
# >
# > - [ ] Which variable will you use **to explain** the target?
# >
# > - [ ] Is something extrange in the `instructions manual` of the function?
# -
# ### Data Visualization to Analyize Patterns
# > - Visualize the 2 variables with a `scatterplot()`
# > - And decide *how many `clusters`* you'd like to calculate
sns.scatterplot(x='alcohol', y='ins_premium', data=df);
# ### Finally `fit()` the Model
model = KMeans(n_clusters=3, verbose=1)
model.__dict__
model.fit(X=df[['alcohol', 'ins_premium']])
model.__dict__
# ## `predict()` the Cluster for One `USA State`
# > **Programming thiking:**
# >
# > - Which `function()` can we use to make a prediction?
# > - How can you answer yourself **without searching in Google**?
df[:1]
model.predict(X=df.loc[['AL'], ['alcohol', 'ins_premium']])
# ## Get the `cluster` for all USA States
# > - `model.` + `↹`
grupos = model.predict(X=df[['alcohol', 'ins_premium']])
# > - Create a `dfsel` DataFrame
# > - That contains the **columns you used for the model**
dfsel = df[['alcohol', 'ins_premium']].copy()
# > - Add a **new column**
# > - That **contains the `cluster` prediction** for every USA State
dfsel["grupo"]= grupos
# ## Model Visualization
# > - You may `hue=` the points with the `cluster` column
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
import matplotlib.pyplot as plt
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
plt.xlim(-20, 1400)
plt.ylim(0, 1400)
# ## Model Interpretation
# > - Do you think the model **makes sense**?
# > - Which **variable is the most important** to determine the cluster?
# +
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/4b5d3muPQmA" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# -
# > - [ ] Is it necessary to **normalize the data** in the [`DecisionTreeClassifier()`](<../06 | Decision Tree. A Supervised Classification Model/06session.ipynb>) as it is in the `KMeans()`?
# # Conclusion
#
# > - You need to `scale` the data
# > - Every time the algorithm computes `distances`
# > - Between `different variables`
# > - Because it's **not the same to increase 1kg of weight than 1m of height**
# +
# Draw Weight Height Axes Min Max Scaler 0 - 1
# -
# # `MinMaxScaler()` the data
# > - `scaler.fit_transform()`
dfsel.agg(['min', 'max'])
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.__dict__
type(scaler)
scaler.fit(X=df)
scaler.__dict__
datanorm = scaler.transform(X=df)
import pandas as pd
dfnorm = pd.DataFrame(datanorm, columns=df.columns, index=df.index)
dfnorm.head()
# # `KMeans()` Model with *Scaled Data*
model = KMeans(n_clusters=3)
model.fit(X=dfnorm[['alcohol', 'ins_premium']])
# ## Get the `cluster` for all USA States
# > - `model.` + `↹`
grupos = model.predict(X=dfnorm[['alcohol', 'ins_premium']])
# > - Create a `dfsel` DataFrame
# > - That contains the **columns you used for the model**
dfsel = df[['alcohol', 'ins_premium']].copy()
# > - Add a **new column**
# > - That **contains the `cluster` prediction** for every USA State
dfsel["grupo"]= grupos
# ## Model Visualization
# > - You may `hue=` the points with the `cluster` column
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
import matplotlib.pyplot as plt
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
plt.xlim(-20, 1400)
plt.ylim(0, 1400)
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue='grupo', palette='Set1');
plt.xlim(-20, 1400)
plt.ylim(0, 1400)
# # Other `Clustering` Models in Python
# > - Visit the `sklearn` website [here ↗](https://scikit-learn.org/stable/)
# > - **Pick 2 new models** and compute the *Clustering*
# ## Other Model 1
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.1)
db.fit(X=dfnorm[['alcohol', 'ins_premium']])
db.fit_predict(dfnorm[['alcohol', 'ins_premium']])
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue=db.fit_predict(dfnorm[['alcohol', 'ins_premium']]), palette='Set1');
# ## Other Model 2
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3)
grupos = ac.fit_predict(X=dfnorm[['alcohol', 'ins_losses']])
sns.scatterplot(x='alcohol', y='ins_premium', data=dfsel, hue=grupos, palette='Set1');
| II Machine Learning & Deep Learning/05_Cluster Analysis con k-Means/05session_cluster-kmeans.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="ReHpB8MPGzDo" outputId="cfeaddfe-fb1c-4637-ce74-7c3dc5bcaf29"
from google.colab import drive
drive.mount('/content/gdrive')
# + [markdown] id="t7zEUteUcwym"
# ## Importing library
# + id="SRmuViCkHGYJ"
import pandas as pd
# + [markdown] id="Pi3u_z9nc1aF"
# ## Loading Datasets from gdrive
# + id="zuK-gwpmHaaE"
# df = pd.read_csv("/content/gdrive/MyDrive/college_project/data_p1.csv")
df = pd.read_csv("data_p1.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="J7-oEE0mHm5Y" outputId="6b2caf02-a72a-4d23-e5fc-daa403701806"
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="Ce_UWthCHo0Y" outputId="329ffd15-9347-488f-e319-06a2ba9474e5"
df.info()
# + [markdown] id="DgXtn6H-c6e9"
# ## Checking NAN value
# + colab={"base_uri": "https://localhost:8080/"} id="7GffCRXgMbnq" outputId="739c56b6-b852-4e7d-b74c-a88b48efeff2"
df.isna().any()
# + [markdown] id="2tczDHBIc-Us"
# ## Drop NAN value
# + id="EQPpW96VNCsN"
df = df.dropna()
# + colab={"base_uri": "https://localhost:8080/"} id="xR-owk8bNFGA" outputId="e410a64d-0fed-4474-a03a-9197d6708de4"
df.isna().any()
# + colab={"base_uri": "https://localhost:8080/"} id="dHDP-DexNH4q" outputId="b51c3655-6102-42df-8af5-63a2f62ea0ae"
df.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="x5MRmD_-Yw1d" outputId="7f11563e-cdce-45a4-aaf6-b64a51a3e600"
df.head()
# + id="duZoL2zcYkBL"
df['director_name'] = df['director_name'].str.lower()
df['actor_1_name'] = df['actor_1_name'].str.lower()
df['actor_2_name'] = df['actor_2_name'].str.lower()
df['actor_3_name'] = df['actor_3_name'].str.lower()
df['genres'] = df['genres'].str.lower()
df['movie_title'] = df['movie_title'].str.lower()
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="gF_3FcpvZCoA" outputId="fd8199aa-0e7c-41cc-c6a2-f01e301f70da"
df.head()
# + id="vrb2orW9PtKf"
index = []
for i in range(0 , df.shape[0]):
index.append(i)
# + id="1kwHGizPP4kZ"
df["index"] = index
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="gBcUcFTDQP2D" outputId="09ff684b-712b-4250-f577-4a21b1c5c1bf"
df.head()
# + id="JVvM10TWJTGr"
df['director_name'] = df['director_name'].str.replace('\d+', '')
df['actor_1_name'] = df['actor_1_name'].str.replace('\d+', '')
df['actor_2_name'] = df['actor_2_name'].str.replace('\d+', '')
df['actor_3_name'] = df['actor_3_name'].str.replace('\d+', '')
df['genres'] = df['genres'].str.replace('\d+', '')
df['movie_title'] = df['movie_title'].str.replace('\d+', '')
# + id="5ATECcEEHvrQ"
def combined_features(row):
return row['director_name']+" "+row['actor_1_name']+" "+row['actor_2_name']+" "+row['actor_3_name']+" "+row["genres"]+" "+row["movie_title"]
df["combined_features"] = df.apply(combined_features, axis =1)
# + colab={"base_uri": "https://localhost:8080/", "height": 270} id="wr_DWYwlImA9" outputId="dc56e68a-ac42-4cc6-b435-499b35138651"
df.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 270} id="KBaWYgiza60T" outputId="cf3157c5-376a-49c2-d34d-5732d86d459b"
df['movie_title'] = df['movie_title'].str.strip()
df.head()
# -
df
new_df=pd.DataFrame()
new_df['index']=df['index']
new_df['movie_title']=df['movie_title']
new_df
new_df.to_csv('find_index.csv')
| index_find_df.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# +
import os
import tensorflow as tf
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt
print("TensorFlow version: {}".format(tf.__version__))
print("TensorFlow Datasets version: ",tfds.__version__)
# -
ds_preview, info = tfds.load('penguins/simple', split='train', with_info=True)
df = tfds.as_dataframe(ds_preview.take(5), info)
print(df)
print(info.features)
class_names = ['Adélie', 'Chinstrap', 'Gentoo']
# +
ds_split, info = tfds.load("penguins/processed", split=['train[:20%]', 'train[20%:]'], as_supervised=True, with_info=True)
ds_test = ds_split[0]
ds_train = ds_split[1]
assert isinstance(ds_test, tf.data.Dataset)
print(info.features)
df_test = tfds.as_dataframe(ds_test.take(5), info)
print("Test dataset sample: ")
print(df_test)
df_train = tfds.as_dataframe(ds_train.take(5), info)
print("Train dataset sample: ")
print(df_train)
ds_train_batch = ds_train.batch(32)
# +
features, labels = next(iter(ds_train_batch))
print(features)
print(labels)
# +
plt.scatter(features[:,0],
features[:,2],
c=labels,
cmap='viridis')
plt.xlabel("Body Mass")
plt.ylabel("Culmen Length")
plt.show()
# -
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)), # input shape required
tf.keras.layers.Dense(10, activation=tf.nn.relu),
tf.keras.layers.Dense(3)
])
predictions = model(features)
predictions[:5]
tf.nn.softmax(predictions[:5])
print("Prediction: {}".format(tf.argmax(predictions, axis=1)))
print(" Labels: {}".format(labels))
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
# +
def loss(model, x, y, training):
# training=training is needed only if there are layers with different
# behavior during training versus inference (e.g. Dropout).
y_ = model(x, training=training)
return loss_object(y_true=y, y_pred=y_)
l = loss(model, features, labels, training=False)
print("Loss test: {}".format(l))
# -
def grad(model, inputs, targets):
with tf.GradientTape() as tape:
loss_value = loss(model, inputs, targets, training=True)
return loss_value, tape.gradient(loss_value, model.trainable_variables)
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
# +
loss_value, grads = grad(model, features, labels)
print("Step: {}, Initial Loss: {}".format(optimizer.iterations.numpy(),
loss_value.numpy()))
optimizer.apply_gradients(zip(grads, model.trainable_variables))
print("Step: {}, Loss: {}".format(optimizer.iterations.numpy(),
loss(model, features, labels, training=True).numpy()))
# +
# Training loop
# With all the pieces in place, the model is ready for training! A training loop feeds the dataset examples into the model to help it make better predictions. The following code block sets up these training steps:
# Iterate each epoch. An epoch is one pass through the dataset.
# Within an epoch, iterate over each example in the training Dataset grabbing its features (x) and label (y).
# Using the example's features, make a prediction and compare it with the label. Measure the inaccuracy of the prediction and use that to calculate the model's loss and gradients.
# Use an optimizer to update the model's parameters.
# Keep track of some stats for visualization.
# Repeat for each epoch.
## Note: Rerunning this cell uses the same model parameters
# Keep results for plotting
train_loss_results = []
train_accuracy_results = []
num_epochs = 201
for epoch in range(num_epochs):
epoch_loss_avg = tf.keras.metrics.Mean()
epoch_accuracy = tf.keras.metrics.SparseCategoricalAccuracy()
# Training loop - using batches of 32
for x, y in ds_train_batch:
# Optimize the model
loss_value, grads = grad(model, x, y)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# Track progress
epoch_loss_avg.update_state(loss_value) # Add current batch loss
# Compare predicted label to actual label
# training=True is needed only if there are layers with different
# behavior during training versus inference (e.g. Dropout).
epoch_accuracy.update_state(y, model(x, training=True))
# End epoch
train_loss_results.append(epoch_loss_avg.result())
train_accuracy_results.append(epoch_accuracy.result())
if epoch % 50 == 0:
print("Epoch {:03d}: Loss: {:.3f}, Accuracy: {:.3%}".format(epoch,
epoch_loss_avg.result(),
epoch_accuracy.result()))
# +
fig, axes = plt.subplots(2, sharex=True, figsize=(12, 8))
fig.suptitle('Training Metrics')
axes[0].set_ylabel("Loss", fontsize=14)
axes[0].plot(train_loss_results)
axes[1].set_ylabel("Accuracy", fontsize=14)
axes[1].set_xlabel("Epoch", fontsize=14)
axes[1].plot(train_accuracy_results)
plt.show()
# +
test_accuracy = tf.keras.metrics.Accuracy()
ds_test_batch = ds_test.batch(10)
for (x, y) in ds_test_batch:
# training=False is needed only if there are layers with different
# behavior during training versus inference (e.g. Dropout).
logits = model(x, training=False)
prediction = tf.argmax(logits, axis=1, output_type=tf.int64)
test_accuracy(prediction, y)
print("Test set accuracy: {:.3%}".format(test_accuracy.result()))
# -
tf.stack([y,prediction],axis=1)
# +
predict_dataset = tf.convert_to_tensor([
[0.3, 0.8, 0.4, 0.5,],
[0.4, 0.1, 0.8, 0.5,],
[0.7, 0.9, 0.8, 0.4]
])
# training=False is needed only if there are layers with different
# behavior during training versus inference (e.g. Dropout).
predictions = model(predict_dataset, training=False)
for i, logits in enumerate(predictions):
class_idx = tf.argmax(logits).numpy()
p = tf.nn.softmax(logits)[class_idx]
name = class_names[class_idx]
print("Example {} prediction: {} ({:4.1f}%)".format(i, name, 100*p))
| src/ml_basic/custom_training_loop.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from keras.datasets import cifar100
from keras.utils import np_utils
import numpy as np
(X_train, y_train), (X_test, y_test) = cifar100.load_data()
X_train = X_train.astype(np.float32) / 255
X_test = X_test.astype(np.float32) / 255
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
# +
from keras.models import Sequential
from keras.layers import Dense, Flatten, Dropout
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.optimizers import Adam
from keras.wrappers.scikit_learn import KerasClassifier
batch_size = 32
training_size = X_train.shape[0]
def create_model(learning_rate=1e-3, dropout_rate=0.2, units=8):
model = Sequential()
model.add(Conv2D(filters=units, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(MaxPooling2D(pool_size=(3, 3)))
model.add(Conv2D(filters=2 * units, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(3, 3)))
model.add(Flatten())
model.add(Dense(units=4 * units, activation='relu'))
model.add(Dropout(dropout_rate))
model.add(Dense(units=8 * units, activation='relu'))
model.add(Dropout(dropout_rate))
model.add(Dense(units=100, activation='softmax'))
model.compile(optimizer=Adam(lr=learning_rate), loss='categorical_crossentropy', metrics=['accuracy'])
return model
model = KerasClassifier(
build_fn=create_model,
epochs=5,
steps_per_epoch=training_size//batch_size,
verbose=0)
# +
from sklearn.model_selection import GridSearchCV
param_grid = {
'learning_rate': [1e-4, 1e-3, 1e-2, 1e-1],
'dropout_rate': [0.2, 0.3, 0.4, 0.5],
'units': [4, 8, 16, 32]
}
grid = GridSearchCV(estimator=model, param_grid=param_grid, n_jobs=-1)
grid.fit(X_train, y_train)
# -
print(f'Best: {grid.best_score_} using {grid.best_params_}')
means = grid.cv_results_['mean_test_score']
params = grid.cv_results_['params']
for mean, param in zip(means, params):
print(f'{mean:.3f} with: {param}')
| main.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#In-this-notebook," data-toc-modified-id="In-this-notebook,-1"><span class="toc-item-num">1 </span>In this notebook,</a></span></li><li><span><a href="#Expected-utility-via-Monte-Carlo" data-toc-modified-id="Expected-utility-via-Monte-Carlo-2"><span class="toc-item-num">2 </span>Expected utility via Monte Carlo</a></span><ul class="toc-item"><li><span><a href="#Plotting-the-exact-solution" data-toc-modified-id="Plotting-the-exact-solution-2.1"><span class="toc-item-num">2.1 </span>Plotting the exact solution</a></span></li><li><span><a href="#MC-implementation" data-toc-modified-id="MC-implementation-2.2"><span class="toc-item-num">2.2 </span>MC implementation</a></span></li></ul></li><li><span><a href="#Exercise" data-toc-modified-id="Exercise-3"><span class="toc-item-num">3 </span>Exercise</a></span></li></ul></div>
# + [markdown] slideshow={"slide_type": "slide"}
# # 4. Expected utility and Monte Carlo in Python
# **<NAME> - 2020**
#
# ---
# -
# ## In this notebook,
# - we look at the Monte Carlo method and how to use it to approximate expected utilities or certainty equivalents.
# - we use Python to plot information using matplotlib, including a histogram and a regression
# ---
# Let us import some packages: math, numpy, matplotlib and scipy
# +
import math
import numpy as np
import scipy as sp
from numpy.random import default_rng # pseudo-random number generator
import matplotlib.pyplot as plt
# This is an indicator to tell jupyter notebook to show us all plots inline:
# %matplotlib inline
# + [markdown] slideshow={"slide_type": "slide"}
# ## Expected utility via Monte Carlo
#
# To compute the expected utility of a wealth gamble $W$ we can use he law of large numbers. Indeed, if $E[|u(W)|]<\infty$, we have
# $$ \frac{1}{N} \sum_{i=1}^N u(W_i) \rightarrow \mathbb E[u(W)] \text{ as } N\rightarrow \infty,$$
# where $(W_i)$ is a family of independent draws of random variables with $W_i \sim W$ for each $i$.
#
# The Monte Carlo method relies on this equality to produce an approximation to the expectation (by choosing a large N and calculating the empirical average).
#
# + [markdown] slideshow={"slide_type": "slide"}
# To see how this works, let us start with $W$ being normally distributed, that is $W = \sigma N + \mu$, where $\mu, \sigma \in \mathbb R$ and $N$ is standard normally distributed.
#
# Now, let us suppose first we want to compute expected utility of a CARA utility $u(x) = 1-\exp(-\alpha * x)$. We can calculate explicitly
# $$ \mathbb E[u(W)] = \mathbb E[1- \exp(-\alpha \sigma N - \alpha \mu ))] =1- \exp\left(-\alpha \mu + \frac 1 2 \alpha^2 \sigma^2 \right).$$
#
# We use this value to compare to the value approximated by Monte Carlo as explained before. Let us build a plot of this function in some given domain.
# -
# ### Plotting the exact solution
# + [markdown] slideshow={"slide_type": "slide"}
# There are several libraries allowing us to plot in Python. We will use one of the simplest: Matplotlib.
#
# A simple way to plot in this library is to provide it with vectors of input and output. To try it, let us simply plot the result of the (exact) expected utility when the CARA coefficient changes.
#
# We start by sampling the space of coefficients of risk aversion:
# -
x = np.linspace(0.001,3,100) # creates a vector of size 100 with numbers between 0.1 and 30
print(x)
# We now implement the exact solution expected CARA utility under normal assumptions. Since it is a simple expression, we can use a lambda function as introduced before.
# The operations in expected_u are well defined for vectors as long as mu,sd,x broadcast correctly together.
expected_u = lambda mu,sigma,alpha: 1-np.exp(-alpha*mu+0.5*alpha**2*sigma**2)
# Note that we use 'np.exp' and not 'math.exp': this is because we want the function to be 'vectorial', that is, to accept vectors as an input
#
# (try changing np.exp for math.exp, run the code and then run the code below... there will be an error).
sd, mu = 2,5 # Equivalently sd=2 and mu=5
y=expected_u(mu,sd,x) # Note that x is a vector
print(y) # And so is y
# If for some reason you cannot implement directly a vectorial function, it is possible to use a loop or the function np.vectorize to render the function vector ready.
# We are ready to make the plot:
plt.plot(x,y) # Make a plot between x and y
plt.title('Expected utility as a function of coefficient of absolute risk aversion - Gaussian case') # Add a title
plt.xlabel('Coefficient of risk aversion') # Add a label on the x axis
plt.ylabel('Expected utility') # Add a label on the y axis
# ### MC implementation
# Let us now look at the Monte Carlo approximation of the above function. We start by defining a function that calculates the CARA utility:
# + slideshow={"slide_type": "fragment"}
cara_utility = lambda x,alpha: 1-np.exp(-alpha*x)
# -
# Some tests on our function
assert cara_utility(1,1)== 1-1./math.e , "Failed test with x=1, alpha =1"
assert cara_utility(5,2)== 1-math.e**-10., "Failed test with x=5, alpha=2"
# We can now generate a sample of wealths, distributed like a $\mathcal N (\mu,\sigma^2)$.
sd, mu = 2,5 # Equivalently sd=2 and mu=5
N = 10000
rng = default_rng()
sample_gaussian = rng.normal(mu,sd,N)
print(sample_gaussian)
# How can we check that these are Gaussian? We can plot the histogram of the empirical distribution defined. The package matplotlib has a convenient function for this: *plt.hist* (recall that plt is our alias for pyplot)
plt.hist(sample_gaussian, density=True) # Plots the histogram, normalising to obtain a pdf.
plt.title('Histogram of our sample') # Add a title to the plot
plt.xlabel('sample_gaussian') # Add a label on the X axis
plt.ylabel('density') # Add a label on the Y axis
# It looks like a good Gaussian sample with our parameters (centred in 5 and with standard deviation 2). In later notebooks we will learn some alternative ways for checking Gaussianity.
# We can now calculate a Monte Carlo approximation of our expected utility. Examine the code below:
cara_utility(sample_gaussian,1).mean()
# In one line, we evaluate the cara utility for each entry of the sample, and then calculate the mean of the resulting vector
# Observe now the following: the estimation is random. To see this, let us run the estimation with another sample
cara_utility(rng.normal(mu,sd,N),1).mean()
# As expected, the two values are close but different. Indeed, this estimator is **random**, because it depends on the sample, which is itself random. This is something to be taken into account when using Monte Carlo estimators.
#
# In fairness, the Python implementation of the MC estimator can only produce a pseudo-random generation. To see this, we can fix the seed of the pseudo-random generation algorithm and compare the answers
rng = default_rng(1234)
sample_gaussian = rng.normal(mu,sd,N)
mc_eu1 = cara_utility(sample_gaussian,1).mean()
rng = default_rng(1234)
sample_gaussian2 = rng.normal(mu,sd,N)
mc_eu2 = cara_utility(sample_gaussian2,1).mean()
print(mc_eu1-mc_eu2)
# Setting the random states allows us to repeat the same sequence on the pseudo-random generation.
# Now, let us remind ourselves of the closed form solution:
expected_u(mu,sd,1)
# We see that the value is very close to the value(s) estimated via MC. Indeed, this error can be explained via the central limit theorem, which give us a control on the L_2 norm and is of the form
#
# $$\left \|\mathbb E[u(W)] - \frac 1 N \sum_{i=1}^N u(W_i) \right \|_{L_2} \leq \frac{C}{N^{1/2}} {\rm sd}(X_1) $$
#
# Let us verify this empirically, using a plot and a regression. We want to retrieve the rate of convergence, which is the power 1/2 in the above control. To do this we use a log-log plot (think why).
# +
n_vec = 2**np.arange(10,20) # The number of MC simulations, we take powers of 2
rng = default_rng(1) # Fix the seed to "1", so that the plot looks the same every time you run it
u = np.array([cara_utility(rng.normal(mu,sd,N),1).mean() for N in n_vec]) # Create an MC expected utility for the sizes above
error = np.abs(u - expected_u(mu, sd, 1)) # Calculate the error
plt.loglog(n_vec, error, 'ro', label='Error') # Make a log log plot
plt.title('Error in Monte Carlo Expected utility as a function of size of sample - Gaussian case')
plt.xlabel('N')
plt.ylabel('Error')
# Let us also add a reference line. To do so, we need to calculate a simple regression. We can use the polyfit function
m, b = np.polyfit( np.log(n_vec), np.log(error), 1)
plt.loglog(n_vec, np.exp(b+m*np.log(n_vec)), 'g--', label='Best fit: Error ='+ "%.2f N^(%.2f)" % (math.exp(b),m))
plt.legend()
# -
# The hardest line of code in the plot above is possibly
# ```python
# plt.loglog(n_vec, np.exp(b+m*np.log(n_vec)), 'g--', label='Best fit: Error ='+ "%.2f N^(%.2f)" % (math.exp(b),m))
# ```
#
# Let us look at two parts in particular:
#
# ```python
# 'g--'
# ```
# Means make a green dashed line.
#
# while
# ```python
# label='Best fit: Error ='+ "%.2f N^(%.2f)" % (math.exp(b),m))
# ```
# means: take the value of exp(b), round it to a float with two decimal figures, do the same with m, and write a string that contains exp(b) N^ m with this format. This is saved on a variable label that is used by matplotlib to assign the legends in a plot.
#
# Check that you understand the other lines of code.
# Note that the best fit slope is close to -1/2 as expected. This is consistent with the theoretical error given before. **Write the equations to be sure you understand why.**
# + [markdown] slideshow={"slide_type": "slide"}
# ## Exercise
#
# 1. Compute, via a Monte-Carlo simulation, the expected utility of a CRRA investor for the following gambles.
# - $W_1 \sim |aN + b|$, where $N$ is standard normally distributed and $a,b \in R$.
# - $W_2 \sim \text{Exp}(\lambda_2)$ where $\lambda_2>0$.
#
# You might have to look up online the commands for the corresponding random number generators. (Use the ones in numpy.random).
# +
#Gambler1
a0 = 2
b0 = 5
crra_utility = lambda x, alpha, beta: alpha * np.log(x) + beta
sd, mu = a0, b0
N = 100000
W1 = np.abs(np.random.randn(N) * sd + mu)
rng = default_rng(1234)
# -
# 2. Write a function that computes the certainty equivalent for a CRRA investor. (Hint: You might have to compute, on a piece of paper, $u^{-1}$ for the different relative risk aversions $\rho$.)
# 3. With $a = 1$ and $b = 2$, plot the certainty equivalent of a CRRA investor as a function of relative risk aversion $\rho$, using gamble $W_1$.
| 4. Expected utility.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Artificial Intelligence Nanodegree
#
# ## Voice User Interfaces
#
# ## Project: Speech Recognition with Neural Networks
#
# ---
#
# In this notebook, some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this project. You will not need to modify the included code beyond what is requested. Sections that begin with **'(IMPLEMENTATION)'** in the header indicate that the following blocks of code will require additional functionality which you must provide. Please be sure to read the instructions carefully!
#
# > **Note**: Once you have completed all of the code implementations, you need to finalize your work by exporting the Jupyter Notebook as an HTML document. Before exporting the notebook to html, all of the code cells need to have been run so that reviewers can see the final implementation and output. You can then export the notebook by using the menu above and navigating to \n",
# "**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
#
# In addition to implementing code, there will be questions that you must answer which relate to the project and your implementation. Each section where you will answer a question is preceded by a **'Question X'** header. Carefully read each question and provide thorough answers in the following text boxes that begin with **'Answer:'**. Your project submission will be evaluated based on your answers to each of the questions and the implementation you provide.
#
# >**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. Markdown cells can be edited by double-clicking the cell to enter edit mode.
#
# The rubric contains _optional_ "Stand Out Suggestions" for enhancing the project beyond the minimum requirements. If you decide to pursue the "Stand Out Suggestions", you should include the code in this Jupyter notebook.
#
# ---
#
# ## Introduction
#
# In this notebook, you will build a deep neural network that functions as part of an end-to-end automatic speech recognition (ASR) pipeline! Your completed pipeline will accept raw audio as input and return a predicted transcription of the spoken language. The full pipeline is summarized in the figure below.
#
# <img src="images/pipeline.png">
#
# - **STEP 1** is a pre-processing step that converts raw audio to one of two feature representations that are commonly used for ASR.
# - **STEP 2** is an acoustic model which accepts audio features as input and returns a probability distribution over all potential transcriptions. After learning about the basic types of neural networks that are often used for acoustic modeling, you will engage in your own investigations, to design your own acoustic model!
# - **STEP 3** in the pipeline takes the output from the acoustic model and returns a predicted transcription.
#
# Feel free to use the links below to navigate the notebook:
# - [The Data](#thedata)
# - [**STEP 1**](#step1): Acoustic Features for Speech Recognition
# - [**STEP 2**](#step2): Deep Neural Networks for Acoustic Modeling
# - [Model 0](#model0): RNN
# - [Model 1](#model1): RNN + TimeDistributed Dense
# - [Model 2](#model2): CNN + RNN + TimeDistributed Dense
# - [Model 3](#model3): Deeper RNN + TimeDistributed Dense
# - [Model 4](#model4): Bidirectional RNN + TimeDistributed Dense
# - [Models 5+](#model5)
# - [Compare the Models](#compare)
# - [Final Model](#final)
# - [**STEP 3**](#step3): Obtain Predictions
#
# <a id='thedata'></a>
# ## The Data
#
# We begin by investigating the dataset that will be used to train and evaluate your pipeline. [LibriSpeech](http://www.danielpovey.com/files/2015_icassp_librispeech.pdf) is a large corpus of English-read speech, designed for training and evaluating models for ASR. The dataset contains 1000 hours of speech derived from audiobooks. We will work with a small subset in this project, since larger-scale data would take a long while to train. However, after completing this project, if you are interested in exploring further, you are encouraged to work with more of the data that is provided [online](http://www.openslr.org/12/).
#
# In the code cells below, you will use the `vis_train_features` module to visualize a training example. The supplied argument `index=0` tells the module to extract the first example in the training set. (You are welcome to change `index=0` to point to a different training example, if you like, but please **DO NOT** amend any other code in the cell.) The returned variables are:
# - `vis_text` - transcribed text (label) for the training example.
# - `vis_raw_audio` - raw audio waveform for the training example.
# - `vis_mfcc_feature` - mel-frequency cepstral coefficients (MFCCs) for the training example.
# - `vis_spectrogram_feature` - spectrogram for the training example.
# - `vis_audio_path` - the file path to the training example.
# +
from data_generator import vis_train_features
# extract label and audio features for a single training example
vis_text, vis_raw_audio, vis_mfcc_feature, vis_spectrogram_feature, vis_audio_path = vis_train_features()
# -
# The following code cell visualizes the audio waveform for your chosen example, along with the corresponding transcript. You also have the option to play the audio in the notebook!
from workspace_utils import active_session
# +
from IPython.display import Markdown, display
from data_generator import vis_train_features, plot_raw_audio
from IPython.display import Audio
# %matplotlib inline
# plot audio signal
plot_raw_audio(vis_raw_audio)
# print length of audio signal
display(Markdown('**Shape of Audio Signal** : ' + str(vis_raw_audio.shape)))
# print transcript corresponding to audio clip
display(Markdown('**Transcript** : ' + str(vis_text)))
# play the audio file
Audio(vis_audio_path)
# -
# <a id='step1'></a>
# ## STEP 1: Acoustic Features for Speech Recognition
#
# For this project, you won't use the raw audio waveform as input to your model. Instead, we provide code that first performs a pre-processing step to convert the raw audio to a feature representation that has historically proven successful for ASR models. Your acoustic model will accept the feature representation as input.
#
# In this project, you will explore two possible feature representations. _After completing the project_, if you'd like to read more about deep learning architectures that can accept raw audio input, you are encouraged to explore this [research paper](https://pdfs.semanticscholar.org/a566/cd4a8623d661a4931814d9dffc72ecbf63c4.pdf).
#
# ### Spectrograms
#
# The first option for an audio feature representation is the [spectrogram](https://www.youtube.com/watch?v=_FatxGN3vAM). In order to complete this project, you will **not** need to dig deeply into the details of how a spectrogram is calculated; but, if you are curious, the code for calculating the spectrogram was borrowed from [this repository](https://github.com/baidu-research/ba-dls-deepspeech). The implementation appears in the `utils.py` file in your repository.
#
# The code that we give you returns the spectrogram as a 2D tensor, where the first (_vertical_) dimension indexes time, and the second (_horizontal_) dimension indexes frequency. To speed the convergence of your algorithm, we have also normalized the spectrogram. (You can see this quickly in the visualization below by noting that the mean value hovers around zero, and most entries in the tensor assume values close to zero.)
# +
from data_generator import plot_spectrogram_feature
# plot normalized spectrogram
plot_spectrogram_feature(vis_spectrogram_feature)
# print shape of spectrogram
display(Markdown('**Shape of Spectrogram** : ' + str(vis_spectrogram_feature.shape)))
# -
# ### Mel-Frequency Cepstral Coefficients (MFCCs)
#
# The second option for an audio feature representation is [MFCCs](https://en.wikipedia.org/wiki/Mel-frequency_cepstrum). You do **not** need to dig deeply into the details of how MFCCs are calculated, but if you would like more information, you are welcome to peruse the [documentation](https://github.com/jameslyons/python_speech_features) of the `python_speech_features` Python package. Just as with the spectrogram features, the MFCCs are normalized in the supplied code.
#
# The main idea behind MFCC features is the same as spectrogram features: at each time window, the MFCC feature yields a feature vector that characterizes the sound within the window. Note that the MFCC feature is much lower-dimensional than the spectrogram feature, which could help an acoustic model to avoid overfitting to the training dataset.
# +
from data_generator import plot_mfcc_feature
# plot normalized MFCC
plot_mfcc_feature(vis_mfcc_feature)
# print shape of MFCC
display(Markdown('**Shape of MFCC** : ' + str(vis_mfcc_feature.shape)))
# -
# When you construct your pipeline, you will be able to choose to use either spectrogram or MFCC features. If you would like to see different implementations that make use of MFCCs and/or spectrograms, please check out the links below:
# - This [repository](https://github.com/baidu-research/ba-dls-deepspeech) uses spectrograms.
# - This [repository](https://github.com/mozilla/DeepSpeech) uses MFCCs.
# - This [repository](https://github.com/buriburisuri/speech-to-text-wavenet) also uses MFCCs.
# - This [repository](https://github.com/pannous/tensorflow-speech-recognition/blob/master/speech_data.py) experiments with raw audio, spectrograms, and MFCCs as features.
# <a id='step2'></a>
# ## STEP 2: Deep Neural Networks for Acoustic Modeling
#
# In this section, you will experiment with various neural network architectures for acoustic modeling.
#
# You will begin by training five relatively simple architectures. **Model 0** is provided for you. You will write code to implement **Models 1**, **2**, **3**, and **4**. If you would like to experiment further, you are welcome to create and train more models under the **Models 5+** heading.
#
# All models will be specified in the `sample_models.py` file. After importing the `sample_models` module, you will train your architectures in the notebook.
#
# After experimenting with the five simple architectures, you will have the opportunity to compare their performance. Based on your findings, you will construct a deeper architecture that is designed to outperform all of the shallow models.
#
# For your convenience, we have designed the notebook so that each model can be specified and trained on separate occasions. That is, say you decide to take a break from the notebook after training **Model 1**. Then, you need not re-execute all prior code cells in the notebook before training **Model 2**. You need only re-execute the code cell below, that is marked with **`RUN THIS CODE CELL IF YOU ARE RESUMING THE NOTEBOOK AFTER A BREAK`**, before transitioning to the code cells corresponding to **Model 2**.
# +
#####################################################################
# RUN THIS CODE CELL IF YOU ARE RESUMING THE NOTEBOOK AFTER A BREAK #
#####################################################################
# allocate 50% of GPU memory (if you like, feel free to change this)
from keras.backend.tensorflow_backend import set_session
import tensorflow as tf
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 0.5
set_session(tf.Session(config=config))
# watch for any changes in the sample_models module, and reload it automatically
# %load_ext autoreload
# %autoreload 2
# import NN architectures for speech recognition
from sample_models import *
# import function for training acoustic model
from train_utils import train_model
# -
# <a id='model0'></a>
# ### Model 0: RNN
#
# Given their effectiveness in modeling sequential data, the first acoustic model you will use is an RNN. As shown in the figure below, the RNN we supply to you will take the time sequence of audio features as input.
#
# <img src="images/simple_rnn.png" width="50%">
#
# At each time step, the speaker pronounces one of 28 possible characters, including each of the 26 letters in the English alphabet, along with a space character (" "), and an apostrophe (').
#
# The output of the RNN at each time step is a vector of probabilities with 29 entries, where the $i$-th entry encodes the probability that the $i$-th character is spoken in the time sequence. (The extra 29th character is an empty "character" used to pad training examples within batches containing uneven lengths.) If you would like to peek under the hood at how characters are mapped to indices in the probability vector, look at the `char_map.py` file in the repository. The figure below shows an equivalent, rolled depiction of the RNN that shows the output layer in greater detail.
#
# <img src="images/simple_rnn_unrolled.png" width="60%">
#
# The model has already been specified for you in Keras. To import it, you need only run the code cell below.
model_0 = simple_rnn_model(input_dim=161) # change to 13 if you would like to use MFCC features
# As explored in the lesson, you will train the acoustic model with the [CTC loss](http://www.cs.toronto.edu/~graves/icml_2006.pdf) criterion. Custom loss functions take a bit of hacking in Keras, and so we have implemented the CTC loss function for you, so that you can focus on trying out as many deep learning architectures as possible :). If you'd like to peek at the implementation details, look at the `add_ctc_loss` function within the `train_utils.py` file in the repository.
#
# To train your architecture, you will use the `train_model` function within the `train_utils` module; it has already been imported in one of the above code cells. The `train_model` function takes three **required** arguments:
# - `input_to_softmax` - a Keras model instance.
# - `pickle_path` - the name of the pickle file where the loss history will be saved.
# - `save_model_path` - the name of the HDF5 file where the model will be saved.
#
# If we have already supplied values for `input_to_softmax`, `pickle_path`, and `save_model_path`, please **DO NOT** modify these values.
#
# There are several **optional** arguments that allow you to have more control over the training process. You are welcome to, but not required to, supply your own values for these arguments.
# - `minibatch_size` - the size of the minibatches that are generated while training the model (default: `20`).
# - `spectrogram` - Boolean value dictating whether spectrogram (`True`) or MFCC (`False`) features are used for training (default: `True`).
# - `mfcc_dim` - the size of the feature dimension to use when generating MFCC features (default: `13`).
# - `optimizer` - the Keras optimizer used to train the model (default: `SGD(lr=0.02, decay=1e-6, momentum=0.9, nesterov=True, clipnorm=5)`).
# - `epochs` - the number of epochs to use to train the model (default: `20`). If you choose to modify this parameter, make sure that it is *at least* 20.
# - `verbose` - controls the verbosity of the training output in the `model.fit_generator` method (default: `1`).
# - `sort_by_duration` - Boolean value dictating whether the training and validation sets are sorted by (increasing) duration before the start of the first epoch (default: `False`).
#
# The `train_model` function defaults to using spectrogram features; if you choose to use these features, note that the acoustic model in `simple_rnn_model` should have `input_dim=161`. Otherwise, if you choose to use MFCC features, the acoustic model should have `input_dim=13`.
#
# We have chosen to use `GRU` units in the supplied RNN. If you would like to experiment with `LSTM` or `SimpleRNN` cells, feel free to do so here. If you change the `GRU` units to `SimpleRNN` cells in `simple_rnn_model`, you may notice that the loss quickly becomes undefined (`nan`) - you are strongly encouraged to check this for yourself! This is due to the [exploding gradients problem](http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/). We have already implemented [gradient clipping](https://arxiv.org/pdf/1211.5063.pdf) in your optimizer to help you avoid this issue.
#
# __IMPORTANT NOTE:__ If you notice that your gradient has exploded in any of the models below, feel free to explore more with gradient clipping (the `clipnorm` argument in your optimizer) or swap out any `SimpleRNN` cells for `LSTM` or `GRU` cells. You can also try restarting the kernel to restart the training process.
with active_session():
train_model(input_to_softmax=model_0,
pickle_path='model_0.pickle',
save_model_path='model_0.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# <a id='model1'></a>
# ### (IMPLEMENTATION) Model 1: RNN + TimeDistributed Dense
#
# Read about the [TimeDistributed](https://keras.io/layers/wrappers/) wrapper and the [BatchNormalization](https://keras.io/layers/normalization/) layer in the Keras documentation. For your next architecture, you will add [batch normalization](https://arxiv.org/pdf/1510.01378.pdf) to the recurrent layer to reduce training times. The `TimeDistributed` layer will be used to find more complex patterns in the dataset. The unrolled snapshot of the architecture is depicted below.
#
# <img src="images/rnn_model.png" width="60%">
#
# The next figure shows an equivalent, rolled depiction of the RNN that shows the (`TimeDistrbuted`) dense and output layers in greater detail.
#
# <img src="images/rnn_model_unrolled.png" width="60%">
#
# Use your research to complete the `rnn_model` function within the `sample_models.py` file. The function should specify an architecture that satisfies the following requirements:
# - The first layer of the neural network should be an RNN (`SimpleRNN`, `LSTM`, or `GRU`) that takes the time sequence of audio features as input. We have added `GRU` units for you, but feel free to change `GRU` to `SimpleRNN` or `LSTM`, if you like!
# - Whereas the architecture in `simple_rnn_model` treated the RNN output as the final layer of the model, you will use the output of your RNN as a hidden layer. Use `TimeDistributed` to apply a `Dense` layer to each of the time steps in the RNN output. Ensure that each `Dense` layer has `output_dim` units.
#
# Use the code cell below to load your model into the `model_1` variable. Use a value for `input_dim` that matches your chosen audio features, and feel free to change the values for `units` and `activation` to tweak the behavior of your recurrent layer.
model_1 = rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
units=200,
activation='relu')
# Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_1.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_1.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
with active_session():
train_model(input_to_softmax=model_1,
pickle_path='model_1.pickle',
save_model_path='model_1.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# <a id='model2'></a>
# ### (IMPLEMENTATION) Model 2: CNN + RNN + TimeDistributed Dense
#
# The architecture in `cnn_rnn_model` adds an additional level of complexity, by introducing a [1D convolution layer](https://keras.io/layers/convolutional/#conv1d).
#
# <img src="images/cnn_rnn_model.png" width="100%">
#
# This layer incorporates many arguments that can be (optionally) tuned when calling the `cnn_rnn_model` module. We provide sample starting parameters, which you might find useful if you choose to use spectrogram audio features.
#
# If you instead want to use MFCC features, these arguments will have to be tuned. Note that the current architecture only supports values of `'same'` or `'valid'` for the `conv_border_mode` argument.
#
# When tuning the parameters, be careful not to choose settings that make the convolutional layer overly small. If the temporal length of the CNN layer is shorter than the length of the transcribed text label, your code will throw an error.
#
# Before running the code cell below, you must modify the `cnn_rnn_model` function in `sample_models.py`. Please add batch normalization to the recurrent layer, and provide the same `TimeDistributed` layer as before.
model_2 = cnn_rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
filters=200,
kernel_size=11,
conv_stride=2,
conv_border_mode='valid',
units=200)
# Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_2.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_2.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
with active_session():
train_model(input_to_softmax=model_2,
pickle_path='model_2.pickle',
save_model_path='model_2.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# <a id='model3'></a>
# ### (IMPLEMENTATION) Model 3: Deeper RNN + TimeDistributed Dense
#
# Review the code in `rnn_model`, which makes use of a single recurrent layer. Now, specify an architecture in `deep_rnn_model` that utilizes a variable number `recur_layers` of recurrent layers. The figure below shows the architecture that should be returned if `recur_layers=2`. In the figure, the output sequence of the first recurrent layer is used as input for the next recurrent layer.
#
# <img src="images/deep_rnn_model.png" width="80%">
#
# Feel free to change the supplied values of `units` to whatever you think performs best. You can change the value of `recur_layers`, as long as your final value is greater than 1. (As a quick check that you have implemented the additional functionality in `deep_rnn_model` correctly, make sure that the architecture that you specify here is identical to `rnn_model` if `recur_layers=1`.)
model_3 = deep_rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
units=200,
recur_layers=2)
# Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_3.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_3.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
with active_session():
train_model(input_to_softmax=model_3,
pickle_path='model_3.pickle',
save_model_path='model_3.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# <a id='model4'></a>
# ### (IMPLEMENTATION) Model 4: Bidirectional RNN + TimeDistributed Dense
#
# Read about the [Bidirectional](https://keras.io/layers/wrappers/) wrapper in the Keras documentation. For your next architecture, you will specify an architecture that uses a single bidirectional RNN layer, before a (`TimeDistributed`) dense layer. The added value of a bidirectional RNN is described well in [this paper](http://www.cs.toronto.edu/~hinton/absps/DRNN_speech.pdf).
# > One shortcoming of conventional RNNs is that they are only able to make use of previous context. In speech recognition, where whole utterances are transcribed at once, there is no reason not to exploit future context as well. Bidirectional RNNs (BRNNs) do this by processing the data in both directions with two separate hidden layers which are then fed forwards to the same output layer.
#
# <img src="images/bidirectional_rnn_model.png" width="80%">
#
# Before running the code cell below, you must complete the `bidirectional_rnn_model` function in `sample_models.py`. Feel free to use `SimpleRNN`, `LSTM`, or `GRU` units. When specifying the `Bidirectional` wrapper, use `merge_mode='concat'`.
model_4 = bidirectional_rnn_model(input_dim=161, # change to 13 if you would like to use MFCC features
units=200)
# Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_4.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_4.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
with active_session():
train_model(input_to_softmax=model_4,
pickle_path='model_4.pickle',
save_model_path='model_4.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# <a id='model5'></a>
# ### (OPTIONAL IMPLEMENTATION) Models 5+
#
# If you would like to try out more architectures than the ones above, please use the code cell below. Please continue to follow the same convention for saving the models; for the $i$-th sample model, please save the loss at **`model_i.pickle`** and saving the trained model at **`model_i.h5`**.
# +
## (Optional) TODO: Try out some more models!
### Feel free to use as many code cells as needed.
# -
# <a id='compare'></a>
# ### Compare the Models
#
# Execute the code cell below to evaluate the performance of the drafted deep learning models. The training and validation loss are plotted for each model.
# +
from glob import glob
import numpy as np
import _pickle as pickle
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
sns.set_style(style='white')
# obtain the paths for the saved model history
all_pickles = sorted(glob("results/*.pickle"))
# extract the name of each model
model_names = [item[8:-7] for item in all_pickles]
# extract the loss history for each model
valid_loss = [pickle.load( open( i, "rb" ) )['val_loss'] for i in all_pickles]
train_loss = [pickle.load( open( i, "rb" ) )['loss'] for i in all_pickles]
# save the number of epochs used to train each model
num_epochs = [len(valid_loss[i]) for i in range(len(valid_loss))]
fig = plt.figure(figsize=(16,5))
# plot the training loss vs. epoch for each model
ax1 = fig.add_subplot(121)
for i in range(len(all_pickles)):
ax1.plot(np.linspace(1, num_epochs[i], num_epochs[i]),
train_loss[i], label=model_names[i])
# clean up the plot
ax1.legend()
ax1.set_xlim([1, max(num_epochs)])
plt.xlabel('Epoch')
plt.ylabel('Training Loss')
# plot the validation loss vs. epoch for each model
ax2 = fig.add_subplot(122)
for i in range(len(all_pickles)):
ax2.plot(np.linspace(1, num_epochs[i], num_epochs[i]),
valid_loss[i], label=model_names[i])
# clean up the plot
ax2.legend()
ax2.set_xlim([1, max(num_epochs)])
plt.xlabel('Epoch')
plt.ylabel('Validation Loss')
plt.show()
# -
# __Question 1:__ Use the plot above to analyze the performance of each of the attempted architectures. Which performs best? Provide an explanation regarding why you think some models perform better than others.
#
# __Answer:__:
#
# Model_0: It's a very basic model consisting of simple GRU layer. The model didn't generalize well as evident from high training and validation loss
#
# Model_1: Batch Normalization and Time Distributed Layer is added to existing architecture of model_0. The model generalize better than model_0 as both training and validation loss plummeted quickly and are comparatively much lower than model_0 values.
#
# Model_2: The model has an added CNN layer to the existing model_1 architecture. The loss values are lower than model_1 while the convergence is faster probably due to the added batch normalization.
#
# Model_3: The model adds one more RNN layer to existing model_1 architecture. The model performs similar to model_2.
#
# Model_4: It consist of bidirectional RNN followed by Time Distributed Dense Layer. Compared to model_0, this model has enormous improvement in terms of reduction in training and validation loss. Given the complex nature of the model, its speed remains slow.
#
# Conclusion: Model_2 outperforms the rest while the performance of model_1, model_3 and model_4 remains comparable. Batch Normalization seems to effect the convergence speed.
# <a id='final'></a>
# ### (IMPLEMENTATION) Final Model
#
# Now that you've tried out many sample models, use what you've learned to draft your own architecture! While your final acoustic model should not be identical to any of the architectures explored above, you are welcome to merely combine the explored layers above into a deeper architecture. It is **NOT** necessary to include new layer types that were not explored in the notebook.
#
# However, if you would like some ideas for even more layer types, check out these ideas for some additional, optional extensions to your model:
#
# - If you notice your model is overfitting to the training dataset, consider adding **dropout**! To add dropout to [recurrent layers](https://faroit.github.io/keras-docs/1.0.2/layers/recurrent/), pay special attention to the `dropout_W` and `dropout_U` arguments. This [paper](http://arxiv.org/abs/1512.05287) may also provide some interesting theoretical background.
# - If you choose to include a convolutional layer in your model, you may get better results by working with **dilated convolutions**. If you choose to use dilated convolutions, make sure that you are able to accurately calculate the length of the acoustic model's output in the `model.output_length` lambda function. You can read more about dilated convolutions in Google's [WaveNet paper](https://arxiv.org/abs/1609.03499). For an example of a speech-to-text system that makes use of dilated convolutions, check out this GitHub [repository](https://github.com/buriburisuri/speech-to-text-wavenet). You can work with dilated convolutions [in Keras](https://keras.io/layers/convolutional/) by paying special attention to the `padding` argument when you specify a convolutional layer.
# - If your model makes use of convolutional layers, why not also experiment with adding **max pooling**? Check out [this paper](https://arxiv.org/pdf/1701.02720.pdf) for example architecture that makes use of max pooling in an acoustic model.
# - So far, you have experimented with a single bidirectional RNN layer. Consider stacking the bidirectional layers, to produce a [deep bidirectional RNN](https://www.cs.toronto.edu/~graves/asru_2013.pdf)!
#
# All models that you specify in this repository should have `output_length` defined as an attribute. This attribute is a lambda function that maps the (temporal) length of the input acoustic features to the (temporal) length of the output softmax layer. This function is used in the computation of CTC loss; to see this, look at the `add_ctc_loss` function in `train_utils.py`. To see where the `output_length` attribute is defined for the models in the code, take a look at the `sample_models.py` file. You will notice this line of code within most models:
# ```
# model.output_length = lambda x: x
# ```
# The acoustic model that incorporates a convolutional layer (`cnn_rnn_model`) has a line that is a bit different:
# ```
# model.output_length = lambda x: cnn_output_length(
# x, kernel_size, conv_border_mode, conv_stride)
# ```
#
# In the case of models that use purely recurrent layers, the lambda function is the identity function, as the recurrent layers do not modify the (temporal) length of their input tensors. However, convolutional layers are more complicated and require a specialized function (`cnn_output_length` in `sample_models.py`) to determine the temporal length of their output.
#
# You will have to add the `output_length` attribute to your final model before running the code cell below. Feel free to use the `cnn_output_length` function, if it suits your model.
model_end = final_model(input_dim=161,
filters=200,
kernel_size=11,
conv_stride=2,
conv_border_mode='valid',
units=200)
# Please execute the code cell below to train the neural network you specified in `input_to_softmax`. After the model has finished training, the model is [saved](https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model) in the HDF5 file `model_end.h5`. The loss history is [saved](https://wiki.python.org/moin/UsingPickle) in `model_end.pickle`. You are welcome to tweak any of the optional parameters while calling the `train_model` function, but this is not required.
with active_session():
train_model(input_to_softmax=model_end,
pickle_path='model_end.pickle',
save_model_path='model_end.h5',
spectrogram=True) # change to False if you would like to use MFCC features
# __Question 2:__ Describe your final model architecture and your reasoning at each step.
#
# __Answer:__
#
# The final model uses architectures from model_2 and model_4 and is a combination of CNNs and RNNs. It has CNN_1d layer followed by a maxpool layer and a bidirectional RNN layer. The CNN extracts the latent features. Between each layer, batch normalization is added to increase the convergence rate. GRUs are used to overcome exploding gradient problem.
# <a id='step3'></a>
# ## STEP 3: Obtain Predictions
#
# We have written a function for you to decode the predictions of your acoustic model. To use the function, please execute the code cell below.
# +
import numpy as np
from data_generator import AudioGenerator
from keras import backend as K
from utils import int_sequence_to_text
from IPython.display import Audio
def get_predictions(index, partition, input_to_softmax, model_path):
""" Print a model's decoded predictions
Params:
index (int): The example you would like to visualize
partition (str): One of 'train' or 'validation'
input_to_softmax (Model): The acoustic model
model_path (str): Path to saved acoustic model's weights
"""
# load the train and test data
data_gen = AudioGenerator()
data_gen.load_train_data()
data_gen.load_validation_data()
# obtain the true transcription and the audio features
if partition == 'validation':
transcr = data_gen.valid_texts[index]
audio_path = data_gen.valid_audio_paths[index]
data_point = data_gen.normalize(data_gen.featurize(audio_path))
elif partition == 'train':
transcr = data_gen.train_texts[index]
audio_path = data_gen.train_audio_paths[index]
data_point = data_gen.normalize(data_gen.featurize(audio_path))
else:
raise Exception('Invalid partition! Must be "train" or "validation"')
# obtain and decode the acoustic model's predictions
input_to_softmax.load_weights(model_path)
prediction = input_to_softmax.predict(np.expand_dims(data_point, axis=0))
output_length = [input_to_softmax.output_length(data_point.shape[0])]
pred_ints = (K.eval(K.ctc_decode(
prediction, output_length)[0][0])+1).flatten().tolist()
# play the audio file, and display the true and predicted transcriptions
print('-'*80)
Audio(audio_path)
print('True transcription:\n' + '\n' + transcr)
print('-'*80)
print('Predicted transcription:\n' + '\n' + ''.join(int_sequence_to_text(pred_ints)))
print('-'*80)
# -
# Use the code cell below to obtain the transcription predicted by your final model for the first example in the training dataset.
get_predictions(index=0,
partition='train',
input_to_softmax=final_model(input_dim=161,
filters=200,
kernel_size=11,
conv_stride=2,
conv_border_mode='valid',
units=200),
model_path='results/model_end.h5')
# Use the next code cell to visualize the model's prediction for the first example in the validation dataset.
get_predictions(index=0,
partition='validation',
input_to_softmax=final_model(input_dim=161,
filters=200,
kernel_size=11,
conv_stride=2,
conv_border_mode='valid',
units=200),
model_path='results/model_end.h5')
# One standard way to improve the results of the decoder is to incorporate a language model. We won't pursue this in the notebook, but you are welcome to do so as an _optional extension_.
#
# If you are interested in creating models that provide improved transcriptions, you are encouraged to download [more data](http://www.openslr.org/12/) and train bigger, deeper models. But beware - the model will likely take a long while to train. For instance, training this [state-of-the-art](https://arxiv.org/pdf/1512.02595v1.pdf) model would take 3-6 weeks on a single GPU!
| vui_notebook.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Channels" data-toc-modified-id="Channels-1"><span class="toc-item-num">1 </span>Channels</a></span></li><li><span><a href="#Differential-Insertion-Loss" data-toc-modified-id="Differential-Insertion-Loss-2"><span class="toc-item-num">2 </span>Differential Insertion Loss</a></span></li><li><span><a href="#Impulse-Responses" data-toc-modified-id="Impulse-Responses-3"><span class="toc-item-num">3 </span>Impulse Responses</a></span></li><li><span><a href="#Step-Responses" data-toc-modified-id="Step-Responses-4"><span class="toc-item-num">4 </span>Step Responses</a></span></li></ul></div>
# -
# # S-parameter Checking
#
# Original author: <NAME> <<EMAIL>>
# Original date: November 30, 2017
#
# Copyright © 2017 <NAME>; all rights reserved World wide.
#
# This [Jupyter](http://jupyter.org) notebook can be used to sanity check a batch of 4-port single-ended [Touchstone](https://en.wikipedia.org/wiki/Touchstone_file) files, and generate their equivalent differential step responses, for use w/ [PyBERT](https://github.com/capn-freako/PyBERT/wiki).
# +
# %matplotlib inline
from matplotlib import pyplot as plt
import skrf as rf
import numpy as np
import scipy.signal as sig
# -
# ## Channels
#
# Load the channels of interest and sanity check them.
# +
plt.figure(figsize=(16, 8))
def sdd_21(ntwk):
"""
Given a 4-port single-ended network, return its differential throughput."
Note that the following connectivity is assumed:
- 1 ==> 2
- 3 ==> 4
"""
return 0.5*(ntwk.s21 - ntwk.s23 + ntwk.s43 - ntwk.s41)
# Load the channels of interest.
chnls = []
# chnls.append(('ch1', rf.Network('../channels/802.3bj_COM_Cisco/kochuparambil_3bj_02_0913/Beth_longSmooth_THRU.s4p')))
# chnls.append(('ch2', rf.Network('../channels/802.3bj_COM_Cisco/kochuparambil_3bj_02_0913/Beth_shortReflective_THRU.s4p')))
# chnls.append(('ch5', rf.Network('../channels/shanbhag_01_0511/TEC_Whisper27in_THRU_G14G15.s4p')))
chnls.append(('se', rf.Network('../Support/DoriItzhaki/tx_se.s4p')))
# Create diagonal mask, for checking passivity, below.
n = chnls[0][1]
m = np.zeros(n.s[0].shape, dtype=bool)
np.fill_diagonal(m, True)
# Check them against several criteria.
passivities = []
clrs = ['r','g','b','c','m','y']
for (lbl, ntwk), clr in zip(chnls, clrs):
passivity = np.array(list(map(lambda x: max(x[m]), ntwk.passivity)))
# passivities.append(ntwk.is_passive()) # Apparently, not implemented, yet.
if(max(passivity) <= 1.0):
passivities.append(True)
else:
passivities.append(False)
plt.subplot(121)
plt.plot(ntwk.f / 1e9, passivity, clr, label=lbl)
plt.subplot(122)
plt.plot(ntwk.f / 1e9, sdd_21(ntwk).group_delay.flatten(), clr, label=lbl)
#Plot passivities.
plt.subplot(121)
plt.title("Passivity Plots")
plt.xlabel("f (GHz)")
plt.grid()
plt.legend(loc='upper right')
#Plot group delays.
plt.subplot(122)
plt.title("Group Delay")
plt.xlabel("f (GHz)")
plt.grid()
plt.legend(loc='upper right')
# Print a summary of the results.
print("{:10s} {:10s}".format('Channel','Passive'))
print('_'*21)
for ((lbl, ntwk), passive) in zip(chnls, passivities):
print("{:^10s} {:^10s}".format(lbl, str(passive)))
# -
# Channel is passive, but has a serious anomaly in its group delay.
#
# ## Differential Insertion Loss
#
# Convert to mixed mode and display Sdd[2,1].
# Plot their differential insertion losses.
sdd_21s = []
plt.figure(figsize=(16, 8))
for (lbl, ntwk), clr in zip(chnls, clrs):
H = sdd_21(ntwk)
sdd_21s.append(H)
plt.semilogx(ntwk.f, 20 * np.log10(abs(H.s[:,0,0])), clr, label=lbl)
plt.title("SDD[2,1]")
plt.xlabel("f (Hz)")
plt.ylabel("|Sdd21| (dB)")
plt.grid()
plt.legend(loc='upper right')
plt.axis(ymin=-40)
plt.show()
# This does *not* look correct.
# The anomaly in the *Sdd[2,1]* plot, above, corresponds in frequency with the anomaly in the *group delay* plot, above.
#
# ## Impulse Responses
# +
# Here, I calculate the impulse response myself,
# as opposed to using the 'Network.s_time()' function provided by skrf,
# because I've found I get better results.
ts = []
fs = []
hs = []
ss = []
trefs = []
frefs = []
hrefs = []
srefs = []
for (lbl, _), sdd_21, clr in zip(chnls, sdd_21s, clrs):
# Testing/comparing one-line solution, using scikit-rf.
sdd_21_ref = sdd_21.extrapolate_to_dc().windowed()
Href = sdd_21_ref.s[:,0,0]
fref = sdd_21_ref.f
Fref = rf.Frequency.from_f(fref / 1e9) ## skrf.Frequency.from_f() expects its argument to be in units of GHz.
print("{} ref. frequencies: {}".format(lbl, Fref))
# Hrefp = Href.copy()
# if(fref[0] != 0): # Add the d.c. point, if necessary.
# Hrefp = np.pad(Hrefp, (1,0), 'constant', constant_values=1.0) # Presume d.c. value = 1.
href = np.fft.irfft(Href)
href /= np.abs(href.sum()) # Equivalent to assuming that step response settles at 1.
# Form frequency vector.
f = sdd_21.f
fmin = f[0]
if(fmin == 0): # Correct, if d.c. point was included in original data.
fmin = f[1]
fmax = f[-1]
f = np.arange(fmin, fmax + fmin, fmin)
F = rf.Frequency.from_f(f / 1e9) ## skrf.Frequency.from_f() expects its argument to be in units of GHz.
print("{} frequencies: {}".format(lbl, F))
# Form impulse response from frequency response.
sdd_21 = sdd_21.interpolate_from_f(F)
H = sdd_21.s[:,0,0]
# H = np.concatenate((H, np.conj(np.flip(H[:-1], 0)))) # Forming the vector that fft() would've outputted.
Hp = H.copy()
Hp = np.pad(Hp, (1,0), 'constant', constant_values=1.0) # Presume d.c. value = 1.
# h = np.real(np.fft.ifft(H))
h = np.fft.irfft(Hp)
h /= np.abs(h.sum()) # Equivalent to assuming that step response settles at 1.
# Form step response from impulse response.
s = np.cumsum(h)
sref = np.cumsum(href)
# Form time vector.
t0 = 1. / (2. * fmax) # Sampling interval = 1 / (2 fNyquist).
t = np.array([n * t0 for n in range(len(h))])
tref = np.array([n * t0 for n in range(len(href))])
# Save results.
ts.append(t)
fs.append(f)
hs.append(h)
ss.append(s)
trefs.append(tref)
frefs.append(fref)
hrefs.append(href)
srefs.append(sref)
# Plot results.
def shift_peak(t, x, new_peak_loc=1e-9):
t_peak = t[np.argmax(x)]
delta_t = new_peak_loc - t_peak
return np.roll(x, int(delta_t / t[1]))
plt.figure(1, figsize=(16, 8))
plt.semilogx(fref, 20. * np.log10(np.abs(Href)), clr+'--', label=lbl+'_ref')
plt.semilogx(f, 20. * np.log10(np.abs(H)), clr, label=lbl)
plt.figure(2, figsize=(16, 8))
plt.plot(tref * 1e9, href / t0 * 1e-9, clr+'--', label=lbl+'_ref')
plt.plot(t * 1e9, h / t0 * 1e-9, clr, label=lbl)
plt.figure(3, figsize=(16, 8))
plt.plot(tref * 1e9, shift_peak(tref, href) / t0 * 1e-9, clr+'--', label=lbl+'_ref')
plt.plot(t * 1e9, shift_peak(t, h) / t0 * 1e-9, clr, label=lbl)
# Annotate the plots.
plt.figure(1, figsize=(16, 8))
plt.title("Frequency Response")
plt.xlabel("f (Hz)")
plt.ylabel("|H(f)| (dB)")
plt.grid()
plt.legend(loc='lower left')
plt.axis(xmin=1e7, xmax=40e9);
plt.figure(2, figsize=(16, 8))
plt.title("Impulse Response")
plt.xlabel("t (ns)")
plt.ylabel("h(t) (V/ns)")
plt.grid()
plt.legend(loc='upper right')
plt.axis(xmin=0, xmax=10);
plt.figure(3, figsize=(16, 8))
plt.title("Impulse Response - Shifted and Zoomed")
plt.xlabel("t (ns)")
plt.ylabel("h(t) (V/ns)")
plt.grid()
plt.legend(loc='upper right')
plt.axis(xmin=0.5, xmax=1.5);
# -
# Hmmm, I think this file has some problems. :(
# ## Step Responses
plt.figure(figsize=(16, 8))
for (lbl, _), t, s, tref, sref, clr in zip(chnls, ts, ss, trefs, srefs, clrs):
plt.plot(tref * 1e9, sref, clr+'--', label=lbl+'_ref')
plt.plot(t * 1e9, s, clr, label=lbl)
plt.title("Step Response")
plt.xlabel("t (ns)")
plt.ylabel("s(t) (V)")
plt.grid()
plt.legend(loc='lower right');
# plt.axis(xmin=1.8, xmax=2.0)
# This doesn't look right.
# Save the step responses.
for (lbl, _), t, s in zip(chnls, trefs, srefs):
with open(lbl+'_s.csv', 'wt') as file:
for x, y in zip(t, s):
# print >> file, "{:014.12f}, {:05.3f}".format(x, y)
print("{:014.12f}, {:05.3f}".format(x, y), file=file)
# +
# Take them back into the frequency domain and compare to original data.
hps = []
plt.figure(figsize=(16, 8))
for f, s, (lbl, _), Href, clr in zip(frefs, srefs, chnls, sdd_21s, clrs):
h = np.diff(s)
h = np.pad(h, (1, 0), 'constant', constant_values=0)
H = np.fft.fft(h)
# Using [1], as opposed to [0], to accomodate ch1. (See, below.)
# I'm assuming the strange behavior in ch1 is due to me forcing d.c. values of 1.
H *= abs(Href.s[:,0,0][1]) / abs(H[1]) # Normalize the "d.c." levels.
plt.semilogx(Href.f, 20 * np.log10(abs(Href.s[:,0,0])), clr+'--', label=lbl+'_ref')
plt.semilogx(f, 20 * np.log10(abs(H[:len(f)])), clr, label=lbl)
plt.title("SDD[2,1]")
plt.xlabel("f (Hz)")
plt.ylabel("|Sdd21| (dB)")
plt.grid()
plt.legend(loc='upper right')
plt.axis(ymin=-40);
# -
# This Touchstone file has serious problems!
| misc/scikit-rf/S-param Check.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ENZYMES contraction coefficient changes
#
# +
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
coefficientsSecond=[0.2,0.4,0.6,0.8,0.9]
coefficientsFirst=[512]
dataset="ENZYMES"
file_constraited="ENZYMESConvergence/TrainConvergence"
save_png_name='ContractionCoefficientsCompare_{}.png'.format(dataset)
start_plot=30
epochs=70
args=coefficientsSecond
PlotMonteCalorsTimesConvergenceNpy(dataset,file_constraited,coefficientsFirst,coefficientsSecond,save_png_name,start_plot,epochs,*args)
# -
# # ENZYMES batch size changes
#
# # Cora Batch size change
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
coefficientsFirst=[16,32,64,128] #
coefficientsSecond=[0.6]
dataset="Cora"
file_constraited="CoraConvergence/TrainConvergence"
save_png_name='BatchSizeChangesCompare_{}.png'.format(dataset)
start_plot=30
epochs=70
args=coefficientsFirst
PlotMonteCalorsTimesConvergenceNpy(dataset,file_constraited,coefficientsFirst,coefficientsSecond,save_png_name,start_plot,epochs,*args)
# # Cora contraction coefficient changes
# +
coefficientsFirst=[1, 2, 3, 4, 5, 6]
coefficientsSecond=[0.5]
dataset="Cora"
file_constraited="TrainConvergence"
save_png_name='LayerNumCompare_{}.png'.format(dataset)
start_plot=0
epochs=200
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
args=coefficientsFirst
PlotMonteCalorsTimesConvergenceNpy(dataset,file_constraited,coefficientsFirst,coefficientsSecond,save_png_name,start_plot,epochs,*args)
# +
coefficientsSecond=[0.7]
coefficientsFirst=[1, 2, 3, 4, 5, 6]
dataset="Cora"
file_constraited="TrainConvergence"
save_png_name='LayerNumCompare_{}.png'.format(dataset)
start_plot=0
epochs=200
args=[3,4,5,6,7,8]
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
PlotMonteCalorsTimesConvergenceNpy(dataset,file_constraited,coefficientsFirst,coefficientsSecond,save_png_name,start_plot,epochs,*args)
# +
coefficientsSecond=[0.8]
coefficientsFirst=[1,2,4,6]
dataset="ENZYMES"
file_constraited="TrainConvergence"
save_png_name='LayerNumCompare_{}.png'.format(dataset)
start_plot=0
epochs=150
args=[3,4,6,8]
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
PlotMonteCalorsTimesConvergenceNpy(dataset,file_constraited,coefficientsFirst,coefficientsSecond,save_png_name,start_plot,epochs,*args)
# -
# # LR comparison
# # Layer number change
# +
import matplotlib.pyplot as plt
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
coefficientsFirst=[128]
coefficientsSecond=[1,2,3]
coefficientsThree=[0.8]
coefficientsFour=[0.1]
modelName="GCN"
Prefix="TrainConvergence"
datasets=["Citeseer","Cora",'Pubmed']
#dataset="Pubmed"
start_plot=0
epochs=200
args=[3,4,5]
plt.rc('font', family='serif', serif='Times')
fig=plt.figure(figsize=(8,2),dpi=300)
fig.tight_layout()
for i, dataset in enumerate(datasets):
plt.subplot(1,4, i+1)
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
PlotMonteCalorsTimesConvergenceNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,*args)
if i==0:
plt.xlabel('Epoches', fontsize=8)
plt.ylabel('Error', fontsize=8)
if i==2:
plt.subplots_adjust(wspace=0.3,hspace=0)
dataset="CoraFull"
modelName="ChebConvNet"
coefficientsThree=[0.99]
coefficientsFour=[0.2]
plt.subplot(1,4, 4)
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
PlotMonteCalorsTimesConvergenceNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,*args)
save_png_name='Results/NumberLayerCompare-{}.png'.format(modelName)
plt.savefig(save_png_name,dpi=600)
# -
# # Network Size Adjust
# +
import matplotlib.pyplot as plt
from PlotNetworkContraction import PlotNetworkContractionNpy
import matplotlib.font_manager
coefficientsFirst=[128]
coefficientsSecond=[1,2,3]
coefficientsThree=[0.8]
coefficientsFour=[0.1]
modelName="GCN"
Prefix="NewNetworkSizeAdjust"
dataset="Pubmed"
datasets=["Cora","Citeseer",'Pubmed']
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
start_plot=0
epochs=200
args=[3,4,5]
plt.rcParams["xtick.labelsize"]=7
plt.rcParams["ytick.labelsize"]=7
plt.rcParams["font.family"] = "Times New Roman"
fig=plt.figure(figsize=(8,1.8),dpi=300)
for i, dataset in enumerate(datasets):
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
plt.subplot(1,4,i+1)
PlotNetworkContractionNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,*args)
if i==1 or i==3:
plt.subplots_adjust(wspace=0.4,hspace=0)
if i==0:
plt.legend(args,loc="upper right")
modelName="GCN"
dataset="CoraFull"
coefficientsThree=[0.99]
coefficientsFour=[0.2]
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
plt.subplot(1,4,4)
PlotNetworkContractionNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,*args)
fig.text(0.495,0.02, 'Depth', va='center',fontdict={'family' : 'Times New Roman', 'size':7})
fig.text(0.08, 0.557, 'Width', ha='center',fontdict={'family' : 'Times New Roman', 'size':7},rotation='vertical')
save_png_name='Results/NewNetworkSizeAdjustCompare-{}.png'.format(modelName)
print(save_png_name)
plt.savefig(save_png_name,dpi=600)
plt.show()
plt.close()
# -
# # LR compare
# +
import matplotlib.pyplot as plt
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
coefficientsFirst=[128]
coefficientsSecond=[2]
coefficientsThree=[0.8]
coefficientsFour=[0.001, 0.01,0.1,0.2,0]
modelName="GCN"
Prefix="TrainConvergence"
dataset="Pubmed"
datasets=["Cora","Citeseer",'Pubmed','CoraFull']
start_plot=0
epochs=200
fig=plt.figure(figsize=(8,1.8),dpi=300)
#fig.tight_layout()
plt.rcParams["xtick.labelsize"]=6
plt.rcParams["ytick.labelsize"]=6
for i, dataset in enumerate(datasets):
plt.subplot(1,4,i+1)
if i==0:
coefficientsFour=[0.001, 0.01,0.1,0.5]
if i==2:
coefficientsFour=[0.001, 0.01,0.1,0.2]
if i==3:
coefficientsFour=[0.001, 0.01,0.1,0.5]
coefficientsThree=[0.99]
args=coefficientsFour
FileName="Results/"+dataset+"Convergence/"
file_constraited=FileName+Prefix
PlotMonteCalorsTimesConvergenceNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,*args)
if i==2:
plt.legend(coefficientsFour,loc="center left",prop = {'size':6})
else:
plt.legend(coefficientsFour,loc="center right",prop = {'size':6})
fig.text(0.52,-0.02, 'Epochs', ha='center',fontsize=7)
fig.text(0.09, 0.58, 'Error', ha='center',fontsize=7,rotation='vertical')
save_png_name='Results/LRCompare-{}.png'.format(modelName)
print(save_png_name)
plt.savefig(save_png_name,dpi=600)
plt.show()
plt.close()
# -
# # Dynamics evolution
# +
import numpy as np
import glob
import matplotlib.pyplot as plt
import matplotlib.font_manager
import ipdb
colors=[(248/255,25/255,25/255),(40/255,172/255,82/255),(161/255,80/255,159/255),(0/255,127/255,182/255),(251/255,181/255,80/255)]
SaveFiles="DiagElement"
dataset="Cora"
modelName="GCN"
NumLayers=2
FileConstrant2="param"
num_epochs=300
interal=40
fig=plt.figure(figsize=(12,2),dpi=300)
#fig, axes = plt.subplots(1, 4, sharex=True, sharey=True, figsize=(12,2),dpi=300)
fig.tight_layout()
epochs=[0,40,120,200,240,299]
#epochs=[0,299]
for k,epoch in enumerate(epochs):
EvolutionDynamics=np.load("Results/{}Convergence/DiagElement-{}-{}-{}_1024_{}_0.99_0.1-monte_0-{}.npy".format(dataset,dataset,modelName,FileConstrant2,NumLayers,epoch),allow_pickle=True)
ax=fig.add_subplot(1,len(epochs),k+1)
with plt.style.context(['science','seaborn-white','no-latex']):
for i in range(EvolutionDynamics.shape[1]):
tmp=np.array(EvolutionDynamics.T)[i]
ax.plot([1,2],tmp,c=colors[i],marker="o",lw=2)
if k==0:
ax.legend([1,2,3,4,5],borderpad=0.01,loc="upper right")
else:
pass
fig.text(0.52,-0.02, 'Layer', ha='center',fontsize="medium")
save_png_name="Results/{}-{}.png".format(SaveFiles,modelName)
print(save_png_name)
plt.savefig(save_png_name,dpi=600)
plt.show()
plt.close()
# -
# # link rewiring
# +
import matplotlib.pyplot as plt
from PlotMonteCalorsConvergence import PlotMonteCalorsTimesConvergenceNpy
coefficientsFirst=[512]
coefficientsSecond=[0.001,0.01,0.1]
coefficientsThree=[0.1]
coefficientsFour=[1]
datasets=["Cora","Citeseer",'Pubmed','CoraFull']
modelName="GCN"
start_plot=40
epochs=40
args=[0.001,0.01,0.1]
fig=plt.figure(figsize=(8,1.7),dpi=300)
plt.rcParams["xtick.labelsize"]=7
plt.rcParams["ytick.labelsize"]=7
for i, dataset in enumerate(datasets):
if i==0:
add=0.2*1e-2
if i==1:
add=0.08*1e-2
plt.subplots_adjust(wspace=0.5,hspace=0)
if i==2:
add=1*1e-2
plt.subplots_adjust(wspace=0.3,hspace=0)
if i==3:
add =0.2*1e-2
plt.subplots_adjust(wspace=0.3,hspace=0)
fig.add_subplot(1,4,i+1)
file_constraited="Results/{}Convergence/LinkCorrection/AlgebraicConectivityTestConvergence".format(dataset)
PlotMonteCalorsTimesConvergenceNpy(dataset,modelName,file_constraited,coefficientsFirst,coefficientsSecond,coefficientsThree,coefficientsFour,start_plot,epochs,add,*args)
if i==0:
plt.legend(args,prop = {'size':7},loc="lower left")
fig.text(0.51,-0.00, 'Epochs', ha='center',fontsize=7)
fig.text(0.08, 0.63, 'Test error', ha='center',fontsize=7,rotation='vertical')
save_png_name='Results/WeightRewiringCoefficientCompare-{}.png'.format(modelName)
print(save_png_name)
plt.savefig(save_png_name,dpi=600)
# +
import numpy as np
mu1=np.array([1.94615606, 1.94629677, 1.9464798 , 1.94666795, 1.94681017,
1.946848 , 1.94672942, 1.9464188 , 1.94590696, 1.94521161,
1.94437174, 1.9434404 , 1.94247254, 1.94151676, 1.94060938,
1.93977368, 1.93902107, 1.93835354, 1.93776739, 1.93725197,
1.93679233, 1.93636811, 1.93595477, 1.9355255 , 1.9350551 ,
1.93452509, 1.9339271 , 1.93326346, 1.93254813, 1.93180184,
1.93104756, 1.93030719, 1.92959734, 1.92892909, 1.92830511,
1.92772404, 1.92717791, 1.92665486, 1.9261409 , 1.92561885,
1.92507434, 1.92449681, 1.92388129, 1.92322886, 1.92254635,
1.92184377, 1.92113074, 1.92041639, 1.91970563, 1.91900114,
1.91830111, 1.91760115, 1.91689459, 1.91617274, 1.91542729,
1.91465072, 1.91383882, 1.91298918, 1.91210274, 1.91118189,
1.91022988, 1.90925014, 1.90824513, 1.90721687, 1.9061652 ,
1.90508978, 1.90398705, 1.90285393, 1.90168496, 1.90047598,
1.89922285, 1.89792224, 1.89657207, 1.89517196, 1.89372341,
1.89222757, 1.89068786, 1.88910623, 1.88748368, 1.88582015,
1.88411248, 1.8823568 , 1.88054729, 1.87867844, 1.87674586,
1.8747464 , 1.87267975, 1.87054773, 1.86835305, 1.8660992 ,
1.86378761, 1.86141777, 1.85898713, 1.85649029, 1.85392078,
1.85127338, 1.84854408, 1.84573146, 1.84283638, 1.83986123,
1.8368084 , 1.83367836, 1.83046977, 1.82717808, 1.82379878,
1.820327 , 1.81675879, 1.8130933 , 1.80933134, 1.80547333,
1.80152011, 1.79747001, 1.79332014, 1.78906568, 1.78470373,
1.78023211, 1.7756507 , 1.77096009, 1.76616049, 1.76125121,
1.75622936, 1.75109136, 1.74583427, 1.74045674, 1.7349596 ,
1.72934337, 1.72360845, 1.71775369, 1.71177673, 1.70567576,
1.69945097, 1.69310236, 1.68663096, 1.68003706, 1.67331922,
1.66647716, 1.65951157, 1.6524243 , 1.6452173 , 1.63789157,
1.63044639, 1.62288241, 1.61520155, 1.60740729, 1.59950284,
1.59149007, 1.5833691 , 1.57514238, 1.5668141 , 1.55838887,
1.54987101, 1.54126203, 1.53256468, 1.52378345, 1.51492449,
1.50599297, 1.49699152, 1.48792473, 1.47879807, 1.46961844,
1.46039093, 1.45111938, 1.4418087 , 1.43246615, 1.42309801,
1.41371 , 1.40430629, 1.39489333, 1.3854777 , 1.37606537,
1.36666071, 1.35726972, 1.347899 , 1.33855438, 1.32923957,
1.31996032, 1.31072191, 1.30152969, 1.2923882 , 1.28330179,
1.27427495, 1.26531204, 1.2564166 , 1.24759205, 1.23884348,
1.23017339, 1.22158436, 1.21307957, 1.20466177, 1.19633377,
1.18809748, 1.17995493, 1.17190786, 1.16395783, 1.15610663,
1.14835536, 1.14070499, 1.13315618, 1.12570997, 1.11836684])+1.7
mu2=np.array([1.94616814, 1.94622215, 1.94629431, 1.94636444, 1.94639826,
1.94635185, 1.94618297, 1.94586229, 1.94537882, 1.94474518,
1.94399083, 1.94315708, 1.94228713, 1.94141893, 1.94058128,
1.93979323, 1.93906327, 1.9383953 , 1.93778869, 1.93723842,
1.9367365 , 1.93626904, 1.93581824, 1.93536222, 1.93487982,
1.9343526 , 1.93377058, 1.93313289, 1.93244851, 1.93173254,
1.93100373, 1.93028073, 1.92957775, 1.92890445, 1.92826549,
1.92766082, 1.927085 , 1.92652984, 1.92598367, 1.92543308,
1.92486505, 1.92426972, 1.92364212, 1.92298234, 1.92229565,
1.92158997, 1.92087364, 1.92015378, 1.91943463, 1.91871687,
1.91799891, 1.91727626, 1.91654249, 1.91579052, 1.91501323,
1.91420523, 1.91336377, 1.91248802, 1.91157969, 1.91064143,
1.90967556, 1.90868402, 1.90766668, 1.9066232 , 1.90555175,
1.90444962, 1.90331399, 1.90214217, 1.90093187, 1.89968141,
1.89838946, 1.89705499, 1.89567713, 1.89425508, 1.89278682,
1.89127159, 1.8897082 , 1.88809677, 1.8864363 , 1.88472772,
1.88297021, 1.88116292, 1.87930437, 1.87739178, 1.8754214 ,
1.87338956, 1.87129315, 1.86912954, 1.86689826, 1.86460026,
1.86223706, 1.85981011, 1.85732031, 1.85476589, 1.85214376,
1.84944892, 1.84667623, 1.84382045, 1.84087912, 1.83785192,
1.8347402 , 1.83154647, 1.82827234, 1.82491712, 1.82147853,
1.81795136, 1.81432986, 1.81060946, 1.80678761, 1.80286423,
1.79884152, 1.79472093, 1.79050291, 1.7861853 , 1.78176347,
1.77723225, 1.77258841, 1.76783085, 1.7629602 , 1.75797872,
1.75288761, 1.74768488, 1.74236659, 1.73692946, 1.73137005,
1.72568854, 1.7198865 , 1.71396617, 1.70792826, 1.7017711 ,
1.69549211, 1.6890891 , 1.68256215, 1.6759127 , 1.66914284,
1.66225394, 1.65524554, 1.64811798, 1.6408716 , 1.63350828,
1.6260289 , 1.61843566, 1.61073061, 1.60291545, 1.59499323,
1.58696636, 1.57883644, 1.57060643, 1.56227922, 1.55385959,
1.5453517 , 1.53675842, 1.52808261, 1.51932828, 1.51050131,
1.50160686, 1.49264908, 1.48363193, 1.47456002, 1.4654398 ,
1.45627773, 1.44707803, 1.43784535, 1.42858537, 1.41930481,
1.4100097 , 1.40070478, 1.39139529, 1.38208739, 1.37278759,
1.3635006 , 1.35423132, 1.34498513, 1.33576882, 1.32658692,
1.31744365, 1.30834333, 1.29929201, 1.29029365, 1.28135268,
1.27247302, 1.26365829, 1.25491246, 1.24623895, 1.23764094,
1.2291218 , 1.22068421, 1.21233046, 1.20406314, 1.19588443,
1.18779643, 1.17980119, 1.17190015, 1.16409377, 1.15638439,
1.14877307, 1.14126035, 1.1338466 , 1.12653275, 1.1193196 ])+1.7
mu3=np.array([1.94581223, 1.9459579 , 1.94614303, 1.94632864, 1.9464649 ,
1.94649684, 1.94637501, 1.94606686, 1.94556308, 1.94488025,
1.94405353, 1.94313312, 1.94217026, 1.94121265, 1.94029713,
1.93944776, 1.93867862, 1.93799365, 1.93738961, 1.9368577 ,
1.93638325, 1.93594801, 1.9355278 , 1.93509865, 1.93463516,
1.93411958, 1.93354118, 1.93289971, 1.93220448, 1.93147266,
1.9307251 , 1.92998207, 1.92926073, 1.92857301, 1.92792487,
1.92731798, 1.92674673, 1.92620289, 1.92567396, 1.92514563,
1.92460465, 1.92403901, 1.92344058, 1.92280734, 1.9221431 ,
1.92145288, 1.92074537, 1.92002833, 1.91930723, 1.91858685,
1.91786826, 1.91715002, 1.91642797, 1.9156965 , 1.91494823,
1.91417646, 1.91337442, 1.91253793, 1.91166592, 1.91075718,
1.90981317, 1.90883648, 1.90783 , 1.90679491, 1.90573502,
1.90464962, 1.90353894, 1.90239978, 1.90122867, 1.90002084,
1.89877141, 1.89747596, 1.89613163, 1.89473629, 1.89329076,
1.89179647, 1.89025545, 1.88867104, 1.88704467, 1.88537526,
1.88366187, 1.88189995, 1.88008404, 1.87820995, 1.87627268,
1.87427032, 1.87220252, 1.8700707 , 1.86787653, 1.865623 ,
1.86330962, 1.86093485, 1.85849512, 1.85598564, 1.8534019 ,
1.85074031, 1.84799922, 1.84517872, 1.84227967, 1.83930373,
1.83624959, 1.83311629, 1.82989883, 1.82659352, 1.82319617,
1.81970525, 1.81611967, 1.81244087, 1.80866921, 1.80480468,
1.80084348, 1.79678249, 1.79261625, 1.78834248, 1.78396082,
1.77947032, 1.77487385, 1.77017009, 1.76535678, 1.76043057,
1.75538743, 1.75022554, 1.74494493, 1.73954713, 1.73403227,
1.72839952, 1.72264588, 1.71676791, 1.71076417, 1.70463586,
1.69838464, 1.69201267, 1.68551791, 1.67889798, 1.67215228,
1.66528094, 1.65828598, 1.65117085, 1.64393449, 1.63657689,
1.62909687, 1.62149799, 1.61378336, 1.60595536, 1.59801579,
1.58996451, 1.58180392, 1.57353723, 1.56516981, 1.55670357,
1.54814112, 1.53948581, 1.53074276, 1.52191782, 1.51301396,
1.50403309, 1.49498045, 1.48586261, 1.47668636, 1.46745598,
1.45817482, 1.44884944, 1.43948662, 1.43009126, 1.4206686 ,
1.41122448, 1.40176582, 1.39229929, 1.38282979, 1.37336218,
1.36390328, 1.35445952, 1.34503531, 1.33563685, 1.32627034,
1.31694102, 1.30765295, 1.29841077, 1.28922045, 1.28008747,
1.27101529, 1.26200736, 1.25306845, 1.24420285, 1.23541319,
1.22670388, 1.21807802, 1.20953739, 1.20108485, 1.19272351,
1.18445635, 1.17628443, 1.1682092 , 1.1602329 , 1.15235698,
1.14458251, 1.13691103, 1.12934268, 1.12187827, 1.1145184 ])+1.7
# -
mu=[mu1,mu2,mu3]
coefficientsFirst=[512]
coefficientsSecond=[0.001,0.01,0.1]
coefficientsThree=[0.1]
coefficientsFour=[1]
savepath="Results"
dataset="CoraFull"
for i in range(3):
FileName="{}-{}-param_{}_{}_{}_{}-monte_{}".format(dataset,modelName,coefficientsFirst[0],coefficientsSecond[i],coefficientsThree[0],coefficientsFour[0],0)
np.save("{}/{}Convergence/LinkCorrection/AlgebraicConectivityTestConvergence-{}".format(savepath,dataset,FileName),mu[i])
for i in range(len(coefficients)):
TrainConvergenceAll=[]
FileNames="{}-{}*{}*{}_{}*{}*{}*.npy".format(file_constraited,dataset,modelName,coefficientsFirst[i],coefficientsSecond[0],coefficientsThree[0],coefficientsFour[0])
print(FileNames)
for file in glob.glob(FileNames):
print(file)
TrainConvergence=np.load(file).tolist()
if max(TrainConvergence)>20:
print("{} maximum is:{}".format(file,max(TrainConvergence)))
os.remove(file)
if len(TrainConvergence)>40 and max(TrainConvergence)<=20:
TrainConvergenceAll.append(TrainConvergence)
print("coefficient of {} num is: {}".format(coefficients[i],len(TrainConvergenceAll)))
mu = np.array(TrainConvergenceAll).mean(axis=0)
standard_dev = np.array(TrainConvergenceAll).std(axis=0)
import networkx as nx
import matplotlib.pyplot as plt
from SpectralAnalysis import community_layout
import pickle
dataset="Pubmed"
modelName="GCN"
for epoch in range(40,80,20):
"""classiResultsFiles="Results/PartitionResults/{}-{}-oneClassNodeEpoch_{}.pkl".format(dataset,modelName,str(epoch))
GraphResultsFiles="Results/PartitionResults/{}-{}-GraphEpoch_{}.pkl".format(dataset,modelName,str(epoch))
with open(GraphResultsFiles,'rb') as f:
G=pickle.loads(f.read())
with open(classiResultsFiles, 'rb') as f:
partition=pickle.loads(f.read())"""
WS = nx.random_graphs.watts_strogatz_graph(20, 4, 0.3)
partitionNew={}
for key in partition:
for value in partition[key]:
partitionNew.update({value: key})
for node in G.nodes():
if node not in partitionNew.keys():
partitionNew.update({node:1})
print(set(partitionNew.values()))
pos = community_layout(G, partitionNew)
nx.draw(G, pos, cmap = plt.cm.get_cmap('viridis'),node_color=list(partitionNew.values()))
plt.show()
plt.savefig("GraphPartitionVisualization-{}_{}-{}.png".format(dataset,modelName,epoch))
# # graph partition visualization
# +
import networkx as nx
import community
import matplotlib.pyplot as plt
from SpectralAnalysis import community_layout
from community import community_louvain
from matplotlib.colors import ListedColormap
G = nx.karate_club_graph() # load a default graph
G =nx.erdos_renyi_graph(500,0.1)
cmap=ListedColormap(BeatutifulColors)
partition = community.best_partition(G) # compute communities
pos = community_layout(G, partition)
#pos = nx.spring_layout(G) # compute graph layout
plt.figure(figsize=(8, 8)) # image is 8 x 8 inches
plt.axis('off')
nx.draw_networkx_nodes(G, pos, node_size=30, cmap=cmap, node_color=list(partition.values()))
nx.draw_networkx_edges(G, pos, alpha=0.01)
plt.savefig("GraphPartitionResults.png",dpi=600)
plt.show(G)
| PlotConvergenceCompare.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + deletable=true editable=true slideshow={"slide_type": "skip"} language="html"
# <style>
# .output_wrapper, .output {
# height:auto !important;
# max-height:300px; /* your desired max-height here */
# }
# .output_scroll {
# box-shadow:none !important;
# webkit-box-shadow:none !important;
# }
# </style>
# + deletable=true editable=true slideshow={"slide_type": "skip"}
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Import Pandas
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
import pandas as pd
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Read in the dataset
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
zillow = pd.read_table('data-zillow.csv', sep=',')
zillow.head()
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Simple sort
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
zillow.sort_values('Metro')
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Changing the sort order
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
sorted = zillow.sort_values('Metro', ascending=False)
sorted.head()
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Sort by more than one column
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
sorted = zillow.sort_values(by=['Metro','County'])
sorted.head()
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Sort by multiple columns and mixed ascending order
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
sorted = zillow.sort_values(by=['Metro','County', 'Zhvi'],
ascending=[True, True, False])
sorted.head()
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ## Sort a Series
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ### Let's create a Series object
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
regions = zillow.RegionID
type(regions)
# + [markdown] deletable=true editable=true slideshow={"slide_type": "slide"}
# ### Let's sort the series
# + [markdown] deletable=true editable=true slideshow={"slide_type": "fragment"}
# #### Original Series
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
regions.head()
# + [markdown] deletable=true editable=true slideshow={"slide_type": "fragment"}
# #### Sorted
# + deletable=true editable=true slideshow={"slide_type": "fragment"}
regions.sort_values().head()
# + deletable=true editable=true slideshow={"slide_type": "skip"}
| Chapter02/Sorting a pandas DataFrame or a Series.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
EPOCSH = 5
test_index = 0
from load_data import *
# +
# load_data()
# -
from load_data import *
X_train,X_test,y_train,y_test = load_data()
len(X_train),len(y_train)
len(X_test),len(y_test)
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
class Test_Model(nn.Module):
def __init__(self) -> None:
super().__init__()
self.c1 = nn.Conv2d(1,64,5)
self.c2 = nn.Conv2d(64,128,5)
self.c3 = nn.Conv2d(128,256,5)
self.fc4 = nn.Linear(256*10*10,256)
self.fc6 = nn.Linear(256,128)
self.fc5 = nn.Linear(128,4)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.c1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.c2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.c3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,256*10*10)
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc6(preds))
preds = self.fc5(preds)
return preds
device = torch.device('cuda')
BATCH_SIZE = 32
IMG_SIZE = 112
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
EPOCHS = 125
from tqdm import tqdm
PROJECT_NAME = 'Weather-Clf'
import wandb
# +
# test_index += 1
# wandb.init(project=PROJECT_NAME,name=f'test')
# for _ in tqdm(range(EPOCHS)):
# for i in range(0,len(X_train),BATCH_SIZE):
# X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
# y_batch = y_train[i:i+BATCH_SIZE].to(device)
# model.to(device)
# preds = model(X_batch.float())
# preds.to(device)
# loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
# optimizer.zero_grad()
# loss.backward()
# optimizer.step()
# wandb.log({'loss':loss.item()})
# wandb.finish()
# +
# for index in range(10):
# print(torch.argmax(preds[index]))
# print(y_batch[index])
# print('\n')
# -
class Test_Model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1,16,5)
self.conv2 = nn.Conv2d(16,32,5)
self.conv3 = nn.Conv2d(32,64,5)
self.fc1 = nn.Linear(64*10*10,16)
self.fc2 = nn.Linear(16,32)
self.fc3 = nn.Linear(32,64)
self.fc4 = nn.Linear(64,32)
self.fc5 = nn.Linear(32,6)
def forward(self,X):
preds = F.max_pool2d(F.relu(self.conv1(X)),(2,2))
preds = F.max_pool2d(F.relu(self.conv2(preds)),(2,2))
preds = F.max_pool2d(F.relu(self.conv3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,64*10*10)
preds = F.relu(self.fc1(preds))
preds = F.relu(self.fc2(preds))
preds = F.relu(self.fc3(preds))
preds = F.relu(self.fc4(preds))
preds = F.relu(self.fc5(preds))
return preds
model = Test_Model().to(device)
optimizer = optim.SGD(model.parameters(),lr=0.1)
criterion = nn.CrossEntropyLoss()
# +
# test_index += 1
# wandb.init(project=PROJECT_NAME,name=f'test-{test_index}')
# for _ in tqdm(range(EPOCHS)):
# for i in range(0,len(X_train),BATCH_SIZE):
# X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
# y_batch = y_train[i:i+BATCH_SIZE].to(device)
# model.to(device)
# preds = model(X_batch.float())
# preds.to(device)
# loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
# optimizer.zero_grad()
# loss.backward()
# optimizer.step()
# wandb.log({'loss':loss.item()})
# wandb.finish()
# -
class Test_Model(nn.Module):
def __init__(self,conv1_output=16,conv2_output=32,conv3_output=64,fc1_output=16,fc2_output=32,fc3_output=64,activation=F.relu):
super().__init__()
self.conv3_output = conv3_output
self.conv1 = nn.Conv2d(1,conv1_output,5)
self.conv2 = nn.Conv2d(conv1_output,conv2_output,5)
self.conv3 = nn.Conv2d(conv2_output,conv3_output,5)
self.fc1 = nn.Linear(conv3_output*10*10,fc1_output)
self.fc2 = nn.Linear(fc1_output,fc2_output)
self.fc3 = nn.Linear(fc2_output,fc3_output)
self.fc4 = nn.Linear(fc3_output,fc2_output)
self.fc5 = nn.Linear(fc2_output,6)
self.activation = activation
def forward(self,X):
preds = F.max_pool2d(self.activation(self.conv1(X)),(2,2))
preds = F.max_pool2d(self.activation(self.conv2(preds)),(2,2))
preds = F.max_pool2d(self.activation(self.conv3(preds)),(2,2))
# print(preds.shape)
preds = preds.view(-1,self.conv3_output*10*10)
preds = self.activation(self.fc1(preds))
preds = self.activation(self.fc2(preds))
preds = self.activation(self.fc3(preds))
preds = self.activation(self.fc4(preds))
preds = self.activation(self.fc5(preds))
return preds
# +
# conv1_output = 32
# conv2_output = 8
# conv3_output = 64
# fc1_output = 512
# fc2_output = 512
# fc3_output = 256
# activation
# optimizer
# loss
# lr
# num of epochs
# -
def get_loss(criterion,y,model,X):
model.to('cpu')
preds = model(X.view(-1,1,112,112).to('cpu').float())
preds.to('cpu')
loss = criterion(preds,torch.tensor(y,dtype=torch.long).to('cpu'))
loss.backward()
return loss.item()
def test(net,X,y):
device = 'cpu'
net.to(device)
correct = 0
total = 0
net.eval()
with torch.no_grad():
for i in range(len(X)):
real_class = torch.argmax(y[i]).to(device)
net_out = net(X[i].view(-1,1,112,112).to(device).float())
net_out = net_out[0]
predictied_class = torch.argmax(net_out)
if predictied_class == real_class:
correct += 1
total += 1
net.train()
net.to('cuda')
return round(correct/total,3)
EPOCHS = 3
EPOCSH = 5
# +
lrs = [1.0,0.1,0.01,0.001,0.0001,0.125,0.25,0.5,0.75]
for lr in lrs:
model = Test_Model(conv1_output=32,conv2_output=8,conv3_output=64,fc1_output=512,fc3_output=256,fc2_output=512,activation=nn.CELU()).to(device)
optimizer = optim.SGD(model.parameters(),lr=lr)
criterion = nn.CrossEntropyLoss()
wandb.init(project=PROJECT_NAME,name=f'lr-{lr}')
for _ in tqdm(range(EPOCHS)):
for i in range(0,len(X_train),BATCH_SIZE):
X_batch = X_train[i:i+BATCH_SIZE].view(-1,1,112,112).to(device)
y_batch = y_train[i:i+BATCH_SIZE].to(device)
model.to(device)
preds = model(X_batch.float())
preds.to(device)
loss = criterion(preds,torch.tensor(y_batch,dtype=torch.long))
optimizer.zero_grad()
loss.backward()
optimizer.step()
wandb.log({'loss':get_loss(criterion,y_train,model,X_train),'accuracy':test(model,X_train,y_train),'val_accuracy':test(model,X_test,y_test),'val_loss':get_loss(criterion,y_test,model,X_test)})
for index in range(10):
print(torch.argmax(preds[index]))
print(y_batch[index])
print('\n')
wandb.finish()
| wandb/run-20210519_171202-20j3w5aa/tmp/code/_session_history.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Merge Two Sorted Lists
# + active=""
# Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.
# Example:
# Input: 1->2->4, 1->3->4
# Output: 1->1->2->3->4->4
# +
class ListNode: # 條件鏈表
def __init__(self, x):
self.val = x
self.next = None
def list2node(lst): # 生成鏈表
res = ListNode(lst[0])
var = res
for x in lst[1:]:
var.next = ListNode(x)
var = var.next
return res
def node2list(l): # 顯使鏈表
lst = []
node = l
while node != None:
lst.append(node.val)
node = node.next
return lst
class Solution:
def mergeTwoLists(self, l1, l2): # 遞迴 89.83%
if not l1: # l1 = None
return l2
if not l2: # l2 = Nome
return l1
if l1.val <= l2.val:
l1.next = self.mergeTwoLists(l1.next, l2)
return l1
else:
l2.next = self.mergeTwoLists(l1, l2.next)
return l2
def mergeTwoLists2(self, l1, l2): # 51.92%
lst = self.node2list(l1) + self.node2list(l2)
if lst == []: # l1 = l2 = emtpy
return l1
lst.sort()
res = ListNode(lst[0])
var = res
for x in lst[1:]:
var.next = ListNode(x)
var = var.next
return res
def node2list(self, l): # 作弊 提取出來 lst
lst = []
node = l
while node != None:
lst.append(node.val)
node = node.next
return lst
# -
l1 = ListNode.list2node([1, 2, 4])
l2 = ListNode.list2node([1, 3, 4])
ans = Solution()
node = ans.mergeTwoLists(l1, l2)
ListNode.node2list(node)
# %%timeit
l1 = ListNode.list2node([i for i in range(100) if i % 3 == 1])
l2 = ListNode.list2node([i for i in range(100) if i % 2 == 1])
ans.mergeTwoLists(l1, l2)
# %%timeit
l1 = ListNode.list2node([i for i in range(100) if i % 3 == 1])
l2 = ListNode.list2node([i for i in range(100) if i % 2 == 1])
ans.mergeTwoLists2(l1, l2)
hea
| 021. Merge Two Sorted Lists.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Build your own tensor type
#
# We present here a core concept of the PySyft library. It is the ability to add new custom tensor types that can provide specific behaviors such as encryption or traceability. This feature makes our library very generic and completely open to new innovations in the field of privacy-preserving machine learning.
#
# We will go through a very simple example which could be the base for a traceability feature that would keep track of the operations performed on the data in a verifiable way. This new tensor type will log all operations executed on tensors of its type. Let's call this type the CustomLoggingTensor.
#
# Authors:
# - <NAME> - Twitter: [@theoryffel](https://twitter.com/theoryffel)
# ## 0. Preliminaries
#
# We use the sandbox that we have already discovered.
#
import torch as th
import syft as sy
sy.create_sandbox(globals(), verbose=False)
# Let's first recall the notions of Torch and Syft tensors. All the object the end user manipulates are torch tensors. This is of course the case when it's a pure torch tensor (ex: `x = th.tensor([1., 2])`), but also when you deal with syft objects, such as the pointer tensor which is a particular case of syft tensor.
ptr = th.tensor([1., 2]).send(bob)
ptr
# The wrapper object you see is actually an empty torch tensor with a child argument which is a PointerTensor:
isinstance(ptr, th.Tensor)
type(ptr.child)
# This is also true for more complex objects, where you also see this wrapper at the beginning. You can then have multiple Syft or Torch tensors chained through the `.child` attribute.
x = th.tensor([1., 2]).fix_prec().share(alice, bob)
x
x.child
x.child.child.child
# Recall that the general behaviour is the following: each time a command in called on the top object, it goes down the chain where it can be modified, it is then executed at the bottom and the result is wrapped back to have exactly the some chain structure, to keep the same properties (such as traceability for example).
# What we're going to do here is to create our own syft Tensor type that we will be able to put in this chain!
# ## 1. The MVP of the CustomLoggingTensor
#
# ### 1.1 Declare the class type
# To get started, there isn't much things to do. First, we need to create the tensor class.
#
# This is done in `syft/frameworks/torch/tensors/`, choose the folder:
# - `interpreters` if the functionality you want to build will modify the results or functions, or
# - `decorators` if the functionality is just ... decorative.
#
# > _The `interpreters` / `decorators` might be removed in the future, in which case just put your tensor in `syft/frameworks/torch/tensors/`_
#
# Here we'll put it in the decorator folder. Choose a simple **but explicit** name, for now `decorators/custom_logging.py` will be sufficient.
#
# Write there the minimal class definition, where our tensor inherits from `AbstractTensor`, an abstraction which gives default bahaviours to Syft tensors:
# +
from syft.generic.tensor import AbstractTensor
class CustomLoggingTensor(AbstractTensor):
def __init__(self, **kwargs):
super().__init__(**kwargs)
# -
# This was quite fast, wasn't it?
# ### 1.2 Add to the hooks
#
# #### 1.2.1 Allow imports
# You now need to declare this type in the imports so that you can use it in real. Add it in the files:
# ```
# - syft/frameworks/torch/tensors/[decorators|interpreters]/__init__.py
# - syft/__init__.py
# ```
# You should now be able to import the tensor type: `from syft import CustomLoggingTensor`
#
# #### 1.2.2 Hook tensor to add torch operations
# In the `syft/frameworks/torch/hook/hook.py` file:
# - Add an import line at the top
# - Add the following in the TorchHook `__init__`: `self._hook_syft_tensor_methods(CustomLoggingTensor)`
#
# All instances of CustomLoggingTensor now have for example a `.add(...)` method. We should now explain how to use it.
#
# #### 1.2.3 Hook tensor to correctly forward arguments to the torch operations
#
# In particular we would like that arguments provided as CustomLoggingTensor be unwrapped and replaced with their .child attribute, do go down the chain.
#
# In the `syft/frameworks/torch/hook/hook_args.py` file:
# - Add an import line at the top
# - Extend the `type_rule` dict with `CustomLoggingTensor: one,` (means that this type of tensors supports (un)wrapping)
# - Extend the `forward_func` dict with `CustomLoggingTensor: lambda i: i.child,` (explains how to unwrap)
# - Extend the `backward_func` dict with `CustomLoggingTensor: lambda i, **kwargs: CustomLoggingTensor(**kwargs).on(i, wrap=False),` (explains how to wrap)
#
#
# Et voilà! You can already do many things with your new tensor!
x = CustomLoggingTensor()
x
# Ok this is not super useful, but it comes with a `.on` method which works as follow:
x = th.tensor([1., 2])
x = CustomLoggingTensor().on(x)
x
# `.on` simply inserts the tensor node into a tensor chain. As we always need to have a torch tensor at the top of the chain, a wrapper was automatically added.
#
# ### Ready to use!
# As this point, if you want to have the behaviour desired, you should make the code changes in the repository: integrating the code in the repository allows you to benefit from the hooking functionalities.
# In particular, after re-instantiating the hook, your `CustomLoggingTensor` should have the methods a pure torch tensor has.
#
# > **Make the change and re-run the notebook up to here**
# This time, we add the `sy.` meaning the code is from the repo.
x = th.tensor([1., 2])
x = sy.CustomLoggingTensor().on(x)
x
# You can do computations on this chain such as `x * 2`, and for example the call `__mul__` made will be forwarded all through the chain down to the last node which is a pure torch tensor, whose value is doubled.
x * 2
# If you correctly obtained `(Wrapper)>CustomLoggingTensor>tensor([2., 4.])`, you're all set!
# ## 2. Adding special functionalities
# Now that you have defined your own tensor type, you should specify it's behaviour, as by default it won't do anything thing special and will just act passively.
#
# In this part, we will see how to specify custom functionalities. We'll use for the execution parts the already existing `LoggingTensor` instead of the `CustomLoggingTensor` and highlight which part of code produces which functionalities, so that you can run code in this notebook without reloading the kernel. If you want to practice more, you can report the code changes in the `CustomLoggingTensor` class definition and you'll observe the same behaviours (just reload the notebook each time you perform a modification in the library code)
from syft import LoggingTensor
# ### 2.1 Default behaviour for functions
#
# You can add a special functionality each time a (hooked) torch **function** is called on `LoggingTensor`: here we just print the call.
#
# Note that this is for functions exclusively and not for methods, but applies for all hooked torch functions
class CustomLoggingTensor(AbstractTensor):
def __init__(self, **kwargs):
super().__init__(**kwargs)
@classmethod
def on_function_call(cls, command):
"""
Override this to perform a specific action for each call of a torch
function with arguments containing syft tensors of the class doing
the overloading
"""
cmd, _, args, kwargs = command
print("Default log", cmd)
# +
x = th.tensor([1., 2])
x = LoggingTensor().on(x)
th.div(x, x)
th.nn.functional.celu(x) # celu is a variant of the activation function relu(x) = max(0, x)
# -
# > Note: this `on_function_call` is called by `handle_func_command` which comes from the `AbstractTensor`: it explains how to propagate functions down the chain, and in some cases you might also need to change it.
# ### 2.2 Overloading torch methods
#
# We introduce here an important decorator object which is @overloaded:
from syft.generic.frameworks.overload import overloaded
# You can directly overwrite torch methods like this, where we overload the `.add` method so that we first print that it was called and then forward the call to the .child attributes.
class CustomLoggingTensor(AbstractTensor):
def __init__(self, **kwargs):
super().__init__(**kwargs)
@overloaded.method
def add(self, _self, *args, **kwargs):
print("Log method add")
response = _self.add(*args, **kwargs)
return response
# Here is an example of how to use the `@` `overloaded.method` decorator. To see
# what this decorator do, just look at the next method manual_add: it does
# exactly the same but without the decorator.
#
# Note the subtlety between `self` and `_self`: you should use `_self` and **NOT** `self`. We kept `self` because it can hold useful attributes that you might want to access (for example, for the fixed precision tensor it stores the field size)
#
# Here is the version of the add method without the decorator: as you can see
# it is much more complicated. However you might need sometimes to use it to specify
# some particular behaviour: so here where to start from if needed!
class CustomLoggingTensor(AbstractTensor):
# [...]
def manual_add(self, *args, **kwargs):
# Replace all syft tensor with their child attribute
new_self, new_args, new_kwargs = syft.frameworks.torch.hook_args.hook_method_args(
"add", self, args, kwargs
)
print("Log method manual_add")
# Send it to the appropriate class and get the response
response = getattr(new_self, "add")(*new_args, **new_kwargs)
# Put back SyftTensor on the tensors found in the response
response = syft.frameworks.torch.hook_args.hook_response(
"add", response, wrap_type=type(self)
)
return response
# They behave exactly the same and print a line when called
# +
x = LoggingTensor().on(th.tensor([1., 2]))
print(x)
r = x.add(x)
# -
# _You might want to try to run_ `r = x.manual_add(x)` _but this will fail: if the LoggingTensor which is `x.child` had a_ `.manual_add` _method, this is not the case for the wrapper `x` as torch tensor don't have_ `.manual_add` _by default._
# ### 2.3 Overloading torch functions
#
# We will still use the @overloaded decorator but now with:
#
# ```
# - @overloaded.module
# - @overloaded.function
# ```
#
# What we want to do is to overload
#
# ```
# - torch.add
# - torch.nn.functional.relu
# ```
class CustomLoggingTensor(AbstractTensor):
# [...]
@staticmethod
@overloaded.module
def torch(module):
"""
We use the @overloaded.module to specify we're writing here
a function which should overload the function with the same
name in the <torch> module
:param module: object which stores the overloading functions
Note that we used the @staticmethod decorator as we're in a
class
"""
def add(x, y):
"""
You can write the function to overload in the most natural
way, so this will be called whenever you call torch.add on
Logging Tensors, and the x and y you get are also Logging
Tensors, so compared to the @overloaded.method, you see
that the @overloaded.module does not hook the arguments.
"""
print("Log function torch.add")
return x + y
# Just register it using the module variable
module.add = add
@overloaded.function
def mul(x, y):
"""
You can also add the @overloaded.function decorator to also
hook arguments, ie all the LoggingTensor are replaced with
their child attribute
"""
print("Log function torch.mul")
return x * y
# Just register it using the module variable
module.mul = mul
# You can also overload functions in submodules!
@overloaded.module
def nn(module):
"""
The syntax is the same, so @overloaded.module handles recursion
Note that we don't need to add the @staticmethod decorator
"""
@overloaded.module
def functional(module):
@overloaded.function
def relu(x):
print("Log function torch.nn.functional.relu")
return x * (x > 0).float()
module.relu = relu
module.functional = functional
# Modules should be registered just like functions
module.nn = nn
# Note the diffence between `def add` and `def mul`: `def add` doesn't have `@` `overloaded.function` which means that the args inside are not unwrapped: there are CustomLoggingTensors, while in `def mul` they are unwrapped and replaced by the child attributes, so Torch tensors in our case.
# Look how it changes compared to 2.1: the behaviour is not much different but now the functions modified are very precisely targetted:
# +
x = th.tensor([1., 2])
x = LoggingTensor().on(x)
# Default overloading made in 2.1
r = th.div(x, x)
# Targetted overloading made in 2.3
r = th.add(x, x)
# -
# Also, compared to 2.1, we changed the function behaviour: for relu for example instead of running the built-in relu we run `x * (x > 0)`, even if the output is the same. We could have also called inside the native relu if we wanted, provided that we unwrap the args using `@` `overloaded.function`, otherwise we would loop indefinitely.
# ```python
# @overloaded.module
# def functional(module):
# @overloaded.function
# def relu(x):
# print("Log function torch.nn.functional.relu")
# return torch.nn.functional.relu(x)
# ```
# ### 2.4 Adding custom tensor attributes
#
# Sometimes you need to add special attributes to your Syft Tensor, like the FixedPrecisionTensor which has a field attribute for example:
fp = th.tensor([1., 2]).fix_precision()
print(fp)
print("Field:", fp.child.field)
# Just declare them in the `__init__`, like for example a `log_max_size`:
class CustomLoggingTensor(AbstractTensor):
def __init__(self, log_max_size=64, **kwargs):
super().__init__(**kwargs)
self.log_max_size = log_max_size
# [...]
# To make sure this value gets correctly added to the response of an operation, when the chain is rebuilt and that a CustomLoggingTensor is wrapped on top of the result, you should declare `get_class_attributes`:
class CustomLoggingTensor(AbstractTensor):
# [...]
def get_class_attributes(self):
"""
Return all elements which defines an instance of a certain class.
"""
return {
'log_max_size': self.log_max_size
}
# ### 2.5 Sending CustomLoggingTensors
# Last thing we love to do, is to sent tensors across workers!
#
#
# To do so, you need to add a serializer and a deserializer to the class:
# +
# Add these new imports
import syft
from syft.workers import AbstractWorker
class CustomLoggingTensor(AbstractTensor):
# [...]
@staticmethod
def simplify(tensor: "CustomLoggingTensor") -> tuple:
"""Takes the attributes of a CustomLoggingTensor and saves them in a tuple.
Args:
tensor: a CustomLoggingTensor.
Returns:
tuple: a tuple holding the unique attributes of the CustomLoggingTensor.
"""
chain = None
if hasattr(tensor, "child"):
chain = syft.serde._simplify(tensor.child)
return (
syft.serde._simplify(tensor.id),
tensor.log_max_size,
syft.serde._simplify(tensor.tags),
syft.serde._simplify(tensor.description),
chain,
)
@staticmethod
def detail(worker: AbstractWorker, tensor_tuple: tuple) -> "CustomLoggingTensor":
"""
This function reconstructs a CustomLoggingTensor given it's attributes in form of a tuple.
Args:
worker: the worker doing the deserialization
tensor_tuple: a tuple holding the attributes of the CustomLoggingTensor
Returns:
CustomLoggingTensor: a CustomLoggingTensor
Examples:
shared_tensor = detail(data)
"""
tensor_id, log_max_size, tags, description, chain = tensor_tuple
tensor = CustomLoggingTensor(
owner=worker,
id=syft.serde._detail(worker, tensor_id),
log_max_size=log_max_size,
tags=syft.serde._detail(worker, tags),
description=syft.serde._detail(worker, description),
)
if chain is not None:
chain = syft.serde._detail(worker, chain)
tensor.child = chain
return tensor
# -
# And to declare this new tensor to the ser/deser module: in `serde/serde.py`:
# - Add an import for CustomLoggingTensor
# - Append CustomLoggingTensor to the `OBJ_SIMPLIFIER_AND_DETAILERS` list
#
# Everyting should now work correctly:
# +
x = th.tensor([1., 2])
x = sy.LoggingTensor().on(x)
p = x.send(alice)
print(p)
p2 = p + p
x2 = p2.get()
print(x2)
# -
# And here you are, you should now understand all the tools we've builded so that you can easily build new tensor types and focus on their behaviour rather than on their integration in the PySyft library.
# # Congratulations!!! - Time to Join the Community!
#
# Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the movement toward privacy preserving, decentralized ownership of AI and the AI supply chain (data), you can do so in the following ways!
#
# ### Star PySyft on GitHub
#
# The easiest way to help our community is just by starring the Repos! This helps raise awareness of the cool tools we're building.
#
# - [Star PySyft](https://github.com/OpenMined/PySyft)
#
# ### Join our Slack!
#
# The best way to keep up to date on the latest advancements is to join our community! You can do so by filling out the form at [http://slack.openmined.org](http://slack.openmined.org)
#
# ### Join a Code Project!
#
# The best way to contribute to our community is to become a code contributor! At any time you can go to PySyft GitHub Issues page and filter for "Projects". This will show you all the top level Tickets giving an overview of what projects you can join! If you don't want to join a project, but you would like to do a bit of coding, you can also look for more "one off" mini-projects by searching for GitHub issues marked "good first issue".
#
# - [PySyft Projects](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3AProject)
# - [Good First Issue Tickets](https://github.com/OpenMined/PySyft/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
#
# ### Donate
#
# If you don't have time to contribute to our codebase, but would still like to lend support, you can also become a Backer on our Open Collective. All donations go toward our web hosting and other community expenses such as hackathons and meetups!
#
# [OpenMined's Open Collective Page](https://opencollective.com/openmined)
| examples/tutorials/advanced/Build your own tensor type (advanced).ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# <font size="4" style="color:red;"> **IMPORTANT: ** When submitting this notebook as homework, make sure you Only modify cells which have the following comment</font>
#
# ```python
# # modify this cell
# ```
#
#
# ## Setup Notebook
# %pylab inline
from scipy import *
from numpy.linalg import norm
from math import sqrt,sin,cos
import pandas as pd
import numpy as np
from numpy import arange,array,ones,linalg
# Below is a **helper function** that outputs a predicted value from a regression fit:
def f(x, reg):
return reg[0]+ x*reg[1]
# # Regression
# It is now your turn to try out all of the above code. For this exercise you will measure the relationship between hours studyig and student grades for a simulated dataset. Below is a scatter plot of the data.
# +
data = pd.read_csv('data/hw_regression_data.csv')
print(data.shape)
data.head()
ax= data.plot(kind='scatter',s=1.4,x="study_hours",y="grades",figsize=[10,8]);
# -
# ## Exercise 1: Get Averages
#
# Write a function, <code><font color="blue">get_averages</font>(data)</code>, that:
# 1. For all data points round the student's study hours to the nearest whole number.
# 2. Compute the mean grade for each rounded whole number of study hours.
#
# The function should return a pandas dataframe of the mean grades for each existing rounded whole number. The beginning of the panda dataframe is provided for you below:
#
# <font style="color:blue"> * **Code:** *</font>
# ```python
# grade_means = get_averages(data)
#
# print type( grade_means )
# print grade_means.shape
# print grade_means.columns
# grade_means.head()
# ```
#
# <font style="color:magenta"> * **Output:** *</font>
# ```
# <class 'pandas.core.frame.DataFrame'>
# (38, 1)
# Index([u'grades'], dtype='object')
# ```
# <img src="data/reg_ex_table.png" style="width: 190px;"/>
df = pd.read_csv('data/hw_regression_data.csv')
df['round_study_hours'] = df['study_hours'].round()
df = df.groupby('round_study_hours').mean()[['grades']]
df.head()
# +
# modify this cell
def get_averages(data):
data['round_study_hours'] = data['study_hours'].round()
data = data.groupby('round_study_hours').mean()[['grades']]
return data
# input: the HW's dataset
# output: a pandas dataframe yielding the mean grade for each rounded number of study hours
#
# YOUR CODE HERE
#
# + nbgrader={"grade": true, "grade_id": "ex1", "locked": true, "points": "5", "solution": false}
# check student function
grade_means = get_averages(data)
assert grade_means.shape == (38, 1)
assert str(type(grade_means)) == "<class 'pandas.core.frame.DataFrame'>"
try: assert grade_means.columns[0] == "grades"
except: raise ValueError('the column in "grade_means" must be named grades')
try: assert sum(abs( grade_means.tail()["grades"].values - \
np.array([ 90.77739,90.02272,92.97258,91.87963,93.48365]) )) < 10**-4
except: raise ValueError('some values are incorrect in grade_means')
# plot Graph
ax= data.plot(kind='scatter',s=1.4,x="study_hours",y="grades",figsize=[10,8]);
grade_means.plot(y='grades',style='ro', ax=ax,legend=False)
_xlim = xlim()
_ylim =ylim()
for _x in arange(_xlim[0]+0.5,_xlim[1],1):
plot([_x,_x],[_ylim[0],_ylim[1]],'g')
#
# AUTOGRADER TEST - DO NOT REMOVE
#
# -
# ## Exercise 2: Simple Linear Regression
#
# Write a function, <code><font color="blue">do_regression</font>(data)</code>, that performs linear regression to return
# $ \;
# {\bf w} = \begin{pmatrix}
# w_0\\
# w_1
# \end{pmatrix}
# $
# for the equation:
#
# $$
# \text{grades}= w_0 + w_1 \cdot \text{study_hours}
# $$
#
# ** *Hint* **: Use the function `linalg.lstsq`
#
#
# <font style="color:blue"> * **Code:** *</font>
# ```python
# w = do_regression(data)
# print type(w)
# print w.shape
# ```
#
# <font style="color:magenta"> * **Output:** *</font>
# ```
# <type 'numpy.ndarray'>
# (2,)
# ```
df = pd.read_csv('data/hw_regression_data.csv')
df.head()
# +
df = pd.read_csv('data/hw_regression_data.csv')
A=np.array(df['study_hours'])
A=np.array([ones(len(A)),A])
y=np.array(df['grades'])
A.shape,y.shape
w1 = linalg.lstsq(A.T,y)[0] # finding the optimal parameters
print type(w1)
print w1.shape
# +
# modify this cell
def do_regression(data):
A=np.array(data['study_hours'])
A=np.array([ones(len(A)),A])
y=np.array(data['grades'])
A.shape,y.shape
w = linalg.lstsq(A.T,y)[0] # finding the optimal parameters
return w1
# input: the HW's dataset
# output: a numpy array yielding w=(w0,w1) from linear regression
#
# YOUR CODE HERE
#
# + nbgrader={"grade": true, "grade_id": "ex2", "locked": true, "points": "5", "solution": false}
# check student function
w1_hw = do_regression(data)
assert str(type(w1_hw)) == "<class 'numpy.ndarray'>"
assert w1_hw.shape == (2,)
assert abs(w1_hw[0] - 48.0694704904) < 10**-5
# plot Means
print(w1_hw)
ax= data.plot(kind='scatter',s=1.4,x="study_hours",y="grades",figsize=[10,8]);
x0,x1=xlim()
print(x0, x1)
ax.plot([x0,x1],[f(x0,w1_hw),f(x1,w1_hw)],'k');
#
# AUTOGRADER TEST - DO NOT REMOVE
#
# -
# ## Exercise 3: Reversed Regression
#
# Write a function, <code><font color="blue">reverse_regression</font>(data)</code>, that again performs linear regression to return
# $ \;
# {\bf w} = \begin{pmatrix}
# w_0\\
# w_1
# \end{pmatrix}
# $
# but this time for:
#
# $$
# \text{study_hours}= w_0 + w_1 \cdot \text{grades}
# $$
#
#
# <font style="color:blue"> * **Code:** *</font>
# ```python
# w = reverse_regression(data)
# print type(w)
# print w.shape
# ```
#
# <font style="color:magenta"> * **Output:** *</font>
# ```
# <type 'numpy.ndarray'>
# (2,)
# ```
# +
# modify this cell
def reverse_regression(data):
A=np.array(data['grades'])
A=np.array([ones(len(A)),A])
y=np.array(data['study_hours'])
A.shape,y.shape
w = linalg.lstsq(A.T,y)[0] # finding the optimal parameters
return w1
# input: the HW's dataset
# output: a numpy array yielding w=(w0,w1) for the reversed linear regression
#
# YOUR CODE HERE
#
# +
reverse_regression(data)[1]
df = pd.read_csv('data/hw_regression_data.csv')
A=np.array(df['grades'])
A=np.array([ones(len(A)),A])
y=np.array(df['study_hours'])
A.shape,y.shape
w1 = linalg.lstsq(A.T,y)[0] # finding the optimal parameters
w1
# + nbgrader={"grade": true, "grade_id": "ex3", "locked": true, "points": "5", "solution": false}
# check answer
w2_hw = reverse_regression(data)
assert str(type(w2_hw)) == "<class 'numpy.ndarray'>"
assert w2_hw.shape == (2,)
assert abs(w2_hw[0] - -31.85141332) < 10**-5
# plot graph
ax= data.plot(kind='scatter',s=1.4,x="study_hours",y="grades",figsize=[10,8]);
x0,x1=xlim()
ax.plot([x0,x1],[f(x0,w1_hw),f(x1,w1_hw)],'k');
y0,y1=ylim()
ax.plot([f(y0,w2_hw),f(y1,w2_hw)],[y0,y1],'r');
#
# AUTOGRADER TEST - DO NOT REMOVE
#
# -
# # Regression to the Mean
# It is now your turn to do regression on a dataset. Consider $1000$ datapoints with random variables $x$ and $y$ both sampled from a normal (gaussian) distribution:
# $$ x,y \text{ ~ } \mathcal{N}(0,1) $$
#
# Notice that the graph below looks like a blob, with no clear relationship between $x$ and $y$. This leads intuitively to the idea that $x$ and $y$ are independent from each other. In this particualr case (not always true) this intuition is correct, $x$ and $y$ are mathematically independent variables.
#
# If we were to try to perform linear regression on this data (the <font style="color:red">red line</font>), we would find rather boring results:
# $$ y = 0 + 0 \cdot x = 0 $$
#
# This is due to the fact that $y$ has mean 0 and is independent of $x$. What do you think would happen if we did:
# $$ y-x = w_0 + w_1 \cdot x $$
#
# Is $y$ independent of $x$? Will the graph look like a blob? Will $y-x = 0 ?$ Lets find out!
# +
HW=pd.read_csv('data/gauss_R2.csv')
ax= HW.plot(kind='scatter',s=1.4,x="x",y="y");
x0,x1=xlim()
ax.plot([x0,x1],[0,0],'r');
# -
# ### Exercise 4: Put $\;y-x\;$ in Dataframe
#
# This first exercise's goal is to familarize you with the [pandas](http://pandas.pydata.org/pandas-docs/version/0.15.2/tutorials.html) package.
#
# Your task is to make a new column on the pandas dataframe `HW` where each element of the new column is equal to $y-x$. Write a function <code><font color="blue">y_minus_x</font>(HW)</code> that will create the new column, make sure the column's name is "y-x" . Notice that the function DOES NOT return any output, this is because the `HW` dataframe will be edited "in-place".
#
# <font style="color:blue"> * **Code:** *</font>
# ```python
# print y_minus_x(HW)
# print HW.shape
# print HW.columns
# HW.head()
# ```
#
# <font style="color:magenta"> * **Output:** *</font>
# ```
# None
# (1000, 3)
# Index([u'x', u'y', u'y-x'], dtype='object')
# ```
# <img src="data/reg_mean_pic.png" style="width: 220px;"/>
# +
HW=pd.read_csv('data/gauss_R2.csv')
HW['y-x'] = HW['y']-HW['x']
HW.head()
HW.shape
HW.columns
# -
HW=pd.read_csv('data/gauss_R2.csv')
def y_minus_x(HW):
HW['y-x'] = HW['y']-HW['x']
# input: the HW's dataset
# output: there is NO OUTPUT
#
# YOUR CODE HERE
#
# + nbgrader={"grade": true, "grade_id": "ex4", "locked": true, "points": "5", "solution": false}
# Check Answer
HW=pd.read_csv('data/gauss_R2.csv')
assert y_minus_x(HW) == None
assert HW.shape == (1000, 3)
assert all( HW.columns.values == array(['x', 'y', 'y-x']) )
assert sum(abs( array(HW["y-x"])[0:10] - \
array([0.36236278,-2.37726552,-0.36501525,0.05449746,-0.27705517,1.80807383,-2.07001209,
-0.67536514,0.67519959, 0.97277652]) )) < 10**-5
# Create Graph
ax= HW.plot(kind='scatter',s=1.4,x="x",y="y-x",figsize=[10,8], title="Plot of y-x");
#
# AUTOGRADER TEST - DO NOT REMOVE
#
# -
# Notice in the graph that there is a clear negative relationship between $y-x$ and $x$. As you might have guessed, $y-x$ and $x$ are NOT independent.
#
# We can use linear regression to find the relationship between $y-x$ and $x$ but before we do that, we can derive this mathematicaly. Remember from before, we showed:
# $$ y = 0 + 0 \cdot x $$
#
# Now, we're doing linear regression to find:
# $$ \;\;\;\;\;\;y-x = w_0 + w_1 \cdot x $$
# $$ \iff y = w_0 + (1+w_1) \cdot x $$
#
# Comparing the two eqations for $y$, you can deduce that $w_0=0$ and $w_1=-1$ . Now lets see how close our sampled data is to the true equation for the distribution!
#
# $\;$
# <font style="color:red">*Technical Note:*</font> The derivation is mathematically sound only because $y-x$ is also a gaussian random variable. The sum of two gaussians is a gaussian. Under the laws of linear regression this ensures both the regressors of $y$ and $y-x$ have zero expected error.
# ### Exercise 5: Simple Linear Regression
#
# Write a function, <code><font color ="blue">do_regression</font>(HW)</code>, that performs linear regression to return
# $ \;
# {\bf w} = \begin{pmatrix}
# w_0\\
# w_1
# \end{pmatrix}
# $
# for the equation:
#
# $$
# \text{y-x}= w_0 + w_1 \cdot \text{x}
# $$
#
# <font style="color:blue"> * **Code:** *</font>
# ```python
# w = do_regression(HW)
# print type(w)
# print w.shape
# ```
#
# <font style="color:magenta"> * **Output:** *</font>
# ```
# <type 'numpy.ndarray'>
# (2,)
# ```
HW=pd.read_csv('data/gauss_R2.csv')
HW['y-x'] = HW['y']-HW['x']
A=np.array(HW['x'])
A=np.array([ones(len(A)),A])
y=np.array(HW['y-x'])
w = linalg.lstsq(A.T,y)[0]
w
# +
# modify this cell
def do_regression(HW):
A=np.array(HW['x'])
A=np.array([ones(len(A)),A])
y=np.array(HW['y-x'])
w = linalg.lstsq(A.T,y)[0] # finding the optimal parameters
return w1
# input: the HW's dataset
# output: a numpy array yielding w=(w0,w1) from linear regression
#
# YOUR CODE HERE
#
# + nbgrader={"grade": true, "grade_id": "ex5", "locked": true, "points": "5", "solution": false}
# Check Answer
w_hw = do_regression(HW)
assert str(type(w_hw)) == "<class 'numpy.ndarray'>"
assert w_hw.shape == (2,)
assert sum(abs(w_hw[0] - 0.02173387)) < 10**-5
# Plot Graph
print("LINEAR REGRESSION EQUATION:")
print("y-x = {:.2f} + {:.2f} x".format(w_hw[0],w_hw[1]))
ax= HW.plot(kind='scatter',s=1.4,x="x",y="y-x",figsize=[10,8]);
x0,x1=xlim()
ax.plot([x0,x1],[f(x0,w_hw),f(x1,w_hw)],'k');
#
# AUTOGRADER TEST - DO NOT REMOVE
#
# -
| Week 12 _ Regression and PCA/HW_Topic12.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Nested List Exercises
# ### Problem 1
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
# ### Problem 2
matrix[1][1]
# ### Problem 3
for i in range(3):
for j in range(3):
print(matrix[i][j])
# ### Problem 4
for i in range(3):
print("Row", i+1, "sum:", sum(matrix[i]))
# ## Nested List Comprehension Exercises
# ### Problem 1
matrix = [[0 for j in range(3)] for i in range(3)]
print(*matrix, sep='\n')
# ### Problem 2
matrix = [[i + 1 for j in range(3)] for i in range(3)]
print(*matrix, sep='\n')
# ### Problem 3
matrix = [[i + j for j in range(3)] for i in range(3)]
print(*matrix, sep='\n')
# ### Bonus Problem 1
matrix = [[1 if i < j else 0 for j in range(5)] for i in range(5)]
# alt: matrix = [[int(i < j) for j in range(5)] for i in range(5)]
print(*matrix, sep='\n')
# ### Bonus Problem 2
matrix = [[1 if (i + j) % 2 == 0 else 0 for j in range(5)] for i in range(5)]
print(*matrix, sep='\n')
# ### Bonus Problem 3
matrix = [[abs(i - j) + 1 for j in range(5)] for i in range(5)]
print(*matrix, sep='\n')
# ## Reading Text Files Exercises
# write temporary text file to disk
with open("tmp.txt", 'w') as f:
f.writelines('\n'.join([
'bread 2',
'milk 4',
'egg 10',
'apple 6'
]))
# ### Problem 1
shopping_list = {}
# ### Problem 2
with open("tmp.txt") as f:
lines = f.readlines()
for l in lines:
food, quantity = l.split()
quantity = int(quantity)
# add to dictionary
shopping_list[food] = quantity
print(shopping_list)
# delete temporary file
import os
os.remove('tmp.txt')
# ### Bonus Problem
# Use `shopping_list[food] = shopping_list.get(food, 0) + quantity`
| session_three/session_three_exercise_solutions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## [A Comparison Study of Point-Process Filter and Deep Learning Performance in Estimating Rat Position Using an Ensemble of Place Cells](https://www.researchgate.net/publication/324390955_A_Comparison_Study_of_Point-Process_Filter_and_Deep_Learning_Performance_in_Estimating_Rat_Position_Using_an_Ensemble_of_Place_Cells)
#
# ###### Conference: 40th International Conference of the IEEE Engineering in Medicine and Biology Science (EMBC 2018)At: Hawaii, USA
| Untitled.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="66975503-001" colab_type="text"
# #1. Install Dependencies
# First install the libraries needed to execute recipes, this only needs to be done once, then click play.
#
# + id="66975503-002" colab_type="code"
# !pip install git+https://github.com/google/starthinker
# + [markdown] id="66975503-003" colab_type="text"
# #2. Get Cloud Project ID
# To run this recipe [requires a Google Cloud Project](https://github.com/google/starthinker/blob/master/tutorials/cloud_project.md), this only needs to be done once, then click play.
#
# + id="66975503-004" colab_type="code"
CLOUD_PROJECT = 'PASTE PROJECT ID HERE'
print("Cloud Project Set To: %s" % CLOUD_PROJECT)
# + [markdown] id="66975503-005" colab_type="text"
# #3. Get Client Credentials
# To read and write to various endpoints requires [downloading client credentials](https://github.com/google/starthinker/blob/master/tutorials/cloud_client_installed.md), this only needs to be done once, then click play.
#
# + id="66975503-006" colab_type="code"
CLIENT_CREDENTIALS = 'PASTE CLIENT CREDENTIALS HERE'
print("Client Credentials Set To: %s" % CLIENT_CREDENTIALS)
# + [markdown] id="66975503-007" colab_type="text"
# #4. Enter Airflow Composer Example Parameters
# Demonstration that uses Airflow/Composer native, Airflow/Composer local, and StarThinker tasks in the same generated DAG.
# 1. Execute this using Airflow or Composer, the Colab and UI recipe is for refence only.
# 1. This is an example DAG that will execute and print dates and text.
# 1. Run it once to ensure everything works, then customize it.
# Modify the values below for your use case, can be done multiple times, then click play.
#
# + id="66975503-008" colab_type="code"
FIELDS = {
'auth_read': 'user', # Credentials used for reading data.
}
print("Parameters Set To: %s" % FIELDS)
# + [markdown] id="66975503-009" colab_type="text"
# #5. Execute Airflow Composer Example
# This does NOT need to be modified unless you are changing the recipe, click play.
#
# + id="66975503-010" colab_type="code"
from starthinker.util.configuration import Configuration
from starthinker.util.configuration import execute
from starthinker.util.recipe import json_set_fields
USER_CREDENTIALS = '/content/user.json'
TASKS = [
{
'airflow': {
'__comment__': 'Calls a native Airflow operator.',
'operators': {
'bash_operator': {
'BashOperator': {
'bash_command': 'date'
}
}
}
}
},
{
'starthinker.airflow': {
'__comment__': 'Calls an custom operator, requires import of library.',
'operators': {
'hello': {
'Hello': {
'say': 'Hi, there!'
}
}
}
}
},
{
'hello': {
'__comment__': 'Calls a StarThinker task.',
'auth': 'user',
'say': 'Hello World'
}
}
]
json_set_fields(TASKS, FIELDS)
execute(Configuration(project=CLOUD_PROJECT, client=CLIENT_CREDENTIALS, user=USER_CREDENTIALS, verbose=True), TASKS, force=True)
| colabs/airflow.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Load necessary modules
# +
# uses https://github.com/fizyr/keras-retinanet/
# all credits to https://github.com/hgaiser, https://github.com/de-vri-es
# and the other contributors for their wonderful work
# show images inline
# %matplotlib inline
# automatically reload modules when they have changed
# %load_ext autoreload
# %autoreload 2
# import keras
import keras
# import keras_retinanet
from keras_retinanet import models
from keras_retinanet.utils.image import read_image_bgr, preprocess_image, resize_image
from keras_retinanet.utils.visualization import draw_box, draw_caption
from keras_retinanet.utils.colors import label_color
# import miscellaneous modules
import matplotlib.pyplot as plt
import cv2
import os
import numpy as np
import time
from requests import get
from tqdm import tqdm
# set tf backend to allow memory to grow, instead of claiming everything
import tensorflow as tf
def get_session():
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
return tf.Session(config=config)
# use this environment flag to change which GPU to use
#os.environ["CUDA_VISIBLE_DEVICES"] = "1"
# set the modified tf session as backend in keras
keras.backend.tensorflow_backend.set_session(get_session())
# download file with a progress bar
def download(url, file_name):
# get request
r = get(url, stream=True)
total_size = int(r.headers.get('content-length'))
unit_size = 1024
block_size = unit_size*32
# open in binary mode
with open(file_name, 'wb') as f:
with tqdm(total=np.ceil(total_size // block_size), \
unit='B', unit_scale=True, unit_divisor=unit_size) as pbar:
for data in r.iter_content(block_size):
f.write(data)
pbar.update(len(data))
# -
# ## Load RetinaNet model
# +
# check if model weights are saved locally, otherwise download them
model_path = os.path.join('/snapshots', 'resnet50_coco_best_v2.1.0.h5')
if not(os.path.isfile(model_path)):
# weights not found: download them from https://github.com/fizyr/keras-retinanet/releases
url = "https://github.com/fizyr/keras-retinanet/releases/download/0.5.1/resnet50_coco_best_v2.1.0.h5"
download(url, model_path)
# load retinanet model
model = models.load_model(model_path, backbone_name='resnet50')
# if the model is not converted to an inference model, use the line below
# see: https://github.com/fizyr/keras-retinanet#converting-a-training-model-to-inference-model
# model = models.convert_model(model)
# print(model.summary())
# load label to names mapping for visualization purposes
labels_to_names = {0: 'person', 1: 'bicycle', 2: 'car', 3: 'motorcycle', 4: 'airplane', 5: 'bus', 6: 'train', 7: 'truck', 8: 'boat', 9: 'traffic light', 10: 'fire hydrant', 11: 'stop sign', 12: 'parking meter', 13: 'bench', 14: 'bird', 15: 'cat', 16: 'dog', 17: 'horse', 18: 'sheep', 19: 'cow', 20: 'elephant', 21: 'bear', 22: 'zebra', 23: 'giraffe', 24: 'backpack', 25: 'umbrella', 26: 'handbag', 27: 'tie', 28: 'suitcase', 29: 'frisbee', 30: 'skis', 31: 'snowboard', 32: 'sports ball', 33: 'kite', 34: 'baseball bat', 35: 'baseball glove', 36: 'skateboard', 37: 'surfboard', 38: 'tennis racket', 39: 'bottle', 40: 'wine glass', 41: 'cup', 42: 'fork', 43: 'knife', 44: 'spoon', 45: 'bowl', 46: 'banana', 47: 'apple', 48: 'sandwich', 49: 'orange', 50: 'broccoli', 51: 'carrot', 52: 'hot dog', 53: 'pizza', 54: 'donut', 55: 'cake', 56: 'chair', 57: 'couch', 58: 'potted plant', 59: 'bed', 60: 'dining table', 61: 'toilet', 62: 'tv', 63: 'laptop', 64: 'mouse', 65: 'remote', 66: 'keyboard', 67: 'cell phone', 68: 'microwave', 69: 'oven', 70: 'toaster', 71: 'sink', 72: 'refrigerator', 73: 'book', 74: 'clock', 75: 'vase', 76: 'scissors', 77: 'teddy bear', 78: 'hair drier', 79: 'toothbrush'}
# -
# ## Run detection on example
# +
# load image
image = read_image_bgr('000000008021.jpg')
# # copy to draw on
draw = image.copy()
draw = cv2.cvtColor(draw, cv2.COLOR_BGR2RGB)
# preprocess image for network
image = preprocess_image(image)
image, scale = resize_image(image)
# process image
start = time.time()
boxes, scores, labels = model.predict_on_batch(np.expand_dims(image, axis=0))
print("processing time: ", time.time() - start)
# correct for image scale
boxes /= scale
# visualize detections
for box, score, label in zip(boxes[0], scores[0], labels[0]):
# scores are sorted so we can break
if score < 0.5:
break
color = label_color(label)
b = box.astype(int)
draw_box(draw, b, color=color)
caption = "{} {:.3f}".format(labels_to_names[label], score)
draw_caption(draw, b, caption)
plt.figure(figsize=(15, 15))
plt.axis('off')
plt.imshow(draw)
plt.show()
| notebooks/COCO_evaluation.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# # Deep Learning with CNNs (<NAME> - 001530978)
#
# Abstract : Deep Learning with CNNs is an effective to classsify images of dogs based on their breeds. This study aims to classify dog breeds. Hyperparameter tuning will be done to understand the performance of the hyperparameters. This study looks at the impact of changing the actiovation function, cost function, no. of epochs, gradient estimation, network architecture, network initialization. We will see loss, accuracy and other metrics on TensorBoard to understand performance . We will also see that certain paramerter tuning causes a dramatic difference. The findings from this study indicate that it is important to do hyper parameter tuning for Deep Learning with CNNs.
# +
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
from torchvision.utils import make_grid
import torchvision
from torch.utils.tensorboard import SummaryWriter
import os
import matplotlib.pyplot as plt
import numpy as np
# +
#Data directory
data_dir = os.path.abspath("dog_breeds_cnn.ipynb")[:-len("dog_breeds_cnn.ipynb")]
#Applying Transformation
train_transforms = transforms.Compose([
transforms.Resize(32),
transforms.CenterCrop(32),
transforms.ToTensor()])
test_transforms = transforms.Compose([transforms.Resize(32),
transforms.ToTensor()])
train_data = datasets.ImageFolder(data_dir + 'data/train',
transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + 'data/test',
transform=test_transforms)
# -
#Creating loaders
batch_size = 32
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size, shuffle=True)
#Viewing the images
for images,labels in train_loader:
break
im = make_grid(images[0:10], nrow= 5)
plt.figure(figsize=(10,4))
plt.imshow(np.transpose(im.numpy(),(1,2,0)))
images.shape
class Network(nn.Module):
def __init__ (self, af, weights_init, hd_layers):
super().__init__()
self.af=af
self.weights_init=weights_init
self.hd_layers = hd_layers
self.conv1 = nn.Conv2d(in_channels = 3,out_channels = 5,kernel_size = 5)
if weights_init=='xavier':
torch.nn.init.xavier_uniform(self.conv1.weight)
self.conv2 = nn.Conv2d(in_channels = 5,out_channels = 20,kernel_size = 3)
if self.hd_layers == 3:
self.fc1 = nn.Linear(720,360)
self.fc2 = nn.Linear(360,240)
self.fc3 = nn.Linear(240,120)
else:
self.fc1 = nn.Linear(720,480)
self.fc2 = nn.Linear(480,360)
self.fc3 = nn.Linear(360,240)
self.fc4 = nn.Linear(240,120)
def forward(self,x):
if self.af=='relu':
x = F.relu(self.conv1(x))
x = F.max_pool2d(x,2,2)
x = F.relu(self.conv2(x))
x = F.max_pool2d(x,2,2)
x = x.view(-1,torch.prod(torch.tensor(x.shape[1:])).item())
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.log_softmax(self.fc3(x),dim = 1)
return(x)
else:
x = F.leaky_relu(self.conv1(x))
x = F.max_pool2d(x,2,2)
x = F.leaky_relu(self.conv2(x))
x = F.max_pool2d(x,2,2)
x = x.view(-1,torch.prod(torch.tensor(x.shape[1:])).item())
x = F.leaky_relu(self.fc1(x))
x = F.leaky_relu(self.fc2(x))
x = F.log_softmax(self.fc3(x),dim = 1)
return(x)
def get_num_correct(preds, labels):
return preds.argmax(dim=1).eq(labels).sum().item()
# +
from itertools import product
parameters = dict(
af = ['relu','leaky_relu'],
cf = ['cross_entropy','nll_loss'],
epochs = [5],
ge = ['adam','stochastic'],
hd_layers = [3,4],
weights = ['default','xavier']
)
param_values = [v for v in parameters.values()]
for af,cf,epochs,ge,hd_layers,weights in product(*param_values):
network = Network(af , weights, hd_layers)
images, labels = next(iter(train_loader))
grid = torchvision.utils.make_grid(images)
comment = f' af={af} cf={cf} epochs={epochs} ge ={ge} weights = {weights}'
tb = SummaryWriter(comment=comment)
tb.add_image('images',grid)
tb.add_graph(network,images)
lr = 0.001
if(ge=='adam'):
optimizer = torch.optim.Adam(network.parameters(), lr = lr)
else:
optimizer = torch.optim.SGD(network.parameters(), lr = lr)
print("Activation:",af,"Cost:",cf,"Epochs:",epochs,"Gradient:",ge,"Hidden layers:",hd_layers, "Weights:",weights)
for epoch in range(epochs):
total_loss = 0
total_correct = 0
total_accuracy = 0
# Run the training batches
for batch in train_loader:
b+=1
images,labels = batch
# Apply the model
preds = network(images)
if cf =='nll_loss':
loss = F.cross_entropy(preds,labels)#Calculating loss
else:
loss = F.nll_loss(preds,labels)
# Updating parameters
optimizer.zero_grad()
loss.backward()#Calculating gradients
optimizer.step()#Updating weights
total_loss+=loss.item()
total_correct+=get_num_correct(preds,labels)
total_accuracy+=get_num_correct(preds,labels)/len(preds)
tb.add_scalar("Loss", total_loss, epoch)
tb.add_scalar("Correct", total_correct, epoch)
tb.add_scalar("Accuracy", total_accuracy, epoch)
tb.add_histogram("conv1.bias", network.conv1.bias, epoch)
tb.add_histogram("conv1.weight", network.conv1.weight, epoch)
tb.add_histogram("conv2.bias", network.conv2.bias, epoch)
tb.add_histogram("conv2.weight", network.conv2.weight, epoch)
print("epoch:", epoch, "total_correct:", total_correct, "loss:",total_loss, "accuracy:",total_accuracy)
print()
tb.close()
# -
# ### Changing the activation function
# How does it affect accuracy? How does it affect how quickly the network plateaus?
# ### Changing the cost function
# How does it affect accuracy? How does it affect how quickly the network plateaus?
#
#
# ### Changing the number of epochs
# How does it affect accuracy? How does it affect how quickly the network plateaus?
#
# Increasing from 5 to 10 has increased the accuracy.
# ### Changing the gradient estimation
# How does it affect accuracy? How does it affect how quickly the network plateaus?
#
# Adam seems to always do better than stochasatic gradient here.
# ### Changing the network architecture
# How does it affect accuracy? How does it affect how quickly the network plateaus?
#
#
# ### Changing the network initialization
# How does it affect accuracy? How does it affect how quickly the network plateaus?
#
#
# +
## Conclusion
We can conclude that the Q-learning algorithm is a great way to tackle the problem i.e to balance the Cart Pole. We were getting good rewards but there is a definite need of improvement. We can see that a low learning rate is good as there are not too many updates to the Q table. For this situation, the discount factor being high seems to do the best. This is because intermediary states here will be the tipping of the cart pole and this information is important. Also, decaying the epsilon value gives a good exploration-exploitation tradeoff. Stability seems to be a huge factor from the graphs. Experience Replay and Deep Learning could be used to get better and more stable results.
## References
[1]: Dataset : https://www.kaggle.com/miljan/stanford-dogs-dataset-traintest#
## Licensing
Copyright 2021 <NAME>
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
| .ipynb_checkpoints/dog_breeds_cnn-checkpoint.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # PRMT-2348 Analyse specific CCG data
#
# We’ve done some initial analysis to understand if CCGs undergoing Lloyd George digitisation are generating more failures than the national average - (PRMT 2332). There are a couple of CCGs (shown below) that show they are above average for certain types of failures. This story is to look more in depth for these CCGs at their reasons for failures.
#
# Create the error code combinations table (PRMT 2269) for the following CCGs, with a separate table for May, June, and July
#
# - Fylde and Wyre
# - Birmingham and Solihull
import pandas as pd
import numpy as np
from sklearn.preprocessing import MultiLabelBinarizer
import paths
from data.practice_metadata import read_asid_metadata
from data import gp2gp_response_codes
# +
asid_lookup=read_asid_metadata("prm-gp2gp-ods-metadata-preprod", "v2/2021/7/organisationMetadata.json")
transfer_file_location = "s3://prm-gp2gp-transfer-data-preprod/v4/2021/"
transfer_files = [
"5/transfers.parquet",
"6/transfers.parquet",
"7/transfers.parquet",
]
transfer_input_files = [transfer_file_location + f for f in transfer_files]
transfers_raw = pd.concat((
pd.read_parquet(f)
for f in transfer_input_files
))
transfers = transfers_raw\
.join(asid_lookup.add_prefix("requesting_"), on="requesting_practice_asid", how="left")\
.join(asid_lookup.add_prefix("sending_"), on="sending_practice_asid", how="left")\
transfers['month']=transfers['date_requested'].dt.to_period('M')
transfers["status"] = transfers["status"].str.replace("_", " ").str.title()
# Supplier name mapping
supplier_renaming = {
"SystmOne":"TPP",
None: "Unknown"
}
transfers["sending_supplier"] = transfers["sending_supplier"].replace(supplier_renaming.keys(), supplier_renaming.values())
transfers["requesting_supplier"] = transfers["requesting_supplier"].replace(supplier_renaming.keys(), supplier_renaming.values())
# -
# Filter transfers
ccgs_interested_in = ['NHS Fylde and Wyre CCG'.upper(), 'NHS Birmingham and Solihull CCG'.upper()]
sending_ccg_transfers = transfers[transfers['sending_ccg_name'].isin(ccgs_interested_in)].copy()
requesting_ccg_transfers = transfers[transfers['requesting_ccg_name'].isin(ccgs_interested_in)].copy()
error_code_lookup_file = pd.read_csv(gp2gp_response_codes.path)
error_code_lookup = error_code_lookup_file.set_index("ErrorCode")["ErrorName"]
# +
def convert_error_list_to_tuple(error_code_list, error_code_type):
return [(error_code_type, error_code, error_code_lookup[error_code]) for error_code in set(error_code_list) if not np.isnan(error_code)]
def combine_error_codes(row):
sender_list = convert_error_list_to_tuple(row["sender_error_codes"], "Sender")
intermediate_list = convert_error_list_to_tuple(row["intermediate_error_codes"], "COPC")
final_list = convert_error_list_to_tuple(row["final_error_codes"], "Final")
full_error_code_list = sender_list + intermediate_list + final_list
if len(full_error_code_list) == 0:
return tuple([("No Error Code", "No Error", "N/A")])
else:
return tuple(full_error_code_list)
sending_ccg_transfers["all_error_codes"] = sending_ccg_transfers.apply(combine_error_codes, axis=1)
requesting_ccg_transfers["all_error_codes"] = requesting_ccg_transfers.apply(combine_error_codes, axis=1)
# -
def binarized_error_codes(table_sample):
# keeping this in case we want to consolidate error codes based on the int value rather then combined with error code type
table_sample["error_code_list"]=table_sample["all_error_codes"].apply(lambda error_tuple_list: [error_tuple[1] for error_tuple in error_tuple_list if type(error_tuple[1])!=str])
# split out error codes so we can use them to filter
mlb = MultiLabelBinarizer()
binarized = mlb.fit_transform(table_sample["error_code_list"])
binarized_error_occurences = pd.DataFrame(data=binarized, columns=mlb.classes_, index=table_sample.index)
return pd.concat([table_sample, binarized_error_occurences], axis=1).drop('error_code_list',axis=1)
def generate_high_level_table(transfers_sample, practice_type, ccg_name_field):
# Create High level table
high_level_table=(
transfers_sample
.fillna("N/A")
.groupby([ccg_name_field,practice_type,"requesting_supplier","sending_supplier","status","failure_reason","all_error_codes"])
.size()
.to_frame("Number of Transfers").reset_index()
)
# Count % of transfers
total_number_transfers = transfers_sample.shape[0]
high_level_table["% of Transfers"]=(
high_level_table["Number of Transfers"]/total_number_transfers
).multiply(100)
# Count by supplier pathway
supplier_pathway_counts = (
transfers_sample
.fillna("Unknown")
.groupby(by=["sending_supplier", "requesting_supplier"])
.size()
)
high_level_table["% Supplier Pathway Transfers"]=(
high_level_table
.apply(lambda row: row["Number of Transfers"]/supplier_pathway_counts.loc[(row["sending_supplier"],row["requesting_supplier"])],axis=1)
.multiply(100)
)
# Add in Paper Fallback columns
total_fallback = transfers_sample["failure_reason"].dropna().shape[0]
fallback_bool=high_level_table["status"]!="Integrated On Time"
high_level_table.loc[fallback_bool,"% Paper Fallback"]=(
high_level_table["Number of Transfers"]/total_fallback
).multiply(100)
# % of error codes column
no_error_tuple = tuple([("No Error Code", "No Error", "N/A")])
error_code_bool = transfers_sample["all_error_codes"]!=no_error_tuple
total_number_of_error_code_combinations=error_code_bool.sum()
table_error_code_bool = high_level_table["all_error_codes"]!=no_error_tuple
high_level_table.loc[table_error_code_bool,"% of error codes"]=(
high_level_table.loc[table_error_code_bool, "Number of Transfers"]/total_number_of_error_code_combinations
).multiply(100)
# Select and re-order table
grouping_columns_order=[ccg_name_field,practice_type,"requesting_supplier","sending_supplier","status","failure_reason", "all_error_codes"]
counting_columns_order=["Number of Transfers","% of Transfers","% Supplier Pathway Transfers","% Paper Fallback","% of error codes"]
high_level_table=(
high_level_table[grouping_columns_order+counting_columns_order]
.sort_values(by="Number of Transfers",ascending=False)
)
high_level_table=binarized_error_codes(high_level_table)
return high_level_table
with pd.ExcelWriter("Error Code Combinations Tables CCG Requester View PRMT-2348.xlsx") as writer:
generate_high_level_table(requesting_ccg_transfers.copy(), "requesting_practice_name", "requesting_ccg_name").to_excel(writer, sheet_name="All",index=False)
[generate_high_level_table(requesting_ccg_transfers[(requesting_ccg_transfers['month']==month) & (requesting_ccg_transfers['requesting_ccg_name']==ccg)].copy(),"requesting_practice_name","requesting_ccg_name").to_excel(writer, sheet_name=f"{ccg[0:5]} {month}",index=False) for month in requesting_ccg_transfers['month'].unique() for ccg in ccgs_interested_in]
with pd.ExcelWriter("Error Code Combinations Tables CCG Sender View PRMT-2348.xlsx") as writer:
generate_high_level_table(sending_ccg_transfers.copy(), "sending_practice_name", "sending_ccg_name").to_excel(writer, sheet_name="All",index=False)
[generate_high_level_table(sending_ccg_transfers[(sending_ccg_transfers['month']==month) & (sending_ccg_transfers['sending_ccg_name']==ccg)].copy(),"sending_practice_name","sending_ccg_name").to_excel(writer, sheet_name=f"{ccg[0:5]} {month}",index=False) for month in sending_ccg_transfers['month'].unique() for ccg in ccgs_interested_in]
| notebooks/69-PRMT-2348-ccgs-error-code-combinations.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python2
# ---
# ## Convolutional neural networks
# %matplotlib inline
import tensorflow as tf
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from ipywidgets import FloatProgress
from IPython.display import display
import time
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("../MNIST_data/",one_hot=True)
mnist.train.next_batch(100)[0].shape
n_training_size,n_features = mnist.train.images.shape
n_test_size = mnist.test.images.shape[0]
batch_size = 100
n_epochs = 5
# ## Structure of the Model
# 
tf.reset_default_graph()
with tf.variable_scope("input") as scope:
image = tf.placeholder(dtype=tf.float32,shape=[None,28,28,1],name="image")
y = tf.placeholder(dtype=tf.float32,shape=[None,10],name="label")
with tf.variable_scope("conv1") as scope:
w = tf.get_variable(name="weights",shape=[5,5,1,32],initializer=tf.contrib.layers.xavier_initializer_conv2d())
b = tf.get_variable(name="biases",shape=[32],initializer=tf.random_normal_initializer())
conv = tf.nn.conv2d(image,w,strides=[1,1,1,1],padding="SAME")
relu = tf.nn.relu(conv+b,name=scope.name)
conv1 = tf.nn.max_pool(relu,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
with tf.variable_scope("conv2") as scope:
w = tf.get_variable(name="weights",shape=[5,5,32,64],initializer=tf.contrib.layers.xavier_initializer_conv2d())
b = tf.get_variable(name="biases",shape=[64],initializer=tf.contrib.layers.xavier_initializer_conv2d())
conv = tf.nn.conv2d(conv1,w,strides=[1,1,1,1],padding="SAME")
relu = tf.nn.relu(conv+b,name=scope.name)
conv2 = tf.nn.max_pool(relu,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
with tf.variable_scope("full") as scope:
w = tf.get_variable(name="weights",shape=[7*7*64,1024],initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable(name="biases",shape=[1024],initializer=tf.random_normal_initializer())
flat = tf.reshape(conv2,[-1,7*7*64])
full = tf.nn.relu(tf.matmul(flat,w) + b)
with tf.variable_scope("dropout") as scope:
keep_prob = tf.placeholder(tf.float32)
drop = tf.nn.dropout(full,keep_prob=keep_prob)
with tf.variable_scope("softmax") as scope:
w = tf.get_variable(name="weights",shape=[1024,10],initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable(name="biases",shape=[10],initializer=tf.random_normal_initializer())
out = tf.nn.softmax(tf.matmul(drop,w)+b)
with tf.name_scope("loss") as scope:
loss = tf.reduce_mean(-tf.reduce_sum(y*tf.log(out),reduction_indices=[1]))
with tf.name_scope("optimizer") as scope:
optimizer = tf.train.AdagradOptimizer(0.01).minimize(loss)
with tf.name_scope("predictions") as scope:
correct_preds = tf.equal(tf.arg_max(out,1),tf.arg_max(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_preds,tf.float32))
init = tf.global_variables_initializer()
n_batches = n_training_size/batch_size
with tf.Session() as sess:
sess.run(init)
writer = tf.summary.FileWriter('graphs/',sess.graph)
for i in range(n_epochs):
epoch_loss = 0
epoch_accuracy = 0
for j in range(n_batches):
x_batch,y_batch = mnist.train.next_batch(100)
x_batch = np.reshape(x_batch,(100,28,28,1))
_,l,acc = sess.run([optimizer,loss,accuracy],feed_dict={image:x_batch,y:y_batch,keep_prob:0.5})
epoch_loss += l
epoch_accuracy += acc
print 'Epoch: {}\tLoss: {}\tAccuracy: {}'.format(i,epoch_loss,epoch_accuracy/n_batches)
# 
| CNNs.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 五年人口迁徙图
import re
import pandas as pd
import requests as rq
from iclientpy import viz
# 使用pandas读取数据,但是列错乱,修正后生成新的dataframe
sdf = pd.read_html(rq.get('http://www.stats.gov.cn/tjsj/pcsj/rkpc/6rp/html/B0708.htm', headers={'User-agent': 'Mozilla/5.0'}).content)[0]
df=sdf.iloc[8:39,[0]+list(range(3,34))]
df.columns=['现住地']+sdf.iloc[5,1:32].tolist()
# 从源数据获取各地方迁出总人口的dataframe,然后提取迁出人口最多的五个省份
tdf=sdf.iloc[7:8,3:34]
tdf.columns=sdf.iloc[5,1:32].tolist()
tdf.loc[7]=pd.to_numeric(tdf.loc[7])
ttdf=tdf.T
ttdf.columns=['value']
sttdf=ttdf.sort_values(by='value',ascending=False)
top5_name=sttdf.iloc[0:5].index.tolist()
# 构建geolines所需要的数据格式
def get_data(dataframe):
alldata=[]
for index,series in dataframe.iteritems():
if index != "现住地":
single_data=[]
for ind,value in series.iteritems():
if index != re.sub('\s','',dataframe['现住地'][ind]):
single_data.append([{'name': index},{'name': re.sub('\s','',dataframe['现住地'][ind]),'value':value}])
alldata.append(single_data)
return alldata
data=get_data(df)
# 生成迁徙图
chart=viz.geolines(data=data,address_key='name',value_key='value',names=df.columns[1:].tolist(),max_symbolsize=15,min_symbolsize=5,symbol='arrow',selected_mode='multiple',selected_legend=top5_name)
# 展示迁徙图
chart
# 迁徙出去人口的等级符号专题图
ttdf['地区']=ttdf.index.tolist()
out_chart=viz.ranksymboltheme(data=ttdf,address_key='地区',value_key='value',is_over_lay=False,codomain=(0,400000),fill_opacity=0.5)
out_chart
out_chart.interact()
# 计算各个地区迁入人口的数据
idf=sdf.iloc[8:39,3:34]
idf=idf.apply(pd.to_numeric, errors='ignore')
idf=idf.fillna(0)
itdf=idf.T.apply(sum)
itdf.columns=sdf.iloc[5,1:32].tolist()
idf=pd.DataFrame([sdf.iloc[5,1:32].tolist(),itdf.data.tolist()]).T
idf.columns=['地区','value']
# 各个地区迁入人口的等级符号专题图
in_chart=viz.ranksymboltheme(data=idf,address_key='地区',value_key='value',is_over_lay=False,codomain=(0,400000))
in_chart
in_chart.interact()
| examples/iclientpy/sample-geolines-stats.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" deletable=true editable=true id="4f3CKqFUqL2-" slideshow={"slide_type": "slide"}
# # Custom Estimator
# + [markdown] deletable=true editable=true
# **Learning Objectives:**
# * Use a custom estimator of the `Estimator` class in TensorFlow to predict median housing price
# + [markdown] deletable=true editable=true
# The data is based on 1990 census data from California. This data is at the city block level, so these features reflect the total number of rooms in that block, or the total number of people who live on that block, respectively.
# <p>
# Let's use a set of features to predict house value.
# + [markdown] colab_type="text" deletable=true editable=true id="6TjLjL9IU80G"
# ## Set Up
# In this first cell, we'll load the necessary libraries.
# + deletable=true editable=true
import math
import shutil
import numpy as np
import pandas as pd
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
# + [markdown] colab_type="text" deletable=true editable=true id="ipRyUHjhU80Q"
# Next, we'll load our data set.
# + deletable=true editable=true
df = pd.read_csv("https://storage.googleapis.com/ml_universities/california_housing_train.csv", sep = ",")
# + [markdown] colab_type="text" deletable=true editable=true id="HzzlSs3PtTmt" slideshow={"slide_type": "-"}
# ## Examine the data
#
# It's a good idea to get to know your data a little bit before you work with it.
#
# We'll print out a quick summary of a few useful statistics on each column.
#
# This will include things like mean, standard deviation, max, min, and various quantiles.
# + deletable=true editable=true
df.head()
# + deletable=true editable=true
df.describe()
# + [markdown] deletable=true editable=true
# This data is at the city block level, so these features reflect the total number of rooms in that block, or the total number of people who live on that block, respectively. Let's create a different, more appropriate feature. Because we are predicing the price of a single house, we should try to make all our features correspond to a single house as well
# + deletable=true editable=true
df['num_rooms'] = df['total_rooms'] / df['households']
df['num_bedrooms'] = df['total_bedrooms'] / df['households']
df['persons_per_house'] = df['population'] / df['households']
df.describe()
# + deletable=true editable=true
df.drop(['total_rooms', 'total_bedrooms', 'population', 'households'], axis = 1, inplace = True)
df.describe()
# + [markdown] colab_type="text" deletable=true editable=true id="Lr6wYl2bt2Ep" slideshow={"slide_type": "-"}
# ## Build a custom estimator linear regressor
#
# In this exercise, we'll be trying to predict `median_house_value`. It will be our label. We'll use the remaining columns as our input features.
#
# To train our model, we'll use the Estimator API and create a custom estimator for linear regression.
#
# Note that we don't actually need a custom estimator for linear regression since there is a canned estimator for it, however we're keeping it simple so you can practice creating a custom estimator function.
# + deletable=true editable=true
# Define feature columns
feature_columns = {
colname : tf.feature_column.numeric_column(colname) \
for colname in ['housing_median_age','median_income','num_rooms','num_bedrooms','persons_per_house']
}
# Bucketize lat, lon so it's not so high-res; California is mostly N-S, so more lats than lons
feature_columns['longitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('longitude'), np.linspace(-124.3, -114.3, 5).tolist())
feature_columns['latitude'] = tf.feature_column.bucketized_column(tf.feature_column.numeric_column('latitude'), np.linspace(32.5, 42, 10).tolist())
# + deletable=true editable=true
# Split into train and eval and create input functions
msk = np.random.rand(len(df)) < 0.8
traindf = df[msk]
evaldf = df[~msk]
SCALE = 100000
BATCH_SIZE=128
train_input_fn = tf.estimator.inputs.pandas_input_fn(x = traindf[list(feature_columns.keys())],
y = traindf["median_house_value"] / SCALE,
num_epochs = None,
batch_size = BATCH_SIZE,
shuffle = True)
eval_input_fn = tf.estimator.inputs.pandas_input_fn(x = evaldf[list(feature_columns.keys())],
y = evaldf["median_house_value"] / SCALE, # note the scaling
num_epochs = 1,
batch_size = len(evaldf),
shuffle=False)
# + deletable=true editable=true
# Create the custom estimator
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,1,activation=None)
# 2. Loss function, training/eval ops
if mode == tf.estimator.ModeKeys.TRAIN or mode == tf.estimator.ModeKeys.EVAL:
labels = tf.expand_dims(tf.cast(labels, dtype=tf.float32), -1)
loss = tf.losses.mean_squared_error(labels, predictions)
optimizer = tf.train.FtrlOptimizer(learning_rate=0.2)
train_op = optimizer.minimize(
loss = loss,
global_step = tf.train.get_global_step())
eval_metric_ops = {
"rmse": tf.metrics.root_mean_squared_error(labels*SCALE, predictions*SCALE)
}
else:
loss = None
train_op = None
eval_metric_ops = None
# 3. Create predictions
predictions_dict = {"predicted": predictions}
# 4. Create export outputs
export_outputs = {"regression_export_outputs": tf.estimator.export.RegressionOutput(value = predictions)}
# 5. Return EstimatorSpec
return tf.estimator.EstimatorSpec(
mode = mode,
predictions = predictions_dict,
loss = loss,
train_op = train_op,
eval_metric_ops = eval_metric_ops,
export_outputs = export_outputs)
# + deletable=true editable=true
# Create serving input function
def serving_input_fn():
feature_placeholders = {
colname : tf.placeholder(tf.float32, [None]) for colname in 'housing_median_age,median_income,num_rooms,num_bedrooms,persons_per_house'.split(',')
}
feature_placeholders['longitude'] = tf.placeholder(tf.float32, [None])
feature_placeholders['latitude'] = tf.placeholder(tf.float32, [None])
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
# + deletable=true editable=true
# Create custom estimator's train and evaluate function
def train_and_evaluate(output_dir):
estimator = tf.estimator.Estimator(
model_fn = custom_estimator,
model_dir = output_dir,
params={'feature_columns': list(feature_columns.values())})
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn,
max_steps = 1000)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn,
steps = None,
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
#Run Training
OUTDIR = 'custom_estimator_trained_model'
shutil.rmtree(OUTDIR, ignore_errors = True) # start fresh each time
train_and_evaluate(OUTDIR)
# + [markdown] deletable=true editable=true
# ## Challenge Excercise
# Modify the custom_estimator function to be a neural network with one hidden layer, instead of a linear regressor
# + deletable=true editable=true
def custom_estimator(features, labels, mode, params):
# 0. Extract data from feature columns
input_layer = tf.feature_column.input_layer(features, params['feature_columns'])
# 1. Define Model Architecture
predictions = tf.layers.dense(input_layer,10,activation=tf.nn.relu)
predictions = tf.layers.dense(input_layer,1,activation=None)
.....REST AS BEFORE
| courses/machine_learning/deepdive/05_artandscience/d_customestimator_linear.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] nbsphinx="hidden"
# # The Laplace Transform
#
# *This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to [<EMAIL>](mailto:<EMAIL>).*
# -
# ## Summary of Properties, Theorems and Transforms
#
# The [properties](properties.ipynb), [theorems](theorems.ipynb) and transforms of the two-sided Laplace transform as derived in the previous sections are summarized in the following. The corresponding tables serve as a reference for the application of the Laplace transform in the theory of signals and systems. Please refer to the respective sections for details.
# ### Definition
#
# The two-sided Laplace transform and its inverse are defined as
#
# \begin{align}
# X(s) &= \int_{-\infty}^{\infty} x(t) \, e^{- s t} \; dt \\
# x(t) &= \frac{1}{2 \pi j} \int_{\sigma - j \infty}^{\sigma + j \infty} X(s) \, e^{s t} \; ds
# \end{align}
#
# where $s \in \text{ROC} \{ x(t) \}$.
# ### Properties and Theorems
#
# The properties and theorems of the two-sided Laplace transform are given as
#
# |  | $x(t)$ | $X(s) = \mathcal{L} \{ x(t) \}$ | $\text{ROC}$ |
# |:---|:---:|:---:|:---|
# | [Linearity](properties.ipynb#Linearity) | $A \, x_1(t) + B \, x_2(t)$ | $A \, X_1(s) + B \, X_2(s)$ | $\supseteq \text{ROC}\{x_1(t)\} \cap \text{ROC}\{x_2(t)\}$ |
# | [Real-valued signal](properties.ipynb#Symmetry-for-Real-Valued-Signals) | $x(t) = x^*(t)$ | $X(s) = X^*(s^*)$ | |
# | [Scaling](theorems.ipynb#Temporal-Scaling-Theorem) | $x(a t)$ | $\frac{1}{\lvert a \rvert} X\left( \frac{s}{a} \right)$ | $s: \frac{s}{a} \in \text{ROC}\{x(t)\}$ |
# | [Convolution](theorems.ipynb#Convolution-Theorem) | $x(t) * h(t)$ | $X(s) \cdot H(s)$ | $\supseteq \text{ROC}\{x(t)\} \cap \text{ROC}\{h(t)\}$ |
# | [Shift](theorems.ipynb#Temporal-Shift-Theorem) | $x(t - \tau)$ | $e^{-s \tau} \cdot X(s)$ | $\text{ROC}\{x(t)\}$ |
# | [Differentiation](theorems.ipynb#Differentiation-Theorem) (causal signal) | $\frac{d}{dt} x(t)$ | $s \cdot X(s) - x(0+)$ | $\supseteq \text{ROC}\{x(t)\}$ |
# | [Integration](theorems.ipynb#Integration-Theorem) | $\int_{-\infty}^{t} x(t) \; dt$ | $\frac{1}{s} \cdot X(s)$ | $\supseteq \text{ROC}\{x(t)\} \cap \{s: \Re \{s\} > 0 \}$ |
# | [Modulation](theorems.ipynb#Modulation-Theorem) | $e^{s_0 t}\cdot x(t)$ | $X(s - s_0)$ | $s: s - \Re \{s_0\} \in \text{ROC}\{x(t)\}$ |
#
# where $A, B, s_0 \in \mathbb{C}$, $a \in \mathbb{R} \setminus \{0\}$ and $\tau \in \mathbb{R}$.
# ### Selected Transforms
#
# Two-sided Laplace transforms which are frequently used are given as
#
# | $x(t)$ | $X(s) = \mathcal{L} \{ x(t) \}$ | $\text{ROC}$ |
# |:---:|:---:|:---|
# | $\delta(t)$ | $1$ | $\mathbb{C}$ |
# | $\epsilon(t)$ | $\frac{1}{s}$ | $\Re \{s\} > 0$ |
# | $t \epsilon(t)$ | $\frac{1}{s^2}$ | $\Re \{s\} > 0$ |
# | $e^{- s_0 t} \epsilon(t)$ | $\frac{1}{s + s_0}$ | $\Re \{s\} > \text{Re}\{-s_0\}$ |
# | $\sin(\omega_0 t) \epsilon(t)$ | $\frac{\omega_0}{s^2 + \omega_0^2}$ | $\Re \{s\} > 0$ |
# | $\cos(\omega_0 t) \epsilon(t)$ | $\frac{s}{s^2 + \omega_0^2}$ | $\Re \{s\} > 0$ |
# | $t^n e^{-s_0 t} \epsilon(t)$ | $\frac{n!}{(s+s_0)^{n+1}}$ | $\Re \{s\} > \text{Re}\{-s_0\}$ |
# | $e^{-s_0 t} \cos(\omega_0 t) \epsilon(t)$ | $\frac{s + s_0}{(s+s_0)^2 + \omega_0^2}$ | $\Re \{s\} > \Re \{-s_0\}$ |
# | $e^{-s_0 t} \sin(\omega_0 t) \epsilon(t)$ | $\frac{\omega_0}{(s+s_0)^2 + \omega_0^2}$ | $\Re \{s\} > \Re \{-s_0\}$ |
# | $t \cos(\omega_0 t) \epsilon(t)$ | $\frac{s^2 - \omega_0^2}{(s^2 + \omega_0^2)^2}$ | $\Re \{s\} > 0$ |
# | $t \sin(\omega_0 t) \epsilon(t)$ | $\frac{2 \omega_0 s}{(s^2 + \omega_0^2)^2}$ | $\Re \{s\} > 0$ |
#
# where $s_0 \in \mathbb{C}$, $\omega_0 \in \mathbb{R}$ and $n \in \mathbb{N}$. More one- and two-sided transforms may be found in the literature or [online](https://en.wikipedia.org/wiki/List_of_Laplace_transforms).
# + [markdown] nbsphinx="hidden"
# **Copyright**
#
# This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Continuous- and Discrete-Time Signals and Systems - Theory and Computational Examples*.
| laplace_transform/table_theorems_transforms.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# Change directory to VSCode workspace root so that relative path loads work correctly. Turn this addition off with the DataScience.changeDirOnImportExport setting
# ms-python.python added
import os
try:
os.chdir(os.path.join(os.getcwd(), '../../..'))
print(os.getcwd())
except:
pass
# A string can be viewed as a special kind of array. You should know how strings are represented in memory,
# and understand basic operations on strings such as comparison, copying, joining, splitting, matching, etc.
# Advanced string processing algorithms often use hash tables and dynamic programming.
# time complexity O(n) and space complexity O(1)
def is_palindromic(s):
# Note that s[~i] for i in [0, len(s)-1] is s[-(i+1)]
return all(s[i] == s[~i] for i in range(len(s) // 2))
# ### string libraries
# - key operators and functions:
# - `s[3]`, len(s), s+t, `s[2:4]`, s in t,
# - s.strip(), s.startswith(prefix), s.endswith(suffix),
# - 'Euclid,Axiom 5,Parallel Lines'.split(’,’)
# - 3 * '01', ','.join(('Gauss', 'Prince of Mathematicians', '1777-1855'))
# - s.tolower()
# - 'Name name, Rank rank'.format(name='Archimedes', rank=3)
#
# ### strings are immutable
# This implies that concatenating a single character n times to a string in a for loop has O(n^2) time complexity
# Some implementations of Python use tricks avoid having to do this allocation, reducing the complexity to O(n)
#
# - Strings problems have simple brute-force solutions that use O(n) space, but subtler solutions to reduce space complexity to O(1)
# - Understand the implications of a string type which is immutable
# - Know alternatives to immutable strings, e.g. a list in Python
# - Updating a mutable string from the front is slow, so see if possible to write values from the back
# +
# interconvert strings and integers
def int_to_string(x):
is_negative = False
if x < 0:
x, is_negative = -x, True
s = []
while True:
s.append(chr(ord('0') + x % 10))
x //= 10
if x == 0:
break
# Adds the negative sign back if is_negative
return ('-' if is_negative else '') + ''.join(reversed(s))
# -
int_to_string(19876)
# +
import functools
import string
def string_to_int(s):
return functools.reduce(lambda running_sum, c: running_sum * 10 + string.digits.index(c),
s[s[0] == '-':], 0) * (-1 if s[0] == '-' else 1)
# -
string_to_int('76429')
# +
# Base conversion
# The base b number system: a0*b^0 + a1*b^1 + a2*b^2 + ... + ak * b^k
# convert a string in base b1 to integer type (decimal number) using a sequence of multiply and adds
# and then convert that integer type to a string in base b2 using a sequence of modulus and division
import functools
import string
def convert_base(num_as_string, b1, b2):
def construct_from_base(num_as_int, base):
return ('' if num_as_int == 0 else
construct_from_base(num_as_int // base, base) +
string.hexdigits[num_as_int % base].upper())
is_negative = num_as_string[0] == '-'
num_as_int = functools.reduce(
lambda x, c: x * b1 + string.hexdigits.index(c.lower()),
num_as_string[is_negative:], 0)
return ('-' if is_negative else '') + ('0' if num_as_int == 0 else construct_from_base(num_as_int, b2))
# -
print(convert_base('102', 3, 4))
print(convert_base('1A7', 13, 7))
| python/epi/ipynb/03_strings.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Machine Learning Pipeline - Feature Selection
#
# In this notebook, we pick up the transformed datasets that we saved in the previous notebook.
# ## Reproducibility: Setting the seed
#
# With the aim to ensure reproducibility between runs of the same notebook, but also between the research and production environment, for each step that includes some element of randomness, it is extremely important that we **set the seed**.
# +
# to handle datasets
import pandas as pd
import numpy as np
# for plotting
import matplotlib.pyplot as plt
# to build the models
from sklearn.linear_model import Lasso
from sklearn.feature_selection import SelectFromModel
# to visualise al the columns in the dataframe
pd.pandas.set_option('display.max_columns', None)
# +
# load the train and test set with the engineered variables
# we built and saved these datasets in the previous lecture.
# If you haven't done so, go ahead and check the previous notebook
# to find out how to create these datasets
X_train = pd.read_csv('xtrain.csv')
X_test = pd.read_csv('xtest.csv')
X_train.head()
# +
# load the target (remember that the target is log transformed)
y_train = pd.read_csv('ytrain.csv')
y_test = pd.read_csv('ytest.csv')
y_train.head()
# -
# ### Feature Selection
#
# Let's go ahead and select a subset of the most predictive features. There is an element of randomness in the Lasso regression, so remember to set the seed.
# +
# We will do the model fitting and feature selection
# altogether in a few lines of code
# first, we specify the Lasso Regression model, and we
# select a suitable alpha (equivalent of penalty).
# The bigger the alpha the less features that will be selected.
# Then we use the selectFromModel object from sklearn, which
# will select automatically the features which coefficients are non-zero
# remember to set the seed, the random state in this function
sel_ = SelectFromModel(Lasso(alpha=0.001, random_state=0))
# train Lasso model and select features
sel_.fit(X_train, y_train)
# -
sel_.get_support().sum()
# +
# let's visualise those features that were selected.
# (selected features marked with True)
sel_.get_support()
# +
# let's print the number of total and selected features
# this is how we can make a list of the selected features
selected_feats = X_train.columns[(sel_.get_support())]
# let's print some stats
print('total features: {}'.format((X_train.shape[1])))
print('selected features: {}'.format(len(selected_feats)))
print('features with coefficients shrank to zero: {}'.format(
np.sum(sel_.estimator_.coef_ == 0)))
# -
# print the selected features
selected_feats
pd.Series(selected_feats).to_csv('selected_features.csv', index=False)
# # Additional Resources
#
# - [Feature Selection for Machine Learning](https://www.udemy.com/course/feature-selection-for-machine-learning/?referralCode=186501DF5D93F48C4F71) - Online Course
# - [Feature Selection for Machine Learning: A comprehensive Overview](https://trainindata.medium.com/feature-selection-for-machine-learning-a-comprehensive-overview-bd571db5dd2d) - Article
| section-04-research-and-development/03-machine-learning-pipeline-feature-selection.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Introdução
# ==========
#
# A Covid-19 é uma doença respiratória causada pelo novo coronavírus (SARS-CoV-2). Esse vírus vem causando bastante preocupação no mundo pela sua acelerada disseminação. No Brasil, até a presente data, o
# número de casos confirmados passam de 145 mil e de mortos ultrapassa os 10 mil.
#
# Ao mesmo tempo que essa doença se propaga rapidamente, estou interessado em compreender como a propagação de doenças infecciosas podem acontecer.
# Existe algum modelo que pode descrever com alguma simplicidade esse contágio?
#
# Descobri que sim. Existe um modelo matemático relativamente simples,
# chamado SIR, que descreve a estrutura dessa disseminação. A afirmação do
# modelo é tão interessante que resolvi implementar e avaliar como se
# comporta na minha realidade local.
#
# Este post tem como objetivo fornecer uma visão geral do modelo SIR e o
# resultado da minha simulação usando um conjunto de dados do Covid-19,
# fornecidos pelo [portal do Governo do Estado do Amapá](https://www.portal.ap.gov.br/coronavirus).
#
# O que é o modelo SIR
# --------------------
#
# O modelo SIR é um tipo de modelo que descreve a dinâmica de doenças infecciosas. O modelo divide a população em três compartimentos e
# espera-se que cada compartimento tenhas as mesmas características. Assim, o modelo SIR é segmentado em:
#
# - **S**uscetíveis
# - **I**nfectados
# - **R**emovidos
#
# Os **Suscetíveis** representam a população total que ainda não tem
# imunidade e está vulnerável a exposição da doença. Os **Infectados**
# representam a população atual de infectados. Elas podem espalhar a
# doença para as pessoas suscetíveis e podem ser removidas desse grupo no
# caso de atingirem recuperação (imunidade) ou morte. Já os **Removidos**
# representam a população que já adquiriu imunidade e não estão mais
# suscetíveis a doença. Nesse caso incluem-se também os mortos (que não
# podem disseminar a doença).
#
# 
#
# O modelo SIR permite descrever o número de pessoas em cada compartimento
# com uma equação diferencial ordinária. O parâmetro $\beta$ é a taxa que
# controla o quanto a doença pode ser transmitida através da exposição. É
# determinado pela chance de contato e pela probabilidade de transmissão
# da doença. O parâmetro $\gamma$ expressa a taxa de recuperação da doença
# em um período específico. Uma vez que as pessoas são curadas, elas obtêm
# imunidade. Não há chance de eles voltarem suscetíveis novamente.
#
# $$
# \begin{array}{rcl}
# \dfrac{dS}{dt} &=& -\beta \dfrac{I}{N}S\\[10pt]
# \dfrac{dI}{dt} &=& \beta \dfrac{I}{N}S\\[10pt]
# \dfrac{dR}{dt} &=& \gamma I
# \end{array}
# $$
#
# onde $N$ é a população total. E assim, é importante notar
# que: $$S + I + R = N$$
#
# Isso mostra uma limitação do modelo. Não consideramos o efeito da taxa
# natural de morte ou nascimento, porque o modelo pressupõe que o período
# pendente da doença seja muito menor que o tempo de vida do ser humano.
# Isso nos permite saber a importância de conhecer dois parâmetros,
# $\beta$ e $\gamma$. Quando podemos estimar os dois valores, há várias
# ideias derivadas deles. Se consideramos $D$ a média de dias para se
# recuperar da infecção, temos que $$D = \frac{1}{\gamma}$$
#
# Além disso, podemos estimar a natureza da doença em termos do poder da
# infecção. $$R_0 = \frac{\beta}{\gamma}$$
#
# É chamado de número básico de reprodução. $R_0$ é o número médio de
# pessoas infectadas por outra pessoa. Se for alto, a probabilidade de
# pandemia também é maior. O número também é usado para estimar o nível de
# imunidade do rebanho (HIL, sigla em inglês), isto é, quando uma porção
# crítica da população se torna imune e a doença pode não persistir mais
# na população, se tornando [endêmica](https://en.wikipedia.org/wiki/Endemic_(epidemiology)). Se o número básico de reprodução
# multiplicado pela porcentagem de pessoas não imunes (suscetíveis) for
# igual a 1, isso indica o estado equilibrado. O número de pessoas
# infecciosas é constante. Suponha que a proporção de pessoas imunes seja
# $p$, o estado estável pode ser formulado da seguinte maneira.
#
# $$R_0(1-p) = 1 \rightarrow 1-p = \frac{1}{R_0} \rightarrow p_c = 1- \frac{1}{R_0}$$
#
# Portanto, $p_c$ é o HIT para parar a propagação da doença infecciosa.
# Podemos parar o surto vacinando a população para aumentar a imunidade do
# rebanho. O vídeo fornecido pelo **3Blue1Brown** também é um ótimo
# recurso para aprender visualmente o modelo SIR.
#
# [](https://www.youtube.com/watch?v=gxAaO2rsdIs "3Blue1Brown")
#
# Agora que sabemos o básico sobre o modelo e sobre as principais métricas, vamos partir para a implementação do código.
#
# Simulação com dados do Covid-19 no Amapá
# ----------------------------------------
#
# A fonte de dados que usei neste experimento foram coletados até dia 09 de Maio de 2020, no Portal do
# Governo do Amapá. É possível fazer o download **aqui**. Nesse arquivo os dados coletados iniciam no dia 04 de Maio, quando começa a apresentar indivíduos removidos, e está organizado em:
#
# - *Dia*
# - *Confirmados*
# - *Mortes*
# - *Recuperados*
#
# Nessas simulações se considera a população estimada do Amapá ($N=845.731$), pelo [IBGE em 2019](https://www.ibge.gov.br/cidades-e-estados/ap.html). O que vamos fazer é estimar o $\beta$ e $\gamma$ para ajustar o modelo
# SIR aos casos confirmados reais (o número de pessoas infectadas). Para
# resolver a equação diferencial ordinária como o modelo SIR, podemos usar
# a função `solve_ivp` no módulo `scipy`.
#
# ### Importandos as principais bibliotecas
# Library
import numpy as np
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import pandas as pd
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
from datetime import date, timedelta
# ### Importando os dados
# +
# import data frame
dados = pd.read_csv('https://marleson.github.io/src/ap-covid-19-SIR-09-05-20.csv')
# Amostra dos dias
Dias = dados['Dias']
# Amostra de casos Confirmados
Confirmed = dados['Confirmados']
# Amostra de casos Recuperados
Recovered = dados['Recuperados']
# Amostra do num. de mortos
Deaths = dados['Mortos']
# Quant. de infectados
Infected = Confirmed - Recovered - Deaths
# Quant. de Removidos
Removed = Recovered + Deaths
# Populacao do Amapa, N.
N = 845731
# Número inicial de indivíduos infectados e removidos, I_start e R_start.
I_start, R_start = Infected[0], Removed[0]
# Os demais, S_start, são os indivíduos inicialmente suscetíveis.
S_start = N - I_start - R_start
# Malha de pontos no tempo (em dias)
t = np.arange(0, 150, 1)
# Dias (data de início da simulação: 04 de Abril de 2020)
# este dia foi escolhido, pois nele começam a surgir casos removidos
ddays = pd.date_range(start='4/4/2020', periods=len(t))
dados.tail()
# -
# ### Função para minização
# Esta função `loss` é utilizada para fazer a minimização do problema de valor inicial e posteriormente encontrar os parâmetros que melhor ajustam os dados importados.
def loss(point, data, removed, s_0, i_0, r_0, N):
size = len(data)
beta, gamma = point
def SIR(t, y):
S = y[0]
I = y[1]
R = y[2]
return [-beta*S*I/N, beta*S*I/N-gamma*I, gamma*I]
solution = solve_ivp(SIR, [0, size], [s_0,i_0,r_0], t_eval=np.arange(0, size, 1), vectorized=True)
# the root mean squared error (RMSE) - a raiz do erro quadrado médio
l1 = np.sqrt(np.mean((solution.y[1] - data)**2))
l2 = np.sqrt(np.mean((solution.y[2] - removed)**2))
alpha = 0.7 # ponderamento dos dados
return alpha * l1 + (1 - alpha) * l2
# ### Cálculo do parâmetros
#
# Os paramêtros $\beta$ (taxa contaminação) e $\gamma$ (taxa de recuperação), necessários para a construção da solução, são computados em cada intervalo de integração até a mais recente data. Os valores de $R_0$ (número básico de reprodução) e $p_{c}$ (índice de imunidade de rebanho) também serão calculados, a cada passo, para comparação.
#
# A rotina `minimize` é utilizada para encontrar os parametros $\beta$ e $\gamma$.
# +
beta, gamma = [], []
num_frames = 20 # num. de frames
for k in range(num_frames):
optimal = minimize(loss, [0.001, 0.001], args=(Infected[:17+k], Removed[:17+k], S_start, I_start, R_start, N), method='L-BFGS-B', bounds=[(0.00000001, 0.7), (0.00000001, 0.7)])
beta.append(optimal.x[0])
gamma.append(optimal.x[1])
obj = {'Dia (Integração)': Dias[16:], 'beta': beta, 'gamma': gamma}
output = pd.DataFrame(data=obj)
output['R0'] = output['beta']/output['gamma']
output['Pc'] = 1-1/output['R0']
output.tail()
# -
# ### As equações do modelo SIR
# Abaixo estão definidas o conjunto das 3 equações acopladas que descrevem o comportamento epidemiológico.
#
# \begin{equation}
# S'(t) = -\beta \dfrac{I(t)}{N(t)}S(t); \quad I'(t) = \beta \dfrac{I(t)}{N(t)}S(t) - \gamma I(t) \quad \mbox{e}\quad
# R'(t) = \gamma I(t)
# \end{equation}
# As equações diferenciais do modelo SIR
def deriv(t, y, N, beta, gamma):
S, I, R = y
dSdt = -beta * S * I / N
dIdt = beta * S * I / N - gamma * I
dRdt = gamma * I
return dSdt, dIdt, dRdt
# ### Solução numérica do modelo
# A solução numérica do modelo é aprensentada em seguida, utilizando a biblioteca voltada para equações diferenciais `solve_ivp` em problemas de valor inicial. A cada passo de tempo, as soluções são gravadas nas linhas das matrizes `S`, `I` e `R`.
# +
# Initial conditions vector
y0 = S_start, I_start, R_start
# Set init values
S, I, R = [], [], []
Imax, Ixmax = [], []
for i in range(num_frames):
sol = solve_ivp(deriv, [0, len(t)], y0, vectorized=True, args=(N, beta[i], gamma[i]), t_eval=t)
# Integrate the SIR equations over the time grid, t.
S.append(sol.y[0])
I.append(sol.y[1])
R.append(sol.y[2])
Imax.append(max(I[i]))
Ixmax.append(np.argmax(I[i]))
# Month abbreviation, day and year
d1 = ddays[Ixmax[-1]].strftime("%d %b %Y")
print('No dia ', d1, 'é atingido o número máximo de infectados: ', int(Imax[-1]))
# -
# ### Criar frames
# Nesta seção são criados os frames para cada uma das soluções
frames = []
for frame in range(num_frames):
x_axis_frame = ddays
y_axis_frameS = S[frame]
y_axis_frameI = I[frame]
y_axis_frameR = R[frame]
curr_frame = go.Frame(data = [go.Scatter(x = x_axis_frame, y = y_axis_frameS, mode = 'lines' ),
go.Scatter(x = x_axis_frame, y = y_axis_frameI, mode = 'lines' ),
go.Scatter(x = x_axis_frame, y = y_axis_frameR, mode = 'lines' )])
frames.append(curr_frame)
# ### Criar Figura
# Este é o último passo para a visualização das soluções. A figura é criada colocando a solução inicial, de onde partem as demais soluções. Os frames criados anteriormente são acrescentados, a fim de vizualizar as soluções a cada passo de tempo.
# +
figure = go.Figure(
data = [go.Scatter(x = ddays, y = S[0], mode = 'lines', name = "Sucetíveis", line = dict(color='rgb(20, 158, 217)')),
go.Scatter(x = ddays, y = I[0], mode = 'lines', name = "Infectados", line = dict(color='rgb(227, 50, 88)')),
go.Scatter(x = ddays, y = R[0], mode = 'lines', name = "Removidos", line = dict(color='rgb(0, 153, 137)'))], # list of traces
layout = {
# "title": "Simulação do modelo Epidêmico SIR",
"hovermode":"x",
"legend": {"x":0.2, "y":1.1},
"legend_orientation": "h",
"plot_bgcolor": 'rgba(10,10,10,0)',
"margin":{"t":50, "b":0, "l":0, "r":0},
"updatemenus":[{
"type":"buttons",
"direction": "left",
"pad":{"b":10, "t":10, "l":0},
"x":0.0,
"xanchor":"left",
"y":-0.2,
"yanchor":"bottom",
"buttons":[{
"label": "Play",
"method": "animate",
"args": [None, {'frame': {'duration': 1000, 'redraw': True}, "fromcurrent": True, 'transition': {'duration': 10, 'easing': 'linear'}}]
},
{
'label': 'Pause',
'args': [[None], {'frame': {'duration': 0, 'redraw': False}, 'mode': 'immediate',
'transition': {'duration': 0}}],
'method': 'animate'
}],
}],
"xaxis": {"range": [ddays[0],ddays[-1]], "showspikes": True, "spikemode": "toaxis+marker"},
"yaxis": {"range": [0,N], "title": "População", "side":"right", "showgrid": True, "gridwidth": 1, "gridcolor":"#B6B6B6"}
},
frames = frames
)
figure.show()
# -
# No gráfico animado acima é possível ter uma noção de como a doença pode evoluir nos próximos meses. A animação aprensenta o comportamento das curvas de infectados, removidos (mortos + recuperados) e suscetíveis, levando em conta os últimos 20 dias até o dia 09 de maio.
#
# O gráfico mostra que o pico de infectados pode ser atingido no início do mês de **Julho (02/07)** com mais de **241 mil pessoas infectadas**. Além disso, nota-se que o pico de infectados aumenta, apesar de se afastar ligeiramente.
#
# Os valores de $\alpha$, $\beta$ e, consequentemente, $R_0$ e $p_c$ obtidos até a presente data são mostradas na tabela abaixo:
output.tail(8)
figure.write_html("sir.html")
# Olhando os valores do número de reprodução ($R_0$) na tabela acima, o que mais chama atenção é o seu aumento. O $R_0$ chega a atingir $2.87$, na data mais recente. Isso significa que uma única pessoa pode infectar por volta de $3$ outros indivíduos. Para que a doença seja controlada esse número precisa estar abaixo de $1$.
#
# Com o aumento do número de reprodução, pode-se notar também que para atingir a imunidade de rebanho pelo menos $65\%$ ($p_c=0.65$ ) da população deve passar pela doença.
# ## Conclusões
# Resolvi explicar um pouco do modelo, pois sua compreensão mostra a importância do distanciamento social. Como a Covid-19 ainda não possui vacina para achatar de vez a curva de infectados, a única forma de garantir que mais pessoas possam ter acesso a leitos em hospitais é reduzindo a taxa de transmissão ($\beta$) e isso só pode ser feito com o isolamento e distanciamento social.
#
# As simulações realizadas coletando os dados do estado do Amapá mostram um cenário preocupante para os próximos meses. Apesar de apresentar um leve achatamento da curva no início da simulação, o aumento do pico da curva mostra um relaxamento nas medidas de isolamento pela população. Se o cenário apresentado se confirmar, o estado pode sofrer não somente um colapso de todo o sistema de saúde, mas um colapso do sistema funerário causado pelo alto número de mortes.
#
# Apesar de o modelo mostrar um alto número de infectados, vale lembrar que nem todos os indivíduos manifestam sintomas, mas mesmo assim podem espalhar a doença e acelerar o contágio, caso não realizem o autoisolemento. Além disso, nem todos os infectados precisarão de leitos clínicos ou de UTI. Pela última estimativa que realizei por meio do [Boletim de 09/04](https://www.portal.ap.gov.br/noticia/0905/boletim-informativo-covid-19-amapa-9-de-maio-de-2020), cerca $6,6\%$ dos infectados precisam de algum leito (clínico ou de UTI). Se este número se mantém, no pico da curva de infectados (cerca de 241.112 pessoas), seria necessário por volta de **15.900** leitos em todo o estado.
#
# Pelo relatório divulado pela [*Imperial College London (report 21)*](https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-21-brazil/) sobre o Brasil, no dia 08 de maio, a taxa de mortalidade por infecção do novo Coronavírus está entre $0.7\%$ e $1.2\%$. Se olharmos novamente para o pico de infectados da doença no Amapá esse número de óbitos pode chegar, por baixo, a **1.687** no estado (mesmo que não seja notificado), o que trás também o colapso funerário. Isso sem contar os mortos até que esse pico seja alcançado, que são incluídos como removidos nas simulações. Para minimizar o quantidade de pessoas sem atendimento médico e, consequentemente, o caos de mortos, a solução é "achatar a curva" de infectados e isso, repito, só será alcançado com um forte isolamento e distanciamento social.
#
# Na presente data, o índice de isolamento social no Amapá, estimado pelo [Inloco](https://www.inloco.com.br/pt/), está próximo de $48\%$. O taxa ideal de isolamento é $70\%$, mas em todo país tem-se observado esse baixo índice. Com o pico da curva de infectados se aproximando de forma acelerada e os sistemas de saúde municipais e estadual a beira do colapso o cenário mais provável para as próximas semanas é a adoção, pelo governo e prefeituras, de decretos mais rigorosos em relação a circulação de pessoas.
#
# ## Aviso
# A estimativa do modelo é bem simplificada, pois, pela própria construção, se considera uma população distribuida de forma homogênea (ideal) e sabe-se que isso não é o que ocorre. As pessoas estão agrupadas por cidades, bairros, comunidades, etc. Existem [modelos mais complexos](https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology) que podem considerar esse fatores.
#
# Além disso, o modelo depende da correta notificação de casos infectados e isso não tem ocorrido. O estado do Amapá, assim como outros estados, sofre pela subnotificação e falta de exames. O Amapá ainda tem um agravante em relação aos demais estados, pois depende de exames realizados no [Instituto <NAME>, em Belém-PA](https://www.portal.ap.gov.br/noticia/2403/governo-do-amapa-envia-4-ordf-remessa-de-casos-suspeitos-do-novo-coronavirus), que quando retornam (alguns dias depois) aumentam o notificação de casos Covid-19 naquele dia. Ou seja, não significa que os casos se confirmaram naquele dia, mas que foram notificados naquele dia. O mesmo acontece quando o estado recebe uma remessa grande de testes rápidos (IgG e IgM) e tira da fila os muitos casos suspeitos em um curto período.
#
# Os boletins do governo apenas notificam a quantidade de casos acumulados naquele dia e não atualiza os dados pelo dia em que o exame foi coletado. Isso fica evidente quando o próprio [portal de estatísticas do governo](http://painel.corona.ap.gov.br/) usa os dados acumulados fornecidos pelos boletins diários. No quesito de precisão de dados, a contagem de mortos por Covid-19 talvez sejam mais precisos, mesmo que hajam casos de óbitos que não foram testados e óbitos em residências, que não entram nas estatísticas.
#
# Mesmo que os dados da simulação não sejam os mais precisos e o modelo seja simplificado, a previsão do aumento do pico da curva é real e é provocado pela falta de cumprimentos das medidas de isolamento.
# ## Referências
# 1. [The SIR epidemic model in python](https://scipython.com/book/chapter-8-scipy/additional-examples/the-sir-epidemic-model/)
# 2. [The SIR model - Wikipedia](https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology#The_SIR_model)
# 3. [COVID-19 dynamics with SIR model](https://www.lewuathe.com/covid-19-dynamics-with-sir-model.html)
# 4. [Plotly](https://plotly.com/)
# Agradecimentos
# --------------
#
# - Um agradecimento especial ao **Prof. Dr. <NAME>
# (IFRS-Osório)**, um amigo e colega de trabalho, que me apresentou [este modelo](https://www.youtube.com/watch?v=1sySX-rGKWs) e possibilitou ricas discussões a respeito do tema.
# +
## Print dependences
# %load_ext watermark
# Python, Ipython, packages, machine characteristics
# %watermark -v -m -p numpy,matplotlib,plotly,pandas,scipy
| _jupyter/covid-19-SIR-model-ap.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import csv
import matplotlib.pyplot as plt
import seaborn as sns
#https://altair-viz.github.io/gallery/errorbars_with_std.html
#import altair as alt
#from vega_datasets import data
#defining paths
results_Baseline_IssueTitle_RandomForest = './experiment/dfTeste.csv'
#classifierChain = './experiment/dfTesteClassifierChain_13Labels.csv'
dataBinary = pd.read_csv(results_Baseline_IssueTitle_RandomForest)
#dataClassifier = pd.read_csv(classifierChain)
# -
dataBinary
# +
dd=pd.melt(dataBinary,id_vars=['Algorithm'],value_vars=['Precision','Recall','Fmeasure_Score'],var_name='Evaluation Metrics')
plt.figure(figsize=(10, 8))
ax = sns.boxplot(y='value',x='Algorithm',data=dd,hue='Evaluation Metrics')
plt.ylabel("Performance", size=12)
plt.xlabel("Evaluation Metrics by Algorithm",size=12)
labels=["Precision", "Recall", "F-measure"]
h, l = ax.get_legend_handles_labels()
ax.legend(h, labels, title="Evaluation Metrics",bbox_to_anchor=(1.02, 1), loc=2, borderaxespad=0.)
plt.title("Binary Relevance Evaluation Metrics by Algorithm", size=12)
plt.show()
#plt.savefig("grouped_boxplot_AlgorithmBinary.png")
# -
dataBinary.groupby(['tf-IDF','#_TopTerms']).mean()
dataBinary.nlargest(5,['Precision','Fmeasure_Score'])
plt.figure(figsize=(10, 8))
ax = sns.boxplot(y='AUC-PR',x='Algorithm',data=dataBinary)
plt.ylabel("AUCpr distribution", size=12)
plt.xlabel("Algorithms",size=12)
plt.title("Binary Relevance - AUCpr Analysis", size=12)
plt.show()
plt.figure(figsize=(10, 8))
ax = sns.boxplot(y='hamming_loss_avg',x='Algorithm',data=dataBinary)
plt.ylabel("Hamming Loss Average distribution", size=12)
plt.xlabel("Algorithms",size=12)
plt.title("Binary Relevance - Hamming Loss Analysis", size=12)
plt.show()
plt.figure(figsize=(10, 8))
ax = sns.boxplot(y='Accuracy_Score_not_normalized',x='Algorithm',data=dataBinary)
plt.ylabel("PR's correctly predicted", size=12)
plt.xlabel("Algorithms",size=12)
plt.title("Binary Relevance - Number of PR correctly predict considering all APIs", size=12)
plt.show()
# +
def cliffsDelta(lst1, lst2, **dull):
"""Returns delta and true if there are more than 'dull' differences"""
if not dull:
dull = {'small': 0.147, 'medium': 0.33, 'large': 0.474} # effect sizes from (Hess and Kromrey, 2004)
m, n = len(lst1), len(lst2)
lst2 = sorted(lst2)
j = more = less = 0
for repeats, x in runs(sorted(lst1)):
while j <= (n - 1) and lst2[j] < x:
j += 1
more += j*repeats
while j <= (n - 1) and lst2[j] == x:
j += 1
less += (n - j)*repeats
d = (more - less) / (m*n)
size = lookup_size(d, dull)
return d, size
def lookup_size(delta: float, dull: dict) -> str:
"""
:type delta: float
:type dull: dict, a dictionary of small, medium, large thresholds.
"""
delta = abs(delta)
if delta < dull['small']:
return 'negligible'
if dull['small'] <= delta < dull['medium']:
return 'small'
if dull['medium'] <= delta < dull['large']:
return 'medium'
if delta >= dull['large']:
return 'large'
def runs(lst):
"""Iterator, chunks repeated values"""
for j, two in enumerate(lst):
if j == 0:
one, i = two, 0
if one != two:
yield j - i, one
i = j
one = two
yield j - i + 1, two
# +
#https://machinelearningmastery.com/effect-size-measures-in-python/
#Small Effect Size: d=0.20
#Medium Effect Size: d=0.50
#Large Effect Size: d=0.80
from numpy import mean
from numpy import var
from math import sqrt
def cohend(d1, d2):
# calculate the size of samples
n1, n2 = len(d1), len(d2)
# calculate the variance of the samples
s1, s2 = var(d1, ddof=1), var(d2, ddof=1)
# calculate the pooled standard deviation
s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
# calculate the means of the samples
u1, u2 = mean(d1), mean(d2)
# calculate the effect size
return (u1 - u2) / s
# -
# +
#Subsetting data to compute Stats
RF_binary = dataBinary[dataBinary.Algorithm == 'RandomForest']
RF_FMeasure = RF_binary['Fmeasure_Score']
LogisticRegression_binary = dataBinary[dataBinary.Algorithm == 'LogisticRegression']
LogisticRegression_FMeasure = LogisticRegression_binary['Fmeasure_Score']
MLPC_binary = dataBinary[dataBinary.Algorithm == 'MLPClassifier']
MLPC_FMeasure = MLPC_binary['Fmeasure_Score']
DT_binary = dataBinary[dataBinary.Algorithm == 'DecisionTree']
DT_FMeasure = DT_binary['Fmeasure_Score']
MlkNN_binary = dataBinary[dataBinary.Algorithm == 'MLkNN']
MlkNN_FMeasure = MlkNN_binary['Fmeasure_Score']
# +
#### MANN-U Independent Samples
from scipy.stats import mannwhitneyu
#Fail to Reject H0: Sample distributions are equal.
#Reject H0: Sample distributions are not equal.
##### Defining variables to be comparede
# compare samples
stat, p = mannwhitneyu(RF_FMeasure, LogisticRegression_FMeasure)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distribution (fail to reject H0)')
else:
print('Different distribution (reject H0)')
#Effect_Size RandomForest Vs others
print(cliffsDelta(RF_FMeasure, LogisticRegression_FMeasure))
print(cliffsDelta(RF_FMeasure, MLPC_FMeasure))
print(cliffsDelta(RF_FMeasure, DT_FMeasure))
print(cliffsDelta(RF_FMeasure, MlkNN_FMeasure)) #divisionByZero error
#Effect_Size LogisticRegression Vs others
print(cliffsDelta(LogisticRegression_FMeasure, MLPC_FMeasure))
print(cliffsDelta(LogisticRegression_FMeasure, DT_FMeasure))
print(cliffsDelta(LogisticRegression_FMeasure, MlkNN_FMeasure))
#Effect_Size MLPC Vs others
print(cliffsDelta(MLPC_FMeasure, DT_FMeasure))
print(cliffsDelta(MLPC_FMeasure, MlkNN_FMeasure))
#Effect_Size MlkNN Vs others
print(cliffsDelta(MlkNN_FMeasure,DT_FMeasure))
# +
#Effect_Size RandomForest Vs others
print('Cohens d: %.3f' % cohend(RF_FMeasure, LogisticRegression_FMeasure))
print('Cohens d: %.3f' % cohend(RF_FMeasure, MLPC_FMeasure))
print('Cohens d: %.3f' % cohend(RF_FMeasure, DT_FMeasure))
print('Cohens d: %.3f' % cohend(RF_FMeasure, MlkNN_FMeasure))
#Effect_Size LogisticRegression Vs others
print('Cohens d: %.3f' % cohend(LogisticRegression_FMeasure, MLPC_FMeasure))
print('Cohens d: %.3f' % cohend(LogisticRegression_FMeasure, DT_FMeasure))
print('Cohens d: %.3f' % cohend(LogisticRegression_FMeasure, MlkNN_FMeasure))
#Effect_Size MLPC Vs others
print('Cohens d: %.3f' % cohend(MLPC_FMeasure, DT_FMeasure))
print('Cohens d: %.3f' % cohend(MLPC_FMeasure, MlkNN_FMeasure))
#Effect_Size MlkNN Vs others
print('Cohens d: %.3f' % cohend(MlkNN_FMeasure,DT_FMeasure))
# +
### Wilcoxon paired and dependent samples
#Fail to Reject H0: Sample distributions are equal.
#Reject H0: Sample distributions are not equal.
#from scipy.stats import wilcoxon
#stat, p = wilcoxon(data1, data2)
#print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
#alpha = 0.05
#if p > alpha:
# print('Same distribution (fail to reject H0)')
#else:
# print('Different distribution (reject H0)')
# +
##<NAME> - Group Comparison
#Fail to Reject H0: Paired sample distributions are equal.
#Reject H0: Paired sample distributions are not equal.
from scipy.stats import kruskal
# seed the random number generator
# compare samples
stat, p = kruskal(RF_FMeasure,LogisticRegression_FMeasure, MLPC_FMeasure,DT_FMeasure,MlkNN_FMeasure)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distributions (fail to reject H0)')
else:
print('Different distributions (reject H0)')
# +
#https://machinelearningmastery.com/nonparametric-statistical-significance-tests-in-python/
from scipy.stats import friedmanchisquare
# compare samples
stat, p = friedmanchisquare(RF_FMeasure,LogisticRegression_FMeasure,MLPC_FMeasure,DT_FMeasure,MlkNN_FMeasure)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distributions (fail to reject H0)')
else:
print('Different distributions (reject H0)')
# -
# +
###Precision analysis
#Subsetting data to compute Stats
RF_binary = dataBinary[dataBinary.Algorithm == 'RandomForest']
RF_Precision = RF_binary['Precision']
LogisticRegression_binary = dataBinary[dataBinary.Algorithm == 'LogisticRegression']
LogisticRegression_Precision = LogisticRegression_binary['Precision']
MLPC_binary = dataBinary[dataBinary.Algorithm == 'MLPClassifier']
MLPC_Precision = MLPC_binary['Precision']
DT_binary = dataBinary[dataBinary.Algorithm == 'DecisionTree']
DT_Precision = DT_binary['Precision']
MlkNN_binary = dataBinary[dataBinary.Algorithm == 'MLkNN']
MlkNN_Precision = MlkNN_binary['Precision']
# +
#### MANN-U Independent Samples
from scipy.stats import mannwhitneyu
#Fail to Reject H0: Sample distributions are equal.
#Reject H0: Sample distributions are not equal.
##### Defining variables to be comparede
# compare samples
stat, p = mannwhitneyu(RF_FMeasure, LogisticRegression_FMeasure)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distribution (fail to reject H0)')
else:
print('Different distribution (reject H0)')
#Effect_Size RandomForest Vs others
print(cliffsDelta(RF_Precision, LogisticRegression_Precision))
print(cliffsDelta(RF_Precision, MLPC_Precision))
print(cliffsDelta(RF_Precision, DT_Precision))
print(cliffsDelta(RF_Precision, MlkNN_Precision)) #divisionByZero error
#Effect_Size LogisticRegression Vs others
print(cliffsDelta(LogisticRegression_Precision, MLPC_Precision))
print(cliffsDelta(LogisticRegression_Precision, DT_Precision))
print(cliffsDelta(LogisticRegression_Precision, MlkNN_Precision))
#Effect_Size MLPC Vs others
print(cliffsDelta(MLPC_Precision, DT_Precision))
print(cliffsDelta(MLPC_Precision, MlkNN_Precision))
#Effect_Size MlkNN Vs others
print(cliffsDelta(MlkNN_Precision,DT_Precision))
# +
##<NAME> - Group Comparison
#Fail to Reject H0: Paired sample distributions are equal.
#Reject H0: Paired sample distributions are not equal.
from scipy.stats import kruskal
# seed the random number generator
# compare samples
stat, p = kruskal(RF_Precision,LogisticRegression_Precision, MLPC_Precision,DT_Precision,MlkNN_Precision)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distributions (fail to reject H0)')
else:
print('Different distributions (reject H0)')
# +
#https://machinelearningmastery.com/nonparametric-statistical-significance-tests-in-python/
from scipy.stats import friedmanchisquare
# compare samples
stat, p = friedmanchisquare(RF_Precision,LogisticRegression_Precision, MLPC_Precision,DT_Precision,MlkNN_Precision)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
print('Same distributions (fail to reject H0)')
else:
print('Different distributions (reject H0)')
# +
ConfusionMatrix = './CM(1, 1)900Yes0.2RandomForest0.csv'
#classifierChain = './experiment/dfTesteClassifierChain_13Labels.csv'
CM = pd.read_csv(ConfusionMatrix, sep=",")
# +
#parsing Confusion matrix
list(CM.columns)
type(CM['0'])
columns = ['Label','TN', 'FP','FN','TP']
df = pd.DataFrame(columns=columns)
df['Label'], df['TN'], df['FP'], df['FN'], df['TP'] = CM['0'].str.split(',', 5).str
df = df.drop(0)
# -
df
| experiment/H1/Analysis_H1-MLSMOTE-Rebuttal.ipynb |
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.1.0
# language: julia
# name: julia-1.1
# ---
# ## Background
#
# [JuliaDiffEq](https://github.com/JuliaDiffEq) is a suite of optimized Julia libraries to solve ordinary differential equations (ODE). *JuliaDiffEq* provides a large number of explicit and implicit solvers suited for different types of ODE problems. It is possible to reduce a system of partial differential equations into an ODE problem by employing the [method of lines (MOL)](https://en.wikipedia.org/wiki/Method_of_lines). The essence of MOL is to discretize the spatial derivatives (by finite difference, finite volume or finite element methods) into algebraic equations and to keep the time derivatives as is. The resulting differential equations are left with only one independent variable (time) and can be solved with an ODE solver. [Solving Systems of Stochastic PDEs and using GPUs in Julia](http://www.stochasticlifestyle.com/solving-systems-stochastic-pdes-using-gpus-julia/) is a brief introduction to MOL and using GPUs to accelerate PDE solving in *JuliaDiffEq*. Here we expand on this introduction by developing an implicit/explicit (IMEX) solver for a 2D cardiac electrophysiology model and show how to use [CuArray](https://github.com/JuliaGPU/CuArrays.jl) and [CUDAnative](https://github.com/JuliaGPU/CUDAnative.jl) libraries to run the explicit part of the model on a GPU.
#
# Note that this tutorial does not use the [higher order IMEX methods built into DifferentialEquations.jl](http://docs.juliadiffeq.org/latest/solvers/split_ode_solve.html#Implicit-Explicit-(IMEX)-ODE-1) but instead shows how to hand-split an equation when the explicit portion has an analytical solution (or approxiate), which is common in many scenarios.
#
# There are hundreds of ionic models that describe cardiac electrical activity in various degrees of detail. Most are based on the classic [Hodgkin-Huxley model](https://en.wikipedia.org/wiki/Hodgkin%E2%80%93Huxley_model) and define the time-evolution of different state variables in the form of nonlinear first-order ODEs. The state vector for these models includes the transmembrane potential, gating variables, and ionic concentrations. The coupling between cells is through the transmembrame potential only and is described as a reaction-diffusion equation, which is a parabolic PDE,
#
# $$\partial V / \partial t = \nabla (D \nabla V) - \frac {I_\text{ion}} {C_m},$$
#
# where $V$ is the transmembrane potential, $D$ is a diffusion tensor, $I_\text{ion}$ is the sum of the transmembrane currents and is calculated from the ODEs, and $C_m$ is the membrane capacitance and is usually assumed to be constant. Here we model a uniform and isotropic medium. Therefore, the model can be simplified to,
#
# $$\partial V / \partial t = D \Delta{V} - \frac {I_\text{ion}} {C_m},$$
#
# where $D$ is now a scalar. By nature, these models have to deal with different time scales and are therefore classified as *stiff*. Commonly, they are solved using the explicit Euler method, usually with a closed form for the integration of the gating variables (the Rush-Larsen method, see below). We can also solve these problems using implicit or semi-implicit PDE solvers (e.g., the [Crank-Nicholson method](https://en.wikipedia.org/wiki/Crank%E2%80%93Nicolson_method) combined with an iterative solver). Higher order explicit methods such as Runge-Kutta and linear multi-step methods cannot overcome the stiffness and are not particularly helpful.
#
# In this tutorial, we first develop a CPU-only IMEX solver and then show how to move the explicit part to a GPU.
#
# ### The Beeler-Reuter Model
#
# We have chosen the [Beeler-Reuter ventricular ionic model](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1283659/) as our example. It is a classic model first described in 1977 and is used as a base for many other ionic models. It has eight state variables, which makes it complicated enough to be interesting without obscuring the main points of the exercise. The eight state variables are: the transmembrane potential ($V$), sodium-channel activation and inactivation gates ($m$ and $h$, similar to the Hodgkin-Huxley model), with an additional slow inactivation gate ($j$), calcium-channel activation and deactivations gates ($d$ and $f$), a time-dependent inward-rectifying potassium current gate ($x_1$), and intracellular calcium concentration ($c$). There are four currents: a sodium current ($i_{Na}$), a calcium current ($i_{Ca}$), and two potassium currents, one time-dependent ($i_{x_1}$) and one background time-independent ($i_{K_1}$).
#
# ## CPU-Only Beeler-Reuter Solver
#
# Let's start by developing a CPU only IMEX solver. The main idea is to use the *DifferentialEquations* framework to handle the implicit part of the equation and code the analytical approximation for explicit part separately. If no analytical approximation was known for the explicit part, one could use methods from [this list](http://docs.juliadiffeq.org/latest/solvers/split_ode_solve.html#Implicit-Explicit-(IMEX)-ODE-1).
#
# First, we define the model constants:
# # An Implicit/Explicit CUDA-Accelerated Solver for the 2D Beeler-Reuter Model
# ### <NAME>
const v0 = -84.624
const v1 = 10.0
const C_K1 = 1.0f0
const C_x1 = 1.0f0
const C_Na = 1.0f0
const C_s = 1.0f0
const D_Ca = 0.0f0
const D_Na = 0.0f0
const g_s = 0.09f0
const g_Na = 4.0f0
const g_NaC = 0.005f0
const ENa = 50.0f0 + D_Na
const γ = 0.5f0
const C_m = 1.0f0
# Note that the constants are defined as `Float32` and not `Float64`. The reason is that most GPUs have many more single precision cores than double precision ones. To ensure uniformity between CPU and GPU, we also code most states variables as `Float32` except for the transmembrane potential, which is solved by an implicit solver provided by the Sundial library and needs to be `Float64`.
#
# ### The State Structure
#
# Next, we define a struct to contain our state. `BeelerReuterCpu` is a functor and we will define a deriv function as its associated function.
mutable struct BeelerReuterCpu <: Function
t::Float64 # the last timestep time to calculate Δt
diff_coef::Float64 # the diffusion-coefficient (coupling strength)
C::Array{Float32, 2} # intracellular calcium concentration
M::Array{Float32, 2} # sodium current activation gate (m)
H::Array{Float32, 2} # sodium current inactivation gate (h)
J::Array{Float32, 2} # sodium current slow inactivaiton gate (j)
D::Array{Float32, 2} # calcium current activaiton gate (d)
F::Array{Float32, 2} # calcium current inactivation gate (f)
XI::Array{Float32, 2} # inward-rectifying potassium current (iK1)
Δu::Array{Float64, 2} # place-holder for the Laplacian
function BeelerReuterCpu(u0, diff_coef)
self = new()
ny, nx = size(u0)
self.t = 0.0
self.diff_coef = diff_coef
self.C = fill(0.0001f0, (ny,nx))
self.M = fill(0.01f0, (ny,nx))
self.H = fill(0.988f0, (ny,nx))
self.J = fill(0.975f0, (ny,nx))
self.D = fill(0.003f0, (ny,nx))
self.F = fill(0.994f0, (ny,nx))
self.XI = fill(0.0001f0, (ny,nx))
self.Δu = zeros(ny,nx)
return self
end
end
# ### Laplacian
#
# The finite-difference Laplacian is calculated in-place by a 5-point stencil. The Neumann boundary condition is enforced. Note that we could have also used [DiffEqOperators.jl](https://github.com/JuliaDiffEq/DiffEqOperators.jl) to automate this step.
# 5-point stencil
function laplacian(Δu, u)
n1, n2 = size(u)
# internal nodes
for j = 2:n2-1
for i = 2:n1-1
@inbounds Δu[i,j] = u[i+1,j] + u[i-1,j] + u[i,j+1] + u[i,j-1] - 4*u[i,j]
end
end
# left/right edges
for i = 2:n1-1
@inbounds Δu[i,1] = u[i+1,1] + u[i-1,1] + 2*u[i,2] - 4*u[i,1]
@inbounds Δu[i,n2] = u[i+1,n2] + u[i-1,n2] + 2*u[i,n2-1] - 4*u[i,n2]
end
# top/bottom edges
for j = 2:n2-1
@inbounds Δu[1,j] = u[1,j+1] + u[1,j-1] + 2*u[2,j] - 4*u[1,j]
@inbounds Δu[n1,j] = u[n1,j+1] + u[n1,j-1] + 2*u[n1-1,j] - 4*u[n1,j]
end
# corners
@inbounds Δu[1,1] = 2*(u[2,1] + u[1,2]) - 4*u[1,1]
@inbounds Δu[n1,1] = 2*(u[n1-1,1] + u[n1,2]) - 4*u[n1,1]
@inbounds Δu[1,n2] = 2*(u[2,n2] + u[1,n2-1]) - 4*u[1,n2]
@inbounds Δu[n1,n2] = 2*(u[n1-1,n2] + u[n1,n2-1]) - 4*u[n1,n2]
end
# ### The Rush-Larsen Method
#
# We use an explicit solver for all the state variables except for the transmembrane potential which is solved with the help of an implicit solver. The explicit solver is a domain-specific exponential method, the Rush-Larsen method. This method utilizes an approximation on the model in order to transform the IMEX equation into a form suitable for an implicit ODE solver. This combination of implicit and explicit methods forms a specialized IMEX solver. For general IMEX integration, please see the [IMEX solvers documentation](http://docs.juliadiffeq.org/latest/solvers/split_ode_solve.html#Implicit-Explicit-%28IMEX%29-ODE-1). While we could have used the general model to solve the current problem, for this specific model, the transformation approach is more efficient and is of practical interest.
#
# The [Rush-Larsen](https://ieeexplore.ieee.org/document/4122859/) method replaces the explicit Euler integration for the gating variables with direct integration. The starting point is the general ODE for the gating variables in Hodgkin-Huxley style ODEs,
#
# $$\frac{dg}{dt} = \alpha(V) (1 - g) - \beta(V) g$$
#
# where $g$ is a generic gating variable, ranging from 0 to 1, and $\alpha$ and $\beta$ are reaction rates. This equation can be written as,
#
# $$\frac{dg}{dt} = (g_{\infty} - g) / \tau_g,$$
#
# where $g_\infty$ and $\tau_g$ are
#
# $$g_{\infty} = \frac{\alpha}{(\alpha + \beta)},$$
#
# and,
#
# $$\tau_g = \frac{1}{(\alpha + \beta)}.$$
#
# Assuing that $g_\infty$ and $\tau_g$ are constant for the duration of a single time step ($\Delta{t}$), which is a reasonable assumption for most cardiac models, we can integrate directly to have,
#
# $$g(t + \Delta{t}) = g_{\infty} - \left(g_{\infty} - g(\Delta{t})\right)\,e^{-\Delta{t}/\tau_g}.$$
#
# This is the Rush-Larsen technique. Note that as $\Delta{t} \rightarrow 0$, this equations morphs into the explicit Euler formula,
#
# $$g(t + \Delta{t}) = g(t) + \Delta{t}\frac{dg}{dt}.$$
#
# `rush_larsen` is a helper function that use the Rush-Larsen method to integrate the gating variables.
@inline function rush_larsen(g, α, β, Δt)
inf = α/(α+β)
τ = 1f0 / (α+β)
return clamp(g + (g - inf) * expm1(-Δt/τ), 0f0, 1f0)
end
# The gating variables are updated as below. The details of how to calculate $\alpha$ and $\beta$ are based on the Beeler-Reuter model and not of direct interest to this tutorial.
# +
function update_M_cpu(g, v, Δt)
# the condition is needed here to prevent NaN when v == 47.0
α = isapprox(v, 47.0f0) ? 10.0f0 : -(v+47.0f0) / (exp(-0.1f0*(v+47.0f0)) - 1.0f0)
β = (40.0f0 * exp(-0.056f0*(v+72.0f0)))
return rush_larsen(g, α, β, Δt)
end
function update_H_cpu(g, v, Δt)
α = 0.126f0 * exp(-0.25f0*(v+77.0f0))
β = 1.7f0 / (exp(-0.082f0*(v+22.5f0)) + 1.0f0)
return rush_larsen(g, α, β, Δt)
end
function update_J_cpu(g, v, Δt)
α = (0.55f0 * exp(-0.25f0*(v+78.0f0))) / (exp(-0.2f0*(v+78.0f0)) + 1.0f0)
β = 0.3f0 / (exp(-0.1f0*(v+32.0f0)) + 1.0f0)
return rush_larsen(g, α, β, Δt)
end
function update_D_cpu(g, v, Δt)
α = γ * (0.095f0 * exp(-0.01f0*(v-5.0f0))) / (exp(-0.072f0*(v-5.0f0)) + 1.0f0)
β = γ * (0.07f0 * exp(-0.017f0*(v+44.0f0))) / (exp(0.05f0*(v+44.0f0)) + 1.0f0)
return rush_larsen(g, α, β, Δt)
end
function update_F_cpu(g, v, Δt)
α = γ * (0.012f0 * exp(-0.008f0*(v+28.0f0))) / (exp(0.15f0*(v+28.0f0)) + 1.0f0)
β = γ * (0.0065f0 * exp(-0.02f0*(v+30.0f0))) / (exp(-0.2f0*(v+30.0f0)) + 1.0f0)
return rush_larsen(g, α, β, Δt)
end
function update_XI_cpu(g, v, Δt)
α = (0.0005f0 * exp(0.083f0*(v+50.0f0))) / (exp(0.057f0*(v+50.0f0)) + 1.0f0)
β = (0.0013f0 * exp(-0.06f0*(v+20.0f0))) / (exp(-0.04f0*(v+20.0f0)) + 1.0f0)
return rush_larsen(g, α, β, Δt)
end
# -
# The intracelleular calcium is not technically a gating variable, but we can use a similar explicit exponential integrator for it.
function update_C_cpu(g, d, f, v, Δt)
ECa = D_Ca - 82.3f0 - 13.0278f0 * log(g)
kCa = C_s * g_s * d * f
iCa = kCa * (v - ECa)
inf = 1.0f-7 * (0.07f0 - g)
τ = 1f0 / 0.07f0
return g + (g - inf) * expm1(-Δt/τ)
end
# ### Implicit Solver
#
# Now, it is time to define the derivative function as an associated function of **BeelerReuterCpu**. We plan to use the CVODE_BDF solver as our implicit portion. Similar to other iterative methods, it calls the deriv function with the same $t$ multiple times. For example, these are consecutive $t$s from a representative run:
#
# 0.86830
# 0.86830
# 0.85485
# 0.85485
# 0.85485
# 0.86359
# 0.86359
# 0.86359
# 0.87233
# 0.87233
# 0.87233
# 0.88598
# ...
#
# Here, every time step is called three times. We distinguish between two types of calls to the deriv function. When $t$ changes, the gating variables are updated by calling `update_gates_cpu`:
function update_gates_cpu(u, XI, M, H, J, D, F, C, Δt)
let Δt = Float32(Δt)
n1, n2 = size(u)
for j = 1:n2
for i = 1:n1
v = Float32(u[i,j])
XI[i,j] = update_XI_cpu(XI[i,j], v, Δt)
M[i,j] = update_M_cpu(M[i,j], v, Δt)
H[i,j] = update_H_cpu(H[i,j], v, Δt)
J[i,j] = update_J_cpu(J[i,j], v, Δt)
D[i,j] = update_D_cpu(D[i,j], v, Δt)
F[i,j] = update_F_cpu(F[i,j], v, Δt)
C[i,j] = update_C_cpu(C[i,j], D[i,j], F[i,j], v, Δt)
end
end
end
end
# On the other hand, du is updated at each time step, since it is independent of $\Delta{t}$.
# +
# iK1 is the inward-rectifying potassium current
function calc_iK1(v)
ea = exp(0.04f0*(v+85f0))
eb = exp(0.08f0*(v+53f0))
ec = exp(0.04f0*(v+53f0))
ed = exp(-0.04f0*(v+23f0))
return 0.35f0 * (4f0*(ea-1f0)/(eb + ec)
+ 0.2f0 * (isapprox(v, -23f0) ? 25f0 : (v+23f0) / (1f0-ed)))
end
# ix1 is the time-independent background potassium current
function calc_ix1(v, xi)
ea = exp(0.04f0*(v+77f0))
eb = exp(0.04f0*(v+35f0))
return xi * 0.8f0 * (ea-1f0) / eb
end
# iNa is the sodium current (similar to the classic Hodgkin-Huxley model)
function calc_iNa(v, m, h, j)
return C_Na * (g_Na * m^3 * h * j + g_NaC) * (v - ENa)
end
# iCa is the calcium current
function calc_iCa(v, d, f, c)
ECa = D_Ca - 82.3f0 - 13.0278f0 * log(c) # ECa is the calcium reversal potential
return C_s * g_s * d * f * (v - ECa)
end
function update_du_cpu(du, u, XI, M, H, J, D, F, C)
n1, n2 = size(u)
for j = 1:n2
for i = 1:n1
v = Float32(u[i,j])
# calculating individual currents
iK1 = calc_iK1(v)
ix1 = calc_ix1(v, XI[i,j])
iNa = calc_iNa(v, M[i,j], H[i,j], J[i,j])
iCa = calc_iCa(v, D[i,j], F[i,j], C[i,j])
# total current
I_sum = iK1 + ix1 + iNa + iCa
# the reaction part of the reaction-diffusion equation
du[i,j] = -I_sum / C_m
end
end
end
# -
# Finally, we put everything together is our deriv function, which is a call on `BeelerReuterCpu`.
function (f::BeelerReuterCpu)(du, u, p, t)
Δt = t - f.t
if Δt != 0 || t == 0
update_gates_cpu(u, f.XI, f.M, f.H, f.J, f.D, f.F, f.C, Δt)
f.t = t
end
laplacian(f.Δu, u)
# calculate the reaction portion
update_du_cpu(du, u, f.XI, f.M, f.H, f.J, f.D, f.F, f.C)
# ...add the diffusion portion
du .+= f.diff_coef .* f.Δu
end
# ### Results
#
# Time to test! We need to define the starting transmembrane potential with the help of global constants **v0** and **v1**, which represent the resting and activated potentials.
const N = 192;
u0 = fill(v0, (N, N));
u0[90:102,90:102] .= v1; # a small square in the middle of the domain
# The initial condition is a small square in the middle of the domain.
using Plots
heatmap(u0)
# Next, the problem is defined:
# +
using DifferentialEquations, Sundials
deriv_cpu = BeelerReuterCpu(u0, 1.0);
prob = ODEProblem(deriv_cpu, u0, (0.0, 50.0));
# -
# For stiff reaction-diffusion equations, CVODE_BDF from Sundial library is an excellent solver.
@time sol = solve(prob, CVODE_BDF(linear_solver=:GMRES), saveat=100.0);
heatmap(sol.u[end])
# ## CPU/GPU Beeler-Reuter Solver
#
# GPUs are great for embarrassingly parallel problems but not so much for highly coupled models. We plan to keep the implicit part on CPU and run the decoupled explicit code on a GPU with the help of the CUDAnative library.
#
# ### GPUs and CUDA
#
# It this section, we present a brief summary of how GPUs (specifically NVIDIA GPUs) work and how to program them using the Julia CUDA interface. The readers who are familiar with these basic concepts may skip this section.
#
# Let's start by looking at the hardware of a typical high-end GPU, GTX 1080. It has four Graphics Processing Clusters (equivalent to a discrete CPU), each harboring five Streaming Multiprocessor (similar to a CPU core). Each SM has 128 single-precision CUDA cores. Therefore, GTX 1080 has a total of 4 x 5 x 128 = 2560 CUDA cores. The maximum theoretical throughput for a GTX 1080 is reported as 8.87 TFLOPS. This figure is calculated for a boost clock frequency of 1.733 MHz as 2 x 2560 x 1.733 MHz = 8.87 TFLOPS. The factor 2 is included because two single floating point operations, a multiplication and an addition, can be done in a clock cycle as part of a fused-multiply-addition FMA operation. GTX 1080 also has 8192 MB of global memory accessible to all the cores (in addition to local and shared memory on each SM).
#
# A typical CUDA application has the following flow:
#
# 1. Define and initialize the problem domain tensors (multi-dimensional arrays) in CPU memory.
# 2. Allocate corresponding tensors in the GPU global memory.
# 3. Transfer the input tensors from CPU to the corresponding GPU tensors.
# 4. Invoke CUDA kernels (i.e., the GPU functions callable from CPU) that operate on the GPU tensors.
# 5. Transfer the result tensors from GPU back to CPU.
# 6. Process tensors on CPU.
# 7. Repeat steps 3-6 as needed.
#
# Some libraries, such as [ArrayFire](https://github.com/arrayfire/arrayfire), hide the complexicities of steps 2-5 behind a higher level of abstraction. However, here we take a lower level route. By using [CuArray](https://github.com/JuliaGPU/CuArrays.jl) and [CUDAnative](https://github.com/JuliaGPU/CUDAnative.jl), we achieve a finer-grained control and higher performance. In return, we need to implement each step manually.
#
# *CuArray* is a thin abstraction layer over the CUDA API and allows us to define GPU-side tensors and copy data to and from them but does not provide for operations on tensors. *CUDAnative* is a compiler that translates Julia functions designated as CUDA kernels into ptx (a high-level CUDA assembly language).
#
# ### The CUDA Code
#
# The key to fast CUDA programs is to minimize CPU/GPU memory transfers and global memory accesses. The implicit solver is currently CPU only, but it only needs access to the transmembrane potential. The rest of state variables reside on the GPU memory.
#
# We modify ``BeelerReuterCpu`` into ``BeelerReuterGpu`` by defining the state variables as *CuArray*s instead of standard Julia *Array*s. The name of each variable defined on GPU is prefixed by *d_* for clarity. Note that $\Delta{v}$ is a temporary storage for the Laplacian and stays on the CPU side.
# +
using CUDAnative, CuArrays
mutable struct BeelerReuterGpu <: Function
t::Float64 # the last timestep time to calculate Δt
diff_coef::Float64 # the diffusion-coefficient (coupling strength)
d_C::CuArray{Float32, 2} # intracellular calcium concentration
d_M::CuArray{Float32, 2} # sodium current activation gate (m)
d_H::CuArray{Float32, 2} # sodium current inactivation gate (h)
d_J::CuArray{Float32, 2} # sodium current slow inactivaiton gate (j)
d_D::CuArray{Float32, 2} # calcium current activaiton gate (d)
d_F::CuArray{Float32, 2} # calcium current inactivation gate (f)
d_XI::CuArray{Float32, 2} # inward-rectifying potassium current (iK1)
d_u::CuArray{Float64, 2} # place-holder for u in the device memory
d_du::CuArray{Float64, 2} # place-holder for d_u in the device memory
Δv::Array{Float64, 2} # place-holder for voltage gradient
function BeelerReuterGpu(u0, diff_coef)
self = new()
ny, nx = size(u0)
@assert (nx % 16 == 0) && (ny % 16 == 0)
self.t = 0.0
self.diff_coef = diff_coef
self.d_C = CuArray(fill(0.0001f0, (ny,nx)))
self.d_M = CuArray(fill(0.01f0, (ny,nx)))
self.d_H = CuArray(fill(0.988f0, (ny,nx)))
self.d_J = CuArray(fill(0.975f0, (ny,nx)))
self.d_D = CuArray(fill(0.003f0, (ny,nx)))
self.d_F = CuArray(fill(0.994f0, (ny,nx)))
self.d_XI = CuArray(fill(0.0001f0, (ny,nx)))
self.d_u = CuArray(u0)
self.d_du = CuArray(zeros(ny,nx))
self.Δv = zeros(ny,nx)
return self
end
end
# -
# The Laplacian function remains unchanged. The main change to the explicit gating solvers is that *exp* and *expm1* functions are prefixed by *CUDAnative.*. This is a technical nuisance that will hopefully be resolved in future.
# +
function rush_larsen_gpu(g, α, β, Δt)
inf = α/(α+β)
τ = 1.0/(α+β)
return clamp(g + (g - inf) * CUDAnative.expm1(-Δt/τ), 0f0, 1f0)
end
function update_M_gpu(g, v, Δt)
# the condition is needed here to prevent NaN when v == 47.0
α = isapprox(v, 47.0f0) ? 10.0f0 : -(v+47.0f0) / (CUDAnative.exp(-0.1f0*(v+47.0f0)) - 1.0f0)
β = (40.0f0 * CUDAnative.exp(-0.056f0*(v+72.0f0)))
return rush_larsen_gpu(g, α, β, Δt)
end
function update_H_gpu(g, v, Δt)
α = 0.126f0 * CUDAnative.exp(-0.25f0*(v+77.0f0))
β = 1.7f0 / (CUDAnative.exp(-0.082f0*(v+22.5f0)) + 1.0f0)
return rush_larsen_gpu(g, α, β, Δt)
end
function update_J_gpu(g, v, Δt)
α = (0.55f0 * CUDAnative.exp(-0.25f0*(v+78.0f0))) / (CUDAnative.exp(-0.2f0*(v+78.0f0)) + 1.0f0)
β = 0.3f0 / (CUDAnative.exp(-0.1f0*(v+32.0f0)) + 1.0f0)
return rush_larsen_gpu(g, α, β, Δt)
end
function update_D_gpu(g, v, Δt)
α = γ * (0.095f0 * CUDAnative.exp(-0.01f0*(v-5.0f0))) / (CUDAnative.exp(-0.072f0*(v-5.0f0)) + 1.0f0)
β = γ * (0.07f0 * CUDAnative.exp(-0.017f0*(v+44.0f0))) / (CUDAnative.exp(0.05f0*(v+44.0f0)) + 1.0f0)
return rush_larsen_gpu(g, α, β, Δt)
end
function update_F_gpu(g, v, Δt)
α = γ * (0.012f0 * CUDAnative.exp(-0.008f0*(v+28.0f0))) / (CUDAnative.exp(0.15f0*(v+28.0f0)) + 1.0f0)
β = γ * (0.0065f0 * CUDAnative.exp(-0.02f0*(v+30.0f0))) / (CUDAnative.exp(-0.2f0*(v+30.0f0)) + 1.0f0)
return rush_larsen_gpu(g, α, β, Δt)
end
function update_XI_gpu(g, v, Δt)
α = (0.0005f0 * CUDAnative.exp(0.083f0*(v+50.0f0))) / (CUDAnative.exp(0.057f0*(v+50.0f0)) + 1.0f0)
β = (0.0013f0 * CUDAnative.exp(-0.06f0*(v+20.0f0))) / (CUDAnative.exp(-0.04f0*(v+20.0f0)) + 1.0f0)
return rush_larsen_gpu(g, α, β, Δt)
end
function update_C_gpu(c, d, f, v, Δt)
ECa = D_Ca - 82.3f0 - 13.0278f0 * CUDAnative.log(c)
kCa = C_s * g_s * d * f
iCa = kCa * (v - ECa)
inf = 1.0f-7 * (0.07f0 - c)
τ = 1f0 / 0.07f0
return c + (c - inf) * CUDAnative.expm1(-Δt/τ)
end
# -
# Similarly, we modify the functions to calculate the individual currents by adding CUDAnative prefix.
# +
# iK1 is the inward-rectifying potassium current
function calc_iK1(v)
ea = CUDAnative.exp(0.04f0*(v+85f0))
eb = CUDAnative.exp(0.08f0*(v+53f0))
ec = CUDAnative.exp(0.04f0*(v+53f0))
ed = CUDAnative.exp(-0.04f0*(v+23f0))
return 0.35f0 * (4f0*(ea-1f0)/(eb + ec)
+ 0.2f0 * (isapprox(v, -23f0) ? 25f0 : (v+23f0) / (1f0-ed)))
end
# ix1 is the time-independent background potassium current
function calc_ix1(v, xi)
ea = CUDAnative.exp(0.04f0*(v+77f0))
eb = CUDAnative.exp(0.04f0*(v+35f0))
return xi * 0.8f0 * (ea-1f0) / eb
end
# iNa is the sodium current (similar to the classic Hodgkin-Huxley model)
function calc_iNa(v, m, h, j)
return C_Na * (g_Na * m^3 * h * j + g_NaC) * (v - ENa)
end
# iCa is the calcium current
function calc_iCa(v, d, f, c)
ECa = D_Ca - 82.3f0 - 13.0278f0 * CUDAnative.log(c) # ECa is the calcium reversal potential
return C_s * g_s * d * f * (v - ECa)
end
# -
# ### CUDA Kernels
#
# A CUDA program does not directly deal with GPCs and SMs. The logical view of a CUDA program is in the term of *blocks* and *threads*. We have to specify the number of block and threads when running a CUDA *kernel*. Each thread runs on a single CUDA core. Threads are logically bundled into blocks, which are in turn specified on a grid. The grid stands for the entirety of the domain of interest.
#
# Each thread can find its logical coordinate by using few pre-defined indexing variables (*threadIdx*, *blockIdx*, *blockDim* and *gridDim*) in C/C++ and the corresponding functions (e.g., `threadIdx()`) in Julia. There variables and functions are defined automatically for each thread and may return a different value depending on the calling thread. The return value of these functions is a 1, 2, or 3 dimensional structure whose elements can be accessed as `.x`, `.y`, and `.z` (for a 1-dimensional case, `.x` reports the actual index and `.y` and `.z` simply return 1). For example, if we deploy a kernel in 128 blocks and with 256 threads per block, each thread will see
#
# ```
# gridDim.x = 128;
# blockDim=256;
# ```
#
# while `blockIdx.x` ranges from 0 to 127 in C/C++ and 1 to 128 in Julia. Similarly, `threadIdx.x` will be between 0 to 255 in C/C++ (of course, in Julia the range will be 1 to 256).
#
# A C/C++ thread can calculate its index as
#
# ```
# int idx = blockDim.x * blockIdx.x + threadIdx.x;
# ```
#
# In Julia, we have to take into account base 1. Therefore, we use the following formula
#
# ```
# idx = (blockIdx().x-UInt32(1)) * blockDim().x + threadIdx().x
# ```
#
# A CUDA programmer is free to interpret the calculated index however it fits the application, but in practice, it is usually interpreted as an index into input tensors.
#
# In the GPU version of the solver, each thread works on a single element of the medium, indexed by a (x,y) pair.
# `update_gates_gpu` and `update_du_gpu` are very similar to their CPU counterparts but are in fact CUDA kernels where the *for* loops are replaced with CUDA specific indexing. Note that CUDA kernels cannot return a valve; hence, *nothing* at the end.
# +
function update_gates_gpu(u, XI, M, H, J, D, F, C, Δt)
i = (blockIdx().x-UInt32(1)) * blockDim().x + threadIdx().x
j = (blockIdx().y-UInt32(1)) * blockDim().y + threadIdx().y
v = Float32(u[i,j])
let Δt = Float32(Δt)
XI[i,j] = update_XI_gpu(XI[i,j], v, Δt)
M[i,j] = update_M_gpu(M[i,j], v, Δt)
H[i,j] = update_H_gpu(H[i,j], v, Δt)
J[i,j] = update_J_gpu(J[i,j], v, Δt)
D[i,j] = update_D_gpu(D[i,j], v, Δt)
F[i,j] = update_F_gpu(F[i,j], v, Δt)
C[i,j] = update_C_gpu(C[i,j], D[i,j], F[i,j], v, Δt)
end
nothing
end
function update_du_gpu(du, u, XI, M, H, J, D, F, C)
i = (blockIdx().x-UInt32(1)) * blockDim().x + threadIdx().x
j = (blockIdx().y-UInt32(1)) * blockDim().y + threadIdx().y
v = Float32(u[i,j])
# calculating individual currents
iK1 = calc_iK1(v)
ix1 = calc_ix1(v, XI[i,j])
iNa = calc_iNa(v, M[i,j], H[i,j], J[i,j])
iCa = calc_iCa(v, D[i,j], F[i,j], C[i,j])
# total current
I_sum = iK1 + ix1 + iNa + iCa
# the reaction part of the reaction-diffusion equation
du[i,j] = -I_sum / C_m
nothing
end
# -
# ### Implicit Solver
#
# Finally, the deriv function is modified to copy *u* to GPU and copy *du* back and to invoke CUDA kernels.
function (f::BeelerReuterGpu)(du, u, p, t)
L = 16 # block size
Δt = t - f.t
copyto!(f.d_u, u)
ny, nx = size(u)
if Δt != 0 || t == 0
@cuda blocks=(ny÷L,nx÷L) threads=(L,L) update_gates_gpu(
f.d_u, f.d_XI, f.d_M, f.d_H, f.d_J, f.d_D, f.d_F, f.d_C, Δt)
f.t = t
end
laplacian(f.Δv, u)
# calculate the reaction portion
@cuda blocks=(ny÷L,nx÷L) threads=(L,L) update_du_gpu(
f.d_du, f.d_u, f.d_XI, f.d_M, f.d_H, f.d_J, f.d_D, f.d_F, f.d_C)
copyto!(du, f.d_du)
# ...add the diffusion portion
du .+= f.diff_coef .* f.Δv
end
# Ready to test!
# +
using DifferentialEquations, Sundials
deriv_gpu = BeelerReuterGpu(u0, 1.0);
prob = ODEProblem(deriv_gpu, u0, (0.0, 50.0));
@time sol = solve(prob, CVODE_BDF(linear_solver=:GMRES), saveat=100.0);
# -
heatmap(sol.u[end])
# ## Summary
#
# We achieve around a 6x speedup with running the explicit portion of our IMEX solver on a GPU. The major bottleneck of this technique is the communication between CPU and GPU. In its current form, not all of the internals of the method utilize GPU acceleration. In particular, the implicit equations solved by GMRES are performed on the CPU. This partial CPU nature also increases the amount of data transfer that is required between the GPU and CPU (performed every f call). Compiling the full ODE solver to the GPU would solve both of these issues and potentially give a much larger speedup. [JuliaDiffEq developers are currently working on solutions to alleviate these issues](http://www.stochasticlifestyle.com/solving-systems-stochastic-pdes-using-gpus-julia/), but these will only be compatible with native Julia solvers (and not Sundials).
| notebook/advanced/beeler_reuter.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Homework 5
# Homework 5 exercises 8 and 9. This exercises required a Dataset told to be synthetically generated by the instructions of the task. In order to load the required dataset [*scikit-learn*](http://scikit-learn.org/stable/datasets/) will be used. The library provides a function to create artificial data to be used while studying machine learning problems. In this case the function *make_classification* allows the creation of data following the desired parameters which in this case will be used for the solution of the homework. The number of features is set to 2 so that the problem can be visualized.
# +
# %matplotlib inline
import matplotlib.pyplot as pl
import numpy as np
from sklearn import linear_model, datasets
from random import randint
num_features = 2
learning_rate = 0.1
num_samples = 100
termination_threshold = 0.001
X1, Y1 = (datasets.make_classification(n_samples=num_samples, n_features=num_features,
n_redundant=0, n_informative=1,n_clusters_per_class=1) )
Y1[Y1 == 0] = -1
pl.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)
# -
# Defined draw function to plot a line in the current chart. (taken from [stackoverflow](http://stackoverflow.com/questions/9148927/matplotlib-extended-line-over-2-control-points))
def draw_line_2p(x,y,xlims):
xrange = np.arange(xlims[0],xlims[1],0.1)
A = np.vstack([x, np.ones(len(x))]).T
k, b = np.linalg.lstsq(A, y)[0]
pl.plot(xrange, k * xrange + b, color='m', linestyle='-', linewidth=2)
# The instructions command to add a line with random coordinates to separate between classes. In this case it is not necessary because the generated data is already clustered and classified. In any case the procedure would be as follows. Remove comments to see generated line.
# +
import random
x1 = random.uniform(0, 1)
x2 = random.uniform(0, 1)
y1 = random.uniform(0, 1)
y2 = random.uniform(0, 1)
#pl.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1)
#draw_line_2p([x1, x2], [y1, y2], [np.amin(X1[:, 0]), np.amax(X1[:, 0])])
# -
# Definition of the gradient function for logistic regression
def gradient(w, row_idx):
global X1, Y1
# minus the dot product of Y1_n and X1_n
numerator = (-Y1[row_idx] * np.array(X1[row_idx]))
# 1 + exp(Y1_n.w.X1_n)
denominator = 1 + np.exp(Y1[row_idx] * np.dot(w,X1[row_idx]))
#print("numerator: " + str(numerator))
#print("denominator: " + str(denominator))
return np.divide(np.array(numerator), np.array(denominator))
# Definition of termination condition function. Takes into account the definition of the threshold defined as parameter for the exercise.
def terminate(w_t, w_t1, first_run):
if(first_run):
return False
else:
#if(loop_count % 1 == 0):
#print("arrays:")
#print(np.array(w_t))
#print(np.array(w_t1))
#print("norm")
#print(np.linalg.norm(np.subtract(np.array(w_t), np.array(w_t1))))
return (np.linalg.norm(np.subtract(np.array(w_t), np.array(w_t1)))) < termination_threshold
# Definition of the error function
def error(w, row_idx):
global X1, Y1
return np.log(1 + np.exp(-Y1[row_idx] * np.dot(w,X1[row_idx])))
# Definition of main function for logistic regression
def logistic_regression():
global num_samples, learning_rate
loop_count = 0
sum_error = 0
#Define weights as random to init the algorithm
#w = np.zeros((num_features+1,1))
#w_t = [np.random.randn(), np.random.randn()]
w_t = [0.0, 0.0]
w_t1 = w_t
first_run = True
while(not terminate(w_t, w_t1, first_run)):
if(loop_count % num_samples == 0):
permutation = np.random.permutation(num_samples)
first_run = False
w_t = w_t1
idx = permutation[loop_count % num_samples]
g = gradient(w_t,idx)
w_t1 = np.subtract(w_t,np.multiply(learning_rate, g))
#w_t1 = np.add(w_t,np.multiply(learning_rate, g))
sum_error += error(w_t1, idx)
loop_count = loop_count + 1
#print("loops: "+str(loop_count))
return (sum_error/loop_count, loop_count)
# Main call to the process to obtain final results
#Define random permutation to go through in the algorithm
sum_error = 0
sum_iterations = 0
for num in range(0, 100):
result = logistic_regression()
sum_error += result[0]
sum_iterations += result[1]
print("Out of sample average error: " + str(sum_error/100))
print("Average iterations ran: " + str(sum_iterations/100))
| Homework-5.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# # Extract Job Posts from Indeed
# Before extracting job posts from [Indeed](https://www.indeed.com/), make sure you have checked their [robots.txt](https://www.indeed.com/robots.txt) file.
# ## Create a table in database
import pandas
import configparser
import psycopg2
# Read the database connection info from the config.ini
# +
config = configparser.ConfigParser()
config.read('config.ini')
host = config['myaws']['host']
db = config['myaws']['db']
user = config['myaws']['user']
pwd = config['myaws']['pwd']
# -
# Establish a connection to the databas, and create a cursor.
conn = psycopg2.connect(host = host,
user = user,
password = <PASSWORD>,
dbname = db
)
cur = conn.cursor()
# Design the table in SQL
# replace the schema and table name to your schema and table name
table_sql = """
CREATE TABLE IF NOT EXISTS gp8.Indeed
(
id SERIAL,
job_title VARCHAR(200),
job_company VARCHAR(200),
job_loc VARCHAR(200),
job_salary VARCHAR(200),
job_summary TEXT,
PRIMARY KEY(id)
);
"""
# create the table
cur.execute(table_sql)
conn.commit()
# ## Request HTML
#
# [urllib.request](https://docs.python.org/3/library/urllib.request.html) makes simple HTTP requests to visit a web page and get the content via the Python standard library.
# Here we define the URL to search job pots about Intelligence analyst.
url = 'https://www.indeed.com/jobs?q=intelligence+analyst&start=0'
import urllib.request
response = urllib.request.urlopen(url)
html_data= response.read()
#print(html_data.decode('utf-8'))
# # Parese HTML
# We can use the inspector tool in browsers to analyze webpages and use [beautifulsoup](https://www.crummy.com/software/BeautifulSoup/bs4/doc/) to extract webpage data.
# pip install the beautiful soup if needed.
# !pip install beautifulsoup4
from bs4 import BeautifulSoup
soup = BeautifulSoup(html_data,'html.parser')
#print (soup)
# Use the <code> tag.find_all(‘tag_name’, tage_attr = ‘possible_value’)</code> function to return a list of tags where the attribute equals the possible_value.
# <ul>Common attributes include:
# <li> id</li>
# <li> class<span style ="color:red">_</span></li>
# </ul>
#
# <ul>Common functions include:
# <li> tag.text: return the visible part of the tag</li>
# <li> tag.get(‘attribute’): return the value of the attribute of the tag</li>
# </ul>
# Since all the job posts are in the <code>div tag class = 'jobsearch-Sprep...'</code>, we need to find that div tag from the body tag.
for table_resultsBody in soup.find_all('table', id = 'resultsBody'):
pass
#print(table_resultsBody)
for table_pageContent in table_resultsBody.find_all('table', id = 'pageContent'):
pass
#print(table_pageContent)
for td_resultsCol in table_pageContent.find_all('td', id = 'resultsCol'):
pass
#print(td_resultsCol)
# ## Save Data to Database
# Now we find the div tag contains the job posts. We need to identify the job title, company, ratings, reviews, salary, and summary.
# We can save those records to our table in the database.
# identify the job title, company, ratings, reviews, salary, and summary
for div_row in td_resultsCol.find_all('div', class_='jobsearch-SerpJobCard unifiedRow row result'):
# find job title
job_title = None
job_company = None
job_rating = None
job_loc = None
job_salary = None
job_summary = None
for h2_title in div_row.find_all('h2', class_ = 'title'):
job_title = h2_title.a.text.strip().replace("'","_")
for div_dsc in div_row.find_all('div', class_ = 'sjcl'):
#find company name
for span_company in div_dsc.find_all('span', class_ = 'company'):
job_company = span_company.text.strip().replace("'","_")
# find location
for div_loc in div_dsc.find_all('div', class_ = 'location accessible-contrast-color-location'):
job_loc = div_loc.text.strip().replace("'","_")
# find salary
for div_salary in div_row.find_all('div',class_ ='salarySnippet'):
job_salary = div_salary.text.strip().replace("'","_")
#find summary
for div_summary in div_row.find_all('div', class_ = 'summary'):
job_summary = div_summary.text.strip().replace("'","_")
# insert into database
sql_insert = """
insert into gp8.Indeed(job_title,job_company,job_loc,job_salary,job_summary)
values('{}','{}','{}','{}','{}')
""".format(job_title,job_company,job_loc,job_salary,job_summary)
cur.execute(sql_insert)
conn.commit()
# # View the Table
df = pandas.read_sql_query('select count(*) as count,job_title from gp8.Indeed group by job_title order by count desc', conn)
df[:]
# ## Query the Table
df = pandas.read_sql_query('select count(*) as count,job_title from gp8.Indeed group by job_title order by count desc ', conn)
df.plot.bar(x='job_title')
cur.close()
conn.close()
| lab 6.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from logicqubit.logic import *
import random
import numpy as np
# +
logicQuBit = LogicQuBit(1)
particle = Qubit()
# +
# Alice prepares the state |1>, base Z
particle.X()
logicQuBit.PlotDensityMatrix()
# +
# Eva measure at base X
particle.H()
logicQuBit.PrintState()
value = logicQuBit.Measure_One(particle)
print(value)
logicQuBit.PrintState()
logicQuBit.PlotDensityMatrix()
# +
# Eva prepares her state at base X
logicQuBit = LogicQuBit(1)
new_particle = Qubit()
if(value[0] == 1):
new_particle.X()
new_particle.H()
logicQuBit.PrintState()
logicQuBit.PlotDensityMatrix()
# +
# Bob measure at base Z
measured = logicQuBit.Measure_One(new_particle)
print(measured)
logicQuBit.PlotDensityMatrix()
# -
| BB84.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Set up
import math
import random
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from pandas import DataFrame
from scipy.optimize import minimize
import seaborn as sns
sns.set(style='ticks', context='paper')
colors=["#e3c934","#68c4bf","#c51000","#287271"]
sns.set_palette(colors)
# ## Library
def barkbark(cloud,formants,formantchar='F'):
newcloud=cloud.copy()
for formant in formants:
name = str(formant).replace(formantchar,'z')
newcloud[name] = 26.81/ (1+ 1960/newcloud[formant]) - 0.53
return newcloud
def activation(testset,cloud,dims = {'F0':4,'F1':2,'F2':3,'F3':1},c=0.01,rmspkr=True):
# Get stuff ready
dims.update((x, (y/sum(dims.values()))) for x, y in dims.items()) # Normalize weights to sum to 1
# If the testset happens to have N in it, remove it before joining dfs
test=testset.copy()
if 'N' in test.columns:
test = test.drop(columns='N', axis=1,inplace=True)
exemplars=cloud[~cloud.isin(test)].dropna()
if rmspkr == True:
spkr=test.speaker.iloc[0]
spkrexemps=exemplars[ exemplars['speaker'] == spkr ].index
exemplars.drop(spkrexemps, inplace=True)
# Merge test and exemplars
bigdf = pd.merge(
test.assign(key=1), # Add column named 'key' with all values == 1
exemplars.assign(key=1), # Add column named 'key' with all values == 1
on='key', # Match on 'key' to get cross join (cartesian product)
suffixes=['_t', '_ex']
).drop('key', axis=1) # Drop 'key' column
dimensions=list(dims.keys()) # Get dimensions from dictionary
weights=list(dims.values()) # Get weights from dictionary
tcols = [f'{d}_t' for d in dimensions] # Get names of all test columns
excols = [f'{d}_ex' for d in dimensions] # Get names of all exemplar columns
# Multiply each dimension by weights
i = bigdf.loc[:, tcols].values.astype(float) # Get all the test columns
i *= weights # Multiply test columns by weight
j = bigdf.loc[:, excols].values.astype(float) # Get all the exemplar columns
j *= weights # Multiply exemplar columns by weights
# Get Euclidean distance
bigdf['dist'] = np.sqrt(np.sum((i-j)**2, axis=1))
# get activation: exponent of negative distance * sensitivity c, multiplied by N_j
bigdf['a'] = np.exp(-bigdf.dist*c)*bigdf.N
return bigdf
def reset_N(exemplars, N=1): # Add or override N, default to 1
exemplars['N'] = N
return exemplars
def probs(bigdf,cats):
prs = {}
for cat in cats:
label = cat+'_ex'
cat_a = bigdf.groupby(label).a.sum()
pr = cat_a/sum(cat_a)
pr = pr.rename_axis(cat).reset_index().rename(columns={"a":"probability"})
prs[cat]=pr
return prs
def choose(pr,test,cats,runnerup=False):
newtest = test.copy()
for cat in cats:
choicename = cat + 'Choice'
choiceprobname = cat + 'Prob'
best2 = pr[cat]['probability'].nlargest(n=2).reset_index(drop=True) # Get the two highest probs for each cat type
choiceprob = best2[0] # Match the prob to the category
choice = pr[cat].loc[pr[cat]['probability']==choiceprob,cat].iloc[0]
newtest[choicename] = choice
newtest[choiceprobname] = choiceprob
if runnerup == True:
choice2name = cat + 'Choice2'
choice2probname = cat +'Choice2Prob'
choice2prob = best2[1]
choice2 = pr[cat].loc[pr[cat]['probability']==choice2prob,cat].iloc[0]
newtest[choice2name] = choice2
newtest[choice2probname] = choice2prob
return newtest
def gettestset(cloud,balcat,n): #Gets n number of rows per cat in given cattype
testlist=[]
for cat in list(cloud[balcat].unique()):
samp = cloud[cloud[balcat]==cat].sample(n)
testlist.append(samp)
test=pd.concat(testlist)
return test
def multicat(cloud,testset,cats,dims = {'F0':4,'F1':2,'F2':3,'F3':1},c=0.01):
choicelist=[]
for ix in list(testset.index.values):
test = testset.loc[[ix,]]
#exemplars=cloud[~cloud.isin(test)].dropna()
exemplars=cloud.copy()
reset_N(exemplars)
bigdf=activation(test,exemplars,dims = dims,c=c)
pr=probs(bigdf,cats)
choices = choose(pr,test,cats)
choicelist.append(choices)
choices=pd.concat(choicelist, ignore_index=True)
return choices
def checkaccuracy(choices,cats):
acc = choices.copy() # Make a copy of choices to muck around with
for cat in cats: # Iterate over your list of cats
accname = cat + 'Acc' # Get the right column names
choicename = cat + 'Choice'
# If choice is the same as intended, acc =y, else n
acc[accname] = np.where(acc[cat]==acc[choicename], 'y', 'n')
return acc
def propcorr(acc,cat):
perc = dict(acc.groupby(cat)[cat+'Acc'].value_counts(normalize=True).drop(labels='n',level=1).reset_index(level=1,drop=True))
pc=pd.DataFrame.from_dict(perc, orient='index').reset_index()
pc.columns=[cat,'propcorr']
return pc
def overallacc(acc,cat):
totalcorrect = acc[cat+'Acc'].value_counts(normalize=True)['y']
return totalcorrect
def accplot(pc,cat,acc):
obs=str(len(acc))
pl = sns.barplot(x=cat,y='propcorr',data=pc,palette=colors)
plt.ylim(0,1.01)
pl.set(ylabel='Proportion accurate of '+obs+' trials')
pl.set_xticklabels(
pl.get_xticklabels(),
rotation=45,
horizontalalignment='right',
fontweight='light',
fontsize='x-large')
plt.show()
def continuum (start,end,cloud,dimlist = ['F0','F1','F2','F3'],steps=7,df=False):
vals = {}
norms = {}
rowlist = []
st=cloud[cloud['vowel'] == start].sample().reset_index(drop=True) # randomly sample a row with the some start vowel
spkr = st.speaker.iloc[0] # Get the speaker and gender
gen = st.gender.iloc[0]
en=pb52[(cloud.speaker==spkr) & (cloud['vowel']==end)].sample().reset_index(drop=True) # get a row with the end vowel from same speaker
for dim in dimlist: # Calculate the difference between start and end for each dim
norms[dim] = en[dim] - st[dim]
for i in range (0,steps):
for dim in dimlist:
vals[dim] = st[dim] + (norms[dim] * i/(steps-1)) # the values for each dim = start val + diff by step
row = pd.DataFrame(vals)
row['vowel'] = '?'
row['speaker'] = spkr
row['gender'] = gen
rowlist.append(row)
rowlist[0]['vowel'] = start # Change start and end vowels
rowlist[-1]['vowel'] = end
cont=pd.concat(rowlist,ignore_index=True) # concatenate
if df == True:
return cont
else:
return rowlist
# +
def FCN(exemplars,start,end):
exemplars['N'] = np.where((exemplars['vowel']==start)|(exemplars['vowel']==end), 1, 0)
return exemplars
## Include other speaker characteristics
# -
def choosecontinuum(cont,cloud,cats,start,end,FC=False):
exemplars=cloud.copy()
exemplars=exemplars[~exemplars.isin(cont)].dropna()
choicelist = []
for row in cont:
test=row
if FC == True:
FCN(exemplars,start,end)
else:
reset_N(exemplars)
bigdf=activation(test,exemplars)
pr=probs(bigdf,cats)
choices=choose(pr,test,cats)
choicelist.append(choices)
choices=pd.concat(choicelist,ignore_index=True)
return choices
def resonate(pr,rescats,cloud,beta=0.25,gamma=0.25):
#beta slows influence of first guess down, gives chance to revise guess
exemplars = cloud.copy()
for cat in rescats:
probval = exemplars[cat].map(pr[cat].set_index(cat).to_dict()['probability'])
# change N to existing N + some prop of probability
exemplars['N'] = exemplars['N'] + (beta * probval) - (gamma * (1-probval))
return exemplars
def multirescat(testset,dims,cloud,cats,c,ncycles,rescats,beta=0.25,gamma=0.25):
choicelist=[]
for ix in list(testset.index.values):
#set the test and exemplar cloud for the trial
test = testset.loc[[ix,]]
exemplars=cloud[~cloud.isin(test)].dropna()
reset_N(exemplars)
#do the first categorization
bigdf=activation(test,exemplars,dims = dims,c=c)
pr=probs(bigdf,cats)
#Start the resonance loop
for cycle in range(0,ncycles):
exemplars=resonate(pr,rescats,exemplars,beta=beta,gamma=gamma)
bigdf=activation(test,exemplars,dims=dims,c=c)
pr=probs(bigdf,cats)
#Make a final categorization for that trial
choices = choose(pr,test,cats)
choicelist.append(choices)
choices=pd.concat(choicelist, ignore_index=True)
return choices
def rescat(test,exemplars,dims,cats,c,n_res,rescats,beta=0.25,gamma=0.25):
reset_N(exemplars)
for i in range(0,n_res):
act = activation(test,exemplars,dims=dims,c=c)
prob = probs (act,cats)
exemplars = resonate(prob,rescats,exemplars,beta=beta,gamma=gamma)
choices = choose(prob,test,cats)
return choices
def multiaccplot(choices,cats):
accuracy = checkaccuracy(choices,cats)
for cat in cats:
proportion = propcorr(accuracy,cat)
accplot(proportion,cat,accuracy)
print(proportion)
def errorfunc(x, cloud,testset,dimslist,catslist):
#x = [c,F0,F1,F2,F3]
c=x[0]
dimsdict={dimslist[0]:x[1],dimslist[1]:x[2],dimslist[2]:x[3],dimslist[3]:x[4]}
choices=multicat(cloud,testset,catslist,dims=dimsdict,c=c)
accuracy=checkaccuracy(choices,catslist)
err = accuracy['vowel'+'Acc'].value_counts(normalize=True)['n']
return err
def errorfunc_c(x, cloud,testset,dimsdict,catslist):
c=x[0]
choices=multicat(cloud,testset,catslist,dims=dimsdict,c=c)
accuracy=checkaccuracy(choices,catslist)
err = accuracy['vowel'+'Acc'].value_counts(normalize=True)['n']
return err
def errorfunc_anchor(x, cloud,testset,dimslist,catslist):
#x = [c,F1,F2,F3]
c=x[0]
dimsdict={dimslist[0]:1,dimslist[1]:x[1],dimslist[2]:x[2],dimslist[3]:x[3]}
choices=multicat(cloud,testset,catslist,dims=dimsdict,c=c)
accuracy=checkaccuracy(choices,catslist)
err = accuracy['vowel'+'Acc'].value_counts(normalize=True)['n']
return err
def confusion(choices,cats):
matrices={}
for cat in cats:
matrices[cat]=pd.crosstab(choices[cat],choices[cat+'Choice'],normalize='index').round(2).rename_axis(None)
return matrices
def evalcycles(dictname,cats):
accdict={}
overallaccdict={}
pcdict={}
cmdict={}
for dx in bgch.keys():
name='res'+str(dx)
accdict[name]=checkaccuracy(bgch[dx],['vowel','type'])
overallaccdict[name]=overallacc(accdict[name],'vowel')
pcdict[name]=propcorr(accdict[name],'vowel')
# ## data
pb52=pd.read_csv('pb52.csv')
pbbark=barkbark(pb52,['F0','F1','F2','F3'])
choices52=pd.read_csv('pb52choices.csv')
ch={}
for h in range(0,10):
name='res'+str(h)+'cyc.csv'
ch[h] = pd.read_csv(name)
pbcm = pd.read_csv('pbcm.csv').drop([0]).set_index('vowelChoice').rename_axis(None)
# # For paper
#
# Set parameters
cval=55
dimsvals={'z0':1,'z1':2.953,'z2':.924,'z3':3.420}
catslist=['vowel','type']
pbtest=pbbark.copy()
rescats=['type']
subset=gettestset(pbbark,'vowel',50)
testers= gettestset(pbbark,'vowel',5)
choices = multicat(cloud=pbbark,testset=testers,cats=catslist,dims = dimsvals,c=cval)
choices
propcorr(checkaccuracy(choices,catslist),'vowel')
# ### Resonance
a={}
for h in range(0,3):
a[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=cval,ncycles=h,rescats=rescats,beta=1,gamma=1)
b={}
for h in range(0,3):
b[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=10,ncycles=h,rescats=rescats,beta=1,gamma=1)
c={}
for h in range(0,3):
c[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=cval,ncycles=h,rescats=['type','vowel'],beta=1,gamma=1)
d={}
for h in range(0,3):
d[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=cval,ncycles=h,rescats=rescats,beta=0,gamma=1)
e={}
for h in range(0,3):
e[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=cval,ncycles=h,rescats=rescats,beta=1,gamma=0.5)
f={}
for h in range(0,3):
f[h]=multirescat(testset=subset,dims=dimsvals,cloud=pbbark,cats=catslist,c=1,ncycles=h,rescats=rescats,beta=1,gamma=0.5)
accdict_f={}
pcdict_f={}
for dx in f.keys():
name='res'+str(dx)
accdict_f[name]=checkaccuracy(f[dx],['vowel','type'])
pcdict_f[name]=propcorr(accdict_f[name],'vowel')
accdict_a={}
pcdict_a={}
for dx in a.keys():
name='res'+str(dx)
accdict_a[name]=checkaccuracy(a[dx],['vowel','type'])
pcdict_a[name]=propcorr(accdict_a[name],'vowel')
accdict_b={}
pcdict_b={}
for dx in b.keys():
name='res'+str(dx)
accdict_b[name]=checkaccuracy(b[dx],['vowel','type'])
pcdict_b[name]=propcorr(accdict_b[name],'vowel')
accdict_c={}
pcdict_c={}
for dx in c.keys():
name='res'+str(dx)
accdict_c[name]=checkaccuracy(c[dx],['vowel','type'])
pcdict_c[name]=propcorr(accdict_c[name],'vowel')
accdict_d={}
pcdict_d={}
for dx in d.keys():
name='res'+str(dx)
accdict_d[name]=checkaccuracy(d[dx],['vowel','type'])
pcdict_d[name]=propcorr(accdict_d[name],'vowel')
serieslist=[]
for dx in a.keys():
name='res'+str(dx)
series=pd.Series(pcdict_a[name]['propcorr'],name=name)
serieslist.append(series)
pcres_a = pd.concat(serieslist,axis=1)
serieslist=[]
for dx in b.keys():
name='res'+str(dx)
series=pd.Series(pcdict_b[name]['propcorr'],name=name)
serieslist.append(series)
pcres_b = pd.concat(serieslist,axis=1)
serieslist=[]
for dx in c.keys():
name='res'+str(dx)
series=pd.Series(pcdict_c[name]['propcorr'],name=name)
serieslist.append(series)
pcres_c = pd.concat(serieslist,axis=1)
serieslist=[]
for dx in d.keys():
name='res'+str(dx)
series=pd.Series(pcdict_d[name]['propcorr'],name=name)
serieslist.append(series)
pcres_d = pd.concat(serieslist,axis=1)
serieslist=[]
for dx in f.keys():
name='res'+str(dx)
series=pd.Series(pcdict_f[name]['propcorr'],name=name)
serieslist.append(series)
pcres_f = pd.concat(serieslist,axis=1)
pcres_f
# #### idk
#save each dict
for dx in res5.keys():
name=str(dx)+'_res5.csv'
res5[dx].to_csv(name)
# +
###How to make function???
accdict_res4={}
overallaccdict_res4={}
pcdict_res4={}
cmdict={}
for dx in res4.keys():
name='res'+str(dx)
accdict_res4[name]=checkaccuracy(res4[dx],['vowel','type'])
overallaccdict_res4[name]=overallacc(accdict[name],'vowel')
pcdict_res4[name]=propcorr(accdict[name],'vowel')
# -
pcdict
serieslist=[]
for dx in res3.keys():
name='res'+str(dx)
series=pd.Series(pcdict_res3[name]['propcorr'],name=name)
serieslist.append(series)
pcres = pd.concat(serieslist,axis=1)
print(pcres)
serieslist=[]
for dx in res2.keys():
name='res'+str(dx)
series=pd.Series(pcdict_res2[name]['propcorr'],name=name)
serieslist.append(series)
pcres_res2 = pd.concat(serieslist,axis=1)
print(pcres_res2)
serieslist=[]
for dx in res4.keys():
name='res'+str(dx)
series=pd.Series(pcdict_res4[name]['propcorr'],name=name)
serieslist.append(series)
pcres_res4 = pd.concat(serieslist,axis=1)
print(pcres_res4)
# ## Categorize all data and check accuracy
confs = confusion(choices52,catslist)
modelcm = confs['vowel']
pbcmfl=pd.Series(pbcm.stack(),name="PB")
mcmfl=pd.Series(modelcm.stack(),name="GCM")
cms
cms=pd.concat([pbcmfl,mcmfl],axis=1)
(((cms.PB-cms.GCM)**2).mean())**.5
correlation = cms['PB'].corr(cms['GCM'])
correlation
pb52_acc=checkaccuracy(choices52,catslist)
pb52_pc=propcorr(pb52_acc,'vowel')
pb52_pc
accplot(pb52_pc, 'vowel', pb52_acc)
overallacc(pb52_acc,'vowel')
# ## Try different numbers of resonance?
# +
accdict={}
overallaccdict={}
pcdict={}
cmdict={}
for dx in bgch.keys():
name='res'+str(dx)
accdict[name]=checkaccuracy(bgch[dx],['vowel','type'])
overallaccdict[name]=overallacc(accdict[name],'vowel')
pcdict[name]=propcorr(accdict[name],'vowel')
# -
bgch={}
for h in range(0,5):
bgch[h]=multirescat(pbtest,dimsvals,pbbark,catslist,cval,h,beta=0.5,gamma=0.5)
for dx in bgch.keys():
name=str(dx)+'wGamma_cyc.csv'
bgch[dx].to_csv(name)
ch[9]['vowelProb']-ch[8]['vowelProb']
# +
serieslist=[]
for dx in ch.keys():
name='res'+str(dx)
series=pd.Series(cmdict[name]['vowel'].stack(),name=name)
serieslist.append(series)
rescm = pd.concat(serieslist,axis=1)
# -
rmsedict={}
for dx in ch.keys():
name='res'+str(dx)
rmsedict[name]=(((rescm.res0-rescm[name])**2).mean())**.5
rmsedict
serieslist=[]
for dx in bgch.keys():
name='res'+str(dx)
series=pd.Series(pcdict[name]['propcorr'],name=name)
serieslist.append(series)
pcres = pd.concat(serieslist,axis=1)
pcresdict={}
for dx in ch.keys():
name='res'+str(dx)
pcresdict[name]=(((pcres.res0-pcres[name])**2).mean())**.5
pcres
pcres
for q in pcdict.keys():
accplot(pcdict[q],'vowel',accdict[q])
accdict
for dx in ch.keys():
name='res'+str(dx)+'cyc.csv'
ch[dx].to_csv(name)
ch.to_csv("res_cycles_1.csv")
# ## scratch
continuum ('TRAP','PALM',pbbark,['F0','F1','F2','F3'],steps=7,df=True)
# # Parameter fitting
test=gettestset(pbbark,'vowel',50)
cats = ['vowel','type']
dims={'z0':1,'z1':1,'z2':1,'z3':1}
# +
#z0anchor = 1
z1guess = 3
z2guess = 1
z3guess = 1
cguess = 55 # initial guess of parameters -- better guesses leads to faster fitting
xguess = [cguess,z1guess,z2guess,z3guess]
#bnds = ((0,None),(0,None),(0,None),(0,None),(0,1)) # require parameters to be > 0
result = minimize(errorfunc_anchor,
xguess, # the initial guess array
args=(pbbark,test,['z0','z1','z2','z3'],cats),
method='Powell',
#bounds=bnds, # the bounds on the parameter values
tol=0.01, # a 'tolerance' value, smaller means more function evaluations
#options={'gtol': 1e-6, 'disp': True}
)
print("fitted parameters = ", result.x)
print("number of function evaluations = ", result.nfev)
result
# -
testnoer=test[test['vowel']!='NURSE']
catpb52 = multicat(pbbark,pbbark,catslist,dims = dimsvals,c=cval)
| GCMPy_parameterFitting.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Inspecting Satellite Imagery using Rasterio
# ## A first look at satellite data with Python
#
# At this point, you will have learned different ways of searching for, filtering, and downloading satellite imagery. Now let's use one of these acquired datasets and dig into it a bit with Python.
#
# Here we're going to use a Python library called [Rasterio](https://rasterio.readthedocs.io/en/stable/): you may be familiar with it already, or perhaps with the related C library, [GDAL](https://gdal.org/). If you've used [Numpy](http://www.numpy.org/) before, working with [Rasterio](https://rasterio.readthedocs.io/en/stable/) will feel very familiar.
# +
from __future__ import division
import math
import rasterio
# This notebook explores a single 4 band (blue, green, red, NIR) PlanetScope scene in a UTM projection.
image_file = "example.tif"
satdat = rasterio.open(image_file)
# -
# ## Basic details
# What can we learn about this satellite image using just Python?
# +
# Minimum bounding box in projected units
print(satdat.bounds)
# +
# Get dimensions, in map units (using the example GeoTIFF, that's meters)
width_in_projected_units = satdat.bounds.right - satdat.bounds.left
height_in_projected_units = satdat.bounds.top - satdat.bounds.bottom
print("Width: {}, Height: {}".format(width_in_projected_units, height_in_projected_units))
# +
# Number of rows and columns.
print("Rows: {}, Columns: {}".format(satdat.height, satdat.width))
# +
# This dataset's projection uses meters as distance units. What are the dimensions of a single pixel in meters?
xres = (satdat.bounds.right - satdat.bounds.left) / satdat.width
yres = (satdat.bounds.top - satdat.bounds.bottom) / satdat.height
print(xres, yres)
print("Are the pixels square: {}".format(xres == yres))
# +
# Get coordinate reference system
satdat.crs
# +
# Convert pixel coordinates to world coordinates.
# Upper left pixel
row_min = 0
col_min = 0
# Lower right pixel. Rows and columns are zero indexing.
row_max = satdat.height - 1
col_max = satdat.width - 1
# Transform coordinates with the dataset's affine transformation.
topleft = satdat.transform * (row_min, col_min)
botright = satdat.transform * (row_max, col_max)
print("Top left corner coordinates: {}".format(topleft))
print("Bottom right corner coordinates: {}".format(botright))
# +
# All of the metadata required to create an image of the same dimensions, datatype, format, etc. is stored in
# one location.
print(satdat.meta)
# -
# ## Bands
# So far, we haven't done too much geospatial-raster-specific work yet. Since we know we're inspecting a multispectral satellite image, let's see what we can learn about its bands.
# +
# The dataset reports a band count.
print(satdat.count)
# And provides a sequence of band indexes. These are one indexing, not zero indexing like Numpy arrays.
print(satdat.indexes)
# -
# Because we know we're look at a PlanetScope 4-band analytic satellite image, we can define the bands by their order:
# +
# PlanetScope 4-band band order: BGRN
blue, green, red, nir = satdat.read()
# Or the slightly less efficient:
# blue = satdat.read(1)
# green = satdat.read(2)
# red = satdat.read(3)
# nir = satdat.read(4)
# Or read the entire dataset into a single 3D array:
# data = satdat.read()
# -
# ## Pixels
#
# In a raster dataset, each pixel has a value. Pixels are arranged in a grid, and pixels representing equivalent data have the same value:
#
# 
# +
# Bands are stored as Numpy arrays.
print(type(blue))
# +
# How many dimensions would a single raster band have? Two dimensions: rows and columns.
print(blue.ndim)
# +
# Glimpse at the band's values and datatype.
print(blue)
print(blue.dtype)
# +
# Output a min & max pixel value in each band.
for bidx in satdat.indexes:
data = satdat.read(bidx)
print("Band {bidx} min {min} max {max}".format(bidx=bidx, min=data.min(), max=data.max()))
# And an overall min/max for the entire dataset.
data = satdat.read()
print("Overall min/max: {} {}".format(data.min(), data.max()))
# +
# Let's grab the pixel 2km east and 2km south of the upper left corner
# World coordinates for the desired pixel.
x_coord = satdat.bounds.left - 2000
y_coord = satdat.bounds.top + 2000
# Convert world coordinates to pixel. World coordinates may not transform precisely to row and column indexes,
# but a Numpy array can only be indexed by integer values. The 'op' parameter for 'satdat.index()' determines
# how the transformed values are rounded. In some cases any point falling within a pixel should be considered
# contained, and in other cases only points falling within one portion of the pixels hould be considered contained.
# The 'op' parameter lets users make this decision on their own. The values must still be cast to integers.
col, row = satdat.index(x_coord, y_coord, op=math.floor)
col = int(col)
row = int(row)
# Now let's look at the value of each band at this pixel
print("Red: {}".format(red[row, col]))
print("Green: {}".format(green[row, col]))
print("Blue: {}".format(blue[row, col]))
print("NIR: {}".format(nir[row, col]))
| jupyter-notebooks/getting-to-know-sat-imagery/Inspecting_Satellite_Imagery.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="oKB8YaRk05Sl"
# <a href="https://colab.research.google.com/github/google-research/tapas/blob/master/notebooks/wtq_predictions.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="-07bRHwv0C7L"
# ##### Copyright 2020 The Google AI Language Team Authors
#
# Licensed under the Apache License, Version 2.0 (the "License");
# + colab={} colab_type="code" id="SSpOxRRH0BCU"
# Copyright 2019 The Google AI Language Team Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="j5EACclxE7sP"
# Running a Tapas fine-tuned checkpoint
# ---
# This notebook shows how to load and make predictions with TAPAS model, which was introduced in the paper: [TAPAS: Weakly Supervised Table Parsing via Pre-training](https://arxiv.org/abs/2004.02349)
# + [markdown] colab_type="text" id="Y-m_JoVCFCV0"
# # Clone and install the repository
#
# + [markdown] colab_type="text" id="lF84Z-KayR3Z"
# First, let's install the code.
# + colab={} colab_type="code" id="uI6zyIM20Kw4"
# ! pip install tapas-table-parsing
# + [markdown] colab_type="text" id="7We9ofHuFMuk"
# # Fetch models fom Google Storage
# + [markdown] colab_type="text" id="sA1jUByqyUNB"
# Next we can get pretrained checkpoint from Google Storage. For the sake of speed, this is a medium sized model trained on [WTQ](https://nlp.stanford.edu/blog/wikitablequestions-a-complex-real-world-question-understanding-dataset/). Note that best results in the paper were obtained with a large model.
# + colab={} colab_type="code" id="B10C0Yz6gQyD"
# ! gsutil cp "gs://tapas_models/2020_08_05/tapas_wtq_wikisql_sqa_masklm_medium_reset.zip" "tapas_model.zip" && unzip tapas_model.zip
# ! mv tapas_wtq_wikisql_sqa_masklm_medium_reset tapas_model
# + [markdown] colab_type="text" id="E3107bGlGm7d"
# # Imports
# + colab={} colab_type="code" id="pnUjDlLqDd3m"
import tensorflow.compat.v1 as tf
import os
import shutil
import csv
import pandas as pd
import IPython
tf.get_logger().setLevel('ERROR')
# + colab={} colab_type="code" id="aml6oLFl1dSt"
from tapas.utils import tf_example_utils
from tapas.protos import interaction_pb2
from tapas.utils import number_annotation_utils
from tapas.scripts import prediction_utils
# + [markdown] colab_type="text" id="AbMUYT1bKMp9"
# # Load checkpoint for prediction
# + [markdown] colab_type="text" id="IO0d_wFMy82O"
# Here's the prediction code, which will create and `interaction_pb2.Interaction` protobuf object, which is the datastructure we use to store examples, and then call the prediction script.
# + colab={} colab_type="code" id="UKfxspnVFPsc"
os.makedirs('results/wtq/tf_examples', exist_ok=True)
os.makedirs('results/wtq/model', exist_ok=True)
with open('results/wtq/model/checkpoint', 'w') as f:
f.write('model_checkpoint_path: "model.ckpt-0"')
for suffix in ['.data-00000-of-00001', '.index', '.meta']:
shutil.copyfile(f'tapas_model/model.ckpt{suffix}', f'results/wtq/model/model.ckpt-0{suffix}')
# + colab={} colab_type="code" id="9RlvgDAmCNtP"
max_seq_length = 512
vocab_file = "tapas_model/vocab.txt"
config = tf_example_utils.ClassifierConversionConfig(
vocab_file=vocab_file,
max_seq_length=max_seq_length,
max_column_id=max_seq_length,
max_row_id=max_seq_length,
strip_column_names=False,
add_aggregation_candidates=False,
)
converter = tf_example_utils.ToClassifierTensorflowExample(config)
def convert_interactions_to_examples(tables_and_queries):
"""Calls Tapas converter to convert interaction to example."""
for idx, (table, queries) in enumerate(tables_and_queries):
interaction = interaction_pb2.Interaction()
for position, query in enumerate(queries):
question = interaction.questions.add()
question.original_text = query
question.id = f"{idx}-0_{position}"
for header in table[0]:
interaction.table.columns.add().text = header
for line in table[1:]:
row = interaction.table.rows.add()
for cell in line:
row.cells.add().text = cell
number_annotation_utils.add_numeric_values(interaction)
for i in range(len(interaction.questions)):
try:
yield converter.convert(interaction, i)
except ValueError as e:
print(f"Can't convert interaction: {interaction.id} error: {e}")
def write_tf_example(filename, examples):
with tf.io.TFRecordWriter(filename) as writer:
for example in examples:
writer.write(example.SerializeToString())
def aggregation_to_string(index):
if index == 0:
return "NONE"
if index == 1:
return "SUM"
if index == 2:
return "AVERAGE"
if index == 3:
return "COUNT"
raise ValueError(f"Unknown index: {index}")
def predict(table_data, queries):
table = [list(map(lambda s: s.strip(), row.split("|")))
for row in table_data.split("\n") if row.strip()]
examples = convert_interactions_to_examples([(table, queries)])
write_tf_example("results/wtq/tf_examples/test.tfrecord", examples)
write_tf_example("results/wtq/tf_examples/random-split-1-dev.tfrecord", [])
# ! python -m tapas.run_task_main \
# --task="WTQ" \
# --output_dir="results" \
# --noloop_predict \
# --test_batch_size={len(queries)} \
# --tapas_verbosity="ERROR" \
# --compression_type= \
# --reset_position_index_per_cell \
# --init_checkpoint="tapas_model/model.ckpt" \
# --bert_config_file="tapas_model/bert_config.json" \
# --mode="predict" 2> error
results_path = "results/wtq/model/test.tsv"
all_coordinates = []
df = pd.DataFrame(table[1:], columns=table[0])
display(IPython.display.HTML(df.to_html(index=False)))
print()
with open(results_path) as csvfile:
reader = csv.DictReader(csvfile, delimiter='\t')
for row in reader:
coordinates = sorted(prediction_utils.parse_coordinates(row["answer_coordinates"]))
all_coordinates.append(coordinates)
answers = ', '.join([table[row + 1][col] for row, col in coordinates])
position = int(row['position'])
aggregation = aggregation_to_string(int(row["pred_aggr"]))
print(">", queries[position])
answer_text = str(answers)
if aggregation != "NONE":
answer_text = f"{aggregation} of {answer_text}"
print(answer_text)
return all_coordinates
# + [markdown] colab_type="text" id="Gqu-I-M9QaoA"
# # Predict
# + colab={"base_uri": "https://localhost:8080/", "height": 842} colab_type="code" id="SIE7bTJMVuSh" outputId="08b2c00b-a433-4324-e7a1-92871d18c62e"
# Based on SQA example nu-1000-0
result = predict("""
Pos | No | Driver | Team | Laps | Time/Retired | Grid | Points
1 | 32 | <NAME> | Team Player's | 87 | 1:48:11.023 | 1 | 22
2 | 1 | <NAME> | Newman/Haas Racing | 87 | +0.8 secs | 2 | 17
3 | 3 | <NAME> | Team Player's | 87 | +28.6 secs | 3 | 14
4 | 9 | <NAME>, Jr. | Team Rahal | 87 | +40.8 secs | 13 | 12
5 | 34 | <NAME> | Mi-Jack Conquest Racing | 87 | +42.1 secs | 6 | 10
6 | 20 | <NAME> | Patrick Racing | 87 | +1:00.2 | 10 | 8
7 | 51 | <NAME> | Fernandez Racing | 87 | +1:01.4 | 5 | 6
8 | 12 | <NAME> | American Spirit Team Johansson | 87 | +1:01.8 | 8 | 5
9 | 7 | <NAME> | Fittipaldi-Dingman Racing | 86 | + 1 Lap | 15 | 4
10 | 55 | <NAME> | Herdez Competition | 86 | + 1 Lap | 11 | 3
11 | 27 | <NAME> | PK Racing | 86 | + 1 Lap | 12 | 2
12 | 31 | <NAME> | American Spirit Team Johansson | 86 | + 1 Lap | 17 | 1
13 | 19 | <NAME> | Dale Coyne Racing | 85 | + 2 Laps | 18 | 0
14 | 33 | <NAME> | Rocketsports Racing | 85 | + 2 Laps | 14 | 0
15 | 4 | <NAME> | Herdez Competition | 85 | + 2 Laps | 9 | 0
16 | 11 | <NAME> | Dale Coyne Racing | 83 | Mechanical | 19 | 0
17 | 2 | <NAME> | Newman/Haas Racing | 77 | Mechanical | 4 | 0
18 | 15 | <NAME> | Walker Racing | 12 | Mechanical | 7 | 0
19 | 5 | <NAME> | Walker Racing | 10 | Mechanical | 16 | 0
""", ["Who are the drivers with 87 laps?", "Sum of laps for team Walker Racing?", "Average grid for the drivers with less than 80 laps?",])
| notebooks/wtq_predictions.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# by <NAME>, 08/2019
#5 frames
#cpu = 1, 21.132148265838623s
#cpu = 16
# +
# %matplotlib inline
import numpy as np
import skimage.external.tifffile
import os
import matplotlib.pyplot as plt
from PIL import Image
import multiprocessing
from multiprocessing import Pool
import sys
sys.path.append('/Users/johannesschoeneberg/git/JohSchoeneberg/pyLattice/src/python/pylattice/functions')
import ParallelFunctions
# +
inputFolder = '/Volumes/4TB_SSD/Johannes_Schoeneberg_Berkeley/20190814_Imaging/rotated/Region_4/CPPdecon/001x_000y_002z/chimeraX/'
outputFolder = '/Volumes/4TB_SSD/Johannes_Schoeneberg_Berkeley/20190814_Imaging/rotated/Region_4/CPPdecon/001x_000y_002z/chimeraX_cropped/'
# +
# prepare the input data for the worker pool
center = np.array([700,330,110+45]) # x,y,z
margin = np.array([200,200,45])
parameters_for_workers = []
for file in os.listdir(inputFolder):
if file.endswith(".tif"):
parameters_for_workers.append((inputFolder,outputFolder,file,center,margin))
print(parameters_for_workers)
# +
# run the jobs on parallel processors
print("Number of cpu : ", multiprocessing.cpu_count())
import time
start_time = time.time()
if __name__ == '__main__':
nCPU = multiprocessing.cpu_count()
numberOfCPUsUsed = int(nCPU*0.75) #10
print("Run on {} CPUs".format(numberOfCPUsUsed))
pool = Pool(numberOfCPUsUsed)
results = pool.starmap(ParallelFunctions.cropLatticeFrame, parameters_for_workers)
print(results)
elapsed_time = time.time() - start_time
print("elapsed time {}s".format(elapsed_time))
# +
#rename output files just by their
# e.g.
# make Scan_Iter_0046_CamA_ch0_CAM1_stack0000_488nm_0000000msec_0005849968msecAbs_001x_000y_002z_0046t_decon.tif'
# to 0046.tif
for file in os.listdir(outputFolder):
if file.endswith(".tif"):
newFilename = outputFolder+"/"+file.split("_")[2]+".tif"
os.rename(os.path.join(outputFolder, file), os.path.join(outputFolder, newFilename))
print(newFilename)
#print(file.split("_")[2])
# -
chimeraX_command_open = "open " + outputFolder+ "*.tif"
chimeraX_command_volume = "volume voxelSize 0.108,0.108,0.4"
print(chimeraX_command_open)
print(chimeraX_command_volume)
| src/jupyter/latticeMovie_cropRegion_parallel.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] graffitiCellId="id_2z4498k"
# ### What is Caching?
# + [markdown] graffitiCellId="id_5why725"
# Caching can be defined as the process of storing data into a temporary data storage to avoid recomputation or to avoid reading the data from a relatively slower part of memory again and again. Thus cachig serves as a fast "look-up" storage allowing programs to execute faster.
#
# *Let's use caching to chalk out an efficient solution for **a problem from the Recursion lesson**.*
# + [markdown] graffitiCellId="id_shkaqhm"
# ### Problem Statement - (Recursion) - Repeat Exercise
#
# A child is running up a staircase and can hop either 1 step, 2 steps or 3 steps at a time.
# Given that the staircase has a total `n` steps, write a function to count the number of possible ways in which child can run up the stairs.
#
# For e.g.
#
# * `n == 1` then `answer = 1`
#
# * `n == 3` then `answer = 4`<br>
# The output is `4` because there are four ways we can climb the staircase:
# - 1 step + 1 step + 1 step
# - 1 step + 2 steps
# - 2 steps + 1 step
# - 3 steps
#
# * `n == 5` then `answer = 13`
#
# **Hint**<br>
# You would need to make use of the [Inductive Hypothesis](https://en.wikipedia.org/wiki/Mathematical_induction#Description), which comprises of the following two steps:
# 1. **The Inductive Hypothesis**: Calculate/assume the results for base case. In our problem scenario, the base cases would be when n = 1, 2, and 3.
#
#
# 2. **The Inductive Step**: Prove that for every $n >= 3$, if the results are true for $n$ , then it holds for $(n+1)$ as well. In other words, assume that the statement holds for some arbitrary natural number $n$ , and prove that the statement holds for $(n+1)$.
#
#
# + graffitiCellId="id_qlyd2h9"
def staircase(n):
# Base Case - What holds true for minimum steps possible i.e., n == 1? Return the number of ways the child can climb one step.
if n == 1:
return 1
# Inductive Hypothesis - What holds true for n == 2 or n == 3? Return the number of ways to climb them.
elif n == 2:
return 2
elif n == 3:
return 4
# Inductive Step (n > 3) - use Inductive Hypothesis to formulate a solutio
return staircase(n-1)+staircase(n-2)+staircase(n-3)
# + graffitiCellId="id_mhzqy0u"
def test_function(test_case):
answer = staircase(test_case[0])
if answer == test_case[1]:
print("Pass")
else:
print("Fail")
# + graffitiCellId="id_vgacxhw"
test_case = [4, 7]
test_function(test_case)
# + graffitiCellId="id_vgt831v"
test_case = [5, 13]
test_function(test_case)
# + graffitiCellId="id_335kkgn"
test_case = [3, 4]
test_function(test_case)
# + graffitiCellId="id_j49hev8"
test_case = [20, 121415]
test_function(test_case)
# + [markdown] graffitiCellId="id_r189hz6"
# <span class="graffiti-highlight graffiti-id_r189hz6-id_vtju73f"><i></i><button>Show Solution</button></span>
# + [markdown] graffitiCellId="id_cfownii"
# ### Problem Statement - (Caching)
#
# While using recursion for the above problem, you might have noticed a small problem with efficiency.
#
# Let's take a look at an example.
#
# * Say the total number of steps are `5`. This means that we will have to call at `(n=4), (n=3), and (n=2)`
#
# * To calculate the answer for `n=4`, we would have to call `(n=3), (n=2) and (n=1)`
#
# You can notice that even for a small number of staircases (here 5), we are calling `n=3` and `n=2` multiple times. Each time we call a method, additional time is required to calculate the solution. In contrast, instead of calling on a particular value of `n` again and again, we can **calculate it once and store the result** to speed up our program.
#
# >Which data structure are you thinking to store the results?
#
# Your job is to use any data-structure that you have used until now to write a faster implementation of the function you wrote earlier while using recursion.
#
# + graffitiCellId="id_uw8ttpq"
def staircase1(n):
stair = dict()
return climb_stair(n,stair)
def climb_stair(n,stair):
if n == 1:
method = 1
elif n == 2:
method = 2
elif n == 3:
method = 4
elif n in stair:
method = stair[n]
else:
if n-1 in stair:
first = stair[n-1]
else:
first = climb_stair(n-1,stair)
if n-2 in stair:
second = stair[n-2]
else:
second = climb_stair(n-2,stair)
if n-3 in stair:
third = stair[n-3]
else:
third = climb_stair(n-3,stair)
method = first+second+third
stair[n] = method
return method
staircase1(20)
# + graffitiCellId="id_zcrgimd"
test_case = [4, 7]
test_function(test_case)
# + graffitiCellId="id_01zs3l1"
test_case = [5, 13]
test_function(test_case)
# + graffitiCellId="id_letl51a"
test_case = [3, 4]
test_function(test_case)
# + graffitiCellId="id_eeu996q"
test_case = [20, 121415]
test_function(test_case)
# + graffitiCellId="id_y6c0eu0"
staircase1(6)
# + [markdown] graffitiCellId="id_0n79ls8"
# <span class="graffiti-highlight graffiti-id_0n79ls8-id_6t02ke7"><i></i><button>Hide Solution</button></span>
# + graffitiCellId="id_6t02ke7"
def staircase2(n):
# start with a blank dictionary. It will populate in the recursive call
num_dict = dict({})
return staircase_faster(n, num_dict)
'''Recursice function'''
def staircase_faster(n, num_dict):
'''
Here `n` is a key and `output` would be the corresponding value
to be inserted into the dictionary as a pair
'''
# Base cases
if n == 1:
output = 1
elif n == 2:
output = 2
elif n == 3:
output = 4
else:
# Simply check if the "value" corresponding to "(n-1)" key is already available in the dictionary
if (n - 1) in num_dict:
first_output = num_dict[n - 1]
# Otherwise, calculate and insert the new key-value pair into the dictioanry
else:
first_output = staircase_faster(n - 1, num_dict)
if (n - 2) in num_dict:
second_output = num_dict[n - 2]
else:
second_output = staircase_faster(n - 2, num_dict)
if (n - 3) in num_dict:
third_output = num_dict[n - 3]
else:
third_output = staircase_faster(n - 3, num_dict)
output = first_output + second_output + third_output
num_dict[n] = output; # insert a key-value pair in the ORIGINAL dictionary
return output
staircase2(20)
# + graffitiCellId="id_121ngzm"
import time
# + graffitiCellId="id_sos51lg"
start_time = time.time()
staircase2(20)
print("--- %s seconds ---" % (time.time() - start_time))
# + graffitiCellId="id_6w4qa4p"
start_time = time.time()
staircase1(20)
print("--- %s seconds ---" % (time.time() - start_time))
# + graffitiCellId="id_tsl5kym"
start_time = time.time()
staircase(20)
print("--- %s seconds ---" % (time.time() - start_time))
# + graffitiCellId="id_dqbjzv0"
import timeit
# -
#original method
print(timeit.timeit('''def staircase1(n):
stair = dict()
return climb_stair(n,stair)
def climb_stair(n,stair):
if n == 1:
method = 1
elif n == 2:
method = 2
elif n == 3:
method = 4
elif n in stair:
method = stair[n]
else:
if n-1 in stair:
method = stair[n-1]+stair[n-2]+stair[n-3]
elif n-2 in stair:
method = climb_stair(n-1,stair)+stair[n-2]+stair[n-3]
elif n-3 in stair:
method = climb_stair(n-1,stair)+climb_stair(n-2,stair)+stair[n-3]
else:
method = climb_stair(n-1,stair)+climb_stair(n-2,stair)+climb_stair(n-3,stair)
stair[n] = method
return method
staircase1(20)''',number = 100000))
print(timeit.timeit('''def staircase1(n):
stair = dict()
return climb_stair(n,stair)
def climb_stair(n,stair):
if n == 1:
method = 1
elif n == 2:
method = 2
elif n == 3:
method = 4
elif n in stair:
method = stair[n]
else:
if n-1 in stair:
first = stair[n-1]
else:
first = climb_stair(n-1,stair)
if n-2 in stair:
second = stair[n-2]
else:
second = climb_stair(n-2,stair)
if n-3 in stair:
third = stair[n-3]
else:
third = climb_stair(n-3,stair)
method = first+second+third
stair[n] = method
return method
staircase1(20)
''',number = 100000))
| data_structure/Caching.ipynb |
#!/usr/bin/env python
# ---
# jupyter:
# jupytext:
# cell_metadata_filter: -all
# formats: ipynb,py
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tfrl-cookbook
# language: python
# name: tfrl-cookbook
# ---
# Value-based reinforcement learning
# Chapter 2, TensorFlow 2 Reinforcement Learning Cookbook | <NAME>
from pathlib import Path
import numpy as np
from envs.maze import MazeEnv
from value_function_utils import visualize_maze_values
discount = 0.9
iters = 1000
env = MazeEnv()
state_dim = env.distinct_states
state_values = np.zeros(state_dim)
q_values = np.zeros((state_dim, env.action_space.n)) # Action values
policy = np.zeros(state_dim)
def calculate_values(state, action):
"""Evaluate Value function for given state and action
Args:
state (int): Valid (discrete) state in discrete `env.observation_space`
action (int): Valid (discrete) action in `env.action_space`
Returns:
v_sum: value for given state, action
"""
v_sum = 0
transitions = []
slip_action = env.slip_action_map[action]
env.set_state(state)
slip_next_state, slip_reward, _ = env.step(slip_action, slip=False)
transitions.append((slip_reward, slip_next_state, env.slip_probability))
env.set_state(state)
next_state, reward, _ = env.step(action, slip=False)
transitions.append((reward, next_state, 1 - env.slip_probability))
for reward, next_state, pi in transitions:
v_sum += pi * (reward + discount * state_values[next_state])
return v_sum
# Value Iteration
for i in range(iters):
v_s = np.zeros(state_dim)
for state in range(state_dim):
if env.index_to_coordinate_map[int(state / 8)] == env.goal_pos:
continue
v_max = float("-inf")
for action in range(env.action_space.n):
v_sum = calculate_values(state, action)
v_max = max(v_max, v_sum)
v_s[state] = v_max
state_values = np.copy(v_s)
for state in range(state_dim):
for action in range(env.action_space.n):
q_values[state, action] = calculate_values(state, action)
for state in range(state_dim):
policy[state] = np.argmax(q_values[state, :])
Path("results").mkdir(exist_ok=True)
np.save("results/q_values", q_values)
np.save("results/optimal_policy", policy)
# print(q_values)
print("Action mapping:[0 - UP; 1 - DOWN; 2 - LEFT; 3 - RIGHT")
print("Optimal actions:")
print(policy)
visualize_maze_values(q_values, env)
| Chapter02/2_value_based_rl.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pickle
from sklearn.externals import joblib
import pandas as pd
import itertools as it
file_name = 'rb_model.pkl'
model = joblib.load(file_name)
stats_df = pd.read_csv('representative_statistics.csv', index_col = 0)
def z_score(data_mean, data_std, val):
return (val - data_mean) / data_std
cols = ['rb_college_height_inches', 'rb_hw_ratio','rb_forty', 'rb_vertical', 'rb_bench','rb_broad', 'rb_threecone', 'rb_shuttle','rb_rushing_games', 'rb_rushing_rec_td','rb_rushing_rec_yards', 'rb_rushing_receptions','rb_rushing_rush_att', 'rb_rushing_rush_td','rb_rushing_rush_yds', 'rb_rushing_scrim_plays','rb_rushing_scrim_tds', 'rb_rushing_scrim_yds','rb_rushing_seasons', 'rb_max_madden','rb_rushing_rec_td_pg', 'rb_rushing_rec_yards_pg','rb_rushing_receptions_pg', 'rb_rushing_rush_att_pg','rb_rushing_rush_td_pg', 'rb_rushing_rush_yds_pg','rb_rushing_scrim_plays_pg', 'rb_rushing_scrim_tds_pg','rb_rushing_scrim_yds_pg', 'rb_football_spending','rb_coaches_salaries', 'rb_ticket_sales','rb_rushing_rush_td_pg_cf_scaled','rb_rushing_rush_yds_pg_cf_scaled','rb_rushing_scrim_plays_pg_cf_scaled','rb_rushing_scrim_tds_pg_cf_scaled','rb_rushing_scrim_yds_pg_cf_scaled', 'rb_ann_rain_inch','rb_ann_snow_inch', 'rb_min_jan', 'rb_min_feb','rb_min_mar', 'rb_min_apr', 'rb_min_may','rb_min_jun', 'rb_min_jul', 'rb_min_aug','rb_min_sep', 'rb_min_oct', 'rb_min_nov','rb_min_dec', 'rb_max_jan', 'rb_max_feb','rb_max_mar', 'rb_max_apr', 'rb_max_may','rb_max_jun', 'rb_max_jul', 'rb_max_aug','rb_college_weight_pounds']
stats_df['rb_college_height_inches_zscore']
frame = []
for c in stats_df.columns:
row = []
mean = stats_df[c][0]
sd = stats_df[c][1]
minv = stats_df[c][2]
maxv = stats_df[c][3]
spread = maxv - minv
division = (spread/10)
for i in range(10):
row.append(z_score(mean,sd,(minv + division*i)))
frame.append(row)
#df = pd.DataFrame(frame)
#df = df.T
synth_vals = pd.DataFrame(frame).T
synth_vals.columns = cols
# +
#df.columns = synth_vals.columns
# -
top_vals = ['rb_forty', 'rb_rushing_scrim_tds_pg_cf_scaled', 'rb_college_weight_pounds', 'rb_vertical', 'rb_rushing_scrim_yds_pg_cf_scaled', 'rb_rushing_rush_att', 'rb_ann_rain_inch', 'rb_rushing_rush_td_pg_cf_scaled', 'rb_rushing_receptions', 'rb_bench']
top_df = synth_vals[top_vals]
perms = it.permutations(top_df)
tmpvals = list(perms)
perm_df = pd.DataFrame(tmpvals)
top_df
| ML/create-synthetic-data.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python
# name: conda-env-python-py
# ---
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="http://cocl.us/pytorch_link_top"><img src = "http://cocl.us/Pytorch_top" width = 950, align = "center"></a>
# <img src = "https://ibm.box.com/shared/static/ugcqz6ohbvff804xp84y4kqnvvk3bq1g.png" width = 200, align = "center">
#
# <h1 align=center><font size = 5>Using Dropout for Classification Assignment </font></h1>
# # Table of Contents
# in this lab, you will see how adding dropout to your model will decrease overfitting by using <code>nn.Sequential</code> and Cross Entropy Loss.
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <li><a href="#ref0">Make Some Data</a></li>
# <li><a href="#ref1">Create the Model and Cost Function the Pytorch way</a></li>
# <li><a href="#ref2">Batch Gradient Descent</a></li>
# <br>
# <p></p>
# Estimated Time Needed: <strong>20 min</strong>
# </div>
#
# <hr>
# Import all the libraries that you need for the lab:
import torch
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
from matplotlib.colors import ListedColormap
# Use this function only for plotting:
def plot_decision_regions_3class(data_set,model=None):
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA','#00AAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00','#00AAFF'])
X=data_set.x.numpy()
y=data_set.y.numpy()
h = .02
x_min, x_max = X[:, 0].min()-0.1 , X[:, 0].max()+0.1
y_min, y_max = X[:, 1].min()-0.1 , X[:, 1].max() +0.1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
newdata=np.c_[xx.ravel(), yy.ravel()]
#XX=torch.torch.Tensor(newdata)
#_,yhat=torch.max(model(XX),1)
#yhat=yhat.numpy().reshape(xx.shape)
Z=data_set.fun(newdata).flatten()
f=np.zeros(Z.shape)
f[Z>0]=1
f=f.reshape(xx.shape)
if model!=None:
model.eval()
XX=torch.torch.Tensor(newdata)
_,yhat=torch.max(model(XX),1)
yhat=yhat.numpy().reshape(xx.shape)
plt.pcolormesh(xx, yy, yhat, cmap=cmap_light)
plt.contour(xx, yy, f, cmap=plt.cm.Paired)
else:
plt.contour(xx, yy, f, cmap=plt.cm.Paired)
plt.pcolormesh(xx, yy, f, cmap=cmap_light)
plt.title("decision region vs True decision boundary")
plt.legend()
# Use this function to calculate accuracy:
def accuracy(model,data_set):
_,yhat=torch.max(model(data_set.x),1)
return (yhat==data_set.y).numpy().mean()
# <a id="ref0"></a>
# <h2 align=center>Get Some Data </h2>
# Create a nonlinearly separable dataset:
# +
from torch.utils.data import Dataset, DataLoader
class Data(Dataset):
def __init__(self,N_SAMPLES = 1000,noise_std=0.1,train=True):
a=np.matrix([-1,1,2,1,1,-3,1]).T
self.x = np.matrix(np.random.rand(N_SAMPLES,2))
self.f=np.array(a[0]+(self.x)*a[1:3]+np.multiply(self.x[:,0], self.x[:,1])*a[4]+np.multiply(self.x, self.x)*a[5:7]).flatten()
self.a=a
self.y=np.zeros(N_SAMPLES)
self.y[self.f> 0]=1
self.y=torch.from_numpy(self.y).type(torch.LongTensor)
self.x=torch.from_numpy(self.x).type(torch.FloatTensor)
self.x = self.x+noise_std*torch.randn(self.x.size())
self.f=torch.from_numpy(self.f)
self.a=a
if train==True:
torch.manual_seed(1)
self.x = self.x+noise_std*torch.randn(self.x.size())
torch.manual_seed(0)
def __getitem__(self,index):
return self.x[index],self.y[index]
def __len__(self):
return self.len
def plot(self):
X=data_set.x.numpy()
y=data_set.y.numpy()
h = .02
x_min, x_max = X[:, 0].min() , X[:, 0].max()
y_min, y_max = X[:, 1].min(), X[:, 1].max()
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
Z=data_set.fun(np.c_[xx.ravel(), yy.ravel()]).flatten()
f=np.zeros(Z.shape)
f[Z>0]=1
f=f.reshape(xx.shape)
plt.title('True decision boundary and sample points with noise ')
plt.plot(self.x[self.y==0,0].numpy(),self.x[self.y==0,1].numpy(),'bo',label='y=0' )
plt.plot(self.x[self.y==1,0].numpy(), self.x[self.y==1,1].numpy(),'ro',label='y=1' )
plt.contour(xx, yy, f, cmap=plt.cm.Paired)
plt.xlim(0,1)
plt.ylim(0,1)
plt.legend()
def fun(self,x):
x=np.matrix(x)
out=np.array(self.a[0]+(x)*self.a[1:3]+np.multiply(x[:,0], x[:,1])*self.a[4]+np.multiply(x, x)*self.a[5:7])
out=np.array(out)
return out
# -
# Create a dataset object:
data_set=Data(noise_std=0.2)
data_set.plot()
# Get some validation data:
torch.manual_seed(0)
validation_set=Data(train=False)
# <a id="ref1"></a>
# <h2 align=center>Create the Model, Optimizer, and Total Loss Function (cost)</h2>
# ### Create a three-layer neural network <code>model</code> with a ReLU() activation function for regression. All the appropriate layers should be 300 units.
#
# +
#create a model
n_hidden = 300
model = torch.nn.Sequential(
torch.nn.Linear(2, n_hidden),
torch.nn.ReLU(),
torch.nn.Linear(n_hidden, n_hidden),
torch.nn.ReLU(),
torch.nn.Linear(n_hidden, 2)
)
# -
# ### Create a three-layer neural network <code>model_drop</code> with a ReLU() activation function for regression. All the appropriate layers should be 300 units. Apply dropout to all but the last layer and make the probability of dropout is 50%.
# +
#create a model
n_hidden = 300
model_dropout = torch.nn.Sequential(
torch.nn.Linear(2, n_hidden),
torch.nn.Dropout(0.5),
torch.nn.ReLU(),
torch.nn.Linear(n_hidden, n_hidden),
torch.nn.Dropout(0.5),
torch.nn.ReLU(),
torch.nn.Linear(n_hidden, 2)
)
# -
# <a id="ref2"></a>
# <h2 align=center>Train the Model via Mini-Batch Gradient Descent </h2>
# Set the model by using dropout to training mode; this is the default mode, but it's a good practice.
model_dropout.train()
# Train the model by using the Adam optimizer. See the unit on other optimizers. Use the Cross Entropy Loss:
optimizer_ofit = torch.optim.Adam(model.parameters(), lr=0.01)
optimizer_drop = torch.optim.Adam(model_dropout.parameters(), lr=0.01)
criterion = torch.nn.CrossEntropyLoss()
# ## Create the appropriate loss function.
# <!-- Your answer is below:
# criterion = torch.nn.CrossEntropyLoss()
# -->
#
# Initialize a dictionary that stores the training and validation loss for each model:
LOSS={}
LOSS['training data no dropout']=[]
LOSS['validation data no dropout']=[]
LOSS['training data dropout']=[]
LOSS['validation data dropout']=[]
# Run 500 iterations of batch gradient decent:
# +
epochs=500
for epoch in range(epochs):
#make a prediction for both models
yhat = model(data_set.x)
yhat_drop = model_dropout(data_set.x)
#calculate the lossf or both models
loss = criterion(yhat, data_set.y)
loss_drop = criterion(yhat_drop, data_set.y)
#store the loss for both the training and validation data for both models
LOSS['training data no dropout'].append(loss.item())
LOSS['validation data no dropout'].append(criterion(model(validation_set.x), validation_set.y).item())
LOSS['training data dropout'].append(loss_drop.item())
model_dropout.eval()
LOSS['validation data dropout'].append(criterion(model_dropout(validation_set.x), validation_set.y).item())
model_dropout.train()
#clear gradient
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad()
#Backward pass: compute gradient of the loss with respect to all the learnable parameters
loss.backward()
loss_drop.backward()
#the step function on an Optimizer makes an update to its parameters
optimizer_ofit.step()
optimizer_drop.step()
# -
# Set the model with dropout to evaluation mode:
model_drop.eval()
# ### Test the accuracy of the model without dropout on the validation data.
#test accuracy
test_acc = accuracy(model, validation_set)
print("Test accuracy of the model without dropout: ", test_acc)
# Double-click __here__ for the solution.
# <!-- Your answer is below:
# _,yhat=torch.max(model(validation_set.x),1)
# (yhat==validation_set.y).numpy().mean()
# -->
# ### Test the accuracy of the model with dropout on the validation data.
#test accuracy
test_acc = accuracy(model_dropout, validation_set)
print("Test accuracy of the model with dropout: ", test_acc)
# Double-click __here__ for the solution.
# <!-- Your answer is below:
# _,yhat=torch.max(model_drop(validation_set.x),1)
# (yhat==validation_set.y).numpy().mean()
# -->
#
# You see that the model with dropout performs better on the validation data.
# Plot the decision boundary and the prediction of the networks in different colors:
# ## true function
plot_decision_regions_3class(data_set)
# ## model without dropout
plot_decision_regions_3class(data_set,model)
# ## model with dropout
plot_decision_regions_3class(data_set,model_dropout)
# You can see that the model using dropout does better at tracking the function that generated the data.
# Plot out the loss for training and validation data on both models:
plt.figure(figsize=(6.1, 10))
for key, value in LOSS.items():
plt.plot(np.log(np.array(value)),label=key)
plt.legend()
plt.xlabel("iterations")
plt.ylabel("Log of cost or total loss")
# You see that the model without dropout performs better on the training data, but it performs worse on the validation data. This suggests overfitting. However, the model using dropout performed better on the validation data, but worse on the training data.
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <a href="http://cocl.us/pytorch_link_bottom"><img src = "http://cocl.us/pytorch_image_bottom" width = 950, align = "center"></a>
# ### About the Authors:
#
# [<NAME>]( https://www.linkedin.com/in/joseph-s-50398b136/) has a PhD in Electrical Engineering. His research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition.
#
# Other contributors: [<NAME>]( https://www.linkedin.com/in/michelleccarey/), [Morvan Youtube channel]( https://www.youtube.com/channel/UCdyjiB5H8Pu7aDTNVXTTpcg), [<NAME>]( https://www.linkedin.com/in/jiahui-mavis-zhou-a4537814a/)
# <hr>
# Copyright © 2018 [cognitiveclass.ai](cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu). This notebook and its source code are released under the terms of the [MIT License](https://bigdatauniversity.com/mit-license/).
| 5. Dropout/5.1.2.dropoutAssignment.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# !pip install numpy scikit-learn compress-fasttext xmltodict matplotlib
from ruwordnet import RuWordNet
wn = RuWordNet()
len(wn.synsets), len(wn.senses)
# # Using the thesaurus
for sense in wn.get_senses('замок'):
print(sense.synset)
wn.get_senses('замок')[0].synset.hypernyms
wn.get_senses('спаржа')[0].synset.hypernyms
wn.get_senses('авокадо')
veg = wn.get_senses('спаржа')[0].synset.hypernyms[0]
veg
veg.hyponyms
wn.get_senses('продукт')[0].synset.hyponyms[0].hyponyms[1].hyponyms[0].senses
# ## More relations
# Домен - атрибут
print(wn['мяч'][0].synset.domains)
import random
print(random.sample(wn['спорт'][0].synset.domain_items, 10))
# Часть - целое
print(wn['автомобиль'][0].synset.meronyms)
print(wn['страница'][0].synset.holonyms)
# Класс-экземпляр
print(wn['москва-река'][0].synset.classes)
print(random.sample(wn['областной центр'][0].synset.instances, 10))
# Предпосылки - выводы
print(wn['убить'][0].synset.premises)
print(wn['завоевать'][0].synset.conclusions)
# Причины-следствия
print(wn['устать'][0].synset.causes)
print(wn['убить'][0].synset.effects)
# Частеречные синонимы
[s for ss in wn['убить'][0].synset.pos_synonyms for s in ss.senses]
# антонимы
wn['быстрый'][0].synset.antonyms
# фразы и их составляющие
wn['быстрый'][0].phrases
wn['послужной список'][0].words
# Однокоренные слова
wn['синий'][0].derivations
# # Predicting hypernyms
# +
import numpy as np
import compress_fasttext
from collections import Counter
from sklearn.neighbors import KDTree
import matplotlib.pyplot as plt
# %matplotlib inline
# -
ft = compress_fasttext.models.CompressedFastTextKeyedVectors.load(
'https://github.com/avidale/compress-fasttext/releases/download/v0.0.1/ft_freqprune_100K_20K_pq_100.bin'
)
# +
def vectorize(text):
vec = np.mean([ft[word] for word in text.lower().split() if len(word) >= 3], axis=0)
vec /= sum(vec**2) ** 0.5
return vec
def distance2vote(d, a=3, b=5):
sim = np.maximum(0, 1 - d**2/2)
return np.exp(-d**a) * sim **b
# -
x = np.linspace(0, 1)
plt.plot(x, distance2vote(x))
plt.xlabel('Расстояние до соседа')
plt.ylabel('Вес голоса соседа')
plt.title('Функция взвешивания соседей');
from tqdm.auto import tqdm, trange
words, vectors, synset_ids = [], [], []
for synset in tqdm(wn.synsets):
if synset.part_of_speech != 'V':
continue
for sense in synset.senses:
words.append(sense.name)
vectors.append(vectorize(sense.name))
synset_ids.append(synset.id)
vectors = np.stack(vectors)
tree = KDTree(vectors)
votes = Counter()
dists, ids = tree.query(vectorize('кудахтать').reshape(1, -1), k=100)
for idx, distance in zip(ids[0], dists[0]):
for hyper in wn[synset_ids[idx]].hypernyms:
votes[hyper.id] += distance2vote(distance)
print(words[idx], [t.title for t in wn[synset_ids[idx]].hypernyms])
for sid, score in votes.most_common(10):
print(score, wn[sid].title)
# # Найди лишнее
# ДИВАН, ШКАФ, ЛАМПА, СТОЛ
# +
import math
def get_all_hypernyms(wn, word, max_level=100):
""" Return dict of all hypernyms of a word and their distances """
front = [sense.synset for sense in wn.get_senses(word)]
levels = {}
for level in range(max_level):
if not front:
break
new_front = []
for synset in front:
if synset.id not in levels:
levels[synset.id] = level
new_front.extend(synset.hypernyms)
front = new_front
return levels
def get_closest_common(levels1, levels2):
""" Find the closest common hypernym and sum of distances to it"""
result = None
result_distance = math.inf
for id, distance in levels1.items():
if id in levels2:
total = distance + levels2[id]
if total < result_distance:
result_distance = total
result = id
return result, result_distance
# -
words = ['ДИВАН', 'ШКАФ', 'ЛАМПА', 'СТОЛ']
print('\t\t', '\t'.join(words))
for w1 in words:
print(w1, end='\t')
for w2 in words:
n, d = get_closest_common(get_all_hypernyms(wn, w1), get_all_hypernyms(wn, w2))
print(d, end='\t\t')
print()
name, distance = get_closest_common(get_all_hypernyms(wn, 'лампа'), get_all_hypernyms(wn, 'шкаф'))
print(distance, name, wn[name].title)
for k, v in get_all_hypernyms(wn, 'лампа').items():
print(k, v, wn[k])
wn["149201-N"].hypernyms
for k, v in get_all_hypernyms(wn, 'стол').items():
print(k, v, wn[k])
# # Word sense disambiguation
# зАмок или замОк ?
#
# Примитивный алгоритм: для каждого значения находим синонимы и проверяем, какие ближе по fasttext-эмбеддингу к словам контекста.
#
# Для верности, стоило бы кроме синонимов взять ещё и ко-гипонимы.
import razdel
context = '''Сначала шов слегка уплотняем молоточком, затем прочеканиваем на нём замок
― бороздку, называемую "зигом", которая будет препятствовать расхождению шва при дальнейшем его уплотнении.'''
word = 'замок'
# +
def disambiguate(word, context):
candidates = [s.synset for s in wn[word]]
text_vector = vectorize(' '.join(t.text for t in razdel.tokenize(context) if t.text != word))
candidate_vectors = [
vectorize(' '.join(w for s in c.senses for w in s.name.lower().split() if name != word))
for c in candidates
]
scores = [np.dot(text_vector, v) for v in candidate_vectors]
return dict(zip(scores, candidates))
disambiguate(word, context)
# -
context = '''Издали видны королевский замок Вавель и кафедральный собор Святых Вацлава и Станислава
― настоящие шедевры зодчества.'''
disambiguate(word, context)
| example_for_taxonomy.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Perceptron
#
# Perceptron is a supervised machine learning algorithm and can be regarded as the base of neural network architectures. A perceptron is basically a neuron in NN models. It is also a binary linear classifier. <br>
# Similar to logistic regression, it has a real-valued weight vector w and a real-valued bias b.
# Unlike logistic regression which uses a sigmoid function as its activation function, perceptron has a step function(heaviside) as activation function. <br>
# ### Training Steps
# 1. Initialize weight vector and bias with zero (or very minimal) values
# 2. Calculate $$\boldsymbol{a} = \boldsymbol{X} \cdot \boldsymbol{w} + b $$
# 3. Apply the step function <br>
# $$\hat{y}^{(i)} = 1 \, if \, a^{(i)} \geq 0, \, else \, 0$$
# 4. Compute the weight updates using perceptron learning rule <br>
# $$
# \Delta \boldsymbol{w} = \eta \, \boldsymbol{X}^T \cdot \big(\boldsymbol{\hat{y}} - \boldsymbol{y} \big)
# $$$$ \Delta b = \eta \, \big(\boldsymbol{\hat{y}} - \boldsymbol{y} \big) $$
# 5. Update the weights and bias <br>
# $$w = w + \Delta \boldsymbol{w}$$ <br>
# $$b = b + \Delta \boldsymbol{b}$$
# ### Data
# +
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
np.random.seed(1234)
X, y = make_blobs(n_samples=2000, centers=2)
fig = plt.figure(figsize=(8,6))
plt.scatter(X[:,0], X[:,1], c=y)
plt.title("Dataset")
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
# +
# Reshaping y variable such that it is (n_samples, 1)
# or in other words, making it a column vector
y = y[:, np.newaxis]
X_train, X_test, y_train, y_test = train_test_split(X, y)
print(f'Shape X_train: {X_train.shape}')
print(f'Shape y_train: {y_train.shape}')
print(f'Shape X_test: {X_test.shape}')
print(f'Shape y_test: {y_test.shape}')
# -
# ### Model
class Perceptron:
def __init__(self):
pass
def step_function(self, x):
return np.array([1 if i >= 0 else 0 for i in x])[:, np.newaxis]
def train(self, X, y, alpha=0.001, iterations=100):
# Step 1: Initialize the parameters
n_samples, n_features = X.shape
self.w = np.zeros(shape=(n_features,1))
self.b = 0
for i in range(iterations):
# Step 2 and 3: Computing linear combination of input features
# and then passing through step function
y_hat = self.step_function(np.dot(X, self.w) + self.b)
# Step 4: Compute weight updates
delta_w = alpha * np.dot(X.T, (y - y_hat))
delta_b = alpha * np.sum(y - y_hat)
# Step 5: Update the parameters
self.w += delta_w
self.b += delta_b
return self.w, self.b
def predict(self, X):
return self.step_function(np.dot(X, self.w) + self.b)
# ### Initializing and training the model
perceptron = Perceptron()
w_trained, b_trained = perceptron.train(X_train, y_train, alpha=0.003, iterations=600)
# ### Testing the model
y_pred_train = perceptron.predict(X_train)
y_pred_test = perceptron.predict(X_test)
print(f"train accuracy: {100 - np.mean(np.abs(y_pred_train - y_train)) * 100}%")
print(f"test accuracy: {100 - np.mean(np.abs(y_pred_test - y_test))*100}%")
# ### Visualize decision boundary
# +
def plot_hyperplane(X, y, w, b):
slope = -w[0]/w[1]
intercept = -b/w[1]
x_hyperplane = np.linspace(-10,5,5)
y_hyperplane = slope*x_hyperplane + intercept
fig = plt.figure(figsize=(8,6))
plt.scatter(X[:,0], X[:,1], c=y.ravel())
plt.plot(x_hyperplane, y_hyperplane, '-')
plt.title("Dataset with fitted hyperplane")
plt.xlabel("First feature")
plt.ylabel("Second feature")
plt.show()
plot_hyperplane(X, y, w_trained, b_trained)
# -
| perceptron.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a id='start'></a>
# # Wrangling
#
# In questo notebook vengono spiegati i principali metodi per manipolare i dati di un dataset. <br>
# <br>
# Il notebook è suddiviso nelle seguenti sezioni:<br>
# - [Summary Functions](#section1)<a href='#section1'></a>; <br>
# - [Grouping and Sorting](#section2)<a href='#section2'></a>; <br>
# - [Data types](#section3)<a href='#section3'></a>; <br>
# - [Wrangling Data](#section4)<a href='#section4'></a><br>
# - [Missing Value](#section5)<a href='#section5'></a><br>
#
# Importiamo il dataset del titanic
# +
import pandas as pd
titanic = pd.read_csv("train_dataset_titanic.csv")
# -
# <a id='section1'></a>
# ## Summary Function
# Osserviamo le prime 4 righe del dataset
titanic.head()
# È possibile conoscere la struttura di un dataset attraverso il metodo **shape**, il primo valore indicherà il numero di righe del dataset, mentre il secondo valore indicherà il numero di colonne del dataset:
titanic.shape
print("Il dataset di Train del Titanic ha", titanic.shape[0], "righe e", titanic.shape[1], "colonne")
# È possibile avere una descrizione veloce di un campo di un dataset attraverso il metodo **describe**:
titanic.describe()
# L'output del metodo **describe** sarà differente a seconda del tipo di campo sul quale si vuole avere una descrizione, ad esempio per un campo stringa si avrà la seguente descrizione:
titanic.Embarked.describe()
# Calcoli veloci che possono tornare utili nell'analizzare un campo possono essere la *media* (**mean**), oppure la *mediana* (**median**). Si tratta di metodi tutti già inseriti all'interno della libreria di Pandas.
print("La media dell'età sul Titanic era:", round(titanic.Age.mean(),0), "anni")
print("La mediana dell'età sul Titanic era:", round(titanic.Age.median(),0), "anni")
# Nel caso di un campo contenente stringhe invece, un metodo molto utile che è possibile usare per vedere i valori univoci contenuti nel campo, è **unique**:
titanic.Embarked.unique()
# Se oltre a vedere la lista dei valori univoci volessimo sapere ogni quanto si ripetono possiamo usare il metodo **value_counts**:
titanic.Embarked.value_counts()
# <a id='section2'></a>
# ## Grouping and Sorting
# Spesso potremmo voler raggruppare i nostri dati e poi fare qualcosa di specifico per il gruppo in cui si trovano. <br>
# Per fare ciò, possiamo usare l'operatore **groupby**.
# <br>
# <br>
# Capiamo meglio con un esempio: supponiamo di voler contare quanti maschi e quante femmine ci sono nel nostro dataset del Titanic.
titanic.groupby('Sex').Sex.count()
# La cosa interessante è che l'operatore *groupby* ci permette di rispondere anche a domande più complesse, come ad esempio: <br>
# *Qual è l'età massima all'interno del gruppo dei maschi e delle femmine?*
titanic.groupby('Sex').Age.max()
# È possibile anche calcolare più metriche sulla stessa selezione, grazie al metodo **agg**, come nel seguente esempio:
titanic.columns
# Calcolo l'età massima per ciascun gruppo (femmine e maschi) e conto il numero di femmine e maschi
titanic.groupby(['Pclass', 'Sex']).Age.agg([max, len])
# È possibile ordinare il dataset come vogliamo utilizzando il metodo **sort_values**:
titanic.sort_values(by='Sex').head()
# In automatico, l'operatore **sort_values** ordina il dataset in ordine crescente, se volessimo ordinarlo in ordine descrescente possiamo usare la seguente notazione:
titanic.sort_values(by='Age', ascending=False).head()
# È possibile ordinare anche più colonne alla volta:
titanic.sort_values(by=['Age', 'Sex'], ascending=False).head()
# <a id='section3'></a>
# ## Data Types
# Il metodo per conoscere il tipo di dato contenuto in un campo del dataset è **dtype**
titanic.Age.dtype
# Si usa invece **dtypes** quando vogliamo conoscere le tipologie di dato utilizzato per ciascuna colonna del dataset
titanic.dtypes
# È possibile convertire la tipologia di una colonna in un'altra attraverso la funzione **astype**; ovviamente la tipologia verso il quale si converte un campo deve essere coerente con i valori contenuti in un campo, ad esempio una stringa non potrà mai essere convertita in un numero.
# +
pd.set_option('max_rows', 5) # codice con il quale imposto il numero di righe visualizzate in output a 5
titanic.Survived.astype('float64') # Converto il campo Survived da int64 a float64
# -
# La funzione **astype** è utile anche quando all'interno del dataset abbiamo dei campi categorici, che possono essere ordinati secondo una logica. In questo caso è possibile creare un *mapping* a cui ad ogni categoria viene associata un numero e ogni numero indica l'ordine in cui devono essere considerate i valori contenuti nel campo categorico. <br>
# Ad esempio:
# +
# Creiamo una lista in cui indichiamo la soddisfazione di un cliente
ordered_satisfaction = ['Molto Infelice', 'Infelice', 'Neutrale', 'Felice']
# Creiamo un DataFrame di soddisfazioni possibili
df = pd.DataFrame({'satisfaction':['Pessima', 'Felice', 'Infelice', 'Neutrale']})
df
# -
df.satisfaction = df.satisfaction.astype("category", ordered=True, categories=ordered_satisfaction).cat.codes
df
# Il record 'Pessima' è stato mappato come -1 poichè non era contenuto nel nostro "Dizionario" (ordered_satisfaction).<br>
# L'esempio visto sopra può tornare utile ogni volta che abbiamo un campo categorico che vogliamo ordinare secondo una nostra logica; nel nostro esempio la logica era dettata dalla lista *ordered satisfaction*
# Oltre a determinare un ordinamento di un campo categorico, è possibile trasformare un campo categorico in una serie di colonne booleane, tante quanti sono i valori distinti del campo categorico. <br>
# Ad esempio, considerando nuovamente il dataset sul titanic, potremmo voler codificare il campo Sex in numerico, eliminando la colonna categorica Sex e sostituendola con due colonne. In ognuna delle due colonne ci saranno degli 0 e degli 1 ad indicare la riga corrispondente ad un maschio e viceversa ad una femmina. Per fare ciò dobbiamo usare la funzione **get_dummies**.<br>
# Osserviamo il seguente esempio:
titanic.head()
titanic = pd.get_dummies(titanic, columns=['Sex'])
titanic.head()
# <a id='section4'></a>
# ## Wrangling Data
# Qualora volessimo eliminare una colonna o una particolare riga del nostro dataset possiamo utilizzare il metodo **drop**.
# Cancello la colonna Ticket dal dataset del Titanic
titanic = titanic.drop(labels=['Ticket'], axis = 1)
titanic
# Possiamo anche assicurarci di eliminare eventuali duplicati dal nostro dataset attraverso il metodo **drop_duplicates**, tuttavia in questo caso Pandas ha bisogno che si specifichi in quale colonne effettuare il controllo dei duplicati.
# Eliminiamo tutti i record che sono identici dal punto di vista del campo Pclass e Age
titanic_2 = titanic.drop_duplicates(subset=['Pclass', 'Age'])
titanic_2
# Quando si eliminano dei duplicati si creano dei "buchi" nell'indicizzazione delle righe, per ovviare a questo problema è sempre utile "resettare" l'indicizzazione attraverso la funzione **reset_index**.
titanic_2 = titanic_2.reset_index(drop=True)
titanic_2
# Pandas determina automaticamente la tipologia di dato contenuto in ciascuna *Series* (colonne) di un *DataFrame*. Tuttavia durante il caricamento di un dataset, soprattutto quando questo viene preso dal web (tramite *read_html*), potrebe accadere che Pandas non rilevi correttamente la tipologia dei dati. <br>
# Ad esempio proviamo a lavorare sulla tabella delle statistiche dei giocatori di NHL della stagione 2015 (http://www.espn.com/nhl/statistics/player/_/stat/points/sort/points/year/2015/seasontype/2):
# +
pd.set_option('max_rows', 10) # codice con il quale imposto il numero di righe visualizzate in output a 5
# Carichiamo la tabella
tb_df = pd.read_html('http://www.espn.com/nhl/statistics/player/_/stat/points/sort/points/year/2015/seasontype/2', header=1)[0]
print(tb_df)
# -
# Rinominiamo le colonne
head_table = ['RK', 'PLAYER', 'TEAM', 'GP', 'G', 'A', 'PTS', 'PLUS_MINUS', 'PIM', 'PTS_G', 'SOG', 'PCT', 'GWG', 'PP_G', 'PP_A', 'SH_G', 'SH_A']
tb_df.columns = head_table
print(tb_df)
tb_df = tb_df.drop(labels=['PLUS_MINUS', 'PIM', 'PTS_G', 'SOG', 'PCT', 'GWG', 'PP_G', 'PP_A', 'SH_G', 'SH_A'], axis=1)
tb_df
# Controlliamo che tipo di dati Pandas ha caricato per ciascuna colonna
tb_df.dtypes
# Come possiamo vedere dal codice sopra, durante la fase di caricamento non è stato possibile categorizzare correttamente ciascun campo del dataset; dobbiamo quindi procedere a convertire ciascun campo nella categoria corretta.
tb_df.GP = pd.to_numeric(tb_df.GP, errors='coerce')
tb_df.G = pd.to_numeric(tb_df.G, errors='coerce')
tb_df.A = pd.to_numeric(tb_df.A, errors='coerce')
tb_df.PTS = pd.to_numeric(tb_df.PTS, errors='coerce')
tb_df.dtypes
tb_df.head()
# <a id='section5'></a>
# ### Missing Value
# Ci sono diversi metodi per rilevare, rimuovere e sostituire i valori nulli in un dataset: <br>
#
# - **isnull()** : utilizzato per identificare i missing values all'interno di un dataset <br>
# - **notnull()** : l'opposto di *isnull()* <br>
# - **dropna()** : restituisce il dataset senza i missing values <br>
# - **fillna()** : restituisce una copia del dataset, con i valori mancanti sostituiti da altri parametri decisi dall'utente
# Utilizziamo il dataset dei giocatori di NHL per sfruttare i metodi descritti sopra.
# Identifichiamo gli elementi del dataset che contengono Missing Values
tb_df.isnull()
# Righe in cui non ci sono valori mancanti nella colonna RK del dataset tb_df
tb_df.RK.notnull()
# Visualizziamo tutte le righe del dataset in cui nella colonna RK non c'è un valore mancante
tb_df[tb_df.RK.notnull()]
# Salviamo il dataset tb_df nella variabile prova e poi eliminiamo le righe in cui ci sono dei missing value
prova = tb_df
prova.dropna()
# Come si può notare sopra però, con il metodo *dropna* di default sono state eliminate tutte le righe in cui almeno una colonna aveva un valore mancante, per togliere tutte le colonne in cui è presente almeno un valore mancante, è necessario utilizzare il parametro *axis = 1*.
#Eliminiamo le colonne in cui è presente almeno un valore mancante
prova.dropna(axis=1)
# Per evitare di eliminare troppe righe/colonne dal dataset è possibile utilizzare i parametri *how* e *thresh*. Ad esempio con il parametro *thresh* possiamo indicare il numero di valori mancanti che ci devono essere per ciascuna riga/colonna per poterla eliminare.
# Eliminiamo le righe che hanno più di due valori mancanti per riga
prova.dropna(thresh = 3)
# Potrebbe essere necessario non eliminare troppe righe dal dataset. Per fare ciò è possibile procedere a sostituire i valori mancanti di una o più colonne, con il metodo **fillna()**.
# Sostituiamo i valori mancanti con 0
prova.fillna(0)
# Sostituiamo i valori mancanti con i primi precedenti non nulli
prova.fillna(method="ffill")
# Sostituiamo i valori mancanti con i primi successivi non nulli
prova.fillna(method="bfill")
# **Link Utili:**
# - CheatSheet sul Data Wrangling: https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf
# - GroupBy: https://pandas.pydata.org/pandas-docs/stable/groupby.html
# - Sorting: https://pandas.pydata.org/pandas-docs/stable/basics.html#sorting
# - Introduction to DataType: https://pandas.pydata.org/pandas-docs/stable/dsintro.html
# - Missing Data: https://pandas.pydata.org/pandas-docs/stable/missing_data.html <br>
# - https://jakevdp.github.io/PythonDataScienceHandbook/03.04-missing-values.html
# [Clicca qui per tornare all'inizio della pagina](#start)<a id='start'></a>
# Con questo paragrafo si conclude il notebook "Wrangling", il prossimo notebook sarà "Exploring".
# Per eventuali dubbi ci potete scrivere su Teams!<br>
# A presto!
| 2_Wrangling/Wrangling.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
# %matplotlib inline
import pandas as pd
import seaborn as sns
import numpy as np
reviews = pd.read_csv('../input/wine-reviews/winemag-data-130k-v2.csv', index_col=0)
reviews.head(3)
from plotnine import *
top_wines = reviews[reviews.variety.isin(reviews.variety.value_counts().head(5).index)]
top_wines.head(3)
# +
df = top_wines.head(1000).dropna()
ggplot(df) + aes('points', 'price') + geom_point()
# +
df = top_wines.head(1000).dropna()
(
ggplot(df)
+ aes('points', 'price')
+ geom_point()
+ stat_smooth()
)
# +
df = top_wines.head(1000).dropna()
(
ggplot(df)
+ aes('points', 'price')
+ aes(color='points')
+ geom_point()
+ stat_smooth()
)
# -
df = top_wines.head(1000).dropna()
(
ggplot(df)
+ aes('points', 'price')
+ aes(color='points')
+ geom_point()
+ stat_smooth()
+ facet_wrap('~variety')
)
(ggplot(df)
+ geom_point(aes('points', 'price'))
)
(ggplot(df, aes('points', 'price'))
+ geom_point()
)
(ggplot(top_wines)
+ aes('points')
+ geom_bar()
)
(ggplot(top_wines)
+ aes('points', 'variety')
+ geom_bin2d(bins=20)
)
(ggplot(top_wines)
+ aes('points', 'variety')
+ geom_bin2d(bins=20)
+ coord_fixed(ratio=2)
+ ggtitle("Top Five Most Common Wine Variety Points Awarded")
)
pokemon = pd.read_csv('../input/pokemon/Pokemon.csv')
pokemon.head(3)
(ggplot(pokemon)
+ aes('Attack', 'Defense')
+ geom_point()
)
# +
(ggplot(pokemon)
+ aes('Attack', 'Defense', color='Legendary')
+ geom_point()
+ ggtitle("Pokemon Attack and Defense by Legendary Status")
)
# -
(ggplot(pokemon, aes('Attack'))
+ facet_wrap('~Generation')
+ geom_histogram(bins=20)
)
| kernels/grammer-of-graphics-with-plotnine.ipynb |
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# [](https://mybinder.org/v2/gh/elastic/geneve/main?labpath=docs/events_generation_walk-through.ipynb)
# # Rule-based events generation walk-through
#
# You can access an interactive version of this document by clicking on the "launch binder" badge above. You will be able to edit the `In [ ]` cells below by clicking in the grey area and executing them by pressing `Ctrl+Enter`.
#
# ## Preliminaries
#
# The API for generating events is exposed by module `geneve.events_emitter`, the `SourceEvents` class provides the front-end for the most common use cases.
#
# Here the module imports needed for the rest of this notebook.
# +
import os; os.chdir('..') # use the repo's root as base for importing local modules
from geneve.events_emitter import SourceEvents
from geneve.utils import load_schema, load_rules
from itertools import islice
from pathlib import Path
# -
# ## Schema
#
# Generating documents requires a specification of the fields types, such as `long` or `ip`. This is the duty of the _schema_.
#
# An example of schema defining fields `x`, `y`, and `z` as float numbers is `{'x': {'type': 'float'}, 'y': {'type': 'float'}, 'z': {'type': 'float'}}`. Fields not defined in the schema are considered of type `keyword`, a kind of string.
#
# The default schema is just `{}`, therefore every field is considered of type `keyword`. To change that, assign to `SourceEvents.schema` as follows:
SourceEvents.schema = {'x': {'type': 'float'}, 'y': {'type': 'float'}, 'z': {'type': 'float'}}
# From now on every document generator will use the assigned schema.
a = SourceEvents()
a.schema
b = SourceEvents()
b.schema
# + [markdown] slideshow={"slide_type": "slide"}
# It's also possible to specify the schema on a per-case basis.
# -
c = SourceEvents(schema={'x': {'type': 'float'}})
c.schema
# The rest of the notebook assumes the rich and standardized [ECS](https://www.elastic.co/guide/en/ecs/current/ecs-reference.html) 8.1.0 as default schema, as loaded below.
SourceEvents.schema = load_schema('./etc/ecs-8.1.0.tar.gz', 'generated/ecs/ecs_flat.yml')
# ## Generate documents from queries
#
# In the simplest form, documents can be generated as follows:
next(SourceEvents.from_query('process.name : *.exe'))
# Which is equivalent to
se = SourceEvents()
se.add_query('process.name : *.exe')
next(se)
# + [markdown] slideshow={"slide_type": "slide"}
# In this second form, multiple queries can be added and the generated documents shall match either of them:
# -
se = SourceEvents()
se.add_query('process.name : *.exe')
se.add_query('source.ip : 10.0.0.0/8')
next(se)
# The query language is guessed automatically. While the above are Kuery based, what follows uses EQL
se = SourceEvents()
se.add_query('process where process.name : "*.exe"')
next(se)
# Currently only Kuery and EQL are supported though others will be added.
# ## Generate documents from rules
#
# Similarily to the query cases, it's possible to generate documents from one or more rules.
# +
# use the local copy of detection-rules 8.1.0
rules = load_rules('./etc/detection-rules-8.1.0.tar.gz', (
'rules/network/command_and_control_port_26_activity.toml',
'rules/network/command_and_control_telnet_port_activity.toml',
))
# load the rules
se = SourceEvents()
for rule in rules:
se.add_rule(rule)
# generate one document
next(se)
# -
# ## Generate documents over and over
#
# Adding queries and rules to a `SourceEvents` object triggers some operations like parsing the query, collecting the field constraints, trying to generate documents for the first time.
#
# When it's important to avoid unnecessary computations, the result of such initial operations can be reused by preserving the `SourceEvents` object between the calls to `next`.
# +
se = SourceEvents.from_query('process.name : (*.exe or *.dll)')
[next(se) for n in range(5)]
# + [markdown] slideshow={"slide_type": "fragment"}
# ## Mappings of the generated documents
#
# The `SourceEvents` object can build mappings describing all the fields used in the loaded queries and rules. For this task it's employed the same schema used for the documents generation.
# +
# use the local copy of detection-rules 8.1.0
rules = load_rules('./etc/detection-rules-8.1.0.tar.gz', (
'rules/network/command_and_control_port_26_activity.toml',
'rules/network/command_and_control_telnet_port_activity.toml',
))
# load the rules
se = SourceEvents()
for rule in rules:
se.add_rule(rule)
# generate the mappings
se.mappings()
# -
# ## Query validation
try:
SourceEvents.from_query('destination.port < 1024 and (destination.port > 512 or destination.port > 1024)')
except Exception as e:
print(e)
# ## Using as iterator
#
# The `SourceEvents` class implements the iterator protocol, as the usage of `next` for generating new documents anticipated. Because documents can be generated indefinitely, the iterator is infinite and therefore some care is needed.
#
# Uses like `list(se)` or `for docs in se: print(docs)` are troublesome, the first would sooner or later exhaust all the resources, the second would never terminate spontaneously. You then need to ask yourself how many documents you need or what other conditions will break the loop.
#
# As example, this prints 10 documents:
# +
se = SourceEvents.from_query('process.name : (*.exe or *.dll)')
for docs in islice(se, 10):
print(docs)
| docs/events_generation_walk-through.ipynb |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.