title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python | Math Puzzle | O(n) | sum-game | 0 | 1 | # Code\n```\nclass Solution:\n def sumGame(self, num: str) -> bool:\n n = len(num)\n qcnt1 = s1 = 0\n for i in range(n//2):\n if num[i] == \'?\':\n qcnt1 += 1\n else:\n s1 += int(num[i])\n qcnt2 = s2 = 0\n for i in range(n//2, n):\n if num[i] == \'?\':\n qcnt2 += 1\n else:\n s2 += int(num[i])\n s_diff = s1 - s2\n q_diff = qcnt2 - qcnt1 \n return not((qcnt2 - qcnt1)*9 == 2*(s1 - s2))\n``` | 0 | Alice and Bob take turns playing a game, with **Alice** **starting first**.
You are given a string `num` of **even length** consisting of digits and `'?'` characters. On each turn, a player will do the following if there is still at least one `'?'` in `num`:
1. Choose an index `i` where `num[i] == '?'`.
2. Replace `num[i]` with any digit between `'0'` and `'9'`.
The game ends when there are no more `'?'` characters in `num`.
For Bob to win, the sum of the digits in the first half of `num` must be **equal** to the sum of the digits in the second half. For Alice to win, the sums must **not be equal**.
* For example, if the game ended with `num = "243801 "`, then Bob wins because `2+4+3 = 8+0+1`. If the game ended with `num = "243803 "`, then Alice wins because `2+4+3 != 8+0+3`.
Assuming Alice and Bob play **optimally**, return `true` _if Alice will win and_ `false` _if Bob will win_.
**Example 1:**
**Input:** num = "5023 "
**Output:** false
**Explanation:** There are no moves to be made.
The sum of the first half is equal to the sum of the second half: 5 + 0 = 2 + 3.
**Example 2:**
**Input:** num = "25?? "
**Output:** true
**Explanation:** Alice can replace one of the '?'s with '9' and it will be impossible for Bob to make the sums equal.
**Example 3:**
**Input:** num = "?3295??? "
**Output:** false
**Explanation:** It can be proven that Bob will always win. One possible outcome is:
- Alice replaces the first '?' with '9'. num = "93295??? ".
- Bob replaces one of the '?' in the right half with '9'. num = "932959?? ".
- Alice replaces one of the '?' in the right half with '2'. num = "9329592? ".
- Bob replaces the last '?' in the right half with '7'. num = "93295927 ".
Bob wins because 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7.
**Constraints:**
* `2 <= num.length <= 105`
* `num.length` is **even**.
* `num` consists of only digits and `'?'`. | It is fast enough to check all possible subarrays The end of each ascending subarray will be the start of the next |
Easy solution Python (time performance >90-100%) | minimum-cost-to-reach-destination-in-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis one is particularly tricky since the solution is supersimple but there is a small tip that is needed to avoid MLE and TLE.\n\nThe basic idea is using a priority queue with aggregated cost as key. With this approach you are able to pass basic examples, then comes how to optimize:\n* First if one path is larger than $maxTime$ then we can cut the extension. Easy.\n* Second, and this one is trickier. If you reach node $u_i$ with a path of length $t$ and previously that node was reach with another path of length $t\'$ with $t\' < t$ then you need to keep the traversal. On the other hand, if you reach $u_i$ but the length of that case $t\' > t$ then the path is not worth keep traversing.\n\n# Code\n```\nfrom queue import PriorityQueue\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n n = len(passingFees)\n graph = defaultdict(list)\n\n for u, v, t in edges:\n graph[u].append((v, t))\n graph[v].append((u, t)) \n queue = [(passingFees[0], 0, 0)]\n dist = [float(\'inf\') for i in range(n)]\n while queue:\n cost, time, city = heappop(queue)\n \n if city == n - 1:\n return cost\n \n for neigh, t in graph[city]:\n new_time = time + t\n if (dist[neigh] > t+time) and (new_time <= maxTime):\n heappush(queue, (cost + passingFees[neigh], new_time, neigh))\n dist[neigh] = new_time\n \n return -1\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Easy Python Solution Using heap | 99% Faster | | minimum-cost-to-reach-destination-in-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], fees: List[int]) -> int:\n h = defaultdict(list)\n for i,j,k in edges:\n h[i].append((j,k))\n h[j].append((i,k))\n n = len(fees)\n q = [(fees[0],0,0)]\n dist = [float(\'inf\') for i in range(n)]\n while q:\n cost, time, node = heapq.heappop(q)\n if node == n-1:return cost\n adj = h[node]\n for j, k in adj:\n if dist[j] > k+time and k+time <= maxTime:\n # if j == n-1:return cost+fees[j]\n dist[j] = k+time\n heapq.heappush(q, (cost+fees[j], k+time, j))\n return -1\n\n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Edge Pruning and Priority Queue BFS | Commented and Explained | 100% Time wo comments | minimum-cost-to-reach-destination-in-time | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBased on the problem description our initial set of edges is not suitable for a standard approach (multiple edges of different times but same cost between nodes). This lets us know we will need a pruning approach. The second part of the problem that serves as a hint is that we want the minimal cost, which suggests path prioritization, which suggests a priority queue, for which we choose a heap. The last condition is also a potential hazard, for which we do a light feasability check before continuing after pruning the graph of checking to see if it is even possible to arrive in time considering the edges immediately at source and goal only. If these are possible, we then continue to frontier progression. As we progress through the frontier, since it is a priority queue, we also always get minimal cost, and thus have a guarantee of minimal cost on reaching goal. From this, we know that if we reach the goal, the cost found is the minimal cost. Otherwise, we know that if we exhaust the queue, there is a disjoint in the graph and it is not possible, thus returning -1. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe start by first getting n and goal as the length of the passingFees and the length - 1 respectively. We set a min time for an edge case of 2 cities. Iff we have exactly two cities, \n- for edge in edges get min time of travel \n- if min time of travel is greater than maxTime, return -1, else return min_time\n\nset a graph as a dictionary of dictionaries \nfor edge in edges (split into src, dst, time) \n- if src in graph \n - if dst not in graph[src], graph[src][dst] = [time, passingFees[dst]]\n - otherwise, graph[src][dst][0] is min of itself and time \n- otherwise, graph[src][dst] = [time, passingFees[dst]]\n- and similar for dst to src version \n\nWe now have our feasability check. We find minimal departure from src, and minimal arrival for dst via the graph. Then, \n- if goal in graph[0] \n - if min arrival greater than maxTime, return -1 \n- otherwise, if min_departure + min_arrival is greater than maxTime, return -1 \n\nWe can use these since if we are not able to ever arrive, we never will have a satisfactory path \n\nSatisfying these, we turn to our set up. We set a time to node array of math.inf of size n, and then set time to node of 0 to 0, since we start there. This will let us keep best paths to each node timewise, which lets us hunt the minimal time path to goal. \n\nOur first state in our frontier will be the cost at 0, time at 0 (0) and id of 0 (0). We heappush this into a frontier list. \n\nwhile we have a frontier \n- pop off the cost, time, and node id \n- if node is goal, return cost \n- otherwise, get node neighbors via graph[node] \n- for neighbor in node neighbors \n - travel time and travel cost are graph at node at neighbor \n - if time + travel time is less than or equal to maxTime and time + travel time is strictly less than time to node at neighbor \n - update time to node at neighbor to time plus travel time \n - push new state of cost + travel cost, time + travel time, neighbor into frontier \n - otherwise, continue \n\nif we exhaust the frontier, there was no physical way to reach the goal, return -1 \n\n# Complexity\n- Time complexity: O(E log E)\n - We loop over E edges to make the graph \n - We loop over potentially V-1 vertices twice to get departure check\n - In the frontier loop we again do E work as we may need to travel every edge to determine physical unreachability. This involves pushes into a heap, so this is actually E log E work. \n - This gives us a total time complexity of E log E + E + (V-1)\n - This reduces to E log E \n\n- Space complexity: O(E) \n - We store each edge in the graph \n - and potentially each edge in the frontier \n\n# Code\n```\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:\n # get n and goal \n n = len(passingFees)\n goal = n - 1 \n # set min_time for the use case of only 2 cities \n min_time = math.inf\n # if only two cities \n if n == 2 : \n # find the least time cost route \n for edge in edges : \n min_time = min(edge[2], min_time)\n # if least time is out of bounds, no way to do it with two cities \n if min_time > maxTime : \n return -1 \n else : \n # otherwise, return sum of passing fees \n return sum(passingFees)\n # the minimum cost among paths connecting 0 to n - 1 \n # built in cost is 0 and n-1 \n # all others are optional \n # must be a valid path (less than maxTime) \n # breadth first search with full edge coverage (must consider all valid edges) \n # can be reduced by looking at minimal time edges only and then by getting minimal cost edges \n # this can be done by first pruning graph and then by heap based priority queue \n graph = collections.defaultdict(dict)\n # build graph of edges with costs associated to arrivals \n for [src, dst, time] in edges : \n if src in graph : \n if dst not in graph[src] : \n graph[src][dst] = [time, passingFees[dst]]\n else : \n graph[src][dst][0] = min(time, graph[src][dst][0])\n else : \n graph[src][dst] = [time, passingFees[dst]]\n if dst in graph : \n if src not in graph[dst] : \n graph[dst][src] = [time, passingFees[src]]\n else : \n graph[dst][src][0] = min(time, graph[dst][src][0])\n else : \n graph[dst][src] = [time, passingFees[src]]\n \n # find minimal departure\n min_departure = math.inf\n for node in graph[0] : \n min_departure = min(min_departure, graph[0][node][0]) \n \n # find minimal arrival \n min_arrival = math.inf\n for node in graph[goal] : \n min_arrival = min(min_arrival, graph[goal][node][0])\n \n if goal in graph[0] : \n if min_arrival > maxTime : \n return -1 \n else : \n if min_departure + min_arrival > maxTime : \n return -1 \n\n # set up array of time to reach node \n time_to_node = [math.inf] * n\n # you start here, so your time to reach here is 0 \n time_to_node[0] = 0\n # set up a frontier \n frontier = []\n # your first state is the passing fees of the 0th node at time 0 and node 0 \n first_state = (passingFees[0], 0, 0)\n # heapify on push in \n heapq.heappush(frontier, first_state) \n # while you have a frontier \n while frontier : \n # pop the cost, time and node from the heap \n cost, time, node = heapq.heappop(frontier)\n # if you have reached the goal, based on the priority queue process, cost is your final cost \n if node == goal : \n return cost \n # otherwise, get the neighbors of this node from the graph \n node_neighbors = graph[node]\n # for each of your node neighbors \n for neighbor in node_neighbors : \n # get minimal travel time from here to there and minimal cost \n travel_time, travel_cost = graph[node][neighbor]\n # if travel time is in range and time to node is strictly greater than this time to node \n # then we have an improvement on our current time to node and thus an improvement on \n # potentially reaching the goal. If this is the case, \n if time + travel_time <= maxTime and time_to_node[neighbor] > time + travel_time : \n # update time to node to prevent less succesful trips \n time_to_node[neighbor] = time + travel_time \n # push in a new node of cost + travel cost, time + travel time and neighbor \n heapq.heappush(frontier, ( cost+travel_cost, time + travel_time, neighbor ))\n # if we exhaust the heap but do not reach the goal, we never could have reached the goal \n # in this case, we return -1 \n return -1 \n\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python straight forward DP, easy to understand, but slow and memory consuming | minimum-cost-to-reach-destination-in-time | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(t \\cdot V \\cdot E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V \\cdot E + t \\cdot V)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass MinValue(dict):\n def __setitem__(self, key, value, /):\n if value < self.get(key, inf):\n super().__setitem__(key, value)\n\n\nclass Solution:\n def minCost(self, maxTime: int, edges: List[List[int]], F: List[int]) -> int:\n M = [MinValue() for _ in range(len(F))]\n for i, j, t in edges:\n M[i][j] = M[j][i] = t\n\n @cache\n def dp(t, i):\n if t >= 0 and i == 0:\n return F[0]\n cost = inf\n for j, dt in M[i].items():\n t_ = t - dt\n if t_ >= 0:\n cost = min(cost, dp(t_, j))\n return cost + F[i]\n\n ans = dp(maxTime, len(F)-1)\n return -1 if ans == inf else ans\n``` | 0 | There is a country of `n` cities numbered from `0` to `n - 1` where **all the cities are connected** by bi-directional roads. The roads are represented as a 2D integer array `edges` where `edges[i] = [xi, yi, timei]` denotes a road between cities `xi` and `yi` that takes `timei` minutes to travel. There may be multiple roads of differing travel times connecting the same two cities, but no road connects a city to itself.
Each time you pass through a city, you must pay a passing fee. This is represented as a **0-indexed** integer array `passingFees` of length `n` where `passingFees[j]` is the amount of dollars you must pay when you pass through city `j`.
In the beginning, you are at city `0` and want to reach city `n - 1` in `maxTime` **minutes or less**. The **cost** of your journey is the **summation of passing fees** for each city that you passed through at some moment of your journey (**including** the source and destination cities).
Given `maxTime`, `edges`, and `passingFees`, return _the **minimum cost** to complete your journey, or_ `-1` _if you cannot complete it within_ `maxTime` _minutes_.
**Example 1:**
**Input:** maxTime = 30, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 11
**Explanation:** The path to take is 0 -> 1 -> 2 -> 5, which takes 30 minutes and has $11 worth of passing fees.
**Example 2:**
**Input:** maxTime = 29, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** 48
**Explanation:** The path to take is 0 -> 3 -> 4 -> 5, which takes 26 minutes and has $48 worth of passing fees.
You cannot take path 0 -> 1 -> 2 -> 5 since it would take too long.
**Example 3:**
**Input:** maxTime = 25, edges = \[\[0,1,10\],\[1,2,10\],\[2,5,10\],\[0,3,1\],\[3,4,10\],\[4,5,15\]\], passingFees = \[5,1,2,20,20,3\]
**Output:** -1
**Explanation:** There is no way to reach city 5 from city 0 within 25 minutes.
**Constraints:**
* `1 <= maxTime <= 1000`
* `n == passingFees.length`
* `2 <= n <= 1000`
* `n - 1 <= edges.length <= 1000`
* `0 <= xi, yi <= n - 1`
* `1 <= timei <= 1000`
* `1 <= passingFees[j] <= 1000`
* The graph may contain multiple edges between two nodes.
* The graph does not contain self loops. | Store the backlog buy and sell orders in two heaps, the buy orders in a max heap by price and the sell orders in a min heap by price. Store the orders in batches and update the fields according to new incoming orders. Each batch should only take 1 "slot" in the heap. |
Python3 and C++ solutions | concatenation-of-array | 0 | 1 | # Solution in C++\n```\nclass Solution {\npublic:\n \n vector<int> getConcatenation(vector<int>& nums) {\n vector<int> ans;\n ans = nums;\n for (int i = 0; i < nums.size(); i++) {\n ans.push_back(nums[i]);\n }\n return ans;\n }\n};\n```\n# Solution in Python3\n```\nclass Solution:\n def getConcatenation(self, nums: List[int]) -> List[int]:\n ans = []\n for num in nums:\n ans.append(num)\n ans += nums\n return ans\n``` | 2 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
🥇 C++ | PYTHON | JAVA | O(N) || EXPLAINED || ; ] | unique-length-3-palindromic-subsequences | 1 | 1 | **UPVOTE IF HELPFuuL**\n\n# Intuition\nWe need to find the number of unique of ```PalindromicSubsequence```, hence repitition is not a case to be done here.\n\n# Approach\nFor every char ```$``` in ```[a,b,c...y,z]``` , a palindrome of type ```"$ @ $"``` will exist if there are atleast 2 occurances of ```"$"```.\n\nHence we need to find first and last occurance of every char and for every char we need to count unique ```"@"``` which represents what characters come in middle of palindrome. This is number of unique characters between FIRST and LAST occurance of ```"$"``` char.\n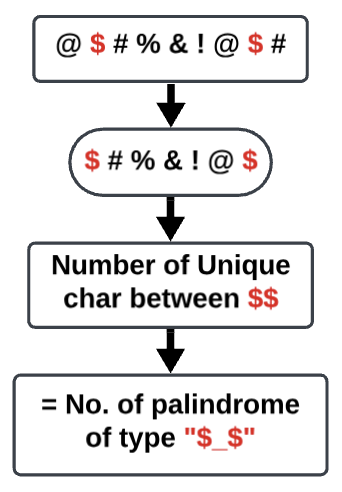\n\n\n# Complexity\n- Time complexity: O(n)\n- O(N) for traversing string to find char occurances.\n- O(26 * N) for slicing string for every lowercase char.\n\n\n# C++ Solution\n```\nclass Solution {\npublic:\n int countPalindromicSubsequence(string inputString) {\n \n int result = 0;\n int firstIndex[26] = {[0 ... 25] = INT_MAX};\n int lastIndex[26] = {};\n\n for (int i = 0; i < inputString.size(); ++i) {\n firstIndex[inputString[i] - \'a\'] = min(firstIndex[inputString[i] - \'a\'], i);\n lastIndex[inputString[i] - \'a\'] = i;\n }\n for (int i = 0; i < 26; ++i)\n if (firstIndex[i] < lastIndex[i])\n result += unordered_set<char>(begin(inputString) + firstIndex[i] + 1, begin(inputString) + lastIndex[i]).size();\n return result;\n}\n};\n\n```\n\n# Python Solution\n```\nclass Solution:\n def countPalindromicSubsequence(self, s):\n res = 0\n\n #string.ascii_lowercase = {a,b,c,d ... x,y,z}\n for k in string.ascii_lowercase:\n first, last = s.find(k), s.rfind(k)\n if first > -1:\n res += len(set(s[first + 1: last]))\n return res\n```\n\n# Java Solution\n```\nclass Solution {\n public int countPalindromicSubsequence(String inputString) {\n int firstIndex[] = new int[26], lastIndex[] = new int[26], result = 0;\n Arrays.fill(firstIndex, Integer.MAX_VALUE);\n for (int i = 0; i < inputString.length(); ++i) {\n firstIndex[inputString.charAt(i) - \'a\'] = Math.min(firstIndex[inputString.charAt(i) - \'a\'], i);\n lastIndex[inputString.charAt(i) - \'a\'] = i;\n }\n for (int i = 0; i < 26; ++i)\n if (firstIndex[i] < lastIndex[i])\n result += inputString.substring(firstIndex[i] + 1, lastIndex[i]).chars().distinct().count();\n return result;\n }\n}\n```\n\n\n | 30 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
🚀 Iterative Solution || Explained Intuition 🚀 | unique-length-3-palindromic-subsequences | 1 | 1 | # Problem Description\n\nGiven a string `s`, calculates the count of **unique** palindromes of length **three** that can be formed as **subsequences** within `s`. \n\nA **palindrome** is a string that reads the **same** forward and backward. In this context, a **subsequence** of a string is a new string formed by **deleting** some characters (possibly none) from the original string without altering the relative **order** of the remaining characters.\n\n**Note** that the count should consider only **unique** palindromes, even if there are multiple ways to derive the same subsequence.\n\n- **Constraints:**\n - $3 <= s.length <= 10^5$\n - `s` consists of only **lowercase** English letters.\n - Count **unique** palindromes\n\n\n---\n\n\n\n# Intuition\n\nHi there,\uD83D\uDE04\n\nHow are you? I hope you are fine \uD83D\uDE03\uD83D\uDCAA\nLet\'s zoom in\uD83D\uDD0E the details of our today\'s interesting problem.\n\nWe have a string\uD83E\uDDF5 and we want to calculate the number of **palindrome** subsequences in this string of length `3` specifically the **unique** number of those subsequences.\n\nOk, seems easy to solve right ?\uD83E\uDD14\nFirst thing that we can think of is our big guy **BRUTE FORCE**\uD83D\uDCAA\uD83D\uDCAA.\nBy **looping** over all the characters of our string and thing look **forward** and **backward** for **similar** characters that can form 3-length palindrome.\uD83D\uDE03\nUnfortunately, this solution will give us $O(N ^ 2)$ time complexity, **TLE** and some **headaches**.\uD83D\uDE02\uD83D\uDE02\n\nHow can we improve this solution atleast to get rid of headaces?\uD83D\uDCA2\nDid you notice something I said earlier ?\uD83E\uDD28\nWe will look for **similar** characters forward and backward for every character in our string.\uD83E\uDD2F\n\nSo why don\'t we change our perspective a little !\uD83E\uDD29\nWe know that we have `26` **unique** characters in English so why don\'t we compute last and first occurences only for each character and then for each **pair** of them let\'s see how many **unique** letters between them.\uD83E\uDD2F\n\nHuh, Does that improve our time complexity ?\uD83E\uDD14\nYes, alot and also remove headaces.\uD83D\uDE02\uD83D\uDCA2\nto compute **first** and **last** occurences of every character of the `26` English characters it will take us to iterate over the input string one time and to look for every **unique** character between them it will take at most to iterate over the whole string for the `26` English characters which is `26 * N` so it is at most `27 * N` iterations which is $O(N)$.\uD83E\uDD29\n\nLet\'s see an example:\n```\ninput = abascba\n\nFirst occurence: a -> 0\n b -> 1\n c -> 4\n s -> 3\nLast occurence: a -> 6\n b -> 5\n c -> 4\n s -> 3\n\nNow for each character of them we calculate number of unique characters between both occurences.\n\nFor a -> 0 : 6\n unique chars -> a, b, c, s -> 4 answers\nFor b -> 1 : 5\n unique chars -> a, c, s -> 3 answers\nFor c -> 4 : 4\n unique chars -> - -> 0 answers\nFor s -> 5 : 5\n unique chars -> - -> 0 answers\n\nFinal asnwer is 4 + 3 + 0 + 0 = 7\n```\n\n```\ninput = bbsasccbaba\n\nFirst occurence: a -> 3\n b -> 0\n c -> 5\n s -> 2\nLast occurence: a -> 10\n b -> 9\n c -> 6\n s -> 4\n\nNow for each character of them we calculate number of unique characters between both occurences.\n\nFor a -> 3 : 10\n unique chars -> a, b, c, s -> 4 answers\nFor b -> 0 : 9\n unique chars -> a, b, c, s -> 4 answers\nFor c -> 5 : 6\n unique chars -> - -> 0 answers\nFor s -> 2 : 4\n unique chars -> a -> 1 answers\n\nFinal asnwer is 4 + 4 + 0 + 1 = 9\n```\nAnd this how will our algorithm work. \u2728\n\n**Bonus part**\uD83E\uDD29\nWhat is the **maximum** answer that can we get for this problem ?\uD83E\uDD14\n<details>\n <summary>Click to show the answer</summary>\n <div>\n It is 676 but why?\uD83E\uDD28 </br>\n <details>\n <summary>Click to show the justification</summary>\n <div>How we got such a number? </br>\n We remember that we have 26 unique chars in English right? </br>\n our palidrome subsequences are formed of 3 places _ _ _ let\'s call them a b c. a and c must have the same value of the 26 chars and b can be any char of the 26 chars so the answer will be 26 * 26 different unique palindromes.\n </div>\n </details>\n </div>\n</details>\n\n</br>\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n# Approach\n1. **Initialize Arrays:** Create arrays `minExist` and `maxExist` with 26 elements each, initialized to `INT_MAX` and `INT_MIN`, respectively.\n2. **Populate Arrays:** Iterate through each character in the input string, updating the minimum and maximum occurrences for each character in the corresponding arrays.\n3. **Count Unique Palindromic Subsequences:**\n - Iterate over each character in the alphabet (26 characters).\n - Check if the character has occurred in the input string. If not, skip to the next character.\n - Create an empty set `uniqueCharsBetween` to store unique characters between the minimum and maximum occurrences of the current character.\n - Iterate over the characters between the minimum and maximum occurrences, adding each character to the set.\n - Add the count of unique characters between occurrences to `uniqueCount`.\n4. **Return Result:** Return the total count of unique palindromic subsequences `uniqueCount`.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nSince we iterating **two** passes, **first** pass to compute first and last occurence for each character with time `N` and **second** pass to compute number of unique palindromes. In the **second** pass we iterate over all the unique characters which are `26` and we iterate between their first and last occurence to compute the number of unique characters which can be at most `N` characters.\nSo time complexity is `26 * N + N` which is `27 * N` which is also `O(N)`.\nWhere `N` is number of characters in our input string.\n\n- **Space complexity:** $O(1)$\nSince we are storing two arrays to compute last and first occurence each one of them is of size `26` and we use hash set that can be at maximum with size `26` so the space complexity is still `O(1)`. Since we have constant space variables.\n\n\n---\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countPalindromicSubsequence(string inputString) {\n // Arrays to store the minimum and maximum occurrences of each character in the input string\n vector<int> minExist(26, INT_MAX);\n vector<int> maxExist(26, INT_MIN);\n\n // Populate minExist and maxExist arrays\n for(int i = 0; i < inputString.size(); i++) {\n int charIndex = inputString[i] - \'a\';\n minExist[charIndex] = min(minExist[charIndex], i);\n maxExist[charIndex] = max(maxExist[charIndex], i);\n }\n\n // Variable to store the final count of unique palindromic subsequences\n int uniqueCount = 0;\n\n // Iterate over each character in the alphabet\n for (int charIndex = 0; charIndex < 26; charIndex++) {\n // Check if the character has occurred in the input string\n if (minExist[charIndex] == INT_MAX || maxExist[charIndex] == INT_MIN) {\n continue; // No occurrences, move to the next character\n }\n\n // Set to store unique characters between the minimum and maximum occurrences\n unordered_set<char> uniqueCharsBetween;\n\n // Iterate over the characters between the minimum and maximum occurrences\n for (int j = minExist[charIndex] + 1; j < maxExist[charIndex]; j++) {\n uniqueCharsBetween.insert(inputString[j]);\n }\n\n // Add the count of unique characters between the occurrences to the final count\n uniqueCount += uniqueCharsBetween.size();\n }\n\n // Return the total count of unique palindromic subsequences\n return uniqueCount;\n }\n};\n```\n```Java []\nclass Solution {\n public int countPalindromicSubsequence(String inputString) {\n // Arrays to store the minimum and maximum occurrences of each character in the input string\n int[] minExist = new int[26];\n int[] maxExist = new int[26];\n for (int i = 0; i < 26; i++) {\n minExist[i] = Integer.MAX_VALUE;\n maxExist[i] = Integer.MIN_VALUE;\n }\n\n // Populate minExist and maxExist arrays\n for (int i = 0; i < inputString.length(); i++) {\n int charIndex = inputString.charAt(i) - \'a\';\n minExist[charIndex] = Math.min(minExist[charIndex], i);\n maxExist[charIndex] = Math.max(maxExist[charIndex], i);\n }\n\n // Variable to store the final count of unique palindromic subsequences\n int uniqueCount = 0;\n\n // Iterate over each character in the alphabet\n for (int charIndex = 0; charIndex < 26; charIndex++) {\n // Check if the character has occurred in the input string\n if (minExist[charIndex] == Integer.MAX_VALUE || maxExist[charIndex] == Integer.MIN_VALUE) {\n continue; // No occurrences, move to the next character\n }\n\n // Set to store unique characters between the minimum and maximum occurrences\n HashSet<Character> uniqueCharsBetween = new HashSet<>();\n\n // Iterate over the characters between the minimum and maximum occurrences\n for (int j = minExist[charIndex] + 1; j < maxExist[charIndex]; j++) {\n uniqueCharsBetween.add(inputString.charAt(j));\n }\n\n // Add the count of unique characters between the occurrences to the final count\n uniqueCount += uniqueCharsBetween.size();\n }\n\n // Return the total count of unique palindromic subsequences\n return uniqueCount;\n }\n}\n```\n```Python []\nclass Solution:\n def countPalindromicSubsequence(self, inputString):\n # Arrays to store the minimum and maximum occurrences of each character in the input string\n min_exist = [float(\'inf\')] * 26\n max_exist = [float(\'-inf\')] * 26\n\n # Populate min_exist and max_exist arrays\n for i in range(len(inputString)):\n char_index = ord(inputString[i]) - ord(\'a\')\n min_exist[char_index] = min(min_exist[char_index], i)\n max_exist[char_index] = max(max_exist[char_index], i)\n\n # Variable to store the final count of unique palindromic subsequences\n unique_count = 0\n\n # Iterate over each character in the alphabet\n for char_index in range(26):\n # Check if the character has occurred in the input string\n if min_exist[char_index] == float(\'inf\') or max_exist[char_index] == float(\'-inf\'):\n continue # No occurrences, move to the next character\n\n # Set to store unique characters between the minimum and maximum occurrences\n unique_chars_between = set()\n\n # Iterate over the characters between the minimum and maximum occurrences\n for j in range(min_exist[char_index] + 1, max_exist[char_index]):\n unique_chars_between.add(inputString[j])\n\n # Add the count of unique characters between the occurrences to the final count\n unique_count += len(unique_chars_between)\n\n # Return the total count of unique palindromic subsequences\n return unique_count\n```\n```C []\nint countPalindromicSubsequence(char* inputString) {\n // Arrays to store the minimum and maximum occurrences of each character in the input string\n int minExist[26];\n int maxExist[26];\n\n // Initialize arrays with default values\n for (int i = 0; i < 26; i++) {\n minExist[i] = INT_MAX;\n maxExist[i] = INT_MIN;\n }\n\n // Populate minExist and maxExist arrays\n for (int i = 0; inputString[i] != \'\\0\'; i++) {\n int charIndex = inputString[i] - \'a\';\n minExist[charIndex] = (minExist[charIndex] < i) ? minExist[charIndex] : i;\n maxExist[charIndex] = (maxExist[charIndex] > i) ? maxExist[charIndex] : i;\n }\n\n // Variable to store the final count of unique palindromic subsequences\n int uniqueCount = 0;\n\n // Iterate over each character in the alphabet\n for (int charIndex = 0; charIndex < 26; charIndex++) {\n // Check if the character has occurred in the input string\n if (minExist[charIndex] == INT_MAX || maxExist[charIndex] == INT_MIN) {\n continue; // No occurrences, move to the next character\n }\n\n // Set to store unique characters between the minimum and maximum occurrences\n char uniqueCharsBetween[CHAR_MAX];\n int uniqueCharsCount = 0;\n\n // Iterate over the characters between the minimum and maximum occurrences\n for (int j = minExist[charIndex] + 1; j < maxExist[charIndex]; j++) {\n int charExists = 0;\n for (int k = 0; k < uniqueCharsCount; k++) {\n if (uniqueCharsBetween[k] == inputString[j]) {\n charExists = 1;\n break;\n }\n }\n if (!charExists) {\n uniqueCharsBetween[uniqueCharsCount++] = inputString[j];\n }\n }\n\n // Add the count of unique characters between the occurrences to the final count\n uniqueCount += uniqueCharsCount;\n }\n\n // Return the total count of unique palindromic subsequences\n return uniqueCount;\n}\n```\n\n\n\n | 144 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Binary search on character positions - beats 100% | unique-length-3-palindromic-subsequences | 0 | 1 | # Intuition\nFor each letter check if there is another letter in between its min and max positions\n\n# Approach\nStore positions for each character\nLoop over combinations of two characters. Take min and max positions from one of them and check if there is a position in between them for the second char using binary search.\n\n# Complexity\n- Time complexity:\nO(N + 26^2 * log(N))\n\n- Space complexity:\nO(N*26) = O(N)\n\n# Code\n```\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n c2pos = defaultdict(list)\n for index, c in enumerate(s):\n c2pos[c].append(index)\n n = len(s)\n res = 0\n for center, center_positions in c2pos.items():\n for candidate, cand_positions in c2pos.items():\n # if its the same character then\n # we only need to have at least three of them\n # to get palindrome\n if candidate == center:\n if len(center_positions) >= 3:\n res += 1\n continue\n # get min and max positions of a char\n left_pos, right_pos = cand_positions[0], cand_positions[-1]\n # check if center char has position in between\n index = bisect.bisect_left(center_positions, left_pos)\n if index < 0 or index > len(center_positions) - 1: continue\n if left_pos < center_positions[index] < right_pos:\n res += 1\n return res\n\n``` | 5 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
[Python3] DP 5 Cases | painting-a-grid-with-three-different-colors | 0 | 1 | **DP 5 Cases**\n\n**Inuition**\n\nThere are only 5 cases to handle (`1 <= m <= 5`). Since `m` is small the recurrence relations per `m` can be discovered and returned.\n\nWith `m` fixed, for each time we increase `n` think in terms of possible `1*m` blocks that can be added to all existing `(n - 1)*m` blocks. \n\n**Case #1: `m == 1`**\n\nEverytime we increment `n` another block is added per existing `n - 1` block. Each 3 color block can only add 2 new blocks (different color blocks) each increment.\n\nResulting relation:\n```\na1 = 3\nan = 2*a(n-1)\n```\n\n**Case #2: `m == 2`**\n\nFrom the second example in the problem we can see that there are initially 6 `1*2` blocks. Each `1*2` block can be appended to 3 other `1*2` blocks (without causing adjacency).\n\n\nResulting relation:\n```\na1 = 6\nan = 3*a(n-1)\n```\n\n**Case #3: `m == 3`**\n\nFrom the problem example ([#1](https://leetcode.com/problems/number-of-ways-to-paint-n-3-grid/description/)) in [1411. Number of Ways to Paint N \xD7 3 Grid](https://leetcode.com/problems/number-of-ways-to-paint-n-3-grid/solutions/2957266/python3-recurrence-relation-to-dp-process/) (same problem but `m==3`) we can see that there are initially 12 `1*3` blocks. There are 2 possible patterns of `1*3` blocks complying with the adjacency restriction (divided into columns - seen below). Pattern `a` consists of 3 different colors. Pattern `b` consists of a single middle color and 2 matching end colors. When incrementing `n` each `1*3` block from the first group `a` can append 3 of its own kind and 2 from the second group `b` (without causing adjacency). When incrementing `n` each `1*3` block from the second group can append 2 of its own kind and 2 from the first group (without causing adjacency). One can brute force find the recurrence relation by taking an arbitrary block in the initial group `a` and visually examine how many blocks in the initial group `b` appended would not cause adjacency issues. One would do the same but for group `a` to itself (getting the `a` relation). One would then repeat the process with group `b` (getting the `b` relation).\n\n\n\nResulting relation:\n```\na1 = 6; b1 = 6\nan = 3*a(n-1) + 2*b(n-1)\nbn = 2*a(n-1) + 2*b(n-1)\n```\n\n**Case #4: `m == 4`**\n\nThe same methodology for `m == 3` can be performed for `m == 4` with the following groups after calculating the coefficients. Count from the following image:\n\n\n\nResulting relation:\n```\na1 = 6; b1 = 6; c1 = 6; d1 = 6\nan = 3*a(n-1) + b(n-1) + 2*c(n-1) + 2*d(n-1)\nbn = a(n-1) + 2*b(n-1) + c(n-1) + d(n-1)\ncn = 2*a(n-1) + b(n-1) + 2*c(n-1) + 2*d(n-1)\ndn = 2*a(n-1) + b(n-1) + 2*c(n-1) + 2*d(n-1)\n```\n\n**Case #5: `m == 5`**\n\nThe same methodology for `m == 4` can be performed for `m == 5` with the following groups:\n\n\n\nResulting relation:\n```\na1 = 6; b1 = 6; c1 = 6; d1 = 6; e1 = 6; f1 = 6; g1 = 6; h1 = 6 \nan = 2*a(n-1) + b(n-1) + c(n-1) + d(n-1) + 2*e(n-1) + 2*f(n-1) + g(n-1) + h(n-1)\nbn = a(n-1) + 2*b(n-1) + c(n-1) + d(n-1) + g(n-1)\ncn = a(n-1) + b(n-1) + 2*c(n-1) + d(n-1) + e(n-1) + f(n-1) + g(n-1) + h(n-1)\ndn = a(n-1) + b(n-1) + c(n-1) + 2*d(n-1) + 2*e(n-1) + 2*f(n-1) + g(n-1) + h(n-1)\nen = 2*a(n-1) + c(n-1) + 2*d(n-1) + 3*e(n-1) + 2*f(n-1) + g(n-1) + 2*h(n-1)\nfn = 2*a(n-1) + c(n-1) + 2*d(n-1) + 2*e(n-1) + 2*f(n-1) + g(n-1) + 2*h(n-1)\ngn = a(n-1) + b(n-1) + c(n-1) + d(n-1) + e(n-1) + f(n-1) + 2*g(n-1) + h(n-1)\nhn = a(n-1) + c(n-1) + d(n-1) + 2*e(n-1) + 2*f(n-1) + g(n-1) + 2*h(n-1)\n```\n\n**Code**\n```Python3 []\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n \'\'\'\n Solves a given recurrence relation\n @params dp: the nth sum per ith equation\n @params coeff: coefficients for the ith equation\n \'\'\'\n def solve_rel(dp, coeff):\n for _ in range(n - 1):\n for i in range(len(dp)):\n tmp = 0\n for j, c in enumerate(coeff[i]):\n # If j >= i we must add the second last\n #value appended, we already updated that dp.\n tmp += c*dp[j][-1 if j >= i else -2]\n dp[i].append(tmp)\n\n return sum(e[-1] for e in dp) % 1000000007\n\n\n if m == 1:\n return solve_rel([[3]], [[2]])\n if m == 2:\n return solve_rel([[6]], [[3]])\n elif m == 3:\n return solve_rel([[6], [6]], [[3,2], [2,2]])\n elif m == 4:\n return solve_rel(\n [[6], [6], [6], [6]], \n [[3,1,2,2], [1,2,1,1], [2,1,2,2], [2,1,2,2]])\n else:\n return solve_rel(\n [[6], [6], [6], [6], [6], [6], [6], [6]],\n [\n [2,1,1,1,2,2,1,1], \n [1,2,1,1,0,0,1,0], \n [1,1,2,1,1,1,1,1], \n [1,1,1,2,2,2,1,1], \n [2,0,1,2,3,2,1,2], \n [2,0,1,2,2,2,1,2], \n [1,1,1,1,1,1,2,1], \n [1,0,1,1,2,2,1,2]\n ])\n``` | 2 | You are given two integers `m` and `n`. Consider an `m x n` grid where each cell is initially white. You can paint each cell **red**, **green**, or **blue**. All cells **must** be painted.
Return _the number of ways to color the grid with **no two adjacent cells having the same color**_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** m = 1, n = 1
**Output:** 3
**Explanation:** The three possible colorings are shown in the image above.
**Example 2:**
**Input:** m = 1, n = 2
**Output:** 6
**Explanation:** The six possible colorings are shown in the image above.
**Example 3:**
**Input:** m = 5, n = 5
**Output:** 580986
**Constraints:**
* `1 <= m <= 5`
* `1 <= n <= 1000` | The grid is at a maximum 500 x 500, so it is clever to assume that the robot's initial cell is grid[501][501] Run a DFS from the robot's position to make sure that you can reach the target, otherwise you should return -1. Now that you are sure you can reach the target, run BFS to find the shortest path. |
python DP top down | painting-a-grid-with-three-different-colors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n @functools.lru_cache(None)\n def generate(i):\n\n if i == m:\n return [""]\n ans = []\n for s in {"r", "b", "g"}:\n for j in generate(i+1):\n if not j or s != j[0]:\n ans.append(s+j)\n return ans\n \n @functools.lru_cache(None)\n def dp(i, prev):\n if i == n:\n return 1\n ans = 0\n if not prev:\n for p in generate(0):\n ans += dp(i+1, p)\n else:\n for p in generate(0):\n for k in range(len(p)):\n if p[k] == prev[k]:\n break\n else:\n ans += dp(i+1, p)\n return ans \n \n return dp(0, "") % (10**9 + 7)\n``` | 0 | You are given two integers `m` and `n`. Consider an `m x n` grid where each cell is initially white. You can paint each cell **red**, **green**, or **blue**. All cells **must** be painted.
Return _the number of ways to color the grid with **no two adjacent cells having the same color**_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** m = 1, n = 1
**Output:** 3
**Explanation:** The three possible colorings are shown in the image above.
**Example 2:**
**Input:** m = 1, n = 2
**Output:** 6
**Explanation:** The six possible colorings are shown in the image above.
**Example 3:**
**Input:** m = 5, n = 5
**Output:** 580986
**Constraints:**
* `1 <= m <= 5`
* `1 <= n <= 1000` | The grid is at a maximum 500 x 500, so it is clever to assume that the robot's initial cell is grid[501][501] Run a DFS from the robot's position to make sure that you can reach the target, otherwise you should return -1. Now that you are sure you can reach the target, run BFS to find the shortest path. |
No bitmask | painting-a-grid-with-three-different-colors | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nb=[]\ndef gen(s,n):\n global b\n if len(s)==n:\n fl=False\n for i in range(1,n):\n fl|=s[i]==s[i-1]\n if not fl:\n b.append(s)\n return\n gen(s+"0",n)\n gen(s+"1",n)\n gen(s+"2",n)\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n global b\n dp=defaultdict(lambda :-1)\n mod=10**9+7\n b=[]\n gen("",m)\n # print(b)\n def rec(i,prev):\n if i==n:\n return 1\n if dp[i,prev]!=-1:\n return dp[i,prev]\n ans=0\n for cl in b:\n if prev==-1 :\n ans+=rec(i+1,cl)\n ans%=mod\n continue\n fl=False\n for id in range(len(cl)):\n fl|=prev[id]==cl[id]\n if fl==False:\n ans+=rec(i+1,cl)\n ans%=mod\n dp[i,prev]=ans\n return ans\n x=rec(0,-1)\n print(x)\n return x%mod\n``` | 0 | You are given two integers `m` and `n`. Consider an `m x n` grid where each cell is initially white. You can paint each cell **red**, **green**, or **blue**. All cells **must** be painted.
Return _the number of ways to color the grid with **no two adjacent cells having the same color**_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** m = 1, n = 1
**Output:** 3
**Explanation:** The three possible colorings are shown in the image above.
**Example 2:**
**Input:** m = 1, n = 2
**Output:** 6
**Explanation:** The six possible colorings are shown in the image above.
**Example 3:**
**Input:** m = 5, n = 5
**Output:** 580986
**Constraints:**
* `1 <= m <= 5`
* `1 <= n <= 1000` | The grid is at a maximum 500 x 500, so it is clever to assume that the robot's initial cell is grid[501][501] Run a DFS from the robot's position to make sure that you can reach the target, otherwise you should return -1. Now that you are sure you can reach the target, run BFS to find the shortest path. |
Python Solution | painting-a-grid-with-three-different-colors | 0 | 1 | \n\n# Approach\nHere\'s a step-by-step explanation of the solution:\n\n1. Generate all valid rows:\nThe generate_valid_rows function generates all valid rows of length m, with no two adjacent cells having the same color. There are 3 ** m possible row combinations, and we iterate through all of them to find the valid ones. To check the validity of a row, we ensure that no two adjacent cells have the same color.\n\n2. Build an adjacency matrix:\nThe build_adjacency_matrix function constructs an adjacency matrix of size R x R, where R is the number of valid rows. The matrix represents the relationship between valid rows, with adj_matrix[i][j] being True if row i and row j can be adjacent in the grid, following the problem\'s constraints. The matrix will be used in the dynamic programming step to find the number of ways to paint the grid.\n\n3. Dynamic programming:\nThe dynamic programming approach is used to count the number of ways to paint the grid. We initialize a list dp of size R, where each entry represents the number of ways to paint the grid with that specific row at the last row of the grid. Initially, we set all entries in dp to 1, as there is only one way to paint the grid with a single row.\n\nThen, we iterate through the columns (n - 1 times) and update the dp list using the adjacency matrix information. For each valid row i, we check all valid adjacent rows j (using the adjacency matrix) and update the dp list accordingly. We keep track of the number of ways to paint the grid by taking the sum of the dp list at the end and applying the modulo operation.\n\n# Complexity\n- Time complexity:\nTime Complexity:\nThe time complexity of this solution is O(R^2 * n), where R is the number of valid rows. The majority of the time is spent on the dynamic programming step, where we iterate n - 1 times, and for each iteration, we perform R * R operations when updating the dp list.\n\n- Space complexity:\nThe space complexity of the solution is O(R^2 + R * n), which is mainly due to the adjacency matrix and the dynamic programming list dp. We also store a list of valid rows, but the overall space complexity is determined by the adjacency matrix and the dp list.\n\n# More \n\nMore of my LeetCode solutions at https://github.com/aurimas13/Solutions-To-Problems.\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n MOD = 1000000007\n valid_rows = self.generate_valid_rows(m)\n adj_matrix = self.build_adjacency_matrix(valid_rows)\n dp = [1] * len(valid_rows)\n \n for _ in range(n - 1):\n dp_next = [0] * len(valid_rows)\n for i, row in enumerate(valid_rows):\n for j, adj_row in enumerate(valid_rows):\n if adj_matrix[i][j]:\n dp_next[j] += dp[i]\n dp_next[j] %= MOD\n dp = dp_next\n \n return sum(dp) % MOD\n\n def generate_valid_rows(self, m: int) -> list:\n valid_rows = []\n for i in range(3 ** m):\n row = []\n for j in range(m):\n row.append((i // (3 ** j)) % 3)\n if all(row[k] != row[k + 1] for k in range(m - 1)):\n valid_rows.append(tuple(row))\n return valid_rows\n\n def build_adjacency_matrix(self, valid_rows: list) -> list:\n adj_matrix = [[False] * len(valid_rows) for _ in range(len(valid_rows))]\n for i, row1 in enumerate(valid_rows):\n for j, row2 in enumerate(valid_rows):\n if all(row1[k] != row2[k] for k in range(len(row1))):\n adj_matrix[i][j] = True\n return adj_matrix\n\n``` | 0 | You are given two integers `m` and `n`. Consider an `m x n` grid where each cell is initially white. You can paint each cell **red**, **green**, or **blue**. All cells **must** be painted.
Return _the number of ways to color the grid with **no two adjacent cells having the same color**_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** m = 1, n = 1
**Output:** 3
**Explanation:** The three possible colorings are shown in the image above.
**Example 2:**
**Input:** m = 1, n = 2
**Output:** 6
**Explanation:** The six possible colorings are shown in the image above.
**Example 3:**
**Input:** m = 5, n = 5
**Output:** 580986
**Constraints:**
* `1 <= m <= 5`
* `1 <= n <= 1000` | The grid is at a maximum 500 x 500, so it is clever to assume that the robot's initial cell is grid[501][501] Run a DFS from the robot's position to make sure that you can reach the target, otherwise you should return -1. Now that you are sure you can reach the target, run BFS to find the shortest path. |
[Python 3] Bitmask DP | painting-a-grid-with-three-different-colors | 0 | 1 | # Intuition\nsince m is very small so it seems sensible to use Bitmask DP here\n\n# Approach\nwe use first 5 bits for red, next 5 for blue and next 5 bits for green\nand continously check for each position if we can use a specific color.\n\n# Time Compexity:\nO(n\\*m\\*2^(2\\*m))\n\n# Code\n```\nclass Solution:\n def colorTheGrid(self, m: int, n: int) -> int:\n colors=[0,5,10]\n def next(prev,curr,j):\n A=[]\n for color in colors:\n if prev&(1<<(j+color))==0 and (j==0 or curr&(1<<(j+color-1))==0):\n A.append(curr|1<<(j+color))\n return A\n\n mod=10**9+7\n @cache\n def solve(prev,curr,i,j):\n if i==n:\n return 1\n if j==m:return solve(curr,0,i+1,0)\n new=next(prev,curr,j)\n res=0\n if new:\n for final in new:\n res+=solve(prev,final,i,j+1)\n return res%mod\n return solve(0,0,0,0) \n \n``` | 0 | You are given two integers `m` and `n`. Consider an `m x n` grid where each cell is initially white. You can paint each cell **red**, **green**, or **blue**. All cells **must** be painted.
Return _the number of ways to color the grid with **no two adjacent cells having the same color**_. Since the answer can be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** m = 1, n = 1
**Output:** 3
**Explanation:** The three possible colorings are shown in the image above.
**Example 2:**
**Input:** m = 1, n = 2
**Output:** 6
**Explanation:** The six possible colorings are shown in the image above.
**Example 3:**
**Input:** m = 5, n = 5
**Output:** 580986
**Constraints:**
* `1 <= m <= 5`
* `1 <= n <= 1000` | The grid is at a maximum 500 x 500, so it is clever to assume that the robot's initial cell is grid[501][501] Run a DFS from the robot's position to make sure that you can reach the target, otherwise you should return -1. Now that you are sure you can reach the target, run BFS to find the shortest path. |
Python Solution beats 100% Time | merge-bsts-to-create-single-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def canMerge(self, trees: List[TreeNode]) -> Optional[TreeNode]:\n\n leaves = set()\n treeDict = {}\n\n for tree in trees:\n treeDict[tree.val]=tree\n if tree.left:\n leaves.add(tree.left.val)\n if tree.right:\n leaves.add(tree.right.val)\n\n root=None\n\n for tree in trees:\n if tree.val not in leaves:\n root = tree\n break\n \n if not root:\n return None\n \n curleaves = {}\n if root.left:\n curleaves[root.left.val] = (-sys.maxsize,root.val,root,0)\n\n if root.right:\n curleaves[root.right.val] = (root.val,sys.maxsize,root,1)\n\n del treeDict[root.val]\n\n while treeDict:\n findTree = False\n for leaf,(low,high,par,lor) in curleaves.items():\n if leaf in treeDict:\n newTree = treeDict[leaf]\n del curleaves[leaf]\n\n if newTree.left:\n if low < newTree.left.val < high and newTree.left.val not in curleaves:\n curleaves[newTree.left.val] = (low,newTree.val,newTree,0)\n else:\n return None\n if newTree.right:\n if low < newTree.right.val < high and newTree.right.val not in curleaves:\n curleaves[newTree.right.val] = (newTree.val,high,newTree,1)\n else:\n return None\n\n if lor == 0:\n par.left = newTree\n else:\n par.right = newTree\n\n findTree = True\n del treeDict[newTree.val]\n break\n if not findTree:\n return None\n return root\n \n \n\n\n\n\n\n``` | 1 | You are given `n` **BST (binary search tree) root nodes** for `n` separate BSTs stored in an array `trees` (**0-indexed**). Each BST in `trees` has **at most 3 nodes**, and no two roots have the same value. In one operation, you can:
* Select two **distinct** indices `i` and `j` such that the value stored at one of the **leaves** of `trees[i]` is equal to the **root value** of `trees[j]`.
* Replace the leaf node in `trees[i]` with `trees[j]`.
* Remove `trees[j]` from `trees`.
Return _the **root** of the resulting BST if it is possible to form a valid BST after performing_ `n - 1` _operations, or_ `null` _if it is impossible to create a valid BST_.
A BST (binary search tree) is a binary tree where each node satisfies the following property:
* Every node in the node's left subtree has a value **strictly less** than the node's value.
* Every node in the node's right subtree has a value **strictly greater** than the node's value.
A leaf is a node that has no children.
**Example 1:**
**Input:** trees = \[\[2,1\],\[3,2,5\],\[5,4\]\]
**Output:** \[3,2,5,1,null,4\]
**Explanation:**
In the first operation, pick i=1 and j=0, and merge trees\[0\] into trees\[1\].
Delete trees\[0\], so trees = \[\[3,2,5,1\],\[5,4\]\].
In the second operation, pick i=0 and j=1, and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[3,2,5,1,null,4\]\].
The resulting tree, shown above, is a valid BST, so return its root.
**Example 2:**
**Input:** trees = \[\[5,3,8\],\[3,2,6\]\]
**Output:** \[\]
**Explanation:**
Pick i=0 and j=1 and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[5,3,8,2,6\]\].
The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.
**Example 3:**
**Input:** trees = \[\[5,4\],\[3\]\]
**Output:** \[\]
**Explanation:** It is impossible to perform any operations.
**Constraints:**
* `n == trees.length`
* `1 <= n <= 5 * 104`
* The number of nodes in each tree is in the range `[1, 3]`.
* Each node in the input may have children but no grandchildren.
* No two roots of `trees` have the same value.
* All the trees in the input are **valid BSTs**.
* `1 <= TreeNode.val <= 5 * 104`. | null |
Map Tree Conditions | Commented and Explained | merge-bsts-to-create-single-bst | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA binary search tree that is valid is a graph of contracts of node relations. As such, we can use graphs and sets of tree node relations and utilize them to determine validity. Validity needs to agree on a node level, and as a whole tree, and so we use a map for trees and a map for leaves, along with a set for each as well. This then lets us uniquely determine the valid binary search tree, for which there must be only one organization for the result based on the problem description. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMake a set of leaf values, tree values, a map of trees, a max tree and min tree value variable as needed for the problem, a min prob value and max prob value as needed for the problem. \n\nLoop such that \n- For tree in trees \n - map tree value to tree in tree map \n - add tree value to tree values set \n - for each of the tree children \n - if leaf add to the leaves the child values \n - update max tree, min tree as needed related to tree.val \n\nBuild a root set as the difference of tree values set and leaves value set \nSet root as \n- None if len of root set is != 1 (non-unique valid bst) \n- tree_map at root_set.pop() if len of root set is 1 \n\nValid conditions checked as follows \n- If root is None\n - return None \n- elif root.left and root.right is None \n - return root if length of trees is 1 else None \n- elif root.left and not root.right and root.val is not max_tree \n - return None \n- elif root.right and not root.left and root.val is not min_tree \n - return None \n\nIf root is None, no tree. If both left and right are None, no tree unless only one tree. If left and not right or right and not left and the root value is not the max or min tree respectively -> also none \n\nConsider child states as (low value limit, high value limit, parent node, side of placement of parent node). This then lets you understand each child state in relation to parent state, and allows for handedness. A left child will always use a parent value as the high limit, and a right child will always use the parent value as the low limit. \n\nIn all other cases, we now need to traverse \n- Make a leaf map, set left to 0 and right to 1 \n- If root.left add to leaf map at root.left.val the tree state of (min_prob, root.val, root, left) \n- If root.right, add to leaf map at root.right.val the tree state of (root.val, max_prob, root, right) \n- delete tree map at root value \n- While you have a tree map \n - set tree exists to False \n - loop for leaf and leaf (child) state in leaf map items \n - if leaf in tree map \n - set new_tree to tree_map at leaf \n - delete leaf_map at leaf \n - Each of the new_tree\'s children must satisfy that they are in bounds of the leaf state (low < children value < high) and children value not in leaf map \n - For each child, if not satisfactory, return None. Otherwise, set leaf map at child value to appropriate leaf state\n - based on sidedness of child state, set parent on side to new tree \n - mark tree exists as True if a leaf was satisfied \n - delete tree map at new tree value \n - break out of loop \n - if leaf not in tree map, continue until leaf in tree map \n - if tree exists is False return None as no leaf was satisfied \n- if loop completes, return root \n\n# Complexity\n- Time complexity : O(T) \n - O(T) loop trees at start \n - O(T) build root set \n - validity check in O(1) lets lower bound at O(2T) \n - O(T) loop tree map \n - O(L) leaf map items (at most 2 or 3 items each loop) \n - early check available inside \n - early check available oustide L loop\n - Total value is O(cT) where c is a constant -> O(T) \n\n- Space complexity : O(L + T) \n - Leaf set of size L \n - Tree values of size L \n - Tree map of size T -> T \n - Leaf map of size L -> LS (held at constant size by deletes / adds) \n - Total size is L + T \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def canMerge(self, trees: List[TreeNode]) -> Optional[TreeNode]:\n # build set of leaves and map of trees \n # note that all tree roots are unique, but not necessarily leaves\n # find min and max tree for easier short circuits later \n leaves = set() \n tree_map = dict() \n tree_vals = set()\n max_tree = 0 \n min_tree = 10**5\n max_prob = 100000\n min_prob = 0 \n for tree in trees : \n # map each tree val uniquely \n tree_map[tree.val] = tree \n # add each to the tree val set \n tree_vals.add(tree.val)\n # then based on presence of leaves, add uniques as needed \n if tree.left : \n leaves.add(tree.left.val)\n if tree.right : \n leaves.add(tree.right.val) \n # and update maxima and minima of tree values \n max_tree, min_tree = max(max_tree, tree.val), min(min_tree, tree.val)\n \n # build root set from difference of tree vals with leaves \n root_set = tree_vals.difference(leaves)\n root = None if len(root_set) != 1 else tree_map[root_set.pop()]\n \n # if none are valid though, no trees are possible \n # invalid set ups are root is None or root is isolated and not solitary \n # else if isolated and solitary return root, otherwise return None \n # else if one side isolated and not matching maxima -> return None \n # otherwise, traverse tree for resolution \n if root is None : \n return None \n elif root.left is None and root.right is None : \n return root if len(trees) == 1 else None \n elif root.left and not root.right and root.val != max_tree : \n return None \n elif root.right and not root.left and root.val != min_tree : \n return None \n else : \n # make a map of leaves to nodes of leaf states \n # leaf states include low value, high value, parent value and handed-ness \n # assume left handed as 0 and right handed as 1 \n leaf_map = dict() \n # set variables for references minimizing overhead \n left = 0 \n right = 1 \n # if root has a left and right, we can utilize it in the leaf map \n # check left and right and record as needed \n if root.left : \n leaf_map[root.left.val] = (min_prob, root.val, root, left)\n if root.right : \n leaf_map[root.right.val] = (root.val, max_prob, root, right) \n \n # since root is now pinned, remove from map \n del tree_map[root.val]\n \n # while you have a tree map \n while tree_map : \n # determine if a tree exists succesfully for the selected item\n tree_exists = False \n # for leaf key, leaf state in leaf map items \n for leaf, (low, high, parent, side) in leaf_map.items() : \n # if leaf in tree map \n if leaf in tree_map : \n # make a new tree based off of tree map via leaf value and update leaf map\n new_tree = tree_map[leaf] \n del leaf_map[leaf]\n\n # satisfy left and right in bounds of low and high of leaf state \n # on failure to satisfy all, none satisfy, so may return None \n if new_tree.left : \n if low < new_tree.left.val < high and new_tree.left.val not in leaf_map : \n leaf_map[new_tree.left.val] = (low, new_tree.val, new_tree, left)\n else : \n return None \n\n if new_tree.right : \n if low < new_tree.right.val < high and new_tree.right.val not in leaf_map : \n leaf_map[new_tree.right.val] = (new_tree.val, high, new_tree, right)\n else : \n return None \n \n # if side is left, place on left; otherwise place on right \n if side == left : \n parent.left = new_tree \n else : \n parent.right = new_tree\n \n # if a leaf was satisfied, mark as tree exists \n # this may be superseded by failure of any future leaves still \n tree_exists = True \n # remove the value as needed from the tree map \n del tree_map[new_tree.val]\n # once one satisfaction is found, break for loop \n break \n else : \n continue \n # at end of while loop before next iteration, if no leaves satisfied, return None \n if tree_exists == False : \n return None \n # if all leaves satisfied, and all trees satisfied, tree constructed \n return root \n``` | 0 | You are given `n` **BST (binary search tree) root nodes** for `n` separate BSTs stored in an array `trees` (**0-indexed**). Each BST in `trees` has **at most 3 nodes**, and no two roots have the same value. In one operation, you can:
* Select two **distinct** indices `i` and `j` such that the value stored at one of the **leaves** of `trees[i]` is equal to the **root value** of `trees[j]`.
* Replace the leaf node in `trees[i]` with `trees[j]`.
* Remove `trees[j]` from `trees`.
Return _the **root** of the resulting BST if it is possible to form a valid BST after performing_ `n - 1` _operations, or_ `null` _if it is impossible to create a valid BST_.
A BST (binary search tree) is a binary tree where each node satisfies the following property:
* Every node in the node's left subtree has a value **strictly less** than the node's value.
* Every node in the node's right subtree has a value **strictly greater** than the node's value.
A leaf is a node that has no children.
**Example 1:**
**Input:** trees = \[\[2,1\],\[3,2,5\],\[5,4\]\]
**Output:** \[3,2,5,1,null,4\]
**Explanation:**
In the first operation, pick i=1 and j=0, and merge trees\[0\] into trees\[1\].
Delete trees\[0\], so trees = \[\[3,2,5,1\],\[5,4\]\].
In the second operation, pick i=0 and j=1, and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[3,2,5,1,null,4\]\].
The resulting tree, shown above, is a valid BST, so return its root.
**Example 2:**
**Input:** trees = \[\[5,3,8\],\[3,2,6\]\]
**Output:** \[\]
**Explanation:**
Pick i=0 and j=1 and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[5,3,8,2,6\]\].
The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.
**Example 3:**
**Input:** trees = \[\[5,4\],\[3\]\]
**Output:** \[\]
**Explanation:** It is impossible to perform any operations.
**Constraints:**
* `n == trees.length`
* `1 <= n <= 5 * 104`
* The number of nodes in each tree is in the range `[1, 3]`.
* Each node in the input may have children but no grandchildren.
* No two roots of `trees` have the same value.
* All the trees in the input are **valid BSTs**.
* `1 <= TreeNode.val <= 5 * 104`. | null |
Python3 | merge-bsts-to-create-single-bst | 0 | 1 | ```\nfrom typing import List, Optional\n\n\nclass TreeNode:\n def __init__(self, val=0, left=None, right=None):\n self.val = val\n self.left = left\n self.right = right\n\n\nclass Solution:\n def __init__(self):\n self.blacklist = set()\n self.value2node = {}\n self.operation_count = 0\n\n def find_leaf(self, node, root):\n if not node:\n return\n """\n Needs to make sure the only root node doesn\'t get count as a leaf\n """\n if not node.left and not node.right and node != root:\n self.blacklist.add(node.val)\n self.find_leaf(node.left, root)\n self.find_leaf(node.right, root)\n\n def canMerge(self, trees: List[TreeNode]) -> Optional[TreeNode]:\n """\n 1. Find the root for the final BST:\n blacklist: all the leaf nodes\n whitelist: all the root nodes\n\n This root node is unique. \n\n Assume there are two nodes which are both roots, but neither of them exist in the leave nodes. \n Let\'s say A is the final root and B is also can be the root(not exist in the leave nodes), the\n subtree with B as the root will not be able to merge into the final tree, but the problem require\n n - 1 operations for n trees, so all the subtree needs to be merged into the final big tree\n\n 2. build tree while checking if the bst is valid\n use recursive to return the validness of the bst\n 3. Make sure all the tree have been used by count the times of merge operation and compare with the count of the trees\n """\n root_count = 0\n return_root = None\n\n for root in trees:\n self.find_leaf(root, root)\n\n for root in trees:\n if root.val not in self.blacklist:\n return_root = root\n root_count += 1\n self.value2node[root.val] = root\n\n # print(self.blacklist)\n # print(return_root)\n # print(self.value2node.keys())\n\n if root_count != 1:\n return None\n\n ok = self.build(return_root, float(\'-inf\'), float(\'inf\'), None, \'\')\n print(ok)\n print(self.operation_count)\n if ok and len(trees) - 1 == self.operation_count:\n return return_root\n else:\n return None\n\n def build(self, node, min_v, max_v, parent, d) -> bool:\n if not node:\n return True\n\n # print(min_v)\n # print(node.val)\n # print(max_v)\n\n if node.val <= min_v or node.val >= max_v:\n return False\n\n if node.left or node.right:\n return self.build(node.left, min_v, node.val, node, \'left\') and self.build(node.right, node.val, max_v,\n node, \'right\')\n elif not node.left and not node.right and node.val in self.value2node:\n if d == \'\':\n """\n When the root passed in with no direction, should just return True for this subtree\n """\n return True\n self.operation_count += 1\n # print(node.val)\n if d == \'left\':\n parent.left = self.value2node[node.val]\n node = parent.left\n return self.build(node.left, min_v, node.val, node, \'left\') and self.build(node.right, node.val, max_v,\n node, \'right\')\n elif d == \'right\':\n parent.right = self.value2node[node.val]\n node = parent.right\n return self.build(node.left, min_v, node.val, node, \'left\') and self.build(node.right, node.val, max_v,\n node, \'right\')\n else:\n return True\n\n``` | 0 | You are given `n` **BST (binary search tree) root nodes** for `n` separate BSTs stored in an array `trees` (**0-indexed**). Each BST in `trees` has **at most 3 nodes**, and no two roots have the same value. In one operation, you can:
* Select two **distinct** indices `i` and `j` such that the value stored at one of the **leaves** of `trees[i]` is equal to the **root value** of `trees[j]`.
* Replace the leaf node in `trees[i]` with `trees[j]`.
* Remove `trees[j]` from `trees`.
Return _the **root** of the resulting BST if it is possible to form a valid BST after performing_ `n - 1` _operations, or_ `null` _if it is impossible to create a valid BST_.
A BST (binary search tree) is a binary tree where each node satisfies the following property:
* Every node in the node's left subtree has a value **strictly less** than the node's value.
* Every node in the node's right subtree has a value **strictly greater** than the node's value.
A leaf is a node that has no children.
**Example 1:**
**Input:** trees = \[\[2,1\],\[3,2,5\],\[5,4\]\]
**Output:** \[3,2,5,1,null,4\]
**Explanation:**
In the first operation, pick i=1 and j=0, and merge trees\[0\] into trees\[1\].
Delete trees\[0\], so trees = \[\[3,2,5,1\],\[5,4\]\].
In the second operation, pick i=0 and j=1, and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[3,2,5,1,null,4\]\].
The resulting tree, shown above, is a valid BST, so return its root.
**Example 2:**
**Input:** trees = \[\[5,3,8\],\[3,2,6\]\]
**Output:** \[\]
**Explanation:**
Pick i=0 and j=1 and merge trees\[1\] into trees\[0\].
Delete trees\[1\], so trees = \[\[5,3,8,2,6\]\].
The resulting tree is shown above. This is the only valid operation that can be performed, but the resulting tree is not a valid BST, so return null.
**Example 3:**
**Input:** trees = \[\[5,4\],\[3\]\]
**Output:** \[\]
**Explanation:** It is impossible to perform any operations.
**Constraints:**
* `n == trees.length`
* `1 <= n <= 5 * 104`
* The number of nodes in each tree is in the range `[1, 3]`.
* Each node in the input may have children but no grandchildren.
* No two roots of `trees` have the same value.
* All the trees in the input are **valid BSTs**.
* `1 <= TreeNode.val <= 5 * 104`. | null |
Easy to understand Python3 solution | maximum-number-of-words-you-can-type | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n count = 0\n\n for word in text.split(" "):\n check = True\n for char in brokenLetters:\n if char in word:\n check = False\n \n if check:\n count += 1\n \n return count\n \n``` | 1 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
🔥[Python 3] Simple Set intersection 2 lines, beats 89% 🥷🏼 | maximum-number-of-words-you-can-type | 0 | 1 | ```python3 []\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n broken = set(brokenLetters)\n return sum(not set(w) & broken for w in text.split())\n```\n```python3 []\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n res, broken = 0, set(brokenLetters)\n for w in text.split():\n if not set(w) & broken:\n res += 1\n return res\n```\n | 4 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
O(n) solution with set(explanation) python faster than others | maximum-number-of-words-you-can-type | 0 | 1 | \n```\ncounter = 0\nfor i in text.split():\n #{\'a\',\'b\'}.intersection(\'a\') is equal to {\'a\'} \n #according to this if this expression returned empty set then we\'ll increment\n if set(brokenLetters).intersection(set(i)) == set():\n counter+=1\nreturn counter\n``` | 2 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Easy, Fast Python Solutions (2 Approaches - 28ms, 32ms; Faster than 93%) | maximum-number-of-words-you-can-type | 0 | 1 | # Easy, Fast Python Solutions (2 Approaches - 28ms, 32ms; Faster than 93%)\n## Approach 1 - Using Sets\n**Runtime: 28 ms, faster than 93% of Python3 online submissions for Maximum Number of Words You Can Type.**\n**Memory Usage: 14.4 MB**\n```\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n text = text.split()\n length = len(text)\n brokenLetters = set(brokenLetters)\n\n for word in text:\n for char in word:\n if char in brokenLetters:\n length -= 1\n break\n\t\t\t\t\t\n return length\n```\n\n\n## Approach 2 - Using Lists\n**Runtime: 32 ms, faster than 82% of Python3 online submissions for Maximum Number of Words You Can Type.**\n**Memory Usage: 14.4 MB**\n\n```\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n text = text.split()\n length = len(text)\n brokenLetters = list(brokenLetters)\n\t\t\n for i in text:\n temp = 0\n for j in i:\n if j in brokenLetters:\n temp -= 1\n break\n if temp < 0:\n length -= 1\n\t\t\t\t\n return length\n```\n | 13 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
p3 1 line | maximum-number-of-words-you-can-type | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n return sum(1 for word in text.split() if len(set(word) & set(brokenLetters)) == 0 )\n``` | 2 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
python3 | maximum-number-of-words-you-can-type | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def canBeTypedWords(self, text: str, b: str) -> int:\n output = 0\n text = text.split()\n brokenLetters = list(b)\n for elem in text:\n if any(v in brokenLetters for v in elem):\n continue\n else:\n output += 1\n return output\n``` | 3 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Python 1-Liner!! | maximum-number-of-words-you-can-type | 0 | 1 | ```py\nclass Solution:\n def canBeTypedWords(self, text: str, brokenLetters: str) -> int:\n return len([i for i in text.split(\' \') if len(set(i).intersection(brokenLetters))==0])\n | 1 | There is a malfunctioning keyboard where some letter keys do not work. All other keys on the keyboard work properly.
Given a string `text` of words separated by a single space (no leading or trailing spaces) and a string `brokenLetters` of all **distinct** letter keys that are broken, return _the **number of words** in_ `text` _you can fully type using this keyboard_.
**Example 1:**
**Input:** text = "hello world ", brokenLetters = "ad "
**Output:** 1
**Explanation:** We cannot type "world " because the 'd' key is broken.
**Example 2:**
**Input:** text = "leet code ", brokenLetters = "lt "
**Output:** 1
**Explanation:** We cannot type "leet " because the 'l' and 't' keys are broken.
**Example 3:**
**Input:** text = "leet code ", brokenLetters = "e "
**Output:** 0
**Explanation:** We cannot type either word because the 'e' key is broken.
**Constraints:**
* `1 <= text.length <= 104`
* `0 <= brokenLetters.length <= 26`
* `text` consists of words separated by a single space without any leading or trailing spaces.
* Each word only consists of lowercase English letters.
* `brokenLetters` consists of **distinct** lowercase English letters. | It is safe to assume the number of operations isn't more than n The number is small enough to apply a brute force solution. |
Divide gaps by dist | add-minimum-number-of-rungs | 1 | 1 | The only trick here is to use division, as the gap between two rungs could be large. We will get TLE if we add rungs one-by-one.\n\n**Java**\n```java\npublic int addRungs(int[] rungs, int dist) {\n int res = (rungs[0] - 1) / dist;\n for (int i = 1; i < rungs.length; ++i)\n res += (rungs[i] - rungs[i - 1] - 1) / dist;\n return res;\n}\n```\n**C++**\n```cpp\nint addRungs(vector<int>& rungs, int dist) {\n int res = (rungs[0] - 1) / dist;\n for (int i = 1; i < rungs.size(); ++i)\n res += (rungs[i] - rungs[i - 1] - 1) / dist;\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def addRungs(self, rungs: List[int], dist: int) -> int:\n return sum((a - b - 1) // dist for a, b in zip(rungs, [0] + rungs))\n``` | 39 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Simple python code | add-minimum-number-of-rungs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addRungs(self, rungs: List[int], dist: int) -> int:\n count=0\n rungs.insert(0,0)\n for i in range(len(rungs)-1):\n if rungs[i+1]-rungs[i]>dist: \n count+=(rungs[i+1]-rungs[i])//dist\n if (rungs[i+1]-rungs[i])%dist==0:\n count-=1\n return count\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Simple and clear python3 solution | add-minimum-number-of-rungs | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def addRungs(self, rungs: List[int], dist: int) -> int:\n result = 0\n prev = 0\n for elem in rungs:\n delta = elem - prev\n current = (delta - 1) // dist\n result += current\n prev = elem\n return result\n\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Python3, 4 lines only! (yep, a bit tricky ones ;-) ) | add-minimum-number-of-rungs | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def addRungs(self, rungs: List[int], dist: int) -> int:\n rung, result = 0, 0\n for r in rungs:\n rung, result = r, result if r - rung <= dist else result + ((r - rung) // dist + (-1 if (r - rung) % dist == 0 else 0))\n return result\n``` | 0 | You are given a **strictly increasing** integer array `rungs` that represents the **height** of rungs on a ladder. You are currently on the **floor** at height `0`, and you want to reach the last rung.
You are also given an integer `dist`. You can only climb to the next highest rung if the distance between where you are currently at (the floor or on a rung) and the next rung is **at most** `dist`. You are able to insert rungs at any positive **integer** height if a rung is not already there.
Return _the **minimum** number of rungs that must be added to the ladder in order for you to climb to the last rung._
**Example 1:**
**Input:** rungs = \[1,3,5,10\], dist = 2
**Output:** 2
**Explanation:**
You currently cannot reach the last rung.
Add rungs at heights 7 and 8 to climb this ladder.
The ladder will now have rungs at \[1,3,5,7,8,10\].
**Example 2:**
**Input:** rungs = \[3,6,8,10\], dist = 3
**Output:** 0
**Explanation:**
This ladder can be climbed without adding additional rungs.
**Example 3:**
**Input:** rungs = \[3,4,6,7\], dist = 2
**Output:** 1
**Explanation:**
You currently cannot reach the first rung from the ground.
Add a rung at height 1 to climb this ladder.
The ladder will now have rungs at \[1,3,4,6,7\].
**Constraints:**
* `1 <= rungs.length <= 105`
* `1 <= rungs[i] <= 109`
* `1 <= dist <= 109`
* `rungs` is **strictly increasing**. | The number of nice divisors is equal to the product of the count of each prime factor. Then the problem is reduced to: given n, find a sequence of numbers whose sum equals n and whose product is maximized. This sequence can have no numbers that are larger than 4. Proof: if it contains a number x that is larger than 4, then you can replace x with floor(x/2) and ceil(x/2), and floor(x/2) * ceil(x/2) > x. You can also replace 4s with two 2s. Hence, there will always be optimal solutions with only 2s and 3s. If there are three 2s, you can replace them with two 3s to get a better product. Hence, you'll never have more than two 2s. Keep adding 3s as long as n ≥ 5. |
Python: Dynamic Programming O(mn) Solution | maximum-number-of-points-with-cost | 0 | 1 | \n\n```\nclass Solution:\n def maxPoints(self, points: List[List[int]]) -> int:\n m, n = len(points), len(points[0])\n \n dp = points[0]\n \n left = [0] * n ## left side contribution\n right = [0] * n ## right side contribution\n \n for r in range(1, m):\n for c in range(n):\n if c == 0:\n left[c] = dp[c]\n else:\n left[c] = max(left[c - 1] - 1, dp[c])\n \n for c in range(n - 1, -1, -1):\n if c == n-1:\n right[c] = dp[c]\n else:\n right[c] = max(right[c + 1] - 1, dp[c])\n \n for c in range(n):\n dp[c] = points[r][c] + max(left[c], right[c])\n \n return max(dp)\n```\n | 17 | You are given an `m x n` integer matrix `points` (**0-indexed**). Starting with `0` points, you want to **maximize** the number of points you can get from the matrix.
To gain points, you must pick one cell in **each row**. Picking the cell at coordinates `(r, c)` will **add** `points[r][c]` to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows `r` and `r + 1` (where `0 <= r < m - 1`), picking cells at coordinates `(r, c1)` and `(r + 1, c2)` will **subtract** `abs(c1 - c2)` from your score.
Return _the **maximum** number of points you can achieve_.
`abs(x)` is defined as:
* `x` for `x >= 0`.
* `-x` for `x < 0`.
**Example 1:**
**Input:** points = \[\[1,2,3\],\[1,5,1\],\[3,1,1\]\]
**Output:** 9
**Explanation:**
The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
You add 3 + 5 + 3 = 11 to your score.
However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
Your final score is 11 - 2 = 9.
**Example 2:**
**Input:** points = \[\[1,5\],\[2,3\],\[4,2\]\]
**Output:** 11
**Explanation:**
The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
You add 5 + 3 + 4 = 12 to your score.
However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
Your final score is 12 - 1 = 11.
**Constraints:**
* `m == points.length`
* `n == points[r].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `0 <= points[r][c] <= 105` | Consider every possible beauty and its first and last index in flowers. Remove all flowers with negative beauties within those indices. |
easy hashmap solution python 3 | maximum-genetic-difference-query | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:\n adj_map = collections.defaultdict(set)\n root = None\n for i, node in enumerate(parents):\n if node == -1:\n root = i\n else:\n adj_map[node].add(i)\n queries_map = collections.defaultdict(set)\n\n for q in queries:\n queries_map[q[0]].add(q[1])\n self.res_map = {}\n def helperDFS(curr_root,prefix_map):\n\n if curr_root in queries_map:\n for val in queries_map[curr_root]:\n bin_rep = format(val, \'020b\')\n best_bin = ""\n print(bin_rep)\n for i in range(20):\n if prefix_map[best_bin+str(1-int(bin_rep[i]))]:\n best_bin += str(1-int(bin_rep[i]))\n else:\n best_bin += bin_rep[i]\n self.res_map[(curr_root,val)] = int(best_bin,2) ^ val \n for child in adj_map[curr_root]:\n bin_rep = format(child, \'020b\')\n for i in range(1, len(bin_rep)+1):\n prefix_map[bin_rep[0:i]].add(child)\n helperDFS(child, prefix_map)\n for i in range(1, len(bin_rep)+1):\n prefix_map[bin_rep[0:i]].remove(child)\n\n initial_prefixmap = collections.defaultdict(set)\n root_rep = format(root, \'020b\')\n for i in range(1,21):\n initial_prefixmap[root_rep[0:i]].add(root)\n helperDFS(root, initial_prefixmap)\n res = []\n for q in queries:\n res.append(self.res_map[(q[0],q[1])])\n return res\n \n\n``` | 0 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
Python, recursive before-order calculation | maximum-genetic-difference-query | 0 | 1 | # Intuition\nLet\'s rephrase problem little bit: if we have query `node,val` can answer have bit prefix `mask`? This gives us next ideas\n1. valid `mask` is always some bit prefix of `p^val` for some parent `p` of `node` (including `node`) \n2. To get the answer we can incrementally improve `mask` prefix. \nLet\'s say we have `cnt[l,mask]` - count of all `l`-prefixes of all parents of `node` (including `node`). `mask` is valid `l`-prefix for `val` ifff `cnt[l,mask^val[:l]>0` (here `val[:l]` denotes `l`-prefix of val). If `mask` is valid `l`-prefix then either `mask<0>` is valid `l+1`-prefix or `mask<1>` is. So if we can append `1` then we should do it, so we maximize valid prefix. And in the end it will be our answer.\n3. To maintain `cnt[l,mask]` and answer `queries` we use next recursive traversal procedure: increment `cnt` before children with all prefixes of `node`, then answer all queries with `node`, then traverse children, then decrement `cnt` after children. \nSo at each `node` we always have up-to-date `cnt` and can answer all queries with `node`.\n\n\n\n\n# Complexity\n- Time complexity: `O(max_bit * (n+q))`, where `n=len(parents)`, `q=len(queries)`, `max_bit=log2(max(n,val))==17` for given constraints.\n\n- Space complexity: `O(2**max_bit)+O(q)+O(n)`\n\n# Code\n```\nclass Solution:\n def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:\n max_bit=17\n child=defaultdict(list)\n for i,p in enumerate(parents):\n child[p].append(i)\n cnt=defaultdict(int)\n q_by_c=defaultdict(list)\n for i,(c,_) in enumerate(queries):\n q_by_c[c].append(i)\n res=[-1]*len(queries)\n def traverse(p):\n if p>=0:\n for l in range(max_bit+1):\n cnt[l,p>>l]+=1\n for i in q_by_c[p]:\n val=queries[i][1]\n mask=0\n for l in range(max_bit,-1,-1):\n val_l = val>>l\n mask0=mask<<1\n mask1=mask0+1\n mask=mask1 if cnt[l,val_l^mask1]>0 else mask0\n res[i]=mask\n for c in child[p]:\n traverse(c)\n if p>=0:\n for l in range(max_bit+1):\n cnt[l,p>>l]-=1 \n traverse(-1)\n return res\n\n \n``` | 0 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
O(32 * (nlogn+mlogn)) python (tle), can take realtime queries | maximum-genetic-difference-query | 0 | 1 | # Intuition\nFuck this tle based on constraints this should be fine\n\n# Code\n```\nclass Node:\n def __init__(self):\n self.containedRanges = {0: [], 1: []}\n self.children = defaultdict(Node)\n\nclass Solution:\n def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:\n graph = defaultdict(list)\n root = None\n bitTreeRoot = Node()\n highestNode = len(parents) - 1\n maxBits = int(math.log(highestNode, 2)) + 1\n for i,parent in enumerate(parents):\n if parent == -1:\n root = i\n else:\n graph[parent].append(i)\n\n nodeId = {}\n nodeRange = {} # node: [l,r] inclusive\n @cache\n def subtreeSize(curr):\n return 1 + sum(subtreeSize(nxt) for nxt in graph[curr])\n def numberAndRange(curr, l):\n nodeId[curr] = l\n nxtL = l + 1\n for nxt in graph[curr]:\n nxtSize = subtreeSize(nxt)\n numberAndRange(nxt, nxtL)\n nxtL += nxtSize\n nodeRange[curr] = [l,nxtL-1]\n numberAndRange(root, 0)\n\n def findRange(x, ranges):\n # finds if x is in any range\n # find right-most (highest) range where range[0] <= x\n l, r = 0, len(ranges)-1\n found = None\n while l <= r:\n m = l+(r-l)//2\n if ranges[m][0] <= x:\n found = m\n l = m + 1\n else:\n r = m - 1\n if found is not None and ranges[found][1] >= x:\n return found\n return None\n\n def dfs(curr):\n bitTreeNode = bitTreeRoot\n currBit = maxBits - 1\n while currBit >= 0:\n bit = int(bool(curr & 1<<currBit))\n rangeIdx = findRange(nodeId[curr], bitTreeNode.containedRanges[bit])\n if rangeIdx is None:\n bitTreeNode.containedRanges[bit].append(nodeRange[curr])\n currBit -= 1\n bitTreeNode = bitTreeNode.children[bit]\n for nxt in graph[curr]:\n dfs(nxt)\n dfs(root)\n\n seen = {}\n\n ret = []\n for node,val in queries:\n bitTreeNode = bitTreeRoot\n currBit = maxBits - 1\n bestValue = max(0, val - (val & ((1<<maxBits)-1)))\n while currBit >= 0:\n bit = int(bool(val & 1<<currBit))\n rangeIdx = findRange(nodeId[node], bitTreeNode.containedRanges[1-bit])\n good = rangeIdx is not None\n pick = 1-bit if good else bit\n bestValue += (1<<currBit) if good else 0\n currBit -= 1\n bitTreeNode = bitTreeNode.children[pick]\n ret.append(bestValue)\n\n return ret\n``` | 0 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
[Python3] bit trie | maximum-genetic-difference-query | 0 | 1 | \n```\nclass Trie: \n def __init__(self): \n self.root = {}\n \n def insert(self, x): \n node = self.root\n for i in range(18, -1, -1): \n bit = (x >> i) & 1\n node = node.setdefault(bit, {})\n node["mult"] = 1 + node.get("mult", 0)\n node["#"] = x # sentinel \n \n def search(self, x): \n node = self.root\n for i in range(18, -1, -1): \n bit = (x >> i) & 1\n if 1^bit in node: node = node[1^bit]\n else: node = node[bit]\n return x ^ node["#"]\n \n def remove(self, x): \n node = self.root\n for i in range(18, -1, -1): \n bit = (x >> i) & 1\n node[bit]["mult"] -= 1\n if node[bit]["mult"] == 0: \n node.pop(bit)\n break \n node = node[bit]\n \n\nclass Solution:\n def maxGeneticDifference(self, parents: List[int], queries: List[List[int]]) -> List[int]:\n mp = {}\n for i, (node, val) in enumerate(queries): \n mp.setdefault(node, []).append([val, i])\n \n tree, root = {}, -1\n for i, x in enumerate(parents): \n if x == -1: root = i\n else: tree.setdefault(x, []).append(i)\n \n ans = [0]*len(queries)\n trie = Trie()\n \n def fn(x): \n """Collect query results while traversing the tree."""\n trie.insert(x)\n for v, i in mp.get(x, []): ans[i] = trie.search(v)\n for xx in tree.get(x, []): fn(xx)\n trie.remove(x)\n \n fn(root)\n return ans \n``` | 1 | There is a rooted tree consisting of `n` nodes numbered `0` to `n - 1`. Each node's number denotes its **unique genetic value** (i.e. the genetic value of node `x` is `x`). The **genetic difference** between two genetic values is defined as the **bitwise-****XOR** of their values. You are given the integer array `parents`, where `parents[i]` is the parent for node `i`. If node `x` is the **root** of the tree, then `parents[x] == -1`.
You are also given the array `queries` where `queries[i] = [nodei, vali]`. For each query `i`, find the **maximum genetic difference** between `vali` and `pi`, where `pi` is the genetic value of any node that is on the path between `nodei` and the root (including `nodei` and the root). More formally, you want to maximize `vali XOR pi`.
Return _an array_ `ans` _where_ `ans[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** parents = \[-1,0,1,1\], queries = \[\[0,2\],\[3,2\],\[2,5\]\]
**Output:** \[2,3,7\]
**Explanation:** The queries are processed as follows:
- \[0,2\]: The node with the maximum genetic difference is 0, with a difference of 2 XOR 0 = 2.
- \[3,2\]: The node with the maximum genetic difference is 1, with a difference of 2 XOR 1 = 3.
- \[2,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Example 2:**
**Input:** parents = \[3,7,-1,2,0,7,0,2\], queries = \[\[4,6\],\[1,15\],\[0,5\]\]
**Output:** \[6,14,7\]
**Explanation:** The queries are processed as follows:
- \[4,6\]: The node with the maximum genetic difference is 0, with a difference of 6 XOR 0 = 6.
- \[1,15\]: The node with the maximum genetic difference is 1, with a difference of 15 XOR 1 = 14.
- \[0,5\]: The node with the maximum genetic difference is 2, with a difference of 5 XOR 2 = 7.
**Constraints:**
* `2 <= parents.length <= 105`
* `0 <= parents[i] <= parents.length - 1` for every node `i` that is **not** the root.
* `parents[root] == -1`
* `1 <= queries.length <= 3 * 104`
* `0 <= nodei <= parents.length - 1`
* `0 <= vali <= 2 * 105` | nums[i+1] must be at least equal to nums[i] + 1. Think greedily. You don't have to increase nums[i+1] beyond nums[i]+1. Iterate on i and set nums[i] = max(nums[i-1]+1, nums[i]) . |
python solution | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n lst=[]\n for i in s:\n c=s.count(i)\n lst.append(c)\n if min(lst)==max(lst):\n return True\n else:\n return False\n``` | 2 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
Best & Easiest Python Solution | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n j=[]\n for i in set(s):\n j.append(s.count(i))\n if len(set(j))!=1:\n return False\n return True\n``` | 1 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
One liner solution easy using counter to count no of occurrences and then convert into set | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | # Code\n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n return len(set(Counter(s).values()))==1\n``` | 1 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
[Python3] 1-line | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | \n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n return len(set(Counter(s).values())) == 1\n``` | 44 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
Simple one-liner with Counter | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | # Intuition\nUse Counter()\n\n# Approach\nIff string is good then there is only one frequency\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n return len(set(Counter(s).values())) == 1\n``` | 2 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
Beginners method | One liner | python | check-if-all-characters-have-equal-number-of-occurrences | 0 | 1 | The key is using length to check if theres a non dup\n\n# Code\n```\nclass Solution:\n def areOccurrencesEqual(self, s: str) -> bool:\n return len(set(collections.Counter(s).values()))==1\n``` | 2 | Given a string `s`, return `true` _if_ `s` _is a **good** string, or_ `false` _otherwise_.
A string `s` is **good** if **all** the characters that appear in `s` have the **same** number of occurrences (i.e., the same frequency).
**Example 1:**
**Input:** s = "abacbc "
**Output:** true
**Explanation:** The characters that appear in s are 'a', 'b', and 'c'. All characters occur 2 times in s.
**Example 2:**
**Input:** s = "aaabb "
**Output:** false
**Explanation:** The characters that appear in s are 'a' and 'b'.
'a' occurs 3 times while 'b' occurs 2 times, which is not the same number of times.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase English letters. | Note that the operations given describe getting the previous permutation of s To solve this problem you need to solve every suffix separately |
Two heaps simulation | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | # Intuition\nUse to heaps to simulate the process\n\n# Approach\n1 sort the times array by arrival time, preserve the index of friend by creating a new list of tuples(arrival, leave, index)\n2 use two heaps, occupied and available to simulate the process\n3 when the targetFriend arrives (index == targetFriend), return chair number\n\n# Complexity\n- Time complexity:\nO(n^2logn)\n\n- Space complexity:\nO(n)\n# Code\n```\nfrom heapq import heappop, heappush\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n friends = sorted([(a, l, i) for i, (a, l) in enumerate(times)])\n next_chair = 0\n availale = []\n occupied = []\n\n for a, l, i in friends:\n while occupied and occupied[0][0] <= a:\n heappush(availale, heappop(occupied)[1])\n\n chair = next_chair\n if availale:\n chair = heappop(availale)\n else:\n next_chair += 1\n\n if i == targetFriend:\n return chair\n\n heappush(occupied, (l, chair))\n \n return -1\n``` | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
Simulation: 6-Line Python Solution | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | # Notes\n* `available` is a **min heap** of all available seat numbers. `i.e., 0, ... n`, where `n` is the length of `times` array, or the maximum possible seats.\n* `leave_times` is a **min heap** of (time when a person will leave, seat number assigned to this person).\n\n\n# Code\n```python3\ndef smallestChair(self, times: List[List[int]], target: int) -> int:\n available, leave_times = list(range(len(times))), []\n for arrival, leaving in sorted(times):\n while leave_times and leave_times[0][0] <= arrival:\n heappush(available, heappop(leave_times)[1])\n if arrival == times[target][0]: return available[0]\n heappush(leave_times, (leaving, heappop(available)))\n\n```\n\n# Explanation\nSort `times` by arrival time, and simulate the seat assignment process.\n\nFor every new friend that wants a seat assigned, first check whether the `arrival` time of that friend is greater than or equal to the leaving time of some other friends. If so, make those seats available.\n\nSince all arrival times are unique (given in the problem statement), we can use arrival time to tell whether we have reached the target friend. When we reach the target friend, we return the minimum available seat as required (`if arrival == times[target][0]: return available[0]`). | 3 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
Python - Simple Heap Solution with Explanation | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | **Explanation:**\n* Put all arrivals in one heap and all departures in another heap - this helps us to go by the chronogical order of time\n* If smallest time in arrivals heap is less than smallest time in departures heap, then pop from arrivals heap and occupy the 1st available table with the popped element. \n* If popped index/friend is the target friend, then return the occupied index\n* Else if smallest time in departures heap is less than or equal to smallest time in arrivals heap, then pop from departures heap and vacate the table occupied by the popped element\n\n```\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n arrivals = []\n departures = []\n for ind, (x, y) in enumerate(times):\n heappush(arrivals, (x, ind))\n heappush(departures, (y, ind))\n d = {}\n occupied = [0] * len(times)\n while True:\n if arrivals and departures and arrivals[0][0] < departures[0][0]:\n _, ind = heappop(arrivals)\n d[ind] = occupied.index(0)\n occupied[d[ind]] = 1\n if ind == targetFriend:\n return d[ind]\n elif arrivals and departures and arrivals[0][0] >= departures[0][0]:\n _, ind = heappop(departures)\n occupied[d[ind]] = 0\n``` | 21 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
[Python3] sweeping | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | \n```\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n vals = []\n for i, (arrival, leaving) in enumerate(times): \n vals.append((arrival, 1, i))\n vals.append((leaving, 0, i))\n \n k = 0 \n pq = [] # available seats \n mp = {} # player-to-seat mapping \n for _, arrival, i in sorted(vals): \n if arrival: \n if pq: s = heappop(pq)\n else: \n s = k\n k += 1\n if i == targetFriend: return s\n mp[i] = s\n else: heappush(pq, mp[i]) # new seat available\n``` | 21 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
The Number of the Smallest Unoccupied Chair|| Min Heaps || Heavily commented|| | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | \n# Code\n```\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n import heapq as hq\n a=[]\n for i in range(len(times)):a.append([i,times[i][0],times[i][1]])\n a.sort(key=lambda x:[x[1],x[2]])\n """Instead of infinite by the logic at worst case each \n of friend can have a chair if all attending at same time \n every one get seperate chair so we can keep can have \n atmost len(times) chairs for safer side \n i took len(times)*2 chairs"""\n availablechairs=[]\n """assigned chairs in this [[EndTime,chairnumber]] type of fashion\n in assigned heap/List"""\n assigned=[] \n hq.heapify(availablechairs)\n hq.heapify(assigned)\n """make heap of available chairs so avalable chairs will \n be put inside this"""\n for i in range(len(a)*2+1):hq.heappush(availablechairs,i)\n for i in range(len(a)):\n """firstly chq whether any chair will be till the arriving \n time of current frnd if so take out all the chairs for it \n as we already sort time array according to arrival time \n of friends is so then put those chairs inside \n availablechairs heap""" \n while len(assigned) and assigned[0][0]<=a[i][1]:\n x=hq.heappop(assigned)\n hq.heappush(availablechairs,x[1])\n """after taking out all available chairs i tried to \n assigned smaller number chairs to the currently arrived friend"""\n x=hq.heappop(availablechairs)\n hq.heappush(assigned,[a[i][2],x])\n """if i got the target frnd i just \n returned the chair is assigned to him."""\n if(a[i][0]==targetFriend):\n return(x)\n \n \n ***"""SECOND APPREOACH"""**\n # import heapq as hq\n # a=[]\n # for i in range(len(times)):a.append([i,times[i][0],times[i][1]])\n # a.sort(key=lambda x:[x[1],x[2]])\n # # print(a)\n # availablechairs=[]\n # assigned=[] ## [[EndTime,chairnumber]]\n # hq.heapify(availablechairs)\n # hq.heapify(assigned)\n # for i in range(len(a)*2+1):hq.heappush(availablechairs,i)\n # for i in range(len(a)):\n # f=False\n # for j in range(len(assigned)):\n # if assigned[j][1]<=a[i][1]:\n # assigned[j][1]=a[i][2]\n # f=True\n # if (a[i][0]==targetFriend):\n # return assigned[j][0]\n # break\n # if f:\n # f=False\n # continue\n # else:\n # x=hq.heappop(availablechairs)\n # hq.heappush(assigned,[x,a[i][2]])\n # if(a[i][0]==targetFriend):\n # return x\n```* | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
[Python3] - Pushing Friends around - DoubleHeap | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to keep track of the smallest chair available and keep track which friend has which chair and when he leaves.\n\nIn my head, this screams for thwo heaps and a simultion over time. Therefore, we first sort the friends in the order of their arrival, so we can simulate over time. Here we also need to keep track of their original indices, as we need to know when target friend arrives.\n\nThen we go through the arrival times. At each arrival time, we push out all friends that are leaving before this time from the occupied chairs heap. Everytime, we pushed out a friend, we add the free chair back into a minheap keeping track of the smallest numbered chair.\n\nAfter we have done that, we assign the smallest chair to the new friend and push his leaving time and chair number into the occupied chairs heap. Before doing that, we can check whether this friend is the target friend. In this case, we can return the minimum chair.\n\nKeep in mind: Pushing friends out is not a good thing!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTwo heaps, with occupied and free chairs\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N * logN) as we need to sort the friends with their arrival time\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) for chairs or leaving friends (if we ignore sorting)\n# Code\n```\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n\n # sort the friends by their arrival time (and keep the index)\n friends = sorted([(arrival, leave, idx) for idx, (arrival, leave) in enumerate(times)], key=lambda x: x[0])\n \n # keep track of the minimum free chair\n free_chair = 0\n\n # make a heap for the leave times and their occupied chair\n occupied = []\n chairs = [ele for ele in range(len(friends))]\n for arrival, leaving, odx in friends:\n\n # get all the occupied chairs back into the available chairs\n while occupied and occupied[0][0] <= arrival:\n\n # push out the leaving friend\n _, chair = heapq.heappop(occupied)\n\n # push back the occupied chair\n heapq.heappush(chairs, chair)\n \n # check whether we reached our target\n if odx == targetFriend: return chairs[0]\n\n # push the friend into the group of chairs\n heapq.heappush(occupied, (leaving, heapq.heappop(chairs)))\n return -1\n \n``` | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
Python sorting + heap + map + solution | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | ```\nclass Solution:\n def smallestChair(self, times: List[List[int]], targetFriend: int) -> int:\n time_arr = []\n arrive, leave = 1, -1\n for idx, (arrive_time, leave_time) in enumerate(times):\n time_arr.append((arrive_time, arrive, idx))\n time_arr.append((leave_time, leave, idx))\n time_arr.sort()\n\n chair_min_heap = [chair for chair in range(len(times))]\n heapq.heapify(chair_min_heap)\n friend_to_chair = {}\n\n for time, flag, idx in time_arr:\n if idx == targetFriend:\n min_chair = heapq.heappop(chair_min_heap)\n return min_chair\n if flag == arrive:\n min_chair = heapq.heappop(chair_min_heap)\n friend_to_chair[idx] = min_chair\n else:\n occupied_chair = friend_to_chair[idx]\n heapq.heappush(chair_min_heap, occupied_chair)\n``` | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
Python | Greedy | O(nlogn) | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | # Code\n```\nclass Solution:\n def smallestChair(self, times: List[List[int]], target: int) -> int:\n n = len(times)\n h = [i for i in range(n)]\n events = []\n L, R = 1, 0\n for i, (s, e) in enumerate(times):\n events.append((s,L,i))\n events.append((e,R,i))\n events.sort()\n d = defaultdict(lambda: -1)\n for t, typ, i in events:\n if typ == L:\n j = heappop(h)\n d[i] = j\n if target == i: return j\n else:\n heappush(h, d[i])\n \n``` | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
Python (Simple Heap + Hashmap) | the-number-of-the-smallest-unoccupied-chair | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestChair(self, times, targetFriend):\n result = []\n\n for i, (a,b) in enumerate(times):\n result.append([a,1,i])\n result.append([b,0,i])\n\n result.sort()\n\n available, dict1 = list(range(len(times))), defaultdict(int)\n heapq.heapify(result)\n\n for i,j,k in result:\n if j:\n if k == targetFriend:\n return heappop(available)\n\n dict1[k] = heappop(available)\n else:\n heappush(available,dict1.pop(k))\n \n\n\n\n\n\n\n\n\n\n \n\n\n \n\n\n\n\n\n\n\n\n\n\n``` | 0 | There is a party where `n` friends numbered from `0` to `n - 1` are attending. There is an **infinite** number of chairs in this party that are numbered from `0` to `infinity`. When a friend arrives at the party, they sit on the unoccupied chair with the **smallest number**.
* For example, if chairs `0`, `1`, and `5` are occupied when a friend comes, they will sit on chair number `2`.
When a friend leaves the party, their chair becomes unoccupied at the moment they leave. If another friend arrives at that same moment, they can sit in that chair.
You are given a **0-indexed** 2D integer array `times` where `times[i] = [arrivali, leavingi]`, indicating the arrival and leaving times of the `ith` friend respectively, and an integer `targetFriend`. All arrival times are **distinct**.
Return _the **chair number** that the friend numbered_ `targetFriend` _will sit on_.
**Example 1:**
**Input:** times = \[\[1,4\],\[2,3\],\[4,6\]\], targetFriend = 1
**Output:** 1
**Explanation:**
- Friend 0 arrives at time 1 and sits on chair 0.
- Friend 1 arrives at time 2 and sits on chair 1.
- Friend 1 leaves at time 3 and chair 1 becomes empty.
- Friend 0 leaves at time 4 and chair 0 becomes empty.
- Friend 2 arrives at time 4 and sits on chair 0.
Since friend 1 sat on chair 1, we return 1.
**Example 2:**
**Input:** times = \[\[3,10\],\[1,5\],\[2,6\]\], targetFriend = 0
**Output:** 2
**Explanation:**
- Friend 1 arrives at time 1 and sits on chair 0.
- Friend 2 arrives at time 2 and sits on chair 1.
- Friend 0 arrives at time 3 and sits on chair 2.
- Friend 1 leaves at time 5 and chair 0 becomes empty.
- Friend 2 leaves at time 6 and chair 1 becomes empty.
- Friend 0 leaves at time 10 and chair 2 becomes empty.
Since friend 0 sat on chair 2, we return 2.
**Constraints:**
* `n == times.length`
* `2 <= n <= 104`
* `times[i].length == 2`
* `1 <= arrivali < leavingi <= 105`
* `0 <= targetFriend <= n - 1`
* Each `arrivali` time is **distinct**. | null |
[Python] Easy solution in O(n*logn) with detailed explanation | describe-the-painting | 0 | 1 | ### Idea\nwe can iterate on coordinates of each `[start_i, end_i)` from small to large and maintain the current mixed color.\n\n### How can we maintain the mixed color?\nWe can do addition if the current coordinate is the beginning of a segment.\nIn contrast, We do subtraction if the current coordinate is the end of a segment.\n\n### Examples\nLet\'s give the example for understanding it easily.\n\n#### Example 1:\n\n\nThere are 3 coordinates get involved. 1, 4, 7 respetively.\nAt coordinate 1, there are two segment starting here. Thus, the current mixed color will be 5 + 9 = 14\nAt coordinate 4, the segment [1, 4, 5] is end here and the segment [4, 7, 7] also start here. Thus, the current mixed color will be 14 - 5 + 7 = 16\nAt coordinate 7, two segments are end here. Thus, the current mixed color will be 0\nSo we know the final answer should be [1, 4, 14] and [4, 7, 16].\n\n\n#### Example 2:\n\n\nThere are 5 coordinates get involved. 1, 6, 7, 8, 10 respetively.\nAt coordinate 1, only the segment [1, 7, 9] start here. Thus, the current mixed color will be 0 + 9 = 9\nAt coordinate 6, another segment [6, 8, 15] start here. Thus, the current mixed color will be 9 + 15 = 24\nAt coordinate 7, the segment [1, 7, 9] is end here. Thus, the current mixed color will be 24 - 9 = 15\nAt coordinate 8, the segment [6, 8, 15] is end here and the segment [8, 10, 7] also start here. Thus, the current mixed color will be 15 - 15 + 7 = 7\nAt coordinate 10, the segment [8, 10, 7] is end here. Thus, the current mixed color will be 0\nSo we know the final answer should be [1,6,9], [6,7,24], [7,8,15], [8,10,7].\n\n### Complexity\n- Time complexity: O(n * log(n)) # We can use a fixed size array with length 10^5 to replace the default dict and bound the time complexity to O(n).\n- Space complexity: O(n)\n\n### Code\n\n```python\nclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n\t\t# via this mapping, we can easily know which coordinates should be took into consideration.\n mapping = defaultdict(int)\n for s, e, c in segments:\n mapping[s] += c\n mapping[e] -= c\n \n res = []\n prev, color = None, 0\n for now in sorted(mapping):\n if color: # if color == 0, it means this part isn\'t painted.\n res.append((prev, now, color))\n \n color += mapping[now]\n prev = now\n \n return res\n```\n\nPlease upvote if it\'s helpful or leave comments if I can do better. Thank you in advance.\n | 136 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
Line Sweep | describe-the-painting | 1 | 1 | We can use the line sweep approach to compute the sum (color mix) for each point. We use this line to check when a sum changes (a segment starts or finishes) and describe each mix. But there is a catch: different colors could produce the same sum. \n\nI was puzzled for a moment, and then I noticed that the color for each segment is distinct. So, every time a segment starts or ends, the color mix is different (even if the sum is the same). So we also mark `ends` of color segments on our line.\n\n**Java**\n```java\npublic List<List<Long>> splitPainting(int[][] segments) {\n long mix[] = new long[100002], sum = 0, last_i = 0;\n boolean ends[] = new boolean[100002];\n List<List<Long>> res = new ArrayList<>();\n for (var s : segments) {\n mix[s[0]] += s[2];\n mix[s[1]] -= s[2];\n ends[s[0]] = ends[s[1]] = true;\n }\n for (int i = 1; i < 100002; ++i) {\n if (ends[i] && sum > 0)\n res.add(Arrays.asList(last_i, (long)i, sum));\n last_i = ends[i] ? i : last_i;\n sum += mix[i];\n } \n return res;\n}\n```\n**C++**\n```cpp\nvector<vector<long long>> splitPainting(vector<vector<int>>& segments) {\n long long mix[100002] = {}, sum = 0, last_i = 0;\n bool ends[100002] = {};\n vector<vector<long long>> res;\n for (auto &s : segments) {\n mix[s[0]] += s[2];\n mix[s[1]] -= s[2];\n ends[s[0]] = ends[s[1]] = true;\n }\n for (int i = 1; i < 100002; ++i) {\n if (ends[i] && sum)\n res.push_back({last_i, i, sum});\n last_i = ends[i] ? i : last_i;\n sum += mix[i];\n }\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n mix, res, last_i = DefaultDict(int), [], 0\n for start, end, color in segments:\n mix[start] += color\n mix[end] -= color\n for i in sorted(mix.keys()):\n if last_i in mix and mix[last_i]:\n res.append([last_i, i, mix[last_i]])\n mix[i] += mix[last_i]\n last_i = i\n return res\n``` | 72 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
[Python 3] - Difference Array + Sweep Line | describe-the-painting | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n d = collections.defaultdict(int)\n for s, e, p in segments:\n d[s] += p\n d[e] -= p\n res = []\n paints = sorted(d.items())\n print(paints)\n l_prev, p_prev = paints[0]\n for l, p in paints[1:]:\n if p_prev != 0:\n res.append([l_prev, l, p_prev])\n l_prev, p_prev = l, p + p_prev\n return res\n``` | 4 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
[Python3] sweeping again | describe-the-painting | 0 | 1 | \n```\nclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n vals = []\n for start, end, color in segments: \n vals.append((start, +color))\n vals.append((end, -color))\n \n ans = []\n prefix = prev = 0 \n for x, c in sorted(vals): \n if prev < x and prefix: ans.append([prev, x, prefix])\n prev = x\n prefix += c \n return ans \n``` | 14 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
🐍 O(nlogn) || Clean and Concise || 97% faster || Well-Explained with Example 📌📌 | describe-the-painting | 0 | 1 | ## IDEA :\nWe are finding all the starting and ending points. These points score we are storing in our dictinoary and after sorting all the poiints we are making our result array.\n\nEg: segments = [[1,7,9],[6,8,15],[8,10,7]]\nThere are 5 coordinates get involved. 1, 6, 7, 8, 10 respetively.\n* At coordinate 1, only the segment [1, 7, 9] start here. Thus, the current mixed color will be 0 + 9 = 9\n* At coordinate 6, another segment [6, 8, 15] start here. Thus, the current mixed color will be 9 + 15 = 24\n* At coordinate 7, the segment [1, 7, 9] is end here. Thus, the current mixed color will be 24 - 9 = 15\n* At coordinate 8, the segment [6, 8, 15] is end here and the segment [8, 10, 7] also start here. Thus, the current mixed color will be 15 - 15 + 7 = 7\n* At coordinate 10, the segment [8, 10, 7] is end here. Thus, the current mixed color will be 0\n* So we know the final answer should be [1,6,9], [6,7,24], [7,8,15], [8,10,7].\n\n\'\'\'\n\n\tclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n \n dic = defaultdict(int)\n for s,e,c in segments:\n dic[s]+=c\n dic[e]-=c\n \n st=None\n color=0\n res = []\n for p in sorted(dic):\n if st is not None and color!=0:\n res.append([st,p,color])\n color+=dic[p]\n st = p\n \n return res\n\nThanks and Happy Coding !!\uD83E\uDD1E\nFeel free to ask and **Upvote** if you got any help. \uD83E\uDD17 | 11 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
Python, beats 98% 10 lines. | describe-the-painting | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine list of breaking points, calculate effective color as aggretable meausure which changes at breaking points.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:\n changes_points = defaultdict(int)\n ret = []\n for s in segments:\n changes_points[s[0]] += s[2]\n changes_points[s[1]] -= s[2]\n color = 0\n for cr_pos in sorted(changes_points):\n if color != 0:\n ret.append([prev_pos, cr_pos, color])\n prev_pos = cr_pos\n color += changes_points[cr_pos]\n return ret\n``` | 0 | There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a **unique** color. You are given a 2D integer array `segments`, where `segments[i] = [starti, endi, colori]` represents the **half-closed segment** `[starti, endi)` with `colori` as the color.
The colors in the overlapping segments of the painting were **mixed** when it was painted. When two or more colors mix, they form a new color that can be represented as a **set** of mixed colors.
* For example, if colors `2`, `4`, and `6` are mixed, then the resulting mixed color is `{2,4,6}`.
For the sake of simplicity, you should only output the **sum** of the elements in the set rather than the full set.
You want to **describe** the painting with the **minimum** number of non-overlapping **half-closed segments** of these mixed colors. These segments can be represented by the 2D array `painting` where `painting[j] = [leftj, rightj, mixj]` describes a **half-closed segment** `[leftj, rightj)` with the mixed color **sum** of `mixj`.
* For example, the painting created with `segments = [[1,4,5],[1,7,7]]` can be described by `painting = [[1,4,12],[4,7,7]]` because:
* `[1,4)` is colored `{5,7}` (with a sum of `12`) from both the first and second segments.
* `[4,7)` is colored `{7}` from only the second segment.
Return _the 2D array_ `painting` _describing the finished painting (excluding any parts that are **not** painted). You may return the segments in **any order**_.
A **half-closed segment** `[a, b)` is the section of the number line between points `a` and `b` **including** point `a` and **not including** point `b`.
**Example 1:**
**Input:** segments = \[\[1,4,5\],\[4,7,7\],\[1,7,9\]\]
**Output:** \[\[1,4,14\],\[4,7,16\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- \[4,7) is colored {7,9} (with a sum of 16) from the second and third segments.
**Example 2:**
**Input:** segments = \[\[1,7,9\],\[6,8,15\],\[8,10,7\]\]
**Output:** \[\[1,6,9\],\[6,7,24\],\[7,8,15\],\[8,10,7\]\]
**Explanation:** The painting can be described as follows:
- \[1,6) is colored 9 from the first segment.
- \[6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- \[7,8) is colored 15 from the second segment.
- \[8,10) is colored 7 from the third segment.
**Example 3:**
**Input:** segments = \[\[1,4,5\],\[1,4,7\],\[4,7,1\],\[4,7,11\]\]
**Output:** \[\[1,4,12\],\[4,7,12\]\]
**Explanation:** The painting can be described as follows:
- \[1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- \[4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment \[1,7) is incorrect because the mixed color sets are different.
**Constraints:**
* `1 <= segments.length <= 2 * 104`
* `segments[i].length == 3`
* `1 <= starti < endi <= 105`
* `1 <= colori <= 109`
* Each `colori` is distinct. | If the chosen substrings are of size larger than 1, then you can remove all but the first character from both substrings, and you'll get equal substrings of size 1, with the same a but less j. Hence, it's always optimal to choose substrings of size 1. If you choose a specific letter, then it's optimal to choose its first occurrence in firstString, and its last occurrence in secondString, to minimize j-a. |
Solution with Monotonic Stack in Python3 / TypeScript | number-of-visible-people-in-a-queue | 0 | 1 | # Intuition\nHere we have:\n- list of `heights`, a particular `heights[i]`\n- our goal is find for each `heights[i]` **HOW much** other persons from right we could see, and represent it in a list of **visible persons**\n\nOften it helps to iterate **not only** from `left` to `right`, but **vice-versa**.\nThis\'ll be **a key** to implement **monotonic nature** of a stack.\n\n```\n# Example \nheights = [10,6,8,5,11,9]\n\n# Let\'s iterate in 5 to 0:\n# 1. How much persons heights[5] see? 0, stack = [9] \n# 2. How much persons heights[4] see? 1, stack = [11] \n# 3. How much persons heights[3] see? 1, stack = [11, 5] \n# 4. How much persons heights[2] see? 2, stack = [11, 8] \n# 5. How much persons heights[1] see? 1, stack = [11, 8, 6] \n# 6. How much persons heights[0] see? 3, stack = [11] \n```\n\n# Approach\n1. declare a **monotonic** `stack`\n2. define `ans` to store the answer\n3. iterate in reverse direction\n4. pop from `stack` each `heights[i]` if it lower than current `heights[i]`\n5. calculate `ans[i]` as max count of persons you could see\n6. push onto stack `heights[i]` to maintain it monotonic nature\n\n# Complexity\n- Time complexity: **O(N)**, in worst-case scenario\n\n- Space complexity: **O(N**), the same for storing\n\n# Code in Python3\n```\nclass Solution:\n def canSeePersonsCount(self, heights: list[int]) -> list[int]:\n n = len(heights)\n stack = []\n ans = [0] * n\n\n for i in range(n - 1, -1, -1):\n cur = 0\n\n while stack and stack[-1] < heights[i]:\n stack.pop()\n cur += 1\n\n ans[i] = cur + int(len(stack) > 0)\n stack.append(heights[i])\n\n return ans\n```\n# Code in TypeScript\n```\nfunction canSeePersonsCount(heights: number[]): number[] {\n const n = heights.length;\n const stack = []\n const ans = Array(n).fill(0)\n\n for (let i = n - 1; i >= 0; i--) {\n let cur = 0\n\n while (stack && stack[stack.length - 1] < heights[i]) {\n stack.pop()\n cur += 1\n }\n\n ans[i] = cur + Number(stack.length > 0)\n stack.push(heights[i])\n\n }\n\n return ans\n};\n``` | 1 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
Solution with Monotonic Stack in Python3 / TypeScript | number-of-visible-people-in-a-queue | 0 | 1 | # Intuition\nHere we have:\n- list of `heights`, a particular `heights[i]`\n- our goal is find for each `heights[i]` **HOW much** other persons from right we could see, and represent it in a list of **visible persons**\n\nOften it helps to iterate **not only** from `left` to `right`, but **vice-versa**.\nThis\'ll be **a key** to implement **monotonic nature** of a stack.\n\n```\n# Example \nheights = [10,6,8,5,11,9]\n\n# Let\'s iterate in 5 to 0:\n# 1. How much persons heights[5] see? 0, stack = [9] \n# 2. How much persons heights[4] see? 1, stack = [11] \n# 3. How much persons heights[3] see? 1, stack = [11, 5] \n# 4. How much persons heights[2] see? 2, stack = [11, 8] \n# 5. How much persons heights[1] see? 1, stack = [11, 8, 6] \n# 6. How much persons heights[0] see? 3, stack = [11] \n```\n\n# Approach\n1. declare a **monotonic** `stack`\n2. define `ans` to store the answer\n3. iterate in reverse direction\n4. pop from `stack` each `heights[i]` if it lower than current `heights[i]`\n5. calculate `ans[i]` as max count of persons you could see\n6. push onto stack `heights[i]` to maintain it monotonic nature\n\n# Complexity\n- Time complexity: **O(N)**, in worst-case scenario\n\n- Space complexity: **O(N**), the same for storing\n\n# Code in Python3\n```\nclass Solution:\n def canSeePersonsCount(self, heights: list[int]) -> list[int]:\n n = len(heights)\n stack = []\n ans = [0] * n\n\n for i in range(n - 1, -1, -1):\n cur = 0\n\n while stack and stack[-1] < heights[i]:\n stack.pop()\n cur += 1\n\n ans[i] = cur + int(len(stack) > 0)\n stack.append(heights[i])\n\n return ans\n```\n# Code in TypeScript\n```\nfunction canSeePersonsCount(heights: number[]): number[] {\n const n = heights.length;\n const stack = []\n const ans = Array(n).fill(0)\n\n for (let i = n - 1; i >= 0; i--) {\n let cur = 0\n\n while (stack && stack[stack.length - 1] < heights[i]) {\n stack.pop()\n cur += 1\n }\n\n ans[i] = cur + Number(stack.length > 0)\n stack.push(heights[i])\n\n }\n\n return ans\n};\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
Python 3 || 8 lines, stack, w/example || T/M: 88% / 72% | number-of-visible-people-in-a-queue | 0 | 1 | ```\nclass Solution: # *\n def canSeePersonsCount(self, heights: List[int]) -> List[int]: # * *\n # * *\n # * * *\n # * * * *\n # * * * * *\n ans, stack = [0] * len(heights), deque() # Example: heights = [5, 1, 2, 3, 6]\n # heights[::-1] = [6, 3, 2, 1, 5]\n for i, hgt in enumerate(heights[::-1]):\n # i hgt stack ans \n while stack and stack[-1] < hgt: # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\n ans[i]+= 1 # 0 10 [6] [0,0,0,0,0]\n stack.pop() # 1 3 [6,3] [0,1,0,0,0]\n # 2 2 [6,3,2] [0,1,1,0,0] \n if stack: ans[i]+= 1 # 3 1 [6,3,2,1] [0,1,1,1,0]\n # 4 5 [6,5] [0,1,1,1,4]\n stack.append(hgt)\n # ans[::-1] = [4,1,1,1,0] <-- return\n return ans[::-1]\n```\n[https://leetcode.com/problems/number-of-visible-people-in-a-queue/submissions/871467326/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 4 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
Python 3 || 8 lines, stack, w/example || T/M: 88% / 72% | number-of-visible-people-in-a-queue | 0 | 1 | ```\nclass Solution: # *\n def canSeePersonsCount(self, heights: List[int]) -> List[int]: # * *\n # * *\n # * * *\n # * * * *\n # * * * * *\n ans, stack = [0] * len(heights), deque() # Example: heights = [5, 1, 2, 3, 6]\n # heights[::-1] = [6, 3, 2, 1, 5]\n for i, hgt in enumerate(heights[::-1]):\n # i hgt stack ans \n while stack and stack[-1] < hgt: # \u2013\u2013\u2013 \u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\n ans[i]+= 1 # 0 10 [6] [0,0,0,0,0]\n stack.pop() # 1 3 [6,3] [0,1,0,0,0]\n # 2 2 [6,3,2] [0,1,1,0,0] \n if stack: ans[i]+= 1 # 3 1 [6,3,2,1] [0,1,1,1,0]\n # 4 5 [6,5] [0,1,1,1,4]\n stack.append(hgt)\n # ans[::-1] = [4,1,1,1,0] <-- return\n return ans[::-1]\n```\n[https://leetcode.com/problems/number-of-visible-people-in-a-queue/submissions/871467326/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 4 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
[Java/Python 3] Monotonic stack w/ 18 similar problems, brief explanation and analysis. | number-of-visible-people-in-a-queue | 1 | 1 | **Method 1: reverse traversal - save heights into stack** \n\n**Intuition**\nSince we see from left to right and can only see any one higher than the persons between them, it looks simpler to traverse reversely (than from left to right) and use monotonic stack to save heights.\n\nBy keep popping out of stack the higher persons, we can increasing the counter, `ans[i]`, of the current person and do NOT forget to add one more if the stack is NOT empty by the end of the aforementioned popping.\n\n----\n\n1. Reversely traverse the input array `heights`, use a stack to store the heights that are higher than current height. \n2. Therefore, whenever current height is higher than the top of the stack, keep popping out the top of the stack and increase the output array `ans` accordingly, till the stack is empty or current height is lower than the top;\n3. Now if the stack is not empty, the top must be higher than current height and will be visible, so count it in;\n4. Push current height into the stack to maintain the monotonic increading property.\n\n```java\n public int[] canSeePersonsCount(int[] heights) {\n int n = heights.length;\n int[] ans = new int[n];\n Deque<Integer> stk = new ArrayDeque<>();\n for (int i = n - 1; i >= 0; --i) {\n while (!stk.isEmpty() && heights[i] > stk.peek()) {\n ++ans[i];\n stk.pop();\n }\n if (!stk.isEmpty()) {\n ++ans[i];\n }\n stk.push(heights[i]);\n }\n return ans;\n }\n```\n```python\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n, stk = len(heights), []\n ans = [0] * n\n for i, h in enumerate(reversed(heights)):\n while stk and h > stk[-1]:\n stk.pop()\n ans[i] += 1\n if stk:\n ans[i] += 1\n stk.append(h)\n return ans[:: -1]\n```\n\n----\n\n**Method 2: normal traversal - save indices into stack**\n\n```java\n public int[] canSeePersonsCount(int[] heights) {\n int n = heights.length;\n int[] ans = new int[n];\n Deque<Integer> stk = new ArrayDeque<>();\n for (int i = 0; i < n; ++i) {\n while (!stk.isEmpty() && heights[stk.peek()] < heights[i]) {\n ++ans[stk.pop()];\n }\n if (!stk.isEmpty()) {\n ++ans[stk.peek()];\n }\n stk.push(i);\n }\n return ans;\n }\n```\n```python\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n = len(heights)\n ans, stk = [0] * n, []\n for i, h in enumerate(heights):\n while stk and heights[stk[-1]] < h:\n ans[stk.pop()] += 1\n if stk:\n ans[stk[-1]] += 1\n stk.append(i)\n return ans\n```\n\n----\n**Comparison of the 2 methods:**\n\nI myself prefer method 1, because the stack stores the value of `heights` instead of indices of the `heights`, which is more intuitive than the way in method 2.\n\n\n----\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n = heights.length`.\n\n----\nSimilar problems (monotonous stack/queue):\n\n[84 Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram)\n[214 Shortest Palindrome](https://leetcode.com/problems/shortest-palindrome)\n[239 Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum)\n[316 Remove Duplicate Letters](https://leetcode.com/problems/remove-duplicate-letters)\n[321 Create Maximum Number](https://leetcode.com/problems/create-maximum-number)\n[402 Remove K Digits](https://leetcode.com/problems/remove-k-digits)\n[456 132 Pattern](https://leetcode.com/problems/132-pattern)\n[496 Next Greater Element I](https://leetcode.com/problems/next-greater-element-i)\n[503. Next Greater Element II](https://leetcode.com/problems/next-greater-element-ii/description/)\n[654 Maximum Binary Tree](https://leetcode.com/problems/maximum-binary-tree)\n[739. Daily Temperatures](https://leetcode.com/problems/daily-temperatures/description/)\n[768 Max Chunks To Make Sorted II](https://leetcode.com/problems/max-chunks-to-make-sorted-ii)\n[862 Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k)\n[889 Construct Binary Tree from Preorder and Postorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal)\n[901 Online Stock Span](https://leetcode.com/problems/online-stock-span)\n[907 Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums)\n[1019. Next Greater Node In Linked List](https://leetcode.com/problems/next-greater-node-in-linked-list/discuss/267163/Java-9-liner-O(n)-using-Stack-and-ArrayList)\n[1475 Final Prices With a Special Discount in a Shop](https://leetcode.com/problems/final-prices-with-a-special-discount-in-a-shop)\n | 50 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
[Java/Python 3] Monotonic stack w/ 18 similar problems, brief explanation and analysis. | number-of-visible-people-in-a-queue | 1 | 1 | **Method 1: reverse traversal - save heights into stack** \n\n**Intuition**\nSince we see from left to right and can only see any one higher than the persons between them, it looks simpler to traverse reversely (than from left to right) and use monotonic stack to save heights.\n\nBy keep popping out of stack the higher persons, we can increasing the counter, `ans[i]`, of the current person and do NOT forget to add one more if the stack is NOT empty by the end of the aforementioned popping.\n\n----\n\n1. Reversely traverse the input array `heights`, use a stack to store the heights that are higher than current height. \n2. Therefore, whenever current height is higher than the top of the stack, keep popping out the top of the stack and increase the output array `ans` accordingly, till the stack is empty or current height is lower than the top;\n3. Now if the stack is not empty, the top must be higher than current height and will be visible, so count it in;\n4. Push current height into the stack to maintain the monotonic increading property.\n\n```java\n public int[] canSeePersonsCount(int[] heights) {\n int n = heights.length;\n int[] ans = new int[n];\n Deque<Integer> stk = new ArrayDeque<>();\n for (int i = n - 1; i >= 0; --i) {\n while (!stk.isEmpty() && heights[i] > stk.peek()) {\n ++ans[i];\n stk.pop();\n }\n if (!stk.isEmpty()) {\n ++ans[i];\n }\n stk.push(heights[i]);\n }\n return ans;\n }\n```\n```python\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n, stk = len(heights), []\n ans = [0] * n\n for i, h in enumerate(reversed(heights)):\n while stk and h > stk[-1]:\n stk.pop()\n ans[i] += 1\n if stk:\n ans[i] += 1\n stk.append(h)\n return ans[:: -1]\n```\n\n----\n\n**Method 2: normal traversal - save indices into stack**\n\n```java\n public int[] canSeePersonsCount(int[] heights) {\n int n = heights.length;\n int[] ans = new int[n];\n Deque<Integer> stk = new ArrayDeque<>();\n for (int i = 0; i < n; ++i) {\n while (!stk.isEmpty() && heights[stk.peek()] < heights[i]) {\n ++ans[stk.pop()];\n }\n if (!stk.isEmpty()) {\n ++ans[stk.peek()];\n }\n stk.push(i);\n }\n return ans;\n }\n```\n```python\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n = len(heights)\n ans, stk = [0] * n, []\n for i, h in enumerate(heights):\n while stk and heights[stk[-1]] < h:\n ans[stk.pop()] += 1\n if stk:\n ans[stk[-1]] += 1\n stk.append(i)\n return ans\n```\n\n----\n**Comparison of the 2 methods:**\n\nI myself prefer method 1, because the stack stores the value of `heights` instead of indices of the `heights`, which is more intuitive than the way in method 2.\n\n\n----\n\n**Analysis:**\n\nTime & space: `O(n)`, where `n = heights.length`.\n\n----\nSimilar problems (monotonous stack/queue):\n\n[84 Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram)\n[214 Shortest Palindrome](https://leetcode.com/problems/shortest-palindrome)\n[239 Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum)\n[316 Remove Duplicate Letters](https://leetcode.com/problems/remove-duplicate-letters)\n[321 Create Maximum Number](https://leetcode.com/problems/create-maximum-number)\n[402 Remove K Digits](https://leetcode.com/problems/remove-k-digits)\n[456 132 Pattern](https://leetcode.com/problems/132-pattern)\n[496 Next Greater Element I](https://leetcode.com/problems/next-greater-element-i)\n[503. Next Greater Element II](https://leetcode.com/problems/next-greater-element-ii/description/)\n[654 Maximum Binary Tree](https://leetcode.com/problems/maximum-binary-tree)\n[739. Daily Temperatures](https://leetcode.com/problems/daily-temperatures/description/)\n[768 Max Chunks To Make Sorted II](https://leetcode.com/problems/max-chunks-to-make-sorted-ii)\n[862 Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k)\n[889 Construct Binary Tree from Preorder and Postorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal)\n[901 Online Stock Span](https://leetcode.com/problems/online-stock-span)\n[907 Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums)\n[1019. Next Greater Node In Linked List](https://leetcode.com/problems/next-greater-node-in-linked-list/discuss/267163/Java-9-liner-O(n)-using-Stack-and-ArrayList)\n[1475 Final Prices With a Special Discount in a Shop](https://leetcode.com/problems/final-prices-with-a-special-discount-in-a-shop)\n | 50 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
✔ Python3 Solution | O(n) | Stack | number-of-visible-people-in-a-queue | 0 | 1 | `Time Complexity` : `O(n)`\n```\nclass Solution:\n def canSeePersonsCount(self, A):\n n = len(A)\n stack, res = [], [0] * n\n for i in range(n - 1, -1, -1):\n while stack and stack[-1] <= A[i]:\n stack.pop()\n res[i] += 1\n if stack: res[i] += 1\n stack.append(A[i])\n return res\n``` | 1 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
✔ Python3 Solution | O(n) | Stack | number-of-visible-people-in-a-queue | 0 | 1 | `Time Complexity` : `O(n)`\n```\nclass Solution:\n def canSeePersonsCount(self, A):\n n = len(A)\n stack, res = [], [0] * n\n for i in range(n - 1, -1, -1):\n while stack and stack[-1] <= A[i]:\n stack.pop()\n res[i] += 1\n if stack: res[i] += 1\n stack.append(A[i])\n return res\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
[Python3] mono-stack | number-of-visible-people-in-a-queue | 0 | 1 | \n```\nclass Solution:\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n ans = [0]*len(heights)\n stack = [] # mono-stack \n for i in reversed(range(len(heights))): \n while stack and stack[-1] <= heights[i]: \n ans[i] += 1\n stack.pop()\n if stack: ans[i] += 1\n stack.append(heights[i])\n return ans \n``` | 10 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
[Python3] mono-stack | number-of-visible-people-in-a-queue | 0 | 1 | \n```\nclass Solution:\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n ans = [0]*len(heights)\n stack = [] # mono-stack \n for i in reversed(range(len(heights))): \n while stack and stack[-1] <= heights[i]: \n ans[i] += 1\n stack.pop()\n if stack: ans[i] += 1\n stack.append(heights[i])\n return ans \n``` | 10 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
Python3 | O(n) using stack | with comments | number-of-visible-people-in-a-queue | 0 | 1 | # Code\n```\nclass Solution:\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n = len(heights)\n visible_people = [1] * n\n stack=[]\n for i in range(n-1, -1, -1):\n # set the counter to 0\n count = 0\n while stack and heights[stack[-1]] < heights[i]:\n # while the last person in the stack is smaller than the current one\n # pop the last person from the stack and increase the visible count\n stack.pop()\n count += 1\n if stack:\n # if there is someone left in the stack\n # add the count to the current person\'s result\n visible_people[i] += count\n else:\n # if the stack is empty\n # set current person\'s result to count\n visible_people[i] = count\n # add current person to the stack\n stack.append(i)\n return visible_people\n\n``` | 1 | There are `n` people standing in a queue, and they numbered from `0` to `n - 1` in **left to right** order. You are given an array `heights` of **distinct** integers where `heights[i]` represents the height of the `ith` person.
A person can **see** another person to their right in the queue if everybody in between is **shorter** than both of them. More formally, the `ith` person can see the `jth` person if `i < j` and `min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1])`.
Return _an array_ `answer` _of length_ `n` _where_ `answer[i]` _is the **number of people** the_ `ith` _person can **see** to their right in the queue_.
**Example 1:**
**Input:** heights = \[10,6,8,5,11,9\]
**Output:** \[3,1,2,1,1,0\]
**Explanation:**
Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.
**Example 2:**
**Input:** heights = \[5,1,2,3,10\]
**Output:** \[4,1,1,1,0\]
**Constraints:**
* `n == heights.length`
* `1 <= n <= 105`
* `1 <= heights[i] <= 105`
* All the values of `heights` are **unique**. | It's easier to solve this problem on an array of strings so parse the string to an array of words After return the first k words as a sentence |
Python3 | O(n) using stack | with comments | number-of-visible-people-in-a-queue | 0 | 1 | # Code\n```\nclass Solution:\n def canSeePersonsCount(self, heights: List[int]) -> List[int]:\n n = len(heights)\n visible_people = [1] * n\n stack=[]\n for i in range(n-1, -1, -1):\n # set the counter to 0\n count = 0\n while stack and heights[stack[-1]] < heights[i]:\n # while the last person in the stack is smaller than the current one\n # pop the last person from the stack and increase the visible count\n stack.pop()\n count += 1\n if stack:\n # if there is someone left in the stack\n # add the count to the current person\'s result\n visible_people[i] += count\n else:\n # if the stack is empty\n # set current person\'s result to count\n visible_people[i] = count\n # add current person to the stack\n stack.append(i)\n return visible_people\n\n``` | 1 | Given two binary search trees `root1` and `root2`, return _a list containing all the integers from both trees sorted in **ascending** order_.
**Example 1:**
**Input:** root1 = \[2,1,4\], root2 = \[1,0,3\]
**Output:** \[0,1,1,2,3,4\]
**Example 2:**
**Input:** root1 = \[1,null,8\], root2 = \[8,1\]
**Output:** \[1,1,8,8\]
**Constraints:**
* The number of nodes in each tree is in the range `[0, 5000]`.
* `-105 <= Node.val <= 105` | How to solve this problem in quadratic complexity ? For every subarray start at index i, keep finding new maximum values until a value larger than arr[i] is found. Since the limits are high, you need a linear solution. Use a stack to keep the values of the array sorted as you iterate the array from the end to the start. Keep popping from the stack the elements in sorted order until a value larger than arr[i] is found, these are the ones that person i can see. |
Simple python solution for beginners | sum-of-digits-of-string-after-convert | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n res=""\n for i in s:\n n=ord(i)-96\n res+=str(n)\n for i in range(k):\n s=0\n for i in res:\n s+=int(i)\n res=str(s)\n return s\n``` | 1 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
Python Easy Solution || 100% || | sum-of-digits-of-string-after-convert | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n res=[]\n for i in s:\n res.append(str(ord(i)-96))\n s=\'\'.join(res)\n for _ in range(k):\n sm = 0\n for i in s:\n sm+=int(i)\n s=str(sm)\n return int(s)\n``` | 1 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
Simple code beat 90% of python users, Beginner friendly | sum-of-digits-of-string-after-convert | 0 | 1 | # Code\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n num=\'\'\n for i in range(len(s)):\n num+=str(ord(s[i])-ord(\'a\')+1)\n \n for i in range(k):\n count=0\n for j in range(len(num)):\n count+=int(num[j]) \n num=str(count) \n return int(num)\n\n\n \n``` | 1 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
Python Very Easy Solution | sum-of-digits-of-string-after-convert | 0 | 1 | # Code\n```\nclass Solution:\n def digitSum(self, n: int) -> int:\n tot=0\n while(n>0):\n tot+=n%10\n n//=10\n return tot\n \n def getLucky(self, s: str, k: int) -> int:\n num=""\n for i in s:\n num+=str(ord(i)-96)\n num=int(num)\n for i in range(k):\n num=Solution.digitSum(self,num)\n return num\n \n``` | 1 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
sum-of-digits-of-string-after-convert | sum-of-digits-of-string-after-convert | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing dictionary...\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n\n def check(n,k):\n sumi=0\n while(n!=0):\n x=n%10\n sumi+=x\n n=n//10\n k=k-1\n if(k!=0):\n return check(sumi,k)\n else:\n return sumi\n\n d={\'a\':1,\'b\':2,\'c\':3,\'d\':4,\'e\':5,\'f\':6,\'g\':7,\'h\':8,\'i\':9,\'j\':10,\n \'k\':11,\'l\':12,\'m\':13,\'n\':14,\'o\':15,\'p\':16,\'q\':17,\'r\':18,\'s\':19,\n \'t\':20,\'u\':21,\'v\':22,\'w\':23,\'x\':24,\'y\':25,\'z\':26}\n\n s1=\'\'\n for i in s:\n if(i in d):\n s1=s1+str(d[i])\n n=int(s1)\n result=check(n,k)\n return result\n\n \n \n```\n | 1 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
Beats 90 %!!! 35 ms!!!Python solution -_- | sum-of-digits-of-string-after-convert | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n alphabet = {"a" : 1 , "b" : 2 , "c" : 3 , "d" : 4 , "e" : 5 , "f" : 6 , "g" : 7 \\\n , "h" : 8 , "i" : 9 , "j" : 10 , "k" : 11 , "l" : 12 , "m" : 13 , "n" : 14 , "o" : 15 \\\n , "p" : 16 , "q" : 17 , "r" : 18 , "s" : 19 , "t" : 20 , "u" : 21 , "v" : 22 , "w" : 23 \\\n , "x" : 24 , "y" : 25 , "z" : 26}\n answ = ""\n for i in s:\n answ += str(alphabet[i])\n while k != 0:\n answ = sum(int(x) for x in str(answ))\n k -= 1\n return answ\n\n\n``` | 5 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
python3 code | sum-of-digits-of-string-after-convert | 0 | 1 | # Code\n```\nclass Solution:\n def convert(self, s):\n converted = ""\n alphabet = "abcdefghijklmnopqrstuvwxyz"\n for char in s:\n converted += str(alphabet.index(char) + 1)\n return converted\n def getSum(self, converted):\n result = 0\n for char in str(converted):\n result += int(char)\n return str(result)\n def getLucky(self, s: str, k: int) -> int:\n converted = self.convert(s)\n result = converted\n for i in range(k):\n result = self.getSum(result)\n return int(result)\n```\n\n\n | 4 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
[Python3] simulation | sum-of-digits-of-string-after-convert | 0 | 1 | \n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n s = "".join(str(ord(ch) - 96) for ch in s)\n for _ in range(k): \n x = sum(int(ch) for ch in s)\n s = str(x)\n return x \n```\n\n```\nclass Solution:\n def getLucky(self, s: str, k: int) -> int:\n s = "".join(str(ord(ch)-96) for ch in s)\n for _ in range(k): s = str(sum(int(ch) for ch in s))\n return int(s)\n``` | 5 | You are given a string `s` consisting of lowercase English letters, and an integer `k`.
First, **convert** `s` into an integer by replacing each letter with its position in the alphabet (i.e., replace `'a'` with `1`, `'b'` with `2`, ..., `'z'` with `26`). Then, **transform** the integer by replacing it with the **sum of its digits**. Repeat the **transform** operation `k` **times** in total.
For example, if `s = "zbax "` and `k = 2`, then the resulting integer would be `8` by the following operations:
* **Convert**: `"zbax " ➝ "(26)(2)(1)(24) " ➝ "262124 " ➝ 262124`
* **Transform #1**: `262124 ➝ 2 + 6 + 2 + 1 + 2 + 4 ➝ 17`
* **Transform #2**: `17 ➝ 1 + 7 ➝ 8`
Return _the resulting integer after performing the operations described above_.
**Example 1:**
**Input:** s = "iiii ", k = 1
**Output:** 36
**Explanation:** The operations are as follows:
- Convert: "iiii " ➝ "(9)(9)(9)(9) " ➝ "9999 " ➝ 9999
- Transform #1: 9999 ➝ 9 + 9 + 9 + 9 ➝ 36
Thus the resulting integer is 36.
**Example 2:**
**Input:** s = "leetcode ", k = 2
**Output:** 6
**Explanation:** The operations are as follows:
- Convert: "leetcode " ➝ "(12)(5)(5)(20)(3)(15)(4)(5) " ➝ "12552031545 " ➝ 12552031545
- Transform #1: 12552031545 ➝ 1 + 2 + 5 + 5 + 2 + 0 + 3 + 1 + 5 + 4 + 5 ➝ 33
- Transform #2: 33 ➝ 3 + 3 ➝ 6
Thus the resulting integer is 6.
**Example 3:**
**Input:** s = "zbax ", k = 2
**Output:** 8
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= k <= 10`
* `s` consists of lowercase English letters. | Try to find the number of different minutes when action happened for each user. For each user increase the value of the answer array index which matches the UAM for this user. |
[Python3] greedy | largest-number-after-mutating-substring | 0 | 1 | \n```\nclass Solution:\n def maximumNumber(self, num: str, change: List[int]) -> str:\n num = list(num)\n on = False \n for i, ch in enumerate(num): \n x = int(ch)\n if x < change[x]: \n on = True\n num[i] = str(change[x])\n elif x > change[x] and on: break\n return "".join(num)\n``` | 7 | You are given a string `num`, which represents a large integer. You are also given a **0-indexed** integer array `change` of length `10` that maps each digit `0-9` to another digit. More formally, digit `d` maps to digit `change[d]`.
You may **choose** to **mutate a single substring** of `num`. To mutate a substring, replace each digit `num[i]` with the digit it maps to in `change` (i.e. replace `num[i]` with `change[num[i]]`).
Return _a string representing the **largest** possible integer after **mutating** (or choosing not to) a **single substring** of_ `num`.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** num = "132 ", change = \[9,8,5,0,3,6,4,2,6,8\]
**Output:** "832 "
**Explanation:** Replace the substring "1 ":
- 1 maps to change\[1\] = 8.
Thus, "132 " becomes "832 ".
"832 " is the largest number that can be created, so return it.
**Example 2:**
**Input:** num = "021 ", change = \[9,4,3,5,7,2,1,9,0,6\]
**Output:** "934 "
**Explanation:** Replace the substring "021 ":
- 0 maps to change\[0\] = 9.
- 2 maps to change\[2\] = 3.
- 1 maps to change\[1\] = 4.
Thus, "021 " becomes "934 ".
"934 " is the largest number that can be created, so return it.
**Example 3:**
**Input:** num = "5 ", change = \[1,4,7,5,3,2,5,6,9,4\]
**Output:** "5 "
**Explanation:** "5 " is already the largest number that can be created, so return it.
**Constraints:**
* `1 <= num.length <= 105`
* `num` consists of only digits `0-9`.
* `change.length == 10`
* `0 <= change[d] <= 9` | Go through each element and test the optimal replacements. There are only 2 possible replacements for each element (higher and lower) that are optimal. |
python3 solution | largest-number-after-mutating-substring | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumNumber(self, num: str, change: List[int]) -> str:\n c = {}\n for i, e in enumerate(change):\n c[i] = e\n res = ""\n use = False\n for j in num:\n k = int(j)\n if not use:\n if k < c[int(j)]:\n use = True\n res += str(c[int(j)])\n else:\n res += j\n elif use and k > c[int(j)]:\n break\n else:\n res += str(c[int(j)])\n res += num[len(res):]\n return res\n\n\n\n``` | 0 | You are given a string `num`, which represents a large integer. You are also given a **0-indexed** integer array `change` of length `10` that maps each digit `0-9` to another digit. More formally, digit `d` maps to digit `change[d]`.
You may **choose** to **mutate a single substring** of `num`. To mutate a substring, replace each digit `num[i]` with the digit it maps to in `change` (i.e. replace `num[i]` with `change[num[i]]`).
Return _a string representing the **largest** possible integer after **mutating** (or choosing not to) a **single substring** of_ `num`.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** num = "132 ", change = \[9,8,5,0,3,6,4,2,6,8\]
**Output:** "832 "
**Explanation:** Replace the substring "1 ":
- 1 maps to change\[1\] = 8.
Thus, "132 " becomes "832 ".
"832 " is the largest number that can be created, so return it.
**Example 2:**
**Input:** num = "021 ", change = \[9,4,3,5,7,2,1,9,0,6\]
**Output:** "934 "
**Explanation:** Replace the substring "021 ":
- 0 maps to change\[0\] = 9.
- 2 maps to change\[2\] = 3.
- 1 maps to change\[1\] = 4.
Thus, "021 " becomes "934 ".
"934 " is the largest number that can be created, so return it.
**Example 3:**
**Input:** num = "5 ", change = \[1,4,7,5,3,2,5,6,9,4\]
**Output:** "5 "
**Explanation:** "5 " is already the largest number that can be created, so return it.
**Constraints:**
* `1 <= num.length <= 105`
* `num` consists of only digits `0-9`.
* `change.length == 10`
* `0 <= change[d] <= 9` | Go through each element and test the optimal replacements. There are only 2 possible replacements for each element (higher and lower) that are optimal. |
largest-number-after-mutating-substring | largest-number-after-mutating-substring | 0 | 1 | # Code\n```\nclass Solution:\n def maximumNumber(self, num: str, change: List[int]) -> str:\n s = ""\n count = 0\n count1 = 0\n for i in num:\n if int(i) <= change[int(i)] and count == 0:\n s+= str(change[int(i)])\n count1+=1 \n else:\n s+= i\n if count1!=0:\n count+=1\n p = ""\n count = 0\n count1 = 0\n for i in num:\n if int(i) < change[int(i)] and count == 0:\n p+= str(change[int(i)])\n count1+=1 \n else:\n p+= i\n if count1!=0:\n count+=1\n for i,j in zip(p,s):\n if int(i)> int(j):\n return p\n else:\n return s\n\n``` | 0 | You are given a string `num`, which represents a large integer. You are also given a **0-indexed** integer array `change` of length `10` that maps each digit `0-9` to another digit. More formally, digit `d` maps to digit `change[d]`.
You may **choose** to **mutate a single substring** of `num`. To mutate a substring, replace each digit `num[i]` with the digit it maps to in `change` (i.e. replace `num[i]` with `change[num[i]]`).
Return _a string representing the **largest** possible integer after **mutating** (or choosing not to) a **single substring** of_ `num`.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** num = "132 ", change = \[9,8,5,0,3,6,4,2,6,8\]
**Output:** "832 "
**Explanation:** Replace the substring "1 ":
- 1 maps to change\[1\] = 8.
Thus, "132 " becomes "832 ".
"832 " is the largest number that can be created, so return it.
**Example 2:**
**Input:** num = "021 ", change = \[9,4,3,5,7,2,1,9,0,6\]
**Output:** "934 "
**Explanation:** Replace the substring "021 ":
- 0 maps to change\[0\] = 9.
- 2 maps to change\[2\] = 3.
- 1 maps to change\[1\] = 4.
Thus, "021 " becomes "934 ".
"934 " is the largest number that can be created, so return it.
**Example 3:**
**Input:** num = "5 ", change = \[1,4,7,5,3,2,5,6,9,4\]
**Output:** "5 "
**Explanation:** "5 " is already the largest number that can be created, so return it.
**Constraints:**
* `1 <= num.length <= 105`
* `num` consists of only digits `0-9`.
* `change.length == 10`
* `0 <= change[d] <= 9` | Go through each element and test the optimal replacements. There are only 2 possible replacements for each element (higher and lower) that are optimal. |
Python easy solution | largest-number-after-mutating-substring | 0 | 1 | ```\nclass Solution:\n def maximumNumber(self, num: str, change: List[int]) -> str:\n res = \'\'\n d = {str(idx): val for idx, val in enumerate(change)}\n changed = False\n for idx, digit in enumerate(num):\n if d[digit] > int(digit):\n res += str(d[digit])\n changed = True\n continue\n if changed and d[digit] < int(digit):\n break\n else:\n res += digit\n res += num[len(res):]\n return res\n``` | 0 | You are given a string `num`, which represents a large integer. You are also given a **0-indexed** integer array `change` of length `10` that maps each digit `0-9` to another digit. More formally, digit `d` maps to digit `change[d]`.
You may **choose** to **mutate a single substring** of `num`. To mutate a substring, replace each digit `num[i]` with the digit it maps to in `change` (i.e. replace `num[i]` with `change[num[i]]`).
Return _a string representing the **largest** possible integer after **mutating** (or choosing not to) a **single substring** of_ `num`.
A **substring** is a contiguous sequence of characters within the string.
**Example 1:**
**Input:** num = "132 ", change = \[9,8,5,0,3,6,4,2,6,8\]
**Output:** "832 "
**Explanation:** Replace the substring "1 ":
- 1 maps to change\[1\] = 8.
Thus, "132 " becomes "832 ".
"832 " is the largest number that can be created, so return it.
**Example 2:**
**Input:** num = "021 ", change = \[9,4,3,5,7,2,1,9,0,6\]
**Output:** "934 "
**Explanation:** Replace the substring "021 ":
- 0 maps to change\[0\] = 9.
- 2 maps to change\[2\] = 3.
- 1 maps to change\[1\] = 4.
Thus, "021 " becomes "934 ".
"934 " is the largest number that can be created, so return it.
**Example 3:**
**Input:** num = "5 ", change = \[1,4,7,5,3,2,5,6,9,4\]
**Output:** "5 "
**Explanation:** "5 " is already the largest number that can be created, so return it.
**Constraints:**
* `1 <= num.length <= 105`
* `num` consists of only digits `0-9`.
* `change.length == 10`
* `0 <= change[d] <= 9` | Go through each element and test the optimal replacements. There are only 2 possible replacements for each element (higher and lower) that are optimal. |
[Python3] permutations | maximum-compatibility-score-sum | 0 | 1 | **Approach 1 - brute force**\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(students)\n \n score = [[0]*m for _ in range(m)]\n for i in range(m): \n for j in range(m): \n score[i][j] = sum(x == y for x, y in zip(students[i], mentors[j]))\n \n ans = 0 \n for perm in permutations(range(m)): \n ans = max(ans, sum(score[i][j] for i, j in zip(perm, range(m))))\n return ans \n```\n\nEdited on 7/26/2021\n**Approach 2 - dp**\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n m = len(students)\n \n score = [[0]*m for _ in range(m)]\n for i in range(m): \n for j in range(m): \n score[i][j] = sum(x == y for x, y in zip(students[i], mentors[j]))\n \n @cache \n def fn(mask, j): \n """Return max score of assigning students in mask to first j mentors."""\n ans = 0 \n for i in range(m): \n if not mask & (1<<i): \n ans = max(ans, fn(mask^(1<<i), j-1) + score[i][j])\n return ans \n \n return fn(1<<m, m-1)\n``` | 20 | There is a survey that consists of `n` questions where each question's answer is either `0` (no) or `1` (yes).
The survey was given to `m` students numbered from `0` to `m - 1` and `m` mentors numbered from `0` to `m - 1`. The answers of the students are represented by a 2D integer array `students` where `students[i]` is an integer array that contains the answers of the `ith` student (**0-indexed**). The answers of the mentors are represented by a 2D integer array `mentors` where `mentors[j]` is an integer array that contains the answers of the `jth` mentor (**0-indexed**).
Each student will be assigned to **one** mentor, and each mentor will have **one** student assigned to them. The **compatibility score** of a student-mentor pair is the number of answers that are the same for both the student and the mentor.
* For example, if the student's answers were `[1, 0, 1]` and the mentor's answers were `[0, 0, 1]`, then their compatibility score is 2 because only the second and the third answers are the same.
You are tasked with finding the optimal student-mentor pairings to **maximize** the **sum of the compatibility scores**.
Given `students` and `mentors`, return _the **maximum compatibility score sum** that can be achieved._
**Example 1:**
**Input:** students = \[\[1,1,0\],\[1,0,1\],\[0,0,1\]\], mentors = \[\[1,0,0\],\[0,0,1\],\[1,1,0\]\]
**Output:** 8
**Explanation:** We assign students to mentors in the following way:
- student 0 to mentor 2 with a compatibility score of 3.
- student 1 to mentor 0 with a compatibility score of 2.
- student 2 to mentor 1 with a compatibility score of 3.
The compatibility score sum is 3 + 2 + 3 = 8.
**Example 2:**
**Input:** students = \[\[0,0\],\[0,0\],\[0,0\]\], mentors = \[\[1,1\],\[1,1\],\[1,1\]\]
**Output:** 0
**Explanation:** The compatibility score of any student-mentor pair is 0.
**Constraints:**
* `m == students.length == mentors.length`
* `n == students[i].length == mentors[j].length`
* `1 <= m, n <= 8`
* `students[i][k]` is either `0` or `1`.
* `mentors[j][k]` is either `0` or `1`. | Think of how to check if a number x is a gcd of a subsequence. If there is such subsequence, then all of it will be divisible by x. Moreover, if you divide each number in the subsequence by x , then the gcd of the resulting numbers will be 1. Adding a number to a subsequence cannot increase its gcd. So, if there is a valid subsequence for x , then the subsequence that contains all multiples of x is a valid one too. Iterate on all possiblex from 1 to 10^5, and check if there is a valid subsequence for x. |
[Python3] Intuitive Backtracking solution | maximum-compatibility-score-sum | 0 | 1 | \n# Code\n```python3\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n \n result = 0\n\n def get_score(l1, l2):\n score = 0\n index = len(l1) - 1\n while index >= 0:\n if l1[index] == l2[index]:\n score += 1\n index -= 1\n return score\n\n def dfs(students, mentors, score):\n nonlocal result\n= result = max(result, score)\n \n for i, student in enumerate(students):\n curr_max_score = 0\n cutoff_j = None\n for j, mentor in enumerate(mentors): # we only care about the "best match" between student and mentor in each step\n curr_score = get_score(student, mentor)\n if curr_score >= curr_max_score:\n cutoff_j = j\n curr_max_score = curr_score\n \n dfs(students[:i] + students[i+1:], mentors[:cutoff_j] + mentors[cutoff_j+1:], score + curr_max_score)\n \n dfs(students, mentors, 0)\n return result\n\n\n``` | 0 | There is a survey that consists of `n` questions where each question's answer is either `0` (no) or `1` (yes).
The survey was given to `m` students numbered from `0` to `m - 1` and `m` mentors numbered from `0` to `m - 1`. The answers of the students are represented by a 2D integer array `students` where `students[i]` is an integer array that contains the answers of the `ith` student (**0-indexed**). The answers of the mentors are represented by a 2D integer array `mentors` where `mentors[j]` is an integer array that contains the answers of the `jth` mentor (**0-indexed**).
Each student will be assigned to **one** mentor, and each mentor will have **one** student assigned to them. The **compatibility score** of a student-mentor pair is the number of answers that are the same for both the student and the mentor.
* For example, if the student's answers were `[1, 0, 1]` and the mentor's answers were `[0, 0, 1]`, then their compatibility score is 2 because only the second and the third answers are the same.
You are tasked with finding the optimal student-mentor pairings to **maximize** the **sum of the compatibility scores**.
Given `students` and `mentors`, return _the **maximum compatibility score sum** that can be achieved._
**Example 1:**
**Input:** students = \[\[1,1,0\],\[1,0,1\],\[0,0,1\]\], mentors = \[\[1,0,0\],\[0,0,1\],\[1,1,0\]\]
**Output:** 8
**Explanation:** We assign students to mentors in the following way:
- student 0 to mentor 2 with a compatibility score of 3.
- student 1 to mentor 0 with a compatibility score of 2.
- student 2 to mentor 1 with a compatibility score of 3.
The compatibility score sum is 3 + 2 + 3 = 8.
**Example 2:**
**Input:** students = \[\[0,0\],\[0,0\],\[0,0\]\], mentors = \[\[1,1\],\[1,1\],\[1,1\]\]
**Output:** 0
**Explanation:** The compatibility score of any student-mentor pair is 0.
**Constraints:**
* `m == students.length == mentors.length`
* `n == students[i].length == mentors[j].length`
* `1 <= m, n <= 8`
* `students[i][k]` is either `0` or `1`.
* `mentors[j][k]` is either `0` or `1`. | Think of how to check if a number x is a gcd of a subsequence. If there is such subsequence, then all of it will be divisible by x. Moreover, if you divide each number in the subsequence by x , then the gcd of the resulting numbers will be 1. Adding a number to a subsequence cannot increase its gcd. So, if there is a valid subsequence for x , then the subsequence that contains all multiples of x is a valid one too. Iterate on all possiblex from 1 to 10^5, and check if there is a valid subsequence for x. |
Easy to understand solution written in Python using Backtracking and Memoization with bit masking | maximum-compatibility-score-sum | 0 | 1 | # Intuition\nWhen I first read this problem, my first intuition is to draw out the decision tree to see what the decisions are for each state.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each student, we will try to assign to one mentor if that mentor has not yet been assigned by any other students. To keep track of all assigned mentors, we will use bit mask technique where 0 represents unassigned and 1 represents assigned. Once a pair of student-mentor is chosen, we need to compute their compatibility score by loop through all their answers of questions and count how many they are that have a match. Then we will recursively call the function to repeat the same process for the next student and the remaining unassigned mentors, the subproblem will return the compatibility score of the next state and if we sum it with the current score, we will get the overall score. After trying all possible pair matching, we will take the maximum overall score. \n\n# Code\n```\nclass Solution:\n def maxCompatibilitySum(self, students: List[List[int]], mentors: List[List[int]]) -> int:\n\n n = len(students)\n cache = defaultdict(int)\n mask = 0\n\n def getScore(student,mentor):\n questions = len(student)\n matchScore = 0\n for i in range(questions):\n if student[i] == mentor[i]:\n matchScore += 1\n return matchScore\n\n def dp(i,mask):\n nonlocal n\n # Base Case\n if i >= n:\n return 0\n\n if (i,mask) in cache:\n return cache[(i,mask)]\n\n res = -math.inf\n for j in range(n):\n # Check if current mentor has been assigned with a student yet\n if (mask >> j) & 1 == 1:\n continue\n\n # Mark this mentor assigned\n mask = mask | (1 << j)\n currScore = getScore(students[i],mentors[j])\n nextScore = dp(i+1,mask)\n res = max(res,currScore + nextScore)\n # Backtrack\n mask = mask ^ (1 << j)\n\n cache[(i,mask)] = res\n return res\n\n return dp(0,mask)\n \n\n\n\n \n``` | 0 | There is a survey that consists of `n` questions where each question's answer is either `0` (no) or `1` (yes).
The survey was given to `m` students numbered from `0` to `m - 1` and `m` mentors numbered from `0` to `m - 1`. The answers of the students are represented by a 2D integer array `students` where `students[i]` is an integer array that contains the answers of the `ith` student (**0-indexed**). The answers of the mentors are represented by a 2D integer array `mentors` where `mentors[j]` is an integer array that contains the answers of the `jth` mentor (**0-indexed**).
Each student will be assigned to **one** mentor, and each mentor will have **one** student assigned to them. The **compatibility score** of a student-mentor pair is the number of answers that are the same for both the student and the mentor.
* For example, if the student's answers were `[1, 0, 1]` and the mentor's answers were `[0, 0, 1]`, then their compatibility score is 2 because only the second and the third answers are the same.
You are tasked with finding the optimal student-mentor pairings to **maximize** the **sum of the compatibility scores**.
Given `students` and `mentors`, return _the **maximum compatibility score sum** that can be achieved._
**Example 1:**
**Input:** students = \[\[1,1,0\],\[1,0,1\],\[0,0,1\]\], mentors = \[\[1,0,0\],\[0,0,1\],\[1,1,0\]\]
**Output:** 8
**Explanation:** We assign students to mentors in the following way:
- student 0 to mentor 2 with a compatibility score of 3.
- student 1 to mentor 0 with a compatibility score of 2.
- student 2 to mentor 1 with a compatibility score of 3.
The compatibility score sum is 3 + 2 + 3 = 8.
**Example 2:**
**Input:** students = \[\[0,0\],\[0,0\],\[0,0\]\], mentors = \[\[1,1\],\[1,1\],\[1,1\]\]
**Output:** 0
**Explanation:** The compatibility score of any student-mentor pair is 0.
**Constraints:**
* `m == students.length == mentors.length`
* `n == students[i].length == mentors[j].length`
* `1 <= m, n <= 8`
* `students[i][k]` is either `0` or `1`.
* `mentors[j][k]` is either `0` or `1`. | Think of how to check if a number x is a gcd of a subsequence. If there is such subsequence, then all of it will be divisible by x. Moreover, if you divide each number in the subsequence by x , then the gcd of the resulting numbers will be 1. Adding a number to a subsequence cannot increase its gcd. So, if there is a valid subsequence for x , then the subsequence that contains all multiples of x is a valid one too. Iterate on all possiblex from 1 to 10^5, and check if there is a valid subsequence for x. |
[Python3] serialize sub-trees | delete-duplicate-folders-in-system | 0 | 1 | \n```\nclass Solution:\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\n paths.sort()\n \n tree = {"#": -1}\n for i, path in enumerate(paths): \n node = tree\n for x in path: node = node.setdefault(x, {})\n node["#"] = i\n \n seen = {}\n mark = set()\n \n def fn(n): \n """Return serialized value of sub-tree rooted at n."""\n if len(n) == 1: return "$" # leaf node \n vals = []\n for k in n: \n if k != "#": vals.append(f"${k}${fn(n[k])}")\n hs = "".join(vals)\n if hs in seen: \n mark.add(n["#"])\n mark.add(seen[hs])\n if hs != "$": seen[hs] = n["#"]\n return hs\n \n fn(tree)\n \n ans = []\n stack = [tree]\n while stack: \n n = stack.pop()\n if n["#"] >= 0: ans.append(paths[n["#"]])\n for k in n: \n if k != "#" and n[k]["#"] not in mark: stack.append(n[k])\n return ans \n``` | 4 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
python dfs + trie + hasmap | delete-duplicate-folders-in-system | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\n \n\n trie = {}\n\n def insert(s):\n current = trie\n for i in s:\n current = current.setdefault(i, {"#":False})\n \n \n for p in paths:\n insert(p)\n table = {}\n def dfs(root):\n if len(root) == 1 and "#" in root:\n return [""]\n ans = []\n for k in root:\n if k == "#":\n continue\n path = dfs(root[k])\n for p in path:\n ans.append(k+p)\n\n ans.sort()\n s="-".join(ans)\n if s not in table:\n table[s]=[]\n table[s].append(root)\n return ans\n\n\n path = dfs(trie)\n path.sort()\n table.pop("-".join(path))\n for s in table:\n if len(table[s]) > 1:\n for node in table[s]:\n node["#"] = True\n \n\n ans = []\n def construct(root, p):\n if "#" in root and root["#"] == True:\n return\n if len(root) == 1 and "#" in root:\n ans.append(p)\n return\n if p:\n ans.append(p)\n for k in root:\n if k == "#":\n continue\n construct(root[k], p+[k])\n \n \n\n construct(trie, [])\n return ans\n \n\n\n``` | 0 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Python solution: JSON-style hashing of all subtrees | delete-duplicate-folders-in-system | 0 | 1 | # Intuition\r\n<!-- Describe your first thoughts on how to solve this problem. -->\r\nInitially I tried to build a Trie with the words reversed, but very soon I found it gives wrong answers. And there are interesting testcases which essentially requires serialization of subtrees\r\n# Approach\r\n<!-- Describe your approach to solving the problem. -->\r\nI chose the JSON style serialization because it\'s very commonly used. One must remember to use sorted children keys for hashing though. To handle leaves properly, I used a second dfs while keeping track of which node I already trimmed. \r\n# Code\r\n```\r\nfrom typing import List\r\n\r\n\r\nclass Solution:\r\n \'\'\'\r\n This question is about serializing a node\'s children, and removing nodes with identical children\r\n Looking at the example, we notice the answer always is a subset of paths. So we need to decide which to delete.\r\n To serialize a subtree, we use the JSON convention: for example, subtree of the root in examples can be represented by\r\n 1: [{a:b},{c:b},{d:a}]\r\n 2: [{a:{b:{x:y}}},{c:b},{w:y}]\r\n 3: [{a:b},{c:d}]\r\n We can sort paths by length first\r\n Then for each increment length, recognize the parent of each node, build the graph\r\n Then dfs from the top: for eacb children, serialize the subtree.\r\n Save the serialization as key in dict and delete node with keys that appear more than once.\r\n \'\'\'\r\n \r\n def dfs(self, node):\r\n n = len(self.graph[node])\r\n nodesSorted = sorted(self.graph[node], key = lambda x: self.paths[x][-1])\r\n result = ""\r\n if n > 0: result += ":"\r\n if n > 1: result += "["\r\n for i in range(n):\r\n result += "{"\r\n result += self.dfs(nodesSorted[i])\r\n result += "}"\r\n if i < n - 1: result += ","\r\n if n > 1: result += "]"\r\n\r\n if result: \r\n if result not in self.subtreeIndexMap:\r\n self.subtreeIndexMap[result] = set() \r\n self.subtreeIndexMap[result].add(node)\r\n return self.paths[node][-1] + result\r\n\r\n def dfsThrow(self, node):\r\n self.KeysToThrow.add(node)\r\n for child in self.graph[node]:\r\n if child not in self.KeysToThrow:\r\n self.dfsThrow(child)\r\n\r\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\r\n data = [[len(path), i] for i, path in enumerate(paths)]\r\n data.sort()\r\n self.paths = paths\r\n n = len(data)\r\n self.graph = [[] for i in range(n)]\r\n j = 0\r\n cur = 0\r\n prev = set()\r\n serializedPathToIndex = {}\r\n self.subtreeIndexMap = {}\r\n dfsStartNodes = set()\r\n while j < n:\r\n cur += 1\r\n next = set()\r\n while j < n and data[j][0] == cur:\r\n pathSerialized = ",".join(paths[data[j][1]])\r\n parentSerialized = ",".join(paths[data[j][1]][:-1])\r\n if parentSerialized in prev:\r\n self.graph[serializedPathToIndex[parentSerialized]].append(data[j][1])\r\n serializedPathToIndex[pathSerialized] = data[j][1]\r\n next.add(pathSerialized)\r\n j += 1\r\n if cur == 1:\r\n dfsStartNodes = set([serializedPathToIndex[i] for i in next])\r\n prev = next\r\n \r\n for node in dfsStartNodes:\r\n self.dfs(node)\r\n\r\n self.KeysToThrow = set()\r\n for indices in self.subtreeIndexMap.values():\r\n if len(indices) > 1:\r\n for i in indices:\r\n if i not in self.KeysToThrow:\r\n self.dfsThrow(i)\r\n result = []\r\n for i in range(n):\r\n if i not in self.KeysToThrow:\r\n result.append(paths[i])\r\n return result\r\n``` | 0 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Python Clean sultion( DFS, hashmaps, serialization) with explaination | delete-duplicate-folders-in-system | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis code is devised to address the problem of identifying and removing duplicate folder structures within a given set of folder paths. A folder structure is considered duplicate if there exists another folder structure with the exact same structure and folder names.\n\nThe initial intuition for solving this problem is to use a trie (prefix tree) data structure, which allows us to efficiently represent the folder paths in a hierarchical structure. By traversing this trie, we can serialize the folder structures into strings and identify duplicate structures by looking for identical serialized strings.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach followed in the code can be broken down into several steps:\n\n**1. Building the Trie:**\n\n- A trie data structure is built to represent the folder paths. Each node in the trie contains a dictionary representing its children, a boolean variable indicating if it\'s the end of a path, and another boolean variable to mark if it needs to be deleted (if it\'s part of a duplicated folder structure).\n- The insert function is used to insert a path into the trie. It starts from the root and iterates through the folders in the path, adding new nodes as necessary.\n\n**2. Serialization:**\n\n- The serialize function is used to create a string representation of each folder structure in the trie. This function is a recursive function that starts from the root and generates a string representation for each node by concatenating the folder names and the serialized strings of the child nodes (in lexicographical order).\n- All serialized strings are stored in a dictionary, where the key is the serialized string and the value is a list of nodes that have that serialized structure.\n- The serialization process converts the folder structures in the trie into string representations, which can be used to easily identify duplicates. Here\'s a detailed explanation of this process:\n\n - It starts with an opening bracket ( to denote the start of a new folder structure.\n - It then iterates over the child nodes in lexicographical order (hence the sorted function usage). Sorting ensures that two identical folder structures will have the exact same serialized string, facilitating the identification of duplicates.\n - For each child node, it appends the folder name and the serialized string of the child node to the current serialized string.\n - It ends with a closing bracket ) to denote the end of the current folder structure.\n - If the serialized string is not () (which represents an empty folder), it adds the node to the list of nodes with that serialized structure in the dictionary.\n - Finally, it returns the serialized string for the current node.\n\nSerialization is an essential step in this solution because it allows us to convert the hierarchical folder structures into string representations, which can be easily compared to identify duplicates. By representing each folder structure as a unique string, we can efficiently find duplicate structures by looking for identical serialized strings in the dictionary.\n\nSorting the keys (folder names) during the serialization process ensures that two identical folder structures will have the exact same serialized string. Without sorting, the order of child nodes might vary between two identical structures, resulting in different serialized strings and failing to identify them as duplicates. Sorting guarantees a consistent order of child nodes in the serialized string, facilitating the identification of duplicates.\n\n**3. Marking Duplicates:**\n\n- After serialization, nodes that have more than one occurrence in the dictionary (indicating duplicated structures) are marked for deletion by setting their deleted attribute to True.\n\n**4. Extracting Non-Duplicate Paths:**\n\n- Finally, the dfs (Depth-First Search) function traverses the trie to extract the non-duplicate paths. It starts from the root and recursively visits all nodes that are not marked for deletion, collecting the folder names to construct the paths. Here\'s a breakdown of its operations:\n\n - It first checks whether the current node is marked for deletion (deleted = True). If so, it terminates the traversal for the current path since it\'s part of a duplicated folder structure.\n - If the node is not marked for deletion and the current path is not empty, it adds the current path to the result list.\n - It then recursively visits the child nodes that are not marked for deletion, extending the current path with the folder name of each child node.\n\n**5. Result Compilation:**\n\n- The paths collected by the dfs function are then returned as the result.\n\n# Complexity\n**Time complexity:**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time and space complexity of the given code can be analyzed based on the operations being performed at each step. Here\'s the breakdown:\n\n**1.Inserting Paths into the Trie (Step 1):**\n\nIterating over each path and inserting it into the trie takes O(nm) time, where n is the number of paths and m is the maximum length of a path.\n\n**2.Serialization (Step 2):**\n\nThe serialization process involves a depth-first traversal of the trie, visiting each node once. Additionally, at each node, we sort the keys of the children dictionary, which takes \nO(klogk) time, where k is the number of children. Therefore, the time complexity for the serialization process can be approximated to \nO(nmlogm), where \nn is the number of nodes in the trie and \nm is the maximum branching factor (maximum number of children of a node).\n\n**3.Marking Duplicates (Step 3):**\n\nThis step involves iterating over the serialized strings and, for each string with more than one node, marking those nodes as deleted. This takes O(n) time, where n is the number of nodes in the trie.\n\n**4.Extracting Non-Duplicate Paths (Step 5):**\nThis step involves a depth-first traversal of the trie to extract non-duplicate paths, visiting each node once. This takes O(n) time, where n is the number of nodes in the trie.\n\nCombining these, the total time complexity is approximately O(nmlogm).\n\n**Space complexity:**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n**1. Trie Structure:**\n\nThe trie structure itself takes O(nm) space to store all the nodes, where n is the number of paths and m is the maximum length of a path.\n\n**2. Serialized Dictionary:**\n\nThe serialized dictionary stores serialized strings for each node in the trie. The total length of all serialized strings can be \nO(nm), where n is the number of nodes and m is the maximum branching factor.\n\n**3. Result List:**\n\nThe result list stores the non-duplicate paths, which can take up to O(nm) space in the worst case.\n\nCombining these, the total space complexity is O(nm).\n\nReference Video: https://www.youtube.com/watch?v=5UGb889i21Y\n\n# Code\n```\nclass TrieNode:\n def __init__(self):\n self.children = {} # key is or folder name, sub directories or the TrieNode is the value\n self.is_end = False # check if it is the child node of the tree\n self.deleted = False # True ifthe subtree should be deleted\n\nclass Solution:\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\n \n # Setting Up a Basic trie Structure\n def insert(path):\n node = root\n for folder in path:\n if folder not in node.children:\n node.children[folder] = TrieNode()\n node = node.children[folder]\n node.is_end = True\n \n # Serialize or hash the subfolders to find the duplicate ones\n def serialize(node):\n ans = \'(\'\n for folder, child in sorted(node.children.items()):\n ans += folder + serialize(child)\n ans += \')\'\n if ans != "()": \n serialized[ans].append(node)\n return ans\n\n # Travers the trie and append non-duplicated folders to the result\n def dfs(node, path):\n if node.deleted:\n return\n if path:\n result.append(path)\n for folder, child in node.children.items():\n if not child.deleted:\n dfs(child, path + [folder])\n\n # Step 1: Insert paths into the trie and build the Trie\n root = TrieNode()\n\n for path in paths:\n insert(path)\n \n #step 2: initiliaze the serialization and serilize the nodes\n serialized = defaultdict(list)\n serialize(root)\n # Step 3: Find the duplciated and mark them\n for nodes in serialized.values():\n if len(nodes) > 1:\n for node in nodes:\n node.deleted = True\n\n # Step 5: travers the trie and print the non duplicated sub trees\n result = []\n dfs(root, [])\n\n return result\n\n``` | 0 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Python3 with tree hash | delete-duplicate-folders-in-system | 0 | 1 | ```\nimport collections\nfrom typing import List\nfrom sortedcontainers import SortedDict\n\n\nclass TreeNode:\n def __init__(self, val):\n self.val = val\n self.children = SortedDict()\n\n\nclass Solution:\n def __init__(self):\n self.key2Id = {}\n self.key2Count = collections.defaultdict(int)\n self.node2Key = {}\n self.res = []\n\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\n root = TreeNode(\'/\')\n for path in paths:\n node = root\n for c in path:\n if c not in node.children:\n node.children[c] = TreeNode(c)\n node = node.children[c]\n\n self.get_id(root)\n self.dfs(root, [])\n\n return self.res\n\n def get_id(self, node):\n if not node:\n return 0\n key = \'\'\n for child in node.children.values():\n key += str(self.get_id(child)) + \'#\' + child.val + \'#\'\n\n self.node2Key[node] = key\n self.key2Count[key] += 1\n if self.key2Count[key] == 1:\n self.key2Id[key] = len(self.key2Id) + 1\n\n return self.key2Id[key]\n\n def dfs(self, node, path):\n key = self.node2Key[node]\n if self.key2Count[key] >= 2 and key != \'\':\n return\n if node.val != \'/\':\n path.append(node.val)\n self.res.append(path.copy())\n\n for child in node.children.values():\n self.dfs(child, path.copy())\n\n if node.val != \'/\':\n path.pop()\n\n\nif __name__ == \'__main__\':\n s = Solution()\n # print(s.deleteDuplicateFolder([["a"], ["c"], ["d"], ["a", "b"], ["c", "b"], ["d", "a"]]))\n print(s.deleteDuplicateFolder(\n [["b"], ["f"], ["f", "r"], ["f", "r", "g"], ["f", "r", "g", "c"], ["f", "r", "g", "c", "r"], ["f", "o"],\n ["f", "o", "x"], ["f", "o", "x", "t"], ["f", "o", "x", "d"], ["f", "o", "l"], ["l"], ["l", "q"], ["c"], ["h"],\n ["h", "t"], ["h", "o"], ["h", "o", "d"], ["h", "o", "t"]]\n ))\n``` | 0 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Python3 solution - clean code (trie, dfs and Hashmap) | delete-duplicate-folders-in-system | 0 | 1 | ```\nclass TrieNode:\n def __init__(self, char):\n self.children = {}\n self.is_end = False\n self.child_hash = ""\n self.char = char\n\nclass Trie:\n def __init__(self):\n self.root = TrieNode("/")\n self.hashmap = collections.defaultdict(int)\n self.duplicates = []\n\n def insert(self, folder):\n current_node = self.root\n for char in folder:\n if char not in current_node.children:\n current_node.children[char] = TrieNode(char)\n current_node = current_node.children[char]\n current_node.is_end = True\n\n def _hash_children(self, root):\n for char in sorted(root.children.keys()):\n self._hash_children(root.children[char])\n root.child_hash += char + \'|\' + root.children[char].child_hash + \'|\' \n self.hashmap[root.child_hash] += 1\n \n def hash_children(self):\n current_node = self.root\n self._hash_children(current_node)\n \n def _get_duplicates(self, root, path):\n if root.children and self.hashmap[root.child_hash] > 1: \n return\n self.duplicates.append(path + [root.char])\n for char in root.children:\n self._get_duplicates(root.children[char], path + [root.char])\n\n def get_duplicates(self):\n current_node = self.root\n for char in current_node.children:\n self._get_duplicates(current_node.children[char], [])\n return self.duplicates\n\nclass Solution:\n def deleteDuplicateFolder(self, paths: List[List[str]]) -> List[List[str]]:\n trie = Trie()\n for path in paths:\n trie.insert(path)\n trie.hash_children()\n return trie.get_duplicates()\n``` | 1 | Due to a bug, there are many duplicate folders in a file system. You are given a 2D array `paths`, where `paths[i]` is an array representing an absolute path to the `ith` folder in the file system.
* For example, `[ "one ", "two ", "three "]` represents the path `"/one/two/three "`.
Two folders (not necessarily on the same level) are **identical** if they contain the **same non-empty** set of identical subfolders and underlying subfolder structure. The folders **do not** need to be at the root level to be identical. If two or more folders are **identical**, then **mark** the folders as well as all their subfolders.
* For example, folders `"/a "` and `"/b "` in the file structure below are identical. They (as well as their subfolders) should **all** be marked:
* `/a`
* `/a/x`
* `/a/x/y`
* `/a/z`
* `/b`
* `/b/x`
* `/b/x/y`
* `/b/z`
* However, if the file structure also included the path `"/b/w "`, then the folders `"/a "` and `"/b "` would not be identical. Note that `"/a/x "` and `"/b/x "` would still be considered identical even with the added folder.
Once all the identical folders and their subfolders have been marked, the file system will **delete** all of them. The file system only runs the deletion once, so any folders that become identical after the initial deletion are not deleted.
Return _the 2D array_ `ans` _containing the paths of the **remaining** folders after deleting all the marked folders. The paths may be returned in **any** order_.
**Example 1:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "d "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "d ", "a "\]\]
**Output:** \[\[ "d "\],\[ "d ", "a "\]\]
**Explanation:** The file structure is as shown.
Folders "/a " and "/c " (and their subfolders) are marked for deletion because they both contain an empty
folder named "b ".
**Example 2:**
**Input:** paths = \[\[ "a "\],\[ "c "\],\[ "a ", "b "\],\[ "c ", "b "\],\[ "a ", "b ", "x "\],\[ "a ", "b ", "x ", "y "\],\[ "w "\],\[ "w ", "y "\]\]
**Output:** \[\[ "c "\],\[ "c ", "b "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** The file structure is as shown.
Folders "/a/b/x " and "/w " (and their subfolders) are marked for deletion because they both contain an empty folder named "y ".
Note that folders "/a " and "/c " are identical after the deletion, but they are not deleted because they were not marked beforehand.
**Example 3:**
**Input:** paths = \[\[ "a ", "b "\],\[ "c ", "d "\],\[ "c "\],\[ "a "\]\]
**Output:** \[\[ "c "\],\[ "c ", "d "\],\[ "a "\],\[ "a ", "b "\]\]
**Explanation:** All folders are unique in the file system.
Note that the returned array can be in a different order as the order does not matter.
**Constraints:**
* `1 <= paths.length <= 2 * 104`
* `1 <= paths[i].length <= 500`
* `1 <= paths[i][j].length <= 10`
* `1 <= sum(paths[i][j].length) <= 2 * 105`
* `path[i][j]` consists of lowercase English letters.
* No two paths lead to the same folder.
* For any folder not at the root level, its parent folder will also be in the input. | null |
Beats 62.32% || Three Divisors | three-divisors | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n count=0\n for i in range(1,n+1):\n if n%i==0:\n count+=1\n if count==3:\n return True\n else:return False\n``` | 1 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
Simple Solution Using Loop & Condition | three-divisors | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n new=[]\n for i in range(1,n+1):\n if n%i==0:\n new.append(i)\n return len(new)==3\n```\nHope you like the solution and your comments are welcomed :). | 1 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
[Python3] 1-line | three-divisors | 0 | 1 | \n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n return sum(n%i == 0 for i in range(1, n+1)) == 3\n```\n\nAdding `O(N^1/4)` solution \n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n if n == 1: return False # edge case \n \n x = int(sqrt(n))\n if x*x != n: return False \n \n for i in range(2, int(sqrt(x))+1): \n if x % i == 0: return False \n return True\n``` | 17 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
Python Easy Solution | three-divisors | 0 | 1 | # Code\n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n cnt=2\n for i in range(2,n//2+1):\n if n%i==0:\n cnt+=1\n if cnt>3:\n return 0\n if cnt!=3:\n return 0\n return 1\n``` | 2 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
Explained Python Solution using primes, O(1) | Faster than 99% | three-divisors | 0 | 1 | # Explained Python Solution using primes, O(1) | Faster than 99%\n\n**Runtime: 24 ms, faster than 99% of Python3 online submissions for Three Divisors.\nMemory Usage: 14.2 MB, less than 74% of Python3 online submissions for Three Divisors.**\n\n**Original Program**\n```\nimport math\nclass Solution:\n def isThree(self, n: int) -> bool:\n primes = {3:1, 5:1, 7:1, 11:1, 13:1, 17:1, 19:1, 23:1, 29:1, 31:1, 37:1, 41:1, 43:1, 47:1, 53:1, 59:1, 61:1, 67:1, 71:1, 73:1, 79:1, 83:1, 89:1, 97:1}\n if n == 4:\n return True\n else:\n a = math.sqrt(n)\n\n if primes.get(a,0):\n return True\n else:\n return False\n```\n\n## Explanation:\nEvery number `n` has **atleast** two divisors/factors, that are `1` and `n` (the number itself).\n\nA Prime number `n` is a number which has **eactly** two factors, `1` and `n` (the number itself).\n\nTherefore, a number `a` (`n*n`) which is a **square of a prime number** `n` will have three factors, `1` and `n` and `a` (`n*n`).\n\nThe above program uses this logic and checks if the square root of `n` (which is `a`) is in the dictionary or not.\n\n_______________________________________________\n\n**Updated Program for the same Approach**\nAs suggested by @NiklasPrograms in the comments.\n\n**Runtime: 42 ms, faster than 70.97% of Python3 online submissions for Three Divisors.\nMemory Usage: 13.8 MB, less than 55.18% of Python3 online submissions for Three Divisors.**\n\n```\nclass Solution:\n def isThree(self, n: int) -> bool:\n primes = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};\n \n return sqrt(n) in primes\n``` | 7 | Given an integer `n`, return `true` _if_ `n` _has **exactly three positive divisors**. Otherwise, return_ `false`.
An integer `m` is a **divisor** of `n` if there exists an integer `k` such that `n = k * m`.
**Example 1:**
**Input:** n = 2
**Output:** false
**Explantion:** 2 has only two divisors: 1 and 2.
**Example 2:**
**Input:** n = 4
**Output:** true
**Explantion:** 4 has three divisors: 1, 2, and 4.
**Constraints:**
* `1 <= n <= 104` | At a given point, there are only 3 possible states for where the frog can be. Check all the ways to move from one point to the next and update the minimum side jumps for each lane. |
[Python] Solution with detailed explanation & proof & common failure analysis | maximum-number-of-weeks-for-which-you-can-work | 0 | 1 | \n## Solution 1\nThanks [@pgthebigshot](https://leetcode.com/pgthebigshot/) for providing another solution for easier understanding. \nI make some images to explain the idea.\n\n### Idea\nWe can separate projects to two sets.\n1. The project with the most milestones\n2. The rest of the projects.\n\nIf `sum(milestones except the max)) = sum(milestones) - max(milestones)` < `max(milestones)`, we can only finish `2 * (sum(milestones) - max(milestones)) + 1` milestones.\n\n\nElse, we can finish all milestones.\n\n\nThere is a edge case that if more than one project contains the same and the most milestones like [5, 5, 3], but we still be able to finish all of them.\n\n\n\n## Solution 2\n### Idea\nIf there are at least two projects with same number of milestones and there isn\'t a project with more milestones than that two, we can finish all milestones.\nIf not, we can only finish `2 * (sum(milestones) - max(milestones)) + 1` at most.\n\n### Example\nLet\'s say we have milestones like [5, 5, 3, 2].\nWe can take turn working on those projects with the most milestones.\nSo, [5, 5] will become [4, 4], then become [3, 3].\nBecause we have another project with 3 milestones, so we can take turn working on [3, 3, 3].\n[3, 3, 3] after three rounds, will become [2, 2, 2].\n[2, 2, 2, 2] -> [1, 1, 1, 1] -> [0, 0, 0, 0] -> all the milestones are finished\n\n### What to do if no two projects with same number of milestones?\nWe can seperate projects to two parts: (1)project with most milestones (2)the rest of projects\nThe `greedy strategy` here is trying to use the milestones from (2) to form a new project with the same number of milestones as (1)\nIf possible, we can finish all milestones as we demonstrate.\nIf impossible, we can only start to work on the max (1)- > work on others (2) -> work on the max (1) -> etc\n\n### Why the greedy strategy works?\nLet\'s consider the case if n >= 3. (because if n == 1 -> only can finish 1, if n == 2, we can only take turn working on it and `_sum - _max` must < `_max` )\nLet\'s say we have:\n1. A max project with the most milestones: `p milestones`\n2. A project with the second most milestones: `q milestones`\n3. Rest of projects with `r milestones` in total\n\nif `q + r >= p` ( note: `q + r` is the sum of milestones except the max project)\nWe can do `p-q` rounds, each round, we work on the max project first and the any one of the rest projects.\nAfter one round, the milestones will be `p-1`, `q`, `r-1` respectively.\nSo after `p-q` rounds, the milestones will be `p-(p-q) = q`, `q`, `r-(p-q)` respectively.\nBecause the assumption of `q + r >= p`, `r-(p-q) ` will be larger or equal to 0, it\'s valid operations. \nThen we have two projects with `q` milestones each and it means we can finish all the tasks (can refer to `Example` section)\n\n## Code\n\n```python\nclass Solution:\n def numberOfWeeks(self, milestones: List[int]) -> int:\n _sum, _max = sum(milestones), max(milestones)\n\t\t# (_sum - _max) is the sum of milestones from (2) the rest of projects, if True, we can form another project with the same amount of milestones as (1)\n\t\t# can refer to the section `Why the greedy strategy works?` for the proof\n if _sum - _max >= _max: \n return _sum\n return 2 * (_sum - _max) + 1 # start from the project with most milestones (_sum - _max + 1) and work on the the rest of milestones (_sum - _max)\n```\n\n## Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n## Bonus\nI noticed many people are trying to use priority queue to solve this problem, but there are two possible failed reasons.\n\n1. Incorrect strategy\nIf you try to work on the top milestones and until one is all finished. Can consider the test case [100, 100, 100]. (Answer should be 300, but many will get 201 if using the wrong strategy)\n\n2. TLE\nIf you always pick the top two milestones and reduce 1 milestones from each and put them back. Due to 1 <= n <= 10^5, 1 <= milestones[i] <= 10^9. In the worse case, you will need O(10^5 * 10^9 * log(10^5)))\n\nNote: Please upvote if it\'s helpful or leave comments if I can do better. Thank you in advance.\n\n | 243 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
O(n) | maximum-number-of-weeks-for-which-you-can-work | 1 | 1 | I got a working solution using a max heap, then tried to optimized it to push through TLE. No luck. \n\nThis prolem seems to requrie prior knowledge or a very good intuition:\n\n> We can complete all milestones for all projects, unless one project has more milestones then all other projects combined.\n> \n> For the latter case: \n\t>> We can complete all milestones for other projects, \n\t>> plus same number of milestones for the largest project, \n\t>> plus one more milestone for the largest project.\n>\n> After that point, we will not be able to alternate projects anymore.\n\n**C++**\n```cpp\nlong long numberOfWeeks(vector<int>& m) {\n long long sum = accumulate(begin(m), end(m), 0ll), max = *max_element(begin(m), end(m));\n return min(sum, 2 * (sum - max) + 1);\n}\n```\n**Java**\n```java\npublic long numberOfWeeks(int[] m) {\n long sum = IntStream.of(m).asLongStream().sum(), max = IntStream.of(m).max().getAsInt();\n return Math.min(sum, 2 * (sum - max) + 1);\n}\n```\n**Python 3**\n```python\nclass Solution:\n def numberOfWeeks(self, m: List[int]) -> int:\n return min(sum(m), 2 * (sum(m) - max(m)) + 1)\n``` | 50 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
[Java/Python 3] 3/2 line greedy O(n) code w/ brief explanation. | maximum-number-of-weeks-for-which-you-can-work | 1 | 1 | **Intuition:**\nAccording to the rule "cannot work on two milestones from the same project for two consecutive weeks.", we at least need to avoid the consecutive working on the project with the maximum milestones, which are most likely to be involved to violate the rule.\n\n----\n\n1. If the `max` of the `milestones` is no more than the the remaining sum by `1`, `sum(milestones) - max + 1`, we can always use the remaining parts to divide the project with max milestones, hence the answer is `sum(milestones)`; e.g., \n\n`milestones = [1,2,4]`, that is, projects `p0, p1, p2` have `1,2,` and `4` milestones repectively. \n\nWe can separate the `4` milestones using the remaining `1 + 2 = 3` ones: `p2, p0, p2, p1, p2, p1, p2`;\n\n2. Otherwise, get the `remaining part + 1` out of the `max`, together with the remaing part, is the solution: `2 * (sum(milestones) - max) + 1`. e.g., \n\n`milestones = [1,5,2]`, that is, projects `p0, p1, p2` have `1,5,` and `2` milestones repectively. \n\nWe can use the `1 + 2 = 3` milestones from `p0` and `p2` to separate only `3 + 1 = 4` milestones out of the `5` ones from `p1`: `p1, p0, p1, p2, p1, p2, p1`.\n\n```java\n public long numberOfWeeks(int[] milestones) {\n int max = IntStream.of(milestones).max().getAsInt();\n long sum = IntStream.of(milestones).mapToLong(i -> i).sum(), rest = sum - max;\n return max <= rest + 1 ? sum : 2 * rest + 1;\n }\n```\n```python\n def numberOfWeeks(self, milestones: List[int]) -> int:\n mx, sm = max(milestones), sum(milestones)\n return sm if 2 * mx <= sm + 1 else 2 * (sm - mx) + 1\n``` | 9 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Very easy python solution | maximum-number-of-weeks-for-which-you-can-work | 0 | 1 | ```\n def numberOfWeeks(self, milestones: List[int]) -> int:\n \n n=len(milestones)\n if n==1:\n return 1\n s=sum(milestones)\n \n if max(milestones)>s-max(milestones)+1:\n return 2*(s-max(milestones))+1\n return s | 2 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python with details. | maximum-number-of-weeks-for-which-you-can-work | 0 | 1 | Initially I also tried the approach with decrementing the every project with maxiumum number of milestones.\n\nIt works but the complexity is awfull.\n\n\n# Approach\n\nThen used approach with simple logic.\nIf the maximum number of milstones is less or equal than sum of milestones - maximum S - M >= M then all milestones could be completed. That\'s quite abvious.\nIf not then number of weeks will 2 * (S - M) + 1.\nAnd a lot of people provides exactly this formula but nobody explain why it is. The answer is in the second rule of the task - You cannot work on two milestones from the same project for two consecutive weeks.\nIt means that you will be able to work on the project with maximum number of only once per two weeks and other week use for anotehr projects. So, number of completed milestones will be S - M and multiple 2 because every 2 weeks. And plus one because we can start or finish with project with maximum milestones.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def numberOfWeeks(self, milestones: List[int]) -> int:\n s = sum(milestones)\n m = max(milestones)\n if s - m >= m: return s\n return 2 * (s - m) + 1\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python || Sort | maximum-number-of-weeks-for-which-you-can-work | 0 | 1 | # Intuition\n- If you can find the pairs for the max element in the array you are done, because you can insert any number of elements in between the pairs.\n\n# Approach\n- Sort the array\n- Get the max of the array, try and get the pairs for the maximum element\n- Once done return sum(milestones)\n- If we are not able to find it that means sum(other elements) other than the max is lesser than the maxx which means we will not be able to work all the weeks, so we return the 2*summ+1, because we can fill the rest of elements paired up with maxx and there will some element left out\n\n# Complexity\n- Time complexity:\n- O(NlogN)\n\n- Space complexity:\n- O(1)\n\n# Code\n```\nclass Solution:\n def numberOfWeeks(self, milestones: List[int]) -> int:\n milestones.sort()\n def solve():\n maxx = milestones[-1]\n summ = 0\n for i in range(len(milestones)-2,-1,-1):\n summ+=milestones[i]\n if summ >= maxx:\n return sum(milestones)\n return 2*summ+1\n return solve()\n # return 2\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
Python: Math problem | maximum-number-of-weeks-for-which-you-can-work | 0 | 1 | # Intuition\nthis is a hell problem, i figure it by using math finally\n\n# Approach\n1. we know that the max of the work can not more than -> (sum of array - max num in the arry) multiple by 2 plus 1 -> (sum(array) - max_num) * 2 + 1\n\n2. then we need to find the amount to deduct from total, as the max deduct amt should no more than to sum of array[1:]+1, hence deduct amt is sum of arry - max_num - max_num + 1\n\n3. and return the max work - deduct \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def numberOfWeeks(self, milestones: List[int]) -> int:\n #base case\n if len(milestones) == 1:\n return min(milestones[0],1)\n max_num = 0\n total = 0\n for n in milestones:\n total += n\n max_num = max(max_num, n)\n\n total -= max_num\n max_val = total * 2 +1\n deduct = max(0, total - max_num +1)\n return max_val - deduct\n``` | 0 | There are `n` projects numbered from `0` to `n - 1`. You are given an integer array `milestones` where each `milestones[i]` denotes the number of milestones the `ith` project has.
You can work on the projects following these two rules:
* Every week, you will finish **exactly one** milestone of **one** project. You **must** work every week.
* You **cannot** work on two milestones from the same project for two **consecutive** weeks.
Once all the milestones of all the projects are finished, or if the only milestones that you can work on will cause you to violate the above rules, you will **stop working**. Note that you may not be able to finish every project's milestones due to these constraints.
Return _the **maximum** number of weeks you would be able to work on the projects without violating the rules mentioned above_.
**Example 1:**
**Input:** milestones = \[1,2,3\]
**Output:** 6
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 2.
- During the 3rd week, you will work on a milestone of project 1.
- During the 4th week, you will work on a milestone of project 2.
- During the 5th week, you will work on a milestone of project 1.
- During the 6th week, you will work on a milestone of project 2.
The total number of weeks is 6.
**Example 2:**
**Input:** milestones = \[5,2,1\]
**Output:** 7
**Explanation:** One possible scenario is:
- During the 1st week, you will work on a milestone of project 0.
- During the 2nd week, you will work on a milestone of project 1.
- During the 3rd week, you will work on a milestone of project 0.
- During the 4th week, you will work on a milestone of project 1.
- During the 5th week, you will work on a milestone of project 0.
- During the 6th week, you will work on a milestone of project 2.
- During the 7th week, you will work on a milestone of project 0.
The total number of weeks is 7.
Note that you cannot work on the last milestone of project 0 on 8th week because it would violate the rules.
Thus, one milestone in project 0 will remain unfinished.
**Constraints:**
* `n == milestones.length`
* `1 <= n <= 105`
* `1 <= milestones[i] <= 109` | At each query, try to save and update the sum of the elements needed to calculate MKAverage. You can use BSTs for fast insertion and deletion of the elements. |
[Java/Python 3] From O(n ^ (1 / 3)) to O(log(n)), easy codes w/ brief explanation & analysis. | minimum-garden-perimeter-to-collect-enough-apples | 1 | 1 | **Method 1:**\n\nDivide into 3 parts: axis, corner and other:\n\nUse `i`, `corner` and `other` to denote the number of apples on each half axis, each corner and other parts, respectively.\n\nObviously, for any given `i`, each half axis has `i` apples; each of the 4 corners has `2 * i` apples, and the rest part (quadrant) has two times of `(i + 1) + (i + 2) + (i + 3) + ... + (2 * i - 1)` apples, which sums to `((i + 1) + (2 * i - 1)) * ((2 * i - 1) - (i + 1) + 1) / 2 * 2 = 3 * i * (i - 1)`.\n\nSee the below for reference.\n\n----\ni, i + 1, i + 2, ..., 2 * i\n.............................\n.............................\n..........................i + 2\n..........................i + 1\n.............................i\n```java\n public long minimumPerimeter(long neededApples) {\n long perimeter = 0;\n for (long i = 1, apples = 0; apples < neededApples; ++i) {\n long corner = 2 * i, other = 3 * i * (i - 1);\n apples += 4 * (i + corner + other);\n perimeter = 8 * i;\n }\n return perimeter;\n }\n```\n```python\n def minimumPerimeter(self, neededApples: int) -> int:\n apples = i = 0\n while apples < neededApples:\n i += 1\n corner, other = 2 * i, 3 * i * (i - 1)\n apples += 4 * (corner + i + other)\n return 8 * i\n```\n\nSince `4 * (i + corner + other) = 4 * (i + 2 * i + 3 * i * (i - 1)) = 4 * (3 * i * i) = 12 * i * i`, the above codes can be simplified as follows: \n```java\n public long minimumPerimeter(long neededApples) {\n long i = 0;\n while (neededApples > 0) {\n neededApples -= 12 * ++i * i;\n }\n return 8 * i;\n }\n```\n```python\n def minimumPerimeter(self, neededApples: int) -> int:\n i = 0\n while neededApples > 0:\n i += 1\n neededApples -= 12 * i * i\n return 8 * i\n```\n\n\n**Analysis:**\n\nTime: `O(n ^ (1 / 3))`, space: `O(1)`, where `n = neededApples`.\n\n----\n\n**Method 2: Binary Search**\n\n\nThe codes in method 1 actually accumulate `12` times of `i ^ 2`. There is a formula: `sum(1 ^ 2 + 2 ^ 2 + ... + i ^ 2) = i * (i + 1) * (2 * i + 1) / 6`, the `12` times of which is \n\n```\n2 * i * (i + 1) * (2 * i + 1)\n``` \nSince the input is in range `1 - 10 ^ 15`, we can observe that `10 ^ 15 >= 2 * i * (i + 1) * (2 * i + 1) > i ^ 3`. Obviously\n```\ni ^ 3 < 10 ^ 15\n```\nwe have\n```\ni < 10 ^ 5\n```\nTherefore, the range of `i` is `1 ~ 10 ^ 5`, and we can use binary search to dicide the `i`.\n\n```java\n public long minimumPerimeter(long neededApples) {\n long lo = 1, hi = 100_000;\n while (lo < hi) {\n long mid = lo + hi >> 1;\n if (2 * mid * (mid + 1) * (2 * mid + 1) < neededApples) {\n lo = mid + 1;\n }else {\n hi = mid;\n }\n }\n return 8 * hi;\n }\n```\n```python\n\n```\n**Analysis:**\n\nTime complexity : `O(log(n ^ (1 / 3))) = O((1 / 3) * log(n)) = O(log(n))`, Therefore\n\nTime: `O(log(n)), space: `O(1)`, where `n = neededApples`.\n\n | 10 | In a garden represented as an infinite 2D grid, there is an apple tree planted at **every** integer coordinate. The apple tree planted at an integer coordinate `(i, j)` has `|i| + |j|` apples growing on it.
You will buy an axis-aligned **square plot** of land that is centered at `(0, 0)`.
Given an integer `neededApples`, return _the **minimum perimeter** of a plot such that **at least**_ `neededApples` _apples are **inside or on** the perimeter of that plot_.
The value of `|x|` is defined as:
* `x` if `x >= 0`
* `-x` if `x < 0`
**Example 1:**
**Input:** neededApples = 1
**Output:** 8
**Explanation:** A square plot of side length 1 does not contain any apples.
However, a square plot of side length 2 has 12 apples inside (as depicted in the image above).
The perimeter is 2 \* 4 = 8.
**Example 2:**
**Input:** neededApples = 13
**Output:** 16
**Example 3:**
**Input:** neededApples = 1000000000
**Output:** 5040
**Constraints:**
* `1 <= neededApples <= 1015` | We just need to replace every even positioned character with the character s[i] positions ahead of the character preceding it Get the position of the preceeding character in alphabet then advance it s[i] positions and get the character at that position |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.