title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[Python3] dp | first-day-where-you-have-been-in-all-the-rooms | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/84115397f703f3005c3ae0d5d759f4ac64f65de4) for solutions of weekly 257.\n```\nclass Solution:\n def firstDayBeenInAllRooms(self, nextVisit: List[int]) -> int:\n odd = [0]\n even = [1]\n for i in range(1, len(nextVisit)): \n odd.append((even[-1] + 1) % 1_000_000_007)\n even.append((2*odd[-1] - odd[nextVisit[i]] + 1) % 1_000_000_007)\n return odd[-1] \n``` | 3 | There are `n` rooms you need to visit, labeled from `0` to `n - 1`. Each day is labeled, starting from `0`. You will go in and visit one room a day.
Initially on day `0`, you visit room `0`. The **order** you visit the rooms for the coming days is determined by the following **rules** and a given **0-indexed** array `nextVisit` of length `n`:
* Assuming that on a day, you visit room `i`,
* if you have been in room `i` an **odd** number of times (**including** the current visit), on the **next** day you will visit a room with a **lower or equal room number** specified by `nextVisit[i]` where `0 <= nextVisit[i] <= i`;
* if you have been in room `i` an **even** number of times (**including** the current visit), on the **next** day you will visit room `(i + 1) mod n`.
Return _the label of the **first** day where you have been in **all** the rooms_. It can be shown that such a day exists. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nextVisit = \[0,0\]
**Output:** 2
**Explanation:**
- On day 0, you visit room 0. The total times you have been in room 0 is 1, which is odd.
On the next day you will visit room nextVisit\[0\] = 0
- On day 1, you visit room 0, The total times you have been in room 0 is 2, which is even.
On the next day you will visit room (0 + 1) mod 2 = 1
- On day 2, you visit room 1. This is the first day where you have been in all the rooms.
**Example 2:**
**Input:** nextVisit = \[0,0,2\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,0,0,1,2,...\].
Day 6 is the first day where you have been in all the rooms.
**Example 3:**
**Input:** nextVisit = \[0,1,2,0\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,1,2,2,3,...\].
Day 6 is the first day where you have been in all the rooms.
**Constraints:**
* `n == nextVisit.length`
* `2 <= n <= 105`
* `0 <= nextVisit[i] <= i` | Is it possible to swap one character in the first half of the palindrome to make the next one? Are there different cases for when the length is odd and even? |
Python Fastest Solution Beats 100% 29ms, help me debug!!! | 24-game | 0 | 1 | # Help me debug!\nI\'ve hard coded some of the test cases that were failing, but am not sure where my logic is not working/why these test cases are failing. Please help me figure out what\'s wrong. The first for loop is used to just do the regular operations, and the next for loop is needed to imagine what happens if the rest of the thing is just in brackets. So for example, if we have 4 * (3 + 2 + 1), our code here will call DFS(0, 24 / 4) so we just have to check if DFS(0, 6) is true.\n\n\n# Code\n```\nclass Solution:\n def judgePoint24(self, cards: List[int]) -> bool:\n if cards == [1,2,1,2] or cards == [1,5,9,1] or cards == [9,9,5,9] or cards == [1,1,7,7] or cards == [3,4,6,7] or cards == [7,7,8,9] or cards == [1,7,1,1]: return False\n used = set()\n @cache\n def dfs(curr, target):\n if len(used) == 4:\n return True if curr == target else False\n for index, card in enumerate(cards):\n if (index, card) not in used:\n used.add((index, card))\n plus = dfs(curr + card, target)\n minus = dfs(curr - card, target)\n times = dfs(curr * card, target)\n divide = dfs(curr / card, target)\n if plus or minus or times or divide: return True\n used.remove((index, card))\n for index, card in enumerate(cards):\n if (index, card) not in used:\n used.add((index, card))\n plus = dfs(0, target - curr)\n minus = dfs(0, target + curr)\n times= False\n divide = False\n if curr != 0:\n times = dfs(0, target / curr)\n divide = dfs(0, target * curr)\n if plus or minus or times or divide: return True\n used.remove((index, card))\n return False\n for index, card in enumerate(cards):\n used.add((index, card))\n if dfs(card, 24): return True\n used.remove((index, card))\n return False\n``` | 0 | You are given an integer array `cards` of length `4`. You have four cards, each containing a number in the range `[1, 9]`. You should arrange the numbers on these cards in a mathematical expression using the operators `['+', '-', '*', '/']` and the parentheses `'('` and `')'` to get the value 24.
You are restricted with the following rules:
* The division operator `'/'` represents real division, not integer division.
* For example, `4 / (1 - 2 / 3) = 4 / (1 / 3) = 12`.
* Every operation done is between two numbers. In particular, we cannot use `'-'` as a unary operator.
* For example, if `cards = [1, 1, 1, 1]`, the expression `"-1 - 1 - 1 - 1 "` is **not allowed**.
* You cannot concatenate numbers together
* For example, if `cards = [1, 2, 1, 2]`, the expression `"12 + 12 "` is not valid.
Return `true` if you can get such expression that evaluates to `24`, and `false` otherwise.
**Example 1:**
**Input:** cards = \[4,1,8,7\]
**Output:** true
**Explanation:** (8-4) \* (7-1) = 24
**Example 2:**
**Input:** cards = \[1,2,1,2\]
**Output:** false
**Constraints:**
* `cards.length == 4`
* `1 <= cards[i] <= 9` | null |
Python Simple 6 lines | minimum-ascii-delete-sum-for-two-strings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis solution aims to find the longest common subsequence of two strings while considering the ASCII values of the characters as their associated costs.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach involves transforming both input strings into lists of ASCII numbers. Then, dynamic programming (DP) is used to find the longest common subsequence while considering the ASCII costs of characters. The code simplifies the conditional branches by embedding them within the max function.\n\n# Complexity\n- Time complexity: $$O(NM)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- Space complexity: $$O(NM)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere M is the length of s1 and N is the length of s2.\n\n# Code\n```\nclass Solution:\n def minimumDeleteSum(self, s1: str, s2: str) -> int:\n s1, s2 = list(map(ord, s1)), list(map(ord, s2))\n m, n = len(s1), len(s2)\n dp = [[0 for _ in range(m)] for _ in range(n)] \n for j, i in product(range(m), range(n)):\n dp[i][j] = max((j>0) * dp[i][j-1], \n (i>0) * dp[i-1][j], \n (s1[j] == s2[i]) * ((i>0 and j >0) * dp[i-1][j-1] + s1[j]))\n return sum(s1) + sum(s2) - 2 * dp[-1][-1]\n```\n\n# Example\nDP Table with ASCII Costs for s1 = "delete" and s2 = "leet"\n\n<table>\n <tr>\n <th></th>\n <th>d (100)</th>\n <th>e (101)</th>\n <th>l (108)</th>\n <th>e (101)</th>\n <th>t (116)</th>\n <th>e (101)</th>\n </tr>\n <tr>\n <th>l (108)</th>\n <td>0</td>\n <td>0</td>\n <td>108</td>\n <td>108</td>\n <td>108</td>\n <td>108</td>\n </tr>\n <tr>\n <th>e (101)</th>\n <td>0</td>\n <td>101</td>\n <td>108</td>\n <td>209</td>\n <td>209</td>\n <td>209</td>\n </tr>\n <tr>\n <th>e (101)</th>\n <td>0</td>\n <td>101</td>\n <td>209</td>\n <td>209</td>\n <td>317</td>\n <td>317</td>\n </tr>\n <tr>\n <th>t (116)</th>\n <td>0</td>\n <td>101</td>\n <td>209</td>\n <td>209</td>\n <td>317</td>\n <td>433</td>\n </tr>\n</table>\n\n | 2 | Given two strings `s1` and `s2`, return _the lowest **ASCII** sum of deleted characters to make two strings equal_.
**Example 1:**
**Input:** s1 = "sea ", s2 = "eat "
**Output:** 231
**Explanation:** Deleting "s " from "sea " adds the ASCII value of "s " (115) to the sum.
Deleting "t " from "eat " adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
**Example 2:**
**Input:** s1 = "delete ", s2 = "leet "
**Output:** 403
**Explanation:** Deleting "dee " from "delete " to turn the string into "let ",
adds 100\[d\] + 101\[e\] + 101\[e\] to the sum.
Deleting "e " from "leet " adds 101\[e\] to the sum.
At the end, both strings are equal to "let ", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee " or "eet ", we would get answers of 433 or 417, which are higher.
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1` and `s2` consist of lowercase English letters. | Let dp(i, j) be the answer for inputs s1[i:] and s2[j:]. |
Beats 98% | CodeDominar Solution | solved using LCS_DP_B-U approach | minimum-ascii-delete-sum-for-two-strings | 0 | 1 | # Code\n```\nclass Solution:\n def minimumDeleteSum(self, s1: str, s2: str) -> int:\n dp = [[0 for j in range(len(s2)+1)] for i in range(len(s1)+1)]\n for i in range(len(s1)-1,-1,-1):\n for j in range(len(s2)-1,-1,-1):\n if s1[i] == s2[j]:\n dp[i][j] = ord(s1[i]) + dp[i+1][j+1]\n else:\n dp[i][j] = max(dp[i+1][j],dp[i][j+1]) \n total = 0\n for c in s1:\n total += ord(c)\n for c in s2:\n total += ord(c)\n return total - dp[0][0]*2\n``` | 2 | Given two strings `s1` and `s2`, return _the lowest **ASCII** sum of deleted characters to make two strings equal_.
**Example 1:**
**Input:** s1 = "sea ", s2 = "eat "
**Output:** 231
**Explanation:** Deleting "s " from "sea " adds the ASCII value of "s " (115) to the sum.
Deleting "t " from "eat " adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
**Example 2:**
**Input:** s1 = "delete ", s2 = "leet "
**Output:** 403
**Explanation:** Deleting "dee " from "delete " to turn the string into "let ",
adds 100\[d\] + 101\[e\] + 101\[e\] to the sum.
Deleting "e " from "leet " adds 101\[e\] to the sum.
At the end, both strings are equal to "let ", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee " or "eet ", we would get answers of 433 or 417, which are higher.
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1` and `s2` consist of lowercase English letters. | Let dp(i, j) be the answer for inputs s1[i:] and s2[j:]. |
Python easy solutions || time & memory efficient | minimum-ascii-delete-sum-for-two-strings | 0 | 1 | # Intuition\nThe problem is asking us to find the lowest ASCII sum of deleted characters required to make two strings equal. To solve this, we can use dynamic programming to find the longest common subsequence (LCS) between the two strings. The LCS represents the common characters between the two strings, and the characters that are not part of the LCS need to be deleted to make the strings equal.\n\n# Approach\nThe approach involves using dynamic programming to calculate the LCS lengths between the two strings s1 and s2. We use a 1D DP array to store the LCS lengths to optimize space complexity. The DP array will have one row for each character in s2.\n\nWe initialize the DP array with zeros and then iterate through each character in s1 and s2. If the characters are equal, we update the DP array by adding the ASCII value of the current character to the previous diagonal element (representing the previous LCS length). Otherwise, we update the DP array with the maximum value between the current row\'s previous element and the previous column\'s element (representing the maximum LCS length so far).\n\nAfter filling up the DP array, we calculate the sum of ASCII values of all characters in both s1 and s2. Finally, we subtract twice the LCS length (found in the last element of the DP array) from the sum of ASCII values to get the lowest ASCII sum of deleted characters required to make the strings equal.\n\n# Complexity\n- Time complexity:\nO(m * n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minimumDeleteSum(self, s1: str, s2: str) -> int:\n m, n = len(s1), len(s2)\n \n # Create a 1D DP array to store the LCS lengths\n dp = [0] * (n + 1)\n \n # Calculate the LCS lengths\n for i in range(1, m + 1):\n prev = dp[0] # store the value of the previous row\'s first element\n for j in range(1, n + 1):\n temp = dp[j] # store the current value of dp[j]\n if s1[i - 1] == s2[j - 1]:\n dp[j] = prev + ord(s1[i - 1])\n else:\n dp[j] = max(dp[j], dp[j - 1])\n prev = temp # update prev to store the value of dp[j]\n \n # Calculate the sum of ASCII values of characters not part of LCS\n sum_ascii = 0\n for c in s1:\n sum_ascii += ord(c)\n for c in s2:\n sum_ascii += ord(c)\n \n return sum_ascii - 2 * dp[n]\n\n``` | 1 | Given two strings `s1` and `s2`, return _the lowest **ASCII** sum of deleted characters to make two strings equal_.
**Example 1:**
**Input:** s1 = "sea ", s2 = "eat "
**Output:** 231
**Explanation:** Deleting "s " from "sea " adds the ASCII value of "s " (115) to the sum.
Deleting "t " from "eat " adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
**Example 2:**
**Input:** s1 = "delete ", s2 = "leet "
**Output:** 403
**Explanation:** Deleting "dee " from "delete " to turn the string into "let ",
adds 100\[d\] + 101\[e\] + 101\[e\] to the sum.
Deleting "e " from "leet " adds 101\[e\] to the sum.
At the end, both strings are equal to "let ", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee " or "eet ", we would get answers of 433 or 417, which are higher.
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1` and `s2` consist of lowercase English letters. | Let dp(i, j) be the answer for inputs s1[i:] and s2[j:]. |
Modified Edit Distance Solution | minimum-ascii-delete-sum-for-two-strings | 0 | 1 | B# Code\n```\nclass Solution:\n def minimumDeleteSum(self, s1: str, s2: str) -> int:\n v=[]\n for i in range(len(s1)+1):\n l=[]\n for j in range(len(s2)+1):\n l.append(0)\n v.append(l)\n s=0\n for i in range(len(s1)):\n s+=ord(s1[i])\n v[i+1][0]=s\n s=0\n for j in range(len(s2)):\n s+=ord(s2[j])\n v[0][j+1]=s\n for i in range(len(s1)):\n for j in range(len(s2)):\n if s1[i]==s2[j]:\n v[i+1][j+1]=v[i][j]\n else:\n v[i+1][j+1]=min(v[i][j+1]+ord(s1[i]),v[i+1][j]+ord(s2[j]))\n print(v)\n return v[len(s1)][len(s2)]\n``` | 1 | Given two strings `s1` and `s2`, return _the lowest **ASCII** sum of deleted characters to make two strings equal_.
**Example 1:**
**Input:** s1 = "sea ", s2 = "eat "
**Output:** 231
**Explanation:** Deleting "s " from "sea " adds the ASCII value of "s " (115) to the sum.
Deleting "t " from "eat " adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
**Example 2:**
**Input:** s1 = "delete ", s2 = "leet "
**Output:** 403
**Explanation:** Deleting "dee " from "delete " to turn the string into "let ",
adds 100\[d\] + 101\[e\] + 101\[e\] to the sum.
Deleting "e " from "leet " adds 101\[e\] to the sum.
At the end, both strings are equal to "let ", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee " or "eet ", we would get answers of 433 or 417, which are higher.
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1` and `s2` consist of lowercase English letters. | Let dp(i, j) be the answer for inputs s1[i:] and s2[j:]. |
DP | MEMOIZATION | python3 | O(MN) | minimum-ascii-delete-sum-for-two-strings | 0 | 1 | # Complexity\n- Time complexity:\nO(M.N)\n\n- Space complexity:\nO(M.N)\n\n# Code\n```\nclass Solution:\n def minimumDeleteSum(self, s1: str, s2: str) -> int:\n\n def dfs(i, j):\n # suppose we reach the end of one string, the we have to delete the chars from other string\n if i == len(s1): \n return sum([ord(c) for c in s2[j:]])\n \n if j == len(s2):\n return sum([ord(c) for c in s1[i:]])\n \n if (i, j) in dp:\n return dp[(i, j)]\n\n res = float(\'inf\')\n if s1[i] == s2[j]: # if both char same nothing to add just increment the pointers\n res = min(res, dfs(i + 1, j + 1))\n else: # else try both ways, del the char from s1 and del the char from s2\n res = min(res, ord(s1[i]) + dfs(i + 1, j))\n res = min(res, ord(s2[j]) + dfs(i, j + 1))\n dp[(i, j)] = res\n return res\n\n dp = {}\n return dfs(0, 0)\n\n``` | 1 | Given two strings `s1` and `s2`, return _the lowest **ASCII** sum of deleted characters to make two strings equal_.
**Example 1:**
**Input:** s1 = "sea ", s2 = "eat "
**Output:** 231
**Explanation:** Deleting "s " from "sea " adds the ASCII value of "s " (115) to the sum.
Deleting "t " from "eat " adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.
**Example 2:**
**Input:** s1 = "delete ", s2 = "leet "
**Output:** 403
**Explanation:** Deleting "dee " from "delete " to turn the string into "let ",
adds 100\[d\] + 101\[e\] + 101\[e\] to the sum.
Deleting "e " from "leet " adds 101\[e\] to the sum.
At the end, both strings are equal to "let ", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee " or "eet ", we would get answers of 433 or 417, which are higher.
**Constraints:**
* `1 <= s1.length, s2.length <= 1000`
* `s1` and `s2` consist of lowercase English letters. | Let dp(i, j) be the answer for inputs s1[i:] and s2[j:]. |
Python solution using right min and current max | max-chunks-to-make-sorted-ii | 0 | 1 | **Algorithm and Intuition:** We have to maximize the number of chunks or partitions we can make. The idea is suppose we are at index i and we know that the minimum element from i+1 to last element is greater than or equal to the maximum element till index i then we can say that this partition between index i and i+1 is valid. Because in a sorted array, the elements present before index i will remain in the left part (0 to i) only and after index i will remain in right part (i+1 to n-1) only.\n\n**Steps:**\n\n* Create a **rightmin array** storing the **minimum element from i to n-1** (length of the array) by traversing the array backwards.\n* Iterate over the array from front and keep track of the **maximum element till current index** (maxele).\n* If **maxele** till index i is less than the **rightmin[i+1]** than it is a valid partition or chunk, so increment the answer variable.\n\n```\nans = 0\nn = len(arr)\nrightmin = [math.inf]*(n+1)\ncurrmin = math.inf\nmaxele = arr[0]\n\n# loop from backward of the array to get the minimum element from i to n\nfor j in range(n-1, -1, -1):\n\tif arr[j]<currmin:\n\t\tcurrmin = arr[j]\n\trightmin[j] = currmin\n\n#Forward loop to compare with current max element (maxele) and count the valid partitions\nfor i in range(len(arr)):\n\tif maxele<arr[i]:\n\t\tmaxele = arr[i]\n\tif maxele<=rightmin[i+1]:\n\t\tans+=1\nreturn ans\n```\n\nLet me know if there is any issue in understanding the solution. Please upvote if you find it useful :) | 8 | You are given an integer array `arr`.
We split `arr` into some number of **chunks** (i.e., partitions), and individually sort each chunk. After concatenating them, the result should equal the sorted array.
Return _the largest number of chunks we can make to sort the array_.
**Example 1:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 1
**Explanation:**
Splitting into two or more chunks will not return the required result.
For example, splitting into \[5, 4\], \[3, 2, 1\] will result in \[4, 5, 1, 2, 3\], which isn't sorted.
**Example 2:**
**Input:** arr = \[2,1,3,4,4\]
**Output:** 4
**Explanation:**
We can split into two chunks, such as \[2, 1\], \[3, 4, 4\].
However, splitting into \[2, 1\], \[3\], \[4\], \[4\] is the highest number of chunks possible.
**Constraints:**
* `1 <= arr.length <= 2000`
* `0 <= arr[i] <= 108` | Try to greedily choose the smallest partition that includes the first letter. If you have something like "abaccbdeffed", then you might need to add b. You can use an map like "last['b'] = 5" to help you expand the width of your partition. |
Python solution using right min and current max | max-chunks-to-make-sorted-ii | 0 | 1 | **Algorithm and Intuition:** We have to maximize the number of chunks or partitions we can make. The idea is suppose we are at index i and we know that the minimum element from i+1 to last element is greater than or equal to the maximum element till index i then we can say that this partition between index i and i+1 is valid. Because in a sorted array, the elements present before index i will remain in the left part (0 to i) only and after index i will remain in right part (i+1 to n-1) only.\n\n**Steps:**\n\n* Create a **rightmin array** storing the **minimum element from i to n-1** (length of the array) by traversing the array backwards.\n* Iterate over the array from front and keep track of the **maximum element till current index** (maxele).\n* If **maxele** till index i is less than the **rightmin[i+1]** than it is a valid partition or chunk, so increment the answer variable.\n\n```\nans = 0\nn = len(arr)\nrightmin = [math.inf]*(n+1)\ncurrmin = math.inf\nmaxele = arr[0]\n\n# loop from backward of the array to get the minimum element from i to n\nfor j in range(n-1, -1, -1):\n\tif arr[j]<currmin:\n\t\tcurrmin = arr[j]\n\trightmin[j] = currmin\n\n#Forward loop to compare with current max element (maxele) and count the valid partitions\nfor i in range(len(arr)):\n\tif maxele<arr[i]:\n\t\tmaxele = arr[i]\n\tif maxele<=rightmin[i+1]:\n\t\tans+=1\nreturn ans\n```\n\nLet me know if there is any issue in understanding the solution. Please upvote if you find it useful :) | 8 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
Solution | max-chunks-to-make-sorted-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int> rightMin(n+1,0);\n rightMin[n]=INT_MAX;\n for(int i=n-1;i>=0;i--){\n rightMin[i]=min(arr[i],rightMin[i+1]);\n }\n int leftMax=-1;\n int chunks=0;\n for(int i=0;i<n;i++){\n leftMax=max(leftMax,arr[i]);\n if(leftMax<=rightMin[i+1]){\n chunks++;\n }\n }\n return chunks;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxChunksToSorted(self, A: List[int]) -> int:\n A_cp = A.copy()\n A_cp.sort()\n n = len(A)\n res, sum, sum_cp = 0, 0, 0\n for i in range(n):\n sum += A[i]\n sum_cp += A_cp[i]\n if sum == sum_cp:\n res += 1\n return res \n```\n\n```Java []\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n int[] maxOfLeft = new int[n];\n int[] minOfRight = new int[n];\n\n maxOfLeft[0] = arr[0];\n minOfRight[n-1]=arr[n-1];\n for (int i=1;i<n;i++)\n {\n maxOfLeft[i]=Math.max(maxOfLeft[i-1],arr[i]);\n }\n for (int i=n-2;i>=0;i--)\n {\n minOfRight[i]=Math.min(minOfRight[i+1],arr[i]);\n }\n int res=0;\n for (int i=0;i<n-1;i++)\n {\n if (maxOfLeft[i]<=minOfRight[i+1]) res++;\n }\n return res + 1;\n }\n}\n```\n | 2 | You are given an integer array `arr`.
We split `arr` into some number of **chunks** (i.e., partitions), and individually sort each chunk. After concatenating them, the result should equal the sorted array.
Return _the largest number of chunks we can make to sort the array_.
**Example 1:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 1
**Explanation:**
Splitting into two or more chunks will not return the required result.
For example, splitting into \[5, 4\], \[3, 2, 1\] will result in \[4, 5, 1, 2, 3\], which isn't sorted.
**Example 2:**
**Input:** arr = \[2,1,3,4,4\]
**Output:** 4
**Explanation:**
We can split into two chunks, such as \[2, 1\], \[3, 4, 4\].
However, splitting into \[2, 1\], \[3\], \[4\], \[4\] is the highest number of chunks possible.
**Constraints:**
* `1 <= arr.length <= 2000`
* `0 <= arr[i] <= 108` | Try to greedily choose the smallest partition that includes the first letter. If you have something like "abaccbdeffed", then you might need to add b. You can use an map like "last['b'] = 5" to help you expand the width of your partition. |
Solution | max-chunks-to-make-sorted-ii | 1 | 1 | ```C++ []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int> rightMin(n+1,0);\n rightMin[n]=INT_MAX;\n for(int i=n-1;i>=0;i--){\n rightMin[i]=min(arr[i],rightMin[i+1]);\n }\n int leftMax=-1;\n int chunks=0;\n for(int i=0;i<n;i++){\n leftMax=max(leftMax,arr[i]);\n if(leftMax<=rightMin[i+1]){\n chunks++;\n }\n }\n return chunks;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxChunksToSorted(self, A: List[int]) -> int:\n A_cp = A.copy()\n A_cp.sort()\n n = len(A)\n res, sum, sum_cp = 0, 0, 0\n for i in range(n):\n sum += A[i]\n sum_cp += A_cp[i]\n if sum == sum_cp:\n res += 1\n return res \n```\n\n```Java []\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n int[] maxOfLeft = new int[n];\n int[] minOfRight = new int[n];\n\n maxOfLeft[0] = arr[0];\n minOfRight[n-1]=arr[n-1];\n for (int i=1;i<n;i++)\n {\n maxOfLeft[i]=Math.max(maxOfLeft[i-1],arr[i]);\n }\n for (int i=n-2;i>=0;i--)\n {\n minOfRight[i]=Math.min(minOfRight[i+1],arr[i]);\n }\n int res=0;\n for (int i=0;i<n-1;i++)\n {\n if (maxOfLeft[i]<=minOfRight[i+1]) res++;\n }\n return res + 1;\n }\n}\n```\n | 2 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
[Python3] Solution with using monotonic stack with comments | max-chunks-to-make-sorted-ii | 0 | 1 | ```\n"""\nThe main idea is to get longest non-decreasing interval.\n\nFor decreasing interval (such an interval that we need to sort) we must the maximum of such interval.\n\nExample:\n\narr: [3,8,9,4,5]\n\n0. [] - empty stack\n1. [3] - it is non-decreasing interval\n2. [3,8] - it is non-decreasing interval\n3. [3,8,9] - it is non-decreasing interval\n4. [3,8,9,4] - it is decreasing interval (9 > 4)\n 4.1. need find position such we will have non-decreasing interval [3,4,8,9] - we need sort [8,9,4]\n while stack and stack[-1] > a\n 4.2. while we find begin of decreasing interval [8,9,4] we must find max value of such interval\n 4.3. why maximum ?\n 4.3.1. [3,8,9,4,5]. We can insert 5. Now decreasing interval - [8,9,4,5]. We must sort [8,9,4,5]. For [8,9,4] we can stay 9 in stack, and when we will consider element = 5 we will get decreasing interval again [9,5].\n\n"""\n\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n\n for a in arr:\n _max = a\n while stack and stack[-1] > a:\n top = stack.pop()\n _max = max(_max, top)\n \n \n stack.append(_max)\n \n return len(stack)\n``` | 3 | You are given an integer array `arr`.
We split `arr` into some number of **chunks** (i.e., partitions), and individually sort each chunk. After concatenating them, the result should equal the sorted array.
Return _the largest number of chunks we can make to sort the array_.
**Example 1:**
**Input:** arr = \[5,4,3,2,1\]
**Output:** 1
**Explanation:**
Splitting into two or more chunks will not return the required result.
For example, splitting into \[5, 4\], \[3, 2, 1\] will result in \[4, 5, 1, 2, 3\], which isn't sorted.
**Example 2:**
**Input:** arr = \[2,1,3,4,4\]
**Output:** 4
**Explanation:**
We can split into two chunks, such as \[2, 1\], \[3, 4, 4\].
However, splitting into \[2, 1\], \[3\], \[4\], \[4\] is the highest number of chunks possible.
**Constraints:**
* `1 <= arr.length <= 2000`
* `0 <= arr[i] <= 108` | Try to greedily choose the smallest partition that includes the first letter. If you have something like "abaccbdeffed", then you might need to add b. You can use an map like "last['b'] = 5" to help you expand the width of your partition. |
[Python3] Solution with using monotonic stack with comments | max-chunks-to-make-sorted-ii | 0 | 1 | ```\n"""\nThe main idea is to get longest non-decreasing interval.\n\nFor decreasing interval (such an interval that we need to sort) we must the maximum of such interval.\n\nExample:\n\narr: [3,8,9,4,5]\n\n0. [] - empty stack\n1. [3] - it is non-decreasing interval\n2. [3,8] - it is non-decreasing interval\n3. [3,8,9] - it is non-decreasing interval\n4. [3,8,9,4] - it is decreasing interval (9 > 4)\n 4.1. need find position such we will have non-decreasing interval [3,4,8,9] - we need sort [8,9,4]\n while stack and stack[-1] > a\n 4.2. while we find begin of decreasing interval [8,9,4] we must find max value of such interval\n 4.3. why maximum ?\n 4.3.1. [3,8,9,4,5]. We can insert 5. Now decreasing interval - [8,9,4,5]. We must sort [8,9,4,5]. For [8,9,4] we can stay 9 in stack, and when we will consider element = 5 we will get decreasing interval again [9,5].\n\n"""\n\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n\n for a in arr:\n _max = a\n while stack and stack[-1] > a:\n top = stack.pop()\n _max = max(_max, top)\n \n \n stack.append(_max)\n \n return len(stack)\n``` | 3 | We build a table of `n` rows (**1-indexed**). We start by writing `0` in the `1st` row. Now in every subsequent row, we look at the previous row and replace each occurrence of `0` with `01`, and each occurrence of `1` with `10`.
* For example, for `n = 3`, the `1st` row is `0`, the `2nd` row is `01`, and the `3rd` row is `0110`.
Given two integer `n` and `k`, return the `kth` (**1-indexed**) symbol in the `nth` row of a table of `n` rows.
**Example 1:**
**Input:** n = 1, k = 1
**Output:** 0
**Explanation:** row 1: 0
**Example 2:**
**Input:** n = 2, k = 1
**Output:** 0
**Explanation:**
row 1: 0
row 2: 01
**Example 3:**
**Input:** n = 2, k = 2
**Output:** 1
**Explanation:**
row 1: 0
row 2: 01
**Constraints:**
* `1 <= n <= 30`
* `1 <= k <= 2n - 1` | Each k for which some permutation of arr[:k] is equal to sorted(arr)[:k] is where we should cut each chunk. |
DFS Marking Every Islands | Full Explanation + Hints | 99.87% faster | making-a-large-island | 0 | 1 | # Intuition\nWe can mark all the islands in one full loop. Then we can count all the unique changed indices around an unchanged (zeroes) index one by one and compare to return the maximum of all.\n\n# Approach\nTreat all these points as separate hints and try the problem again after reading a single point (for best results ;)).\n- We change the index of an island from one to negative of the `currIslands` i.e. if no islands are found then the value of `currIslands` will be `0` and as soon as we come across our first `1`, we will decrement the `currIslands` and change the value of the index to that of `currIslands`. \n- We can mark these through a dfs function and it will return the number of changed indices, which we will store in a list.\n- After that we will traverse the indices having the value `0`, and check their neighbouring four indices for unique islands.\n- We can now calculate the total landmass around the current index (if it were also land) by using the unique neighbouring islands stored landmass value.\n- Compare it with a variable for maximum result and return the final answer.\n\nYou can now try doing the problem, if still in problem, continue reading the code.\n\nPS: Please upvote if you liked my explanation, it encourages me to write more.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\ndef largestIsland(grid: List[List[int]]) -> int:\n n = len(grid)\n\n # A dfs function to mark all the connected indices to \n # the passed index to the value of currIslands and\n # return the number of connected indices having 1 as its value\n def dfs(i: int, j: int) -> int:\n if i < 0 or j < 0 or i >= n or j >= n or grid[i][j] != 1:\n return 0\n grid[i][j] = currIsland\n return 1 + dfs(i + 1, j) + dfs(i - 1, j) + dfs(i, j + 1) + dfs(i, j - 1)\n\n # counting the number of islands found\n currIsland = 0\n # this array stores the landmass of each island\n islands = [0]\n # marking and finding the landmasses of all the islands\n for i in range(n):\n for j in range(n):\n if grid[i][j] == 1:\n currIsland -= 1\n islands.append(dfs(i, j))\n\n maxIsland = max(islands)\n for i in range(n):\n for j in range(n):\n if grid[i][j] == 0:\n # This set checks for all the unique islands \n # on the neighbouring four square\n islandsAround = set()\n if i > 0 and grid[i - 1][j] < 0:\n islandsAround.add(grid[i - 1][j])\n if i < n - 1 and grid[i + 1][j] < 0:\n islandsAround.add(grid[i + 1][j])\n if j > 0 and grid[i][j - 1] < 0:\n islandsAround.add(grid[i][j - 1])\n if j < n - 1 and grid[i][j + 1] < 0:\n islandsAround.add(grid[i][j + 1])\n\n # calculating the total landmass if this\n # index was to be a landmass by using \n # previously stored landmasses of all islands\n totalLandAround = 1\n for k in islandsAround:\n totalLandAround += islands[-k]\n maxIsland = max(maxIsland, totalLandAround)\n return maxIsland\n```\n | 2 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
DFS Marking Every Islands | Full Explanation + Hints | 99.87% faster | making-a-large-island | 0 | 1 | # Intuition\nWe can mark all the islands in one full loop. Then we can count all the unique changed indices around an unchanged (zeroes) index one by one and compare to return the maximum of all.\n\n# Approach\nTreat all these points as separate hints and try the problem again after reading a single point (for best results ;)).\n- We change the index of an island from one to negative of the `currIslands` i.e. if no islands are found then the value of `currIslands` will be `0` and as soon as we come across our first `1`, we will decrement the `currIslands` and change the value of the index to that of `currIslands`. \n- We can mark these through a dfs function and it will return the number of changed indices, which we will store in a list.\n- After that we will traverse the indices having the value `0`, and check their neighbouring four indices for unique islands.\n- We can now calculate the total landmass around the current index (if it were also land) by using the unique neighbouring islands stored landmass value.\n- Compare it with a variable for maximum result and return the final answer.\n\nYou can now try doing the problem, if still in problem, continue reading the code.\n\nPS: Please upvote if you liked my explanation, it encourages me to write more.\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n\n- Space complexity: $$O(n^2)$$\n\n# Code\n```\ndef largestIsland(grid: List[List[int]]) -> int:\n n = len(grid)\n\n # A dfs function to mark all the connected indices to \n # the passed index to the value of currIslands and\n # return the number of connected indices having 1 as its value\n def dfs(i: int, j: int) -> int:\n if i < 0 or j < 0 or i >= n or j >= n or grid[i][j] != 1:\n return 0\n grid[i][j] = currIsland\n return 1 + dfs(i + 1, j) + dfs(i - 1, j) + dfs(i, j + 1) + dfs(i, j - 1)\n\n # counting the number of islands found\n currIsland = 0\n # this array stores the landmass of each island\n islands = [0]\n # marking and finding the landmasses of all the islands\n for i in range(n):\n for j in range(n):\n if grid[i][j] == 1:\n currIsland -= 1\n islands.append(dfs(i, j))\n\n maxIsland = max(islands)\n for i in range(n):\n for j in range(n):\n if grid[i][j] == 0:\n # This set checks for all the unique islands \n # on the neighbouring four square\n islandsAround = set()\n if i > 0 and grid[i - 1][j] < 0:\n islandsAround.add(grid[i - 1][j])\n if i < n - 1 and grid[i + 1][j] < 0:\n islandsAround.add(grid[i + 1][j])\n if j > 0 and grid[i][j - 1] < 0:\n islandsAround.add(grid[i][j - 1])\n if j < n - 1 and grid[i][j + 1] < 0:\n islandsAround.add(grid[i][j + 1])\n\n # calculating the total landmass if this\n # index was to be a landmass by using \n # previously stored landmasses of all islands\n totalLandAround = 1\n for k in islandsAround:\n totalLandAround += islands[-k]\n maxIsland = max(maxIsland, totalLandAround)\n return maxIsland\n```\n | 2 | Strings `s1` and `s2` are `k`**\-similar** (for some non-negative integer `k`) if we can swap the positions of two letters in `s1` exactly `k` times so that the resulting string equals `s2`.
Given two anagrams `s1` and `s2`, return the smallest `k` for which `s1` and `s2` are `k`**\-similar**.
**Example 1:**
**Input:** s1 = "ab ", s2 = "ba "
**Output:** 1
**Explanation:** The two string are 1-similar because we can use one swap to change s1 to s2: "ab " --> "ba ".
**Example 2:**
**Input:** s1 = "abc ", s2 = "bca "
**Output:** 2
**Explanation:** The two strings are 2-similar because we can use two swaps to change s1 to s2: "abc " --> "bac " --> "bca ".
**Constraints:**
* `1 <= s1.length <= 20`
* `s2.length == s1.length`
* `s1` and `s2` contain only lowercase letters from the set `{'a', 'b', 'c', 'd', 'e', 'f'}`.
* `s2` is an anagram of `s1`. | null |
Python || Easy || DSU | making-a-large-island | 0 | 1 | ```\nclass Solution:\n def largestIsland(self, grid: List[List[int]]) -> int:\n def find(u):\n if u==parent[u]:\n return u\n else:\n parent[u]=find(parent[u])\n return parent[u]\n def union(u,v):\n pu,pv=find(u),find(v)\n if pu==pv:\n return \n if size[pv]>size[pu]:\n parent[pu]=pv\n size[pv]+=size[pu]\n else:\n parent[pv]=pu\n size[pu]+=size[pv]\n \n n=len(grid)\n parent=[i for i in range(n*n)]\n size=[1 for i in range(n*n)]\n for i in range(n):\n for j in range(n):\n if grid[i][j]:\n a=i*n+j\n for u,v in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:\n if 0<=u<n and 0<=v<n and grid[u][v]:\n b=u*n+v\n union(a,b)\n m=0 \n for i in range(n):\n for j in range(n):\n if grid[i][j]==0:\n#adjacent elemnts can have the same parent that\'s why we are using set\n t=set()\n c=1\n for u,v in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:\n if 0<=u<n and 0<=v<n and grid[u][v]:\n a=u*n+v\n t.add(find(a))\n for x in t:\n c+=size[x]\n if c>m:\n m=c\n for i in range(n*n):\n m=max(m,size[find(i)])\n return m\n```\n\n**An upvote will be encouraging** | 4 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
Python || Easy || DSU | making-a-large-island | 0 | 1 | ```\nclass Solution:\n def largestIsland(self, grid: List[List[int]]) -> int:\n def find(u):\n if u==parent[u]:\n return u\n else:\n parent[u]=find(parent[u])\n return parent[u]\n def union(u,v):\n pu,pv=find(u),find(v)\n if pu==pv:\n return \n if size[pv]>size[pu]:\n parent[pu]=pv\n size[pv]+=size[pu]\n else:\n parent[pv]=pu\n size[pu]+=size[pv]\n \n n=len(grid)\n parent=[i for i in range(n*n)]\n size=[1 for i in range(n*n)]\n for i in range(n):\n for j in range(n):\n if grid[i][j]:\n a=i*n+j\n for u,v in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:\n if 0<=u<n and 0<=v<n and grid[u][v]:\n b=u*n+v\n union(a,b)\n m=0 \n for i in range(n):\n for j in range(n):\n if grid[i][j]==0:\n#adjacent elemnts can have the same parent that\'s why we are using set\n t=set()\n c=1\n for u,v in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:\n if 0<=u<n and 0<=v<n and grid[u][v]:\n a=u*n+v\n t.add(find(a))\n for x in t:\n c+=size[x]\n if c>m:\n m=c\n for i in range(n*n):\n m=max(m,size[find(i)])\n return m\n```\n\n**An upvote will be encouraging** | 4 | Strings `s1` and `s2` are `k`**\-similar** (for some non-negative integer `k`) if we can swap the positions of two letters in `s1` exactly `k` times so that the resulting string equals `s2`.
Given two anagrams `s1` and `s2`, return the smallest `k` for which `s1` and `s2` are `k`**\-similar**.
**Example 1:**
**Input:** s1 = "ab ", s2 = "ba "
**Output:** 1
**Explanation:** The two string are 1-similar because we can use one swap to change s1 to s2: "ab " --> "ba ".
**Example 2:**
**Input:** s1 = "abc ", s2 = "bca "
**Output:** 2
**Explanation:** The two strings are 2-similar because we can use two swaps to change s1 to s2: "abc " --> "bac " --> "bca ".
**Constraints:**
* `1 <= s1.length <= 20`
* `s2.length == s1.length`
* `s1` and `s2` contain only lowercase letters from the set `{'a', 'b', 'c', 'd', 'e', 'f'}`.
* `s2` is an anagram of `s1`. | null |
89% TC and 50% SC easy python solution | making-a-large-island | 0 | 1 | ```\ndef largestIsland(self, grid: List[List[int]]) -> int:\n\t@lru_cache(None)\n\tdef dfs(i, j, c):\n\t\tgrid[i][j] = c\n\t\ttemp = 1\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<n and 0<=j+y<n and grid[i+x][j+y] == 1):\n\t\t\t\ttemp += dfs(i+x, j+y, c)\n\t\treturn temp\n\tn = len(grid)\n\tdir = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\tarea = dict()\n\tc = 2\n\tpos = []\n\tfor i in range(n):\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j] == 1):\n\t\t\t\tarea[c] = dfs(i, j, c)\n\t\t\t\tc += 1\n\t\t\telif(grid[i][j] == 0):\n\t\t\t\tpos.append((i, j))\n\tans = 0\n\tif not(pos): return n**2\n\tfor i, j in pos:\n\t\tneigh = set()\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<n and 0<=j+y<n and grid[i+x][j+y] != 0):\n\t\t\t\tneigh.add(grid[i+x][j+y])\n\t\tneigh = list(neigh)\n\t\tneigh = [area[i] for i in neigh]\n\t\tans = max(ans, 1 + sum(neigh))\n\treturn ans\n``` | 1 | You are given an `n x n` binary matrix `grid`. You are allowed to change **at most one** `0` to be `1`.
Return _the size of the largest **island** in_ `grid` _after applying this operation_.
An **island** is a 4-directionally connected group of `1`s.
**Example 1:**
**Input:** grid = \[\[1,0\],\[0,1\]\]
**Output:** 3
**Explanation:** Change one 0 to 1 and connect two 1s, then we get an island with area = 3.
**Example 2:**
**Input:** grid = \[\[1,1\],\[1,0\]\]
**Output:** 4
**Explanation:** Change the 0 to 1 and make the island bigger, only one island with area = 4.
**Example 3:**
**Input:** grid = \[\[1,1\],\[1,1\]\]
**Output:** 4
**Explanation:** Can't change any 0 to 1, only one island with area = 4.
**Constraints:**
* `n == grid.length`
* `n == grid[i].length`
* `1 <= n <= 500`
* `grid[i][j]` is either `0` or `1`. | null |
89% TC and 50% SC easy python solution | making-a-large-island | 0 | 1 | ```\ndef largestIsland(self, grid: List[List[int]]) -> int:\n\t@lru_cache(None)\n\tdef dfs(i, j, c):\n\t\tgrid[i][j] = c\n\t\ttemp = 1\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<n and 0<=j+y<n and grid[i+x][j+y] == 1):\n\t\t\t\ttemp += dfs(i+x, j+y, c)\n\t\treturn temp\n\tn = len(grid)\n\tdir = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n\tarea = dict()\n\tc = 2\n\tpos = []\n\tfor i in range(n):\n\t\tfor j in range(n):\n\t\t\tif(grid[i][j] == 1):\n\t\t\t\tarea[c] = dfs(i, j, c)\n\t\t\t\tc += 1\n\t\t\telif(grid[i][j] == 0):\n\t\t\t\tpos.append((i, j))\n\tans = 0\n\tif not(pos): return n**2\n\tfor i, j in pos:\n\t\tneigh = set()\n\t\tfor x, y in dir:\n\t\t\tif(0<=i+x<n and 0<=j+y<n and grid[i+x][j+y] != 0):\n\t\t\t\tneigh.add(grid[i+x][j+y])\n\t\tneigh = list(neigh)\n\t\tneigh = [area[i] for i in neigh]\n\t\tans = max(ans, 1 + sum(neigh))\n\treturn ans\n``` | 1 | Strings `s1` and `s2` are `k`**\-similar** (for some non-negative integer `k`) if we can swap the positions of two letters in `s1` exactly `k` times so that the resulting string equals `s2`.
Given two anagrams `s1` and `s2`, return the smallest `k` for which `s1` and `s2` are `k`**\-similar**.
**Example 1:**
**Input:** s1 = "ab ", s2 = "ba "
**Output:** 1
**Explanation:** The two string are 1-similar because we can use one swap to change s1 to s2: "ab " --> "ba ".
**Example 2:**
**Input:** s1 = "abc ", s2 = "bca "
**Output:** 2
**Explanation:** The two strings are 2-similar because we can use two swaps to change s1 to s2: "abc " --> "bac " --> "bca ".
**Constraints:**
* `1 <= s1.length <= 20`
* `s2.length == s1.length`
* `s1` and `s2` contain only lowercase letters from the set `{'a', 'b', 'c', 'd', 'e', 'f'}`.
* `s2` is an anagram of `s1`. | null |
Python short and clean. O(n * k). Functional programming. | verifying-an-alien-dictionary | 0 | 1 | # Approach\n1. Create an `ordinal` hashmap which maps alien characters to an integer such that `ordinal[x] < ordinal[y] implies x comes before y`.\nAdd an `EMPTY` character at the lowest ordinal to make comparisions easier.\n\n2. Define `is_lexico` which takes `s1` and `s2` and returns `true` if `s1` comes before `s2` in the alien dictionary. This can be done by:\n 1. Skip prefix characters which are equal in `s1` and `s2`.\n 2. Take the next pair `(ch1, ch2)`.\n 3. Return `true` if `ordinals[ch1] < ordinals[ch2]` else `false`\n\n3. Check if each adjacent pair in `words` satisfy `is_lexico`.\n\n# Complexity\n- Time complexity: $$O(n * k)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is number of words`, `k is max number of characters per word`\n\n# Code\n```python\nclass Solution:\n def isAlienSorted(self, words: list[str], order: str) -> bool:\n EMPTY = ""\n ordinals = {ch: i for i, ch in enumerate(chain((EMPTY,), order))}\n\n def is_lexico(s1: str, s2: str) -> bool:\n pairs = zip_longest(s1, s2, fillvalue=EMPTY)\n ch1, ch2 = next(dropwhile(lambda chs: eq(*chs), pairs), (EMPTY, "z"))\n return ordinals[ch1] < ordinals[ch2]\n \n return all(starmap(is_lexico, pairwise(words)))\n \n``` | 1 | In an alien language, surprisingly, they also use English lowercase letters, but possibly in a different `order`. The `order` of the alphabet is some permutation of lowercase letters.
Given a sequence of `words` written in the alien language, and the `order` of the alphabet, return `true` if and only if the given `words` are sorted lexicographically in this alien language.
**Example 1:**
**Input:** words = \[ "hello ", "leetcode "\], order = "hlabcdefgijkmnopqrstuvwxyz "
**Output:** true
**Explanation:** As 'h' comes before 'l' in this language, then the sequence is sorted.
**Example 2:**
**Input:** words = \[ "word ", "world ", "row "\], order = "worldabcefghijkmnpqstuvxyz "
**Output:** false
**Explanation:** As 'd' comes after 'l' in this language, then words\[0\] > words\[1\], hence the sequence is unsorted.
**Example 3:**
**Input:** words = \[ "apple ", "app "\], order = "abcdefghijklmnopqrstuvwxyz "
**Output:** false
**Explanation:** The first three characters "app " match, and the second string is shorter (in size.) According to lexicographical rules "apple " > "app ", because 'l' > '∅', where '∅' is defined as the blank character which is less than any other character ([More info](https://en.wikipedia.org/wiki/Lexicographical_order)).
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 20`
* `order.length == 26`
* All characters in `words[i]` and `order` are English lowercase letters. | This problem is exactly like reversing a normal string except that there are certain characters that we have to simply skip. That should be easy enough to do if you know how to reverse a string using the two-pointer approach. |
Python short and clean. O(n * k). Functional programming. | verifying-an-alien-dictionary | 0 | 1 | # Approach\n1. Create an `ordinal` hashmap which maps alien characters to an integer such that `ordinal[x] < ordinal[y] implies x comes before y`.\nAdd an `EMPTY` character at the lowest ordinal to make comparisions easier.\n\n2. Define `is_lexico` which takes `s1` and `s2` and returns `true` if `s1` comes before `s2` in the alien dictionary. This can be done by:\n 1. Skip prefix characters which are equal in `s1` and `s2`.\n 2. Take the next pair `(ch1, ch2)`.\n 3. Return `true` if `ordinals[ch1] < ordinals[ch2]` else `false`\n\n3. Check if each adjacent pair in `words` satisfy `is_lexico`.\n\n# Complexity\n- Time complexity: $$O(n * k)$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is number of words`, `k is max number of characters per word`\n\n# Code\n```python\nclass Solution:\n def isAlienSorted(self, words: list[str], order: str) -> bool:\n EMPTY = ""\n ordinals = {ch: i for i, ch in enumerate(chain((EMPTY,), order))}\n\n def is_lexico(s1: str, s2: str) -> bool:\n pairs = zip_longest(s1, s2, fillvalue=EMPTY)\n ch1, ch2 = next(dropwhile(lambda chs: eq(*chs), pairs), (EMPTY, "z"))\n return ordinals[ch1] < ordinals[ch2]\n \n return all(starmap(is_lexico, pairwise(words)))\n \n``` | 1 | You are given an array of strings `equations` that represent relationships between variables where each string `equations[i]` is of length `4` and takes one of two different forms: `"xi==yi "` or `"xi!=yi "`.Here, `xi` and `yi` are lowercase letters (not necessarily different) that represent one-letter variable names.
Return `true` _if it is possible to assign integers to variable names so as to satisfy all the given equations, or_ `false` _otherwise_.
**Example 1:**
**Input:** equations = \[ "a==b ", "b!=a "\]
**Output:** false
**Explanation:** If we assign say, a = 1 and b = 1, then the first equation is satisfied, but not the second.
There is no way to assign the variables to satisfy both equations.
**Example 2:**
**Input:** equations = \[ "b==a ", "a==b "\]
**Output:** true
**Explanation:** We could assign a = 1 and b = 1 to satisfy both equations.
**Constraints:**
* `1 <= equations.length <= 500`
* `equations[i].length == 4`
* `equations[i][0]` is a lowercase letter.
* `equations[i][1]` is either `'='` or `'!'`.
* `equations[i][2]` is `'='`.
* `equations[i][3]` is a lowercase letter. | null |
Easy Python Solution - Concatenation | concatenation-of-array | 0 | 1 | \n# Code\n```\nclass Solution:\n def getConcatenation(self, nums: List[int]) -> List[int]:\n return 2*nums\n``` | 3 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Two Python Solutions | Concatenate or Repeat | concatenation-of-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to return a new array that repeats the original array twice.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n### Approach 1\nWe can concatenate the original `nums` array with itself using the `+` operator.\n\n> `+` \u2192 it concatenates two lists in Python:\nExample: `[1, 2, 3] + [1, 2, 3] = [1, 2, 3, 1, 2, 3]`\n\n### Approach 2\nWe can repeat the the original `nums` array `2` times using the `*` operator.\n\n> `*` \u2192 it repeats a list a specified number of times in Python:\nExample: `[1, 2, 3] * 2 = [1, 2, 3, 1, 2, 3]`\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n`n` is the length of the `nums` array. Both solutions require going through each element of the input list once, and the time they take scales linearly with the size of the input list.\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n`n` is the length of the `nums` array. Both solutions create a new list to store the concatenated list, and the space used for this is directly proportional to the size of the input list.\n\n# Code\n## Approach 1 Solution:\n```\nclass Solution:\n def getConcatenation(self, nums: List[int]) -> List[int]:\n return nums + nums\n \n```\n\n## Approach 2 Solution:\n```\nclass Solution:\n def getConcatenation(self, nums: List[int]) -> List[int]:\n return nums * 2 \n``` | 6 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
simple 2 lines code python | concatenation-of-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nsimple multiply\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getConcatenation(self, nums: List[int]) -> List[int]:\n d=nums*2\n return d\n \n``` | 0 | Given an integer array `nums` of length `n`, you want to create an array `ans` of length `2n` where `ans[i] == nums[i]` and `ans[i + n] == nums[i]` for `0 <= i < n` (**0-indexed**).
Specifically, `ans` is the **concatenation** of two `nums` arrays.
Return _the array_ `ans`.
**Example 1:**
**Input:** nums = \[1,2,1\]
**Output:** \[1,2,1,1,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[0\],nums\[1\],nums\[2\]\]
- ans = \[1,2,1,1,2,1\]
**Example 2:**
**Input:** nums = \[1,3,2,1\]
**Output:** \[1,3,2,1,1,3,2,1\]
**Explanation:** The array ans is formed as follows:
- ans = \[nums\[0\],nums\[1\],nums\[2\],nums\[3\],nums\[0\],nums\[1\],nums\[2\],nums\[3\]\]
- ans = \[1,3,2,1,1,3,2,1\]
**Constraints:**
* `n == nums.length`
* `1 <= n <= 1000`
* `1 <= nums[i] <= 1000` | What if the problem was instead determining if you could generate a valid array with nums[index] == target? To generate the array, set nums[index] to target, nums[index-i] to target-i, and nums[index+i] to target-i. Then, this will give the minimum possible sum, so check if the sum is less than or equal to maxSum. n is too large to actually generate the array, so you can use the formula 1 + 2 + ... + n = n * (n+1) / 2 to quickly find the sum of nums[0...index] and nums[index...n-1]. Binary search for the target. If it is possible, then move the lower bound up. Otherwise, move the upper bound down. |
Python 9 line concise code With intuition explained using example.(Beats 87%) | unique-length-3-palindromic-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSo this problem might be difficult to grasp even after seeing the solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can observe that for a pallindrome with 3 length(note this)\nonly requirement is the first and last element should be equal.\nExample: aba,bcb....etc\n\nNow the most confusing part might be why we are calculationg the first and last index and calculating there length.\nSo take a look at an example.\n\n"bacdefb"\n\nremind you we are looking for subsequences not substring.\nnow we see that first and last element is same i.e. b.\n\nso \nbab,bcb,bdb,beb,bfb are all pallindromes of 3 length.\n\nand the reason we are using a set is because we want "unique" subsequences.\n\nNote : characters is a set of all lower case alphabets..\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n res = 0\n characters = {chr(x) for x in range(97,123,1)}\n for k in characters:\n first,last = s.find(k),s.rfind(k)\n if first!=-1:\n res+=len(set(s[first+1:last]))\n return res\n``` | 4 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
【Video】Give me 8 minutes - How we think about a solution | unique-length-3-palindromic-subsequences | 1 | 1 | # Intuition\nFind the same characters at the both sides.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/Tencj59MHAc\n\n\u203B Since I recorded that video last year, there might be parts that could be unclear. If you have any questions, feel free to leave a comment.\n\n\u25A0 Timeline of the video\n\n`0:00` Read the question of Unique Length-3 Palindromic Subsequences\n`1:03` Explain a basic idea to solve Unique Length-3 Palindromic Subsequences\n`4:48` Coding\n`8:01` Summarize the algorithm of Unique Length-3 Palindromic Subsequences\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,083\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n## How we think about a solution\n\nWe know that we create strings which are length of `3`. So simply if we find the same characters at the both sides, we can create Unique Length-3 Palindromic Subsequences, because Length-3 palindrome has only one pattern.\n\nFor example\n```\naba: OK\nxyx: OK\nctc: OK\naaa: OK\n\naab: not good\nbaa: not good\n\n```\n\n---\n\n\u2B50\uFE0F Points\n\nWe will create and count this pattern.\n```\na _ a\nz _ z\n```\nBoth sides of characters are the same.\n\n---\n\n\n\n\n##### How can you create the strings?\n\nLet\'s say\n\n```\nInput: ababcad\n```\nLet\'s find the frist `a` from beginning and from the last.\n```\nababcad\n\u2191 \u2191\n```\n\nNext, look at the characters between `a`.\n\n```\nbabc\n```\nNow we find `a` at the both sides. So if we can make each character unique between `a`, that means we can create Unique Length-3 Palindromic Subsequences.\n\nIn this case,\n\n```\n(a)babc(a) \u2192 (a)bac(a)\naba\naaa\naca\n``` \n---\n\n\u2B50\uFE0F Points\n\nIterate through input string from the beginning and from the last. Try to find the same characters at the both sides. Then we make each character unique between the same characters.\n\n--- \n\n##### How many times do you have to find the same characters at the both sides.\n\nThe answer is number of unique characters in input string.\n```\nInput: ababcad\n```\nIn this case, we should find `a`,`b`,`c`,`d` 4 times, because there is posibility that we can create Unique Length-3 Palindromic Subsequences with each unique character.\n\nLet\'s see the rest of characters `b`,`c`,`d`\n```\ntarget = b\n\nababcad\n \u2191 \u2191\n\nFound bab\n```\n```\ntarget = c\n\nababcad\n \u2191\n \u2191\n\nThere is no Unique Length-3 Palindromic Subsequences.\n```\n```\ntarget = d\n\nababcad\n \u2191\n \u2191\n\nThere is no Unique Length-3 Palindromic Subsequences.\n```\nIn the end, we found\n```\naba\naaa\naca\nbab\n```\nOutput should be total number of unique characters between specific characters at the both sides.\n```\nbetween a, we have 3 unique characters (= b, a and c)\nbetween b, we have 1 unique character (= a)\nbetween c, we have 0 unique characters\nbetween d, we have 0 unique characters\n```\n```\nOutput: 4\n```\n\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm.\n\n\n---\n\n### Algorithm Overview:\n\n1. Initialization\n\n2. Loop through unique characters\n\n3. Find the first and last occurrence of the character\n\n4. Check if there is a valid range\n\n5. Count unique characters within the valid range\n\n6. Return the result\n\n### Detailed Explanation:\n\n1. **Initialization**:\n ```python\n res = 0\n uniq = set(s)\n ```\n\n - Initialize `res` to 0, which will store the final result.\n - Create a set `uniq` containing unique characters from the string `s`.\n\n2. **Loop through unique characters**:\n ```python\n for c in uniq:\n ```\n\n - Iterate through each unique character in the set `uniq`.\n\n3. **Find the first and last occurrence of the character**:\n ```python\n start = s.find(c)\n end = s.rfind(c)\n ```\n\n - Use `find` to locate the first occurrence of the character `c`.\n - Use `rfind` to locate the last occurrence of the character `c`.\n\n4. **Check if there is a valid range**:\n ```python\n if start < end:\n ```\n\n - Verify that the first occurrence index is less than the last occurrence index.\n\n5. **Count unique characters within the valid range**:\n ```python\n res += len(set(s[start+1:end]))\n ```\n\n - If there is a valid range, calculate the length of the set of characters within the substring between `start+1` and `end` (excluding the character at `start`).\n - Add this length to the result.\n\n6. **Return the result**:\n ```python\n return res\n ```\n\n - After iterating through all unique characters, return the final result.\n \n\n# Complexity\n- Time complexity: $$O(26 * (n+n+n))$$ \u2192 $$O(n)$$\n3n is start, end, set in the for loop.\n\n- Space complexity: $$O(26)$$ \u2192 $$O(1)$$\n`uniq` variable has potentially 26 unique characters.\n\n\n```python []\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n \n res = 0\n uniq = set(s)\n \n for c in uniq:\n start = s.find(c) # search a character from the beginning\n end = s.rfind(c) # search a character from the last index\n \n if start < end:\n res += len(set(s[start+1:end]))\n \n return res\n```\n```javascript []\nvar countPalindromicSubsequence = function(s) {\n let res = 0;\n const uniq = new Set(s);\n\n for (const c of uniq) {\n const start = s.indexOf(c);\n const end = s.lastIndexOf(c);\n\n if (start < end) {\n res += new Set(s.slice(start + 1, end)).size;\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int countPalindromicSubsequence(String s) {\n int res = 0;\n Set<Character> uniq = new HashSet<>();\n\n for (char c : s.toCharArray()) {\n uniq.add(c);\n }\n\n for (char c : uniq) {\n int start = s.indexOf(c);\n int end = s.lastIndexOf(c);\n\n if (start < end) {\n Set<Character> charSet = new HashSet<>();\n for (int i = start + 1; i < end; i++) {\n charSet.add(s.charAt(i));\n }\n res += charSet.size();\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int countPalindromicSubsequence(string s) {\n int res = 0;\n unordered_set<char> uniq;\n\n for (char c : s) {\n uniq.insert(c);\n }\n\n for (char c : uniq) {\n int start = s.find(c);\n int end = s.rfind(c);\n\n if (start < end) {\n unordered_set<char> charSet;\n for (int i = start + 1; i < end; i++) {\n charSet.insert(s[i]);\n }\n res += charSet.size();\n }\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-element-after-decreasing-and-rearranging/solutions/4290299/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/1XhaQo-cDVg\n\n\u25A0 Timeline of the video\n\n`0:04` Explain a key point of the question\n`0:19` Important condition\n`0:56` Demonstrate how it works\n`3:08` What if we have a lot of the same numbers in input array?\n`4:10` Coding\n`4:55` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sort-vowels-in-a-string/solutions/4285226/give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/fVv8R93DaTc\n\n\u25A0 Timeline of the video\n\n`0:04` Explain a key point of the question\n`1:19` Demonstrate how it works\n`3:09` Coding\n`5:02` Time Complexity and Space Complexity\n | 82 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
✅☑[C++/Java/Python/JavaScript] || 2 Approaches || Easy Approaches || EXPLAINED🔥 | unique-length-3-palindromic-subsequences | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n\n#### ***Approach 1(Counting in Between)***\n1. **Initialization and Index Storage:**\n\n - The code begins by initializing variables, such as `n` (size of the input string s) and `result` (the count of palindromic subsequences).\n - It uses an unordered map `indices` to store the indices of characters in the string `s`. Each character key in the map is associated with a pair of integers representing the first and last occurrence indices in the string.\n1. **Character Index Update:**\n\n - The code then iterates through the string `s` and updates the `indices` of characters in the indices map. For each character `s[i]` encountered, it updates its first occurrence index if it\'s not set, otherwise updates the second occurrence index.\n1. **Palindromic Subsequence Calculation:**\n\n - After indexing all characters, the code loops through the map entries.\n - For each character\'s pair of indices (first and last occurrence), if both indices are valid (not -1), it calculates the unique characters present between these two indices (excluding the characters at the indices).\n - It uses an unordered set `unique_chars` to store these unique characters and increments the `result` by the size of this set. This count represents the number of unique subsequences that can be formed between the first and last occurrences of the character, assuming they are part of a palindrome.\n1. **Returning the Result:**\n\n - Finally, the code returns the accumulated count of distinct palindromic subsequences.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countPalindromicSubsequence(std::string s) {\n int n = s.size();\n int result = 0;\n\n // Store the indices of characters in the string\n std::unordered_map<char, std::pair<int, int>> indices;\n\n // Initializing indices with -1 (not visited yet)\n for (char c = \'a\'; c <= \'z\'; ++c) {\n indices[c] = std::make_pair(-1, -1);\n }\n\n // Iterate through the string\n for (int i = 0; i < n; ++i) {\n if (indices[s[i]].first == -1) {\n indices[s[i]].first = i;\n } else {\n indices[s[i]].second = i;\n }\n }\n\n // Calculate palindromic subsequences\n for (auto &[c, idx] : indices) {\n if (idx.first != -1 && idx.second != -1) {\n std::unordered_set<char> unique_chars;\n for (int i = idx.first + 1; i < idx.second; ++i) {\n unique_chars.insert(s[i]);\n }\n result += unique_chars.size();\n }\n }\n\n return result;\n }\n};\n\n --------------------------------------------\nclass Solution {\npublic:\n int countPalindromicSubsequence(string s) {\n unordered_set<char> letters;\n for (char c : s) {\n letters.insert(c);\n }\n \n int ans = 0;\n for (char letter : letters) {\n int i = -1;\n int j = 0;\n \n for (int k = 0; k < s.size(); k++) {\n if (s[k] == letter) {\n if (i == -1) {\n i = k;\n }\n \n j = k;\n }\n }\n \n unordered_set<char> between;\n for (int k = i + 1; k < j; k++) {\n between.insert(s[k]);\n }\n \n ans += between.size();\n }\n \n return ans;\n }\n};\n\n\n\n\n```\n```C []\n\n\nstruct Pair {\n int first;\n int second;\n};\n\nint countPalindromicSubsequence(char* s) {\n int n = strlen(s);\n int result = 0;\n\n struct Pair indices[26];\n for (int i = 0; i < 26; ++i) {\n indices[i].first = -1;\n indices[i].second = -1;\n }\n\n for (int i = 0; i < n; ++i) {\n int idx = s[i] - \'a\';\n if (indices[idx].first == -1) {\n indices[idx].first = i;\n } else {\n indices[idx].second = i;\n }\n }\n\n for (int i = 0; i < 26; ++i) {\n if (indices[i].first != -1 && indices[i].second != -1) {\n int unique_chars[26] = {0};\n for (int j = indices[i].first + 1; j < indices[i].second; ++j) {\n unique_chars[s[j] - \'a\'] = 1;\n }\n for (int j = 0; j < 26; ++j) {\n result += unique_chars[j];\n }\n }\n }\n\n return result;\n}\n\n```\n```Java []\nclass Solution {\n public int countPalindromicSubsequence(String s) {\n int n = s.length();\n int result = 0;\n\n Map<Character, int[]> indices = new HashMap<>();\n\n for (char c = \'a\'; c <= \'z\'; ++c) {\n indices.put(c, new int[]{-1, -1});\n }\n\n for (int i = 0; i < n; ++i) {\n char ch = s.charAt(i);\n if (indices.get(ch)[0] == -1) {\n indices.get(ch)[0] = i;\n } else {\n indices.get(ch)[1] = i;\n }\n }\n\n for (Map.Entry<Character, int[]> entry : indices.entrySet()) {\n int[] idx = entry.getValue();\n if (idx[0] != -1 && idx[1] != -1) {\n Set<Character> uniqueChars = new HashSet<>();\n for (int i = idx[0] + 1; i < idx[1]; ++i) {\n uniqueChars.add(s.charAt(i));\n }\n result += uniqueChars.size();\n }\n }\n\n return result;\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n n = len(s)\n result = 0\n indices = {c: [-1, -1] for c in \'abcdefghijklmnopqrstuvwxyz\'}\n\n for i in range(n):\n if indices[s[i]][0] == -1:\n indices[s[i]][0] = i\n else:\n indices[s[i]][1] = i\n\n for c, idx in indices.items():\n if idx[0] != -1 and idx[1] != -1:\n unique_chars = set(s[idx[0] + 1:idx[1]])\n result += len(unique_chars)\n\n return result\n\n\n--------------------------------------------\n\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n return sum([len(set(s[s.index(letter)+1:s.rindex(letter)])) for letter in set(s)])\n\n```\n```javascript []\nvar countPalindromicSubsequence = function(s) {\n const n = s.length;\n let result = 0;\n const indices = {};\n\n for (let c = \'a\'; c <= \'z\'; ++c) {\n indices[c] = [-1, -1];\n }\n\n for (let i = 0; i < n; ++i) {\n if (indices[s[i]][0] === -1) {\n indices[s[i]][0] = i;\n } else {\n indices[s[i]][1] = i;\n }\n }\n\n for (const [c, idx] of Object.entries(indices)) {\n if (idx[0] !== -1 && idx[1] !== -1) {\n const uniqueChars = new Set(s.slice(idx[0] + 1, idx[1]));\n result += uniqueChars.size;\n }\n }\n\n return result;\n};\n\n\n```\n\n---\n\n\n#### ***Approach 2(Pre-Counting indices)***\n1. **Initialization:**\n\n - Two vectors `first` and `last` of size 26 (one for each letter in the English alphabet) are created and initialized with `-1`. These vectors will store the first and last occurrences of each letter in the string.\n1. **Finding First and Last Occurrences:**\n\n - Loop through each character in the input string `s`.\n - For each character, calculate its index in the `first` and `last` vectors based on its ASCII value. Update `first` with the current index if it\'s the first occurrence of the character. Always update `last` with the current index to keep track of the latest occurrence.\n1. **Counting Unique Characters:**\n\n - Initialize `ans` to store the total count of unique characters.\n - Iterate over each letter from \'a\' to \'z\'.\n - For each letter, if `first[i]` is not equal to `-1`, meaning the letter exists in the string:\n - Create an unordered set `between` to store unique characters between the first and last occurrences of the current letter.\n - Iterate from the index after the first occurrence (`first[i] + 1`) to the index before the last occurrence (`last[i] - 1`) of the current letter and insert each character into the `between` set.\n - Increase `ans` by the size of the `between` set, which represents the count of unique characters between the first and last occurrences of the current letter.\n1. **Return:**\n\n - Return the final count of unique characters (`ans`) between the first and last occurrences of each letter in the input string.\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int countPalindromicSubsequence(string s) {\n vector<int> first = vector(26, -1);\n vector<int> last = vector(26, -1);\n \n for (int i = 0; i < s.size(); i++) {\n int curr = s[i] - \'a\';\n if (first[curr] == - 1) {\n first[curr] = i;\n }\n \n last[curr] = i;\n }\n \n int ans = 0;\n for (int i = 0; i < 26; i++) {\n if (first[i] == -1) {\n continue;\n }\n \n unordered_set<char> between;\n for (int j = first[i] + 1; j < last[i]; j++) {\n between.insert(s[j]);\n }\n \n ans += between.size();\n }\n \n return ans;\n }\n};\n\n\n```\n```C []\nstruct Solution {\n int countPalindromicSubsequence(char *s) {\n int first[26], last[26];\n for (int i = 0; i < 26; ++i) {\n first[i] = -1;\n last[i] = -1;\n }\n \n int i = 0;\n while (s[i] != \'\\0\') {\n int curr = s[i] - \'a\';\n if (first[curr] == -1) {\n first[curr] = i;\n }\n last[curr] = i;\n ++i;\n }\n \n int ans = 0;\n for (int i = 0; i < 26; ++i) {\n if (first[i] == -1) {\n continue;\n }\n \n int between[26] = {0};\n for (int j = first[i] + 1; j < last[i]; ++j) {\n between[s[j] - \'a\'] = 1;\n }\n \n int count = 0;\n for (int j = 0; j < 26; ++j) {\n count += between[j];\n }\n \n ans += count;\n }\n \n return ans;\n }\n};\n\n\n\n\n```\n```Java []\n\n\n\nclass Solution {\n public int countPalindromicSubsequence(String s) {\n int[] first = new int[26];\n int[] last = new int[26];\n Arrays.fill(first, -1);\n Arrays.fill(last, -1);\n\n for (int i = 0; i < s.length(); i++) {\n int curr = s.charAt(i) - \'a\';\n if (first[curr] == -1) {\n first[curr] = i;\n }\n last[curr] = i;\n }\n\n int ans = 0;\n for (int i = 0; i < 26; i++) {\n if (first[i] == -1) {\n continue;\n }\n Set<Character> between = new HashSet<>();\n for (int j = first[i] + 1; j < last[i]; j++) {\n between.add(s.charAt(j));\n }\n ans += between.size();\n }\n\n return ans;\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n first = [-1] * 26\n last = [-1] * 26\n\n for i in range(len(s)):\n curr = ord(s[i]) - ord(\'a\')\n if first[curr] == -1:\n first[curr] = i\n last[curr] = i\n\n ans = 0\n for i in range(26):\n if first[i] == -1:\n continue\n between = set(s[first[i] + 1:last[i]])\n ans += len(between)\n\n return ans\n\n\n```\n```javascript []\nvar countPalindromicSubsequence = function(s) {\n let first = new Array(26).fill(-1);\n let last = new Array(26).fill(-1);\n\n for (let i = 0; i < s.length; i++) {\n let curr = s.charCodeAt(i) - \'a\'.charCodeAt(0);\n if (first[curr] === -1) {\n first[curr] = i;\n }\n last[curr] = i;\n }\n\n let ans = 0;\n for (let i = 0; i < 26; i++) {\n if (first[i] === -1) {\n continue;\n }\n let between = new Set(s.slice(first[i] + 1, last[i]));\n ans += between.size;\n }\n\n return ans;\n};\n\n\n```\n\n---\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
[Python, Rust] Elegant & Short | O(n) | 99.67% Faster | Left & Right Index | unique-length-3-palindromic-subsequences | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```python []\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n subsequences = 0\n\n for c in ascii_lowercase:\n left, right = s.find(c), s.rfind(c)\n if left != right:\n subsequences += len(set(s[left + 1:right]))\n\n return subsequences\n```\n```rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn count_palindromic_subsequence(s: String) -> i32 {\n let mut subsequences: i32 = 0;\n\n for c in b\'a\'..=b\'z\' {\n let c_char = c as char;\n\n if let (Some(left), Some(right)) = (s.find(c_char), s.rfind(c_char)) {\n if left != right {\n let subsequence_set: HashSet<_> = s[left + 1..right].chars().collect();\n subsequences += subsequence_set.len() as i32;\n }\n }\n }\n\n subsequences\n }\n}\n```\n\n# Results\n\n | 2 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Python3 Solution | unique-length-3-palindromic-subsequences | 0 | 1 | \n```\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n ans=0\n for i in range(0,26):\n c=chr(i+ord(\'a\'))\n if c in s:\n first=s.index(c)\n last=s.rindex(c)\n if first!=last:\n u=set()\n for index in range(first+1,last):\n u.add(s[index])\n ans+=len(u)\n return ans \n``` | 2 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Easy Solution with intuition in C++ and Python | unique-length-3-palindromic-subsequences | 0 | 1 | # Intuition\nWe only need palindromic subsequences of length three. Which means the first and last characters will be same and there is only one other character in between them. Our job is to find if two characters are same from the left and right end and if they are, add the unique characters (which will form unique palindromic subsequences) in between them to our result.\n\n# Approach\n1. Create two vectors to store the first occurence from left and first occurence from right.\n2. Traverse through the string and get the first occurence from left and right for each character.\n3. For every character, if the left and right occurences are different, then the character appears more than once.\n4. Go to every character, if its left and right most occurences are different, then add the characters between them into a set(to get the unique characters).\n5. Add the size of the set to the result and clear the set for next iteration.\n\n# Complexity\n- Time complexity:\nO(n) because we traverse the string a fixed number of times.\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int countPalindromicSubsequence(string s) {\n set<char> st;\n vector<int> leftmost(26,INT_MAX);\n vector<int> rightmost(26,0);\n for(int i=0;i<s.length();i++){\n leftmost[s[i]-\'a\']=min(leftmost[s[i]-\'a\'],i);\n rightmost[s[i]-\'a\']=i;\n }\n int res=0;\n for(int i=0;i<26;i++){\n if(leftmost[i]>rightmost[i]){\n int firstoccurence=leftmost[i];\n int lastoccurence=rightmost[i];\n for(int j=firstoccurence+1;j<lastoccurence;j++){\n st.insert(s[j]);\n }\n res+=st.size();\n st.clear();\n }\n }\n return res;\n }\n};\n\n```\n# Python \n```\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n st = set()\n leftmost = [1e5]*26\n rightmost = [0] * 26\n\n for i in range(len(s)):\n leftmost[ord(s[i]) - ord(\'a\')] = min(leftmost[ord(s[i]) - ord(\'a\')], i)\n rightmost[ord(s[i]) - ord(\'a\')] = i\n\n res = 0\n\n for i in range(26):\n if leftmost[i] < rightmost[i]:\n first_occurrence = leftmost[i]\n last_occurrence = rightmost[i]\n for j in range(first_occurrence + 1, last_occurrence):\n st.add(s[j])\n res += len(st)\n st.clear()\n\n return res\n\n``` | 1 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Go/Python/JavaScript/Java O(n) time | O(1) space | unique-length-3-palindromic-subsequences | 1 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc countPalindromicSubsequence(s string) int {\n pos := make(map[rune][]int)\n for i,letter := range(s){\n if _,ok := pos[letter]; !ok{\n pos[letter] = []int{i,i}\n }else{\n pos[letter][1] = i\n }\n }\n \n answer := 0\n for _,pair := range(pos){\n left := pair[0]\n right := pair[1]\n counter := make(map[byte]bool)\n for i:=left+1;i<right;i++{\n counter[s[i]] = true\n }\n answer+=len(counter)\n }\n return answer\n}\n```\n```python []\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n pos = {}\n for i,letter in enumerate(s):\n if letter not in pos:\n pos[letter] = [i,i]\n else:\n pos[letter][1] = i\n \n answer = 0\n for left,right in pos.values():\n counter = set()\n for i in range(left+1,right):\n counter.add(s[i])\n answer+=len(counter)\n\n return answer\n```\n```javascript []\n/**\n * @param {string} s\n * @return {number}\n */\nvar countPalindromicSubsequence = function(s) {\n let pos = new Map()\n for (let i=0;i<s.length;i++){\n let letter = s.charAt(i)\n if (!pos.has(letter)){\n pos.set(letter, [i,i])\n }else{\n pos.get(letter)[1] = i\n }\n }\n \n let answer = 0\n for (let [left,right] of pos.values()){\n let counter = new Set()\n for (i=left+1;i<right;i++){\n counter.add(s.charAt(i))\n }\n answer+=counter.size\n }\n return answer\n};\n```\n```java []\nclass Solution {\n public int countPalindromicSubsequence(String s) {\n HashMap<Character,int[]> pos = new HashMap<>();\n for (int i=0;i<s.length();i++){\n char letter = s.charAt(i);\n if (!pos.containsKey(letter)){\n pos.put(letter, new int[]{i,i});\n }else{\n pos.get(letter)[1] = i;\n }\n }\n \n int answer = 0;\n for (int[] value : pos.values()){\n int left = value[0];\n int right = value[1];\n HashSet<Character> counter = new HashSet<>();\n for (int i=left+1;i<right;i++){\n counter.add(s.charAt(i));\n }\n answer+=counter.size();\n }\n return answer;\n }\n}\n```\n\n# Bitwise mask\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n n = len(s)\n\n pref = [0 for _ in range(n)]\n pref[0] = 1<<ord(s[0])-97\n for i in range(1,n):\n pref[i] = pref[i-1] | 1<<ord(s[i])-97\n\n suff = [0 for _ in range(n)]\n suff[n-1] = 1<<ord(s[n-1])-97\n for i in range(n-2,-1,-1):\n suff[i] = suff[i+1] | 1<<ord(s[i])-97\n \n bits = defaultdict(int)\n\n for i in range(1,n-1):\n letter = s[i]\n bits[letter] |= pref[i-1]&suff[i+1]\n\n answer = 0\n for _,value in bits.items():\n answer+=value.bit_count()\n\n return answer\n``` | 2 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
Python Solution | unique-length-3-palindromic-subsequences | 0 | 1 | # Approach\nTry to find the starting index and ending index of each letter and try to find the unique element between the indexes and add the that to the result this gives you the solution.\n\n# Code\n```\nclass Solution:\n def countPalindromicSubsequence(self, s: str) -> int:\n d=dict()\n for i in range(len(s)):\n if s[i] in d.keys():\n l=d.get(s[i])\n l[1]=i\n d[s[i]]=l\n else:\n d[s[i]]=[i,i]\n res=0\n for y in d.values():\n st=set()\n for j in range(y[0]+1,y[1]):\n st.add(s[j])\n res+=len(st)\n return res\n``` | 1 | Given a string `s`, return _the number of **unique palindromes of length three** that are a **subsequence** of_ `s`.
Note that even if there are multiple ways to obtain the same subsequence, it is still only counted **once**.
A **palindrome** is a string that reads the same forwards and backwards.
A **subsequence** of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.
* For example, `"ace "` is a subsequence of `"abcde "`.
**Example 1:**
**Input:** s = "aabca "
**Output:** 3
**Explanation:** The 3 palindromic subsequences of length 3 are:
- "aba " (subsequence of "aabca ")
- "aaa " (subsequence of "aabca ")
- "aca " (subsequence of "aabca ")
**Example 2:**
**Input:** s = "adc "
**Output:** 0
**Explanation:** There are no palindromic subsequences of length 3 in "adc ".
**Example 3:**
**Input:** s = "bbcbaba "
**Output:** 4
**Explanation:** The 4 palindromic subsequences of length 3 are:
- "bbb " (subsequence of "bbcbaba ")
- "bcb " (subsequence of "bbcbaba ")
- "bab " (subsequence of "bbcbaba ")
- "aba " (subsequence of "bbcbaba ")
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of only lowercase English letters. | If you can make the first x values and you have a value v, then you can make all the values ≤ v + x Sort the array of coins. You can always make the value 0 so you can start with x = 0. Process the values starting from the smallest and stop when there is a value that cannot be achieved with the current x. |
O(1) time | O(1) space | solution explained | check-if-move-is-legal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA move is legal if after changing the color of the cell, the cell becomes the end point of a good line. \n\nA line can be vertical, horizontal, or diagonal. A line is a good line if:\n- has at least 3 blocks/cells\n- starting and ending cells are of the same color\n- starting or ending consecutive cells are not of the same color\n- has no empty cell\n\nExplore all directions for the move and search for a good line.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- create a list and add all eight directions (bottom, top, right, left, bottom right, bottom left, top right, top left)\n- explore all directions to check all lines \nfor each direction (x, y)\n - set size = 2 to track cells in the current line\n - get coordinates (row, column) of the current cell in the current line\n set r = input move row number + x, c = input move column number + y\n - loop to check all cells in a line (max can be 8 because it is an 8 x 8 matrix)\n while indices are inbound\n - if the current cell is empty, the current line is not good, break the while loop to check the next line\n - if the current line size is 2, the current cell is consecutive. If it is of the same color as the move cell, the line is not good, break\n - else the current cell is not consecutive, if it is of the same color, we found a good line, return true\n - increment row and column to check the next cell in the line\n - increment size of the line\n- if the loop completes without returning true, there\'s no good line, the move is illegal, return false\n\n# Complexity\n- Time complexity: O(directions * cells) \u2192 O(8 * 8) \u2192 O(64) \u2192 O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(directions list) \u2192 O(rows * columns) \u2192 O(8 * 2) \u2192 O(16) \u2192 O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def checkMove(self, board: List[List[str]], rMove: int, cMove: int, color: str) -> bool:\n irections = [[1, 0], [-1, 0], [0, 1], [0, -1], \n [1, 1], [1, -1], [-1, 1], [-1, -1]]\n for x, y in directions:\n size = 2\n r = rMove + x\n c = cMove + y\n while 0 <= r < 8 and 0 <= c < 8:\n if board[r][c] == \'.\':\n break\n if size == 2 and board[r][c] == color:\n break\n if board[r][c] == color:\n return True\n r += x\n c += y\n size += 1\n return False\n\n\n``` | 0 | You are given a **0-indexed** `8 x 8` grid `board`, where `board[r][c]` represents the cell `(r, c)` on a game board. On the board, free cells are represented by `'.'`, white cells are represented by `'W'`, and black cells are represented by `'B'`.
Each move in this game consists of choosing a free cell and changing it to the color you are playing as (either white or black). However, a move is only **legal** if, after changing it, the cell becomes the **endpoint of a good line** (horizontal, vertical, or diagonal).
A **good line** is a line of **three or more cells (including the endpoints)** where the endpoints of the line are **one color**, and the remaining cells in the middle are the **opposite color** (no cells in the line are free). You can find examples for good lines in the figure below:
Given two integers `rMove` and `cMove` and a character `color` representing the color you are playing as (white or black), return `true` _if changing cell_ `(rMove, cMove)` _to color_ `color` _is a **legal** move, or_ `false` _if it is not legal_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ "W ", "B ", "B ", ". ", "W ", "W ", "W ", "B "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\]\], rMove = 4, cMove = 3, color = "B "
**Output:** true
**Explanation:** '.', 'W', and 'B' are represented by the colors blue, white, and black respectively, and cell (rMove, cMove) is marked with an 'X'.
The two good lines with the chosen cell as an endpoint are annotated above with the red rectangles.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "B ", ". ", ". ", "W ", ". ", ". ", ". "\],\[ ". ", ". ", "W ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", "B ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", "B ", "W ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", "W ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", "B "\]\], rMove = 4, cMove = 4, color = "W "
**Output:** false
**Explanation:** While there are good lines with the chosen cell as a middle cell, there are no good lines with the chosen cell as an endpoint.
**Constraints:**
* `board.length == board[r].length == 8`
* `0 <= rMove, cMove < 8`
* `board[rMove][cMove] == '.'`
* `color` is either `'B'` or `'W'`. | null |
Best Python3 Solution. Beats 50% | check-if-move-is-legal | 0 | 1 | Just Enumerate all possible directions\n\n# Code\n```\nclass Solution:\n def checkMove(self, board: List[List[str]], rMove: int, cMove: int, color: str) -> bool:\n m=len(board)\n n=len(board[0])\n \n lin=[[0,1],[0,-1],[1,0],[-1,0],[1,1],[-1,1],[-1,-1],[1,-1]]\n\n def other(x):\n if x==\'W\':\n return \'B\'\n if x==\'B\':\n return \'W\'\n\n def valid(i,j):\n if i<0 or j<0 or i==m or j==n:\n return False\n return True\n \n final=0\n for i in lin:\n x,y=rMove,cMove\n c=1\n while valid(x+i[0],y+i[1]) and board[x+i[0]][y+i[1]]==other(color):\n x+=i[0]\n y+=i[1]\n c+=1\n \n if not valid(x+i[0],y+i[1]):\n continue\n if board[x+i[0]][y+i[1]]==color:\n c+=1\n if c>=3:\n return True\n return False\n\n \n\n\n \n``` | 0 | You are given a **0-indexed** `8 x 8` grid `board`, where `board[r][c]` represents the cell `(r, c)` on a game board. On the board, free cells are represented by `'.'`, white cells are represented by `'W'`, and black cells are represented by `'B'`.
Each move in this game consists of choosing a free cell and changing it to the color you are playing as (either white or black). However, a move is only **legal** if, after changing it, the cell becomes the **endpoint of a good line** (horizontal, vertical, or diagonal).
A **good line** is a line of **three or more cells (including the endpoints)** where the endpoints of the line are **one color**, and the remaining cells in the middle are the **opposite color** (no cells in the line are free). You can find examples for good lines in the figure below:
Given two integers `rMove` and `cMove` and a character `color` representing the color you are playing as (white or black), return `true` _if changing cell_ `(rMove, cMove)` _to color_ `color` _is a **legal** move, or_ `false` _if it is not legal_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ "W ", "B ", "B ", ". ", "W ", "W ", "W ", "B "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\]\], rMove = 4, cMove = 3, color = "B "
**Output:** true
**Explanation:** '.', 'W', and 'B' are represented by the colors blue, white, and black respectively, and cell (rMove, cMove) is marked with an 'X'.
The two good lines with the chosen cell as an endpoint are annotated above with the red rectangles.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "B ", ". ", ". ", "W ", ". ", ". ", ". "\],\[ ". ", ". ", "W ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", "B ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", "B ", "W ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", "W ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", "B "\]\], rMove = 4, cMove = 4, color = "W "
**Output:** false
**Explanation:** While there are good lines with the chosen cell as a middle cell, there are no good lines with the chosen cell as an endpoint.
**Constraints:**
* `board.length == board[r].length == 8`
* `0 <= rMove, cMove < 8`
* `board[rMove][cMove] == '.'`
* `color` is either `'B'` or `'W'`. | null |
🧐 Try 8 possible directions | check-if-move-is-legal | 0 | 1 | # Intuition\nThe cell `board[rMove][cMove]` should be one of the endpoints, so we just try all possible paths(vertical, horizontal, and diagonal). There are 8 possible directions in total.\n\nAnd we **maintain an invariant that** - we only add the cell with opposite color along the direction.\n\n| go top-left | go up | go top-right |\n| -------------- | ---------------- | --------------- |\n| go left | `(rMove, cMove)` | go right |\n| go bottom-left | go down | go bottom-right |\n\n# Code\n```\nclass Solution:\n def checkMove(self, board: List[List[str]], rMove: int, cMove: int, color: str) -> bool:\n def collect(dx: int, dy: int):\n """Return true if we find a good line"""\n path = [board[rMove][cMove]]\n\n x, y = rMove, cMove\n while 0 <= x < m and 0 <= y < n:\n x += dx\n y += dy\n\n # case 1. we are out of bounds before we find a good line\n if x < 0 or x >= m or y < 0 or y >= n:\n return False\n # case 2. we meet a free cell before we find a good line\n if board[x][y] == ".":\n return False\n # case 3. we find (x, y) and (rMove, cMove) have same color\n # , let\'s check the length\n if board[x][y] == board[rMove][cMove]:\n if len(path) < 2:\n # do not need to go further because all cells in the middle\n # should be the oppsite color\n return False\n else:\n return True\n else:\n # invariant: we only add the opposite color\n path.append(board[x][y])\n return True\n\n m, n = len(board), len(board[0])\n board[rMove][cMove] = color\n for dx, dy in [\n (-1, -1),\n (-1, 0),\n (-1, 1),\n (0, 1),\n (0, -1),\n (1, -1),\n (1, 0),\n (1, 1),\n ]:\n if collect(dx, dy):\n return True\n return False\n\n\n``` | 0 | You are given a **0-indexed** `8 x 8` grid `board`, where `board[r][c]` represents the cell `(r, c)` on a game board. On the board, free cells are represented by `'.'`, white cells are represented by `'W'`, and black cells are represented by `'B'`.
Each move in this game consists of choosing a free cell and changing it to the color you are playing as (either white or black). However, a move is only **legal** if, after changing it, the cell becomes the **endpoint of a good line** (horizontal, vertical, or diagonal).
A **good line** is a line of **three or more cells (including the endpoints)** where the endpoints of the line are **one color**, and the remaining cells in the middle are the **opposite color** (no cells in the line are free). You can find examples for good lines in the figure below:
Given two integers `rMove` and `cMove` and a character `color` representing the color you are playing as (white or black), return `true` _if changing cell_ `(rMove, cMove)` _to color_ `color` _is a **legal** move, or_ `false` _if it is not legal_.
**Example 1:**
**Input:** board = \[\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\],\[ "W ", "B ", "B ", ". ", "W ", "W ", "W ", "B "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "B ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", ". ", ". ", ". ", ". "\]\], rMove = 4, cMove = 3, color = "B "
**Output:** true
**Explanation:** '.', 'W', and 'B' are represented by the colors blue, white, and black respectively, and cell (rMove, cMove) is marked with an 'X'.
The two good lines with the chosen cell as an endpoint are annotated above with the red rectangles.
**Example 2:**
**Input:** board = \[\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", "B ", ". ", ". ", "W ", ". ", ". ", ". "\],\[ ". ", ". ", "W ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", "W ", "B ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", "B ", "W ", ". ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", "W ", ". "\],\[ ". ", ". ", ". ", ". ", ". ", ". ", ". ", "B "\]\], rMove = 4, cMove = 4, color = "W "
**Output:** false
**Explanation:** While there are good lines with the chosen cell as a middle cell, there are no good lines with the chosen cell as an endpoint.
**Constraints:**
* `board.length == board[r].length == 8`
* `0 <= rMove, cMove < 8`
* `board[rMove][cMove] == '.'`
* `color` is either `'B'` or `'W'`. | null |
[c++ & Python] short and concise | find-greatest-common-divisor-of-array | 0 | 1 | \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n + log(phi)(min(min, max)))$$\n the log one is of Euclidean Algorithm for GCD\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# C++\n```\nclass Solution {\npublic:\n int findGCD(vector<int>& nums) {\n int min = nums[0], maxy = nums[0];\n for(auto i : nums) {\n if(i < min) min = i;\n if(i > maxy) maxy = i;\n }\n // GCD of min and max\n // Euclidean algorithm\n while(min && maxy) {\n if(maxy > min) maxy %= min;\n else min %= maxy;\n }\n return max(maxy, min);\n }\n};\n```\n\n# Python / Python3\n```\nclass Solution:\n def findGCD(self, nums: List[int]) -> int:\n min = max = nums[0]\n for i in nums:\n if i < min:\n min = i\n if i > max:\n max = i\n \n # GCD of min and max\n # Euclidean Algorithm\n while max and min:\n if max > min:\n max %= min\n else:\n min %= max\n return max if max > min else min\n``` | 1 | Given an integer array `nums`, return _the **greatest common divisor** of the smallest number and largest number in_ `nums`.
The **greatest common divisor** of two numbers is the largest positive integer that evenly divides both numbers.
**Example 1:**
**Input:** nums = \[2,5,6,9,10\]
**Output:** 2
**Explanation:**
The smallest number in nums is 2.
The largest number in nums is 10.
The greatest common divisor of 2 and 10 is 2.
**Example 2:**
**Input:** nums = \[7,5,6,8,3\]
**Output:** 1
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 8.
The greatest common divisor of 3 and 8 is 1.
**Example 3:**
**Input:** nums = \[3,3\]
**Output:** 3
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 3.
The greatest common divisor of 3 and 3 is 3.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | Try to use as much of the range of a person who is "it" as possible. Find the leftmost person who is "it" that has not caught anyone yet, and the leftmost person who is not "it" that has not been caught yet. If the person who is not "it" can be caught, pair them together and repeat the process. If the person who is not "it" cannot be caught, and the person who is not "it" is on the left of the person who is "it", find the next leftmost person who is not "it". If the person who is not "it" cannot be caught, and the person who is "it" is on the left of the person who is not "it", find the next leftmost person who is "it". |
Simple Python Solution ||O(N) | find-greatest-common-divisor-of-array | 0 | 1 | Time Complexcity O(N)\nSpace complexcity O(1)\n```\nclass Solution:\n def findGCD(self, nums: List[int]) -> int:\n m=max(nums)\n n=min(nums)\n ans=1\n for i in range(2,n+1):\n print(i)\n if m%i==0 and n%i==0:\n ans=i\n return ans\n``` | 1 | Given an integer array `nums`, return _the **greatest common divisor** of the smallest number and largest number in_ `nums`.
The **greatest common divisor** of two numbers is the largest positive integer that evenly divides both numbers.
**Example 1:**
**Input:** nums = \[2,5,6,9,10\]
**Output:** 2
**Explanation:**
The smallest number in nums is 2.
The largest number in nums is 10.
The greatest common divisor of 2 and 10 is 2.
**Example 2:**
**Input:** nums = \[7,5,6,8,3\]
**Output:** 1
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 8.
The greatest common divisor of 3 and 8 is 1.
**Example 3:**
**Input:** nums = \[3,3\]
**Output:** 3
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 3.
The greatest common divisor of 3 and 3 is 3.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | Try to use as much of the range of a person who is "it" as possible. Find the leftmost person who is "it" that has not caught anyone yet, and the leftmost person who is not "it" that has not been caught yet. If the person who is not "it" can be caught, pair them together and repeat the process. If the person who is not "it" cannot be caught, and the person who is not "it" is on the left of the person who is "it", find the next leftmost person who is not "it". If the person who is not "it" cannot be caught, and the person who is "it" is on the left of the person who is not "it", find the next leftmost person who is "it". |
Python3 || 1 lined beginner solution || Beats 81.80%. | find-greatest-common-divisor-of-array | 0 | 1 | # Code\n```\nclass Solution:\n def findGCD(self, nums: List[int]) -> int:\n return gcd(min(nums),max(nums))\n\n```\n# Please upvote if you find the solution helpful.\uD83D\uDE4F | 3 | Given an integer array `nums`, return _the **greatest common divisor** of the smallest number and largest number in_ `nums`.
The **greatest common divisor** of two numbers is the largest positive integer that evenly divides both numbers.
**Example 1:**
**Input:** nums = \[2,5,6,9,10\]
**Output:** 2
**Explanation:**
The smallest number in nums is 2.
The largest number in nums is 10.
The greatest common divisor of 2 and 10 is 2.
**Example 2:**
**Input:** nums = \[7,5,6,8,3\]
**Output:** 1
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 8.
The greatest common divisor of 3 and 8 is 1.
**Example 3:**
**Input:** nums = \[3,3\]
**Output:** 3
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 3.
The greatest common divisor of 3 and 3 is 3.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | Try to use as much of the range of a person who is "it" as possible. Find the leftmost person who is "it" that has not caught anyone yet, and the leftmost person who is not "it" that has not been caught yet. If the person who is not "it" can be caught, pair them together and repeat the process. If the person who is not "it" cannot be caught, and the person who is not "it" is on the left of the person who is "it", find the next leftmost person who is not "it". If the person who is not "it" cannot be caught, and the person who is "it" is on the left of the person who is not "it", find the next leftmost person who is "it". |
Math solution Python MAANG | find-greatest-common-divisor-of-array | 0 | 1 | # Intuition\nFor finding GCD we can use math formula: a * b // lcd(a, b)\n\n# Approach\nInitially finding min and max values in array. Then find LCD and return answer.\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n# Code\n```\nclass Solution:\n def findGCD(self, nums: List[int]) -> int:\n mi, ma = float(\'inf\'), 0\n for i in nums:\n if i > ma:\n ma = i\n if i < mi:\n mi = i\n lcd = 1\n while True:\n if ma * lcd % mi == 0:\n lcd *= ma\n break\n lcd += 1\n return ma * mi // lcd\n``` | 2 | Given an integer array `nums`, return _the **greatest common divisor** of the smallest number and largest number in_ `nums`.
The **greatest common divisor** of two numbers is the largest positive integer that evenly divides both numbers.
**Example 1:**
**Input:** nums = \[2,5,6,9,10\]
**Output:** 2
**Explanation:**
The smallest number in nums is 2.
The largest number in nums is 10.
The greatest common divisor of 2 and 10 is 2.
**Example 2:**
**Input:** nums = \[7,5,6,8,3\]
**Output:** 1
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 8.
The greatest common divisor of 3 and 8 is 1.
**Example 3:**
**Input:** nums = \[3,3\]
**Output:** 3
**Explanation:**
The smallest number in nums is 3.
The largest number in nums is 3.
The greatest common divisor of 3 and 3 is 3.
**Constraints:**
* `2 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000` | Try to use as much of the range of a person who is "it" as possible. Find the leftmost person who is "it" that has not caught anyone yet, and the leftmost person who is not "it" that has not been caught yet. If the person who is not "it" can be caught, pair them together and repeat the process. If the person who is not "it" cannot be caught, and the person who is not "it" is on the left of the person who is "it", find the next leftmost person who is not "it". If the person who is not "it" cannot be caught, and the person who is "it" is on the left of the person who is not "it", find the next leftmost person who is "it". |
C++/Python bit Manip vs Cantor method||0ms beats 100%||w Math proof | find-unique-binary-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nHere are 2 methods, 3 C++ & 1 python solutions, provided.\nOne is very standard. Define a function `int toInt(string& nums)` converting a binary string to its int number `x`.\n\nThere are numbers for choice, say `[0, 1,..., 2**len-1]`. \nSet a boolean array `hasX` to store the status whether number `x` is already in `nums`.\n\nFinally find any number `N` which is not in `nums`, and convert it to the desired binary string. \n\nA variant using bitset & C++ string::substr is also provided.\n# Cantor\'s Diagonal Approach\n<!-- Describe your approach to solving the problem. -->\n[I give a Math proof in this film on Cantor\'s diagonal mehod. Please turn on English subtitles if necessary]\n[https://youtu.be/0iFR8nafMWE?si=AFOy4iBrd0TVQKul](https://youtu.be/0iFR8nafMWE?si=AFOy4iBrd0TVQKul)\nCantor diagonal argument is the learning stuff for the set theory, purely math. But it can be applied for solving this question. Quite amazing.\n\n2nd method is using the Cantor diagonal argument. This argument I learned from the set theory & advanced Calculus. It is used for proving that the set of real numbers is uncountable. Of course, a Math argument.\n\nA python version is also provided.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(len*n)$$\nCantor method $O(n)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(len)$\nCantor method extra space $O(1)$ \n# Code\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int len;\n int toInt(string& nums){\n int x=0;\n #pragma unroll\n for(char c: nums){\n x=(x<<1)+(c-\'0\');\n }\n return x;\n }\n string findDifferentBinaryString(vector<string>& nums) {\n len=nums[0].size();\n vector<bool> hasX(1<<len, 0);\n\n #pragma unroll \n for(auto& x: nums)\n hasX[toInt(x)]=1;\n int N=0;//find N\n\n #pragma unroll\n for(; N<(1<<len) && hasX[N]; N++);\n // cout<<N<<endl;\n string ans=string(len, \'0\');\n\n #pragma unroll\n for(int i=len-1; i>=0 && N>0; i--){\n ans[i]=(N&1)+\'0\';\n N>>=1;\n }\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Code using bitset & substr\n```\nclass Solution {\npublic:\n string findDifferentBinaryString(vector<string>& nums) {\n const int len=nums[0].size();\n vector<bool> hasX(1<<len, 0);\n\n #pragma unroll \n for(auto& x: nums)\n hasX[bitset<16>(x).to_ulong()]=1;\n int N=0;//find N\n\n #pragma unroll\n for(; N<(1<<len) && hasX[N]; N++);\n // cout<<N<<endl;\n return bitset<16>(N).to_string().substr(16-len,len);\n }\n};\n```\n# Cantor diagonal argument runs in 0ms\n```\n// Use Cantor argument\n// Cantor argument is used to prove that the set of real numbers\n// is uncountable\n// I think that it is the learning stuff for set theory or \n// advanced calculus, pure Math\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n string findDifferentBinaryString(vector<string>& nums) {\n int n=nums.size(), len=nums[0].size();\n string ans=string(len, \'1\');\n #pragma unroll\n for(int i=0; i<n; i++)\n ans[i]=(\'1\'-nums[i][i])+\'0\';\n return ans;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Python code\n```\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n n=len(nums[0])\n ans=[\'0\']*n\n for i, x in enumerate(nums):\n if x[i]==\'0\':\n ans[i]=\'1\'\n else:\n ans[i]=\'0\'\n return "".join(ans)\n \n```\n\n\nSuppose that the real number within $[0,1)$ was countable many. All numbers are expressed in therir binary expansion.\n\nSo, list them as $a_0, a_1,\\cdots, a_n,\\cdots$.\nConstruct a number $ans=0.x_0x_1\\cdots x_n\\cdots$ with $x_i=1-a_{ii}$\n\nThen $ans\\not=a_i \\forall i$. $ans$ can not be in the list. A contradiction.\n | 9 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
Elegant, greedy, short | find-unique-binary-string | 0 | 1 | # Approach\nGiven an array nums consisting of binary strings, we need to find a binary string that differs from all the binary strings in the array. We can achieve this by iterating through each position in the binary strings and flipping the bit at that position. This will ensure that the resulting binary string is different from each binary string in the array. \n\n### why?\nBecause `len(nums) == len(nums[i])`\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```py\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n res = []\n for i in range(len(nums)):\n if nums[i][i] == \'1\':\n res.append(\'0\')\n else:\n res.append(\'1\')\n return "".join(res)\n```\nplease upvote :D | 22 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
【Video】Give me 7 minutes - How we think about a solution | find-unique-binary-string | 1 | 1 | # Intuition\nConvert input strings to integer.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/tJ_Eu2S4334\n\n\u25A0 Timeline of the video\n\n`0:04` Explain a key point of the question\n`1:39` Why you need to iterate through input array with len(nums) + 1?\n`2:25` Coding\n`3:56` Explain part of my solution code.\n`3:08` What if we have a lot of the same numbers in input array?\n`6:11` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,123\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n\n### How we think about a solution\n\nBefore I explain my solution, I don\'t take this solution. This is a smart solution but probably nobody will come up with this solution in such a short real interview, if you don\'t know "Cantor\'s diagonal argument". We need a [mathematical proof](https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument) if you use it in the interviews. At least I didn\'t come up with it.\n\n```\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n ans = []\n for i in range(len(nums)):\n curr = nums[i][i]\n ans.append("1" if curr == "0" else "0")\n \n return "".join(ans)\n```\n\nLet\'s talk about another solution.\n\nMy idea is simply to convert binary strings to decimal, because creating and comparing decimal numbers is easier than creating and comparing binary strings, especially creating. For example, we get `"00"` as a `0` of binary string. Typical biarny is just `0`, so we need to add `0` until we meet length of `n`. It\'s time comsuming and complicated.\n\n```\nInput: nums = ["00","01"]\n```\nConvert the binary strings to decimal\n```\n"00" \u2192 0\n"01" \u2192 1\n\nset = {0, 1}\n```\nThen iterate through decimal numbers from `0` to `len(nums) + 1`.\n\nLet\'s start.\n\n```\nWe have 0 in set.\nWe have 1 in set.\nWe don\'t have 2 in set.\n```\nThen we need to convert `2` to a binary string\n```\nOutput: "10"\n```\n\n### Why len(nums) + 1?\n\nThe description says "Given an array of strings nums containing n unique binary strings each of length n".\n\nSo all possible answers of binary string for the input array should be `00`,`01`, `10`, `11`. but we have the first two numbers of binary strings(= 0, 1).\n\nThere are cases where we already have the first a few numbers. In that case, we need to find larger number than length of input. In this case, `2` or `3`. \n\n`+1` enables us to find a output definitely.\n\n### What if the first answer we found is `0` or `1`?\n\n```\nInput: nums = ["00","11"]\n```\nSince we iterate through from `0` to `len(nums) + 1`, the output should be\n```\nOutput: "01"\n```\nThis is a binary list.\n```\ndecimal \u2192 binary\n\n0 \u2192 0\n1 \u2192 1\n2 \u2192 10\n3 \u2192 11\n```\nWe found `1` as a output. If we return binary string of `1`, we will return `"1"`. But for this question, we need to fill blanks with `0`, because length of output is also length of `n`.\n\nLook at this Python code.\n```\nreturn bin(i)[2:].zfill(n) \n```\n`zfill` is build-in function to fill the blanks with `0`. The reason why we start from `[2:]` is that when we convert decimal to binary with bin function, there is some prefix which we don\'t need this time. `[2:]` enables us to remove the first two chracters then `zfill` function will fill the blanks with `0` until we reach length of `n`.\n\nEasy! \uD83D\uDE04\nLet\'s see a real algorithm!\n\n---\n\n\n### Algorithm Overview:\n\nConvert input strings to integer, then compare one by one.\n\n### Detailed Explanation:\n\n1. **Initialize an empty set `seen`:**\n - `seen` is a set to store integers that have been encountered.\n\n ```python\n seen = set()\n ```\n\n2. **Convert each binary string in `nums` to an integer and add to `seen`:**\n - Iterate through each binary string in `nums`, convert it to an integer in base 2, and add it to the `seen` set.\n\n ```python\n for binary_string in nums:\n seen.add(int(binary_string, 2))\n ```\n\n3. **Get the length `n` of the binary strings:**\n - Utilize the fact that all binary strings in `nums` have the same length to get the value of `n`.\n\n ```python\n n = len(nums[0])\n ```\n\n4. **Inspect integers from 0 to `len(nums)`:**\n - Loop `len(nums) + 1` times to inspect integers from 0 to `len(nums)`.\n\n ```python\n for i in range(len(nums) + 1):\n ```\n\n5. **If the integer is not in the `seen` set:**\n - If `i` is not in the `seen` set (not encountered yet), generate a new binary string representation and return it.\n\n ```python\n if i not in seen:\n return bin(i)[2:].zfill(n)\n ```\n\nIn the end, find the first integer not present in the `seen` set, convert it to a binary string, and return it.\n\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\nIterate through input array n times and fill the blank with n times at most. But $$O(n^2)$$ will happen only when we found the answer number. For the most part, we have $$O(n)$$ time.\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n\n seen = set()\n\n for binary_string in nums:\n seen.add(int(binary_string, 2))\n\n n = len(nums[0])\n\n for i in range(len(nums) + 1):\n if i not in seen:\n return bin(i)[2:].zfill(n) \n```\n```javascript []\nvar findDifferentBinaryString = function(nums) {\n const seen = new Set();\n\n for (const binaryString of nums) {\n seen.add(parseInt(binaryString, 2));\n }\n\n const n = nums[0].length;\n\n for (let i = 0; i <= nums.length; i++) {\n if (!seen.has(i)) {\n return i.toString(2).padStart(n, \'0\');\n }\n } \n};\n```\n```java []\nclass Solution {\n public String findDifferentBinaryString(String[] nums) {\n HashSet<Integer> seen = new HashSet<>();\n\n for (String binaryString : nums) {\n seen.add(Integer.parseInt(binaryString, 2));\n }\n\n int n = nums[0].length();\n\n for (int i = 0; i <= n; i++) {\n if (!seen.contains(i)) {\n StringBuilder binaryStringBuilder = new StringBuilder(Integer.toBinaryString(i));\n while (binaryStringBuilder.length() < n) {\n binaryStringBuilder.insert(0, \'0\');\n }\n return binaryStringBuilder.toString();\n }\n }\n\n return ""; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string findDifferentBinaryString(vector<string>& nums) {\n unordered_set<int> seen;\n\n for (const auto& binaryString : nums) {\n seen.insert(stoi(binaryString, nullptr, 2));\n }\n\n int n = nums[0].length();\n\n for (int i = 0; i <= nums.size(); i++) {\n if (seen.find(i) == seen.end()) {\n return bitset<32>(i).to_string().substr(32 - n);\n }\n }\n\n return ""; \n }\n};\n```\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/minimize-maximum-pair-sum-in-array/solutions/4297828/video-give-me-u-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/DzzjWJdhNhI\n\n\u25A0 Timeline of the video\n\n`0:04` Explain how we can solve Minimize Maximum Pair Sum in Array\n`2:21` Check with other pair combinations\n`4:12` Let\'s see another example!\n`5:37` Find Common process of the two examples\n`6:45` Coding\n`7:55` Time Complexity and Space Complexity\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/maximum-element-after-decreasing-and-rearranging/solutions/4290299/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/1XhaQo-cDVg\n\n\u25A0 Timeline of the video\n\n`0:04` Explain a key point of the question\n`0:19` Important condition\n`0:56` Demonstrate how it works\n`3:08` What if we have a lot of the same numbers in input array?\n`4:10` Coding\n`4:55` Time Complexity and Space Complexity\n\n\n | 28 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
🚀 Sorting & Cantor's Diagonal Argument || Explained Intuition 🚀 | find-unique-binary-string | 1 | 1 | # Problem Description\n\nWrite a function that takes an array of length `n` of **unique** **binary** strings, each of length `n`, as input. The task is to **find** and return a binary string of length `n` that does not **exist** in the given array. \nIn case there are multiple valid answers, the function is allowed to return any of them.\n\n- Constraints:\n - $n == nums.length$\n - $1 <= n <= 16$\n - $nums[i].length == n$\n - nums[i][j] is either \'0\' or \'1\'.\n - All the strings of nums are **unique**.\n\n---\n\n\n\n# Intuition\n\nHi there,\uD83D\uDE00\n\nLet\'s take a look\uD83D\uDC40 on our today\'s problem.\nIn our today\'s problem, We have array of **binary** strings of size `n` and each string in it has length `n` and our task is to return any binary string og length `n` that doesn\'t **appear** in our array.\uD83E\uDD14\n\nSeem pretty easy !\uD83D\uDCAA\n\nWe can notice that `n` isn\'t that large $1 <= n <= 16$ so there are at most `2^16` possible binary strings. Our **Brute Force** guy can be used here !\uD83D\uDCAA\uD83D\uDCAA\nWe can **generate** all **possible** strings and see when string of them doesn\'t exist then we can return it as an answer.\uD83E\uDD29\nbut we can try a neat solution using **Sorting**.\uD83E\uDD2F\n\n### Sorting\nWhy not we **sort** the array then **initialize** pointer variable that **expects** the next element in sequence of binary strings and return that pointer if it doesn\'t match with current element in the array.... How ?\uD83E\uDD28\n\nLet\'s see some examples\n```\nnums = ["111","011","001"]\nDecimal = [7, 3, 1]\nSorted = [1, 3, 7]\n\nPointer = 0 \nFirst element = 1 -> 1 != Pointer\n\nReturn 0 which is 000\n```\n```\nnums = ["1110","0000", "0001", "1100"]\nDecimal = [14, 0, 1, 12]\nSorted = [0, 1, 12, 14]\n\nPointer = 0 \nFirst element = 0 -> 0 == Pointer\n\nPointer = 1\nSecond element = 1 -> 1 == Pointer\n\nPointer = 2\nThird element = 12 -> 12 != Pointer\n\nReturn 2 which is 0010\n```\n\nSince the input array is **smaller** than the whole sequence of binary strings of length `n` then we are sure that at some point our pointer won\'t match the sorted array.\uD83E\uDD29\nAnd is a neat solution and has good complexity of $O(N * log(N))$.\uD83D\uDE0E\n\nThere is another pretty solution using a **mathematical** proof from the world of set theory called **Cantor\'s diagonal argument**.\n\n### Cantor\'s diagonal argument\nThis mathimatical proof was published in `1891` by **Georg Cantor**. \nPretty old proof.\uD83D\uDE05\n\nThis was a mathematical proof that set of **Real numbers** are **uncountable** sets which means that we **can\'t count** all the numbers in this set.\uD83E\uDD2F\n\nHow does that relate to our problem?\uD83E\uDD14\nThe proof started by **mapping** each binary string `X` to a real number and said that if the set of binary strings are **countable** then the set of real numbers are **countable**.\nWhat next\u2753\nIt was proven by **contradiction** that the set of binary strings in **uncountable**.\nBy simply, construct a new string `Xn` that doesn\'t exist in this set and that what we will use in our problem.\uD83E\uDD2F\n\nSince we want a new string that is **different** from all strings in our array then why don\'t we **alter** some character from each string so that the result is **different** from each string in the array in some **position**.\uD83D\uDE00\nAnd these positions are the **diagonal** of the matrix formed by our input.\uD83E\uDD28\n\nLet\'s see some examples\n\n```\nnums = ["111","011","001"]\n\nnums = ["1 1 1",\n "0 1 1",\n "0 0 1"]\n\nresult = "000"\n```\n```\nnums = ["1011","1001","0001", "1100"]\n\nnums = ["1 011",\n "1 0 01",\n "00 0 1", \n "110 0"]\n\nresult = "0111"\n```\nYou can see the **pattern** right?\nour result is **different** from all of the strings in the array. Actually it is **formed** from the **input** itself to ensure that it is different from it.\uD83E\uDD29\n\n\n### Bonus Part\nThere is pretty **observation**. You noticed that the array length is `n` right ? and the binary string length is also `n` ?\uD83E\uDD14\nThat means that can exist $2^n - n$ answers to return.\n|Input Size | Possible strings of lengths n | Number of Answers |\n| :---:| :---: | :---: | \n| 1 | 2 | 1 |\n| 2 | 4 | 2 |\n| 3 | 8 | 5 |\n| 4 | 16 | 12 |\n| 5 | 32 | 27 |\n| ... | ... | ... |\n| 16 | 65536 | 65520 | \n\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n---\n\n\n\n# Approach\n## 1. Sorting\n\n1. Declare an integer `pointer` to track the expected decimal value for the next binary string.\n2. Sort the input vector `nums` in lexicographical order.\n\n3. Iterate through the sorted binary strings using a for loop:\n - Convert the current binary string to decimal.\n - Check if the decimal value matches the expected value (`pointer`).\n - If they **match**, increment `pointer`.\n - If **not**, return the binary representation of the expected value with the appropriate length.\n4. If no binary string is found during the iteration, return the binary representation of the next expected value.\n\n\n\n## Complexity\n- **Time complexity:** $O(N ^ 2)$\nWe are sorting the input array which takes `O(N * log(N))` generally in all programming languages then we are iterating over all of its elements in `O(N)` and converting each string to its equivalent integer in `O(N)` Which cost us total `O(N^2)` for the for loop then total complexity is `O(N^2 + N * log(N))` which is `O(N^2)`.\n- **Space complexity:** $O(log(N))$ or $O(N)$\nThe space complexity depends on the used sorting algorithm. In Java which uses **Dual-Pivot Quick Sort** and C++ which uses **Intro Sort** the complexity of their algorithms are `O(log(N))` space which in Python which uses **Timsort** it uses `O(N)`.\n\n\n\n---\n\n## 2. Cantor\'s Diagonal Argument\n\n1. Create an empty string called `result` to store the binary string.\n2. Use a **loop** to iterate through each binary string in the vector:\n - For each binary string, access the character at the current index (`i`) and **append** the **opposite** binary value to the `result` string.\n - If the current character is `0`, append `1`; otherwise, append `0`.\n4. The final **result** is the binary string formed by appending the **opposite** binary values from each binary string.\n\n\n## Complexity\n- **Time complexity:** $O(N)$\nWe are iterating over the input using for loop which cost us `O(N)`.\n- **Space complexity:** $O(1)$\nWithout considering the result then we are using constant variables.\n\n\n---\n\n\n\n# Code\n## 1. Sorting\n```C++ []\nclass Solution {\npublic:\n\n string findDifferentBinaryString(vector<string>& nums) {\n const int size = nums.size(); // Number of binary strings in the input vector\n\n // Sort the input vector in lexicographical order\n sort(nums.begin(), nums.end());\n\n int pointer = 0; // Pointer to track the expected decimal value for the next binary string\n\n // Iterate through the sorted binary strings\n for(int i = 0; i < size; ++i) {\n // Convert the current binary string to decimal\n unsigned long decimalValue = bitset<16>(nums[i]).to_ulong();\n\n // Check if the decimal value matches the expected value\n if(decimalValue == pointer)\n pointer++;\n else\n // If not, return the binary representation of the expected value with appropriate length\n return bitset<16>(pointer).to_string().substr(16 - size);\n }\n\n // If no unique binary string is found, return the binary representation of the next expected value\n return bitset<16>(pointer).to_string().substr(16 - size);\n }\n};\n```\n```Java []\npublic class Solution {\n public String findDifferentBinaryString(String[] nums) {\n int size = nums.length; // Number of binary strings in the input array\n\n // Sort the input array in lexicographical order\n Arrays.sort(nums);\n\n int pointer = 0; // Pointer to track the expected decimal value for the next binary string\n\n // Iterate through the sorted binary strings\n for (int i = 0; i < size; ++i) {\n // Convert the current binary string to decimal\n long decimalValue = Long.parseLong(nums[i], 2);\n\n // Check if the decimal value matches the expected value\n if (decimalValue == pointer)\n pointer++;\n else\n // If not, return the binary representation of the expected value with appropriate length\n return String.format("%" + size + "s", Long.toBinaryString(pointer)).replace(\' \', \'0\');\n }\n\n // If no unique binary string is found, return the binary representation of the next expected value\n return String.format("%" + size + "s", Long.toBinaryString(pointer)).replace(\' \', \'0\');\n }\n}\n```\n```Python []\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n size = len(nums) # Number of binary strings in the input list\n\n # Sort the input list in lexicographical order\n nums.sort()\n\n pointer = 0 # Pointer to track the expected decimal value for the next binary string\n\n # Iterate through the sorted binary strings\n for i in range(size):\n # Convert the current binary string to decimal\n decimal_value = int(nums[i], 2)\n\n # Check if the decimal value matches the expected value\n if decimal_value == pointer:\n pointer += 1\n else:\n # If not, return the binary representation of the expected value with appropriate length\n return format(pointer, f\'0{size}b\')\n\n # If no unique binary string is found, return the binary representation of the next expected value\n return format(pointer, f\'0{size}b\')\n```\n\n\n---\n\n## 2. Cantor\'s Diagonal Argument\n```C++ []\nclass Solution {\npublic:\n string findDifferentBinaryString(vector<string>& nums) {\n string result;\n\n // Iterate through each binary string in the vector\n for (int i = 0; i < nums.size(); ++i) {\n // Access the i-th character of the i-th binary string\n char currentCharacter = nums[i][i];\n\n // Append the opposite binary value to the result string\n result += (currentCharacter == \'0\' ? \'1\' : \'0\');\n }\n\n // Return the resulting binary string\n return result;\n }\n};\n```\n```Java []\npublic class Solution {\n public String findDifferentBinaryString(String[] nums) {\n StringBuilder result = new StringBuilder();\n\n // Iterate through each binary string in the array\n for (int i = 0; i < nums.length; ++i) {\n // Access the i-th character of the i-th binary string\n char currentCharacter = nums[i].charAt(i);\n\n // Append the opposite binary value to the result string\n result.append((currentCharacter == \'0\' ? \'1\' : \'0\'));\n }\n\n // Return the resulting binary string\n return result.toString();\n }\n}\n```\n```Python []\nclass Solution:\n def findDifferentBinaryString(self, binaryStrings: List[str]) -> str:\n result = []\n\n # Iterate through each binary string in the list\n for i in range(len(binaryStrings)):\n # Access the i-th character of the i-th binary string\n current_character = binaryStrings[i][i]\n\n # Append the opposite binary value to the result string\n result.append(\'1\' if current_character == \'0\' else \'0\')\n\n # Return the resulting binary string\n return \'\'.join(result)\n```\n\n\n\n\n\n\n\n | 37 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
Python3 Solution | find-unique-binary-string | 0 | 1 | \n```\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n n=len(nums)\n s=set(int(x,2) for x in nums)\n def pod(x,n):\n n1=len(x)\n return ("0"*(n-n1))+x\n for x in range(1<<n):\n if x not in s:\n return pod(bin(x)[2:],n)\n return "0"*n \n``` | 4 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
[Python, Java, Rust] Elegant & Short | O(n) | Cantor Diagonal Argument | find-unique-binary-string | 1 | 1 | # Approach\nGet more about Cantor diagonal argument [here](https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument)\n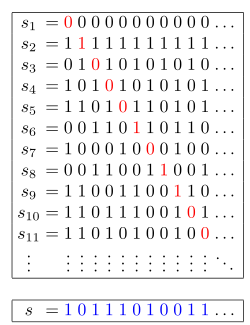\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```python []\nclass Solution:\n def findDifferentBinaryString(self, nums: list[str]) -> str:\n return \'\'.join(\'1\' if row[i] == \'0\' else \'0\' for i, row in enumerate(nums))\n```\n```java []\npublic class Solution {\n public String findDifferentBinaryString(String[] nums) {\n StringBuilder result = new StringBuilder();\n\n for (int i = 0; i < nums[0].length(); ++i)\n result.append(nums[i].charAt(i) == \'0\' ? \'1\' : \'0\');\n\n return result.toString();\n }\n}\n```\n```rust []\nimpl Solution {\n pub fn find_different_binary_string(nums: Vec<String>) -> String {\n nums.iter()\n .enumerate()\n .fold(String::new(), |acc, (i, row)| {\n acc + if row.chars().nth(i).unwrap() == \'0\' { "1" } else { "0" }\n })\n }\n}\n``` | 3 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
HEART BREAKiNG SOLUTiON by PRODONiK (Java, C#, Python, C++, Ruby) | find-unique-binary-string | 1 | 1 | \n\n# Intuition\nThe intuition behind this solution is to construct a binary string that is different from each binary string in the given array.\n\n# Approach\nIterate through the binary representations of the given numbers and flip the bit at the current position to construct a different binary string.\n\n# Complexity\n- Time complexity: O(n * m), where n is the number of binary strings, and m is the length of each binary string.\n- Space complexity: O(m), where m is the length of each binary string.\n\n# Code\n```java []\nclass Solution {\n public String findDifferentBinaryString(String[] nums) {\n int length = nums.length;\n StringBuilder number = new StringBuilder();\n for (int i = 0; i < length; i ++) {\n number.append(nums[i].charAt(i) == \'1\' ? \'0\' : \'1\');\n }\n return number.toString();\n }\n}\n```\n``` C# []\npublic class Solution {\n public string FindDifferentBinaryString(string[] nums) {\n int length = nums.Length;\n StringBuilder number = new StringBuilder();\n for (int i = 0; i < length; i++) {\n number.Append(nums[i][i] == \'1\' ? \'0\' : \'1\');\n }\n return number.ToString();\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n string findDifferentBinaryString(vector<string>& nums) {\n int length = nums.size();\n string number;\n for (int i = 0; i < length; i++) {\n number.push_back(nums[i][i] == \'1\' ? \'0\' : \'1\');\n }\n return number;\n }\n};\n```\n``` Python []\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n length = len(nums)\n number = []\n for i in range(length):\n number.append(\'0\' if nums[i][i] == \'1\' else \'1\')\n return \'\'.join(number)\n```\n``` Ruby []\n# @param {String[]} nums\n# @return {String}\ndef find_different_binary_string(nums)\n length = nums.length\n number = \'\'\n (0...length).each do |i|\n number += (nums[i][i] == \'1\' ? \'0\' : \'1\')\n end\n number\nend\n``` | 2 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
faster than 100 percent solutions | find-unique-binary-string | 0 | 1 | # Intuition:\nThe goal is to find a binary string that does not appear in the given list of binary strings. One approach is to iterate through each position of the binary strings and choose the opposite digit. If the digit at position i is \'1\', we can choose \'0\', and if it\'s \'0\', we can choose \'1\'. This way, we can guarantee that the resulting binary string is different from all the strings in the given list.\n\n# Approach:\n\nInitialize an empty list res to store the result.\nIterate through each position i in the binary strings.\nIf the digit at position i is \'1\', append \'0\' to res.\nIf the digit at position i is \'0\', append \'1\' to res.\nJoin the elements of res to form the final binary string and return it.\n# Complexity:\n\n# Time complexity: \n\n# O(n)\n\nn is the length of the binary strings in the input list.\n# Space complexity: \n\n# O(n) \nCode:\n\n# python\n\n```\nfrom typing import List\n\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n res = []\n for i in range(len(nums)):\n if nums[i][i] == \'1\':\n res.append(\'0\')\n else:\n res.append(\'1\')\n return "".join(res)\n```\n | 2 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
Simple Easy Python Solution | Beats 99% | Accepted 🔥🚀✅✅✅ | find-unique-binary-string | 0 | 1 | # Code\n```\nclass Solution:\n def findDifferentBinaryString(self, x: List[str]) -> str:\n t,i,x=len(x[0]),0,sorted([int(j,2) for j in x])\n while i<len(x) and i==x[i]: i+=1\n return "0"*(t-len(bin(i))+2)+bin(i)[2:]\n``` | 1 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
Simple solution in Python3 | find-unique-binary-string | 0 | 1 | # Intuition\nHere we have:\n- `nums` as list of integers in **binary** representation\n- our goal is to find **the unique combination** of integers with length of `nums`\n\nThis\'s achievable with a **mathematical proof**: if you use for each bit **an opposite bit** by **XOR** operator, you\'ll get a unique combination.\n\n# Approach\n1. declare `ans`\n2. iterate over `nums` and reverse a bit for each combination as `nums[i][i]`\n3. return stringified `ans`\n\n# Complexity\n- Time complexity: **O(N)** to iterate over `nums`\n\n- Space complexity: **O(N)** to store the unique combination\n\n# Code\n```\nclass Solution:\n def findDifferentBinaryString(self, nums: List[str]) -> str:\n ans = []\n\n for i in range(len(nums)):\n ans.append(str(int(nums[i][i]) ^ 1))\n\n return \'\'.join(ans)\n``` | 1 | Given an array of strings `nums` containing `n` **unique** binary strings each of length `n`, return _a binary string of length_ `n` _that **does not appear** in_ `nums`_. If there are multiple answers, you may return **any** of them_.
**Example 1:**
**Input:** nums = \[ "01 ", "10 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "00 " would also be correct.
**Example 2:**
**Input:** nums = \[ "00 ", "01 "\]
**Output:** "11 "
**Explanation:** "11 " does not appear in nums. "10 " would also be correct.
**Example 3:**
**Input:** nums = \[ "111 ", "011 ", "001 "\]
**Output:** "101 "
**Explanation:** "101 " does not appear in nums. "000 ", "010 ", "100 ", and "110 " would also be correct.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 16`
* `nums[i].length == n`
* `nums[i]` is either `'0'` or `'1'`.
* All the strings of `nums` are **unique**. | Check for a common prefix of the two arrays. After this common prefix, there should be one array similar to the other but shifted by one. If both arrays can be shifted, return -1. |
[Python3] greedy | find-array-given-subset-sums | 0 | 1 | Please check this [commit](https://github.com/gaosanyong/leetcode/commit/12942515a0e681f7ed804e66ec8de2b3423cadb0) for solutions of weekly 255. \n```\nclass Solution:\n def recoverArray(self, n: int, sums: List[int]) -> List[int]:\n sums.sort()\n ans = []\n for _ in range(n): \n diff = sums[1] - sums[0]\n ss0, ss1 = [], []\n freq = defaultdict(int)\n on = False \n for i, x in enumerate(sums): \n if not freq[x]: \n ss0.append(x)\n freq[x+diff] += 1\n if x == 0: on = True \n else: \n ss1.append(x)\n freq[x] -= 1\n if on: \n ans.append(diff)\n sums = ss0 \n else: \n ans.append(-diff)\n sums = ss1\n return ans \n``` | 0 | You are given an integer `n` representing the length of an unknown array that you are trying to recover. You are also given an array `sums` containing the values of all `2n` **subset sums** of the unknown array (in no particular order).
Return _the array_ `ans` _of length_ `n` _representing the unknown array. If **multiple** answers exist, return **any** of them_.
An array `sub` is a **subset** of an array `arr` if `sub` can be obtained from `arr` by deleting some (possibly zero or all) elements of `arr`. The sum of the elements in `sub` is one possible **subset sum** of `arr`. The sum of an empty array is considered to be `0`.
**Note:** Test cases are generated such that there will **always** be at least one correct answer.
**Example 1:**
**Input:** n = 3, sums = \[-3,-2,-1,0,0,1,2,3\]
**Output:** \[1,2,-3\]
**Explanation:** \[1,2,-3\] is able to achieve the given subset sums:
- \[\]: sum is 0
- \[1\]: sum is 1
- \[2\]: sum is 2
- \[1,2\]: sum is 3
- \[-3\]: sum is -3
- \[1,-3\]: sum is -2
- \[2,-3\]: sum is -1
- \[1,2,-3\]: sum is 0
Note that any permutation of \[1,2,-3\] and also any permutation of \[-1,-2,3\] will also be accepted.
**Example 2:**
**Input:** n = 2, sums = \[0,0,0,0\]
**Output:** \[0,0\]
**Explanation:** The only correct answer is \[0,0\].
**Example 3:**
**Input:** n = 4, sums = \[0,0,5,5,4,-1,4,9,9,-1,4,3,4,8,3,8\]
**Output:** \[0,-1,4,5\]
**Explanation:** \[0,-1,4,5\] is able to achieve the given subset sums.
**Constraints:**
* `1 <= n <= 15`
* `sums.length == 2n`
* `-104 <= sums[i] <= 104` | Is there a way we can know beforehand which nodes to delete? Count the number of appearances for each number. |
Python | Backtracking | 664ms | 100% time and space | Explanation | minimum-number-of-work-sessions-to-finish-the-tasks | 0 | 1 | * I think the test cases are little weak, because I just did backtracking and a little pruning and seems to be 4x faster than bitmask solutions.\n* The question boils down to finding minimum number of subsets such that each subset sum <= sessionTime. I maintain a list called subsets, where I track each subset sum. For each tasks[i] try to fit it into one of the existing subsets or create a new subset with this tasks[i] and recurse further. Once I reach the end of the list, I compare the length of the subsets list with current best and record minimum.\n* For pruning, I do the following - Once the length of subsets is larger than current best length, I backtrack. This doesn\'t decrease complexity in mathematical terms but I think in implementation, it helps a lot.\n\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n subsets = []\n self.ans = len(tasks)\n \n def func(idx):\n if len(subsets) >= self.ans:\n return\n \n if idx == len(tasks):\n self.ans = min(self.ans, len(subsets))\n return\n \n for i in range(len(subsets)):\n if subsets[i] + tasks[idx] <= sessionTime:\n subsets[i] += tasks[idx]\n func(idx + 1)\n subsets[i] -= tasks[idx]\n \n subsets.append(tasks[idx])\n func(idx + 1)\n subsets.pop()\n \n func(0)\n return self.ans | 26 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python DP + Bitmask | minimum-number-of-work-sessions-to-finish-the-tasks | 0 | 1 | # Intuition\nTry to pack as many hours into a session as possible\nbitmasking: dp(space_left_in_cur_bag, mask): return the smallest n.o bags required to pack the remaning tasks, including the current bag.\n```\ndp(space_left_in_cur_bag, mask) = \n 1 if mask == 0, i.e no tasks left,\n 1 + dp(sessionTime, mask) if space_left_in_cur_bag == 0,\n min(\n 1 + dp(sessionTime - tasks[i], mask flipped at ith) if tasks[i] > space_left_in_cur_bag \n dp(space_left_in_cur_bag - tasks[i], mask flipped at ith) otherwise\n for i where i is a remaining task\'s index\n )\n```\n# Code\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n def clearBit(x, k):\n return x ^ (1<<k)\n def checkBit(x, k):\n return x & (1<<k)\n @lru_cache(None)\n def dp(space_left, mask):\n if mask == 0: return 1\n if space_left == 0: return 1 + dp(sessionTime, mask)\n ans = math.inf\n for i in range(len(tasks)):\n if checkBit(mask, i):\n flipped = clearBit(mask, i)\n if space_left < tasks[i]: \n ans = min(ans, 1+dp(sessionTime - tasks[i], flipped))\n else:\n ans = min(ans, dp(space_left - tasks[i], flipped))\n return ans\n \n return dp(sessionTime, (1<<len(tasks)) - 1)\n``` | 0 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Simple python backtrack, no bitmask | minimum-number-of-work-sessions-to-finish-the-tasks | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n n = len(tasks)\n res = math.inf\n bucket = [0]\n\n # assign to any valid prev bucket or create new bucket\n def backtrack(i):\n nonlocal res\n if len(bucket) > res:\n return\n if i >= n:\n res = min(res, len(bucket))\n return\n\n for j in range(len(bucket)):\n if bucket[j] + tasks[i] <= sessionTime:\n bucket[j] += tasks[i]\n backtrack(i+1)\n bucket[j] -= tasks[i]\n\n # if cant fit in any prev bucket, try creating new bucket\n bucket.append(tasks[i])\n backtrack(i+1)\n bucket.pop()\n\n backtrack(0)\n return res\n``` | 0 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python 30 ms: Sort task first and then Backtracking | minimum-number-of-work-sessions-to-finish-the-tasks | 0 | 1 | # Complexity\n- Time complexity:\nWorst case: O(n!)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minSessions(self, tasks: List[int], sessionTime: int) -> int:\n self.tasks = sorted(tasks, reverse = True)\n self.nTasks = len(tasks)\n self.minSession = self.nTasks\n self.sessions = []\n self.sessionTime = sessionTime\n self.dfs(0)\n return self.minSession\n \n def dfs(self, i):\n """\n For each task, it can be added to either current sessions or a new session \n """\n if i == self.nTasks:\n self.minSession = min(self.minSession, len(self.sessions))\n return\n if len(self.sessions) >= self.minSession:\n return\n for j in range(len(self.sessions)):\n if self.tasks[i] + self.sessions[j] <= self.sessionTime:\n self.sessions[j] += self.tasks[i]\n self.dfs(i+1)\n self.sessions[j] -= self.tasks[i]\n \n self.sessions.append(self.tasks[i])\n self.dfs(i+1)\n self.sessions.pop() \n \n\n\n\n\n \n``` | 0 | There are `n` tasks assigned to you. The task times are represented as an integer array `tasks` of length `n`, where the `ith` task takes `tasks[i]` hours to finish. A **work session** is when you work for **at most** `sessionTime` consecutive hours and then take a break.
You should finish the given tasks in a way that satisfies the following conditions:
* If you start a task in a work session, you must complete it in the **same** work session.
* You can start a new task **immediately** after finishing the previous one.
* You may complete the tasks in **any order**.
Given `tasks` and `sessionTime`, return _the **minimum** number of **work sessions** needed to finish all the tasks following the conditions above._
The tests are generated such that `sessionTime` is **greater** than or **equal** to the **maximum** element in `tasks[i]`.
**Example 1:**
**Input:** tasks = \[1,2,3\], sessionTime = 3
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish the first and the second tasks in 1 + 2 = 3 hours.
- Second work session: finish the third task in 3 hours.
**Example 2:**
**Input:** tasks = \[3,1,3,1,1\], sessionTime = 8
**Output:** 2
**Explanation:** You can finish the tasks in two work sessions.
- First work session: finish all the tasks except the last one in 3 + 1 + 3 + 1 = 8 hours.
- Second work session: finish the last task in 1 hour.
**Example 3:**
**Input:** tasks = \[1,2,3,4,5\], sessionTime = 15
**Output:** 1
**Explanation:** You can finish all the tasks in one work session.
**Constraints:**
* `n == tasks.length`
* `1 <= n <= 14`
* `1 <= tasks[i] <= 10`
* `max(tasks[i]) <= sessionTime <= 15` | Use topological sort. let dp[u][c] := the maximum count of vertices with color c of any path starting from vertex u. (by JerryJin2905) |
Python (Simple Dynamic Programming) | first-day-where-you-have-been-in-all-the-rooms | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def firstDayBeenInAllRooms(self, nextVisit):\n n, mod = len(nextVisit), 10**9 + 7\n dp = [0]*n \n\n for i in range(1,n):\n dp[i] = (dp[i-1] + (dp[i-1] - dp[nextVisit[i-1]] + 1) + 1)%mod\n\n return dp[-1]\n\n\n\n\n \n \n \n \n``` | 0 | There are `n` rooms you need to visit, labeled from `0` to `n - 1`. Each day is labeled, starting from `0`. You will go in and visit one room a day.
Initially on day `0`, you visit room `0`. The **order** you visit the rooms for the coming days is determined by the following **rules** and a given **0-indexed** array `nextVisit` of length `n`:
* Assuming that on a day, you visit room `i`,
* if you have been in room `i` an **odd** number of times (**including** the current visit), on the **next** day you will visit a room with a **lower or equal room number** specified by `nextVisit[i]` where `0 <= nextVisit[i] <= i`;
* if you have been in room `i` an **even** number of times (**including** the current visit), on the **next** day you will visit room `(i + 1) mod n`.
Return _the label of the **first** day where you have been in **all** the rooms_. It can be shown that such a day exists. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nextVisit = \[0,0\]
**Output:** 2
**Explanation:**
- On day 0, you visit room 0. The total times you have been in room 0 is 1, which is odd.
On the next day you will visit room nextVisit\[0\] = 0
- On day 1, you visit room 0, The total times you have been in room 0 is 2, which is even.
On the next day you will visit room (0 + 1) mod 2 = 1
- On day 2, you visit room 1. This is the first day where you have been in all the rooms.
**Example 2:**
**Input:** nextVisit = \[0,0,2\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,0,0,1,2,...\].
Day 6 is the first day where you have been in all the rooms.
**Example 3:**
**Input:** nextVisit = \[0,1,2,0\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,1,2,2,3,...\].
Day 6 is the first day where you have been in all the rooms.
**Constraints:**
* `n == nextVisit.length`
* `2 <= n <= 105`
* `0 <= nextVisit[i] <= i` | Is it possible to swap one character in the first half of the palindrome to make the next one? Are there different cases for when the length is odd and even? |
Python | Two Solutions | first-day-where-you-have-been-in-all-the-rooms | 0 | 1 | # Approach\nFirst approach (at the bottom of the code) was to directly simulate the process using caching. We keep track of the last day a room was visited in ```last_day``` and the number of times a room has been visited in ```visits```. The calculations performed coalesce into the dynamic programming solution at the top.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def firstDayBeenInAllRooms2(self, next_visit: List[int]) -> int:\n p = 10**9 + 7\n n = len(next_visit)\n dp = [0]*n\n\n for i in range(1,n):\n dp[i] = (2 * dp[i-1] - dp[next_visit[i-1]] + 2) % p\n\n return dp[-1]\n\n def firstDayBeenInAllRooms(self, next_visit: List[int]) -> int:\n p = 10**9 + 7\n n = len (next_visit)\n not_visited = set(range(n))\n\n visits = [0] * n\n last_day = [float(\'-inf\')] * n\n\n def simulate (room, day):\n not_visited.discard(room)\n while not_visited:\n visits[room] += 1\n last_day[room] = day\n if visits[room] & 1:\n # This room has been visited an odd number of times.\n day = (2*day - last_day[next_visit[room]] + 1) % p\n\n # This room has been visited an even number of times.\n day += 1\n room = (room + 1) % n\n not_visited.discard(room)\n\n return day\n\n return simulate (0, 0) % p\n``` | 0 | There are `n` rooms you need to visit, labeled from `0` to `n - 1`. Each day is labeled, starting from `0`. You will go in and visit one room a day.
Initially on day `0`, you visit room `0`. The **order** you visit the rooms for the coming days is determined by the following **rules** and a given **0-indexed** array `nextVisit` of length `n`:
* Assuming that on a day, you visit room `i`,
* if you have been in room `i` an **odd** number of times (**including** the current visit), on the **next** day you will visit a room with a **lower or equal room number** specified by `nextVisit[i]` where `0 <= nextVisit[i] <= i`;
* if you have been in room `i` an **even** number of times (**including** the current visit), on the **next** day you will visit room `(i + 1) mod n`.
Return _the label of the **first** day where you have been in **all** the rooms_. It can be shown that such a day exists. Since the answer may be very large, return it **modulo** `109 + 7`.
**Example 1:**
**Input:** nextVisit = \[0,0\]
**Output:** 2
**Explanation:**
- On day 0, you visit room 0. The total times you have been in room 0 is 1, which is odd.
On the next day you will visit room nextVisit\[0\] = 0
- On day 1, you visit room 0, The total times you have been in room 0 is 2, which is even.
On the next day you will visit room (0 + 1) mod 2 = 1
- On day 2, you visit room 1. This is the first day where you have been in all the rooms.
**Example 2:**
**Input:** nextVisit = \[0,0,2\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,0,0,1,2,...\].
Day 6 is the first day where you have been in all the rooms.
**Example 3:**
**Input:** nextVisit = \[0,1,2,0\]
**Output:** 6
**Explanation:**
Your room visiting order for each day is: \[0,0,1,1,2,2,3,...\].
Day 6 is the first day where you have been in all the rooms.
**Constraints:**
* `n == nextVisit.length`
* `2 <= n <= 105`
* `0 <= nextVisit[i] <= i` | Is it possible to swap one character in the first half of the palindrome to make the next one? Are there different cases for when the length is odd and even? |
[Python3] union-find | gcd-sort-of-an-array | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/84115397f703f3005c3ae0d5d759f4ac64f65de4) for solutions of weekly 257.\n```\nclass UnionFind:\n \n def __init__(self, n): \n self.parent = list(range(n))\n self.rank = [1] * n\n \n def find(self, p): \n if p != self.parent[p]: \n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p, q):\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt\n self.parent[prt] = qrt\n self.rank[qrt] += self.rank[prt]\n return True \n \n\nclass Solution:\n def gcdSort(self, nums: List[int]) -> bool:\n m = max(nums)\n uf = UnionFind(m+1)\n \n seen = set(nums)\n \n # modified sieve of eratosthenes\n sieve = [1]*(m+1)\n sieve[0] = sieve[1] = 0\n for k in range(m//2 + 1): \n if sieve[k]: \n for x in range(2*k, m+1, k): \n sieve[x] = 0\n if x in seen: uf.union(k, x)\n return all(uf.find(x) == uf.find(y) for x, y in zip(nums, sorted(nums)))\n```\n\n**Related problems**\n[952. Largest Component Size by Common Factor](https://leetcode.com/problems/largest-component-size-by-common-factor/discuss/1546345/Python3-union-find)\n[1998. GCD Sort of an Array](https://leetcode.com/problems/gcd-sort-of-an-array/discuss/1445278/Python3-union-find) | 11 | You are given an integer array `nums`, and you can perform the following operation **any** number of times on `nums`:
* Swap the positions of two elements `nums[i]` and `nums[j]` if `gcd(nums[i], nums[j]) > 1` where `gcd(nums[i], nums[j])` is the **greatest common divisor** of `nums[i]` and `nums[j]`.
Return `true` _if it is possible to sort_ `nums` _in **non-decreasing** order using the above swap method, or_ `false` _otherwise._
**Example 1:**
**Input:** nums = \[7,21,3\]
**Output:** true
**Explanation:** We can sort \[7,21,3\] by performing the following operations:
- Swap 7 and 21 because gcd(7,21) = 7. nums = \[**21**,**7**,3\]
- Swap 21 and 3 because gcd(21,3) = 3. nums = \[**3**,7,**21**\]
**Example 2:**
**Input:** nums = \[5,2,6,2\]
**Output:** false
**Explanation:** It is impossible to sort the array because 5 cannot be swapped with any other element.
**Example 3:**
**Input:** nums = \[10,5,9,3,15\]
**Output:** true
We can sort \[10,5,9,3,15\] by performing the following operations:
- Swap 10 and 15 because gcd(10,15) = 5. nums = \[**15**,5,9,3,**10**\]
- Swap 15 and 3 because gcd(15,3) = 3. nums = \[**3**,5,9,**15**,10\]
- Swap 10 and 15 because gcd(10,15) = 5. nums = \[3,5,9,**10**,**15**\]
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `2 <= nums[i] <= 105` | null |
Beats 88%, solution with detailed explanation and intuition! | gcd-sort-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We can exchange 2 numbers if and only if they have gcd > 1\n- If we want the minimum number in the array to reach the 0 index we need to be able to do a sequence of swaps which results in the min number and the present number in index 0 having gcd > 1\n- The numbers that the initial nums[0] can be switched with are those that have gcd with it > 1 and in the subsequent rounds it would be the numbers whose gcd with the current nums[0] > 1. \n- So basically we can indirectly swap 2 numbers if they belong to the same connected component in the graph where the nodes are the elements of the array and we have an edge if gcd > 1.\n- Note that gcd > 1 is equivalent to sharing a prime factor\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Looking at the constraints on how large the numbers can go we see that it is feasible to use the sieve algorithm to find the smallest prime factor (spf) for all numbers in 1 to 10**5\n2. For each number in the array we can then find all its distinct prime factors by iteratively dividing it by the corresponding spf in each iteration\n3. For each prime we create a list where we store the array index of numbers that are multiples of it. Every pair of elements in these lists would have an edge beetween them\n4. For each prime we would do a union over all the elements in the corresponding list\n5. For each element in the sorted array we would check if the union find component it belongs to is the same as the union find component of the orifinal number in that index. This is because this indicates that they belong to the same connected component and hence have a path from one to the other\n6. If it is not the same for any index we return False\n\n# Complexity\n- Time complexity: $$O(N\\log(M) + M\\log(M))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: $$O(M+N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nM = 10 ** 5 + 1\nspf = [x for x in range(M)]\nfor i in range(2, M):\n if spf[i] != i:\n continue\n j = i ** 2\n while j < M:\n spf[j] = min(spf[j], i)\n j += i\n\n\nclass Solution:\n def gcdSort(self, nums: List[int]) -> bool:\n n = len(nums)\n\n divides = defaultdict(set)\n for i, x in enumerate(nums):\n num = x\n while num > 1:\n divides[spf[num]].add(i)\n num //= spf[num]\n \n parents = [x for x in range(n)]\n def find(a):\n if parents[a] != a:\n parents[a] = find(parents[a])\n return parents[a]\n def union(a, b):\n ua, ub = find(a), find(b)\n parents[ua] = ub\n \n for prime in divides:\n arr = list(divides[prime])\n for x in arr:\n union(x, arr[0])\n\n poss = defaultdict(int)\n for i, x in enumerate(nums):\n poss[x] = i\n sortednums = sorted(nums)\n for i in range(n):\n if find(poss[sortednums[i]]) != find(i):\n return False\n return True\n``` | 0 | You are given an integer array `nums`, and you can perform the following operation **any** number of times on `nums`:
* Swap the positions of two elements `nums[i]` and `nums[j]` if `gcd(nums[i], nums[j]) > 1` where `gcd(nums[i], nums[j])` is the **greatest common divisor** of `nums[i]` and `nums[j]`.
Return `true` _if it is possible to sort_ `nums` _in **non-decreasing** order using the above swap method, or_ `false` _otherwise._
**Example 1:**
**Input:** nums = \[7,21,3\]
**Output:** true
**Explanation:** We can sort \[7,21,3\] by performing the following operations:
- Swap 7 and 21 because gcd(7,21) = 7. nums = \[**21**,**7**,3\]
- Swap 21 and 3 because gcd(21,3) = 3. nums = \[**3**,7,**21**\]
**Example 2:**
**Input:** nums = \[5,2,6,2\]
**Output:** false
**Explanation:** It is impossible to sort the array because 5 cannot be swapped with any other element.
**Example 3:**
**Input:** nums = \[10,5,9,3,15\]
**Output:** true
We can sort \[10,5,9,3,15\] by performing the following operations:
- Swap 10 and 15 because gcd(10,15) = 5. nums = \[**15**,5,9,3,**10**\]
- Swap 15 and 3 because gcd(15,3) = 3. nums = \[**3**,5,9,**15**,10\]
- Swap 10 and 15 because gcd(10,15) = 5. nums = \[3,5,9,**10**,**15**\]
**Constraints:**
* `1 <= nums.length <= 3 * 104`
* `2 <= nums[i] <= 105` | null |
Easiest and Fast Python Solution | reverse-prefix-of-word | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def reversePrefix(self, word: str, ch: str) -> str:\n if ch not in word:\n return word\n ind = list(word).index(ch)\n l = (word[:ind+1][::-1])\n word = list(word)\n word[:ind+1] = l\n # print(word)\n \n \n return \'\'.join(word)\n``` | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
python | Two pointers - easy solution | reverse-prefix-of-word | 0 | 1 | ```\nclass Solution:\n def reversePrefix(self, word: str, ch: str) -> str:\n ## Two pointers\n res = list(word)\n left = 0\n \n for i in range(len(word)):\n if res[i] == ch:\n while left <= i:\n res[i], res[left] = res[left], res[i]\n left += 1\n i -= 1\n return "".join(res)\n return word | 1 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
reverse prefix python3 | reverse-prefix-of-word | 0 | 1 | # Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def reversePrefix(self, word: str, ch: str) -> str:\n prefix = \'\'\n for i, c in enumerate(word):\n if c == ch:\n return (prefix + c)[::-1] + word[i+1:]\n prefix += c\n return prefix\n``` | 4 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
two methods || python || easy to understand | reverse-prefix-of-word | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def reversePrefix(self, word: str, ch: str) -> str:\n """\n #method 1:\n for i in range(len(word)):\n if word[i]==ch:\n return word[:i+1][::-1]+word[i+1:]\n return word"""\n #method 2:\n l=0\n r=word.find(ch)\n word=list(word)\n while l<r:\n word[l],word[r]=word[r],word[l]\n l+=1\n r-=1\n return "".join(word)\n \n\n \n\n\n \n\n \n``` | 8 | Given a **0-indexed** string `word` and a character `ch`, **reverse** the segment of `word` that starts at index `0` and ends at the index of the **first occurrence** of `ch` (**inclusive**). If the character `ch` does not exist in `word`, do nothing.
* For example, if `word = "abcdefd "` and `ch = "d "`, then you should **reverse** the segment that starts at `0` and ends at `3` (**inclusive**). The resulting string will be `"dcbaefd "`.
Return _the resulting string_.
**Example 1:**
**Input:** word = "abcdefd ", ch = "d "
**Output:** "dcbaefd "
**Explanation:** The first occurrence of "d " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "dcbaefd ".
**Example 2:**
**Input:** word = "xyxzxe ", ch = "z "
**Output:** "zxyxxe "
**Explanation:** The first and only occurrence of "z " is at index 3.
Reverse the part of word from 0 to 3 (inclusive), the resulting string is "zxyxxe ".
**Example 3:**
**Input:** word = "abcd ", ch = "z "
**Output:** "abcd "
**Explanation:** "z " does not exist in word.
You should not do any reverse operation, the resulting string is "abcd ".
**Constraints:**
* `1 <= word.length <= 250`
* `word` consists of lowercase English letters.
* `ch` is a lowercase English letter. | Given the speed the trains are traveling at, can you find the total time it takes for you to arrive? Is there a cutoff where any speeds larger will always allow you to arrive on time? |
[Python3] Math GCD + Hash Table - Concise and Simple | number-of-pairs-of-interchangeable-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def interchangeableRectangles(self, rectangles: List[List[int]]) -> int:\n c = collections.Counter()\n for x, y in rectangles:\n gcd = math.gcd(x, y)\n c[(x // gcd, y // gcd)] += 1\n \n res = 0\n for k, v in c.items():\n res += v * (v - 1) // 2\n return res\n``` | 2 | You are given `n` rectangles represented by a **0-indexed** 2D integer array `rectangles`, where `rectangles[i] = [widthi, heighti]` denotes the width and height of the `ith` rectangle.
Two rectangles `i` and `j` (`i < j`) are considered **interchangeable** if they have the **same** width-to-height ratio. More formally, two rectangles are **interchangeable** if `widthi/heighti == widthj/heightj` (using decimal division, not integer division).
Return _the **number** of pairs of **interchangeable** rectangles in_ `rectangles`.
**Example 1:**
**Input:** rectangles = \[\[4,8\],\[3,6\],\[10,20\],\[15,30\]\]
**Output:** 6
**Explanation:** The following are the interchangeable pairs of rectangles by index (0-indexed):
- Rectangle 0 with rectangle 1: 4/8 == 3/6.
- Rectangle 0 with rectangle 2: 4/8 == 10/20.
- Rectangle 0 with rectangle 3: 4/8 == 15/30.
- Rectangle 1 with rectangle 2: 3/6 == 10/20.
- Rectangle 1 with rectangle 3: 3/6 == 15/30.
- Rectangle 2 with rectangle 3: 10/20 == 15/30.
**Example 2:**
**Input:** rectangles = \[\[4,5\],\[7,8\]\]
**Output:** 0
**Explanation:** There are no interchangeable pairs of rectangles.
**Constraints:**
* `n == rectangles.length`
* `1 <= n <= 105`
* `rectangles[i].length == 2`
* `1 <= widthi, heighti <= 105` | Consider for each reachable index i the interval [i + a, i + b]. Use partial sums to mark the intervals as reachable. |
O(n) time and O(1) space complexity | number-of-pairs-of-interchangeable-rectangles | 0 | 1 | class Solution:\n def interchangeableRectangles(self, nums: List[List[int]]) -> int:\n \n for i in range(0,len(nums)):\n nums[i]=nums[i][0]/nums[i][1]\n \n dic={}\n for i in nums:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n ans=0\n l=dic.values()\n for i in l:\n ans+=(i*(i-1)//2)\n return ans | 0 | You are given `n` rectangles represented by a **0-indexed** 2D integer array `rectangles`, where `rectangles[i] = [widthi, heighti]` denotes the width and height of the `ith` rectangle.
Two rectangles `i` and `j` (`i < j`) are considered **interchangeable** if they have the **same** width-to-height ratio. More formally, two rectangles are **interchangeable** if `widthi/heighti == widthj/heightj` (using decimal division, not integer division).
Return _the **number** of pairs of **interchangeable** rectangles in_ `rectangles`.
**Example 1:**
**Input:** rectangles = \[\[4,8\],\[3,6\],\[10,20\],\[15,30\]\]
**Output:** 6
**Explanation:** The following are the interchangeable pairs of rectangles by index (0-indexed):
- Rectangle 0 with rectangle 1: 4/8 == 3/6.
- Rectangle 0 with rectangle 2: 4/8 == 10/20.
- Rectangle 0 with rectangle 3: 4/8 == 15/30.
- Rectangle 1 with rectangle 2: 3/6 == 10/20.
- Rectangle 1 with rectangle 3: 3/6 == 15/30.
- Rectangle 2 with rectangle 3: 10/20 == 15/30.
**Example 2:**
**Input:** rectangles = \[\[4,5\],\[7,8\]\]
**Output:** 0
**Explanation:** There are no interchangeable pairs of rectangles.
**Constraints:**
* `n == rectangles.length`
* `1 <= n <= 105`
* `rectangles[i].length == 2`
* `1 <= widthi, heighti <= 105` | Consider for each reachable index i the interval [i + a, i + b]. Use partial sums to mark the intervals as reachable. |
Python HashMap Solution | number-of-pairs-of-interchangeable-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def interchangeableRectangles(self, rectangles: List[List[int]]) -> int:\n l1=[]\n for i,j in rectangles:\n sk=i/j\n l1.append(sk)\n \n count=0\n sums=0\n l2={}\n for i in l1:\n l2[i]=l2.get(i,0)+1\n for i in l2.values():\n if(i>1):\n sums+=i*(i-1)//2\n \n \n \n\n return sums\n\n\n``` | 2 | You are given `n` rectangles represented by a **0-indexed** 2D integer array `rectangles`, where `rectangles[i] = [widthi, heighti]` denotes the width and height of the `ith` rectangle.
Two rectangles `i` and `j` (`i < j`) are considered **interchangeable** if they have the **same** width-to-height ratio. More formally, two rectangles are **interchangeable** if `widthi/heighti == widthj/heightj` (using decimal division, not integer division).
Return _the **number** of pairs of **interchangeable** rectangles in_ `rectangles`.
**Example 1:**
**Input:** rectangles = \[\[4,8\],\[3,6\],\[10,20\],\[15,30\]\]
**Output:** 6
**Explanation:** The following are the interchangeable pairs of rectangles by index (0-indexed):
- Rectangle 0 with rectangle 1: 4/8 == 3/6.
- Rectangle 0 with rectangle 2: 4/8 == 10/20.
- Rectangle 0 with rectangle 3: 4/8 == 15/30.
- Rectangle 1 with rectangle 2: 3/6 == 10/20.
- Rectangle 1 with rectangle 3: 3/6 == 15/30.
- Rectangle 2 with rectangle 3: 10/20 == 15/30.
**Example 2:**
**Input:** rectangles = \[\[4,5\],\[7,8\]\]
**Output:** 0
**Explanation:** There are no interchangeable pairs of rectangles.
**Constraints:**
* `n == rectangles.length`
* `1 <= n <= 105`
* `rectangles[i].length == 2`
* `1 <= widthi, heighti <= 105` | Consider for each reachable index i the interval [i + a, i + b]. Use partial sums to mark the intervals as reachable. |
Python3 solution, beats 100%, 2 solutions. | number-of-pairs-of-interchangeable-rectangles | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def interchangeableRectangles(self, rectangles: List[List[int]]) -> int:\n # solution 1 (w math formula)\n res = 0\n hashmap = {}\n for r in rectangles:\n rate = r[0] / r[1]\n hashmap[rate] = hashmap.get(rate, 0) + 1\n for c in hashmap.values():\n res += c * (c - 1) // 2\n return res\n\n # solution 2 (w/o math formula)\n res = 0\n hashmap = {} # for the rates: rate : count\n for r in rectangles:\n rate = r[0] / r[1]\n if rate in hashmap:\n res += hashmap[rate]\n hashmap[rate] += 1\n else:\n hashmap[rate] = 1\n return res\n``` | 0 | You are given `n` rectangles represented by a **0-indexed** 2D integer array `rectangles`, where `rectangles[i] = [widthi, heighti]` denotes the width and height of the `ith` rectangle.
Two rectangles `i` and `j` (`i < j`) are considered **interchangeable** if they have the **same** width-to-height ratio. More formally, two rectangles are **interchangeable** if `widthi/heighti == widthj/heightj` (using decimal division, not integer division).
Return _the **number** of pairs of **interchangeable** rectangles in_ `rectangles`.
**Example 1:**
**Input:** rectangles = \[\[4,8\],\[3,6\],\[10,20\],\[15,30\]\]
**Output:** 6
**Explanation:** The following are the interchangeable pairs of rectangles by index (0-indexed):
- Rectangle 0 with rectangle 1: 4/8 == 3/6.
- Rectangle 0 with rectangle 2: 4/8 == 10/20.
- Rectangle 0 with rectangle 3: 4/8 == 15/30.
- Rectangle 1 with rectangle 2: 3/6 == 10/20.
- Rectangle 1 with rectangle 3: 3/6 == 15/30.
- Rectangle 2 with rectangle 3: 10/20 == 15/30.
**Example 2:**
**Input:** rectangles = \[\[4,5\],\[7,8\]\]
**Output:** 0
**Explanation:** There are no interchangeable pairs of rectangles.
**Constraints:**
* `n == rectangles.length`
* `1 <= n <= 105`
* `rectangles[i].length == 2`
* `1 <= widthi, heighti <= 105` | Consider for each reachable index i the interval [i + a, i + b]. Use partial sums to mark the intervals as reachable. |
O(n) beats 99.75% single for loop no if statements needed | number-of-pairs-of-interchangeable-rectangles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nKeep track of how many ratios we have seen. This can be used to calculate how many pairs of interchangeable rectangles.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCalculate the ratio for a given rectangle. Update result by adding to it however many of that ratio we have seen previously. Update the count for number of those ratios.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def interchangeableRectangles(self, rectangles: List[List[int]]) -> int:\n hmap = {}\n res = 0\n\n for rect in rectangles:\n ratio = rect[0]/rect[1]\n res += hmap.get(ratio, 0)\n hmap[ratio] = 1 + hmap.get(ratio, 0)\n\n return res\n``` | 0 | You are given `n` rectangles represented by a **0-indexed** 2D integer array `rectangles`, where `rectangles[i] = [widthi, heighti]` denotes the width and height of the `ith` rectangle.
Two rectangles `i` and `j` (`i < j`) are considered **interchangeable** if they have the **same** width-to-height ratio. More formally, two rectangles are **interchangeable** if `widthi/heighti == widthj/heightj` (using decimal division, not integer division).
Return _the **number** of pairs of **interchangeable** rectangles in_ `rectangles`.
**Example 1:**
**Input:** rectangles = \[\[4,8\],\[3,6\],\[10,20\],\[15,30\]\]
**Output:** 6
**Explanation:** The following are the interchangeable pairs of rectangles by index (0-indexed):
- Rectangle 0 with rectangle 1: 4/8 == 3/6.
- Rectangle 0 with rectangle 2: 4/8 == 10/20.
- Rectangle 0 with rectangle 3: 4/8 == 15/30.
- Rectangle 1 with rectangle 2: 3/6 == 10/20.
- Rectangle 1 with rectangle 3: 3/6 == 15/30.
- Rectangle 2 with rectangle 3: 10/20 == 15/30.
**Example 2:**
**Input:** rectangles = \[\[4,5\],\[7,8\]\]
**Output:** 0
**Explanation:** There are no interchangeable pairs of rectangles.
**Constraints:**
* `n == rectangles.length`
* `1 <= n <= 105`
* `rectangles[i].length == 2`
* `1 <= widthi, heighti <= 105` | Consider for each reachable index i the interval [i + a, i + b]. Use partial sums to mark the intervals as reachable. |
Easy Understand | Simple Method | Java | Python ✅ | maximum-product-of-the-length-of-two-palindromic-subsequences | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse mask to save all combination in hashmap and use "&" bit manipulation to check if two mask have repeated letter.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O((2^n)^2)$ => $O(4^n)$ \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe worst case is need save every combination, for example the string of length 12 that only contains one kind of letter.\n$O(2^n)$\n\n# Code\nMathod using bit mask\n``` java []\nclass Solution {\n public int maxProduct(String s) {\n char[] strArr = s.toCharArray();\n int n = strArr.length;\n Map<Integer, Integer> pali = new HashMap<>();\n // save all elligible combination into hashmap\n for (int mask = 0; mask < 1<<n; mask++){\n String subseq = "";\n for (int i = 0; i < 12; i++){\n if ((mask & 1<<i) > 0)\n subseq += strArr[i];\n }\n if (isPalindromic(subseq))\n pali.put(mask, subseq.length());\n }\n // use & opertion between any two combination\n int res = 0;\n for (int mask1 : pali.keySet()){\n for (int mask2 : pali.keySet()){\n if ((mask1 & mask2) == 0)\n res = Math.max(res, pali.get(mask1)*pali.get(mask2));\n }\n }\n\n return res;\n }\n\n public boolean isPalindromic(String str){\n int j = str.length() - 1;\n char[] strArr = str.toCharArray();\n for (int i = 0; i < j; i ++){\n if (strArr[i] != strArr[j])\n return false;\n j--;\n }\n return true;\n }\n}\n```\n``` python3 []\nclass Solution:\n def maxProduct(self, s: str) -> int:\n n, pali = len(s), {} # bitmask : length\n for mask in range(1, 1 << n):\n subseq = ""\n for i in range(n):\n if mask & (1 << i):\n subseq += s[i]\n if subseq == subseq[::-1]: # valid is palindromic\n pali[mask] = len(subseq)\n res = 0\n for mask1, length1 in pali.items():\n for mask2, length2 in pali.items():\n if mask1 & mask2 == 0: \n res = max(res, length1 * length2)\n return res\n```\n\nThere is another method using recursion\n``` java []\nclass Solution {\n int res = 0;\n \n public int maxProduct(String s) {\n char[] strArr = s.toCharArray();\n dfs(strArr, 0, "", "");\n return res;\n }\n\n public void dfs(char[] strArr, int i, String s1, String s2){\n if(i >= strArr.length){\n if(isPalindromic(s1) && isPalindromic(s2))\n res = Math.max(res, s1.length()*s2.length());\n return;\n }\n dfs(strArr, i+1, s1 + strArr[i], s2);\n dfs(strArr, i+1, s1, s2 + strArr[i]);\n dfs(strArr, i+1, s1, s2);\n }\n\n public boolean isPalindromic(String str){\n int j = str.length() - 1;\n char[] strArr = str.toCharArray();\n for (int i = 0; i < j; i ++){\n if (strArr[i] != strArr[j])\n return false;\n j--;\n }\n return true;\n }\n}\n```\n\n**Please upvate if helpful!!**\n\n | 9 | Given a string `s`, find two **disjoint palindromic subsequences** of `s` such that the **product** of their lengths is **maximized**. The two subsequences are **disjoint** if they do not both pick a character at the same index.
Return _the **maximum** possible **product** of the lengths of the two palindromic subsequences_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** s = "leetcodecom "
**Output:** 9
**Explanation**: An optimal solution is to choose "ete " for the 1st subsequence and "cdc " for the 2nd subsequence.
The product of their lengths is: 3 \* 3 = 9.
**Example 2:**
**Input:** s = "bb "
**Output:** 1
**Explanation**: An optimal solution is to choose "b " (the first character) for the 1st subsequence and "b " (the second character) for the 2nd subsequence.
The product of their lengths is: 1 \* 1 = 1.
**Example 3:**
**Input:** s = "accbcaxxcxx "
**Output:** 25
**Explanation**: An optimal solution is to choose "accca " for the 1st subsequence and "xxcxx " for the 2nd subsequence.
The product of their lengths is: 5 \* 5 = 25.
**Constraints:**
* `2 <= s.length <= 12`
* `s` consists of lowercase English letters only. | Let's note that the only thing that matters is how many stones were removed so we can maintain dp[numberOfRemovedStones] dp[x] = max(sum of all elements up to y - dp[y]) for all y > x |
Brute Force Appro | maximum-product-of-the-length-of-two-palindromic-subsequences | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n N,pali = len(s),{} # bitmask = length\n\n for mask in range(1,1<<N): # 1 << N == 2**N\n subseq = ""\n for i in range(N):\n if mask & (1<<i):\n subseq+=s[i]\n\n if subseq == subseq[::-1]:\n pali[mask] = len(subseq)\n\n \n res = 0\n for m1 in pali:\n for m2 in pali:\n if m1 & m2 == 0:\n res = max(res,pali[m1]*pali[m2])\n\n return res\n\n\n``` | 1 | Given a string `s`, find two **disjoint palindromic subsequences** of `s` such that the **product** of their lengths is **maximized**. The two subsequences are **disjoint** if they do not both pick a character at the same index.
Return _the **maximum** possible **product** of the lengths of the two palindromic subsequences_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** s = "leetcodecom "
**Output:** 9
**Explanation**: An optimal solution is to choose "ete " for the 1st subsequence and "cdc " for the 2nd subsequence.
The product of their lengths is: 3 \* 3 = 9.
**Example 2:**
**Input:** s = "bb "
**Output:** 1
**Explanation**: An optimal solution is to choose "b " (the first character) for the 1st subsequence and "b " (the second character) for the 2nd subsequence.
The product of their lengths is: 1 \* 1 = 1.
**Example 3:**
**Input:** s = "accbcaxxcxx "
**Output:** 25
**Explanation**: An optimal solution is to choose "accca " for the 1st subsequence and "xxcxx " for the 2nd subsequence.
The product of their lengths is: 5 \* 5 = 25.
**Constraints:**
* `2 <= s.length <= 12`
* `s` consists of lowercase English letters only. | Let's note that the only thing that matters is how many stones were removed so we can maintain dp[numberOfRemovedStones] dp[x] = max(sum of all elements up to y - dp[y]) for all y > x |
Unleash the Power of Bit Manipulation: Maximize Product of Palindromic Subsequences! | maximum-product-of-the-length-of-two-palindromic-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking to find the maximum product of the lengths of two non-intersecting palindromic subsequences. My first thought is to generate all possible subsequences and check which ones are palindromes. Then, I can iterate over all pairs of these palindromic subsequences and find the pair that has no overlap and gives the maximum product of lengths.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI start by generating all possible subsequences of the given string and store them along with their corresponding masks. The mask of a subsequence is a binary number where the i-th bit is set if the i-th character of the original string is included in the subsequence. I also check if each subsequence is a palindrome and if so, I store it in a separate list.\n\nThen, I iterate over all pairs of palindromic subsequences. For each pair, I check if they have any overlap by performing a bitwise AND operation on their masks. If the result is zero, it means there is no overlap. In this case, I calculate the product of the lengths of the two subsequences and update the result if it\u2019s greater than the current result.\n\n# Complexity\n- Time complexity: The time complexity is `O(2^n\u22C5n)` because there are `2n` possible subsequences and for each subsequence, we spend `O(n)` time to check if it\u2019s a palindrome and to calculate its length.\n- Space complexity: The space complexity is `O(2^n)`\n because we need to store all subsequences and their masks.\n\n# Code\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n masks = [] # masks for subsequences\n subs = [] # corresponding subsequences\n palSubs = [] # palindromic subsequences\n\n # Generate all possible subsequences\n for i in range(len(s) - 1, -1, -1):\n length = len(masks)\n\n for j in range(length):\n # Add the current character to the subsequence\n sub = subs[j] + s[len(s) - i - 1]\n # Update the mask to include the current character\n mask = masks[j] | 1 << i\n\n # If the subsequence is a palindrome, add it to the list of palindromic subsequences\n if self.isPalindrom(sub):\n palSubs.append((sub, mask))\n\n # Add the subsequence and its mask to the lists\n subs.append(sub)\n masks.append(mask)\n\n # Add the current character as a single-character subsequence\n palSubs.append((s[len(s) - i - 1], 1 << i))\n masks.append(1 << i)\n subs.append(s[len(s) - i - 1])\n\n result = 1\n # Iterate over all pairs of palindromic subsequences\n for i in range(len(palSubs)):\n sub1, mask1 = palSubs[i]\n\n for j in range(len(palSubs)):\n if i == j:\n continue\n sub2, mask2 = palSubs[j]\n # If the subsequences have no overlap, calculate the product of their lengths\n if mask1 & mask2 == 0: # no overlap\n result = max(result, len(sub1) * len(sub2))\n\n return result\n\n def isPalindrom(self, _str):\n left, right = 0, len(_str) - 1\n result = True\n # Check if the string is a palindrome\n while left < right:\n if _str[left] != _str[right]:\n result = False\n break\n left += 1\n right -= 1\n\n return result\n``` | 0 | Given a string `s`, find two **disjoint palindromic subsequences** of `s` such that the **product** of their lengths is **maximized**. The two subsequences are **disjoint** if they do not both pick a character at the same index.
Return _the **maximum** possible **product** of the lengths of the two palindromic subsequences_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** s = "leetcodecom "
**Output:** 9
**Explanation**: An optimal solution is to choose "ete " for the 1st subsequence and "cdc " for the 2nd subsequence.
The product of their lengths is: 3 \* 3 = 9.
**Example 2:**
**Input:** s = "bb "
**Output:** 1
**Explanation**: An optimal solution is to choose "b " (the first character) for the 1st subsequence and "b " (the second character) for the 2nd subsequence.
The product of their lengths is: 1 \* 1 = 1.
**Example 3:**
**Input:** s = "accbcaxxcxx "
**Output:** 25
**Explanation**: An optimal solution is to choose "accca " for the 1st subsequence and "xxcxx " for the 2nd subsequence.
The product of their lengths is: 5 \* 5 = 25.
**Constraints:**
* `2 <= s.length <= 12`
* `s` consists of lowercase English letters only. | Let's note that the only thing that matters is how many stones were removed so we can maintain dp[numberOfRemovedStones] dp[x] = max(sum of all elements up to y - dp[y]) for all y > x |
Python3 DP solution, faster than 99% Python3 | maximum-product-of-the-length-of-two-palindromic-subsequences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the maximum string length is just 12, we can generate all possible subsequence then calculate the longest Palindromic Subsequences\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use DP to find the longest Palindromic Subsequences of a given string.\n2. Recursively generate all possible subsequence and the complement subsequence of the given string.\nFor example, the given string is "abcdefgh", one possible subsequence is "acfg" and the complement subsequence should be "bdeh".\n3. Run DP on these two subsequence and mulpily the result. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(2^n)\n# Code\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n @cache\n def dp(s):\n if len(s) == 0:\n return 0\n if len(s) == 1:\n return 1\n else:\n if s[0]==s[-1]:\n return dp(s[1:-1])+2\n else:\n return max(dp(s[1:]),dp(s[:-1]))\n ans = 0\n def generate(s1,s2,ind):\n if ind == len(s):\n nonlocal ans\n ans=max(ans,dp(s1)*dp(s2))\n return\n generate(s1+s[ind],s2,ind+1)\n generate(s1,s2+s[ind],ind+1)\n \n generate(\'\',\'\',0)\n return ans\n \n\n``` | 0 | Given a string `s`, find two **disjoint palindromic subsequences** of `s` such that the **product** of their lengths is **maximized**. The two subsequences are **disjoint** if they do not both pick a character at the same index.
Return _the **maximum** possible **product** of the lengths of the two palindromic subsequences_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** s = "leetcodecom "
**Output:** 9
**Explanation**: An optimal solution is to choose "ete " for the 1st subsequence and "cdc " for the 2nd subsequence.
The product of their lengths is: 3 \* 3 = 9.
**Example 2:**
**Input:** s = "bb "
**Output:** 1
**Explanation**: An optimal solution is to choose "b " (the first character) for the 1st subsequence and "b " (the second character) for the 2nd subsequence.
The product of their lengths is: 1 \* 1 = 1.
**Example 3:**
**Input:** s = "accbcaxxcxx "
**Output:** 25
**Explanation**: An optimal solution is to choose "accca " for the 1st subsequence and "xxcxx " for the 2nd subsequence.
The product of their lengths is: 5 \* 5 = 25.
**Constraints:**
* `2 <= s.length <= 12`
* `s` consists of lowercase English letters only. | Let's note that the only thing that matters is how many stones were removed so we can maintain dp[numberOfRemovedStones] dp[x] = max(sum of all elements up to y - dp[y]) for all y > x |
Python Solution | maximum-product-of-the-length-of-two-palindromic-subsequences | 0 | 1 | # Complexity\n- Time complexity: O(2 ** N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(2 ** N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProduct(self, s: str) -> int:\n N, pali = len(s), {} # bitmask: length\n\n for mask in range(1, 1 << N): # 1 << N == 2 ** N\n subseq = ""\n for i in range(N):\n if mask & (1 << i): #1 shifted to the left by i position\n subseq += s[i]\n if subseq == subseq[::-1]:\n pali[mask] = len(subseq)\n \n mxm = 1\n\n for m1 in pali:\n for m2 in pali:\n if m1 & m2 == 0:\n mxm = max(mxm, pali[m1] * pali[m2])\n \n return mxm\n``` | 0 | Given a string `s`, find two **disjoint palindromic subsequences** of `s` such that the **product** of their lengths is **maximized**. The two subsequences are **disjoint** if they do not both pick a character at the same index.
Return _the **maximum** possible **product** of the lengths of the two palindromic subsequences_.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** s = "leetcodecom "
**Output:** 9
**Explanation**: An optimal solution is to choose "ete " for the 1st subsequence and "cdc " for the 2nd subsequence.
The product of their lengths is: 3 \* 3 = 9.
**Example 2:**
**Input:** s = "bb "
**Output:** 1
**Explanation**: An optimal solution is to choose "b " (the first character) for the 1st subsequence and "b " (the second character) for the 2nd subsequence.
The product of their lengths is: 1 \* 1 = 1.
**Example 3:**
**Input:** s = "accbcaxxcxx "
**Output:** 25
**Explanation**: An optimal solution is to choose "accca " for the 1st subsequence and "xxcxx " for the 2nd subsequence.
The product of their lengths is: 5 \* 5 = 25.
**Constraints:**
* `2 <= s.length <= 12`
* `s` consists of lowercase English letters only. | Let's note that the only thing that matters is how many stones were removed so we can maintain dp[numberOfRemovedStones] dp[x] = max(sum of all elements up to y - dp[y]) for all y > x |
Python (Simple DFS + Union Find) | smallest-missing-genetic-value-in-each-subtree | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestMissingValueSubtree(self, parents, nums):\n dict1 = defaultdict(int)\n\n def find(x):\n if x not in dict1:\n return x\n else:\n if x != dict1[x]:\n dict1[x] = find(dict1[x])\n return dict1[x]\n\n def union(x,y):\n a,b = find(x),find(y)\n\n if a == b: return 0\n\n dict1[b] = a\n\n return a\n\n\n def dfs(tree):\n smallest = max({dfs(subtree) for subtree in graph[tree]}|{1})\n\n for subtree in graph[tree]:\n union(nums[tree],nums[subtree])\n\n for i in range(smallest,n+1):\n if find(i) != find(nums[tree]):\n res[tree] = i\n return i\n \n return i+1\n\n\n n, graph = len(nums), defaultdict(list)\n res = [1]*n\n\n for i,p in enumerate(parents):\n graph[p].append(i)\n\n res[0] = dfs(0)\n\n return res\n\n \n\n\n\n\n\n\n\n\n \n\n\n\n\n \n\n\n\n\n \n\n\n\n \n \n``` | 0 | There is a **family tree** rooted at `0` consisting of `n` nodes numbered `0` to `n - 1`. You are given a **0-indexed** integer array `parents`, where `parents[i]` is the parent for node `i`. Since node `0` is the **root**, `parents[0] == -1`.
There are `105` genetic values, each represented by an integer in the **inclusive** range `[1, 105]`. You are given a **0-indexed** integer array `nums`, where `nums[i]` is a **distinct** genetic value for node `i`.
Return _an array_ `ans` _of length_ `n` _where_ `ans[i]` _is_ _the **smallest** genetic value that is **missing** from the subtree rooted at node_ `i`.
The **subtree** rooted at a node `x` contains node `x` and all of its **descendant** nodes.
**Example 1:**
**Input:** parents = \[-1,0,0,2\], nums = \[1,2,3,4\]
**Output:** \[5,1,1,1\]
**Explanation:** The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes \[0,1,2,3\] with values \[1,2,3,4\]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes \[2,3\] with values \[3,4\]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.
**Example 2:**
**Input:** parents = \[-1,0,1,0,3,3\], nums = \[5,4,6,2,1,3\]
**Output:** \[7,1,1,4,2,1\]
**Explanation:** The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes \[0,1,2,3,4,5\] with values \[5,4,6,2,1,3\]. 7 is the smallest missing value.
- 1: The subtree contains nodes \[1,2\] with values \[4,6\]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes \[3,4,5\] with values \[2,1,3\]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.
**Example 3:**
**Input:** parents = \[-1,2,3,0,2,4,1\], nums = \[2,3,4,5,6,7,8\]
**Output:** \[1,1,1,1,1,1,1\]
**Explanation:** The value 1 is missing from all the subtrees.
**Constraints:**
* `n == parents.length == nums.length`
* `2 <= n <= 105`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents[0] == -1`
* `parents` represents a valid tree.
* `1 <= nums[i] <= 105`
* Each `nums[i]` is distinct. | Keep a frequency map of the elements in each window. When the frequency of the element is 0, remove it from the map. The answer to each window is the size of the map. |
[Python3] dfs | smallest-missing-genetic-value-in-each-subtree | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/0de189059bd6af4dabe23d9066dde1655f3334fc) for solutions of weekly 258. \n```\nclass Solution:\n def smallestMissingValueSubtree(self, parents: List[int], nums: List[int]) -> List[int]:\n ans = [1] * len(parents)\n if 1 in nums: \n tree = {}\n for i, x in enumerate(parents): \n tree.setdefault(x, []).append(i)\n \n k = nums.index(1)\n val = 1\n seen = set()\n \n while k != -1: \n stack = [k]\n while stack: \n x = stack.pop()\n seen.add(nums[x])\n for xx in tree.get(x, []): \n if nums[xx] not in seen: \n stack.append(xx)\n seen.add(nums[xx])\n while val in seen: val += 1\n ans[k] = val\n k = parents[k]\n return ans \n``` | 1 | There is a **family tree** rooted at `0` consisting of `n` nodes numbered `0` to `n - 1`. You are given a **0-indexed** integer array `parents`, where `parents[i]` is the parent for node `i`. Since node `0` is the **root**, `parents[0] == -1`.
There are `105` genetic values, each represented by an integer in the **inclusive** range `[1, 105]`. You are given a **0-indexed** integer array `nums`, where `nums[i]` is a **distinct** genetic value for node `i`.
Return _an array_ `ans` _of length_ `n` _where_ `ans[i]` _is_ _the **smallest** genetic value that is **missing** from the subtree rooted at node_ `i`.
The **subtree** rooted at a node `x` contains node `x` and all of its **descendant** nodes.
**Example 1:**
**Input:** parents = \[-1,0,0,2\], nums = \[1,2,3,4\]
**Output:** \[5,1,1,1\]
**Explanation:** The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes \[0,1,2,3\] with values \[1,2,3,4\]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes \[2,3\] with values \[3,4\]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.
**Example 2:**
**Input:** parents = \[-1,0,1,0,3,3\], nums = \[5,4,6,2,1,3\]
**Output:** \[7,1,1,4,2,1\]
**Explanation:** The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes \[0,1,2,3,4,5\] with values \[5,4,6,2,1,3\]. 7 is the smallest missing value.
- 1: The subtree contains nodes \[1,2\] with values \[4,6\]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes \[3,4,5\] with values \[2,1,3\]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.
**Example 3:**
**Input:** parents = \[-1,2,3,0,2,4,1\], nums = \[2,3,4,5,6,7,8\]
**Output:** \[1,1,1,1,1,1,1\]
**Explanation:** The value 1 is missing from all the subtrees.
**Constraints:**
* `n == parents.length == nums.length`
* `2 <= n <= 105`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents[0] == -1`
* `parents` represents a valid tree.
* `1 <= nums[i] <= 105`
* Each `nums[i]` is distinct. | Keep a frequency map of the elements in each window. When the frequency of the element is 0, remove it from the map. The answer to each window is the size of the map. |
[Python] Clean & concise. Dictionary T.C O(N) | count-number-of-pairs-with-absolute-difference-k | 0 | 1 | ```\nclass Solution:\n def countKDifference(self, nums: List[int], k: int) -> int:\n seen = defaultdict(int)\n counter = 0\n for num in nums:\n tmp, tmp2 = num - k, num + k\n if tmp in seen:\n counter += seen[tmp]\n if tmp2 in seen:\n counter += seen[tmp2]\n \n seen[num] += 1\n \n return counter\n```\n\nShorter version\n\n```\nclass Solution:\n def countKDifference(self, nums: List[int], k: int) -> int:\n seen = defaultdict(int)\n counter = 0\n for num in nums:\n counter += seen[num-k] + seen[num+k]\n seen[num] += 1\n return counter\n``` | 47 | Given an integer array `nums` and an integer `k`, return _the number of pairs_ `(i, j)` _where_ `i < j` _such that_ `|nums[i] - nums[j]| == k`.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,2,2,1\], k = 1
**Output:** 4
**Explanation:** The pairs with an absolute difference of 1 are:
- \[**1**,**2**,2,1\]
- \[**1**,2,**2**,1\]
- \[1,**2**,2,**1**\]
- \[1,2,**2**,**1**\]
**Example 2:**
**Input:** nums = \[1,3\], k = 3
**Output:** 0
**Explanation:** There are no pairs with an absolute difference of 3.
**Example 3:**
**Input:** nums = \[3,2,1,5,4\], k = 2
**Output:** 3
**Explanation:** The pairs with an absolute difference of 2 are:
- \[**3**,2,**1**,5,4\]
- \[**3**,2,1,**5**,4\]
- \[3,**2**,1,5,**4**\]
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100`
* `1 <= k <= 99` | Subtract the sum of chalk[i] from k until k is less than that sum Now just iterate over the array if chalk[i] is less thank k this is your answer otherwise this i is the answer |
2 Approach Python Solution O(n) & O(n2) | count-number-of-pairs-with-absolute-difference-k | 0 | 1 | O(n)\n```\nclass Solution:\n def countKDifference(self, nums: List[int], k: int) -> int:\n count = 0\n \n hash = {}\n \n for i in nums:\n if i in hash:\n hash[i] +=1\n else:\n hash[i] = 1\n \n for i in hash:\n if i+k in hash:\n count+=hash[i]*hash[i+k]\n \n return count\n```\nO(n2)\n```\nclass Solution:\n def countKDifference(self, nums: List[int], k: int) -> int:\n \n count = 0\n i = 0\n j = len(nums)-1\n nums.sort()\n while i<len(nums):\n if abs(nums[j]-nums[i])==k:\n count+=1\n j-=1\n \n \n elif abs(nums[j]-nums[i])<k:\n i+=1\n j=len(nums)-1\n else:\n j-=1\n \n return count\n\t\n\t\t | 8 | Given an integer array `nums` and an integer `k`, return _the number of pairs_ `(i, j)` _where_ `i < j` _such that_ `|nums[i] - nums[j]| == k`.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,2,2,1\], k = 1
**Output:** 4
**Explanation:** The pairs with an absolute difference of 1 are:
- \[**1**,**2**,2,1\]
- \[**1**,2,**2**,1\]
- \[1,**2**,2,**1**\]
- \[1,2,**2**,**1**\]
**Example 2:**
**Input:** nums = \[1,3\], k = 3
**Output:** 0
**Explanation:** There are no pairs with an absolute difference of 3.
**Example 3:**
**Input:** nums = \[3,2,1,5,4\], k = 2
**Output:** 3
**Explanation:** The pairs with an absolute difference of 2 are:
- \[**3**,2,**1**,5,4\]
- \[**3**,2,1,**5**,4\]
- \[3,**2**,1,5,**4**\]
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100`
* `1 <= k <= 99` | Subtract the sum of chalk[i] from k until k is less than that sum Now just iterate over the array if chalk[i] is less thank k this is your answer otherwise this i is the answer |
Python3, Time: O(n), Using dictionary | count-number-of-pairs-with-absolute-difference-k | 0 | 1 | ```\nclass Solution:\n def countKDifference(self, nums: List[int], k: int) -> int:\n count=0\n from collections import Counter\n mydict=Counter(nums) \n for i in mydict:\n if i+k in mydict:\n count=count+ mydict[i]*mydict[i+k] \n return count\n``` | 5 | Given an integer array `nums` and an integer `k`, return _the number of pairs_ `(i, j)` _where_ `i < j` _such that_ `|nums[i] - nums[j]| == k`.
The value of `|x|` is defined as:
* `x` if `x >= 0`.
* `-x` if `x < 0`.
**Example 1:**
**Input:** nums = \[1,2,2,1\], k = 1
**Output:** 4
**Explanation:** The pairs with an absolute difference of 1 are:
- \[**1**,**2**,2,1\]
- \[**1**,2,**2**,1\]
- \[1,**2**,2,**1**\]
- \[1,2,**2**,**1**\]
**Example 2:**
**Input:** nums = \[1,3\], k = 3
**Output:** 0
**Explanation:** There are no pairs with an absolute difference of 3.
**Example 3:**
**Input:** nums = \[3,2,1,5,4\], k = 2
**Output:** 3
**Explanation:** The pairs with an absolute difference of 2 are:
- \[**3**,2,**1**,5,4\]
- \[**3**,2,1,**5**,4\]
- \[3,**2**,1,5,**4**\]
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i] <= 100`
* `1 <= k <= 99` | Subtract the sum of chalk[i] from k until k is less than that sum Now just iterate over the array if chalk[i] is less thank k this is your answer otherwise this i is the answer |
Python3 || 9 lines, Counter, with explanation || T/M: 99.6%/81% | find-original-array-from-doubled-array | 0 | 1 | Pretty much explains itself. It uses a Counter, handles the zeros separately, then iterates\nthrough the keys of the Counter to check the doubles and to build the answer array.\n\nI\'m no expert, but I guess time/space to be *O*(*n*)/*O*(*n*). (Counter is *O*(*n*) on both I believe.)\n[edit: @jacobquicksilver--oops, you\'re correct, thank you; you get my upvote. *O*(*n*log(*n*)/*O*(*n*log(*n*)\nis mitigated a little because the sort is on the keys, not the whole list. ]\n\n```\nclass Solution:\n def findOriginalArray(self, changed: List[int]) -> List[int]:\n c = Counter(changed)\n\n zeros, m = divmod(c[0], 2)\n if m: return []\n ans = [0]*zeros \n\n for n in sorted(c.keys()):\n if c[n] > c[2*n]: return []\n c[2*n]-= c[n]\n ans.extend([n]*c[n])\n\n return ans\n\n```\n[https://leetcode.com/submissions/detail/800041728/](http://)\n\t\t | 5 | An integer array `original` is transformed into a **doubled** array `changed` by appending **twice the value** of every element in `original`, and then randomly **shuffling** the resulting array.
Given an array `changed`, return `original` _if_ `changed` _is a **doubled** array. If_ `changed` _is not a **doubled** array, return an empty array. The elements in_ `original` _may be returned in **any** order_.
**Example 1:**
**Input:** changed = \[1,3,4,2,6,8\]
**Output:** \[1,3,4\]
**Explanation:** One possible original array could be \[1,3,4\]:
- Twice the value of 1 is 1 \* 2 = 2.
- Twice the value of 3 is 3 \* 2 = 6.
- Twice the value of 4 is 4 \* 2 = 8.
Other original arrays could be \[4,3,1\] or \[3,1,4\].
**Example 2:**
**Input:** changed = \[6,3,0,1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Example 3:**
**Input:** changed = \[1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Constraints:**
* `1 <= changed.length <= 105`
* `0 <= changed[i] <= 105` | null |
Python Solution | find-original-array-from-doubled-array | 0 | 1 | ### 1\n```py\nclass Solution:\n def findOriginalArray(self, changed: List[int]) -> List[int]:\n if len(changed) % 2 == 1:\n return []\n data = Counter(changed)\n result = []\n for k in sorted(data):\n if data[k] < 0:\n return []\n elif k == 0:\n x, y = divmod(data[k], 2)\n if y == 1:\n return []\n result += [0] * x\n elif data[k] > 0:\n value = k * 2\n if data[value] == 0:\n return []\n min_value = min(value, data[k])\n result += [k] * min_value\n data[k] -= min_value\n data[value] -= min_value\n return result\n```\n\n\n### 2\n```py\nclass Solution:\n def findOriginalArray(self, changed: List[int]) -> List[int]:\n if len(changed) % 2 == 1:\n return []\n data = Counter(changed)\n result = []\n for k in sorted(data):\n if data[k] < 0:\n return []\n value = k * 2\n while data[k] > 0:\n if data[value] == 0:\n return []\n result.append(k)\n data[k] -= 1\n data[value] -= 1\n return result\n``` | 3 | An integer array `original` is transformed into a **doubled** array `changed` by appending **twice the value** of every element in `original`, and then randomly **shuffling** the resulting array.
Given an array `changed`, return `original` _if_ `changed` _is a **doubled** array. If_ `changed` _is not a **doubled** array, return an empty array. The elements in_ `original` _may be returned in **any** order_.
**Example 1:**
**Input:** changed = \[1,3,4,2,6,8\]
**Output:** \[1,3,4\]
**Explanation:** One possible original array could be \[1,3,4\]:
- Twice the value of 1 is 1 \* 2 = 2.
- Twice the value of 3 is 3 \* 2 = 6.
- Twice the value of 4 is 4 \* 2 = 8.
Other original arrays could be \[4,3,1\] or \[3,1,4\].
**Example 2:**
**Input:** changed = \[6,3,0,1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Example 3:**
**Input:** changed = \[1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Constraints:**
* `1 <= changed.length <= 105`
* `0 <= changed[i] <= 105` | null |
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | find-original-array-from-doubled-array | 1 | 1 | Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**C++ - HashMap Approach**\n\n```cpp\n// Time Complexity: O(N + NlogN)\n// Space Complexity: O(N)\n// where N is the number of elements in `changed` \nclass Solution {\npublic:\n // hashmap approach\n vector<int> findOriginalArray(vector<int>& changed) {\n // if the length of the input is odd, then return {}\n // because doubled array must have even length\n if (changed.size() & 1) return {};\n // count the frequency of each number\n unordered_map<int, int> m;\n for (auto x: changed) m[x]++;\n vector<int> ans;\n // sort in ascending order\n sort(changed.begin(), changed.end());\n // keep the unique elements only in changed\n // think of test cases like [0,0,0,0]\n // alternatively you can handle it like\n // - check if the frequency of 0 is odd, if so, return {}\n // - push `0` `m[0] / 2` times to ans\n changed.erase(unique(changed.begin(), changed.end()), changed.end());\n // so that we can iterate `changed` from smallest to largest\n for (auto x : changed) {\n // if the number of m[x] is greater than than m[x * 2]\n // then there would be some m[x] left\n // therefore, return {} here as changed is not a doubled array\n if (m[x] > m[x * 2]) return {};\n for (int i = 0; i < m[x]; i++) {\n // otherwise, we put the element `x` `m[x]` times to ans\n ans.push_back(x);\n // at the same time we decrease the count of m[x * 2] by 1\n // we don\'t need to decrease m[x] by 1 as we won\'t use it again\n m[x * 2] -= 1;\n }\n }\n return ans;\n }\n};\n```\n\n```cpp\n// Time Complexity: O(N + KlogK)\n// Space Complexity: O(N)\n// where N is the number of elements in `changed` \n// and K is the number of elements in `uniqueNumbers`\nclass Solution {\npublic:\n // hashmap approach\n vector<int> findOriginalArray(vector<int>& changed) {\n // if the length of the input is odd, then return {}\n // because doubled array must have even length\n if (changed.size() & 1) return {};\n // count the frequency of each number\n unordered_map<int, int> m;\n for (auto x: changed) m[x]++;\n vector<int> ans;\n vector<int> uniqueNumbers;\n\t\t// push all unuque numbers to `uniqueNumbers`\n for (auto x : m) uniqueNumbers.push_back(x.first);\n // sort in ascending order\n sort(uniqueNumbers.begin(), uniqueNumbers.end());\n // so that we can iterate `changed` from smallest to largest\n for (auto x : uniqueNumbers) {\n // if the number of m[x] is greater than than m[x * 2]\n // then there would be some m[x] left\n // therefore, return {} here as changed is not a doubled array\n if (m[x] > m[x * 2]) return {};\n for (int i = 0; i < m[x]; i++) {\n // otherwise, we put the element `x` `m[x]` times to ans\n ans.push_back(x);\n // at the same time we decrease the count of m[x * 2] by 1\n // we don\'t need to decrease m[x] by 1 as we won\'t use it again\n m[x * 2] -= 1;\n }\n }\n return ans;\n }\n};\n```\n\n**C++ - Multiset Approach**\n\n```cpp\n// Time Complexity: O(NlogN)\n// Space Complexity: O(N)\n// where N is the number of elements in `changed` \nclass Solution {\npublic:\n // multiset approach\n vector<int> findOriginalArray(vector<int>& changed) {\n // if the length of the input is odd, then return {}\n // because doubled array must have even length\n if (changed.size() & 1) return {};\n vector<int> ans;\n // put all the elements to a multiset\n multiset<int> s(changed.begin(), changed.end());\n // keep doing the following logic when there is an element in the multiset\n while (s.size()) {\n // get the smallest element\n int smallest = *s.begin();\n ans.push_back(smallest);\n // remove the smallest element in multiset\n s.erase(s.begin());\n // if the doubled value of smallest doesn\'t exist in the multiset\n // then return {}\n if (s.find(smallest * 2) == s.end()) return {};\n // otherwise we can remove its doubled element\n else s.erase(s.find(smallest * 2)); \n }\n return ans;\n }\n};\n```\n\n**Python**\n\n```py\n# Time Complexity: O(NlogN)\n# Space Complextiy O(N)\n# where N is the number of elements in `changed` \nclass Solution:\n def findOriginalArray(self, changed):\n # use Counter to count the frequency of each element in `changed`\n cnt, ans = Counter(changed), []\n # if the length of the input is odd, then return []\n # because doubled array must have even length\n if len(changed) % 2: return []\n # sort in ascending order\n for x in sorted(cnt.keys()):\n # if the number of cnt[x] is greater than than cnt[x * 2]\n # then there would be some cnt[x] left\n # therefore, return [] here as changed is not a doubled array\n if cnt[x] > cnt[x * 2]: return []\n # handle cases like [0,0,0,0]\n if x == 0:\n # similarly, odd length -> return []\n if cnt[x] % 2:\n return []\n else: \n # add `0` `cnt[x] // 2` times \n ans += [0] * (cnt[x] // 2)\n else:\n # otherwise, we put the element `x` `cnt[x]` times to ans\n ans += [x] * cnt[x]\n cnt[2 * x] -= cnt[x]\n return ans\n```\n\n**Java - Counting Sort**\n\n```java\nclass Solution {\n // counting sort approach\n public int[] findOriginalArray(int[] changed) {\n int n = changed.length, j = 0;\n // if the length of the input is odd, then return []\n // because doubled array must have even length\n if (n % 2 == 1) return new int[]{};\n int[] ans = new int[n / 2];\n // alternatively, you can find the max number in `changed`\n // then use new int[2 * mx + 1]\n int[] cnt = new int[200005];\n // count the frequency of each number\n for (int x : changed) cnt[x] += 1;\n // iterate from 0 to max number\n for (int i = 0; i < 200005; i++) {\n // check if the count of number i is greater than 0\n if (cnt[i] > 0) {\n // number i exists, decrease by 1\n cnt[i] -= 1;\n // look for the doubled value\n if (cnt[i * 2] > 0) {\n // doubled value exists, decrease by 1\n cnt[i * 2] -= 1;\n // add this number to ans\n ans[j++] = i--;\n } else {\n // cannot pair up, return []\n return new int[]{};\n }\n }\n }\n return ans;\n }\n}\n``` | 46 | An integer array `original` is transformed into a **doubled** array `changed` by appending **twice the value** of every element in `original`, and then randomly **shuffling** the resulting array.
Given an array `changed`, return `original` _if_ `changed` _is a **doubled** array. If_ `changed` _is not a **doubled** array, return an empty array. The elements in_ `original` _may be returned in **any** order_.
**Example 1:**
**Input:** changed = \[1,3,4,2,6,8\]
**Output:** \[1,3,4\]
**Explanation:** One possible original array could be \[1,3,4\]:
- Twice the value of 1 is 1 \* 2 = 2.
- Twice the value of 3 is 3 \* 2 = 6.
- Twice the value of 4 is 4 \* 2 = 8.
Other original arrays could be \[4,3,1\] or \[3,1,4\].
**Example 2:**
**Input:** changed = \[6,3,0,1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Example 3:**
**Input:** changed = \[1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Constraints:**
* `1 <= changed.length <= 105`
* `0 <= changed[i] <= 105` | null |
Python | Math + Sort + Counter | find-original-array-from-doubled-array | 0 | 1 | ## Intuition\nAll numbers are non-negative, so if a double is present, it must be greater than or equal. We can sort the numbers from greatest to least, and pair the numbers with their doubles greedily.\n\n## Approach\nWe will use a `collections.Counter()` to keep track of how many of each number we have not paired yet.\n\nFor each `num` in `changed`:\n* If `num` is half some number in the counter, it should be on the original array. We save it and update the count of `2 * num`.\n* If `num` is not half some number in the counter, and it is even, then we save it in the counter as a possible number to be paired.\n* If `num` is not half some number in the counter, and it is not even, it would not be possible to pair it and `changed` is not a double array. We return `[]`.\n\nWe need to be careful with the `0`s, as `2 * 0 == 0`. We just need to make sure that in the end we have an even number of `0`\'s if `changed` is to be a double array.\n\nIf in the end there are no more numbers to be paired, then we had a double array.\n\n## Complexity\n- Time complexity: *O(n)* where *n* is the number of elements in `changed`; we visit each number once, saving checking if it can be paired or saving it in the counter takes *O(1)* time. \n\n- Space complexity: *O(n)* in the worst case, since we could have all numbers are different.\n\n## Possible quick improvements\nWe would not need to wait until the end to check if there were any unpaired numbers. Since we are sorting the array, if there is an unpaired even number that is larger than twice the current number we are looking at, no number would be able to be paired with it.\n\n## Code\n```python\nclass Solution:\n def findOriginalArray(self, changed: List[int]) -> List[int]:\n if len(changed) % 2 != 0:\n return []\n\n changed.sort(reverse = True)\n unpaired = Counter(); original = []\n for i, num in enumerate(changed):\n if num != 0:\n if unpaired[2 * num] > 0:\n unpaired[2 * num] -= 1\n original.append(num)\n elif num % 2 == 0:\n unpaired[num] += 1\n else:\n return []\n else:\n unpaired[num] += 1\n \n if unpaired[0] % 2 == 0:\n original += [0] * (unpaired[0] // 2)\n unpaired[0] = 0\n \n return original if all(count == 0 for count in unpaired.values()) else []\n``` | 3 | An integer array `original` is transformed into a **doubled** array `changed` by appending **twice the value** of every element in `original`, and then randomly **shuffling** the resulting array.
Given an array `changed`, return `original` _if_ `changed` _is a **doubled** array. If_ `changed` _is not a **doubled** array, return an empty array. The elements in_ `original` _may be returned in **any** order_.
**Example 1:**
**Input:** changed = \[1,3,4,2,6,8\]
**Output:** \[1,3,4\]
**Explanation:** One possible original array could be \[1,3,4\]:
- Twice the value of 1 is 1 \* 2 = 2.
- Twice the value of 3 is 3 \* 2 = 6.
- Twice the value of 4 is 4 \* 2 = 8.
Other original arrays could be \[4,3,1\] or \[3,1,4\].
**Example 2:**
**Input:** changed = \[6,3,0,1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Example 3:**
**Input:** changed = \[1\]
**Output:** \[\]
**Explanation:** changed is not a doubled array.
**Constraints:**
* `1 <= changed.length <= 105`
* `0 <= changed[i] <= 105` | null |
python3 sorting+dynamic programming(with explicit explanation + test case) | maximum-earnings-from-taxi | 0 | 1 | # Intuition\nthis question is similar to [leetcode 80: maximum number of events that can be attended](https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/), the two question uses simiar sorting and usage of stack/heap. In this solution, I used dynamic programming to use an array to keep track of whats the maximum amount of money the driver has made by the time he switched to direction ```i```\n\n# Approach\nfirst we sort the rides based on the end direction, and break ties using the starting direction. In Python3, we can do the sorting using ```rides = sorted(rides, key=lambda x: (x[1], x[0]))```\n\nnext we build a array of size ```n+1``` to keep track of whats the maximum amount of money the drive can make by the time he switched to direction ```i```\n\nthen we began the algorithm\'s iterative part where we iterate over each direction, at each direction we store in our stack the rides that ends in current direction, then the maximum money the driver can make at index ```i``` is ```dp[i] = max(dp[start]+end-start+tip, dp[d])```\n\nthen in the end, compare the current ```dp[i]``` with previous value ```dp[i-1]```, and set ```dp[i] = max(dp[i], dp[i-1])```\n\nfor a detailed example, for test case:\n```sol = Solution()\nn = 10\nrides = [[2,3,6],[8,9,8],[5,9,7],[8,9,1],[2,9,2],[9,10,6],[7,10,10],[6,7,9],[4,9,7],[2,3,1]]\n```\n\nafter sorting, rides becomes:\n```\nrides = [[2, 3, 6], [2, 3, 1], [6, 7, 9], [2, 9, 2], [4, 9, 7], [5, 9, 7], [8, 9, 8], [8, 9, 1], [7, 10, 10], [9, 10, 6]]\n```\n\nthe dp array looks like this:\n```\ndp = [0, 0, 0, 7, 7, 7, 7, 17, 17, 26, 33]\n```\n\nthen we simply ```return max(dp)```\n\n# Complexity\n- Time complexity:\nlet ```k = len(rides)```\n$$O(max(n, k))$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n # rides based on the end direction, and break ties using the starting direction\n rides = sorted(rides, key=lambda x: (x[1], x[0]))\n l = []\n dp = [0] * (n+1)\n idx = 0\n\n # iterate over each end direction\n for d in range(1, n+1):\n\n stack = []\n # store all rides that ends up in current direction\n while idx < len(rides) and rides[idx][1] == d:\n stack.append(rides[idx])\n idx += 1\n\n # calculate the maximum money that can me made in current direction\n while stack:\n start, end, tip = stack.pop()\n dp[d] = max(dp[d], dp[start]+end-start+tip)\n # compare with last direction and keeping the maximum\n dp[d] = max(dp[d], dp[d-1])\n return max(dp)\n```\n\nif my solution has helped you, please consider upvoting my anwser, thank you :)\n\n | 2 | There are `n` points on a road you are driving your taxi on. The `n` points on the road are labeled from `1` to `n` in the direction you are going, and you want to drive from point `1` to point `n` to make money by picking up passengers. You cannot change the direction of the taxi.
The passengers are represented by a **0-indexed** 2D integer array `rides`, where `rides[i] = [starti, endi, tipi]` denotes the `ith` passenger requesting a ride from point `starti` to point `endi` who is willing to give a `tipi` dollar tip.
For **each** passenger `i` you pick up, you **earn** `endi - starti + tipi` dollars. You may only drive **at most one** passenger at a time.
Given `n` and `rides`, return _the **maximum** number of dollars you can earn by picking up the passengers optimally._
**Note:** You may drop off a passenger and pick up a different passenger at the same point.
**Example 1:**
**Input:** n = 5, rides = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 7
**Explanation:** We can pick up passenger 0 to earn 5 - 2 + 4 = 7 dollars.
**Example 2:**
**Input:** n = 20, rides = \[\[1,6,1\],\[3,10,2\],\[10,12,3\],\[11,12,2\],\[12,15,2\],\[13,18,1\]\]
**Output:** 20
**Explanation:** We will pick up the following passengers:
- Drive passenger 1 from point 3 to point 10 for a profit of 10 - 3 + 2 = 9 dollars.
- Drive passenger 2 from point 10 to point 12 for a profit of 12 - 10 + 3 = 5 dollars.
- Drive passenger 5 from point 13 to point 18 for a profit of 18 - 13 + 1 = 6 dollars.
We earn 9 + 5 + 6 = 20 dollars in total.
**Constraints:**
* `1 <= n <= 105`
* `1 <= rides.length <= 3 * 104`
* `rides[i].length == 3`
* `1 <= starti < endi <= n`
* `1 <= tipi <= 105` | How many possible states are there for a given expression? Is there a data structure that we can use to solve the problem optimally? |
[Python] Solution - Maximum Earnings from Taxi | maximum-earnings-from-taxi | 0 | 1 | \n**Problem** : To find the maximum earnings.\n\n**Idea** : Start to think in this way that we can track the maximum earning at each point .\neg : n = 20, rides = [[1,6,1],[3,10,2],[10,12,3],[11,12,2],[12,15,2],[13,18,1]]\n\nWe want to loop from i = 1 to n and at each step check if this i is an end point or not .\nif it is an end point then we check all of its corresponding start points and get the maximum earning we can make .\n\n i | 0 | 1 | 2 | 3 | 4 | 5\ndp| 0 | 0 | 0 | 0 | 0 | 0\n\nWhen i=6 ,\nwe check if 6 is an end point in the given array of rides \nyes it is \n(Note : -In order to quickly check if this number is an end point or not I am maintaining a dictionary where \nkey=end point and the value is [start_point,tip])\n\nnow I loop through all the corresponding start points whose end point is i\ntemp_profit = i(end_point) - start_point + tip \nbut in order to get the total profit at this end point (i) I also have to consider adding dp[start_point]\n\nWhat this means is **max_profit achieved till the start point (i.e dp[start])+ profit achieved from start_point to this end_point(i)\n(i.e end_point(i)-start_point+tip)**\n\nHence the eqn : \n****\n dp[i] = max(dp[i-1],end_point-start_point+tip+dp[start])\n****\n\nSolution :\n\n```\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n \n d = {}\n for start,end,tip in rides:\n if end not in d:\n d[end] =[[start,tip]]\n else:\n d[end].append([start,tip])\n \n \n dp = [0]*(n+1)\n dp[0] = 0\n \n for i in range(1,n+1):\n dp[i] = dp[i-1]\n if i in d:\n temp_profit = 0\n for start,tip in d[i]:\n if (i-start)+tip+dp[start] > temp_profit:\n temp_profit = i-start+tip+dp[start]\n dp[i] = max(dp[i],temp_profit)\n \n \n return dp[-1]\n```\nT.C : O(n)\n | 4 | There are `n` points on a road you are driving your taxi on. The `n` points on the road are labeled from `1` to `n` in the direction you are going, and you want to drive from point `1` to point `n` to make money by picking up passengers. You cannot change the direction of the taxi.
The passengers are represented by a **0-indexed** 2D integer array `rides`, where `rides[i] = [starti, endi, tipi]` denotes the `ith` passenger requesting a ride from point `starti` to point `endi` who is willing to give a `tipi` dollar tip.
For **each** passenger `i` you pick up, you **earn** `endi - starti + tipi` dollars. You may only drive **at most one** passenger at a time.
Given `n` and `rides`, return _the **maximum** number of dollars you can earn by picking up the passengers optimally._
**Note:** You may drop off a passenger and pick up a different passenger at the same point.
**Example 1:**
**Input:** n = 5, rides = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 7
**Explanation:** We can pick up passenger 0 to earn 5 - 2 + 4 = 7 dollars.
**Example 2:**
**Input:** n = 20, rides = \[\[1,6,1\],\[3,10,2\],\[10,12,3\],\[11,12,2\],\[12,15,2\],\[13,18,1\]\]
**Output:** 20
**Explanation:** We will pick up the following passengers:
- Drive passenger 1 from point 3 to point 10 for a profit of 10 - 3 + 2 = 9 dollars.
- Drive passenger 2 from point 10 to point 12 for a profit of 12 - 10 + 3 = 5 dollars.
- Drive passenger 5 from point 13 to point 18 for a profit of 18 - 13 + 1 = 6 dollars.
We earn 9 + 5 + 6 = 20 dollars in total.
**Constraints:**
* `1 <= n <= 105`
* `1 <= rides.length <= 3 * 104`
* `rides[i].length == 3`
* `1 <= starti < endi <= n`
* `1 <= tipi <= 105` | How many possible states are there for a given expression? Is there a data structure that we can use to solve the problem optimally? |
DP solution | O(m+n) | Python Kotlin Javascript Java | maximum-earnings-from-taxi | 1 | 1 | # Intuition\nUse dynamic programming to solve this problem. \n\n# Approach\nUse a array dp to record best solution. dp[i] means the best solution end with index i. dp[i] >= dp[i-1]. If there is a ride end with index i, if we take this, the money we can get is `dp[start_i] + end_i - start_i + tip_i` , if it is greater than dp[i], we can update dp[i].\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(m+n)$$ \n\nm is the number of rides and n is the number of points on road.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(m+n)$$\n\n# Code\n```python []\nclass Solution:\n def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:\n mp = dict()\n for ride in rides:\n if ride[1] not in mp:\n mp[ride[1]] = [ride]\n else:\n mp[ride[1]].append(ride)\n \n dp = [0] * (n+1)\n for i in range(1, n+1) :\n dp[i] = dp[i-1]\n if i not in mp:\n continue\n for ride in mp[i]:\n dp[i] = max(dp[i], dp[ride[0]] + ride[1] - ride[0] + ride[2])\n return dp[n]\n \n```\n```kotlin []\nclass Solution {\n fun maxTaxiEarnings(n: Int, rides: Array<IntArray>): Long {\n val map = HashMap<Int,ArrayList<IntArray>>()\n for(ride in rides) {\n var list = map[ride[1]]\n if(list == null) {\n list = ArrayList<IntArray>()\n list.add(ride)\n map[ride[1]] = list\n } else {\n list.add(ride)\n }\n }\n\n val dp = LongArray(n+1)\n for(i in 1..n) {\n dp[i] = dp[i-1]\n val list = map[i]\n if(list == null) {\n continue\n }\n for(ride in list) {\n dp[i] = Math.max(dp[i], dp[ride[0]] + ride[1] - ride[0] + ride[2])\n }\n }\n return dp[n]\n }\n}\n```\n```javascript []\nvar maxTaxiEarnings = function(n, rides) {\n let map = new Map();\n for(let ride of rides) {\n if(!map.has(ride[1])) {\n map.set(ride[1], [ride]);\n } else {\n map.get(ride[1]).push(ride);\n }\n \n }\n\n let dp = [0];\n for(let i=1; i<=n; i++) {\n dp.push(dp[dp.length-1]);\n if(!map.has(i)) {\n continue;\n }\n for(let ride of map.get(i)){\n dp[i] = Math.max(dp[i], dp[ride[0]] + ride[1] - ride[0] + ride[2]);\n }\n }\n return dp[n];\n}\n```\n```java []\nclass Solution {\n public long maxTaxiEarnings(int n, int[][] rides) {\n var map = new HashMap<Integer,ArrayList<int[]>>();\n for(var ride : rides) {\n map.putIfAbsent(ride[1], new ArrayList<>());\n map.get(ride[1]).add(ride);\n }\n\n var dp = new long[n+1];\n for(int i=1; i<=n; i++) {\n dp[i] = dp[i-1];\n var arr = map.get(i);\n if(arr == null) {\n continue;\n }\n for(var ride : arr) {\n dp[i] = Math.max(dp[i], dp[ride[0]] + ride[1] - ride[0] + ride[2]);\n }\n }\n return dp[n];\n }\n}\n``` | 0 | There are `n` points on a road you are driving your taxi on. The `n` points on the road are labeled from `1` to `n` in the direction you are going, and you want to drive from point `1` to point `n` to make money by picking up passengers. You cannot change the direction of the taxi.
The passengers are represented by a **0-indexed** 2D integer array `rides`, where `rides[i] = [starti, endi, tipi]` denotes the `ith` passenger requesting a ride from point `starti` to point `endi` who is willing to give a `tipi` dollar tip.
For **each** passenger `i` you pick up, you **earn** `endi - starti + tipi` dollars. You may only drive **at most one** passenger at a time.
Given `n` and `rides`, return _the **maximum** number of dollars you can earn by picking up the passengers optimally._
**Note:** You may drop off a passenger and pick up a different passenger at the same point.
**Example 1:**
**Input:** n = 5, rides = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 7
**Explanation:** We can pick up passenger 0 to earn 5 - 2 + 4 = 7 dollars.
**Example 2:**
**Input:** n = 20, rides = \[\[1,6,1\],\[3,10,2\],\[10,12,3\],\[11,12,2\],\[12,15,2\],\[13,18,1\]\]
**Output:** 20
**Explanation:** We will pick up the following passengers:
- Drive passenger 1 from point 3 to point 10 for a profit of 10 - 3 + 2 = 9 dollars.
- Drive passenger 2 from point 10 to point 12 for a profit of 12 - 10 + 3 = 5 dollars.
- Drive passenger 5 from point 13 to point 18 for a profit of 18 - 13 + 1 = 6 dollars.
We earn 9 + 5 + 6 = 20 dollars in total.
**Constraints:**
* `1 <= n <= 105`
* `1 <= rides.length <= 3 * 104`
* `rides[i].length == 3`
* `1 <= starti < endi <= n`
* `1 <= tipi <= 105` | How many possible states are there for a given expression? Is there a data structure that we can use to solve the problem optimally? |
From Dumb to Pro with Just One Visit-My Promise to You with A Smart Approach to Minimize Operations | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | # Intuition\n\nThe goal is to determine the minimum number of operations needed to make the numbers consecutive. To do this, we want to find the maximum unique element within a certain range, specifically from \'n\' to \'n + nums.size() - 1\', where \'n\' can be any element from the array. \n\nThe idea is that if we choose \'n\' as an element in the array, we have found the maximum value that doesn\'t need to be changed to make the numbers consecutive. Therefore, the result can be calculated as \'nums.size() - maximum unique element in the range (n to n + nums.size() - 1)\'. This will give us the minimum number of operations required to make the numbers consecutive, as we are subtracting the count of numbers that don\'t need to be changed from the total count of numbers.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. **Sort the Array**: The first step is to sort the input `nums` array in ascending order. This is done using `sort(nums.begin(), nums.end())`.\n\n2. **Remove Duplicates**: After sorting, the code iterates through the sorted array to remove duplicate elements while maintaining a modified length in the variable `l`. This ensures that the array contains only unique elements in ascending order.\n\n3. **Choose a Reference Number \'n\'**: The algorithm selects a reference number \'n\' from the modified array. This \'n\' represents the starting point for our consecutive sequence. The code starts with \'n\' as the first element of the array.\n\n4. **Find the Maximum Consecutive Sequence**: The code iterates through the modified array, keeping track of the maximum consecutive sequence that includes \'n\'. It calculates the count of consecutive elements by comparing the difference between the current element and \'n\' and incrementing the count until the difference exceeds the maximum possible difference \'n\'. The maximum count is stored in the variable `maxi`.\n\n5. **Calculate the Minimum Operations**: The minimum number of operations needed to make the numbers consecutive is determined by subtracting the maximum count `maxi` from the total number of unique elements in the modified array, which is represented by `l`.\n\n6. **Return the Result**: Finally, the code returns the minimum number of operations as the result.\n\nThis approach ensures that we find the reference number \'n\' that, when used as the starting point, maximizes the consecutive sequence within the array. Subtracting this maximum count from the total unique elements gives us the minimum number of operations required to make the numbers consecutive.\n\n# Complexity\nHere are the time and space complexities for the given code:\n\n**Time Complexity:**\n\n1. Sorting the `nums` array takes O(n log n) time, where \'n\' is the number of elements in the array.\n2. Removing duplicates while iterating through the sorted array takes O(n) time, where \'n\' is the number of elements in the array.\n3. The consecutive sequence calculation also takes O(n) time in the worst case because for each element, we perform a while loop that goes through a portion of the array.\n4. The overall time complexity is dominated by the sorting step, so the total time complexity is O(n log n).\n\n**Space Complexity:**\n\n1. The code modifies the input `nums` array in place, so there is no additional space used for storing a separate copy of the array.\n2. The space used for variables like `maxi`, `count`, `n`, `l`, and loop indices is constant and not dependent on the size of the input array.\n3. Therefore, the space complexity of the code is O(1), which means it uses a constant amount of extra space.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums)\n {\n int maxi = 0; // Initialize a variable to store the maximum count of consecutive numbers\n int count = 0; // Initialize a variable to keep track of the current count of consecutive numbers\n int n = nums.size() - 1; // Calculate the maximum possible difference between numbers\n int l = 0; // Initialize a variable to keep track of the modified length of the \'nums\' vector\n\n sort(nums.begin(), nums.end()); // Sort the input vector \'nums\' in ascending order\n\n // Remove duplicates in \'nums\' and update \'l\' with the modified length\n for(int i = 0; i < nums.size(); i++) {\n if(i+1 < nums.size() && nums[i] == nums[i+1]) continue;\n nums[l++] = nums[i];\n }\n\n // Calculate the maximum count of consecutive numbers\n for(int i = 0, j = 0; i < l; i++) {\n while(j < l && (nums[j] - nums[i]) <= n) {\n count++;\n j++;\n }\n maxi = max(maxi, count);\n count--;\n }\n\n // Calculate and return the minimum number of operations needed to make the numbers consecutive\n return nums.size() - maxi;\n }\n};\n\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums) {\n int maxi = 0; // Initialize a variable to store the maximum count of consecutive numbers\n int count = 0; // Initialize a variable to keep track of the current count of consecutive numbers\n int n = nums.length - 1; // Calculate the maximum possible difference between numbers\n int l = 0; // Initialize a variable to keep track of the modified length of the \'nums\' array\n\n Arrays.sort(nums); // Sort the input array \'nums\' in ascending order\n\n // Remove duplicates in \'nums\' and update \'l\' with the modified length\n for (int i = 0; i < nums.length; i++) {\n if (i + 1 < nums.length && nums[i] == nums[i + 1]) {\n continue;\n }\n nums[l++] = nums[i];\n }\n\n // Calculate the maximum count of consecutive numbers\n for (int i = 0, j = 0; i < l; i++) {\n while (j < l && (nums[j] - nums[i]) <= n) {\n count++;\n j++;\n }\n maxi = Math.max(maxi, count);\n count--;\n }\n\n // Calculate and return the minimum number of operations needed to make the numbers consecutive\n return nums.length - maxi;\n }\n}\n```\n```python3 []\nclass Solution:\n def minOperations(self, nums):\n maxi = 0 # Initialize a variable to store the maximum count of consecutive numbers\n count = 0 # Initialize a variable to keep track of the current count of consecutive numbers\n n = len(nums) - 1 # Calculate the maximum possible difference between numbers\n l = 0 # Initialize a variable to keep track of the modified length of the \'nums\' list\n\n nums.sort() # Sort the input list \'nums\' in ascending order\n\n # Remove duplicates in \'nums\' and update \'l\' with the modified length\n i = 0\n while i < len(nums):\n if i + 1 < len(nums) and nums[i] == nums[i + 1]:\n i += 1\n continue\n nums[l] = nums[i]\n l += 1\n i += 1\n\n # Calculate the maximum count of consecutive numbers\n i = 0\n j = 0\n while i < l:\n while j < l and (nums[j] - nums[i]) <= n:\n count += 1\n j += 1\n maxi = max(maxi, count)\n count -= 1\n i += 1\n\n # Calculate and return the minimum number of operations needed to make the numbers consecutive\n return len(nums) - maxi\n```\n*Thank you for taking the time to read my post in its entirety. I appreciate your attention and hope you found it informative and helpful.*\n\n**PLEASE UPVOTE THIS POST IF YOU FOUND IT HELPFUL** | 12 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Easy To Understand || Sliding Window || C++ || Java | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSorting and Removing Duplicates:\nFirst, the code sorts the input array nums in ascending order. This is done to make it easier to find the maximum and minimum elements.\nIt also removes any duplicate elements, ensuring that all elements are unique. This addresses the first condition.\n\nSliding Window Approach:\nThe core of the code is a sliding window approach, where the code iterates through potential "start" elements and extends a "window" to find a valid continuous subarray.\nFor each potential "start" element, it uses a while loop to find the maximum possible "end" element such that the difference between nums[end] and nums[start] is less than n (the length of the array).\n\nCalculating Operations:\nOnce the valid subarray is found, the code calculates the number of operations needed to make it continuous.\nThe number of operations is calculated as n - (end - start + 1). This formula considers the length of the array and the size of the valid subarray.\n\nTracking Minimum Operations:\nThe code keeps track of the minimum operations found so far using the ans variable.\nFor each potential "start" element, it updates ans with the minimum of the current ans and the calculated operations.\n\nFinal Result:\nAfter iterating through all potential "start" elements, the code returns the final value of ans, which represents the minimum number of operations needed to make the entire array continuous.\n\n# Complexity\n- Time complexity:\no(n*log(n))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```c++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums) {\n int n = nums.size();\n int ans=INT_MAX;\n sort(nums.begin(), nums.end());\n nums.erase(unique(begin(nums),end(nums)),end(nums));\n int end = 0;\n for(int start=0,end=0; start<nums.size(); ++start)\n {\n while (end < nums.size() && nums[end] < nums[start] + n) \n {\n ans=min(ans,n-(++end -start));\n }\n }\n\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n n = len(nums)\n nums = sorted(set(nums))\n ans = sys.maxsize\n for i, s in enumerate(nums):\n e = s + n - 1\n idx = bisect_right(nums, e)\n ans = min(ans, n - (idx - i))\n return ans\n\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums) {\n Arrays.sort(nums);\n int uniqueLen = 1;\n for (int i = 1; i < nums.length; ++i) {\n if (nums[i] != nums[i - 1]) {\n nums[uniqueLen++] = nums[i];\n }\n }\n \n int ans = nums.length;\n for (int i = 0, j = 0; i < uniqueLen; ++i) {\n while (j < uniqueLen && nums[j] - nums[i] <= nums.length - 1) {\n ++j;\n }\n ans = Math.min(ans, nums.length - (j - i));\n }\n \n return ans;\n }\n}\n```\n | 6 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Simple Solution || Beginner Friendly || Easy to Understand ✅ | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort the input array `nums` in ascending order.\n- Traverse the sorted array to remove duplicates and count unique elements in `uniqueLen`.\n- Initialize `ans` to the length of the input array, representing the maximum operations initially.\n- Iterate over unique elements using an outer loop.\n- Use an inner while loop with two pointers to find subarrays where the difference between the maximum and minimum element is within the array\'s length.\n- Calculate the number of operations needed to make all elements distinct within each subarray.\n- Update `ans` with the minimum operations found among all subarrays.\n- Return the minimum operations as the final result.\n# Complexity\n- Time complexity: `O(N*lgN + N + N*lgN)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minOperations(int[] nums) {\n Arrays.sort(nums);\n int uniqueLen = 1;\n for (int i = 1; i < nums.length; ++i) {\n if (nums[i] != nums[i - 1]) {\n nums[uniqueLen++] = nums[i];\n }\n }\n \n int ans = nums.length;\n for (int i = 0, j = 0; i < uniqueLen; ++i) {\n while (j < uniqueLen && nums[j] - nums[i] <= nums.length - 1) {\n ++j;\n }\n ans = Math.min(ans, nums.length - (j - i));\n }\n \n return ans;\n }\n}\n```\n```python3 []\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n n = len(nums)\n nums = sorted(set(nums))\n\t\t\n answer = float("+inf")\n for i, start in enumerate(nums):\n \n search = start + n - 1 # number to search\n start, end = 0, len(nums)-1\n \n while start <= end:\n mid = start + (end - start) // 2\n if nums[mid] <= search:\n idx = mid\n start = mid + 1\n else:\n end = mid - 1\n \n changes = idx - i + 1\n answer = min(answer, n - changes)\n return answer\n \n```\n```python []\nclass Solution(object):\n def minOperations(self, nums):\n # Sort the input list in ascending order.\n nums.sort()\n \n # Initialize variables to keep track of unique elements and minimum operations.\n unique_len = 1\n ans = len(nums)\n \n # Traverse the sorted list to remove duplicates and count unique elements.\n for i in range(1, len(nums)):\n if nums[i] != nums[i - 1]:\n nums[unique_len] = nums[i]\n unique_len += 1\n \n # Initialize pointers for calculating operations within subarrays.\n i, j = 0, 0\n \n # Iterate over unique elements to find minimum operations.\n for i in range(unique_len):\n while j < unique_len and nums[j] - nums[i] <= len(nums) - 1:\n j += 1\n ans = min(ans, len(nums) - (j - i))\n \n return ans\n\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums) {\n // Sort the vector in ascending order\n sort(nums.begin(), nums.end());\n\n // Initialize variables\n int n = nums.size(); // Number of elements in the vector\n int left = 0; // Left pointer for the sliding window\n int maxCount = 1; // Initialize the maximum count of distinct elements\n int currentCount = 1; // Initialize the count of distinct elements in the current window\n\n // Iterate through the vector to find the minimum operations\n for (int right = 1; right < n; ++right) {\n // Check if the current element is equal to the previous one\n if (nums[right] == nums[right - 1]) {\n continue; // Skip duplicates\n }\n\n // Check if the current window size is less than or equal to the difference between the maximum and minimum values\n while (nums[right] - nums[left] > n - 1) {\n // Move the left pointer to shrink the window\n if(left<n && nums[left+1]==nums[left]){\ncurrentCount++;\n}\n left++;\n currentCount--;\n }\n\n // Update the count of distinct elements in the current window\n currentCount++;\n\n // Update the maximum count\n maxCount = max(maxCount, currentCount);\n }\n\n // Calculate the minimum operations\n int minOps = n - maxCount;\n\n return minOps;\n }\n};\n```\n```C []\n// Function prototype for the comparison function\nint compare(const void* a, const void* b);\n\nint minOperations(int* nums, int numsSize) {\n // Define the maximum size of the sliding window\n int k = numsSize - 1;\n\n // Sort the array in ascending order\n qsort(nums, numsSize, sizeof(int), compare);\n\n // Remove adjacent duplicates\n int newLen = 1;\n for (int i = 1; i < numsSize; ++i) {\n if (nums[i] != nums[i - 1]) {\n nums[newLen++] = nums[i];\n }\n }\n\n int l = 0, r = 0, fin = 1;\n\n while (r < newLen) {\n if (l == r)\n r++;\n else if (nums[r] - nums[l] > k)\n l++;\n else {\n fin = (fin > r - l + 1) ? fin : r - l + 1;\n r++;\n }\n }\n\n return k - fin + 1;\n}\n\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n```\n# If you like the solution please Upvote !!\n\n\n | 82 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
[Python] Simple sort & queue, 2-liner | minimum-number-of-operations-to-make-array-continuous | 0 | 1 | # Intuition\n\nThe continuous array that the problem asks for is simply an array with the form `[x, x + 1, x + 2, x + 3, ..., x + n - 1]`, but scrambled. Let\'s call that original sorted form **sorted continuous**.\n\nTo simplify the problem, we simply need to find the longest incomplete **sorted continuous** array from the given array.\n\nWe can keep a queue of the current longest incomplete **sorted continuous** array. Whenever adding a new element would make the queue an invalid incomplete **sorted continuous** array (i.e. the added element is larger than `queue[0] + N - 1`), we pop the first element of the queue.\n\nWhatever numbers that aren\'t included in the longest incomplete **sorted continuous** must be replaced. That\'s the number of operations we\'re looking for.\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n N = len(nums)\n queue = deque()\n max_length = 1\n\n for num in sorted(set(nums)):\n while queue and num - queue[0] >= N:\n queue.popleft()\n\n queue.append(num)\n max_length = max(max_length, len(queue))\n\n return N - max_length\n\n```\n\n## Time complexity\nSorting: O(NlogN)\nLoop: O(N)\n-> O(NlogN)\n\n## Note\n\nFor each `num` in `sorted(set(nums))`, we can also just binary search for the expected `num + N - 1` ending number. This will take O(logN) per loop iteration instead of O(1), but won\'t affect the final time complexity, which is bounded by the O(NlogN) sort anyway.\n\n## 2-liner using binary search, just for fun\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n sn = sorted(set(nums))\n return min(len(nums) - (bisect_right(sn, sn[i] + len(nums) - 1) - i) for i in range(len(sn)))\n\n``` | 8 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
【Video】Give me 15 minutes - How we think about a solution | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\nSorting input array.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/9DLAvMurzbU\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Minimum Number of Operations to Make Array Continuous\n`0:42` How we think about a solution\n`4:33` Demonstrate solution with an example\n`8:10` Why the window has all valid numbers?\n`8:36` We don\'t have to reset the right pointer to 0 or something\n`10:36` Why we need to start window from each number?\n`12:24` What if we have duplicate numbers in input array?\n`14:50` Coding\n`17:11` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,643\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n### How we think about a solution\nWe have two constraints.\n\n\n---\n- All elements in nums are unique.\n- The difference between the maximum element and the minimum element in nums equals nums.length - 1.\n---\n\nFor example, `nums = [1,2,3,4,5]` need `0` opearation because \n\n```\nminimum number is 1\nmaximum number is 5 \u2192 1 + len(nums) - 1(= 4) \n```\nHow about `nums = [4,1,3,2,5]`? we need `0` operation because The array `[4,1,3,2,5]` is simply a shuffled version of `[1,2,3,4,5]`. But shuffuled version makes us feel more diffucult and seems hard to solve the question.\n\nThat\'s why it\'s good idea to sort input array first then try to solve the question. Because we know that we create an array and value range should be `len(nums) - 1`. Seems sorting make the question easy.\n\n---\n\n\u2B50\uFE0F Points\n\nSort input array at first.\n\n---\n\n\nLet\'s think about this input\n```\nInput: [1,2,3,5]\n```\nIn this case, it\'s easy.\n```\n[1,2,3] is good, becuase they are in range 1 to 4.\n[5] should be changed to 4\n\nCalculation is 4 - 3 = 1\n4: length of nums\n3: length of [1,2,3]\n\nOutput: 1 (operation)\n```\nHow about this.\n```\nInput: [1,2,3,5,6]\n\nCalculation is 5 - 3 = 2\n5: length of nums\n3: length of [1,2,3]\n\nOutput: 2 (operations)\n\n```\n##### This is a wrong answer.\n\nThat\'s because if we change `1` to `4` or `6` to `4`, we can create `[2,3,4,5,6]` or `[1,2,3,4,5]`, so just one operation instead of two operations.\n\nFrom those examples, problem is we don\'t know which numbers we should keep and which number we should change.\n\n---\n\n\u2B50\uFE0F Points\n\nSo, we\'re determining the length of a subarray where all numbers are valid. The starting point of subarray should be each respective number.\n\nSince we check length of valid subarray, seems like we can use `sliding window` technique.\n\n---\n\n### How it works\n\nLet\'s see how it works. Initialize a left pointer and a right pointer with `0`.\n```\nInput: nums = [1,2,3,5,6]\n\nleft = 0\nright = 0\noperations = 5 (= len(nums))\n```\nEvery time we check like this.\n```\nnums[right] < nums[left] + length\n```\nBecuase `left pointer` is current starting point of window and valid numbers for current staring point should be `nums[left] + length - 1`.\n\nIf the condition is `true`, increament `right pointer` by `1`.\n\n```\nInput: nums = [1,2,3,5,6]\n\nvalid number is from 1 to 5.\nleft = 0\nright = 4 (until index 3, they are valid)\noperations = 5 (= len(nums)), we don\'t calcuate yet.\n```\nNow `right pointer` is index `4` and we don\'t meet \n```\nnums[right] < nums[left] + length\n= 6 < 1 + 5\n```\nThen, it\'s time to compare mininum operations. Condition should be\n```\n min_operations = min(min_operations, length - (right - left))\n```\n`right - left` is valid part, so if we subtract it from whole length of input array, we can get invalid part which is places where we should change. \n\n\n---\n\n\u2B50\uFE0F Points\n\nThat\'s because we sorted input array at first, so when we find invalid number which means later numbers are also invalid. we are sure that they are out of valid range.\n\n---\n\n\n```\nmin(min_operations, length - (right - left))\n= min(5, 5 - 4)\n= 1 \n```\nWe repeated this process from each index.\n\nBut one more important thing is \n\n---\n\n\u2B50\uFE0F Points\n\nWe can continue to use current right pointer position when we change staring position. we don\'t have to reset right pointer to 0 or something. Because previous starting point number is definitely smaller than current number.\n\n[1,2,3,5,6]\n\nLet\'s say current starting point is at index 1(2). In this case, index 0(1) is smaller than index 1(2) because we sorted the input array.\n\nWhen we start from index 0, we reach index 4(6) and index 4 is invalid. That means we are sure that at least until index 3, we know that all numbers are valid when we start from index 1 becuase\n\nfrom value 1, valid max number is 5 (1 + len(nums) - 1)\nfrom value 2, valid max number is 6 (2 + len(nums) - 1)\n\nIn this case, 6 includes range 2 to 5 from 1 to 5.\n\nThat\'s why we can use current right position when starting point is changed.\n\n---\n\n### Why do we need to start from each number?\n\nAs I told you, problem is we don\'t know which numbers we should keep and which number we should change. But there is another reason.\n\nLet\'s think about this case.\n```\nInput: [1,10,11,12]\n```\nWhen start from index `0`\n```\nvalid: [1]\ninvalid: [10,11,12]\n\n4 - 1 = 3\n\n4: total length of input\n1: valid length\n\nwe need 3 operations.\n```\nWhen start from index `1`\n```\nvalid: [10,11,12]\ninvalid: [1]\n\n4 - 3 = 1\n\n4: total length of input\n3: valid length\n\nwe need 1 operation.\n```\n\n---\n\n\u2B50\uFE0F Points\n\nStarting index 0 is not always minimum operation.\n\n---\n\n### What if we have duplicate numbers in input array?\n\nOne more important point is when we have duplicate numbers in the input array.\n```\nInput: [1,2,3,5,5]\n```\nLet\'s start from index 0, in this case, valid max value is \n```\n1 + (5 - 1) = 5\n```\nWe go through entire array and reach out of bounds from index 0. So output is `0`?\n\nIt\'s not. Do you rememeber we have two constraints and one of them says "All elements in nums are unique", so it\'s a wrong answer.\n\nHow can we avoid this? My idea is to remove duplicate by `Set` before interation.\n\n```\n[1,2,3,5,5]\n\u2193\n[1,2,3,5]\n```\nAfter removing duplicate number, valid range from index 0 should be from `1` to `4`\n\n```\nvalid: [1,2,3]\ninvalid: [5]\n\noperation = 4 - 3 = 1\n```\n\nIf we change one of 5s to 4, we can create `[1,2,3,4,5]` from `[1,2,3,5,5]`.\n\n---\n\n\u2B50\uFE0F Points\n\nRemove duplicate numbers from input array.\n\n---\n\nThat is long thought process. I spent 2 hours to write this.\nI felt like crying halfway through LOL.\n\nOkay, now I hope you have knowledge of important points. Let\'s see a real algorithm!\n\n### Algorithm Overview:\n\n1. Calculate the length of the input array.\n2. Initialize `min_operations` with the length of the array.\n3. Create a sorted set of unique elements from the input array.\n4. Initialize a variable `right` to 0.\n5. Iterate through the sorted unique elements:\n - For each element, find the rightmost index within the range `[element, element + length]`.\n - Calculate the minimum operations needed for the current element.\n6. Return the minimum operations.\n\n### Detailed Explanation:\n\n1. Calculate the length of the input array:\n - `length = len(nums)`\n\n2. Initialize `min_operations` with the length of the array:\n - `min_operations = length`\n\n3. Create a sorted set of unique elements from the input array:\n - `unique_nums = sorted(set(nums))`\n - This ensures that we have a sorted list of unique elements to work with.\n\n4. Initialize a variable `right` to 0:\n - `right = 0`\n - This will be used to keep track of the right pointer in our traversal.\n\n5. Iterate through the sorted unique elements:\n - `for left in range(len(unique_nums)):`\n\n - For each element, find the rightmost index within the range `[element, element + length]`:\n - While `right` is within bounds and the element at `right` is less than `element + length`, increment `right`.\n\n - Calculate the minimum operations needed for the current element:\n - Update `min_operations` as the minimum of its current value and `length - (right - left)`.\n\n6. Return the minimum operations:\n - `return min_operations`\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n\nFor just in case, somebody might think this is $$O(n^2)$$ because of nested loop.\n\nActually the left pointer and the right pointer touch each number once because the left pointer is obvious and we don\'t reset the right pointer with 0 or something. we continue to use the right pointer from previous loop.\n\nSo, this nested loop works like $$O(2n)$$ instead of $$O(n^2)$$. That\'s why time complexity of this nested loop is $$O(n)$$.\n\n- Space complexity: $$O(n)$$\n\n\n```python []\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n length = len(nums)\n min_operations = length\n unique_nums = sorted(set(nums))\n right = 0\n \n for left in range(len(unique_nums)):\n while right < len(unique_nums) and unique_nums[right] < unique_nums[left] + length:\n right += 1\n \n min_operations = min(min_operations, length - (right - left))\n\n return min_operations\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minOperations = function(nums) {\n const length = nums.length;\n let minOperations = length;\n const uniqueNums = new Set(nums);\n const sortedUniqueNums = Array.from(uniqueNums).sort((a, b) => a - b);\n let right = 0;\n\n for (let left = 0; left < sortedUniqueNums.length; left++) {\n while (right < sortedUniqueNums.length && sortedUniqueNums[right] < sortedUniqueNums[left] + length) {\n right++;\n }\n\n minOperations = Math.min(minOperations, length - (right - left));\n }\n\n return minOperations; \n};\n```\n```java []\nclass Solution {\n public int minOperations(int[] nums) {\n int length = nums.length;\n int minOperations = length;\n Set<Integer> uniqueNums = new HashSet<>();\n for (int num : nums) {\n uniqueNums.add(num);\n }\n Integer[] sortedUniqueNums = uniqueNums.toArray(new Integer[uniqueNums.size()]);\n Arrays.sort(sortedUniqueNums);\n int right = 0;\n\n for (int left = 0; left < sortedUniqueNums.length; left++) {\n while (right < sortedUniqueNums.length && sortedUniqueNums[right] < sortedUniqueNums[left] + length) {\n right++;\n }\n\n minOperations = Math.min(minOperations, length - (right - left));\n }\n\n return minOperations; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums) {\n int length = nums.size();\n int minOperations = length;\n sort(nums.begin(), nums.end());\n nums.erase(unique(nums.begin(), nums.end()), nums.end());\n int right = 0;\n\n for (int left = 0; left < nums.size(); left++) {\n while (right < nums.size() && nums[right] < nums[left] + length) {\n right++;\n }\n\n minOperations = min(minOperations, length - (right - left));\n }\n\n return minOperations; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u2B50\uFE0F Next daily coding challenge post and video\n\nPost\n\nhttps://leetcode.com/problems/number-of-flowers-in-full-bloom/solutions/4156243/video-give-me-15-minutes-how-we-can-think-about-a-solution-python-javascript-java-c/\n\n\nhttps://youtu.be/kiIYG6drNZo\n\nMy previous post for daily coding challenge\n\nPost\nhttps://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/solutions/4147878/video-give-me-10-minutes-how-we-think-about-a-solution-binary-search/\n\n\u2B50\uFE0F Yesterday\'s daily challenge video\n\nhttps://youtu.be/441pamgku74\n | 85 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Video Solution | Explanation With Drawings | In Depth | Java | C++ | Python 3 | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | # Intuition, approach and complexity dicsussed in detail in video solution\nhttps://youtu.be/W_2-2Ee7y-s\n# Code\nPython 3\n```\nclass Solution:\n def minOperations(self, nums):\n unqEles = set()\n unqs = []\n for num in nums:\n if num not in unqEles:\n unqs.append(num)\n unqEles.add(num)\n unqs.sort()\n endIndx = 0\n sz = len(unqs)\n minOps = float(\'inf\')\n for startIndx in range(sz):\n while endIndx < sz and unqs[endIndx] - unqs[startIndx] < len(nums):\n endIndx += 1\n opReq = len(nums) - (endIndx - startIndx)\n minOps = min(minOps, opReq)\n return minOps\n```\nJava\n```\nclass Solution {\n public int minOperations(int nums[]) {\n HashSet<Integer> unqEles = new HashSet<>();\n ArrayList<Integer> unqs = new ArrayList<>();\n for(int num : nums){\n if(!unqEles.contains(num)){\n unqs.add(num);\n unqEles.add(num);\n }\n }\n Collections.sort(unqs);\n int endIndx = 0; \n int sz = unqs.size();\n int minOps = Integer.MAX_VALUE;\n for(int startIndx = 0; startIndx < sz; startIndx++){\n while(endIndx < sz && unqs.get(endIndx) - unqs.get(startIndx) < nums.length)endIndx++;\n int opReq = nums.length - (endIndx - startIndx);\n minOps = Math.min(minOps, opReq);\n }\n return minOps;\n }\n}\n\n```\nC++\n```\nclass Solution {\npublic:\n int minOperations(vector<int>& nums) {\n \n unordered_set<int> unqEles;\n\n vector<int> unqs;\n for(auto num : nums){\n if(unqEles.find(num) == unqEles.end()){\n unqs.push_back(num);\n unqEles.insert(num);\n }\n }\n sort(unqs.begin(), unqs.end());\n int endIndx = 0; \n\n int sz = unqs.size();\n int minOps = INT_MAX;\n\n \n for(int startIndx = 0; startIndx < sz; startIndx++){\n while(endIndx < sz && unqs[endIndx] - unqs[startIndx] < nums.size())endIndx++;\n int opReq = nums.size() - (endIndx - startIndx);\n minOps = min(minOps, opReq);\n }\n return minOps;\n }\n};\n``` | 1 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
✅☑[C++/C/Java/Python/JavaScript] || O(nlogn) || Sliding Window || EXPLAINED🔥 | minimum-number-of-operations-to-make-array-continuous | 1 | 1 | # *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n# Approaches\n***(Also explained in the code)***\n1. The code aims to find the minimum operations required to make the array "consecutive," where consecutive elements have a difference of at most `n-1`.\n\n1. We first insert all unique elements from the input array `nums` into a set `s`. This step ensures that we have a sorted and unique set of elements.\n\n1. We convert the set `s` back into a vector `unique` to work with the elements in sorted order.\n\n1. We iterate through the `unique` vector and use a pointer `j` to find the rightmost element within the current range (defined by `unique[i]` and `unique[i] + n)`.\n\n1. For each range, we calculate the minimum operations required by subtracting the count of elements within the range (`j - i`) from `n`.\n\n1. Finally, we return the minimum operations required as the answer.\n\n*Let\'s illustrate the approach with an example:*\n\n**Example:**\nInput: **[1, 3, 6, 2, 7]**\n\n- After sorting and removing duplicates, `unique` becomes **[1, 2, 3, 6, 7]**.\n\n- The code will iterate through the `unique` vector and determine the minimum operations for each range:\n\n - Range **[1, 2, 3]** requires `2` operations to make them consecutive.\n - Range **[6, 7]** requires `0` operations as they are already consecutive.\n- The final answer is the minimum of the operations required for these two ranges, which is `0`.\n\n# Complexity\n- **Time complexity:**\n$$O(nlogn)$$\n\n- **Space complexity:**\n$$O(n)$$\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minOperations(vector<int>& nums) {\n int n = nums.size();\n int ans = n; // Initialize the answer as the maximum possible value \'n\'.\n set<int> s; // Create a set to store unique elements from \'nums\'.\n\n // Step 1: Insert all unique elements from \'nums\' into the set \'s\'.\n for (auto a : nums) {\n s.insert(a);\n }\n\n // Step 2: Convert the set \'s\' back to a vector \'unique\'.\n vector<int> unique(s.begin(), s.end());\n\n int j = 0; // Initialize a pointer \'j\'.\n int m = unique.size(); // Get the size of the \'unique\' vector.\n\n // Step 3: Iterate through the \'unique\' vector.\n for (int i = 0; i < m; i++) {\n // Step 4: Move the pointer \'j\' to find the rightmost element within the current range.\n while (j < m && unique[j] < unique[i] + n) {\n j++;\n }\n // Step 5: Calculate the minimum operations required for the current range.\n ans = min(ans, n - (j - i));\n }\n // Step 6: Return the minimum operations required.\n return ans;\n }\n};\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint compare(const void *a, const void *b) {\n return (*(int *)a - *(int *)b);\n}\n\nint minOperations(int *nums, int numsSize) {\n int n = numsSize;\n int ans = n; // Initialize the answer as the maximum possible value \'n\'.\n int *unique = (int *)malloc(n * sizeof(int));\n if (unique == NULL) {\n return -1; // Memory allocation failed.\n }\n\n // Step 1: Sort \'nums\' array to make duplicate elements adjacent.\n qsort(nums, n, sizeof(int), compare);\n\n int j = 0; // Initialize a pointer \'j\'.\n int m = 0; // Initialize the size of the \'unique\' array.\n\n // Step 2: Create an array \'unique\' containing unique elements from \'nums\'.\n for (int i = 0; i < n; i++) {\n if (i == 0 || nums[i] != nums[i - 1]) {\n unique[m++] = nums[i];\n }\n }\n\n // Step 3: Iterate through the \'unique\' array.\n for (int i = 0; i < m; i++) {\n // Step 4: Move the pointer \'j\' to find the rightmost element within the current range.\n while (j < m && unique[j] < unique[i] + n) {\n j++;\n }\n // Step 5: Calculate the minimum operations required for the current range.\n ans = (ans < (n - (j - i))) ? ans : (n - (j - i));\n }\n\n // Step 6: Release memory allocated for \'unique\' array.\n free(unique);\n\n // Step 7: Return the minimum operations required.\n return ans;\n}\n\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n public int minOperations(int[] nums) {\n int n = nums.length;\n int ans = n; // Initialize the answer as the maximum possible value \'n\'.\n Set<Integer> s = new HashSet<>(); // Create a set to store unique elements from \'nums\'.\n\n // Step 1: Insert all unique elements from \'nums\' into the set \'s\'.\n for (int a : nums) {\n s.add(a);\n }\n\n // Step 2: Convert the set \'s\' back to a list \'unique\'.\n List<Integer> unique = new ArrayList<>(s);\n\n int j = 0; // Initialize a pointer \'j\'.\n int m = unique.size(); // Get the size of the \'unique\' list.\n\n // Step 3: Iterate through the \'unique\' list.\n for (int i = 0; i < m; i++) {\n // Step 4: Move the pointer \'j\' to find the rightmost element within the current range.\n while (j < m && unique.get(j) < unique.get(i) + n) {\n j++;\n }\n // Step 5: Calculate the minimum operations required for the current range.\n ans = Math.min(ans, n - (j - i));\n }\n // Step 6: Return the minimum operations required.\n return ans;\n }\n}\n\n```\n```Python []\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n n = len(nums)\n ans = n # Initialize the answer as the maximum possible value \'n\'.\n s = set() # Create a set to store unique elements from \'nums\'.\n\n # Step 1: Insert all unique elements from \'nums\' into the set \'s\'.\n for a in nums:\n s.add(a)\n\n # Step 2: Convert the set \'s\' back to a list \'unique\'.\n unique = list(s)\n\n j = 0 # Initialize a pointer \'j\'.\n m = len(unique) # Get the size of the \'unique\' list.\n\n # Step 3: Iterate through the \'unique\' list.\n for i in range(m):\n # Step 4: Move the pointer \'j\' to find the rightmost element within the current range.\n while j < m and unique[j] < unique[i] + n:\n j += 1\n # Step 5: Calculate the minimum operations required for the current range.\n ans = min(ans, n - (j - i))\n # Step 6: Return the minimum operations required.\n return ans\n\n```\n\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minOperations = function(nums) {\n const n = nums.length;\n let ans = n; // Initialize the answer as the maximum possible value \'n\'.\n const s = new Set(); // Create a set to store unique elements from \'nums\'.\n\n // Step 1: Insert all unique elements from \'nums\' into the set \'s\'.\n for (const a of nums) {\n s.add(a);\n }\n\n // Step 2: Convert the set \'s\' back to an array \'unique\'.\n const unique = [...s];\n\n let j = 0; // Initialize a pointer \'j\'.\n const m = unique.length; // Get the size of the \'unique\' array.\n\n // Step 3: Iterate through the \'unique\' array.\n for (let i = 0; i < m; i++) {\n // Step 4: Move the pointer \'j\' to find the rightmost element within the current range.\n while (j < m && unique[j] < unique[i] + n) {\n j++;\n }\n // Step 5: Calculate the minimum operations required for the current range.\n ans = Math.min(ans, n - (j - i));\n }\n // Step 6: Return the minimum operations required.\n return ans;\n};\n\n```\n# *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n---\n\n | 2 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Easy Solution using python | minimum-number-of-operations-to-make-array-continuous | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, nums: List[int]) -> int:\n n = len(nums)\n ans = n\n nums = sorted(set(nums))\n\n for i, start in enumerate(nums):\n end = start + n - 1\n index = bisect_right(nums, end)\n uniqueLength = index - i\n ans = min(ans, n - uniqueLength)\n\n return ans\n\n``` | 1 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Python super easy solution with intuition. Concept( set & binary search) | minimum-number-of-operations-to-make-array-continuous | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n If you observe the question carefully you can see that\n1. the frequency of the numbers does not matter the same number comes up once or many times does not matter in the end you just need to find maximum **unique** numbers that are agreable with the given condition.\n2. the position of the numbers does not matter\n\n# Approach\n\nAt first take a **sorted set** of the numbers. Now imagine the 1st element in the set is your starting element of your answer. Then the last element would be n+s[0]-1 (total length required + value of the 1st element). \nAs the set is sorted just binary search this value to check how many elements in between the first and last element you have. Do the same for, 2nd element in the set is your starting element of your answer. And so on ...\n\n\n# Complexity\n- Time complexity:\nO(nlog(n))\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n\n def minOperations(self, nums: List[int]) -> int:\n if len(nums)==1:\n return 0\n n=len(nums)\n s=set(nums)\n s=list(s)\n s.sort()\n maax=0\n for i in range(len(s)-1):\n lo=i\n hi=len(s)-1\n ans=-1\n target=s[i]+n-1\n while lo<=hi:\n mid=(lo+hi)//2\n if s[mid]<=target:\n ans=mid\n lo=mid+1\n else:\n hi=mid-1\n maax=max(maax,ans-i+1)\n return n-maax\n\n\n\n``` | 1 | You are given an integer array `nums`. In one operation, you can replace **any** element in `nums` with **any** integer.
`nums` is considered **continuous** if both of the following conditions are fulfilled:
* All elements in `nums` are **unique**.
* The difference between the **maximum** element and the **minimum** element in `nums` equals `nums.length - 1`.
For example, `nums = [4, 2, 5, 3]` is **continuous**, but `nums = [1, 2, 3, 5, 6]` is **not continuous**.
Return _the **minimum** number of operations to make_ `nums` **_continuous_**.
**Example 1:**
**Input:** nums = \[4,2,5,3\]
**Output:** 0
**Explanation:** nums is already continuous.
**Example 2:**
**Input:** nums = \[1,2,3,5,6\]
**Output:** 1
**Explanation:** One possible solution is to change the last element to 4.
The resulting array is \[1,2,3,5,4\], which is continuous.
**Example 3:**
**Input:** nums = \[1,10,100,1000\]
**Output:** 3
**Explanation:** One possible solution is to:
- Change the second element to 2.
- Change the third element to 3.
- Change the fourth element to 4.
The resulting array is \[1,2,3,4\], which is continuous.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Add all the words to a trie. Check the longest path where all the nodes are words. |
Python3 - Easy Solution for Beginners! | final-value-of-variable-after-performing-operations | 0 | 1 | \n# Code\n```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n result = 0\n for i in range(len(operations)):\n if(operations[i] == \'++X\' or operations[i] == \'X++\'):\n result = result + 1\n else:\n result = result - 1\n return result\n``` | 1 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Solution of final value of variable after performing operations problem | final-value-of-variable-after-performing-operations | 0 | 1 | # Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n\n- Space complexity:\n$$O(1)$$ - as we use extra space for answer equal to a constant\n\n# Solution_1\n```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n answer = 0\n for i in operations:\n if \'-\' in i:\n answer -= 1\n else:\n answer += 1\n return answer\n```\n\n# Solution_2\n```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n A = operations.count(\'++X\')\n B = operations.count(\'X++\')\n return A + B - (len(operations) - A - B)\n``` | 1 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Simple Solutions in Py and Cpp😉 | final-value-of-variable-after-performing-operations | 0 | 1 | # Solution in C++\n```\nclass Solution {\npublic:\n int finalValueAfterOperations(vector<string>& operations) {\n int answer = 0;\n for (int i = 0; i < operations.size(); i++ ){\n if (operations[i] == "X++" || operations[i] == "++X"){answer++;}\n else if (operations[i] == "--X" || operations[i] == "X--"){answer--;}\n }\n return answer;\n }\n};\n```\n# Solution in Python\n```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n answer = 0\n for operation in operations:\n if operation in {\'X--\', \'--X\'}:\n answer -= 1\n elif operation in {\'X++\', \'++X\'}:\n answer += 1\n return answer\n``` | 2 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Very easy solution | final-value-of-variable-after-performing-operations | 0 | 1 | # Best Solution very Easy\n\n# Code\n```\nclass Solution:\n def finalValueAfterOperations(self, arr: List[str]) -> int:\n a=0\n for i in arr:\n if i[0]=="+" or i[-1]=="+":\n a+=1\n else:\n a-=1\n return a\n``` | 1 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Very Easy Python3 Count Function Use 5 Lines Codes | final-value-of-variable-after-performing-operations | 0 | 1 | We can use simple python count function to get count value of given conditions\nand solve it very easily and with compact solution :\n\n```class Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n \n \n A=operations.count("++X")\n B=operations.count("X++")\n C=operations.count("--X") \n D=operations.count("X--")\n\t\t\n return A+B-C-D #it will automatically return the required results value\n```\n\nPlease Upvote if You Find this solution helpful\n | 37 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Easy 💥 C++ Solution [ TESLA 🚘 SDE Intern Interview😳 ] | final-value-of-variable-after-performing-operations | 1 | 1 | \n## Please Upvote if it Helps \uD83D\uDE4F\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int finalValueAfterOperations(vector<string>& operations) {\n int n = operations.size() , X=0;\n for(int i=0;i<n;i++){\n if(operations[i]=="--X" || operations[i]=="X--" ) X--;\n else X++;\n }\n return X;\n }\n};\n``` | 9 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
[Python 3] Using reduce, 1 line | final-value-of-variable-after-performing-operations | 0 | 1 | ```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n return reduce(lambda a, b: a + (1 if b[1] == \'+\' else -1) , operations, 0)\n``` | 13 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.