title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
[PYTHON] Comments | Simple | minimum-number-of-moves-to-seat-everyone | 0 | 1 | ```\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats = sorted(seats)\n students = sorted(students)\n # redefine the varaibles to be sorted [min->max]\n\n counter = 0\n # set up the counter for amount of moves\n\n for x in range(len(seats)):\n counter += abs(seats[x]-students[x])\n # add the amount of moves that the person moved\n # use absolute in the case seats[x]<students[x]\n \n return counter\n # return the amount of moves\n``` | 2 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
Python Easiest Solution With Explanation | Sorting | Beg to adv | minimum-number-of-moves-to-seat-everyone | 0 | 1 | ```python\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n total_moves = 0 # taking a int variable to store the value\n sorted_seats = sorted(seats) # sorting the seat list\n sorted_students = sorted(students) #sorting the student list\n \n diff_1 = [] # taking empty list for storing difference of both the list\n for i in range(len(seats)):\n diff = abs(sorted_seats[i] - sorted_students[i]) # calculating diff of both the list elements, to calculate numbers of move. \n diff_1.append(diff) # appending the Difference to the empty list declared by us. \n \n for i in diff_1: # loop for traversing the diff of elems from both the lists.\n total_moves += i # adding them to calculate the moves. \n \n return total_moves\n```\n\n```python\n\t\t"""\n Short form of above solution:-\n """\n #first sort both the lists\n seats.sort() \n students.sort()\n \n res = 0 # variable to store the result\n \n for i in range(len(seats)): \n res += abs(students[i] - seats[i]) # calculating diff of both the list and adding it to the variable , rather then adding it to the list, and then to traverse that list for the total moves.\n \n return res\n```\n\n***Found helpful, Do upvote !!*** | 4 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
O(n) counting sort in Python | minimum-number-of-moves-to-seat-everyone | 0 | 1 | trivial `O(nlogn)` solution, using `sort()` w/o hesitation:\n```python\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats.sort()\n students.sort()\n return sum(abs(seat - student) for seat, student in zip(seats, students))\n```\n`O(m+n)` solution, using counting sort where `m` and `n` are respectively the maximum digit of `students` and `seats`:\nnote that for better understanding, you may replace `i` and `j` with `student` and `seat`.\n```python\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats_cnt, students_cnt = [0] * (max(seats) + 1), [0] * (max(students) + 1)\n for seat in seats:\n seats_cnt[seat] += 1\n for student in students:\n students_cnt[student] += 1\n ans = 0\n i = j = 1\n while i < len(students_cnt):\n if students_cnt[i]:\n # find the next available seat\n while j < len(seats_cnt) and not seats_cnt[j]:\n j += 1\n ans += abs(i - j)\n seats_cnt[j] -= 1\n students_cnt[i] -= 1\n else:\n i += 1\n return ans\n``` | 9 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
Python || 99.81% Faster || 5 Lines || Sorting | minimum-number-of-moves-to-seat-everyone | 0 | 1 | ```\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats.sort()\n students.sort()\n c,n=0,len(seats)\n for i in range(n): c+=abs(seats[i]-students[i])\n return c\n```\n\n**Upvote if you like the solution or ask if there is any query** | 4 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
✅ 99.81% 2-Approaches RegEx & Iterative Count | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Interview Guide: "Remove Colored Pieces if Both Neighbors are the Same Color" Problem\n\n## Problem Understanding\n\nIn the "Remove Colored Pieces if Both Neighbors are the Same Color" problem, you are given a string `colors` where each piece is colored either by \'A\' or by \'B\'. Alice and Bob play a game where they take alternating turns removing pieces from the line. Alice can only remove a piece colored \'A\' if both its neighbors are also colored \'A\' and vice versa for Bob with color \'B\'. Alice moves first, and if a player cannot make a move on their turn, that player loses. The goal is to determine if Alice can win the game.\n\n## Key Points to Consider\n\n### 1. Understand the Constraints\n\nThe length of the string `colors` can be up to $$10^5$$, indicating the need for a solution with a time complexity better than $$O(n^2)$$.\n\n### 2. Multiple Approaches\n\nThere are several methods to solve this problem:\n\n - Regular Expressions (RegEx)\n - Iterative Count\n \nEach method has its own nuances, and understanding the logic behind each can provide multiple tools to tackle similar problems.\n\n### 3. Patterns are Key\n\nIn this problem, the solution heavily relies on recognizing patterns within the string. Identifying sequences of \'A\'s and \'B\'s and understanding how they influence the game\'s outcome is crucial.\n\n### 4. Explain Your Thought Process\n\nArticulate your reasoning behind each approach and the steps involved. This showcases clarity of thought and can help in discussing the problem\'s nuances.\n\n## Conclusion\n\nThe "Remove Colored Pieces if Both Neighbors are the Same Color" problem is a fascinating blend of string manipulation and game theory. By employing pattern recognition and iterative techniques, one can efficiently determine the game\'s outcome. Discussing and demonstrating multiple approaches reflects a comprehensive understanding and adaptability to problem-solving.\n\n---\n\n# Live Coding & Explaining 2 Approaches\nhttps://youtu.be/e3qHIM0byhc?si=td8fkcbWHzQ4x39-\n\n# Approach: Iterative Count\n\nThe iterative count approach involves traversing the `colors` string and counting consecutive \'A\'s and \'B\'s.\n\n## Key Data Structures:\n- **Counters**: Utilized to keep track of consecutive occurrences.\n\n## Enhanced Breakdown:\n\n1. **Initialization**:\n - Initialize counters for Alice\'s and Bob\'s plays. Start a count for consecutive colors.\n \n2. **Iterate through the String**:\n - Traverse the `colors` string. For every character, check if it\'s the same as the previous one to identify consecutive sequences.\n - When the sequence breaks or changes, calculate plays for Alice or Bob based on the color of the sequence.\n \n3. **Handle the Last Segment**:\n - After iterating, handle the last segment of colors and calculate plays for Alice or Bob as needed.\n \n4. **Determine the Winner**:\n - Compare the number of plays for both players. If Alice has more plays, she wins.\n\n## Complexity:\n\n**Time Complexity**: \n- The solution requires a single traversal of the `colors` string, leading to a time complexity of $$O(n)$$, where $$n$$ is the length of the string.\n\n**Space Complexity**: \n- We only utilize a few integer counters to keep track of the sequences and plays, so the space complexity is $$O(1)$$.\n\n# Code Iterative Count\n``` Python []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n alice_plays, bob_plays = 0, 0\n count = 1 \n \n for i in range(1, len(colors)):\n if colors[i] == colors[i - 1]:\n count += 1\n else:\n if colors[i - 1] == \'A\':\n alice_plays += max(0, count - 2)\n else:\n bob_plays += max(0, count - 2)\n count = 1\n \n if colors[-1] == \'A\':\n alice_plays += max(0, count - 2)\n else:\n bob_plays += max(0, count - 2)\n \n return alice_plays > bob_plays\n```\n``` Rust []\nimpl Solution {\n pub fn winner_of_game(colors: String) -> bool {\n let mut alice_plays = 0;\n let mut bob_plays = 0;\n let mut count = 0;\n let chars: Vec<char> = colors.chars().collect();\n \n for i in 1..chars.len() {\n if chars[i] == chars[i - 1] {\n count += 1;\n } else {\n if chars[i - 1] == \'A\' {\n alice_plays += (count - 1).max(0);\n } else {\n bob_plays += (count - 1).max(0);\n }\n count = 0;\n }\n }\n\n if chars[chars.len() - 1] == \'A\' {\n alice_plays += (count - 1).max(0);\n } else {\n bob_plays += (count - 1).max(0);\n }\n \n alice_plays > bob_plays\n }\n}\n```\n``` Go []\npackage main\n\nfunc winnerOfGame(colors string) bool {\n alice_plays, bob_plays, count := 0, 0, 0\n \n for i := 1; i < len(colors); i++ {\n if colors[i] == colors[i-1] {\n count++\n } else {\n if colors[i-1] == \'A\' {\n alice_plays += max(0, count - 1)\n } else {\n bob_plays += max(0, count - 1)\n }\n count = 0\n }\n }\n\n if colors[len(colors)-1] == \'A\' {\n alice_plays += max(0, count - 1)\n } else {\n bob_plays += max(0, count - 1)\n }\n \n return alice_plays > bob_plays\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` C++ []\nclass Solution {\npublic:\n bool winnerOfGame(std::string colors) {\n int alice_plays = 0, bob_plays = 0, count = 0;\n \n for (int i = 1; i < colors.size(); i++) {\n if (colors[i] == colors[i - 1]) {\n count++;\n } else {\n if (colors[i - 1] == \'A\') {\n alice_plays += std::max(0, count - 1);\n } else {\n bob_plays += std::max(0, count - 1);\n }\n count = 0;\n }\n }\n\n if (colors.back() == \'A\') {\n alice_plays += std::max(0, count - 1);\n } else {\n bob_plays += std::max(0, count - 1);\n }\n \n return alice_plays > bob_plays;\n }\n};\n```\n``` Java []\npublic class Solution {\n public boolean winnerOfGame(String colors) {\n int alice_plays = 0, bob_plays = 0, count = 0;\n \n for (int i = 1; i < colors.length(); i++) {\n if (colors.charAt(i) == colors.charAt(i - 1)) {\n count++;\n } else {\n if (colors.charAt(i - 1) == \'A\') {\n alice_plays += Math.max(0, count - 1);\n } else {\n bob_plays += Math.max(0, count - 1);\n }\n count = 0;\n }\n }\n\n if (colors.charAt(colors.length() - 1) == \'A\') {\n alice_plays += Math.max(0, count - 1);\n } else {\n bob_plays += Math.max(0, count - 1);\n }\n \n return alice_plays > bob_plays;\n }\n}\n```\n``` PHP []\nclass Solution {\n function winnerOfGame($colors) {\n $alice_plays = 0; $bob_plays = 0; $count = 0;\n \n for ($i = 1; $i < strlen($colors); $i++) {\n if ($colors[$i] == $colors[$i - 1]) {\n $count++;\n } else {\n if ($colors[$i - 1] == \'A\') {\n $alice_plays += max(0, $count - 1);\n } else {\n $bob_plays += max(0, $count - 1);\n }\n $count = 0;\n }\n }\n\n if ($colors[strlen($colors) - 1] == \'A\') {\n $alice_plays += max(0, $count - 1);\n } else {\n $bob_plays += max(0, $count - 1);\n }\n \n return $alice_plays > $bob_plays;\n }\n}\n```\n``` JavaScript []\n/**\n * @param {string} colors\n * @return {boolean}\n */\nvar winnerOfGame = function(colors) {\n let alice_plays = 0, bob_plays = 0, count = 0;\n \n for (let i = 1; i < colors.length; i++) {\n if (colors[i] == colors[i - 1]) {\n count++;\n } else {\n if (colors[i - 1] == \'A\') {\n alice_plays += Math.max(0, count - 1);\n } else {\n bob_plays += Math.max(0, count - 1);\n }\n count = 0;\n }\n }\n\n if (colors.charAt(colors.length - 1) == \'A\') {\n alice_plays += Math.max(0, count - 1);\n } else {\n bob_plays += Math.max(0, count - 1);\n }\n \n return alice_plays > bob_plays;\n }\n```\n``` C# []\npublic class Solution {\n public bool WinnerOfGame(string colors) {\n int alice_plays = 0, bob_plays = 0, count = 0;\n \n for (int i = 1; i < colors.Length; i++) {\n if (colors[i] == colors[i - 1]) {\n count++;\n } else {\n if (colors[i - 1] == \'A\') {\n alice_plays += Math.Max(0, count - 1);\n } else {\n bob_plays += Math.Max(0, count - 1);\n }\n count = 0;\n }\n }\n\n if (colors[colors.Length - 1] == \'A\') {\n alice_plays += Math.Max(0, count - 1);\n } else {\n bob_plays += Math.Max(0, count - 1);\n }\n \n return alice_plays > bob_plays;\n }\n}\n```\n\n# Approach: RegEx\n\nTo solve this problem using RegEx, we search for patterns within the `colors` string that match consecutive \'A\'s or \'B\'s of length 3 or more.\n\n## Key Data Structures:\n- **Regular Expressions**: Utilized to identify patterns within the string.\n\n## Enhanced Breakdown:\n\n1. **Identify Alice\'s Plays**:\n - Use regular expressions to find all matches of \'A\'s of length 3 or more.\n - For each match, calculate how many times Alice can play (length of match - 2) and aggregate them.\n \n2. **Identify Bob\'s Plays**:\n - Similarly, use regular expressions to find all matches of \'B\'s of length 3 or more.\n - For each match, calculate how many times Bob can play and aggregate them.\n \n3. **Determine the Winner**:\n - Compare the number of plays for Alice and Bob. If Alice has more plays, she wins.\n\n## Complexity:\n\n**Time Complexity**: \n- Regular expressions generally operate in $$O(n)$$ time complexity for simple patterns. However, for complex patterns and longer strings, the time complexity can be worse. In our case, since the patterns are straightforward (repeated \'A\'s or \'B\'s), the time complexity is roughly $$O(n)$$ for each RegEx search, where $$n$$ is the length of the string. Overall, considering two searches (one for \'A\'s and one for \'B\'s), the time complexity remains $$O(n)$$.\n\n**Space Complexity**: \n- The space complexity is mainly dependent on the number of matches found by the RegEx search. In the worst case, if every alternate character is an \'A\' or \'B\', the number of matches would be $$n/3$$. However, these matches are processed sequentially, and we only store the count, making the space complexity $$O(1)$$.\n\n# Code RegEx \n``` Python []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n alice_plays = sum(len(match.group()) - 2 for match in re.finditer(r\'A{3,}\', colors))\n \n bob_plays = sum(len(match.group()) - 2 for match in re.finditer(r\'B{3,}\', colors))\n \n return alice_plays > bob_plays\n```\n\n## Performance\n| Language | Time (ms) | Space (MB) | Approach |\n|------------|-----------|------------|----------|\n| Rust | 6 | 2.7 | Counter |\n| Go | 13 | 6.5 | Counter |\n| Java | 14 | 44.4 | Counter |\n| C++ | 34 | 13.6 | Counter |\n| JavaScript | 55 | 47.8 | Counter |\n| Python3 | 77 | 17.3 | RegEx |\n| C# | 71 | 42.2 | Counter |\n| PHP | 68 | 19.6 | Counter |\n| Python3 | 201 | 17.4 | Counter |\n\n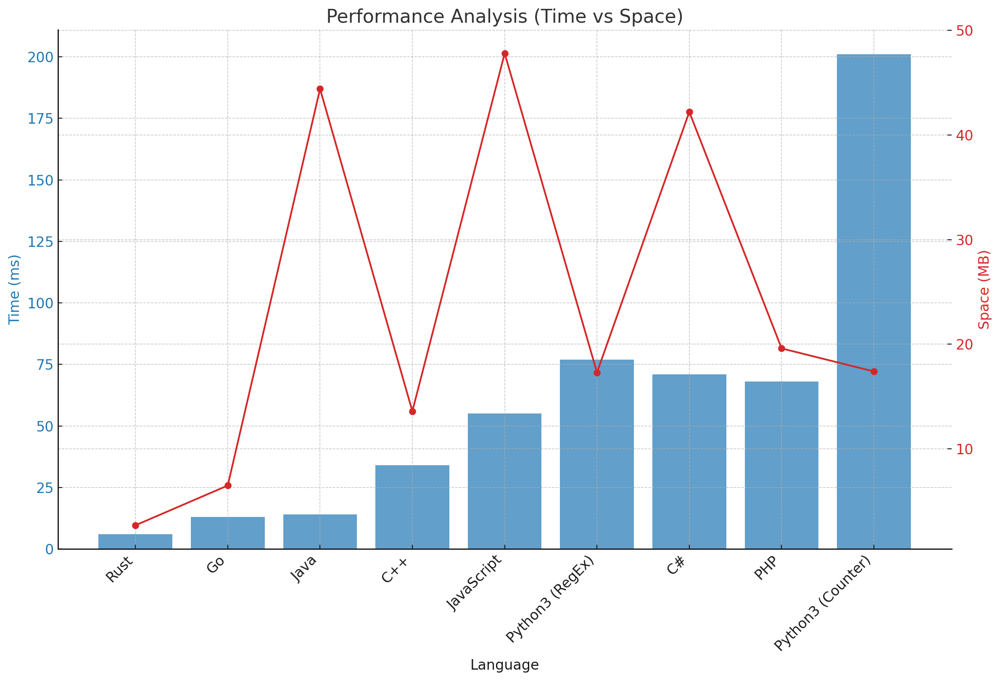\n\n\nBoth the provided approaches offer a clear and efficient solution to the problem. The RegEx approach capitalizes on Python\'s powerful string manipulation capabilities, while the iterative count offers a more intuitive step-by-step breakdown. Understanding both methods provides a holistic view of the problem and its possible solutions. \uD83D\uDCA1\uD83C\uDF20\uD83D\uDC69\u200D\uD83D\uDCBB\uD83D\uDC68\u200D\uD83D\uDCBB | 41 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
✅96.44%🔥Easy Solution🔥Game Theory & Greedy | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Problem Explanation:\n#### In this problem, you are given a string colors representing a line of colored pieces, where each piece is either colored \'A\' or \'B\'. Alice and Bob are playing a game where they take alternating turns removing pieces from the line. Alice goes first, and they have certain rules for removing pieces:\n\n- Alice can only remove a piece colored \'A\' if both its neighbors are also colored \'A\'. She cannot remove pieces that are colored \'B\'.\n- Bob can only remove a piece colored \'B\' if both its neighbors are also colored \'B\'. He cannot remove pieces that are colored \'A\'.\n- They cannot remove pieces from the edge of the line.\n\n#### The game continues until one of the players cannot make a move, and in that case, the other player wins.\n\n#### You need to determine, assuming both Alice and Bob play optimally, whether Alice can win the game or not.\n---\n# Solution Approach:\n#### The given solution approach uses a Counter object to count how many valid moves Alice can make and how many valid moves Bob can make. It iterates through the input string colors to count these moves.\n\n- The collections.Counter() is used to count the occurrences of characters in the string.\n- The groupby(colors) function groups consecutive characters in the string.\n- It iterates through the groups and counts how many \'A\'s and \'B\'s can be removed according to the game rules. Specifically, it counts the number of \'A\'s and \'B\'s that have at least two neighbors of the same color.\n- Finally, it compares the counts of valid moves for Alice (\'A\') and Bob (\'B\'). If Alice has more valid moves, it returns True; otherwise, it returns False.\n\n#### The idea is that if Alice can make more valid moves than Bob, she has a winning strategy because she will eventually force Bob into a position where he can\'t make a move.\n\n#### This solution works under the assumption that both players play optimally and is a good approach to solve the problem efficiently.\n\n\n---\n# Code\n```python []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n c = collections.Counter()\n for x, t in groupby(colors):\n c[x] += max(len(list(t)) - 2, 0)\n\n if c[\'A\'] > c[\'B\']:\n return True\n return False\n```\n```C# []\npublic class Solution {\n public bool WinnerOfGame(string colors) {\n int countA = 0;\n int countB = 0;\n \n for (int i = 0; i < colors.Length; i++) {\n char x = colors[i];\n int count = 0;\n \n while (i < colors.Length && colors[i] == x) {\n i++;\n count++;\n }\n \n if (x == \'A\') {\n countA += Math.Max(count - 2, 0);\n } else if (x == \'B\') {\n countB += Math.Max(count - 2, 0);\n }\n \n i--;\n }\n\n return countA > countB;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n map<char, int> c;\n for (auto it = colors.begin(); it != colors.end(); ) {\n char x = *it;\n auto t = it;\n while (t != colors.end() && *t == x) {\n t++;\n }\n c[x] += max(int(distance(it, t) - 2), 0);\n it = t;\n }\n\n if (c[\'A\'] > c[\'B\']) {\n return true;\n }\n return false;\n }\n};\n\n```\n```C []\nbool winnerOfGame(char *colors) {\n int len = strlen(colors);\n int countA = 0, countB = 0;\n\n for (int i = 0; i < len; i++) {\n char x = colors[i];\n int count = 0;\n\n while (i < len && colors[i] == x) {\n i++;\n count++;\n }\n\n if (x == \'A\') {\n countA += (count - 2 > 0) ? count - 2 : 0;\n } else if (x == \'B\') {\n countB += (count - 2 > 0) ? count - 2 : 0;\n }\n\n i--; \n }\n\n return countA > countB;\n}\n```\n```Java []\npublic class Solution {\n public boolean winnerOfGame(String colors) {\n Map<Character, Integer> c = new HashMap<>();\n c.put(\'A\', 0);\n c.put(\'B\', 0);\n \n for (int i = 0; i < colors.length(); i++) {\n char x = colors.charAt(i);\n int count = 0;\n \n while (i < colors.length() && colors.charAt(i) == x) {\n i++;\n count++;\n }\n \n c.put(x, c.get(x) + Math.max(count - 2, 0));\n i--;\n }\n\n return c.get(\'A\') > c.get(\'B\');\n }\n}\n\n```\n```javascript []\nvar winnerOfGame = function(colors) {\n let countA = 0;\n let countB = 0;\n\n for (let i = 0; i < colors.length; i++) {\n const x = colors[i];\n let count = 0;\n\n while (i < colors.length && colors[i] === x) {\n i++;\n count++;\n }\n\n if (x === \'A\') {\n countA += Math.max(count - 2, 0);\n } else if (x === \'B\') {\n countB += Math.max(count - 2, 0);\n }\n\n i--;\n }\n\n return countA > countB;\n};\n```\n```Typescript []\nfunction winnerOfGame(colors: string): boolean {\n let countA = 0;\n let countB = 0;\n\n for (let i = 0; i < colors.length; i++) {\n const x = colors[i];\n let count = 0;\n\n while (i < colors.length && colors[i] === x) {\n i++;\n count++;\n }\n\n if (x === \'A\') {\n countA += Math.max(count - 2, 0);\n } else if (x === \'B\') {\n countB += Math.max(count - 2, 0);\n }\n\n i--;\n }\n\n return countA > countB;\n}\n\n```\n```Go []\nfunc winnerOfGame(colors string) bool {\n countA := 0\n countB := 0\n\n for i := 0; i < len(colors); i++ {\n x := colors[i]\n count := 0\n\n for i < len(colors) && colors[i] == x {\n i++\n count++\n }\n\n if x == \'A\' {\n countA += max(count-2, 0)\n } else if x == \'B\' {\n countB += max(count-2, 0)\n }\n\n i--\n }\n\n return countA > countB\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\n```\n\n\n | 130 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
100% Acceptance rate with O(n) Solution - Detailed explanation Ever Check it out | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem presents a game played between Alice and Bob on a line of colored pieces, represented by the string colors. Each piece is colored either \'A\' or \'B\', and the players take alternating turns to remove pieces according to certain rules. Alice can remove a piece \'A\' if both its neighbors are also \'A\', and Bob can remove a piece \'B\' if both its neighbors are also \'B\'. The game continues until a player cannot make a valid move, and the one who cannot move loses the game. The task is to determine if Alice will win or if Bob will win when both play optimally.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two variables, aliceWins and bobWins, to keep track of the number of consecutive valid moves each player can make.\n\n2. Iterate through the string colors from the second character to the second-to-last character. This ensures that we do not consider the edge pieces (the first and last characters), as the rules for removal require pieces to have both neighbors.\n\n3. For each position i, check if there are three consecutive \'A\'s or three consecutive \'B\'s. If there are, increment the corresponding counter (aliceWins or bobWins). This means that Alice can remove the \'A\' piece or Bob can remove the \'B\' piece at that position.\n\n4. After iterating through the string, compare the counts of aliceWins and bobWins. If aliceWins is greater than bobWins, Alice wins the game, so return true. Otherwise, Bob wins the game, so return false.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(n), where n is the length of the input string colors. This is because we iterate through the string once, visiting each character once.\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because we only use a constant amount of extra space to store the two counters aliceWins and bobWins. Regardless of the size of the input string, the space required remains constant.\n\n---\n\n# Code\n```\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int n = colors.length();\n int aliceWins = 0, bobWins = 0;\n \n // Count the number of consecutive \'A\'s and \'B\'s.\n for (int i = 1; i < n - 1; ++i) {\n if (colors[i - 1] == \'A\' && colors[i] == \'A\' && colors[i + 1] == \'A\') {\n aliceWins++;\n } else if (colors[i - 1] == \'B\' && colors[i] == \'B\' && colors[i + 1] == \'B\') {\n bobWins++;\n }\n }\n \n // Alice starts, so if she has more opportunities to remove \'A\', she wins.\n if (aliceWins > bobWins) {\n return true;\n }\n \n return false;\n }\n};\n\n``` | 5 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
✅Easy explanation ever - O(n) solution | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this code is to determine the winner of a game played by Alice and Bob, where they take alternating turns removing pieces based on specific rules about adjacent colors in the input string.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n The approach involves iterating through the input string to count the consecutive valid moves each player can make and then comparing these counts to determine the winner.\n\n---\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe code\'s time complexity is O(n), where n is the length of the input string colors, as it iterates through the entire string once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because it uses a constant amount of extra space to store the counts of valid moves for Alice and Bob, regardless of the input string\'s size.\n\n---\n# Do upvote if you like the explanation and solution \u2705\n# Code\n```\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int n = colors.length();\n int aliceWins = 0, bobWins = 0;\n for (int i = 1; i < n - 1; ++i) {\n if (colors[i - 1] == \'A\' && colors[i] == \'A\' && colors[i + 1] == \'A\') {\n aliceWins++;\n } else if (colors[i - 1] == \'B\' && colors[i] == \'B\' && colors[i + 1] == \'B\') {\n bobWins++;\n }\n }\n if (aliceWins > bobWins) {\n return true;\n }\n return false;\n }\n};\n``` | 5 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
Video Solution | Explanation With Drawings | In Depth | C++ | Java | Python 3 | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Intuition and approach discussed in detail in video solution\nhttps://youtu.be/Pkywd65nA6Q\n\n# Code\nC++\n```\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int threeA = 0;\n int threeB = 0;\n int sz = colors.size();\n for(int indx = 1; indx < sz - 1; indx++){\n if(colors[indx] == \'A\' && colors[indx+1] == \'A\' && colors[indx-1] == \'A\'){\n\n threeA++;\n }else if(colors[indx] == \'B\' && colors[indx+1] == \'B\' && colors[indx-1] == \'B\'){\n threeB++;\n }\n }\n return threeA > threeB;\n }\n};\n```\nJava\n```\nclass Solution {\n public boolean winnerOfGame(String clrs) {\n int threeA = 0;\n int threeB = 0;\n int sz = clrs.length();\n char colors[] = clrs.toCharArray();\n for(int indx = 1; indx < sz - 1; indx++){\n if(colors[indx] == \'A\' && colors[indx+1] == \'A\' && colors[indx-1] == \'A\'){\n\n threeA++;\n }else if(colors[indx] == \'B\' && colors[indx+1] == \'B\' && colors[indx-1] == \'B\'){\n threeB++;\n }\n }\n return threeA > threeB;\n }\n}\n```\nPython 3\n```\nclass Solution:\n def winnerOfGame(self, clrs: str) -> bool:\n threeA = 0\n threeB = 0\n sz = len(clrs)\n colors = list(clrs)\n for indx in range(1, sz - 1):\n if colors[indx] == \'A\' and colors[indx+1] == \'A\' and colors[indx-1] == \'A\':\n threeA += 1\n elif colors[indx] == \'B\' and colors[indx+1] == \'B\' and colors[indx-1] == \'B\':\n threeB += 1\n return threeA > threeB\n``` | 3 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
🐍😱 Really Scary Python One-Liner! 🎃 | remove-colored-pieces-if-both-neighbors-are-the-same-color | 0 | 1 | **Faster than 98.94% of all solutions**\n\n# Code\n```\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n return sum((len(i) - 2)*(1 if i[0] is \'A\' else -1) for i in filter(lambda x: len(x) > 2, colors.replace(\'AB\', \'AxB\').replace(\'BA\', \'BxA\').split("x"))) > 0\n``` | 2 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
✅ O(n) Solution with detailed explanation ever - Beats 100% with runtime and memory acceptance 😎 | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to determine the winner of a game played by Alice and Bob based on certain rules about removing pieces from a string. Alice can only remove \'A\' pieces if both neighbors are also \'A\', and Bob can only remove \'B\' pieces if both neighbors are \'B\'. They take alternating turns, and the player who cannot make a move loses the game.\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two variables, aliceWins and bobWins, to keep track of the count of consecutive valid moves each player can make.\n\n2. Iterate through the string colors from the second character to the second-to-last character (indices from 1 to n - 2).\n\n3. For each position i, check if there are three consecutive \'A\'s or three consecutive \'B\'s. If yes, increment the corresponding counter (aliceWins or bobWins).\n\n4. After iterating through the string, compare the counts of aliceWins and bobWins. If aliceWins is greater than bobWins, Alice wins the game, so return true; otherwise, Bob wins the game, so return false.\n\n---\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this code is O(n), where n is the length of the input string colors. This is because we iterate through the string once.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because we only use a constant amount of extra space to store aliceWins and bobWins, regardless of the size of the input string.\n\n---\n# Do upvote if you like the solution and explanation please \uD83D\uDE04\n# Code\n```\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int n = colors.length();\n int aliceWins = 0, bobWins = 0;\n \n // Iterate through the string colors.\n for (int i = 1; i < n - 1; ++i) {\n if (colors[i - 1] == \'A\' && colors[i] == \'A\' && colors[i + 1] == \'A\') {\n aliceWins++;\n } else if (colors[i - 1] == \'B\' && colors[i] == \'B\' && colors[i + 1] == \'B\') {\n bobWins++;\n }\n }\n \n // Alice starts, so if she has more opportunities to remove \'A\', she wins.\n if (aliceWins > bobWins) {\n return true;\n }\n \n return false;\n }\n};\n\n``` | 5 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
🔥Beats 100% | ✅ Line by Line Expl. | [PY/Java/C++/C#/C/JS/Rust/Go] | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | ```python []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n totalA = 0 # Initialize a variable to store the total points of player A.\n totalB = 0 # Initialize a variable to store the total points of player B.\n currA = 0 # Initialize a variable to count the current consecutive colors of A.\n currB = 0 # Initialize a variable to count the current consecutive colors of B.\n\n # Iterate through the characters in the \'colors\' string.\n for char in colors:\n if char == \'A\': # If the current character is \'A\':\n currA += 1 # Increment the count of consecutive \'A\' colors.\n if currB > 2: # If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2 # Add the excess consecutive \'B\' colors to totalB.\n currB = 0 # Reset the consecutive \'B\' count since there\'s an \'A\'.\n else: # If the current character is \'B\':\n currB += 1 # Increment the count of consecutive \'B\' colors.\n if currA > 2: # If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2 # Add the excess consecutive \'A\' colors to totalA.\n currA = 0 # Reset the consecutive \'A\' count since there\'s a \'B\'.\n\n # After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if currA > 2:\n totalA += currA - 2\n if currB > 2:\n totalB += currB - 2\n\n # Compare the total points for \'A\' and \'B\' to determine the winner.\n return totalA > totalB # If \'A\' has more points, return True (A wins); otherwise, return False (B wins or it\'s a tie).\n\n```\n```Java []\npublic class Solution {\n public boolean winnerOfGame(String colors) {\n int totalA = 0; // Initialize a variable to store the total points of player A.\n int totalB = 0; // Initialize a variable to store the total points of player B.\n int currA = 0; // Initialize a variable to count the current consecutive colors of A.\n int currB = 0; // Initialize a variable to count the current consecutive colors of B.\n\n // Iterate through the characters in the \'colors\' string.\n for (char c : colors.toCharArray()) {\n if (c == \'A\') { // If the current character is \'A\':\n currA++; // Increment the count of consecutive \'A\' colors.\n if (currB > 2) // If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2; // Add the excess consecutive \'B\' colors to totalB.\n currB = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n currB++; // Increment the count of consecutive \'B\' colors.\n if (currA > 2) // If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2; // Add the excess consecutive \'A\' colors to totalA.\n currA = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if (currA > 2)\n totalA += currA - 2;\n if (currB > 2)\n totalB += currB - 2;\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n return totalA > totalB; // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int totalA = 0, totalB = 0; // Initialize counters for the total points of players A and B.\n int currA = 0, currB = 0; // Initialize counters for the current consecutive colors of A and B.\n\n // Iterate through the characters in the \'colors\' string.\n for (int i = 0; i < colors.size(); i++) {\n if (colors[i] == \'A\') { // If the current character is \'A\':\n currA++; // Increment the count of consecutive \'A\' colors.\n if (currB > 2) // If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2; // Add the excess consecutive \'B\' colors to totalB.\n currB = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n currB++; // Increment the count of consecutive \'B\' colors.\n if (currA > 2) // If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2; // Add the excess consecutive \'A\' colors to totalA.\n currA = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if (currA > 2)\n totalA += currA - 2;\n if (currB > 2)\n totalB += currB - 2;\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n if (totalA > totalB)\n return true; // If \'A\' has more points, return true (A wins).\n return false; // Otherwise, return false (B wins or it\'s a tie).\n }\n};\n\n```\n```C# []\npublic class Solution {\n public bool WinnerOfGame(string colors) {\n int totalA = 0; // Initialize a variable to store the total points of player A.\n int totalB = 0; // Initialize a variable to store the total points of player B.\n int currA = 0; // Initialize a variable to count the current consecutive colors of A.\n int currB = 0; // Initialize a variable to count the current consecutive colors of B.\n\n // Iterate through the characters in the \'colors\' string.\n foreach (char c in colors) {\n if (c == \'A\') { // If the current character is \'A\':\n currA++; // Increment the count of consecutive \'A\' colors.\n if (currB > 2) // If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2; // Add the excess consecutive \'B\' colors to totalB.\n currB = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n currB++; // Increment the count of consecutive \'B\' colors.\n if (currA > 2) // If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2; // Add the excess consecutive \'A\' colors to totalA.\n currA = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if (currA > 2)\n totalA += currA - 2;\n if (currB > 2)\n totalB += currB - 2;\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n return totalA > totalB; // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n }\n}\n\n```\n```C []\n#include <stdbool.h> // Include the header for boolean data type.\n\nbool winnerOfGame(char *colors) {\n int totalA = 0; // Initialize a variable to store the total points of player A.\n int totalB = 0; // Initialize a variable to store the total points of player B.\n int currA = 0; // Initialize a variable to count the current consecutive colors of A.\n int currB = 0; // Initialize a variable to count the current consecutive colors of B.\n\n // Iterate through the characters in the \'colors\' string.\n for (int i = 0; colors[i] != \'\\0\'; i++) {\n char currentChar = colors[i];\n if (currentChar == \'A\') { // If the current character is \'A\':\n currA++; // Increment the count of consecutive \'A\' colors.\n if (currB > 2) // If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2; // Add the excess consecutive \'B\' colors to totalB.\n currB = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n currB++; // Increment the count of consecutive \'B\' colors.\n if (currA > 2) // If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2; // Add the excess consecutive \'A\' colors to totalA.\n currA = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if (currA > 2)\n totalA += currA - 2;\n if (currB > 2)\n totalB += currB - 2;\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n return totalA > totalB; // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n}\n\n```\n```JavaScript []\nclass Solution {\n winnerOfGame(colors) {\n let totalA = 0; // Initialize a variable to store the total points of player A.\n let totalB = 0; // Initialize a variable to store the total points of player B.\n let currA = 0; // Initialize a variable to count the current consecutive colors of A.\n let currB = 0; // Initialize a variable to count the current consecutive colors of B.\n\n // Iterate through the characters in the \'colors\' string.\n for (let i = 0; i < colors.length; i++) {\n const char = colors[i];\n if (char === \'A\') { // If the current character is \'A\':\n currA++; // Increment the count of consecutive \'A\' colors.\n if (currB > 2) { // If there were more than 2 consecutive \'B\' colors before this \'A\':\n totalB += currB - 2; // Add the excess consecutive \'B\' colors to totalB.\n }\n currB = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n currB++; // Increment the count of consecutive \'B\' colors.\n if (currA > 2) { // If there were more than 2 consecutive \'A\' colors before this \'B\':\n totalA += currA - 2; // Add the excess consecutive \'A\' colors to totalA.\n }\n currA = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if (currA > 2) {\n totalA += currA - 2;\n }\n if (currB > 2) {\n totalB += currB - 2;\n }\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n return totalA > totalB; // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n }\n}\n\n```\n```Rust []\nstruct Solution;\n\nimpl Solution {\n pub fn winner_of_game(colors: &str) -> bool {\n let mut total_a = 0; // Initialize a variable to store the total points of player A.\n let mut total_b = 0; // Initialize a variable to store the total points of player B.\n let mut curr_a = 0; // Initialize a variable to count the current consecutive colors of A.\n let mut curr_b = 0; // Initialize a variable to count the current consecutive colors of B.\n\n // Iterate through the characters in the \'colors\' string.\n for char in colors.chars() {\n if char == \'A\' { // If the current character is \'A\':\n curr_a += 1; // Increment the count of consecutive \'A\' colors.\n if curr_b > 2 { // If there were more than 2 consecutive \'B\' colors before this \'A\':\n total_b += curr_b - 2; // Add the excess consecutive \'B\' colors to total_b.\n }\n curr_b = 0; // Reset the consecutive \'B\' count since there\'s an \'A\'.\n } else { // If the current character is \'B\':\n curr_b += 1; // Increment the count of consecutive \'B\' colors.\n if curr_a > 2 { // If there were more than 2 consecutive \'A\' colors before this \'B\':\n total_a += curr_a - 2; // Add the excess consecutive \'A\' colors to total_a.\n }\n curr_a = 0; // Reset the consecutive \'A\' count since there\'s a \'B\'.\n }\n }\n\n // After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n if curr_a > 2 {\n total_a += curr_a - 2;\n }\n if curr_b > 2 {\n total_b += curr_b - 2;\n }\n\n // Compare the total points for \'A\' and \'B\' to determine the winner.\n total_a > total_b // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n }\n}\n\nfn main() {\n let colors = "AABBBBAAABBAA"; // Example input string.\n let result = Solution::winner_of_game(colors);\n println!("Is player A the winner? {}", result);\n}\n\n```\n```Go []\npackage main\n\nimport "fmt"\n\nfunc winnerOfGame(colors string) bool {\n\ttotalA := 0 // Initialize a variable to store the total points of player A.\n\ttotalB := 0 // Initialize a variable to store the total points of player B.\n\tcurrA := 0 // Initialize a variable to count the current consecutive colors of A.\n\tcurrB := 0 // Initialize a variable to count the current consecutive colors of B.\n\n\t// Iterate through the characters in the \'colors\' string.\n\tfor _, char := range colors {\n\t\tif char == \'A\' { // If the current character is \'A\':\n\t\t\tcurrA++ // Increment the count of consecutive \'A\' colors.\n\t\t\tif currB > 2 { // If there were more than 2 consecutive \'B\' colors before this \'A\':\n\t\t\t\ttotalB += currB - 2 // Add the excess consecutive \'B\' colors to totalB.\n\t\t\t}\n\t\t\tcurrB = 0 // Reset the consecutive \'B\' count since there\'s an \'A\'.\n\t\t} else { // If the current character is \'B\':\n\t\t\tcurrB++ // Increment the count of consecutive \'B\' colors.\n\t\t\tif currA > 2 { // If there were more than 2 consecutive \'A\' colors before this \'B\':\n\t\t\t\ttotalA += currA - 2 // Add the excess consecutive \'A\' colors to totalA.\n\t\t\t}\n\t\t\tcurrA = 0 // Reset the consecutive \'A\' count since there\'s a \'B\'.\n\t\t}\n\t}\n\n\t// After the loop, add any remaining consecutive \'A\' and \'B\' colors to their respective totals.\n\tif currA > 2 {\n\t\ttotalA += currA - 2\n\t}\n\tif currB > 2 {\n\t\ttotalB += currB - 2\n\t}\n\n\t// Compare the total points for \'A\' and \'B\' to determine the winner.\n\treturn totalA > totalB // If \'A\' has more points, return true (A wins); otherwise, return false (B wins or it\'s a tie).\n}\n\nfunc main() {\n\tcolors := "AAABBB"\n\tresult := winnerOfGame(colors)\n\tfmt.Println(result) // Output: true (A wins)\n}\n\n``` | 2 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
Most optimal solution with complete exaplanation | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | \n# Approach\nThe solution iterates through the input string colors. For each position i, it checks if the character at that position and its neighboring characters (at positions i-1 and i+1) satisfy the conditions mentioned in the game rules. If the conditions are met, Alice or Bob can make a move, and their corresponding counter (alice or bob) is incremented.\n\nFinally, the function compares the counts of valid moves made by Alice and Bob. If Alice has made more valid moves, the function returns true, indicating that Alice wins; otherwise, it returns false, indicating that Bob wins.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n```java []\nclass Solution {\n public boolean winnerOfGame(String colors) {\n int alice = 0, bob = 0;\n for (int i = 1; i < colors.length() - 1; i++) {\n char next = colors.charAt(i + 1);\n char prev = colors.charAt(i - 1);\n char curr = colors.charAt(i);\n if (curr == \'A\' && next == \'A\' && prev == \'A\') {\n alice++;\n }\n if (curr == \'B\' && next == \'B\' && prev == \'B\') {\n bob++;\n }\n }\n return alice > bob;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n alice, bob = 0, 0\n for i in range(1, len(colors) - 1):\n next_char = colors[i + 1]\n prev_char = colors[i - 1]\n curr_char = colors[i]\n if curr_char == \'A\' and next_char == \'A\' and prev_char == \'A\':\n alice += 1\n if curr_char == \'B\' and next_char == \'B\' and prev_char == \'B\':\n bob += 1\n return alice > bob\n\n```\n```C++ []\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int alice = 0, bob = 0;\n for(int i = 1; i< colors.size()-1; i++) {\n char next = colors[i+1];\n char prev = colors[i-1];\n char curr = colors[i];\n if(curr == \'A\' && next == \'A\' && prev == \'A\') alice++;\n if(curr == \'B\' && next == \'B\' && prev == \'B\') bob++;\n }\n return alice>bob;\n }\n};\n```\n | 2 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
NOOB CODE : Easy to Understand | remove-colored-pieces-if-both-neighbors-are-the-same-color | 0 | 1 | # Approach\n\n1. It initializes two variables `al` and `bo` to 0 to keep track of the number of consecutive colors for player \'A\' and player \'B\', respectively.\n\n2. It then iterates through the string `colors` from the second character (index 1) to the second-to-last character (index `len(colors) - 2`).\n\n3. Inside the loop, it checks if the current character is \'A\' and if it\'s the same as the previous and next characters. If all these conditions are met, it increments the `al` counter. Similarly, it checks for \'B\' and increments the `bo` counter.\n\n4. Finally, it compares the `al` and `bo` counters and returns `True` if `al` is greater than `bo`, indicating that player \'A\' is the winner, or `False` otherwise.\n\n# Complexity\n- Time complexity: ***O(n)***\n\n- Space complexity: ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n al=0\n bo=0\n for i in range(1,len(colors)-1):\n if (colors[i]==\'A\' and colors[i]==colors[i-1] and colors[i]==colors[i+1]):\n al+=1\n elif (colors[i]==\'B\' and colors[i]==colors[i-1] and colors[i]==colors[i+1]):\n bo+=1\n if(al>bo):\n return(True)\n else:\n return(False)\n``` | 2 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
🚀Count Solution || Explained Intuition || Commented Code🚀 | remove-colored-pieces-if-both-neighbors-are-the-same-color | 1 | 1 | # Problem Description\nIn brief, The problem involves a **game** between `Alice` and `Bob` where they take **turns** **removing** pieces from a line of `A` and `B` colored pieces. `Alice` can only remove `A` pieces if **both** neighbors are also `A`, and `Bob` can only remove `B` pieces if **both** neighbors are `B`. The game **starts** with `Alice` moving **first**. If a player **can\'t** make a move on **their turn**, they **lose**. The task is to determine if `Alice` can win the game assuming **optimal** play.\n\n- **Constraints:**\n - `1 <= colors.length <= 10e5`\n - `colors consists of only the letters A and B`\n - Player only remove piece if its neighbors are the **same** like it\n - Who **can\'t** play in its turn loses\n\n\n---\n\n\n\n# Intuition\nHi there\uD83D\uDE03,\n\nToday\'s problem may seem tough first but it is **very easy** once you **understand** some observations. \uD83D\uDE80\n\nIn our today\'s problem, We have **two** of our friends `Alice` and `Bob` and they are playing some game (a Weird game\uD83D\uDE02). `Alice` only can **remove** piece with letter `A` and its **neighbors** have also letter `A` and `Bob` only can **remove** piece with letter `B` and its **neighbors** have also letter `B`. `Alice` **starts** first and the player who **can\'t** move any more pieces **lose**. \uD83E\uDD14\n\nFrom the description, It seems that we will have to do **many** calculations and go through **many** steps but **actually we won\'t**.\uD83E\uDD29\nLet\'s see some **exapmles**.\n\n```\nEX1: colors = BBAAABBA\n \nAlice\'s Turn -> removes BBA`A`ABBA\ncolors = BBAABBA\n \nBob\'s Turn -> can\'t remove any piece\nAlice wins \n```\n```\nEX2: colors = ABBBABAAAB\n\nAlice\'s Turn -> removes ABBBABA`A`AB\ncolors = ABBBABAAB\n \nBob\'s Turn -> removes AB`B`BABAAB\ncolors = ABBABAAB\n\nAlice\'s Turn -> can\'t remove any piece\nBob wins \n```\n\nI think this is enough for the problem.\nFrom these two examples we can see two important **observations**:\n\n**First** observation, If someone **removed** a piece from its place (Let\'s say Alice) It won\'t give the other player **more** moves to help him play more.\uD83E\uDD14\nEx -> `BBAAABB` -> Alice plays -> `BBAABB` -> Bob loses\nWe can see that from the **begining** of the game, Bob doesn\'t have any pieces to move and **Alice\'s move** didn\'t give hime extra moves like it didn\'t make the string `BBBB`.\uD83E\uDD2F\n\n**Second** observation, From first observation we can **conclude** and I **mentioned** it in the first one also, Every player have **dedicated** number of moves in the **begining** of the game and it **can\'t** be increased or decreased.\uD83D\uDE14\n\nFrom these **two observations** the solution become **much easier**. Only **count** the moves for each player and if Alice has more moves then she wins and if Bob has more or equal moves then he wins.\uD83D\uDE80\uD83D\uDE80\n\nBut Why the last line?\uD83E\uDD2F\uD83E\uDD14\nLets assume that we are playing and see in each turn if the current player has no more moves who wins.\n\n| Turn | Alice\'s Moves | Bob\'s Moves | Who wins | \n| :--- | :---: | :---: | :---: |\n| Alice\'s Turn | 0 | 0 or more |Bob |\n| Bob\'s Turn | 1 or more | 0 |Alice |\n| Alice\'s Turn | 1 | 1 or more | Bob |\n| Bob\'s Turn | 2 or more | 1 |Alice |\n\nAnd we can continue further, But the point that if Alice has more moves then she wins and if Bob has more or equal moves then he wins.\n\nAnd this is the solution for our today problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n# Approach\n1. **Initialize** scores for Alice and Bob (`aliceScore` and `bobScore`) to `zero`.\n2. **Iterate** through the colors (**excluding** edge pieces) using a loop. For **each** piece in the iteration:\n - Check if it\'s `A` and its **neighboring** pieces are also `A`.\n - If **yes**, **increment** `aliceScore` as Alice can remove the current piece.\n - Check if it\'s `B` and its **neighboring** pieces are also `B`.\n - If **yes**, **increment** `bobScore` as Bob can remove the current piece.\n3. Return **true** if Alice\'s score is **greater** than Bob\'s score; otherwise, return **false**.\n\n# Complexity\n- **Time complexity:** $$O(N)$$\nSince we are iterating over all the pieaces then it is **linear** complexity which is `O(N)`.\n- **Space complexity:** $$O(1)$$\nSince we are only storing couple of **constant** variables then complexity is `O(1)`.\n\n---\n\n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n bool winnerOfGame(string colors) {\n int aliceScore = 0, bobScore = 0; // Initialize scores for Alice and Bob\n\n // Iterate through the colors, excluding the edge pieces\n for (int i = 1; i < colors.size() - 1; i++) {\n char currentColor = colors[i];\n char prevColor = colors[i - 1];\n char nextColor = colors[i + 1];\n\n // Check if Alice can make a move here\n if (currentColor == \'A\' && prevColor == \'A\' && nextColor == \'A\')\n aliceScore++; // Alice can remove \'A\'\n\n // Check if Bob can make a move here\n else if (currentColor == \'B\' && prevColor == \'B\' && nextColor == \'B\')\n bobScore++; // Bob can remove \'B\'\n }\n\n // Determine the winner based on the scores\n return aliceScore > bobScore;\n }\n};\n```\n```Java []\npublic class Solution {\n public boolean winnerOfGame(String colors) {\n int aliceScore = 0;\n int bobScore = 0;\n\n // Iterate through the colors, excluding the edge pieces\n for (int i = 1; i < colors.length() - 1; i++) {\n char currentColor = colors.charAt(i);\n char prevColor = colors.charAt(i - 1);\n char nextColor = colors.charAt(i + 1);\n\n // Check if Alice can make a move here\n if (currentColor == \'A\' && prevColor == \'A\' && nextColor == \'A\')\n aliceScore++; // Alice can remove \'A\'\n\n // Check if Bob can make a move here\n else if (currentColor == \'B\' && prevColor == \'B\' && nextColor == \'B\')\n bobScore++; // Bob can remove \'B\'\n }\n\n // Determine the winner based on the scores\n return aliceScore > bobScore;\n }\n}\n```\n```Python []\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n alice_score = 0\n bob_score = 0\n\n # Iterate through the colors, excluding the edge pieces\n for i in range(1, len(colors) - 1):\n current_color = colors[i]\n prev_color = colors[i - 1]\n next_color = colors[i + 1]\n\n # Check if Alice can make a move here\n if current_color == \'A\' and prev_color == \'A\' and next_color == \'A\':\n alice_score += 1 # Alice can remove \'A\'\n\n # Check if Bob can make a move here\n elif current_color == \'B\' and prev_color == \'B\' and next_color == \'B\':\n bob_score += 1 # Bob can remove \'B\'\n\n # Determine the winner based on the scores\n return alice_score > bob_score\n```\n\n\n\n | 99 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
🐢Slow and Unintuitive Python Solution | Slower than 95%🐢 | remove-colored-pieces-if-both-neighbors-are-the-same-color | 0 | 1 | \nThe top solution explains how this game is not very complicated and you can determine the winner by counting the number of As and Bs. This is like a more complicated version of that solution.\uD83D\uDE0E \n\n```\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n count = 0 # 0 if Alice\'s turn, 1 if it is Bob\'s turn\n\n chunks = []\n i = 0\n # we start by breaking the input into groups of As and Bs\n while i < len(colors):\n new_chunk = [colors[i]]\n while i < len(colors) - 1 and colors[i + 1] == colors[i]:\n i += 1\n new_chunk.append(colors[i])\n\n if new_chunk:\n chunks.append(new_chunk)\n i += 1\n\n # We filter the chunks into valid chunks, which contain\n # three or more of a color\n alice_valid_chunks = [chunk for chunk in chunks if chunk[0] == "A" and len(chunk) > 2]\n bob_valid_chunks = [chunk for chunk in chunks if chunk[0] == "B" and len(chunk) > 2]\n \n # we simulate the game.\n for i in range(len(colors)):\n if count == 0: # Alice\'s turn\n if alice_valid_chunks and len(alice_valid_chunks[-1]) > 2:\n alice_valid_chunks[-1].pop()\n if len(alice_valid_chunks[-1]) < 3:\n alice_valid_chunks.pop()\n else: # she has run out of moves\n return False\n else: # Bob\'s turn\n if bob_valid_chunks and len(bob_valid_chunks[-1]) > 2:\n bob_valid_chunks[-1].pop()\n if len(bob_valid_chunks[-1]) < 3:\n bob_valid_chunks.pop()\n else: # he has run out of moves\n return True\n \n count ^= 1\n \n return False\n``` | 1 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
Simple Approach and Answer. No fancy code | remove-colored-pieces-if-both-neighbors-are-the-same-color | 0 | 1 | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSimply we can count the number of times Alice can pop and the number of times Bob can pop. And return whether Alice has the more count or not.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def winnerOfGame(self, colors: str) -> bool:\n a=b=0\n for i in range(1,len(colors)-1):\n if colors[i]==colors[i-1] and colors[i]==colors[i+1]:\n if colors[i]==\'A\':\n a+=1\n else:\n b+=1\n return a>b\n``` | 1 | There are `n` pieces arranged in a line, and each piece is colored either by `'A'` or by `'B'`. You are given a string `colors` of length `n` where `colors[i]` is the color of the `ith` piece.
Alice and Bob are playing a game where they take **alternating turns** removing pieces from the line. In this game, Alice moves **first**.
* Alice is only allowed to remove a piece colored `'A'` if **both its neighbors** are also colored `'A'`. She is **not allowed** to remove pieces that are colored `'B'`.
* Bob is only allowed to remove a piece colored `'B'` if **both its neighbors** are also colored `'B'`. He is **not allowed** to remove pieces that are colored `'A'`.
* Alice and Bob **cannot** remove pieces from the edge of the line.
* If a player cannot make a move on their turn, that player **loses** and the other player **wins**.
Assuming Alice and Bob play optimally, return `true` _if Alice wins, or return_ `false` _if Bob wins_.
**Example 1:**
**Input:** colors = "AAABABB "
**Output:** true
**Explanation:**
AAABABB -> AABABB
Alice moves first.
She removes the second 'A' from the left since that is the only 'A' whose neighbors are both 'A'.
Now it's Bob's turn.
Bob cannot make a move on his turn since there are no 'B's whose neighbors are both 'B'.
Thus, Alice wins, so return true.
**Example 2:**
**Input:** colors = "AA "
**Output:** false
**Explanation:**
Alice has her turn first.
There are only two 'A's and both are on the edge of the line, so she cannot move on her turn.
Thus, Bob wins, so return false.
**Example 3:**
**Input:** colors = "ABBBBBBBAAA "
**Output:** false
**Explanation:**
ABBBBBBBAAA -> ABBBBBBBAA
Alice moves first.
Her only option is to remove the second to last 'A' from the right.
ABBBBBBBAA -> ABBBBBBAA
Next is Bob's turn.
He has many options for which 'B' piece to remove. He can pick any.
On Alice's second turn, she has no more pieces that she can remove.
Thus, Bob wins, so return false.
**Constraints:**
* `1 <= colors.length <= 105`
* `colors` consists of only the letters `'A'` and `'B'` | Which type of traversal lets you find the distance from a point? Try using a Breadth First Search. |
Python bfs || fast and very easy to understand | the-time-when-the-network-becomes-idle | 0 | 1 | The idea is very simple:\n1. First we calculate the shortest latency ( amount of time it takes for a message to reach the master server plus the time it takes for a reply to reach back the server ) for every node.\n2. Then from their patience time, we calculate for each node, the last time it sends a message before it recieves a reply.\n3. Finally our answer is the maximum of the time for each node from the time they send the first message to the time they recieve a reply for their last message\n\n```\nclass Solution:\n def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:\n graph = defaultdict(set)\n for a, b in edges:\n graph[a].add(b)\n graph[b].add(a)\n \n dis = {}\n queue = deque([(0, 0)])\n visited = set([0])\n while queue:\n cur, length = queue.popleft()\n dis[cur] = length * 2\n for nxt in graph[cur]:\n if nxt not in visited:\n queue.append((nxt, length + 1))\n visited.add(nxt)\n \n ans = -float("inf")\n for i in range(1, len(patience)):\n if patience[i] < dis[i]:\n rem = dis[i] % patience[i]\n lastCall = dis[i] - (rem) if rem > 0 else dis[i] - patience[i]\n ans = max(ans, lastCall + dis[i]) \n else:\n ans = max(ans, dis[i])\n return ans + 1\n\n# time and space complexity\n# time: O(n + m)\n# space: O(n)\n# n = number of nodes\n# m = len(edges)\n \n``` | 1 | There is a network of `n` servers, labeled from `0` to `n - 1`. You are given a 2D integer array `edges`, where `edges[i] = [ui, vi]` indicates there is a message channel between servers `ui` and `vi`, and they can pass **any** number of messages to **each other** directly in **one** second. You are also given a **0-indexed** integer array `patience` of length `n`.
All servers are **connected**, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled `0` is the **master** server. The rest are **data** servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers **optimally**, so every message takes the **least amount of time** to arrive at the master server. The master server will process all newly arrived messages **instantly** and send a reply to the originating server via the **reversed path** the message had gone through.
At the beginning of second `0`, each data server sends its message to be processed. Starting from second `1`, at the **beginning** of **every** second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
* If it has not, it will **resend** the message periodically. The data server `i` will resend the message every `patience[i]` second(s), i.e., the data server `i` will resend the message if `patience[i]` second(s) have **elapsed** since the **last** time the message was sent from this server.
* Otherwise, **no more resending** will occur from this server.
The network becomes **idle** when there are **no** messages passing between servers or arriving at servers.
Return _the **earliest second** starting from which the network becomes **idle**_.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\]\], patience = \[0,2,1\]
**Output:** 8
**Explanation:**
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.
At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience\[1\] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience\[2\] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
**Example 2:**
**Input:** edges = \[\[0,1\],\[0,2\],\[1,2\]\], patience = \[0,10,10\]
**Output:** 3
**Explanation:** Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.
**Constraints:**
* `n == patience.length`
* `2 <= n <= 105`
* `patience[0] == 0`
* `1 <= patience[i] <= 105` for `1 <= i < n`
* `1 <= edges.length <= min(105, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no duplicate edges.
* Each server can directly or indirectly reach another server. | Bob can always make the total sum of both sides equal in mod 9. Why does the difference between the number of question marks on the left and right side matter? |
Clear BFS solution (beats 100% Python, 96.5% Java) | the-time-when-the-network-becomes-idle | 1 | 1 | # Intuition\nAfter using BFS to determine the distance between the start node and every other node, we can calculate when the last messages will be sent and received.\n\n# Approach\n1. Convert the edge list into an adjacency list.\n2. Use BFS to compute the distance from the start node to every other node.\n3. Use a helper method `getLastSend()` to determine when the last message will be sent by a node `n`.\n 1. If `patience[n]` is greater than the round trip message latency (`2 * distance[n]`), only the original message will be sent at time 0.\n 2. If the round trip time is a multiple of `patience[n]`, the last message will be sent at `patience[n]` ticks before the arrival of the response to the original message.\n 3. Otherwise, the last message will be sent at time `2 * distance[n] - (2 * distance[n] % patience[n])\n4. Compute the maximum time for a node to receive a response to its last message. For each node, this is the sum of:\n - the last send time (computed by the helper method)\n - the round trip latency (`2 * distance[n]`)\n3. Add 1 to find when the network will become idle.\n\n# Complexity\n- Time complexity: $$O(E+V)$$\n - Building the adjacency list: $$O(E)$$\n - Calculating the distances: $$O(E)$$\n - Calculating the max time: $$O(V)$$\n\n- Space complexity: $$O(E+V)$$\n - The adjacency list: $$O(E+V)$$\n - The distance array: $$O(V)$$\n - The BFS queue: $$O(V)$$\n\nAny of the $O(E+V)$ terms above can be replaced with $O(E)$ because the graph is connected, implying that $V < E + 1$.\n\n# Python Code\n```\nclass Solution:\n def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:\n # Build adjacency list.\n graph = defaultdict(list)\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n\n # Perform BFS to find distances.\n distance = [None] * len(patience)\n distance[0] = 0\n queue = deque()\n queue.append(0)\n # Instance of explicitly keeping track of which nodes are\n # visited, use None as the distance to unvisited nodes.\n while queue:\n node = queue.popleft()\n for neighbor in graph[node]:\n if not distance[neighbor]:\n distance[neighbor] = 1 + distance[node]\n queue.append(neighbor)\n\n def getLastSend(n: int) -> int:\n """Compute when the last message is sent by node n."""\n if patience[n] >= 2 * distance[n]:\n return 0\n if (2 * distance[n]) % patience[n] == 0:\n return 2 * distance[n] - patience[n]\n return 2 * distance[n] - (2 * distance[n] % patience[n])\n\n # Calculate the max time for a node to receive its last response.\n maxTime = 0\n for n in range(1, len(patience)):\n lastSend = getLastSend(n)\n lastReceive = lastSend + 2 * distance[n]\n maxTime = max(maxTime, lastReceive)\n # The above loop can be replaced by a single line with a list comprehension:\n maxTime = max(getLastSend(n) + 2 * distance[n] for n in range(1, len(patience)))\n\n return maxTime + 1\n```\n\n# Java Code\n```\nclass Solution {\n private int getLastSend(int d, int p) {\n if (p >= 2 * d) {\n return 0;\n }\n if ((2 * d) % p == 0) {\n return 2 * d - p;\n }\n return 2 * d - (2 * d) % p;\n }\n\n public int networkBecomesIdle(int[][] edges, int[] patience) {\n // Build adjacency list.\n List<List<Integer>> graph = new ArrayList<>();\n for (int i = 0; i < patience.length; i++) {\n graph.add(new ArrayList<>());\n }\n for (int[] edge : edges) {\n int u = edge[0];\n int v = edge[1];\n graph.get(u).add(v);\n graph.get(v).add(u);\n }\n\n // Perform BFS to find the min distance of each node from the root.\n int[] distance = new int[patience.length];\n boolean[] visited = new boolean[patience.length];\n visited[0] = true;\n Queue<Integer> queue = new LinkedList<>();\n queue.add(0);\n while (!queue.isEmpty()) {\n int node = queue.remove();\n for (int neighbor : graph.get(node)) {\n if (!visited[neighbor]) {\n distance[neighbor] = 1 + distance[node];\n queue.add(neighbor);\n visited[neighbor] = true;\n }\n }\n }\n\n int maxTime = 0;\n for (int n = 1; n < patience.length; n++) {\n int lastSend = getLastSend(distance[n], patience[n]);\n int lastReceive = lastSend + 2 * distance[n];\n maxTime = Math.max(maxTime, lastReceive);\n }\n return maxTime + 1;\n }\n}\n``` | 2 | There is a network of `n` servers, labeled from `0` to `n - 1`. You are given a 2D integer array `edges`, where `edges[i] = [ui, vi]` indicates there is a message channel between servers `ui` and `vi`, and they can pass **any** number of messages to **each other** directly in **one** second. You are also given a **0-indexed** integer array `patience` of length `n`.
All servers are **connected**, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled `0` is the **master** server. The rest are **data** servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers **optimally**, so every message takes the **least amount of time** to arrive at the master server. The master server will process all newly arrived messages **instantly** and send a reply to the originating server via the **reversed path** the message had gone through.
At the beginning of second `0`, each data server sends its message to be processed. Starting from second `1`, at the **beginning** of **every** second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
* If it has not, it will **resend** the message periodically. The data server `i` will resend the message every `patience[i]` second(s), i.e., the data server `i` will resend the message if `patience[i]` second(s) have **elapsed** since the **last** time the message was sent from this server.
* Otherwise, **no more resending** will occur from this server.
The network becomes **idle** when there are **no** messages passing between servers or arriving at servers.
Return _the **earliest second** starting from which the network becomes **idle**_.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\]\], patience = \[0,2,1\]
**Output:** 8
**Explanation:**
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.
At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience\[1\] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience\[2\] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
**Example 2:**
**Input:** edges = \[\[0,1\],\[0,2\],\[1,2\]\], patience = \[0,10,10\]
**Output:** 3
**Explanation:** Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.
**Constraints:**
* `n == patience.length`
* `2 <= n <= 105`
* `patience[0] == 0`
* `1 <= patience[i] <= 105` for `1 <= i < n`
* `1 <= edges.length <= min(105, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no duplicate edges.
* Each server can directly or indirectly reach another server. | Bob can always make the total sum of both sides equal in mod 9. Why does the difference between the number of question marks on the left and right side matter? |
[Python3] graph | the-time-when-the-network-becomes-idle | 0 | 1 | \n```\nclass Solution:\n def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:\n graph = {}\n for u, v in edges: \n graph.setdefault(u, []).append(v)\n graph.setdefault(v, []).append(u)\n \n dist = [-1]*len(graph)\n dist[0] = 0 \n val = 0\n queue = [0]\n while queue: \n val += 2\n newq = []\n for u in queue: \n for v in graph[u]: \n if dist[v] == -1: \n dist[v] = val\n newq.append(v)\n queue = newq\n \n ans = 0\n for d, p in zip(dist, patience): \n if p: \n k = d//p - int(d%p == 0)\n ans = max(ans, d + k*p)\n return ans + 1\n``` | 5 | There is a network of `n` servers, labeled from `0` to `n - 1`. You are given a 2D integer array `edges`, where `edges[i] = [ui, vi]` indicates there is a message channel between servers `ui` and `vi`, and they can pass **any** number of messages to **each other** directly in **one** second. You are also given a **0-indexed** integer array `patience` of length `n`.
All servers are **connected**, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled `0` is the **master** server. The rest are **data** servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers **optimally**, so every message takes the **least amount of time** to arrive at the master server. The master server will process all newly arrived messages **instantly** and send a reply to the originating server via the **reversed path** the message had gone through.
At the beginning of second `0`, each data server sends its message to be processed. Starting from second `1`, at the **beginning** of **every** second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
* If it has not, it will **resend** the message periodically. The data server `i` will resend the message every `patience[i]` second(s), i.e., the data server `i` will resend the message if `patience[i]` second(s) have **elapsed** since the **last** time the message was sent from this server.
* Otherwise, **no more resending** will occur from this server.
The network becomes **idle** when there are **no** messages passing between servers or arriving at servers.
Return _the **earliest second** starting from which the network becomes **idle**_.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\]\], patience = \[0,2,1\]
**Output:** 8
**Explanation:**
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.
At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience\[1\] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience\[2\] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
**Example 2:**
**Input:** edges = \[\[0,1\],\[0,2\],\[1,2\]\], patience = \[0,10,10\]
**Output:** 3
**Explanation:** Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.
**Constraints:**
* `n == patience.length`
* `2 <= n <= 105`
* `patience[0] == 0`
* `1 <= patience[i] <= 105` for `1 <= i < n`
* `1 <= edges.length <= min(105, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no duplicate edges.
* Each server can directly or indirectly reach another server. | Bob can always make the total sum of both sides equal in mod 9. Why does the difference between the number of question marks on the left and right side matter? |
Python3 || Shortest Path | the-time-when-the-network-becomes-idle | 0 | 1 | # Intuition\n- Shortest Path to trace the distance to each vertex to calculcate the distance\n\n# Approach\n- Shortest Path to calculate the time take to reach vertex\n- Calculate the last packet that would leave the node due to no response\n- Calculate it\'s arrival\n\n# Complexity\n- Time complexity:\n- O(V^2) worst case\n\n- Space complexity:\n- O(N)\n# Code\n```\nclass Solution:\n def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:\n\n graph = {}\n for i in range(len(edges)):\n if edges[i][0] not in graph:\n graph[edges[i][0]] = []\n if edges[i][1] not in graph:\n graph[edges[i][1]] = [] \n graph[edges[i][0]].append(edges[i][1])\n graph[edges[i][1]].append(edges[i][0])\n\n def solve():\n heap = []\n dist = [float(\'inf\') for _ in range(len(patience))]\n dist[0] = 0\n heapq.heappush(heap,(0,0))\n while len(heap)!=0:\n # print(heap)\n ele = heapq.heappop(heap)\n ver = ele[0]\n dis = ele[1]\n\n for n in graph[ver]:\n if dis+1 < dist[n]:\n dist[n] = dis+1\n heapq.heappush(heap,(n,dis+1))\n \n maxx = -1\n print(dist)\n for i in range(1,len(patience)):\n t = 2*dist[i]\n _rS = patience[i]\n if t%_rS == 0:\n times = (t//_rS)-1\n else:\n times = t//_rS\n if times!=0:\n arrival = times*_rS + t\n maxx = max(maxx,arrival)\n else:\n maxx = max(maxx,t)\n return maxx\n return solve()+1\n # return 2\n\n``` | 0 | There is a network of `n` servers, labeled from `0` to `n - 1`. You are given a 2D integer array `edges`, where `edges[i] = [ui, vi]` indicates there is a message channel between servers `ui` and `vi`, and they can pass **any** number of messages to **each other** directly in **one** second. You are also given a **0-indexed** integer array `patience` of length `n`.
All servers are **connected**, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled `0` is the **master** server. The rest are **data** servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers **optimally**, so every message takes the **least amount of time** to arrive at the master server. The master server will process all newly arrived messages **instantly** and send a reply to the originating server via the **reversed path** the message had gone through.
At the beginning of second `0`, each data server sends its message to be processed. Starting from second `1`, at the **beginning** of **every** second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
* If it has not, it will **resend** the message periodically. The data server `i` will resend the message every `patience[i]` second(s), i.e., the data server `i` will resend the message if `patience[i]` second(s) have **elapsed** since the **last** time the message was sent from this server.
* Otherwise, **no more resending** will occur from this server.
The network becomes **idle** when there are **no** messages passing between servers or arriving at servers.
Return _the **earliest second** starting from which the network becomes **idle**_.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\]\], patience = \[0,2,1\]
**Output:** 8
**Explanation:**
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.
At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience\[1\] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience\[2\] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
**Example 2:**
**Input:** edges = \[\[0,1\],\[0,2\],\[1,2\]\], patience = \[0,10,10\]
**Output:** 3
**Explanation:** Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.
**Constraints:**
* `n == patience.length`
* `2 <= n <= 105`
* `patience[0] == 0`
* `1 <= patience[i] <= 105` for `1 <= i < n`
* `1 <= edges.length <= min(105, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no duplicate edges.
* Each server can directly or indirectly reach another server. | Bob can always make the total sum of both sides equal in mod 9. Why does the difference between the number of question marks on the left and right side matter? |
Python BFS | the-time-when-the-network-becomes-idle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind distance from each data node to master node, then use some math to calculate how long does it take for a data server to finish sending messages, taken into consideration its patience. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def networkBecomesIdle(self, edges: List[List[int]], patience: List[int]) -> int:\n graph = defaultdict(list)\n for u,v in edges:\n graph[u].append(v)\n graph[v].append(u)\n\n # find distance between each node and master node\n distances = defaultdict(int)\n bfs = [0]\n distance = -1\n visited = set()\n while bfs:\n distance += 1\n next_round = []\n for node in bfs:\n if node in visited:\n continue\n\n if node != 0:\n distances[node] = distance\n \n visited.add(node)\n next_round.extend(graph[node])\n bfs = next_round\n \n # calculate idle time\n ans = 0\n for i, v in distances.items():\n round_trip = 2 * v\n remainder = round_trip % patience[i]\n if remainder == 0:\n subtrahend = patience[i]\n else:\n if patience[i] >= round_trip:\n subtrahend = round_trip\n else:\n subtrahend = remainder\n\n ans = max(ans, round_trip + round_trip - subtrahend)\n\n return ans + 1\n``` | 0 | There is a network of `n` servers, labeled from `0` to `n - 1`. You are given a 2D integer array `edges`, where `edges[i] = [ui, vi]` indicates there is a message channel between servers `ui` and `vi`, and they can pass **any** number of messages to **each other** directly in **one** second. You are also given a **0-indexed** integer array `patience` of length `n`.
All servers are **connected**, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled `0` is the **master** server. The rest are **data** servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers **optimally**, so every message takes the **least amount of time** to arrive at the master server. The master server will process all newly arrived messages **instantly** and send a reply to the originating server via the **reversed path** the message had gone through.
At the beginning of second `0`, each data server sends its message to be processed. Starting from second `1`, at the **beginning** of **every** second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
* If it has not, it will **resend** the message periodically. The data server `i` will resend the message every `patience[i]` second(s), i.e., the data server `i` will resend the message if `patience[i]` second(s) have **elapsed** since the **last** time the message was sent from this server.
* Otherwise, **no more resending** will occur from this server.
The network becomes **idle** when there are **no** messages passing between servers or arriving at servers.
Return _the **earliest second** starting from which the network becomes **idle**_.
**Example 1:**
**Input:** edges = \[\[0,1\],\[1,2\]\], patience = \[0,2,1\]
**Output:** 8
**Explanation:**
At (the beginning of) second 0,
- Data server 1 sends its message (denoted 1A) to the master server.
- Data server 2 sends its message (denoted 2A) to the master server.
At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience\[1\] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience\[2\] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
...
At second 4,
- The reply 2A arrives at server 2. No more resending will occur from server 2.
...
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
**Example 2:**
**Input:** edges = \[\[0,1\],\[0,2\],\[1,2\]\], patience = \[0,10,10\]
**Output:** 3
**Explanation:** Data servers 1 and 2 receive a reply back at the beginning of second 2.
From the beginning of the second 3, the network becomes idle.
**Constraints:**
* `n == patience.length`
* `2 <= n <= 105`
* `patience[0] == 0`
* `1 <= patience[i] <= 105` for `1 <= i < n`
* `1 <= edges.length <= min(105, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `0 <= ui, vi < n`
* `ui != vi`
* There are no duplicate edges.
* Each server can directly or indirectly reach another server. | Bob can always make the total sum of both sides equal in mod 9. Why does the difference between the number of question marks on the left and right side matter? |
[Python3] binary search | kth-smallest-product-of-two-sorted-arrays | 0 | 1 | \n```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n \n def fn(val):\n """Return count of products <= val."""\n ans = 0\n for x in nums1: \n if x < 0: ans += len(nums2) - bisect_left(nums2, ceil(val/x))\n elif x == 0: \n if 0 <= val: ans += len(nums2)\n else: ans += bisect_right(nums2, floor(val/x))\n return ans \n \n lo, hi = -10**10, 10**10 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if fn(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n```\n\n```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n neg = [x for x in nums1 if x < 0]\n pos = [x for x in nums1 if x >= 0]\n \n def fn(val):\n """Return count of products <= val."""\n ans = 0\n lo, hi = 0, len(nums2)-1\n for x in neg[::-1] + pos if val >= 0 else neg + pos[::-1]: \n if x < 0: \n while lo < len(nums2) and x*nums2[lo] > val: lo += 1\n ans += len(nums2) - lo\n elif x == 0: \n if 0 <= val: ans += len(nums2)\n else: \n while 0 <= hi and x*nums2[hi] > val: hi -= 1\n ans += hi+1\n return ans \n \n lo, hi = -10**10, 10**10 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if fn(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n``` | 9 | Given two **sorted 0-indexed** integer arrays `nums1` and `nums2` as well as an integer `k`, return _the_ `kth` _(**1-based**) smallest product of_ `nums1[i] * nums2[j]` _where_ `0 <= i < nums1.length` _and_ `0 <= j < nums2.length`.
**Example 1:**
**Input:** nums1 = \[2,5\], nums2 = \[3,4\], k = 2
**Output:** 8
**Explanation:** The 2 smallest products are:
- nums1\[0\] \* nums2\[0\] = 2 \* 3 = 6
- nums1\[0\] \* nums2\[1\] = 2 \* 4 = 8
The 2nd smallest product is 8.
**Example 2:**
**Input:** nums1 = \[-4,-2,0,3\], nums2 = \[2,4\], k = 6
**Output:** 0
**Explanation:** The 6 smallest products are:
- nums1\[0\] \* nums2\[1\] = (-4) \* 4 = -16
- nums1\[0\] \* nums2\[0\] = (-4) \* 2 = -8
- nums1\[1\] \* nums2\[1\] = (-2) \* 4 = -8
- nums1\[1\] \* nums2\[0\] = (-2) \* 2 = -4
- nums1\[2\] \* nums2\[0\] = 0 \* 2 = 0
- nums1\[2\] \* nums2\[1\] = 0 \* 4 = 0
The 6th smallest product is 0.
**Example 3:**
**Input:** nums1 = \[-2,-1,0,1,2\], nums2 = \[-3,-1,2,4,5\], k = 3
**Output:** -6
**Explanation:** The 3 smallest products are:
- nums1\[0\] \* nums2\[4\] = (-2) \* 5 = -10
- nums1\[0\] \* nums2\[3\] = (-2) \* 4 = -8
- nums1\[4\] \* nums2\[0\] = 2 \* (-3) = -6
The 3rd smallest product is -6.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 5 * 104`
* `-105 <= nums1[i], nums2[j] <= 105`
* `1 <= k <= nums1.length * nums2.length`
* `nums1` and `nums2` are sorted. | Consider a new graph where each node is one of the old nodes at a specific time. For example, node 0 at time 5. You need to find the shortest path in the new graph. |
Python 3 AC Solution with detailed math derivation | kth-smallest-product-of-two-sorted-arrays | 0 | 1 | ```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n """\n Binary Search\n find first number that makes countSmallerOrEqual(number) >= k\n return number\n """\n boundary = [nums1[0]*nums2[0], nums1[0] * nums2[-1], nums1[-1] * nums2[0], nums1[-1] * nums2[-1]]\n low, high = min(boundary), max(boundary)\n while low + 1 < high:\n mid = low + (high - low) // 2\n if self.countSmallerOrEqual(mid, nums1, nums2) >= k:\n high = mid\n else:\n low = mid + 1\n if self.countSmallerOrEqual(low, nums1, nums2) >= k:\n return low\n else:\n return high\n \n def countSmallerOrEqual(self, m, nums1, nums2):\n """\n Two pointers solution\n use monotonic property of both nums1 and nums2\n return the number of products nums1[i] * nums2[j] <= m\n l1, l2 = len(nums1), len(nums2)\n \n 1) if m >= 0, \n ***Given nums1[i] < 0***\n find j such that nums2[j] >= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] decreases -> index j decreases\n j monotonically moves left\n return j:l2 -> l2 - j + 1\n *** Given nums1[i] = 0\n return l2\n ***Given nums1[i] > 0***\n find j such that nums2[j] <= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] decreases -> index j decreases\n j monotonically moves left\n return 0:j -> j + 1\n\n 2) if m < 0, \n ***Given nums1[i] < 0***\n find j such that nums2[j] >= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] increases -> index j increases\n j monotonically moves right\n return j:l2 -> l2 - j + 1\n *** Given nums1[i] = 0\n return 0\n ***Given nums1[i] > 0***\n find j such that nums2[j] <= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] increases -> index j increases\n j monotonically moves right\n return 0:j -> j + 1\n \n """\n l1, l2 = len(nums1), len(nums2)\n ans = 0\n if m >= 0:\n j1, j2 = l2-1, l2-1\n for i in range(l1):\n if nums1[i] < 0:\n while j1 >=0 and nums2[j1] >= m/nums1[i]:\n j1 -= 1\n ans += l2 - j1 - 1\n elif nums1[i] > 0:\n while j2 >=0 and nums2[j2] > m/nums1[i]:\n j2 -= 1\n ans += j2 + 1\n else:\n ans += l2\n else:\n j1, j2 = 0, 0\n for i in range(l1):\n if nums1[i] < 0:\n while j1 < l2 and nums2[j1] < m/nums1[i]:\n j1 += 1\n ans += l2 - j1\n elif nums1[i] > 0:\n while j2 < l2 and nums2[j2] <= m/nums1[i]:\n j2 += 1\n ans += j2\n return ans\n```\n \n | 2 | Given two **sorted 0-indexed** integer arrays `nums1` and `nums2` as well as an integer `k`, return _the_ `kth` _(**1-based**) smallest product of_ `nums1[i] * nums2[j]` _where_ `0 <= i < nums1.length` _and_ `0 <= j < nums2.length`.
**Example 1:**
**Input:** nums1 = \[2,5\], nums2 = \[3,4\], k = 2
**Output:** 8
**Explanation:** The 2 smallest products are:
- nums1\[0\] \* nums2\[0\] = 2 \* 3 = 6
- nums1\[0\] \* nums2\[1\] = 2 \* 4 = 8
The 2nd smallest product is 8.
**Example 2:**
**Input:** nums1 = \[-4,-2,0,3\], nums2 = \[2,4\], k = 6
**Output:** 0
**Explanation:** The 6 smallest products are:
- nums1\[0\] \* nums2\[1\] = (-4) \* 4 = -16
- nums1\[0\] \* nums2\[0\] = (-4) \* 2 = -8
- nums1\[1\] \* nums2\[1\] = (-2) \* 4 = -8
- nums1\[1\] \* nums2\[0\] = (-2) \* 2 = -4
- nums1\[2\] \* nums2\[0\] = 0 \* 2 = 0
- nums1\[2\] \* nums2\[1\] = 0 \* 4 = 0
The 6th smallest product is 0.
**Example 3:**
**Input:** nums1 = \[-2,-1,0,1,2\], nums2 = \[-3,-1,2,4,5\], k = 3
**Output:** -6
**Explanation:** The 3 smallest products are:
- nums1\[0\] \* nums2\[4\] = (-2) \* 5 = -10
- nums1\[0\] \* nums2\[3\] = (-2) \* 4 = -8
- nums1\[4\] \* nums2\[0\] = 2 \* (-3) = -6
The 3rd smallest product is -6.
**Constraints:**
* `1 <= nums1.length, nums2.length <= 5 * 104`
* `-105 <= nums1[i], nums2[j] <= 105`
* `1 <= k <= nums1.length * nums2.length`
* `nums1` and `nums2` are sorted. | Consider a new graph where each node is one of the old nodes at a specific time. For example, node 0 at time 5. You need to find the shortest path in the new graph. |
simple python | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | \nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n s=s.split(" ")\n l=[]\n for i in s:\n if i.isdigit():\n l.append(int(i))\n print(l)\n l1=sorted(l)\n if(l==l1):\n s1=set(l1)\n if(len(s1)==len(l1)):\n return True\n else:\n return False\n else:\n return False\n\n``` | 1 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
[Python3] 2-line | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | \n```\nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n nums = [int(w) for w in s.split() if w.isdigit()]\n return all(nums[i-1] < nums[i] for i in range(1, len(nums)))\n``` | 29 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
One line Python solution | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n return [int(i) for i in s.split() if i.isnumeric()] == sorted(set(int(i) for i in s.split() if i.isnumeric()))\n``` | 2 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
Beat 94.70% 23 ms Python 3 | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n b = 0\n for i in s.split():\n if i.isdigit():\n if int(i) <= b: return False\n else: b = int(i)\n return True\n\n``` | 2 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
Python simple solution | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | **Python :**\n\n```\ndef areNumbersAscending(self, s: str) -> bool:\n\tprev = -1\n\n\tfor w in s.split():\n\t\tif w.isdigit():\n\t\t\tif int(w) <= prev:\n\t\t\t\treturn False\n\t\t\tprev = int(w)\n\n\treturn True\n```\n\n**Like it ? please upvote !** | 13 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
Very simple python solution - O(n) | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | \n# Code\n```\nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n l = s.split(\' \') # split string into list of words\n max = 0 # keep track of current maximum\n for i in l:\n if i.isdigit(): # check if i is a number\n if int(i) <= max: # check if the number < max\n return False # Return False if true\n max = int(i)\n return True # Return True\n\n\n\n\n``` | 2 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
Python3|| Beats 93.33% || Simple solution & O(n*logn). | check-if-numbers-are-ascending-in-a-sentence | 0 | 1 | # **Please do upvote if you like the solution.**\n# Code\n```\nclass Solution:\n def areNumbersAscending(self, s: str) -> bool:\n l=[]\n for i in s.split():\n if i.isnumeric():\n l.append(int(i))\n return l == sorted(set(l))\n``` | 2 | A sentence is a list of **tokens** separated by a **single** space with no leading or trailing spaces. Every token is either a **positive number** consisting of digits `0-9` with no leading zeros, or a **word** consisting of lowercase English letters.
* For example, `"a puppy has 2 eyes 4 legs "` is a sentence with seven tokens: `"2 "` and `"4 "` are numbers and the other tokens such as `"puppy "` are words.
Given a string `s` representing a sentence, you need to check if **all** the numbers in `s` are **strictly increasing** from left to right (i.e., other than the last number, **each** number is **strictly smaller** than the number on its **right** in `s`).
Return `true` _if so, or_ `false` _otherwise_.
**Example 1:**
**Input:** s = "1 box has 3 blue 4 red 6 green and 12 yellow marbles "
**Output:** true
**Explanation:** The numbers in s are: 1, 3, 4, 6, 12.
They are strictly increasing from left to right: 1 < 3 < 4 < 6 < 12.
**Example 2:**
**Input:** s = "hello world 5 x 5 "
**Output:** false
**Explanation:** The numbers in s are: **5**, **5**. They are not strictly increasing.
**Example 3:**
**Input:** s = "sunset is at 7 51 pm overnight lows will be in the low 50 and 60 s "
**Output:** false
**Explanation:** The numbers in s are: 7, **51**, **50**, 60. They are not strictly increasing.
**Constraints:**
* `3 <= s.length <= 200`
* `s` consists of lowercase English letters, spaces, and digits from `0` to `9`, inclusive.
* The number of tokens in `s` is between `2` and `100`, inclusive.
* The tokens in `s` are separated by a single space.
* There are at least **two** numbers in `s`.
* Each number in `s` is a **positive** number **less** than `100`, with no leading zeros.
* `s` contains no leading or trailing spaces. | If you only had to find the maximum product of 2 numbers in an array, which 2 numbers should you choose? We only need to worry about 4 numbers in the array. |
Python decorator | simple-bank-system | 0 | 1 | \n# Code\n```\ndef validator(function):\n def wrapper(self, *args, **kwargs):\n if len(args) == 3:\n account1, account2, money = args\n if (account1 not in self.balance_map) or (account2 not in self.balance_map):\n return False\n elif len(args) == 2:\n account, money = args\n if account not in self.balance_map:\n return False\n return function(self, *args, **kwargs)\n return wrapper\n\n\nclass Bank:\n def __init__(self, balance: List[int]):\n self.balance_map = {}\n for i in range(1, len(balance) + 1):\n self.balance_map[i] = balance[i - 1] \n\n @validator\n def transfer(self, account1: int, account2: int, money: int) -> bool:\n if self.balance_map[account1] >= money: \n self.balance_map[account1] -= money\n self.balance_map[account2] += money\n return True\n else:\n return False\n\n @validator\n def deposit(self, account: int, money: int) -> bool: \n self.balance_map[account] += money\n return True\n\n @validator\n def withdraw(self, account: int, money: int) -> bool:\n if self.balance_map[account] >= money:\n self.balance_map[account] -= money\n return True\n else:\n return False\n\n\n``` | 1 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
[Python3] just do what's told | simple-bank-system | 0 | 1 | \n```\nclass Bank:\n\n def __init__(self, balance: List[int]):\n self.balance = balance\n\n def transfer(self, account1: int, account2: int, money: int) -> bool:\n if self.withdraw(account1, money): \n if self.deposit(account2, money): return True \n self.deposit(account1, money)\n\n def deposit(self, account: int, money: int) -> bool:\n if 1 <= account <= len(self.balance): \n self.balance[account-1] += money\n return True \n \n def withdraw(self, account: int, money: int) -> bool:\n if 1 <= account <= len(self.balance) and self.balance[account-1] >= money: \n self.balance[account-1] -= money\n return True \n``` | 8 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
Easy Python Solution | Faster than 100% | With Comments | simple-bank-system | 0 | 1 | # Easy Python Solution | Faster than 100% | With Comments\n\n**Runtime: 673 ms, faster than 100.00% of Python3 online submissions for Simple Bank System.\nMemory Usage: 43.8 MB.**\n\n```\nclass Bank:\n\n def __init__(self, bal: List[int]):\n self.store = bal # storage list\n\n\n def transfer(self, a1: int, a2: int, money: int) -> bool:\n try:\n # checking if both accounts exist. and if the transaction would be valid\n if self.store[a1 - 1] >= money and self.store[a2 - 1] >= 0:\n # performing the transaction\n self.store[a1 - 1] -= money\n self.store[a2 - 1] += money\n return True\n else:\n # retrning false on invalid transaction\n return False\n except:\n # returning false when accounts don\'t exist\n return False\n\n\n def deposit(self, ac: int, mn: int) -> bool:\n try:\n # if account exists performing transaction\n self.store[ac - 1] += mn\n return True\n except:\n # returning false when account doesn\'t exist\n return False\n\n\n def withdraw(self, ac: int, mn: int) -> bool:\n try:\n # checking if transaction is valid\n if self.store[ac - 1] >= mn:\n # performing the transaction\n self.store[ac - 1] -= mn\n return True\n else:\n # returning false in case on invalid transaction\n return False\n except:\n # returning false when account doesn\'t exist\n return False\n```\n\n\n | 2 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
✅ Easy to understand Python solution | simple-bank-system | 0 | 1 | # Code\n```\nclass Bank:\n\n def __init__(self, balance: List[int]):\n self.balance = balance\n \n def transfer(self, account1: int, account2: int, money: int) -> bool:\n if account1 <= len(self.balance) and account2 <= len(self.balance) and self.balance[account1 - 1] >= money:\n self.balance[account2 - 1] += money\n self.balance[account1 - 1] -= money\n return True\n return False\n \n\n def deposit(self, account: int, money: int) -> bool:\n if account <= len(self.balance):\n self.balance[account - 1] += money\n return True\n return False\n\n def withdraw(self, account: int, money: int) -> bool:\n if account <= len(self.balance) and self.balance[account - 1] >= money:\n self.balance[account - 1] -= money\n return True\n return False\n \n\n\n# Your Bank object will be instantiated and called as such:\n# obj = Bank(balance)\n# param_1 = obj.transfer(account1,account2,money)\n# param_2 = obj.deposit(account,money)\n# param_3 = obj.withdraw(account,money)\n``` | 0 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
python3 simulation | simple-bank-system | 0 | 1 | \n\n# Code\n```\nclass Bank:\n\n def __init__(self, balance: List[int]):\n self.balance = balance\n\n def transfer(self, account1: int, account2: int, money: int) -> bool:\n if account1 > len(self.balance) or account2 > len(self.balance):\n return False\n if self.balance[account1-1] < money:\n return False\n self.balance[account1-1] -= money\n self.balance[account2-1] += money\n return True\n\n def deposit(self, account: int, money: int) -> bool:\n if account > len(self.balance):\n return False\n self.balance[account-1]+=money\n return True\n\n def withdraw(self, account: int, money: int) -> bool:\n if account > len(self.balance):\n return False\n if self.balance[account-1] < money:\n return False\n self.balance[account-1]-=money\n return True\n\n\n# Your Bank object will be instantiated and called as such:\n# obj = Bank(balance)\n# param_1 = obj.transfer(account1,account2,money)\n# param_2 = obj.deposit(account,money)\n# param_3 = obj.withdraw(account,money)\n``` | 0 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
Easy Python Solution | simple-bank-system | 0 | 1 | # Code\n```\nclass Bank:\n\n def __init__(self, balance: List[int]):\n self.bankAccounts = balance\n self.length = len(self.bankAccounts)\n \n\n def transfer(self, account1: int, account2: int, money: int) -> bool:\n if 1 <= account1 <= self.length and 1 <= account2 <= self.length:\n if money <= self.bankAccounts[account1 - 1]:\n self.bankAccounts[account1 - 1] = self.bankAccounts[account1 - 1] - money\n self.bankAccounts[account2 - 1] = self.bankAccounts[account2 - 1] + money\n return True\n return False\n\n\n def deposit(self, account: int, money: int) -> bool:\n if 1 <= account <= self.length:\n self.bankAccounts[account - 1] = self.bankAccounts[account - 1] + money\n return True\n return False\n \n\n def withdraw(self, account: int, money: int) -> bool:\n if 1 <= account <= self.length:\n if money <= self.bankAccounts[account - 1]:\n self.bankAccounts[account - 1] = self.bankAccounts[account - 1] - money\n return True\n return False\n\n\n# Your Bank object will be instantiated and called as such:\n# obj = Bank(balance)\n# param_1 = obj.transfer(account1,account2,money)\n# param_2 = obj.deposit(account,money)\n# param_3 = obj.withdraw(account,money)\n``` | 0 | You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has `n` accounts numbered from `1` to `n`. The initial balance of each account is stored in a **0-indexed** integer array `balance`, with the `(i + 1)th` account having an initial balance of `balance[i]`.
Execute all the **valid** transactions. A transaction is **valid** if:
* The given account number(s) are between `1` and `n`, and
* The amount of money withdrawn or transferred from is **less than or equal** to the balance of the account.
Implement the `Bank` class:
* `Bank(long[] balance)` Initializes the object with the **0-indexed** integer array `balance`.
* `boolean transfer(int account1, int account2, long money)` Transfers `money` dollars from the account numbered `account1` to the account numbered `account2`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean deposit(int account, long money)` Deposit `money` dollars into the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
* `boolean withdraw(int account, long money)` Withdraw `money` dollars from the account numbered `account`. Return `true` if the transaction was successful, `false` otherwise.
**Example 1:**
**Input**
\[ "Bank ", "withdraw ", "transfer ", "deposit ", "transfer ", "withdraw "\]
\[\[\[10, 100, 20, 50, 30\]\], \[3, 10\], \[5, 1, 20\], \[5, 20\], \[3, 4, 15\], \[10, 50\]\]
**Output**
\[null, true, true, true, false, false\]
**Explanation**
Bank bank = new Bank(\[10, 100, 20, 50, 30\]);
bank.withdraw(3, 10); // return true, account 3 has a balance of $20, so it is valid to withdraw $10.
// Account 3 has $20 - $10 = $10.
bank.transfer(5, 1, 20); // return true, account 5 has a balance of $30, so it is valid to transfer $20.
// Account 5 has $30 - $20 = $10, and account 1 has $10 + $20 = $30.
bank.deposit(5, 20); // return true, it is valid to deposit $20 to account 5.
// Account 5 has $10 + $20 = $30.
bank.transfer(3, 4, 15); // return false, the current balance of account 3 is $10,
// so it is invalid to transfer $15 from it.
bank.withdraw(10, 50); // return false, it is invalid because account 10 does not exist.
**Constraints:**
* `n == balance.length`
* `1 <= n, account, account1, account2 <= 105`
* `0 <= balance[i], money <= 1012`
* At most `104` calls will be made to **each** function `transfer`, `deposit`, `withdraw`. | First, you need to consider each layer separately as an array. Just cycle this array and then re-assign it. |
Hashmap | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport functools\nclass Solution:\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n mapping = collections.defaultdict(int)\n for count in range(1,len(nums)+1):\n subsets = list(itertools.combinations(nums,count))\n for ele in subsets:\n mapping[functools.reduce(lambda a,b: a|b,list(ele))] += 1\n return mapping[max(mapping.keys())]\n\n``` | 1 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
[Python3] top-down dp | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | \n```\nclass Solution:\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n target = reduce(or_, nums)\n \n @cache\n def fn(i, mask): \n """Return number of subsets to get target."""\n if mask == target: return 2**(len(nums)-i)\n if i == len(nums): return 0 \n return fn(i+1, mask | nums[i]) + fn(i+1, mask)\n \n return fn(0, 0)\n``` | 9 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
Easy python solution using recursion and backtracking | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | # Code\n```\nclass Solution:\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n def subs(idx,nums,N,lst,l):\n if idx>=N:\n val=0\n for i in lst:\n val |= i\n l.append(val)\n return\n lst.append(nums[idx])\n subs(idx+1,nums,N,lst,l)\n lst.pop()\n subs(idx+1,nums,N,lst,l)\n return \n \n lst=[]\n l=[]\n subs(0,nums,len(nums),lst,l)\n cnt=Counter(l)\n return max([i for i in cnt.values()])\n \n``` | 2 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
Python3 | Solved using Recursion + Backtracking | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | ```\nclass Solution:\n #Let n = len(nums) array!\n #Time-Complexity: O(n * 2^n), since we make 2^n rec. calls to generate\n #all 2^n different subsets and for each rec. call, we call helper function that\n #computes Bitwise Or Lienarly!\n #Space-Complexity: O(n), since max stack depth is n!\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n \n \n \n #helper function!\n def calculate_BWOR(arr):\n if(len(arr) == 1):\n return arr[0]\n else:\n n = len(arr)\n res = arr[0]\n for i in range(1, n):\n #take the bitwise or operation on two integers: ans and i!\n res = res | arr[i]\n return res\n \n \n \n \n \n #Approach: Utilize backtracking to generate all possible subsets!\n #Even if two sets contain same elements, it can be considered different\n #if we choose elements of differing indices!\n \n #I can keep track in answer all of the subset(s) that posseses the maximum\n #bitwise or!\n \n #At the end, I simply have to return number of subsets in answer!\n \n ans = []\n n = len(nums)\n #since the range of integers in input array nums is at least 1,\n #I will initialize maximum bitwise or value to 1!\n maximum = 1\n #parameters: i -> index that we are considering from\n #cur -> array of elements in current subset we built up so far!\n def helper(i, cur):\n nonlocal nums, ans, maximum, n\n #base case -> if index i == n and current subset is not None, we know we made #decision to include or not include for each and every of the n elements!\n if(i == n):\n if(not cur):\n return\n #once we hit base case, get the bitwise or of cur and compare\n #against max!\n #1. If it matches max, add it to ans!\n #2. If it beats current max, update maximum and update ans to\n #have only cur element!\n #3. Otherwise, ignore!\n current = calculate_BWOR(cur)\n if(current > maximum):\n maximum = current\n #make sure to add deep copy!\n ans = [cur[::]]\n return\n elif(current == maximum):\n #make sure to add deep copy! Contents of cur might change\n #as we return to parent rec. call from current call to helper!\n ans.append(cur[::])\n return\n else:\n return\n #if it\'s not the base case, we have to make 2 rec. calls!\n cur.append(nums[i])\n helper(i+1, cur)\n #once the prev. rec.call finishes, we generated all subsets that\n #does contain nums[i]!\n \n cur.pop()\n #this rec. call generates all subsets that do not contain nums[i]\n helper(i+1, cur)\n \n helper(0, [])\n return len(ans) | 1 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
Backtracking solution | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n\n OR = 0\n for num in nums:\n OR |= num\n\n def perform_or(li):\n or_cumilative = 0\n for num in li:\n or_cumilative |= num\n \n return or_cumilative\n\n \n ans = []\n N = len(nums)\n\n def f(i, res):\n\n if perform_or(res) == OR:\n ans.append(res)\n\n \n \n for j in range(i, N):\n res.append(nums[j])\n f(j+1, res)\n res.pop()\n \n f(0, [])\n return len(ans)\n\n\n \n``` | 0 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
BackTracking using python Easy Solution..! | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n d={}\n def backtrack(nums,c,curror):\n if(c>=len(nums)):\n if curror not in d:\n d[curror]=1\n else:\n d[curror]+=1\n return\n backtrack(nums,c+1,curror | nums[c])\n backtrack(nums,c+1,curror)\n backtrack(nums,0,0)\n return max(d.values()) \n \n \n``` | 0 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
python straightforward backtracking solution | count-number-of-maximum-bitwise-or-subsets | 0 | 1 | # Code\n```\nclass Solution:\n def backtracking(self, nums, startIndex, path, result):\n if len(path) > 0: result.append(path[:])\n for i in range(startIndex, len(nums)):\n self.backtracking(nums, i + 1, path + [nums[i]], result)\n \n def find_or_max_count(self, subsets):\n max_ = float(\'-inf\')\n or_sum = lambda lst: functools.reduce(lambda a, b: a | b, lst)\n count = 0\n\n for subset in subsets:\n curr_sum = or_sum(subset)\n if curr_sum == max_:\n count += 1\n elif curr_sum > max_:\n max_ = curr_sum\n count = 1\n else:\n continue\n return count\n\n def countMaxOrSubsets(self, nums: List[int]) -> int:\n result = []\n self.backtracking(nums, 0, [], result)\n return self.find_or_max_count(result)\n \n``` | 0 | Given an integer array `nums`, find the **maximum** possible **bitwise OR** of a subset of `nums` and return _the **number of different non-empty subsets** with the maximum bitwise OR_.
An array `a` is a **subset** of an array `b` if `a` can be obtained from `b` by deleting some (possibly zero) elements of `b`. Two subsets are considered **different** if the indices of the elements chosen are different.
The bitwise OR of an array `a` is equal to `a[0] **OR** a[1] **OR** ... **OR** a[a.length - 1]` (**0-indexed**).
**Example 1:**
**Input:** nums = \[3,1\]
**Output:** 2
**Explanation:** The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- \[3\]
- \[3,1\]
**Example 2:**
**Input:** nums = \[2,2,2\]
**Output:** 7
**Explanation:** All non-empty subsets of \[2,2,2\] have a bitwise OR of 2. There are 23 - 1 = 7 total subsets.
**Example 3:**
**Input:** nums = \[3,2,1,5\]
**Output:** 6
**Explanation:** The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- \[3,5\]
- \[3,1,5\]
- \[3,2,5\]
- \[3,2,1,5\]
- \[2,5\]
- \[2,1,5\]
**Constraints:**
* `1 <= nums.length <= 16`
* `1 <= nums[i] <= 105` | For each prefix of the string, check which characters are of even frequency and which are not and represent it by a bitmask. Find the other prefixes whose masks differs from the current prefix mask by at most one bit. |
[Python3] Dijkstra & BFS | second-minimum-time-to-reach-destination | 0 | 1 | \n```\nclass Solution:\n def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u-1].append(v-1)\n graph[v-1].append(u-1)\n pq = [(0, 0)]\n seen = [[] for _ in range(n)]\n least = None\n while pq: \n t, u = heappop(pq)\n if u == n-1: \n if least is None: least = t\n elif least < t: return t \n if (t//change) & 1: t = (t//change+1)*change # waiting for green\n t += time\n for v in graph[u]: \n if not seen[v] or len(seen[v]) == 1 and seen[v][0] != t: \n seen[v].append(t)\n heappush(pq, (t, v))\n```\n\nEdited on 2021-10-20\nDijkstra\'s algo is an overkill for this problem as the weights on edges are identical per the one `time` variable. BFS is enough for this problem. \n```\nclass Solution:\n def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:\n graph = [[] for _ in range(n)]\n for u, v in edges: \n graph[u-1].append(v-1)\n graph[v-1].append(u-1)\n \n least = None\n queue = deque([(0, 0)])\n seen = [[] for _ in range(n)]\n while queue: \n t, u = queue.popleft()\n if u == n-1: \n if least is None: least = t\n elif least < t: return t \n if (t//change) & 1: t = (t//change+1)*change # waiting for green\n t += time\n for v in graph[u]: \n if not seen[v] or len(seen[v]) == 1 and seen[v][0] != t: \n seen[v].append(t)\n queue.append((t, v))\n``` | 9 | A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes.
Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time**, but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**.
The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value.
* For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`.
Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`.
**Notes:**
* You can go through any vertex **any** number of times, **including** `1` and `n`.
* You can assume that when the journey **starts**, all signals have just turned **green**.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2\],\[1,3\],\[1,4\],\[3,4\],\[4,5\]\], time = 3, change = 5
**Output:** 13
**Explanation:**
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.
The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\], time = 3, change = 2
**Output:** 11
**Explanation:**
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
**Constraints:**
* `2 <= n <= 104`
* `n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no duplicate edges.
* Each vertex can be reached directly or indirectly from every other vertex.
* `1 <= time, change <= 103` | Use binary search on the answer. You can get l/m branches of length m from a branch with length l. |
heap based solution | second-minimum-time-to-reach-destination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:\n # graph construction\n graph = defaultdict(list)\n for u, v in edges:\n graph[u].append(v)\n graph[v].append(u)\n\n # initialization\n distances = [[float(\'inf\')] * 2] * (n + 1)\n\n # relaxation\n pq = [(0, 1)]\n while pq:\n curr_time, node = heappop(pq)\n if node == n and distances[n][1] != float(\'inf\'):\n return distances[n][1]\n for neighbor in graph[node]:\n next_time = curr_time + time if not (curr_time // change) % 2 else (curr_time // change + 1) * change + time\n min_time, second_min_time = distances[neighbor]\n if next_time < min_time or (min_time != next_time < second_min_time):\n if next_time < min_time:\n min_time = next_time\n else:\n second_min_time = next_time\n heappush(pq, (next_time, neighbor))\n distances[neighbor] = [min_time, second_min_time]\n return -1\n``` | 0 | A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes.
Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time**, but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**.
The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value.
* For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`.
Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`.
**Notes:**
* You can go through any vertex **any** number of times, **including** `1` and `n`.
* You can assume that when the journey **starts**, all signals have just turned **green**.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2\],\[1,3\],\[1,4\],\[3,4\],\[4,5\]\], time = 3, change = 5
**Output:** 13
**Explanation:**
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.
The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\], time = 3, change = 2
**Output:** 11
**Explanation:**
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
**Constraints:**
* `2 <= n <= 104`
* `n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no duplicate edges.
* Each vertex can be reached directly or indirectly from every other vertex.
* `1 <= time, change <= 103` | Use binary search on the answer. You can get l/m branches of length m from a branch with length l. |
[Python] BFS solution with Japanese explanation. | second-minimum-time-to-reach-destination | 0 | 1 | # Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\n- 2nd\u6700\u77ED\u3082\u7BA1\u7406\u3059\u308B\u3088\u3046\u306BBFS\uFF08DP\uFF09\u3092\u884C\u3046\u3002\n - BFS\u3092\u884C\u3063\u3066\u3044\u308B\u304C\u3001\u672C\u8CEA\u7684\u306B\u306F\u52D5\u7684\u8A08\u753B\u6CD5\u3082\u884C\u3063\u3066\u3044\u308B\u3002\uFF08\u3053\u306E\u69D8\u306B\u30B0\u30E9\u30D5\u3068DP\u306B\u306F\u5BC6\u63A5\u306A\u95A2\u4FC2\u304C\u3042\u308B\uFF09\n - BFS\uFF08DP\uFF09\u306B\u3088\u3063\u3066\u5C0F\u3055\u3044\u9806\u306B\u5404\u30CE\u30FC\u30C9\u306E\u6700\u77ED\u30682nd\u6700\u77ED\u304C\u6C7A\u307E\u308B\u3002\n - \u3042\u308B\u30CE\u30FC\u30C9\u306E\u6700\u77ED\u30682nd\u6700\u77ED\u304B\u3089\u96A3\u63A5\u3059\u308B\u30CE\u30FC\u30C9\u306E\u6700\u77ED\u30682nd\u6700\u77ED\u3092\u6C42\u3081\u308B\u3002\uFF08\u914D\u308BDP\u306E\u30A4\u30E1\u30FC\u30B8\u3002)\n- 2nd\u6700\u77ED\u306E\u7D4C\u8DEF\u306E\u9577\u3055\u304C\u6C7A\u307E\u308C\u3070\u5F8C\u306F\u305D\u308C\u306B\u304B\u304B\u308B\u6642\u9593\u3092\u8A08\u7B97\u3059\u308B\u3060\u3051\u3002\n - signal\u306E\u5909\u5316\u56DE\u6570\u306B\u7740\u76EE\u3059\u308C\u3070\u305D\u308C\u307B\u3069\u96E3\u3057\u304F\u306A\u3044\u3002\n\n# Complexity\n$$e$$: ```len(edges)```\n- Time complexity: $$O(n+e)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nBFS\u306E$$O(n+e)$$\u304C\u30DC\u30C8\u30EB\u30CD\u30C3\u30AF\u3002\u6642\u9593\u306E\u8A08\u7B97\u306F\u7D4C\u8DEF\u9577\u306B\u4F9D\u5B58\u3057\u3066\u3044\u3066$$O(e)$$\u3002\n\n- Space complexity: $$O(n+e)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\ngraph\u304C\u30DC\u30C8\u30EB\u30CD\u30C3\u30AF\u3067$$O(n+e)$$\u4F7F\u7528\u3002\n\n# Code\n```\nfrom collections import deque\n\nINF = float(\'inf\')\n\n# \u7D4C\u8DEF\u9577l\u9032\u3080\u306E\u306B\u3069\u308C\u304F\u3089\u3044\u304B\u304B\u308B\u304B\u3092\u8FD4\u3059\ndef calc(l, time, change):\n # print(l, time, change)\n cur_time = 0\n while l:\n # signal\u304C\u5909\u5316\u3057\u305F\u56DE\u6570\n flip = cur_time // change\n if flip & 1: # flip\u304C\u5947\u6570\u3001\u3064\u307E\u308A\u901A\u308C\u306A\u3044\n # \u901A\u308C\u306A\u3044\u306E\u3067\u6B21\u306Bsignal\u304C\u5909\u5316\u3057\u3066\u901A\u308C\u308B\u307E\u3067\u5F85\u3064\n cur_time = (flip + 1) * change\n\n cur_time += time\n l -= 1\n\n return cur_time \n\nclass Solution:\n def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:\n graph = [[] for _ in range(n)]\n\n for edge in edges:\n u, v = edge\n u -= 1\n v -= 1\n graph[u].append(v)\n graph[v].append(u)\n\n # \u6700\u77ED\u30682nd\u6700\u77ED\u306E\uFF12\u3064\u3092\u8A18\u9332\u3059\u308B\uFF08\u6700\u77ED < 2nd\u6700\u77ED\uFF09\n # dp[i][0]: 0\u304B\u3089i\u307E\u3067\u306E\u6700\u77ED, dp[i][1]: 0\u304B\u3089i\u307E\u3067\u306E2nd\u6700\u77ED\n # dp\u306F\u6700\u77ED\u30012nd\u6700\u77ED\u3092\u767A\u898B\u3057\u305F\u304B\u3069\u3046\u304B\u306E\u8A18\u9332\u3068\u3057\u3066\u3082\u4F7F\u3048\u308B\uFF08\u521D\u671F\u5024\u306EINF\u3068\u3044\u3046\u3053\u3068\u306F\u672A\u767A\u898B\uFF09\n dp = [[INF, INF] for _ in range(n)] \n dp[0][0] = 0\n\n # \u8DDD\u96E2\uFF08\u6700\u77ED or 2nd\u6700\u77ED\uFF09, \u30CE\u30FC\u30C9id\n que = deque([(0, 0)])\n\n # \u91CD\u307F\u306A\u3057\u306E\u30B0\u30E9\u30D5\u306B\u5BFE\u3059\u308BBFS\u306A\u306E\u3067\u3001\u30AD\u30E5\u30FC\u5185\u3067\u306F\u5E38\u306B\u8DDD\u96E2\u304C\u5C0F\u3055\u3044\u9806\u306B\u306A\u3063\u3066\u3044\u308B\u3053\u3068\u306B\u6CE8\u610F\uFF01\n # \u5C0F\u3055\u3044\u9806\u6700\u77ED\u30682nd\u6700\u77ED\u3092\u6C7A\u5B9A\u3057\u3066dp\u3057\u3066\u3044\u304F\u30A4\u30E1\u30FC\u30B8\n while que:\n u, ud = que.popleft()\n for v in graph[u]:\n # \u6700\u77ED\u304C\u672A\u5B9A\n if dp[v][0] == INF:\n # \u3053\u3053\u3067\u6700\u77ED\u304C\u6C7A\u5B9A\n dp[v][0] = ud + 1\n que.append((v, dp[v][0])) \n elif dp[v][1] == INF: # \u6700\u77ED\u306F\u6C7A\u5B9A\u6E08\u307F\u3060\u304C2nd\u6700\u77ED\u306F\u672A\u5B9A\n # 2nd\u6700\u77ED\u306E\u5019\u88DC\u306F\u6700\u77ED\u3068\u7B49\u3057\u304F\u7121\u3044\u5FC5\u8981\u304C\u3042\u308B\n if ud + 1 != dp[v][0]:\n # \u3053\u3053\u30672nd\u6700\u77ED\u304C\u6C7A\u5B9A\n dp[v][1] = ud + 1 \n # 0\u304B\u3089v\u3078\u306E2nd\u6700\u77ED\u7D4C\u8DEF\u3092\u901A\u308B\u3053\u3068\u3067\u4ED6\u306E\u30CE\u30FC\u30C9\u3078\u306E2nd\u6700\u77ED\u304C\u6C42\u307E\u3063\u3066\u3044\u304F\u53EF\u80FD\u6027\u304C\u3042\u308B\n # \u3088\u3063\u3066\u30AD\u30E5\u30FC\u306B2nd\u6700\u77ED\u306E\u8DDD\u96E2\u3067\u30CE\u30FC\u30C9\u3092\u8FFD\u52A0\n que.append((v, dp[v][1]))\n\n\n return calc(dp[n-1][1], time, change)\n\n``` | 0 | A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes.
Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time**, but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**.
The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value.
* For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`.
Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`.
**Notes:**
* You can go through any vertex **any** number of times, **including** `1` and `n`.
* You can assume that when the journey **starts**, all signals have just turned **green**.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2\],\[1,3\],\[1,4\],\[3,4\],\[4,5\]\], time = 3, change = 5
**Output:** 13
**Explanation:**
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.
The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\], time = 3, change = 2
**Output:** 11
**Explanation:**
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
**Constraints:**
* `2 <= n <= 104`
* `n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no duplicate edges.
* Each vertex can be reached directly or indirectly from every other vertex.
* `1 <= time, change <= 103` | Use binary search on the answer. You can get l/m branches of length m from a branch with length l. |
Simple BFS in Python, Faster than 95% | second-minimum-time-to-reach-destination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this problem, a vertex can be visited more than one time. In fact, only the first two visits should be considered since the goal is to find the second shortest path. This is the key to solve this problem efficiently. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis problem can solved by a slightly revised BFS graph traversal algorithm. A state in the search space is $(v, t, r)$, where $v$ is the current staying vertex, $t$ is the time to leave $v$, and $r$ is the times of $v$ being visited. \nOnly the first time and the second time of visits should be considered, so all the state with $r>2$ can be ignored. As a result, the size of the search space is only $2 \\times |V|$, which is manageable.\n\n# Complexity\n- Time complexity: $$O(|E| + |V|)$$, where $|E|$ is the number of edges and $|V|$ is the number of vertices. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(|E| + |V|)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:\n graph = defaultdict(set)\n for u, v in edges:\n graph[v].add(u)\n graph[u].add(v)\n\n ans = inf\n q = deque([(1, 0)])\n visited = defaultdict(set)\n visited[1].add(0)\n\n while q:\n v, t = q.popleft()\n next_t = t + time\n if next_t // change % 2 == 1:\n next_t = (next_t // change + 1) * change\n for u in graph[v]:\n if u == n:\n if ans == inf:\n ans = t + time\n elif t + time > ans:\n return t + time\n if len(visited[u]) < 2 and next_t not in visited[u]:\n visited[u].add(next_t)\n q.append((u, next_t))\n return -1\n\n\n\n``` | 0 | A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes.
Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time**, but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**.
The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value.
* For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`.
Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`.
**Notes:**
* You can go through any vertex **any** number of times, **including** `1` and `n`.
* You can assume that when the journey **starts**, all signals have just turned **green**.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2\],\[1,3\],\[1,4\],\[3,4\],\[4,5\]\], time = 3, change = 5
**Output:** 13
**Explanation:**
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.
The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\], time = 3, change = 2
**Output:** 11
**Explanation:**
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
**Constraints:**
* `2 <= n <= 104`
* `n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no duplicate edges.
* Each vertex can be reached directly or indirectly from every other vertex.
* `1 <= time, change <= 103` | Use binary search on the answer. You can get l/m branches of length m from a branch with length l. |
Python (Simple modified Dijkstra's algorithm) | second-minimum-time-to-reach-destination | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def secondMinimum(self, n, edges, time, change):\n dict1 = collections.defaultdict(list)\n\n for i,j in edges:\n dict1[i-1].append((j-1,time))\n dict1[j-1].append((i-1,time))\n\n d1, d2 = {i:float("inf") for i in range(n)}, {i:float("inf") for i in range(n)}\n\n d1[0], freq = 0, collections.defaultdict(int)\n\n stack = [(0,0)]\n\n while stack:\n cur_time, node = heapq.heappop(stack)\n\n freq[node] += 1\n\n if freq[node] == 2 and node == n-1:\n return cur_time\n\n if ((cur_time//change)%2):\n cur_time = change*(cur_time//change + 1)\n\n for neighbor,t in dict1[node]:\n if freq[neighbor] == 2: continue\n if d1[neighbor] > cur_time + t:\n d2[neighbor] = d1[neighbor]\n d1[neighbor] = cur_time + t\n heapq.heappush(stack,(cur_time + t,neighbor))\n\n elif d2[neighbor] > cur_time + t and d1[neighbor] != cur_time + t:\n d2[neighbor] = cur_time + t\n heapq.heappush(stack,(cur_time + t,neighbor))\n\n\n\n \n\n``` | 0 | A city is represented as a **bi-directional connected** graph with `n` vertices where each vertex is labeled from `1` to `n` (**inclusive**). The edges in the graph are represented as a 2D integer array `edges`, where each `edges[i] = [ui, vi]` denotes a bi-directional edge between vertex `ui` and vertex `vi`. Every vertex pair is connected by **at most one** edge, and no vertex has an edge to itself. The time taken to traverse any edge is `time` minutes.
Each vertex has a traffic signal which changes its color from **green** to **red** and vice versa every `change` minutes. All signals change **at the same time**. You can enter a vertex at **any time**, but can leave a vertex **only when the signal is green**. You **cannot wait** at a vertex if the signal is **green**.
The **second minimum value** is defined as the smallest value **strictly larger** than the minimum value.
* For example the second minimum value of `[2, 3, 4]` is `3`, and the second minimum value of `[2, 2, 4]` is `4`.
Given `n`, `edges`, `time`, and `change`, return _the **second minimum time** it will take to go from vertex_ `1` _to vertex_ `n`.
**Notes:**
* You can go through any vertex **any** number of times, **including** `1` and `n`.
* You can assume that when the journey **starts**, all signals have just turned **green**.
**Example 1:**
**Input:** n = 5, edges = \[\[1,2\],\[1,3\],\[1,4\],\[3,4\],\[4,5\]\], time = 3, change = 5
**Output:** 13
**Explanation:**
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.
The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.
**Example 2:**
**Input:** n = 2, edges = \[\[1,2\]\], time = 3, change = 2
**Output:** 11
**Explanation:**
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.
**Constraints:**
* `2 <= n <= 104`
* `n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)`
* `edges[i].length == 2`
* `1 <= ui, vi <= n`
* `ui != vi`
* There are no duplicate edges.
* Each vertex can be reached directly or indirectly from every other vertex.
* `1 <= time, change <= 103` | Use binary search on the answer. You can get l/m branches of length m from a branch with length l. |
Python | Easy Solution✅ | number-of-valid-words-in-a-sentence | 0 | 1 | # Code\u2705\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n sentence_list = sentence.split()\n count = 0\n for i, word in enumerate(sentence_list):\n valid = True\n hyphen_count = 0 \n for j, letter in enumerate(word):\n if letter.isdigit():\n valid = False \n break\n if letter in ("!",".",",") and j != len(word)-1:\n valid = False \n break\n if (letter == "-" and (j == len(word)-1 or j == 0)) or (letter == "-" and (not word[j-1].isalpha() or not word[j+1].isalpha())):\n valid = False \n break\n if letter == "-":\n hyphen_count +=1\n if hyphen_count >1:\n valid = False \n break\n if valid:\n count +=1\n return count\n\n \n``` | 6 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
✔️ PYTHON || EXPLAINED || ;] CORNER CASE | number-of-valid-words-in-a-sentence | 0 | 1 | **UPVOTE IF HELPFuuL**\n\nSolution is just implementation provided below.\n\nThe case that people miss is ```"example-!"``` -> where there is hypen and puntuation at the end.\n\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n a = list(sentence.split())\n res=0\n punc = [\'!\',\'.\',\',\']\n \n for s in a:\n if s!="":\n num=0\n for i in range(0,10):\n num+=s.count(str(i))\n if num==0:\n k=s.count(\'-\')\n if k==0 or (k==1 and s.index(\'-\')!=0 and s.index(\'-\')!=len(s)-1):\n num=0\n for i in punc:\n num+=s.count(i)\n if num==0 or (num==1 and s[-1] in punc and (len(s)==1 or s[-2]!=\'-\')):\n res+=1\n return res\n```\n\n | 6 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
[Python3] check words | number-of-valid-words-in-a-sentence | 0 | 1 | \n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n \n def fn(word): \n """Return true if word is valid."""\n seen = False \n for i, ch in enumerate(word): \n if ch.isdigit() or ch in "!.," and i != len(word)-1: return False\n elif ch == \'-\': \n if seen or i == 0 or i == len(word)-1 or not word[i+1].isalpha(): return False \n seen = True \n return True \n \n return sum(fn(word) for word in sentence.split())\n```\n\nAdding a regex solution by @yo1995\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n pattern = re.compile(r\'(^[a-z]+(-[a-z]+)?)?[,.!]?$\')\n return sum(bool(pattern.match(word)) for word in sentence.split())\n``` | 24 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
Python by regex [w/ Comment] | number-of-valid-words-in-a-sentence | 0 | 1 | Python by [regula expression aka regex](https://docs.python.org/3/library/re.html)\n\n[Online regex debugger](https://regex101.com/)\n\n---\n\n```\nimport re\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n \n # parse and get each word from sentence\n words = sentence.split()\n \n # regular expression pattern for valid words\n pattern = re.compile( r\'^([a-z]+\\-?[a-z]+[!\\.,]?)$|^([a-z]*[!\\.,]?)$\' )\n \n # valid word count\n count = 0\n \n # scan each word from word pool\n for word in words:\n \n # judge whether current word is valid or not\n match = re.match(pattern, word)\n \n if match:\n count+=1\n \n return count\n```\n\n---\n\nReference:\n\n[1] [Python official docs about regular expression and *re* module](https://docs.python.org/3/library/re.html) | 7 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
python with regex | number-of-valid-words-in-a-sentence | 0 | 1 | ```\nimport re\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n count = 0\n pattern = "^([a-z]+(-?[a-z]+)?)?(!|\\.|,)?$"\n sentence_list = sentence.split()\n for word in sentence_list:\n result = re.match(pattern, word)\n if result:\n count += 1\n return count\n``` | 2 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
Python | REGEX pattern matching Explained | Faster than 98.86% | number-of-valid-words-in-a-sentence | 0 | 1 | A rule of thumb is that when you need to filter strings based on multiple conditions, `regex` will be your friend. The regex pattern we want to search for is: \n```\n(^[a-z]+(-[a-z]+)?)?[,.!]?$\n```\nThis pattern consists of many parts: \n\n- `^` denotes the beginning of a string.\n- `[a-z]` matches any character in the range of \'a\' to \'z\'.\n- `+` matches the previous token between one and unlimited times, so `[a-z]+` will match any string that has at least one of the characters in the range \'a-z\'.\n- `?` matches the previous group exactly zero or one time, so `(-[a-z]+)?` will match string that either has one pattern of a hyphen followed by any number of characters, or does not contain this pattern at all.\n- similarly, `(^[a-z]+(-[a-z]+)?)?` matches any string that has all these previous patterns zero or one times.\n- `[,.!]?` matches any string that has zero or one of these punctuation characters.\n- `$` matches the end of the string.\n\nNow we can search for words that match the desired pattern:\n```python\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n pattern = re.compile(r\'(^[a-z]+(-[a-z]+)?)?[,.!]?$\')\n count = 0\n \n for token in sentence.split():\n if pattern.match(token):\n count += 1\n \n return count\n```\n\nBonus one-liner version:\n```python\n return sum(bool(re.compile(r\'(^[a-z]+(-[a-z]+)?)?[,.!]?$\').match(token)) for token in sentence.split())\n``` | 3 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
Fastest Python Solution | 100%, 35ms | number-of-valid-words-in-a-sentence | 0 | 1 | # Fastest Python Solution | 100%, 35ms\n**Runtime: 35 ms, faster than 100.00% of Python3 online submissions for Number of Valid Words in a Sentence.\nMemory Usage: 14.3 MB.**\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n sen = sentence.split()\n r, m = 0, 0\n _digits = re.compile(\'\\d\')\n \n def increment(s):\n a, b, c = 0, 0, 0\n a = s.count(\'!\')\n b = s.count(\',\') \n c = s.count(\'.\')\n \n if (a+b+c) == 0:\n return 1\n elif (a+b+c) == 1:\n if s[-1] in [\'!\',\',\',\'.\']:\n return 1\n return 0\n \n for s in sen:\n if not bool(_digits.search(s)):\n m = s.count(\'-\')\n if m == 1:\n a = s.index(\'-\')\n if a != 0 and a != len(s)-1 and s[a+1].isalpha():\n r += increment(s)\n elif m == 0:\n r += increment(s)\n return r\n```\n\n\n | 5 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
python, net | number-of-valid-words-in-a-sentence | 0 | 1 | # Code\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n ls = list(sentence.split())\n punctuations = set("!., ")\n \n cnt = 0\n for i in ls:\n alphabet_cnt = 0\n numbers_cnt = 0\n punc_cnt = 0\n hyphens_cnt = 0\n for j in i:\n if j.isalpha():\n alphabet_cnt += 1\n elif j.isdigit():\n numbers_cnt += 1\n elif j in punctuations:\n punc_cnt += 1\n elif j == "-":\n hyphens_cnt += 1\n if numbers_cnt >= 1:\n continue\n elif alphabet_cnt >= 1 and punc_cnt == 0 and hyphens_cnt == 0:\n cnt += 1\n elif alphabet_cnt >= 1 and punc_cnt == 1 or hyphens_cnt == 1:\n if punc_cnt == 1 and hyphens_cnt == 1:\n ind = i.index(\'-\')\n if i[-1] in punctuations and i[0] != \'-\' and i[ind+1].isalpha() and i[ind-1].isalpha():\n cnt += 1\n elif punc_cnt == 1 and hyphens_cnt == 0:\n if i[-1] in punctuations:\n cnt += 1\n elif punc_cnt == 0 and hyphens_cnt == 1:\n ind = i.index(\'-\')\n if i[0] != \'-\' and i[-1] != \'-\' and i[ind+1].isalpha() and i[ind-1].isalpha():\n cnt += 1\n elif len(i) == 1 and i[-1] in punctuations:\n cnt += 1\n\n return cnt\n``` | 0 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
Two line solution with using regex | number-of-valid-words-in-a-sentence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countValidWords(self, sentence: str) -> int:\n ptr = re.compile(r"^[a-z]+\\-?[a-z]+[!,.]?$|^[a-z]*[!,.]?$")\n \n return sum((bool(ptr.fullmatch(word)) for word in sentence.split()))\n \n``` | 0 | A sentence consists of lowercase letters (`'a'` to `'z'`), digits (`'0'` to `'9'`), hyphens (`'-'`), punctuation marks (`'!'`, `'.'`, and `','`), and spaces (`' '`) only. Each sentence can be broken down into **one or more tokens** separated by one or more spaces `' '`.
A token is a valid word if **all three** of the following are true:
* It only contains lowercase letters, hyphens, and/or punctuation (**no** digits).
* There is **at most one** hyphen `'-'`. If present, it **must** be surrounded by lowercase characters ( `"a-b "` is valid, but `"-ab "` and `"ab- "` are not valid).
* There is **at most one** punctuation mark. If present, it **must** be at the **end** of the token ( `"ab, "`, `"cd! "`, and `". "` are valid, but `"a!b "` and `"c., "` are not valid).
Examples of valid words include `"a-b. "`, `"afad "`, `"ba-c "`, `"a! "`, and `"! "`.
Given a string `sentence`, return _the **number** of valid words in_ `sentence`.
**Example 1:**
**Input:** sentence = "cat and dog "
**Output:** 3
**Explanation:** The valid words in the sentence are "cat ", "and ", and "dog ".
**Example 2:**
**Input:** sentence = "!this 1-s b8d! "
**Output:** 0
**Explanation:** There are no valid words in the sentence.
"!this " is invalid because it starts with a punctuation mark.
"1-s " and "b8d " are invalid because they contain digits.
**Example 3:**
**Input:** sentence = "alice and bob are playing stone-game10 "
**Output:** 5
**Explanation:** The valid words in the sentence are "alice ", "and ", "bob ", "are ", and "playing ".
"stone-game10 " is invalid because it contains digits.
**Constraints:**
* `1 <= sentence.length <= 1000`
* `sentence` only contains lowercase English letters, digits, `' '`, `'-'`, `'!'`, `'.'`, and `','`.
* There will be at least `1` token. | Let's assume that the width of the array is bigger than the height, otherwise, we will split in another direction. Split the array into three parts: central column left side and right side. Go through the central column and two neighbor columns and look for maximum. If it's in the central column - this is our peak. If it's on the left side, run this algorithm on subarray left_side + central_column. If it's on the right side, run this algorithm on subarray right_side + central_column |
Python Using permutations (very simple solution)-->96% Faster | next-greater-numerically-balanced-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n from itertools import permutations\n mylist = [1, 22, 122, 333, 1333, 4444, 14444, 22333, 55555, 122333, 155555, 224444, 666666,1224444]\n res=[]\n def digit_combination(a,length):\n a = list(str(a))\n comb = permutations(a, length)\n for each in comb:\n s = [str(i) for i in each]\n result = int("".join(s))\n res.append(result)\n for every in mylist:\n digit_combination(every,len(str(every)))\n res.sort()\n print(res)\n for idx in res:\n if(idx>n):\n return idx\n``` | 1 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
[Python3] brute-force | next-greater-numerically-balanced-number | 0 | 1 | \n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n while True: \n n += 1\n nn = n \n freq = defaultdict(int)\n while nn: \n nn, d = divmod(nn, 10)\n freq[d] += 1\n if all(k == v for k, v in freq.items()): return n \n```\n\nBacktracking\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n \n def fn(i, x):\n if i == k:\n if all(d == v for d, v in freq.items() if v): yield x\n else: \n for d in range(1, k+1):\n if freq[d] < d <= freq[d] + k - i: \n freq[d] += 1\n yield from fn(i+1, 10*x+d)\n freq[d] -= 1\n\n for k in (len(str(n)), len(str(n))+1):\n freq = Counter()\n for val in fn(0, 0):\n if val > n: return val\n``` | 3 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Python - Generate Numeric Balanced Numbers with Prune | next-greater-numerically-balanced-number | 0 | 1 | **Idea**\n\n- The idea is that we generate all possible numeric balanced numbers with numLen start from |n|.\n- While backtracking to generate we can prune some invalid combination, they are\n- if counter[d] >= d: continue # Prune if number of occurrences of d is greater than d\n- if counter[d] + (numLen - i) < d: continue # Prune if not enough number of occurrences of d\nSince n <= 10^6, in the worst case, there are up to 7 digits, each digits must be values from [1..7], so it can run up to 7^7 = 823543.\n\n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n def backtracking(i, numLen, curNum, counter):\n if i == numLen:\n isBalanceNumber = True\n for d, freq in counter.items():\n if freq != 0 and d != freq:\n isBalanceNumber = False\n if isBalanceNumber:\n yield curNum\n return\n\n for d in range(1, numLen+1):\n if counter[d] >= d: continue # Prune if number of occurrences of `d` is greater than `d`\n if counter[d] + (numLen - i) < d: continue # Prune if not enough number of occurrences of `d`\n counter[d] += 1\n yield from backtracking(i + 1, numLen, curNum * 10 + d, counter)\n counter[d] -= 1\n\n for numLen in range(len(str(n)), len(str(n)) + 2):\n for num in backtracking(0, numLen, 0, Counter()):\n if num > n:\n return num\n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Python3|| backtracking | next-greater-numerically-balanced-number | 0 | 1 | # Intuition\n- We will need to know all the numbers that we can use, So hence I have created a method getNums\n- Get all the permutations with the values we can use and get the lowest among the values that is greater than n\n\n# Approach\n- Intuition pretty much explains the approach\n\n# Complexity\n- Time complexity:\n- O(pos!) - this is to generate all the possibilities with permutations\n\n- Space complexity:\n- O(permutations)\n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n if n == 0:\n return 1\n def getNums(mask,places,vals):\n if places < 0:\n return \n elif places == 0:\n vals.add(mask)\n else:\n for i in range(1,places+1):\n cmask = 1 << i\n if not(cmask & mask):\n getNums(mask ^ cmask,places-i,vals)\n\n def solve(n):\n # calc the positions\n curr = 1\n pos = 0\n while curr <= n:\n pos+=1\n curr=curr*10\n\n #getting the numbers that can be used\n vals=set()\n getNums(0,pos,vals)\n getNums(0,pos+1,vals)\n values = set()\n res = float(\'inf\')\n for num in vals:\n bin_val = bin(num).replace(\'0b\',\'\')[-1::-1]\n arr = []\n for i in range(len(bin_val)):\n if bin_val[i]!=\'0\':\n for j in range(i):\n arr.append(i)\n for p in permutations(arr):\n s = \'\'\n for k in p:\n s+=str(k)\n if int(s) > n and int(s) < res:\n res = int(s)\n return res\n return solve(n)\n # return 2\n\n \n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Solution Using Dictionary | next-greater-numerically-balanced-number | 0 | 1 | # Intuition\nCreate function to check whether a number is balanced. and then iterate from n+1 to find the next balanced number.\n\n# Approach\nisbalanced function checks whether the digit value is equal to the number of occurences using a dictionary and then returns True or False.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(n)\n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n def isbalanced(n):\n d={}\n while n>0:\n d[n%10]=d.get(n%10,0)+1\n n=n//10\n for i in d:\n if d[i]!=i:\n return False\n return True\n i=n+1\n while not isbalanced(i):\n i+=1\n return i\n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Python Easy Solution | next-greater-numerically-balanced-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def is_next_balance(self,n):\n val = str(n)\n counts = [val.count(i) for i in val]\n return all(count == int(d) for d,count in zip(val,counts))\n # val = str(n)\n # counts = []\n # for digit in val:\n # counts.append(val.count(digit))\n\n # temp = []\n # for digit,count in zip(val,counts ):\n # if int(digit) == count:\n # temp.append(True)\n # else:\n # temp.append(False)\n\n # return all(temp)\n\n def nextBeautifulNumber(self, n: int) -> int:\n n = n+1\n while True:\n if self.is_next_balance(n):\n return n\n n += 1\n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
python | next-greater-numerically-balanced-number | 0 | 1 | Not an intuitive question\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n i = n+1\n while True:\n if i % 10 == 0:\n i += 1\n continue\n\n c = Counter(str(i))\n \n flag = False\n for k, v in c.items():\n if k != str(v):\n flag = True\n break\n if flag:\n i += 1\n continue\n else:\n return i\n\n i += 1\n \n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Easy to understand | |Next Greater Numerically Balanced Number Simple iterative Solution | next-greater-numerically-balanced-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, a: int) -> int:\n def is_safe(s):\n for i in s:\n if s.count(i)!=int(i):\n return False\n return True\n while True:\n a+=1\n s=str(a)\n if is_safe(s):\n break\n return(a)\n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
Python3 brute force | next-greater-numerically-balanced-number | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def nextBeautifulNumber(self, n: int) -> int:\n \n def isValid(x):\n count=Counter(str(x))\n for k,v in count.items():\n if int(k)!=v:\n return False\n \n return True\n\n \n start=n+1\n \n while True:\n if isValid(start):\n return start\n start+=1\n \n \n \n``` | 0 | An integer `x` is **numerically balanced** if for every digit `d` in the number `x`, there are **exactly** `d` occurrences of that digit in `x`.
Given an integer `n`, return _the **smallest numerically balanced** number **strictly greater** than_ `n`_._
**Example 1:**
**Input:** n = 1
**Output:** 22
**Explanation:**
22 is numerically balanced since:
- The digit 2 occurs 2 times.
It is also the smallest numerically balanced number strictly greater than 1.
**Example 2:**
**Input:** n = 1000
**Output:** 1333
**Explanation:**
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.
**Example 3:**
**Input:** n = 3000
**Output:** 3133
**Explanation:**
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.
**Constraints:**
* `0 <= n <= 106` | Just apply what's said in the statement. Notice that you can't apply it on the same array directly since some elements will change after application |
✔ Python3 Solution | DFS | O(n) | count-nodes-with-the-highest-score | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n scores = [1] * n\n graph = [[] for _ in range(n)]\n for e, i in enumerate(parents):\n if e: graph[i].append(e)\n def dfs(i):\n res = 1\n for j in graph[i]:\n val = dfs(j)\n res += val\n scores[i] *= val\n if i: scores[i] *= (n - res)\n return res\n dfs(0)\n return scores.count(max(scores))\n``` | 1 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Python Easy Recursive Solution | count-nodes-with-the-highest-score | 0 | 1 | ## Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n\n sizes = [[0]*2 for _ in range(len(parents))]\n dic = defaultdict(list)\n\n def rec(root):\n\n if not dic[root]:\n return 1\n\n if len(dic[root]) == 1:\n sizes[root][0] = rec(dic[root][0])\n elif len(dic[root]) == 2:\n sizes[root][0] = rec(dic[root][0])\n sizes[root][1] = rec(dic[root][1])\n\n return 1 + sizes[root][0] + sizes[root][1]\n\n for i in range(1,len(parents)):\n dic[parents[i]].append(i)\n\n total = rec(0)\n\n res = []\n for x,y in sizes:\n res.append(max(x,1) * max(y,1) * max(total-x-y-1,1))\n\n return res.count(max(res))\n\n``` | 1 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Python 3 | Graph, DFS, Post-order Traversal, O(N) | Explanation | count-nodes-with-the-highest-score | 0 | 1 | ### Explanation\n- Intuition: Maximum product of 3 branches, need to know how many nodes in each branch, use `DFS` to start with\n- Build graph\n- Find left, right, up (number of nodes) for each node\n\t- left: use recursion\n\t- right: use recursion\n\t- up: `n - 1 - left - right`\n- Calculate score store in a dictinary\n- Return count of max key\n- Time: `O(n)`\n### Implementation \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n graph = collections.defaultdict(list)\n for node, parent in enumerate(parents): # build graph\n graph[parent].append(node)\n n = len(parents) # total number of nodes\n d = collections.Counter()\n def count_nodes(node): # number of children node + self\n p, s = 1, 0 # p: product, s: sum\n for child in graph[node]: # for each child (only 2 at maximum)\n res = count_nodes(child) # get its nodes count\n p *= res # take the product\n s += res # take the sum\n p *= max(1, n - 1 - s) # times up-branch (number of nodes other than left, right children ans itself)\n d[p] += 1 # count the product\n return s + 1 # return number of children node + 1 (self)\n count_nodes(0) # starting from root (0)\n return d[max(d.keys())] # return max count\n``` | 81 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
✔️ PYTHON || EXPLAINED || ;] | count-nodes-with-the-highest-score | 0 | 1 | **UPVOTE IF HELPFuuL**\n\n**Observation** : \nscore = ```number of above nodes * number of nodes of 1 child * number of nodes ofother child```\n\nWe are provided with the parents of nodes, For convenience we keep mapping of chilren of nodes.\n\n* First task : Create a dictionary to keep the children of nodes.\n* Secondly, with recurssion we find number of nodes below and including itself for ```node i``` and store in ```nums```\n\nNow use formula :\n* Number of nodes above node i = Total nodes - ```nums[i]``` . -> nums [ i ] is number of nodes below it + 1.\n* Number of nodes for children are provided directly stored in nums dictionary.\n\n**UPVOTE IF HELPFuuL**\n\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n \n def fin(n):\n k=1\n for i in child[n]:\n k += fin(i)\n nums[n]=k\n return k\n \n child = {}\n for i in range(len(parents)):\n child[i]=[]\n for i in range(1,len(parents)):\n child[parents[i]].append(i)\n \n nums={}\n fin(0)\n k=1\n for i in child[0]:\n k*=nums[i]\n score=[k]\n for i in range(1,len(nums)):\n k=1\n k*=(nums[0]-nums[i])\n for j in child[i]:\n k*=nums[j]\n score.append(k)\n \n return score.count(max(score))\n```\n![Uploading file...]()\n | 5 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
[Python3] post-order dfs | count-nodes-with-the-highest-score | 0 | 1 | \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in parents]\n for i, x in enumerate(parents): \n if x >= 0: tree[x].append(i)\n \n freq = defaultdict(int)\n \n def fn(x): \n """Return count of tree nodes."""\n left = right = 0\n if tree[x]: left = fn(tree[x][0])\n if len(tree[x]) > 1: right = fn(tree[x][1])\n score = (left or 1) * (right or 1) * (len(parents) - 1 - left - right or 1)\n freq[score] += 1\n return 1 + left + right\n \n fn(0)\n return freq[max(freq)]\n```\n\nAlternatively \n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in parents]\n for i, x in enumerate(parents): \n if x >= 0: tree[x].append(i)\n \n def fn(x): \n """Return count of tree nodes."""\n count = score = 1\n for xx in tree[x]: \n cc = fn(xx)\n count += cc\n score *= cc\n score *= len(parents) - count or 1\n freq[score] += 1\n return count\n \n freq = defaultdict(int)\n fn(0)\n return freq[max(freq)]\n``` | 17 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Using DFS | count-nodes-with-the-highest-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n d = {} # store the childs for each node.\n root = None\n for i in range(len(parents)):\n p = parents[i]\n if p == -1:\n root = i\n else:\n d.setdefault(p, [])\n d[p].append(i)\n\n\n max_d = collections.defaultdict(int) # store the count for each N\n\n # if remove node, there will be maximum 3 parts left. \n # which are node.left subtree, node.right subtree and whatever in the parent tree\n def dfs(node):\n # this dfs function returns the number of nodes for the subtree starting\n # at `node`\n \n if node not in d:\n # leaf\n n = len(parents) - 1\n max_d[n] += 1\n return 1\n childs = d[node]\n n = 1\n child_t = 0\n for child in d[node]:\n child_c = dfs(child) # number of nodes for the subtree\n child_t += child_c\n n = n * child_c\n if child_t + 1 < len(parents):\n # if number of nodes in left&right subtree is smaller than the number\n # of nodes of the whole tree. Then there is another len(parents) - child_t - 1 nodes left\n n = n * (len(parents) - child_t - 1)\n max_d[n] += 1\n return child_t + 1\n\n dfs(root)\n max_n = max(max_d)\n return max_d[max_n]\n\n``` | 0 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
DFS | count-nodes-with-the-highest-score | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n d = {} # store the childs for each node.\n root = None\n for i in range(len(parents)):\n p = parents[i]\n if p == -1:\n root = i\n else:\n d.setdefault(p, [])\n d[p].append(i)\n\n\n max_d = collections.defaultdict(int) # store the count for each N\n\n # if remove node, there will be maximum 3 parts left. \n # which are node.left subtree, node.right subtree and whatever in the parent tree\n def dfs(node):\n # this dfs function returns the number of nodes for the subtree starting\n # at `node`\n \n if node not in d:\n # leaf\n n = len(parents) - 1\n max_d[n] += 1\n return 1\n childs = d[node]\n n = 1\n child_t = 0\n for child in d[node]:\n child_c = dfs(child) # number of nodes for the subtree\n child_t += child_c\n n = n * child_c\n if child_t + 1 < len(parents):\n # if number of nodes in left&right subtree is smaller than the number\n # of nodes of the whole tree. Then there is another len(parents) - child_t - 1 nodes left\n n = n * (len(parents) - child_t - 1)\n max_d[n] += 1\n return child_t + 1\n\n dfs(root)\n max_n = max(max_d)\n return max_d[max_n]\n\n``` | 0 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Simple DFS solution. Runtime > 99%!!! | count-nodes-with-the-highest-score | 0 | 1 | \n```\nclass Solution:\n def dfs(self, root, tree, cnt):\n if not tree[root]:\n cnt[root] = len(tree)-1\n return 1\n score, sum_children_nodes = 1, 0\n for child in tree[root]:\n cnt_children_nodes = self.dfs(child, tree, cnt)\n score *= cnt_children_nodes\n sum_children_nodes += cnt_children_nodes\n cnt[root] = score * (len(tree) - sum_children_nodes - 1 if root else 1)\n return sum_children_nodes + 1\n \n\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n tree = [[] for _ in range(len(parents))]\n cnt = [0]*len(parents)\n for child, parent in enumerate(islice(parents, 1, None), start = 1):\n tree[parent].append(child)\n self.dfs(0, tree, cnt)\n return cnt.count(max(cnt))\n\n \n \n``` | 0 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Iterate with stack --- O(n), 98% Time + 100% space | count-nodes-with-the-highest-score | 0 | 1 | # Intuition\nFor every node removed there will always be 1, 2 or 3 subtrees: One for each child (2 at most) and one for the parent.\nTo compute a score of a node V, we must know the size of each of its child nodes AND the size of the upper part of the free.\nNote: The size of the upper part is: `size[0] - size[v]` (size[0] is the size of the whole tree without removing any node).\n\nWe need to calculate the score of all nodes, find the highest score, and count how many nodes have this score. The idea is that we must find the `size[v]` of each node. \n\nYou can find how this is done with DFS on any other submitted solution. However, this Solution explains how can this be done with minimal memory usage and no recursion, which automatically makes it faster too.\n\n\n# Approach\nThe idea is that we will compute the score of all nodes whose child nodes have already been processed. Initially, these are all leaf nodes.\nOnce a node has been processed, we will know its `size[v]`, so we will update the parent size too: `size[parents[v]] += size[v]`.\nIt\'s important to note that `size[v]` does not contain the information of each child size separately, which is needed to compute the score (multiply `score=size[child1]*size[child2]*uppersize`).\nWe can easily solve this requirement by creating a new `multipliers[v]` with one of the following values:\n- `size[child1] * size[child2]` if `v` has 2 child nodes\n- `size[child1]` if `v` has 1 child nodes\n- `1` if `v` has no child nodes\n\nSo, for each processed node, we will:\n- Compute its score (with `size[v]` and `multipliers[v]`)\n- Update parent node values (`size[parent] += size[v]` and `multipliers[v] *= size[v]`)\n- Add parent to the queue if it has no more child nodes pending to be processed.\n\nOne way to find both the leaf nodes and how many child nodes are pending to be processed is by counting the number of child nodes for a given node `v`.\nAfter initialising the `child_counts` array, we add all nodes `v` with `child_counts[v] == 0`, which are all the leaf nodes.\nThen, after processing every node, we will decrease the `child_counts[v]` by 1. When it reaches 0, we know all the parent childs have been processed, so we can add it to the queue and process it because we have `size[parent]` and `multiplier[parent]` ready to use.\n\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\nTwo lists of N elements and one stack with N appends and pops.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n child_counts = [0] * n\n for v in range(1, n):\n child_counts[parents[v]] += 1\n \n # Process leafs first\n highest_score = cnt = 0\n size = [0] * n # sum of child node sizes\n mult = [1] * n # multiplication of child node sizes\n q = [v for v in range(n) if child_counts[v] == 0]\n while q:\n v = q.pop()\n vsize = size[v] + 1\n\n # Check score\n score = mult[v] * max(n - vsize, 1)\n if score > highest_score:\n highest_score = score\n cnt= 1\n elif score == highest_score:\n cnt += 1\n\n if v != 0:\n # Update parent data + maybe enqueue it\n p = parents[v]\n size[p] += vsize\n mult[p] *= vsize\n child_counts[p] -= 1\n if child_counts[p] == 0:\n q.append(p)\n return cnt\n\n``` | 0 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Python3 Solution Easy to Understand with O(n) | DFS | count-nodes-with-the-highest-score | 0 | 1 | # Code\n```\nclass Solution:\n def countHighestScoreNodes(self, parents: List[int]) -> int:\n n = len(parents)\n\n cntChilds = [0 for _ in range(n)]\n # buld graph\n graph = [[] for _ in range(n)]\n for i in range(1,n):\n graph[parents[i]].append(i)\n ##\n countChilds = [0 for _ in range(n)]\n def countChildNodes(root):\n if root == None:\n return 0\n if len(graph[root]) >= 1:\n countChilds[root] += countChildNodes(graph[root][0])\n if len(graph[root]) == 2:\n countChilds[root] += countChildNodes(graph[root][1])\n return countChilds[root] + 1\n countChildNodes(0)\n\n ansMax = 0\n ans = 0\n for i in range(n):\n numLeft = numRight = 0\n if len(graph[i]) >= 1:\n numLeft = countChilds[graph[i][0]] + 1\n if len(graph[i]) == 2:\n numRight = countChilds[graph[i][1]] + 1\n numRestOf = max(1, n - 1 - numLeft - numRight)\n numLeft = max(1, numLeft)\n numRight = max(1, numRight)\n currCnt = numRestOf * numLeft * numRight\n if currCnt > ansMax:\n ansMax = currCnt\n ans = 1\n elif currCnt == ansMax:\n ans += 1\n return ans\n``` | 0 | There is a **binary** tree rooted at `0` consisting of `n` nodes. The nodes are labeled from `0` to `n - 1`. You are given a **0-indexed** integer array `parents` representing the tree, where `parents[i]` is the parent of node `i`. Since node `0` is the root, `parents[0] == -1`.
Each node has a **score**. To find the score of a node, consider if the node and the edges connected to it were **removed**. The tree would become one or more **non-empty** subtrees. The **size** of a subtree is the number of the nodes in it. The **score** of the node is the **product of the sizes** of all those subtrees.
Return _the **number** of nodes that have the **highest score**_.
**Example 1:**
**Input:** parents = \[-1,2,0,2,0\]
**Output:** 3
**Explanation:**
- The score of node 0 is: 3 \* 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 \* 1 \* 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
**Example 2:**
**Input:** parents = \[-1,2,0\]
**Output:** 2
**Explanation:**
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 \* 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
**Constraints:**
* `n == parents.length`
* `2 <= n <= 105`
* `parents[0] == -1`
* `0 <= parents[i] <= n - 1` for `i != 0`
* `parents` represents a valid binary tree. | Find the amount of time it takes each monster to arrive. Find the order in which the monsters will arrive. |
Original Heap-Based Approach | parallel-courses-iii | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n)*c)$$, n - number of courses, c - avg number of connections between courses.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n # List of successors\n nodeToNext = {node: [] for node in range(n)}\n # Number of prerequisites\n nodeToPrev = {node: 0 for node in range(n)}\n for prev, nextt in relations:\n nodeToNext[prev-1].append(nextt-1)\n nodeToPrev[nextt-1] += 1\n \n heap = []\n # Find start nodes without prerequisites\n for node, prevCnt in nodeToPrev.items():\n if prevCnt == 0:\n heappush(heap, (time[node], node))\n \n while heap:\n # Get the node with the earliest endtime\n tm, node = heappop(heap)\n for nextt in nodeToNext[node]:\n # Decrease counter of successor\n nodeToPrev[nextt] -= 1\n if nodeToPrev[nextt] == 0:\n # If there are no prerequisites \n # add successor to processing\n heappush(heap, (tm + time[nextt], nextt))\n \n return tm\n``` | 5 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
✅☑[C++/Java/Python/JavaScript] || Beats 100% || 2 Approaches || EXPLAINED🔥 | parallel-courses-iii | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1 (Sort + Kahn\'s Algorithm)***\n\n***Kahn\'s Algorithm :***\nKahn\'s algorithm, also known as Kahn\'s topological sort algorithm, is used to find a topological ordering of the nodes in a directed acyclic graph (DAG). A topological ordering is a linear ordering of the nodes in a way that for every directed edge (u, v), node u comes before node v in the ordering. This algorithm is particularly useful for scheduling tasks or dependencies in a way that ensures that no task is executed before its dependencies are completed.\n\n***Explaination :***\n1. **Data Structures:** The code uses an unordered map called `graph` to represent the graph, where the keys are nodes, and the values are lists of their neighbors. It also uses vectors to store information about in-degrees, maximum time, and task completion times.\n\n1. **Input and Initialization:**\n\n - The function `minimumTime` takes the following inputs: `n` (the number of tasks), `relations` (a list of dependencies between tasks), and `time` (a list of times required for each task).\n - The `graph` is initially empty.\n - A vector `indegree` of size `n` is initialized with all values set to 0. It represents the in-degrees of each node.\n1. **Building the Graph:**\n\n - A loop iterates through the `relations` vector, which contains pairs of tasks (dependencies).\n - For each relation, it extracts the tasks `x` and `y` and decreases them by 1 to adjust for 0-based indexing.\n - It populates the `graph` with edges, indicating dependencies from task `x` to task `y`.\n - It also increments the in-degree of task `y` to track the number of incoming edges.\n1. **Topological Sorting and Max Time Calculation:**\n\n - Create an empty queue for topological sorting.\n - Initialize a vector `maxTime` to store the maximum time required to complete each task. Initially, all values are set to 0.\n - Iterate through the tasks (nodes) to find tasks with no incoming edges (in-degree equals 0). These tasks are enqueued and their `maxTime` is set to their own completion time.\n - The code then performs a topological sort by processing nodes with no dependencies and updating the `maxTime` for their neighbors. It also decreases the in-degrees of their neighbors and enqueues them when their in-degree becomes 0.\n - The process continues until the queue is empty, and all tasks have been processed.\n1. **Finding the Answer:**\n\n - After the topological sorting is completed, the code calculates the maximum time required for all tasks by finding the maximum value in the `maxTime` vector.\n1. **Output:**\n\n - The code returns the maximum time required to complete all tasks, which represents the minimum time needed to complete all tasks considering their dependencies.\n\n# Complexity\n- *Time complexity:*\n $$O(n + e)$$\n \n\n- *Space complexity:*\n $$O(n + e)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n unordered_map<int, vector<int>> graph;\n \n int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) { \n unordered_map<int, vector<int>> graph;\n vector<int> indegree = vector(n, 0);\n\n for (vector<int>& edge: relations) {\n int x = edge[0] - 1;\n int y = edge[1] - 1;\n graph[x].push_back(y);\n indegree[y]++;\n }\n \n queue<int> queue;\n vector<int> maxTime = vector(n, 0);\n \n for (int node = 0; node < n; node++) {\n if (indegree[node] == 0) {\n queue.push(node);\n maxTime[node] = time[node];\n }\n }\n \n while (!queue.empty()) {\n int node = queue.front();\n queue.pop();\n for (int neighbor: graph[node]) {\n maxTime[neighbor] = max(maxTime[neighbor], maxTime[node] + time[neighbor]);\n indegree[neighbor]--;\n if (indegree[neighbor] == 0) {\n queue.push(neighbor);\n }\n }\n }\n \n int ans = 0;\n for (int node = 0; node < n; node++) {\n ans = max(ans, maxTime[node]);\n }\n \n return ans;\n }\n};\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n#include <stdbool.h>\n\n// Structure to represent a node in the graph\nstruct Node {\n int value;\n struct Node* next;\n};\n\n// Function to create a new node\nstruct Node* createNode(int value) {\n struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));\n newNode->value = value;\n newNode->next = NULL;\n return newNode;\n}\n\n// Function to initialize a graph with \'n\' nodes\nstruct Node** initializeGraph(int n) {\n struct Node** graph = (struct Node**)malloc(n * sizeof(struct Node*));\n for (int i = 0; i < n; i++) {\n graph[i] = NULL;\n }\n return graph;\n}\n\n// Function to add a directed edge from node \'x\' to node \'y\' in the graph\nvoid addEdge(struct Node** graph, int x, int y) {\n struct Node* newNode = createNode(y);\n newNode->next = graph[x];\n graph[x] = newNode;\n}\n\n// Function to find the indegrees of all nodes in the graph\nint* calculateIndegrees(int n, struct Node** graph) {\n int* indegree = (int*)malloc(n * sizeof(int));\n for (int i = 0; i < n; i++) {\n indegree[i] = 0;\n struct Node* current = graph[i];\n while (current != NULL) {\n indegree[current->value]++;\n current = current->next;\n }\n }\n return indegree;\n}\n\n// Function to perform topological sorting using Kahn\'s algorithm\nbool topologicalSort(int n, struct Node** graph, int* indegree, int* maxTime, int* time) {\n int* queue = (int*)malloc(n * sizeof(int));\n int front = 0, rear = 0;\n\n // Initialize the queue with nodes having indegree 0\n for (int i = 0; i < n; i++) {\n if (indegree[i] == 0) {\n queue[rear++] = i;\n maxTime[i] = time[i];\n }\n }\n\n while (front != rear) {\n int node = queue[front++];\n struct Node* current = graph[node];\n while (current != NULL) {\n int neighbor = current->value;\n indegree[neighbor]--;\n\n // Update maxTime for the neighbor\n maxTime[neighbor] = (maxTime[neighbor] > maxTime[node] + time[neighbor])\n ? maxTime[neighbor]\n : maxTime[node] + time[neighbor];\n\n if (indegree[neighbor] == 0) {\n queue[rear++] = neighbor;\n }\n current = current->next;\n }\n }\n\n // Check if there\'s a cycle in the graph (indicating no topological order)\n if (front != n) {\n free(queue);\n return false;\n }\n\n free(queue);\n return true;\n}\n\n// Function to find the minimum time to complete all tasks\nint minimumTime(int n, int** relations, int* time) {\n // Initialize the graph and add edges\n struct Node** graph = initializeGraph(n);\n for (int i = 0; i < n - 1; i++) {\n int x = relations[i][0] - 1;\n int y = relations[i][1] - 1;\n addEdge(graph, x, y);\n }\n\n // Calculate indegrees of nodes\n int* indegree = calculateIndegrees(n, graph);\n\n // Arrays to store the maximum time for each node\n int* maxTime = (int*)malloc(n * sizeof(int));\n\n // Perform topological sorting\n bool isPossible = topologicalSort(n, graph, indegree, maxTime, time);\n\n // Find the maximum time among all nodes\n int ans = 0;\n for (int i = 0; i < n; i++) {\n ans = (ans > maxTime[i]) ? ans : maxTime[i];\n }\n\n free(indegree);\n free(maxTime);\n for (int i = 0; i < n; i++) {\n struct Node* current = graph[i];\n while (current != NULL) {\n struct Node* temp = current;\n current = current->next;\n free(temp);\n }\n }\n free(graph);\n\n return isPossible ? ans : -1; // Return -1 if there is a cycle (no valid topological order)\n}\n\nint main() {\n int n = 4;\n int relations[][2] = {{1, 2}, {2, 3}, {2, 4}};\n int time[] = {3, 2, 1, 4};\n int** relPtr = (int**)relations;\n\n int result = minimumTime(n, relPtr, time);\n printf("Minimum time: %d\\n", result);\n\n return 0;\n}\n\n\n```\n\n\n```Java []\nclass Solution {\n public int minimumTime(int n, int[][] relations, int[] time) {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n for (int i = 0; i < n; i++) {\n graph.put(i, new ArrayList<>());\n }\n \n int[] indegree = new int[n];\n for (int[] edge: relations) {\n int x = edge[0] - 1;\n int y = edge[1] - 1;\n graph.get(x).add(y);\n indegree[y]++;\n }\n \n Queue<Integer> queue = new LinkedList<>();\n int[] maxTime = new int[n];\n \n for (int node = 0; node < n; node++) {\n if (indegree[node] == 0) {\n queue.add(node);\n maxTime[node] = time[node];\n }\n }\n \n while (!queue.isEmpty()) {\n int node = queue.remove();\n for (int neighbor: graph.get(node)) {\n maxTime[neighbor] = Math.max(maxTime[neighbor], maxTime[node] + time[neighbor]);\n indegree[neighbor]--;\n if (indegree[neighbor] == 0) {\n queue.add(neighbor);\n }\n }\n }\n \n int ans = 0;\n for (int node = 0; node < n; node++) {\n ans = Math.max(ans, maxTime[node]);\n }\n\n return ans;\n }\n \n}\n\n```\n\n```python3 []\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n graph = defaultdict(list)\n indegree = [0] * n\n \n for (x, y) in relations:\n graph[x - 1].append(y - 1)\n indegree[y - 1] += 1\n \n queue = deque()\n max_time = [0] * n\n for node in range(n):\n if indegree[node] == 0:\n queue.append(node)\n max_time[node] = time[node]\n\n while queue:\n node = queue.popleft()\n for neighbor in graph[node]:\n max_time[neighbor] = max(max_time[neighbor], max_time[node] + time[neighbor])\n indegree[neighbor] -= 1\n if indegree[neighbor] == 0:\n queue.append(neighbor)\n\n return max(max_time)\n```\n\n\n```javascript []\nfunction minimumTime(n, relations, time) {\n const graph = Array(n).fill(null).map(() => []);\n const indegree = Array(n).fill(0);\n \n // Build the graph and calculate indegrees\n for (const relation of relations) {\n const x = relation[0] - 1;\n const y = relation[1] - 1;\n graph[x].push(y);\n indegree[y]++;\n }\n \n const queue = [];\n const maxTime = Array(n).fill(0);\n \n // Initialize the queue with nodes having indegree 0\n for (let node = 0; node < n; node++) {\n if (indegree[node] === 0) {\n queue.push(node);\n maxTime[node] = time[node];\n }\n }\n \n while (queue.length > 0) {\n const node = queue.shift();\n for (const neighbor of graph[node]) {\n maxTime[neighbor] = Math.max(maxTime[neighbor], maxTime[node] + time[neighbor]);\n indegree[neighbor]--;\n if (indegree[neighbor] === 0) {\n queue.push(neighbor);\n }\n }\n }\n \n let ans = 0;\n for (let node = 0; node < n; node++) {\n ans = Math.max(ans, maxTime[node]);\n }\n \n return ans;\n}\n\n// Example usage\nconst n = 4;\nconst relations = [[1, 2], [2, 3], [2, 4]];\nconst time = [3, 2, 1, 4];\n\nconst result = minimumTime(n, relations, time);\nconsole.log("Minimum time:", result);\n\n\n```\n\n---\n\n#### ***Approach 2 DFS + Memoization (Top-Down DP)***\n1. **Graph Construction:**\n\n - The code begins by constructing a graph using a vector of vectors called `relations`. Each `relations` entry represents a directed edge from one node to another. It\'s essentially constructing an adjacency list representation of the graph.\n1. **Memoization:**\n\n - A vector called `memo` is used for memoization. It will store the maximum time needed for each node. It\'s initialized to -1 for all nodes, indicating that no nodes have been visited yet.\n1. **DFS for Maximum Time:**\n\n - The primary logic for calculating the minimum time is implemented in a Depth-First Search (DFS) function called `dfs`.\n - `dfs` takes two parameters: the current node and the `time` vector which represents the time required for each task.\n1. **Memoization Check:**\n\n - In the `dfs` function, it first checks whether the result for the current node has already been computed and stored in the `memo` vector. If so, it returns the memoized result.\n - This is a common optimization technique to avoid redundant calculations for the same node.\n1. **Base Case:**\n\n - If the current node has no outgoing edges, it\'s considered a leaf node in the graph, representing a task that can be executed without any dependency. In this case, the time required for the task itself (given in the `time` vector) is returned as there are no dependencies.\n1. **Recursive Maximum Time Calculation:**\n\n - If the current node has outgoing edges (dependencies), the code recursively explores all its neighbors.\n - For each neighbor, it calls `dfs` to calculate the maximum time required to complete that neighbor\'s tasks.\n - It selects the maximum time among its neighbors and adds the time required for the current task (node) itself.\n1. **Memoization Update:**\n\n - The calculated maximum time for the current node is stored in the `memo` vector to avoid recalculating it in case the same node is encountered later in the traversal.\n1. **Overall Maximum Time Calculation:**\n\n - Finally, the code iterates through all nodes and calculates the maximum time required to complete all tasks.\n - The overall maximum time among all nodes is stored in the variable `ans` and returned as the result.\n\n# Complexity\n- *Time complexity:*\n $$O(n + e)$$\n \n\n- *Space complexity:*\n $$O(n + e)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n unordered_map<int, vector<int>> graph;\n vector<int> memo;\n \n int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) { \n for (vector<int>& edge: relations) {\n int x = edge[0] - 1;\n int y = edge[1] - 1;\n graph[x].push_back(y);\n }\n \n memo = vector(n, -1);\n int ans = 0;\n for (int node = 0; node < n; node++) {\n ans = max(ans, dfs(node, time));\n }\n \n return ans;\n }\n \n int dfs(int node, vector<int>& time) {\n if (memo[node] != -1) {\n return memo[node];\n }\n \n if (graph[node].size() == 0) {\n return time[node];\n }\n \n int ans = 0;\n for (int neighbor: graph[node]) {\n ans = max(ans, dfs(neighbor, time));\n }\n \n memo[node] = time[node] + ans;\n return time[node] + ans;\n }\n};\n\n```\n\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nint** graph;\nint* memo;\n\nint dfs(int node, int* time) {\n if (memo[node] != -1) {\n return memo[node];\n }\n\n if (graph[node][0] == -1) {\n return time[node];\n }\n\n int ans = 0;\n for (int i = 0; graph[node][i] != -1; i++) {\n ans = ans > dfs(graph[node][i], time) ? ans : dfs(graph[node][i], time);\n }\n\n memo[node] = time[node] + ans;\n return time[node] + ans;\n}\n\nint minimumTime(int n, int relations[][2], int time[]) {\n graph = (int**)malloc(n * sizeof(int*));\n memo = (int*)malloc(n * sizeof(int));\n\n for (int i = 0; i < n; i++) {\n graph[i] = (int*)malloc(n * sizeof(int));\n memo[i] = -1;\n\n for (int j = 0; j < n; j++) {\n graph[i][j] = -1;\n }\n }\n\n for (int i = 0; i < n - 1; i++) {\n int x = relations[i][0] - 1;\n int y = relations[i][1] - 1;\n\n int j = 0;\n while (graph[x][j] != -1) {\n j++;\n }\n graph[x][j] = y;\n }\n\n int ans = 0;\n for (int node = 0; node < n; node++) {\n ans = ans > dfs(node, time) ? ans : dfs(node, time);\n }\n\n for (int i = 0; i < n; i++) {\n free(graph[i]);\n }\n free(graph);\n free(memo);\n\n return ans;\n}\n\nint main() {\n int n = 4;\n int relations[][2] = {{1, 2}, {1, 3}, {2, 4}};\n int time[] = {3, 2, 4, 2};\n\n int result = minimumTime(n, relations, time);\n printf("Minimum time: %d\\n", result);\n\n return 0;\n}\n\n\n```\n\n\n```Java []\nclass Solution {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n Map<Integer, Integer> memo = new HashMap<>();\n \n public int minimumTime(int n, int[][] relations, int[] time) {\n for (int i = 0; i < n; i++) {\n graph.put(i, new ArrayList<>());\n }\n \n for (int[] edge: relations) {\n int x = edge[0] - 1;\n int y = edge[1] - 1;\n graph.get(x).add(y);\n }\n \n int ans = 0;\n for (int node = 0; node < n; node++) {\n ans = Math.max(ans, dfs(node, time));\n }\n\n return ans;\n }\n \n public int dfs(int node, int[] time) {\n if (memo.containsKey(node)) {\n return memo.get(node);\n }\n \n if (graph.get(node).size() == 0) {\n return time[node];\n }\n \n int ans = 0;\n for (int neighbor: graph.get(node)) {\n ans = Math.max(ans, dfs(neighbor, time));\n }\n \n memo.put(node, time[node] + ans);\n return time[node] + ans;\n }\n}\n\n```\n\n```python3 []\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n @cache\n def dfs(node):\n if not graph[node]:\n return time[node]\n \n ans = 0\n for neighbor in graph[node]:\n ans = max(ans, dfs(neighbor))\n\n return time[node] + ans\n \n graph = defaultdict(list)\n for (x, y) in relations:\n graph[x - 1].append(y - 1)\n \n ans = 0\n for node in range(n):\n ans = max(ans, dfs(node))\n\n return ans\n```\n\n\n```javascript []\nfunction minimumTime(n, relations, time) {\n let graph = Array(n);\n let memo = Array(n).fill(-1);\n\n for (let i = 0; i < n; i++) {\n graph[i] = [];\n }\n\n for (let i = 0; i < n - 1; i++) {\n let x = relations[i][0] - 1;\n let y = relations[i][1] - 1;\n graph[x].push(y);\n }\n\n function dfs(node) {\n if (memo[node] !== -1) {\n return memo[node];\n }\n\n if (graph[node].length === 0) {\n return time[node];\n }\n\n let ans = 0;\n for (let neighbor of graph[node]) {\n ans = Math.max(ans, dfs(neighbor));\n }\n\n memo[node] = time[node] + ans;\n return time[node] + ans;\n }\n\n let ans = 0;\n for (let node = 0; node < n; node++) {\n ans = Math.max(ans, dfs(node));\n }\n\n return ans;\n}\n\nconst n = 4;\nconst relations = [[1, 2], [1, 3], [2, 4]];\nconst time = [3, 2, 4, 2];\n\nconst result = minimumTime(n, relations, time);\nconsole.log("Minimum time:", result);\n\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 4 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
✨✅💯 Simple Solution | Beats 100% | Kahn's Agorithm ✨✅💯 | parallel-courses-iii | 0 | 1 | # Proof:\n\n# Intuition And Approach:\nRelax Time by taking the max of its current value and previous neighbour+time[curr] while applying Kahn\'s Algo ( Toposort using BFS and Indegrees )\nMight be new terms for you if you are a beginner in graphs.(Like Me \uD83E\uDEF6 ) Time to learn this algo is today. I will recommend. Channel Name TUF (Take u Forward) Striver\'s video , Pepcoding video on this topic is also great if you understand Hindi.\n\n# Complexity\n- Time complexity:O(N+E)\n\n- Space complexity:O(N+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]],time: List[int]) -> int:\n t=[0]*(n+1)#ans\n indegrees=[0]*(n+1)\n graph=[[] for _ in range(n+1)]\n for edge in relations:\n node1,node2=edge\n # node1->node2\n graph[node1].append(node2)\n indegrees[node2]+=1\n q=deque()\n for i in range(1,n+1):\n if indegrees[i]==0:\n q.append(i)\n t[i]=time[i-1]\n # print(q,graph,indegrees,t)\n while q:\n top=q.popleft()\n topTime=t[top]\n for neigh in graph[top]:\n t[neigh]=max(t[neigh],topTime+time[neigh-1])\n indegrees[neigh]-=1\n if indegrees[neigh]==0:\n q.append(neigh)\n # print(t)\n return max(t)\n```\nAll suggestions are welcome.\nIf you have any query or suggestion please comment below.\nPlease upvote\uD83D\uDC4D if you like\uD83D\uDC97\uD83E\uDEF6\uD83E\uDEF6\uD83D\uDC97 it. Thank you:-)\nHappy Learning, Cheers Guys \uD83D\uDE0A\nKeep Grinding \uD83D\uDE00\uD83D\uDE00 | 2 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
✅ 92.65% BFS in Directed Acyclic Graph | parallel-courses-iii | 1 | 1 | # Intuition\nWhen we first encounter this problem, it is evident that the courses have dependencies among themselves. The first intuition that should come to mind when seeing such dependencies is a directed graph, where an edge from one course to another signifies a prerequisite relationship. Since the problem guarantees no cycles (Directed Acyclic Graph or DAG), the thought should naturally progress towards topological ordering. This is because a topological order of a DAG ensures that every node (course, in this context) comes before its dependents.\n\n## Live Coding + Explein\nhttps://youtu.be/dtBSjB924kU?si=IDRT9XR09r9jdRyL\n\n# Approach\n1. **Graph Representation**: We start by representing the courses and their relationships as a graph where each node represents a course, and each edge represents a relationship between two courses.\n \n2. **Calculate In-degrees**: For each course, we calculate its in-degree, which is the number of prerequisites it has.\n \n3. **Topological Sort Using BFS**: We perform a BFS-based topological sort. We start with courses that have no prerequisites (in-degree of 0). For each course, we calculate the earliest time it can be completed. This is based on its prerequisites\' completion times.\n \n - For each course, the start time is determined by its prerequisites. The start time is the maximum of the finish times of its prerequisites. The finish time of a course is its start time plus its duration (given in the `time` array).\n - We keep track of these times in the `dist` array.\n - As we determine the finish time for a course, we decrease the in-degree of its dependents (courses that have it as a prerequisite). If the in-degree of a course becomes 0, it means all its prerequisites are completed, and it\'s added to the queue.\n \n4. **Result**: The answer to the problem is the maximum value in the `dist` array, which represents the earliest finish time for all courses.\n\n# Complexity\n- **Time complexity**: $O(N + M)$\n - $O(N)$ for initializing the in-degrees and dist arrays.\n - $O(M)$ for constructing the graph from the relations array, where $M$ is the length of the relations array.\n\n- **Space complexity**: $O(N + M)$\n - $O(N)$ for the in-degrees and dist arrays.\n - $O(M)$ for the graph.\n\n# Code\n``` Python []\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n # Build the graph and calculate in-degrees\n graph = defaultdict(list)\n in_degree = [0] * (n + 1)\n for u, v in relations:\n graph[u].append(v)\n in_degree[v] += 1\n \n # Initialize the dist array and queue\n dist = [0] + time\n queue = deque([i for i in range(1, n+1) if in_degree[i] == 0])\n \n # Perform Topological Sort\n while queue:\n course = queue.popleft()\n for next_course in graph[course]:\n dist[next_course] = max(dist[next_course], dist[course] + time[next_course-1])\n in_degree[next_course] -= 1\n if in_degree[next_course] == 0:\n queue.append(next_course)\n \n return max(dist)\n```\n``` C++ []\nclass Solution {\npublic:\n int minimumTime(int n, std::vector<std::vector<int>>& relations, std::vector<int>& time) {\n std::unordered_map<int, std::vector<int>> graph;\n std::vector<int> in_degree(n + 1, 0);\n for (auto& relation : relations) {\n graph[relation[0]].push_back(relation[1]);\n in_degree[relation[1]]++;\n }\n\n std::vector<int> dist = time;\n dist.insert(dist.begin(), 0);\n std::queue<int> q;\n for (int i = 1; i <= n; i++) {\n if (in_degree[i] == 0) {\n q.push(i);\n }\n }\n\n while (!q.empty()) {\n int course = q.front(); q.pop();\n for (int next_course : graph[course]) {\n dist[next_course] = std::max(dist[next_course], dist[course] + time[next_course - 1]);\n in_degree[next_course]--;\n if (in_degree[next_course] == 0) {\n q.push(next_course);\n }\n }\n }\n\n return *std::max_element(dist.begin(), dist.end());\n }\n};\n```\n``` Java []\npublic class Solution {\n public int minimumTime(int n, int[][] relations, int[] time) {\n Map<Integer, List<Integer>> graph = new HashMap<>();\n int[] in_degree = new int[n + 1];\n for (int[] relation : relations) {\n graph.computeIfAbsent(relation[0], k -> new ArrayList<>()).add(relation[1]);\n in_degree[relation[1]]++;\n }\n\n int[] dist = new int[n + 1];\n System.arraycopy(time, 0, dist, 1, n);\n Queue<Integer> q = new LinkedList<>();\n for (int i = 1; i <= n; i++) {\n if (in_degree[i] == 0) {\n q.add(i);\n }\n }\n\n while (!q.isEmpty()) {\n int course = q.poll();\n if (graph.containsKey(course)) {\n for (int next_course : graph.get(course)) {\n dist[next_course] = Math.max(dist[next_course], dist[course] + time[next_course - 1]);\n in_degree[next_course]--;\n if (in_degree[next_course] == 0) {\n q.add(next_course);\n }\n }\n }\n }\n\n int maxVal = 0;\n for (int val : dist) {\n maxVal = Math.max(maxVal, val);\n }\n return maxVal;\n }\n}\n```\n``` Go []\nfunc minimumTime(n int, relations [][]int, time []int) int {\n graph := make(map[int][]int)\n in_degree := make([]int, n+1)\n for _, relation := range relations {\n graph[relation[0]] = append(graph[relation[0]], relation[1])\n in_degree[relation[1]]++\n }\n\n dist := make([]int, n+1)\n copy(dist[1:], time)\n queue := []int{}\n for i := 1; i <= n; i++ {\n if in_degree[i] == 0 {\n queue = append(queue, i)\n }\n }\n\n for len(queue) > 0 {\n course := queue[0]\n queue = queue[1:]\n for _, next_course := range graph[course] {\n dist[next_course] = max(dist[next_course], dist[course] + time[next_course-1])\n in_degree[next_course]--\n if in_degree[next_course] == 0 {\n queue = append(queue, next_course)\n }\n }\n }\n\n maxVal := 0\n for _, val := range dist {\n maxVal = max(maxVal, val)\n }\n return maxVal\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n``` Rust []\nuse std::collections::HashMap;\nuse std::collections::VecDeque;\n\nimpl Solution {\n pub fn minimum_time(n: i32, relations: Vec<Vec<i32>>, time: Vec<i32>) -> i32 {\n let mut graph: HashMap<i32, Vec<i32>> = HashMap::new();\n let mut in_degree = vec![0; (n + 1) as usize];\n for relation in &relations {\n graph.entry(relation[0]).or_insert(Vec::new()).push(relation[1]);\n in_degree[relation[1] as usize] += 1;\n }\n\n let mut dist: Vec<i32> = vec![0];\n dist.extend(&time);\n let mut queue: VecDeque<i32> = VecDeque::new();\n for i in 1..=n {\n if in_degree[i as usize] == 0 {\n queue.push_back(i);\n }\n }\n\n while let Some(course) = queue.pop_front() {\n if let Some(neighbors) = graph.get(&course) {\n for &next_course in neighbors {\n dist[next_course as usize] = std::cmp::max(dist[next_course as usize], dist[course as usize] + time[(next_course - 1) as usize]);\n in_degree[next_course as usize] -= 1;\n if in_degree[next_course as usize] == 0 {\n queue.push_back(next_course);\n }\n }\n }\n }\n\n *dist.iter().max().unwrap()\n }\n}\n```\n``` JavaScript []\nvar minimumTime = function(n, relations, time) {\n let graph = {};\n let in_degree = Array(n + 1).fill(0);\n for (let relation of relations) {\n if (!graph[relation[0]]) {\n graph[relation[0]] = [];\n }\n graph[relation[0]].push(relation[1]);\n in_degree[relation[1]]++;\n }\n\n let dist = [0].concat(time);\n let queue = [];\n for (let i = 1; i <= n; i++) {\n if (in_degree[i] === 0) {\n queue.push(i);\n }\n }\n\n while (queue.length) {\n let course = queue.shift();\n if (graph[course]) {\n for (let next_course of graph[course]) {\n dist[next_course] = Math.max(dist[next_course], dist[course] + time[next_course - 1]);\n in_degree[next_course]--;\n if (in_degree[next_course] === 0) {\n queue.push(next_course);\n }\n }\n }\n }\n\n return Math.max(...dist);\n};\n```\n``` PHP []\nclass Solution {\n function minimumTime($n, $relations, $time) {\n $graph = [];\n $in_degree = array_fill(0, $n + 1, 0);\n foreach ($relations as $relation) {\n if (!isset($graph[$relation[0]])) {\n $graph[$relation[0]] = [];\n }\n array_push($graph[$relation[0]], $relation[1]);\n $in_degree[$relation[1]]++;\n }\n\n $dist = array_merge([0], $time);\n $queue = [];\n for ($i = 1; $i <= $n; $i++) {\n if ($in_degree[$i] === 0) {\n array_push($queue, $i);\n }\n }\n\n while (count($queue) > 0) {\n $course = array_shift($queue);\n if (isset($graph[$course])) {\n foreach ($graph[$course] as $next_course) {\n $dist[$next_course] = max($dist[$next_course], $dist[$course] + $time[$next_course - 1]);\n $in_degree[$next_course]--;\n if ($in_degree[$next_course] === 0) {\n array_push($queue, $next_course);\n }\n }\n }\n }\n\n return max($dist);\n }\n}\n```\n``` C# []\nusing System;\nusing System.Collections.Generic;\nusing System.Linq;\n\npublic class Solution {\n public int MinimumTime(int n, int[][] relations, int[] time) {\n Dictionary<int, List<int>> graph = new Dictionary<int, List<int>>();\n int[] in_degree = new int[n + 1];\n foreach (var relation in relations) {\n if (!graph.ContainsKey(relation[0])) {\n graph[relation[0]] = new List<int>();\n }\n graph[relation[0]].Add(relation[1]);\n in_degree[relation[1]]++;\n }\n\n int[] dist = new int[n + 1];\n Array.Copy(time, 0, dist, 1, n);\n Queue<int> q = new Queue<int>();\n for (int i = 1; i <= n; i++) {\n if (in_degree[i] == 0) {\n q.Enqueue(i);\n }\n }\n\n while (q.Count > 0) {\n int course = q.Dequeue();\n if (graph.ContainsKey(course)) {\n foreach (int next_course in graph[course]) {\n dist[next_course] = Math.Max(dist[next_course], dist[course] + time[next_course - 1]);\n in_degree[next_course]--;\n if (in_degree[next_course] == 0) {\n q.Enqueue(next_course);\n }\n }\n }\n }\n\n return dist.Max();\n }\n}\n```\n\n## Performance\n| Language | Execution Time (ms) | Memory Usage |\n|-----------|---------------------|--------------|\n| Java | 31 | 73 MB |\n| Rust | 57 | 10.3 MB |\n| JavaScript| 222 | 78.5 MB |\n| Go | 243 | 15.6 MB |\n| C++ | 350 | 145.6 MB |\n| C# | 446 | 73.6 MB |\n| PHP | 672 | 85.8 MB |\n| Python3 | 1393 | 45.7 MB |\n\n\n\n\n# Why it works?\nThe approach relies on the properties of a Directed Acyclic Graph (DAG). In a DAG, there exists a topological order where every node comes before its dependents. By processing the courses in topological order, we ensure that we only start a course when all its prerequisites are completed. This guarantees that the resulting time for each course is the earliest possible completion time. | 34 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
✅98.44%🔥Easy Solution🔥with explanation🔥 | parallel-courses-iii | 1 | 1 | # Problem Explanation: \uD83E\uDDAF\n\n##### You are given a list of courses with prerequisites and a duration for each course. You want to complete all the courses while adhering to the prerequisites. The goal is to minimize the time it takes to complete all the courses.\n\n---\n\n# DFS + Memoization (Top-Down DP): \uD83D\uDE80\n\n##### 1. Create a graph to represent the prerequisites using an adjacency list.\n\n##### 2. Create a memoization table (an array) to store the minimum time needed to complete each course.\n##### 3. Define a recursive function to calculate the minimum time to complete a course:\n- a. If the course has already been calculated, return its value from the memoization table.\n- b. If the course has no prerequisites, its time is simply its own duration.\n- c. Otherwise, calculate the time to complete this course as the maximum time among its prerequisites plus its own duration.\n- d. Store this calculated time in the memoization table and return it.\n\n\n##### 4. Initialize a variable to keep track of the overall minimum time.\n##### 5. For each course, calculate its minimum time using the recursive function and update the overall minimum time if necessary.\n##### 6. The overall minimum time is the answer.\n---\n\n# Time and Space Complexity Analysis: \u23F2\uFE0F\n\n- **Time Complexity:** $$O(V + E)$$, where V is the number of courses and E is the number of prerequisite relations. The memoization table ensures that each course\'s time is calculated only once.\n- **Space Complexity:** $$O(V)$$ for the memoization table and $$O(E)$$ for the graph.\n---\n\n# Code\n\n```python []\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n graph = [[] for _ in range(n)]\n\n for prev, next in relations:\n graph[prev - 1].append(next - 1)\n\n memo = [-1] * n\n\n def calculateTime(course):\n if memo[course] != -1:\n return memo[course]\n\n if not graph[course]:\n memo[course] = time[course]\n return memo[course]\n\n max_prerequisite_time = 0\n for prereq in graph[course]:\n max_prerequisite_time = max(max_prerequisite_time, calculateTime(prereq))\n\n memo[course] = max_prerequisite_time + time[course]\n return memo[course]\n\n overall_min_time = 0\n for course in range(n):\n overall_min_time = max(overall_min_time, calculateTime(course))\n\n return overall_min_time\n\n```\n```C++ []\nclass Solution {\npublic:\n int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {\n vector<vector<int>> graph(n);\n\n for (const vector<int>& relation : relations) {\n int prev = relation[0] - 1;\n int next = relation[1] - 1;\n graph[prev].push_back(next);\n }\n\n vector<int> memo(n, -1);\n\n function<int(int)> calculateTime = [&](int course) {\n if (memo[course] != -1) {\n return memo[course];\n }\n\n if (graph[course].empty()) {\n memo[course] = time[course];\n return memo[course];\n }\n\n int maxPrerequisiteTime = 0;\n for (int prereq : graph[course]) {\n maxPrerequisiteTime = max(maxPrerequisiteTime, calculateTime(prereq));\n }\n\n memo[course] = maxPrerequisiteTime + time[course];\n return memo[course];\n };\n\n int overallMinTime = 0;\n for (int course = 0; course < n; course++) {\n overallMinTime = max(overallMinTime, calculateTime(course));\n }\n\n return overallMinTime;\n }\n};\n\n```\n```javascript []\nvar minimumTime = function(n, relations, time) {\n const graph = Array(n).fill(null).map(() => []);\n \n for (const [prev, next] of relations) {\n graph[next - 1].push(prev - 1);\n }\n \n const memo = new Array(n).fill(0);\n let overallMinTime = 0;\n \n for (let course = 0; course < n; course++) {\n overallMinTime = Math.max(overallMinTime, calculateTime(course, graph, time, memo));\n }\n \n return overallMinTime;\n \n function calculateTime(course, graph, time, memo) {\n if (memo[course] !== 0) {\n return memo[course];\n }\n \n let maxPrerequisiteTime = 0;\n for (const prereq of graph[course]) {\n maxPrerequisiteTime = Math.max(maxPrerequisiteTime, calculateTime(prereq, graph, time, memo));\n }\n \n memo[course] = maxPrerequisiteTime + time[course];\n return memo[course];\n }\n};\n\n```\n```java []\n\npublic class Solution {\n public int minimumTime(int n, int[][] relations, int[] time) {\n List<List<Integer>> graph = new ArrayList<>();\n for (int i = 0; i < n; i++) {\n graph.add(new ArrayList<>());\n }\n\n for (int[] relation : relations) {\n int prev = relation[0] - 1;\n int next = relation[1] - 1;\n graph.get(next).add(prev);\n }\n\n int[] memo = new int[n];\n int overallMinTime = 0;\n\n for (int i = 0; i < n; i++) {\n overallMinTime = Math.max(overallMinTime, calculateTime(i, graph, time, memo));\n }\n\n return overallMinTime;\n }\n\n private int calculateTime(int course, List<List<Integer> > graph, int[] time, int[] memo) {\n if (memo[course] != 0) {\n return memo[course];\n }\n\n int maxPrerequisiteTime = 0;\n for (int prereq : graph.get(course)) {\n maxPrerequisiteTime = Math.max(maxPrerequisiteTime, calculateTime(prereq, graph, time, memo));\n }\n\n memo[course] = maxPrerequisiteTime + time[course];\n return memo[course];\n }\n}\n\n```\n```C# []\npublic class Solution {\n public int MinimumTime(int n, int[][] relations, int[] time) {\n List<List<int>> graph = new List<List<int>>();\n for (int i = 0; i < n; i++) {\n graph.Add(new List<int>());\n }\n\n foreach (int[] relation in relations) {\n int prev = relation[0] - 1;\n int next = relation[1] - 1;\n graph[next].Add(prev);\n }\n\n int[] memo = new int[n];\n int overallMinTime = 0;\n\n for (int course = 0; course < n; course++) {\n overallMinTime = Math.Max(overallMinTime, CalculateTime(course, graph, time, memo));\n }\n\n return overallMinTime;\n }\n\n private int CalculateTime(int course, List<List<int>> graph, int[] time, int[] memo) {\n if (memo[course] != 0) {\n return memo[course];\n }\n\n int maxPrerequisiteTime = 0;\n foreach (int prereq in graph[course]) {\n maxPrerequisiteTime = Math.Max(maxPrerequisiteTime, CalculateTime(prereq, graph, time, memo));\n }\n\n memo[course] = maxPrerequisiteTime + time[course];\n return memo[course];\n }\n}\n\n```\n---\n\n\n---\n\n\n | 77 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
🚀 Topological Sort using Kahn's Algorithm || Explained Intuition🚀 | parallel-courses-iii | 1 | 1 | # Problem Description\n\nGiven an integer `n` representing the number of courses labeled from `1` to `n`, a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` indicates that course `prevCoursej` must be completed before course `nextCoursej` (prerequisite relationship), and a 0-indexed integer array `time` where `time[i]` denotes the duration in months to complete the `(i+1)th` course. Find the **minimum** number of months required to **complete** all courses, considering the given prerequisites and course durations.\n\n- **Rules:**\n 1. Courses can be started at any time if prerequisites are met.\n 2. Multiple courses can be taken simultaneously.\n\nReturn the **minimum** number of months needed to **complete** all the courses, ensuring the given graph is a **directed acyclic** graph and it is possible to complete every course.\n\n- **Constraints:**\n - `1 <= n <= 5 * 10e4`\n - `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10e4)`\n - `relations[j].length == 2`\n - `1 <= prevCoursej, nextCoursej <= n`\n - `prevCoursej != nextCoursej`\n - `All the pairs [prevCoursej, nextCoursej] are unique.`\n - `time.length == n`\n - `1 <= time[i] <= 10e4`\n - `The given graph is a directed acyclic graph.`\n\n\n---\n\n\n# Intuition\n\nHi there, my friends \uD83D\uDE03\nLet\'s take a look at today\'s problem \uD83D\uDC40\n\nIn our problem, we have a graph of courses\uD83D\uDCCA. Each edge in the graph represents a **dependency**. The task is to find the **minimum** time to finish all the courses with respect to their **dependencies**.\n\nLook challenging ?\u2694\nActually not \u270C\uD83D\uDE80\nFirst thing, we need an algorithm to deal with dependencies, a **topological sort** algorithm.\uD83E\uDD14\nI will pretend that I didn\'t say it in the title.\uD83D\uDE02\n\nOue hero is **Kahn\'s Algorithm** \uD83E\uDDB8\u200D\u2642\uFE0F\nBut wait, **Kahn\'s algorithm** really is good with topological sorting but not if there is a time.\uD83E\uDD28\nCan we edit it to do our task \u2753\nLet\'s these examples and note that each node represents the time needed to finish it\n\n\nWe can see here that last node which is `4` will finish after `max(3, 5) + 4` which is `9`.\n\n \n\nWe can see here that node `4` will finish after `max(3, max(1, 2) + 5) + 4` which is `11`.\n\n\nWe can see here that node `4` will finish after `max(6 + 3, max(1, 2, 6) + 5) + 4` which is `15`.\n\n\nThis is tricky one. We can see that node `5` will have to wait for node `3` which is the longest so node `4` will finish after `18` which is `max(1, 2, 6 + 3) + 5 + 4`.\n\nI think we have something here. We can use **Kahn\'s Algorithm** by make the time each node waits for is the **maximum** time of its **parents**.\nHow ? \uD83E\uDD14\n- By compare by **two things:**\n - How much the **current** course **waited** so far to finish.\n - How much the **parent** that finihsed now **waited** + How much the **current** course will **take**.\n\nSince each course can have **many parents** then each time one of them finishes we must compare between these two things.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n\n\n---\n\n\n\n# Approach\n1. **Adjacency List and In-Degrees Setup:**\n - **Initialize** an `adjacency list` to represent the graph and `in-degrees` array to track the number of prerequisites for each course.\n - **Update** the `adjacency list` and `in-degrees` based on the prerequisites.\n2. **Topological Sort using Kahn\'s Algorithm:**\n - **Initialize** a `queue` to keep track of the courses to be taken.\n - Iterate through each course:\n - If a course has **no prerequisites** (in-degree is 0), **add** it to the `queue` with its time.\n - **While** the `queue` is **not empty**:\n - **Pop** a course from the `queue`.\n - **Update** the `maximum wait time` if needed.\n - Process each course that depends on the current course:\n - **Decrease** the `in-degree` of the dependent course.\n - **Update** its `total wait time`.\n - If all prerequisites are completed, add the dependent course to the priority queue with updated time.\n - **Return** the `maximum wait time`.\n\n\n# Complexity\n- **Time complexity:** $O(N + E)$ \nSince we are building the `adjacencyList` by looping over all relations then apply topological sorting to find the maximum time by looping over all courses.\nWhere `E` is the number of relations and `N` is the number of courses.\n- **Space complexity:** $O(N + E)$ \nSince we are building the `adjacencyList` by which has the all relations then when applying topological sorting using the `queue` it can have at maximum `N` elements.\n\n\n---\n\n# Code\n## Kahn\'s Algorithm\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> adjacencyList; // Adjacency list to represent the course prerequisites\n vector<int> inDegrees; // In-degree of each course (number of prerequisites)\n\n // Kahn\'s Algorithm\n int calculateMinimumTime(int n, vector<int>& time) {\n vector<int> waitTime(n + 1) ; // keep track of wait time for each course\n queue<int> q; // queue for topological sort\n int maxWaitTime = 0; // Maximum wait time for completing all courses\n\n // Initialize the queue with courses that have no prerequisites\n for (int i = 1; i <= n; i++) {\n if (inDegrees[i] == 0) {\n q.push(i);\n waitTime[i] = time[i - 1] ;\n maxWaitTime = max(maxWaitTime, waitTime[i]);\n }\n }\n\n // Perform topological sort\n while (!q.empty()) {\n int currentCourse = q.front();\n q.pop();\n\n // Process each course that depends on the current course\n for (auto childCourse : adjacencyList[currentCourse]) {\n inDegrees[childCourse]--;\n waitTime[childCourse] = max(time[childCourse - 1] + waitTime[currentCourse], waitTime[childCourse]);\n maxWaitTime = max(maxWaitTime, waitTime[childCourse]);\n\n // If all prerequisites are completed, update the wait time and add to the queue\n if (inDegrees[childCourse] == 0) \n q.push(childCourse);\n }\n }\n\n return maxWaitTime;\n }\n\n int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {\n adjacencyList.resize(n + 1);\n inDegrees.resize(n + 1);\n\n // Build the adjacency list and calculate in-degrees for each course\n for (int i = 0; i < relations.size(); i++) {\n auto prerequisitePair = relations[i];\n adjacencyList[prerequisitePair[0]].push_back(prerequisitePair[1]);\n inDegrees[prerequisitePair[1]]++;\n }\n\n return calculateMinimumTime(n, time);\n }\n};\n```\n```Java []\nclass Solution {\n List<List<Integer>> adjacencyList; // Adjacency list to represent the course prerequisites\n List<Integer> inDegrees; // In-degree of each course (number of prerequisites)\n\n // Kahn\'s Algorithm\n public int calculateMinimumTime(int n, int[] time) {\n int[] waitTime = new int[n + 1]; // keep track of wait time for each course\n Queue<Integer> q = new LinkedList<>(); // queue for topological sort\n int maxWaitTime = 0; // Maximum wait time for completing all courses\n\n // Initialize the queue with courses that have no prerequisites\n for (int i = 1; i <= n; i++) {\n if (inDegrees.get(i) == 0) {\n q.offer(i);\n waitTime[i] = time[i - 1];\n maxWaitTime = Math.max(maxWaitTime, waitTime[i]);\n }\n }\n\n // Perform topological sort\n while (!q.isEmpty()) {\n int currentCourse = q.poll();\n\n // Process each course that depends on the current course\n for (int childCourse : adjacencyList.get(currentCourse)) {\n inDegrees.set(childCourse, inDegrees.get(childCourse) - 1);\n waitTime[childCourse] = Math.max(time[childCourse - 1] + waitTime[currentCourse], waitTime[childCourse]);\n maxWaitTime = Math.max(maxWaitTime, waitTime[childCourse]);\n\n // If all prerequisites are completed, update the wait time and add to the queue\n if (inDegrees.get(childCourse) == 0)\n q.offer(childCourse);\n }\n }\n\n return maxWaitTime;\n }\n\n public int minimumTime(int n, int[][] relations, int[] time) {\n adjacencyList = new ArrayList<>(n + 1);\n inDegrees = new ArrayList<>(n + 1);\n\n for (int i = 0; i <= n; i++) {\n adjacencyList.add(new ArrayList<>());\n inDegrees.add(0);\n }\n\n // Build the adjacency list and calculate in-degrees for each course\n for (int i = 0; i < relations.length; i++) {\n int[] prerequisitePair = relations[i];\n adjacencyList.get(prerequisitePair[0]).add(prerequisitePair[1]);\n inDegrees.set(prerequisitePair[1], inDegrees.get(prerequisitePair[1]) + 1);\n }\n\n return calculateMinimumTime(n, time);\n }\n}\n```\n```Python []\nfrom queue import Queue\n\nclass Solution:\n def __init__(self):\n self.adjacencyList = [] # Adjacency list to represent the course prerequisites\n self.inDegrees = [] # In-degree of each course (number of prerequisites)\n\n # Kahn\'s Algorithm\n def calculateMinimumTime(self, n: int, time: List[int]) -> int:\n waitTime = [0] * (n + 1) # keep track of wait time for each course\n q = Queue() # queue for topological sort\n maxWaitTime = 0 # Maximum wait time for completing all courses\n\n # Initialize the queue with courses that have no prerequisites\n for i in range(1, n + 1):\n if self.inDegrees[i] == 0:\n q.put(i)\n waitTime[i] = time[i - 1]\n maxWaitTime = max(maxWaitTime, waitTime[i])\n\n # Perform topological sort\n while not q.empty():\n currentCourse = q.get()\n\n # Process each course that depends on the current course\n for childCourse in self.adjacencyList[currentCourse]:\n self.inDegrees[childCourse] -= 1\n waitTime[childCourse] = max(time[childCourse - 1] + waitTime[currentCourse], waitTime[childCourse])\n maxWaitTime = max(maxWaitTime, waitTime[childCourse])\n\n # If all prerequisites are completed, update the wait time and add to the queue\n if self.inDegrees[childCourse] == 0:\n q.put(childCourse)\n\n return maxWaitTime\n\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n self.adjacencyList = [[] for _ in range(n + 1)]\n self.inDegrees = [0] * (n + 1)\n\n # Build the adjacency list and calculate in-degrees for each course\n for prereqPair in relations:\n self.adjacencyList[prereqPair[0]].append(prereqPair[1])\n self.inDegrees[prereqPair[1]] += 1\n\n return self.calculateMinimumTime(n, time)\n```\n\n\n\n\n\n\n\n | 35 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
[python3] BFS and keep track of max value of children | parallel-courses-iii | 0 | 1 | ```\nclass Solution:\n def minimumTime(self, n: int, rel: List[List[int]], time: List[int]) -> int:\n indegree = [0]*(n+1)\n maxi = [0]*(n+1)\n ans = 0\n stack = []\n \n G = defaultdict(list)\n \n for s,e in rel:\n indegree[e] += 1\n G[s].append(e)\n\n for i in range(1, n+1):\n if indegree[i] == 0:\n stack.append(i)\n \n while stack:\n n = stack.pop()\n time[n-1] = maxi[n] + time[n-1]\n \n if not G[n]:\n ans = max(ans, time[n-1])\n \n for nxt in G[n]:\n indegree[nxt] -= 1\n if indegree[nxt] == 0:\n stack.append(nxt)\n maxi[nxt] = max(maxi[nxt], time[n-1])\n \n return ans\n | 1 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
Python || Stack || DFS || Recursive | parallel-courses-iii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n children, total_time, visited, result = [[] for i in range(n)], [0] * n, set(range(n)), 0\n for u, v in relations:\n children[u - 1].append(v - 1)\n visited.discard(v - 1)\n stack = list(visited)\n while stack:\n tmp = stack[-1]\n total_time[tmp] = time[tmp]\n for child in children[tmp]:\n if total_time[child] <= 0: stack.append(child)\n else: total_time[tmp] = max(total_time[tmp], time[tmp] + total_time[child])\n if tmp == stack[-1]: \n result = max(result, total_time[tmp])\n stack.pop(-1)\n return result \n``` | 1 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
Python3 Solution | parallel-courses-iii | 0 | 1 | \n```\nclass Solution:\n def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:\n graph=defaultdict(list)\n for required,course in relations:\n graph[course].append(required)\n\n @cache\n def dp (i):\n if not graph.get(i,False):\n return time[i-1]\n ans=-1\n for j in graph[i]:\n ans=max(ans,dp(j))\n return ans+time[i-1]\n return max([dp(i+1) for i in range(n)]) \n``` | 1 | You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course.
You must find the **minimum** number of months needed to complete all the courses following these rules:
* You may start taking a course at **any time** if the prerequisites are met.
* **Any number of courses** can be taken at the **same time**.
Return _the **minimum** number of months needed to complete all the courses_.
**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
**Example 1:**
**Input:** n = 3, relations = \[\[1,3\],\[2,3\]\], time = \[3,2,5\]
**Output:** 8
**Explanation:** The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
**Example 2:**
**Input:** n = 5, relations = \[\[1,5\],\[2,5\],\[3,5\],\[3,4\],\[4,5\]\], time = \[1,2,3,4,5\]
**Output:** 12
**Explanation:** The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
**Constraints:**
* `1 <= n <= 5 * 104`
* `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)`
* `relations[j].length == 2`
* `1 <= prevCoursej, nextCoursej <= n`
* `prevCoursej != nextCoursej`
* All the pairs `[prevCoursej, nextCoursej]` are **unique**.
* `time.length == n`
* `1 <= time[i] <= 104`
* The given graph is a directed acyclic graph. | Is there a formula we can use to find the count of all the good numbers? Exponentiation can be done very fast if we looked at the binary bits of n. |
Python solution | kth-distinct-string-in-an-array | 0 | 1 | # Code\n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n uni = []\n copies = []\n for item in arr:\n if item not in uni:\n if item in copies:\n pass\n else:\n uni.append(item)\n else:\n copies.append(item)\n uni.remove(item)\n \n return "" if k > len(uni) else uni[k - 1]\n``` | 1 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
Python Hash Table | kth-distinct-string-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n\n dicts = {}\n ans = []\n\n for i in range(len(arr)):\n if arr[i] in dicts:\n dicts[arr[i]] += 1\n else:\n dicts[arr[i]] = 1\n \n for i in dicts:\n if dicts[i] == 1:\n ans.append([i, dicts[i]])\n \n if len(ans) <k:\n return ""\n return ans[k-1][0]\n\n\n\n \n\n\n\n\n``` | 1 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
Easy to Understand , beats 85.8% of solution in Python. Beginner Friendly Solution | kth-distinct-string-in-an-array | 0 | 1 | \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) is the time complexity as Counter takes O(N) time complexity.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) is the worst space complexity where all the elements are unique\n\n# Code\n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n l = []\n x = Counter(arr)\n for i, j in x.items():\n if j==1:\n l.append(i)\n if len(l)<k:\n return ""\n return l[k-1]\n```\n\nFor understanding Python from Scratch, Learning Complex Libraries, need help with solving questions or want to learn MACHINE LEARNING for FREE\n\nSubscribe to Bolt Coding Channel - https://www.youtube.com/@boltcoding | 1 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
4 liner code very easy beats 98.33% | kth-distinct-string-in-an-array | 0 | 1 | # Best Code Easy To understand beats 98.33% for true\n\n# Code\n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n for val,c in Counter(arr).items():\n if c==1:\n k-=1\n if k==0: return val\n return ""\n``` | 1 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
Python simple 2 lines solution | kth-distinct-string-in-an-array | 0 | 1 | **Python :**\n\n```\ndef kthDistinct(self, arr: List[str], k: int) -> str:\n\tarr = [i for i in arr if arr.count(i) == 1]\n\treturn "" if k > len(arr) else arr[k - 1]\n```\n\n**Like it ? please upvote !** | 27 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
[Python3] freq table | kth-distinct-string-in-an-array | 0 | 1 | \n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n freq = Counter(arr)\n for x in arr: \n if freq[x] == 1: k -= 1\n if k == 0: return x\n return ""\n``` | 19 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
Python Easy Solution || Hash Table | kth-distinct-string-in-an-array | 0 | 1 | # Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def kthDistinct(self, arr: List[str], k: int) -> str:\n dic={}\n for i in arr:\n if i in dic:\n dic[i]+=1\n else:\n dic[i]=1\n for i in arr:\n if dic[i]==1:\n k-=1\n if k==0:\n return i\n return ""\n``` | 1 | A **distinct string** is a string that is present only **once** in an array.
Given an array of strings `arr`, and an integer `k`, return _the_ `kth` _**distinct string** present in_ `arr`. If there are **fewer** than `k` distinct strings, return _an **empty string**_ `" "`.
Note that the strings are considered in the **order in which they appear** in the array.
**Example 1:**
**Input:** arr = \[ "d ", "b ", "c ", "b ", "c ", "a "\], k = 2
**Output:** "a "
**Explanation:**
The only distinct strings in arr are "d " and "a ".
"d " appears 1st, so it is the 1st distinct string.
"a " appears 2nd, so it is the 2nd distinct string.
Since k == 2, "a " is returned.
**Example 2:**
**Input:** arr = \[ "aaa ", "aa ", "a "\], k = 1
**Output:** "aaa "
**Explanation:**
All strings in arr are distinct, so the 1st string "aaa " is returned.
**Example 3:**
**Input:** arr = \[ "a ", "b ", "a "\], k = 3
**Output:** " "
**Explanation:**
The only distinct string is "b ". Since there are fewer than 3 distinct strings, we return an empty string " ".
**Constraints:**
* `1 <= k <= arr.length <= 1000`
* `1 <= arr[i].length <= 5`
* `arr[i]` consists of lowercase English letters. | Build a dictionary containing the frequency of each character appearing in s Check if all values in the dictionary are the same. |
[Python3] binary search | two-best-non-overlapping-events | 0 | 1 | \n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n time = []\n vals = []\n ans = prefix = 0\n for st, et, val in sorted(events, key=lambda x: x[1]): \n prefix = max(prefix, val)\n k = bisect_left(time, st)-1\n if k >= 0: val += vals[k]\n ans = max(ans, val)\n time.append(et)\n vals.append(prefix)\n return ans \n```\n\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n ans = most = 0 \n pq = []\n for st, et, val in sorted(events): \n heappush(pq, (et, val))\n while pq and pq[0][0] < st: \n _, vv = heappop(pq)\n most = max(most, vv)\n ans = max(ans, most + val)\n return ans \n``` | 15 | You are given a **0-indexed** 2D integer array of `events` where `events[i] = [startTimei, endTimei, valuei]`. The `ith` event starts at `startTimei` and ends at `endTimei`, and if you attend this event, you will receive a value of `valuei`. You can choose **at most** **two** **non-overlapping** events to attend such that the sum of their values is **maximized**.
Return _this **maximum** sum._
Note that the start time and end time is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time `t`, the next event must start at or after `t + 1`.
**Example 1:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[2,4,3\]\]
**Output:** 4
**Explanation:** Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
**Example 2:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[1,5,5\]\]
**Output:** 5
**Explanation:** Choose event 2 for a sum of 5.
**Example 3:**
**Input:** events = \[\[1,5,3\],\[1,5,1\],\[6,6,5\]\]
**Output:** 8
**Explanation:** Choose events 0 and 2 for a sum of 3 + 5 = 8.
**Constraints:**
* `2 <= events.length <= 105`
* `events[i].length == 3`
* `1 <= startTimei <= endTimei <= 109`
* `1 <= valuei <= 106` | Sort times by arrival time. for each arrival_i find the smallest unoccupied chair and mark it as occupied until leaving_i. |
📌📌 Heap || very-Easy || Well-Explained 🐍 | two-best-non-overlapping-events | 0 | 1 | ## IDEA:\n**This question is same as https://leetcode.com/problems/maximum-profit-in-job-scheduling/ .**\n\n* In this we have to consider atmost two events. So we will only put the cureent profit in heap.\n\n* Maintain one variable res1 for storing the maximum value among all the events ending before the current event gets start.\n* Another variable res2 store the maximum profit according the given condition.\n\n\'\'\'\n\n\tclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n \n events.sort()\n heap = []\n res2,res1 = 0,0\n for s,e,p in events:\n while heap and heap[0][0]<s:\n res1 = max(res1,heapq.heappop(heap)[1])\n \n res2 = max(res2,res1+p)\n heapq.heappush(heap,(e,p))\n \n return res2\n\n### Thanks and Upvote If you like the Idea !!\uD83E\uDD1E | 14 | You are given a **0-indexed** 2D integer array of `events` where `events[i] = [startTimei, endTimei, valuei]`. The `ith` event starts at `startTimei` and ends at `endTimei`, and if you attend this event, you will receive a value of `valuei`. You can choose **at most** **two** **non-overlapping** events to attend such that the sum of their values is **maximized**.
Return _this **maximum** sum._
Note that the start time and end time is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time `t`, the next event must start at or after `t + 1`.
**Example 1:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[2,4,3\]\]
**Output:** 4
**Explanation:** Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
**Example 2:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[1,5,5\]\]
**Output:** 5
**Explanation:** Choose event 2 for a sum of 5.
**Example 3:**
**Input:** events = \[\[1,5,3\],\[1,5,1\],\[6,6,5\]\]
**Output:** 8
**Explanation:** Choose events 0 and 2 for a sum of 3 + 5 = 8.
**Constraints:**
* `2 <= events.length <= 105`
* `events[i].length == 3`
* `1 <= startTimei <= endTimei <= 109`
* `1 <= valuei <= 106` | Sort times by arrival time. for each arrival_i find the smallest unoccupied chair and mark it as occupied until leaving_i. |
Binary Search + Right Max | two-best-non-overlapping-events | 0 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$.\n\n- Space complexity: $$O(n)$$.\n\n# Code\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n START, END, VAL = 0, 1, 2\n\n events.sort()\n maxRightVal = [0]*len(events)\n maxRightVal[-1] = events[-1][VAL]\n for i in range(len(events)-2, -1, -1):\n maxRightVal[i] = max(events[i][VAL], maxRightVal[i+1])\n\n max2Sum = max(val for _, _, val in events)\n for start, end, val in events:\n j = bisect_right(events, end, key=lambda x: x[START])\n if j < len(events):\n if end < events[j][START]:\n max2Sum = max(max2Sum, val + maxRightVal[j])\n elif end == events[j][START] and j < len(events)-1:\n max2Sum = max(max2Sum, val + maxRightVal[j+1])\n \n return max2Sum\n``` | 0 | You are given a **0-indexed** 2D integer array of `events` where `events[i] = [startTimei, endTimei, valuei]`. The `ith` event starts at `startTimei` and ends at `endTimei`, and if you attend this event, you will receive a value of `valuei`. You can choose **at most** **two** **non-overlapping** events to attend such that the sum of their values is **maximized**.
Return _this **maximum** sum._
Note that the start time and end time is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time `t`, the next event must start at or after `t + 1`.
**Example 1:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[2,4,3\]\]
**Output:** 4
**Explanation:** Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
**Example 2:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[1,5,5\]\]
**Output:** 5
**Explanation:** Choose event 2 for a sum of 5.
**Example 3:**
**Input:** events = \[\[1,5,3\],\[1,5,1\],\[6,6,5\]\]
**Output:** 8
**Explanation:** Choose events 0 and 2 for a sum of 3 + 5 = 8.
**Constraints:**
* `2 <= events.length <= 105`
* `events[i].length == 3`
* `1 <= startTimei <= endTimei <= 109`
* `1 <= valuei <= 106` | Sort times by arrival time. for each arrival_i find the smallest unoccupied chair and mark it as occupied until leaving_i. |
Python heap Sol beats 90% | two-best-non-overlapping-events | 0 | 1 | So, notice that if we sort events, then we always have the left bound increasing. Therefore, we can keep a heap of (right_bound, value) tuples from events that we have seen so far. Whenever the current left bound becomes larger than the right_bound on the stack, that means we can start poppping from the heap to look for the next possible interval pairing. We simply record the best value seen so far, and since every next event has a larger left, we can always pair with the values that have popped off the heap.\n\n# Code\n```\nclass Solution:\n def maxTwoEvents(self, events: List[List[int]]) -> int:\n events.sort()\n res = 0\n best_value_to_the_left_of_all_intervals = 0\n intervals_seen_so_far = []\n for left, r, v in events:\n heappush(intervals_seen_so_far, (r, v))\n while intervals_seen_so_far and intervals_seen_so_far[0][0] < left:\n R, V = heappop(intervals_seen_so_far)\n best_value_to_the_left_of_all_intervals = max(best_value_to_the_left_of_all_intervals, V)\n res = max(res, best_value_to_the_left_of_all_intervals + v)\n return res\n``` | 0 | You are given a **0-indexed** 2D integer array of `events` where `events[i] = [startTimei, endTimei, valuei]`. The `ith` event starts at `startTimei` and ends at `endTimei`, and if you attend this event, you will receive a value of `valuei`. You can choose **at most** **two** **non-overlapping** events to attend such that the sum of their values is **maximized**.
Return _this **maximum** sum._
Note that the start time and end time is **inclusive**: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time `t`, the next event must start at or after `t + 1`.
**Example 1:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[2,4,3\]\]
**Output:** 4
**Explanation:** Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.
**Example 2:**
**Input:** events = \[\[1,3,2\],\[4,5,2\],\[1,5,5\]\]
**Output:** 5
**Explanation:** Choose event 2 for a sum of 5.
**Example 3:**
**Input:** events = \[\[1,5,3\],\[1,5,1\],\[6,6,5\]\]
**Output:** 8
**Explanation:** Choose events 0 and 2 for a sum of 3 + 5 = 8.
**Constraints:**
* `2 <= events.length <= 105`
* `events[i].length == 3`
* `1 <= startTimei <= endTimei <= 109`
* `1 <= valuei <= 106` | Sort times by arrival time. for each arrival_i find the smallest unoccupied chair and mark it as occupied until leaving_i. |
Python Simple + Explanation | plates-between-candles | 0 | 1 | \n# Code\n```\n# Slightly modified Binary search\n# Say you have an array [3, 5, 7, 9, 15] and you have an element\n# 6 and you want to find closest elements on the left and right\n# of 6 in the array. You can run binary search and ultimately\n# r will point to 5 and l will point to 7, i.e r, l gives the boundary\n# However, if the query is 5, both r, l will point to 5 (note)\n# Also, if q is 16, r will point to 15 but l will point to an element\n# at index = len(array) + 1 ( which doesn\'t exist) -- so need to handle\n# these cases.\n\n# Using this logic in this problem we\'ll use Binary Search to find \n# the closest candle on the right of the first element in the \n# query and the closest candle on the left of the second element in the query.\n# The we\'ll use the prefix sum already computed to compute the \n# sum of the plates between these candles\n\nclass Solution:\n def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:\n look_up, pre_sum, res = [], [], []\n for i, e in enumerate(s):\n if s[i] == \'|\':\n look_up.append(i)\n pre_sum.append(pre_sum[-1] if pre_sum else 0)\n else:\n pre_sum.append(pre_sum[-1] + 1 if pre_sum else 1)\n \n for st, end in queries:\n _, r = self.range_bs(look_up, st)\n l, _ = self.range_bs(look_up, end)\n if st < end and 0<= r < len(look_up) and 0 <= l < len(look_up):\n res.append(\n max(pre_sum[look_up[l]] - pre_sum[look_up[r]], 0)\n )\n else:\n res.append(0)\n \n return res\n \n \n def range_bs(self, look_up, q):\n l, r = 0, len(look_up) - 1\n while l <= r:\n mid = (l+r)//2\n if look_up[mid] == q:\n return mid, mid\n elif look_up[mid] < q:\n l = mid+1\n else:\n r = mid-1\n return r, l\n``` | 1 | There is a long table with a line of plates and candles arranged on top of it. You are given a **0-indexed** string `s` consisting of characters `'*'` and `'|'` only, where a `'*'` represents a **plate** and a `'|'` represents a **candle**.
You are also given a **0-indexed** 2D integer array `queries` where `queries[i] = [lefti, righti]` denotes the **substring** `s[lefti...righti]` (**inclusive**). For each query, you need to find the **number** of plates **between candles** that are **in the substring**. A plate is considered **between candles** if there is at least one candle to its left **and** at least one candle to its right **in the substring**.
* For example, `s = "||**||**|* "`, and a query `[3, 8]` denotes the substring `"*||******| "`. The number of plates between candles in this substring is `2`, as each of the two plates has at least one candle **in the substring** to its left **and** right.
Return _an integer array_ `answer` _where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** s = "\*\*|\*\*|\*\*\*| ", queries = \[\[2,5\],\[5,9\]\]
**Output:** \[2,3\]
**Explanation:**
- queries\[0\] has two plates between candles.
- queries\[1\] has three plates between candles.
**Example 2:**
**Input:** s = "\*\*\*|\*\*|\*\*\*\*\*|\*\*||\*\*|\* ", queries = \[\[1,17\],\[4,5\],\[14,17\],\[5,11\],\[15,16\]\]
**Output:** \[9,0,0,0,0\]
**Explanation:**
- queries\[0\] has nine plates between candles.
- The other queries have zero plates between candles.
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of `'*'` and `'|'` characters.
* `1 <= queries.length <= 105`
* `queries[i].length == 2`
* `0 <= lefti <= righti < s.length` | Can we sort the segments in a way to help solve the problem? How can we dynamically keep track of the sum of the current segment(s)? |
[Python 3] - Prefix Sum + Binary Search - Simple | plates-between-candles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n1. Binary Search\n```\nclass Solution:\n def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:\n candies = [i for i, c in enumerate(s) if c == "|"]\n \n def bns(x: int) -> int:\n l, r = 0, len(candies) - 1\n while l <= r:\n m = (l + r) // 2\n if candies[m] < x: l = m + 1\n else: r = m - 1\n return l\n\n ans = []\n for a, b in queries:\n l, r = bns(a), bns(b + 1) - 1\n ans.append(candies[r] - candies[l] - (r - l) if l < r else 0)\n return ans\n```\n- TC: $$O(NlogN)$$\n- SC: $$O(N)$$\n\n2. Prefix Sum\n```\nclass Solution:\n def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:\n psum, next, prev = [0] * (len(s) + 1), [float("inf")] * (len(s) + 1), [0] * (len(s) + 1)\n res = []\n for i, ch in enumerate(s):\n psum[i + 1] = psum[i] + (ch == \'|\')\n prev[i + 1] = i if ch == \'|\' else prev[i]\n for i, ch in reversed(list(enumerate(s))):\n next[i] = i if ch == \'|\' else next[i + 1]\n for q in queries:\n l, r = next[q[0]], prev[q[1] + 1]\n res.append(r - l - (psum[r] - psum[l]) if l < r else 0)\n return res\n```\n- TC: $$O(N)$$\n- SC: $$O(N)$$ | 2 | There is a long table with a line of plates and candles arranged on top of it. You are given a **0-indexed** string `s` consisting of characters `'*'` and `'|'` only, where a `'*'` represents a **plate** and a `'|'` represents a **candle**.
You are also given a **0-indexed** 2D integer array `queries` where `queries[i] = [lefti, righti]` denotes the **substring** `s[lefti...righti]` (**inclusive**). For each query, you need to find the **number** of plates **between candles** that are **in the substring**. A plate is considered **between candles** if there is at least one candle to its left **and** at least one candle to its right **in the substring**.
* For example, `s = "||**||**|* "`, and a query `[3, 8]` denotes the substring `"*||******| "`. The number of plates between candles in this substring is `2`, as each of the two plates has at least one candle **in the substring** to its left **and** right.
Return _an integer array_ `answer` _where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** s = "\*\*|\*\*|\*\*\*| ", queries = \[\[2,5\],\[5,9\]\]
**Output:** \[2,3\]
**Explanation:**
- queries\[0\] has two plates between candles.
- queries\[1\] has three plates between candles.
**Example 2:**
**Input:** s = "\*\*\*|\*\*|\*\*\*\*\*|\*\*||\*\*|\* ", queries = \[\[1,17\],\[4,5\],\[14,17\],\[5,11\],\[15,16\]\]
**Output:** \[9,0,0,0,0\]
**Explanation:**
- queries\[0\] has nine plates between candles.
- The other queries have zero plates between candles.
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of `'*'` and `'|'` characters.
* `1 <= queries.length <= 105`
* `queries[i].length == 2`
* `0 <= lefti <= righti < s.length` | Can we sort the segments in a way to help solve the problem? How can we dynamically keep track of the sum of the current segment(s)? |
Python bisect | plates-between-candles | 0 | 1 | A short solution using bisect (built in library bisect [source code](https://github.com/python/cpython/blob/3.10/Lib/bisect.py)):\n\n`p` stores the index for each candle, \n`p[j] - p[i]` returns how many plates there are between the two candles.\n`j - i` returns how many candles are between these two candles\njust be careful about the boundary conditions\n\n import bisect \n class Solution:\n\t\tdef platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:\n\t\t\tp = [i for i in range(len(s)) if s[i] == \'|\']\n\n\t\t\tres = []\n\t\t\tfor f,t in queries: \n\t\t\t\tl = bisect.bisect_left(p, f)\n\t\t\t\tr = bisect.bisect_right(p, t)\n\t\t\t\tres.append(p[r-1] - p[l] - (r-1-l) if r > l else 0)\n\n\t\t\treturn res\n\n(credits: Raymond for using bisect) | 9 | There is a long table with a line of plates and candles arranged on top of it. You are given a **0-indexed** string `s` consisting of characters `'*'` and `'|'` only, where a `'*'` represents a **plate** and a `'|'` represents a **candle**.
You are also given a **0-indexed** 2D integer array `queries` where `queries[i] = [lefti, righti]` denotes the **substring** `s[lefti...righti]` (**inclusive**). For each query, you need to find the **number** of plates **between candles** that are **in the substring**. A plate is considered **between candles** if there is at least one candle to its left **and** at least one candle to its right **in the substring**.
* For example, `s = "||**||**|* "`, and a query `[3, 8]` denotes the substring `"*||******| "`. The number of plates between candles in this substring is `2`, as each of the two plates has at least one candle **in the substring** to its left **and** right.
Return _an integer array_ `answer` _where_ `answer[i]` _is the answer to the_ `ith` _query_.
**Example 1:**
**Input:** s = "\*\*|\*\*|\*\*\*| ", queries = \[\[2,5\],\[5,9\]\]
**Output:** \[2,3\]
**Explanation:**
- queries\[0\] has two plates between candles.
- queries\[1\] has three plates between candles.
**Example 2:**
**Input:** s = "\*\*\*|\*\*|\*\*\*\*\*|\*\*||\*\*|\* ", queries = \[\[1,17\],\[4,5\],\[14,17\],\[5,11\],\[15,16\]\]
**Output:** \[9,0,0,0,0\]
**Explanation:**
- queries\[0\] has nine plates between candles.
- The other queries have zero plates between candles.
**Constraints:**
* `3 <= s.length <= 105`
* `s` consists of `'*'` and `'|'` characters.
* `1 <= queries.length <= 105`
* `queries[i].length == 2`
* `0 <= lefti <= righti < s.length` | Can we sort the segments in a way to help solve the problem? How can we dynamically keep track of the sum of the current segment(s)? |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.