title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python | Simulation | Simple Solution | O(mn) | decode-the-slanted-ciphertext | 0 | 1 | # Code\n```\nclass Solution:\n def decodeCiphertext(self, encodedText: str, rows: int) -> str:\n cols = len(encodedText)//rows\n matrix = [[0]*cols for _ in range(rows)]\n for i in range(rows):\n for j in range(cols):\n matrix[i][j] = encodedText[i*cols + j]\n i,j = 0,0\n res = []\n while 0<=i<rows and 0<=j<cols:\n res.append(matrix[i][j])\n i = (i+1)%rows\n j += 1\n j = j-(rows-1)*(i==0)\n return "".join(res).rstrip()\n \n``` | 0 | A string `originalText` is encoded using a **slanted transposition cipher** to a string `encodedText` with the help of a matrix having a **fixed number of rows** `rows`.
`originalText` is placed first in a top-left to bottom-right manner.
The blue cells are filled first, followed by the red cells, then the yellow cells, and so on, until we reach the end of `originalText`. The arrow indicates the order in which the cells are filled. All empty cells are filled with `' '`. The number of columns is chosen such that the rightmost column will **not be empty** after filling in `originalText`.
`encodedText` is then formed by appending all characters of the matrix in a row-wise fashion.
The characters in the blue cells are appended first to `encodedText`, then the red cells, and so on, and finally the yellow cells. The arrow indicates the order in which the cells are accessed.
For example, if `originalText = "cipher "` and `rows = 3`, then we encode it in the following manner:
The blue arrows depict how `originalText` is placed in the matrix, and the red arrows denote the order in which `encodedText` is formed. In the above example, `encodedText = "ch ie pr "`.
Given the encoded string `encodedText` and number of rows `rows`, return _the original string_ `originalText`.
**Note:** `originalText` **does not** have any trailing spaces `' '`. The test cases are generated such that there is only one possible `originalText`.
**Example 1:**
**Input:** encodedText = "ch ie pr ", rows = 3
**Output:** "cipher "
**Explanation:** This is the same example described in the problem description.
**Example 2:**
**Input:** encodedText = "iveo eed l te olc ", rows = 4
**Output:** "i love leetcode "
**Explanation:** The figure above denotes the matrix that was used to encode originalText.
The blue arrows show how we can find originalText from encodedText.
**Example 3:**
**Input:** encodedText = "coding ", rows = 1
**Output:** "coding "
**Explanation:** Since there is only 1 row, both originalText and encodedText are the same.
**Constraints:**
* `0 <= encodedText.length <= 106`
* `encodedText` consists of lowercase English letters and `' '` only.
* `encodedText` is a valid encoding of some `originalText` that **does not** have trailing spaces.
* `1 <= rows <= 1000`
* The testcases are generated such that there is **only one** possible `originalText`. | Convert lights into an array of ranges representing the range where each street light can light up and sort the start and end points of the ranges. Do we need to traverse all possible positions on the street? No, we don't, we only need to go to the start and end points of the ranges for each streetlight. |
python3 simple union find | process-restricted-friend-requests | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n res = []\n self.parent = list(range(n))\n for a,b in requests:\n temp = self.parent.copy()\n self.union(a,b)\n flag = True\n for x,y in restrictions:\n if self.find(x)==self.find(y):\n flag = False\n break\n if flag:\n res.append(True)\n else:\n res.append(False)\n self.parent = temp\n \n return res\n\n def find(self, a):\n acopy = a\n while a != self.parent[a]:\n a = self.parent[a]\n while acopy != a:\n self.parent[acopy], acopy = a, self.parent[acopy]\n return a\n \n def union(self, a, b):\n self.parent[self.find(b)] = self.find(a)\n\n``` | 1 | You are given an integer `n` indicating the number of people in a network. Each person is labeled from `0` to `n - 1`.
You are also given a **0-indexed** 2D integer array `restrictions`, where `restrictions[i] = [xi, yi]` means that person `xi` and person `yi` **cannot** become **friends**, either **directly** or **indirectly** through other people.
Initially, no one is friends with each other. You are given a list of friend requests as a **0-indexed** 2D integer array `requests`, where `requests[j] = [uj, vj]` is a friend request between person `uj` and person `vj`.
A friend request is **successful** if `uj` and `vj` can be **friends**. Each friend request is processed in the given order (i.e., `requests[j]` occurs before `requests[j + 1]`), and upon a successful request, `uj` and `vj` **become direct friends** for all future friend requests.
Return _a **boolean array**_ `result`, _where each_ `result[j]` _is_ `true` _if the_ `jth` _friend request is **successful** or_ `false` _if it is not_.
**Note:** If `uj` and `vj` are already direct friends, the request is still **successful**.
**Example 1:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[0,2\],\[2,1\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 0 and person 2 can be friends, so they become direct friends.
Request 1: Person 2 and person 1 cannot be friends since person 0 and person 1 would be indirect friends (1--2--0).
**Example 2:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[1,2\],\[0,2\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 1 and person 2 can be friends, so they become direct friends.
Request 1: Person 0 and person 2 cannot be friends since person 0 and person 1 would be indirect friends (0--2--1).
**Example 3:**
**Input:** n = 5, restrictions = \[\[0,1\],\[1,2\],\[2,3\]\], requests = \[\[0,4\],\[1,2\],\[3,1\],\[3,4\]\]
**Output:** \[true,false,true,false\]
**Explanation:**
Request 0: Person 0 and person 4 can be friends, so they become direct friends.
Request 1: Person 1 and person 2 cannot be friends since they are directly restricted.
Request 2: Person 3 and person 1 can be friends, so they become direct friends.
Request 3: Person 3 and person 4 cannot be friends since person 0 and person 1 would be indirect friends (0--4--3--1).
**Constraints:**
* `2 <= n <= 1000`
* `0 <= restrictions.length <= 1000`
* `restrictions[i].length == 2`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= requests.length <= 1000`
* `requests[j].length == 2`
* `0 <= uj, vj <= n - 1`
* `uj != vj` | First, let's note that after the first transform the value will be at most 100 * 9 which is not much After The first transform, we can just do the rest of the transforms by brute force |
[Python] [272 ms,36 MB] Maintain connected components of the graph | process-restricted-friend-requests | 0 | 1 | Maintain two lists of sets ```connected_components``` and ```banned_by_comps``` to store the connected components the restrictions of nodes in each connected component. Maintain a dictionary ```connected_comp_dict``` to map each node to its connected compoent. Update them when a new edge is added.\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]: \n result = [False for _ in requests]\n \n connected_components = [{i} for i in range(n)]\n \n connected_comp_dict = {}\n for i in range(n):\n connected_comp_dict[i] = i\n \n banned_by_comps = [set() for i in range(n)]\n for res in restrictions:\n banned_by_comps[res[0]].add(res[1])\n banned_by_comps[res[1]].add(res[0])\n for i,r in enumerate(requests):\n n1, n2 = r[0], r[1]\n c1, c2 = connected_comp_dict[n1], connected_comp_dict[n2]\n if c1 == c2:\n result[i] = True\n else:\n if not (connected_components[c1].intersection(banned_by_comps[c2]) or connected_components[c2].intersection(banned_by_comps[c1])):\n connected_components[c1].update(connected_components[c2])\n banned_by_comps[c1].update(banned_by_comps[c2])\n for node in connected_components[c2]:\n connected_comp_dict[node] = c1\n result[i] = True\n \n return result\n\n``` | 2 | You are given an integer `n` indicating the number of people in a network. Each person is labeled from `0` to `n - 1`.
You are also given a **0-indexed** 2D integer array `restrictions`, where `restrictions[i] = [xi, yi]` means that person `xi` and person `yi` **cannot** become **friends**, either **directly** or **indirectly** through other people.
Initially, no one is friends with each other. You are given a list of friend requests as a **0-indexed** 2D integer array `requests`, where `requests[j] = [uj, vj]` is a friend request between person `uj` and person `vj`.
A friend request is **successful** if `uj` and `vj` can be **friends**. Each friend request is processed in the given order (i.e., `requests[j]` occurs before `requests[j + 1]`), and upon a successful request, `uj` and `vj` **become direct friends** for all future friend requests.
Return _a **boolean array**_ `result`, _where each_ `result[j]` _is_ `true` _if the_ `jth` _friend request is **successful** or_ `false` _if it is not_.
**Note:** If `uj` and `vj` are already direct friends, the request is still **successful**.
**Example 1:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[0,2\],\[2,1\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 0 and person 2 can be friends, so they become direct friends.
Request 1: Person 2 and person 1 cannot be friends since person 0 and person 1 would be indirect friends (1--2--0).
**Example 2:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[1,2\],\[0,2\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 1 and person 2 can be friends, so they become direct friends.
Request 1: Person 0 and person 2 cannot be friends since person 0 and person 1 would be indirect friends (0--2--1).
**Example 3:**
**Input:** n = 5, restrictions = \[\[0,1\],\[1,2\],\[2,3\]\], requests = \[\[0,4\],\[1,2\],\[3,1\],\[3,4\]\]
**Output:** \[true,false,true,false\]
**Explanation:**
Request 0: Person 0 and person 4 can be friends, so they become direct friends.
Request 1: Person 1 and person 2 cannot be friends since they are directly restricted.
Request 2: Person 3 and person 1 can be friends, so they become direct friends.
Request 3: Person 3 and person 4 cannot be friends since person 0 and person 1 would be indirect friends (0--4--3--1).
**Constraints:**
* `2 <= n <= 1000`
* `0 <= restrictions.length <= 1000`
* `restrictions[i].length == 2`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= requests.length <= 1000`
* `requests[j].length == 2`
* `0 <= uj, vj <= n - 1`
* `uj != vj` | First, let's note that after the first transform the value will be at most 100 * 9 which is not much After The first transform, we can just do the rest of the transforms by brute force |
Hash Table + Union Find | 661 ms - faster than 71.86% solutions | process-restricted-friend-requests | 0 | 1 | # Complexity\n- Time complexity: $$O(m \\cdot\\log(m) + k \\cdot m \\cdot \\alpha(n))$$\n- Space complexity: $$O(n + m + k)$$\n\nwhere `m = restrictions.length, k = requests.length`,\n$\\alpha(n)$ is inverse Ackermann function ([wiki](https://en.wikipedia.org/wiki/Ackermann_function#Inverse)).\n\nBecause `n < 1000, m < 1000, k < 1000`, let `p = max(n, m, k)`.\n\n- Time complexity: $$O(p^2 \\cdot \\alpha(p))$$\n- Space complexity: $$O(p)$$\n\n# Code\n``` python3 []\nclass DJS:\n def __init__(self, n):\n self._d = list(range(n))\n \n def find(self, a):\n aa = self._d[a]\n if a == aa:\n return aa\n self._d[a] = self.find(aa)\n return self._d[a]\n\n def union(self, a, b):\n aa = self.find(a)\n bb = self.find(b)\n if aa != bb:\n self._d[aa] = bb\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n pairs = defaultdict(set)\n for x, y in sorted(restrictions):\n x, y = min(x, y), max(x, y)\n pairs[x].add(y)\n \n djs = DJS(n)\n\n def check(uu, vv):\n for x, ys in pairs.items():\n xx = djs.find(x)\n if xx != uu and xx != vv:\n continue\n for y in ys: \n yy = djs.find(y)\n if yy == uu or yy == vv:\n return False\n return True\n\n result = []\n for u, v in requests: \n uu = djs.find(u)\n vv = djs.find(v)\n if uu == vv:\n result.append(True)\n continue\n \n current = check(uu, vv)\n result.append(current)\n if current:\n djs.union(uu, vv)\n \n return result\n\n``` | 0 | You are given an integer `n` indicating the number of people in a network. Each person is labeled from `0` to `n - 1`.
You are also given a **0-indexed** 2D integer array `restrictions`, where `restrictions[i] = [xi, yi]` means that person `xi` and person `yi` **cannot** become **friends**, either **directly** or **indirectly** through other people.
Initially, no one is friends with each other. You are given a list of friend requests as a **0-indexed** 2D integer array `requests`, where `requests[j] = [uj, vj]` is a friend request between person `uj` and person `vj`.
A friend request is **successful** if `uj` and `vj` can be **friends**. Each friend request is processed in the given order (i.e., `requests[j]` occurs before `requests[j + 1]`), and upon a successful request, `uj` and `vj` **become direct friends** for all future friend requests.
Return _a **boolean array**_ `result`, _where each_ `result[j]` _is_ `true` _if the_ `jth` _friend request is **successful** or_ `false` _if it is not_.
**Note:** If `uj` and `vj` are already direct friends, the request is still **successful**.
**Example 1:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[0,2\],\[2,1\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 0 and person 2 can be friends, so they become direct friends.
Request 1: Person 2 and person 1 cannot be friends since person 0 and person 1 would be indirect friends (1--2--0).
**Example 2:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[1,2\],\[0,2\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 1 and person 2 can be friends, so they become direct friends.
Request 1: Person 0 and person 2 cannot be friends since person 0 and person 1 would be indirect friends (0--2--1).
**Example 3:**
**Input:** n = 5, restrictions = \[\[0,1\],\[1,2\],\[2,3\]\], requests = \[\[0,4\],\[1,2\],\[3,1\],\[3,4\]\]
**Output:** \[true,false,true,false\]
**Explanation:**
Request 0: Person 0 and person 4 can be friends, so they become direct friends.
Request 1: Person 1 and person 2 cannot be friends since they are directly restricted.
Request 2: Person 3 and person 1 can be friends, so they become direct friends.
Request 3: Person 3 and person 4 cannot be friends since person 0 and person 1 would be indirect friends (0--4--3--1).
**Constraints:**
* `2 <= n <= 1000`
* `0 <= restrictions.length <= 1000`
* `restrictions[i].length == 2`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= requests.length <= 1000`
* `requests[j].length == 2`
* `0 <= uj, vj <= n - 1`
* `uj != vj` | First, let's note that after the first transform the value will be at most 100 * 9 which is not much After The first transform, we can just do the rest of the transforms by brute force |
Union Find + small trick | process-restricted-friend-requests | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBasic union find data structure to be used. The part to tell if the a restriction would be violated before a connection can be made needs some thinking, which is the hardest part of this problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAfter figuring out how to resolve the above problem in the intuition by comparing the bosses/heads of the 2 sets requested to be joint and bosses/heads in every restrictions, it\'s just a union find problem.\n\nUse `for/else` probably for the first time in python\n\n# Complexity\n- Time complexity:\nAs unionfind\n\n- Space complexity:\nUsed a recursive function so probably not very good\n\n# Code\n```\nclass UnionFind:\n def __init__(self, n):\n self.head = [i for i in range(n)]\n\n def connect(self, a, b):\n head_a, head_b = self.find(a), self.find(b)\n\n if head_a == head_b:\n return\n\n self.head[head_a] = self.find(head_b)\n \n def find(self, a):\n if self.head[a] == a:\n return a\n\n self.head[a] = self.find(self.head[a])\n return self.head[a]\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n groups = UnionFind(n)\n res = []\n\n for a, b in requests:\n boss_a, boss_b = groups.find(a), groups.find(b)\n\n if boss_a == boss_b:\n res.append(True)\n continue\n\n for c, d in restrictions:\n boss_c, boss_d = groups.find(c), groups.find(d)\n\n if (boss_a == boss_c and boss_b == boss_d) or (boss_a == boss_d and boss_b == boss_c):\n res.append(False)\n break\n else:\n res.append(True)\n groups.connect(a, b)\n \n return res\n\n\n\n\n \n \n\n``` | 0 | You are given an integer `n` indicating the number of people in a network. Each person is labeled from `0` to `n - 1`.
You are also given a **0-indexed** 2D integer array `restrictions`, where `restrictions[i] = [xi, yi]` means that person `xi` and person `yi` **cannot** become **friends**, either **directly** or **indirectly** through other people.
Initially, no one is friends with each other. You are given a list of friend requests as a **0-indexed** 2D integer array `requests`, where `requests[j] = [uj, vj]` is a friend request between person `uj` and person `vj`.
A friend request is **successful** if `uj` and `vj` can be **friends**. Each friend request is processed in the given order (i.e., `requests[j]` occurs before `requests[j + 1]`), and upon a successful request, `uj` and `vj` **become direct friends** for all future friend requests.
Return _a **boolean array**_ `result`, _where each_ `result[j]` _is_ `true` _if the_ `jth` _friend request is **successful** or_ `false` _if it is not_.
**Note:** If `uj` and `vj` are already direct friends, the request is still **successful**.
**Example 1:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[0,2\],\[2,1\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 0 and person 2 can be friends, so they become direct friends.
Request 1: Person 2 and person 1 cannot be friends since person 0 and person 1 would be indirect friends (1--2--0).
**Example 2:**
**Input:** n = 3, restrictions = \[\[0,1\]\], requests = \[\[1,2\],\[0,2\]\]
**Output:** \[true,false\]
**Explanation:**
Request 0: Person 1 and person 2 can be friends, so they become direct friends.
Request 1: Person 0 and person 2 cannot be friends since person 0 and person 1 would be indirect friends (0--2--1).
**Example 3:**
**Input:** n = 5, restrictions = \[\[0,1\],\[1,2\],\[2,3\]\], requests = \[\[0,4\],\[1,2\],\[3,1\],\[3,4\]\]
**Output:** \[true,false,true,false\]
**Explanation:**
Request 0: Person 0 and person 4 can be friends, so they become direct friends.
Request 1: Person 1 and person 2 cannot be friends since they are directly restricted.
Request 2: Person 3 and person 1 can be friends, so they become direct friends.
Request 3: Person 3 and person 4 cannot be friends since person 0 and person 1 would be indirect friends (0--4--3--1).
**Constraints:**
* `2 <= n <= 1000`
* `0 <= restrictions.length <= 1000`
* `restrictions[i].length == 2`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= requests.length <= 1000`
* `requests[j].length == 2`
* `0 <= uj, vj <= n - 1`
* `uj != vj` | First, let's note that after the first transform the value will be at most 100 * 9 which is not much After The first transform, we can just do the rest of the transforms by brute force |
Constant Space | two-furthest-houses-with-different-colors | 1 | 1 | The maximum distance will always include either first or the last house. This can be proven by a contradiction.\n\nTherefore, we need to return the maximum of two cases: `max(j, n - i - 1)`, where\n- `i` is the leftmost position of the color different from the last color.\n- `j` is the rightmost position of the color different from the first one.\n\n\n\n**C++**\n```cpp\nint maxDistance(vector<int>& cs) {\n int n = cs.size(), i = 0, j = n - 1;\n while (cs[0] == cs[j])\n --j;\n while (cs[n - 1] == cs[i])\n ++i;\n return max(j, n - i - 1);\n}\n```\n**Java**\n```java\npublic int maxDistance(int[] cs) {\n int n = cs.length, i = 0, j = n - 1;\n while (cs[0] == cs[j])\n --j;\n while (cs[n - 1] == cs[i])\n ++i;\n return Math.max(j, n - i - 1); \n}\n```\n\n#### Alternative Solution\nWe only care about two positions: `0` for the first color, and the first position for some other color (`p`).\n\nIt works since we are looking for a maximum distance:\n- If color `i` is different than the first one, the maximum distance is `i`.\n- If color `i` is the same as the first one, the maximum distance is `i - p`.\n\n**Python 3**\n```python\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n p, res = inf, 0\n for i, c in enumerate(colors):\n if (c != colors[0]):\n res = i\n p = min(p, i)\n else:\n res = max(res, i - p)\n return res\n```\n**C++**\n```cpp\nint maxDistance(vector<int>& cs) {\n int p = INT_MAX, res = 1;\n for (int i = 1; i < cs.size(); ++i) {\n if (cs[i] != cs[0])\n p = min(i, p);\n res = max({res, cs[i] == cs[0] ? 0 : i, i - p });\n }\n return res;\n}\n```\n**Java**\n```java\npublic int maxDistance(int[] cs) {\n int p_col2 = Integer.MAX_VALUE, res = 1;\n for (int i = 1; i < cs.length; ++i) {\n if (cs[i] != cs[0]) {\n p_col2 = Math.min(i, p_col2);\n res = i;\n }\n else\n res = Math.max(res, i - p_col2);\n }\n return res; \n}\n``` | 80 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Easy Python solution | Beats 89.95% | two-furthest-houses-with-different-colors | 0 | 1 | \n# Code\n```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n ind1, ind2 = 0, -1\n size = len(colors)\n while ind1 < size:\n front = colors[ind1]\n if front != colors[-1]:\n return size - ind1 - 1\n last = colors[ind2]\n if last != colors[0]:\n return size + ind2\n ind1 += 1\n ind2 -= 1\n\n``` | 2 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
[Python3] one of end points will be used | two-furthest-houses-with-different-colors | 0 | 1 | Downvoters, lease a comment! \n\nIt is not difficult to find out that at least one of the end points will be used. \n\nPlease check out this [commit](https://github.com/gaosanyong/leetcode/commit/b5ca73e6f7d317e9f30f7e67a499b0bf489ec019) for the solutions of weekly 268. \n```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n ans = 0 \n for i, x in enumerate(colors): \n if x != colors[0]: ans = max(ans, i)\n if x != colors[-1]: ans = max(ans, len(colors)-1-i)\n return ans \n``` | 33 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Python3 | both side checking | fastest | two-furthest-houses-with-different-colors | 0 | 1 | ```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n clr1=colors[0]\n clr2=colors[-1]\n mx=0\n for i in range(len(colors)-1,-1,-1):\n if clr1!=colors[i]:\n mx=max(mx,i)\n break\n for i in range(len(colors)):\n if clr2!=colors[i]:\n mx=max(mx,len(colors)-i-1)\n return mx\n``` | 4 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
90% O(n) - Fast & Easy 2-pointer / Greedy | two-furthest-houses-with-different-colors | 0 | 1 | Easiest way to do a scan like this is with two pointers. Fix a left pointer, and while they\'re equal, move the right pointer from the end, inward until they arent. Then, take the distance by index. However, that will only solve the example cases. To correctly solve an edge case (where Greedy comes in to play), do the same thing but from the other end. Fix the right pointer at the end and move the left pointer by one every time. Since you\'re making two separate passes, time complexity isn\'t compounding so it is just O(n). No extra space, either O(1). \n\n\n```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n\t\t#first pass\n l, r = 0, len(colors)-1\n dist = 0\n \n while r > l:\n if colors[r] != colors[l]:\n dist = r-l\n\t\t\t\t#slight performance increase, break out if you find it \n\t\t\t\t#because it can\'t get bigger than this\n break \n r -= 1\n\t\t\t\n #second pass, backwards\n l, r = 0, len(colors)-1\n while r > l:\n if colors[r] != colors[l]:\n dist = max(dist, r-l)\n break\n l += 1\n \n return dist\n\t\n\t | 6 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Easy Python Solution | two-furthest-houses-with-different-colors | 0 | 1 | ```\ndef maxDistance(self, colors: List[int]) -> int:\n m=0\n for i in range(0,len(colors)):\n for j in range(len(colors)-1,0,-1):\n if colors[i]!=colors[j] and j>i:\n m=max(m,j-i)\n return m\n``` | 6 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Python3 simple solution | two-furthest-houses-with-different-colors | 0 | 1 | ```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n x = []\n for i in range(len(colors)-1):\n for j in range(i+1,len(colors)):\n if colors[i] != colors[j]:\n x.append(j-i)\n return max(x)\n```\n**If you like this solution, please upvote for this** | 2 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Simple Python Solution: O(n) | two-furthest-houses-with-different-colors | 0 | 1 | ## INTUITION:\n\n- __Target__: Compute the maximum distance between two houses of different colors\n- __Assumption__: \n\t- The distance between any two houses is uniform and equal to one.\n\t- There has to be atleast two elements in the array/list to compute the distance.\n- Maximum possible distance is observed when the house on the two ends are of different color\n - In such a scenario, we can simply look up the first and last elements of the array/list and return the distance as `length_of _array - 1 `\n- If the first and last houses are of the same color, \n\t- We need to traverse the array to find a house of different color\n\t- Compute the distance from the houses on either ends and take the maximum of it.\n\t- Update a Counter Variable that maintains the largest distance for any such house of different color\n\n## CODE:\n```python\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n n = len(colors)\n if n < 2:\n return 0 \n if colors[0]!=colors[-1]:\n return n-1\n d = 0\n for i in range(n):\n if colors[i] != colors[0]:\n d = max(d,i)\n if colors[i] != colors[-1]:\n d = max(d,n-1-i)\n return d\n```\n\n ## TIME COMPLEXITY:\n- O(n)\n- In the worst case scenario, we have to iterate through the entire list/array of colors for n houses\n\n## SPACE COMPLEXITY:\n- O(1) | 3 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
Two solutions O(n) and O(n^2) | two-furthest-houses-with-different-colors | 0 | 1 | O(n)\n```\nclass Solution:\n def maxDistance(self, colors: List[int]) -> int:\n i=0\n l=len(colors)\n j=l-1\n while colors[j] == colors[0]:\n j-=1\n \n while colors[-1] == colors[i]:\n i+=1\n return max(j,l-1-i)\n```\nO(n^2)\n```\n max_dist=0\n l=len(colors)\n for i in range(l):\n for j in range(l):\n if colors[i]!=colors[j]:\n max_dist = max(max_dist,abs(j-i))\n return max_dist\n```\n | 4 | There are `n` houses evenly lined up on the street, and each house is beautifully painted. You are given a **0-indexed** integer array `colors` of length `n`, where `colors[i]` represents the color of the `ith` house.
Return _the **maximum** distance between **two** houses with **different** colors_.
The distance between the `ith` and `jth` houses is `abs(i - j)`, where `abs(x)` is the **absolute value** of `x`.
**Example 1:**
**Input:** colors = \[**1**,1,1,**6**,1,1,1\]
**Output:** 3
**Explanation:** In the above image, color 1 is blue, and color 6 is red.
The furthest two houses with different colors are house 0 and house 3.
House 0 has color 1, and house 3 has color 6. The distance between them is abs(0 - 3) = 3.
Note that houses 3 and 6 can also produce the optimal answer.
**Example 2:**
**Input:** colors = \[**1**,8,3,8,**3**\]
**Output:** 4
**Explanation:** In the above image, color 1 is blue, color 8 is yellow, and color 3 is green.
The furthest two houses with different colors are house 0 and house 4.
House 0 has color 1, and house 4 has color 3. The distance between them is abs(0 - 4) = 4.
**Example 3:**
**Input:** colors = \[**0**,**1**\]
**Output:** 1
**Explanation:** The furthest two houses with different colors are house 0 and house 1.
House 0 has color 0, and house 1 has color 1. The distance between them is abs(0 - 1) = 1.
**Constraints:**
* `n == colors.length`
* `2 <= n <= 100`
* `0 <= colors[i] <= 100`
* Test data are generated such that **at least** two houses have different colors. | Calculate the compatibility score for each student-mentor pair. Try every permutation of students with the original mentors array. |
[Python3] simulation | watering-plants | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b5ca73e6f7d317e9f30f7e67a499b0bf489ec019) for the solutions of weekly 268. \n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n ans = 0\n can = capacity\n for i, x in enumerate(plants): \n if can < x: \n ans += 2*i\n can = capacity\n ans += 1\n can -= x\n return ans \n``` | 25 | You want to water `n` plants in your garden with a watering can. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`. There is a river at `x = -1` that you can refill your watering can at.
Each plant needs a specific amount of water. You will water the plants in the following way:
* Water the plants in order from left to right.
* After watering the current plant, if you do not have enough water to **completely** water the next plant, return to the river to fully refill the watering can.
* You **cannot** refill the watering can early.
You are initially at the river (i.e., `x = -1`). It takes **one step** to move **one unit** on the x-axis.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and an integer `capacity` representing the watering can capacity, return _the **number of steps** needed to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacity = 5
**Output:** 14
**Explanation:** Start at the river with a full watering can:
- Walk to plant 0 (1 step) and water it. Watering can has 3 units of water.
- Walk to plant 1 (1 step) and water it. Watering can has 1 unit of water.
- Since you cannot completely water plant 2, walk back to the river to refill (2 steps).
- Walk to plant 2 (3 steps) and water it. Watering can has 2 units of water.
- Since you cannot completely water plant 3, walk back to the river to refill (3 steps).
- Walk to plant 3 (4 steps) and water it.
Steps needed = 1 + 1 + 2 + 3 + 3 + 4 = 14.
**Example 2:**
**Input:** plants = \[1,1,1,4,2,3\], capacity = 4
**Output:** 30
**Explanation:** Start at the river with a full watering can:
- Water plants 0, 1, and 2 (3 steps). Return to river (3 steps).
- Water plant 3 (4 steps). Return to river (4 steps).
- Water plant 4 (5 steps). Return to river (5 steps).
- Water plant 5 (6 steps).
Steps needed = 3 + 3 + 4 + 4 + 5 + 5 + 6 = 30.
**Example 3:**
**Input:** plants = \[7,7,7,7,7,7,7\], capacity = 8
**Output:** 49
**Explanation:** You have to refill before watering each plant.
Steps needed = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 5 + 6 + 6 + 7 = 49.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 1000`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacity <= 109` | Can we use a trie to build the folder structure? Can we utilize hashing to hash the folder structures? |
[Python3] simulation | watering-plants | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b5ca73e6f7d317e9f30f7e67a499b0bf489ec019) for the solutions of weekly 268. \n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n ans = 0\n can = capacity\n for i, x in enumerate(plants): \n if can < x: \n ans += 2*i\n can = capacity\n ans += 1\n can -= x\n return ans \n``` | 25 | You are given an array `arr` of positive integers. You are also given the array `queries` where `queries[i] = [lefti, righti]`.
For each query `i` compute the **XOR** of elements from `lefti` to `righti` (that is, `arr[lefti] XOR arr[lefti + 1] XOR ... XOR arr[righti]` ).
Return an array `answer` where `answer[i]` is the answer to the `ith` query.
**Example 1:**
**Input:** arr = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[0,3\],\[3,3\]\]
**Output:** \[2,7,14,8\]
**Explanation:**
The binary representation of the elements in the array are:
1 = 0001
3 = 0011
4 = 0100
8 = 1000
The XOR values for queries are:
\[0,1\] = 1 xor 3 = 2
\[1,2\] = 3 xor 4 = 7
\[0,3\] = 1 xor 3 xor 4 xor 8 = 14
\[3,3\] = 8
**Example 2:**
**Input:** arr = \[4,8,2,10\], queries = \[\[2,3\],\[1,3\],\[0,0\],\[0,3\]\]
**Output:** \[8,0,4,4\]
**Constraints:**
* `1 <= arr.length, queries.length <= 3 * 104`
* `1 <= arr[i] <= 109`
* `queries[i].length == 2`
* `0 <= lefti <= righti < arr.length` | Simulate the process. Return to refill the container once you meet a plant that needs more water than you have. |
Awesome Logic problem | watering-plants | 0 | 1 | ```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n stored=capacity\n ans=0\n for i,v in enumerate(plants):\n if capacity>=v:\n ans+=1\n capacity-=v\n else:\n\t\t\t# main Logic\n ans+=i+(i+1) \n capacity=stored-v\n return ans\n```\n# please upvote me it would encourage me alot\n\n\t\t | 2 | You want to water `n` plants in your garden with a watering can. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`. There is a river at `x = -1` that you can refill your watering can at.
Each plant needs a specific amount of water. You will water the plants in the following way:
* Water the plants in order from left to right.
* After watering the current plant, if you do not have enough water to **completely** water the next plant, return to the river to fully refill the watering can.
* You **cannot** refill the watering can early.
You are initially at the river (i.e., `x = -1`). It takes **one step** to move **one unit** on the x-axis.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and an integer `capacity` representing the watering can capacity, return _the **number of steps** needed to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacity = 5
**Output:** 14
**Explanation:** Start at the river with a full watering can:
- Walk to plant 0 (1 step) and water it. Watering can has 3 units of water.
- Walk to plant 1 (1 step) and water it. Watering can has 1 unit of water.
- Since you cannot completely water plant 2, walk back to the river to refill (2 steps).
- Walk to plant 2 (3 steps) and water it. Watering can has 2 units of water.
- Since you cannot completely water plant 3, walk back to the river to refill (3 steps).
- Walk to plant 3 (4 steps) and water it.
Steps needed = 1 + 1 + 2 + 3 + 3 + 4 = 14.
**Example 2:**
**Input:** plants = \[1,1,1,4,2,3\], capacity = 4
**Output:** 30
**Explanation:** Start at the river with a full watering can:
- Water plants 0, 1, and 2 (3 steps). Return to river (3 steps).
- Water plant 3 (4 steps). Return to river (4 steps).
- Water plant 4 (5 steps). Return to river (5 steps).
- Water plant 5 (6 steps).
Steps needed = 3 + 3 + 4 + 4 + 5 + 5 + 6 = 30.
**Example 3:**
**Input:** plants = \[7,7,7,7,7,7,7\], capacity = 8
**Output:** 49
**Explanation:** You have to refill before watering each plant.
Steps needed = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 5 + 6 + 6 + 7 = 49.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 1000`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacity <= 109` | Can we use a trie to build the folder structure? Can we utilize hashing to hash the folder structures? |
Awesome Logic problem | watering-plants | 0 | 1 | ```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n stored=capacity\n ans=0\n for i,v in enumerate(plants):\n if capacity>=v:\n ans+=1\n capacity-=v\n else:\n\t\t\t# main Logic\n ans+=i+(i+1) \n capacity=stored-v\n return ans\n```\n# please upvote me it would encourage me alot\n\n\t\t | 2 | You are given an array `arr` of positive integers. You are also given the array `queries` where `queries[i] = [lefti, righti]`.
For each query `i` compute the **XOR** of elements from `lefti` to `righti` (that is, `arr[lefti] XOR arr[lefti + 1] XOR ... XOR arr[righti]` ).
Return an array `answer` where `answer[i]` is the answer to the `ith` query.
**Example 1:**
**Input:** arr = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[0,3\],\[3,3\]\]
**Output:** \[2,7,14,8\]
**Explanation:**
The binary representation of the elements in the array are:
1 = 0001
3 = 0011
4 = 0100
8 = 1000
The XOR values for queries are:
\[0,1\] = 1 xor 3 = 2
\[1,2\] = 3 xor 4 = 7
\[0,3\] = 1 xor 3 xor 4 xor 8 = 14
\[3,3\] = 8
**Example 2:**
**Input:** arr = \[4,8,2,10\], queries = \[\[2,3\],\[1,3\],\[0,0\],\[0,3\]\]
**Output:** \[8,0,4,4\]
**Constraints:**
* `1 <= arr.length, queries.length <= 3 * 104`
* `1 <= arr[i] <= 109`
* `queries[i].length == 2`
* `0 <= lefti <= righti < arr.length` | Simulate the process. Return to refill the container once you meet a plant that needs more water than you have. |
[PYTHON 3] FASTER THAN 96.9% | LESS THAN 84.8% | watering-plants | 0 | 1 | Runtime: **47 ms, faster than 96.80%** of Python3 online submissions for Watering Plants.\nMemory Usage: **14 MB, less than 84.80%** of Python3 online submissions for Watering Plants.\n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n s, p, c = 0, -1, capacity\n for i, e in enumerate(plants):\n if e <= c: s += i - p; c -= e\n else: s += p + i + 2; c = capacity - e\n p = i\n return s | 2 | You want to water `n` plants in your garden with a watering can. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`. There is a river at `x = -1` that you can refill your watering can at.
Each plant needs a specific amount of water. You will water the plants in the following way:
* Water the plants in order from left to right.
* After watering the current plant, if you do not have enough water to **completely** water the next plant, return to the river to fully refill the watering can.
* You **cannot** refill the watering can early.
You are initially at the river (i.e., `x = -1`). It takes **one step** to move **one unit** on the x-axis.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and an integer `capacity` representing the watering can capacity, return _the **number of steps** needed to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacity = 5
**Output:** 14
**Explanation:** Start at the river with a full watering can:
- Walk to plant 0 (1 step) and water it. Watering can has 3 units of water.
- Walk to plant 1 (1 step) and water it. Watering can has 1 unit of water.
- Since you cannot completely water plant 2, walk back to the river to refill (2 steps).
- Walk to plant 2 (3 steps) and water it. Watering can has 2 units of water.
- Since you cannot completely water plant 3, walk back to the river to refill (3 steps).
- Walk to plant 3 (4 steps) and water it.
Steps needed = 1 + 1 + 2 + 3 + 3 + 4 = 14.
**Example 2:**
**Input:** plants = \[1,1,1,4,2,3\], capacity = 4
**Output:** 30
**Explanation:** Start at the river with a full watering can:
- Water plants 0, 1, and 2 (3 steps). Return to river (3 steps).
- Water plant 3 (4 steps). Return to river (4 steps).
- Water plant 4 (5 steps). Return to river (5 steps).
- Water plant 5 (6 steps).
Steps needed = 3 + 3 + 4 + 4 + 5 + 5 + 6 = 30.
**Example 3:**
**Input:** plants = \[7,7,7,7,7,7,7\], capacity = 8
**Output:** 49
**Explanation:** You have to refill before watering each plant.
Steps needed = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 5 + 6 + 6 + 7 = 49.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 1000`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacity <= 109` | Can we use a trie to build the folder structure? Can we utilize hashing to hash the folder structures? |
[PYTHON 3] FASTER THAN 96.9% | LESS THAN 84.8% | watering-plants | 0 | 1 | Runtime: **47 ms, faster than 96.80%** of Python3 online submissions for Watering Plants.\nMemory Usage: **14 MB, less than 84.80%** of Python3 online submissions for Watering Plants.\n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n s, p, c = 0, -1, capacity\n for i, e in enumerate(plants):\n if e <= c: s += i - p; c -= e\n else: s += p + i + 2; c = capacity - e\n p = i\n return s | 2 | You are given an array `arr` of positive integers. You are also given the array `queries` where `queries[i] = [lefti, righti]`.
For each query `i` compute the **XOR** of elements from `lefti` to `righti` (that is, `arr[lefti] XOR arr[lefti + 1] XOR ... XOR arr[righti]` ).
Return an array `answer` where `answer[i]` is the answer to the `ith` query.
**Example 1:**
**Input:** arr = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[0,3\],\[3,3\]\]
**Output:** \[2,7,14,8\]
**Explanation:**
The binary representation of the elements in the array are:
1 = 0001
3 = 0011
4 = 0100
8 = 1000
The XOR values for queries are:
\[0,1\] = 1 xor 3 = 2
\[1,2\] = 3 xor 4 = 7
\[0,3\] = 1 xor 3 xor 4 xor 8 = 14
\[3,3\] = 8
**Example 2:**
**Input:** arr = \[4,8,2,10\], queries = \[\[2,3\],\[1,3\],\[0,0\],\[0,3\]\]
**Output:** \[8,0,4,4\]
**Constraints:**
* `1 <= arr.length, queries.length <= 3 * 104`
* `1 <= arr[i] <= 109`
* `queries[i].length == 2`
* `0 <= lefti <= righti < arr.length` | Simulate the process. Return to refill the container once you meet a plant that needs more water than you have. |
Simple Python Solution 8 Lines 63 % | watering-plants | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n right, water,steps = 0, capacity, 0, \n while right < len(plants):\n water = capacity\n while right < len(plants) and water >= plants[right]:\n steps += 1\n water -= plants[right]\n right += 1\n\n if right <len(plants): \n steps += (2* (right))\n return steps \n\n\n``` | 1 | You want to water `n` plants in your garden with a watering can. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`. There is a river at `x = -1` that you can refill your watering can at.
Each plant needs a specific amount of water. You will water the plants in the following way:
* Water the plants in order from left to right.
* After watering the current plant, if you do not have enough water to **completely** water the next plant, return to the river to fully refill the watering can.
* You **cannot** refill the watering can early.
You are initially at the river (i.e., `x = -1`). It takes **one step** to move **one unit** on the x-axis.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and an integer `capacity` representing the watering can capacity, return _the **number of steps** needed to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacity = 5
**Output:** 14
**Explanation:** Start at the river with a full watering can:
- Walk to plant 0 (1 step) and water it. Watering can has 3 units of water.
- Walk to plant 1 (1 step) and water it. Watering can has 1 unit of water.
- Since you cannot completely water plant 2, walk back to the river to refill (2 steps).
- Walk to plant 2 (3 steps) and water it. Watering can has 2 units of water.
- Since you cannot completely water plant 3, walk back to the river to refill (3 steps).
- Walk to plant 3 (4 steps) and water it.
Steps needed = 1 + 1 + 2 + 3 + 3 + 4 = 14.
**Example 2:**
**Input:** plants = \[1,1,1,4,2,3\], capacity = 4
**Output:** 30
**Explanation:** Start at the river with a full watering can:
- Water plants 0, 1, and 2 (3 steps). Return to river (3 steps).
- Water plant 3 (4 steps). Return to river (4 steps).
- Water plant 4 (5 steps). Return to river (5 steps).
- Water plant 5 (6 steps).
Steps needed = 3 + 3 + 4 + 4 + 5 + 5 + 6 = 30.
**Example 3:**
**Input:** plants = \[7,7,7,7,7,7,7\], capacity = 8
**Output:** 49
**Explanation:** You have to refill before watering each plant.
Steps needed = 1 + 1 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 5 + 6 + 6 + 7 = 49.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 1000`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacity <= 109` | Can we use a trie to build the folder structure? Can we utilize hashing to hash the folder structures? |
Simple Python Solution 8 Lines 63 % | watering-plants | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def wateringPlants(self, plants: List[int], capacity: int) -> int:\n right, water,steps = 0, capacity, 0, \n while right < len(plants):\n water = capacity\n while right < len(plants) and water >= plants[right]:\n steps += 1\n water -= plants[right]\n right += 1\n\n if right <len(plants): \n steps += (2* (right))\n return steps \n\n\n``` | 1 | You are given an array `arr` of positive integers. You are also given the array `queries` where `queries[i] = [lefti, righti]`.
For each query `i` compute the **XOR** of elements from `lefti` to `righti` (that is, `arr[lefti] XOR arr[lefti + 1] XOR ... XOR arr[righti]` ).
Return an array `answer` where `answer[i]` is the answer to the `ith` query.
**Example 1:**
**Input:** arr = \[1,3,4,8\], queries = \[\[0,1\],\[1,2\],\[0,3\],\[3,3\]\]
**Output:** \[2,7,14,8\]
**Explanation:**
The binary representation of the elements in the array are:
1 = 0001
3 = 0011
4 = 0100
8 = 1000
The XOR values for queries are:
\[0,1\] = 1 xor 3 = 2
\[1,2\] = 3 xor 4 = 7
\[0,3\] = 1 xor 3 xor 4 xor 8 = 14
\[3,3\] = 8
**Example 2:**
**Input:** arr = \[4,8,2,10\], queries = \[\[2,3\],\[1,3\],\[0,0\],\[0,3\]\]
**Output:** \[8,0,4,4\]
**Constraints:**
* `1 <= arr.length, queries.length <= 3 * 104`
* `1 <= arr[i] <= 109`
* `queries[i].length == 2`
* `0 <= lefti <= righti < arr.length` | Simulate the process. Return to refill the container once you meet a plant that needs more water than you have. |
Arrays of Indices | range-frequency-queries | 1 | 1 | Since the value is limited to 10,000, we can just store positions for each value and then binary-search for the range.\n\n> Note: a lot of folks got TLE because they collected frequencies for each number and each position. This allows answering queries in O(1), but populating the array takes O(n * m) time and space.\n\n**Java**\n```java\nList<Integer>[] ids = new ArrayList[10001];\nFunction<Integer, Integer> lower_bound = (pos) -> pos < 0 ? ~pos : pos;\npublic RangeFreqQuery(int[] arr) {\n for (int i = 0; i < ids.length; ++i)\n ids[i] = new ArrayList<>();\n for (int i = 0; i < arr.length; ++i)\n ids[arr[i]].add(i);\n}\npublic int query(int l, int r, int v) {\n return lower_bound.apply(Collections.binarySearch(ids[v], r + 1)) - lower_bound.apply(Collections.binarySearch(ids[v], l));\n}\n```\n\n**Python 3**\n```python\nclass RangeFreqQuery:\n def __init__(self, arr: List[int]):\n self.l = [[] for _ in range(10001)]\n for i, v in enumerate(arr):\n self.l[v].append(i)\n def query(self, left: int, right: int, v: int) -> int:\n return bisect_right(self.l[v], right) - bisect_left(self.l[v], left)\n```\n\n**C++**\n```cpp\nvector<int> ids[10001] = {};\nRangeFreqQuery(vector<int>& arr) {\n for (int i = 0; i < arr.size(); ++i)\n ids[arr[i]].push_back(i);\n}\nint query(int left, int right, int v) {\n return upper_bound(begin(ids[v]), end(ids[v]), right) - \n lower_bound(begin(ids[v]), end(ids[v]), left);\n}\n``` | 41 | Design a data structure to find the **frequency** of a given value in a given subarray.
The **frequency** of a value in a subarray is the number of occurrences of that value in the subarray.
Implement the `RangeFreqQuery` class:
* `RangeFreqQuery(int[] arr)` Constructs an instance of the class with the given **0-indexed** integer array `arr`.
* `int query(int left, int right, int value)` Returns the **frequency** of `value` in the subarray `arr[left...right]`.
A **subarray** is a contiguous sequence of elements within an array. `arr[left...right]` denotes the subarray that contains the elements of `nums` between indices `left` and `right` (**inclusive**).
**Example 1:**
**Input**
\[ "RangeFreqQuery ", "query ", "query "\]
\[\[\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]\], \[1, 2, 4\], \[0, 11, 33\]\]
**Output**
\[null, 1, 2\]
**Explanation**
RangeFreqQuery rangeFreqQuery = new RangeFreqQuery(\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]);
rangeFreqQuery.query(1, 2, 4); // return 1. The value 4 occurs 1 time in the subarray \[33, 4\]
rangeFreqQuery.query(0, 11, 33); // return 2. The value 33 occurs 2 times in the whole array.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], value <= 104`
* `0 <= left <= right < arr.length`
* At most `105` calls will be made to `query` | For each line starting at the given cell check if it's a good line To do that iterate over all directions horizontal, vertical, and diagonals then check good lines naively |
[Python3] binary search | range-frequency-queries | 0 | 1 | Downvoters, leave a comment! \n\nPlease check out this [commit](https://github.com/gaosanyong/leetcode/commit/b5ca73e6f7d317e9f30f7e67a499b0bf489ec019) for the solutions of weekly 268. \n```\nclass RangeFreqQuery:\n\n def __init__(self, arr: List[int]):\n self.loc = defaultdict(list)\n for i, x in enumerate(arr): self.loc[x].append(i)\n\n def query(self, left: int, right: int, value: int) -> int:\n if value not in self.loc: return 0 \n lo = bisect_left(self.loc[value], left)\n hi = bisect_right(self.loc[value], right)\n return hi - lo \n``` | 9 | Design a data structure to find the **frequency** of a given value in a given subarray.
The **frequency** of a value in a subarray is the number of occurrences of that value in the subarray.
Implement the `RangeFreqQuery` class:
* `RangeFreqQuery(int[] arr)` Constructs an instance of the class with the given **0-indexed** integer array `arr`.
* `int query(int left, int right, int value)` Returns the **frequency** of `value` in the subarray `arr[left...right]`.
A **subarray** is a contiguous sequence of elements within an array. `arr[left...right]` denotes the subarray that contains the elements of `nums` between indices `left` and `right` (**inclusive**).
**Example 1:**
**Input**
\[ "RangeFreqQuery ", "query ", "query "\]
\[\[\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]\], \[1, 2, 4\], \[0, 11, 33\]\]
**Output**
\[null, 1, 2\]
**Explanation**
RangeFreqQuery rangeFreqQuery = new RangeFreqQuery(\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]);
rangeFreqQuery.query(1, 2, 4); // return 1. The value 4 occurs 1 time in the subarray \[33, 4\]
rangeFreqQuery.query(0, 11, 33); // return 2. The value 33 occurs 2 times in the whole array.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], value <= 104`
* `0 <= left <= right < arr.length`
* At most `105` calls will be made to `query` | For each line starting at the given cell check if it's a good line To do that iterate over all directions horizontal, vertical, and diagonals then check good lines naively |
Easy solution - Python | range-frequency-queries | 0 | 1 | Please upvote if you like the solution\n\n# Code\n```\nclass RangeFreqQuery:\n \n \n def __init__(self, arr: List[int]):\n self.arr = arr\n self.mydict = {}\n \n\n def query(self, left: int, right: int, value: int) -> int:\n if value in self.mydict and self.mydict[value][0]==left and self.mydict[value][1]==right:\n return self.mydict[value][2]\n else:\n freq = self.arr[left:right+1].count(value)\n self.mydict[value] = [left,right,freq] \n return freq \n\n \n\n \n \n\n\n# Your RangeFreqQuery object will be instantiated and called as such:\n# obj = RangeFreqQuery(arr)\n# param_1 = obj.query(left,right,value)\n``` | 0 | Design a data structure to find the **frequency** of a given value in a given subarray.
The **frequency** of a value in a subarray is the number of occurrences of that value in the subarray.
Implement the `RangeFreqQuery` class:
* `RangeFreqQuery(int[] arr)` Constructs an instance of the class with the given **0-indexed** integer array `arr`.
* `int query(int left, int right, int value)` Returns the **frequency** of `value` in the subarray `arr[left...right]`.
A **subarray** is a contiguous sequence of elements within an array. `arr[left...right]` denotes the subarray that contains the elements of `nums` between indices `left` and `right` (**inclusive**).
**Example 1:**
**Input**
\[ "RangeFreqQuery ", "query ", "query "\]
\[\[\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]\], \[1, 2, 4\], \[0, 11, 33\]\]
**Output**
\[null, 1, 2\]
**Explanation**
RangeFreqQuery rangeFreqQuery = new RangeFreqQuery(\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]);
rangeFreqQuery.query(1, 2, 4); // return 1. The value 4 occurs 1 time in the subarray \[33, 4\]
rangeFreqQuery.query(0, 11, 33); // return 2. The value 33 occurs 2 times in the whole array.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], value <= 104`
* `0 <= left <= right < arr.length`
* At most `105` calls will be made to `query` | For each line starting at the given cell check if it's a good line To do that iterate over all directions horizontal, vertical, and diagonals then check good lines naively |
Binary Search, Count Dict, DP Python | range-frequency-queries | 0 | 1 | # Complexity\n- Time complexity:\n\n O(N + qlog(N)) \n\n O(N) to build count list.\n log(N) for each q queries.\n\n- Space complexity:\n\n O(N)\n\n# Code\n```\nfrom bisect import bisect_right, bisect_left\nclass RangeFreqQuery:\n \n def __init__(self, arr: List[int]):\n self.count = [[] for _ in range(10001)]\n for i, num in enumerate(arr):\n self.count[num].append(i)\n\n \n def query(self, left: int, right: int, value: int) -> int:\n # make sure that left and right do not pass each other\n return bisect_right(self.count[value], right) - bisect_left(self.count[value], left)\n \n \n"""\nThis works but stores a lot of memory\n\nclass RangeFreqQuery:\n \n def __init__(self, arr: List[int]):\n self.count = []\n curr_dict = {}\n for num in arr:\n curr_dict[num] = curr_dict.get(num, 0) + 1\n\n self.count.append(curr_dict.copy())\n self.count.append({})\n \n def query(self, left: int, right: int, value: int) -> int:\n # make sure that left and right do not pass each other\n return self.count[right].get(value, 0) - self.count[left - 1].get(value, 0)\n\n---\n\nThis is a DP version that takes a lot of memory\nThis is pretty much like a segment tree without updates\nclass RangeFreqQuery:\n # This is pretty much like a segment tree without updates\n def __init__(self, arr: List[int]):\n self.arr = arr\n \n @lru_cache(maxsize=None)\n def query(self, left: int, right: int, value: int) -> int:\n # make sure that left and right do not pass each other\n if left == right:\n return int(self.arr[left] == value)\n \n mid = (right + left) // 2 \n return self.query(left, mid, value) + self.query(mid + 1, right, value)\n\n"""\n \n\n\n\n\n\n# Your RangeFreqQuery object will be instantiated and called as such:\n# obj = RangeFreqQuery(arr)\n# param_1 = obj.query(left,right,value)\n``` | 0 | Design a data structure to find the **frequency** of a given value in a given subarray.
The **frequency** of a value in a subarray is the number of occurrences of that value in the subarray.
Implement the `RangeFreqQuery` class:
* `RangeFreqQuery(int[] arr)` Constructs an instance of the class with the given **0-indexed** integer array `arr`.
* `int query(int left, int right, int value)` Returns the **frequency** of `value` in the subarray `arr[left...right]`.
A **subarray** is a contiguous sequence of elements within an array. `arr[left...right]` denotes the subarray that contains the elements of `nums` between indices `left` and `right` (**inclusive**).
**Example 1:**
**Input**
\[ "RangeFreqQuery ", "query ", "query "\]
\[\[\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]\], \[1, 2, 4\], \[0, 11, 33\]\]
**Output**
\[null, 1, 2\]
**Explanation**
RangeFreqQuery rangeFreqQuery = new RangeFreqQuery(\[12, 33, 4, 56, 22, 2, 34, 33, 22, 12, 34, 56\]);
rangeFreqQuery.query(1, 2, 4); // return 1. The value 4 occurs 1 time in the subarray \[33, 4\]
rangeFreqQuery.query(0, 11, 33); // return 2. The value 33 occurs 2 times in the whole array.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], value <= 104`
* `0 <= left <= right < arr.length`
* At most `105` calls will be made to `query` | For each line starting at the given cell check if it's a good line To do that iterate over all directions horizontal, vertical, and diagonals then check good lines naively |
[Python3] enumerate k-symmetric numbers | sum-of-k-mirror-numbers | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b5ca73e6f7d317e9f30f7e67a499b0bf489ec019) for the solutions of weekly 268. \n\n```\nclass Solution:\n def kMirror(self, k: int, n: int) -> int:\n \n def fn(x):\n """Return next k-symmetric number."""\n n = len(x)//2\n for i in range(n, len(x)): \n if int(x[i])+1 < k: \n x[i] = x[~i] = str(int(x[i])+1)\n for ii in range(n, i): x[ii] = x[~ii] = \'0\'\n return x\n return ["1"] + ["0"]*(len(x)-1) + ["1"]\n \n x = ["0"]\n ans = 0\n for _ in range(n): \n while True: \n x = fn(x)\n val = int("".join(x), k)\n if str(val)[::-1] == str(val): break\n ans += val\n return ans \n``` | 48 | A **k-mirror number** is a **positive** integer **without leading zeros** that reads the same both forward and backward in base-10 **as well as** in base-k.
* For example, `9` is a 2-mirror number. The representation of `9` in base-10 and base-2 are `9` and `1001` respectively, which read the same both forward and backward.
* On the contrary, `4` is not a 2-mirror number. The representation of `4` in base-2 is `100`, which does not read the same both forward and backward.
Given the base `k` and the number `n`, return _the **sum** of the_ `n` _**smallest** k-mirror numbers_.
**Example 1:**
**Input:** k = 2, n = 5
**Output:** 25
**Explanation:**
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
base-10 base-2
1 1
3 11
5 101
7 111
9 1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25.
**Example 2:**
**Input:** k = 3, n = 7
**Output:** 499
**Explanation:**
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
base-10 base-3
1 1
2 2
4 11
8 22
121 11111
151 12121
212 21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.
**Example 3:**
**Input:** k = 7, n = 17
**Output:** 20379000
**Explanation:** The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 30` | Given a range, how can you find the minimum waste if you can't perform any resize operations? Can we build our solution using dynamic programming using the current index and the number of resizing operations performed as the states? |
[Python3] Easy Python Brute Force with comment | sum-of-k-mirror-numbers | 0 | 1 | ```python\nclass Solution:\n def kMirror(self, k: int, n: int) -> int:\n\n def numberToBase(n, b):\n if n == 0:\n return [0]\n digits = []\n while n:\n digits.append(n % b)\n n //= b\n return digits[::-1]\n \n # not used\n def baseToNumber(arr, b):\n ans = 0\n for x in arr:\n ans = ans * b + int(x)\n return ans\n \n def is_mirror(s):\n l, r = 0, len(s)-1\n while l <= r:\n if s[l] != s[r]:\n return False\n l += 1\n r -= 1\n return True\n \n def gen():\n \'\'\'\n generate for value with different length\n when i == 0: num\uFF1A[1, 10)\n size of num: 1, 2 -> 1 or 11\n when i == 1: [10, 100)\n size of num: 3, 4 -> 10 or 101\n when i == 2: [100, 1000)\n size of num: 5, 6 -> 10001 or 100001\n \n the num will be increasing\n \'\'\'\n for i in range(30):\n for num in range(10**i, 10**(i+1)):\n s = str(num) + str(num)[::-1][1:]\n yield int(s)\n for num in range(10**i, 10**(i+1)):\n s = str(num) + str(num)[::-1]\n yield int(s)\n \n ans = 0\n left = n\n for num in gen():\n base = numberToBase(num, k)\n\t\t\t# if is_mirror(base):\n if base == base[::-1]:\n ans += num\n left -= 1\n if left == 0:\n break\n\n return ans\n``` | 10 | A **k-mirror number** is a **positive** integer **without leading zeros** that reads the same both forward and backward in base-10 **as well as** in base-k.
* For example, `9` is a 2-mirror number. The representation of `9` in base-10 and base-2 are `9` and `1001` respectively, which read the same both forward and backward.
* On the contrary, `4` is not a 2-mirror number. The representation of `4` in base-2 is `100`, which does not read the same both forward and backward.
Given the base `k` and the number `n`, return _the **sum** of the_ `n` _**smallest** k-mirror numbers_.
**Example 1:**
**Input:** k = 2, n = 5
**Output:** 25
**Explanation:**
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
base-10 base-2
1 1
3 11
5 101
7 111
9 1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25.
**Example 2:**
**Input:** k = 3, n = 7
**Output:** 499
**Explanation:**
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
base-10 base-3
1 1
2 2
4 11
8 22
121 11111
151 12121
212 21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.
**Example 3:**
**Input:** k = 7, n = 17
**Output:** 20379000
**Explanation:** The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 30` | Given a range, how can you find the minimum waste if you can't perform any resize operations? Can we build our solution using dynamic programming using the current index and the number of resizing operations performed as the states? |
Python Itertools Product base k generation | sum-of-k-mirror-numbers | 0 | 1 | # Intuition\nGenerate all base-k palindromes in order, then convert them to base 10 to check if they are also palidromes there\n\n# Approach\nPalindromes come in two forms- even length and odd length. \n\nTo generate an even palindrome, first generate the first half of the palindrome, then mirror it around the middle. For k = 3, the palidromes of length 4 are\n```\n1001\n1111\n1221\n2002\n2112\n2222\n```\nSo the values that have to be generated are:\n```\n10\n11\n12\n20\n21\n22\n```\n\n\nItertools product can be used to generate these:\n```py\nfor product in itertools.product(range(k), repeat=<length of sequence>):\n```\nand skipping over values with leading 0\'s\n\nOdd values can be generated in a similar method by removing the middle value of the front or the back\n\n\n# Code\n```\nfrom itertools import product\n\nclass Solution:\n def kMirror(self, k: int, n: int) -> int:\n\n sumOf = 0\n length = 1\n\n while n:\n gen_len = (1 + length) // 2\n for x in product(range(k), repeat=gen_len):\n if x[0] == 0: continue\n\n string_product = \'\'.join(str(val) for val in x)\n\n curr = \'\'\n if length % 2 == 0:\n curr = string_product + string_product[::-1]\n else:\n curr = string_product[:-1] + string_product[::-1]\n\n base10 = int(curr, k)\n \n if str(base10) == str(base10)[::-1]:\n n -= 1\n sumOf += base10\n if n == 0:\n break\n length += 1\n\n\n return sumOf\n\n``` | 0 | A **k-mirror number** is a **positive** integer **without leading zeros** that reads the same both forward and backward in base-10 **as well as** in base-k.
* For example, `9` is a 2-mirror number. The representation of `9` in base-10 and base-2 are `9` and `1001` respectively, which read the same both forward and backward.
* On the contrary, `4` is not a 2-mirror number. The representation of `4` in base-2 is `100`, which does not read the same both forward and backward.
Given the base `k` and the number `n`, return _the **sum** of the_ `n` _**smallest** k-mirror numbers_.
**Example 1:**
**Input:** k = 2, n = 5
**Output:** 25
**Explanation:**
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
base-10 base-2
1 1
3 11
5 101
7 111
9 1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25.
**Example 2:**
**Input:** k = 3, n = 7
**Output:** 499
**Explanation:**
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
base-10 base-3
1 1
2 2
4 11
8 22
121 11111
151 12121
212 21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.
**Example 3:**
**Input:** k = 7, n = 17
**Output:** 20379000
**Explanation:** The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 30` | Given a range, how can you find the minimum waste if you can't perform any resize operations? Can we build our solution using dynamic programming using the current index and the number of resizing operations performed as the states? |
69th Solution | sum-of-k-mirror-numbers | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kMirror(self, k: int, n: int) -> int:\n \n # start from single digit base k\n cands = [str(i) for i in range(1, k)]\n ans = 0\n \n while n > 0:\n # check current canddiates to see if base 10 is also mirroring\n for cand in cands:\n b10 = str(int(cand, k))\n if b10 == b10[::-1]:\n ans += int(b10)\n n -= 1\n if n == 0: return ans\n\n new_cands = []\n for cand in cands:\n m = len(cand)\n for i in range(k):\n if m % 2 == 0:\n new_cands.append(cand[:m//2] + str(i) + cand[m//2:])\n else:\n left, right = cand[:m//2+1], cand[m//2+1:]\n if str(i) == left[-1]:\n new_cands.append(left + str(i) + right)\n cands = new_cands\n\n return ans\n``` | 0 | A **k-mirror number** is a **positive** integer **without leading zeros** that reads the same both forward and backward in base-10 **as well as** in base-k.
* For example, `9` is a 2-mirror number. The representation of `9` in base-10 and base-2 are `9` and `1001` respectively, which read the same both forward and backward.
* On the contrary, `4` is not a 2-mirror number. The representation of `4` in base-2 is `100`, which does not read the same both forward and backward.
Given the base `k` and the number `n`, return _the **sum** of the_ `n` _**smallest** k-mirror numbers_.
**Example 1:**
**Input:** k = 2, n = 5
**Output:** 25
**Explanation:**
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
base-10 base-2
1 1
3 11
5 101
7 111
9 1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25.
**Example 2:**
**Input:** k = 3, n = 7
**Output:** 499
**Explanation:**
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
base-10 base-3
1 1
2 2
4 11
8 22
121 11111
151 12121
212 21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.
**Example 3:**
**Input:** k = 7, n = 17
**Output:** 20379000
**Explanation:** The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 30` | Given a range, how can you find the minimum waste if you can't perform any resize operations? Can we build our solution using dynamic programming using the current index and the number of resizing operations performed as the states? |
python3 (generating all palindromes) | sum-of-k-mirror-numbers | 0 | 1 | 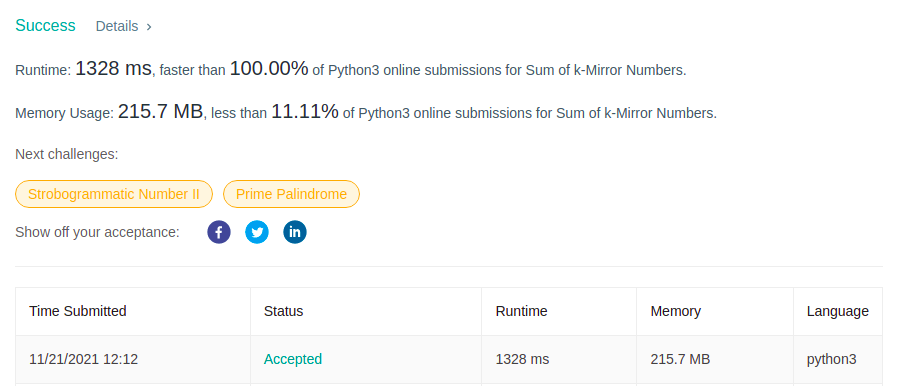\n\n\n```\n def kMirror(self, k: int, n: int) -> int:\n @cache \n def helper(start, n): \n if n == 1:\n return [str(i) for i in range(start, k)]\n if n == 2: \n return [str(i) + str(i) for i in range(start, k)]\n else: \n arr = []\n for elem in [str(i) for i in range(start, k)]:\n for center in helper(0, n - 2):\n arr.append(elem + center + elem[::-1])\n\n return arr\n \n digits = 1\n counter = 0\n ans = 0 \n while True:\n for num in helper(1, digits):\n numBase = str(int(num, k))\n if numBase == numBase[::-1]:\n ans += int(numBase)\n counter += 1\n if counter == n: \n return ans\n \n digits += 1 \n \n``` | 2 | A **k-mirror number** is a **positive** integer **without leading zeros** that reads the same both forward and backward in base-10 **as well as** in base-k.
* For example, `9` is a 2-mirror number. The representation of `9` in base-10 and base-2 are `9` and `1001` respectively, which read the same both forward and backward.
* On the contrary, `4` is not a 2-mirror number. The representation of `4` in base-2 is `100`, which does not read the same both forward and backward.
Given the base `k` and the number `n`, return _the **sum** of the_ `n` _**smallest** k-mirror numbers_.
**Example 1:**
**Input:** k = 2, n = 5
**Output:** 25
**Explanation:**
The 5 smallest 2-mirror numbers and their representations in base-2 are listed as follows:
base-10 base-2
1 1
3 11
5 101
7 111
9 1001
Their sum = 1 + 3 + 5 + 7 + 9 = 25.
**Example 2:**
**Input:** k = 3, n = 7
**Output:** 499
**Explanation:**
The 7 smallest 3-mirror numbers are and their representations in base-3 are listed as follows:
base-10 base-3
1 1
2 2
4 11
8 22
121 11111
151 12121
212 21212
Their sum = 1 + 2 + 4 + 8 + 121 + 151 + 212 = 499.
**Example 3:**
**Input:** k = 7, n = 17
**Output:** 20379000
**Explanation:** The 17 smallest 7-mirror numbers are:
1, 2, 3, 4, 5, 6, 8, 121, 171, 242, 292, 16561, 65656, 2137312, 4602064, 6597956, 6958596
**Constraints:**
* `2 <= k <= 9`
* `1 <= n <= 30` | Given a range, how can you find the minimum waste if you can't perform any resize operations? Can we build our solution using dynamic programming using the current index and the number of resizing operations performed as the states? |
One line solution | count-common-words-with-one-occurrence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n x=[x for x in words1 if x in words2 and words1.count(x)==1 and words2.count(x)==1];return len(x)\n``` | 2 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
Count common words with one occurrence | count-common-words-with-one-occurrence | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n count=0\n for i in words1:\n if words1.count(i)==1 and words2.count(i)==1 and i in words2:\n print(i)\n count+=1\n return count\n``` | 2 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
Python3 solution, clean code with full comments. | count-common-words-with-one-occurrence | 0 | 1 | ```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n \n counter = 0\n \n count_words_1 = convert(words1)\n \n count_words_2 = convert(words2) \n \n count_words_1 = remove_multipel_occurences(count_words_1)\n \n count_words_2 = remove_multipel_occurences(count_words_2) \n \n # Check if two dictionarys have same keys and if so, counts them.\n \n for i in count_words_2.keys():\n \n if i in count_words_1:\n \n counter += 1 \n \n return counter\n \n # Helper function that will convert a list into a dictionary.\n # List elements represented as KEYS and list element\'s occurence represented as VALUES.\n \ndef convert(array: List[str]):\n \n d = dict()\n \n for i in array:\n \n if i in d:\n \n d[i] += 1\n \n else:\n \n d[i] = 1\n \n return d \n\n# Helper method that search and deletes keys that have a value that is not 1.\n\ndef remove_multipel_occurences(dict):\n \n for key in list(dict.keys()):\n \n if dict[key] != 1:\n \n del dict[key]\n \n return dict \n\t\n # If you like my work, then I\'ll appreciate your like. Thanks.\n\t``` | 1 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
[Python3] 2-line freq table | count-common-words-with-one-occurrence | 0 | 1 | Downvoters, leave a comment! \n\nFor solutions of biweekly 66, please check out this [commit](https://github.com/gaosanyong/leetcode/commit/2efa877859ad8f79f212b8ebde3edf5730d457ad)\n```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n freq1, freq2 = Counter(words1), Counter(words2)\n return len({w for w, v in freq1.items() if v == 1} & {w for w, v in freq2.items() if v == 1}) \n``` | 14 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
Python | 2-liner solution | count-common-words-with-one-occurrence | 0 | 1 | ```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n fix = lambda w: set(filter(lambda x: x[1] == 1, Counter(w).items()))\n\n return len(fix(words1) & fix(words2))\n``` | 1 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
Python Easy Solution | count-common-words-with-one-occurrence | 0 | 1 | ```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n w1,w2,r = words1 , words2 , 0\n for i in w1:\n if w1.count(i) == w2.count(i) == 1:\n r += 1\n return r\n``` | 5 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
2 Liner Python Solution || 110ms (50 %) || Memory (82 %) | count-common-words-with-one-occurrence | 0 | 1 | ```\nclass Solution:\n\tdef countWords(self, words1: List[str], words2: List[str]) -> int:\n\t\tcount = Counter(words1 + words2)\n\t\treturn len([word for word in count if count[word] == 2 and word in words1 and word in words2])\n```\n-------------------\n***----- Taha Choura -----***\n*[email protected]* | 3 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
✅ Beats 98.84% solutions,✅ Python easy to understand code with explanation --- ✅ By BOLT CODING ✅ | count-common-words-with-one-occurrence | 0 | 1 | # Explanation\nHere we are creating 2 Counter objects and keeping track of all the words.\nWe can iterate through either of the counter and check if number == 1, if this case passes we check if the occurence of same word is 1 in the other counter. If both condition satisfies we will update the count and return that value\n\n# Code\n```\nclass Solution:\n def countWords(self, words1: List[str], words2: List[str]) -> int:\n count = 0\n x = Counter(words1)\n y = Counter(words2)\n for i, j in x.items():\n if j==1 and y[i] == 1:\n count+=1\n\n return count\n\n```\n\n# Learning\nFor understanding code in such simpler ways, for learning more about python, for knowing tricks to solve question, for wanting to learn ways to crack interview, to work on resume level projects, to learn modules in python or want to be a data scientiest.\nSubscribe to BOLT CODING - https://www.youtube.com/@boltcoding \uD83E\uDD29 | 3 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
Python Solution | Faster than 99% | O(n) time complexity | count-common-words-with-one-occurrence | 0 | 1 | \n\nExplanation can be found after full solution code block.\nFull Solution:\n```\ncount1 = {}\nfor i in words1:\n\tif i in count1:\n\t\t\tcount1[i] += 1\n\telse:\n\t\tcount1[i] = 1\n ans = 0\n count2 = {}\n for i in words2:\n\tif i in count2:\n\t\tif count2[i] == \'added\':\n\t\t\tans -= 1\n\t\t\tcount2[i] = \'processed\'\n\telse:\n\t\tif i in count1 and count1[i] == 1:\n\t\t\tcount2[i] = \'added\'\n\t\t\tans += 1 \nreturn ans\n```\n\nFirst we use a dictionary `count1` to get the frequencies of each word in the first word array `words1`. \n```\ncount1 = {}\nfor i in words1: # for loop to iterate through each element directly, does not use the value of index \n\tif i in count1: # if the word is found in the count i.e already seen earlier\n\t\tcount1[i] += 1 # increment the count by 1\n\telse: # if the word is not in count i.e. not seen before\n\t\tcount1[i] = 1 # set the count of the word to 1\n```\nThen we initialize our answer variable `ans` and another dictionary `count2` to process the second word array `words2`\n```\nans = 0\ncount2 = {}\n```\nSo under what conditions do we increment our answer?\n1. Must occur only once in both `words1` and `words2`\n2. Must occur in both `words1` and `words2`\n\nInitially, I considered counting the frequencies of both arrays then seeing if a word with a count of 1 found in `count1` existed in `count2` with a count of 1. While this is also a O(n) solution, we are increasing the run time by having to, in the worst case, iterate through every word again. So I came up with a solution that increments the answer while processing `count2`.\n\nIterating through `words2`, if we come across a word which we have never seen before, we can initally assume its frequency is 1 and increment our answer by 1. To signify that we have already incremented our answer because of this word, we will set the value of the word in `count2` as "added". \nIf you are wondering why we are doing that:\n<img src="https://assets.leetcode.com/users/images/ec29fc95-fb14-42cb-8701-a3cd93b3e178_1647473173.7593021.png" alt="drawing" width="350"/>\nThen if we come across a word that we have seen before, it can either be of two situations:\n1. We have seen it before and we have incremented our answer because if it\n2. We have seen it before and we have done nothing because of it.\n\nIn this case we don\'t really care about the second case because nothing has happened to our precious answer so we can just ignore any instance of our second case.\nWhat we really care about is the first case, because this ensures that we are only adding words that are of frequency 1 and more importantly we are getting the correct answer. So how do we handle the first case? Remember that we used "added"? If we see that the value of a word in count2 is "added", it means that we have already seen it and have incremented our answer which is our first case. So if we encounter "added" we have to decrement our answer then add another flag to show that we have taken care of it.\n```\nfor i in words2: # for each word in words2 \n\tif i in count2: # if the word is in count2 i.e we have already seen it before\n\t\tif count2[i] == \'added\': # if we have already seen the word and added to answer\n\t\t\tans -= 1 # decrement our lovely answer\n\t\t\tcount2[i] = \'processed\' # set value of word in dictionary to something other than "added"\n\telse: # if the word is not in count2 i.e we have not seen it before.\n\t\tif i in count1 and count1[i] == 1: # if the word is also found in count1 and if of frequency 1\n\t\t\tcount2[i] = \'added\' # set value of word in dictionary to "added"\n\t\t\tans += 1 # increment our lovely answer\n```\n\nand of course, remember to return your answer.\n```\nreturn ans\n```\nTime complexity:\nWe go through `words1` exactly once while building our `count1`. We also go through `words2` exactly once while building our `count2`. \nLet n = length of words1 + length of words2\nTherefore time complexity is O(n)\n\nIf you found my answer helpful, please upvote and leave a like!\n\n\n | 7 | Given two string arrays `words1` and `words2`, return _the number of strings that appear **exactly once** in **each** of the two arrays._
**Example 1:**
**Input:** words1 = \[ "leetcode ", "is ", "amazing ", "as ", "is "\], words2 = \[ "amazing ", "leetcode ", "is "\]
**Output:** 2
**Explanation:**
- "leetcode " appears exactly once in each of the two arrays. We count this string.
- "amazing " appears exactly once in each of the two arrays. We count this string.
- "is " appears in each of the two arrays, but there are 2 occurrences of it in words1. We do not count this string.
- "as " appears once in words1, but does not appear in words2. We do not count this string.
Thus, there are 2 strings that appear exactly once in each of the two arrays.
**Example 2:**
**Input:** words1 = \[ "b ", "bb ", "bbb "\], words2 = \[ "a ", "aa ", "aaa "\]
**Output:** 0
**Explanation:** There are no strings that appear in each of the two arrays.
**Example 3:**
**Input:** words1 = \[ "a ", "ab "\], words2 = \[ "a ", "a ", "a ", "ab "\]
**Output:** 1
**Explanation:** The only string that appears exactly once in each of the two arrays is "ab ".
**Constraints:**
* `1 <= words1.length, words2.length <= 1000`
* `1 <= words1[i].length, words2[j].length <= 30`
* `words1[i]` and `words2[j]` consists only of lowercase English letters. | A number can be the average of its neighbors if one neighbor is smaller than the number and the other is greater than the number. We can put numbers smaller than the median on odd indices and the rest on even indices. |
[Python3] greedy | minimum-number-of-food-buckets-to-feed-the-hamsters | 0 | 1 | \nDownvoters, leave a comment! \n\nFor solutions of biweekly 66, please check out this [commit](https://github.com/gaosanyong/leetcode/commit/2efa877859ad8f79f212b8ebde3edf5730d457ad)\n```\nclass Solution:\n def minimumBuckets(self, street: str) -> int:\n street = list(street)\n ans = 0 \n for i, ch in enumerate(street): \n if ch == \'H\' and (i == 0 or street[i-1] != \'#\'): \n if i+1 < len(street) and street[i+1] == \'.\': street[i+1] = \'#\'\n elif i and street[i-1] == \'.\': street[i-1] = \'#\'\n else: return -1\n ans += 1\n return ans \n``` | 12 | You are given a **0-indexed** string `hamsters` where `hamsters[i]` is either:
* `'H'` indicating that there is a hamster at index `i`, or
* `'.'` indicating that index `i` is empty.
You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index `i` can be fed if you place a food bucket at index `i - 1` **and/or** at index `i + 1`.
Return _the minimum number of food buckets you should **place at empty indices** to feed all the hamsters or_ `-1` _if it is impossible to feed all of them_.
**Example 1:**
**Input:** hamsters = "H..H "
**Output:** 2
**Explanation:** We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.
**Example 2:**
**Input:** hamsters = ".H.H. "
**Output:** 1
**Explanation:** We place one food bucket at index 2.
**Example 3:**
**Input:** hamsters = ".HHH. "
**Output:** -1
**Explanation:** If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.
**Constraints:**
* `1 <= hamsters.length <= 105`
* `hamsters[i]` is either`'H'` or `'.'`. | Can we first solve a simpler problem? Counting the number of subsequences with 1s followed by 0s. How can we keep track of the partially matched subsequences to help us find the answer? |
python 3 | one pass greedy solution | O(n)/O(1) | minimum-number-of-food-buckets-to-feed-the-hamsters | 0 | 1 | ```\nclass Solution:\n def minimumBuckets(self, street: str) -> int:\n n = len(street)\n buckets = 0\n prevBucket = -2\n for i, c in enumerate(street):\n if c == \'.\' or prevBucket == i - 1:\n continue\n \n buckets += 1\n if i != n - 1 and street[i + 1] == \'.\':\n prevBucket = i + 1\n elif not i or street[i - 1] == \'H\':\n return -1\n \n return buckets | 1 | You are given a **0-indexed** string `hamsters` where `hamsters[i]` is either:
* `'H'` indicating that there is a hamster at index `i`, or
* `'.'` indicating that index `i` is empty.
You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index `i` can be fed if you place a food bucket at index `i - 1` **and/or** at index `i + 1`.
Return _the minimum number of food buckets you should **place at empty indices** to feed all the hamsters or_ `-1` _if it is impossible to feed all of them_.
**Example 1:**
**Input:** hamsters = "H..H "
**Output:** 2
**Explanation:** We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.
**Example 2:**
**Input:** hamsters = ".H.H. "
**Output:** 1
**Explanation:** We place one food bucket at index 2.
**Example 3:**
**Input:** hamsters = ".HHH. "
**Output:** -1
**Explanation:** If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.
**Constraints:**
* `1 <= hamsters.length <= 105`
* `hamsters[i]` is either`'H'` or `'.'`. | Can we first solve a simpler problem? Counting the number of subsequences with 1s followed by 0s. How can we keep track of the partially matched subsequences to help us find the answer? |
[Python3] pattern match | minimum-number-of-food-buckets-to-feed-the-hamsters | 0 | 1 | ```python\nclass Solution:\n def minimumBuckets(self, street: str) -> int:\n \n patterns = [\'H.H\', \'.H\', \'H.\', \'H\'] # 4 patterns (excluding \'.\' cuz it costs 0 )\n costs = [1, 1, 1, -1] # corresponding costs\n res = 0\n for p, c in zip(patterns, costs): # firstly, detect \'H.H\'; secondly, detect \'.H\' and \'H.\'; ...\n t = street.count(p) # occurences\n if (t >= 1):\n if (c == -1): # if found an impossible case...\n return -1\n res += c * t # accumulate the cost\n street = street.replace(p, \'#\') # erase such arrangement\n return res\n \n``` | 2 | You are given a **0-indexed** string `hamsters` where `hamsters[i]` is either:
* `'H'` indicating that there is a hamster at index `i`, or
* `'.'` indicating that index `i` is empty.
You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index `i` can be fed if you place a food bucket at index `i - 1` **and/or** at index `i + 1`.
Return _the minimum number of food buckets you should **place at empty indices** to feed all the hamsters or_ `-1` _if it is impossible to feed all of them_.
**Example 1:**
**Input:** hamsters = "H..H "
**Output:** 2
**Explanation:** We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.
**Example 2:**
**Input:** hamsters = ".H.H. "
**Output:** 1
**Explanation:** We place one food bucket at index 2.
**Example 3:**
**Input:** hamsters = ".HHH. "
**Output:** -1
**Explanation:** If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.
**Constraints:**
* `1 <= hamsters.length <= 105`
* `hamsters[i]` is either`'H'` or `'.'`. | Can we first solve a simpler problem? Counting the number of subsequences with 1s followed by 0s. How can we keep track of the partially matched subsequences to help us find the answer? |
Basic steps detailed explaination mentioned - Python | minimum-number-of-food-buckets-to-feed-the-hamsters | 0 | 1 | \n\n# Approach\nDetailed explaination inline in the code\n\n# Complexity\n- Time complexity:\nO(n+m)\nm - size of list of indices of hamsters\n\n\n# Code\n```\nclass Solution:\n def minimumBuckets(self, hamsters: str) -> int:\n\n #check if there is no empty place in string\n if \'.\' not in hamsters:\n return -1\n foodbucket = []\n #find all hamsters indices\n hamsterIdx = [i for i,v in enumerate(hamsters) if v==\'H\']\n\n #Now check for all hamsters whether they can be fed or not \n for i in range(len(hamsterIdx)):\n #check first for right side for every hamster , if its empty then put index in food bucket\n if hamsterIdx[i]+1 < len(hamsters) and hamsters[hamsterIdx[i]+1]!=\'H\':\n #if right side is empty check if left side of hamster already have food as it be can shared between hamsters\n if foodbucket and foodbucket[-1]==hamsterIdx[i]-1:\n print("food already present")\n else:\n foodbucket.append(hamsterIdx[i]+1) \n #if right is not empty than check left if empty put index in foodbucket \n elif hamsterIdx[i]-1 >=0 and hamsters[hamsterIdx[i]-1]!=\'H\':\n #if left side is empty check if left side of hamster already have food as it be can shared between hamsters\n if foodbucket and foodbucket[-1]==hamsterIdx[i]-1:\n print("food already present")\n else:\n foodbucket.append(hamsterIdx[i]-1)\n \n #if both sides are not empty it means one of the hamster can not be fed and we have to return -1\n else:\n return -1 \n return len(foodbucket)\n``` | 0 | You are given a **0-indexed** string `hamsters` where `hamsters[i]` is either:
* `'H'` indicating that there is a hamster at index `i`, or
* `'.'` indicating that index `i` is empty.
You will add some number of food buckets at the empty indices in order to feed the hamsters. A hamster can be fed if there is at least one food bucket to its left or to its right. More formally, a hamster at index `i` can be fed if you place a food bucket at index `i - 1` **and/or** at index `i + 1`.
Return _the minimum number of food buckets you should **place at empty indices** to feed all the hamsters or_ `-1` _if it is impossible to feed all of them_.
**Example 1:**
**Input:** hamsters = "H..H "
**Output:** 2
**Explanation:** We place two food buckets at indices 1 and 2.
It can be shown that if we place only one food bucket, one of the hamsters will not be fed.
**Example 2:**
**Input:** hamsters = ".H.H. "
**Output:** 1
**Explanation:** We place one food bucket at index 2.
**Example 3:**
**Input:** hamsters = ".HHH. "
**Output:** -1
**Explanation:** If we place a food bucket at every empty index as shown, the hamster at index 2 will not be able to eat.
**Constraints:**
* `1 <= hamsters.length <= 105`
* `hamsters[i]` is either`'H'` or `'.'`. | Can we first solve a simpler problem? Counting the number of subsequences with 1s followed by 0s. How can we keep track of the partially matched subsequences to help us find the answer? |
One Liner Beats 98.90% | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, sp: List[int], hp: List[int], rc: List[int], cc: List[int]) -> int:\n return (sum(cc[hp[1]:sp[1]]) if hp[1]<sp[1] else sum(cc[sp[1]+1:hp[1]+1])) + (sum(rc[hp[0]:sp[0]]) if hp[0]<sp[0] else sum(rc[sp[0]+1:hp[0]+1]))\n``` | 1 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
[Python 3] Greedy - Simple + Easy to Understand | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity $$O(M + N)$$\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n sx, sy = startPos\n hx, hy = homePos\n return sum(rowCosts[min(sx, hx): max(sx, hx) + 1]) + \\\n sum(colCosts[min(sy, hy): max(sy, hy) + 1]) - \\\n rowCosts[sx] - colCosts[sy]\n``` | 1 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
EASY SOLUTION in Python with DETAILED EXPLANATION || Beats 95.4% | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the question asks about the minimum cost, You just have to go straight to the Home without any extra moves, by directly changing the position of Robot to required Row and Column accordingly. Do refer to the Hint if you don\'t understand what I mean.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMy approach was to simply traverse through the rows and columns between the Start and Home locations and add the cost of corresponding rows and columns to the `cost` variable.\n- When the Robot starts at a lower indexed row than the Home, We have to add the cost of the indexes starting from the index of Start\'s next row, since the Robot is moving to that particular index, including the index of Home\'s row.\n- On the contrary, if the Robot starts at a higher indexed row than the Home,We have to add the cost of the indexes starting from the index of the Home to the index of the row, which is just above the Start. The point of this is that the Robot will start to move to the row just above the Home and continue moving upto Home\'s row. So we are adding the costs of this, just in the Reverse way.\n- The logic is pretty much same for the Columns.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n i,j=startPos\n a,b=homePos\n cost=0\n if i<a:\n for k in range(i,a):\n cost+=rowCosts[k+1]\n else:\n for m in range(a,i):\n cost+=rowCosts[m]\n if j<b:\n for l in range(j,b):\n cost+=colCosts[l+1]\n else:\n for n in range(b,j):\n cost+=colCosts[n]\n \n return cost\n\n``` | 3 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
75% TC and 67% SC easy python solution | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | ```\ndef minCost(self, startPos: List[int], homePos: List[int], rowC: List[int], colC: List[int]) -> int:\n\tm, n = len(rowC), len(colC)\n\ti1, j1 = startPos\n\ti2, j2 = homePos\n\tans = 0\n\tif(i1 <= i2):\n\t\tfor i in range(i1+1, i2+1):\n\t\t\tans += rowC[i]\n\telse:\n\t\tfor i in range(i1-1, i2-1, -1):\n\t\t\tans += rowC[i]\n\tif(j1 <= j2):\n\t\tfor j in range(j1+1, j2+1):\n\t\t\tans += colC[j]\n\telse:\n\t\tfor j in range(j1-1, j2-1, -1):\n\t\t\tans += colC[j]\n\treturn ans\n``` | 1 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
📌📌 Greedy Approach || Well-Coded and Explained || 95% faster 🐍 | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | ## IDEA : \n In this Question directly we can find the cost for rows and column from source to target and add in last. \n* From going starting rows to target rows we have to add cost of the up or down path. \n\n* Similarly, for going from starting column to target column we have to add all the costs of coming column in path either towards left or right,\n\n**Implementation:**\n\'\'\'\n\n\tclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n src_x,src_y = startPos[0],startPos[1]\n end_x,end_y = homePos[0], homePos[1]\n \n if src_x < end_x:\n rc = sum(rowCosts[src_x+1:end_x+1])\n elif src_x > end_x:\n rc = sum(rowCosts[end_x:src_x])\n else:\n rc=0\n \n if src_y < end_y:\n cc = sum(colCosts[src_y+1:end_y+1])\n elif src_y > end_y:\n cc = sum(colCosts[end_y:src_y])\n else:\n cc=0\n \n return cc+rc\n\n### Thanks and Upvote if you like the Idea!!\u270C | 3 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
Python 2-liner Beat 97% | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(m + n)\n\n- Space complexity:\nO(1) can be\n\n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n dist = lambda x, y, costs, d: sum(costs[i] for i in range(x + d, y + d, d))\n return sum(dist(x, y, costs, 1 if x < y else -1) for x, y, costs in zip(startPos, homePos, [rowCosts, colCosts]))\n \n # dir = 1 if startPos[0] < homePos[0] else -1\n # x_distance = sum(rowCosts[i] for i in range(startPos[0] + dir, homePos[0] + dir, dir))\n # dir = 1 if startPos[1] < homePos[1] else -1\n # y_distance = sum(colCosts[i] for i in range(startPos[1] + dir, homePos[1] + dir, dir))\n # return x_distance + y_distance\n```\n\nAnd my TLE Dijkstra for amusement. Right, you are not the only one:\n```\n\nclass Solution {\n\n class Entry {\n int x;\n int y;\n int cost;\n public Entry(int x, int y, int cost) {\n this.x = x;\n this.y = y;\n this.cost = cost;\n }\n }\n\n private static final int[][] moveVert = {{1, 0}, {-1, 0}};\n private static final int[][] moveHori = {{0, 1}, {0, -1}};\n private int m;\n private int n;\n\n public int minCost(int[] startPos, int[] homePos, int[] rowCosts, int[] colCosts) {\n m = rowCosts.length;\n n = colCosts.length;\n\n int[][] costs = new int[m][n];\n for (int[] row : costs) Arrays.fill(row, Integer.MAX_VALUE);\n PriorityQueue<Entry> pq = new PriorityQueue<>((a, b)->(a.cost - b.cost));\n\n pq.offer(new Entry(startPos[0], startPos[1], 0));\n costs[startPos[0]][startPos[1]] = 0;\n while (!pq.isEmpty()) {\n Entry currEntry = pq.poll();\n if (currEntry.x == homePos[0] && currEntry.y == homePos[1]) return currEntry.cost;\n extendQueue(currEntry, moveHori, colCosts, true, pq, costs);\n extendQueue(currEntry, moveVert, rowCosts, false, pq, costs);\n }\n return -1;\n }\n\n private void extendQueue(Entry entry, int[][] moves, int[]moveCost, boolean moveHori, PriorityQueue<Entry> pq, int[][] costs) {\n int cx = entry.x;\n int cy = entry.y;\n int cost = entry.cost;\n for (int[] move : moves) {\n int nx = cx + move[0];\n int ny = cy + move[1];\n if (!isValid(nx, ny)) continue;\n int newCost = cost + moveCost[moveHori ? ny : nx];\n if (costs[nx][ny] <= newCost) continue;\n costs[nx][ny] = newCost;\n pq.offer(new Entry(nx, ny, newCost));\n }\n }\n\n private boolean isValid(int x, int y) {return 0 <= x && x < m && 0 <= y && y < n;}\n}\n``` | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
Python | Simple Solution With Explanation | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | \n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n cost = 0\n """\n Since the robot can\'t walk in the diagonals hence whhatever path the robot takes, \n it has to cover all the intermediate rows and columns.\n Hence just calculate the cost for taking all the intermediate rows anc columns and that would be the minimum cost.\n """\n r1, r2 = startPos[0], homePos[0]\n c1, c2 = startPos[1], homePos[1]\n if r1 < r2:\n for r in range(r1+1, r2+1):\n cost += rowCosts[r]\n else:\n for r in range(r1-1, r2-1, -1):\n cost += rowCosts[r]\n if c1 < c2:\n for c in range(c1+1, c2+1):\n cost += colCosts[c]\n else:\n for c in range(c1-1, c2-1, -1):\n cost += colCosts[c]\n return cost\n```\n\n**If you liked the above solution then please upvote!** | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
Python Solution with Greedy Approach | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n row_offset = 1 if startPos[0] < homePos[0] else -1\n col_offset = 1 if startPos[1] < homePos[1] else -1\n row_cost, col_cost = 0, 0\n for i in range(startPos[0], homePos[0], row_offset):\n row_cost += rowCosts[i+row_offset]\n for j in range(startPos[1], homePos[1], col_offset):\n col_cost += colCosts[j+col_offset]\n return row_cost + col_cost\n\n\n \n``` | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
python3 1 liner beats 94% | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | \n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n return sum(rowCosts[startPos[0]+1:homePos[0]+1]) + sum(colCosts[startPos[1]+1:homePos[1]+1])+sum(rowCosts[homePos[0]:startPos[0]]) + sum(colCosts[homePos[1]:startPos[1]])\n``` | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
Python easy sol... | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | # Code\n```\nclass Solution:\n def minCost(self, s: List[int], h: List[int], r: List[int], c: List[int]) -> int:\n res=0\n while s!=h:\n m=float(inf)\n if s[0]<h[0] or s[1]<h[1]:\n if s[0]<h[0]:\n m=min(m,r[s[0]+1])\n s[0]+=1\n elif s[1]<h[1]:\n m=min(m,c[s[1]+1])\n s[1]+=1\n elif s[0]>h[0] or s[1]>h[1]:\n if s[0]>h[0]:\n m=min(m,r[s[0]-1])\n s[0]-=1\n elif s[1]>h[1]:\n m=min(m,c[s[1]-1])\n s[1]-=1\n res+=m\n return res\n``` | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
Easy basic solution - Python | minimum-cost-homecoming-of-a-robot-in-a-grid | 0 | 1 | \n\n# Approach\nExplained inline in code\n\n# Complexity\n- Time complexity:\nO(n+m)\n\n\n# Code\n```\nclass Solution:\n def minCost(self, startPos: List[int], homePos: List[int], rowCosts: List[int], colCosts: List[int]) -> int:\n\n if startPos==homePos:\n return 0\n \n mincost = 0\n #rows calculation\n if startPos[0] <= homePos[0]:\n start = startPos[0]+1\n while start <= homePos[0]:\n mincost += rowCosts[start]\n start += 1\n else:\n start = startPos[0]-1\n while start >= homePos[0]:\n mincost += rowCosts[start]\n start -= 1\n \n #columns calculation\n if startPos[1] <= homePos[1]:\n start = startPos[1]+1\n while start <= homePos[1]:\n mincost += colCosts[start]\n start += 1\n else:\n start = startPos[1]-1\n while start >= homePos[1]:\n mincost += colCosts[start]\n start -= 1\n \n\n return mincost\n``` | 0 | There is an `m x n` grid, where `(0, 0)` is the top-left cell and `(m - 1, n - 1)` is the bottom-right cell. You are given an integer array `startPos` where `startPos = [startrow, startcol]` indicates that **initially**, a **robot** is at the cell `(startrow, startcol)`. You are also given an integer array `homePos` where `homePos = [homerow, homecol]` indicates that its **home** is at the cell `(homerow, homecol)`.
The robot needs to go to its home. It can move one cell in four directions: **left**, **right**, **up**, or **down**, and it can not move outside the boundary. Every move incurs some cost. You are further given two **0-indexed** integer arrays: `rowCosts` of length `m` and `colCosts` of length `n`.
* If the robot moves **up** or **down** into a cell whose **row** is `r`, then this move costs `rowCosts[r]`.
* If the robot moves **left** or **right** into a cell whose **column** is `c`, then this move costs `colCosts[c]`.
Return _the **minimum total cost** for this robot to return home_.
**Example 1:**
**Input:** startPos = \[1, 0\], homePos = \[2, 3\], rowCosts = \[5, 4, 3\], colCosts = \[8, 2, 6, 7\]
**Output:** 18
**Explanation:** One optimal path is that:
Starting from (1, 0)
-> It goes down to (**2**, 0). This move costs rowCosts\[2\] = 3.
-> It goes right to (2, **1**). This move costs colCosts\[1\] = 2.
-> It goes right to (2, **2**). This move costs colCosts\[2\] = 6.
-> It goes right to (2, **3**). This move costs colCosts\[3\] = 7.
The total cost is 3 + 2 + 6 + 7 = 18
**Example 2:**
**Input:** startPos = \[0, 0\], homePos = \[0, 0\], rowCosts = \[5\], colCosts = \[26\]
**Output:** 0
**Explanation:** The robot is already at its home. Since no moves occur, the total cost is 0.
**Constraints:**
* `m == rowCosts.length`
* `n == colCosts.length`
* `1 <= m, n <= 105`
* `0 <= rowCosts[r], colCosts[c] <= 104`
* `startPos.length == 2`
* `homePos.length == 2`
* `0 <= startrow, homerow < m`
* `0 <= startcol, homecol < n` | null |
[Python3] just count | count-fertile-pyramids-in-a-land | 0 | 1 | Downvoters, leave a comment! \n\nFor solutions of biweekly 66, please check out this [commit](https://github.com/gaosanyong/leetcode/commit/2efa877859ad8f79f212b8ebde3edf5730d457ad)\n```\nclass Solution:\n def countPyramids(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n vals = [[inf]*n for _ in range(m)]\n for i in range(m):\n for j in range(n): \n if grid[i][j] == 0: vals[i][j] = 0\n elif j == 0: vals[i][j] = 1\n else: vals[i][j] = min(vals[i][j], 1 + vals[i][j-1])\n if grid[i][~j] == 0: vals[i][~j] = 0\n elif j == 0: vals[i][~j] = 1\n else: vals[i][~j] = min(vals[i][~j], 1 + vals[i][~j+1])\n \n def fn(vals): \n """Return count of pyramid in given grid."""\n ans = 0 \n for j in range(n):\n width = 0\n for i in range(m): \n if vals[i][j]: width = min(width+1, vals[i][j])\n else: width = 0\n ans += max(0, width-1)\n return ans \n \n return fn(vals) + fn(vals[::-1])\n```\n\n**AofA**\ntime complexity `O(MN)`\nspace complexity `O(MN)` | 5 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Depth First Search Recursive - Dynamic Programming Solution | count-fertile-pyramids-in-a-land | 0 | 1 | # Complexity\n- Time complexity: If I don\'t use DP to store results then the TC = m * n * 2^(min(m,n)). With DP our TC is : o(m * n). \n- Because worst case all elements will be fertile. Which means we will get all dp results in the first iteration itself as we traverse through all the land. \n- And for the remainder iterations we just fetch the dp results. \n- 1st iteration - m * n calls to dfs. Remaining iterations: O(1) lookup. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m*n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPyramids(self, grid: List[List[int]]) -> int:\n\n m=len(grid)\n n=len(grid[0])\n \n # To keep track of positive pyramids\n posDp={}\n # To keep track of negative pyramids\n negDp={}\n\n def dfs(i, j, dr, dp):\n \n # If the pyramid height is already present in dp for this apex then return \n if dp.get((i,j)) is not None:\n return dp[(i,j)]\n\n # Otherwise perform dfs\n if grid[i][j]==1 and 0<=i+dr<m and (j-1)>=0 and (j+1)<n and grid[i+dr][j]==1:\n \n height=min(dfs(i+dr,j-1,dr, dp), dfs(i+dr, j+1,dr, dp)) +1\n dp[(i,j)]=height\n return height\n\n # Else just store the value of that element\n dp[(i,j)]=grid[i][j]\n return grid[i][j]\n\n count=0\n for i in range(m):\n for j in range(n):\n \n # Have we already computed the pyramid height for this apex\n if posDp.get((i,j)) is not None:\n posHeight=posDp.get((i,j))\n # Else compute height\n else:\n posHeight=dfs(i,j,1, posDp)\n \n # Have we already computed the negative pyramid height for this apex\n if negDp.get((i,j)) is not None:\n negHeight=negDp.get((i,j))\n else:\n negHeight=dfs(i,j,-1, negDp)\n\n # Add\n count+=max(0, posHeight-1)\n count+=max(0, negHeight-1)\n\n return count\n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Python DP with clear naming | count-fertile-pyramids-in-a-land | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def countPyramids(self, G):\n \n num_rows = len(G)\n num_cols = len(G[0])\n\n @cache\n def get_height_with_apex(row, col, dir):\n\n if G[row][col] == 1 and 0 <= row + dir <= num_rows - 1 and col - 1 >= 0 and col + 1 <= num_cols - 1 and G[row + dir][col] == 1:\n return min(get_height_with_apex(row + dir, col - 1, dir), get_height_with_apex(row + dir, col + 1, dir)) + 1\n \n return G[row][col]\n\n total_num_pyriads = 0\n for row in range(num_rows):\n for col in range(num_cols):\n top_apex_height = get_height_with_apex(row, col, 1)\n # num pyriads with this (row, col) as apex\n num_pyriads_with_top_apex = max(0, top_apex_height - 1)\n\n total_num_pyriads += num_pyriads_with_top_apex \n\n bot_apex_height = get_height_with_apex(row, col, -1)\n num_pyriads_with_bot_apex = max(0, bot_apex_height - 1)\n\n total_num_pyriads += num_pyriads_with_bot_apex\n\n return total_num_pyriads\n\n \n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Python, DP 97%, 97% | count-fertile-pyramids-in-a-land | 0 | 1 | # Intuition\nFirst of all the direct and inverted pyramids are just the same problem, solved with direct and reversed order or rows.\n\n# Approach\nThe smallest pyramind is a single cell (not counted in the result)\nEach pyramid step sits on 3 other overlapping pyramids and can extend below as far as the shortest of those 3 pyramids below. So build a DP trying to send the pyramid height. On the very left and right sides only pyramids of height 1 is possible.\nAs you go sum how many pyramids there were seen with height 2 or larger\n\n# Complexity\n- Time complexity:\n$$O(nRows*nCols)$$\n\n- Space complexity:\n$$O(nCols)$$\n\n# Code\n```\nclass Solution:\n def countPyramids(self, grid: List[List[int]]) -> int:\n nCols = len(grid[0])\n\n result = 0\n dp0 = [0] * nCols\n dp1 = [0] * nCols\n nCols -= 1\n\n for g in (iter(grid), reversed(grid)):\n dp0[:] = next(g)\n \n for r in g:\n dp1[0] = r[0]\n dp1[-1] = r[-1]\n for ci in range(1, nCols):\n if r[ci]:\n dp1[ci] = 1 + min(dp0[ci - 1], dp0[ci], dp0[ci + 1])\n result += dp1[ci] - 1\n else:\n dp1[ci] = 0\n dp1, dp0 = dp0, dp1\n\n\n\n return result\n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Python3 || Faster than 100% || O(m*n) time || O(n) space || no in-place grid modification | count-fertile-pyramids-in-a-land | 0 | 1 | # Intuition\nLarger pyramids contain smaller pyramids suggesting recursion.\n\nThere are two key notions: \nIf a cell hosts some pyramid then it also hosts any pyramid of smaller size. Most solutions look at the apex, while I prefer the base\n\nTo decide if a cell hosts a pyramid of height $H$ we need knowledge about neighbors in same row and which pyramids are hosted by cells of the previous row\n\nCombining these two observations we see that we can run from the top to bottom once for plain pyramids and another time back from bottom to top for inverse pyramids.\n\nSince we only need results of the previous row to solve the current row, we only need to store $$O(n)$$ worth of data.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWe want to calculate how many pyramids each cell hosts. We say a cell hosts a pyramid if there\'s a valid pyramid with it\'s mid-base located at the given cell. \n\nIf the heighest pyramid hosted has height $$H$$, then the cell hosts $$H-1$$ distinct pyramids total (height $$1$$ pyramids are single blocks and are not counted)\n\nTo host a pyramid of height $$H$$ a cell must have $$H-1$$ fertile cells on each side (left and right) and the cell immediately above it must host a size $$H-1$$ pyramid. Thus, we can go from top row to bottom row of grid, writing down $$H$$ for each cell in a row and storing this info to use when handling the next row.\n\nWe use a single row "prev" of data storing $H$ for the previous row, i.e. $O(n)$ memory. This could be avoided by in-place modifications, however 1) in-place modifications are uncalled for here 2) this might mess up the backwards run counting inverse pyramids\n\nThere is no recursion here and thus no stack memory costs\n\nInverse pyramids are treated similarly by inversing the scanning order. This is technically implemented within the function "runDown2" and controlled by a "reverse" argument.\n\nWhen working on a row we try to be as efficient as possible by hopping over cells that cannot host pyramids (e.g. if cell $i$ is infertile then the next cell that might host pyramids is $i+2$). Whenever a promising streak (i.e. $3+$ cells) of fertile cells is encountered we directly calculate its length. The memory row "prev" is updated with new values on the fly, cell by cell, to avoid using another row-worth of memory (though obviously $$O(n)=O(2n)$$).\n\nSorry for the messy code. This is my first solution submission :)\nPartially, the mess is due to incorporating different increments in the row scan and the cell-by-cell update process for "prev".\n\n# Complexity\n- Time complexity:\n$$O(m*n)$$\n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\nclass Solution:\n def countPyramids(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n def runDown2(g, reverse=False):\n \'\'\'\n look for pyramids starting with top row (row 0)\n reverse=True commands to start from bottom and look for inverse pyramids\n \'\'\'\n if reverse: prev = g[m-1].copy() #prev will be written over to store recent row data\n else: prev = g[0].copy()\n total = 0 #pyramid counter\n for h in range(1,m):\n if reverse: l = g[m-h-1].copy()\n else: l = g[h].copy()\n i = 1 #edges do not host pyramids, thus 0 and L-1 are excluded from run\n while i < n-1: \n if l[i+1] == 0: \n prev[i], prev[i+1] = l[i], 0 #update prev to the left of pointer i\n if i+2 < n: prev[i+2] = l[i+2] #update prev (note edges are irrelevant)\n i += 3 #barrens to the right: skip current, skip barrens, skip next\n elif l[i] == 0: #barrens here: skip current, skip next\n prev[i], prev[i+1] = 0, l[i+1]\n i += 2 \n elif l[i-1] == 0: #barrens to the left: skip current\n prev[i] = l[i]\n i += 1 \n else: #now i-1, i, i+1 are 3 fertile in a row -- pyramid possible\n first = i-1 #first fertile cell in current 3+ fertile streak\n j = i+2 #pointer to seek ahead for end of fertile streak\n while (j < n) and l[j]: j+=1 #while fertile and on-grid move right\n last = j-1 #last fertile cell of current fertile streak\n for i in range(first+1,last): #run over fertile streak\n l[i] = 1 + min(i-first, last-i, prev[i]) #how many pyrs -1\n prev[i] = l[i] #update prev[i], we already used its info in this run\n if l[i] > 1: \n total += l[i] - 1 #count pyramids buildable here\n prev[last] = 1\n if last+1 < n: \n prev[last+1] = 0\n if last+2 < n: \n prev[last+2] = l[last+2]\n i = last + 3 #last+1 = barren => last+3 is the first posible inner fertile\n return total\n\n if m < 2 or n < 3: return 0 #if too shallow or too narrow for any pyramids to fit\n return runDown2(grid) + runDown2(grid, reverse = True)\n \n \n\n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Python (Simple DP) | count-fertile-pyramids-in-a-land | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPyramids(self, grid):\n m, n, total = len(grid), len(grid[0]), 0\n\n @lru_cache(None)\n def dfs(i,j,df):\n if grid[i][j] == 1 and 0 <= i + df < m and j > 0 and j + 1 < n and grid[i+df][j] == 1:\n return min(dfs(i+df,j-1,df),dfs(i+df,j+1,df)) + 1\n return grid[i][j]\n\n for i in range(m):\n for j in range(n):\n total += max(0,dfs(i,j,1)-1)\n total += max(0,dfs(i,j,-1)-1)\n\n return total\n\n\n\n \n\n\n\n \n \n \n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
Python3 beats 90% short solution | count-fertile-pyramids-in-a-land | 0 | 1 | # Code\n```\nclass Solution:\n def countPyramids(self, G):\n m, n, ans = len(G), len(G[0]), 0\n \n @lru_cache(None)\n def dp(i, j, dr):\n if G[i][j] == 1 and 0 <= i + dr < m and j > 0 and j + 1 < n and G[i+dr][j] == 1:\n return min(dp(i+dr, j-1, dr), dp(i+dr, j+1, dr)) + 1\n return G[i][j]\n \n for i, j in product(range(m), range(n)):\n ans += max(0, dp(i, j, 1) - 1)\n ans += max(0, dp(i, j, -1) - 1)\n \n return ans\n``` | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
2 Python Approach - Brute Force to most Optimized Solution | count-fertile-pyramids-in-a-land | 1 | 1 | \tclass Solution:\n\t\tdef countPyramids(self, grid: List[List[int]]) -> int:\n\t\t\t#Simple Idea one - Brute Force\n\t\t\t#This will give us tle sometime and sometimes passes\n\t\t\t#F-LC\n\t\t\t"""\n\t\t\tn = len(grid)\n\t\t\tm = len(grid[0])\n\t\t\tprefix = [[0 for _ in range(m+1)] for i in range(n+1)]\n\t\t\tfor i in range(1,n+1):\n\t\t\t\tfor j in range(1,m+1):\n\t\t\t\t\tprefix[i][j] = grid[i-1][j-1]+prefix[i][j-1]\n\t\t\tans = 0\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m):\n\t\t\t\t\tx = i\n\t\t\t\t\ty1 = j\n\t\t\t\t\ty2 = j\n\t\t\t\t\tcnt = 1\n\t\t\t\t\twhile x<n and y1>=0 and y2<m:\n\t\t\t\t\t\tval = prefix[x+1][y2+1] - prefix[x+1][y1]\n\t\t\t\t\t\tif val==cnt:\n\t\t\t\t\t\t\tif cnt>1: ans+=1\n\t\t\t\t\t\t\tcnt+=2\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tbreak\n\t\t\t\t\t\tx+=1\n\t\t\t\t\t\ty1-=1\n\t\t\t\t\t\ty2+=1\n\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m):\n\t\t\t\t\tx = i\n\t\t\t\t\ty1 = j\n\t\t\t\t\ty2 = j\n\t\t\t\t\tcnt = 1\n\t\t\t\t\twhile x>=0 and y1>=0 and y2<m:\n\t\t\t\t\t\tval = prefix[x+1][y2+1] - prefix[x+1][y1]\n\t\t\t\t\t\tif val==cnt:\n\t\t\t\t\t\t\tif cnt>1: ans+=1\n\t\t\t\t\t\t\tcnt+=2\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\tbreak\n\t\t\t\t\t\tx-=1\n\t\t\t\t\t\ty1-=1\n\t\t\t\t\t\ty2+=1\n\t\t\treturn ans\n\t\t\t"""\n\t\t\t#Here we are using dp concept\n\t\t\t#It is like a pyramid question\n\t\t\t#0 0 1 0 0\n\t\t\t#0 1 1 1 0\n\t\t\t#1 1 1 1 1\n\t\t\t#If we take idea of this example then we can get our answer easily\n\t\t\t#First we are processing from the last row and checking all four directions such as \n\t\t\t#down left, down ,down right and own\n\t\t\t#Same idea for the inverse\n\n\t\t\tdef findPyramids(mat):\n\t\t\t\trows,cols = len(mat),len(mat[0])\n\t\t\t\tres = 0\n\t\t\t\tfor r in range(rows-2,-1,-1):\n\t\t\t\t\tfor c in range(1,cols-1):\n\t\t\t\t\t\tif mat[r][c] and mat[r+1][c] and mat[r+1][c-1] and mat[r+1][c+1] :\n\t\t\t\t\t\t\tmat[r][c] = min(mat[r+1][c-1],mat[r+1][c],mat[r+1][c+1]) + 1\n\t\t\t\t\t\t\tres += (mat[r][c] - 1)\n\t\t\t\treturn res\n\n\n\t\t\treverseGrid = []\n\t\t\tfor i in range(len(grid)-1,-1,-1) :\n\t\t\t\treverseGrid.append(list(grid[i]))\n\t\t\tres = findPyramids(grid)\n\t\t\tres += findPyramids(reverseGrid)\n\t\t\treturn res | 0 | A farmer has a **rectangular grid** of land with `m` rows and `n` columns that can be divided into unit cells. Each cell is either **fertile** (represented by a `1`) or **barren** (represented by a `0`). All cells outside the grid are considered barren.
A **pyramidal plot** of land can be defined as a set of cells with the following criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of a pyramid is the **topmost** cell of the pyramid. The **height** of a pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r <= i <= r + h - 1` **and** `c - (i - r) <= j <= c + (i - r)`.
An **inverse pyramidal plot** of land can be defined as a set of cells with similar criteria:
1. The number of cells in the set has to be **greater than** `1` and all cells must be **fertile**.
2. The **apex** of an inverse pyramid is the **bottommost** cell of the inverse pyramid. The **height** of an inverse pyramid is the number of rows it covers. Let `(r, c)` be the apex of the pyramid, and its height be `h`. Then, the plot comprises of cells `(i, j)` where `r - h + 1 <= i <= r` **and** `c - (r - i) <= j <= c + (r - i)`.
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.
Given a **0-indexed** `m x n` binary matrix `grid` representing the farmland, return _the **total number** of pyramidal and inverse pyramidal plots that can be found in_ `grid`.
**Example 1:**
**Input:** grid = \[\[0,1,1,0\],\[1,1,1,1\]\]
**Output:** 2
**Explanation:** The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid.
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.
**Example 2:**
**Input:** grid = \[\[1,1,1\],\[1,1,1\]\]
**Output:** 2
**Explanation:** The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red.
Hence the total number of plots is 1 + 1 = 2.
**Example 3:**
**Input:** grid = \[\[1,1,1,1,0\],\[1,1,1,1,1\],\[1,1,1,1,1\],\[0,1,0,0,1\]\]
**Output:** 13
**Explanation:** There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 1000`
* `1 <= m * n <= 105`
* `grid[i][j]` is either `0` or `1`. | There are only two possible directions you can go when you move to the next letter. When moving to the next letter, you will always go in the direction that takes the least amount of time. |
NO SEARCHING | NO SORTING 👑 | BEATS 100% | find-target-indices-after-sorting-array | 0 | 1 | # Intuition\nwe dont need actual indices, we dont care about sequence or order so we don\'t need sort.\nbinary search \n# Approach\nJust count number of elements which are less than or equal to given target. say lessThanOrEqualCount\nThen count number of elements which are strictly less than given target onlyLessThanCount\n\nif lessThanOrEqualCount = onlyLessThanCount: return empty\nor else all numbers between them\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n- Space complexity: O(1)\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def targetIndices(self, nums: List[int], target: int) -> List[int]:\n lessThanEqual = 0\n onlyLess = 0\n for i in nums:\n if i <= target:\n lessThanEqual += 1\n if i < target:\n onlyLess += 1\n return list(range(onlyLess, lessThanEqual))\n```\n\nPlease upvote if you like the solution.\n | 10 | You are given a **0-indexed** integer array `nums` and a target element `target`.
A **target index** is an index `i` such that `nums[i] == target`.
Return _a list of the target indices of_ `nums` after _sorting_ `nums` _in **non-decreasing** order_. If there are no target indices, return _an **empty** list_. The returned list must be sorted in **increasing** order.
**Example 1:**
**Input:** nums = \[1,2,5,2,3\], target = 2
**Output:** \[1,2\]
**Explanation:** After sorting, nums is \[1,**2**,**2**,3,5\].
The indices where nums\[i\] == 2 are 1 and 2.
**Example 2:**
**Input:** nums = \[1,2,5,2,3\], target = 3
**Output:** \[3\]
**Explanation:** After sorting, nums is \[1,2,2,**3**,5\].
The index where nums\[i\] == 3 is 3.
**Example 3:**
**Input:** nums = \[1,2,5,2,3\], target = 5
**Output:** \[4\]
**Explanation:** After sorting, nums is \[1,2,2,3,**5**\].
The index where nums\[i\] == 5 is 4.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], target <= 100` | Try to use the operation so that each row has only one negative number. If you have only one negative element you cannot convert it to positive. |
Python3 || Easy beginner solution. | find-target-indices-after-sorting-array | 0 | 1 | # Please upvote if you find the solution helpful\n\n# Code\n```\nclass Solution:\n def targetIndices(self, nums: List[int], target: int) -> List[int]:\n l=[]\n nums.sort()\n for i in range(len(nums)):\n if nums[i]==target:\n l.append(i)\n return l\n \n``` | 4 | You are given a **0-indexed** integer array `nums` and a target element `target`.
A **target index** is an index `i` such that `nums[i] == target`.
Return _a list of the target indices of_ `nums` after _sorting_ `nums` _in **non-decreasing** order_. If there are no target indices, return _an **empty** list_. The returned list must be sorted in **increasing** order.
**Example 1:**
**Input:** nums = \[1,2,5,2,3\], target = 2
**Output:** \[1,2\]
**Explanation:** After sorting, nums is \[1,**2**,**2**,3,5\].
The indices where nums\[i\] == 2 are 1 and 2.
**Example 2:**
**Input:** nums = \[1,2,5,2,3\], target = 3
**Output:** \[3\]
**Explanation:** After sorting, nums is \[1,2,2,**3**,5\].
The index where nums\[i\] == 3 is 3.
**Example 3:**
**Input:** nums = \[1,2,5,2,3\], target = 5
**Output:** \[4\]
**Explanation:** After sorting, nums is \[1,2,2,3,**5**\].
The index where nums\[i\] == 5 is 4.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], target <= 100` | Try to use the operation so that each row has only one negative number. If you have only one negative element you cannot convert it to positive. |
Easiest solution in python u will ever find | find-target-indices-after-sorting-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def targetIndices(self, nums: List[int], target: int) -> List[int]:\n res=[]\n nums.sort()\n index1=bisect.bisect_left(nums,target)\n index2=bisect.bisect_right(nums,target)\n return list(range(index1,index2))\n \n \n``` | 2 | You are given a **0-indexed** integer array `nums` and a target element `target`.
A **target index** is an index `i` such that `nums[i] == target`.
Return _a list of the target indices of_ `nums` after _sorting_ `nums` _in **non-decreasing** order_. If there are no target indices, return _an **empty** list_. The returned list must be sorted in **increasing** order.
**Example 1:**
**Input:** nums = \[1,2,5,2,3\], target = 2
**Output:** \[1,2\]
**Explanation:** After sorting, nums is \[1,**2**,**2**,3,5\].
The indices where nums\[i\] == 2 are 1 and 2.
**Example 2:**
**Input:** nums = \[1,2,5,2,3\], target = 3
**Output:** \[3\]
**Explanation:** After sorting, nums is \[1,2,2,**3**,5\].
The index where nums\[i\] == 3 is 3.
**Example 3:**
**Input:** nums = \[1,2,5,2,3\], target = 5
**Output:** \[4\]
**Explanation:** After sorting, nums is \[1,2,2,3,**5**\].
The index where nums\[i\] == 5 is 4.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], target <= 100` | Try to use the operation so that each row has only one negative number. If you have only one negative element you cannot convert it to positive. |
2 Lines of Code--->Using BST Logic | find-target-indices-after-sorting-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def targetIndices(self, nums: List[int], target: int) -> List[int]:\n n=sorted(nums)\n index1,index2=bisect.bisect_left(n,target),bisect.bisect_right(n,target)\n return list(range(index1,index2))\n #please upvote me it would encourage me alot\n\n\n\n``` | 3 | You are given a **0-indexed** integer array `nums` and a target element `target`.
A **target index** is an index `i` such that `nums[i] == target`.
Return _a list of the target indices of_ `nums` after _sorting_ `nums` _in **non-decreasing** order_. If there are no target indices, return _an **empty** list_. The returned list must be sorted in **increasing** order.
**Example 1:**
**Input:** nums = \[1,2,5,2,3\], target = 2
**Output:** \[1,2\]
**Explanation:** After sorting, nums is \[1,**2**,**2**,3,5\].
The indices where nums\[i\] == 2 are 1 and 2.
**Example 2:**
**Input:** nums = \[1,2,5,2,3\], target = 3
**Output:** \[3\]
**Explanation:** After sorting, nums is \[1,2,2,**3**,5\].
The index where nums\[i\] == 3 is 3.
**Example 3:**
**Input:** nums = \[1,2,5,2,3\], target = 5
**Output:** \[4\]
**Explanation:** After sorting, nums is \[1,2,2,3,**5**\].
The index where nums\[i\] == 5 is 4.
**Constraints:**
* `1 <= nums.length <= 100`
* `1 <= nums[i], target <= 100` | Try to use the operation so that each row has only one negative number. If you have only one negative element you cannot convert it to positive. |
w Explanation||C++/Python/C solutions Sliding Window|| Beats 98.25% | k-radius-subarray-averages | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis function calculates sliding window averages for a given input vector nums and window size k. It first checks if there are enough elements in the input vector to form a valid window. If not, it returns a vector with all elements set to -1. If there are enough elements, it proceeds to calculate the sliding window averages.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPlease turn english subtitles if neccessary\n[https://youtu.be/u5p1dEiaAPw](https://youtu.be/u5p1dEiaAPw)\nTo calculate the averages, the code initializes a vector avg of the same size as the input vector, with all elements initially set to -1.\n\nIt uses a loop to iterate over the input vector, summing up the first 2 * k + 1 elements. It then calculates the average of these elements and stores it in the avg vector at the index k, representing the center of the window.\n\nNext, the code enters another loop that starts from k + 1 and iterates until n - k - 1, where n is the size of the input vector.\n\nWithin this loop, it updates the sum by subtracting the element that moved out of the window (at index i - k - 1) and adding the element that enters the window (at index k + i). It then calculates the average based on the updated sum and stores it in the avg vector at the current index i.\n\nFinally, the function returns the avg vector, which contains the sliding window averages for each position in the input vector. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code Runtime 229 ms Beats 94.77%\n```\nclass Solution {\npublic:\n vector<int> getAverages(vector<int>& nums, int k) {\n int n=nums.size();\n vector<int> avg(n, -1);\n if (2*k+1>n) return avg;\n unsigned long long sum=0;\n //sum=accumulate(nums.begin(), nums.begin()+(k*2+1), 0L);\n for(int i=0; i<=2*k; i++){\n sum+=nums[i];\n }\n avg[k]=sum/(2*k+1);\n for(int i=k+1; i<n-k; i++){\n sum+=nums[k+i]-nums[i-k-1];\n avg[i]=sum/(2*k+1);\n }\n return avg;\n }\n};\n```\n# Python solution\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n n=len(nums)\n avg=[-1]*n\n k2_1=2*k+1\n if k2_1>n: return avg\n # wsum=sum(nums[0:k2_1])\n wsum=0\n for x in nums[0:k2_1]:\n wsum+=x\n # Can replace by sum()\n avg[k]=wsum//k2_1\n for i in range(k+1, n-k):\n wsum+=nums[k+i]-nums[i-k-1]\n avg[i]=sum//k2_1\n return avg\n```\n# C solution\n```\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint* getAverages(int* nums, int n, int k, int* returnSize){\n int* avg=(int*)malloc(sizeof(int)*n);\n memset(avg, -1, sizeof(int)*n);\n *returnSize=n;\n int k2_1=2*k+1;\n if (k2_1>n) return avg;\n unsigned long long sum=0;\n for(register int i=0; i<k2_1; i++){\n sum+=nums[i];\n }\n avg[k]=sum/k2_1;\n for(register int i=k+1; i<n-k; i++){\n sum+=nums[k+i]-nums[i-k-1];\n avg[i]=sum/k2_1;\n }\n return avg;\n\n}\n``` | 6 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Python3 Solution | k-radius-subarray-averages | 0 | 1 | \n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n n=len(nums)\n counts=(2*k+1)\n prefix=[0]\n for x in nums:\n prefix.append(prefix[-1]+x)\n\n ans=[]\n for i in range(n):\n if i-k>=0 and i+k<n:\n ans.append((prefix[i+k+1]-prefix[i-k])//counts)\n\n else:\n ans.append(-1)\n\n return ans \n``` | 2 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Sliding_Window.py | k-radius-subarray-averages | 0 | 1 | # Approach\nSliding_Window\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n\n# Code\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n a=k # number of \'-1\'\n k=2*k+1\n if len(nums)<k:return [-1]*len(nums)\n ans,sm=[-1]*a,0\n for i in range(k):sm+=nums[i]\n ans.append(sm//k)\n for i in range(len(nums)-k): # Sliding window start\n sm-=nums[i]\n sm+=nums[i+k]\n ans.append(sm//k)\n for i in range(a):ans.append(-1)\n return ans\n\n``` | 4 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Python3 soln | k-radius-subarray-averages | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nHave a helper function that calculates the average and run it through the List for all n items in the array.\n\nHowever, there time limit was exceeded for this initial thought process, hence the solution shifted to having an additional List that stored the sums of all the elements in nums for O(1) access.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Declare the list that stores the sums\n2. Add all the sums to the list declared above\n4. return a list that contains the averages (-1 if the average does not exist)\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n a = [0]\n for i in range(len(nums)): a.append(a[i] + nums[i])\n return [-1 if i < k or i > len(nums) - 1 - k else (a[i + k + 1] - a[i - k]) // (2 * k + 1) for i in range(len(nums))]\n\n\n``` | 1 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Python Easy Code. Beats 90%. O(n) | k-radius-subarray-averages | 0 | 1 | # Intuition\n\nSliding window approach will be used to get the sum and change it as we keep propagating with the array. If k==0 we return nums itself. if 2*k + 1 > n : we return [-1]*n (n being len(nums)). Otherwise we calculate average for indexes k to n - k -1.\n\n# Complexity \nO(n)\n\n# Code\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n if k==0:\n return nums\n n = len(nums)\n ans = [-1]*n\n if 2*k + 1> n:\n return ans\n val = 0\n if(2*k < n):\n val = sum(nums[:2*k+1])\n avg = val//(2*k +1)\n ans[k] = avg\n for i in range(k+1,n-k):\n if(i-k-1>=0 and i+k<n):\n val -= nums[i-k-1]\n val += nums[i+k]\n avg = val//(2*k +1)\n ans[i] = avg\n return ans\n \n \n \n``` | 1 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Python3, one pass, 100% faster, 53% less mem. | k-radius-subarray-averages | 0 | 1 | # Intuition\nJust scan the input.\nKeep track of sum of sliding window sum.\n\n# Approach\n1. start with `[-1, -1, ..., -1]` of size `n`\n2. calculate the initial window sum `s := sum(nums[:r])`\n3. store int(sum / radius)\n4. slide the window by adding element from the right and removing from the left.\n5. repeat from step 3 until window gets to the end of `nums`\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$ (we don\'t count the output!) \n\nIf you like it, please up-vote. Thanks!\n\n# Code\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n n = len(nums)\n ans = [-1] * n\n r = 2*k + 1\n if r > n:\n return ans\n s = 0\n for i in range(r):\n s+=nums[i]\n span = k+k+1-n # -n so wo dont have to deal with last iteration \n for i in range(n-k-k):\n ans[i+k] = s // r\n s += nums[i+span] - nums[i]\n return ans\n``` | 1 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
Simple Two Pointers Python3 Solution | O(N) Beats 96.34% | Sliding Window with Detailed Explanation | k-radius-subarray-averages | 0 | 1 | Initialized a result array **res** with a length equal to the input array nums, filled with -1s. This array will store the average values of the subarrays. The variables **left** and **windowSum** are initialized to 0, representing the left pointer of the sliding window and the sum of elements within the window, respectively.\n\n**windowLength** is calculated as **2 * k + 1**, which represents the total length of each window.\nThen iterating over the nums array using the variable **right** as the right pointer of the sliding window.\nIn each iteration, the current element is added to the **windowSum** to update the sum of elements within the window. If the length of the current window is equal to **windowLength**, it means the window is complete and we can calculate the average.\n\nThe average is obtained by dividing the **windowSum** by **windowLength**, and it is stored in the **res** array at the corresponding index **(left + k)**. Next, we adjust the window by subtracting the element at the left pointer from the **windowSum** and moving the left pointer to the right by incrementing it by 1.\n\nFinally, the res array is returned, which contains the averages of all the subarrays!\n\n**Time Complexity:** The algorithm iterates over the nums array once using the right pointer, resulting in a time complexity of **O(N)**, where N is the length of the input array.\n\n**Space Complexity:** The algorithm uses additional space to store the res array, which has the same length as the input array. Therefore, the space complexity is **O(N)**, where N is the length of the input array.\n\n**Please Upvote if you like the solution!**\n\n```\nclass Solution:\n def getAverages(self, nums: List[int], k: int) -> List[int]:\n res, left, windowSum, windowLength = [-1] * len(nums), 0, 0, 2 * k + 1\n \n for right in range(len(nums)):\n windowSum += nums[right] # Add the current element to the window sum\n \n # Check if the window length is reached\n if right - left + 1 == windowLength:\n # Calculate the average of the window and store it in the result array\n res[left + k] = windowSum // windowLength\n \n # Adjust the window sum and move the left pointer\n windowSum -= nums[left]\n left += 1\n \n return res\n``` | 1 | You are given a **0-indexed** array `nums` of `n` integers, and an integer `k`.
The **k-radius average** for a subarray of `nums` **centered** at some index `i` with the **radius** `k` is the average of **all** elements in `nums` between the indices `i - k` and `i + k` (**inclusive**). If there are less than `k` elements before **or** after the index `i`, then the **k-radius average** is `-1`.
Build and return _an array_ `avgs` _of length_ `n` _where_ `avgs[i]` _is the **k-radius average** for the subarray centered at index_ `i`.
The **average** of `x` elements is the sum of the `x` elements divided by `x`, using **integer division**. The integer division truncates toward zero, which means losing its fractional part.
* For example, the average of four elements `2`, `3`, `1`, and `5` is `(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75`, which truncates to `2`.
**Example 1:**
**Input:** nums = \[7,4,3,9,1,8,5,2,6\], k = 3
**Output:** \[-1,-1,-1,5,4,4,-1,-1,-1\]
**Explanation:**
- avg\[0\], avg\[1\], and avg\[2\] are -1 because there are less than k elements **before** each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
Using **integer division**, avg\[3\] = 37 / 7 = 5.
- For the subarray centered at index 4, avg\[4\] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg\[5\] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg\[6\], avg\[7\], and avg\[8\] are -1 because there are less than k elements **after** each index.
**Example 2:**
**Input:** nums = \[100000\], k = 0
**Output:** \[100000\]
**Explanation:**
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
avg\[0\] = 100000 / 1 = 100000.
**Example 3:**
**Input:** nums = \[8\], k = 100000
**Output:** \[-1\]
**Explanation:**
- avg\[0\] is -1 because there are less than k elements before and after index 0.
**Constraints:**
* `n == nums.length`
* `1 <= n <= 105`
* `0 <= nums[i], k <= 105` | First use any shortest path algorithm to get edges where dist[u] + weight = dist[v], here dist[x] is the shortest distance between node 0 and x Using those edges only the graph turns into a dag now we just need to know the number of ways to get from node 0 to node n - 1 on a dag using dp |
[Python 3] Remove from left, right, both sides || beats 99% || 766ms 🥷🏼 | removing-minimum-and-maximum-from-array | 0 | 1 | ```python3 []\nclass Solution:\n def minimumDeletions(self, nums: List[int]) -> int:\n minp, maxp, minel, maxel, L = 0, 0, float(\'inf\'), float(\'-inf\'), len(nums)\n for i, n in enumerate(nums):\n if n > maxel:\n maxel = n\n maxp = i\n if n < minel:\n minel = n\n minp = i\n \n left, right = min(minp, maxp), max(minp, maxp)\n\n return min(right + 1, L - left, left + 1 + (L - right))\n```\n\n | 2 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
one liner and easy for beginners | removing-minimum-and-maximum-from-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, nums: List[int]) -> int:\n return min((min(nums.index(min(nums))+1,len(nums)-nums.index(min(nums)))+min(nums.index(max(nums))+1,len(nums)-nums.index(max(nums)))),max(nums.index(min(nums))+1,nums.index(max(nums))+1),max(len(nums)-nums.index(min(nums)),len(nums)-nums.index(max(nums))))\n``` | 4 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
best python3 code beats up to 93% | removing-minimum-and-maximum-from-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBest easy to understand code of python\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, nums: List[int]) -> int:\n maximum = nums.index(max(nums))\n minimum = nums.index(min(nums))\n if maximum > minimum:\n middle_list = nums[minimum+1:maximum]\n else:\n middle_list = nums[maximum+1:minimum]\n if maximum < minimum:\n addition = minimum+1\n else:\n addition = maximum+1\n if maximum < minimum:\n subtracting = len(nums)-maximum\n else:\n subtracting = len(nums)-minimum\n return(min(subtracting,addition,len(nums)-len(middle_list)))\n``` | 2 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
Basic nested lf-else(97.54% beats) | removing-minimum-and-maximum-from-array | 0 | 1 | # Intuition\nWe need to remove the min and max element from the list in such a way that the no.of deletions is the least. \n\n# Approach\nFor starters we need to find out from which end we need to start out deletions.\n\nFor finding that:\n1)Find out the index\'s of both the elements\n2)Check the distance the extreme elements are from the left end and right end\n3)Consider the element which is closest to any of the end\n\nNow we need to follow similar procedure to eliminate the remaining element\n\nFor finding that:\n1)Know the index of the remaining element\n2)Check the distance of that element from both the ends in the new list\n3)Consider deletion from the side with the lesser distance.\n\nBy using nested if we can understand the exact way the control has to work and the problem can be broken down into parts for simplification.\n\nThe code may be long,but it is very simple to understand.Please go through it thorougly.\n\n# Complexity\n- Time complexity:\n0(1)\n\n- Space complexity:\nidk how to find space complexity :(\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, nums: List[int]) -> int:\n si=nums.index(min(nums))#index of smallest number\n li=nums.index(max(nums))#index of biggest number\n if si<li:\n if si<len(nums)-li-1:\n #removes from the start to the smallest element\n sum=si+1\n if li-si<len(nums)-li-1:\n sum+=li-si\n else:\n sum+=len(nums)-li\n else:\n #removes from end to the biggest element\n sum=len(nums)-li\n if si<li-si-1:\n sum+=si+1\n else:\n sum+=li-si\n else:\n if li<len(nums)-si-1:\n #removing from the start to the biggest element\n sum=li+1\n if si-li<len(nums)-si-1:\n sum+=si-li\n else:\n sum+=len(nums)-si\n else:\n #removing from back to the smallest element\n sum=len(nums)-si\n if li<si-li-1:\n sum+=li+1\n else:\n sum+=si-li\n return sum\n``` | 1 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
python3 solution easy to under stand | removing-minimum-and-maximum-from-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumDeletions(self, a: List[int]) -> int:\n# a=[2,10,7,5,4,1,8,6]\n b=a.index(max(a))\n c=a.index(min(a))\n if b>c:\n d=a[c+1:b]\n else:\n d=a[b+1:c]\n print(d)\n if b>c:\n y=b+1\n else:\n y=c+1\n print(y)\n if b>c:\n u=len(a)-c\n else:\n u=len(a)-b\n print(u)\n return(min(u,y,len(a)-len(d)))\n \n``` | 2 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
Basic Python Solution | removing-minimum-and-maximum-from-array | 0 | 1 | simply find the minimum of the two options available. first option is going one way to the larger index and deleting the smaller along the way (consider this from both sides). second option is going from left for the smaller index and going from right for the larger index.\n\n```\nclass Solution:\n def minimumDeletions(self, nums: List[int]) -> int:\n n = len(nums)\n x = nums.index(min(nums)) + 1\n y = nums.index(max(nums)) + 1\n \n res = min(max(n-x+1, n-y+1) , max(x,y)) #minimum of going from right and going from left\n if x > y: #exchange if needed so as to do one operation later assuming x is the smaller index\n x, y = y, x\n \n option = x + (n - y) + 1 #going left for smaller and right for larger\n res = min(res, option)\n \n return res if n > 2 else n\n\t\t\n``` | 3 | You are given a **0-indexed** array of **distinct** integers `nums`.
There is an element in `nums` that has the **lowest** value and an element that has the **highest** value. We call them the **minimum** and **maximum** respectively. Your goal is to remove **both** these elements from the array.
A **deletion** is defined as either removing an element from the **front** of the array or removing an element from the **back** of the array.
Return _the **minimum** number of deletions it would take to remove **both** the minimum and maximum element from the array._
**Example 1:**
**Input:** nums = \[2,**10**,7,5,4,**1**,8,6\]
**Output:** 5
**Explanation:**
The minimum element in the array is nums\[5\], which is 1.
The maximum element in the array is nums\[1\], which is 10.
We can remove both the minimum and maximum by removing 2 elements from the front and 3 elements from the back.
This results in 2 + 3 = 5 deletions, which is the minimum number possible.
**Example 2:**
**Input:** nums = \[0,**\-4**,**19**,1,8,-2,-3,5\]
**Output:** 3
**Explanation:**
The minimum element in the array is nums\[1\], which is -4.
The maximum element in the array is nums\[2\], which is 19.
We can remove both the minimum and maximum by removing 3 elements from the front.
This results in only 3 deletions, which is the minimum number possible.
**Example 3:**
**Input:** nums = \[**101**\]
**Output:** 1
**Explanation:**
There is only one element in the array, which makes it both the minimum and maximum element.
We can remove it with 1 deletion.
**Constraints:**
* `1 <= nums.length <= 105`
* `-105 <= nums[i] <= 105`
* The integers in `nums` are **distinct**. | If we know the current number has d digits, how many digits can the previous number have? Is there a quick way of calculating the number of possibilities for the previous number if we know that it must have less than or equal to d digits? Try to do some pre-processing. |
[Python3] BFS or DFS by group | find-all-people-with-secret | 0 | 1 | Pleaes check out this [commit](https://github.com/gaosanyong/leetcode/commit/b3dd8d234940d5e4afc6a22cc8fc1f4a2e69dd3d) for solutions of weekly 269.\n\n```\nclass Solution:\n def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n can = {0, firstPerson}\n for _, grp in groupby(sorted(meetings, key=lambda x: x[2]), key=lambda x: x[2]): \n queue = set()\n graph = defaultdict(list)\n for x, y, _ in grp: \n graph[x].append(y)\n graph[y].append(x)\n if x in can: queue.add(x)\n if y in can: queue.add(y)\n \n queue = deque(queue)\n while queue: \n x = queue.popleft()\n for y in graph[x]: \n if y not in can: \n can.add(y)\n queue.append(y)\n return can\n```\n\nor \n```\nclass Solution:\n def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n can = {0, firstPerson}\n for _, grp in groupby(sorted(meetings, key=lambda x: x[2]), key=lambda x: x[2]): \n stack = set()\n graph = defaultdict(list)\n for x, y, _ in grp: \n graph[x].append(y)\n graph[y].append(x)\n if x in can: stack.add(x)\n if y in can: stack.add(y)\n \n stack = list(stack)\n while stack: \n x = stack.pop()\n for y in graph[x]: \n if y not in can: \n can.add(y)\n stack.append(y)\n return can\n```\n\nAdding union-find implementation inspired by @lzl124631x\'s post.\n```\nclass UnionFind:\n\n\tdef __init__(self, n: int):\n\t\tself.parent = list(range(n))\n\t\tself.rank = [1] * n\n\n\tdef find(self, p: int) -> int:\n\t\t"""Find with path compression"""\n\t\tif p != self.parent[p]:\n\t\t\tself.parent[p] = self.find(self.parent[p])\n\t\treturn self.parent[p]\n\n\tdef union(self, p: int, q: int) -> bool:\n\t\t"""Union with rank"""\n\t\tprt, qrt = self.find(p), self.find(q)\n\t\tif prt == qrt: return False\n\t\tif self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt \n\t\tself.parent[prt] = qrt\n\t\tself.rank[qrt] += self.rank[prt]\n\t\treturn True\n\n\nclass Solution:\n def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n uf = UnionFind(n)\n uf.union(0, firstPerson)\n for _, grp in groupby(sorted(meetings, key=lambda x: x[2]), key=lambda x: x[2]): \n seen = set()\n for x, y, _ in grp: \n seen.add(x)\n seen.add(y)\n uf.union(x, y)\n for x in seen: \n if uf.find(x) != uf.find(0): uf.parent[x] = x # reset \n return [x for x in range(n) if uf.find(x) == uf.find(0)]\n``` | 29 | You are given an integer `n` indicating there are `n` people numbered from `0` to `n - 1`. You are also given a **0-indexed** 2D integer array `meetings` where `meetings[i] = [xi, yi, timei]` indicates that person `xi` and person `yi` have a meeting at `timei`. A person may attend **multiple meetings** at the same time. Finally, you are given an integer `firstPerson`.
Person `0` has a **secret** and initially shares the secret with a person `firstPerson` at time `0`. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person `xi` has the secret at `timei`, then they will share the secret with person `yi`, and vice versa.
The secrets are shared **instantaneously**. That is, a person may receive the secret and share it with people in other meetings within the same time frame.
Return _a list of all the people that have the secret after all the meetings have taken place._ You may return the answer in **any order**.
**Example 1:**
**Input:** n = 6, meetings = \[\[1,2,5\],\[2,3,8\],\[1,5,10\]\], firstPerson = 1
**Output:** \[0,1,2,3,5\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.
**Example 2:**
**Input:** n = 4, meetings = \[\[3,1,3\],\[1,2,2\],\[0,3,3\]\], firstPerson = 3
**Output:** \[0,1,3\]
**Explanation:**
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.
**Example 3:**
**Input:** n = 5, meetings = \[\[3,4,2\],\[1,2,1\],\[2,3,1\]\], firstPerson = 1
**Output:** \[0,1,2,3,4\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.
**Constraints:**
* `2 <= n <= 105`
* `1 <= meetings.length <= 105`
* `meetings[i].length == 3`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= timei <= 105`
* `1 <= firstPerson <= n - 1` | null |
📌📌 Really the Simplest answer I came through || BFS or DFS 🐍 | find-all-people-with-secret | 0 | 1 | ## IDEA :\n* Firstly group all the meetings with the key as time on which meeting is happening.\n\n* So one by one go through all the groups (timing by increasing order) and add all the persons to whom secrets got get shared.\n* Here `sh` denotes the persons having secret with them.\n* Going through each group find the persons with whom secrets got shared and add them in `sh` .\n* At last return the `sh` as a list.\n\n**Implementation :**\n\n## BFS :\n\'\'\'\n\n\tclass Solution:\n def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n \n meetings.sort(key=lambda x:x[2])\n groups = itertools.groupby(meetings,key = lambda x:x[2])\n \n sh = {0,firstPerson}\n for key,grp in groups:\n seen = set()\n graph = defaultdict(list)\n for a,b,t in grp:\n graph[a].append(b)\n graph[b].append(a)\n if a in sh:\n seen.add(a)\n if b in sh:\n seen.add(b)\n \n queue = deque(seen)\n while queue:\n node = queue.popleft()\n for neig in graph[node]:\n if neig not in sh:\n sh.add(neig)\n queue.append(neig)\n \n return list(sh)\n\n## DFS :\n\'\'\'\n\n\tclass Solution:\n\t\tdef findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n\n\t\t\tmeetings.sort(key=lambda x:x[2])\n\t\t\tgroups = itertools.groupby(meetings,key = lambda x:x[2])\n\n\t\t\tsh = {0,firstPerson}\n\t\t\tfor key,grp in groups:\n\t\t\t\tseen = set()\n\t\t\t\tgraph = defaultdict(list)\n\t\t\t\tfor a,b,t in grp:\n\t\t\t\t\tgraph[a].append(b)\n\t\t\t\t\tgraph[b].append(a)\n\t\t\t\t\tif a in sh:\n\t\t\t\t\t\tseen.add(a)\n\t\t\t\t\tif b in sh:\n\t\t\t\t\t\tseen.add(b)\n\n\t\t\t\tst = list(seen)[::]\n\t\t\t\twhile st:\n\t\t\t\t\tnode = st.pop()\n\t\t\t\t\tfor neig in graph[node]:\n\t\t\t\t\t\tif neig not in sh:\n\t\t\t\t\t\t\tsh.add(neig)\n\t\t\t\t\t\t\tst.append(neig)\n\n\t\t\treturn list(sh)\n\n**Thanks & Upvote if you got any help !!\uD83E\uDD1E** | 12 | You are given an integer `n` indicating there are `n` people numbered from `0` to `n - 1`. You are also given a **0-indexed** 2D integer array `meetings` where `meetings[i] = [xi, yi, timei]` indicates that person `xi` and person `yi` have a meeting at `timei`. A person may attend **multiple meetings** at the same time. Finally, you are given an integer `firstPerson`.
Person `0` has a **secret** and initially shares the secret with a person `firstPerson` at time `0`. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person `xi` has the secret at `timei`, then they will share the secret with person `yi`, and vice versa.
The secrets are shared **instantaneously**. That is, a person may receive the secret and share it with people in other meetings within the same time frame.
Return _a list of all the people that have the secret after all the meetings have taken place._ You may return the answer in **any order**.
**Example 1:**
**Input:** n = 6, meetings = \[\[1,2,5\],\[2,3,8\],\[1,5,10\]\], firstPerson = 1
**Output:** \[0,1,2,3,5\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.
**Example 2:**
**Input:** n = 4, meetings = \[\[3,1,3\],\[1,2,2\],\[0,3,3\]\], firstPerson = 3
**Output:** \[0,1,3\]
**Explanation:**
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.
**Example 3:**
**Input:** n = 5, meetings = \[\[3,4,2\],\[1,2,1\],\[2,3,1\]\], firstPerson = 1
**Output:** \[0,1,2,3,4\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.
**Constraints:**
* `2 <= n <= 105`
* `1 <= meetings.length <= 105`
* `meetings[i].length == 3`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= timei <= 105`
* `1 <= firstPerson <= n - 1` | null |
Python BFS | find-all-people-with-secret | 0 | 1 | ```\nclass Solution:\n def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:\n g = defaultdict(dict)\n for p1, p2, t in meetings:\n g[t][p1] = g[t].get(p1, [])\n g[t][p1].append(p2)\n g[t][p2] = g[t].get(p2, [])\n g[t][p2].append(p1)\n known = {0, firstPerson}\n for t in sorted(g.keys()):\n seen = set()\n for p in g[t]:\n if p in known and p not in seen:\n q = deque([p])\n seen.add(p)\n while q:\n cur = q.popleft()\n for nxt in g[t][cur]:\n if nxt not in seen:\n q.append(nxt)\n seen.add(nxt)\n known.add(nxt)\n return known\n```\nEdited to make it more concise. \n__________________________\nInterestingly, for this part\n```\n g[t][p1] = g[t].get(p1, [])\n g[t][p1].append(p2)\n g[t][p2] = g[t].get(p2, [])\n g[t][p2].append(p1)\n```\nIf we write it as below, we would get TLE\n```\n g[t][p1] = g[t].get(p1, [])+[p2]\n g[t][p2] = g[t].get(p2, [])+[p1]\n```\nThe main reason is that `g[t].get(p1, [])+[p2]` creates a new array whereas `g[t][p1].append(p2)` simply adds `p2` to the original array | 7 | You are given an integer `n` indicating there are `n` people numbered from `0` to `n - 1`. You are also given a **0-indexed** 2D integer array `meetings` where `meetings[i] = [xi, yi, timei]` indicates that person `xi` and person `yi` have a meeting at `timei`. A person may attend **multiple meetings** at the same time. Finally, you are given an integer `firstPerson`.
Person `0` has a **secret** and initially shares the secret with a person `firstPerson` at time `0`. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person `xi` has the secret at `timei`, then they will share the secret with person `yi`, and vice versa.
The secrets are shared **instantaneously**. That is, a person may receive the secret and share it with people in other meetings within the same time frame.
Return _a list of all the people that have the secret after all the meetings have taken place._ You may return the answer in **any order**.
**Example 1:**
**Input:** n = 6, meetings = \[\[1,2,5\],\[2,3,8\],\[1,5,10\]\], firstPerson = 1
**Output:** \[0,1,2,3,5\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.
**Example 2:**
**Input:** n = 4, meetings = \[\[3,1,3\],\[1,2,2\],\[0,3,3\]\], firstPerson = 3
**Output:** \[0,1,3\]
**Explanation:**
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.
**Example 3:**
**Input:** n = 5, meetings = \[\[3,4,2\],\[1,2,1\],\[2,3,1\]\], firstPerson = 1
**Output:** \[0,1,2,3,4\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.
**Constraints:**
* `2 <= n <= 105`
* `1 <= meetings.length <= 105`
* `meetings[i].length == 3`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= timei <= 105`
* `1 <= firstPerson <= n - 1` | null |
[With Pictures] Easy to Understand Union-Find Approach | find-all-people-with-secret | 0 | 1 | **Intuition**\n\nThe key to this problem is observing that:\n1. We need to keep track of all people who know the secret (i.e., this is the disjoint set containing person `0`); and\n2. When we have people meeting at the same time, we will connect the people who meet each other. \n\t* However, this can result in disjoint sets of size greater than 1 of people who don\'t know the secret.\n\t* Therefore, before we move on to process the next point in time, we need to make sure that we have **only one** disjoint set of size greater than 1 -- that is the people who know the secret.\n\t* This will help us avoiding to connect wrong people unintentionally in the future.\n\nProcedure `unset_nodes` will unset all nodes that are not connected to node `0` (i.e., people who don\'t know the secret). It will ensure that we leave a particular time with **only one** disjoint set of size greater than 1 -- the people who know the secret.\n\n\n\n**Algorithm**\nFirst, we implement the algorithm to unset all people who don\'t know the secret as follows:\n```python\ndef unset_nodes(self, uf: UnionFind, nodes: Set[int]) -> None:\n\tfor p in nodes:\n\t\tif uf.is_connected(0, p):\n\t\t\tcontinue\n\t\t# This person does not know the secret, so disconnect\n\t\t# this person from any other people. Note that we will\n\t\t# NOT mess up the ranks of nodes, because we unset every\n\t\t# person who is not knowing the secret. At the end of the\n\t\t# operation, there will only be one "connected component".\n\t\tuf.root[p], uf.rank[p] = p, 1\n```\n\nThen, the main algorithm that utilized union find, as follows:\n**NOTE:** `UnionFind` is just a standard implementation of union find with ranks and path compression. You can learn more about this in the LeetCode official Union Find card.\n```python\ndef findAllPeople(self, n: int, meetings: List[List[int]], first: int) -> List[int]:\n\t# Initialize union find and connect people who initially know the secret;\n\t# Since person 0 will tell the secret to person `first`, this will be a set\n\t# of two people: 0 and `first`.\n\tuf = UnionFind(n)\n\tuf.union(0, first)\n\n\t# Process meeting sorted by time in ascending order; this is very intuitive.\n\tmeetings.sort(key=lambda meeting: meeting[2])\n\n\t# `prev_time` allows us to tell whether we are moving on to a new time period;\n\t# `processed` allows us to record the nodes that we have processed for this\n\t# point in time.\n\tprev_time, processed = None, set()\n\n\t# Reads: person `x` meets person `y` at time `time`.\n\tfor x, y, time in meetings:\n\t\t# When we enter into a new point in time, we keep **only** the\n\t\t# people knowing the secret connected. This means all people (nodes)\n\t\t# not knowing the secret must be disconnected.\n\t\tif prev_time != time:\n\t\t\tprev_time = time\n\t\t\t# `unset_nodes` finds all people in `processed` that is not knowing\n\t\t\t# the secret; i.e., not connected with node 0.\n\t\t\tself.unset_nodes(uf, processed)\n\t\t\tprocessed = set()\n\n\t\t# Marks that person `x` meets with person `y`, and we "processed" person\n\t\t# `x` and `y`.\n\t\tuf.union(x, y)\n\t\tprocessed.update([x, y])\n\n\t# Find all people who are knows the secret.\n\tres = []\n\tfor i in range(n):\n\t\tif uf.is_connected(0, i):\n\t\t\tres.append(i)\n\treturn res\n```\n\n**Please...**\n\nPlease **upvote** this post if you find it helpful. It motivates me to create more helpful content for the community. | 3 | You are given an integer `n` indicating there are `n` people numbered from `0` to `n - 1`. You are also given a **0-indexed** 2D integer array `meetings` where `meetings[i] = [xi, yi, timei]` indicates that person `xi` and person `yi` have a meeting at `timei`. A person may attend **multiple meetings** at the same time. Finally, you are given an integer `firstPerson`.
Person `0` has a **secret** and initially shares the secret with a person `firstPerson` at time `0`. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person `xi` has the secret at `timei`, then they will share the secret with person `yi`, and vice versa.
The secrets are shared **instantaneously**. That is, a person may receive the secret and share it with people in other meetings within the same time frame.
Return _a list of all the people that have the secret after all the meetings have taken place._ You may return the answer in **any order**.
**Example 1:**
**Input:** n = 6, meetings = \[\[1,2,5\],\[2,3,8\],\[1,5,10\]\], firstPerson = 1
**Output:** \[0,1,2,3,5\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.
**Example 2:**
**Input:** n = 4, meetings = \[\[3,1,3\],\[1,2,2\],\[0,3,3\]\], firstPerson = 3
**Output:** \[0,1,3\]
**Explanation:**
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.
**Example 3:**
**Input:** n = 5, meetings = \[\[3,4,2\],\[1,2,1\],\[2,3,1\]\], firstPerson = 1
**Output:** \[0,1,2,3,4\]
**Explanation:**
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.
**Constraints:**
* `2 <= n <= 105`
* `1 <= meetings.length <= 105`
* `meetings[i].length == 3`
* `0 <= xi, yi <= n - 1`
* `xi != yi`
* `1 <= timei <= 105`
* `1 <= firstPerson <= n - 1` | null |
Three Cycles | finding-3-digit-even-numbers | 0 | 1 | **C++**\n```cpp\nvector<int> findEvenNumbers(vector<int>& digits) {\n vector<int> res;\n int cnt[10] = {};\n for (auto d : digits)\n ++cnt[d];\n for (int i = 1; i < 10; ++i)\n for (int j = 0; cnt[i] > 0 && j < 10; ++j)\n for (int k = 0; cnt[j] > (i == j) && k < 10; k += 2)\n if (cnt[k] > (k == i) + (k == j))\n res.push_back(i * 100 + j * 10 + k);\n return res;\n}\n```\n**Python 3**\nFor brevity, we check for `cnt` at the very end. It is faster to prune earier, but here we only need to check 450 numbers. \n\n```python\nclass Solution:\n def findEvenNumbers(self, digits: List[int]) -> List[int]:\n res, cnt = [], Counter(digits)\n for i in range(1, 10):\n for j in range(0, 10):\n for k in range(0, 10, 2):\n if cnt[i] > 0 and cnt[j] > (i == j) and cnt[k] > (k == i) + (k == j):\n res.append(i * 100 + j * 10 + k)\n return res\n``` | 73 | You are given an integer array `digits`, where each element is a digit. The array may contain duplicates.
You need to find **all** the **unique** integers that follow the given requirements:
* The integer consists of the **concatenation** of **three** elements from `digits` in **any** arbitrary order.
* The integer does not have **leading zeros**.
* The integer is **even**.
For example, if the given `digits` were `[1, 2, 3]`, integers `132` and `312` follow the requirements.
Return _a **sorted** array of the unique integers._
**Example 1:**
**Input:** digits = \[2,1,3,0\]
**Output:** \[102,120,130,132,210,230,302,310,312,320\]
**Explanation:** All the possible integers that follow the requirements are in the output array.
Notice that there are no **odd** integers or integers with **leading zeros**.
**Example 2:**
**Input:** digits = \[2,2,8,8,2\]
**Output:** \[222,228,282,288,822,828,882\]
**Explanation:** The same digit can be used as many times as it appears in digits.
In this example, the digit 8 is used twice each time in 288, 828, and 882.
**Example 3:**
**Input:** digits = \[3,7,5\]
**Output:** \[\]
**Explanation:** No **even** integers can be formed using the given digits.
**Constraints:**
* `3 <= digits.length <= 100`
* `0 <= digits[i] <= 9` | Choose the pile with the maximum number of stones each time. Use a data structure that helps you find the mentioned pile each time efficiently. One such data structure is a Priority Queue. |
[Python3] brute-force | finding-3-digit-even-numbers | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b1948f8814bebeca475cbb354cd44d19092dff59) for solutions of weekly 270.\n\n```\nclass Solution:\n def findEvenNumbers(self, digits: List[int]) -> List[int]:\n ans = set()\n for x, y, z in permutations(digits, 3): \n if x != 0 and z & 1 == 0: \n ans.add(100*x + 10*y + z) \n return sorted(ans)\n```\n\nAlternative `O(N)` approach \n```\nclass Solution:\n def findEvenNumbers(self, digits: List[int]) -> List[int]:\n ans = []\n freq = Counter(digits)\n for x in range(100, 1000, 2): \n if not Counter(int(d) for d in str(x)) - freq: ans.append(x)\n return ans \n``` | 33 | You are given an integer array `digits`, where each element is a digit. The array may contain duplicates.
You need to find **all** the **unique** integers that follow the given requirements:
* The integer consists of the **concatenation** of **three** elements from `digits` in **any** arbitrary order.
* The integer does not have **leading zeros**.
* The integer is **even**.
For example, if the given `digits` were `[1, 2, 3]`, integers `132` and `312` follow the requirements.
Return _a **sorted** array of the unique integers._
**Example 1:**
**Input:** digits = \[2,1,3,0\]
**Output:** \[102,120,130,132,210,230,302,310,312,320\]
**Explanation:** All the possible integers that follow the requirements are in the output array.
Notice that there are no **odd** integers or integers with **leading zeros**.
**Example 2:**
**Input:** digits = \[2,2,8,8,2\]
**Output:** \[222,228,282,288,822,828,882\]
**Explanation:** The same digit can be used as many times as it appears in digits.
In this example, the digit 8 is used twice each time in 288, 828, and 882.
**Example 3:**
**Input:** digits = \[3,7,5\]
**Output:** \[\]
**Explanation:** No **even** integers can be formed using the given digits.
**Constraints:**
* `3 <= digits.length <= 100`
* `0 <= digits[i] <= 9` | Choose the pile with the maximum number of stones each time. Use a data structure that helps you find the mentioned pile each time efficiently. One such data structure is a Priority Queue. |
98% Runtime 91% Memory One liner with 3 loops and counter solution | finding-3-digit-even-numbers | 0 | 1 | \n\n\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findEvenNumbers(self, digits: List[int]) -> List[int]:\n c = Counter(digits)\n \n return [\n i*100+j*10+k \n for i in range(1,10) \n for j in range(0,10) \n for k in range(0,10,2) \n if c[i]>0 and c[j]>(i==j) and c[k]>(k==i)+(k==j)\n ]\n\n``` | 1 | You are given an integer array `digits`, where each element is a digit. The array may contain duplicates.
You need to find **all** the **unique** integers that follow the given requirements:
* The integer consists of the **concatenation** of **three** elements from `digits` in **any** arbitrary order.
* The integer does not have **leading zeros**.
* The integer is **even**.
For example, if the given `digits` were `[1, 2, 3]`, integers `132` and `312` follow the requirements.
Return _a **sorted** array of the unique integers._
**Example 1:**
**Input:** digits = \[2,1,3,0\]
**Output:** \[102,120,130,132,210,230,302,310,312,320\]
**Explanation:** All the possible integers that follow the requirements are in the output array.
Notice that there are no **odd** integers or integers with **leading zeros**.
**Example 2:**
**Input:** digits = \[2,2,8,8,2\]
**Output:** \[222,228,282,288,822,828,882\]
**Explanation:** The same digit can be used as many times as it appears in digits.
In this example, the digit 8 is used twice each time in 288, 828, and 882.
**Example 3:**
**Input:** digits = \[3,7,5\]
**Output:** \[\]
**Explanation:** No **even** integers can be formed using the given digits.
**Constraints:**
* `3 <= digits.length <= 100`
* `0 <= digits[i] <= 9` | Choose the pile with the maximum number of stones each time. Use a data structure that helps you find the mentioned pile each time efficiently. One such data structure is a Priority Queue. |
Python - Short & Simple (dict + sorting) | finding-3-digit-even-numbers | 0 | 1 | ```\ndef findEvenNumbers(self, digits: List[int]) -> List[int]:\n res = []\n dic = Counter(digits) \n for num in range(100,1000,2):\n flag = 0\n for i,j in Counter(str(num)).items():\n if dic[int(i)] < j:\n flag = 1\n if flag == 0:\n res.append(num)\n return res\n``` | 1 | You are given an integer array `digits`, where each element is a digit. The array may contain duplicates.
You need to find **all** the **unique** integers that follow the given requirements:
* The integer consists of the **concatenation** of **three** elements from `digits` in **any** arbitrary order.
* The integer does not have **leading zeros**.
* The integer is **even**.
For example, if the given `digits` were `[1, 2, 3]`, integers `132` and `312` follow the requirements.
Return _a **sorted** array of the unique integers._
**Example 1:**
**Input:** digits = \[2,1,3,0\]
**Output:** \[102,120,130,132,210,230,302,310,312,320\]
**Explanation:** All the possible integers that follow the requirements are in the output array.
Notice that there are no **odd** integers or integers with **leading zeros**.
**Example 2:**
**Input:** digits = \[2,2,8,8,2\]
**Output:** \[222,228,282,288,822,828,882\]
**Explanation:** The same digit can be used as many times as it appears in digits.
In this example, the digit 8 is used twice each time in 288, 828, and 882.
**Example 3:**
**Input:** digits = \[3,7,5\]
**Output:** \[\]
**Explanation:** No **even** integers can be formed using the given digits.
**Constraints:**
* `3 <= digits.length <= 100`
* `0 <= digits[i] <= 9` | Choose the pile with the maximum number of stones each time. Use a data structure that helps you find the mentioned pile each time efficiently. One such data structure is a Priority Queue. |
[Python] Simple HashMap Solution, O(n) | finding-3-digit-even-numbers | 0 | 1 | * We need 3 digit numbers so we travese form 100 to 999\n* For every num in range we check if its digits are in digits array and frequency of its digits is less than or equal to frequency of digits in digits array.\n```\nclass Solution:\n def findEvenNumbers(self, digits: List[int]) -> List[int]:\n hmap, res = defaultdict(int), []\n for num in digits:\n hmap[num] += 1 #counting frequency of digits of digits array\n \n for num in range(100, 999, 2): #step 2 because we need even numbers\n checker = defaultdict(int)\n for digit in str(num):\n checker[int(digit)] += 1 #counting frequency of digits of num\n \n\t\t\t#check if every digit in num is in digits array and its frequency is less than or equal to its frequency in digits array\n if all(map(lambda x: x in hmap and checker[x] <= hmap[x], checker)):\n res.append(num)\n \n return res\n``` | 8 | You are given an integer array `digits`, where each element is a digit. The array may contain duplicates.
You need to find **all** the **unique** integers that follow the given requirements:
* The integer consists of the **concatenation** of **three** elements from `digits` in **any** arbitrary order.
* The integer does not have **leading zeros**.
* The integer is **even**.
For example, if the given `digits` were `[1, 2, 3]`, integers `132` and `312` follow the requirements.
Return _a **sorted** array of the unique integers._
**Example 1:**
**Input:** digits = \[2,1,3,0\]
**Output:** \[102,120,130,132,210,230,302,310,312,320\]
**Explanation:** All the possible integers that follow the requirements are in the output array.
Notice that there are no **odd** integers or integers with **leading zeros**.
**Example 2:**
**Input:** digits = \[2,2,8,8,2\]
**Output:** \[222,228,282,288,822,828,882\]
**Explanation:** The same digit can be used as many times as it appears in digits.
In this example, the digit 8 is used twice each time in 288, 828, and 882.
**Example 3:**
**Input:** digits = \[3,7,5\]
**Output:** \[\]
**Explanation:** No **even** integers can be formed using the given digits.
**Constraints:**
* `3 <= digits.length <= 100`
* `0 <= digits[i] <= 9` | Choose the pile with the maximum number of stones each time. Use a data structure that helps you find the mentioned pile each time efficiently. One such data structure is a Priority Queue. |
Beats 100% || Detailed explanation || Two pointer || [Java/C++/Python] | delete-the-middle-node-of-a-linked-list | 1 | 1 | # Intuition\n1. If a point with a speed s moves n units in a given time, a point with speed 2 * s will move 2 * n units at the same time. It means when a pointer with 2*s speed reaches the end, the pointer will s speed will be at exactly the mid point.\n\n# Approach\n1. **Base Case Check:**\n - If the linked list is empty or has only one node, there is no middle node to delete, so the method returns `null`.\n2. **Two-Pointer Approach (Slow and Fast Pointers):**\n - Two pointers, slow and fast, are initialized. The slow pointer advances one node at a time, while the fast pointer advances two nodes at a time.\n4. **Find the Middle Node:**\n - The loop iterates until the `fast` pointer reaches the end of the list (`null`) or the second-to-last node. At each iteration, the `slow` pointer moves one step, and the `fast` pointer moves two steps. As a result, the `slow` pointer will be at the middle node when the loop exits.\n5. **Delete the Middle Node:**\n - The middle node is deleted by updating the next reference of the node before the middle node (`slow.next`) to skip the middle node.\n6. Return the Updated Head:\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode deleteMiddle(ListNode head) {\n // return bruteApproach(head);\n\n if(head==null || head.next==null) return null;\n\n ListNode slow = head;\n ListNode fast = head.next.next;\n\n while(fast!=null && fast.next!=null) {\n slow = slow.next;\n fast = fast.next.next;\n }\n slow.next = slow.next.next;\n return head;\n }\n}\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n \nstruct ListNode {\n int val;\n ListNode* next;\n ListNode() : val(0), next(nullptr) {}\n ListNode(int x) : val(x), next(nullptr) {}\n ListNode(int x, ListNode* next) : val(x), next(next) {}\n};\n*/\n\nclass Solution {\npublic:\n ListNode* deleteMiddle(ListNode* head) {\n // Base Case Check\n if (head == nullptr || head->next == nullptr)\n return nullptr;\n\n ListNode* slow = head;\n ListNode* fast = head->next->next;\n\n // Two-Pointer Approach to Find the Middle Node\n while (fast != nullptr && fast->next != nullptr) {\n slow = slow->next;\n fast = fast->next->next;\n }\n\n // Delete the Middle Node\n slow->next = slow->next->next;\n\n // Return the Updated Head\n return head;\n }\n};\n```\n```Python []\n# Definition for singly-linked list.\n#class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\n\nclass Solution:\n def deleteMiddle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n # Base Case Check\n if head is None or head.next is None:\n return None\n\n slow = head\n fast = head.next.next\n\n # Two-Pointer Approach to Find the Middle Node\n while fast is not None and fast.next is not None:\n slow = slow.next\n fast = fast.next.next\n\n # Delete the Middle Node\n slow.next = slow.next.next\n\n # Return the Updated Head\n return head\n``` | 2 | You are given the `head` of a linked list. **Delete** the **middle node**, and return _the_ `head` _of the modified linked list_.
The **middle node** of a linked list of size `n` is the `⌊n / 2⌋th` node from the **start** using **0-based indexing**, where `⌊x⌋` denotes the largest integer less than or equal to `x`.
* For `n` = `1`, `2`, `3`, `4`, and `5`, the middle nodes are `0`, `1`, `1`, `2`, and `2`, respectively.
**Example 1:**
**Input:** head = \[1,3,4,7,1,2,6\]
**Output:** \[1,3,4,1,2,6\]
**Explanation:**
The above figure represents the given linked list. The indices of the nodes are written below.
Since n = 7, node 3 with value 7 is the middle node, which is marked in red.
We return the new list after removing this node.
**Example 2:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,2,4\]
**Explanation:**
The above figure represents the given linked list.
For n = 4, node 2 with value 3 is the middle node, which is marked in red.
**Example 3:**
**Input:** head = \[2,1\]
**Output:** \[2\]
**Explanation:**
The above figure represents the given linked list.
For n = 2, node 1 with value 1 is the middle node, which is marked in red.
Node 0 with value 2 is the only node remaining after removing node 1.
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`.
* `1 <= Node.val <= 105` | Iterate over the string and keep track of the number of opening and closing brackets on each step. If the number of closing brackets is ever larger, you need to make a swap. Swap it with the opening bracket closest to the end of s. |
✅✅✅Easy python3 solution. | delete-the-middle-node-of-a-linked-list | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def deleteMiddle(self, head: Optional[ListNode]) -> Optional[ListNode]:\n if head == None:\n return \n if head.next == None:\n return \n\n slow = head\n fast = head\n fast = fast.next.next\n\n while fast != None and fast.next != None:\n fast = fast.next.next\n slow = slow.next\n \n slow.next = slow.next.next\n\n return head\n``` | 2 | You are given the `head` of a linked list. **Delete** the **middle node**, and return _the_ `head` _of the modified linked list_.
The **middle node** of a linked list of size `n` is the `⌊n / 2⌋th` node from the **start** using **0-based indexing**, where `⌊x⌋` denotes the largest integer less than or equal to `x`.
* For `n` = `1`, `2`, `3`, `4`, and `5`, the middle nodes are `0`, `1`, `1`, `2`, and `2`, respectively.
**Example 1:**
**Input:** head = \[1,3,4,7,1,2,6\]
**Output:** \[1,3,4,1,2,6\]
**Explanation:**
The above figure represents the given linked list. The indices of the nodes are written below.
Since n = 7, node 3 with value 7 is the middle node, which is marked in red.
We return the new list after removing this node.
**Example 2:**
**Input:** head = \[1,2,3,4\]
**Output:** \[1,2,4\]
**Explanation:**
The above figure represents the given linked list.
For n = 4, node 2 with value 3 is the middle node, which is marked in red.
**Example 3:**
**Input:** head = \[2,1\]
**Output:** \[2\]
**Explanation:**
The above figure represents the given linked list.
For n = 2, node 1 with value 1 is the middle node, which is marked in red.
Node 0 with value 2 is the only node remaining after removing node 1.
**Constraints:**
* The number of nodes in the list is in the range `[1, 105]`.
* `1 <= Node.val <= 105` | Iterate over the string and keep track of the number of opening and closing brackets on each step. If the number of closing brackets is ever larger, you need to make a swap. Swap it with the opening bracket closest to the end of s. |
Beat 100% - Easy to understand and implement - DFS | step-by-step-directions-from-a-binary-tree-node-to-another | 0 | 1 | # Intuition\nFind a path from the root to the start node and another path from the root to the destination node. Identify the node where these two paths intersect. Then, add the path from that node to the start value and the path from that node to the destination value to the result.\n\n\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\'\'\'\nIdea: Find a path from the root to the start node and another path from the root to the destination node. Identify the node where these two paths intersect. Then, add the path from that node to the start value and the path from that node to the destination value to the result.\n\'\'\'\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n directionToStartValue = []\n directionToDestValue = []\n # find path from root to start node and dest node\n self.hasPath(root, directionToStartValue, startValue)\n self.hasPath(root, directionToDestValue, destValue)\n\n # reverse\n directionToStartValue = directionToStartValue[::-1]\n directionToDestValue = directionToDestValue[::-1]\n\n rs = ""\n i = 0\n\n # Find the index where the path starts in a different direction.\n while i < len(directionToStartValue):\n if i >= len(directionToDestValue) or directionToStartValue[i] != directionToDestValue[i]:\n break\n i += 1\n\n # add path from i to start value to result\n for j in range(i, len(directionToStartValue)): \n rs += "U"\n\n # add path from i to dest value to result\n for j in range(i, len(directionToDestValue)): \n rs += directionToDestValue[j]\n\n return rs\n \n def hasPath(self, root: Optional[TreeNode], direction: List[str], x: int) -> bool:\n if not root:\n return False\n\n if root.val == x:\n return True\n\n if self.hasPath(root.left, direction, x):\n direction.append("L")\n return True\n\n if self.hasPath(root.right, direction, x):\n direction.append("R")\n return True\n \n return False\n \n``` | 3 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
3 Steps | step-by-step-directions-from-a-binary-tree-node-to-another | 1 | 1 | 1. Build directions for both start and destination from the root.\n\t- Say we get "LLRRL" and "LRR".\n2. Remove common prefix path.\n\t- We remove "L", and now start direction is "LRRL", and destination - "RR"\n3. Replace all steps in the start direction to "U" and add destination direction.\n\t- The result is "UUUU" + "RR".\n\n**C++**\nHere, we build path in the reverse order to avoid creating new strings.\n\n```cpp\nbool find(TreeNode* n, int val, string &path) {\n if (n->val == val)\n return true;\n if (n->left && find(n->left, val, path))\n path.push_back(\'L\');\n else if (n->right && find(n->right, val, path))\n path.push_back(\'R\');\n return !path.empty();\n}\nstring getDirections(TreeNode* root, int startValue, int destValue) {\n string s_p, d_p;\n find(root, startValue, s_p);\n find(root, destValue, d_p);\n while (!s_p.empty() && !d_p.empty() && s_p.back() == d_p.back()) {\n s_p.pop_back();\n d_p.pop_back();\n }\n return string(s_p.size(), \'U\') + string(rbegin(d_p), rend(d_p));\n}\n```\n**Java**\n```java\nprivate boolean find(TreeNode n, int val, StringBuilder sb) {\n if (n.val == val) \n return true;\n if (n.left != null && find(n.left, val, sb))\n sb.append("L");\n else if (n.right != null && find(n.right, val, sb))\n sb.append("R");\n return sb.length() > 0;\n}\npublic String getDirections(TreeNode root, int startValue, int destValue) {\n StringBuilder s = new StringBuilder(), d = new StringBuilder();\n find(root, startValue, s);\n find(root, destValue, d);\n int i = 0, max_i = Math.min(d.length(), s.length());\n while (i < max_i && s.charAt(s.length() - i - 1) == d.charAt(d.length() - i - 1))\n ++i;\n return "U".repeat(s.length() - i) + d.reverse().toString().substring(i);\n}\n```\n**Python 3**\nLists in Python are mutable and passed by a reference.\n\n```python\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n def find(n: TreeNode, val: int, path: List[str]) -> bool:\n if n.val == val:\n return True\n if n.left and find(n.left, val, path):\n path += "L"\n elif n.right and find(n.right, val, path):\n path += "R"\n return path\n s, d = [], []\n find(root, startValue, s)\n find(root, destValue, d)\n while len(s) and len(d) and s[-1] == d[-1]:\n s.pop()\n d.pop()\n return "".join("U" * len(s)) + "".join(reversed(d))\n``` | 775 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
[Python3] lca | step-by-step-directions-from-a-binary-tree-node-to-another | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b1948f8814bebeca475cbb354cd44d19092dff59) for solutions of weekly 270.\n\n```\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n \n def lca(node): \n """Return lowest common ancestor of start and dest nodes."""\n if not node or node.val in (startValue , destValue): return node \n left, right = lca(node.left), lca(node.right)\n return node if left and right else left or right\n \n root = lca(root) # only this sub-tree matters\n \n ps = pd = ""\n stack = [(root, "")]\n while stack: \n node, path = stack.pop()\n if node.val == startValue: ps = path \n if node.val == destValue: pd = path\n if node.left: stack.append((node.left, path + "L"))\n if node.right: stack.append((node.right, path + "R"))\n return "U"*len(ps) + pd\n``` | 120 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
Python3 BFS | step-by-step-directions-from-a-binary-tree-node-to-another | 0 | 1 | \n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n \n adj=defaultdict(list)\n \n def dfs(root):\n if not root:\n return\n if root.left:\n adj[root.val].append((root.left.val,"L"))\n adj[root.left.val].append((root.val,"U"))\n dfs(root.left)\n if root.right:\n adj[root.val].append((root.right.val,"R"))\n adj[root.right.val].append((root.val,"U"))\n dfs(root.right)\n \n dfs(root)\n\n \n q=deque()\n q.append((startValue,""))\n visited=set([startValue])\n \n \n \n while q:\n for i in range(len(q)):\n node,s=q.popleft()\n if node==destValue:\n return s\n\n for child,st in adj[node]:\n if child not in visited:\n visited.add(child)\n q.append((child,s+st))\n \n \n \n \n \n \n \n \n \n \n \n \n \n \n``` | 1 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
Python3 || easiest explanation|| LCA Method | step-by-step-directions-from-a-binary-tree-node-to-another | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Find common parent and navigate.**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- find least common parent of start and destination.\n- now find height of start from lca.\n- append hheight times \'U\' in answer string.\n- now traverse from lca for destination node.\n- check in both left and right sub-tree, if destination found in left append \'L\' and if found in right append \'R\'.\n- return answer.\n\n# Complexity\n- Time complexity: O(3*height of tree)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n lca = None\n def get_lca(curr=None):\n nonlocal lca\n if curr:\n ans = 0\n if curr.val == startValue:ans += 1\n if curr.val == destValue:ans += 1\n ans += get_lca(curr.left)\n ans += get_lca(curr.right)\n if ans == 2 and not lca:\n lca = curr\n return 0\n else: return ans\n return 0\n get_lca(root)\n def get_height_from(curr=None):\n if curr:\n if curr.val == startValue: return 1\n ans = get_height_from(curr.left)+get_height_from(curr.right)\n if ans: return ans + 1\n return ans\n return 0\n height = get_height_from(lca) - 1\n asf = []\n for i in range(height):asf.append(\'U\') \n def find_dest(curr=None):\n nonlocal asf\n if curr:\n if curr.val == destValue:return True\n asf.append(\'L\')\n if not find_dest(curr.left):asf.pop()\n else:return True\n asf.append(\'R\')\n if not find_dest(curr.right):asf.pop()\n else:return True\n return False\n return False\n find_dest(lca)\n return \'\'.join(asf)\n```\n# Please like and comment. | 2 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
2 Python 🐍 solutions: Graph-based, LCA | step-by-step-directions-from-a-binary-tree-node-to-another | 0 | 1 | #### **Solution 1: Graph Based, passed**\n#### Space=O(N) for building graph and queue. Time= O(N) for traversing the tree and for the BFS\nThe idea is build an undirected graph, the directions from Node1--> Node2 is either L or R, and the opposite Node2-->1 is always U\n```\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n\t\n graph=defaultdict(list) \n stack=[(root)]\n\t\t\n\t\t#Step1: Build Graph\n while stack:\n node=stack.pop()\n \n if node.left:\n graph[node.val].append((node.left.val,"L"))\n graph[node.left.val].append((node.val,"U"))\n stack.append(node.left)\n if node.right:\n graph[node.val].append((node.right.val,"R"))\n graph[node.right.val].append((node.val,"U"))\n stack.append(node.right)\n #Step 2: Normal BFS\n q=deque([(startValue,"")])\n seen=set()\n seen.add(startValue)\n \n while q:\n node,path=q.popleft()\n if node==destValue:\n return path\n \n for neigh in graph[node]:\n v,d=neigh\n if v not in seen:\n q.append((v,path+d))\n seen.add(v)\n return -1\n```\n\n#### **Solution 2: LCA with getPath recursion: Memory Limit Exceded**\n#### When I tried the LCA solution, I got the path from LCA to start and LCA to end recursively which is correct, but didn\'t pass memory constraint\nThe idea is that the 2 nodes must have a LCA, if you get the LCA, then the answer is startNode to LCA + LCA to dest node, but if you notice the first part start to LCA is always \'U\', but I do care about the length, how many U\'\'s? so I still get the path from start to LCA then I relace the path with U\'s\n```\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n \n def getLCA(root,p,q):\n if not root: return None\n if root.val==p or root.val==q:\n return root\n L=getLCA(root.left,p,q)\n R=getLCA(root.right,p,q)\n if L and R:\n return root\n return L or R\n \n \n def getPath(node1,node2,path): #---> Problem here\n if not node1: return\n if node1.val==node2: return path\n return getPath(node1.left,node2,path+["L"]) or getPath(node1.right,node2,path+["R"])\n \n \n LCA=getLCA(root,startValue,destValue)\n path1=getPath(LCA,startValue,[]) \n path2=getPath(LCA,destValue,[])\n path=["U"]*len(path1) + path2 if path1 else path2 \n return "".join(path)\n \n```\n\n#### **Solution 2 Revisited: LCA then get path iterative*\nExact same idea as above, the only change is getPath,\n```\nclass Solution:\n def getDirections(self, root: Optional[TreeNode], startValue: int, destValue: int) -> str:\n \n #soltion 2 LCA\n def getLCA(root,p,q):\n if not root: return None\n if root.val==p or root.val==q:\n return root\n L=getLCA(root.left,p,q)\n R=getLCA(root.right,p,q)\n if L and R:\n return root\n return L or R\n \n \n \n LCA=getLCA(root,startValue,destValue)\n ps,pd="",""\n stack = [(LCA, "")]\n while stack: \n node, path = stack.pop()\n if node.val == startValue: ps = path \n if node.val == destValue: pd = path\n if node.left: stack.append((node.left, path + "L"))\n if node.right: stack.append((node.right, path + "R"))\n \n return "U"*len(ps) + pd\n```\n\n**A 3rd solution is getting the depth of each node from the root, then removing the common prefix.\n** | 19 | You are given the `root` of a **binary tree** with `n` nodes. Each node is uniquely assigned a value from `1` to `n`. You are also given an integer `startValue` representing the value of the start node `s`, and a different integer `destValue` representing the value of the destination node `t`.
Find the **shortest path** starting from node `s` and ending at node `t`. Generate step-by-step directions of such path as a string consisting of only the **uppercase** letters `'L'`, `'R'`, and `'U'`. Each letter indicates a specific direction:
* `'L'` means to go from a node to its **left child** node.
* `'R'` means to go from a node to its **right child** node.
* `'U'` means to go from a node to its **parent** node.
Return _the step-by-step directions of the **shortest path** from node_ `s` _to node_ `t`.
**Example 1:**
**Input:** root = \[5,1,2,3,null,6,4\], startValue = 3, destValue = 6
**Output:** "UURL "
**Explanation:** The shortest path is: 3 -> 1 -> 5 -> 2 -> 6.
**Example 2:**
**Input:** root = \[2,1\], startValue = 2, destValue = 1
**Output:** "L "
**Explanation:** The shortest path is: 2 -> 1.
**Constraints:**
* The number of nodes in the tree is `n`.
* `2 <= n <= 105`
* `1 <= Node.val <= n`
* All the values in the tree are **unique**.
* `1 <= startValue, destValue <= n`
* `startValue != destValue` | Can you keep track of the minimum height for each obstacle course length? You can use binary search to find the longest previous obstacle course length that satisfies the conditions. |
[Python3] Hierholzer's algo | valid-arrangement-of-pairs | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b1948f8814bebeca475cbb354cd44d19092dff59) for solutions of weekly 270.\n\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n graph = defaultdict(list)\n degree = defaultdict(int) # net out degree \n for x, y in pairs: \n graph[x].append(y)\n degree[x] += 1\n degree[y] -= 1\n \n for k in degree: \n if degree[k] == 1: \n x = k\n break \n \n ans = []\n\n def fn(x): \n """Return Eulerian path via dfs."""\n while graph[x]: fn(graph[x].pop()) \n ans.append(x)\n \n fn(x)\n ans.reverse()\n return [[ans[i], ans[i+1]] for i in range(len(ans)-1)]\n```\n\nAdding an iterative implementation of Hieholzer\'s algo from @delphih\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n graph = defaultdict(list)\n degree = defaultdict(int) # net out degree \n for x, y in pairs: \n graph[x].append(y)\n degree[x] += 1\n degree[y] -= 1\n \n for k in degree: \n if degree[k] == 1: \n x = k\n break \n \n ans = []\n stack = [x]\n while stack: \n while graph[stack[-1]]: \n stack.append(graph[stack[-1]].pop())\n ans.append(stack.pop())\n ans.reverse()\n return [[ans[i], ans[i+1]] for i in range(len(ans)-1)]\n``` | 39 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
Eulerian path linear time | valid-arrangement-of-pairs | 0 | 1 | Read this tutorial on Eulerian path for undirected graph https://cp-algorithms.com/graph/euler_path.html\n\nThe algorithm can be extended to directed graph by looking at indegrees and outdegrees as described here https://math.stackexchange.com/a/2433946\n\nThe idea is we check if the graph makes an Eulerian cycle or path. If cycle, the indegree = outdegree for all nodes (a number in each pair is a node here). If it\'s a path, there must be one node with (out-in)=1 and one node with (in-out)=1. If it\'s the latter, create a fake path between those 2 to make it a cycle. For a cycle, we can start from any node and follow the algorithm in cp-algorithms link above. The idea of the algorithm is if in=out then we can just follow the out path to any node it must continue to another node. I cannot explain better than the link, just read it. \n\nOnce we finish, the output from the stack forms the path (list of nodes) we\'ve gone through. Each pair of consecutive nodes is a path. We must remove the fake path if any.\n\n# Code\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n from collections import defaultdict, Counter\n curr = None\n maps = defaultdict(list)\n out_minus_in = Counter()\n for a, b in pairs:\n curr = a\n maps[a].append(b)\n out_minus_in[a] += 1\n out_minus_in[b] -= 1\n \n ends = []\n for node in out_minus_in:\n if out_minus_in[node] != 0:\n ends.append(node)\n \n if ends:\n a, b = ends\n if out_minus_in[a] < out_minus_in[b]:\n a, b = b, a\n fake = (b, a)\n maps[b].append(a)\n else:\n fake = None\n \n stack = [curr]\n res = []\n while stack:\n top = stack[-1]\n if not maps[top]:\n res.append(stack.pop())\n else:\n nxt = maps[top].pop()\n stack.append(nxt)\n \n res = res[::-1]\n if fake:\n i = 1\n while i < len(res):\n if tuple([res[i - 1], res[i]]) == fake:\n break\n i += 1\n \n res = res[i:] + res[1:i]\n\n path = []\n for i in range(1, len(res)):\n path.append([res[i - 1], res[i]])\n return path\n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
Eulerian Circuit | valid-arrangement-of-pairs | 0 | 1 | Almost same as Q332, but the key point here is where to start.\n\nIf there is no eulerian cycle, there must be a point where there is one more vertex out than vertexes in, which is where we should start. If not such point exists, then there must be a eulerian cycle, in which case we may start anywhere we want.\n\n# Code\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n graph = {}\n indegs = {}\n outdegs = {}\n for s,e in pairs:\n if s not in graph:\n graph[s] = []\n if e not in graph:\n graph[e] = []\n if s not in outdegs:\n outdegs[s] = 0 \n if e not in outdegs:\n outdegs[e] = 0 \n if s not in indegs:\n indegs[s] = 0\n if e not in indegs:\n indegs[e] = 0\n graph[s].append(e)\n indegs[e] += 1\n outdegs[s] += 1\n N = len(pairs)\n \n \n def dfs(node):\n while graph[node]:\n dfs(graph[node].pop())\n self.route.append(node)\n s = pairs[0][0]\n for a in graph:\n if outdegs[a] - indegs[a] == 1:\n s = a\n break\n self.route = []\n dfs(s)\n t = self.route[::-1]\n if len(t) == N+1:\n return [[t[i],t[i+1]] for i in range(N)]\n \n \n \n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.