title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Tried 2 methods to solve...Using algorithm and without using algorithm | valid-arrangement-of-pairs | 0 | 1 | ## Code 1 (TLE)\n\nTried out the concept in this question [332. Reconstruct Itinerary](https://leetcode.com/problems/reconstruct-itinerary/description/) to solve this problem. But got TLE although it did pass some testcases.\n\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n def findDFS():\n adj = { src : [] for src, dest in pairs }\n n = len(pairs)\n for src, des in pairs:\n adj[src].append(des)\n def dfs(src):\n if len(res) == n:\n return True\n if src not in adj:\n return False\n temp = list(adj[src])\n for i,des in enumerate(temp):\n res.append([ src, des ])\n adj[src].pop(i)\n if dfs(des): return True\n res.remove([ src, des ])\n adj[src].insert(i, des)\n return False\n\n for src, des in pairs:\n res = []\n if src in adj and dfs(src): return res\n return findDFS()\n\n```\n\n## Code 2 (Solved using Hierholzer\'s Algorithm - Accepted)\n\n```\nimport collections\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n graph = defaultdict(list)\n degree = defaultdict(int)\n for src, des in pairs:\n graph[src].append(des)\n degree[src] += 1\n degree[des] -= 1\n\n # In Line 12 we find out the pendent vertex to start the Euler path \n for start in degree:\n if degree[start]==1:\n break\n\n # Line 19 onwards, we visit each node and try to traverse any circuits \n # that start and end at that node, the proceed to the other cicuits arising \n # from that node or move to the next node and thus do the DFS procedure.\n res = []\n def dfs(node):\n while graph[node]:\n child = graph[node].pop()\n dfs(child)\n res.append(node)\n dfs(start)\n res.reverse()\n return [[res[i],res[i+1]] for i in range(len(res)-1)]\n\n\n \n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
[Python3] Eulerian path explanation | valid-arrangement-of-pairs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a pretty standard eulerian path problem. If you haven\'t solved this type of problem, I recommend just googling that to get a gist of the idea. It is also very similar to leetcode #332.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe are given pairs, which are the connection between two nodes. This means we are given a list of **edges**.\n\nWe want to build an adjacency matrix the contains the neighbors of each node, stored in a queue. Then, we visit each node using recursion (or a stack if you want to do it iteratively). This effectively plays out the traversal as we travel along each edge.\n\nWith eulerian paths, there is the concept of **degrees**, which are either the inward connecting edges (in_degrees) or the outward connecting edges(out_degrees).\n\nTo find the start node, you need one of two things to be true:\n1. out_degrees[i] == in_degrees[i] for every node i\n2. out_degrees[i] == in_degrees[i] + 1 for exactly one node i\n\nIn the case of 1, any node can be the start. We pick [0][0] for simplicity.\n\nIn the case of 2, that node is your start node.\n\nAfter the traversal, we have to remember that we need to return pairs. An easy way to do this is just to pair each index of the result with index-1. But since I used recursion in my solution, we have to reverse the result first to be in the correct order.\n\n# Complexity\n- Time complexity: O(n), where n is the amount of edges we are given\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(3n) = O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n adjacencyMatrix = defaultdict(deque)\n in_degree = defaultdict(int)\n out_degree = defaultdict(int)\n\n # Build the adjacencyMatrix\n # Keep track of the degrees so we can find the start node\n for start, end in pairs:\n adjacencyMatrix[start].append(end)\n out_degree[start] += 1\n in_degree[end] += 1\n \n # Now, have each node visit its neighbors\n self.result = []\n def visit(node):\n while adjacencyMatrix[node]:\n nextNode = adjacencyMatrix[node].popleft()\n visit(nextNode)\n self.result.append(node)\n\n # Find the node where out == in + 1\n # Standard method of finding start in eulerian path\n start_node = None\n for node in adjacencyMatrix.keys():\n if out_degree[node] == in_degree[node] + 1:\n start_node = node\n break\n\n if start_node == None:\n start_node = pairs[0][0]\n\n visit(start_node)\n\n # Reverse visit because recursion\n self.result = self.result[::-1]\n\n # Convert to pairs\n paired_result = []\n for i in range(1, len(self.result)):\n paired_result.append([self.result[i-1], self.result[i]])\n\n return paired_result\n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
98.18/98.18 % in Both speed and memory | valid-arrangement-of-pairs | 0 | 1 | # Approach\n**Graph\nDepth-First Search\nEulerian Circuit\nRecursion\nHash Table\nQueue\nGreedy**\n\n# Code\n```\nfrom array import array\nclass Solution:\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n graph = defaultdict(lambda: array(\'I\'))\n degree = defaultdict(int)\n for y, x in pairs:\n graph[x].append(y)\n degree[x] += 1\n degree[y] -= 1\n stack = array(\'I\', [next((k for k in graph if degree[k]==1), x)])\n while (l := graph[stack[-1]]):\n stack.append(l.pop())\n prev = stack.pop()\n while stack:\n while (l := graph[stack[-1]]):\n stack.append(l.pop())\n yield (prev, (prev := stack.pop()))\n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
Solution using Dijkstra O(PlogP) | valid-arrangement-of-pairs | 0 | 1 | I did not know of Hierholzer so came up with another approach. It is less efficient but kinda funky and no solutions here have described it yet.\n\n# Intuition\n\nTLDR: Always pick the longest route to get to some end vertex that you\'ve chosen.\n\nWe can represent the pairs as a graph, and we want to neatly travel each edge from some start vertex to some end vertex in one go. At some points, we\'ll have to make a choice between two routes, e.g. the picture below.\n\n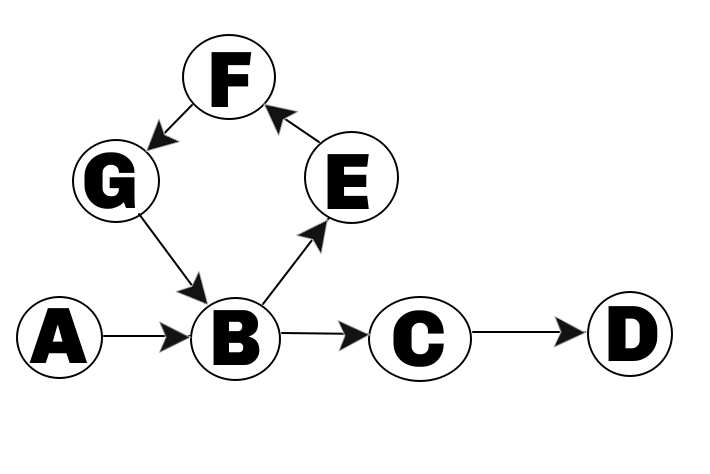\n\nAt B, we can either go to C or E. If we pick C, we\'ll go straight to the end node (D) and miss a bunch of edges. Therefore we want to pick E instead.\n\nThe way we can tell that E is the right choice is because the shortest path from E to D is longer than that from C to D, therefore we are less likely to miss edges.\n\nBecause we are guaranteed that there\'s at least one valid solution, once we pick the start and end nodes we shouldn\'t be able to make a wrong call.\n\n\n# Approach\nStep 1: pick the start node. This is the vertex that has fewer incoming than outgoing edges, or a random vertex if all vertices are balanced.\n\nStep 2: pick the end node. This is the opposite of Step 1.\n\nStep 3: Construct forward and backward versions of the graph. Use Dijkstra on the backward one to calculate the shortest path from each node to the end node.\n\nStep 4: Navigate the graph from the start node to end node, always choosing the neighbor with the largest distance given by the Dijkstra above.\n\nStep 5: Profit.\n\n# Complexity\n- Time complexity: O(E + VlogV) for Dijkstra, then O(V+E) for constructing the graph, another worst case O(ElogE) for sorting the neighbours or each node once we\'ve calculated the distances.\n \n For this problem, E=P and V<=P, so it boils down to O(PlogP) where P is the number of pairs.\n\n- Space complexity: O(P) to store the graphs and relevant data structures.\n\n# Code\n```\nclass Solution:\n\n # simple Dijkstra\n def dijkstra(self, graph, start):\n distances = {}\n heap = [(0, start)]\n\n while heap:\n dist, node = heappop(heap)\n if node in distances:\n continue\n distances[node] = dist\n for neighbor in graph[node]:\n if neighbor not in distances:\n heappush(heap, (dist + 1, neighbor))\n\n return distances\n\n\n def validArrangement(self, pairs: List[List[int]]) -> List[List[int]]:\n # Convert the pairs into and ajdacency list represented graph\n adj_list = defaultdict(list)\n reverse_adj_list = defaultdict(list)\n for s, e in pairs:\n adj_list[s].append(e)\n reverse_adj_list[e].append(s)\n\n # Determine start and end values by counting the incoming and outgoing\n # edges of each vertex.\n start = pairs[0][0]\n end = None\n end_count = defaultdict(int)\n for s, e in pairs:\n end_count[e] += 1\n if e == start:\n # if the graph has no explicit start, the route should\n # end at the randomly picked starting point\n end = s\n\n for k, l in adj_list.items():\n if len(l) > end_count[k]:\n # print(f"start change to {k} because it has appeared as start of {l} which is more times than as end {end_count[k]}")\n start = k\n break\n \n for k, count in end_count.items():\n if len(adj_list[k]) < count:\n # print(f"end change to {k} because it has appeared as end {count} times which is more than the start of {adj_list[k]}")\n end = k\n break\n\n # dijkstra calculating the distance from end to all nodes\n distances = self.dijkstra(reverse_adj_list, end)\n\n\n # For each vertex, store the edges in an ascending order by distance to\n # the end node so that we can pop them off efficiently starting from largest\n for k in adj_list:\n adj_list[k].sort(key=lambda e: distances[e])\n\n # Now simply navigate the graph from the start node by always taking the\n # route that will take longer to the end\n r = []\n curr = start\n for i in range(len(pairs)):\n nxt = adj_list[curr].pop()\n\n r.append([curr, nxt])\n curr = nxt\n\n return r\n\n``` | 0 | You are given a **0-indexed** 2D integer array `pairs` where `pairs[i] = [starti, endi]`. An arrangement of `pairs` is **valid** if for every index `i` where `1 <= i < pairs.length`, we have `endi-1 == starti`.
Return _**any** valid arrangement of_ `pairs`.
**Note:** The inputs will be generated such that there exists a valid arrangement of `pairs`.
**Example 1:**
**Input:** pairs = \[\[5,1\],\[4,5\],\[11,9\],\[9,4\]\]
**Output:** \[\[11,9\],\[9,4\],\[4,5\],\[5,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 9 == 9 = start1
end1 = 4 == 4 = start2
end2 = 5 == 5 = start3
**Example 2:**
**Input:** pairs = \[\[1,3\],\[3,2\],\[2,1\]\]
**Output:** \[\[1,3\],\[3,2\],\[2,1\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 3 == 3 = start1
end1 = 2 == 2 = start2
The arrangements \[\[2,1\],\[1,3\],\[3,2\]\] and \[\[3,2\],\[2,1\],\[1,3\]\] are also valid.
**Example 3:**
**Input:** pairs = \[\[1,2\],\[1,3\],\[2,1\]\]
**Output:** \[\[1,2\],\[2,1\],\[1,3\]\]
**Explanation:**
This is a valid arrangement since endi-1 always equals starti.
end0 = 2 == 2 = start1
end1 = 1 == 1 = start2
**Constraints:**
* `1 <= pairs.length <= 105`
* `pairs[i].length == 2`
* `0 <= starti, endi <= 109`
* `starti != endi`
* No two pairs are exactly the same.
* There **exists** a valid arrangement of `pairs`. | null |
[Java/Python 3] From O(n * logn) to average O(n) w/ brief explanation and analysis. | find-subsequence-of-length-k-with-the-largest-sum | 1 | 1 | **Method 1: Sort**\n\n*Sort the whole array*\n1. Combine each index with its corresponding value to create a 2-d array;\n2. Sort the 2-d array reversely by value, then copy the largest k ones;\n3. Sort the largest k ones by index, then return the corresponding values by index order.\n\n```java\n public int[] maxSubsequence(int[] nums, int k) {\n int n = nums.length;\n int[][] indexAndVal = new int[n][2];\n for (int i = 0; i < n; ++i) {\n indexAndVal[i] = new int[]{i, nums[i]};\n }\n // Reversely sort by value.\n Arrays.sort(indexAndVal, Comparator.comparingInt(a -> -a[1]));\n int[][] maxK = Arrays.copyOf(indexAndVal, k);\n // Sort by index.\n Arrays.sort(maxK, Comparator.comparingInt(a -> a[0]));\n int[] seq = new int[k];\n for (int i = 0; i < k; ++i) {\n seq[i] = maxK[i][1];\n }\n return seq;\n }\n```\n```python\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n val_and_index = sorted([(num, i) for i, num in enumerate(nums)])\n return [num for num, i in sorted(val_and_index[-k :], key=lambda x: x[1])]\n```\n\n**Analysis:**\n\nTime: `O(n * logn)`, space: `O(n)`.\n\n----\n\n**Method 2: PriorityQueue/heap**\n\n**Two Passes**\n\n1. Travse input and use PriorityQueue / heap to store `k` largest items, poll out if its size bigger than `k`;\n2. Use Map/dict to store the `k` items in 1.;\n3. Traverse input again, if encounter any item in the afore-mentioned Map/ dict, save it into the output array, then remove the item from the Map/dict.\n```java\n public int[] maxSubsequence(int[] nums, int k) {\n PriorityQueue<Integer> pq = new PriorityQueue<>(k + 1);\n for (int n : nums) {\n pq.offer(n);\n if (pq.size() > k) {\n pq.poll();\n }\n }\n Map<Integer, Integer> freq = new HashMap<>();\n for (int n : pq) {\n freq.merge(n, 1, Integer::sum);\n }\n int[] seq = new int[k]; \n int i = 0;\n for (int n : nums) {\n if (freq.merge(n, -1, Integer::sum) >= 0) {\n seq[i++] = n;\n }\n }\n return seq;\n }\n```\n```python\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n heap = []\n for n in nums:\n heapq.heappush(heap, n)\n if len(heap) > k:\n heapq.heappop(heap)\n cnt = Counter(heap)\n res = []\n for n in nums:\n if cnt[n] > 0:\n cnt[n] -= 1\n res.append(n)\n return res\n```\n\n----\n\n*Simplified the above to **One pass*** - credit to **@climberig**\n\nStore indexes of the input array by PriorityQueue/heap, and get rid of Map/dict.\n\n```java\n public int[] maxSubsequence(int[] nums, int k) {\n PriorityQueue<Integer> pq = new PriorityQueue<>\n (Comparator.comparingInt(i -> nums[i]));\n for (int i = 0; i < nums.length; ++i) {\n pq.offer(i);\n if (pq.size() > k) {\n pq.poll();\n }\n }\n return pq.stream().sorted().mapToInt(i -> nums[i]).toArray();\n }\n```\n```python\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n heap = []\n for i, n in enumerate(nums):\n heapq.heappush(heap, (n, i))\n if len(heap) > k:\n heapq.heappop(heap)\n return [a[0] for a in sorted(heap, key=lambda x: x[1])] \n```\n\nTime: `O(n * logk)`, space: `O(k)`\n\n----\n\n**Method 3: Quick Select**\n\n```java\n public int[] maxSubsequence(int[] nums, int k) {\n int n = nums.length;\n int[] index = new int[n];\n for (int i = 0; i < n; ++i) {\n index[i] = i;\n }\n \n // Use Quick Select to put the indexes of the \n // max k items to the left of index array. \n int lo = 0, hi = n - 1;\n while (lo < hi) {\n int idx = quickSelect(nums, index, lo, hi);\n if (idx < k) {\n lo = idx + 1;\n }else {\n hi = idx;\n }\n }\n \n // Count the occurrencs of the kth largest items\n // within the k largest ones.\n int kthVal = nums[index[k - 1]], freqOfkthVal = 0;\n for (int i : Arrays.copyOf(index, k)) {\n freqOfkthVal += nums[i] == kthVal ? 1 : 0;\n }\n \n // Greedily copy the subsequence into output array seq.\n int[] seq = new int[k];\n int i = 0;\n for (int num : nums) {\n if (num > kthVal || num == kthVal && freqOfkthVal-- > 0) {\n seq[i++] = num;\n }\n }\n return seq;\n }\n \n // Divide index[lo...hi] into two parts: larger and less than \n // the pivot; Then return the position of the pivot;\n private int quickSelect(int[] nums, int[] index, int lo, int hi) {\n int pivot = index[lo];\n while (lo < hi) {\n while (lo < hi && nums[index[hi]] <= nums[pivot]) {\n --hi;\n }\n index[lo] = index[hi];\n while (lo < hi && nums[index[lo]] >= nums[pivot]) {\n ++lo;\n }\n index[hi] = index[lo];\n } \n index[lo] = pivot;\n return lo;\n }\n```\n```python\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n \n # Divide index[lo...hi] into two parts: larger and less than \n # the pivot; Then return the position of the pivot;\n def quickSelect(lo: int, hi: int) -> int:\n pivot = index[lo]\n while lo < hi:\n while lo < hi and nums[index[hi]] <= nums[pivot]:\n hi -= 1\n index[lo] = index[hi]\n while lo < hi and nums[index[lo]] >= nums[pivot]:\n lo += 1\n index[hi] = index[lo]\n index[lo] = pivot\n return lo\n\n n = len(nums)\n index = list(range(n))\n \n # Use Quick Select to put the indexes of the \n # max k items to the left of index array.\n left, right = 0, n - 1\n while left < right:\n idx = quickSelect(left, right)\n if idx < k:\n left = idx + 1\n else:\n right = idx\n \n # Count the occurrencs of the kth largest items\n # within the k largest ones.\n kth_val, freq_of_kth_val = nums[index[k - 1]], 0\n for i in index[ : k]:\n if nums[i] == kth_val:\n freq_of_kth_val += 1\n \n # Greedily copy the subsequence into output array seq.\n seq = []\n for num in nums:\n if num > kth_val or num == kth_val and freq_of_kth_val > 0:\n seq.append(num)\n if num == kth_val:\n freq_of_kth_val -= 1\n return seq\n```\nTime: average `O(n)`, worst `O(n ^ 2)`, space: `O(n)`.\n\n----\n\n***Please feel free to let me know if you can make the codes better.*** | 59 | You are given an integer array `nums` and an integer `k`. You want to find a **subsequence** of `nums` of length `k` that has the **largest** sum.
Return _**any** such subsequence as an integer array of length_ `k`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[2,1,3,3\], k = 2
**Output:** \[3,3\]
**Explanation:**
The subsequence has the largest sum of 3 + 3 = 6.
**Example 2:**
**Input:** nums = \[-1,-2,3,4\], k = 3
**Output:** \[-1,3,4\]
**Explanation:**
The subsequence has the largest sum of -1 + 3 + 4 = 6.
**Example 3:**
**Input:** nums = \[3,4,3,3\], k = 2
**Output:** \[3,4\]
**Explanation:**
The subsequence has the largest sum of 3 + 4 = 7.
Another possible subsequence is \[4, 3\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `-105 <= nums[i] <= 105`
* `1 <= k <= nums.length` | Deal with each of the patterns individually. Use the built-in function in the language you are using to find if the pattern exists as a substring in word. |
One liner code very easy | find-subsequence-of-length-k-with-the-largest-sum | 0 | 1 | # Code\n```\nclass Solution:\n def maxSubsequence(self, arr: List[int], k: int) -> List[int]:\n return [j[1] for j in sorted(sorted(enumerate(arr),reverse=True,key=lambda x:x[1])[:k],key=lambda x:x[0])]\n \n``` | 1 | You are given an integer array `nums` and an integer `k`. You want to find a **subsequence** of `nums` of length `k` that has the **largest** sum.
Return _**any** such subsequence as an integer array of length_ `k`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[2,1,3,3\], k = 2
**Output:** \[3,3\]
**Explanation:**
The subsequence has the largest sum of 3 + 3 = 6.
**Example 2:**
**Input:** nums = \[-1,-2,3,4\], k = 3
**Output:** \[-1,3,4\]
**Explanation:**
The subsequence has the largest sum of -1 + 3 + 4 = 6.
**Example 3:**
**Input:** nums = \[3,4,3,3\], k = 2
**Output:** \[3,4\]
**Explanation:**
The subsequence has the largest sum of 3 + 4 = 7.
Another possible subsequence is \[4, 3\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `-105 <= nums[i] <= 105`
* `1 <= k <= nums.length` | Deal with each of the patterns individually. Use the built-in function in the language you are using to find if the pattern exists as a substring in word. |
Concise Python solution | find-subsequence-of-length-k-with-the-largest-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n while len(nums) > k:\n nums.remove(min(nums))\n return nums\n``` | 8 | You are given an integer array `nums` and an integer `k`. You want to find a **subsequence** of `nums` of length `k` that has the **largest** sum.
Return _**any** such subsequence as an integer array of length_ `k`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[2,1,3,3\], k = 2
**Output:** \[3,3\]
**Explanation:**
The subsequence has the largest sum of 3 + 3 = 6.
**Example 2:**
**Input:** nums = \[-1,-2,3,4\], k = 3
**Output:** \[-1,3,4\]
**Explanation:**
The subsequence has the largest sum of -1 + 3 + 4 = 6.
**Example 3:**
**Input:** nums = \[3,4,3,3\], k = 2
**Output:** \[3,4\]
**Explanation:**
The subsequence has the largest sum of 3 + 4 = 7.
Another possible subsequence is \[4, 3\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `-105 <= nums[i] <= 105`
* `1 <= k <= nums.length` | Deal with each of the patterns individually. Use the built-in function in the language you are using to find if the pattern exists as a substring in word. |
Python Simple Solution | 100% Time | find-subsequence-of-length-k-with-the-largest-sum | 0 | 1 | ## Code:\n```\nclass Solution:\n def maxSubsequence(self, nums: List[int], k: int) -> List[int]:\n tuple_heap = [] # Stores (value, index) as min heap\n for i, val in enumerate(nums):\n if len(tuple_heap) == k:\n heappushpop(tuple_heap, (val, i)) # To prevent size of heap growing larger than k\n else:\n heappush(tuple_heap, (val, i))\n\t\t# heap now contains only the k largest elements with their indices as well.\n tuple_heap.sort(key=lambda x: x[1]) # To get the original order of values. That is why we sort it by index(x[1]) & not value(x[0])\n ans = []\n for i in tuple_heap:\n ans.append(i[0])\n return ans\n```\nGive an \u2B06\uFE0Fupvote if you found this article helpful. | 14 | You are given an integer array `nums` and an integer `k`. You want to find a **subsequence** of `nums` of length `k` that has the **largest** sum.
Return _**any** such subsequence as an integer array of length_ `k`.
A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[2,1,3,3\], k = 2
**Output:** \[3,3\]
**Explanation:**
The subsequence has the largest sum of 3 + 3 = 6.
**Example 2:**
**Input:** nums = \[-1,-2,3,4\], k = 3
**Output:** \[-1,3,4\]
**Explanation:**
The subsequence has the largest sum of -1 + 3 + 4 = 6.
**Example 3:**
**Input:** nums = \[3,4,3,3\], k = 2
**Output:** \[3,4\]
**Explanation:**
The subsequence has the largest sum of 3 + 4 = 7.
Another possible subsequence is \[4, 3\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `-105 <= nums[i] <= 105`
* `1 <= k <= nums.length` | Deal with each of the patterns individually. Use the built-in function in the language you are using to find if the pattern exists as a substring in word. |
[Python3] Prefix Sum - Simple Solution | find-good-days-to-rob-the-bank | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def goodDaysToRobBank(self, security: List[int], time: int) -> List[int]:\n n = len(security)\n res = []\n incr, dcr = [0], [0]\n for i in range(1, n):\n if security[i] > security[i - 1]:\n incr.append(incr[-1] + 1)\n dcr.append(0)\n elif security[i] < security[i - 1]:\n dcr.append(dcr[-1] + 1)\n incr.append(0)\n else:\n incr.append(incr[-1] + 1)\n dcr.append(dcr[-1] + 1)\n \n for i in range(time, n - time):\n if dcr[i] >= time and incr[i + time] >= time: res.append(i)\n\n return res\n``` | 1 | You and a gang of thieves are planning on robbing a bank. You are given a **0-indexed** integer array `security`, where `security[i]` is the number of guards on duty on the `ith` day. The days are numbered starting from `0`. You are also given an integer `time`.
The `ith` day is a good day to rob the bank if:
* There are at least `time` days before and after the `ith` day,
* The number of guards at the bank for the `time` days **before** `i` are **non-increasing**, and
* The number of guards at the bank for the `time` days **after** `i` are **non-decreasing**.
More formally, this means day `i` is a good day to rob the bank if and only if `security[i - time] >= security[i - time + 1] >= ... >= security[i] <= ... <= security[i + time - 1] <= security[i + time]`.
Return _a list of **all** days **(0-indexed)** that are good days to rob the bank_. _The order that the days are returned in does **not** matter._
**Example 1:**
**Input:** security = \[5,3,3,3,5,6,2\], time = 2
**Output:** \[2,3\]
**Explanation:**
On day 2, we have security\[0\] >= security\[1\] >= security\[2\] <= security\[3\] <= security\[4\].
On day 3, we have security\[1\] >= security\[2\] >= security\[3\] <= security\[4\] <= security\[5\].
No other days satisfy this condition, so days 2 and 3 are the only good days to rob the bank.
**Example 2:**
**Input:** security = \[1,1,1,1,1\], time = 0
**Output:** \[0,1,2,3,4\]
**Explanation:**
Since time equals 0, every day is a good day to rob the bank, so return every day.
**Example 3:**
**Input:** security = \[1,2,3,4,5,6\], time = 2
**Output:** \[\]
**Explanation:**
No day has 2 days before it that have a non-increasing number of guards.
Thus, no day is a good day to rob the bank, so return an empty list.
**Constraints:**
* `1 <= security.length <= 105`
* `0 <= security[i], time <= 105` | Try to minimize each element by swapping bits with any of the elements after it. If you swap out all the 1s in some element, this will lead to a product of zero. |
[Python3] prefix & suffix | find-good-days-to-rob-the-bank | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/b553623546e2799477b8bca6b5c89f22c83a4d08) for solutions of weekly 67. \n\n```\nclass Solution:\n def goodDaysToRobBank(self, security: List[int], time: int) -> List[int]:\n suffix = [0]*len(security)\n for i in range(len(security)-2, 0, -1): \n if security[i] <= security[i+1]: suffix[i] = suffix[i+1] + 1\n \n ans = []\n prefix = 0\n for i in range(len(security)-time): \n if i and security[i-1] >= security[i]: prefix += 1\n else: prefix = 0\n if prefix >= time and suffix[i] >= time: ans.append(i)\n return ans \n``` | 6 | You and a gang of thieves are planning on robbing a bank. You are given a **0-indexed** integer array `security`, where `security[i]` is the number of guards on duty on the `ith` day. The days are numbered starting from `0`. You are also given an integer `time`.
The `ith` day is a good day to rob the bank if:
* There are at least `time` days before and after the `ith` day,
* The number of guards at the bank for the `time` days **before** `i` are **non-increasing**, and
* The number of guards at the bank for the `time` days **after** `i` are **non-decreasing**.
More formally, this means day `i` is a good day to rob the bank if and only if `security[i - time] >= security[i - time + 1] >= ... >= security[i] <= ... <= security[i + time - 1] <= security[i + time]`.
Return _a list of **all** days **(0-indexed)** that are good days to rob the bank_. _The order that the days are returned in does **not** matter._
**Example 1:**
**Input:** security = \[5,3,3,3,5,6,2\], time = 2
**Output:** \[2,3\]
**Explanation:**
On day 2, we have security\[0\] >= security\[1\] >= security\[2\] <= security\[3\] <= security\[4\].
On day 3, we have security\[1\] >= security\[2\] >= security\[3\] <= security\[4\] <= security\[5\].
No other days satisfy this condition, so days 2 and 3 are the only good days to rob the bank.
**Example 2:**
**Input:** security = \[1,1,1,1,1\], time = 0
**Output:** \[0,1,2,3,4\]
**Explanation:**
Since time equals 0, every day is a good day to rob the bank, so return every day.
**Example 3:**
**Input:** security = \[1,2,3,4,5,6\], time = 2
**Output:** \[\]
**Explanation:**
No day has 2 days before it that have a non-increasing number of guards.
Thus, no day is a good day to rob the bank, so return an empty list.
**Constraints:**
* `1 <= security.length <= 105`
* `0 <= security[i], time <= 105` | Try to minimize each element by swapping bits with any of the elements after it. If you swap out all the 1s in some element, this will lead to a product of zero. |
✅ 🔥 Python3 || ⚡easy solution | detonate-the-maximum-bombs | 0 | 1 | # Code\n```\nfrom typing import List\nimport collections\n\nclass Solution:\n def maximumDetonation(self, bombs: List[List[int]]) -> int:\n n2nxt = collections.defaultdict(set)\n lb = len(bombs)\n\n for i in range(lb): # i is the source\n xi, yi, ri = bombs[i]\n\n for j in range(lb):\n if i == j:\n continue\n\n xj, yj, rj = bombs[j]\n\n if ri ** 2 >= (xi - xj) ** 2 + (yi - yj) ** 2: # reachable from i\n n2nxt[i].add(j)\n\n def dfs(n, seen): # return None\n if n in seen:\n return\n seen.add(n)\n for nxt in n2nxt[n]:\n dfs(nxt, seen)\n\n ans = 0\n for i in range(lb):\n seen = set()\n dfs(i, seen)\n ans = max(ans, len(seen))\n return ans\n\n``` | 1 | You are given a list of bombs. The **range** of a bomb is defined as the area where its effect can be felt. This area is in the shape of a **circle** with the center as the location of the bomb.
The bombs are represented by a **0-indexed** 2D integer array `bombs` where `bombs[i] = [xi, yi, ri]`. `xi` and `yi` denote the X-coordinate and Y-coordinate of the location of the `ith` bomb, whereas `ri` denotes the **radius** of its range.
You may choose to detonate a **single** bomb. When a bomb is detonated, it will detonate **all bombs** that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of `bombs`, return _the **maximum** number of bombs that can be detonated if you are allowed to detonate **only one** bomb_.
**Example 1:**
**Input:** bombs = \[\[2,1,3\],\[6,1,4\]\]
**Output:** 2
**Explanation:**
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.
**Example 2:**
**Input:** bombs = \[\[1,1,5\],\[10,10,5\]\]
**Output:** 1
**Explanation:**
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
**Example 3:**
**Input:** bombs = \[\[1,2,3\],\[2,3,1\],\[3,4,2\],\[4,5,3\],\[5,6,4\]\]
**Output:** 5
**Explanation:**
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.
**Constraints:**
* `1 <= bombs.length <= 100`
* `bombs[i].length == 3`
* `1 <= xi, yi, ri <= 105` | What graph algorithm allows us to find whether a path exists? Can we use binary search to help us solve the problem? |
EASY PYTHON SOLUTION USING BFS TRAVERSAL | detonate-the-maximum-bombs | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumDetonation(self, bombs: List[List[int]]) -> int:\n mx=0\n n=len(bombs)\n for i in range(n):\n vis=[0]*n\n ct=1\n queue=[(bombs[i])]\n vis[i]=1\n while queue:\n x=queue.pop(0)\n # print(x,ct)\n for j in range(n):\n if vis[j]==0 and((x[0]-bombs[j][0])**2+(x[1]-bombs[j][1])**2)<=x[2]**2:\n ct+=1\n queue.append((bombs[j]))\n vis[j]=1\n mx=max(mx,ct)\n return mx\n \n\n \n``` | 1 | You are given a list of bombs. The **range** of a bomb is defined as the area where its effect can be felt. This area is in the shape of a **circle** with the center as the location of the bomb.
The bombs are represented by a **0-indexed** 2D integer array `bombs` where `bombs[i] = [xi, yi, ri]`. `xi` and `yi` denote the X-coordinate and Y-coordinate of the location of the `ith` bomb, whereas `ri` denotes the **radius** of its range.
You may choose to detonate a **single** bomb. When a bomb is detonated, it will detonate **all bombs** that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of `bombs`, return _the **maximum** number of bombs that can be detonated if you are allowed to detonate **only one** bomb_.
**Example 1:**
**Input:** bombs = \[\[2,1,3\],\[6,1,4\]\]
**Output:** 2
**Explanation:**
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.
**Example 2:**
**Input:** bombs = \[\[1,1,5\],\[10,10,5\]\]
**Output:** 1
**Explanation:**
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
**Example 3:**
**Input:** bombs = \[\[1,2,3\],\[2,3,1\],\[3,4,2\],\[4,5,3\],\[5,6,4\]\]
**Output:** 5
**Explanation:**
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.
**Constraints:**
* `1 <= bombs.length <= 100`
* `bombs[i].length == 3`
* `1 <= xi, yi, ri <= 105` | What graph algorithm allows us to find whether a path exists? Can we use binary search to help us solve the problem? |
python 3 - dfs | detonate-the-maximum-bombs | 0 | 1 | # Intuition\nCan\'t do DSU for this question because explosion\'s effect should be unidirection. eg. bomb A can affect bomb B doesn\'t implies bomb B can also affect bomb A.\n\nYou can go either DFS/BFS.\n\n# Approach\nDFS\n\n# My mistake\nI chose DSU in the beginning. But later I realized the single direction effect. A couple of minutes had gone at that time...\n\n# Complexity\n- Time complexity:\nO(n^2) -> double loops preprocess / dfs both comsumes n^2 time\n\n- Space complexity:\nO(n^2) -> n2nxt map\n\nn = len(bombs)\n\n# Code\n```\nclass Solution:\n def maximumDetonation(self, bombs: List[List[int]]) -> int:\n \n import collections\n\n n2nxt = collections.defaultdict(set)\n lb = len(bombs)\n\n\n for i in range(lb): # i is source\n xi, yi, ri = bombs[i]\n\n for j in range(lb):\n if i == j: continue\n\n xj, yj, rj = bombs[j]\n\n if ri ** 2 >= (xi - xj) ** 2 + (yi - yj) ** 2: # reachable from i\n n2nxt[i].add(j)\n \n def dfs(n): # return None\n if n in seen: return\n seen.add(n)\n for nxt in n2nxt[n]:\n dfs(nxt)\n\n ans = 0\n for i in range(lb):\n seen = set()\n dfs(i)\n ans = max(ans, len(seen))\n return ans\n``` | 1 | You are given a list of bombs. The **range** of a bomb is defined as the area where its effect can be felt. This area is in the shape of a **circle** with the center as the location of the bomb.
The bombs are represented by a **0-indexed** 2D integer array `bombs` where `bombs[i] = [xi, yi, ri]`. `xi` and `yi` denote the X-coordinate and Y-coordinate of the location of the `ith` bomb, whereas `ri` denotes the **radius** of its range.
You may choose to detonate a **single** bomb. When a bomb is detonated, it will detonate **all bombs** that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of `bombs`, return _the **maximum** number of bombs that can be detonated if you are allowed to detonate **only one** bomb_.
**Example 1:**
**Input:** bombs = \[\[2,1,3\],\[6,1,4\]\]
**Output:** 2
**Explanation:**
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.
**Example 2:**
**Input:** bombs = \[\[1,1,5\],\[10,10,5\]\]
**Output:** 1
**Explanation:**
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
**Example 3:**
**Input:** bombs = \[\[1,2,3\],\[2,3,1\],\[3,4,2\],\[4,5,3\],\[5,6,4\]\]
**Output:** 5
**Explanation:**
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.
**Constraints:**
* `1 <= bombs.length <= 100`
* `bombs[i].length == 3`
* `1 <= xi, yi, ri <= 105` | What graph algorithm allows us to find whether a path exists? Can we use binary search to help us solve the problem? |
Python short and clean. DFS. Functional programming. | detonate-the-maximum-bombs | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial Solution](https://leetcode.com/problems/detonate-the-maximum-bombs/editorial/) but shorter and cleaner.\n\n# Complexity\n- Time complexity: $$O(n ^ 3)$$\n\n- Space complexity: $$O(n ^ 2)$$\n\n# Code\n```python\nclass Solution:\n def maximumDetonation(self, bombs: list[list[int]]) -> int:\n Bomb = tuple[int, int, int]\n T = Hashable\n Graph = Mapping[T, Collection[T]]\n\n def in_range(b1: Bomb, b2: Bomb) -> bool:\n return (b1[0] - b2[0]) ** 2 + (b1[1] - b2[1]) ** 2 <= b1[2] ** 2\n\n def connections(graph: Graph, src: T, seen: set[T]) -> int:\n return seen.add(src) or 1 + sum(connections(graph, x, seen) for x in graph[src] if x not in seen)\n\n g = {i: tuple(j for j, b2 in enumerate(bombs) if in_range(b1, b2)) for i, b1 in enumerate(bombs)}\n return max(connections(g, x, set()) for x in g)\n\n\n``` | 2 | You are given a list of bombs. The **range** of a bomb is defined as the area where its effect can be felt. This area is in the shape of a **circle** with the center as the location of the bomb.
The bombs are represented by a **0-indexed** 2D integer array `bombs` where `bombs[i] = [xi, yi, ri]`. `xi` and `yi` denote the X-coordinate and Y-coordinate of the location of the `ith` bomb, whereas `ri` denotes the **radius** of its range.
You may choose to detonate a **single** bomb. When a bomb is detonated, it will detonate **all bombs** that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of `bombs`, return _the **maximum** number of bombs that can be detonated if you are allowed to detonate **only one** bomb_.
**Example 1:**
**Input:** bombs = \[\[2,1,3\],\[6,1,4\]\]
**Output:** 2
**Explanation:**
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.
**Example 2:**
**Input:** bombs = \[\[1,1,5\],\[10,10,5\]\]
**Output:** 1
**Explanation:**
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
**Example 3:**
**Input:** bombs = \[\[1,2,3\],\[2,3,1\],\[3,4,2\],\[4,5,3\],\[5,6,4\]\]
**Output:** 5
**Explanation:**
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.
**Constraints:**
* `1 <= bombs.length <= 100`
* `bombs[i].length == 3`
* `1 <= xi, yi, ri <= 105` | What graph algorithm allows us to find whether a path exists? Can we use binary search to help us solve the problem? |
Python | Two Solutions | sortedContainers and minHeap+maxHeap with Explanation | sequentially-ordinal-rank-tracker | 0 | 1 | First Solution (Using sortedcontainers):\nHere we use SortedList which is implemented using divide & conquer and binary search, sortedlist always maintain the sorted order, so we can just query the ith index nd get the Ithe best location\nMore at: https://github.com/grantjenks/python-sortedcontainers/blob/master/src/sortedcontainers/sortedlist.py\n\n```\nfrom sortedcontainers import SortedList\nclass SORTracker1:\n def __init__(self):\n self.storage=SortedList()\n self.queryNum=0\n \n def add(self, name: str, score: int) -> None:\n self.storage.add((-score,name)) \n\n def get(self) -> str:\n ans=self.storage[self.queryNum]\n self.queryNum+=1\n return ans[1]\n```\n\nSecond Solution (using heaps):\nIdea: \n1. First lets suppose, there is no condition of returing the ith best location. So, in this scenario we just have to use a maxheap and return the top element of the maxheap every time the get function is called.\nBut the catch in the question is that we have to return the ith best so, in this case we can not pop the top most element from the heap and just return it because in some cases we might need the popped location. Refer to provided example in the question description for more insight.\n2. So, we also need the popped locations to be used further. To solve this scenario what we can do is use two heaps. \n3. See the diagram below:\n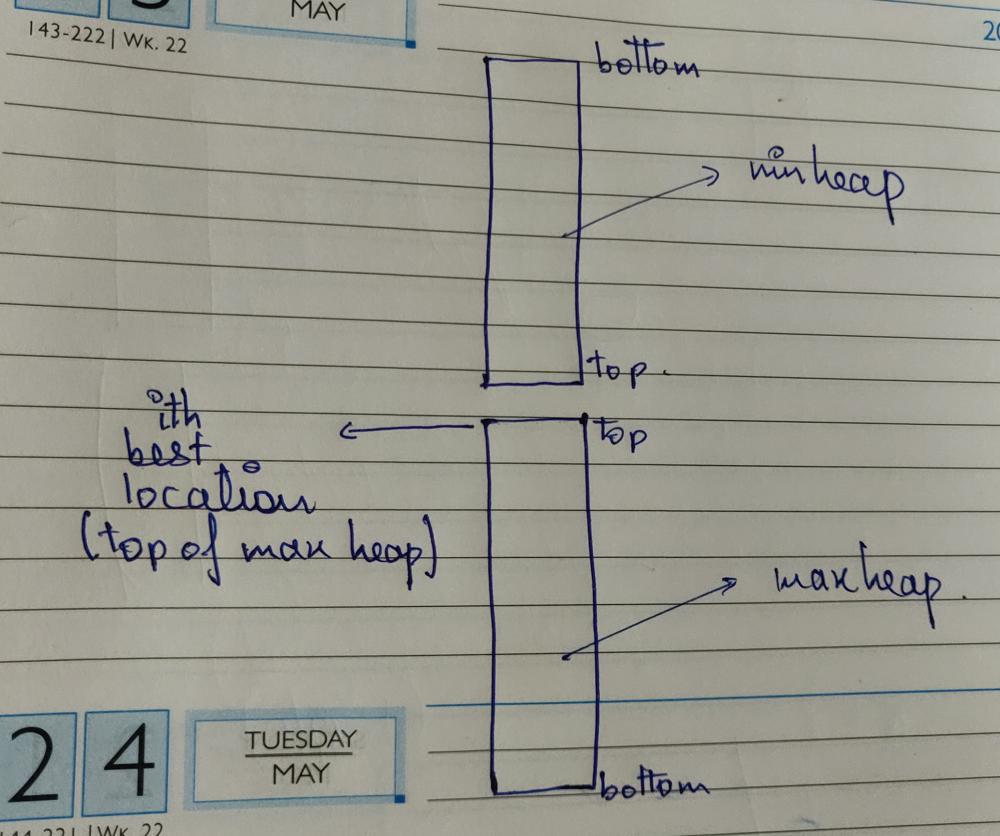\n\n4. In the diagram we can see, if we think of the min heap in inverted fashion then combining it with the max heap will give us the tracker. Because when we pop the ith best location, before returning it we will also push that to the min heap namely upper part of the tracker, so that the order of the best locations is maintained, now when we add a new location we will check if the new location is better than the top of min heap or i-1th location, if it is better than we will add the new location in the min heap or the upper part of the tracker and remove the top of min heap or the i-1 th location and push it to max heap or lower part of the tracker, in simple terms we have two parts, upper part contains 1 to (i-1)th locations and lower part contains i to nth locations, so whenever we get a location that fits in the upper part we push the new location there, now it has 1 to i locations so we push the (i-1)th location in the upper part, so that top of maxheap remains the ith best location. As we are using heaps so the order is maintained.\n\nNote: In python, maxheap do not exist, so I have used a custom string class that will sort the location names in decreasing order in minheap if scores are equal. We do not need it in maxHeap, as the best location is decided by a big score and a lexicographically smaller name.\n\n```\nclass CString:\n def __init__(self,word):\n self.word=word\n \n def __lt__(self,other):\n return self.word>other.word\n \n def __eq__(self,other):\n return self.word==other.word\n \nclass SORTracker:\n def __init__(self):\n self.upperPart=[] #minHeap\n self.lowerPart=[] #maxHeap\n \n def add(self, name, score):\n name=CString(name)\n\t\t#first check if there is any element in minHeap\n if self.upperPart:\n upperScore,upperName=self.upperPart[0]\n\t\t\t#check if we got a better location than the i-1th location\n if (upperScore<score) or (upperScore==score and upperName.word>name.word):\n heapq.heappop(self.upperPart)\n heapq.heappush(self.upperPart,(score,name))\n\t\t\t\t#negative score used below because its a maxheap\n heapq.heappush(self.lowerPart,(-upperScore,upperName.word))\n \n else:\n\t\t\t#if not we just add the new location to lower part\n heapq.heappush(self.lowerPart,(-score,name.word))\n else:\n\t\t#if not we just add the new location to lower part\n heapq.heappush(self.lowerPart,(-score,name.word)) \n \n def get(self):\n\t\t#remove from the ith position\n score,name=heapq.heappop(self.lowerPart)\n\t\t#add to the upper part of the tracker or minHeap\n heapq.heappush(self.upperPart,(-score,CString(name)))\n return name\n \n```\n\nTime Complexity (same for both solution):\nadd function: O(logn)\nget function: O(logn)\n\nPlease upvote, if you like the explanation!\n | 2 | A scenic location is represented by its `name` and attractiveness `score`, where `name` is a **unique** string among all locations and `score` is an integer. Locations can be ranked from the best to the worst. The **higher** the score, the better the location. If the scores of two locations are equal, then the location with the **lexicographically smaller** name is better.
You are building a system that tracks the ranking of locations with the system initially starting with no locations. It supports:
* **Adding** scenic locations, **one at a time**.
* **Querying** the `ith` **best** location of **all locations already added**, where `i` is the number of times the system has been queried (including the current query).
* For example, when the system is queried for the `4th` time, it returns the `4th` best location of all locations already added.
Note that the test data are generated so that **at any time**, the number of queries **does not exceed** the number of locations added to the system.
Implement the `SORTracker` class:
* `SORTracker()` Initializes the tracker system.
* `void add(string name, int score)` Adds a scenic location with `name` and `score` to the system.
* `string get()` Queries and returns the `ith` best location, where `i` is the number of times this method has been invoked (including this invocation).
**Example 1:**
**Input**
\[ "SORTracker ", "add ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "get "\]
\[\[\], \[ "bradford ", 2\], \[ "branford ", 3\], \[\], \[ "alps ", 2\], \[\], \[ "orland ", 2\], \[\], \[ "orlando ", 3\], \[\], \[ "alpine ", 2\], \[\], \[\]\]
**Output**
\[null, null, null, "branford ", null, "alps ", null, "bradford ", null, "bradford ", null, "bradford ", "orland "\]
**Explanation**
SORTracker tracker = new SORTracker(); // Initialize the tracker system.
tracker.add( "bradford ", 2); // Add location with name= "bradford " and score=2 to the system.
tracker.add( "branford ", 3); // Add location with name= "branford " and score=3 to the system.
tracker.get(); // The sorted locations, from best to worst, are: branford, bradford.
// Note that branford precedes bradford due to its **higher score** (3 > 2).
// This is the 1st time get() is called, so return the best location: "branford ".
tracker.add( "alps ", 2); // Add location with name= "alps " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford.
// Note that alps precedes bradford even though they have the same score (2).
// This is because "alps " is **lexicographically smaller** than "bradford ".
// Return the 2nd best location "alps ", as it is the 2nd time get() is called.
tracker.add( "orland ", 2); // Add location with name= "orland " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford, orland.
// Return "bradford ", as it is the 3rd time get() is called.
tracker.add( "orlando ", 3); // Add location with name= "orlando " and score=3 to the system.
tracker.get(); // Sorted locations: branford, orlando, alps, bradford, orland.
// Return "bradford ".
tracker.add( "alpine ", 2); // Add location with name= "alpine " and score=2 to the system.
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "bradford ".
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "orland ".
**Constraints:**
* `name` consists of lowercase English letters, and is unique among all locations.
* `1 <= name.length <= 10`
* `1 <= score <= 105`
* At any time, the number of calls to `get` does not exceed the number of calls to `add`.
* At most `4 * 104` calls **in total** will be made to `add` and `get`. | Could we go from left to right and check to see if an index is a middle index? Do we need to sum every number to the left and right of an index each time? Use a prefix sum array where prefix[i] = nums[0] + nums[1] + ... + nums[i]. |
Python 2 heap easy to understand best solution | sequentially-ordinal-rank-tracker | 0 | 1 | \tclass MinHeapItem:\n\t\tdef __init__(self, name, score):\n\t\t\tself.name = name\n\t\t\tself.score = score\n\t\tdef __lt__(self, other):\n\t\t\treturn self.score < other.score or \\\n\t\t\t\t (self.score == other.score and self.name > other.name)\n\n\tclass MaxHeapItem:\n\t\tdef __init__(self, name, score):\n\t\t\tself.name = name\n\t\t\tself.score = score\n\t\tdef __lt__(self, other):\n\t\t\treturn self.score > other.score or \\\n\t\t\t\t (self.score == other.score and self.name < other.name)\n\n\tclass SORTracker:\n\t\tdef __init__(self):\n\t\t\tself.min_heap = []\n\t\t\tself.max_heap = []\n\t\t\tself.k = 0\n\n\t\tdef add(self, name: str, score: int) -> None:\n\t\t\theappush(self.min_heap, MinHeapItem(name, score)) \n\t\t\tif len(self.min_heap) > self.k + 1:\n\t\t\t\ttemp = heappop(self.min_heap)\n\t\t\t\theappush(self.max_heap, MaxHeapItem(temp.name, temp.score))\n\n\t\tdef get(self) -> str:\n\t\t\tans = self.min_heap[0].name\n\t\t\tself.k += 1 \n\t\t\tif self.max_heap:\n\t\t\t\ttemp = heappop(self.max_heap)\n\t\t\t\theappush(self.min_heap, MinHeapItem(temp.name, temp.score))\n\t\t\treturn ans | 0 | A scenic location is represented by its `name` and attractiveness `score`, where `name` is a **unique** string among all locations and `score` is an integer. Locations can be ranked from the best to the worst. The **higher** the score, the better the location. If the scores of two locations are equal, then the location with the **lexicographically smaller** name is better.
You are building a system that tracks the ranking of locations with the system initially starting with no locations. It supports:
* **Adding** scenic locations, **one at a time**.
* **Querying** the `ith` **best** location of **all locations already added**, where `i` is the number of times the system has been queried (including the current query).
* For example, when the system is queried for the `4th` time, it returns the `4th` best location of all locations already added.
Note that the test data are generated so that **at any time**, the number of queries **does not exceed** the number of locations added to the system.
Implement the `SORTracker` class:
* `SORTracker()` Initializes the tracker system.
* `void add(string name, int score)` Adds a scenic location with `name` and `score` to the system.
* `string get()` Queries and returns the `ith` best location, where `i` is the number of times this method has been invoked (including this invocation).
**Example 1:**
**Input**
\[ "SORTracker ", "add ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "get "\]
\[\[\], \[ "bradford ", 2\], \[ "branford ", 3\], \[\], \[ "alps ", 2\], \[\], \[ "orland ", 2\], \[\], \[ "orlando ", 3\], \[\], \[ "alpine ", 2\], \[\], \[\]\]
**Output**
\[null, null, null, "branford ", null, "alps ", null, "bradford ", null, "bradford ", null, "bradford ", "orland "\]
**Explanation**
SORTracker tracker = new SORTracker(); // Initialize the tracker system.
tracker.add( "bradford ", 2); // Add location with name= "bradford " and score=2 to the system.
tracker.add( "branford ", 3); // Add location with name= "branford " and score=3 to the system.
tracker.get(); // The sorted locations, from best to worst, are: branford, bradford.
// Note that branford precedes bradford due to its **higher score** (3 > 2).
// This is the 1st time get() is called, so return the best location: "branford ".
tracker.add( "alps ", 2); // Add location with name= "alps " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford.
// Note that alps precedes bradford even though they have the same score (2).
// This is because "alps " is **lexicographically smaller** than "bradford ".
// Return the 2nd best location "alps ", as it is the 2nd time get() is called.
tracker.add( "orland ", 2); // Add location with name= "orland " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford, orland.
// Return "bradford ", as it is the 3rd time get() is called.
tracker.add( "orlando ", 3); // Add location with name= "orlando " and score=3 to the system.
tracker.get(); // Sorted locations: branford, orlando, alps, bradford, orland.
// Return "bradford ".
tracker.add( "alpine ", 2); // Add location with name= "alpine " and score=2 to the system.
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "bradford ".
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "orland ".
**Constraints:**
* `name` consists of lowercase English letters, and is unique among all locations.
* `1 <= name.length <= 10`
* `1 <= score <= 105`
* At any time, the number of calls to `get` does not exceed the number of calls to `add`.
* At most `4 * 104` calls **in total** will be made to `add` and `get`. | Could we go from left to right and check to see if an index is a middle index? Do we need to sum every number to the left and right of an index each time? Use a prefix sum array where prefix[i] = nums[0] + nums[1] + ... + nums[i]. |
[Python3] brute-force | sequentially-ordinal-rank-tracker | 0 | 1 | Kinda cheating for Python3 as `insort` is fast enough for such problems. \n\nPlease check out this [commit](https://github.com/gaosanyong/leetcode/commit/b553623546e2799477b8bca6b5c89f22c83a4d08) for solutions of weekly 67. \n\n```\nclass SORTracker:\n\n def __init__(self):\n self.k = 0 \n self.data = []\n\n def add(self, name: str, score: int) -> None:\n insort(self.data, (-score, name))\n\n def get(self) -> str:\n self.k += 1\n return self.data[self.k-1][1]\n``` | 2 | A scenic location is represented by its `name` and attractiveness `score`, where `name` is a **unique** string among all locations and `score` is an integer. Locations can be ranked from the best to the worst. The **higher** the score, the better the location. If the scores of two locations are equal, then the location with the **lexicographically smaller** name is better.
You are building a system that tracks the ranking of locations with the system initially starting with no locations. It supports:
* **Adding** scenic locations, **one at a time**.
* **Querying** the `ith` **best** location of **all locations already added**, where `i` is the number of times the system has been queried (including the current query).
* For example, when the system is queried for the `4th` time, it returns the `4th` best location of all locations already added.
Note that the test data are generated so that **at any time**, the number of queries **does not exceed** the number of locations added to the system.
Implement the `SORTracker` class:
* `SORTracker()` Initializes the tracker system.
* `void add(string name, int score)` Adds a scenic location with `name` and `score` to the system.
* `string get()` Queries and returns the `ith` best location, where `i` is the number of times this method has been invoked (including this invocation).
**Example 1:**
**Input**
\[ "SORTracker ", "add ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "get "\]
\[\[\], \[ "bradford ", 2\], \[ "branford ", 3\], \[\], \[ "alps ", 2\], \[\], \[ "orland ", 2\], \[\], \[ "orlando ", 3\], \[\], \[ "alpine ", 2\], \[\], \[\]\]
**Output**
\[null, null, null, "branford ", null, "alps ", null, "bradford ", null, "bradford ", null, "bradford ", "orland "\]
**Explanation**
SORTracker tracker = new SORTracker(); // Initialize the tracker system.
tracker.add( "bradford ", 2); // Add location with name= "bradford " and score=2 to the system.
tracker.add( "branford ", 3); // Add location with name= "branford " and score=3 to the system.
tracker.get(); // The sorted locations, from best to worst, are: branford, bradford.
// Note that branford precedes bradford due to its **higher score** (3 > 2).
// This is the 1st time get() is called, so return the best location: "branford ".
tracker.add( "alps ", 2); // Add location with name= "alps " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford.
// Note that alps precedes bradford even though they have the same score (2).
// This is because "alps " is **lexicographically smaller** than "bradford ".
// Return the 2nd best location "alps ", as it is the 2nd time get() is called.
tracker.add( "orland ", 2); // Add location with name= "orland " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford, orland.
// Return "bradford ", as it is the 3rd time get() is called.
tracker.add( "orlando ", 3); // Add location with name= "orlando " and score=3 to the system.
tracker.get(); // Sorted locations: branford, orlando, alps, bradford, orland.
// Return "bradford ".
tracker.add( "alpine ", 2); // Add location with name= "alpine " and score=2 to the system.
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "bradford ".
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "orland ".
**Constraints:**
* `name` consists of lowercase English letters, and is unique among all locations.
* `1 <= name.length <= 10`
* `1 <= score <= 105`
* At any time, the number of calls to `get` does not exceed the number of calls to `add`.
* At most `4 * 104` calls **in total** will be made to `add` and `get`. | Could we go from left to right and check to see if an index is a middle index? Do we need to sum every number to the left and right of an index each time? Use a prefix sum array where prefix[i] = nums[0] + nums[1] + ... + nums[i]. |
SortedList | sequentially-ordinal-rank-tracker | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom sortedcontainers import SortedList\nclass SORTracker:\n\n def __init__(self):\n self.arr=SortedList()\n self.index=-1\n def add(self, name: str, score: int) -> None:\n self.arr.add([-score,name])\n \n def get(self) -> str:\n \n self.index+=1\n return self.arr[self.index][1]\n\n\n# Your SORTracker object will be instantiated and called as such:\n# obj = SORTracker()\n# obj.add(name,score)\n# param_2 = obj.get()\n``` | 0 | A scenic location is represented by its `name` and attractiveness `score`, where `name` is a **unique** string among all locations and `score` is an integer. Locations can be ranked from the best to the worst. The **higher** the score, the better the location. If the scores of two locations are equal, then the location with the **lexicographically smaller** name is better.
You are building a system that tracks the ranking of locations with the system initially starting with no locations. It supports:
* **Adding** scenic locations, **one at a time**.
* **Querying** the `ith` **best** location of **all locations already added**, where `i` is the number of times the system has been queried (including the current query).
* For example, when the system is queried for the `4th` time, it returns the `4th` best location of all locations already added.
Note that the test data are generated so that **at any time**, the number of queries **does not exceed** the number of locations added to the system.
Implement the `SORTracker` class:
* `SORTracker()` Initializes the tracker system.
* `void add(string name, int score)` Adds a scenic location with `name` and `score` to the system.
* `string get()` Queries and returns the `ith` best location, where `i` is the number of times this method has been invoked (including this invocation).
**Example 1:**
**Input**
\[ "SORTracker ", "add ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "get "\]
\[\[\], \[ "bradford ", 2\], \[ "branford ", 3\], \[\], \[ "alps ", 2\], \[\], \[ "orland ", 2\], \[\], \[ "orlando ", 3\], \[\], \[ "alpine ", 2\], \[\], \[\]\]
**Output**
\[null, null, null, "branford ", null, "alps ", null, "bradford ", null, "bradford ", null, "bradford ", "orland "\]
**Explanation**
SORTracker tracker = new SORTracker(); // Initialize the tracker system.
tracker.add( "bradford ", 2); // Add location with name= "bradford " and score=2 to the system.
tracker.add( "branford ", 3); // Add location with name= "branford " and score=3 to the system.
tracker.get(); // The sorted locations, from best to worst, are: branford, bradford.
// Note that branford precedes bradford due to its **higher score** (3 > 2).
// This is the 1st time get() is called, so return the best location: "branford ".
tracker.add( "alps ", 2); // Add location with name= "alps " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford.
// Note that alps precedes bradford even though they have the same score (2).
// This is because "alps " is **lexicographically smaller** than "bradford ".
// Return the 2nd best location "alps ", as it is the 2nd time get() is called.
tracker.add( "orland ", 2); // Add location with name= "orland " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford, orland.
// Return "bradford ", as it is the 3rd time get() is called.
tracker.add( "orlando ", 3); // Add location with name= "orlando " and score=3 to the system.
tracker.get(); // Sorted locations: branford, orlando, alps, bradford, orland.
// Return "bradford ".
tracker.add( "alpine ", 2); // Add location with name= "alpine " and score=2 to the system.
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "bradford ".
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "orland ".
**Constraints:**
* `name` consists of lowercase English letters, and is unique among all locations.
* `1 <= name.length <= 10`
* `1 <= score <= 105`
* At any time, the number of calls to `get` does not exceed the number of calls to `add`.
* At most `4 * 104` calls **in total** will be made to `add` and `get`. | Could we go from left to right and check to see if an index is a middle index? Do we need to sum every number to the left and right of an index each time? Use a prefix sum array where prefix[i] = nums[0] + nums[1] + ... + nums[i]. |
Short Python faster than 80%🔥🔥 SortedList | sequentially-ordinal-rank-tracker | 0 | 1 | ```\nfrom sortedcontainers import SortedList\n\nclass SORTracker:\n\n def __init__(self):\n self.scores = SortedList()\n self.i = 0\n\n\n def add(self, name: str, score: int) -> None:\n self.scores.add((-score, name))\n\n def get(self) -> str:\n self.i += 1\n return self.scores[self.i - 1][1]\n\n\n# Your SORTracker object will be instantiated and called as such:\n# obj = SORTracker()\n# obj.add(name,score)\n# param_2 = obj.get()\n``` | 0 | A scenic location is represented by its `name` and attractiveness `score`, where `name` is a **unique** string among all locations and `score` is an integer. Locations can be ranked from the best to the worst. The **higher** the score, the better the location. If the scores of two locations are equal, then the location with the **lexicographically smaller** name is better.
You are building a system that tracks the ranking of locations with the system initially starting with no locations. It supports:
* **Adding** scenic locations, **one at a time**.
* **Querying** the `ith` **best** location of **all locations already added**, where `i` is the number of times the system has been queried (including the current query).
* For example, when the system is queried for the `4th` time, it returns the `4th` best location of all locations already added.
Note that the test data are generated so that **at any time**, the number of queries **does not exceed** the number of locations added to the system.
Implement the `SORTracker` class:
* `SORTracker()` Initializes the tracker system.
* `void add(string name, int score)` Adds a scenic location with `name` and `score` to the system.
* `string get()` Queries and returns the `ith` best location, where `i` is the number of times this method has been invoked (including this invocation).
**Example 1:**
**Input**
\[ "SORTracker ", "add ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "add ", "get ", "get "\]
\[\[\], \[ "bradford ", 2\], \[ "branford ", 3\], \[\], \[ "alps ", 2\], \[\], \[ "orland ", 2\], \[\], \[ "orlando ", 3\], \[\], \[ "alpine ", 2\], \[\], \[\]\]
**Output**
\[null, null, null, "branford ", null, "alps ", null, "bradford ", null, "bradford ", null, "bradford ", "orland "\]
**Explanation**
SORTracker tracker = new SORTracker(); // Initialize the tracker system.
tracker.add( "bradford ", 2); // Add location with name= "bradford " and score=2 to the system.
tracker.add( "branford ", 3); // Add location with name= "branford " and score=3 to the system.
tracker.get(); // The sorted locations, from best to worst, are: branford, bradford.
// Note that branford precedes bradford due to its **higher score** (3 > 2).
// This is the 1st time get() is called, so return the best location: "branford ".
tracker.add( "alps ", 2); // Add location with name= "alps " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford.
// Note that alps precedes bradford even though they have the same score (2).
// This is because "alps " is **lexicographically smaller** than "bradford ".
// Return the 2nd best location "alps ", as it is the 2nd time get() is called.
tracker.add( "orland ", 2); // Add location with name= "orland " and score=2 to the system.
tracker.get(); // Sorted locations: branford, alps, bradford, orland.
// Return "bradford ", as it is the 3rd time get() is called.
tracker.add( "orlando ", 3); // Add location with name= "orlando " and score=3 to the system.
tracker.get(); // Sorted locations: branford, orlando, alps, bradford, orland.
// Return "bradford ".
tracker.add( "alpine ", 2); // Add location with name= "alpine " and score=2 to the system.
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "bradford ".
tracker.get(); // Sorted locations: branford, orlando, alpine, alps, bradford, orland.
// Return "orland ".
**Constraints:**
* `name` consists of lowercase English letters, and is unique among all locations.
* `1 <= name.length <= 10`
* `1 <= score <= 105`
* At any time, the number of calls to `get` does not exceed the number of calls to `add`.
* At most `4 * 104` calls **in total** will be made to `add` and `get`. | Could we go from left to right and check to see if an index is a middle index? Do we need to sum every number to the left and right of an index each time? Use a prefix sum array where prefix[i] = nums[0] + nums[1] + ... + nums[i]. |
Simple Python Solution: beats 94.5% | rings-and-rods | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countPoints(self, rings: str) -> int:\n lst=[]\n rgb=[]\n count=0\n for i in range(1,len(rings),2):\n rgb=[]\n if rings[i] not in lst:\n lst.append(rings[i])\n for j in range(1,len(rings),2):\n if rings[j]==rings[i]:\n if rings[j-1]==\'R\':\n rgb.append(rings[j-1])\n if rings[j-1]==\'G\':\n rgb.append(rings[j-1])\n if rings[j-1]==\'B\':\n rgb.append(rings[j-1])\n if len(set(rgb))==3:\n count+=1\n return count\n\n``` | 1 | There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.
You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:
* The **first** character of the `ith` pair denotes the `ith` ring's **color** (`'R'`, `'G'`, `'B'`).
* The **second** character of the `ith` pair denotes the **rod** that the `ith` ring is placed on (`'0'` to `'9'`).
For example, `"R3G2B1 "` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.
Return _the number of rods that have **all three colors** of rings on them._
**Example 1:**
**Input:** rings = "B0B6G0R6R0R6G9 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.
**Example 2:**
**Input:** rings = "B0R0G0R9R0B0G0 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.
**Example 3:**
**Input:** rings = "G4 "
**Output:** 0
**Explanation:**
Only one ring is given. Thus, no rods have all three colors.
**Constraints:**
* `rings.length == 2 * n`
* `1 <= n <= 100`
* `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
* `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**). | Since every group of farmland is rectangular, the top left corner of each group will have the smallest x-coordinate and y-coordinate of any farmland in the group. Similarly, the bootm right corner of each group will have the largest x-coordinate and y-coordinate of any farmland in the group. Use DFS to traverse through different groups of farmlands and keep track of the smallest and largest x-coordinate and y-coordinates you have seen in each group. |
Python simple solution | rings-and-rods | 0 | 1 | ```\nclass Solution:\n def countPoints(self, r: str) -> int:\n ans = 0\n for i in range(10):\n i = str(i)\n if \'R\'+i in r and \'G\'+i in r and \'B\'+i in r:\n ans += 1\n return ans\n``` | 24 | There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.
You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:
* The **first** character of the `ith` pair denotes the `ith` ring's **color** (`'R'`, `'G'`, `'B'`).
* The **second** character of the `ith` pair denotes the **rod** that the `ith` ring is placed on (`'0'` to `'9'`).
For example, `"R3G2B1 "` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.
Return _the number of rods that have **all three colors** of rings on them._
**Example 1:**
**Input:** rings = "B0B6G0R6R0R6G9 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.
**Example 2:**
**Input:** rings = "B0R0G0R9R0B0G0 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.
**Example 3:**
**Input:** rings = "G4 "
**Output:** 0
**Explanation:**
Only one ring is given. Thus, no rods have all three colors.
**Constraints:**
* `rings.length == 2 * n`
* `1 <= n <= 100`
* `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
* `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**). | Since every group of farmland is rectangular, the top left corner of each group will have the smallest x-coordinate and y-coordinate of any farmland in the group. Similarly, the bootm right corner of each group will have the largest x-coordinate and y-coordinate of any farmland in the group. Use DFS to traverse through different groups of farmlands and keep track of the smallest and largest x-coordinate and y-coordinates you have seen in each group. |
Python Short & Simple | rings-and-rods | 0 | 1 | ```\nclass Solution:\n def countPoints(self, rings: str) -> int:\n count = 0\n for i in range(10):\n c = str(i)\n if "B"+c in rings and "G"+c in rings and "R"+c in rings:\n count += 1\n return count\n \n``` | 3 | There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.
You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:
* The **first** character of the `ith` pair denotes the `ith` ring's **color** (`'R'`, `'G'`, `'B'`).
* The **second** character of the `ith` pair denotes the **rod** that the `ith` ring is placed on (`'0'` to `'9'`).
For example, `"R3G2B1 "` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.
Return _the number of rods that have **all three colors** of rings on them._
**Example 1:**
**Input:** rings = "B0B6G0R6R0R6G9 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.
**Example 2:**
**Input:** rings = "B0R0G0R9R0B0G0 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.
**Example 3:**
**Input:** rings = "G4 "
**Output:** 0
**Explanation:**
Only one ring is given. Thus, no rods have all three colors.
**Constraints:**
* `rings.length == 2 * n`
* `1 <= n <= 100`
* `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
* `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**). | Since every group of farmland is rectangular, the top left corner of each group will have the smallest x-coordinate and y-coordinate of any farmland in the group. Similarly, the bootm right corner of each group will have the largest x-coordinate and y-coordinate of any farmland in the group. Use DFS to traverse through different groups of farmlands and keep track of the smallest and largest x-coordinate and y-coordinates you have seen in each group. |
PYTHON3 || BEGINNER-FRIENDLY || DICTIONARY | rings-and-rods | 0 | 1 | # PYTHON3 || BEGINNER-FRIENDLY || DICTIONARY\n\n# Code\n```\nclass Solution:\n def countPoints(self, rings: str) -> int:\n count=0\n arr=[]\n for i in range(0,len(rings),2):\n arr.append(rings[i:i+2])\n print(arr)\n\n dicc={}\n\n for j in range(len(arr)):\n if int(arr[j][1]) in dicc:\n dicc[int(arr[j][1])]+=arr[j][0]\n else:\n dicc[int(arr[j][1])]=arr[j][0]\n print(dicc)\n for k,v in dicc.items():\n sss=set(list(v))\n print(sss)\n if len(sss)==3:\n count+=1\n \n return count\n\n``` | 1 | There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.
You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:
* The **first** character of the `ith` pair denotes the `ith` ring's **color** (`'R'`, `'G'`, `'B'`).
* The **second** character of the `ith` pair denotes the **rod** that the `ith` ring is placed on (`'0'` to `'9'`).
For example, `"R3G2B1 "` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.
Return _the number of rods that have **all three colors** of rings on them._
**Example 1:**
**Input:** rings = "B0B6G0R6R0R6G9 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.
**Example 2:**
**Input:** rings = "B0R0G0R9R0B0G0 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.
**Example 3:**
**Input:** rings = "G4 "
**Output:** 0
**Explanation:**
Only one ring is given. Thus, no rods have all three colors.
**Constraints:**
* `rings.length == 2 * n`
* `1 <= n <= 100`
* `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
* `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**). | Since every group of farmland is rectangular, the top left corner of each group will have the smallest x-coordinate and y-coordinate of any farmland in the group. Similarly, the bootm right corner of each group will have the largest x-coordinate and y-coordinate of any farmland in the group. Use DFS to traverse through different groups of farmlands and keep track of the smallest and largest x-coordinate and y-coordinates you have seen in each group. |
Simplest Python solution using sets | rings-and-rods | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countPoints(self, rings: str) -> int:\n r,g,b = [],[],[]\n for i in range(len(rings)):\n if rings[i] == "R": r.append(rings[i+1])\n if rings[i] == "G": g.append(rings[i+1])\n if rings[i] == "B": b.append(rings[i+1])\n return len((set(r).intersection(set(g))).intersection(set(b)))\n``` | 3 | There are `n` rings and each ring is either red, green, or blue. The rings are distributed **across ten rods** labeled from `0` to `9`.
You are given a string `rings` of length `2n` that describes the `n` rings that are placed onto the rods. Every two characters in `rings` forms a **color-position pair** that is used to describe each ring where:
* The **first** character of the `ith` pair denotes the `ith` ring's **color** (`'R'`, `'G'`, `'B'`).
* The **second** character of the `ith` pair denotes the **rod** that the `ith` ring is placed on (`'0'` to `'9'`).
For example, `"R3G2B1 "` describes `n == 3` rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.
Return _the number of rods that have **all three colors** of rings on them._
**Example 1:**
**Input:** rings = "B0B6G0R6R0R6G9 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.
**Example 2:**
**Input:** rings = "B0R0G0R9R0B0G0 "
**Output:** 1
**Explanation:**
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.
**Example 3:**
**Input:** rings = "G4 "
**Output:** 0
**Explanation:**
Only one ring is given. Thus, no rods have all three colors.
**Constraints:**
* `rings.length == 2 * n`
* `1 <= n <= 100`
* `rings[i]` where `i` is **even** is either `'R'`, `'G'`, or `'B'` (**0-indexed**).
* `rings[i]` where `i` is **odd** is a digit from `'0'` to `'9'` (**0-indexed**). | Since every group of farmland is rectangular, the top left corner of each group will have the smallest x-coordinate and y-coordinate of any farmland in the group. Similarly, the bootm right corner of each group will have the largest x-coordinate and y-coordinate of any farmland in the group. Use DFS to traverse through different groups of farmlands and keep track of the smallest and largest x-coordinate and y-coordinates you have seen in each group. |
Python Stack O(n) Solution with inline explanation | sum-of-subarray-ranges | 0 | 1 | ```python\n\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n n = len(nums)\n \n # the answer will be sum{ Max(subarray) - Min(subarray) } over all possible subarray\n # which decomposes to sum{Max(subarray)} - sum{Min(subarray)} over all possible subarray\n # so totalsum = maxsum - minsum\n # we calculate minsum and maxsum in two different loops\n minsum = maxsum = 0\n \n # first calculate sum{ Min(subarray) } over all subarrays\n # sum{ Min(subarray) } = sum(f(i) * nums[i]) ; i=0..n-1\n # where f(i) is number of subarrays where nums[i] is the minimum value\n # f(i) = (i - index of the previous smaller value) * (index of the next smaller value - i) * nums[i]\n # we can claculate these indices in linear time using a monotonically increasing stack.\n stack = []\n for next_smaller in range(n + 1):\n\t\t\t# we pop from the stack in order to satisfy the monotonically increasing order property\n\t\t\t# if we reach the end of the iteration and there are elements present in the stack, we pop all of them\n while stack and (next_smaller == n or nums[stack[-1]] > nums[next_smaller]):\n i = stack.pop()\n prev_smaller = stack[-1] if stack else -1\n minsum += nums[i] * (next_smaller - i) * (i - prev_smaller)\n stack.append(next_smaller)\n \n # then calculate sum{ Max(subarray) } over all subarrays\n # sum{ Max(subarray) } = sum(f\'(i) * nums[i]) ; i=0..n-1\n # where f\'(i) is number of subarrays where nums[i] is the maximum value\n # f\'(i) = (i - index of the previous larger value) - (index of the next larger value - i) * nums[i]\n # this time we use a monotonically decreasing stack.\n stack = []\n for next_larger in range(n + 1):\n\t\t\t# we pop from the stack in order to satisfy the monotonically decreasing order property\n\t\t\t# if we reach the end of the iteration and there are elements present in the stack, we pop all of them\n while stack and (next_larger == n or nums[stack[-1]] < nums[next_larger]):\n i = stack.pop()\n prev_larger = stack[-1] if stack else -1\n maxsum += nums[i] * (next_larger - i) * (i - prev_larger)\n stack.append(next_larger)\n \n return maxsum - minsum\n``` | 45 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
[Python3] stack | sum-of-subarray-ranges | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/f57038d6cca9ccb356a137b3af67fba615a067dd) for solutions of weekly 271. \n\n```\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n \n def fn(op): \n """Return min sum (if given gt) or max sum (if given lt)."""\n ans = 0 \n stack = []\n for i in range(len(nums) + 1): \n while stack and (i == len(nums) or op(nums[stack[-1]], nums[i])): \n mid = stack.pop()\n ii = stack[-1] if stack else -1 \n ans += nums[mid] * (i - mid) * (mid - ii)\n stack.append(i)\n return ans \n \n return fn(lt) - fn(gt)\n```\n\n**Related problems**\n[907. Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums/discuss/949064/Python3-stack-O(N)) | 17 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
Python3 | Monotonus Stack | O(n) | sum-of-subarray-ranges | 0 | 1 | ```\n"""\nif you are not sure what is monotonous stack go through the concept given in this post:\n\nhttps://leetcode.com/problems/sum-of-subarray-minimums/discuss/178876/stack-solution-with-very-detailed-explanation-step-by-step\n\nhttps://leetcode.com/problems/sum-of-subarray-ranges/discuss/1624268/Reformulate-Problem-O(n)\n"""\n\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n """\n [4,-2,-3,4,1]\n \n """\n n = len(nums)\n \n min_stack = []\n min_sum = 0\n\n for i in range(n + 1):\n while min_stack and nums[min_stack[-1]] > (nums[i] if i < n else -float(\'Inf\')):\n j = min_stack.pop()\n k = min_stack[-1] if min_stack else -1\n min_sum += (j - k) * (i - j) * nums[j]\n min_stack.append(i)\n \n max_stack = []\n max_sum = 0\n for i in range(n + 1):\n while max_stack and nums[max_stack[-1]] < (nums[i] if i < n else float(\'Inf\')):\n j = max_stack.pop()\n k = max_stack[-1] if max_stack else -1\n max_sum += (j - k) * (i - j) * nums[j]\n\n max_stack.append(i)\n \n ans = max_sum - min_sum\n \n return ans\n``` | 8 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
Python 3, two monotonic stacks, O(n) time, O(n) space | sum-of-subarray-ranges | 0 | 1 | ```\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n res = 0\n min_stack, max_stack = [], []\n n = len(nums)\n nums.append(0)\n for i, num in enumerate(nums):\n while min_stack and (i == n or num < nums[min_stack[-1]]):\n top = min_stack.pop()\n starts = top - min_stack[-1] if min_stack else top + 1\n ends = i - top\n res -= starts * ends * nums[top] \n min_stack.append(i) \n while max_stack and (i == n or num > nums[max_stack[-1]]):\n top = max_stack.pop()\n starts = top - max_stack[-1] if max_stack else top + 1\n ends = i - top\n res += starts * ends * nums[top] \n max_stack.append(i) \n return res | 11 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
Python3 || Monotonic Stack || O(n) time complexity | sum-of-subarray-ranges | 0 | 1 | ```\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n mon = monotonicStack()\n \n # for each element, check in how many sub-arrays arrays, it can be max\n # find the prev and next greater element\n\n # for each element, check in how many sub-arrays arrays, it can be min\n # find the prev and next smaller element\n \n nse_l = mon.nextSmaller_left_idx(nums)\n nse_r = mon.nextSmaller_right_idx(nums)\n nge_l = mon.nextGreater_left_idx(nums)\n nge_r = mon.nextGreater_right_idx(nums)\n \n ans = 0\n \n for idx in range(len(nums)):\n smaller_left, smaller_right = nse_l[idx], nse_r[idx]\n greater_left, greater_right = nge_l[idx], nge_r[idx]\n \n if smaller_right == -1:\n smaller_right = len(nums)\n if greater_right == -1:\n greater_right = len(nums)\n \n min_val = (idx - smaller_left) * (smaller_right - idx) * nums[idx]\n max_val = (idx - greater_left) * (greater_right - idx) * nums[idx]\n \n ans += (max_val - min_val)\n return ans\n \nclass monotonicStack:\n def nextGreater_right_idx(self,arr):\n ans = [None] * len(arr)\n stack = []\n for idx in range(len(arr)-1,-1,-1):\n while stack and arr[stack[-1]] < arr[idx]:\n stack.pop()\n if not stack:\n #no greater element\n ans[idx] = -1\n else:\n ans[idx] = stack[-1]\n stack.append(idx)\n return ans\n \n def nextGreater_left_idx(self,arr):\n ans = [None] * len(arr)\n stack = []\n for idx in range(len(arr)):\n while stack and arr[stack[-1]] <= arr[idx]:\n stack.pop()\n if not stack:\n #no greater element\n ans[idx] = -1\n else:\n ans[idx] = stack[-1]\n stack.append(idx)\n return ans \n \n def nextSmaller_right_idx(self,arr):\n ans = [None] * len(arr)\n stack = []\n for idx in range(len(arr)-1,-1,-1):\n while stack and arr[stack[-1]] > arr[idx]:\n stack.pop()\n if not stack:\n #no smaller element\n ans[idx] = -1\n else:\n ans[idx] = stack[-1]\n stack.append(idx)\n return ans \n \n def nextSmaller_left_idx(self,arr):\n ans = [None] * len(arr)\n stack = []\n for idx in range(len(arr)):\n while stack and arr[stack[-1]] >= arr[idx]:\n stack.pop()\n if not stack:\n #no smaller element\n ans[idx] = -1\n else:\n ans[idx] = stack[-1]\n stack.append(idx)\n return ans \n``` | 5 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
[Python] Monostack explanation O(n) time and space | sum-of-subarray-ranges | 0 | 1 | \'\'\'\nThere are alot of good answers that explains max_sum and min_sum initiative \nHere I will try to explain how I analyzed and solved this monotonic stack problem\n\nAssuming you are familiar with monotonic stack but don\'t know how to write the "while" part that pops the stack\n\nLet\'s go with an example:\n\nnums = [2,3,4,1,5]\n\n5|----------X\n4|----X\n3| --X \n2| X \n1|-------X \n---------------------------\n\nStep 1: Let\'s see how many ranges do we have and what they are\n\n2: [2] [2,3] [2,4] [2,1] [2,5]\n3: [3] [3,4] [3,1] [3,5]\n4: [4] [4,1] [4,5]\n1: [1] [1,5]\n2: [5]\n\nStep 2: Let\'s maintain a monotonicly increasing stack to keep the minimum of ranges\nas a thump of rule, we always process a number when we pop it\nso if we add 2 and then 3 and then 4 to our stack, we don\'t process anything\n\nSo let\'s write down the structure\n\nStep 3: Let\'s pop!\nwhen we reach to 1 (remember we never process the current item in mono stack problems)\nwe pop 4 and so we can say [4] is found here\nnow let\'s pop 3, at this point we know that there is no element less than 3 after index of 3 cause if it was we didn\'t have 3\nin our stack so i (index of current element in for) minus index of 3 is the range that we can surely say everything in between doesn\'t matter and 3 is the minimum for them\nso we have [3] and [3,4] here\nnow we pop 2 and same as above we have [2] and [2,3] and [2,3,4]\n\nAs you can see, if we just care about the minimum, we might as well just say the sum of min for all of these fetched ranges are:\n\n2: [2] [2,3] [2,4] min in all ranges is 2\n3: [3] [3,4] min in all ranges is 3\n4: [4] min in all ranges is 4\n\nSo the formula would be poped_item * (poped_index - i)\n\nwe push 1 to the stack BTW ATM :D\n\nStep 4:\nNow that we have 1 in stack we can put 5 in the stack but we just need to process these items\nSo like others we can just add a Integer.MIN_VALUE or float("-inf") to or input array to do the trick\n\nNo let\'s pop!\nJust like step 3 we can pop 5 and then 1 and after this round we have checked and know the min for all of the following ranges:\n2: [2] [2,3] [2,4]\n3: [3] [3,4]\n4: [4] \n1: [1] [1,5]\n2: [5]\n\nBut we should have come up with the following list!\n\n2: [2] [2,3] [2,4] [2,1] [2,5]\n3: [3] [3,4] [3,1] [3,5]\n4: [4] [4,1] [4,5]\n1: [1] [1,5]\n2: [5]\n\nTo find the missed ranges we should have looked into our stack and see what\'s on the top (that\'s our minimum for missed ranges) and then multiply them by their distance to i\nand if the stack is empty then we might have some elements in the stack that we already poped. we don\'t care what they were cause the were obviously greater than 1 (in this case)\nSo it\'s safe to say that the INDEX of whatever is on top of the stack or -1 should be multipled by the element that we poped from the stack (min of all of those ranges)\n\nSame goes with sum_max (second pass with min mono stack)\n\n\'\'\'\nclass Solution:\n def subArrayRanges(self, nums: List[int]) -> int:\n \n st = []\n sum_min = 0\n for i,n in enumerate(nums+[float("-inf")]):\n while st and nums[st[-1]] > n:\n j = st.pop()\n poped = nums[j]\n k = -1\n if st:\n k = st[-1]\n sum_min += poped * (i - j)*(j - k)\n st.append(i)\n \n st = []\n sum_max = 0\n for i,n in enumerate(nums+[float("inf")]):\n while st and nums[st[-1]] < n:\n j = st.pop()\n poped = nums[j]\n k = -1\n if st:\n k = st[-1]\n sum_max += poped * (i - j)*(j - k)\n st.append(i)\n \n return sum_max - sum_min | 6 | You are given an integer array `nums`. The **range** of a subarray of `nums` is the difference between the largest and smallest element in the subarray.
Return _the **sum of all** subarray ranges of_ `nums`_._
A subarray is a contiguous **non-empty** sequence of elements within an array.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[2\], range = 2 - 2 = 0
\[3\], range = 3 - 3 = 0
\[1,2\], range = 2 - 1 = 1
\[2,3\], range = 3 - 2 = 1
\[1,2,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4.
**Example 2:**
**Input:** nums = \[1,3,3\]
**Output:** 4
**Explanation:** The 6 subarrays of nums are the following:
\[1\], range = largest - smallest = 1 - 1 = 0
\[3\], range = 3 - 3 = 0
\[3\], range = 3 - 3 = 0
\[1,3\], range = 3 - 1 = 2
\[3,3\], range = 3 - 3 = 0
\[1,3,3\], range = 3 - 1 = 2
So the sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4.
**Example 3:**
**Input:** nums = \[4,-2,-3,4,1\]
**Output:** 59
**Explanation:** The sum of all subarray ranges of nums is 59.
**Constraints:**
* `1 <= nums.length <= 1000`
* `-109 <= nums[i] <= 109`
**Follow-up:** Could you find a solution with `O(n)` time complexity? | How can we use the small constraints to help us solve the problem? How can we traverse the ancestors and descendants of a node? |
[Python3] 2 pointers | watering-plants-ii | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/f57038d6cca9ccb356a137b3af67fba615a067dd) for solutions of weekly 271. \n\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n ans = 0 \n lo, hi = 0, len(plants)-1\n canA, canB = capacityA, capacityB\n while lo < hi: \n if canA < plants[lo]: ans += 1; canA = capacityA\n canA -= plants[lo]\n if canB < plants[hi]: ans += 1; canB = capacityB\n canB -= plants[hi]\n lo, hi = lo+1, hi-1\n if lo == hi and max(canA, canB) < plants[lo]: ans += 1\n return ans \n``` | 8 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
python beats 98% | watering-plants-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n# Code\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n count = 0\n left = 0\n right = len(plants)-1\n capA = capacityA\n capB = capacityB\n while left<=right:\n if left == right:\n if plants[left]>max(capA, capB):\n count+=1\n return count\n if plants[left]<=capA:\n capA -= plants[left]\n left+=1\n else:\n count+=1\n capA = capacityA-plants[left]\n left+=1\n if plants[right]<=capB:\n capB -= plants[right]\n right-=1\n else:\n count+=1\n capB = capacityB-plants[right]\n right-=1\n return count \n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
CLEAN PYTHON SOLUTION || WITH COMMENTS | watering-plants-ii | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimumRefill(self, plant: List[int], capacityA: int, capacityB: int) -> int:\n refill = 0\n canA = capacityA\n canB = capacityB\n left = 0\n right = len(plant) - 1\n while left <= right:\n if left == right: # when pointing to same index\n if plant[left] > max(canA, canB): # the one which has more water in can will water it\n refill += 1\n break\n\n if plant[left] > canA or plant[right] > canB: # if due to any plant cans need refill\n if plant[left] > canA: # if alice-can need refill\n canA = capacityA\n refill += 1\n if plant[right] > canB: #if bob-can need refill\n canB = capacityB\n refill += 1\n canA -= plant[left] # rem amount after watering\n canB -= plant[right]\n left += 1\n right -= 1\n # print(refill)\n return refill\n \n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
python3 - simple | watering-plants-ii | 0 | 1 | # Intuition\neither it\'s an even count of plants \n\nor an odd count => Alice and Bob will meet at one plant \n\nin either case, half of the plants will be served by one of them.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(len(plants)), time to iterate through the array\n- Space complexity: \nO(n), u can optimize to be O(1) \n \n# Code\n```\nclass Solution:\n\n def get_refill_cnt_and_capacity_left(self,plants, capacity,left_to_right_direction):\n serving_cnt=0\n current_capacity = capacity\n if not left_to_right_direction:\n plants = plants[::-1]\n for plant in plants:\n if current_capacity>=plant:\n current_capacity -= plant\n else:\n current_capacity = capacity\n current_capacity -= plant\n serving_cnt +=1\n return serving_cnt,current_capacity\n\n\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n \n is_even_plant_count = len(plants) % 2 == 0\n half_plants_cnt = len(plants) // 2\n\n first_half_of_plants = plants[0:half_plants_cnt]\n second_half_of_plants_index = half_plants_cnt if is_even_plant_count else half_plants_cnt +1\n second_half_of_plants = plants[second_half_of_plants_index:]\n\n serving_cnt_a,current_capacity_a = self.get_refill_cnt_and_capacity_left(first_half_of_plants,capacityA, True)\n serving_cnt_b,current_capacity_b = self.get_refill_cnt_and_capacity_left(second_half_of_plants,capacityB, False)\n \n serving_cnt = serving_cnt_a + serving_cnt_b \n\n if not is_even_plant_count:\n final_plant = plants[half_plants_cnt]\n if not (current_capacity_a>=final_plant or current_capacity_b>=final_plant):\n serving_cnt +=1\n\n return serving_cnt\n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
many conditionals | watering-plants-ii | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n i=0\n j=len(plants)-1\n count=0\n ia=capacityA\n ib=capacityB\n while i<=j:\n if i==j:\n # print(\'1\')\n if capacityA>=capacityB:\n if capacityA<plants[i]:\n count+=1\n capacityA=ia\n if capacityA>=plants[i]:\n capacityA-=plants[i]\n elif capacityA<capacityB:\n if capacityB<plants[j]:\n count+=1\n capacityB=ib\n if capacityB>=plants[j]:\n capacityB-=plants[j]\n break\n if capacityA<plants[i]:\n # print(\'2\')\n count+=1\n capacityA=ia\n if capacityA>=plants[i]:\n # print(\'3\')\n capacityA-=plants[i]\n if capacityB<plants[j]:\n # print(\'4\')\n count+=1\n capacityB=ib\n if capacityB>=plants[j]:\n # print(\'5\')\n capacityB-=plants[j]\n i+=1\n j-=1\n return count\n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
Python easy sol. | watering-plants-ii | 0 | 1 | # Code\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], ca: int, cb: int) -> int:\n a,b=0,len(plants)-1\n alice,bob=ca,cb\n res=0\n while a<=b:\n if a==b:\n if alice>=bob:\n if alice<plants[a]:\n res+=1\n return res\n else:\n if bob<plants[b]:\n res+=1\n return res\n if plants[a]>alice:\n alice=ca\n res+=1\n if plants[b]>bob:\n bob=cb\n res+=1\n alice-=plants[a]\n bob-=plants[b]\n a+=1\n b-=1\n return res\n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
Python, 2 pointers with explanation | watering-plants-ii | 0 | 1 | # Intuition\nWe know that both Alice and Bob start from both ends and water them at the same time. The only tricky part about this problem is to determine the order of when both alice and bob reach the same plant.\n\n# Approach\nWe generate a separate array to contain True and False values, This is used to check which plants have been watered.\n\nAt each iteration, we check for both Alice and Bob if they are able to water the plants and if a refill is required and update the left and right pointers.\n\n```python\nif capacityA >= plants[l] and not watered[l]:\n if a < plants[l]:\n refills += 1\n a = capacityA\n a -= plants[l]\n watered[l] = True\nl += 1\n\nif capacityB >= plants[r] and not watered[r]:\n if b < plants[r]:\n refills += 1\n b = capacityB\n b -= plants[r]\n watered[r] = True\nr -= 1\n```\n\nNote that when Alice and Bob reach the same plant, the person who has the more water will water the plant. For the case of when they have both the same amount of water, it is already covered in this section of the code here:\n```python\nif capacityA >= plants[l] and not watered[l]:\n if a < plants[l]:\n refills += 1\n a = capacityA\n a -= plants[l]\n watered[l] = True\nl += 1\n```\nTherefore we will only need to state the condition where Bob is required to water the plant when he has more water than Alice. Note that for the case when they both do not have enough to water the plants, Alice will first have to refill and water the plant.\n```python\nif l == r and b > a and b >= plants[l]:\n b -= plants[l]\n watered[l] = True\n```\n\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n\n l, r = 0 , len(plants) - 1\n\n refills = 0\n a, b = capacityA, capacityB\n watered = [False] * len(plants)\n while l < len(plants) and r >= 0:\n \n # if both reach the same plant, determine who to water the plant\n if l == r and b > a and b >= plants[l]:\n b -= plants[l]\n watered[l] = True\n\n if capacityA >= plants[l] and not watered[l]:\n if a < plants[l]:\n refills += 1\n a = capacityA\n a -= plants[l]\n watered[l] = True\n l += 1\n\n if capacityB >= plants[r] and not watered[r]:\n if b < plants[r]:\n refills += 1\n b = capacityB\n b -= plants[r]\n watered[r] = True\n r -= 1\n\n return refills\n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
Easy Python Solution beats 91.30% run time | watering-plants-ii | 0 | 1 | # Approach\nCompute if refill is needed at each plant[i].\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:\n a = 0\n b = len(plants)-1\n r = 0\n ca, cb = capacityA, capacityB\n while a<b:\n if ca < plants[a]:\n ca = capacityA\n r+=1\n\n if cb < plants[b]:\n cb = capacityB\n r+=1\n\n ca -= plants[a]\n cb -= plants[b]\n \n a+=1\n b-=1\n \n if a == b:\n if ca >= cb:\n if ca < plants[a]:\n ca = capacityA\n r+=1\n ca -= plants[a]\n \n elif ca < cb:\n if cb < plants[b]:\n cb = capacityB\n r+=1\n cb -= plants[b]\n\n return r\n``` | 0 | Alice and Bob want to water `n` plants in their garden. The plants are arranged in a row and are labeled from `0` to `n - 1` from left to right where the `ith` plant is located at `x = i`.
Each plant needs a specific amount of water. Alice and Bob have a watering can each, **initially full**. They water the plants in the following way:
* Alice waters the plants in order from **left to right**, starting from the `0th` plant. Bob waters the plants in order from **right to left**, starting from the `(n - 1)th` plant. They begin watering the plants **simultaneously**.
* It takes the same amount of time to water each plant regardless of how much water it needs.
* Alice/Bob **must** water the plant if they have enough in their can to **fully** water it. Otherwise, they **first** refill their can (instantaneously) then water the plant.
* In case both Alice and Bob reach the same plant, the one with **more** water currently in his/her watering can should water this plant. If they have the same amount of water, then Alice should water this plant.
Given a **0-indexed** integer array `plants` of `n` integers, where `plants[i]` is the amount of water the `ith` plant needs, and two integers `capacityA` and `capacityB` representing the capacities of Alice's and Bob's watering cans respectively, return _the **number of times** they have to refill to water all the plants_.
**Example 1:**
**Input:** plants = \[2,2,3,3\], capacityA = 5, capacityB = 5
**Output:** 1
**Explanation:**
- Initially, Alice and Bob have 5 units of water each in their watering cans.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 3 units and 2 units of water respectively.
- Alice has enough water for plant 1, so she waters it. Bob does not have enough water for plant 2, so he refills his can then waters it.
So, the total number of times they have to refill to water all the plants is 0 + 0 + 1 + 0 = 1.
**Example 2:**
**Input:** plants = \[2,2,3,3\], capacityA = 3, capacityB = 4
**Output:** 2
**Explanation:**
- Initially, Alice and Bob have 3 units and 4 units of water in their watering cans respectively.
- Alice waters plant 0, Bob waters plant 3.
- Alice and Bob now have 1 unit of water each, and need to water plants 1 and 2 respectively.
- Since neither of them have enough water for their current plants, they refill their cans and then water the plants.
So, the total number of times they have to refill to water all the plants is 0 + 1 + 1 + 0 = 2.
**Example 3:**
**Input:** plants = \[5\], capacityA = 10, capacityB = 8
**Output:** 0
**Explanation:**
- There is only one plant.
- Alice's watering can has 10 units of water, whereas Bob's can has 8 units. Since Alice has more water in her can, she waters this plant.
So, the total number of times they have to refill is 0.
**Constraints:**
* `n == plants.length`
* `1 <= n <= 105`
* `1 <= plants[i] <= 106`
* `max(plants[i]) <= capacityA, capacityB <= 109` | Consider only the numbers which have a good prime factorization. Use brute force to find all possible good subsets and then calculate its frequency in nums. |
Python (Simple Prefix Sum) | maximum-fruits-harvested-after-at-most-k-steps | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxTotalFruits(self, fruits, start, k):\n def dfs(i,j):\n return fruits[j][0]-fruits[i][0]+min(abs(start-fruits[i][0]),abs(start-fruits[j][0]))\n\n ans = [0]\n\n for i,j in fruits:\n ans.append(ans[-1]+j)\n\n j, max_val, n = 0, 0, len(fruits)\n\n for i in range(n):\n j = max(i,j)\n\n while j < n and dfs(i,j) <= k:\n j += 1\n\n max_val = max(max_val,ans[j]-ans[i])\n\n return max_val\n\n\n\n \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 0 | Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array `fruits` where `fruits[i] = [positioni, amounti]` depicts `amounti` fruits at the position `positioni`. `fruits` is already **sorted** by `positioni` in **ascending order**, and each `positioni` is **unique**.
You are also given an integer `startPos` and an integer `k`. Initially, you are at the position `startPos`. From any position, you can either walk to the **left or right**. It takes **one step** to move **one unit** on the x-axis, and you can walk **at most** `k` steps in total. For every position you reach, you harvest all the fruits at that position, and the fruits will disappear from that position.
Return _the **maximum total number** of fruits you can harvest_.
**Example 1:**
**Input:** fruits = \[\[2,8\],\[6,3\],\[8,6\]\], startPos = 5, k = 4
**Output:** 9
**Explanation:**
The optimal way is to:
- Move right to position 6 and harvest 3 fruits
- Move right to position 8 and harvest 6 fruits
You moved 3 steps and harvested 3 + 6 = 9 fruits in total.
**Example 2:**
**Input:** fruits = \[\[0,9\],\[4,1\],\[5,7\],\[6,2\],\[7,4\],\[10,9\]\], startPos = 5, k = 4
**Output:** 14
**Explanation:**
You can move at most k = 4 steps, so you cannot reach position 0 nor 10.
The optimal way is to:
- Harvest the 7 fruits at the starting position 5
- Move left to position 4 and harvest 1 fruit
- Move right to position 6 and harvest 2 fruits
- Move right to position 7 and harvest 4 fruits
You moved 1 + 3 = 4 steps and harvested 7 + 1 + 2 + 4 = 14 fruits in total.
**Example 3:**
**Input:** fruits = \[\[0,3\],\[6,4\],\[8,5\]\], startPos = 3, k = 2
**Output:** 0
**Explanation:**
You can move at most k = 2 steps and cannot reach any position with fruits.
**Constraints:**
* `1 <= fruits.length <= 105`
* `fruits[i].length == 2`
* `0 <= startPos, positioni <= 2 * 105`
* `positioni-1 < positioni` for any `i > 0` (**0-indexed**)
* `1 <= amounti <= 104`
* `0 <= k <= 2 * 105` | Find the minimum and maximum in one iteration. Let them be mn and mx. Try all the numbers in the range [1, mn] and check the largest number which divides both of them. |
Python3 code. | maximum-fruits-harvested-after-at-most-k-steps | 0 | 1 | # **Bold**# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:\n arr = [0 for _ in range(2*k+1)]\n for pos, numOfFruit in fruits:\n if pos < startPos-k or pos > startPos+k:\n continue\n arr[pos-(startPos-k)] += numOfFruit\n \n left, right = sum(arr[:k+1]), sum(arr[k:])\n maxSeen = max(left, right)\n \n turn = 1 # turning point\n for i in range(2, k+1, 2):\n left = left-arr[i-2]-arr[i-1]+arr[k+turn]\n right = right-arr[~(i-2)]-arr[~(i-1)]+arr[k-turn]\n maxSeen = max(maxSeen, left, right)\n turn += 1\n \n return maxSeen\n``` | 0 | Fruits are available at some positions on an infinite x-axis. You are given a 2D integer array `fruits` where `fruits[i] = [positioni, amounti]` depicts `amounti` fruits at the position `positioni`. `fruits` is already **sorted** by `positioni` in **ascending order**, and each `positioni` is **unique**.
You are also given an integer `startPos` and an integer `k`. Initially, you are at the position `startPos`. From any position, you can either walk to the **left or right**. It takes **one step** to move **one unit** on the x-axis, and you can walk **at most** `k` steps in total. For every position you reach, you harvest all the fruits at that position, and the fruits will disappear from that position.
Return _the **maximum total number** of fruits you can harvest_.
**Example 1:**
**Input:** fruits = \[\[2,8\],\[6,3\],\[8,6\]\], startPos = 5, k = 4
**Output:** 9
**Explanation:**
The optimal way is to:
- Move right to position 6 and harvest 3 fruits
- Move right to position 8 and harvest 6 fruits
You moved 3 steps and harvested 3 + 6 = 9 fruits in total.
**Example 2:**
**Input:** fruits = \[\[0,9\],\[4,1\],\[5,7\],\[6,2\],\[7,4\],\[10,9\]\], startPos = 5, k = 4
**Output:** 14
**Explanation:**
You can move at most k = 4 steps, so you cannot reach position 0 nor 10.
The optimal way is to:
- Harvest the 7 fruits at the starting position 5
- Move left to position 4 and harvest 1 fruit
- Move right to position 6 and harvest 2 fruits
- Move right to position 7 and harvest 4 fruits
You moved 1 + 3 = 4 steps and harvested 7 + 1 + 2 + 4 = 14 fruits in total.
**Example 3:**
**Input:** fruits = \[\[0,3\],\[6,4\],\[8,5\]\], startPos = 3, k = 2
**Output:** 0
**Explanation:**
You can move at most k = 2 steps and cannot reach any position with fruits.
**Constraints:**
* `1 <= fruits.length <= 105`
* `fruits[i].length == 2`
* `0 <= startPos, positioni <= 2 * 105`
* `positioni-1 < positioni` for any `i > 0` (**0-indexed**)
* `1 <= amounti <= 104`
* `0 <= k <= 2 * 105` | Find the minimum and maximum in one iteration. Let them be mn and mx. Try all the numbers in the range [1, mn] and check the largest number which divides both of them. |
Simple python solution | find-first-palindromic-string-in-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def firstPalindrome(self, words: List[str]) -> str:\n for i in words:\n s=\'\'\n for j in range(len(i)):\n s=i[j]+s\n if s==i:\n return i\n return \'\'\n``` | 1 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
4 liner code beats 99.83% in Runtime | find-first-palindromic-string-in-the-array | 0 | 1 | # Proof:\n\nsee my image\n\n# Code\n```\nclass Solution:\n def firstPalindrome(self, words: List[str]) -> str:\n for i in words:\n if i==i[::-1]:\n return i\n return ""\n``` | 1 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
Python Easy Solution || word==word[::-1] | find-first-palindromic-string-in-the-array | 0 | 1 | # Code\n```\nclass Solution:\n def firstPalindrome(self, words: List[str]) -> str:\n for i in words:\n if i==i[::-1]:\n return i\n return ""\n``` | 3 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
Python Solution ||O(N) | find-first-palindromic-string-in-the-array | 0 | 1 | Time Complexcity O(N)\nSpace Complexcity O(1)\n```\nclass Solution:\n def firstPalindrome(self, words: List[str]) -> str:\n for word in words:\n print(word)\n if word==word[::-1]:\n return word\n return ""\n \n``` | 1 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
simple sol in python | find-first-palindromic-string-in-the-array | 0 | 1 | \n```\nclass Solution:\n def firstPalindrome(self, words: List[str]) -> str:\n for i in words:\n if(i[::-1]==i):\n return i\n break\n else:\n return ""\n``` | 1 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
Python | Reverse String | find-first-palindromic-string-in-the-array | 0 | 1 | \n def firstPalindrome(self, words: List[str]) -> str:\n for w in words:\n if w == w[::-1]:\n return w\n return "" | 1 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
Python - Clean and Simple + One-Liner! | find-first-palindromic-string-in-the-array | 0 | 1 | **Solution**:\n```\nclass Solution:\n def firstPalindrome(self, words):\n for word in words:\n if word == word[::-1]: return word\n return ""\n```\n\n**Solution with custom palindrome checker (Two-Pointer approach)**:\n```\nclass Solution:\n def firstPalindrome(self, words):\n for word in words:\n if self.isPalindrome(word): return word\n return ""\n \n def isPalindrome(self, word):\n l, r = 0, len(word)-1\n while l < r:\n if word[l] != word[r]: return False\n l += 1\n r -= 1\n return True\n```\n\n**One-Liner**:\n```\nclass Solution:\n def firstPalindrome(self, words):\n return next((word for word in words if word==word[::-1]), "")\n``` | 3 | Given an array of strings `words`, return _the first **palindromic** string in the array_. If there is no such string, return _an **empty string**_ `" "`.
A string is **palindromic** if it reads the same forward and backward.
**Example 1:**
**Input:** words = \[ "abc ", "car ", "ada ", "racecar ", "cool "\]
**Output:** "ada "
**Explanation:** The first string that is palindromic is "ada ".
Note that "racecar " is also palindromic, but it is not the first.
**Example 2:**
**Input:** words = \[ "notapalindrome ", "racecar "\]
**Output:** "racecar "
**Explanation:** The first and only string that is palindromic is "racecar ".
**Example 3:**
**Input:** words = \[ "def ", "ghi "\]
**Output:** " "
**Explanation:** There are no palindromic strings, so the empty string is returned.
**Constraints:**
* `1 <= words.length <= 100`
* `1 <= words[i].length <= 100`
* `words[i]` consists only of lowercase English letters. | The sum of chosen elements will not be too large. Consider using a hash set to record all possible sums while iterating each row. Instead of keeping track of all possible sums, since in each row, we are adding positive numbers, only keep those that can be a candidate, not exceeding the target by too much. |
8 Line Python Code || One Pass | adding-spaces-to-a-string | 0 | 1 | # Intuition\nMaintain a lastAdded upto pointer -> this pointer will store the last index we have added in res of s.\nIterate in spaces and add chars from last seen index till i and then add space & update last idx added upto.\nreturn res.\n\n# Code\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n res = ""\n lastIdx = 0\n for i in spaces:\n res += s[lastIdx:i]\n res += " "\n lastIdx = i\n res += s[lastIdx:]\n return(res)\n\n #TLE ->\n # s = list(s)\n # for i in range(len(spaces)):\n # idx = spaces[i] + i\n # s.insert(idx, " ")\n # res = \'\'.join(s)\n # return(res)\n``` | 2 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
[Java/Python 3] Traverse input. | adding-spaces-to-a-string | 1 | 1 | Reversely traverse input.\n\n```java\n public String addSpaces(String s, int[] spaces) {\n StringBuilder ans = new StringBuilder();\n for (int i = s.length() - 1, j = spaces.length - 1; i >= 0; --i) {\n ans.append(s.charAt(i));\n if (j >= 0 && spaces[j] == i) {\n --j;\n ans.append(\' \');\n }\n }\n return ans.reverse().toString();\n }\n```\n```python\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n ans = []\n i = len(s) - 1\n while i >= 0:\n ans.append(s[i])\n if spaces and i == spaces[-1]:\n ans.append(\' \')\n spaces.pop()\n i -= 1 \n return \'\'.join(ans[:: -1])\n```\n\n----\n\nTraverse input from left to right.\n```java\n public String addSpaces(String s, int[] spaces) {\n StringBuilder ans = new StringBuilder();\n for (int i = 0, j = 0; i < s.length(); ++i) {\n if (j < spaces.length && spaces[j] == i) {\n ans.append(\' \');\n ++j;\n }\n ans.append(s.charAt(i));\n }\n return ans.toString();\n }\n```\n```python\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n ans = []\n j = 0\n for i, c in enumerate(s):\n if j < len(spaces) and i == spaces[j]:\n ans.append(\' \')\n j += 1\n ans.append(c)\n return \'\'.join(ans)\n``` | 15 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
[Python] Split and Join to the rescue. From TLE to Accepted ! Straightforward | adding-spaces-to-a-string | 0 | 1 | Just do what the question said i.e \nAdd spaces at that index \n\nIn the first solution i guess due to python\'s way of working with strings we are getting a TLE error\n```\n#TLE SOLUTION\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n\t\tspaces_idx = len(spaces)-1\n\n\t\tdef addString(index,s):\n\t\t\ts = s[:index]+" "+s[index:] \n\t\t\t#This changes the string at every instance hence taking so much time\n\t\t\treturn s\n\t\t\t\n\t\twhile spaces_idx>=0:\n\t\t\ts = addString(spaces[spaces_idx],s)\n\t\t\tspaces_idx-=1\n\t\treturn s\n```\nTo tackle this I **split** the required words and then used the **join** method to combine it with a whitespaces\n\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n \n arr = []\n prev = 0\n for space in spaces:\n arr.append(s[prev:space])\n prev = space\n arr.append(s[space:])\n \n return " ".join(arr)\n``` | 8 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
** Python code: Adding Spaces to a String | adding-spaces-to-a-string | 0 | 1 | ```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n arr=[]\n prev=0\n for i in spaces:\n arr.append(s[prev:i])\n prev=i\n arr.append(s[i:])\n return " ".join(arr)\n``` | 6 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Python simple and clean solution | adding-spaces-to-a-string | 0 | 1 | **Python :**\n\n```\ndef addSpaces(self, s: str, spaces: List[int]) -> str:\n\tres = s[:spaces[0]] + " "\n\n\tfor j in range(1, len(spaces)):\n\t\tres += s[spaces[j- 1]:spaces[j]] + " "\n\n\tres += s[spaces[-1]:] \n\treturn res\n```\n\n**Like it ? please upvote !** | 8 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Python3 Easy understanding | adding-spaces-to-a-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n a = []\n string = 0\n for i in spaces:\n a.append(s[string:i])\n a.append(" ")\n string = i\n a.append(s[string:])\n return "".join(a)\n``` | 1 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
[Python3] forward & backward | adding-spaces-to-a-string | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/55c6a88797eef9ac745a3dbbff821a2aac735a70) for solutions of weekly 272. \n\n**Approach 1 -- forward**\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n ans = []\n j = 0 \n for i, ch in enumerate(s): \n if j < len(spaces) and i == spaces[j]: \n ans.append(\' \')\n j += 1\n ans.append(ch)\n return \'\'.join(ans)\n```\n\n**Approach 2 -- backward**\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n ans = []\n for i in reversed(range(len(s))): \n ans.append(s[i])\n if spaces and spaces[-1] == i: \n ans.append(\' \')\n spaces.pop()\n return "".join(reversed(ans))\n``` | 5 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Python Using String Comprehension vs Copying to another string | adding-spaces-to-a-string | 0 | 1 | The basic idea here is to do it inplace using string comprehension (Giving TLE) :\n\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n j = 0\n for i in spaces:\n s = s[:i+j]+" "+s[i+j:]\n j += 1\n return s \n```\n\nIt says - \n***66 / 66 test cases passed, but took too long.***\n***Time Limit Exceeded***\n\nNow copying to another string (Pass):\n\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n res = s[:spaces[0]]+" "\n for i in range(1, len(spaces)):\n res += s[spaces[i-1]:spaces[i]]+" "\n prev = spaces[i]\n return res+s[spaces[len(spaces)-1]:] \n```\n\nThanks for reading \uD83D\uDE0A | 2 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Python3 || Simple Solution | adding-spaces-to-a-string | 0 | 1 | # Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n spaces.append(len(s))\n result = ""\n idx = 0\n for i in range(len(s)):\n if spaces[idx] == i:\n result += " "\n idx += 1\n result += s[i]\n return result\n``` | 0 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Simple Python Solution | adding-spaces-to-a-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to add the space at the given indices. If we directly add it to s, then with each addition, the length of s will change and the spaces position will differ. So, take an empty string and add the part of s and spaces respectively.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n-> First if it is first space we are adding, then:\n```\np=p+s[0:spaces[0]]+" "\n```\n-> After first space addition we need to get the sub parts between (i-1) and (i) index in s to add to p along with a space.\n```\np=p+s[spaces[i-1]:s[spaces[i]]+" "\n```\n-> After completion of loop add the last remaining part of s to p and return it.\n```\np=p+s[spaces[-1]::]\n```\n# Code\n```\nclass Solution:\n def addSpaces(self, s: str, spaces: List[int]) -> str:\n p=\'\'\n for i in range(len(spaces)):\n if (i==0):\n p+=(s[0:spaces[0]]+" ")\n else:\n p+=(s[spaces[i-1]:spaces[i]]+" ")\n p+=s[spaces[-1]::]\n return p\n``` | 0 | You are given a **0-indexed** string `s` and a **0-indexed** integer array `spaces` that describes the indices in the original string where spaces will be added. Each space should be inserted **before** the character at the given index.
* For example, given `s = "EnjoyYourCoffee "` and `spaces = [5, 9]`, we place spaces before `'Y'` and `'C'`, which are at indices `5` and `9` respectively. Thus, we obtain `"Enjoy **Y**our **C**offee "`.
Return _the modified string **after** the spaces have been added._
**Example 1:**
**Input:** s = "LeetcodeHelpsMeLearn ", spaces = \[8,13,15\]
**Output:** "Leetcode Helps Me Learn "
**Explanation:**
The indices 8, 13, and 15 correspond to the underlined characters in "Leetcode**H**elps**M**e**L**earn ".
We then place spaces before those characters.
**Example 2:**
**Input:** s = "icodeinpython ", spaces = \[1,5,7,9\]
**Output:** "i code in py thon "
**Explanation:**
The indices 1, 5, 7, and 9 correspond to the underlined characters in "i**c**ode**i**n**p**y**t**hon ".
We then place spaces before those characters.
**Example 3:**
**Input:** s = "spacing ", spaces = \[0,1,2,3,4,5,6\]
**Output:** " s p a c i n g "
**Explanation:**
We are also able to place spaces before the first character of the string.
**Constraints:**
* `1 <= s.length <= 3 * 105`
* `s` consists only of lowercase and uppercase English letters.
* `1 <= spaces.length <= 3 * 105`
* `0 <= spaces[i] <= s.length - 1`
* All the values of `spaces` are **strictly increasing**. | What information do the two largest elements tell us? Can we use recursion to check all possible states? |
Easy approach || O(n) | number-of-smooth-descent-periods-of-a-stock | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getDescentPeriods(self, prices: List[int]) -> int:\n dp=[]\n for i in range(1,len(prices)):\n if(prices[i]-prices[i-1]==-1):\n dp.append(1)\n else:\n dp.append(0)\n c=[]\n res=0\n count=0\n for i in range(len(dp)):\n if(dp[i]==1):\n count+=1\n else:\n c.append(count)\n count=0\n c.append(count)\n for i in c:\n if(i==1):\n res+=1\n else:\n res+=(i*(i+1))//2\n res+=len(prices)\n return(res)\n \n``` | 3 | You are given an integer array `prices` representing the daily price history of a stock, where `prices[i]` is the stock price on the `ith` day.
A **smooth descent period** of a stock consists of **one or more contiguous** days such that the price on each day is **lower** than the price on the **preceding day** by **exactly** `1`. The first day of the period is exempted from this rule.
Return _the number of **smooth descent periods**_.
**Example 1:**
**Input:** prices = \[3,2,1,4\]
**Output:** 7
**Explanation:** There are 7 smooth descent periods:
\[3\], \[2\], \[1\], \[4\], \[3,2\], \[2,1\], and \[3,2,1\]
Note that a period with one day is a smooth descent period by the definition.
**Example 2:**
**Input:** prices = \[8,6,7,7\]
**Output:** 4
**Explanation:** There are 4 smooth descent periods: \[8\], \[6\], \[7\], and \[7\]
Note that \[8,6\] is not a smooth descent period as 8 - 6 ≠ 1.
**Example 3:**
**Input:** prices = \[1\]
**Output:** 1
**Explanation:** There is 1 smooth descent period: \[1\]
**Constraints:**
* `1 <= prices.length <= 105`
* `1 <= prices[i] <= 105` | null |
[Java/Python 3] Time O(n) space O(1) code. | number-of-smooth-descent-periods-of-a-stock | 1 | 1 | For each descent periods ending at `i`, use `cnt` to count the # of the the periods and add to the output variable `ans`.\n```java\n public long getDescentPeriods(int[] prices) {\n long ans = 0;\n int cnt = 0, prev = -1;\n for (int cur : prices) {\n if (prev - cur == 1) {\n ++cnt; \n }else {\n cnt = 1;\n }\n ans += cnt;\n prev = cur;\n }\n return ans;\n }\n```\n```python\n def getDescentPeriods(self, prices: List[int]) -> int:\n ans = cnt = 0\n prev = -math.inf\n for cur in prices:\n if prev - cur == 1:\n cnt += 1\n else:\n cnt = 1\n ans += cnt\n prev = cur\n return ans\n``` | 11 | You are given an integer array `prices` representing the daily price history of a stock, where `prices[i]` is the stock price on the `ith` day.
A **smooth descent period** of a stock consists of **one or more contiguous** days such that the price on each day is **lower** than the price on the **preceding day** by **exactly** `1`. The first day of the period is exempted from this rule.
Return _the number of **smooth descent periods**_.
**Example 1:**
**Input:** prices = \[3,2,1,4\]
**Output:** 7
**Explanation:** There are 7 smooth descent periods:
\[3\], \[2\], \[1\], \[4\], \[3,2\], \[2,1\], and \[3,2,1\]
Note that a period with one day is a smooth descent period by the definition.
**Example 2:**
**Input:** prices = \[8,6,7,7\]
**Output:** 4
**Explanation:** There are 4 smooth descent periods: \[8\], \[6\], \[7\], and \[7\]
Note that \[8,6\] is not a smooth descent period as 8 - 6 ≠ 1.
**Example 3:**
**Input:** prices = \[1\]
**Output:** 1
**Explanation:** There is 1 smooth descent period: \[1\]
**Constraints:**
* `1 <= prices.length <= 105`
* `1 <= prices[i] <= 105` | null |
Little Maths, Little Sliding Window Without DP! | number-of-smooth-descent-periods-of-a-stock | 0 | 1 | In order to solve this problem I would prefer you take a pen and paper and make few testcases of your own.\nDuring that youll find some similarities\nLet me illustrate:\n[3,2,1] - [3,2] , [2,1] , [3,2,1] and singular values\n3+3 = 6\nNow when we have 4 numbers\n[4,3,2,1] \nwhen we take two numbers at once\n[4,3] ,[3,2] ,[2,1] 3 cases-.\nwhen we take 3 numbers at once\n[4,3,2] , [3,2,1] - 2 cases\nwhen we take 4 numbers at once\n[4,3,2,1] - 1 cases\n\nTo add we sum it i.e **sum of natural numbers **\n**(N*(N+1))//2**\nHere N is size of the **(contiguous valid array - 1)**\nAlso we will add all singualar values as they also satisfy the condition\nThus **ans+=len(arr)**.\n\n**So all different contiguous arrays which satisfy + size of array** \nIn the code we keep track of contiguous array using the value of k \nAnd calculate the value using the sum of natural numbers.\n\n```\nimport sys\nclass Solution:\n def getDescentPeriods(self, prices: List[int]) -> int: \n def calculate(k,ans):\n if k>1:\n ans+=((k-1)*(k))//2 \n\t\t\t\t#Sum of Natural Numbers\n return ans\n else:\n return ans\n end = 0\n start = 0\n prev= sys.maxsize\n k= 0\n ans = 0\n while end<len(prices): \n if prev- prices[end]==1 or prev == sys.maxsize:\n k+=1\n prev = prices[end]\n end+=1 \n else: \n ans = calculate(k,ans)\n start = end\n if end<len(prices):\n prev = sys.maxsize\n k=0\n if k>1:\n ans = calculate(k,ans)\n\t\t\t\n return ans+len(prices)\n``` | 5 | You are given an integer array `prices` representing the daily price history of a stock, where `prices[i]` is the stock price on the `ith` day.
A **smooth descent period** of a stock consists of **one or more contiguous** days such that the price on each day is **lower** than the price on the **preceding day** by **exactly** `1`. The first day of the period is exempted from this rule.
Return _the number of **smooth descent periods**_.
**Example 1:**
**Input:** prices = \[3,2,1,4\]
**Output:** 7
**Explanation:** There are 7 smooth descent periods:
\[3\], \[2\], \[1\], \[4\], \[3,2\], \[2,1\], and \[3,2,1\]
Note that a period with one day is a smooth descent period by the definition.
**Example 2:**
**Input:** prices = \[8,6,7,7\]
**Output:** 4
**Explanation:** There are 4 smooth descent periods: \[8\], \[6\], \[7\], and \[7\]
Note that \[8,6\] is not a smooth descent period as 8 - 6 ≠ 1.
**Example 3:**
**Input:** prices = \[1\]
**Output:** 1
**Explanation:** There is 1 smooth descent period: \[1\]
**Constraints:**
* `1 <= prices.length <= 105`
* `1 <= prices[i] <= 105` | null |
[Python3] counting | number-of-smooth-descent-periods-of-a-stock | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/55c6a88797eef9ac745a3dbbff821a2aac735a70) for solutions of weekly 272. \n\n```\nclass Solution:\n def getDescentPeriods(self, prices: List[int]) -> int:\n ans = 0 \n for i, x in enumerate(prices): \n if i == 0 or prices[i-1] != x + 1: cnt = 0\n cnt += 1\n ans += cnt \n return ans \n``` | 8 | You are given an integer array `prices` representing the daily price history of a stock, where `prices[i]` is the stock price on the `ith` day.
A **smooth descent period** of a stock consists of **one or more contiguous** days such that the price on each day is **lower** than the price on the **preceding day** by **exactly** `1`. The first day of the period is exempted from this rule.
Return _the number of **smooth descent periods**_.
**Example 1:**
**Input:** prices = \[3,2,1,4\]
**Output:** 7
**Explanation:** There are 7 smooth descent periods:
\[3\], \[2\], \[1\], \[4\], \[3,2\], \[2,1\], and \[3,2,1\]
Note that a period with one day is a smooth descent period by the definition.
**Example 2:**
**Input:** prices = \[8,6,7,7\]
**Output:** 4
**Explanation:** There are 4 smooth descent periods: \[8\], \[6\], \[7\], and \[7\]
Note that \[8,6\] is not a smooth descent period as 8 - 6 ≠ 1.
**Example 3:**
**Input:** prices = \[1\]
**Output:** 1
**Explanation:** There is 1 smooth descent period: \[1\]
**Constraints:**
* `1 <= prices.length <= 105`
* `1 <= prices[i] <= 105` | null |
Python (Simple LIS) | minimum-operations-to-make-the-array-k-increasing | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kIncreasing(self, arr, k):\n def dfs(nums):\n vals = []\n\n for x in nums:\n k = bisect_right(vals,x)\n if k == len(vals): vals.append(x)\n else: vals[k] = x\n\n return len(nums) - len(vals)\n\n return sum([dfs(arr[i:len(arr):k]) for i in range(k)])\n\n\n\n \n\n\n\n\n \n``` | 0 | You are given a **0-indexed** array `arr` consisting of `n` positive integers, and a positive integer `k`.
The array `arr` is called **K-increasing** if `arr[i-k] <= arr[i]` holds for every index `i`, where `k <= i <= n-1`.
* For example, `arr = [4, 1, 5, 2, 6, 2]` is K-increasing for `k = 2` because:
* `arr[0] <= arr[2] (4 <= 5)`
* `arr[1] <= arr[3] (1 <= 2)`
* `arr[2] <= arr[4] (5 <= 6)`
* `arr[3] <= arr[5] (2 <= 2)`
* However, the same `arr` is not K-increasing for `k = 1` (because `arr[0] > arr[1]`) or `k = 3` (because `arr[0] > arr[3]`).
In one **operation**, you can choose an index `i` and **change** `arr[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array K-increasing for the given_ `k`.
**Example 1:**
**Input:** arr = \[5,4,3,2,1\], k = 1
**Output:** 4
**Explanation:**
For k = 1, the resultant array has to be non-decreasing.
Some of the K-increasing arrays that can be formed are \[5,**6**,**7**,**8**,**9**\], \[**1**,**1**,**1**,**1**,1\], \[**2**,**2**,3,**4**,**4**\]. All of them require 4 operations.
It is suboptimal to change the array to, for example, \[**6**,**7**,**8**,**9**,**10**\] because it would take 5 operations.
It can be shown that we cannot make the array K-increasing in less than 4 operations.
**Example 2:**
**Input:** arr = \[4,1,5,2,6,2\], k = 2
**Output:** 0
**Explanation:**
This is the same example as the one in the problem description.
Here, for every index i where 2 <= i <= 5, arr\[i-2\] <= arr\[i\].
Since the given array is already K-increasing, we do not need to perform any operations.
**Example 3:**
**Input:** arr = \[4,1,5,2,6,2\], k = 3
**Output:** 2
**Explanation:**
Indices 3 and 5 are the only ones not satisfying arr\[i-3\] <= arr\[i\] for 3 <= i <= 5.
One of the ways we can make the array K-increasing is by changing arr\[3\] to 4 and arr\[5\] to 5.
The array will now be \[4,1,5,**4**,6,**5**\].
Note that there can be other ways to make the array K-increasing, but none of them require less than 2 operations.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], k <= arr.length` | The target will not be found if it is removed from the sequence. When does this occur? If a pivot is to the left of and is greater than the target, then the target will be removed. The same occurs when the pivot is to the right of and is less than the target. Since any element can be chosen as the pivot, for any target NOT to be removed, the condition described in the previous hint must never occur. |
[Python3] almost LIS | minimum-operations-to-make-the-array-k-increasing | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/55c6a88797eef9ac745a3dbbff821a2aac735a70) for solutions of weekly 272. \n\n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n \n def fn(sub): \n """Return ops to make sub non-decreasing."""\n vals = []\n for x in sub: \n k = bisect_right(vals, x)\n if k == len(vals): vals.append(x)\n else: vals[k] = x\n return len(sub) - len(vals)\n \n return sum(fn(arr[i:len(arr):k]) for i in range(k))\n```\n\nAlternative implementation \n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n ans = 0 \n for _ in range(k): \n vals = []\n for i in range(_, len(arr), k): \n if not vals or vals[-1] <= arr[i]: vals.append(arr[i])\n else: vals[bisect_right(vals, arr[i])] = arr[i]\n ans += len(vals)\n return len(arr) - ans\n``` | 2 | You are given a **0-indexed** array `arr` consisting of `n` positive integers, and a positive integer `k`.
The array `arr` is called **K-increasing** if `arr[i-k] <= arr[i]` holds for every index `i`, where `k <= i <= n-1`.
* For example, `arr = [4, 1, 5, 2, 6, 2]` is K-increasing for `k = 2` because:
* `arr[0] <= arr[2] (4 <= 5)`
* `arr[1] <= arr[3] (1 <= 2)`
* `arr[2] <= arr[4] (5 <= 6)`
* `arr[3] <= arr[5] (2 <= 2)`
* However, the same `arr` is not K-increasing for `k = 1` (because `arr[0] > arr[1]`) or `k = 3` (because `arr[0] > arr[3]`).
In one **operation**, you can choose an index `i` and **change** `arr[i]` into **any** positive integer.
Return _the **minimum number of operations** required to make the array K-increasing for the given_ `k`.
**Example 1:**
**Input:** arr = \[5,4,3,2,1\], k = 1
**Output:** 4
**Explanation:**
For k = 1, the resultant array has to be non-decreasing.
Some of the K-increasing arrays that can be formed are \[5,**6**,**7**,**8**,**9**\], \[**1**,**1**,**1**,**1**,1\], \[**2**,**2**,3,**4**,**4**\]. All of them require 4 operations.
It is suboptimal to change the array to, for example, \[**6**,**7**,**8**,**9**,**10**\] because it would take 5 operations.
It can be shown that we cannot make the array K-increasing in less than 4 operations.
**Example 2:**
**Input:** arr = \[4,1,5,2,6,2\], k = 2
**Output:** 0
**Explanation:**
This is the same example as the one in the problem description.
Here, for every index i where 2 <= i <= 5, arr\[i-2\] <= arr\[i\].
Since the given array is already K-increasing, we do not need to perform any operations.
**Example 3:**
**Input:** arr = \[4,1,5,2,6,2\], k = 3
**Output:** 2
**Explanation:**
Indices 3 and 5 are the only ones not satisfying arr\[i-3\] <= arr\[i\] for 3 <= i <= 5.
One of the ways we can make the array K-increasing is by changing arr\[3\] to 4 and arr\[5\] to 5.
The array will now be \[4,1,5,**4**,6,**5**\].
Note that there can be other ways to make the array K-increasing, but none of them require less than 2 operations.
**Constraints:**
* `1 <= arr.length <= 105`
* `1 <= arr[i], k <= arr.length` | The target will not be found if it is removed from the sequence. When does this occur? If a pivot is to the left of and is greater than the target, then the target will be removed. The same occurs when the pivot is to the right of and is less than the target. Since any element can be chosen as the pivot, for any target NOT to be removed, the condition described in the previous hint must never occur. |
Python and C++ Solutions | 2D array | maximum-number-of-words-found-in-sentences | 0 | 1 | # Code\n```C++ []\nclass Solution {\npublic:\n int mostWordsFound(vector<string>& sentences) {\n int answer = 1;\n int maxx = 0;\n for (int i = 0; i < sentences.size(); i++){\n for (int j = 0; j < sentences[i].size(); j++){\n if (sentences[i][j] == \' \'){answer += 1; }\n }\n maxx = max(maxx, answer);\n answer = 1;\n }\n\n\n\n return maxx;\n }\n};\n```\n```python3 []\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n answer = 0\n for sentence in sentences:\n answer = max(answer, len(sentence.split()))\n\n\n return answer\n```\n\n | 1 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
2 One-Liner solution | maximum-number-of-words-found-in-sentences | 0 | 1 | # Code\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n return max(len(x.split(" ")) for x in sentences)\n\n```\n# Counting " ", but its less efficient\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n return max(x.count(" ") for x in sentences)+1\n\n``` | 1 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
Space-Based Word Count in Python | maximum-number-of-words-found-in-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs included in the problem constraints:\n1. None of the sentences have leading or trailing spaces.\n2. All the words in sentences are separated by a single space.\n\nFrom these constraints, we can conclude that:\n> The more spaces there are in the sentence, the more words it has.\n\nTherefore, we can count spaces in each sentence to find the sentence with the maximum word count.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Count the number of spaces in each sentence within the input list.\n2. Find the sentence with the maximum count of spaces.\n3. Add 1 to the sentence with highest count of spaces to find the total number of words.\n4. Return the final answer.\n\n# Complexity\n- Time complexity: O(n * m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nIt iterates through each element in each sentence and then finds the maximum count. Therefore, time complexity is `O(n * m)`, where `n` is the number of sentences and `m` is the maximum number of spaces in a sentence.\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nIt only uses a constant amount of memory to store intermediate values and return the result. Therefore, the space complexity is O(1), indicating constant space complexity.\n\n# Code\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n return max(s.count(\' \') for s in sentences) + 1\n``` | 2 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
Beginner Friendly! | maximum-number-of-words-found-in-sentences | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n count = 0\n for i in sentences:\n c = len(i.split())\n if(c > count):\n count = c\n return count\n``` | 2 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
(47 ms runtime) Best for Beginners (--) Simple logic | maximum-number-of-words-found-in-sentences | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->My approch is straight forward as words are seperated by spaces count the number of spaces append it to a list and max of that list and add one to it and return it\n\n# Approach\n<!-- Describe your approach to solving the problem. -->Simple Code refer intuition.If found helpful do UPVOTE\n\n# Complexity\n- Time complexity:O(n) (47ms)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:16.32mb\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n c=[]\n for i in sentences:\n c.append(i.count(" "))\n return max(c)+1\n``` | 2 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
Python3 using enumerate | maximum-number-of-words-found-in-sentences | 0 | 1 | # Intuition\nUsed .split() to separate string \n\n# Approach\nWe know sentences is a list and we have to go through the list thus we need a for loop. We also need a variable to keep track of the length of the strings. Once were going through the loop we need to check the length of every string and compare to our previous value. If the the current string is longer than our previous value we replace it with the current length of the string. Once we are done with the loop we return the int which is the longest value for a string.\n\n# Complexity\n- Time complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n new_length = 0\n for index, val in enumerate(sentences):\n length = len(sentences[index].split(" "))\n if length > new_length:\n new_length = length\n return new_length\n#use .split()to find length of sentence \n``` | 0 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
Count Spaces | maximum-number-of-words-found-in-sentences | 1 | 1 | Count spaces in each sentence, and return `max + 1`. The benefit (comparing to a split method) is that we do not create temporary strings.\n\n**Python 3**\n```python\nclass Solution:\n def mostWordsFound(self, ss: List[str]) -> int:\n return max(s.count(" ") for s in ss) + 1\n```\n\n**C++**\n```cpp\nint mostWordsFound(vector<string>& s) {\n return 1 + accumulate(begin(s), end(s), 0, [](int res, const auto &s) {\n return max(res, (int)count(begin(s), end(s), \' \')); });\n}\n```\n\n**Java**\n```java\npublic int mostWordsFound(String[] sentences) {\n return 1 + Stream.of(sentences).mapToInt(s -> (int)s.chars().filter(ch -> ch == \' \').count()).max().getAsInt();\n}\n``` | 101 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
Solution of maximum number of words found in sentences problem | maximum-number-of-words-found-in-sentences | 0 | 1 | # Complexity\n- Time complexity:\n$$O(n * m)$$ - as loop takes linear time $$O(n)$$ and split() function takes $$O(m)$$. This is because the method needs to iterate through the entire string to find all occurrences of the delimiter\n\n- Space complexity:\n$$O(1)$$ - as we use extra space for answer equal to a constant\n\n# Gigachad solution\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n answer = 0\n for i in sentences:\n answer = max(answer, len(i.split()))\n return max_space \n```\n# Complexity\n- Time complexity:\n$$O(n * m)$$ - as loop takes linear time $$O(n)$$ and count() function takes $$O(m)$$. \n- Space complexity:\n$$O(1)$$ - as we use extra space for answer equal to a constant\n# NotGigachad solution\n```\nclass Solution:\n def mostWordsFound(self, sentences: List[str]) -> int:\n max_space = 0\n for i in sentences:\n max_space = max(max_space, i.count(" ") + 1)\n return max_space\n``` | 1 | A **sentence** is a list of **words** that are separated by a single space with no leading or trailing spaces.
You are given an array of strings `sentences`, where each `sentences[i]` represents a single **sentence**.
Return _the **maximum number of words** that appear in a single sentence_.
**Example 1:**
**Input:** sentences = \[ "alice and bob love leetcode ", "i think so too ", "this is great thanks very much "\]
**Output:** 6
**Explanation:**
- The first sentence, "alice and bob love leetcode ", has 5 words in total.
- The second sentence, "i think so too ", has 4 words in total.
- The third sentence, "this is great thanks very much ", has 6 words in total.
Thus, the maximum number of words in a single sentence comes from the third sentence, which has 6 words.
**Example 2:**
**Input:** sentences = \[ "please wait ", "continue to fight ", "continue to win "\]
**Output:** 3
**Explanation:** It is possible that multiple sentences contain the same number of words.
In this example, the second and third sentences (underlined) have the same number of words.
**Constraints:**
* `1 <= sentences.length <= 100`
* `1 <= sentences[i].length <= 100`
* `sentences[i]` consists only of lowercase English letters and `' '` only.
* `sentences[i]` does not have leading or trailing spaces.
* All the words in `sentences[i]` are separated by a single space. | Try all possible ways of assignment. If we can store the assignments in form of a state then we can reuse that state and solve the problem in a faster way. |
SIMPLE PYTHON SOLUTION | find-all-possible-recipes-from-given-supplies | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findAllRecipes(self, recepies: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n dct=defaultdict(lambda :[])\n indegree={}\n n=len(recepies)\n\n for i in recepies:\n indegree[i]=0\n\n for i in range(n):\n for j in ingredients[i]:\n indegree[j]=0\n\n for i in range(n):\n for j in ingredients[i]:\n dct[j].append(recepies[i])\n indegree[recepies[i]]+=1\n\n st=[]\n for i in indegree:\n if indegree[i]==0:\n st.append(i)\n flst=[]\n ans=defaultdict(lambda :[])\n while st:\n x=st.pop(0)\n for i in dct[x]:\n # if ans[x]!=[]:\n # for j in ans[x]:\n # if j not in ans[i]:\n # ans[i].append(j)\n ans[i].append(x)\n indegree[i]-=1\n if indegree[i]==0:\n st.append(i)\n if x in recepies:\n for k in ans[x]:\n if k not in supplies:\n break\n else:\n flst.append(x)\n supplies.append(x)\n\n return flst\n``` | 1 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
SIMPLE PYTHON TOPOLOGICAL SORT SOLUTION | find-all-possible-recipes-from-given-supplies | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findAllRecipes(self, recepies: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n dct=defaultdict(lambda :[])\n indegree={}\n n=len(recepies)\n\n for i in recepies:\n indegree[i]=0\n\n for i in range(n):\n for j in ingredients[i]:\n indegree[j]=0\n\n for i in range(n):\n for j in ingredients[i]:\n dct[j].append(recepies[i])\n indegree[recepies[i]]+=1\n\n st=[]\n for i in indegree:\n if indegree[i]==0:\n st.append(i)\n flst=[]\n ans=defaultdict(lambda :[])\n while st:\n x=st.pop(0)\n for i in dct[x]:\n # if ans[x]!=[]:\n for j in ans[x]:\n if j not in ans[i]:\n ans[i].append(j)\n ans[i].append(x)\n indegree[i]-=1\n if indegree[i]==0:\n st.append(i)\n if x in recepies:\n for k in ans[x]:\n if k not in supplies:\n break\n else:\n flst.append(x)\n supplies.append(x)\n\n return flst\n``` | 1 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
[Java/Python 3] Toplogical Sort w/ brief explanation. | find-all-possible-recipes-from-given-supplies | 1 | 1 | **Method 1: Bruteforce**\nRepeated BFS till no any more finding\n\n1. Put all supplies into a HashSet, `seen`, for checking the availability in `O(1)` time;\n2. Put into a Queue all indexes of the recipes;\n3. BFS and put into `seen` all recipes that we currently can create; put back into the Queue if a recipe we currently can not create;\n4. After any round of breadth search, if no any more recipe we can create, return the recipes we found so far.\n\n```java\n public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {\n Set<String> seen = new HashSet<>();\n for (String sup : supplies) {\n seen.add(sup);\n }\n Queue<Integer> q = new LinkedList<>();\n for (int i = 0; i < recipes.length; ++i) {\n q.offer(i);\n }\n List<String> ans = new ArrayList<>();\n int prevSize = seen.size() - 1;\n while (seen.size() > prevSize) {\n prevSize = seen.size();\n mid:\n for (int sz = q.size(); sz > 0; --sz) {\n int i = q.poll();\n for (String ing : ingredients.get(i)) {\n if (!seen.contains(ing)) {\n q.offer(i);\n continue mid;\n }\n }\n seen.add(recipes[i]);\n ans.add(recipes[i]);\n }\n }\n return ans;\n }\n```\n```python\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n \n ans = []\n seen = set(supplies)\n dq = deque([(r, ing) for r, ing in zip(recipes, ingredients)])\n \n # dummy value for prev_size, just to make sure \n # the initial value of prev_size < len(seen) \n prev_size = len(seen) - 1 \n \n # Keep searching if we have any new finding(s).\n while len(seen) > prev_size:\n prev_size = len(seen)\n for _ in range(len(dq)):\n r, ing = dq.popleft()\n if all(i in seen for i in ing):\n ans.append(r)\n seen.add(r)\n else:\n dq.append((r, ing))\n return ans\n```\n\n----\n\n**Method 2: Topological sort**\n1. For each recipe, count its non-available ingredients as in degree; Store (non-available ingredient, dependent recipes) as HashMap; \n2. Store all 0-in-degree recipes into a list as the starting points of topological sort;\n3. Use topogical sort to decrease the in degree of recipes, whenever the in-degree reaches `0`, add it to return list.\n\n```java\n public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {\n List<String> ans = new ArrayList<>();\n // Put all supplies into HashSet.\n Set<String> available = Stream.of(supplies).collect(Collectors.toCollection(HashSet::new));\n Map<String, Set<String>> ingredientToRecipes = new HashMap<>();\n Map<String, Integer> inDegree = new HashMap<>();\n for (int i = 0; i < recipes.length; ++i) {\n int nonAvailable = 0;\n for (String ing : ingredients.get(i)) {\n if (!available.contains(ing)) {\n ingredientToRecipes.computeIfAbsent(ing, s -> new HashSet<>()).add(recipes[i]);\n ++nonAvailable;\n }\n }\n if (nonAvailable == 0) {\n ans.add(recipes[i]);\n }else {\n inDegree.put(recipes[i], nonAvailable);\n }\n }\n // Toplogical Sort.\n for (int i = 0; i < ans.size(); ++i) {\n String recipe = ans.get(i);\n if (ingredientToRecipes.containsKey(recipe)) {\n for (String rcp : ingredientToRecipes.remove(recipe)) {\n if (inDegree.merge(rcp, -1, Integer::sum) == 0) {\n ans.add(rcp);\n }\n }\n }\n }\n return ans;\n }\n```\n```python\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n available = set(supplies)\n ans, ingredient_to_recipe, in_degree = [], defaultdict(set), Counter()\n for rcp, ingredient in zip(recipes, ingredients):\n non_available = 0\n for ing in ingredient:\n if ing not in available:\n non_available += 1\n ingredient_to_recipe[ing].add(rcp)\n if non_available == 0:\n ans.append(rcp)\n else:\n in_degree[rcp] = non_available\n for rcp in ans:\n for recipe in ingredient_to_recipe.pop(rcp, set()):\n in_degree[recipe] -= 1\n if in_degree[recipe] == 0:\n ans.append(recipe)\n return ans\n```\n\nSimpler version is as follows:\n\nAssumption: `ingredients do not contain any recipe`.\n1. For each recipe, count its dependent ingredients as in degree; Store (ingredient, recipes that dependent on it) as HashMap; \n2. Use the `supplies` as the starting points of topological sort;\n3. Use topogical sort to decrease the in degree of recipes, whenever the in-degree reaches `0`, add it to return list.\n```java\n public List<String> findAllRecipes(String[] recipes, List<List<String>> ingredients, String[] supplies) {\n // Construct directed graph and count in-degrees.\n Map<String, Set<String>> ingredientToRecipes = new HashMap<>();\n Map<String, Integer> inDegree = new HashMap<>();\n for (int i = 0; i < recipes.length; ++i) {\n for (String ing : ingredients.get(i)) {\n ingredientToRecipes.computeIfAbsent(ing, s -> new HashSet<>()).add(recipes[i]);\n }\n inDegree.put(recipes[i], ingredients.get(i).size());\n }\n // Toplogical Sort.\n List<String> ans = new ArrayList<>();\n Queue<String> available = Stream.of(supplies).collect(Collectors.toCollection(LinkedList::new));\n while (!available.isEmpty()) {\n String ing = available.poll();\n if (ingredientToRecipes.containsKey(ing)) {\n for (String rcp : ingredientToRecipes.remove(ing)) {\n if (inDegree.merge(rcp, -1, Integer::sum) == 0) {\n available.offer(rcp);\n ans.add(rcp);\n }\n }\n }\n }\n return ans;\n }\n```\n\n```python\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n # Construct directed graph and count the in-degrees\n ingredient_to_recipe, in_degree = defaultdict(set), Counter()\n for rcp, ingredient in zip(recipes, ingredients):\n for ing in ingredient:\n ingredient_to_recipe[ing].add(rcp)\n in_degree[rcp] = len(ingredient)\n # Topological sort. \n available, ans = deque(supplies), []\n while available:\n ing = available.popleft()\n for rcp in ingredient_to_recipe.pop(ing, set()):\n in_degree[rcp] -= 1\n if in_degree[rcp] == 0:\n available.append(rcp)\n ans.append(rcp)\n return ans\n```\n\nWe can further simplify a bit the above Python 3 code, if you do NOT mind modifying the input `supplies`: get rid of the deque `available` and use `supplies` instead.\n\n```python\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n # Construct directed graph and count the in-degrees\n ingredient_to_recipe, in_degree = defaultdict(set), Counter()\n for rcp, ingredient in zip(recipes, ingredients):\n for ing in ingredient:\n ingredient_to_recipe[ing].add(rcp)\n in_degree[rcp] = len(ingredient)\n # Topological sort. \n ans = []\n for ing in supplies:\n for rcp in ingredient_to_recipe.pop(ing, set()):\n in_degree[rcp] -= 1\n if in_degree[rcp] == 0:\n supplies.append(rcp)\n ans.append(rcp)\n return ans\n```\n\n----\n\n**Q & A**\nQ1: Please explain the below statement(particularly how these set() funtion here).\n\n```python\n for rcp in ingredient_to_recipe.pop(ing, set()):\n```\nA1: `ingredient_to_recipe.pop(ing, set())`: If existing, the dict will remove the entry (key, value) and return the value corresponding to the key; if not, the dict will return the default value, a empty set.\n\nTherefore, if the key `ing` is in the dict, `ingredient_to_recipe`, the statement will one by one traverse the value, the set corresponding to `ing`; if not, it will NOT iterate into a empty set.\n\nQ2: Can you explain the intuition behind mapping ingredients to recipes instead of recipes to ingredients?\nA2: Mapping ingredients to recipes is an iterative way, and from recipes to ingredients is a recursive way. Topological Sort I used is an iterative algorithm to handle the problem.\n\nSince the problem ask us to find all of the possible recipes, and it says that "Ingredients to a recipe may need to be created from other recipes", we build nonavailable ingredient to its dependent recipe mapping to implement the Topological Sort algorithm. You may need to learn the algorithm if you are not familiar with it. \n\n**End of Q & A**\n | 110 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
DFS | find-all-possible-recipes-from-given-supplies | 0 | 1 | This problem is not complex but "hairy".\n\nSince we only care if a recipe can be made or not (regarless of in which order), we do not need a topological sort. \n\nWe can use a simple DFS; we just need to track `can_make` for each recipe (undefined, yes or no), so that we traverse each node only once.\n\nTo simplify the DFS logic, we check `supplies` when generating `graph`, and create a self-loop for recipes without needed `supplies`. This ensures that those `recipes` cannot be made.\n\n**Python 3**\n```python\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n graph, can_make, supplies = {recipe : [] for recipe in recipes}, {}, set(supplies)\n def dfs(recipe : str) -> bool:\n if recipe not in can_make:\n can_make[recipe] = False\n can_make[recipe] = all([dfs(ingr) for ingr in graph[recipe]])\n return can_make[recipe]\n for i, recipe in enumerate(recipes):\n for ingr in ingredients[i]:\n if ingr not in supplies:\n graph[recipe].append(ingr if ingr in graph else recipe)\n return [recipe for recipe in recipes if dfs(recipe)]\n``` | 74 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
[Python3] topological sort (Kahn's algo) | find-all-possible-recipes-from-given-supplies | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/8bba95f803d58a5e571fa13de6635c96f5d1c1ee) for solutions of biweekly 68. \n\n```\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n indeg = defaultdict(int)\n graph = defaultdict(list)\n for r, ing in zip(recipes, ingredients): \n indeg[r] = len(ing)\n for i in ing: graph[i].append(r)\n \n ans = []\n queue = deque(supplies)\n recipes = set(recipes)\n while queue: \n x = queue.popleft()\n if x in recipes: ans.append(x)\n for xx in graph[x]: \n indeg[xx] -= 1\n if indeg[xx] == 0: queue.append(xx)\n return ans \n``` | 68 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
[Python3] Topological Sort -Simple Solution | find-all-possible-recipes-from-given-supplies | 0 | 1 | # Intuition\nSome Recipe depends on some other Recipe that is cooked before -> Sound very similar to course schedule -> Topological sort\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N * M)$$ with N is the number of recipes, M is number of ingredients/recipes requires for each recipes\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(M * N + S)$$ with N is the number of recipes, M is number of ingredients/recipes requires for each recipes and S is number of supplies\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n not_supplied_needs = collections.Counter()\n ingredients_needs = collections.defaultdict(list)\n supplies_set = set(supplies)\n\n for i in range(len(recipes)):\n recipe = recipes[i]\n for ingredient in ingredients[i]:\n if ingredient not in supplies:\n not_supplied_needs[recipe] += 1\n ingredients_needs[ingredient].append(recipe)\n \n\n q = collections.deque()\n for recipe in recipes:\n if not_supplied_needs[recipe] == 0: q.append(recipe)\n\n res = []\n while q:\n recipe = q.popleft()\n res.append(recipe)\n for new_recipe in ingredients_needs[recipe]:\n not_supplied_needs[new_recipe] -= 1\n if not_supplied_needs[new_recipe] == 0: q.append(new_recipe)\n \n return res\n``` | 5 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
📌📌 Beginners Friendly || Well-Explained || 94% Faster 🐍 | find-all-possible-recipes-from-given-supplies | 0 | 1 | ## IDEA :\n*Yeahh, This question is little tricky. But when we come to question in which one element is dependent on others element to complete then we have to first think of Graph.*\nHere, All the recipes and supplies ingredients should be made node and Edges `a->b` to be defined as for completion of recipe `b` we should have ingredients `a`.\n\nTaking the first Example:\n\'\'\'\n\n\trecipes = ["bread"], ingredients = [["yeast","flour"]], supplies = ["yeast","flour","corn"]\n\t\n\twe can now draw the graph first. (Consider the graph directed from upper nodes to downwards)\n\t\n\t\t\t\t\tyeast flour\n\t\t\t\t\t\t \\ /\n\t\t\t\tmeat Bread\n\t\t\t\t \\ /\n\t\t\t\t SandWhich\n\nSo From here, we can clearly see that we have to do topological sort, Since our graph will be always DAG.\n\n**Topological Sort :-** Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.\n****\n### Implementation :\n\'\'\'\n\n\tclass Solution:\n\t\tdef findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n\n\t\t\tgraph = defaultdict(list)\n\t\t\tin_degree = defaultdict(int)\n\t\t\tfor r,ing in zip(recipes,ingredients):\n\t\t\t\tfor i in ing:\n\t\t\t\t\tgraph[i].append(r)\n\t\t\t\t\tin_degree[r]+=1\n\n\t\t\tqueue = supplies[::]\n\t\t\tres = []\n\t\t\twhile queue:\n\t\t\t\ting = queue.pop(0)\n\t\t\t\tif ing in recipes:\n\t\t\t\t\tres.append(ing)\n\n\t\t\t\tfor child in graph[ing]:\n\t\t\t\t\tin_degree[child]-=1\n\t\t\t\t\tif in_degree[child]==0:\n\t\t\t\t\t\tqueue.append(child)\n\n\t\t\treturn res\n\t\t\n### Feel free to ask if you have any doubts!! \uD83E\uDD17\n### **Thanks & Upvote if you like the Idea !!** \uD83E\uDD1E | 47 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
✅Python Easy Solution with explanation | Beginner Friendly | Kahn's Algorithm 🚀😀👍🏻 | find-all-possible-recipes-from-given-supplies | 0 | 1 | # Approach\nUsing Kahn\'s Algorithm / Topological Sort\n# Video Explanation\nhttps://youtu.be/jsSq5_h-6vE\n\n# Code\n```\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n # indegree = {"bread" : 2}\n indegree = defaultdict(int)\n # graph = {"flour" : ["bread", " ", ""]}\n graph = defaultdict(list)\n for recipe, ing in zip(recipes, ingredients):\n for i in ing:\n indegree[recipe] += 1\n graph[i].append(recipe)\n \n answer = []\n queue = deque(supplies)\n recipes = set(recipes)\n while queue:\n x = queue.popleft()\n if x in recipes:\n answer.append(x)\n for i in graph[x]:\n indegree[i] -= 1\n if indegree[i] == 0:\n queue.append(i)\n return answer\n``` | 4 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
[PYTHON3] BFS -EASY TO UNDERSTAND | find-all-possible-recipes-from-given-supplies | 0 | 1 | ```\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n adj=defaultdict(list)\n ind=defaultdict(int)\n \n for i in range(len(ingredients)):\n for j in range(len(ingredients[i])):\n adj[ingredients[i][j]].append(recipes[i])\n ind[recipes[i]]+=1\n ans=[]\n q=deque()\n for i in range(len(supplies)):\n q.append(supplies[i])\n while q:\n node=q.popleft()\n for i in adj[node]:\n ind[i]-=1\n if ind[i]==0:\n q.append(i)\n ans.append(i)\n return ans\n\n``` | 9 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
TOPOLOGICAL | Python Explained | find-all-possible-recipes-from-given-supplies | 0 | 1 | # Intuition\ntreat this problem as one of the standard topological problem finding ancestors.\nWhere if you can create the parent then u can create the child recipe too.\nNow the trick of the problem is to curate the graph.\n`1. Think of it as what can be the parents? The ingredients required to make a recipe.`\n`2. And how to get indegrees? If a ingredient required to make a recipe isnt available in supplies then its dependent on the parent i.e if u cannot make parent the child cant be prepared.`\n\nNow solve it as topological\nif indegrees[recipe] == 0 #it can be made as all the items required are available/ created before\neg -> \n1. bread -> yeast (already available)\n2. sandwich -> (bread, meat) (meat -> already available, bread -> created before)\n\nand those whose indegrees become 0 are created thus add it to ans.\n\n# Code\n```\nclass Solution:\n def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:\n menu = list(zip(recipes, ingredients))\n graph = defaultdict(list)\n indegrees = {r: 0 for r in recipes}\n for r, ing in menu:\n for i in ing:\n graph[i].append(r) # parent is ing required to make child recipe \n if i not in supplies:\n indegrees[r] += 1 #if not present the child is dependent\n \n q = deque()\n possibleRecipe = []\n for r, v in indegrees.items():\n if v == 0:\n q.append(r)\n possibleRecipe.append(r)\n \n while q:\n currRecipe = q.popleft()\n for neiRecipe in graph[currRecipe]:\n indegrees[neiRecipe] -= 1\n if indegrees[neiRecipe] == 0:\n possibleRecipe.append(neiRecipe) # the parent was possible to made so now the child can be made too\n q.append(neiRecipe)\n return(possibleRecipe)\n``` | 3 | You have information about `n` different recipes. You are given a string array `recipes` and a 2D string array `ingredients`. The `ith` recipe has the name `recipes[i]`, and you can **create** it if you have **all** the needed ingredients from `ingredients[i]`. Ingredients to a recipe may need to be created from **other** recipes, i.e., `ingredients[i]` may contain a string that is in `recipes`.
You are also given a string array `supplies` containing all the ingredients that you initially have, and you have an infinite supply of all of them.
Return _a list of all the recipes that you can create._ You may return the answer in **any order**.
Note that two recipes may contain each other in their ingredients.
**Example 1:**
**Input:** recipes = \[ "bread "\], ingredients = \[\[ "yeast ", "flour "\]\], supplies = \[ "yeast ", "flour ", "corn "\]
**Output:** \[ "bread "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
**Example 2:**
**Input:** recipes = \[ "bread ", "sandwich "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
**Example 3:**
**Input:** recipes = \[ "bread ", "sandwich ", "burger "\], ingredients = \[\[ "yeast ", "flour "\],\[ "bread ", "meat "\],\[ "sandwich ", "meat ", "bread "\]\], supplies = \[ "yeast ", "flour ", "meat "\]
**Output:** \[ "bread ", "sandwich ", "burger "\]
**Explanation:**
We can create "bread " since we have the ingredients "yeast " and "flour ".
We can create "sandwich " since we have the ingredient "meat " and can create the ingredient "bread ".
We can create "burger " since we have the ingredient "meat " and can create the ingredients "bread " and "sandwich ".
**Constraints:**
* `n == recipes.length == ingredients.length`
* `1 <= n <= 100`
* `1 <= ingredients[i].length, supplies.length <= 100`
* `1 <= recipes[i].length, ingredients[i][j].length, supplies[k].length <= 10`
* `recipes[i], ingredients[i][j]`, and `supplies[k]` consist only of lowercase English letters.
* All the values of `recipes` and `supplies` combined are unique.
* Each `ingredients[i]` does not contain any duplicate values. | The number of unique good subsequences is equal to the number of unique decimal values there are for all possible subsequences. Find the answer at each index based on the previous indexes' answers. |
Left-to-right and right-to-left | check-if-a-parentheses-string-can-be-valid | 1 | 1 | A useful trick (when doing any parentheses validation) is to greedily check balance left-to-right, and then right-to-left.\n- Left-to-right check ensures that we do not have orphan \')\' parentheses.\n- Right-to-left checks for orphan \'(\' parentheses.\n\nWe go left-to-right:\n- Count `wild` (not locked) characters. \n- Track the balance `bal` for locked parentheses. \n\t- If the balance goes negative, we check if we have enough `wild` characters to compensate.\n- In the end, check that we have enough `wild` characters to cover positive balance (open parentheses). \n\nThis approach alone, however, will fail for `["))((", "0011"]` test case. That is why we also need to do the same going right-to-left.\n\n**Python 3**\n```python\nclass Solution:\n def canBeValid(self, s: str, locked: str) -> bool:\n def validate(s: str, locked: str, op: str) -> bool:\n bal, wild = 0, 0\n for i in range(len(s)):\n if locked[i] == "1":\n bal += 1 if s[i] == op else -1\n else:\n wild += 1\n if wild + bal < 0:\n return False\n return bal <= wild\n return len(s) % 2 == 0 and validate(s, locked, \'(\') and validate(s[::-1], locked[::-1], \')\')\n```\n\n**Java**\n```java\nboolean validate(String s, String locked, char op) {\n int bal = 0, wild = 0, sz = s.length();\n int start = op == \'(\' ? 0 : sz - 1, dir = op == \'(\' ? 1 : - 1;\n for (int i = start; i >= 0 && i < sz && wild + bal >= 0; i += dir)\n if (locked.charAt(i) == \'1\')\n bal += s.charAt(i) == op ? 1 : -1;\n else\n ++wild;\n return Math.abs(bal) <= wild;\n}\npublic boolean canBeValid(String s, String locked) {\n return s.length() % 2 == 0 && validate(s, locked, \'(\') && validate(s, locked, \')\');\n}\n```\n**C++**\n```cpp\nbool canBeValid(string s, string locked) {\n auto validate = [&](char op) {\n int bal = 0, wild = 0, sz = s.size();\n int start = op == \'(\' ? 0 : sz - 1, dir = op == \'(\' ? 1 : - 1;\n for (int i = start; i >= 0 && i < sz && wild + bal >= 0; i += dir)\n if (locked[i] == \'1\')\n bal += s[i] == op ? 1 : -1;\n else\n ++wild;\n return abs(bal) <= wild;\n };\n return s.size() % 2 == 0 && validate(\'(\') && validate(\')\');\n}\n``` | 207 | A parentheses string is a **non-empty** string consisting only of `'('` and `')'`. It is valid if **any** of the following conditions is **true**:
* It is `()`.
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid parentheses strings.
* It can be written as `(A)`, where `A` is a valid parentheses string.
You are given a parentheses string `s` and a string `locked`, both of length `n`. `locked` is a binary string consisting only of `'0'`s and `'1'`s. For **each** index `i` of `locked`,
* If `locked[i]` is `'1'`, you **cannot** change `s[i]`.
* But if `locked[i]` is `'0'`, you **can** change `s[i]` to either `'('` or `')'`.
Return `true` _if you can make `s` a valid parentheses string_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "))())) ", locked = "010100 "
**Output:** true
**Explanation:** locked\[1\] == '1' and locked\[3\] == '1', so we cannot change s\[1\] or s\[3\].
We change s\[0\] and s\[4\] to '(' while leaving s\[2\] and s\[5\] unchanged to make s valid.
**Example 2:**
**Input:** s = "()() ", locked = "0000 "
**Output:** true
**Explanation:** We do not need to make any changes because s is already valid.
**Example 3:**
**Input:** s = ") ", locked = "0 "
**Output:** false
**Explanation:** locked permits us to change s\[0\].
Changing s\[0\] to either '(' or ')' will not make s valid.
**Constraints:**
* `n == s.length == locked.length`
* `1 <= n <= 105`
* `s[i]` is either `'('` or `')'`.
* `locked[i]` is either `'0'` or `'1'`.
x if x >= 0, or -x if x < 0. | Can we check every possible pair? Can we use a nested for loop to solve this problem? |
[Python3, Java, C++] Counting Brackets O(n) | check-if-a-parentheses-string-can-be-valid | 1 | 1 | * We iterate over the string s twice. \n* Count of variable brackets is maintained using `tot`\n* Count of fixed open brackets is maintained using `op`\n* Count of fixed closed brackets is maintained using `cl`\n* In forward iteration we are checking if we have too many fixed closed brackets `)`, this is achieved using: `if tot + op - cl < 0: return False `\n* In backward iteration we are checking if we have too many fixed open brackets `(`, this is achieved using: `if tot - op + cl < 0: return False`\n\n**Python3**:\n```\n def canBeValid(self, s: str, l: str) -> bool:\n if len(s) % 2 == 1: return False\n tot = op = cl = 0 # tot -> Total variable brackets, op -> Open, cl -> Closed\n for i in range(len(s) - 1, -1, -1):\n if l[i] == \'0\': tot += 1\n elif s[i] == \'(\': op += 1\n elif s[i] == \')\': cl += 1\n if tot - op + cl < 0: return False\n tot = op = cl = 0\n for i in range(len(s)):\n if l[i] == \'0\': tot += 1\n elif s[i] == \'(\': op += 1\n elif s[i] == \')\': cl += 1\n if tot + op - cl < 0: return False \n return True\n```\n\n<iframe src="https://leetcode.com/playground/HfZuXCuy/shared" frameBorder="0" width="700" height="490"></iframe>\n\n | 120 | A parentheses string is a **non-empty** string consisting only of `'('` and `')'`. It is valid if **any** of the following conditions is **true**:
* It is `()`.
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid parentheses strings.
* It can be written as `(A)`, where `A` is a valid parentheses string.
You are given a parentheses string `s` and a string `locked`, both of length `n`. `locked` is a binary string consisting only of `'0'`s and `'1'`s. For **each** index `i` of `locked`,
* If `locked[i]` is `'1'`, you **cannot** change `s[i]`.
* But if `locked[i]` is `'0'`, you **can** change `s[i]` to either `'('` or `')'`.
Return `true` _if you can make `s` a valid parentheses string_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "))())) ", locked = "010100 "
**Output:** true
**Explanation:** locked\[1\] == '1' and locked\[3\] == '1', so we cannot change s\[1\] or s\[3\].
We change s\[0\] and s\[4\] to '(' while leaving s\[2\] and s\[5\] unchanged to make s valid.
**Example 2:**
**Input:** s = "()() ", locked = "0000 "
**Output:** true
**Explanation:** We do not need to make any changes because s is already valid.
**Example 3:**
**Input:** s = ") ", locked = "0 "
**Output:** false
**Explanation:** locked permits us to change s\[0\].
Changing s\[0\] to either '(' or ')' will not make s valid.
**Constraints:**
* `n == s.length == locked.length`
* `1 <= n <= 105`
* `s[i]` is either `'('` or `')'`.
* `locked[i]` is either `'0'` or `'1'`.
x if x >= 0, or -x if x < 0. | Can we check every possible pair? Can we use a nested for loop to solve this problem? |
[Python3] greedy 2-pass | check-if-a-parentheses-string-can-be-valid | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/8bba95f803d58a5e571fa13de6635c96f5d1c1ee) for solutions of biweekly 68. \n\n```\nclass Solution:\n def canBeValid(self, s: str, locked: str) -> bool:\n if len(s)&1: return False\n bal = 0\n for ch, lock in zip(s, locked):\n if lock == \'0\' or ch == \'(\': bal += 1\n elif ch == \')\': bal -= 1\n if bal < 0: return False \n bal = 0\n for ch, lock in zip(reversed(s), reversed(locked)): \n if lock == \'0\' or ch == \')\': bal += 1\n elif ch == \'(\': bal -= 1\n if bal < 0: return False\n return True\n```\n\nNote: zip object is not reversable but reversed object is zippable. | 9 | A parentheses string is a **non-empty** string consisting only of `'('` and `')'`. It is valid if **any** of the following conditions is **true**:
* It is `()`.
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid parentheses strings.
* It can be written as `(A)`, where `A` is a valid parentheses string.
You are given a parentheses string `s` and a string `locked`, both of length `n`. `locked` is a binary string consisting only of `'0'`s and `'1'`s. For **each** index `i` of `locked`,
* If `locked[i]` is `'1'`, you **cannot** change `s[i]`.
* But if `locked[i]` is `'0'`, you **can** change `s[i]` to either `'('` or `')'`.
Return `true` _if you can make `s` a valid parentheses string_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "))())) ", locked = "010100 "
**Output:** true
**Explanation:** locked\[1\] == '1' and locked\[3\] == '1', so we cannot change s\[1\] or s\[3\].
We change s\[0\] and s\[4\] to '(' while leaving s\[2\] and s\[5\] unchanged to make s valid.
**Example 2:**
**Input:** s = "()() ", locked = "0000 "
**Output:** true
**Explanation:** We do not need to make any changes because s is already valid.
**Example 3:**
**Input:** s = ") ", locked = "0 "
**Output:** false
**Explanation:** locked permits us to change s\[0\].
Changing s\[0\] to either '(' or ')' will not make s valid.
**Constraints:**
* `n == s.length == locked.length`
* `1 <= n <= 105`
* `s[i]` is either `'('` or `')'`.
* `locked[i]` is either `'0'` or `'1'`.
x if x >= 0, or -x if x < 0. | Can we check every possible pair? Can we use a nested for loop to solve this problem? |
✔ Python3 Solution | Clean & Concise | check-if-a-parentheses-string-can-be-valid | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def canBeValid(self, s, locked):\n cmin, cmax = 0, 0\n for i, j in zip(s, locked):\n cmin -= 1 if cmin and (j == \'0\' or i == \')\') else -1\n cmax += 1 if j == \'0\' or i == \'(\' else -1\n if cmax < 0: return False\n return cmin == 0\n``` | 3 | A parentheses string is a **non-empty** string consisting only of `'('` and `')'`. It is valid if **any** of the following conditions is **true**:
* It is `()`.
* It can be written as `AB` (`A` concatenated with `B`), where `A` and `B` are valid parentheses strings.
* It can be written as `(A)`, where `A` is a valid parentheses string.
You are given a parentheses string `s` and a string `locked`, both of length `n`. `locked` is a binary string consisting only of `'0'`s and `'1'`s. For **each** index `i` of `locked`,
* If `locked[i]` is `'1'`, you **cannot** change `s[i]`.
* But if `locked[i]` is `'0'`, you **can** change `s[i]` to either `'('` or `')'`.
Return `true` _if you can make `s` a valid parentheses string_. Otherwise, return `false`.
**Example 1:**
**Input:** s = "))())) ", locked = "010100 "
**Output:** true
**Explanation:** locked\[1\] == '1' and locked\[3\] == '1', so we cannot change s\[1\] or s\[3\].
We change s\[0\] and s\[4\] to '(' while leaving s\[2\] and s\[5\] unchanged to make s valid.
**Example 2:**
**Input:** s = "()() ", locked = "0000 "
**Output:** true
**Explanation:** We do not need to make any changes because s is already valid.
**Example 3:**
**Input:** s = ") ", locked = "0 "
**Output:** false
**Explanation:** locked permits us to change s\[0\].
Changing s\[0\] to either '(' or ')' will not make s valid.
**Constraints:**
* `n == s.length == locked.length`
* `1 <= n <= 105`
* `s[i]` is either `'('` or `')'`.
* `locked[i]` is either `'0'` or `'1'`.
x if x >= 0, or -x if x < 0. | Can we check every possible pair? Can we use a nested for loop to solve this problem? |
Python (Simple Maths) | abbreviating-the-product-of-a-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left, right):\n string = str(prod(list(range(left,right+1))))\n n_string = string.rstrip("0")\n zeros = len(string) - len(n_string)\n\n if len(n_string) <= 10:\n return n_string + "e" + str(zeros)\n else:\n return n_string[:5] + "..." + n_string[-5:] + "e" + str(zeros)\n\n \n \n``` | 2 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
[Python3] quasi brute-force | abbreviating-the-product-of-a-range | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/8bba95f803d58a5e571fa13de6635c96f5d1c1ee) for solutions of biweekly 68. \n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n ans = prefix = suffix = 1\n trailing = 0 \n flag = False \n for x in range(left, right+1): \n if not flag: \n ans *= x\n while ans % 10 == 0: ans //= 10 \n if ans >= 1e10: flag = True \n prefix *= x\n suffix *= x\n while prefix >= 1e12: prefix //= 10 \n while suffix % 10 == 0: \n trailing += 1\n suffix //= 10 \n if suffix >= 1e10: suffix %= 10_000_000_000\n while prefix >= 100000: prefix //= 10 \n suffix %= 100000\n if flag: return f"{prefix}...{suffix:>05}e{trailing}"\n return f"{ans}e{trailing}"\n``` | 10 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Simple (5-line) Python solution beats 100% || 5 line solution || beats 100% | abbreviating-the-product-of-a-range | 0 | 1 | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach: Simple and step by step approach as mentiones in problem description \nstep 1: calculate the product of the given range (left, right)\nrange(left, right+1) will give us a range object or the range which is converted into list by list() function and then to calculate the product of whole list we use prod() function \nso till here the 1st line is explained \n**prod(list(range(left, right+1)))** and converting the result into string with the help of str() function as we have to print our solution in string format and for later opertions\n\nstep 2: removing the trailing zeros form the end of the calculated product with the help of rstrip() method which removes the white space in case of no string is given to it (i.e. "hii ".rstrip() will become "hii" if we give it any string/parameter it will remove all occurence till any other charater apper for example- "hii00000000000000".rstrip("0") will become "hii")\n\nstep 3: count of traling zeros of the string \nthe experssion goes like this **lenght of string with zeros - length of string without zeros**\n\nstep 4: as there is 2 way to output the result if the lenght of string (without zeros) is less then or equal to 10 the we will output it as it is string (without zeros)+"e"+ count of zeros\n\nstep 5: if the lenght of string after removing zeros is greater then > 10 then we have to print the it in 2 parts the starting 5 digits and the last 5 digits \nexample 123456789987654 consider this as our non zero string \nso we have to print the starting 5 digits which is 12345 and the last 5 digits if it which is 87654 in the given format \nstarting 5 digits + "..." + last 5 digits + "e" + count of zeros\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1) \n- as we have not used any loops or recursion call so i think the TC will be O(1) **correct me if i\'m wrong** \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n- as for space complexity, we are not doing any recursion and using only 3 veriables to store our calculation so i think this solution uses constant space \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n summ = str(prod(list(range(left, right+1))))\n su = summ.rstrip("0")\n zeros = len(summ)-len(su)\n if len(su)<=10: return (su+"e"+str(zeros))\n else: return (su[:5]+"..."+su[-5:]+"e"+str(zeros))\n``` | 1 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Very straightforward completely beginner friendly Python solution | abbreviating-the-product-of-a-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFairly easy. Just find the product and convert it to str\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou just find the product and convert to string to slice it\n\n# Complexity\n- Time complexity: 51%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 70%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport sys \nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n sys.set_int_max_str_digits(20000000)\n p = 1\n for i in range(left, right+1):\n p *= i\n s = str(p)\n c = len(s) \n s = s.rstrip(\'0\')\n c = c - len(s)\n if len(s) > 10:\n return \'%s...%se%s\' % (s[:5], s[-5:], str(c))\n return \'%se%s\' % (s, str(c))\n``` | 0 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Understandable Python Solution with linear time complexity | abbreviating-the-product-of-a-range | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the above code is to efficiently calculate and represent the product of all integers in the given range in a human-readable format. The product can be very large and contain many trailing zeros, which can make it difficult to read and understand. So this code aims to simplify the representation of the product by removing trailing zeros and truncating the number to the first 5 and last 5 digits, if it has more than 10 digits.\n\n# Approach\n1. Initialize a variable \'product\' to 1 and a variable \'trailing_zeros\' to 0.\n2. Use a for loop to iterate over all integers in the range [left, right]. For each integer in the range, multiply it with the current value of \'product\'\n3. While the last digit of product is zero, count number of trailing zeros and divide product by 10\n4. Convert product to a string, store the number of digits of product in a variable \'digits\'\n5. If the number of digits of the product is greater than 10, return the first 5 digits followed by \'...\' and the last 5 digits, followed by \'e\' and the number of trailing zeros.\n6. If the number of digits of the product is less than or equal to 10, return the original number followed by \'e\' and the number of trailing zeros.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product = 1\n for i in range(left, right + 1):\n product *= i\n trailing_zeros = 0\n while product % 10 == 0:\n trailing_zeros += 1\n product //= 10\n product_str = str(product)\n digits = len(product_str)\n if digits > 10:\n pre = product_str[:5]\n suf = product_str[-5:]\n return f"{pre}...{suf}e{trailing_zeros}"\n else:\n return f"{product_str}e{trailing_zeros}"\n``` | 0 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Python, almost brute force | abbreviating-the-product-of-a-range | 0 | 1 | There are 2 steps:\nStep1: Calculate the number of trailing zeros\nStep2: Multiply & Keep track of the first 12 numbers and the last 5 numbers\n\nFor step1, we need to know the number of factors 2 and 5 in [right, left], because 10 = 2 * 5. The minimum of the two will be the number of trailing zeros.\n\nFor step2, If the final number is less than 10 ** 10, I just output the number without abbreviation, but if the number exceeds 10 ** 10, then I switch to the calculation of the "big" number which needs abbreviation. For each, step, I only keep track of the first and last few numbers because they don\'t change by multiplication. \n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n #Step1: count the num of trailing zeros\n factor_two, factor_five = 0, 0\n curr_factor = 2\n while curr_factor <= right:\n factor_two += (right // curr_factor) - ((left - 1) // curr_factor)\n curr_factor *= 2\n curr_factor = 5\n while curr_factor <= right:\n factor_five += (right // curr_factor) - ((left - 1) // curr_factor)\n curr_factor *= 5\n trailing_zeros = min(factor_two, factor_five)\n \n #Step2: Multiply until it gets too big, while dividing 2 and 5\n\t\tdivide_two_so_far, divide_five_so_far = 0, 0\n curr_num = 1\n for i in range(left, right + 1):\n multiply = i\n while multiply % 2 == 0 and divide_two_so_far < trailing_zeros:\n multiply //= 2\n divide_two_so_far += 1\n while multiply % 5 == 0 and divide_five_so_far < trailing_zeros:\n multiply //= 5\n divide_five_so_far += 1\n curr_num *= multiply\n if curr_num >= 10 ** 10:\n break\n \n #if the number doesn\'t get too large (less than or equal to 10 digits)\n if curr_num < 10 ** 10:\n return str(curr_num) + \'e\' + str(trailing_zeros)\n \n #Step2: if the number exceeds 10 ** 10, then keep track of the first and last digits\n first_digits, last_digits = int(str(curr_num)[:12]), int(str(curr_num)[-5:])\n start = i + 1\n for i in range(start, right + 1):\n multiply = i\n while multiply % 2 == 0 and divide_two_so_far < trailing_zeros:\n multiply //= 2\n divide_two_so_far += 1\n while multiply % 5 == 0 and divide_five_so_far < trailing_zeros:\n multiply //= 5\n divide_five_so_far += 1\n first_digits = int(str(first_digits * multiply)[:12])\n last_digits = int(str(last_digits * multiply)[-5:])\n \n\t\t#output\n return str(first_digits)[:5] + \'...\' + \'{:>05d}\'.format(last_digits) + \'e\' + str(trailing_zeros)\n``` | 2 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Non-bruteforce algorithm in Python3 with numpy | abbreviating-the-product-of-a-range | 0 | 1 | As suggested in the hints, the three parts are calculated separately. The precision issue in the Python built-in floating numbers happen, so I use numpy.float128 instead of the built-in floats. \n\n```\nimport numpy\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n log_prod = numpy.float128(0)\n last = 1\n num_zeros = 0\n for x in range(left, right+1):\n log_prod += numpy.log10(x)\n last *= x\n while last % 10 == 0:\n last //= 10\n num_zeros += 1\n last %= 1000000000000\n x = floor(log_prod)\n if x - num_zeros < 10:\n return "%de%d" % (last % 10000000000, num_zeros)\n return "%.0f...%05de%d" % (floor(numpy.power(10, (4 + log_prod - x))), last % 100000, num_zeros)\n \n | 0 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Python3 accepted solution (using rstrip) | abbreviating-the-product-of-a-range | 0 | 1 | ```\n class Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product=1\n for i in range(left,right+1):\n product *= i\n if(len(str(product).rstrip("0"))<=10):\n return str(product).rstrip("0") + "e" + str(len(str(product)) - len(str(product).rstrip("0")))\n else:\n return str(product).rstrip("0")[:5] +"..."+ str(product).rstrip("0")[-5:]+"e" + str(len(str(product)) - len(str(product).rstrip("0")))\n \n ``` | 0 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
Brute Force Approach Python3 (Accepted) (Commented) | abbreviating-the-product-of-a-range | 0 | 1 | ```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n ans = 1 //Initialise the product with 1\n while left <= right: // Start the multiplying numbers in\n if left == right: // Exception case when left is right else the number will be multiplied 2 times\n ans *= left //then only multiply either left or right\n else:\n ans *= left * right // Else multiply left and right numbers and multiply with ans\n left += 1 // Increment left by one\n right -= 1 //Decrement right by 1\n count = 0 // Initialise count of trailing zeroes\n ans = str(ans) // Converting integer to string\n i = len(ans) - 1 // Start the pointer with end of string\n while i >= 0 and ans[i] == \'0\': // Decrement pointer by one while the value at pointer is 0\n count += 1 //and increase the count of trailing zeroes\n i -= 1\n fans = \'\' //Empty string which will store the number without the trailing zeroes\n for j in range(i+1): // will use the i pointer which stored the last location of the trailing zero\n fans += ans[j] //store each character until the trailing zero isn\'t reached\n final = \'\' //Final ans which will give the required result \n if len(fans) > 10: //If the length of the number without the trailing zeroes has a length greater than 10\n temp1 = \'\' //Will store the first 5 character of the number\n for j in range(5): // Adding the first 5 characters\n temp1 += fans[j]\n temp2 = \'\' //Will store the last 5 characters of the number\n for j in range(-5,0): // Add the last 5 characters\n temp2 += fans[j]\n final = temp1 + \'...\' + temp2 + \'e\' + str(count) //Final ans with first 5 character, last 5 characters + e + count of trailing zeroes\n else: //If length of the number is less than 10\n final = fans + \'e\' + str(count) // Final ans with number without trailing zeroes + e + count of trailing zeroes\n return final //Return the final string\n \n``` | 0 | You are given two positive integers `left` and `right` with `left <= right`. Calculate the **product** of all integers in the **inclusive** range `[left, right]`.
Since the product may be very large, you will **abbreviate** it following these steps:
1. Count all **trailing** zeros in the product and **remove** them. Let us denote this count as `C`.
* For example, there are `3` trailing zeros in `1000`, and there are `0` trailing zeros in `546`.
2. Denote the remaining number of digits in the product as `d`. If `d > 10`, then express the product as
...
3. Finally, represent the product as a **string** `"`
...eC "
Return _a string denoting the **abbreviated product** of all integers in the **inclusive** range_ `[left, right]`.
**Example 1:**
**Input:** left = 1, right = 4
**Output:** "24e0 "
**Explanation:** The product is 1 \* 2 \* 3 \* 4 = 24.
There are no trailing zeros, so 24 remains the same. The abbreviation will end with "e0 ".
Since the number of digits is 2, which is less than 10, we do not have to abbreviate it further.
Thus, the final representation is "24e0 ".
**Example 2:**
**Input:** left = 2, right = 11
**Output:** "399168e2 "
**Explanation:** The product is 39916800.
There are 2 trailing zeros, which we remove to get 399168. The abbreviation will end with "e2 ".
The number of digits after removing the trailing zeros is 6, so we do not abbreviate it further.
Hence, the abbreviated product is "399168e2 ".
**Example 3:**
**Input:** left = 371, right = 375
**Output:** "7219856259e3 "
**Explanation:** The product is 7219856259000.
**Constraints:**
* `1 <= left <= right <= 104` | If changed is a doubled array, you should be able to delete elements and their doubled values until the array is empty. Which element is guaranteed to not be a doubled value? It is the smallest element. After removing the smallest element and its double from changed, is there another number that is guaranteed to not be a doubled value? |
one string solution | a-number-after-a-double-reversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n return False if num % 10 == 0 and num != 0 else True \n``` | 1 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
Efficient O(1) check in Python3 | a-number-after-a-double-reversal | 0 | 1 | # Intuition\nHere we have:\n- `num` as an integer\n- our goal is to **double reverse** and check, if reversed version is equal to original `num`\n\n# Approach\n1. simple check for `zero` (**true**) and `num % 10 != 0` \n\n# Complexity\n- Time complexity: **O(1)**\n\n- Space complexity: **O(1)**\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n return num == 0 or num % 10 != 0\n``` | 1 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
string convert and then convert it to integer again; | a-number-after-a-double-reversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n s = str(num)\n s1 = int(s[::-1])\n s2 = str(s1)\n print(s2[::-1])\n return int(s2[::-1])==int(s)\n``` | 1 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
Beats 93.42% || A number after a double reversal | a-number-after-a-double-reversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n original=num\n reverse1=0\n while num!=0:\n reverse1=(num%10)+reverse1*10\n num//=10\n reverse2=0\n while reverse1!=0:\n reverse2=(reverse1%10)+reverse2*10\n reverse1//=10\n if(reverse2==original):\n return True\n else:\n return False\n \n``` | 1 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
Solution of a number after a double reversal problem | a-number-after-a-double-reversal | 0 | 1 | # Approach\nThere are two options:\n- If the last digit is 0 --> False\n- In another situatiion --> True\n\n# Complexity\n\n- Space complexity:\n$$O(1)$$ - as, no extra space is required.\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n if len(str(num)) > 1 and str(num)[-1] == "0":\n return False\n else:\n return True\n``` | 1 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
A Number After a Double Reversal | a-number-after-a-double-reversal | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def isSameAfterReversals(self, num: int) -> bool:\n def reverse(number):\n result = 0\n while number:\n result = result * 10 + number % 10\n number //= 10\n return result\n\n return reverse(reverse(num)) == num \n``` | 3 | **Reversing** an integer means to reverse all its digits.
* For example, reversing `2021` gives `1202`. Reversing `12300` gives `321` as the **leading zeros are not retained**.
Given an integer `num`, **reverse** `num` to get `reversed1`, **then reverse** `reversed1` to get `reversed2`. Return `true` _if_ `reversed2` _equals_ `num`. Otherwise return `false`.
**Example 1:**
**Input:** num = 526
**Output:** true
**Explanation:** Reverse num to get 625, then reverse 625 to get 526, which equals num.
**Example 2:**
**Input:** num = 1800
**Output:** false
**Explanation:** Reverse num to get 81, then reverse 81 to get 18, which does not equal num.
**Example 3:**
**Input:** num = 0
**Output:** true
**Explanation:** Reverse num to get 0, then reverse 0 to get 0, which equals num.
**Constraints:**
* `0 <= num <= 106` | Sort the array. For every index do a binary search to get the possible right end of the window and calculate the possible answer. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.