title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Simple python3 solution || beats 80% || 💻🧑💻🤖 | final-value-of-variable-after-performing-operations | 0 | 1 | # ***These 2 solutions are Basically same***\n**Please upvote\nGuys if you have better solution please comment it**\n\n# Code 1\n```\nclass Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n x=0\n for i in operations:\n if i=="--X" or i=="X--":\n x=x-1\n else:\n x=x+1\n return x\n \n```\n# Code 2\n```class Solution:\n def finalValueAfterOperations(self, operations: List[str]) -> int:\n x=0\n for i in operations:\n if "-" in i:\n x=x-1\n else:\n x=x+1\n return x```\n | 3 | There is a programming language with only **four** operations and **one** variable `X`:
* `++X` and `X++` **increments** the value of the variable `X` by `1`.
* `--X` and `X--` **decrements** the value of the variable `X` by `1`.
Initially, the value of `X` is `0`.
Given an array of strings `operations` containing a list of operations, return _the **final** value of_ `X` _after performing all the operations_.
**Example 1:**
**Input:** operations = \[ "--X ", "X++ ", "X++ "\]
**Output:** 1
**Explanation:** The operations are performed as follows:
Initially, X = 0.
--X: X is decremented by 1, X = 0 - 1 = -1.
X++: X is incremented by 1, X = -1 + 1 = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
**Example 2:**
**Input:** operations = \[ "++X ", "++X ", "X++ "\]
**Output:** 3
**Explanation:** The operations are performed as follows:
Initially, X = 0.
++X: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
X++: X is incremented by 1, X = 2 + 1 = 3.
**Example 3:**
**Input:** operations = \[ "X++ ", "++X ", "--X ", "X-- "\]
**Output:** 0
**Explanation:** The operations are performed as follows:
Initially, X = 0.
X++: X is incremented by 1, X = 0 + 1 = 1.
++X: X is incremented by 1, X = 1 + 1 = 2.
--X: X is decremented by 1, X = 2 - 1 = 1.
X--: X is decremented by 1, X = 1 - 1 = 0.
**Constraints:**
* `1 <= operations.length <= 100`
* `operations[i]` will be either `"++X "`, `"X++ "`, `"--X "`, or `"X-- "`. | Note that if the number is negative it's the same as positive but you look for the minimum instead. In the case of maximum, if s[i] < x it's optimal that x is put before s[i]. In the case of minimum, if s[i] > x it's optimal that x is put before s[i]. |
Python Accumulate Max and Min | sum-of-beauty-in-the-array | 0 | 1 | ```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n nums1 = list(accumulate(nums, lambda x, y: max(x, y)))\n nums2 = list(accumulate(nums[::-1], lambda x, y: min(x, y)))[::-1]\n cnt = 0\n for i in range(1, len(nums) - 1):\n if nums1[i - 1] < nums[i] < nums2[i + 1]:\n cnt += 2\n elif nums[i - 1] < nums[i] < nums[i + 1]:\n cnt += 1\n return cnt\n```\n | 1 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
python3 precomputation | sum-of-beauty-in-the-array | 0 | 1 | \n\n\n\n* **Case1**: for each index in nums if every element before this is smaller and every element after this is bigger \nthan we have to increase count by 2\nfor this can we can make two array which will store minimum and maximum till now for each index\n* **Case2**: simply compare with left and right neighbour ,if condition satisfies we will increase count by 1\n\n```\n\ndef sumOfBeauties(self, nums) :\n N=len(nums)\n \n # for each index we have to check if all element before it is smaller than this\n min_=[None for _ in range(N)]\n mi_=float(\'-inf\')\n for i in range(N):\n min_[i]=mi_\n mi_=max(nums[i],mi_)\n \n # for each index we have to check if all element after it is bigger than this \n max_=[None for _ in range(N)]\n mx_=float(\'inf\')\n for i in range(N-1,-1,-1):\n max_[i]=mx_\n mx_=min(mx_,nums[i])\n \n ans=0\n for i in range(1,N-1):\n if min_[i]<nums[i]<max_[i]:\n ans+=2\n elif nums[i-1]<nums[i]<nums[i+1]:\n ans+=1\n return ans\n```\n\t\t\n* **TC - O(N)** | 18 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
Python | Two Passes | O(n) | sum-of-beauty-in-the-array | 0 | 1 | # Code\n```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n n = len(nums)\n d = [0]*n\n d[-1] = nums[-1]\n for i in range(n-2,-1,-1):\n d[i] = min(d[i+1], nums[i])\n curmax = nums[0]\n res = 0\n for i in range(1,n-1):\n if curmax < nums[i] < d[i+1]:\n res += 2\n elif nums[i-1] < nums[i] < nums[i+1]:\n res += 1\n curmax = max(curmax, nums[i])\n return res\n \n\n``` | 2 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
intuitive approach | sum-of-beauty-in-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can simply keep track of the maximum value to the left of every index and minimum value to the RIGHT of every index in 2 seperate arrays, maxLeft and minRight. for every index, if the maximum to its left is LESS than it, every element on its left is less than it. Similarly, if the minimum element to its right is greater than it, EVERY element on its right must be greater than it. Thus it satisfies the first property and we add +2 to the sum of beauty.\n\nIf the conditions above do not hold, we can simply compare the current element to its direct neighbours in order to check if the second property holds, and if it does add +1 to the sum of beauty.\n\nif both properties do not hold, we do not increment the beauty.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n maxLeft = [0] * len(nums)\n minRight = [0] * len(nums)\n currMax = nums[0]\n for i in range(1, len(nums)):\n maxLeft[i] = currMax\n currMax = max(currMax, nums[i])\n \n currMin = nums[-1]\n for i in range(len(nums) - 2, -1, -1):\n minRight[i] = currMin\n currMin = min(currMin, nums[i])\n total = 0\n for i in range(1, len(nums) - 1):\n if maxLeft[i] < nums[i] and nums[i] < minRight[i]:\n total += 2\n elif nums[i-1] < nums[i] and nums[i] < nums[i+1]:\n total += 1\n \n return total\n\n``` | 0 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
Python Simple Solution Explained | sum-of-beauty-in-the-array | 0 | 1 | # Intuition\nSo, to basically find beauty of an array we need to check for two conditions at each element of array.\n1. nums[j] < nums[i] < nums[k] -> for all j < i < k\n2. nums[i-1] < nums[i] < nums[i+1] \n\nLets break down the first condition,\nIt means for all the elements seen before i they all must be smaller than nums[i] and for all the elements after i they all must be greater than nums[i]\ni.e max(elements before i) < nums[i] < max(elements after i)\n\nif first condition satisfies summ += 2 \nif second condition satisfies summ += 1\nelse summ += 0\n\n\n# Code\n```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n # 1 -> nums[i-1] < nums[i] < nums[i+1]\n # 2 -> nums[j] < nums[i] < nums[k] -> j < i < k\n # 0 -> if none\n \n # to find the min on every position seen yet\n mini = [0] * len(nums)\n mini[-1] = nums[-1]\n for i in range(len(nums)-2, -1, -1):\n mini[i] = min(nums[i], mini[i+1])\n \n # to find maxi on every position seen yet\n maxi = [0] * len(nums)\n maxi[0] = nums[0]\n for i in range(1, len(nums)):\n maxi[i] = max(nums[i], maxi[i-1])\n \n summ = 0\n for i in range(1, len(nums)-1):\n if maxi[i-1] < nums[i] < mini[i+1]:\n summ += 2\n continue\n elif nums[i-1] < nums[i] < nums[i+1]:\n summ += 1\n continue\n return summ\n\n \n``` | 0 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
space exchange for time, Beats 100.00%of users with Python3 | sum-of-beauty-in-the-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nBeats 100.00%of users with Python3\n\n- Space complexity:\nBeats 25.84%of users with Python3\n\n# Code\n```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n res = 0\n lmax = [nums[0]] * len(nums)\n rmin = [nums[-1]] * len(nums)\n lm = nums[0]\n rm = nums[-1]\n for i in range(0, len(nums)):\n if lm < nums[i]:\n lm = nums[i]\n lmax[i] = lm\n if rm > nums[-i-1]:\n rm = nums[-i-1]\n rmin[-i-1] = rm\n for i in range(0, len(nums)-2):\n if nums[i+1]>lmax[i] and nums[i+1]<rmin[i+2]:\n res += 2\n elif nums[i+1]>nums[i] and nums[i+1]<nums[i+2]:\n res += 1\n else:\n res += 0\n return res\n \n``` | 0 | You are given a **0-indexed** integer array `nums`. For each index `i` (`1 <= i <= nums.length - 2`) the **beauty** of `nums[i]` equals:
* `2`, if `nums[j] < nums[i] < nums[k]`, for **all** `0 <= j < i` and for **all** `i < k <= nums.length - 1`.
* `1`, if `nums[i - 1] < nums[i] < nums[i + 1]`, and the previous condition is not satisfied.
* `0`, if none of the previous conditions holds.
Return _the **sum of beauty** of all_ `nums[i]` _where_ `1 <= i <= nums.length - 2`.
**Example 1:**
**Input:** nums = \[1,2,3\]
**Output:** 2
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 2.
**Example 2:**
**Input:** nums = \[2,4,6,4\]
**Output:** 1
**Explanation:** For each index i in the range 1 <= i <= 2:
- The beauty of nums\[1\] equals 1.
- The beauty of nums\[2\] equals 0.
**Example 3:**
**Input:** nums = \[3,2,1\]
**Output:** 0
**Explanation:** For each index i in the range 1 <= i <= 1:
- The beauty of nums\[1\] equals 0.
**Constraints:**
* `3 <= nums.length <= 105`
* `1 <= nums[i] <= 105` | You can maintain a Heap of available Servers and a Heap of unavailable servers Note that the tasks will be processed in the input order so you just need to find the x-th server that will be available according to the rules |
Python3 | Simple, Fast, Elegant | Beats 90% | detect-squares | 0 | 1 | # Please upvote if helpful!\n\n# Approach\n**Adding Points** - Since duplicate points can be used to form distinct, countable squares, we will use a dictionary to track the number of times that point has been added. In order for us to track the point in a dictionary, it must be hashable, so we will convert the point from a list (non-hashable) to a tuple (hashable).\n\n*Note: `defaultdict(int)` defaults to 0 for new values*\n\n\n**Counting Squares** - To reduce the amount of iterating, we loop through the items of `self.points` searching for points that can serve as the opposite corner of a square. For each such point found, we check if `self.points` contains the other two necessary corners. If so, we calculate how many identical squares can be created by multiplying the instances of each of the three points in `self.points`. We add this number to the running count, which we return once the for loop is completed.\n\n\n# Code\n```\nclass DetectSquares:\n\n def __init__(self):\n self.points = collections.defaultdict(int)\n\n def add(self, point: List[int]) -> None:\n self.points[tuple(point)] += 1\n\n def count(self, point: List[int]) -> int:\n square_count = 0\n x1, y1 = point\n\n for (x2, y2), n in self.points.items():\n x_dist, y_dist = abs(x1 - x2), abs(y1 - y2)\n if x_dist == y_dist and x_dist > 0:\n corner1 = (x1, y2)\n corner2 = (x2, y1)\n if corner1 in self.points and corner2 in self.points:\n square_count += n * self.points[corner1] * self.points[corner2]\n\n return square_count\n \n``` | 8 | You are given a stream of points on the X-Y plane. Design an algorithm that:
* **Adds** new points from the stream into a data structure. **Duplicate** points are allowed and should be treated as different points.
* Given a query point, **counts** the number of ways to choose three points from the data structure such that the three points and the query point form an **axis-aligned square** with **positive area**.
An **axis-aligned square** is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the `DetectSquares` class:
* `DetectSquares()` Initializes the object with an empty data structure.
* `void add(int[] point)` Adds a new point `point = [x, y]` to the data structure.
* `int count(int[] point)` Counts the number of ways to form **axis-aligned squares** with point `point = [x, y]` as described above.
**Example 1:**
**Input**
\[ "DetectSquares ", "add ", "add ", "add ", "count ", "count ", "add ", "count "\]
\[\[\], \[\[3, 10\]\], \[\[11, 2\]\], \[\[3, 2\]\], \[\[11, 10\]\], \[\[14, 8\]\], \[\[11, 2\]\], \[\[11, 10\]\]\]
**Output**
\[null, null, null, null, 1, 0, null, 2\]
**Explanation**
DetectSquares detectSquares = new DetectSquares();
detectSquares.add(\[3, 10\]);
detectSquares.add(\[11, 2\]);
detectSquares.add(\[3, 2\]);
detectSquares.count(\[11, 10\]); // return 1. You can choose:
// - The first, second, and third points
detectSquares.count(\[14, 8\]); // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add(\[11, 2\]); // Adding duplicate points is allowed.
detectSquares.count(\[11, 10\]); // return 2. You can choose:
// - The first, second, and third points
// - The first, third, and fourth points
**Constraints:**
* `point.length == 2`
* `0 <= x, y <= 1000`
* At most `3000` calls **in total** will be made to `add` and `count`. | Is there something you can keep track of from one road to another? How would knowing the start time for each state help us solve the problem? |
O(n) time | O(1) space | solution explained | detect-squares | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse a hashmap to add and count the points.\n\nWe are given a query point and need to choose the other three points and find the number of squares with a positive area. \n\nFor a square, we need four points. 1st point P1 is the query point\nSearch for a diagonal point P2 in the hashmap. P1 and P2 can form a diagonal if the width and height difference is the same i.e P1x - P2x == P1y - P2y. We can get the other two points as:\n P3 = P1x - P2y\n P4 = P2x - P1y\n\nFor positive area, the points shouldn\'t be in the same spot. No need to check all points, only check the x or y coordinates of P1 and P2.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- init()\n - create a hashmap \n - hashmap key = point coordinates i.e x, y and value = frequency\n- add()\n - increment the count of the point(x, y) in the hashmap\n- count()\n - set a result variable res=0 to count the number of squares\n - get the coordinates x, y of the 1st point\n - iterate the points hashmap \n - if the 2nd point is not at the same spot, the 1st & 2nd points are diagonal, and the 3rd & 4th points are there, we can create a square\n - multiply the count of the three points (2nd, 3rd, and 4th) to get the number of squares and update the res\n *No need to multiply all 4 points count because the count of the 1st point (query point) is always 1*\n - return res\n\n# Complexity\n- Time complexity:\n - init() O(1)\n - add() O(1)\n - count O(hashmap iteration) \u2192 O(hashmap size) \u2192 O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n - init() O(1)\n - add() O(1)\n - count O(1)\n - O(1) for all operations because the functions don\'t need extra space for the computation. Size of hashmap will be n after n calls to add()\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass DetectSquares:\n\n def __init__(self):\n self.points = defaultdict(int)\n\n def add(self, point: List[int]) -> None:\n self.points[tuple(point)] += 1\n\n def count(self, point: List[int]) -> int:\n res = 0\n px, py = point\n for (x, y), count in self.points.items():\n if x != px and abs(px - x) == abs(py - y) and (px, y) in self.points and (x, py) in self.points:\n res += self.points[(px, y)] * self.points[(x, py)] * count\n return res\n \n\n\n# Your DetectSquares object will be instantiated and called as such:\n# obj = DetectSquares()\n# obj.add(point)\n# param_2 = obj.count(point)\n``` | 2 | You are given a stream of points on the X-Y plane. Design an algorithm that:
* **Adds** new points from the stream into a data structure. **Duplicate** points are allowed and should be treated as different points.
* Given a query point, **counts** the number of ways to choose three points from the data structure such that the three points and the query point form an **axis-aligned square** with **positive area**.
An **axis-aligned square** is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.
Implement the `DetectSquares` class:
* `DetectSquares()` Initializes the object with an empty data structure.
* `void add(int[] point)` Adds a new point `point = [x, y]` to the data structure.
* `int count(int[] point)` Counts the number of ways to form **axis-aligned squares** with point `point = [x, y]` as described above.
**Example 1:**
**Input**
\[ "DetectSquares ", "add ", "add ", "add ", "count ", "count ", "add ", "count "\]
\[\[\], \[\[3, 10\]\], \[\[11, 2\]\], \[\[3, 2\]\], \[\[11, 10\]\], \[\[14, 8\]\], \[\[11, 2\]\], \[\[11, 10\]\]\]
**Output**
\[null, null, null, null, 1, 0, null, 2\]
**Explanation**
DetectSquares detectSquares = new DetectSquares();
detectSquares.add(\[3, 10\]);
detectSquares.add(\[11, 2\]);
detectSquares.add(\[3, 2\]);
detectSquares.count(\[11, 10\]); // return 1. You can choose:
// - The first, second, and third points
detectSquares.count(\[14, 8\]); // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add(\[11, 2\]); // Adding duplicate points is allowed.
detectSquares.count(\[11, 10\]); // return 2. You can choose:
// - The first, second, and third points
// - The first, third, and fourth points
**Constraints:**
* `point.length == 2`
* `0 <= x, y <= 1000`
* At most `3000` calls **in total** will be made to `add` and `count`. | Is there something you can keep track of from one road to another? How would knowing the start time for each state help us solve the problem? |
[Python3] bfs | longest-subsequence-repeated-k-times | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/acb743eb49f794773b70483bbd90cd6403c367b3) for solutions of weekly 259. \n```\nclass Solution:\n def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:\n freq = [0] * 26\n for ch in s: freq[ord(ch)-97] += 1\n \n cand = [chr(i+97) for i, x in enumerate(freq) if x >= k] # valid candidates \n \n def fn(ss): \n """Return True if ss is a k-repeated sub-sequence of s."""\n i = cnt = 0\n for ch in s: \n if ss[i] == ch: \n i += 1\n if i == len(ss): \n if (cnt := cnt + 1) == k: return True \n i = 0\n return False \n \n ans = ""\n queue = deque([""])\n while queue: \n x = queue.popleft()\n for ch in cand: \n xx = x + ch\n if fn(xx): \n ans = xx\n queue.append(xx)\n return ans\n``` | 11 | You are given a string `s` of length `n`, and an integer `k`. You are tasked to find the **longest subsequence repeated** `k` times in string `s`.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A subsequence `seq` is **repeated** `k` times in the string `s` if `seq * k` is a subsequence of `s`, where `seq * k` represents a string constructed by concatenating `seq` `k` times.
* For example, `"bba "` is repeated `2` times in the string `"bababcba "`, because the string `"bbabba "`, constructed by concatenating `"bba "` `2` times, is a subsequence of the string `"**b**a**bab**c**ba** "`.
Return _the **longest subsequence repeated**_ `k` _times in string_ `s`_. If multiple such subsequences are found, return the **lexicographically largest** one. If there is no such subsequence, return an **empty** string_.
**Example 1:**
**Input:** s = "letsleetcode ", k = 2
**Output:** "let "
**Explanation:** There are two longest subsequences repeated 2 times: "let " and "ete ".
"let " is the lexicographically largest one.
**Example 2:**
**Input:** s = "bb ", k = 2
**Output:** "b "
**Explanation:** The longest subsequence repeated 2 times is "b ".
**Example 3:**
**Input:** s = "ab ", k = 2
**Output:** " "
**Explanation:** There is no subsequence repeated 2 times. Empty string is returned.
**Constraints:**
* `n == s.length`
* `2 <= n, k <= 2000`
* `2 <= n < k * 8`
* `s` consists of lowercase English letters. | null |
simple python bfs implementation | longest-subsequence-repeated-k-times | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nn = len(s)\nlongestSubsequenceRepeatedK is O(n)\nso total time complexity will be O(n * 2 ^ (n/k))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:\n if k == 1:\n return s\n def is_subseq(subseq, full):\n full_iter = iter(full)\n return all(c in full_iter for c in subseq)\n at_least_k = {key:value for key,value in filter(lambda x:x[1] >= k, collections.Counter(s).items())}\n queue = deque([""])\n curr_max = ""\n while queue:\n string = queue.popleft()\n curr_count = collections.Counter(string)\n for key in at_least_k:\n if k * (curr_count[key] + 1) <= at_least_k[key]:\n subseq = string + key\n if is_subseq(subseq * k, s):\n queue.append(subseq)\n if len(subseq) < len(curr_max):\n continue \n if len(subseq) == len(curr_max) and subseq > curr_max:\n curr_max = subseq\n continue\n if len(subseq) > len(curr_max):\n curr_max = subseq\n return curr_max\n \n``` | 0 | You are given a string `s` of length `n`, and an integer `k`. You are tasked to find the **longest subsequence repeated** `k` times in string `s`.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A subsequence `seq` is **repeated** `k` times in the string `s` if `seq * k` is a subsequence of `s`, where `seq * k` represents a string constructed by concatenating `seq` `k` times.
* For example, `"bba "` is repeated `2` times in the string `"bababcba "`, because the string `"bbabba "`, constructed by concatenating `"bba "` `2` times, is a subsequence of the string `"**b**a**bab**c**ba** "`.
Return _the **longest subsequence repeated**_ `k` _times in string_ `s`_. If multiple such subsequences are found, return the **lexicographically largest** one. If there is no such subsequence, return an **empty** string_.
**Example 1:**
**Input:** s = "letsleetcode ", k = 2
**Output:** "let "
**Explanation:** There are two longest subsequences repeated 2 times: "let " and "ete ".
"let " is the lexicographically largest one.
**Example 2:**
**Input:** s = "bb ", k = 2
**Output:** "b "
**Explanation:** The longest subsequence repeated 2 times is "b ".
**Example 3:**
**Input:** s = "ab ", k = 2
**Output:** " "
**Explanation:** There is no subsequence repeated 2 times. Empty string is returned.
**Constraints:**
* `n == s.length`
* `2 <= n, k <= 2000`
* `2 <= n < k * 8`
* `s` consists of lowercase English letters. | null |
python3: 2 solutions | longest-subsequence-repeated-k-times | 0 | 1 | * In both solutions the helper functions do the same thing. It calculates if the **subString** belongs to **string** but the second (that uses an iterator) is fastest.\n\n\n**First solution**\n```\nclass Solution:\n def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:\n def helper(subString, string):\n n, m = len(subString), len(string)\n i, j = 0, 0\n while i < n and j < m: \n if subString[i] == string[j]:\n i += 1\n j += 1\n \n return i == n\n \n counter = defaultdict(lambda: 0)\n \n for char in s: \n counter[char] += 1\n \n chars = [key for key in counter if counter[key] >= k]\n chars.sort()\n \n ans = ""\n stack = [""]\n while stack: \n prefix = stack.pop(0)\n for char in chars: \n word = prefix + char\n if helper(word*k, s): \n stack.append(word)\n ans = word\n \n return ans\n```\n**Second solution**\n```\nclass Solution:\n def longestSubsequenceRepeatedK(self, s: str, k: int) -> str:\n def helper(subString, string):\n string = iter(string)\n return all(c in string for c in subString)\n \n counter = defaultdict(lambda: 0)\n \n for char in s: \n counter[char] += 1\n \n chars = ""\n for key in counter: \n if counter[key]//k: \n chars += key*(counter[key]//k)\n \n for i in range(len(chars), 0, -1):\n possibilities = set() \n for comb in combinations(chars, i):\n for perm in permutations(comb): \n subString = "".join(perm)\n possibilities.add(subString)\n \n possibilities = sorted(possibilities, key = lambda item: (len(item), item), reverse = True)\n \n for pos in possibilities: \n if helper(pos*k, s):\n return pos\n \n return "" \n```\n | 0 | You are given a string `s` of length `n`, and an integer `k`. You are tasked to find the **longest subsequence repeated** `k` times in string `s`.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A subsequence `seq` is **repeated** `k` times in the string `s` if `seq * k` is a subsequence of `s`, where `seq * k` represents a string constructed by concatenating `seq` `k` times.
* For example, `"bba "` is repeated `2` times in the string `"bababcba "`, because the string `"bbabba "`, constructed by concatenating `"bba "` `2` times, is a subsequence of the string `"**b**a**bab**c**ba** "`.
Return _the **longest subsequence repeated**_ `k` _times in string_ `s`_. If multiple such subsequences are found, return the **lexicographically largest** one. If there is no such subsequence, return an **empty** string_.
**Example 1:**
**Input:** s = "letsleetcode ", k = 2
**Output:** "let "
**Explanation:** There are two longest subsequences repeated 2 times: "let " and "ete ".
"let " is the lexicographically largest one.
**Example 2:**
**Input:** s = "bb ", k = 2
**Output:** "b "
**Explanation:** The longest subsequence repeated 2 times is "b ".
**Example 3:**
**Input:** s = "ab ", k = 2
**Output:** " "
**Explanation:** There is no subsequence repeated 2 times. Empty string is returned.
**Constraints:**
* `n == s.length`
* `2 <= n, k <= 2000`
* `2 <= n < k * 8`
* `s` consists of lowercase English letters. | null |
Simple python solution | maximum-difference-between-increasing-elements | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumDifference(self, nums: List[int]) -> int:\n m=0\n k=0\n for i in range(len(nums)):\n for j in range(i+1,len(nums)):\n if nums[j]>nums[i]:\n k=nums[j]-nums[i]\n if k>=m:\n m=k\n if m==0:\n return -1\n return m\n``` | 1 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
Simple Solution and Simple Logic in Python | maximum-difference-between-increasing-elements | 0 | 1 | # Code\n```\nclass Solution:\n def maximumDifference(self, nums: List[int]) -> int:\n difference = 0\n for i in range(len(nums)):\n for j in range(i,len(nums)):\n if nums[j]-nums[i]>difference:\n difference = nums[j]-nums[i]\n if difference == 0:\n return -1\n return difference\n\n \n``` | 0 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
Python simple one pass solution | maximum-difference-between-increasing-elements | 0 | 1 | **Python :**\n\n```\ndef maximumDifference(self, nums: List[int]) -> int:\n\tmaxDiff = -1\n\n\tminNum = nums[0]\n\n\tfor i in range(len(nums)):\n\t\tmaxDiff = max(maxDiff, nums[i] - minNum)\n\t\tminNum = min(minNum, nums[i])\n\n\treturn maxDiff if maxDiff != 0 else -1\n```\n\n**Like it ? please upvote !** | 35 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
[Java/Python 3] Time O(n) space O(1) codes w/ brief explanation and a similar problem. | maximum-difference-between-increasing-elements | 1 | 1 | **Similar Problem:** [121. Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock)\n\n----\n\nTraverse input, compare current number to the minimum of the previous ones. then update the max difference.\n```java\n public int maximumDifference(int[] nums) {\n int diff = -1;\n for (int i = 1, min = nums[0]; i < nums.length; ++i) {\n if (nums[i] > min) {\n diff = Math.max(diff, nums[i] - min);\n }\n min = Math.min(min, nums[i]);\n }\n return diff;\n }\n```\n```python\n def maximumDifference(self, nums: List[int]) -> int:\n diff, mi = -1, math.inf\n for i, n in enumerate(nums):\n if i > 0 and n > mi:\n diff = max(diff, n - mi) \n mi = min(mi, n)\n return diff \n``` | 30 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
[Python3] prefix min | maximum-difference-between-increasing-elements | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/fa0bb65b4cb428452e2b4192ad53e56393b8fb8d) for solutions of weekly 260. \n```\nclass Solution:\n def maximumDifference(self, nums: List[int]) -> int:\n ans = -1 \n prefix = inf\n for i, x in enumerate(nums): \n if i and x > prefix: ans = max(ans, x - prefix)\n prefix = min(prefix, x)\n return ans \n``` | 6 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
[Python3] Straightforward O(n) no extra space w comments | maximum-difference-between-increasing-elements | 0 | 1 | ```py\nclass Solution:\n def maximumDifference(self, nums: List[int]) -> int:\n output = -1\n low = 10**9 # Set because of question constraints\n \n for i in range(len(nums)):\n # If we come across a new lowest number, keep track of it\n low = min(low, nums[i])\n \n # If the current number is greater than our lowest - and if their difference is greater than\n # the largest distance seen yet, save this distance\n if nums[i] > low: output = max(output, nums[i] - low)\n return output | 2 | Given a **0-indexed** integer array `nums` of size `n`, find the **maximum difference** between `nums[i]` and `nums[j]` (i.e., `nums[j] - nums[i]`), such that `0 <= i < j < n` and `nums[i] < nums[j]`.
Return _the **maximum difference**._ If no such `i` and `j` exists, return `-1`.
**Example 1:**
**Input:** nums = \[7,**1**,**5**,4\]
**Output:** 4
**Explanation:**
The maximum difference occurs with i = 1 and j = 2, nums\[j\] - nums\[i\] = 5 - 1 = 4.
Note that with i = 1 and j = 0, the difference nums\[j\] - nums\[i\] = 7 - 1 = 6, but i > j, so it is not valid.
**Example 2:**
**Input:** nums = \[9,4,3,2\]
**Output:** -1
**Explanation:**
There is no i and j such that i < j and nums\[i\] < nums\[j\].
**Example 3:**
**Input:** nums = \[**1**,5,2,**10**\]
**Output:** 9
**Explanation:**
The maximum difference occurs with i = 0 and j = 3, nums\[j\] - nums\[i\] = 10 - 1 = 9.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 1000`
* `1 <= nums[i] <= 109` | Sort the array. Try to reduce all elements with maximum value to the next maximum value in one operation. |
linear time constant space 96% beat time complexity | grid-game | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gridGame(self, grid: List[List[int]]) -> int: \n result = float("inf")\n left,right = 0,sum(grid[0])\n\n for a,b in zip(grid[0],grid[1]):\n right-=a\n\n result = min(result,max(left,right))\n left+=b\n \n return result\n\n# time & space - O(n),O(1)\n\n\n``` | 1 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
[Java/Python 3] Prefix and Suffix sum O(n) code, w/ brief explanation and analysis. | grid-game | 1 | 1 | Key observation: **Robot 2 can ONLY choose the lower left part or the upper right part of the the column that Rob 1 traversed.** Therefore, we compute the *max values* of the two parts when traversing the two-cell-columns from left and right. The mininum out of the afore-mentioned *max values* is the solution.\n```java\n public long gridGame(int[][] grid) {\n long ans = Long.MAX_VALUE, lowerLeft = 0, upperRight = IntStream.of(grid[0]).mapToLong(i -> i).sum();\n for (int i = 0; i < grid[0].length; ++i) {\n upperRight -= grid[0][i];\n ans = Math.min(ans, Math.max(upperRight, lowerLeft));\n lowerLeft += grid[1][i];\n }\n return ans;\n }\n```\nPer **@aravinth3108**\'s suggestion, the following code might be more friendly to the beginners:\n\n```java\n public long gridGame(int[][] grid) {\n long ans = Long.MAX_VALUE, lowerLeft = 0, upperRight = 0;\n for (int cell : grid[0]) {\n upperRight += cell;\n }\n for (int i = 0; i < grid[0].length; ++i) {\n upperRight -= grid[0][i];\n ans = Math.min(ans, Math.max(upperRight, lowerLeft));\n lowerLeft += grid[1][i];\n }\n return ans;\n }\n```\n\n----\n\n```python\n def gridGame(self, grid: List[List[int]]) -> int:\n upper_right, lower_left, ans = sum(grid[0]), 0, math.inf\n for upper, lower in zip(grid[0], grid[1]):\n upper_right -= upper\n ans = min(ans, max(upper_right, lower_left))\n lower_left += lower\n return ans\n```\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = grid[0].length`. | 13 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Practice - DP solution that would work if A wasn't an A-hole. | grid-game | 0 | 1 | Note: **Dynamic-Programming approach does not work for this problem.** The idea behind a DP approach is to let Robot A go first, get the highest score it can get and then reduce all the grid-cells it passed through to 0. Then let Robot B go and get the highest score it can get. (the code below) But the question wants Robot A to minimize B\'s score; even if that means A itself doesn\'t get the most optimal score. These posts ([link1](https://leetcode.com/problems/grid-game/discuss/1486340/C%2B%2BJavaPython-Robot1-Minimize-TopSum-and-BottomSum-of-Robot-2-Picture-Explained), [link2](https://leetcode.com/problems/grid-game/discuss/1486399/Can-anyone-explain-one-of-the-LC-Test-cases)) do a great job of expaining the difference with edge cases.\n\n def gridGame(self, grid: List[List[int]]) -> int:\n As = self.get_best_score_n_path(grid)\n A_path, A_score = As[0], As[1]\n\t\t# now we have the path and score for robot A. We have to empty all the cells that A visited to get max score\n for cell in A_path:\n row,col = cell\n grid[row][col] = 0\n Bs = self.get_best_score_n_path(grid)\n return Bs[1]\n \n def get_best_score_n_path(self, grid):\n rl, cl = len(grid), len(grid[0])\n dp = [[[[(row,col)],grid[row][col]] for col in range(cl)] for row in range(rl)] \n # each cell in dp grid = [(row1,col1),(row2,col2)], score_till_now (i.e. path and score)\n for row in range(rl):\n for col in range(cl):\n if row > 0 and col > 0:\n above_score = dp[row-1][col][1]\n left_score = dp[row][col-1][1]\n if above_score >= left_score: # this leads to the optimal path\n dp[row][col][1] = grid[row][col]+above_score\n dp[row][col][0] += dp[row-1][col][0]\n else:\n dp[row][col][1] = grid[row][col]+left_score\n dp[row][col][0] += dp[row][col-1][0]\n elif row > 0 and col == 0: # leftmost col\n above_score = dp[row-1][col][1]\n dp[row][col][1] = grid[row][col]+above_score\n dp[row][col][0] += dp[row-1][col][0]\n elif row == 0 and col > 0: # topmost col\n left_score = dp[row][col-1][1]\n dp[row][col][1] = grid[row][col]+left_score\n dp[row][col][0] += dp[row][col-1][0]\n return dp[-1][-1] | 6 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Simple python3 solution | Prefix sum + Suffix_sum | grid-game | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def gridGame(self, grid: List[List[int]]) -> int:\n suffix_first = sum(grid[0])\n prefix_second = 0\n\n result = float(\'inf\')\n\n for first, second in zip(*grid):\n suffix_first -= first\n\n current = max(suffix_first, prefix_second)\n result = min(result, current)\n\n prefix_second += second\n\n return result\n``` | 0 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Sliding Window or Prefix Sum | grid-game | 0 | 1 | \n# Code\n```\nclass Solution:\n def gridGame(self, grid: List[List[int]]) -> int:\n mPoints = float(\'inf\')\n p1 = sum(grid[0])\n p2= -grid[1][-1]\n for i in range(len(grid[0])):\n p1 -=grid[0][i]\n p2 += grid[1][i-1]\n mPoints = min(mPoints, max(p1, p2))\n return mPoints\n \n\n\n\n\n \n``` | 0 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Python3 solution | grid-game | 0 | 1 | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gridGame(self, grid: List[List[int]]) -> int:\n N = len(grid[0])\n pre1,pre2 = grid[0].copy(),grid[1].copy()\n for i in range(1,N):\n pre1[i] += pre1[i-1] \n pre2[i] += pre2[i-1] \n res = float(\'inf\')\n for i in range(N):\n top = pre1[-1]-pre1[i]\n bottom = pre2[i-1] if i>0 else 0\n second = max(top,bottom)\n res = min(res,second)\n return res\n``` | 0 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Using Prefix Sum | grid-game | 0 | 1 | # Intuition\nFor every index calculating maximum score second robot can achieve and returning minimum score among all the indices.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def gridGame(self, grid: List[List[int]]) -> int:\n s1, s2 = [grid[0][0]], [grid[1][0]]\n n = len(grid[0])\n for i in range(1, n):\n s1.append(s1[-1] + grid[0][i])\n s2.append(s2[-1] + grid[1][i])\n\n sec_robot_min = s1[-1] - s1[0]\n for i in range(1, n):\n sec_robot_min = min(sec_robot_min, max(s1[-1] - s1[i], s2[i-1]))\n return sec_robot_min \n \n``` | 0 | You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix.
Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`).
At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another.
The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return _the **number of points** collected by the **second** robot._
**Example 1:**
**Input:** grid = \[\[2,5,4\],\[1,5,1\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.
**Example 2:**
**Input:** grid = \[\[3,3,1\],\[8,5,2\]\]
**Output:** 4
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.
**Example 3:**
**Input:** grid = \[\[1,3,1,15\],\[1,3,3,1\]\]
**Output:** 7
**Explanation:** The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.
**Constraints:**
* `grid.length == 2`
* `n == grid[r].length`
* `1 <= n <= 5 * 104`
* `1 <= grid[r][c] <= 105` | Note what actually matters is how many 0s and 1s are in odd and even positions For every cyclic shift we need to count how many 0s and 1s are at each parity and convert the minimum between them for each parity |
Easiest Python | check-if-word-can-be-placed-in-crossword | 0 | 1 | # Intuition\ncheck all the valid spaces where this condition is met\n(previous cell is # or out of bounds and curr cell is not \'#\')\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n M,N = len(board),len(board[0])\n L = len(word)\n def canPlace(r,c,dirX,dirY,i):\n # check all the chars in board starting for r,c\n while i<L:\n if r<0 or c<0 or r>=M or c>=N or board[r][c] == \'#\' or (board[r][c] != \' \' and board[r][c] != word[i]):\n return False\n r+=dirX\n c+=dirY\n i+=1\n # check if it is end of blank space\n if r<0 or c<0 or r>=M or c>=N or board[r][c] == \'#\':\n return True\n return False\n\n for i in range(M):\n for j in range(N):\n # down\n if (i-1<0 or board[i-1][j] == \'#\') and board[i][j] != \'#\':\n if canPlace(i,j,1,0,0):\n return True\n # right\n if (j-1<0 or board[i][j-1] == \'#\') and board[i][j] != \'#\':\n if canPlace(i,j,0,1,0):\n return True\n # up\n if (i+1>=M or board[i+1][j] == \'#\') and board[i][j] != \'#\':\n if canPlace(i,j,-1,0,0):\n return True\n # left\n if (j+1>=N or board[i][j+1] == \'#\') and board[i][j] != \'#\':\n if canPlace(i,j,0,-1,0):\n return True\n return False\n \n \n \n \n\n\n\n\n \n \n``` | 0 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
Python 3 || 7 lines, with a brief explanation || T/M: 87% / 20% | check-if-word-can-be-placed-in-crossword | 0 | 1 | Here\'s the intuition:\n\nThe problem reduces to finding all vertical or horizontal lines of consecutive cells with elements that consist of letters or spaces only and that are the same length as`word`. We can further reduce the problem by only considering whether the rows, left-to-right, allow the word to be placed. We achieve this reduction by considering both`word`and its reverse, and by considering the rows of both`board`and its tranpose`zip(*board)`\n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n\n n, words = len(word), [word,word[::-1]]\n\n for brd in (board, zip(*board)):\n\n brd = chain(*[\'\'.join(row).split(\'#\') for row in brd])\n \n for s, w in product(brd,words):\n if len(s) == n and all(s[i] in [\' \', w[i]] for i in range(n)):\n return True\n \n return False\n```\n[https://leetcode.com/problems/check-if-word-can-be-placed-in-crossword/submissions/939691455/](http://)\n\n\nI\'m most likely wrong considering the wide range of testcases, but I think that time complexity is *O*(*MN*)-ish and space complexity is *O*(*M+N*)-ish.\n | 4 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
[Python3] row-by-row & col-by-col | check-if-word-can-be-placed-in-crossword | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/fa0bb65b4cb428452e2b4192ad53e56393b8fb8d) for solutions of weekly 260. \n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n for x in board, zip(*board): \n for row in x: \n for s in "".join(row).split("#"): \n for w in word, word[::-1]: \n if len(s) == len(w) and all(ss in (" ", ww) for ss, ww in zip(s, w)): return True \n return False\n```\n\n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n for x in board, zip(*board): \n for row in x:\n for k, grp in groupby(row, key=lambda x: x != "#"): \n grp = list(grp)\n if k and len(grp) == len(word): \n for w in word, word[::-1]: \n if all(gg in (" ", ww) for gg, ww in zip(grp, w)): return True \n return False\n``` | 10 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
Python | 2 Methods | check-if-word-can-be-placed-in-crossword | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n1. Just follow the rules and search\n2. transpose the board and perform the match row by row\n\n# Code\n```\nimport itertools\n\nclass Solution:\n\n # method 1: just follow the rules\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n m, n = len(board), len(board[0])\n dirs = {\n # left\n -1: (-1, 0),\n # right\n 1: (1, 0),\n # top\n -2: (0, -1),\n # down\n 2: (0, 1)\n }\n \n def check(i, j, k, direction):\n if i < 0 or j < 0 or i >= m or j >= n:\n return k >= len(word)\n if k >= len(word):\n return board[i][j] == \'#\'\n if board[i][j] == \' \' or board[i][j] == word[k]:\n dx, dy = dirs[direction]\n return check(i + dx, j + dy, k + 1, direction)\n return False\n \n for i in range(m):\n for j in range(n):\n if board[i][j] == \' \' or board[i][j] == word[0]:\n # move left\n if (i + 1 >= m or board[i+1][j] == \'#\') and check(i, j, 0, -1):\n return True\n # move right\n if (i - 1 < 0 or board[i-1][j] == \'#\') and check(i, j, 0, 1):\n return True\n # move top\n if (j +1 >= n or board[i][j+1] == \'#\') and check(i, j, 0, -2):\n return True\n # move bottom\n if (j - 1 < 0 or board[i][j-1] == \'#\') and check(i, j, 0, 2):\n return True\n return False\n\n # method 2: transpose and reverse for easy comparison\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n for row in itertools.chain(board, zip(*board)):\n for w in [word, word[::-1]]:\n for s in \'\'.join(row).split(\'#\'):\n if len(s) == len(word) and all(s[i] == w[i] or s[i] == \' \' for i in range(len(word))):\n return True\n return False\n\n``` | 0 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
Simple intuitive approach using sets | check-if-word-can-be-placed-in-crossword | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nthe words need to fit perfectly between 2 #s or between a # and the end of a row / col or perfectly into a row or col\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart by finding where are the blocks in the board where the word can fit, gaps of exactly length of word between 2 #s \nStore those points in a set (one for left to right, one for top to bottom)\n\nThen for each of those points, call the helper function to check if the word can fit in that gap, helper function also takes a parameter reversed to see if we want to check the opposite direction (right to left or bottom to top). \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO( m * n * length(word))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(m * n) to store the sets of potential starting points\n\n# Code\n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n rows,cols = len(board), len(board[0])\n target = len(word)\n\n rowStarts = set()\n #O( m * n )\n for row in range(rows):\n count = 0\n col = 0\n start = col\n for col in range(cols):\n if board[row][col] != "#":\n count += 1\n else:\n if count == target:\n rowStarts.add((row, start))\n \n \n count = 0\n start = col+1\n if count == target:\n rowStarts.add((row, start))\n \n #O(m * n)\n colStarts = set()\n for col in range(cols):\n count = 0\n row = 0\n start = row\n for row in range(rows):\n if board[row][col] != "#":\n count += 1\n else:\n if count == target:\n colStarts.add((start, col))\n count = 0\n start = row + 1\n if count == target:\n colStarts.add((start, col))\n\n\n def checkWordRow(r, c, reversed):\n curr = 0\n if not reversed:\n for i in range(c, c+len(word)):\n if board[r][i] == word[curr] or board[r][i] == " ":\n curr += 1\n else:\n return False\n else:\n for i in range(c, c+len(word)):\n if board[r][i] == word[len(word) - 1 - curr] or board[r][i] == " ":\n curr += 1\n else:\n return False\n return True\n\n def checkWordCol(r, c, reversed):\n curr = 0\n if not reversed:\n for i in range(r, r+len(word)):\n if board[i][c] == word[curr] or board[i][c] == " ":\n curr += 1\n else:\n return False\n else:\n for i in range(r, r+len(word)):\n if board[i][c] == word[len(word) - 1 - curr] or board[i][c] == " ":\n curr += 1\n else:\n return False\n \n return True\n\n #O(m*n * k) k = len(word)\n for startRow, startCol in rowStarts:\n if checkWordRow(startRow,startCol, False):\n return True\n if checkWordRow(startRow, startCol, True):\n return True\n for startRow, startCol in colStarts:\n if checkWordCol(startRow, startCol, False):\n return True\n if checkWordCol(startRow, startCol, True):\n return True\n return False\n \n \n \n\n``` | 0 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
Index Math [100 % Time] | check-if-word-can-be-placed-in-crossword | 0 | 1 | # Approach\nAssume `k` is the length of the word\n\nFor each row, attempt to place horizontally starting from column `c`. For the current row, if both the cells in `(c - 1)th` column and `(c + k)th` column are not either `#` or out of bounds, check the next value of `c`.\nReturn `True` if word or reverse word can be placed in `board[row][c] ... board[row][c + k - 1]`\n\nFor each column, attempt to place vertically starting from row `r`. For the current column, if both the cells in `(r - 1)th` row and `(r + k)th` column are not either `#` or out of bounds, check the next value of `r`.\nReturn `True` if word or reverse word can be placed in `board[r][column] ... board[r + k -1][column]`\n\n# Code\n```\nclass Solution:\n def placeWordInCrossword(self, board: List[List[str]], word: str) -> bool:\n m = len(board)\n n = len(board[0])\n k = len(word)\n\n if n >= k:\n for row in range(m):\n for col in range(n - k + 1):\n if (col > 0 and board[row][col - 1] != \'#\') or (col + k - 1 < n - 1 and board[row][col + k] != \'#\'):\\\n continue\n for i in range(k):\n if board[row][col + i] not in [word[i], \' \']:\n break\n else:\n return True\n for i in range(k):\n if board[row][col + k - 1 - i] not in [word[i], \' \']:\n break\n else:\n return True\n if m >= k:\n for col in range(n):\n for row in range(m - k + 1):\n if (row > 0 and board[row - 1][col] != \'#\') or (row + k - 1 < m - 1 and board[row + k][col] != \'#\'):\n continue\n for i in range(k):\n if board[row + i][col] not in [word[i], \' \']:\n break\n else:\n return True\n for i in range(k):\n if board[row + k - 1 - i][col] not in [word[i], \' \']:\n break\n else:\n return True\n return False\n\n``` | 0 | You are given an `m x n` matrix `board`, representing the **current** state of a crossword puzzle. The crossword contains lowercase English letters (from solved words), `' '` to represent any **empty** cells, and `'#'` to represent any **blocked** cells.
A word can be placed **horizontally** (left to right **or** right to left) or **vertically** (top to bottom **or** bottom to top) in the board if:
* It does not occupy a cell containing the character `'#'`.
* The cell each letter is placed in must either be `' '` (empty) or **match** the letter already on the `board`.
* There must not be any empty cells `' '` or other lowercase letters **directly left or right** of the word if the word was placed **horizontally**.
* There must not be any empty cells `' '` or other lowercase letters **directly above or below** the word if the word was placed **vertically**.
Given a string `word`, return `true` _if_ `word` _can be placed in_ `board`_, or_ `false` _**otherwise**_.
**Example 1:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", "c ", " "\]\], word = "abc "
**Output:** true
**Explanation:** The word "abc " can be placed as shown above (top to bottom).
**Example 2:**
**Input:** board = \[\[ " ", "# ", "a "\], \[ " ", "# ", "c "\], \[ " ", "# ", "a "\]\], word = "ac "
**Output:** false
**Explanation:** It is impossible to place the word because there will always be a space/letter above or below it.
**Example 3:**
**Input:** board = \[\[ "# ", " ", "# "\], \[ " ", " ", "# "\], \[ "# ", " ", "c "\]\], word = "ca "
**Output:** true
**Explanation:** The word "ca " can be placed as shown above (right to left).
**Constraints:**
* `m == board.length`
* `n == board[i].length`
* `1 <= m * n <= 2 * 105`
* `board[i][j]` will be `' '`, `'#'`, or a lowercase English letter.
* `1 <= word.length <= max(m, n)`
* `word` will contain only lowercase English letters. | Given a fixed size box, is there a way to quickly query which packages (i.e., count and sizes) should end up in that box size? Do we have to order the boxes a certain way to allow us to answer the query quickly? |
[Python3] somewhat dp | the-score-of-students-solving-math-expression | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/fa0bb65b4cb428452e2b4192ad53e56393b8fb8d) for solutions of weekly 260. \n```\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n \n @cache\n def fn(lo, hi): \n """Return possible answers of s[lo:hi]."""\n if lo+1 == hi: return {int(s[lo])}\n ans = set()\n for mid in range(lo+1, hi, 2): \n for x in fn(lo, mid): \n for y in fn(mid+1, hi): \n if s[mid] == "+" and x + y <= 1000: ans.add(x + y)\n elif s[mid] == "*" and x * y <= 1000: ans.add(x * y)\n return ans \n \n target = eval(s)\n cand = fn(0, len(s))\n ans = 0 \n for x in answers: \n if x == target: ans += 5\n elif x in cand: ans += 2\n return ans \n``` | 6 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
DP with memo | the-score-of-students-solving-math-expression | 0 | 1 | # Intuition\n\nOne need to get all possible answers for arithmatically correct computations. To get these you need to split the expression at an operand compute all possible left and right values and combine them with the given opearations. So it is natural to use top down approach here with memoization.\n\n\n# Complexity\n\nThe major factor in runtime is the computation of not totally wrong possible answers. Since there are at most $m=1000$ different possible values to consider the computation of `memo[(i,j)]` takes $ m^2\\cdot(j-i)/2$ operations at most. The total number of operations is at most $n^2m^2$, where `n=len(s)//2`.\n\n- Time complexity: $$O((nm)^2)$$.\n\n- Space complexity: $$O(n^2)$$.\n\n# Code\n```\ndef eval_tokens(tokens):\n stack = [int(tokens[0])]\n for arg1, op in zip(tokens[2::2], tokens[1::2]):\n stack.append(int(arg1))\n if op == "*":\n stack.append(stack.pop()*stack.pop()) \n return sum(stack)\n\ndef eval_all(s, memo, i, j):\n values = memo.get((i,j))\n if values is None:\n values = set()\n for k in range(i+1, j, 2):\n left_values = eval_all(s, memo, i, k)\n right_values = eval_all(s, memo, k+1, j)\n op = s[k]\n if op == "+":\n values.update(c for a in left_values for b in right_values if (c := a+b) <= 1000)\n else:\n values.update(c for a in left_values for b in right_values if (c := a*b) <= 1000)\n memo[(i,j)] = values\n return values \n\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n memo = {(i,i+1): {int(s[i])} for i in range(0, len(s), 2)}\n score = [0]*(1001)\n for val in eval_all(s, memo, 0, len(s)):\n score[val] = 2\n score[eval_tokens(s)] = 5\n return sum(score[answer] for answer in answers)\n \n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
DP with Frequency Domain Reductions | the-score-of-students-solving-math-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is a dp problem. As such, we should look for speedups to make it in under the time complexity limits. One of the most common is a shift to a frequency domain. The first shift is by shifting answers from a list to a map of frequency of answers uniquely. \n\nThen, we need to consider the process from both sides. If we imagine one operation going left to right and one going right to left from the mid point we can see that we can build a range of values up nice and easily. We do this to establish our result array of 2D first by taking even steps of 2 * i up to midpoint of the expression. \n\nThen, we need to loop over our expression. We know the correct answer is bound by 1000 and as such we know we can use that as an upper bound definitively for our operations. We also know we want one track to left and the other right, and we know that we need to do this for the subrange of our values as needed. This leads to the formation of a quintuple loop (ugly but necessary) \n\n- We first loop up to our midpoint on a difference pointer \n - Within that, we loop i up to midpoint minus difference \n - Within this, we set j to i + difference or basically the other side of midpoint (looking left and right) \n - We want the current answers here, so we make a set \n - We now loop k from 2 * i + 1 to 2 * j in steps of 2 \n - this keeps k stepping on the operands \n - In here, if we are not at a + or a * it\'s a space, skip \n - If it\'s a + or a *, check concerning \n - for x in result at i at k // 2 \n - for y in result at k//2 + 1 at j \n - if operation of x, y is lte 1000 add operation result to current answer \n\nNext we need to figure out how to get answer. \nLet answer be 0. \nUse python evaluator to evaluate expression. \nGet the correct answer frequency from results first row and last column (must be here since we looked left and right simultaneously) \n\n- For each correct answer in correct answer frequency \n - if it\'s actually correct, add 5 * frequency of answer * correct answer frequency \n - if it\'s not actually correct, add 2 * frequency of answer * correct answer frequency \n\nThis gives us the frequency transformed answer \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSee intuition \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n # frequency transform \n answer_frequency = collections.Counter(answers)\n # find length midpoint \n midpoint = len(s)//2 + 1 \n # build 2D dp array \n result = [[set() for _ in range(midpoint)] for __ in range(midpoint)]\n # for i in range midpoint -> equal spot placement hits evens -> add component as needed \n for i in range(midpoint) : \n result[i][i].add(int(s[2*i]))\n \n # loop 1 to midpoint \n for difference in range(1, midpoint) : \n # and use that to build a difference range for i \n for i in range(midpoint - difference) : \n # so that you can set j on the appropriate side of the midpoint \n j = i + difference \n current_answers = set() \n # and from there build up on steps of 2*i + 1 to 2*j in steps of 2 \n # only considering those appropriate and checking mathematics for the subarray components \n # in the result dp array \n for k in range(2*i + 1, 2*j, 2) : \n if s[k] != "+" and s[k] != "*" : \n continue \n elif s[k] == "+" : \n for x in result[i][k//2]: \n for y in result[k//2 + 1][j] : \n if x + y <= 1000 : \n current_answers.add(x+y)\n else : \n for x in result[i][k//2] : \n for y in result[k//2 + 1][j] : \n if x * y <= 1000 : \n current_answers.add(x*y)\n # and then storing the resulting component as needed \n result[i][j] = current_answers\n\n # build up the answer \n ans = 0\n # by first evaluating s to get the correct answer\n crt = eval(s)\n # then for each entry in results final analysis (which must cover the whole string!) build a frequency domain\n correct_answer_frequency = collections.Counter(result[0][-1])\n # calculate appropriately using double frequency time reduction \n for correct_answer in correct_answer_frequency : \n if correct_answer == crt : \n ans += (5 * answer_frequency[correct_answer] * correct_answer_frequency[correct_answer])\n else : \n ans += (2 * answer_frequency[correct_answer] * correct_answer_frequency[correct_answer])\n\n # return answer when done \n return ans\n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
Top-down DP solution | the-score-of-students-solving-math-expression | 0 | 1 | # Complexity\n- Time complexity: $$O(n^2 \\cdot 2^{n - 1} + m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n \\cdot n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nwhere `n = s.length`, `m = answers.length`\n\n# Code\n``` python3 []\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n add = lambda x, y: x + y\n multi = lambda x, y: x * y\n \n def get_tokens(s):\n tokens = []\n for char in s:\n if char == \'+\':\n value = add\n elif char == \'*\':\n value = multi\n else:\n value = int(char)\n tokens.append(value)\n return tokens\n \n tokens = get_tokens(s)\n\n def calc(tokens):\n stack = []\n for elem in tokens:\n if stack and stack[-1] is multi:\n _ = stack.pop()\n stack[-1] *= elem\n else:\n stack.append(elem)\n return sum(\n stack[i]\n for i in range(0, len(stack), 2)\n )\n \n @cache\n def dp(left, right):\n if left + 1 == right:\n return {tokens[left]}\n \n result = set()\n for middle in range(left + 1, right, 2):\n op = tokens[middle]\n left_options = dp(left, middle)\n right_options = dp(middle + 1, right)\n for a in left_options:\n for b in right_options:\n current = op(a, b)\n if current <= 1000:\n result.add(current)\n return result\n \n correct_answer = calc(tokens)\n wrong_answers = dp(0, len(tokens))\n\n result = 0\n for answer in answers:\n if answer == correct_answer:\n result += 5\n elif answer in wrong_answers:\n result += 2\n return result\n\n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
Short DP in Python Faster than 97% | the-score-of-students-solving-math-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing the top-down DP to generate all the possible outcomes in the range of `[0, 1000]`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGiven a substring of `s`, we enumerate all possible orders of operators (`+` and `*`), and collect all of their outcomes. The procedure can be speeded up by using memoization that is as simple as adding the `@cache` decorator.\n\n# Code\n```\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n @cache\n def valid(l, r):\n if l == r - 1:\n return {int(s[l])}\n res = set()\n for i in range(l, r):\n if s[i] == \'*\':\n res |= set(v * u for v, u in product(valid(l, i), valid(i+1, r)) if v * u <= 1000) \n elif s[i] == \'+\':\n res |= set(v + u for v, u in product(valid(l, i), valid(i+1, r)) if v + u <= 1000)\n return res\n\n ans = 0\n golden = eval(s)\n partial_corrects = valid(0, len(s))\n for test in answers:\n if test == golden:\n ans += 5\n elif test in partial_corrects:\n ans += 2\n return ans\n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
My solution... | the-score-of-students-solving-math-expression | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport operator\nfrom functools import cache\nfrom itertools import product\n\n\nclass Solution:\n def getOperation(self, op, lst1, lst2):\n """\n This function applies the operation to all possible pairs\n of numbers in the two lists.\n """\n ops = {"+": operator.add, "*": operator.mul} # Operation mapping\n return {\n result for a, b in product(lst1, lst2) if (result := ops[op](a, b)) <= 1000\n }\n\n @cache\n def getResults(self, s, start, end):\n """\n This function gets all possible results of the subexpression denoted by the interval [start, end].\n It uses recursion and dynamic programming for better efficiency.\n """\n # Base case: if start equals end, it\'s just a single number\n if start == end:\n return {int(s[start])}\n\n # Get all possible results\n results = set()\n for i in range(\n start + 1, end, 2\n ): # Choose every possible operator as the final operator\n # Use the chosen operator to split the expression into two parts\n left_results = self.getResults(s, start, i - 1)\n right_results = self.getResults(s, i + 1, end)\n # Combine the results of the two parts\n results |= self.getOperation(s[i], left_results, right_results)\n return results\n\n def scoreOfStudents(self, s: str, answers: list[int]) -> int:\n """\n This function calculates total score answers of students.\n """\n # Correct answer\n correct_answer = eval(s)\n\n # All possible results\n all_possible_results = self.getResults(s, 0, len(s) - 1)\n\n # Score each student\'s answer\n total_score = 0\n for answer in answers:\n if answer == correct_answer:\n total_score += 5 # 5 points for correct answer\n elif answer in all_possible_results:\n total_score += 2 # 2 points for valid but incorrect answer\n\n return total_score\n\n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
Top-down DP, short & clean | the-score-of-students-solving-math-expression | 0 | 1 | # Intuition\nSo main challenge is to calculate all possible outcomes (e.g. any valid `(...)` expression). So let\'s decompose what does that mean\nLet `f(l,r)` be the set of all possible outcomes of `s[l:r]` (assuming it stars and ends withs a digit). Then all possibilities could be defined as trying to chose any operator inside and put it as \'last order\'. Let `s[l:r]==\'<d_l><op_l+1>...<op_r-1><d_r>`, then we try to choose `<op_i>` from `[<op_l+1>,...,<op_r-1>]` and apply `<op_i>` to all possibilities from left substring `f(s:i-1)` and right substring `f(i+1:r)` (basically a cartesian product); and then combine all possibilities. \n\n# Approach\nImplement the idea from intuition via top-down recursive function. Use `@cache`. Limit all possibile outcomes by `1000` as in statement, since so that possibilites don\'t grow exponentially. Since all digits and operator are `1-char` string, things are really simplified here - each digit is on odd position, each operator is on even.\nUse `eval` to get correct answer in scoring. \n\n# Complexity\n- Time complexity: `O(len(s)^3 * C^2)` where `C=1000`\n- Space complexity: `O(len(s)^2 * C)`\n\n# Code\n```\nclass Solution:\n def scoreOfStudents(self, s: str, answers: List[int]) -> int:\n n=len(s)\n ops={\'+\':operator.add, \'*\':operator.mul}\n def apply(op,lst1,lst2):\n return {y for a,b in product(lst1,lst2) if (y:=op(a,b)) <= 1000}\n @cache\n def f(l,r):\n if r==l: return {int(s[l])}\n return reduce(set.union, (apply(ops[s[i]], f(l,i-1), f(i+1,r)) for i in range(l+1,r,2)), set())\n ans=eval(s)\n return sum(5 if a==ans else 2*(a in f(0,n-1)) for a in answers)\n \n``` | 0 | You are given a string `s` that contains digits `0-9`, addition symbols `'+'`, and multiplication symbols `'*'` **only**, representing a **valid** math expression of **single digit numbers** (e.g., `3+5*2`). This expression was given to `n` elementary school students. The students were instructed to get the answer of the expression by following this **order of operations**:
1. Compute **multiplication**, reading from **left to right**; Then,
2. Compute **addition**, reading from **left to right**.
You are given an integer array `answers` of length `n`, which are the submitted answers of the students in no particular order. You are asked to grade the `answers`, by following these **rules**:
* If an answer **equals** the correct answer of the expression, this student will be rewarded `5` points;
* Otherwise, if the answer **could be interpreted** as if the student applied the operators **in the wrong order** but had **correct arithmetic**, this student will be rewarded `2` points;
* Otherwise, this student will be rewarded `0` points.
Return _the sum of the points of the students_.
**Example 1:**
**Input:** s = "7+3\*1\*2 ", answers = \[20,13,42\]
**Output:** 7
**Explanation:** As illustrated above, the correct answer of the expression is 13, therefore one student is rewarded 5 points: \[20,**13**,42\]
A student might have applied the operators in this wrong order: ((7+3)\*1)\*2 = 20. Therefore one student is rewarded 2 points: \[**20**,13,42\]
The points for the students are: \[2,5,0\]. The sum of the points is 2+5+0=7.
**Example 2:**
**Input:** s = "3+5\*2 ", answers = \[13,0,10,13,13,16,16\]
**Output:** 19
**Explanation:** The correct answer of the expression is 13, therefore three students are rewarded 5 points each: \[**13**,0,10,**13**,**13**,16,16\]
A student might have applied the operators in this wrong order: ((3+5)\*2 = 16. Therefore two students are rewarded 2 points: \[13,0,10,13,13,**16**,**16**\]
The points for the students are: \[5,0,0,5,5,2,2\]. The sum of the points is 5+0+0+5+5+2+2=19.
**Example 3:**
**Input:** s = "6+0\*1 ", answers = \[12,9,6,4,8,6\]
**Output:** 10
**Explanation:** The correct answer of the expression is 6.
If a student had incorrectly done (6+0)\*1, the answer would also be 6.
By the rules of grading, the students will still be rewarded 5 points (as they got the correct answer), not 2 points.
The points for the students are: \[0,0,5,0,0,5\]. The sum of the points is 10.
**Constraints:**
* `3 <= s.length <= 31`
* `s` represents a valid expression that contains only digits `0-9`, `'+'`, and `'*'` only.
* All the integer operands in the expression are in the **inclusive** range `[0, 9]`.
* `1 <=` The count of all operators (`'+'` and `'*'`) in the math expression `<= 15`
* Test data are generated such that the correct answer of the expression is in the range of `[0, 1000]`.
* `n == answers.length`
* `1 <= n <= 104`
* `0 <= answers[i] <= 1000` | Keep track of the indices on both RLE arrays and join the parts together. What is the maximum number of segments if we took the minimum number of elements left on both the current segments every time? |
Python Easy Solution | convert-1d-array-into-2d-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n ans=[]\n if m*n==len(original):\n a=0\n for i in range(0,m):\n t=[]\n for j in range(0,n):\n t.append(original[a])\n a=a+1\n ans.append(t)\n #return ans\n return ans\n``` | 5 | You are given a **0-indexed** 1-dimensional (1D) integer array `original`, and two integers, `m` and `n`. You are tasked with creating a 2-dimensional (2D) array with `m` rows and `n` columns using **all** the elements from `original`.
The elements from indices `0` to `n - 1` (**inclusive**) of `original` should form the first row of the constructed 2D array, the elements from indices `n` to `2 * n - 1` (**inclusive**) should form the second row of the constructed 2D array, and so on.
Return _an_ `m x n` _2D array constructed according to the above procedure, or an empty 2D array if it is impossible_.
**Example 1:**
**Input:** original = \[1,2,3,4\], m = 2, n = 2
**Output:** \[\[1,2\],\[3,4\]\]
**Explanation:** The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, \[1,2\], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, \[3,4\], becomes the second row in the constructed 2D array.
**Example 2:**
**Input:** original = \[1,2,3\], m = 1, n = 3
**Output:** \[\[1,2,3\]\]
**Explanation:** The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
**Example 3:**
**Input:** original = \[1,2\], m = 1, n = 1
**Output:** \[\]
**Explanation:** There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
**Constraints:**
* `1 <= original.length <= 5 * 104`
* `1 <= original[i] <= 105`
* `1 <= m, n <= 4 * 104` | Is only tracking a single sum enough to solve the problem? How does tracking an odd sum and an even sum reduce the number of states? |
Python Easy Solution | convert-1d-array-into-2d-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n ans=[]\n if m*n==len(original):\n a=0\n for i in range(0,m):\n t=[]\n for j in range(0,n):\n t.append(original[a])\n a=a+1\n ans.append(t)\n #return ans\n return ans\n``` | 1 | You are given a **0-indexed** 1-dimensional (1D) integer array `original`, and two integers, `m` and `n`. You are tasked with creating a 2-dimensional (2D) array with `m` rows and `n` columns using **all** the elements from `original`.
The elements from indices `0` to `n - 1` (**inclusive**) of `original` should form the first row of the constructed 2D array, the elements from indices `n` to `2 * n - 1` (**inclusive**) should form the second row of the constructed 2D array, and so on.
Return _an_ `m x n` _2D array constructed according to the above procedure, or an empty 2D array if it is impossible_.
**Example 1:**
**Input:** original = \[1,2,3,4\], m = 2, n = 2
**Output:** \[\[1,2\],\[3,4\]\]
**Explanation:** The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, \[1,2\], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, \[3,4\], becomes the second row in the constructed 2D array.
**Example 2:**
**Input:** original = \[1,2,3\], m = 1, n = 3
**Output:** \[\[1,2,3\]\]
**Explanation:** The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
**Example 3:**
**Input:** original = \[1,2\], m = 1, n = 1
**Output:** \[\]
**Explanation:** There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
**Constraints:**
* `1 <= original.length <= 5 * 104`
* `1 <= original[i] <= 105`
* `1 <= m, n <= 4 * 104` | Is only tracking a single sum enough to solve the problem? How does tracking an odd sum and an even sum reduce the number of states? |
6 Lines Of Code-->Powerful Math Approach | convert-1d-array-into-2d-array | 0 | 1 | \n\n# 1. Math Approach\n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n if len(original)!=m*n:\n return []\n matrix=[]\n for i in range(0,len(original),n):\n matrix.append(original[i:i+n])\n return matrix\n\n\n```\n# please upvote me it would encourage me alot\n | 2 | You are given a **0-indexed** 1-dimensional (1D) integer array `original`, and two integers, `m` and `n`. You are tasked with creating a 2-dimensional (2D) array with `m` rows and `n` columns using **all** the elements from `original`.
The elements from indices `0` to `n - 1` (**inclusive**) of `original` should form the first row of the constructed 2D array, the elements from indices `n` to `2 * n - 1` (**inclusive**) should form the second row of the constructed 2D array, and so on.
Return _an_ `m x n` _2D array constructed according to the above procedure, or an empty 2D array if it is impossible_.
**Example 1:**
**Input:** original = \[1,2,3,4\], m = 2, n = 2
**Output:** \[\[1,2\],\[3,4\]\]
**Explanation:** The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, \[1,2\], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, \[3,4\], becomes the second row in the constructed 2D array.
**Example 2:**
**Input:** original = \[1,2,3\], m = 1, n = 3
**Output:** \[\[1,2,3\]\]
**Explanation:** The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
**Example 3:**
**Input:** original = \[1,2\], m = 1, n = 1
**Output:** \[\]
**Explanation:** There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
**Constraints:**
* `1 <= original.length <= 5 * 104`
* `1 <= original[i] <= 105`
* `1 <= m, n <= 4 * 104` | Is only tracking a single sum enough to solve the problem? How does tracking an odd sum and an even sum reduce the number of states? |
[Python3] simulation | convert-1d-array-into-2d-array | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/182350e41572fb26ffb8c44204b037cc9f0e5035) for solutions of biweekly 62. \n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n ans = []\n if len(original) == m*n: \n for i in range(0, len(original), n): \n ans.append(original[i:i+n])\n return ans \n``` | 42 | You are given a **0-indexed** 1-dimensional (1D) integer array `original`, and two integers, `m` and `n`. You are tasked with creating a 2-dimensional (2D) array with `m` rows and `n` columns using **all** the elements from `original`.
The elements from indices `0` to `n - 1` (**inclusive**) of `original` should form the first row of the constructed 2D array, the elements from indices `n` to `2 * n - 1` (**inclusive**) should form the second row of the constructed 2D array, and so on.
Return _an_ `m x n` _2D array constructed according to the above procedure, or an empty 2D array if it is impossible_.
**Example 1:**
**Input:** original = \[1,2,3,4\], m = 2, n = 2
**Output:** \[\[1,2\],\[3,4\]\]
**Explanation:** The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, \[1,2\], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, \[3,4\], becomes the second row in the constructed 2D array.
**Example 2:**
**Input:** original = \[1,2,3\], m = 1, n = 3
**Output:** \[\[1,2,3\]\]
**Explanation:** The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
**Example 3:**
**Input:** original = \[1,2\], m = 1, n = 1
**Output:** \[\]
**Explanation:** There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
**Constraints:**
* `1 <= original.length <= 5 * 104`
* `1 <= original[i] <= 105`
* `1 <= m, n <= 4 * 104` | Is only tracking a single sum enough to solve the problem? How does tracking an odd sum and an even sum reduce the number of states? |
Python one line | convert-1d-array-into-2d-array | 0 | 1 | One line:\n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n return [original[i:i+n] for i in range(0, len(original), n)] if m*n == len(original) else []\n \n```\n\nWhich is equivalent to\n```\nclass Solution:\n def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:\n if m*n != len(original):\n return []\n \n q = []\n\n for i in range(0, len(original), n):\n q.append(original[i:i+n])\n \n return q\n \n``` | 16 | You are given a **0-indexed** 1-dimensional (1D) integer array `original`, and two integers, `m` and `n`. You are tasked with creating a 2-dimensional (2D) array with `m` rows and `n` columns using **all** the elements from `original`.
The elements from indices `0` to `n - 1` (**inclusive**) of `original` should form the first row of the constructed 2D array, the elements from indices `n` to `2 * n - 1` (**inclusive**) should form the second row of the constructed 2D array, and so on.
Return _an_ `m x n` _2D array constructed according to the above procedure, or an empty 2D array if it is impossible_.
**Example 1:**
**Input:** original = \[1,2,3,4\], m = 2, n = 2
**Output:** \[\[1,2\],\[3,4\]\]
**Explanation:** The constructed 2D array should contain 2 rows and 2 columns.
The first group of n=2 elements in original, \[1,2\], becomes the first row in the constructed 2D array.
The second group of n=2 elements in original, \[3,4\], becomes the second row in the constructed 2D array.
**Example 2:**
**Input:** original = \[1,2,3\], m = 1, n = 3
**Output:** \[\[1,2,3\]\]
**Explanation:** The constructed 2D array should contain 1 row and 3 columns.
Put all three elements in original into the first row of the constructed 2D array.
**Example 3:**
**Input:** original = \[1,2\], m = 1, n = 1
**Output:** \[\]
**Explanation:** There are 2 elements in original.
It is impossible to fit 2 elements in a 1x1 2D array, so return an empty 2D array.
**Constraints:**
* `1 <= original.length <= 5 * 104`
* `1 <= original[i] <= 105`
* `1 <= m, n <= 4 * 104` | Is only tracking a single sum enough to solve the problem? How does tracking an odd sum and an even sum reduce the number of states? |
Noob Code : Easy to Understand | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | 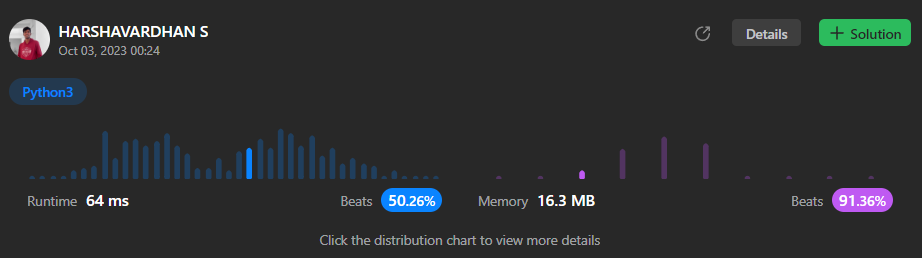\n\n\n# Approach\n1. Initialize a counter variable `c` to 0. This variable will be used to keep track of the count of valid pairs.\n\n2. Create a copy of the `nums` list and store it in the `l` variable. This copy is created to avoid modifying the original list while iterating through it.\n\n3. Initialize a temporary variable `temp` to an empty string. This variable will be used to store the string temporarily while iterating through the list.\n\n4. Use a `for` loop to iterate through the `nums` list. The loop variable `i` represents the index of the current element being considered.\n\n5. Inside the loop, store the current element (string) in the `temp` variable.\n\n6. Remove the current element from the `l` list using the `pop` method. This is done to ensure that we don\'t use the same element twice to form a pair.\n\n7. Use another `for` loop to iterate through the remaining elements in the `l` list. The loop variable `j` represents the current element from the remaining elements.\n\n8. Check if concatenating the current element from the original `nums` list (at index `i`) with the current element `j` from the `l` list results in the `target` string. If `nums[i] + j` equals `target`, it means we have found a valid pair.\n\n9. If a valid pair is found, increment the counter variable `c` by 1.\n\n10. After the inner loop completes, insert the temporarily removed element (`temp`) back into the `l` list at its original index `i`. This is done to restore the original state of the list.\n\n11. Continue the outer loop to consider the next element in the `nums` list and repeat the process.\n\n12. Finally, return the value of the counter variable `c`, which represents the count of pairs that can be concatenated to form the `target` string.\n\n\n# Complexity\n- Time complexity: ***O(n^2)***\n- Space complexity: ***O(n)***\n\n# Code\n```\nclass Solution:\n def numOfPairs(self, nums: List[str], target: str) -> int:\n c=0\n l=nums.copy()\n temp=\'\'\n for i in range (0,len(nums)):\n temp=l[i]\n l.pop(i)\n for j in l:\n if nums[i]+j==target:\n c+=1\n l.insert(i,temp)\n return(c)\n``` | 1 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
Dictionary & List || Python | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | # Code\n```\nclass Solution:\n def numOfPairs(self, nums: List[str], target: str) -> int:\n d = defaultdict(int)\n for char in nums:\n d[char] += 1\n \n arr = []\n for char in target:\n arr.append(char)\n \n pairs = 0\n num = ""\n while len(arr) > 1:\n num += arr.pop()\n findNum = "".join(arr)\n if num[::-1] not in d or findNum not in d:\n continue\n\n c1 = d[num[::-1]]\n d[num[::-1]] -= 1 #reduce the count as we dont want to count it again if the other part is also same.\n \n c2 = d[findNum]\n d[num[::-1]] += 1 # make the count again same.\n\n pairs += c1 * c2\n return pairs\n \n``` | 1 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
[Java/Python 3] One pass O(NM) HashTable codes w/ analysis. | number-of-pairs-of-strings-with-concatenation-equal-to-target | 1 | 1 | ```java\n public int numOfPairs(String[] nums, String target) {\n int cnt = 0, n = target.length();\n Map<Integer, Integer> prefix = new HashMap<>(), suffix = new HashMap<>();\n for (String num : nums) {\n int sz = num.length();\n if (target.startsWith(num)) {\n cnt += suffix.getOrDefault(n - sz, 0);\n }\n if (target.endsWith(num)) {\n cnt += prefix.getOrDefault(n - sz, 0);\n }\n if (target.startsWith(num)) {\n prefix.put(sz, 1 + prefix.getOrDefault(sz, 0));\n }\n if (target.endsWith(num)) {\n suffix.put(sz, 1 + suffix.getOrDefault(sz, 0));\n }\n }\n return cnt;\n }\n```\n```python\n def numOfPairs(self, nums: List[str], target: str) -> int:\n prefix, suffix = Counter(), Counter()\n cnt = 0\n for num in nums:\n if target.startswith(num):\n cnt += suffix[len(target) - len(num)]\n if target.endswith(num):\n cnt += prefix[len(target) - len(num)]\n if target.startswith(num):\n prefix[len(num)] += 1\n if target.endswith(num):\n suffix[len(num)] += 1\n return cnt\n```\n**Analysis:**\n\nLet `N = nums.length`, `M` be the average size of the digits in `nums`, and `T = target.length()`, then each `startsWith()` cost time O(min(M, T)), therefore the total time is `O(N * M)`, space cost `O(N)`. | 20 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
[Python3] freq table | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/182350e41572fb26ffb8c44204b037cc9f0e5035) for solutions of biweekly 62. \n```\nclass Solution:\n def numOfPairs(self, nums: List[str], target: str) -> int:\n freq = Counter(nums)\n ans = 0 \n for k, v in freq.items(): \n if target.startswith(k): \n suffix = target[len(k):]\n ans += v * freq[suffix]\n if k == suffix: ans -= freq[suffix]\n return ans \n``` | 45 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
python3 Solution | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | \n```\nclass Solution:\n def numOfPairs(self,nums:List[str],target:str)->int:\n n=len(nums)\n count=0\n for i in range(n):\n for j in range(n):\n if i!=j:\n if nums[i]+nums[j]==target:\n count+=1\n\n return count \n``` | 1 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
Python3|| Beats 94.22% | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | # Please upvote guys!\n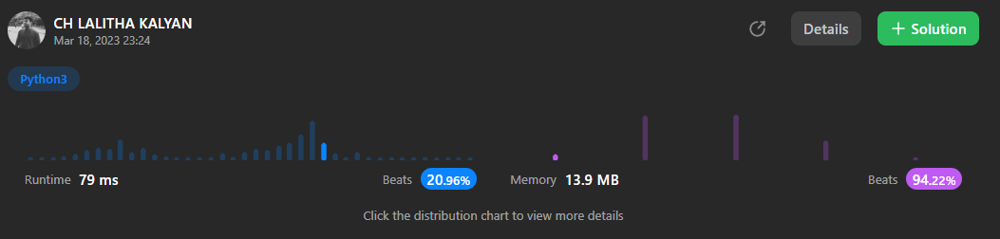\n\n# Code\n```\nclass Solution:\n def numOfPairs(self, nums: List[str], target: str) -> int:\n count=0\n for i in range(len(nums)):\n for j in range(len(nums)):\n if nums[i]+nums[j] == target and i!=j:\n count+=1\n return count\n``` | 2 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
[Python 3] Simple one-liner using permutations() | Straightforward | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | ```\nclass Solution:\n def numOfPairs(self, nums, target):\n return sum(i + j == target for i, j in permutations(nums, 2))\n``` | 5 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
Beste Easy Solution Bruteforce | number-of-pairs-of-strings-with-concatenation-equal-to-target | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nIterate And Slicing\n\n# Complexity\n- Time complexity:\nO(N^2)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def numOfPairs(self, nums: List[str], target: str) -> int:\n c=0\n for i in range(len(nums)): \n lst=[] \n lst=nums[:i]+nums[i+1:]\n for j in lst:\n if nums[i]+j==target:\n c+=1\n return c \n``` | 1 | Given an array of **digit** strings `nums` and a **digit** string `target`, return _the number of pairs of indices_ `(i, j)` _(where_ `i != j`_) such that the **concatenation** of_ `nums[i] + nums[j]` _equals_ `target`.
**Example 1:**
**Input:** nums = \[ "777 ", "7 ", "77 ", "77 "\], target = "7777 "
**Output:** 4
**Explanation:** Valid pairs are:
- (0, 1): "777 " + "7 "
- (1, 0): "7 " + "777 "
- (2, 3): "77 " + "77 "
- (3, 2): "77 " + "77 "
**Example 2:**
**Input:** nums = \[ "123 ", "4 ", "12 ", "34 "\], target = "1234 "
**Output:** 2
**Explanation:** Valid pairs are:
- (0, 1): "123 " + "4 "
- (2, 3): "12 " + "34 "
**Example 3:**
**Input:** nums = \[ "1 ", "1 ", "1 "\], target = "11 "
**Output:** 6
**Explanation:** Valid pairs are:
- (0, 1): "1 " + "1 "
- (1, 0): "1 " + "1 "
- (0, 2): "1 " + "1 "
- (2, 0): "1 " + "1 "
- (1, 2): "1 " + "1 "
- (2, 1): "1 " + "1 "
**Constraints:**
* `2 <= nums.length <= 100`
* `1 <= nums[i].length <= 100`
* `2 <= target.length <= 100`
* `nums[i]` and `target` consist of digits.
* `nums[i]` and `target` do not have leading zeros. | You need to maintain a sorted list for each movie and a sorted list for rented movies When renting a movie remove it from its movies sorted list and added it to the rented list and vice versa in the case of dropping a movie |
Python easy solution using collections | maximize-the-confusion-of-an-exam | 0 | 1 | \n# Code\n```\nimport collections\n\nclass Solution:\n def maxConsecutiveAnswers(self, answerKey: str, k: int) -> int:\n\n max_freq = i = 0\n char_count = collections.Counter()\n\n for j in range(len(answerKey)):\n char_count[answerKey[j]] += 1\n max_freq = max(max_freq, char_count[answerKey[j]])\n\n if j - i + 1 > max_freq + k:\n char_count[answerKey[i]] -= 1\n i += 1\n return len(answerKey) - i\n``` | 1 | A teacher is writing a test with `n` true/false questions, with `'T'` denoting true and `'F'` denoting false. He wants to confuse the students by **maximizing** the number of **consecutive** questions with the **same** answer (multiple trues or multiple falses in a row).
You are given a string `answerKey`, where `answerKey[i]` is the original answer to the `ith` question. In addition, you are given an integer `k`, the maximum number of times you may perform the following operation:
* Change the answer key for any question to `'T'` or `'F'` (i.e., set `answerKey[i]` to `'T'` or `'F'`).
Return _the **maximum** number of consecutive_ `'T'`s or `'F'`s _in the answer key after performing the operation at most_ `k` _times_.
**Example 1:**
**Input:** answerKey = "TTFF ", k = 2
**Output:** 4
**Explanation:** We can replace both the 'F's with 'T's to make answerKey = "TTTT ".
There are four consecutive 'T's.
**Example 2:**
**Input:** answerKey = "TFFT ", k = 1
**Output:** 3
**Explanation:** We can replace the first 'T' with an 'F' to make answerKey = "FFFT ".
Alternatively, we can replace the second 'T' with an 'F' to make answerKey = "TFFF ".
In both cases, there are three consecutive 'F's.
**Example 3:**
**Input:** answerKey = "TTFTTFTT ", k = 1
**Output:** 5
**Explanation:** We can replace the first 'F' to make answerKey = "TTTTTFTT "
Alternatively, we can replace the second 'F' to make answerKey = "TTFTTTTT ".
In both cases, there are five consecutive 'T's.
**Constraints:**
* `n == answerKey.length`
* `1 <= n <= 5 * 104`
* `answerKey[i]` is either `'T'` or `'F'`
* `1 <= k <= n` | null |
Simple Python || O(N) || Concise || Two Pointers ✅✅ | maximize-the-confusion-of-an-exam | 0 | 1 | # Approach\n> Calculating the minimum of the number of `T`s and `F`s. And, Trying to keep it smaller than `K`.\n\n> If it is greater than `K`, the size of the window is decreased.\nHere, the sliding window starts at `i` and ends at `j-1`\n# Code\n```\nclass Solution:\n def maxConsecutiveAnswers(self, answerKey: str, k: int) -> int:\n res=0; i=0; j=0; ans={\'T\':0, \'F\':0}\n while j<len(answerKey):\n while min(ans[\'T\'], ans[\'F\'])>k:\n ans[answerKey[i]]-=1\n i+=1\n ans[answerKey[j]]+=1\n j+=1\n if min(ans[\'T\'], ans[\'F\'])<=k:\n res=max(res, j-i)\n \n return res\n```\n\n\n | 1 | A teacher is writing a test with `n` true/false questions, with `'T'` denoting true and `'F'` denoting false. He wants to confuse the students by **maximizing** the number of **consecutive** questions with the **same** answer (multiple trues or multiple falses in a row).
You are given a string `answerKey`, where `answerKey[i]` is the original answer to the `ith` question. In addition, you are given an integer `k`, the maximum number of times you may perform the following operation:
* Change the answer key for any question to `'T'` or `'F'` (i.e., set `answerKey[i]` to `'T'` or `'F'`).
Return _the **maximum** number of consecutive_ `'T'`s or `'F'`s _in the answer key after performing the operation at most_ `k` _times_.
**Example 1:**
**Input:** answerKey = "TTFF ", k = 2
**Output:** 4
**Explanation:** We can replace both the 'F's with 'T's to make answerKey = "TTTT ".
There are four consecutive 'T's.
**Example 2:**
**Input:** answerKey = "TFFT ", k = 1
**Output:** 3
**Explanation:** We can replace the first 'T' with an 'F' to make answerKey = "FFFT ".
Alternatively, we can replace the second 'T' with an 'F' to make answerKey = "TFFF ".
In both cases, there are three consecutive 'F's.
**Example 3:**
**Input:** answerKey = "TTFTTFTT ", k = 1
**Output:** 5
**Explanation:** We can replace the first 'F' to make answerKey = "TTTTTFTT "
Alternatively, we can replace the second 'F' to make answerKey = "TTFTTTTT ".
In both cases, there are five consecutive 'T's.
**Constraints:**
* `n == answerKey.length`
* `1 <= n <= 5 * 104`
* `answerKey[i]` is either `'T'` or `'F'`
* `1 <= k <= n` | null |
[Python3] Counter of (Left - Right) at Each Pivot | maximum-number-of-ways-to-partition-an-array | 0 | 1 | ```python\nclass Solution:\n def waysToPartition(self, nums: List[int], k: int) -> int:\n """This is a good problem. It\'s not difficult, but is quite complex.\n\n The idea is that once we change a position at i, for all the pivots at\n 1...i, the sum of the left half stay the same whereas the sum of\n the right half changes by delta = k - nums[i]. Similarly, for all the\n pivots at i + 1...n - 1, the left half changes by delta, whereas the\n right half stay the same.\n\n We can pre-compute all the differences at each pivot position and make\n that into a diffs = [d1, d2, .... , dn-1]\n\n Then after a change at i, if we want the pivots at 1...i to form a good\n partition, we must have left - (right + delta) = 0 => delta = left - right\n In other words, the number of good partitions is the count of d1, d2, ...\n di that are equal to delta. Similarly, if we want the pivots at i + 1...\n n - 1 to form a good partition, we must have left + delta - right = 0\n => left - right = -delta. In other words, the number of good partitions\n is the count of di+1, ...., dn-1 that are equal to -delta.\n\n Based on this, we progressively build a left sum and right sum to\n compute the diffs array. And then progressively build a left counter\n and right counter to compute the number of matches to delta and -delta.\n\n The difficulty is in the implementation, especially with the indices.\n\n O(N), 7339 ms, faster than 32.20%\n """\n N = len(nums)\n diffs = []\n sl, sr = 0, sum(nums)\n for i in range(N - 1):\n sl += nums[i]\n sr -= nums[i]\n diffs.append(sl - sr)\n diffs.append(math.inf) # to prevent error in the counter arithemtic\n \n cl, cr = Counter(), Counter(diffs)\n res = cl[0] + cr[0]\n for i in range(N):\n d = k - nums[i]\n res = max(res, cl[d] + cr[-d])\n cl[diffs[i]] += 1\n cr[diffs[i]] -= 1\n return res\n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`. The number of ways to **partition** `nums` is the number of `pivot` indices that satisfy both conditions:
* `1 <= pivot < n`
* `nums[0] + nums[1] + ... + nums[pivot - 1] == nums[pivot] + nums[pivot + 1] + ... + nums[n - 1]`
You are also given an integer `k`. You can choose to change the value of **one** element of `nums` to `k`, or to leave the array **unchanged**.
Return _the **maximum** possible number of ways to **partition**_ `nums` _to satisfy both conditions after changing **at most** one element_.
**Example 1:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 1
**Explanation:** One optimal approach is to change nums\[0\] to k. The array becomes \[**3**,-1,2\].
There is one way to partition the array:
- For pivot = 2, we have the partition \[3,-1 | 2\]: 3 + -1 == 2.
**Example 2:**
**Input:** nums = \[0,0,0\], k = 1
**Output:** 2
**Explanation:** The optimal approach is to leave the array unchanged.
There are two ways to partition the array:
- For pivot = 1, we have the partition \[0 | 0,0\]: 0 == 0 + 0.
- For pivot = 2, we have the partition \[0,0 | 0\]: 0 + 0 == 0.
**Example 3:**
**Input:** nums = \[22,4,-25,-20,-15,15,-16,7,19,-10,0,-13,-14\], k = -33
**Output:** 4
**Explanation:** One optimal approach is to change nums\[2\] to k. The array becomes \[22,4,**\-33**,-20,-15,15,-16,7,19,-10,0,-13,-14\].
There are four ways to partition the array.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `-105 <= k, nums[i] <= 105` | Characters are independent—only the frequency of characters matters. It is possible to distribute characters if all characters can be divided equally among all strings. |
78% TC and 56% SC easy python solution | maximum-number-of-ways-to-partition-an-array | 0 | 1 | 1. Create a map of list , going thru the indices and make diff between right half and left half as key.\n2. Store all the indices in the list having the diff as x, as you gonna need it it later.\n3. Now try to change all the indices and check how many indices could now become your pivot.\n4. So you are changing a num, nums[i] to k.\n5. Let\'s assume this i index is in the left of pivot. So by changing nums[i] to k, you are increasing the sum of left half by k-nums[i].\n6. So all the pivots where the right half\'s sum was (k-nums[i]) grater than left half\'s sum, would now be balanced, as you have added that (k-nums[i]) to the left. So just find out how many indices are in the RIGHT of index i, having such diff. Now, those all will be counted as pivots.\n7. Now go back to step 5. We had assumed the index i to be in the left of pivot. Nows the time to take it the other way.\n8. Now the index i is inthe right of pivot. By changing nums[i] to k, we have increased right half by (k-nums[i]).\n9. So search for all the indices having left half\'s sum more than rights\'s half by (k-nums[i]). \n10. The ans for the index i would be the sum of the both assumptions we have taken.\n11. Do the same for all the indices. Max of all will be your answer. :)\n ```\ndef waysToPartition(self, nums: List[int], k: int) -> int:\n\tl, r = 0, sum(nums)\n\td = defaultdict(list)\n\tprev = nums[0]\n\tn = len(nums)\n\tans = 0\n\tfor i in range(1, n):\n\t\tl += prev\n\t\tr -= prev\n\t\tif(l == r): ans += 1\n\t\td[r-l].append(i)\n\t\tprev = nums[i]\n\tfor i in range(n):\n\t\tdiff = k-nums[i]\n\t\tleft = right = 0\n\t\tif(diff in d):\n\t\t\tright = len(d[diff]) - bisect_left(d[diff], i+1)\n\t\tif(d[-diff] and d[-diff][0] <= i):\n\t\t\tleft = bisect_right(d[-diff], i)\n\t\tans = max(ans, left+right)\n\treturn ans\n``` | 2 | You are given a **0-indexed** integer array `nums` of length `n`. The number of ways to **partition** `nums` is the number of `pivot` indices that satisfy both conditions:
* `1 <= pivot < n`
* `nums[0] + nums[1] + ... + nums[pivot - 1] == nums[pivot] + nums[pivot + 1] + ... + nums[n - 1]`
You are also given an integer `k`. You can choose to change the value of **one** element of `nums` to `k`, or to leave the array **unchanged**.
Return _the **maximum** possible number of ways to **partition**_ `nums` _to satisfy both conditions after changing **at most** one element_.
**Example 1:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 1
**Explanation:** One optimal approach is to change nums\[0\] to k. The array becomes \[**3**,-1,2\].
There is one way to partition the array:
- For pivot = 2, we have the partition \[3,-1 | 2\]: 3 + -1 == 2.
**Example 2:**
**Input:** nums = \[0,0,0\], k = 1
**Output:** 2
**Explanation:** The optimal approach is to leave the array unchanged.
There are two ways to partition the array:
- For pivot = 1, we have the partition \[0 | 0,0\]: 0 == 0 + 0.
- For pivot = 2, we have the partition \[0,0 | 0\]: 0 + 0 == 0.
**Example 3:**
**Input:** nums = \[22,4,-25,-20,-15,15,-16,7,19,-10,0,-13,-14\], k = -33
**Output:** 4
**Explanation:** One optimal approach is to change nums\[2\] to k. The array becomes \[22,4,**\-33**,-20,-15,15,-16,7,19,-10,0,-13,-14\].
There are four ways to partition the array.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `-105 <= k, nums[i] <= 105` | Characters are independent—only the frequency of characters matters. It is possible to distribute characters if all characters can be divided equally among all strings. |
Prefix Sum + 2 hash tables in python3 | maximum-number-of-ways-to-partition-an-array | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def waysToPartition(self, nums: List[int], k: int) -> int:\n s = sum(nums)\n n = len(nums)\n prefix = []\n suffix = []\n currsum = 0\n diff = {}\n for i,a in enumerate(nums[:-1]):\n currsum += a\n prefix.append(currsum)\n suffix.append(s-currsum)\n d = currsum - (s-currsum)\n if i < n-1:# empty partition is not allowed\n if d not in diff:\n diff[d] = 0\n diff[d] += 1\n #first, iterate through the array to construct the prefix array and the suffix array\n prediff = {}\n res = 0\n if 0 in diff:\n res = diff[0]\n # this is the case when we don\'t change any element in the array\n for i,a in enumerate(nums):\n currmax = 0\n # when the element at the current index is changed to k, :\n #1.all prefixes before it does not change while the suffixes after it increases by k-a, leading to a change in the difference of a-k, thus look for all differences of k-a before i\n #2.all prefixes after it increase by k-a while the suffixes do not change, leading to a change in differnce of k-a, we look for all differences a-k after index i by subtracting the two values in the two hashtables\n if k-a in prediff:\n currmax += prediff[k-a]\n if a-k in diff:\n currmax += diff[a-k]\n if a-k in prediff:\n currmax -= prediff[a-k]\n #currmax is the best result we can get by changing arr[i] to k\n res = max(res,currmax)\n # update the difference hastable so far\n p = prefix[i]\n s = suffix[i]\n currd = p - s\n if currd not in prediff:\n prediff[currd] = 0\n prediff[currd] += 1\n return res\n\n\n \n``` | 0 | You are given a **0-indexed** integer array `nums` of length `n`. The number of ways to **partition** `nums` is the number of `pivot` indices that satisfy both conditions:
* `1 <= pivot < n`
* `nums[0] + nums[1] + ... + nums[pivot - 1] == nums[pivot] + nums[pivot + 1] + ... + nums[n - 1]`
You are also given an integer `k`. You can choose to change the value of **one** element of `nums` to `k`, or to leave the array **unchanged**.
Return _the **maximum** possible number of ways to **partition**_ `nums` _to satisfy both conditions after changing **at most** one element_.
**Example 1:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 1
**Explanation:** One optimal approach is to change nums\[0\] to k. The array becomes \[**3**,-1,2\].
There is one way to partition the array:
- For pivot = 2, we have the partition \[3,-1 | 2\]: 3 + -1 == 2.
**Example 2:**
**Input:** nums = \[0,0,0\], k = 1
**Output:** 2
**Explanation:** The optimal approach is to leave the array unchanged.
There are two ways to partition the array:
- For pivot = 1, we have the partition \[0 | 0,0\]: 0 == 0 + 0.
- For pivot = 2, we have the partition \[0,0 | 0\]: 0 + 0 == 0.
**Example 3:**
**Input:** nums = \[22,4,-25,-20,-15,15,-16,7,19,-10,0,-13,-14\], k = -33
**Output:** 4
**Explanation:** One optimal approach is to change nums\[2\] to k. The array becomes \[22,4,**\-33**,-20,-15,15,-16,7,19,-10,0,-13,-14\].
There are four ways to partition the array.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `-105 <= k, nums[i] <= 105` | Characters are independent—only the frequency of characters matters. It is possible to distribute characters if all characters can be divided equally among all strings. |
[Python3] binary search | maximum-number-of-ways-to-partition-an-array | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/182350e41572fb26ffb8c44204b037cc9f0e5035) for solutions of biweekly 62. \n```\nclass Solution:\n def waysToPartition(self, nums: List[int], k: int) -> int:\n prefix = [0]\n loc = defaultdict(list)\n for i, x in enumerate(nums): \n prefix.append(prefix[-1] + x)\n if i < len(nums)-1: loc[prefix[-1]].append(i)\n \n ans = 0 \n if prefix[-1] % 2 == 0: ans = len(loc[prefix[-1]//2]) # unchanged \n \n total = prefix[-1]\n for i, x in enumerate(nums): \n cnt = 0 \n diff = k - x\n target = total + diff \n if target % 2 == 0: \n target //= 2\n cnt += bisect_left(loc[target], i)\n cnt += len(loc[target-diff]) - bisect_left(loc[target-diff], i)\n ans = max(ans, cnt)\n return ans \n``` | 2 | You are given a **0-indexed** integer array `nums` of length `n`. The number of ways to **partition** `nums` is the number of `pivot` indices that satisfy both conditions:
* `1 <= pivot < n`
* `nums[0] + nums[1] + ... + nums[pivot - 1] == nums[pivot] + nums[pivot + 1] + ... + nums[n - 1]`
You are also given an integer `k`. You can choose to change the value of **one** element of `nums` to `k`, or to leave the array **unchanged**.
Return _the **maximum** possible number of ways to **partition**_ `nums` _to satisfy both conditions after changing **at most** one element_.
**Example 1:**
**Input:** nums = \[2,-1,2\], k = 3
**Output:** 1
**Explanation:** One optimal approach is to change nums\[0\] to k. The array becomes \[**3**,-1,2\].
There is one way to partition the array:
- For pivot = 2, we have the partition \[3,-1 | 2\]: 3 + -1 == 2.
**Example 2:**
**Input:** nums = \[0,0,0\], k = 1
**Output:** 2
**Explanation:** The optimal approach is to leave the array unchanged.
There are two ways to partition the array:
- For pivot = 1, we have the partition \[0 | 0,0\]: 0 == 0 + 0.
- For pivot = 2, we have the partition \[0,0 | 0\]: 0 + 0 == 0.
**Example 3:**
**Input:** nums = \[22,4,-25,-20,-15,15,-16,7,19,-10,0,-13,-14\], k = -33
**Output:** 4
**Explanation:** One optimal approach is to change nums\[2\] to k. The array becomes \[22,4,**\-33**,-20,-15,15,-16,7,19,-10,0,-13,-14\].
There are four ways to partition the array.
**Constraints:**
* `n == nums.length`
* `2 <= n <= 105`
* `-105 <= k, nums[i] <= 105` | Characters are independent—only the frequency of characters matters. It is possible to distribute characters if all characters can be divided equally among all strings. |
Python3 Neat Code | minimum-moves-to-convert-string | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n ans=i=0\n while i<len(s):\n if s[i]==\'O\':i+=1\n else:\n i+=3\n ans+=1\n return ans\n``` | 1 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
[Python3] scan | minimum-moves-to-convert-string | 0 | 1 | \n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n ans = i = 0\n while i < len(s): \n if s[i] == "X": \n ans += 1\n i += 3\n else: i += 1\n return ans \n``` | 35 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
✅ 99% beats || Python3 || While loop | minimum-moves-to-convert-string | 0 | 1 | # Intuition\n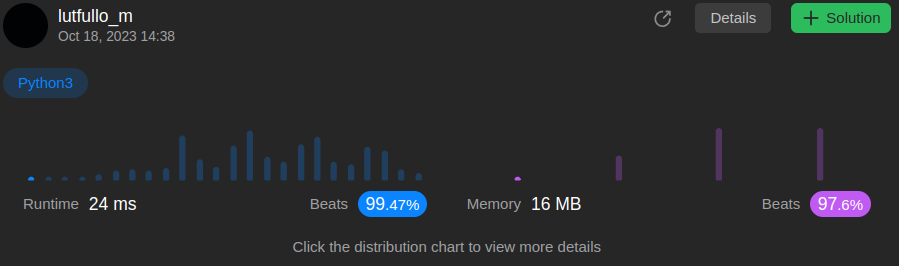\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n Use while.\n\n 1.Assign i pointer to while loop as given word`s index.\n\n 2.Ckeck if word`s char is "X", if so incraese i to 3 when it turns out "X" each time otherwise increase 1 and count each operation.\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n counter = 0\n length = len(s)\n i = 0\n\n while i < length:\n\n if s[i] == "X":\n counter += 1\n i += 3\n else:\n i += 1\n return counter\n\n\nobj = Solution()\nprint(obj.minimumMoves(s="OXOXXOXX"))\n\n``` | 1 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
2027. Run time - 95.42% | Memory - 87% | minimum-moves-to-convert-string | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n ind, moves = 0, 0\n n = len(s)\n while ind < n:\n if s[ind] == \'X\':\n ind += 3\n moves += 1\n else:\n ind += 1\n return moves\n\n``` | 2 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
Easy Python Solution | Faster than 99% (24 ms) | minimum-moves-to-convert-string | 0 | 1 | # Easy Python Solution | Faster than 99% (24 ms)\n**Runtime: 24 ms, faster than 99% of Python3 online submissions for Minimum Moves to Convert String.\nMemory Usage: 14.2 MB.**\n\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n i, m = 0, 0\n l = len(s)\n\n while i < l:\n if s[i] != \'X\':\n i += 1\n elif \'X\' not in s[i:i+1]:\n i += 2\n elif \'X\' in s[i:i+2]:\n m += 1\n i += 3\n return m\n``` | 6 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
Python fast and simple solution | minimum-moves-to-convert-string | 0 | 1 | \n# Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n count = 0\n last = None\n for index,item in enumerate(s):\n if item == \'X\' and (last == None or abs(last - index) > 2):\n last = index\n count +=1 \n \n return count\n``` | 0 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
Simple solutions for begineer | minimum-moves-to-convert-string | 0 | 1 | # Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n # bruteforce solutions\n # 33ms\n # Beats 88.92% of users with Python3\n """\n ret, l = 0, 0\n while l < len(s):\n if s[l] == "X":\n if l+3 > len(s):\n s = s[:l] + "0" * (len(s) - l)\n else:\n s = s[:l] + "000" + s[l+3:]\n ret += 1\n l += 2\n \n l += 1\n \n return ret\n """\n\n # we can use without changing s\n ret, l = 0, 0\n while l < len(s):\n if s[l] == "X":\n ret += 1\n l += 2\n \n l += 1\n \n return ret\n``` | 0 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
Not easy but works | minimum-moves-to-convert-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumMoves(self, s: str) -> int:\n l = len(s)\n sm = 0\n i = 0\n while(i<l):\n if s[i] ==\'O\':\n i+=1\n\n else:\n p = s[i:i+3]\n print(p)\n if "X" in p:\n sm +=1\n s[i:i+3].replace(\'X\',\'0\')\n i+=3\n print(i) \n\n return sm \n \n \n``` | 0 | You are given a string `s` consisting of `n` characters which are either `'X'` or `'O'`.
A **move** is defined as selecting **three** **consecutive characters** of `s` and converting them to `'O'`. Note that if a move is applied to the character `'O'`, it will stay the **same**.
Return _the **minimum** number of moves required so that all the characters of_ `s` _are converted to_ `'O'`.
**Example 1:**
**Input:** s = "XXX "
**Output:** 1
**Explanation:** XXX -> OOO
We select all the 3 characters and convert them in one move.
**Example 2:**
**Input:** s = "XXOX "
**Output:** 2
**Explanation:** XXOX -> OOOX -> OOOO
We select the first 3 characters in the first move, and convert them to `'O'`.
Then we select the last 3 characters and convert them so that the final string contains all `'O'`s.
**Example 3:**
**Input:** s = "OOOO "
**Output:** 0
**Explanation:** There are no `'X's` in `s` to convert.
**Constraints:**
* `3 <= s.length <= 1000`
* `s[i]` is either `'X'` or `'O'`. | First, we need to think about solving an easier problem, If we remove a set of indices from the string does P exist in S as a subsequence We can binary search the K and check by solving the above problem. |
Python Easy Solution || Logic | find-missing-observations | 0 | 1 | # Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n curSum=sum(rolls)\n obv=n+len(rolls)\n missSum=mean*obv-curSum\n if missSum>6*n or missSum<0 or missSum<n:\n return []\n x=missSum//n\n res=[x]*n\n remain=missSum-x*n\n if remain>0:\n more=6-x\n add=remain//more\n res=res[add:]+[6]*add\n final=remain%more\n res[0]+=final\n return res\n \n``` | 1 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
Easy to Understand || 72% || Python3 | find-missing-observations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n m = len(rolls)\n sums = mean * (m+n) - sum(rolls)\n\n if sums < n or not ( 1 <= sums / n <= 6):\n return list()\n if sums % n == 0:\n return [sums // n] * n\n else:\n k = sums % n\n res = [sums//n] * n\n for i in range(k):\n res[i] += 1\n return res\n \n``` | 2 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
O(m+n) time | O(n) space | solution explained | find-missing-observations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind the sum of missing n rolls\n*missing sum = target sum - sum of m rolls = mean * (m + n) - sum of m rolls*\n\nCheck if the missing sum can be distributed to n rolls. If yes, find the average *(missing sum / n)* and distribute it. Distribute the remainder also if any.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- compute the target sum i.e mean * (m + n)\n- compute the missing sum i.e target sum - sum of m rolls\n- if the missing sum is less than n or more than n * 6, return an empty list because it can\'t be distributed\n- find the average n_avg and remainder n_mod\n- create a result list of size n and initialize it with n_avg to give each roll distribution of the average\n- distribute the remainder\n - loop in range n_mod\n - increment the value in the result list by 1\n- return the result list\n\n# Complexity\n- Time complexity: O(finding sum of m rolls + creating result list to distribute the average + distributing remainder) \u2192 O(m + n + n) \u2192 O(m + n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(result list) \u2192 O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n target_sum = (len(rolls) + n) * mean\n missing_sum = target_sum - sum(rolls)\n if missing_sum < n or missing_sum > n * 6:\n return []\n n_avg, n_mod = missing_sum // n, missing_sum % n\n res = [n_avg] * n\n for i in range(n_mod):\n res[i] += 1\n return res\n``` | 2 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
beats 97% easy to understand | find-missing-observations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfirst calculate if the sum is achevable, then calculate the dice value by average and modulos\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n diff = (mean * (n + len(rolls))) - sum(rolls)\n ans = []\n if diff < n or diff > n * 6:\n return ans\n \n av = diff//n\n mod = diff%n\n for x in range(n):\n if mod > x:\n ans.append(av + 1)\n else: \n ans.append(av)\n return ans\n\n``` | 0 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
Python beats 95% 1 loop subtract from sum as you go | find-missing-observations | 0 | 1 | ```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n #rolls has the m rolls\n #mean is the mean of m + n rolls\n #n is the len of missing rolls\n #return all n rolls\n #sum_m = sum(rolls)\n #sum_n = (mean*n)\n #mean = sum (m+n) / len (m + n)\n #sum = mean*len\n #sum_all = mean*(sum(rolls)+n)\n des_sum = (len(rolls) + n)*mean\n n_sum = des_sum - sum(rolls)\n returner = []\n \n while n_sum > 0:\n appender = n_sum // (n-len(returner))\n #print(appender)\n if appender > 6 or appender < 1:\n return []\n returner.append(appender)\n n_sum -= appender\n #print("returner",returner,"len(returner)",len(returner))\n #print("n_sum",n_sum)\n \n return returner\n``` | 0 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
Fastest Python solution. Beat 100% | find-missing-observations | 0 | 1 | # Intuition\nFirst check if the problem is solvable by calculating the max. and min. change in mean possible. Then calculate the missing sum and the dice throws within that.\n\n# Approach\nSince the programm is supposed to run as fast as possible, it makes sense to first calculate if the problem has a solution at all. To do that we check if the current mean of rolls is below or over the obserevd mean. If it is lower we de the maximum amount possible (n times six) the the sum and take the mean again. If it is still lower the problem has no solution. Same for the case of a higher mean. There we add the lowest possible sum (n times one) and check again.\nIf there is no solution we should return the empty array. \nNow that we are certain that there is a solution we can start the search for the missing dice rolls.\n\nFirst we calulate the missing sl (sum left) which we get by multiplying the mean by the sum of n and the length of rolls and then subtracting the sum we already have from rolls.\nThe sum now has to be distributed to n dice rolls.\n\nThe algorithm I chose for this follows 3 rules:\nIf the sl - 6 is bigger or equal to the number of dices rolls that still have to be determined: Then add a dice roll of 6 to the return and decrease sl by 6\nIf sl - 6 is exactly equal to the number of dice rolls that still have to be determined: Just fill all of them with a 1\nThe only case left is that sl - 6 is bigger than the number of dice rolls left but not by 6. This will only happen once. So we just make sl equal to the number of rolls left by choosing this roll to be the difference of sl that the number of dice rolls left. \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n+c)$$\n\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n l = len(rolls)\n sr = sum(rolls)\n mr = sr / l\n if mr > mean: \n if (sr + n) / (l + n) > mean: return []\n elif mr < mean:\n if (sr + (6 * n)) / (l + n) < mean: return []\n sl = mean * (n + l) - sr\n ra = []\n for i in range(n):\n if (sl - 6) >= (n - i - 1):\n sl -= 6\n ra.append(6)\n elif sl == (n - i - 1): \n sl -= 1\n ra.append(1)\n else:\n t = sl - (n - i - 1)\n ra.append(t)\n sl -= t\n return ra\n``` | 0 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
O(N) solution beats 100% | find-missing-observations | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n \n #this is kind of interesting\n val = sum(rolls)\n missing = mean * (n + len(rolls)) - val\n\n if missing/n > float(6):\n return []\n if missing < 0:\n return []\n if missing < n:\n return []\n\n ans = []\n val = missing//n\n\n\n for i in range(n):\n ans.append(val)\n \n additional = missing - sum(ans)\n for i in range(missing - sum(ans)):\n ans[i] += 1\n\n\n\n return ans\n``` | 0 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
Python Simple Solution | 90% | 4 lines | find-missing-observations | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nFind the target sum of the unknown observations by using the average calculation. Ensure the target sum is reachable by checking targetSum > n (roll 1 each time) and targetSum < 6*n (roll 6 each time).\n\nThen, it\'s simply a matter of finding a combination of dice rolls that sums to targetSum. Divide targetSum by n to get a \'base\' number, and store the remainder. \n\nFor example, if targetSum = 28 and n = 5, our base is 5 and remainder is 3. Our base result would be `[5,5,5,5,5]`, then \'top up\' the remainder amount to turn it into `[6,6,6,5,5]`.\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N+M)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def missingRolls(self, rolls: List[int], mean: int, n: int) -> List[int]:\n targetSum = mean * (n + len(rolls)) - sum(rolls)\n if 6 * n < targetSum or targetSum < n: return []\n base,remainder = divmod(targetSum,n)\n return [base]*(n-remainder) + [base+1]*remainder\n\n``` | 0 | You have observations of `n + m` **6-sided** dice rolls with each face numbered from `1` to `6`. `n` of the observations went missing, and you only have the observations of `m` rolls. Fortunately, you have also calculated the **average value** of the `n + m` rolls.
You are given an integer array `rolls` of length `m` where `rolls[i]` is the value of the `ith` observation. You are also given the two integers `mean` and `n`.
Return _an array of length_ `n` _containing the missing observations such that the **average value** of the_ `n + m` _rolls is **exactly**_ `mean`. If there are multiple valid answers, return _any of them_. If no such array exists, return _an empty array_.
The **average value** of a set of `k` numbers is the sum of the numbers divided by `k`.
Note that `mean` is an integer, so the sum of the `n + m` rolls should be divisible by `n + m`.
**Example 1:**
**Input:** rolls = \[3,2,4,3\], mean = 4, n = 2
**Output:** \[6,6\]
**Explanation:** The mean of all n + m rolls is (3 + 2 + 4 + 3 + 6 + 6) / 6 = 4.
**Example 2:**
**Input:** rolls = \[1,5,6\], mean = 3, n = 4
**Output:** \[2,3,2,2\]
**Explanation:** The mean of all n + m rolls is (1 + 5 + 6 + 2 + 3 + 2 + 2) / 7 = 3.
**Example 3:**
**Input:** rolls = \[1,2,3,4\], mean = 6, n = 4
**Output:** \[\]
**Explanation:** It is impossible for the mean to be 6 no matter what the 4 missing rolls are.
**Constraints:**
* `m == rolls.length`
* `1 <= n, m <= 105`
* `1 <= rolls[i], mean <= 6` | Brute force using bitmasks and simulate the rounds. Calculate each state one time and save its solution. |
[Python3] freq table | stone-game-ix | 0 | 1 | **Intuition**\nHere, the specific numbers don\'t matter. Only the modulos do. \nIn order for Alice to win, the sequence would be like \n1) 1(12)(12)...(12)2 with even number of 0\'s between first 1 and final 2\n2) 1(12)(12)...(12)11 with odd number of 0\'s between first 1 and final 1\n\nwhere 1\'s and 2\'s are interchangable due to symmetry. So the strategy is \n1) if there are even number of 0\'s, Alice would choose 1 or 2 whoever is less or equal frequent as long as they both exist. Without loss of generality, let\'s say 1 is less frequent. In this case, it is guranteed to be Bob\'s turn to place the last number 2 when they run out of 1\'s. \n2) if there are odd number of 0\'s, Alice would choose 1 or 2 whoever is more frequent. Let\'s say 1 is more frequent in the input. In this case, Alice need three extra 1\'s to win. Besides, it is not difficult to figure out that as long as there are three (or more) extra 1\'s Alice will win. \n\n```\nclass Solution:\n def stoneGameIX(self, stones: List[int]) -> bool:\n freq = defaultdict(int)\n for x in stones: freq[x % 3] += 1\n \n if freq[0]%2 == 0: return freq[1] and freq[2]\n return abs(freq[1] - freq[2]) >= 3\n``` | 4 | Alice and Bob continue their games with stones. There is a row of n stones, and each stone has an associated value. You are given an integer array `stones`, where `stones[i]` is the **value** of the `ith` stone.
Alice and Bob take turns, with **Alice** starting first. On each turn, the player may remove any stone from `stones`. The player who removes a stone **loses** if the **sum** of the values of **all removed stones** is divisible by `3`. Bob will win automatically if there are no remaining stones (even if it is Alice's turn).
Assuming both players play **optimally**, return `true` _if Alice wins and_ `false` _if Bob wins_.
**Example 1:**
**Input:** stones = \[2,1\]
**Output:** true
**Explanation:** The game will be played as follows:
- Turn 1: Alice can remove either stone.
- Turn 2: Bob removes the remaining stone.
The sum of the removed stones is 1 + 2 = 3 and is divisible by 3. Therefore, Bob loses and Alice wins the game.
**Example 2:**
**Input:** stones = \[2\]
**Output:** false
**Explanation:** Alice will remove the only stone, and the sum of the values on the removed stones is 2.
Since all the stones are removed and the sum of values is not divisible by 3, Bob wins the game.
**Example 3:**
**Input:** stones = \[5,1,2,4,3\]
**Output:** false
**Explanation:** Bob will always win. One possible way for Bob to win is shown below:
- Turn 1: Alice can remove the second stone with value 1. Sum of removed stones = 1.
- Turn 2: Bob removes the fifth stone with value 3. Sum of removed stones = 1 + 3 = 4.
- Turn 3: Alices removes the fourth stone with value 4. Sum of removed stones = 1 + 3 + 4 = 8.
- Turn 4: Bob removes the third stone with value 2. Sum of removed stones = 1 + 3 + 4 + 2 = 10.
- Turn 5: Alice removes the first stone with value 5. Sum of removed stones = 1 + 3 + 4 + 2 + 5 = 15.
Alice loses the game because the sum of the removed stones (15) is divisible by 3. Bob wins the game.
**Constraints:**
* `1 <= stones.length <= 105`
* `1 <= stones[i] <= 104` | Is there a particular way we should order the arrays such that the product sum is minimized? Would you want to multiply two numbers that are closer to one another or further? |
python clean and short solution | stone-game-ix | 0 | 1 | ```\nclass Solution:\n def stoneGameIX(self, stones: List[int]) -> bool:\n stones = [v % 3 for v in stones]\n \n d = defaultdict(int)\n for v in stones:\n d[v] += 1\n \n while d[1] >= 2 and d[2] >= 2:\n d[2] -= 1\n d[1] -= 1\n \n if d[0] % 2 == 0: # number of 0s will not influent the result\n if (d[1] == 1 and d[2] >= 1) or (d[2] == 1 and d[1] >= 1):\n return True\n else:\n if (d[1] == 0 and d[2] >= 3) or (d[2] == 0 and d[1] >= 3):\n return True\n if (d[1] == 1 and d[2] >= 4) or (d[2] == 1 and d[1] >= 4):\n return True\n\n return False\n````\t\t | 1 | Alice and Bob continue their games with stones. There is a row of n stones, and each stone has an associated value. You are given an integer array `stones`, where `stones[i]` is the **value** of the `ith` stone.
Alice and Bob take turns, with **Alice** starting first. On each turn, the player may remove any stone from `stones`. The player who removes a stone **loses** if the **sum** of the values of **all removed stones** is divisible by `3`. Bob will win automatically if there are no remaining stones (even if it is Alice's turn).
Assuming both players play **optimally**, return `true` _if Alice wins and_ `false` _if Bob wins_.
**Example 1:**
**Input:** stones = \[2,1\]
**Output:** true
**Explanation:** The game will be played as follows:
- Turn 1: Alice can remove either stone.
- Turn 2: Bob removes the remaining stone.
The sum of the removed stones is 1 + 2 = 3 and is divisible by 3. Therefore, Bob loses and Alice wins the game.
**Example 2:**
**Input:** stones = \[2\]
**Output:** false
**Explanation:** Alice will remove the only stone, and the sum of the values on the removed stones is 2.
Since all the stones are removed and the sum of values is not divisible by 3, Bob wins the game.
**Example 3:**
**Input:** stones = \[5,1,2,4,3\]
**Output:** false
**Explanation:** Bob will always win. One possible way for Bob to win is shown below:
- Turn 1: Alice can remove the second stone with value 1. Sum of removed stones = 1.
- Turn 2: Bob removes the fifth stone with value 3. Sum of removed stones = 1 + 3 = 4.
- Turn 3: Alices removes the fourth stone with value 4. Sum of removed stones = 1 + 3 + 4 = 8.
- Turn 4: Bob removes the third stone with value 2. Sum of removed stones = 1 + 3 + 4 + 2 = 10.
- Turn 5: Alice removes the first stone with value 5. Sum of removed stones = 1 + 3 + 4 + 2 + 5 = 15.
Alice loses the game because the sum of the removed stones (15) is divisible by 3. Bob wins the game.
**Constraints:**
* `1 <= stones.length <= 105`
* `1 <= stones[i] <= 104` | Is there a particular way we should order the arrays such that the product sum is minimized? Would you want to multiply two numbers that are closer to one another or further? |
Monotonic Stack | smallest-k-length-subsequence-with-occurrences-of-a-letter | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBased on the increasing monotonic stack, keep the smallest letter in the stack.\nFor this problem, require the specified letters for repetition times.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstack pop:\nwhen current stack last letter is smaller than current letter and the stack size combined with leftover letters that have not been visited is still enough to compose a string of length k,and:\n1 if current letter is the specified letter, we can pop the element in the stack\n2 if current letter is not the specified letter, but the leftover string still have enough specified letters \n\nthis element could be poped.\n\nstack push:\nwhen current letter is the specified letter, push it\nwhen current letter is not the specified letter, just make sure there are enough spaces for pushing the specified letter.\n\nwhenever the specified letter is visited, reduce the leftover letter that could be available for pushing to the stack. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(K)\n# Code\n```\nclass Solution:\n def smallestSubsequence(self, s: str, k: int, letter: str, repetition: int) -> str:\n m, n = Counter(s), len(s)\n stack = []\n cnt = m[letter]\n for i, c in enumerate(s):\n while stack and stack[-1] > c and len(stack) + n - i - 1 >= k and (stack[-1] !=letter or cnt > repetition):\n top_c = stack[-1]\n if top_c == letter:\n repetition += 1\n stack.pop()\n \n if len(stack) < k:\n if c == letter:\n stack.append(c)\n repetition -= 1\n elif k - len(stack) > repetition:\n stack.append(c)\n if c== letter:\n cnt = cnt - 1\n return "".join(stack)\n\n \n \n \n``` | 0 | You are given a string `s`, an integer `k`, a letter `letter`, and an integer `repetition`.
Return _the **lexicographically smallest** subsequence of_ `s` _of length_ `k` _that has the letter_ `letter` _appear **at least**_ `repetition` _times_. The test cases are generated so that the `letter` appears in `s` **at least** `repetition` times.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A string `a` is **lexicographically smaller** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`.
**Example 1:**
**Input:** s = "leet ", k = 3, letter = "e ", repetition = 1
**Output:** "eet "
**Explanation:** There are four subsequences of length 3 that have the letter 'e' appear at least 1 time:
- "lee " (from "**lee**t ")
- "let " (from "**le**e**t** ")
- "let " (from "**l**e**et** ")
- "eet " (from "l**eet** ")
The lexicographically smallest subsequence among them is "eet ".
**Example 2:**
**Input:** s = "leetcode ", k = 4, letter = "e ", repetition = 2
**Output:** "ecde "
**Explanation:** "ecde " is the lexicographically smallest subsequence of length 4 that has the letter "e " appear at least 2 times.
**Example 3:**
**Input:** s = "bb ", k = 2, letter = "b ", repetition = 2
**Output:** "bb "
**Explanation:** "bb " is the only subsequence of length 2 that has the letter "b " appear at least 2 times.
**Constraints:**
* `1 <= repetition <= k <= s.length <= 5 * 104`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter, and appears in `s` at least `repetition` times. | null |
Python Heap based solution | smallest-k-length-subsequence-with-occurrences-of-a-letter | 0 | 1 | # Complexity\n- Time complexity:\n$$O(N * log(N))$$\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```\nclass Solution:\n def smallestSubsequence(self, s: str, k: int, letter: str, repetition: int) -> str:\n suffix_count = [0 for _ in range(len(s) + 1)]\n\n for i in range(len(s) - 1, -1, -1):\n suffix_count[i] = suffix_count[i + 1] + int(s[i] == letter)\n \n heap = []\n result = []\n in_result = right = left = 0\n \n while len(result) < k:\n while heap and heap[0][1] < left:\n ch = heappop(heap)\n \n while right < len(s) and len(s) - right >= k - len(result) and suffix_count[right] >= repetition - in_result:\n heappush(heap, (s[right], right))\n right += 1\n\n ch, idx = heappop(heap)\n \n in_result += int(ch == letter)\n if ch == letter or k - len(result) > repetition - in_result:\n result.append(ch)\n left = idx + 1\n \n return "".join(result)\n``` | 0 | You are given a string `s`, an integer `k`, a letter `letter`, and an integer `repetition`.
Return _the **lexicographically smallest** subsequence of_ `s` _of length_ `k` _that has the letter_ `letter` _appear **at least**_ `repetition` _times_. The test cases are generated so that the `letter` appears in `s` **at least** `repetition` times.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A string `a` is **lexicographically smaller** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`.
**Example 1:**
**Input:** s = "leet ", k = 3, letter = "e ", repetition = 1
**Output:** "eet "
**Explanation:** There are four subsequences of length 3 that have the letter 'e' appear at least 1 time:
- "lee " (from "**lee**t ")
- "let " (from "**le**e**t** ")
- "let " (from "**l**e**et** ")
- "eet " (from "l**eet** ")
The lexicographically smallest subsequence among them is "eet ".
**Example 2:**
**Input:** s = "leetcode ", k = 4, letter = "e ", repetition = 2
**Output:** "ecde "
**Explanation:** "ecde " is the lexicographically smallest subsequence of length 4 that has the letter "e " appear at least 2 times.
**Example 3:**
**Input:** s = "bb ", k = 2, letter = "b ", repetition = 2
**Output:** "bb "
**Explanation:** "bb " is the only subsequence of length 2 that has the letter "b " appear at least 2 times.
**Constraints:**
* `1 <= repetition <= k <= s.length <= 5 * 104`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter, and appears in `s` at least `repetition` times. | null |
Python (Simple Stack Solution) | smallest-k-length-subsequence-with-occurrences-of-a-letter | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestSubsequence(self, s, k, letter, repetition):\n n, count, stack = len(s), sum(x == letter for x in s), []\n\n for i,j in enumerate(s):\n while stack and stack[-1] > j and len(stack) + n - i > k and (stack[-1] != letter or repetition < count):\n if stack.pop() == letter: repetition += 1\n\n if len(stack) < k and (j == letter or len(stack) + repetition < k):\n stack.append(j)\n if j == letter: repetition -= 1\n\n if j == letter: count -= 1\n\n return "".join(stack)\n\n \n\n\n\n\n\n\n \n \n``` | 1 | You are given a string `s`, an integer `k`, a letter `letter`, and an integer `repetition`.
Return _the **lexicographically smallest** subsequence of_ `s` _of length_ `k` _that has the letter_ `letter` _appear **at least**_ `repetition` _times_. The test cases are generated so that the `letter` appears in `s` **at least** `repetition` times.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A string `a` is **lexicographically smaller** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`.
**Example 1:**
**Input:** s = "leet ", k = 3, letter = "e ", repetition = 1
**Output:** "eet "
**Explanation:** There are four subsequences of length 3 that have the letter 'e' appear at least 1 time:
- "lee " (from "**lee**t ")
- "let " (from "**le**e**t** ")
- "let " (from "**l**e**et** ")
- "eet " (from "l**eet** ")
The lexicographically smallest subsequence among them is "eet ".
**Example 2:**
**Input:** s = "leetcode ", k = 4, letter = "e ", repetition = 2
**Output:** "ecde "
**Explanation:** "ecde " is the lexicographically smallest subsequence of length 4 that has the letter "e " appear at least 2 times.
**Example 3:**
**Input:** s = "bb ", k = 2, letter = "b ", repetition = 2
**Output:** "bb "
**Explanation:** "bb " is the only subsequence of length 2 that has the letter "b " appear at least 2 times.
**Constraints:**
* `1 <= repetition <= k <= s.length <= 5 * 104`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter, and appears in `s` at least `repetition` times. | null |
[PYTHON3] O(n) using stack with explanation | smallest-k-length-subsequence-with-occurrences-of-a-letter | 0 | 1 | First, we need to count how many time `letter` occurs in the whole string.\nNext, we enumerate and keep track of how many times `letter` occurred (and how many are remaining) and greedily add the current character with some condition. \n\nIf we need to remove the top element of the stack, we need to have these three conditions satisfied:\n1) current stack top is greater than the `current character`\n2) if we remove the top of stack and add the `current character`, we can still have k total characters\n3) if we remove the top of stack and add the `current character`, we can still have repetition of `letter` character.\n\nNext, we may add the the `current character` based on these condition:\n1) if the current character is `letter`, we check how many times `letter` occcurs later; if it is not enough for the length constraint, we need to add it. Otherwise, we can always add the `letter` later.\n2) if the `current character` is not the `letter`, we can try to greedily add this character keeping space for the `letter` repetition number of times. If better alternatives come, we can always pop this. Thus we need to keep track how many time the character `letter` was added in the stack too using variable `occ`. \n\n```\nclass Solution:\n def smallestSubsequence(self, s: str, k: int, letter: str, repetition: int) -> str:\n counts,total = 0, 0\n n = len(s)\n for ch in s:\n if ch==letter:\n total +=1\n stack = []\n occ = 0\n for idx,ch in enumerate(s):\n if ch==letter:\n counts +=1\n while stack and stack[-1]>ch and len(stack)+ (n-1-idx)>=k and (occ+total-counts-(stack[-1]==letter)+(ch==letter)>=repetition ): \n occ -= stack.pop()==letter\n if ch!=letter and len(stack)< k-max(0,(repetition-occ)):\n stack.append(ch)\n elif ch==letter and len(stack)+(total-counts)<k:\n stack.append(ch)\n occ +=1\n return \'\'.join(stack)\n``` | 2 | You are given a string `s`, an integer `k`, a letter `letter`, and an integer `repetition`.
Return _the **lexicographically smallest** subsequence of_ `s` _of length_ `k` _that has the letter_ `letter` _appear **at least**_ `repetition` _times_. The test cases are generated so that the `letter` appears in `s` **at least** `repetition` times.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A string `a` is **lexicographically smaller** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`.
**Example 1:**
**Input:** s = "leet ", k = 3, letter = "e ", repetition = 1
**Output:** "eet "
**Explanation:** There are four subsequences of length 3 that have the letter 'e' appear at least 1 time:
- "lee " (from "**lee**t ")
- "let " (from "**le**e**t** ")
- "let " (from "**l**e**et** ")
- "eet " (from "l**eet** ")
The lexicographically smallest subsequence among them is "eet ".
**Example 2:**
**Input:** s = "leetcode ", k = 4, letter = "e ", repetition = 2
**Output:** "ecde "
**Explanation:** "ecde " is the lexicographically smallest subsequence of length 4 that has the letter "e " appear at least 2 times.
**Example 3:**
**Input:** s = "bb ", k = 2, letter = "b ", repetition = 2
**Output:** "bb "
**Explanation:** "bb " is the only subsequence of length 2 that has the letter "b " appear at least 2 times.
**Constraints:**
* `1 <= repetition <= k <= s.length <= 5 * 104`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter, and appears in `s` at least `repetition` times. | null |
Python Stack solution | smallest-k-length-subsequence-with-occurrences-of-a-letter | 0 | 1 | ```\nclass Solution:\n def smallestSubsequence(self, s: str, k: int, letter: str, repetition: int) -> str:\n s = list(s)\n stack = []\n countAll = s.count(letter)\n count = 0\n for ind, i in enumerate(s):\n while stack and stack[-1] > i:\n if stack[-1] == letter and i != letter:\n if countAll+count-1 < repetition:\n break\n if len(stack)+len(s)-ind-1 < k:\n break\n if stack[-1] == letter:\n count-=1\n stack.pop()\n stack.append(i)\n if i == letter:\n count+=1\n countAll-=1\n temp = 0\n while len(stack)+temp > k:\n if stack[-1] == letter and count <= repetition:\n temp+=1\n if stack[-1] == letter:\n count-=1\n stack.pop()\n return "".join(stack)+temp*letter\n```\n | 1 | You are given a string `s`, an integer `k`, a letter `letter`, and an integer `repetition`.
Return _the **lexicographically smallest** subsequence of_ `s` _of length_ `k` _that has the letter_ `letter` _appear **at least**_ `repetition` _times_. The test cases are generated so that the `letter` appears in `s` **at least** `repetition` times.
A **subsequence** is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.
A string `a` is **lexicographically smaller** than a string `b` if in the first position where `a` and `b` differ, string `a` has a letter that appears earlier in the alphabet than the corresponding letter in `b`.
**Example 1:**
**Input:** s = "leet ", k = 3, letter = "e ", repetition = 1
**Output:** "eet "
**Explanation:** There are four subsequences of length 3 that have the letter 'e' appear at least 1 time:
- "lee " (from "**lee**t ")
- "let " (from "**le**e**t** ")
- "let " (from "**l**e**et** ")
- "eet " (from "l**eet** ")
The lexicographically smallest subsequence among them is "eet ".
**Example 2:**
**Input:** s = "leetcode ", k = 4, letter = "e ", repetition = 2
**Output:** "ecde "
**Explanation:** "ecde " is the lexicographically smallest subsequence of length 4 that has the letter "e " appear at least 2 times.
**Example 3:**
**Input:** s = "bb ", k = 2, letter = "b ", repetition = 2
**Output:** "bb "
**Explanation:** "bb " is the only subsequence of length 2 that has the letter "b " appear at least 2 times.
**Constraints:**
* `1 <= repetition <= k <= s.length <= 5 * 104`
* `s` consists of lowercase English letters.
* `letter` is a lowercase English letter, and appears in `s` at least `repetition` times. | null |
Counter Python solution | two-out-of-three | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n counter = Counter(list(set(nums1)) + list(set(nums2)) + list(set(nums3)))\n result = []\n for i in counter:\n if counter[i] > 1:\n result.append(i)\n return result \n``` | 1 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
python easy solution ! | two-out-of-three | 0 | 1 | # Intuition\n # Iterate through the combined iterable of all three arrays and find values that are present in at least two arrays.\n \n\n\n# Approach\n\n \n \n # - Combine all three arrays into a single iterable.\n # - For each value in the combined iterable, check if it is present in at least two arrays.\n # - If yes, append the value to the \'unique\' list.\n # - Return the set of unique values to ensure uniqueness.\n \n\n\n\n# Complexity\n \n # - Time complexity: O(n), where n is the total number of elements in all three arrays.\n # - Space complexity: O(n), as the \'unique\' list stores unique values.\n\n\n\n# Code\n```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n unique = []\n for i in nums1+nums2+nums3:\n if i in nums1 and i in nums2 or i in nums2 and i in nums3 or i in nums1 and i in nums3:\n unique.append(i)\n\n return set(unique)\n \n``` | 4 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
Python one line simple solution | two-out-of-three | 0 | 1 | **Python :**\n\n```\ndef twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n\treturn set(nums1) & set(nums2) | set(nums2) & set(nums3) | set(nums1) & set(nums3)\n```\n\n**Like it ? please upvote !** | 67 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
🔥100% EASY TO UNDERSTAND/SIMPLE/CLEAN🔥 | two-out-of-three | 0 | 1 | ```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n output = []\n for i in nums1:\n if i in nums2 or i in nums3:\n if i not in output:\n output.append(i)\n for j in nums2:\n if j in nums3 or j in nums1:\n if j not in output:\n output.append(j)\n return output | 0 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
[Python3] set | two-out-of-three | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/933e9b50b2532374ab8252f431da84b6675663a8) for solutions of weekly 262.\n```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n s1, s2, s3 = set(nums1), set(nums2), set(nums3)\n return (s1&s2) | (s2&s3) | (s1&s3)\n```\n\nAdding an approach by @SunnyvaleCA\n```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n freq = Counter()\n for nums in nums1, nums2, nums3: freq.update(set(nums))\n return [k for k, v in freq.items() if v >= 2]\n``` | 26 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
Easy Python Solution | Faster than 97% (64 ms) | two-out-of-three | 0 | 1 | # Easy Python Solution | Faster than 97% (64 ms)\n**Runtime: 64 ms, faster than 97% of Python3 online submissions for Two Out of Three.\nMemory Usage: 14.2 MB.**\n\n```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n ret = []\n\n ret += set(nums1).intersection(set(nums2))\n ret += set(nums1).intersection(set(nums3))\n ret += set(nums2).intersection(set(nums3))\n\n return set(ret)\n``` | 7 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
PYTHON | Simple python solution | two-out-of-three | 0 | 1 | ```\nclass Solution:\n def twoOutOfThree(self, nums1: List[int], nums2: List[int], nums3: List[int]) -> List[int]:\n countMap = {}\n \n for i in set(nums1):\n countMap[i] = 1 + countMap.get(i, 0)\n \n for i in set(nums2):\n countMap[i] = 1 + countMap.get(i, 0)\n \n for i in set(nums3):\n countMap[i] = 1 + countMap.get(i, 0)\n \n res = []\n \n for i in countMap:\n if countMap[i] >= 2:\n res.append(i)\n \n return res\n``` | 2 | Given three integer arrays `nums1`, `nums2`, and `nums3`, return _a **distinct** array containing all the values that are present in **at least two** out of the three arrays. You may return the values in **any** order_.
**Example 1:**
**Input:** nums1 = \[1,1,3,2\], nums2 = \[2,3\], nums3 = \[3\]
**Output:** \[3,2\]
**Explanation:** The values that are present in at least two arrays are:
- 3, in all three arrays.
- 2, in nums1 and nums2.
**Example 2:**
**Input:** nums1 = \[3,1\], nums2 = \[2,3\], nums3 = \[1,2\]
**Output:** \[2,3,1\]
**Explanation:** The values that are present in at least two arrays are:
- 2, in nums2 and nums3.
- 3, in nums1 and nums2.
- 1, in nums1 and nums3.
**Example 3:**
**Input:** nums1 = \[1,2,2\], nums2 = \[4,3,3\], nums3 = \[5\]
**Output:** \[\]
**Explanation:** No value is present in at least two arrays.
**Constraints:**
* `1 <= nums1.length, nums2.length, nums3.length <= 100`
* `1 <= nums1[i], nums2[j], nums3[k] <= 100` | In what order should you iterate through the digits? If an odd number exists, where must the number start from? |
[Python3] median 4-line | minimum-operations-to-make-a-uni-value-grid | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/933e9b50b2532374ab8252f431da84b6675663a8) for solutions of weekly 262.\n```\nclass Solution:\n def minOperations(self, grid: List[List[int]], x: int) -> int:\n vals = [x for row in grid for x in row]\n if len(set(val%x for val in vals)) > 1: return -1 # impossible\n median = sorted(vals)[len(vals)//2] # O(N) possible via "quick select"\n return sum(abs(val - median)//x for val in vals)\n``` | 22 | You are given a 2D integer `grid` of size `m x n` and an integer `x`. In one operation, you can **add** `x` to or **subtract** `x` from any element in the `grid`.
A **uni-value grid** is a grid where all the elements of it are equal.
Return _the **minimum** number of operations to make the grid **uni-value**_. If it is not possible, return `-1`.
**Example 1:**
**Input:** grid = \[\[2,4\],\[6,8\]\], x = 2
**Output:** 4
**Explanation:** We can make every element equal to 4 by doing the following:
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.
**Example 2:**
**Input:** grid = \[\[1,5\],\[2,3\]\], x = 1
**Output:** 5
**Explanation:** We can make every element equal to 3.
**Example 3:**
**Input:** grid = \[\[1,2\],\[3,4\]\], x = 2
**Output:** -1
**Explanation:** It is impossible to make every element equal.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= x, grid[i][j] <= 104` | Consider the day as 48 hours instead of 24. For each round check if you were playing. |
[Python3] Why median is optimal | Detailed Explanation | minimum-operations-to-make-a-uni-value-grid | 0 | 1 | So I have seen a few posts showing the code but none of them go to the mathematical detail of this problem.\nHere\'s my attempt at explaining this problem and how the solution is derived.\n\nPoints to note:\n1. We dont really care about the matrix itself. We just want the values, so we can just safely ignore the matrix and **treat it like an array**.\n2. We can do **as many operations** as we want with x as increment/decrement (hypothetically).\n\nPoint 2 helps prove an important concept.\nIf we can do infinte operations on any number with x, we should get **all the possible numbers in the matrix**. Think on it :)\nIf we dont get all the possible numbers, that means the **solution doesnt exist**\n\nHence, this helps us derive this,\nlet A, B be any numbers in the matrix.\n**(A-B) % x == 0**\n\nNow we just have to optimize the value to be subtracted from each number.\nThe simplest way of doing that is **sorting the array** (converted from the matrix) and **finding the middle value**.\nThe middle value will be **equidistant** from the start and end and this will help minimize the operations.\nAs we do not **overcompensate** in addition as well as the subtraction aspect.\n\n```\nclass Solution:\n def minOperations(self, grid: List[List[int]], x: int) -> int:\n li = []\n \n # convert matrix to array, we dont care about the structure itself. We just want the values\n for val in grid:\n li+= val\n \n # sort the array\n li.sort()\n \n # get the middle value, which is equidistant from both sides\n median = li[len(li)//2]\n ops = 0\n \n # run the loop over all the elements to calculate the number of operations needed\n for val in li:\n \n # this is the condtion which determines if our number can reach the other number with adding/subtracting k\n if abs(val-median)%x != 0:\n return -1\n ops += abs(val-median)//x\n return ops\n```\n\nResults:\n\n | 5 | You are given a 2D integer `grid` of size `m x n` and an integer `x`. In one operation, you can **add** `x` to or **subtract** `x` from any element in the `grid`.
A **uni-value grid** is a grid where all the elements of it are equal.
Return _the **minimum** number of operations to make the grid **uni-value**_. If it is not possible, return `-1`.
**Example 1:**
**Input:** grid = \[\[2,4\],\[6,8\]\], x = 2
**Output:** 4
**Explanation:** We can make every element equal to 4 by doing the following:
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.
**Example 2:**
**Input:** grid = \[\[1,5\],\[2,3\]\], x = 1
**Output:** 5
**Explanation:** We can make every element equal to 3.
**Example 3:**
**Input:** grid = \[\[1,2\],\[3,4\]\], x = 2
**Output:** -1
**Explanation:** It is impossible to make every element equal.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= x, grid[i][j] <= 104` | Consider the day as 48 hours instead of 24. For each round check if you were playing. |
Numpy 4-liner beats 100% in speed | minimum-operations-to-make-a-uni-value-grid | 0 | 1 | # Intuition\nPython is slow, numpy delegates some operations to internal C implementation, which is way faster\n\n# Approach\nJust use numpy\n\n# Complexity\n- Time complexity: $O(n)$\nmultiple operasions that traverses whole matrix\n\n- Space complexity: $O(n)$\nConversion to numpy array traverses whole matrix\n\n$n$ here is $width\\times height$ of a materi\n\n# Code\n```\nimport numpy as np\n\nclass Solution:\n def minOperations(self, grid: List[List[int]], x: int) -> int:\n grid = np.array(grid, dtype=int).reshape(-1)\n\n if 0 != np.ptp(np.mod(grid, x)):\n return -1\n return int(np.abs(grid - np.median(grid)).sum() / x)\n\n``` | 0 | You are given a 2D integer `grid` of size `m x n` and an integer `x`. In one operation, you can **add** `x` to or **subtract** `x` from any element in the `grid`.
A **uni-value grid** is a grid where all the elements of it are equal.
Return _the **minimum** number of operations to make the grid **uni-value**_. If it is not possible, return `-1`.
**Example 1:**
**Input:** grid = \[\[2,4\],\[6,8\]\], x = 2
**Output:** 4
**Explanation:** We can make every element equal to 4 by doing the following:
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.
**Example 2:**
**Input:** grid = \[\[1,5\],\[2,3\]\], x = 1
**Output:** 5
**Explanation:** We can make every element equal to 3.
**Example 3:**
**Input:** grid = \[\[1,2\],\[3,4\]\], x = 2
**Output:** -1
**Explanation:** It is impossible to make every element equal.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= x, grid[i][j] <= 104` | Consider the day as 48 hours instead of 24. For each round check if you were playing. |
Ternary Search | minimum-operations-to-make-a-uni-value-grid | 0 | 1 | # Approach\nThe grid can be made uni-value if each value of the grid mod x is uni-value. We can use a set to detect that.\n\nThe function f defines the number of operations to shift all value to k.\nSince f is unimodal, we could utilize ternary search shrink interval [min, max] small enough and then brute force it.\n \n\n\n\n# Complexity\n- Time complexity: O(MNlgK) M:#rows in grid N:#cols in grid K:range of grid value\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(MN)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minOperations(self, grid: List[List[int]], x: int) -> int:\n m = len(grid)\n n = len(grid[0])\n S = set()\n L = []\n\n for r in range(m):\n for c in range(n):\n S.add(grid[r][c] % x)\n\n if len(S) > 1:\n return -1\n \n L.append(grid[r][c] // x)\n\n #print(L)\n def f(k):\n return sum(abs(x-k) for x in L)\n \n l, r = min(L), max(L)\n\n while r - l > 3:\n #print(l, r)\n m1 = l + (r-l) // 3\n m2 = r - (r-l) // 3\n\n if f(m1) < f(m2):\n r = m2\n else:\n l = m1\n\n ret = f(l)\n\n for i in range(l+1, r+1):\n ret = min(ret, f(i))\n \n return ret\n``` | 0 | You are given a 2D integer `grid` of size `m x n` and an integer `x`. In one operation, you can **add** `x` to or **subtract** `x` from any element in the `grid`.
A **uni-value grid** is a grid where all the elements of it are equal.
Return _the **minimum** number of operations to make the grid **uni-value**_. If it is not possible, return `-1`.
**Example 1:**
**Input:** grid = \[\[2,4\],\[6,8\]\], x = 2
**Output:** 4
**Explanation:** We can make every element equal to 4 by doing the following:
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.
**Example 2:**
**Input:** grid = \[\[1,5\],\[2,3\]\], x = 1
**Output:** 5
**Explanation:** We can make every element equal to 3.
**Example 3:**
**Input:** grid = \[\[1,2\],\[3,4\]\], x = 2
**Output:** -1
**Explanation:** It is impossible to make every element equal.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= x, grid[i][j] <= 104` | Consider the day as 48 hours instead of 24. For each round check if you were playing. |
[Python3] hash map & 2 heaps | stock-price-fluctuation | 0 | 1 | Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/933e9b50b2532374ab8252f431da84b6675663a8) for solutions of weekly 262.\n```\nclass StockPrice:\n\n def __init__(self):\n self.mp = {}\n self.maxp = [] # max-heap \n self.minp = [] # min-heap \n self.latest = 0 # latest timestamp\n\n def update(self, timestamp: int, price: int) -> None:\n self.mp[timestamp] = price \n if self.latest <= timestamp: self.latest = timestamp\n heappush(self.maxp, (-price, timestamp))\n heappush(self.minp, (price, timestamp))\n\n def current(self) -> int:\n return self.mp[self.latest]\n\n def maximum(self) -> int:\n while self.mp[self.maxp[0][1]] != -self.maxp[0][0]: heappop(self.maxp)\n return -self.maxp[0][0]\n\n def minimum(self) -> int:\n while self.mp[self.minp[0][1]] != self.minp[0][0]: heappop(self.minp)\n return self.minp[0][0]\n``` | 41 | You are given a stream of **records** about a particular stock. Each record contains a **timestamp** and the corresponding **price** of the stock at that timestamp.
Unfortunately due to the volatile nature of the stock market, the records do not come in order. Even worse, some records may be incorrect. Another record with the same timestamp may appear later in the stream **correcting** the price of the previous wrong record.
Design an algorithm that:
* **Updates** the price of the stock at a particular timestamp, **correcting** the price from any previous records at the timestamp.
* Finds the **latest price** of the stock based on the current records. The **latest price** is the price at the latest timestamp recorded.
* Finds the **maximum price** the stock has been based on the current records.
* Finds the **minimum price** the stock has been based on the current records.
Implement the `StockPrice` class:
* `StockPrice()` Initializes the object with no price records.
* `void update(int timestamp, int price)` Updates the `price` of the stock at the given `timestamp`.
* `int current()` Returns the **latest price** of the stock.
* `int maximum()` Returns the **maximum price** of the stock.
* `int minimum()` Returns the **minimum price** of the stock.
**Example 1:**
**Input**
\[ "StockPrice ", "update ", "update ", "current ", "maximum ", "update ", "maximum ", "update ", "minimum "\]
\[\[\], \[1, 10\], \[2, 5\], \[\], \[\], \[1, 3\], \[\], \[4, 2\], \[\]\]
**Output**
\[null, null, null, 5, 10, null, 5, null, 2\]
**Explanation**
StockPrice stockPrice = new StockPrice();
stockPrice.update(1, 10); // Timestamps are \[1\] with corresponding prices \[10\].
stockPrice.update(2, 5); // Timestamps are \[1,2\] with corresponding prices \[10,5\].
stockPrice.current(); // return 5, the latest timestamp is 2 with the price being 5.
stockPrice.maximum(); // return 10, the maximum price is 10 at timestamp 1.
stockPrice.update(1, 3); // The previous timestamp 1 had the wrong price, so it is updated to 3.
// Timestamps are \[1,2\] with corresponding prices \[3,5\].
stockPrice.maximum(); // return 5, the maximum price is 5 after the correction.
stockPrice.update(4, 2); // Timestamps are \[1,2,4\] with corresponding prices \[3,5,2\].
stockPrice.minimum(); // return 2, the minimum price is 2 at timestamp 4.
**Constraints:**
* `1 <= timestamp, price <= 109`
* At most `105` calls will be made **in total** to `update`, `current`, `maximum`, and `minimum`.
* `current`, `maximum`, and `minimum` will be called **only after** `update` has been called **at least once**. | How does the maximum value being 100 help us? How can we tell if a number exists in a given range? |
Python | Easy Explanation | Meet in the Middle | partition-array-into-two-arrays-to-minimize-sum-difference | 0 | 1 | **NOTE** - This is question was very easy, if you had done this https://leetcode.com/problems/closest-subsequence-sum/. So Please first go and try that.\n\nHere we have to find 2 groups of equal length (N).\nLet\'s say, left_ans is required the N elements required for first group, and right_ans is the other N elements for second group.\n\n**Intuition ->**\nThe main and only intuition which is required here is,\nnums = [1,3,6,5,4,2]\nSo, let\'s divide into 2 parts\nleft_part = [1,3,6]\nright_part = [5,4,2]\nN = len(nums) // 2, i.e. no. of elements in each group. Here 3.\nSo here, to make left_ans either we can take all 3 from left_part and 0 from right_part, or 1 from left_part and 2(N-1) from right_part, 2 from left_part and 1(N-2) from right_part.\n\nSo how this works is, if we take 1 from left_part, so this means we have taken one group of element, so its sum is taken from l_sum = left_sums[1], now to make is closer to half = total // 2, we need to add req_sum = half - l_sum, so we will binary search the value of it in right_sums. So now lest_ans_sum will become l_sum + r_sum(the binary search sum we got closest go req_sum).\nNote - Above we are just finding the best possible sum of left_ans, as right_ans sum will then be total - left_ans_sum.\n\nThe get_sums function generate all possible subset sums using k elements from nums.\nnums = [1,3,6]\nget_sums(nums) will give,\n{1: [1, 3, 6], # using only 1 elements from nums\n2: [4, 7, 9], # using only 2\n3: [10]} # using all 3\n\n**Why not TLE ->**\nAnd why this works is, because we are generating all possible subset sums using only k elements, where k is from 1 to N. Which is in total 2\\**k, and as max value of k is 15, so 2\\**15 is 32,000. Which is easy to work with. While if you try to make all subset sums, it becomes 2\\**30 is 1,073,741,824 which will give TLE.\n\n**Meet in the Middle ->**\nThis technique is called meet in the middle. Here we are halving the max array size from 30, to 15. As generating all possible subset sums is feasible, ie 2\\**15. And to complete left_ans, we are taking subset sum of k from left_part, and N-k from right_part.\n\n**Time Complexity ->** \nFor N elements, there are 2\\**N subset possible. Then we also sum those each of those subset. O(N * 2^N)\nFor each k from 1 to 15, there are 2\\**M1 subset sums for left, then we are sorting right O(M2 * logM2), then we are finding its other part using binary search logM2. \nO(2\\**M1 * logM2 + M2 * logM2), \nwhere,\nM1 = no. of elements in left_sums[k], \nM2 = no. of elements in right_sums[N-k]\n\n**Space Complexity ->**\nAs there are 2\\**N subsets, for left and right. So, O(2 * 2^N), where max value of N is 15.\n\n```\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n N = len(nums) // 2 # Note this is N/2, ie no. of elements required in each.\n \n def get_sums(nums): # generate all combinations sum of k elements\n ans = {}\n N = len(nums)\n for k in range(1, N+1): # takes k element for nums\n sums = []\n for comb in combinations(nums, k):\n s = sum(comb)\n sums.append(s)\n ans[k] = sums\n return ans\n \n left_part, right_part = nums[:N], nums[N:]\n left_sums, right_sums = get_sums(left_part), get_sums(right_part)\n ans = abs(sum(left_part) - sum(right_part)) # the case when taking all N from left_part for left_ans, and vice versa\n total = sum(nums) \n half = total // 2 # the best sum required for each, we have to find sum nearest to this\n for k in range(1, N):\n left = left_sums[k] # if taking k no. from left_sums\n right = right_sums[N-k] # then we have to take remaining N-k from right_sums.\n right.sort() # sorting, so that we can binary search the required value\n for x in left:\n r = half - x # required, how much we need to add in x to bring it closer to half.\n p = bisect.bisect_left(right, r) # we are finding index of value closest to r, present in right, using binary search\n for q in [p, p-1]:\n if 0 <= q < len(right):\n left_ans_sum = x + right[q]\n right_ans_sum = total - left_ans_sum\n diff = abs(left_ans_sum - right_ans_sum)\n ans = min(ans, diff) \n return ans\n```\n\n\nPlease give this a **UPVOTE** , if you liked my effort.\nAnd feel free to let me know if you have any doubts or suggestions. | 161 | You are given an integer array `nums` of `2 * n` integers. You need to partition `nums` into **two** arrays of length `n` to **minimize the absolute difference** of the **sums** of the arrays. To partition `nums`, put each element of `nums` into **one** of the two arrays.
Return _the **minimum** possible absolute difference_.
**Example 1:**
**Input:** nums = \[3,9,7,3\]
**Output:** 2
**Explanation:** One optimal partition is: \[3,9\] and \[7,3\].
The absolute difference between the sums of the arrays is abs((3 + 9) - (7 + 3)) = 2.
**Example 2:**
**Input:** nums = \[-36,36\]
**Output:** 72
**Explanation:** One optimal partition is: \[-36\] and \[36\].
The absolute difference between the sums of the arrays is abs((-36) - (36)) = 72.
**Example 3:**
**Input:** nums = \[2,-1,0,4,-2,-9\]
**Output:** 0
**Explanation:** One optimal partition is: \[2,4,-9\] and \[-1,0,-2\].
The absolute difference between the sums of the arrays is abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0.
**Constraints:**
* `1 <= n <= 15`
* `nums.length == 2 * n`
* `-107 <= nums[i] <= 107` | Let's use floodfill to iterate over the islands of the second grid Let's note that if all the cells in an island in the second grid if they are represented by land in the first grid then they are connected hence making that island a sub-island |
Very fast python3 solution | 698 ms - faster than 100% solutions | meet-in-middle + 2 pointers | partition-array-into-two-arrays-to-minimize-sum-difference | 0 | 1 | # Complexity\n- Time complexity: $$O(2^n \\cdot n^{1.5})$$\n<!-- Add your time complexity here, e.g. $$O(2^n)$$ -->\n\n- Space complexity: $$O(2^n)$$\n<!-- Add your space complexity here, e.g. $$O(2^n)$$ -->\n\n\nTime complexity of `get_subsets_sums` is $$O(2^n)$$,\ntime complexity of `calc` is $$O(n \\cdot k \\cdot log(k))$$,\nwhere $$k = O(C^{n/2}_n)$$.\n\nUsing Stirling\'s approximation ([wiki](https://en.wikipedia.org/wiki/Stirling%27s_approximation)) got $$k = O(2^n \\cdot n ^ {-0.5})$$, and $$log(k) = O(n)$$.\n\nAnd finally\n$$n \\cdot k \\cdot log(k) = O(n) \\cdot O(2^n \\cdot n ^ {-0.5}) \\cdot O(n) = O(2^n \\cdot n^{1.5})$$.\n\n\n# Code\n``` python3 []\nclass Solution:\n def minimumDifference(self, nums: List[int]) -> int:\n n = len(nums)\n half = n // 2\n\n full_sum = sum(nums)\n half_sum = full_sum // 2\n\n # check if left and right part is optimal\n if sum(nums[: half]) == half_sum:\n # here and further\n # (full_sum - 2 * half_sum) is equivalent (full_sum % 2) and isn\'t equivalent (0)\n # because sum(nums) may be odd \n return full_sum - 2 * half_sum\n if sum(nums[half :]) == half_sum:\n return full_sum - 2 * half_sum\n\n def get_subsets_sums(elems):\n result = defaultdict(set)\n result[0] = {0}\n for elem in elems:\n for cnt in reversed(list(result)):\n result[cnt + 1].update(\n value + elem\n for value in result[cnt]\n )\n return result\n\n left = get_subsets_sums(nums[: half])\n right = get_subsets_sums(nums[half :])\n\n def calc(left, right):\n # initial var result\n # find max of n-subset of nums, if sum of subset is equal or less than half_sum\n result = min(min(left[half]), min(right[half]))\n \n for left_cnt, left_sums in left.items():\n right_cnt = half - left_cnt\n right_sums = right[right_cnt]\n\n a = sorted(left_sums)\n b = sorted(right_sums)\n m = len(a)\n l = len(b)\n i = 0\n j = l - 1\n \n # use 2 pointers instead of a loop in a loop\n while i < m and j >= 0:\n current = a[i] + b[j]\n if current == half_sum:\n return full_sum - 2 * current\n if current > half_sum:\n j -= 1\n else:\n result = max(result, current)\n i += 1\n \n return full_sum - 2 * result\n\n return calc(left, right)\n```\n\n#### If you found this useful or interesting, please upvote! | 1 | You are given an integer array `nums` of `2 * n` integers. You need to partition `nums` into **two** arrays of length `n` to **minimize the absolute difference** of the **sums** of the arrays. To partition `nums`, put each element of `nums` into **one** of the two arrays.
Return _the **minimum** possible absolute difference_.
**Example 1:**
**Input:** nums = \[3,9,7,3\]
**Output:** 2
**Explanation:** One optimal partition is: \[3,9\] and \[7,3\].
The absolute difference between the sums of the arrays is abs((3 + 9) - (7 + 3)) = 2.
**Example 2:**
**Input:** nums = \[-36,36\]
**Output:** 72
**Explanation:** One optimal partition is: \[-36\] and \[36\].
The absolute difference between the sums of the arrays is abs((-36) - (36)) = 72.
**Example 3:**
**Input:** nums = \[2,-1,0,4,-2,-9\]
**Output:** 0
**Explanation:** One optimal partition is: \[2,4,-9\] and \[-1,0,-2\].
The absolute difference between the sums of the arrays is abs((2 + 4 + -9) - (-1 + 0 + -2)) = 0.
**Constraints:**
* `1 <= n <= 15`
* `nums.length == 2 * n`
* `-107 <= nums[i] <= 107` | Let's use floodfill to iterate over the islands of the second grid Let's note that if all the cells in an island in the second grid if they are represented by land in the first grid then they are connected hence making that island a sub-island |
Intuitive Greedy solution with Python3 | minimum-number-of-moves-to-seat-everyone | 0 | 1 | # Intuition\nHere we have:\n- `seats` and `students` lists\n- our goal is to move `students` to `seats` **optimally**\n\nThere\'re some `students`, who we don\'t need to move, as they\'re sitting in the right place.\n\nTo make an **optimal decision** we should map `seats` to `students` and minimize a distance between `seats[i]` and `students[i]`.\n\nThis is achievable with **sorting in non-decreasing order** for both collections and finding **absolute difference**. \n\n# Approach\n1. sort both collections\n2. find sum of distances, for a particular student we have `abs(seats[i] - students[i])`\n\n# Complexity\n- Time complexity: **O(N log N)** for sorting\n\n- Space complexity: **O(N)**, since we apply **list comprehension**.\n\n# Code\n```\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats.sort()\n students.sort()\n\n return sum([abs(seats[i] - students[i]) for i in range(len(seats))])\n``` | 1 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
PYHTON SOLUTION FOR BEGGINERS || VERY EASY USING | minimum-number-of-moves-to-seat-everyone | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n qadam = 0\n seats.sort()\n students.sort()\n for st in range(len(students)):\n qadam += abs(students[st] - seats[st])\n return qadam\n\n\n\n\n\n\n\n\n \n \n \n\n\n\n \n \n\n \n``` | 3 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
Python ✅✅✅ || Faster than 86.11%, Memory Beats 97.69% | minimum-number-of-moves-to-seat-everyone | 0 | 1 | # Code\n```\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n moves = 0\n seats.sort()\n students.sort()\n for s in range(len(students)):\n moves += abs(students[s]-seats[s])\n return moves\n```\n\n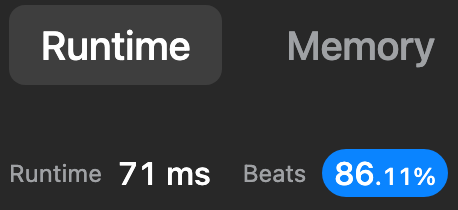\n\n | 2 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
[Java/Python 3] Sort both and sum the corresponding difference. | minimum-number-of-moves-to-seat-everyone | 1 | 1 | ```java\n public int minMovesToSeat(int[] seats, int[] students) {\n Arrays.sort(seats);\n Arrays.sort(students);\n int moves = 0;\n for (int i = 0; i < seats.length; ++i) {\n moves += Math.abs(seats[i] - students[i]);\n }\n return moves;\n }\n```\n```python\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats.sort()\n students.sort()\n return sum(abs(e - t) for e, t in zip(seats, students))\n```\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(S)`, where `n = seats.length, S = space cost during sorting`. | 26 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
✅✔🔥 EASY PYTHON3 SOLUTION 🔥✅✔ ONE-LINE | minimum-number-of-moves-to-seat-everyone | 0 | 1 | if it is helpful please **Upvote** me\n ``` \n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n seats.sort()\n students.sort()\n count = 0\n for i in range(len(seats)):\n count += abs(seats[i]-students[i])\n return count\n``` \n**One line approach **\n``` \n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n return sum(abs(a-b) for a,b in zip(sorted(students),sorted(seats)))\n``` | 1 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
Math Bazooka | 1 liner | Earthmover Distance Solution | minimum-number-of-moves-to-seat-everyone | 0 | 1 | Today we will be nuking mosquitos by using the [Earthmover distance](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wasserstein_distance.html). \n\nExcluding an import, this yields a 1-liner.\n\nIs that overkill? Yes, absolutely.\n\n```\nfrom scipy.stats import wasserstein_distance as EMD\nclass Solution:\n def minMovesToSeat(self, seats: List[int], students: List[int]) -> int:\n return round( len(seats)*EMD(seats, students) )\n```\n\n# Intuition\n\n**TLDR:** The Earthmover distance (EMD) is a measure of statistical distance coming from the theory of optimal transport which basically tells you the minimal effort it would take to reshape one probability distribution into another. Reframing our inputs as probability distributions, we can compute their EMD and rescale to get the answer in 1-line. You can learn more about the specific implementation the code used from the [documentation](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.wasserstein_distance.html).\n\n**Q:** But where are the probability distributions?\n**A:** To turn our `seats` position data into a probability distribution, we can just imagine we pick seats at random. So each seat has a uniform $$1/n$$ chance of being selected. That\'s it, that\'s the distribution. It\'s called the *empirical distribution*. We can do the same thing for `students`. \n\nIn our case, the EMD of two 1D empirical distributions with equal number of points will tell us on ***average*** how much each point will need to move in the optimal transport plan. The scipy implemention with defaults assumes this, so that means `EMD(seats,students)` equals `answer/n`. So if we just multiply by the number of points (i.e. array length) then we should have the answer. However, because of the limited precision of floats, we\'ll need to actually round after that multiplication. \n\n# Complexity\n\nDidn\'t vet the implementation so dunno. The differences of sorted values solution is surely much faster though since it avoids floats and requires no import. It would be interesting to see how that solution fares against the EMD approach if the seat/student positions were allowed to be floats.\n\n**Bonus Background:** Among many reasons the EMD is nice is because it is well-defined for higher dimensions (possibly infinite), curved geometry (spheres), and wacky distributions (you can compare discrete and continuous distributions and mixes of the two). It has lots of applications ranging from statistics, physics, biology, and machine learning as well (see Wasserstein GANs).\n\n**Minor technical notes:** I\'ve been saying probability distribution but I really mean probability measure to be precise. \n\n | 3 | There are `n` seats and `n` students in a room. You are given an array `seats` of length `n`, where `seats[i]` is the position of the `ith` seat. You are also given the array `students` of length `n`, where `students[j]` is the position of the `jth` student.
You may perform the following move any number of times:
* Increase or decrease the position of the `ith` student by `1` (i.e., moving the `ith` student from position `x` to `x + 1` or `x - 1`)
Return _the **minimum number of moves** required to move each student to a seat_ _such that no two students are in the same seat._
Note that there may be **multiple** seats or students in the **same** position at the beginning.
**Example 1:**
**Input:** seats = \[3,1,5\], students = \[2,7,4\]
**Output:** 4
**Explanation:** The students are moved as follows:
- The first student is moved from from position 2 to position 1 using 1 move.
- The second student is moved from from position 7 to position 5 using 2 moves.
- The third student is moved from from position 4 to position 3 using 1 move.
In total, 1 + 2 + 1 = 4 moves were used.
**Example 2:**
**Input:** seats = \[4,1,5,9\], students = \[1,3,2,6\]
**Output:** 7
**Explanation:** The students are moved as follows:
- The first student is not moved.
- The second student is moved from from position 3 to position 4 using 1 move.
- The third student is moved from from position 2 to position 5 using 3 moves.
- The fourth student is moved from from position 6 to position 9 using 3 moves.
In total, 0 + 1 + 3 + 3 = 7 moves were used.
**Example 3:**
**Input:** seats = \[2,2,6,6\], students = \[1,3,2,6\]
**Output:** 4
**Explanation:** Note that there are two seats at position 2 and two seats at position 6.
The students are moved as follows:
- The first student is moved from from position 1 to position 2 using 1 move.
- The second student is moved from from position 3 to position 6 using 3 moves.
- The third student is not moved.
- The fourth student is not moved.
In total, 1 + 3 + 0 + 0 = 4 moves were used.
**Constraints:**
* `n == seats.length == students.length`
* `1 <= n <= 100`
* `1 <= seats[i], students[j] <= 100` | Iterate over all possible pairs (a,b) and check that the square root of a * a + b * b is an integers less than or equal n You can check that the square root of an integer is an integer using binary seach or a builtin function like sqrt |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.