title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
🔥🔥EASY BEGINNER FRIENDLY SOLUTION USING FREQUENCY HASHMAP !! 🔥🔥 | check-if-number-has-equal-digit-count-and-digit-value | 0 | 1 | # Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfrom collections import Counter\nclass Solution:\n def digitCount(self, num: str) -> bool:\n dic=Counter(num)\n c=0\n for i in range(len(num)):\n if dic[str(i)]==int(num[i]):\n c+=1\n \n if c==len(num):\n return 1\n return 0\n\n``` | 2 | You are given a **0-indexed** string `num` of length `n` consisting of digits.
Return `true` _if for **every** index_ `i` _in the range_ `0 <= i < n`_, the digit_ `i` _occurs_ `num[i]` _times in_ `num`_, otherwise return_ `false`.
**Example 1:**
**Input:** num = "1210 "
**Output:** true
**Explanation:**
num\[0\] = '1'. The digit 0 occurs once in num.
num\[1\] = '2'. The digit 1 occurs twice in num.
num\[2\] = '1'. The digit 2 occurs once in num.
num\[3\] = '0'. The digit 3 occurs zero times in num.
The condition holds true for every index in "1210 ", so return true.
**Example 2:**
**Input:** num = "030 "
**Output:** false
**Explanation:**
num\[0\] = '0'. The digit 0 should occur zero times, but actually occurs twice in num.
num\[1\] = '3'. The digit 1 should occur three times, but actually occurs zero times in num.
num\[2\] = '0'. The digit 2 occurs zero times in num.
The indices 0 and 1 both violate the condition, so return false.
**Constraints:**
* `n == num.length`
* `1 <= n <= 10`
* `num` consists of digits. | Try to separate the elements at odd indices from the elements at even indices. Sort the two groups of elements individually. Combine them to form the resultant array. |
🔥[Python 3] 4 lines using dictionary, beats 97% 🥷🏼 | sender-with-largest-word-count | 0 | 1 | ```python3 []\nclass Solution:\n def largestWordCount(self, messages: List[str], senders: List[str]) -> str:\n d = defaultdict(int)\n for m, n in zip(messages, senders):\n d[n] += len(m.split())\n return max(d, key = lambda k: (d[k], k))\n``` | 3 | You have a chat log of `n` messages. You are given two string arrays `messages` and `senders` where `messages[i]` is a **message** sent by `senders[i]`.
A **message** is list of **words** that are separated by a single space with no leading or trailing spaces. The **word count** of a sender is the total number of **words** sent by the sender. Note that a sender may send more than one message.
Return _the sender with the **largest** word count_. If there is more than one sender with the largest word count, return _the one with the **lexicographically largest** name_.
**Note:**
* Uppercase letters come before lowercase letters in lexicographical order.
* `"Alice "` and `"alice "` are distinct.
**Example 1:**
**Input:** messages = \[ "Hello userTwooo ", "Hi userThree ", "Wonderful day Alice ", "Nice day userThree "\], senders = \[ "Alice ", "userTwo ", "userThree ", "Alice "\]
**Output:** "Alice "
**Explanation:** Alice sends a total of 2 + 3 = 5 words.
userTwo sends a total of 2 words.
userThree sends a total of 3 words.
Since Alice has the largest word count, we return "Alice ".
**Example 2:**
**Input:** messages = \[ "How is leetcode for everyone ", "Leetcode is useful for practice "\], senders = \[ "Bob ", "Charlie "\]
**Output:** "Charlie "
**Explanation:** Bob sends a total of 5 words.
Charlie sends a total of 5 words.
Since there is a tie for the largest word count, we return the sender with the lexicographically larger name, Charlie.
**Constraints:**
* `n == messages.length == senders.length`
* `1 <= n <= 104`
* `1 <= messages[i].length <= 100`
* `1 <= senders[i].length <= 10`
* `messages[i]` consists of uppercase and lowercase English letters and `' '`.
* All the words in `messages[i]` are separated by **a single space**.
* `messages[i]` does not have leading or trailing spaces.
* `senders[i]` consists of uppercase and lowercase English letters only. | For positive numbers, the leading digit should be the smallest nonzero digit. Then the remaining digits follow in ascending order. For negative numbers, the digits should be arranged in descending order. |
Python3 | Hash word count associated with a sender's name then return max | sender-with-largest-word-count | 0 | 1 | ```\nclass Solution:\n def largestWordCount(self, messages: List[str], senders: List[str]) -> str:\n words_count = defaultdict(int)\n for m, person in zip(messages, senders):\n words_count[person] += len(m.split())\n \n max_len = max(words_count.values())\n \n names = sorted([name for name, words in words_count.items() if words == max_len], reverse=True)\n return names[0]\n``` | 1 | You have a chat log of `n` messages. You are given two string arrays `messages` and `senders` where `messages[i]` is a **message** sent by `senders[i]`.
A **message** is list of **words** that are separated by a single space with no leading or trailing spaces. The **word count** of a sender is the total number of **words** sent by the sender. Note that a sender may send more than one message.
Return _the sender with the **largest** word count_. If there is more than one sender with the largest word count, return _the one with the **lexicographically largest** name_.
**Note:**
* Uppercase letters come before lowercase letters in lexicographical order.
* `"Alice "` and `"alice "` are distinct.
**Example 1:**
**Input:** messages = \[ "Hello userTwooo ", "Hi userThree ", "Wonderful day Alice ", "Nice day userThree "\], senders = \[ "Alice ", "userTwo ", "userThree ", "Alice "\]
**Output:** "Alice "
**Explanation:** Alice sends a total of 2 + 3 = 5 words.
userTwo sends a total of 2 words.
userThree sends a total of 3 words.
Since Alice has the largest word count, we return "Alice ".
**Example 2:**
**Input:** messages = \[ "How is leetcode for everyone ", "Leetcode is useful for practice "\], senders = \[ "Bob ", "Charlie "\]
**Output:** "Charlie "
**Explanation:** Bob sends a total of 5 words.
Charlie sends a total of 5 words.
Since there is a tie for the largest word count, we return the sender with the lexicographically larger name, Charlie.
**Constraints:**
* `n == messages.length == senders.length`
* `1 <= n <= 104`
* `1 <= messages[i].length <= 100`
* `1 <= senders[i].length <= 10`
* `messages[i]` consists of uppercase and lowercase English letters and `' '`.
* All the words in `messages[i]` are separated by **a single space**.
* `messages[i]` does not have leading or trailing spaces.
* `senders[i]` consists of uppercase and lowercase English letters only. | For positive numbers, the leading digit should be the smallest nonzero digit. Then the remaining digits follow in ascending order. For negative numbers, the digits should be arranged in descending order. |
Easy Python Solution With Dictionary | sender-with-largest-word-count | 0 | 1 | ```\nclass Solution:\n def largestWordCount(self, messages: List[str], senders: List[str]) -> str:\n d={}\n l=[]\n for i in range(len(messages)):\n if senders[i] not in d:\n d[senders[i]]=len(messages[i].split())\n else:\n d[senders[i]]+=len(messages[i].split())\n x=max(d.values())\n for k,v in d.items():\n if v==x :\n l.append(k)\n if len(l)==1:\n return l[0]\n else:\n l=sorted(l)[::-1] #Lexigograhical sorting of list\n return l[0]\n```\n\n***Please Upvote if you like it.*** | 7 | You have a chat log of `n` messages. You are given two string arrays `messages` and `senders` where `messages[i]` is a **message** sent by `senders[i]`.
A **message** is list of **words** that are separated by a single space with no leading or trailing spaces. The **word count** of a sender is the total number of **words** sent by the sender. Note that a sender may send more than one message.
Return _the sender with the **largest** word count_. If there is more than one sender with the largest word count, return _the one with the **lexicographically largest** name_.
**Note:**
* Uppercase letters come before lowercase letters in lexicographical order.
* `"Alice "` and `"alice "` are distinct.
**Example 1:**
**Input:** messages = \[ "Hello userTwooo ", "Hi userThree ", "Wonderful day Alice ", "Nice day userThree "\], senders = \[ "Alice ", "userTwo ", "userThree ", "Alice "\]
**Output:** "Alice "
**Explanation:** Alice sends a total of 2 + 3 = 5 words.
userTwo sends a total of 2 words.
userThree sends a total of 3 words.
Since Alice has the largest word count, we return "Alice ".
**Example 2:**
**Input:** messages = \[ "How is leetcode for everyone ", "Leetcode is useful for practice "\], senders = \[ "Bob ", "Charlie "\]
**Output:** "Charlie "
**Explanation:** Bob sends a total of 5 words.
Charlie sends a total of 5 words.
Since there is a tie for the largest word count, we return the sender with the lexicographically larger name, Charlie.
**Constraints:**
* `n == messages.length == senders.length`
* `1 <= n <= 104`
* `1 <= messages[i].length <= 100`
* `1 <= senders[i].length <= 10`
* `messages[i]` consists of uppercase and lowercase English letters and `' '`.
* All the words in `messages[i]` are separated by **a single space**.
* `messages[i]` does not have leading or trailing spaces.
* `senders[i]` consists of uppercase and lowercase English letters only. | For positive numbers, the leading digit should be the smallest nonzero digit. Then the remaining digits follow in ascending order. For negative numbers, the digits should be arranged in descending order. |
Very simple Python solution O(nlog(n)) | maximum-total-importance-of-roads | 0 | 1 | ```\nclass Solution:\n def maximumImportance(self, n: int, roads: List[List[int]]) -> int:\n Arr = [0] * n # i-th city has Arr[i] roads\n for A,B in roads:\n Arr[A] += 1 # Each road increase the road count\n Arr[B] += 1\n Arr.sort() # Cities with most road should receive the most score\n summ = 0\n for i in range(len(Arr)):\n summ += Arr[i] * (i+1) # Multiply city roads with corresponding score\n \n return summ\n``` | 20 | You are given an integer `n` denoting the number of cities in a country. The cities are numbered from `0` to `n - 1`.
You are also given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional** road connecting cities `ai` and `bi`.
You need to assign each city with an integer value from `1` to `n`, where each value can only be used **once**. The **importance** of a road is then defined as the **sum** of the values of the two cities it connects.
Return _the **maximum total importance** of all roads possible after assigning the values optimally._
**Example 1:**
**Input:** n = 5, roads = \[\[0,1\],\[1,2\],\[2,3\],\[0,2\],\[1,3\],\[2,4\]\]
**Output:** 43
**Explanation:** The figure above shows the country and the assigned values of \[2,4,5,3,1\].
- The road (0,1) has an importance of 2 + 4 = 6.
- The road (1,2) has an importance of 4 + 5 = 9.
- The road (2,3) has an importance of 5 + 3 = 8.
- The road (0,2) has an importance of 2 + 5 = 7.
- The road (1,3) has an importance of 4 + 3 = 7.
- The road (2,4) has an importance of 5 + 1 = 6.
The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
It can be shown that we cannot obtain a greater total importance than 43.
**Example 2:**
**Input:** n = 5, roads = \[\[0,3\],\[2,4\],\[1,3\]\]
**Output:** 20
**Explanation:** The figure above shows the country and the assigned values of \[4,3,2,5,1\].
- The road (0,3) has an importance of 4 + 5 = 9.
- The road (2,4) has an importance of 2 + 1 = 3.
- The road (1,3) has an importance of 3 + 5 = 8.
The total importance of all roads is 9 + 3 + 8 = 20.
It can be shown that we cannot obtain a greater total importance than 20.
**Constraints:**
* `2 <= n <= 5 * 104`
* `1 <= roads.length <= 5 * 104`
* `roads[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi`
* There are no duplicate roads. | Note that flipping a bit twice does nothing. In order to determine the value of a bit, consider how you can efficiently count the number of flips made on the bit since its latest update. |
Python3 | Easy understanding | Faster than 100% time and memory | maximum-total-importance-of-roads | 0 | 1 | **UPVOTE IF YOU LIKE IT**\n```\nclass Solution:\n def maximumImportance(self, n: int, roads: List[List[int]]) -> int:\n \n \'\'\'The main idea is to count the frequency of the cities connected to roads and then \n keep on assigning the integer value from one to n to each cities after sorting it. \'\'\'\n \n f = [0 for _ in range(n)] # for storing the frequency of each city connected to pathways\n \n for x, y in roads:\n f[x] += 1\n f[y] += 1\n \n f.sort()\n s = 0\n for i in range(len(f)):\n s += f[i] * (i+1) # assigning and storing the integer value to each cities frequency in ascending order\n return s\n``` | 2 | You are given an integer `n` denoting the number of cities in a country. The cities are numbered from `0` to `n - 1`.
You are also given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional** road connecting cities `ai` and `bi`.
You need to assign each city with an integer value from `1` to `n`, where each value can only be used **once**. The **importance** of a road is then defined as the **sum** of the values of the two cities it connects.
Return _the **maximum total importance** of all roads possible after assigning the values optimally._
**Example 1:**
**Input:** n = 5, roads = \[\[0,1\],\[1,2\],\[2,3\],\[0,2\],\[1,3\],\[2,4\]\]
**Output:** 43
**Explanation:** The figure above shows the country and the assigned values of \[2,4,5,3,1\].
- The road (0,1) has an importance of 2 + 4 = 6.
- The road (1,2) has an importance of 4 + 5 = 9.
- The road (2,3) has an importance of 5 + 3 = 8.
- The road (0,2) has an importance of 2 + 5 = 7.
- The road (1,3) has an importance of 4 + 3 = 7.
- The road (2,4) has an importance of 5 + 1 = 6.
The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
It can be shown that we cannot obtain a greater total importance than 43.
**Example 2:**
**Input:** n = 5, roads = \[\[0,3\],\[2,4\],\[1,3\]\]
**Output:** 20
**Explanation:** The figure above shows the country and the assigned values of \[4,3,2,5,1\].
- The road (0,3) has an importance of 4 + 5 = 9.
- The road (2,4) has an importance of 2 + 1 = 3.
- The road (1,3) has an importance of 3 + 5 = 8.
The total importance of all roads is 9 + 3 + 8 = 20.
It can be shown that we cannot obtain a greater total importance than 20.
**Constraints:**
* `2 <= n <= 5 * 104`
* `1 <= roads.length <= 5 * 104`
* `roads[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi`
* There are no duplicate roads. | Note that flipping a bit twice does nothing. In order to determine the value of a bit, consider how you can efficiently count the number of flips made on the bit since its latest update. |
Python Easy Solution using Sort | maximum-total-importance-of-roads | 0 | 1 | The main idea is:\n1. Find the number of roads that are connecting to each city. Let\'s call it `degrees` \n2. Sort the `degrees` in ascending order such that the city is the least number of connecting roads comes to the top. This will be assigned the least score.\n3. Sum the importance of all the cities. The importance of a city is : \n\n```\nthe number of connecting roads \'degree\' * the \'position\' of the city in the sorted \'degrees\'.\n```\nBelow is my implementation\n```\nclass Solution:\n def maximumImportance(self, n: int, roads: List[List[int]]) -> int:\n degrees = [0] * n \n for x,y in roads:\n degrees[x] += 1 \n degrees[y] += 1\n degrees.sort() # Cities with most roads would receive the most score \n return sum(degrees[i] * (i+1) for i in range(len(degrees)))\n```\n\n**Time - O(nlogn)** - for sorting the `degrees`\n**Space - O(n)**\n\n---\n\n***Please upvote if you find it useful*** | 2 | You are given an integer `n` denoting the number of cities in a country. The cities are numbered from `0` to `n - 1`.
You are also given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional** road connecting cities `ai` and `bi`.
You need to assign each city with an integer value from `1` to `n`, where each value can only be used **once**. The **importance** of a road is then defined as the **sum** of the values of the two cities it connects.
Return _the **maximum total importance** of all roads possible after assigning the values optimally._
**Example 1:**
**Input:** n = 5, roads = \[\[0,1\],\[1,2\],\[2,3\],\[0,2\],\[1,3\],\[2,4\]\]
**Output:** 43
**Explanation:** The figure above shows the country and the assigned values of \[2,4,5,3,1\].
- The road (0,1) has an importance of 2 + 4 = 6.
- The road (1,2) has an importance of 4 + 5 = 9.
- The road (2,3) has an importance of 5 + 3 = 8.
- The road (0,2) has an importance of 2 + 5 = 7.
- The road (1,3) has an importance of 4 + 3 = 7.
- The road (2,4) has an importance of 5 + 1 = 6.
The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
It can be shown that we cannot obtain a greater total importance than 43.
**Example 2:**
**Input:** n = 5, roads = \[\[0,3\],\[2,4\],\[1,3\]\]
**Output:** 20
**Explanation:** The figure above shows the country and the assigned values of \[4,3,2,5,1\].
- The road (0,3) has an importance of 4 + 5 = 9.
- The road (2,4) has an importance of 2 + 1 = 3.
- The road (1,3) has an importance of 3 + 5 = 8.
The total importance of all roads is 9 + 3 + 8 = 20.
It can be shown that we cannot obtain a greater total importance than 20.
**Constraints:**
* `2 <= n <= 5 * 104`
* `1 <= roads.length <= 5 * 104`
* `roads[i].length == 2`
* `0 <= ai, bi <= n - 1`
* `ai != bi`
* There are no duplicate roads. | Note that flipping a bit twice does nothing. In order to determine the value of a bit, consider how you can efficiently count the number of flips made on the bit since its latest update. |
Python | Simple | Explained | 3 Lines | rearrange-characters-to-make-target-string | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\nI approached this problem by dividing the count of letters in both given string and target string. I take the minimum of b because we need to get the maximum amount of target strings we can make that using minimum of one letter.\n\n# Example\ns : ilovecodingonleetcode\ntarget : code\n\n- No. of c in s = 2\n- No. of o in s = 4\n- No. of d in s = 2\n- No. of e in s = 4\nAs we can see here we can only form 2 words "code" by rearraging it\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n\n# Code\n```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n res=101\n for i in target:\n res=min(res,s.count(i)//target.count(i))\n return res\n``` | 1 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Easy Python solution with Counter() | rearrange-characters-to-make-target-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n cntTarget = Counter(target)\n cntS = Counter(s)\n ans = 10000\n for i in cntTarget:\n ans = min(ans , cntS[i] // cntTarget[i])\n return ans\n``` | 1 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Python | Easy Solution✅ | rearrange-characters-to-make-target-string | 0 | 1 | ```\ndef rearrangeCharacters(self, s: str, target: str) -> int:\n maxx = []\n for i in range(len(set(target))):\n t_count = target.count(target[i]) # count the no of occurrence of letter in target string\n s_count = s.count(target[i]) # count the no of occurrence of target letter in s\n if t_count <= s_count:\n maxx.append(s_count // t_count)\n else:\n return 0\n return min(maxx)\n``` | 10 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Python Two Liner Beats ~95% | rearrange-characters-to-make-target-string | 0 | 1 | ```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n counter_s = Counter(s) \n return min(counter_s[c] // count for c,count in Counter(target).items())\n```\n\n**Time - O(n)\nSpace - O(n)**\n\n--- \n***Please upvote if you find it useful*** | 18 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Python | Easy Solution | Loops | Hashmap | rearrange-characters-to-make-target-string | 0 | 1 | # Code\n```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n hashmap = defaultdict(int)\n for i in s:\n hashmap[i] += 1\n count = 0\n flag = 0\n while True:\n if flag:\n break\n for i in target:\n if hashmap[i] == 0:\n flag = 1\n break\n hashmap[i] -= 1\n count += 1\n return count-1\n```\nDo upvote if you like the solution :) | 4 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
✅ 96% || Python3 || Counter and calculation | rearrange-characters-to-make-target-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\n\n\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n counter = Counter(s)\n s_count = Counter(target)\n min_letter = []\n for key, val in s_count.items():\n min_letter.append(counter[key] // val)\n min_letter.sort()\n return min_letter[0]\n\n\nobj = Solution()\nprint(obj.rearrangeCharacters( s = "abbaccaddaeea", target = "aaaaa"))\n``` | 1 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Python, two Counters | rearrange-characters-to-make-target-string | 0 | 1 | ```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n s = Counter(s)\n target = Counter(target)\n return min(s[c] // target[c] for c in target)\n``` | 2 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Python | Stright Forward | rearrange-characters-to-make-target-string | 0 | 1 | ```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n counter_s = Counter(s)\n res = float(\'inf\')\n for k, v in Counter(target).items():\n res = min(res, counter_s[k] // v)\n return res\n``` | 2 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Two Counters | rearrange-characters-to-make-target-string | 0 | 1 | **Python 3**\n```python\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n cnt, cnt1 = Counter(s), Counter(target)\n return min(cnt[ch] // cnt1[ch] for ch in cnt1.keys())\n``` | 2 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Simple Python solution | rearrange-characters-to-make-target-string | 0 | 1 | ```\nclass Solution:\n def rearrangeCharacters(self, s: str, target: str) -> int:\n freqs = {} # count the letter ffrequency of string s\n for char in s:\n freqs[char] = freqs.get(char,0) + 1\n \n freqTarget = {} # count the letter ffrequency of target s\n for c in target:\n freqTarget[c] = freqTarget.get(c,0) + 1\n \n mini = len(s) #Minimum value to be updated\n for c in target:\n mini = min(mini, freqs.get(c,0) // freqTarget[c]) # Don\'t forget to use freqs.get(c,0). freqs[c] can give you keyError\n return mini\n\t\t``` | 3 | You are given two **0-indexed** strings `s` and `target`. You can take some letters from `s` and rearrange them to form new strings.
Return _the **maximum** number of copies of_ `target` _that can be formed by taking letters from_ `s` _and rearranging them._
**Example 1:**
**Input:** s = "ilovecodingonleetcode ", target = "code "
**Output:** 2
**Explanation:**
For the first copy of "code ", take the letters at indices 4, 5, 6, and 7.
For the second copy of "code ", take the letters at indices 17, 18, 19, and 20.
The strings that are formed are "ecod " and "code " which can both be rearranged into "code ".
We can make at most two copies of "code ", so we return 2.
**Example 2:**
**Input:** s = "abcba ", target = "abc "
**Output:** 1
**Explanation:**
We can make one copy of "abc " by taking the letters at indices 0, 1, and 2.
We can make at most one copy of "abc ", so we return 1.
Note that while there is an extra 'a' and 'b' at indices 3 and 4, we cannot reuse the letter 'c' at index 2, so we cannot make a second copy of "abc ".
**Example 3:**
**Input:** s = "abbaccaddaeea ", target = "aaaaa "
**Output:** 1
**Explanation:**
We can make one copy of "aaaaa " by taking the letters at indices 0, 3, 6, 9, and 12.
We can make at most one copy of "aaaaa ", so we return 1.
**Constraints:**
* `1 <= s.length <= 100`
* `1 <= target.length <= 10`
* `s` and `target` consist of lowercase English letters. | What is the highest possible answer for a set of n points? The highest possible answer is n / 2 (rounded up). This is because you can cover at least two points with a line, and if n is odd, you need to add one extra line to cover the last point. Suppose you have a line covering two points, how can you quickly check if a third point is also covered by that line? Calculate the slope from the first point to the second point. If the slope from the first point to the third point is the same, then it is also covered by that line. |
Simple Python with explanation | apply-discount-to-prices | 0 | 1 | ```\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n s = sentence.split() # convert to List to easily update\n m = discount / 100 \n for i,word in enumerate(s):\n if word[0] == "$" and word[1:].isdigit(): # Check whether it is in correct format\n num = int(word[1:]) * (1-m) # discounted price\n w = "$" + "{:.2f}".format(num) #correctly format\n s[i] = w #Change inside the list\n \n return " ".join(s) #Combine the updated list\n\t\t``` | 9 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
Self Explanatory Python3 using startswith and string.split( | apply-discount-to-prices | 0 | 1 | \n# Code\n```\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n words = sentence.split()\n for i, word in enumerate(words):\n if word.startswith(\'\n```) and word[1:].isdigit():\n price = int(word[1:])\n discounted_price = round(price * (100 - discount) / 100, 2)\n new_word = "$" + format(discounted_price, ".2f")\n words[i] = new_word\n return \' \'.join(words)\n``` | 1 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
Regex sub, 92% speed | apply-discount-to-prices | 0 | 1 | \n```\nfrom re import compile\nclass Solution:\n pat = compile(r"(?<= [$])(\\d+)(?= )")\n def discountPrices(self, sentence: str, discount: int) -> str:\n coeff = 1 - discount / 100\n return (Solution.pat.\n sub(lambda m: f"{float(m.group(1)) * coeff:0.2f}",\n f" {sentence} ").strip(" "))\n``` | 0 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
[Python3] Regex substitution | apply-discount-to-prices | 0 | 1 | ```python\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n """If you use regex, now you have two problems. \n\n Lots of trial and error on regex101.com\n\n 254 ms, faster than 40.17%\n """\n \n def repl(m):\n rep = float(m.group(2)) * (100 - discount) / 100\n return f\'${rep:.2f}\'\n\n return re.sub(r\'(^|(?<=\\s))\\$(\\d+)(?=\\s|$)\', repl, sentence)\n``` | 1 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
Python | Easy ✅ | apply-discount-to-prices | 0 | 1 | ```python\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n words = sentence.split()\n calc_price = lambda cost, discount: cost * (discount / 100)\n\n for i, w in enumerate(words):\n if w.startswith("$"):\n price = w[1:]\n if price and "$" not in price and price.isdigit():\n words[i] = f\'${int(price) - calc_price(int(price), discount):.2f}\'\n\n return " ".join(words)\n```\n**Time**: `O(n)`\n**Space**: `O(1)` | 1 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
Easy Python Solution | apply-discount-to-prices | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n arr=sentence.split()\n for i in range(len(arr)):\n if arr[i][:1]==\'\n``` and arr[i][1:].isnumeric():\n val=format((float(arr[i][1:])*(100-discount))/100,".2f")\n arr[i]="$"+str(val)\n return \' \'.join(arr)\n``` | 0 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
2288. Apply Discount to Prices | apply-discount-to-prices | 0 | 1 | # Intuition\nThe array approach makes handling valid prices much easier compared to the iteration of the entire string. \n\n# Approach\n1. Split into array, elements with prices will be either valid or invalid \n2. Check whether it is a valid price by checking if element starts with `$`\nand whether the entire string after `$` is a digit.\n3. Perform the discount logic, and update the element\n4. Returned the joined array\n\n# Code\n```\nclass Solution:\n def discountPrices(self, sentence: str, discount: int) -> str:\n words = sentence.split()\n\n for index, word in enumerate(words):\n if word.startswith("$") and word[1:].isdigit():\n val = int(word[1:])\n words[index] = "$" + str("%.2f" % (val - (discount / 100) * val))\n\n return " ".join(words)\n\n``` | 0 | A **sentence** is a string of single-space separated words where each word can contain digits, lowercase letters, and the dollar sign `'$'`. A word represents a **price** if it is a sequence of digits preceded by a dollar sign.
* For example, `"$100 "`, `"$23 "`, and `"$6 "` represent prices while `"100 "`, `"$ "`, and `"$1e5 "` do not.
You are given a string `sentence` representing a sentence and an integer `discount`. For each word representing a price, apply a discount of `discount%` on the price and **update** the word in the sentence. All updated prices should be represented with **exactly two** decimal places.
Return _a string representing the modified sentence_.
Note that all prices will contain **at most** `10` digits.
**Example 1:**
**Input:** sentence = "there are $1 $2 and 5$ candies in the shop ", discount = 50
**Output:** "there are $0.50 $1.00 and 5$ candies in the shop "
**Explanation:**
The words which represent prices are "$1 " and "$2 ".
- A 50% discount on "$1 " yields "$0.50 ", so "$1 " is replaced by "$0.50 ".
- A 50% discount on "$2 " yields "$1 ". Since we need to have exactly 2 decimal places after a price, we replace "$2 " with "$1.00 ".
**Example 2:**
**Input:** sentence = "1 2 $3 4 $5 $6 7 8$ $9 $10$ ", discount = 100
**Output:** "1 2 $0.00 4 $0.00 $0.00 7 8$ $0.00 $10$ "
**Explanation:**
Applying a 100% discount on any price will result in 0.
The words representing prices are "$3 ", "$5 ", "$6 ", and "$9 ".
Each of them is replaced by "$0.00 ".
**Constraints:**
* `1 <= sentence.length <= 105`
* `sentence` consists of lowercase English letters, digits, `' '`, and `'$'`.
* `sentence` does not have leading or trailing spaces.
* All words in `sentence` are separated by a single space.
* All prices will be **positive** numbers without leading zeros.
* All prices will have **at most** `10` digits.
* `0 <= discount <= 100` | Try simulating the process until either of the two integers is zero. Count the number of operations done. |
[Python3] Increasing Stack | steps-to-make-array-non-decreasing | 0 | 1 | Reverse scan from right to left, maintain an increasing stack.\nFor i<j and nums[i]>nums[j], the number of rounds for nums[i] to remove nums[j] is:\n 1. If nums[j] takes 3 rounds to remove all smaller numbers on its right, then it will also take nums[i] same 3 rounds to remove nums[j], not 1 round. \n 2. If nums[j] has nothing to remove on its right side, then nums[i] will take at least 1 round to remove nums[j].\n\n```\n def totalSteps(self, nums: List[int]) -> int:\n res,stack = 0, []\n for i in range(len(nums)-1,-1,-1):\n cur = 0\n while stack and nums[stack[-1][0]]<nums[i]:\n _,v = stack.pop()\n cur=max(cur+1,v)\n res = max(res,cur)\n stack.append([i,cur])\n return res\n``` | 14 | You are given a **0-indexed** integer array `nums`. In one step, **remove** all elements `nums[i]` where `nums[i - 1] > nums[i]` for all `0 < i < nums.length`.
Return _the number of steps performed until_ `nums` _becomes a **non-decreasing** array_.
**Example 1:**
**Input:** nums = \[5,3,4,4,7,3,6,11,8,5,11\]
**Output:** 3
**Explanation:** The following are the steps performed:
- Step 1: \[5,**3**,4,4,7,**3**,6,11,**8**,**5**,11\] becomes \[5,4,4,7,6,11,11\]
- Step 2: \[5,**4**,4,7,**6**,11,11\] becomes \[5,4,7,11,11\]
- Step 3: \[5,**4**,7,11,11\] becomes \[5,7,11,11\]
\[5,7,11,11\] is a non-decreasing array. Therefore, we return 3.
**Example 2:**
**Input:** nums = \[4,5,7,7,13\]
**Output:** 0
**Explanation:** nums is already a non-decreasing array. Therefore, we return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Count the frequency of each element in odd positions in the array. Do the same for elements in even positions. To minimize the number of operations we need to maximize the number of elements we keep from the original array. What are the possible combinations of elements we can choose from odd indices and even indices so that the number of unchanged elements is maximized? |
Python3 easiest solution beats 90% | steps-to-make-array-non-decreasing | 0 | 1 | # Code\n```\nclass Solution:\n def totalSteps(self, A: List[int]) -> int: \n st = [[A[0], 0]]\n ans = 0\n \n for a in A[1:]:\n t = 0\n while st and st[-1][0] <= a:\n t = max(t, st[-1][1])\n st.pop()\n if st: \n t += 1\n else:\n t = 0\n ans = max(ans, t)\n st.append([a, t])\n \n return ans\n``` | 2 | You are given a **0-indexed** integer array `nums`. In one step, **remove** all elements `nums[i]` where `nums[i - 1] > nums[i]` for all `0 < i < nums.length`.
Return _the number of steps performed until_ `nums` _becomes a **non-decreasing** array_.
**Example 1:**
**Input:** nums = \[5,3,4,4,7,3,6,11,8,5,11\]
**Output:** 3
**Explanation:** The following are the steps performed:
- Step 1: \[5,**3**,4,4,7,**3**,6,11,**8**,**5**,11\] becomes \[5,4,4,7,6,11,11\]
- Step 2: \[5,**4**,4,7,**6**,11,11\] becomes \[5,4,7,11,11\]
- Step 3: \[5,**4**,7,11,11\] becomes \[5,7,11,11\]
\[5,7,11,11\] is a non-decreasing array. Therefore, we return 3.
**Example 2:**
**Input:** nums = \[4,5,7,7,13\]
**Output:** 0
**Explanation:** nums is already a non-decreasing array. Therefore, we return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Count the frequency of each element in odd positions in the array. Do the same for elements in even positions. To minimize the number of operations we need to maximize the number of elements we keep from the original array. What are the possible combinations of elements we can choose from odd indices and even indices so that the number of unchanged elements is maximized? |
Easy Python Linked List Simulation Solution | steps-to-make-array-non-decreasing | 0 | 1 | **Walkthrough**\nThis is def not as elegant as the DP solution. But personally I find it easier to understand and a little bit more intuitive. What it is is recognizing the fact that linked list can help us for this problem because we keep deleting adjacent elements. \n\nThere are mostly 3 steps:\n1. Convert the array list to a singly linked list\n2. Get all peaks, where a peak is defined as any point in nums such that nums[i] > nums[i+1].\n3. This is the simulation step. We keep deleting adjacent numbers to the peaks as long as they are smaller than the peaks, until no such peak exist any more. \n\n\tNote that here we traverse backwards and that\'s because in situation like [6,5,4] it can actually be deleted in one iteration if we traverse backwards. But if we traverse forward, 6 would delete 5 and 5 hasn\'t had to chance to delete 4 yet, therefore yielding incorrect result. \n\n**Code**\n```\nclass Node:\n def __init__(self, val):\n self.val = val\n self.next = None\n\nclass Solution:\n def totalSteps(self, nums: List[int]) -> int:\n head = Node(-1)\n curr = head\n \n # 1. Convert the list to a singly linked list\n for num in nums:\n curr.next = Node(num)\n curr = curr.next\n \n # 2. Get all the peaks, where a peak is defined if nums[i] > nums[i+1]\n curr = head\n peaks = []\n \n while curr.next:\n if curr.val > curr.next.val:\n peaks.append(curr)\n curr = curr.next\n \n # 3. Simulation. Keep getting rid of the peaks until there\'s no more. \n steps = 0\n while peaks: \n nextPeaks = []\n \n for node in reversed(peaks):\n if node.next and node.val > node.next.val:\n node.next = node.next.next\n nextPeaks.append(node)\n \n if not nextPeaks:\n return steps\n \n peaks = list(reversed(nextPeaks))\n steps += 1\n return steps\n```\t\t\n\n**Time/Space Complexity**\n\n* Time: O(N), as each number can at be deleted once at most \n* Space: O(N), we use linear space to convert the array list to a linked list\n | 3 | You are given a **0-indexed** integer array `nums`. In one step, **remove** all elements `nums[i]` where `nums[i - 1] > nums[i]` for all `0 < i < nums.length`.
Return _the number of steps performed until_ `nums` _becomes a **non-decreasing** array_.
**Example 1:**
**Input:** nums = \[5,3,4,4,7,3,6,11,8,5,11\]
**Output:** 3
**Explanation:** The following are the steps performed:
- Step 1: \[5,**3**,4,4,7,**3**,6,11,**8**,**5**,11\] becomes \[5,4,4,7,6,11,11\]
- Step 2: \[5,**4**,4,7,**6**,11,11\] becomes \[5,4,7,11,11\]
- Step 3: \[5,**4**,7,11,11\] becomes \[5,7,11,11\]
\[5,7,11,11\] is a non-decreasing array. Therefore, we return 3.
**Example 2:**
**Input:** nums = \[4,5,7,7,13\]
**Output:** 0
**Explanation:** nums is already a non-decreasing array. Therefore, we return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Count the frequency of each element in odd positions in the array. Do the same for elements in even positions. To minimize the number of operations we need to maximize the number of elements we keep from the original array. What are the possible combinations of elements we can choose from odd indices and even indices so that the number of unchanged elements is maximized? |
Efficient Algorithm for Making an Array Non-Decreasing with Step-by-Step Visualization | steps-to-make-array-non-decreasing | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to find the minimum number of steps required to make the input array non-decreasing. One way to approach this problem is to keep track of the elements in the array that need to be removed in order to make it non-decreasing.\n\nTo make the given array non-decreasing, we need to remove the elements that violate the non-decreasing condition. The idea is to make the smallest possible modifications to the array to make it non-decreasing. Therefore, we can choose to remove the elements that are smaller than the previous element and make them equal to the previous element. This way, we only need to modify the array elements that violate the non-decreasing condition. We can count the number of modifications made to the array to make it non-decreasing, which gives us the number of steps required to solve the problem.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo implement the above intuition, we can iterate over the input array and check if the current element is smaller than the previous element. If it is smaller, we remove the current element and make it equal to the previous element. We also update the steps count by the difference between the previous element and the current element. At the end of the loop, we would have made all necessary modifications to the array to make it non-decreasing. The steps count gives us the number of modifications made to the array to achieve this condition. We return this count as the final result.\n\n\nWe can use a stack to keep track of the elements in the array that need to be removed. We iterate through the input array and for each element, we check if it is greater than or equal to the top element of the stack. If it is, we pop elements from the stack until we find an element that is greater than the current element or until the stack is empty. We then update a variable temp with the maximum value of the second element of the tuples in the stack. If the stack is not empty, we increment temp by 1. Otherwise, we set temp to 0. We then update a variable steps with the maximum value of steps and temp. Finally, we append a tuple containing the current element and temp to the stack.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity: The time complexity of our approach is O(n), where n is the length of the input array. We are iterating over the input array only once, and the time taken to modify an element is constant. Therefore, the overall time complexity of our approach is linear.\n\nTime complexity: O(n)\n\nThe time complexity of this solution is linear because we iterate through the input array once and for each element, we perform a constant number of operations.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity: The space complexity of our approach is O(1), as we are not using any extra data structures to store the intermediate results. We are modifying the input array in-place, so there is no extra space used apart from the input array itself. Therefore, the space complexity of our approach is constant.\n\n\nSpace complexity: O(n)\n\nThe space complexity of this solution is linear because we use a stack to keep track of the elements in the array that need to be removed.\n\n\n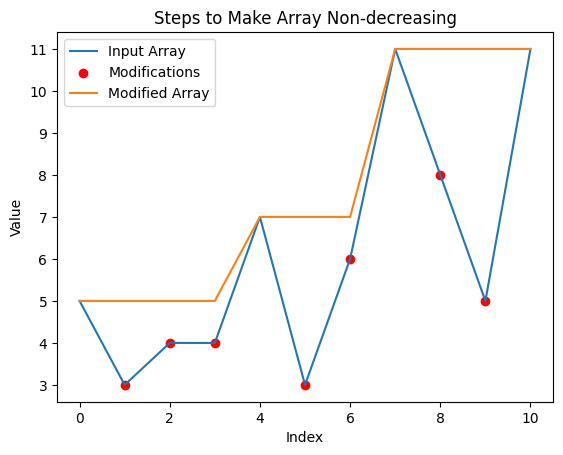\n\n\n\n\n\n# Code\n```C++ []\n\npublic:\n int totalSteps(vector<int>& nums) {\n stack<pair<int, int>> stack;\n stack.push({nums[0], 0});\n int steps = 0;\n for (int i = 1; i < nums.size(); i++) {\n int temp = 0;\n while (!stack.empty() && stack.top().first <= nums[i]) {\n temp = max(temp, stack.top().second);\n stack.pop();\n }\n if (!stack.empty()) {\n temp += 1;\n } else {\n temp = 0;\n }\n steps = max(steps, temp);\n stack.push({nums[i], temp});\n }\n return steps;\n }\n};\n\n```\n```python []\nclass Solution:\n def totalSteps(self, nums: List[int]) -> int:\n stack = [[nums[0], 0]]\n steps = 0\n for num in nums[1:]:\n temp = 0\n while stack and stack[-1][0] <= num:\n temp = max(temp, stack[-1][1])\n stack.pop()\n if stack:\n temp += 1\n else:\n temp = 0\n steps = max(steps, temp)\n stack.append([num, temp])\n return steps\n\n```\n```java []\nclass Solution {\n public int totalSteps(int[] nums) {\n Stack<int[]> stack = new Stack<>();\n stack.push(new int[]{nums[0], 0});\n int steps = 0;\n for (int i = 1; i < nums.length; i++) {\n int temp = 0;\n while (!stack.isEmpty() && stack.peek()[0] <= nums[i]) {\n temp = Math.max(temp, stack.peek()[1]);\n stack.pop();\n }\n if (!stack.isEmpty()) {\n temp += 1;\n } else {\n temp = 0;\n }\n steps = Math.max(steps, temp);\n stack.push(new int[]{nums[i], temp});\n }\n return steps;\n }\n}\n\n```\n | 2 | You are given a **0-indexed** integer array `nums`. In one step, **remove** all elements `nums[i]` where `nums[i - 1] > nums[i]` for all `0 < i < nums.length`.
Return _the number of steps performed until_ `nums` _becomes a **non-decreasing** array_.
**Example 1:**
**Input:** nums = \[5,3,4,4,7,3,6,11,8,5,11\]
**Output:** 3
**Explanation:** The following are the steps performed:
- Step 1: \[5,**3**,4,4,7,**3**,6,11,**8**,**5**,11\] becomes \[5,4,4,7,6,11,11\]
- Step 2: \[5,**4**,4,7,**6**,11,11\] becomes \[5,4,7,11,11\]
- Step 3: \[5,**4**,7,11,11\] becomes \[5,7,11,11\]
\[5,7,11,11\] is a non-decreasing array. Therefore, we return 3.
**Example 2:**
**Input:** nums = \[4,5,7,7,13\]
**Output:** 0
**Explanation:** nums is already a non-decreasing array. Therefore, we return 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 109` | Count the frequency of each element in odd positions in the array. Do the same for elements in even positions. To minimize the number of operations we need to maximize the number of elements we keep from the original array. What are the possible combinations of elements we can choose from odd indices and even indices so that the number of unchanged elements is maximized? |
[Python 3] 0-1 BFS - Easy to understand | minimum-obstacle-removal-to-reach-corner | 0 | 1 | # Intuition\nFind the shortest path with the weight is only 0 or 1 => 0-1 BFS\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\ncan refer 0-1 BFS [here](https://cp-algorithms.com/graph/01_bfs.html#algorithm)\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(E)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumObstacles(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n distance = [[float(\'inf\') for _ in range(n)] for _ in range(m)]\n distance[0][0] = 0\n q = collections.deque([(0, 0, 0)])\n while q:\n d, i, j = q.popleft()\n if i == m - 1 and j == n - 1: return d\n for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n ci, cj = i + di, j + dj\n if 0 <= ci < m and 0 <= cj < n:\n if d + grid[ci][cj] < distance[ci][cj]:\n distance[ci][cj] = d + grid[ci][cj]\n if grid[ci][cj] == 1: q.append((distance[ci][cj], ci, cj))\n else: q.appendleft((distance[ci][cj], ci, cj))\n return distance[m - 1][n - 1]\n``` | 3 | You are given a **0-indexed** 2D integer array `grid` of size `m x n`. Each cell has one of two values:
* `0` represents an **empty** cell,
* `1` represents an **obstacle** that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return _the **minimum** number of **obstacles** to **remove** so you can move from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)`.
**Example 1:**
**Input:** grid = \[\[0,1,1\],\[1,1,0\],\[1,1,0\]\]
**Output:** 2
**Explanation:** We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.
**Example 2:**
**Input:** grid = \[\[0,1,0,0,0\],\[0,1,0,1,0\],\[0,0,0,1,0\]\]
**Output:** 0
**Explanation:** We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Notice that if we choose to make x bags of beans empty, we should choose the x bags with the least amount of beans. Notice that if the minimum number of beans in a non-empty bag is m, then the best way to make all bags have an equal amount of beans is to reduce all the bags to have m beans. Can we iterate over how many bags we should remove and choose the one that minimizes the total amount of beans to remove? Sort the bags of beans first. |
[Java/Python 3] 2 codes: Shortest Path & BFS, w/ brief explanation, analysis and similar problems. | minimum-obstacle-removal-to-reach-corner | 1 | 1 | **Q & A**\n\nQ1: Why do we not need to keep track of which nodes we\'ve already visited? Is this code perhaps already implicitly tracking the nodes we\'ve visited? According to the implementation of Lazy Dijkstra [here](http://nmamano.com/blog/dijkstra/dijkstra.html), we need to keep track of which nodes we\'ve already visited. \nA1: The `PriorityQueue/heap` always keep track of the cell that we currently can reach with shortest path, and `grid[i][j] + o < dist[i][j]` makes sure we don\'t need to visit the cell again if we can not reach it with less obstacles. \nQ2: .Is it possible to optimize backtracking code with dp for this problem?\n[@Mikey98](https://leetcode.com/Mikey98) [@Adithya_U_Bhat](https://leetcode.com/Adithya_U_Bhat) contributed the following anwer.\nA2: No. In this question `1 <= m, n <= 10`<sup>5</sup>, which is toooo big for backtracking; You cannot use dp here as there are 4 directions and revisiting a node again can give you minimum answer so dp fails here , remember one thing if its given 4 direction always go with graphs\n\n**End of Q & A**\n\n----\n\n**Method 1: Shortest Path**\n\n1. Initialize `dist` with `Integer.MAX_VALUE/math.inf`, and use `dist[i][j]` to indicate the currently minimum obstacles need to remove to reach `(i, j)`;\n2. Starting from `(0, 0)`, put `[grid[0][0], 0, 0]` into a `PriorityQueue/heap` to begin to search by **Shortest Path**; Once we can reach any `(i, j)` from its neighbor with fewer obstacles, we update it with the less value and put the corresponding information array `[dist[i][j], i, j]` into `PriorityQueue/heap`, repeat till we find a path to `(m - 1, n - 1)`.\n\n```java\n private static final int[] d = {0, 1, 0, -1, 0};\n public int minimumObstacles(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] dist = new int[m][n];\n for (int[] di : dist) {\n Arrays.fill(di, Integer.MAX_VALUE);\n }\n dist[0][0] = grid[0][0];\n PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));\n pq.offer(new int[]{dist[0][0], 0, 0});\n while (!pq.isEmpty()) {\n int[] cur = pq.poll();\n int o = cur[0], r = cur[1], c = cur[2];\n if (r == m - 1 && c == n - 1) {\n return o;\n }\n for (int k = 0; k < 4; ++k) {\n int i = r + d[k], j = c + d[k + 1];\n if (0 <= i && i < m && 0 <= j && j < n && o + grid[i][j] < dist[i][j]) {\n dist[i][j] = o + grid[i][j];\n pq.offer(new int[]{dist[i][j], i, j});\n }\n }\n }\n return dist[m - 1][n - 1];\n }\n```\n```python\n def minimumObstacles(self, grid: List[List[int]]) -> int:\n m, n = map(len, (grid, grid[0]))\n dist = [[inf] * n for _ in range(m)]\n dist[0][0] = grid[0][0]\n hp = [(dist[0][0], 0, 0)]\n while hp:\n o, r, c = heappop(hp)\n if (r, c) == (m - 1, n - 1):\n return o\n for i, j in (r + 1, c), (r - 1, c), (r, c + 1), (r, c - 1):\n if m > i >= 0 <= j < n and grid[i][j] + o < dist[i][j]:\n dist[i][j] = grid[i][j] + o\n heappush(hp, (dist[i][j], i, j))\n```\n\n**Analysis:**\n\nTime: `O(m * n log(m * n))`, space: `O(m * n)`.\n\n----\n\n**Method 2: Modified BFS** -- credit to **@Doskarin**.\n1. Initialize `dist` with `Integer.MAX_VALUE/math.inf`, and use `dist[i][j]` to indicate the currently minimum obstacles need to remove to reach `(i, j)`;\n2. Starting from `(0, 0)`, put `[grid[0][0], 0, 0]` into a `Deque` to begin BFS, and use `dist` value to avoid duplicates;\n3. **Whenever encountering an empty cell neighbor, the `dist` value is same and hence we can put it to the front of the `Deque`;** Otherwise, put it to the back of the `Deque`;\n4. Repeat 2. and 3. and update `dist` accordingly till the `Deque` is empty;\n5. return `dist[m - 1][n - 1]` as solution.\n\n```java\n private static final int[] d = {0, 1, 0, -1, 0};\n private static final int M = Integer.MAX_VALUE;\n public int minimumObstacles(int[][] grid) {\n int m = grid.length, n = grid[0].length;\n int[][] dist = new int[m][n];\n for (int[] di : dist) {\n Arrays.fill(di, M);\n }\n dist[0][0] = 0;\n Deque<int[]> dq = new ArrayDeque<>();\n dq.offer(new int[3]);\n while (!dq.isEmpty()) {\n int[] cur = dq.poll();\n int o = cur[0], r = cur[1], c = cur[2];\n for (int k = 0; k < 4; ++k) {\n int i = r + d[k], j = c + d[k + 1];\n if (0 <= i && i < m && 0 <= j && j < n && dist[i][j] == M) {\n if (grid[i][j] == 1) {\n dist[i][j] = o + 1;\n dq.offer(new int[]{o + 1, i, j});\n }else {\n dist[i][j] = o;\n dq.offerFirst(new int[]{o, i, j});\n }\n }\n }\n }\n return dist[m - 1][n - 1];\n }\n```\n```python\n def minimumObstacles(self, grid: List[List[int]]) -> int:\n m, n = map(len, (grid, grid[0]))\n dist = [[inf] * n for _ in range(m)]\n dist[0][0] = 0\n dq = deque([(0, 0, 0)])\n while dq:\n o, r, c = dq.popleft()\n for i, j in (r + 1, c), (r - 1, c), (r, c + 1), (r, c - 1):\n if m > i >= 0 <= j < n and dist[i][j] == inf:\n if grid[i][j] == 1:\n dist[i][j] = o + 1\n dq.append((o + 1, i, j))\n else:\n dist[i][j] = o\n dq.appendleft((o, i, j)) \n return dist[-1][-1]\n```\n**Analysis:**\n\nSince each cell is visited at most once, therefore\n\nTime & space: `O(m * n)`.\n\n----\n\nIn case you are NOT familiar with Bellman Ford and Dijkstra\'s algorithm, the following links are excellent materials for you to learn:\n\n**Bellman Ford algorithm:**\nhttps://algs4.cs.princeton.edu/44sp/\nhttps://algs4.cs.princeton.edu/44sp/BellmanFordSP.java.html\nhttps://web.stanford.edu/class/archive/cs/cs161/cs161.1168/lecture14.pdf\nhttps://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm\nhttps://www.geeks for geeks.org/bellman-ford-algorithm-dp-23/(remove the 2 spaces among the links to make it valid)\n\n**Dijkstra\'s algorithm:**\nhttps://algs4.cs.princeton.edu/44sp/\nhttps://algs4.cs.princeton.edu/44sp/DijkstraSP.java.html\nhttps://en.wikipedia.org/wiki/Dijkstra%27s_algorithm\nhttps://www.geeks for geeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/ (remove the 2 spaces among the links to make it valid)\n\nSimilar problems:\n\n[407. Trapping Rain Water II](https://leetcode.com/problems/trapping-rain-water-ii)\n[499. The Maze III](https://leetcode.com/problems/the-maze-iii)\n[505. The Maze II](https://leetcode.com/problems/the-maze-ii)\n[743. Network Delay Time](https://leetcode.com/problems/network-delay-time/)\n[778. Swim in Rising Water](https://leetcode.com/problems/swim-in-rising-water/description/)\n[787. Cheapest Flights Within K Stops](https://leetcode.com/problems/cheapest-flights-within-k-stops/)\n[1102. Path With Maximum Minimum Value](https://leetcode.com/problems/path-with-maximum-minimum-value) **Premium**\n[1514. Path with Maximum Probability](https://leetcode.com/problems/path-with-maximum-probability/discuss/731767/JavaPython-3-2-codes%3A-Bellman-Ford-and-Dijkstra\'s-algorithm-w-brief-explanation-and-analysis.)\n[1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/discuss/909002/JavaPython-3-3-codes%3A-Binary-Search-Bellman-Ford-and-Dijkstra-w-brief-explanation-and-analysis.)\n[2290. Minimum Obstacle Removal to Reach Corner](https://leetcode.com/problems/minimum-obstacle-removal-to-reach-corner/discuss/2085640/JavaPython-3-Shortest-Path-w-brief-explanation-and-analysis.) | 85 | You are given a **0-indexed** 2D integer array `grid` of size `m x n`. Each cell has one of two values:
* `0` represents an **empty** cell,
* `1` represents an **obstacle** that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return _the **minimum** number of **obstacles** to **remove** so you can move from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)`.
**Example 1:**
**Input:** grid = \[\[0,1,1\],\[1,1,0\],\[1,1,0\]\]
**Output:** 2
**Explanation:** We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.
**Example 2:**
**Input:** grid = \[\[0,1,0,0,0\],\[0,1,0,1,0\],\[0,0,0,1,0\]\]
**Output:** 0
**Explanation:** We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Notice that if we choose to make x bags of beans empty, we should choose the x bags with the least amount of beans. Notice that if the minimum number of beans in a non-empty bag is m, then the best way to make all bags have an equal amount of beans is to reduce all the bags to have m beans. Can we iterate over how many bags we should remove and choose the one that minimizes the total amount of beans to remove? Sort the bags of beans first. |
[Python3] Dijkstra's algo | minimum-obstacle-removal-to-reach-corner | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7a598e64fb507fc966a3025d8edd0c8e7caf0bec) for solutions of weekly 295. \n\n```\nclass Solution:\n def minimumObstacles(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n dist = [[inf]*n for _ in range(m)]\n dist[0][0] = 0\n pq = [(0, 0, 0)]\n while pq: \n x, i, j = heappop(pq)\n if i == m-1 and j == n-1: return x\n for ii, jj in (i-1, j), (i, j-1), (i, j+1), (i+1, j): \n if 0 <= ii < m and 0 <= jj < n and x + grid[ii][jj] < dist[ii][jj]: \n dist[ii][jj] = x + grid[ii][jj]\n heappush(pq, (dist[ii][jj], ii, jj))\n``` | 1 | You are given a **0-indexed** 2D integer array `grid` of size `m x n`. Each cell has one of two values:
* `0` represents an **empty** cell,
* `1` represents an **obstacle** that may be removed.
You can move up, down, left, or right from and to an empty cell.
Return _the **minimum** number of **obstacles** to **remove** so you can move from the upper left corner_ `(0, 0)` _to the lower right corner_ `(m - 1, n - 1)`.
**Example 1:**
**Input:** grid = \[\[0,1,1\],\[1,1,0\],\[1,1,0\]\]
**Output:** 2
**Explanation:** We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.
**Example 2:**
**Input:** grid = \[\[0,1,0,0,0\],\[0,1,0,1,0\],\[0,0,0,1,0\]\]
**Output:** 0
**Explanation:** We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `grid[i][j]` is either `0` **or** `1`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Notice that if we choose to make x bags of beans empty, we should choose the x bags with the least amount of beans. Notice that if the minimum number of beans in a non-empty bag is m, then the best way to make all bags have an equal amount of beans is to reduce all the bags to have m beans. Can we iterate over how many bags we should remove and choose the one that minimizes the total amount of beans to remove? Sort the bags of beans first. |
🔥[Python 3] Simple recursion with diapason pass | min-max-game | 0 | 1 | ```python3 []\nclass Solution:\n def minMaxGame(self, nums: List[int]) -> int:\n def getMinMax(l, r, func):\n if r - l == 1: return nums[l]\n mid = l + (r-l)//2\n return func(getMinMax(l, mid, min), getMinMax(mid, r, max))\n \n return getMinMax(0, len(nums), min)\n``` | 3 | You are given a **0-indexed** integer array `nums` whose length is a power of `2`.
Apply the following algorithm on `nums`:
1. Let `n` be the length of `nums`. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n / 2`.
2. For every **even** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `min(nums[2 * i], nums[2 * i + 1])`.
3. For every **odd** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `max(nums[2 * i], nums[2 * i + 1])`.
4. **Replace** the array `nums` with `newNums`.
5. **Repeat** the entire process starting from step 1.
Return _the last number that remains in_ `nums` _after applying the algorithm._
**Example 1:**
**Input:** nums = \[1,3,5,2,4,8,2,2\]
**Output:** 1
**Explanation:** The following arrays are the results of applying the algorithm repeatedly.
First: nums = \[1,5,4,2\]
Second: nums = \[1,4\]
Third: nums = \[1\]
1 is the last remaining number, so we return 1.
**Example 2:**
**Input:** nums = \[3\]
**Output:** 3
**Explanation:** 3 is already the last remaining number, so we return 3.
**Constraints:**
* `1 <= nums.length <= 1024`
* `1 <= nums[i] <= 109`
* `nums.length` is a power of `2`. | Notice that for anagrams, the order of the letters is irrelevant. For each letter, we can count its frequency in s and t. For each letter, its contribution to the answer is the absolute difference between its frequency in s and t. |
✅ Python Easy Approach | min-max-game | 0 | 1 | ```\nclass Solution:\n def minMaxGame(self, nums: List[int]) -> int: \n l=nums\n while len(l)>1:\n is_min=True \n tmp=[]\n for i in range(0, len(l), 2):\n if is_min:\n tmp.append(min(l[i:i+2]))\n else:\n tmp.append(max(l[i:i+2]))\n is_min=not is_min \n l=tmp \n return l[0] \n```\n\n**Time - O(nlogn)** - The input space is reduced by half after each iteration. \n**Space - O(n)**\n\n**Note**: The space can be reduced to `O(1)` if you use input array as the space to store the next list of elements. But I don\'t like the idea of modifying the input array.\n\n---\n\n***Please upvote if you find it useful*** | 11 | You are given a **0-indexed** integer array `nums` whose length is a power of `2`.
Apply the following algorithm on `nums`:
1. Let `n` be the length of `nums`. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n / 2`.
2. For every **even** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `min(nums[2 * i], nums[2 * i + 1])`.
3. For every **odd** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `max(nums[2 * i], nums[2 * i + 1])`.
4. **Replace** the array `nums` with `newNums`.
5. **Repeat** the entire process starting from step 1.
Return _the last number that remains in_ `nums` _after applying the algorithm._
**Example 1:**
**Input:** nums = \[1,3,5,2,4,8,2,2\]
**Output:** 1
**Explanation:** The following arrays are the results of applying the algorithm repeatedly.
First: nums = \[1,5,4,2\]
Second: nums = \[1,4\]
Third: nums = \[1\]
1 is the last remaining number, so we return 1.
**Example 2:**
**Input:** nums = \[3\]
**Output:** 3
**Explanation:** 3 is already the last remaining number, so we return 3.
**Constraints:**
* `1 <= nums.length <= 1024`
* `1 <= nums[i] <= 109`
* `nums.length` is a power of `2`. | Notice that for anagrams, the order of the letters is irrelevant. For each letter, we can count its frequency in s and t. For each letter, its contribution to the answer is the absolute difference between its frequency in s and t. |
✅ EASY SOLUTION PYTHON || BEATS 99% RUNTIME ✅ | min-max-game | 0 | 1 | Here: \n1. count is the counter inside a function set to maintain the max min pattern ( if count is odd => find min; else => find max)\n2. final [] returns the modified list with max min values as list values which replaces the nums\n3. repeating the process until we get only one element in nums\n# Code\n```\nclass Solution:\n def minMaxGame(self, nums: List[int]) -> int:\n def minmax(lis):\n final = []\n count = 1\n for i in range(0,len(lis),2):\n temp = lis[i:i+2]\n if count%2 !=0:\n final.append(min(temp))\n else:\n final.append(max(temp)) \n count+=1\n return final\n while(len(nums)!=1):\n nums = minmax(nums)\n return nums[0]\n \n``` | 2 | You are given a **0-indexed** integer array `nums` whose length is a power of `2`.
Apply the following algorithm on `nums`:
1. Let `n` be the length of `nums`. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n / 2`.
2. For every **even** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `min(nums[2 * i], nums[2 * i + 1])`.
3. For every **odd** index `i` where `0 <= i < n / 2`, **assign** the value of `newNums[i]` as `max(nums[2 * i], nums[2 * i + 1])`.
4. **Replace** the array `nums` with `newNums`.
5. **Repeat** the entire process starting from step 1.
Return _the last number that remains in_ `nums` _after applying the algorithm._
**Example 1:**
**Input:** nums = \[1,3,5,2,4,8,2,2\]
**Output:** 1
**Explanation:** The following arrays are the results of applying the algorithm repeatedly.
First: nums = \[1,5,4,2\]
Second: nums = \[1,4\]
Third: nums = \[1\]
1 is the last remaining number, so we return 1.
**Example 2:**
**Input:** nums = \[3\]
**Output:** 3
**Explanation:** 3 is already the last remaining number, so we return 3.
**Constraints:**
* `1 <= nums.length <= 1024`
* `1 <= nums[i] <= 109`
* `nums.length` is a power of `2`. | Notice that for anagrams, the order of the letters is irrelevant. For each letter, we can count its frequency in s and t. For each letter, its contribution to the answer is the absolute difference between its frequency in s and t. |
[Python 3] Sort + Greedy - Simple Solution | partition-array-such-that-maximum-difference-is-k | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def partitionArray(self, nums: List[int], k: int) -> int:\n nums.sort()\n j = 0\n res = 1\n for i, num in enumerate(nums):\n if num - nums[j] > k:\n res += 1\n j = i\n return res\n``` | 3 | You are given an integer array `nums` and an integer `k`. You may partition `nums` into one or more **subsequences** such that each element in `nums` appears in **exactly** one of the subsequences.
Return _the **minimum** number of subsequences needed such that the difference between the maximum and minimum values in each subsequence is **at most**_ `k`_._
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[3,6,1,2,5\], k = 2
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[3,1,2\] and \[6,5\].
The difference between the maximum and minimum value in the first subsequence is 3 - 1 = 2.
The difference between the maximum and minimum value in the second subsequence is 6 - 5 = 1.
Since two subsequences were created, we return 2. It can be shown that 2 is the minimum number of subsequences needed.
**Example 2:**
**Input:** nums = \[1,2,3\], k = 1
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[1,2\] and \[3\].
The difference between the maximum and minimum value in the first subsequence is 2 - 1 = 1.
The difference between the maximum and minimum value in the second subsequence is 3 - 3 = 0.
Since two subsequences were created, we return 2. Note that another optimal solution is to partition nums into the two subsequences \[1\] and \[2,3\].
**Example 3:**
**Input:** nums = \[2,2,4,5\], k = 0
**Output:** 3
**Explanation:**
We can partition nums into the three subsequences \[2,2\], \[4\], and \[5\].
The difference between the maximum and minimum value in the first subsequences is 2 - 2 = 0.
The difference between the maximum and minimum value in the second subsequences is 4 - 4 = 0.
The difference between the maximum and minimum value in the third subsequences is 5 - 5 = 0.
Since three subsequences were created, we return 3. It can be shown that 3 is the minimum number of subsequences needed.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105`
* `0 <= k <= 105` | For a given amount of time, how can we count the total number of trips completed by all buses within that time? Consider using binary search. |
Python Easy Solution using Sorting | partition-array-such-that-maximum-difference-is-k | 0 | 1 | ### Explanation:\n\nInitially I did think it as a DP problem because of the word "**subsequence**" and "**minimum**". But after analysing the array and output I realized we are more concerned about "**at most difference should be K**", and the at most difference is of min element and max element of subsequence, so what\'s better than sorting? Sorting gives min and max element.\n\nYes, we are changing the order of elements but it wouldnt matter because we dont need to return the exact subsequences, we need to return the count of subsequences.\n\n**Example:**\n\n*before sort:*\nnums -> [3, 6, 1, 2, 5]\nsubsequences -> [3, 1, 2], [6, 5]\noutput -> 2\n\n*after sort:*\nnums -> [1, 2, 3, 5, 6]\nsubsequences -> [1, 2, 3], [5, 6]\noutput -> 2\n\nSo the order of elements would change but the elements inside each subsequence would remain same.\n\n\n```\nclass Solution:\n def partitionArray(self, nums: List[int], k: int) -> int:\n nums.sort()\n ans = 1\n\t\t# To keep track of starting element of each subsequence\n start = nums[0]\n \n for i in range(1, len(nums)):\n diff = nums[i] - start\n if diff > k:\n\t\t\t\t# If difference of starting and current element of subsequence is greater\n\t\t\t\t# than K, then only start new subsequence\n ans += 1\n start = nums[i]\n \n return ans | 22 | You are given an integer array `nums` and an integer `k`. You may partition `nums` into one or more **subsequences** such that each element in `nums` appears in **exactly** one of the subsequences.
Return _the **minimum** number of subsequences needed such that the difference between the maximum and minimum values in each subsequence is **at most**_ `k`_._
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[3,6,1,2,5\], k = 2
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[3,1,2\] and \[6,5\].
The difference between the maximum and minimum value in the first subsequence is 3 - 1 = 2.
The difference between the maximum and minimum value in the second subsequence is 6 - 5 = 1.
Since two subsequences were created, we return 2. It can be shown that 2 is the minimum number of subsequences needed.
**Example 2:**
**Input:** nums = \[1,2,3\], k = 1
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[1,2\] and \[3\].
The difference between the maximum and minimum value in the first subsequence is 2 - 1 = 1.
The difference between the maximum and minimum value in the second subsequence is 3 - 3 = 0.
Since two subsequences were created, we return 2. Note that another optimal solution is to partition nums into the two subsequences \[1\] and \[2,3\].
**Example 3:**
**Input:** nums = \[2,2,4,5\], k = 0
**Output:** 3
**Explanation:**
We can partition nums into the three subsequences \[2,2\], \[4\], and \[5\].
The difference between the maximum and minimum value in the first subsequences is 2 - 2 = 0.
The difference between the maximum and minimum value in the second subsequences is 4 - 4 = 0.
The difference between the maximum and minimum value in the third subsequences is 5 - 5 = 0.
Since three subsequences were created, we return 3. It can be shown that 3 is the minimum number of subsequences needed.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105`
* `0 <= k <= 105` | For a given amount of time, how can we count the total number of trips completed by all buses within that time? Consider using binary search. |
Simple Python Solution | partition-array-such-that-maximum-difference-is-k | 0 | 1 | # Intuition\nSort Your given array. Why? Because we need to find subsequence so order isnt define for them.\nWe are asked to return minimum number of subsequence we need to form so our aim is to add as many number as possible in one array with limit(k).\n`How limit is defined? largest ele - Smallest ele`\nAs we sorted our array so for each subsequence the first element will be smallest and just check if by adding curr element if we are still in our limit. (The problem is reduced in finding subarrays within limit)\n`If yes -> add the element\nIf not -> add the by far collected ans in res and reset your ans as empty to start finding new subarray.`\nRes carries all the possible subsequnces thus, return its length as the min no of subsequences required.\n\n# Code\n```\nclass Solution:\n def partitionArray(self, nums: List[int], k: int) -> int:\n nums.sort()\n \n # Base Case\n if nums[-1] - nums[0] <= k:\n return 1\n\n ans = []\n ans.append(nums[0])\n res = []\n for i in range(len(nums)-1):\n if nums[i + 1] - ans[0] <= k:\n ans.append(nums[i + 1])\n else:\n res.append(ans)\n ans = []\n ans.append(nums[i + 1])\n res.append(ans)\n # print(res)\n return len(res)\n\n``` | 2 | You are given an integer array `nums` and an integer `k`. You may partition `nums` into one or more **subsequences** such that each element in `nums` appears in **exactly** one of the subsequences.
Return _the **minimum** number of subsequences needed such that the difference between the maximum and minimum values in each subsequence is **at most**_ `k`_._
A **subsequence** is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.
**Example 1:**
**Input:** nums = \[3,6,1,2,5\], k = 2
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[3,1,2\] and \[6,5\].
The difference between the maximum and minimum value in the first subsequence is 3 - 1 = 2.
The difference between the maximum and minimum value in the second subsequence is 6 - 5 = 1.
Since two subsequences were created, we return 2. It can be shown that 2 is the minimum number of subsequences needed.
**Example 2:**
**Input:** nums = \[1,2,3\], k = 1
**Output:** 2
**Explanation:**
We can partition nums into the two subsequences \[1,2\] and \[3\].
The difference between the maximum and minimum value in the first subsequence is 2 - 1 = 1.
The difference between the maximum and minimum value in the second subsequence is 3 - 3 = 0.
Since two subsequences were created, we return 2. Note that another optimal solution is to partition nums into the two subsequences \[1\] and \[2,3\].
**Example 3:**
**Input:** nums = \[2,2,4,5\], k = 0
**Output:** 3
**Explanation:**
We can partition nums into the three subsequences \[2,2\], \[4\], and \[5\].
The difference between the maximum and minimum value in the first subsequences is 2 - 2 = 0.
The difference between the maximum and minimum value in the second subsequences is 4 - 4 = 0.
The difference between the maximum and minimum value in the third subsequences is 5 - 5 = 0.
Since three subsequences were created, we return 3. It can be shown that 3 is the minimum number of subsequences needed.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105`
* `0 <= k <= 105` | For a given amount of time, how can we count the total number of trips completed by all buses within that time? Consider using binary search. |
✅ Python Simple Map Approach | replace-elements-in-an-array | 0 | 1 | The core logic for this is the reversed iteration to construct the final replacements list.The reversed iteration helps to link the last replacement.\n\nThere can be chain of `operations` which will replace the same index in the array.\neg:\n> **operations = [[1,2], [2,3], [3,4]], nums = [1, 7, 9, 10]**\n\nIf you consider this example, the chain of operations are: `1-> 2 -> 3 -> 4`. So by transitive property we only care only about this replacement: `1->4`. The reversed iteration helps me to connect this link in `O(1)` with `replacements[x] = replacements.get(y, y)` logic. If I start from first, I would need a `O(n)` search.\n\n```\nclass Solution:\n def arrayChange(self, nums: List[int], operations: List[List[int]]) -> List[int]:\n replacements = {}\n for x, y in reversed(operations):\n replacements[x] = replacements.get(y, y)\n for idx, val in enumerate(nums):\n if val in replacements:\n nums[idx] = replacements[val]\n return nums\n```\n\n**Time - O(n)**\n**Space - O(n)** - space for storing positions of each element in input `nums`\n\n---\n***Please upvote if you find it useful*** | 29 | You are given a **0-indexed** array `nums` that consists of `n` **distinct** positive integers. Apply `m` operations to this array, where in the `ith` operation you replace the number `operations[i][0]` with `operations[i][1]`.
It is guaranteed that in the `ith` operation:
* `operations[i][0]` **exists** in `nums`.
* `operations[i][1]` does **not** exist in `nums`.
Return _the array obtained after applying all the operations_.
**Example 1:**
**Input:** nums = \[1,2,4,6\], operations = \[\[1,3\],\[4,7\],\[6,1\]\]
**Output:** \[3,2,7,1\]
**Explanation:** We perform the following operations on nums:
- Replace the number 1 with 3. nums becomes \[**3**,2,4,6\].
- Replace the number 4 with 7. nums becomes \[3,2,**7**,6\].
- Replace the number 6 with 1. nums becomes \[3,2,7,**1**\].
We return the final array \[3,2,7,1\].
**Example 2:**
**Input:** nums = \[1,2\], operations = \[\[1,3\],\[2,1\],\[3,2\]\]
**Output:** \[2,1\]
**Explanation:** We perform the following operations to nums:
- Replace the number 1 with 3. nums becomes \[**3**,2\].
- Replace the number 2 with 1. nums becomes \[3,**1**\].
- Replace the number 3 with 2. nums becomes \[**2**,1\].
We return the array \[2,1\].
**Constraints:**
* `n == nums.length`
* `m == operations.length`
* `1 <= n, m <= 105`
* All the values of `nums` are **distinct**.
* `operations[i].length == 2`
* `1 <= nums[i], operations[i][0], operations[i][1] <= 106`
* `operations[i][0]` will exist in `nums` when applying the `ith` operation.
* `operations[i][1]` will not exist in `nums` when applying the `ith` operation. | What is the maximum number of times we would want to go around the track without changing tires? Can we precompute the minimum time to go around the track x times without changing tires? Can we use dynamic programming to solve this efficiently using the precomputed values? |
O(n) space, O(n) time solution using a map | replace-elements-in-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def arrayChange(self, nums: List[int], operations: List[List[int]]) -> List[int]:\n index_map = defaultdict(int)\n for i, n in enumerate(nums):\n index_map[n] = i\n \n for op in operations:\n n1, n2 = op\n nums[index_map[n1]] = n2\n index_map[n2] = index_map[n1]\n \n return nums\n\n``` | 1 | You are given a **0-indexed** array `nums` that consists of `n` **distinct** positive integers. Apply `m` operations to this array, where in the `ith` operation you replace the number `operations[i][0]` with `operations[i][1]`.
It is guaranteed that in the `ith` operation:
* `operations[i][0]` **exists** in `nums`.
* `operations[i][1]` does **not** exist in `nums`.
Return _the array obtained after applying all the operations_.
**Example 1:**
**Input:** nums = \[1,2,4,6\], operations = \[\[1,3\],\[4,7\],\[6,1\]\]
**Output:** \[3,2,7,1\]
**Explanation:** We perform the following operations on nums:
- Replace the number 1 with 3. nums becomes \[**3**,2,4,6\].
- Replace the number 4 with 7. nums becomes \[3,2,**7**,6\].
- Replace the number 6 with 1. nums becomes \[3,2,7,**1**\].
We return the final array \[3,2,7,1\].
**Example 2:**
**Input:** nums = \[1,2\], operations = \[\[1,3\],\[2,1\],\[3,2\]\]
**Output:** \[2,1\]
**Explanation:** We perform the following operations to nums:
- Replace the number 1 with 3. nums becomes \[**3**,2\].
- Replace the number 2 with 1. nums becomes \[3,**1**\].
- Replace the number 3 with 2. nums becomes \[**2**,1\].
We return the array \[2,1\].
**Constraints:**
* `n == nums.length`
* `m == operations.length`
* `1 <= n, m <= 105`
* All the values of `nums` are **distinct**.
* `operations[i].length == 2`
* `1 <= nums[i], operations[i][0], operations[i][1] <= 106`
* `operations[i][0]` will exist in `nums` when applying the `ith` operation.
* `operations[i][1]` will not exist in `nums` when applying the `ith` operation. | What is the maximum number of times we would want to go around the track without changing tires? Can we precompute the minimum time to go around the track x times without changing tires? Can we use dynamic programming to solve this efficiently using the precomputed values? |
Python two solutions with explanation | replace-elements-in-an-array | 0 | 1 | **Solution 1: Index mapping**\nWe buid a hashmap that contains {value: index} key pairs. Based on the index looked up from that hashmap, for each operation, we update both the replaced value in nums, and the {updated num: index} key-value pair in the hashmap\nTotal runtime: `O(len(nums))` to build the hashmap + `O(len(operations))` to update the output array => `O(max(len(nums), len(operations))`\n```\n def arrayChange(self, nums: List[int], operations: List[List[int]]) -> List[int]:\n dic = {num: i for i, num in enumerate(nums)}\n for s, e in operations:\n i = dic[s]\n nums[i] = e\n dic[e] = i\n del dic[s]\n return nums\n```\n**Solution 2: Swap mapping**\nLet say we have the following operations: a -> b, b -> c, c -> d, we know that in the end a will be transformed to d\nSo we want to build a hashmap that contains a -> d key-value pair\nWe can do this by traversing the operations backward and with this line `swaps[s] = swaps[e] if e in swaps else e`, the dictionary will be updated each iteration. Example:\nIteration 1: {c -> d}\nIteration 2: {c -> d, b -> d}\nIteration 3: {c -> d, b -> d, a -> d}\nTotal runtime: `O(len(operations))` to build the hashmap + `O(len(nums))` to update the output array => `O(max(len(operations), len(nums))`\n```\ndef arrayChange(self, nums: List[int], operations: List[List[int]]) -> List[int]:\n\tswaps = {}\n\tfor s, e in reversed(operations):\n\t\tswaps[s] = swaps[e] if e in swaps else e\n\tfor i, num in enumerate(nums):\n\t\tif num in swaps:\n\t\t\tnums[i] = swaps[num]\n\treturn nums\n``` | 9 | You are given a **0-indexed** array `nums` that consists of `n` **distinct** positive integers. Apply `m` operations to this array, where in the `ith` operation you replace the number `operations[i][0]` with `operations[i][1]`.
It is guaranteed that in the `ith` operation:
* `operations[i][0]` **exists** in `nums`.
* `operations[i][1]` does **not** exist in `nums`.
Return _the array obtained after applying all the operations_.
**Example 1:**
**Input:** nums = \[1,2,4,6\], operations = \[\[1,3\],\[4,7\],\[6,1\]\]
**Output:** \[3,2,7,1\]
**Explanation:** We perform the following operations on nums:
- Replace the number 1 with 3. nums becomes \[**3**,2,4,6\].
- Replace the number 4 with 7. nums becomes \[3,2,**7**,6\].
- Replace the number 6 with 1. nums becomes \[3,2,7,**1**\].
We return the final array \[3,2,7,1\].
**Example 2:**
**Input:** nums = \[1,2\], operations = \[\[1,3\],\[2,1\],\[3,2\]\]
**Output:** \[2,1\]
**Explanation:** We perform the following operations to nums:
- Replace the number 1 with 3. nums becomes \[**3**,2\].
- Replace the number 2 with 1. nums becomes \[3,**1**\].
- Replace the number 3 with 2. nums becomes \[**2**,1\].
We return the array \[2,1\].
**Constraints:**
* `n == nums.length`
* `m == operations.length`
* `1 <= n, m <= 105`
* All the values of `nums` are **distinct**.
* `operations[i].length == 2`
* `1 <= nums[i], operations[i][0], operations[i][1] <= 106`
* `operations[i][0]` will exist in `nums` when applying the `ith` operation.
* `operations[i][1]` will not exist in `nums` when applying the `ith` operation. | What is the maximum number of times we would want to go around the track without changing tires? Can we precompute the minimum time to go around the track x times without changing tires? Can we use dynamic programming to solve this efficiently using the precomputed values? |
✅ Python3 solution | replace-elements-in-an-array | 0 | 1 | ```\nclass Solution:\n def arrayChange(self, nums: List[int], operations: List[List[int]]) -> List[int]:\n d = {} \n for i,num in enumerate(nums):\n d[num] = i #Save index of all elements in dictionary for O(1) lookup\n \n for x,r in operations:\n where = d[x] # Find location of operation from dictionary\n nums[where] = r # Complete the operation (Change number)\n del d[x] # Update dictionary\n d[r] = where # Update dictionary\n \n return nums\n``` | 4 | You are given a **0-indexed** array `nums` that consists of `n` **distinct** positive integers. Apply `m` operations to this array, where in the `ith` operation you replace the number `operations[i][0]` with `operations[i][1]`.
It is guaranteed that in the `ith` operation:
* `operations[i][0]` **exists** in `nums`.
* `operations[i][1]` does **not** exist in `nums`.
Return _the array obtained after applying all the operations_.
**Example 1:**
**Input:** nums = \[1,2,4,6\], operations = \[\[1,3\],\[4,7\],\[6,1\]\]
**Output:** \[3,2,7,1\]
**Explanation:** We perform the following operations on nums:
- Replace the number 1 with 3. nums becomes \[**3**,2,4,6\].
- Replace the number 4 with 7. nums becomes \[3,2,**7**,6\].
- Replace the number 6 with 1. nums becomes \[3,2,7,**1**\].
We return the final array \[3,2,7,1\].
**Example 2:**
**Input:** nums = \[1,2\], operations = \[\[1,3\],\[2,1\],\[3,2\]\]
**Output:** \[2,1\]
**Explanation:** We perform the following operations to nums:
- Replace the number 1 with 3. nums becomes \[**3**,2\].
- Replace the number 2 with 1. nums becomes \[3,**1**\].
- Replace the number 3 with 2. nums becomes \[**2**,1\].
We return the array \[2,1\].
**Constraints:**
* `n == nums.length`
* `m == operations.length`
* `1 <= n, m <= 105`
* All the values of `nums` are **distinct**.
* `operations[i].length == 2`
* `1 <= nums[i], operations[i][0], operations[i][1] <= 106`
* `operations[i][0]` will exist in `nums` when applying the `ith` operation.
* `operations[i][1]` will not exist in `nums` when applying the `ith` operation. | What is the maximum number of times we would want to go around the track without changing tires? Can we precompute the minimum time to go around the track x times without changing tires? Can we use dynamic programming to solve this efficiently using the precomputed values? |
✅Just String Slicing Nothing Else✅ | design-a-text-editor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI also use "|" like the actual case, It helps you to understand Better.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\u2B06**Please Upvote If it helps**\u2B06\n# Code\n```\nclass TextEditor:\n\n def __init__(self):\n self.ans = "|"\n\n def addText(self, text: str) -> None:\n index = self.ans.index(\'|\')\n self.ans = self.ans[:index]+text+"|"+self.ans[index+1:]\n \n\n def deleteText(self, k: int) -> int:\n temp = self.ans\n index = self.ans.index("|")\n if len(self.ans[:index])>=k: \n self.ans = self.ans[:index-k]+self.ans[index:]\n else:\n self.ans = self.ans[index:]\n return len(temp) - len(self.ans)\n \n\n def cursorLeft(self, k: int) -> str:\n index = self.ans.index(\'|\')\n if index<k:\n self.ans = self.ans.replace("|","")\n self.ans = "|"+self.ans\n else:\n self.ans = self.ans.replace("|","")\n self.ans = self.ans[:index-k]+"|"+self.ans[index-k:]\n \n index = self.ans.index(\'|\')\n if self.ans.index("|")>10:\n return self.ans[index-10:index]\n return self.ans[:self.ans.index("|")]\n \n\n def cursorRight(self, k: int) -> str:\n index = self.ans.index(\'|\')\n if len(self.ans)-index<k:\n self.ans = self.ans.replace("|","")\n self.ans = self.ans+"|"\n else:\n self.ans = self.ans.replace("|","")\n self.ans = self.ans[:index+k]+"|"+self.ans[index+k:]\n \n index = self.ans.index(\'|\')\n if self.ans.index("|")>10:\n return self.ans[index-10:index]\n return self.ans[:self.ans.index("|")]\n\n\n\n# Your TextEditor object will be instantiated and called as such:\n# obj = TextEditor()\n# obj.addText(text)\n# param_2 = obj.deleteText(k)\n# param_3 = obj.cursorLeft(k)\n# param_4 = obj.cursorRight(k)\n```\n\u2B06**Please Upvote If it helps**\u2B06\n | 1 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
Simple O(k) Python solution in 11 lines of code, beats 95% | design-a-text-editor | 0 | 1 | # Complexity\n- Time complexities: $$\\begin{matrix}\n\\textrm{\\_\\_init\\_\\_} & \\mathcal O(1) \\\\\n\\textrm{addText} & \\mathcal O(len(text)) \\\\\n\\textrm{deleteText} & \\mathcal O(k) \\\\\n\\textrm{cursorLeft} & \\mathcal O(k) \\\\\n\\textrm{cursorRight} & \\mathcal O(k)\n\\end{matrix}$$\n\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $\\mathcal O(max(len(currentText)))$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TextEditor:\n\n def __init__(self):\n # Two stacks that are relative to the cursor, r is in reverse\n self.l, self.r = [], []\n\n def addText(self, text: str) -> None:\n self.l.extend(list(text))\n\n def deleteText(self, k: int) -> int:\n for _ in range((d := min(k, len(self.l)))):\n self.l.pop()\n return d\n\n def cursorLeft(self, k: int) -> str:\n for _ in range(min(k, len(self.l))):\n self.r.append(self.l.pop())\n return \'\'.join(self.l[-10:])\n\n def cursorRight(self, k: int) -> str:\n for _ in range(min(k, len(self.r))):\n self.l.append(self.r.pop())\n return \'\'.join(self.l[-10:])\n \n\n# Your TextEditor object will be instantiated and called as such:\n# obj = TextEditor()\n# obj.addText(text)\n# param_2 = obj.deleteText(k)\n# param_3 = obj.cursorLeft(k)\n# param_4 = obj.cursorRight(k)\n``` | 1 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
Solution | design-a-text-editor | 1 | 1 | ```C++ []\nclass TextEditor {\npublic:\n string ltext = "", rtext="";\n TextEditor() {}\n \n void addText(string text) {\n ltext += text;\n }\n \n int deleteText(int k) {\n k = min(k, (int) ltext.size());\n ltext.resize(ltext.size() - k);\n return k;\n }\n \n string cursorLeft(int k) {\n for(;k > 0 && !ltext.empty(); ltext.pop_back(), k--)\n rtext.push_back(ltext.back());\n \n return ltext.size() >= 10 ? ltext.substr(ltext.size()-10, 10): ltext;\n }\n \n string cursorRight(int k) {\n for(;k > 0 && !rtext.empty(); rtext.pop_back(), k--)\n ltext.push_back(rtext.back());\n \n return ltext.size() >= 10 ? ltext.substr(ltext.size()-10, 10): ltext;\n }\n};\n```\n\n```Python3 []\nclass TextEditor:\n\n def __init__(self):\n self.left = []\n self.right = deque([])\n \n def addText(self, text: str) -> None:\n self.left.append(text)\n \n def deleteText(self, k: int) -> int:\n total = 0\n while k:\n if not self.left:\n break\n s = self.left.pop()\n if len(s) > k:\n s = s[:-k]\n self.left.append(s)\n total +=k\n break\n k -= len(s)\n total += len(s)\n return total\n\n def cursorLeft(self, k: int) -> str:\n total = 0\n while k:\n if not self.left:\n break\n s = self.left.pop()\n if len(s) > k:\n self.left.append(s[:-k])\n self.right.appendleft(s[-k:])\n break\n self.right.appendleft(s)\n k -= len(s)\n return self.get()\n \n\n def cursorRight(self, k: int) -> str:\n total = 0\n while k:\n if not self.right:\n break\n s = self.right.popleft()\n if len(s) > k:\n self.left.append(s[:k])\n self.right.appendleft(s[k:])\n break\n self.left.append(s)\n k -= len(s)\n return self.get()\n \n def get(self):\n ans = \'\'\n i = len(self.left) - 1\n while i >= 0 and len(ans) < 10:\n ans = self.left[i] + ans\n i -= 1\n return ans[-10:]\n```\n\n```Java []\nclass TextEditor {\n char buffer[];\n int left;\n int right;\n public TextEditor() {\n buffer = new char[800000];\n left = 0;\n right = buffer.length-1;\n }\n \n public void addText(String text) {\n for(char c : text.toCharArray()){\n buffer[left] = c;\n left++;\n }\n }\n \n public int deleteText(int k) {\n if(k>left)k=left;\n left-=k;\n return k;\n }\n \n public String cursorLeft(int k) { \n k = Math.min(k,left);\n while(k>0){\n left--;k--;\n buffer[right] = buffer[left];\n right--;\n }\n int len = Math.min(10,left);\n StringBuilder sb = new StringBuilder();\n int i = left;\n while(len!=0){\n len--;i--;\n sb.append(buffer[i]);\n }\n return sb.reverse().toString(); \n }\n \n public String cursorRight(int k) {\n int charOnRight = buffer.length - right -1;\n k = Math.min(k,charOnRight);\n while(k>0){\n k--;\n right++; \n buffer[left] = buffer[right];\n left++;\n }\n int len = Math.min(10,left);\n int i = left;\n StringBuilder sb = new StringBuilder();\n while(len!=0){\n len--;i--;\n sb.append(buffer[i]);\n }\n return sb.reverse().toString();\n\n }\n}\n```\n | 27 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
Python 3 solution beat 95% using stack and queue | design-a-text-editor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\naddText: O(n)\ndeleteText: O(k)\ncursorLeft: O(k)\ncursorRight: O(k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\n\nclass TextEditor:\n def __init__(self):\n self.stack = []\n self.q = deque([])\n \n def addText(self, text: str) -> None:\n for c in text:\n self.stack.append(c)\n\n #return "".join(self.stack)\n \n def deleteText(self, k: int) -> int:\n i = 0\n while self.stack and i < k:\n self.stack.pop()\n i += 1\n return i\n \n def cursorLeft(self, k: int) -> str:\n i = 0\n while self.stack and i < k:\n self.q.appendleft(self.stack.pop())\n i += 1\n return "".join(self.stack[-10:]) if len(self.stack) >= 10 else "".join(self.stack)\n def cursorRight(self, k: int) -> str:\n i = 0\n while self.q and i < k:\n self.stack.append(self.q.popleft())\n i += 1\n return "".join(self.stack[-10:]) if len(self.stack) >= 10 else "".join(self.stack) \n \n\n\n\n \n \n\n\n# Your TextEditor object will be instantiated and called as such:\n# obj = TextEditor()\n# obj.addText(text)\n# param_2 = obj.deleteText(k)\n# param_3 = obj.cursorLeft(k)\n# param_4 = obj.cursorRight(k)\n``` | 8 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
Python Easy Logical Starightforward | design-a-text-editor | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse python functions to manipulate strings\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe tricky part is to figure which index location is our cursor present..\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass TextEditor:\n\n def __init__(self):\n self.tex=""\n self.pos=0\n\n def addText(self, text: str) -> None:\n self.tex=self.tex[:self.pos]+text+self.tex[self.pos:]\n self.pos+=len(text)\n\n def deleteText(self, k: int) -> int:\n de=max(self.pos-k,0)\n d=min(self.pos,k)\n self.tex=self.tex[:de]+self.tex[self.pos:]\n self.pos=de\n return d\n\n def cursorLeft(self, k: int) -> str:\n self.pos=max(0,self.pos-k)\n return self.tex[max(0,self.pos-10):self.pos]\n\n def cursorRight(self, k: int) -> str:\n self.pos=min(len(self.tex),self.pos+k)\n return self.tex[max(0,self.pos-10):self.pos]\n``` | 1 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
✅ Python Simple Solution | design-a-text-editor | 0 | 1 | The approach that I am using is string slicing. So that would end up with `O(n)` time for all the operations. The following implementation seems to pass without any TLE. I will update this post once I find a more optimized solution.\n\n```\nclass TextEditor:\n\n def __init__(self):\n self.s = \'\'\n self.cursor = 0\n\n def addText(self, text: str) -> None:\n self.s = self.s[:self.cursor] + text + self.s[self.cursor:]\n self.cursor += len(text)\n\n def deleteText(self, k: int) -> int:\n new_cursor = max(0, self.cursor - k)\n noOfChars = k if self.cursor - k >= 0 else self.cursor\n self.s = self.s[:new_cursor] + self.s[self.cursor:]\n self.cursor = new_cursor\n return noOfChars\n\n def cursorLeft(self, k: int) -> str:\n self.cursor = max(0, self.cursor - k)\n start = max(0, self.cursor-10)\n return self.s[start:self.cursor]\n\n def cursorRight(self, k: int) -> str:\n self.cursor = min(len(self.s), self.cursor + k)\n start = max(0, self.cursor - 10)\n return self.s[start:self.cursor]\n```\n\n**Time - O(n)** - for all operations\n**Space - O(n)** - store the string\n\n\n---\n\n\n***Please upvote if you find it useful*** | 20 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
[Python] Easy to Understand Solution String Operation | design-a-text-editor | 0 | 1 | ```\nclass TextEditor:\n\n def __init__(self):\n self.txt = \'\' \n self.ptr = 0 \n\n def addText(self, text: str) -> None:\n self.txt = self.txt[:self.ptr] + text + self.txt[self.ptr:]\n self.ptr += len(text) \n\n def deleteText(self, k: int) -> int:\n org = len(self.txt) \n self.txt = self.txt[:max(self.ptr - k, 0)] + self.txt[self.ptr:]\n self.ptr = max(self.ptr - k, 0) \n return org - len(self.txt)\n\n def cursorLeft(self, k: int) -> str:\n self.ptr = max(self.ptr - k, 0) \n return self.txt[max(0, self.ptr - 10):self.ptr]\n\n def cursorRight(self, k: int) -> str:\n self.ptr = min(self.ptr + k, len(self.txt)) \n return self.txt[max(0, self.ptr - 10):self.ptr]\n\n``` | 5 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
[Explained] Easy Python Solution using String slicing | design-a-text-editor | 0 | 1 | # [Explained] Easy Python Solution using String slicing\n\n```\nclass TextEditor:\n\n def __init__(self):\n """\n\t\tstring storage\n\t\t"""\n\t\tself.txt = \'\' \n\t\t\n\t\t"""\n\t\tcursor/pointer location storage\n\t\t"""\n self.ptr = 0 \n \n\n def addText(self, text: str) -> None:\n\t\t"""\n\t\tslicing the previously added text and \n\t\tadding the new text after pointer location\n\t\t"""\n self.txt = self.txt[:self.ptr] + text + self.txt[self.ptr:]\n\t\t\n\t\t"""\n\t\tincrementing the pointer/cursor \n\t\tlocation by the length of the added text\n\t\t"""\n self.ptr += len(text) \n \n\n def deleteText(self, k: int) -> int:\n\t\t"""\n\t\toriginal length of the string before deletion\n\t\t"""\n\t\torg = len(self.txt) \n\t\t\n\t\t"""\n\t\tdeleting the text to the left of pointer, \n\t\twhile checking that the pointer value stays above or equal to 0\n\t\t"""\n self.txt = self.txt[:max(self.ptr - k, 0)] + self.txt[self.ptr:]\n\t\t\n\t\t"""\n\t\tupdating the pointer/cursor to the current value\n\t\t"""\n self.ptr = max(self.ptr - k, 0) \n \n\t\t"""\n\t\treturning the difference in lengths of original and new string\n\t\t"""\n return org - len(self.txt)\n\n \n def cursorLeft(self, k: int) -> str:\n """\n\t\tgetting the new value of pointer/cursor\n\t\t"""\n\t\tself.ptr = max(self.ptr - k, 0) \n \n\t\t"""\n\t\tbased on the new value returning \n\t\tthe string of minimum length to the left of pointer/cursor\n\t\t"""\n return self.txt[max(0, self.ptr - 10):self.ptr]\n \n\n def cursorRight(self, k: int) -> str:\n """\n\t\tgetting the new value of pointer/cursor\n\t\t"""\n\t\tself.ptr = min(self.ptr + k, len(self.txt)) \n\n\t\t"""\n\t\tbased on the new value returning\n\t\tthe string of minimum length to the left of pointer/cursor\n\t\t"""\n return self.txt[max(0, self.ptr - 10):self.ptr]\n``` | 2 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
✅Python clean and easy solution: 2 stacks solution | design-a-text-editor | 0 | 1 | The idea is very simple: divide the text into two parts: left (text before the cursor) and right(text after the cursor)\n```\nclass TextEditor:\n\n def __init__(self):\n self.left = []\n self.right = []\n\n def addText(self, text: str) -> None:\n self.left.extend(text)\n\n def deleteText(self, k: int) -> int:\n for i in range(k):\n if self.left:\n self.left.pop()\n else:\n return i\n return k\n\n def cursorLeft(self, k: int) -> str:\n for i in range(k):\n if self.left:\n self.right.append(self.left.pop())\n else:\n break\n return \'\'.join(self.left[-10:])\n\n def cursorRight(self, k: int) -> str:\n for i in range(k):\n if self.right:\n self.left.append(self.right.pop())\n else:\n break\n return \'\'.join(self.left[-10:])\n``` | 6 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
Simple Python Solution - 2 stacks - O(K) time (where K<N), O(N) space complexity | design-a-text-editor | 0 | 1 | Basic idea:\n=====\n1. Create two stacks, left and right. The "left" stack is left of cursor, while the "right" stack is right of cursor.\n2. addText - we append characters to the "left" stack.\n3. deleteText - we delete text by popping characters from the "left" stack.\n4. cursorLeft - we move the cursor to the left by popping characters from the "left" stack, and pushing it to the "right" stack\n5. cursorRight - we move the cursor to the right by popping characters from the "right" stack and pushing it to the "left" stack\n\nTime complexity is O(K) - where K is the length of the affected operations, e.g. number of characters of text to add / delete, number of times to move cursor left / right\nSpace complexity is O(N)\n\n```\nclass TextEditor:\n\n def __init__(self):\n self.left = []\n self.right = []\n\n def addText(self, text: str) -> None:\n for c in text:\n self.left.append(c)\n\n def deleteText(self, k: int) -> int:\n count = 0\n while len(self.left) > 0 and count < k:\n self.left.pop()\n count += 1\n return count\n\n def cursorLeft(self, k: int) -> str:\n count = 0\n while len(self.left) > 0 and count < k:\n self.right.append(self.left.pop())\n count += 1\n return \'\'.join(self.left[max(0, len(self.left) - 10):])\n\n def cursorRight(self, k: int) -> str:\n count = 0\n while len(self.right) > 0 and count < k:\n self.left.append(self.right.pop())\n count += 1\n return \'\'.join(self.left[max(0, len(self.left) - 10):])\n``` | 11 | Design a text editor with a cursor that can do the following:
* **Add** text to where the cursor is.
* **Delete** text from where the cursor is (simulating the backspace key).
* **Move** the cursor either left or right.
When deleting text, only characters to the left of the cursor will be deleted. The cursor will also remain within the actual text and cannot be moved beyond it. More formally, we have that `0 <= cursor.position <= currentText.length` always holds.
Implement the `TextEditor` class:
* `TextEditor()` Initializes the object with empty text.
* `void addText(string text)` Appends `text` to where the cursor is. The cursor ends to the right of `text`.
* `int deleteText(int k)` Deletes `k` characters to the left of the cursor. Returns the number of characters actually deleted.
* `string cursorLeft(int k)` Moves the cursor to the left `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
* `string cursorRight(int k)` Moves the cursor to the right `k` times. Returns the last `min(10, len)` characters to the left of the cursor, where `len` is the number of characters to the left of the cursor.
**Example 1:**
**Input**
\[ "TextEditor ", "addText ", "deleteText ", "addText ", "cursorRight ", "cursorLeft ", "deleteText ", "cursorLeft ", "cursorRight "\]
\[\[\], \[ "leetcode "\], \[4\], \[ "practice "\], \[3\], \[8\], \[10\], \[2\], \[6\]\]
**Output**
\[null, null, 4, null, "etpractice ", "leet ", 4, " ", "practi "\]
**Explanation**
TextEditor textEditor = new TextEditor(); // The current text is "| ". (The '|' character represents the cursor)
textEditor.addText( "leetcode "); // The current text is "leetcode| ".
textEditor.deleteText(4); // return 4
// The current text is "leet| ".
// 4 characters were deleted.
textEditor.addText( "practice "); // The current text is "leetpractice| ".
textEditor.cursorRight(3); // return "etpractice "
// The current text is "leetpractice| ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// "etpractice " is the last 10 characters to the left of the cursor.
textEditor.cursorLeft(8); // return "leet "
// The current text is "leet|practice ".
// "leet " is the last min(10, 4) = 4 characters to the left of the cursor.
textEditor.deleteText(10); // return 4
// The current text is "|practice ".
// Only 4 characters were deleted.
textEditor.cursorLeft(2); // return " "
// The current text is "|practice ".
// The cursor cannot be moved beyond the actual text and thus did not move.
// " " is the last min(10, 0) = 0 characters to the left of the cursor.
textEditor.cursorRight(6); // return "practi "
// The current text is "practi|ce ".
// "practi " is the last min(10, 6) = 6 characters to the left of the cursor.
**Constraints:**
* `1 <= text.length, k <= 40`
* `text` consists of lowercase English letters.
* At most `2 * 104` calls **in total** will be made to `addText`, `deleteText`, `cursorLeft` and `cursorRight`.
**Follow-up:** Could you find a solution with time complexity of `O(k)` per call? | null |
[Java/Python 3] 2 codes w/ brief explanation and analysis. | strong-password-checker-ii | 1 | 1 | **Method 1: Use HashSet to count conditions**\n\n**Q & A**\n\nQ: Does the `HashSet` in the codes really cost space `O(1)`?\nA: Java `HashSet` is implemented on `HashMap`, which has an initial size of `16`. The size will not increase since the load factor `4 / 16 < 0.75`. Generally speaking, space `O(16) = O(1)`. \n\nIf you really wanted to optimize space, which is not really needed here, you could call `new HashSet<>(4, 1)`, here `4` and `1` are initial size and load factor respectively. -- credit to **@Ricola**.\n\n**End of Q & A**\n\n----\n\nUse `s`, `l`, `u`, and `d` to indicate special characters, lower case, upper case and digits respectively; Put the characters into a `HashSet` to count the conditions met.\n\n```java\n public boolean strongPasswordCheckerII(String password) {\n Set<Character> seen = new HashSet<>();\n for (int i = 0; i < password.length(); ++i) {\n char c = password.charAt(i);\n if (i > 0 && c == password.charAt(i - 1)) {\n return false;\n }\n if (Character.isLowerCase(c)) {\n seen.add(\'l\');\n }else if (Character.isUpperCase(c)) {\n seen.add(\'u\');\n }else if (Character.isDigit(c)) {\n seen.add(\'d\');\n }else {\n seen.add(\'s\');\n }\n }\n return password.length() >= 8 && seen.size() == 4;\n }\n```\n```python\n def strongPasswordCheckerII(self, password: str) -> bool:\n seen = set()\n for i, c in enumerate(password):\n if i > 0 and c == password[i - 1]:\n return False\n if c.isupper():\n seen.add(\'u\')\n elif c.islower():\n seen.add(\'l\')\n elif c.isdigit():\n seen.add(\'d\') \n else:\n seen.add(\'s\')\n return len(password) > 7 and len(seen) == 4\n```\n\n----\n\n**Method 2: 6 passes**\n\n```java\n public boolean strongPasswordCheckerII(String password) {\n for (int i = 1; i < password.length(); ++i) {\n if (password.charAt(i - 1) == password.charAt(i)) {\n return false;\n }\n }\n return password.chars().anyMatch(i -> "!@#$%^&*()-+".contains("" + (char)i)) && \n password.chars().anyMatch(i -> Character.isDigit((char)i)) &&\n password.chars().anyMatch(i -> Character.isLowerCase((char)i)) && \n password.chars().anyMatch(i -> Character.isUpperCase((char)i)) && \n password.length() > 7;\n }\n```\nCredit to **@SunnyvaleCA** for the following Python 3 code:\n```python\n def strongPasswordCheckerII(self, password: str) -> bool:\n return any(c.isdigit() for c in password) and \\\n any(c.islower() for c in password) and \\\n any(c.isupper() for c in password) and \\\n any(c in \'!@#$%^&*()-+\' for c in password) and \\\n all(a != b for a, b in pairwise(password)) and \\\n len(password) > 7\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = password.length()`. | 33 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
Nothing Special | strong-password-checker-ii | 0 | 1 | We do not need to check for a special character. \n\nWe just count lowercase/uppercase letters and digits. The rest of the characters are special.\n\n**C++**\n```cpp\nbool strongPasswordCheckerII(string p) {\n int lo = 0, up = 0, digit = 0, sz = p.size();\n for (int i = 0; i < sz; ++i) {\n if (i > 0 && p[i - 1] == p[i])\n return false;\n lo += islower(p[i]) ? 1 : 0;\n up += isupper(p[i]) ? 1 : 0;\n digit += isdigit(p[i]) ? 1 : 0;\n }\n return sz > 7 && lo && up && digit && (sz - lo - up - digit > 0);\n}\n```\n\nHere is a shorter version when we count character types using an array.\n\n**C++**\n```cpp\nbool strongPasswordCheckerII(string p) {\n int cnt[4] = {}, sz = p.size();\n for (int i = 0; i < sz; ++i) {\n if (i > 0 && p[i - 1] == p[i])\n return false;\n ++cnt[islower(p[i]) ? 1 : isupper(p[i]) ? 2 : isdigit(p[i]) ? 3 : 0];\n }\n return sz > 7 && all_of(begin(cnt), end(cnt), bind(greater<int>(), placeholders::_1, 0));\n}\n```\n\n**Python 3**\n```python\nclass Solution:\n def strongPasswordCheckerII(self, pwd: str) -> bool:\n return (\n len(pwd) > 7\n and max(len(list(p[1])) for p in groupby(pwd)) == 1\n and reduce(\n lambda a, b: a | (1 if b.isdigit() else 2 if b.islower() else 4 if b.isupper() else 8), pwd, 0\n ) == 15\n )\n``` | 24 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
[Python/Java/C++/C#/JavaScript/PHP] Regex | strong-password-checker-ii | 1 | 1 | ### Just for fun ( \u02C6_\u02C6 ) \u2013 [don\'t do regex](https://softwareengineering.stackexchange.com/questions/113237/when-you-should-not-use-regular-expressions) for interviews! \n\n1. Hyphen or minus sign `-` has to be placed at the end or at the begining of the character class (`[]`), for special chars (i.e., `[!@#$%^&*()+-]` or `[-!@#$%^&*()+]`). Otherwise, `[!@#$%^&*()-+]` will not work, because `-` in the middle is a reserved meta char for ranges (i.e., `[d-y]`).\n\n### First readable version\n\n```\n^ # start\n(?!.*([0-9])\\1) # 2 same consecutive digits not allowed\n(?!.*([a-z])\\2) # 2 same consecutive lowercase letters not allowed\n(?!.*([A-Z])\\3) # 2 same consecutive uppercase letters not allowed\n(?!.*([!@#$%^&*()+-])\\4) # 2 same consecutive special chars not allowed\n(?=.*[a-z])\\ # must have at least one lowercase letter\n(?=.*[A-Z])\\ # must have at least one uppercase letter\n(?=.*[0-9])\\ # must have at least one digit\n(?=.*[!@#$%^&*()+-]) # must have at least one special char\n[A-Za-z0-9!@#$%^&*()+-]{8,} # allowed chars \u2013 8 or more times (using {8,})\n$ # end\n\n```\n\n2. We can further simplify that to:\n\n```\n^ # start\n(?!.*(.)\\1) # 2 same consecutive chars not allowed\n(?=.*[a-z])\\ # must have at least one lowercase letter\n(?=.*[A-Z])\\ # must have at least one uppercase letter\n(?=.*[0-9])\\ # must have at least one digit\n(?=.*[!@#$%^&*()+-]) # must have at least one special char\n.{8,} # any char \u2013 8 or more times (using {8,})\n$ # end\n\n```\n\n\n### Python:\n\n```\nclass Solution:\n def strongPasswordCheckerII(self, password):\n return re.match(r\'^(?!.*(.)\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$\', password)\n```\n\n### Java:\n\n```\nimport java.util.regex.Matcher;\nimport java.util.regex.Pattern;\n\nclass Solution {\n public boolean strongPasswordCheckerII(String password) {\n final String regex = "^(?!.*(.)\\\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$";\n final Pattern pattern = Pattern.compile(regex);\n final Matcher matcher = pattern.matcher(password);\n return matcher.find();\n }\n}\n```\n\n### C#\n\n```\nusing System.Text.RegularExpressions;\n\npublic class Solution {\n public bool StrongPasswordCheckerII(string password) {\n string pattern = @"^(?!.*(.)\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$";\n \n return Regex.Match(password, pattern).Success;\n }\n}\n```\n\n### C++:\n\n```\n#include <regex>\n\nclass Solution {\npublic:\n bool strongPasswordCheckerII(string password) {\n string pattern = "^(?!.*(.)\\\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$";\n return regex_match (password, regex(pattern));\n }\n};\n```\n\n### JavaScript:\n\n```\nconst strongPasswordCheckerII = function(password) {\n const regex = new RegExp("^(?!.*(.)\\\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$", \'g\')\n return regex.exec(password) !== null\n};\n```\n\n### PHP:\n\n```\nclass Solution {\n\n /**\n * @param String $password\n * @return Boolean\n */\n function strongPasswordCheckerII($password) {\n $re = \'/^(?!.*(.)\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$/s\';\n\n return preg_match($re, $password);\n }\n}\n```\n\n### TypeScript\n\n```\nfunction strongPasswordCheckerII(password: string): boolean {\n const regex = new RegExp("^(?!.*(.)\\\\1)(?=.*[a-z])(?=.*[A-Z])(?=.*[0-9])(?=.*[!@#$%^&*()+-]).{8,}$", \'g\')\n return regex.exec(password) !== null\n};\n\n```\n\n### RegEx Visualizer\n\n[jex.im](https://jex.im/regulex/#!flags=&re=%5E(a%7Cb)*%3F%24) visualizes regular expressions:\n\n\n\n\n\n\n---------\n\nIf you wish to simplify/update/explore the expression, it\'s been explained on the top right panel of [regex101.com](https://regex101.com/r/1Lvfla/1/). You can watch the matching steps or modify them in [this debugger link](https://regex101.com/r/1Lvfla/1/debugger), if you\'d be interested. The debugger demonstrates that how [a RegEx engine](https://en.wikipedia.org/wiki/Comparison_of_regular_expression_engines) might step by step consume some sample input strings and would perform the matching process.\n\n--------- | 6 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
Python | Easy Solution✅ | strong-password-checker-ii | 0 | 1 | ```\ndef strongPasswordCheckerII(self, password: str) -> bool:\n if len(password) < 8:\n return False\n lowercase, uppercase, digit, special = False, False, False, False\n special_char = "!@#$%^&*()-+"\n for i in range(len(password)):\n if i != len(password)-1 and password[i] == password[i+1]: \n # checking for same character in adjacent positions\n return False\n # not lowercase because we have to search for at least one lowercase letter only.\n if not lowercase: \n lowercase = password[i].islower()\n if not uppercase:\n uppercase = password[i].isupper()\n if not digit:\n digit = password[i].isdigit()\n if not special:\n special = password[i] in special_char\n return lowercase and uppercase and digit and special\n``` | 7 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
Easy Python Solution (using count approach) | strong-password-checker-ii | 0 | 1 | ```\ndef strongPasswordCheckerII(self, password: str) -> bool:\n u,l,d,s=0,0,0,0\n if len(password)<8: return False\n for i in range(0,len(password)):\n if i>0 and password[i-1]==password[i]: return False\n if password[i].isdigit(): d+=1\n elif password[i].islower(): l+=1\n elif password[i].isupper(): u+=1\n elif password[i] in "!@#$%^&*()-+": s+=1\n if u!=0 and l!=0 and d!=0 and s!=0: return True\n``` | 5 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
Python, regex, easy to understand | strong-password-checker-ii | 0 | 1 | bool(re.search(r"(.)\\1+", s)) --> backreference in regex to check if two adjacent chars are equal or not.\n```\nimport re\nclass Solution:\n def strongPasswordCheckerII(self, s: str) -> bool:\n \n if len(s)<8:\n return False\n \n if (bool(re.search(r\'[a-z]\',s)) and \n bool(re.search(r\'[A-Z]\',s)) and \n bool(re.search(r\'[0-9]\',s)) and \n bool(re.search(r\'[^a-zA-Z0-9]\',s)) and \n not bool(re.search(r"(.)\\1+", s))):\n return True\n return False\n``` | 2 | A password is said to be **strong** if it satisfies all the following criteria:
* It has at least `8` characters.
* It contains at least **one lowercase** letter.
* It contains at least **one uppercase** letter.
* It contains at least **one digit**.
* It contains at least **one special character**. The special characters are the characters in the following string: `"!@#$%^&*()-+ "`.
* It does **not** contain `2` of the same character in adjacent positions (i.e., `"aab "` violates this condition, but `"aba "` does not).
Given a string `password`, return `true` _if it is a **strong** password_. Otherwise, return `false`.
**Example 1:**
**Input:** password = "IloveLe3tcode! "
**Output:** true
**Explanation:** The password meets all the requirements. Therefore, we return true.
**Example 2:**
**Input:** password = "Me+You--IsMyDream "
**Output:** false
**Explanation:** The password does not contain a digit and also contains 2 of the same character in adjacent positions. Therefore, we return false.
**Example 3:**
**Input:** password = "1aB! "
**Output:** false
**Explanation:** The password does not meet the length requirement. Therefore, we return false.
**Constraints:**
* `1 <= password.length <= 100`
* `password` consists of letters, digits, and special characters: `"!@#$%^&*()-+ "`. | How can you use two pointers to modify the original list into the new list? Have a pointer traverse the entire linked list, while another pointer looks at a node that is currently being modified. Keep on summing the values of the nodes between the traversal pointer and the modifying pointer until the former comes across a ‘0’. In that case, the modifying pointer is incremented to modify the next node. Do not forget to have the next pointer of the final node of the modified list point to null. |
Simple Python Code | Binary Search | successful-pairs-of-spells-and-potions | 0 | 1 | # Approach: `Binary Search`\n\n# Complexity\n- Time complexity: `O(N LogN)`\n\n- Space complexity: ` O(N) `\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n potions.sort()\n x = []\n for i in spells:\n l,r,ans = 0,len(potions)-1,0\n while l<=r:\n m = (l+r)//2\n if (potions[m]*i)>=success:\n ans+=(r-m+1)\n r=m-1\n else: l=m+1\n x.append(ans);\n return x\n \n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
Clear Python Solution--Using Binary Search | successful-pairs-of-spells-and-potions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n #We have to sort the potions.\n potions.sort()\n #create a empty list for result.\n res=[]\n for i in spells:\n #make left pointer as 0 and right pointer as len(potions)-1\n l=0\n r=len(potions)-1\n ans=len(potions)\n while l<=r:\n #M denotes the mid of the array.\n m=(l+r)//2\n if potions[m]*i>=success:\n #ans will store the exact point that is greaterthen or equal to the success.\n r=m-1\n ans=m\n else:\n l=m+1\n #append the ans that is decrement of length of the potions that is remaining elements that are greater than or equal to the success.\n res.append((len(potions))-ans)\n return res\n \n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
Python solution | successful-pairs-of-spells-and-potions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n n, m = len(spells), len(potions)\n pairs = [0]*n\n potions.sort()\n for i in range(n):\n spell = spells[i]\n left = 0\n right = m - 1\n while left <= right:\n mid = left+(right-left)//2\n product = spell*potions[mid]\n if product >= success:\n right = mid - 1\n else:\n left = mid + 1\n pairs[i] = m - left\n return pairs\n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
Python O(mlogn) solution for reference | successful-pairs-of-spells-and-potions | 0 | 1 | \n# Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n # We find the lowest value of potion that is needed for\n # a spell to be sucess, that is \'x\' here\n # now we can sort the potions, search for the value\n # just greater or equal to x, all the values right to it\n # will also result in success\n potions.sort()\n res = []\n for i in range(0,len(spells)):\n x = ceil( success/spells[i]); \n j = bisect.bisect_left(potions,x);\n res.append(len(potions)-j)\n \n return res\n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
Easy Python Solution for beginners | successful-pairs-of-spells-and-potions | 0 | 1 | # Code\n```\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n def binary_search(temp,m,target):\n l = 0\n r = m-1\n while l < r:\n mid = l + (r-l)//2\n if temp[mid] >= target:\n r = mid\n else:\n l = mid+1 \n if temp[l] >= target:\n return l\n else:\n return m\n n = len(spells)\n m = len(potions)\n ans = [0]*n\n potions = sorted(potions)\n for i in range(n):\n if spells[i] >= success :\n ans[i] = m\n else:\n if success%spells[i] == 0:\n target = success//spells[i]\n else:\n target = success//spells[i] + 1\n ans[i] = m - binary_search(potions,m,target)\n return ans\n\n\n \n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
o(1) space solution beats 100% space and 100% time | successful-pairs-of-spells-and-potions | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nsimply use sort potions and use binary search.\n# Complexity\n- Time complexity:\nO(nlog(n)+m)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nimport bisect\nclass Solution:\n def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:\n n=len(potions)\n potions.sort()\n for i in range(len(spells)):\n spells[i]=n-bisect.bisect_left(potions,math.ceil(success/spells[i]))\n return spells\n``` | 1 | You are given two positive integer arrays `spells` and `potions`, of length `n` and `m` respectively, where `spells[i]` represents the strength of the `ith` spell and `potions[j]` represents the strength of the `jth` potion.
You are also given an integer `success`. A spell and potion pair is considered **successful** if the **product** of their strengths is **at least** `success`.
Return _an integer array_ `pairs` _of length_ `n` _where_ `pairs[i]` _is the number of **potions** that will form a successful pair with the_ `ith` _spell._
**Example 1:**
**Input:** spells = \[5,1,3\], potions = \[1,2,3,4,5\], success = 7
**Output:** \[4,0,3\]
**Explanation:**
- 0th spell: 5 \* \[1,2,3,4,5\] = \[5,**10**,**15**,**20**,**25**\]. 4 pairs are successful.
- 1st spell: 1 \* \[1,2,3,4,5\] = \[1,2,3,4,5\]. 0 pairs are successful.
- 2nd spell: 3 \* \[1,2,3,4,5\] = \[3,6,**9**,**12**,**15**\]. 3 pairs are successful.
Thus, \[4,0,3\] is returned.
**Example 2:**
**Input:** spells = \[3,1,2\], potions = \[8,5,8\], success = 16
**Output:** \[2,0,2\]
**Explanation:**
- 0th spell: 3 \* \[8,5,8\] = \[**24**,15,**24**\]. 2 pairs are successful.
- 1st spell: 1 \* \[8,5,8\] = \[8,5,8\]. 0 pairs are successful.
- 2nd spell: 2 \* \[8,5,8\] = \[**16**,10,**16**\]. 2 pairs are successful.
Thus, \[2,0,2\] is returned.
**Constraints:**
* `n == spells.length`
* `m == potions.length`
* `1 <= n, m <= 105`
* `1 <= spells[i], potions[i] <= 105`
* `1 <= success <= 1010` | Start constructing the string in descending order of characters. When repeatLimit is reached, pick the next largest character. |
✅ Python Precalculation O(n*k) without TLE | match-substring-after-replacement | 0 | 1 | I have added comments to help understand better. I have seen many python solutions getting TLE. To avoid that, I have added a precalculation logic. Please let me know if there is a better way. :)\n\n```\nclass Solution:\n def matchReplacement(self, s: str, sub: str, mappings: List[List[str]]) -> bool:\n s_maps = defaultdict(lambda : set())\n for x,y in mappings:\n s_maps[x].add(y)\n \n # build a sequence of set for substring match\n # eg: sub=leet, mappings = {e: 3, t:7}\n # subs = [{l}, {e, 3}, {e, 3}, {t, 7}]\n # precalculation helps to eliminate TLE\n subs = [s_maps[c] | {c} for c in sub] \n \n for i in range(len(s)-len(sub) + 1):\n c=s[i] \n j=i\n # Try to match substring\n while j-i<len(sub) and s[j] in subs[j-i]: \n j+=1\n if j-i==len(sub): # a valid match if iterated through the whole length of substring\n return True\n \n return False \n```\nIf `n` is the length of `s`, `k` is the length of `sub` and `m` is number of keys in `s_maps` , then\nTime - O(n * k ) \nSpace - O(k * m) \n\n---\n\n***Please upvote if you find it useful*** | 7 | You are given two strings `s` and `sub`. You are also given a 2D character array `mappings` where `mappings[i] = [oldi, newi]` indicates that you may perform the following operation **any** number of times:
* **Replace** a character `oldi` of `sub` with `newi`.
Each character in `sub` **cannot** be replaced more than once.
Return `true` _if it is possible to make_ `sub` _a substring of_ `s` _by replacing zero or more characters according to_ `mappings`. Otherwise, return `false`.
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "fool3e7bar ", sub = "leet ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\]\]
**Output:** true
**Explanation:** Replace the first 'e' in sub with '3' and 't' in sub with '7'.
Now sub = "l3e7 " is a substring of s, so we return true.
**Example 2:**
**Input:** s = "fooleetbar ", sub = "f00l ", mappings = \[\[ "o ", "0 "\]\]
**Output:** false
**Explanation:** The string "f00l " is not a substring of s and no replacements can be made.
Note that we cannot replace '0' with 'o'.
**Example 3:**
**Input:** s = "Fool33tbaR ", sub = "leetd ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\],\[ "d ", "b "\],\[ "p ", "b "\]\]
**Output:** true
**Explanation:** Replace the first and second 'e' in sub with '3' and 'd' in sub with 'b'.
Now sub = "l33tb " is a substring of s, so we return true.
**Constraints:**
* `1 <= sub.length <= s.length <= 5000`
* `0 <= mappings.length <= 1000`
* `mappings[i].length == 2`
* `oldi != newi`
* `s` and `sub` consist of uppercase and lowercase English letters and digits.
* `oldi` and `newi` are either uppercase or lowercase English letters or digits.
0 <= i < j < n and nums\[i\] % k + nums\[j\] % k == k. | For any element in the array, what is the smallest number it should be multiplied with such that the product is divisible by k? The smallest number which should be multiplied with nums[i] so that the product is divisible by k is k / gcd(k, nums[i]). Now think about how you can store and update the count of such numbers present in the array efficiently. |
[Python3] Easy to understand Solution using Dictionary and HashSet | match-substring-after-replacement | 0 | 1 | ```\nclass Solution:\n def matchReplacement(self, s: str, sub: str, mappings: List[List[str]]) -> bool:\n dic = {}\n for m in mappings:\n if m[0] not in dic:\n dic[m[0]] = {m[1]}\n else:\n dic[m[0]].add(m[1])\n \n for i in range(len(s)-len(sub)+1):\n j = 0\n while j < len(sub) and (s[i+j] == sub[j] or \n (sub[j] in dic and s[i+j] in dic[sub[j]])):\n j += 1\n\n if j == len(sub): return True\n \n return False\n \n# Time: O(len(s) * len(sub))\n# Space: O(len(mapping))\n``` | 4 | You are given two strings `s` and `sub`. You are also given a 2D character array `mappings` where `mappings[i] = [oldi, newi]` indicates that you may perform the following operation **any** number of times:
* **Replace** a character `oldi` of `sub` with `newi`.
Each character in `sub` **cannot** be replaced more than once.
Return `true` _if it is possible to make_ `sub` _a substring of_ `s` _by replacing zero or more characters according to_ `mappings`. Otherwise, return `false`.
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "fool3e7bar ", sub = "leet ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\]\]
**Output:** true
**Explanation:** Replace the first 'e' in sub with '3' and 't' in sub with '7'.
Now sub = "l3e7 " is a substring of s, so we return true.
**Example 2:**
**Input:** s = "fooleetbar ", sub = "f00l ", mappings = \[\[ "o ", "0 "\]\]
**Output:** false
**Explanation:** The string "f00l " is not a substring of s and no replacements can be made.
Note that we cannot replace '0' with 'o'.
**Example 3:**
**Input:** s = "Fool33tbaR ", sub = "leetd ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\],\[ "d ", "b "\],\[ "p ", "b "\]\]
**Output:** true
**Explanation:** Replace the first and second 'e' in sub with '3' and 'd' in sub with 'b'.
Now sub = "l33tb " is a substring of s, so we return true.
**Constraints:**
* `1 <= sub.length <= s.length <= 5000`
* `0 <= mappings.length <= 1000`
* `mappings[i].length == 2`
* `oldi != newi`
* `s` and `sub` consist of uppercase and lowercase English letters and digits.
* `oldi` and `newi` are either uppercase or lowercase English letters or digits.
0 <= i < j < n and nums\[i\] % k + nums\[j\] % k == k. | For any element in the array, what is the smallest number it should be multiplied with such that the product is divisible by k? The smallest number which should be multiplied with nums[i] so that the product is divisible by k is k / gcd(k, nums[i]). Now think about how you can store and update the count of such numbers present in the array efficiently. |
[Python 3]KMP Algorithm | match-substring-after-replacement | 0 | 1 | \n```\nclass Solution:\n def matchReplacement(self, s: str, p: str, mappings: List[List[str]]) -> bool:\n m = defaultdict(set)\n for a, b in mappings:\n m[a].add(b) \n \n\t\t# build pattern array\n i, j = 0, 1\n arr = [0] * len(p)\n while j < len(p):\n if p[i] == p[j]:\n arr[j] = arr[j-1] + 1\n i += 1\n j += 1\n else:\n\t\t\t\t# no need to go to beginning of pattern (only need to go to previous arr index)\n while i > 0 and p[j] != p[i]:\n i = arr[i-1]\n if p[i] == p[j]:\n arr[j] = arr[i] + 1\n j += 1\n \n i = j = 0\n while i < len(s):\n if s[i] == p[j] or s[i] in m[p[j]]:\n i += 1\n j += 1\n if j == len(p): return True\n else:\n\t\t\t # find previous latest index as long as two characters matched or convertible\n\t\t\t\torigin_j = j\n while j > 0 and not (s[i] == p[j] or s[i] in m[p[j]]):\n j = arr[j - 1]\n\t\t\t\ti = i - (origin_j - j) + 1\n # if s[i] != p[j]:\n # i += 1\n \n return False\n\t\t\n```\n\nCorrections made for the pointer of `s` need to go back `origin_j - j` after `j` jump to the latest index. But this will get TLE for case 106. Though local run will pass.\n\n\n\n | 0 | You are given two strings `s` and `sub`. You are also given a 2D character array `mappings` where `mappings[i] = [oldi, newi]` indicates that you may perform the following operation **any** number of times:
* **Replace** a character `oldi` of `sub` with `newi`.
Each character in `sub` **cannot** be replaced more than once.
Return `true` _if it is possible to make_ `sub` _a substring of_ `s` _by replacing zero or more characters according to_ `mappings`. Otherwise, return `false`.
A **substring** is a contiguous non-empty sequence of characters within a string.
**Example 1:**
**Input:** s = "fool3e7bar ", sub = "leet ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\]\]
**Output:** true
**Explanation:** Replace the first 'e' in sub with '3' and 't' in sub with '7'.
Now sub = "l3e7 " is a substring of s, so we return true.
**Example 2:**
**Input:** s = "fooleetbar ", sub = "f00l ", mappings = \[\[ "o ", "0 "\]\]
**Output:** false
**Explanation:** The string "f00l " is not a substring of s and no replacements can be made.
Note that we cannot replace '0' with 'o'.
**Example 3:**
**Input:** s = "Fool33tbaR ", sub = "leetd ", mappings = \[\[ "e ", "3 "\],\[ "t ", "7 "\],\[ "t ", "8 "\],\[ "d ", "b "\],\[ "p ", "b "\]\]
**Output:** true
**Explanation:** Replace the first and second 'e' in sub with '3' and 'd' in sub with 'b'.
Now sub = "l33tb " is a substring of s, so we return true.
**Constraints:**
* `1 <= sub.length <= s.length <= 5000`
* `0 <= mappings.length <= 1000`
* `mappings[i].length == 2`
* `oldi != newi`
* `s` and `sub` consist of uppercase and lowercase English letters and digits.
* `oldi` and `newi` are either uppercase or lowercase English letters or digits.
0 <= i < j < n and nums\[i\] % k + nums\[j\] % k == k. | For any element in the array, what is the smallest number it should be multiplied with such that the product is divisible by k? The smallest number which should be multiplied with nums[i] so that the product is divisible by k is k / gcd(k, nums[i]). Now think about how you can store and update the count of such numbers present in the array efficiently. |
Sliding Window | count-subarrays-with-score-less-than-k | 1 | 1 | This problem is similar to [713. Subarray Product Less Than K](https://leetcode.com/problems/subarray-product-less-than-k/).\n\nWe use a sliding window technique, tracking the sum of the subarray in the window.\n\nThe score of the subarray in the window is `sum * (i - j + 1)`. We move the left side of the window, decreasing `sum`, if that score is equal or greater than `k`.\n\nNote that element `i` forms `i - j + 1` valid subarrays. This is because subarrays `[j + 1, i]`, `[j + 2, i]` ... `[i, i]` are valid if subarray `[j, i]` is valid.\n\n**C++**\n```cpp\nlong long countSubarrays(vector<int>& nums, long long k) {\n long long sum = 0, res = 0;\n for (int i = 0, j = 0; i < nums.size(); ++i) {\n sum += nums[i];\n while (sum * (i - j + 1) >= k)\n sum -= nums[j++];\n res += i - j + 1;\n }\n return res;\n}\n```\nMinimalizm version (just for kicks):\n```cpp\nlong long countSubarrays(vector<int>& n, long long k) {\n long long s = 0, res = 0, sz = n.size();\n for (int i = 0, j = 0; i < sz; res += (i++) - j + 1)\n for (s = s + n[i]; s * (i - j + 1) >= k; s -= n[j++]);\n return res;\n}\n```\n**Java**\n```cpp\npublic long countSubarrays(int[] nums, long k) {\n long sum = 0, res = 0;\n for (int i = 0, j = 0; i < nums.length; ++i) {\n sum += nums[i];\n while (sum * (i - j + 1) >= k)\n sum -= nums[j++];\n res += i - j + 1;\n }\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def countSubarrays(self, nums: List[int], k: int) -> int:\n sum, res, j = 0, 0, 0\n for i, n in enumerate(nums):\n sum += n\n while sum * (i - j + 1) >= k:\n sum -= nums[j]\n j += 1\n res += i - j + 1\n return res\n``` | 133 | The **score** of an array is defined as the **product** of its sum and its length.
* For example, the score of `[1, 2, 3, 4, 5]` is `(1 + 2 + 3 + 4 + 5) * 5 = 75`.
Given a positive integer array `nums` and an integer `k`, return _the **number of non-empty subarrays** of_ `nums` _whose score is **strictly less** than_ `k`.
A **subarray** is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** nums = \[2,1,4,3,5\], k = 10
**Output:** 6
**Explanation:**
The 6 subarrays having scores less than 10 are:
- \[2\] with score 2 \* 1 = 2.
- \[1\] with score 1 \* 1 = 1.
- \[4\] with score 4 \* 1 = 4.
- \[3\] with score 3 \* 1 = 3.
- \[5\] with score 5 \* 1 = 5.
- \[2,1\] with score (2 + 1) \* 2 = 6.
Note that subarrays such as \[1,4\] and \[4,3,5\] are not considered because their scores are 10 and 36 respectively, while we need scores strictly less than 10.
**Example 2:**
**Input:** nums = \[1,1,1\], k = 5
**Output:** 5
**Explanation:**
Every subarray except \[1,1,1\] has a score less than 5.
\[1,1,1\] has a score (1 + 1 + 1) \* 3 = 9, which is greater than 5.
Thus, there are 5 subarrays having scores less than 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* `1 <= k <= 1015` | null |
[Java/Python 3] Sliding window T O(n) S O(1) code w/ brief explanation and analysis. | count-subarrays-with-score-less-than-k | 1 | 1 | Similar Problems and study materials on leedcode:\n\n[Sliding Window Problems](https://leetcode.com/tag/sliding-window/)\n[Sliding Window for Beginners [Problems | Template | Sample Solutions]](https://leetcode.com/discuss/general-discussion/657507/Sliding-Window-for-Beginners-Problems-or-Template-or-Sample-Solutions)\n\n----\n\nMaintain a sliding window and keep calculating its score and shrinking its size so that the score is less than `k`.\n```java\n public long countSubarrays(int[] nums, long k) {\n long winSum = 0, cnt = 0;\n for (int lo = -1, hi = 0; hi < nums.length; ++hi) {\n winSum += nums[hi];\n while (lo < hi && winSum * (hi - lo) >= k) {\n winSum -= nums[++lo];\n }\n cnt += hi - lo;\n }\n return cnt;\n }\n```\n```python\n def countSubarrays(self, nums: List[int], k: int) -> int:\n win_sum = cnt = 0\n lo = -1\n for hi, num in enumerate(nums):\n win_sum += num\n while lo < hi and win_sum * (hi - lo) >= k:\n lo += 1\n win_sum -= nums[lo]\n cnt += hi - lo\n return cnt\n```\n\n**Analysis:**\n\nEach element in `nums` at most visited twice, therefore:\n\nTime: `O(n)`, space: `O(1)`, where `n = nums.length`. | 7 | The **score** of an array is defined as the **product** of its sum and its length.
* For example, the score of `[1, 2, 3, 4, 5]` is `(1 + 2 + 3 + 4 + 5) * 5 = 75`.
Given a positive integer array `nums` and an integer `k`, return _the **number of non-empty subarrays** of_ `nums` _whose score is **strictly less** than_ `k`.
A **subarray** is a contiguous sequence of elements within an array.
**Example 1:**
**Input:** nums = \[2,1,4,3,5\], k = 10
**Output:** 6
**Explanation:**
The 6 subarrays having scores less than 10 are:
- \[2\] with score 2 \* 1 = 2.
- \[1\] with score 1 \* 1 = 1.
- \[4\] with score 4 \* 1 = 4.
- \[3\] with score 3 \* 1 = 3.
- \[5\] with score 5 \* 1 = 5.
- \[2,1\] with score (2 + 1) \* 2 = 6.
Note that subarrays such as \[1,4\] and \[4,3,5\] are not considered because their scores are 10 and 36 respectively, while we need scores strictly less than 10.
**Example 2:**
**Input:** nums = \[1,1,1\], k = 5
**Output:** 5
**Explanation:**
Every subarray except \[1,1,1\] has a score less than 5.
\[1,1,1\] has a score (1 + 1 + 1) \* 3 = 9, which is greater than 5.
Thus, there are 5 subarrays having scores less than 5.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* `1 <= k <= 1015` | null |
[Python3] bracket by bracket | calculate-amount-paid-in-taxes | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e59b5d5832483707a595ae92b9aa1fb456986009) for solutions of weekly 297\n\n```\nclass Solution:\n def calculateTax(self, brackets: List[List[int]], income: int) -> float:\n ans = prev = 0 \n for hi, pct in brackets: \n hi = min(hi, income)\n ans += (hi - prev)*pct/100\n prev = hi \n return ans \n``` | 15 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
[Java/Python 3] Simple O(n) codes. | calculate-amount-paid-in-taxes | 1 | 1 | ```java\n public double calculateTax(int[][] brackets, int income) {\n double tax = 0;\n int prev = 0;\n for (int[] bracket : brackets) {\n int upper = bracket[0], percent = bracket[1];\n if (income >= upper) {\n tax += (upper - prev) * percent / 100d;\n prev = upper;\n }else {\n tax += (income - prev) * percent / 100d;\n return tax;\n } \n }\n return tax;\n }\n```\n```python\n def calculateTax(self, brackets: List[List[int]], income: int) -> float:\n tax = prev = 0\n for upper, p in brackets:\n if income >= upper:\n tax += (upper - prev) * p / 100\n prev = upper\n else:\n tax += (income - prev) * p / 100\n return tax\n return tax \n``` | 33 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
Python Doesn't get any easier than this | calculate-amount-paid-in-taxes | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def calculateTax(self, brackets: List[List[int]], income: int) -> float:\n tax = 0\n brackets.insert(0, [0,0])\n for i in range(1, len(brackets)):\n diff = brackets[i][0] - brackets[i-1][0]\n if income < diff: return income*(brackets[i][1]/100) + tax\n tax += diff*(brackets[i][1]/100)\n income -= diff\n return tax\n``` | 1 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
Simple Python Solution | calculate-amount-paid-in-taxes | 0 | 1 | ```\nclass Solution:\n def calculateTax(self, brackets: List[List[int]], income: int) -> float:\n brackets.sort(key=lambda x: x[0])\n res = 0 # Total Tax \n prev = 0 # Prev Bracket Upperbound\n for u, p in brackets:\n if income >= u: # \n res += ((u-prev) * p) / 100\n prev = u\n else:\n res += ((income-prev) * p) / 100\n break # As total income has been taxed at this point.\n return res\n``` | 2 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
Python3 solution | Easy to understand | concise and simple code | | calculate-amount-paid-in-taxes | 0 | 1 | ```\nclass Solution:\n def calculateTax(self, brackets: List[List[int]], income: int) -> float:\n lower = 0; \n\t\ttax = 0; \n\t\tleft = income # amount left to be taxed\n for i in brackets:\n k = i[0]-lower # amount being taxed\n if k<= left:\n tax+=k*i[1]/100; left-=k; lower=i[0]\n else:\n tax+= left*i[1]/100\n break\n return tax\n``` | 1 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
Python || Simple 6-Liner | calculate-amount-paid-in-taxes | 0 | 1 | ```\nclass Solution:\n def calculateTax(self, l: List[List[int]], k: int) -> float:\n prev=sol=0\n for x,y in l:\n t, prev = min(x,k)-prev, x\n if t<0:break\n sol+=t*y/100\n return sol\n```\n\n**Happy Coding !!** | 1 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
O(n) Solution in python | calculate-amount-paid-in-taxes | 0 | 1 | ```\n\t\tleng = len(brackets)\n\t\t\'\'\' if income is 0, no tax \'\'\'\n if income == 0:\n return float(0)\n \n tax = 0\n\t\t\'\'\' here we calculate tax for 1st bracket i.e. at index \'\'\'\n if (income > brackets[0][0]):\n tax = brackets[0][0] * (brackets[0][1] * 0.01)\n else:\n tax = income * (brackets[0][1] * 0.01)\n \n\t\t\'\'\'\n\t\trem_inc is for checking upto what limit we have to keep checking\n\t\t(what if our income for which we # have to calculate tax is done, in this case our iteration should stop.)\n\t\t\'\'\'\n rem_inc = income - brackets[0][0]\n \n i = 1\n while rem_inc > 0 and i < leng:\n\t\t\t\'\'\' Here we check the bracket on which we have to calculate the tax depends on the difference of last 2 brackets\'\'\'\n principal = (brackets[i][0] - brackets[i-1][0]) if brackets[i][0] <= income else (income - brackets[i-1][0])\n rem_inc -= principal\n tax += principal * (brackets[i][1] * 0.01)\n i += 1\n \n return tax\n``` | 1 | You are given a **0-indexed** 2D integer array `brackets` where `brackets[i] = [upperi, percenti]` means that the `ith` tax bracket has an upper bound of `upperi` and is taxed at a rate of `percenti`. The brackets are **sorted** by upper bound (i.e. `upperi-1 < upperi` for `0 < i < brackets.length`).
Tax is calculated as follows:
* The first `upper0` dollars earned are taxed at a rate of `percent0`.
* The next `upper1 - upper0` dollars earned are taxed at a rate of `percent1`.
* The next `upper2 - upper1` dollars earned are taxed at a rate of `percent2`.
* And so on.
You are given an integer `income` representing the amount of money you earned. Return _the amount of money that you have to pay in taxes._ Answers within `10-5` of the actual answer will be accepted.
**Example 1:**
**Input:** brackets = \[\[3,50\],\[7,10\],\[12,25\]\], income = 10
**Output:** 2.65000
**Explanation:**
Based on your income, you have 3 dollars in the 1st tax bracket, 4 dollars in the 2nd tax bracket, and 3 dollars in the 3rd tax bracket.
The tax rate for the three tax brackets is 50%, 10%, and 25%, respectively.
In total, you pay $3 \* 50% + $4 \* 10% + $3 \* 25% = $2.65 in taxes.
**Example 2:**
**Input:** brackets = \[\[1,0\],\[4,25\],\[5,50\]\], income = 2
**Output:** 0.25000
**Explanation:**
Based on your income, you have 1 dollar in the 1st tax bracket and 1 dollar in the 2nd tax bracket.
The tax rate for the two tax brackets is 0% and 25%, respectively.
In total, you pay $1 \* 0% + $1 \* 25% = $0.25 in taxes.
**Example 3:**
**Input:** brackets = \[\[2,50\]\], income = 0
**Output:** 0.00000
**Explanation:**
You have no income to tax, so you have to pay a total of $0 in taxes.
**Constraints:**
* `1 <= brackets.length <= 100`
* `1 <= upperi <= 1000`
* `0 <= percenti <= 100`
* `0 <= income <= 1000`
* `upperi` is sorted in ascending order.
* All the values of `upperi` are **unique**.
* The upper bound of the last tax bracket is greater than or equal to `income`. | With the constraints, could we try every substring? Yes, checking every substring has runtime O(n^2), which will pass. How can we make sure we only count unique substrings? Use a set to store previously counted substrings. Hashing a string s of length m takes O(m) time. Is there a fast way to compute the hash of s if we know the hash of s[0..m - 2]? Use a rolling hash. |
Python Recursion + Memoization | minimum-path-cost-in-a-grid | 0 | 1 | **Observations:**\n1. This problem can be solved using recursion but simple recursion will lead to TLE.\n2. If we make the recursion tree we can easily see that we will have a lot of redundant computations.\n\n**For this example: *grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]***\n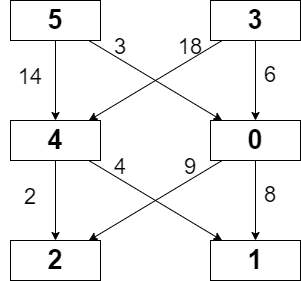\n**We can see that as we go from 5 to 4 and compute all paths for 4. In future we again reach 4 from 3 and compute all paths for 4 again. The computations made for 4 can be memoized be maintaining a dp array for each node. This will store the min cost path from that node and its node value. For 4 it will be path with cost 2 to Node 2. So dp[1][0] = dp for Node 4 = 2(Target Path Cost) + 2(Target Node Val) + 4 (Its Own Value).**\n```\nclass Solution:\n def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:\n max_row, max_col = len(grid), len(grid[0])\n dp = [[-1] * max_col for _ in range(max_row)] \n\n def recursion(row, col):\n if row == max_row - 1: # If last row then return nodes value\n return grid[row][col]\n if dp[row][col] == -1: # If DP for this node is not computed then we will do so now.\n current = grid[row][col] # Current Node Value\n res = float(\'inf\') # To store best path from Current Node\n for c in range(max_col): # Traverse all path from Current Node\n val = moveCost[current][c] + recursion(row + 1, c) # Move cost + Target Node Value\n res = min(res, val)\n dp[row][col] = res + current # DP[current node] = Best Path + Target Node Val + Current Node Val\n return dp[row][col]\n\n for c in range(max_col):\n recursion(0, c) # Start recursion from all nodes in 1st row\n return min(dp[0]) # Return min value from 1st row\n``` | 13 | You are given a **0-indexed** `m x n` integer matrix `grid` consisting of **distinct** integers from `0` to `m * n - 1`. You can move in this matrix from a cell to any other cell in the **next** row. That is, if you are in cell `(x, y)` such that `x < m - 1`, you can move to any of the cells `(x + 1, 0)`, `(x + 1, 1)`, ..., `(x + 1, n - 1)`. **Note** that it is not possible to move from cells in the last row.
Each possible move has a cost given by a **0-indexed** 2D array `moveCost` of size `(m * n) x n`, where `moveCost[i][j]` is the cost of moving from a cell with value `i` to a cell in column `j` of the next row. The cost of moving from cells in the last row of `grid` can be ignored.
The cost of a path in `grid` is the **sum** of all values of cells visited plus the **sum** of costs of all the moves made. Return _the **minimum** cost of a path that starts from any cell in the **first** row and ends at any cell in the **last** row._
**Example 1:**
**Input:** grid = \[\[5,3\],\[4,0\],\[2,1\]\], moveCost = \[\[9,8\],\[1,5\],\[10,12\],\[18,6\],\[2,4\],\[14,3\]\]
**Output:** 17
**Explanation:** The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
**Example 2:**
**Input:** grid = \[\[5,1,2\],\[4,0,3\]\], moveCost = \[\[12,10,15\],\[20,23,8\],\[21,7,1\],\[8,1,13\],\[9,10,25\],\[5,3,2\]\]
**Output:** 6
**Explanation:** The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 50`
* `grid` consists of distinct integers from `0` to `m * n - 1`.
* `moveCost.length == m * n`
* `moveCost[i].length == n`
* `1 <= moveCost[i][j] <= 100` | From the given string, find the corresponding rows and columns. Iterate through the columns in ascending order and for each column, iterate through the rows in ascending order to obtain the required cells in sorted order. |
[Java/Python 3] 2 DP codes: space O(m * n) and O(n), w/ analysis. | minimum-path-cost-in-a-grid | 1 | 1 | ```java\n public int minPathCost(int[][] grid, int[][] moveCost) {\n int m = grid.length, n = grid[0].length;\n int[][] cost = new int[m][n];\n for (int c = 0; c < n; ++c) {\n cost[0][c] = grid[0][c];\n }\n for (int r = 1; r < m; ++r) {\n for (int c = 0; c < n; ++c) {\n int mi = Integer.MAX_VALUE;\n for (int j = 0; j < n; ++j) {\n mi = Math.min(mi, cost[r - 1][j] + moveCost[grid[r - 1][j]][c]);\n }\n cost[r][c] = mi + grid[r][c];\n }\n }\n return IntStream.of(cost[m - 1]).min().getAsInt();\n }\n```\n```python\n def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:\n m, n = map(len, (grid, grid[0]))\n min_cost = 0\n cost = [grid[0][:]]\n for r, row in enumerate(grid):\n if r > 0:\n cost.append([])\n for c, cell in enumerate(row):\n cost[-1].append(cell + min(cost[-2][j] + moveCost[i][c] for j, i in enumerate(grid[r - 1])))\n return min(cost[-1]) \n```\n\n**Analysis:**\n\nTime: `O(m * n * n)`, space: `O(m * n)`.\n\n----\n\nSpace optimization to `O(n)`:\n```java\n public int minPathCost(int[][] grid, int[][] moveCost) {\n int m = grid.length, n = grid[0].length;\n int[][] cost = new int[2][n];\n cost[0] = grid[0].clone();\n for (int r = 1; r < m; ++r) {\n for (int c = 0; c < n; ++c) {\n int min = Integer.MAX_VALUE;\n for (int j = 0; j < n; ++j) {\n min = Math.min(min, cost[1 - r % 2][j] + moveCost[grid[r - 1][j]][c]);\n }\n cost[r % 2][c] = min + grid[r][c];\n }\n }\n return IntStream.of(cost[1 - m % 2]).min().getAsInt();\n }\n```\n\n```python\n def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n cost = [grid[0][:], [0] * n]\n for r, row in enumerate(grid):\n for c, cell in enumerate(row):\n if r > 0:\n cost[r % 2][c] = cell + min(cost[1 - r % 2][j] + moveCost[i][c] for j, i in enumerate(grid[r - 1]))\n return min(cost[1 - m % 2])\n```\n\n**Analysis:**\n\nTime: `O(m * n * n)`, space: `O(n)`.\n\n----\n\nFeel free to let me know if you have any questions, and please **upvote** if the post is helpful. | 24 | You are given a **0-indexed** `m x n` integer matrix `grid` consisting of **distinct** integers from `0` to `m * n - 1`. You can move in this matrix from a cell to any other cell in the **next** row. That is, if you are in cell `(x, y)` such that `x < m - 1`, you can move to any of the cells `(x + 1, 0)`, `(x + 1, 1)`, ..., `(x + 1, n - 1)`. **Note** that it is not possible to move from cells in the last row.
Each possible move has a cost given by a **0-indexed** 2D array `moveCost` of size `(m * n) x n`, where `moveCost[i][j]` is the cost of moving from a cell with value `i` to a cell in column `j` of the next row. The cost of moving from cells in the last row of `grid` can be ignored.
The cost of a path in `grid` is the **sum** of all values of cells visited plus the **sum** of costs of all the moves made. Return _the **minimum** cost of a path that starts from any cell in the **first** row and ends at any cell in the **last** row._
**Example 1:**
**Input:** grid = \[\[5,3\],\[4,0\],\[2,1\]\], moveCost = \[\[9,8\],\[1,5\],\[10,12\],\[18,6\],\[2,4\],\[14,3\]\]
**Output:** 17
**Explanation:** The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
**Example 2:**
**Input:** grid = \[\[5,1,2\],\[4,0,3\]\], moveCost = \[\[12,10,15\],\[20,23,8\],\[21,7,1\],\[8,1,13\],\[9,10,25\],\[5,3,2\]\]
**Output:** 6
**Explanation:** The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 50`
* `grid` consists of distinct integers from `0` to `m * n - 1`.
* `moveCost.length == m * n`
* `moveCost[i].length == n`
* `1 <= moveCost[i][j] <= 100` | From the given string, find the corresponding rows and columns. Iterate through the columns in ascending order and for each column, iterate through the rows in ascending order to obtain the required cells in sorted order. |
Python | Memoization | minimum-path-cost-in-a-grid | 0 | 1 | ```\nclass Solution:\n def minPathCost(self, grid: list[list[int]], moveCost: list[list[int]]) -> int:\n\n @lru_cache()\n def helper(i, j):\n if i >= len(grid) - 1:\n return grid[i][j]\n \n m_cost = 9999999999\n cost = 0\n\n for k in range(len(grid[0])):\n cost = grid[i][j] + moveCost[grid[i][j]][k] + helper(i + 1, k)\n m_cost = min(cost, m_cost)\n\n return m_cost\n\n cost, min_cost = 0, 999999999999\n n = len(grid[0])\n for j in range(n):\n cost = helper(0, j)\n min_cost = min(cost, min_cost)\n\n return min_cost\n```\n\nA much cleaner code provided by @feng4\n```\nclass Solution:\n def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n @lru_cache()\n def helper(i, j):\n if i == 0:\n return grid[i][j]\n else:\n return grid[i][j] + min(moveCost[grid[i - 1][k]][j] + helper(i - 1, k) for k in range(n))\n \n return min(helper(m - 1, j) for j in range(n))\n``` | 11 | You are given a **0-indexed** `m x n` integer matrix `grid` consisting of **distinct** integers from `0` to `m * n - 1`. You can move in this matrix from a cell to any other cell in the **next** row. That is, if you are in cell `(x, y)` such that `x < m - 1`, you can move to any of the cells `(x + 1, 0)`, `(x + 1, 1)`, ..., `(x + 1, n - 1)`. **Note** that it is not possible to move from cells in the last row.
Each possible move has a cost given by a **0-indexed** 2D array `moveCost` of size `(m * n) x n`, where `moveCost[i][j]` is the cost of moving from a cell with value `i` to a cell in column `j` of the next row. The cost of moving from cells in the last row of `grid` can be ignored.
The cost of a path in `grid` is the **sum** of all values of cells visited plus the **sum** of costs of all the moves made. Return _the **minimum** cost of a path that starts from any cell in the **first** row and ends at any cell in the **last** row._
**Example 1:**
**Input:** grid = \[\[5,3\],\[4,0\],\[2,1\]\], moveCost = \[\[9,8\],\[1,5\],\[10,12\],\[18,6\],\[2,4\],\[14,3\]\]
**Output:** 17
**Explanation:** The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
**Example 2:**
**Input:** grid = \[\[5,1,2\],\[4,0,3\]\], moveCost = \[\[12,10,15\],\[20,23,8\],\[21,7,1\],\[8,1,13\],\[9,10,25\],\[5,3,2\]\]
**Output:** 6
**Explanation:** The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 50`
* `grid` consists of distinct integers from `0` to `m * n - 1`.
* `moveCost.length == m * n`
* `moveCost[i].length == n`
* `1 <= moveCost[i][j] <= 100` | From the given string, find the corresponding rows and columns. Iterate through the columns in ascending order and for each column, iterate through the rows in ascending order to obtain the required cells in sorted order. |
[Python3] top-down dp | minimum-path-cost-in-a-grid | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e59b5d5832483707a595ae92b9aa1fb456986009) for solutions of weekly 297\n\n```\nclass Solution:\n def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n \n @cache\n def fn(i, j):\n """Return min cost of moving from (i, j) to bottom row."""\n if i == m-1: return grid[i][j]\n ans = inf \n for jj in range(n): \n ans = min(ans, grid[i][j] + fn(i+1, jj) + moveCost[grid[i][j]][jj])\n return ans \n \n return min(fn(0, j) for j in range(n))\n``` | 7 | You are given a **0-indexed** `m x n` integer matrix `grid` consisting of **distinct** integers from `0` to `m * n - 1`. You can move in this matrix from a cell to any other cell in the **next** row. That is, if you are in cell `(x, y)` such that `x < m - 1`, you can move to any of the cells `(x + 1, 0)`, `(x + 1, 1)`, ..., `(x + 1, n - 1)`. **Note** that it is not possible to move from cells in the last row.
Each possible move has a cost given by a **0-indexed** 2D array `moveCost` of size `(m * n) x n`, where `moveCost[i][j]` is the cost of moving from a cell with value `i` to a cell in column `j` of the next row. The cost of moving from cells in the last row of `grid` can be ignored.
The cost of a path in `grid` is the **sum** of all values of cells visited plus the **sum** of costs of all the moves made. Return _the **minimum** cost of a path that starts from any cell in the **first** row and ends at any cell in the **last** row._
**Example 1:**
**Input:** grid = \[\[5,3\],\[4,0\],\[2,1\]\], moveCost = \[\[9,8\],\[1,5\],\[10,12\],\[18,6\],\[2,4\],\[14,3\]\]
**Output:** 17
**Explanation:** The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
**Example 2:**
**Input:** grid = \[\[5,1,2\],\[4,0,3\]\], moveCost = \[\[12,10,15\],\[20,23,8\],\[21,7,1\],\[8,1,13\],\[9,10,25\],\[5,3,2\]\]
**Output:** 6
**Explanation:** The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 50`
* `grid` consists of distinct integers from `0` to `m * n - 1`.
* `moveCost.length == m * n`
* `moveCost[i].length == n`
* `1 <= moveCost[i][j] <= 100` | From the given string, find the corresponding rows and columns. Iterate through the columns in ascending order and for each column, iterate through the rows in ascending order to obtain the required cells in sorted order. |
Python3 Solution | fair-distribution-of-cookies | 0 | 1 | \n```\nclass Solution:\n def distributeCookies(self, cookies: List[int], k: int) -> int:\n n=len(cookies)\n\n @cache\n def fn(mask,k):\n if mask==0:\n return 0\n\n if k==0:\n return inf\n\n ans=inf\n orig=mask\n\n while mask:\n mask=orig &(mask-1)\n res=sum(cookies[i] for i in range(n) if (orig^mask) & 1<<i)\n ans=min(ans,max(res,fn(mask,k-1)))\n\n return ans\n\n return fn((1<<n)-1,k) \n``` | 2 | You are given an integer array `cookies`, where `cookies[i]` denotes the number of cookies in the `ith` bag. You are also given an integer `k` that denotes the number of children to distribute **all** the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The **unfairness** of a distribution is defined as the **maximum** **total** cookies obtained by a single child in the distribution.
Return _the **minimum** unfairness of all distributions_.
**Example 1:**
**Input:** cookies = \[8,15,10,20,8\], k = 2
**Output:** 31
**Explanation:** One optimal distribution is \[8,15,8\] and \[10,20\]
- The 1st child receives \[8,15,8\] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives \[10,20\] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
**Example 2:**
**Input:** cookies = \[6,1,3,2,2,4,1,2\], k = 3
**Output:** 7
**Explanation:** One optimal distribution is \[6,1\], \[3,2,2\], and \[4,1,2\]
- The 1st child receives \[6,1\] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives \[3,2,2\] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives \[4,1,2\] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
**Constraints:**
* `2 <= cookies.length <= 8`
* `1 <= cookies[i] <= 105`
* `2 <= k <= cookies.length` | The k smallest numbers that do not appear in nums will result in the minimum sum. Recall that the sum of the first n positive numbers is equal to n * (n+1) / 2. Initialize the answer as the sum of 1 to k. Then, adjust the answer depending on the values in nums. |
Best Solution | fair-distribution-of-cookies | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*2^k)$$\n\n\n# Code\n```\nclass Solution:\n def solve(self,index,bucket,cookies):\n if index==len(cookies):\n if bucket:\n return max(bucket)\n mini=inf\n for choice in range(len(bucket)):\n bucket[choice]+=cookies[index]\n mini=min(mini,self.solve(index+1,bucket,cookies))\n bucket[choice]-=cookies[index]\n """\n since the position of the maximum element doesn\'t matter \n to avoid the repetitions of the permutations we stop them by bucket[choice]==0 which states the call has returned to the initial position \n\n if bucket[choice]==0:\n return mini\n\n\n\n return mini\n \n def distributeCookies(self, cookies: List[int], k: int) -> int:\n bucket=[0 for i in range(k)]\n return self.solve(0,bucket,cookies)\n \n``` | 1 | You are given an integer array `cookies`, where `cookies[i]` denotes the number of cookies in the `ith` bag. You are also given an integer `k` that denotes the number of children to distribute **all** the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The **unfairness** of a distribution is defined as the **maximum** **total** cookies obtained by a single child in the distribution.
Return _the **minimum** unfairness of all distributions_.
**Example 1:**
**Input:** cookies = \[8,15,10,20,8\], k = 2
**Output:** 31
**Explanation:** One optimal distribution is \[8,15,8\] and \[10,20\]
- The 1st child receives \[8,15,8\] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives \[10,20\] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
**Example 2:**
**Input:** cookies = \[6,1,3,2,2,4,1,2\], k = 3
**Output:** 7
**Explanation:** One optimal distribution is \[6,1\], \[3,2,2\], and \[4,1,2\]
- The 1st child receives \[6,1\] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives \[3,2,2\] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives \[4,1,2\] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
**Constraints:**
* `2 <= cookies.length <= 8`
* `1 <= cookies[i] <= 105`
* `2 <= k <= cookies.length` | The k smallest numbers that do not appear in nums will result in the minimum sum. Recall that the sum of the first n positive numbers is equal to n * (n+1) / 2. Initialize the answer as the sum of 1 to k. Then, adjust the answer depending on the values in nums. |
EASY PYTHON SOLUTION USING BACKTRACKING AND DP | fair-distribution-of-cookies | 0 | 1 | # Code\n```\nclass Solution: \n def dp(self,i,dist,cookies,k,dct):\n if i<0:\n return max(dist)\n if (i,tuple(dist)) in dct:\n return dct[(i,tuple(dist))]\n ans=float("infinity")\n for j in range(k):\n dist[j]+=cookies[i]\n if max(dist)<ans:\n x=self.dp(i-1,dist,cookies,k,dct)\n ans=min(ans,x)\n dist[j]-=cookies[i]\n dct[(i,tuple(dist))]=ans\n return ans\n def distributeCookies(self, cookies: List[int], k: int) -> int:\n dist=[0]*k\n n=len(cookies)\n return self.dp(n-1,dist,cookies,k,{})\n\n``` | 1 | You are given an integer array `cookies`, where `cookies[i]` denotes the number of cookies in the `ith` bag. You are also given an integer `k` that denotes the number of children to distribute **all** the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The **unfairness** of a distribution is defined as the **maximum** **total** cookies obtained by a single child in the distribution.
Return _the **minimum** unfairness of all distributions_.
**Example 1:**
**Input:** cookies = \[8,15,10,20,8\], k = 2
**Output:** 31
**Explanation:** One optimal distribution is \[8,15,8\] and \[10,20\]
- The 1st child receives \[8,15,8\] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives \[10,20\] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
**Example 2:**
**Input:** cookies = \[6,1,3,2,2,4,1,2\], k = 3
**Output:** 7
**Explanation:** One optimal distribution is \[6,1\], \[3,2,2\], and \[4,1,2\]
- The 1st child receives \[6,1\] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives \[3,2,2\] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives \[4,1,2\] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
**Constraints:**
* `2 <= cookies.length <= 8`
* `1 <= cookies[i] <= 105`
* `2 <= k <= cookies.length` | The k smallest numbers that do not appear in nums will result in the minimum sum. Recall that the sum of the first n positive numbers is equal to n * (n+1) / 2. Initialize the answer as the sum of 1 to k. Then, adjust the answer depending on the values in nums. |
Python optimization needed to avoid TLE | fair-distribution-of-cookies | 0 | 1 | # Intuition\nSince data size is small, just brutal force it using backtracking; however, for python3 time constraint is tight. \n\nTo make it work, each time I sort the current count for each child to break symmetry of the state. For example, if we have 2 children and 30 candies, then allocation (10, 20) equal (20, 10), we only need to compute one of them to save time.\n\n\n\n# Code\n```\nclass Solution:\n def distributeCookies(self, cookies: List[int], k: int) -> int:\n # distribute as even as possible\n # brutal force it: \n\n self.res = float(\'inf\')\n\n @cache\n def dfs(start, state):\n # Given the state which is the count for each kid, return the result\n if start == len(cookies):\n self.res = min(self.res, max(state))\n return max(state)\n \n if max(state) > self.res:\n # early stopping\n return float(\'inf\')\n \n # break the symmetry for state\n lst = sorted(state)\n res = float(\'inf\')\n\n for i in range(k):\n lst[i] += cookies[start]\n res = min(res, dfs(start+1, tuple(lst)))\n lst[i] -= cookies[start]\n\n return res\n \n return dfs(0, tuple([0]*k))\n``` | 1 | You are given an integer array `cookies`, where `cookies[i]` denotes the number of cookies in the `ith` bag. You are also given an integer `k` that denotes the number of children to distribute **all** the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The **unfairness** of a distribution is defined as the **maximum** **total** cookies obtained by a single child in the distribution.
Return _the **minimum** unfairness of all distributions_.
**Example 1:**
**Input:** cookies = \[8,15,10,20,8\], k = 2
**Output:** 31
**Explanation:** One optimal distribution is \[8,15,8\] and \[10,20\]
- The 1st child receives \[8,15,8\] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives \[10,20\] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
**Example 2:**
**Input:** cookies = \[6,1,3,2,2,4,1,2\], k = 3
**Output:** 7
**Explanation:** One optimal distribution is \[6,1\], \[3,2,2\], and \[4,1,2\]
- The 1st child receives \[6,1\] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives \[3,2,2\] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives \[4,1,2\] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
**Constraints:**
* `2 <= cookies.length <= 8`
* `1 <= cookies[i] <= 105`
* `2 <= k <= cookies.length` | The k smallest numbers that do not appear in nums will result in the minimum sum. Recall that the sum of the first n positive numbers is equal to n * (n+1) / 2. Initialize the answer as the sum of 1 to k. Then, adjust the answer depending on the values in nums. |
Python short and clean. Backtracking. DFS. | fair-distribution-of-cookies | 0 | 1 | # Approach\nTL;DR, Similar to [Editorial Solution](https://leetcode.com/problems/fair-distribution-of-cookies/editorial/) with an additional `average` based pruning.\n\n# Complexity\n- Time complexity: $$O(k^n)$$\n\n- Space complexity: $$O(k + n)$$\n\nwhere, `n is number of cookies(bags)`.\n\n# Code\n```python\nclass Solution:\n def distributeCookies(self, cookies: list[int], k: int) -> int:\n average = sum(cookies) // k\n\n def min_unfairness(i: int, kids: list[int], zero_count: int) -> int:\n if i == len(cookies): return max(kids)\n unfairness = inf\n\n if len(cookies) - i < zero_count: return unfairness # Prune if #cookies_left < #kids_with_zero\n optimal_next_kids = filter(lambda j: kids[j] < average, range(len(kids))) # Prune if kid_j has more cookies than average\n\n for j in optimal_next_kids:\n is_kid_j_zero = int(kids[j] == 0)\n \n kids[j] += cookies[i]\n unfairness = min(unfairness, min_unfairness(i + 1, kids, zero_count - is_kid_j_zero))\n kids[j] -= cookies[i]\n \n return unfairness\n \n return min_unfairness(0, [0] * k, k)\n\n\n``` | 2 | You are given an integer array `cookies`, where `cookies[i]` denotes the number of cookies in the `ith` bag. You are also given an integer `k` that denotes the number of children to distribute **all** the bags of cookies to. All the cookies in the same bag must go to the same child and cannot be split up.
The **unfairness** of a distribution is defined as the **maximum** **total** cookies obtained by a single child in the distribution.
Return _the **minimum** unfairness of all distributions_.
**Example 1:**
**Input:** cookies = \[8,15,10,20,8\], k = 2
**Output:** 31
**Explanation:** One optimal distribution is \[8,15,8\] and \[10,20\]
- The 1st child receives \[8,15,8\] which has a total of 8 + 15 + 8 = 31 cookies.
- The 2nd child receives \[10,20\] which has a total of 10 + 20 = 30 cookies.
The unfairness of the distribution is max(31,30) = 31.
It can be shown that there is no distribution with an unfairness less than 31.
**Example 2:**
**Input:** cookies = \[6,1,3,2,2,4,1,2\], k = 3
**Output:** 7
**Explanation:** One optimal distribution is \[6,1\], \[3,2,2\], and \[4,1,2\]
- The 1st child receives \[6,1\] which has a total of 6 + 1 = 7 cookies.
- The 2nd child receives \[3,2,2\] which has a total of 3 + 2 + 2 = 7 cookies.
- The 3rd child receives \[4,1,2\] which has a total of 4 + 1 + 2 = 7 cookies.
The unfairness of the distribution is max(7,7,7) = 7.
It can be shown that there is no distribution with an unfairness less than 7.
**Constraints:**
* `2 <= cookies.length <= 8`
* `1 <= cookies[i] <= 105`
* `2 <= k <= cookies.length` | The k smallest numbers that do not appear in nums will result in the minimum sum. Recall that the sum of the first n positive numbers is equal to n * (n+1) / 2. Initialize the answer as the sum of 1 to k. Then, adjust the answer depending on the values in nums. |
Python3 easy solution | naming-a-company | 0 | 1 | # Approach\n<!-- Describe your approach to solving the problem. -->\n- make array of size 26*26.\n- i will represent first incident alphabet of ideas.\n- j will be our replacement for i alphabet.\n- value of $$match[i][j]$$ will decide that how many times replacing current idea\'s incident with another word\'s incident is correct.\n- at end we want answer for match[i][j] and match[j][i], because it represents if we can **replace c with b** and **creates one new word, then viseversa is also correct.**\n- return answer\n\n# Complexity\n- Time complexity: $$O(N*26+26*26)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N+1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n answer = 0\n ideasSet = {i for i in ideas}\n match = [[0 for _ in range(26)] for __ in range(26)]\n for i in ideas:\n for j in range(ord(\'a\'), ord(\'z\')+1):\n newIdea = chr(j)+i[1:]\n if newIdea not in ideasSet:\n match[ord(i[0]) - ord(\'a\')][j - ord(\'a\')] += 1\n for i in range(26):\n for j in range(26):\n answer += match[i][j]*match[j][i]\n return answer\n```\n# Please like this solution and comment any suggestion :-) | 3 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
Python3 👍||⚡96/98 T/M beats, only 10 lines 🔥|| Optimization Simple explain ||attach a TLE solution | naming-a-company | 0 | 1 | \n\n# Approach\nCreate Hash table with \nkey: > prefix_word , in other words words[0]\nvalue: > suffux_word , in other words words[1:]\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\nCreate table time , need traverse ideas\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\nThe Max table size is O(26)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n hashmap = defaultdict(set)\n for name in set(ideas):\n hashmap[name[0]].add(name[1:])\n ans=0\n for index_1 , (pre_a,suf_a) in enumerate(hashmap.items()):\n for index_2 , (pre_b,suf_b) in enumerate(hashmap.items()): # name_a name_b is same name_b name_a \n if index_2>index_1: # so you dont need calculate it double times\n both_have = len(suf_a.intersection(suf_b)) # count the suffix_words that appear in both groups\n ans += (len(suf_a)-both_have) * (len(suf_b)-both_have) \n return 2*ans\n\n```\n# Old Code (TLE with pairs of words)\nWhy TLE ?\nGiven the size of the input array ideas as n, we need to try O(n ^ 2) pairs of words.(n <=5 * 10_4) This approach is likely to exceed the time limit, implying that we should look for a better approach.\n\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n def check_naming(name_list,ht):\n name_a,name_b = name_list[0],name_list[1]\n if name_a[0] == name_b[0]:\n return 0\n if name_b[1:] in ht[name_a[0]] or name_a[1:] in ht[name_b[0]]:\n return 0\n return 2\n n = len(ideas)\n hashmap = defaultdict(list)\n for name in ideas:\n hashmap[name[0]].append(name[1:])\n cur_list,ans=[],0\n for index_a in range(n):\n cur_list.append(ideas.pop(0))\n for index_b in range(index_a+1,n):\n cur_list.append(ideas.pop(0))\n ans += check_naming(cur_list,hashmap)\n ideas.append(cur_list.pop())\n cur_list.pop()\n return ans\n```\n | 2 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
O(n) | O(n) | Python Solution | Explained | naming-a-company | 0 | 1 | Hello **Tenno Leetcoders**, \n\nFor this problem, we are giving an array of strings `ideas`, we want to return `valid distinct names for companies`\n\nThe restrictions are as follows:\n1) If both of the new names are not found in the original ideas, then the name ideaA ideaB (the concatenation of ideaA and ideaB, separated by a space) is a valid company name.\n\n2) Otherwise, it is not a valid name.\n\n### Explanation\nWe can use `Hashset` to help us validate distinct names. If we want to know the number of distinct company names formed by ideas array, we only need to pay attention to the first character of our two words as that will be our key to help us group suffixes together.\n\nFor each set of grouped suffixes based on the first character, we will now look at their suffixes to see if any other group have the same suffix, If so, we will subtract it to make our grouped suffix to be distinct\n\n#### Example: \n\n```\nc -> [at, offee] -> 2 - 1(offee) = 1 distinct suffix\n\nd -> [onuts] -> 1 distinct suffix\n \nt -> [ime, offee] -> 2 - 1 (offee) = 1 distinct suffix\n```\n\n#### Algorithm steps:\n\n1) Group ideas based on the first letter\n\n2) When comparing two words, if same words appears in both set(), then the word must not be a valid name\n\n3) Remove the same words then calculate how many unique suffix are in the list\n\n4) To make a valid name with two words: \n\n - Multiply the first suffix\n \n - Multiply the second suffix * 2\n \nWe are multiplying by `2` is because once we found a distinct suffix, we can use the suffix to also create another pair of words. \n\n **Example**: **``coffee, donuts` -> `doffee conuts`, `conuts doffee``**\n \n### Code\t \n\t \n```\n def distinctNames(self, ideas: List[str]) -> int:\n \n nameMap = collections.defaultdict(set)\n result = 0\n\n for word in ideas: \n # first char as keys - nameMap[word[0]]\n # suffixes as values - word[1:]\n nameMap[word[0]].add(word[1:])\n \n keys = list(nameMap.keys())\n n = len(keys)\n \n # traverse through first char\n for char1 in range(n):\n \n for char2 in range(char1 + 1, n):\n key1, key2 = keys[char1], keys[char2]\n \n value1, value2 = nameMap[key1], nameMap[key2]\n \n duplicated_suffixes = len(value1 & value2)\n \n if key1 == key2: continue\n \n result += (len(value1) - duplicated_suffixes) * (len(value2) - duplicated_suffixes) * 2\n\n return result\n```\n\n#### Time complexity: O(n)\n#### Space complexity: O(n)\n\n***Upvote if this tenno\'s discussion helped you in some type of way***\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 1 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
Python 11 lines, faster than 98% | naming-a-company | 0 | 1 | <!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nTODO\n<!-- - Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n\n# Code\n```\nclass Solution:\n def distinctNames(self, xs: List[str]) -> int:\n idx = defaultdict(lambda: len(idx))\n grp = defaultdict(set)\n for x in xs:\n grp[x[0]].add(idx[x[1:]])\n n = 0\n for a, b in combinations(grp.values(), 2):\n d = len(a&b)\n n += (len(a)-d) * (len(b)-d)\n return n * 2\n```\nOr just:\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n S = [set() for _ in range(26)]\n for x in ideas:\n S[ord(x[0])-97].add(x[1:])\n n = 0\n for x, y in combinations(S, 2):\n a = len(x&y)\n n += (len(x)-a) * (len(y)-a)\n return n * 2\n```\n^ Same speed, less memory. | 1 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
Python3 dictionary solution 96.74% | naming-a-company | 0 | 1 | # Idea\nConstruct a dictionary `d` with keys the alphabats `x` where the values are set of strings `s` such that `x+s` is in `ideas`. One can then derive the result by computing pairwise intersections.\n\n# Code\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n d = defaultdict(set)\n for idea in ideas:\n d[idea[0]].add(idea[1:])\n result = 0\n for (x, y) in combinations(d, 2):\n temp = len(d[x] & d[y])\n result += (len(d[x]) - temp) * (len(d[y]) - temp)\n return result * 2\n```\n\n##### Example\nSay we have `[\'ab\',\'ac\',\'bc\',\'bd\']`, then `d={\'a\':{\'b\',\'c\'},\'b\':{\'c\',\'d\'}}`. The only available swap is between `\'ab\',\'bd\'`, so this should output `2`. The formula for computing this can be seen in the code above.\n\n##### Note on implementation in Python\n`collections.defaultdict` is pretty handy to avoid getting KeyErrors and specify how to initialize a dictionary key value, while `itertools.combinations` is also convenient when we want to iterate over pairs of elements in an iterable. | 1 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
🐸Python|| begineer friendly|| well explained | naming-a-company | 0 | 1 | # Intitution\nElement with same first letter cannot form valid combination as replecing them create the same name again.\nTherefore, there is no relation between element with same first letter. So, we will divide them into different set with same first letter.\nThen we will compare every set and and check the common element because common element also leads to same invalid sequence **if we have "cat","car" and "rat" so replacing c with r in "cat" and "rat"will make the same letters again and even if we replace "car" and "rat" thet will also creat "cat" that is invalid**. So we will simply dont count them in result .\ntake intersection and dont count them while calculating the combination.\n# Code\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n d={}\n #creating a dictionary with first letter as key\n for i in ideas:\n if ord(i[0]) in d:\n d[ord(i[0])].add(i[1:])\n else:\n d[ord(i[0])]={i[1:]}\n r=0 \n #comparing every set with each other \n for i in range(97,123):\n if i not in d:\n continue\n for j in range(i+1,123):\n if j not in d:\n continue\n # we dont need common element because that will lead to invalid sequence\n a=len(d[i].intersection(d[j]))\n #removing common element and add total combinations it to result \n r+=((len(d[i])-a)*(len(d[j])-a))*2 \n return r \n```\n **UPVOTE IF YOU FIND THIS HELPFUL AND DO COMMENT IF YOU GET CONFUSED SOMEWHERE** | 1 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
Hash - beating 95% in speed | naming-a-company | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe length of ideas is at 10^4 level, which means we cannot just loop twice, as the limit is at 10^6 level. \nGiven we need to find the unoverlapped rest of strings other than the initial, we can use hash - to keep the length of substrings per initial and get the length of substring intersection of two initials, and finally get the result\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse hash, i.e. set to keep the unique substrings per initial and loop it twice (at most 26 * 26 loops).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) where n is the length of ideas. The count of loops is at most 26 * 26. Per loop we take intersection of two sets, whose complexity is O(min(len1, len2)) where len1 and len2 are the lengths of the two sets. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) where n is the length of ideas. A list to keep sets and the sets contains all elements in ideas. \n\n# Code\n```\nclass Solution:\n def distinctNames(self, ideas: List[str]) -> int:\n ls = [set() for _ in range(26)]\n for idea in ideas: \n init = idea[0]\n rest = idea[1:]\n ls[ord(init) - 97].add(rest)\n res = 0\n for i in range(25): \n st1 = ls[i]\n len1 = len(st1)\n if not len1: \n continue\n for j in range(i + 1, 26): \n st2 = ls[j]\n len2 = len(st2)\n if not len2: \n continue\n len_int = len(st1.intersection(st2))\n res += 2 * (len1 - len_int) * (len2 - len_int)\n return res\n\n\n``` | 1 | You are given an array of strings `ideas` that represents a list of names to be used in the process of naming a company. The process of naming a company is as follows:
1. Choose 2 **distinct** names from `ideas`, call them `ideaA` and `ideaB`.
2. Swap the first letters of `ideaA` and `ideaB` with each other.
3. If **both** of the new names are not found in the original `ideas`, then the name `ideaA ideaB` (the **concatenation** of `ideaA` and `ideaB`, separated by a space) is a valid company name.
4. Otherwise, it is not a valid name.
Return _the number of **distinct** valid names for the company_.
**Example 1:**
**Input:** ideas = \[ "coffee ", "donuts ", "time ", "toffee "\]
**Output:** 6
**Explanation:** The following selections are valid:
- ( "coffee ", "donuts "): The company name created is "doffee conuts ".
- ( "donuts ", "coffee "): The company name created is "conuts doffee ".
- ( "donuts ", "time "): The company name created is "tonuts dime ".
- ( "donuts ", "toffee "): The company name created is "tonuts doffee ".
- ( "time ", "donuts "): The company name created is "dime tonuts ".
- ( "toffee ", "donuts "): The company name created is "doffee tonuts ".
Therefore, there are a total of 6 distinct company names.
The following are some examples of invalid selections:
- ( "coffee ", "time "): The name "toffee " formed after swapping already exists in the original array.
- ( "time ", "toffee "): Both names are still the same after swapping and exist in the original array.
- ( "coffee ", "toffee "): Both names formed after swapping already exist in the original array.
**Example 2:**
**Input:** ideas = \[ "lack ", "back "\]
**Output:** 0
**Explanation:** There are no valid selections. Therefore, 0 is returned.
**Constraints:**
* `2 <= ideas.length <= 5 * 104`
* `1 <= ideas[i].length <= 10`
* `ideas[i]` consists of lowercase English letters.
* All the strings in `ideas` are **unique**. | Could you represent and store the descriptions more efficiently? Could you find the root node? The node that is not a child in any of the descriptions is the root node. |
Counter | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | **Python 3**\n```python\nclass Solution:\n def greatestLetter(self, s: str) -> str:\n cnt = Counter(s)\n return next((u for u in reversed(ascii_uppercase) if cnt[u] and cnt[u.lower()]), "")\n```\n**C++**\n```cpp\nstring greatestLetter(string s) {\n int cnt[128] = {};\n for (auto ch : s)\n ++cnt[ch];\n for (auto ch = \'Z\'; ch >= \'A\'; --ch)\n if (cnt[ch] && cnt[ch + \'a\' - \'A\'])\n return string(1, ch);\n return "";\n}\n``` | 46 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Python Elegant & Short | 98.51% faster | Two solutions | O(n*log(n)) and O(n) | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | \n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(2*26*log(2*26))\n\t\tMemory: O(2*26)\n\t\t"""\n\n\t\tdef greatestLetter(self, s: str) -> str:\n\t\t\tletters = set(s)\n\n\t\t\tfor ltr in sorted(letters, reverse=True):\n\t\t\t\tif ltr.isupper() and ltr.lower() in letters:\n\t\t\t\t\treturn ltr\n\n\t\t\treturn \'\'\n\n\n\tclass Solution:\n\t\t"""\n\t\tTime: O(2*26)\n\t\tMemory: O(2*26)\n\t\t"""\n\n\t\tdef greatestLetter(self, s: str) -> str:\n\t\t\tletters = set(s)\n\t\t\tgreatest = \'\'\n\n\t\t\tfor ltr in letters:\n\t\t\t\tif ltr.isupper() and ltr.lower() in letters:\n\t\t\t\t\tgreatest = max(ltr, greatest)\n\n\t\t\treturn greatest\n | 2 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Python || Hash Map || O(N) || Easy Solution | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | # Code\n```\nclass Solution:\n def greatestLetter(self, s: str) -> str:\n dic={}\n res=""\n for i in s:\n if i>=\'A\' and i<=\'Z\':\n if i in dic and dic[i]%2==1:\n dic[i]+=2\n elif i not in dic:\n dic[i]=2\n if i>=\'a\' and i<=\'z\':\n i=i.upper()\n if i in dic and dic[i]%2==0:\n dic[i]+=1\n elif i not in dic:\n dic[i]=1\n for i in dic:\n if dic[i]>=3:\n res=max(i,res)\n return res \n```\n\n***Please Upvote*** | 2 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Python 1-liner | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | The intersection between the uppercase and lowercase string results the characters of interest.\n\n```\nclass Solution:\n def greatestLetter(self, s: str) -> str:\n return max(Counter(s) & Counter(s.swapcase()), default="").upper()\n``` | 1 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Simple Python 2-liner | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def greatestLetter(self, s: str) -> str:\n a = [x for x in s if x.upper() in s and x.lower() in s] + [""]\n return max(a).upper()\n```\n | 3 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Easy python solution | greatest-english-letter-in-upper-and-lower-case | 0 | 1 | ```\ndef greatestLetter(self, s: str) -> str:\n c="abcdefghijklmnopqrstuvwxyz"\n l=[""]\n for i in c:\n if i in s and i.upper() in s:\n l.append(i.upper())\n l.sort()\n return l[-1]\n``` | 2 | Given a string of English letters `s`, return _the **greatest** English letter which occurs as **both** a lowercase and uppercase letter in_ `s`. The returned letter should be in **uppercase**. If no such letter exists, return _an empty string_.
An English letter `b` is **greater** than another letter `a` if `b` appears **after** `a` in the English alphabet.
**Example 1:**
**Input:** s = "l**Ee**TcOd**E** "
**Output:** "E "
**Explanation:**
The letter 'E' is the only letter to appear in both lower and upper case.
**Example 2:**
**Input:** s = "a**rR**AzFif "
**Output:** "R "
**Explanation:**
The letter 'R' is the greatest letter to appear in both lower and upper case.
Note that 'A' and 'F' also appear in both lower and upper case, but 'R' is greater than 'F' or 'A'.
**Example 3:**
**Input:** s = "AbCdEfGhIjK "
**Output:** " "
**Explanation:**
There is no letter that appears in both lower and upper case.
**Constraints:**
* `1 <= s.length <= 1000`
* `s` consists of lowercase and uppercase English letters. | Find the optimal position to add pattern[0] so that the number of subsequences is maximized. Similarly, find the optimal position to add pattern[1]. For each of the above cases, count the number of times the pattern occurs as a subsequence in text. The larger count is the required answer. |
Python Math Solution | Only Looking at Unit Digit | Clean & Concise | sum-of-numbers-with-units-digit-k | 0 | 1 | ```\nclass Solution:\n def minimumNumbers(self, num: int, k: int) -> int:\n if num == 0:\n return 0\n unit = num % 10\n for i in range(1, 11):\n if (i * k) % 10 == unit:\n if i * k <= num:\n return i\n else:\n break\n return -1\n``` | 1 | Given two integers `num` and `k`, consider a set of positive integers with the following properties:
* The units digit of each integer is `k`.
* The sum of the integers is `num`.
Return _the **minimum** possible size of such a set, or_ `-1` _if no such set exists._
Note:
* The set can contain multiple instances of the same integer, and the sum of an empty set is considered `0`.
* The **units digit** of a number is the rightmost digit of the number.
**Example 1:**
**Input:** num = 58, k = 9
**Output:** 2
**Explanation:**
One valid set is \[9,49\], as the sum is 58 and each integer has a units digit of 9.
Another valid set is \[19,39\].
It can be shown that 2 is the minimum possible size of a valid set.
**Example 2:**
**Input:** num = 37, k = 2
**Output:** -1
**Explanation:** It is not possible to obtain a sum of 37 using only integers that have a units digit of 2.
**Example 3:**
**Input:** num = 0, k = 7
**Output:** 0
**Explanation:** The sum of an empty set is considered 0.
**Constraints:**
* `0 <= num <= 3000`
* `0 <= k <= 9` | It is always optimal to halve the largest element. What data structure allows for an efficient query of the maximum element? Use a heap or priority queue to maintain the current elements. |
Python solution | Constant Time-Complexity | Simple Solution | No DP nor Greedy | | sum-of-numbers-with-units-digit-k | 0 | 1 | The Approach is quite simple, You\'ve to understand that inorder to get the sum "num" from numbers ending with digit "k", you need to check the last digit of the multiple of the "k" upto 10 and these digits will repeat after 10 again. so if the ending digit exists in the dictionary of "k"s multiples that means the sum is possible otherwise its not. For example if the num ends with 6 and the "k" is 7 then the 6 is in the 8th position in 7th list and you need to have 8 numbers ending with 7 to get the number ending with 6 and other constraints is to separate the 0 of 10 and the 10th multiple of "k"\n\n```\nclass Solution:\n def minimumNumbers(self, num: int, k: int) -> int:\n if num==0:\n return 0 \n if k==0:\n if num%10==0:\n return 1\n return -1\n if num<k:\n return -1 \n d = {\n 1:[1,2,3,4,5,6,7,8,9,0],\n 2:[2,4,6,8,0],\n 3:[3,6,9,2,5,8,1,4,7,0],\n 4:[4,8,2,6,0],\n 5:[5,0],\n 6:[6,2,8,4,0],\n 7:[7,4,1,8,5,2,9,6,3,0],\n 8:[8,6,4,2,0],\n 9:[9,8,7,6,5,4,3,2,1,0]\n }\n if num%10 not in d[k]:\n return -1 \n else:\n i = d[k].index(num%10) + 1 \n if num<i*k:\n return -1 \n return i\n``` | 1 | Given two integers `num` and `k`, consider a set of positive integers with the following properties:
* The units digit of each integer is `k`.
* The sum of the integers is `num`.
Return _the **minimum** possible size of such a set, or_ `-1` _if no such set exists._
Note:
* The set can contain multiple instances of the same integer, and the sum of an empty set is considered `0`.
* The **units digit** of a number is the rightmost digit of the number.
**Example 1:**
**Input:** num = 58, k = 9
**Output:** 2
**Explanation:**
One valid set is \[9,49\], as the sum is 58 and each integer has a units digit of 9.
Another valid set is \[19,39\].
It can be shown that 2 is the minimum possible size of a valid set.
**Example 2:**
**Input:** num = 37, k = 2
**Output:** -1
**Explanation:** It is not possible to obtain a sum of 37 using only integers that have a units digit of 2.
**Example 3:**
**Input:** num = 0, k = 7
**Output:** 0
**Explanation:** The sum of an empty set is considered 0.
**Constraints:**
* `0 <= num <= 3000`
* `0 <= k <= 9` | It is always optimal to halve the largest element. What data structure allows for an efficient query of the maximum element? Use a heap or priority queue to maintain the current elements. |
O(1) Python | sum-of-numbers-with-units-digit-k | 0 | 1 | ```\n\tdef minimumNumbers(self, num: int, k: int) -> int:\n t = num%10\n if num==0:\n return 0\n if num<k:\n return -1\n for i in range(1,11):\n if (i*k)%10 == t:\n if i*k <= num:\n return i\n return -1\n``` | 1 | Given two integers `num` and `k`, consider a set of positive integers with the following properties:
* The units digit of each integer is `k`.
* The sum of the integers is `num`.
Return _the **minimum** possible size of such a set, or_ `-1` _if no such set exists._
Note:
* The set can contain multiple instances of the same integer, and the sum of an empty set is considered `0`.
* The **units digit** of a number is the rightmost digit of the number.
**Example 1:**
**Input:** num = 58, k = 9
**Output:** 2
**Explanation:**
One valid set is \[9,49\], as the sum is 58 and each integer has a units digit of 9.
Another valid set is \[19,39\].
It can be shown that 2 is the minimum possible size of a valid set.
**Example 2:**
**Input:** num = 37, k = 2
**Output:** -1
**Explanation:** It is not possible to obtain a sum of 37 using only integers that have a units digit of 2.
**Example 3:**
**Input:** num = 0, k = 7
**Output:** 0
**Explanation:** The sum of an empty set is considered 0.
**Constraints:**
* `0 <= num <= 3000`
* `0 <= k <= 9` | It is always optimal to halve the largest element. What data structure allows for an efficient query of the maximum element? Use a heap or priority queue to maintain the current elements. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.