title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python simple solution both recursive and iterative | calculate-digit-sum-of-a-string | 0 | 1 | ***Recursive:***\n```\nclass Solution:\n def digitSum(self, s: str, k: int) -> str:\n def str_sum(s):\n return str(sum([int(i) for i in s]))\n\n if len(s) <= k:\n return s\n tmp = []\n for i in range(0, len(s), k):\n tmp.append(str_sum(s[i:i + k]))\n s = \'\'.join(tmp)\n return self.digitSum(s, k)\n```\n\n***Iterative:***\n```\nclass Solution:\n def digitSum(self, s: str, k: int) -> str:\n def str_sum(s):\n return str(sum([int(i) for i in s]))\n\n while len(s) > k:\n tmp = []\n for i in range(0, len(s), k):\n tmp.append(str_sum(s[i:i + k]))\n s = \'\'.join(tmp)\n return s\n``` | 1 | You are given a string `s` consisting of digits and an integer `k`.
A **round** can be completed if the length of `s` is greater than `k`. In one round, do the following:
1. **Divide** `s` into **consecutive groups** of size `k` such that the first `k` characters are in the first group, the next `k` characters are in the second group, and so on. **Note** that the size of the last group can be smaller than `k`.
2. **Replace** each group of `s` with a string representing the sum of all its digits. For example, `"346 "` is replaced with `"13 "` because `3 + 4 + 6 = 13`.
3. **Merge** consecutive groups together to form a new string. If the length of the string is greater than `k`, repeat from step `1`.
Return `s` _after all rounds have been completed_.
**Example 1:**
**Input:** s = "11111222223 ", k = 3
**Output:** "135 "
**Explanation:**
- For the first round, we divide s into groups of size 3: "111 ", "112 ", "222 ", and "23 ".
Then we calculate the digit sum of each group: 1 + 1 + 1 = 3, 1 + 1 + 2 = 4, 2 + 2 + 2 = 6, and 2 + 3 = 5.
So, s becomes "3 " + "4 " + "6 " + "5 " = "3465 " after the first round.
- For the second round, we divide s into "346 " and "5 ".
Then we calculate the digit sum of each group: 3 + 4 + 6 = 13, 5 = 5.
So, s becomes "13 " + "5 " = "135 " after second round.
Now, s.length <= k, so we return "135 " as the answer.
**Example 2:**
**Input:** s = "00000000 ", k = 3
**Output:** "000 "
**Explanation:**
We divide s into "000 ", "000 ", and "00 ".
Then we calculate the digit sum of each group: 0 + 0 + 0 = 0, 0 + 0 + 0 = 0, and 0 + 0 = 0.
s becomes "0 " + "0 " + "0 " = "000 ", whose length is equal to k, so we return "000 ".
**Constraints:**
* `1 <= s.length <= 100`
* `2 <= k <= 100`
* `s` consists of digits only. | You can check the opposite: check if there is a ‘b’ before an ‘a’. Then, negate and return that answer. s should not have any occurrences of “ba” as a substring. |
Python3 O(n+k) || O(n) Runtime: 52ms 41.96% || Memory: 13.0mb 70.32% | calculate-digit-sum-of-a-string | 0 | 1 | Hope I didn\'t coded this in hardcore.\n```\nclass Solution:\n# O(n+k) where n is the elements present in the string\n# and k is the number of steps\n# O(N) space\n# Runtime: 52ms 41.96% || Memory: 13.0mb 70.32%\n def digitSum(self, string: str, k: int) -> str:\n if not string:\n return string\n stringLength = len(string)\n k %= stringLength \n if stringLength == k or k == 0 or k == 1:\n return string\n\n return helper(string, k)\n\ndef helper(string, k):\n newStringList = list(string)\n newNum = 0\n tempList = list()\n for i in range(0, len(newStringList), k):\n newNum = sum(map(int, newStringList[i:k+i]))\n tempList += list(str(newNum))\n\n result = \'\'.join(tempList)\n if len(result) > k:\n return helper(result, k)\n return result\n``` | 1 | You are given a string `s` consisting of digits and an integer `k`.
A **round** can be completed if the length of `s` is greater than `k`. In one round, do the following:
1. **Divide** `s` into **consecutive groups** of size `k` such that the first `k` characters are in the first group, the next `k` characters are in the second group, and so on. **Note** that the size of the last group can be smaller than `k`.
2. **Replace** each group of `s` with a string representing the sum of all its digits. For example, `"346 "` is replaced with `"13 "` because `3 + 4 + 6 = 13`.
3. **Merge** consecutive groups together to form a new string. If the length of the string is greater than `k`, repeat from step `1`.
Return `s` _after all rounds have been completed_.
**Example 1:**
**Input:** s = "11111222223 ", k = 3
**Output:** "135 "
**Explanation:**
- For the first round, we divide s into groups of size 3: "111 ", "112 ", "222 ", and "23 ".
Then we calculate the digit sum of each group: 1 + 1 + 1 = 3, 1 + 1 + 2 = 4, 2 + 2 + 2 = 6, and 2 + 3 = 5.
So, s becomes "3 " + "4 " + "6 " + "5 " = "3465 " after the first round.
- For the second round, we divide s into "346 " and "5 ".
Then we calculate the digit sum of each group: 3 + 4 + 6 = 13, 5 = 5.
So, s becomes "13 " + "5 " = "135 " after second round.
Now, s.length <= k, so we return "135 " as the answer.
**Example 2:**
**Input:** s = "00000000 ", k = 3
**Output:** "000 "
**Explanation:**
We divide s into "000 ", "000 ", and "00 ".
Then we calculate the digit sum of each group: 0 + 0 + 0 = 0, 0 + 0 + 0 = 0, and 0 + 0 = 0.
s becomes "0 " + "0 " + "0 " = "000 ", whose length is equal to k, so we return "000 ".
**Constraints:**
* `1 <= s.length <= 100`
* `2 <= k <= 100`
* `s` consists of digits only. | You can check the opposite: check if there is a ‘b’ before an ‘a’. Then, negate and return that answer. s should not have any occurrences of “ba” as a substring. |
Python easy iterative solution for beginners | calculate-digit-sum-of-a-string | 0 | 1 | ```\nclass Solution:\n def digitSum(self, s: str, k: int) -> str:\n while len(s) > k:\n groups = [s[x:x+k] for x in range(0, len(s), k)]\n temp = ""\n for i in groups:\n dig = [int(y) for y in i]\n temp += str(sum(dig))\n s = temp\n return s | 2 | You are given a string `s` consisting of digits and an integer `k`.
A **round** can be completed if the length of `s` is greater than `k`. In one round, do the following:
1. **Divide** `s` into **consecutive groups** of size `k` such that the first `k` characters are in the first group, the next `k` characters are in the second group, and so on. **Note** that the size of the last group can be smaller than `k`.
2. **Replace** each group of `s` with a string representing the sum of all its digits. For example, `"346 "` is replaced with `"13 "` because `3 + 4 + 6 = 13`.
3. **Merge** consecutive groups together to form a new string. If the length of the string is greater than `k`, repeat from step `1`.
Return `s` _after all rounds have been completed_.
**Example 1:**
**Input:** s = "11111222223 ", k = 3
**Output:** "135 "
**Explanation:**
- For the first round, we divide s into groups of size 3: "111 ", "112 ", "222 ", and "23 ".
Then we calculate the digit sum of each group: 1 + 1 + 1 = 3, 1 + 1 + 2 = 4, 2 + 2 + 2 = 6, and 2 + 3 = 5.
So, s becomes "3 " + "4 " + "6 " + "5 " = "3465 " after the first round.
- For the second round, we divide s into "346 " and "5 ".
Then we calculate the digit sum of each group: 3 + 4 + 6 = 13, 5 = 5.
So, s becomes "13 " + "5 " = "135 " after second round.
Now, s.length <= k, so we return "135 " as the answer.
**Example 2:**
**Input:** s = "00000000 ", k = 3
**Output:** "000 "
**Explanation:**
We divide s into "000 ", "000 ", and "00 ".
Then we calculate the digit sum of each group: 0 + 0 + 0 = 0, 0 + 0 + 0 = 0, and 0 + 0 = 0.
s becomes "0 " + "0 " + "0 " = "000 ", whose length is equal to k, so we return "000 ".
**Constraints:**
* `1 <= s.length <= 100`
* `2 <= k <= 100`
* `s` consists of digits only. | You can check the opposite: check if there is a ‘b’ before an ‘a’. Then, negate and return that answer. s should not have any occurrences of “ba” as a substring. |
Easy and very short solution | minimum-rounds-to-complete-all-tasks | 0 | 1 | # Intuition\nOnly one case the result will be -1. If frequency of any number is 1. If not then the answer is always \n\n ```\n int((frequency+2)/3)\n```\nFor example:\n if 2 then answer is (2+2)/3 => 1 same for others\n- 3 (3+2)/3 => 1\n- 4 (4+2)/3 => 2\n- 5 (5+2)/3 => 3\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumRounds(self, tasks: List[int]) -> int:\n countFreq = Counter(tasks)\n res = 0\n for element in countFreq:\n if countFreq[element] == 1:\n return -1\n res += int((countFreq[element]+2)/3)\n return res\n \n \n``` | 2 | You are given a **0-indexed** integer array `tasks`, where `tasks[i]` represents the difficulty level of a task. In each round, you can complete either 2 or 3 tasks of the **same difficulty level**.
Return _the **minimum** rounds required to complete all the tasks, or_ `-1` _if it is not possible to complete all the tasks._
**Example 1:**
**Input:** tasks = \[2,2,3,3,2,4,4,4,4,4\]
**Output:** 4
**Explanation:** To complete all the tasks, a possible plan is:
- In the first round, you complete 3 tasks of difficulty level 2.
- In the second round, you complete 2 tasks of difficulty level 3.
- In the third round, you complete 3 tasks of difficulty level 4.
- In the fourth round, you complete 2 tasks of difficulty level 4.
It can be shown that all the tasks cannot be completed in fewer than 4 rounds, so the answer is 4.
**Example 2:**
**Input:** tasks = \[2,3,3\]
**Output:** -1
**Explanation:** There is only 1 task of difficulty level 2, but in each round, you can only complete either 2 or 3 tasks of the same difficulty level. Hence, you cannot complete all the tasks, and the answer is -1.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= tasks[i] <= 109` | What is the commonality between security devices on the same row? Each device on the same row has the same number of beams pointing towards the devices on the next row with devices. If you were given an integer array where each element is the number of security devices on each row, can you solve it? Convert the input to such an array, skip any row with no security device, then find the sum of the product between adjacent elements. |
✅ ✅ Python Greedy Solution | Dictionary ✅ ✅ | minimum-rounds-to-complete-all-tasks | 0 | 1 | # Intuition\nWhenever we encounter with frequency 1 then we can\'t able finish our task any number of rounds. While in other cases we see that every three number there minimum is always comes same.\nEx - for 2 with freq 4,5,6, we always get minimum round is 2\n for 2 with freq 7,8,9, we always get minimum round is 3\n for 2 with freq 10,11,12, we always get minimum round is 4\nHence, we conclude frequency of element greater than 1 will always required minimum round ceiling value of (freq(n) / 3). Where n represent the diffulty level. \n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def minimumRounds(self, tasks: List[int]) -> int:\n hashTable = defaultdict(int)\n for task in tasks:\n hashTable[task] += 1\n\n ans = 0\n for key in hashTable:\n if hashTable[key] == 1: return -1\n ans += ceil(hashTable[key]/3)\n return ans\n\n``` | 2 | You are given a **0-indexed** integer array `tasks`, where `tasks[i]` represents the difficulty level of a task. In each round, you can complete either 2 or 3 tasks of the **same difficulty level**.
Return _the **minimum** rounds required to complete all the tasks, or_ `-1` _if it is not possible to complete all the tasks._
**Example 1:**
**Input:** tasks = \[2,2,3,3,2,4,4,4,4,4\]
**Output:** 4
**Explanation:** To complete all the tasks, a possible plan is:
- In the first round, you complete 3 tasks of difficulty level 2.
- In the second round, you complete 2 tasks of difficulty level 3.
- In the third round, you complete 3 tasks of difficulty level 4.
- In the fourth round, you complete 2 tasks of difficulty level 4.
It can be shown that all the tasks cannot be completed in fewer than 4 rounds, so the answer is 4.
**Example 2:**
**Input:** tasks = \[2,3,3\]
**Output:** -1
**Explanation:** There is only 1 task of difficulty level 2, but in each round, you can only complete either 2 or 3 tasks of the same difficulty level. Hence, you cannot complete all the tasks, and the answer is -1.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= tasks[i] <= 109` | What is the commonality between security devices on the same row? Each device on the same row has the same number of beams pointing towards the devices on the next row with devices. If you were given an integer array where each element is the number of security devices on each row, can you solve it? Convert the input to such an array, skip any row with no security device, then find the sum of the product between adjacent elements. |
[Python \ C++ \ Rust] | HashMap | minimum-rounds-to-complete-all-tasks | 0 | 1 | Python\n```\nclass Solution:\n def minimumRounds(self, tasks: List[int]) -> int:\n diffCount = defaultdict(int)\n for t in tasks:\n diffCount[t] += 1\n \n rounds = 0\n for v in diffCount.values():\n if v == 1:\n return -1\n rounds += ceil(v/3)\n \n return rounds\n```\n\nC++\n```\nclass Solution {\npublic:\n int minimumRounds(vector<int>& tasks) {\n unordered_map<int,int> diffCount;\n for (int& t:tasks) diffCount[t]++;\n\n int rounds = 0;\n for (auto& [_,v]:diffCount) {\n if (v == 1) return -1;\n rounds += ceil(v/3.0);\n }\n \n return rounds;\n }\n};\n```\n\nRust\n```\nuse std::collections::HashMap;\n\nimpl Solution {\n pub fn minimum_rounds(tasks: Vec<i32>) -> i32 {\n let mut diffCount = HashMap::new();\n for t in tasks {\n *diffCount.entry(t).or_insert(0) += 1;\n }\n\n let mut rounds = 0i32;\n let countVec: Vec<i32> = diffCount.into_values().collect();\n for c in countVec {\n if c == 1 {\n return -1;\n } else {\n rounds += (c as f32/3.0).ceil() as i32;\n }\n }\n\n rounds\n }\n}\n```\n\nPlease upvote if you found helpful! | 1 | You are given a **0-indexed** integer array `tasks`, where `tasks[i]` represents the difficulty level of a task. In each round, you can complete either 2 or 3 tasks of the **same difficulty level**.
Return _the **minimum** rounds required to complete all the tasks, or_ `-1` _if it is not possible to complete all the tasks._
**Example 1:**
**Input:** tasks = \[2,2,3,3,2,4,4,4,4,4\]
**Output:** 4
**Explanation:** To complete all the tasks, a possible plan is:
- In the first round, you complete 3 tasks of difficulty level 2.
- In the second round, you complete 2 tasks of difficulty level 3.
- In the third round, you complete 3 tasks of difficulty level 4.
- In the fourth round, you complete 2 tasks of difficulty level 4.
It can be shown that all the tasks cannot be completed in fewer than 4 rounds, so the answer is 4.
**Example 2:**
**Input:** tasks = \[2,3,3\]
**Output:** -1
**Explanation:** There is only 1 task of difficulty level 2, but in each round, you can only complete either 2 or 3 tasks of the same difficulty level. Hence, you cannot complete all the tasks, and the answer is -1.
**Constraints:**
* `1 <= tasks.length <= 105`
* `1 <= tasks[i] <= 109` | What is the commonality between security devices on the same row? Each device on the same row has the same number of beams pointing towards the devices on the next row with devices. If you were given an integer array where each element is the number of security devices on each row, can you solve it? Convert the input to such an array, skip any row with no security device, then find the sum of the product between adjacent elements. |
Python 3 || w/ some explanation || T/M: 94% / 93% | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | - We construct a prefix sum of 4-tuples, writing over`grid`as we go. For each cell, we determine `(up2, up5, left2, right5)`, the accummulated factors of two and five for the up-direction and the left-direction respectively.\n\n- We use the transformed`grid`to determine for each cell the count of zeros over the four paths: up-left, down-left, up-right, down-right.\n- We determine the max zeros for each cell along the four paths, and then determine the overall max from those cell maxs.\n```\nclass Solution:\n def maxTrailingZeros(self, grid: list[list[int]]) -> int:\n\n m, n = len(grid)+1, len(grid[0])+1\n grid = [[(0,0,0,0)]*n]+[[(0,0,0,0)]+row for row in grid]\n\n def pref(row: int,col: int)-> tuple: # <-- prefix for each cell\n \n val = grid[row][col]\n for f2 in range(19):\n if val%2: break\n val//= 2\n \n for f5 in range(6):\n if val%5: break\n val//= 5\n \n (u2, u5, _,_), (_,_, l2, l5) = grid[row-1][col], grid[row][col-1]\n return (f2 + u2, f5 + u5, f2 + l2, f5 + l5)\n \n def countZeros(r: int,c: int)-> int: # <--Count the zeros \n up2 ,up5 = grid[r][c][0],grid[r][c][1]\n down2 ,down5 = grid[m-1][c][0]-grid[r-1][c][0],grid[m-1][c][1]-grid[r-1][c][1]\n \n left2 ,left5 = grid[r][c-1][2],grid[r][c-1][3]\n right2,right5 = grid[r][n-1][2]-grid[r][c][2],grid[r][n-1][3]-grid[r][c][3] \n\n return max(min(up2+left2 ,up5+left5 ), min(down2+left2 ,down5+left5 ),\n min(up2+right2,up5+right5), min(down2+right2,down5+right5))\n\n for r in range(1,m):\n for c in range(1,n):grid[r][c] = pref(r,c)\n\n return max(countZeros(r,c) for c in range(1,n) for r in range(1,m))\n```\n[https://leetcode.com/problems/maximum-trailing-zeros-in-a-cornered-path/submissions/908601238/](http://)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) (wnere*N* is *mn* and space complexity is probably *O*(*N*) but maybe *O*(1). I\'m just not sure.\n | 3 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
[Python] Prefix Sum, O(m * n) | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | **Intuition**\nStore the prefix sum matrices of rows and columns, where each entry is `[a, b]` representing the cumulative count of (1) the factors of 2 and (2) the factors of 5.\n\n\n**Complexity**\nTime: `O(m * n)`\nSpace: `O(m * n)`\n\nBelow is my slightly-modified in-contest solution. Please upvote if you find this solution helpful. Thanks!\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n ans = 0\n m, n = len(grid), len(grid[0])\n prefixH = [[[0] * 2 for _ in range(n + 1)] for __ in range(m)]\n prefixV = [[[0] * 2 for _ in range(n)] for __ in range(m + 1)]\n for i in range(m):\n for j in range(n):\n temp= grid[i][j]\n while temp % 2 == 0:\n prefixH[i][j + 1][0] += 1\n prefixV[i + 1][j][0] += 1\n temp //= 2\n while temp % 5 == 0:\n prefixH[i][j + 1][1] += 1\n prefixV[i + 1][j][1] += 1\n temp //= 5\n for k in range(2):\n prefixH[i][j + 1][k] += prefixH[i][j][k]\n prefixV[i + 1][j][k] += prefixV[i][j][k]\n for i in range(m):\n for j in range(n):\n left = prefixH[i][j]\n up = prefixV[i][j]\n right, down, center = [0] * 2, [0] * 2, [0] * 2\n for k in range(2):\n right[k] = prefixH[i][n][k] - prefixH[i][j + 1][k]\n down[k] = prefixV[m][j][k] - prefixV[i + 1][j][k]\n center[k] = prefixH[i][j + 1][k] - prefixH[i][j][k]\n LU, LD, RU, RD = [0] * 2, [0] * 2, [0] * 2, [0] * 2\n for k in range(2):\n LU[k] += left[k] + up[k] + center[k]\n LD[k] += left[k] + down[k] + center[k]\n RU[k] += right[k] + up[k] + center[k]\n RD[k] += right[k] + down[k] + center[k]\n ans = max(ans,\n min(LU[0], LU[1]),\n min(LD[0], LD[1]),\n min(RU[0], RU[1]),\n min(RD[0], RD[1]))\n return ans\n``` | 7 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
[Python] Self-explain code using Prefix sum | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | # Intuition\nSince product of numbers and its trailing zeros will never go down with additional numbers. The problem becomes "**for each point (i,j) in the grid, compute the max trailling zeros of product of 4 L-shape pathes(till boundary). Then find the max num of trailling zeros over all points**" That\'s definately a prefix sum problem.\n\n# Approach\nTrailing zeros can be calculated by the min count of factor 2 and factor 5. Hence, we can maintain a tup of counts of factor 2 and factor 5 and calculate prefix sum. Than scan over the grid, ultilize the prefix sums to get the max.\n\nThe code below create a class for demostration(though slow down the caculation). It also minimize the memory needed to hold prefix sum. Other parts are self-explianed.\n\n# Complexity\n- Time complexity: O(mn)\n\n- Space complexity: O(n)\n (Ignore the ngrid which cab be transferred on the fly)\n\n# Code\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n class BaseTup:\n def __init__(self, a=0, b=0):\n self.a, self.b = a, b\n\n @classmethod\n def from_num(cls, n): \n c2 = c5 = 0\n while n and n%2==0:\n c2 += 1\n n = n>>1\n while n and n%5==0:\n c5 += 1\n n //= 5\n return BaseTup(c2, c5)\n\n @classmethod\n def sum(cls, iterable):\n return sum(iterable, start = BaseTup())\n\n def __add__(self, o):\n return BaseTup(self.a + o.a, self.b + o.b)\n\n def __sub__(self, o):\n return BaseTup(self.a - o.a, self.b - o.b)\n\n @property\n def trail_zeros(self):\n return min(self.a, self.b)\n\n \n m,n = len(grid), len(grid[0])\n ngrid = [[ BaseTup.from_num(grid[i][j]) for j in range(n)] for i in range(m)]\n\n up_sum = [BaseTup() for _ in range(n)]\n down_sum = [BaseTup.sum(ngrid[i][j] for i in range(m)) for j in range(n)]\n\n zmax = 0\n for i in range(m):\n rsum = BaseTup.sum(ngrid[i])\n lsum = BaseTup()\n for j in range(n):\n t = ngrid[i][j]\n lsum += t\n down_sum[j] -= t\n\n zmax = max(zmax, \n (lsum+up_sum[j]).trail_zeros,\n (rsum+up_sum[j]).trail_zeros,\n (lsum+down_sum[j]).trail_zeros,\n (rsum+down_sum[j]).trail_zeros)\n\n rsum -= t\n up_sum[j] += t\n \n return zmax\n\n``` | 0 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
Python3 Vectorized Solution | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | I hope this answer is helpful to those who prefer more formal explanations (like myself).\n___\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI made the following two observations:\n1. Let $g(x)$ denote the number of trailing zeros of a number $x$. Then \n$g(x) = \\min_{p\\in\\{2,5\\}} f(x,p),$ \nwhere $f(x, p)$ is the number of times that prime number $p$ appears in the prime factorization of $x$.\n2. The solution can always be represented by a cornered path which extends all the way to the edges of the grid. This is because the entries are non-negative, and so adding more cells can never harm the solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine a _leg_ $(i,j,d)$ to be a path of cells from (_excluding_) $(i,j)$ to the edge of the grid, following direction $d\\in\\{{\\rm up,down,left,right}\\}$. WLOG, we only consider cornered paths which extend all the way to the edges of the grid, so that each cornered path can be decomposed into a corner and two legs. We encode each cornered path by a tuple $(i,j,d_1,d_2)$, where $(i,j)$ is the location of the path\'s corner, and $(d_1,d_2)$ are the directions of the its legs, $(i,j,d_1)$ and $(i,j,d_2)$.\n\nDefine the _gain_ $g(\\pi)$ of $\\pi$ to be the number of trailing zeros in the product of the path, i.e. $g(\\pi) = g(\\Pi_{ij\\in\\pi}x_{ij})$, and let $f(\\pi, p) = \\sum_{ij\\in\\pi} f(x_{ij}, p)$ be the number of times prime number $p$ appears along a path $\\pi$. Then,\n$g(\\pi) = g(\\Pi_{ij\\in\\pi}x_{ij}) \\\\ = \\min_{p\\in\\{2,5\\}} f(\\Pi_{ij\\in\\pi}x_{ij}, p) \\\\ = \\min_{p\\in\\{2,5\\}} \\sum_{ij\\in\\pi} f(x_{ij}, p) \\\\ = \\min_{p\\in\\{2,5\\}} f(\\pi, p).$\nOur objective is to find a cornered path $\\pi$ which maximizes $g(\\pi)$. First, we need to compute $f(\\pi, p)$ for all cornered paths $\\pi$ and $p\\in\\{2,5\\}$.\n\nNotice that, for a cornered path, $\\pi=(i,j,d_1,d_2)$, the quantity $f(\\pi,p)$ can be decomposed over $\\pi$\'s corner and two legs:\n$f((i,j,d_1,d_2), p) = f(x_{ij}, p) + f((i,j,d_1), p) + f((i,j,d_2), p).$\n\nThese leg counts, $f((i,j,d), p)$, are our building blocks, so I computed them for each possible leg $(i,j,d)$. Since a leg may be a sub-leg of a longer leg, I stored and reused intermediate results in a dynamic programming style. I then used these leg counts to compute $f(\\pi, 2)$ and $f(\\pi, 5)$ for each possible cornered path $\\pi$, which together yield $g(\\pi)$. Finally, I computed $\\max_\\pi g(\\pi)$ by searching over all cornered paths $\\pi$. Crucially, I vectorized this search over $(i,j)$ using NumPy; without doing so, my solution exceeded the time limit.\n\n# Complexity\n- Time complexity: $O(mn)$, because $O(1)$ visits per cell\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(mn)$, because $O(1)$ values stored per cell\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport numpy as np\n\n# directions\nU = 0 # Up\nD = 1 # Down\nL = 2 # Left\nR = 3 # Right\nN_dir = 4\n\n# factors\nT = 0 # Two\nF = 1 # Five\nN_fac = 2\n\ndef f(x, p):\n \'\'\'returns the highest power of `p` that divides `x`\'\'\'\n c = 0\n while x % p == 0:\n c += 1\n x //= p\n return c\n\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n grid = np.array(grid)\n\n # y[i, j, p] = \n # highest power of `p` that divides `grid[i, j]`\n y = np.zeros((m, n, N_fac), dtype=int)\n for i in range(m):\n for j in range(n):\n y[i, j, T] = f(grid[i, j], 2)\n y[i, j, F] = f(grid[i, j], 5)\n\n # x[i, j, d, p] = \n # count of times that `p` appears in leg `(i,j,d)`\n x = np.zeros((m, n, N_dir, N_fac), dtype=int)\n for i in range(m):\n for j in range(n):\n if i > 0:\n x[i, j, U] = y[i-1, j] + x[i-1, j, U]\n x[m-1-i, j, D] = y[m-i, j] + x[m-i, j, D]\n if j > 0:\n x[i, j, L] = y[i, j-1] + x[i, j-1, L]\n x[i, n-1-j, R] = y[i, n-j] + x[i, n-j, R]\n\n # the cornered path\'s legs can be oriented in one of four ways\n path_orientations = [(U,R), (U,L), (D,R), (D,L)]\n\n # for each orientation `(d1, d2)`, \n # for each corner `(i, j)` (vectorized):\n # find the the number of trailing zeros in the product\n # of the path `(i, j, d1, d2)`.\n # max-reduce over corners (vectorized)\n # max-reduce over orientations.\n return max(\n (y + x[:, :, d1] + x[:, :, d2]).min(-1).max()\n for d1, d2 in path_orientations\n )\n``` | 0 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
Python | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | \n```\nclass Solution:\n def maxTrailingZeros(self, grid) :\n matrix = grid \n self.ans,prefix,suffix = 0,[i[:] for i in matrix ],[i[:] for i in matrix ]\n \n def f(n):\n x,y =0,0\n while n%2==0:\n n = n//2\n x+=1\n while n% 5==0:\n n = n // 5\n y+=1\n return x,y\n\n for i in prefix:\n for n,v in enumerate(i):\n if n==0 : i[0] =f(v)\n else:\n x,y = f(v)\n a,b = i[n-1]\n i[n]=x+a,y+b\n\n for i in suffix :\n for n in range(len(i)-1,-1,-1):\n if n == len(i)-1:i[n]=f(i[n])\n else:\n x,y = f(i[n])\n a,b= i[n+1]\n i[n]=x+a,y+b\n\n for j in range(len(matrix[0])):\n two,five =0,0\n for i in range(len(matrix)):\n self.ans = max(self.ans,min(two+prefix[i][j][0],five + prefix[i][j][1]))\n self.ans = max(self.ans , min(two + suffix[i][j][0] , five + suffix[i][j][1]))\n\n x,y = f(matrix[i][j])\n two +=x\n five +=y \n \n two,five = 0,0\n for i in range(len(matrix)-1,-1,-1):\n self.ans = max(self.ans,min(two+prefix[i][j][0],five + prefix[i][j][1]))\n self.ans = max(self.ans , min(two + suffix[i][j][0] , five + suffix[i][j][1]))\n x,y = f(matrix[i][j])\n two +=x\n five +=y \n \n return self.ans \n``` | 0 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
Python | Simple Solution | O(mn) | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | # Code\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n def factors(num):\n res = [0,0]\n while num > 1 and num%2 == 0:\n num //= 2\n res[0] += 1\n while num > 1 and num%5 == 0:\n num //= 5\n res[1] += 1\n return res\n def zeros(a, b, c):\n return min(a[0]+b[0]-c[0], a[1]+b[1]-c[1])\n m, n = len(grid), len(grid[0])\n UD = [[0 for i in range(n)] for _ in range(m)]\n LR = [[0 for i in range(n)] for _ in range(m)]\n for i in range(m):\n for j in range(n):\n UD[i][j] = factors(grid[i][j])\n LR[i][j] = factors(grid[i][j])\n UD[i][j][0] += UD[i-1][j][0] if i else 0\n UD[i][j][1] += UD[i-1][j][1] if i else 0\n LR[i][j][0] += LR[i][j-1][0] if j else 0\n LR[i][j][1] += LR[i][j-1][1] if j else 0\n DU = [[0 for i in range(n)] for _ in range(m)]\n RL = [[0 for i in range(n)] for _ in range(m)]\n for i in range(m-1,-1,-1):\n for j in range(n-1,-1,-1):\n DU[i][j] = factors(grid[i][j])\n RL[i][j] = factors(grid[i][j])\n DU[i][j][0] += DU[i+1][j][0] if i < m - 1 else 0\n DU[i][j][1] += DU[i+1][j][1] if i < m - 1 else 0\n RL[i][j][0] += RL[i][j+1][0] if j < n - 1 else 0\n RL[i][j][1] += RL[i][j+1][1] if j < n - 1 else 0\n res = 0\n for i in range(m):\n for j in range(n):\n f = factors(grid[i][j])\n cur = max(zeros(UD[i][j],LR[i][j],f), zeros(UD[i][j],RL[i][j],f), zeros(DU[i][j],LR[i][j],f), zeros(DU[i][j],RL[i][j],f))\n res = max(res, cur)\n return res\n \n \n``` | 0 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
[Python3] prefix sums | maximum-trailing-zeros-in-a-cornered-path | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/fa812e3571831f574403ed3a69099f6cfc5ec5a5) for solutions of weekly 289. \n\n```\nclass Solution:\n def maxTrailingZeros(self, grid: List[List[int]]) -> int:\n m, n = len(grid), len(grid[0])\n f2 = [[0]*n for _ in range(m)]\n f5 = [[0]*n for _ in range(m)]\n for i in range(m): \n for j in range(n): \n x = grid[i][j]\n while x % 2 == 0: \n f2[i][j] += 1\n x //= 2 \n x = grid[i][j]\n while x % 5 == 0: \n f5[i][j] += 1\n x //= 5 \n \n h = [[[0, 0] for j in range(n+1)] for i in range(m+1)]\n v = [[[0, 0] for j in range(n+1)] for i in range(m+1)]\n\n for i in range(m): \n for j in range(n): \n h[i][j+1][0] = h[i][j][0] + f2[i][j]\n h[i][j+1][1] = h[i][j][1] + f5[i][j]\n v[i+1][j][0] = v[i][j][0] + f2[i][j]\n v[i+1][j][1] = v[i][j][1] + f5[i][j]\n \n ans = 0 \n for i in range(m): \n for j in range(n): \n hh = [h[i][n][0] - h[i][j][0], h[i][n][1] - h[i][j][1]]\n vv = [v[m][j][0] - v[i][j][0], v[m][j][1] - v[i][j][1]]\n ans = max(ans, min(h[i][j][0]+v[i][j][0]+f2[i][j], h[i][j][1]+v[i][j][1]+f5[i][j]))\n ans = max(ans, min(h[i][j][0]+vv[0], h[i][j][1]+vv[1]))\n ans = max(ans, min(hh[0]+v[i][j][0], hh[1]+v[i][j][1]))\n ans = max(ans, min(hh[0]+vv[0]-f2[i][j], hh[1]+vv[1]-f5[i][j]))\n return ans\n``` | 1 | You are given a 2D integer array `grid` of size `m x n`, where each cell contains a positive integer.
A **cornered path** is defined as a set of adjacent cells with **at most** one turn. More specifically, the path should exclusively move either **horizontally** or **vertically** up to the turn (if there is one), without returning to a previously visited cell. After the turn, the path will then move exclusively in the **alternate** direction: move vertically if it moved horizontally, and vice versa, also without returning to a previously visited cell.
The **product** of a path is defined as the product of all the values in the path.
Return _the **maximum** number of **trailing zeros** in the product of a cornered path found in_ `grid`.
Note:
* **Horizontal** movement means moving in either the left or right direction.
* **Vertical** movement means moving in either the up or down direction.
**Example 1:**
**Input:** grid = \[\[23,17,15,3,20\],\[8,1,20,27,11\],\[9,4,6,2,21\],\[40,9,1,10,6\],\[22,7,4,5,3\]\]
**Output:** 3
**Explanation:** The grid on the left shows a valid cornered path.
It has a product of 15 \* 20 \* 6 \* 1 \* 10 = 18000 which has 3 trailing zeros.
It can be shown that this is the maximum trailing zeros in the product of a cornered path.
The grid in the middle is not a cornered path as it has more than one turn.
The grid on the right is not a cornered path as it requires a return to a previously visited cell.
**Example 2:**
**Input:** grid = \[\[4,3,2\],\[7,6,1\],\[8,8,8\]\]
**Output:** 0
**Explanation:** The grid is shown in the figure above.
There are no cornered paths in the grid that result in a product with a trailing zero.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `1 <= m, n <= 105`
* `1 <= m * n <= 105`
* `1 <= grid[i][j] <= 1000` | Choosing the asteroid to collide with can be done greedily. If an asteroid will destroy the planet, then every bigger asteroid will also destroy the planet. You only need to check the smallest asteroid at each collision. If it will destroy the planet, then every other asteroid will also destroy the planet. Sort the asteroids in non-decreasing order by mass, then greedily try to collide with the asteroids in that order. |
[python3] dfs solution for reference | longest-path-with-different-adjacent-characters | 0 | 1 | At every node, there are three strings to consider.\n- Longest child string whose last char == parent_char\n- Longest child string whose last char != parent_char\n- Two longest child strings whose last char != parent_char - joined by parent char in the middle.\n\nThe code below uses a dfs traversal in the graph, that will - at everynode checks and keep track of the longest string.\n\n```\nclass Solution:\n def longestPath(self, parent: List[int], s: str) -> int:\n g = defaultdict(list)\n \n for i in range(1, len(parent)):\n g[parent[i]].append(i)\n \n ans = 0 \n \n def dfs(node, parent):\n nonlocal ans\n \n\t\t\t## required for keeping track of two longest child paths that dont match \n\t\t\t## the label in case there is a case (iii) from the list above.\n\t\t\t\n fir,sec = 0,0 \n \n for nei in g[node]:\n st = dfs(nei, node)\n if s[nei] != s[node]:\n if st > fir: \n sec = fir\n fir = st\n elif st == fir or st > sec: \n sec = st\n \n ans = max(ans, fir+sec+1)\n return fir+1\n \n dfs(0, -1)\n \n return ans | 3 | You are given a **tree** (i.e. a connected, undirected graph that has no cycles) **rooted** at node `0` consisting of `n` nodes numbered from `0` to `n - 1`. The tree is represented by a **0-indexed** array `parent` of size `n`, where `parent[i]` is the parent of node `i`. Since node `0` is the root, `parent[0] == -1`.
You are also given a string `s` of length `n`, where `s[i]` is the character assigned to node `i`.
Return _the length of the **longest path** in the tree such that no pair of **adjacent** nodes on the path have the same character assigned to them._
**Example 1:**
**Input:** parent = \[-1,0,0,1,1,2\], s = "abacbe "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
**Example 2:**
**Input:** parent = \[-1,0,0,0\], s = "aabc "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
**Constraints:**
* `n == parent.length == s.length`
* `1 <= n <= 105`
* `0 <= parent[i] <= n - 1` for all `i >= 1`
* `parent[0] == -1`
* `parent` represents a valid tree.
* `s` consists of only lowercase English letters. | From the given array favorite, create a graph where for every index i, there is a directed edge from favorite[i] to i. The graph will be a combination of cycles and chains of acyclic edges. Now, what are the ways in which we can choose employees to sit at the table? The first way by which we can choose employees is by selecting a cycle of the graph. It can be proven that in this case, the employees that do not lie in the cycle can never be seated at the table. The second way is by combining acyclic chains. At most two chains can be combined by a cycle of length 2, where each chain ends on one of the employees in the cycle. |
Simple Python Solution with explanation 🔥 | longest-path-with-different-adjacent-characters | 0 | 1 | # Approach\n\n* Create adjacency list since its easier to traverse with adjacency list\n\n* Lets solve this recursively using Depth First Search (DFS)\n\n 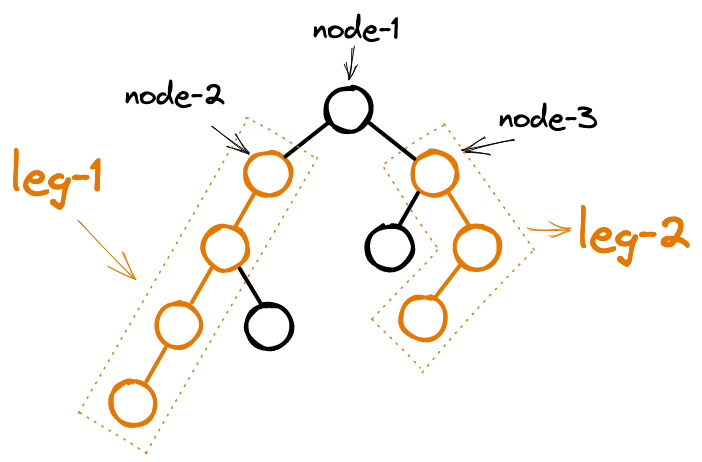\n \n\n * Lets assume, there is no condition on adjacent nodes, they can have the same value.\n Now, for node-1, max_value will be maximum of \n 1) max value of node-2 (child sub tree can have the max value, in this case 4)\n 2) max value of node-3 (in this case also 4)\n 3) max leg of node-2 + max leg of node-3 + 1 (in this case 8)\n\n * Lets bring back the condition on adjacent nodes, in the image, lets say, node-1 and node-2 have same value,\n Now, for node-1, max_value will be maximum of \n 1) max value of node-2 (in this case 4)\n 2) max value of node-3 (in this case 4)\n 3) ~~max leg of node-2 +~~ max leg of node-3 + 1 (in this case 4)\n\n So, for any node, if the child and the node has same value, we won\'t consider its max leg, the max leg value becomes zero\n\n * So our resursive function will return max value of the leg from the root node of the sub tree and the max_value for the sub-tree \n\n * Since this is not a binary tree, the root node can have multiple children, hence we keep track of max_leg1 and max_leg2 to make a path between two children \n\n\n \n\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$ -> function stack, adj_list\n\n# Code (with comments)\n```python []\nclass Solution:\n def longestPath(self, parent: List[int], s: str) -> int:\n n = len(parent)\n\n # constructing adjacency list\n adj_list = {i: [] for i in range(n)}\n for i in range(1, n):\n adj_list[parent[i]].append(i)\n\n # depth first search\n def dfs(node):\n max_value = max_leg1 = max_leg2 = 0\n for child in adj_list[node]:\n # get max leg and max value of the child tree\n (leg, value) = dfs(child)\n if s[child] == s[node]:\n leg = 0\n\n # max_leg1 is the max leg length \n # max_leg2 is the second max leg length\n if leg > max_leg1:\n max_leg2, max_leg1 = max_leg1, leg\n elif leg > max_leg2:\n max_leg2 = leg\n\n # max value of child trees\n max_value = max(value, max_value)\n\n # value which includes max_leg1, max_leg2 and the root of this subtree\n max_value = max(max_value, (max_leg1 + max_leg2 + 1))\n return (max_leg1 + 1, max_value)\n\n _, max_value = dfs(0)\n return max_value\n\n``` | 2 | You are given a **tree** (i.e. a connected, undirected graph that has no cycles) **rooted** at node `0` consisting of `n` nodes numbered from `0` to `n - 1`. The tree is represented by a **0-indexed** array `parent` of size `n`, where `parent[i]` is the parent of node `i`. Since node `0` is the root, `parent[0] == -1`.
You are also given a string `s` of length `n`, where `s[i]` is the character assigned to node `i`.
Return _the length of the **longest path** in the tree such that no pair of **adjacent** nodes on the path have the same character assigned to them._
**Example 1:**
**Input:** parent = \[-1,0,0,1,1,2\], s = "abacbe "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
**Example 2:**
**Input:** parent = \[-1,0,0,0\], s = "aabc "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
**Constraints:**
* `n == parent.length == s.length`
* `1 <= n <= 105`
* `0 <= parent[i] <= n - 1` for all `i >= 1`
* `parent[0] == -1`
* `parent` represents a valid tree.
* `s` consists of only lowercase English letters. | From the given array favorite, create a graph where for every index i, there is a directed edge from favorite[i] to i. The graph will be a combination of cycles and chains of acyclic edges. Now, what are the ways in which we can choose employees to sit at the table? The first way by which we can choose employees is by selecting a cycle of the graph. It can be proven that in this case, the employees that do not lie in the cycle can never be seated at the table. The second way is by combining acyclic chains. At most two chains can be combined by a cycle of length 2, where each chain ends on one of the employees in the cycle. |
DFS solution with explanations(What two options are for each recursive call). | longest-path-with-different-adjacent-characters | 0 | 1 | # Intuition\n1. The path here is counting the number of nodes on a path instead of edges.\n2. Similar to 543. Diameter of Binary Tree, the longest path may or may not pass through the root.\n3. This leaves us with two options: \n a . The longest path passes the current node, and in the subtree which is rooted by the current node, so that we find top two of the longest paths plus the current node. \n b. The longest path does may or may not pass the current root, but it is not in the subtree which is rooted by the current node, then we pass the longest path that passes the root back to upper level for further use. \n\n# Approach\nDFS\n\n# Complexity\n- Time complexity:\nO(m+n)\n\n- Space complexity:\nO(m+n)\n\n# Code\n```\nclass Solution:\n def longestPath(self, parent: List[int], s: str) -> int:\n graph = collections.defaultdict(list)\n for i in range(1, len(parent)):\n graph[i].append(parent[i])\n graph[parent[i]].append(i)\n ans=0\n def dfs(root,parent):\n nonlocal ans\n res = 0\n first_path=0\n second_path=0\n for v in graph[root]:\n if v != parent :\n cur_path = dfs(v,root)\n #####################################\n #option1 : The longest path is under this subtree\n #Then we find the top 2 longest path under this subtree\n #and add them with the subtree root(current node)\n if cur_path > first_path:\n second_path = first_path\n first_path=cur_path\n \n elif cur_path > second_path:\n second_path = cur_path\n #####################################\n #Option 2: The longest path is not under this subtree\n #But since one of the branchs of the subtree may be part of the longest path,\n # We pass the best among all branches back to upper level for future use.\n res=max(res,cur_path)\n #compare two options for the best, ans is a global var\n ans = max(ans,first_path+second_path+1)\n if s[root]!=s[parent]:\n return res +1\n else:\n return 0\n \n\n dfs(0,0)\n return ans\n\n``` | 2 | You are given a **tree** (i.e. a connected, undirected graph that has no cycles) **rooted** at node `0` consisting of `n` nodes numbered from `0` to `n - 1`. The tree is represented by a **0-indexed** array `parent` of size `n`, where `parent[i]` is the parent of node `i`. Since node `0` is the root, `parent[0] == -1`.
You are also given a string `s` of length `n`, where `s[i]` is the character assigned to node `i`.
Return _the length of the **longest path** in the tree such that no pair of **adjacent** nodes on the path have the same character assigned to them._
**Example 1:**
**Input:** parent = \[-1,0,0,1,1,2\], s = "abacbe "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
**Example 2:**
**Input:** parent = \[-1,0,0,0\], s = "aabc "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
**Constraints:**
* `n == parent.length == s.length`
* `1 <= n <= 105`
* `0 <= parent[i] <= n - 1` for all `i >= 1`
* `parent[0] == -1`
* `parent` represents a valid tree.
* `s` consists of only lowercase English letters. | From the given array favorite, create a graph where for every index i, there is a directed edge from favorite[i] to i. The graph will be a combination of cycles and chains of acyclic edges. Now, what are the ways in which we can choose employees to sit at the table? The first way by which we can choose employees is by selecting a cycle of the graph. It can be proven that in this case, the employees that do not lie in the cycle can never be seated at the table. The second way is by combining acyclic chains. At most two chains can be combined by a cycle of length 2, where each chain ends on one of the employees in the cycle. |
Python, DFS | longest-path-with-different-adjacent-characters | 0 | 1 | ```\nclass Solution:\n def longestPath(self, parent: List[int], s: str) -> int:\n def dfs(node):\n node_char = s[node] \n longest = second_longest = 0\n for child in children[node]:\n child_path = dfs(child)\n if s[child] != node_char: \n if child_path >= longest:\n second_longest = longest\n longest = child_path \n elif child_path > second_longest:\n second_longest = child_path\n \n self.result = max(self.result, 1 + longest + second_longest) \n return 1 + longest\n \n children = defaultdict(list)\n for n in range(1, len(parent)):\n children[parent[n]].append(n)\n \n self.result = 0\n dfs(0)\n \n return self.result\n``` | 2 | You are given a **tree** (i.e. a connected, undirected graph that has no cycles) **rooted** at node `0` consisting of `n` nodes numbered from `0` to `n - 1`. The tree is represented by a **0-indexed** array `parent` of size `n`, where `parent[i]` is the parent of node `i`. Since node `0` is the root, `parent[0] == -1`.
You are also given a string `s` of length `n`, where `s[i]` is the character assigned to node `i`.
Return _the length of the **longest path** in the tree such that no pair of **adjacent** nodes on the path have the same character assigned to them._
**Example 1:**
**Input:** parent = \[-1,0,0,1,1,2\], s = "abacbe "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
**Example 2:**
**Input:** parent = \[-1,0,0,0\], s = "aabc "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
**Constraints:**
* `n == parent.length == s.length`
* `1 <= n <= 105`
* `0 <= parent[i] <= n - 1` for all `i >= 1`
* `parent[0] == -1`
* `parent` represents a valid tree.
* `s` consists of only lowercase English letters. | From the given array favorite, create a graph where for every index i, there is a directed edge from favorite[i] to i. The graph will be a combination of cycles and chains of acyclic edges. Now, what are the ways in which we can choose employees to sit at the table? The first way by which we can choose employees is by selecting a cycle of the graph. It can be proven that in this case, the employees that do not lie in the cycle can never be seated at the table. The second way is by combining acyclic chains. At most two chains can be combined by a cycle of length 2, where each chain ends on one of the employees in the cycle. |
✅ python- EasySolution-BEATS 95% | longest-path-with-different-adjacent-characters | 0 | 1 | Easy Approach \uD83D\uDCAF. Enjoy the day.\n```\nclass Solution:\n def longestPath(self, parent: List[int], s: str) -> int:\n t={}\n for i in range(1,len(parent)):\n if parent[i] not in t:\n t[parent[i]]=[i]\n else:\n t[parent[i]].append(i)\n \n self.ans=1\n def fun(i):\n if i not in t:\n return 1\n res = 1\n for j in t[i]:\n length=fun(j)\n if s[i] != s[j]:\n self.ans = max(self.ans,length+res)\n res = max(res,length+1)\n return res\n \n fun(0)\n return self.ans\n```\n**If you like my Content please \uD83D\uDC4D REPUTATE ME \uD83D\uDC4D \u2705**\nFROM TOMORROW I WILL EXPLAIN THE CODE CLEARLY..SORYY FOR TODAY WHAT I HAVE DONE..\n | 16 | You are given a **tree** (i.e. a connected, undirected graph that has no cycles) **rooted** at node `0` consisting of `n` nodes numbered from `0` to `n - 1`. The tree is represented by a **0-indexed** array `parent` of size `n`, where `parent[i]` is the parent of node `i`. Since node `0` is the root, `parent[0] == -1`.
You are also given a string `s` of length `n`, where `s[i]` is the character assigned to node `i`.
Return _the length of the **longest path** in the tree such that no pair of **adjacent** nodes on the path have the same character assigned to them._
**Example 1:**
**Input:** parent = \[-1,0,0,1,1,2\], s = "abacbe "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters in the tree is the path: 0 -> 1 -> 3. The length of this path is 3, so 3 is returned.
It can be proven that there is no longer path that satisfies the conditions.
**Example 2:**
**Input:** parent = \[-1,0,0,0\], s = "aabc "
**Output:** 3
**Explanation:** The longest path where each two adjacent nodes have different characters is the path: 2 -> 0 -> 3. The length of this path is 3, so 3 is returned.
**Constraints:**
* `n == parent.length == s.length`
* `1 <= n <= 105`
* `0 <= parent[i] <= n - 1` for all `i >= 1`
* `parent[0] == -1`
* `parent` represents a valid tree.
* `s` consists of only lowercase English letters. | From the given array favorite, create a graph where for every index i, there is a directed edge from favorite[i] to i. The graph will be a combination of cycles and chains of acyclic edges. Now, what are the ways in which we can choose employees to sit at the table? The first way by which we can choose employees is by selecting a cycle of the graph. It can be proven that in this case, the employees that do not lie in the cycle can never be seated at the table. The second way is by combining acyclic chains. At most two chains can be combined by a cycle of length 2, where each chain ends on one of the employees in the cycle. |
simple python solution | intersection-of-multiple-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n l=[]\n for i in nums:\n l.extend(i)\n s=[]\n k=len(nums)\n for i in l:\n if l.count(i)==k:\n s.append(i)\n s=list(set(s))\n s.sort()\n return s\n\n\n \n``` | 1 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
[Python] good looking solution, easy to understand | intersection-of-multiple-arrays | 0 | 1 | \n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n\n ll = []\n sortedNums = sorted(nums)\n\n for num in sortedNums[0]:\n cou = 1\n\n for listNums in sortedNums[1:]:\n if num not in listNums:\n cou = 0\n break\n \n if cou:\n ll.append(num)\n\n return sorted(ll)\n``` | 2 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
[Python3] - 1 LINE Solution || Simple Explanation | intersection-of-multiple-arrays | 0 | 1 | # **Idea**\n<br>\n\n##### To solve this question easily, we can take advantage of one of the specifications:\n\n*nums[i] is a non-empty array of **distinct** positive integers*\n\n<br>\n\n##### Since the integers in each sub-list of nums are distinct (i.e. unique), we can count the number of occurences of every integer in nums.\n<br>\n\n##### Suppose it happens that the number of occurences for some integer x is equal to the length of nums (the number of sub-lists).\n##### It would mean, that x must have appeared in every single sub-list of nums (because it could appear in each of the sub-lists at most 1 time).\n\n<br>\n\n##### Notice, that the result is a list of integers like x, so we just need to find all of them.\n\n<br>\n<br>\n\n# **Code**\n<br>\n\n```\n\nclass Solution:\n def intersection(self, A: List[List[int]]) -> List[int]:\n return sorted([k for k,v in Counter([x for l in A for x in l]).items() if v==len(A)])\n\t\t\n```\n\n<br>\n<br>\n\n# **Breakdown**\n\n##### Here\'s a breakdown of each operation that\'s happening in the line above:\n\n<br>\n\n```\n\nclass Solution:\n def intersection(self, A: List[List[int]]) -> List[int]:\n # Flattening the list A\n # For example, if A = [[3, 5, 1], [2, 3, 1]] then flat_list = [3, 5, 1, 2, 3, 1]\n flat_list = [x for lst in A for x in lst]\n\n # Counter - a container from the collections module\n # Here, it is pretty much a dictionary, where:\n # keys - the integers from flat_list\n # values - the number of occurences of the keys\n\n # counts from the above flat_list would be equal to {3: 2, 5: 1, 1: 2, 2: 1}\n counts = Counter(flat_list)\n\n # dict.items() is a method that returns a list of pairs that look like (key, value)\n # Here, items would be equal to [(3, 2), (5, 1), (1, 2), (2, 1)]\n items = counts.items()\n\n # result array created by taking every key from items array\n # which has the value (number of key\'s occurences) equal to the length of A (here, 2)\n # The result would be equal to [3, 1]\n result = [key for (key, value) in items if value == len(A)]\n\n # Sort the result array and return it\n # The result is [1, 3]\n return sorted(result)\n\t\t\n```\n\n<br>\n\n---\n\n<br>\n\n\n### Thanks for reading, and have an amazing day! \uFF3C(\uFF3E\u25BD\uFF3E)\uFF0F\n\n<br> | 39 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
No set, sort, or hashmap: use Masks | intersection-of-multiple-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* It\'s highlighted that the integers in each sublist are **distinct**.\n* The result must be sorted in ascending order.\n * I think the point is to build your result in a way that it turns out to be ascending.\n * Not that you build however and finally sort it!\n* Use the constraint: `1 <= nums[i] <= 1000`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* For each sublist create a `mask`\n* `mask` is an integer.\n* See it as an array of bits.\n\t* 0-indexed from the right.\n* The length of this array is limited by the range of elements in each sublist of `nums`.\n\t* In this particular problem, `mask` can be, atmost, an array of 1000 bits.\n\t\t* Now that could be a pretty large number. But Python can handle arbitrarily large numbers!\n* Let `arr` be a sublist of `nums`\n* For each `n` in `arr`\n\t* Set the `n-1`-th bit from the right.\t \n\t * The right-most bit is the `0`-th bit.\n\t * When we "set a bit", we mean we set it to `1`.\n\n* Take the intersection of all these masks.\n* The bits that are set in `intersection` correspond to the desired numbers that are common in all the sublists.\n* Iterate over each bit in `intersection` to check if the bit is set or not.\n * If set, add the corresponding element to the result.\n\n\n# Complexity\n- Time complexity: `O(n)`, where `n = len(nums)`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`, where `n = len(nums)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n minVal = 1 \n \n def generateMask(arr):\n mask = 0\n for n in arr:\n mask |= (1 << (n - minVal))\n return mask\n\n intersection = reduce(lambda x, y: x & y, map(generateMask, nums))\n\n result = []\n ele = 0\n while intersection:\n if intersection & 1:\n result.append(ele + minVal)\n intersection >>= 1\n ele += 1\n\n return result\n``` | 1 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
94.58% faster using set and & operator in Python | intersection-of-multiple-arrays | 0 | 1 | \n\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n res = set(nums[0])\n for i in range(1, len(nums)):\n res &= set(nums[i])\n res = list(res)\n res.sort()\n return res\n \n``` | 12 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python Solution || Hashmap | intersection-of-multiple-arrays | 0 | 1 | ```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n d = {}\n \n for i in range(len(nums)):\n for j in nums[i]:\n if j not in d:\n d[j] = 1\n else:\n d[j]+=1\n \n res = []\n for k,v in d.items():\n if v == len(nums):\n res.append(k)\n \n return sorted(res)\n``` | 6 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python - Short & Simple - Set | intersection-of-multiple-arrays | 0 | 1 | ```\ndef intersection(self, nums: List[List[int]]) -> List[int]:\n temp = set(nums[0])\n for i in range(1,len(nums)):\n temp = (temp & set(nums[i]))\n \n return list(sorted(temp))\n``` | 2 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python 2 beginner friendly approaches | intersection-of-multiple-arrays | 0 | 1 | ### Method 1\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n res = []\n concat = []\n for i in range(len(nums)):\n concat += nums[i]\n for i in set(concat):\n if concat.count(i) == len(nums):\n res.append(i)\n return sorted(res)\n```\n\n### Method 2\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n res = []\n nums = sorted(nums, key=len)\n check = 0\n for i in nums[0]:\n for j in nums:\n if i in j:\n check += 1\n if check == len(nums):\n res.append(i)\n check = 0\n return sorted(res)\n``` | 4 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
97.81% faster using set and set.intersection | intersection-of-multiple-arrays | 0 | 1 | \n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n inter = set(nums[0])\n for i in range(1, len(nums)):\n inter = inter.intersection(set(nums[i]))\n inter = sorted(list(inter))\n return inter\n``` | 1 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python3 | intersection-of-multiple-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n d = {}\n \n for i in range(len(nums)):\n for j in nums[i]:\n if j not in d:\n d[j] = 1\n else:\n d[j]+=1\n \n res = []\n for k,v in d.items():\n if v == len(nums):\n res.append(k)\n \n return sorted(res)\n``` | 2 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python solution 3 line | intersection-of-multiple-arrays | 0 | 1 | ```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n a=set(nums[0])\n inters=a.intersection(*nums)\n return sorted(list(inters))\n\n\n``` | 3 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Python Easy Understanding | intersection-of-multiple-arrays | 0 | 1 | ```\nclass Solution:\n def intersection(self, nums: List[List[int]]) -> List[int]:\n \n intersection = nums[0]\n \n for i in range(1,len(nums)):\n intersection = set(nums[i]) & set(intersection)\n \n return sorted(list(intersection))\n``` | 2 | Given a 2D integer array `nums` where `nums[i]` is a non-empty array of **distinct** positive integers, return _the list of integers that are present in **each array** of_ `nums` _sorted in **ascending order**_.
**Example 1:**
**Input:** nums = \[\[**3**,1,2,**4**,5\],\[1,2,**3**,**4**\],\[**3**,**4**,5,6\]\]
**Output:** \[3,4\]
**Explanation:**
The only integers present in each of nums\[0\] = \[**3**,1,2,**4**,5\], nums\[1\] = \[1,2,**3**,**4**\], and nums\[2\] = \[**3**,**4**,5,6\] are 3 and 4, so we return \[3,4\].
**Example 2:**
**Input:** nums = \[\[1,2,3\],\[4,5,6\]\]
**Output:** \[\]
**Explanation:**
There does not exist any integer present both in nums\[0\] and nums\[1\], so we return an empty list \[\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= sum(nums[i].length) <= 1000`
* `1 <= nums[i][j] <= 1000`
* All the values of `nums[i]` are **unique**. | If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? If we consider costs from high to low, what is the maximum cost of a single candy that we can get for free? How can we generalize this approach to maximize the costs of the candies we get for free? Can “sorting” the array help us find the minimum cost? |
Worst Memory Solution|| Recursion Approach||Python | count-lattice-points-inside-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI guess you already know the question , its quite understandable .\nI don\'t know why i am obsessed with recursion , the first approach came to my mind after seeing most question is if i can somehow use memoization. So here is result of that.\n# This solution uses 56.2MB of space \nDon\'t ask me how just see the solution you will get why.\n\n\nIt\'s okay with run time i guess beats 55%.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We start from the center and move in all four directions\n2. If we already visited the point for current circle , we return 0\n3. If we have already encountered the point in any other circle , we don\'t count it\n4. and if point is out of circle , we return 0\n\nPlease Suggest any methods to optimise the code.\nThanks\n# Code\n```\nclass Solution:\n def countLatticePoints(self, circles: List[List[int]]) -> int:\n circle=[]\n for i in circles:\n if i not in circle:\n circle.append(i)\n dic={}\n visited={}\n def fun(i,x,y):\n if (x,y) in visited:\n return 0\n if (i[0]-x)**2+(i[1]-y)**2<=i[2]**2 and (x,y) not in dic:\n dic[x,y]=1\n visited[x,y]=1\n return 1+fun(i,x+1,y)+fun(i,x-1,y)+fun(i,x,y+1)+fun(i,x,y-1)\n if (i[0]-x)**2+(i[1]-y)**2<=i[2]**2 and (x,y) not in visited:\n visited[x,y]=1\n return fun(i,x+1,y)+fun(i,x-1,y)+fun(i,x,y+1)+fun(i,x,y-1)\n return 0\n ans=0\n for i in (circle):\n ans+=fun(i,i[0],i[1])\n visited={}\n return ans\n \n \n``` | 1 | Given a 2D integer array `circles` where `circles[i] = [xi, yi, ri]` represents the center `(xi, yi)` and radius `ri` of the `ith` circle drawn on a grid, return _the **number of lattice points**_ _that are present inside **at least one** circle_.
**Note:**
* A **lattice point** is a point with integer coordinates.
* Points that lie **on the circumference of a circle** are also considered to be inside it.
**Example 1:**
**Input:** circles = \[\[2,2,1\]\]
**Output:** 5
**Explanation:**
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.
**Example 2:**
**Input:** circles = \[\[2,2,2\],\[3,4,1\]\]
**Output:** 16
**Explanation:**
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
**Constraints:**
* `1 <= circles.length <= 200`
* `circles[i].length == 3`
* `1 <= xi, yi <= 100`
* `1 <= ri <= min(xi, yi)` | Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array. We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this. We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper. Answer is (upper - lower + 1) - (range of sequence) |
[Java/C++/Python] O(1) Space | count-lattice-points-inside-a-circle | 1 | 1 | Updated this post, \nsince I noticed almost every solutions will use `set`,\nwith extra space complexity.\n<br>\n# **Solution 1: Set**\n## **Explanation**\nFor each circle `(x, y)`,\nenumerate `i` from `x - r` to `x + r`\nenumerate `j` from `y - r` to `y + r`\nCheck if `(i, j)` in this circle.\n\nIf so, add the point to a set `res` to de-duplicate.\n<br>\n\n## **Complexity**\nTime `O(NRR)`\nSpace `O(XY)`\nwhere `R = 100` is maximum radius of circles.\n\nActual run time depends on circles area in test cases.\n<br>\n\n**Java**\n```java\n public int countLatticePoints(int[][] circles) {\n Set<Integer> res = new HashSet<>();\n for (int[] c : circles)\n for (int i = -c[2]; i <= c[2]; i++)\n for (int j = -c[2]; j <= c[2]; j++)\n if (i * i + j * j <= c[2] * c[2])\n res.add((c[0] + i) * 1000 + c[1] + j);\n return res.size();\n }\n```\n**C++**\n```cpp\n int countLatticePoints(vector<vector<int>> circles) {\n unordered_set<int> res;\n for (auto& c : circles)\n for (int i = -c[2]; i <= c[2]; i++)\n for (int j = -c[2]; j <= c[2]; j++)\n if (i * i + j * j <= c[2] * c[2])\n res.insert((c[0] + i) * 1000 + c[1] + j);\n return res.size();\n }\n```\n**Python3**\n```py\n def countLatticePoints(self, A: List[List[int]]) -> int:\n res = set()\n for x,y,r in A:\n for i in range(x - r,x + r + 1):\n for j in range(y - r, y + r + 1):\n if (x - i) ** 2 + (y - j) ** 2 <= r * r:\n res.add((i,j))\n return len(res)\n```\n\n# **Solution 2: Check all points, O(1) space**\n## **Explanation**\nFor each point `(i, j)` in the plan,\nenumerate `i` from `0` to `200`\nenumerate `j` from `0` to `200`\nCheck if `(i, j)` in any circle.\n<br>\n\n## **Complexity**\nSame time complexity, `O(1)` space.\n\nTime `O(NXY)`\nSpace `O(1)`\nwhere `X = 100` is the range of `xi`\nwhere `Y = 100` is the range of `yi`\n<br>\n\n**Java**\n```java\n public int countLatticePoints(int[][] circles) {\n int res = 0;\n for (int i = 0; i <= 200; i++) {\n for (int j = 0; j <= 200; j++) {\n for (int[] c : circles) {\n if ((c[0] - i) * (c[0] - i) + (c[1] - j) * (c[1] - j) <= c[2] * c[2]) {\n res++;\n break;\n }\n }\n }\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n int countLatticePoints(vector<vector<int>>& circles) {\n int res = 0;\n for (int i = 0; i <= 200; i++)\n for (int j = 0; j <= 200; j++) {\n for (auto& c : circles) {\n if ((c[0] - i) * (c[0] - i) + (c[1] - j) * (c[1] - j) <= c[2] * c[2]) {\n res++;\n break;\n }\n }\n }\n return res;\n }\n```\n | 37 | Given a 2D integer array `circles` where `circles[i] = [xi, yi, ri]` represents the center `(xi, yi)` and radius `ri` of the `ith` circle drawn on a grid, return _the **number of lattice points**_ _that are present inside **at least one** circle_.
**Note:**
* A **lattice point** is a point with integer coordinates.
* Points that lie **on the circumference of a circle** are also considered to be inside it.
**Example 1:**
**Input:** circles = \[\[2,2,1\]\]
**Output:** 5
**Explanation:**
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.
**Example 2:**
**Input:** circles = \[\[2,2,2\],\[3,4,1\]\]
**Output:** 16
**Explanation:**
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
**Constraints:**
* `1 <= circles.length <= 200`
* `circles[i].length == 3`
* `1 <= xi, yi <= 100`
* `1 <= ri <= min(xi, yi)` | Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array. We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this. We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper. Answer is (upper - lower + 1) - (range of sequence) |
Python set solution, Easy | count-lattice-points-inside-a-circle | 0 | 1 | # Intuition\nThe "Count Lattice Points" problem involves counting the number of lattice points that lie within or on the boundary of a given set of circles. A lattice point is a point in the plane with integer coordinates. Our initial thoughts are to iterate through the lattice points and determine whether each point is inside any of the circles.\n\n# Approach\nTo solve this problem, we adopt the following approach:\n\n1. Define a function `distance(x, y, r, xo, yo)` to calculate the distance between a lattice point at coordinates `(x, y)` and a circle with center `(xo, yo)` and radius `r`. We use the Pythagorean theorem to compute the square of the distance and check if it\'s less than or equal to the square of the circle\'s radius.\n\n2. Initialize a set `lattice` to store unique lattice points.\n\n3. Iterate through each circle in the `circles` list, denoted by `(x, y, r)`. For each circle, we perform the following steps:\n - Iterate through the x-coordinates from `x - r` to `x + r`, and for each x-coordinate, iterate through the y-coordinates from `y - r` to `y + r`.\n - For each combination of x and y, use the `distance` function to check if the lattice point `(i, j)` is within the circle. If it is, add the lattice point to the `lattice` set.\n\n4. After processing all circles, the `lattice` set contains all unique lattice points that are within or on the boundary of at least one circle.\n\n5. Return the count of lattice points by taking the length of the `lattice` set.\n\n# Complexity\n- Time complexity: The time complexity depends on the number of lattice points generated while iterating through the circles. In the worst case, where circles are large and overlap, the time complexity can be quadratic. Specifically, it is O(c * r^2), where \'c\' is the number of circles and \'r\' is the radius of the largest circle in the worst case.\n- Space complexity: The space complexity is O(k), where \'k\' is the number of unique lattice points within or on the boundary of the circles. We store these points in the `lattice` set.\n\n# Code\n```python\nclass Solution:\n def countLatticePoints(self, circles: List[List[int]) -> int:\n\n def distance(x, y, r, xo, yo):\n res = (x - xo) ** 2 + (y - yo) ** 2\n return sqrt(res) <= r\n\n lattice = set()\n\n for x, y, r in circles:\n for i in range(x - r, x + r + 1):\n for j in range(y - r, y + r + 1):\n if distance(x, y, r, i, j):\n lattice.add((i, j))\n return len(lattice)\n``` | 0 | Given a 2D integer array `circles` where `circles[i] = [xi, yi, ri]` represents the center `(xi, yi)` and radius `ri` of the `ith` circle drawn on a grid, return _the **number of lattice points**_ _that are present inside **at least one** circle_.
**Note:**
* A **lattice point** is a point with integer coordinates.
* Points that lie **on the circumference of a circle** are also considered to be inside it.
**Example 1:**
**Input:** circles = \[\[2,2,1\]\]
**Output:** 5
**Explanation:**
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.
**Example 2:**
**Input:** circles = \[\[2,2,2\],\[3,4,1\]\]
**Output:** 16
**Explanation:**
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
**Constraints:**
* `1 <= circles.length <= 200`
* `circles[i].length == 3`
* `1 <= xi, yi <= 100`
* `1 <= ri <= min(xi, yi)` | Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array. We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this. We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper. Answer is (upper - lower + 1) - (range of sequence) |
[Python] Optimized time/space complexity solution without using set | count-lattice-points-inside-a-circle | 0 | 1 | > **number of circles**: N\n**length of range of xi, yi and r**: M \n\n\n# Intuition\nThis problem can easily be solved by calculating points inside each circle and using Set to get union, or scan through all possible points and check each circle. However, the theoritical time complexity $$O(NM^2)$$ is not optimized. We can transform the question into layers of one-dimension problem and solve with better time complexity $$min(O(M(M+N)), O(M(NLogN))))$$.\n\n# Approach\nConsider 1-dimension problem: \n> Given a line of length M, and N periods [start,end], calculate the number of integer points inside any period.\n\nThis is a simple problem which can be resolved either in $$O(M+N)$$ or $$O(NlogN)$$. Once we transfer the original problem into layers of this 1-dimension problems. We can get a solution with better time complexity. \n\n# Complexity\n- Time complexity: $$min(O(M(M+N)), O(M(NLogN))))$$\n\n- Space complexity: $$min(M,N)$$\nThis space complexity is not as good as the full area scan method $$O(1)$$, but is definately better than the set one $$O(M^2)$$ \n\n# Code\n```\nfrom math import ceil, floor, sqrt, log2\nclass Solution:\n def countLatticePoints(self, circles: List[List[int]]) -> int:\n xd = yd = 100\n xu = yu = 0\n for x,y,r in circles:\n xd = min(xd, x-r)\n yd = min(yd, y-r)\n xu = max(xu, x+r)\n yu = max(yu, y+r)\n\n m = xu - xd +1\n\n def count_line_dense(periods):\n li = [0]*(m+1)\n for l,r in periods:\n li[l-xd] += 1\n li[r-xd] -=1\n res = su = 0\n for i in range(m):\n su += li[i]\n res += (su>0)\n return res \n\n def count_line_sparse(periods):\n periods.sort()\n res = s = e = 0\n for l,r in periods:\n if e<l:\n res += e-s\n s,e = l,r\n else:\n e = max(e,r)\n return res + e-s\n\n def count_line(periods):\n if not periods:\n return 0\n n = len(periods)\n if n*log2(n) > m:\n return count_line_dense(periods)\n return count_line_sparse(periods)\n\n res = 0\n # print(xd,yd,xu, yu)\n for h in range(yd, yu+1):\n periods = []\n for x,y,r in circles:\n if abs(h-y)>r:\n continue\n dx = sqrt(r**2 - (h-y)**2)\n periods.append([ceil(x-dx), floor(x+dx)+1])\n # print(h, periods)\n res += count_line(periods)\n return res\n\n\n``` | 0 | Given a 2D integer array `circles` where `circles[i] = [xi, yi, ri]` represents the center `(xi, yi)` and radius `ri` of the `ith` circle drawn on a grid, return _the **number of lattice points**_ _that are present inside **at least one** circle_.
**Note:**
* A **lattice point** is a point with integer coordinates.
* Points that lie **on the circumference of a circle** are also considered to be inside it.
**Example 1:**
**Input:** circles = \[\[2,2,1\]\]
**Output:** 5
**Explanation:**
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.
**Example 2:**
**Input:** circles = \[\[2,2,2\],\[3,4,1\]\]
**Output:** 16
**Explanation:**
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
**Constraints:**
* `1 <= circles.length <= 200`
* `circles[i].length == 3`
* `1 <= xi, yi <= 100`
* `1 <= ri <= min(xi, yi)` | Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array. We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this. We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper. Answer is (upper - lower + 1) - (range of sequence) |
numpy is all you needed. | count-lattice-points-inside-a-circle | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nJust use numpy. np.mgrid\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nO(n * 500 * 500)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countLatticePoints(self, circles: List[List[int]]) -> int:\n import numpy as np\n xx, yy = np.mgrid[-200:300,-200:300]\n arr = np.full(shape=(500,500),fill_value=False,dtype=bool)\n for x,y,r in circles:\n arr |= (xx - x) ** 2 + (yy - y) ** 2 <= r ** 2\n return arr.sum()\n```\n | 0 | Given a 2D integer array `circles` where `circles[i] = [xi, yi, ri]` represents the center `(xi, yi)` and radius `ri` of the `ith` circle drawn on a grid, return _the **number of lattice points**_ _that are present inside **at least one** circle_.
**Note:**
* A **lattice point** is a point with integer coordinates.
* Points that lie **on the circumference of a circle** are also considered to be inside it.
**Example 1:**
**Input:** circles = \[\[2,2,1\]\]
**Output:** 5
**Explanation:**
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.
**Example 2:**
**Input:** circles = \[\[2,2,2\],\[3,4,1\]\]
**Output:** 16
**Explanation:**
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle.
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
**Constraints:**
* `1 <= circles.length <= 200`
* `circles[i].length == 3`
* `1 <= xi, yi <= 100`
* `1 <= ri <= min(xi, yi)` | Fix the first element of the hidden sequence to any value x and ignore the given bounds. Notice that we can then determine all the other elements of the sequence by using the differences array. We will also be able to determine the difference between the minimum and maximum elements of the sequence. Notice that the value of x does not affect this. We now have the ‘range’ of the sequence (difference between min and max element), we can then calculate how many ways there are to fit this range into the given range of lower to upper. Answer is (upper - lower + 1) - (range of sequence) |
Python BS O(n log n) | count-number-of-rectangles-containing-each-point | 0 | 1 | - Time complexity: O(n log n)\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:\n\n def bs(arr, a):\n left = 0\n right = len(arr) - 1\n\n while left <= right:\n mid = (left + right) // 2\n\n if arr[mid] == a:\n return mid\n elif arr[mid] < a:\n left = mid + 1\n else:\n right = mid - 1\n return left\n\n dict_rectangles = defaultdict(list)\n result = []\n\n for x, y in rectangles:\n dict_rectangles[y].append(x)\n\n for value in dict_rectangles.values():\n value.sort()\n\n max_heigh = max(dict_rectangles.keys())\n\n for a, b in points:\n counts = 0\n for i in range(b, max_heigh + 1):\n if dict_rectangles[i]:\n counts += len(dict_rectangles[i]) - bs(dict_rectangles[i], a)\n result.append(counts)\n\n return result\n``` | 1 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
5-lines easy solution with explanation and analysis | count-number-of-rectangles-containing-each-point | 0 | 1 | Notice the constraints of y-axis: `1 <= hi, yj <= 100`.\nWe can sort rectangles by x-axis and separate them by y-axis.\nWhen we search for the answer of a point (x, y) we can search only in all lists with `height >= y`, and with the fact that lengths (x\'s) are already sorted, we can use binary search to find the number of rectangles with height y that contain the given point.\n\n**Python:**\n\n```\ndef countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:\n rectangles.sort()\n length = defaultdict(list)\n for l, h in rectangles:\n length[h].append(l)\n return [sum(len(length[h]) - bisect.bisect_left(length[h], x) for h in range(y, 101)) for x, y in points]\n```\n\n**Complexity: O(nlogn)** | 4 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
[Python3] binary search | count-number-of-rectangles-containing-each-point | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/c2730559a4a05cfc912d81e5d7a3d4d607079401) for solutions of weekly 290.\n\n```\nclass Solution:\n def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:\n mp = defaultdict(list)\n for l, h in rectangles: mp[h].append(l)\n for v in mp.values(): v.sort()\n ans = []\n for x, y in points: \n cnt = 0 \n for yy in range(y, 101): \n if yy in mp: cnt += len(mp[yy]) - bisect_left(mp[yy], x)\n ans.append(cnt)\n return ans \n``` | 3 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
[Python] Binary Search (detailed explanation) | count-number-of-rectangles-containing-each-point | 0 | 1 | ### Idea\n\n- `Point (px, py)` should be counted when `px <= length and py <= height`\n- We can start with a simpler question -> If the point is not 2D, and it\'s just a 1D integer, how can we solve this?\n\n### Simpler question (1D)\n- Question: \n\t- Given a list of point `xi` and a list of rectangle\'s length `li`. For each point, how many rectangles contain it?\n- Brute Force: \n\t- We can travese each point and compare with each rectangle.\n```Python\nres = []\nfor xi in points:\n\tcount = 0 \n\tfor li in rectangles: \n\t\tif li >= xi:\n\t\t\tcount +=1\n\tres.append(count)\n\n# Time Complexity: O(P * R) #assume P points and R rectangles \n```\n- Better approach: \n\t- We know the Brute Force is not efficient enough because it check all rectangles for each points again and again. \n\t- Instead, we can do some preprocessing in advance to make the rectangle\'s states easier to be reused before starting traversing points. \n\t- The common *preprocessing* are like building map, creating prefix sum, sorting, etc. Here, a simple sorting helps because then we can use a binary search to find the first index which\'s rectangle is larger than the point.\n\n```Python\nrectangles.sort() \nres = []\nfor xi in points:\n\tidx = bisect.bisect_left(rectangles, xi) #index of first rectangle which is >= xi \n\tres.append(len(rectangles) - idx)\n\t\n# Time Complexity: O(RlogR + PlogR) #Sorting: RlogR / Binary search in rectangle for P times: PlogR \n```\n\n### Back to the original question (2D)\n- Similar to the 1D question, if either the height or weight is static, we can use the same approach `sorting + binary search` to solve. \n- After checking the constraint, we noticed one important fact - the height is limited !\n```\n1 <= li, xj <= 10^9\n1 <= hi, yj <= 100\n```\n- Then the story becomes easy. It\'s almost the same as the 1D question. We just need to find the possible heights first, then do the binary search for each possible heights, and sum them up. \n\n```\nclass Solution:\n def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:\n maxH = 101 \n hToL = [[] for _ in range(maxH)]\n \n\t\t# Create the 100 list (0 is not used) \n for l, h in rectangles:\n hToL[h].append(l)\n\t\t\t\n # Sort the 100 list\n for h in range(1, maxH):\n hToL[h].sort()\n \n\t\tres = []\n for px, py in points:\n count = 0\n # Only search the height (y) which equals to or greater than given py \n for h in range(py, maxH):\n if len(hToL[h]) == 0:\n continue\n # Find the first index of length (x) which equals to or greater than given px in the sorted array\n idx = bisect.bisect_left(hToL[h], px) \n count += len(hToL[h]) - idx\n res.append(count)\n return res\n\n# Time Complexity: O(100*RlogR + P*100*logR) = O(RlogR + PlogR) //if we consider 100 is a constant\n# Space Complexity: O(R)\n```\n\nPracticing leetcode problem is tough and lonely (at least for me).\nI hope this solution helps you a bit :) \n\n | 8 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
Python: Array dictionary and Binary search. beats 99 % other solutions. | count-number-of-rectangles-containing-each-point | 0 | 1 | # Intuition\nGroup rectangle widths by height ```h```. Height is chosen because the maximum value of ```h``` is 100. Thus it is easy to use array as dictionary. \n\nBinary search on the grouped widths.\n\n# Approach\n\n\n# Complexity\n- Time complexity: \n```n = len(rectangles), m = len(points), y = len(ydict[x])``` \n O(n + m.log y)\n\n- Space complexity:\n Constant space. constant O(100) is allocated.\n\n\n# Code\n```\nclass Solution: \n\n def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]: \n ydict = [[] for _ in range(101)]\n for x,y in rectangles:\n ydict[y].append(x) \n \n ydict[100].sort()\n for i in range(99,0,-1):\n ydict[i] += ydict[i+1]\n ydict[i].sort()\n\n ans = []\n for x,y in points:\n i = bisect.bisect_left(ydict[y],x)\n n = len(ydict[y]) - i\n ans.append(n)\n\n return ans\n``` | 0 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
python3 binary search on heights | count-number-of-rectangles-containing-each-point | 0 | 1 | \n\n# Code\n```\nimport bisect\nclass Solution:\n def countRectangles(self, rectangles: List[List[int]], points: List[List[int]]) -> List[int]:\n heights = defaultdict(list)\n for x,y in rectangles:\n heights[y].append(x)\n for k,v in heights.items():\n heights[k] = sorted(heights[k])\n res = []\n for x,y in points:\n temp = 0\n for i in range(y,101):\n temp+=len(heights[i]) - bisect.bisect_left(heights[i],x)\n res.append(temp)\n return res\n``` | 0 | You are given a 2D integer array `rectangles` where `rectangles[i] = [li, hi]` indicates that `ith` rectangle has a length of `li` and a height of `hi`. You are also given a 2D integer array `points` where `points[j] = [xj, yj]` is a point with coordinates `(xj, yj)`.
The `ith` rectangle has its **bottom-left corner** point at the coordinates `(0, 0)` and its **top-right corner** point at `(li, hi)`.
Return _an integer array_ `count` _of length_ `points.length` _where_ `count[j]` _is the number of rectangles that **contain** the_ `jth` _point._
The `ith` rectangle **contains** the `jth` point if `0 <= xj <= li` and `0 <= yj <= hi`. Note that points that lie on the **edges** of a rectangle are also considered to be contained by that rectangle.
**Example 1:**
**Input:** rectangles = \[\[1,2\],\[2,3\],\[2,5\]\], points = \[\[2,1\],\[1,4\]\]
**Output:** \[2,1\]
**Explanation:**
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return \[2, 1\].
**Example 2:**
**Input:** rectangles = \[\[1,1\],\[2,2\],\[3,3\]\], points = \[\[1,3\],\[1,1\]\]
**Output:** \[1,3\]
**Explanation:**
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return \[1, 3\].
**Constraints:**
* `1 <= rectangles.length, points.length <= 5 * 104`
* `rectangles[i].length == points[j].length == 2`
* `1 <= li, xj <= 109`
* `1 <= hi, yj <= 100`
* All the `rectangles` are **unique**.
* All the `points` are **unique**. | Could you determine the rank of every item efficiently? We can perform a breadth-first search from the starting position and know the length of the shortest path from start to every item. Sort all the items according to the conditions listed in the problem, and return the first k (or all if less than k exist) items as the answer. |
python3 Solution | number-of-flowers-in-full-bloom | 0 | 1 | \n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n start=sorted(flowers,key=lambda x:x[0])\n end=sorted(flowers,key=lambda x:x[1])\n ans=[]\n for man in people:\n i=bisect_left(end,man,key=lambda x:x[1])\n j=bisect_right(start,man,key=lambda x:x[0])\n ans.append(j-i)\n\n return ans \n``` | 3 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
🚀 Priority Queue || Explained Intuition || Commented Code🚀 | number-of-flowers-in-full-bloom | 1 | 1 | # Problem Description\n\nThe problem involves processing data about the **bloom time** of flowers and the arrival times of people to determine the **number** of flowers in full bloom at each person\'s arrival time.\n\nGiven a 2D array `flowers` representing the bloom intervals for each flower and an array `people` representing the arrival times of individuals, the task is to **calculate**, for each person, the **count** of flowers in **full bloom** at their respective arrival times.\n\n---\n\n\n\n# Intuition\nHi There! \uD83D\uDE03\n\nLet\'s deep in our today\'s problem.\uD83E\uDD3F\nThe problem says that we have flowers which bloom in some interval from `[a, b]` and there are people arriving in **specific** time. Our task is to **calculate** for each person how many blooming flowers he would **see**.\nSeems tough.\uD83D\uDCAA\n\n**First Solution** that would pop into mind \uD83C\uDF7F is to iterate on every arrival time and for each arrival time iterate over all flowers and **count** the number of flowers for that time.\nFor sure, It is **correct** answer but it is **inefficient** solution since its Time complexity is `O(N * M)`.\n\nHow can we improve this solution or come with more efficient one?\uD83E\uDD14\n\nLet\'s look at the first example of the problem.\n```\nflowers = [[1,6],[3,7],[9,12],[4,13]], poeple = [2,3,7,11]\nAnswer -> [1,2,2,2]\n```\n\n\n\nwe can imagine that in the picture there is a certain data structure **storing** which flowers are blooming in the **current interval** and based on that we put it as an answer for **current person**.\n\nCan we implement something like this?\uD83E\uDD14\nHopefully, we can !\uD83D\uDE03\uD83D\uDCAA\n\n**First**, we will **sort** **people** based on their arrival time and the **flowers** based on the starting of the blooming interval, but why?\uD83E\uDD14\nso we can **process** them **one by one** with the **same** data structure without iterate over all the flowers again for each person.\nlike if we have two persons arrived at time = 2 then they will have the **same** answer from the **same** data structure.\uD83E\uDD2F\n\n**Second**, the data structure which we want it to maintain a scheme like the above picture. I will pretend that I didn\'t say its name in the title.\uD83D\uDE02\n- For **each person**, We want to **maintain** two things for the flowers in the data structure:\n - The **starting** of blooming interval of all flowers are less than or equal the current person `(meaning it started blooming before the current person arrival)`.\n - The **ending** of blooming interval of all flowers are more than or equal the current person `(meaning it ended blooming after the current person arrival)`.\n \nOur hero for this job is the **Priority Queue** (Min Heap) \uD83E\uDDB8\u200D\u2642\uFE0F but how we will use it?\uD83E\uDD14\nwe will check for each flower that it **started** blooming before or as just as the person arrived then we will **push** its **ending** time in the Priority Queue so we maintained the **first feature**.\nwe will see the top of Priority Queue and check the ending time of it and pop it if the flower ended blooming before the persong arrived so \nwe maintained the **second feature**.\nNow, we are **sure** that for a **specific time** that the flowers in the Priority Queue are **blooming** in that time.\uD83C\uDF38\n\nLast Thing, How will we store the answers ?\uD83E\uDD14\nIn a **dictionary** such that for each arrival time of a person we will store how many flowers in our Priority Queue that we are sure that thery are blooming in the arrival time of the person.\n\nAnd this is the solution for our today\'S problem I hope that you understood it\uD83D\uDE80\uD83D\uDE80\n\n\n---\n\n\n\n# Approach\n1. **Sort** the arrival times of people `people` and the flower intervals `flowers` based on their starting in **ascending** order.\n3. **Initialize** an empty dictionary `bloom_counts` to store **counts** of flowers in bloom for each arrival time and an empty **min heap** `bloom_end_times` to track flower bloom end times.\n4. **Iterate** through the sorted arrival times and For each arrival time:\n - **Add** flowers that are in bloom at the current arrival time by pushing bloom end times into the min heap `bloom_end_times`.\n - **Remove** flowers that are no longer in bloom by popping the min heap.\n - **Store** the count of flowers in bloom for the current person\'s arrival time in the `bloom_counts` dictionary.\n5. **Return** `flowerCounts`, which contains the counts of flowers in bloom for each person\'s arrival time.\n\n# Complexity\n- **Time complexity:** $O(N * log(N) + M * (log(M) + log(N)))$\nSince we are **sorting** people array and flowers array then this cost `O(M * log(M))` and `O(N * log(N))` then we have a **for loop** which we iterate over all people and in each iteration we do some operations using the min heap then its complexity is `O(M * log(N))` so total time complexity is `O(N * log(N) + M * log(M) + M * log(N))` which is `O(N * log(N) + M * (log(M) + log(N)))`.\nWhere `M` is the size of perple array and `N` is the soze of flower array.\n- **Space complexity:** $O(M + N)$\nSince we are storing **sorted arrival times** which has space of `M` and storing the **dictionary** for all arival times also has space `M` and the **min heap** for storing the flowers blooming intervals which has space of `N`. So total space is `N + 2 * M` which is `O(N + M)`. \n\n\n---\n\n\n\n# Code\n\n```C++ []\nclass Solution {\npublic:\n vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {\n vector<int> sortedArrivalTimes(people.begin(), people.end());\n sort(sortedArrivalTimes.begin(), sortedArrivalTimes.end());\n\n // Sort the flower intervals based on their start times.\n sort(flowers.begin(), flowers.end()) ;\n \n unordered_map<int, int> bloomCounts; // Map to store counts of flowers in bloom for each arrival time.\n priority_queue<int, vector<int>, greater<int>> bloomEndTimes; // Min heap to track flower bloom end times.\n\n int flowerIdx = 0 ;\n for(int personTime: sortedArrivalTimes){\n // Add flowers that are in bloom at the person\'s arrival time.\n while(flowerIdx < flowers.size() && flowers[flowerIdx][0] <= personTime)\n bloomEndTimes.push(flowers[flowerIdx++][1]);\n\n // Remove flowers that are no longer in bloom.\n while(!bloomEndTimes.empty() && bloomEndTimes.top() < personTime)\n bloomEndTimes.pop();\n\n // Store the count of flowers in bloom for the person\'s arrival time.\n bloomCounts[personTime] = bloomEndTimes.size();\n }\n\n vector<int> flowerCounts; // Resulting array to store flower counts for each person.\n for(int arrivalTime: people)\n flowerCounts.push_back(bloomCounts[arrivalTime]);\n\n return flowerCounts; // Return the counts of flowers in bloom for each person\'s arrival time.\n }\n};\n```\n```Java []\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] people) {\n int[] sortedArrivalTimes = Arrays.copyOf(people, people.length);\n Arrays.sort(sortedArrivalTimes);\n\n // Sort the flower intervals based on their start times.\n Arrays.sort(flowers, Comparator.comparingInt(flower -> flower[0]));\n\n Map<Integer, Integer> bloomCounts = new HashMap<>(); // Map to store counts of flowers in bloom for each arrival time.\n PriorityQueue<Integer> bloomEndTimes = new PriorityQueue<>(); // Min heap to track flower bloom end times.\n\n int flowerIdx = 0;\n for (int personTime : sortedArrivalTimes) {\n // Add flowers that are in bloom at the person\'s arrival time.\n while (flowerIdx < flowers.length && flowers[flowerIdx][0] <= personTime) {\n bloomEndTimes.offer(flowers[flowerIdx][1]);\n flowerIdx++;\n }\n\n // Remove flowers that are no longer in bloom.\n while (!bloomEndTimes.isEmpty() && bloomEndTimes.peek() < personTime) {\n bloomEndTimes.poll();\n }\n\n // Store the count of flowers in bloom for the person\'s arrival time.\n bloomCounts.put(personTime, bloomEndTimes.size());\n }\n\n int[] flowerCounts = new int[people.length]; // Resulting array to store flower counts for each person.\n for (int i = 0; i < people.length; i++) {\n flowerCounts[i] = bloomCounts.get(people[i]);\n }\n\n return flowerCounts; // Return the counts of flowers in bloom for each person\'s arrival time.\n }\n}\n```\n```Python []\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n sorted_arrival_times = sorted(people)\n flowers.sort() # Sort the flower intervals based on their start times.\n \n bloom_counts = {} # Dictionary to store counts of flowers in bloom for each arrival time.\n bloom_end_times = [] # Min heap to track flower bloom end times.\n\n flower_idx = 0\n for person_time in sorted_arrival_times:\n # Add flowers that are in bloom at the person\'s arrival time.\n while flower_idx < len(flowers) and flowers[flower_idx][0] <= person_time:\n heapq.heappush(bloom_end_times, flowers[flower_idx][1])\n flower_idx += 1\n\n # Remove flowers that are no longer in bloom.\n while bloom_end_times and bloom_end_times[0] < person_time:\n heapq.heappop(bloom_end_times)\n\n # Store the count of flowers in bloom for the person\'s arrival time.\n bloom_counts[person_time] = len(bloom_end_times)\n\n # Resulting list to store flower counts for each person.\n flower_counts = [bloom_counts[arrival_time] for arrival_time in people]\n\n return flower_counts # Return the counts of flowers in bloom for each person\'s arrival time.\n```\n\n\n\n\n | 27 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
【Video】Give me 15 minutes - How we can think about a solution - Python, JavaScript, Java, C++ | number-of-flowers-in-full-bloom | 1 | 1 | Welcome to my post! This post starts with "How we think about a solution". In other words, that is my thought process to solve the question. This post explains how I get to my solution instead of just posting solution codes or out of blue algorithms. I hope it is helpful for someone.\n\n# Intuition\ncalculate how many flowers are available in days\n\n---\n\n# Solution Video\n\nI\'m sure you understand how to solve this question in 15 minutes by the video.\n\nhttps://youtu.be/kiIYG6drNZo\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Number of Flowers in Full Bloom\n`0:35` How we think about a solution\n`2:50` Demonstrate solution with an example\n`6:09` Find available flowers\n`8:36` We don\'t have to reset the right pointer to 0 or something\n`9:32` Coding\n`13:31` Time Complexity and Space Complexity\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 2,664\nMy initial goal is 10,000\nThank you for your support!\n\n---\n\n\n# Approach\n\n### How we think about a solution\n\nFirst of all, I try brute force like this.\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n hash = {}\n for f in flowers:\n for day in range(f[0], f[1] + 1):\n hash[day] = 1 + hash.get(day, 0)\n \n res = []\n\n for p in people:\n res.append(hash.get(p, 0))\n \n return res\n```\nI just keep flower counts in all available days in `hash`, then try to check visit days...but I got memory limit exceeded...lol\n\nThat\'s how I think about $$O(n)$$ space solution.\n\nBut I felt like I can solve this question with straightforward solution, because even though the brute force solution didn\'t pass all test cases, the algorithm works except a memory.\n\nThat\'s why simply, I tried to create a `list` or `hashMap` containing number of new flowers or not available flowers in `start day` and `end day + 1`.\n\n```\nflowers = [[1,6],[3,7],[9,12],[4,13]]\npeople = [2,3,7,11]\n```\nIn the end, I created this `HashMap` from Input above.\n```\n{1: 1, 7: -1, 3: 1, 8: -1, 9: 1, 13: -1, 4: 1, 14: -1}\n\nkey is start day or end day + 1\nvalue is number of new flowers or not available flowers from the day\n```\nwhen I added the key and value to `HashMap`, I added `+1 with start day` and `-1 with end day + 1`\n\n---\n\n\u2B50\uFE0F Points\n\n- Why `end day + 1`?\nThat\'s because description says end day is inclusive, so number of flowers is changed next day of end day.\n\n- Why `-1 with end day + 1` instead of `+1 with end day + 1`?\nSimply from next day of end day, flowers will finish full bloom days, so in the next day, at least one flower is not available. If we have the same end day for multiple flowers, value should be -2 or -3....\n\n---\n\nNext, I took all days regardless of `start days` or `end days + 1` with ascending order.\n```\ndays = [1, 3, 4, 7, 8, 9, 13, 14]\n```\nWe know that number of flowers will be changed in the days. Let\'s count exact number of flowers in each day. The values are `accumulative number including postive and negative`.\n\n```\n{1: 1, 7: -1, 3: 1, 8: -1, 9: 1, 13: -1, 4: 1, 14: -1}\n\nday 1\n\ntotal flowers are 1 (= 0 + 1)\n\n+1: [1,6] flower starts from day 1\n```\n```\nday 3\n\ntotal flowers are 2 (= 1 + 1)\n\n1: from day 1\n+1: [3,7] flower starts from day 3\n```\n```\nday 4\n\ntotal flowers are 3 (= 2 + 1)\n\n2: from day 3\n+1: [4,13] flower starts from day 4\n```\n```\nday 7\n\ntotal flowers are 2 (= 3 - 1)\n\n3: from day 4\n-1: [1,6] flower finish in day 7\n```\n```\nday 8\n\ntotal flowers are 1 (= 2 - 1)\n\n2: from day 7\n-1: [3,7] flower finish in day 8\n```\n```\nday 9\n\ntotal flowers are 2 (= 1 + 1)\n\n1: from day 8\n+1: [9,12] flower starts from day 9\n```\n```\nday 13\n\ntotal flowers are 1 (= 2 - 1)\n\n2: from day 9\n-1: [9,12] flower finish from day 13\n```\n```\nday 14\n\ntotal flowers are 0 (= 1 - 1)\n\n1: from day 13\n-1: [4,13] flower finish from day 14\n```\nIn the end, we have this `HashMap`\n```\nflower_count = {1: 1, 7: 2, 3: 2, 8: 1, 9: 2, 13: 1, 4: 3, 14: 0}\n```\nWe can use the same `HashMap` because we iterate through with keys from this `HashMap` when we count exact number of flowers in each day.\n\nAt last, we iterate through `people` and get each `visit day`.\n```\npeople = [2,3,7,11]\ndays = [1, 3, 4, 7, 8, 9, 13, 14]\n```\nSince days are sorted, we can use binary search to find visit day.\n\n```\nvisit day: 2\n```\nThere is not a exact day in `days`.\n\n---\n\n\u2B50\uFE0F Points\n\nIf you don\'t find a exact day, use `previous changing day`. when visit day is `2`, use `day 1`, because the flower state remains unchanged until `day 3` from `day 1`.\n\nThat\'s why we try to find index of right position of the exact day.\n\n`days list` doesn\'t have `day 2`, so binary search should return `index 1`, so that we can access `index 0` easily with `index - 1`\n\n---\n\nAgain,\n```\npeople = [2, 3, 7, 11]\ndays = [1, 3, 4, 7, 8, 9, 13, 14]\nflower_count = {1: 1, 7: 2, 3: 2, 8: 1, 9: 2, 13: 1, 4: 3, 14: 0}\n```\n\n```\nvisit day: 2\nbinary search return 1 (index)\ntarget index = 1 - 1 (index from binary search - 1) \n\nflower_count[days[0]] = 1\nres = [1]\n```\n\n```\nvisit day: 3\nbinary search return 2 (right position of index 1)\ntarget index = 2 - 1\n\nflower_count[days[1]] = 2\nres = [1, 2]\n```\n\n```\nvisit day: 7\nbinary search return 4 (right position of index 3)\ntarget index = 4 - 1\n\nflower_count[days[3]] = 2\nres = [1, 2, 2]\n```\n\n```\nvisit day: 11\nbinary search return 6\ntarget index = 6 - 1\n\nflower_count[days[5]] = 2\nres = [1, 2, 2, 2]\n```\n\n```\nOutput: [1, 2, 2, 2]\n```\n\nThat is my thought process to solve this question. It\'s a very straightforward solution.\n\nYesterday\'s post was really tough. lol\n\nLet\'s see real algorithm!\n\n### Algorithm Overview:\n\nThis is based on Python code. Other might be different a bit.\n\n1. Initialize a dictionary `flower_count` using `defaultdict` from the collections module to store the count of flowers for each day.\n2. Iterate through the `flowers` list and increment the count of flowers for the start day and decrement for the day after the end day in the `flower_count` dictionary.\n3. Sort the unique days (start and end days) from the `flower_count` keys and accumulate the flower count efficiently for each day.\n4. For each person\'s time in the `people` list, use binary search (`bisect_right`) to find the index of the closest day in the `days` list and append the accumulated flower count for that day to the answer list.\n\n### Detailed Explanation:\n\n1. Initialize a dictionary `flower_count` using `defaultdict(int)` to store the count of flowers for each day. This dictionary will have keys representing the days and values representing the count of flowers for that day.\n\n2. **Iterate through the `flowers` list:**\n a. For each flower range (start, end), increment the count of flowers for the start day in the `flower_count` dictionary.\n b. Decrement the count of flowers for the day after the end day in the `flower_count` dictionary.\n\n3. Sort the unique days (start and end days) from the `flower_count` keys. This sorted list of days will be stored in the variable `days`.\n\n4. **Accumulate the flower count efficiently for each day:**\n a. Initialize a variable `total_flowers` to keep track of the total flower count.\n b. Iterate through the sorted `days`:\n - Add the count of flowers for the current day to the `total_flowers`.\n - Update the `flower_count` for the current day with the accumulated `total_flowers`.\n\n5. **For each person\'s time in the `people` list:**\n a. Use binary search (`bisect_right`) on the sorted `days` list to find the index of the closest day that is greater than the person\'s time.\n b. If the index is 0 (meaning the person\'s time is before the first day with flowers), append 0 to the answer list.\n c. If the index is not 0, append the accumulated flower count for the day before the found index to the answer list.\n\n6. Return the answer list, which contains the accumulated flower counts for each person\'s time.\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O((n + m) log n)$$\n\nWe sorted `key` for `flower_count` which is $$O(n * log n)$$.\nWe iterate through `visit days` and every time we use `binary search` which is $$O(m * log n)$$\n\nSo, total time compelxity should be $$O((n + m) log n)$$\n\n- Space complexity: $$O(n)$$\n\n`flower_count` has $$O(2n)$$, because we put all start days and end days to `flower_count`, which is $$O(n)$$\n\n# Python Code\n\n```python []\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n flower_count = defaultdict(int)\n\n for start, end in flowers:\n flower_count[start] += 1\n flower_count[end + 1] -= 1\n\n days = sorted(flower_count.keys())\n total_flowers = 0\n for day in days:\n total_flowers += flower_count[day]\n flower_count[day] = total_flowers\n\n answer = []\n for person_time in people:\n index = bisect_right(days, person_time)\n if index == 0:\n answer.append(0)\n else:\n answer.append(flower_count[days[index - 1]])\n\n return answer\n```\n```javascript []\n/**\n * @param {number[][]} flowers\n * @param {number[]} people\n * @return {number[]}\n */\nvar fullBloomFlowers = function(flowers, people) {\n const flower_count = new Map();\n\n for (const [start, end] of flowers) {\n flower_count.set(start, (flower_count.get(start) || 0) + 1);\n flower_count.set(end + 1, (flower_count.get(end + 1) || 0) - 1);\n }\n\n const days = Array.from(flower_count.keys()).sort((a, b) => a - b);\n\n let total_flowers = 0;\n for (const day of days) {\n total_flowers += flower_count.get(day) || 0; // Use 0 if flower count is undefined\n flower_count.set(day, total_flowers);\n }\n\n const answer = [];\n for (const person_time of people) {\n const index = days.findIndex(day => day > person_time);\n\n if (index === -1) {\n answer.push(0);\n } else {\n answer.push(flower_count.get(days[index - 1]) || 0); // Use 0 if flower count is undefined\n }\n }\n\n return answer; \n};\n```\n```java []\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] people) {\n TreeMap<Integer, Integer> flowerCount = new TreeMap<>();\n\n for (int[] flower : flowers) {\n flowerCount.put(flower[0], flowerCount.getOrDefault(flower[0], 0) + 1);\n flowerCount.put(flower[1] + 1, flowerCount.getOrDefault(flower[1] + 1, 0) - 1);\n }\n\n int totalFlowers = 0;\n\n for (Map.Entry<Integer, Integer> entry : flowerCount.entrySet()) {\n int day = entry.getKey();\n int flowersDelta = entry.getValue();\n\n totalFlowers += flowersDelta;\n flowerCount.put(day, totalFlowers);\n }\n\n int[] answer = new int[people.length];\n for (int i = 0; i < people.length; i++) {\n int personTime = people[i];\n Integer floorKey = flowerCount.floorKey(personTime);\n answer[i] = (floorKey != null) ? flowerCount.get(floorKey) : 0;\n }\n\n return answer;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {\n map<int, int> flowerCount;\n\n for (const auto& flower : flowers) {\n flowerCount[flower[0]]++;\n flowerCount[flower[1] + 1]--;\n }\n\n vector<int> days;\n for (const auto& entry : flowerCount) {\n days.push_back(entry.first);\n }\n sort(days.begin(), days.end());\n\n int totalFlowers = 0;\n for (int day : days) {\n totalFlowers += flowerCount[day];\n flowerCount[day] = totalFlowers;\n }\n\n vector<int> answer;\n for (int personTime : people) {\n auto it = upper_bound(days.begin(), days.end(), personTime);\n int index = distance(days.begin(), it);\n if (index == 0)\n answer.push_back(0);\n else\n answer.push_back(flowerCount[days[index - 1]]);\n }\n\n return answer; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u2B50\uFE0F next post for daily coding challenge\nhttps://leetcode.com/problems/find-in-mountain-array/solutions/4159293/video-give-me-10-minutes-how-we-think-about-a-solution-python-javascript-java-c/\n\n\u2B50\uFE0F next daily challenge video\n\nhttps://youtu.be/09RZINmppQI\n\n\u25A0 Timeline of the video\n`0:04` How we think about a solution\n`2:45` An important point when you find peak index\n`4:47` An important point when you find peak index\n`6:13` Coding\n`11:45` Time Complexity and Space Complexity\n\n\u2B50\uFE0F previous post for daily coding challenge\nhttps://leetcode.com/problems/minimum-number-of-operations-to-make-array-continuous/solutions/4152964/video-give-me-15-minutes-how-we-think-about-a-solution/\n\n\u2B50\uFE0F previous daily challenge video\n\nhttps://youtu.be/9DLAvMurzbU\n\n\u25A0 Timeline of the video\n`0:00` Read the question of Minimum Number of Operations to Make Array Continuous\n`0:42` How we think about a solution\n`4:33` Demonstrate solution with an example\n`8:10` Why the window has all valid numbers?\n`8:36` We don\'t have to reset the right pointer to 0 or something\n`10:36` Why we need to start window from each number?\n`12:24` What if we have duplicate numbers in input array?\n`14:50` Coding\n`17:11` Time Complexity and Space Complexity\n\n | 48 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
✅100%🔥Easy Solution🔥With explanation🔥|| Binary Search || Beginner Friendly ✅ | number-of-flowers-in-full-bloom | 0 | 1 | # Intuition\n\nThe problem aims to determine the number of flowers that are in full bloom at specific dates. To achieve this, the code utilizes binary search to find the positions where the given dates fall in the flower blooming date ranges. The problem is solved by sorting the flowers by their bloom start and bloom end dates and then performing binary searches to count the flowers that are in full bloom at the given dates.\n\n# Approach\n1. Create an empty list `ans` to store the results, which will indicate the number of flowers in full bloom for each person.\n2. Create two lists, `flower_bloom_start` and `flower_bloom_end`, by sorting the flowers list based on the start and end bloom dates, respectively. These lists represent the start and end dates of flower blooms.\n3. Define a binary search function `binary_search(array, date)` that searches for the index at which the date can be inserted in the array while maintaining the sorted order. This function returns the position where the date is greater than or equal to the elements in the array.\n4. Iterate through the people list, and for each `person\'s date`, use the binary search function to find the positions where the person\'s date falls in both flower_bloom_start and flower_bloom_end lists. These positions represent the flowers whose bloom dates include the person\'s date.\n5. Calculate the `difference` between the two positions `(a - b)` and store the result in the corresponding `index` of the `ans` list.\n6. Finally, `return the ans list`, which contains the counts of flowers in full bloom for each person.\n\n# Complexity\n- **Time complexity**:\nThe most time-consuming part of the algorithm is the sorting of the flowers list, which has a time complexity of **O(n * log(n))**, where n is the number of flowers. The binary search is performed for each person, resulting in **O(m * log(n))** complexity, where m is the number of people. Therefore, the overall time complexity is **O(n * log(n) + m * log(n))**.\n\n- **Space complexity**:\nThe code uses additional space to store the flower_bloom_start and flower_bloom_end lists, which have a combined space complexity of **O(n)**. The ans list also has a space complexity of **O(m)**, where m is the number of people. Therefore, the overall space complexity is **O(n + m)**.\n\n# Code\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n ans=[0]*len(people)\n flower_bloom_start=[x[0] for x in sorted(flowers,key=lambda x:x[0])]\n flower_bloom_end=[x[1]+1 for x in sorted(flowers,key=lambda x:x[1])]\n def binary_search(array,date):\n low,high=0,len(array)\n while low<high:\n mid=(low+high)//2\n\n if array[mid]>date:\n high=mid\n else:\n low=mid+1\n return low\n for i in range(len(people)):\n a=binary_search(flower_bloom_start,people[i])\n b=binary_search(flower_bloom_end,people[i])\n ans[i]=a-b\n return ans\n\n \n``` | 2 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
|| Beginner Friendly || Easy Solution Line By Line Explanation || Beats 100 % || PYTHON || C++ || | number-of-flowers-in-full-bloom | 1 | 1 | # BEATS 100% Python And Ruby\n\n\n\n# Intuition\nThe intuition for this problem is to track the bloom intervals of flowers and determine the bloom status for each person. This involves processing the intervals and persons in a way that efficiently calculates the bloom status.\n\n# Approach\nThe approach used in this solution involves maintaining a defaultdict to track bloom intervals of flowers. The code iterates through the flower intervals, updates the intervals in the dictionary, and processes the persons in reverse order of their bloom time. It calculates the bloom count at each time step and records the bloom status for each person. The result is returned as a list of bloom statuses for each person.\n\n# Complexity\n- Time complexity:\nThe time complexity of this solution is determined by sorting the bloom times and processing the persons. In the worst case, it\'s O(n*log(n)) for sorting the bloom times and O(n) for processing the persons, resulting in a time complexity of O(n*log(n)).\n\n- Space complexity:\nThe space complexity primarily depends on the dictionaries used to track bloom intervals and bloom status. The space complexity is O(n) to store bloom intervals, bloom statuses, and the remaining persons.\n\n# Code\n# PYTHON\n```python\nfrom collections import defaultdict\n\nclass Solution:\n def fullBloomFlowers(self, flowers, persons):\n # Create a defaultdict to track bloom intervals\n blooming_intervals = defaultdict(int)\n\n # Iterate through the flower intervals and update bloom_intervals\n for start, end in flowers:\n blooming_intervals[start] += 1\n blooming_intervals[end + 1] -= 1\n\n # Initialize dictionaries and variables\n blooming_status, bloom_count = {}, 0\n remaining_persons = sorted(persons, reverse=True) # Sort persons in reverse order\n\n # Iterate through sorted bloom times\n for time in sorted(blooming_intervals.keys()):\n bloom_change = blooming_intervals[time] # Get bloom change at this time\n\n # Process persons whose bloom time has arrived\n while remaining_persons and time > remaining_persons[-1]:\n blooming_status[remaining_persons.pop()] = bloom_count\n\n # If there are no remaining persons, exit the loop\n if not remaining_persons:\n break\n\n bloom_count += bloom_change # Update bloom count\n\n # Create a list of bloom statuses for each person\n return [blooming_status[p] if p in blooming_status else 0 for p in persons]\n```\n# JAVA\n```\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] persons) {\n int n = persons.length;\n int[] result = new int[n];\n \n // Create a TreeMap to track flower intervals and their frequencies.\n TreeMap<Integer, Integer> treeMap = new TreeMap<>();\n for (int i = 0; i < flowers.length; i++) {\n // Increment the start time frequency.\n treeMap.put(flowers[i][0], treeMap.getOrDefault(flowers[i][0], 0) + 1);\n // Decrement the end time frequency (add 1 to end time to indicate the end of the interval).\n treeMap.put(flowers[i][1] + 1, treeMap.getOrDefault(flowers[i][1] + 1, 0) - 1);\n }\n \n // Create another TreeMap to accumulate the frequencies and track the number of flowers blooming at each moment.\n TreeMap<Integer, Integer> sum = new TreeMap<>();\n int prev = 0;\n for (Map.Entry<Integer, Integer> entry : treeMap.entrySet()) {\n prev += entry.getValue();\n sum.put(entry.getKey(), prev);\n }\n \n // Calculate bloom statuses for each person.\n for (int i = 0; i < n; i++) {\n // Find the floor entry for the person\'s bloom time.\n Map.Entry<Integer, Integer> entry = sum.floorEntry(persons[i]);\n if (entry != null) {\n result[i] = entry.getValue(); // Store the number of blooming flowers at that time.\n }\n }\n return result;\n }\n}\n\n```\n# C++\n```\nclass Solution {\npublic:\n vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {\n vector<int> st, bl; // Initialize vectors to store start and bloom times.\n int n = flowers.size();\n\n // Extract start and bloom times from the flowers array and store them in separate vectors.\n for (auto i : flowers) {\n int x = i[0];\n int y = i[1];\n st.push_back(x);\n bl.push_back(y);\n }\n\n // Sort the start and bloom time vectors in ascending order.\n sort(st.begin(), st.end());\n sort(bl.begin(), bl.end());\n\n vector<int> v; // Initialize a result vector to store bloom statuses.\n\n // Iterate through each person\'s bloom time.\n for (int i = 0; i < people.size(); i++) {\n // Calculate the number of flowers blooming at or before the person\'s bloom time.\n int p = st.size() - (upper_bound(st.begin(), st.end(), people[i]) - st.begin());\n\n // Calculate the number of flowers blooming at or after the person\'s bloom time.\n int q = bl.size() - (lower_bound(bl.begin(), bl.end(), people[i]) - bl.begin());\n\n // Calculate the bloom status for the person and store it in the result vector.\n v.push_back(q - p);\n }\n\n return v; // Return the vector containing bloom statuses for each person.\n }\n};\n\n```\n# Ruby\n```\n# Define a function full_bloom_flowers that takes two arrays as input: flowers and people.\n# It calculates the bloom status for each person based on their bloom time and flower intervals.\n\ndef full_bloom_flowers(flowers, people)\n flowers_size = flowers.size # Get the total number of flower intervals.\n \n # Extract and sort the start and end indices of flower intervals.\n start_indices = flowers.map(&:first).sort\n end_indices = flowers.map(&:last).sort\n\n # Initialize an array to store bloom statuses for each person and iterate through each person.\n people.map do |num|\n # Calculate the number of flowers starting after the person\'s bloom time.\n # Use bsearch_index to find the first start index greater than the person\'s bloom time.\n # If not found, use flowers_size (all intervals are valid).\n\n start_index = start_indices.bsearch_index { |start_index| start_index > num }\n start_index ||= flowers_size\n\n # Calculate the number of flowers blooming after or at the person\'s bloom time.\n # Use bsearch_index to find the first end index greater than or equal to the person\'s bloom time.\n # If not found, use flowers_size (all intervals are valid).\n\n end_index = end_indices.bsearch_index { |end_index| end_index >= num }\n end_index ||= flowers_size\n\n # Calculate the bloom status for the person by subtracting the end index from the start index.\n # This represents the number of flowers blooming in the person\'s desired time range.\n\n bloom_status = start_index - end_index\n\n # Return the calculated bloom status for the current person.\n bloom_status\n end\nend\n\n```\n | 24 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
Video Solution | Explanation With Drawings | In Depth | Java | C++ | Python 3 | number-of-flowers-in-full-bloom | 1 | 1 | # Intuition, approach and complexity discussed in detail in video solution\nhttps://youtu.be/s3pk2n_Fi3g\n\n# Code\nJava\n```\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] persons) {\n int n = flowers.length;\n int[] bloomStartTime = new int[n], bloomEndTime = new int[n];\n \n for (int indx = 0; indx < n; indx++) {\n bloomStartTime[indx] = flowers[indx][0];\n bloomEndTime[indx] = flowers[indx][1];\n }\n \n Arrays.sort(bloomStartTime);\n Arrays.sort(bloomEndTime);\n \n int[] res = new int[persons.length];\n \n for (int indx = 0; indx < persons.length; indx++) {\n int t = persons[indx];\n int bloomStartNumber = upper_bound(bloomStartTime, t);\n int bloomEndNumber = lower_bound(bloomEndTime, t);\n res[indx] = bloomStartNumber - bloomEndNumber;\n }\n \n return res;\n }\n \n private int upper_bound(int[] arr, int target) {\n int left = 0;\n int right = arr.length;\n \n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] <= target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return left;\n }\n \n private int lower_bound(int[] arr, int target) {\n int left = 0;\n int right = arr.length;\n \n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return left;\n }\n}\n```\n\nC++\n```\nclass Solution {\npublic:\n vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {\n int sz = people.size();\n vector<int> answers(sz, 0), bloomStartTime, bloomEndTime;\n for(auto × : flowers){\n bloomStartTime.push_back(times[0]);\n bloomEndTime.push_back(times[1]);\n }\n sort(bloomStartTime.begin(), bloomStartTime.end());\n sort(bloomEndTime.begin(), bloomEndTime.end());\n for(int indx = 0; indx < sz; indx++){\n int arrivalTime = people[indx]; \n //index of first time value in bloomStartTime array which is having value greater than current arrival time\n int bloomStartNumber = upper_bound(bloomStartTime.begin(), bloomStartTime.end(), arrivalTime) - bloomStartTime.begin();\n\n //index of first time value in bloomEndTime array which is having value atleast equal current arrival Time\n int bloomEndNumber = lower_bound(bloomEndTime.begin(), bloomEndTime.end(), arrivalTime) - bloomEndTime.begin();\n answers[indx] = bloomStartNumber - bloomEndNumber;\n }\n return answers;\n } \n};\n```\nPython 3\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n bloomStartTime = sorted([s for s, e in flowers])\n bloomEndTime = sorted([e for s, e in flowers])\n return [bisect_right(bloomStartTime, arrivalTime) - bisect_left(bloomEndTime, arrivalTime) for arrivalTime in people]\n``` | 1 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
A True Classic Line Sweep Algo | number-of-flowers-in-full-bloom | 0 | 1 | \n# Code\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n\n sweep = collections.defaultdict(int)\n\n for s,e in flowers:\n sweep[s]+=1\n sweep[e+1]-=1\n\n flowers_in_bloom = 0\n times = []\n for time in sorted(sweep):\n flowers_in_bloom+=sweep[time]\n times.append((time,flowers_in_bloom))\n\n ans = []\n for person in people:\n \n idx = bisect_left(times,person,key = lambda x: x[0])\n if person not in sweep:\n idx-=1\n ans.append(times[idx][1])\n return ans\n\n\n\n\n\n\n``` | 1 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
🧩 "Blooming Flowers Problem: A Step-by-Step Guide with Simple Code Explanation 🌼📝" | number-of-flowers-in-full-bloom | 0 | 1 | # Intuition:\n\nIn simple terms, this code sorts the flowers by their start and end times and then counts how many flowers are blooming at the preferred times of each person. It returns a list of counts for each person. The time complexity is reasonably efficient, while the space complexity depends on the number of flowers.\n\n# Approach:\n\n1. First, the code sorts the list of flowers twice, once by their start times and once by their end times, resulting in two lists: `flowersStartTime` and `flowersEndTime`.\n\n2. Then, it iterates through each person\'s preference, denoted by the variable `people[i]`.\n\n3. Inside the loop, it uses the `bisect_right` and `bisect_left` functions from the `bisect` module. These functions are used to find the rightmost and leftmost indices where `people[i]` could be inserted into the `flowersStartTime` and `flowersEndTime` lists without disrupting their sorted order. This effectively finds how many flowers are currently blooming at the time preferred by the current person.\n\n4. It calculates the difference between the right index and the left index, which represents the number of blooming flowers matching the person\'s preference.\n\n5. Finally, it updates the `people[i]` with the count of blooming flowers that match their preference.\n\n6. The function returns the modified `people` list with the counts of blooming flowers for each person.\n\n#Complexity:\n\n- Time complexity: The sorting steps take O(N * log(N)) time, where N is the number of flowers. The loop through people takes O(M) time, where M is the number of people. Therefore, the overall time complexity is O(N * log(N) + M), which can be approximated as O(N * log(N)) if M is much smaller than N.\n\n- Space complexity: The additional space used for the two sorted lists (`flowersStartTime` and `flowersEndTime`) is O(N) as they store the start and end times of each flower. The space complexity of the input and output lists is not considered in the space complexity analysis.\n\n\n\n# Code\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n flowersStartTime = sorted(startTime for startTime, endTime in flowers)\n flowersEndTime = sorted(endTime for startTime, endTime in flowers)\n print(flowersStartTime, flowersEndTime)\n for i in range(len(people)):\n rightIndex = bisect_right(flowersStartTime, people[i]) \n leftIndex = bisect_left(flowersEndTime, people[i])\n people[i] = rightIndex - leftIndex\n\n return people\n\n\t \n``` | 1 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
Go/Python/JavaScript/Java O(n*log(n)) time | O(n) space | number-of-flowers-in-full-bloom | 1 | 1 | # Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```golang []\nfunc fullBloomFlowers(flowers [][]int, people []int) []int {\n starts := make([]int,len(flowers))\n ends := make([]int,len(flowers))\n for i,f := range(flowers){\n starts[i] = f[0]\n ends[i] = f[1]\n }\n sort.Ints(starts)\n sort.Ints(ends)\n memo := make(map[int][2]int)\n answer := make([]int,len(people))\n\n for i,item := range(people){\n var left int\n var right int\n if v,ok := memo[item];ok{\n left = v[0]\n right = v[1]\n }else{\n left = bisect_right(starts,item)\n right = bisect_left(ends,item)\n memo[item] = [2]int{left,right}\n }\n answer[i] = left-right\n }\n \n return answer\n}\n\nfunc bisect_left(arr []int,target int) int{\n left := 0\n right := len(arr)-1\n for left <= right{\n mid := (left+right)/2\n if arr[mid] >= target{\n right = mid-1\n }else{\n left = mid+1\n }\n }\n return left\n}\n\nfunc bisect_right(arr []int,target int) int{\n left := 0\n right := len(arr)-1\n for left <= right{\n mid := (left+right)/2\n if arr[mid] <= target{\n left = mid+1\n }else{\n right = mid-1\n }\n }\n return left\n}\n```\n```python []\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n starts = [f[0] for f in flowers]\n ends = [f[1] for f in flowers]\n starts.sort()\n ends.sort()\n memo = {}\n answer = [0 for _ in range(len(people))]\n\n for i,item in enumerate(people):\n if item in memo:\n left,right = memo[item]\n else:\n left = bisect_right(starts,item)\n right = bisect_left(ends,item)\n memo[item] = [left,right]\n print(left,right)\n answer[i] = left-right\n \n return answer\n\n\ndef bisect_left(arr,target):\n left = 0\n right = len(arr)-1\n while left <= right:\n mid = (left+right)//2\n if arr[mid] >= target:\n right = mid-1\n else:\n left = mid+1\n return left\n\ndef bisect_right(arr,target):\n left = 0\n right = len(arr)-1\n while left <= right:\n mid = (left+right)//2\n if arr[mid] <= target:\n left = mid+1\n else:\n right = mid-1\n return left\n```\n```javascript []\n/**\n * @param {number[][]} flowers\n * @param {number[]} people\n * @return {number[]}\n */\nvar fullBloomFlowers = function(flowers, people) {\n let starts = Array(flowers.length)\n let ends = Array(flowers.length)\n for (let i=0;i<flowers.length;i++){\n starts[i] = flowers[i][0]\n ends[i] = flowers[i][1]\n }\n starts.sort((a,b) => a-b)\n ends.sort((a,b) => a-b)\n let memo = new Map()\n let answer = Array(people.length)\n\n for (let i=0;i<people.length;i++){\n let item = people[i]\n let left\n let right\n if (memo.has(item)){\n left = memo.get(item)[0]\n right = memo.get(item)[1]\n }else{\n left = bisect_right(starts,item)\n right = bisect_left(ends,item)\n memo.set(item,[left,right])\n }\n answer[i] = left-right\n }\n \n return answer\n};\n\nfunction bisect_left(arr,target){\n let left = 0\n let right = arr.length-1\n while (left <= right){\n let mid = Math.floor((left+right)/2)\n if (arr[mid] >= target){\n right = mid-1\n }else{\n left = mid+1\n }\n }\n return left\n}\n\nfunction bisect_right(arr,target){\n let left = 0\n let right = arr.length-1\n while (left <= right){\n let mid = Math.floor((left+right)/2)\n if (arr[mid] <= target){\n left = mid+1\n }else{\n right = mid-1\n }\n }\n return left\n}\n```\n```java []\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] people) {\n int[] starts = new int[flowers.length];\n int[] ends = new int[flowers.length];\n for (int i=0;i<flowers.length;i++){\n starts[i] = flowers[i][0];\n ends[i] = flowers[i][1];\n }\n Arrays.sort(starts);\n Arrays.sort(ends);\n HashMap<Integer,int[]> memo = new HashMap<>();\n int[] answer = new int[people.length];\n\n for (int i=0;i<people.length;i++){\n int item = people[i];\n int left;\n int right;\n if (memo.containsKey(item)){\n left = memo.get(item)[0];\n right = memo.get(item)[1];\n }else{\n left = bisect_right(starts,item);\n right = bisect_left(ends,item);\n memo.put(item, new int[]{left,right});\n }\n answer[i] = left-right;\n }\n \n return answer;\n };\n\n public int bisect_left(int[] arr, int target){\n int left = 0;\n int right = arr.length-1;\n while (left <= right){\n int mid = (int) Math.floor((left+right)/2);\n if (arr[mid] >= target){\n right = mid-1;\n }else{\n left = mid+1;\n }\n }\n return left;\n }\n\n public int bisect_right(int[] arr, int target){\n int left = 0;\n int right = arr.length-1;\n while (left <= right){\n int mid = (int) Math.floor((left+right)/2);\n if (arr[mid] <= target){\n left = mid+1;\n }else{\n right = mid-1;\n }\n }\n return left;\n }\n}\n``` | 1 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
sweep line | number-of-flowers-in-full-bloom | 1 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) \n {\n vector<vector<int>> arr;\n for (auto flower : flowers)\n {\n arr.push_back({flower[0], 1});\n arr.push_back({flower[1] + 1, -1});\n }\n vector<vector<int>> persons;\n for (int i = 0; i < people.size(); ++i)\n {\n persons.push_back({people[i], i});\n }\n sort(arr.begin(), arr.end(), compare);\n sort(persons.begin(), persons.end(), compare);\n\n int i = 0, j = 0, cnt = 0;\n vector<int> res;\n for (int x = 0; x < people.size(); ++x)\n {\n res.push_back(0);\n }\n\n while (i < persons.size())\n {\n int time = persons[i][0];\n int idx = persons[i][1];\n while (j < arr.size() && arr[j][0] <= time)\n {\n cnt += arr[j][1];\n cnt = max(cnt, 0);\n j++;\n }\n res[idx] = cnt;\n i++;\n }\n return res;\n }\n\nprivate:\n static bool compare(const vector<int>& a, const vector<int>& b)\n {\n return a[0] == b[0] ? a[1] < b[1] : a[0] < b[0];\n }\n};\n```\n```\nclass Solution:\n def fullBloomFlowers(self, flowers: List[List[int]], people: List[int]) -> List[int]:\n arr = []\n for flower in flowers:\n arr.append([flower[0], 1])\n arr.append([flower[1] + 1 , -1])\n arr = sorted(arr, key = lambda x : (x[0], x[1]))\n persons = [[j, i] for i, j in enumerate(people)]\n persons = sorted(persons, key = lambda x : x[0])\n res = [0] * len(people)\n\n i, j, cnt = 0, 0, 0\n while i < len(persons):\n time, idx = persons[i]\n while j < len(arr) and arr[j][0] <= time:\n cnt += arr[j][1]\n cnt = max(cnt, 0)\n j += 1\n\n res[idx] = cnt\n i += 1\n return res\n```\n\n```\nclass Solution {\n public int[] fullBloomFlowers(int[][] flowers, int[] people) {\n List<int[]> flower = new ArrayList<>();\n for (int[] f : flowers) {\n flower.add(new int[]{f[0], 1});\n flower.add(new int[]{f[1] + 1, -1});\n }\n Collections.sort(flower, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o1[0] - o2[0]);\n List<int[]> persons = new ArrayList<>();\n for (int i = 0; i < people.length; ++i) {\n persons.add(new int[]{people[i], i});\n }\n int[] res = new int[people.length];\n Collections.sort(persons, (o1, o2) -> o1[0] - o2[0]);\n\n int i = 0, j = 0, cnt = 0;\n while (i < persons.size()) {\n int time = persons.get(i)[0];\n int idx = persons.get(i)[1];\n while (j < flower.size() && flower.get(j)[0] <= time) {\n cnt += flower.get(j)[1];\n cnt = Math.max(0, cnt);\n j++;\n }\n if (time >= flower.get(flower.size() - 1)[0]) {\n res[idx] = 0;\n } else {\n res[idx] = cnt;\n }\n i++;\n }\n return res;\n }\n}\n```\n\n\n\n\n | 1 | You are given a **0-indexed** 2D integer array `flowers`, where `flowers[i] = [starti, endi]` means the `ith` flower will be in **full bloom** from `starti` to `endi` (**inclusive**). You are also given a **0-indexed** integer array `people` of size `n`, where `poeple[i]` is the time that the `ith` person will arrive to see the flowers.
Return _an integer array_ `answer` _of size_ `n`_, where_ `answer[i]` _is the **number** of flowers that are in full bloom when the_ `ith` _person arrives._
**Example 1:**
**Input:** flowers = \[\[1,6\],\[3,7\],\[9,12\],\[4,13\]\], poeple = \[2,3,7,11\]
**Output:** \[1,2,2,2\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Example 2:**
**Input:** flowers = \[\[1,10\],\[3,3\]\], poeple = \[3,3,2\]
**Output:** \[2,2,1\]
**Explanation:** The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.
**Constraints:**
* `1 <= flowers.length <= 5 * 104`
* `flowers[i].length == 2`
* `1 <= starti <= endi <= 109`
* `1 <= people.length <= 5 * 104`
* `1 <= people[i] <= 109` | Divide the corridor into segments. Each segment has two seats, starts precisely with one seat, and ends precisely with the other seat. How many dividers can you install between two adjacent segments? You must install precisely one. Otherwise, you would have created a section with not exactly two seats. If there are k plants between two adjacent segments, there are k + 1 positions (ways) you could install the divider you must install. The problem now becomes: Find the product of all possible positions between every two adjacent segments. |
python ||O(N) | count-prefixes-of-a-given-string | 0 | 1 | Time Complexcity O(N)\nspace Complexcity O(1)\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n count=0\n for word in words:\n n=len(word)\n if s[0:n]==word:\n count+=1\n return count\n \n``` | 1 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
Python simple solution | count-prefixes-of-a-given-string | 0 | 1 | # Approach\nCheck for each word if is prefix of s.\n\n# Code\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n res = 0\n\n for word in words:\n if s.startswith(word):\n res += 1\n\n return res\n```\n\nLike it? Please upvote! | 6 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
Python one line solution | count-prefixes-of-a-given-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n return len([i for i in words if s.startswith(i)])\n``` | 2 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
one line solution | count-prefixes-of-a-given-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n return sum(1 for x in words if s.startswith(x))\n``` | 3 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
Easy python solution | count-prefixes-of-a-given-string | 0 | 1 | ```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n count=0\n for i in words:\n if (s[:len(i)]==i):\n count+=1\n return count\n``` | 15 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
Pyhton3 oneliner using startswith() | count-prefixes-of-a-given-string | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n count = 0\n for i in words:\n if s.startswith(i):\n count += 1\n return count\n\n #One Liner\n\n return sum(1 for i in words if s.startswith(i))\n``` | 1 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
Easy Python solution | count-prefixes-of-a-given-string | 0 | 1 | ```\ndef countPrefixes(self, words: List[str], s: str) -> int:\n c=0\n for i in words:\n l=len(i)\n if i==s[:l]:\n c+=1\n return c\n``` | 3 | You are given a string array `words` and a string `s`, where `words[i]` and `s` comprise only of **lowercase English letters**.
Return _the **number of strings** in_ `words` _that are a **prefix** of_ `s`.
A **prefix** of a string is a substring that occurs at the beginning of the string. A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** words = \[ "a ", "b ", "c ", "ab ", "bc ", "abc "\], s = "abc "
**Output:** 3
**Explanation:**
The strings in words which are a prefix of s = "abc " are:
"a ", "ab ", and "abc ".
Thus the number of strings in words which are a prefix of s is 3.
**Example 2:**
**Input:** words = \[ "a ", "a "\], s = "aa "
**Output:** 2
**Explanation:**
Both of the strings are a prefix of s.
Note that the same string can occur multiple times in words, and it should be counted each time.
**Constraints:**
* `1 <= words.length <= 1000`
* `1 <= words[i].length, s.length <= 10`
* `words[i]` and `s` consist of lowercase English letters **only**. | Notice that the number of 1’s to be grouped together is fixed. It is the number of 1's the whole array has. Call this number total. We should then check for every subarray of size total (possibly wrapped around), how many swaps are required to have the subarray be all 1’s. The number of swaps required is the number of 0’s in the subarray. To eliminate the circular property of the array, we can append the original array to itself. Then, we check each subarray of length total. How do we avoid recounting the number of 0’s in the subarray each time? The Sliding Window technique can help. |
💡Python O(n) simple solution | minimum-average-difference | 0 | 1 | # Intuition\nAccording to constraint `1 <= nums.length <= 10 ** 5` we cannot re-calculate avg values for sub-arrays every time.\n\n# Approach\n\n1. Right handside area\n 1. Calculate a sum for all elements in `nums` for the further tracking\n 2. Remember `nums` len\n2. Left handside area\n 1. Set placeholders because we begin with the first index `0` we have nothing on the left area so it is `0` as well as the count of elements is `0`\n3. On each step of iteration we need to transfer numbers from the right area to the left area. We can do it by substituion the current number from the right area sum and adding it to the left area. Also we update the numbers of integers accordingly.\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution:\n def minimumAverageDifference(self, nums: List[int]) -> int:\n\n sum_right = sum(nums)\n len_right = len(nums)\n sum_left = 0\n len_left = 0\n\n min_avg = inf\n index = 0\n\n for i in range(len(nums)):\n \n sum_left += nums[i]\n len_left += 1\n\n sum_right -= nums[i]\n len_right -= 1\n\n #in case of only zeroes left on right\n if sum_right == 0:\n v = sum_left // len_left\n else:\n v = abs(\n sum_left // len_left - sum_right // len_right\n )\n\n if v < min_avg:\n min_avg = v\n index = i\n\n return index\n\n``` | 2 | You are given a **0-indexed** integer array `nums` of length `n`.
The **average difference** of the index `i` is the **absolute** **difference** between the average of the **first** `i + 1` elements of `nums` and the average of the **last** `n - i - 1` elements. Both averages should be **rounded down** to the nearest integer.
Return _the index with the **minimum average difference**_. If there are multiple such indices, return the **smallest** one.
**Note:**
* The **absolute difference** of two numbers is the absolute value of their difference.
* The **average** of `n` elements is the **sum** of the `n` elements divided (**integer division**) by `n`.
* The average of `0` elements is considered to be `0`.
**Example 1:**
**Input:** nums = \[2,5,3,9,5,3\]
**Output:** 3
**Explanation:**
- The average difference of index 0 is: |2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3.
- The average difference of index 1 is: |(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2.
- The average difference of index 2 is: |(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2.
- The average difference of index 3 is: |(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0.
- The average difference of index 4 is: |(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1.
- The average difference of index 5 is: |(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4.
The average difference of index 3 is the minimum average difference so return 3.
**Example 2:**
**Input:** nums = \[0\]
**Output:** 0
**Explanation:**
The only index is 0 so return 0.
The average difference of index 0 is: |0 / 1 - 0| = |0 - 0| = 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | Which data structure can be used to efficiently check if a string exists in startWords? After appending a letter, all letters of a string can be rearranged in any possible way. How can we use this to reduce our search space while checking if a string in targetWords can be obtained from a string in startWords? |
Python || 91.23 % Faster || Prefix Sum || O(n) Solution | minimum-average-difference | 0 | 1 | ```\nclass Solution:\n def minimumAverageDifference(self, nums: List[int]) -> int:\n n=len(nums)\n pre,post=[nums[0]]*n,[nums[n-1]]*n\n for i in range(1,n):\n pre[i]=(nums[i]+pre[i-1])\n for i in range(n-2,-1,-1):\n post[i]=(nums[i]+post[i+1])\n m,f=1000000,n-1\n for i in range(n):\n x=pre[i]//(i+1)\n if i==n-1:\n y=0\n else:\n y=post[i+1]//(n-i-1)\n if m>abs(x-y):\n m=abs(x-y)\n f=i\n return f\n```\n\n**An upvote will be encouraging** | 2 | You are given a **0-indexed** integer array `nums` of length `n`.
The **average difference** of the index `i` is the **absolute** **difference** between the average of the **first** `i + 1` elements of `nums` and the average of the **last** `n - i - 1` elements. Both averages should be **rounded down** to the nearest integer.
Return _the index with the **minimum average difference**_. If there are multiple such indices, return the **smallest** one.
**Note:**
* The **absolute difference** of two numbers is the absolute value of their difference.
* The **average** of `n` elements is the **sum** of the `n` elements divided (**integer division**) by `n`.
* The average of `0` elements is considered to be `0`.
**Example 1:**
**Input:** nums = \[2,5,3,9,5,3\]
**Output:** 3
**Explanation:**
- The average difference of index 0 is: |2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3.
- The average difference of index 1 is: |(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2.
- The average difference of index 2 is: |(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2.
- The average difference of index 3 is: |(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0.
- The average difference of index 4 is: |(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1.
- The average difference of index 5 is: |(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4.
The average difference of index 3 is the minimum average difference so return 3.
**Example 2:**
**Input:** nums = \[0\]
**Output:** 0
**Explanation:**
The only index is 0 so return 0.
The average difference of index 0 is: |0 / 1 - 0| = |0 - 0| = 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | Which data structure can be used to efficiently check if a string exists in startWords? After appending a letter, all letters of a string can be rearranged in any possible way. How can we use this to reduce our search space while checking if a string in targetWords can be obtained from a string in startWords? |
Python | SImple iterative solution | minimum-average-difference | 0 | 1 | # Approach\n1) Calculate initial sum of all elements in array\n2) On each iteration step calculate prefix and suffix (initila sum - prefix) and recalculate answer!\n\n# Complexity\n- Time complexity: $$O(N)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution:\n def minimumAverageDifference(self, nums: List[int]) -> int:\n first_half, second_half = 0, sum(nums)\n num_first_half = 0\n ans, min_ind = 1e18, 1e18\n for i in range(len(nums)):\n first_half += nums[i]\n num_first_half += 1\n if i < len(nums) - 1:\n carry = abs((first_half // num_first_half) - ((second_half - first_half)//(len(nums) - i - 1)))\n else:\n carry = abs(first_half // num_first_half)\n if carry < ans:\n ans = carry\n min_ind = i\n return min_ind \n``` | 1 | You are given a **0-indexed** integer array `nums` of length `n`.
The **average difference** of the index `i` is the **absolute** **difference** between the average of the **first** `i + 1` elements of `nums` and the average of the **last** `n - i - 1` elements. Both averages should be **rounded down** to the nearest integer.
Return _the index with the **minimum average difference**_. If there are multiple such indices, return the **smallest** one.
**Note:**
* The **absolute difference** of two numbers is the absolute value of their difference.
* The **average** of `n` elements is the **sum** of the `n` elements divided (**integer division**) by `n`.
* The average of `0` elements is considered to be `0`.
**Example 1:**
**Input:** nums = \[2,5,3,9,5,3\]
**Output:** 3
**Explanation:**
- The average difference of index 0 is: |2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3.
- The average difference of index 1 is: |(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2.
- The average difference of index 2 is: |(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2.
- The average difference of index 3 is: |(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0.
- The average difference of index 4 is: |(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1.
- The average difference of index 5 is: |(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4.
The average difference of index 3 is the minimum average difference so return 3.
**Example 2:**
**Input:** nums = \[0\]
**Output:** 0
**Explanation:**
The only index is 0 so return 0.
The average difference of index 0 is: |0 / 1 - 0| = |0 - 0| = 0.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | Which data structure can be used to efficiently check if a string exists in startWords? After appending a letter, all letters of a string can be rearranged in any possible way. How can we use this to reduce our search space while checking if a string in targetWords can be obtained from a string in startWords? |
[Python] DFS solution with explaination | count-unguarded-cells-in-the-grid | 0 | 1 | Idea is to mark all locations which the guard can see with \'X\' value. Then later just count the non marked cells.\n\nDefines a named tuple called "Directions" with two fields x and y, which represents the movement directions on a 2D grid.\n\n\nCreates a matrix with zeros of size m x n and fills it with \'G\' and \'W\' for the guard and wall locations, respectively.\n\nIt then performs a depth-first search starting from each guard location, moving in each of the four directions specified by the Directions named tuple.\n\nDuring the depth-first search, if the search goes out of bounds, hits a wall or another guard, it stops. Otherwise, it marks the current cell as \'X\' to indicate it has been visited and continues the search in the specified direction.\n\nAfter the search is complete, the method counts the number of cells in the matrix that are still 0 (i.e., unguarded) and returns the count.\n\n\n```\nfrom collections import namedtuple\nfrom typing import List\n\nDirections = namedtuple(\'Directions\', [\'x\', \'y\'])\nup = Directions(-1, 0)\ndown = Directions(1, 0)\nleft = Directions(0, -1)\nright = Directions(0, 1)\n\n\ndef countUnguarded(m: int, n: int, guards: List[List[int]], walls: List[List[int]]) -> int:\n matrix = [[0 for _ in range(n)] for _ in range(m)]\n for x, y in guards:\n matrix[x][y] = \'G\'\n for x, y in walls:\n matrix[x][y] = \'W\'\n\n def dfs(row, col, direction):\n if row < 0 or row >= m or col < 0 or col >= n or matrix[row][col] == \'W\' or matrix[row][col] == \'G\':\n return\n\n matrix[row][col] = \'X\'\n dfs(row + direction.x, col + direction.y, direction)\n\n for x in range(m):\n for y in range(n):\n if matrix[x][y] == \'G\':\n dfs(x + 1, y, down)\n dfs(x - 1, y, up)\n dfs(x, y + 1, right)\n dfs(x, y - 1, left)\n\n counter = 0\n for x in range(m):\n for y in range(n):\n if matrix[x][y] == 0:\n counter += 1\n\n return counter\n\n\n```\n | 1 | You are given two integers `m` and `n` representing a **0-indexed** `m x n` grid. You are also given two 2D integer arrays `guards` and `walls` where `guards[i] = [rowi, coli]` and `walls[j] = [rowj, colj]` represent the positions of the `ith` guard and `jth` wall respectively.
A guard can see **every** cell in the four cardinal directions (north, east, south, or west) starting from their position unless **obstructed** by a wall or another guard. A cell is **guarded** if there is **at least** one guard that can see it.
Return _the number of unoccupied cells that are **not** **guarded**._
**Example 1:**
**Input:** m = 4, n = 6, guards = \[\[0,0\],\[1,1\],\[2,3\]\], walls = \[\[0,1\],\[2,2\],\[1,4\]\]
**Output:** 7
**Explanation:** The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.
**Example 2:**
**Input:** m = 3, n = 3, guards = \[\[1,1\]\], walls = \[\[0,1\],\[1,0\],\[2,1\],\[1,2\]\]
**Output:** 4
**Explanation:** The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.
**Constraints:**
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `1 <= guards.length, walls.length <= 5 * 104`
* `2 <= guards.length + walls.length <= m * n`
* `guards[i].length == walls[j].length == 2`
* `0 <= rowi, rowj < m`
* `0 <= coli, colj < n`
* All the positions in `guards` and `walls` are **unique**. | List the planting like the diagram above shows, where a row represents the timeline of a seed. A row i is above another row j if the last day planting seed i is ahead of the last day for seed j. Does it have any advantage to spend some days to plant seed j before completely planting seed i? No. It does not help seed j but could potentially delay the completion of seed i, resulting in a worse final answer. Remaining focused is a part of the optimal solution. Sort the seeds by their growTime in descending order. Can you prove why this strategy is the other part of the optimal solution? Note the bloom time of a seed is the sum of plantTime of all seeds preceding this seed plus the growTime of this seed. There is no way to improve this strategy. The seed to bloom last dominates the final answer. Exchanging the planting of this seed with another seed with either a larger or smaller growTime will result in a potentially worse answer. |
Python solution using DFS. | count-unguarded-cells-in-the-grid | 0 | 1 | \n```\nclass Solution:\n def countUnguarded(self, m: int, n: int, guards: List[List[int]], walls: List[List[int]]) -> int:\n \n #Create a matrix, hint from question\n mat = [[0 for _ in range(n)] for _ in range(m)] \n \n for [i,j] in guards:\n mat[i][j] = 1 \n for [i,j] in walls:\n mat[i][j] = -1\n \n #dfs for marking paths.\n def dfs(i,j,di):\n if i<0 or i>=m or j<0 or j>=n or mat[i][j] == 1 or mat[i][j] == -1:\n return\n else:\n mat[i][j] = 2\n i = i + lst[di]\n j = j + lst[di+1]\n dfs(i,j,di)\n \n lst = [1,0,-1,0,1]\n for [i,j] in guards:\n for idx in range(4): \n k = i + lst[idx]\n l = j + lst[idx+1]\n dfs(k,l,idx)\n \n #count uncovered cells.\n count = 0\n for i in range(m):\n for j in range(n):\n if mat[i][j]==0:\n count +=1\n return count\n``` | 1 | You are given two integers `m` and `n` representing a **0-indexed** `m x n` grid. You are also given two 2D integer arrays `guards` and `walls` where `guards[i] = [rowi, coli]` and `walls[j] = [rowj, colj]` represent the positions of the `ith` guard and `jth` wall respectively.
A guard can see **every** cell in the four cardinal directions (north, east, south, or west) starting from their position unless **obstructed** by a wall or another guard. A cell is **guarded** if there is **at least** one guard that can see it.
Return _the number of unoccupied cells that are **not** **guarded**._
**Example 1:**
**Input:** m = 4, n = 6, guards = \[\[0,0\],\[1,1\],\[2,3\]\], walls = \[\[0,1\],\[2,2\],\[1,4\]\]
**Output:** 7
**Explanation:** The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.
**Example 2:**
**Input:** m = 3, n = 3, guards = \[\[1,1\]\], walls = \[\[0,1\],\[1,0\],\[2,1\],\[1,2\]\]
**Output:** 4
**Explanation:** The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.
**Constraints:**
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `1 <= guards.length, walls.length <= 5 * 104`
* `2 <= guards.length + walls.length <= m * n`
* `guards[i].length == walls[j].length == 2`
* `0 <= rowi, rowj < m`
* `0 <= coli, colj < n`
* All the positions in `guards` and `walls` are **unique**. | List the planting like the diagram above shows, where a row represents the timeline of a seed. A row i is above another row j if the last day planting seed i is ahead of the last day for seed j. Does it have any advantage to spend some days to plant seed j before completely planting seed i? No. It does not help seed j but could potentially delay the completion of seed i, resulting in a worse final answer. Remaining focused is a part of the optimal solution. Sort the seeds by their growTime in descending order. Can you prove why this strategy is the other part of the optimal solution? Note the bloom time of a seed is the sum of plantTime of all seeds preceding this seed plus the growTime of this seed. There is no way to improve this strategy. The seed to bloom last dominates the final answer. Exchanging the planting of this seed with another seed with either a larger or smaller growTime will result in a potentially worse answer. |
it works | count-unguarded-cells-in-the-grid | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countUnguarded(self, m: int, n: int, guards: List[List[int]], walls: List[List[int]]) -> int:\n dirs = [(-1,0), (1,0), (0,-1), (0,1)]\n guarded = set()\n guardset = set(tuple(g) for g in guards)\n wallset = set(tuple(w) for w in walls)\n for gx, gy in guards:\n for dx, dy in dirs:\n x = gx\n y = gy\n while (0 <= dx + x < m) and (0 <= dy + y < n) and (tuple([x+dx, y+dy]) not in wallset) and (tuple([x+dx, y+dy]) not in guardset):\n guarded.add(tuple([x+dx, y+dy]))\n x += dx\n y += dy\n \n return m*n - len(guardset) - len(wallset) - len(guarded)\n``` | 0 | You are given two integers `m` and `n` representing a **0-indexed** `m x n` grid. You are also given two 2D integer arrays `guards` and `walls` where `guards[i] = [rowi, coli]` and `walls[j] = [rowj, colj]` represent the positions of the `ith` guard and `jth` wall respectively.
A guard can see **every** cell in the four cardinal directions (north, east, south, or west) starting from their position unless **obstructed** by a wall or another guard. A cell is **guarded** if there is **at least** one guard that can see it.
Return _the number of unoccupied cells that are **not** **guarded**._
**Example 1:**
**Input:** m = 4, n = 6, guards = \[\[0,0\],\[1,1\],\[2,3\]\], walls = \[\[0,1\],\[2,2\],\[1,4\]\]
**Output:** 7
**Explanation:** The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.
**Example 2:**
**Input:** m = 3, n = 3, guards = \[\[1,1\]\], walls = \[\[0,1\],\[1,0\],\[2,1\],\[1,2\]\]
**Output:** 4
**Explanation:** The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.
**Constraints:**
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `1 <= guards.length, walls.length <= 5 * 104`
* `2 <= guards.length + walls.length <= m * n`
* `guards[i].length == walls[j].length == 2`
* `0 <= rowi, rowj < m`
* `0 <= coli, colj < n`
* All the positions in `guards` and `walls` are **unique**. | List the planting like the diagram above shows, where a row represents the timeline of a seed. A row i is above another row j if the last day planting seed i is ahead of the last day for seed j. Does it have any advantage to spend some days to plant seed j before completely planting seed i? No. It does not help seed j but could potentially delay the completion of seed i, resulting in a worse final answer. Remaining focused is a part of the optimal solution. Sort the seeds by their growTime in descending order. Can you prove why this strategy is the other part of the optimal solution? Note the bloom time of a seed is the sum of plantTime of all seeds preceding this seed plus the growTime of this seed. There is no way to improve this strategy. The seed to bloom last dominates the final answer. Exchanging the planting of this seed with another seed with either a larger or smaller growTime will result in a potentially worse answer. |
27 lines easy to understand | count-unguarded-cells-in-the-grid | 0 | 1 | # Intuition\nThe usual walk in 4 directions from each guard and mark space as guarded.\n\nHowever, can optimise time by stopping the walk when you encounter a guard (and of course wall).\n\nTo avoid the final extra iteration over the space grid to count unguarded cells, can include a counter of empty space that is decremented as spaces are marked as guarded.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countUnguarded(self, m: int, n: int, guards: List[List[int]], walls: List[List[int]]) -> int:\n space = [[\'e\' for _ in range(n)] for _ in range(m)]\n empty = m*n - len(guards) - len(walls)\n for guard in guards:\n space[guard[0]][guard[1]] = \'o\'\n\n for wall in walls:\n space[wall[0]][wall[1]] = \'o\'\n\n def walk(r, c):\n for dx, dy in [(0, -1), (0, 1), (1, 0), (-1, 0)]:\n row, col = r + dy, c + dx\n\n while row >= 0 and row < m and col >= 0 and col < n:\n if space[row][col] == \'e\':\n space[row][col] = \'g\'\n nonlocal empty\n empty -= 1\n elif space[row][col] == \'o\':\n break\n row, col = row + dy, col + dx\n\n for guard in guards:\n walk(guard[0], guard[1])\n\n return empty\n\n``` | 0 | You are given two integers `m` and `n` representing a **0-indexed** `m x n` grid. You are also given two 2D integer arrays `guards` and `walls` where `guards[i] = [rowi, coli]` and `walls[j] = [rowj, colj]` represent the positions of the `ith` guard and `jth` wall respectively.
A guard can see **every** cell in the four cardinal directions (north, east, south, or west) starting from their position unless **obstructed** by a wall or another guard. A cell is **guarded** if there is **at least** one guard that can see it.
Return _the number of unoccupied cells that are **not** **guarded**._
**Example 1:**
**Input:** m = 4, n = 6, guards = \[\[0,0\],\[1,1\],\[2,3\]\], walls = \[\[0,1\],\[2,2\],\[1,4\]\]
**Output:** 7
**Explanation:** The guarded and unguarded cells are shown in red and green respectively in the above diagram.
There are a total of 7 unguarded cells, so we return 7.
**Example 2:**
**Input:** m = 3, n = 3, guards = \[\[1,1\]\], walls = \[\[0,1\],\[1,0\],\[2,1\],\[1,2\]\]
**Output:** 4
**Explanation:** The unguarded cells are shown in green in the above diagram.
There are a total of 4 unguarded cells, so we return 4.
**Constraints:**
* `1 <= m, n <= 105`
* `2 <= m * n <= 105`
* `1 <= guards.length, walls.length <= 5 * 104`
* `2 <= guards.length + walls.length <= m * n`
* `guards[i].length == walls[j].length == 2`
* `0 <= rowi, rowj < m`
* `0 <= coli, colj < n`
* All the positions in `guards` and `walls` are **unique**. | List the planting like the diagram above shows, where a row represents the timeline of a seed. A row i is above another row j if the last day planting seed i is ahead of the last day for seed j. Does it have any advantage to spend some days to plant seed j before completely planting seed i? No. It does not help seed j but could potentially delay the completion of seed i, resulting in a worse final answer. Remaining focused is a part of the optimal solution. Sort the seeds by their growTime in descending order. Can you prove why this strategy is the other part of the optimal solution? Note the bloom time of a seed is the sum of plantTime of all seeds preceding this seed plus the growTime of this seed. There is no way to improve this strategy. The seed to bloom last dominates the final answer. Exchanging the planting of this seed with another seed with either a larger or smaller growTime will result in a potentially worse answer. |
Solution + Intuition + Explanation with Pictures 🏞 | escape-the-spreading-fire | 1 | 1 | \n\n\n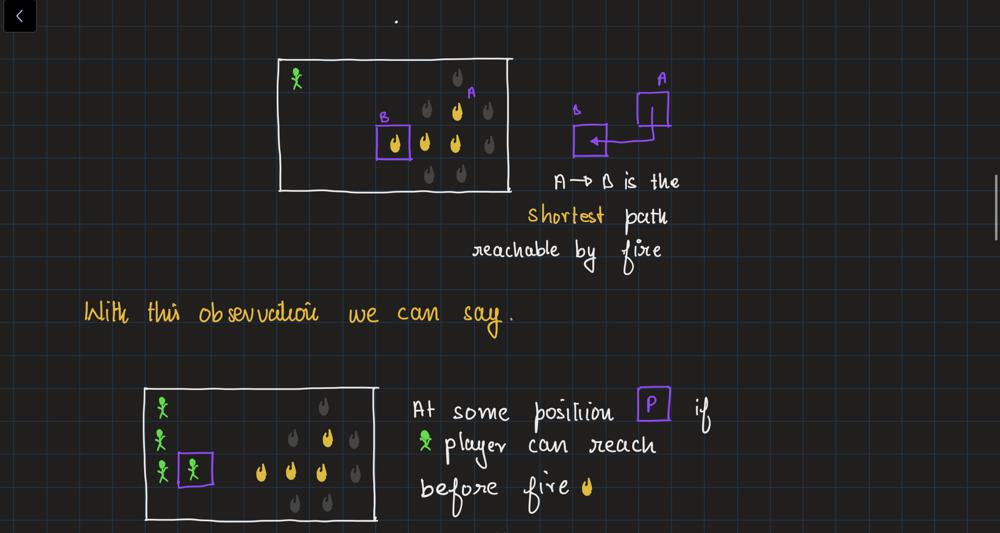\n\n\n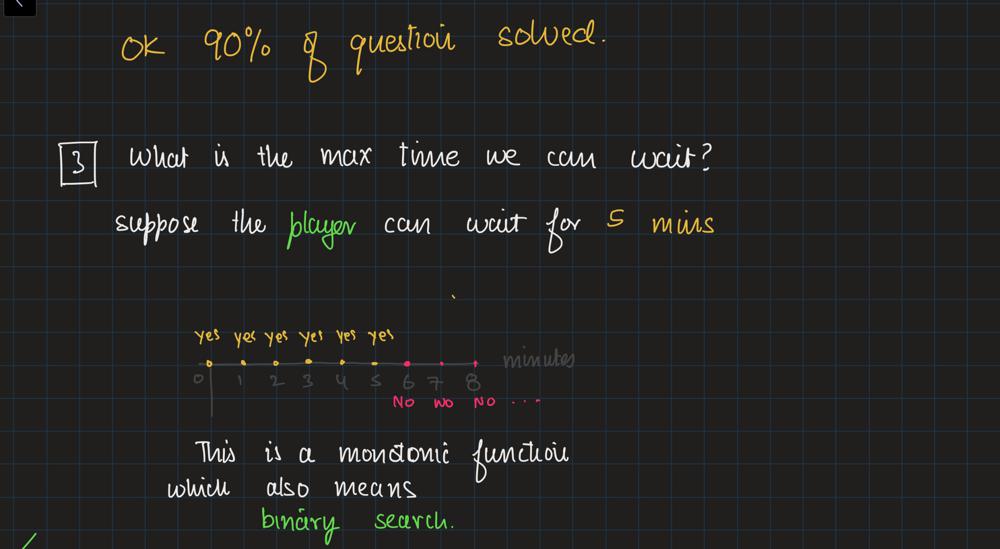\n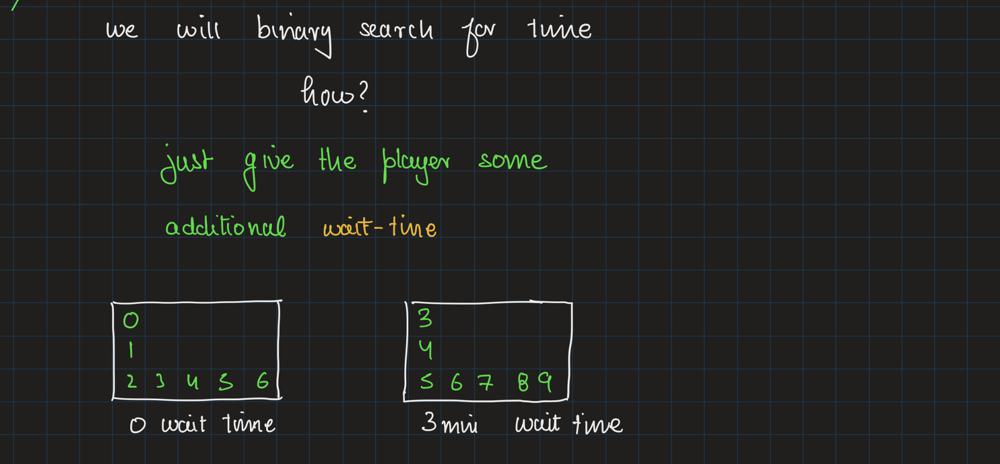\n\n\n\nCode - \n\n```java\n\nimport java.util.Arrays;\nimport java.util.LinkedList;\nimport java.util.Queue;\n\nclass Solution {\n\n public boolean ok(int[][] grid, int[][] dist, int wait_time) {\n int n = grid.length;\n int m = grid[0].length;\n\n Queue<Pair<Integer, Integer, Integer>> Q = new LinkedList<>();\n Q.add(new Pair<>(0, 0, wait_time));\n\n int[][] visited = new int[n][m];\n visited[0][0] = 1;\n\n while (!Q.isEmpty()) {\n Pair<Integer, Integer, Integer> at = Q.poll();\n int[][] moves = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};\n\n for (int[] to : moves) {\n int ii = at.first + to[0];\n int jj = at.second + to[1];\n if (!inBounds(ii, jj, n, m) || visited[ii][jj] == 1 || grid[ii][jj] == 2) continue;\n if (ii == n - 1 && jj == m - 1 && dist[ii][jj] >= at.third + 1) return true;\n if (dist[ii][jj] <= at.third + 1) continue;\n Q.add(new Pair<>(ii, jj, 1 + at.third));\n visited[ii][jj] = 1;\n }\n }\n return false;\n }\n\n public boolean inBounds(int i, int j, int n, int m) {\n return (0 <= i && i < n && 0 <= j && j < m);\n }\n\n public int maximumMinutes(int[][] grid) {\n int n = grid.length;\n int m = grid[0].length;\n\n int[][] dist = new int[n][m];\n\n for (int[] r : dist) Arrays.fill(r, Integer.MAX_VALUE);\n\n Queue<Pair<Integer, Integer, Integer>> Q = new LinkedList<>();\n\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (grid[i][j] == 1) {\n Q.add(new Pair<>(i, j, 0));\n dist[i][j] = 0;\n }\n }\n }\n\n while (!Q.isEmpty()) {\n Pair<Integer, Integer, Integer> at = Q.poll();\n int[][] moves = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};\n for (int[] to : moves) {\n int ii = at.first + to[0];\n int jj = at.second + to[1];\n if (!inBounds(ii, jj, n, m) || grid[ii][jj] == 2 || dist[ii][jj] <= at.third + 1) continue;\n dist[ii][jj] = 1 + at.third;\n Q.add(new Pair<>(ii, jj, 1 + at.third));\n }\n }\n\n int left = 0;\n int right = 1_000_000_000;\n\n int ans = -1;\n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (ok(grid, dist, mid)) {\n ans = mid;\n left = mid + 1;\n } else right = mid - 1;\n }\n\n return ans;\n }\n\n static class Pair<T, K, L> {\n T first;\n K second;\n L third;\n\n public Pair(T first, K second, L third) {\n this.first = first;\n this.second = second;\n this.third = third;\n }\n }\n\n}\n``` | 95 | You are given a **0-indexed** 2D integer array `grid` of size `m x n` which represents a field. Each cell has one of three values:
* `0` represents grass,
* `1` represents fire,
* `2` represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, `(0, 0)`, and you want to travel to the safehouse at the bottom-right cell, `(m - 1, n - 1)`. Every minute, you may move to an **adjacent** grass cell. **After** your move, every fire cell will spread to all **adjacent** cells that are not walls.
Return _the **maximum** number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse_. If this is impossible, return `-1`. If you can **always** reach the safehouse regardless of the minutes stayed, return `109`.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is **adjacent** to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
**Example 1:**
**Input:** grid = \[\[0,2,0,0,0,0,0\],\[0,0,0,2,2,1,0\],\[0,2,0,0,1,2,0\],\[0,0,2,2,2,0,2\],\[0,0,0,0,0,0,0\]\]
**Output:** 3
**Explanation:** The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.
**Example 2:**
**Input:** grid = \[\[0,0,0,0\],\[0,1,2,0\],\[0,2,0,0\]\]
**Output:** -1
**Explanation:** The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.
**Example 3:**
**Input:** grid = \[\[0,0,0\],\[2,2,0\],\[1,2,0\]\]
**Output:** 1000000000
**Explanation:** The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 300`
* `4 <= m * n <= 2 * 104`
* `grid[i][j]` is either `0`, `1`, or `2`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Try to find a pattern in how nums changes. Let m be the original length of nums. If time_i / m (integer division) is even, then nums is at its original size or decreasing in size. If it is odd, then it is empty, or increasing in size. time_i % m can be used to find how many elements are in nums at minute time_i. |
Useing binary search on the answer and BFS | escape-the-spreading-fire | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst try to solve this problem.\nSuppose you start without waiting. Can you find out if you will be able to reach destination? (Simple multisource BFS right?)\nNow notice this,\nIf you can escape from the fire after x minitues of waiting you can also escape the fire waiting less than that (ie x-1, x-2, .. ,0)\nSo you can simply binary search on the answer and everytime check if it is reachable after this many minitues of waiting. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def check(self,a,b):\n if a>=0 and a<self.n and b>=0 and b<self.m and self.grid[a][b]==0:\n return True\n return False\n def check2(self,a,b):\n if a>=0 and a<self.n and b>=0 and b<self.m and self.grid[a][b]==0 and self.vis[a][b]==0:\n return True\n return False\n def isReachable(self):\n if self.grid[0][0]!=0 or self.grid[self.n-1][self.m-1]!=0:\n return False\n self.stF.appendleft((0,0,-1))\n x=[0,1,-1,0]\n y=[1,0,0,-1]\n tot=1\n while len(self.stF) and tot!=0:\n a,b,depth=self.stF.popleft()\n if depth<0:\n tot-=1\n if a==self.n-1 and b==self.m-1:\n return True\n if self.vis[a][b] or self.grid[a][b]==1:\n continue\n self.vis[a][b]=1\n \n for dx,dy in zip(x,y):\n if self.check2(a+dx,b+dy):\n self.stF.append((a+dx,b+dy,-1))\n tot+=1\n else:\n for dx,dy in zip(x,y):\n if self.check(a+dx,b+dy):\n self.grid[a+dx][b+dy]=1\n self.stF.append((a+dx,b+dy,depth+1))\n return False\n def spread(self,count):\n x=[0,1,-1,0]\n y=[1,0,0,-1]\n while len(self.stF):\n a,b,depth=self.stF.popleft()\n self.grid[a][b]=1\n if self.grid[0][0]!=0 or self.grid[self.n-1][self.m-1]!=0:\n return\n if count==depth:\n self.stF.append((a,b,depth))\n return\n for dx,dy in zip(x,y):\n if self.check(a+dx,b+dy):\n self.stF.append((a+dx,b+dy,depth+1))\n return\n\n\n \n def maximumMinutes(self, grid: List[List[int]]) -> int:\n \n self.n=len(grid)\n self.m=len(grid[0])\n stFire=deque()\n for i in range(self.n):\n for j in range(self.m):\n if grid[i][j]==1:\n stFire.append((i,j,0))\n\n lo=0\n hi=((self.n*self.m)//2+5)\n ans=-1\n while lo<=hi:\n mid=(lo+hi)//2\n self.grid=[grid[i][::] for i in range(len(grid))]\n self.vis=[[0 for i in range(self.m)] for j in range(self.n)]\n self.stF=stFire.copy()\n self.spread(mid)\n if self.isReachable():\n ans=mid\n lo=mid+1\n else:\n hi=mid-1\n if ans==((self.n*self.m)//2+5):\n return 10**9\n return ans\n\n \n``` | 0 | You are given a **0-indexed** 2D integer array `grid` of size `m x n` which represents a field. Each cell has one of three values:
* `0` represents grass,
* `1` represents fire,
* `2` represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, `(0, 0)`, and you want to travel to the safehouse at the bottom-right cell, `(m - 1, n - 1)`. Every minute, you may move to an **adjacent** grass cell. **After** your move, every fire cell will spread to all **adjacent** cells that are not walls.
Return _the **maximum** number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse_. If this is impossible, return `-1`. If you can **always** reach the safehouse regardless of the minutes stayed, return `109`.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is **adjacent** to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
**Example 1:**
**Input:** grid = \[\[0,2,0,0,0,0,0\],\[0,0,0,2,2,1,0\],\[0,2,0,0,1,2,0\],\[0,0,2,2,2,0,2\],\[0,0,0,0,0,0,0\]\]
**Output:** 3
**Explanation:** The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.
**Example 2:**
**Input:** grid = \[\[0,0,0,0\],\[0,1,2,0\],\[0,2,0,0\]\]
**Output:** -1
**Explanation:** The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.
**Example 3:**
**Input:** grid = \[\[0,0,0\],\[2,2,0\],\[1,2,0\]\]
**Output:** 1000000000
**Explanation:** The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 300`
* `4 <= m * n <= 2 * 104`
* `grid[i][j]` is either `0`, `1`, or `2`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Try to find a pattern in how nums changes. Let m be the original length of nums. If time_i / m (integer division) is even, then nums is at its original size or decreasing in size. If it is odd, then it is empty, or increasing in size. time_i % m can be used to find how many elements are in nums at minute time_i. |
Escape set up with alternate test cases | Commented and Explained | escape-the-spreading-fire | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNice version of robot movement with changing terrain. Useful in a number of cases (imagine your battery gets less juice as time goes on instead of fires sprouting up... same idea different implementation details). \n\nAs such, we know that BFS is going to provide us with the best possible set up for the answer. This is not optimally implemented at the moment (likely an A* or similar could speed it up a bit). Additionally, we also know that we have the cases of walls adding a common hurdle. \n\nFinally, we need to account for the chances of fire never beating us, us never reaching there, and why not add in the fun (this was a tack on in an interview) of considering multiple but non-conflicting agents? \n\nTo start, it should be apparent that we have two movers in this case, an agent and a fire. As such, we could try to model both simultaneously (don\'t do it! If asked why not in an interview, talk about unnecessary added complexity. If they insist they want both at the same time, be ready to defend your choice -> bring up the issue of simultaneous movement adding code complexity for likely no time benefit). \n\nAs we have two movers, two BFS will suffice. As we care about fire, let\'s do fire first. \n\nWe also have a max time to consider, and have a grid. Easier to have a secondary grid marked with values as you go along than to devise a storage in place. Still, for those who ask for storage in place, can be done (not here) with negative valuations if you are careful about the implications at the end (Again, complexity vs brevity of code) \n\nAlright, implementation time \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGet your rows and cols, and check your start and end are not invalid at the start. \nThen, build your queues, and set your max time as advised \nBuild a modifying grid (chose a dict of a dict with lists. More advanced scenarios might call for a dict of dict of dicts, where each of the final dicts is either agents or enemies. Fun stuff there, and good to recognize in interview) \n\nAlright, add in your start position(s) to your agent(s) queue, and mark their start position(s) appropriately. I did the obstacle finding in the above loop for the modifying grid init, and could have done this agent portion there as well. If walls are to be set aside in some manner could conserve some space there if needed. \n\nDo your bfs for your queues for your axis, enemies first than agents. \n\nGet the destination arrival times as needed and check the following \n- If enemies get to base before us, or we never can make it to base, we lose, return -1 \n- Else if enemies never reach us and we reach base, win, return max time \n- Otherwise \n - both enemies and allies can reach base, and we do win \n - calculate level of win based on time difference of arrival \n\n# Complexity\n- Time complexity : O(G) \n - Need at least grid space currently to set up modifying grid, so grid space time, O(G) \n - each bfs may cover whole graph, O(G) \n\n- Space complexity : O(G) \n - See above \n\n# Code\n```\nclass Solution:\n def maximumMinutes(self, grid: List[List[int]], src=(0, 0)) -> int:\n # get rows and cols \n rows = len(grid)\n cols = len(grid[0])\n # check for dummy cases \n if grid[src[0]][src[1]] != 0 and grid[rows - 1][cols - 1] != 0 : \n return -1 \n else : \n # build some queues for movement \n moq = collections.deque()\n maq = collections.deque() \n # set max time according to problem statement \n max_time = 10**9\n # build a grid of modifying nature -> needs axis within cells -> axis is obstacle, agent \n self.modifying_grid = collections.defaultdict(dict)\n # loop to build \n for row in range(rows) : \n for col in range(cols) : \n # if obstacle, mark as such (obstacle axis is 0, agent is set to max time (could alter if needed for more advanced scenarios))\n if grid[row][col] == 1 : \n self.modifying_grid[row][col] = [0, max_time]\n moq.append((row, col)) \n else : \n # otherwise, simply mark and move on \n self.modifying_grid[row][col] = [max_time, max_time]\n\n # set up agent queue to contain source \n maq.append(src)\n # and mark singular agent as needed (if multiple agents, could mark above with different value for agents)\n self.modifying_grid[src[0]][src[1]][1] = 0 \n # directions as needed \n self.directions = [(1, 0), (0, 1), (-1, 0), (0, -1)] \n\n # bfs queue set up \n def bfs(queue, axis) : \n # while queue exists \n while queue : \n # pop, and then iterate directions \n r, c = queue.popleft()\n for dr, dc in self.directions : \n nr, nc = r + dr, c + dc \n # if in bounds and unvisited for this axis and the grid is not a wall \n if 0 <=nr<rows and 0<=nc<cols and self.modifying_grid[nr][nc][axis] == max_time and grid[nr][nc] != 2 : \n # update, visit \n self.modifying_grid[nr][nc][axis] = self.modifying_grid[r][c][axis] + 1 \n queue.append((nr, nc))\n \n # process queues \n queues = [moq, maq] \n for i in range(2) : \n bfs(queues[i], i) \n\n # get obstacle and agent dest time \n fire_dest_time, agent_dest_time = self.modifying_grid[rows - 1][cols-1]\n\n # if we\'ll be beat, say so. If we\'re stuck say so. Otherwise if fire never gets there, say so. \n if fire_dest_time < agent_dest_time or agent_dest_time == max_time: \n return -1 \n elif fire_dest_time == max_time and fire_dest_time > agent_dest_time : \n return 10**9 \n else : \n # otherwise, get the difference in arrival based on one row off or one col off \n time_delta = fire_dest_time - agent_dest_time \n one_row_off = self.modifying_grid[rows-2][cols-1]\n row_time_delta = one_row_off[0] - one_row_off[1]\n one_col_off = self.modifying_grid[rows-1][cols-2]\n col_time_delta = one_col_off[0] - one_col_off[1] \n # if either row or col time delta is gt time delta, just return time delta. Otherwise, one is lt or equal, so return one less. \n if row_time_delta > time_delta or col_time_delta > time_delta : \n return time_delta \n return time_delta - 1 \n``` | 0 | You are given a **0-indexed** 2D integer array `grid` of size `m x n` which represents a field. Each cell has one of three values:
* `0` represents grass,
* `1` represents fire,
* `2` represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, `(0, 0)`, and you want to travel to the safehouse at the bottom-right cell, `(m - 1, n - 1)`. Every minute, you may move to an **adjacent** grass cell. **After** your move, every fire cell will spread to all **adjacent** cells that are not walls.
Return _the **maximum** number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse_. If this is impossible, return `-1`. If you can **always** reach the safehouse regardless of the minutes stayed, return `109`.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is **adjacent** to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
**Example 1:**
**Input:** grid = \[\[0,2,0,0,0,0,0\],\[0,0,0,2,2,1,0\],\[0,2,0,0,1,2,0\],\[0,0,2,2,2,0,2\],\[0,0,0,0,0,0,0\]\]
**Output:** 3
**Explanation:** The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.
**Example 2:**
**Input:** grid = \[\[0,0,0,0\],\[0,1,2,0\],\[0,2,0,0\]\]
**Output:** -1
**Explanation:** The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.
**Example 3:**
**Input:** grid = \[\[0,0,0\],\[2,2,0\],\[1,2,0\]\]
**Output:** 1000000000
**Explanation:** The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 300`
* `4 <= m * n <= 2 * 104`
* `grid[i][j]` is either `0`, `1`, or `2`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Try to find a pattern in how nums changes. Let m be the original length of nums. If time_i / m (integer division) is even, then nums is at its original size or decreasing in size. If it is odd, then it is empty, or increasing in size. time_i % m can be used to find how many elements are in nums at minute time_i. |
Python BFS , NO BS , corner case explained FAST AF | escape-the-spreading-fire | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe use binary search to track distance of each cell\'s shortes pat from out desired locations : Fire and Agent.\n\nThe idea is at the location of the safehouse, we know time taken by the person and fire to reach there, so the wait time would be fireTime-agentTime\n\nThe corner cases are as follows:\n\n- fire spreads faster than agent can reach \n```\n if fireTime < agentTime:\n return -1\n```\n- fire cant reach\n```\n if fireTime == 10**9 and fireTime > agentTime :\n return 10**9\n```\n- agnet walled off and cant reach\n```\n if agentTime == 10**9:\n return -1\n```\n- fire reches before agent\n```\n diff = fireTime - agentTime\n \n if diff <0:\n return -1\n```\n\nThe most complicated cases are when fire and agent have seperate paths and only converge at the safehouse\n\nShoutout to https://leetcode.com/problems/escape-the-spreading-fire/solutions/2653210/96-faster-java-sol-no-bs-required-edge-cases-explained-double-bfs-method/ for giving the code behind this\n\n- **when they arrive through differenet paths , we assume the agent moves in asynchronously first, then the fire catches on** \n - we calculate the difference between the two at a cell above and cell to the left\n - if either of these values are greater than diff , then they come in different paths\n - here we do not subtract -1\n- else we subtract res by 1 as they come in same path and agent must be ahead of the flames\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(mxn)\n\n# Code\n```\nclass Solution:\n def maximumMinutes(self, grid: List[List[int]]) -> int: \n \n # for row in range(len(grid)):\n # print(grid[row])\n\n\n height = len(grid)\n width = len(grid[0])\n \n src = (0,0)\n dest = (height-1,width-1)\n \n src_i , src_j = src\n dest_i, dest_j = dest\n\n # Game rigged from the start\n if grid[src_i][src_j] != 0 and grid[dest_i][dest_j] != 0:\n print("missfire?")\n return -1\n\n # BFSQ for fire\n fireQ = collections.deque() \n\n fire_plane = [[10**9 for _ in range(width)] for _ in range(height)]\n agent_plane = [[10**9 for _ in range(width)] for _ in range(height)]\n \n\n # bfsQ for our agent\n agentQ = collections.deque()\n agent_plane[src_i][src_j]=0\n agentQ.append(src)\n\n # populate initial matrices\n for h in range(height):\n for w in range(width):\n # multisourceBFS for fore\n if grid[h][w]==1:\n fire_plane[h][w] = 0 \n fireQ.append((h,w))\n\n def bfs(queue , board , isAgent):\n directions = [(1,0),(0,1),(-1,0),(0,-1)]\n\n # BFS to obtain shortest path to destination\n while len(queue)>0:\n i,j = queue.popleft()\n\n for dir_i , dir_j in directions:\n\n di = i + dir_i \n dj = j + dir_j\n\n if 0<=di<height and 0<=dj<width and board[di][dj] == 10**9 and grid[di][dj] != 2 :\n\n board[di][dj] = board[i][j]+1 \n queue.append((di,dj))\n \n # print("isAgent",isAgent)\n # for row in range(len(board)):\n # print(board[row])\n # print("/////////////////////////////")\n\n # bfs for fire\n bfs(fireQ,fire_plane,False)\n # bfs for agent\n bfs(agentQ,agent_plane,True)\n\n \n\n fireTime = fire_plane[-1][-1]\n agentTime = agent_plane[-1][-1]\n\n # fire spreads faster than agent can reach \n if fireTime < agentTime:\n return -1\n\n # fire cant reach\n if fireTime == 10**9 and fireTime > agentTime :\n return 10**9\n\n # agnet walled off and cant reach\n if agentTime == 10**9:\n return -1\n\n diff = fireTime - agentTime\n \n if diff <0:\n return -1\n # both reach safehouse from 2nd last row \n downDiff = fire_plane[-2][-1] - agent_plane[-2][-1]\n\n # both reach safehouse from last row \n rightDiff = fire_plane[-1][-2] - agent_plane[-1][-2]\n\n\n\n if downDiff > diff or rightDiff > diff:\n return diff\n\n return diff -1\n\n # return -1\n\n\n``` | 0 | You are given a **0-indexed** 2D integer array `grid` of size `m x n` which represents a field. Each cell has one of three values:
* `0` represents grass,
* `1` represents fire,
* `2` represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, `(0, 0)`, and you want to travel to the safehouse at the bottom-right cell, `(m - 1, n - 1)`. Every minute, you may move to an **adjacent** grass cell. **After** your move, every fire cell will spread to all **adjacent** cells that are not walls.
Return _the **maximum** number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse_. If this is impossible, return `-1`. If you can **always** reach the safehouse regardless of the minutes stayed, return `109`.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is **adjacent** to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
**Example 1:**
**Input:** grid = \[\[0,2,0,0,0,0,0\],\[0,0,0,2,2,1,0\],\[0,2,0,0,1,2,0\],\[0,0,2,2,2,0,2\],\[0,0,0,0,0,0,0\]\]
**Output:** 3
**Explanation:** The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.
**Example 2:**
**Input:** grid = \[\[0,0,0,0\],\[0,1,2,0\],\[0,2,0,0\]\]
**Output:** -1
**Explanation:** The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.
**Example 3:**
**Input:** grid = \[\[0,0,0\],\[2,2,0\],\[1,2,0\]\]
**Output:** 1000000000
**Explanation:** The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 300`
* `4 <= m * n <= 2 * 104`
* `grid[i][j]` is either `0`, `1`, or `2`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Try to find a pattern in how nums changes. Let m be the original length of nums. If time_i / m (integer division) is even, then nums is at its original size or decreasing in size. If it is odd, then it is empty, or increasing in size. time_i % m can be used to find how many elements are in nums at minute time_i. |
[Python3][BFS+Heap] Beats 95% Runtime | escape-the-spreading-fire | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst use BFS to calculate each cell\'s last day it can ba passed\nThen use a heap started from the last cell with the last day we can pass to the cell until reached the start point.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst use BFS to calculate each cell\'s last day it can ba passed\nThen use a heap started from the last cell with the last day we can pass to the cell\nIn each iteration, we add the neighbor of the current cell with the last day which be the maximum of `current last day - 1` (as it takes 1 day to pass to next cell) or `the neighbor\'s last day`.\nOnce we reached the start point, we check:\n1. if the last day we can pass is less than 0 which means it does not exists a path\n2. if the last day equals to INF means it can take as longer as it wants, we return 10 ** 9\n3. Return the last day\n# Complexity\nThe time complexity of this code is determined by the breadth-first search (BFS) and heap operations. Let\'s break down the major parts of the code:\n\n1. Building the `last_day_pass` array using BFS: This step visits each cell in the grid once, and for each cell, it explores its neighbors in the grid. So, the time complexity for this step is O(m * n), where m is the number of rows and n is the number of columns in the grid.\n\n2. Building the heap: The heap is built by adding cells to the heap based on their `last_day_pass` values. In the worst case, all cells are added to the heap, which would result in O(m * n * log(m * n)) time complexity due to the heap operations.\n\n3. Extracting cells from the heap: The while loop extracts cells from the heap until it\'s empty. In the worst case, it can extract all cells in the heap, which would also result in O(m * n * log(m * n)) time complexity due to the heap operations.\n\nCombining these time complexities, the overall time complexity of the code is dominated by the heap operations, which is O(m * n * log(m * n)).\n\nAs for space complexity, the major space-consuming data structures are:\n\n- `last_day_pass`: O(m * n) space\n- `q`: The BFS queue, in the worst case, could store all cells in the grid, so O(m * n) space\n- `heap`: The heap, in the worst case, could store all cells in the grid, so O(m * n) space\n- `visited`: A set to track visited cells, in the worst case, could store all cells in the grid, so O(m * n) space\n\nThe overall space complexity is O(m * n) due to these data structures.\n- Time complexity: O(m * n * log(m * n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(m * n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumMinutes(self, grid: List[List[int]]) -> int:\n m = len(grid)\n n = len(grid[0])\n INF = float(\'inf\')\n last_day_pass = [[INF] * n for _ in range(m)]\n q = deque()\n visited = set() \n for i in range(m):\n for j in range(n):\n if grid[i][j] > 0:\n if grid[i][j] == 1:\n q.append((i, j))\n visited.add((i, j))\n last_day_pass[i][j] = -1\n dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]\n \n while q:\n x, y = q.popleft()\n for d0, d1 in dirs:\n if not 0 <= x+d0 < m or not 0 <= y+d1 < n or (x+d0, y+d1) in visited:\n continue\n visited.add((x+d0, y+d1))\n last_day_pass[x+d0][y+d1] = last_day_pass[x][y] + 1\n q.append((x+d0, y+d1))\n\n heap = [(-last_day_pass[m-1][n-1]-1, m-1, n-1)]\n visited = set()\n while heap:\n last_day, x, y = heapq.heappop(heap)\n if x == 0 and y == 0:\n if -last_day < 0:\n return -1 \n return -last_day if -last_day != INF else 10 ** 9\n for d0, d1 in dirs:\n if not 0 <= x+d0 < m or not 0 <= y+d1 < n or grid[x+d0][y+d1] > 0 or (x+d0, y+d1) in visited:\n continue\n visited.add((x+d0, y+d1))\n heapq.heappush(heap, (max(last_day+1, -last_day_pass[x+d0][y+d1]), x+d0, y+d1))\n return -1\n \n``` | 0 | You are given a **0-indexed** 2D integer array `grid` of size `m x n` which represents a field. Each cell has one of three values:
* `0` represents grass,
* `1` represents fire,
* `2` represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, `(0, 0)`, and you want to travel to the safehouse at the bottom-right cell, `(m - 1, n - 1)`. Every minute, you may move to an **adjacent** grass cell. **After** your move, every fire cell will spread to all **adjacent** cells that are not walls.
Return _the **maximum** number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse_. If this is impossible, return `-1`. If you can **always** reach the safehouse regardless of the minutes stayed, return `109`.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is **adjacent** to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
**Example 1:**
**Input:** grid = \[\[0,2,0,0,0,0,0\],\[0,0,0,2,2,1,0\],\[0,2,0,0,1,2,0\],\[0,0,2,2,2,0,2\],\[0,0,0,0,0,0,0\]\]
**Output:** 3
**Explanation:** The figure above shows the scenario where you stay in the initial position for 3 minutes.
You will still be able to safely reach the safehouse.
Staying for more than 3 minutes will not allow you to safely reach the safehouse.
**Example 2:**
**Input:** grid = \[\[0,0,0,0\],\[0,1,2,0\],\[0,2,0,0\]\]
**Output:** -1
**Explanation:** The figure above shows the scenario where you immediately move towards the safehouse.
Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse.
Thus, -1 is returned.
**Example 3:**
**Input:** grid = \[\[0,0,0\],\[2,2,0\],\[1,2,0\]\]
**Output:** 1000000000
**Explanation:** The figure above shows the initial grid.
Notice that the fire is contained by walls and you will always be able to safely reach the safehouse.
Thus, 109 is returned.
**Constraints:**
* `m == grid.length`
* `n == grid[i].length`
* `2 <= m, n <= 300`
* `4 <= m * n <= 2 * 104`
* `grid[i][j]` is either `0`, `1`, or `2`.
* `grid[0][0] == grid[m - 1][n - 1] == 0` | Try to find a pattern in how nums changes. Let m be the original length of nums. If time_i / m (integer division) is even, then nums is at its original size or decreasing in size. If it is odd, then it is empty, or increasing in size. time_i % m can be used to find how many elements are in nums at minute time_i. |
2259. Checking the next digit | Beats 96.72% | remove-digit-from-number-to-maximize-result | 0 | 1 | # Code\n```\nclass Solution:\n def removeDigit(self, number: str, digit: str) -> str:\n n = len(number)\n for x in range(1, n):\n prev, cur = number[x-1], number[x]\n if prev == digit:\n last_ind = x-1\n if cur > prev:\n ind = x - 1\n return number[:ind] + number[ind+1:]\n else:\n if number[-1] == digit:\n last_ind = n-1\n if last_ind < n-1:\n return number[:last_ind] + number[last_ind+1:]\n return number[:last_ind]\n\n``` | 1 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
🔥🔥🔥Python O(N) solution || Faster than 99% submissions || Detailed explanation. | remove-digit-from-number-to-maximize-result | 0 | 1 | ***Please Upvote, comment and share if you like the detailed explanation and the solution***\n\nLet us understand with an example: \n`Number = 9515901 and digit = 9`\n\n1. Since the occurence of the number `9` is happening twice in the string(number), and we can only remove one `9` from the string, we can achieve the Maximum possible outcome in the below cases:\n\t* `Case 1`: If the first occurence of 9 `is greater than` the next element at index `i+1`.\n\t* `Case 2`: If not the first occurence, we iterate till next/last occurence, and the next occurence has number 9 less than the index `i+1`.\n\t* `Case 3`: This would be if there is a number `9` present at the end of the string.\n\t\n\n2. In the given example we have 2 possiblities: `515901` and `951501`.\n\n3. As per the condition of the problem, the maximum returned value from the above sample should be `951501` as per **case 2**. \n4. Since `9` is less than `5` (if we consider the outcome `515901`), it would have resulted in a string with lower value. Hence we keep moving forward till we find this condition to be true `number[i]` is greater than `number[i-1]`. And remove the character from from that position.\n\n5. `Edge Case`: This is the scenario where none of the above two cases holds true. In this case, we have to remove the last occurence of the digit, hence, `case 3` is added to find the last occurence of `9` and remove it.\n\n```\nclass Solution:\n def removeDigit(self, number: str, digit: str) -> str:\n \n # Initializing the last index as zero\n last_index = 0\n \n #iterating each number to find the occurences, \\\n # and to find if the number is greater than the next element \\ \n\n for num in range(1, len(number)):\n \n # Handling [case 1] and [case 2]\n if number[num-1] == digit:\n if int(number[num]) > int(number[num-1]):\n return number[:num-1] + number[num:]\n else:\n last_index = num - 1\n \n # If digit is the last number (last occurence) in the string [case 3]\n if number[-1] == digit:\n last_index = len(number) - 1\n\n return number[:last_index] + number[last_index + 1:]\n```\n\nBetter and faster than **99% of submissions** \uD83D\uDD25\uD83D\uDD25\uD83D\uDD25\uD83D\uDD25\uD83D\uDD25\uD83D\uDD25\n\n\n | 25 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
Python | Easy Solution✅ | remove-digit-from-number-to-maximize-result | 0 | 1 | ```\ndef removeDigit(self, number: str, digit: str) -> str:\n output = []\n for i in range(len(number)):\n if number[i] == digit:\n output.append(number[:i]+number[i+1:])\n return max(output)\n``` | 12 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
[Python 3] Brute Force Easy Solution | remove-digit-from-number-to-maximize-result | 0 | 1 | **Approach:** For all the occurences, remove it and find the maximum of all the possible numbers generated.\n\n**DO UPVOTE IF YOU FOUND IT HELPFUL.**\n\n```\nclass Solution:\n def removeDigit(self, number: str, digit: str) -> str:\n ans = 0\n for i, dig in enumerate(list(number)):\n if dig == digit:\n ans = max(ans, int(number[:i]+number[i+1:]))\n \n return str(ans)\n``` | 16 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
Python3 ✅✅✅ || 2-line Faster than 99.25% | remove-digit-from-number-to-maximize-result | 0 | 1 | # Code\n```\nclass Solution:\n def removeDigit(self, number: str, digit: str) -> str:\n nums = [ int(number[:n] + number[n+1:]) for n in range(len(number)) if number[n] == digit]\n return str(max(nums))\n```\n\n | 1 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
Easy Solution || O(n) | remove-digit-from-number-to-maximize-result | 0 | 1 | ```\nclass Solution:\n def removeDigit(self, number: str, digit: str) -> str:\n l=[]\n for i in range(len(number)):\n if number[i]==digit:\n l.append(int(number[:i]+number[i+1:]))\n return str(max(l))\n``` | 2 | You are given a string `number` representing a **positive integer** and a character `digit`.
Return _the resulting string after removing **exactly one occurrence** of_ `digit` _from_ `number` _such that the value of the resulting string in **decimal** form is **maximized**_. The test cases are generated such that `digit` occurs at least once in `number`.
**Example 1:**
**Input:** number = "123 ", digit = "3 "
**Output:** "12 "
**Explanation:** There is only one '3' in "123 ". After removing '3', the result is "12 ".
**Example 2:**
**Input:** number = "1231 ", digit = "1 "
**Output:** "231 "
**Explanation:** We can remove the first '1' to get "231 " or remove the second '1' to get "123 ".
Since 231 > 123, we return "231 ".
**Example 3:**
**Input:** number = "551 ", digit = "5 "
**Output:** "51 "
**Explanation:** We can remove either the first or second '5' from "551 ".
Both result in the string "51 ".
**Constraints:**
* `2 <= number.length <= 100`
* `number` consists of digits from `'1'` to `'9'`.
* `digit` is a digit from `'1'` to `'9'`.
* `digit` occurs at least once in `number`. | Consider each cell containing a 1 as a vertex whose neighbors are the cells 4-directionally connected to it. The grid then becomes a bipartite graph. You want to find the smallest set of vertices such that every edge in the graph has an endpoint in this set. If you remove every vertex in this set from the graph, then all the 1’s will be disconnected. Are there any well-known algorithms for finding this set? This set of vertices is called a minimum vertex cover. You can find the size of a minimum vertex cover by finding the size of a maximum matching (Konig’s theorem). There are well-known algorithms such as Kuhn’s algorithm and Hopcroft-Karp-Karzanov algorithm which can find a maximum matching in a bipartite graph quickly. |
Beating 85.16% Python Easiest Solution | minimum-consecutive-cards-to-pick-up | 0 | 1 | \n\n\n# Code\n```\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n if len(set(cards))==len(cards):\n return -1\n dic={} \n ma=1000000\n for i in range (len(cards)):\n if cards[i] not in dic:\n dic[cards[i]]=i\n else:\n if ma>(i-(dic[cards[i]])):\n ma=(i-dic[cards[i]])\n dic[cards[i]]=i\n return ma+1\n\n\n``` | 1 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
🚀🚀🚀Three ways to solve(99 beating) | minimum-consecutive-cards-to-pick-up | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n #enumerate; time O(n), space O(n)\n d = defaultdict(list)\n res = float(\'inf\')\n for i, val in enumerate(cards):\n if val in d:\n res = min(res, i - d[val] + 1)\n d[val] = i\n\n return res if res != float(\'inf\') else -1 \n\n #sliding window; time O(n), space O(m)\n l = 0\n res = float(\'inf\')\n d = defaultdict(int)\n for r in range(len(cards)):\n d[cards[r]] += 1\n if d[cards[r]] == 2: \n while cards[l] != cards[r]:\n d[cards[l]] -= 1\n l += 1\n res = min(res, r - l + 1)\n d[cards[l]] -= 1\n l += 1\n\n return res if res != float(\'inf\') else -1\n\n #storing indices; time O(n + m * k), space O(n + m)\n d = defaultdict(list)\n res = float(\'inf\')\n for i in range(len(cards)):\n d[cards[i]].append(i)\n\n for key in d:\n ans = d[key]\n for i in range(len(ans) - 1):\n res = min(res, ans[i + 1] - ans[i] + 1)\n\n return res if res != float(\'inf\') else -1\n\n\n\n``` | 2 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
Hashing and then using the indexes(Algorithm) | minimum-consecutive-cards-to-pick-up | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirstly store the indexes the elements repeated and donnot forget to update the indexes...\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\nlinear traversal\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n uni=set(cards)\n if(len(uni)==len(cards)):\n return -1\n d={}\n mini=len(cards)\n for i in range(0,len(cards)):\n if cards[i] in d:\n mini=min(mini,i-d[cards[i]]+1)\n d[cards[i]]=i\n else:\n d[cards[i]]=i\n return mini\n``` | 2 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
Python3 | Beginner-friendly explained | | minimum-consecutive-cards-to-pick-up | 0 | 1 | **Thought Process:**\n\nSo we want to find the minimum difference between current character\'s position and previously seen position. And only keep the minimum!\n\n1.\tKeep the index of visiting number (We will always update the index to latest since we are looking for minimum length)\n2.\tIf your current number is seen before, then calculate the length from previously seen index, and update if its difference is smaller than what we have seen so far\n3.\tAt the end of iteration, if we didn\u2019t find any duplicate, return -1; otherwise, return the minimum distance you found\n\n**Complexity**\nTime \u2013 O(N) as we iterate over the input only once\nSpace \u2013 O(N) at worst case we will be storing all the numbers in the input to our index hashmap. (in case of all distinct numbers in input array)\n\n```\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n minPick = float(\'inf\')\n seen = {}\n for i, n in enumerate(cards):\n if n in seen:\n if i - seen[n] + 1 < minPick:\n minPick = i - seen[n] + 1\n seen[n] = i\n if minPick == float(\'inf\'):\n return -1\n return minPick\n```\n\n**Please correct me if I am wrong !\nPlease UPVOTE if you find this solution helpful !\nHappy algo!**\n | 29 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
[Python 3] Using dictionary || beats 99% || 694ms 🥷🏼 | minimum-consecutive-cards-to-pick-up | 0 | 1 | ```python3 []\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n res, pos = 10**6+1, {}\n for i, c in enumerate(cards):\n if c in pos:\n res = min(res, i - pos[c] + 1)\n pos[c] = i\n \n return res % (10**6+1) or -1\n```\n\n | 3 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
python solution | minimum-consecutive-cards-to-pick-up | 0 | 1 | # class Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n d = {}\n ans = float(\'inf\')\n \n for i in range(len(cards)):\n if cards[i] not in d:\n d[cards[i]] = i\n else:\n ans = min(ans, i - d[cards[i]])\n d[cards[i]] = i\n \n return -1 if ans == float(\'inf\') else ans + 1 | 3 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
Python3 | HashMaps | minimum-consecutive-cards-to-pick-up | 0 | 1 | ```\nclass Solution:\n def minimumCardPickup(self, cards: List[int]) -> int:\n HashMap={}\n lengths=[]\n for i,j in enumerate(cards):\n if j in HashMap:\n lengths.append(abs(HashMap[j]-i)+1)\n HashMap[j]=i\n else:\n HashMap[j]=i\n if len(lengths)>0:\n return min(lengths)\n else:\n return -1``\n``` | 2 | You are given an integer array `cards` where `cards[i]` represents the **value** of the `ith` card. A pair of cards are **matching** if the cards have the **same** value.
Return _the **minimum** number of **consecutive** cards you have to pick up to have a pair of **matching** cards among the picked cards._ If it is impossible to have matching cards, return `-1`.
**Example 1:**
**Input:** cards = \[3,4,2,3,4,7\]
**Output:** 4
**Explanation:** We can pick up the cards \[3,4,2,3\] which contain a matching pair of cards with value 3. Note that picking up the cards \[4,2,3,4\] is also optimal.
**Example 2:**
**Input:** cards = \[1,0,5,3\]
**Output:** -1
**Explanation:** There is no way to pick up a set of consecutive cards that contain a pair of matching cards.
**Constraints:**
* `1 <= cards.length <= 105`
* `0 <= cards[i] <= 106` | Using the length of the string and k, can you count the number of groups the string can be divided into? Try completing each group using characters from the string. If there aren’t enough characters for the last group, use the fill character to complete the group. |
✅ Python - Simple Count all combinations | k-divisible-elements-subarrays | 0 | 1 | ```\nclass Solution:\n def countDistinct(self, nums: List[int], k: int, p: int) -> int:\n n = len(nums) \n sub_arrays = set()\n \n\t\t# generate all combinations of subarray\n for start in range(n):\n cnt = 0\n temp = \'\'\n for i in range(start, n):\n if nums[i]%p == 0:\n cnt+=1 \n temp+=str(nums[i]) + \',\' # build the sequence subarray in CSV format \n if cnt>k: # check for termination \n break\n sub_arrays.add(temp) \n \n return len(sub_arrays)\n```\n\n**T = O(N^3)**\n**S = O(N^2)**\n\n---\n\n***Please upvote if you find it useful*** | 23 | Given an integer array `nums` and two integers `k` and `p`, return _the number of **distinct subarrays** which have **at most**_ `k` _elements divisible by_ `p`.
Two arrays `nums1` and `nums2` are said to be **distinct** if:
* They are of **different** lengths, or
* There exists **at least** one index `i` where `nums1[i] != nums2[i]`.
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[**2**,3,3,**2**,**2**\], k = 2, p = 2
**Output:** 11
**Explanation:**
The elements at indices 0, 3, and 4 are divisible by p = 2.
The 11 distinct subarrays which have at most k = 2 elements divisible by 2 are:
\[2\], \[2,3\], \[2,3,3\], \[2,3,3,2\], \[3\], \[3,3\], \[3,3,2\], \[3,3,2,2\], \[3,2\], \[3,2,2\], and \[2,2\].
Note that the subarrays \[2\] and \[3\] occur more than once in nums, but they should each be counted only once.
The subarray \[2,3,3,2,2\] should not be counted because it has 3 elements that are divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 4, p = 1
**Output:** 10
**Explanation:**
All element of nums are divisible by p = 1.
Also, every subarray of nums will have at most 4 elements that are divisible by 1.
Since all subarrays are distinct, the total number of subarrays satisfying all the constraints is 10.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i], p <= 200`
* `1 <= k <= nums.length`
**Follow up:**
Can you solve this problem in O(n2) time complexity? | When you iterate the array, maintain the number of zeros and ones on the left side. Can you quickly calculate the number of ones on the right side? The number of ones on the right side equals the number of ones in the whole array minus the number of ones on the left side. Alternatively, you can quickly calculate it by using a prefix sum array. |
Easily implemented using Trie | k-divisible-elements-subarrays | 0 | 1 | ```\nclass Solution:\n def countDistinct(self, nums: List[int], k: int, p: int) -> int:\n trie = {}\n cnt = 0\n for i in range(len(nums)):\n count = 0\n divis = 0 #contain count of element in array divisible by p\n d = trie\n for j in range(i,len(nums)):\n if nums[j] % p == 0:\n divis += 1\n if divis > k:\n break\n if nums[j] not in d:\n d[nums[j]] = {}\n count += 1\n d = d[nums[j]]\n cnt += count #count contain all subarrays that can be made from nums[i:j]\n return cnt``` | 2 | Given an integer array `nums` and two integers `k` and `p`, return _the number of **distinct subarrays** which have **at most**_ `k` _elements divisible by_ `p`.
Two arrays `nums1` and `nums2` are said to be **distinct** if:
* They are of **different** lengths, or
* There exists **at least** one index `i` where `nums1[i] != nums2[i]`.
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[**2**,3,3,**2**,**2**\], k = 2, p = 2
**Output:** 11
**Explanation:**
The elements at indices 0, 3, and 4 are divisible by p = 2.
The 11 distinct subarrays which have at most k = 2 elements divisible by 2 are:
\[2\], \[2,3\], \[2,3,3\], \[2,3,3,2\], \[3\], \[3,3\], \[3,3,2\], \[3,3,2,2\], \[3,2\], \[3,2,2\], and \[2,2\].
Note that the subarrays \[2\] and \[3\] occur more than once in nums, but they should each be counted only once.
The subarray \[2,3,3,2,2\] should not be counted because it has 3 elements that are divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 4, p = 1
**Output:** 10
**Explanation:**
All element of nums are divisible by p = 1.
Also, every subarray of nums will have at most 4 elements that are divisible by 1.
Since all subarrays are distinct, the total number of subarrays satisfying all the constraints is 10.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i], p <= 200`
* `1 <= k <= nums.length`
**Follow up:**
Can you solve this problem in O(n2) time complexity? | When you iterate the array, maintain the number of zeros and ones on the left side. Can you quickly calculate the number of ones on the right side? The number of ones on the right side equals the number of ones in the whole array minus the number of ones on the left side. Alternatively, you can quickly calculate it by using a prefix sum array. |
Sliding Window Technique: O(N^2) | k-divisible-elements-subarrays | 0 | 1 | # Intuition\nSince the problem is about subarrays, I felt like the sliding window method is great at dealing with subarrays.\n\n# Approach\nWe\'re gonna run through the list with two pointers, i and j. They both start at the beginning, but we keep moving j ahead until we hit more than k numbers in the nums[i:j+1] section that can be divided by p. Every time we find a section that fits the requirements, we add it into a set. Once we can\'t push j any more without breaking the rules, we increase i up a spot and repeat the process.\n\n# Complexity\n- Time complexity: O(N^2)\nThe sliding window approach goes through the list twice, once for each "start" point and once for each "end" point of a subarray. Since we\'re looping twice for each item in the list, we say it takes O(N^2).\n\n- Space complexity: O(N)\nThe main thing taking up extra space is the set where we keep track of the subarrays. Given we might end up storing a bunch of subarrays in the set, and each subarray can be as big as the original list, our space usage can be roughly proportional to the size of the list, making it O(N).\n\n# Code\n```\nclass Solution:\n def countDistinct(self, nums: List[int], k: int, p: int) -> int:\n res = set()\n N = len(nums)\n\n for i in range(N):\n count = 0\n\n for j in range(i, N):\n if nums[j] % p == 0:\n count += 1\n if count > k:\n break\n \n res.add(tuple(nums[i:j + 1]))\n\n return len(res)\n``` | 2 | Given an integer array `nums` and two integers `k` and `p`, return _the number of **distinct subarrays** which have **at most**_ `k` _elements divisible by_ `p`.
Two arrays `nums1` and `nums2` are said to be **distinct** if:
* They are of **different** lengths, or
* There exists **at least** one index `i` where `nums1[i] != nums2[i]`.
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[**2**,3,3,**2**,**2**\], k = 2, p = 2
**Output:** 11
**Explanation:**
The elements at indices 0, 3, and 4 are divisible by p = 2.
The 11 distinct subarrays which have at most k = 2 elements divisible by 2 are:
\[2\], \[2,3\], \[2,3,3\], \[2,3,3,2\], \[3\], \[3,3\], \[3,3,2\], \[3,3,2,2\], \[3,2\], \[3,2,2\], and \[2,2\].
Note that the subarrays \[2\] and \[3\] occur more than once in nums, but they should each be counted only once.
The subarray \[2,3,3,2,2\] should not be counted because it has 3 elements that are divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 4, p = 1
**Output:** 10
**Explanation:**
All element of nums are divisible by p = 1.
Also, every subarray of nums will have at most 4 elements that are divisible by 1.
Since all subarrays are distinct, the total number of subarrays satisfying all the constraints is 10.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i], p <= 200`
* `1 <= k <= nums.length`
**Follow up:**
Can you solve this problem in O(n2) time complexity? | When you iterate the array, maintain the number of zeros and ones on the left side. Can you quickly calculate the number of ones on the right side? The number of ones on the right side equals the number of ones in the whole array minus the number of ones on the left side. Alternatively, you can quickly calculate it by using a prefix sum array. |
[Python3] Backtracking | k-divisible-elements-subarrays | 0 | 1 | ```\nclass Solution:\n def countDistinct(self, nums: List[int], k: int, p: int) -> int:\n def dfs(idx, k, path):\n nonlocal res, visited\n if idx == len(nums):\n visited.add(tuple(path[:]))\n return\n \n if nums[idx] % p == 0 and k > 0:\n path.append(nums[idx])\n if tuple(path) not in visited:\n visited.add(tuple(path))\n res += 1\n dfs(idx + 1, k - 1, path)\n elif nums[idx] % p != 0:\n path.append(nums[idx])\n if tuple(path) not in visited:\n visited.add(tuple(path))\n res += 1\n dfs(idx + 1, k, path)\n \n res = 0\n visited = set()\n for i in range(len(nums)):\n dfs(i, k, [])\n return res\n``` | 2 | Given an integer array `nums` and two integers `k` and `p`, return _the number of **distinct subarrays** which have **at most**_ `k` _elements divisible by_ `p`.
Two arrays `nums1` and `nums2` are said to be **distinct** if:
* They are of **different** lengths, or
* There exists **at least** one index `i` where `nums1[i] != nums2[i]`.
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[**2**,3,3,**2**,**2**\], k = 2, p = 2
**Output:** 11
**Explanation:**
The elements at indices 0, 3, and 4 are divisible by p = 2.
The 11 distinct subarrays which have at most k = 2 elements divisible by 2 are:
\[2\], \[2,3\], \[2,3,3\], \[2,3,3,2\], \[3\], \[3,3\], \[3,3,2\], \[3,3,2,2\], \[3,2\], \[3,2,2\], and \[2,2\].
Note that the subarrays \[2\] and \[3\] occur more than once in nums, but they should each be counted only once.
The subarray \[2,3,3,2,2\] should not be counted because it has 3 elements that are divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 4, p = 1
**Output:** 10
**Explanation:**
All element of nums are divisible by p = 1.
Also, every subarray of nums will have at most 4 elements that are divisible by 1.
Since all subarrays are distinct, the total number of subarrays satisfying all the constraints is 10.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i], p <= 200`
* `1 <= k <= nums.length`
**Follow up:**
Can you solve this problem in O(n2) time complexity? | When you iterate the array, maintain the number of zeros and ones on the left side. Can you quickly calculate the number of ones on the right side? The number of ones on the right side equals the number of ones in the whole array minus the number of ones on the left side. Alternatively, you can quickly calculate it by using a prefix sum array. |
[Python3] Rolling Hash Simple Solution | k-divisible-elements-subarrays | 0 | 1 | ```python\nclass Solution:\n POW = 397\n MODULO = 100000000069\n def countDistinct(self, nums: List[int], k: int, p: int) -> int:\n arr = list(map(lambda x: 1 if x % p == 0 else 0, nums))\n ans_set = set[int]()\n for i in range(len(arr)):\n cnt_one = 0\n hash1 = 0\n for j in range(i, len(arr)):\n hash1 = (hash1 * Solution.POW + nums[j] + (j + 1 - i)) % Solution.MODULO\n if arr[j] == 1:\n cnt_one += 1\n if cnt_one <= k:\n ans_set.add(hash1)\n else:\n break\n\n return len(ans_set)\n```\n\n | 3 | Given an integer array `nums` and two integers `k` and `p`, return _the number of **distinct subarrays** which have **at most**_ `k` _elements divisible by_ `p`.
Two arrays `nums1` and `nums2` are said to be **distinct** if:
* They are of **different** lengths, or
* There exists **at least** one index `i` where `nums1[i] != nums2[i]`.
A **subarray** is defined as a **non-empty** contiguous sequence of elements in an array.
**Example 1:**
**Input:** nums = \[**2**,3,3,**2**,**2**\], k = 2, p = 2
**Output:** 11
**Explanation:**
The elements at indices 0, 3, and 4 are divisible by p = 2.
The 11 distinct subarrays which have at most k = 2 elements divisible by 2 are:
\[2\], \[2,3\], \[2,3,3\], \[2,3,3,2\], \[3\], \[3,3\], \[3,3,2\], \[3,3,2,2\], \[3,2\], \[3,2,2\], and \[2,2\].
Note that the subarrays \[2\] and \[3\] occur more than once in nums, but they should each be counted only once.
The subarray \[2,3,3,2,2\] should not be counted because it has 3 elements that are divisible by 2.
**Example 2:**
**Input:** nums = \[1,2,3,4\], k = 4, p = 1
**Output:** 10
**Explanation:**
All element of nums are divisible by p = 1.
Also, every subarray of nums will have at most 4 elements that are divisible by 1.
Since all subarrays are distinct, the total number of subarrays satisfying all the constraints is 10.
**Constraints:**
* `1 <= nums.length <= 200`
* `1 <= nums[i], p <= 200`
* `1 <= k <= nums.length`
**Follow up:**
Can you solve this problem in O(n2) time complexity? | When you iterate the array, maintain the number of zeros and ones on the left side. Can you quickly calculate the number of ones on the right side? The number of ones on the right side equals the number of ones in the whole array minus the number of ones on the left side. Alternatively, you can quickly calculate it by using a prefix sum array. |
DP | total-appeal-of-a-string | 1 | 1 | > Note: there is even a simpler [combinatorics solution](https://leetcode.com/problems/total-appeal-of-a-string/discuss/1999226/Combinatorics), proposed by [geekykant](https://leetcode.com/geekykant/).\n\nWhat is the appeal of all substrings that end at `i`-th position?\n- It is the same as the appeal of all substrings that end at `i - 1` position, plus: \n- number of substrings (ending at `i`-th position) that do not contain `s[i]` character.\n\t- to count those substrings, we just track the previous (`prev`) position of `s[i]` character.\n\n\n\n**C++**\nSince we initialize `last` with zero, we need to do `+ 1` \n```cpp\nlong long appealSum(string s) {\n long long res = 0, cur = 0, prev[26] = {};\n for (int i = 0; i < s.size(); ++i) {\n cur += i + 1 - prev[s[i] - \'a\'];\n prev[s[i] - \'a\'] = i + 1;\n res += cur;\n }\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def appealSum(self, s: str) -> int:\n res, cur, prev = 0, 0, defaultdict(lambda: -1)\n for i, ch in enumerate(s):\n cur += i - prev[ch]\n prev[ch] = i\n res += cur\n return res \n```\n**Java**\n```java\npublic long appealSum(String s) {\n long res = 0, cur = 0, prev[] = new long[26];\n for (int i = 0; i < s.length(); ++i) {\n cur += i + 1 - prev[s.charAt(i) - \'a\'];\n prev[s.charAt(i) - \'a\'] = i + 1;\n res += cur;\n } \n return res;\n}\n``` | 266 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
Python3 | O(N) / O(1) | detail for beginners | total-appeal-of-a-string | 0 | 1 | **Thought Process**\n\nThe constraints of length of input is 10^5, then we would like to do it linear time.\nSo started filling this table to observe pattern. (to visually see what are my possible subarrays are as iterating only once)\n\nAssume our example input is **S = \'ababba\'**\n\n\n\n\n\n\nSo to store the previously seen characters\u2019s index, we can use hashmap.\n**It makes sense because we know that we just need to increment the number of current candidates that does not have duplicate characters that we are looking at i.**\nSo we are basically doing => previous points **+ (** number of candidates for current index **\u2013** index where this character was shown before **)**.\n\nHope this makes sense, then implement gets simple.\n\n```\nclass Solution:\n def appealSum(self, s: str) -> int:\n lastSeenMap = {s[0]: 0}\n prev, curr, res = 1, 0, 1\n \n for i in range(1, len(s)):\n if s[i] in lastSeenMap:\n curr = prev + (i - lastSeenMap[s[i]])\n else:\n curr = prev + (i + 1)\n res += curr\n prev = curr\n lastSeenMap[s[i]] = i\n return res\n```\n\n**Complexity:**\nTime \u2013 O(N) because we are only iterating over the input once\nSpace \u2013 O(26) -> O(1) as input consist of lowercase English letters only\n\n**Please correct me if I am wrong !\nPlease UPVOTE if you find this solution helpful !\nHappy algo!**\n\n**UPDATES** - I found that the way how I started is useful when you are looking for all possible subarrays.\nWorking on the two problems greatly helped me to understand such a problem like this, so please take a look\nhttps://leetcode.com/problems/sum-of-subarray-ranges/\nhttps://leetcode.com/problems/sum-of-subarray-minimums/\n | 115 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
Combinatorics | total-appeal-of-a-string | 0 | 1 | This is similar to [2063. Vowels of All Substrings](https://leetcode.com/problems/vowels-of-all-substrings/discuss/1563701/(i-%2B-1)-*-(sz-i)). \n\nFrom that problem, we use the fact that each character appears in `(i + 1) * (n - i)` substrings. However, it does not contribute to the appeal of substrings on the left that already include that character. For example, for string "abc**a**b", the second \'a\' character contributes to the appeal of 6 substrings: \n- ~~"abca"~~ and ~~"abcab"~~ (first \'a\' character is already counted)\n- "bca" and "bcab"\n- "ca" and "cab"\n- "a" and "ab"\n\nTo exclude previously counted substrings, we just track the previous (prev) position of s[i] character. So, the final formula is `(i - prev[ch]) * (n - i)`.\n\n> For a different way to solve it, check out this [DP solution](https://leetcode.com/problems/total-appeal-of-a-string/discuss/1996203/DP).\n\n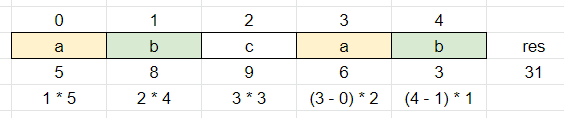\n\n**Python 3**\n```python\nclass Solution:\n def appealSum(self, s: str) -> int:\n res, n, prev = 0, len(s), defaultdict(lambda: -1)\n for i, ch in enumerate(s):\n res += (i - prev[ch]) * (n - i)\n prev[ch] = i\n return res\n```\n\n**C++**\n```cpp\nlong long appealSum(string s) {\n long long res = 0, n = s.size(), prev[26] = {};\n for (int i = 0; i < n; ++i) {\n res += (i + 1 - prev[s[i] - \'a\']) * (n - i);\n prev[s[i] - \'a\'] = i + 1;\n }\n return res;\n}\n```\n\n | 76 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
Easy to Understand || Detailed solution || Combinatorics || O(N) | total-appeal-of-a-string | 0 | 1 | # Intuition\nThe intuition is to think about the **contribution** of each element in the **to the total appeal**. By contribution I mean how much appeal is the element going to bring from all the subarrays it is a part of.\n\n# Approach\nConsider the given testcase from the problem `"abbca"`. Let\'s consider two more things `left` & `right`. `left` is the number of subarrays ending at the number (including it) and `right` is the number of subarrays starting from the number to the end. Our target is the count how many of these are actually meaningful for us.\nBack to the test case `"abbca"`, let\'s consider the first element `a` at the index 0:\nFor `a` the number of subarrays starting from beginning including `a` is only 1 i.e `a` itself. Therefore here `left = 1`. So far so good, now let\'s think about the right part, we have the following possibilities: `a`,`ab`,`abb`,`abbc`,`abbca`. Let us not think about duplicates right now. So we get `right = 5`. Now the number of subarrays that this `a` contributes to is given by `left * right` which is 5. This is pretty self intuitive for any number in an array, the total number of subarrays it can be a part of is given by `left * right`.\n\nLet\'s consider the case of `b`. In the left part we either take `ab` or simply `b` so `left = 2`. For the right part we have `b`,`bb`,`bbc`,`bbca`. Therefore, `right = 4`. Contribution of this `b` is `4*2 = 8`.\n\nHere comes the *logic*, sorry to keep you hanging \uD83D\uDE42. So the second `b` is the curious case, do I calculate `left` and `right` normally?\nNo, I would not because this is no longer unique. According to the question **each letter in the alphabet can only contribute at max 1**. Since this b\'s brother ( the first `b`) already contributed in *some* of the subarrays as 1. This one cannot do that in *those* subarrays. So how do we find out which subarrays to **NOT** count??\nWe find the unique subarrays which the previous `b` was not a part of.\nThese are `b`, `bc`, `bca`. What would the `left` and `right` look like? Left\'s new definition is *the number of subarrays starting after the previous duplicate and ending on this `b`*. While we don\'t need to bother about right, because we will be traversing from left to right and the present `b` will take care of all the previous `b`\'s and use all the other right side oppurtunities where it can be a part of. So anymore `b`\'s to the right will only have to worry about the previous ones.\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N) for the dictionary/hashMap\n\n# Code (Python)\n```\nclass Solution:\n def appealSum(self, s: str) -> int:\n N = len(s)\n seen = {}; appeal = 0 # this dict keeps track of the just previous duplicate we have seen. We just worry about this one, and not earlier ones because the previous dupe already took care of its previous ones\n for idx, char in enumerate(s):\n left, right = -1, -1\n if char in seen: left = idx - seen[char] # we have to include elements starting from 0\n else: left = idx + 1 # include elements starting after the duplicate\n \n right = N - idx\n appeal += left * right\n seen[char] = idx\n return appeal\n \n```\n# Code (C++)\n```cpp\nclass Solution{\n public:\n int appealSum(string &s){\n int N = s.size()\n unordered_map<char, int> seen;\n int appeal = 0;\n for(int i = 0; i < N; i++){\n int left{}, right{};\n if(seen.find(s[i]) != seen.end())\n left = i - seen[s[i]];\n else\n left = i + 1;\n right = N - i;\n appeal += left * right;\n seen[s[i]] = i;\n }\n return appeal;\n }\n};\n``` | 1 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
[Python] Hashmap O(N) Solution with Detailed Explanations, Clean & Concise | total-appeal-of-a-string | 0 | 1 | **Intuition**\nThe given constraint has `1 <= s.length <= 10^5`, indicating `O(N^2)` solutions would get TLE. A natural idea is to use 1-D DP.\n\n**Explanation**\nWe use an array `dp` of length `N`, where `dp[i]` represents the total appeal of all of substrings ending at index `i` of the original string `s`. We also use a hashmap to record the most recent index with the current letter. Now, two conditions needs to be considered:\n(1) If the current letter does not exist in the hashmap, meaning that it is a *new* appearance. Hence, the current letter can contribute to the appeals of all substrings ending at it, which implies `dp[i] = dp[i - 1] + (i + 1)`;\n(2) If the current letter does exist in the hashmap, meaning that it is not a new appearance. Hence, the current letter can contribute to the appeals of all substrings starting after the previous appearance and ending at it, which implies `dp[i] = dp[i - 1] + (i - hashmap[s[i]])`.\nThe final answer is `sum(dp)`.\n\n**Complexity**\nTime: `O(N)`, where `N = s.length` since we perform a linear scan\nSpace `O(N)`, for the use of `dp` array (and the hashmap)\n\nBelow is my in-contest solution. Please upvote if you find this solution helpful. Thanks!\n```\nclass Solution:\n def appealSum(self, s: str) -> int:\n n = len(s)\n dp = [0] * n\n dp[0] = 1\n hashmap = {s[0]: 0}\n for i in range(1, n):\n if s[i] not in hashmap:\n dp[i] = dp[i - 1] + (i + 1)\n hashmap[s[i]] = i\n else:\n dp[i] = dp[i - 1] + (i - hashmap[s[i]])\n hashmap[s[i]] = i\n return sum(dp)\n```\n\n**Follow up**: The above solution can be further optimized to save the use of `dp` array given as follows, which makes the code even more clean and concise.\n\n**Complexity**\nTime: `O(N)`, where `N = s.length` since we perform a linear scan\nSpace `O(26) = O(1)`, for the use of hashmap only\n\n```\nclass Solution:\n def appealSum(self, s: str) -> int:\n n = len(s)\n curSum, cumSum = 1, 1\n hashmap = {s[0]: 0}\n for i in range(1, n):\n if s[i] not in hashmap:\n curSum += i + 1\n else:\n curSum += i - hashmap[s[i]]\n cumSum += curSum\n hashmap[s[i]] = i\n return cumSum\n``` | 7 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
✔️ [Python3] 7-LINES DP (•̀ᴗ•́)و , Explained | total-appeal-of-a-string | 0 | 1 | **UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.**\n\nThe idea is to iterate over all characters and for every one of them calculate the amount of substrings where this character contribute to the score. The formula is as follows:\n`X + Y - Z`, where\n* X - the amount of substrings where current characters appears if the string started from this characters `n - i`\n* Y - the amount of substrings that the previous character can form with the current one ` dp[i-1] - i`\n* Z - correction for the previously seen same characters (just substruct amount of substrings where those two appears together) `last_seen[ch] + 1`\n\nTo know when the same characters appeared before. we use a hash map `last_seen`\n\nSo resulting formula is `(n - i) + (dp[i - 1] - i) - (last_seen[ch] + 1)`. Result is equal to sum of the dp table.\n\n\n```\ndef appealSum(self, s: str) -> int:\n\tn = len(s) \n\tdp = [0]*(n + 1)\n\tlast_seen = defaultdict(lambda: -1)\n\tfor i, ch in enumerate(s):\n\t\tdp[i] = (n - i) + (dp[i - 1] - i) - (last_seen[ch] + 1)\n\t\tlast_seen[ch] = i\n\n\treturn sum(dp)\n```\n\n**UPVOTE if you like (\uD83C\uDF38\u25E0\u203F\u25E0), If you have any question, feel free to ask.** | 8 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
Python | Hashtable One Pass O(n) with Illustration | total-appeal-of-a-string | 0 | 1 | \n\n```\nclass Solution:\n def appealSum(self, s: str) -> int:\n prev = {}\n total, curr = 0, 0\n for i, c in enumerate(s):\n if c in prev:\n curr += i + 1 - (prev[c])\n prev[c] = (i + 1)\n else:\n prev[c] = (i+1)\n curr += i + 1\n total += curr\n return total\n``` | 3 | The **appeal** of a string is the number of **distinct** characters found in the string.
* For example, the appeal of `"abbca "` is `3` because it has `3` distinct characters: `'a'`, `'b'`, and `'c'`.
Given a string `s`, return _the **total appeal of all of its **substrings**.**_
A **substring** is a contiguous sequence of characters within a string.
**Example 1:**
**Input:** s = "abbca "
**Output:** 28
**Explanation:** The following are the substrings of "abbca ":
- Substrings of length 1: "a ", "b ", "b ", "c ", "a " have an appeal of 1, 1, 1, 1, and 1 respectively. The sum is 5.
- Substrings of length 2: "ab ", "bb ", "bc ", "ca " have an appeal of 2, 1, 2, and 2 respectively. The sum is 7.
- Substrings of length 3: "abb ", "bbc ", "bca " have an appeal of 2, 2, and 3 respectively. The sum is 7.
- Substrings of length 4: "abbc ", "bbca " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 5: "abbca " has an appeal of 3. The sum is 3.
The total sum is 5 + 7 + 7 + 6 + 3 = 28.
**Example 2:**
**Input:** s = "code "
**Output:** 20
**Explanation:** The following are the substrings of "code ":
- Substrings of length 1: "c ", "o ", "d ", "e " have an appeal of 1, 1, 1, and 1 respectively. The sum is 4.
- Substrings of length 2: "co ", "od ", "de " have an appeal of 2, 2, and 2 respectively. The sum is 6.
- Substrings of length 3: "cod ", "ode " have an appeal of 3 and 3 respectively. The sum is 6.
- Substrings of length 4: "code " has an appeal of 4. The sum is 4.
The total sum is 4 + 6 + 6 + 4 = 20.
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters. | For each question, we can either solve it or skip it. How can we use Dynamic Programming to decide the most optimal option for each problem? We store for each question the maximum points we can earn if we started the exam on that question. If we skip a question, then the answer for it will be the same as the answer for the next question. If we solve a question, then the answer for it will be the points of the current question plus the answer for the next solvable question. The maximum of these two values will be the answer to the current question. |
string & loop||0ms beats 100% | largest-3-same-digit-number-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIterate over the string `num` & look for 3 consecutive identical letters!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nOne pass & set `maxd` to record the max seen 3 consecutive identical letters.\n\nPython code is provided in the same manner.\n\nPure C code is rare which is also implemented.\n\n[Please turn on English subtitles if necessary]\n[https://youtu.be/YzDhxIp8OxQ?si=iTSkkpEGtbRzVtSf](https://youtu.be/YzDhxIp8OxQ?si=iTSkkpEGtbRzVtSf)\n\nLeetcode posted several simple questions for several days in a row.However simple problems should also be solved in an appropriate way. The solution is best to be scalable, so use something like a sliding window.\n\nLet\'s consider the testcase `num ="30000777133339"`. The process is as follows\n```\n3 count=1\n0 count=1\n0 count=2\n0 count=3\nmaxd=0\n0 count=4\n7 count=1\n7 count=2\n7 count=3\nmaxd=7\n1 count=1\n3 count=1\n3 count=2\n3 count=3\nmaxd=7\n3 count=4\n9 count=1\n```\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code 0ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n string largestGoodInteger(string& num) {\n int count=0;\n char prev=\'X\', maxd=\' \';\n for(char c: num){\n if (c==prev) count++;\n else count=1;\n if (count==3)\n maxd=max(maxd, c);\n prev=move(c);\n }\n return (maxd==\' \')?"":string(3, maxd);\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# C code 0ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nchar* largestGoodInteger(char* num) {\n int count=1;\n char prev=num[0], maxd=\' \';\n for (register int i=1; num[i]!=\'\\0\'; i++){\n char c=num[i];\n if (c==prev) count++;\n else count=1;\n if (count==3 && c>maxd)\n maxd=c;\n prev=c;\n }\n if (maxd==\' \') return "";\n char* ans=malloc(4);\n memset(ans, maxd, 3);\n ans[3]=\'\\0\';\n return ans;\n}\n```\n# Python code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n count=0\n prev=\'X\'\n maxd=\' \'\n for c in num:\n if c==prev: count+=1\n else: count=1\n if count==3: maxd=max(c, maxd)\n prev=c\n if maxd==\' \': return ""\n return maxd*3\n``` | 7 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
✅☑[C++/Java/Python/JavaScript] || 3 Approaches || Beats 100% || EXPLAINED🔥 | largest-3-same-digit-number-in-string | 1 | 1 | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(With Basics)***\n1. It uses a flag `check` to verify if the condition of finding the triplet is met.\n1. The `temp` variable stores the largest digit found within the triplet.\n1. If a triplet is found (`check == false`), the largest digit is appended three times to the ans string.\n1. If no triplet is found, it returns an empty string.\n1. The `main` function demonstrates how to use this method by providing an example input string and displaying the largest good integer found in it.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find the largest good integer in a given string\n string largestGoodInteger(string num) {\n string ans = ""; // Initialize an empty string to store the result\n string empty = ""; // Initialize an empty string for a special case\n int temp = 0; // Initialize a variable to store the largest digit found\n bool check = true; // Initialize a flag to check for a specific condition\n\n // Loop through the string to find the largest digit occurring thrice consecutively\n for (int i = 0; i < num.size() - 2; i++) {\n // Check if the current digit is the same as the next two digits\n if (i + 2 < num.size() && num[i] == num[i + 1] && num[i] == num[i + 2]) {\n // Convert the character digit to its integer equivalent and update \'temp\'\n temp = max(temp, num[i] - \'0\');\n check = false; // Update the flag to indicate the condition was met\n }\n }\n\n // If the condition was met (i.e., a triplet was found)\n if (check == false) {\n // Append the largest digit found three times to the \'ans\' string\n for (int i = 0; i < 3; i++) {\n ans += to_string(temp);\n }\n } else { // If no such triplet found\n return empty; // Return the empty string\n }\n\n return ans; // Return the result containing the largest good integer\n }\n};\n\n\n```\n```C []\n#include <stdio.h>\n#include <string.h>\n\nchar* largestGoodInteger(char* num) {\n char* ans = ""; // Initialize an empty string to store the result\n char* empty = ""; // Initialize an empty string for a special case\n int temp = 0; // Initialize a variable to store the largest digit found\n int check = 1; // Initialize a flag to check for a specific condition\n\n // Loop through the string to find the largest digit occurring thrice consecutively\n for (int i = 0; i < strlen(num) - 2; i++) {\n // Check if the current digit is the same as the next two digits\n if (i + 2 < strlen(num) && num[i] == num[i + 1] && num[i] == num[i + 2]) {\n // Convert the character digit to its integer equivalent and update \'temp\'\n temp = (temp > (num[i] - \'0\')) ? temp : (num[i] - \'0\');\n check = 0; // Update the flag to indicate the condition was met\n }\n }\n\n // If the condition was met (i.e., a triplet was found)\n if (check == 0) {\n // Append the largest digit found three times to the \'ans\' string\n for (int i = 0; i < 3; i++) {\n // Convert integer \'temp\' back to character and append to \'ans\'\n char buffer[2];\n snprintf(buffer, sizeof(buffer), "%d", temp);\n strcat(ans, buffer);\n }\n } else { // If no such triplet found\n return empty; // Return the empty string\n }\n\n return ans; // Return the result containing the largest good integer\n}\n\n\n\n\n\n\n```\n```Java []\npublic class Solution {\n public String largestGoodInteger(String num) {\n String ans = ""; // Initialize an empty string to store the result\n String empty = ""; // Initialize an empty string for a special case\n int temp = 0; // Initialize a variable to store the largest digit found\n boolean check = true; // Initialize a flag to check for a specific condition\n\n // Loop through the string to find the largest digit occurring thrice consecutively\n for (int i = 0; i < num.length() - 2; i++) {\n // Check if the current digit is the same as the next two digits\n if (i + 2 < num.length() && num.charAt(i) == num.charAt(i + 1) && num.charAt(i) == num.charAt(i + 2)) {\n // Convert the character digit to its integer equivalent and update \'temp\'\n temp = Math.max(temp, num.charAt(i) - \'0\');\n check = false; // Update the flag to indicate the condition was met\n }\n }\n\n // If the condition was met (i.e., a triplet was found)\n if (!check) {\n // Append the largest digit found three times to the \'ans\' string\n for (int i = 0; i < 3; i++) {\n ans += temp;\n }\n } else { // If no such triplet found\n return empty; // Return the empty string\n }\n\n return ans; // Return the result containing the largest good integer\n } \n}\n\n\n\n```\n```python3 []\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n ans = "" # Initialize an empty string to store the result\n empty = "" # Initialize an empty string for a special case\n temp = 0 # Initialize a variable to store the largest digit found\n check = True # Initialize a flag to check for a specific condition\n\n # Loop through the string to find the largest digit occurring thrice consecutively\n for i in range(len(num) - 2):\n # Check if the current digit is the same as the next two digits\n if i + 2 < len(num) and num[i] == num[i + 1] == num[i + 2]:\n # Convert the character digit to its integer equivalent and update \'temp\'\n temp = max(temp, int(num[i]))\n check = False # Update the flag to indicate the condition was met\n\n # If the condition was met (i.e., a triplet was found)\n if not check:\n # Append the largest digit found three times to the \'ans\' string\n ans += str(temp) * 3\n\n else: # If no such triplet found\n return empty # Return the empty string\n\n return ans # Return the result containing the largest good integer\n\n\n```\n```javascript []\nfunction largestGoodInteger(num) {\n let ans = ""; // Initialize an empty string to store the result\n let empty = ""; // Initialize an empty string for a special case\n let temp = 0; // Initialize a variable to store the largest digit found\n let check = true; // Initialize a flag to check for a specific condition\n\n // Loop through the string to find the largest digit occurring thrice consecutively\n for (let i = 0; i < num.length - 2; i++) {\n // Check if the current digit is the same as the next two digits\n if (i + 2 < num.length && num[i] == num[i + 1] && num[i] == num[i + 2]) {\n // Convert the character digit to its integer equivalent and update \'temp\'\n temp = Math.max(temp, parseInt(num[i]));\n check = false; // Update the flag to indicate the condition was met\n }\n }\n\n // If the condition was met (i.e., a triplet was found)\n if (check == false) {\n // Append the largest digit found three times to the \'ans\' string\n for (let i = 0; i < 3; i++) {\n ans += temp.toString();\n }\n } else { // If no such triplet found\n return empty; // Return the empty string\n }\n\n return ans; // Return the result containing the largest good integer\n}\n\n\n```\n\n---\n#### ***Approach 2(Multiple Iterations, One For Each Digit)***\n1. **List of Same Digit Numbers:** The code has a list called `sameDigitNumbers` containing strings like "999", "888", "777", and so on down to "000".\n\n1. **Checking Function (contains):** There\'s a function called `contains` that takes two strings as input - a three-digit number and another larger string (`num`). It checks if the three-digit number appears as a consecutive sequence within the larger string.\n\n1. **Main Function (largestGoodInteger):** This function iterates through each three-digit number in the `sameDigitNumbers` list. For each number, it uses the `contains` function to see if that three-digit number is present in the input string `num`.\n\n1. **Return:**\n\n - If a three-digit number from `sameDigitNumbers` is found within `num`, the function returns that number.\n - If none of the numbers from `sameDigitNumbers` are found in `num`, it returns an empty string.\n\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\n vector<string> sameDigitNumbers = {"999", "888", "777", "666", "555", "444", "333", "222", "111", "000"};\n\n // Check whether the \'num\' string contains the \'sameDigitNumber\' string or not.\n bool contains(string sameDigitNumber, string num) {\n for (int index = 0; index <= num.size() - 3; ++index) {\n if (num[index] == sameDigitNumber[0] and \n num[index + 1] == sameDigitNumber[1] and \n num[index + 2] == sameDigitNumber[2]) {\n return true;\n }\n }\n return false;\n }\n\npublic:\n string largestGoodInteger(string num) {\n // Iterate on all \'sameDigitNumbers\' and check if the string \'num\' contains it.\n for (auto& sameDigitNumber: sameDigitNumbers) {\n if (contains(sameDigitNumber, num)) {\n // Return the current \'sameDigitNumbers\'.\n return sameDigitNumber;\n }\n }\n // No 3 consecutive same digits are present in the string \'num\'.\n return "";\n }\n};\n\n```\n```C []\n\n// Check whether the \'num\' string contains the \'sameDigitNumber\' string or not.\nint contains(const char *sameDigitNumber, const char *num) {\n int len = strlen(num);\n int sameDigitLen = strlen(sameDigitNumber);\n \n for (int index = 0; index <= len - sameDigitLen; ++index) {\n if (num[index] == sameDigitNumber[0] &&\n num[index + 1] == sameDigitNumber[1] &&\n num[index + 2] == sameDigitNumber[2]) {\n return 1;\n }\n }\n return 0;\n}\n\nchar* largestGoodInteger(const char *num) {\n char *sameDigitNumbers[] = {"999", "888", "777", "666", "555", "444", "333", "222", "111", "000"};\n int totalNumbers = sizeof(sameDigitNumbers) / sizeof(sameDigitNumbers[0]);\n \n // Iterate on all \'sameDigitNumbers\' and check if the string \'num\' contains it.\n for (int i = 0; i < totalNumbers; ++i) {\n if (contains(sameDigitNumbers[i], num)) {\n // Return the current \'sameDigitNumbers\'.\n return sameDigitNumbers[i];\n }\n }\n // No 3 consecutive same digits are present in the string \'num\'.\n return "";\n}\n\n\n```\n```Java []\nclass Solution {\n private List<String> sameDigitNumbers = List.of("999", "888", "777", "666", "555", "444", "333", "222", "111", "000");\n\n // Check whether the \'num\' string contains the \'sameDigitNumber\' string or not.\n private boolean contains(String sameDigitNumber, String num) {\n for (int index = 0; index <= num.length() - 3; ++index) {\n if (num.charAt(index) == sameDigitNumber.charAt(0) &&\n num.charAt(index + 1) == sameDigitNumber.charAt(1) &&\n num.charAt(index + 2) == sameDigitNumber.charAt(2)) {\n return true;\n }\n }\n return false;\n }\n\n public String largestGoodInteger(String num) {\n // Iterate on all \'sameDigitNumbers\' and check if the string \'num\' contains it.\n for (String sameDigitNumber : sameDigitNumbers) {\n if (contains(sameDigitNumber, num)) {\n // Return the current \'sameDigitNumbers\'.\n return sameDigitNumber;\n }\n }\n // No 3 consecutive same digits are present in the string \'num\'.\n return "";\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n same_digit_numbers = ["999", "888", "777", "666", "555", "444", "333", "222", "111", "000"]\n\n # Check whether the \'num\' string contains the \'same_digit_number\' string or not.\n def contains(same_digit_number):\n for index in range(len(num) - 2):\n if num[index] == same_digit_number[0] and \\\n num[index + 1] == same_digit_number[1] and \\\n num[index + 2] == same_digit_number[2]:\n return True\n return False\n\n # Iterate on all \'same_digit_numbers\' and check if the string \'num\' contains it.\n for same_digit_number in same_digit_numbers:\n if contains(same_digit_number):\n # Return the current \'same_digit_number\'.\n return same_digit_number\n # No 3 consecutive same digits are present in the string \'num\'.\n return ""\n\n\n```\n```javascript []\nconst sameDigitNumbers = ["999", "888", "777", "666", "555", "444", "333", "222", "111", "000"];\n\n// Check whether the \'num\' string contains the \'sameDigitNumber\' string or not.\nlet contains = (sameDigitNumber, num) => {\n for (let index = 0; index <= num.length - 3; ++index) {\n if (num[index] === sameDigitNumber[0] &&\n num[index + 1] === sameDigitNumber[1] &&\n num[index + 2] === sameDigitNumber[2]) {\n return true;\n }\n }\n return false;\n};\n\nlet largestGoodInteger = num => {\n // Iterate on all \'sameDigitNumbers\' and check if the string \'num\' contains it.\n for (const sameDigitNumber of sameDigitNumbers) {\n if (contains(sameDigitNumber, num)) {\n // Return the current \'sameDigitNumber\'.\n return sameDigitNumber;\n }\n }\n // No 3 consecutive same digits are present in the string \'num\'.\n return "";\n};\n\n```\n\n---\n#### ***Approach 3(Single Iteration)***\n\n\n1. **Initialization of maxDigit:** It initializes the variable `maxDigit` with the NUL character `\'\\0\'`, which is the smallest character based on ASCII value.\n1. **Iteration over num string:** It loops through the characters of the `num` string, considering sequences of three consecutive characters.\n1. **Finding the largest identical digit sequence:** Within the loop, it checks if three consecutive characters are the same.\n - If they are the same, it updates `maxDigit` to the maximum value between its current value and the current character in the sequence (if it\'s larger).\n1. **Return:** After iterating through the string, the function returns:\n - If `maxDigit` remains `\'\\0\'` (i.e., no sequence of three identical digits was found), it returns an empty string `""`.\n - Otherwise, it constructs and returns a string of size 3 with `maxDigit` characters, representing the largest sequence of three identical digits found in the input string `num`.\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n string largestGoodInteger(string num) {\n // Assign \'maxDigit\' to the NUL character (smallest ASCII value character)\n char maxDigit = \'\\0\';\n\n // Iterate on characters of the num string.\n for (int index = 0; index <= num.size() - 3; ++index) {\n // If 3 consecutive characters are the same,\n // store the character in \'maxDigit\' if bigger than what it already stores.\n if (num[index] == num[index + 1] && num[index] == num[index + 2]) {\n maxDigit = max(maxDigit, num[index]);\n }\n }\n\n // If \'maxDigit\' is NUL return an empty string, otherwise string of size 3 with \'maxDigit\' characters.\n return maxDigit == \'\\0\' ? "" : string(3, maxDigit);\n }\n};\n\n```\n```C []\n\nchar* largestGoodInteger(const char* num) {\n char maxDigit = \'\\0\'; // Assign \'maxDigit\' to the NUL character (smallest ASCII value character)\n int len = strlen(num);\n\n // Iterate on characters of the num string.\n for (int index = 0; index <= len - 3; ++index) {\n // If 3 consecutive characters are the same,\n // store the character in \'maxDigit\' if bigger than what it already stores.\n if (num[index] == num[index + 1] && num[index] == num[index + 2]) {\n maxDigit = (maxDigit > num[index]) ? maxDigit : num[index];\n }\n }\n\n // If \'maxDigit\' is NUL return an empty string, otherwise return string of size 4 with \'maxDigit\' characters.\n char* result = (char*)malloc(4 * sizeof(char));\n if (maxDigit == \'\\0\') {\n result[0] = \'\\0\';\n } else {\n for (int i = 0; i < 3; ++i) {\n result[i] = maxDigit;\n }\n result[3] = \'\\0\'; // Null-terminate the string\n }\n return result;\n}\n\n\n```\n```Java []\nclass Solution {\n public String largestGoodInteger(String num) {\n // Assign \'maxDigit\' to the NUL character (smallest ASCII value character)\n char maxDigit = \'\\0\';\n\n // Iterate on characters of the num string.\n for (int index = 0; index <= num.length() - 3; ++index) {\n // If 3 consecutive characters are the same, \n // store the character in \'maxDigit\' if it\'s bigger than what it already stores.\n if (num.charAt(index) == num.charAt(index + 1) && num.charAt(index) == num.charAt(index + 2)) {\n maxDigit = (char) Math.max(maxDigit, num.charAt(index));\n }\n }\n\n // If \'maxDigit\' is NUL, return an empty string; otherwise, return a string of size 3 with \'maxDigit\' characters.\n return maxDigit == \'\\0\' ? "" : new String(new char[]{maxDigit, maxDigit, maxDigit});\n }\n}\n\n\n```\n```python3 []\n\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n # Assign \'max_digit\' to NUL character (smallest ASCII value character)\n max_digit = \'\\0\'\n\n # Iterate on characters of the num string.\n for index in range(len(num) - 2):\n # If 3 consecutive characters are the same,\n # store the character in \'max_digit\' if it\'s bigger than what it already stores.\n if num[index] == num[index + 1] == num[index + 2]:\n max_digit = max(max_digit, num[index])\n\n # If \'max_digit\' is NUL, return an empty string; otherwise, return a string of size 3 with \'max_digit\' characters.\n return \'\' if max_digit == \'\\0\' else max_digit * 3\n\n```\n```javascript []\nvar largestGoodInteger = function(num) {\n // Assign \'maxDigit\' to the NUL character (smallest ASCII value character)\n let maxDigit = \'\\0\';\n\n // Iterate on characters of the num string.\n for (let index = 0; index <= num.length - 3; ++index) {\n // If 3 consecutive characters are the same,\n // store the character in \'maxDigit\' if it\'s bigger than what it already stores.\n if (num[index] === num[index + 1] && num[index] === num[index + 2]) {\n maxDigit = String.fromCharCode(Math.max(maxDigit.charCodeAt(0), num.charCodeAt(index)));\n }\n }\n\n // If \'maxDigit\' is NUL, return an empty string; otherwise, return a string of size 3 with \'maxDigit\' characters.\n return maxDigit === \'\\0\' ? \'\' : maxDigit.repeat(3);\n};\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 5 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Python Solution | largest-3-same-digit-number-in-string | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n s=""\n for i in range(len(num)-2):\n if num[i]==num[i+1] and num[i]==num[i+2]:\n if num[i]>s:\n s=num[i]\n return s*3\n \n``` | 4 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Python3 Solution | largest-3-same-digit-number-in-string | 0 | 1 | \n```\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n n=len(num)\n ans=""\n for i in range(n):\n if i+2<n and num[i]==num[i+1] and num[i]==num[i+2]:\n ans=max(ans,num[i:i+3])\n return ans \n``` | 3 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Easy solution with comment on each line. TC = O(n), SC = O1 | largest-3-same-digit-number-in-string | 0 | 1 | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O1\n\n# Code\n```Python\nclass Solution:\n def largestGoodInteger(self, num: str) -> str:\n # Initialize max_num to -1, to track the largest triplet\n max_num = -1\n \n # Set the left pointer to the start of the string\n l = 0\n \n # Set the right pointer next to the left pointer\n r = l + 1\n\n # Iterate as long as the right pointer is within the string\n while r < len(num):\n # If current characters at left and right pointers are different\n if num[l] != num[r]:\n # Move left pointer to the right pointer\'s position\n l = r\n \n # Move right pointer to one position after the new left pointer\n r = l + 1\n\n # If current characters at left and right pointers are the same\n else:\n # If a triplet is formed\n if r - l == 2:\n # Update max_num with the largest digit among the found triplets\n max_num = max(max_num, int(num[l]))\n \n # Move left pointer to the position after the current triplet\n l = r + 1\n \n # Reset right pointer to one position after the new left pointer\n r = l + 1\n \n else:\n # If a triplet is not formed yet, increment the right pointer\n r += 1\n \n # Return an empty string if no triplet is found, otherwise return the largest triplet\n return "" if max_num == -1 else f"{max_num}" * 3 \n``` | 10 | You are given a string `num` representing a large integer. An integer is **good** if it meets the following conditions:
* It is a **substring** of `num` with length `3`.
* It consists of only one unique digit.
Return _the **maximum good** integer as a **string** or an empty string_ `" "` _if no such integer exists_.
Note:
* A **substring** is a contiguous sequence of characters within a string.
* There may be **leading zeroes** in `num` or a good integer.
**Example 1:**
**Input:** num = "6**777**133339 "
**Output:** "777 "
**Explanation:** There are two distinct good integers: "777 " and "333 ".
"777 " is the largest, so we return "777 ".
**Example 2:**
**Input:** num = "23**000**19 "
**Output:** "000 "
**Explanation:** "000 " is the only good integer.
**Example 3:**
**Input:** num = "42352338 "
**Output:** " "
**Explanation:** No substring of length 3 consists of only one unique digit. Therefore, there are no good integers.
**Constraints:**
* `3 <= num.length <= 1000`
* `num` only consists of digits. | Notice that the most optimal way to obtain the minimum possible sum using 4 digits is by summing up two 2-digit numbers. We can use the two smallest digits out of the four as the digits found in the tens place respectively. Similarly, we use the final 2 larger digits as the digits found in the ones place. |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.