title
stringlengths 1
100
| titleSlug
stringlengths 3
77
| Java
int64 0
1
| Python3
int64 1
1
| content
stringlengths 28
44.4k
| voteCount
int64 0
3.67k
| question_content
stringlengths 65
5k
| question_hints
stringclasses 970
values |
|---|---|---|---|---|---|---|---|
Python in-place w/ Stack | replace-non-coprime-numbers-in-array | 0 | 1 | # Intuition\nNote that we can greedily merge elements since the problem explicitly states that it can be shown that the order of merge does not matter. \n# Approach\nGiven that we can implement a greedy approach, we just need to keep track of the last number we have merged as we iterate over the array.\n# Complexity\n- Time complexity:\n$O(n \\log(n))$\nAlgorithm completes in one loop w/ a log(n) cost per iteration.\n- Space complexity:\n$O(n)$\n# Code\n```\nimport math \nclass Solution:\n def replaceNonCoprimes(self, nums: List[int]) -> List[int]:\n n = len(nums)\n i = 0\n stack = []\n while i < n:\n while stack and math.gcd(stack[-1][0], nums[i]) > 1:\n num, j = stack.pop()\n nums[i] = math.lcm(num, nums[i])\n nums[j] = float(\'inf\')\n stack.append([nums[i], i])\n i += 1\n return [ele for ele in nums if ele != float(\'inf\')]\n``` | 0 | You are given an array of integers `nums`. Perform the following steps:
1. Find **any** two **adjacent** numbers in `nums` that are **non-coprime**.
2. If no such numbers are found, **stop** the process.
3. Otherwise, delete the two numbers and **replace** them with their **LCM (Least Common Multiple)**.
4. **Repeat** this process as long as you keep finding two adjacent non-coprime numbers.
Return _the **final** modified array._ It can be shown that replacing adjacent non-coprime numbers in **any** arbitrary order will lead to the same result.
The test cases are generated such that the values in the final array are **less than or equal** to `108`.
Two values `x` and `y` are **non-coprime** if `GCD(x, y) > 1` where `GCD(x, y)` is the **Greatest Common Divisor** of `x` and `y`.
**Example 1:**
**Input:** nums = \[6,4,3,2,7,6,2\]
**Output:** \[12,7,6\]
**Explanation:**
- (6, 4) are non-coprime with LCM(6, 4) = 12. Now, nums = \[**12**,3,2,7,6,2\].
- (12, 3) are non-coprime with LCM(12, 3) = 12. Now, nums = \[**12**,2,7,6,2\].
- (12, 2) are non-coprime with LCM(12, 2) = 12. Now, nums = \[**12**,7,6,2\].
- (6, 2) are non-coprime with LCM(6, 2) = 6. Now, nums = \[12,7,**6**\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[12,7,6\].
Note that there are other ways to obtain the same resultant array.
**Example 2:**
**Input:** nums = \[2,2,1,1,3,3,3\]
**Output:** \[2,1,1,3\]
**Explanation:**
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**,3\].
- (3, 3) are non-coprime with LCM(3, 3) = 3. Now, nums = \[2,2,1,1,**3**\].
- (2, 2) are non-coprime with LCM(2, 2) = 2. Now, nums = \[**2**,1,1,3\].
There are no more adjacent non-coprime numbers in nums.
Thus, the final modified array is \[2,1,1,3\].
Note that there are other ways to obtain the same resultant array.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 105`
* The test cases are generated such that the values in the final array are **less than or equal** to `108`. | How can you use rows and encodedText to find the number of columns of the matrix? Once you have the number of rows and columns, you can create the matrix and place encodedText in it. How should you place it in the matrix? How should you traverse the matrix to "decode" originalText? |
✅Python easy to understand || Beginner friendly | find-all-k-distant-indices-in-an-array | 0 | 1 | ```\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n ind_j = []\n for ind, elem in enumerate(nums):\n if elem == key:\n ind_j.append(ind)\n res = []\n for i in range(len(nums)):\n for j in ind_j:\n if abs(i - j) <= k:\n res.append(i)\n break\n return sorted(res)\n``` | 8 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
O(N) two-pass solution in Python | find-all-k-distant-indices-in-an-array | 0 | 1 | for each index `i`, we check for two possible key indexes - `keys[left]` and `keys[left + 1]`. If either of them is less than or equal to k, then add to `res`.\n\nIn order to handle the edges, I added negative and positive infinity to both sides.\n\n```\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n keys = [-math.inf] + [idx for idx, num in enumerate(nums) if num == key] + [math.inf]\n N = len(nums)\n res = []\n left = 0\n \n for i in range(N):\n if i - keys[left] <= k or keys[left + 1] - i <= k:\n res.append(i)\n if keys[left + 1] == i:\n left += 1\n return res\n``` | 3 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
python Beginner friendly soln.. | find-all-k-distant-indices-in-an-array | 0 | 1 | ```class Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n temp=[]\n result=[]\n for u,v in enumerate(nums):\n if v==key:\n temp.append(u)\n for i in range(0,len(nums)):\n for j in temp:\n if abs(j-i)<=k:\n result.append(i)\n break\n return result | 0 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
Python easy solution without using external function | Fast and single pass | find-all-k-distant-indices-in-an-array | 0 | 1 | Time :0(n) | Space : 0(n)\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n \n res_idx = set()\n n = len(nums)\n for idx in range(n):\n if key==nums[idx]:\n sp = idx - k if idx - k > 0 else 0\n ep = idx + k if idx + k < n else n-1\n for val in range(sp,ep+1):\n res_idx.add(val)\n \n return list(res_idx) | 1 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
Python 5 lines | find-all-k-distant-indices-in-an-array | 0 | 1 | ```\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n ans = set()\n for i, num in enumerate(nums):\n if num == key:\n ans.update(range(max(0, i-k), min(i+k+1, len(nums))))\n return sorted(list(res))\n``` | 1 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
Clean Python Brute Force Solution | find-all-k-distant-indices-in-an-array | 0 | 1 | ```\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n n, ans = len(nums), []\n keys_index = [i for i in range(n) if nums[i] == key] # Holds the indices of all elements equal to key.\n m = len(keys_index)\n for i in range(n):\n for j in range(m):\n if abs(i - keys_index[j]) <= k: # If the conditions are met then add ith index to the answer array.\n ans.append(i)\n break\n return sorted(ans) # Return sorted ans according to problem\n```\n | 1 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
O(N) 5-line one pass without sorting | find-all-k-distant-indices-in-an-array | 0 | 1 | # Code\n```python\nclass Solution:\n def findKDistantIndices(self, nums: List[int], key: int, k: int) -> List[int]:\n k_d_indices = set()\n for i, num in enumerate(nums):\n if num == key:\n k_d_indices.update(range(max(0, i-k), min(len(nums), i+k+1)))\n return list(k_d_indices)\n\n``` | 0 | You are given a **0-indexed** integer array `nums` and two integers `key` and `k`. A **k-distant index** is an index `i` of `nums` for which there exists at least one index `j` such that `|i - j| <= k` and `nums[j] == key`.
Return _a list of all k-distant indices sorted in **increasing order**_.
**Example 1:**
**Input:** nums = \[3,4,9,1,3,9,5\], key = 9, k = 1
**Output:** \[1,2,3,4,5,6\]
**Explanation:** Here, `nums[2] == key` and `nums[5] == key. - For index 0, |0 - 2| > k and |0 - 5| > k, so there is no j` where `|0 - j| <= k` and `nums[j] == key. Thus, 0 is not a k-distant index. - For index 1, |1 - 2| <= k and nums[2] == key, so 1 is a k-distant index. - For index 2, |2 - 2| <= k and nums[2] == key, so 2 is a k-distant index. - For index 3, |3 - 2| <= k and nums[2] == key, so 3 is a k-distant index. - For index 4, |4 - 5| <= k and nums[5] == key, so 4 is a k-distant index. - For index 5, |5 - 5| <= k and nums[5] == key, so 5 is a k-distant index. - For index 6, |6 - 5| <= k and nums[5] == key, so 6 is a k-distant index.`
Thus, we return \[1,2,3,4,5,6\] which is sorted in increasing order.
**Example 2:**
**Input:** nums = \[2,2,2,2,2\], key = 2, k = 2
**Output:** \[0,1,2,3,4\]
**Explanation:** For all indices i in nums, there exists some index j such that |i - j| <= k and nums\[j\] == key, so every index is a k-distant index.
Hence, we return \[0,1,2,3,4\].
**Constraints:**
* `1 <= nums.length <= 1000`
* `1 <= nums[i] <= 1000`
* `key` is an integer from the array `nums`.
* `1 <= k <= nums.length` | We can check if every empty cell is a part of a consecutive row of empty cells that has a width of at least stampWidth as well as a consecutive column of empty cells that has a height of at least stampHeight. We can prove that this condition is sufficient and necessary to fit the stamps while following the given restrictions and requirements. For each row, find every consecutive row of empty cells, and mark all the cells where the consecutive row is at least stampWidth wide. Do the same for the columns with stampHeight. Then, you can check if every cell is marked twice. |
📌 [VISUAL] | [Python] | Easy to Understand | O(N^2) Time | O(N^2) Space | count-artifacts-that-can-be-extracted | 0 | 1 | \uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A\n\n**Approach**\nHere we want to check if each part of an artifact is completely dug up. To do this we check each artifact, comparing it to what has been dug to see if it is completely excavated.\n\n**Visual**\nHere is a visual for the example in the question description where red and blue are two seperate artifacts. In this example:\nn = 2\nartifacts = [[0,0,0,0],[0,1,1,1]]\ndig = [[0,0],[0,1],[1,1]]\n\n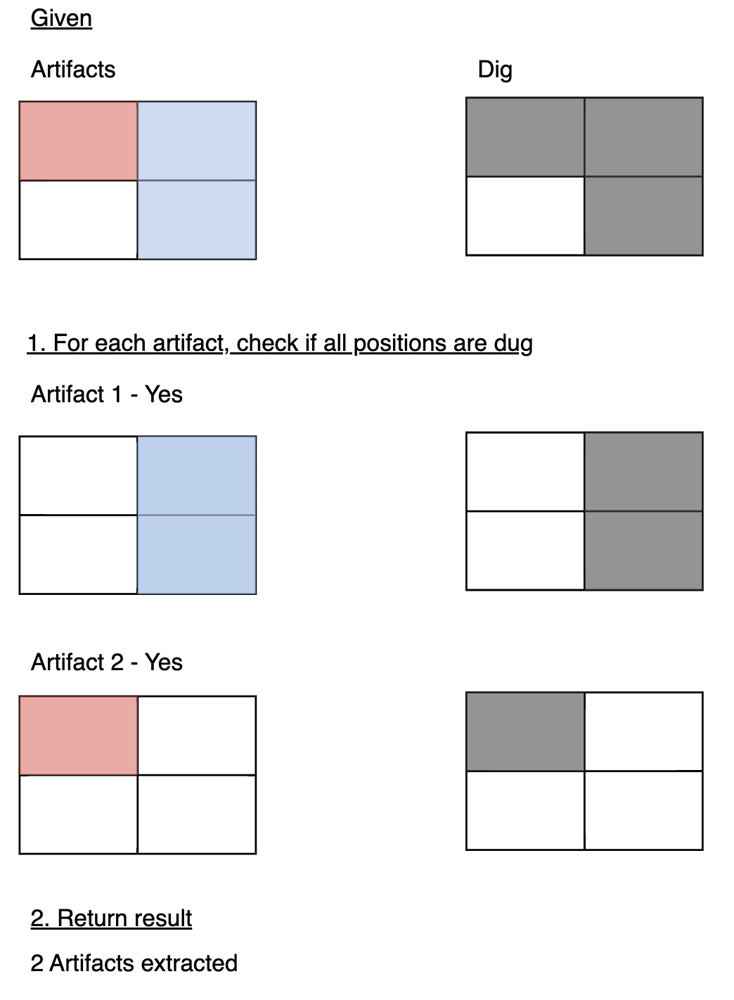\n\n\n**Code**\nSee below for code related to this visual.\n<iframe src="https://leetcode.com/playground/MFdGPhTs/shared" frameBorder="0" width="800" height="600"></iframe>\n\n\uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A | 26 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
📌 [VISUAL] | [Python] | Easy to Understand | O(N^2) Time | O(N^2) Space | count-artifacts-that-can-be-extracted | 0 | 1 | \uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A\n\n**Approach**\nHere we want to check if each part of an artifact is completely dug up. To do this we check each artifact, comparing it to what has been dug to see if it is completely excavated.\n\n**Visual**\nHere is a visual for the example in the question description where red and blue are two seperate artifacts. In this example:\nn = 2\nartifacts = [[0,0,0,0],[0,1,1,1]]\ndig = [[0,0],[0,1],[1,1]]\n\n\n\n\n**Code**\nSee below for code related to this visual.\n<iframe src="https://leetcode.com/playground/MFdGPhTs/shared" frameBorder="0" width="800" height="600"></iframe>\n\n\uD83D\uDD3A**Please UPVOTE: Can we hit 20?** \uD83D\uDD3A | 26 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
💯 Python elegant, short and simple to understand with explanations | count-artifacts-that-can-be-extracted | 0 | 1 | ## Solution 1 - Hash dig positions\n\n1. Since we know all the dig spots, we add all of them into a set for fast lookup. \n1. Then we go through each artifact and check if all the positions for that artifact exist in the dig spots set. \n - If they do, we increment our results counter, otherwise proceed to the next artifact\n\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n\t # Time: O(max(artifacts, dig)) which is O(N^2) as every position in the grid can be in dig\n\t\t# Space: O(dig) which is O(N^2)\n result, dig_pos = 0, set(tuple(pos) for pos in dig)\n for pos in artifacts:\n if all((x, y) in dig_pos for x in range(pos[0], pos[2] + 1) for y in range(pos[1], pos[3] + 1)): \n result += 1\n return result\n```\n\n## Solution 2 - Hash artifact positions\n\nWe make use of two hashmaps in this solution. \n\n1. The first would be a map of positions to the artifacts, uniquely identified by their index in the `artifacts` array\n2. The second would be a map of artifact index to how many spots left for artifact that is undug\n\nOur first loop would be to go through the artifacts and add their positions to the first hashmap, and add how many positions are there into the second hashmap.\n\nThe second loop goes through the dig positions, find the artifact corresponding to each position (if it exists), then update the second hashmap for how many positions left to dig for that artifact. If the remaining count is 0, the artifact is entirely dug up and we can increment our results counter.\n\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n pos_to_artifacts = {} # (x, y) => artifact unique index\n artifacts_to_remaining = {} # artifact unique index to remaining spots for artifact to dig up\n results = 0\n \n\t\t# Each artifact is identified by a unique index.\n for id, artifact in enumerate(artifacts):\n start, end = (artifact[0], artifact[1]), (artifact[2], artifact[3])\n size = 0\n for x in range(start[0], end[0] + 1):\n for y in range(start[1], end[1] + 1):\n pos_to_artifacts[(x, y)] = id\n size += 1\n artifacts_to_remaining[id] = size\n \n for pos in dig:\n if tuple(pos) not in pos_to_artifacts:\n continue\n id = pos_to_artifacts[tuple(pos)]\n artifacts_to_remaining[id] = artifacts_to_remaining[id] - 1\n if artifacts_to_remaining[id] == 0:\n results += 1\n\n return results\n``` | 6 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
💯 Python elegant, short and simple to understand with explanations | count-artifacts-that-can-be-extracted | 0 | 1 | ## Solution 1 - Hash dig positions\n\n1. Since we know all the dig spots, we add all of them into a set for fast lookup. \n1. Then we go through each artifact and check if all the positions for that artifact exist in the dig spots set. \n - If they do, we increment our results counter, otherwise proceed to the next artifact\n\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n\t # Time: O(max(artifacts, dig)) which is O(N^2) as every position in the grid can be in dig\n\t\t# Space: O(dig) which is O(N^2)\n result, dig_pos = 0, set(tuple(pos) for pos in dig)\n for pos in artifacts:\n if all((x, y) in dig_pos for x in range(pos[0], pos[2] + 1) for y in range(pos[1], pos[3] + 1)): \n result += 1\n return result\n```\n\n## Solution 2 - Hash artifact positions\n\nWe make use of two hashmaps in this solution. \n\n1. The first would be a map of positions to the artifacts, uniquely identified by their index in the `artifacts` array\n2. The second would be a map of artifact index to how many spots left for artifact that is undug\n\nOur first loop would be to go through the artifacts and add their positions to the first hashmap, and add how many positions are there into the second hashmap.\n\nThe second loop goes through the dig positions, find the artifact corresponding to each position (if it exists), then update the second hashmap for how many positions left to dig for that artifact. If the remaining count is 0, the artifact is entirely dug up and we can increment our results counter.\n\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n pos_to_artifacts = {} # (x, y) => artifact unique index\n artifacts_to_remaining = {} # artifact unique index to remaining spots for artifact to dig up\n results = 0\n \n\t\t# Each artifact is identified by a unique index.\n for id, artifact in enumerate(artifacts):\n start, end = (artifact[0], artifact[1]), (artifact[2], artifact[3])\n size = 0\n for x in range(start[0], end[0] + 1):\n for y in range(start[1], end[1] + 1):\n pos_to_artifacts[(x, y)] = id\n size += 1\n artifacts_to_remaining[id] = size\n \n for pos in dig:\n if tuple(pos) not in pos_to_artifacts:\n continue\n id = pos_to_artifacts[tuple(pos)]\n artifacts_to_remaining[id] = artifacts_to_remaining[id] - 1\n if artifacts_to_remaining[id] == 0:\n results += 1\n\n return results\n``` | 6 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
Python Solution using Matrix and Simple Counting | count-artifacts-that-can-be-extracted | 0 | 1 | We number each artifact differently in a grid matrix of size n * n. Then we set the value of each grid[r][c] for r, c in dig to -1 meaning that they have been dug up. Now traverse the grid matrix finally and see which artifact numbers still remains. Those artifacts are the once which were not fully excavated. Now subrtact the number of total artifacts to the number of artifacts remaining, this gives us the artifacts which were successfully dug up completely.\n\n**STEPS:**\n1. Make a grid matrix of size n * n denoting our ground of operation.\n2. Now populate each individual artifact (all of its blocks) with a unique number.\n3. Now traverse the dig array and set grid[r][c] to -1 deonting that that index is now dug up.\n4. Now traverse the grid completely and check which artifacts number still remains as they were not dug up yet since their value was set to -1 if they were. Add these artifact numbers to a set to avoid redundant values.\n5. Artifacts Excavated Fully = Total Artifacts - Artifacts that still remain\n\n***NOTE: `artifacts_remaining` set contains the artifacts that are not yet dug by their unique number given to each artifact in the first loop.***\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n grid, artifact_id = [[-1] * n for _ in range(n)], 0 # Making the grid\n for r1, c1, r2, c2 in artifacts: # Populate the grid matrix\n for r in range(r1, r2 + 1):\n for c in range(c1, c2 + 1):\n grid[r][c] = artifact_id\n artifact_id += 1\n for r, c in dig: # Change the grid row, col to -1 by traversing dig array.\n if grid[r][c] >= 0:\n grid[r][c] = -1\n artifacts_remaining = set() \n for r in range(n):\n for c in range(n):\n if grid[r][c] >= 0: # > 0 means that there still remains an artifact underneath, thus add it to the array\n artifacts_remaining.add(grid[r][c])\n return artifact_id - len(artifacts_remaining)\n``` | 3 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
Python Solution using Matrix and Simple Counting | count-artifacts-that-can-be-extracted | 0 | 1 | We number each artifact differently in a grid matrix of size n * n. Then we set the value of each grid[r][c] for r, c in dig to -1 meaning that they have been dug up. Now traverse the grid matrix finally and see which artifact numbers still remains. Those artifacts are the once which were not fully excavated. Now subrtact the number of total artifacts to the number of artifacts remaining, this gives us the artifacts which were successfully dug up completely.\n\n**STEPS:**\n1. Make a grid matrix of size n * n denoting our ground of operation.\n2. Now populate each individual artifact (all of its blocks) with a unique number.\n3. Now traverse the dig array and set grid[r][c] to -1 deonting that that index is now dug up.\n4. Now traverse the grid completely and check which artifacts number still remains as they were not dug up yet since their value was set to -1 if they were. Add these artifact numbers to a set to avoid redundant values.\n5. Artifacts Excavated Fully = Total Artifacts - Artifacts that still remain\n\n***NOTE: `artifacts_remaining` set contains the artifacts that are not yet dug by their unique number given to each artifact in the first loop.***\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n grid, artifact_id = [[-1] * n for _ in range(n)], 0 # Making the grid\n for r1, c1, r2, c2 in artifacts: # Populate the grid matrix\n for r in range(r1, r2 + 1):\n for c in range(c1, c2 + 1):\n grid[r][c] = artifact_id\n artifact_id += 1\n for r, c in dig: # Change the grid row, col to -1 by traversing dig array.\n if grid[r][c] >= 0:\n grid[r][c] = -1\n artifacts_remaining = set() \n for r in range(n):\n for c in range(n):\n if grid[r][c] >= 0: # > 0 means that there still remains an artifact underneath, thus add it to the array\n artifacts_remaining.add(grid[r][c])\n return artifact_id - len(artifacts_remaining)\n``` | 3 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
Python 6 lines | count-artifacts-that-can-be-extracted | 0 | 1 | ```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n dig = set((r, c) for r, c in dig)\n ans = 0\n for r0, c0, r1, c1 in artifacts:\n if all((r, c) in dig for r in range(r0, r1 + 1) for c in range(c0, c1 + 1)):\n ans += 1\n return ans\n``` | 2 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
Python 6 lines | count-artifacts-that-can-be-extracted | 0 | 1 | ```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n dig = set((r, c) for r, c in dig)\n ans = 0\n for r0, c0, r1, c1 in artifacts:\n if all((r, c) in dig for r in range(r0, r1 + 1) for c in range(c0, c1 + 1)):\n ans += 1\n return ans\n``` | 2 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
4 Line super simple | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n dig = set([tuple(i) for i in dig])\n ret = 0\n for x1, y1, x2, y2 in artifacts:\n if all((r, c) in dig for r in range(x1, x2+1) for c in range(y1, y2+1)):\n ret += 1\n return ret\n\n``` | 0 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
4 Line super simple | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n dig = set([tuple(i) for i in dig])\n ret = 0\n for x1, y1, x2, y2 in artifacts:\n if all((r, c) in dig for r in range(x1, x2+1) for c in range(y1, y2+1)):\n ret += 1\n return ret\n\n``` | 0 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
Can you dig it? | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince this is not an online problem -- "how many artifacts are uncovered after each shovel-ful in \'dig\'?" -- we can process all of ```dig``` to build a binary map of which cells are uncovered.\n\nThen, it\'s a matter of seeing, for each ```artifact``` whether the cell(s) it occupies are uncovered, counting one for each such ```artifact```.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code is pretty straightforward. The only tricky part is getting the indexing right in the per-artifact loop.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nPreparing the binary map takes $$O(d)$$ where $$d$$ is the size of ```dig```. Processing of the artifacts to see if they\'re uncovered takes $$O(c)$$ where $$c$$ is the number of cells covered by artifacts. It\'s reasonable to assume that the density of the artifacts is roughly constant; in that case, the number of cells covered by artifacts is $$O(n*n)$$.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only storage created by the program (ignoring the inputs) is the binary map of which cells are uncovered. This will be $$O(n)$$.\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: list[list[int]], dig: list[list[int]]) -> int:\n # Process all the cells in "dig" to produce a map of which cells are uncovered:\n uncovered = [[0] * n for i in range(n)]\n for r, c in dig:\n uncovered[r][c] = 1\n n_extracted = 0\n for r1, c1, r2, c2 in artifacts:\n extractable = True\n for r in range(r1, r2 + 1):\n for c in range(c1, c2 + 1):\n extractable &= uncovered[r][c]\n if not extractable:\n break\n if not extractable:\n break\n if extractable:\n n_extracted += 1\n return n_extracted\n\n``` | 0 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
Can you dig it? | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince this is not an online problem -- "how many artifacts are uncovered after each shovel-ful in \'dig\'?" -- we can process all of ```dig``` to build a binary map of which cells are uncovered.\n\nThen, it\'s a matter of seeing, for each ```artifact``` whether the cell(s) it occupies are uncovered, counting one for each such ```artifact```.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code is pretty straightforward. The only tricky part is getting the indexing right in the per-artifact loop.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nPreparing the binary map takes $$O(d)$$ where $$d$$ is the size of ```dig```. Processing of the artifacts to see if they\'re uncovered takes $$O(c)$$ where $$c$$ is the number of cells covered by artifacts. It\'s reasonable to assume that the density of the artifacts is roughly constant; in that case, the number of cells covered by artifacts is $$O(n*n)$$.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe only storage created by the program (ignoring the inputs) is the binary map of which cells are uncovered. This will be $$O(n)$$.\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: list[list[int]], dig: list[list[int]]) -> int:\n # Process all the cells in "dig" to produce a map of which cells are uncovered:\n uncovered = [[0] * n for i in range(n)]\n for r, c in dig:\n uncovered[r][c] = 1\n n_extracted = 0\n for r1, c1, r2, c2 in artifacts:\n extractable = True\n for r in range(r1, r2 + 1):\n for c in range(c1, c2 + 1):\n extractable &= uncovered[r][c]\n if not extractable:\n break\n if not extractable:\n break\n if extractable:\n n_extracted += 1\n return n_extracted\n\n``` | 0 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
Python | Prefix Sum | count-artifacts-that-can-be-extracted | 0 | 1 | # Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n g = [[0] * n for _ in range(n)]\n for r, c in dig:\n g[r][c] = 1\n for r in range(n):\n for c in range(n):\n g[r][c] += (g[r - 1][c] if r else 0) + (g[r][c - 1] if c else 0) - (g[r - 1][c - 1] if r and c else 0)\n res = 0\n for tr, tc, br, bc in artifacts:\n cnt = g[br][bc] - (g[tr - 1][bc] if tr else 0) - (g[br][tc - 1] if tc else 0) + (g[tr - 1][tc - 1] if tr and tc else 0)\n res += (br - tr + 1) * (bc - tc + 1) == cnt\n return res\n``` | 0 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
Python | Prefix Sum | count-artifacts-that-can-be-extracted | 0 | 1 | # Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n g = [[0] * n for _ in range(n)]\n for r, c in dig:\n g[r][c] = 1\n for r in range(n):\n for c in range(n):\n g[r][c] += (g[r - 1][c] if r else 0) + (g[r][c - 1] if c else 0) - (g[r - 1][c - 1] if r and c else 0)\n res = 0\n for tr, tc, br, bc in artifacts:\n cnt = g[br][bc] - (g[tr - 1][bc] if tr else 0) - (g[br][tc - 1] if tc else 0) + (g[tr - 1][tc - 1] if tr and tc else 0)\n res += (br - tr + 1) * (bc - tc + 1) == cnt\n return res\n``` | 0 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
Simple solution using prefix sums | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing prefix sums,calculating if all the squares that occupy the treasure are dug or not\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*n) for the prefix sum\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n*n) for storing the prefix array\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n \n\n dug = [[0]*n for i in range(n)]\n\n for i,j in dig:\n dug[i][j] = 1\n \n\n for i in range(n):\n for j in range(1,n):\n dug[i][j] += dug[i][j-1]\n \n for j in range(n):\n for i in range(1,n):\n dug[i][j] += dug[i-1][j]\n \n\n ans = 0\n\n for x1,y1,x2,y2 in artifacts:\n add1 = 0\n add2 = 0\n min1 = 0\n min2 = 0\n\n if x1-1 >= 0 and y1 - 1 >= 0:\n add1 += dug[x1-1][y1-1]\n \n if x1 - 1 >= 0:\n min1 += dug[x1-1][y2]\n \n if y1 - 1 >= 0:\n min2 += dug[x2][y1-1]\n \n add2 += dug[x2][y2]\n\n occu = (x2-x1+1)*(y2-y1+1)\n # print(occu,add1 + add2 - min1 - min2)\n if occu == add1 + add2 - min1 - min2:\n ans += 1\n \n return ans\n\n``` | 0 | There is an `n x n` **0-indexed** grid with some artifacts buried in it. You are given the integer `n` and a **0-indexed** 2D integer array `artifacts` describing the positions of the rectangular artifacts where `artifacts[i] = [r1i, c1i, r2i, c2i]` denotes that the `ith` artifact is buried in the subgrid where:
* `(r1i, c1i)` is the coordinate of the **top-left** cell of the `ith` artifact and
* `(r2i, c2i)` is the coordinate of the **bottom-right** cell of the `ith` artifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a **0-indexed** 2D integer array `dig` where `dig[i] = [ri, ci]` indicates that you will excavate the cell `(ri, ci)`, return _the number of artifacts that you can extract_.
The test cases are generated such that:
* No two artifacts overlap.
* Each artifact only covers at most `4` cells.
* The entries of `dig` are unique.
**Example 1:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\]\]
**Output:** 1
**Explanation:**
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.
**Example 2:**
**Input:** n = 2, artifacts = \[\[0,0,0,0\],\[0,1,1,1\]\], dig = \[\[0,0\],\[0,1\],\[1,1\]\]
**Output:** 2
**Explanation:** Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
**Constraints:**
* `1 <= n <= 1000`
* `1 <= artifacts.length, dig.length <= min(n2, 105)`
* `artifacts[i].length == 4`
* `dig[i].length == 2`
* `0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1`
* `r1i <= r2i`
* `c1i <= c2i`
* No two artifacts will overlap.
* The number of cells covered by an artifact is **at most** `4`.
* The entries of `dig` are unique. | Could you convert this into a graph problem? Consider the pairs as edges and each number as a node. We have to find an Eulerian path of this graph. Hierholzer’s algorithm can be used. |
Simple solution using prefix sums | count-artifacts-that-can-be-extracted | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing prefix sums,calculating if all the squares that occupy the treasure are dug or not\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n*n) for the prefix sum\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n*n) for storing the prefix array\n# Code\n```\nclass Solution:\n def digArtifacts(self, n: int, artifacts: List[List[int]], dig: List[List[int]]) -> int:\n \n\n dug = [[0]*n for i in range(n)]\n\n for i,j in dig:\n dug[i][j] = 1\n \n\n for i in range(n):\n for j in range(1,n):\n dug[i][j] += dug[i][j-1]\n \n for j in range(n):\n for i in range(1,n):\n dug[i][j] += dug[i-1][j]\n \n\n ans = 0\n\n for x1,y1,x2,y2 in artifacts:\n add1 = 0\n add2 = 0\n min1 = 0\n min2 = 0\n\n if x1-1 >= 0 and y1 - 1 >= 0:\n add1 += dug[x1-1][y1-1]\n \n if x1 - 1 >= 0:\n min1 += dug[x1-1][y2]\n \n if y1 - 1 >= 0:\n min2 += dug[x2][y1-1]\n \n add2 += dug[x2][y2]\n\n occu = (x2-x1+1)*(y2-y1+1)\n # print(occu,add1 + add2 - min1 - min2)\n if occu == add1 + add2 - min1 - min2:\n ans += 1\n \n return ans\n\n``` | 0 | Given a string `s`. In one step you can insert any character at any index of the string.
Return _the minimum number of steps_ to make `s` palindrome.
A **Palindrome String** is one that reads the same backward as well as forward.
**Example 1:**
**Input:** s = "zzazz "
**Output:** 0
**Explanation:** The string "zzazz " is already palindrome we do not need any insertions.
**Example 2:**
**Input:** s = "mbadm "
**Output:** 2
**Explanation:** String can be "mbdadbm " or "mdbabdm ".
**Example 3:**
**Input:** s = "leetcode "
**Output:** 5
**Explanation:** Inserting 5 characters the string becomes "leetcodocteel ".
**Constraints:**
* `1 <= s.length <= 500`
* `s` consists of lowercase English letters. | Check if each coordinate of each artifact has been excavated. How can we do this quickly without iterating over the dig array every time? Consider marking all excavated cells in a 2D boolean array. |
[Python 3] Find Maximum of first k-1 elements or (k+1)th element | Beats 100% | maximize-the-topmost-element-after-k-moves | 0 | 1 | The num after the kth element do not matter as they can\'t be accessed.\nSo, handling some corner cases like:\n1. If len(num) == 1.\n2. if k == 0\n3. Comparing k and len(nums)\n\n**DO UPVOTE if you found it useful.**\n```\nclass Solution:\n def maximumTop(self, nums: List[int], k: int) -> int:\n if len(nums) == 1:\n if k%2 != 0:\n return -1\n return nums[0]\n \n if k == 0:\n return nums[0]\n if k == len(nums):\n return max(nums[:-1])\n if k > len(nums):\n return max(nums)\n if k == 1:\n return nums[1]\n m = max(nums[:k-1])\n m = max(m, nums[k])\n return m\n```\nTime Complexity: O(n) - finding max\nSpace Complexity: O(1) | 10 | You are given a **0-indexed** integer array `nums` representing the contents of a **pile**, where `nums[0]` is the topmost element of the pile.
In one move, you can perform **either** of the following:
* If the pile is not empty, **remove** the topmost element of the pile.
* If there are one or more removed elements, **add** any one of them back onto the pile. This element becomes the new topmost element.
You are also given an integer `k`, which denotes the total number of moves to be made.
Return _the **maximum value** of the topmost element of the pile possible after **exactly**_ `k` _moves_. In case it is not possible to obtain a non-empty pile after `k` moves, return `-1`.
**Example 1:**
**Input:** nums = \[5,2,2,4,0,6\], k = 4
**Output:** 5
**Explanation:**
One of the ways we can end with 5 at the top of the pile after 4 moves is as follows:
- Step 1: Remove the topmost element = 5. The pile becomes \[2,2,4,0,6\].
- Step 2: Remove the topmost element = 2. The pile becomes \[2,4,0,6\].
- Step 3: Remove the topmost element = 2. The pile becomes \[4,0,6\].
- Step 4: Add 5 back onto the pile. The pile becomes \[5,4,0,6\].
Note that this is not the only way to end with 5 at the top of the pile. It can be shown that 5 is the largest answer possible after 4 moves.
**Example 2:**
**Input:** nums = \[2\], k = 1
**Output:** -1
**Explanation:**
In the first move, our only option is to pop the topmost element of the pile.
Since it is not possible to obtain a non-empty pile after one move, we return -1.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i], k <= 109` | Since we need to reduce search space, instead of checking if every number is a palindrome in base-10, can we try to "generate" the palindromic numbers? If you are provided with a d digit number, how can you generate a palindrome with 2*d or 2*d - 1 digit? Try brute-forcing and checking if the palindrome you generated is a "k-Mirror" number. |
[Python 3] Find Maximum of first k-1 elements or (k+1)th element | Beats 100% | maximize-the-topmost-element-after-k-moves | 0 | 1 | The num after the kth element do not matter as they can\'t be accessed.\nSo, handling some corner cases like:\n1. If len(num) == 1.\n2. if k == 0\n3. Comparing k and len(nums)\n\n**DO UPVOTE if you found it useful.**\n```\nclass Solution:\n def maximumTop(self, nums: List[int], k: int) -> int:\n if len(nums) == 1:\n if k%2 != 0:\n return -1\n return nums[0]\n \n if k == 0:\n return nums[0]\n if k == len(nums):\n return max(nums[:-1])\n if k > len(nums):\n return max(nums)\n if k == 1:\n return nums[1]\n m = max(nums[:k-1])\n m = max(m, nums[k])\n return m\n```\nTime Complexity: O(n) - finding max\nSpace Complexity: O(1) | 10 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
Python 9 lines | maximize-the-topmost-element-after-k-moves | 0 | 1 | ```\nclass Solution:\n def maximumTop(self, nums: List[int], k: int) -> int:\n if len(nums) == 1:\n return -1 if k % 2 == 1 else nums[0]\n if k <= 1:\n return nums[k]\n if k < len(nums):\n return max(max(nums[:k-1]), nums[k])\n if k < len(nums) + 2: \n return max(nums[:k-1])\n return max(nums)\n``` | 2 | You are given a **0-indexed** integer array `nums` representing the contents of a **pile**, where `nums[0]` is the topmost element of the pile.
In one move, you can perform **either** of the following:
* If the pile is not empty, **remove** the topmost element of the pile.
* If there are one or more removed elements, **add** any one of them back onto the pile. This element becomes the new topmost element.
You are also given an integer `k`, which denotes the total number of moves to be made.
Return _the **maximum value** of the topmost element of the pile possible after **exactly**_ `k` _moves_. In case it is not possible to obtain a non-empty pile after `k` moves, return `-1`.
**Example 1:**
**Input:** nums = \[5,2,2,4,0,6\], k = 4
**Output:** 5
**Explanation:**
One of the ways we can end with 5 at the top of the pile after 4 moves is as follows:
- Step 1: Remove the topmost element = 5. The pile becomes \[2,2,4,0,6\].
- Step 2: Remove the topmost element = 2. The pile becomes \[2,4,0,6\].
- Step 3: Remove the topmost element = 2. The pile becomes \[4,0,6\].
- Step 4: Add 5 back onto the pile. The pile becomes \[5,4,0,6\].
Note that this is not the only way to end with 5 at the top of the pile. It can be shown that 5 is the largest answer possible after 4 moves.
**Example 2:**
**Input:** nums = \[2\], k = 1
**Output:** -1
**Explanation:**
In the first move, our only option is to pop the topmost element of the pile.
Since it is not possible to obtain a non-empty pile after one move, we return -1.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i], k <= 109` | Since we need to reduce search space, instead of checking if every number is a palindrome in base-10, can we try to "generate" the palindromic numbers? If you are provided with a d digit number, how can you generate a palindrome with 2*d or 2*d - 1 digit? Try brute-forcing and checking if the palindrome you generated is a "k-Mirror" number. |
Python 9 lines | maximize-the-topmost-element-after-k-moves | 0 | 1 | ```\nclass Solution:\n def maximumTop(self, nums: List[int], k: int) -> int:\n if len(nums) == 1:\n return -1 if k % 2 == 1 else nums[0]\n if k <= 1:\n return nums[k]\n if k < len(nums):\n return max(max(nums[:k-1]), nums[k])\n if k < len(nums) + 2: \n return max(nums[:k-1])\n return max(nums)\n``` | 2 | Given an array `arr` of integers, check if there exist two indices `i` and `j` such that :
* `i != j`
* `0 <= i, j < arr.length`
* `arr[i] == 2 * arr[j]`
**Example 1:**
**Input:** arr = \[10,2,5,3\]
**Output:** true
**Explanation:** For i = 0 and j = 2, arr\[i\] == 10 == 2 \* 5 == 2 \* arr\[j\]
**Example 2:**
**Input:** arr = \[3,1,7,11\]
**Output:** false
**Explanation:** There is no i and j that satisfy the conditions.
**Constraints:**
* `2 <= arr.length <= 500`
* `-103 <= arr[i] <= 103` | For each index i, how can we check if nums[i] can be present at the top of the pile or not after k moves? For which conditions will we end up with an empty pile? |
[Python3] - Dijkstra - Simple solution | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | # Intuition\nShortest path in positive weight graph -> Dijkstra\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThe idea is the following: paths from `s1` to `dest` and from `s2` to `dest` can have common point `x`. Then we need to reach:\n\nFrom `s1` to `x`, for this we use Dijkstra\nFrom `s2` to `x`, same.\nFrom `x` to `dest`, for this we use Dijkstra on the reversed graph.\nFinally, we check all possible `x`.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(ElogV)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V + E)$$ ~ $$O(E)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n g1 = collections.defaultdict(list)\n g2 = collections.defaultdict(list)\n for u, v , w in edges:\n g1[u].append((v, w))\n g2[v].append((u, w))\n\n def get_distance(node: int, g: dict) -> List[float | int]:\n distance = [float(\'inf\') for _ in range(n)]\n distance[node] = 0\n q = [(0, node)]\n while q:\n d, u = heapq.heappop(q)\n if d > distance[u]: continue\n for v, w in g[u]:\n if d + w < distance[v]:\n distance[v] = d + w\n heapq.heappush(q, (distance[v], v))\n return distance\n \n l1, l2, l3 = get_distance(src1, g1), get_distance(src2, g1), get_distance(dest, g2)\n ans = float("inf")\n for i in range(n):\n ans = min(ans, l1[i] + l2[i] + l3[i])\n \n return ans if ans != float("inf") else -1\n``` | 2 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
Dijkstra of Graph and Dual | Commented and Explained | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBy using a graph and it\'s dual we can solve a meeting vertext problem like this. This allows us to find the join of the two solution spaces, and can lead to optimizations on time as detailed herein. \n\nFirst, if we can never reach our destination from either of our starting nodes, we can not get an answer. We should implement dijkstra\'s to get the distances of each node reachable, and then use that figure out if we can reach the destination. If not, return -1. \n\nAfter that, we need to use the dual graph and find the distances for each point in the dual as well. The sum of the two forwards and one dual values allows us to find the minimal value, but only if they are all present. On a miss we should continue and at the end minimize if able. We should use a set of the travel costs, as this lets us avoid a very large list otherwise. \n\nWe can also sort our three lists of distances rather quickly by simply comparing their length, and optomize based on the length of the list (shortest to least as that skips the most non-useful nodes)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproach uses a graph and its dual as well as dijkstra\'s algorithm. Write up in comments is not present on dijkstra as it should be a fairly common implement on hard problems. \n\n# Complexity\n- Time complexity : \n - Takes O(E) to build graph and dual \n - Takes O(E log V) for dijkstras \n - Takes O(v) for building travel costs \n - Total is O( Max(V, E log V)) : sparsity of graph may cause O(V) to dominate if lowest connected v is equivalent to V \n\n- Space complexity : O(e + v)\n - O(e) for the graphs as we keep only the min edge cost \n - O(v) for the distances \n - O(e + v) total \n\n# Code\n```\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n # weighted directed graph \n # edges is src, dst, weight \n # build graph and it\'s dual \n graph = collections.defaultdict(dict)\n dualg = collections.defaultdict(dict)\n for index, edge in enumerate(edges) : \n src, dst, cost = edge \n graph[src][dst] = min(cost, graph[src].get(dst, inf))\n dualg[dst][src] = min(cost, dualg[dst].get(src, inf))\n \n # conduct dijkstra\'s algorithm using priority queue and heaping based on min cost of travel\n def dijkstra(graph_i, src) : \n distance = {} \n pq = [(0, src)]\n while pq : \n cost, node = heapq.heappop(pq)\n if node not in distance : \n distance[node] = cost \n for neighbor in graph_i[node] : \n if neighbor not in distance : \n heapq.heappush(pq, (cost + graph_i[node][neighbor], neighbor))\n return distance \n \n # get src1 distance and src2 distance \n src1_distance = dijkstra(graph, src1)\n src2_distance = dijkstra(graph, src2)\n # if both of them does not have dest -> auto fail doesn\'t matter if we can go backward\n if dest not in src1_distance and dest not in src2_distance : \n return -1 \n else : \n # otherwise get the dual distance \n dest_distance = dijkstra(dualg, dest)\n # build travel costs lists \n travel_costs = set()\n # in order of the distances based on shortest to longest list \n distance_list = [src1_distance, src2_distance, dest_distance]\n distance_list.sort(key = lambda listing : len(listing))\n # loop over nodes in range n \n for k in distance_list[0] : \n cost = distance_list[0][k]\n # if k in second listing \n if k in distance_list[1] : \n cost += distance_list[1][k] \n # if k in largest listing (least skipped, do last) \n if k in distance_list[2] : \n cost += distance_list[2][k]\n travel_costs.add(cost)\n else : \n continue \n else : \n continue \n # return min of travel cost if you built it otherwise -1 \n return min(travel_costs) if travel_costs else -1 \n``` | 0 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
Triple Dijkstra in Python, Faster than 92% | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis problem can be re-framed as the problem to find a meeting vertex `k` so that $$\\delta_{s_1, k} + \\delta_{s_2, k} + \\delta_{k, d}$$ is minimized, where $$\\delta_{s_1, k}$$ is the shortest distance between `src1` and `k`, $$\\delta_{s_2, k}$$ is the shortest distance between `src2` and `k`, and $$\\delta_{k, d}$$ is the shortest distance between `k` and `dest`. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTherefore, we can do the efficient Dijkstra algorithm to find the distances from `src1` and `src2` to all vertices. We can also find the distances from all vertices to `dest` by composing a graph with reversed edges. Finally, exploring each vertex as the meeting point `k` to find the minimum. Each Dijkstra algorithm spends $$O(|E| \\log |V|)$$ (with usual binary heap), and the last step spends $$O(|V|)$$ since all the $$\\delta_{s_1, k}$$, $$\\delta_{s_2, k}$$, and $$\\delta_{k, d}$$ are precomputed. \n\n# Complexity\n- Time complexity: $$O(|E| \\log |V|)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n graph, reversed_graph = defaultdict(dict), defaultdict(dict)\n for u, v, w in edges:\n graph[u][v] = min(w, graph[u].get(v, inf))\n reversed_graph[v][u] = min(w, reversed_graph[v].get(u, inf))\n \n def dijkstra(g, src):\n dist = {}\n h = [(0, src)]\n while h:\n d, v = heappop(h)\n if v not in dist:\n dist[v] = d\n for u in g[v]:\n if u not in dist:\n heappush(h, (d+g[v][u], u))\n return dist\n\n src1_dist = dijkstra(graph, src1)\n src2_dist = dijkstra(graph, src2)\n dest_dist = dijkstra(reversed_graph, dest)\n return min((src1_dist[k] + src2_dist[k] + dest_dist[k] for k in range(n) \n if k in src1_dist and k in src2_dist and k in dest_dist), \n default=-1)\n``` | 0 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
80+ beats in both | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport heapq\nfrom typing import List\nfrom collections import defaultdict\n\ndef dijk(s, g, n):\n dis = [float("inf")] * n\n par = [-1] * n\n dis[s] = 0\n q = [(0, s)]\n while q:\n wt, t = heapq.heappop(q)\n if wt != dis[t]:\n continue\n for i, w in g[t]:\n if w + wt < dis[i]:\n dis[i] = w + wt\n heapq.heappush(q, (w + wt, i))\n par[i] = t\n return dis, par\n\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n g = defaultdict(list)\n gr = defaultdict(list)\n for x, y, w in edges:\n g[x].append((y, w))\n gr[y].append((x, w))\n \n d1, p1 = dijk(src1, g, n)\n d2, p2 = dijk(src2, g, n)\n \n ans = float("inf")\n for i, w in gr[dest]:\n ans = min(ans, d1[i] + d2[i] + w, d1[dest] + d2[i] + w)\n \n ed = dest\n while ed != -1:\n ans = min(ans, d1[dest] + d2[ed])\n ed = p1[ed]\n \n ed = dest\n while ed != -1:\n ans = min(ans, d2[dest] + d1[ed])\n ed = p2[ed]\n \n ans = min(ans, d1[dest] + d2[dest])\n \n if ans == float("inf"):\n ans = -1\n \n return ans\n``` | 0 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
2 dijkstras HACK me :) | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef dijk(s,g,n):\n dis=[float("inf")]*n\n par=[-1]*n\n dis[s]=0\n q=[(0,s)]\n while q:\n wt,t=heapq.heappop(q)\n if wt!=dis[t]:\n continue\n for i,w in g[t]:\n if w+wt<dis[i]:\n dis[i]=w+wt\n heapq.heappush(q,(w+wt,i))\n par[i]=t\n return dis,par\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n g=defaultdict(list)\n gr=defaultdict(list)\n for x,y,w in edges:\n g[x].append((y,w))\n gr[y].append((x,w))\n # print(x,y,w)\n d1,p1=dijk(src1,g,n)\n d2,p2=dijk(src2,g,n)\n ans=float("inf")\n for i,w in gr[dest]:\n ans=min(ans,d1[i]+d2[i]+w,d1[dest]+d2[i]+w)\n ed=dest\n # print(p1)\n # print(p2)\n while ed!=-1:\n ans=min(ans,d1[dest]+d2[ed])\n # print("dis1",d1[dest],d2[ed],dest,ed)\n ed=p1[ed]\n ed=dest\n while ed!=-1:\n ans=min(ans,d2[dest]+d1[ed])\n # print("dis",d2[dest],d1[ed],dest,ed)\n ed=p2[ed]\n ans=min(ans,d1[dest]+d2[dest])\n # ans=min(ans,d1[src2]+d2[dest],d2[src1]+d1[dest],d1[dest]+d2[dest])\n if ans==float("inf"):\n ans=-1\n return ans\n``` | 0 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
could be faster than dijkstra in average | minimum-weighted-subgraph-with-the-required-paths | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf there is a subgraph comply, there should exist at least one node that, src1 and src2 both reach that node and that node reach dest. The dest is one of them.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstrat from for both src1 and src2 travel the graph to caculate the cost to reach any node that is reachable\nstart from dest travel the reversed (reverse all edges\' direction) graph to caculate the cost from any node\n\n# special note\nThis looks like a dijkstra, but it is not. \ndijkstra use prioritied heap queue, which has O(n*log(N)) time complexity\nFor this problem just use a stack. as average time complexity will be O(n) though in the worst combination every single node will be recaculated when a less cost path has been found. The worst case could be O(N**2) when recaculate could happen to every single node. While I believe that will be very rare.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nE is the amount of edges\nO(E)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(E)\n\n# Code\n```\nclass Solution:\n def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:\n g = defaultdict(dict)\n r = defaultdict(dict)\n for f,t,w in edges:\n g[f][t] = min(w, g[f].get(t,inf))\n r[t][f] = min(w, r[t].get(f,inf))\n wt = {}\n ws1 = {}\n ws2 = {}\n def t(s, g, w):\n sk = [(s,0)]\n while sk:\n s, c = sk.pop()\n if c < w.get(s,inf):\n w[s] = c\n for i, w0 in g[s].items():\n sk.append((i, w0 + c))\n # print(s, w)\n \n t(dest, r, wt)\n t(src1, g, ws1)\n t(src2, g, ws2)\n if dest not in ws1 or dest not in ws2:\n return -1\n return min (ws1[i] + ws2[i] + wt[i] for i in ws1 if i in wt and i in ws2)\n # return min (ws1[i] + ws2[i] + wt[i] for i in range(n) if i in ws1 and i in ws2 and i in wt)\n``` | 0 | You are given an integer `n` denoting the number of nodes of a **weighted directed** graph. The nodes are numbered from `0` to `n - 1`.
You are also given a 2D integer array `edges` where `edges[i] = [fromi, toi, weighti]` denotes that there exists a **directed** edge from `fromi` to `toi` with weight `weighti`.
Lastly, you are given three **distinct** integers `src1`, `src2`, and `dest` denoting three distinct nodes of the graph.
Return _the **minimum weight** of a subgraph of the graph such that it is **possible** to reach_ `dest` _from both_ `src1` _and_ `src2` _via a set of edges of this subgraph_. In case such a subgraph does not exist, return `-1`.
A **subgraph** is a graph whose vertices and edges are subsets of the original graph. The **weight** of a subgraph is the sum of weights of its constituent edges.
**Example 1:**
**Input:** n = 6, edges = \[\[0,2,2\],\[0,5,6\],\[1,0,3\],\[1,4,5\],\[2,1,1\],\[2,3,3\],\[2,3,4\],\[3,4,2\],\[4,5,1\]\], src1 = 0, src2 = 1, dest = 5
**Output:** 9
**Explanation:**
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph \[\[1,0,3\],\[0,5,6\]\] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.
**Example 2:**
**Input:** n = 3, edges = \[\[0,1,1\],\[2,1,1\]\], src1 = 0, src2 = 1, dest = 2
**Output:** -1
**Explanation:**
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.
**Constraints:**
* `3 <= n <= 105`
* `0 <= edges.length <= 105`
* `edges[i].length == 3`
* `0 <= fromi, toi, src1, src2, dest <= n - 1`
* `fromi != toi`
* `src1`, `src2`, and `dest` are pairwise distinct.
* `1 <= weight[i] <= 105` | Simulate how the robot moves and keep track of how many spaces it has cleaned so far. When can we stop the simulation? When the robot reaches a space that it has already cleaned and is facing the same direction as before, we can stop the simulation. |
divide-array-into-equal-pairs | divide-array-into-equal-pairs | 0 | 1 | \n# Code\n```\nclass Solution:\n def divideArray(self, nums: List[int]) -> bool:\n if len(nums)%2!=0:\n return False\n else:\n for i in nums:\n if nums.count(i)%2!=0:\n return False\n else:\n return True\n``` | 1 | You are given an integer array `nums` consisting of `2 * n` integers.
You need to divide `nums` into `n` pairs such that:
* Each element belongs to **exactly one** pair.
* The elements present in a pair are **equal**.
Return `true` _if nums can be divided into_ `n` _pairs, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[3,2,3,2,2,2\]
**Output:** true
**Explanation:**
There are 6 elements in nums, so they should be divided into 6 / 2 = 3 pairs.
If nums is divided into the pairs (2, 2), (3, 3), and (2, 2), it will satisfy all the conditions.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:**
There is no way to divide nums into 4 / 2 = 2 pairs such that the pairs satisfy every condition.
**Constraints:**
* `nums.length == 2 * n`
* `1 <= n <= 500`
* `1 <= nums[i] <= 500` | How can we model the relationship between different bombs? Can "graphs" help us? Bombs are nodes and are connected to other bombs in their range by directed edges. If we know which bombs will be affected when any bomb is detonated, how can we find the total number of bombs that will be detonated if we start from a fixed bomb? Run a Depth First Search (DFS) from every node, and all the nodes it reaches are the bombs that will be detonated. |
[Java/Python 3] 4/1 liner O(n) code. | divide-array-into-equal-pairs | 1 | 1 | **Method 1: Count and check parity**\n\n```java\n public boolean divideArray(int[] nums) {\n int[] cnt = new int[501];\n for (int n : nums)\n ++cnt[n];\n return IntStream.of(cnt).allMatch(n -> n % 2 == 0);\n }\n```\n\n```python\n def divideArray(self, nums: List[int]) -> bool:\n return all(v % 2 == 0 for v in Counter(nums).values())\n```\n\n---\n\n**Method 2: check parity by boolean array**\n\n```java\n public boolean divideArray(int[] nums) {\n boolean[] odd = new boolean[501];\n for (int n : nums)\n odd[n] = !odd[n];\n return Arrays.equals(odd, new boolean[501]);\n }\n```\n```python\n def divideArray(self, nums: List[int]) -> bool:\n odd = [False] * 501\n for n in nums:\n odd[n] = not odd[n]\n return not any(odd)\n```\n\n---\n\n**Method 3: HashSet** - credit to **@SunnyvaleCA**.\n\n```java\n public boolean divideArray(int[] nums) {\n Set<Integer> seen = new HashSet<>();\n for (int num : nums) {\n if (!seen.add(num)) {\n seen.remove(num);\n }\n }\n return seen.isEmpty();\n }\n```\n```python\n def divideArray(self, nums: List[int]) -> bool:\n seen = set()\n for num in nums:\n if num in seen:\n seen.discard(num)\n else:\n seen.add(num)\n return not seen\n```\nor simplify it to follows: - credit to **@stefan4trivia**\n\n```python\nclass stefan4trivia:\n def divideArray(self, nums: List[int], test_case_number = [0]) -> bool:\n seen = set()\n for n in nums:\n seen ^= {n}\n return not seen\n```\n\n**Analysis:**\n\nTime & space: `O(n)`. | 41 | You are given an integer array `nums` consisting of `2 * n` integers.
You need to divide `nums` into `n` pairs such that:
* Each element belongs to **exactly one** pair.
* The elements present in a pair are **equal**.
Return `true` _if nums can be divided into_ `n` _pairs, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[3,2,3,2,2,2\]
**Output:** true
**Explanation:**
There are 6 elements in nums, so they should be divided into 6 / 2 = 3 pairs.
If nums is divided into the pairs (2, 2), (3, 3), and (2, 2), it will satisfy all the conditions.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:**
There is no way to divide nums into 4 / 2 = 2 pairs such that the pairs satisfy every condition.
**Constraints:**
* `nums.length == 2 * n`
* `1 <= n <= 500`
* `1 <= nums[i] <= 500` | How can we model the relationship between different bombs? Can "graphs" help us? Bombs are nodes and are connected to other bombs in their range by directed edges. If we know which bombs will be affected when any bomb is detonated, how can we find the total number of bombs that will be detonated if we start from a fixed bomb? Run a Depth First Search (DFS) from every node, and all the nodes it reaches are the bombs that will be detonated. |
Simplest Python 1 liner | divide-array-into-equal-pairs | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def divideArray(self, nums: List[int]) -> bool:\n return all(not x&1 for x in Counter(nums).values())\n``` | 2 | You are given an integer array `nums` consisting of `2 * n` integers.
You need to divide `nums` into `n` pairs such that:
* Each element belongs to **exactly one** pair.
* The elements present in a pair are **equal**.
Return `true` _if nums can be divided into_ `n` _pairs, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[3,2,3,2,2,2\]
**Output:** true
**Explanation:**
There are 6 elements in nums, so they should be divided into 6 / 2 = 3 pairs.
If nums is divided into the pairs (2, 2), (3, 3), and (2, 2), it will satisfy all the conditions.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:**
There is no way to divide nums into 4 / 2 = 2 pairs such that the pairs satisfy every condition.
**Constraints:**
* `nums.length == 2 * n`
* `1 <= n <= 500`
* `1 <= nums[i] <= 500` | How can we model the relationship between different bombs? Can "graphs" help us? Bombs are nodes and are connected to other bombs in their range by directed edges. If we know which bombs will be affected when any bomb is detonated, how can we find the total number of bombs that will be detonated if we start from a fixed bomb? Run a Depth First Search (DFS) from every node, and all the nodes it reaches are the bombs that will be detonated. |
Easy Python Solution | divide-array-into-equal-pairs | 0 | 1 | ```\ndef divideArray(self, nums: List[int]) -> bool:\n for i in nums:\n if nums.count(i)%2==1:\n return False\n return True\n``` | 3 | You are given an integer array `nums` consisting of `2 * n` integers.
You need to divide `nums` into `n` pairs such that:
* Each element belongs to **exactly one** pair.
* The elements present in a pair are **equal**.
Return `true` _if nums can be divided into_ `n` _pairs, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[3,2,3,2,2,2\]
**Output:** true
**Explanation:**
There are 6 elements in nums, so they should be divided into 6 / 2 = 3 pairs.
If nums is divided into the pairs (2, 2), (3, 3), and (2, 2), it will satisfy all the conditions.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:**
There is no way to divide nums into 4 / 2 = 2 pairs such that the pairs satisfy every condition.
**Constraints:**
* `nums.length == 2 * n`
* `1 <= n <= 500`
* `1 <= nums[i] <= 500` | How can we model the relationship between different bombs? Can "graphs" help us? Bombs are nodes and are connected to other bombs in their range by directed edges. If we know which bombs will be affected when any bomb is detonated, how can we find the total number of bombs that will be detonated if we start from a fixed bomb? Run a Depth First Search (DFS) from every node, and all the nodes it reaches are the bombs that will be detonated. |
Python ||O(N)|| simple solution | divide-array-into-equal-pairs | 0 | 1 | Time Complexcity : best -> O(N)\n wrost -> O(NlogN)\nSpace Complexcity O(N)\n```\nclass Solution:\n def divideArray(self, nums: List[int]) -> bool:\n if len(nums)%2!=0:\n return False\n n=len(nums)\n nums.sort()\n p1,p2=[],[]\n for i in range(n):\n if i%2==0:\n p1.append(nums[i])\n else:\n p2.append(nums[i])\n for i in range(len(p1)):\n if p1[i]!=p2[i]:\n return False\n return True\n```\n**pls vote if helpfull** | 2 | You are given an integer array `nums` consisting of `2 * n` integers.
You need to divide `nums` into `n` pairs such that:
* Each element belongs to **exactly one** pair.
* The elements present in a pair are **equal**.
Return `true` _if nums can be divided into_ `n` _pairs, otherwise return_ `false`.
**Example 1:**
**Input:** nums = \[3,2,3,2,2,2\]
**Output:** true
**Explanation:**
There are 6 elements in nums, so they should be divided into 6 / 2 = 3 pairs.
If nums is divided into the pairs (2, 2), (3, 3), and (2, 2), it will satisfy all the conditions.
**Example 2:**
**Input:** nums = \[1,2,3,4\]
**Output:** false
**Explanation:**
There is no way to divide nums into 4 / 2 = 2 pairs such that the pairs satisfy every condition.
**Constraints:**
* `nums.length == 2 * n`
* `1 <= n <= 500`
* `1 <= nums[i] <= 500` | How can we model the relationship between different bombs? Can "graphs" help us? Bombs are nodes and are connected to other bombs in their range by directed edges. If we know which bombs will be affected when any bomb is detonated, how can we find the total number of bombs that will be detonated if we start from a fixed bomb? Run a Depth First Search (DFS) from every node, and all the nodes it reaches are the bombs that will be detonated. |
✅ ✅ Python3 O(NlogN) Solution || Max Heap ✅ ✅ | minimum-operations-to-halve-array-sum | 0 | 1 | # Complexity\n- Time complexity:\nO(N logN)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def halveArray(self, nums: List[int]) -> int:\n heap = []\n for num in nums:\n heappush(heap,-1 * num)\n\n initalSum = sum(nums)\n targetSum = initalSum / 2\n k = 0\n\n while initalSum > targetSum:\n val = heappop(heap)\n heappush(heap,val / 2)\n initalSum -= (-1 * (val / 2))\n k = k + 1\n \n return k\n``` | 1 | You are given an array `nums` of positive integers. In one operation, you can choose **any** number from `nums` and reduce it to **exactly** half the number. (Note that you may choose this reduced number in future operations.)
Return _the **minimum** number of operations to reduce the sum of_ `nums` _by **at least** half._
**Example 1:**
**Input:** nums = \[5,19,8,1\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is \[5, 4.75, 4, 1\] with a total sum of 5 + 4.75 + 4 + 1 = 14.75.
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Example 2:**
**Input:** nums = \[3,8,20\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is \[1.5, 8, 5\] with a total sum of 1.5 + 8 + 5 = 14.5.
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 15.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
[Java/Python 3] PriorityQueue/heap w/ brief explanation and analysis. | minimum-operations-to-halve-array-sum | 1 | 1 | **Q & A**\n*Q1:* Why in `PriorityQueue<Double> pq=new PriorityQueue<>((a,b)->b-a);` the lambda expression does not work with `double`?\n*A1:* Not very sure, but I guess it is because that in Java `Comparator` interface there is only one `int compare(T o1, T o2)` method, of which the return type is `int`. Please refer to [Java 8 Comparator](https://docs.oracle.com/javase/8/docs/api/java/util/Comparator.html).\n\nYou can use `Math.signum` to convert `double` to `int` as follows:\n```java\n PriorityQueue<Double> pq = new PriorityQueue<Double>((a, b) -> (int)Math.signum(b - a));\n```\n\n\n*Q2:* `Math.signum()` returns only 3 values(double) i.e `1.0, -1.0, 0.0`. Then how exactly sorting is happening in above lambda expression `(a, b) -> (int)Math.signum(b - a)`?\n*A2:* The returning 3 values are enough for comparing `2` elements in the array.\n\n`Arrays.sort(Object[])` uses Tim sort. The sorting algorithms like Tim Sort, Merge Sort, Quick Sort, and Heap Sort, etc., are comparison (of `2` elements) based. Therefore, we only need to know the result of each comparison between `2` elements: `<`, `=`, `>`, which we can get conclusion from the returning values `-1.0`, `0.0`, `1.0`.\n\n\n*Q3:* How does this work?\n```java\nPriorityQueue pq = new PriorityQueue((a, b) -> b.compareTo(a));\n```\n*A3:* `compareTo` is the method in `Comparable` interface and you can refer to [Java 8 Comparable Interface](https://docs.oracle.com/javase/8/docs/api/java/lang/Comparable.html).\n\n`int compareTo(T o)`\n\n"Compares this object with the specified object for order. Returns a negative integer, zero, or a positive integer as this object is less than, equal to, or greater than the specified object.\n\n..."\n\n\n*Q4:* And when to use `(b-a)` and when to use `b.compareTo(a)` in lambda expressions?\n*A4:* I would choose `b.compareTo(a)` if `(b - a)` could cause overflow. e.g, `a` and `b` are both `int` or `long` and `a = Integer.MIN_VALUE or Long.MIN_VALUE`.\n\nHowever, in case of no overflow, either is good to use.\n\n**Correct me if I am wrong.**\n\n\n**End of Q & A**\n\n----\n\nAlways reduce current max value by half.\n\n1. Compute the `half` of the sum of the input `nums`;\n2. Put all `nums` into a PriorityQueue/heap by reverse order;\n3. Poll out and cut the current max value by half and add it back to PriorityQueue/ heap, deduct the `half` of the sum accordingly and increase the counter `ops` by 1;\n4. Repeat 3 till `half <= 0`, then return `ops`.\n```java\n public int halveArray(int[] nums) {\n PriorityQueue<Double> pq = new PriorityQueue<>(Comparator.reverseOrder()); \n double half = IntStream.of(nums).mapToLong(i -> i).sum() / 2d;\n for (int n : nums) {\n pq.offer((double)n);\n }\n int ops = 0;\n while (half > 0) {\n double d = pq.poll();\n d /= 2;\n half -= d;\n pq.offer(d);\n ++ops;\n }\n return ops;\n }\n```\n\n```python\n def halveArray(self, nums: List[int]) -> int:\n half, ops = sum(nums) / 2, 0\n heap = [-num for num in nums]\n heapify(heap)\n while half > 0:\n num = -heappop(heap)\n num /= 2.0\n half -= num\n heappush(heap, -num)\n ops += 1\n return ops\n```\n\n**Analysis:**\n\nTime: `O(nlogn)`, space: `O(n)`, where `n = nums.length`. | 18 | You are given an array `nums` of positive integers. In one operation, you can choose **any** number from `nums` and reduce it to **exactly** half the number. (Note that you may choose this reduced number in future operations.)
Return _the **minimum** number of operations to reduce the sum of_ `nums` _by **at least** half._
**Example 1:**
**Input:** nums = \[5,19,8,1\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is \[5, 4.75, 4, 1\] with a total sum of 5 + 4.75 + 4 + 1 = 14.75.
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Example 2:**
**Input:** nums = \[3,8,20\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is \[1.5, 8, 5\] with a total sum of 1.5 + 8 + 5 = 14.5.
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 15.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
python 3 || priority queue | minimum-operations-to-halve-array-sum | 0 | 1 | ```\nclass Solution:\n def halveArray(self, nums: List[int]) -> int:\n s = sum(nums)\n goal = s / 2\n res = 0\n \n for i, num in enumerate(nums):\n nums[i] = -num\n heapq.heapify(nums)\n \n while s > goal:\n halfLargest = -heapq.heappop(nums) / 2\n s -= halfLargest\n heapq.heappush(nums, -halfLargest)\n res += 1\n \n return res | 2 | You are given an array `nums` of positive integers. In one operation, you can choose **any** number from `nums` and reduce it to **exactly** half the number. (Note that you may choose this reduced number in future operations.)
Return _the **minimum** number of operations to reduce the sum of_ `nums` _by **at least** half._
**Example 1:**
**Input:** nums = \[5,19,8,1\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is \[5, 4.75, 4, 1\] with a total sum of 5 + 4.75 + 4 + 1 = 14.75.
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Example 2:**
**Input:** nums = \[3,8,20\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is \[1.5, 8, 5\] with a total sum of 1.5 + 8 + 5 = 14.5.
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 15.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
Max Heap Python3 Short Solution | minimum-operations-to-halve-array-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first thought you can notice that you constantly want to be picking the largest possible number after each halving to minimize the number of operations. The brute force solution would be to sort the list and then pop the last element and the add that halved element back into the list again and then resort it. However, with all that resorting the algorithm becomes efficient when all you are really looking for is just the max element. This is where the max heap becomes useful. We can use a max heap to heapify our nums list and then just pop out the max from that which is more efficient.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor this approach you have to first calculate the total sum as this is when you want your while loop to stop. Then, in python the heapq library is supported for minHeap however, by multiplying every value by negative one you essentially turn it into a maxHeap you just have to remember to multiply the -1 back when actually using the data. The while loop will run as long as the current sum is greater than the totalSum/2. You want to pop out the largest element and store that number. Make sure to push the largest element/2 back in so you arent forgetting about any largest values. Then subtract half of the largest element so you account for popping it out of the heap. Don\'t forget to multiply this by -1 as we are actually processing the data. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn) -> heapify runtime\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) -> space that the heap will take\n# Code\n```\nclass Solution:\n def halveArray(self, nums: List[int]) -> int:\n arraySum = currSum = sum(nums)\n nums = [-1*num for num in nums]\n heapq.heapify(nums)\n minOperations = 0\n\n while currSum > arraySum/2:\n largestNum = heapq.heappop(nums)\n heapq.heappush(nums, largestNum/2)\n currSum -= (-1 * largestNum)/2\n minOperations += 1\n\n return minOperations\n \n``` | 1 | You are given an array `nums` of positive integers. In one operation, you can choose **any** number from `nums` and reduce it to **exactly** half the number. (Note that you may choose this reduced number in future operations.)
Return _the **minimum** number of operations to reduce the sum of_ `nums` _by **at least** half._
**Example 1:**
**Input:** nums = \[5,19,8,1\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is \[5, 4.75, 4, 1\] with a total sum of 5 + 4.75 + 4 + 1 = 14.75.
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Example 2:**
**Input:** nums = \[3,8,20\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is \[1.5, 8, 5\] with a total sum of 1.5 + 8 + 5 = 14.5.
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 15.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
Easy Problem with simple Intuition and Approcah Explanation | minimum-operations-to-halve-array-sum | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy intuition is that the task is to reduce the sum of an array to half by performing the minimum number of operations. To achieve this, select the largest value in the array, halve it, and subtract this halved value from the total sum.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing a max heap is the best option because it always returns the maximum value. After popping the maximum value, halve it and add it back to the heap. Ensure to use `abs()` to maintain the integrity of the max heap. Keep a close eye on the value while doing this.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe sum(nums) operation is O(n), where n is the length of the nums array.\nThe heapify(nums) operation has a time complexity of O(n).\nThe while loop is the most complex part. In the worst case, this loop runs until the sum of the array is halved. The number of iterations depends on the values in nums.\nWithin the loop, heappop(nums) and heappush(nums, -val) are O(log n) operations because both popping and pushing in a heap have a logarithmic time complexity.\nThe total time complexity of the loop is a bit harder to determine exactly since it depends on the values in the array and how quickly the sum reduces to half. However, in the worst case, if we assume that the loop runs for k iterations, the overall time complexity within the loop is O(k log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace Complexity:\nThe space complexity primarily depends on the size of the nums array, which is converted into a max heap.\nSince no additional data structures are used that grow with the size of the input, the space complexity is O(n), where n is the length of the nums array.\n\n> **PS: This is an Easy question rather than Medium one. Please UPVOTE if you like this explainationa and code.**\n# Code\n```\nfrom heapq import *\nclass Solution:\n def halveArray(self, nums: List[int]) -> int:\n sum1=sum(nums)\n sum2=sum1/2\n nums=[-num for num in nums]\n heapify(nums)\n count=0\n while(sum1>sum2):\n val=abs(heappop(nums))\n val=val/2\n sum1-=val\n heappush(nums,-val)\n count+=1\n return count\n \n``` | 0 | You are given an array `nums` of positive integers. In one operation, you can choose **any** number from `nums` and reduce it to **exactly** half the number. (Note that you may choose this reduced number in future operations.)
Return _the **minimum** number of operations to reduce the sum of_ `nums` _by **at least** half._
**Example 1:**
**Input:** nums = \[5,19,8,1\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 5 + 19 + 8 + 1 = 33.
The following is one of the ways to reduce the sum by at least half:
Pick the number 19 and reduce it to 9.5.
Pick the number 9.5 and reduce it to 4.75.
Pick the number 8 and reduce it to 4.
The final array is \[5, 4.75, 4, 1\] with a total sum of 5 + 4.75 + 4 + 1 = 14.75.
The sum of nums has been reduced by 33 - 14.75 = 18.25, which is at least half of the initial sum, 18.25 >= 33/2 = 16.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Example 2:**
**Input:** nums = \[3,8,20\]
**Output:** 3
**Explanation:** The initial sum of nums is equal to 3 + 8 + 20 = 31.
The following is one of the ways to reduce the sum by at least half:
Pick the number 20 and reduce it to 10.
Pick the number 10 and reduce it to 5.
Pick the number 3 and reduce it to 1.5.
The final array is \[1.5, 8, 5\] with a total sum of 1.5 + 8 + 5 = 14.5.
The sum of nums has been reduced by 31 - 14.5 = 16.5, which is at least half of the initial sum, 16.5 >= 31/2 = 15.5.
Overall, 3 operations were used so we return 3.
It can be shown that we cannot reduce the sum by at least half in less than 3 operations.
**Constraints:**
* `1 <= nums.length <= 105`
* `1 <= nums[i] <= 107` | null |
[Python3] dp | minimum-white-tiles-after-covering-with-carpets | 0 | 1 | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/7e91381aab0f51486f380f703245463c99fed635) for solutions of biweekly 74. \n\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n \n @cache\n def fn(i, n):\n """Return min while tiles at k with n carpets left."""\n if n < 0: return inf \n if i >= len(floor): return 0 \n if floor[i] == \'1\': return min(fn(i+carpetLen, n-1), 1 + fn(i+1, n))\n return fn(i+1, n)\n \n return fn(0, numCarpets)\n```\n\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n dp = [[0]*(1 + numCarpets) for _ in range(len(floor)+1)]\n for i in range(len(floor)-1, -1, -1): \n for j in range(0, numCarpets+1): \n if floor[i] == \'1\': \n dp[i][j] = 1 + dp[i+1][j] \n if j: \n if i+carpetLen >= len(floor): dp[i][j] = 0 \n else: dp[i][j] = min(dp[i+carpetLen][j-1], dp[i][j])\n else: dp[i][j] = dp[i+1][j]\n return dp[0][numCarpets]\n``` | 2 | You are given a **0-indexed binary** string `floor`, which represents the colors of tiles on a floor:
* `floor[i] = '0'` denotes that the `ith` tile of the floor is colored **black**.
* On the other hand, `floor[i] = '1'` denotes that the `ith` tile of the floor is colored **white**.
You are also given `numCarpets` and `carpetLen`. You have `numCarpets` **black** carpets, each of length `carpetLen` tiles. Cover the tiles with the given carpets such that the number of **white** tiles still visible is **minimum**. Carpets may overlap one another.
Return _the **minimum** number of white tiles still visible._
**Example 1:**
**Input:** floor = "10110101 ", numCarpets = 2, carpetLen = 2
**Output:** 2
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that only 2 white tiles are visible.
No other way of covering the tiles with the carpets can leave less than 2 white tiles visible.
**Example 2:**
**Input:** floor = "11111 ", numCarpets = 2, carpetLen = 3
**Output:** 0
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that no white tiles are visible.
Note that the carpets are able to overlap one another.
**Constraints:**
* `1 <= carpetLen <= floor.length <= 1000`
* `floor[i]` is either `'0'` or `'1'`.
* `1 <= numCarpets <= 1000` | The brute force solution is to check every substring, which would TLE. How can we improve this solution? In an equal count substring, the first character appears count times, the second character appears count times, and so on. The length of an equal count substring is the number of unique characters multiplied by count. The length of all equal count substrings are multiples of count. |
Simple Explanation and Solution (Memoization) [Python] | minimum-white-tiles-after-covering-with-carpets | 0 | 1 | # Intuition\nBacktracking memoization solution. At every step we either place a carpet or don\'t - we do whatever minimizes the number of exposed white tiles. For every tile we make a binary choice, which means complexity $O(2^n)$, but with memoization we reduce that to $O(n^2)$.\n\n# Complexity\n- Time complexity: $$\\mathcal{O}(n^2)$$\n- Space complexity: $$\\mathcal{O}(n \\cdot k)$$\n\nWhere $n = nums.length$ and $k = numCarpets$.\n\n# Code\n```\nclass Solution:\n\n def minimumWhiteTiles(self, floor: str, carpets: int, length: int) -> int:\n \n floor = [int(tile) for tile in floor]\n \n @cache # O(floor.length * numCarpets) memory\n def backtrack(i: int, carpets: int) -> int:\n\n # there is no more floor to carpet\n if i >= len(floor):\n return 0\n\n # we have no more carpets to place\n if carpets == 0:\n # this tile and all remaining tiles could be visible\n return floor[i] + backtrack(i + 1, carpets)\n else: \n # we have some carpets to place\n # we can either:\n # 1. place a carpet to hide the tiles under it (ignore them, skip one carpet-length ahead), or\n # 2. keep the carpet, saving one for later but exposing the current tile (which could be white)\n # simply do both and pick whichever one is better\n place = backtrack(i + length, carpets - 1)\n dont = floor[i] + backtrack(i + 1, carpets)\n return min(place, dont)\n \n return backtrack(0, carpets)\n``` | 0 | You are given a **0-indexed binary** string `floor`, which represents the colors of tiles on a floor:
* `floor[i] = '0'` denotes that the `ith` tile of the floor is colored **black**.
* On the other hand, `floor[i] = '1'` denotes that the `ith` tile of the floor is colored **white**.
You are also given `numCarpets` and `carpetLen`. You have `numCarpets` **black** carpets, each of length `carpetLen` tiles. Cover the tiles with the given carpets such that the number of **white** tiles still visible is **minimum**. Carpets may overlap one another.
Return _the **minimum** number of white tiles still visible._
**Example 1:**
**Input:** floor = "10110101 ", numCarpets = 2, carpetLen = 2
**Output:** 2
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that only 2 white tiles are visible.
No other way of covering the tiles with the carpets can leave less than 2 white tiles visible.
**Example 2:**
**Input:** floor = "11111 ", numCarpets = 2, carpetLen = 3
**Output:** 0
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that no white tiles are visible.
Note that the carpets are able to overlap one another.
**Constraints:**
* `1 <= carpetLen <= floor.length <= 1000`
* `floor[i]` is either `'0'` or `'1'`.
* `1 <= numCarpets <= 1000` | The brute force solution is to check every substring, which would TLE. How can we improve this solution? In an equal count substring, the first character appears count times, the second character appears count times, and so on. The length of an equal count substring is the number of unique characters multiplied by count. The length of all equal count substrings are multiples of count. |
python3 dp beats 93% | minimum-white-tiles-after-covering-with-carpets | 0 | 1 | \n\n# Code\n```\nclass Solution:\n def minimumWhiteTiles(self, floor: str, numCarpets: int, carpetLen: int) -> int:\n floor = \'0\'+floor\n dp = [[inf for x in range(len(floor))] for y in range(numCarpets+1)]\n c = 0\n for i in range(len(floor)):\n if floor[i]==\'1\':\n c+=1\n dp[0][i] = c\n\n \n for r in range(1,numCarpets+1):\n for c in range(len(floor)):\n if c==0:\n dp[r][c]=0\n continue\n if floor[c]==\'0\':\n dp[r][c] = dp[r][c-1]\n else:\n dp[r][c] = min(dp[r][c-1]+1,dp[r-1][max(0,c-carpetLen)])\n\n return dp[-1][-1]\n\n \n``` | 0 | You are given a **0-indexed binary** string `floor`, which represents the colors of tiles on a floor:
* `floor[i] = '0'` denotes that the `ith` tile of the floor is colored **black**.
* On the other hand, `floor[i] = '1'` denotes that the `ith` tile of the floor is colored **white**.
You are also given `numCarpets` and `carpetLen`. You have `numCarpets` **black** carpets, each of length `carpetLen` tiles. Cover the tiles with the given carpets such that the number of **white** tiles still visible is **minimum**. Carpets may overlap one another.
Return _the **minimum** number of white tiles still visible._
**Example 1:**
**Input:** floor = "10110101 ", numCarpets = 2, carpetLen = 2
**Output:** 2
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that only 2 white tiles are visible.
No other way of covering the tiles with the carpets can leave less than 2 white tiles visible.
**Example 2:**
**Input:** floor = "11111 ", numCarpets = 2, carpetLen = 3
**Output:** 0
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that no white tiles are visible.
Note that the carpets are able to overlap one another.
**Constraints:**
* `1 <= carpetLen <= floor.length <= 1000`
* `floor[i]` is either `'0'` or `'1'`.
* `1 <= numCarpets <= 1000` | The brute force solution is to check every substring, which would TLE. How can we improve this solution? In an equal count substring, the first character appears count times, the second character appears count times, and so on. The length of an equal count substring is the number of unique characters multiplied by count. The length of all equal count substrings are multiples of count. |
Dp Super Detailed Explanation and Process | minimum-white-tiles-after-covering-with-carpets | 0 | 1 | \n## Initial thoughts \n\nIt looks like initially, me an others considered a greedy approach to optimize the placement of carpets to cover the most white tiles at each step. With counterexamples It became clear though that the approach didn\'t yield the optimal solution. From the solutions section it seemed was rather necessary to find the optimal solution at each step and sum those together to get the minimum possible white tiles visible at the end.\n\nMy first approach the first time I encountered this problem 6 months ago was likely manipulating arrays somehow. Trying the greedy this second time and finding a couple counter examples, I discarded it quickly.\n\nIt was kind of interesting to see this kind of problem the first time around. Labelled as \'hard\' the difficulty was a bit intimidating.\n\nIf I recall correctly, it was probably the first time I saw the use of diagrams to explain the problem statement.\n\n## Past experiences\n\nI\'ve come across similar problems or topics related to dynamic programming before, but this is likely the first of its kind I tackled. The concept often feels confusing, especially around the pre-computation of values to be reused later. Understanding solutions is complex on its on, but devising my own can and still to this day does feel hellish.\n\nI\'ve seen similar problems with tags strings and prefix sum (another term for cumulative sum). The problem made me recall the latter concept, and [the wikipedia](https://en.wikipedia.org/wiki/Prefix_sum) article I first clarified it with.\n\nThe dynamic programming approach required here keeps a sum of the remaining visible white tiles in a two-dimensional array at each position, which is a bit reminiscent of problems with prefix sum I\'ve encountered before.\n\n## ChatGPT interaction\n\nWith ChatGPT I usually follow a couple prompting patterns for seeking tag explanations and understanding tricky solutions on LeetCode, often times from specific recurrent LeetCode users like Lee215 whose English may be tricky to read but solutions are spot on. I find ChatGPT useful in elaborating on those solutions, explaining the logic and code involved in a structured manner, to enhance understanding\n\n\n\nI prefer to ask ChatGPT to clarify existing human made solutions rather than asking it to provide new ones himself, as it can sometimes hallucinate or offer less optimal solutions.\n\nInitially, I thought a greedy approach might work but soon realized it led to suboptimal solutions. \n\nThrough interactions and reviewing different submissions, I explored solutions with different approaches to dynamic programming, learning more about bottom-up and top-down strategies, and when to use dynamic programming.\n\nI didn\'t get to ask all my questions to it due to time constraints. The problem is significantly more difficult to process than others I\'ve written about and confronted before, and in such cases my method\'s cue to move on is placed to the test.\n\nMy experience has been that the quicker I move away from frustration, while actively seeking it through making and testing assumptions, the faster I learn.\n\nI also wondered if the problem could be approached as a sliding window scenario, considering each carpet\'s starting index rather than a greedy placement. Initially, I pursued a wrong route based on this insight. This evolved through discovering a crucial example in the discussion section and self-discovery in isolation, leading me to understand that the problem had a larger search space with more possibilities for carpet placement combinations.\n\nI also used ChatGPT to tweak around a more in-depth second solution compared to user Lee215\'s succinct, Pythonic solution.\n\n## Tricky Parts\n\nAs I said, it was tricky figuring out how to traverse the space of carpet placement combinations. Dynamic programming (DP) is always a bit daunting on its difficulty to grasp and for me it often is the case that it doesn\'t intuitively come to mind as a solution.\n\nAlthough there weren\'t any tricky coding constraints, understanding the DP approach and the problem\'s optimal substructure was challenging still. The goal is to minimize something by finding minima in sub-sequences, which in general is hard to visualize.\n\nWith more learning and a closer look, I might get better at it, but I still don\'t feel strong on this one and for that reason haven\'t been able to mark it as understood on my database just yet.\n\n## Solution\n\n\n```python\nclass Solution:\n def minimumWhiteTiles(self, floor, k, l):\n\n @lru_cache(None)\n def dp(i, k):\n if i <= 0: return 0\n return min(int(floor[i - 1]) + dp(i - 1, k), dp(i - l, k - 1) if k else 1000)\n \n return dp(len(floor), k) \n\n```\n\nAs mentioned, the solution revolves around a DP approach to minimize the number of visible white tiles after placing a given number of carpets on a floor represented by the string `floor`. The core of this solution is the `dp` function, which is memoized using `lru_cache` to improve performance by storing the results of previous computations -that\'s what memoization means.\n\nThe `dp` function takes two arguments: `i`, the current index in the string representing the `floor`, and `k`, the number of carpets left to lay. The function is called recursively, working from right to left across the string, considering two main choices at each step: placing a carpet or not:\n\n1. **Not Placing a Carpet:** If a carpet isn\'t placed at the current index, the function adds `1` to the count if a white tile is present (`int(A[i - 1])` converts the character at the current index to an integer, adding `1` if it\'s a white tile), and then `dp` calls itself recursively with `i - 1`, moving one step to the left, keeping the count of carpets `k` left to place unchanged.\n\n2. **Placing a Carpet:** If a carpet is placed, the function calls itself also with `i - l`, jumping by the length of a carpet (we skip `l` positions because a carpet is there), and `k - 1`, reducing the count of remaining carpets by `1`. However, this choice is only considered if there are carpets left to place (`k` is not zero), otherwise, a large value (`1000`) is used to represent an undesirable choice, effectively ignoring this option, and always going for the other side of `min`. \n\nThe recursion continues until the left end of the string is reached (`i <= 0`), at which point `0` is returned, serving as the base case to terminate the recursion.\n\nThe main method initiates the dynamic programming process by calling `dp` with the initial index set to the length of the string `floor`, and the initial count of carpets `k`, and returns the result, representing the minimum number of visible white tiles after placing all carpets optimally.\n\n## Optimization\n\nJust understanding the actual complexity as described by these guys was initially challenging. With dynamic programming, it seems like the states are built around the indexes or tiles and the number of carpets `k`. So, the states are essentially what happens at a particular index after placing a certain number of carpets.\n\nThe complexity arises as we consider all positions from 0 to n (length of `floor`) and all carpet counts from 0 to k, leading to n times k states.\n\nThere are weird scenarios, like stacking a bunch of carpets at index 0, which feels illogical and calls for optimization to eliminate such considerations. These states seemed to inflate the space complexity and possibly the time complexity too.\n\n## Learned\n\nThis problem dives into the core of dynamic programming and gave me an opportunity to work on its fundamental concepts. I got to grasp, perhaps to an intermediate extent, the essence of recursiveness, tabulation, and memoization, and how the same ideas can be implemented with iterative rather than recursive code, essentially tabulating states.\n\nI got a little bit of an initial handle on optimally solving problems, understanding how tackling larger problems with optimal solutions to smaller sub-problems aligns with dynamic programming.\n\nI was able to expose the inadequacy of a greedy approach, affirming that dynamic programming, is the suitable strategy for such problems that are optimal in structure. I think this was the most significant realization of the session.\n\n## Further\n\nThe resources I used were basically the [convo with ChatGPT](https://chat.openai.com/share/f2df59ac-f8e5-4a2e-85fe-2b41ab8f9615) on this topic that I had today and yesterday. And the couple solutions ([first](https://leetcode.com/problems/minimum-white-tiles-after-covering-with-carpets/solutions/1863955/java-c-python-dp-solution/) and [second](https://leetcode.com/problems/minimum-white-tiles-after-covering-with-carpets/solutions/1872882/python-readable-and-easy-understand-bottom-up-dp-solution-in-python/))from users on LeetCode I feed as context to ChatGPT and drew understanding from.\n | 0 | You are given a **0-indexed binary** string `floor`, which represents the colors of tiles on a floor:
* `floor[i] = '0'` denotes that the `ith` tile of the floor is colored **black**.
* On the other hand, `floor[i] = '1'` denotes that the `ith` tile of the floor is colored **white**.
You are also given `numCarpets` and `carpetLen`. You have `numCarpets` **black** carpets, each of length `carpetLen` tiles. Cover the tiles with the given carpets such that the number of **white** tiles still visible is **minimum**. Carpets may overlap one another.
Return _the **minimum** number of white tiles still visible._
**Example 1:**
**Input:** floor = "10110101 ", numCarpets = 2, carpetLen = 2
**Output:** 2
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that only 2 white tiles are visible.
No other way of covering the tiles with the carpets can leave less than 2 white tiles visible.
**Example 2:**
**Input:** floor = "11111 ", numCarpets = 2, carpetLen = 3
**Output:** 0
**Explanation:**
The figure above shows one way of covering the tiles with the carpets such that no white tiles are visible.
Note that the carpets are able to overlap one another.
**Constraints:**
* `1 <= carpetLen <= floor.length <= 1000`
* `floor[i]` is either `'0'` or `'1'`.
* `1 <= numCarpets <= 1000` | The brute force solution is to check every substring, which would TLE. How can we improve this solution? In an equal count substring, the first character appears count times, the second character appears count times, and so on. The length of an equal count substring is the number of unique characters multiplied by count. The length of all equal count substrings are multiples of count. |
Python Clean solution || Simple and easy | count-hills-and-valleys-in-an-array | 0 | 1 | We start by taking a for loop which goes from 1 to length of array -1.\nSince we cannot take 2 adjacent values such that nums[i] == nums[j]. \nSo, we update the current value to previous value which will help us in counting the next hill or valley. \n\nTime complexity = O(n)\nSpace complexity = O(1)\n\n```class Solution:\n def countHillValley(self, nums: List[int]) -> int:\n hillValley = 0\n for i in range(1, len(nums)-1):\n if nums[i] == nums[i+1]:\n nums[i] = nums[i-1]\n if nums[i] > nums[i-1] and nums[i] > nums[i+1]: #hill check\n hillValley += 1\n if nums[i] < nums[i-1] and nums[i] < nums[i+1]: #valley check\n hillValley += 1\n return hillValley\n``` | 56 | You are given a **0-indexed** integer array `nums`. An index `i` is part of a **hill** in `nums` if the closest non-equal neighbors of `i` are smaller than `nums[i]`. Similarly, an index `i` is part of a **valley** in `nums` if the closest non-equal neighbors of `i` are larger than `nums[i]`. Adjacent indices `i` and `j` are part of the **same** hill or valley if `nums[i] == nums[j]`.
Note that for an index to be part of a hill or valley, it must have a non-equal neighbor on **both** the left and right of the index.
Return _the number of hills and valleys in_ `nums`.
**Example 1:**
**Input:** nums = \[2,4,1,1,6,5\]
**Output:** 3
**Explanation:**
At index 0: There is no non-equal neighbor of 2 on the left, so index 0 is neither a hill nor a valley.
At index 1: The closest non-equal neighbors of 4 are 2 and 1. Since 4 > 2 and 4 > 1, index 1 is a hill.
At index 2: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 2 is a valley.
At index 3: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 3 is a valley, but note that it is part of the same valley as index 2.
At index 4: The closest non-equal neighbors of 6 are 1 and 5. Since 6 > 1 and 6 > 5, index 4 is a hill.
At index 5: There is no non-equal neighbor of 5 on the right, so index 5 is neither a hill nor a valley.
There are 3 hills and valleys so we return 3.
**Example 2:**
**Input:** nums = \[6,6,5,5,4,1\]
**Output:** 0
**Explanation:**
At index 0: There is no non-equal neighbor of 6 on the left, so index 0 is neither a hill nor a valley.
At index 1: There is no non-equal neighbor of 6 on the left, so index 1 is neither a hill nor a valley.
At index 2: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 2 is neither a hill nor a valley.
At index 3: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 3 is neither a hill nor a valley.
At index 4: The closest non-equal neighbors of 4 are 5 and 1. Since 4 < 5 and 4 > 1, index 4 is neither a hill nor a valley.
At index 5: There is no non-equal neighbor of 1 on the right, so index 5 is neither a hill nor a valley.
There are 0 hills and valleys so we return 0.
**Constraints:**
* `3 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Try "sorting" the array first. Now find all indices in the array whose values are equal to target. |
Python Clean solution & explanation of an edge case | count-hills-and-valleys-in-an-array | 0 | 1 | # Intuition\nWe are iterating from 1st to last -1 element.\nFor each one determine is it hill or velly:\nelement-1 < element > element + 1 or element-1 > element < element + 1\n\n# Approach\nImportant to not count the same velly [4, ***1,1,1*** ,4] multiple times.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def countHillValley(self, nums: List[int]) -> int:\n result = 0\n for i in range(1, len(nums)-1):\n # edge case, the same velly!\n # adjacent indexes should be considered as one velly or hill\n # to handle this, we can check if next value is the same as current\n # for example in [4,1,1,6]\n # [4, 1(we are here), 1(detected next value), 6]\n # replace the first 1 by 4 (4 is a previous value)\n # as result we get: [4,4,1,6]\n # so thet at the next iteration the second 1 will be detected as a valley\n # [4,4,1(we are here),6] \n # 4 > 1 < 6\n if nums[i] == nums[i+1]:\n nums[i] = nums[i-1]\n elif nums[i-1] > nums[i] < nums[i+1] or nums[i-1] < nums[i] > nums[i+1]:\n result += 1\n return result\n \n\n \n\n\n \n\n``` | 2 | You are given a **0-indexed** integer array `nums`. An index `i` is part of a **hill** in `nums` if the closest non-equal neighbors of `i` are smaller than `nums[i]`. Similarly, an index `i` is part of a **valley** in `nums` if the closest non-equal neighbors of `i` are larger than `nums[i]`. Adjacent indices `i` and `j` are part of the **same** hill or valley if `nums[i] == nums[j]`.
Note that for an index to be part of a hill or valley, it must have a non-equal neighbor on **both** the left and right of the index.
Return _the number of hills and valleys in_ `nums`.
**Example 1:**
**Input:** nums = \[2,4,1,1,6,5\]
**Output:** 3
**Explanation:**
At index 0: There is no non-equal neighbor of 2 on the left, so index 0 is neither a hill nor a valley.
At index 1: The closest non-equal neighbors of 4 are 2 and 1. Since 4 > 2 and 4 > 1, index 1 is a hill.
At index 2: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 2 is a valley.
At index 3: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 3 is a valley, but note that it is part of the same valley as index 2.
At index 4: The closest non-equal neighbors of 6 are 1 and 5. Since 6 > 1 and 6 > 5, index 4 is a hill.
At index 5: There is no non-equal neighbor of 5 on the right, so index 5 is neither a hill nor a valley.
There are 3 hills and valleys so we return 3.
**Example 2:**
**Input:** nums = \[6,6,5,5,4,1\]
**Output:** 0
**Explanation:**
At index 0: There is no non-equal neighbor of 6 on the left, so index 0 is neither a hill nor a valley.
At index 1: There is no non-equal neighbor of 6 on the left, so index 1 is neither a hill nor a valley.
At index 2: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 2 is neither a hill nor a valley.
At index 3: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 3 is neither a hill nor a valley.
At index 4: The closest non-equal neighbors of 4 are 5 and 1. Since 4 < 5 and 4 > 1, index 4 is neither a hill nor a valley.
At index 5: There is no non-equal neighbor of 1 on the right, so index 5 is neither a hill nor a valley.
There are 0 hills and valleys so we return 0.
**Constraints:**
* `3 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Try "sorting" the array first. Now find all indices in the array whose values are equal to target. |
[Python3] One pass || O(1) space | count-hills-and-valleys-in-an-array | 0 | 1 | ```\nclass Solution:\n def countHillValley(self, nums: List[int]) -> int:\n \n #cnt: An integer to store total hills and valleys\n #left: Highest point of hill or lowest point of valley left of the current index\n cnt, left = 0, nums[0]\n \n for i in range(1, len(nums)-1):\n if (left<nums[i] and nums[i]>nums[i+1]) or (left>nums[i] and nums[i]<nums[i+1]):\n cnt+=1\n left=nums[i]\n return cnt\n``` | 3 | You are given a **0-indexed** integer array `nums`. An index `i` is part of a **hill** in `nums` if the closest non-equal neighbors of `i` are smaller than `nums[i]`. Similarly, an index `i` is part of a **valley** in `nums` if the closest non-equal neighbors of `i` are larger than `nums[i]`. Adjacent indices `i` and `j` are part of the **same** hill or valley if `nums[i] == nums[j]`.
Note that for an index to be part of a hill or valley, it must have a non-equal neighbor on **both** the left and right of the index.
Return _the number of hills and valleys in_ `nums`.
**Example 1:**
**Input:** nums = \[2,4,1,1,6,5\]
**Output:** 3
**Explanation:**
At index 0: There is no non-equal neighbor of 2 on the left, so index 0 is neither a hill nor a valley.
At index 1: The closest non-equal neighbors of 4 are 2 and 1. Since 4 > 2 and 4 > 1, index 1 is a hill.
At index 2: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 2 is a valley.
At index 3: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 3 is a valley, but note that it is part of the same valley as index 2.
At index 4: The closest non-equal neighbors of 6 are 1 and 5. Since 6 > 1 and 6 > 5, index 4 is a hill.
At index 5: There is no non-equal neighbor of 5 on the right, so index 5 is neither a hill nor a valley.
There are 3 hills and valleys so we return 3.
**Example 2:**
**Input:** nums = \[6,6,5,5,4,1\]
**Output:** 0
**Explanation:**
At index 0: There is no non-equal neighbor of 6 on the left, so index 0 is neither a hill nor a valley.
At index 1: There is no non-equal neighbor of 6 on the left, so index 1 is neither a hill nor a valley.
At index 2: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 2 is neither a hill nor a valley.
At index 3: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 3 is neither a hill nor a valley.
At index 4: The closest non-equal neighbors of 4 are 5 and 1. Since 4 < 5 and 4 > 1, index 4 is neither a hill nor a valley.
At index 5: There is no non-equal neighbor of 1 on the right, so index 5 is neither a hill nor a valley.
There are 0 hills and valleys so we return 0.
**Constraints:**
* `3 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Try "sorting" the array first. Now find all indices in the array whose values are equal to target. |
python | count-hills-and-valleys-in-an-array | 0 | 1 | ```\ndef countHillValley(self, nums: List[int]) -> int:\n nums1 = [nums[0]]\n for i in range(1, len(nums)):\n if nums[i] != nums1[-1]:\n nums1.append(nums[i])\n cnt = 0\n for i in range(1, len(nums1) - 1):\n if nums1[i - 1] < nums1[i] > nums1[i + 1] or nums1[i - 1] > nums1[i] < nums1[i + 1]:\n cnt += 1\n return cnt\n``` | 2 | You are given a **0-indexed** integer array `nums`. An index `i` is part of a **hill** in `nums` if the closest non-equal neighbors of `i` are smaller than `nums[i]`. Similarly, an index `i` is part of a **valley** in `nums` if the closest non-equal neighbors of `i` are larger than `nums[i]`. Adjacent indices `i` and `j` are part of the **same** hill or valley if `nums[i] == nums[j]`.
Note that for an index to be part of a hill or valley, it must have a non-equal neighbor on **both** the left and right of the index.
Return _the number of hills and valleys in_ `nums`.
**Example 1:**
**Input:** nums = \[2,4,1,1,6,5\]
**Output:** 3
**Explanation:**
At index 0: There is no non-equal neighbor of 2 on the left, so index 0 is neither a hill nor a valley.
At index 1: The closest non-equal neighbors of 4 are 2 and 1. Since 4 > 2 and 4 > 1, index 1 is a hill.
At index 2: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 2 is a valley.
At index 3: The closest non-equal neighbors of 1 are 4 and 6. Since 1 < 4 and 1 < 6, index 3 is a valley, but note that it is part of the same valley as index 2.
At index 4: The closest non-equal neighbors of 6 are 1 and 5. Since 6 > 1 and 6 > 5, index 4 is a hill.
At index 5: There is no non-equal neighbor of 5 on the right, so index 5 is neither a hill nor a valley.
There are 3 hills and valleys so we return 3.
**Example 2:**
**Input:** nums = \[6,6,5,5,4,1\]
**Output:** 0
**Explanation:**
At index 0: There is no non-equal neighbor of 6 on the left, so index 0 is neither a hill nor a valley.
At index 1: There is no non-equal neighbor of 6 on the left, so index 1 is neither a hill nor a valley.
At index 2: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 2 is neither a hill nor a valley.
At index 3: The closest non-equal neighbors of 5 are 6 and 4. Since 5 < 6 and 5 > 4, index 3 is neither a hill nor a valley.
At index 4: The closest non-equal neighbors of 4 are 5 and 1. Since 4 < 5 and 4 > 1, index 4 is neither a hill nor a valley.
At index 5: There is no non-equal neighbor of 1 on the right, so index 5 is neither a hill nor a valley.
There are 0 hills and valleys so we return 0.
**Constraints:**
* `3 <= nums.length <= 100`
* `1 <= nums[i] <= 100` | Try "sorting" the array first. Now find all indices in the array whose values are equal to target. |
Not a stupid problem! | count-collisions-on-a-road | 1 | 1 | **Similar Question :-** [ https://leetcode.com/problems/asteroid-collision/]\n**C++ Solution**\n\n```\nclass Solution {\npublic:\n int countCollisions(string dir) {\n \n int res(0), n(size(dir)), i(0), carsFromRight(0);\n \n while (i < n and dir[i] == \'L\') i++; // skipping all the cars going to left from beginning as they will never collide\n \n for ( ; i<n; i++) {\n if (dir[i] == \'R\') carsFromRight++;\n else {\n // if dir[i] == \'S\' then there will be carsFromRight number of collission\n // if dir[i] == \'L\' then there will be carsFromRight+1 number of collision (one collision for the rightmost cars and carsFromRight collision for the cars coming from left)\n res += (dir[i] == \'S\') ? carsFromRight : carsFromRight+1;\n carsFromRight = 0;\n }\n }\n return res;\n }\n};\n```\n\n**Java Solution**\n\n```\nclass Solution {\n public int countCollisions(String dir) {\n \n int res = 0, n = dir.length(), i = 0, carsFromRight = 0;\n \n while (i < n && dir.charAt(i) == \'L\') i++;\n \n for ( ; i<n; i++) {\n if (dir.charAt(i) == \'R\') carsFromRight++;\n else {\n res += (dir.charAt(i) == \'S\') ? carsFromRight : carsFromRight+1;\n carsFromRight = 0;\n }\n }\n return res;\n }\n}\n```\n**Python Solution**\n```\nclass Solution:\n def countCollisions(self, directions: str) -> int:\n \n res, n, i, carsFromRight = 0, len(directions), 0, 0\n \n while i < n and directions[i] == \'L\':\n i+=1\n \n while i<n:\n if directions[i] == \'R\':\n carsFromRight+=1\n else:\n res += carsFromRight if directions[i] == \'S\' else carsFromRight+1;\n carsFromRight = 0\n i+=1\n \n return res\n```\n**Upvote if it helps :)** | 124 | There are `n` cars on an infinitely long road. The cars are numbered from `0` to `n - 1` from left to right and each car is present at a **unique** point.
You are given a **0-indexed** string `directions` of length `n`. `directions[i]` can be either `'L'`, `'R'`, or `'S'` denoting whether the `ith` car is moving towards the **left**, towards the **right**, or **staying** at its current point respectively. Each moving car has the **same speed**.
The number of collisions can be calculated as follows:
* When two cars moving in **opposite** directions collide with each other, the number of collisions increases by `2`.
* When a moving car collides with a stationary car, the number of collisions increases by `1`.
After a collision, the cars involved can no longer move and will stay at the point where they collided. Other than that, cars cannot change their state or direction of motion.
Return _the **total number of collisions** that will happen on the road_.
**Example 1:**
**Input:** directions = "RLRSLL "
**Output:** 5
**Explanation:**
The collisions that will happen on the road are:
- Cars 0 and 1 will collide with each other. Since they are moving in opposite directions, the number of collisions becomes 0 + 2 = 2.
- Cars 2 and 3 will collide with each other. Since car 3 is stationary, the number of collisions becomes 2 + 1 = 3.
- Cars 3 and 4 will collide with each other. Since car 3 is stationary, the number of collisions becomes 3 + 1 = 4.
- Cars 4 and 5 will collide with each other. After car 4 collides with car 3, it will stay at the point of collision and get hit by car 5. The number of collisions becomes 4 + 1 = 5.
Thus, the total number of collisions that will happen on the road is 5.
**Example 2:**
**Input:** directions = "LLRR "
**Output:** 0
**Explanation:**
No cars will collide with each other. Thus, the total number of collisions that will happen on the road is 0.
**Constraints:**
* `1 <= directions.length <= 105`
* `directions[i]` is either `'L'`, `'R'`, or `'S'`. | To calculate the average of a subarray, you need the sum and the K. K is already given. How could you quickly calculate the sum of a subarray? Use the Prefix Sums method to calculate the subarray sums. It is possible that the sum of all the elements does not fit in a 32-bit integer type. Be sure to use a 64-bit integer type for the prefix sum array. |
One-liner in Python | count-collisions-on-a-road | 0 | 1 | All the cars that move to the middle will eventually collide.... \n\n```\nclass Solution:\n def countCollisions(self, directions: str) -> int:\n return sum(d!=\'S\' for d in directions.lstrip(\'L\').rstrip(\'R\'))\n``` | 74 | There are `n` cars on an infinitely long road. The cars are numbered from `0` to `n - 1` from left to right and each car is present at a **unique** point.
You are given a **0-indexed** string `directions` of length `n`. `directions[i]` can be either `'L'`, `'R'`, or `'S'` denoting whether the `ith` car is moving towards the **left**, towards the **right**, or **staying** at its current point respectively. Each moving car has the **same speed**.
The number of collisions can be calculated as follows:
* When two cars moving in **opposite** directions collide with each other, the number of collisions increases by `2`.
* When a moving car collides with a stationary car, the number of collisions increases by `1`.
After a collision, the cars involved can no longer move and will stay at the point where they collided. Other than that, cars cannot change their state or direction of motion.
Return _the **total number of collisions** that will happen on the road_.
**Example 1:**
**Input:** directions = "RLRSLL "
**Output:** 5
**Explanation:**
The collisions that will happen on the road are:
- Cars 0 and 1 will collide with each other. Since they are moving in opposite directions, the number of collisions becomes 0 + 2 = 2.
- Cars 2 and 3 will collide with each other. Since car 3 is stationary, the number of collisions becomes 2 + 1 = 3.
- Cars 3 and 4 will collide with each other. Since car 3 is stationary, the number of collisions becomes 3 + 1 = 4.
- Cars 4 and 5 will collide with each other. After car 4 collides with car 3, it will stay at the point of collision and get hit by car 5. The number of collisions becomes 4 + 1 = 5.
Thus, the total number of collisions that will happen on the road is 5.
**Example 2:**
**Input:** directions = "LLRR "
**Output:** 0
**Explanation:**
No cars will collide with each other. Thus, the total number of collisions that will happen on the road is 0.
**Constraints:**
* `1 <= directions.length <= 105`
* `directions[i]` is either `'L'`, `'R'`, or `'S'`. | To calculate the average of a subarray, you need the sum and the K. K is already given. How could you quickly calculate the sum of a subarray? Use the Prefix Sums method to calculate the subarray sums. It is possible that the sum of all the elements does not fit in a 32-bit integer type. Be sure to use a 64-bit integer type for the prefix sum array. |
Short Easy Python Solution With Explanation | count-collisions-on-a-road | 0 | 1 | We can transform this problem into whether go right or go left cars will stop and count the sum of stops. After transformation, we just need to check the situation of each go left and go right car individually.\n\nStarting from left->right,\n\nIf there is no car at the beginning go right or stop, then go left car after them will never stop.\nExample\nLLLLL -> No one car will stop\nIf there one car stop or go right at the beginning, then go left car after them is bound to stop\nExample\nLR | LLL -> After R, three L will stop there are **three** left car stop\nLS | LLL -> After S, three L will stop\n\n\nStarting from right->left,\nIf there is no car at the beginning go left or stop, then go right car after them will never stop.\nExample\nRRRRR -> No one car will stop\n\nIf there is one car stop or go left at the beginning, then go right car after them is bound to stop\nExample\nRRR | LR -> After L, three RRR will stop \nRRR | SR -> After S, three R will stop\n\nThen we check wether left car will stop by (left->right) and then check wether right car will stop by (right->left). The answer is the sum\n\n\n\n```\nclass Solution:\n def countCollisions(self, directions: str) -> int:\n ans = 0\n # At the beginning, leftest car can go without collide\n # At the beginning, rightest car can go without collide\n \n leftc = rightc = 0\n \n for c in directions:\n # if left side, no car stop or right answer + 0\n # if left side start to have car go right or stop\n # then cars after that are bound to be stopped so answer + 1\n if c == "L":\n ans += leftc\n else:\n leftc = 1\n \n for c in directions[::-1]:\n # if right side, no car stop or left answer + 0\n # if right side start to have car go left or stop\n # then cars after that are bound to be stopped so answer + 1\n if c == "R":\n ans += rightc\n else:\n rightc = 1\n \n return ans\n``` | 13 | There are `n` cars on an infinitely long road. The cars are numbered from `0` to `n - 1` from left to right and each car is present at a **unique** point.
You are given a **0-indexed** string `directions` of length `n`. `directions[i]` can be either `'L'`, `'R'`, or `'S'` denoting whether the `ith` car is moving towards the **left**, towards the **right**, or **staying** at its current point respectively. Each moving car has the **same speed**.
The number of collisions can be calculated as follows:
* When two cars moving in **opposite** directions collide with each other, the number of collisions increases by `2`.
* When a moving car collides with a stationary car, the number of collisions increases by `1`.
After a collision, the cars involved can no longer move and will stay at the point where they collided. Other than that, cars cannot change their state or direction of motion.
Return _the **total number of collisions** that will happen on the road_.
**Example 1:**
**Input:** directions = "RLRSLL "
**Output:** 5
**Explanation:**
The collisions that will happen on the road are:
- Cars 0 and 1 will collide with each other. Since they are moving in opposite directions, the number of collisions becomes 0 + 2 = 2.
- Cars 2 and 3 will collide with each other. Since car 3 is stationary, the number of collisions becomes 2 + 1 = 3.
- Cars 3 and 4 will collide with each other. Since car 3 is stationary, the number of collisions becomes 3 + 1 = 4.
- Cars 4 and 5 will collide with each other. After car 4 collides with car 3, it will stay at the point of collision and get hit by car 5. The number of collisions becomes 4 + 1 = 5.
Thus, the total number of collisions that will happen on the road is 5.
**Example 2:**
**Input:** directions = "LLRR "
**Output:** 0
**Explanation:**
No cars will collide with each other. Thus, the total number of collisions that will happen on the road is 0.
**Constraints:**
* `1 <= directions.length <= 105`
* `directions[i]` is either `'L'`, `'R'`, or `'S'`. | To calculate the average of a subarray, you need the sum and the K. K is already given. How could you quickly calculate the sum of a subarray? Use the Prefix Sums method to calculate the subarray sums. It is possible that the sum of all the elements does not fit in a 32-bit integer type. Be sure to use a 64-bit integer type for the prefix sum array. |
Efficient Python solution O(N) time O(1) space with clear explanation | count-collisions-on-a-road | 0 | 1 | This question is similar to the [Asteroid Collision](https://leetcode.com/problems/asteroid-collision/) question.\n\nWe need a few variables:\n- has_stationary - determines if there stationary objects which will result in collisions\n- number of cars moving towards the right - when they hit a left/stationary car, they will result in collisions\n\n```py\nclass Solution:\n def countCollisions(self, directions: str) -> int:\n has_stationary, right, collisions = False, 0, 0\n for direction in directions:\n if direction == \'R\':\n\t\t\t # Just record number of right-moving cars. We will resolve them when we encounter a left-moving/stationary car.\n right += 1\n elif direction == \'L\' and (has_stationary or right > 0): \n\t\t\t # Left-moving cars which don\'t have any existing right-moving/stationary cars to their left can be ignored. They won\'t hit anything.\n\t\t\t\t# But if there are right-moving/stationary cars, it will result in collisions and we can resolve them.\n\t\t\t\t# We reset right to 0 because they have collided and will become stationary cars.\n collisions += 1 + right\n right = 0\n has_stationary = True\n elif direction == \'S\':\n\t\t\t # Resolve any right-moving cars and reset right to 0 because they are now stationary.\n collisions += right\n right = 0\n has_stationary = True\n return collisions\n```\n\nShorter solution (but less readable IMO)\n\n```\nclass Solution:\n def countCollisions(self, directions: str) -> int:\n has_stationary, right, collisions = False, 0, 0\n for direction in directions:\n if direction == \'R\':\n right += 1\n elif (direction == \'L\' and (has_stationary or right > 0)) or direction == \'S\':\n collisions += (1 if direction == \'L\' else 0) + right\n right = 0\n has_stationary = True\n return collisions\n``` | 5 | There are `n` cars on an infinitely long road. The cars are numbered from `0` to `n - 1` from left to right and each car is present at a **unique** point.
You are given a **0-indexed** string `directions` of length `n`. `directions[i]` can be either `'L'`, `'R'`, or `'S'` denoting whether the `ith` car is moving towards the **left**, towards the **right**, or **staying** at its current point respectively. Each moving car has the **same speed**.
The number of collisions can be calculated as follows:
* When two cars moving in **opposite** directions collide with each other, the number of collisions increases by `2`.
* When a moving car collides with a stationary car, the number of collisions increases by `1`.
After a collision, the cars involved can no longer move and will stay at the point where they collided. Other than that, cars cannot change their state or direction of motion.
Return _the **total number of collisions** that will happen on the road_.
**Example 1:**
**Input:** directions = "RLRSLL "
**Output:** 5
**Explanation:**
The collisions that will happen on the road are:
- Cars 0 and 1 will collide with each other. Since they are moving in opposite directions, the number of collisions becomes 0 + 2 = 2.
- Cars 2 and 3 will collide with each other. Since car 3 is stationary, the number of collisions becomes 2 + 1 = 3.
- Cars 3 and 4 will collide with each other. Since car 3 is stationary, the number of collisions becomes 3 + 1 = 4.
- Cars 4 and 5 will collide with each other. After car 4 collides with car 3, it will stay at the point of collision and get hit by car 5. The number of collisions becomes 4 + 1 = 5.
Thus, the total number of collisions that will happen on the road is 5.
**Example 2:**
**Input:** directions = "LLRR "
**Output:** 0
**Explanation:**
No cars will collide with each other. Thus, the total number of collisions that will happen on the road is 0.
**Constraints:**
* `1 <= directions.length <= 105`
* `directions[i]` is either `'L'`, `'R'`, or `'S'`. | To calculate the average of a subarray, you need the sum and the K. K is already given. How could you quickly calculate the sum of a subarray? Use the Prefix Sums method to calculate the subarray sums. It is possible that the sum of all the elements does not fit in a 32-bit integer type. Be sure to use a 64-bit integer type for the prefix sum array. |
No Segment Tree and NOT Pretty [100%, 48%] | longest-substring-of-one-repeating-character | 0 | 1 | # Complexity\n- Time complexity: $O(nlogn)$ (*assuming* array resizing is const time)\n\n- Space complexity: $(On)$\n\n# Code\n```python\nfrom heapq import heappush, heappop\nclass Solution:\n def longestRepeating(self, A: str, C: str, I: List[int]) -> List[int]:\n ii = [[0, 0, 1, A[0]]]\n for i in range(1, len(A)):\n if A[i] == A[i - 1]:\n ii[-1][1] = i\n ii[-1][2] += 1\n else:\n ii.append([i, i, 1, A[i]])\n\n hh = [-(ln) for _, _, ln, _ in ii]\n cc = defaultdict(int)\n for _, _, ln, _ in ii: cc[ln] += 1\n heapq.heapify(hh)\n\n rr = []\n for i in range(len(C)):\n idx = bisect_left(ii, I[i], key=lambda x: x[1])\n if ii[idx][3] == C[i]: \n rr.append(-hh[0])\n continue\n if ii[idx][0] == ii[idx][1]:\n ii[idx][3] = C[i]\n elif ii[idx][0] == I[i]:\n ii[idx][0] = I[i] + 1\n cc[ii[idx][2]] -= 1\n ii[idx][2] -= 1\n cc[ii[idx][2]] += 1\n cc[1] += 1\n heappush(hh, -ii[idx][2])\n heappush(hh, -1)\n ii[idx:idx + 1] = [[I[i], I[i], 1, C[i]], ii[idx]]\n elif ii[idx][1] == I[i]:\n cc[ii[idx][2]] -= 1\n ii[idx][2] -= 1\n cc[ii[idx][2]] += 1\n cc[1] += 1\n heappush(hh, -ii[idx][2])\n heappush(hh, -1)\n ii[idx][1] = I[i] - 1\n ii[idx:idx + 1] = [ii[idx], [I[i], I[i], 1, C[i]]]\n idx += 1\n else:\n cc[ii[idx][2]] -= 1\n ii[idx:idx + 1] = [\n [ii[idx][0], I[i] - 1, I[i] - ii[idx][0], ii[idx][3]],\n [I[i], I[i], 1, C[i]], \n [I[i] + 1, ii[idx][1], ii[idx][1] - I[i], ii[idx][3]],\n ]\n cc[ii[idx][2]] += 1\n cc[ii[idx + 2][2]] += 1\n cc[1] += 1\n heappush(hh, -ii[idx][2])\n heappush(hh, -ii[idx + 2][2])\n heappush(hh, -1)\n idx += 1\n \n if idx + 1 < len(ii) and ii[idx + 1][3] == C[i]:\n cc[ii[idx][2]] -= 1\n cc[ii[idx + 1][2]] -= 1\n ii[idx + 1][0] = ii[idx][0]\n ii[idx + 1][2] += ii[idx][2]\n ii[idx:idx + 2] = ii[idx + 1:idx + 2]\n cc[ii[idx][2]] += 1\n heappush(hh, -ii[idx][2])\n if idx > 0 and ii[idx - 1][3] == C[i]:\n cc[ii[idx][2]] -= 1\n cc[ii[idx - 1][2]] -= 1\n ii[idx - 1][1] = ii[idx][1]\n ii[idx - 1][2] += ii[idx][2]\n ii[idx - 1:idx + 1] = ii[idx - 1:idx]\n cc[ii[idx - 1][2]] += 1\n heappush(hh, -ii[idx - 1][2])\n \n while hh and not cc[-hh[0]]:\n heappop(hh)\n rr.append(-hh[0])\n return rr\n \n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n``` | 0 | You are given a **0-indexed** string `s`. You are also given a **0-indexed** string `queryCharacters` of length `k` and a **0-indexed** array of integer **indices** `queryIndices` of length `k`, both of which are used to describe `k` queries.
The `ith` query updates the character in `s` at index `queryIndices[i]` to the character `queryCharacters[i]`.
Return _an array_ `lengths` _of length_ `k` _where_ `lengths[i]` _is the **length** of the **longest substring** of_ `s` _consisting of **only one repeating** character **after** the_ `ith` _query_ _is performed._
**Example 1:**
**Input:** s = "babacc ", queryCharacters = "bcb ", queryIndices = \[1,3,3\]
**Output:** \[3,3,4\]
**Explanation:**
- 1st query updates s = "b**b**bacc ". The longest substring consisting of one repeating character is "bbb " with length 3.
- 2nd query updates s = "bbb**c**cc ".
The longest substring consisting of one repeating character can be "bbb " or "ccc " with length 3.
- 3rd query updates s = "bbb**b**cc ". The longest substring consisting of one repeating character is "bbbb " with length 4.
Thus, we return \[3,3,4\].
**Example 2:**
**Input:** s = "abyzz ", queryCharacters = "aa ", queryIndices = \[2,1\]
**Output:** \[2,3\]
**Explanation:**
- 1st query updates s = "ab**a**zz ". The longest substring consisting of one repeating character is "zz " with length 2.
- 2nd query updates s = "a**a**azz ". The longest substring consisting of one repeating character is "aaa " with length 3.
Thus, we return \[2,3\].
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `k == queryCharacters.length == queryIndices.length`
* `1 <= k <= 105`
* `queryCharacters` consists of lowercase English letters.
* `0 <= queryIndices[i] < s.length` | Could you model all the meetings happening at the same time as a graph? What data structure can you use to efficiently share the secret? You can use the union-find data structure to quickly determine who knows the secret and share the secret. |
longest substring with one repeating charecter | longest-substring-of-one-repeating-character | 0 | 1 | # Intuition \n<!-- Describe your first thoughts on how to solve this problem. -->sliding window approach \n\n# Approach\n<!-- Describe your approach to solving the problem. -->can refer to the longest substring with k unique charecter here it can be k=1\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# def longestKSubstr(s,k):\n# i=0\n# j=0\n# maxi=-float(\'inf\')\n# d=dict()\n# while j<len(s):\n# d[s[j]]=1+d.get(s[j],0)\n# if len(d)<k:\n# j+=1\n# elif len(d)==k:\n# maxi=max(maxi,(j-i+1))\n# j+=1\n# elif len(d)>k:\n# while len(d)>k:\n# d[s[i]]-=1\n# if d[s[i]]==0:\n# del d[s[i]]\n# i+=1\n# if len(d)==k:\n# maxi=max(maxi,j-i+1)\n# j+=1\n# return maxi if maxi>0 else -1\n# class Solution:\n# def longestRepeating(self, s: str, queryCharacters: str, queryIndices: List[int]) -> List[int]:\n \n# # # m=list(s)\n# # # q=list(queryCharacters)\n# # res=[]\n# # for i in range(len(queryIndices)):\n# # s=s[:queryIndices[i]] + queryCharacters[i] + s[queryIndices[i]+1:]\n# # res.append(longestKSubstr(s,1))\n# # # m[queryIndices[i]]=q[i]\n# # # res.append(longestKSubstr(\'\'.join(m),1))\n# # return res\n\n# res=[]\n# for i in range(len(queryIndices)):\n# s=s[:queryIndices[i]] + queryCharacters[i] + s[queryIndices[i]+1:]\n# res.append(longestKSubstr(s,1))\n# return res\n\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def longestRepeating(self, s: str, queryCharacters: str, queryIndices: List[int]) -> List[int]:\n sl = SortedList()\n length = SortedList()\n curr = 0\n for char, it in itertools.groupby(s):\n c = sum(1 for _ in it)\n length.add(c)\n sl.add((curr, curr + c, char))\n curr += c\n ans = []\n for char, i in zip(queryCharacters, queryIndices):\n t = (i, math.inf, \'a\')\n index = sl.bisect_right(t) - 1\n to_remove = [sl[index]]\n to_add = []\n left, right, original_char = to_remove[0]\n if original_char != char:\n length.remove(right - left)\n if right - left > 1:\n if i == left:\n left += 1\n to_add.append((left, right, original_char))\n length.add(right - left)\n elif i == right - 1:\n right -= 1\n to_add.append((left, right, original_char))\n length.add(right - left)\n else:\n to_add.append((left, i, original_char))\n length.add(i - left)\n to_add.append((i + 1, right, original_char))\n length.add(right - (i + 1))\n \n l, r = i, i + 1\n if index - 1 >= 0 and sl[index - 1][1:3] == (i, char):\n l, old_r, _ = sl[index - 1]\n to_remove.append(sl[index - 1])\n length.remove(old_r - l)\n if index + 1 < len(sl) and sl[index + 1][0] == i + 1 and sl[index + 1][2] == char:\n old_l, r, old_length = sl[index + 1]\n to_remove.append(sl[index + 1])\n length.remove(r - old_l)\n length.add(r - l)\n sl.add((l, r, char))\n for t in to_remove:\n sl.remove(t)\n sl.update(to_add)\n # print(sl)\n # print(length)\n ans.append(length[-1])\n\n return ans\n\n``` | 0 | You are given a **0-indexed** string `s`. You are also given a **0-indexed** string `queryCharacters` of length `k` and a **0-indexed** array of integer **indices** `queryIndices` of length `k`, both of which are used to describe `k` queries.
The `ith` query updates the character in `s` at index `queryIndices[i]` to the character `queryCharacters[i]`.
Return _an array_ `lengths` _of length_ `k` _where_ `lengths[i]` _is the **length** of the **longest substring** of_ `s` _consisting of **only one repeating** character **after** the_ `ith` _query_ _is performed._
**Example 1:**
**Input:** s = "babacc ", queryCharacters = "bcb ", queryIndices = \[1,3,3\]
**Output:** \[3,3,4\]
**Explanation:**
- 1st query updates s = "b**b**bacc ". The longest substring consisting of one repeating character is "bbb " with length 3.
- 2nd query updates s = "bbb**c**cc ".
The longest substring consisting of one repeating character can be "bbb " or "ccc " with length 3.
- 3rd query updates s = "bbb**b**cc ". The longest substring consisting of one repeating character is "bbbb " with length 4.
Thus, we return \[3,3,4\].
**Example 2:**
**Input:** s = "abyzz ", queryCharacters = "aa ", queryIndices = \[2,1\]
**Output:** \[2,3\]
**Explanation:**
- 1st query updates s = "ab**a**zz ". The longest substring consisting of one repeating character is "zz " with length 2.
- 2nd query updates s = "a**a**azz ". The longest substring consisting of one repeating character is "aaa " with length 3.
Thus, we return \[2,3\].
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `k == queryCharacters.length == queryIndices.length`
* `1 <= k <= 105`
* `queryCharacters` consists of lowercase English letters.
* `0 <= queryIndices[i] < s.length` | Could you model all the meetings happening at the same time as a graph? What data structure can you use to efficiently share the secret? You can use the union-find data structure to quickly determine who knows the secret and share the secret. |
[Python] AC Merge Intervals Explain | SortedContainers | longest-substring-of-one-repeating-character | 0 | 1 | # Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can use segment tree but it didn\'t work for me in python TLE :(\nWe can also think this problem as merging intervals, each interval will represent range of repeated characters.\ninterval - [start,end,character]\nFor each query update these intervals accordingly.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(NlogN)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n# Code\n```\nfrom sortedcontainers import SortedList,SortedDict\nclass Solution:\n def longestRepeating(self, s: str, queryCharacters: str, queryIndices: List[int]) -> List[int]:\n n = len(s)\n lens = SortedDict() # lengths sorted order\n m = SortedList() # contain repeated intervals (start,end,char)\n m.add((-1,-1,\'\')) # handle edge case\n m.add((n,n,\'\'))\n # helper functions\n def add(start,end,c): # add interval \n m.add((start,end,c))\n lens[end-start+1] =lens.get(end-start+1,0) + 1\n def rm(ival): # remove interval\n m.remove(ival)\n ln = ival[1]-ival[0] + 1\n lens[ln] -=1\n if(lens[ln]<=0): del lens[ln]\n # building the m and lens\n i = 0\n while(i<n):\n c = s[i]\n start = i\n while(i<n and s[i]==c): i += 1\n add(start,i-1,c)\n def query(index,nc): # replace character at specific index\n pos = m.bisect_right((index,index,\'\'))\n if(m[pos][0]>index): pos -=1 \n ival = m[pos]\n if(ival[2]==nc): return lens.peekitem()[0]; # no change if same as old character\n prev,nxt = m[pos-1],m[pos+1] # get adjacent interval for possible merge\n cur = [index,index,nc]\n if(ival[0]==index and prev[2]==nc): # try to merge with prev\n cur[0] = prev[0]\n rm(prev)\n if(ival[1]==index and nxt[2]==nc): # merge with next\n cur[1] = nxt[1]\n rm(nxt)\n rm(ival)\n if(cur): add(*cur)\n if(ival[0]<cur[0]): add(ival[0],cur[0]-1,ival[2]) # split left\n if(ival[1]>cur[1]): add(cur[1]+1,ival[1],ival[2]) # split right\n return lens.peekitem()[0]\n return [query(j,queryCharacters[i]) for i,j in enumerate(queryIndices)]\n``` | 0 | You are given a **0-indexed** string `s`. You are also given a **0-indexed** string `queryCharacters` of length `k` and a **0-indexed** array of integer **indices** `queryIndices` of length `k`, both of which are used to describe `k` queries.
The `ith` query updates the character in `s` at index `queryIndices[i]` to the character `queryCharacters[i]`.
Return _an array_ `lengths` _of length_ `k` _where_ `lengths[i]` _is the **length** of the **longest substring** of_ `s` _consisting of **only one repeating** character **after** the_ `ith` _query_ _is performed._
**Example 1:**
**Input:** s = "babacc ", queryCharacters = "bcb ", queryIndices = \[1,3,3\]
**Output:** \[3,3,4\]
**Explanation:**
- 1st query updates s = "b**b**bacc ". The longest substring consisting of one repeating character is "bbb " with length 3.
- 2nd query updates s = "bbb**c**cc ".
The longest substring consisting of one repeating character can be "bbb " or "ccc " with length 3.
- 3rd query updates s = "bbb**b**cc ". The longest substring consisting of one repeating character is "bbbb " with length 4.
Thus, we return \[3,3,4\].
**Example 2:**
**Input:** s = "abyzz ", queryCharacters = "aa ", queryIndices = \[2,1\]
**Output:** \[2,3\]
**Explanation:**
- 1st query updates s = "ab**a**zz ". The longest substring consisting of one repeating character is "zz " with length 2.
- 2nd query updates s = "a**a**azz ". The longest substring consisting of one repeating character is "aaa " with length 3.
Thus, we return \[2,3\].
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `k == queryCharacters.length == queryIndices.length`
* `1 <= k <= 105`
* `queryCharacters` consists of lowercase English letters.
* `0 <= queryIndices[i] < s.length` | Could you model all the meetings happening at the same time as a graph? What data structure can you use to efficiently share the secret? You can use the union-find data structure to quickly determine who knows the secret and share the secret. |
best python sol | longest-substring-of-one-repeating-character | 0 | 1 | \n# Code\n```\n\nfrom sortedcontainers import SortedList\nclass Solution:\n def longestRepeating(self, s: str, qc: str, qi):\n qr = list(zip(list(qc), qi))\n srt = SortedList([])\n mx = SortedList([])\n cr = s[0]\n sz = 1\n start, end = 0, 0\n for i in range(1, len(s)):\n if s[i] == cr:\n sz += 1\n end = i\n else:\n srt.add((start, end, sz, cr))\n mx.add(sz)\n cr = s[i]\n start = i\n end = i\n sz = 1\n srt.add((start, end, sz, cr))\n mx.add(sz)\n s = list(s)\n n = len(s)\n ans = [0] * len(qr)\n for id, (ch, ind) in enumerate(qr):\n if s[ind] == ch:\n ans[id] = mx[-1]\n continue\n s[ind] = ch\n\n ll = srt.bisect_left((ind, n + 1, n + 1, "z")) - 1\n start, end, sz, cho = srt[ll]\n srt.pop(ll)\n # todo start==end\n if start == end:\n\n mx.remove(sz)\n if ind + 1 < n and s[ind + 1] == ch and ind - 1 >= 0 and s[ind - 1] == ch:\n ll = srt.bisect_left((ind + 1, n + 1, n + 1, "z")) - 1\n sr, endr, szr, chr = srt[ll]\n srt.pop(ll)\n mx.remove(szr)\n ll = srt.bisect_left((ind - 1, n + 1, n + 1, "z")) - 1\n sl, endl, szl, chl = srt[ll]\n srt.pop(ll)\n mx.remove(szl)\n mid = (sl, endr, szr+szl+1, ch)\n srt.add(mid)\n mx.add(szr+szl+1)\n elif ind + 1 < n and s[ind + 1] == ch:\n ll = srt.bisect_left((ind + 1, n + 1, n + 1, "z")) - 1\n sr, endr, szr, chr = srt[ll]\n srt.pop(ll)\n right = (ind, endr, szr + 1, chr)\n srt.add(right)\n mx.remove(szr)\n mx.add(szr + 1)\n elif ind - 1 >= 0 and s[ind - 1] == ch:\n ll = srt.bisect_left((ind - 1, n + 1, n + 1, "z")) - 1\n sl, endl, szl, chl = srt[ll]\n srt.pop(ll)\n left = (sl, ind, szl + 1, ch)\n srt.add(left)\n mx.remove(szl)\n mx.add(szl + 1)\n else:\n srt.add((start, end, sz, ch))\n mx.add(sz)\n\n elif ind == end:\n left = (start, end - 1, sz - 1, cho)\n srt.add(left)\n mx.remove(sz)\n mx.add(sz - 1)\n if ind + 1 < n and s[ind + 1] == ch:\n ll = srt.bisect_left((ind + 1, n + 1, n + 1, "z")) - 1\n sr, endr, szr, chr = srt[ll]\n srt.pop(ll)\n right = (ind, endr, szr + 1, chr)\n srt.add(right)\n mx.remove(szr)\n mx.add(szr + 1)\n else:\n right = (ind, ind, 1, ch)\n srt.add(right)\n mx.add(1)\n elif ind == start:\n right = (start + 1, end, sz - 1, cho)\n srt.add(right)\n mx.remove(sz)\n mx.add(sz-1)\n if ind - 1 >= 0 and s[ind - 1] == ch:\n ll = srt.bisect_left((ind - 1, n + 1, n + 1, "z")) - 1\n sl, endl, szl, chl = srt[ll]\n srt.pop(ll)\n left = (sl, ind, szl + 1, ch)\n mx.remove(szl)\n srt.add(left)\n mx.add(szl + 1)\n else:\n left = (ind, ind, 1, ch)\n srt.add(left)\n mx.add(1)\n else:\n left = (start, ind - 1, ((ind - 1)-start + 1), cho)\n mid = (ind, ind, 1, ch)\n right = (ind + 1, end, (end - (ind + 1) +1), cho)\n srt.add(left)\n srt.add(right)\n srt.add(mid)\n mx.remove(sz)\n mx.add(left[2])\n mx.add(right[2])\n mx.add(1)\n\n ans[id] = mx[-1]\n return ans\n\n``` | 0 | You are given a **0-indexed** string `s`. You are also given a **0-indexed** string `queryCharacters` of length `k` and a **0-indexed** array of integer **indices** `queryIndices` of length `k`, both of which are used to describe `k` queries.
The `ith` query updates the character in `s` at index `queryIndices[i]` to the character `queryCharacters[i]`.
Return _an array_ `lengths` _of length_ `k` _where_ `lengths[i]` _is the **length** of the **longest substring** of_ `s` _consisting of **only one repeating** character **after** the_ `ith` _query_ _is performed._
**Example 1:**
**Input:** s = "babacc ", queryCharacters = "bcb ", queryIndices = \[1,3,3\]
**Output:** \[3,3,4\]
**Explanation:**
- 1st query updates s = "b**b**bacc ". The longest substring consisting of one repeating character is "bbb " with length 3.
- 2nd query updates s = "bbb**c**cc ".
The longest substring consisting of one repeating character can be "bbb " or "ccc " with length 3.
- 3rd query updates s = "bbb**b**cc ". The longest substring consisting of one repeating character is "bbbb " with length 4.
Thus, we return \[3,3,4\].
**Example 2:**
**Input:** s = "abyzz ", queryCharacters = "aa ", queryIndices = \[2,1\]
**Output:** \[2,3\]
**Explanation:**
- 1st query updates s = "ab**a**zz ". The longest substring consisting of one repeating character is "zz " with length 2.
- 2nd query updates s = "a**a**azz ". The longest substring consisting of one repeating character is "aaa " with length 3.
Thus, we return \[2,3\].
**Constraints:**
* `1 <= s.length <= 105`
* `s` consists of lowercase English letters.
* `k == queryCharacters.length == queryIndices.length`
* `1 <= k <= 105`
* `queryCharacters` consists of lowercase English letters.
* `0 <= queryIndices[i] < s.length` | Could you model all the meetings happening at the same time as a graph? What data structure can you use to efficiently share the secret? You can use the union-find data structure to quickly determine who knows the secret and share the secret. |
Superb Questions--->Python3 | find-the-difference-of-two-arrays | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findDifference(self, nums1: List[int], nums2: List[int]) -> List[List[int]]:\n list1,list2,list3=[],[],[]\n for i in nums1:\n if i in nums2:\n continue\n else:\n list2.append(i)\n for j in nums2:\n if j in nums1:\n continue\n else:\n list3.append(j)\n list1.append(list(set(list2)))\n list1.append(list(set(list3)))\n return list1\n```\n```\nclass Solution:\n def findDifference(self, nums1: List[int], nums2: List[int]) -> List[List[int]]:\n m,n=set(nums1),set(nums2)\n return [list(m-n),list(n-m)]\n\n``` | 4 | Given two **0-indexed** integer arrays `nums1` and `nums2`, return _a list_ `answer` _of size_ `2` _where:_
* `answer[0]` _is a list of all **distinct** integers in_ `nums1` _which are **not** present in_ `nums2`_._
* `answer[1]` _is a list of all **distinct** integers in_ `nums2` _which are **not** present in_ `nums1`.
**Note** that the integers in the lists may be returned in **any** order.
**Example 1:**
**Input:** nums1 = \[1,2,3\], nums2 = \[2,4,6\]
**Output:** \[\[1,3\],\[4,6\]\]
**Explanation:**
For nums1, nums1\[1\] = 2 is present at index 0 of nums2, whereas nums1\[0\] = 1 and nums1\[2\] = 3 are not present in nums2. Therefore, answer\[0\] = \[1,3\].
For nums2, nums2\[0\] = 2 is present at index 1 of nums1, whereas nums2\[1\] = 4 and nums2\[2\] = 6 are not present in nums2. Therefore, answer\[1\] = \[4,6\].
**Example 2:**
**Input:** nums1 = \[1,2,3,3\], nums2 = \[1,1,2,2\]
**Output:** \[\[3\],\[\]\]
**Explanation:**
For nums1, nums1\[2\] and nums1\[3\] are not present in nums2. Since nums1\[2\] == nums1\[3\], their value is only included once and answer\[0\] = \[3\].
Every integer in nums2 is present in nums1. Therefore, answer\[1\] = \[\].
**Constraints:**
* `1 <= nums1.length, nums2.length <= 1000`
* `-1000 <= nums1[i], nums2[i] <= 1000` | The range of possible answers includes all even numbers between 100 and 999 inclusive. Could you check each possible answer to see if it could be formed from the digits in the array? |
Python | Greedy | minimum-deletions-to-make-array-beautiful | 0 | 1 | ```\nclass Solution:\n def minDeletion(self, nums: List[int]) -> int:\n # Greedy !\n # we first only consider requirement 2: nums[i] != nums[i + 1] for all i % 2 == 0\n # at the begining, we consider the num on the even index\n # when we delete a num, we need consider the num on the odd index\n # then repeat this process\n # at the end we check the requirement 1: nums.length is even or not\n \n n = len(nums)\n count = 0\n # flag is true then check the even index\n # flag is false then check the odd index\n flag = True\n \n for i in range(n):\n # check the even index\n if flag:\n if i % 2 == 0 and i != n -1 and nums[i] == nums[i + 1]:\n count += 1\n flag = False\n # check the odd index\n elif not flag:\n if i % 2 == 1 and i != n -1 and nums[i] == nums[i + 1]:\n count += 1\n flag = True\n \n curLength = n - count\n \n return count if curLength % 2 == 0 else count + 1 | 15 | You are given a **0-indexed** integer array `nums`. The array `nums` is **beautiful** if:
* `nums.length` is even.
* `nums[i] != nums[i + 1]` for all `i % 2 == 0`.
Note that an empty array is considered beautiful.
You can delete any number of elements from `nums`. When you delete an element, all the elements to the right of the deleted element will be **shifted one unit to the left** to fill the gap created and all the elements to the left of the deleted element will remain **unchanged**.
Return _the **minimum** number of elements to delete from_ `nums` _to make it_ _beautiful._
**Example 1:**
**Input:** nums = \[1,1,2,3,5\]
**Output:** 1
**Explanation:** You can delete either `nums[0]` or `nums[1]` to make `nums` = \[1,2,3,5\] which is beautiful. It can be proven you need at least 1 deletion to make `nums` beautiful.
**Example 2:**
**Input:** nums = \[1,1,2,2,3,3\]
**Output:** 2
**Explanation:** You can delete `nums[0]` and `nums[5]` to make nums = \[1,2,2,3\] which is beautiful. It can be proven you need at least 2 deletions to make nums beautiful.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | If a point with a speed s moves n units in a given time, a point with speed 2 * s will move 2 * n units at the same time. Can you use this to find the middle node of a linked list? If you are given the middle node, the node before it, and the node after it, how can you modify the linked list? |
Python Simple Solution O(n) Time and O(1) Space | minimum-deletions-to-make-array-beautiful | 0 | 1 | We iterate over nums from left to right and **greedily choose elements** which satisfy the given condition in our final array. While iterating, we need to **keep a count** of how many elements we have chosen so far to make greedy choices.\n\n### Idea:\n1. Iterate from left to right uptil second last element:\n 1.1 If `count` is even and current element is same as next one, we delete it.\n 1.2 Otherise we take that element and increase `count`.\n2. Take the last element as it is and increment `count`.\n3. If our final `count` is odd, delete the last element as well.\n\n**Time Complexity:** *O(n)*\n**Space Complexity:** *O(1)*\n\n```\nclass Solution:\n def minDeletion(self, nums: List[int]) -> int:\n n = len(nums)\n dels = cnt = 0\n\n for i in range(n - 1):\n if (cnt % 2) == 0 and (nums[i] == nums[i + 1]):\n dels += 1\n else:\n cnt += 1\n \n cnt += 1 # Take the last element as it is.\n dels += cnt & 1 # If final count is odd, delete last element.\n return dels\n```\n\n***Do upvote if you like the solution. Have a nice day!***\n\n\n | 9 | You are given a **0-indexed** integer array `nums`. The array `nums` is **beautiful** if:
* `nums.length` is even.
* `nums[i] != nums[i + 1]` for all `i % 2 == 0`.
Note that an empty array is considered beautiful.
You can delete any number of elements from `nums`. When you delete an element, all the elements to the right of the deleted element will be **shifted one unit to the left** to fill the gap created and all the elements to the left of the deleted element will remain **unchanged**.
Return _the **minimum** number of elements to delete from_ `nums` _to make it_ _beautiful._
**Example 1:**
**Input:** nums = \[1,1,2,3,5\]
**Output:** 1
**Explanation:** You can delete either `nums[0]` or `nums[1]` to make `nums` = \[1,2,3,5\] which is beautiful. It can be proven you need at least 1 deletion to make `nums` beautiful.
**Example 2:**
**Input:** nums = \[1,1,2,2,3,3\]
**Output:** 2
**Explanation:** You can delete `nums[0]` and `nums[5]` to make nums = \[1,2,2,3\] which is beautiful. It can be proven you need at least 2 deletions to make nums beautiful.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | If a point with a speed s moves n units in a given time, a point with speed 2 * s will move 2 * n units at the same time. Can you use this to find the middle node of a linked list? If you are given the middle node, the node before it, and the node after it, how can you modify the linked list? |
[Python 3] Two Pointer Greedy Solution | minimum-deletions-to-make-array-beautiful | 0 | 1 | **Approach**:\nInitialise steps to 0.\nUse two pointers, one to iterate through the array and other to keep track of the index in the updated list after removing (as the indices will change because of shifting).\n\nIf the index is not divisible by 2, then increment the index by 1. Otherwise, taking care of an edge case of i=len(nums)-1 and if the element is equal to the next element, then increment steps by 1 and keep the index the same (as this element would be deleted), otherwise, increment the index by 1.\n\nIn the end, if the len of the updated list (index) is divisible by 2, then return steps, otherwise, we would need to delete another element and hence return steps+1.\n\n**Time Complexity**: O(n) - we iterate the list once\n**Space Complexity**: O(1) \n\n**DO UPVOTE IF YOU FOUND IT HELPFUL.**\n\n**Code**:\n```\nclass Solution:\n def minDeletion(self, nums: List[int]) -> int:\n i = index = steps = 0\n while i < len(nums):\n if index%2 != 0:\n index += 1\n else:\n if i == len(nums)-1:\n index += 1\n break\n if nums[i] == nums[i+1]:\n steps += 1\n else:\n index += 1\n i += 1\n \n return steps if index%2 == 0 else steps+1\n``` | 2 | You are given a **0-indexed** integer array `nums`. The array `nums` is **beautiful** if:
* `nums.length` is even.
* `nums[i] != nums[i + 1]` for all `i % 2 == 0`.
Note that an empty array is considered beautiful.
You can delete any number of elements from `nums`. When you delete an element, all the elements to the right of the deleted element will be **shifted one unit to the left** to fill the gap created and all the elements to the left of the deleted element will remain **unchanged**.
Return _the **minimum** number of elements to delete from_ `nums` _to make it_ _beautiful._
**Example 1:**
**Input:** nums = \[1,1,2,3,5\]
**Output:** 1
**Explanation:** You can delete either `nums[0]` or `nums[1]` to make `nums` = \[1,2,3,5\] which is beautiful. It can be proven you need at least 1 deletion to make `nums` beautiful.
**Example 2:**
**Input:** nums = \[1,1,2,2,3,3\]
**Output:** 2
**Explanation:** You can delete `nums[0]` and `nums[5]` to make nums = \[1,2,2,3\] which is beautiful. It can be proven you need at least 2 deletions to make nums beautiful.
**Constraints:**
* `1 <= nums.length <= 105`
* `0 <= nums[i] <= 105` | If a point with a speed s moves n units in a given time, a point with speed 2 * s will move 2 * n units at the same time. Can you use this to find the middle node of a linked list? If you are given the middle node, the node before it, and the node after it, how can you modify the linked list? |
Python simple solution beats 100.00% | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n res=[]\n ln=ceil(intLength/2)\n odd=intLength%2==1\n base=10**(ln-1)\n def getLalindrome(k:int)->int:\n val=str(k-1+base)\n if len(val)>ln:\n return -1\n return int(val+val[-2::-1]) if odd else int(val+val[::-1])\n for q in queries:\n res.append(getLalindrome(q)) \n return res \n``` | 1 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
Python simple solution beats 100.00% | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n res=[]\n ln=ceil(intLength/2)\n odd=intLength%2==1\n base=10**(ln-1)\n def getLalindrome(k:int)->int:\n val=str(k-1+base)\n if len(val)>ln:\n return -1\n return int(val+val[-2::-1]) if odd else int(val+val[::-1])\n for q in queries:\n res.append(getLalindrome(q)) \n return res \n``` | 1 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python | simple and straightforward | find-palindrome-with-fixed-length | 0 | 1 | ```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n # think the palindromes in half\n # e.g. len = 4 we only consider the first 2 digits\n # half: 10, 11, 12, 13, 14, ..., 19, 20, \n # full: 1001, 1111, 1221, 1331, ...\n # e.g. len = 5 we consider the first 3 digits\n # half: 100, 101, 102, ...\n # full: 10001, 10101, 10201, ...\n \n result = []\n \n for i in queries:\n result.append(self.generatePalindrome(intLength, i))\n \n return result\n \n def generatePalindrome(self, length, num):\n # index start from 0\n\t\t# e.g. num =1 means we want to find the most smallest palindrome, then its index is 0\n\t\t# e.g. num =2 means we want to find the second most smallest palindrome, then its index is 1\n index = num -1\n \n\t\t# if the length is even\n\t\t# we only think about the fisrt half of digits\n if length % 2 == 0:\n cur = int(\'1\' + \'0\' * (length // 2 -1))\n maxLength = len(str(cur))\n cur += index\n \n if len(str(cur)) > maxLength:\n return -1\n \n else:\n cur = str(cur)\n cur = cur + cur[::-1]\n cur = int(cur)\n return cur\n\t\t\t\t\n # if the length is odd\n\t\t# we consider first (length // 2 + 1) digits\n else:\n cur = int(\'1\' + \'0\' * (length // 2))\n maxLength = len(str(cur))\n cur += index\n \n if len(str(cur)) > maxLength:\n return -1\n \n else:\n cur = str(cur)\n temp = str(cur)[:-1]\n cur = cur + temp[::-1]\n cur = int(cur)\n return cur | 7 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
Python | simple and straightforward | find-palindrome-with-fixed-length | 0 | 1 | ```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n # think the palindromes in half\n # e.g. len = 4 we only consider the first 2 digits\n # half: 10, 11, 12, 13, 14, ..., 19, 20, \n # full: 1001, 1111, 1221, 1331, ...\n # e.g. len = 5 we consider the first 3 digits\n # half: 100, 101, 102, ...\n # full: 10001, 10101, 10201, ...\n \n result = []\n \n for i in queries:\n result.append(self.generatePalindrome(intLength, i))\n \n return result\n \n def generatePalindrome(self, length, num):\n # index start from 0\n\t\t# e.g. num =1 means we want to find the most smallest palindrome, then its index is 0\n\t\t# e.g. num =2 means we want to find the second most smallest palindrome, then its index is 1\n index = num -1\n \n\t\t# if the length is even\n\t\t# we only think about the fisrt half of digits\n if length % 2 == 0:\n cur = int(\'1\' + \'0\' * (length // 2 -1))\n maxLength = len(str(cur))\n cur += index\n \n if len(str(cur)) > maxLength:\n return -1\n \n else:\n cur = str(cur)\n cur = cur + cur[::-1]\n cur = int(cur)\n return cur\n\t\t\t\t\n # if the length is odd\n\t\t# we consider first (length // 2 + 1) digits\n else:\n cur = int(\'1\' + \'0\' * (length // 2))\n maxLength = len(str(cur))\n cur += index\n \n if len(str(cur)) > maxLength:\n return -1\n \n else:\n cur = str(cur)\n temp = str(cur)[:-1]\n cur = cur + temp[::-1]\n cur = int(cur)\n return cur | 7 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
[Python3] Math solution with explanation | find-palindrome-with-fixed-length | 0 | 1 | Taking into account the palindrome property, we want to work with only half of the digits, and get the rest as the same half, but in reverse order. For this purpose, we have a **helper** function, in which for even numbers the order of the left side is changed to receive the right part, and for odd numbers the last digit is removed and the order is also changed.\nAlso, we want to precompute the number of palindromes for a given length **intLength** to avoid the case where the ordinal exceeds the possible number of palindromes.\nRuntime leaves a lot to be desired, but hopefully the explanations will be helpful.\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n ans = []\n limit = [10, 19]\n\n for i in range(3, intLength + 1):\n limit.append(limit[-1] + 9 * (10 ** int((i - 1) / 2)))\n \n def helper(num):\n left = str(num)\n \n if intLength % 2 == 0:\n right = str(num)[::-1]\n else:\n right = str(num)[:-1][::-1]\n \n return int(left + right)\n\t\t \n if intLength % 2 == 0:\n digits = intLength // 2 - 1\n else:\n digits = intLength // 2\n\t\t\n for i in queries:\n if i <= limit[intLength - 1]:\n half = 10 ** digits + i - 1\n tmp = helper(half)\n \n if len(str(tmp)) <= intLength:\n ans.append(tmp)\n else:\n ans.append(-1)\n else:\n ans.append(-1)\n \n return ans\n```\n\n | 3 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
[Python3] Math solution with explanation | find-palindrome-with-fixed-length | 0 | 1 | Taking into account the palindrome property, we want to work with only half of the digits, and get the rest as the same half, but in reverse order. For this purpose, we have a **helper** function, in which for even numbers the order of the left side is changed to receive the right part, and for odd numbers the last digit is removed and the order is also changed.\nAlso, we want to precompute the number of palindromes for a given length **intLength** to avoid the case where the ordinal exceeds the possible number of palindromes.\nRuntime leaves a lot to be desired, but hopefully the explanations will be helpful.\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n ans = []\n limit = [10, 19]\n\n for i in range(3, intLength + 1):\n limit.append(limit[-1] + 9 * (10 ** int((i - 1) / 2)))\n \n def helper(num):\n left = str(num)\n \n if intLength % 2 == 0:\n right = str(num)[::-1]\n else:\n right = str(num)[:-1][::-1]\n \n return int(left + right)\n\t\t \n if intLength % 2 == 0:\n digits = intLength // 2 - 1\n else:\n digits = intLength // 2\n\t\t\n for i in queries:\n if i <= limit[intLength - 1]:\n half = 10 ** digits + i - 1\n tmp = helper(half)\n \n if len(str(tmp)) <= intLength:\n ans.append(tmp)\n else:\n ans.append(-1)\n else:\n ans.append(-1)\n \n return ans\n```\n\n | 3 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Simple Solution python | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N*intLength)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(N*intLength)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n@cache for duplicated queries if any\n\n# Code\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n \n @cache\n def get(count, length):\n mid = ceil(length / 2) - 1\n\n if count > 10**(mid+1) - 10**mid - 1:\n return -1\n\n arr = [0] * length\n arr[0] = 1\n arr[-1] = 1\n\n\n for i in range(mid, -1, -1):\n arr[i] += count % 10\n arr[length - 1 - i] = arr[i]\n count //= 10\n \n res = 0\n for e in arr:\n res = 10*res + e\n return res\n\n res = [0] * len(queries)\n for i, query in enumerate(queries):\n res[i] = get(query - 1, intLength)\n \n return res\n\n``` | 0 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
Simple Solution python | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N*intLength)\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n\n- Space complexity: O(N*intLength)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n@cache for duplicated queries if any\n\n# Code\n```\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n \n @cache\n def get(count, length):\n mid = ceil(length / 2) - 1\n\n if count > 10**(mid+1) - 10**mid - 1:\n return -1\n\n arr = [0] * length\n arr[0] = 1\n arr[-1] = 1\n\n\n for i in range(mid, -1, -1):\n arr[i] += count % 10\n arr[length - 1 - i] = arr[i]\n count //= 10\n \n res = 0\n for e in arr:\n res = 10*res + e\n return res\n\n res = [0] * len(queries)\n for i, query in enumerate(queries):\n res[i] = get(query - 1, intLength)\n \n return res\n\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Python | Straightforward Solution | Half Palin | find-palindrome-with-fixed-length | 0 | 1 | # Code\n```\nfrom math import log10\nfrom bisect import bisect_left\n\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n # num of palindrome with intLength\n # k = (intLength + 1) // 2\n # total cnt of palindrome with intLength = 9 * 10 ** (k - 1)\n ans = []\n k = (intLength + 1) // 2\n n = 9 * 10 ** (k - 1) # total count\n base = 10 ** (k - 1)\n for query in queries:\n if query > n:\n ans.append(-1)\n else:\n half = str(base + query - 1)\n ans.append(int(half + half[:intLength//2][::-1]))\n return ans\n\n``` | 0 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
Python | Straightforward Solution | Half Palin | find-palindrome-with-fixed-length | 0 | 1 | # Code\n```\nfrom math import log10\nfrom bisect import bisect_left\n\nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n # num of palindrome with intLength\n # k = (intLength + 1) // 2\n # total cnt of palindrome with intLength = 9 * 10 ** (k - 1)\n ans = []\n k = (intLength + 1) // 2\n n = 9 * 10 ** (k - 1) # total count\n base = 10 ** (k - 1)\n for query in queries:\n if query > n:\n ans.append(-1)\n else:\n half = str(base + query - 1)\n ans.append(int(half + half[:intLength//2][::-1]))\n return ans\n\n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
Math way: construct the prefix half | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\nConstruct the prefix half of Palindrome in increasing order. \n\n# Approach\nGiven the half-palindrome\'s lenght = k, so number must no less than \n10**(k-1). The index=1 should 10**k-1. Distinct half-paalindrome will contribute to one paalindrome in incresing order. \n\nExample: \nintLength =4, half-length = 2 \nthe first element: [10] --> [10001]\nthe second element: [11] ---> [1111]\nthe third element: [12] --> [1221]\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import ceil \nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n\n ln = ceil(intLength/2) \n odd =intLength%2==1\n base = 10**(ln-1)\n\n def get_palindrome(query: int):\n val = str(query-1+base)\n if len(val) > ln:\n return -1 \n\n if odd:\n return int(val+val[-2::-1])\n else:\n return int(val+val[::-1])\n \n return [\n get_palindrome(query)\n for query in queries\n ]\n\n \n``` | 0 | Given an integer array `queries` and a **positive** integer `intLength`, return _an array_ `answer` _where_ `answer[i]` _is either the_ `queries[i]th` _smallest **positive palindrome** of length_ `intLength` _or_ `-1` _if no such palindrome exists_.
A **palindrome** is a number that reads the same backwards and forwards. Palindromes cannot have leading zeros.
**Example 1:**
**Input:** queries = \[1,2,3,4,5,90\], intLength = 3
**Output:** \[101,111,121,131,141,999\]
**Explanation:**
The first few palindromes of length 3 are:
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, ...
The 90th palindrome of length 3 is 999.
**Example 2:**
**Input:** queries = \[2,4,6\], intLength = 4
**Output:** \[1111,1331,1551\]
**Explanation:**
The first six palindromes of length 4 are:
1001, 1111, 1221, 1331, 1441, and 1551.
**Constraints:**
* `1 <= queries.length <= 5 * 104`
* `1 <= queries[i] <= 109`
* `1 <= intLength <= 15` | The shortest path between any two nodes in a tree must pass through their Lowest Common Ancestor (LCA). The path will travel upwards from node s to the LCA and then downwards from the LCA to node t. Find the path strings from root → s, and root → t. Can you use these two strings to prepare the final answer? Remove the longest common prefix of the two path strings to get the path LCA → s, and LCA → t. Each step in the path of LCA → s should be reversed as 'U'. |
Math way: construct the prefix half | find-palindrome-with-fixed-length | 0 | 1 | # Intuition\nConstruct the prefix half of Palindrome in increasing order. \n\n# Approach\nGiven the half-palindrome\'s lenght = k, so number must no less than \n10**(k-1). The index=1 should 10**k-1. Distinct half-paalindrome will contribute to one paalindrome in incresing order. \n\nExample: \nintLength =4, half-length = 2 \nthe first element: [10] --> [10001]\nthe second element: [11] ---> [1111]\nthe third element: [12] --> [1221]\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import ceil \nclass Solution:\n def kthPalindrome(self, queries: List[int], intLength: int) -> List[int]:\n\n ln = ceil(intLength/2) \n odd =intLength%2==1\n base = 10**(ln-1)\n\n def get_palindrome(query: int):\n val = str(query-1+base)\n if len(val) > ln:\n return -1 \n\n if odd:\n return int(val+val[-2::-1])\n else:\n return int(val+val[::-1])\n \n return [\n get_palindrome(query)\n for query in queries\n ]\n\n \n``` | 0 | You have a **1-indexed** binary string of length `n` where all the bits are `0` initially. We will flip all the bits of this binary string (i.e., change them from `0` to `1`) one by one. You are given a **1-indexed** integer array `flips` where `flips[i]` indicates that the bit at index `i` will be flipped in the `ith` step.
A binary string is **prefix-aligned** if, after the `ith` step, all the bits in the **inclusive** range `[1, i]` are ones and all the other bits are zeros.
Return _the number of times the binary string is **prefix-aligned** during the flipping process_.
**Example 1:**
**Input:** flips = \[3,2,4,1,5\]
**Output:** 2
**Explanation:** The binary string is initially "00000 ".
After applying step 1: The string becomes "00100 ", which is not prefix-aligned.
After applying step 2: The string becomes "01100 ", which is not prefix-aligned.
After applying step 3: The string becomes "01110 ", which is not prefix-aligned.
After applying step 4: The string becomes "11110 ", which is prefix-aligned.
After applying step 5: The string becomes "11111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 2 times, so we return 2.
**Example 2:**
**Input:** flips = \[4,1,2,3\]
**Output:** 1
**Explanation:** The binary string is initially "0000 ".
After applying step 1: The string becomes "0001 ", which is not prefix-aligned.
After applying step 2: The string becomes "1001 ", which is not prefix-aligned.
After applying step 3: The string becomes "1101 ", which is not prefix-aligned.
After applying step 4: The string becomes "1111 ", which is prefix-aligned.
We can see that the string was prefix-aligned 1 time, so we return 1.
**Constraints:**
* `n == flips.length`
* `1 <= n <= 5 * 104`
* `flips` is a permutation of the integers in the range `[1, n]`. | For any value of queries[i] and intLength, how can you check if there exists at least queries[i] palindromes of length intLength? Since a palindrome reads the same forwards and backwards, consider how you can efficiently find the first half (ceil(intLength/2) digits) of the palindrome. |
python3 Solution | maximum-value-of-k-coins-from-piles | 0 | 1 | \n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @functools.lru_cache(None)\n def dp(i,K):\n if k==0 or i==len(piles):\n return 0\n\n res,cur=dp(i+1,K),0\n\n for j in range(min(len(piles[i]),K)):\n cur+=piles[i][j]\n res=max(res,cur+dp(i+1,K-j-1))\n\n return res\n\n\n return dp(0,k) \n``` | 4 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
Python 3 || 9 lines, recursion || T/M: 91% / 33% | maximum-value-of-k-coins-from-piles | 0 | 1 | ```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @lru_cache(None)\n def dfs(coins, moves):\n if len(piles) == coins: return 0\n\n ans, curr, pile = dfs(coins+1, moves), 0, piles[coins]\n\n for j in range(min(len(pile), moves)):\n curr += pile[j]\n ans = max(ans, curr + dfs(coins+1, moves-j-1))\n\n return ans\n \n return dfs(0,k)\n```\n[https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/submissions/934256020/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*^2). | 3 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
Python 3 || 9 lines, recursion || T/M: 91% / 33% | maximum-value-of-k-coins-from-piles | 0 | 1 | ```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @lru_cache(None)\n def dfs(coins, moves):\n if len(piles) == coins: return 0\n\n ans, curr, pile = dfs(coins+1, moves), 0, piles[coins]\n\n for j in range(min(len(pile), moves)):\n curr += pile[j]\n ans = max(ans, curr + dfs(coins+1, moves-j-1))\n\n return ans\n \n return dfs(0,k)\n```\n[https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/submissions/934247436/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*^2) and space complexity is *O*(*N*^2). | 3 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
prefix sum + 2d DP | maximum-value-of-k-coins-from-piles | 0 | 1 | # Intuition\nUse DP and prefix sum\n\n# Approach\nFirst for each pile, build a prefix sum (aka cummulative sum) up to k elements (we can just trim/ignore if there is more).\n\nThen focus on the first pile.\nWe can take first coin, or two, or ... k and then deal with smaller problem (one less pile and same or less coins to consider).\n\nSo the base cases are:\n- we have considered all piles\n- we have no more coins to take\n\nIn the meoized helper DP function, we take two parameters:\n`start_pile` - index of the pile we focus on (and later deal only with piles with bigger index)\n`hp` - the helper version of k, that is remaining coins we need to consider\n\nOn the helper function we looking for the maximum,\nconsidering taking from the start_pile 0 up to hk coins and remaining coins from the next piles recursively.\n\nHaving such helper function, the answer will be found by `helper(start_pile=0, hk=k)`\n\nIf you find it helpful please up-vote. Thank you!\n\n# Complexity\n- Time complexity: $$O(n\\times k)$$ I think...\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n\\times k)$$ I think...\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n n = len(piles)\n\n # Turn each pile to cummulative sum trimmed to k elements\n for pi in range(n):\n piles[pi] = list(accumulate(piles[pi][:k]))\n \n @cache\n def helper(start_pile: int, hk: int):\n if start_pile >= n or hk == 0:\n return 0\n # Consider we don\'t take anything from start_pile\n ans = helper(start_pile + 1, hk)\n for i, v in enumerate(piles[start_pile], start=1):\n # Consider we take first i coins from start_pile\n ans = max(ans, v + helper(start_pile + 1, hk - i))\n if i == hk:\n break\n return ans\n \n return helper(0, k)``` | 2 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
PYTHON || easy solution with explanation || recursion with caching | maximum-value-of-k-coins-from-piles | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ndynamic programming problem \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- we first skip all nodes to start from last assume i have 4 piles (try last piles , then try 3rd and last pile , etc)\n- with base case if i ==n or k ==0 return 0\n- in for loop i try all possible coins in cur pile to last pile in limit with k\n- cur_val save the value of cur try , ans res save max res of all tries \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n# Code\n```\nclass Solution(object):\n def maxValueOfCoins(self, piles, k):\n """\n :type piles: List[List[int]]\n :type k: int\n :rtype: int\n """\n cache ={}\n def dfs(i,k ):\n if (i,k) in cache:\n return cache[(i,k)]\n if k==0 or i == len(piles):\n return 0\n # skip piles until reach end , then try all possible from last to first \n dfs(i+1 , k) \n res , cur_val = dfs(i+1 , k),0\n for j in range(min(k , len(piles[i]))):\n cur_val += piles[i][j]\n # print(cur_val ,res )\n res = max(res , cur_val + dfs(i+1 , k-j-1))\n cache[(i,k)]=res\n return cache[(i,k)]\n return dfs(0,k)\n\n``` | 2 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
Easy python solution | maximum-value-of-k-coins-from-piles | 0 | 1 | ```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n presum = [list(accumulate(p, initial=0)) for p in piles]\n n = len(piles)\n dp = [[0] * (k + 1) for _ in range(n + 1)]\n for i, s in enumerate(presum, 1):\n for j in range(k + 1):\n for idx, v in enumerate(s):\n if j >= idx:\n dp[i][j] = max(dp[i][j], dp[i - 1][j - idx] + v)\n return dp[-1][-1]\n \n``` | 1 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
No-brainer DFS solution with cache | maximum-value-of-k-coins-from-piles | 0 | 1 | # Intuition\nIntuition 1: for pile i, I can pick l = 0, 1, ..., min(k, len(pile[i])) coins from pile i;\nIntuition 2: when I pick l coins on pile i, I then can pick k-l coins from i+1 to N-1 piles.\n \n# Approach\nSolve a subproblem: Find the maximum total value if we are picking from ith pile upto (N-1)th pile for a total of k coins.\n\n# Complexity\n- Time complexity:\n$$O(Nmk)$$ - N is the length of piles, m is the number of coins in each pile.\n\n- Space complexity:\n$$O(Nk)$$ - N is the length of piles.\n\n# Code\n```python\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n """\n Intuition 1: for pile i, I can pick l = 0, 1, ..., min(k, len(pile[i])) coins from pile i;\n Intuition 2: when I pick l coins on pile i, from i+1 to N-1 piles, I then can k-l coins.\n Subproblem: Find the maximum total value if we pick from i-th pile and up for a total of k coins.\n """\n @cache\n def solve(i: int, k: int) -> int:\n # end of piles or no more room for any coin\n if i == len(piles) or k == 0:\n return 0\n\n # don\'t pick this pile\n res = solve(i+1, k)\n cur_total = 0\n\n # If we pick this pile, try all possible number of coins that we can pick, e.g. 1, 2, ..., or\n # up to k or the total number of coins in piles[i] whenever which one comes first.\n for l in range(min(k, len(piles[i]))):\n cur_total += piles[i][l]\n\n # once I pick l+1 coins in i-th pile, then solve the subproblem\n # for (i+1)th and onward piles, with k-l-1 room left to fill.\n res = max(res, cur_total + solve(i+1, k-l-1))\n\n return res\n\n return solve(0,k)\n``` | 1 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
python 3 - top-down DP | maximum-value-of-k-coins-from-piles | 0 | 1 | # Intuition\nFrom the question, you need to exhaust the possibilities of:\n1.picking certain number of coin from a pile\n2.loop the remaining piles with k_remain\n\nThese are the 2 state variables.\n\nFrom eg.2, you know you can\'t do greedy. Previous choice affect future choice. So DP is the only solution.\n\n# Approach\ntop-down DP\n\n# Complexity\n- Time complexity:\nO(nk) -> need to do all state variables combination\n\n- Space complexity:\nO(nk) -> cache size\n\n# Code\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n\n import collections\n ind2sumdict = collections.defaultdict(collections.defaultdict) # ind: {coin token: sum}\n\n for i in range(len(piles)):\n ind2sumdict[i][0] = 0\n end = min(k, len(piles[i]))\n total = 0\n for j in range(end):\n total += piles[i][j]\n ind2sumdict[i][j+1] = total\n \n @lru_cache(None)\n def dp(i, k_remain):\n if k_remain == 0 or i == len(piles): # can\'t take / exceed piles len\n return 0\n end = min(len(ind2sumdict[i]) - 1, k_remain)\n ans = 0\n for take_coin in range(end+1):\n ans = max(ans, ind2sumdict[i][take_coin] + dp(i+1, k_remain - take_coin))\n return ans\n\n return dp(0, k)\n \n``` | 1 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
Bottom-Up DP Python | maximum-value-of-k-coins-from-piles | 0 | 1 | \n\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n n = len(piles)\n dp = [[0 for _ in range(k + 1)] for _ in range(n + 1)]\n for i in range(1, n + 1):\n for coins in range(0, k + 1):\n currSum = 0\n for currCoins in range(0, min(len(piles[i - 1]), coins) + 1):\n if currCoins > 0:\n currSum += piles[i - 1][currCoins - 1]\n dp[i][coins] = max(dp[i][coins], dp[i - 1][coins - currCoins] + currSum)\n return dp[n][k]\n``` | 1 | There are `n` **piles** of coins on a table. Each pile consists of a **positive number** of coins of assorted denominations.
In one move, you can choose any coin on **top** of any pile, remove it, and add it to your wallet.
Given a list `piles`, where `piles[i]` is a list of integers denoting the composition of the `ith` pile from **top to bottom**, and a positive integer `k`, return _the **maximum total value** of coins you can have in your wallet if you choose **exactly**_ `k` _coins optimally_.
**Example 1:**
**Input:** piles = \[\[1,100,3\],\[7,8,9\]\], k = 2
**Output:** 101
**Explanation:**
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.
**Example 2:**
**Input:** piles = \[\[100\],\[100\],\[100\],\[100\],\[100\],\[100\],\[1,1,1,1,1,1,700\]\], k = 7
**Output:** 706
**Explanation:**
The maximum total can be obtained if we choose all coins from the last pile.
**Constraints:**
* `n == piles.length`
* `1 <= n <= 1000`
* `1 <= piles[i][j] <= 105`
* `1 <= k <= sum(piles[i].length) <= 2000` | If the path starts at room i, what properties must the other two rooms in the cycle have? The other two rooms must be connected to room i, and must be connected to each other. |
[Python/Java/C++] Solution without XOR | minimum-bit-flips-to-convert-number | 0 | 1 | # Divmod Remainder Approach:\n#### Time Complexity: O(log(min(s,g))) --> O(log(n)) \n#### Space Complexity: O(1)\n\nWe divide s and q by 2 until either s or g equals zero.\nDuring this process, if the remainder of either of them **do not** equal eachother, we increment the counter.\n\n***This process is similar to converting a decimal number to binary***\n\n**Example:** s=10 g=7\n\n| iterations | s (binary) | g (binary) | counter | explaination\n| - | --- | --- | --- | ---- |\n1| 1010 |0111|+1| The last digit of s and g are ***different***\n2| 0101 |0011|+0| The last digits are the **same** so we do nothing\n3| 0010 |0001|+1| The last digit of s and g are ***different***\n4| 0001 |0000|+1|The last digit of s and g are ***different***\n\n```Python []\nclass Solution:\n def minBitFlips(self, s: int, g: int) -> int:\n count = 0 \n while s or g:\n if s%2 != g%2: count+=1\n s, g = s//2, g//2\n return count\n```\n```Java []\nclass Solution {\n public int minBitFlips(int s, int g) {\n int count = 0;\n while(s > 0 || g > 0){\n if(s%2 != g%2) count++;\n s = s/2;\n g = g/2;\n }\n return count;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minBitFlips(int s, int g) {\n int count = 0;\n while(s > 0 || g > 0){\n if(s%2 != g%2) count++;\n s = s/2;\n g = g/2;\n }\n return count;\n }\n};\n```\n```PsudoCode []\nfunction minBitFlips(integer s, integer g){\n\tinitilize counter integer to 0\n\tloop until s or g is equal to zero{\n\t\tif the s mod 2 and g mod 2 have the same remainder, increment counter\n\t\tdivide s and g by 2 every pass\n\t}\n\treturn counter\n}\n```\n\n# PLEASE UPVOTE IF THIS HELPED YOU :)\n | 17 | A **bit flip** of a number `x` is choosing a bit in the binary representation of `x` and **flipping** it from either `0` to `1` or `1` to `0`.
* For example, for `x = 7`, the binary representation is `111` and we may choose any bit (including any leading zeros not shown) and flip it. We can flip the first bit from the right to get `110`, flip the second bit from the right to get `101`, flip the fifth bit from the right (a leading zero) to get `10111`, etc.
Given two integers `start` and `goal`, return _the **minimum** number of **bit flips** to convert_ `start` _to_ `goal`.
**Example 1:**
**Input:** start = 10, goal = 7
**Output:** 3
**Explanation:** The binary representation of 10 and 7 are 1010 and 0111 respectively. We can convert 10 to 7 in 3 steps:
- Flip the first bit from the right: 1010 -> 1011.
- Flip the third bit from the right: 1011 -> 1111.
- Flip the fourth bit from the right: 1111 -> 0111.
It can be shown we cannot convert 10 to 7 in less than 3 steps. Hence, we return 3.
**Example 2:**
**Input:** start = 3, goal = 4
**Output:** 3
**Explanation:** The binary representation of 3 and 4 are 011 and 100 respectively. We can convert 3 to 4 in 3 steps:
- Flip the first bit from the right: 011 -> 010.
- Flip the second bit from the right: 010 -> 000.
- Flip the third bit from the right: 000 -> 100.
It can be shown we cannot convert 3 to 4 in less than 3 steps. Hence, we return 3.
**Constraints:**
* `0 <= start, goal <= 109` | Can we use a data structure to quickly query whether we have a certain ingredient? Once we verify that we can make a recipe, we can add it to our ingredient data structure. We can then check if we can make more recipes as a result of this. |
✔ python | easy | interview thinking | minimum-bit-flips-to-convert-number | 0 | 1 | The given question requires us to count the total number of flips we need to do inorder to make `start -> goal`.\nEx: \n7 - 0111\n10 - 1010\nHere, we only flip the bits which are different in both **start** and **goal**, i.e. `01` or `10`. And, what helps us to find if the bits are different? **XOR**. \nNow, we count these bits (i.e. different bits). And how do we calculate the number of `1\'s` in a number? `n & (n-1)` technique.\n\nSo, the number of flips required is **3**.\n\nTherefore, the solution is divided into two parts - identify the distinct bits in both numbers and then, count these bits.\n\nSolution:\n```python\nclass Solution(object):\n def minBitFlips(self, start, goal):\n res = start ^ goal\n cnt = 0\n while res:\n res &= res - 1\n cnt += 1\n return cnt\n```\n\n | 7 | A **bit flip** of a number `x` is choosing a bit in the binary representation of `x` and **flipping** it from either `0` to `1` or `1` to `0`.
* For example, for `x = 7`, the binary representation is `111` and we may choose any bit (including any leading zeros not shown) and flip it. We can flip the first bit from the right to get `110`, flip the second bit from the right to get `101`, flip the fifth bit from the right (a leading zero) to get `10111`, etc.
Given two integers `start` and `goal`, return _the **minimum** number of **bit flips** to convert_ `start` _to_ `goal`.
**Example 1:**
**Input:** start = 10, goal = 7
**Output:** 3
**Explanation:** The binary representation of 10 and 7 are 1010 and 0111 respectively. We can convert 10 to 7 in 3 steps:
- Flip the first bit from the right: 1010 -> 1011.
- Flip the third bit from the right: 1011 -> 1111.
- Flip the fourth bit from the right: 1111 -> 0111.
It can be shown we cannot convert 10 to 7 in less than 3 steps. Hence, we return 3.
**Example 2:**
**Input:** start = 3, goal = 4
**Output:** 3
**Explanation:** The binary representation of 3 and 4 are 011 and 100 respectively. We can convert 3 to 4 in 3 steps:
- Flip the first bit from the right: 011 -> 010.
- Flip the second bit from the right: 010 -> 000.
- Flip the third bit from the right: 000 -> 100.
It can be shown we cannot convert 3 to 4 in less than 3 steps. Hence, we return 3.
**Constraints:**
* `0 <= start, goal <= 109` | Can we use a data structure to quickly query whether we have a certain ingredient? Once we verify that we can make a recipe, we can add it to our ingredient data structure. We can then check if we can make more recipes as a result of this. |
Curious Logic Python3 | minimum-bit-flips-to-convert-number | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minBitFlips(self, start: int, goal: int) -> int:\n s=bin(start)[2:].zfill(50)\n g=bin(goal)[2:].zfill(50)\n count=0\n for i in range(50):\n if s[i]!=g[i]:\n count+=1\n return count\n``` | 5 | A **bit flip** of a number `x` is choosing a bit in the binary representation of `x` and **flipping** it from either `0` to `1` or `1` to `0`.
* For example, for `x = 7`, the binary representation is `111` and we may choose any bit (including any leading zeros not shown) and flip it. We can flip the first bit from the right to get `110`, flip the second bit from the right to get `101`, flip the fifth bit from the right (a leading zero) to get `10111`, etc.
Given two integers `start` and `goal`, return _the **minimum** number of **bit flips** to convert_ `start` _to_ `goal`.
**Example 1:**
**Input:** start = 10, goal = 7
**Output:** 3
**Explanation:** The binary representation of 10 and 7 are 1010 and 0111 respectively. We can convert 10 to 7 in 3 steps:
- Flip the first bit from the right: 1010 -> 1011.
- Flip the third bit from the right: 1011 -> 1111.
- Flip the fourth bit from the right: 1111 -> 0111.
It can be shown we cannot convert 10 to 7 in less than 3 steps. Hence, we return 3.
**Example 2:**
**Input:** start = 3, goal = 4
**Output:** 3
**Explanation:** The binary representation of 3 and 4 are 011 and 100 respectively. We can convert 3 to 4 in 3 steps:
- Flip the first bit from the right: 011 -> 010.
- Flip the second bit from the right: 010 -> 000.
- Flip the third bit from the right: 000 -> 100.
It can be shown we cannot convert 3 to 4 in less than 3 steps. Hence, we return 3.
**Constraints:**
* `0 <= start, goal <= 109` | Can we use a data structure to quickly query whether we have a certain ingredient? Once we verify that we can make a recipe, we can add it to our ingredient data structure. We can then check if we can make more recipes as a result of this. |
Pascal Triangle | find-triangular-sum-of-an-array | 0 | 1 | We can do a simulation for a O(n * n) solution, but it\'s not interesting. Instead, we will use a bit of math to look at more efficient solutions.\n\nEach number in the array contributes to the final sum a certain number of times. We can visualize how to figure out factors for each number using [Pascal\'s triangle](https://en.wikipedia.org/wiki/Pascal%27s_triangle):\n\n\n\nFor test case `[1, 2, 3, 4, 5]`, we will get `1 * 1 + 2 * 4 + 3 * 6 + 4 * 4 + 5 * 1` = `1 + 8 + 18 + 16 + 5` = `48`, or `8` after modulo `10`.\n\nThe bottom row of Pascal\'s triangle are [binomial coefficients](https://en.wikipedia.org/wiki/Binomial_coefficient), which can be computed as `nCr(n - 1, i)`. \n\n## Approach 1: comb\nUsing the built-in `comb` Python function to compute `nCr`.\n**Python 3**\n```python\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n return sum(n * comb(len(nums) - 1, i) for i, n in enumerate(nums)) % 10\n```\n\n## Approach 2: Iterative nCr\nThe `nCr` can be computed iteratively as `nCr(r + 1) = nCr(r) * (n - r) / (r + 1)`.\n**Python 3**\n```python\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n res, nCr, n = 0, 1, len(nums) - 1\n for r, num in enumerate(nums):\n res = (res + num * nCr) % 10\n nCr = nCr * (n - r) // (r + 1)\n return res\n```\n## Approach 3: Pascal Triangle\nThe approach 2 above won\'t work for C++ as `nCr` can get quite large. \n\n> We could use modular arithmetic with inverse modulo for the division. However, for modulus `10`, we need to put co-primes `5` and `2` out of brackets before computing the inverse modulo. Check out [this post](https://leetcode.com/problems/find-triangular-sum-of-an-array/discuss/1907380/O(n)-time-O(1)-space-Python-189-ms-C%2B%2B-22-ms-Java-4-ms) by [StefanPochmann](https://leetcode.com/StefanPochmann/) to see how to do it.\n\nInstead, we can build the entire Pascal Triangle once (for array sizes 1..1000) and store it in a static array. From that point, we can compute the result for any array in O(n). The runtime of the code below is 12 ms.\n\n**C++**\nNote that here we populate the Pascal Triangle lazilly. \n```cpp\nint c[1001][1001] = {}, n = 1;\nclass Solution {\npublic:\nint triangularSum(vector<int>& nums) {\n for (; n <= nums.size(); ++n) // compute once for all test cases.\n for (int r = 0; r < n; ++r) \n c[n][r] = r == 0 ? 1 : (c[n - 1][r - 1] + c[n - 1][r]) % 10;\n return inner_product(begin(nums), end(nums), begin(c[nums.size()]), 0) % 10;\n}\n};\n``` | 35 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
Clean Python 3 Solution O(n) | find-triangular-sum-of-an-array | 0 | 1 | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nOnce the pascal\'s triangle/binomial coefficients idea is clear the implementation is easy as follows, for each term in the initial array calculate its contribution in the final array.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) but nCr may cause overflow in some languages\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom math import comb\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n ans = 0\n n = len(nums) - 1\n for i,j in enumerate(nums):\n ncr = comb(n,i)\n ans = (ans + ncr*j)%10\n return ans\n``` | 1 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
nested loop solution | find-triangular-sum-of-an-array | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n n=len(nums)\n while n>0:\n for i in range(n-1):\n nums[i]=(nums[i]+nums[i+1])%10\n n-=1\n return nums[0]\n``` | 7 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
Python 2265 ms, faster than 86.98% of Python3 online submissions | find-triangular-sum-of-an-array | 0 | 1 | ```\ndef triangularSum(self, nums: List[int]) -> int:\n if not nums:\n return 0\n if len(nums) == 1:\n return nums[0]\n \n n = len(nums)\n \n while n != 1:\n nums = [(nums[i] + nums[i+1]) % 10 for i in range(n-1)]\n n = len(nums)\n return nums[0]\n```\n\nLogic is simple. I create new array at every iteration until len(array) == 1, which replace the ith index to (nums[i] + nums[i+1]) % 10. Finally when array has length of 1 that will be the final answer. | 2 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
[Java/Python 3] Compute in-place w/ analysis. | find-triangular-sum-of-an-array | 1 | 1 | ```java\n public int triangularSum(int[] nums) {\n for (int n = nums.length; n > 0; --n) {\n for (int i = 1; i < n; ++i) {\n nums[i - 1] += nums[i];\n nums[i - 1] %= 10;\n }\n }\n return nums[0];\n }\n```\n```python\n def triangularSum(self, nums: List[int]) -> int:\n for j in range(len(nums), 0, -1):\n for i in range(1, j):\n nums[i - 1] += nums[i]\n nums[i - 1] %= 10\n return nums[0]\n```\n**Analysis:**\n\nTime: `O(n ^ 2)`, extra space: `O(1)`, where `n = nums.length`. | 22 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
Python 3 | Intuitive | Brute Force + Optimal | find-triangular-sum-of-an-array | 0 | 1 | # Approach\nGoals: return the single element of triangular sum\n\n\n\n\nWe can see from the image that we will sum up the first cell and the second cell. Then, since it\'s triangular, the length of the top row is greater (+1) than the next row. \n\n## Brute Force\n\n```python\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n n = len(nums)\n\n if n == 0: return 0\n if n == 1: return nums[0]\n\n prev = list(nums)\n while n > 1:\n cur = [0]*(n-1)\n for i in range(1, len(prev)):\n cur[i-1] = (prev[i] + prev[i-1]) % 10\n prev = cur\n n -= 1\n return cur[n//2]\n```\n\n## Optimal\n\n```python\nclass Solution:\n def triangularSum(self, nums: List[int]) -> int:\n n = len(nums)\n while n > 0:\n for i in range(n-1):\n nums[i] = (nums[i] + nums[i+1]) % 10\n n -= 1\n return nums[0]\n``` | 8 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
Python3 with helper | find-triangular-sum-of-an-array | 0 | 1 | ```\nclass Solution:\n def helper(self, nums: List[int]) -> List[int]:\n dp = []\n i = 0\n while i < len(nums) - 1:\n dp.append((nums[i] + nums[i + 1]) % 10)\n i += 1\n return dp\n \n def triangularSum(self, nums: List[int]) -> int:\n while len(nums) > 1:\n nums = self.helper(nums)\n return nums[0]\n``` | 5 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
9 lines Easy python solution | find-triangular-sum-of-an-array | 0 | 1 | **PLEASE UPVOTE IF YOU FIND THIS SOLUTION HELPFUL **\n\tclass Solution:\n\t\tdef triangularSum(self, nums: List[int]) -> int:\n\t\t\n\t\t\tarr=nums.copy()\n\t\t\tlst=[]\n\t\t\twhile len(arr)!=1:\n\t\t\t\tfor i in range(0,len(arr)-1):\n\t\t\t\t\ts=arr[i]+arr[i+1]\n\t\t\t\t\tlst.append(s%10) #to get the last digit of integer sum\n\t\t\t\tarr=lst.copy()\n\t\t\t\tlst=[]\n\t\t\treturn arr[0] | 1 | You are given a **0-indexed** integer array `nums`, where `nums[i]` is a digit between `0` and `9` (**inclusive**).
The **triangular sum** of `nums` is the value of the only element present in `nums` after the following process terminates:
1. Let `nums` comprise of `n` elements. If `n == 1`, **end** the process. Otherwise, **create** a new **0-indexed** integer array `newNums` of length `n - 1`.
2. For each index `i`, where `0 <= i < n - 1`, **assign** the value of `newNums[i]` as `(nums[i] + nums[i+1]) % 10`, where `%` denotes modulo operator.
3. **Replace** the array `nums` with `newNums`.
4. **Repeat** the entire process starting from step 1.
Return _the triangular sum of_ `nums`.
**Example 1:**
**Input:** nums = \[1,2,3,4,5\]
**Output:** 8
**Explanation:**
The above diagram depicts the process from which we obtain the triangular sum of the array.
**Example 2:**
**Input:** nums = \[5\]
**Output:** 5
**Explanation:**
Since there is only one element in nums, the triangular sum is the value of that element itself.
**Constraints:**
* `1 <= nums.length <= 1000`
* `0 <= nums[i] <= 9` | Can an odd length string ever be valid? From left to right, if a locked ')' is encountered, it must be balanced with either a locked '(' or an unlocked index on its left. If neither exist, what conclusion can be drawn? If both exist, which one is more preferable to use? After the above, we may have locked indices of '(' and additional unlocked indices. How can you balance out the locked '(' now? What if you cannot balance any locked '('? |
[Java/Python 3] One pass S O(1) T O(n) codes and follow up, w/ brief explanation and analysis. | number-of-ways-to-select-buildings | 1 | 1 | Traverse the input `s`:\n1. If encontering `0`, count subsequences ending at current `0`: `0`, `10` and `010`\'s; The number of `10` depends on how many `1`s before current `0`, and the number of `010` depends on how many `01` before current `0`;\n\nSimilarly, \n\n2. If encontering `1`, count subsequences ending at current `1`: `1`, `01` and `101`\'s; The number of `01` depends on how many `0`s before current `1`, and the number of `101` depends on how many `10` before current `1`.\n\n```java\n public long numberOfWays(String s) {\n long one = 0, zero = 0, oneZero = 0, zeroOne = 0, ways = 0;\n for (int i = 0; i < s.length(); ++i) {\n if (s.charAt(i) == \'0\') {\n ++zero;\n oneZero += one; // Count in \'10\'.\n ways += zeroOne; // Count in \'010\'.\n }else {\n ++one;\n zeroOne += zero; // Count in \'01\'.\n ways += oneZero; // Count in \'101\'.\n }\n }\n return ways;\n }\n```\n```python\n def numberOfWays(self, s: str) -> int:\n ways = 0\n one = zero = zero_one = one_zero = 0\n for c in s:\n if c == \'0\':\n zero += 1\n one_zero += one\n ways += zero_one\n else:\n one += 1 \n zero_one += zero \n ways += one_zero\n return ways\n```\n\n**Analysis:**\n\nTime: `O(n)`, space: `O(1)`, where `n = s.length()`.\n\n----\n\n**Follow-up**\nWhat if the city official would like to select `k`, instead of `3`, buildings?\n\n~~~If **the upvotes can reach `25`**, I will provide time `O(k * n)` space `O(k)` code for the follow-up.~~~\n\nTraverse the input `s`:\n1. If encontering `0`, count subsequences ending at current `0`: `0`, `10` and `010`, `1010`\'s, ...,; The number of `10` depends on how many `1`s before current `0`, the number of `010` depends on how many `01` before current `0`, and the number of `1010` depends on how many `101` before current `0`...;\n\nSimilarly,\n\n2. If encontering `1`, count subsequences ending at current `1`: `1`, `01`, `101`, and `0101`\'s; The number of `01` depends on how many `0`s before current `1`, the number of `101` depends on how many `10` before current `1`, and the number of `0101` depends on how many `010` before current `1`...\n3. We can observe the above patterns and use a 2-D array `ways` to record the corresponding subsequences, e.g., \n \n\t ways[0][0] - number of `0`\'s;\n\t ways[1][0] - number of `10`\'s;\n\t ways[2][0] - number of `010`\'s;\n\t ways[3][0] - number of `1010`\'s;\n\t ...\n\t ways[0][1] - number of `1`\'s;\n\t ways[1][1] - number of `01`\'s;\n\t ways[2][1] - number of `101`\'s;\n\t ways[3][1] - number of `0101`\'s;\n\t ...\n\t \n```java\n public long numberOfWays(String s, int k) {\n // int k = 3;\n long[][] ways = new long[k][2]; \n for (int i = 0; i < s.length(); ++i) {\n int idx = s.charAt(i) - \'0\';\n ++ways[0][idx];\n for (int j = 1; j < k; ++j) {\n ways[j][idx] += ways[j - 1][1 - idx];\n }\n }\n return ways[k - 1][0] + ways[k - 1][1];\n }\n```\n```python\n def numberOfWays(self, s: str, k: int) -> int:\n # k = 3\n ways = [[0, 0] for _ in range(k)]\n for c in s:\n idx = ord(c) - ord(\'0\')\n ways[0][idx] += 1\n for i in range(1, k):\n ways[i][idx] += ways[i - 1][1 - idx]\n return sum(ways[-1])\n```\n**Analysis:**\n\nTime: `O(k * n)`, space: `O(k)`, where `n = s.length()`.\n\n**Do let me know** if you have an algorithm better than `O(k * n)` time or `O(k)` space for the follow-up. | 131 | You are given a **0-indexed** binary string `s` which represents the types of buildings along a street where:
* `s[i] = '0'` denotes that the `ith` building is an office and
* `s[i] = '1'` denotes that the `ith` building is a restaurant.
As a city official, you would like to **select** 3 buildings for random inspection. However, to ensure variety, **no two consecutive** buildings out of the **selected** buildings can be of the same type.
* For example, given `s = "0**0**1**1**0**1** "`, we cannot select the `1st`, `3rd`, and `5th` buildings as that would form `"0**11** "` which is **not** allowed due to having two consecutive buildings of the same type.
Return _the **number of valid ways** to select 3 buildings._
**Example 1:**
**Input:** s = "001101 "
**Output:** 6
**Explanation:**
The following sets of indices selected are valid:
- \[0,2,4\] from "**0**0**1**1**0**1 " forms "010 "
- \[0,3,4\] from "**0**01**10**1 " forms "010 "
- \[1,2,4\] from "0**01**1**0**1 " forms "010 "
- \[1,3,4\] from "0**0**1**10**1 " forms "010 "
- \[2,4,5\] from "00**1**1**01** " forms "101 "
- \[3,4,5\] from "001**101** " forms "101 "
No other selection is valid. Thus, there are 6 total ways.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:** It can be shown that there are no valid selections.
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Calculating the number of trailing zeros, the last five digits, and the first five digits can all be done separately. Use a prime factorization property to find the number of trailing zeros. Use modulo to find the last 5 digits. Use a logarithm property to find the first 5 digits. The number of trailing zeros C is nothing but the number of times the product is completely divisible by 10. Since 2 and 5 are the only prime factors of 10, C will be equal to the minimum number of times 2 or 5 appear in the prime factorization of the product. Iterate through the integers from left to right. For every integer, keep dividing it by 2 as long as it is divisible by 2 and C occurrences of 2 haven't been removed in total. Repeat this process for 5. Finally, multiply the integer under modulo of 10^5 with the product obtained till now to obtain the last five digits. The product P can be represented as P=10^(x+y) where x is the integral part and y is the fractional part of x+y. Using the property "if S = A * B, then log(S) = log(A) + log(B)", we can write x+y = log_10(P) = sum(log_10(i)) for each integer i in [left, right]. Once we obtain the sum, the first five digits can be represented as floor(10^(y+4)). |
[Python 3] BEATS 100% | number-of-ways-to-select-buildings | 0 | 1 | # Intuition\nFor each house calculate how many inspections where this house is the last one\n\n# Approach\n1. Iterate over houses\n2. If house is \'1\' $\\Longrightarrow$ previous house should be \'0\'\n 2.1 We can choose any previous \'0\' as the 2nd house and any \'1\' before that \'0\' as the 1st\n 2.2 Because of that when we see \'0\' we add count of previous ones in special sum \u2014 `options_for_ones` (options_for_ones, because we will use it when we see house \'1\')\n 2.3 So when we see current house, `options_for_ones` indicates the exact number of combinations of choosing any previously seen \'0\' and any \'1\' before that $\\Longrightarrow$ ans += options_for_ones\n3. If house is \'0\' \u2014 similarly\n\n# Code\n```\nclass Solution:\n def numberOfWays(self, s: str) -> int:\n ans = 0\n ones = 0\n zeros = 0\n options_for_zeros = 0\n options_for_ones = 0\n for x in s:\n if x == \'1\':\n ans += options_for_ones\n options_for_zeros += zeros\n ones += 1\n else:\n ans += options_for_zeros\n options_for_ones += ones\n zeros += 1\n return ans\n```\n\n\n# Complexity\n- Time complexity: $O(n)$\n\n- Space complexity: $O(1)$ | 3 | You are given a **0-indexed** binary string `s` which represents the types of buildings along a street where:
* `s[i] = '0'` denotes that the `ith` building is an office and
* `s[i] = '1'` denotes that the `ith` building is a restaurant.
As a city official, you would like to **select** 3 buildings for random inspection. However, to ensure variety, **no two consecutive** buildings out of the **selected** buildings can be of the same type.
* For example, given `s = "0**0**1**1**0**1** "`, we cannot select the `1st`, `3rd`, and `5th` buildings as that would form `"0**11** "` which is **not** allowed due to having two consecutive buildings of the same type.
Return _the **number of valid ways** to select 3 buildings._
**Example 1:**
**Input:** s = "001101 "
**Output:** 6
**Explanation:**
The following sets of indices selected are valid:
- \[0,2,4\] from "**0**0**1**1**0**1 " forms "010 "
- \[0,3,4\] from "**0**01**10**1 " forms "010 "
- \[1,2,4\] from "0**01**1**0**1 " forms "010 "
- \[1,3,4\] from "0**0**1**10**1 " forms "010 "
- \[2,4,5\] from "00**1**1**01** " forms "101 "
- \[3,4,5\] from "001**101** " forms "101 "
No other selection is valid. Thus, there are 6 total ways.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:** It can be shown that there are no valid selections.
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Calculating the number of trailing zeros, the last five digits, and the first five digits can all be done separately. Use a prime factorization property to find the number of trailing zeros. Use modulo to find the last 5 digits. Use a logarithm property to find the first 5 digits. The number of trailing zeros C is nothing but the number of times the product is completely divisible by 10. Since 2 and 5 are the only prime factors of 10, C will be equal to the minimum number of times 2 or 5 appear in the prime factorization of the product. Iterate through the integers from left to right. For every integer, keep dividing it by 2 as long as it is divisible by 2 and C occurrences of 2 haven't been removed in total. Repeat this process for 5. Finally, multiply the integer under modulo of 10^5 with the product obtained till now to obtain the last five digits. The product P can be represented as P=10^(x+y) where x is the integral part and y is the fractional part of x+y. Using the property "if S = A * B, then log(S) = log(A) + log(B)", we can write x+y = log_10(P) = sum(log_10(i)) for each integer i in [left, right]. Once we obtain the sum, the first five digits can be represented as floor(10^(y+4)). |
5 line Python Solution | Easy + Fast | number-of-ways-to-select-buildings | 0 | 1 | ```\nclass Solution:\n def numberOfWays(self, s: str) -> int:\n x0,x1,x01,x10,ans = 0,0,0,0,0\n for i in s:\n if i=="1": x1+=1;x01+=x0;ans+=x10\n else: x0+=1;x10+=x1;ans+=x01\n return ans | 2 | You are given a **0-indexed** binary string `s` which represents the types of buildings along a street where:
* `s[i] = '0'` denotes that the `ith` building is an office and
* `s[i] = '1'` denotes that the `ith` building is a restaurant.
As a city official, you would like to **select** 3 buildings for random inspection. However, to ensure variety, **no two consecutive** buildings out of the **selected** buildings can be of the same type.
* For example, given `s = "0**0**1**1**0**1** "`, we cannot select the `1st`, `3rd`, and `5th` buildings as that would form `"0**11** "` which is **not** allowed due to having two consecutive buildings of the same type.
Return _the **number of valid ways** to select 3 buildings._
**Example 1:**
**Input:** s = "001101 "
**Output:** 6
**Explanation:**
The following sets of indices selected are valid:
- \[0,2,4\] from "**0**0**1**1**0**1 " forms "010 "
- \[0,3,4\] from "**0**01**10**1 " forms "010 "
- \[1,2,4\] from "0**01**1**0**1 " forms "010 "
- \[1,3,4\] from "0**0**1**10**1 " forms "010 "
- \[2,4,5\] from "00**1**1**01** " forms "101 "
- \[3,4,5\] from "001**101** " forms "101 "
No other selection is valid. Thus, there are 6 total ways.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:** It can be shown that there are no valid selections.
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Calculating the number of trailing zeros, the last five digits, and the first five digits can all be done separately. Use a prime factorization property to find the number of trailing zeros. Use modulo to find the last 5 digits. Use a logarithm property to find the first 5 digits. The number of trailing zeros C is nothing but the number of times the product is completely divisible by 10. Since 2 and 5 are the only prime factors of 10, C will be equal to the minimum number of times 2 or 5 appear in the prime factorization of the product. Iterate through the integers from left to right. For every integer, keep dividing it by 2 as long as it is divisible by 2 and C occurrences of 2 haven't been removed in total. Repeat this process for 5. Finally, multiply the integer under modulo of 10^5 with the product obtained till now to obtain the last five digits. The product P can be represented as P=10^(x+y) where x is the integral part and y is the fractional part of x+y. Using the property "if S = A * B, then log(S) = log(A) + log(B)", we can write x+y = log_10(P) = sum(log_10(i)) for each integer i in [left, right]. Once we obtain the sum, the first five digits can be represented as floor(10^(y+4)). |
Python DP | number-of-ways-to-select-buildings | 0 | 1 | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn this case, the dp should not be initialized as a list, but it should be initalized as a hashmap.\nIf a character in s is \'1\', then the number of ways to select one \'1\' is incremented by 1, the number of ways to select \'101\' is incremented by the number of ways to select \'10\', and the number of ways to select \'01\' is incremented by the number of ways to select \'0\'.\n\n# Code\n```\nclass Solution:\n def numberOfWays(self, s: str) -> int:\n dp = {\'1\':0, \'0\':0, \'10\':0, \'01\':0, \'101\':0, \'010\':0}\n for i in range(len(s)):\n if s[i] == \'0\':\n dp[\'0\'] += 1\n dp[\'10\'] += dp[\'1\']\n dp[\'010\'] += dp[\'01\']\n else:\n dp[\'1\'] += 1\n dp[\'01\'] += dp[\'0\']\n dp[\'101\'] += dp[\'10\']\n \n return dp[\'101\'] + dp[\'010\']\n``` | 1 | You are given a **0-indexed** binary string `s` which represents the types of buildings along a street where:
* `s[i] = '0'` denotes that the `ith` building is an office and
* `s[i] = '1'` denotes that the `ith` building is a restaurant.
As a city official, you would like to **select** 3 buildings for random inspection. However, to ensure variety, **no two consecutive** buildings out of the **selected** buildings can be of the same type.
* For example, given `s = "0**0**1**1**0**1** "`, we cannot select the `1st`, `3rd`, and `5th` buildings as that would form `"0**11** "` which is **not** allowed due to having two consecutive buildings of the same type.
Return _the **number of valid ways** to select 3 buildings._
**Example 1:**
**Input:** s = "001101 "
**Output:** 6
**Explanation:**
The following sets of indices selected are valid:
- \[0,2,4\] from "**0**0**1**1**0**1 " forms "010 "
- \[0,3,4\] from "**0**01**10**1 " forms "010 "
- \[1,2,4\] from "0**01**1**0**1 " forms "010 "
- \[1,3,4\] from "0**0**1**10**1 " forms "010 "
- \[2,4,5\] from "00**1**1**01** " forms "101 "
- \[3,4,5\] from "001**101** " forms "101 "
No other selection is valid. Thus, there are 6 total ways.
**Example 2:**
**Input:** s = "11100 "
**Output:** 0
**Explanation:** It can be shown that there are no valid selections.
**Constraints:**
* `3 <= s.length <= 105`
* `s[i]` is either `'0'` or `'1'`. | Calculating the number of trailing zeros, the last five digits, and the first five digits can all be done separately. Use a prime factorization property to find the number of trailing zeros. Use modulo to find the last 5 digits. Use a logarithm property to find the first 5 digits. The number of trailing zeros C is nothing but the number of times the product is completely divisible by 10. Since 2 and 5 are the only prime factors of 10, C will be equal to the minimum number of times 2 or 5 appear in the prime factorization of the product. Iterate through the integers from left to right. For every integer, keep dividing it by 2 as long as it is divisible by 2 and C occurrences of 2 haven't been removed in total. Repeat this process for 5. Finally, multiply the integer under modulo of 10^5 with the product obtained till now to obtain the last five digits. The product P can be represented as P=10^(x+y) where x is the integral part and y is the fractional part of x+y. Using the property "if S = A * B, then log(S) = log(A) + log(B)", we can write x+y = log_10(P) = sum(log_10(i)) for each integer i in [left, right]. Once we obtain the sum, the first five digits can be represented as floor(10^(y+4)). |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.